| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2.3. Временная дисперсия в объемной среде
В оптике слово «дисперсия» обычно связывают с величиной  а в оптических системах связи с явлением уширения световых импульсов после их прохождения через дисперсионную среду. Ниже будет показано, что за это уширение ответственна не величина
а в оптических системах связи с явлением уширения световых импульсов после их прохождения через дисперсионную среду. Ниже будет показано, что за это уширение ответственна не величина  а величина
а величина  именно эта последняя будет пониматься в данной книге под термином «дисперсия материала».
именно эта последняя будет пониматься в данной книге под термином «дисперсия материала».
Любая помеха или сигнал, налагаемые на световую волну, распространяются не с фазовой скоростью волны, равной

а с групповой скоростью  определяемой соотношением
определяемой соотношением

Доказательство этого утверждения можно найти в большинстве учебников по распространению электромагнитных волн и, в частности, в [1.2] и [2.1]. Итак, в недисперсионной среде фазовая скорость не зависит от частоты волны, вследствие чего групповая и, фазовая скорости становятся одинаковыми:

Однако в дисперсионной среде, где по определению фазовая скорость зависит от частоты,  будут различными:
будут различными:

Это обстоятельство важно, поскольку групповая скорость является скоростью распространения сигнала, с которой постоянно имеют дело в технике связи. Например, световой импульс проходит через дисперсионную среду со скоростью  Рассмотрение вопроса распространения светового импульса усложняется тем обстоятельством, что из-за дисперсии он обязательно ослабляется и в некоторой степени искажается в процессе распространения. Тем не менее можно ввести понятие группового показателя преломления
Рассмотрение вопроса распространения светового импульса усложняется тем обстоятельством, что из-за дисперсии он обязательно ослабляется и в некоторой степени искажается в процессе распространения. Тем не менее можно ввести понятие группового показателя преломления

который в дисперсионной среде будет отличаться от обычного или фазового показателя преломления 
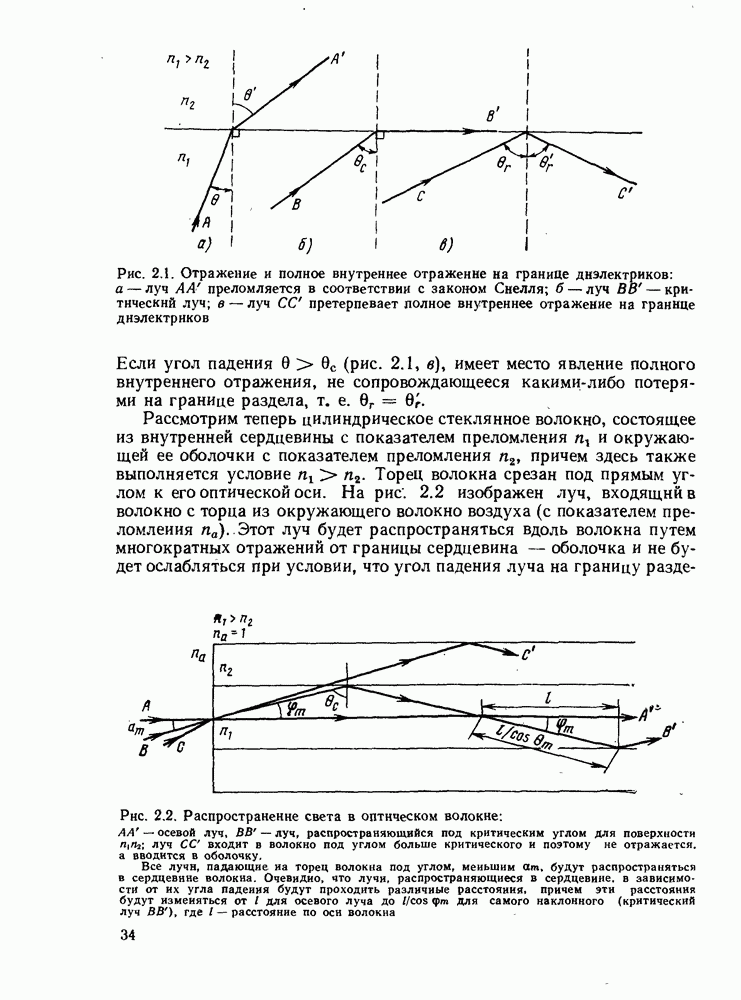
Будет очевидно, что в § 2.1.2 был использован самый простой подход для выражения межмодовой временной дисперсии с помощью формулы (2.1.17). При использовании лучевой модели, изображенной на рис. 2.2, скорость распространения световых импульсов равна  Следовательно, разница времен распространения импульсов вдоль осевого и наиболее наклонного лучей должна быть равна
Следовательно, разница времен распространения импульсов вдоль осевого и наиболее наклонного лучей должна быть равна

где  групповой показатель преломления сердцевины. Однако формула (2.1.17) остается хорошим приближением для обычных ступенчатых волокон. Вопрос о влиянии дисперсии материала на распространение света в градиентных волокнах требует более тщательного рассмотрения и будет описан в гл. 6.
групповой показатель преломления сердцевины. Однако формула (2.1.17) остается хорошим приближением для обычных ступенчатых волокон. Вопрос о влиянии дисперсии материала на распространение света в градиентных волокнах требует более тщательного рассмотрения и будет описан в гл. 6.
Как было показано, дисперсионные свойства оптических материалов традиционно характеризуются зависимостью показателя преломления от длины волны в свободном пространстве, т. е.  Поэтому необходимо выразить величины
Поэтому необходимо выразить величины  через
через  Отметим сначала, что
Отметим сначала, что

Далее

а если учесть, что  то
то

Подставляя полученные выражения в (2.2.37), находим

Таким образом,

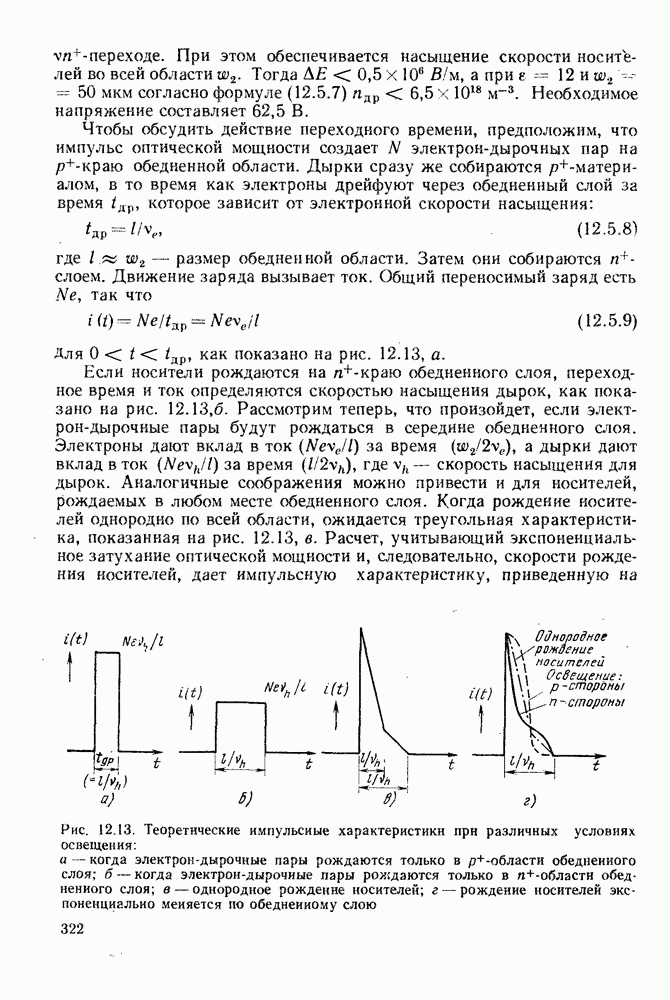
Тогда время прохождения  световым импульсом расстояния I будет равно
световым импульсом расстояния I будет равно

Если свет имеет ширину спектра А к относительно к и если среда дисперсионная, то световой импульс расширяется в процессе
распространения и поступает на выход на протяжении интервала времени  определяемого соотношением
определяемого соотношением

Обычно ширину спектра  источника излучения определяют как диапазон длин волн, в пределах которого излучаемая им мощность превышает 50 % максимального значения. Часто удобно использовать относительную ширину спектра излучения у, равную
источника излучения определяют как диапазон длин волн, в пределах которого излучаемая им мощность превышает 50 % максимального значения. Часто удобно использовать относительную ширину спектра излучения у, равную

Таким образом, после прохождения световым импульсом расстояния I в дисперсионной среде импульс расширяется; причем его длительность  на уровне половинной мощности определяется выражением:
на уровне половинной мощности определяется выражением:

Ее можно написать в таком виде:

где 
представляет собой коэффициент дисперсии материала. Если аппроксимировать ширину полосы частот, занимаемую сигналом в волокне, величиной  то получим
то получим

При определении у и  был введен знак модуля, поскольку обычно интересует абсолютная величина разброса длин волн
был введен знак модуля, поскольку обычно интересует абсолютная величина разброса длин волн  или длительность импульса
или длительность импульса  а не то, какая волна прибудет первой — более короткая или более длинная.
а не то, какая волна прибудет первой — более короткая или более длинная.
Снова подчеркнем, что  это длительность импульса на уровне половинной мощности и что выражение
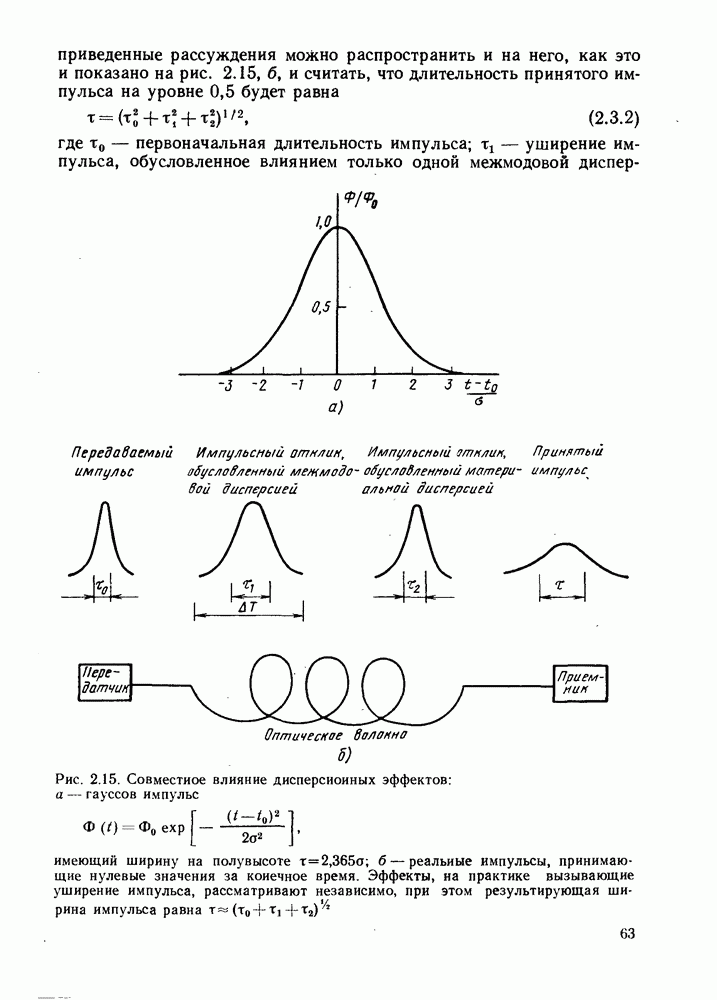
это длительность импульса на уровне половинной мощности и что выражение  является приближением, как и соотношение между шириной полосы частот и общей межмодовой дисперсией вида
является приближением, как и соотношение между шириной полосы частот и общей межмодовой дисперсией вида  полученное в § 2.1.2. Эти вопросы будут предметом дальнейшего рассмотрения и анализа, в частности в § 2.4.
полученное в § 2.1.2. Эти вопросы будут предметом дальнейшего рассмотрения и анализа, в частности в § 2.4.
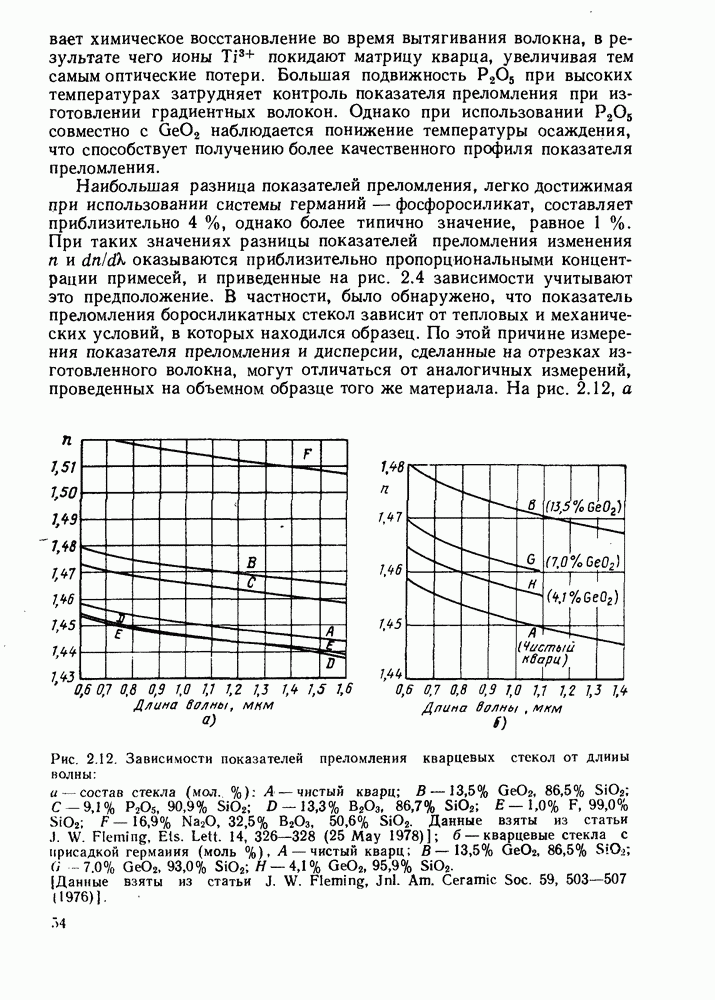
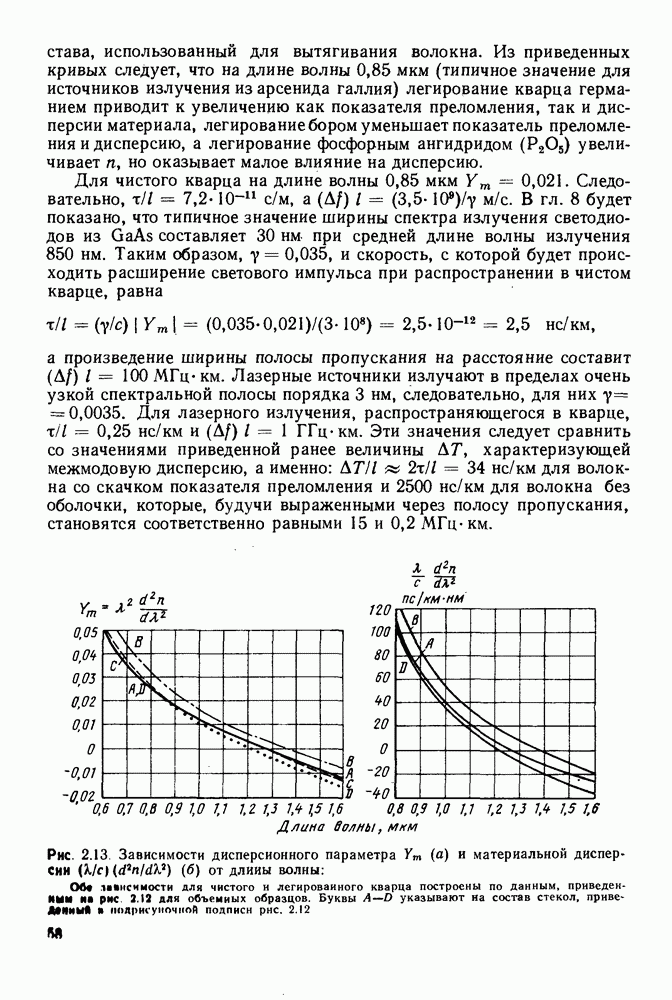
На рис. 2.13 представлены зависимости величин  от длины волны для объемных образцов из чистого и легированного кварца. Приведенные данные получены на основе графиков, изображенных на рис. 2.12. Необходимо подчеркнуть, что эти данные не могут быть непосредственно перенесены на материал аналогичного
от длины волны для объемных образцов из чистого и легированного кварца. Приведенные данные получены на основе графиков, изображенных на рис. 2.12. Необходимо подчеркнуть, что эти данные не могут быть непосредственно перенесены на материал аналогичного
состава, использованный для вытягивания волокна. Из приведенных кривых следует, что на длине волны 0,85 мкм (типичное значение для источников излучения из арсенида галлия) легирование кварца германием приводит к увеличению как показателя преломления, так и дисперсии материала, легирование бором уменьшает показатель преломления и дисперсию, а легирование фосфорным ангидридом  увеличивает
увеличивает  но оказывает малое влияние на дисперсию.
но оказывает малое влияние на дисперсию.
Для чистого кварца на длине волны  . Следовательно,
. Следовательно,  . В гл. 8 будет показано, что типичное значение ширины спектра излучения светодиодов из GaAs составляет 30 нм при средней длине волны излучения
. В гл. 8 будет показано, что типичное значение ширины спектра излучения светодиодов из GaAs составляет 30 нм при средней длине волны излучения  Таким образом,
Таким образом,  и скорость, с которой будет происходить расширение светового импульса при распространении в чистом кварце, равна
и скорость, с которой будет происходить расширение светового импульса при распространении в чистом кварце, равна

а произведение ширины полосы пропускания на расстояние составит  Лазерные источники излучают в пределах очень узкой спектральной полосы порядка
Лазерные источники излучают в пределах очень узкой спектральной полосы порядка  следовательно, для них
следовательно, для них  Для лазерного излучения, распространяющегося в кварце,
Для лазерного излучения, распространяющегося в кварце,  . Эти значения следует сравнить со значениями приведенной ранее величины
. Эти значения следует сравнить со значениями приведенной ранее величины  характеризующей межмодовую дисперсию, а именно:
характеризующей межмодовую дисперсию, а именно:  для волокна со скачком показателя преломления и
для волокна со скачком показателя преломления и  для волокна без оболочки, которые, будучи выраженными через полосу пропускания, становятся соответственно равными 15 и 0,2 МГц-км.
для волокна без оболочки, которые, будучи выраженными через полосу пропускания, становятся соответственно равными 15 и 0,2 МГц-км.

Рис. 2.13. Зависимости дисперсионного параметра  и материальной дисперсии
и материальной дисперсии  от длины волны: Обе зависимости для чистого и легированного кварца построены по данным, приведенным на рис 2.12 для объемных образцов. Буквы
от длины волны: Обе зависимости для чистого и легированного кварца построены по данным, приведенным на рис 2.12 для объемных образцов. Буквы  указывают на состав стекол, приведенный в подрисуночной подписи рис. 2.12
указывают на состав стекол, приведенный в подрисуночной подписи рис. 2.12
Как видно из рис. 2.13, кривая  для чистого кварца изменяет знак на длине волны
для чистого кварца изменяет знак на длине волны  Это значение соответствует точке перегиба кривой
Это значение соответствует точке перегиба кривой  В литературе часто указывают на него, как на «длину волны нулевой дисперсии материала». С практической точки зрения такое определение вводит в заблуждение, поскольку реальный световой импульс содержит в себе спектр длин волн, которые распространяются с групповыми скоростями, лежащими в некотором интервале, даже если самая короткая и самая длинная волны распространяются с одинаковыми скоростями. Эта ситуация проиллюстрирована на рис. 2.14, а. Лежит ли кривая
В литературе часто указывают на него, как на «длину волны нулевой дисперсии материала». С практической точки зрения такое определение вводит в заблуждение, поскольку реальный световой импульс содержит в себе спектр длин волн, которые распространяются с групповыми скоростями, лежащими в некотором интервале, даже если самая короткая и самая длинная волны распространяются с одинаковыми скоростями. Эта ситуация проиллюстрирована на рис. 2.14, а. Лежит ли кривая  выше или ниже нуля, не имеет никакого значения для вопроса о расширении импульса.
выше или ниже нуля, не имеет никакого значения для вопроса о расширении импульса.
Дисперсия материала минимальна для источников, которые излучают на длинах волн, близких к  Такие источники обеспечили бы максимальную пропускную способность волокна, используемого в настоящее время. Несомненно важно знать, что этот предел существует и является причиной, по которой мы будем использовать точные выражения для временной дисперсии в области минимума дисперсии материала.
Такие источники обеспечили бы максимальную пропускную способность волокна, используемого в настоящее время. Несомненно важно знать, что этот предел существует и является причиной, по которой мы будем использовать точные выражения для временной дисперсии в области минимума дисперсии материала.
Спектральная кривая источника, излучающего в диапазоне длин волн  относительно центральной длины волны
относительно центральной длины волны  содержит
содержит  т. е.
т. е.

и можно определить уширение импульса путем разложения времени распространения импульса  в ряд Тейлора в окрестности
в ряд Тейлора в окрестности  Ранее определили
Ранее определили

Пусть

В таком случае

Далее можно записать

и

Следовательно,

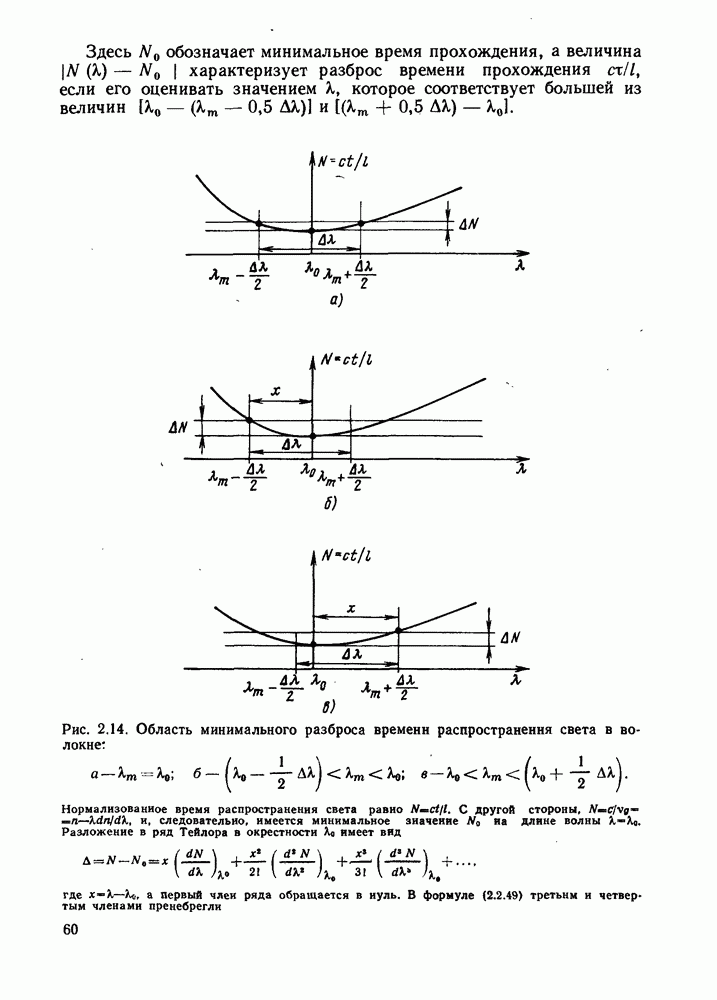
Здесь  обозначает минимальное время прохождения, а величина
обозначает минимальное время прохождения, а величина  характеризует разброс времени прохождения
характеризует разброс времени прохождения  если его оценивать значением к, которое соответствует большей из величин
если его оценивать значением к, которое соответствует большей из величин  и
и 

Рис. 2.14. Область минимального разброса времени распространения света в волокне: а — 
Нормализованное время распространения света равно  С другой стороны,
С другой стороны,  следовательно, имеется минимальное значение
следовательно, имеется минимальное значение  на длине волны
на длине волны  Разложение в ряд Тейлора в окрестности
Разложение в ряд Тейлора в окрестности  имеет вид
имеет вид  где а первый член ряда обращается в нуль. В формуле (2.2.49) третьим и четвертым членами пренебрегли
где а первый член ряда обращается в нуль. В формуле (2.2.49) третьим и четвертым членами пренебрегли
Имеют место два случая:
1.  , как показано на рис. 2.14, б, тогда
, как показано на рис. 2.14, б, тогда

2.  , как изображено на рис. 2.14, в, тогда
, как изображено на рис. 2.14, в, тогда

Неучтенные члены разложения более высокого порядка становятся значительными, если ширина спектра источника излучения  приближается к
приближается к 
При  дисперсия в объеме материала становится минимальной и равной
дисперсия в объеме материала становится минимальной и равной

Для чистого кварца на длине волны 
Следовательно, 

Рассмотрим имеющиеся светодиоды, излучение которых центрировано относительно  Они имеют
Они имеют  Это подразумевает разброс длин волн порядка
Это подразумевает разброс длин волн порядка  относительно
относительно  а также
а также  При использовании лазерного источника излучения значения приведенных величин были бы на два порядка лучше. В любом случае дисперсионный параметр становится очень малым, и это вынуждает разрабатывать источники излучения и фотоприемники для работы в данной области спектра.
При использовании лазерного источника излучения значения приведенных величин были бы на два порядка лучше. В любом случае дисперсионный параметр становится очень малым, и это вынуждает разрабатывать источники излучения и фотоприемники для работы в данной области спектра.
По поводу рис. 2.13 можно также сделать два следующих замечания. Первое — величина  остается весьма малой на длинах волн в окрестности
остается весьма малой на длинах волн в окрестности  Например, для чистого кварца на длине волны
Например, для чистого кварца на длине волны  лежащей, как будет показано в § 2.5, в области минимума потерь,
лежащей, как будет показано в § 2.5, в области минимума потерь,  обеспечивая
обеспечивая  В таком случае при использовании источника излучения с
В таком случае при использовании источника излучения с  получаем
получаем  тогда как
тогда как  будем иметь
будем иметь  Второе замечание состоит в том, что величину
Второе замечание состоит в том, что величину  можно изменять, вводя различные примеси. Как видно из рис. 2.13, введение бора может сделать ее менее
можно изменять, вводя различные примеси. Как видно из рис. 2.13, введение бора может сделать ее менее  а легирование германием позволяет поднять ее до
а легирование германием позволяет поднять ее до 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
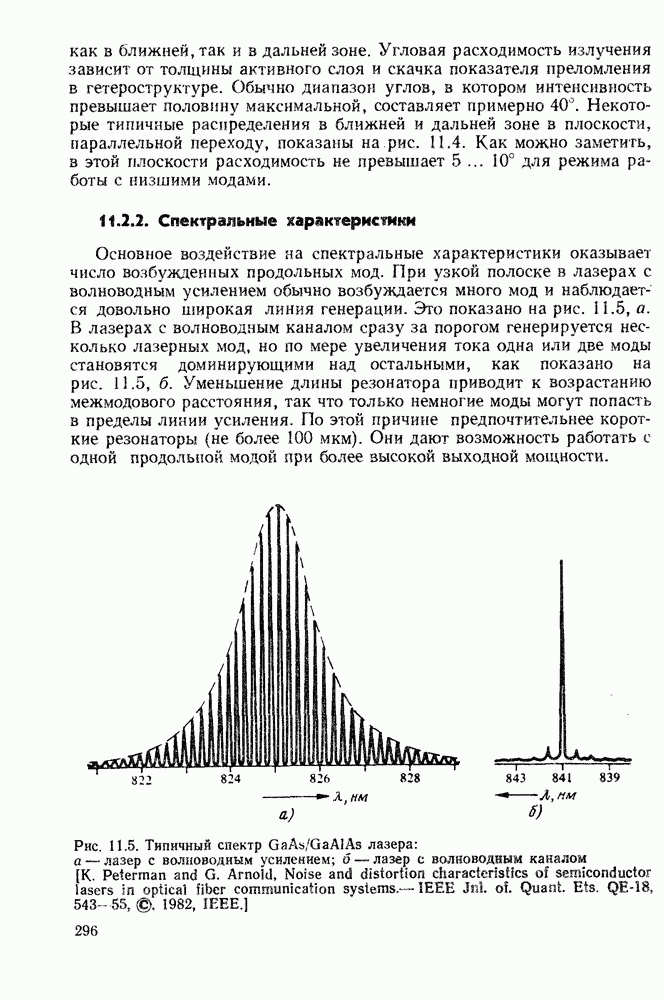
- 11.2.2. Спектральные характеристики
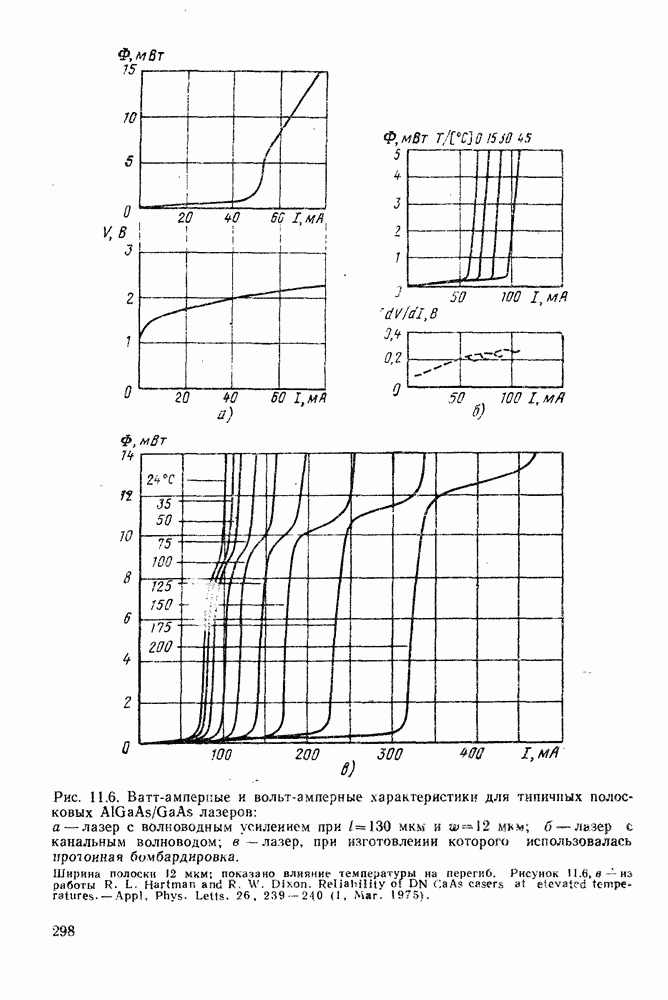
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
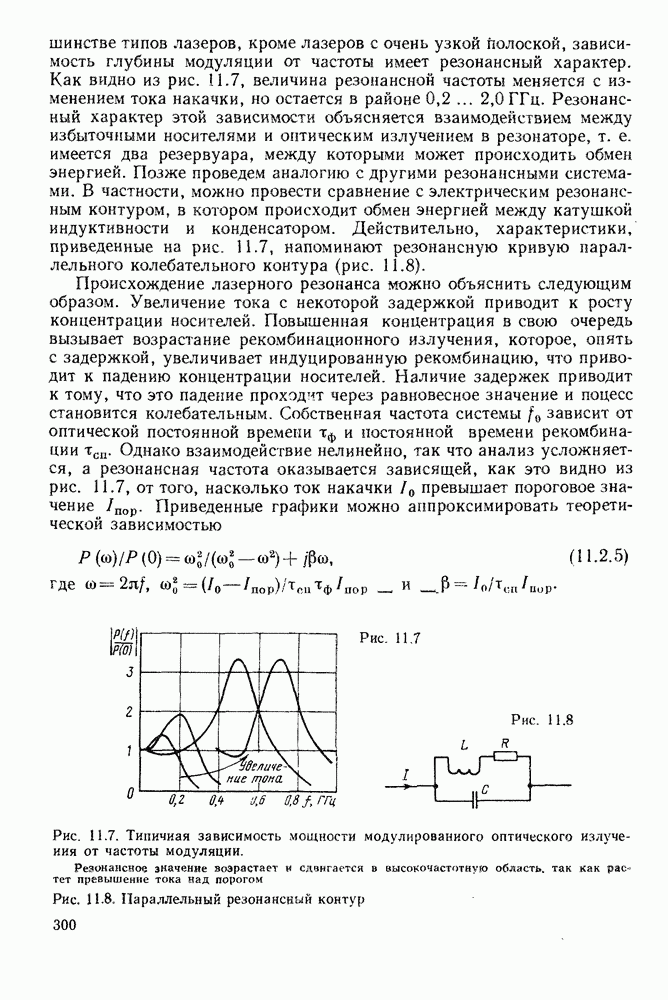
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
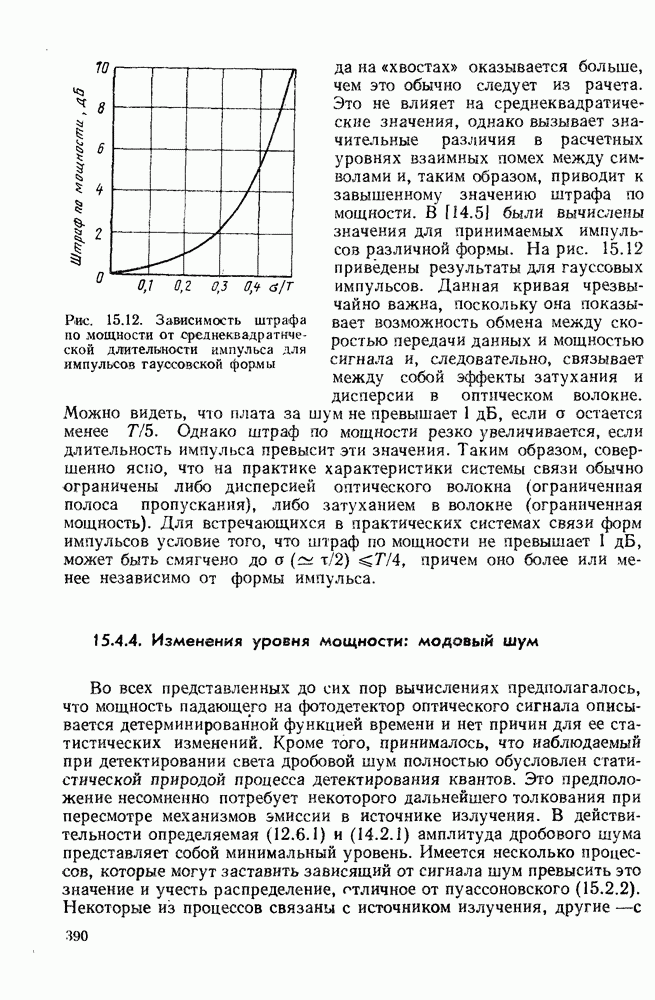
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
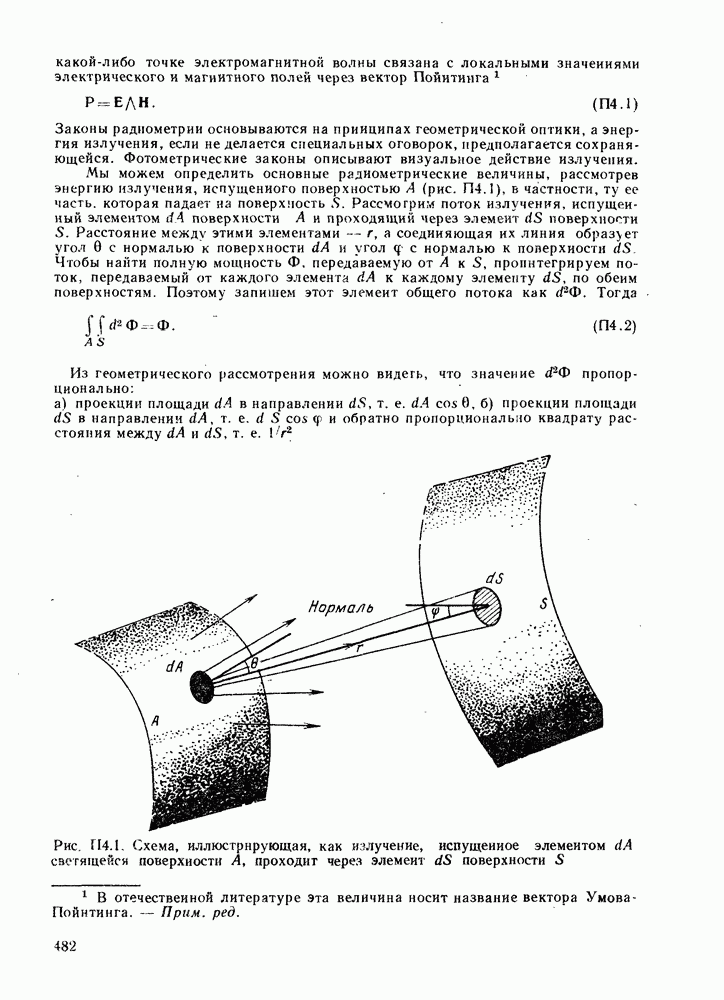
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
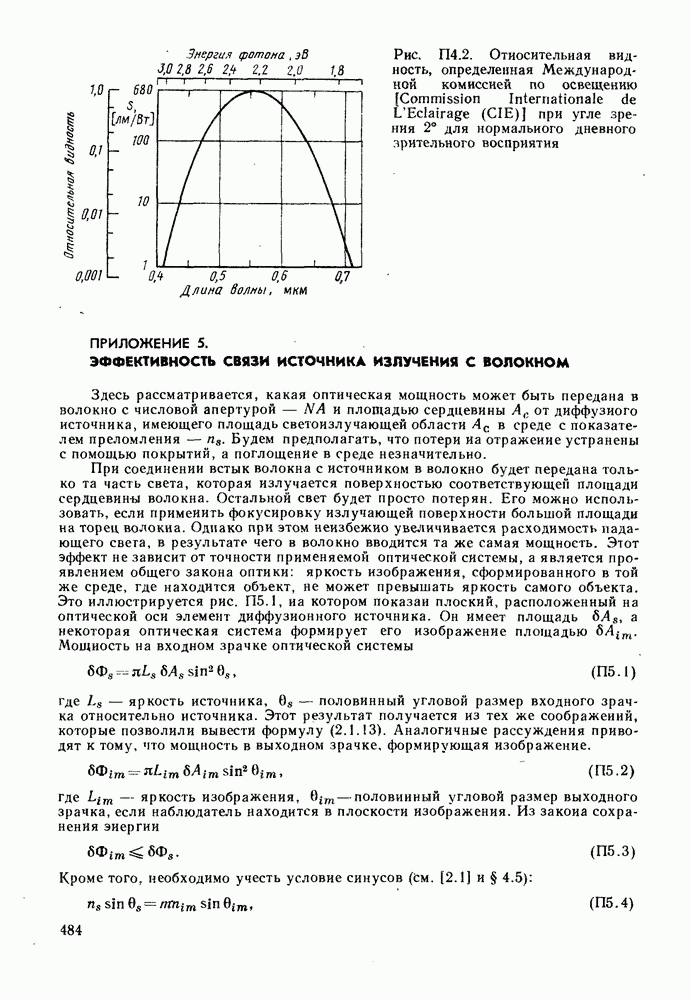
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
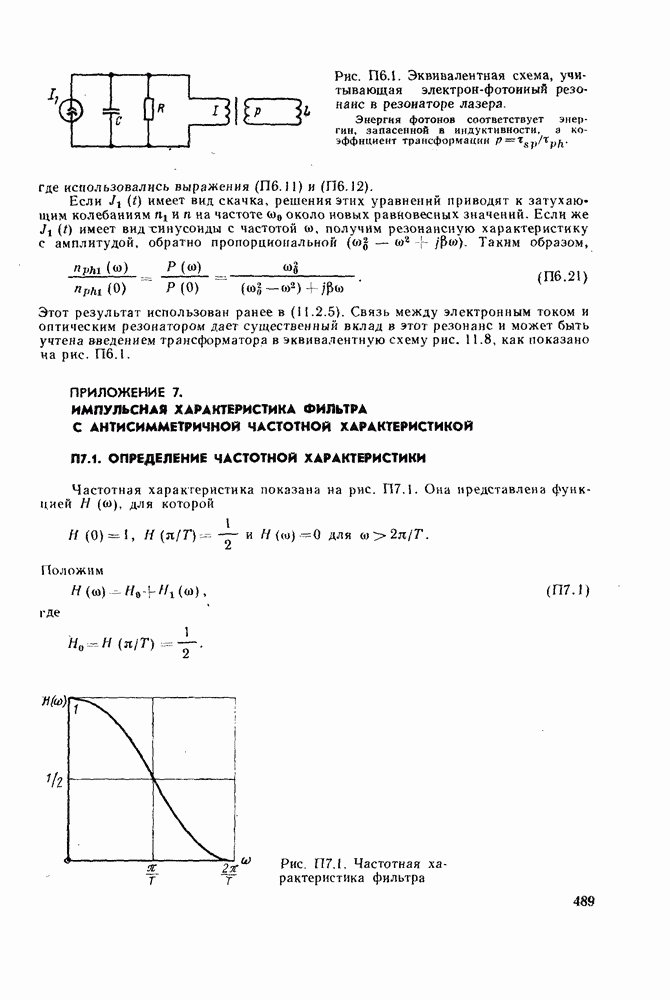
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ