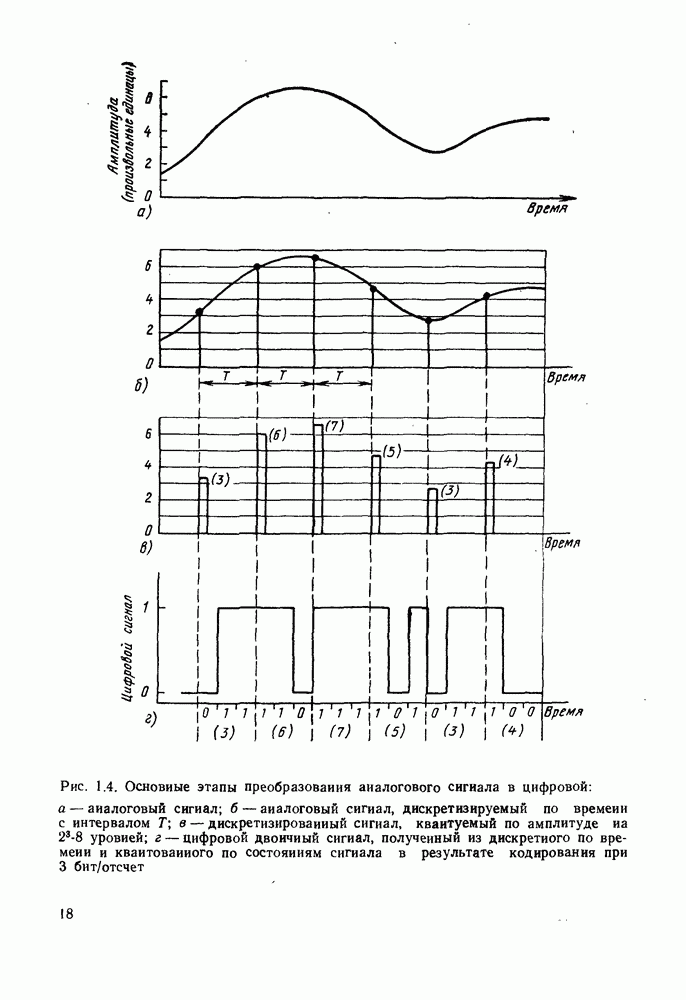
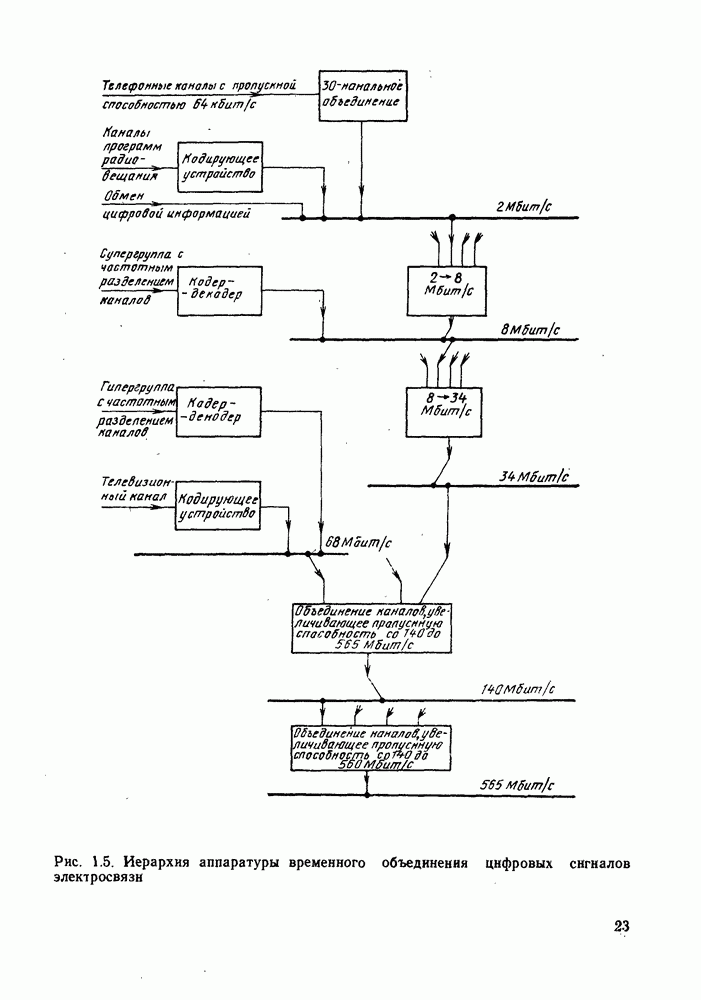
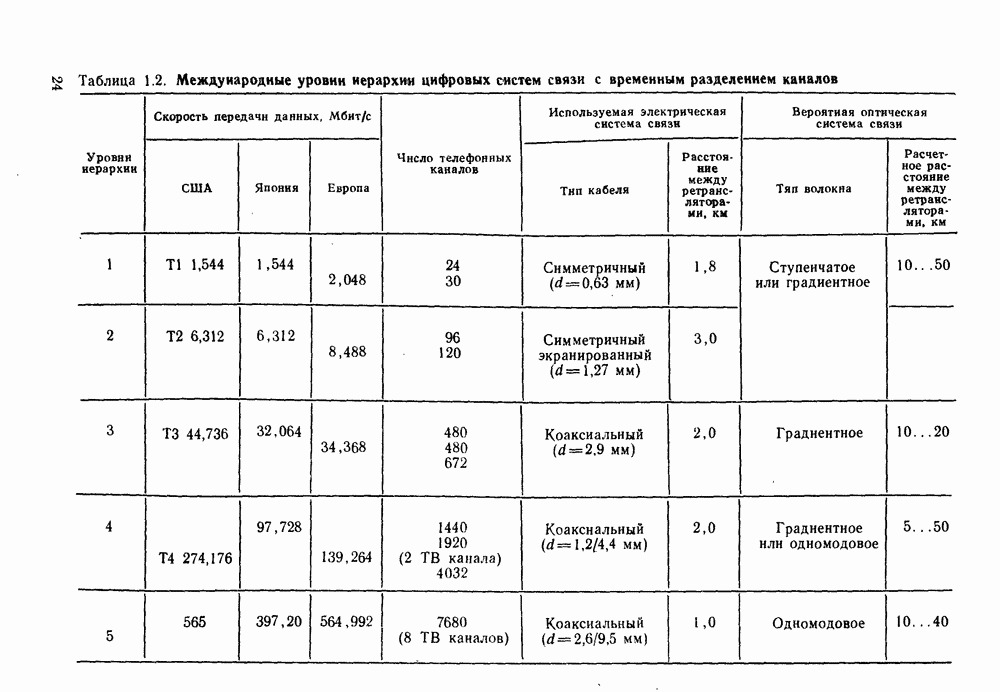
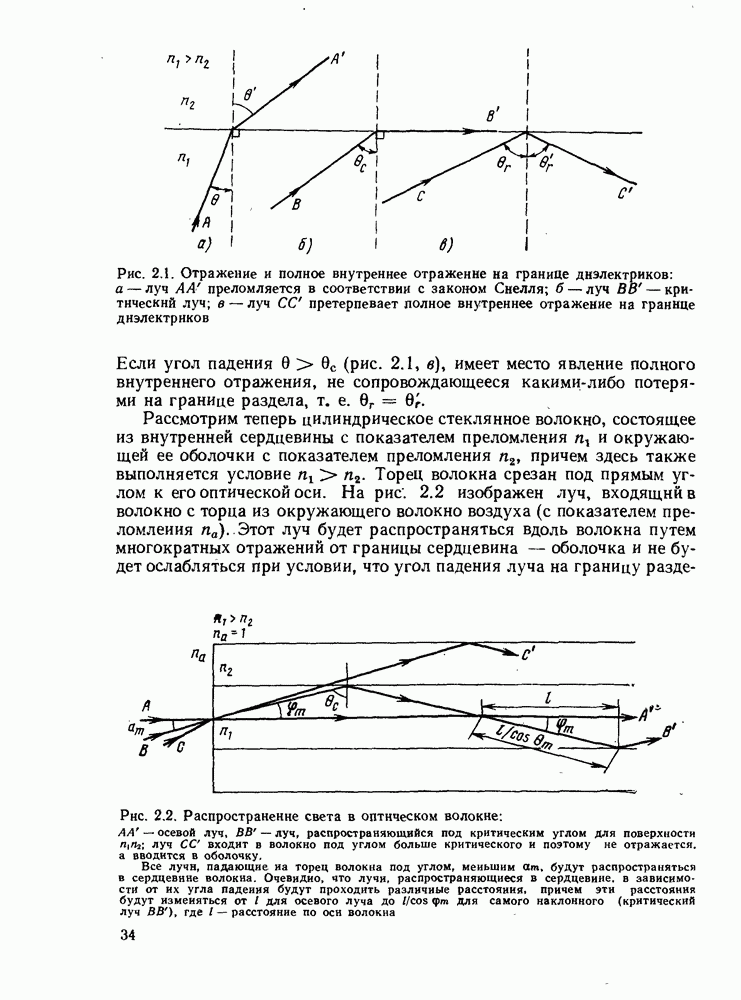
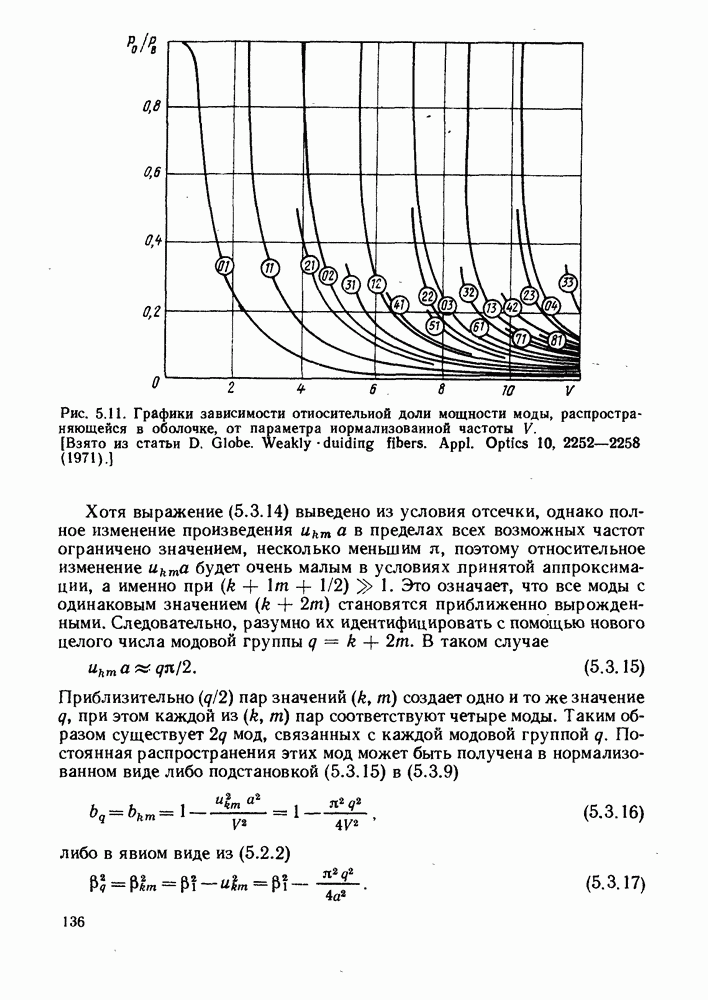
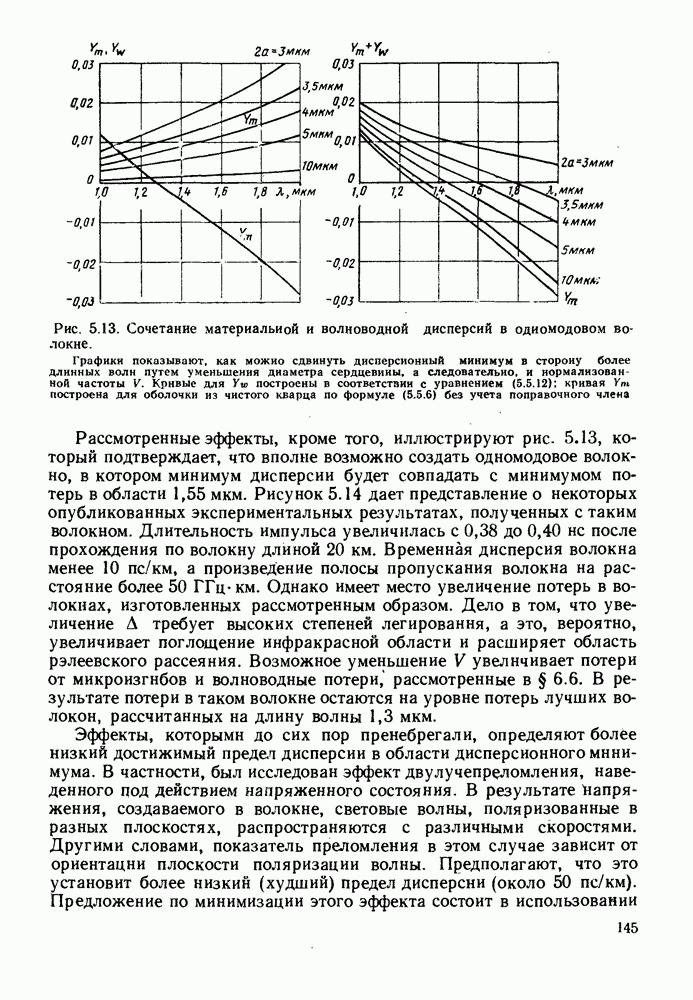
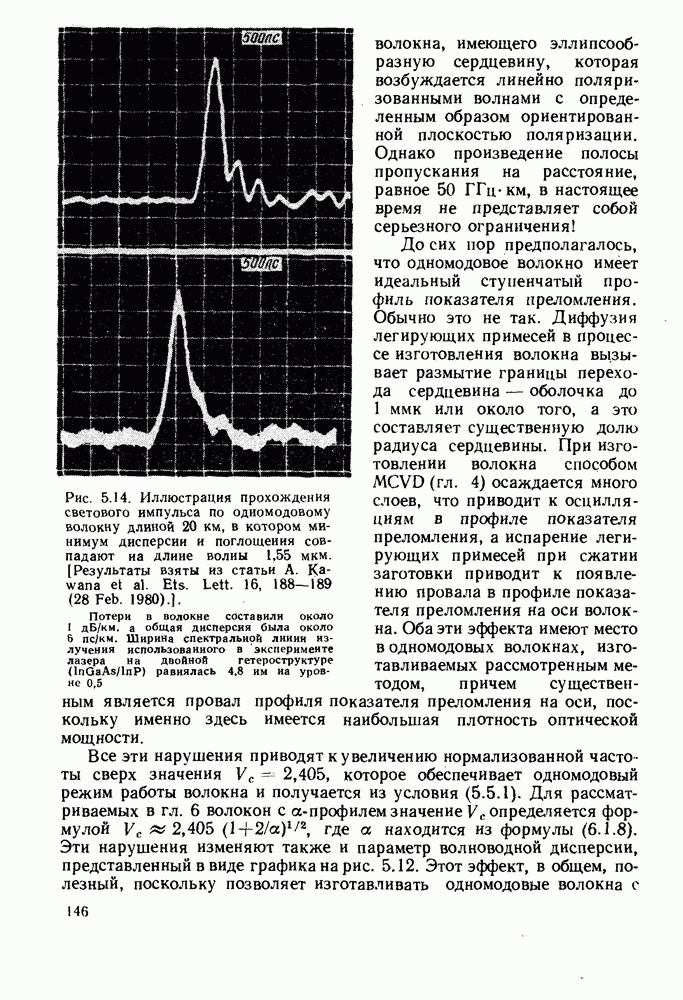
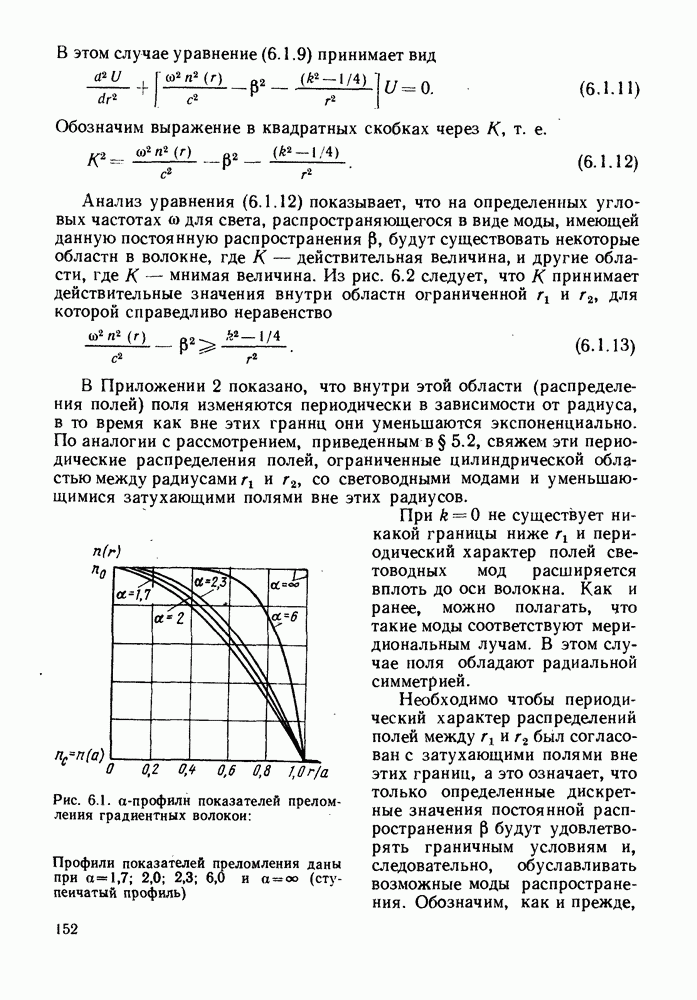
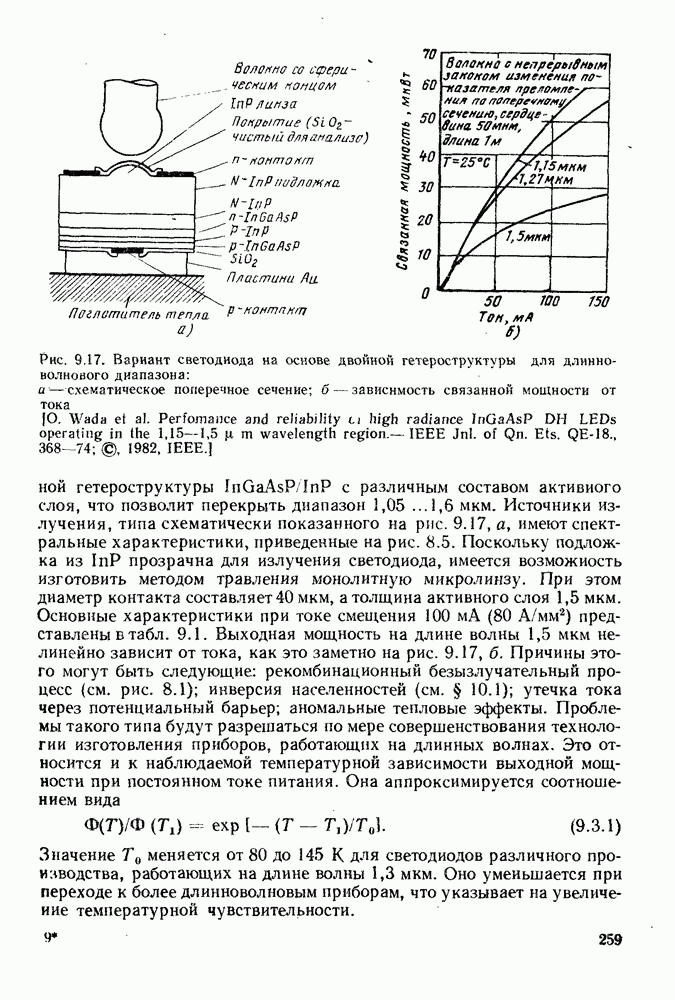
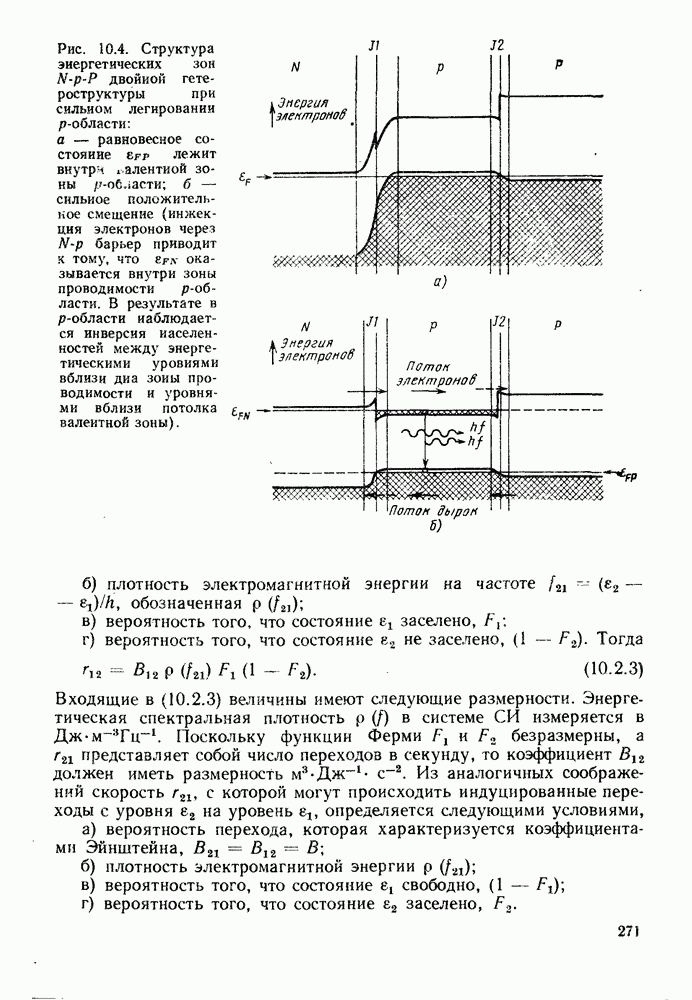
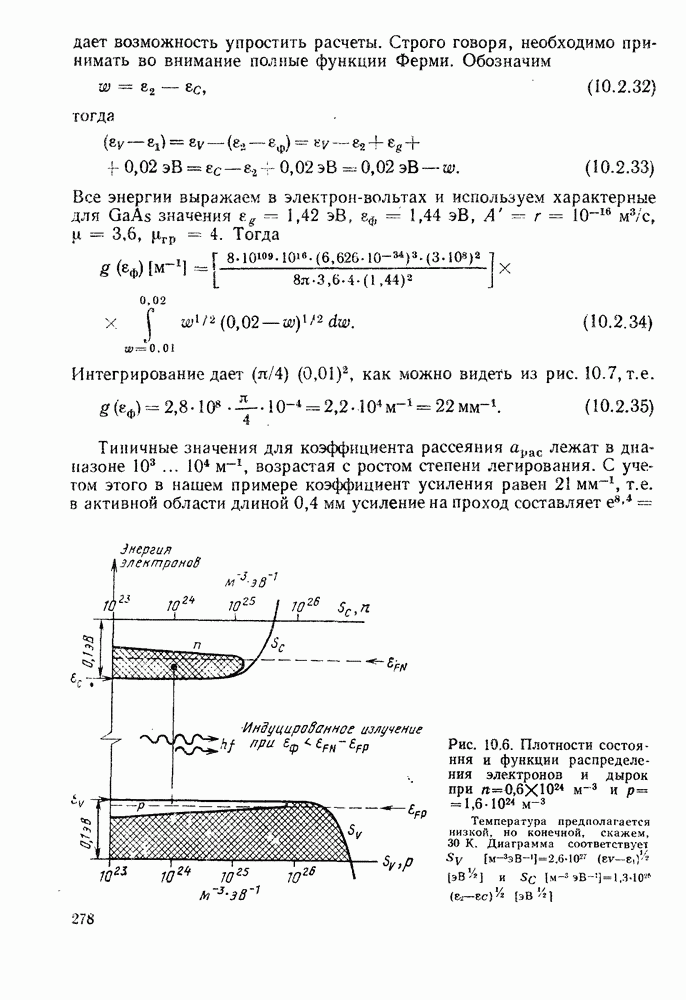
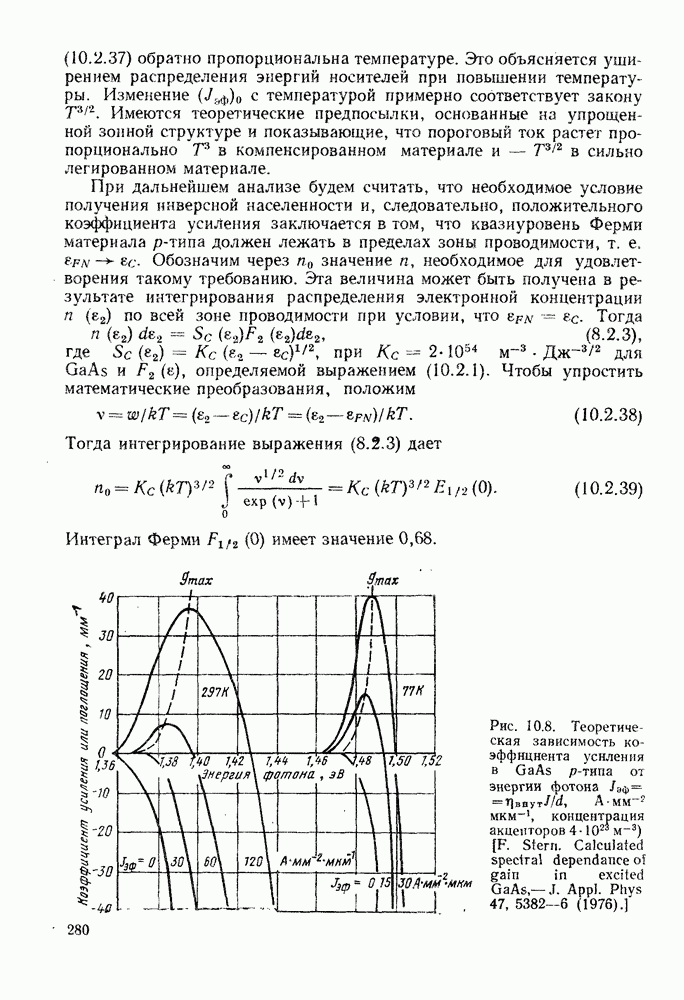
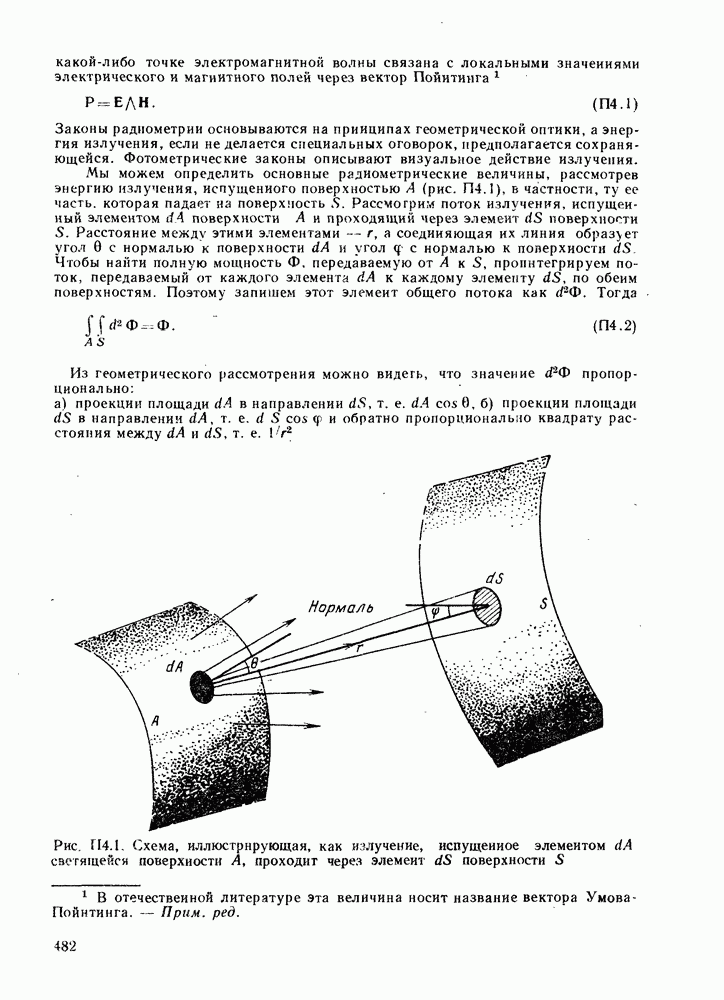
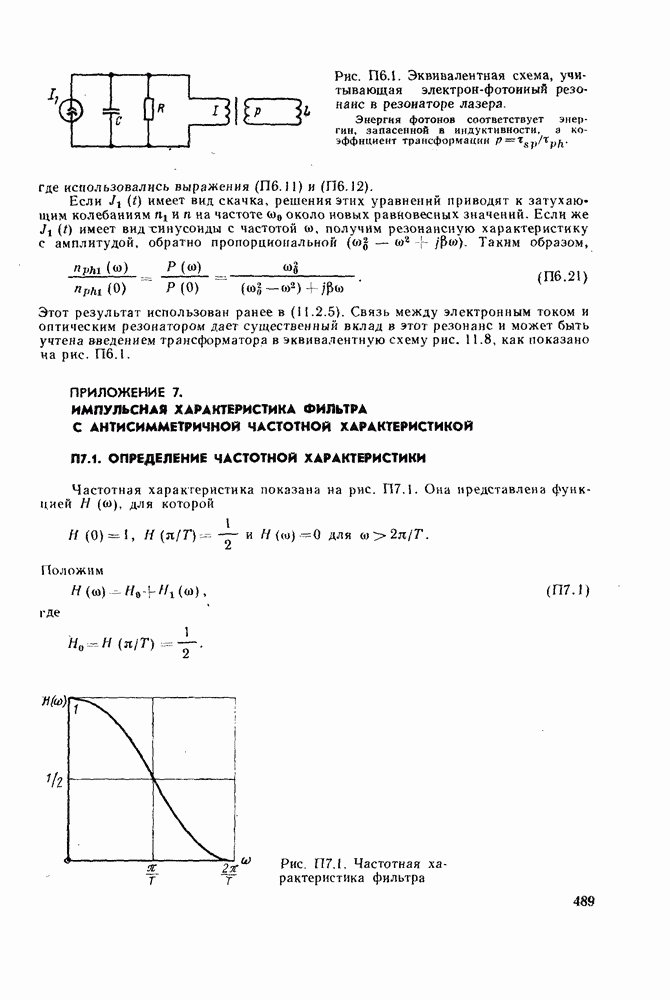
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
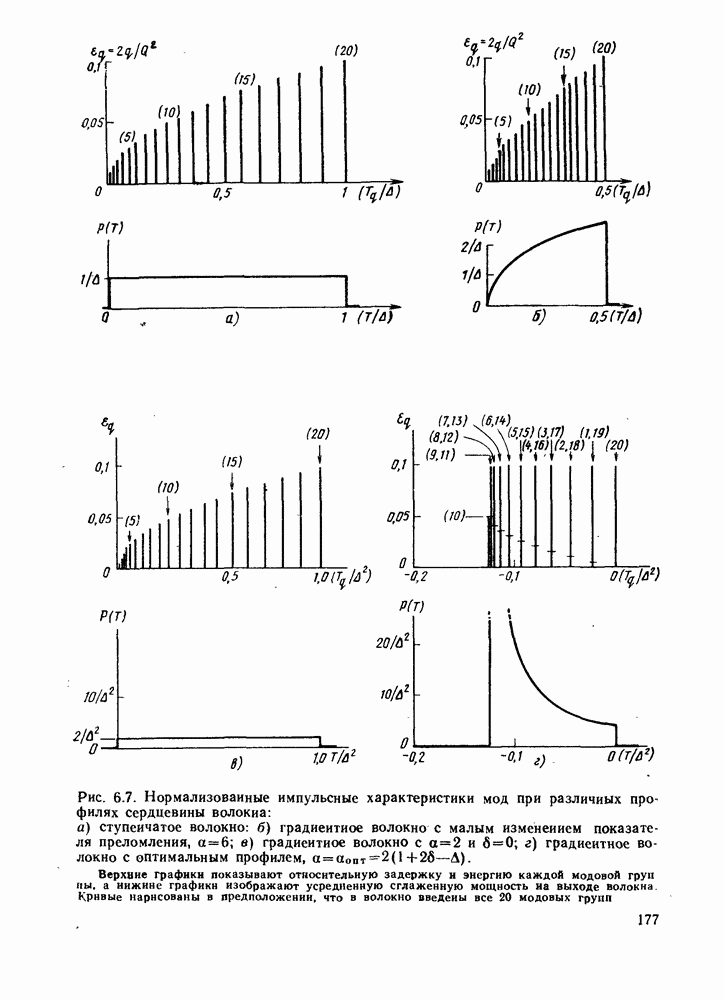
6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
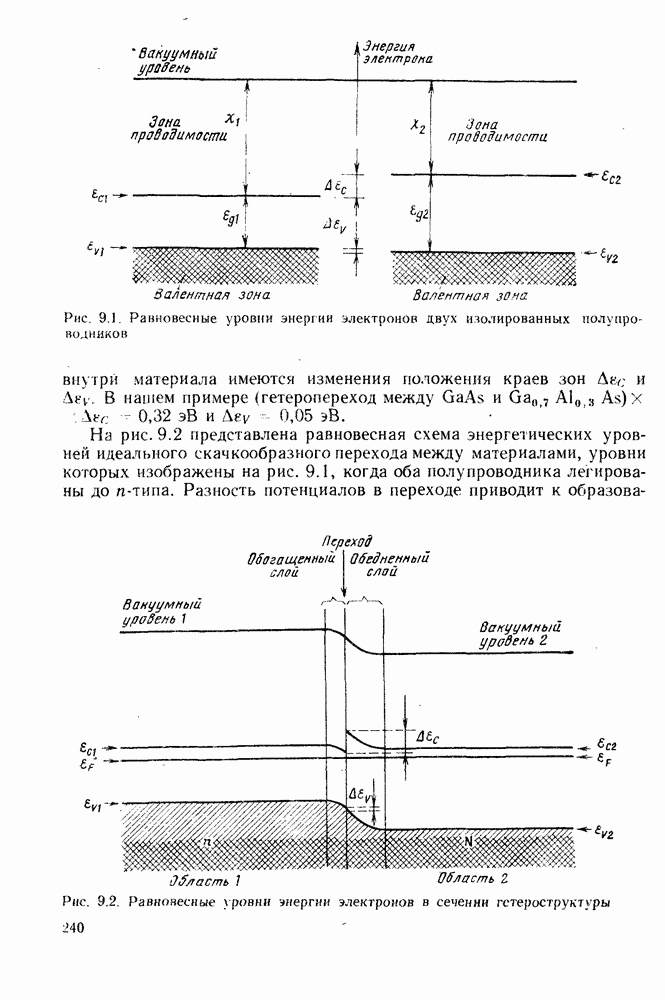
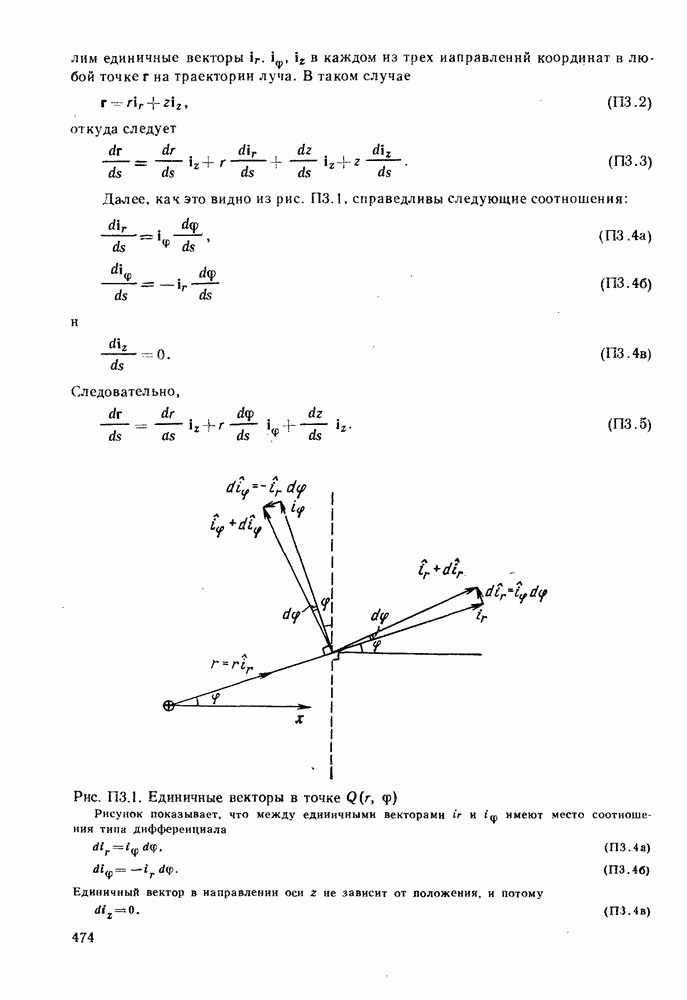
Попытаемся найти оптимальный профиль показателя преломления волокна с учетом дисперсионных свойств материала его сердцевины. Это означает, что необходимо учесть зависимость от частоты величин  входящих в выражение (6.1.40). Приводимое ниже рассмотрение просто повторяет только что сделанное выше для среды без дисперсии, однако математические выкладки становятся существенно более громоздкими. Как и ранее,
входящих в выражение (6.1.40). Приводимое ниже рассмотрение просто повторяет только что сделанное выше для среды без дисперсии, однако математические выкладки становятся существенно более громоздкими. Как и ранее,

Однако теперь

Введем обозначение

где  параметр, не зависящий от частоты
параметр, не зависящий от частоты  Тогда
Тогда 

Учитывая, что 

где

Используя формулу (6.1.20), можно затем упростить выражение (6.3.14) до вида

Представив первый сомножитель в квадратных скобках в виде биномиального ряда, получим

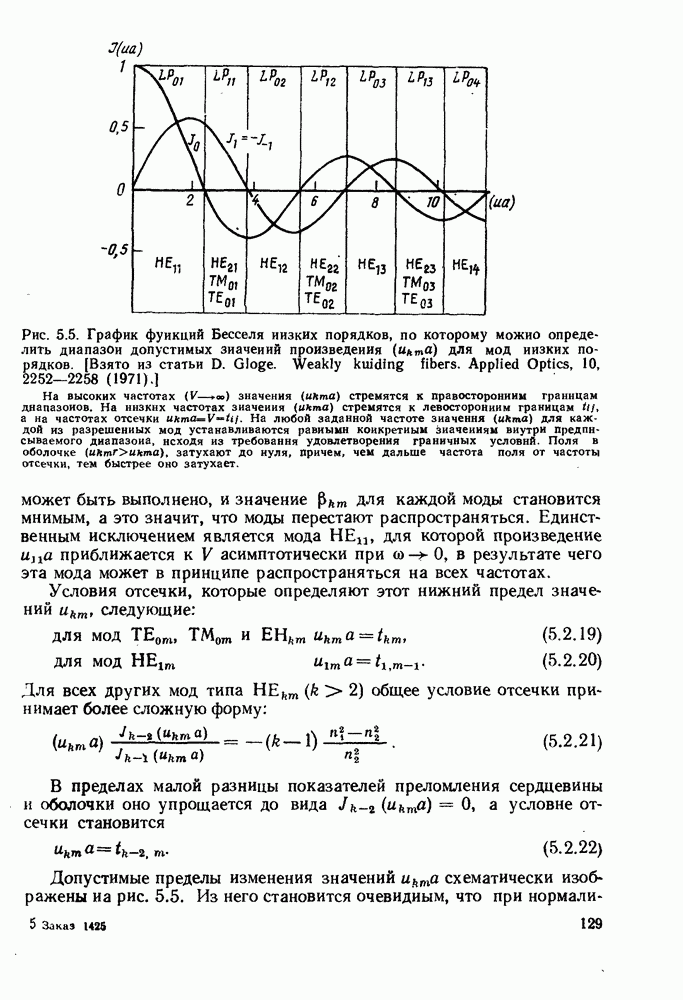
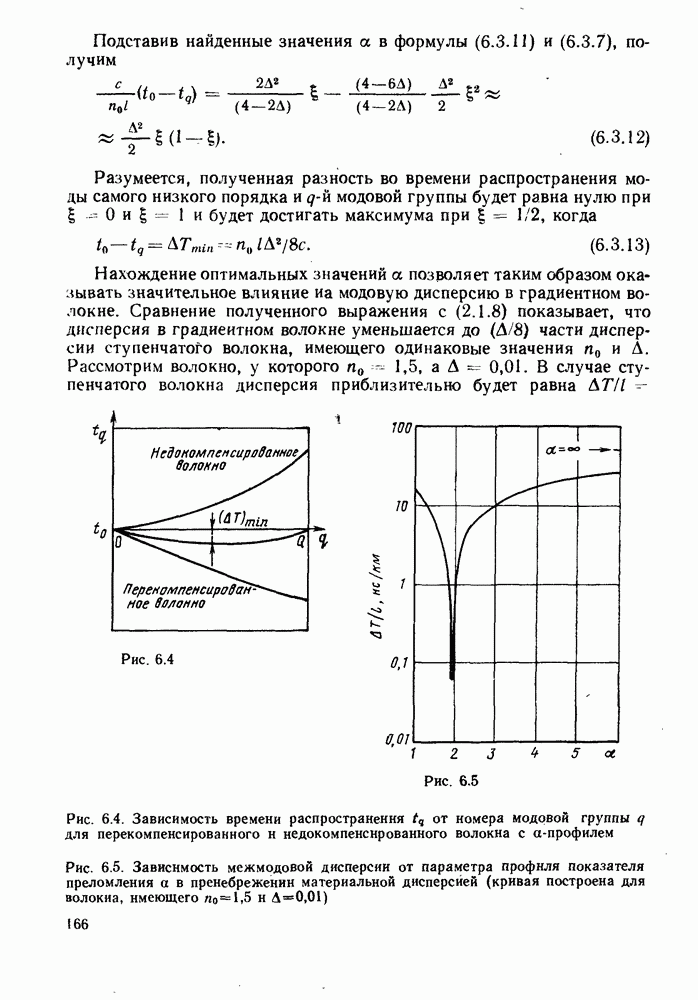
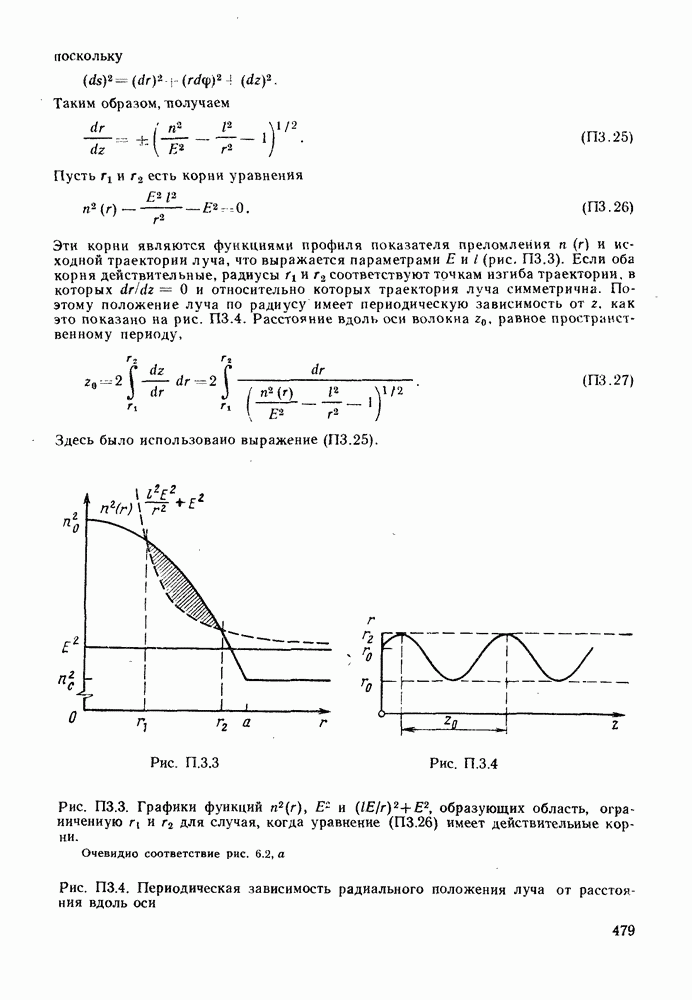
Сиова крайние группы мод соответствуют значениям  Для значений а, удаленных от оптимального, их модовые группы будут такими, которые имеют самое длинное и самое короткое время распространения.
Для значений а, удаленных от оптимального, их модовые группы будут такими, которые имеют самое длинное и самое короткое время распространения.
Тогда, ограничившись только членами первого порядка, находим

Как и в предыдущем случае, минимум временной дисперсии имеет место при  если пренебречь членами третьего порядка,
если пренебречь членами третьего порядка,

Отсюда

В таком случае зависимость групповой задержки от параметра медовой группы  принимает вид
принимает вид

Здесь пренебрегли членами с  по сравнению с 1. Выражение (6.3.22) достигает своего максимума при
по сравнению с 1. Выражение (6.3.22) достигает своего максимума при  когда
когда

Отсюда видно, что наличие материальной дисперсии оказывает двойное влияние на межмодовую дисперсию в градиентных волокнах с  -профилем: приводит к появлению индекса
-профилем: приводит к появлению индекса  группы мод в формуле (6.3.23) для минимума модовой дисперсии и изменяет оптимальное значение а (формула (6.3.21)), требуемое для достижения этого минимума модовой дисперсии, на величину, которая зависит от
группы мод в формуле (6.3.23) для минимума модовой дисперсии и изменяет оптимальное значение а (формула (6.3.21)), требуемое для достижения этого минимума модовой дисперсии, на величину, которая зависит от  а следовательно, и от
а следовательно, и от 
Напомним, что здесь не была учтена внутримодовая дисперсия: эффекты уширения импульса, обусловленные влиянием материальной и волноводной дисперсий для каждой моды. Этот вопрос будет рассмотрен в следующем параграфе.
Осуществление лишь одного легирования материала сердцевины волокна для получения желаемого профиля показателя преломления обычно приводит к нежелательным изменениям дисперсионных свойств стекла вдоль радиуса. Вот почему величина  может стать функцией длины волны. (Так же, как и значение величины а, что уже было учтено при нашем анализе.) Эти эффекты, обусловленные свойствами материала, могут быть скомпенсированы путем управления профилем показателя преломления, т. е. изменением а. Если а меньше 2, моды более высоких порядков (более наклонные лучи) распространяются бы стрее, чем моды низших порядков (осевые лучи). Это может компенсировать разницу показателей преломления между сердцевиной и оболочкой, которая увеличивается с увеличением длины волны. Если же а больше 2, быстрее будут распространяться аксиальные лучи, и это может компенсировать величину
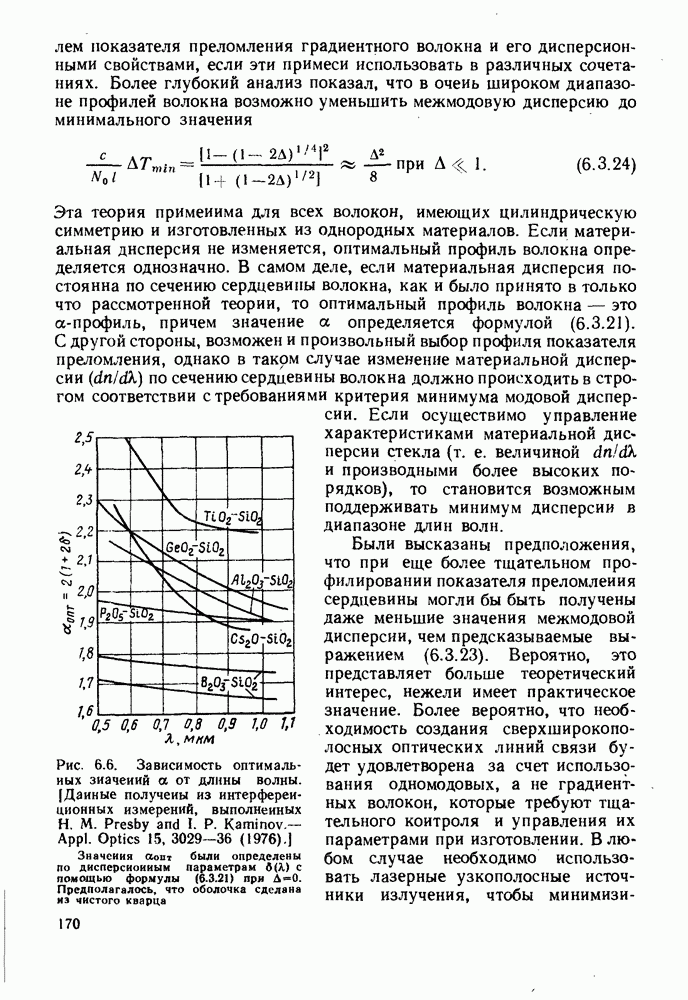
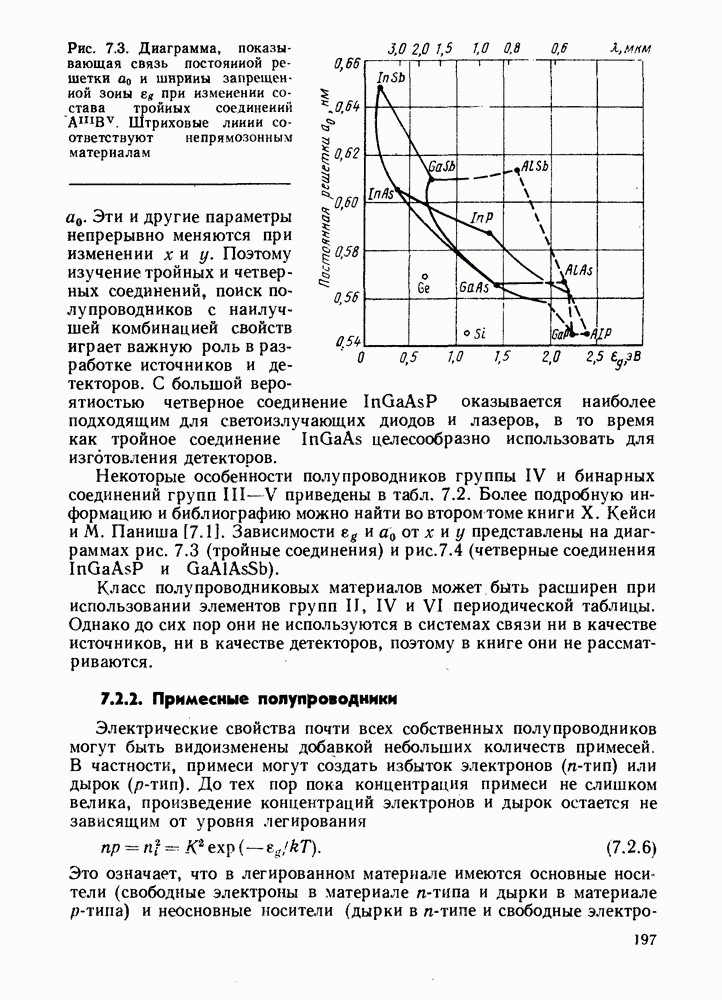
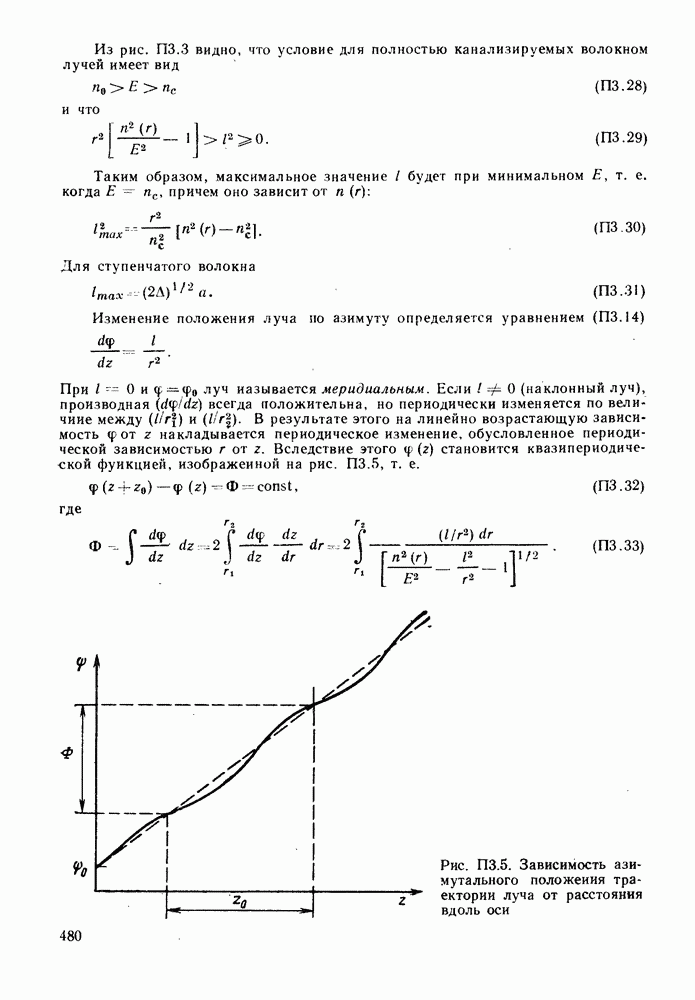
может стать функцией длины волны. (Так же, как и значение величины а, что уже было учтено при нашем анализе.) Эти эффекты, обусловленные свойствами материала, могут быть скомпенсированы путем управления профилем показателя преломления, т. е. изменением а. Если а меньше 2, моды более высоких порядков (более наклонные лучи) распространяются бы стрее, чем моды низших порядков (осевые лучи). Это может компенсировать разницу показателей преломления между сердцевиной и оболочкой, которая увеличивается с увеличением длины волны. Если же а больше 2, быстрее будут распространяться аксиальные лучи, и это может компенсировать величину  которая уменьшается с увеличением длины волны. В результате оптимальное значение а зависит от выбора материала примесей, используемых для получения требуемого изменения показателя преломления, и от длины волны, на которой должно работать волокно. Значения функции 6 (X) для различных легирующих примесей можно определить по известным дисперсионным характеристикам, рассмотренным в § 2.2.2. Затем их можно использовать для нахождения оптимальных значений а на различных длинах волн. Результаты приведены на рис. 6.6.
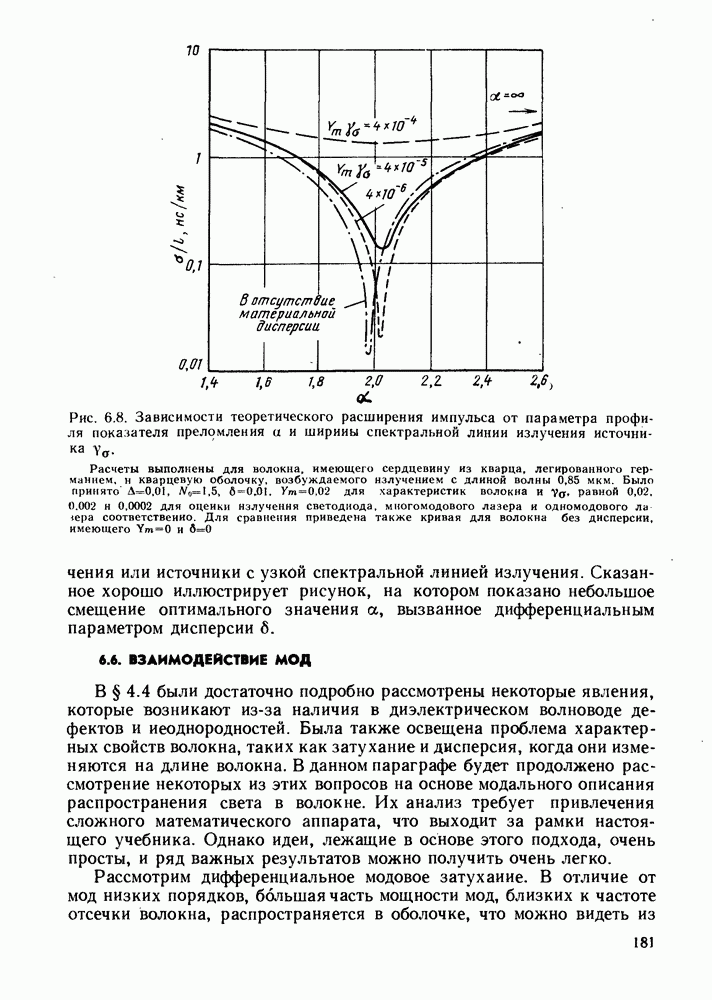
которая уменьшается с увеличением длины волны. В результате оптимальное значение а зависит от выбора материала примесей, используемых для получения требуемого изменения показателя преломления, и от длины волны, на которой должно работать волокно. Значения функции 6 (X) для различных легирующих примесей можно определить по известным дисперсионным характеристикам, рассмотренным в § 2.2.2. Затем их можно использовать для нахождения оптимальных значений а на различных длинах волн. Результаты приведены на рис. 6.6.
Разработчик оптического волокна имеет в своем распоряжении целый ряд легирующих примесей, которые позволят управлять
профилем показателя преломления градиентного волокна и его дисперсионными свойствами, если эти примеси использовать в различных сочетаниях. Более глубокий анализ показал, что в очеиь широком диапазоне профилей волокна возможно уменьшить межмодовую дисперсию до минимального значения

Эта теория применима для всех волокон, имеющих цилиндрическую симметрию и изготовленных из однородных материалов. Если материальная дисперсия не изменяется, оптимальный профиль волокна определяется однозначно. В самом деле, если материальная дисперсия постоянна по сечению сердцевины волокна, как и было принято в только что рассмотренной теории, то оптимальный профиль волокна — это  -профиль, причем значение а определяется формулой (6.3.21). С другой стороны, возможен и произвольный выбор профиля показателя преломления, однако в таком случае изменение материальной дисперсии
-профиль, причем значение а определяется формулой (6.3.21). С другой стороны, возможен и произвольный выбор профиля показателя преломления, однако в таком случае изменение материальной дисперсии  по сечению сердцевины волокна должно происходить в строгом соответствии с требованиями критерия минимума модовой дисперсии. Если осуществимо управление характеристиками материальной дисперсии стекла (т. е. величиной
по сечению сердцевины волокна должно происходить в строгом соответствии с требованиями критерия минимума модовой дисперсии. Если осуществимо управление характеристиками материальной дисперсии стекла (т. е. величиной  и производными более высоких порядков), то становится возможным поддерживать минимум дисперсии в диапазоне длин волн.
и производными более высоких порядков), то становится возможным поддерживать минимум дисперсии в диапазоне длин волн.
Были высказаны предположения, что при еще более тщательном профилировании показателя преломления сердцевины могли бы быть получены даже меньшие значения межмодовой дисперсии, чем предсказываемые выражением (6.3.23). Вероятно, это представляет больше теоретический интерес, нежели имеет практическое значение. Более вероятно, что необходимость создания сверхширокополосных оптических линий связи будет удовлетворена за счет использования одномодовых, а не градиентных волокон, которые требуют тщательного контроля и управления их параметрами при изготовлении. В любом случае необходимо использовать лазерные узкополосные источники излучения, чтобы

Рис. 6.6. Зависимость оптимальных значений о от длины волны. (Данные получены из интерференционных измерений, выполненных Н. М. Presby and I. P. Kaminov.- Appl. Optics 15, 3029-36 (1976).] Значения аопт были определены по дисперсионным параметрам  с помощью формулы (6.3.21) при
с помощью формулы (6.3.21) при  Предполагалось, что оболочка сделана из чистого кварца
Предполагалось, что оболочка сделана из чистого кварца
минимизировать непосредственное влияние материальной дисперсии. Однако возможно одно исключение из этого требования, относящееся к оптическим системам передачи информации, которые используют светодиод, работающий на длине волны около 1,3 мкм, что соответствует минимуму материальной дисперсии. Такая система описана в гл. 17. Она имеет еще и то достоинство, что проста и дешева и обеспечивает широкую полосу пропускания. Однако характеристики этой системы очень сильно зависят от наличия хороших градиентных волокон. Существует и другой тип волокна, который, по-видимому, найдет определенное применение. Это волокно имеет довольно большие числовую апертуру и диаметр сердцевины и сравнительно грубый профиль показателя преломления. При использовании в сочетании с широкополосным светодиодом оно могло бы помочь в реализации дешевой и простой системы связи со средними значениями полосы пропускания. В данном случае целью изменения показателя преломления было бы уменьшение межмодовой дисперсии простого ступенчатого волокна до уровня, сравнимого с материальной дисперсией.
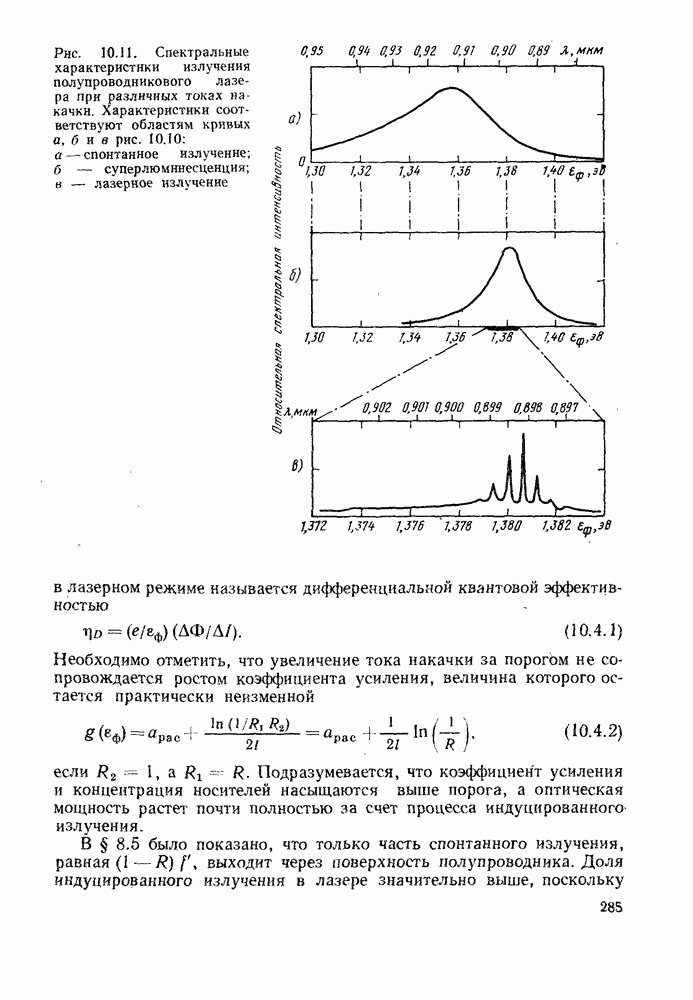
Наконец, необходимо упомянуть о практически важном эффекте, наблюдаемом в длинных волоконных линиях. Обнаружено, что если некоторые отрезки волокна перекомпенсированы (а слишком мало), а другие недокомпенсированы (а слишком велико), то чередование их приводит к уменьшению совокупной дисперсии. Группы мод, которые более медленно распространяются в первом отрезке волокна, будут быстрее распространяться во втором отрезке волокна, и наоборот. В результате этого уменьшается разница во времени распространения мод после прохождения этой пары отрезков волокна.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
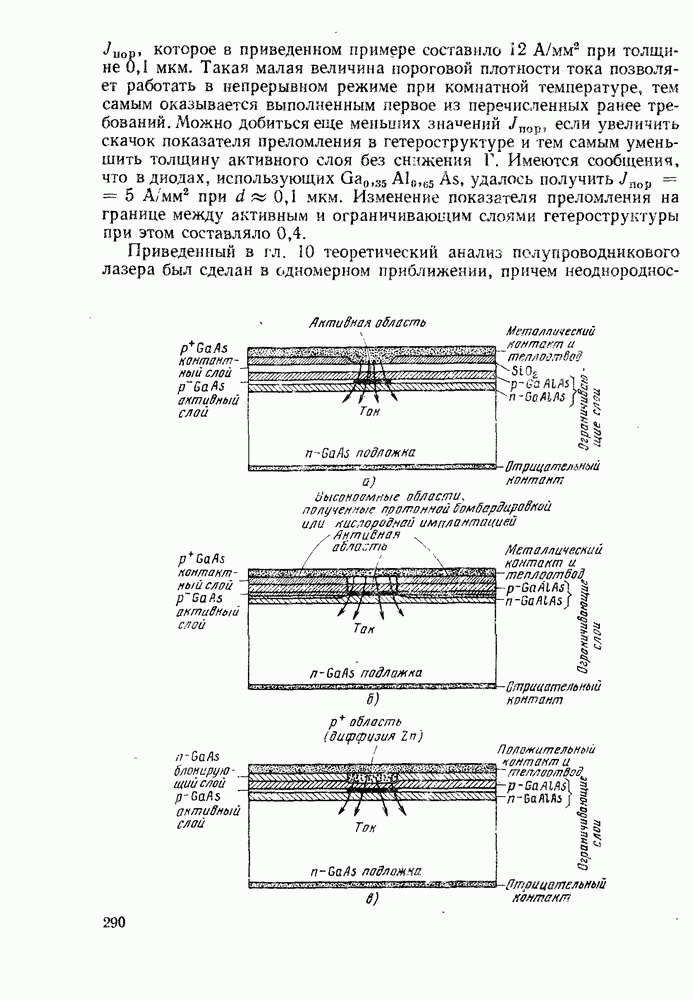
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
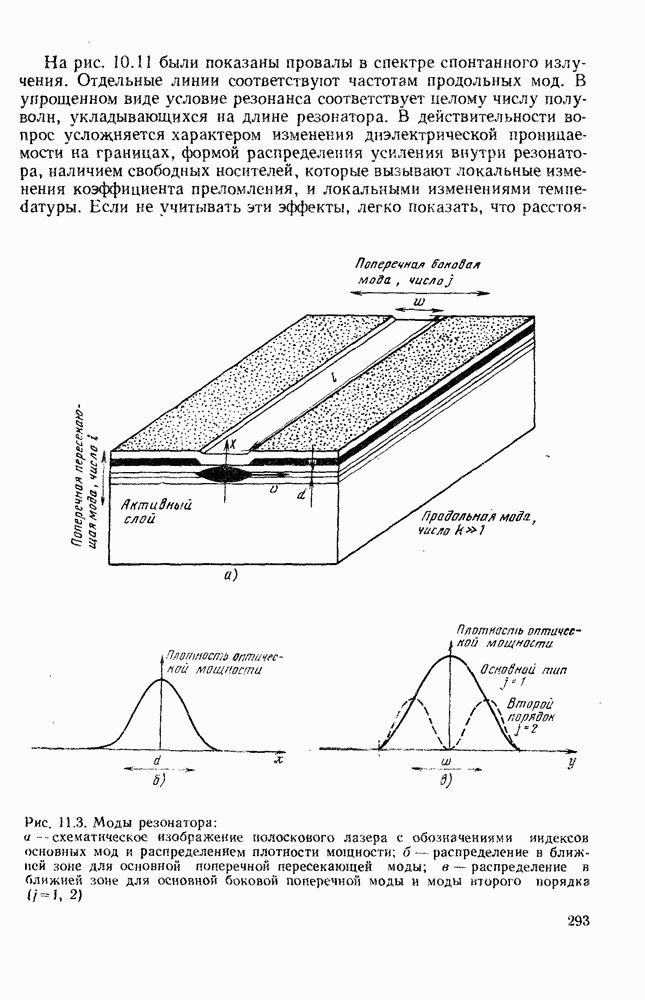
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
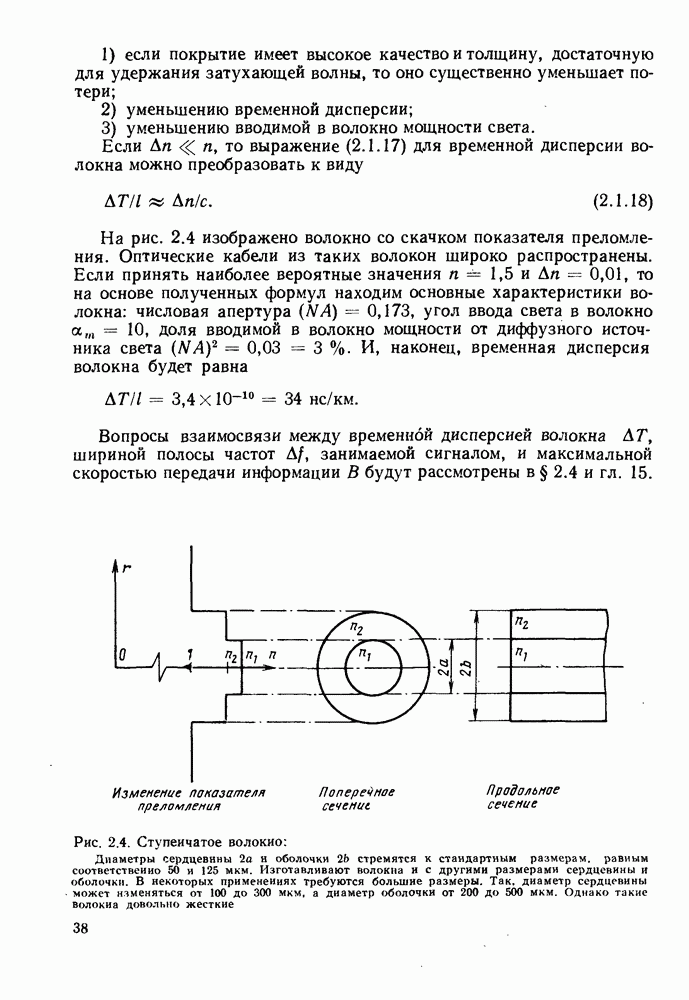
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
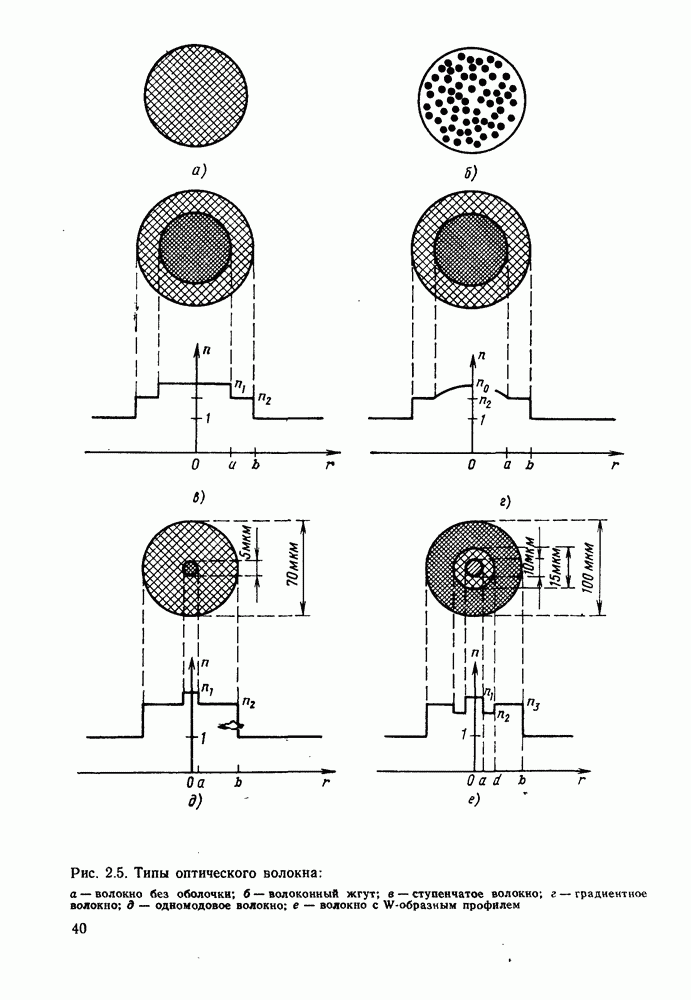
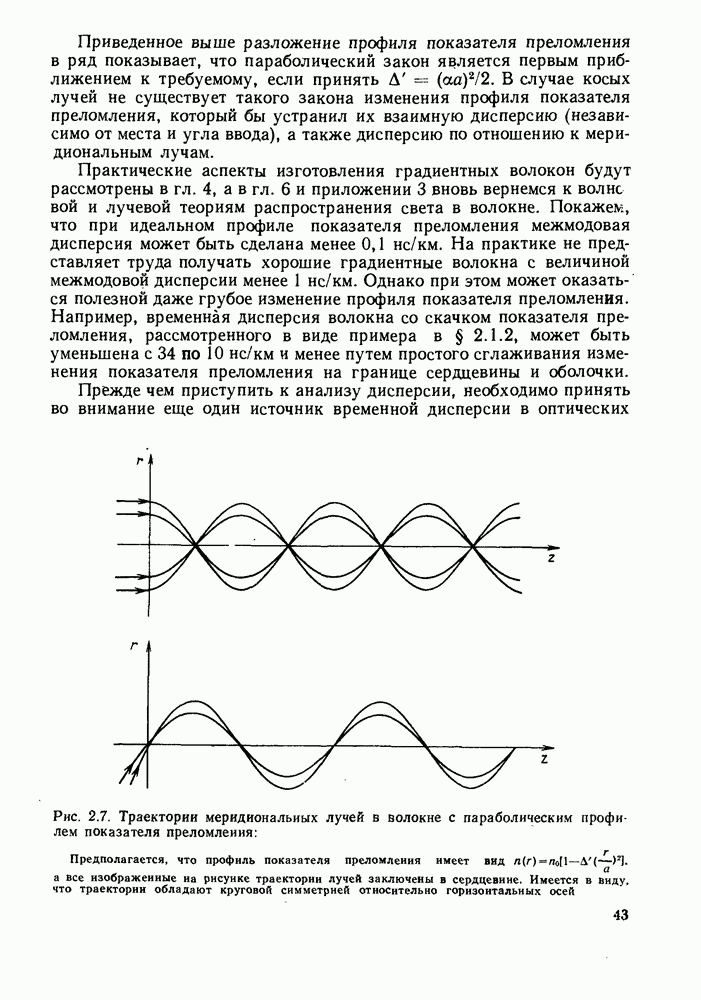
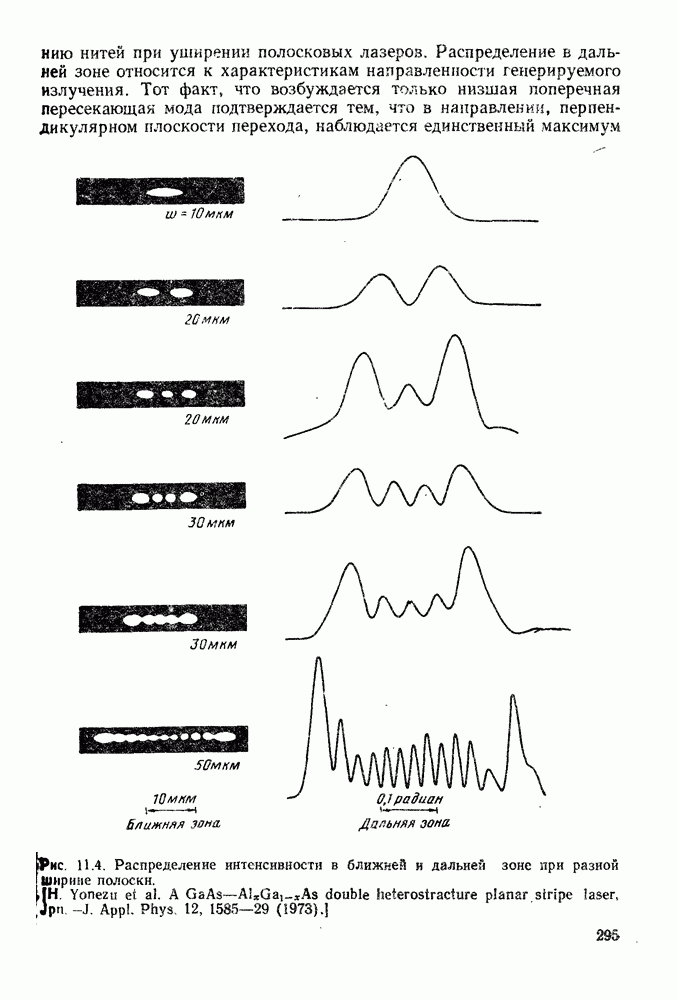
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
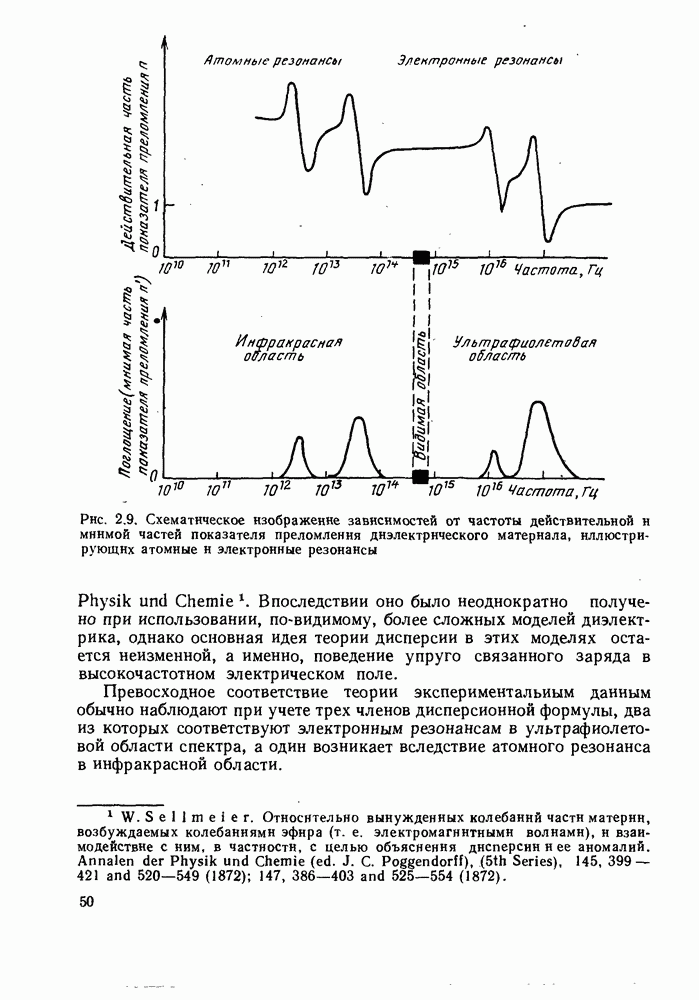
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
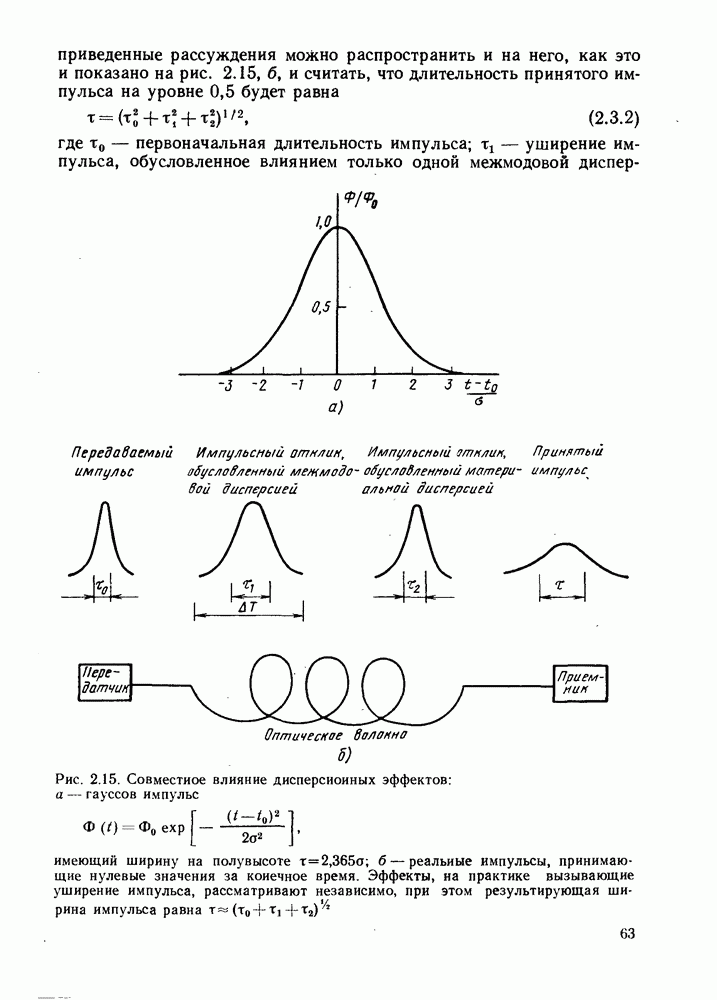
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
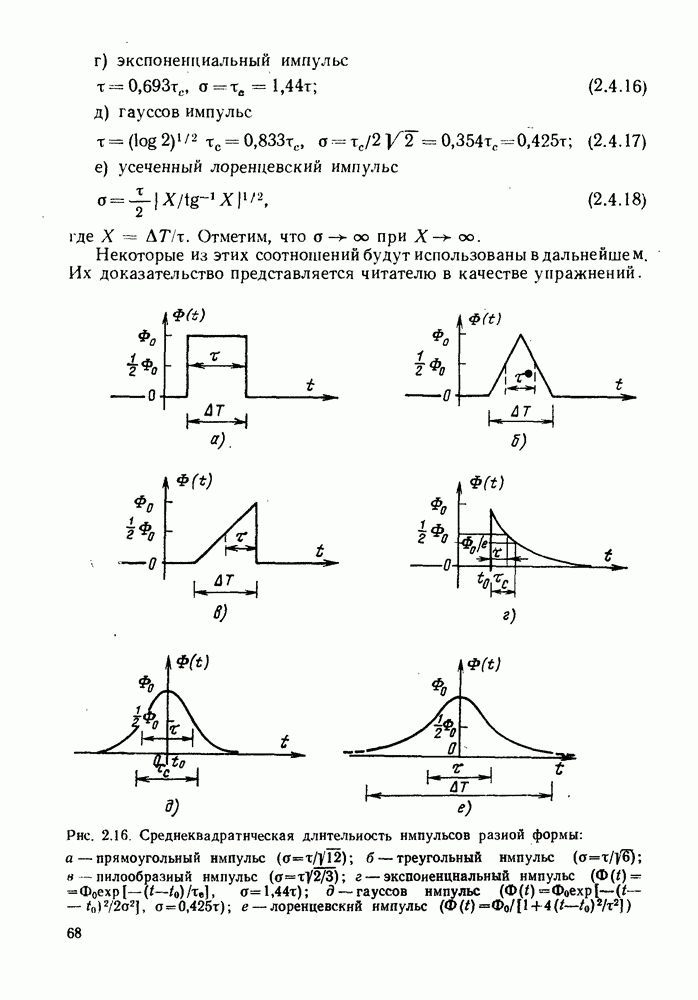
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
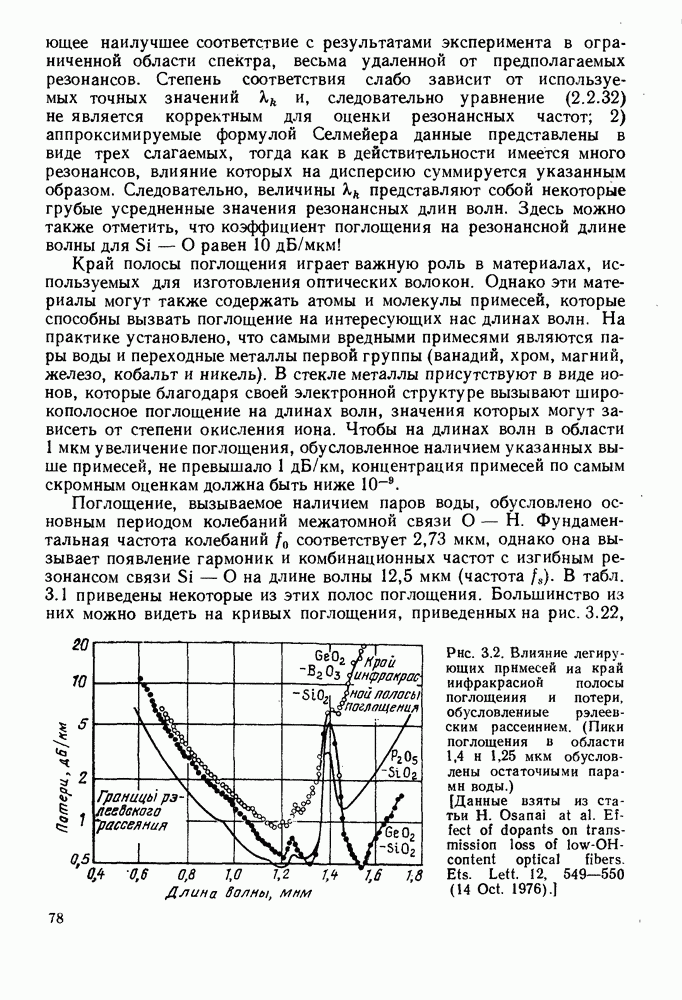
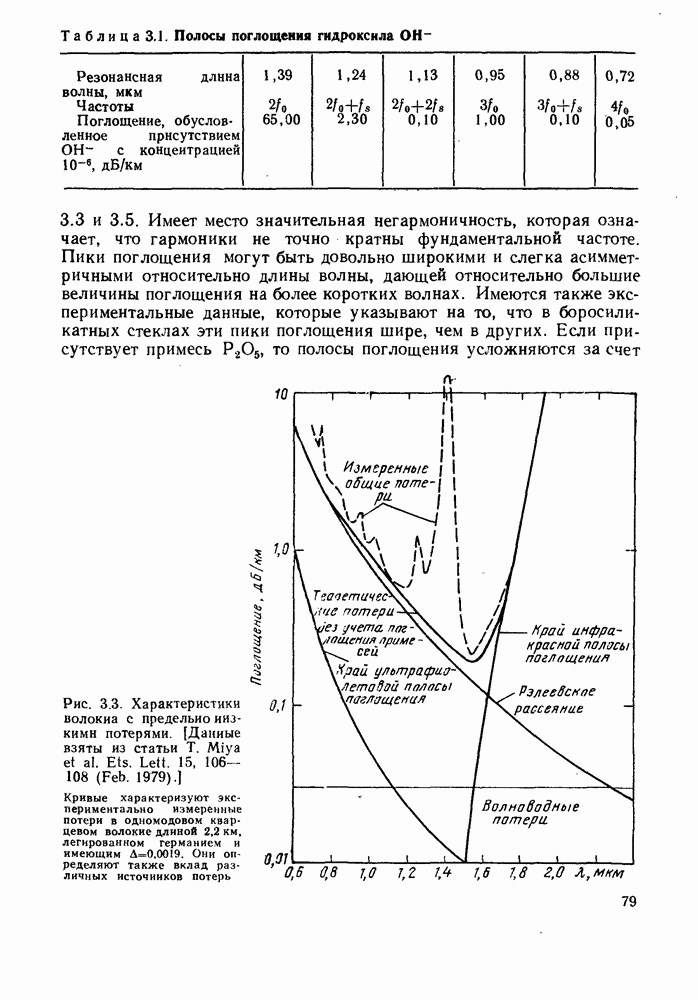
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
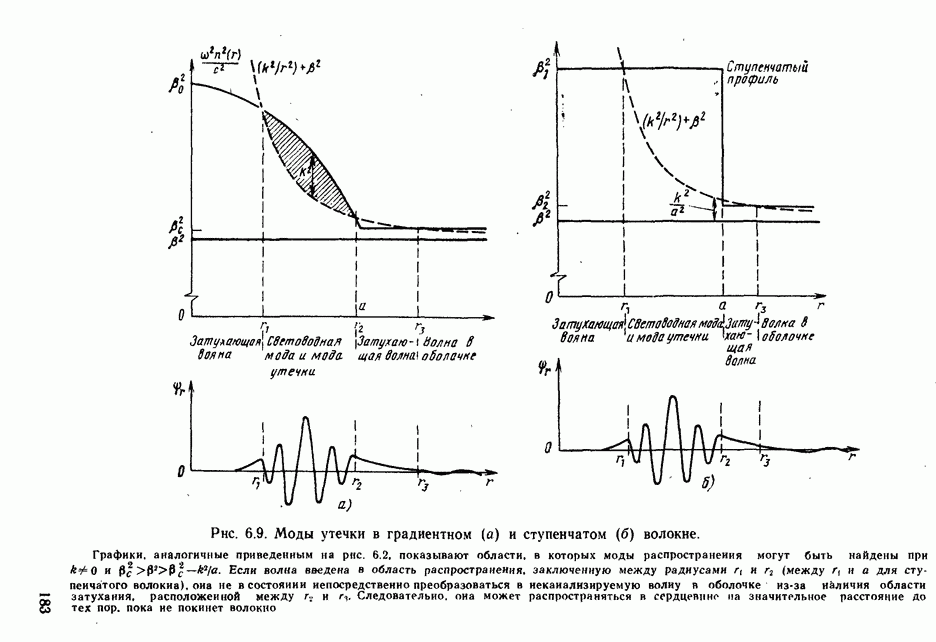
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
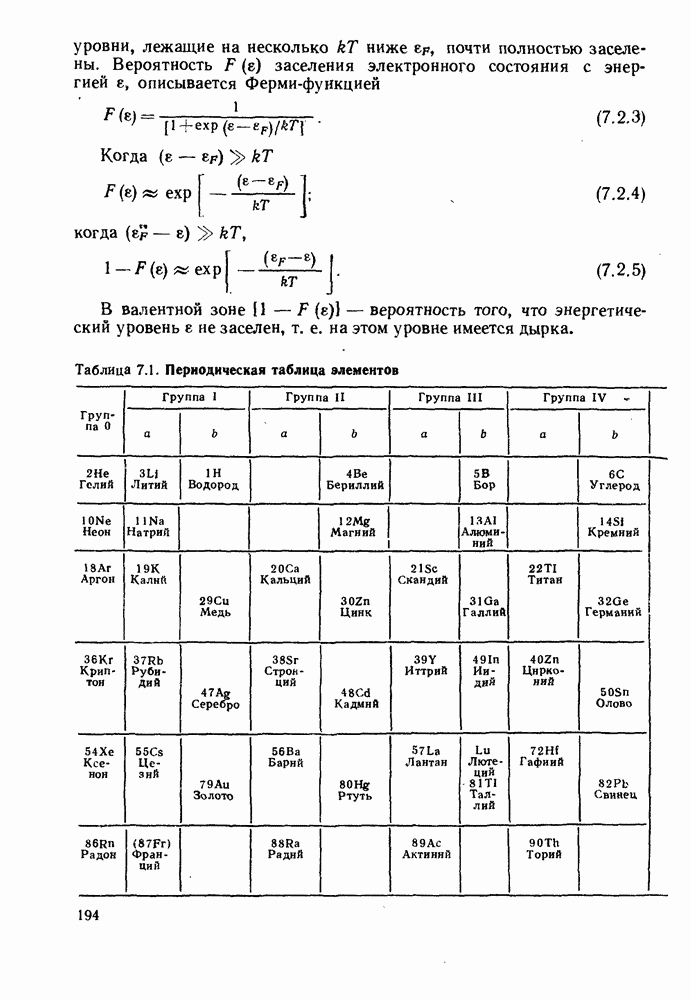
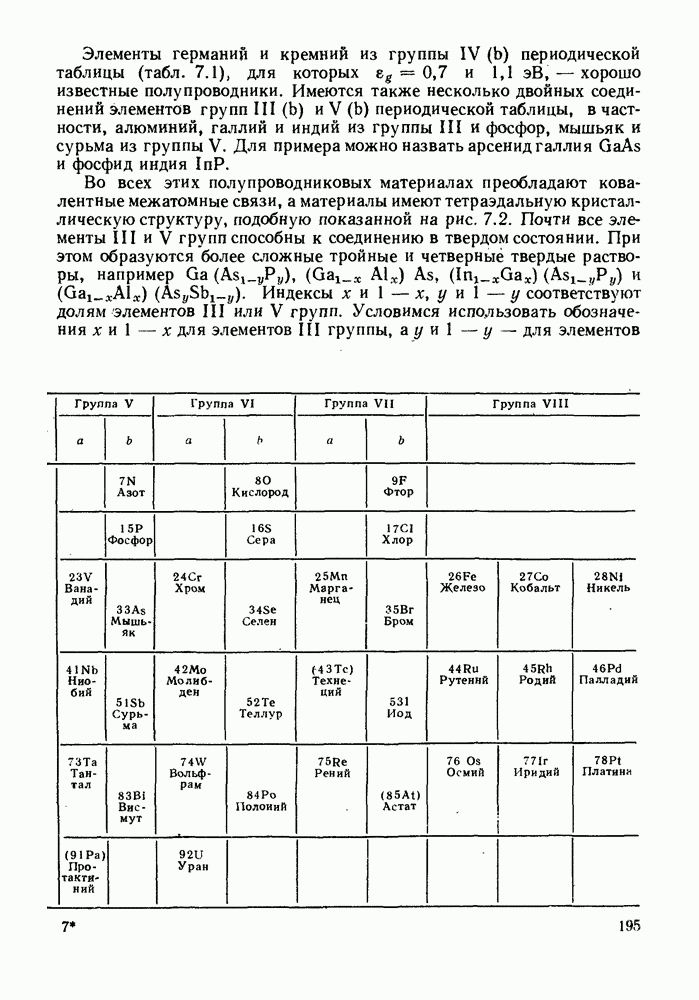
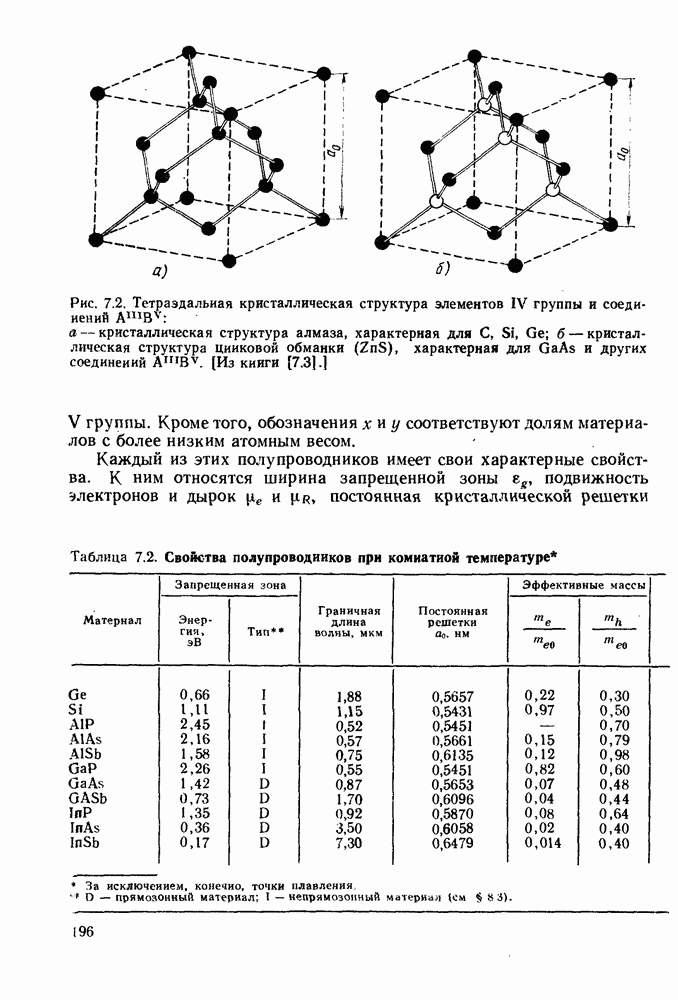
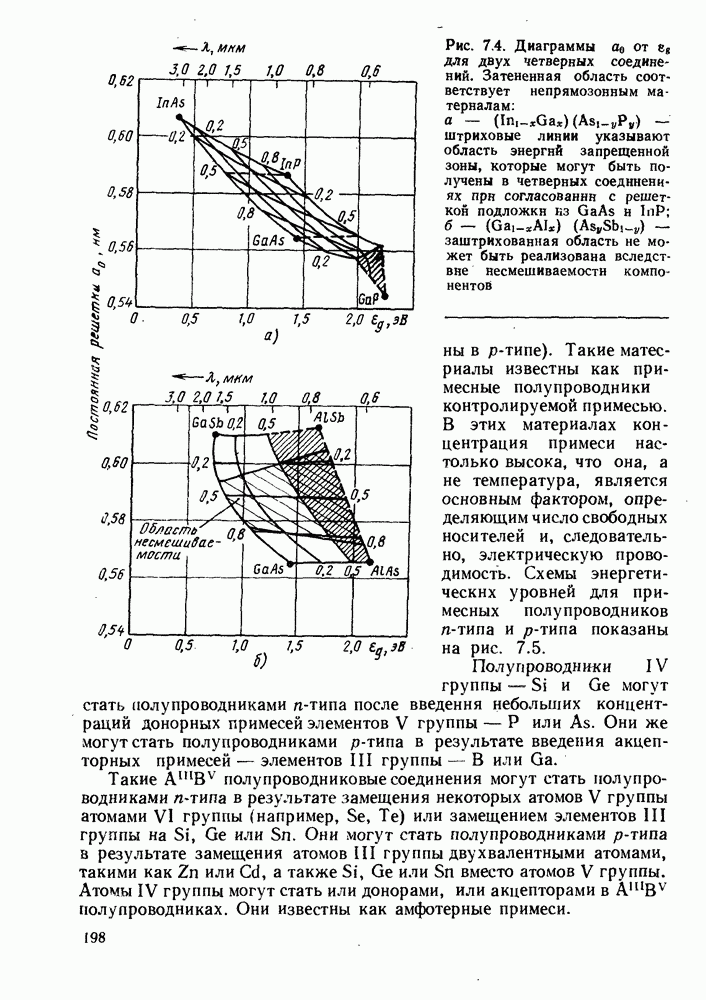
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
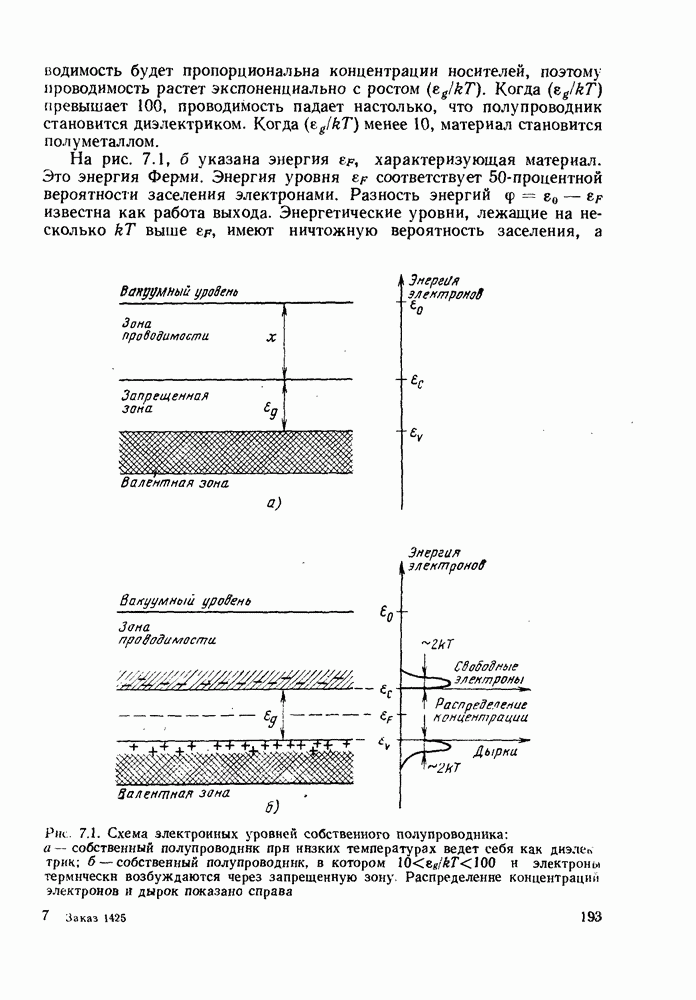
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
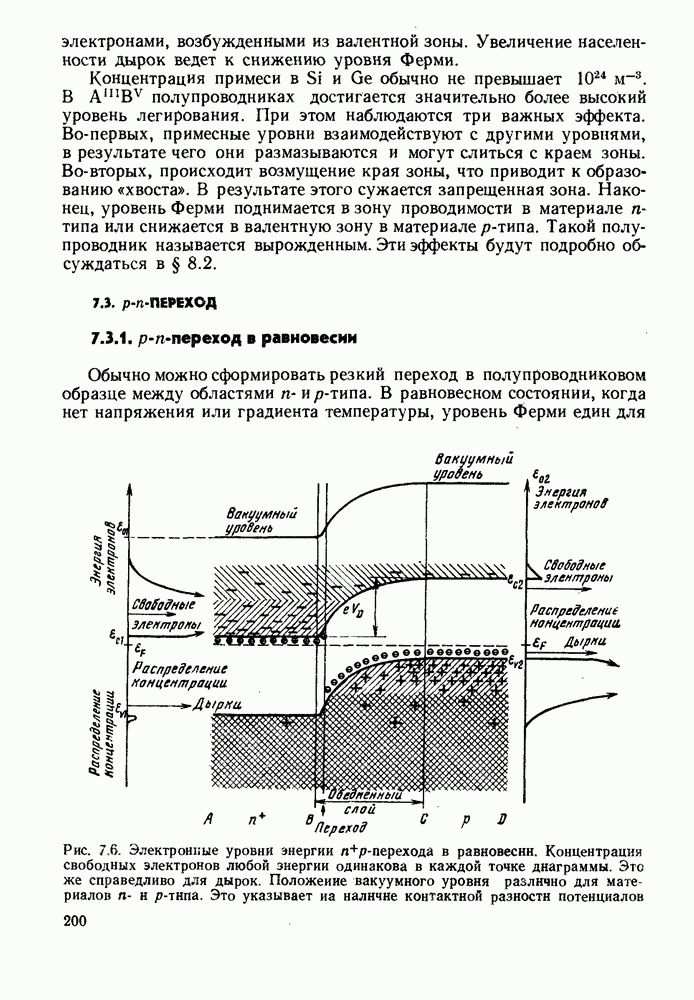
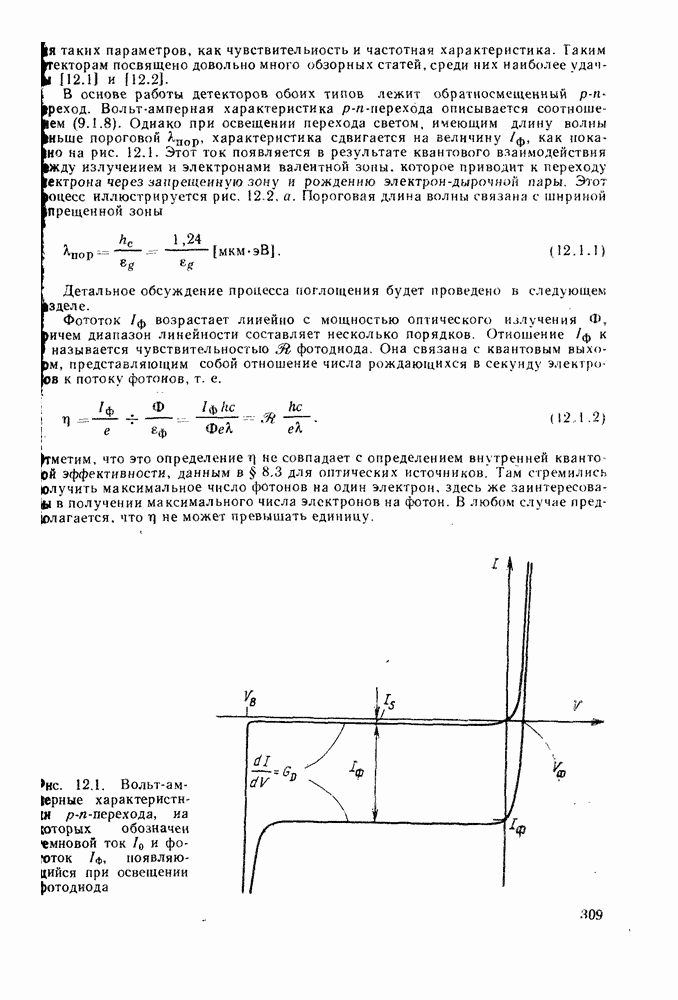
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
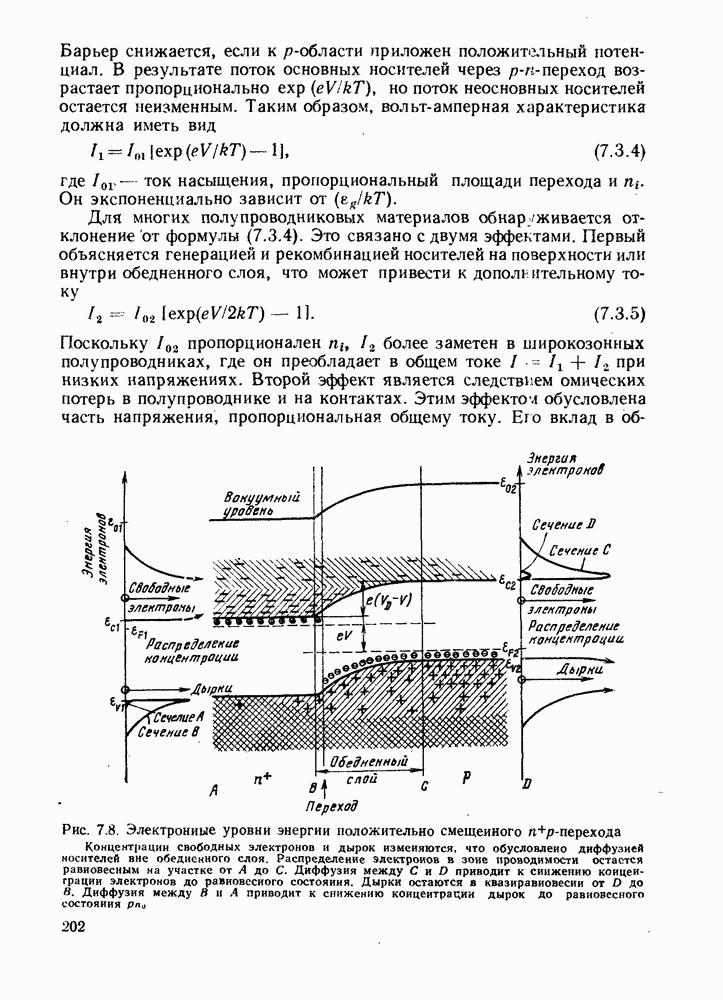
- 7.3.2. Смещенный p-n-переход
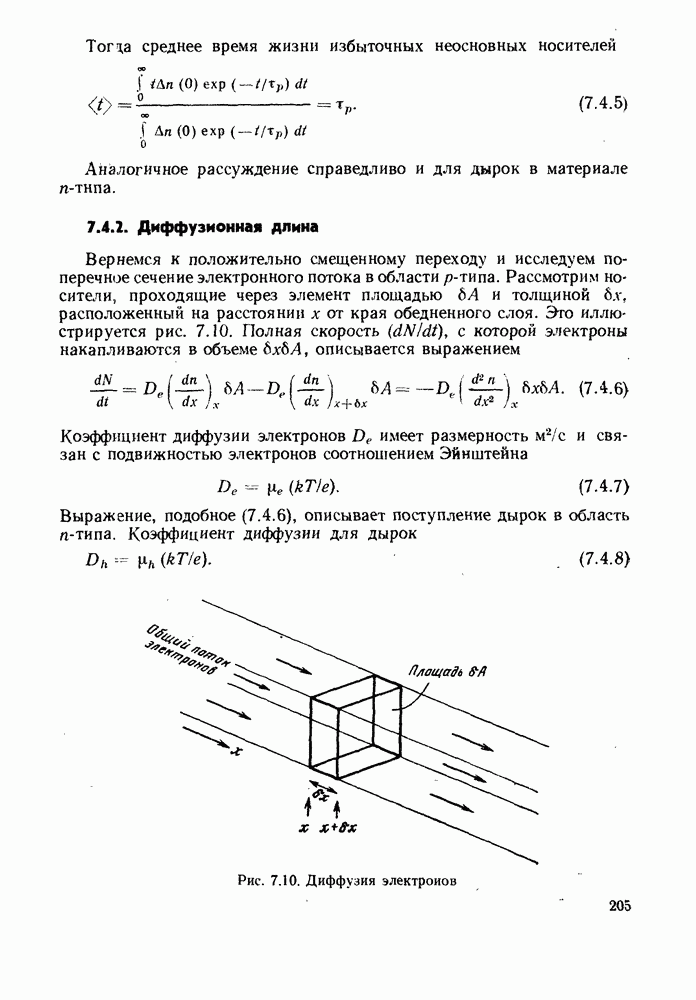
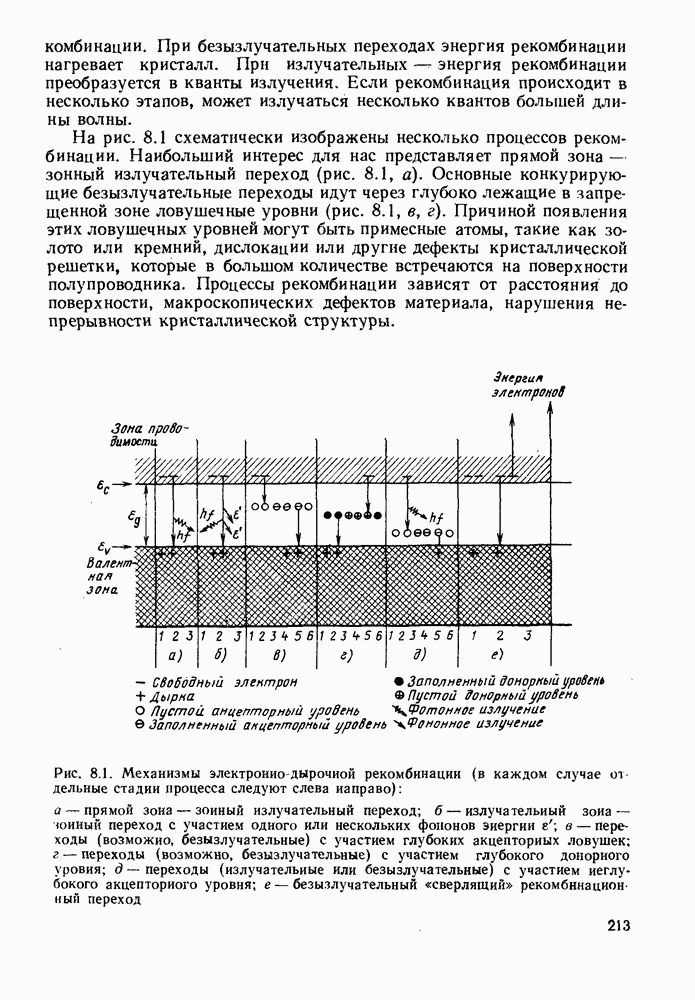
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
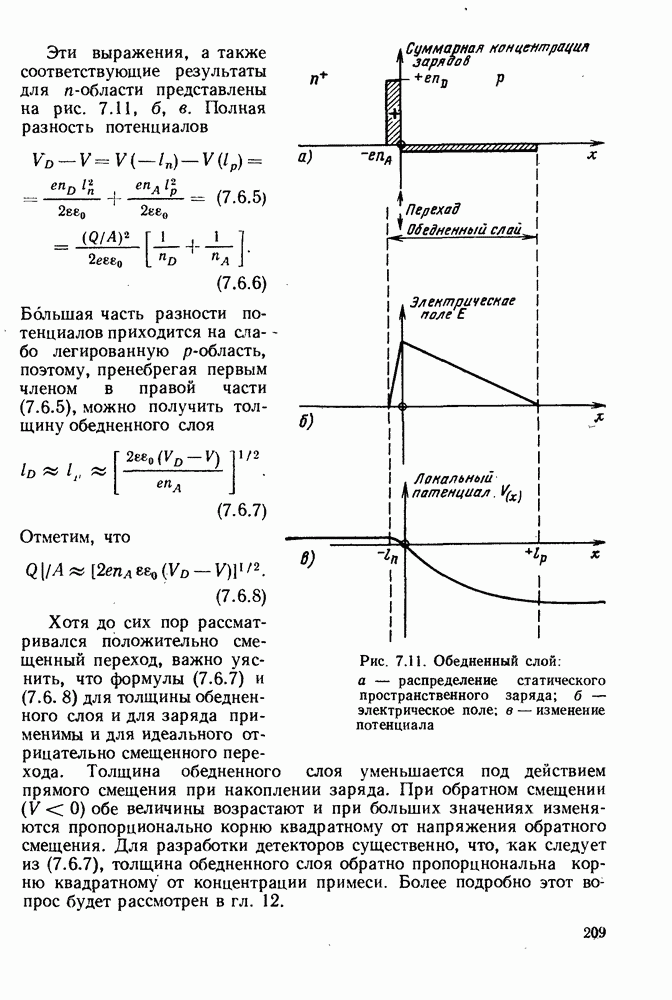
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
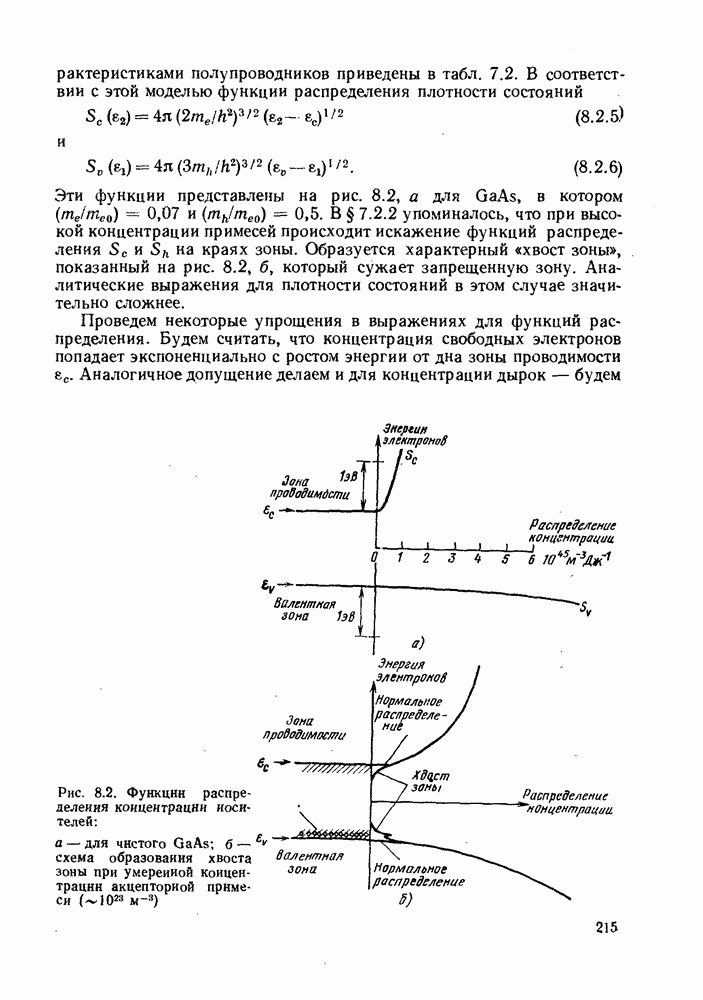
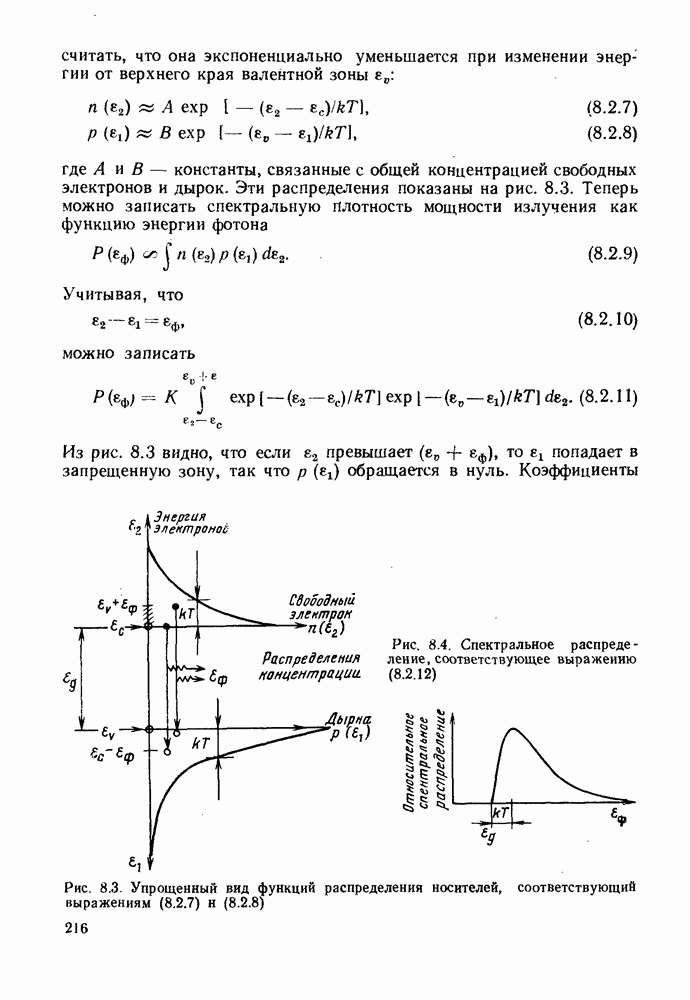
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
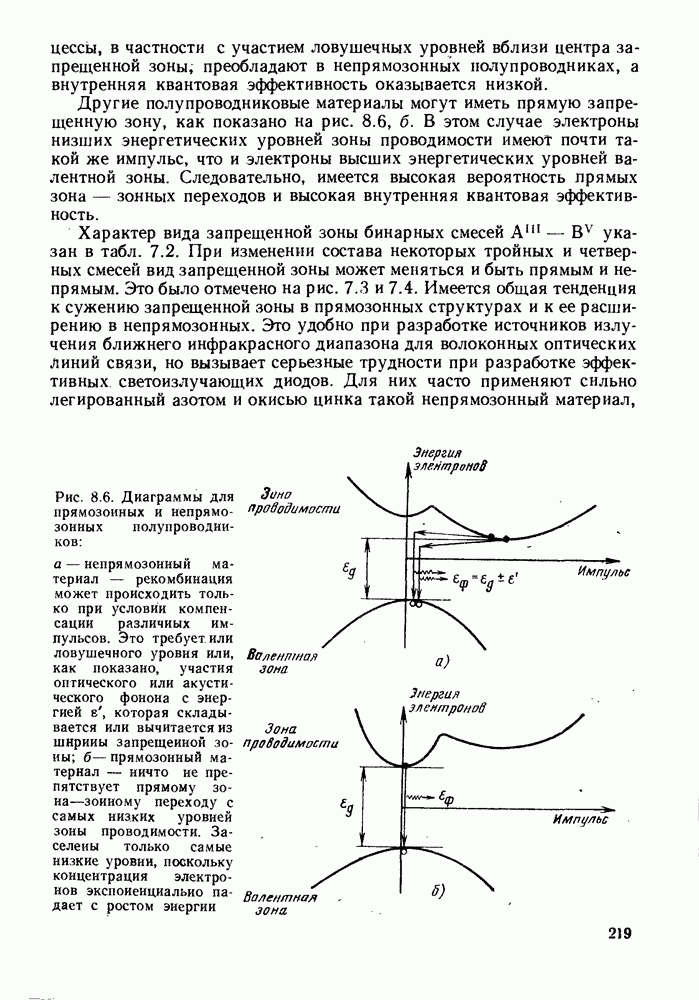
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
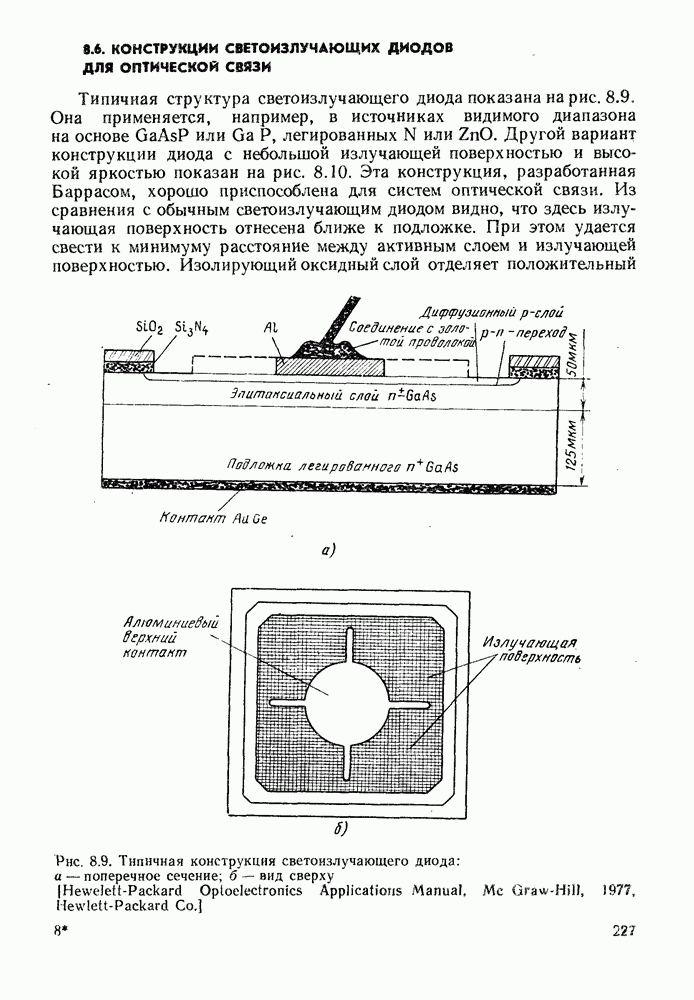
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
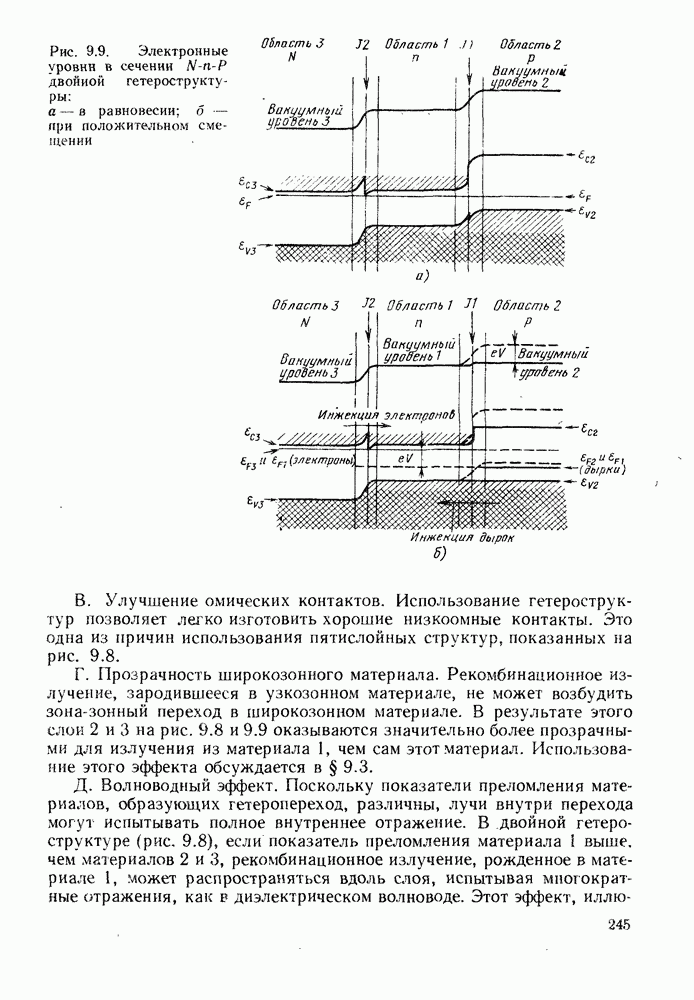
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
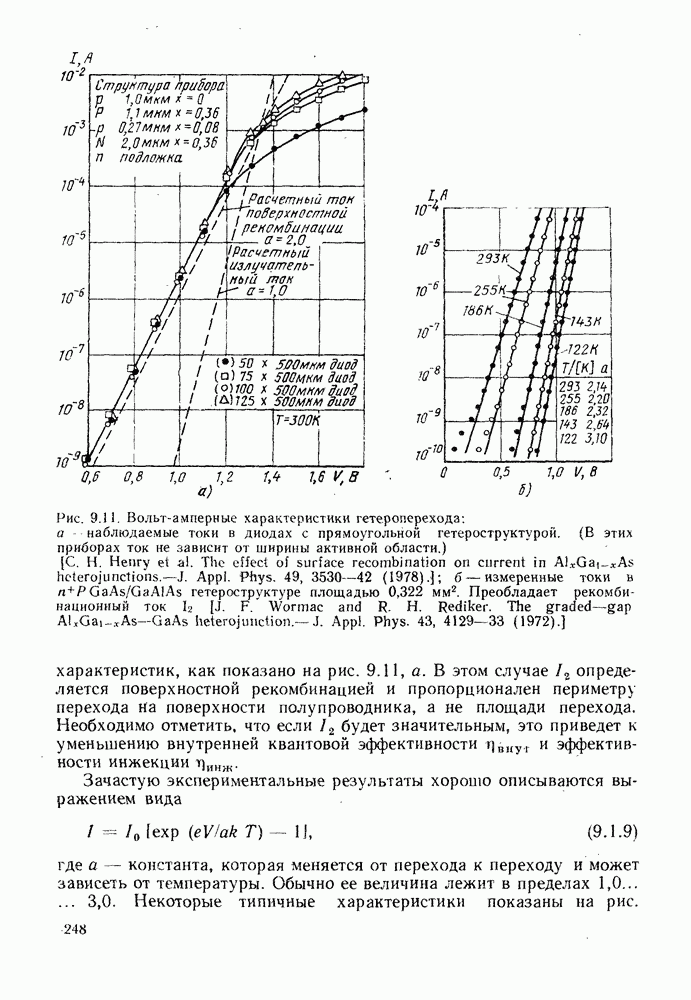
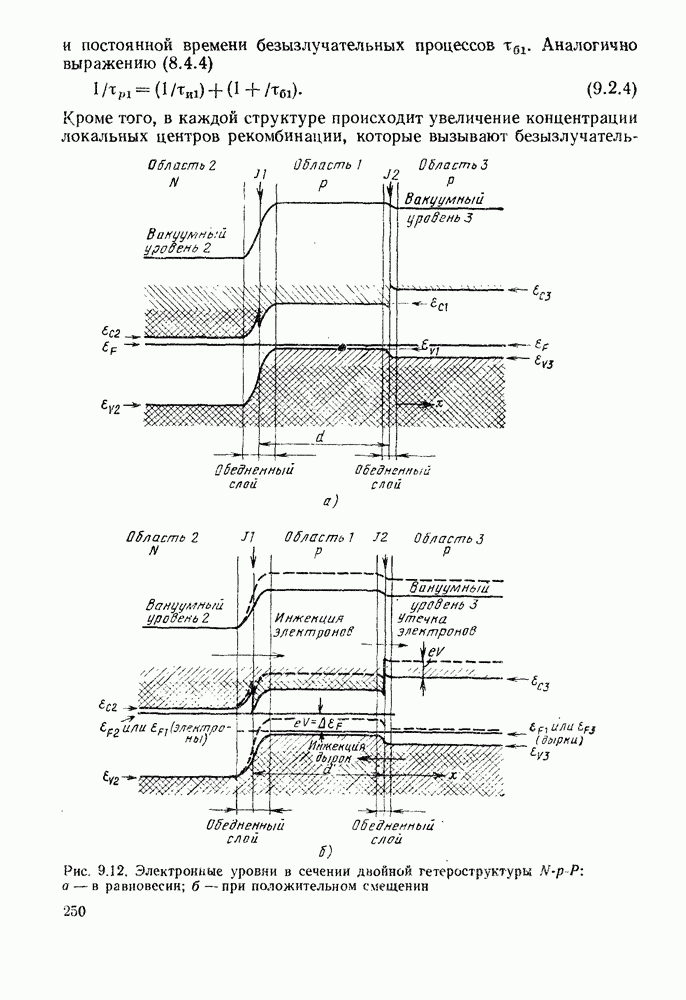
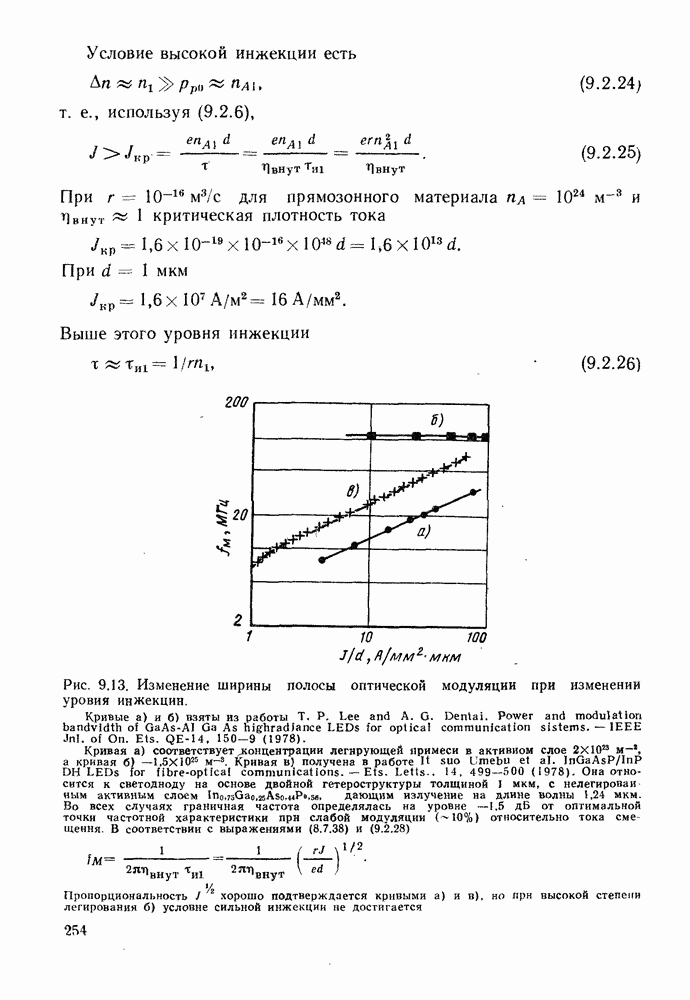
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
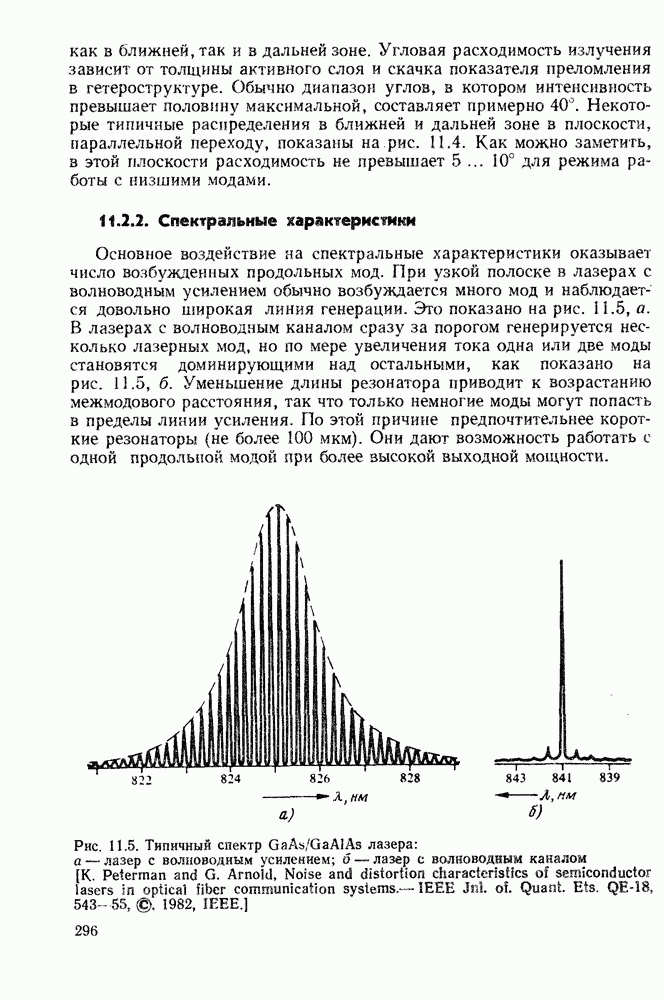
- 11.2.2. Спектральные характеристики
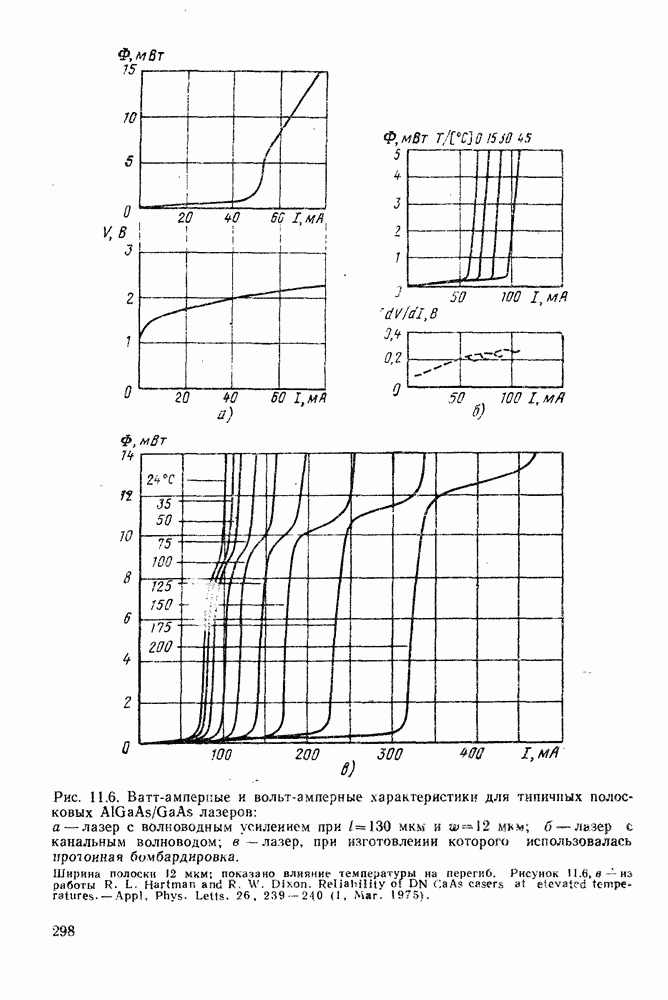
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
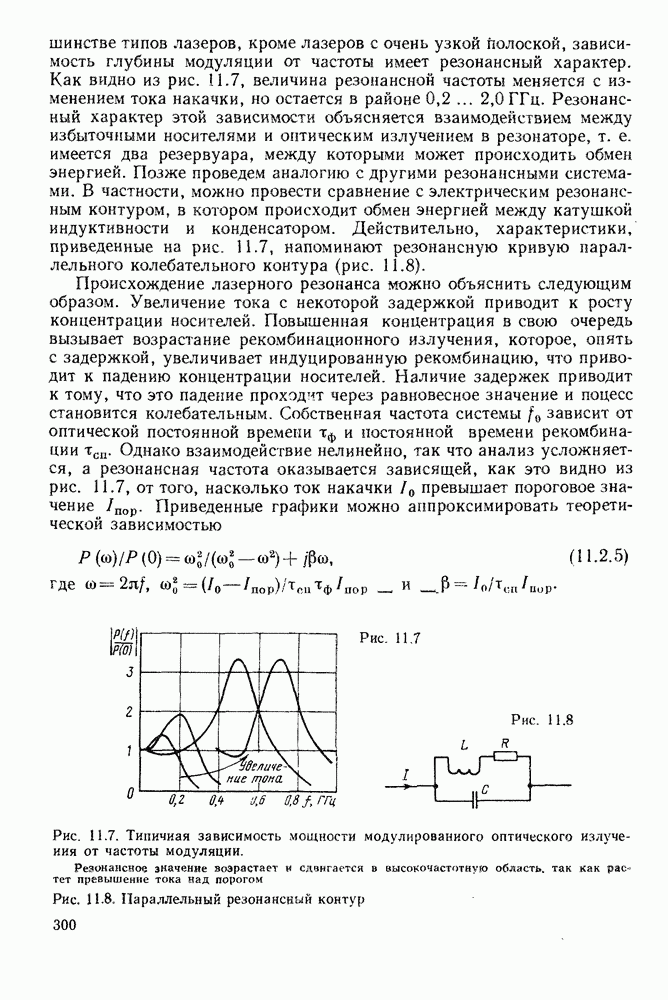
- 11.2.4. Частотные характеристики
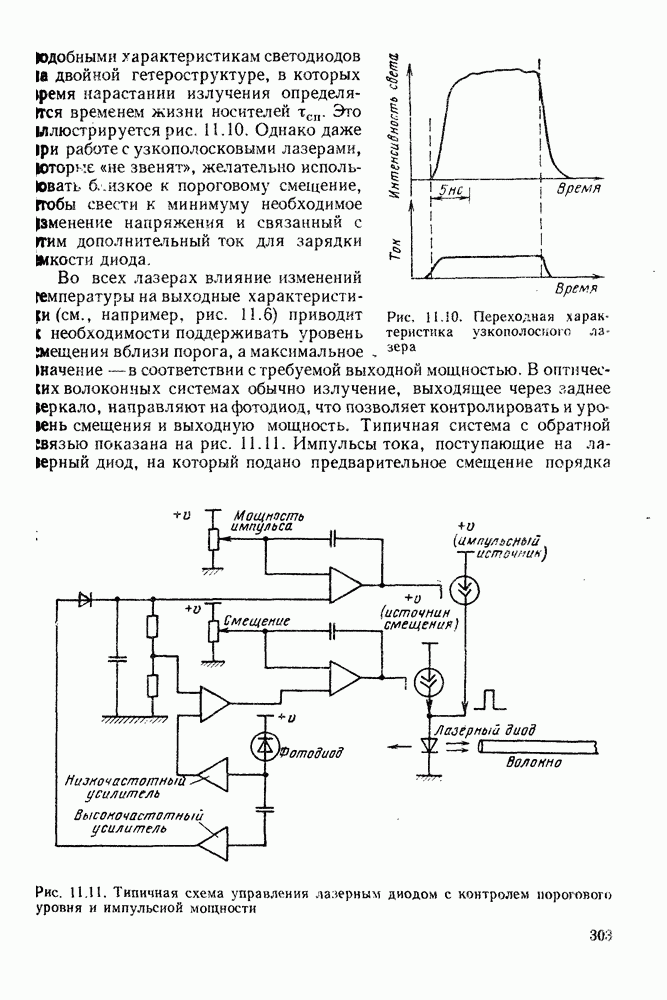
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
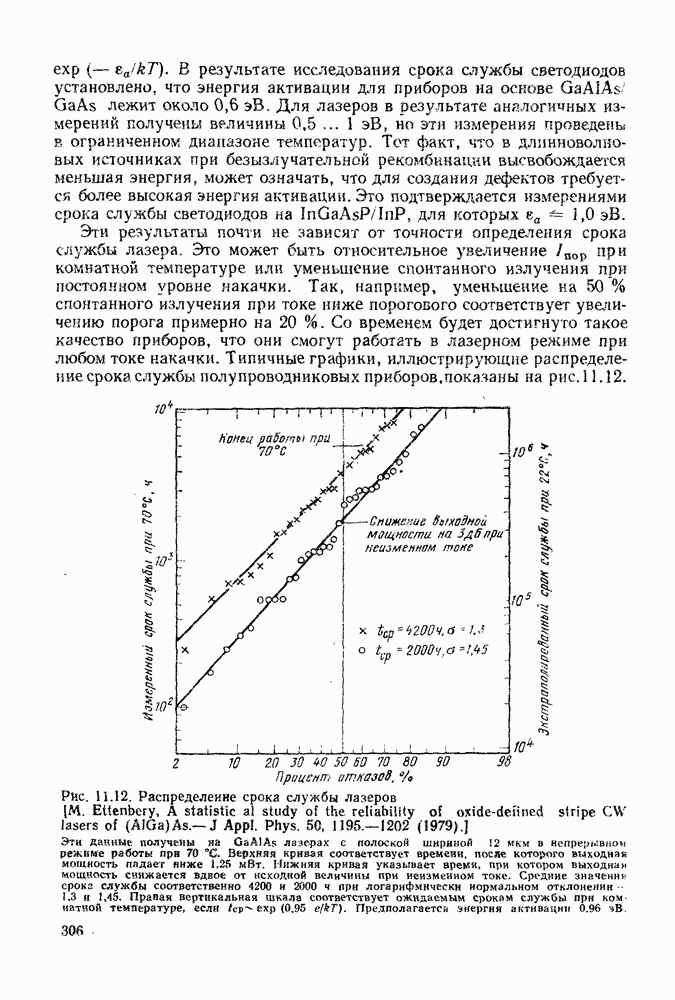
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
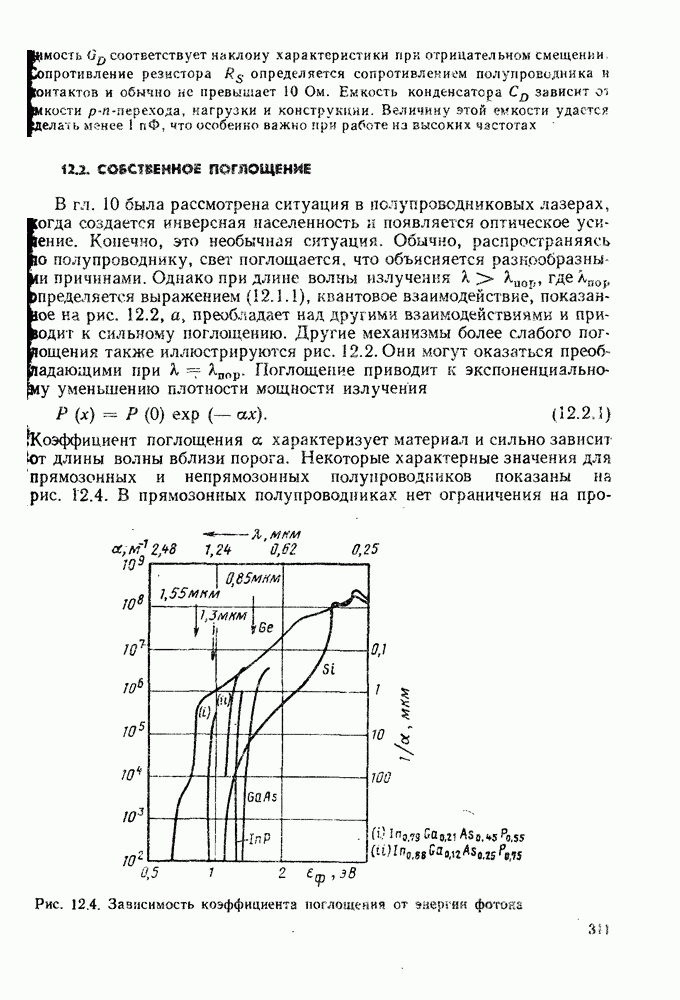
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
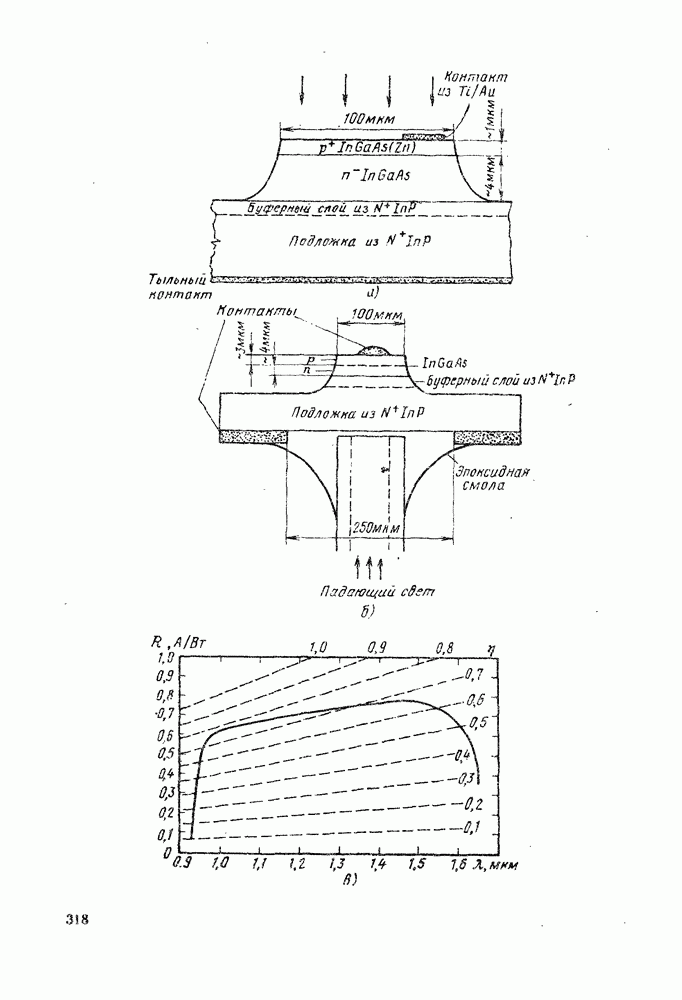
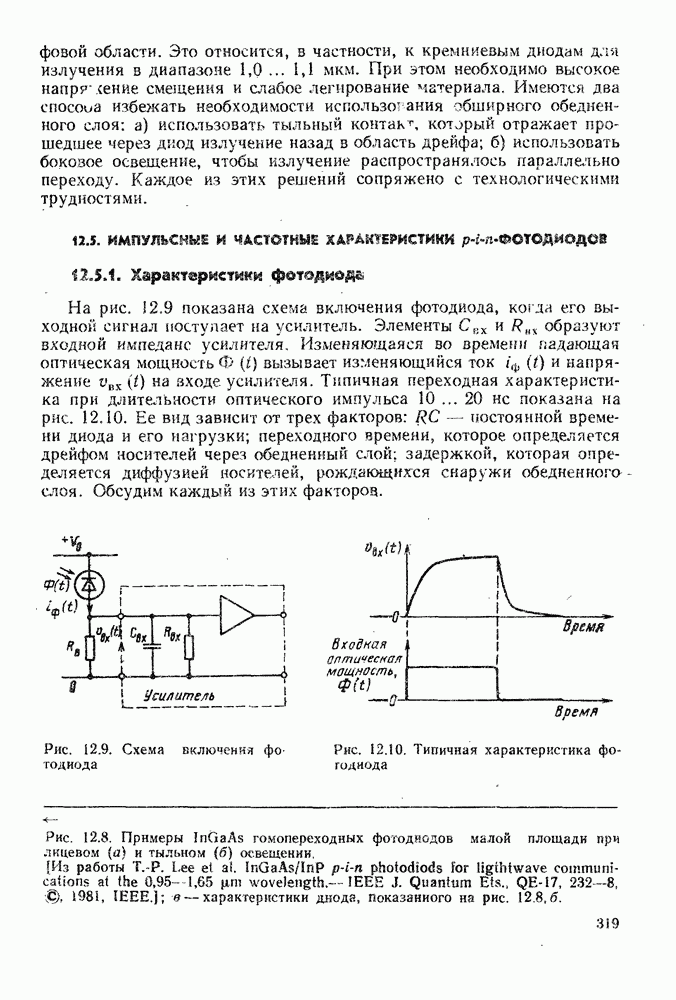
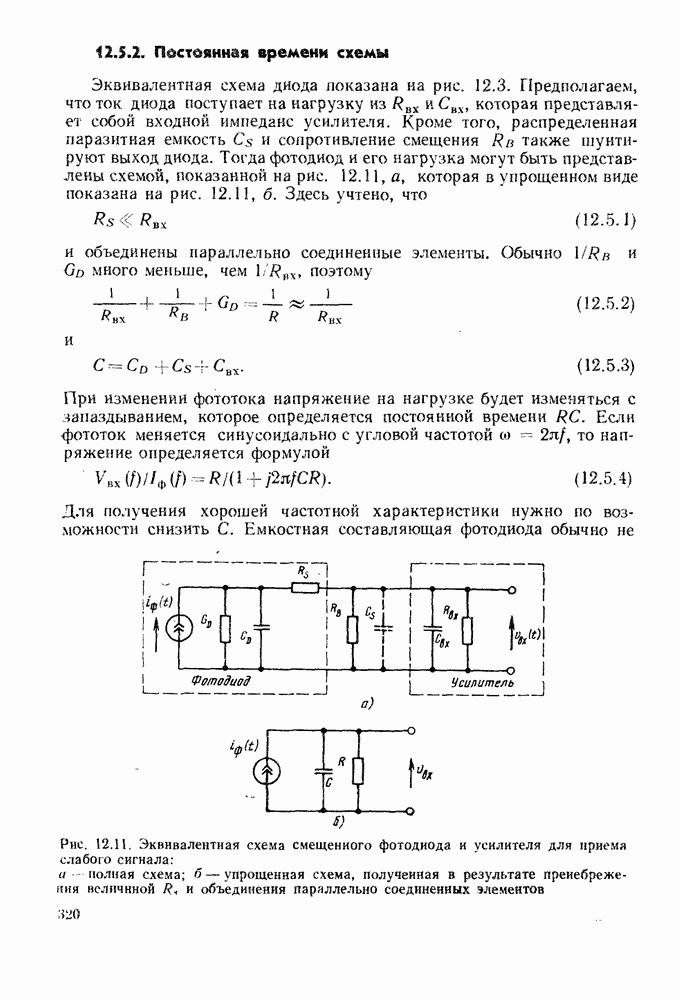
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
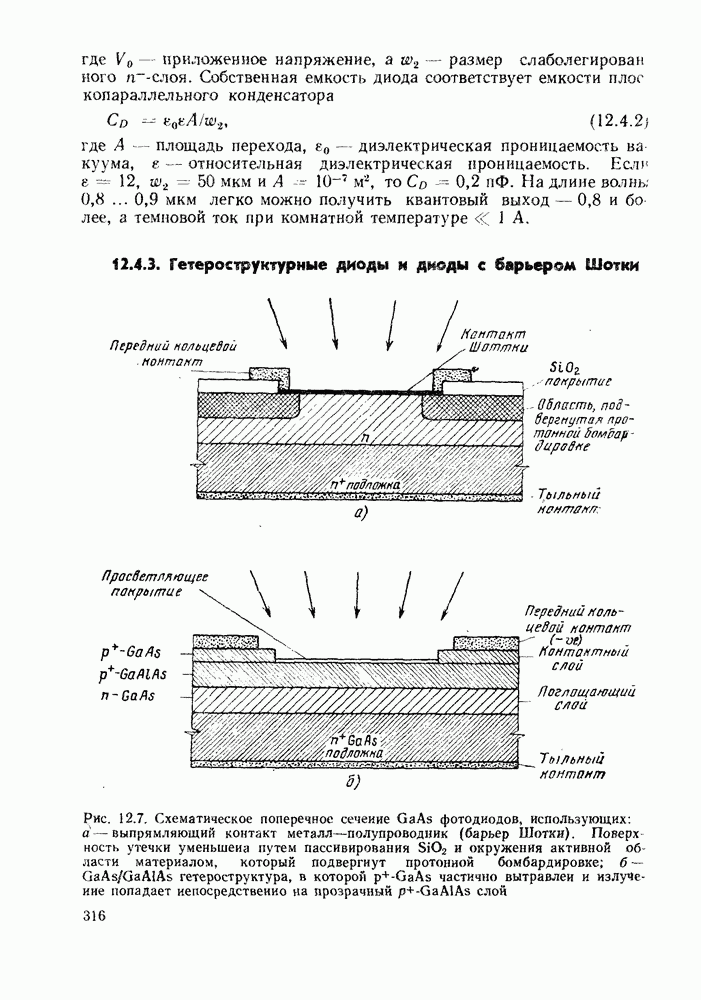
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
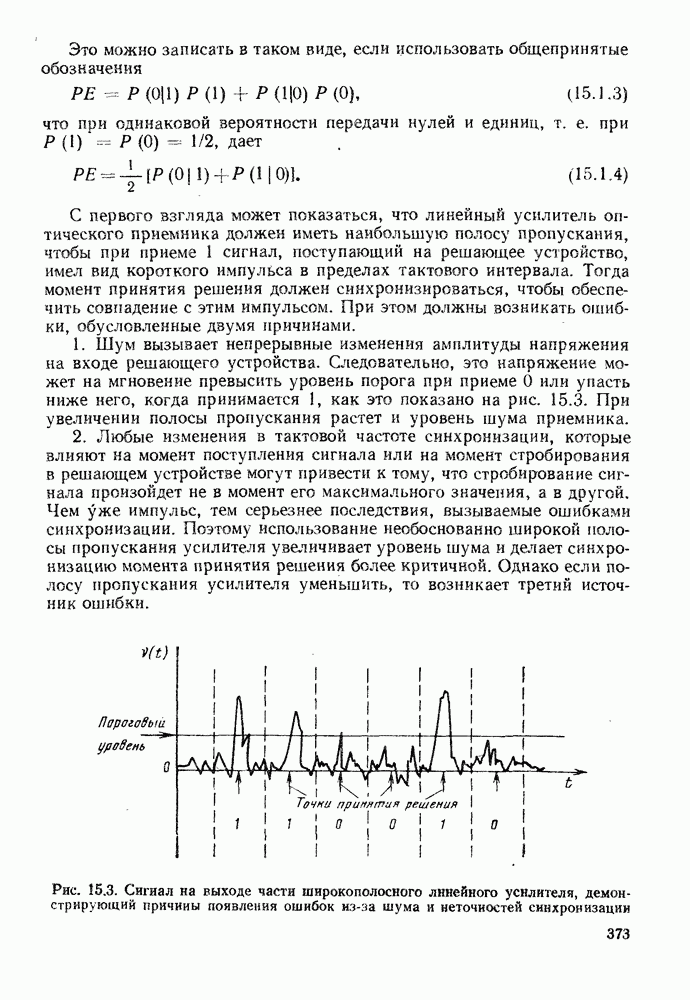
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
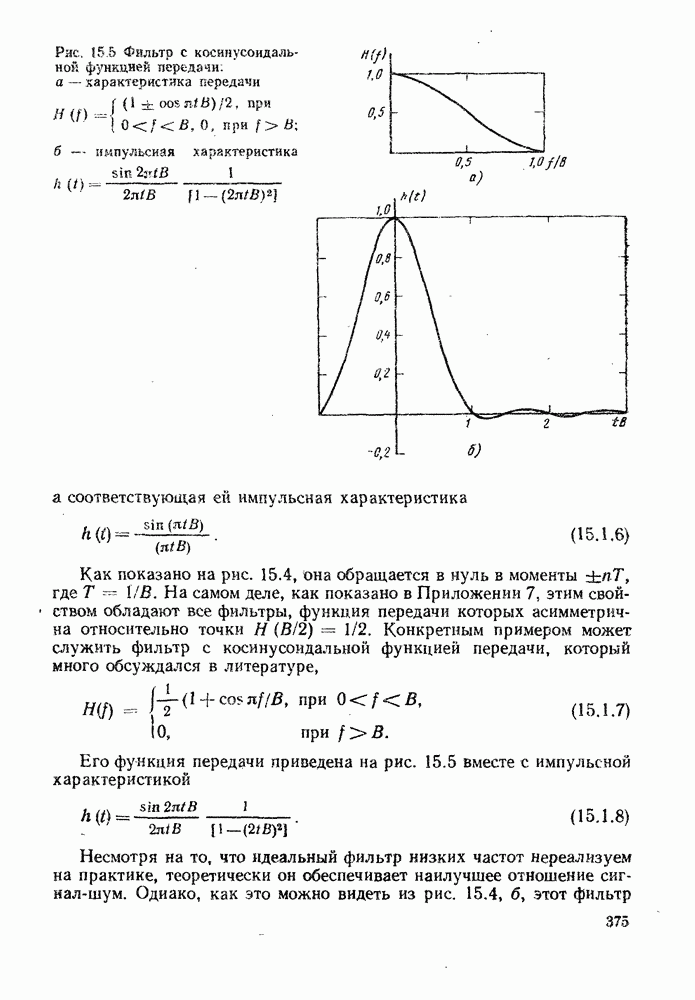
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
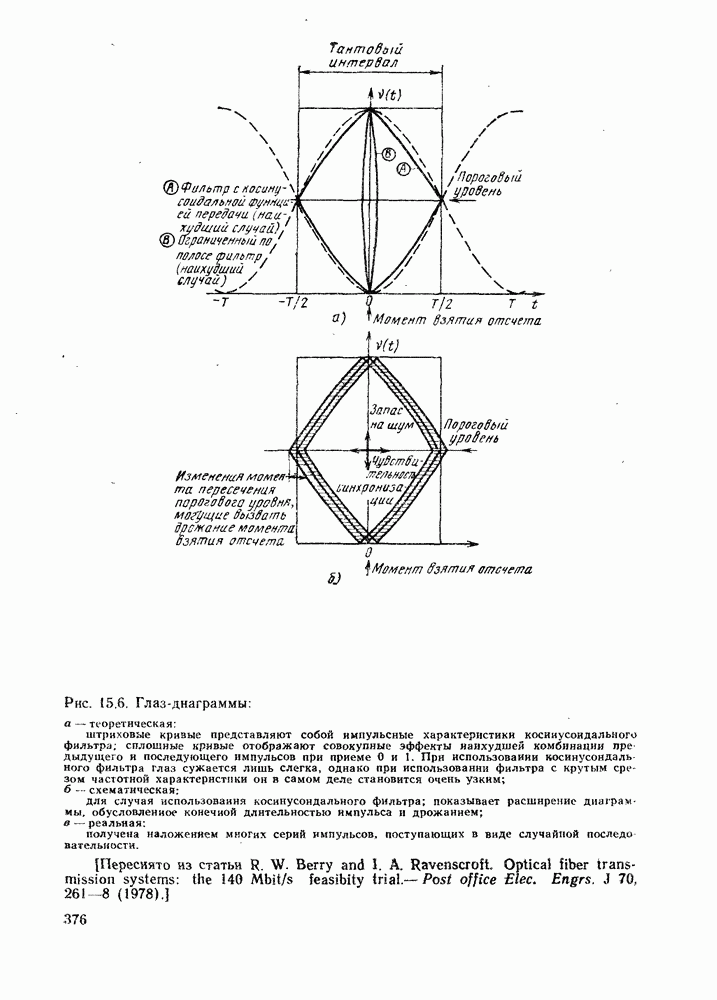
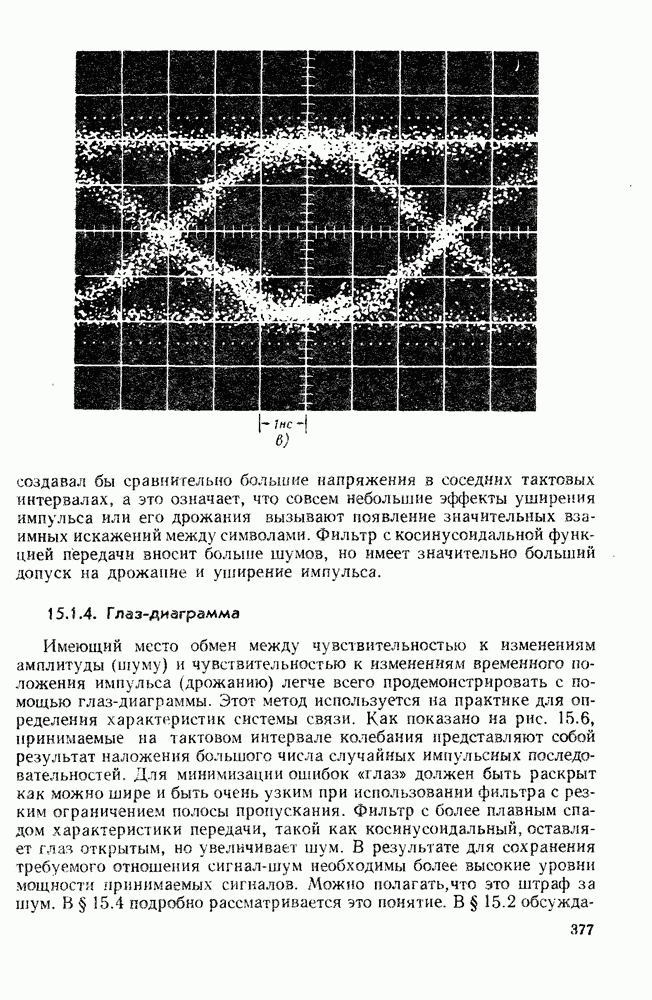
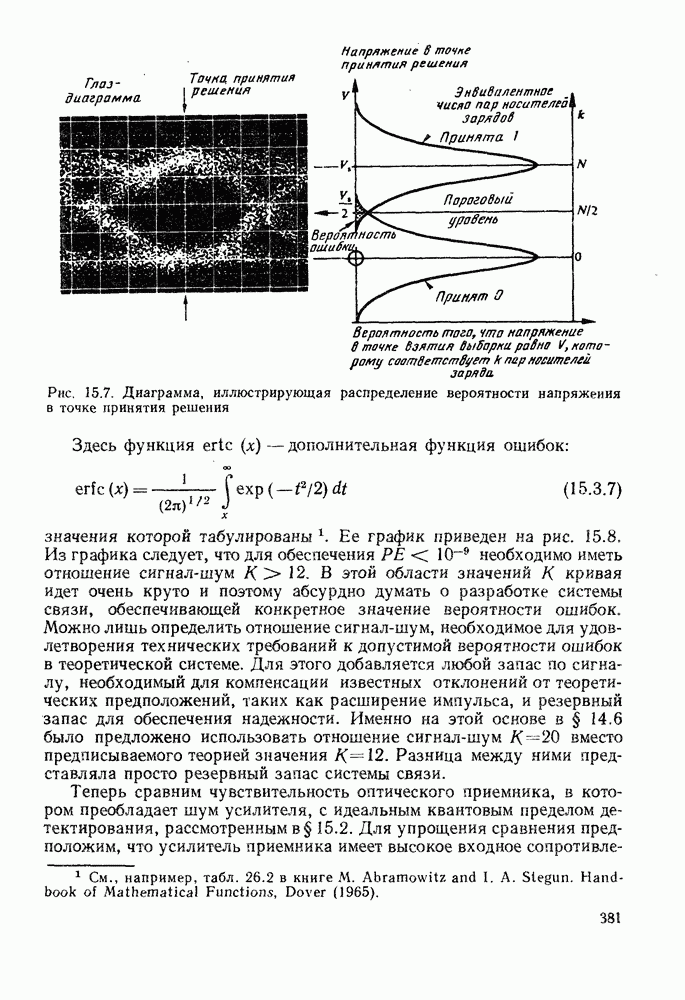
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
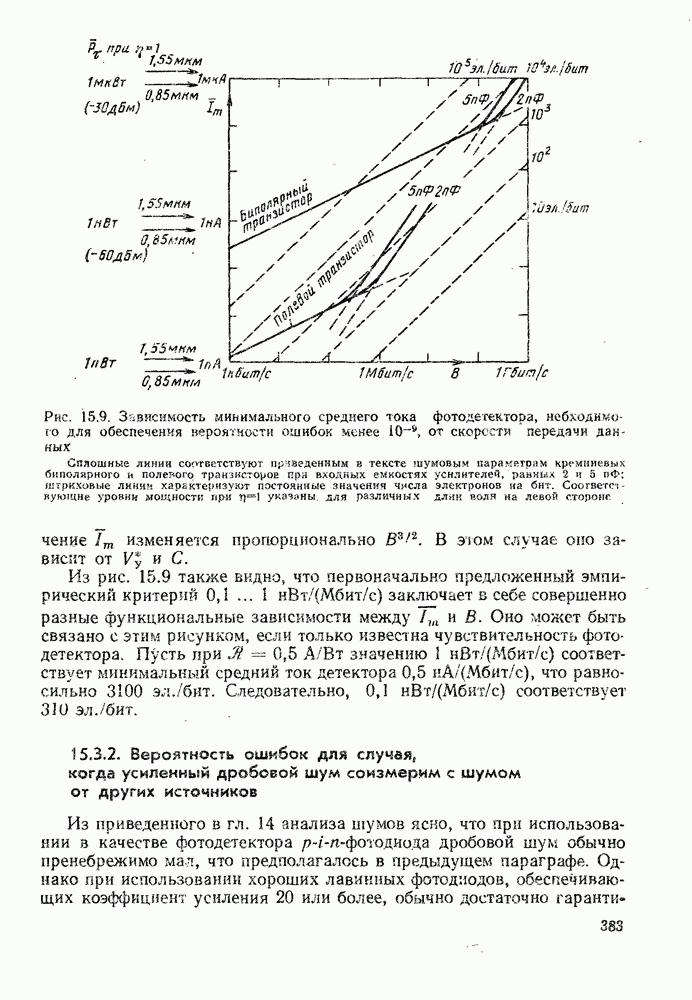
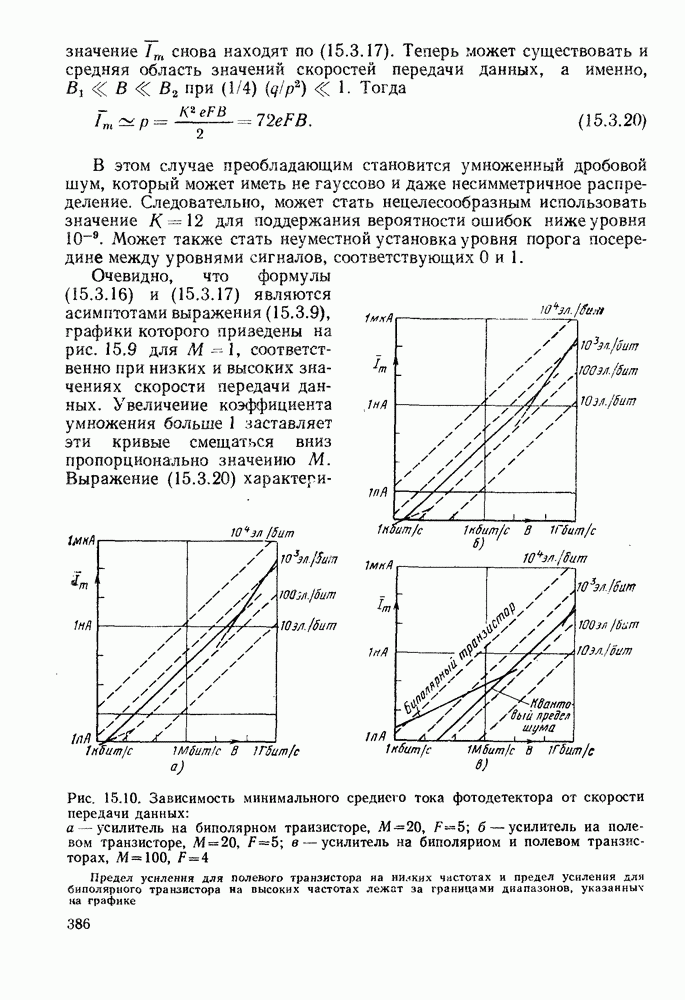
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
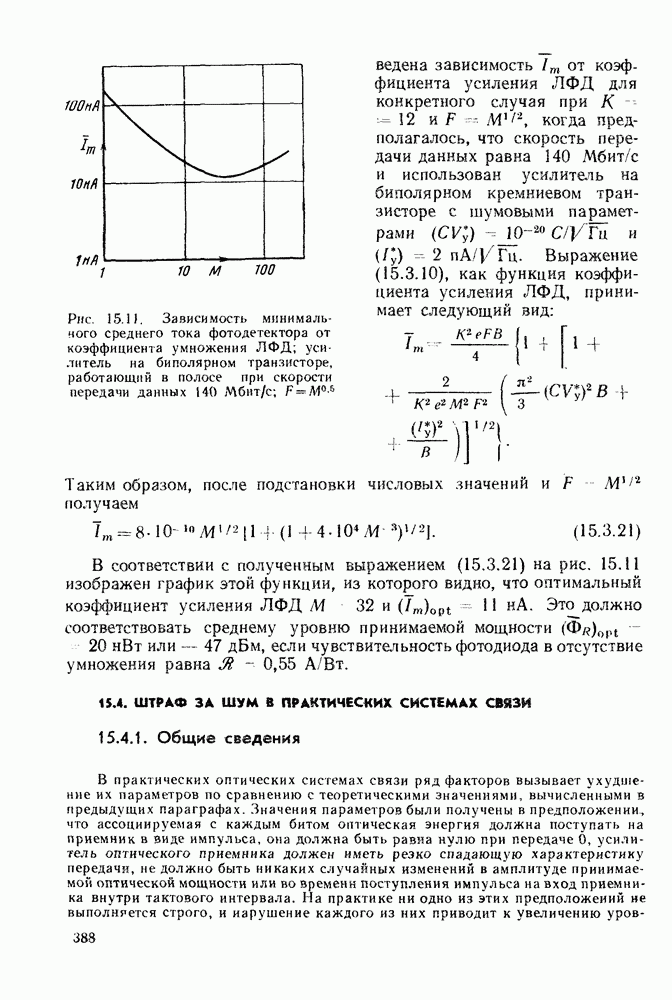
- 15.3.3. Оптимизация оптической системы связи
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
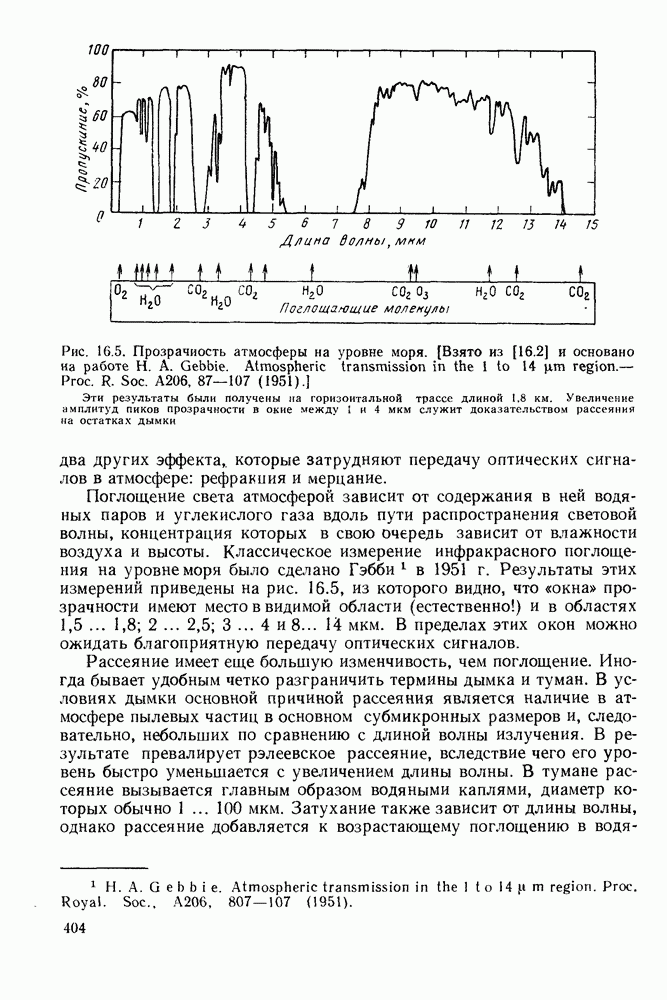
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
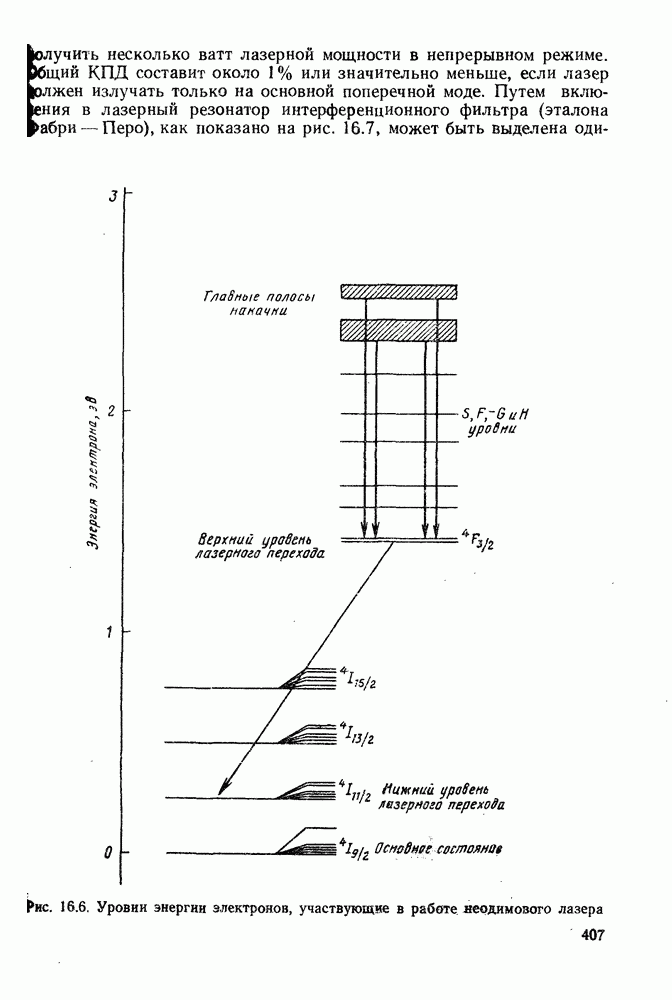
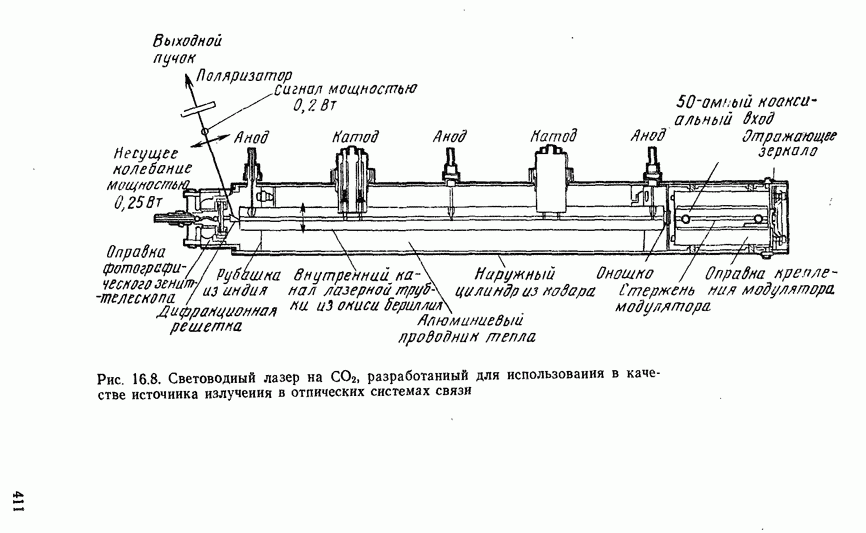
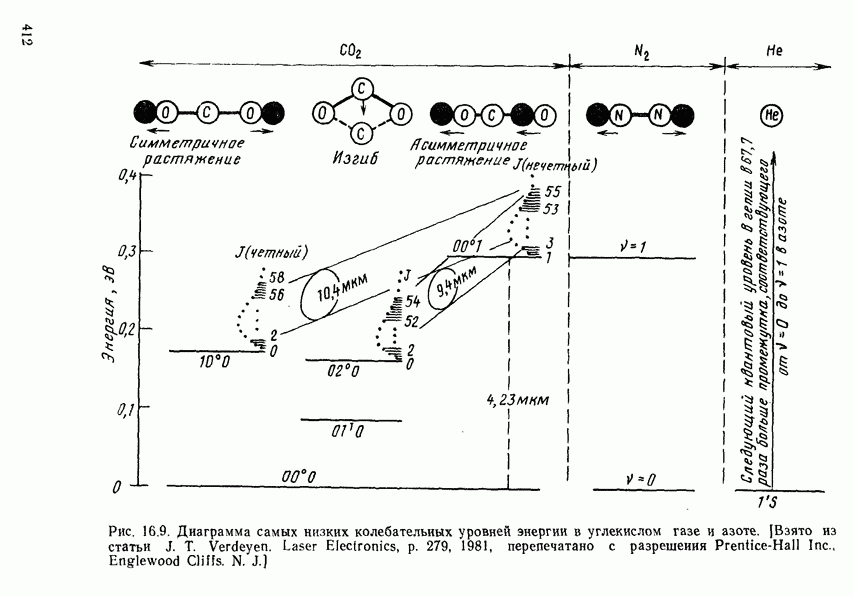
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ