| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
16.2.1. Расходимость пучка
На рис. 16.1 изображена сильно упрощенная идеализированная схема открытой оптической системы связи. Опущены все детали оптической линзовой системы в приемнике и передатчике, и в схеме, как и в последующем обсуждении, для простоты рассмотрения используется приближение тонкой линзы. Предполагается, что источник излучения является диффузным подобно светодиоду и имеет излучающую площадь Интенсивность излучения  считается постоянной для всего света, сколлимированного линзой передатчика. Линза имеет эффективную апертуру
считается постоянной для всего света, сколлимированного линзой передатчика. Линза имеет эффективную апертуру  и фокусное расстояние
и фокусное расстояние  Оптический приемник расположен на расстоянии
Оптический приемник расположен на расстоянии  Его эффективная апертура равна
Его эффективная апертура равна  и считается, что весь падающий на нее свет сфокусирован на активной области фотодетектора. Для того чтобы максимизировать принимаемую мощность изображение источника излучения должно формироваться в плоскости приемной апертуры. Используя элементарную теорию тонкой линзы, можно найти расстояние от источника излучения до центра линзы передатчика из соотношения
и считается, что весь падающий на нее свет сфокусирован на активной области фотодетектора. Для того чтобы максимизировать принимаемую мощность изображение источника излучения должно формироваться в плоскости приемной апертуры. Используя элементарную теорию тонкой линзы, можно найти расстояние от источника излучения до центра линзы передатчика из соотношения

а площадь его изображения определить по формуле

Мощность излучения, собранного линзой передатчика,

Считая, что изображение источника заполняет апертуру  часть мощности
часть мощности  которая достигает фотодетектора, просто равна
которая достигает фотодетектора, просто равна  так что принимаемая мощность
так что принимаемая мощность

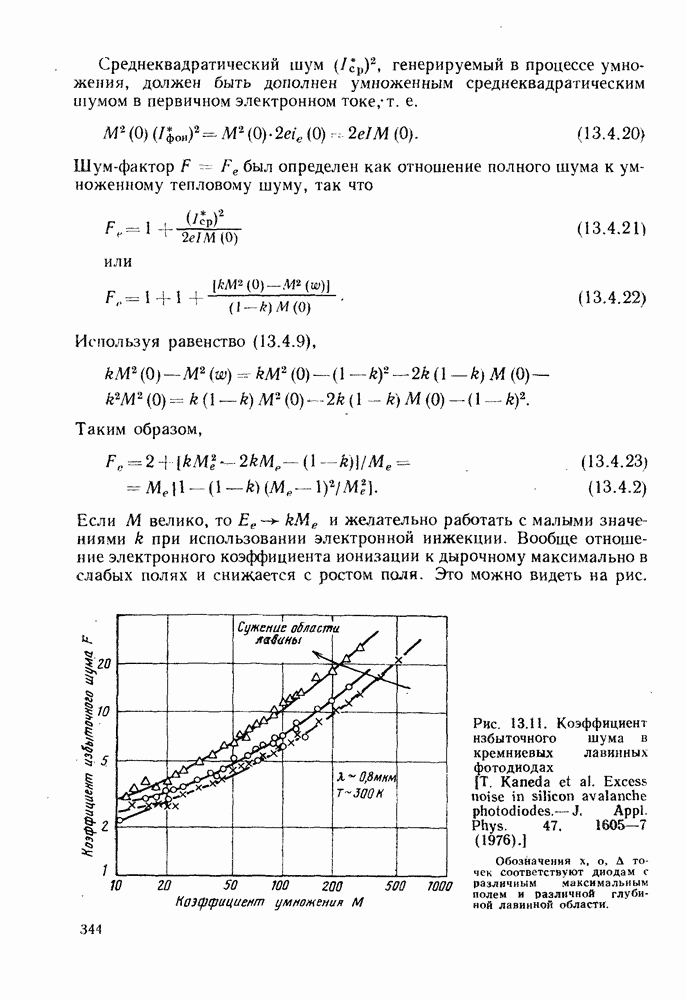
где  энергетическая яркость источника. Отсюда ясно, что требуется источник излучения с высокой энергетической
энергетическая яркость источника. Отсюда ясно, что требуется источник излучения с высокой энергетической

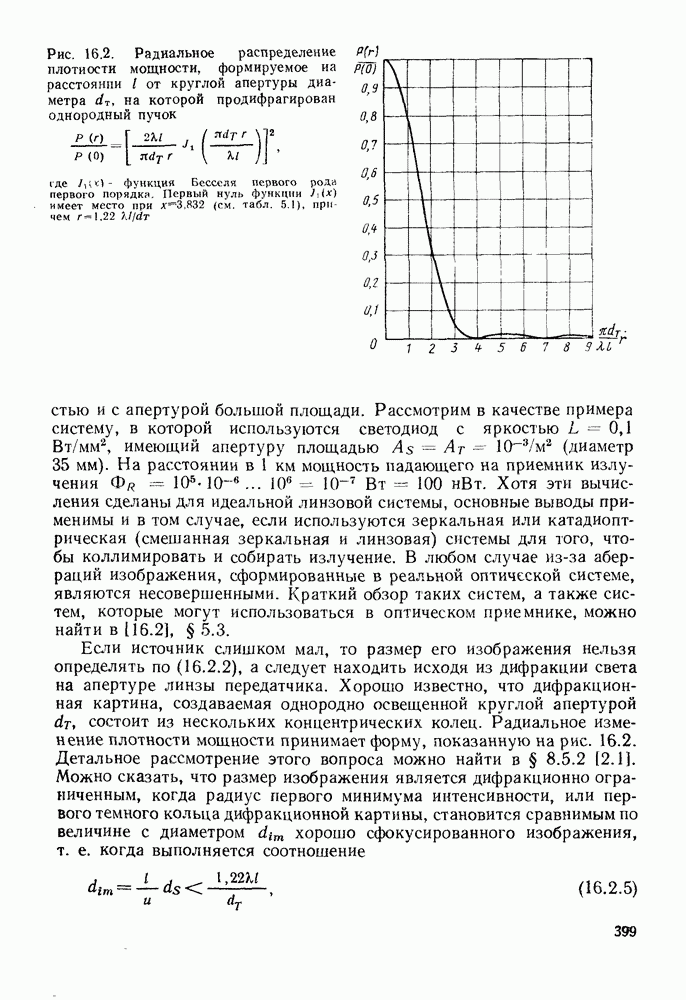
Рис. 16.2. Радиальное распределение плотности мощности, формируемое на расстоянии I от круглой апертуры диаметра  на которой продифрагирован однородный пучок
на которой продифрагирован однородный пучок  где
где  функция Бесселя первого рода первого порядка. Первый нуль функции
функция Бесселя первого рода первого порядка. Первый нуль функции  имеет место при
имеет место при  табл. 5.1), причем
табл. 5.1), причем 
яркостью и с апертурой большой площади. Рассмотрим в качестве примера систему, в которой используются светодиод с яркостью  имеющий апертуру площадью
имеющий апертуру площадью  (диаметр 35 мм). На расстоянии в 1 км мощность падающего на приемник излучения
(диаметр 35 мм). На расстоянии в 1 км мощность падающего на приемник излучения  Хотя эти вычисления сделаны для идеальной линзовой системы, основные выводы применимы и в том случае, если используются зеркальная или катадиоптрическая (смешанная зеркальная и линзовая) системы для того, чтобы коллимировать и собирать излучение. В любом случае из-за аберраций изображения, сформированные в реальной оптической системе, являются несовершенными. Краткий обзор таких систем, а также систем, которые могут использоваться в оптическом приемнике, можно найти в [16.2], § 5.3.
Хотя эти вычисления сделаны для идеальной линзовой системы, основные выводы применимы и в том случае, если используются зеркальная или катадиоптрическая (смешанная зеркальная и линзовая) системы для того, чтобы коллимировать и собирать излучение. В любом случае из-за аберраций изображения, сформированные в реальной оптической системе, являются несовершенными. Краткий обзор таких систем, а также систем, которые могут использоваться в оптическом приемнике, можно найти в [16.2], § 5.3.
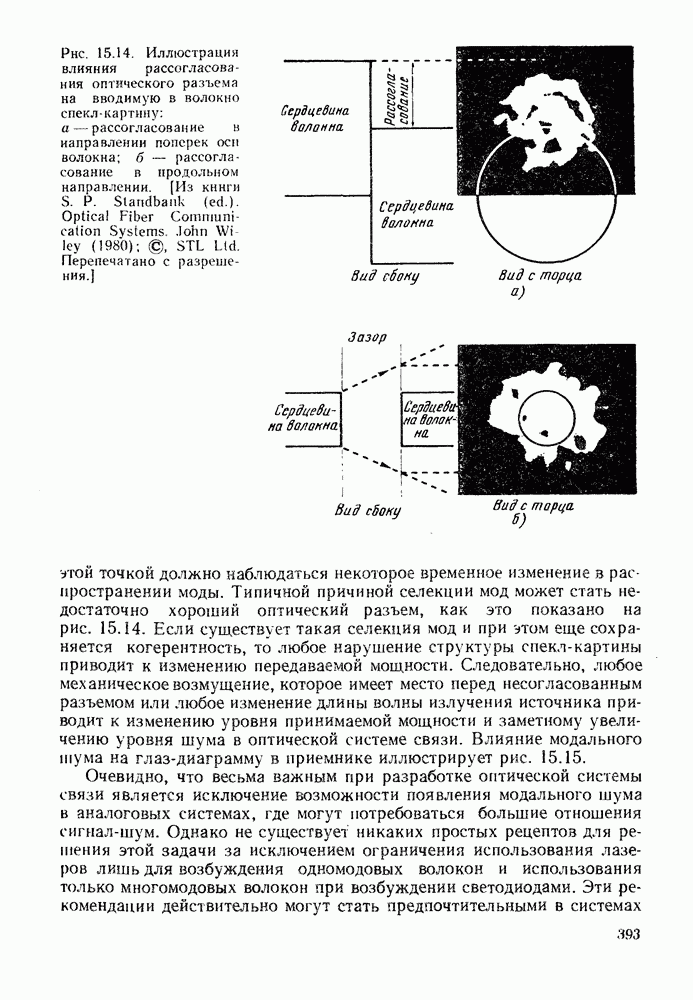
Если источник слишком мал, то размер его изображения нельзя определять по (16.2.2), а следует находить исходя из дифракции света на апертуре линзы передатчика. Хорошо известно, что дифракционная картина, создаваемая однородно освещенной круглой апертурой  состоит из нескольких концентрических колец. Радиальное изменение плотности мощности принимает форму, показанную на рис. 16.2. Детальное рассмотрение этого вопроса можно найти в § 8.5.2 [2.1]. Можно сказать, что размер изображения является дифракционно ограниченным, когда радиус первого минимума интенсивности, или первого темного кольца дифракционной картины, становится сравнимым по величине с диаметром
состоит из нескольких концентрических колец. Радиальное изменение плотности мощности принимает форму, показанную на рис. 16.2. Детальное рассмотрение этого вопроса можно найти в § 8.5.2 [2.1]. Можно сказать, что размер изображения является дифракционно ограниченным, когда радиус первого минимума интенсивности, или первого темного кольца дифракционной картины, становится сравнимым по величине с диаметром  хорошо сфокусированного изображения, т. е. когда выполняется соотношение
хорошо сфокусированного изображения, т. е. когда выполняется соотношение

где  диаметр источника. Отсюда следует
диаметр источника. Отсюда следует

Свет от лазерного источника, будучи по своей природе высэко коллимированным и когерентным, обычно дает дифракционно-ограниченное изображение источника. В любом случае интенсивность излучения в центре дифракционной картины определяется выражением  где
где  общая излучаемая мощность. В случае точечного источника
общая излучаемая мощность. В случае точечного источника  определяется с помощью (16.2.3), а в других случаях —
определяется с помощью (16.2.3), а в других случаях —  произведение плотности мощности в плоскости передающей апертуры на площадь апертуры. Суммарная мощность излучения, собираемого небольшой приемной апертурой площадью
произведение плотности мощности в плоскости передающей апертуры на площадь апертуры. Суммарная мощность излучения, собираемого небольшой приемной апертурой площадью  расположенной в центре дифракционной картины, в общем случае определяется по формуле
расположенной в центре дифракционной картины, в общем случае определяется по формуле

а в случае точечного источника с интенсивностью излучения 

Следует иметь в виду, что приведенные формулы дают завышенные значения мощности и на практике будут иметь место дополнительные потери в оптической системе в результате аберраций. Обсуждение этих вопросов с использованием теории антенн можно найти в [16.3].
Будет полезно рассмотреть обстоятельства, при которых описанная выше оптическая система связи, использующая светодиод  может стать дифракционно-ограниченной. Предположим, что
может стать дифракционно-ограниченной. Предположим, что  и фокусное расстояние линзы передатчика
и фокусное расстояние линзы передатчика  В этом случае из соотношения (16.2.2) следует, что
В этом случае из соотношения (16.2.2) следует, что

Рис. 16.3. Расширитель пучка, используемый для уменьшения его расходимости, обусловленной дифракцией
дифракция будет определять расходимость пучка только тогда, когда диаметр источника  Таким образом, светодиод с торцевым излучением обеспечит выполнение условия дифракционно-ограниченной системы, а с излучающей поверхностью — нет.
Таким образом, светодиод с торцевым излучением обеспечит выполнение условия дифракционно-ограниченной системы, а с излучающей поверхностью — нет.
Для уменьшения дифракционной расходимости лазерного источника излучения можно использовать расширитель пучка (рис. 16.3). В результате апертура, на которой происходит дифракция, увеличивается. В § 11.2 было показано, что расходимость излучения полупроводниковых лазеров обычно не имеет круговой симметрии. Для эффективного введения их излучения в волокно используются цилиндрические линзы. Такие же линзы можно применить и в системе расширения пучка и тогда, как обычно, пользуются (16.2.7). В качестве примера допустим, что излучение полупроводникового лазера мощностью  коллимируется и заполняет объектив расширителя пучка диаметром
коллимируется и заполняет объектив расширителя пучка диаметром  Тогда, приняв, как и раньше,
Тогда, приняв, как и раньше,  находим, что мощность на расстоянии
находим, что мощность на расстоянии 

Если расходимость пучка столь мала, что не превышает 0,1 мрад, то требуемая точность наведения будет предъявлять жесткие требования к системе управления лучом и маханической стабильности любого портативного передатчика.
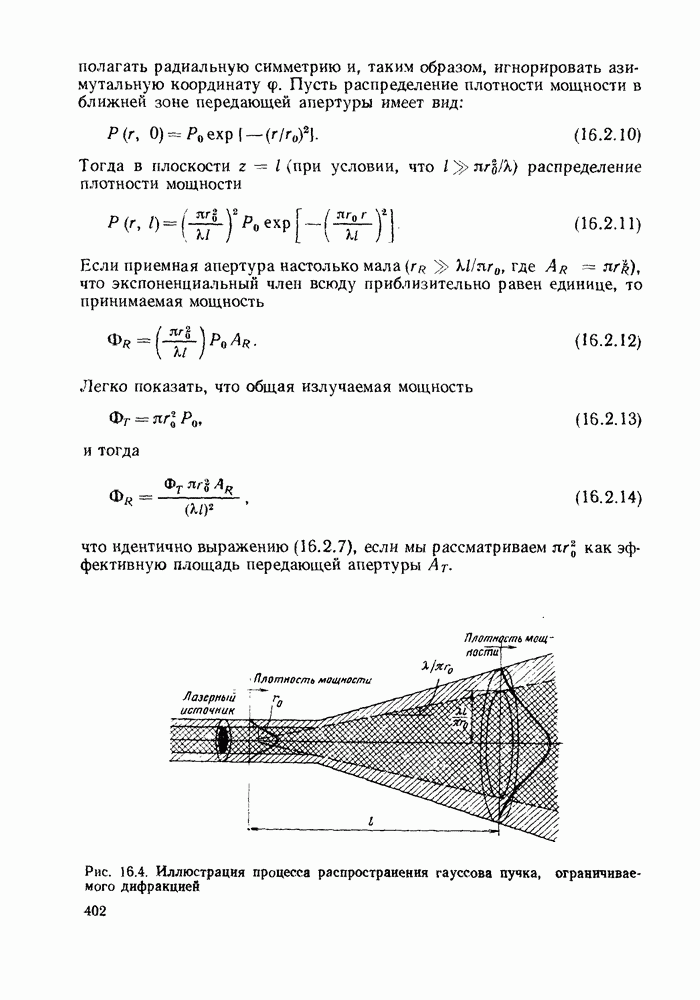
Выражения (16.2.7) и (16.2.8) справедливы при однородном освещении передающей апертуры. Другой случай, в котором обусловленное дифракцией распределение мощности в дальней зоне можно легко вычислить, имеет место, когда плотность мощности в ближней зоне принимает гауссовое распределение, как показано на рис. 16.4. Можно показать, что дифракционно-ограниченный пучок в дальней зоне сохраняет гауссов профиль (см., например, § 4.6.4 в [16.3]). На практике это важно, так как согласно теории основная поперечная мода излучения лазера с цилиндрическим резонатором дает именно такое распределение выходной мощности, и это наблюдается в действительности.
Эту систему лучше всего описать с помощью цилиндрических координат  с началом в центре передающей апертуры. Будем
с началом в центре передающей апертуры. Будем
предполагать радиальную симметрию и, таким образом, игнорировать азимутальную координату  Пусть распределение плотности мощности в ближней зоне передающей апертуры имеет вид:
Пусть распределение плотности мощности в ближней зоне передающей апертуры имеет вид:

Тогда в плоскости  (при условии, что
(при условии, что  распределение плотности мощности
распределение плотности мощности

Если приемная апертура настолько мала  где
где  что экспоненциальный член всюду приблизительно равен единице, то принимаемая мощность
что экспоненциальный член всюду приблизительно равен единице, то принимаемая мощность

Легко показать, что общая излучаемая мощность

и тогда

что идентично выражению (16.2.7), если мы рассматриваем  как эффективную площадь передающей апертуры
как эффективную площадь передающей апертуры 

Рис. 16.4. Иллюстрация процесса распространения гауссова пучка, ограничиваемого дифракцией
Отметим, что радиоинженеры обычно описывают характеристики направленности антенных систем довольно странным способом. Они начинают с обоснованного предположения, что если бы не использование большой апертуры передатчика  мощность источника излучалась бы равномерно во всех направлениях. На расстоянии
мощность источника излучалась бы равномерно во всех направлениях. На расстоянии  она распределилась бы на площади
она распределилась бы на площади  Затем они используют тот факт, что основной приемник с согласованной, абсолютно не направленной антенной обеспечивает принимаемому излучению эффективную площадь апертуры, равную
Затем они используют тот факт, что основной приемник с согласованной, абсолютно не направленной антенной обеспечивает принимаемому излучению эффективную площадь апертуры, равную  Тогда основные потери при передаче
Тогда основные потери при передаче  и являются частью изотропно излучаемой мощности, которая могла бы быть принята основным приемником. Обычно потери выражаются в децибелах. Если для концентрации передаваемого пучка используется направленная антенная решетка с большой апертурой, то интенсивность дифракционно-ограниченного пучка максимально возрастает в
и являются частью изотропно излучаемой мощности, которая могла бы быть принята основным приемником. Обычно потери выражаются в децибелах. Если для концентрации передаваемого пучка используется направленная антенная решетка с большой апертурой, то интенсивность дифракционно-ограниченного пучка максимально возрастает в  раз. Величина
раз. Величина  известна как «коэффициент усиления» антенны передатчика и также выражается в децибелах. Аналогично и в приемнике использование антенной решетки с большой апертурой и эффективной площадью увеличит принимаемую мощность
известна как «коэффициент усиления» антенны передатчика и также выражается в децибелах. Аналогично и в приемнике использование антенной решетки с большой апертурой и эффективной площадью увеличит принимаемую мощность  раз. Выраженная в децибелах величина
раз. Выраженная в децибелах величина  есть «коэффициент усиления» антенны приемника. Эти соотношения выявляют существование принципа обратимости между антеннами приемника и передатчика, что обоснованно, когда речь идет о радиочастотах. Однако они не имеют места на практике в оптическом диапазоне. Общие потери при передаче
есть «коэффициент усиления» антенны приемника. Эти соотношения выявляют существование принципа обратимости между антеннами приемника и передатчика, что обоснованно, когда речь идет о радиочастотах. Однако они не имеют места на практике в оптическом диапазоне. Общие потери при передаче

или с учетом (16.2.7)

Если  основные потери при передаче составят
основные потери при передаче составят  коэффициент усиления антенны передатчика
коэффициент усиления антенны передатчика  коэффициент усиления антенны приемника
коэффициент усиления антенны приемника  что дает общие потери при передаче
что дает общие потери при передаче  Вопрос о том, имеет ли смысл выполнять расчеты таким образом на оптических частотах, остается открытым для обсуждений.
Вопрос о том, имеет ли смысл выполнять расчеты таким образом на оптических частотах, остается открытым для обсуждений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
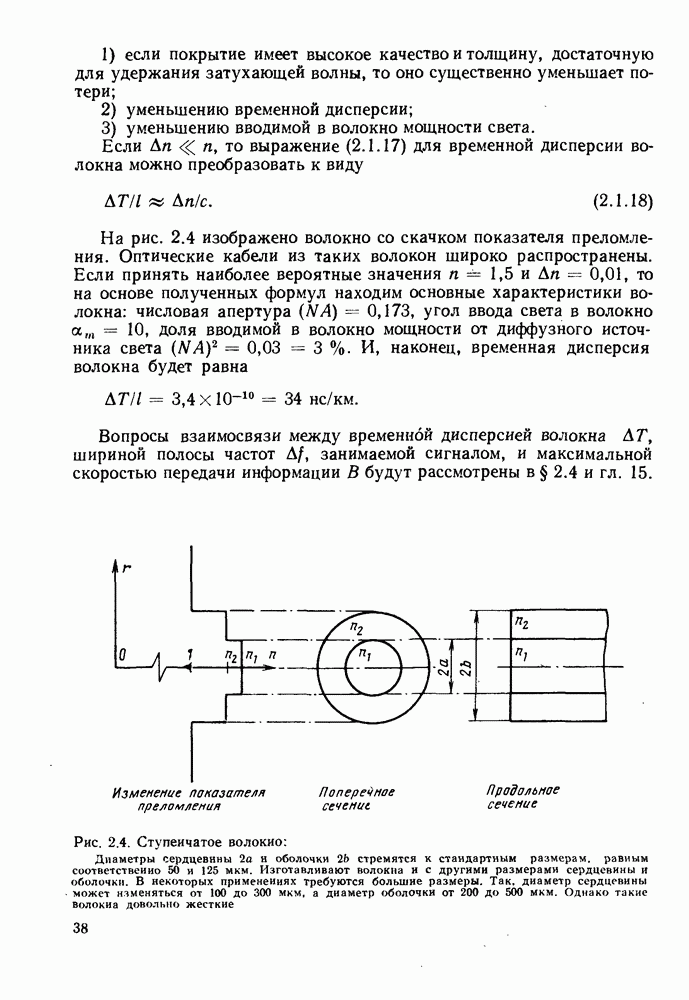
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
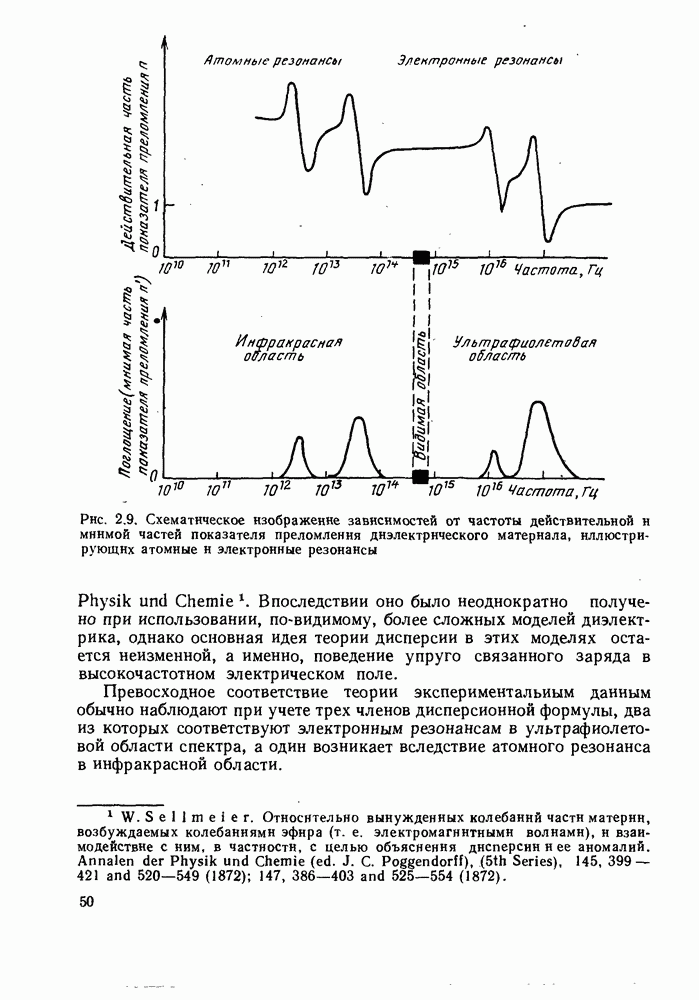
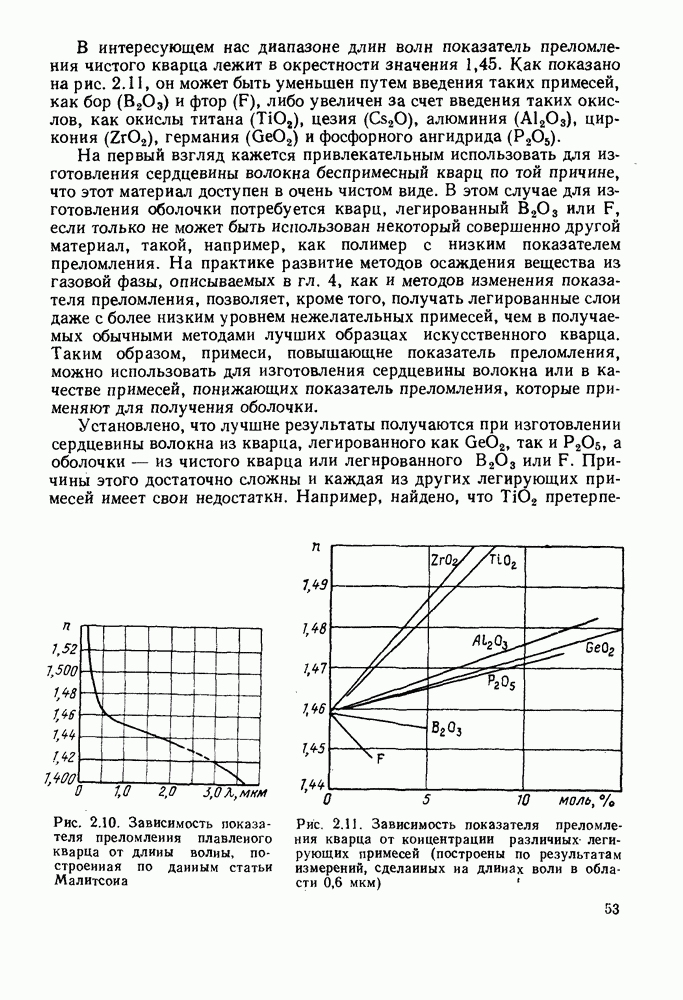
- 2.2.1. Показатель преломления объемной среды: теория
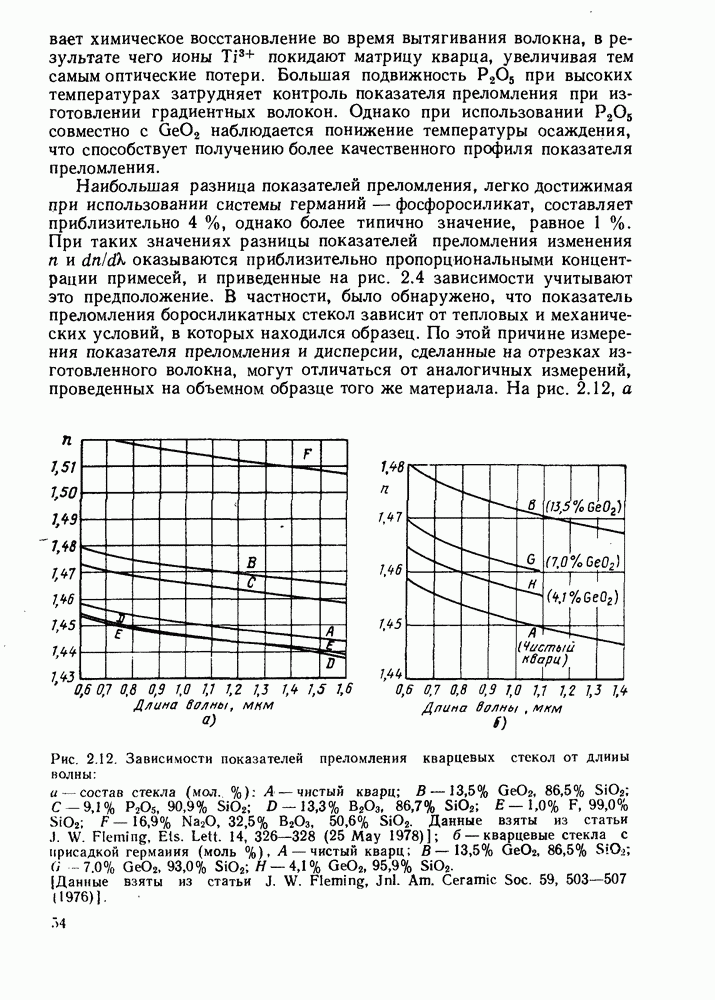
- 2.2.2. Показатель преломления материала: экспериментальные значения
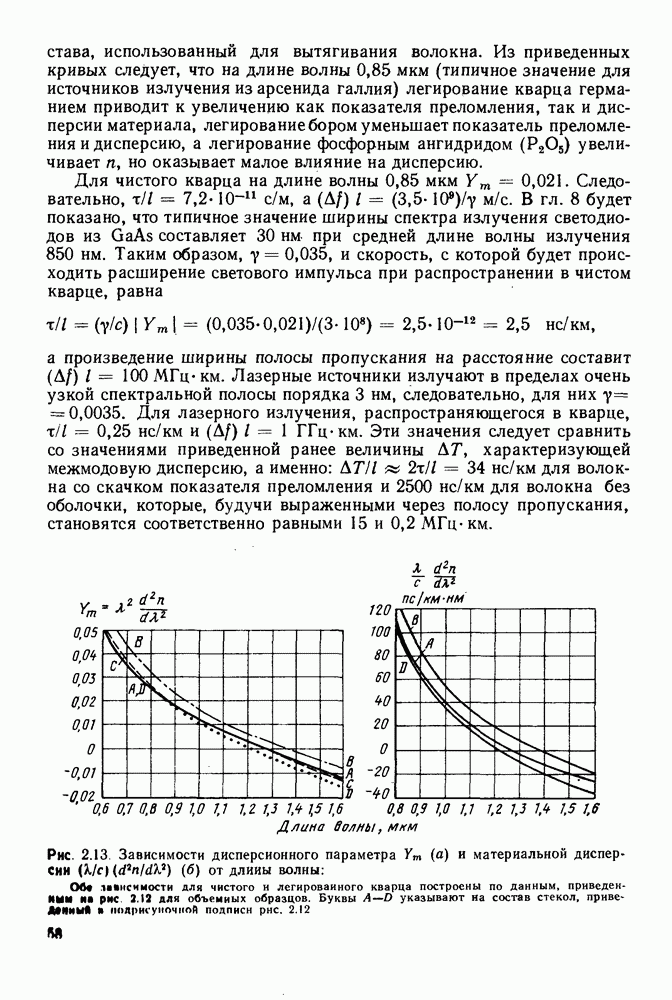
- 2.2.3. Временная дисперсия в объемной среде
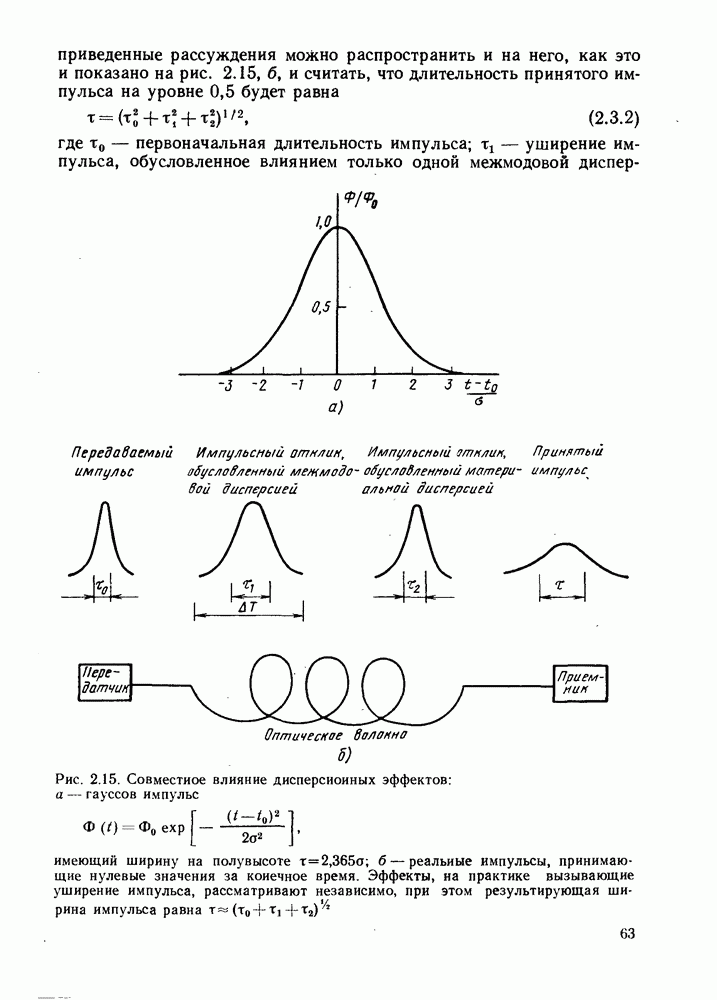
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
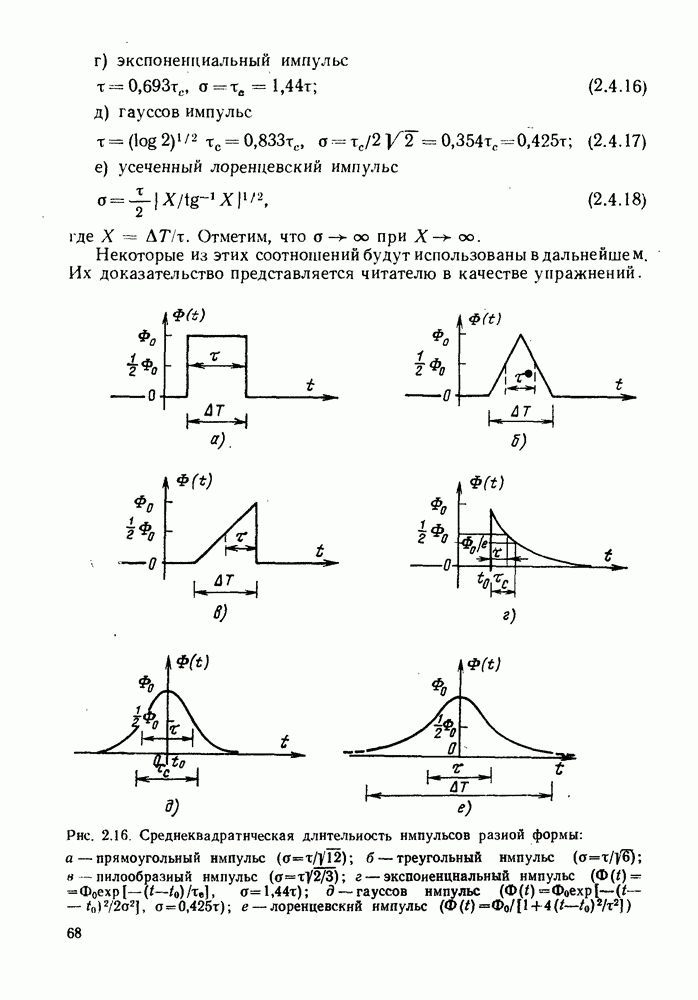
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
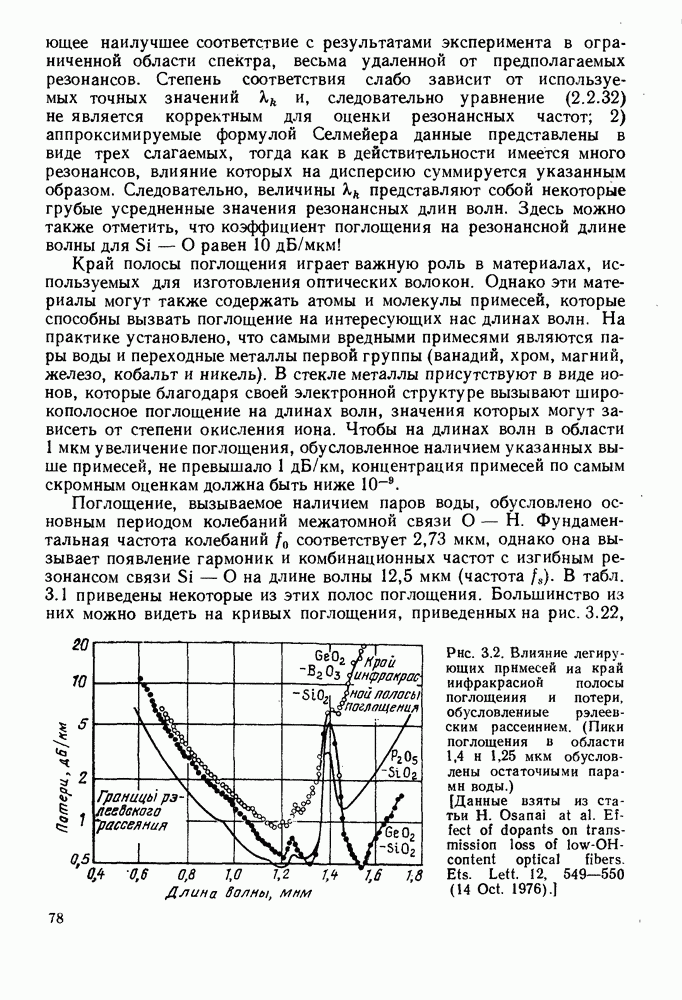
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
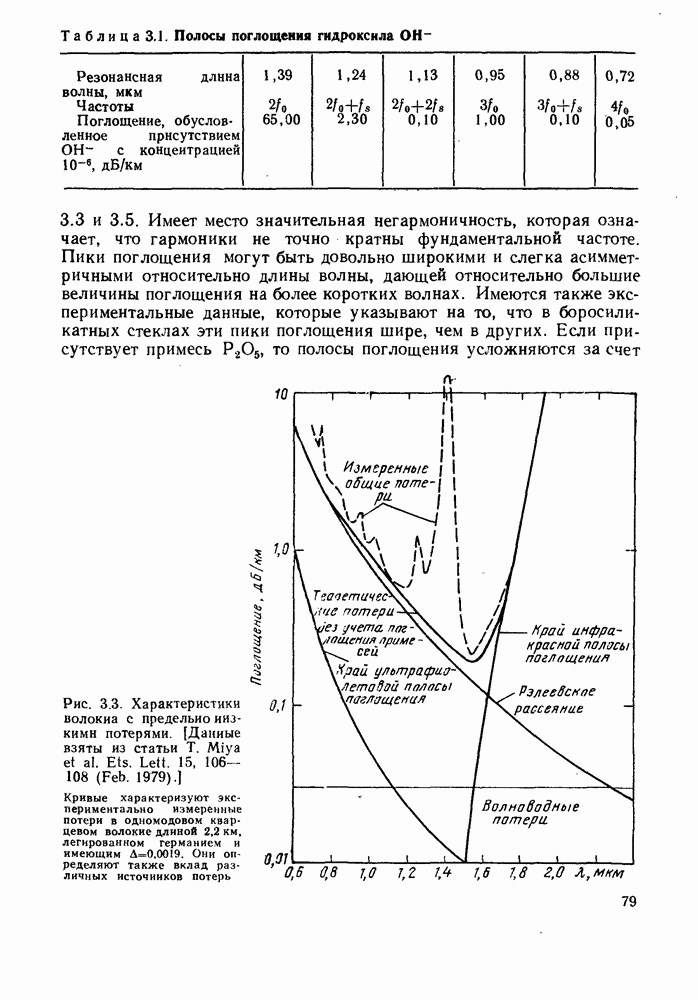
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
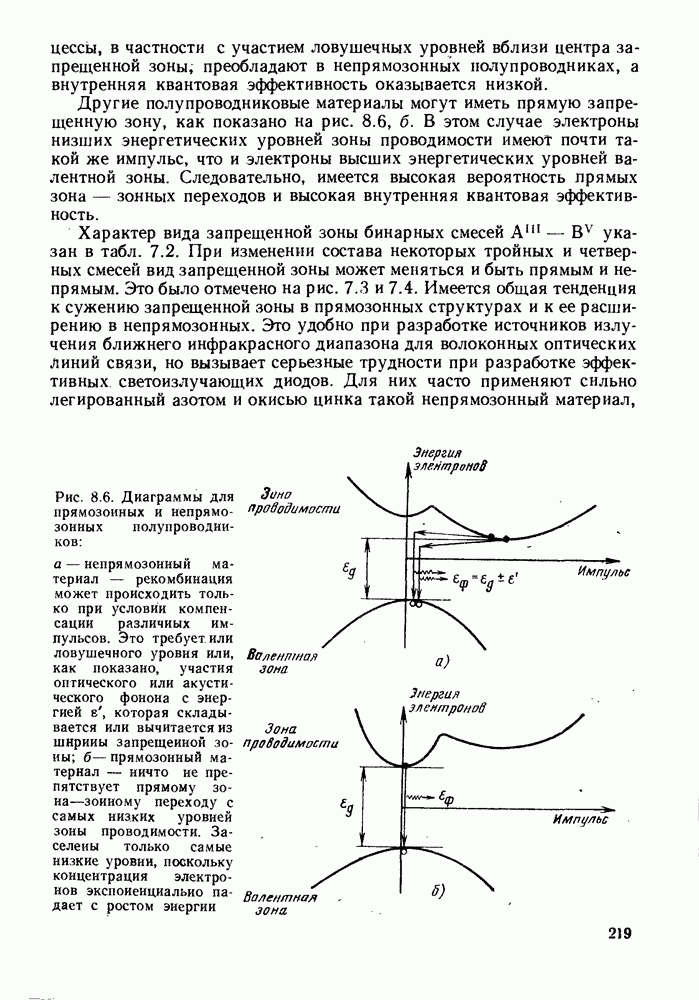
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
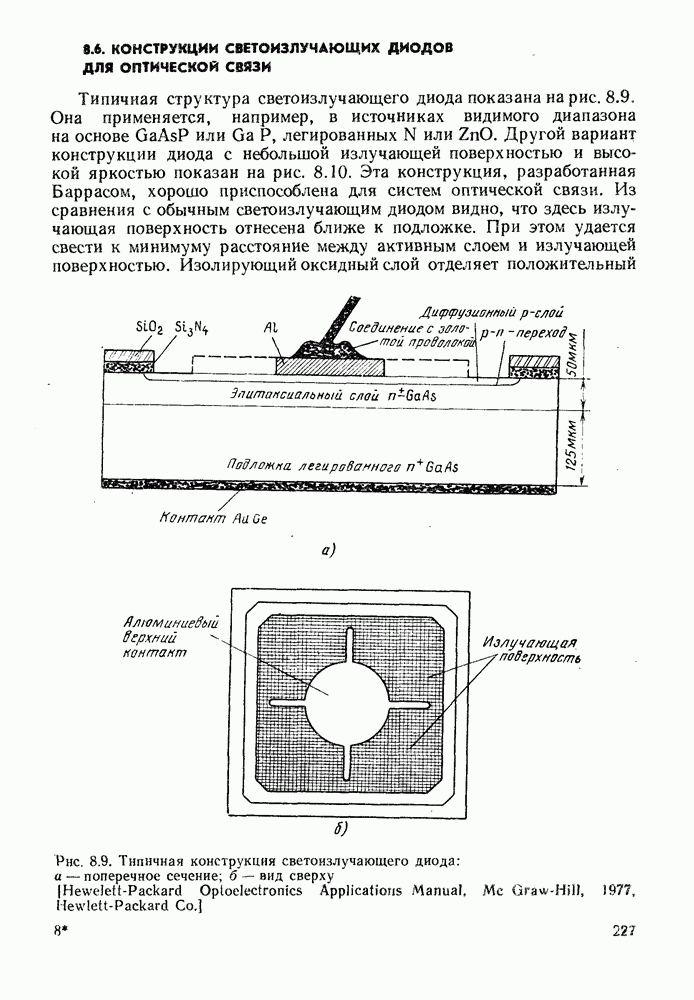
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
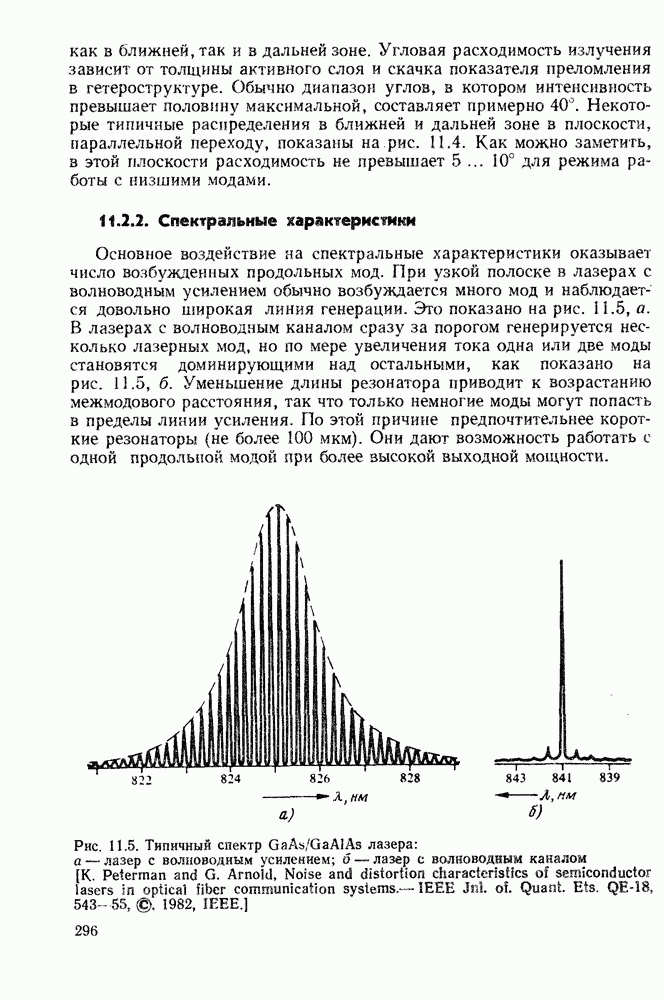
- 11.2.2. Спектральные характеристики
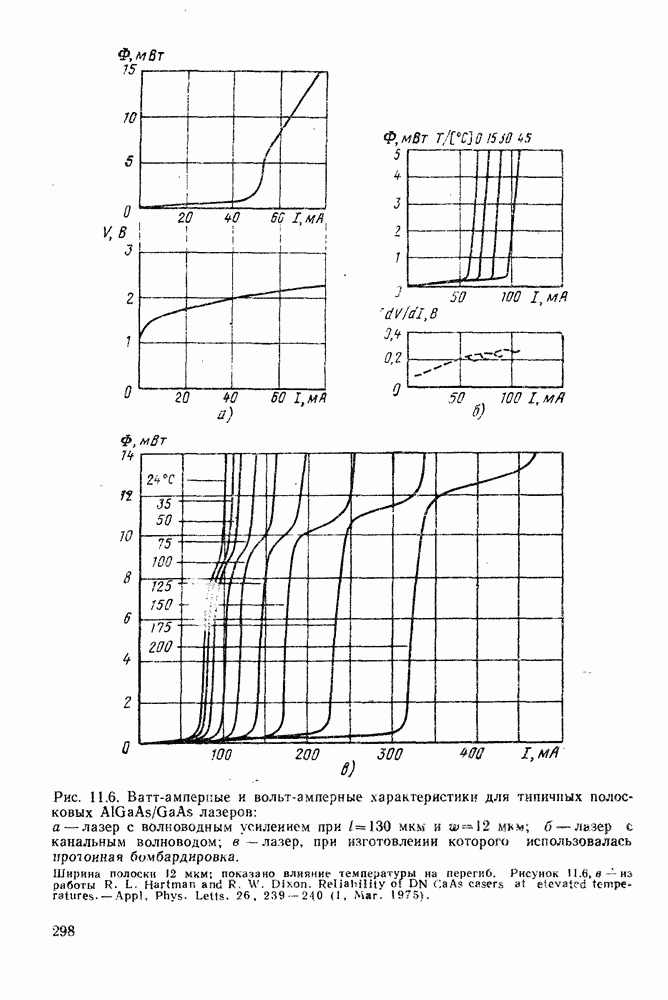
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
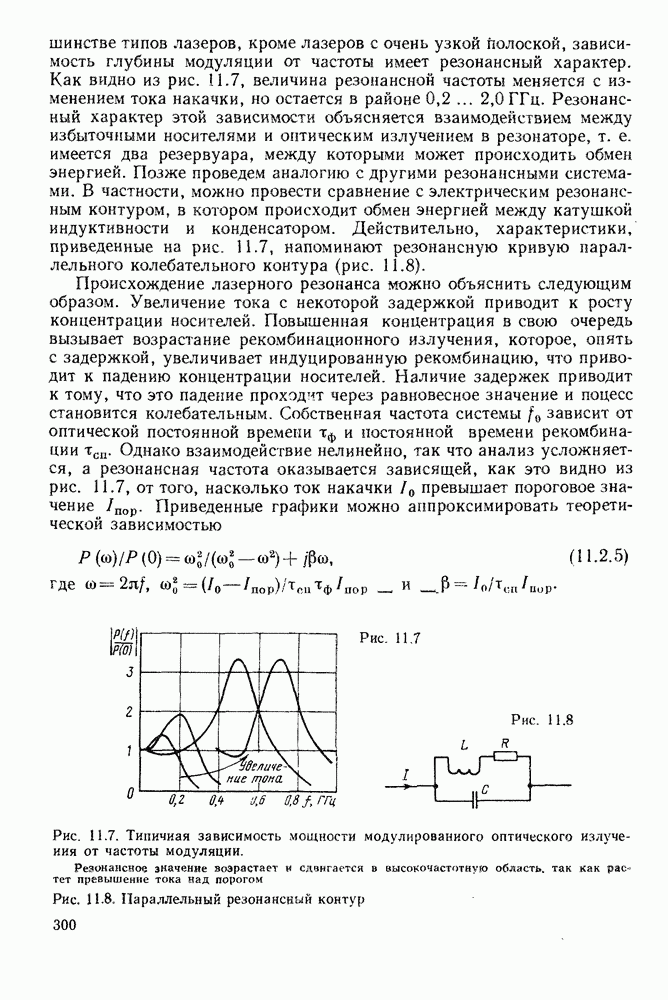
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
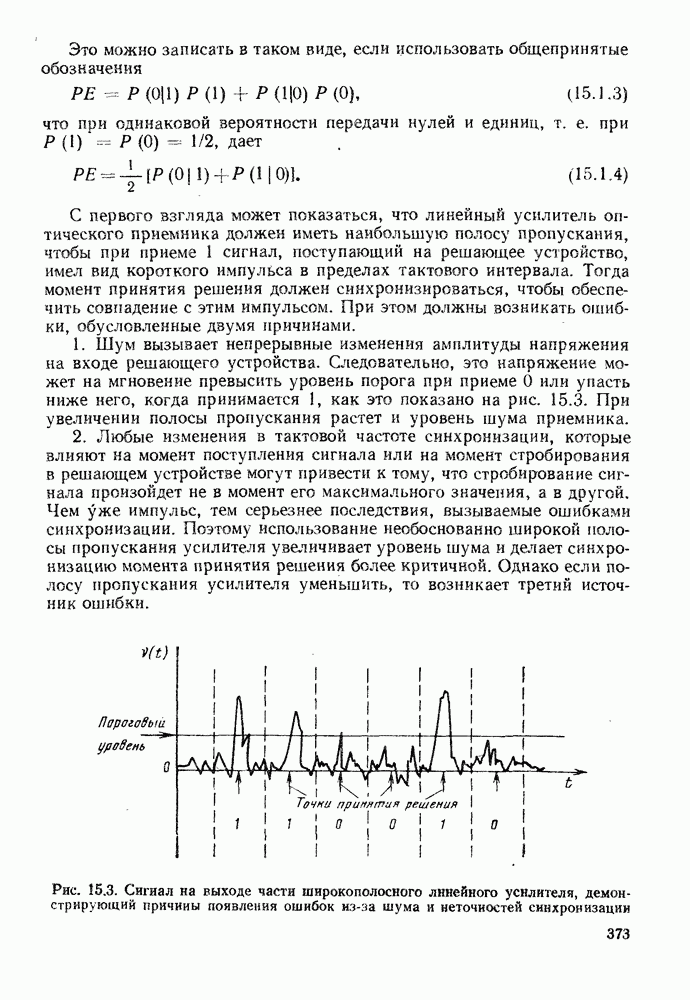
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
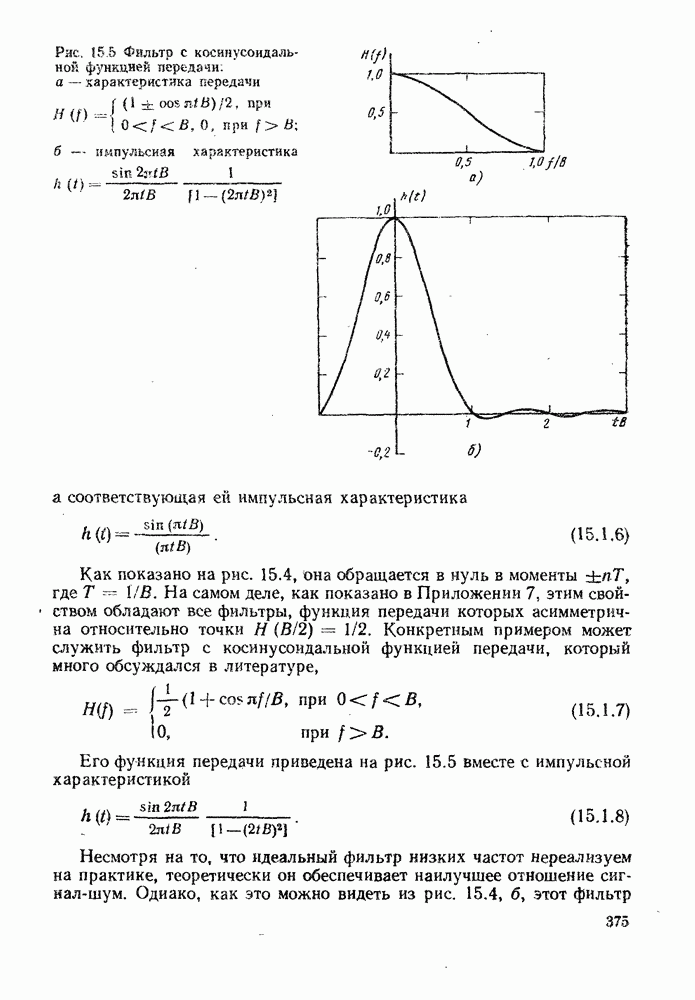
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
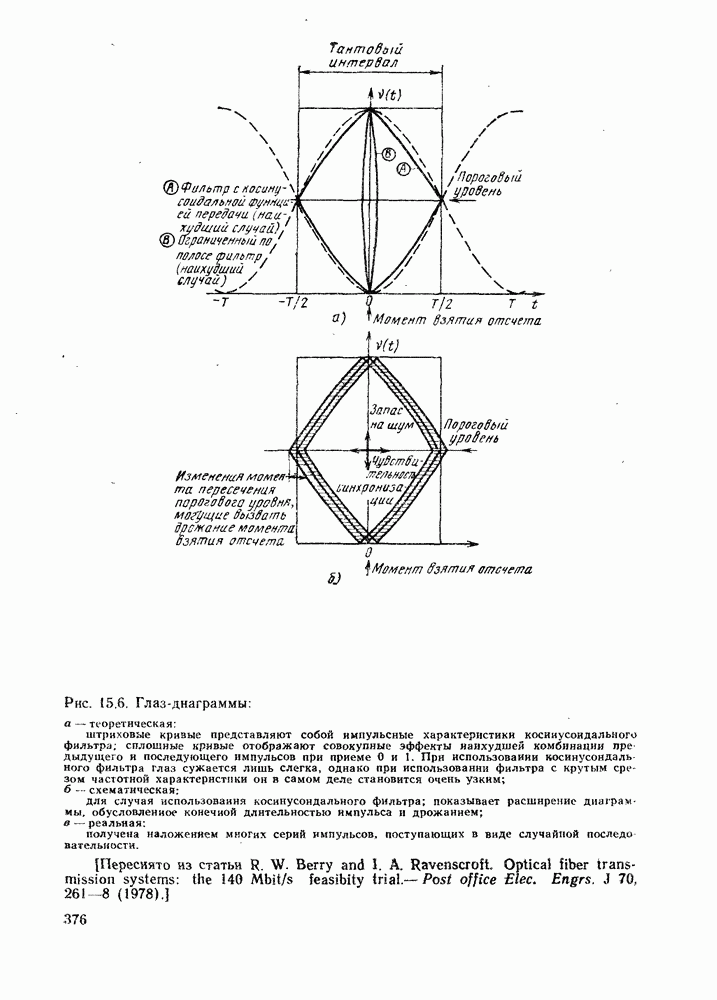
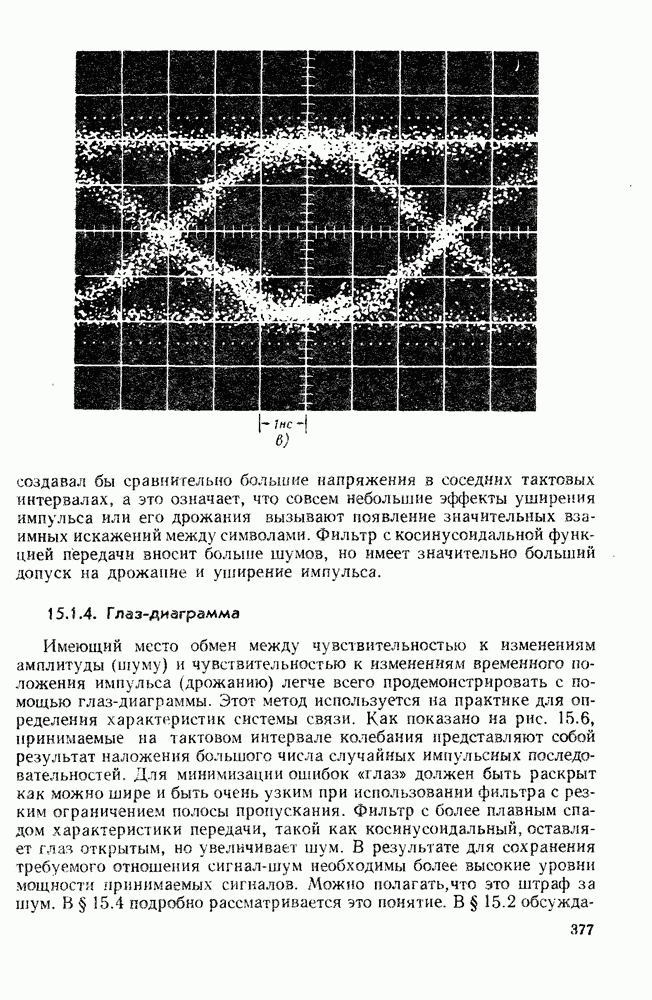
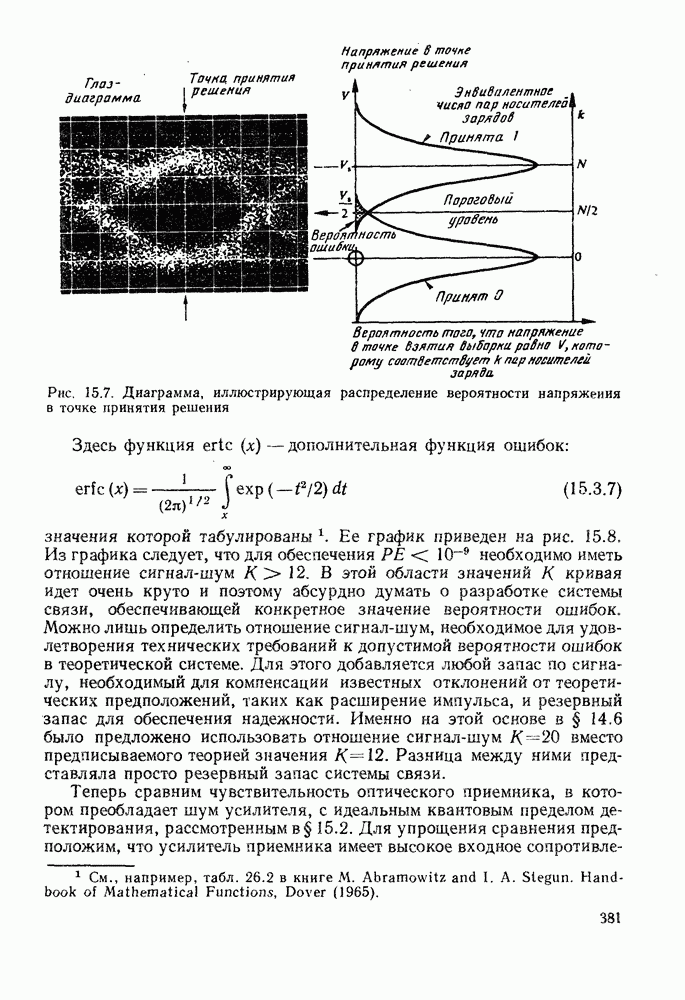
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
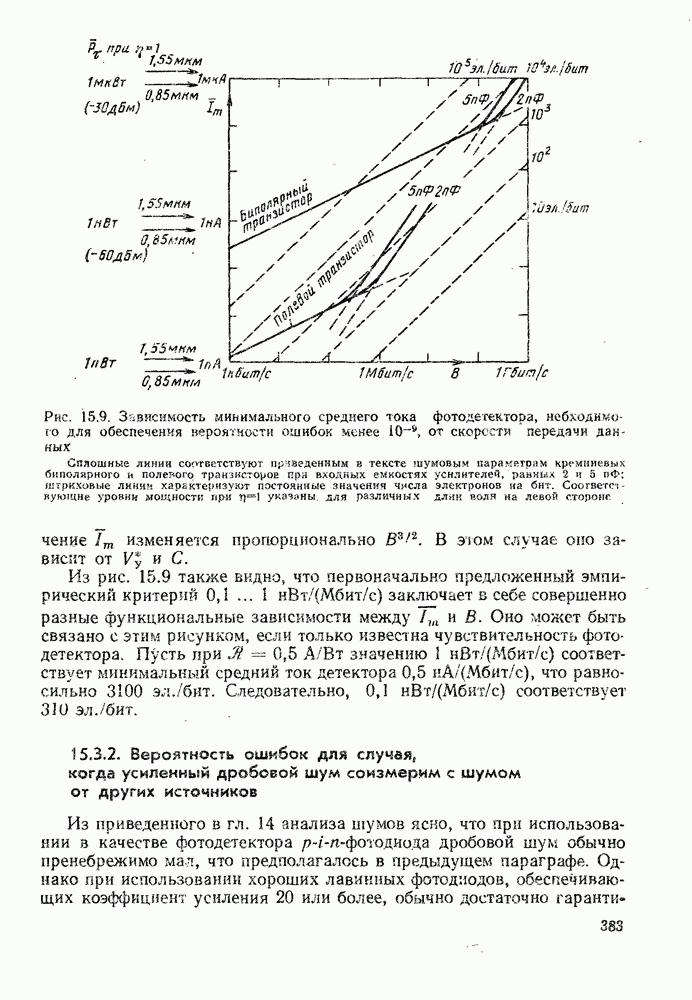
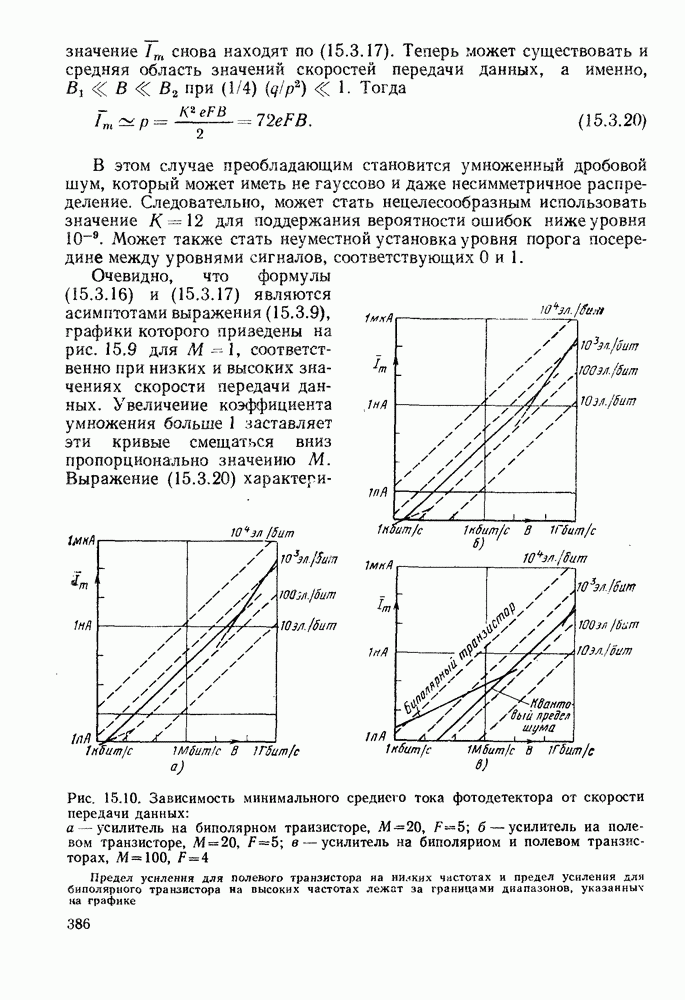
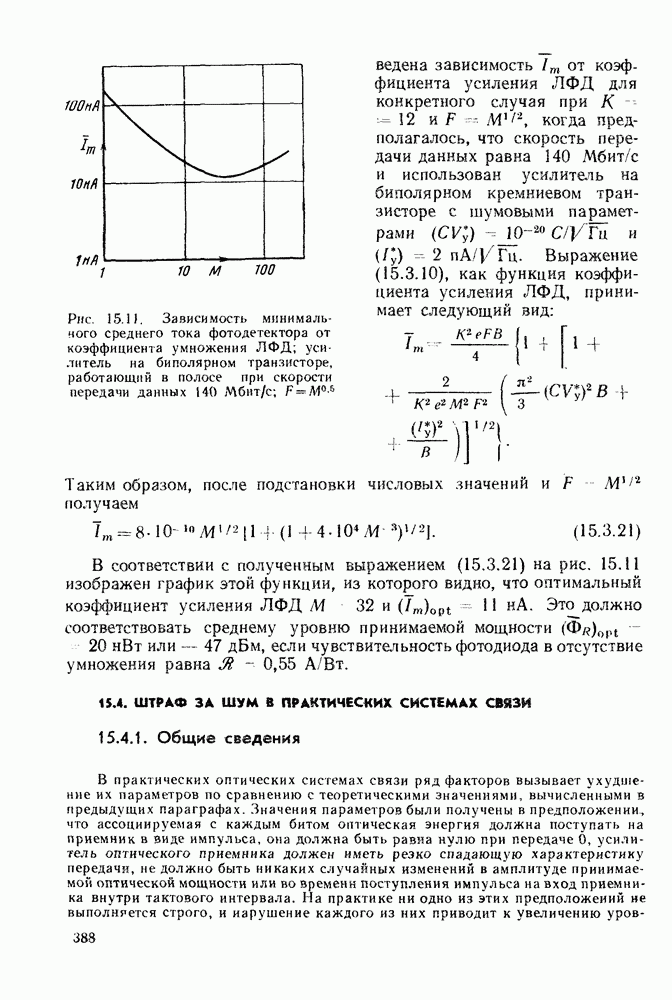
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
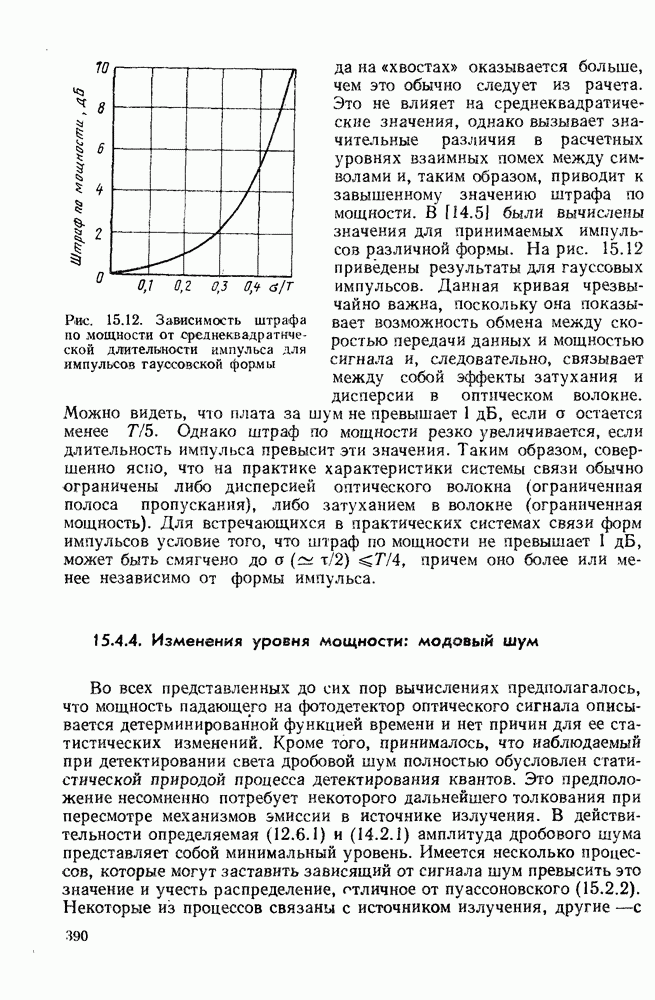
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
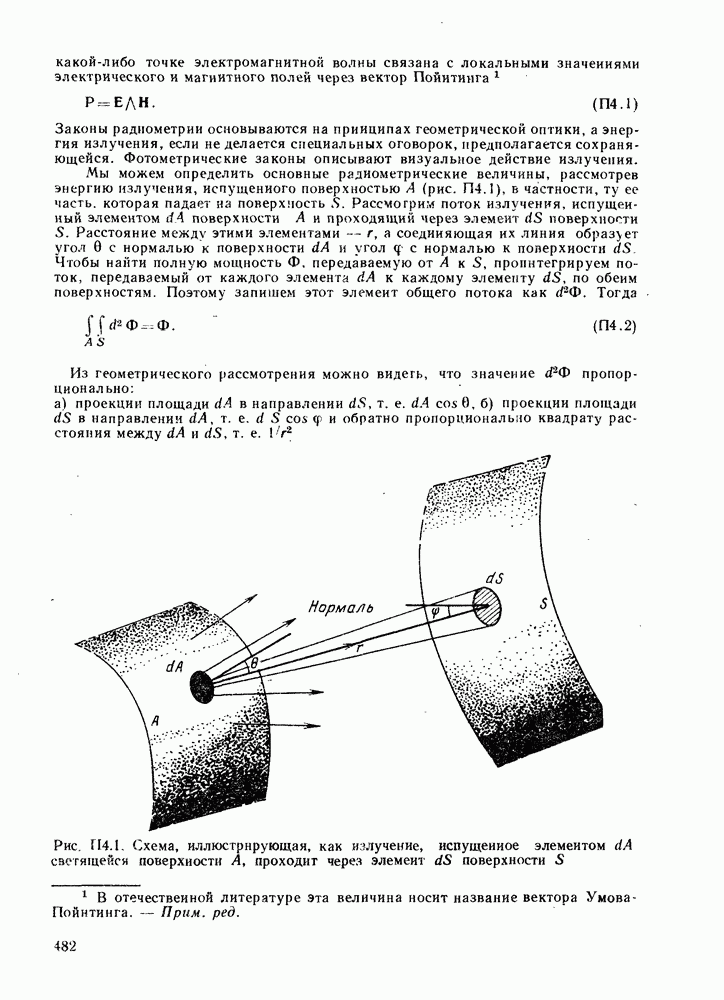
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
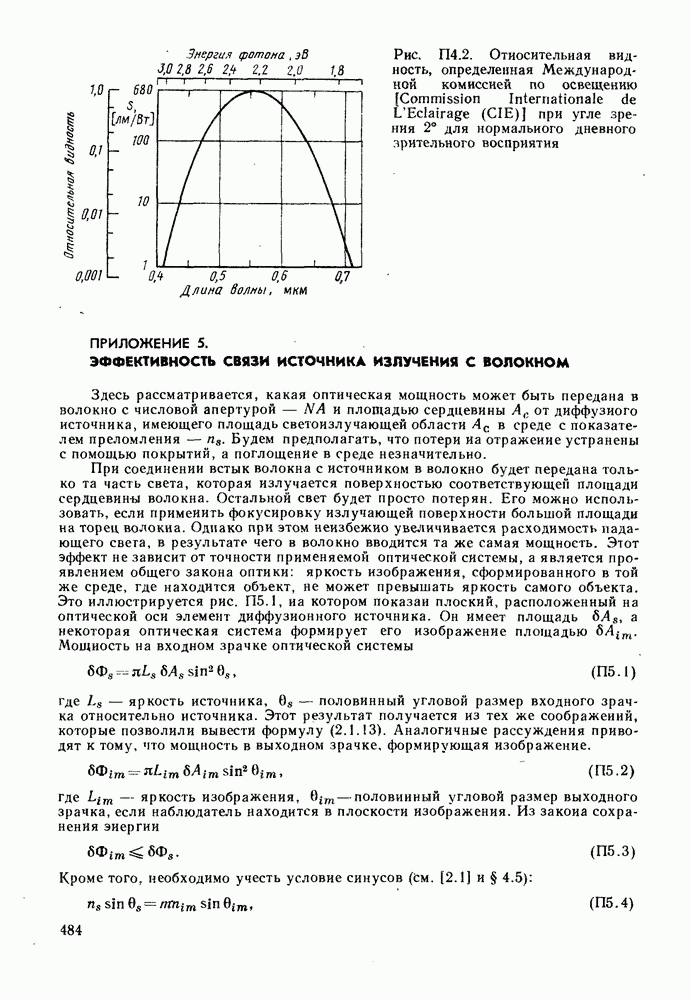
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
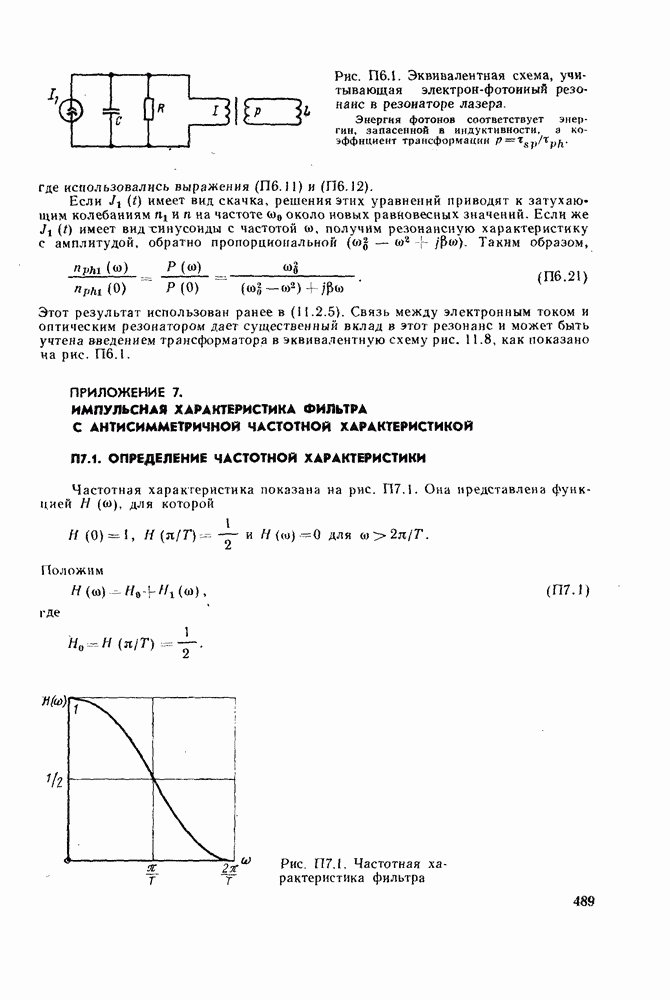
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ