| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
14.4.1. Отношение сигнал-шум
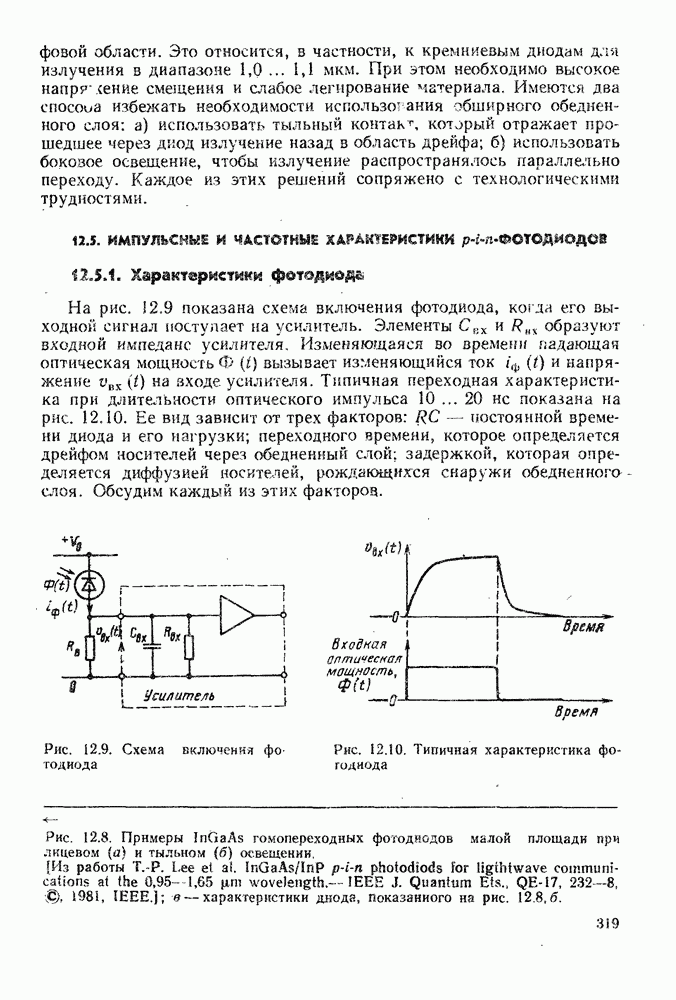
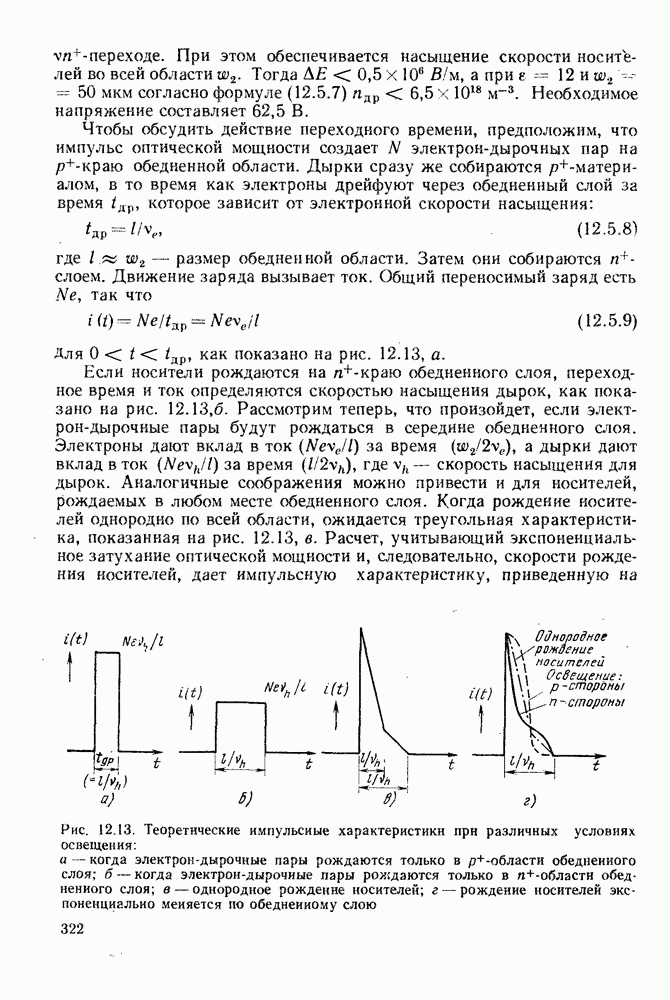
Сначала рассмотрим передаточную функцию усилителя. В § 12.5 была кратко рассмотрена эквивалентная схема оптического приемника для малого сигнала, состоящая из фотодетектора (фотодиода) и усилителя напряжения. Она вновь приведена на рис. 14.3. Как и раньше запишем

так что на выходе усилителя

Результирующая входная емкость С ограничивает полосу пропускания значением  Если сигналы будут изменяться быстрее, чем граничная частота, они будут эффективно интегрироваться (ослабляться) входной цепью. Для случая равномерной суммарной передаточной функции
Если сигналы будут изменяться быстрее, чем граничная частота, они будут эффективно интегрироваться (ослабляться) входной цепью. Для случая равномерной суммарной передаточной функции

Тогда выражение для напряжения на выходе примет вид:

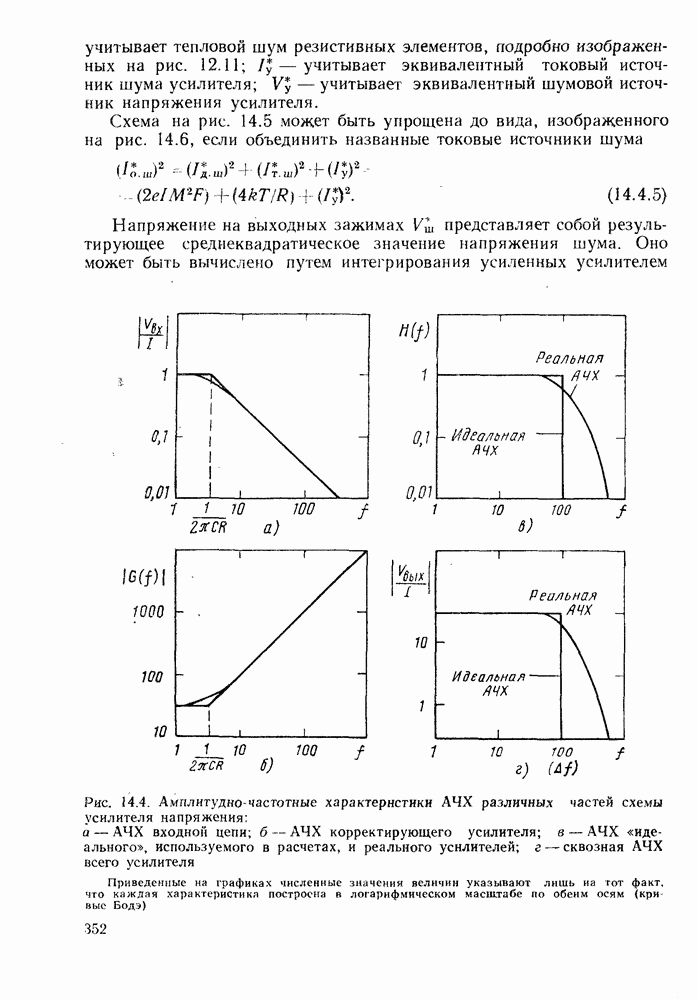
В дальнейшем будем предполагать, что всегда, когда это требуется, после начального усиления имеет место такое выравнивание АЧХ усилителя. В ряде случаев для этой цели полезно использовать дифференцирующую цепочку. На рис. 14.4. приведены АЧХ различных звеньев, включая и АЧХ фильтра  ограничивающего полосу частот.
ограничивающего полосу частот.
Эквивалентная шумовая схема для фотодиода и усилителя напряжения приведена на рис. 14.5. На ней изображены следующие источники шума:  учитывает умноженный дробовый шум фотодиода;
учитывает умноженный дробовый шум фотодиода; 

Рис. 14.3. Схема усилителя напряжения
учитывает тепловой шум резистивных элементов, подробно изображенных на рис. 12.11;  - учитывает эквивалентный токовый источник шума усилителя;
- учитывает эквивалентный токовый источник шума усилителя;  учитывает эквивалентный шумовой источник напряжения усилителя.
учитывает эквивалентный шумовой источник напряжения усилителя.
Схема на рис. 14.5 может быть упрощена до вида, изображенного на рис. 14.6, если объединить названные токовые источники шума

Напряжение на выходных зажимах  представляет собой результирующее среднеквадратическое значение напряжения шума. Оно может быть вычислено путем интегрирования усиленных усилителем
представляет собой результирующее среднеквадратическое значение напряжения шума. Оно может быть вычислено путем интегрирования усиленных усилителем
Рис. 14.4. (см. скан) Амплитудно-частотные характеристики АЧХ различных частей схемы усилителя напряжения: а — АЧХ входной цепи; б - АЧХ корректирующего усилителя; в - АЧХ «идеального», используемого в расчетах, и реального усилителей; г - сквозная АЧХ всего усилителя. Приведенные на графиках численные значения величин указывают лишь на тот факт, что каждая характеристика построена в логарифмическом масштабе по обеим осям (кривые Бодэ)

Рис. 14.5. Эквивалентная шумовая схема усилителя напряжения
среднеквадратических значений  в требуемой полосе частот
в требуемой полосе частот  В результате получаем
В результате получаем

Это выражение упрощается, если в него подставить значение  определяемое (14.4.3), и учесть, что требуемая полоса частот равна
определяемое (14.4.3), и учесть, что требуемая полоса частот равна 

Если же величины  не зависят от частоты в полосе
не зависят от частоты в полосе  то
то

Следовательно, отношение сигнала к среднеквадратическому значению шума

Если теперь представить  в виде суммы составляющих, чтобы сделать зависимость К от отдельных источников шума более наглядной, и подставить в (14.4.9), то получим окончательное выражение для отношения сигнал-шум на выходе усилителя
в виде суммы составляющих, чтобы сделать зависимость К от отдельных источников шума более наглядной, и подставить в (14.4.9), то получим окончательное выражение для отношения сигнал-шум на выходе усилителя

Для удобства последующего анализа каждая из пяти составляющих шума в знаменателе обозначена буквами а  Величина К определяет качество канала связи и при проектировании системы связи минимально допустимое значение отношения сигнал-шум всегда оговаривается особо. Например, для канала с импульсно-кодовой модуляцией оно составляет
Величина К определяет качество канала связи и при проектировании системы связи минимально допустимое значение отношения сигнал-шум всегда оговаривается особо. Например, для канала с импульсно-кодовой модуляцией оно составляет  в то время как для аналогового канала требуется
в то время как для аналогового канала требуется  Поэтому выражение (14.4.10) имеет огромное значение при проектировании оптической системы связи и оценки ее ожидаемых характеристик.
Поэтому выражение (14.4.10) имеет огромное значение при проектировании оптической системы связи и оценки ее ожидаемых характеристик.

Рис. 14, б. Сокращенная эквивалентная шумовая схема усилителя напряжения
Обратим внимание на ряд особенностей выражения (14.4.10).
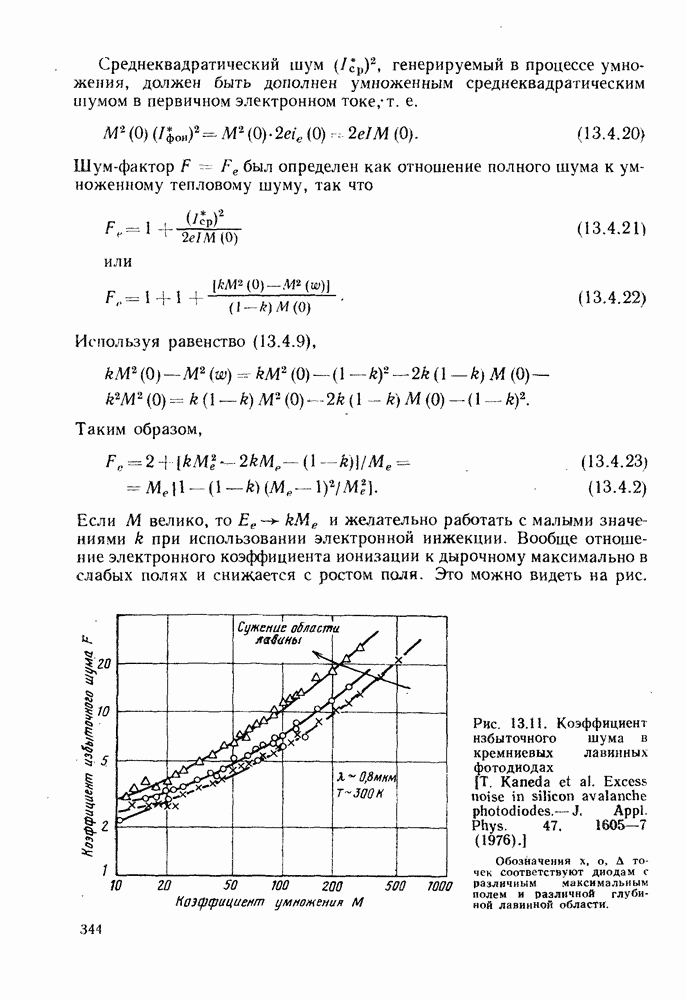
1. Отношение сигнал-шум может быть увеличено за счет увеличения коэффициента умножения  до тех пор, пока учитывающее дробовой шум слагаемое в, увеличенное в число раз, равное коэффициенту шума
до тех пор, пока учитывающее дробовой шум слагаемое в, увеличенное в число раз, равное коэффициенту шума  который сам в свою очередь растет с увеличением
который сам в свою очередь растет с увеличением  не станет преобладать над другими слагаемыми. Поэтому здесь всегда существует оптимальное значение
не станет преобладать над другими слагаемыми. Поэтому здесь всегда существует оптимальное значение 
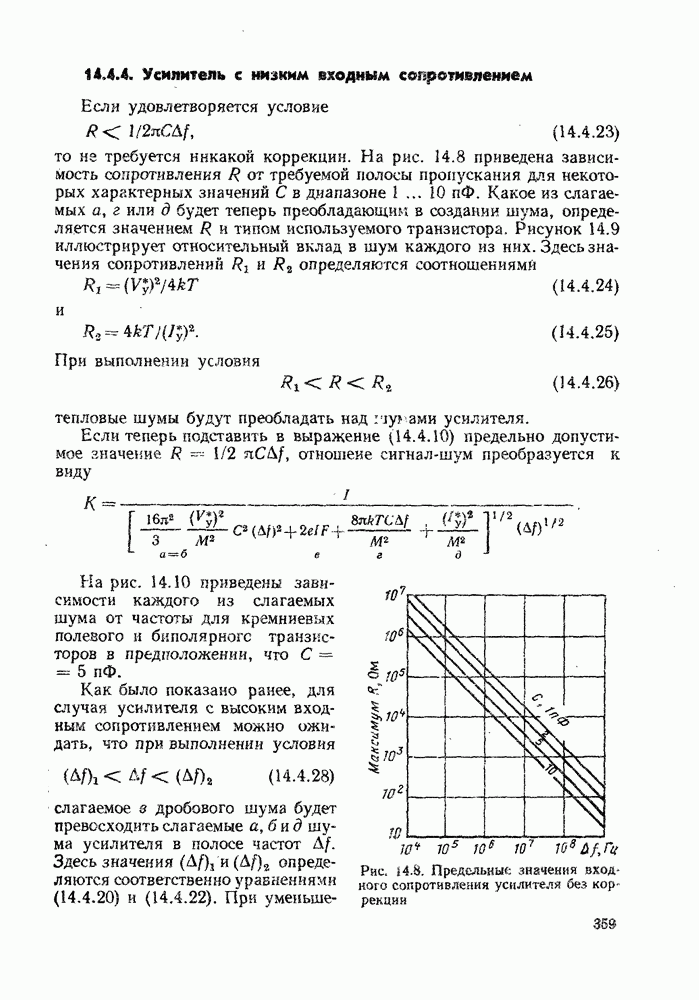
2. Увеличение сопротивления высокочастотного тракта R улучшает отношение сигнал-шум, пока слагаемые а и  значительны по величине. Интересно отметить, что этот результат был «открыт» дважды. Сначала
значительны по величине. Интересно отметить, что этот результат был «открыт» дважды. Сначала  -х годах, когда были впервые опубликованы ранние работы по шумам усилителей, а затем в 50-е годы, когда потребовались малошумящие усилители для высокочувствительных телевизионных систем и усиления сигналов с выходов фотоумножителей. И, наконец, он был вновь «переоткрыт» в 70-е годы, когда стали серьезно исследовать малошумящие усилители для приемников оптических систем связи.
-х годах, когда были впервые опубликованы ранние работы по шумам усилителей, а затем в 50-е годы, когда потребовались малошумящие усилители для высокочувствительных телевизионных систем и усиления сигналов с выходов фотоумножителей. И, наконец, он был вновь «переоткрыт» в 70-е годы, когда стали серьезно исследовать малошумящие усилители для приемников оптических систем связи.
Однако использование большого входного сопротивления приводит к появлению трудностей, наименьшая из которых состоит в необходимости значительной коррекции АЧХ усилителя на высоких частотах. Более подробно эти вопросы будут рассмотрены в § 14.4.3.
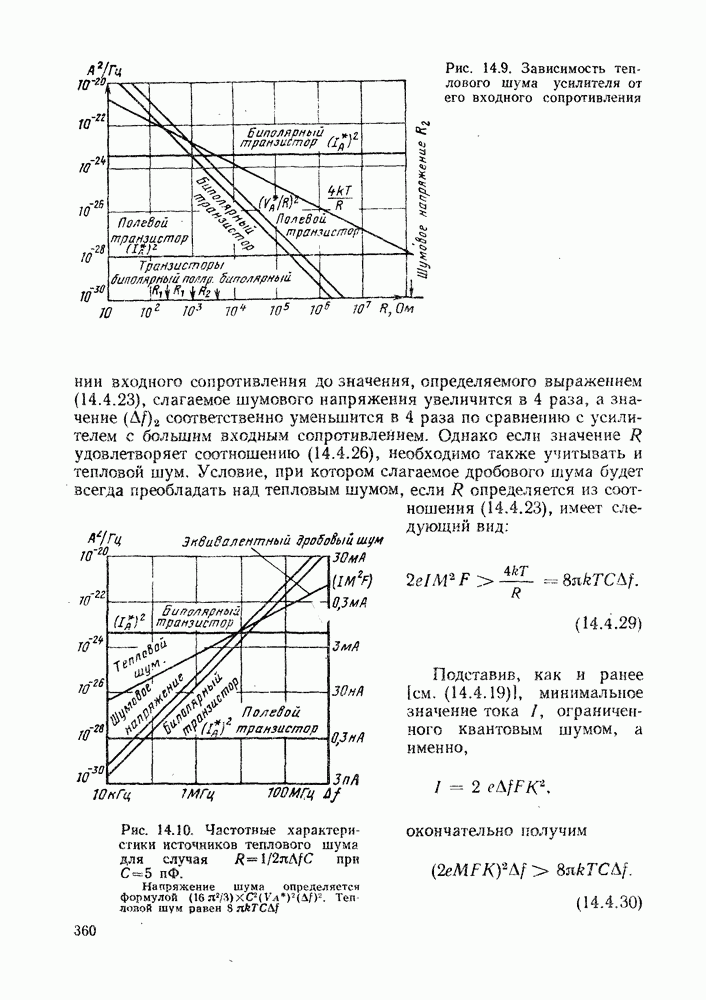
3. При наличии коррекции на высоких частотах слагаемое  становится преобладающим и шум начинает возрастать пропорционально квадрату значения входной емкости. Поэтому весьма важно минимизировать значение С. Это приводит также и к уменьшению величины требуемой коррекции АЧХ усилителя.
становится преобладающим и шум начинает возрастать пропорционально квадрату значения входной емкости. Поэтому весьма важно минимизировать значение С. Это приводит также и к уменьшению величины требуемой коррекции АЧХ усилителя.
4. Наличие слагаемого дробового шума в приводит к тому, что общий уровень шума на выходе усилителя будет зависеть от уровня принимаемого сигнала. Эта характерная особенность отличает оптические системы связи от других и означает, что выражение (14.4.10) квадратично по отношению к  Сначала мы рассмотрим ситуацию, когда слагаемое
Сначала мы рассмотрим ситуацию, когда слагаемое  либо значительно больше, либо значительно меньше других, а затем в § 14.4.5 вернемся к общему случаю.
либо значительно больше, либо значительно меньше других, а затем в § 14.4.5 вернемся к общему случаю.
5. Пять членов в знаменателе выражения (14.4.10) суммируются, поскольку предполагается, что каждое из них представляет гауссов некоррелированный источник шума. На самом деле имеются теоретические границы применимости ожидаемых статистических характеристик некоторых из слагаемых, которые не являются гауссовыми
случайными процессами. Например» дробовой шум является пуассоновским процессом, подчиняющимся пуассоновской статистике, так же, как и некоторые другие, образующие  Кроме того, коэффициент шума лавинного умножения
Кроме того, коэффициент шума лавинного умножения  также может иметь закон распределения, отличный от нормального. Приведенная здесь оценка отношения сигкал-шум К годится как рабочий критерий и обычно вполне достаточна, однако следует помнить, что, как будет показано в § 15.2, в отдельных экстремальных случаях необходимо использовать истинные законы распределения шума, и объединять составляющие шума с гауссовым и негауссовым распределением следует с осторожностью.
также может иметь закон распределения, отличный от нормального. Приведенная здесь оценка отношения сигкал-шум К годится как рабочий критерий и обычно вполне достаточна, однако следует помнить, что, как будет показано в § 15.2, в отдельных экстремальных случаях необходимо использовать истинные законы распределения шума, и объединять составляющие шума с гауссовым и негауссовым распределением следует с осторожностью.
14.4.2. Идеальный случай
В идеальном фотоприемнике коэффициент умножения  должен быть достаточно большим, чтобы слагаемое в, учитывающее дробовой шум, преобладало над другими, а коэффициент шума
должен быть достаточно большим, чтобы слагаемое в, учитывающее дробовой шум, преобладало над другими, а коэффициент шума  должен быть равен единице. В этом случае
должен быть равен единице. В этом случае

откуда требуемый фототок

Это соотношение определяет квантовый предел для чувствительности идеального фотодетектора.
В диапазоне длин волн, где можно использовать высококачественные кремниевые лавинные фотодиоды при не очень высоких модулирующлх частотах, вполне возможна ситуация, когда слагаемое в будет доминирующим, а квантовый предел шума приблизится к коэффицентку шума ЛФД.
В этом случае, потребовав выполнения условия

и учтя чувствительность фотодиода  по (12.1.2), минимальное значение принимаемой мощности сигнала определяется по формуле
по (12.1.2), минимальное значение принимаемой мощности сигнала определяется по формуле

Для кремниевых лавинных фотодиодов, работающих на длине волны 0,85 мкм с квантовой эффективностью  чувствительность
чувствительность  Следовательно, при полосе
Следовательно, при полосе  коэффициенте шума
коэффициенте шума  и минимально допустимом отношении сигнал-шум
и минимально допустимом отношении сигнал-шум  требуемая минимальная мощность сигнала, принимаемого фотодиодом, дожна быть
требуемая минимальная мощность сигнала, принимаемого фотодиодом, дожна быть 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
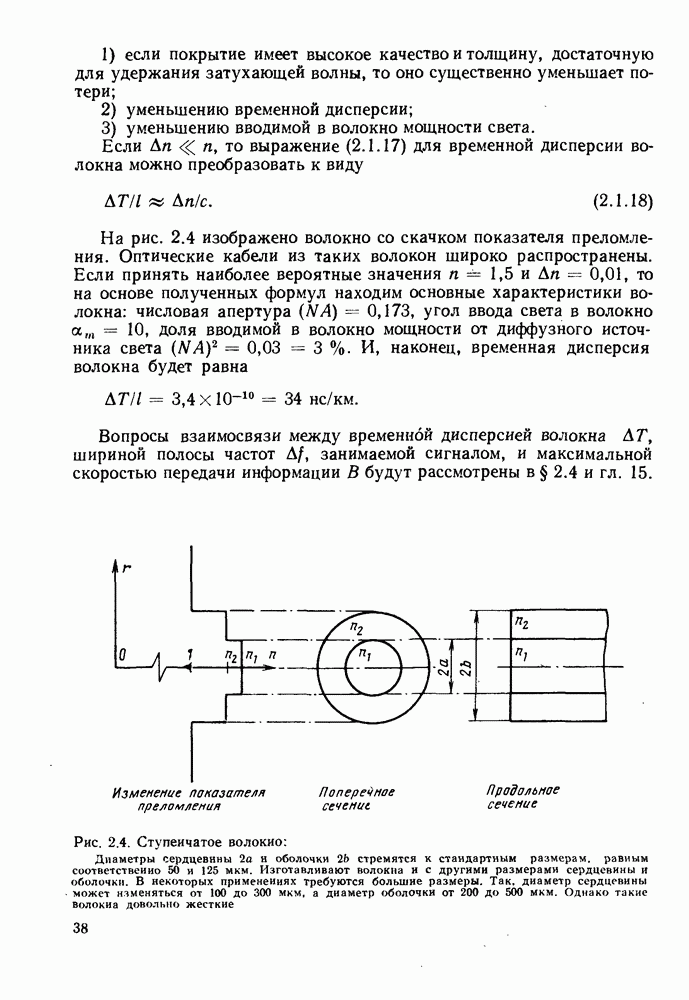
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
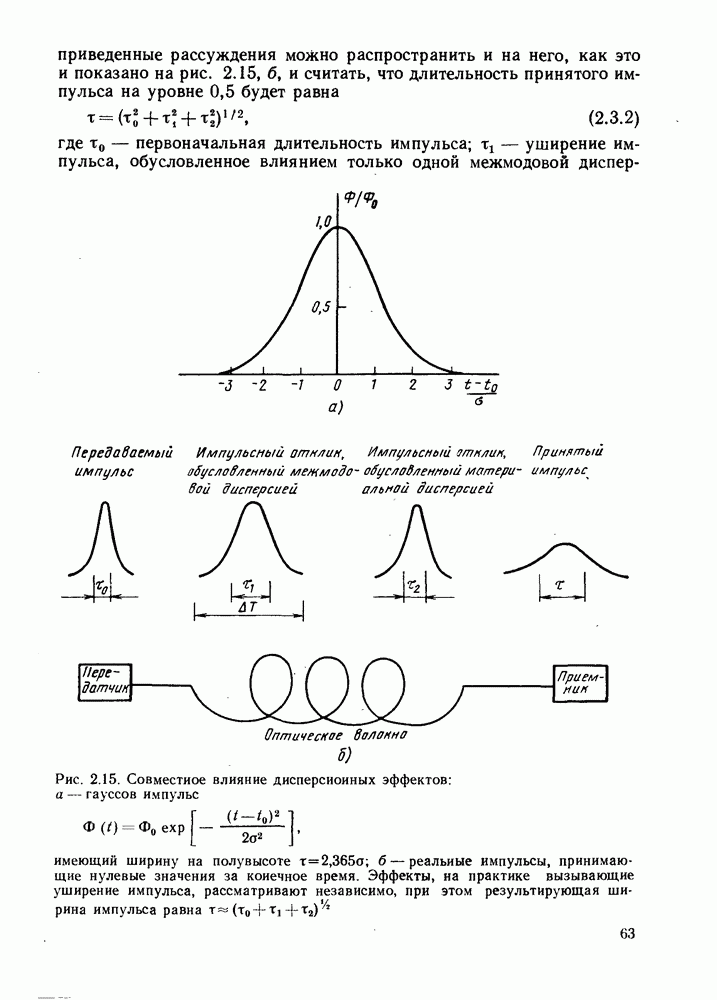
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
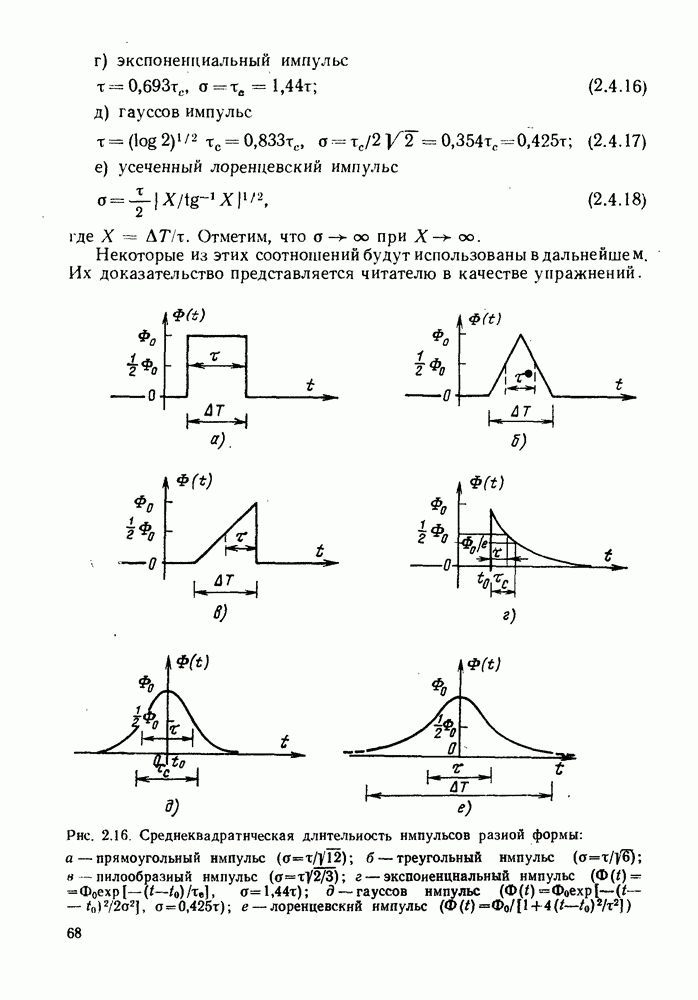
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
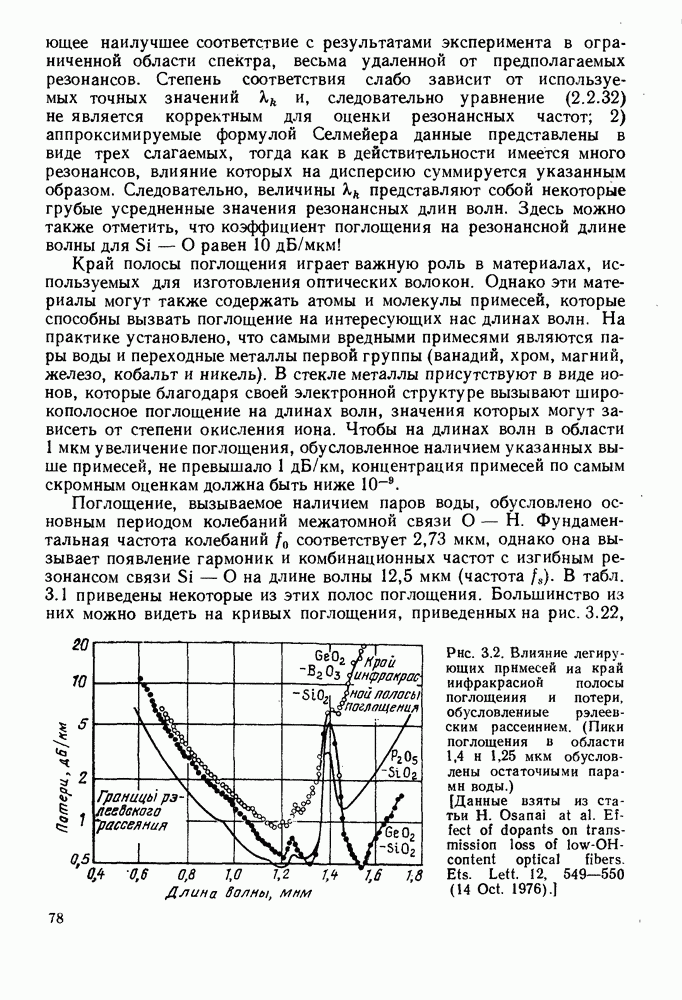
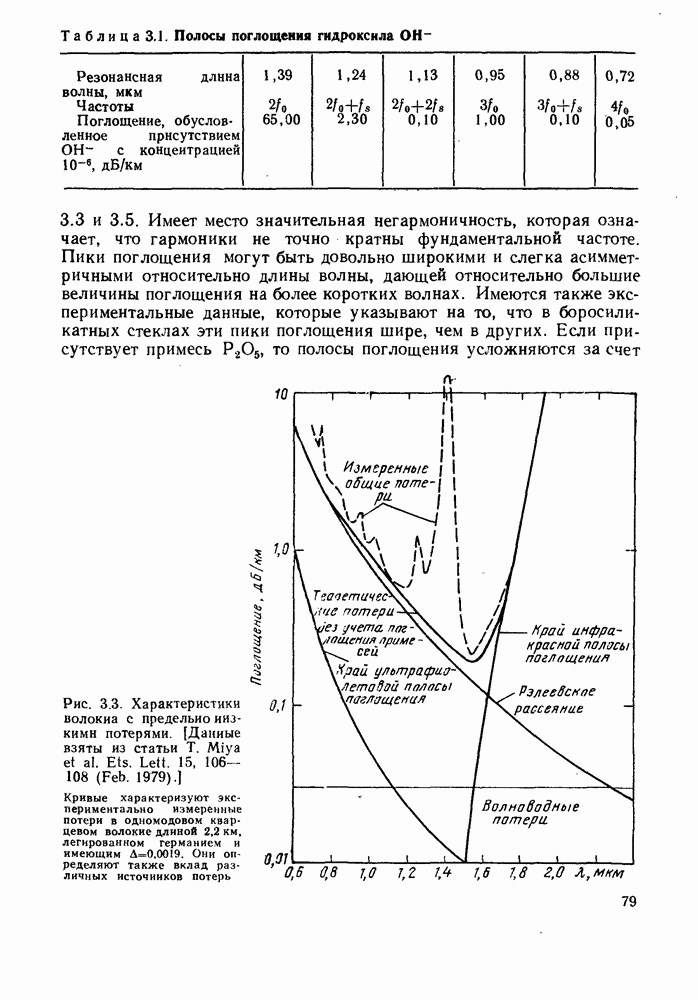
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
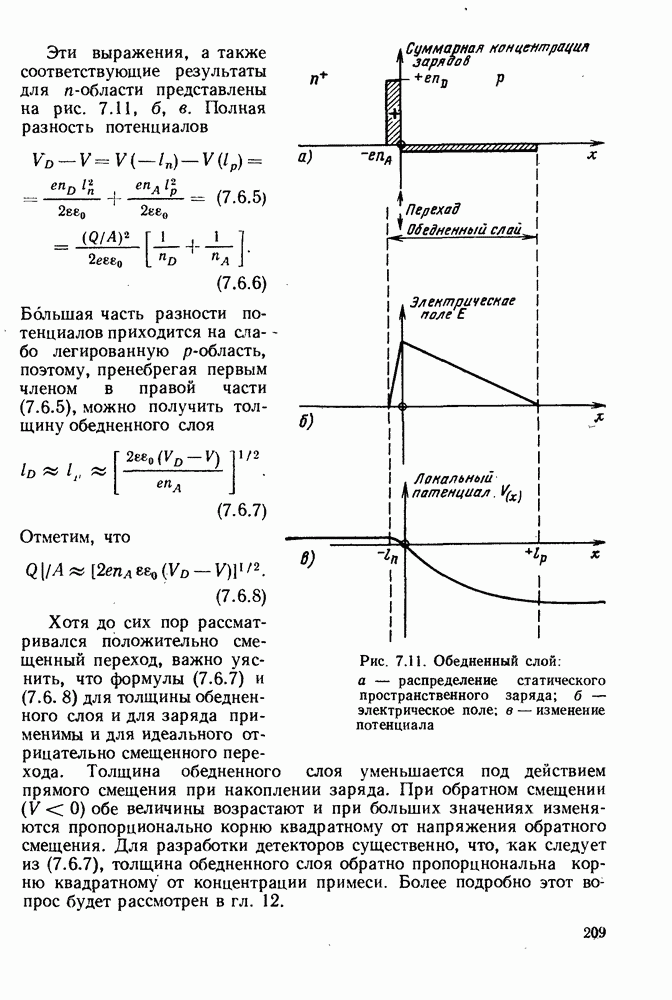
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
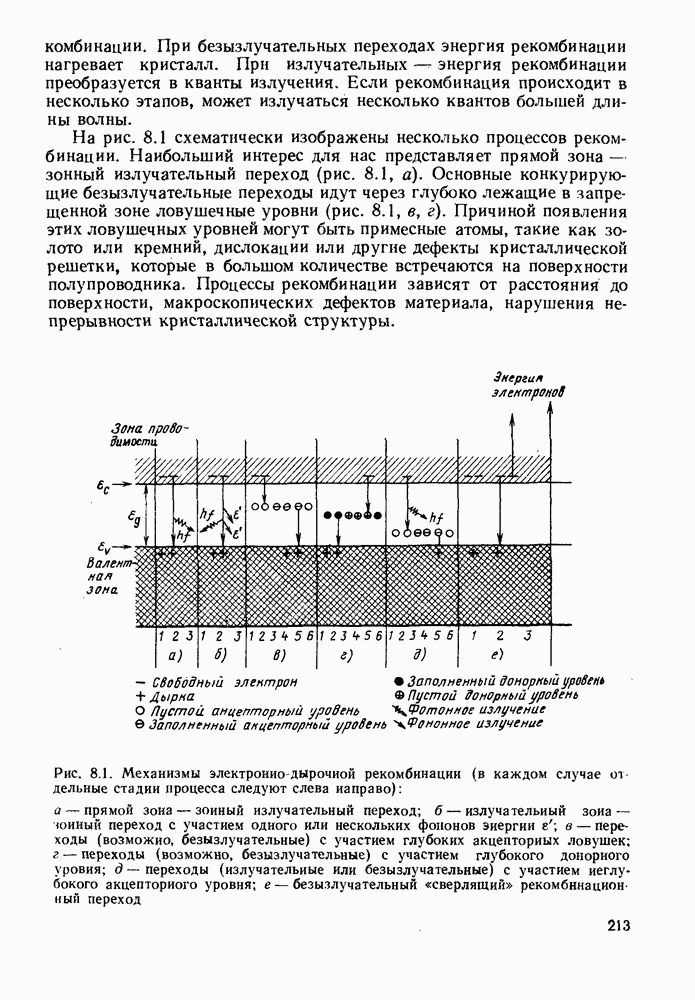
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
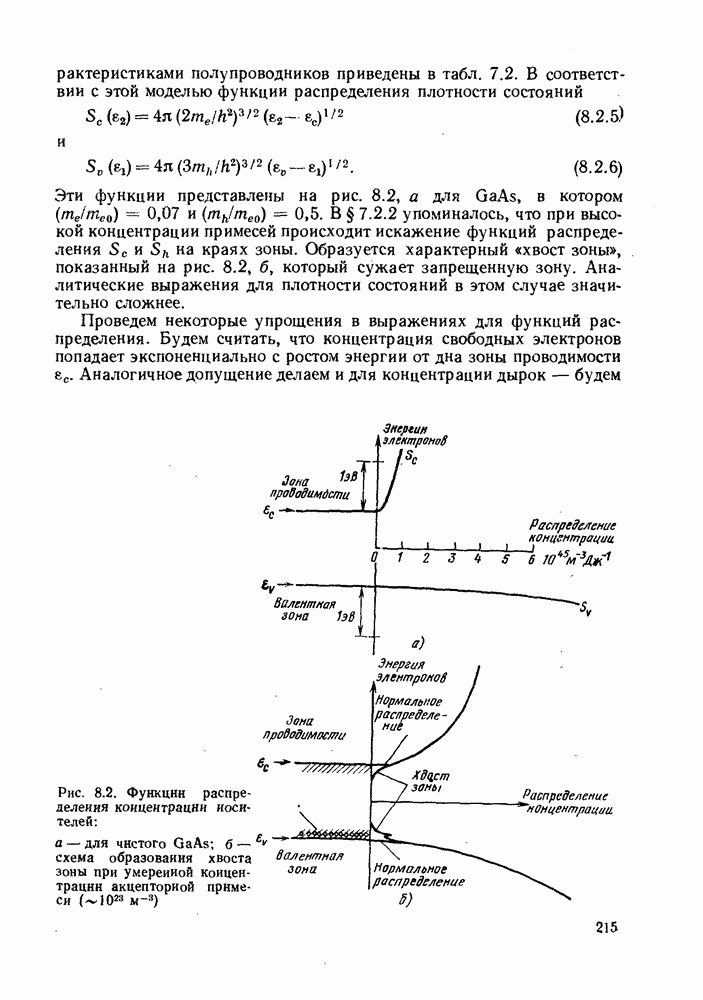
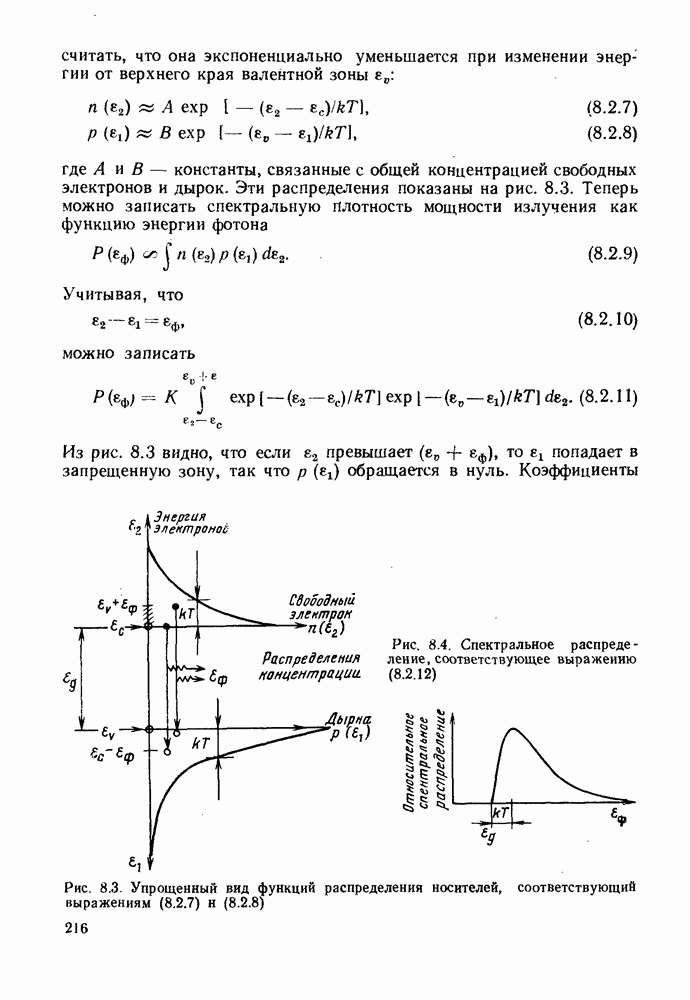
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
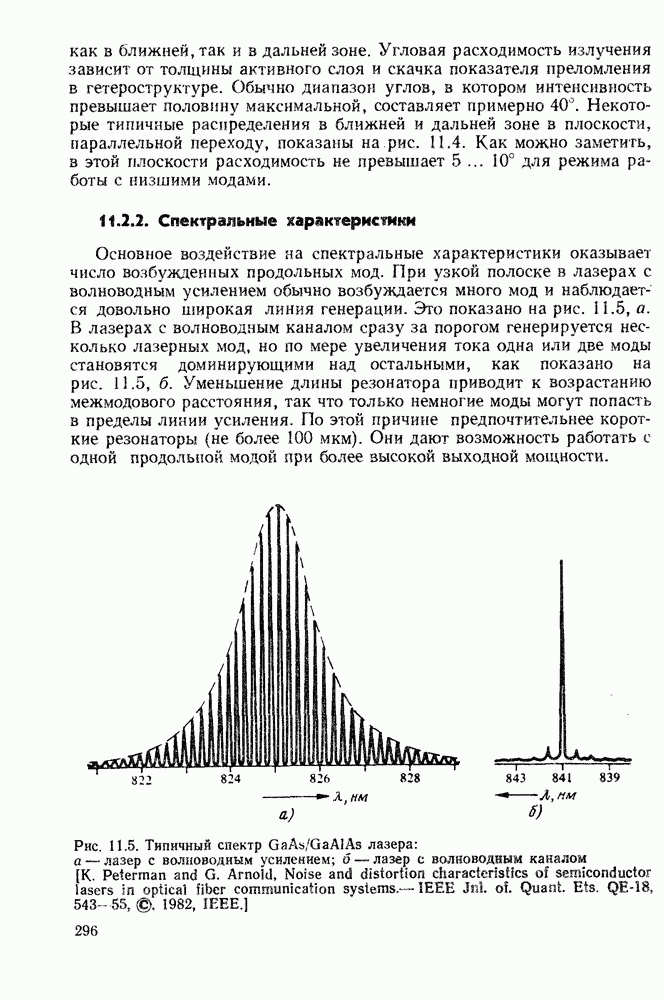
- 11.2.2. Спектральные характеристики
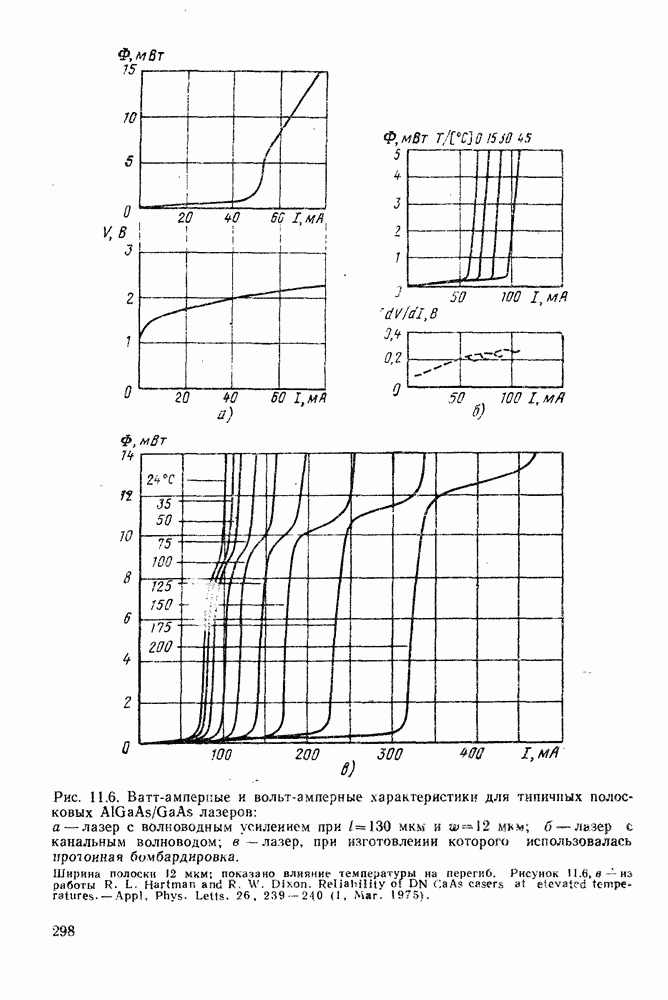
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
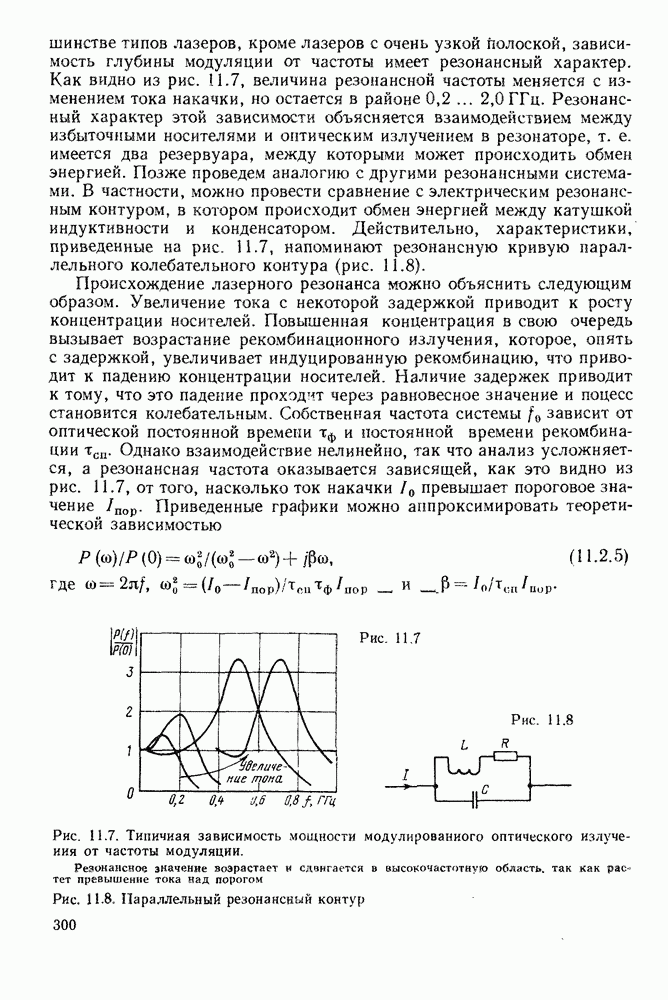
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
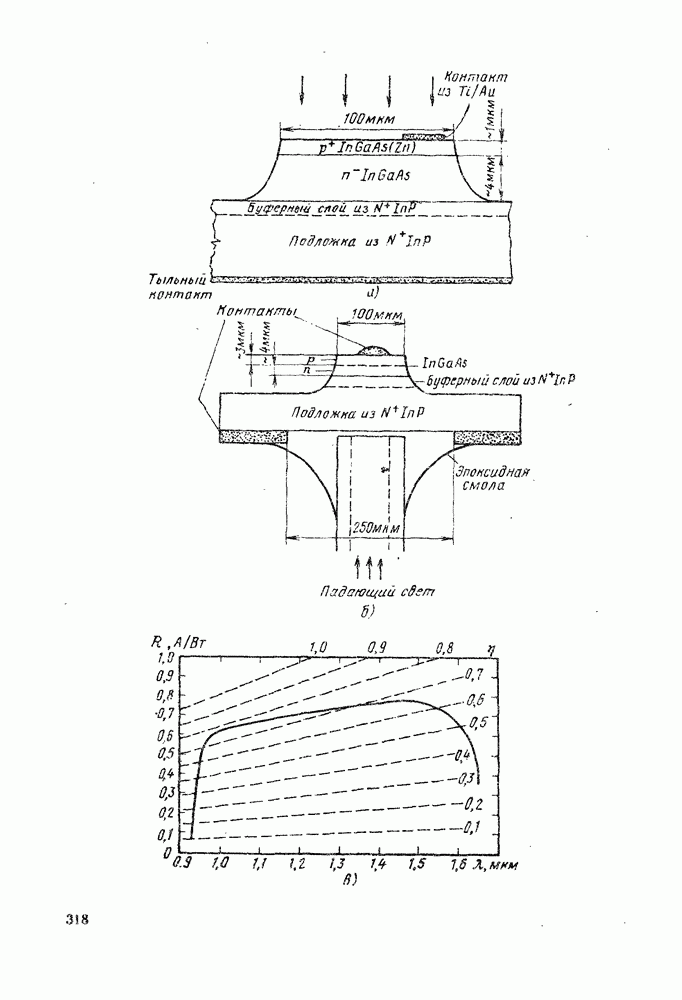
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
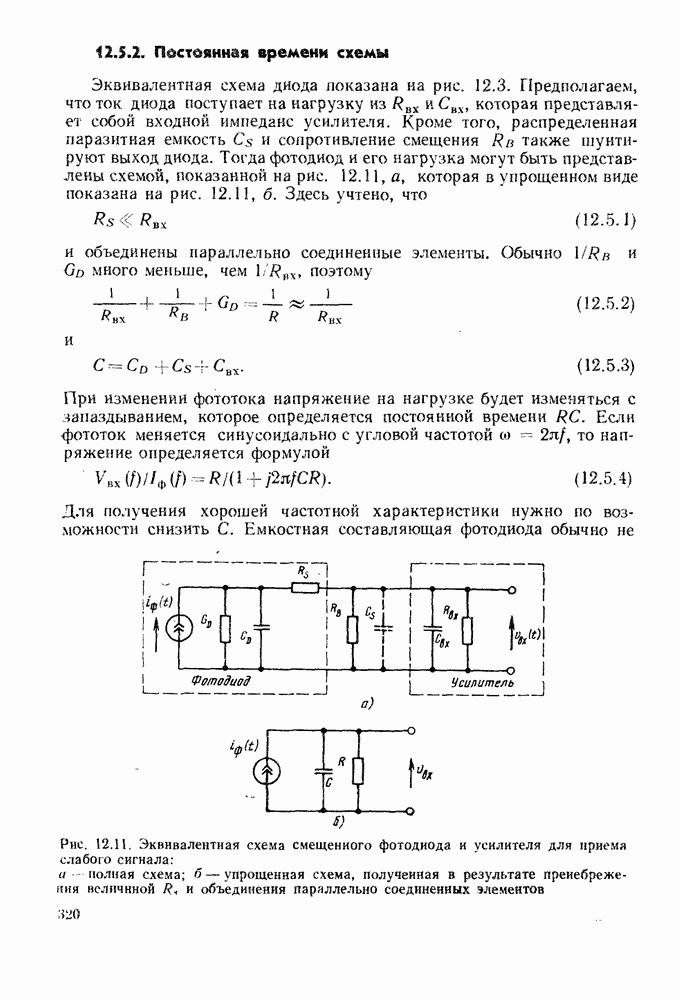
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
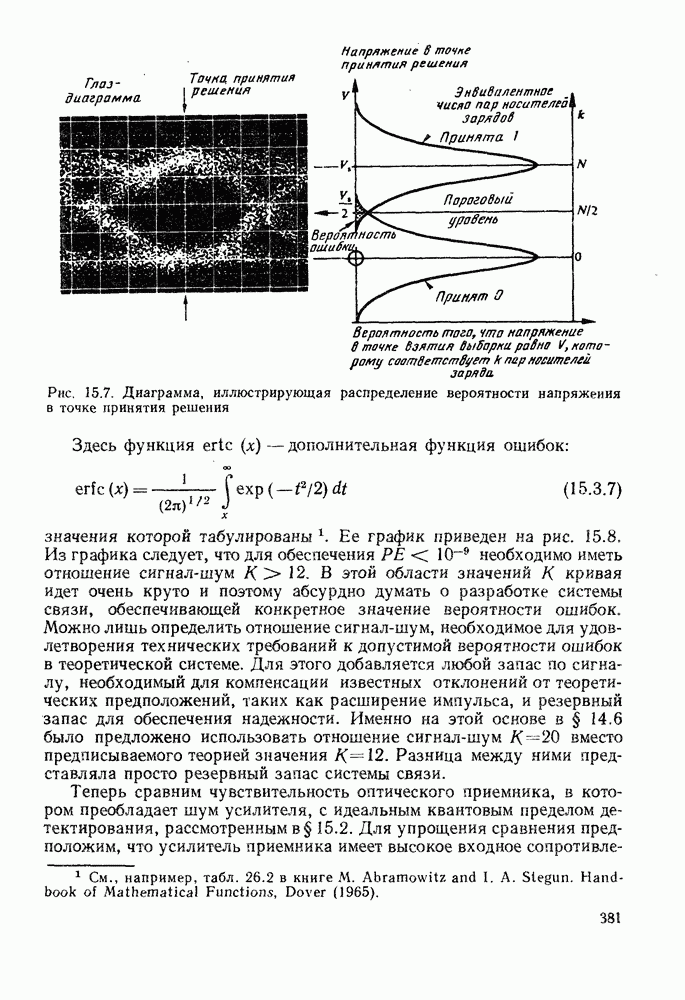
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
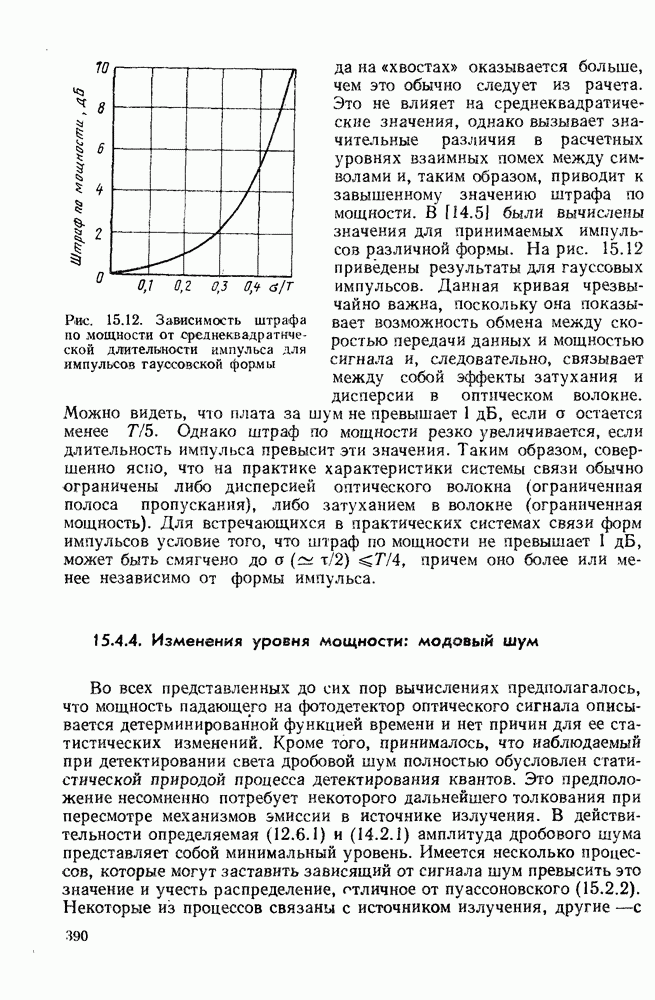
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
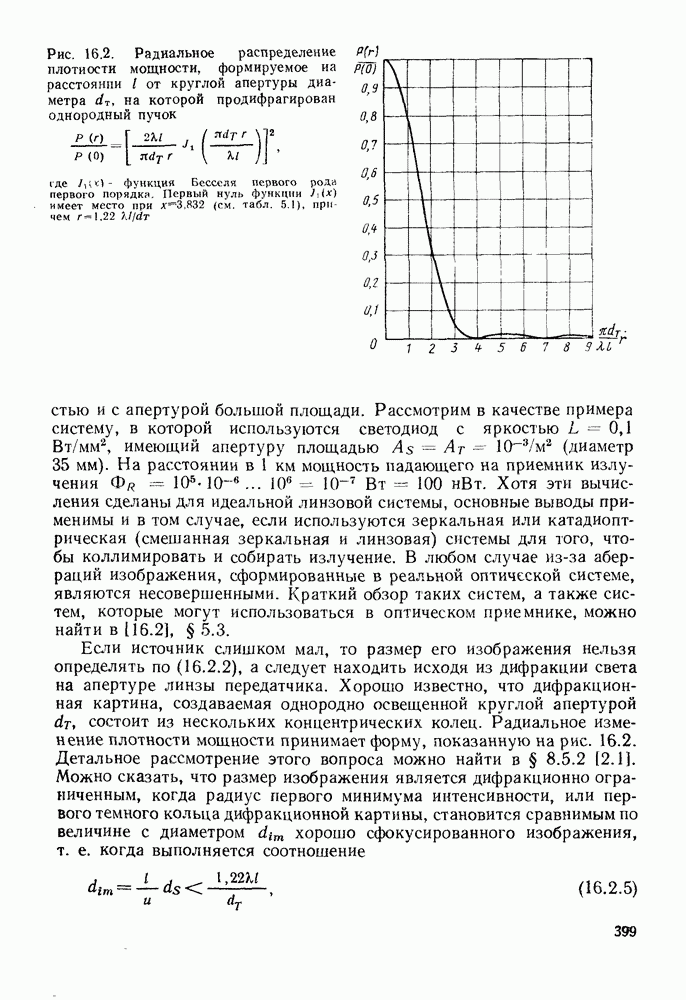
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
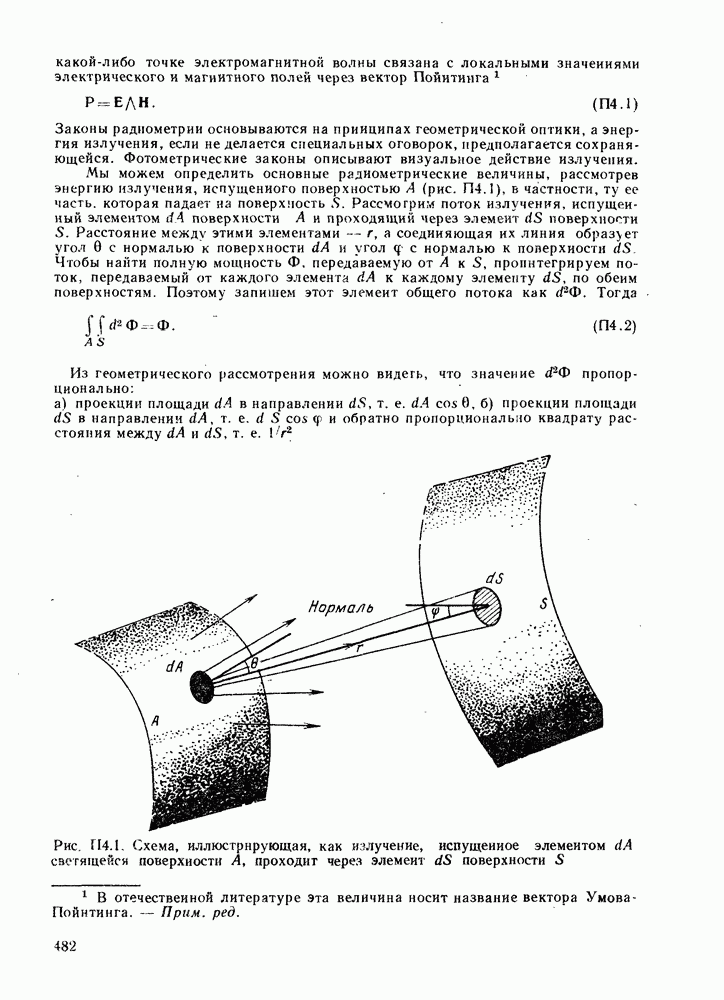
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
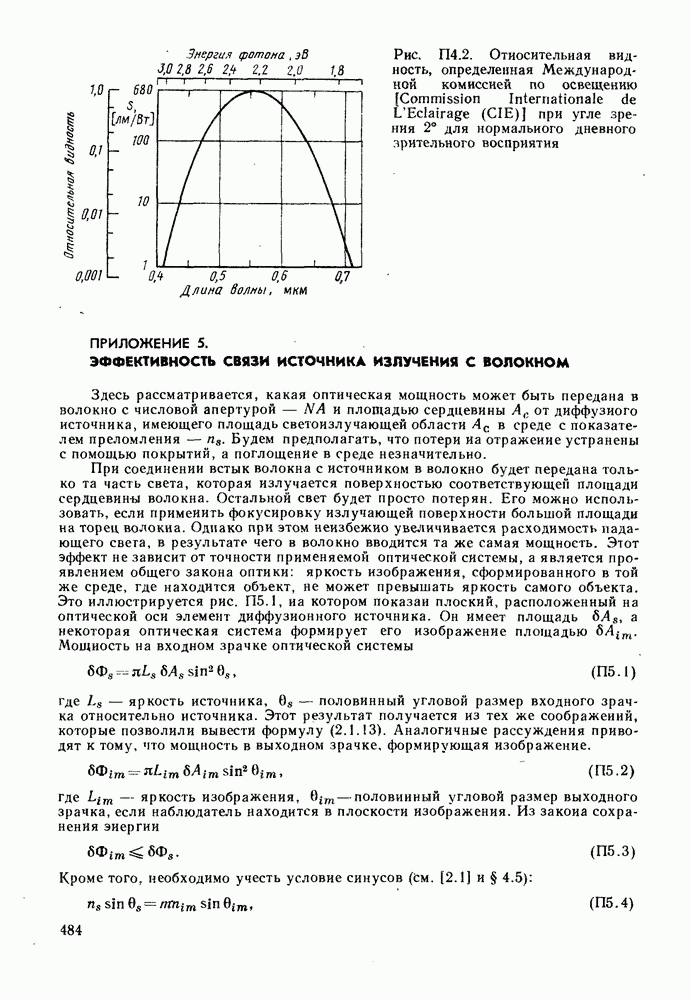
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
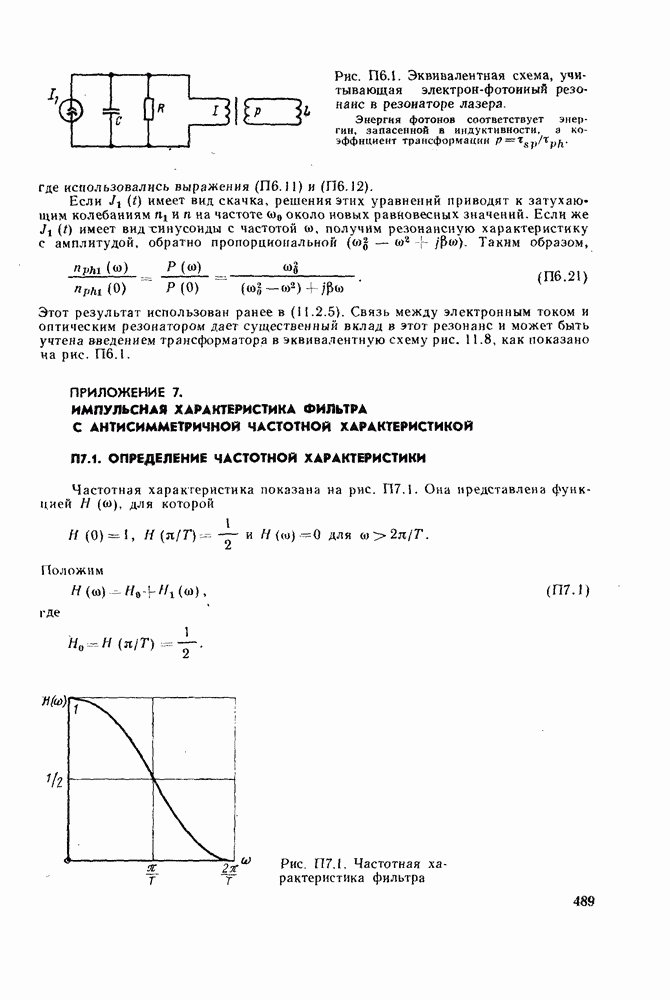
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ