| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
13.1. ЛАВИННОЕ УМНОЖЕНИЕ НОСИТЕЛЕЙ
13.1.1. Общие сведения
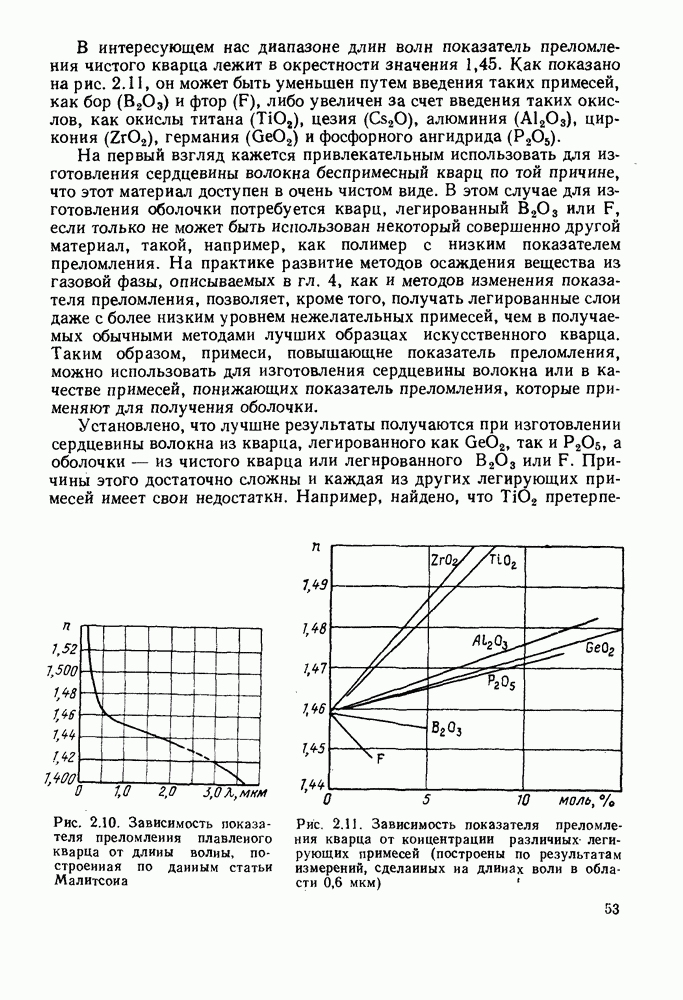
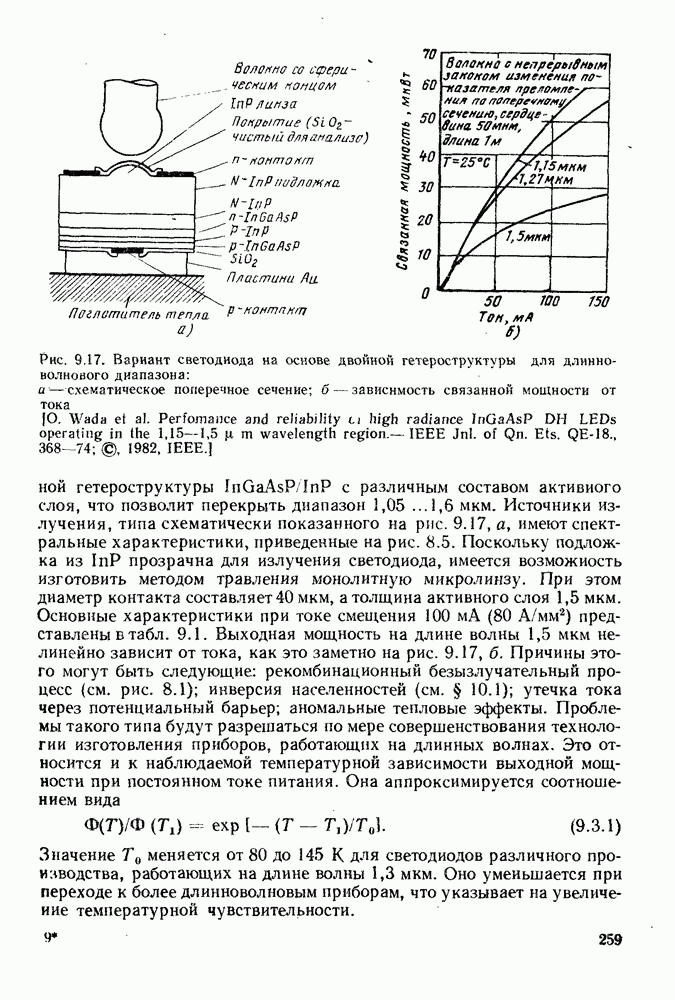
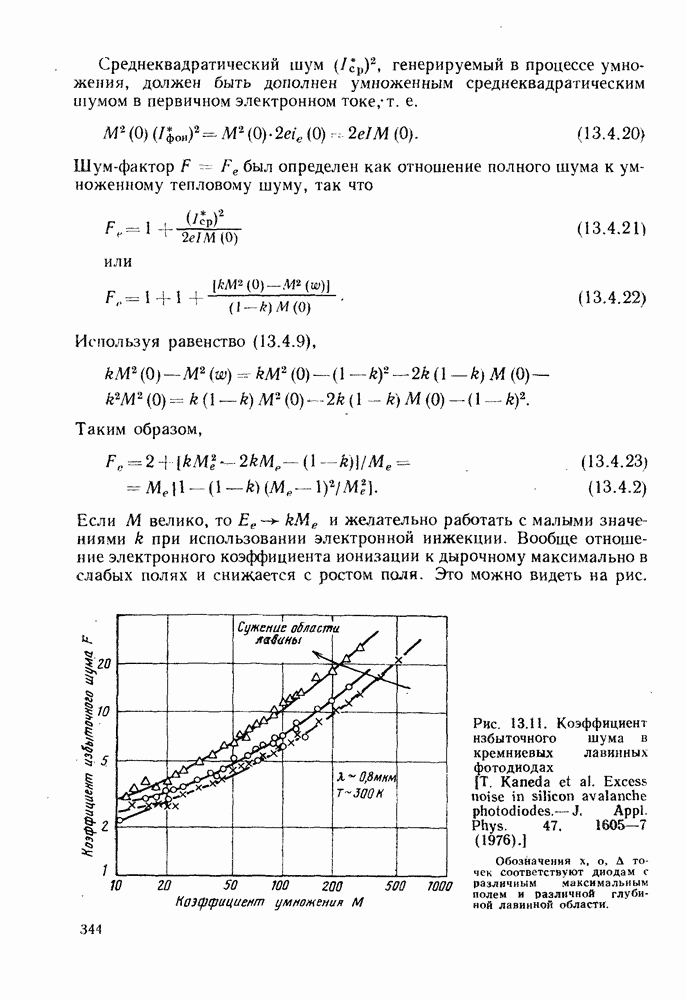
В гл. 12 рассматривалась природа шумов, вносимых фотодиодом в приемную систему. В гл. 14 убедимся, что в случае  -диодов — это тепловой шум и темновой ток, которые подавляются электронным шумом нагрузки и усилителя. Поэтому можно было бы увеличить отношение сигнал-шум, если бы удалось добиться умножения сигнала в самом детекторе. Конечно, при этом умножится и тепловой шум детектора, но суммарный эффект останется положительным. Как уже было упомянуто в гл. 12, такое умножение можно получить в лавинном процессе при высоких значениях электрического поля. Однако сам процесс умножения не свободен от шума. Положим, что каждый фотоноситель порождает в конце процесса умножения в среднем
-диодов — это тепловой шум и темновой ток, которые подавляются электронным шумом нагрузки и усилителя. Поэтому можно было бы увеличить отношение сигнал-шум, если бы удалось добиться умножения сигнала в самом детекторе. Конечно, при этом умножится и тепловой шум детектора, но суммарный эффект останется положительным. Как уже было упомянуто в гл. 12, такое умножение можно получить в лавинном процессе при высоких значениях электрического поля. Однако сам процесс умножения не свободен от шума. Положим, что каждый фотоноситель порождает в конце процесса умножения в среднем  носителей. Любой инициирующий лавину носитель может привести к появлению в результате умножения большего или меньшего
носителей. Любой инициирующий лавину носитель может привести к появлению в результате умножения большего или меньшего  числа носителей. Статистическая природа этого процесса приводит к возрастанию шума. В результате одновременно с возрастанием в
числа носителей. Статистическая природа этого процесса приводит к возрастанию шума. В результате одновременно с возрастанием в  раз сигнального тока в
раз сигнального тока в  раз увеличивается среднеквадратическое значение уровня шума. Шум-фактор
раз увеличивается среднеквадратическое значение уровня шума. Шум-фактор  практически всегда больше единицы и растет с ростом
практически всегда больше единицы и растет с ростом  Следовательно, для любого лавинного диода в конкретном приемнике имеется оптимальная величина
Следовательно, для любого лавинного диода в конкретном приемнике имеется оптимальная величина  при которой достигается наилучшее отношение сигнал-шум. Эти вопросы будут подробно рассмотрены в гл. 14. Здесь же остановимся на физических механизмах процесса умножения и принципах разработки приборов с оптимальными характеристиками.
при которой достигается наилучшее отношение сигнал-шум. Эти вопросы будут подробно рассмотрены в гл. 14. Здесь же остановимся на физических механизмах процесса умножения и принципах разработки приборов с оптимальными характеристиками.
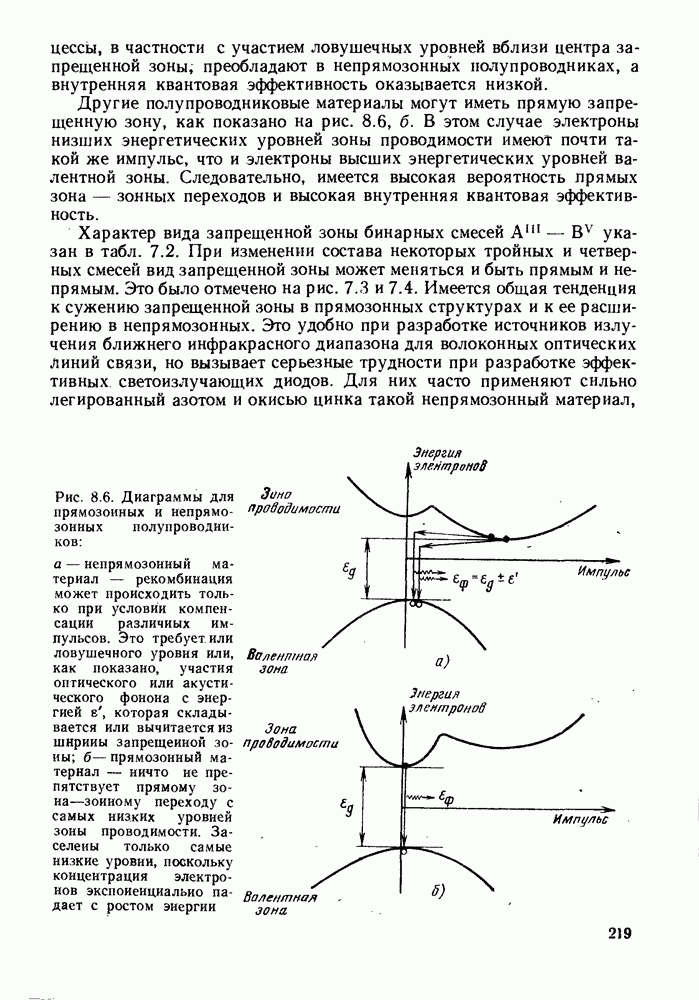
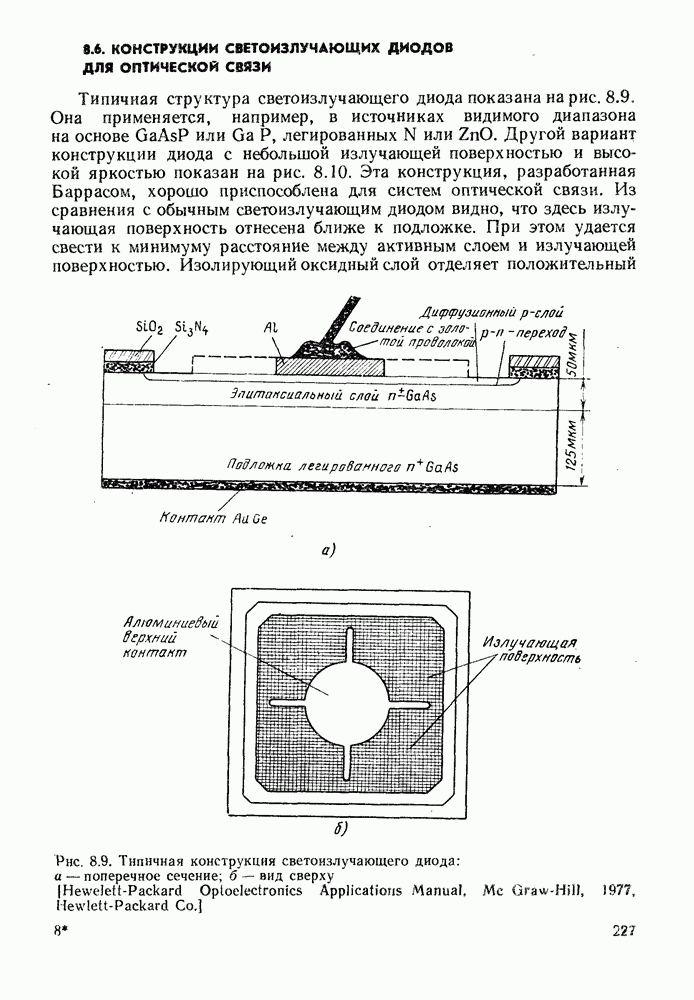
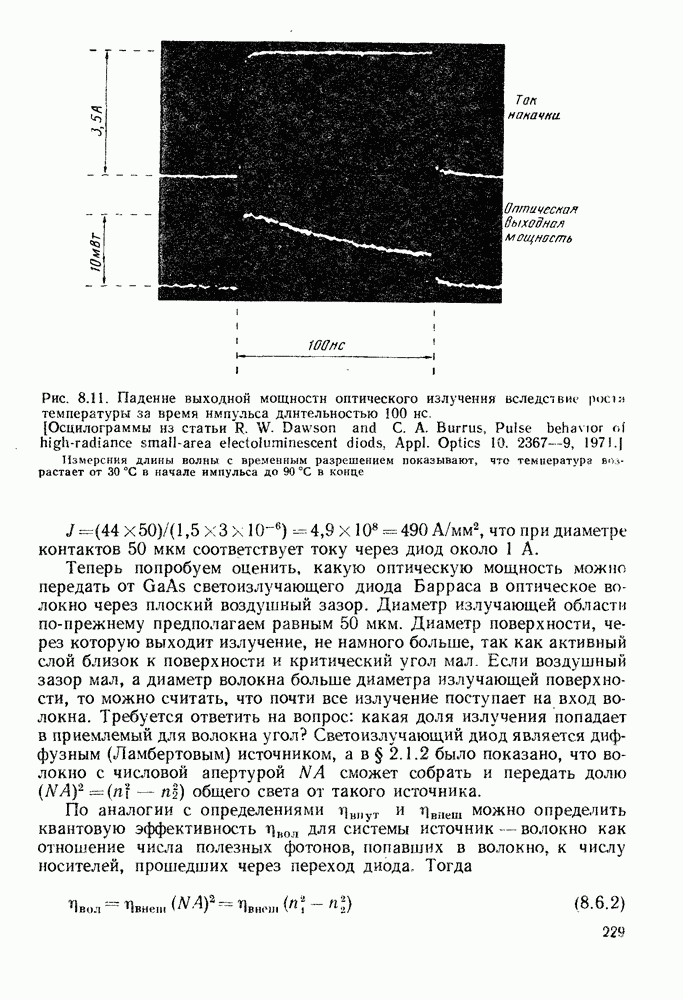
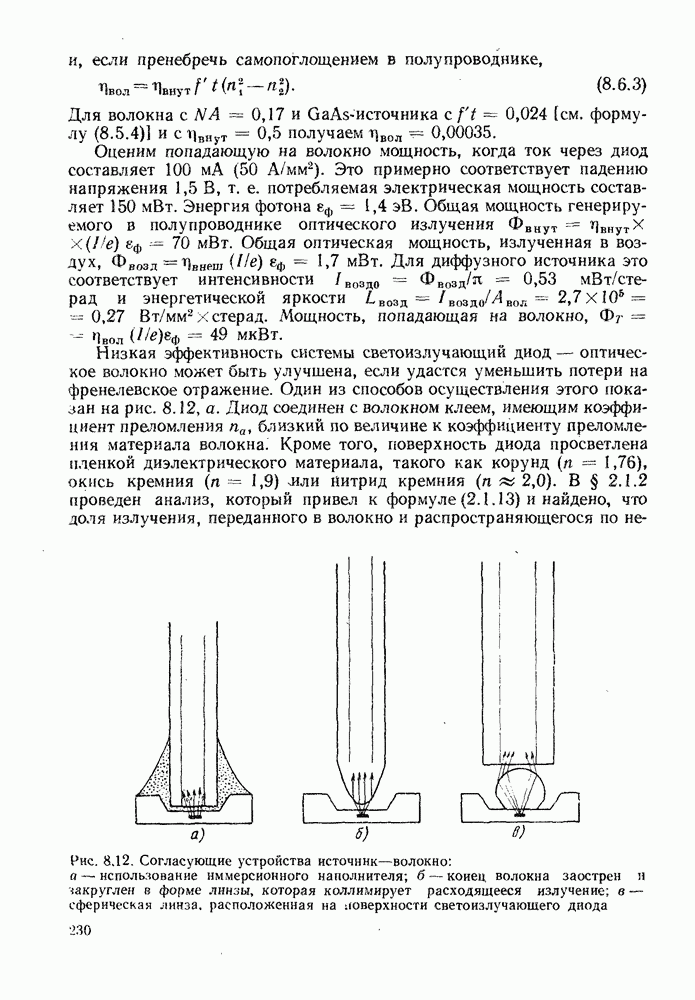
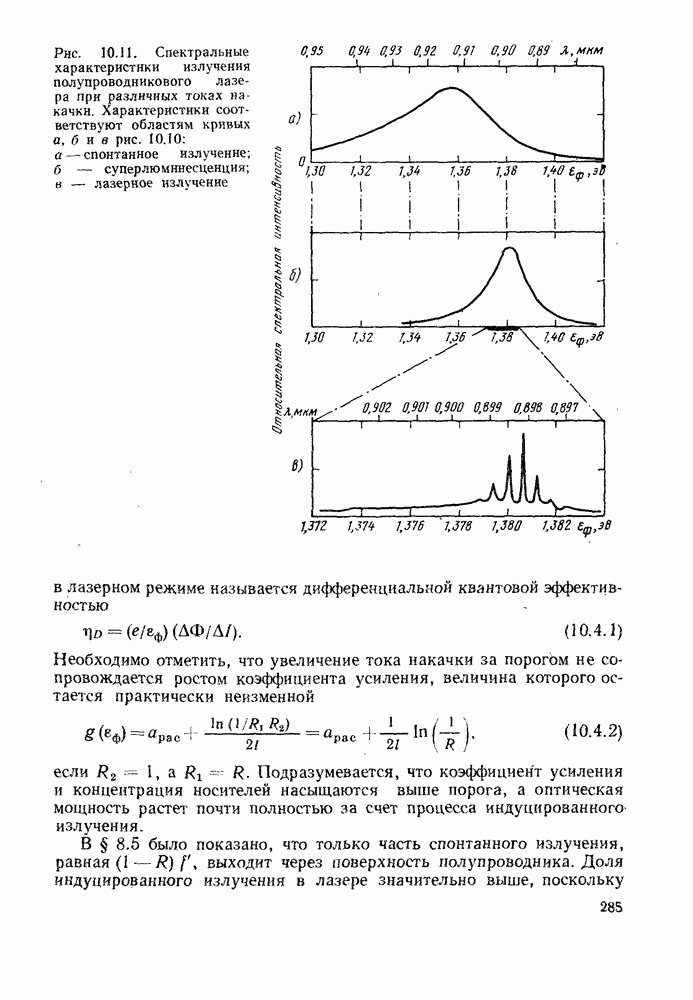
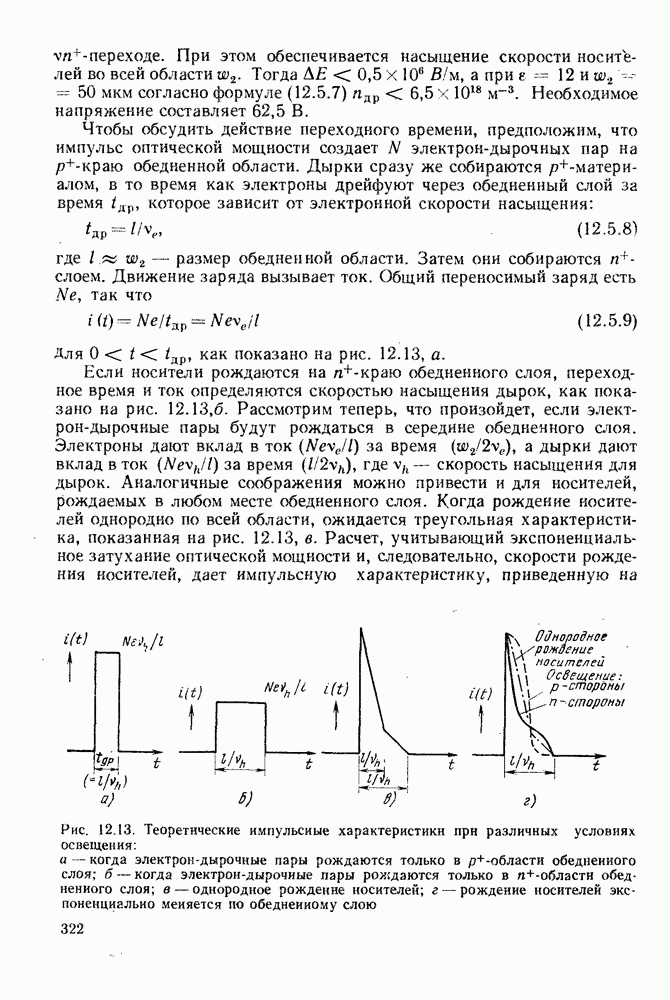
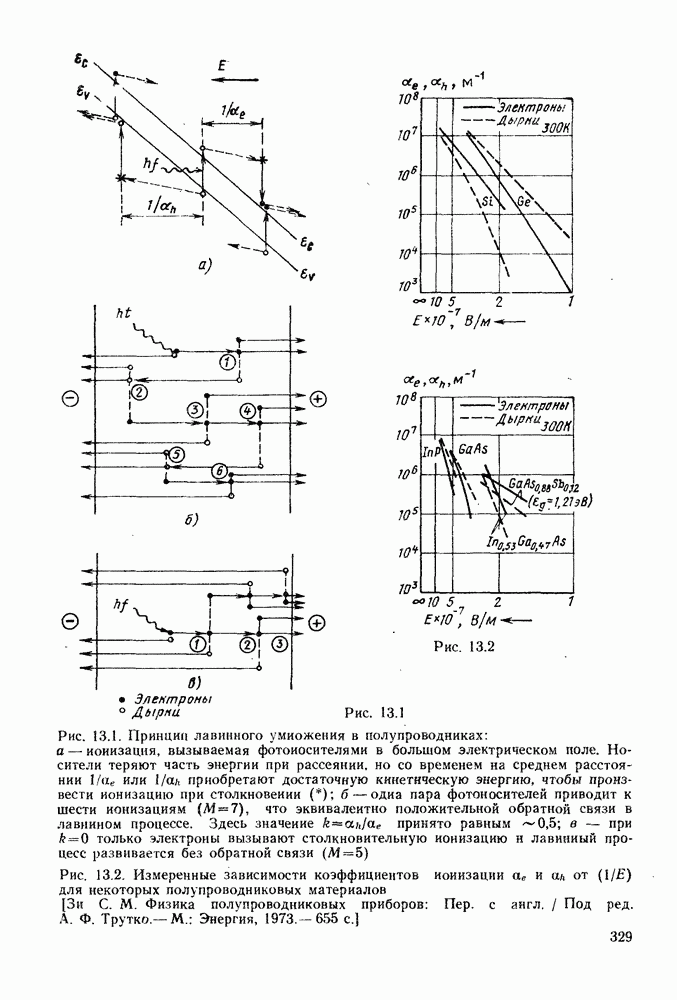
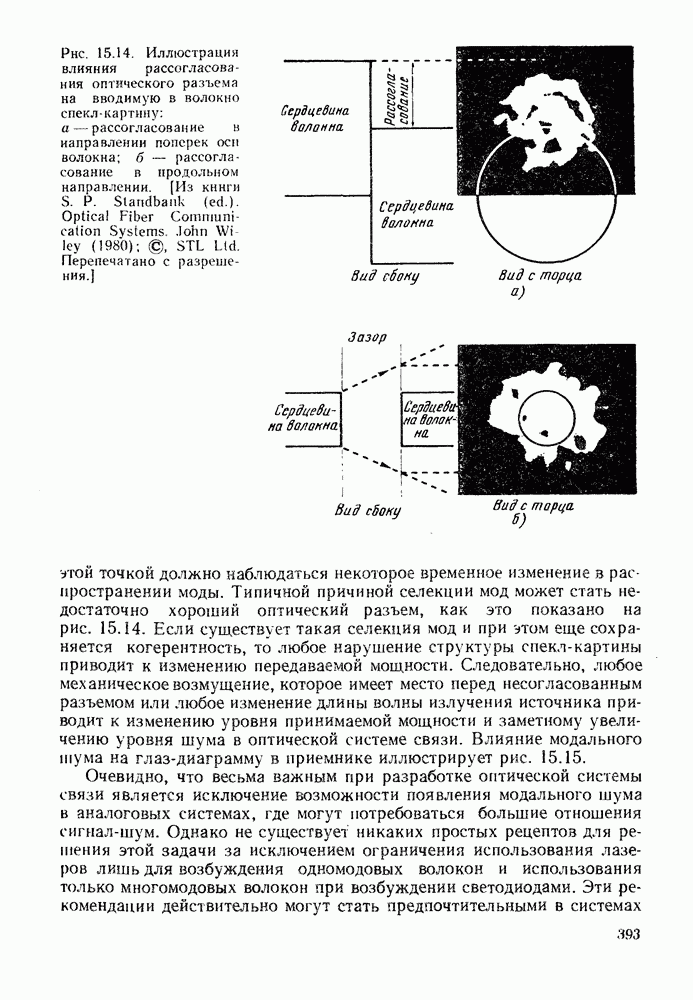
Рисунок 13.1 иллюстрирует два различных процесса генерации лавинного тока. На рис. 13.1, а на схеме зонной структуры показано, как в электрическом поле рождаются электрон-дырочные пары. Хотя средние дрейфовые скорости носителей остаются в области насыщения  в энергетических распределениях появляются высокоэнергетические хвосты, обусловленные ускорением между столкновениями. В достаточно сильном поле заметное число носителей приобретает энергию порядка
в энергетических распределениях появляются высокоэнергетические хвосты, обусловленные ускорением между столкновениями. В достаточно сильном поле заметное число носителей приобретает энергию порядка  что дает возможность вызвать переход через запрещенную зону. Рождающаяся при этом электрон-дырочная пара может участвовать в процессе последующих возбуждений. На рис. 13.1, 6 схематически показано, как одна полученная в результате фоторождения электрон-дырочная пара приводит к появлению шести новых пар.
что дает возможность вызвать переход через запрещенную зону. Рождающаяся при этом электрон-дырочная пара может участвовать в процессе последующих возбуждений. На рис. 13.1, 6 схематически показано, как одна полученная в результате фоторождения электрон-дырочная пара приводит к появлению шести новых пар.

(кликните для просмотра скана)
Можно ввести коэффициенты ионизации соответственно для электронов и дырок  как вероятность возбуждения данным носителем электрон-дырочной пары на единичном расстоянии. Эти коэффициенты быстро возрастают с ростом напряженности электрического поля, поэтому зачастую удобно пользоваться полем пробоя Епроб, при котором лавинное возбуждение становится критическим (скажем, а становится порядка
как вероятность возбуждения данным носителем электрон-дырочной пары на единичном расстоянии. Эти коэффициенты быстро возрастают с ростом напряженности электрического поля, поэтому зачастую удобно пользоваться полем пробоя Епроб, при котором лавинное возбуждение становится критическим (скажем, а становится порядка  Зависимость
Зависимость  от электрического поля для некоторых полупроводников, перспективных для использования в качестве фото детекторов, приведена на рис. 13.2. Эти графики соответствуют комнатной температуре. При повышении температуры значения коэффициентов ионизации уменьшаются, поскольку увеличивается число столкновений, понижающих высокоэнергетические хвосты в распределении энергии носителей, и, следовательно, уменьшается вероятность ионизации. Есть материалы, в которых
от электрического поля для некоторых полупроводников, перспективных для использования в качестве фото детекторов, приведена на рис. 13.2. Эти графики соответствуют комнатной температуре. При повышении температуры значения коэффициентов ионизации уменьшаются, поскольку увеличивается число столкновений, понижающих высокоэнергетические хвосты в распределении энергии носителей, и, следовательно, уменьшается вероятность ионизации. Есть материалы, в которых  в других
в других  а в арсениде и фосфиде галлия оба коэффициента приблизительно равны. Величина отношения
а в арсениде и фосфиде галлия оба коэффициента приблизительно равны. Величина отношения

составляет 0,01 — 100. В предположении, что  зависят только от напряженности электрического поля
зависят только от напряженности электрического поля  можно считать, что в пределах среднего расстояния между ионизирующими столкновениями
можно считать, что в пределах среднего расстояния между ионизирующими столкновениями  изменение
изменение  мало; б) число упругих столкновений велико, так что устанавливается равновесное распределение по скоростям; в) потенциальная энергия носителя велика по сравнению с энергией ионизации
мало; б) число упругих столкновений велико, так что устанавливается равновесное распределение по скоростям; в) потенциальная энергия носителя велика по сравнению с энергией ионизации 
Если ионизация вызывается только носителями одного типа, скажем, электронами  то лавина развивается более простым путем, который иллюстрируется рис. 13.1, в. На интервале, значительно превышающем
то лавина развивается более простым путем, который иллюстрируется рис. 13.1, в. На интервале, значительно превышающем  число электронов растет экспоненциально. В реальных материалах
число электронов растет экспоненциально. В реальных материалах  что соответствует частичной положительной обратной связи в процессе умножения. В результате появляется неопределенность в теоретическом расчете числа электрон-дырочных пар на конечном интервале. (Этот процесс аналогичен пробою Таунсенда в газе, но несколько сложнее. В газе первичный электрон рождает ионы и электроны. Ионы падают на отрицательный электрод, где они с конечной вероятностью вызывают эмиссию вторичных электронов. Если первичный электрон произведет достаточное количество ионов, чтобы в результате эмиссии появилось не менее одного электрона, ток может неограниченно нарастать и наступит пробой. На практике при этом устанавливается новая форма разряда, соответствующая большему току и меньшему напряжению.)
что соответствует частичной положительной обратной связи в процессе умножения. В результате появляется неопределенность в теоретическом расчете числа электрон-дырочных пар на конечном интервале. (Этот процесс аналогичен пробою Таунсенда в газе, но несколько сложнее. В газе первичный электрон рождает ионы и электроны. Ионы падают на отрицательный электрод, где они с конечной вероятностью вызывают эмиссию вторичных электронов. Если первичный электрон произведет достаточное количество ионов, чтобы в результате эмиссии появилось не менее одного электрона, ток может неограниченно нарастать и наступит пробой. На практике при этом устанавливается новая форма разряда, соответствующая большему току и меньшему напряжению.)
13.1.2. Теория лавинного умножения
Рассмотрим лавинное умножение в полупроводнике, находящемся в стационарном состоянии, причем электронный ток  инжектируется в обедненный слой размером
инжектируется в обедненный слой размером  в плоскости
в плоскости  Будем
Будем
предполагать, что напряженность поля достаточно велика, чтобы вызвать лавину, но число тепловых и фотоносителей незначительно. Несколько также убедимся, что эти допущения вполне реальны для лавинных фотодиодов, изготовленных из материалов типа кремния, в которых  В некоторой точке такой, что
В некоторой точке такой, что  скорость генерации носителей
скорость генерации носителей

где  электронный и дырочный ток в точке х. В каждой точке
электронный и дырочный ток в точке х. В каждой точке

Если при  отсутствует инжекция дырок
отсутствует инжекция дырок  то
то  Подставив (13.1.3) в (13.1.2), получим
Подставив (13.1.3) в (13.1.2), получим

Интегрирование этого уравнения 1 даст

Можно определить коэффициент умножения для инжектированных электронов

непосредственной подстановкой в (13.1.5). Перестановка дает

Используя тот факт, что

получим

Условие пробоя

Если в анализе учесть генерацию носителей  и инжекцию дырок
и инжекцию дырок  то получим выражения, подобные (13.1.10), но несколько более сложные. Однако условие пробоя (13.1.11) остается тем же самым. При
то получим выражения, подобные (13.1.10), но несколько более сложные. Однако условие пробоя (13.1.11) остается тем же самым. При  т. е.
т. е.  уравнения упрощаются, и тогда общий ток
уравнения упрощаются, и тогда общий ток

Однако при этих условиях  значения
значения  резко зависят от напряженности электрического поля и меняются поперек площади диода, если имеются слабые изменения распределения примеси. Этот эффект усиливается, когда лавина возбуждается «неправильными» носителями — электронами в материале с
резко зависят от напряженности электрического поля и меняются поперек площади диода, если имеются слабые изменения распределения примеси. Этот эффект усиливается, когда лавина возбуждается «неправильными» носителями — электронами в материале с  или дырками в материале с
или дырками в материале с 
Анализ существенно упрощается, если можно считать, что лавина возбуждается в области с однородным электрическим полем. Тогда  зависят от х, и выражение (13.1.10) приобретает вид
зависят от х, и выражение (13.1.10) приобретает вид

Тогда при 
13.1.3. Экспериментальное поведение
При напряжении, близком к пробойному Упроб, когда  удовлетворяют условию (13.1.11), рост
удовлетворяют условию (13.1.11), рост  ограничивается двумя факторами. Во-первых, это последовательное сопротивление полупроводника
ограничивается двумя факторами. Во-первых, это последовательное сопротивление полупроводника  между переходом и выводами диода. Во-вторых, это рост температуры, связанный с увеличенным выделением тепла при возрастании тока. При этом уменьшаются
между переходом и выводами диода. Во-вторых, это рост температуры, связанный с увеличенным выделением тепла при возрастании тока. При этом уменьшаются  и увеличивается пробойное напряжение. Одновременно возрастает скорость тепловой генерации носителей и темновой ток. Коэффициент умножения связан с приложенным напряжением V
и увеличивается пробойное напряжение. Одновременно возрастает скорость тепловой генерации носителей и темновой ток. Коэффициент умножения связан с приложенным напряжением V

где  сумма сопротивления полупроводника
сумма сопротивления полупроводника  и сопротивления
и сопротивления  обусловленного ростом температуры. Степенной показатель
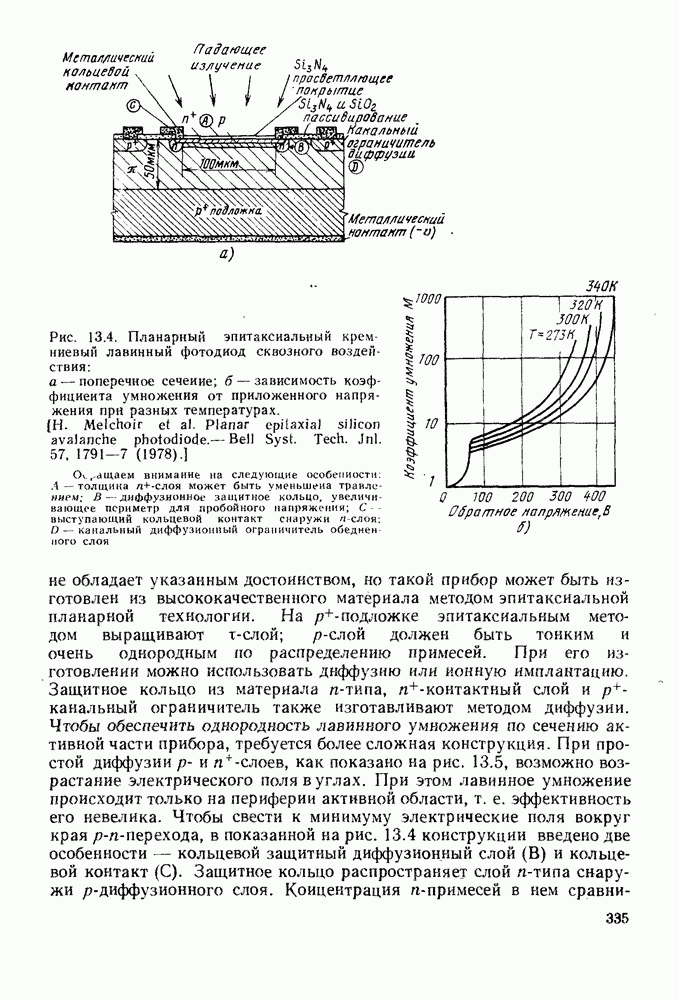
обусловленного ростом температуры. Степенной показатель  зависит от конструкции и материала диода. Некоторые типичные зависимости
зависит от конструкции и материала диода. Некоторые типичные зависимости  для кремниевого лавинного фотодиода показаны на рис. 13.4, б.
для кремниевого лавинного фотодиода показаны на рис. 13.4, б.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
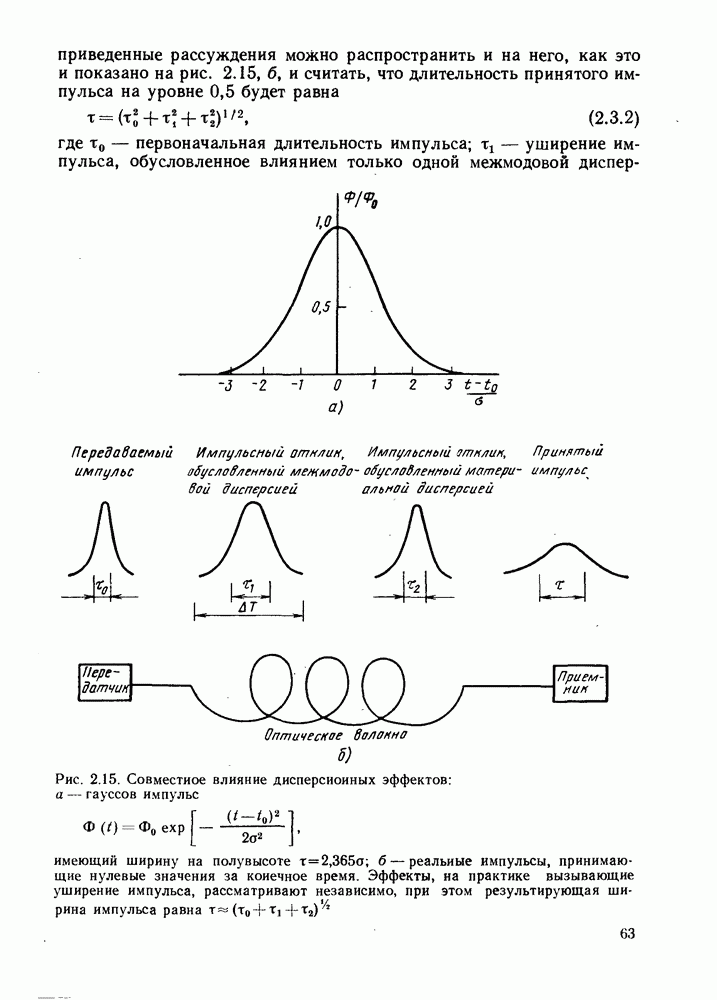
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
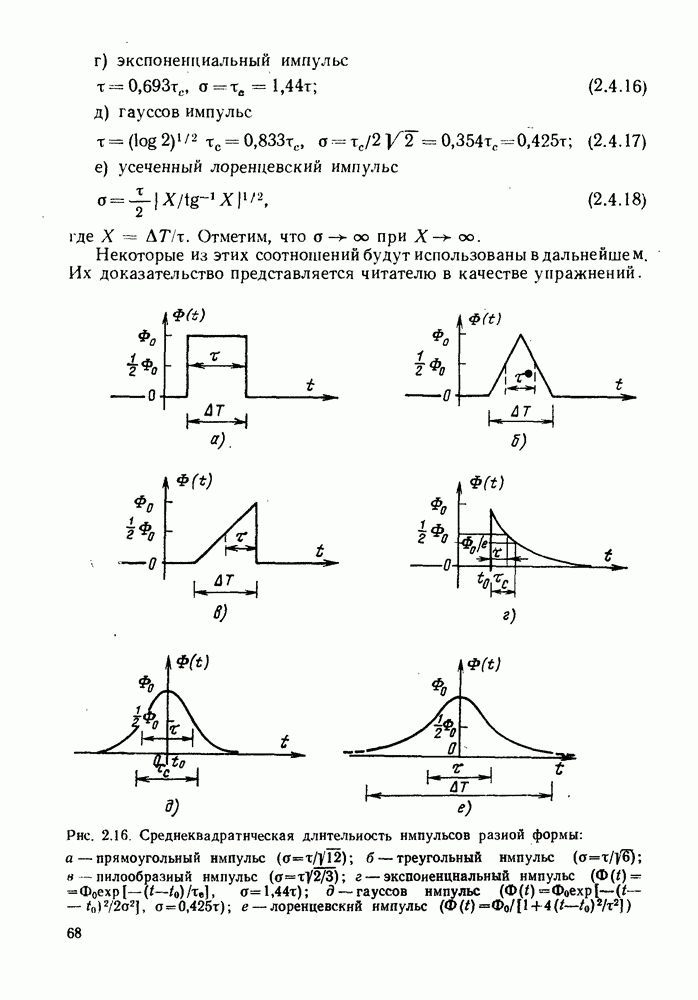
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
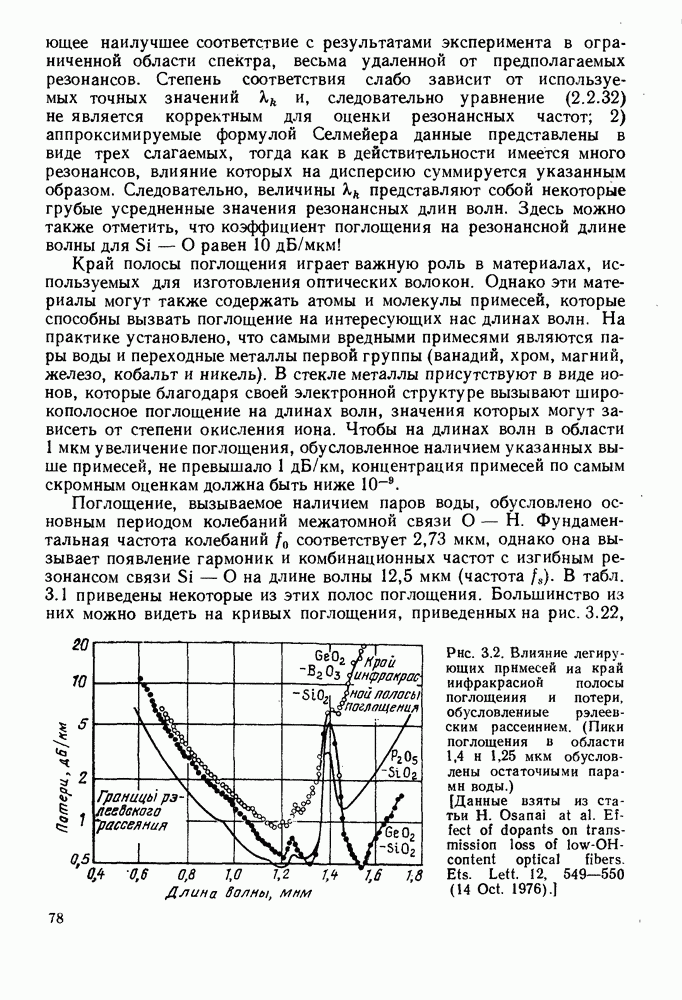
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
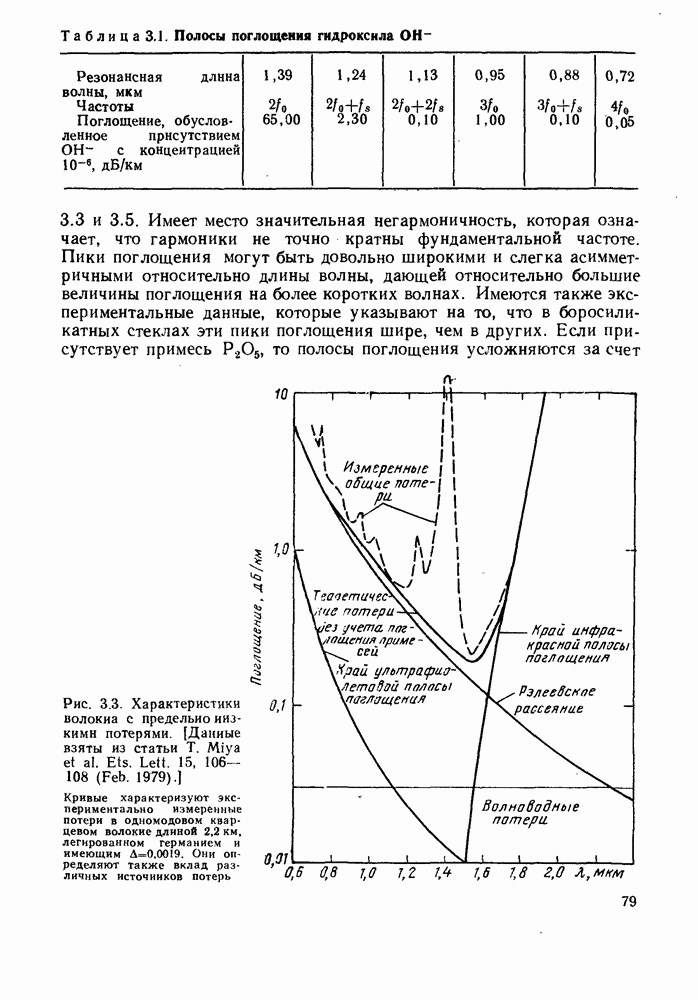
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
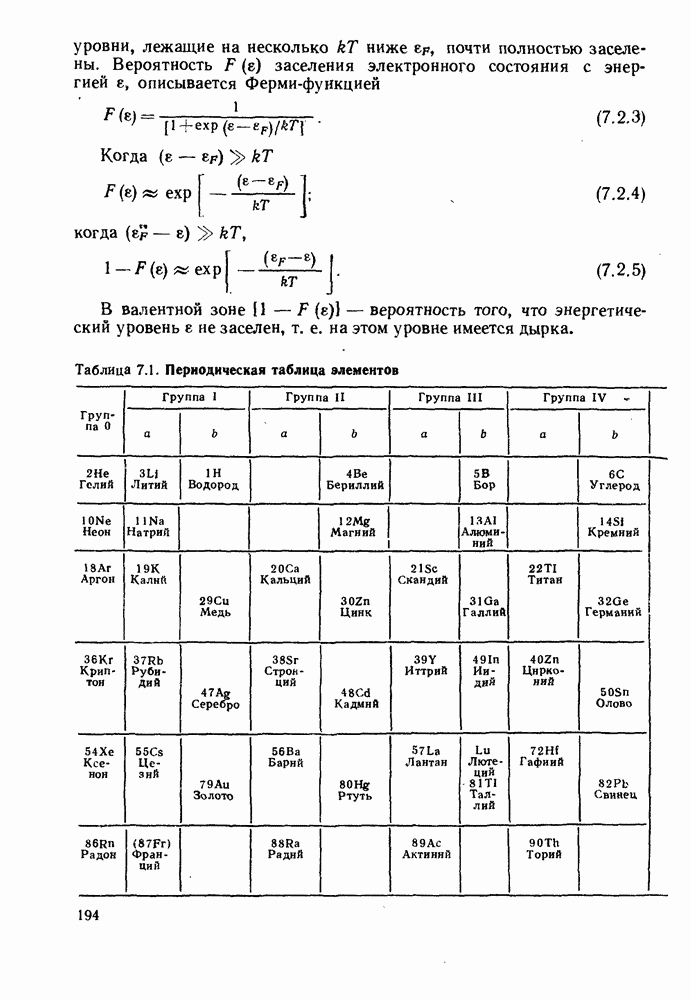
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
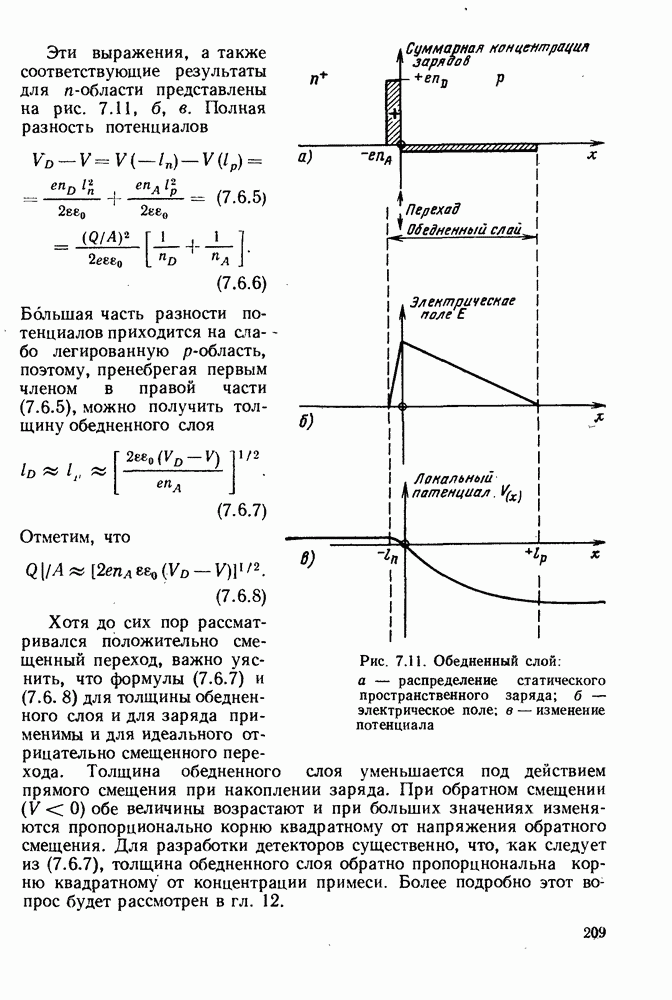
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
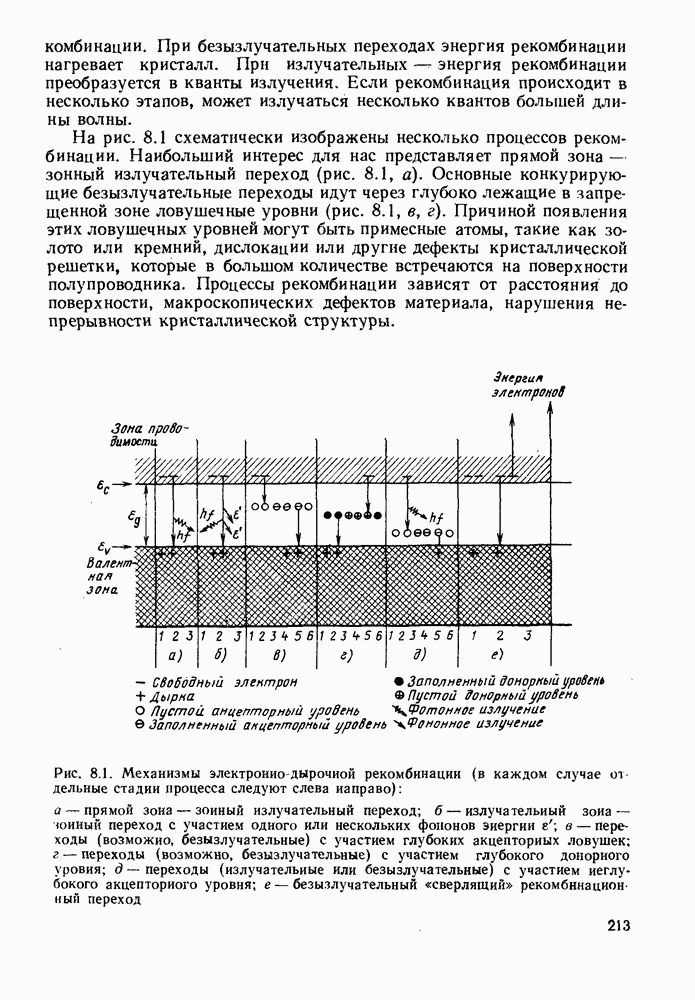
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
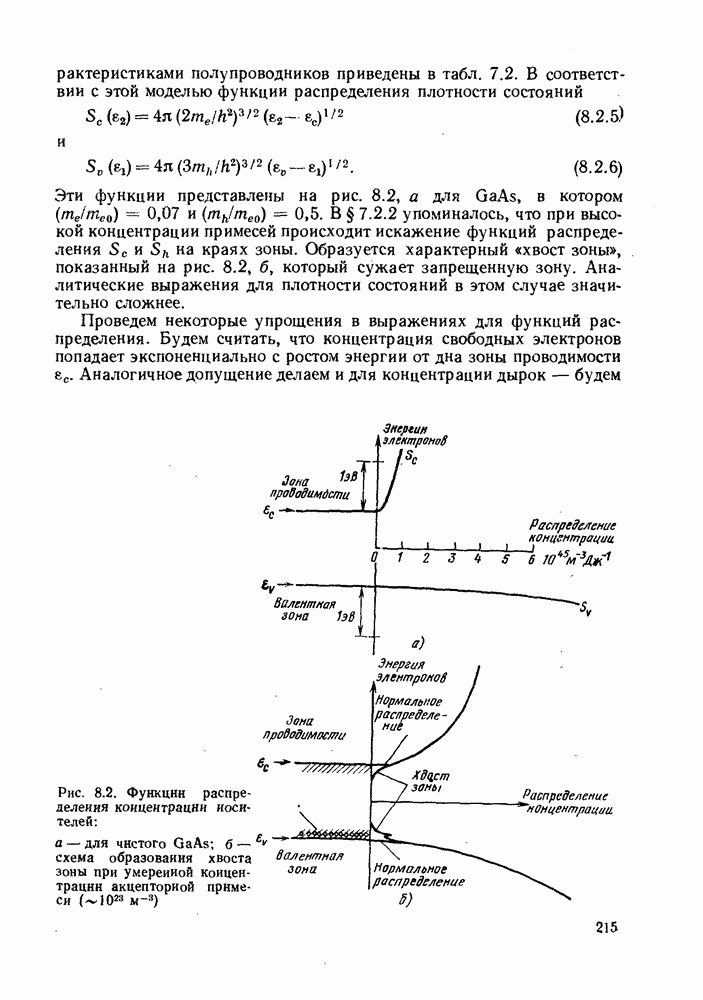
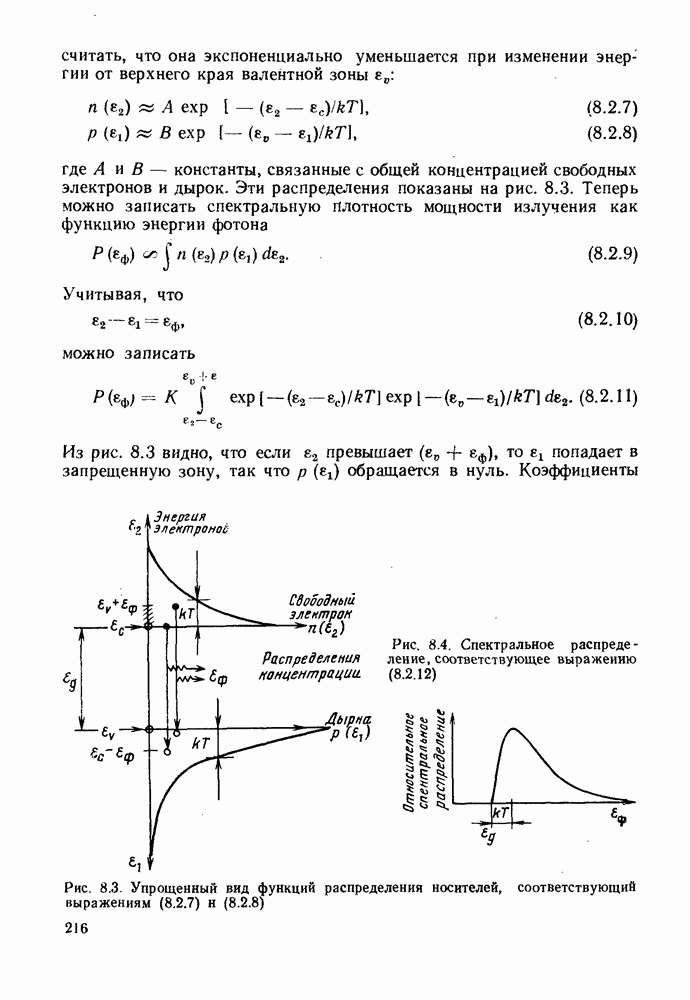
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
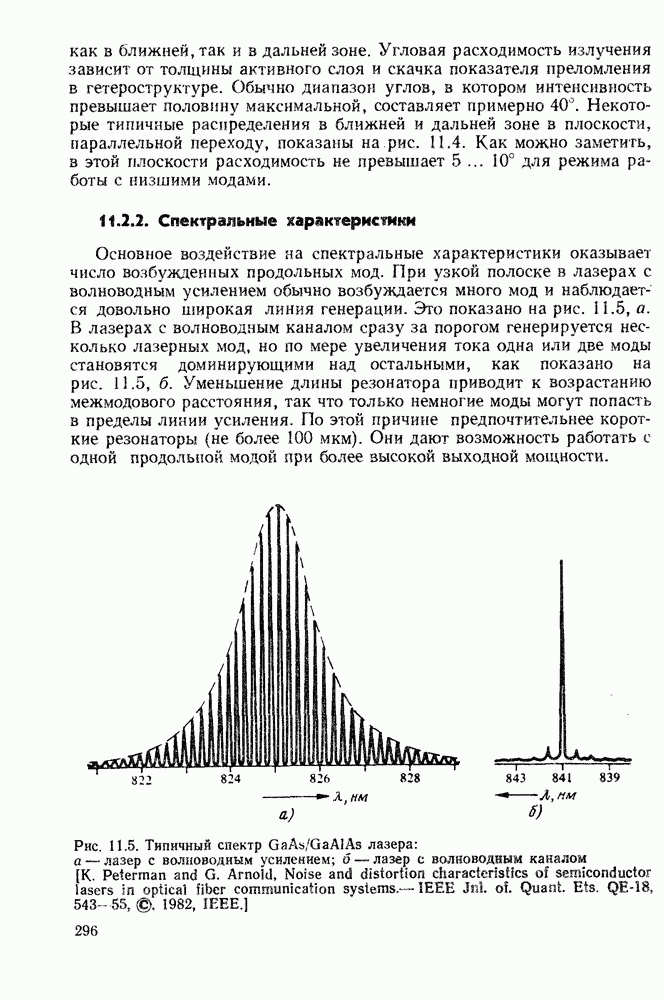
- 11.2.2. Спектральные характеристики
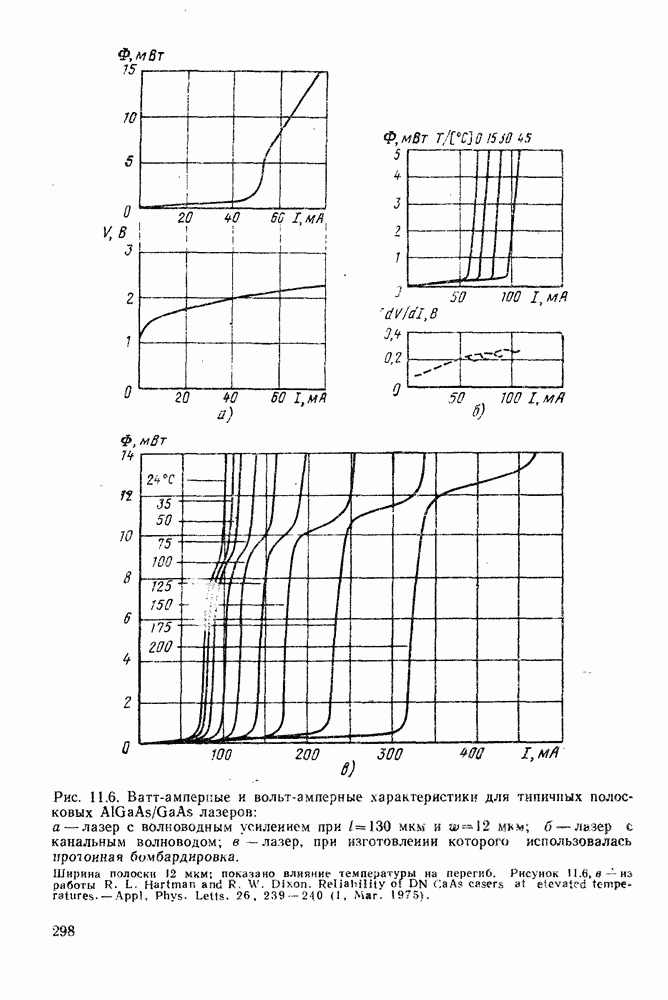
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
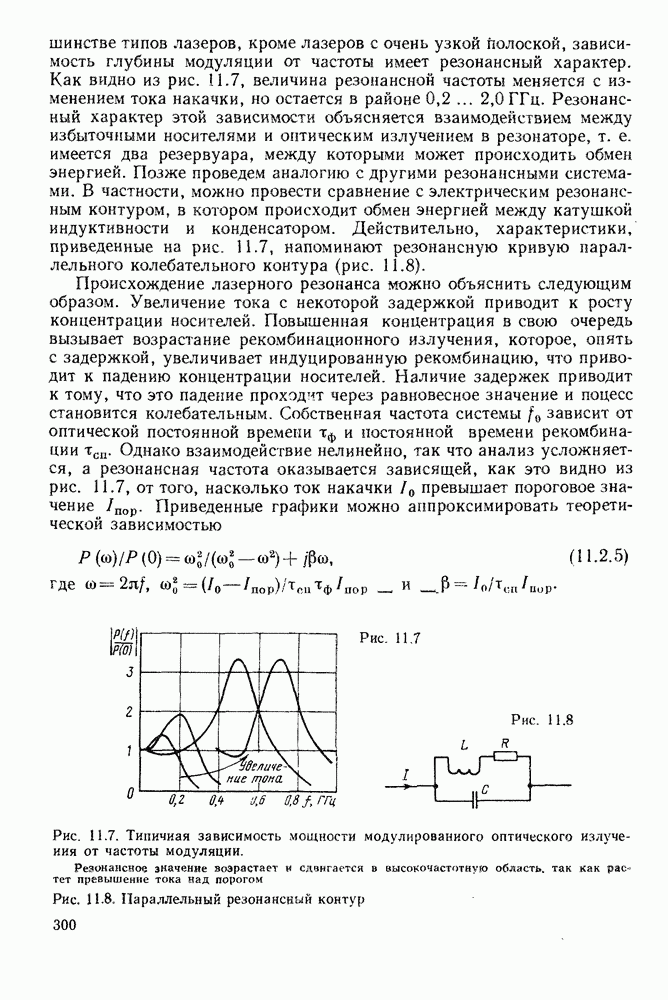
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
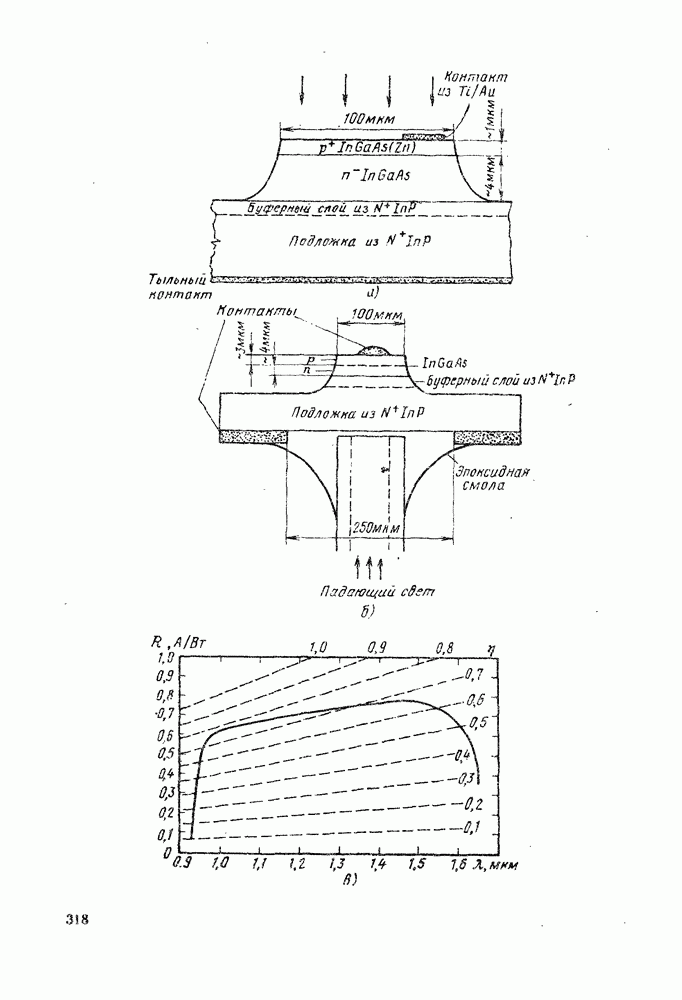
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
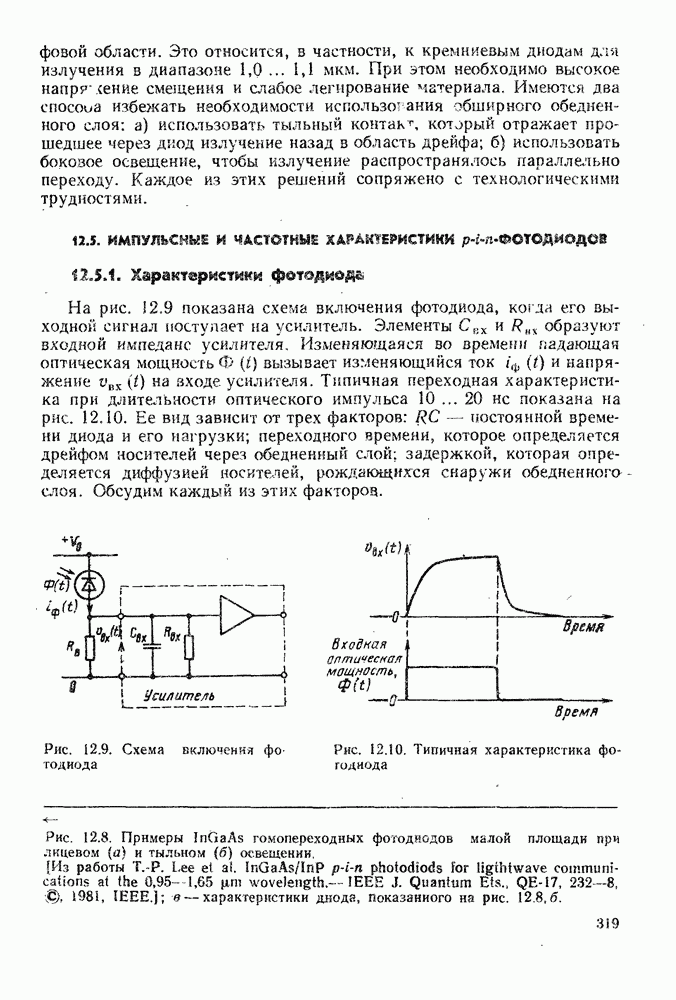
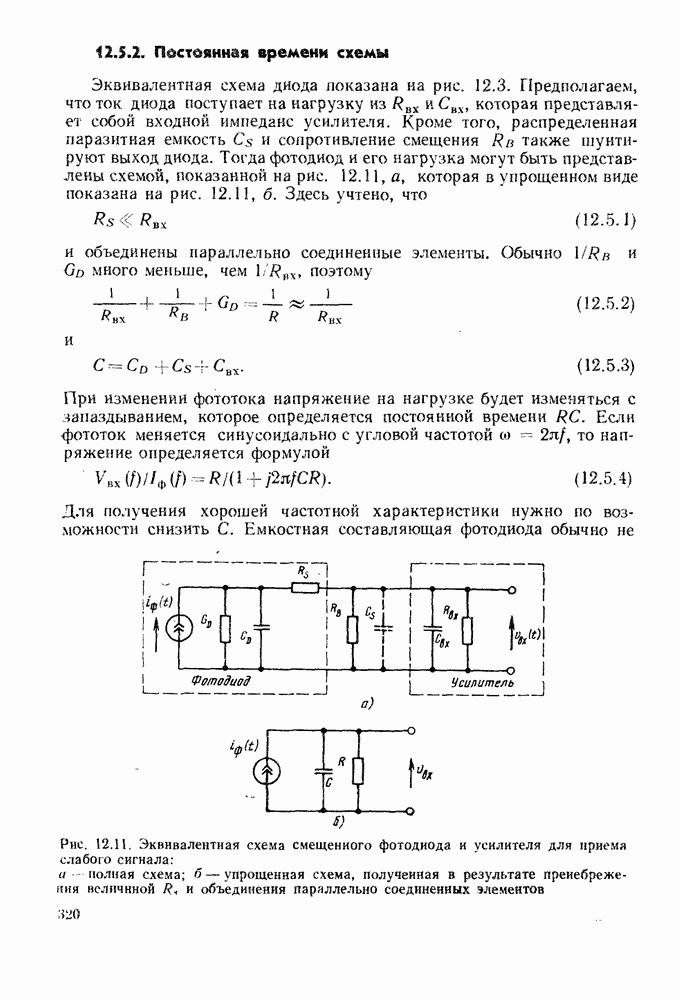
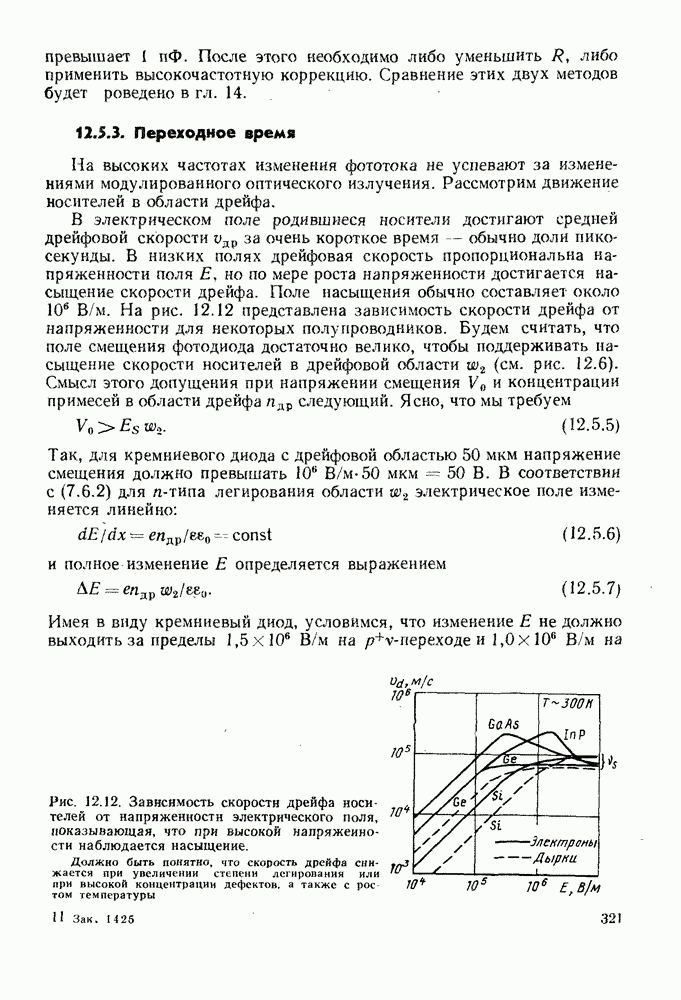
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
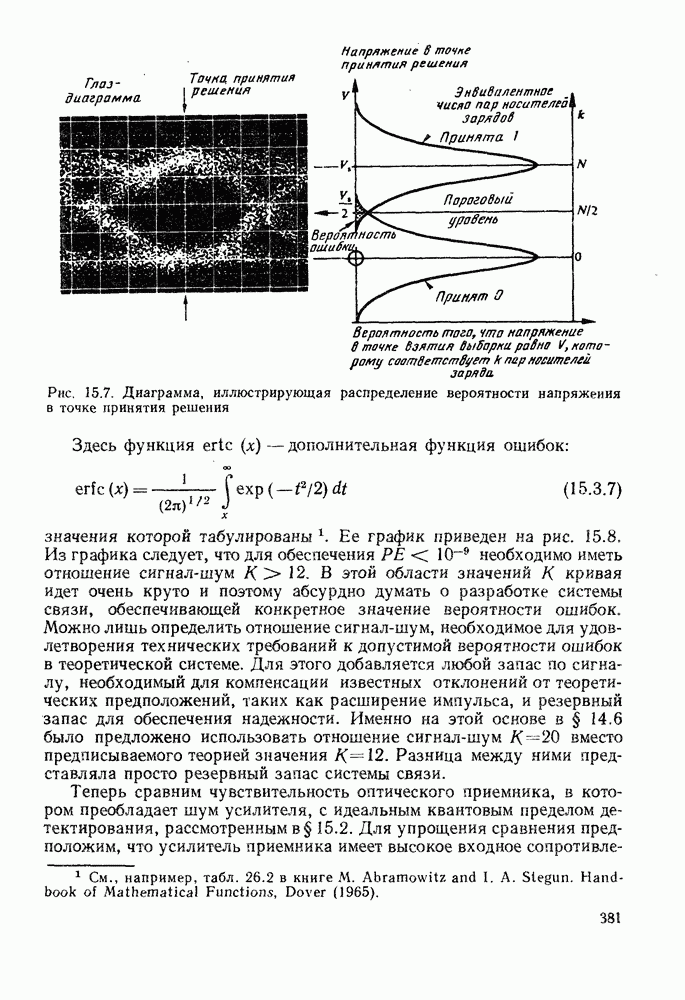
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
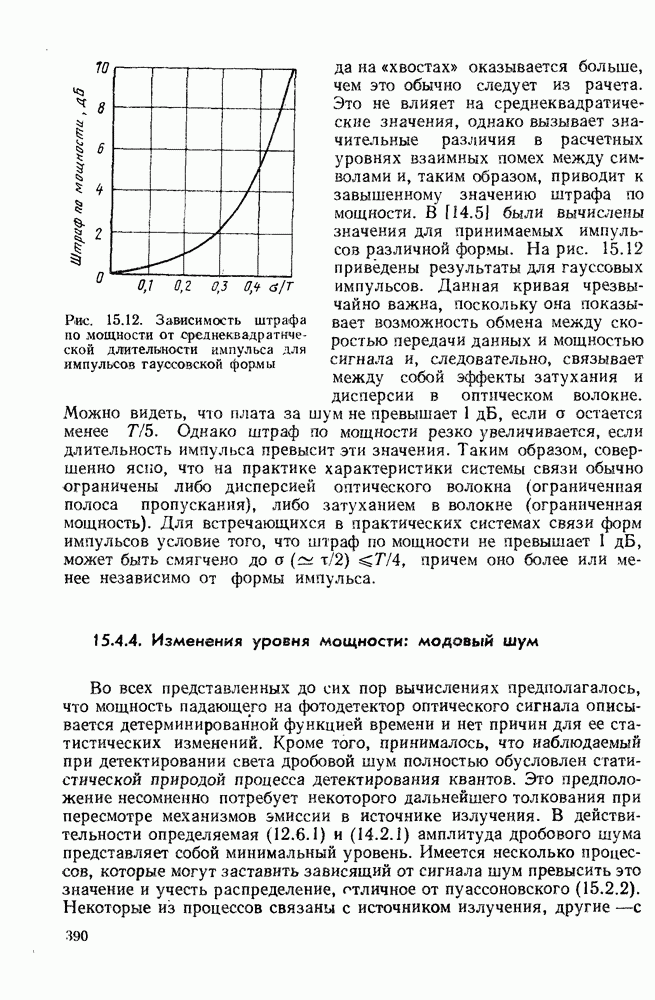
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
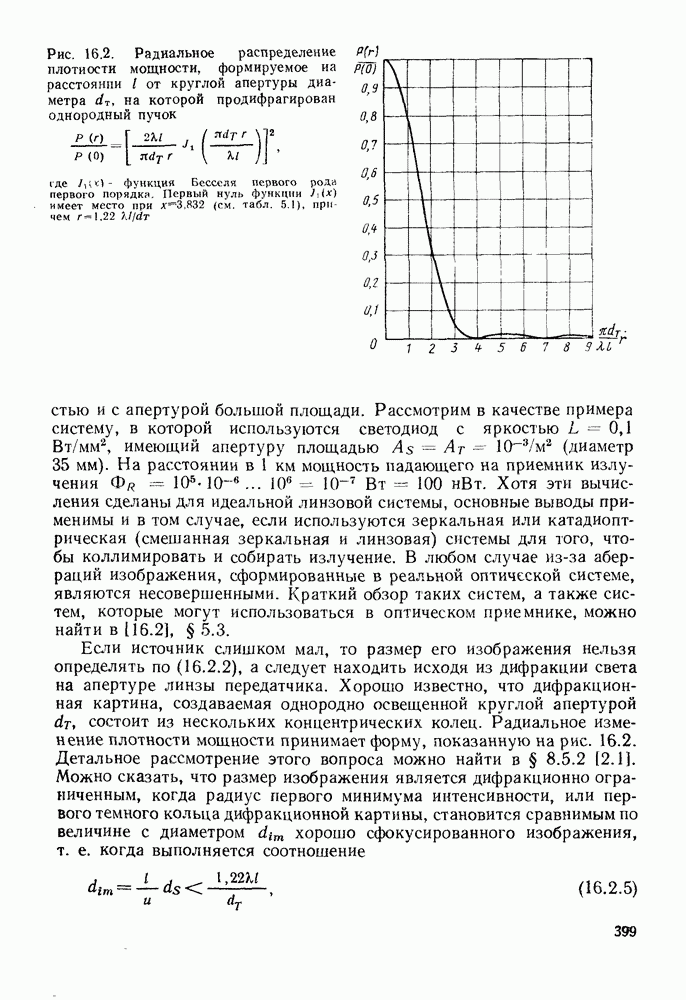
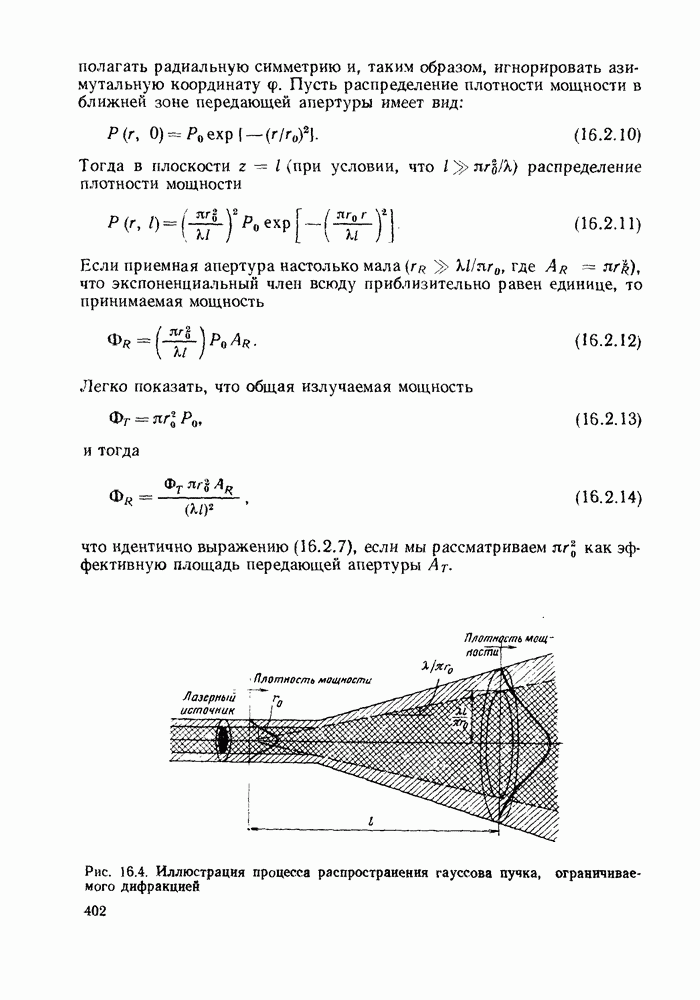
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
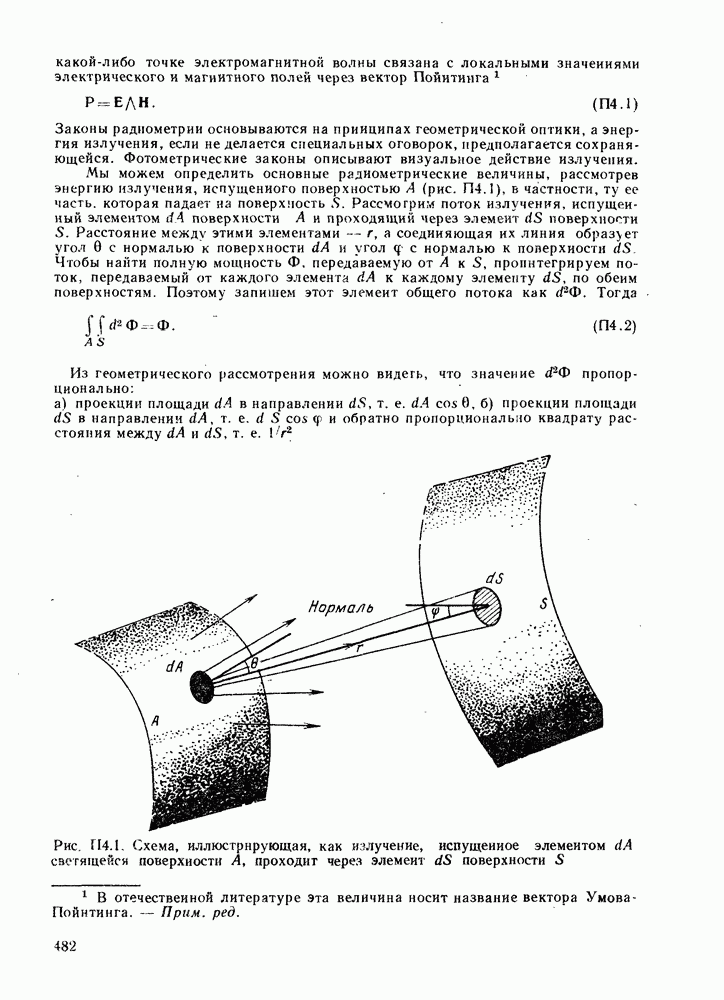
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
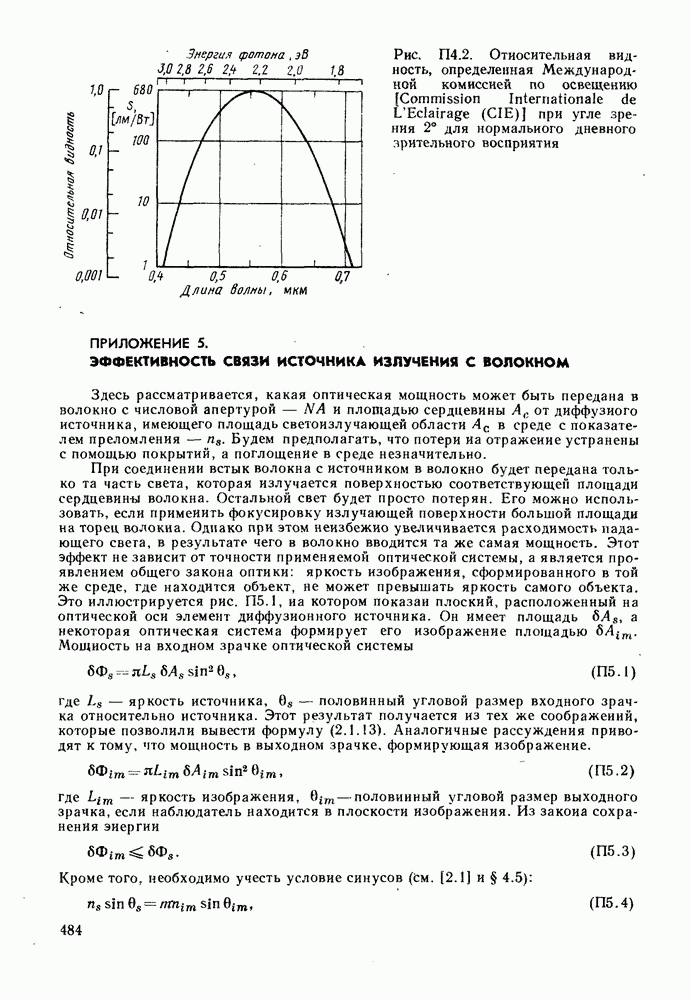
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
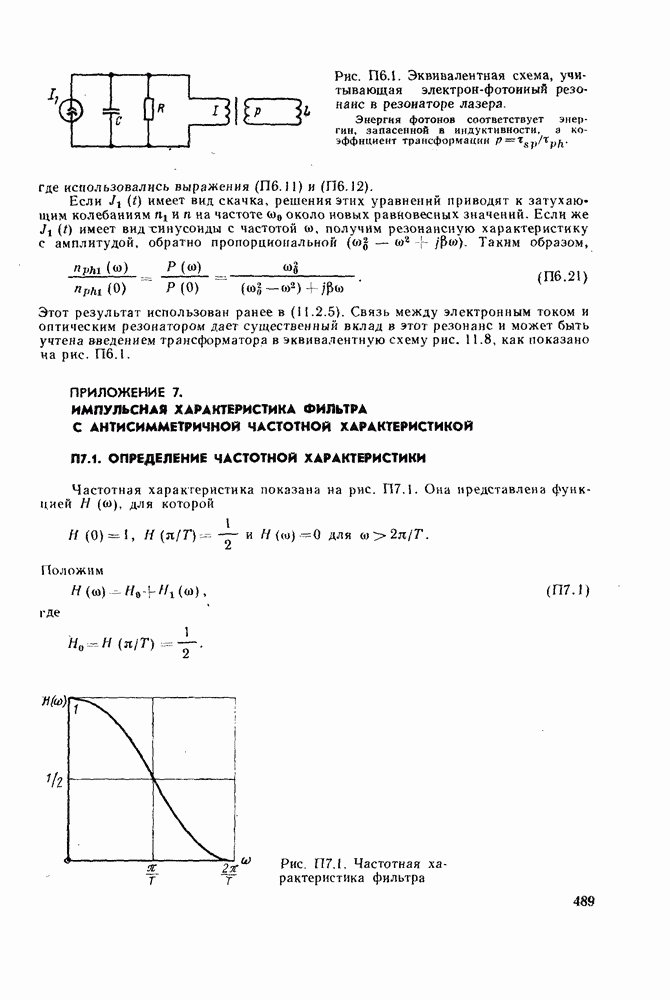
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ