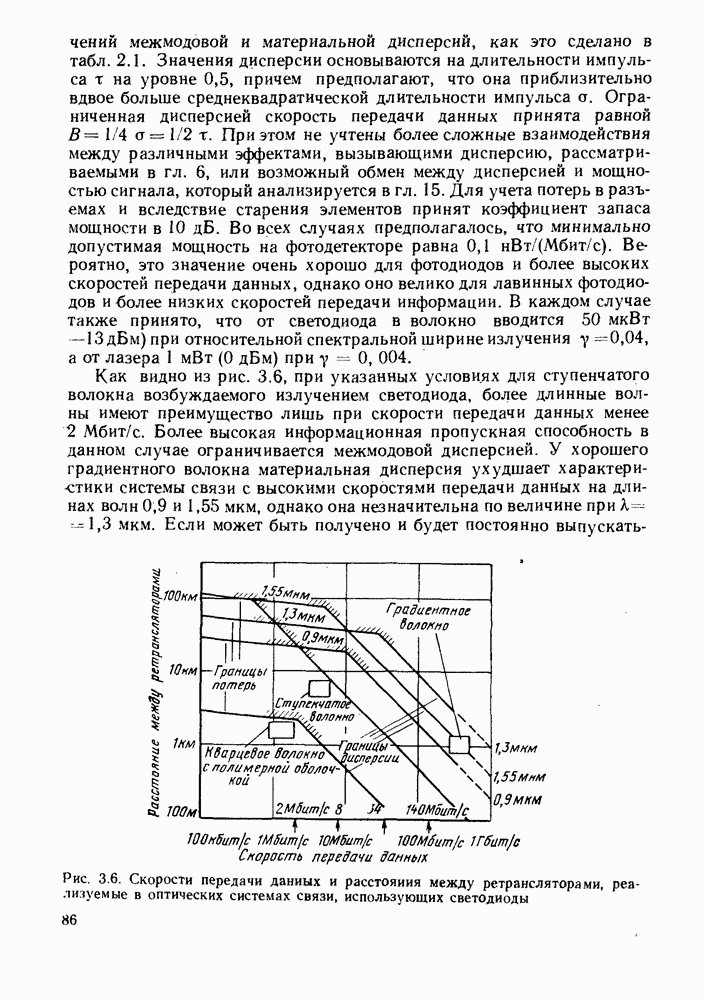
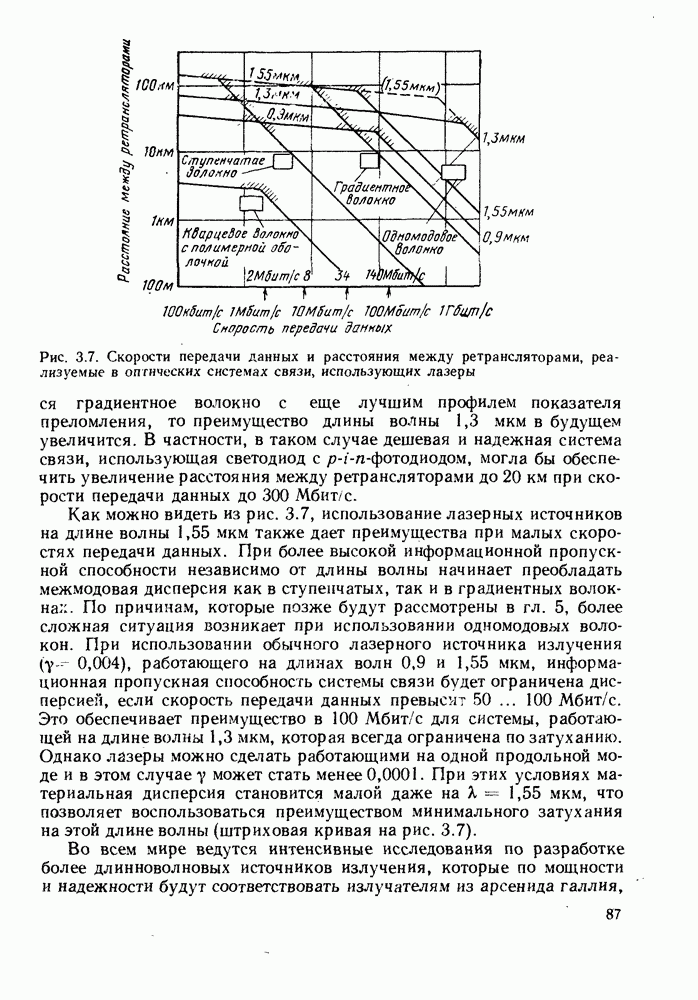
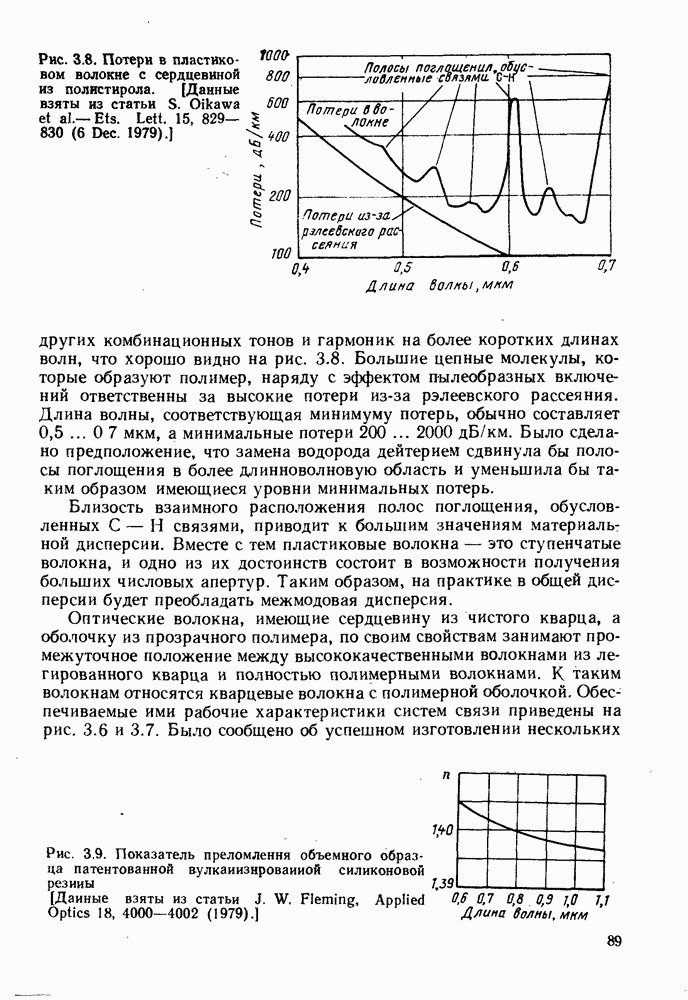
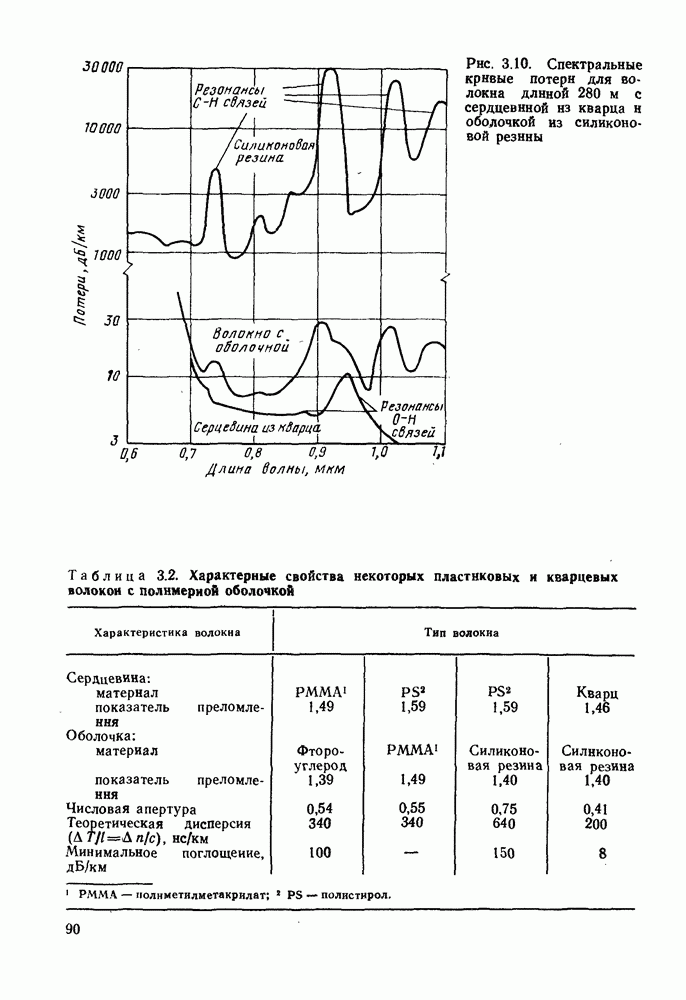
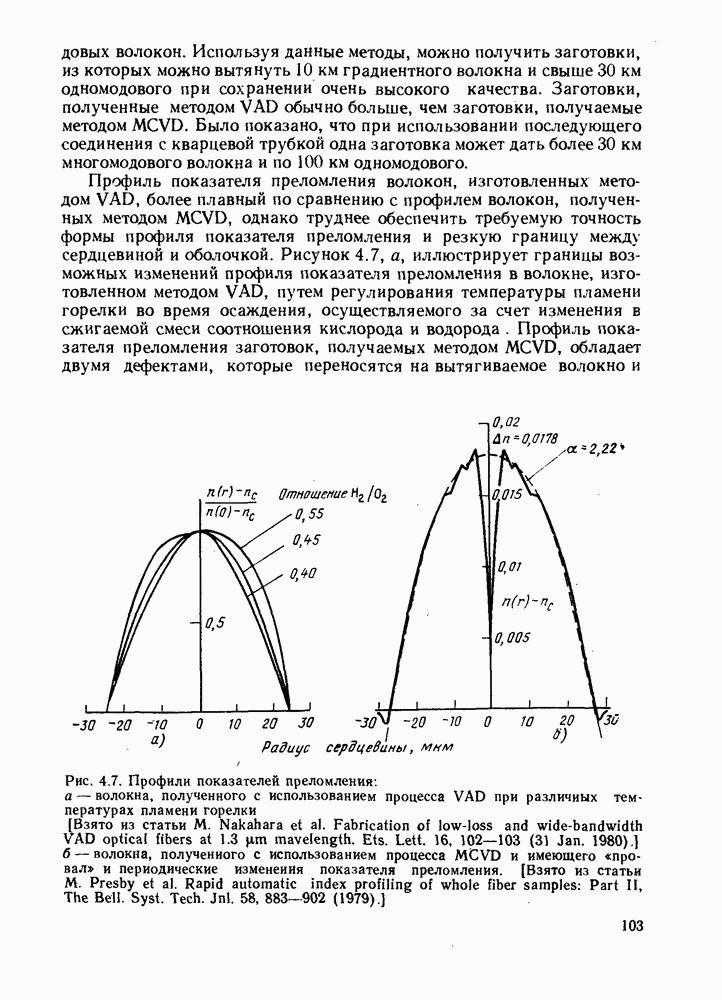
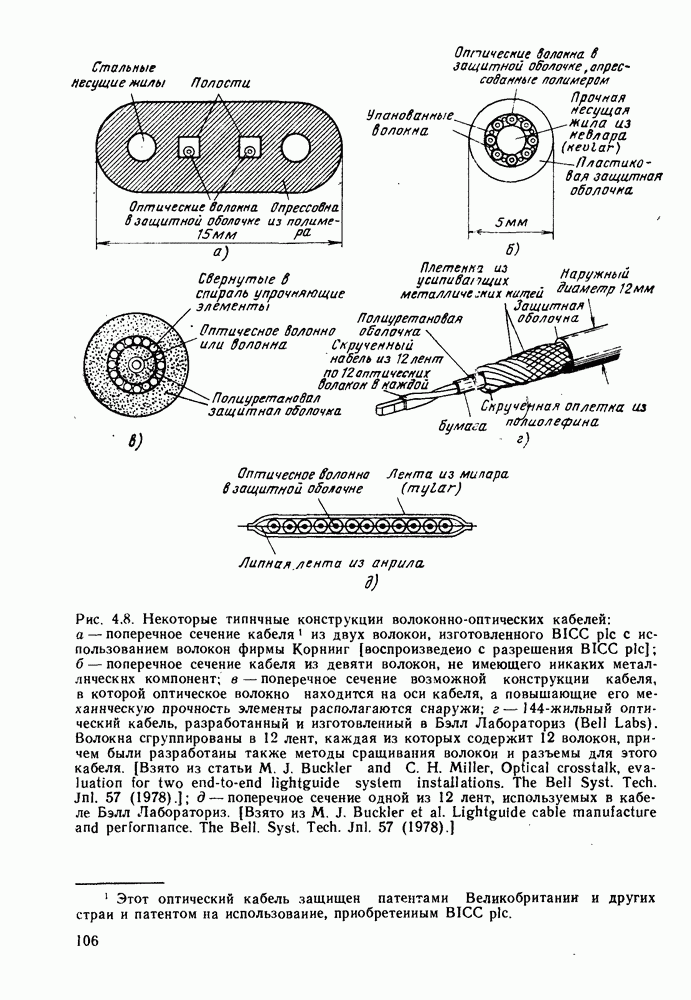
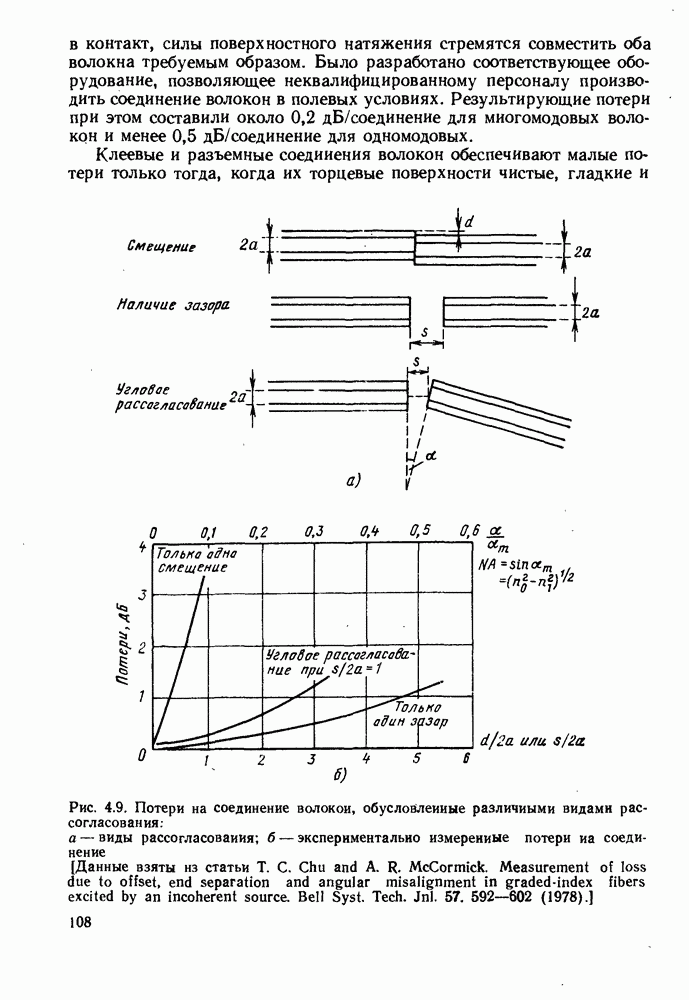
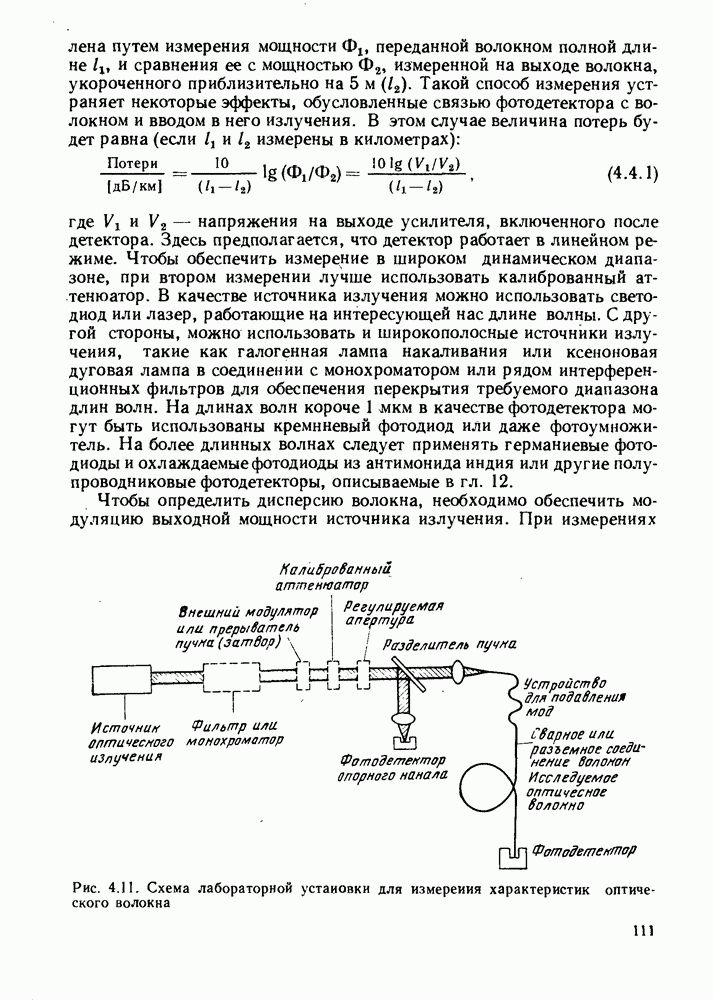
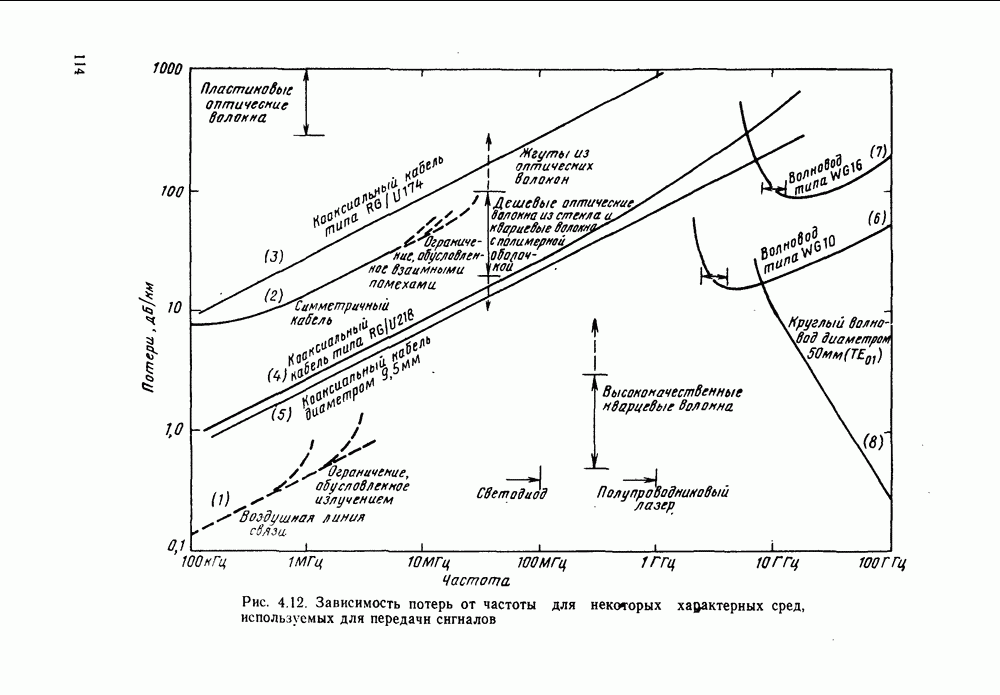
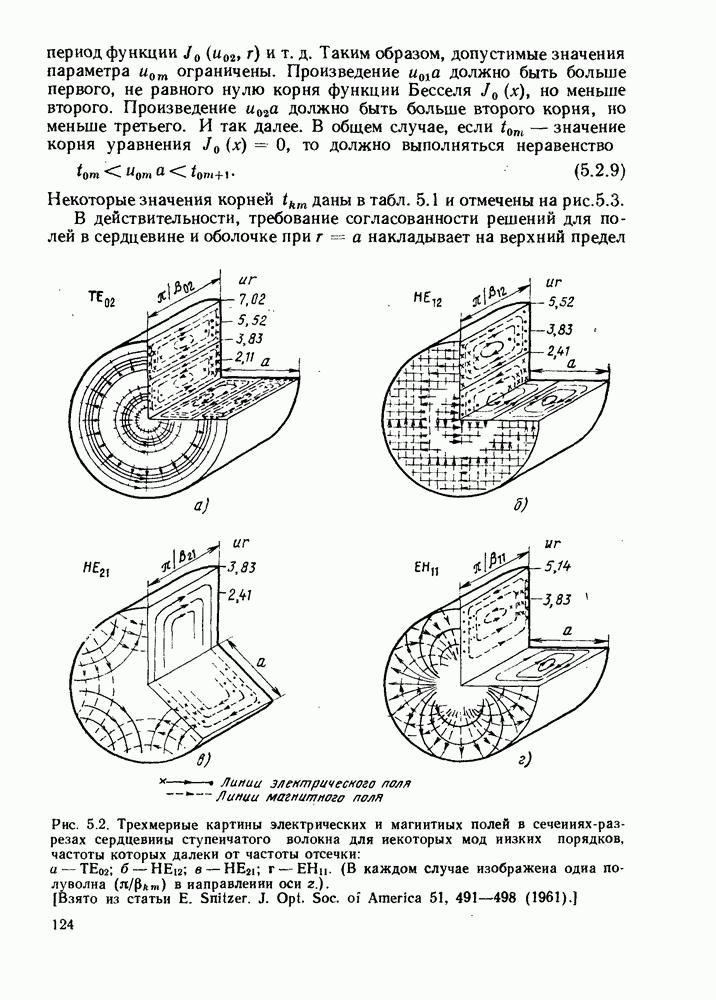
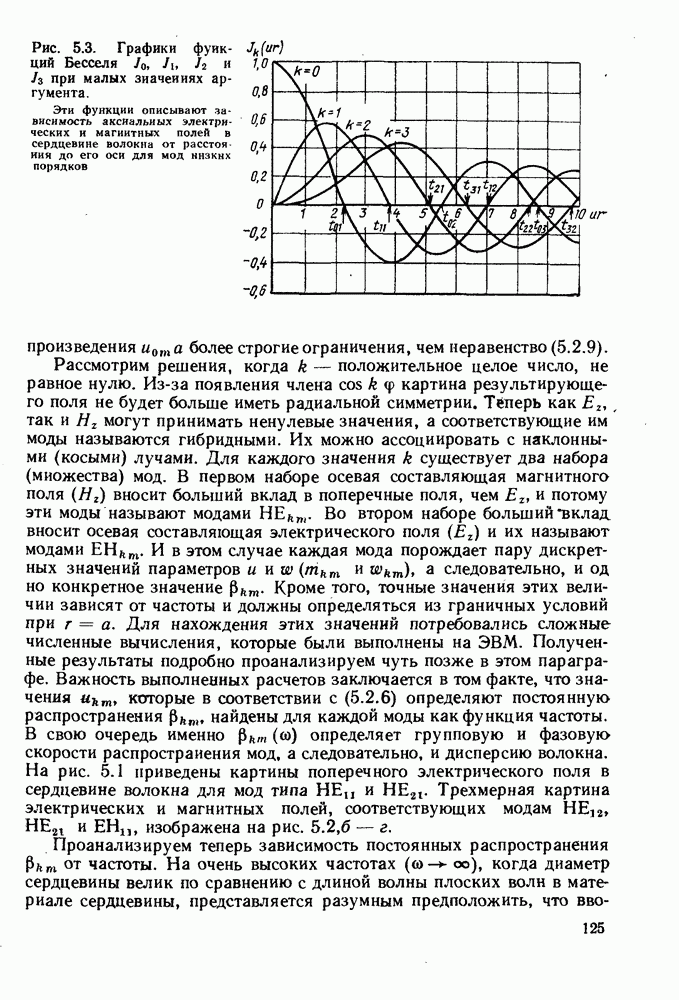
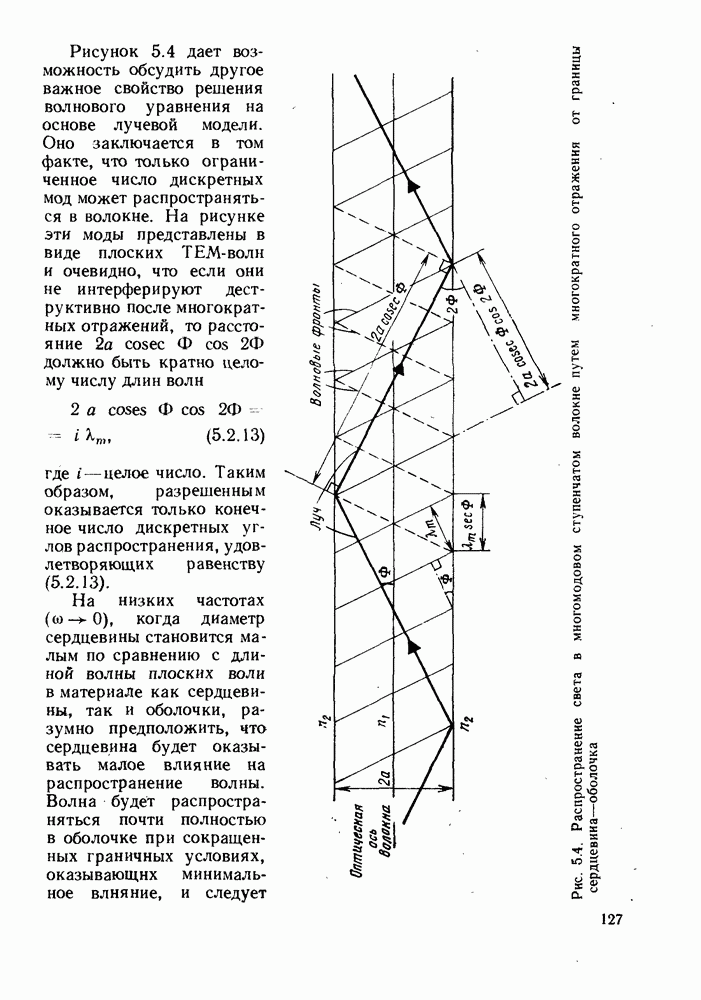
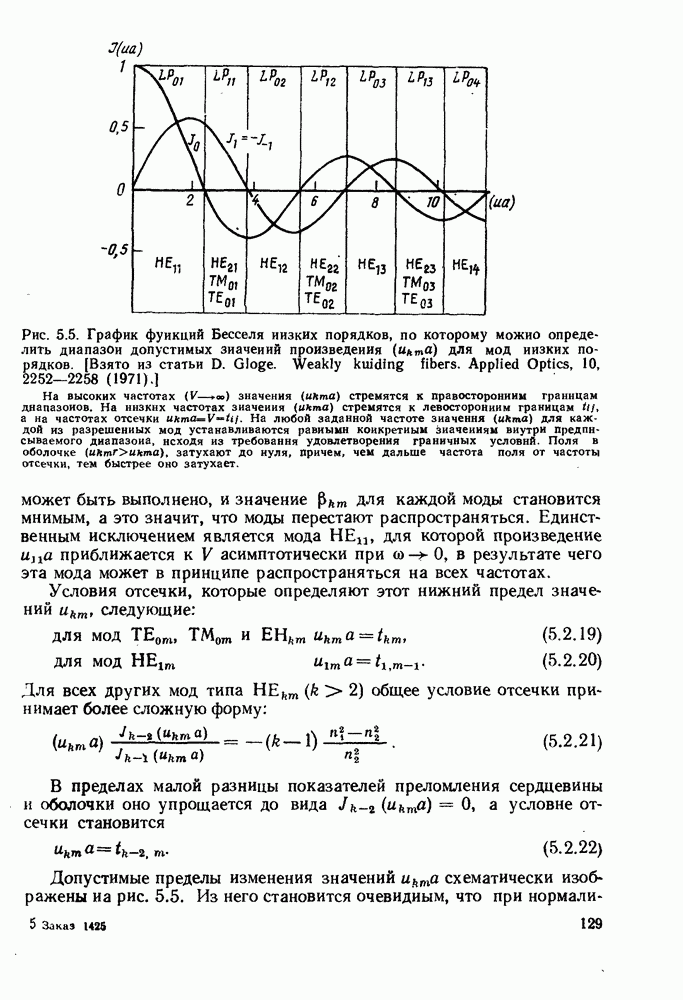
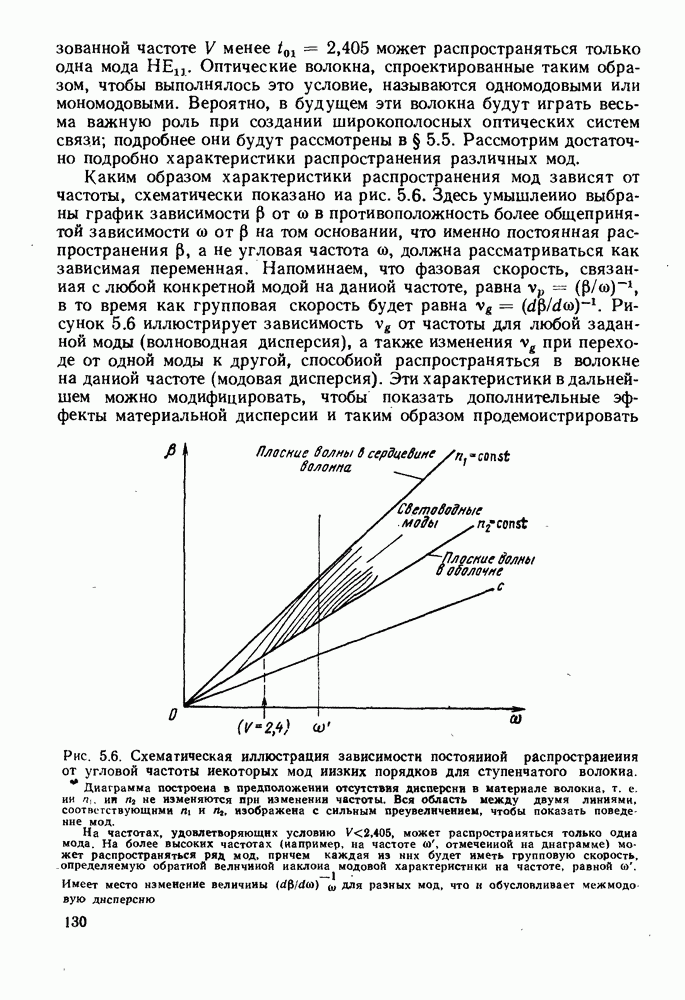
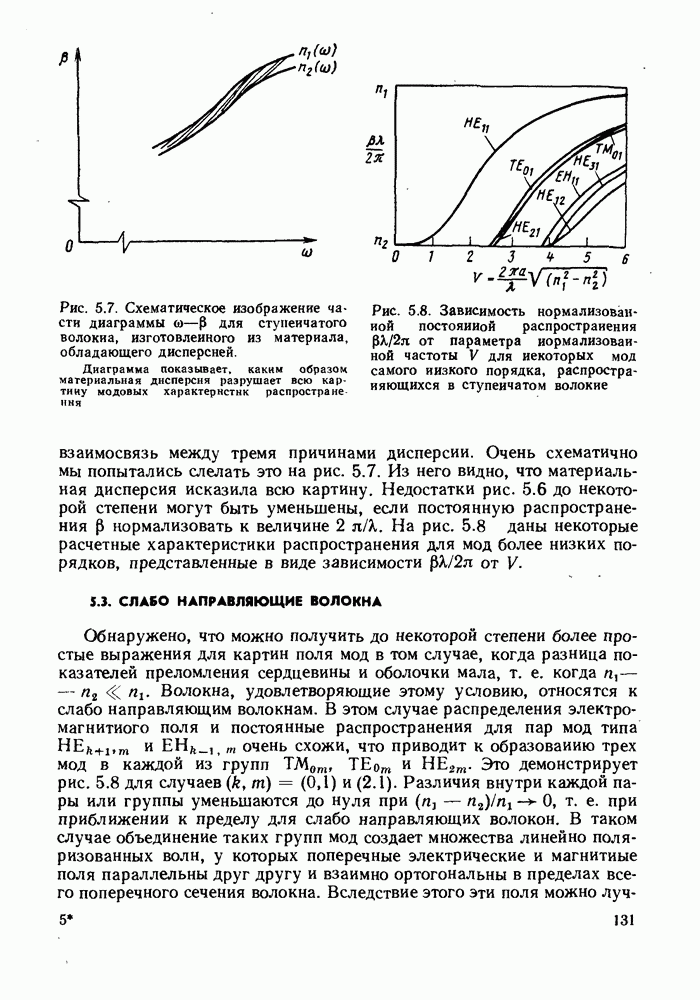
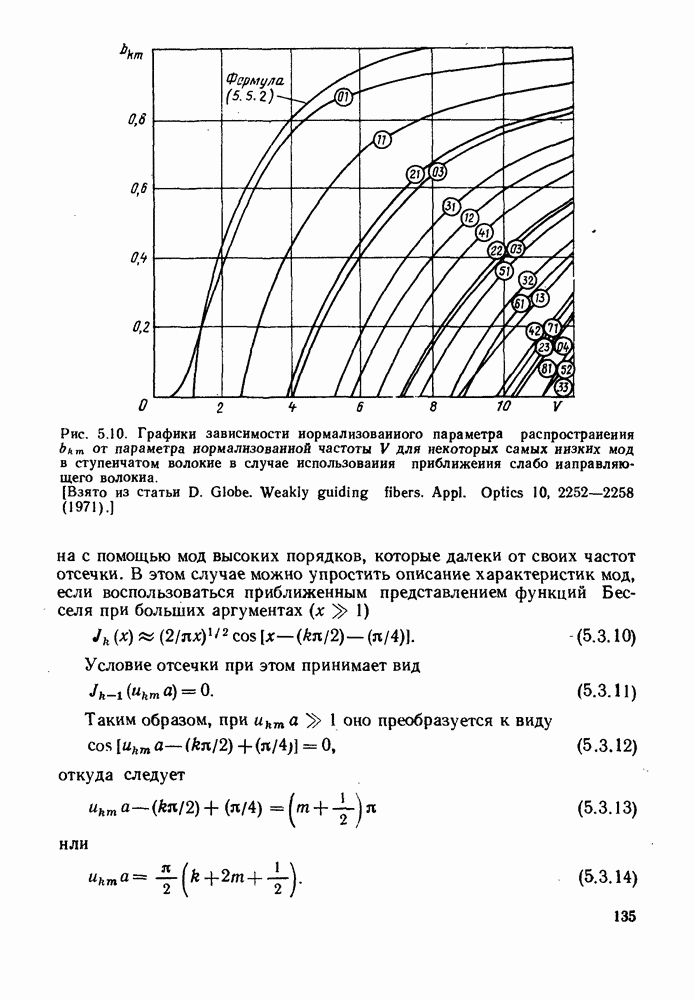
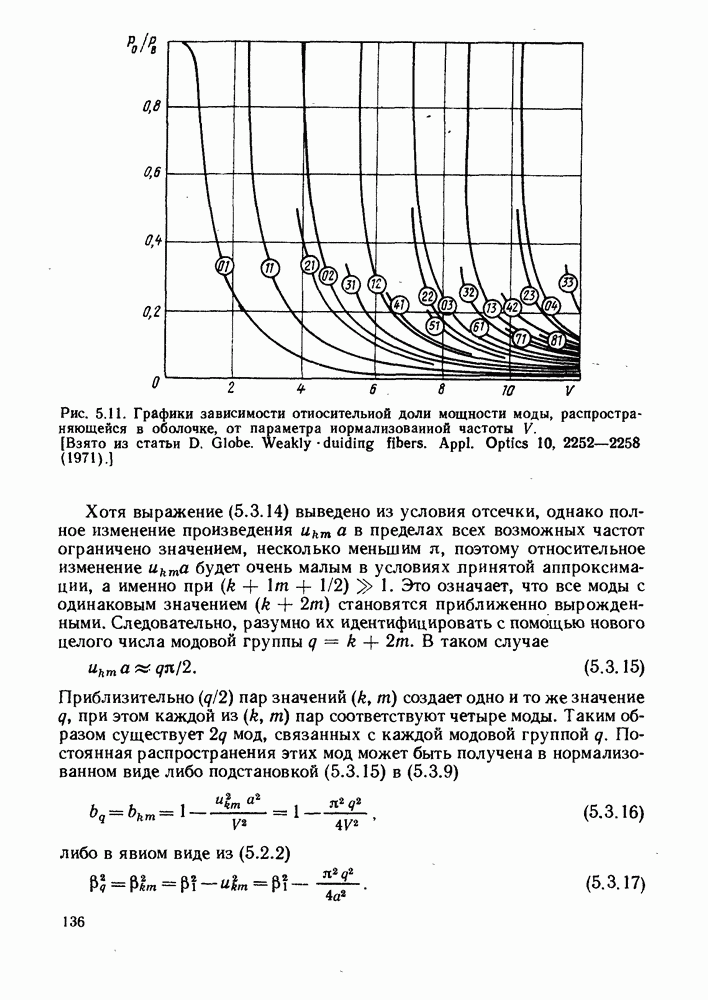
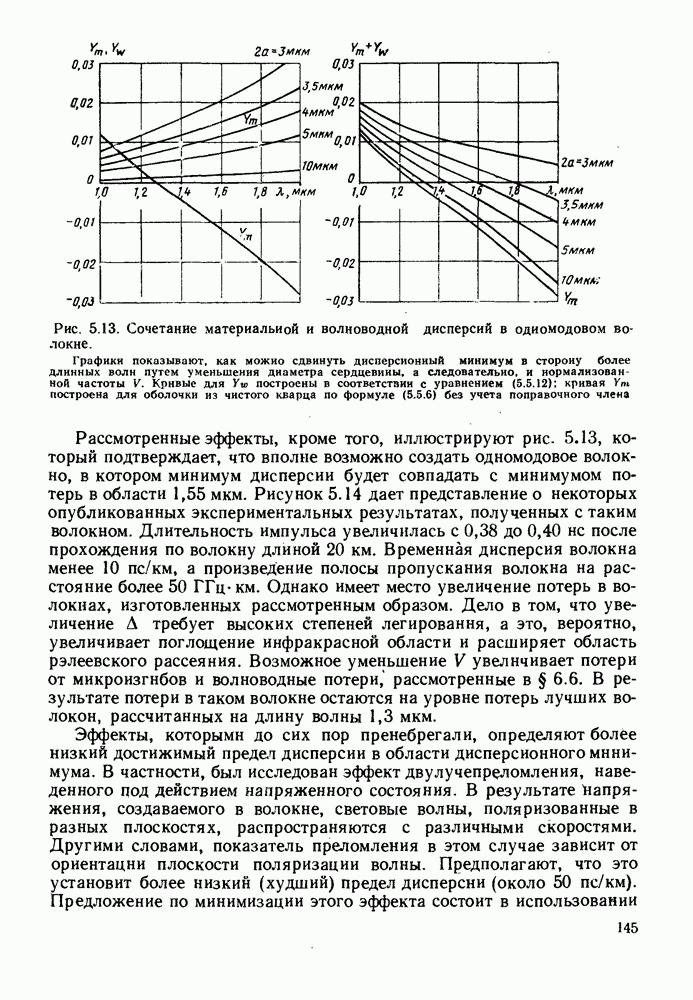
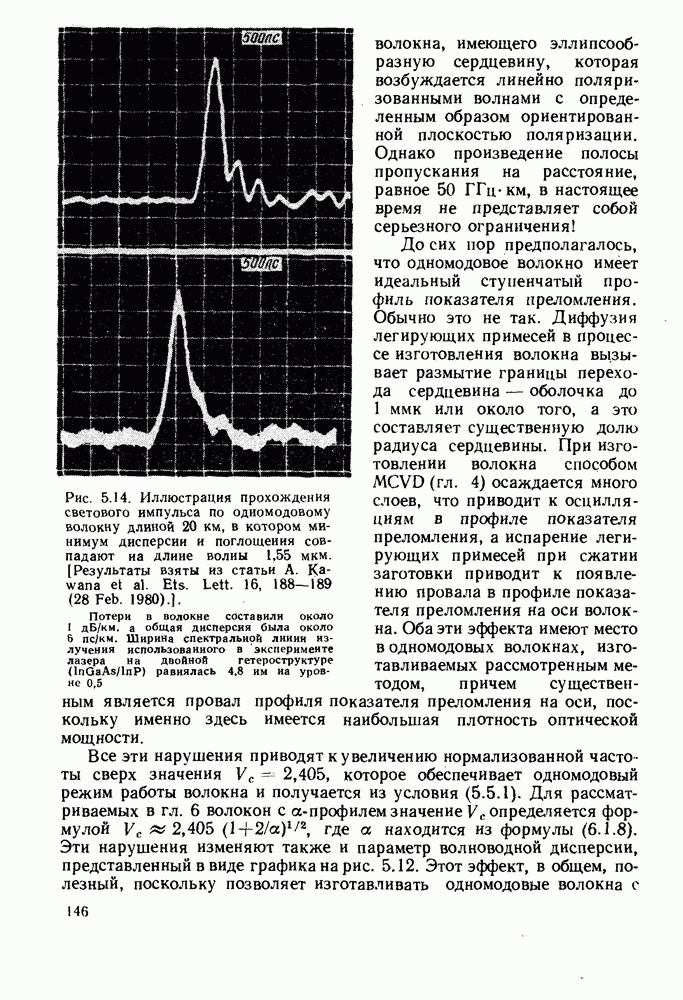
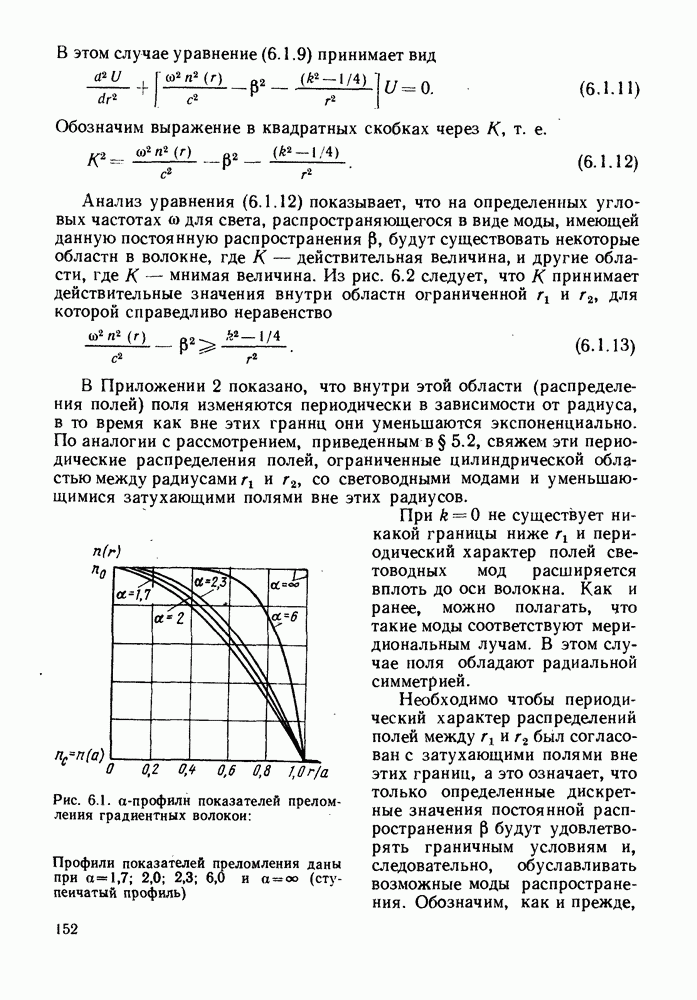
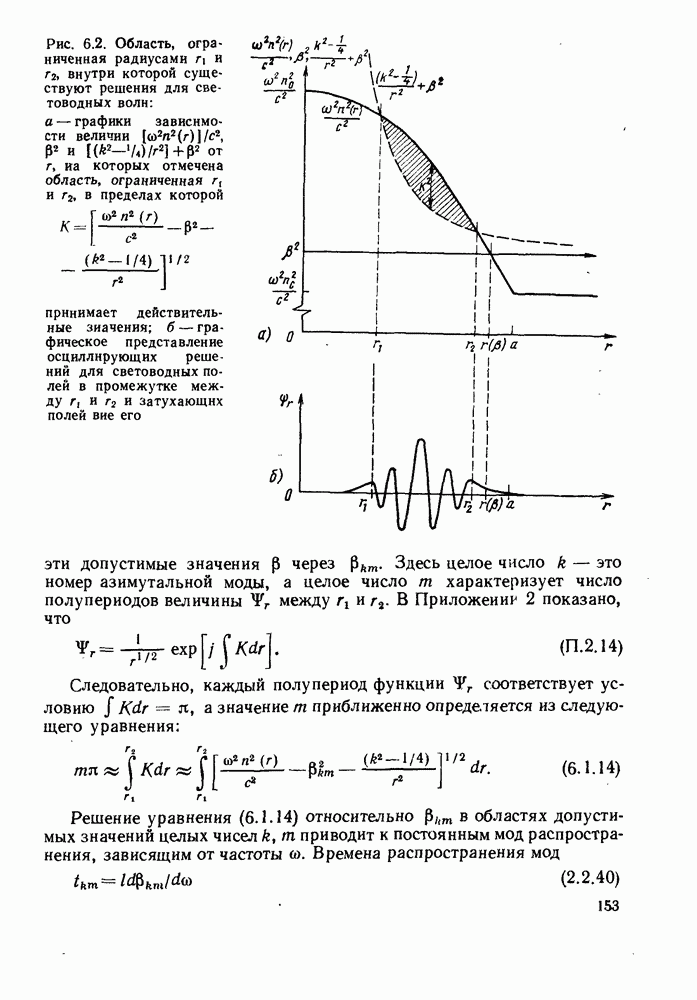
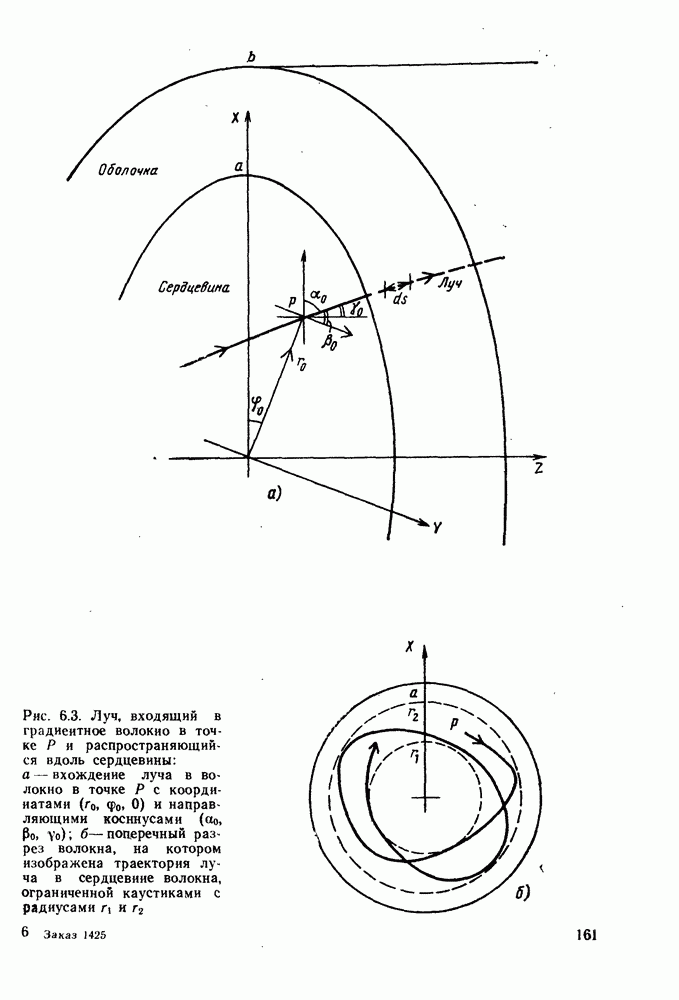
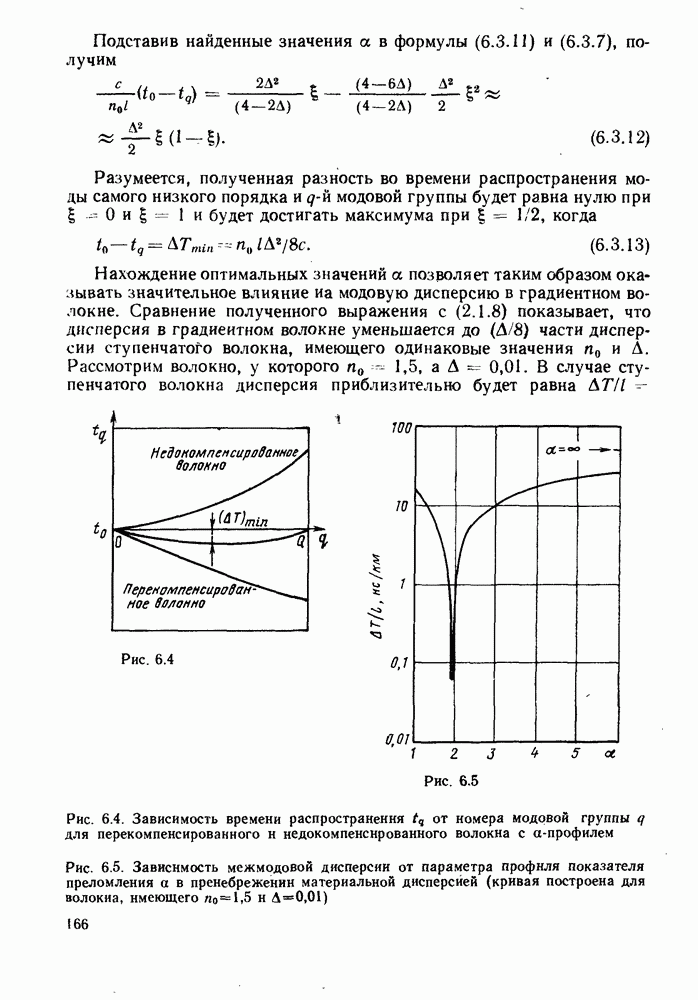
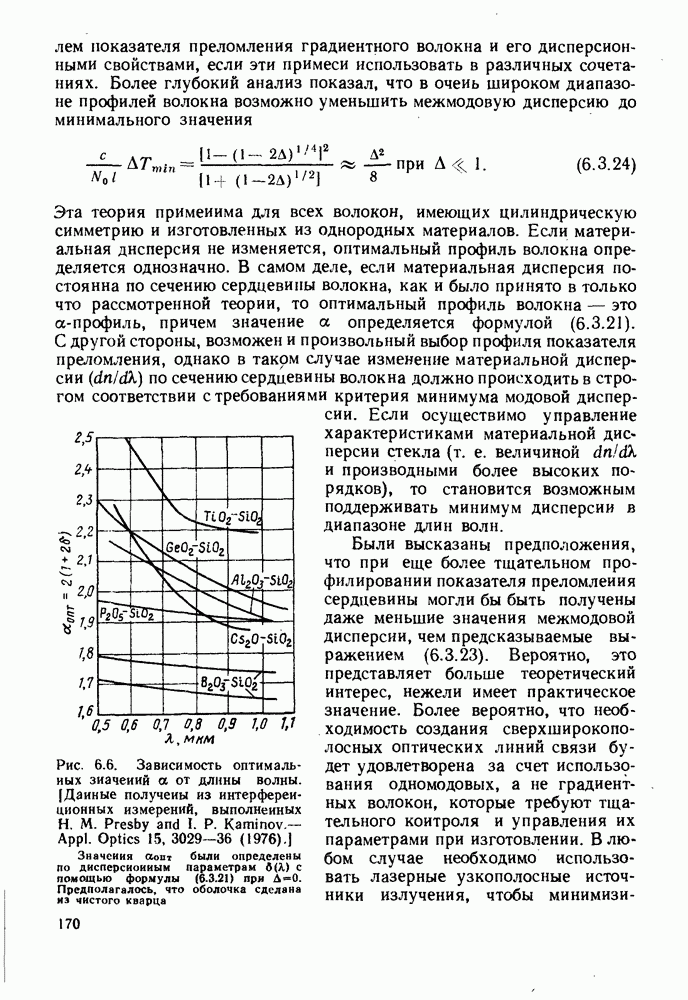
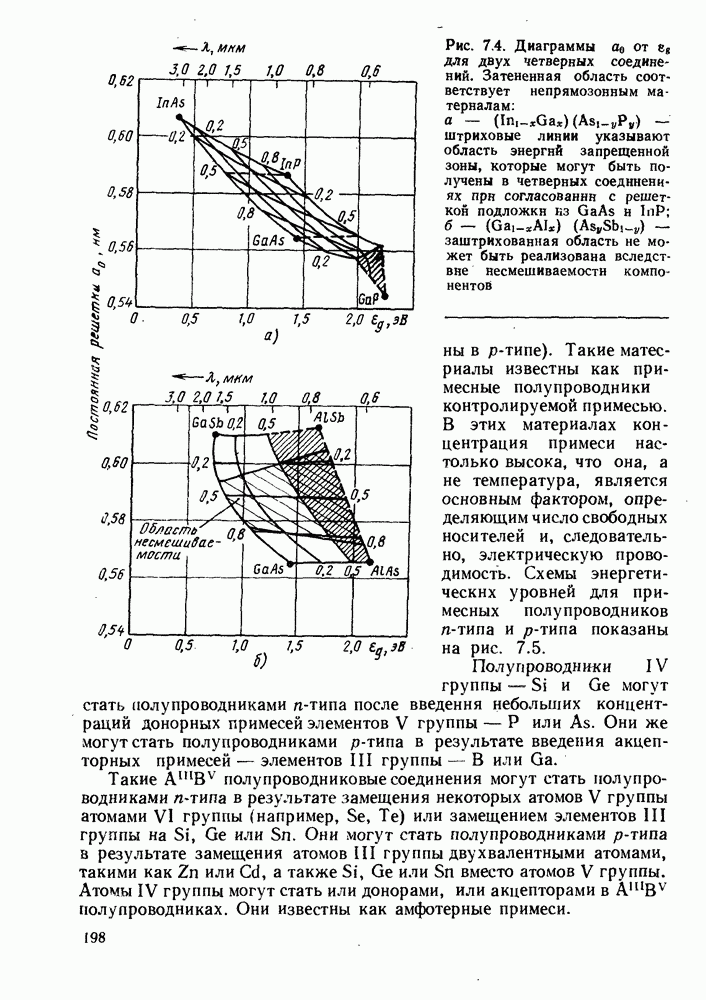
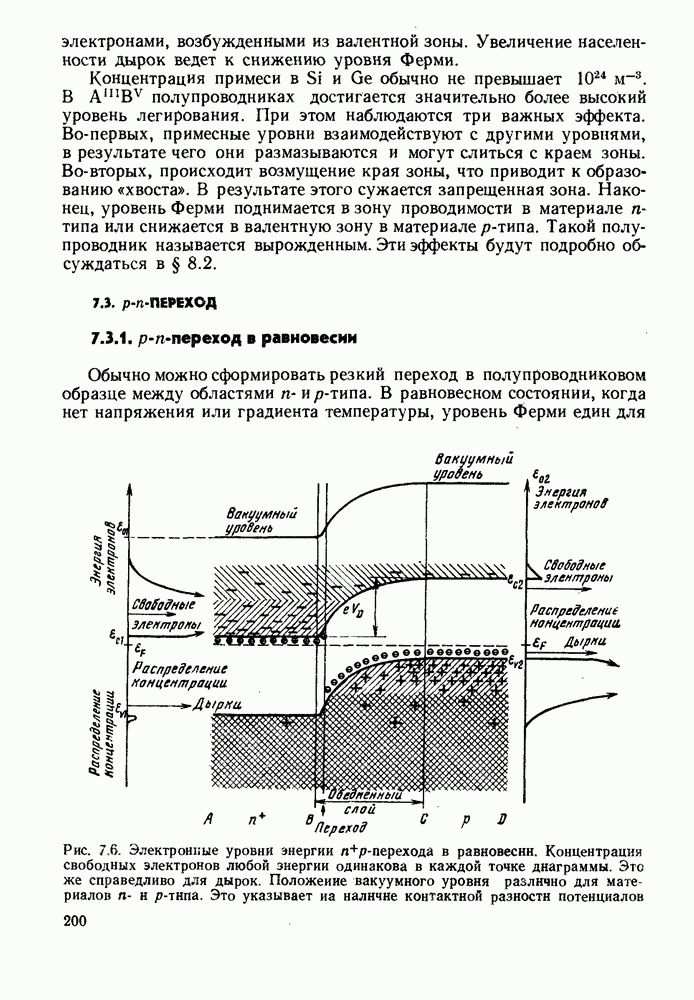
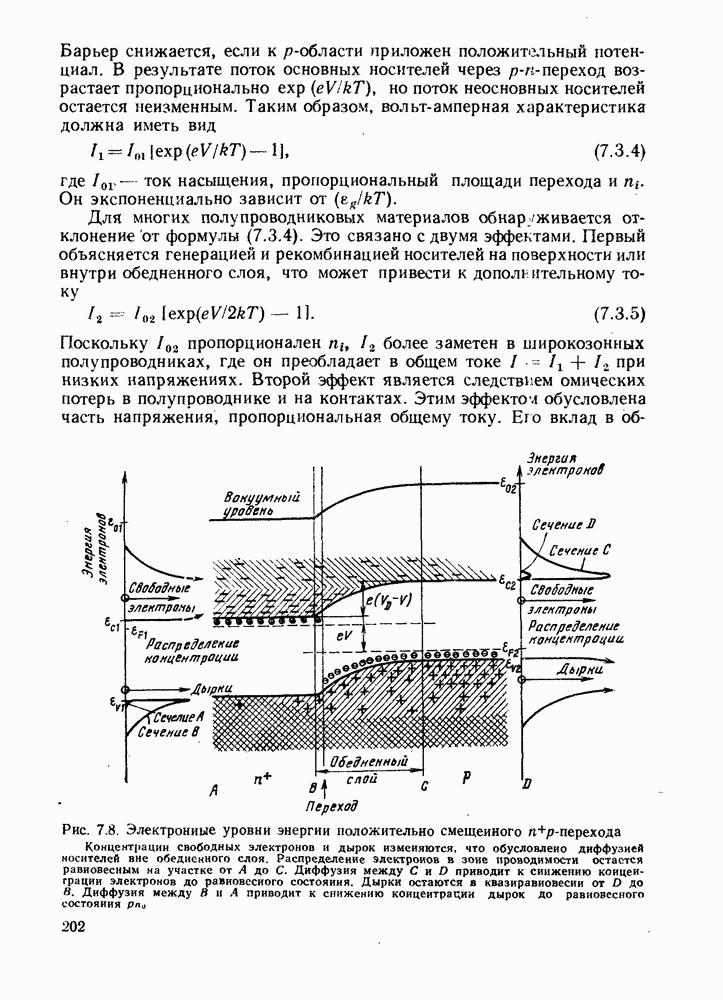
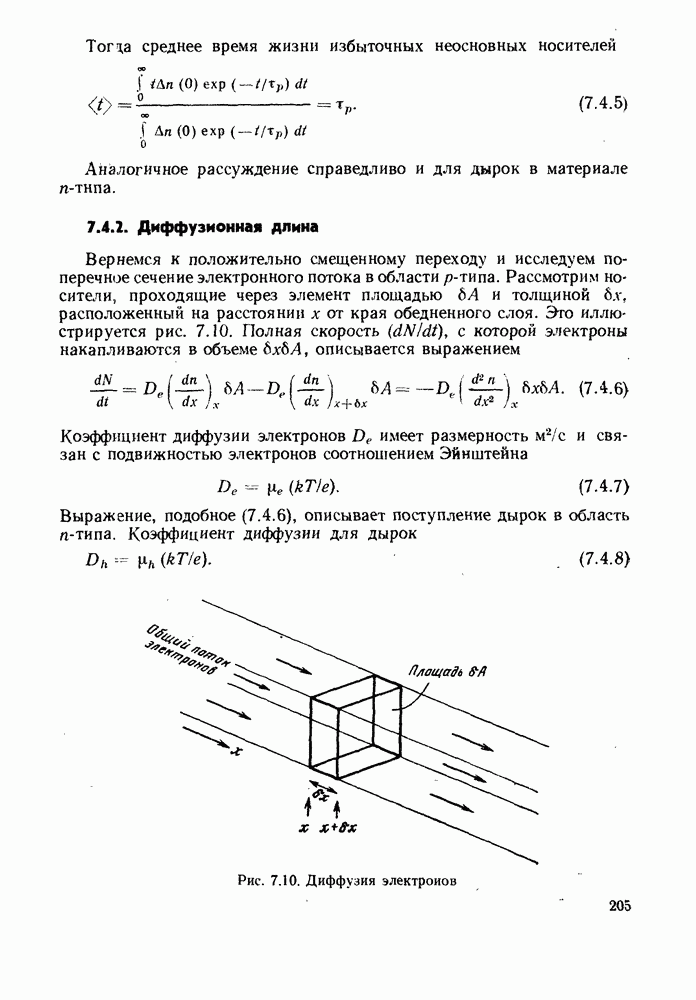
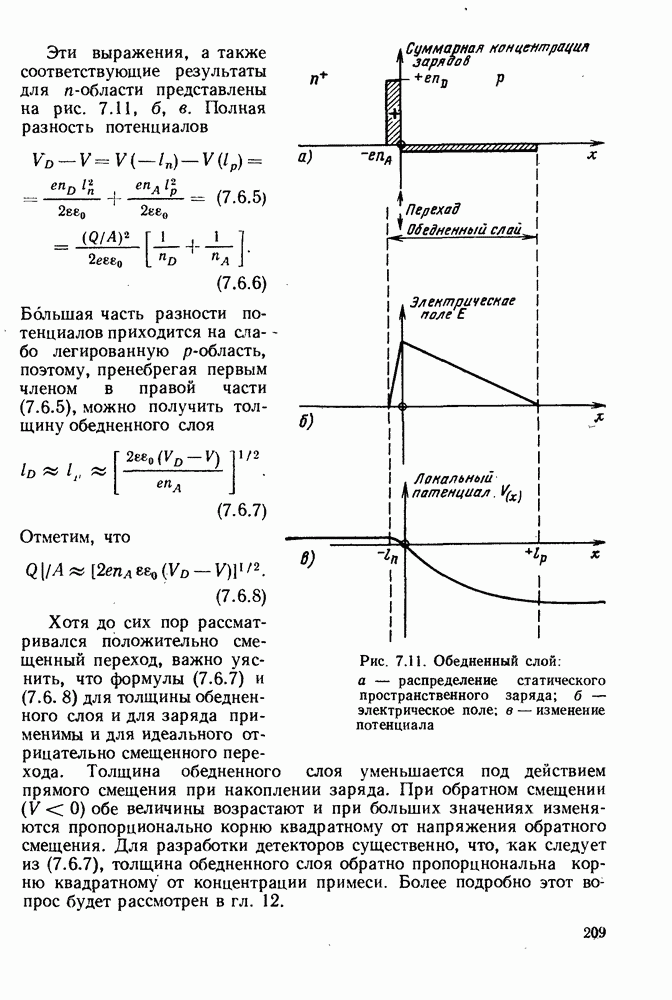
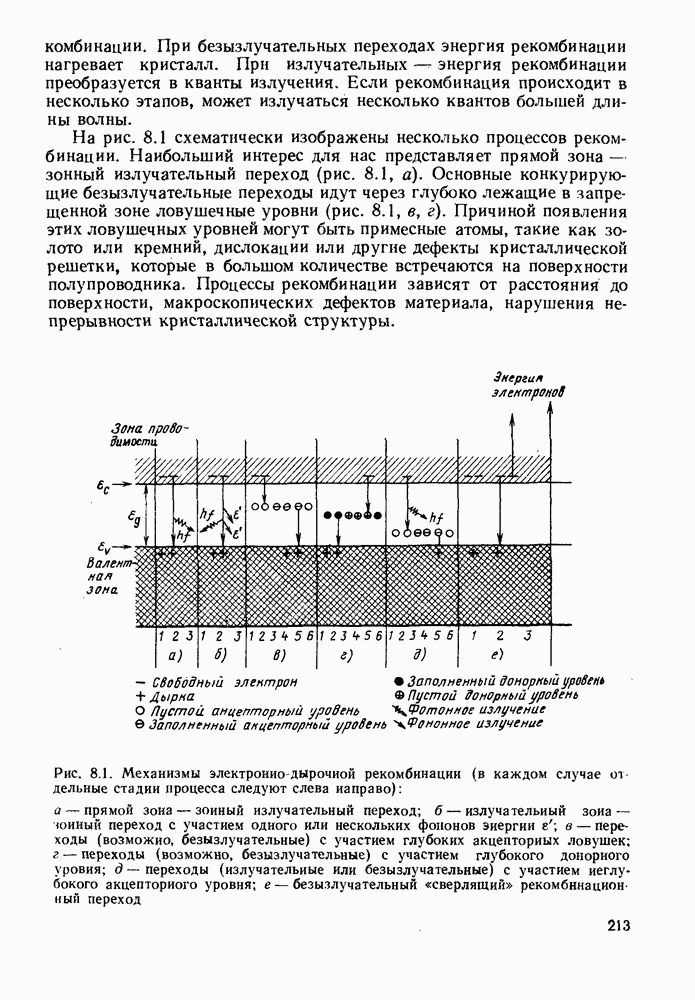
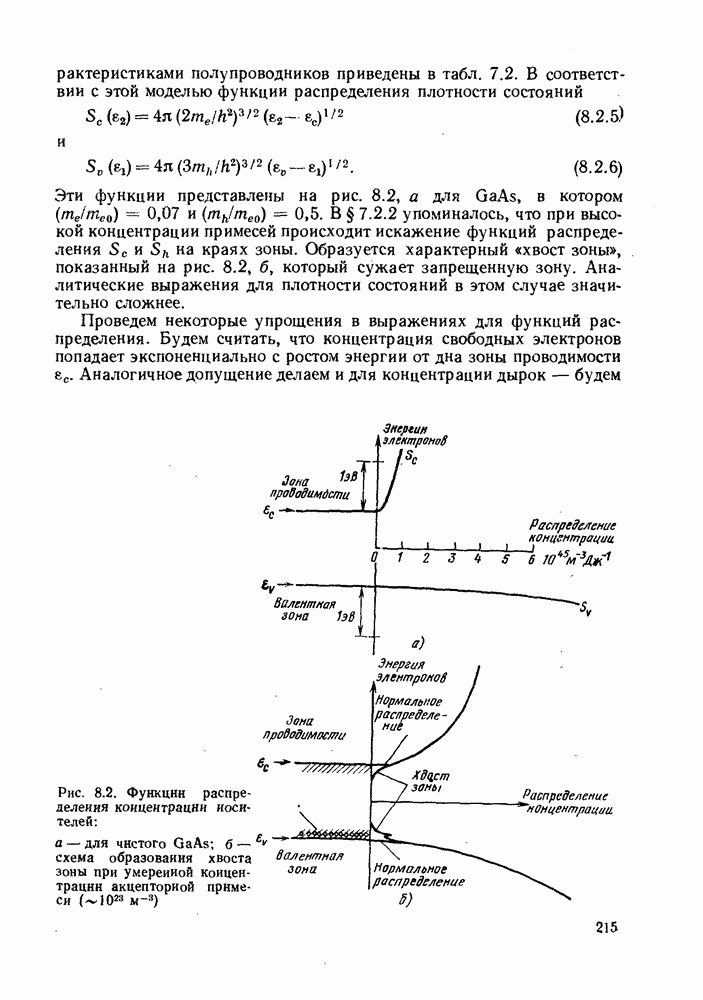
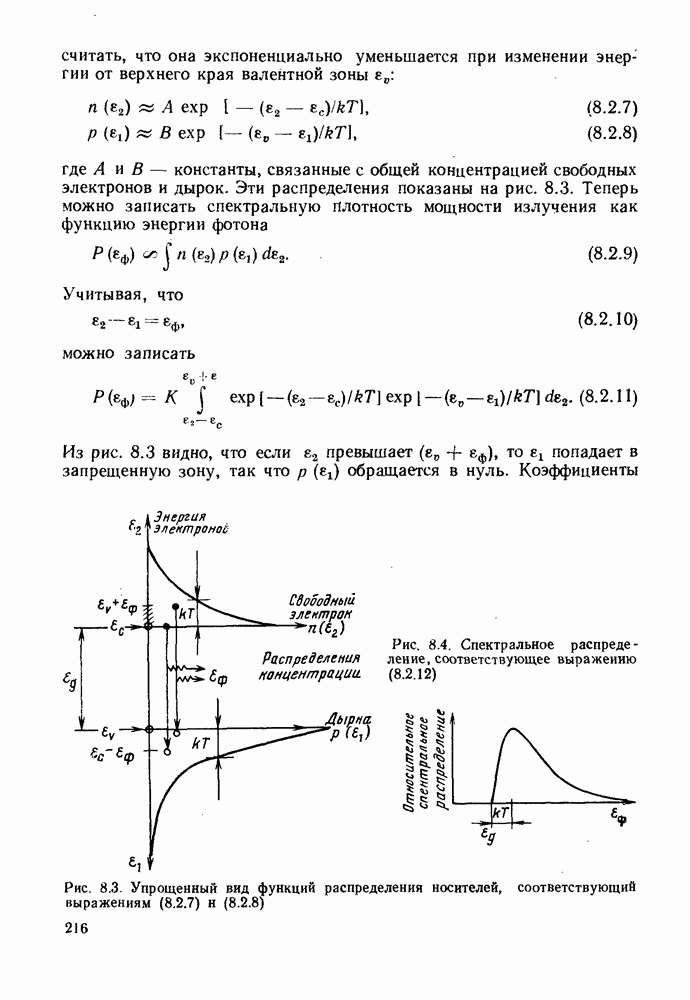
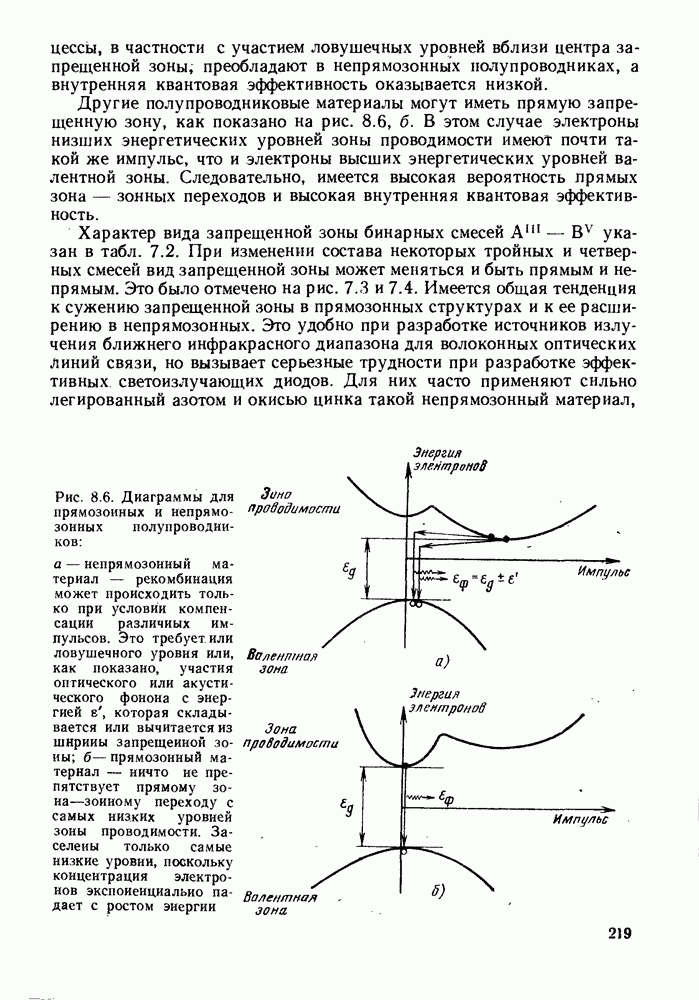
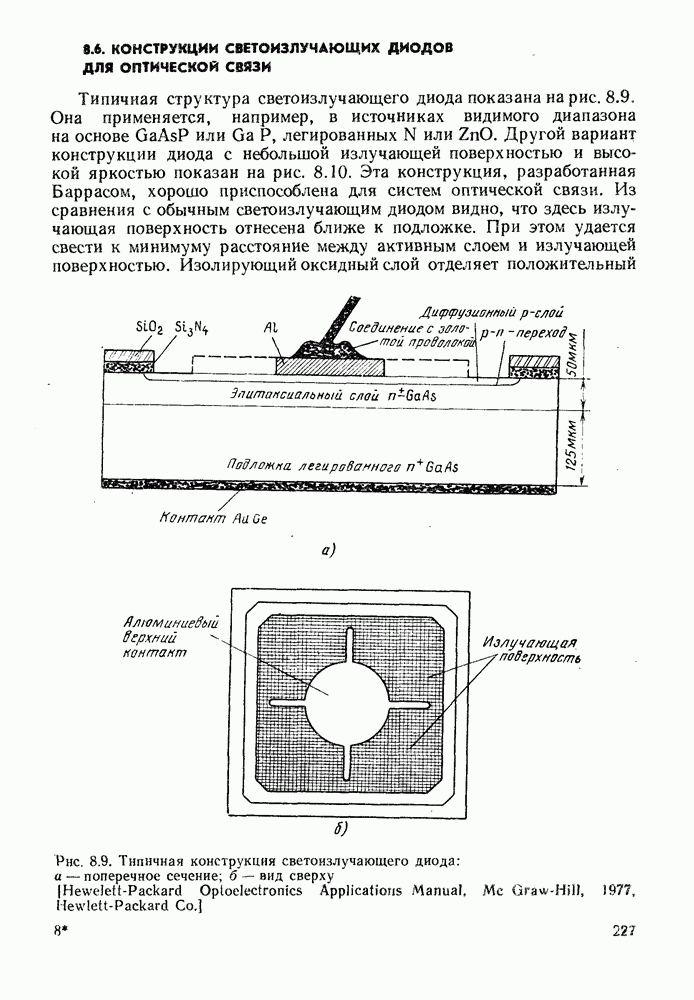
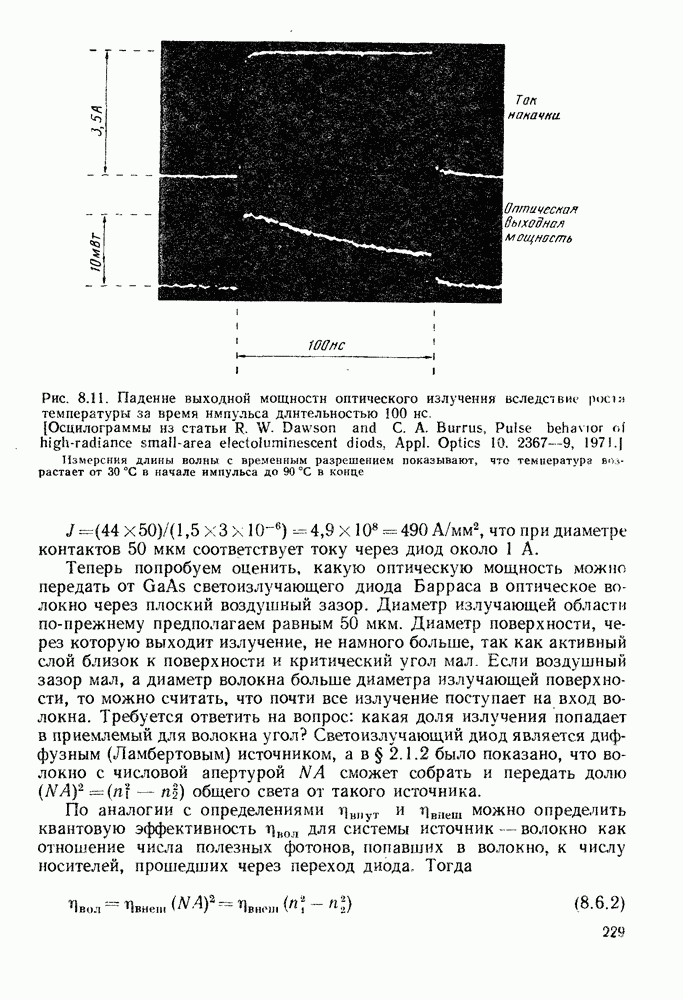
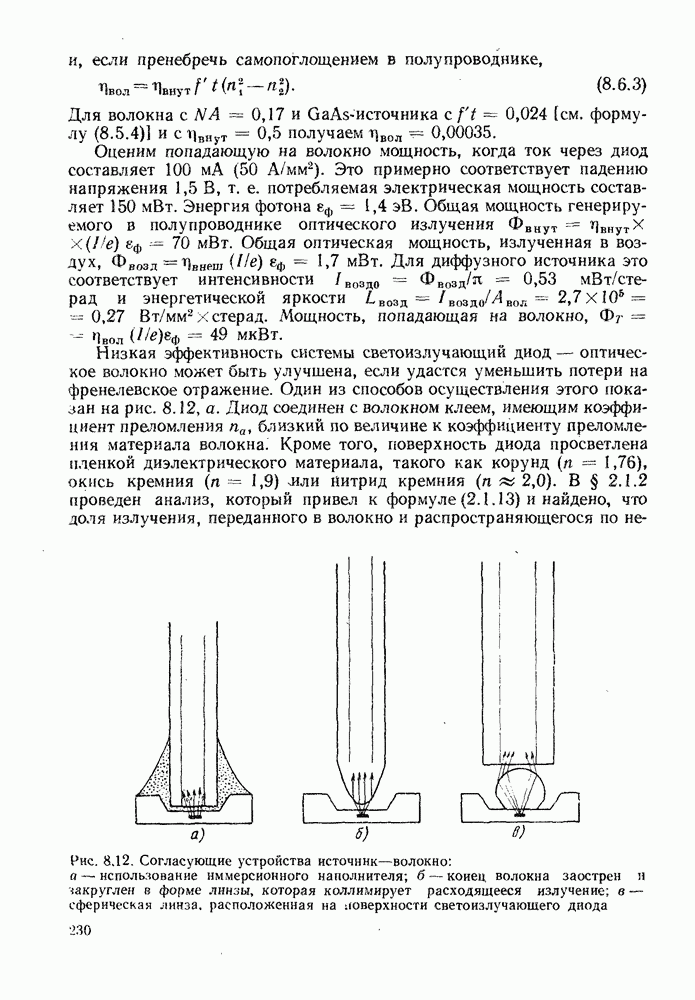
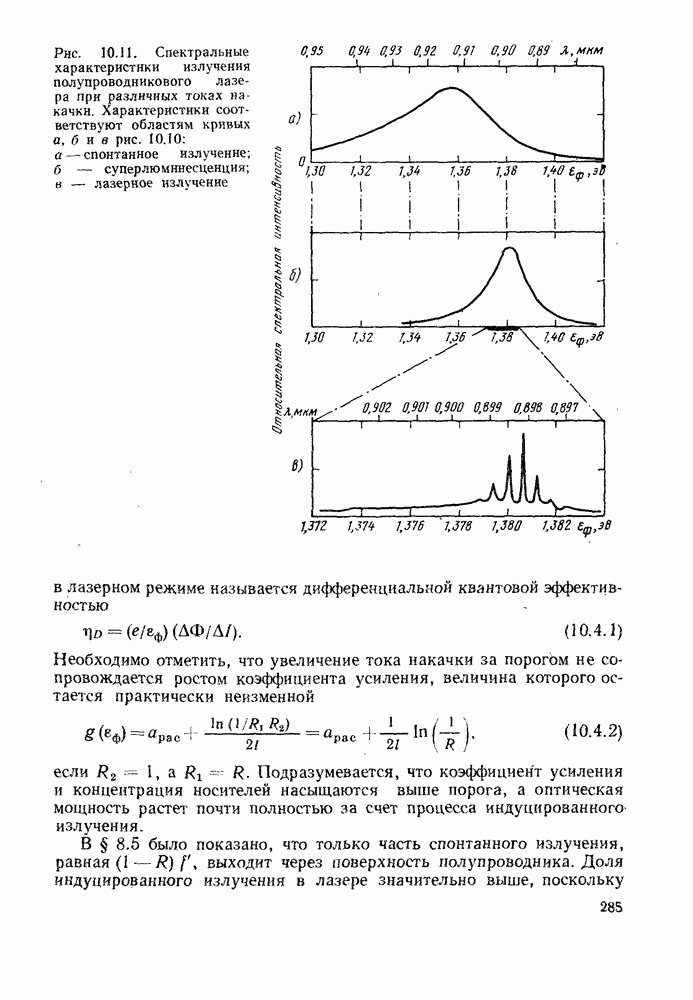
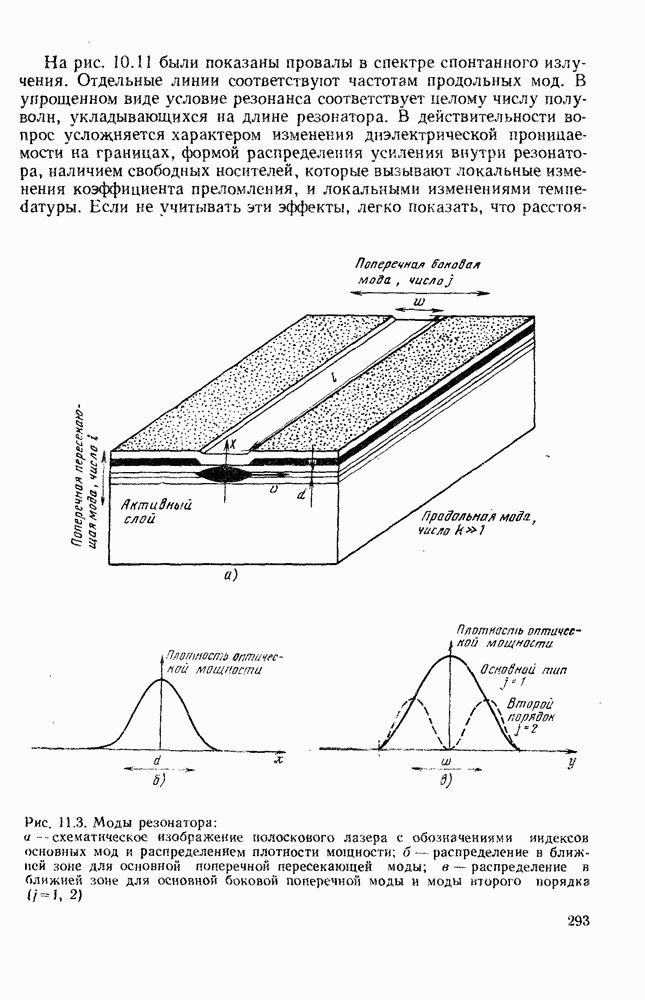
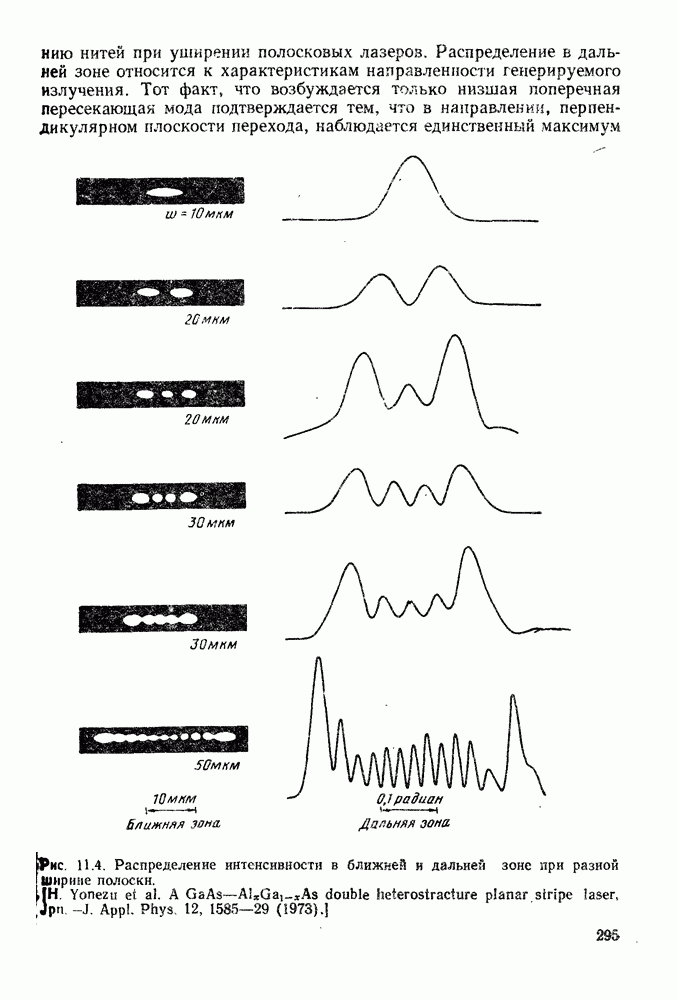
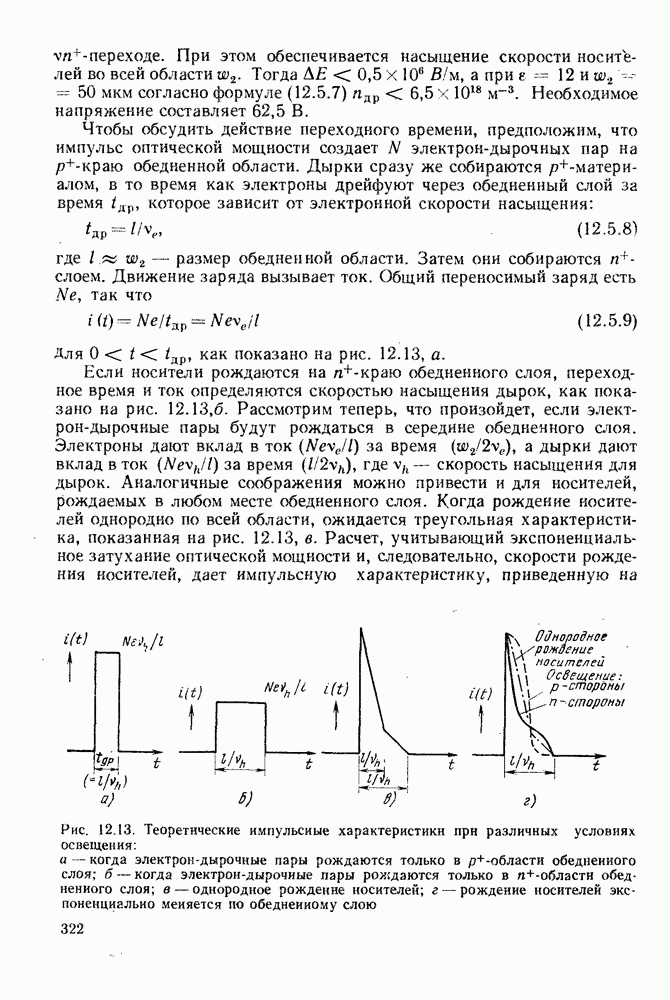
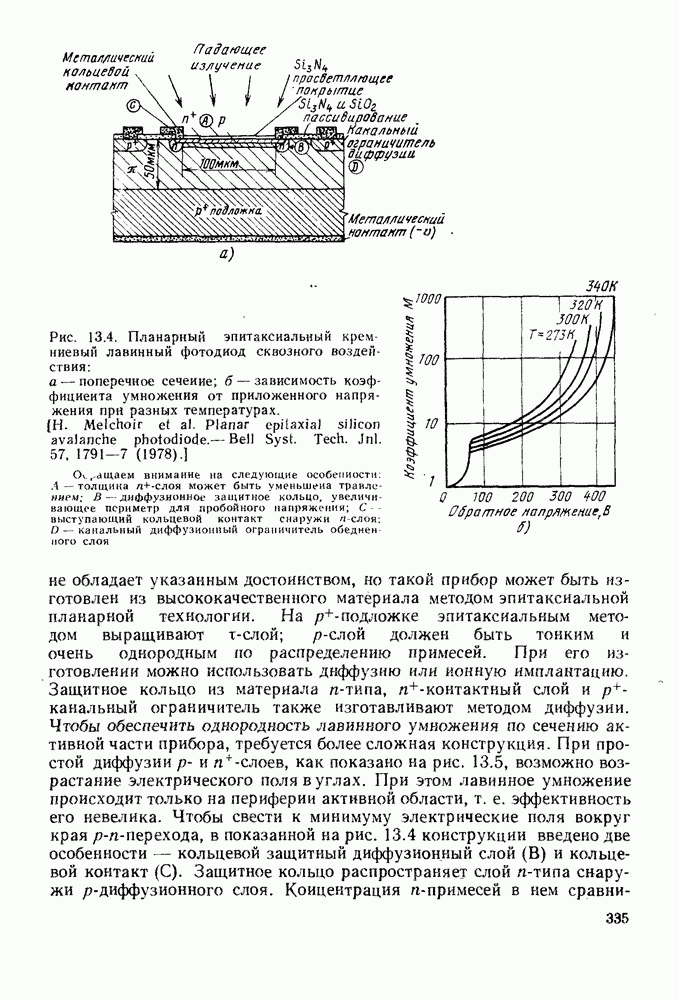
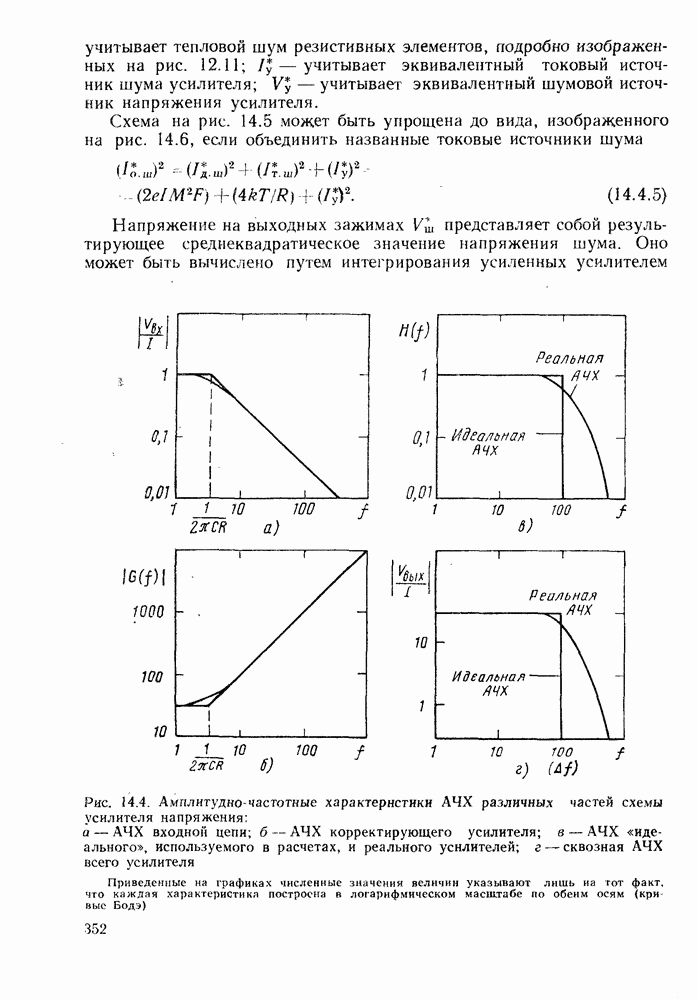
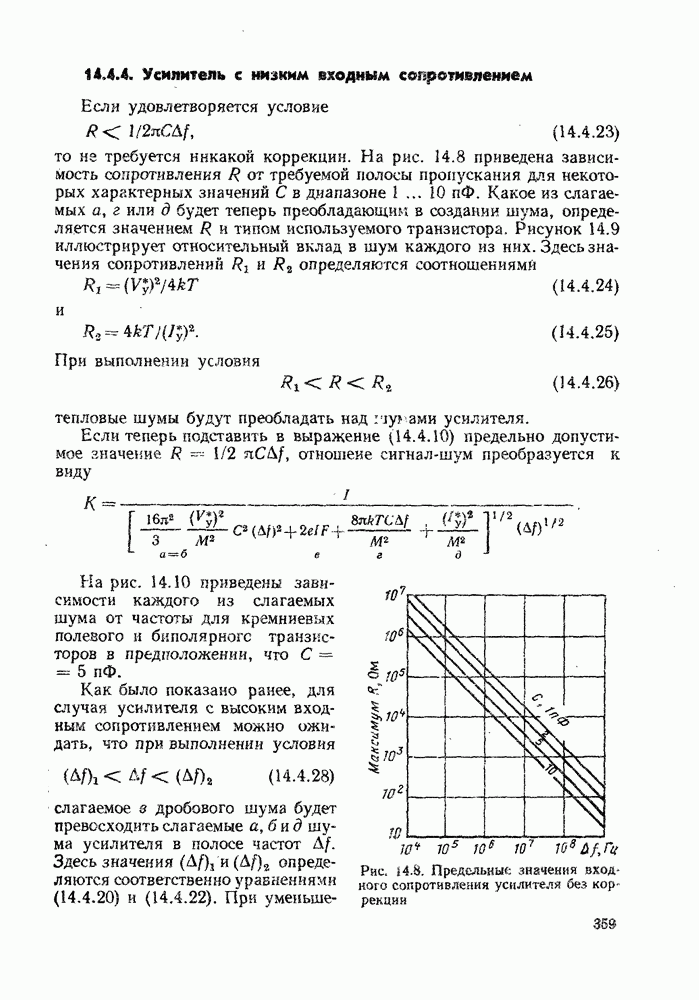
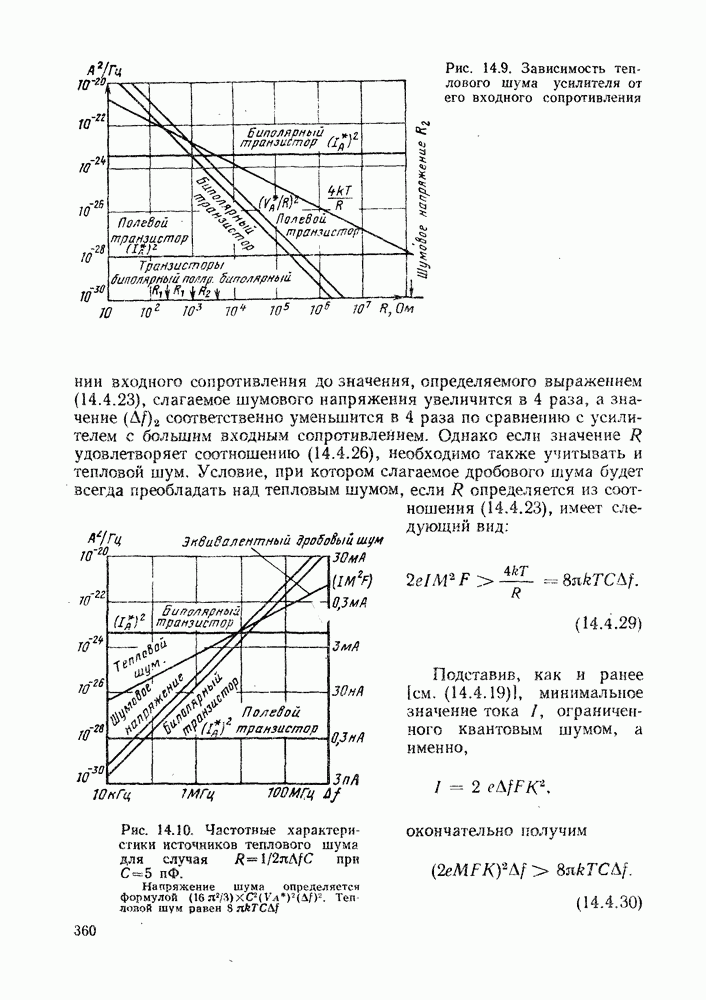
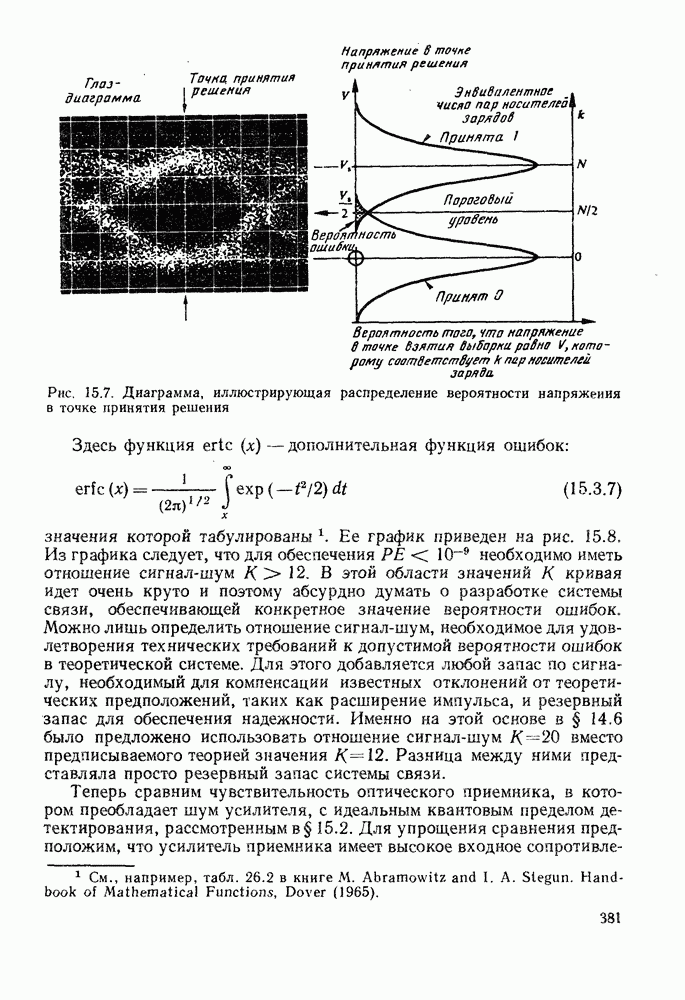
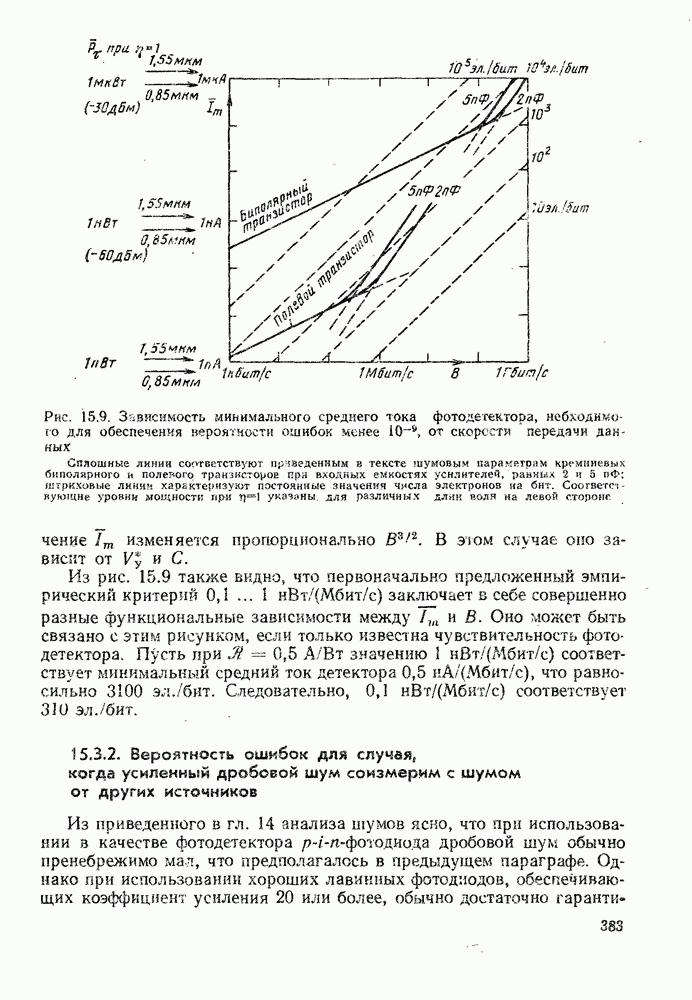
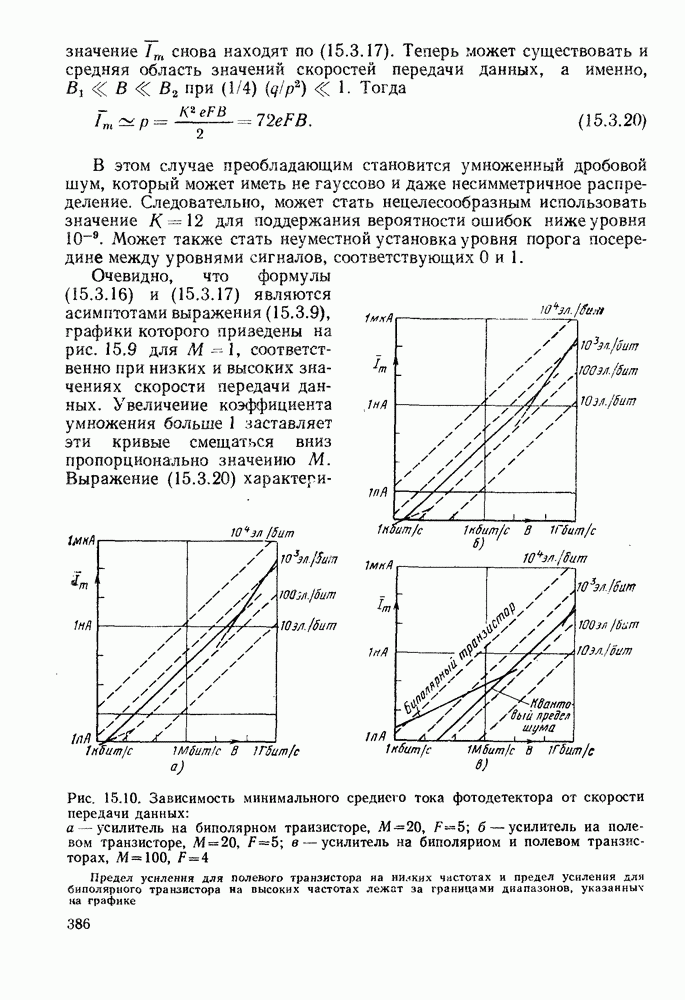
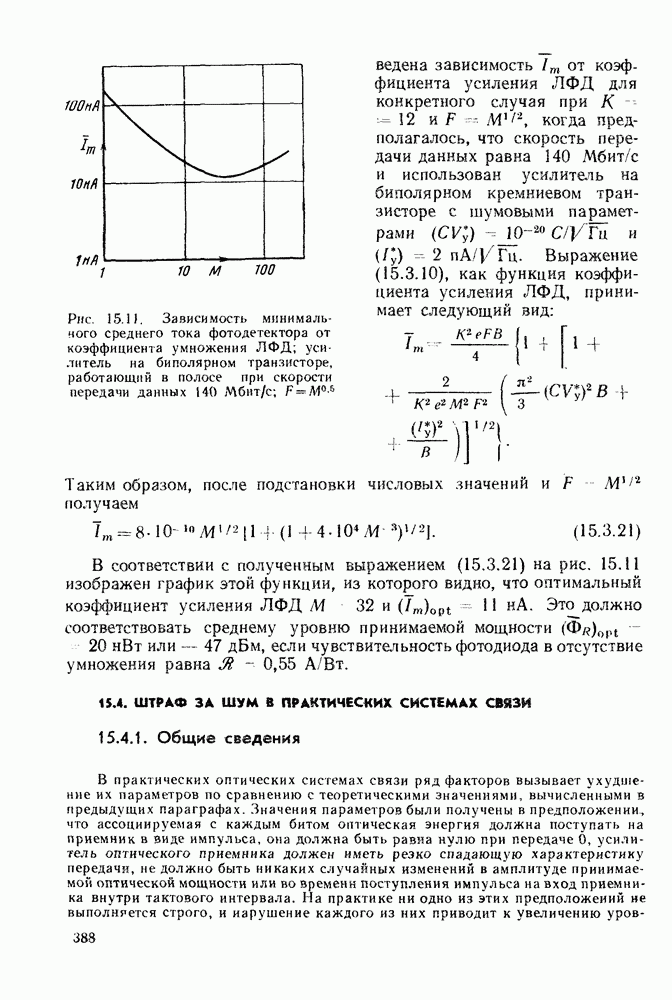
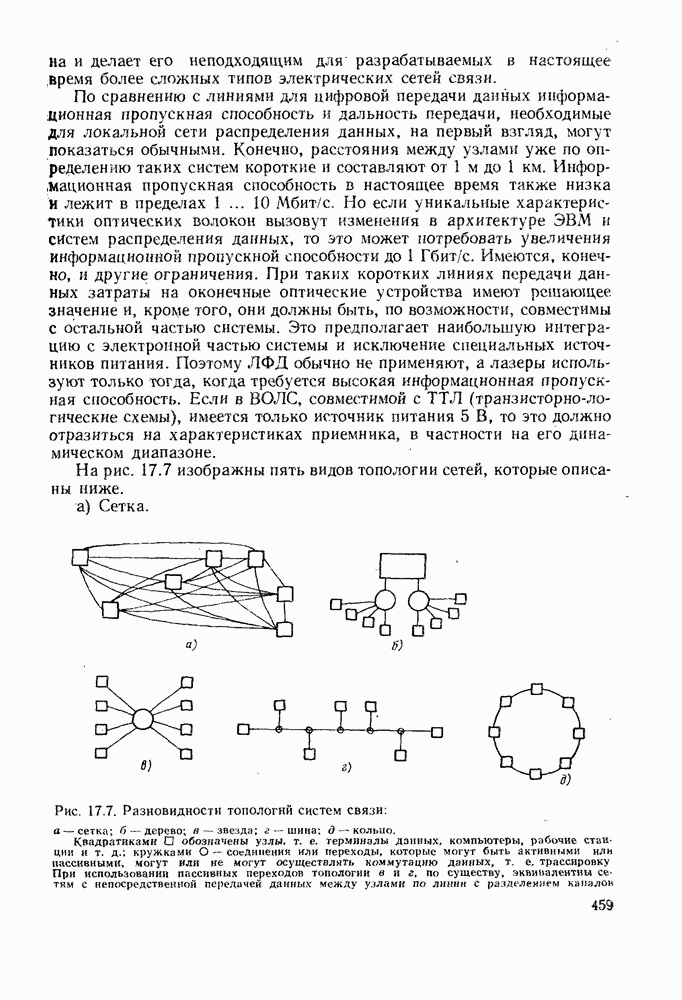
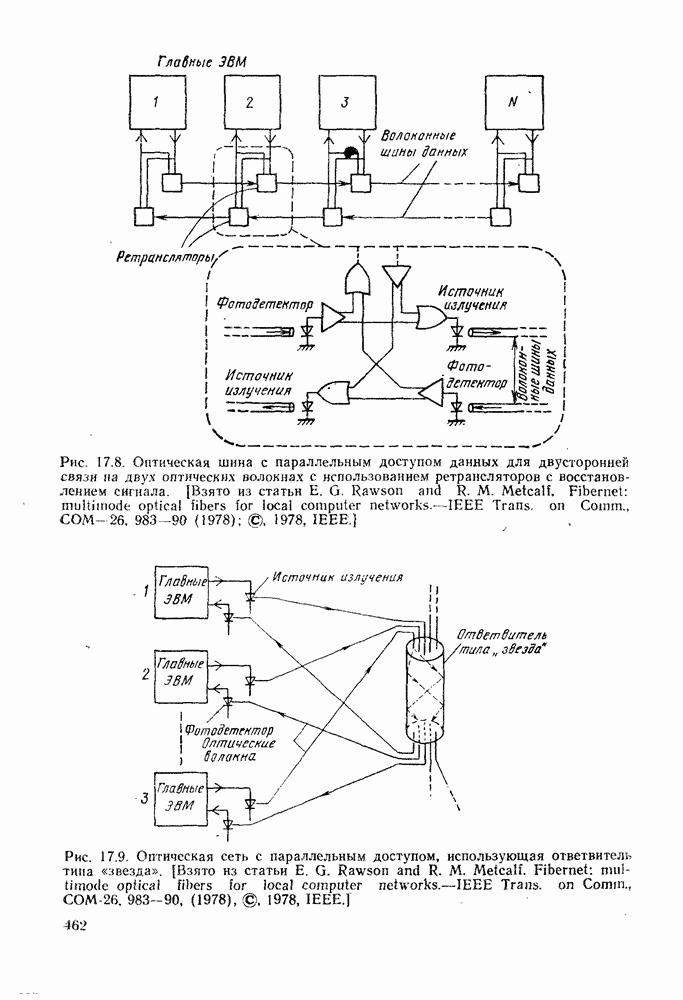
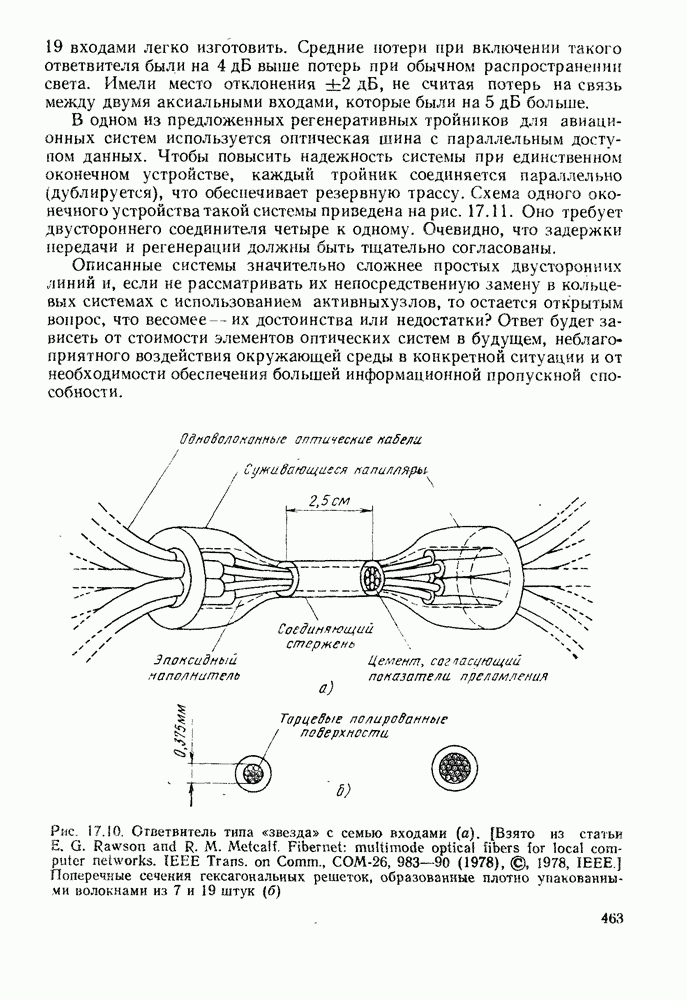
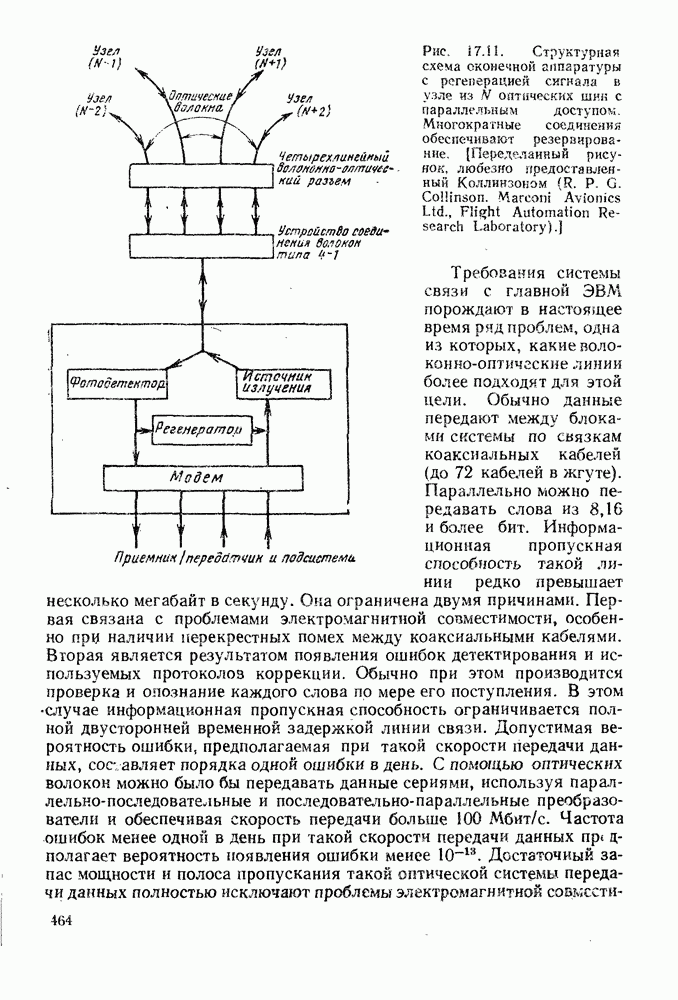
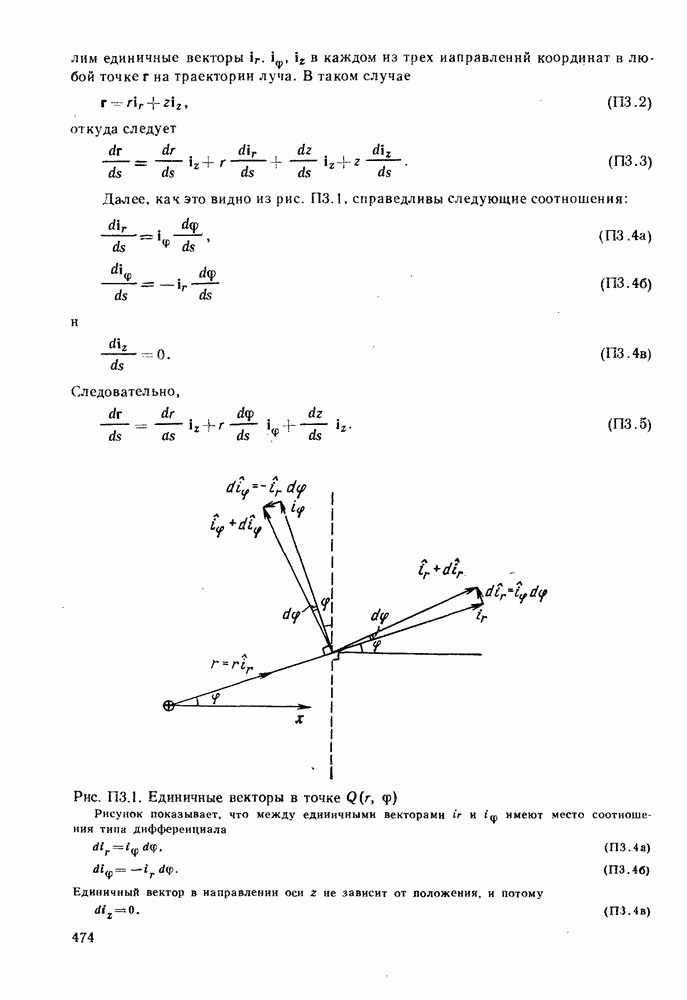
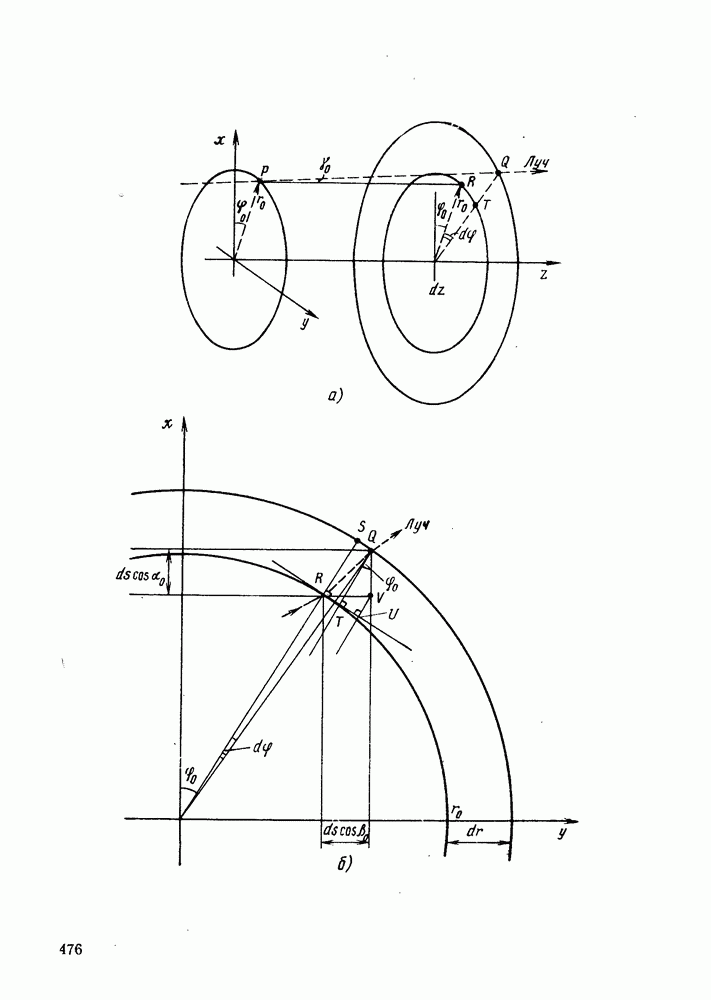
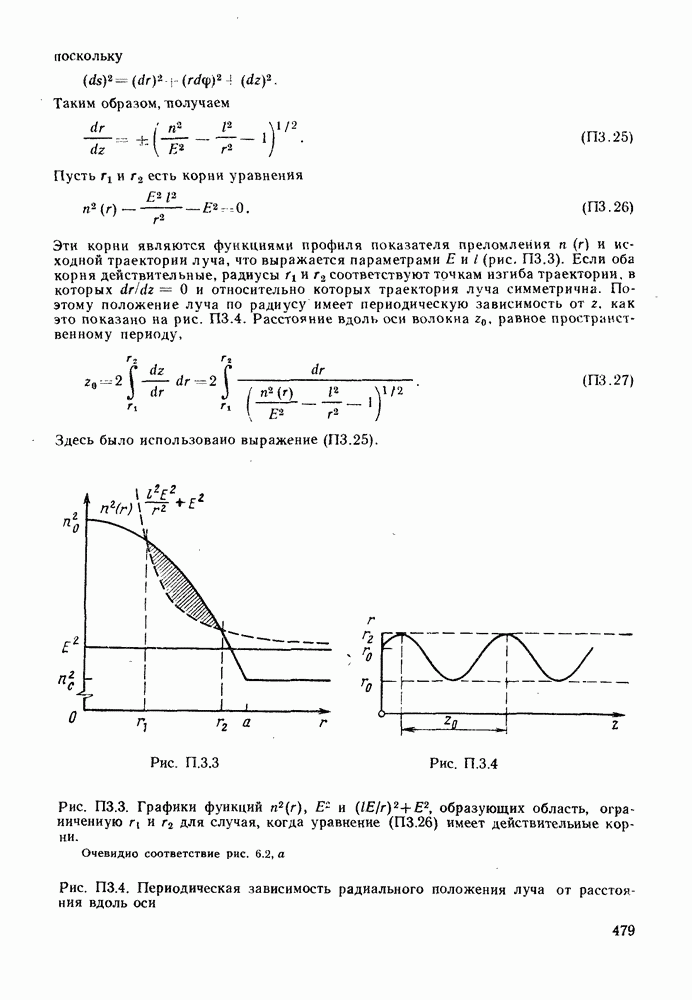
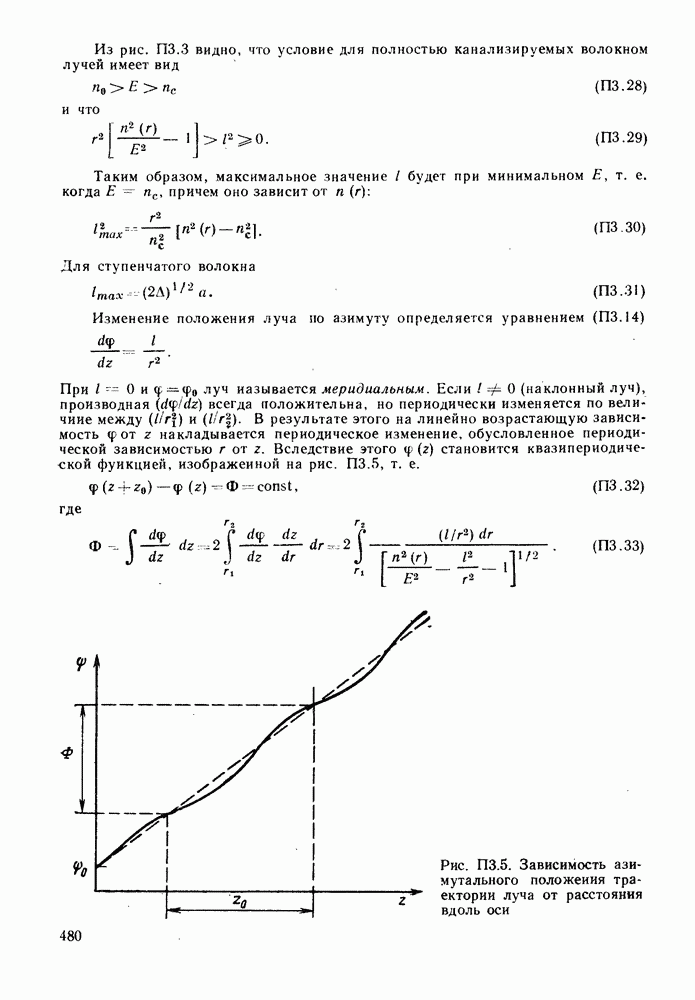
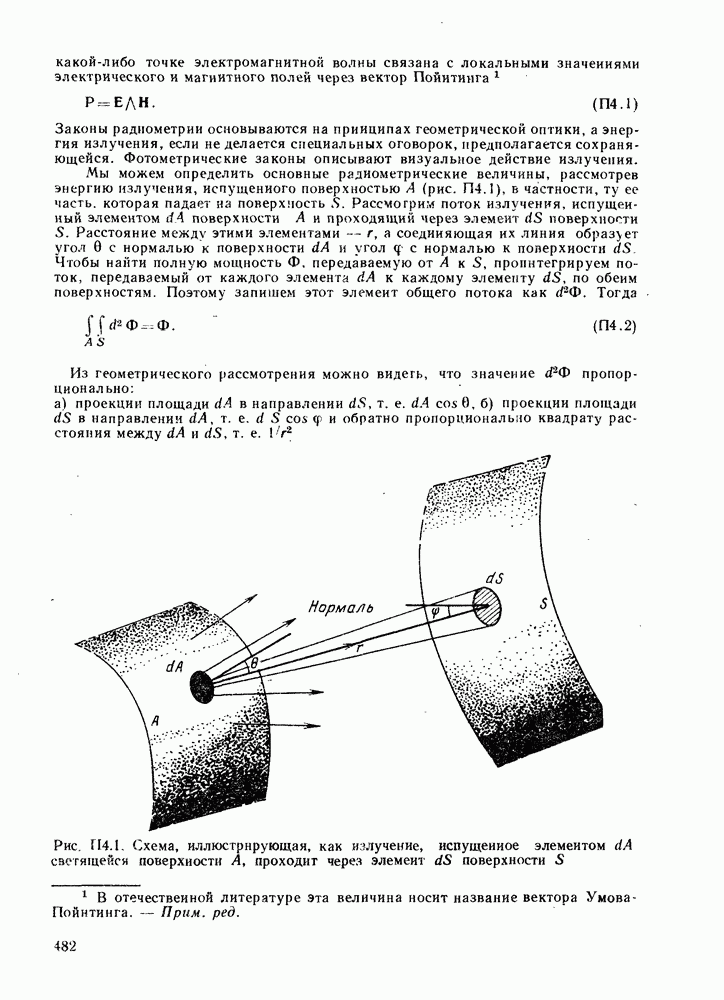
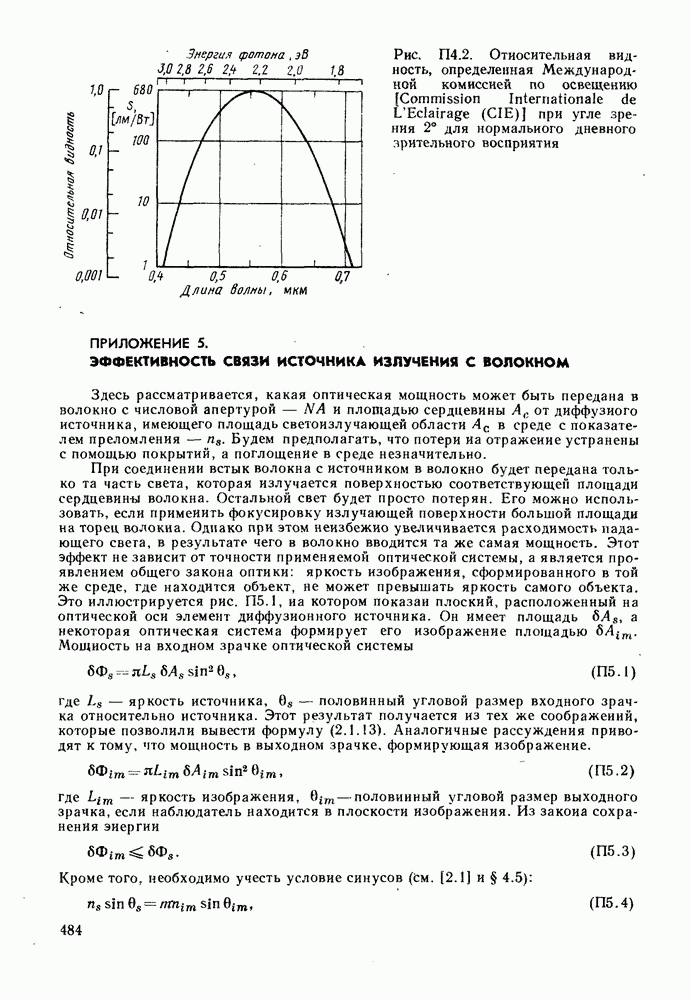
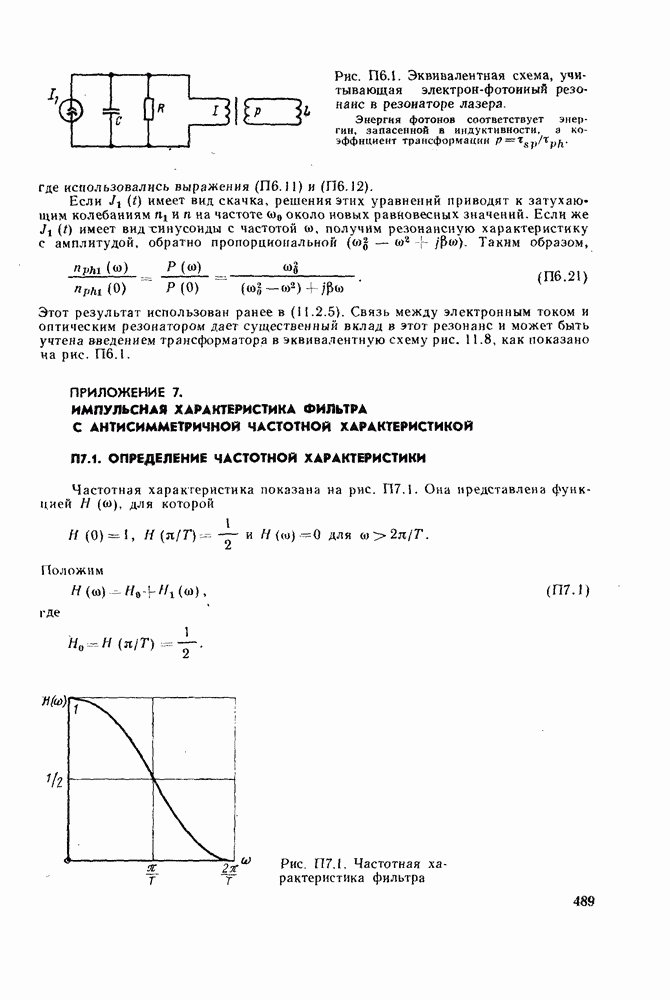
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
Величина шум-фактора  и его зависимость от коэффициента умножения
и его зависимость от коэффициента умножения  имеют большое значение для работы оптических приемников. Зачастую используется аппроксимация
имеют большое значение для работы оптических приемников. Зачастую используется аппроксимация

Типичные значения показателя х лежат в диапазоне между 0,2 и 1,0 в зависимости от материала и типа носителей, вызывающих лавину. Как убедимся позже, соотношение (13.4.1) справедливо во всем диапазоне значений 
В [13.11 получено более сложное выражение. Когда умножение инициируется электронами

Если же лавина вызвана дырками

Графики, соответствующие формулам (13.4.1) и (13.4.2), представлены на рис. 13.9. Можно заметить, что при  в лавине умножается электронный ток, а при
в лавине умножается электронный ток, а при  должны использоваться дырки.
должны использоваться дырки.
Теперь имеются три довода против материалов, в которых к я» 1, и один за выбор вызывающих лавину носителей с высоким коэффициентом ионизации. Как было показано в § 13-1, при этом удается получить более стабильное усиление и единообразные параметры приборов. В § 13.3 убедились, что при этом достигается большая широкополосность. Теперь видим, что и вносимые лавиной шумы при этом также минимизируются.
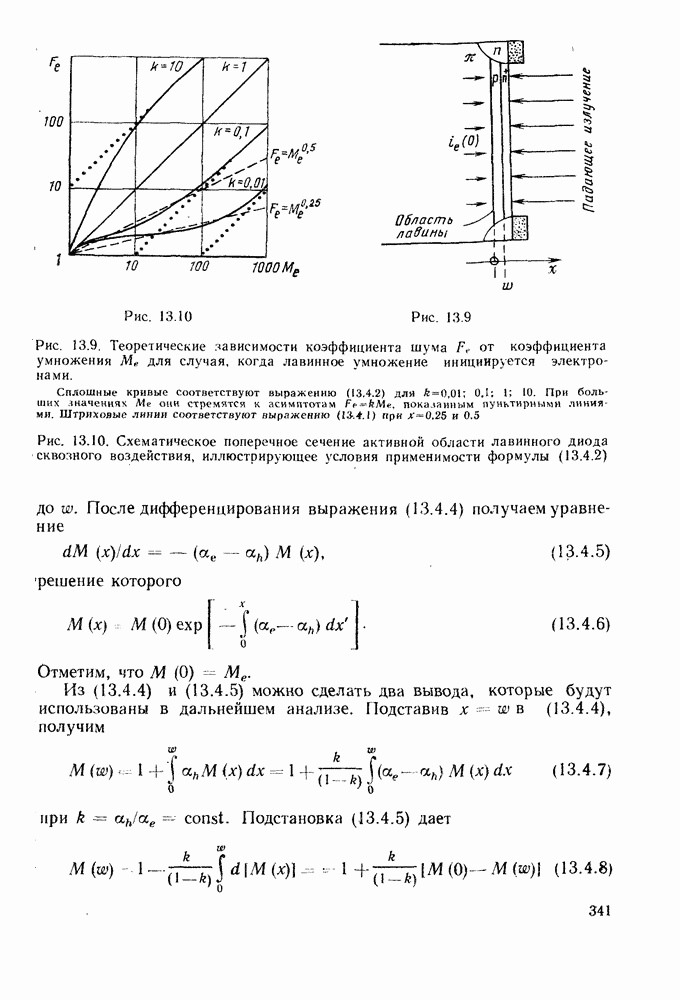
Выведем выражение (13.4.2) для диода, показанного на рис. 13.10, считая, что рожденные при  электроны инициируют лавинный процесс в области
электроны инициируют лавинный процесс в области  Будем пренебрегать инжекцией дырок при
Будем пренебрегать инжекцией дырок при  и генерацией носителей между
и генерацией носителей между  до, исключая долю лавинного процесса, т. е. пренебрегается оптической и тепловой генерацией носителей. В § 13.1 получено выражение (13.1.10) для коэффициента умножения
до, исключая долю лавинного процесса, т. е. пренебрегается оптической и тепловой генерацией носителей. В § 13.1 получено выражение (13.1.10) для коэффициента умножения  который относится к электронам, поступающим при
который относится к электронам, поступающим при  Чтобы получить численное значение коэффициента шума, нужно рассмотреть коэффициент умножения
Чтобы получить численное значение коэффициента шума, нужно рассмотреть коэффициент умножения  для генерации пар носителей в некоторой точке х, лежащей в области лавины. Это
для генерации пар носителей в некоторой точке х, лежащей в области лавины. Это

Второй член в правой части этого выражения описывает умножение дырок, рожденных в точке х, в процессе их продвижения к  Последний член соответствует умножению электронов на интервале от х
Последний член соответствует умножению электронов на интервале от х

Рис. 13.9. Теоретические зависимости коэффициента шума  от коэффициента умножения
от коэффициента умножения  для случая, когда лавинное умножение инициируется электронами. Сплошные кривые соответствуют выражению (13.4.2) для
для случая, когда лавинное умножение инициируется электронами. Сплошные кривые соответствуют выражению (13.4.2) для  При больших значениях
При больших значениях  они стремятся к асимптотам
они стремятся к асимптотам  показанным пунктирными линиями. Штриховые линии соответствуют выражению
показанным пунктирными линиями. Штриховые линии соответствуют выражению  при
при  и 0,5
и 0,5

Рис. 13.10. Схематическое поперечное сечение активной области лавинного диода сквозного воздействия, иллюстрирующее условия применимости формулы (13.4.2)
до  После дифференцирования выражения (13.4.4) получаем уравнение
После дифференцирования выражения (13.4.4) получаем уравнение

решение которого

Отметим, что 
Из (13.4.4) и (13.4.5) можно сделать два вывода, которые будут использованы в дальнейшем анализе. Подставив  в (13.4.4), получим
в (13.4.4), получим

при  Подстановка (13.4.5) дает
Подстановка (13.4.5) дает

или

Сделав аналогичные подстановки в интеграле  получим
получим

Теория лавинных шумов основана на двух предпосылках, связанных с генерацией носителей в точке х, о том, что они будут умножены на коэффициент  и создаются в независимых случайных процессах и, таким образом, имеют природу теплового шума. Пренебрежем всеми переходными эффектами и ограничениями на частотную полосу. Из гл. 12 видно, что среднеквадратическое значение шума в единичной полосе частот, связанное с генерацией среднего случайного тока —
и создаются в независимых случайных процессах и, таким образом, имеют природу теплового шума. Пренебрежем всеми переходными эффектами и ограничениями на частотную полосу. Из гл. 12 видно, что среднеквадратическое значение шума в единичной полосе частот, связанное с генерацией среднего случайного тока —  есть
есть  Будем называть его среднеквадратической спектральной плотностью шума и отмечать звездочкой. Таким образом,
Будем называть его среднеквадратической спектральной плотностью шума и отмечать звездочкой. Таким образом,

На интервале  вблизи точки генерируется электронный ток
вблизи точки генерируется электронный ток

Очевидно, что величина генерируемого дырочного тока та же самая, но мы совершенно произвольно выбрали для анализа электронный ток. С этим током связано среднеквадратическое значение спектральной плотности, шума  Можно предполагать, что как ток
Можно предполагать, что как ток  так и связанный с ним среднеквадратический шум
так и связанный с ним среднеквадратический шум  умножаются в диоде на коэффициент
умножаются в диоде на коэффициент  Генерируемый в элементе
Генерируемый в элементе  шум независим, а значит, некоррелирован с любым шумом, генерируемым в другом месте, так что среднеквадратическое значение спектральной плотности полного шума в лавинной области
шум независим, а значит, некоррелирован с любым шумом, генерируемым в другом месте, так что среднеквадратическое значение спектральной плотности полного шума в лавинной области

Интегрируя по частям,

Подставив пределы в первом слагаемом правой части и упростив, используя (14.4.5), второе слагаемое,

Полный ток

поскольку  а также
а также

Таким образом,

Подставим (13.4.17) в последний член правой части (13.4.15) и проинтегрируем

В первом слагаемом использовано выражение (13.4.16), а во втором

Среднеквадратический шум  генерируемый в процессе умножения, должен быть дополнен умноженным среднеквадратическим шумом в первичном электронном токе,-т. е.
генерируемый в процессе умножения, должен быть дополнен умноженным среднеквадратическим шумом в первичном электронном токе,-т. е.

Шум-фактор  был определен как отношение полного шума к умноженному тепловому шуму, так что
был определен как отношение полного шума к умноженному тепловому шуму, так что

или

Используя равенство (13.4.9),

Таким образом,

Если  велико, то
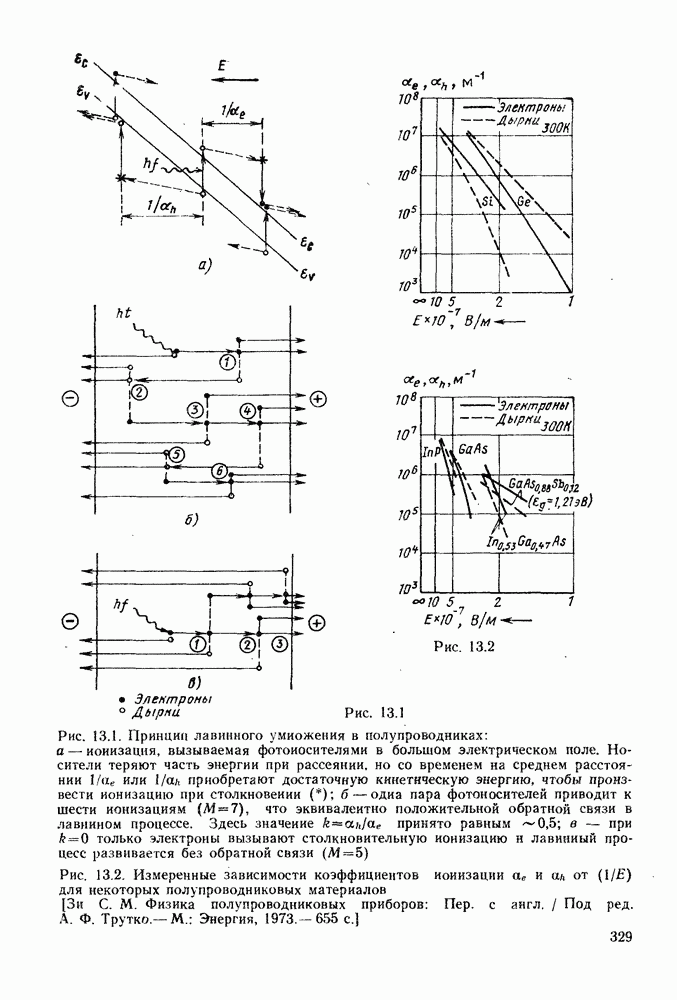
велико, то  и желательно работать с малыми значениями к при использовании электронной инжекции. Вообще отношение электронного коэффициента ионизации к дырочному максимально в слабых полях и снижается с ростом поля. Это можно видеть на рис.
и желательно работать с малыми значениями к при использовании электронной инжекции. Вообще отношение электронного коэффициента ионизации к дырочному максимально в слабых полях и снижается с ростом поля. Это можно видеть на рис.

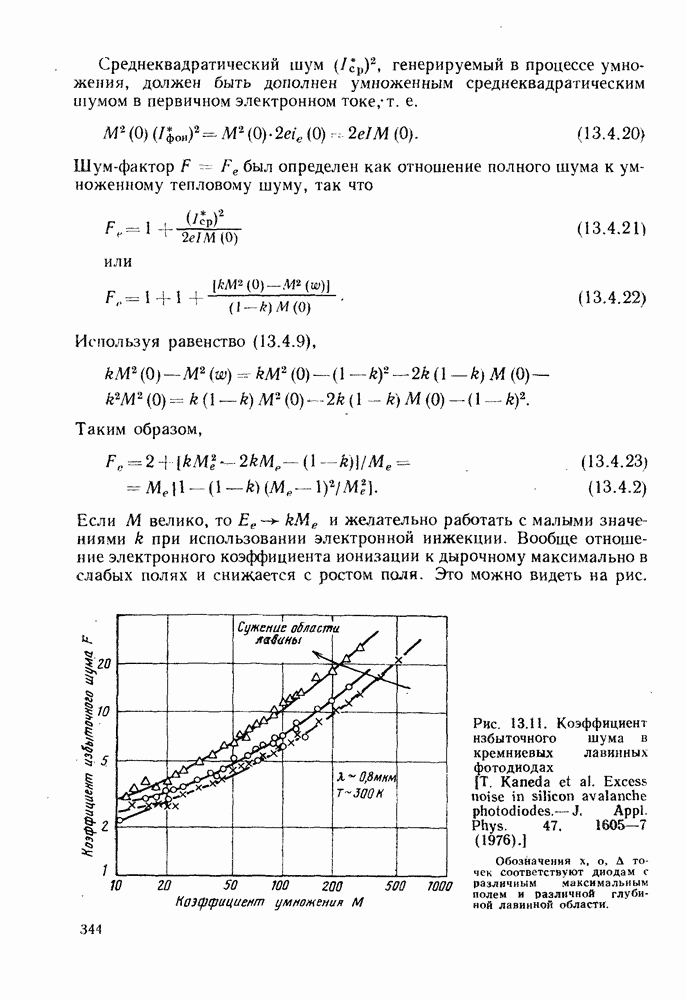
Рис. 13.11. Коэффициент избыточного шума в кремниевых лавинных фотодиодах [Т. Kaneda et al. Excess noise in silicon avalanche photodiodes.- J, Appl. Phys. 47. 1605-7 (1976).] Обозначения  А точек соответствуют диодам с различным максимальным полем и различной глубиной лавинной области.
А точек соответствуют диодам с различным максимальным полем и различной глубиной лавинной области.
13.2 для германия и кремйия. Этот эффект приводит к увеличению шум-фактора при работе с очень тонкой лавинной областью, поскольку в таком случае для получения заданного коэффициента умножения необходимо увеличивать среднюю напряженность поля. Эффект иллюстрируется рис. 13.11.
ЗАДАЧИ
(см. скан)
РЕЗЮМЕ
Первичный фототок в электрических полях в несколько десятков мегавольт на метр умножается в процессе лавинной ионизации электронами и дырками. Коэффициент умножения  ограничивается образованием микроплазмы. Теоретическая зависимость коэффициента шума от
ограничивается образованием микроплазмы. Теоретическая зависимость коэффициента шума от  приведена в § 13.4. На практике может использоваться аппроксимация вида
приведена в § 13.4. На практике может использоваться аппроксимация вида 
В лавине выгоднее использовать инициирующие носители с высоким коэффициентом ионизации. При этом получается самое высокое усиление, самая хорошая частотная характеристика и самый низкий коэффициент шума.
В кремниевых лавинных фотодиодах, особенно при низких полях,  Таким образом, в
Таким образом, в  -диодах со сквозным воздействием, показанных на рис. 13.3 и 13.4, умножается электронный ток. Коэффициент шума может быть снижен до
-диодах со сквозным воздействием, показанных на рис. 13.3 и 13.4, умножается электронный ток. Коэффициент шума может быть снижен до  при
при  но при использовании более высоких электрических полей могут быть достигнуты лучшие квантовая эффективность (которая может приближаться к
но при использовании более высоких электрических полей могут быть достигнуты лучшие квантовая эффективность (которая может приближаться к  и полоса частот (которая может доходить до
и полоса частот (которая может доходить до  а также простота изготовления. При этом коэффициент шума может возрасти до 6—10 при
а также простота изготовления. При этом коэффициент шума может возрасти до 6—10 при  .
.
В германии электронный и дырочный коэффициенты ионизации одного порядка  . В этом случае из теории следует
. В этом случае из теории следует  что наблюдается и на практике. Германиевые лавинные фотодиоды могут иметь
что наблюдается и на практике. Германиевые лавинные фотодиоды могут иметь  и полосу в несколько гигагерц, но для них характерны высокие значения темнового тока.
и полосу в несколько гигагерц, но для них характерны высокие значения темнового тока.
Коэффициент умножения в  полупроводниковых гетероструктурах в настоящее время ограничивается токами утечки и возникновением микроплазмы.
полупроводниковых гетероструктурах в настоящее время ограничивается токами утечки и возникновением микроплазмы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
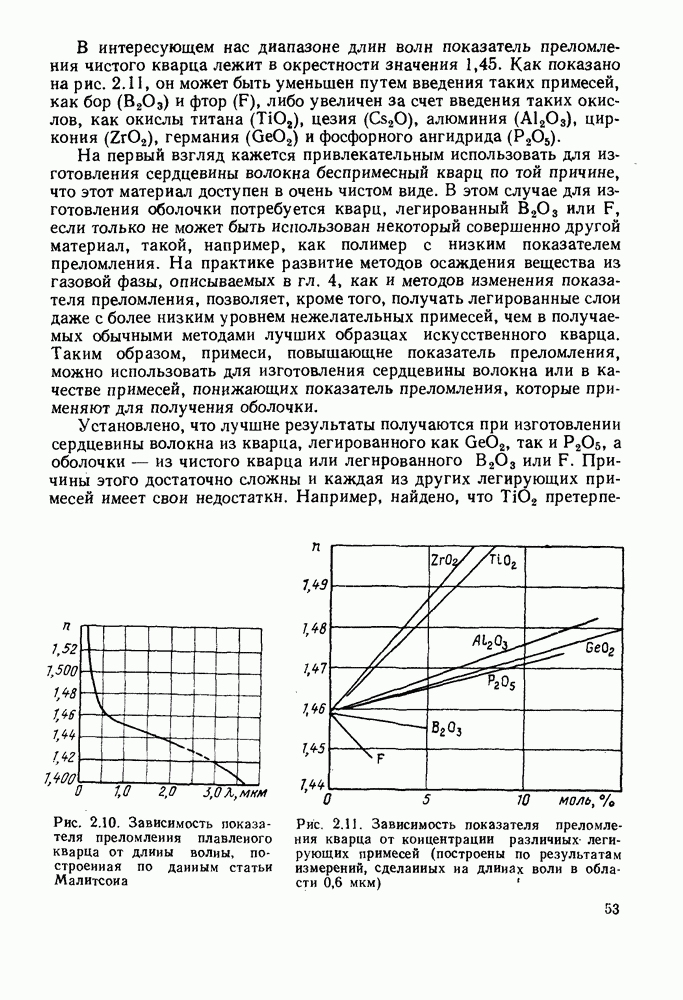
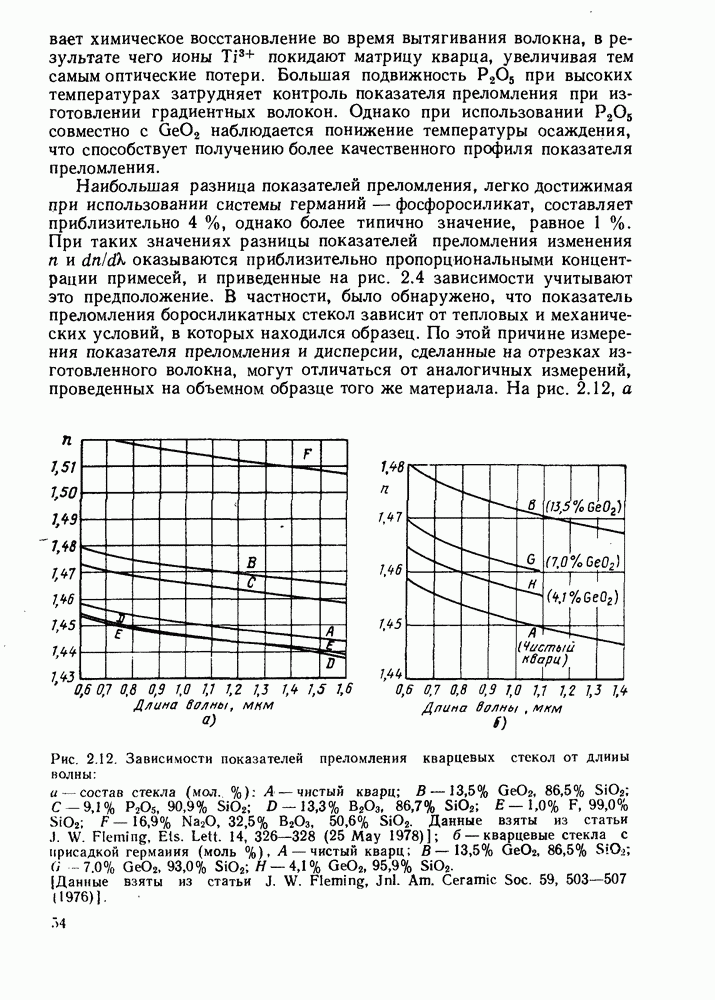
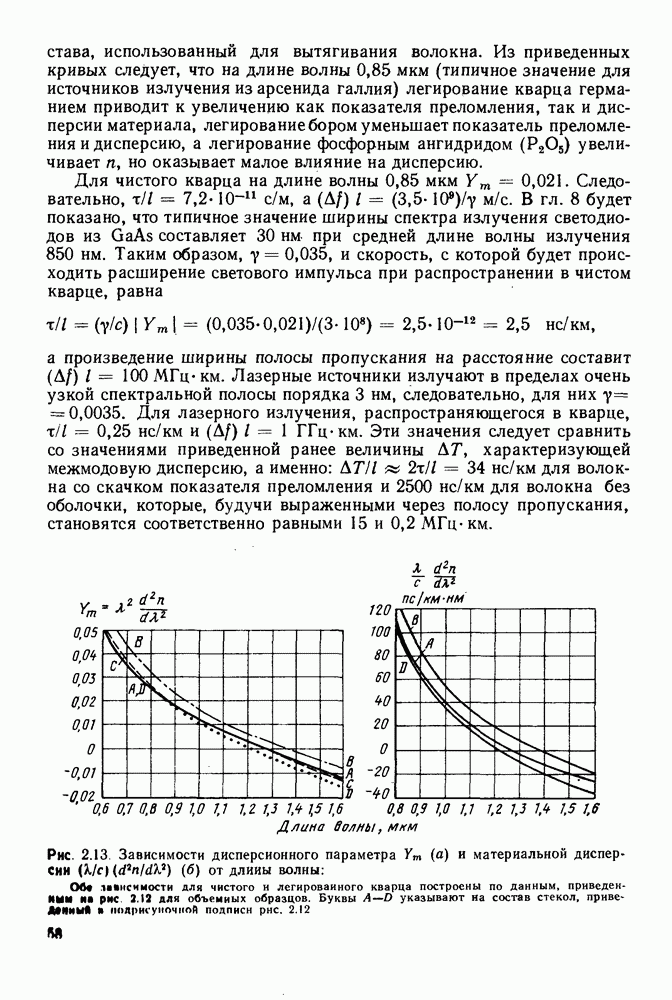
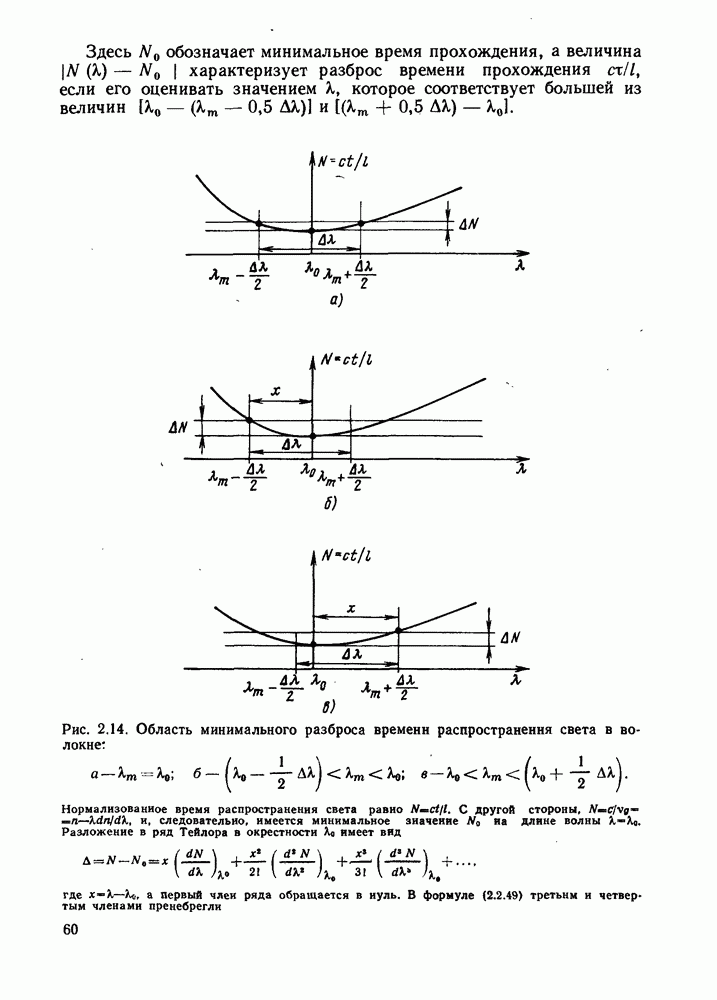
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
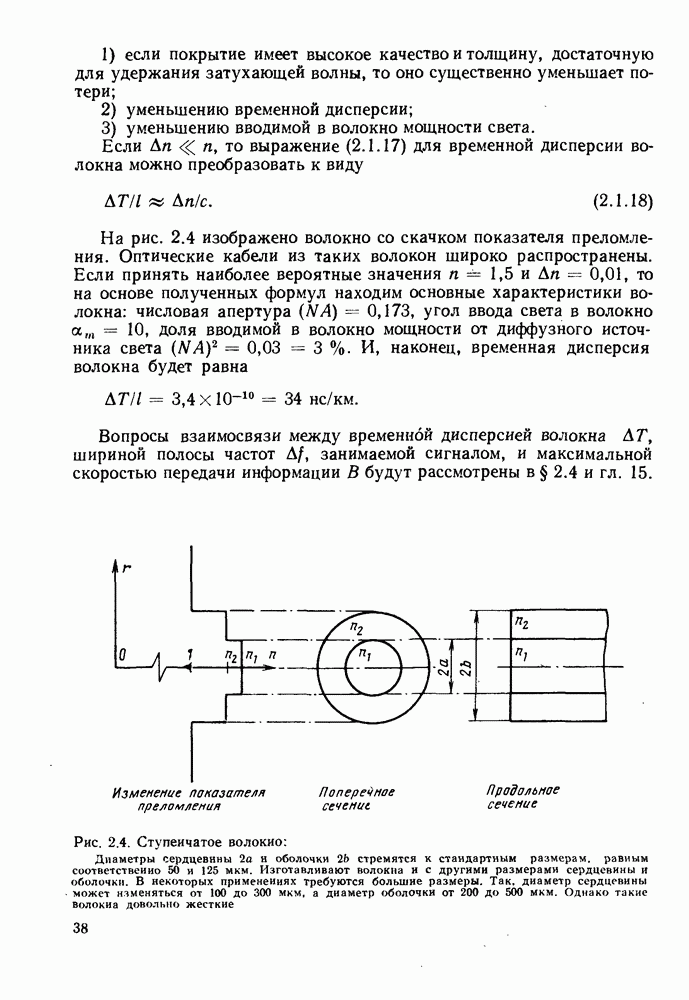
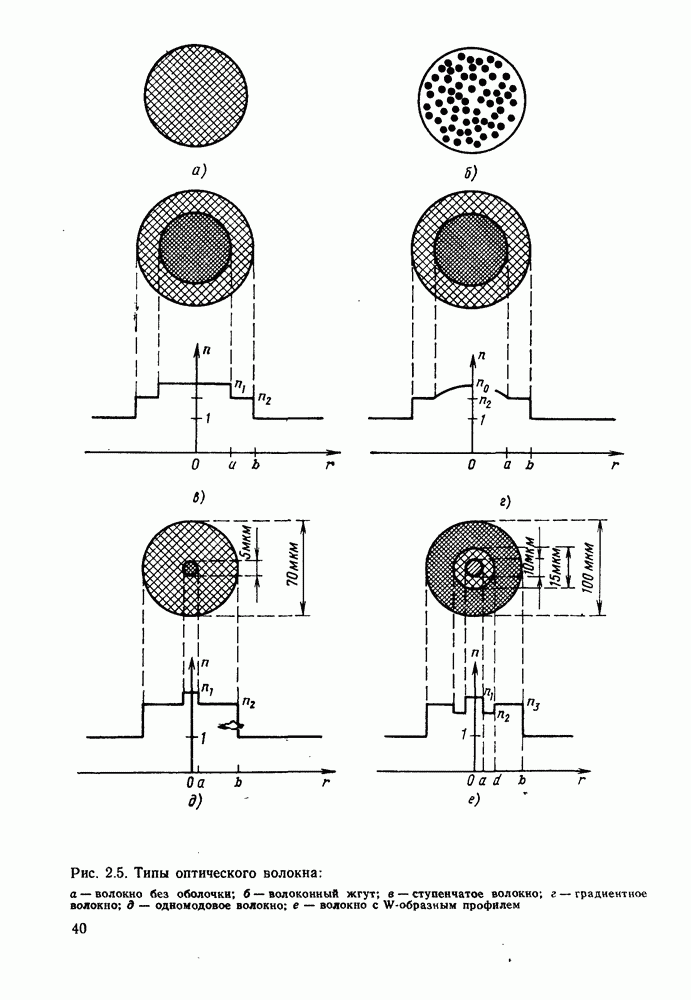
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
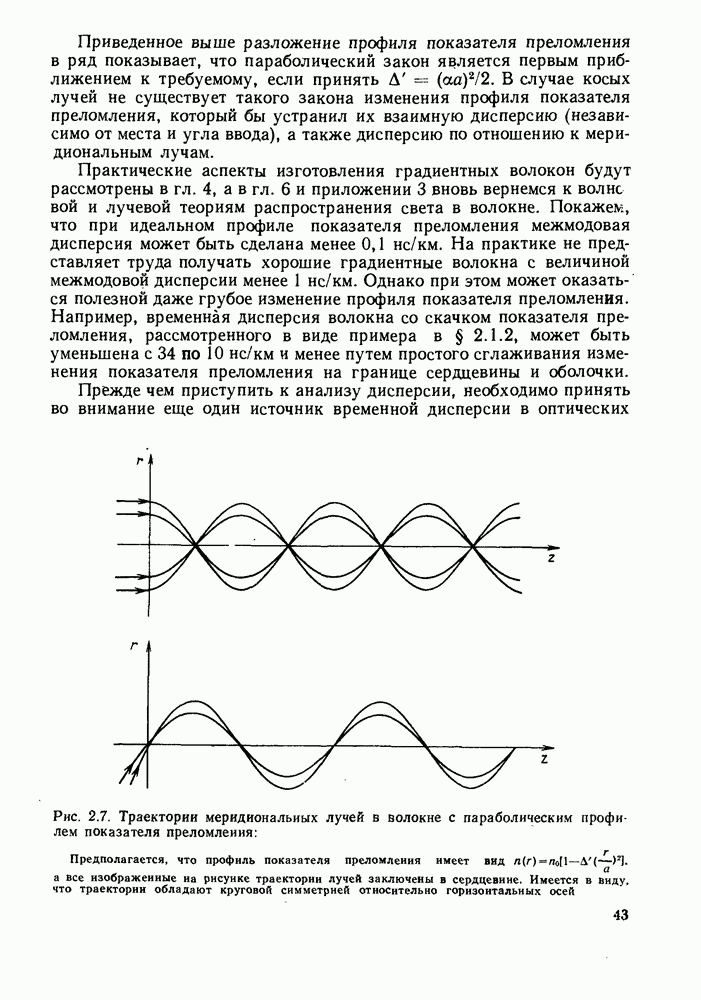
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
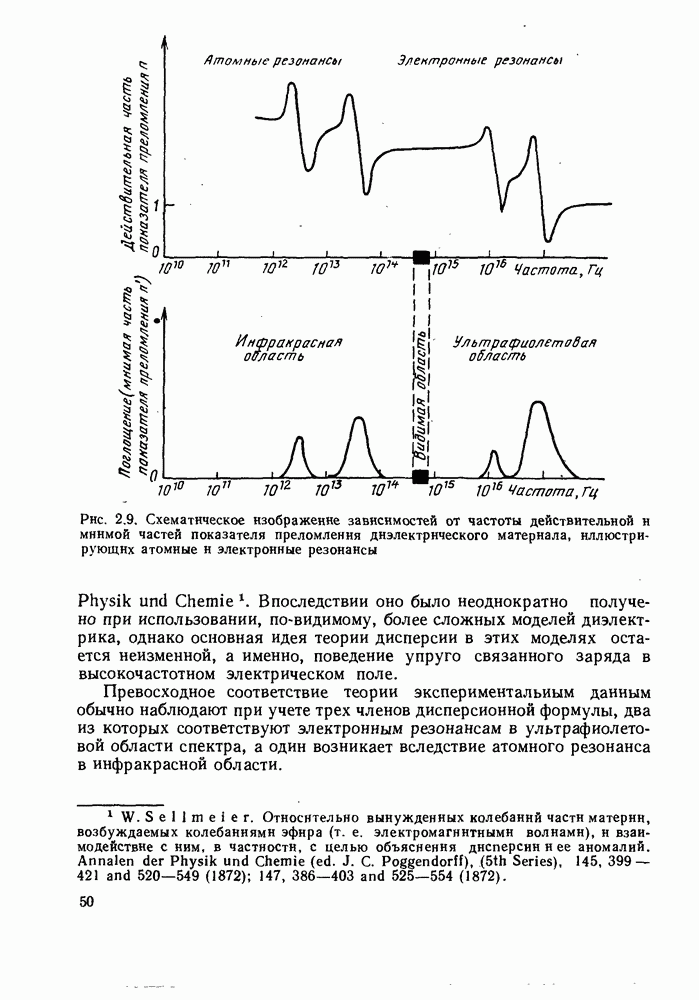
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
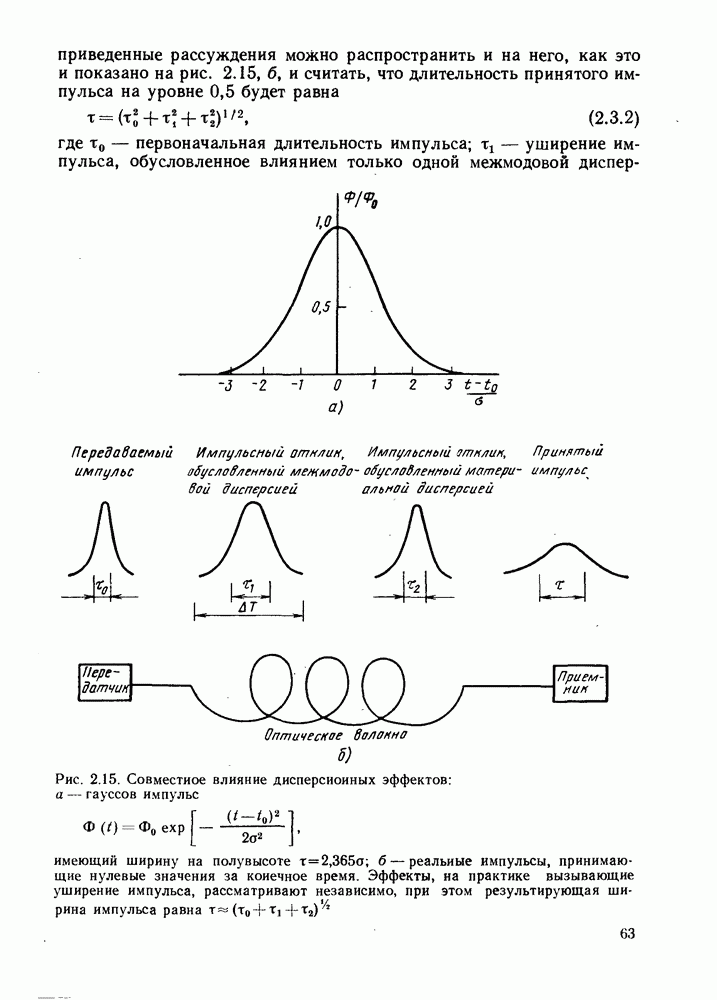
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
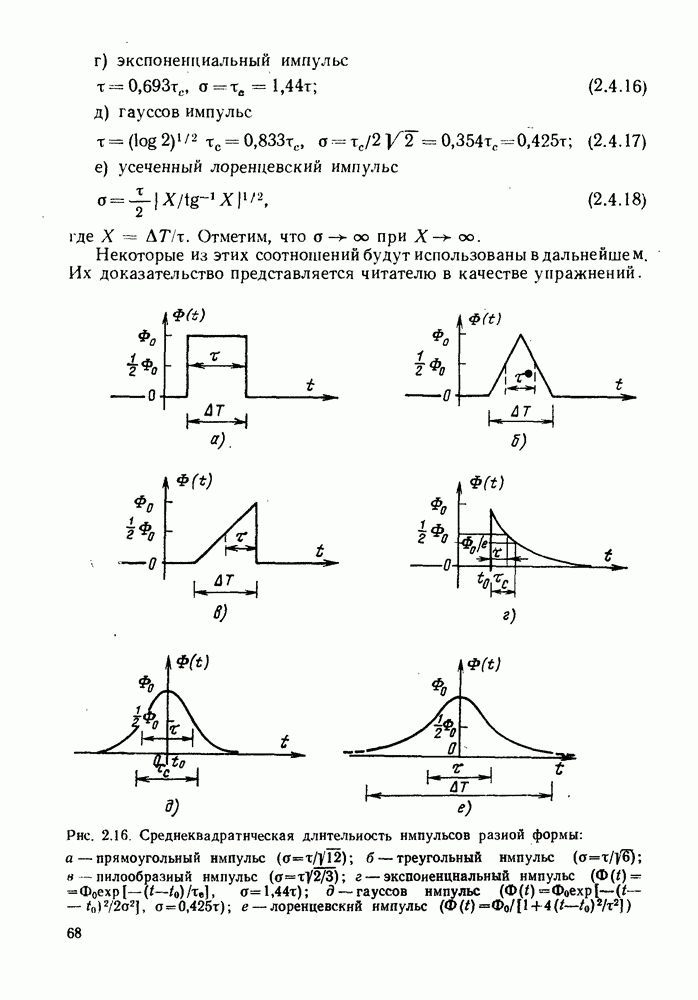
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
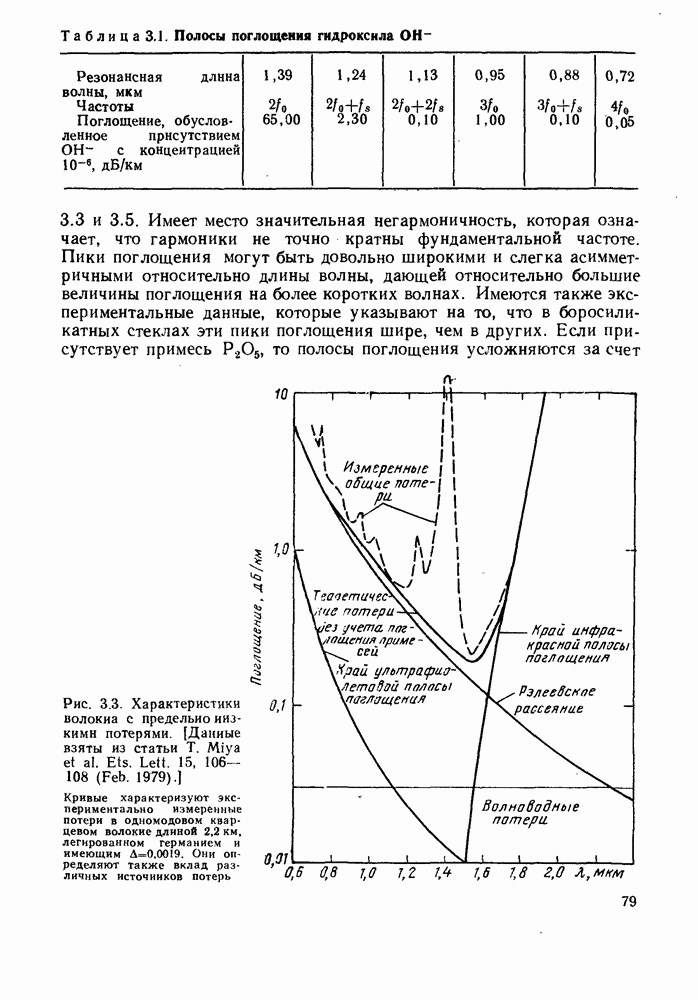
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
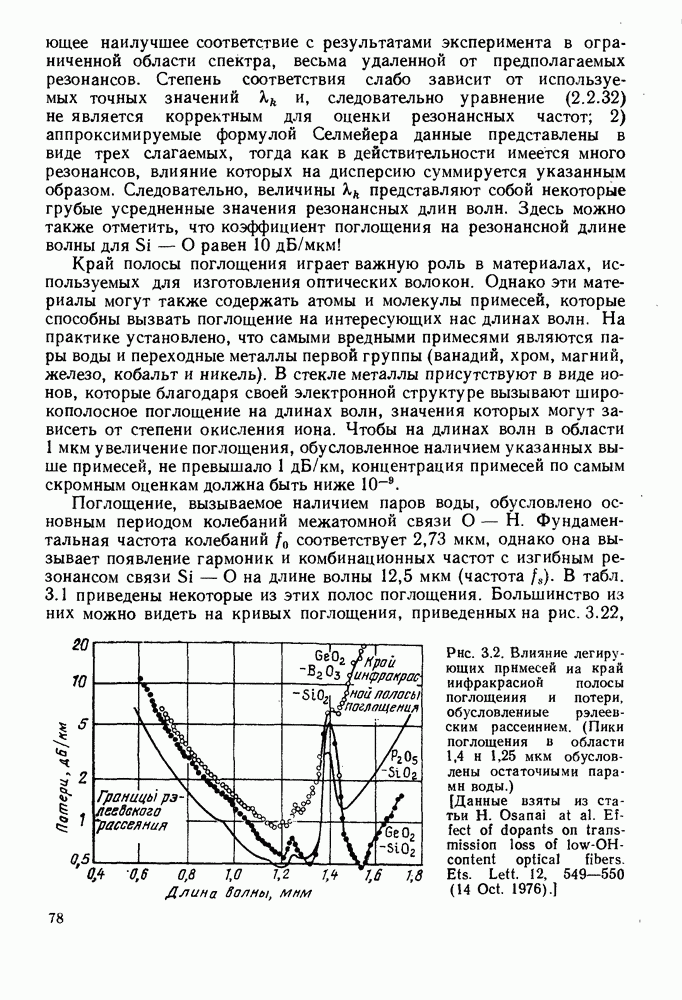
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
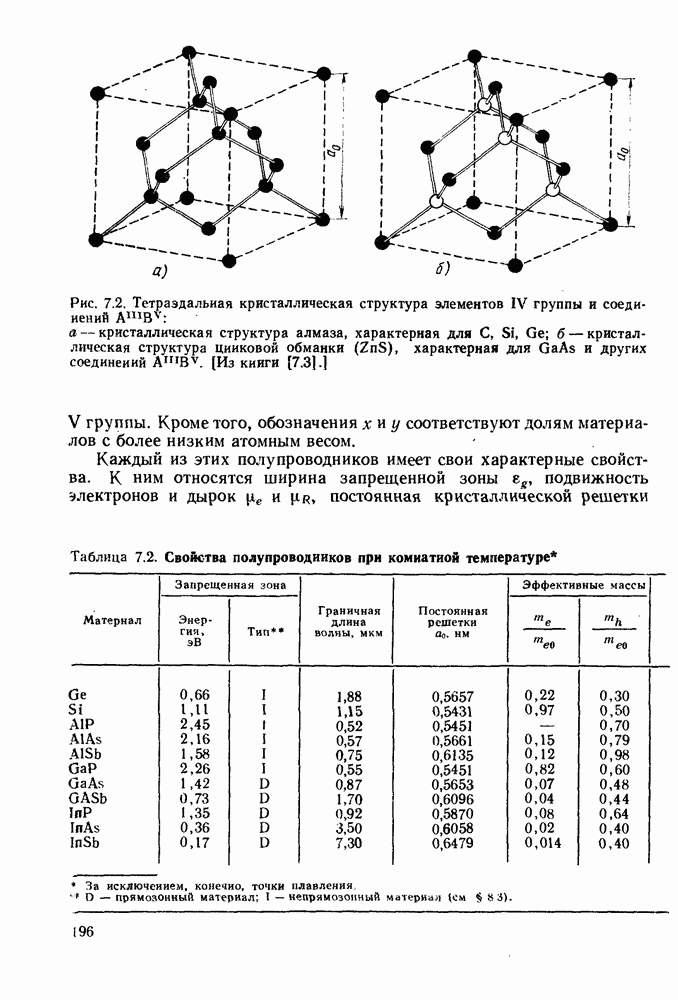
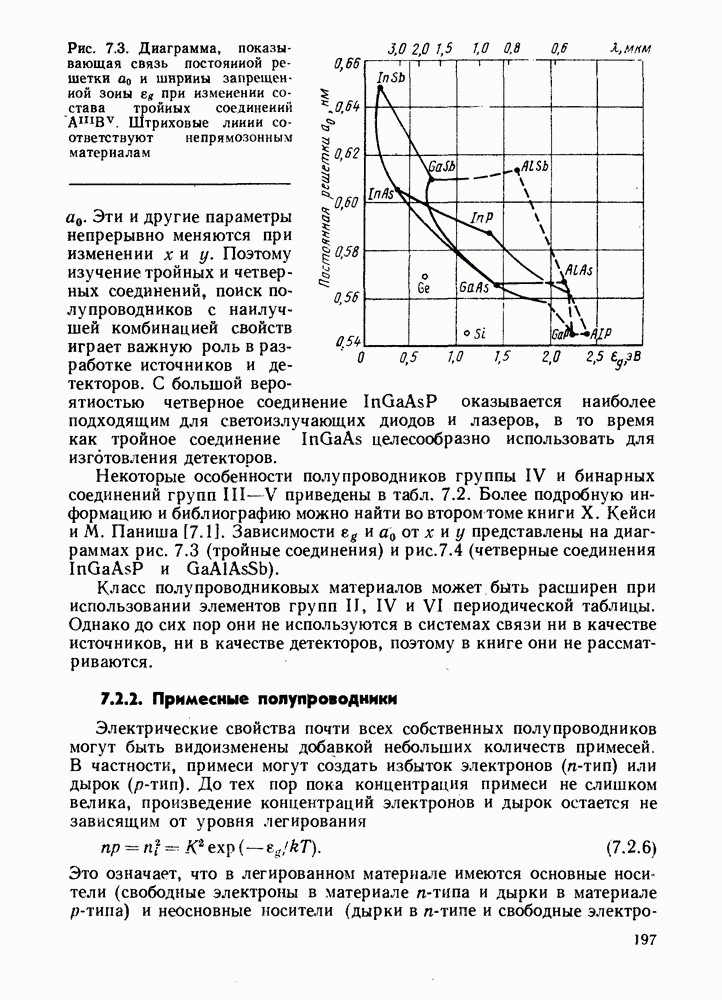
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
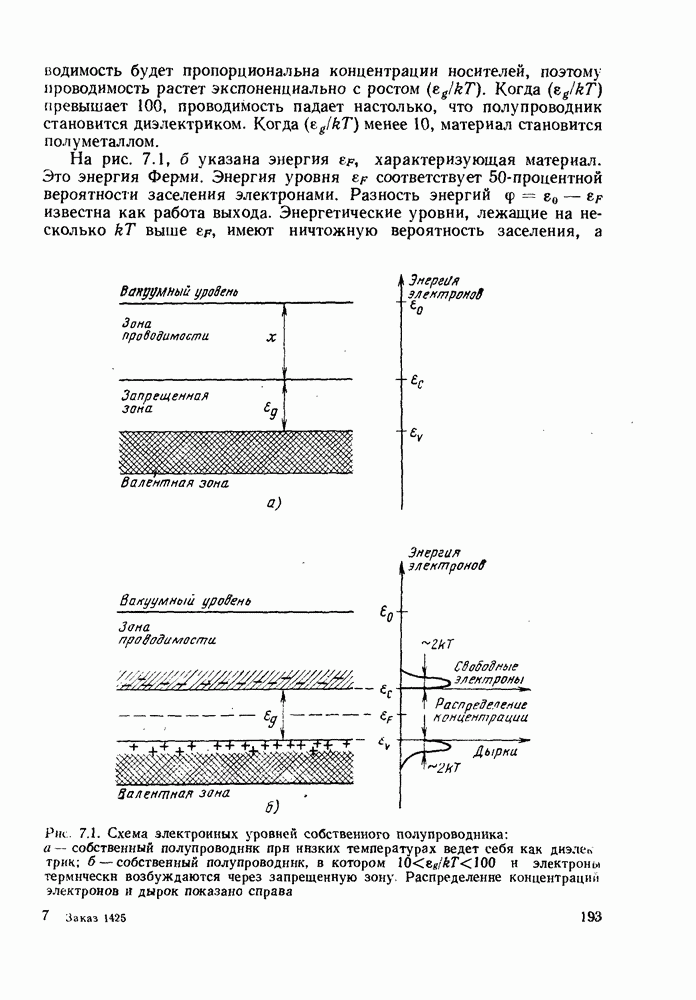
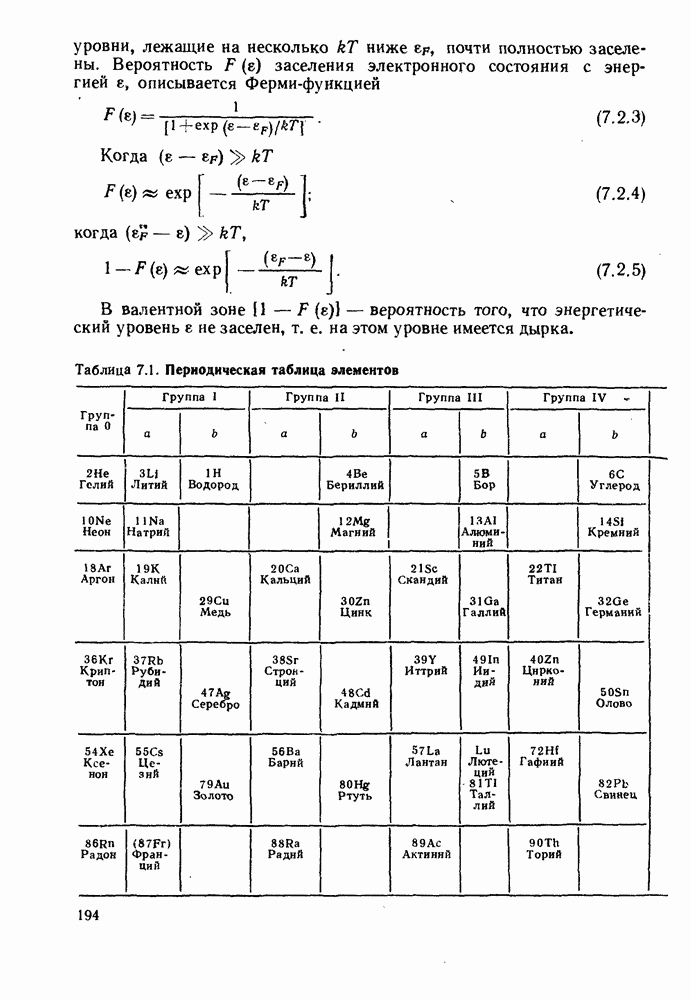
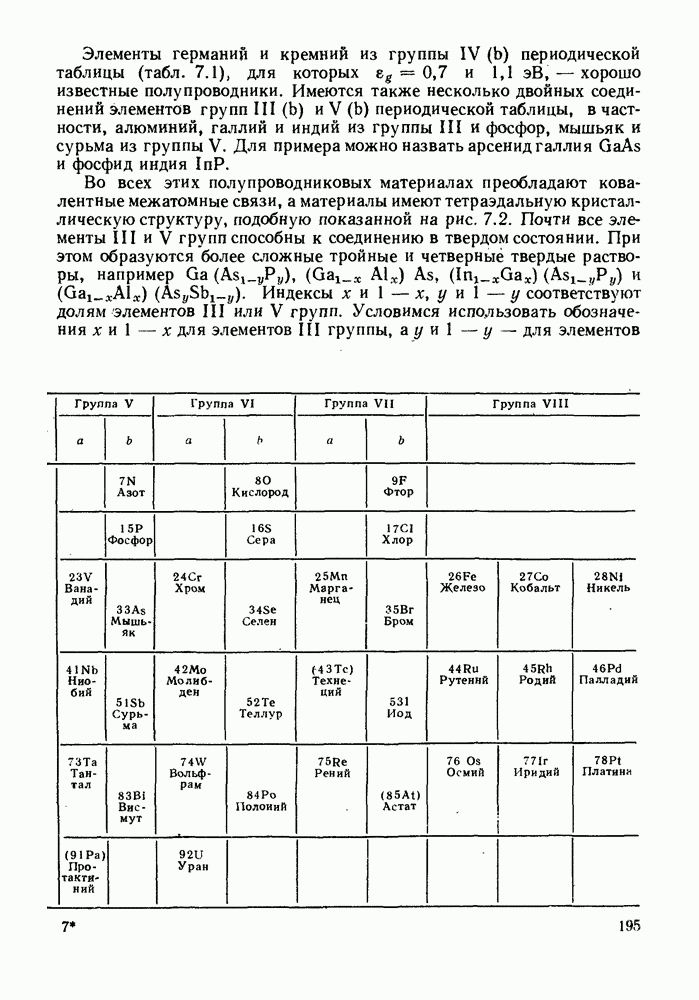
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
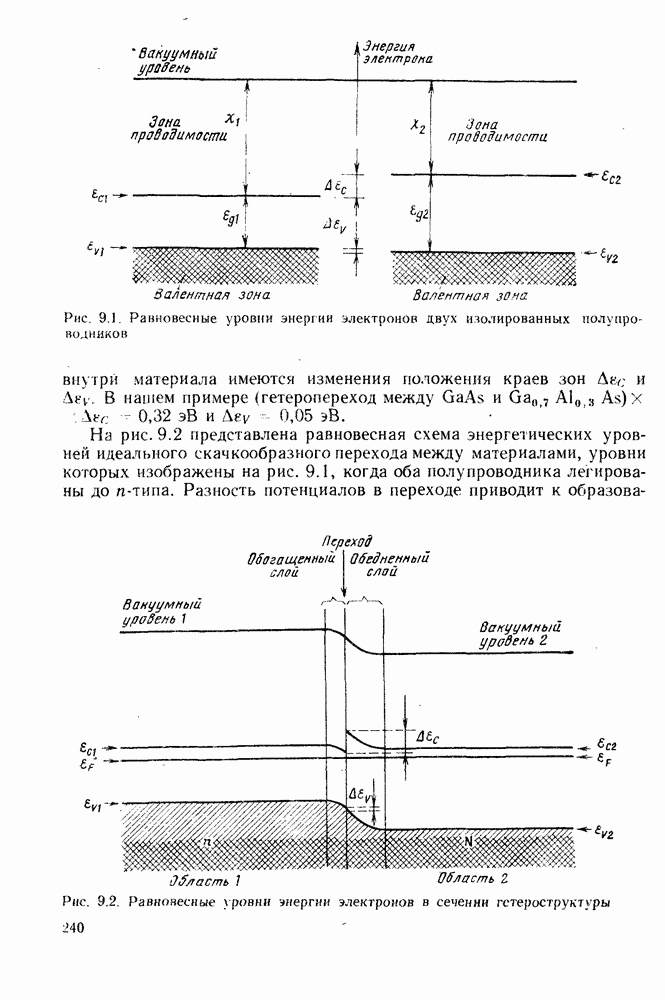
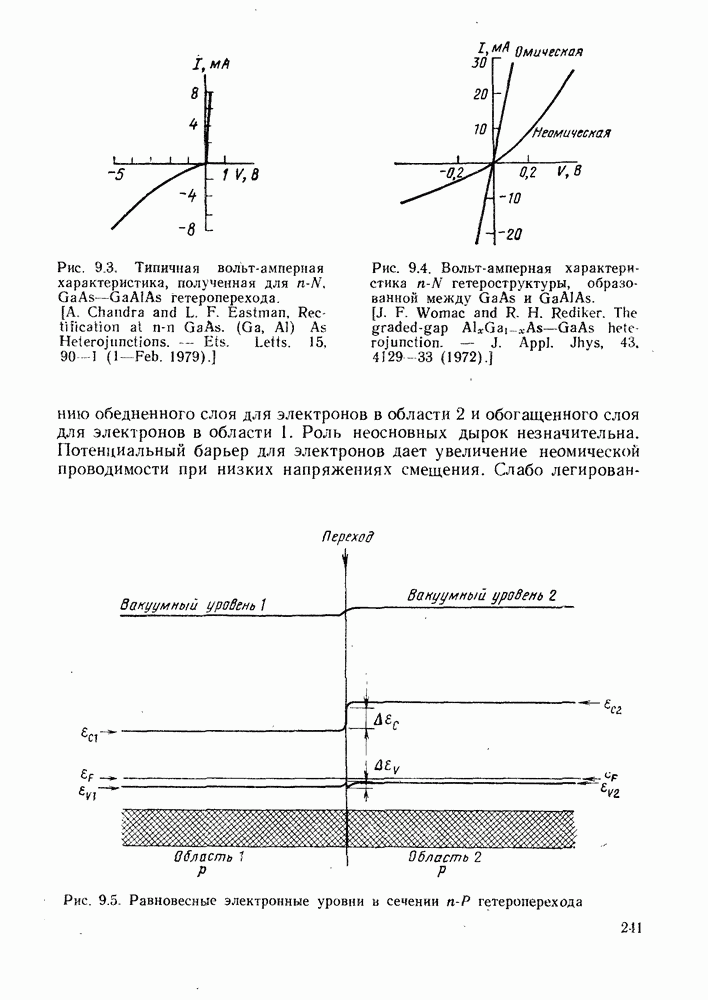
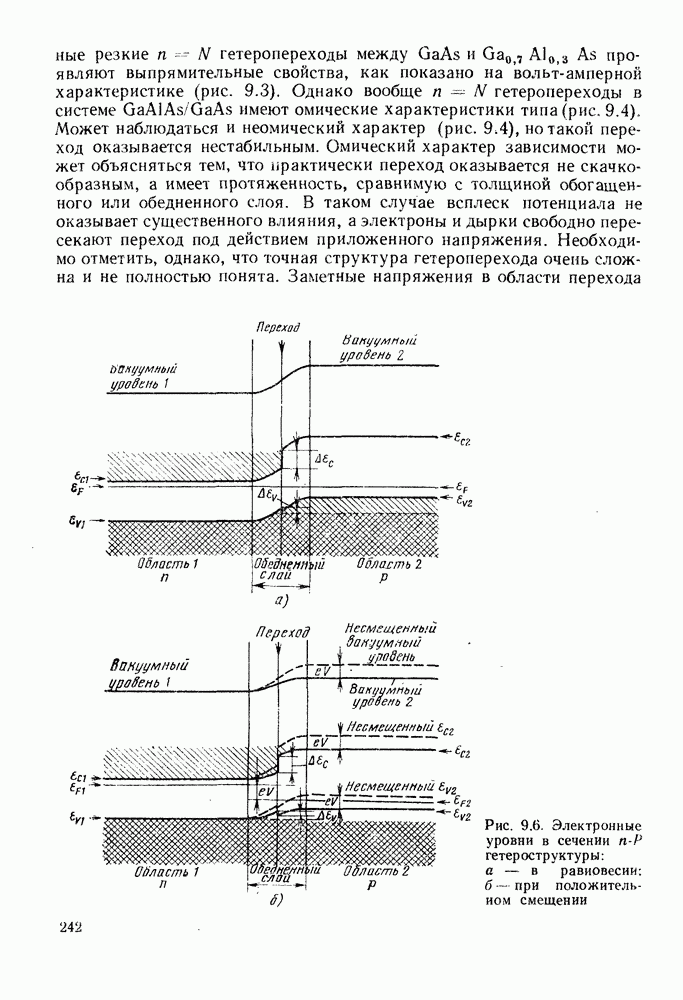
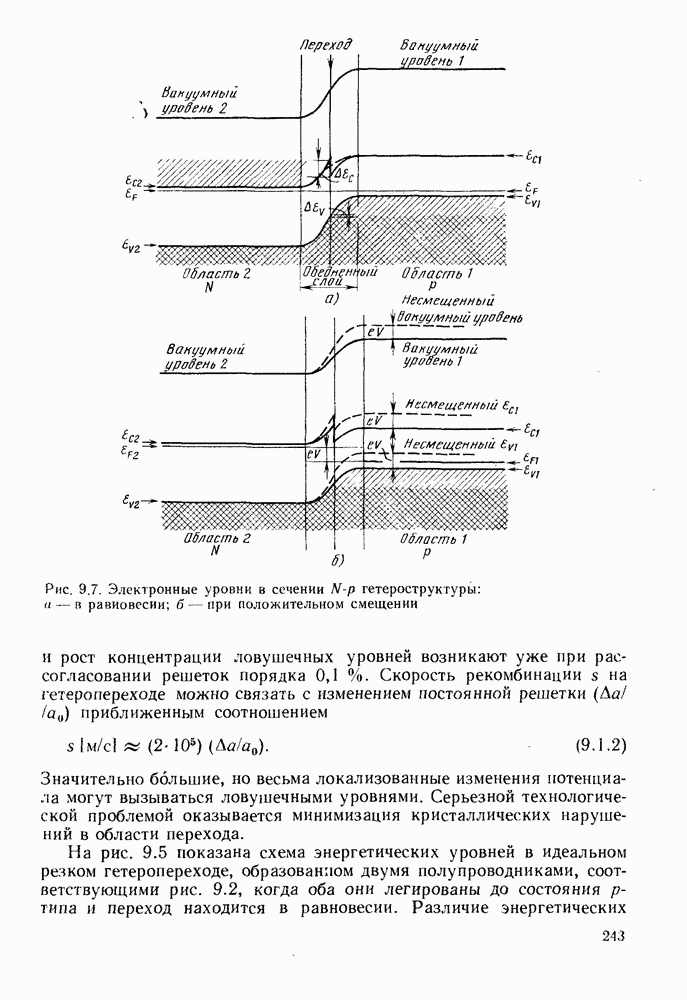
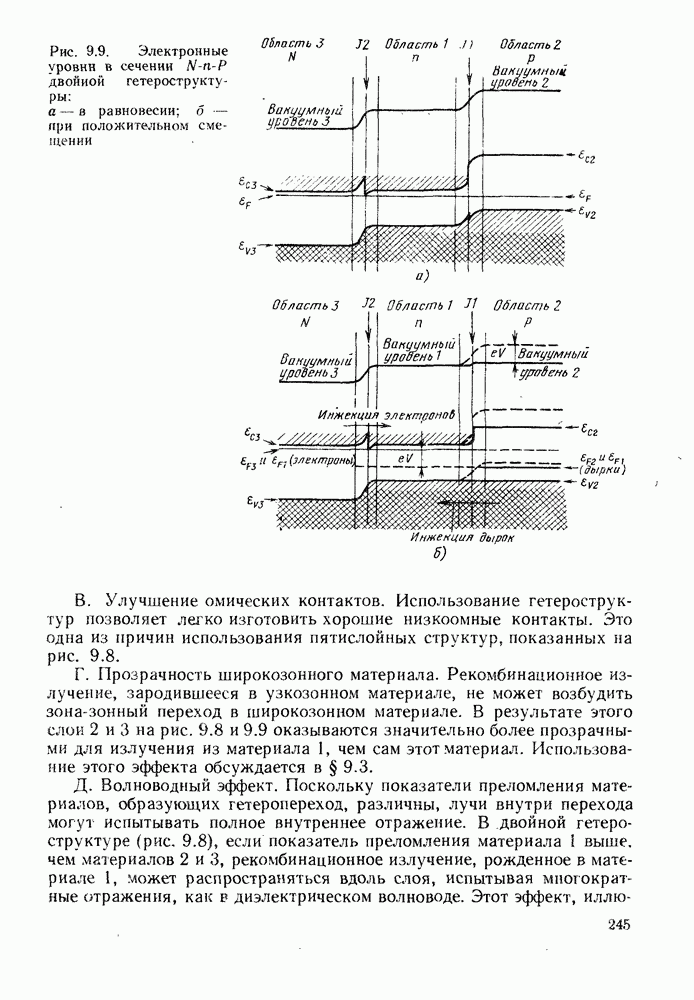
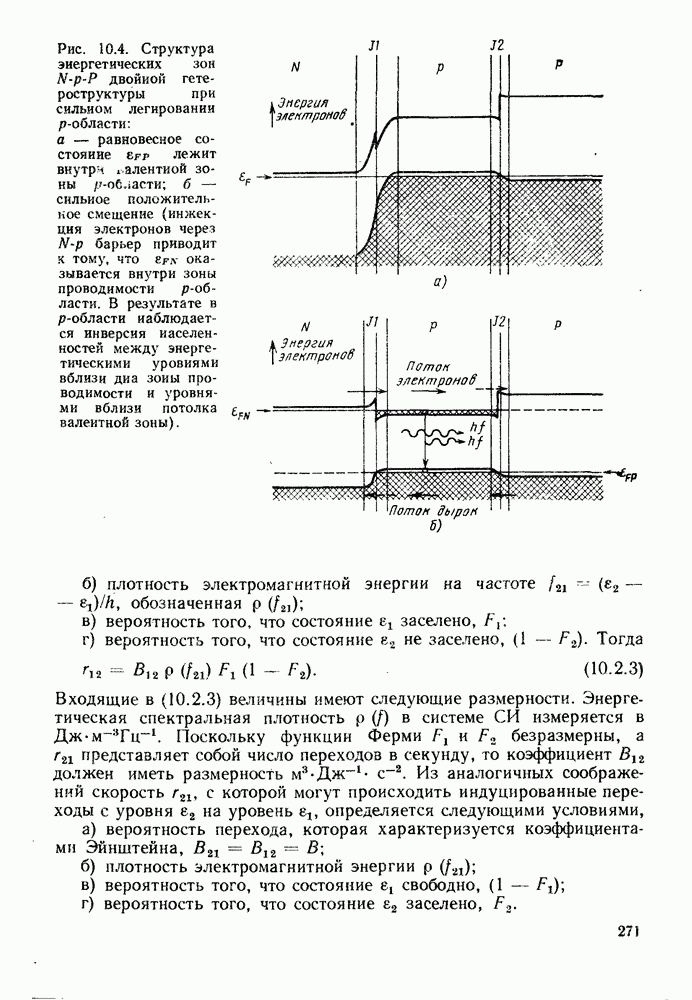
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
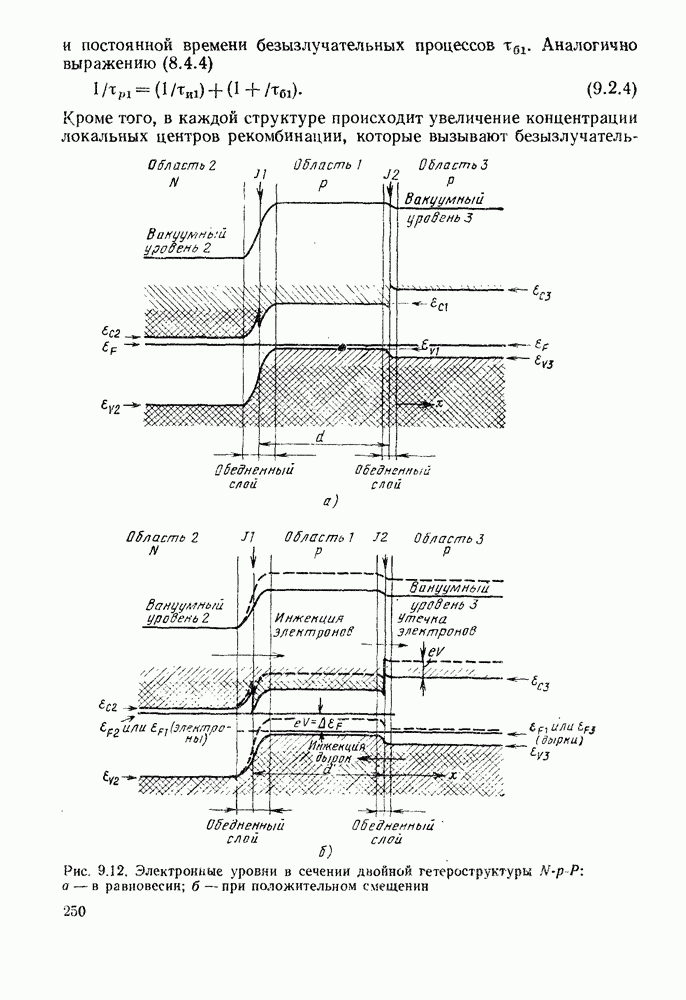
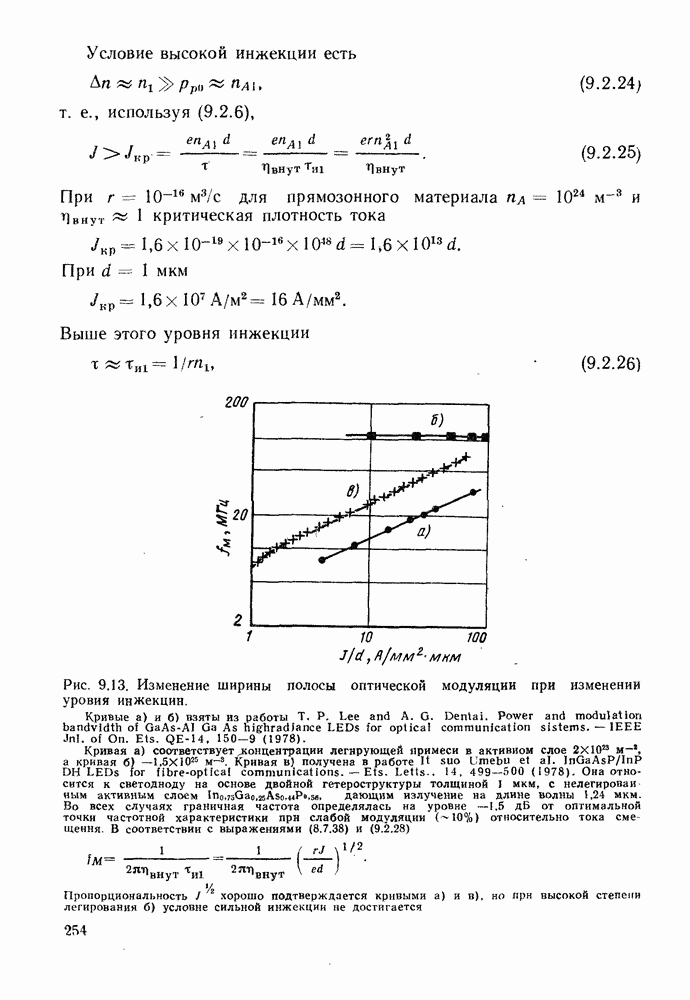
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
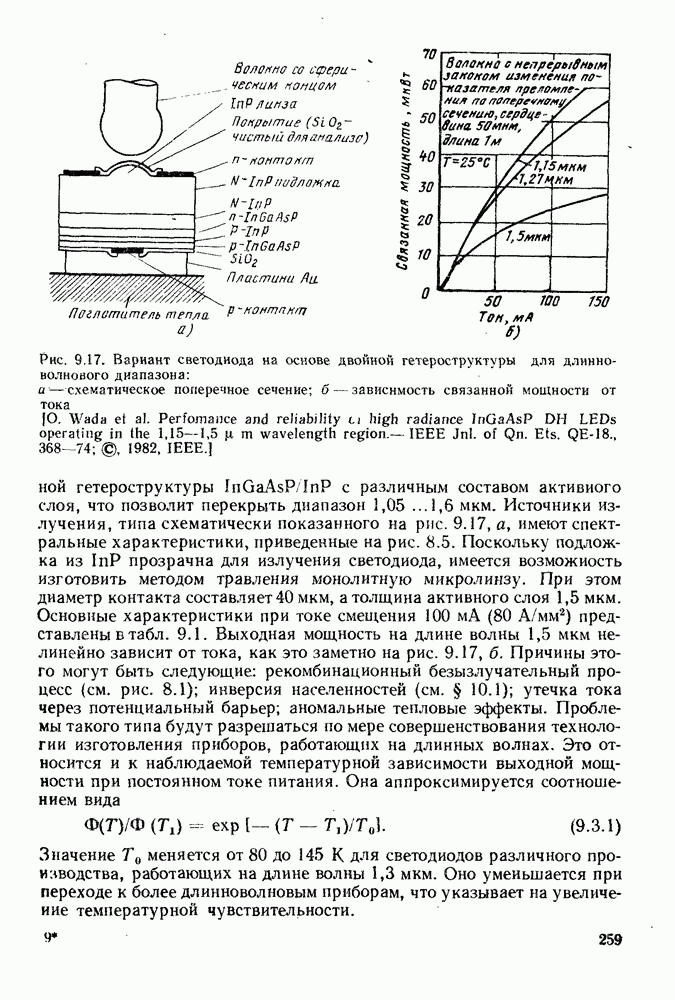
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
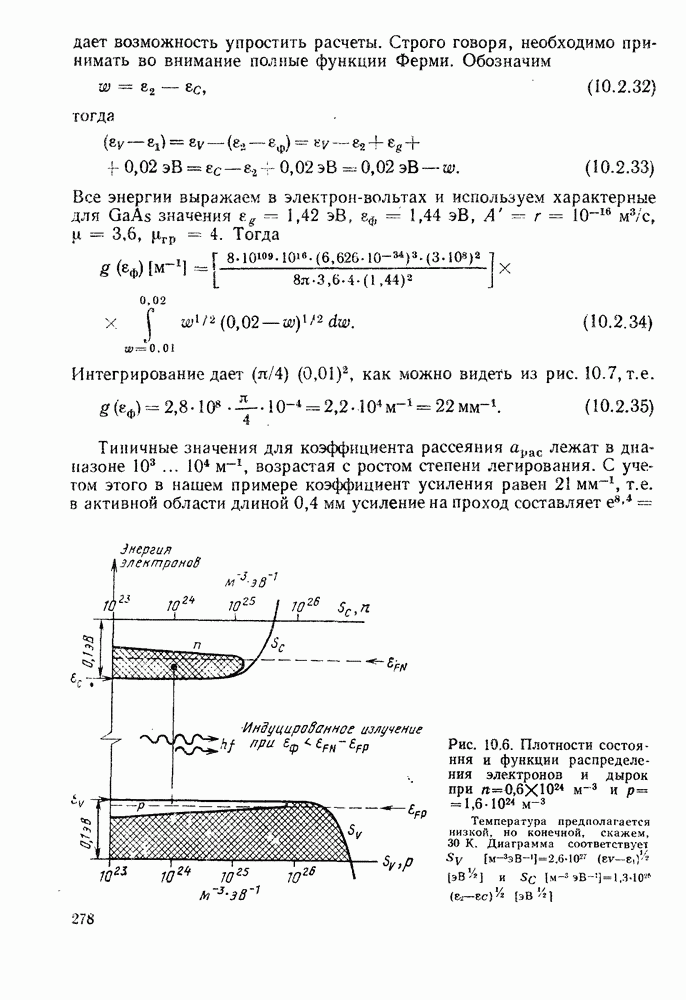
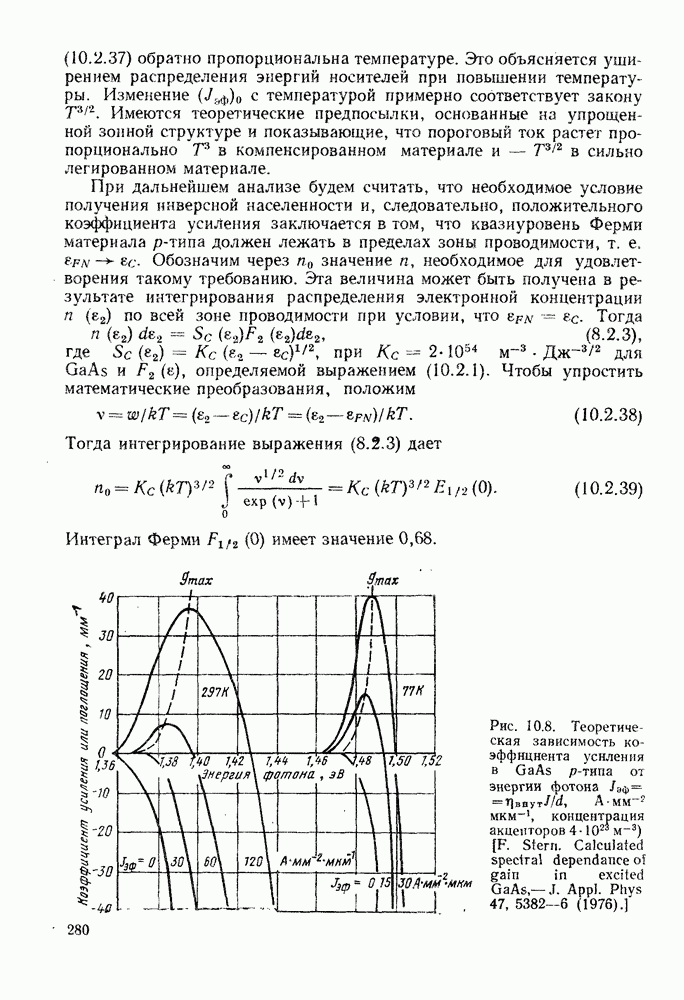
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
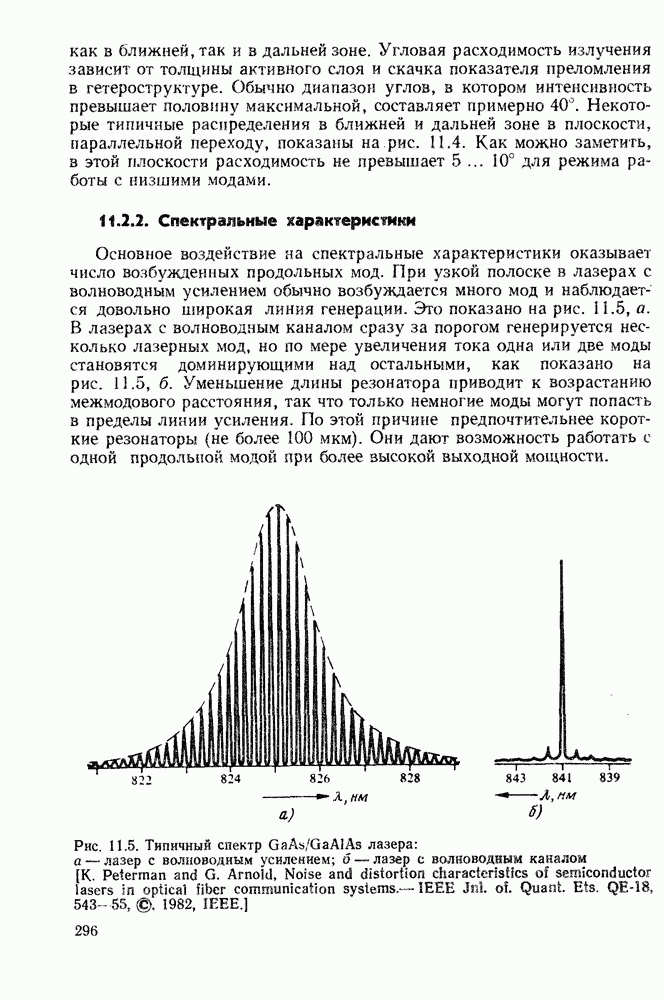
- 11.2.2. Спектральные характеристики
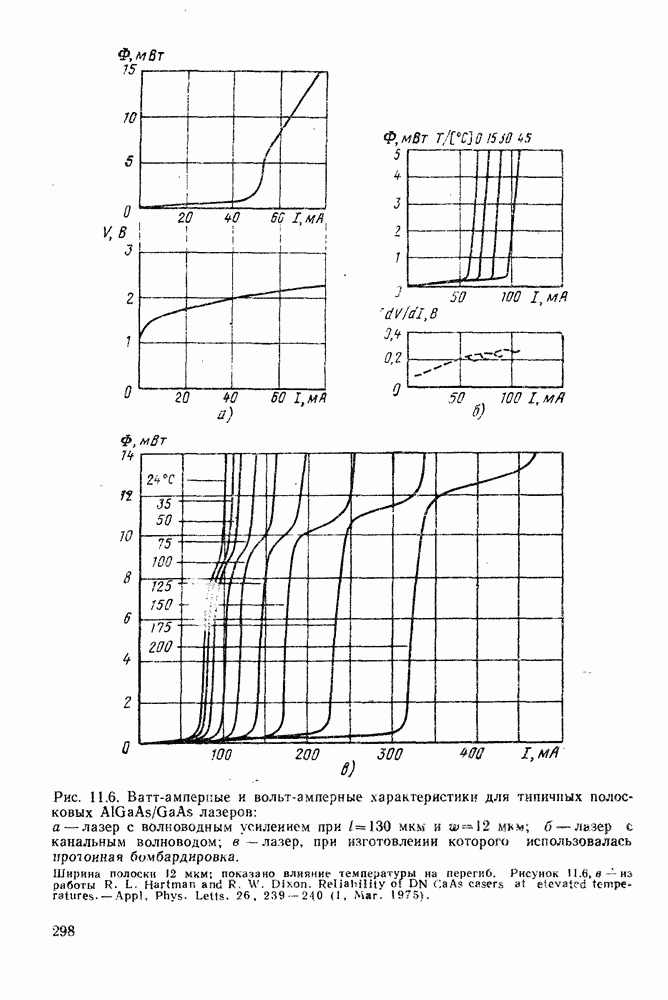
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
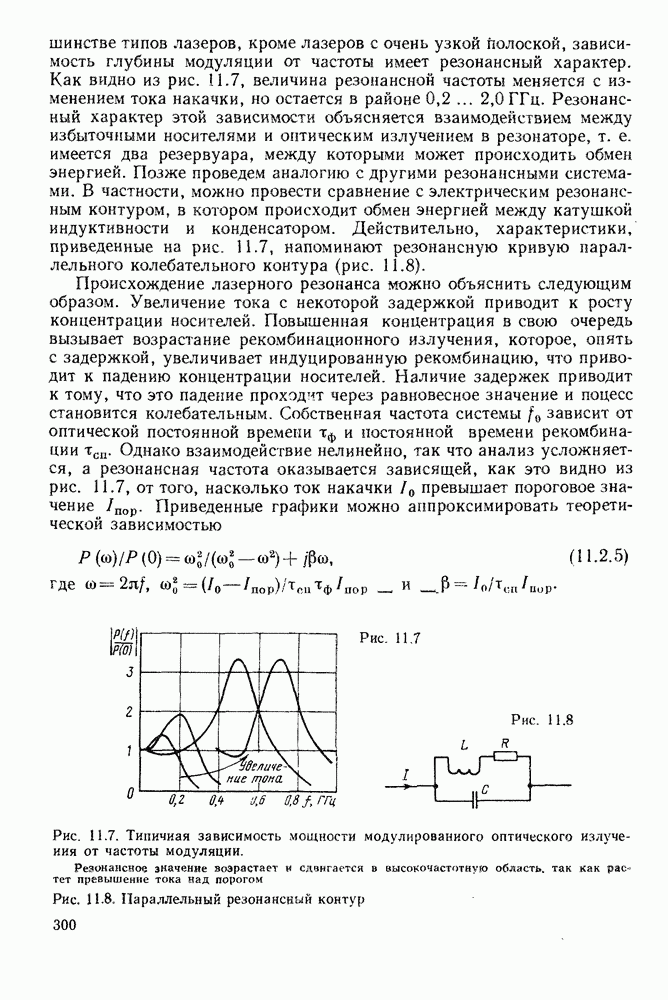
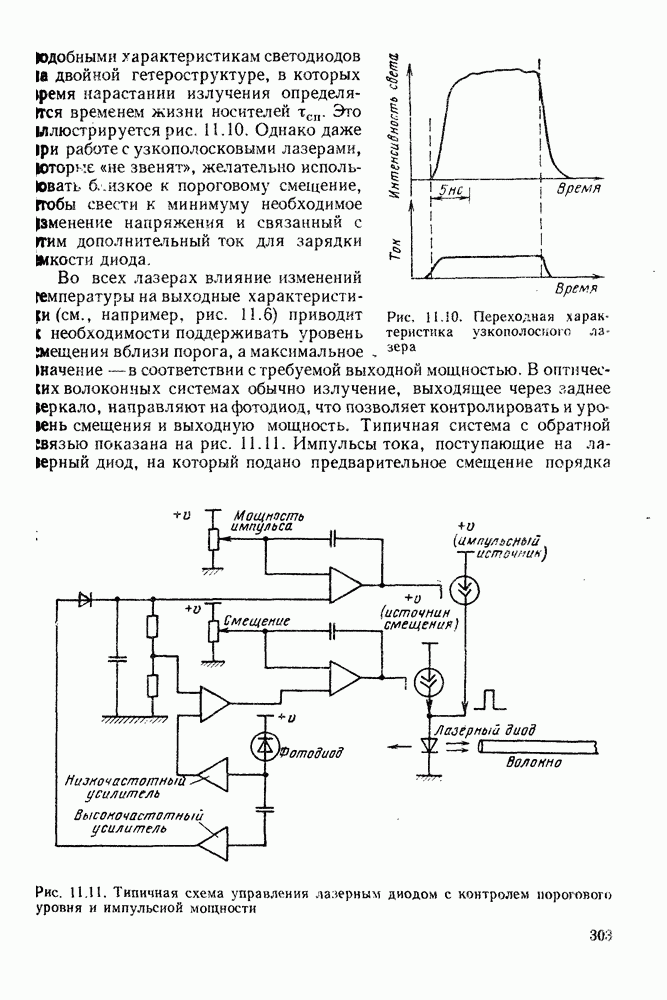
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
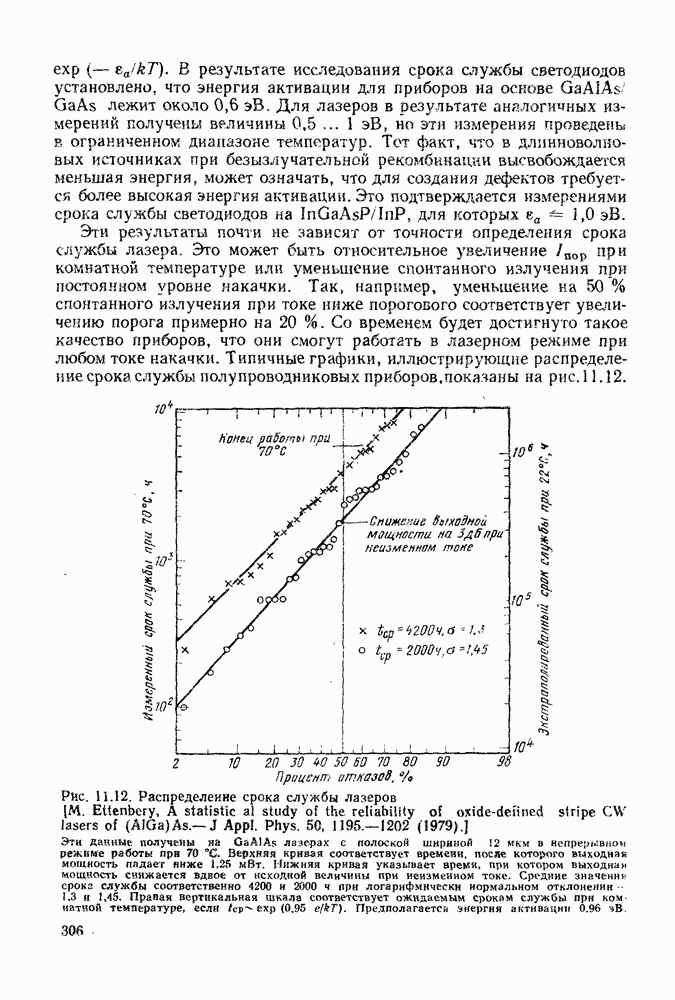
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
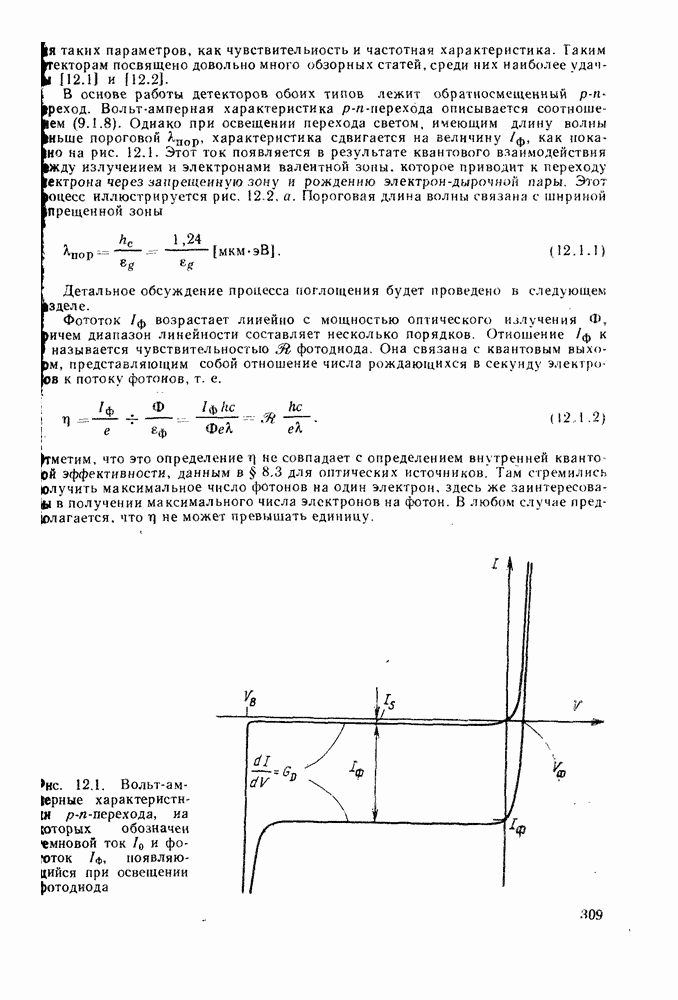
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
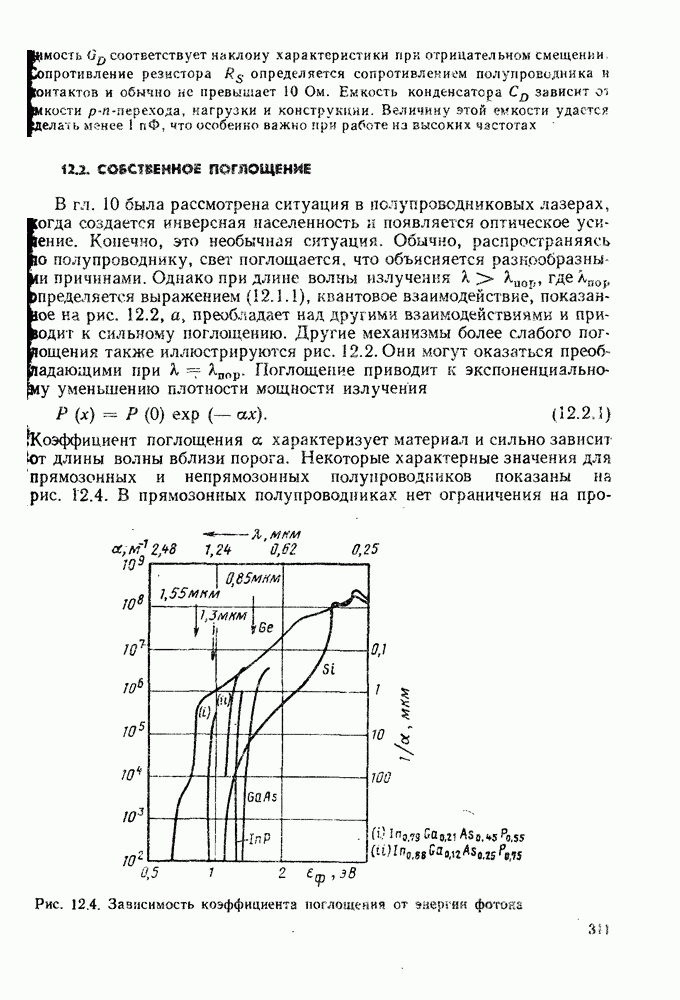
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
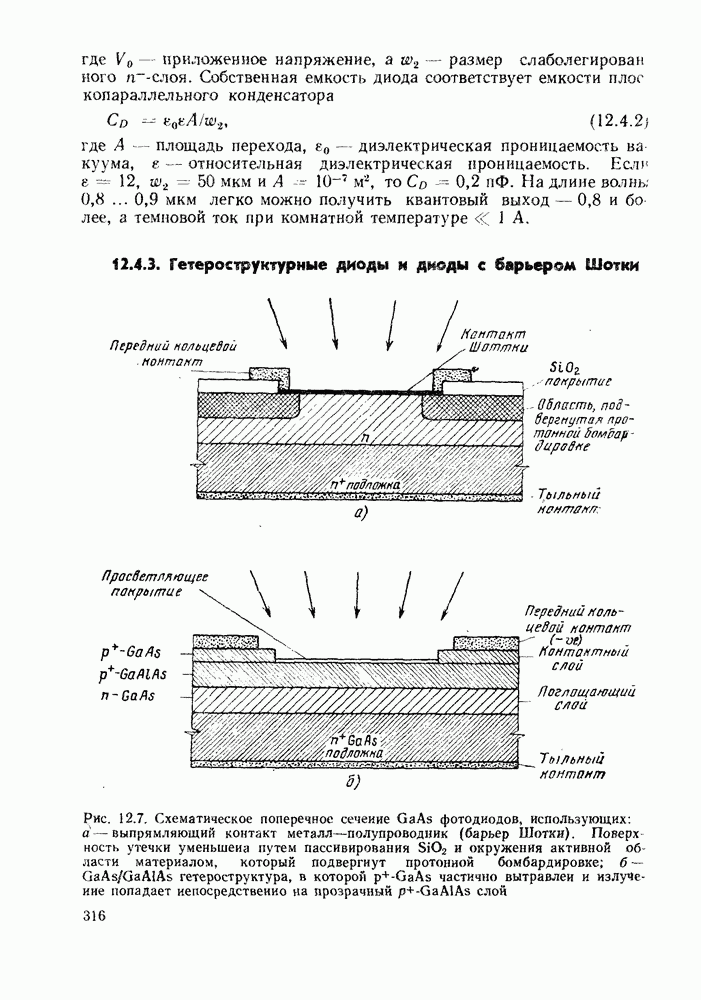
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
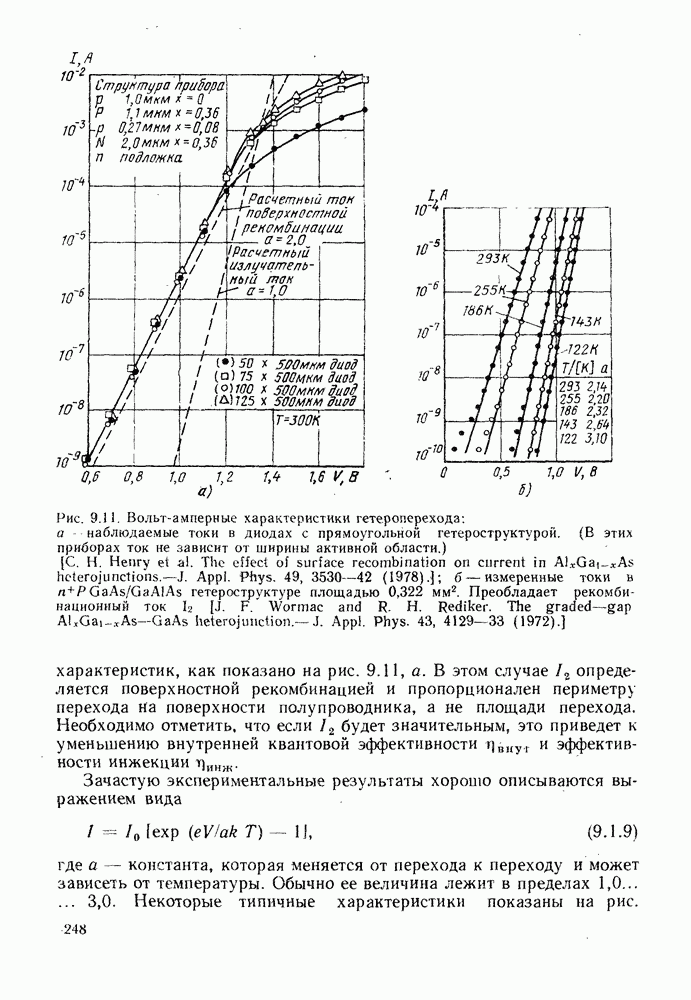
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
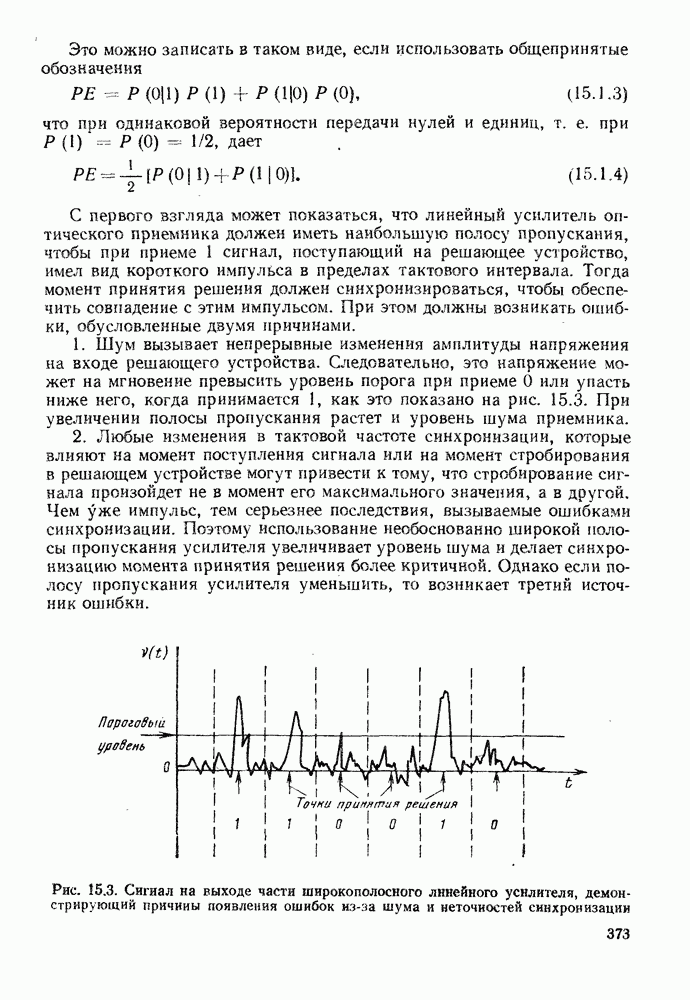
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
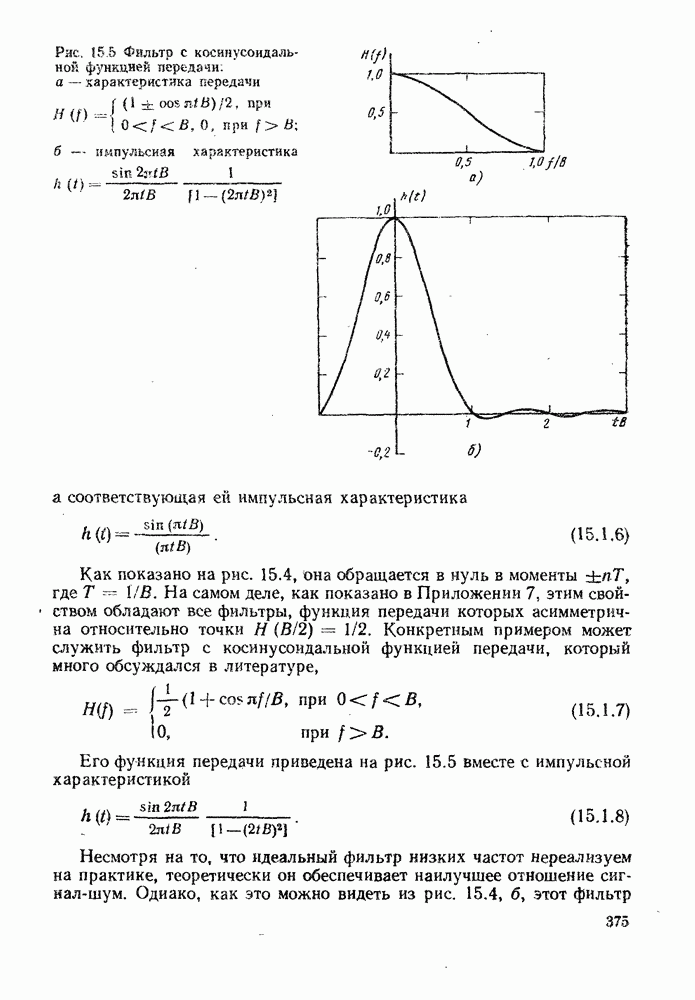
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
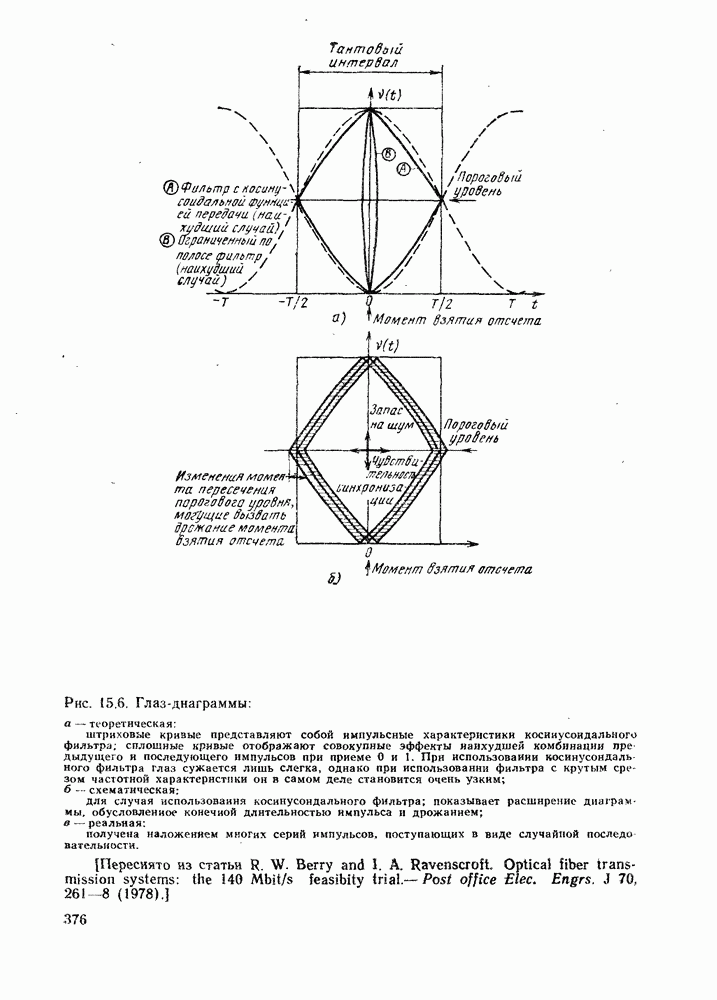
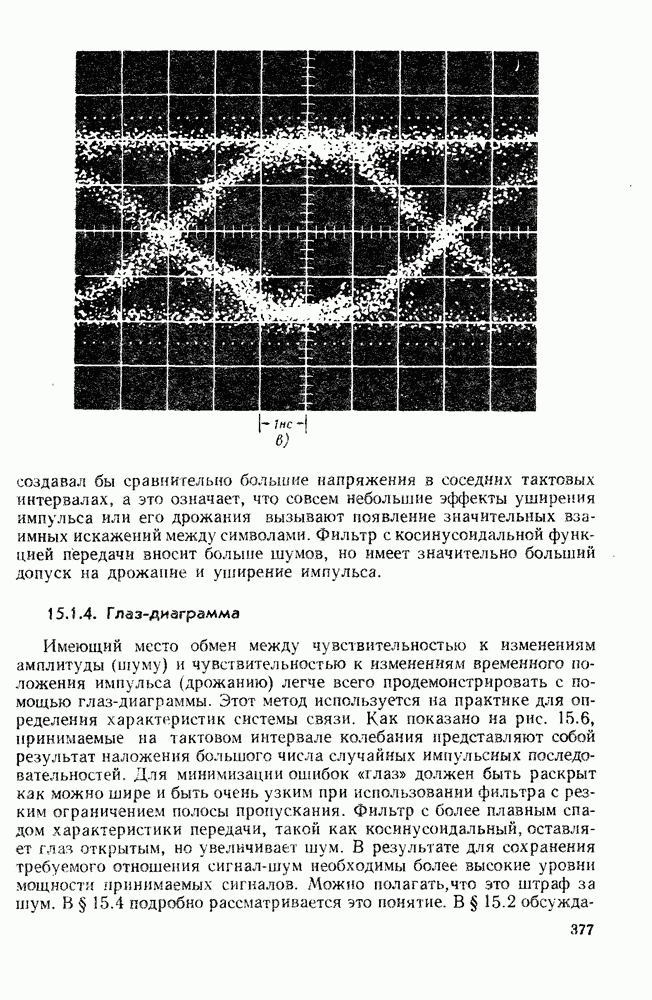
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
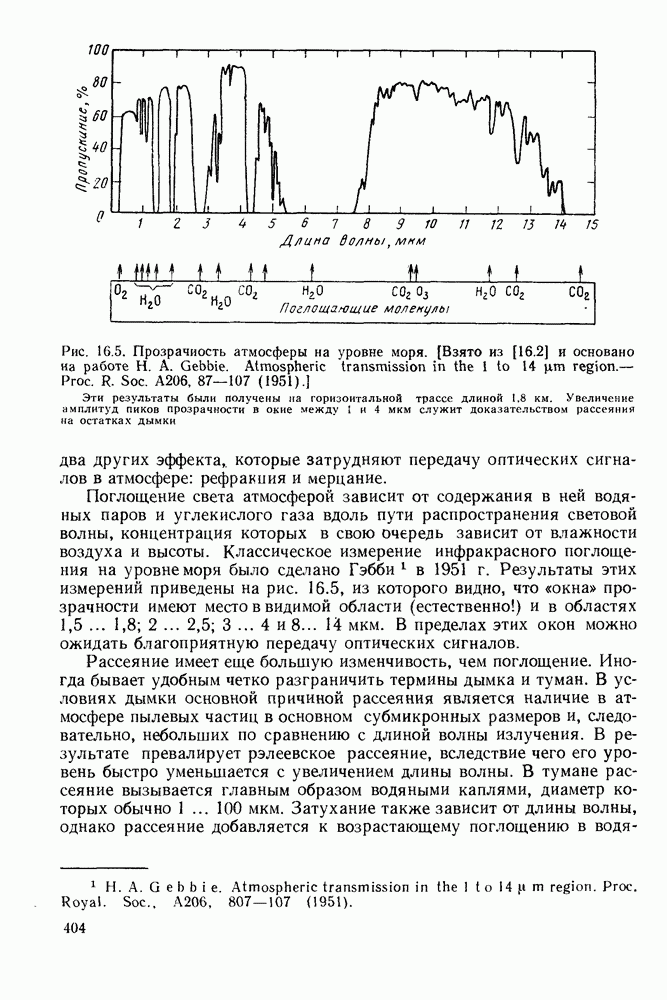
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
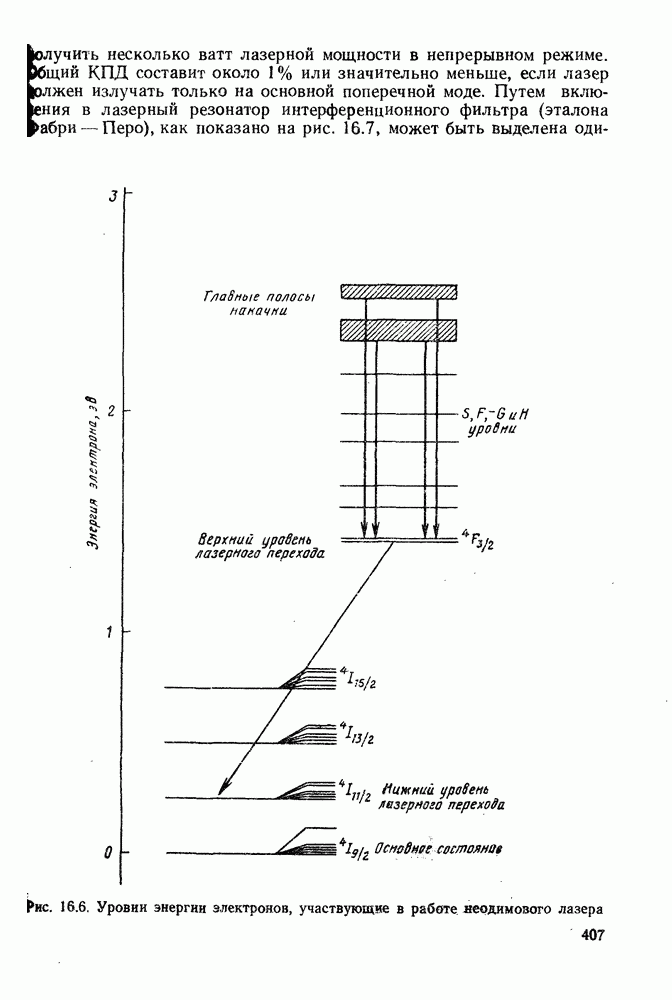
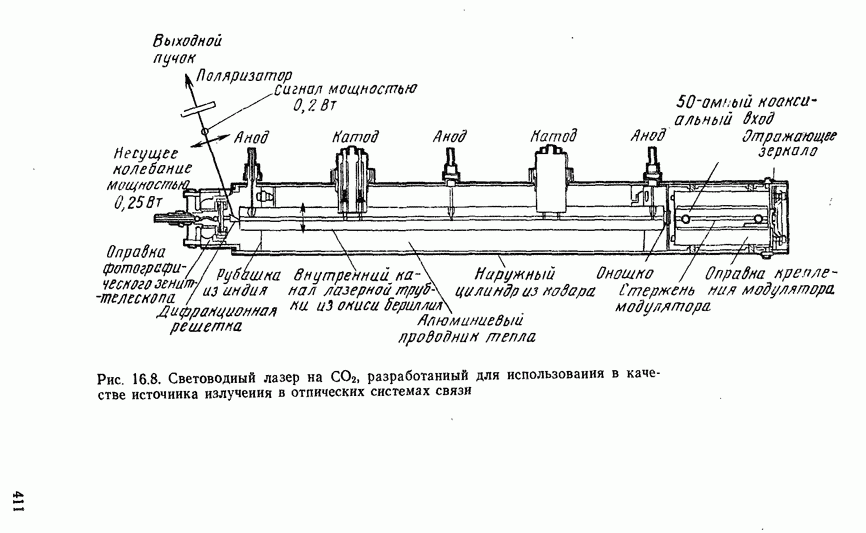
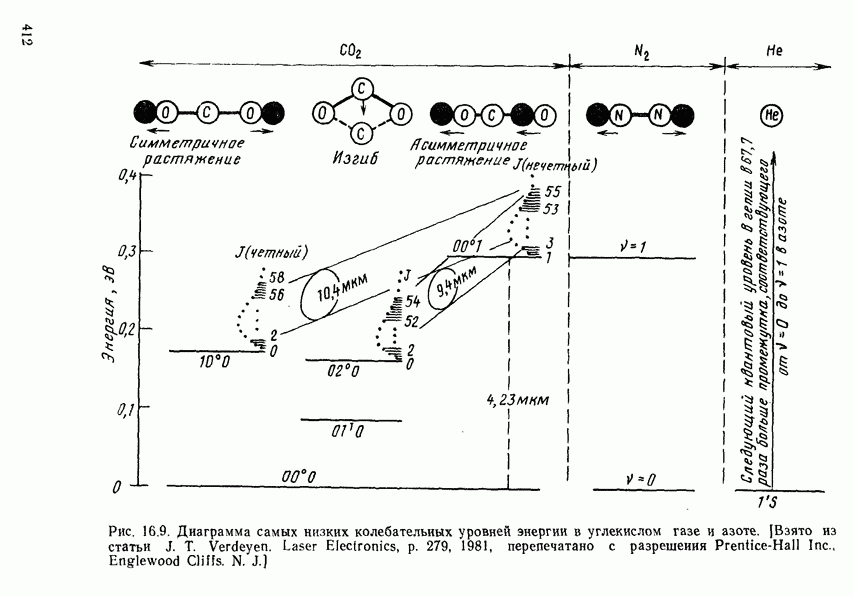
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ