| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
5.1. МОДЫ И ЛУЧИ
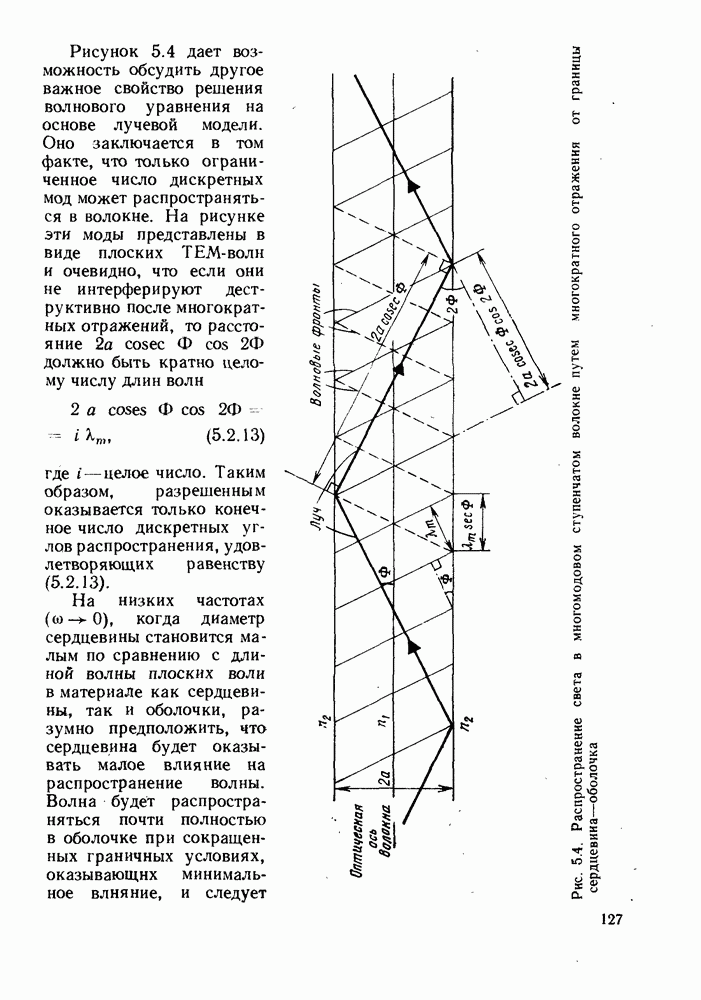
До сих пор использовалась лучевая модель распространения света в оптических волокнах, когда световые лучи, последовательно отражаясь от границы сердцевина — оболочка, распространялись в сердцевине по зигзагообразным траекториям. Такая модель распространения света пригодна для объяснения большинства эффектов, наблюдаемых в оптических системах связи, использующих многомодовые волокна. Однако необходимо помнить, что свет представляет собой электромагнитные волны и его распространение в волокне следует рассматривать в виде мод распространения, а не лучей. Физически понятие луча означает узкий пучок плоских электромагнитных волн в пределе, когда к 0. На практике нечто похожее может быть получено с помощью узкого пучка излучения лазера. В оптических волокнах обычно не выполняется условие малости длины волны распространяющегося света в сравнении с радиусом сердцевины волокна и поэтому лучевая модель должна использоваться с осторожностью, а само оптическое
волокно в действительности следует рассматривать как диэлектрический волновод.
При изучении направленного распространения электромагнитных волн в диэлектрической среде, описываемого в данной главе и гл. 6, не будем излишне усложнять изложение материала. С одной стороны, будем предполагать, что читатель знаком с основами теории электромагнитных колебаний. С другой стороны, подробное и строгое рассмотрение вопроса выходит за рамки данной книги и заинтересованным читателям советуем обратиться к более фундаментальным учебникам, например таким, как [5.1] — [5.3]. Даже в простейшем случае ступенчатого цилиндрического волокна с бесконечно толстой оболочкой решение уравнений Максвелла представляетсложную задачу. Интересно отметить, что разного рода дополнительные предположения и упрощения, к которым обычно прибегают, чтобы рассмотреть более сложные типы волокна, в любом случае формально эквивалентны лучевой модели. Сначала рассмотрим ступенчатые волокна, а затем в гл. 6 изучим распространение световых волн в некоторых видах градиентных волокон. Поскольку многие читатели могут быть знакомы с теорией направленного распространения электромагнитных волн в металлических волноводах, начнем рассмотрение с представления решений волновых уравнений в виде, обычно используемом в теории металлических волноводов. Будем использовать приближения, которые позволяют упростить выражения для волоконных световодов. Некоторые читатели, вероятно, знакомы с приближением Вентцеля, Крамерса, Бриллюэна — WKB (Wentzal, Kramers, Brillouin), которое может быть использовано при решении волновых уравнений. Будет показано, что использование этого приближения, которое будет рассмотрено в гл. 6, весьма эффективно при изучении градиентного волокна.
Воспользуемся решениями уравнений Максвелла для случая распространения электромагнитной волны в непроводящем и свободном от зарядов диэлектрике. Они имеют следующий вид:

где  вектор электрического ноля;
вектор электрического ноля;  вектор электрического смещения; В — вектор магнитной индукции;
вектор электрического смещения; В — вектор магнитной индукции;  вектор магнитного поля;
вектор магнитного поля;  магнитная проницаемость свободного пространства;
магнитная проницаемость свободного пространства;  диэлектрическая проницаемость свободного пространства; — относительная магнитная проницаемость материала, которая предполагается всегда равной 1;
диэлектрическая проницаемость свободного пространства; — относительная магнитная проницаемость материала, которая предполагается всегда равной 1;  относительная диэлектрическая проницаемость материала. Уже были рассмотрены решения этих уравнений для случая плоских волн, распространяющихся в свободном пространстве. Такие волны называются поперечными электромагнитными волнами (ТЕМ), поскольку у них векторы электрического и магнитного полей взаимно перпендикулярны, а оба
относительная диэлектрическая проницаемость материала. Уже были рассмотрены решения этих уравнений для случая плоских волн, распространяющихся в свободном пространстве. Такие волны называются поперечными электромагнитными волнами (ТЕМ), поскольку у них векторы электрического и магнитного полей взаимно перпендикулярны, а оба
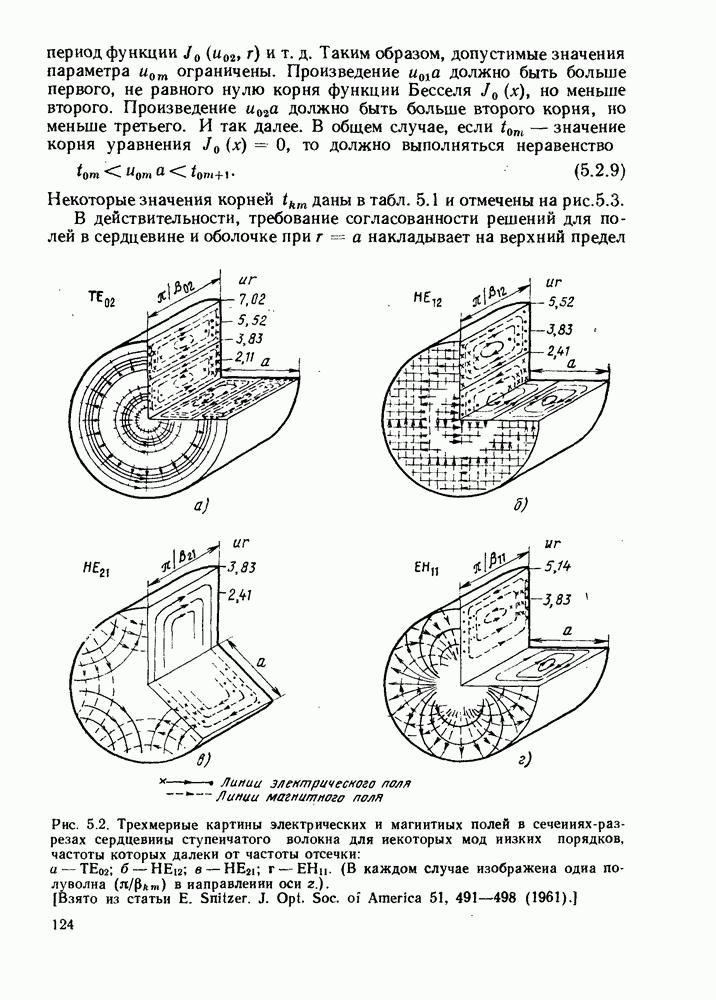
они перпендикулярны направлению распространения. Теперь найдем решения для случая направленного распространения волны в волокне для случая радиально-симметрнчного закона изменения  в нем. Установлено, что в данном случае волны не могут быть чисто поперечными, т. е. волнами типа ТЕМ, а всегда имеют осевую составляющую вектора
в нем. Установлено, что в данном случае волны не могут быть чисто поперечными, т. е. волнами типа ТЕМ, а всегда имеют осевую составляющую вектора  или
или  Из-за наличия радиальной симметрии решения удобно записать в системе цилиндрических полярных координат в следующем виде:
Из-за наличия радиальной симметрии решения удобно записать в системе цилиндрических полярных координат в следующем виде:

где, как и ранее,  угловая частота,
угловая частота,  постоянная распространения. Поскольку как электрический, так и магнитный векторы имеют одинаковую функциональную зависимость, воспользуемся следующим обозначением:
постоянная распространения. Поскольку как электрический, так и магнитный векторы имеют одинаковую функциональную зависимость, воспользуемся следующим обозначением:

где  обозначает локальное значение либо электрического поля
обозначает локальное значение либо электрического поля  либо магнитного поля
либо магнитного поля  Накладываемое волокном граничное условие предписывается законом изменения диэлектрической проницаемости
Накладываемое волокном граничное условие предписывается законом изменения диэлектрической проницаемости  или показателя преломления
или показателя преломления  Решения также подчиняются требованиям, чтобы поля были конечными на оси волокна и обращались в нуль на бесконечности. Другими словами,
Решения также подчиняются требованиям, чтобы поля были конечными на оси волокна и обращались в нуль на бесконечности. Другими словами,  Эти условия обусловливают решения в собственных значениях для
Эти условия обусловливают решения в собственных значениях для  каждое из которых имеет конкретное значение
каждое из которых имеет конкретное значение  Это приводит к дискретным картинам распространяющихся в волокне электромагнитных волн, которые называются модами.
Это приводит к дискретным картинам распространяющихся в волокне электромагнитных волн, которые называются модами.
Оба типа волокна, которые рассматривались до сих пор, а именно ступенчатые и градиентные волокна, способствуют распространению в них многих мод. На самом деле в волокне типичных размеров могут распространяться много сотен мод. Такие волокна являются примерами многомодовых волокон. В некоторой степени различные моды можно ассоциировать с различными траекториями лучей. Поскольку постоянная распространения изменяется от моды к моде, каждая из мод распространяется со своими собственными значениями фазовой и групповой скоростей. Таким образом, свойство волокна, которое до сих пор называли многолучевой дисперсией, по-видимому, лучше называть межмодовой дисперсией. В литературе этот термин сокращенно называется модовой дисперсией.
Модовая теория не только обеспечивает более ясное физическое понимание характеристик распространения света в волокне, но дает возможность изучать распространение света в волокнах с серцевиной очень малого диаметра, позволяет вычислить распределение мощности в волокне и обнаружить дополнительный источник временной дисперсии. Дополнительная дисперсия возникает из-за того, что скорость распространения любой конкретной моды зависит от частоты,
независимо от имеющейся материальной дисперсии. Это эффект известен как внутримодовая дисперсия, которую чаще называют волноводной дисперсией. Хотя она обычно мала по сравнению с материальной дисперсией, однако, как будет показано в § 5.5, она может оказать влияние на смещение минимума дисперсии в сторону более длинных волн.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
- 11.2.2. Спектральные характеристики
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
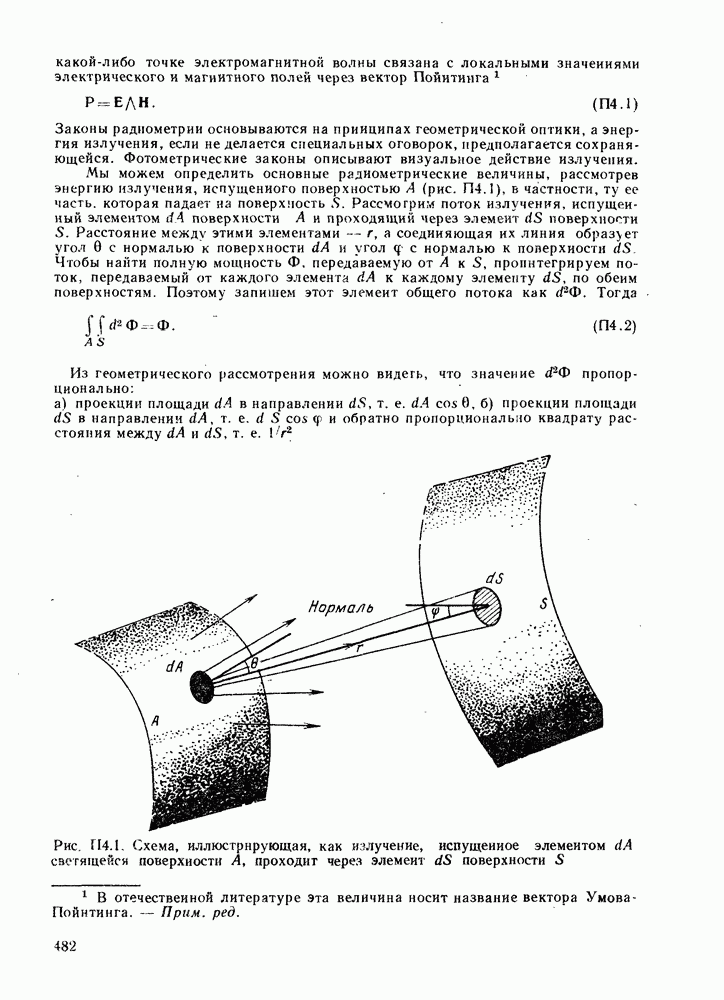
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
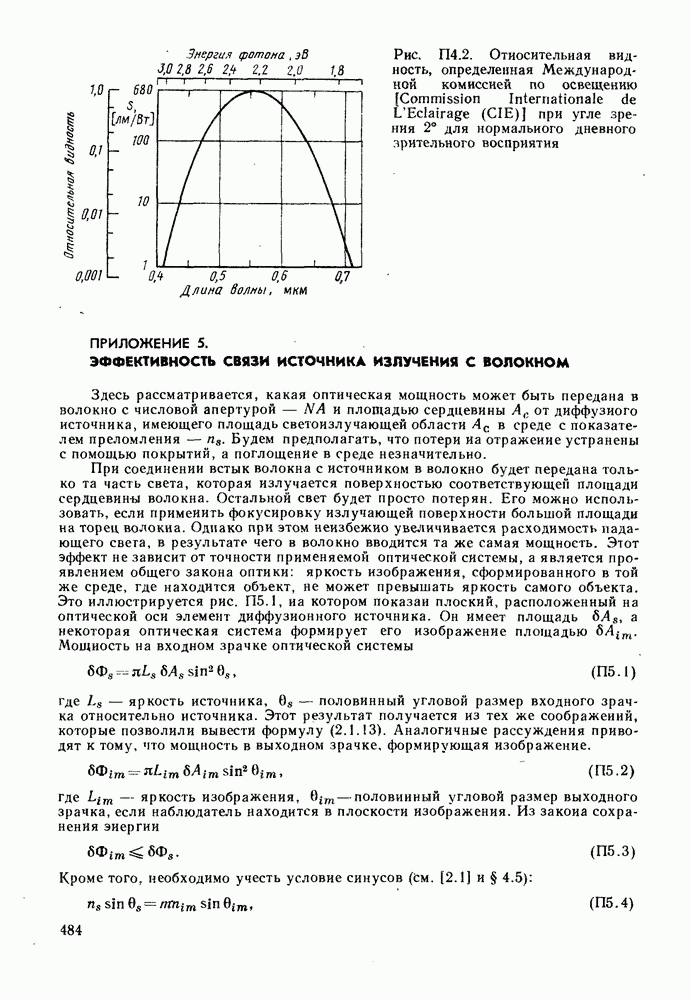
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
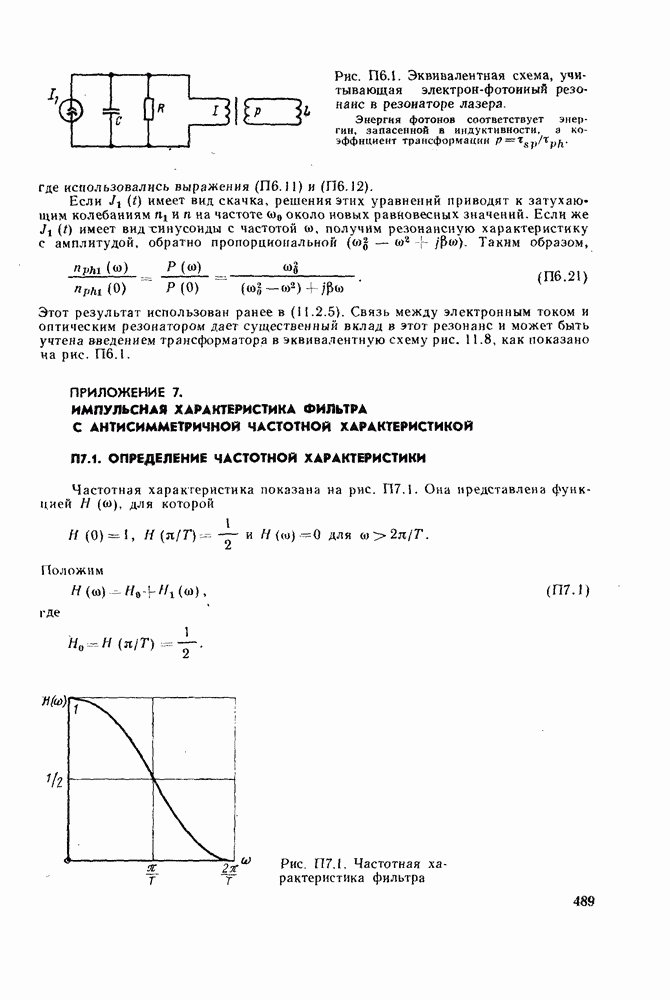
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ