| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
Рассмотрим выходное излучение люминесцентного диода при наличии электрической высокочастотной модуляции. Будем предполагать, что небольшая синусоидальная модуляция наложена на положительно смещающее напряжение. Ограничим обсуждение случаем  -диода, в котором электроны инжекции преобладают в потоке носителей и концентрация избыточных электронов падает до нуля вдали от перехода. В § 7.5 была рассмотрена эквивалентная схема светоизлучающего диода, здесь же рассмотрим элементы
-диода, в котором электроны инжекции преобладают в потоке носителей и концентрация избыточных электронов падает до нуля вдали от перехода. В § 7.5 была рассмотрена эквивалентная схема светоизлучающего диода, здесь же рассмотрим элементы  и
и  этой схемы, чтобы выяснить временные характеристики диода на высоких частотах. Нас будет также интересовать отношение выходной оптической мощности к входной электрической в зависимости от частоты.
этой схемы, чтобы выяснить временные характеристики диода на высоких частотах. Нас будет также интересовать отношение выходной оптической мощности к входной электрической в зависимости от частоты.
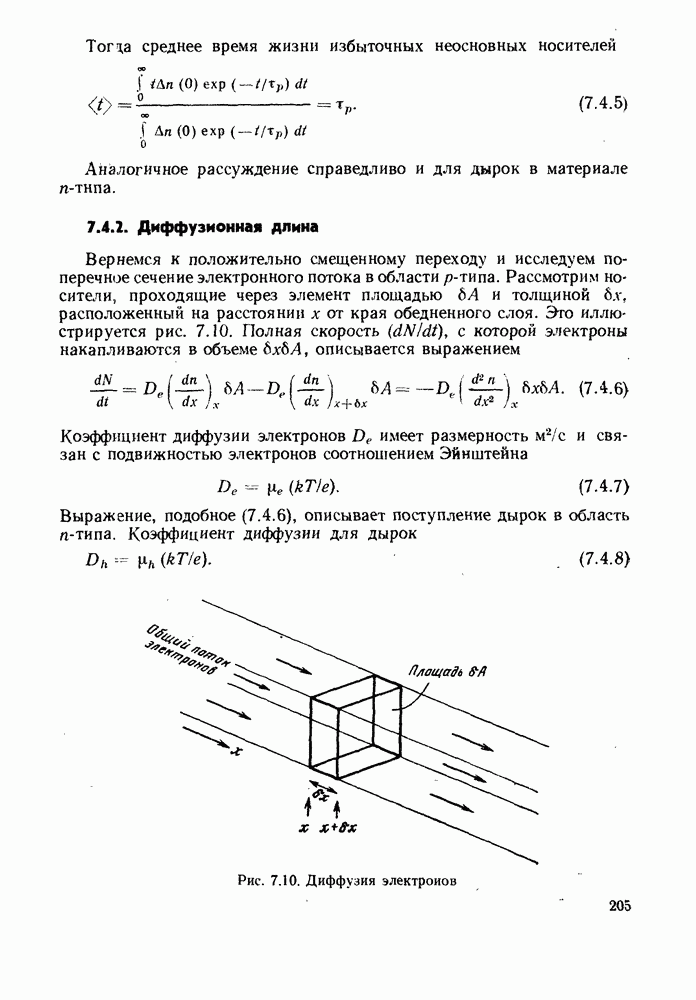
Соответствующее стационарному случаю решение для диффузной области получено в § 7.4.2. Если концентрация носителей в элементе объема  (рис. 7.10) меняется со временем, полученное ранее уравнение (7.4.10) для концентрации носителей преобразуется к виду
(рис. 7.10) меняется со временем, полученное ранее уравнение (7.4.10) для концентрации носителей преобразуется к виду

Как и ранее, предполагаем, что концентрация электронов на краю обедненного слоя в области  -типа
-типа  определяется концентрацией основных электронов в области n-типа и изменением потенциала в обедненном слое. Положим его равным
определяется концентрацией основных электронов в области n-типа и изменением потенциала в обедненном слое. Положим его равным  тогда из формулы (7.5.3) получим
тогда из формулы (7.5.3) получим

Здесь  угловая частота,
угловая частота,  частота модуляции. Представим зависящую от времени часть напряжения как действительную часть
частота модуляции. Представим зависящую от времени часть напряжения как действительную часть  считая
считая  Тогда
Тогда

Не зависящая от времени часть решения

а решение, зависящее от времени,

где

Аналогично и решение уравнения (8.7.1) можно представить в виде двух частей:

Если обозначить концентрацию избыточных носителей  то
то

Тогда уравнение (8.7.1) приобретает вид

Этому уравнению должны удовлетворять обе части выражения (8.7.8). Таким образом, не зависящая от времени часть

откуда

Зависящая от времени часть

Поскольку граничное условие при  определяется (8.7.5), можно записать
определяется (8.7.5), можно записать

Подставляя (8.7.11) в (8.7.10), получаем

где

Итак,

Эффективная зависящая от времени диффузионная длина является комплексной функцией частоты. Будем использовать (8.7.15) для расчета зависящей от времени части плотности тока  и плотности выходной оптической мощности
и плотности выходной оптической мощности 
Плотность тока зависит от градиента концентрации носителей при 

Здесь использована формула (8.7.14). Используя (7.5.4), получаем 

Полная проводимость положительно смещенного диода

где  площадь перехода,
площадь перехода,  переменная составляющая тока. Используя (8.7.17), имеем
переменная составляющая тока. Используя (8.7.17), имеем

Положив  и возведя обе части в квадрат, получим
и возведя обе части в квадрат, получим

Приравниваем действительные части

Так что при 

Приравниваем мнимые части

Тогда

Отметим, что справедливость (8.7.23) и (8.7.25) зависит от сделанного допущения  . На высоких частотах, когда
. На высоких частотах, когда  из (8.7.22) и (8.7.24) легко получить
из (8.7.22) и (8.7.24) легко получить

Таким образом,  на высоких частотах, когда С падает, параметры перехода опять определяются емкостью обедненного слоя
на высоких частотах, когда С падает, параметры перехода опять определяются емкостью обедненного слоя 
Полная интенсивность оптического излучения определяется числом актов излучательной рекомбинации в секунду на единицу площади, умноженным на среднюю энергию фотона, т. е.

Можно разделить  на стационарную компоненту
на стационарную компоненту  и зависящую от времени
и зависящую от времени  Используем определение
Используем определение  данное в § 8.4,
данное в § 8.4,

Тогда

Используя (8.7.8). можно записать

и

Подставляя (7.4.12) в (8.7.29) и интегрируя, получаем стационарную компоненту

учитывая (8.7.18), получаем

С другой стороны, интегрируя (8.7.15), получаем зависящую от времени компоненту

Теперь, используя (8.7.16), можно исключить  :
:

Сравнивая (8.7.32) и (8.7.34), можно получить выражение для частотной характеристики

Экспериментальная частотная характеристика очень близка к (8.7.35), как показано на рис. 8.13. Из такой кривой можно оценить  с точностью порядка 1 не. Необходимо иметь в виду, что на эквивалентной схеме рис.
с точностью порядка 1 не. Необходимо иметь в виду, что на эквивалентной схеме рис.  ток, текущий только через
ток, текущий только через  Эта величина не учитывает составляющей тока, текущего через
Эта величина не учитывает составляющей тока, текущего через  Характеристика управляющей схемы может быть причиной изменения
Характеристика управляющей схемы может быть причиной изменения  в зависимости от частоты, что приведет к падению мощности излучения на частотах выше
в зависимости от частоты, что приведет к падению мощности излучения на частотах выше 
Необходимо отметить, что линейное соотношение между  не зависит от условия малости сигнала, сделанного при выводе (8.7.3). Допущение о малости сигнала существенно только для соотношения между
не зависит от условия малости сигнала, сделанного при выводе (8.7.3). Допущение о малости сигнала существенно только для соотношения между  Если нельзя допустить, что
Если нельзя допустить, что  то положим
то положим

Тогда

 еще должны удовлетворять (8.7.35). Однако очень трудно корректно установить границу между обедненным слоем и диффузионной областью, поэтому допущения, сделанные в этом параграфе, надо использовать с большой осторожностью в случае больших сигналов.
еще должны удовлетворять (8.7.35). Однако очень трудно корректно установить границу между обедненным слоем и диффузионной областью, поэтому допущения, сделанные в этом параграфе, надо использовать с большой осторожностью в случае больших сигналов.
Формула (8.7.35) имеет большое значение для рассмотрения процесса высокочастотной модуляции источника оптического излучения. На частотах выше  эффективность источника падает, как это иллюстрирует рис. 8.13. Уменьшение
эффективность источника падает, как это иллюстрирует рис. 8.13. Уменьшение  приведет к росту этой граничной частоты, но уменьшение
приведет к росту этой граничной частоты, но уменьшение  за счет уменьшения времени жизни при безызлучательной рекомбинации
за счет уменьшения времени жизни при безызлучательной рекомбинации  не дает увеличения оптической мощности на высоких частотах — просто уменьшится мощность на низких частотах, так как понизится внутренняя квантовая эффективность. Это следует из (8.4.5), поскольку
не дает увеличения оптической мощности на высоких частотах — просто уменьшится мощность на низких частотах, так как понизится внутренняя квантовая эффективность. Это следует из (8.4.5), поскольку

Действие уменьшения  при постоянной
при постоянной  иллюстрируется рис. 8.14. Необходимо по возможности уменьшить излучательное время жизни
иллюстрируется рис. 8.14. Необходимо по возможности уменьшить излучательное время жизни  При этом возрастает как квантовая эффективность на низких частотах модуляции, так и высокочастотная граница. Соотношения (8.4.13) и (8.4.14) показывают, что уменьшения
При этом возрастает как квантовая эффективность на низких частотах модуляции, так и высокочастотная граница. Соотношения (8.4.13) и (8.4.14) показывают, что уменьшения  т. е. увеличения
т. е. увеличения  можно добиться, увеличивая степень легирования и уровень инжекции. Ограничение обусловлено тем, что при значительных уровнях легирования уменьшается безызлучательное время жизни и падает
можно добиться, увеличивая степень легирования и уровень инжекции. Ограничение обусловлено тем, что при значительных уровнях легирования уменьшается безызлучательное время жизни и падает

Рис. 8.13. Зависимость выходной мощности светоизлучающего диода от частоты модуляции. Сплошная кривая соответствует выражению (8.7.35) при  . Кружками обозначены экспериментальные точки
. Кружками обозначены экспериментальные точки

Рис. 8.14. Кажущееся увеличение широкопол осности светоизлучающего диода при увеличении скорости безызлучательной рекомбинации. (Оно достигается лишь за счет падения низкочастотной квантовом эффективности. Высокочастотная квантовая эффективность может быть увеличена только при уменьшении 
квантовая эффективность. В случае арсенида галлия это происходит при концентрации примеси порядка  при этом
при этом  нс. То есть частоты модуляции значительно выше
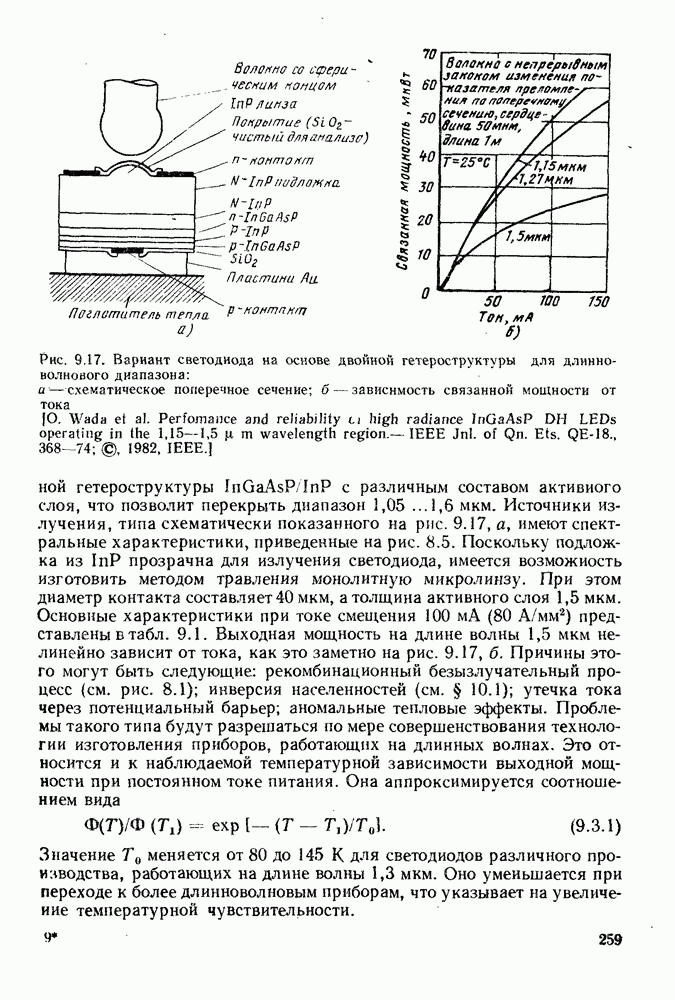
нс. То есть частоты модуляции значительно выше  могут быть достигнуты только за счет квантовой эффективности. Как будет показана в § 9.3, в 4 раза большую полосу модуляции без снижения эффективности удается получить в светоизлучающих диодах на InGaAsP/InP. На рис. 8.5, б показано, что они излучают в области 1,3 или 1,5 мкм.
могут быть достигнуты только за счет квантовой эффективности. Как будет показана в § 9.3, в 4 раза большую полосу модуляции без снижения эффективности удается получить в светоизлучающих диодах на InGaAsP/InP. На рис. 8.5, б показано, что они излучают в области 1,3 или 1,5 мкм.
ЗАДАЧИ
(см. скан)
(см. скан)
РЕЗЮМЕ
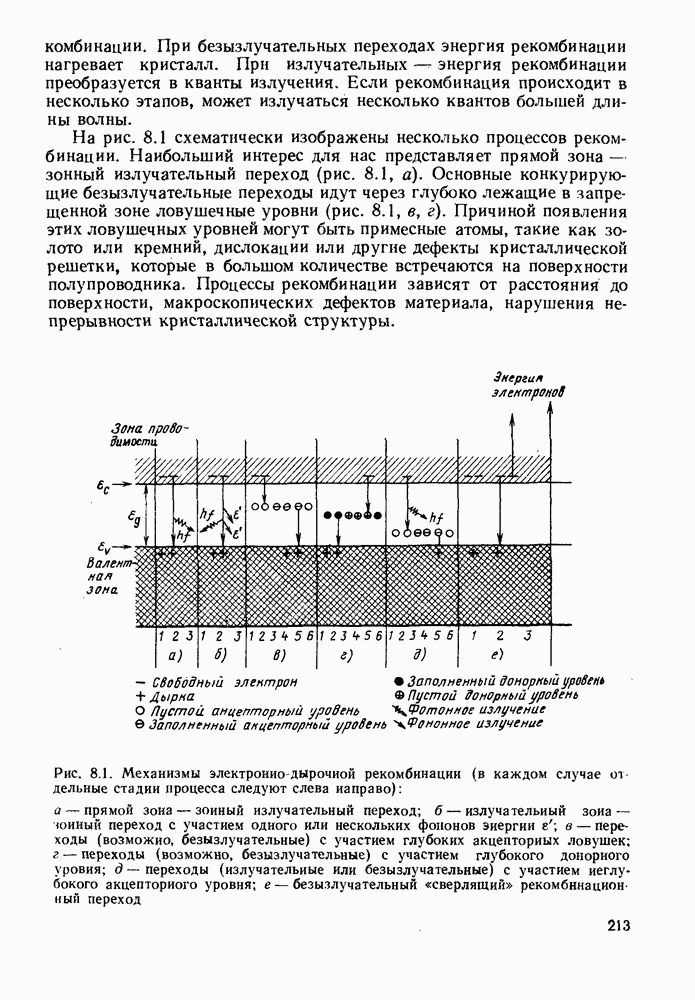
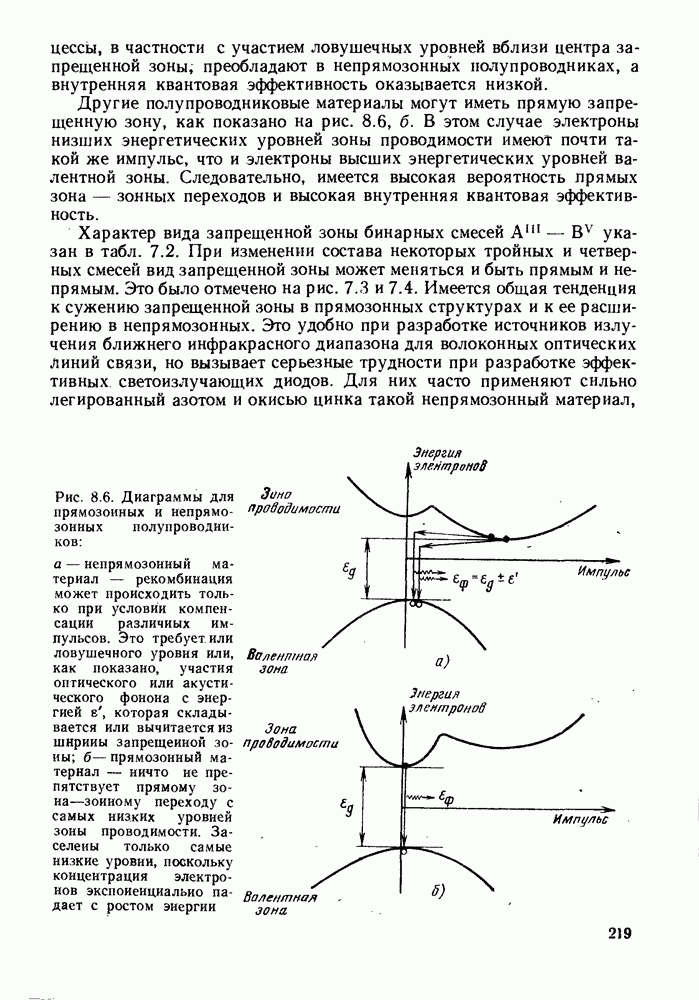
Эффективность инжекционной люминесценции зависит от преобладания прямой зона — зонной излучательной рекомбинации над другими механизмами рекомбинации, показанными на рис. 8.1. Это реализуется в прямозонном материале.
Внутренняя квантовая эффективность

где 
Когда преобладает безызлучательная рекомбинация на ловушках 
Длина волны оптического излучения  при энергии фотона
при энергии фотона 
Потери, вызванные переизлучением, поглощением, френелевским отражением и полным внутренним отражением от поверхности полупроводника снижают достижимую мощность:  Иммерсия и просветление могут уменьшить френелевские потери. Внешняя квантовая эффективность
Иммерсия и просветление могут уменьшить френелевские потери. Внешняя квантовая эффективность 
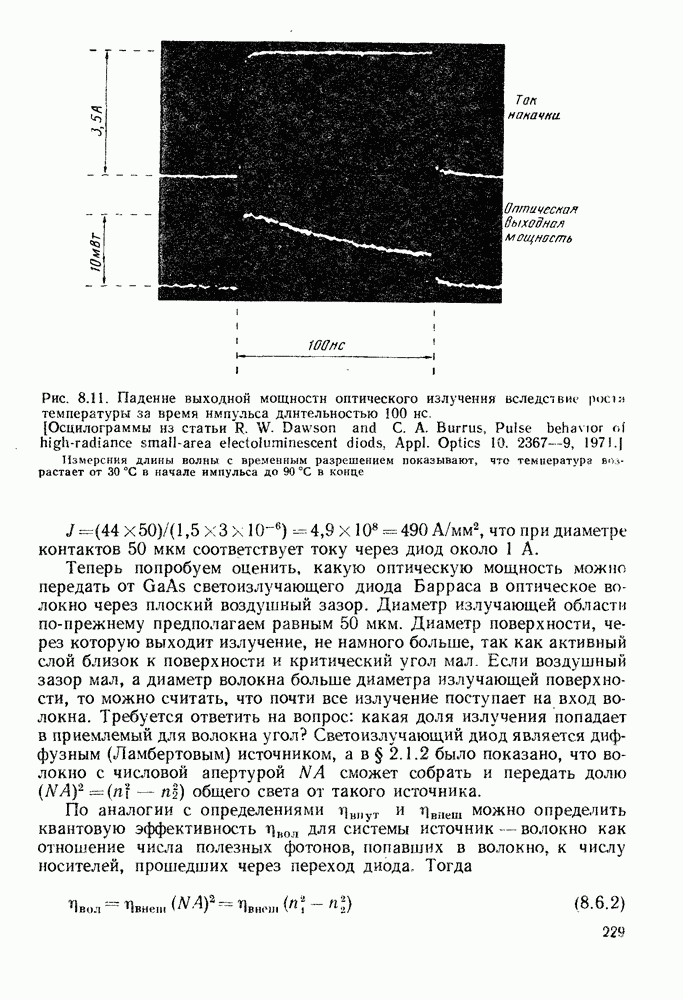
Оптическая выходная мощность первоначально пропорциональна питающему току, но затем появляется тенденция к насыщению. Генерация оптического излучения снижается с ростом температуры.
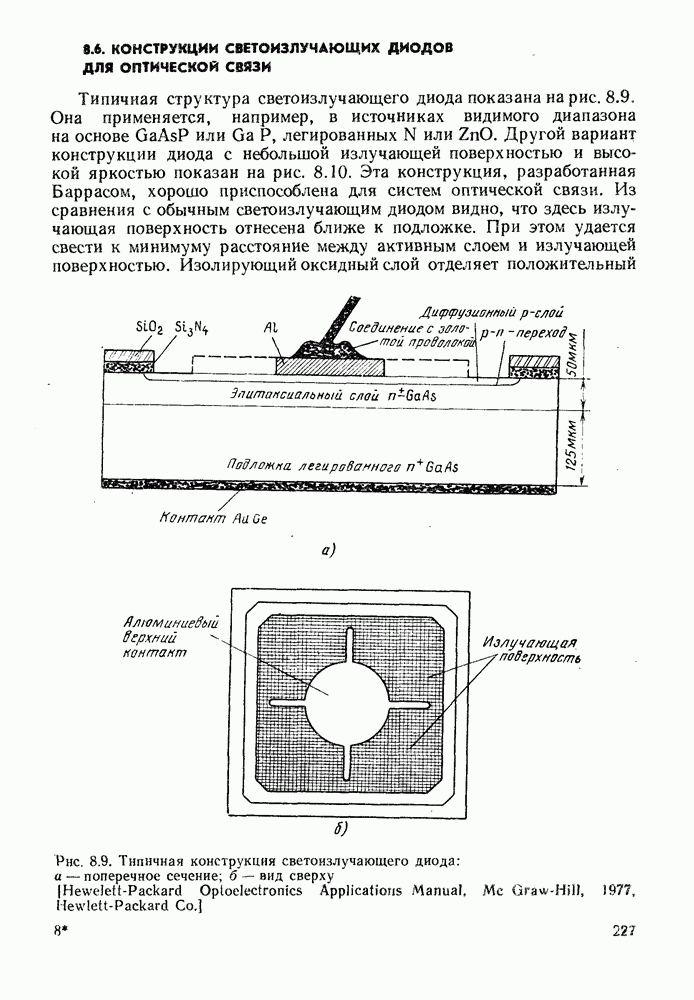
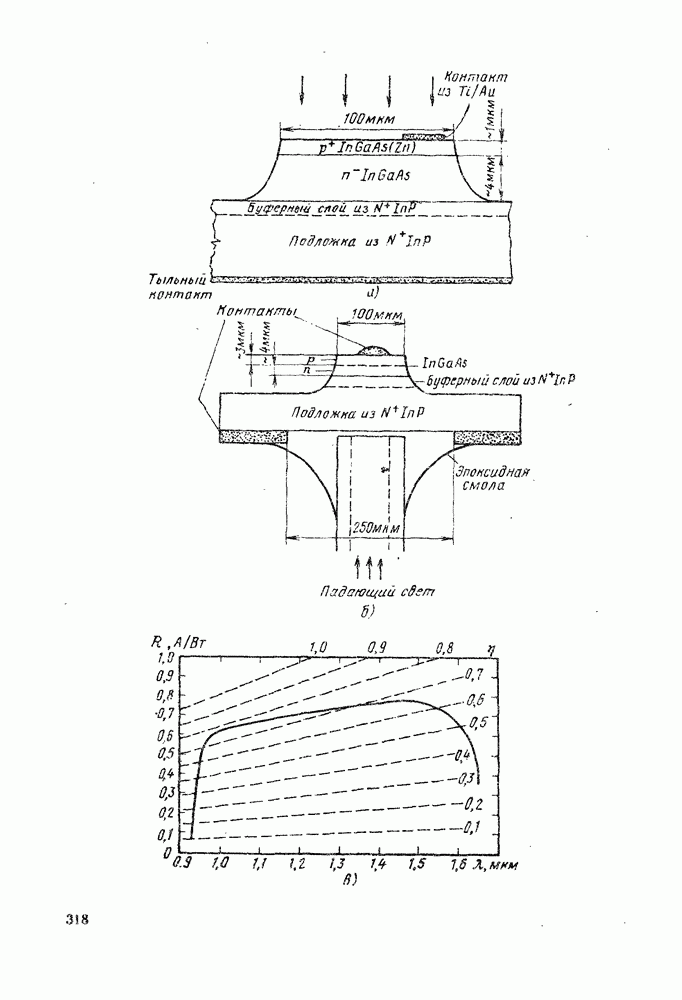
На рис. 8.10 показан диод конструкции Барраса, имеющий малую излучающую поверхность и высокую яркость.
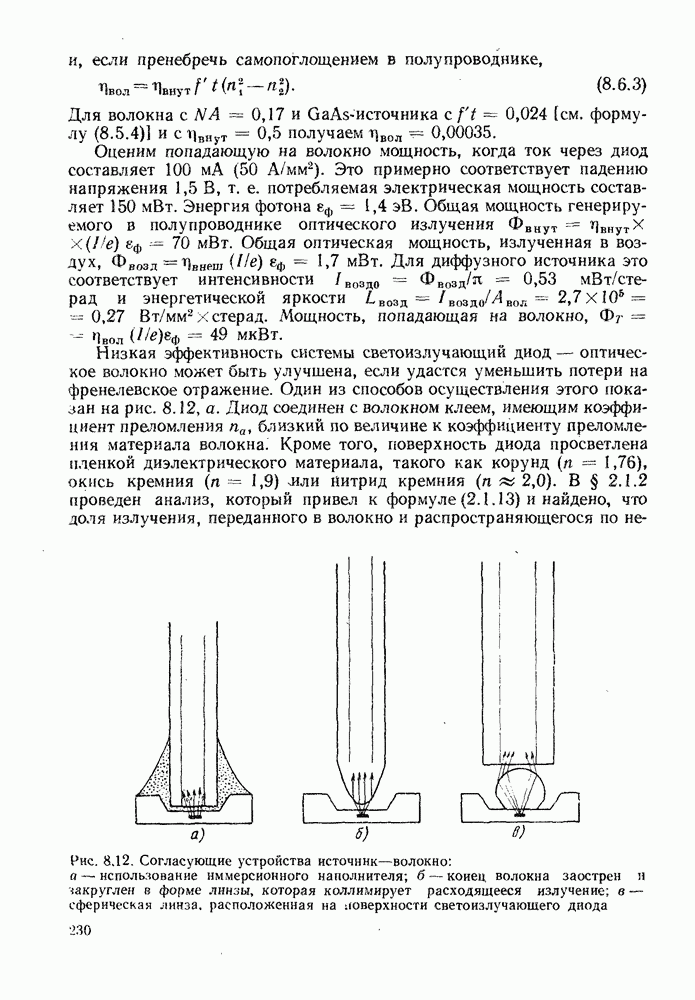
При размере источника меньше диаметра сердцевины волокна передаваемую в волокно мощность можно увеличить, используя линзовые согласующие устройства, которые обеспечивают максимальный коэффициент связи 
Типичная частотная характеристика

где 
Уменьшение  приводит к уменьшению
приводит к уменьшению  и поднимает частотную характеристику за счет снижения квантовой эффективности.
и поднимает частотную характеристику за счет снижения квантовой эффективности.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
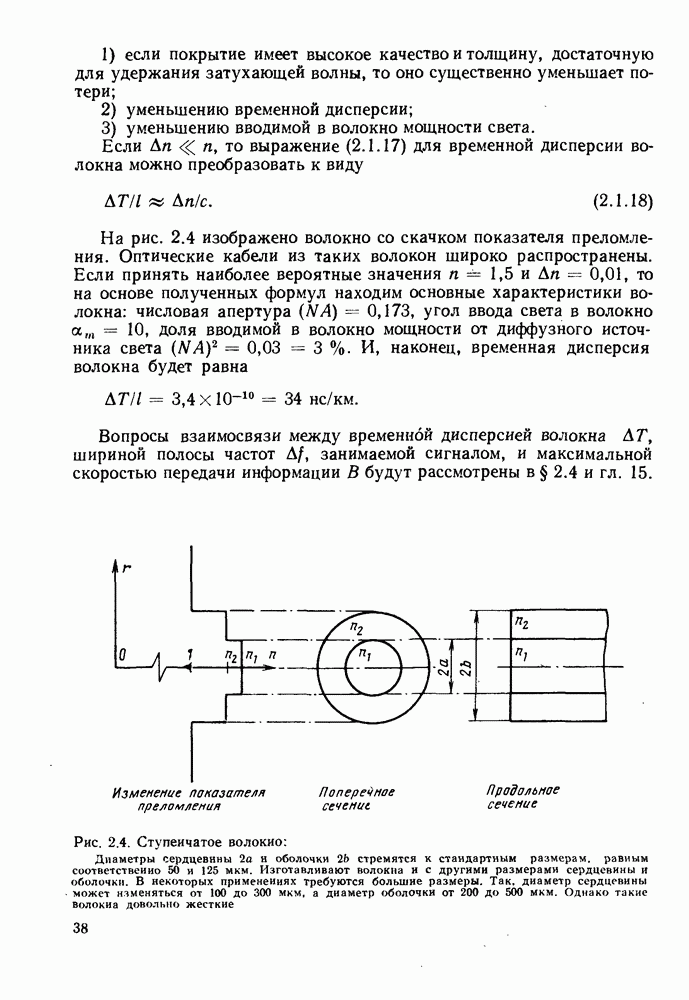
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
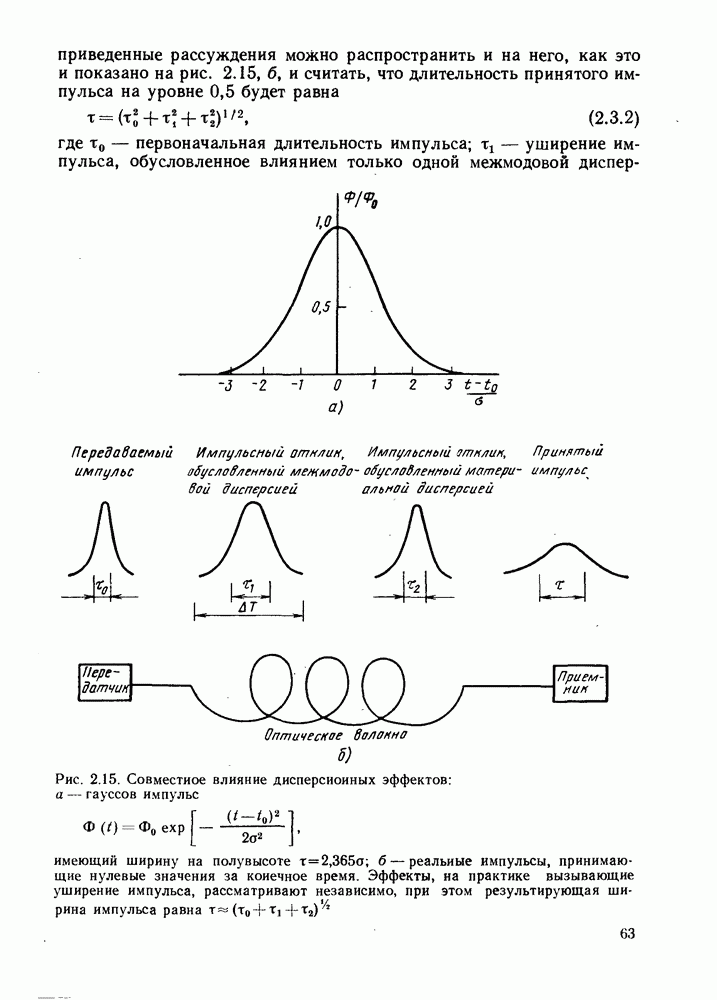
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
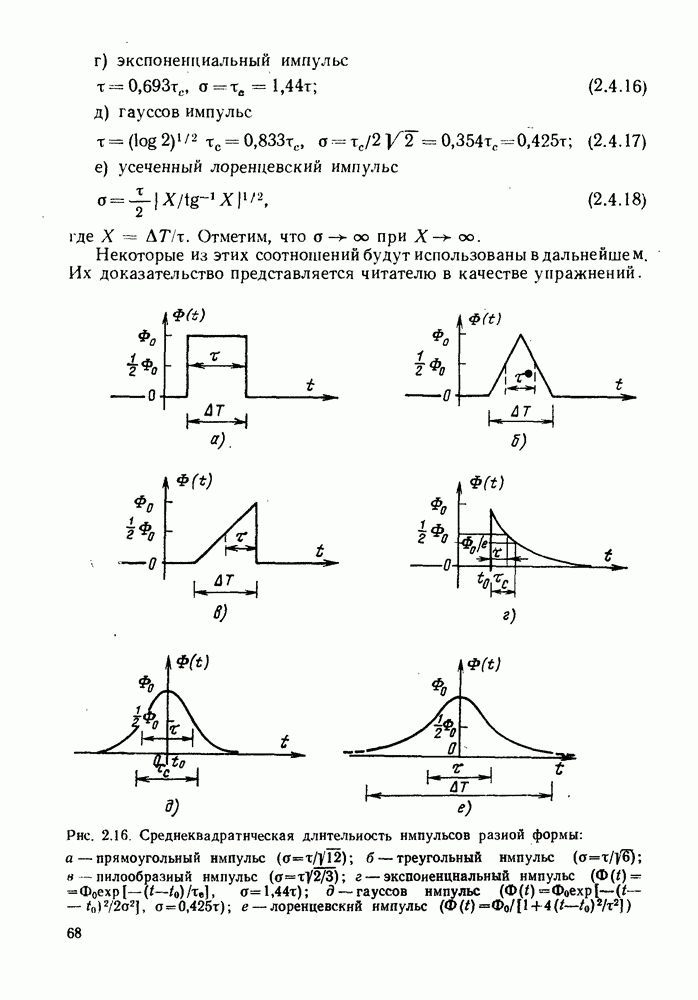
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
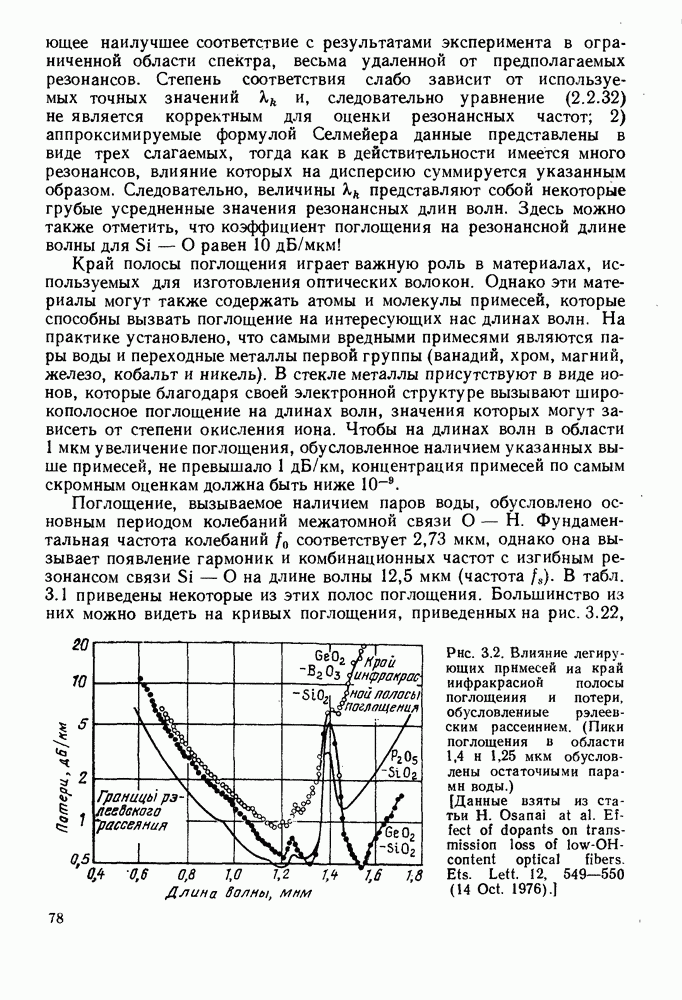
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
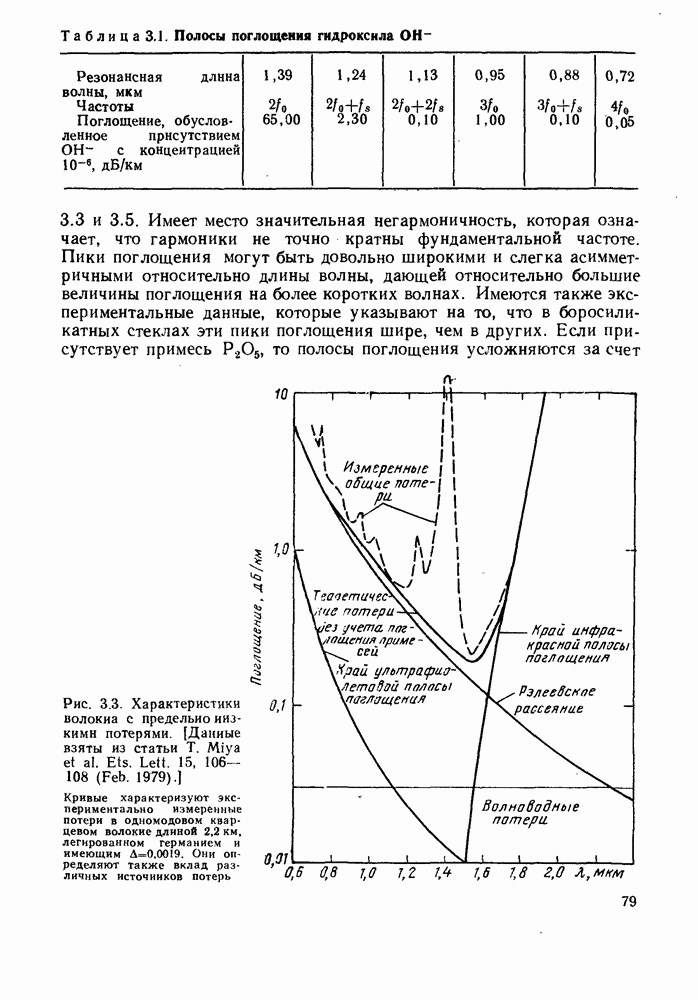
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
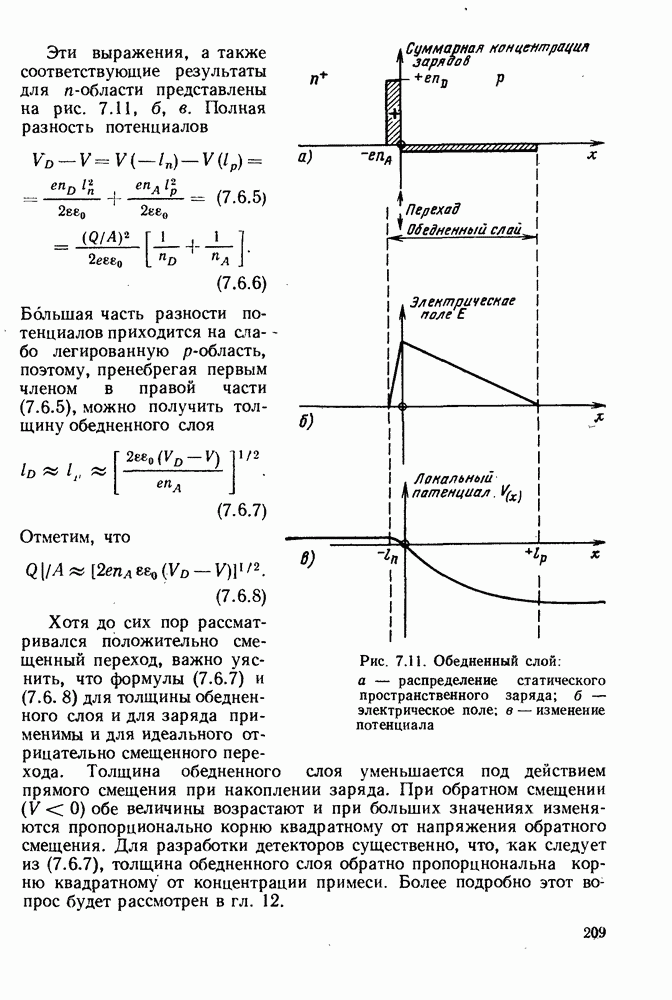
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
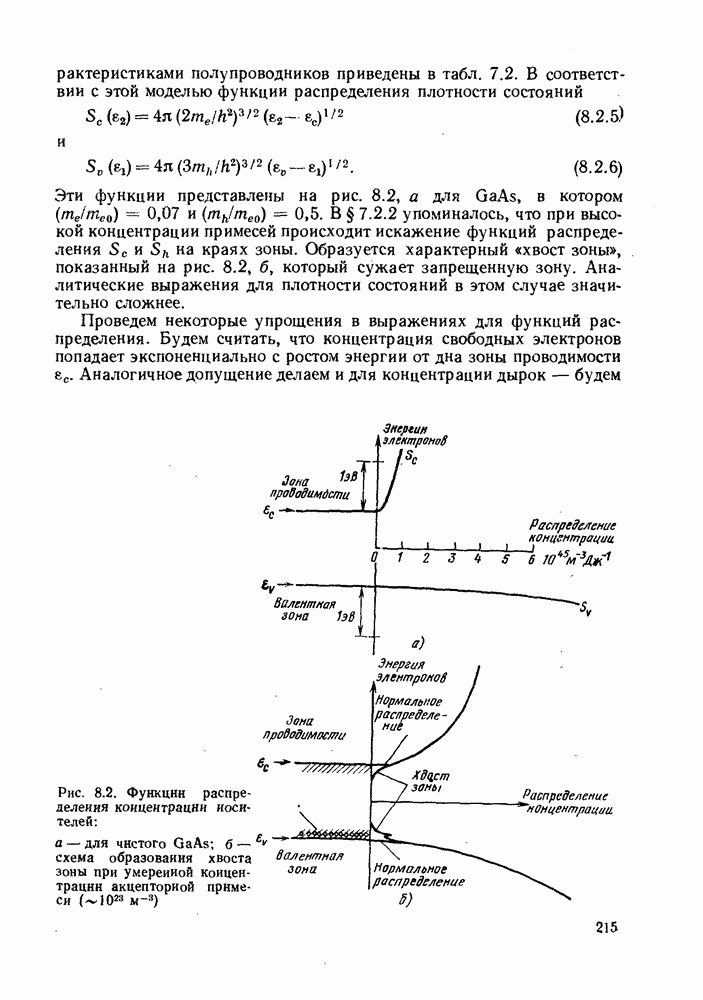
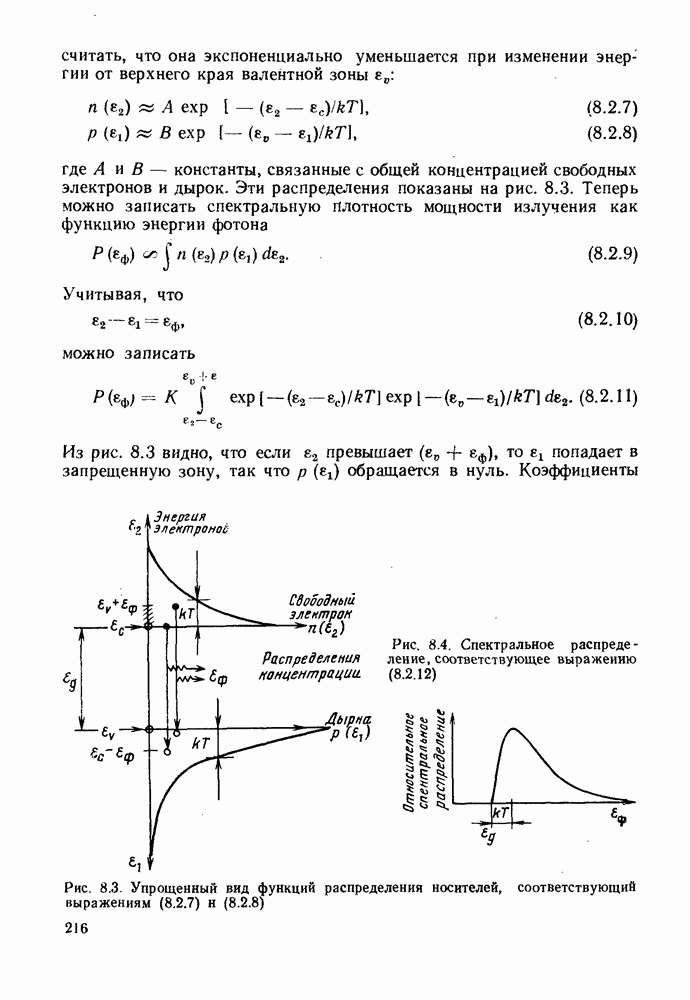
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
- 11.2.2. Спектральные характеристики
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
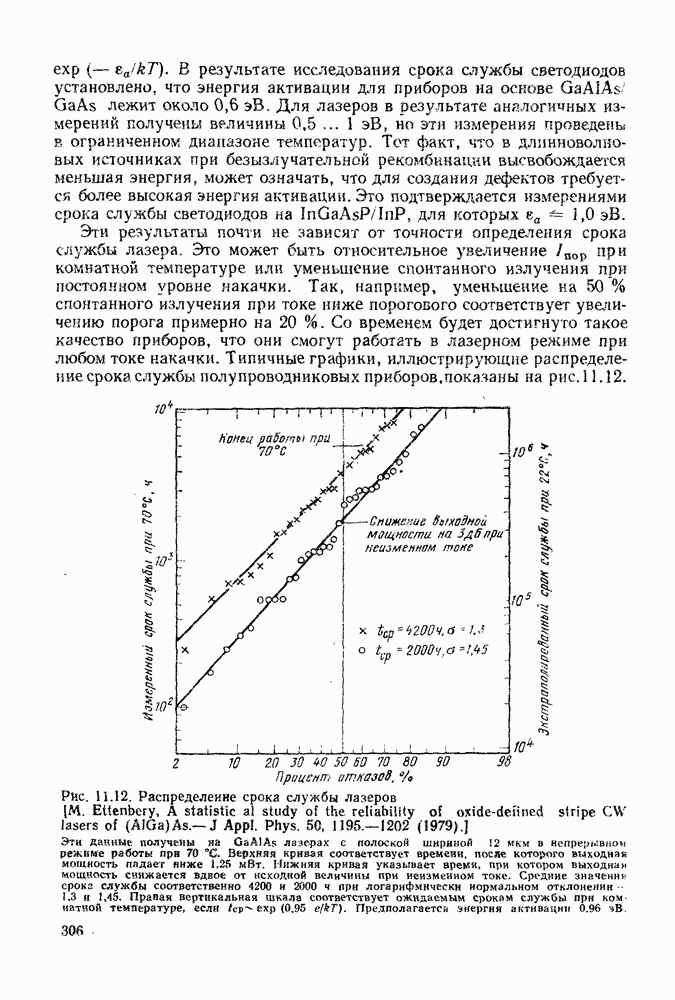
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
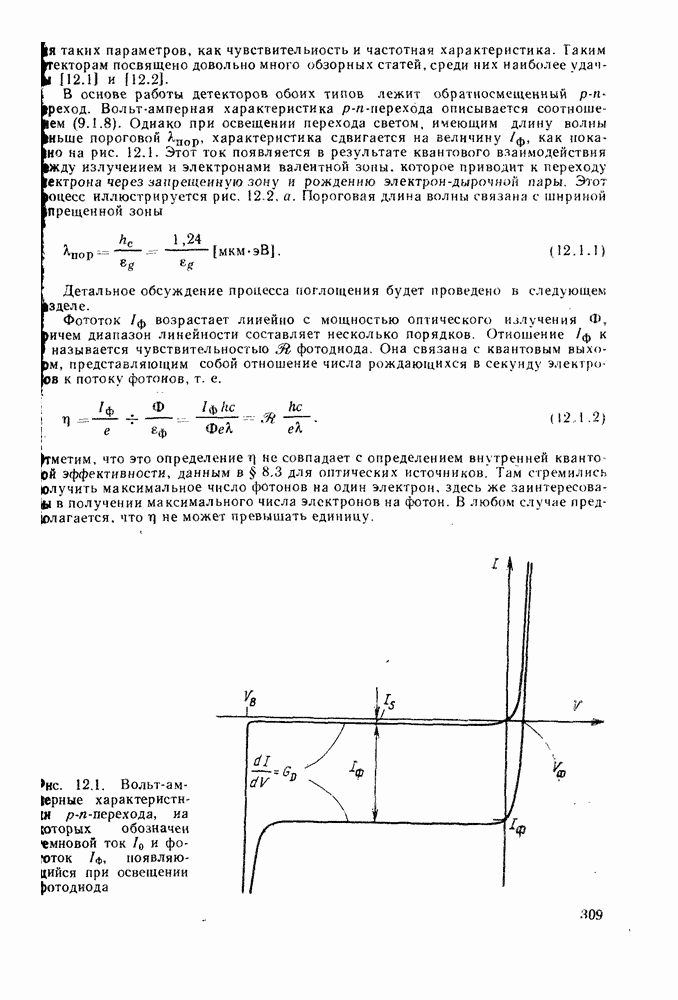
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
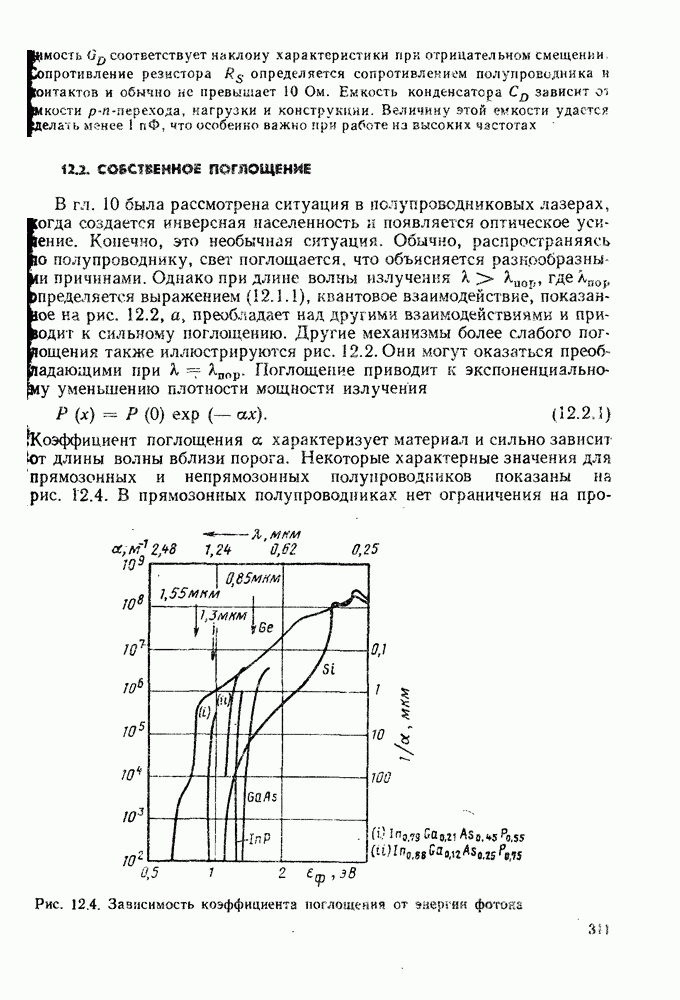
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
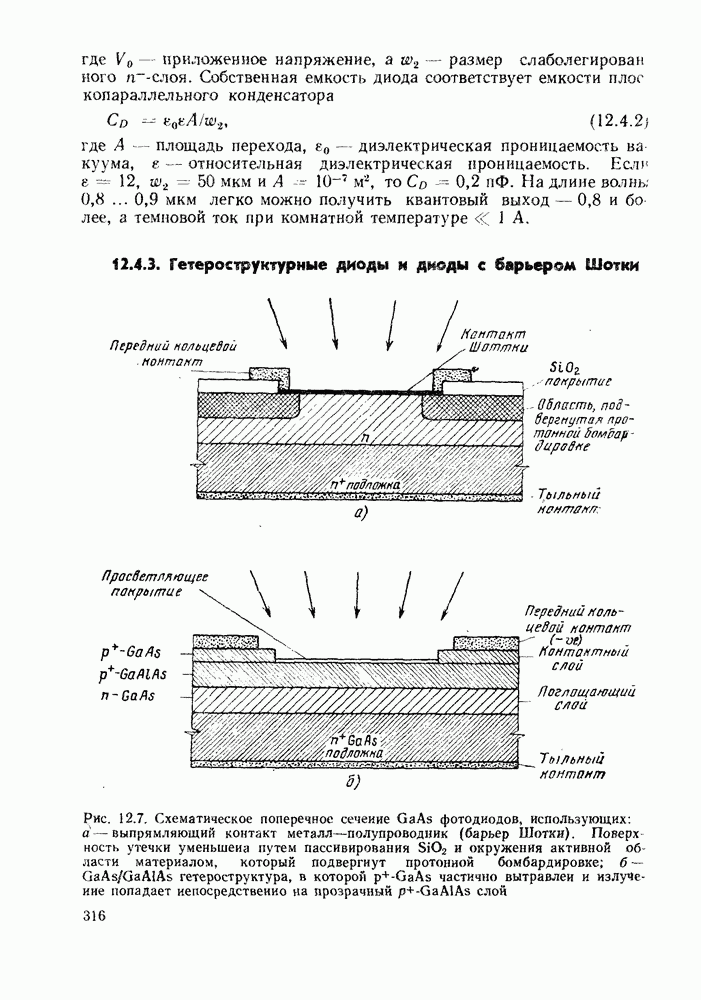
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
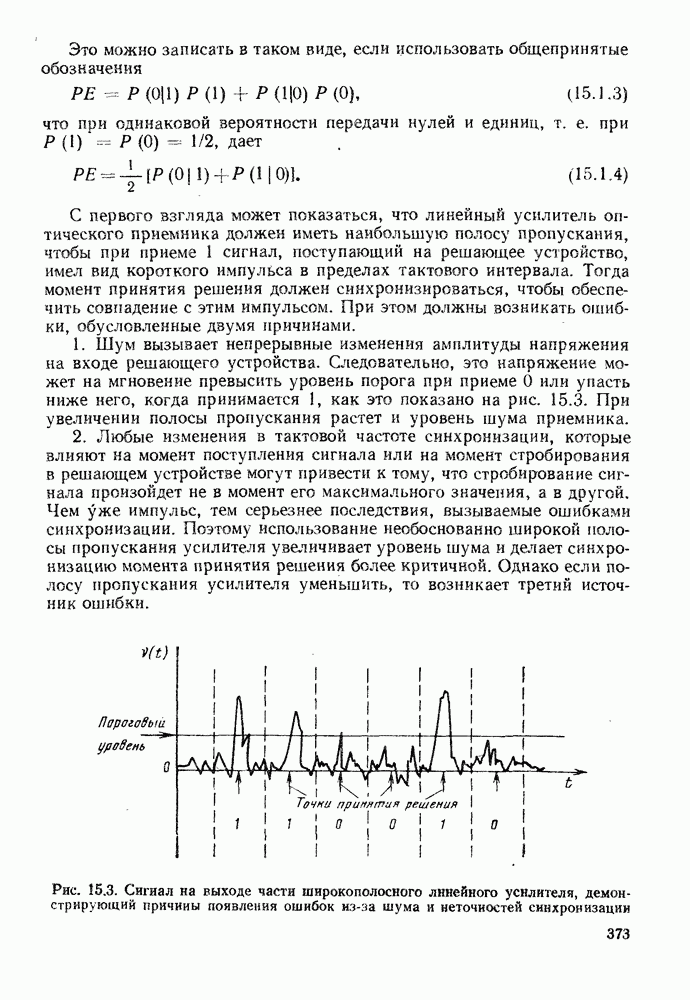
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
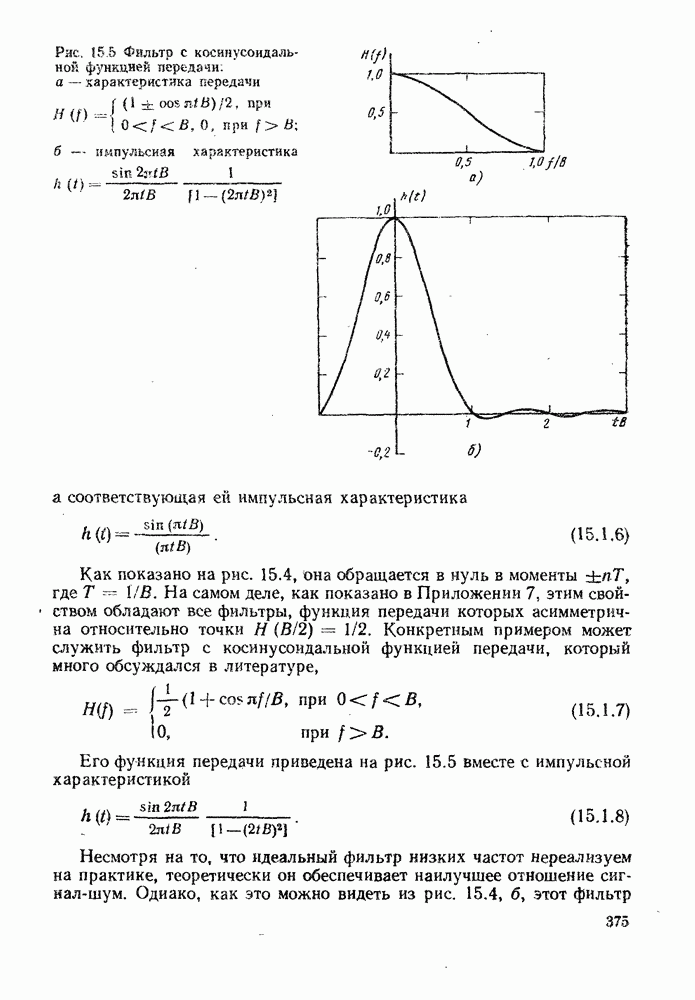
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
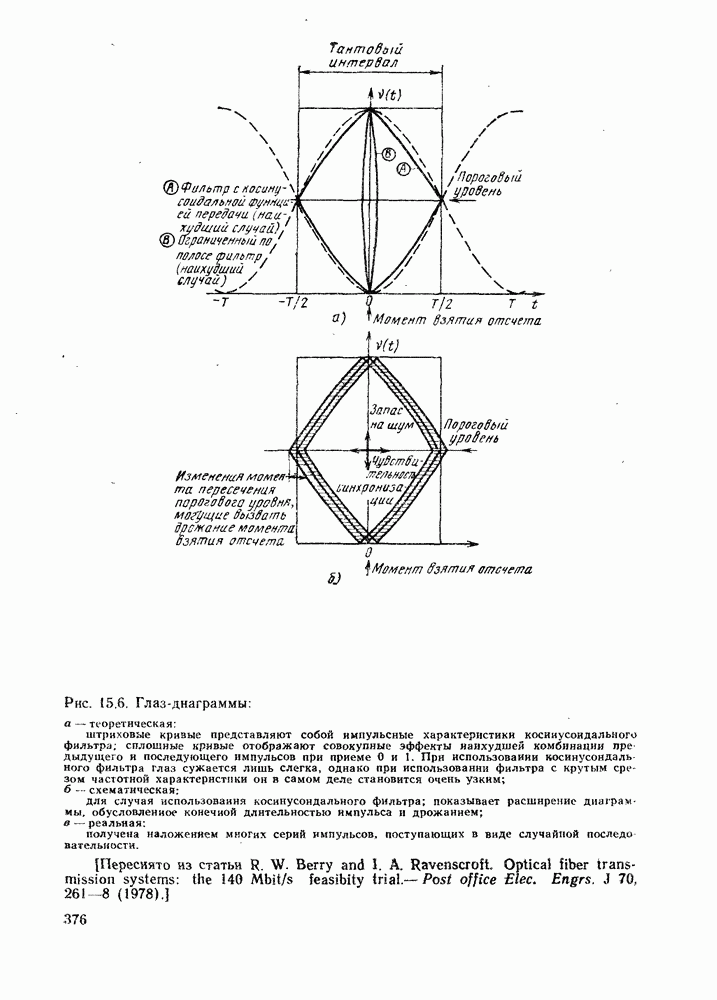
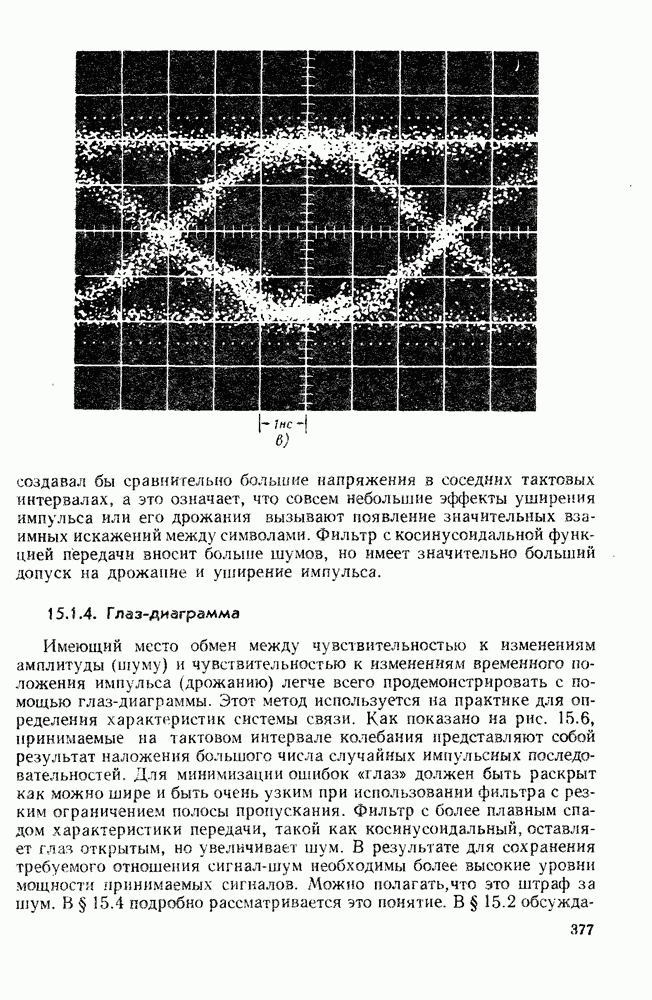
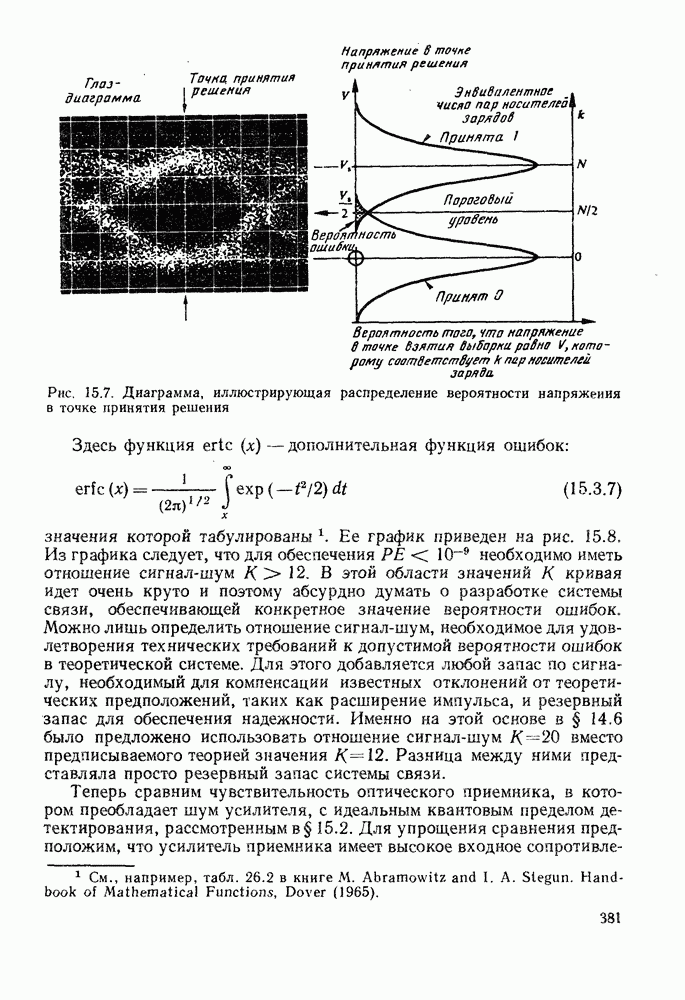
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
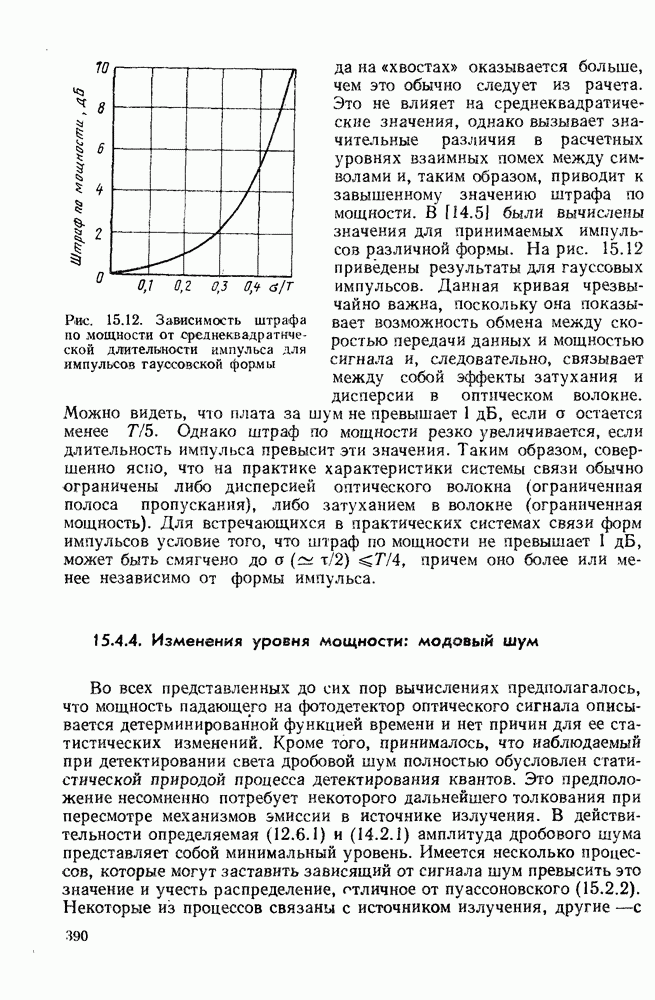
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
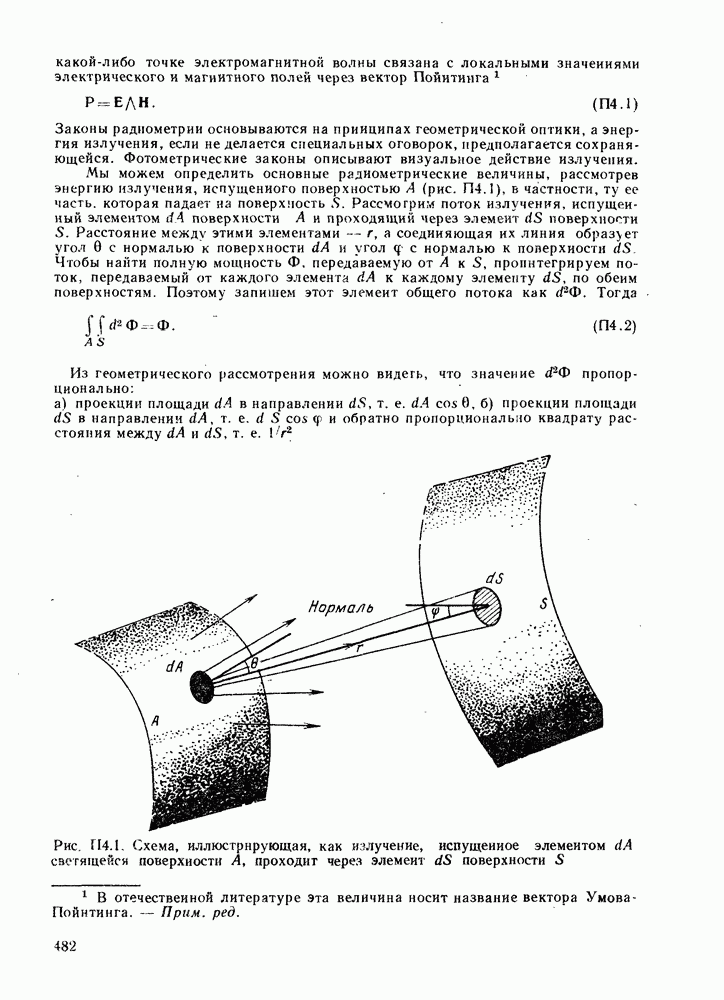
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
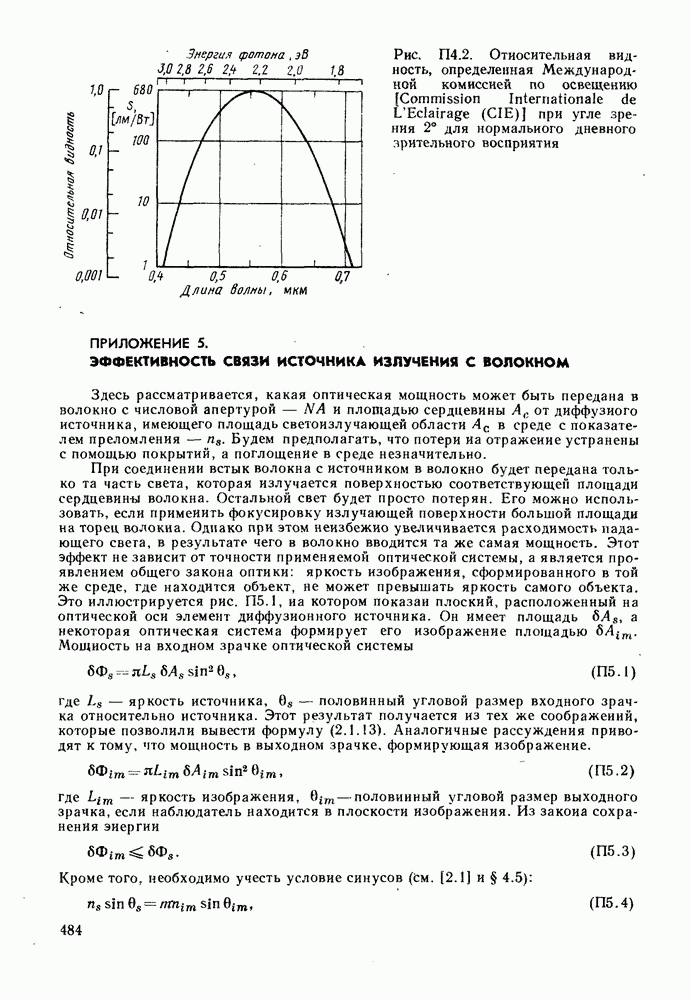
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
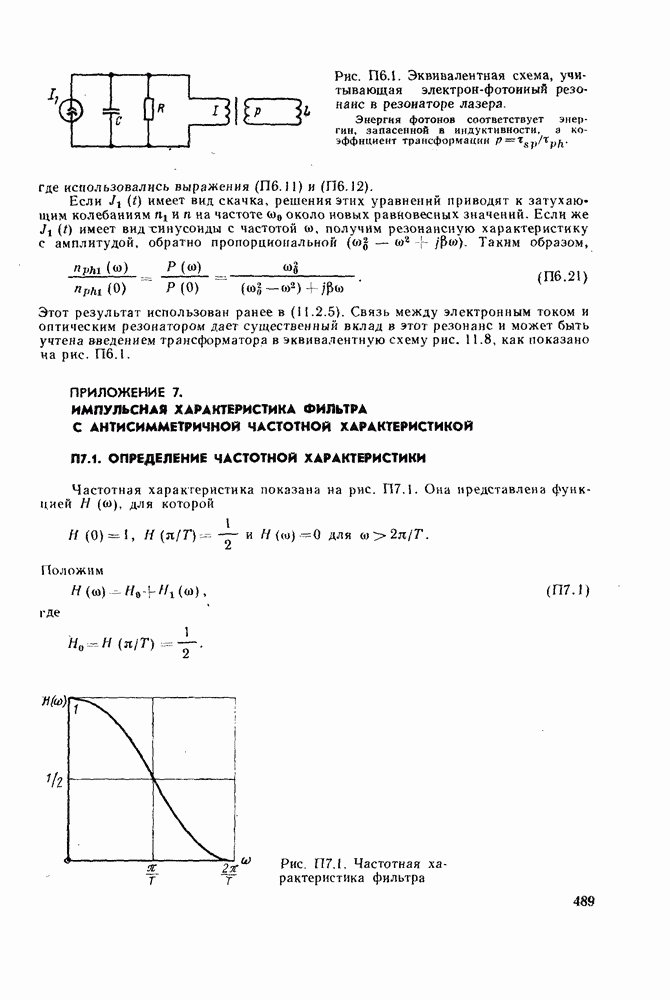
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ