| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
Здесь будем рассматривать волокно, состоящее из однородной сердцевины радиусом а из материала с показателем преломления  и бесконечно толстой оболочки из материала с показателем преломления
и бесконечно толстой оболочки из материала с показателем преломления 
Решения уравнений (5.1.1) должны удовлетворять только разрыву функции  в точке
в точке  а и принимают вид хорошо известных функций, а именно, функций Бесселя
а и принимают вид хорошо известных функций, а именно, функций Бесселя  в области сердцевины и функций Ганкеля
в области сердцевины и функций Ганкеля  в пределах оболочки Аксиальные составляющие поля в оболочке
в пределах оболочки Аксиальные составляющие поля в оболочке  определяются выражением
определяются выражением

где — постоянное электрическое или магнитное поле;  целое число; и — параметр, связанный с еще не определенной нами постоянной распространения § световодной волны следующим соотношением:
целое число; и — параметр, связанный с еще не определенной нами постоянной распространения § световодной волны следующим соотношением:

Отметим, что

— постоянная распространения плоских поперечных электромагнитных волн (ТЕМ) в материале сердцевины волокна.
Осевые составляющие поля в оболочке  определяются формулой
определяются формулой

где  постоянное электрическое или магнитное поле;
постоянное электрическое или магнитное поле;  целое число;
целое число;  параметр, связанный с
параметр, связанный с  соотношением
соотношением

Здесь

— постоянная распространения для плоских поперечных электромагнитных волн (ТЕМ) в материале оболочки. При больших значениях  таких, что при
таких, что при

Это означает, что поля в оболочке затухают экспоненциально на больших радиальных расстояниях от сердцевины. Это те самые поля, которые раньше мы называли затухающей волной.
До сих пор рассматривались решения только для аксиальных составляющих  Поперечные составляющие могут быть найдены с помощью следующих соотношений:
Поперечные составляющие могут быть найдены с помощью следующих соотношений:

где 
Картины распределения электромагнитного поля для различных мод имеют некоторое сходство с теми, которые получаются в круглых металлических волноводах, имея в виду менее резкие граничные условия на поверхности сердцевина — оболочка. В то время как на границе металл — воздух электрическое поле, параллельное ее поверхности, должно быть пренебрежимо мало (обе составляющие  обращаются в нуль), в волокне радиальные поля испытывают лишь небольшой разрыв на поверхности, разделяющей сердцевину и оболочку, причем тангенциальные составляющие поля
обращаются в нуль), в волокне радиальные поля испытывают лишь небольшой разрыв на поверхности, разделяющей сердцевину и оболочку, причем тангенциальные составляющие поля  должны быть здесь непрерывны. Требование удовлетворить этим граничным условиям означает, что для каждого значения
должны быть здесь непрерывны. Требование удовлетворить этим граничным условиям означает, что для каждого значения  в выражениях (5.2.1) и (5.2.3) существует только определенный дискретный набор значений
в выражениях (5.2.1) и (5.2.3) существует только определенный дискретный набор значений  и
и  Обозначим из
Обозначим из  Как и
Как и  индекс
индекс  означает целое число. Отсюда следует, что и постоянная распространения
означает целое число. Отсюда следует, что и постоянная распространения  также принимает лишь дискретные значения, определяемые выражением
также принимает лишь дискретные значения, определяемые выражением

Рассмотрим сначала решения уравнений (5.2.1) и (5.2.3) при  Они имеют вид: в сердцевине
Они имеют вид: в сердцевине

в оболочке

Эти решения представляют собой моды, в которых картины распределения поля имеют радиальную симметрию. Можно полагать, что в рамках лучевой модели каждая из этих мод  соответствует ряду меридиональных лучей, имеющих предписанный угол, наклона к оси волокна. Как и в случае круглого металлического волновода, в данном случае имеются два набора (множества) решений. В первом изних составляющая
соответствует ряду меридиональных лучей, имеющих предписанный угол, наклона к оси волокна. Как и в случае круглого металлического волновода, в данном случае имеются два набора (множества) решений. В первом изних составляющая  равна нулю и такие моды называются поперечными магнитными
равна нулю и такие моды называются поперечными магнитными  а во втором обращается в нуль составляющая
а во втором обращается в нуль составляющая  и такие моды называются поперечными электрическими
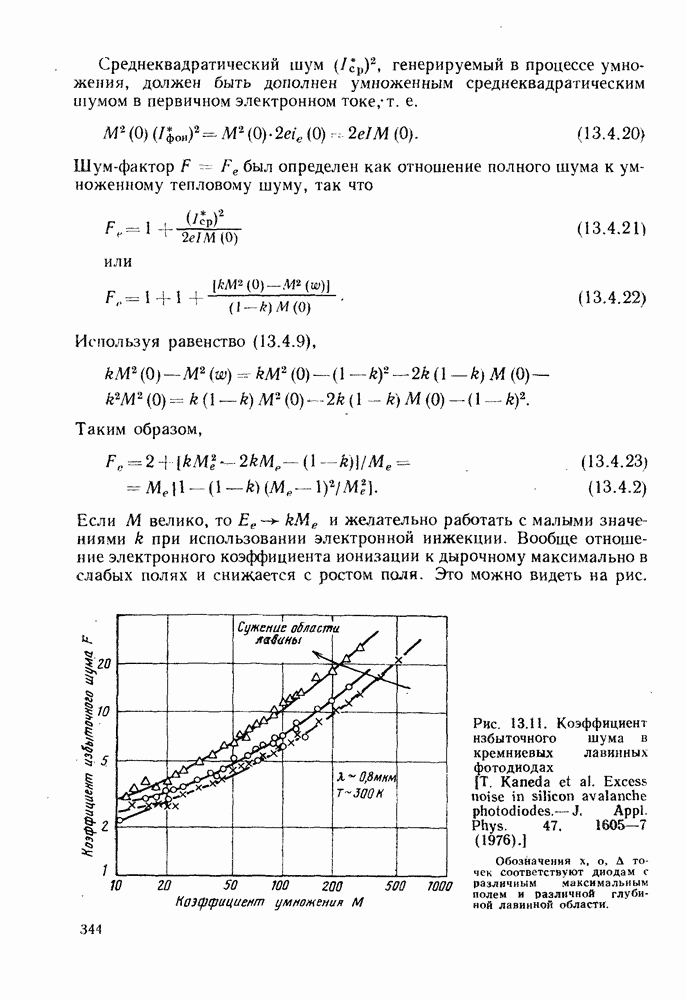
и такие моды называются поперечными электрическими  На рис. 5.1 приведены картины поперечного электрического поля в сердцевине волокна для двух мод, соответствующих
На рис. 5.1 приведены картины поперечного электрического поля в сердцевине волокна для двух мод, соответствующих  Распределения осевых и поперечных составляющих как для электрических, так и магнитных полей, связанных с модой
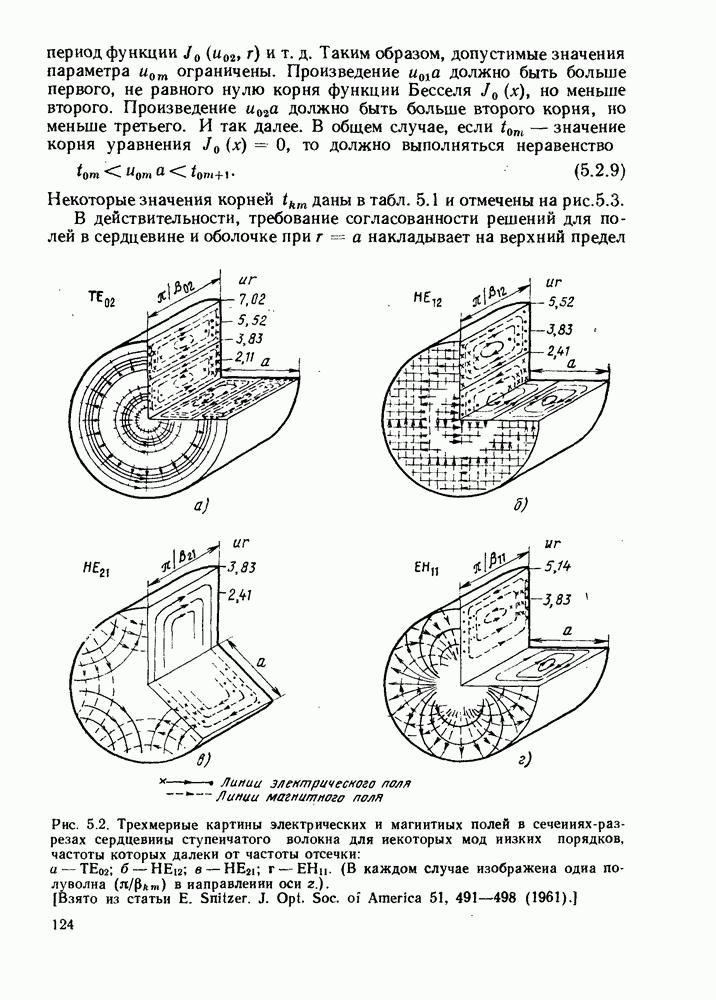
Распределения осевых и поперечных составляющих как для электрических, так и магнитных полей, связанных с модой  изображены на рис. 5.2, а.
изображены на рис. 5.2, а.
Теперь можно понять значение второго параметра моды  Функция Бесселя
Функция Бесселя  описывающая распределение амплитуд поля в. сердцевине, является осциллирующей функцией. Ее график приведен на рис. 5.3. С другой стороны, модифицированная функция Ганкеля, описывающая поля в оболочке, есть монотонно убывающая функция. Для моды с параметрами
описывающая распределение амплитуд поля в. сердцевине, является осциллирующей функцией. Ее график приведен на рис. 5.3. С другой стороны, модифицированная функция Ганкеля, описывающая поля в оболочке, есть монотонно убывающая функция. Для моды с параметрами  значение параметра
значение параметра  должно быть таким, чтобы на поверхности сердцевина — оболочка
должно быть таким, чтобы на поверхности сердцевина — оболочка  оно находилось в области второго полупериода функции
оно находилось в области второго полупериода функции  Для моды
Для моды  при
при  она должна попасть в третий
она должна попасть в третий

Рис. 5.1. Картины векторов поперечного электрического поля в поперечном сечении сердцевины ступенчатого волокна для четырех мод самых низких порядков
полупериод функции  и т. д. Таким образом, допустимые значения параметра
и т. д. Таким образом, допустимые значения параметра  ограничены. Произведение
ограничены. Произведение  должно быть больше первого, не равного нулю корня функции Бесселя
должно быть больше первого, не равного нулю корня функции Бесселя  но меньше второго. Произведение иога должно быть больше второго корня, но меньше третьего. И так далее. В общем случае, если
но меньше второго. Произведение иога должно быть больше второго корня, но меньше третьего. И так далее. В общем случае, если  значение корня уравнения
значение корня уравнения  то должно выполняться неравенство
то должно выполняться неравенство

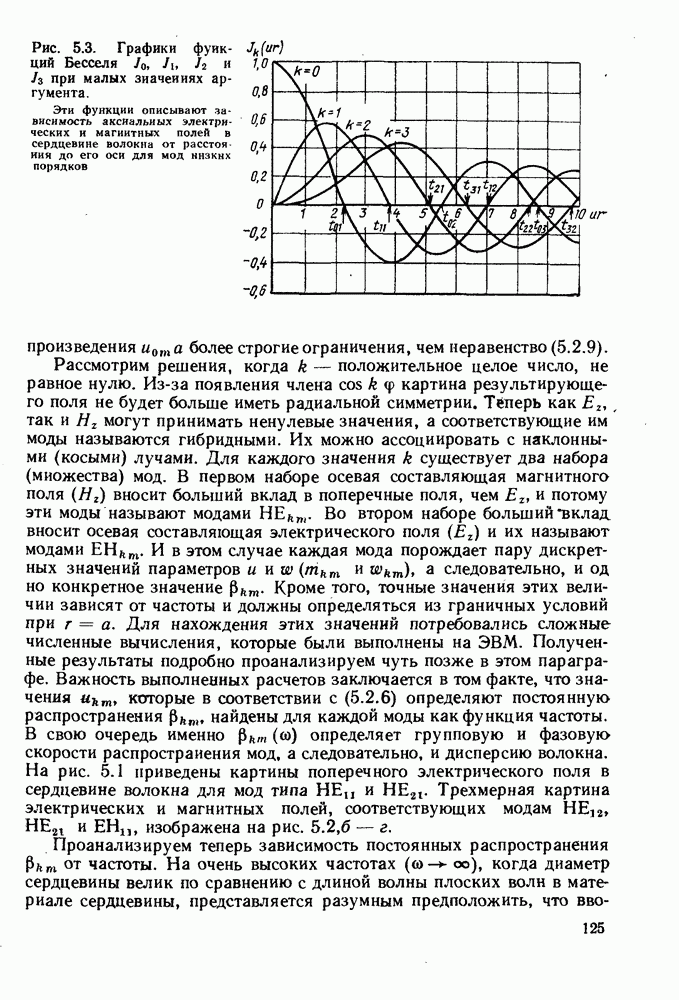
Некоторые значения корней  даны в табл. 5.1 и отмечены на рис. 5.3.
даны в табл. 5.1 и отмечены на рис. 5.3.
В действительности, требование согласованности решений для полей в сердцевине и оболочке при  накладывает на верхний предел
накладывает на верхний предел

Рис. 5.2. Трехмерные картины электрических и магиитиых полей в сечениях-разрезах сердцевины ступенчатого волокна для некоторых мод низких порядков, частоты которых далеки от частоты отсечки: а —  (В каждом случае изображена одна полуволна
(В каждом случае изображена одна полуволна  в направлении оси
в направлении оси  ). [Взято из статьи Е. Snitzer. J. Opt. Soc. of America 51, 491-498 (1961).]
). [Взято из статьи Е. Snitzer. J. Opt. Soc. of America 51, 491-498 (1961).]

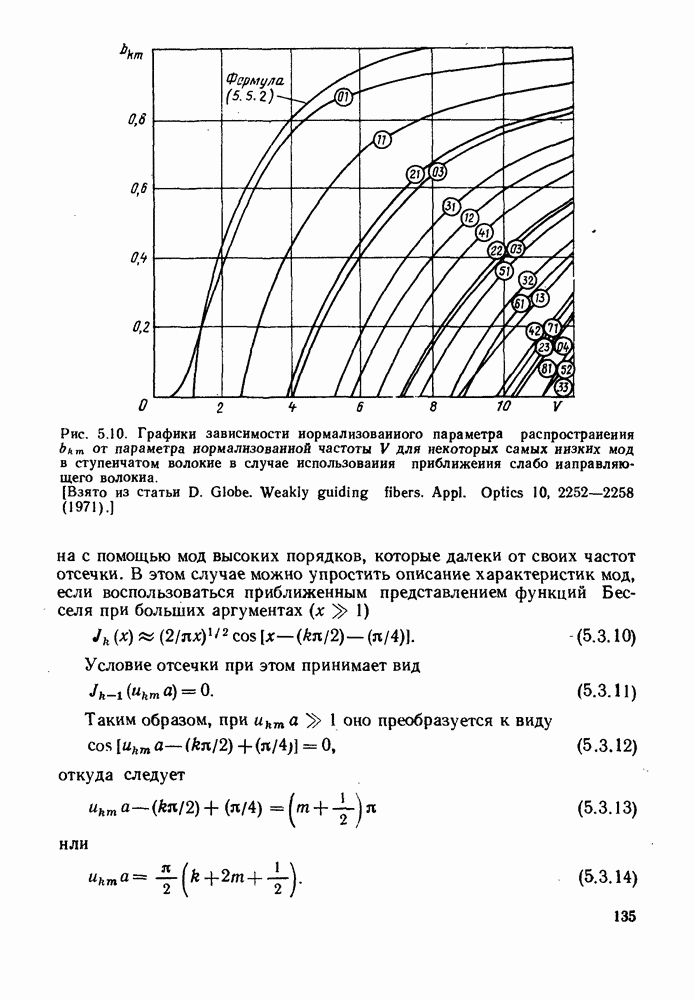
Рис. 5.3. Графики функций Бесселя  при малых значениях аргумента. Эти функции описывают зависимость аксиальных электрических и магнитных полей в сердцевине волокна от расстояния до его оси для мод ннзкнх порядков
при малых значениях аргумента. Эти функции описывают зависимость аксиальных электрических и магнитных полей в сердцевине волокна от расстояния до его оси для мод ннзкнх порядков
произведения  более строгие ограничения, чем неравенство (5.2.9).
более строгие ограничения, чем неравенство (5.2.9).
Рассмотрим решения, когда  положительное целое число, не равное нулю. Из-за появления члена
положительное целое число, не равное нулю. Из-за появления члена  картина результирующего поля не будет больше иметь радиальной симметрии. Теперь как
картина результирующего поля не будет больше иметь радиальной симметрии. Теперь как  так и
так и  могут принимать ненулевые значения, а соответствующие им моды называются гибридными. Их можно ассоциировать с наклонными (косыми) лучами. Для каждого значения
могут принимать ненулевые значения, а соответствующие им моды называются гибридными. Их можно ассоциировать с наклонными (косыми) лучами. Для каждого значения  существует два набора (множества) мод. В первом наборе осевая составляющая магнитного поля
существует два набора (множества) мод. В первом наборе осевая составляющая магнитного поля  вносит больший вклад в поперечные поля, чем
вносит больший вклад в поперечные поля, чем  и потому эти моды называют модами Во втором наборе больший вклад вносит осевая составляющая электрического поля
и потому эти моды называют модами Во втором наборе больший вклад вносит осевая составляющая электрического поля  и их называют модами
и их называют модами  И в этом случае каждая мода порождает пару дискретных значений параметров и и
И в этом случае каждая мода порождает пару дискретных значений параметров и и  а следовательно, и
а следовательно, и  но конкретное значение Кроме того, точные значения этих величии зависят от частоты и должны определяться из граничных условий при
но конкретное значение Кроме того, точные значения этих величии зависят от частоты и должны определяться из граничных условий при  Для нахождения этих значений потребовались сложные численные вычисления, которые были выполнены на ЭВМ. Полученные результаты подробно проанализируем чуть позже в этом параграфе. Важность выполненных расчетов заключается в том факте, что значения
Для нахождения этих значений потребовались сложные численные вычисления, которые были выполнены на ЭВМ. Полученные результаты подробно проанализируем чуть позже в этом параграфе. Важность выполненных расчетов заключается в том факте, что значения  которые в соответствии с (5.2.6) определяют постоянную распространения
которые в соответствии с (5.2.6) определяют постоянную распространения  найдены для каждой моды как функция частоты. В свою очередь именно
найдены для каждой моды как функция частоты. В свою очередь именно  определяет групповую и фазовую скорости распространения мод, а следовательно, и дисперсию волокна. На рис. 5.1 приведены картины поперечного электрического поля в сердцевине волокна для мод типа
определяет групповую и фазовую скорости распространения мод, а следовательно, и дисперсию волокна. На рис. 5.1 приведены картины поперечного электрического поля в сердцевине волокна для мод типа  и
и  Трехмерная картина электрических и магнитных полей, соответствующих модам
Трехмерная картина электрических и магнитных полей, соответствующих модам  изображена на рис. 5.2, б - г.
изображена на рис. 5.2, б - г.
Проанализируем теперь зависимость постоянных распространения  от частоты. На очень высоких частотах
от частоты. На очень высоких частотах  когда диаметр сердцевины велик по сравнению с длиной волны плоских волн в материале сердцевины, представляется разумным предположить, что
когда диаметр сердцевины велик по сравнению с длиной волны плоских волн в материале сердцевины, представляется разумным предположить, что
Таблица 5.1. (см. скан) Корни функций Бесселя
вводимый в сердцевину свет в первом приближении будет распространяться в виде плоской ТЕМ-волны, имеющей постоянную распространения  При этих условиях уместно вернуться к лучевой модели распространения света в волокне. В таком случае можно ассоциировать моды более высоких порядков с теми лучами, которые более наклонены к оси волокна. Параметр распространения моды
При этих условиях уместно вернуться к лучевой модели распространения света в волокне. В таком случае можно ассоциировать моды более высоких порядков с теми лучами, которые более наклонены к оси волокна. Параметр распространения моды  при этом будет определять кажущуюся фазовую скорость
при этом будет определять кажущуюся фазовую скорость  волны вдоль линии, параллельной оси:
волны вдоль линии, параллельной оси:

Свяжем такую моду с лучом, представляющим плоскую ТЕМ-волну, перемещающуюся под углом  к оси волокна и распространяющуюся в направлении оси
к оси волокна и распространяющуюся в направлении оси  путем многократного отражения, как это показано на рис. 5.4. Из рисунка видно, что, хотя фазовая скорость в направлении распространения луча равна
путем многократного отражения, как это показано на рис. 5.4. Из рисунка видно, что, хотя фазовая скорость в направлении распространения луча равна

кажущаяся фазовая скорость, с которой волновой фронт пересекает любую линию, параллельную оси волокна, будет определяться из следующего соотношения

откуда

Как было показано  предельный угол наклона
предельный угол наклона  для лучей, еще распространяющихся в волокне, определялся таким критическим углом
для лучей, еще распространяющихся в волокне, определялся таким критическим углом  что
что

Таким образом,  определяет минимальное значение
определяет минимальное значение  в соответствии с соотношениями
в соответствии с соотношениями

Это означает, что на любой заданной частоте моды самых низких порядков (соответствующие аксиальным лучам) имеют постоянную распространения, близкую к  в то время как мода самого высокого порядка, еще способная распространяться в волокне (и соответствующая самому наклонному лучу), имеет постоянную распространения
в то время как мода самого высокого порядка, еще способная распространяться в волокне (и соответствующая самому наклонному лучу), имеет постоянную распространения  которая соответствует плоским ТЕМ-волнам в оболочке.
которая соответствует плоским ТЕМ-волнам в оболочке.
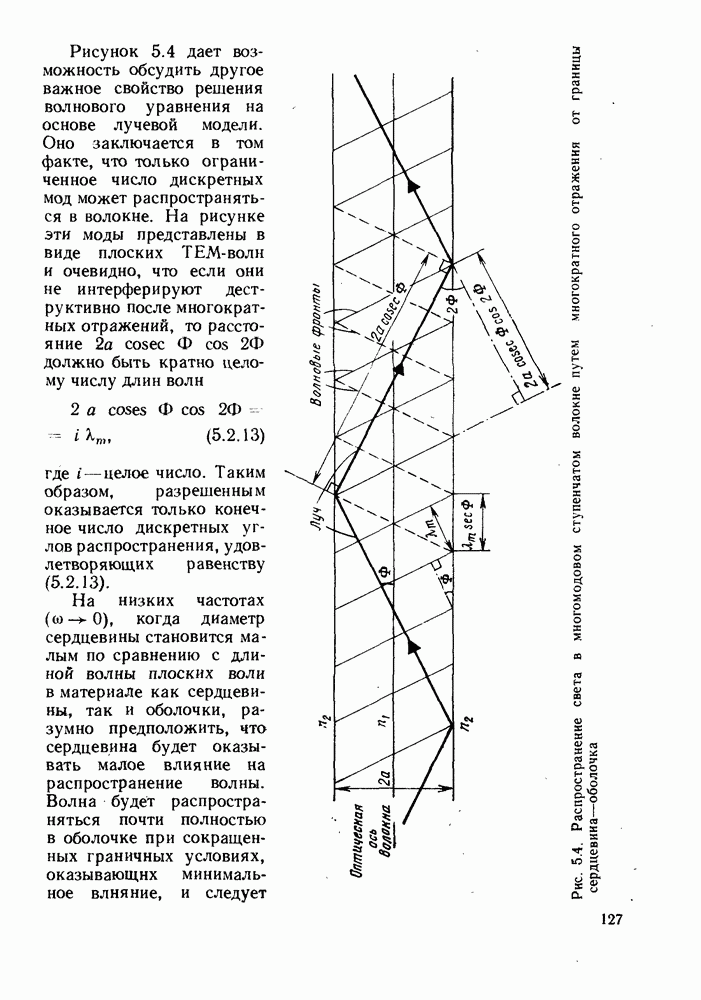
Рисунок 5.4 дает возможность обсудить другое важное свойство решения волнового уравнения на основе лучевой модели. Оно заключается в том факте, что только ограниченное число дискретных мод может распространяться в волокне. На рисунке эти моды представлены в виде плоских ТЕМ-волн и очевидно, что если они не интерферируют деструктивно после многократных отражений, то расстояние  должно быть кратно целому числу длин волн
должно быть кратно целому числу длин волн

где  целое число. Таким образом, разрешенным оказывается только конечное число дискретных углов распространения, удовлетворяющих равенству (5.2.13).
целое число. Таким образом, разрешенным оказывается только конечное число дискретных углов распространения, удовлетворяющих равенству (5.2.13).
На низких частотах  когда диаметр сердцевины становится малым по сравнению с длиной волны плоских воли в материале как сердцевины, так и оболочки, разумно предположить, что сердцевина будет оказывать малое влияние на распространение волны. Волна будет распространяться почти полностью в оболочке при сокращенных граничных условиях, оказывающих минимальное влияние, и следует
когда диаметр сердцевины становится малым по сравнению с длиной волны плоских воли в материале как сердцевины, так и оболочки, разумно предположить, что сердцевина будет оказывать малое влияние на распространение волны. Волна будет распространяться почти полностью в оболочке при сокращенных граничных условиях, оказывающих минимальное влияние, и следует
Рис. 5.4. (см. скан) Распространение света в многомодовом ступенчатом волокне путем многократного отражения от границы сердцевина-оболочка
ожидать неограниченных ненаправленных плоских ТЕМ-волн, имеющих постоянную распространения  . В действительности, существует бесконечно много ненаправленных мод, содержащих, например, и свет, который входит в сердцевину через границу сердцевина — оболочка, проходит через сердцевину и выходит с противоположной стороны волокна.
. В действительности, существует бесконечно много ненаправленных мод, содержащих, например, и свет, который входит в сердцевину через границу сердцевина — оболочка, проходит через сердцевину и выходит с противоположной стороны волокна.
Интуитивно можно предположить, что постоянная распространения для распространяющихся в волокне мод должна лежать между двумя крайними значениями  а на самом деле условие
а на самом деле условие

существования связанных решений для световодных волн выражено в неявном виде в уравнениях (5.2.2) и (5.2.4), если параметры и и  принимают вещественные значения. Эти решения удовлетворяют интересующему нас неравенству (5.2.14).
принимают вещественные значения. Эти решения удовлетворяют интересующему нас неравенству (5.2.14).
На этой стадии удобно ввести в рассмотрение нормализованный параметр частоты V, определяемый соотношением:

где

Таким образом,

Выражение (5.2.2) можно переписать в таком виде

Из него следует, что на высоких частотах, когда  значения
значения  приближаются к следующим предельным значениям:
приближаются к следующим предельным значениям:

В каждом случае величина  при
при  таким образом,
таким образом, 
Предполагаем, что на низких частотах, когда  Воспользовавшись выражениями (5.2.4) и (5.2.17), видим, что
Воспользовавшись выражениями (5.2.4) и (5.2.17), видим, что  Весьма важно отметить, что для всех светодиодных мод, кроме одной, этот предел значений произведений
Весьма важно отметить, что для всех светодиодных мод, кроме одной, этот предел значений произведений  достигается на некоторой не равной нулю частоте отсечки. На частотах ниже частоты отсечки условие (5.2.14) не
достигается на некоторой не равной нулю частоте отсечки. На частотах ниже частоты отсечки условие (5.2.14) не

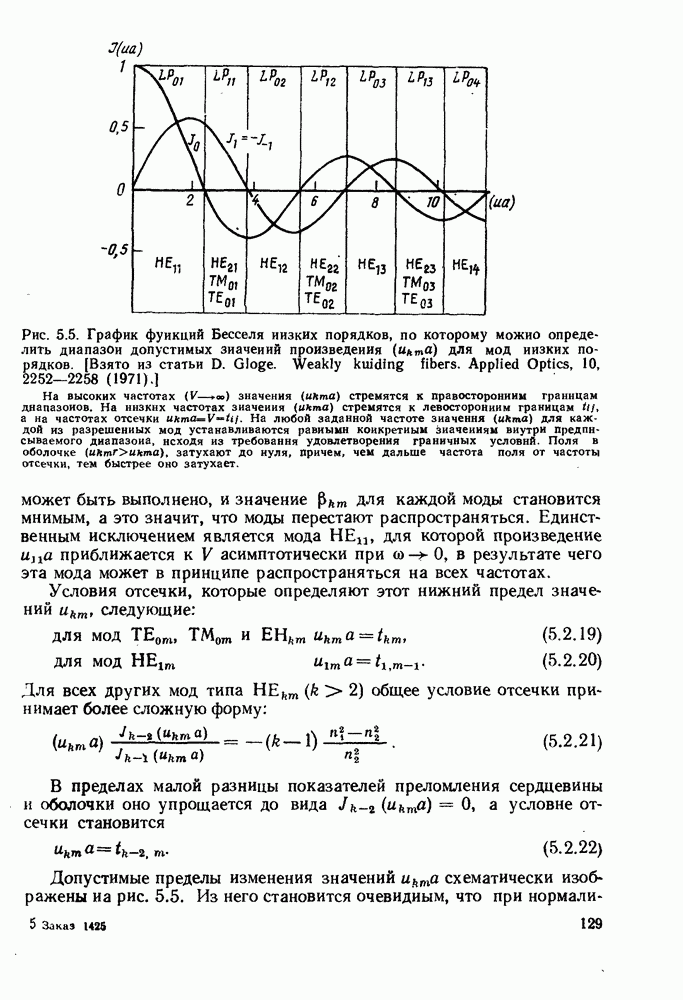
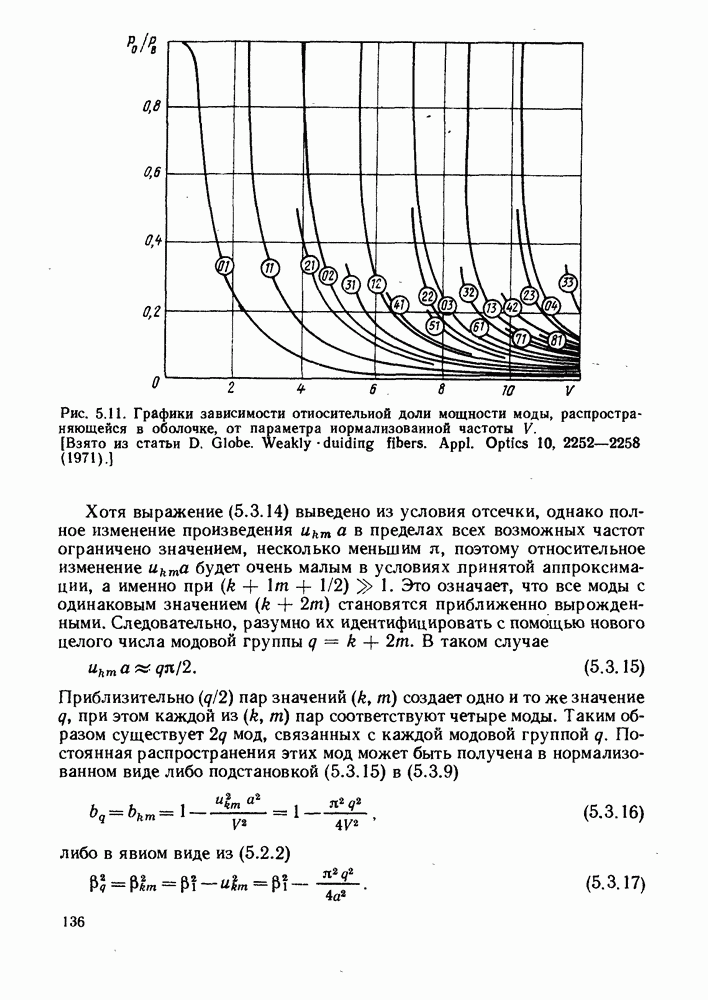
Рис. 5.5. График функций Бесселя низких порядков, по которому можно определить диапазон допустимых значений произведения (иьта) для мод низких порядков. [Взято из статьи D. Gloge. Weakly kuiding fibers. Applied Optics, 10, 2252-2258 (1971).]
На высоких частотах  значения (икта) стремятся к правосторонним границам диапазонов. На ннзкнх частотах значения
значения (икта) стремятся к правосторонним границам диапазонов. На ннзкнх частотах значения  стремятся к левосторонним границам
стремятся к левосторонним границам  а на частотах отсечки
а на частотах отсечки  На любой заданной частоте значения
На любой заданной частоте значения  для каждой из разрешенных мод устанавливаются равными конкретным значениям внутри предписываемого диапазона, исходя из требования удовлетворения граничных условий. Поля в оболочке
для каждой из разрешенных мод устанавливаются равными конкретным значениям внутри предписываемого диапазона, исходя из требования удовлетворения граничных условий. Поля в оболочке  затухают до нуля, причем, чем дальше частота поля от частоты отсечки, тем быстрее оно затухает.
затухают до нуля, причем, чем дальше частота поля от частоты отсечки, тем быстрее оно затухает.
может быть выполнено, и значение  для каждой моды становится мнимым, а это значит, что моды перестают распространяться. Единственным исключением является мода
для каждой моды становится мнимым, а это значит, что моды перестают распространяться. Единственным исключением является мода  для которой произведение
для которой произведение  приближается к V асимптотически при
приближается к V асимптотически при  в результате чего эта мода может в принципе распространяться на всех частотах.
в результате чего эта мода может в принципе распространяться на всех частотах.
Условия отсечки, которые определяют этот нижний предел значений  следующие:
следующие:

Для всех других мод типа  общее условие отсечки принимает более сложную форму:
общее условие отсечки принимает более сложную форму:

В пределах малой разницы показателей преломления сердцевины и оболочки оно упрощается до вида  условие отсечки становится
условие отсечки становится

Допустимые пределы изменения значений икта схематически изображены на рис. 5.5. Из него становится очевидным, что при
нормализованной частоте V менее  может распространяться только одна мода
может распространяться только одна мода  Оптические волокна, спроектированные таким образом, чтобы выполнялось это условие, называются одномодовыми или мономодовыми. Вероятно, в будущем эти волокна будут играть весьма важную роль при создании широкополосных оптических систем связи; подробнее они будут рассмотрены в § 5.5. Рассмотрим достаточно подробно характеристики распространения различных мод.
Оптические волокна, спроектированные таким образом, чтобы выполнялось это условие, называются одномодовыми или мономодовыми. Вероятно, в будущем эти волокна будут играть весьма важную роль при создании широкополосных оптических систем связи; подробнее они будут рассмотрены в § 5.5. Рассмотрим достаточно подробно характеристики распространения различных мод.
Каким образом характеристики распространения мод зависят от частоты, схематически показано на рис. 5.6. Здесь умышленно выбраны график зависимости  от со в противоположность более общепринятой зависимости со от
от со в противоположность более общепринятой зависимости со от  на том основании, что именно постоянная распространения
на том основании, что именно постоянная распространения  а не угловая частота
а не угловая частота  должна рассматриваться как зависимая переменная. Напоминаем, что фазовая скорость, связанная с любой конкретной модой на данной частоте, равна
должна рассматриваться как зависимая переменная. Напоминаем, что фазовая скорость, связанная с любой конкретной модой на данной частоте, равна  в то время как групповая скорость будет равна
в то время как групповая скорость будет равна  Рисунок 5.6 иллюстрирует зависимость
Рисунок 5.6 иллюстрирует зависимость  от частоты для любой заданной моды (волноводная дисперсия), а также изменения
от частоты для любой заданной моды (волноводная дисперсия), а также изменения  при переходе от одной моды к другой, способной распространяться в волокне на данной частоте (модовая дисперсия). Эти характеристики в дальнейшем можно модифицировать, чтобы показать дополнительные эффекты материальной дисперсии и таким образом продемонстрировать
при переходе от одной моды к другой, способной распространяться в волокне на данной частоте (модовая дисперсия). Эти характеристики в дальнейшем можно модифицировать, чтобы показать дополнительные эффекты материальной дисперсии и таким образом продемонстрировать

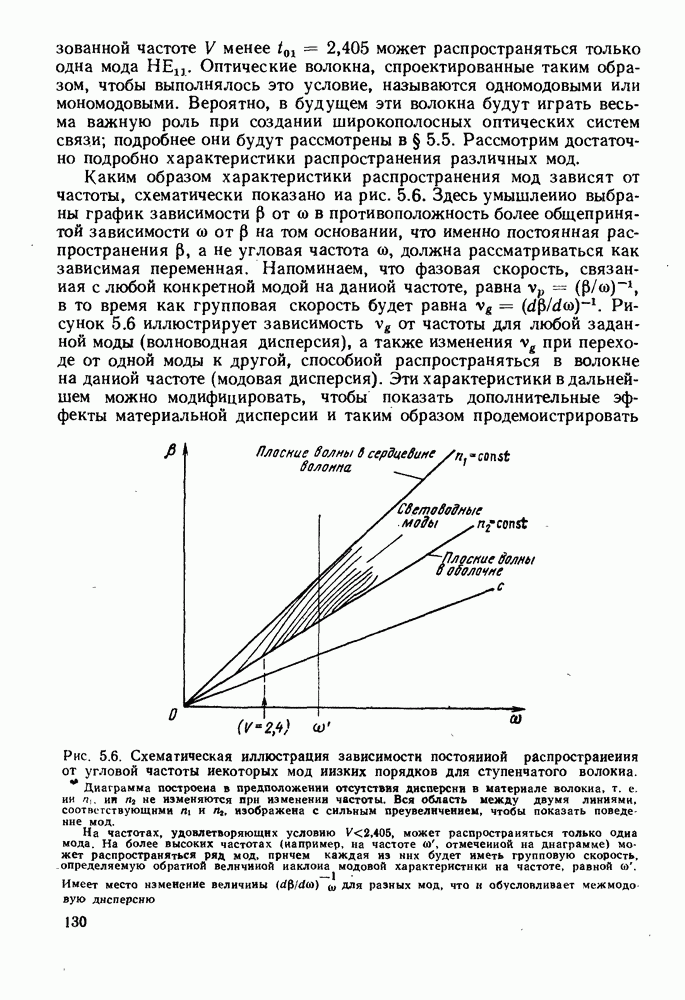
Рис. 5.6. Схематическая иллюстрация зависимости постоянной распространения от угловой частоты некоторых мод низких порядков для ступенчатого волокна. Диаграмма построена в предположении отсутствия дисперсии в материале волокна, т. е. ни  не изменяются при изменении частоты. Вся область между двумя линиями, соответствующими
не изменяются при изменении частоты. Вся область между двумя линиями, соответствующими  изображена с сильным преувеличением, чтобы показать поведение мод. На частотах, удовлетворяющих условию
изображена с сильным преувеличением, чтобы показать поведение мод. На частотах, удовлетворяющих условию  может распространяться только одна мода. На более высоких частотах (например, на частоте
может распространяться только одна мода. На более высоких частотах (например, на частоте  отмеченной на диаграмме) может распространяться ряд мод, причем каждая из них будет иметь групповую скорость, определяемую обратной величиной наклона модовой характеристики на частоте, равной
отмеченной на диаграмме) может распространяться ряд мод, причем каждая из них будет иметь групповую скорость, определяемую обратной величиной наклона модовой характеристики на частоте, равной  Имеет место изменение величины
Имеет место изменение величины  для разных мод, что и обусловливает межмодовую дисперсию
для разных мод, что и обусловливает межмодовую дисперсию

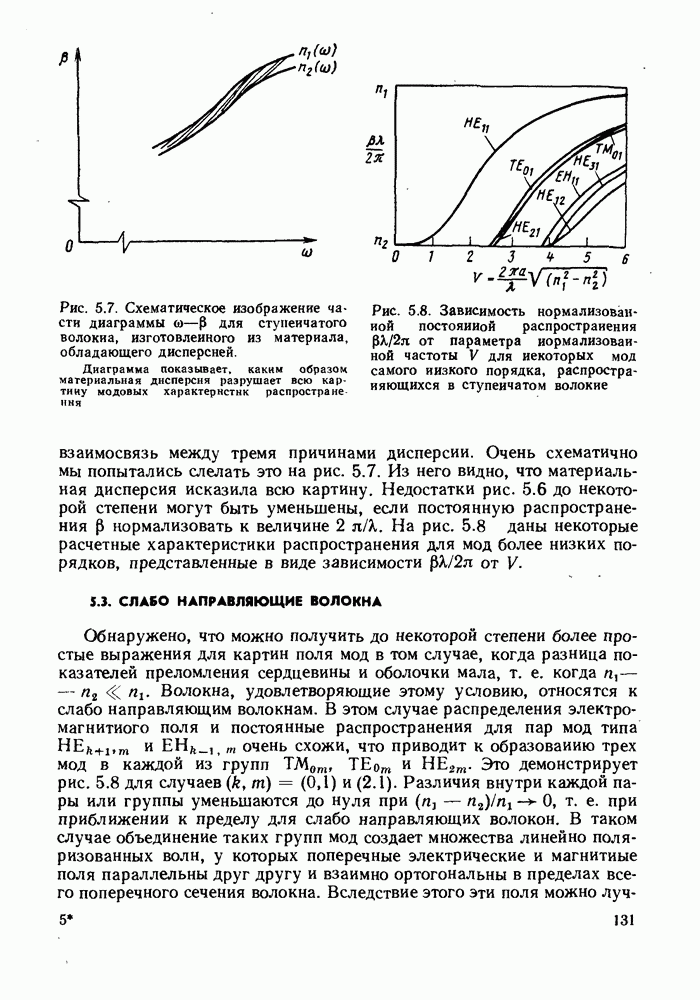
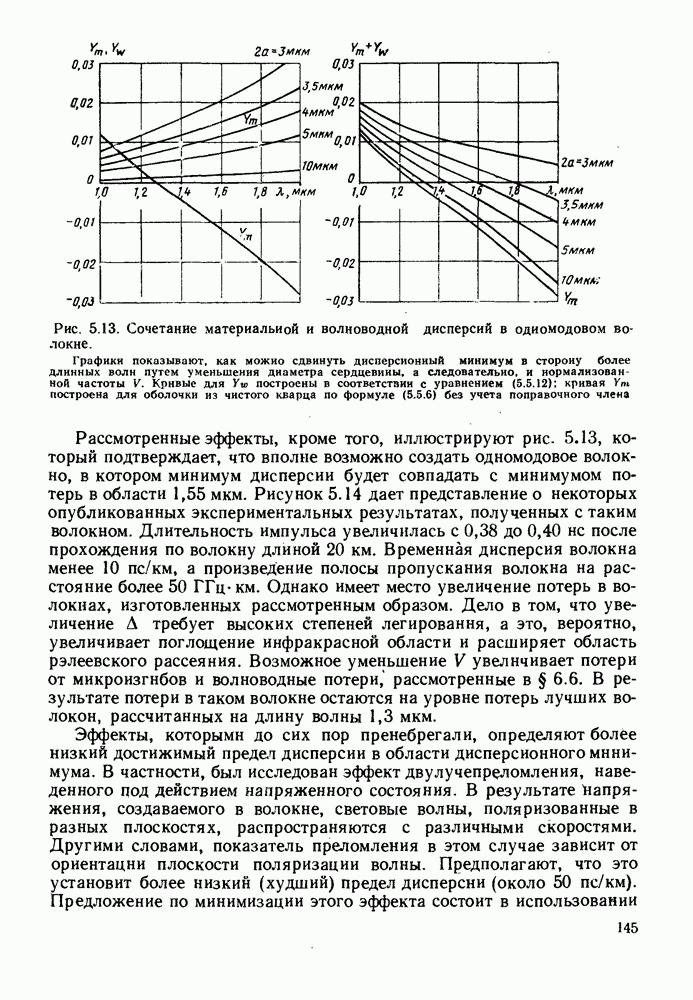
Рис. 5.7. Схематическое изображение части диаграммы  для ступенчатого волокна, изготовленного из материала, обладающего дисперсией. Диаграмма показывает, каким образом материальная дисперсия разрушает всю картину модовых характеристик распространения
для ступенчатого волокна, изготовленного из материала, обладающего дисперсией. Диаграмма показывает, каким образом материальная дисперсия разрушает всю картину модовых характеристик распространения

Рис. 5.8. Зависимость нормализованной постоянной распространения  от параметра нормализованной частоты V для некоторых мод самого низкого порядка, распространяющихся в ступенчатом волокне
от параметра нормализованной частоты V для некоторых мод самого низкого порядка, распространяющихся в ступенчатом волокне
взаимосвязь между тремя причинами дисперсии. Очень схематично мы попытались слелать это на рис. 5.7. Из него видно, что материальная дисперсия исказила всю картину. Недостатки рис. 5.6 до некоторой степени могут быть уменьшены, если постоянную распространения  нормализовать к величине
нормализовать к величине  На рис. 5.8 даны некоторые расчетные характеристики распространения для мод более низких порядков, представленные в виде зависимости
На рис. 5.8 даны некоторые расчетные характеристики распространения для мод более низких порядков, представленные в виде зависимости  от
от 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
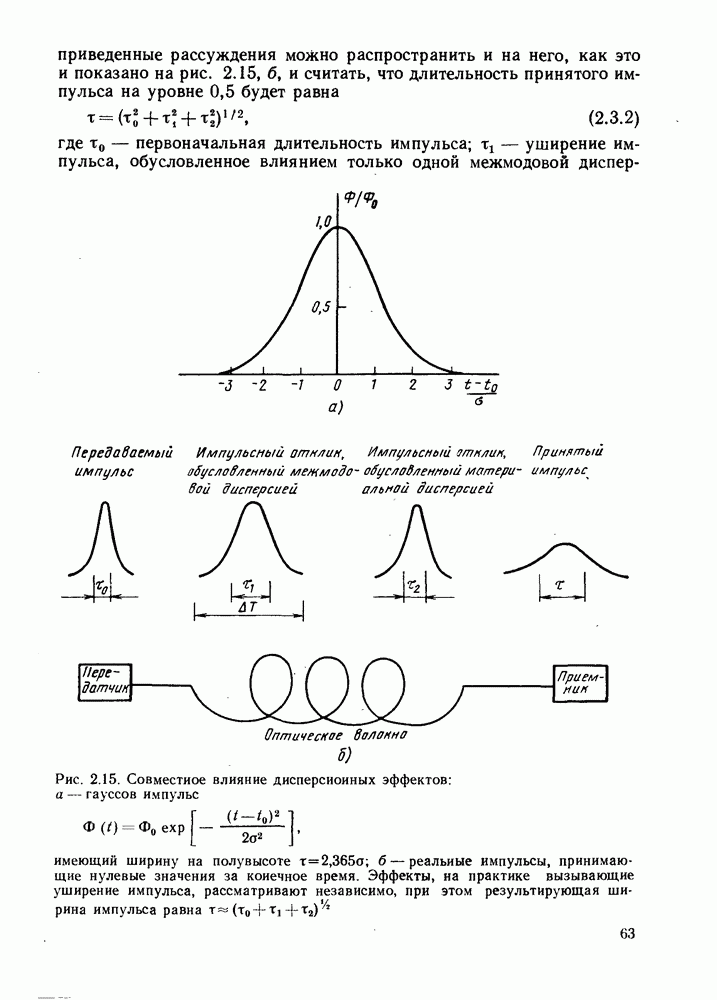
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
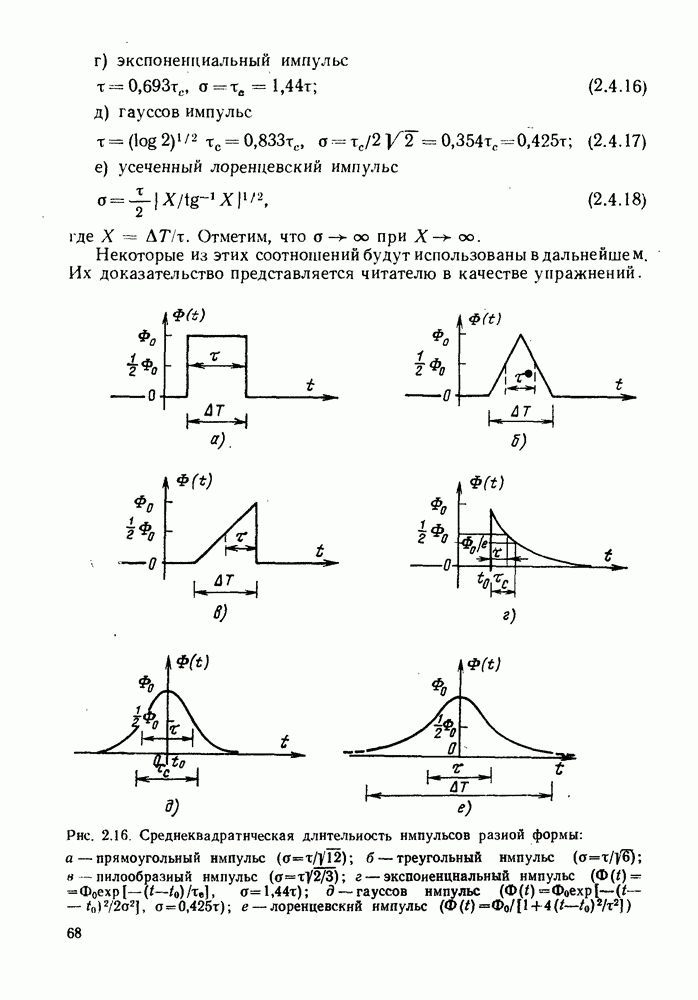
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
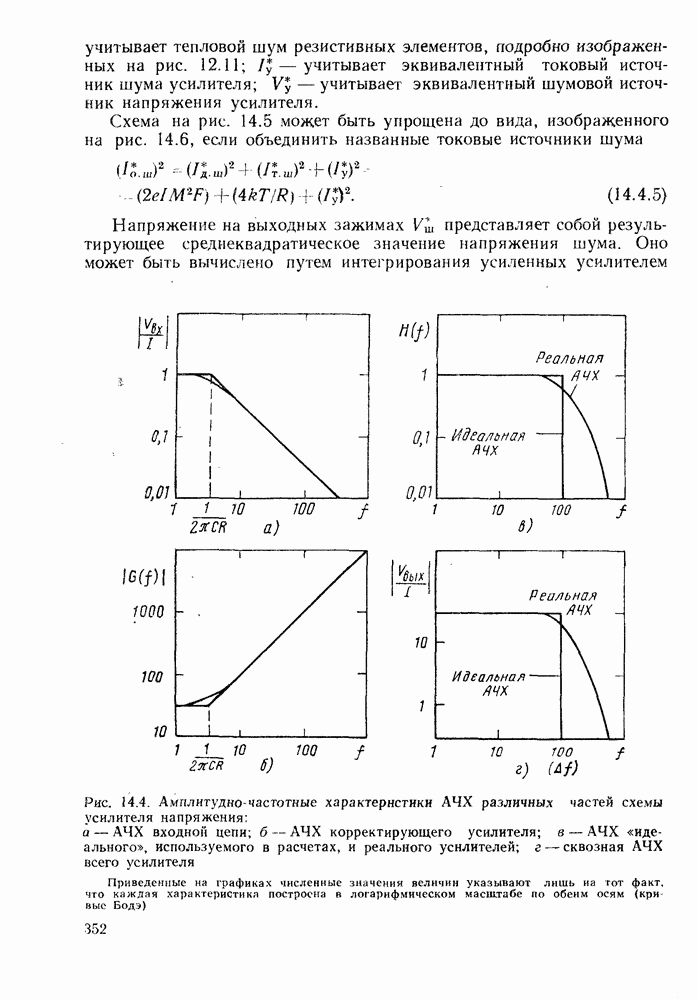
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
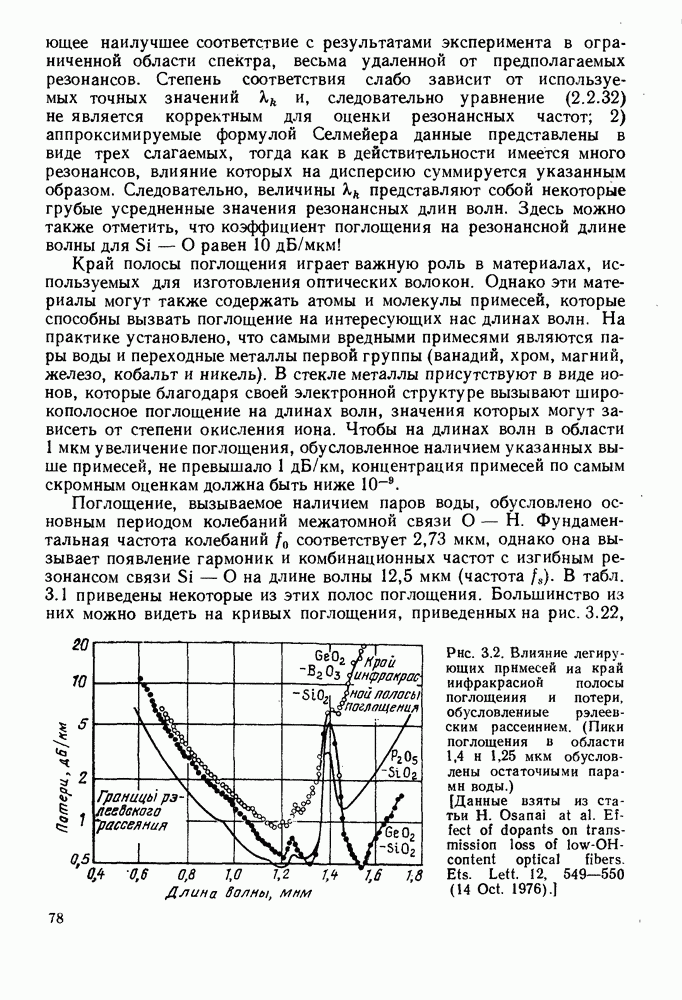
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
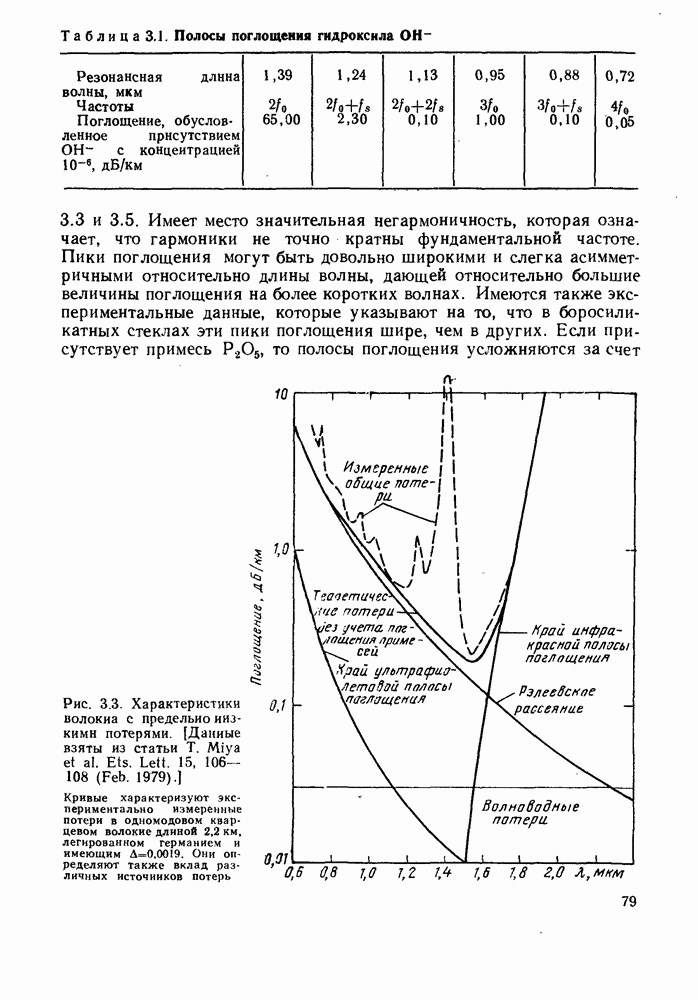
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
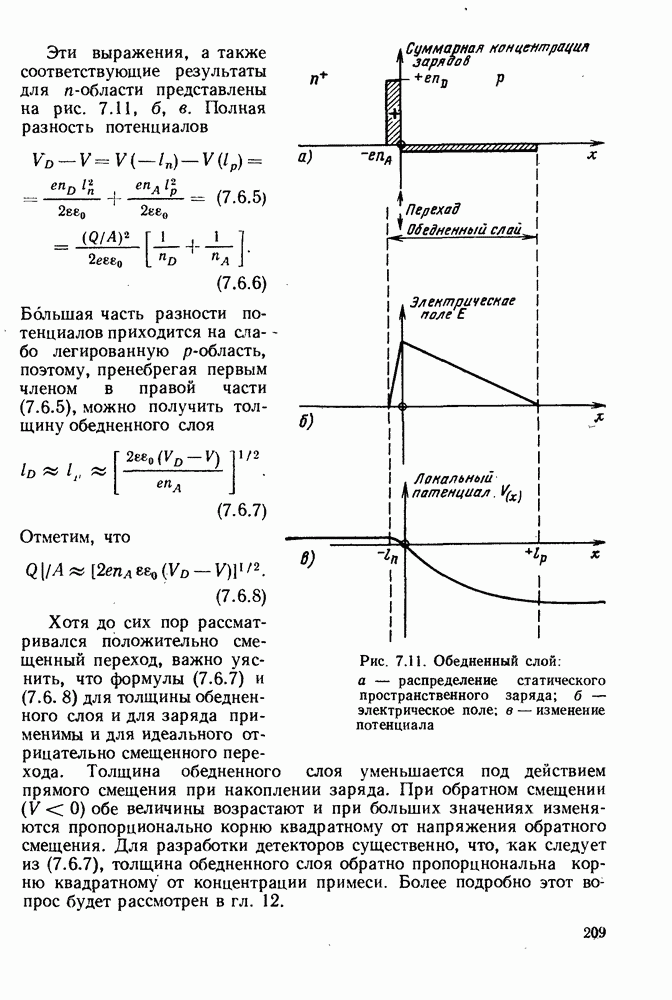
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
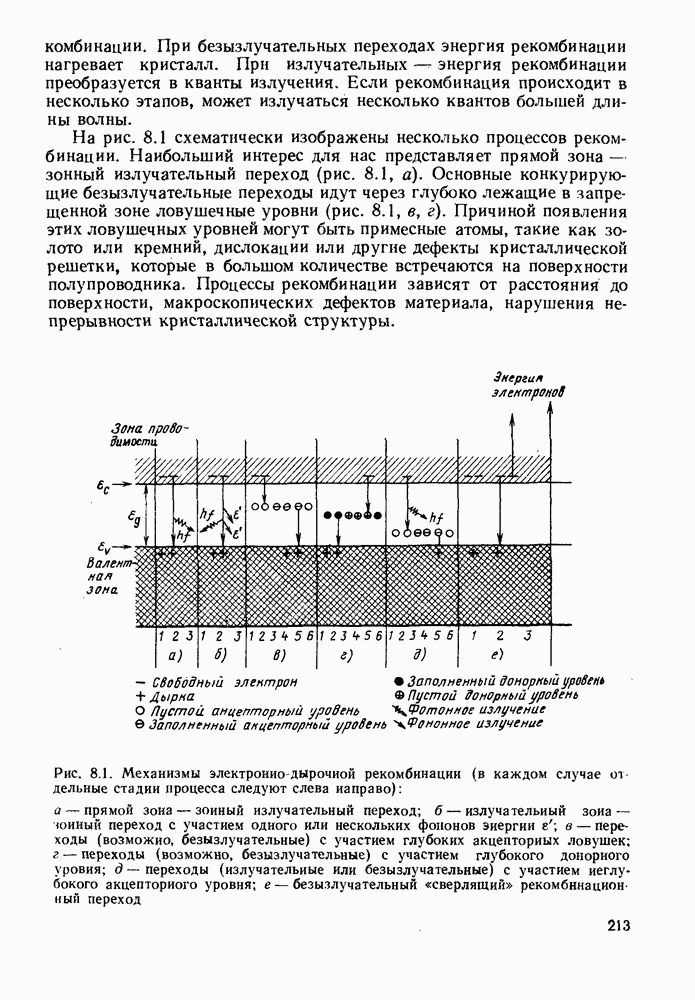
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
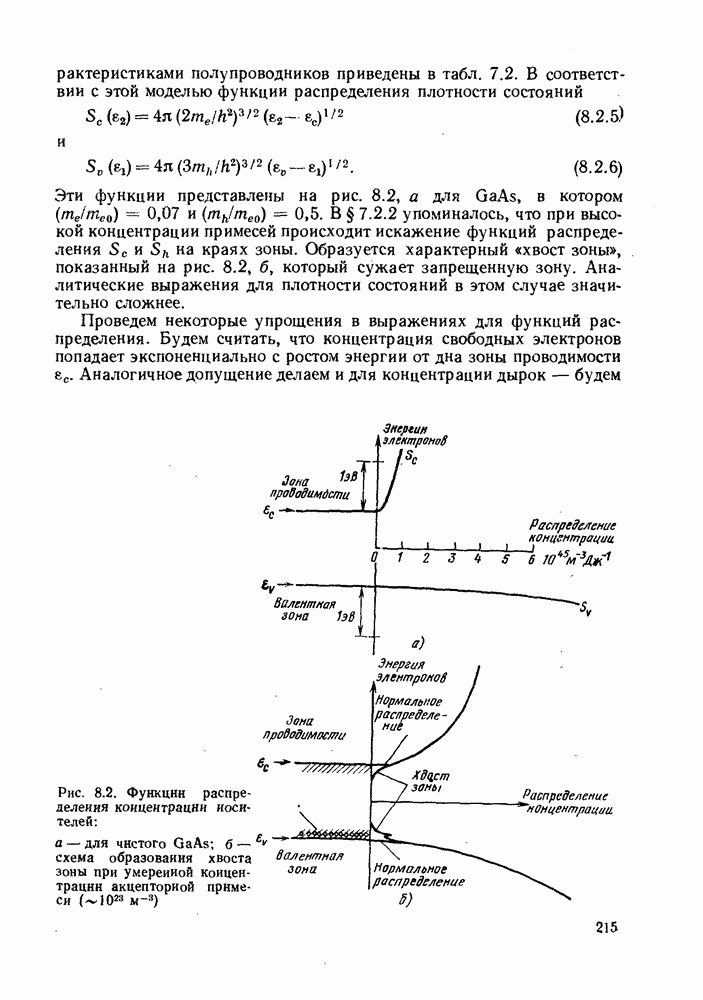
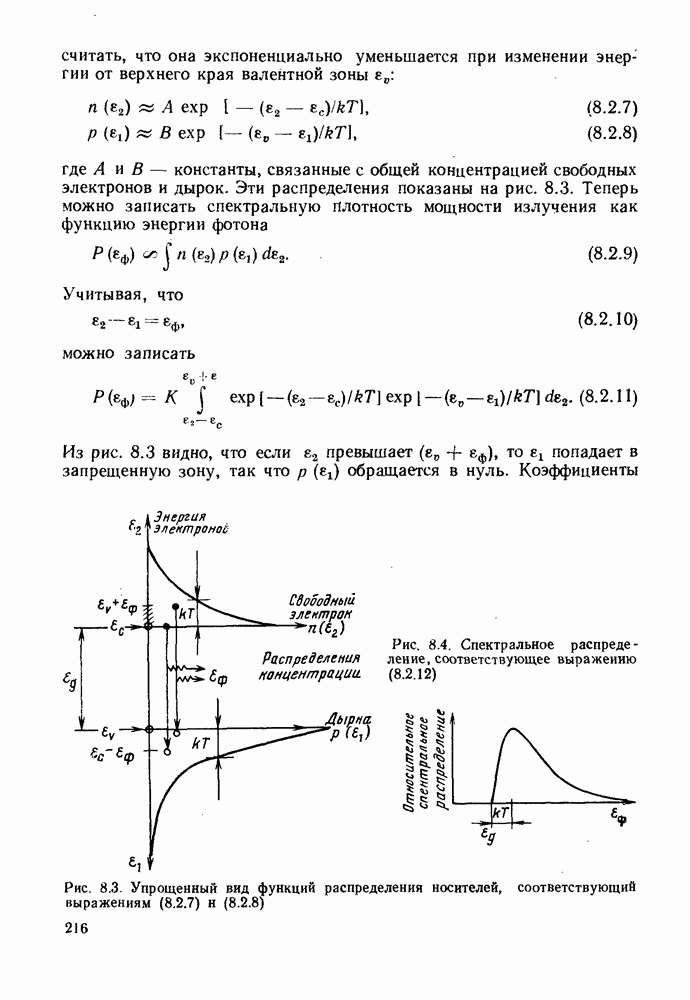
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
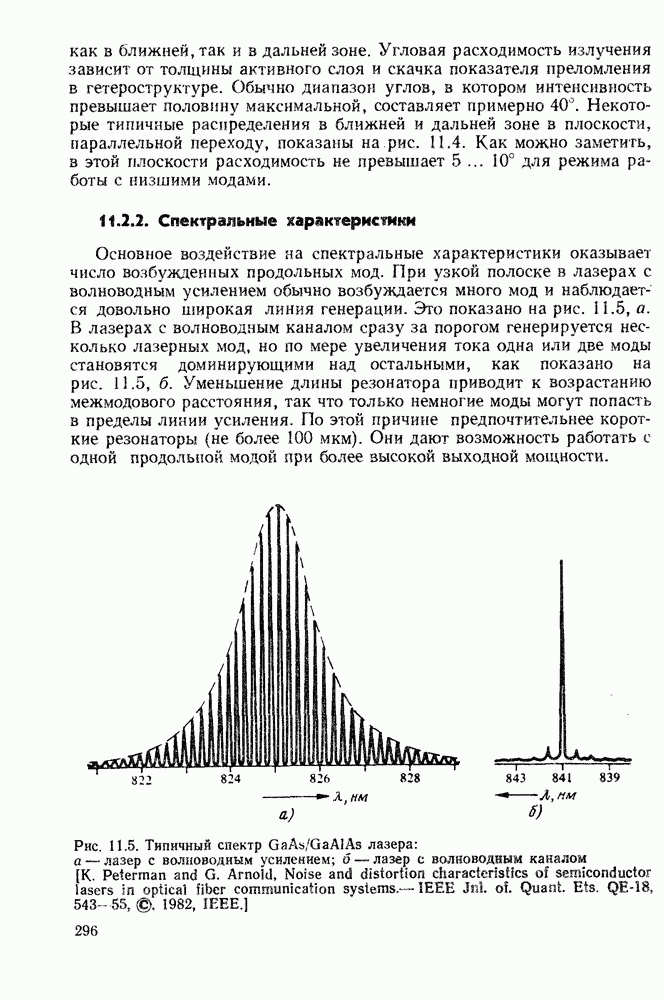
- 11.2.2. Спектральные характеристики
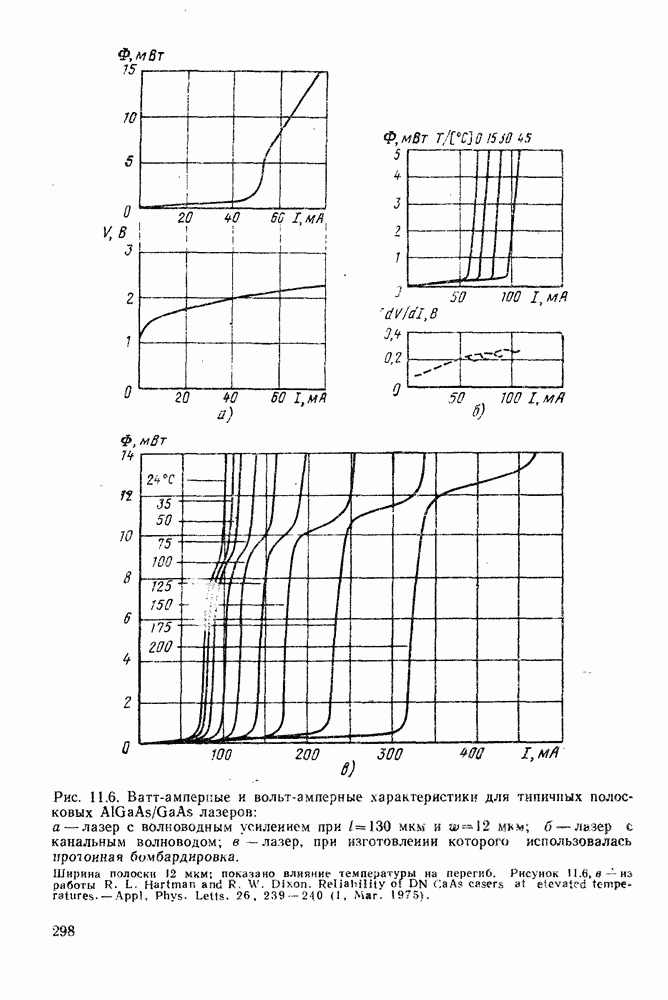
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
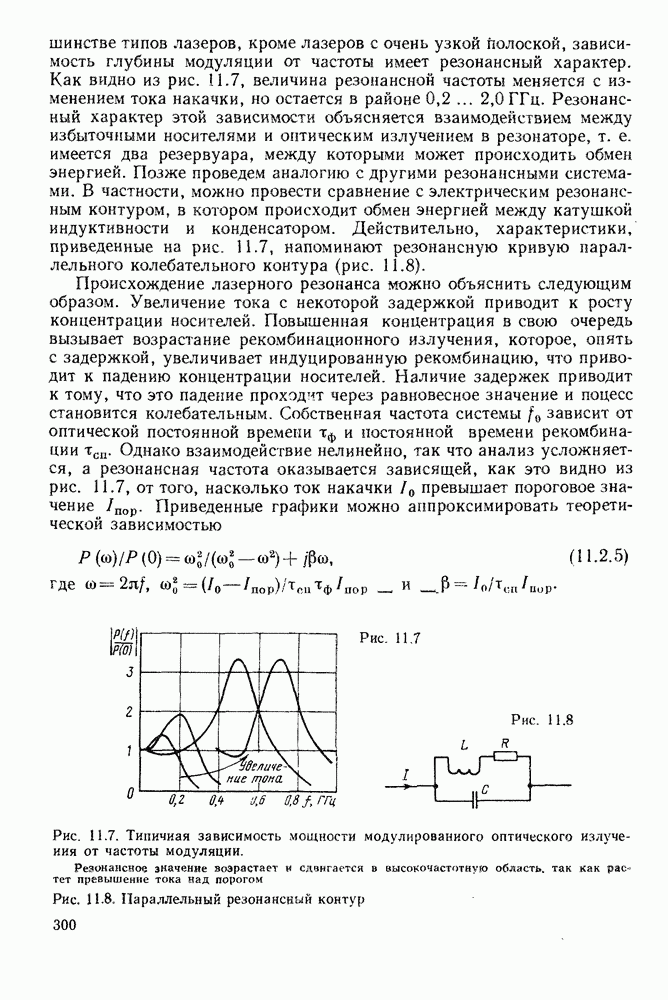
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
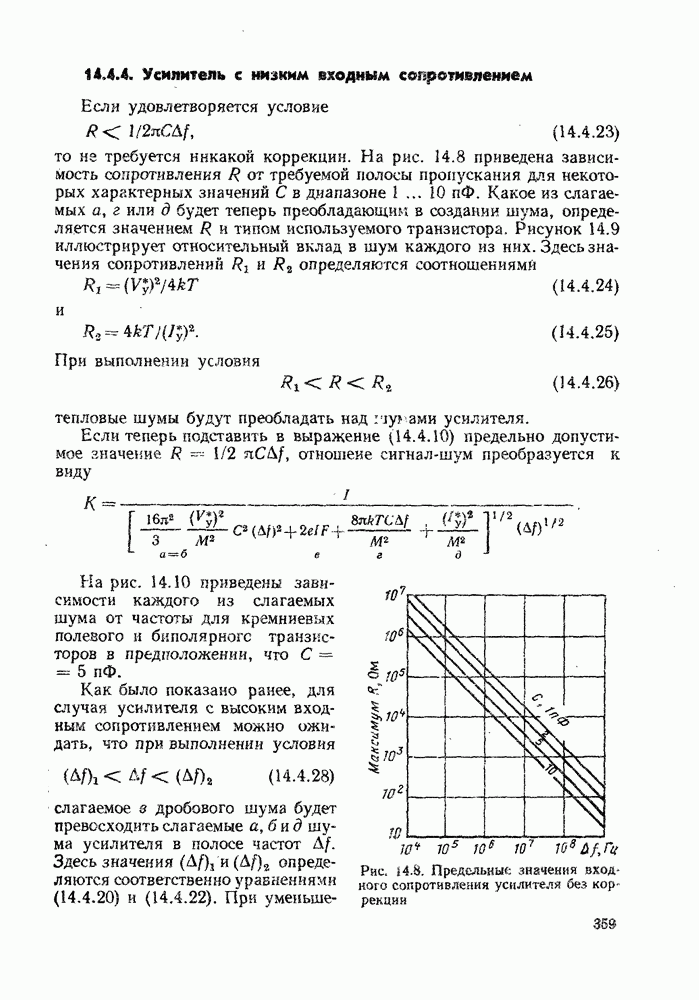
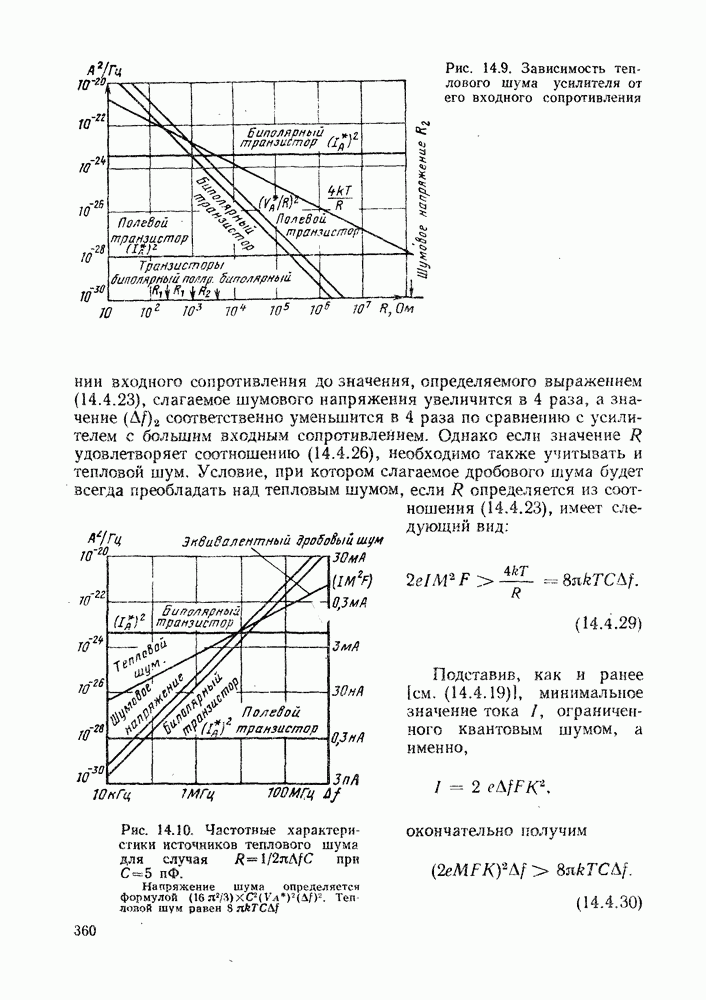
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
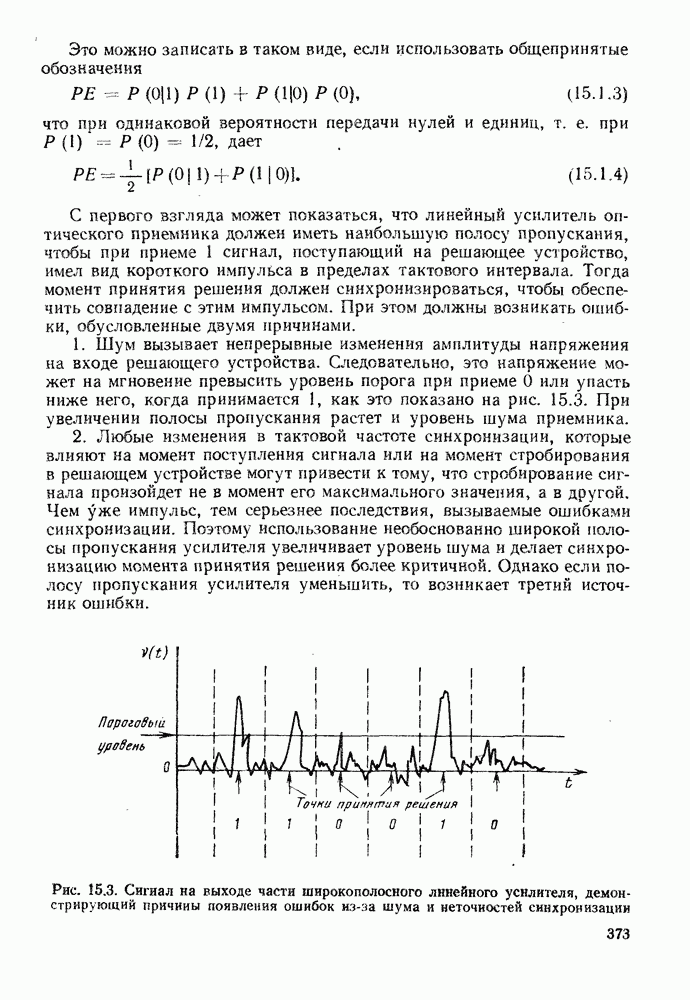
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
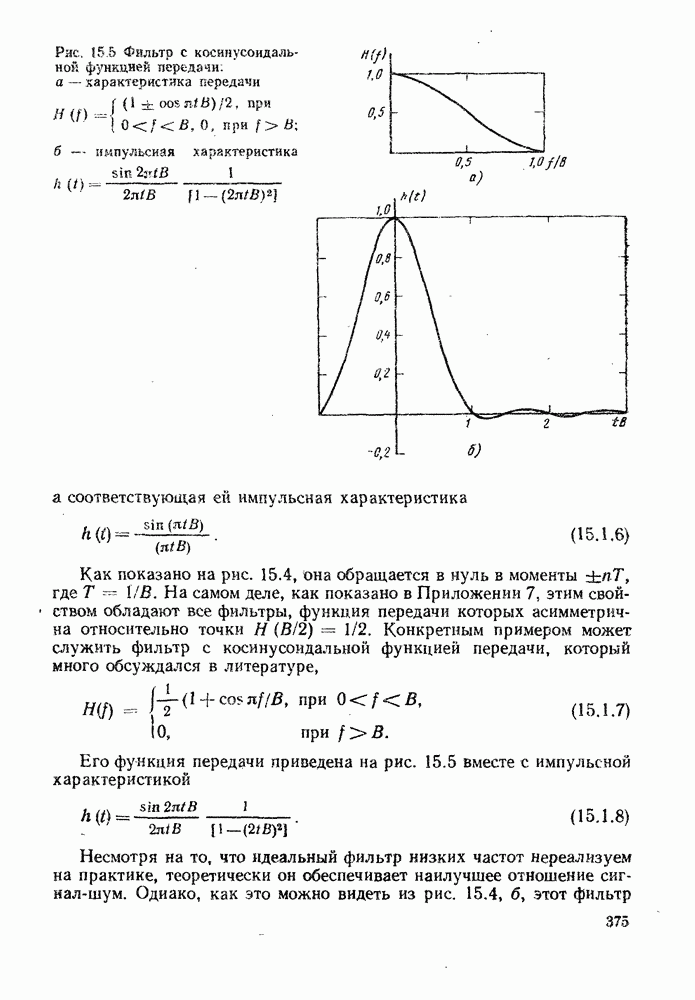
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
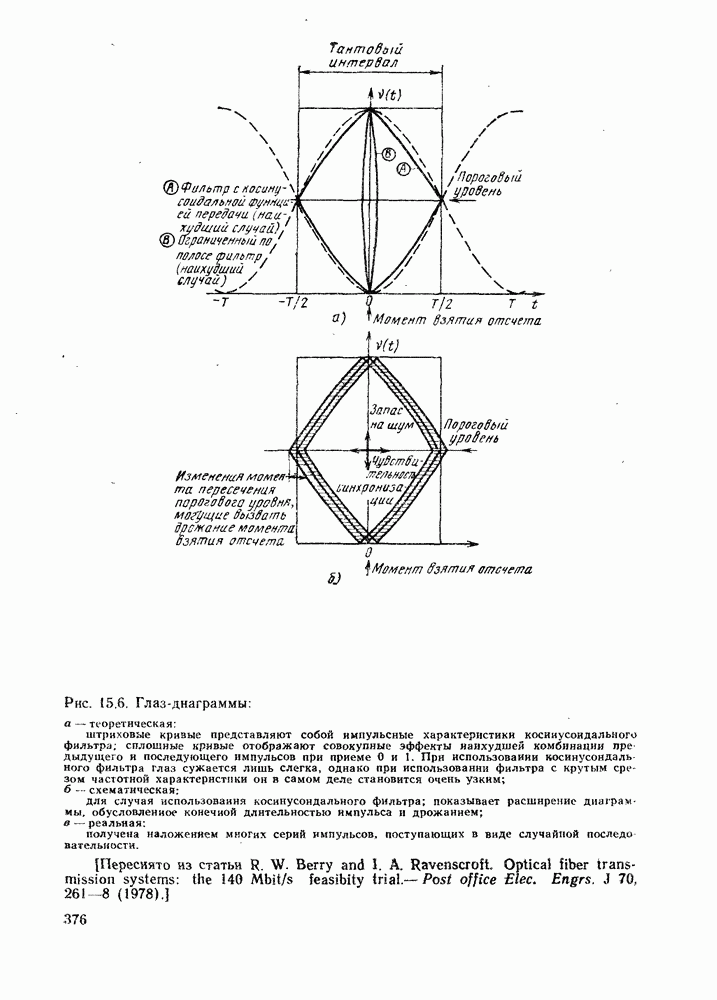
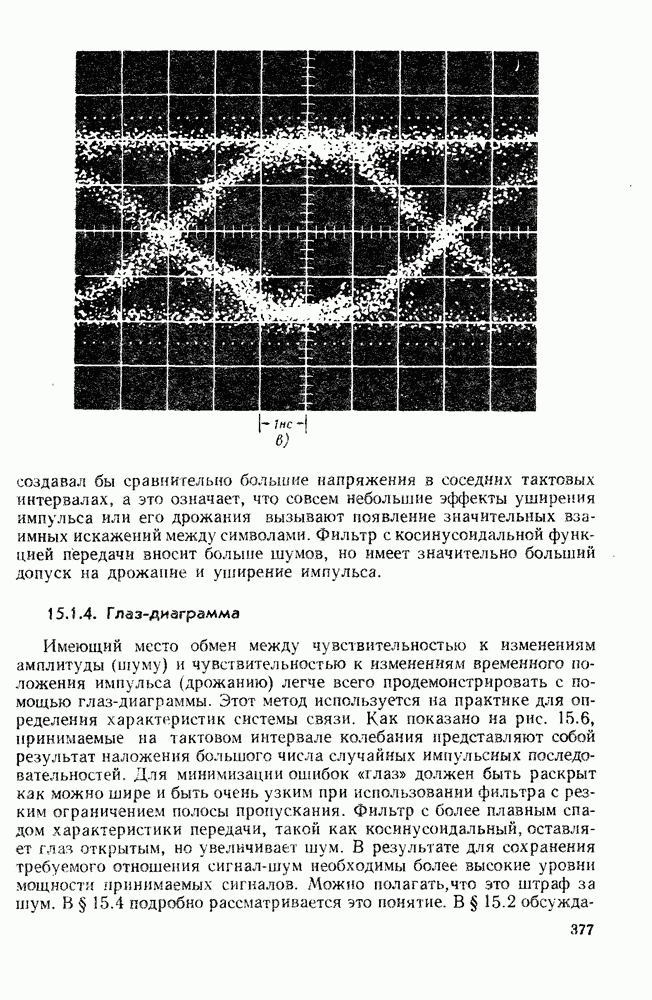
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
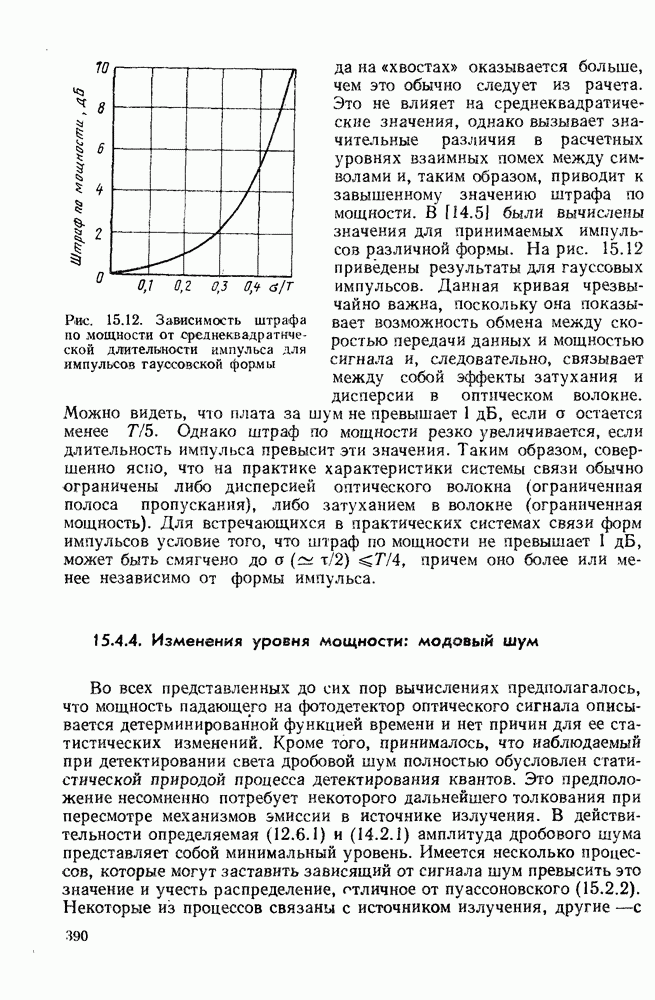
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
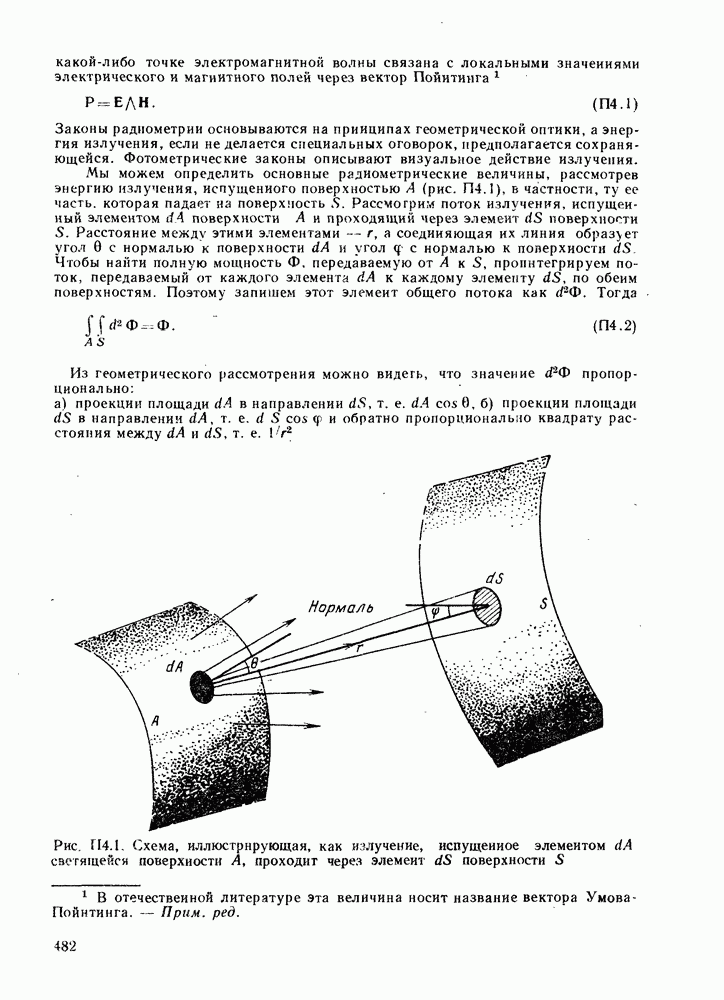
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
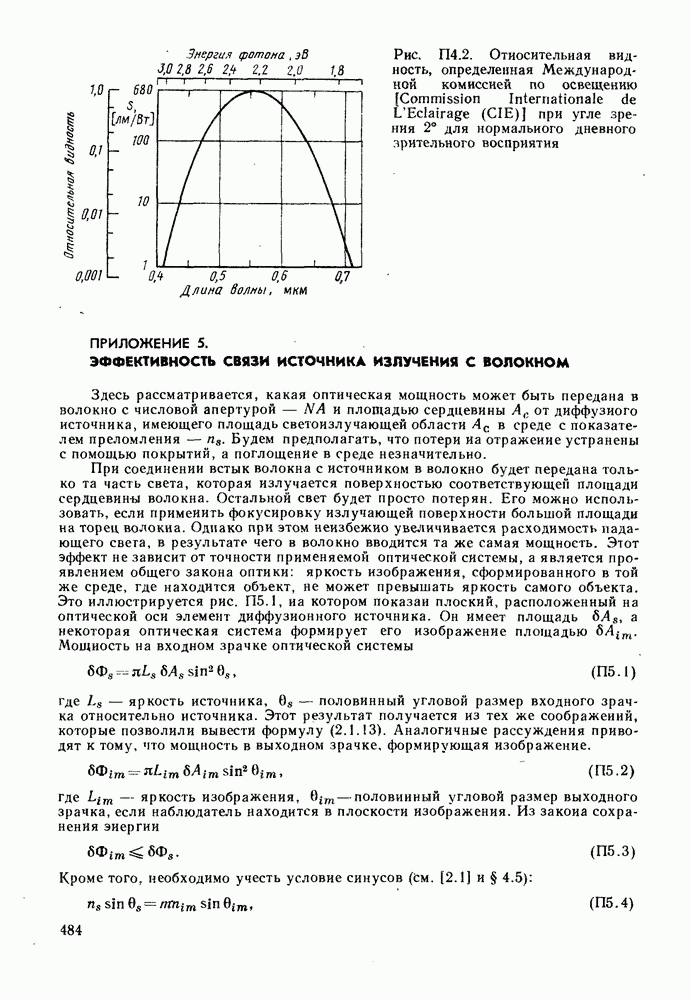
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
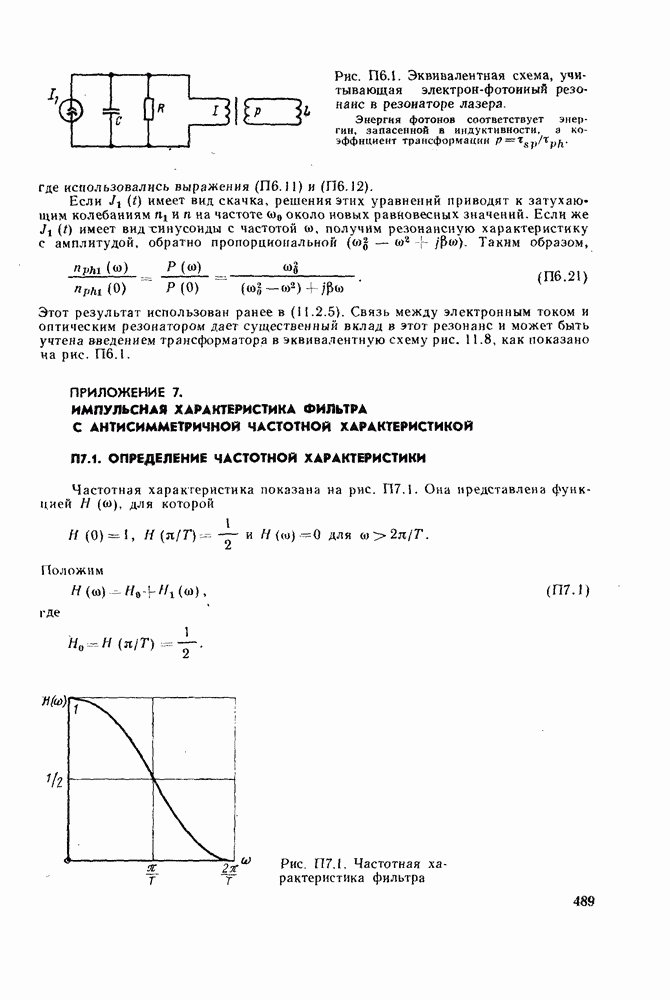
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ