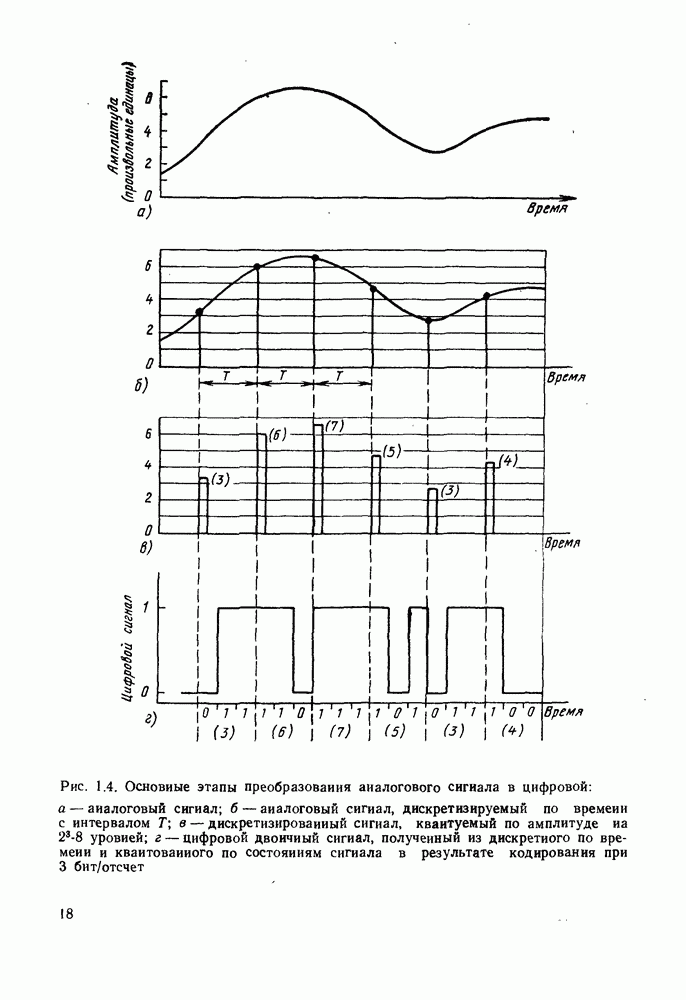
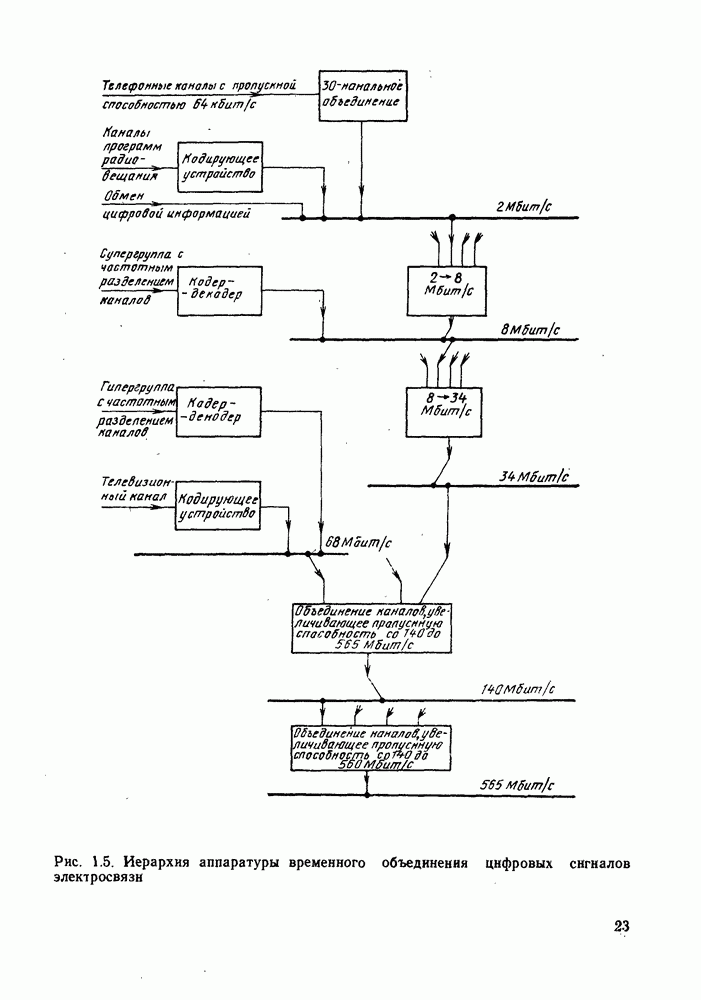
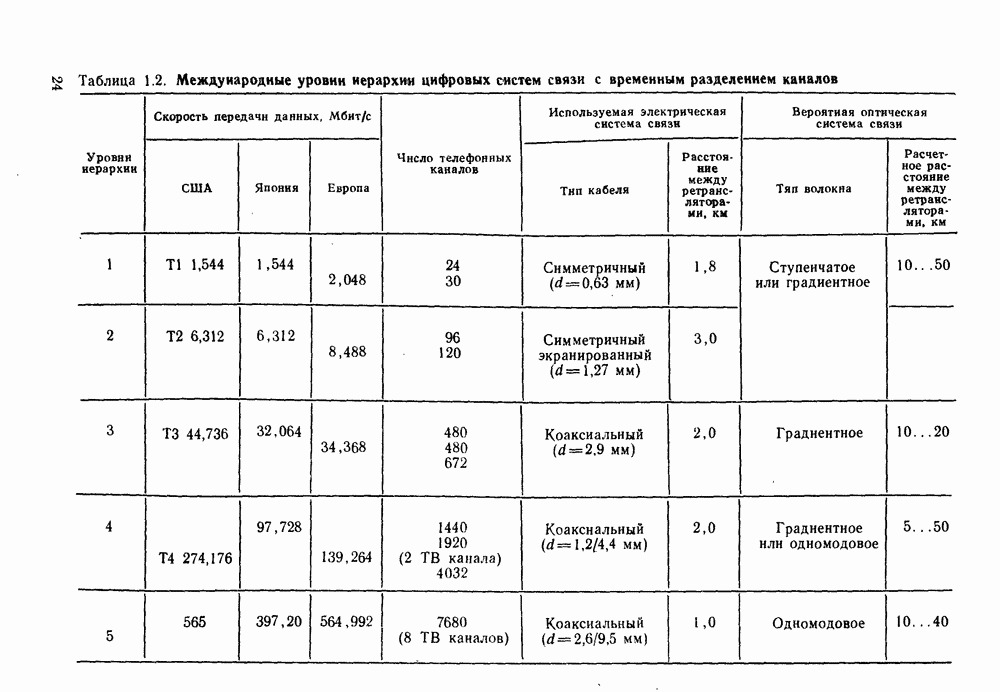
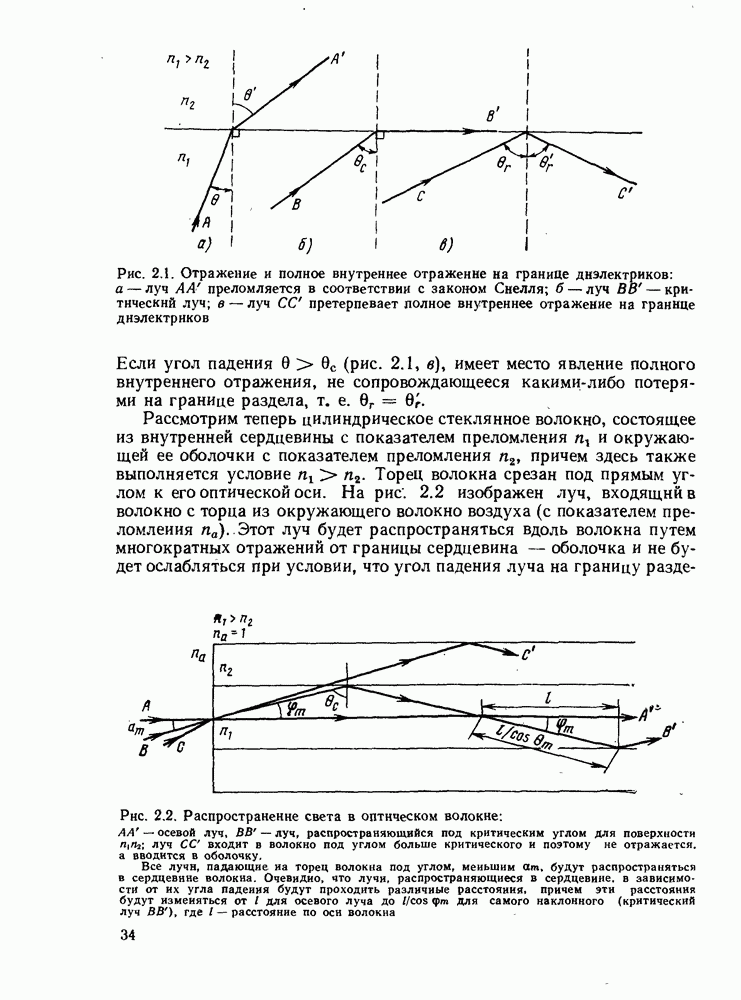
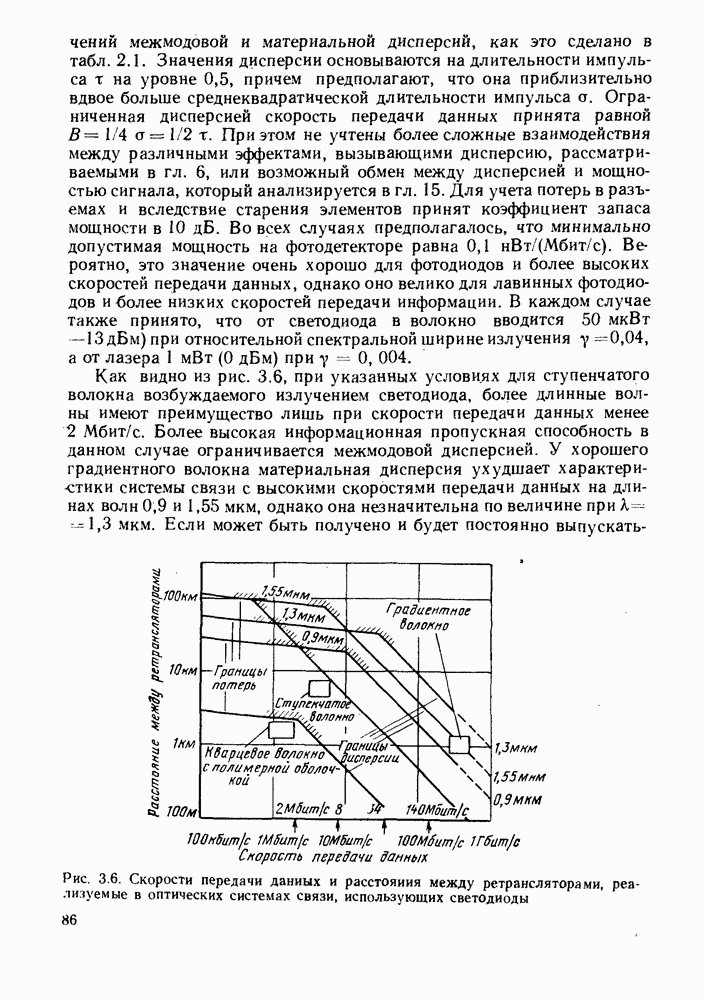
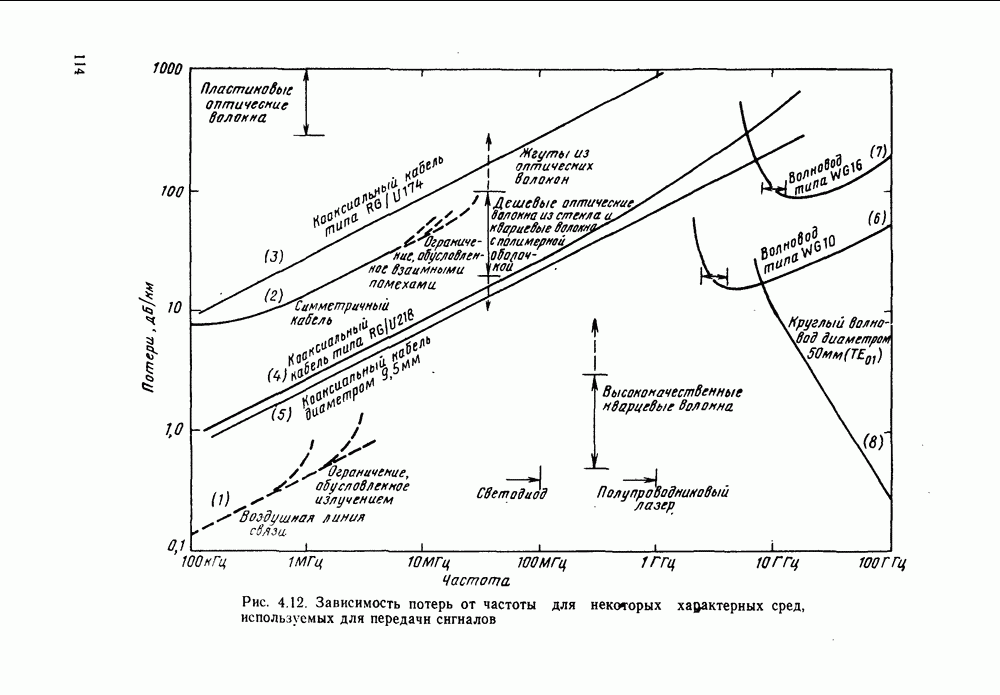
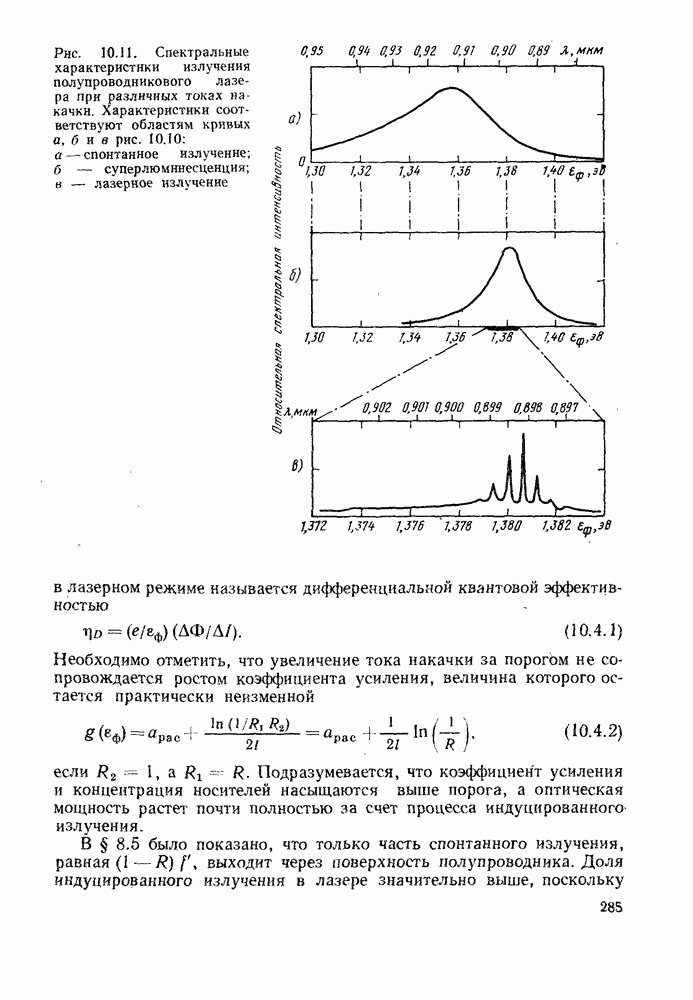
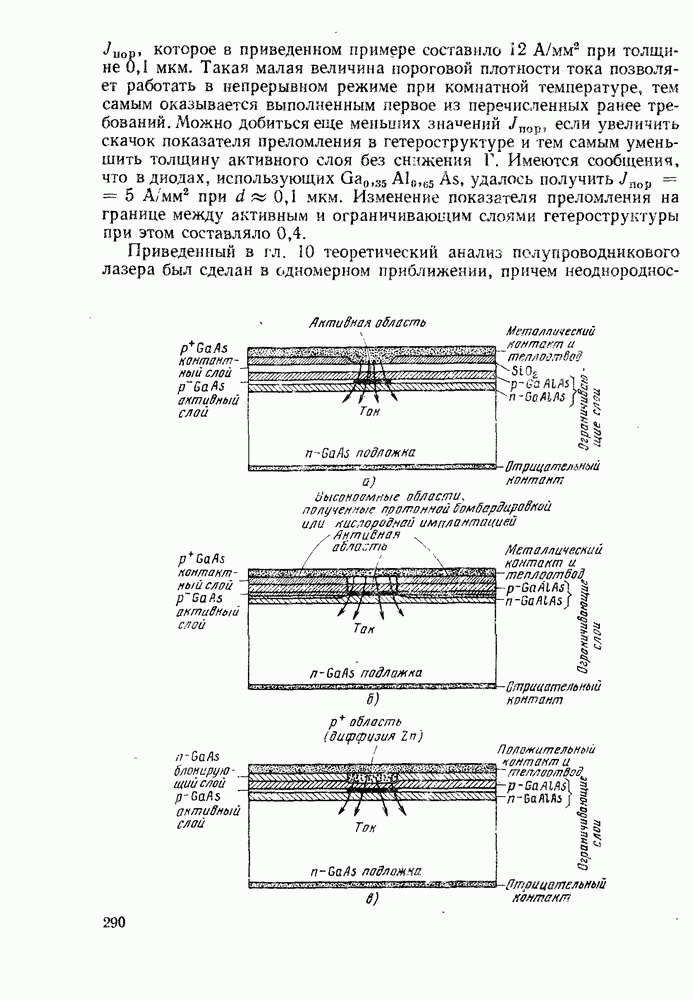
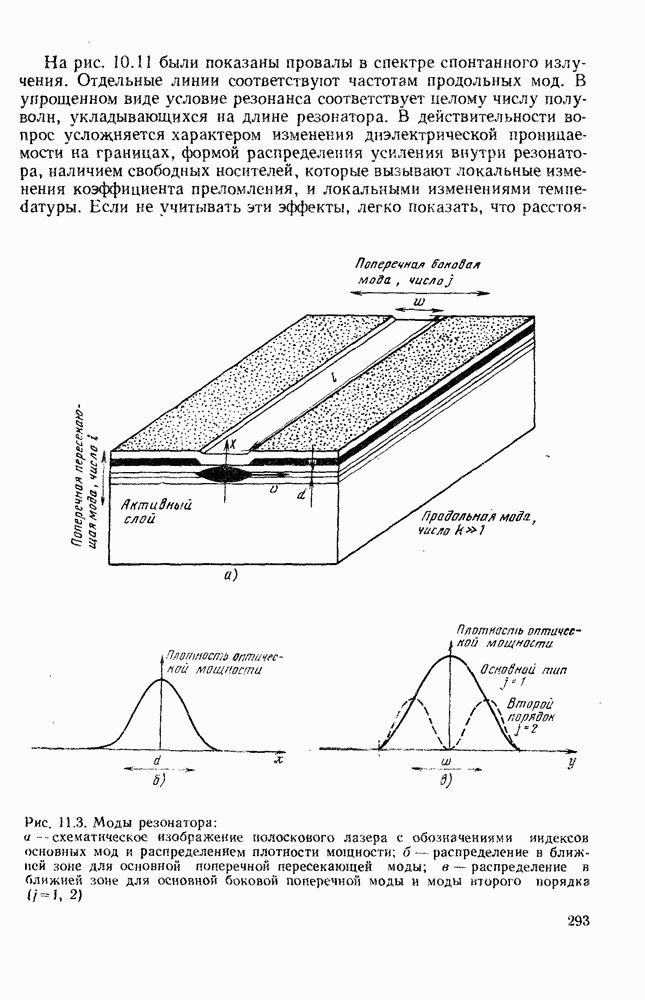
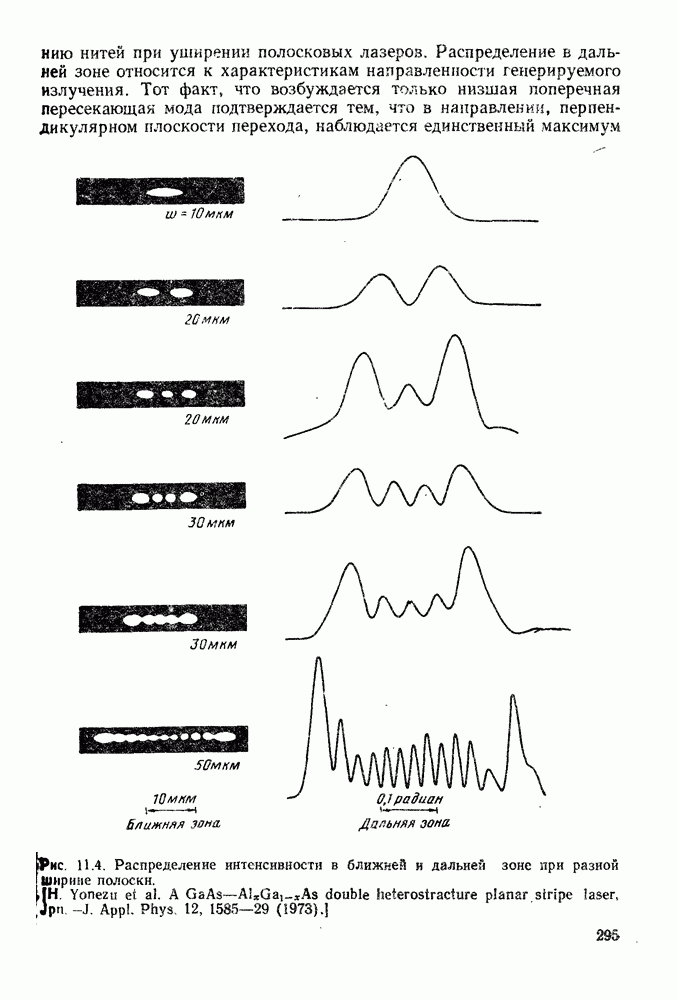
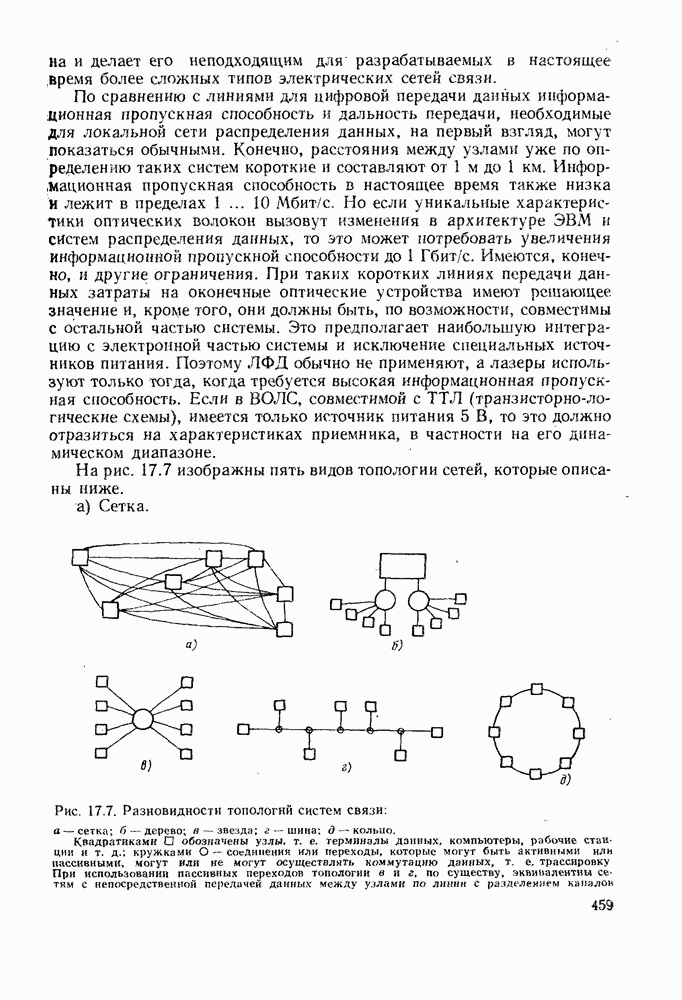
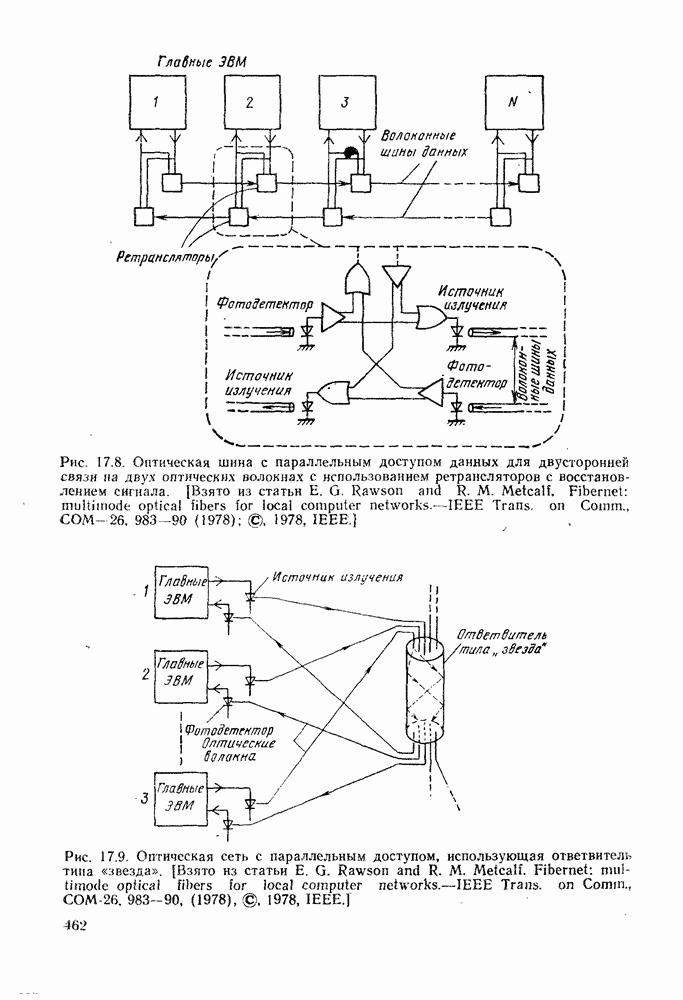
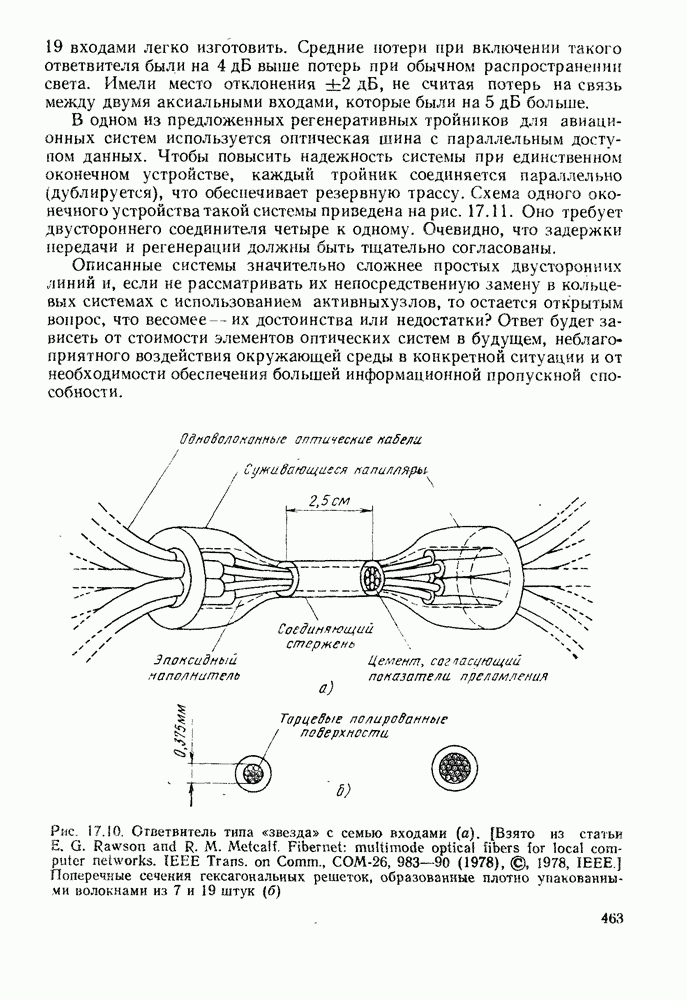
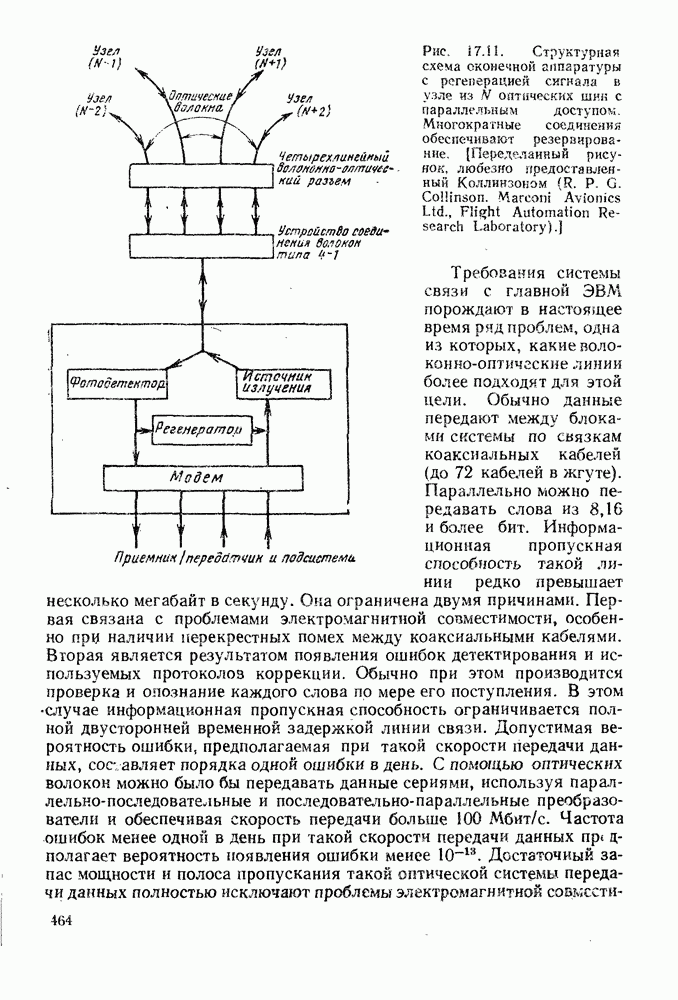
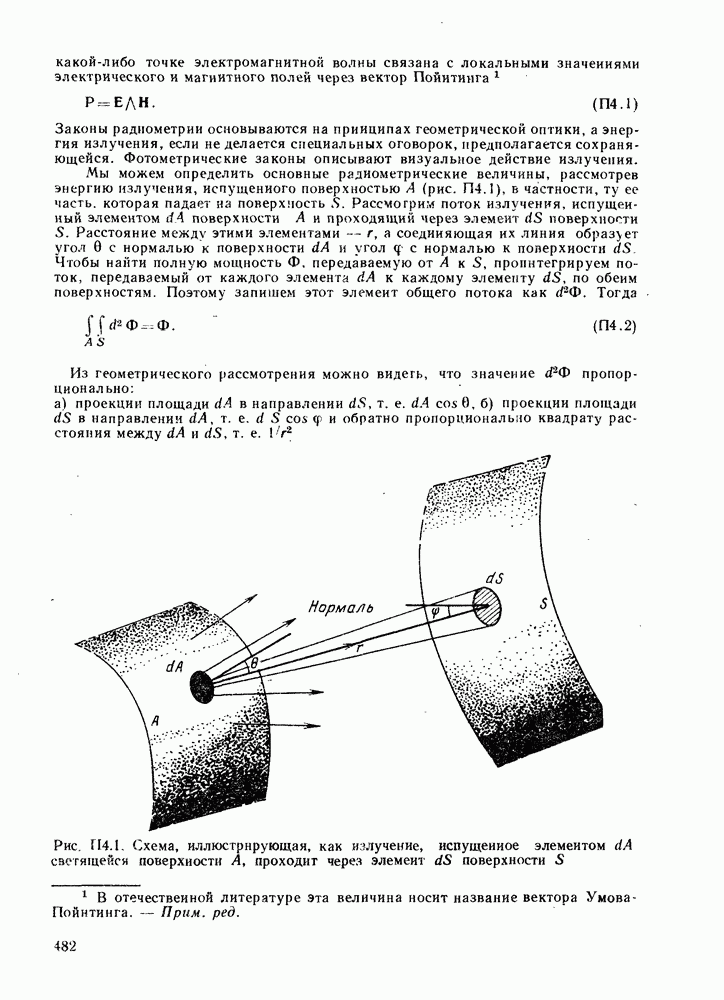
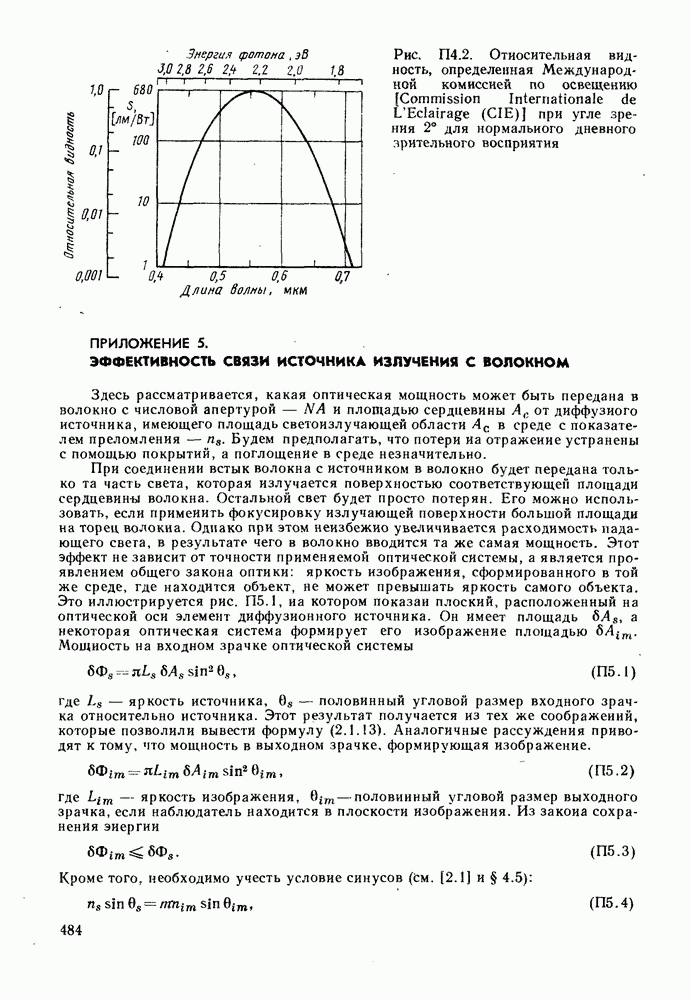
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
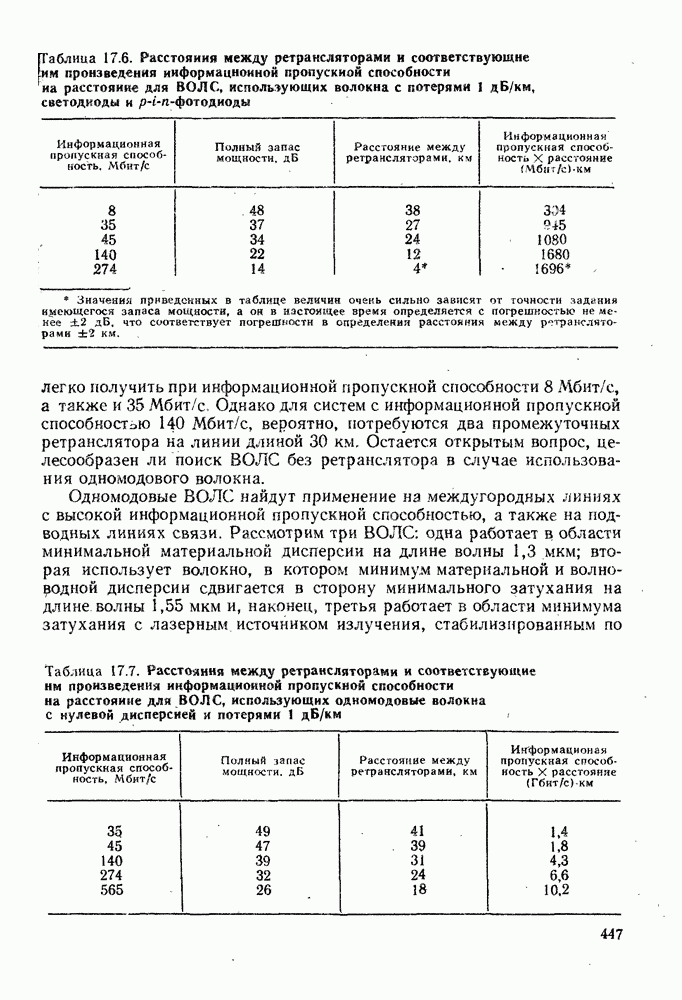
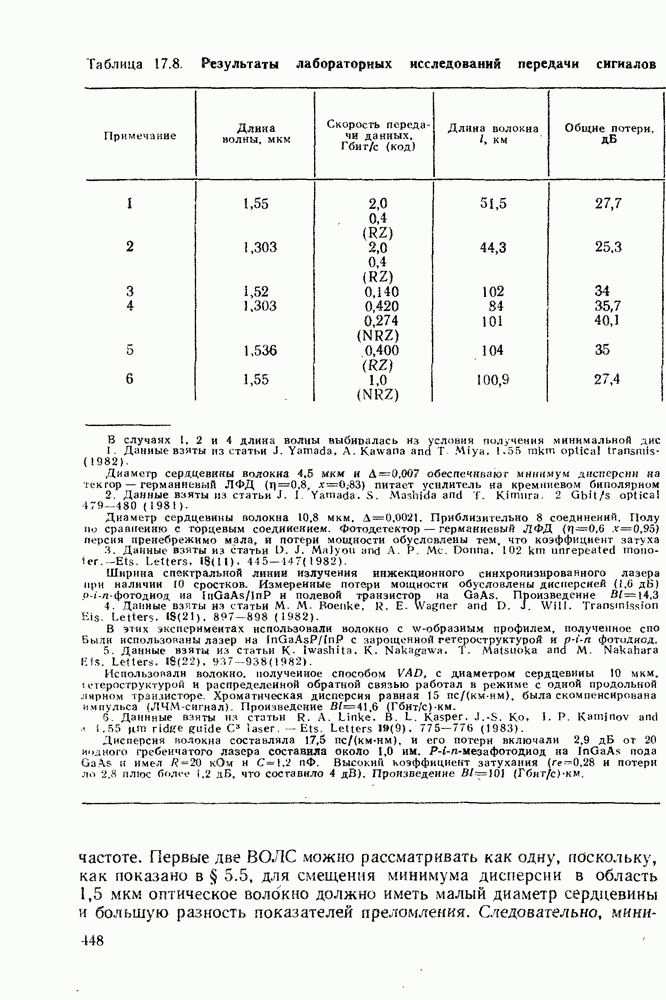
5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
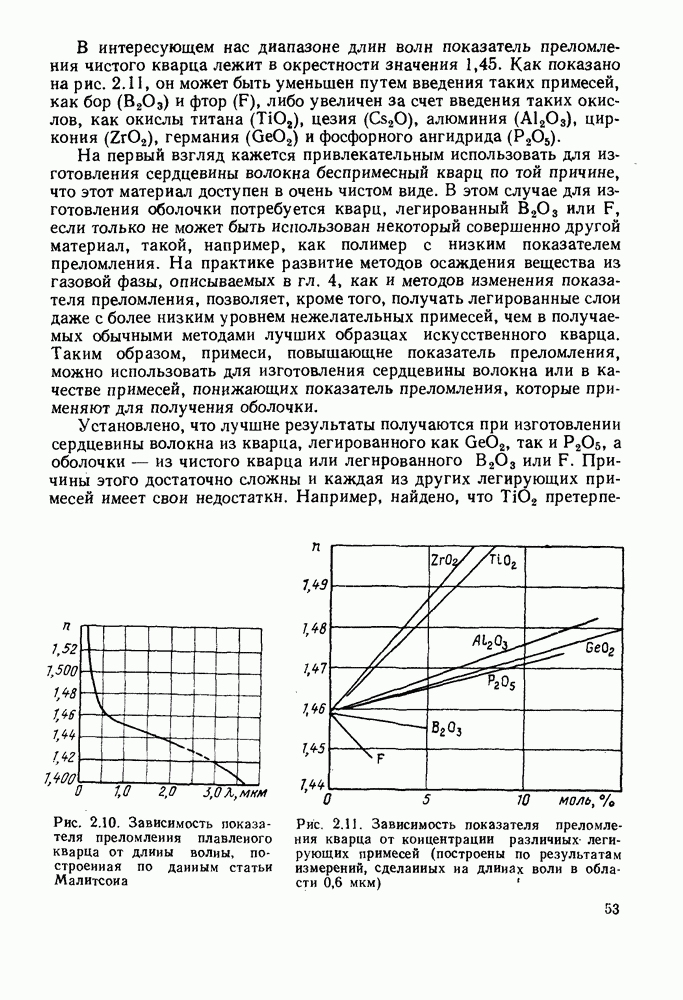
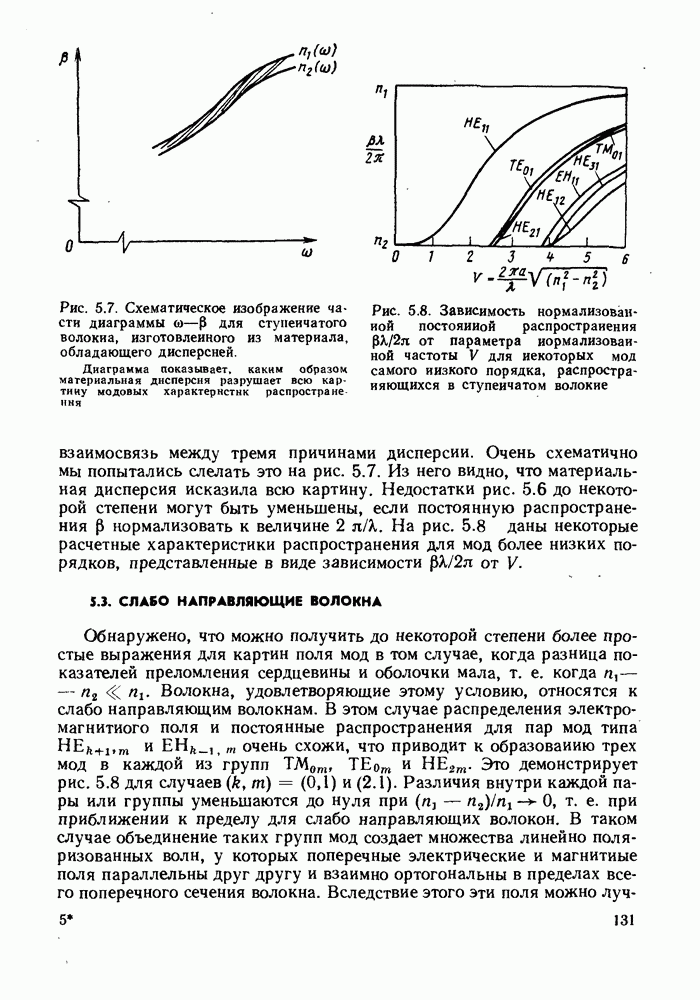
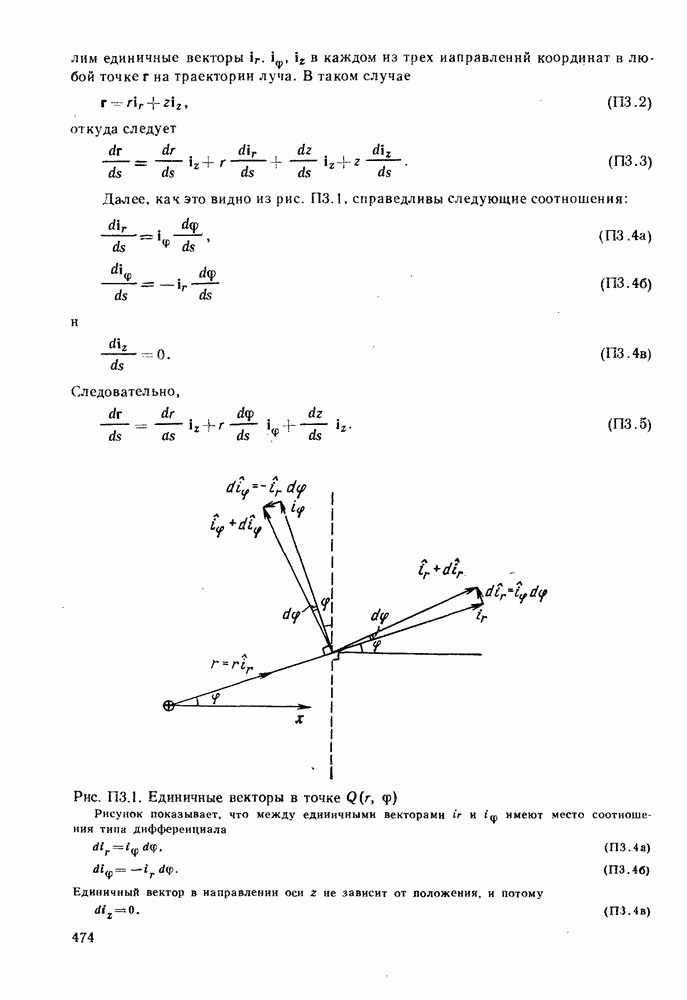
Обнаружено, что можно получить до некоторой степени более простые выражения для картин поля мод в том случае, когда разница показателей преломления сердцевины и оболочки мала, т. е. когда 
Волокна, удовлетворяющие этому условию, относятся к слабо направляющим волокнам. В этом случае распределения электромагнитного поля и постоянные распространения для пар мод типа  очень схожи, что приводит к образованию трех мод в каждой из групп
очень схожи, что приводит к образованию трех мод в каждой из групп  Это демонстрирует рис. 5.8 для случаев
Это демонстрирует рис. 5.8 для случаев  и (2.1). Различия внутри каждой пары или группы уменьшаются до нуля при
и (2.1). Различия внутри каждой пары или группы уменьшаются до нуля при  т. е. при приближении к пределу для слабо направляющих волокон. В таком случае объединение таких групп мод создает множества линейно поляризованных волн, у которых поперечные электрические и магнитные поля параллельны друг другу и взаимно ортогональны в пределах всего поперечного сечения волокна. Вследствие этого эти поля можно
т. е. при приближении к пределу для слабо направляющих волокон. В таком случае объединение таких групп мод создает множества линейно поляризованных волн, у которых поперечные электрические и магнитные поля параллельны друг другу и взаимно ортогональны в пределах всего поперечного сечения волокна. Вследствие этого эти поля можно
лучше описать, используя их составляющие в прямоугольной системе координат, а именно, 

и  где
где  постоянные поля, к и
постоянные поля, к и  целые числа,
целые числа,  а у — прямоугольные координаты, произвольно ориентированные в плоскости, перпендикулярно оси волокна, а
а у — прямоугольные координаты, произвольно ориентированные в плоскости, перпендикулярно оси волокна, а  азимутальный угол;
азимутальный угол;

Здесь снова  постоянные поля,
постоянные поля,  целые числа.
целые числа.
Мода порядка  образуется в результате сложения
образуется в результате сложения  решений для
решений для  Таким образом, используя выражение (5.2.1), получаем для сердцевины
Таким образом, используя выражение (5.2.1), получаем для сердцевины

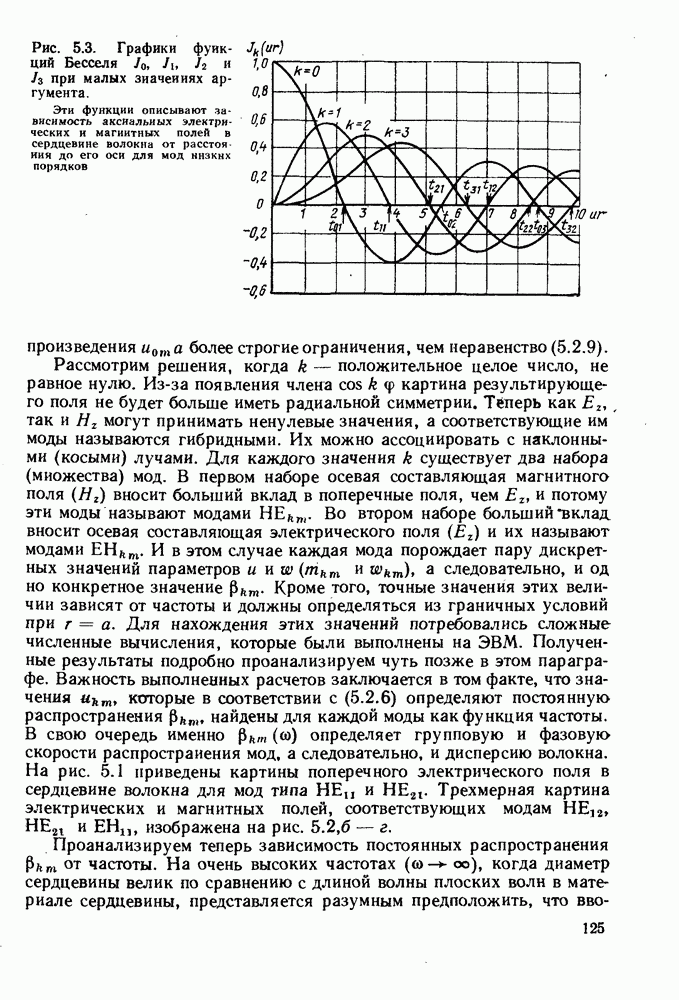
Далее можно воспользоваться рекурсивной формулой для функции Бесселя

Вместо того, чтобы с помощью формулы (5.2.5) определять составляющие поперечных полей  в полярной системе координат, получают составляющие полятрж
в полярной системе координат, получают составляющие полятрж  в прямоугольной системе координат с помощью соотношений
в прямоугольной системе координат с помощью соотношений  Затем обнаруживают, что объединение двух решений вызывает появление составляющих поля
Затем обнаруживают, что объединение двух решений вызывает появление составляющих поля  и Ну, которые почти сходят на нет, когда изменение показателя преломления на границе сердцевина — оболочка мало. Также находят, что продольные составляющие
и Ну, которые почти сходят на нет, когда изменение показателя преломления на границе сердцевина — оболочка мало. Также находят, что продольные составляющие  много меньше основных поперечных компонент
много меньше основных поперечных компонент  Таким образом, существуют решения для почти плоско поляризованных поперечных электромагнитных волн. Они известны как линейно поляризованные моды вида
Таким образом, существуют решения для почти плоско поляризованных поперечных электромагнитных волн. Они известны как линейно поляризованные моды вида  Обычно каждая мода
Обычно каждая мода  получается из моды
получается из моды  каждая мода
каждая мода  из мод
из мод  и
и  каждая мода
каждая мода  из мод и
из мод и 
Таким образом, имеют место следующие преобразования мод:

Подобно множеству решений для  при малых
при малых  и Ну существует эквивалентное множество решений для
и Ну существует эквивалентное множество решений для  и Ну при малых
и Ну при малых  Кроме того, существуют эквивалентные решения для полей обратной полярности, в результате чего каждая мода
Кроме того, существуют эквивалентные решения для полей обратной полярности, в результате чего каждая мода  заключает в себе четыре вырожденные решения. Распределения четырех полей для моды
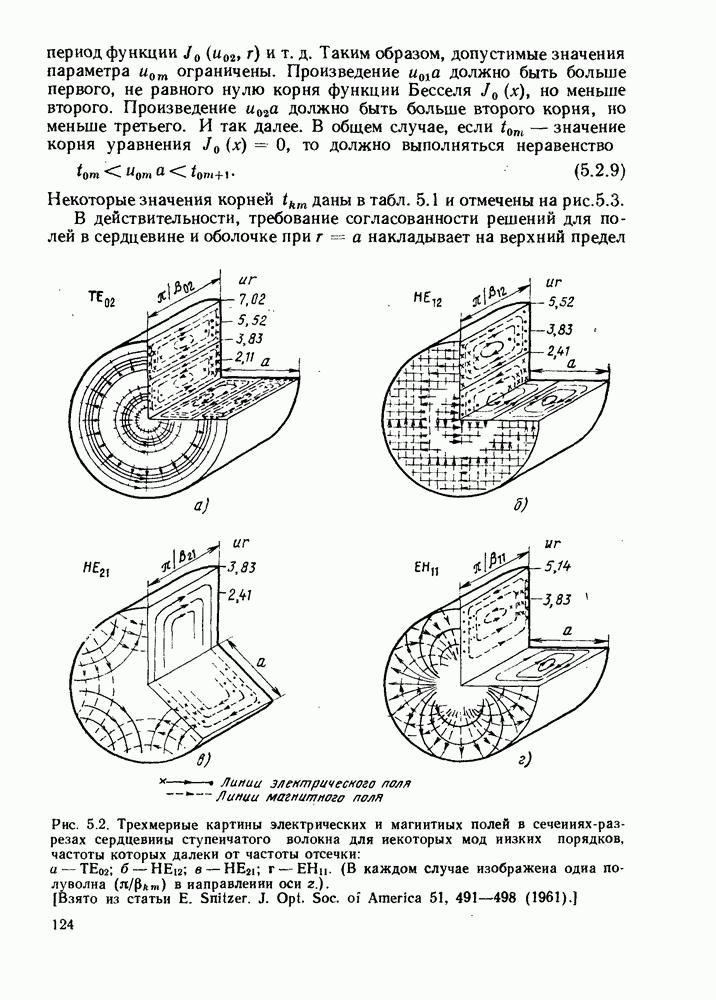
заключает в себе четыре вырожденные решения. Распределения четырех полей для моды  изображены на рис. 5.9. Подробные выводы решений для моды
изображены на рис. 5.9. Подробные выводы решений для моды  приводятся в [5.1] — [5.3].
приводятся в [5.1] — [5.3].
Одним из преимуществ приближения слабо направляющего волокна является относительная простота граничного условия, к которой оно приводит. Теперь это условие принимает вид

Однако оно еще требует численного решения для определения  а следовательно, и
а следовательно, и  для световодных мод.
для световодных мод.
Как видно из (5.3.5), условие отсечки  преобразуется к
преобразуется к

Это означает, что для всех мод за исключением  справедливо равенство
справедливо равенство

Это условие согласуется с условиями отсечки (5.2.19) — (5.2.21) в пределе слабо направляющего волокна. Очевидно, что, как и ранее,

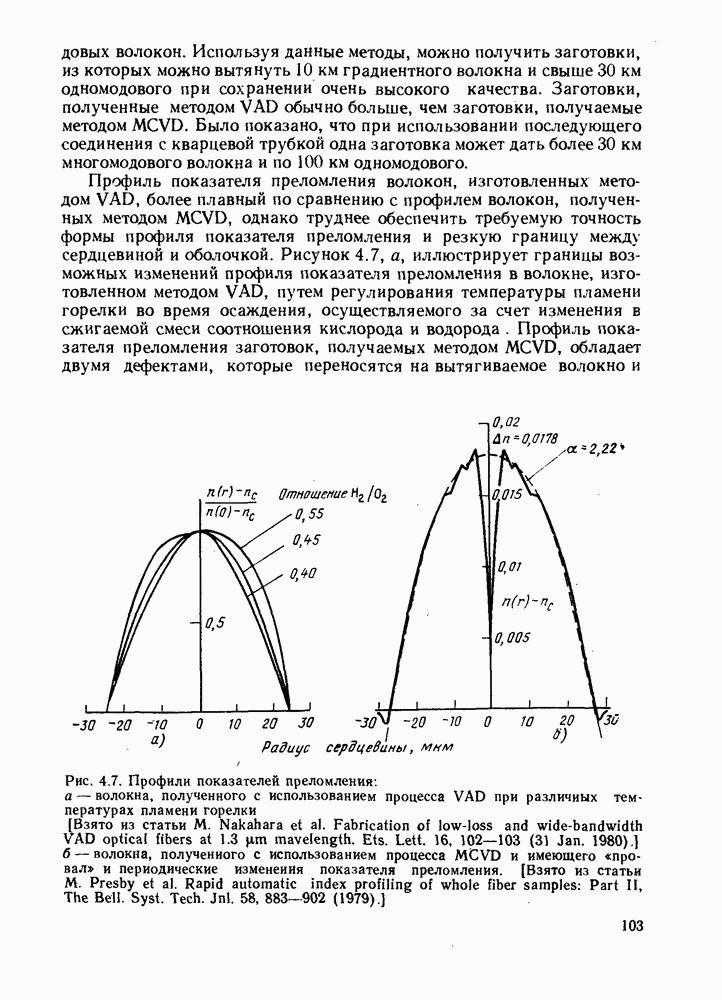
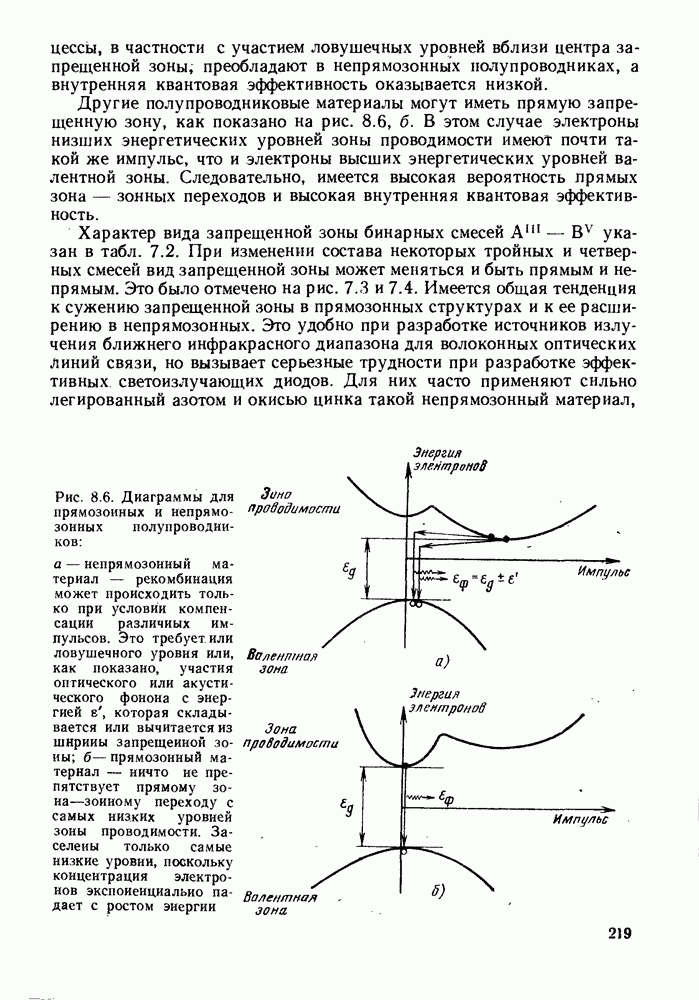
Рис. 5.9. Картины поперечных электрических полей в сердцевине волокна для четырех вырожденных мод 
при  не существует частоты отсечки для моды
не существует частоты отсечки для моды  а для всех других мод
а для всех других мод  частота отсечки определяется из соотношения
частота отсечки определяется из соотношения

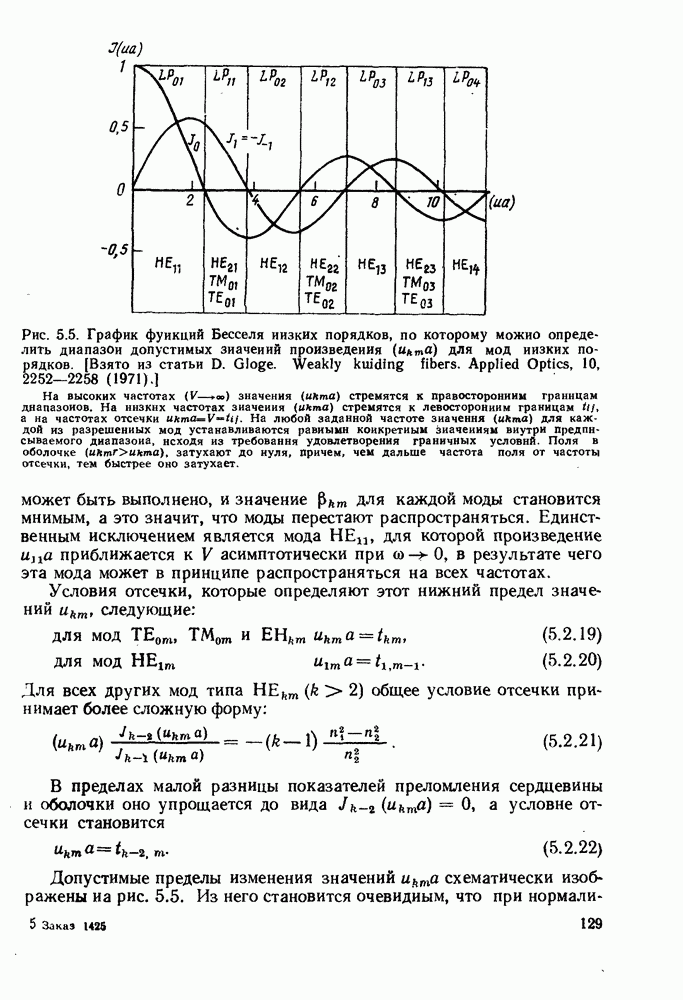
Пределы изменения допустимых значений произведения  а для мод
а для мод  приведены на рис. 5.5.
приведены на рис. 5.5.
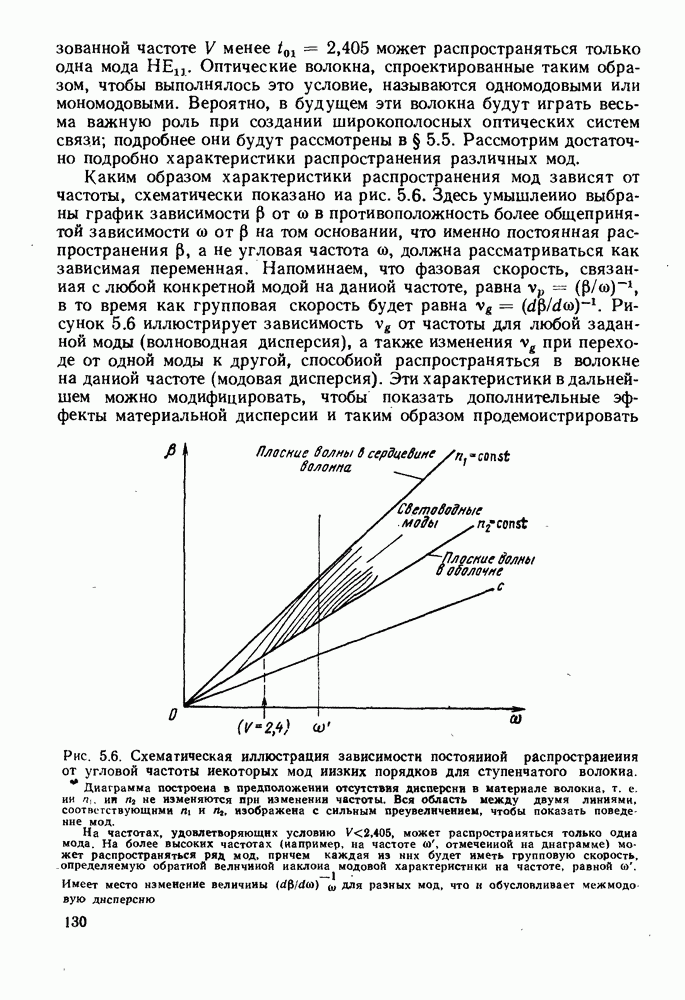
Ранее было показано, что значения постоянных распространения заключены в пределах

а на рис. 5.8 изображена зависимость на высоких частотах нормализованных постоянных распространения  от
от  в пределах от частоты отсечки до
в пределах от частоты отсечки до  Дальнейшая нормализация постоянной распространения дает возможность вычислять характеристики распространения и строить их графики совершенно независимо от параметров волокна
Дальнейшая нормализация постоянной распространения дает возможность вычислять характеристики распространения и строить их графики совершенно независимо от параметров волокна  Введем в рассмотрение величину
Введем в рассмотрение величину  определяемую следующим образом:
определяемую следующим образом:

В таком случае  представляет собой новый параметр распространения, который перекрывает диапазон значений от 0 до 1.
представляет собой новый параметр распространения, который перекрывает диапазон значений от 0 до 1.
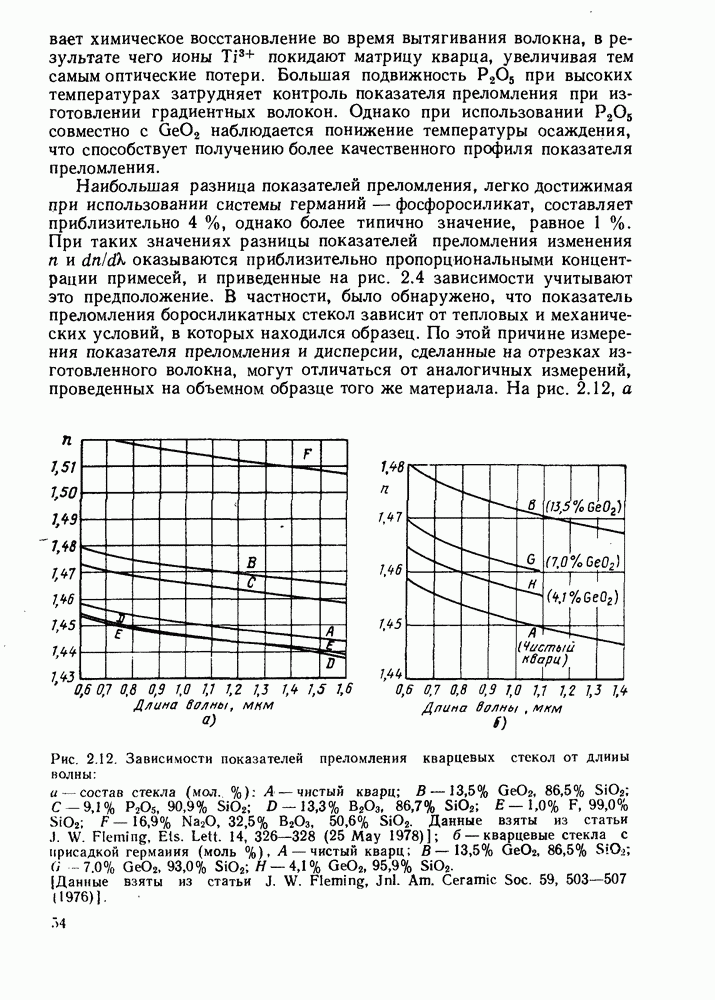
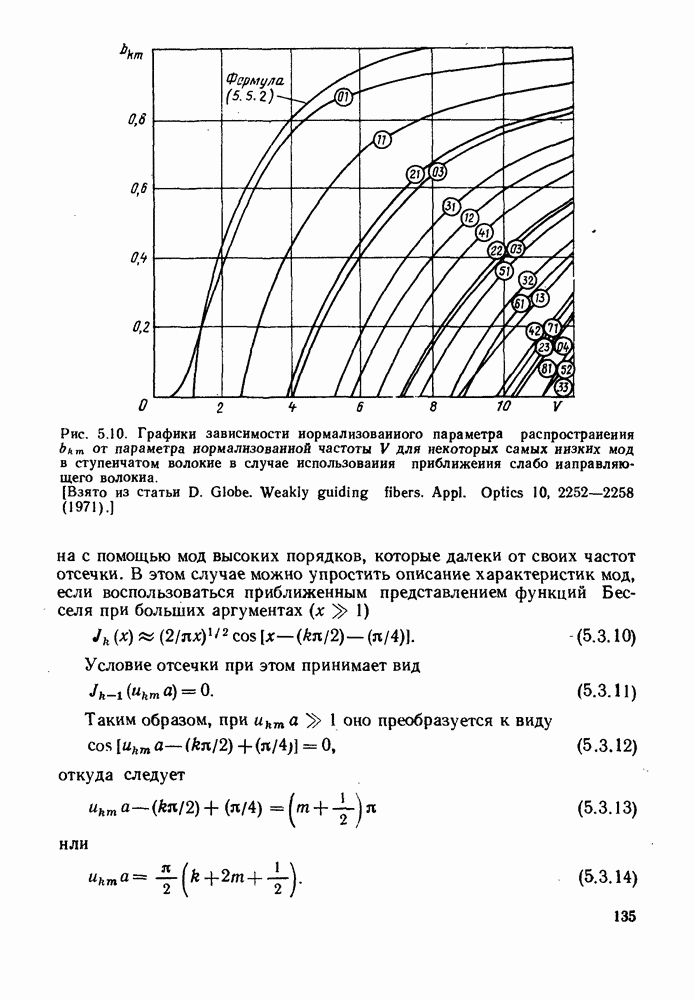
На рис. 5.10 приведены характеристики распространения мод самых низких порядков, вычисленные с использованием приближения, которые построены в виде зависимости  от
от  Между прочим, можно отметить, что
Между прочим, можно отметить, что

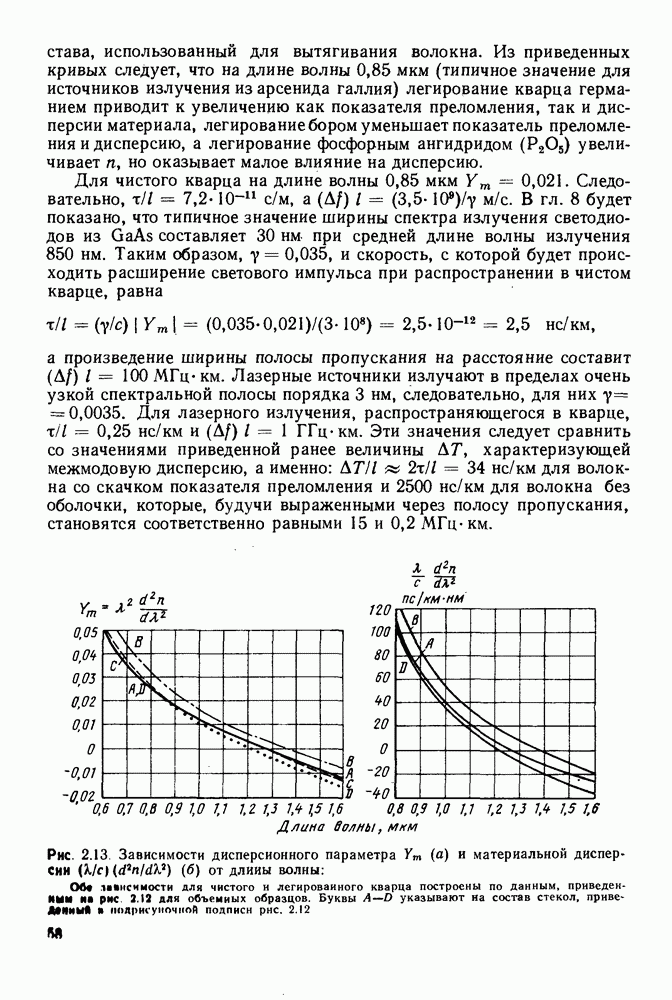
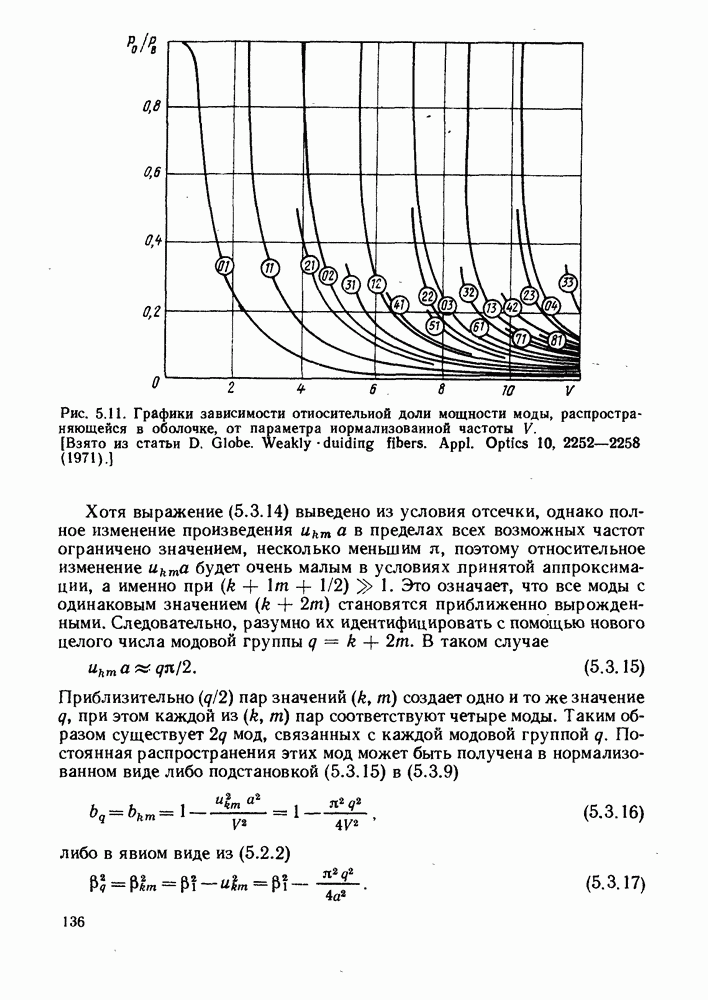
Одно из достоинств модового анализа состоит в том, что он позволяет просто определять распределение плотности мощности в волокне для каждой моды путем вычисления вектора Пойнтинга  для поперечных полей в плоскости поперечного сечения волокна. При этом становится возможным определить то расстояние, на которое электромагнитная волна проникает за поверхность сердцевина — оболочка и рассеивается в оболочке. Интегрируя по сечению сердцевины, можно вычислить ту часть полной мощности каждой моды, которая переносится в сердцевине. Результаты таких вычислений для нескольких мод самых низких порядков, выполненных в приближении слабо направляющего волокна приведены на рис. 5.11. Как и ожидалось, большая часть потока мощности находится в сердцевине волокна за исключением случая, когда моды близки к частоте отсечки.
для поперечных полей в плоскости поперечного сечения волокна. При этом становится возможным определить то расстояние, на которое электромагнитная волна проникает за поверхность сердцевина — оболочка и рассеивается в оболочке. Интегрируя по сечению сердцевины, можно вычислить ту часть полной мощности каждой моды, которая переносится в сердцевине. Результаты таких вычислений для нескольких мод самых низких порядков, выполненных в приближении слабо направляющего волокна приведены на рис. 5.11. Как и ожидалось, большая часть потока мощности находится в сердцевине волокна за исключением случая, когда моды близки к частоте отсечки.
В большинстве многомодовых волокон, используемых в оптических системах связи, одновременно распространяется много мод. Рассмотрим кратко способ оценки числа распространяющихся в волокне мод. Большая часть оптической мощности переносится в сердцевине

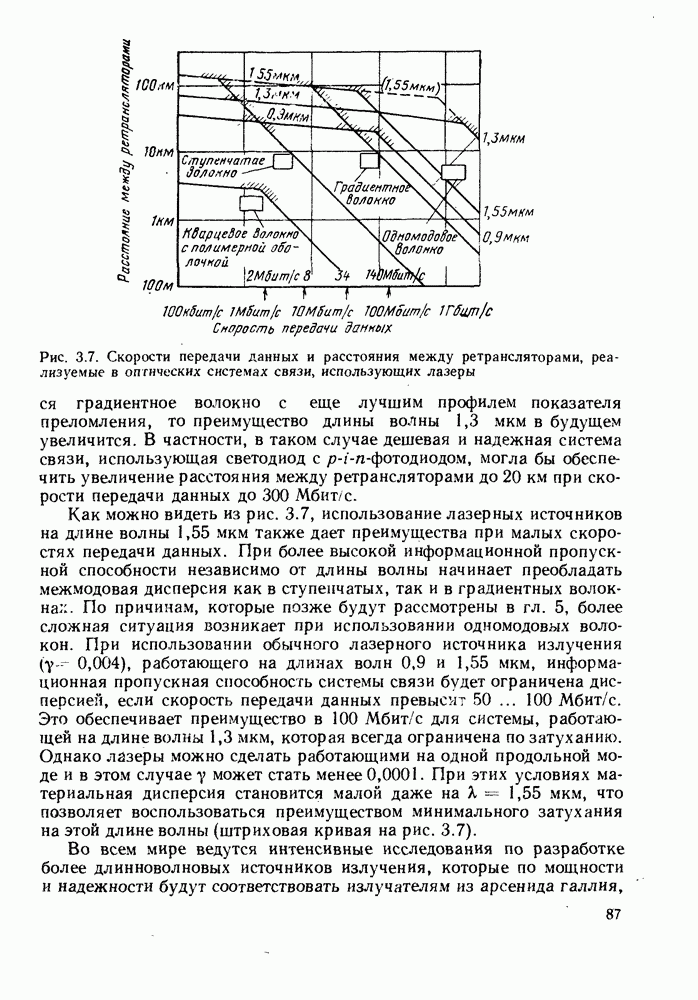
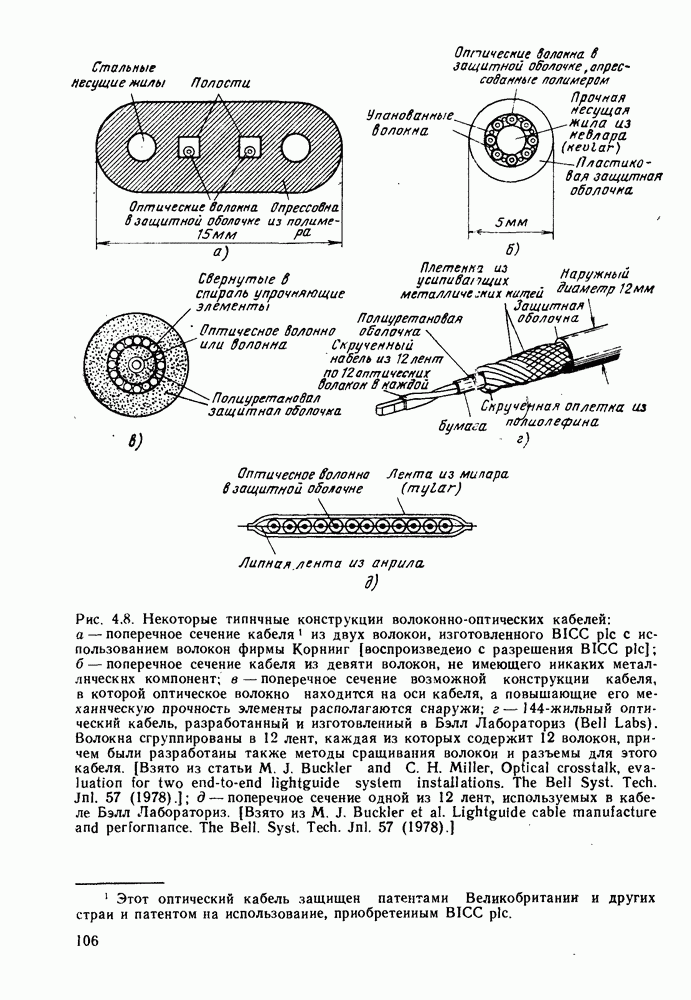
Рис. 5.10. Графики зависимости нормализованного параметра распространения  от параметра нормализованной частоты V для некоторых самых низких мод в ступенчатом волокне в случае использования приближения слабо направляющего волокна. [Взято из статьи D. Globe. Weakly guiding fibers. Appl. Optics 10, 2252-2258 (1971).]
от параметра нормализованной частоты V для некоторых самых низких мод в ступенчатом волокне в случае использования приближения слабо направляющего волокна. [Взято из статьи D. Globe. Weakly guiding fibers. Appl. Optics 10, 2252-2258 (1971).]
волокна с помощью мод высоких порядков, которые далеки от своих частот отсечки. В этом случае можно упростить описание характеристик мод, если воспользоваться приближенным представлением функций Бесселя при больших аргументах 

Условие отсечки при этом принимает вид

Таким образом, при  оно преобразуется к виду
оно преобразуется к виду

откуда следует

или


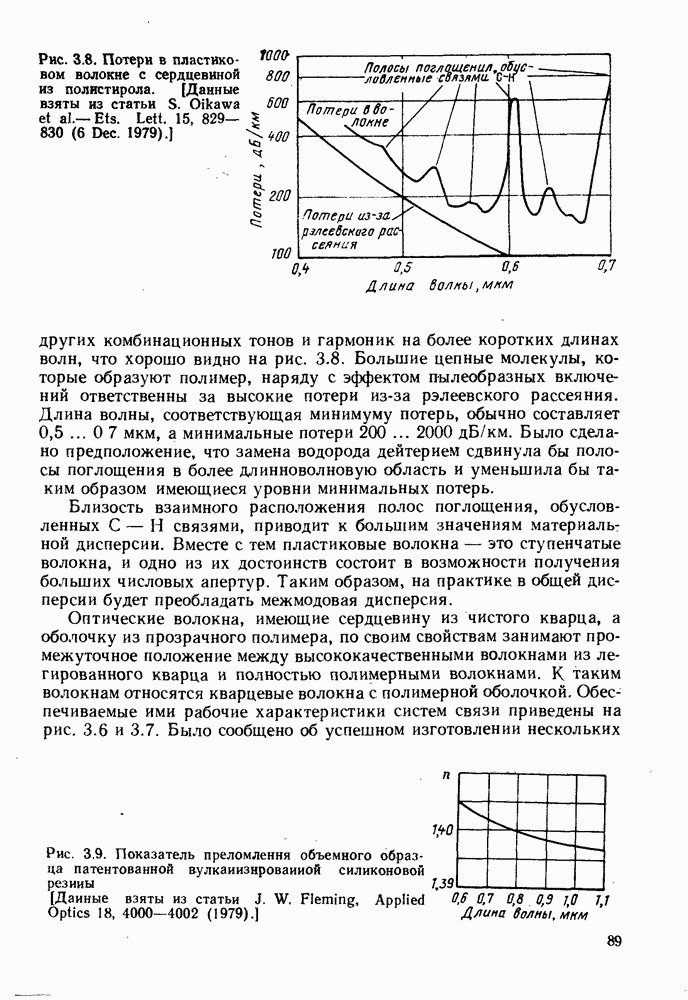
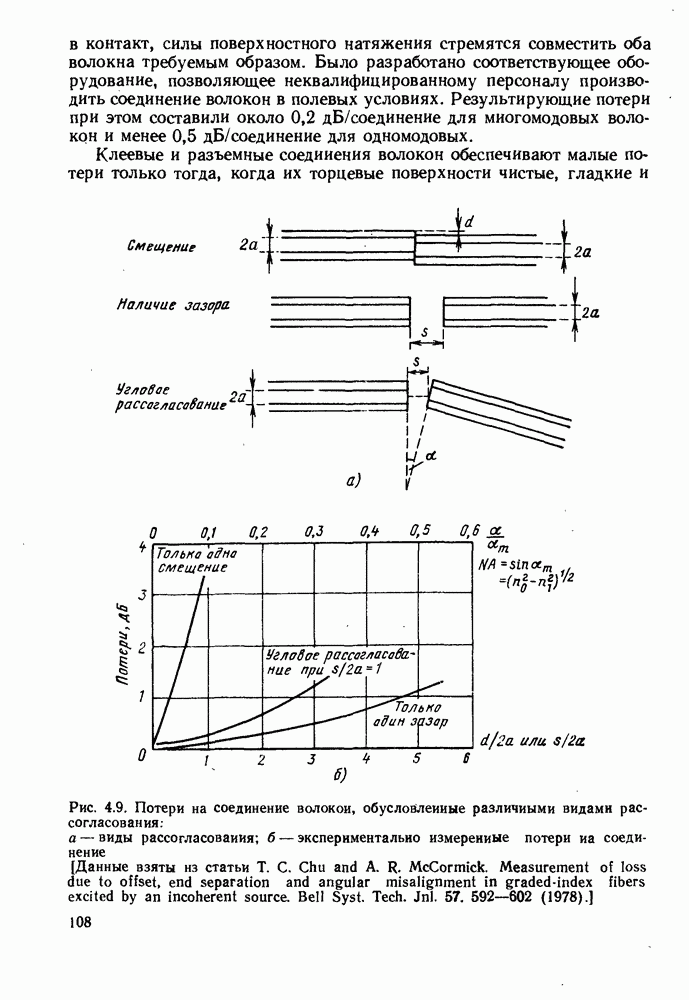
Рис. 5.11. Графики зависимости относительной доли мощности моды, распространяющейся в оболочке, от параметра нормализованной частоты  [Взято из статьи D. Globe. Weakly ? duiding fibers. Appl. Optics 10, 2252-2258 (1971).]
[Взято из статьи D. Globe. Weakly ? duiding fibers. Appl. Optics 10, 2252-2258 (1971).]
Хотя выражение (5.3.14) выведено из условия отсечки, однако полное изменение произведения  а в пределах всех возможных частот ограничено значением, несколько меньшим
а в пределах всех возможных частот ограничено значением, несколько меньшим  поэтому относительное изменение
поэтому относительное изменение  будет очень малым в условиях лринятой аппроксимации, а именно при
будет очень малым в условиях лринятой аппроксимации, а именно при  Это означает, что все моды с одинаковым значением
Это означает, что все моды с одинаковым значением  становятся приближенно вырожденными. Следовательно, разумно их идентифицировать с помощью нового целого числа модовой группы
становятся приближенно вырожденными. Следовательно, разумно их идентифицировать с помощью нового целого числа модовой группы  В таком случае
В таком случае

Приблизительно  пар значений
пар значений  создает одно и то же значение
создает одно и то же значение  при этом каждой из
при этом каждой из  пар соответствуют четыре моды. Таким образом существует
пар соответствуют четыре моды. Таким образом существует  мод, связанных с каждой модовой группой
мод, связанных с каждой модовой группой  Постоянная распространения этих мод может быть получена в нормализованном виде либо подстановкой (5.3.15) в (5.3.9)
Постоянная распространения этих мод может быть получена в нормализованном виде либо подстановкой (5.3.15) в (5.3.9)

либо в явиом виде из (5.2.2)

Наибольшее допустимое значение для  имеет место при
имеет место при  Обозначим это максимальное значение квантованного числа модовой группы буквой
Обозначим это максимальное значение квантованного числа модовой группы буквой  Тогда
Тогда

Откуда следует

И, наконец, воспользовавшись (5.2.16), находим

Когда V велико, что должно быть справедливым в рассматриваемом случае, общее число  мод порядка
мод порядка  которые могут распространяться в волокне, приближенно определяется соотношением
которые могут распространяться в волокне, приближенно определяется соотношением

Несколько лучшее приближение дает формула

Воспользовавшись формулой (5.3.20), получим

где  площадь сердцевины,
площадь сердцевины,  как и ранее, числовая апертура волокна. Данное соотношение не является неожиданным, поскольку квадрат числовой апертуры определяет оптическую мощность, которая может быть введена в волокно, число распространяющихся в нем мод, если все они возбуждаются одинаково, а также полную мощность, которая может распространяться по волокну.
как и ранее, числовая апертура волокна. Данное соотношение не является неожиданным, поскольку квадрат числовой апертуры определяет оптическую мощность, которая может быть введена в волокно, число распространяющихся в нем мод, если все они возбуждаются одинаково, а также полную мощность, которая может распространяться по волокну.
Чтобы вычислить значение  для типичного многомодового ступенчатого волокна, примем
для типичного многомодового ступенчатого волокна, примем  В таком случае
В таком случае  . При длине волны источника 0,85 мкм получаем
. При длине волны источника 0,85 мкм получаем  число модовых групп
число модовых групп  а общее число мод, распространяющихся в волокне и определяемое формулой (5.3.23),
а общее число мод, распространяющихся в волокне и определяемое формулой (5.3.23),  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
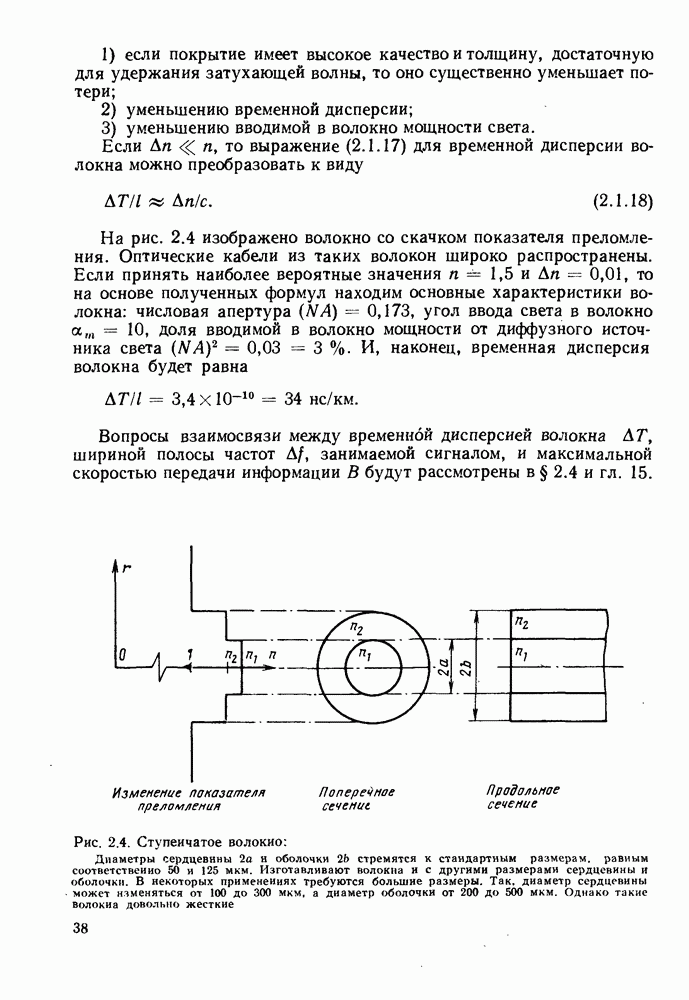
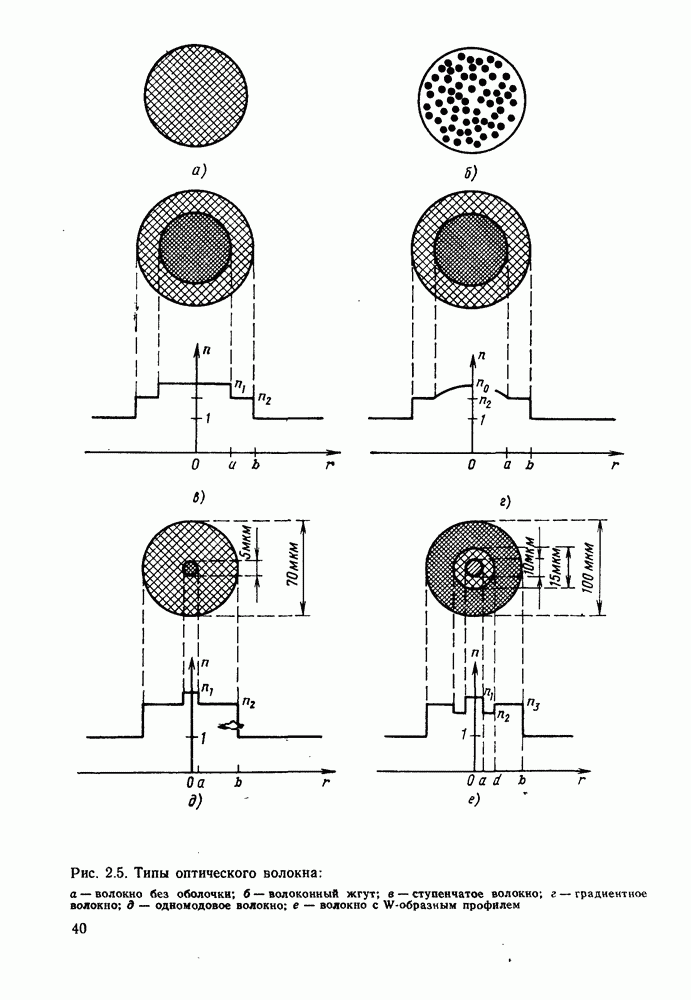
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
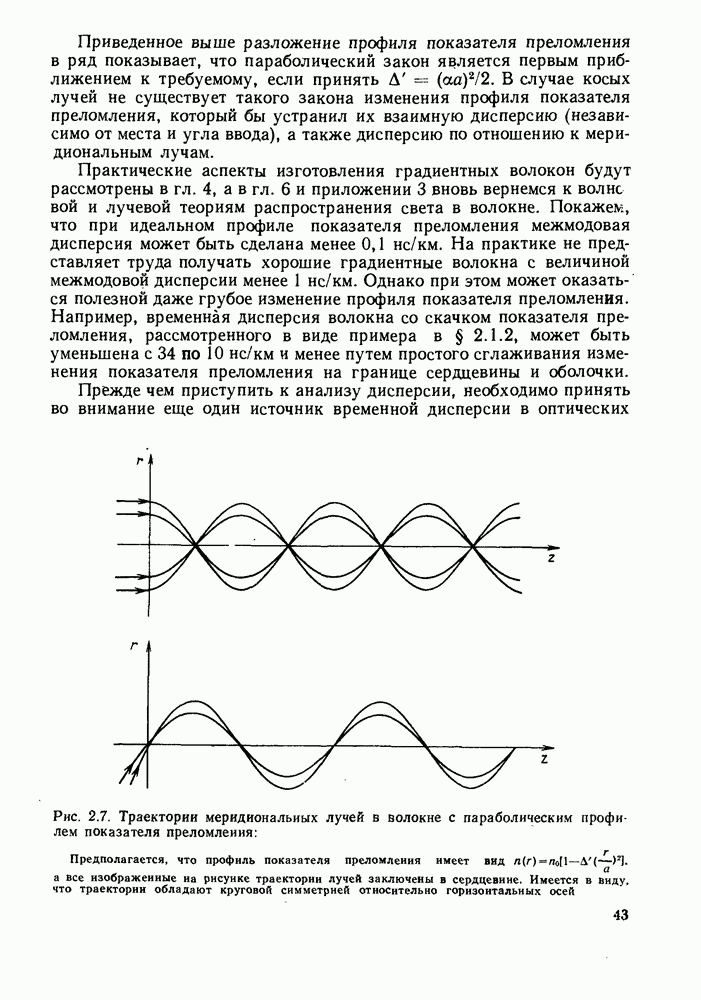
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
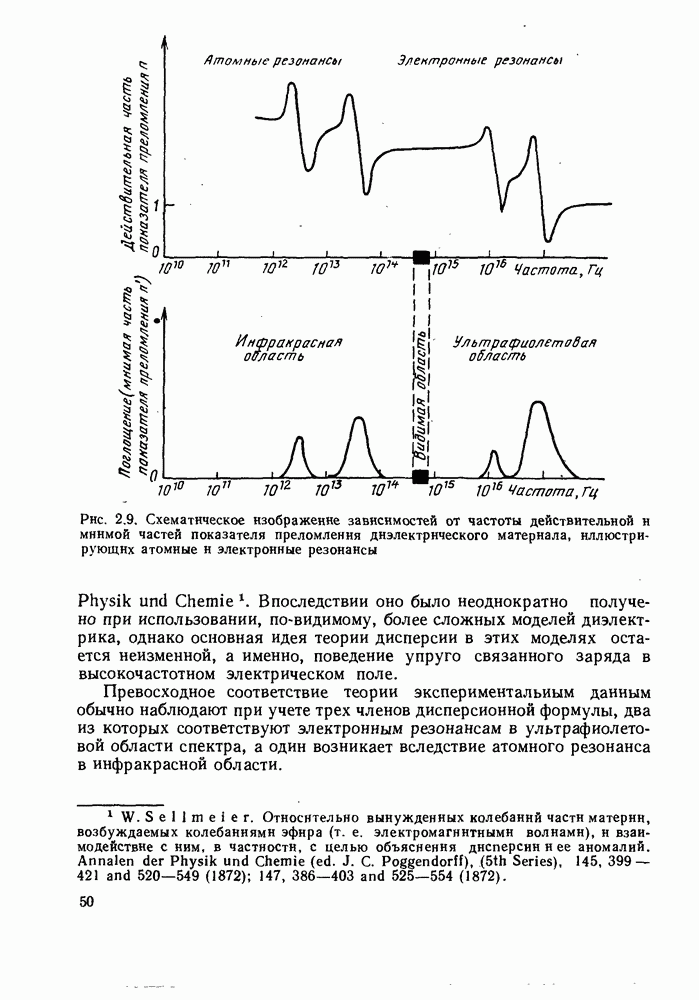
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
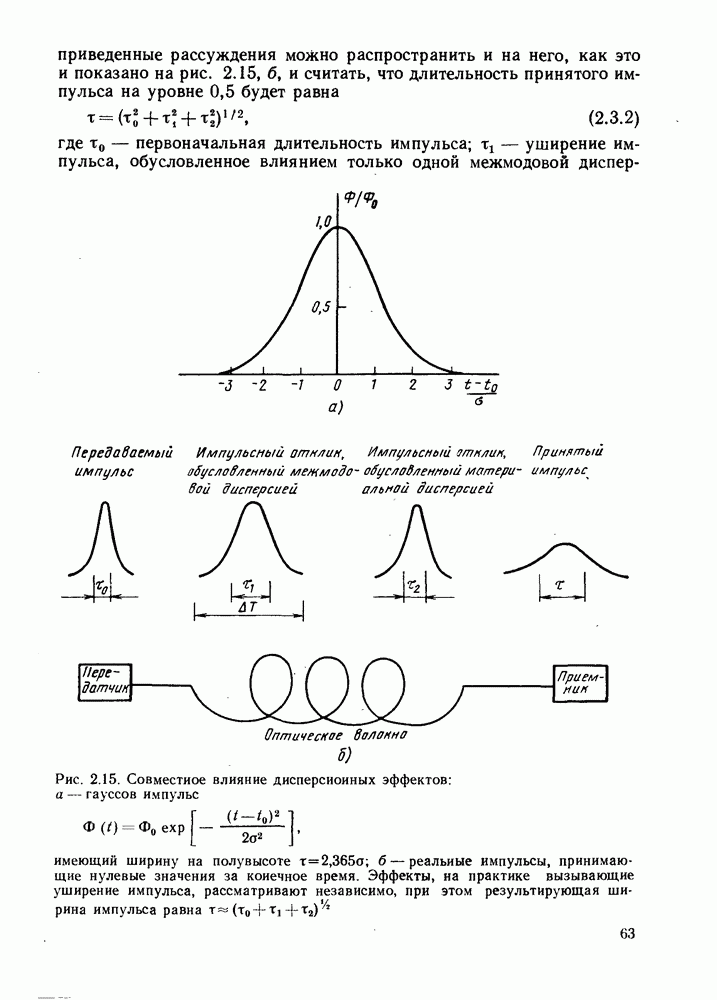
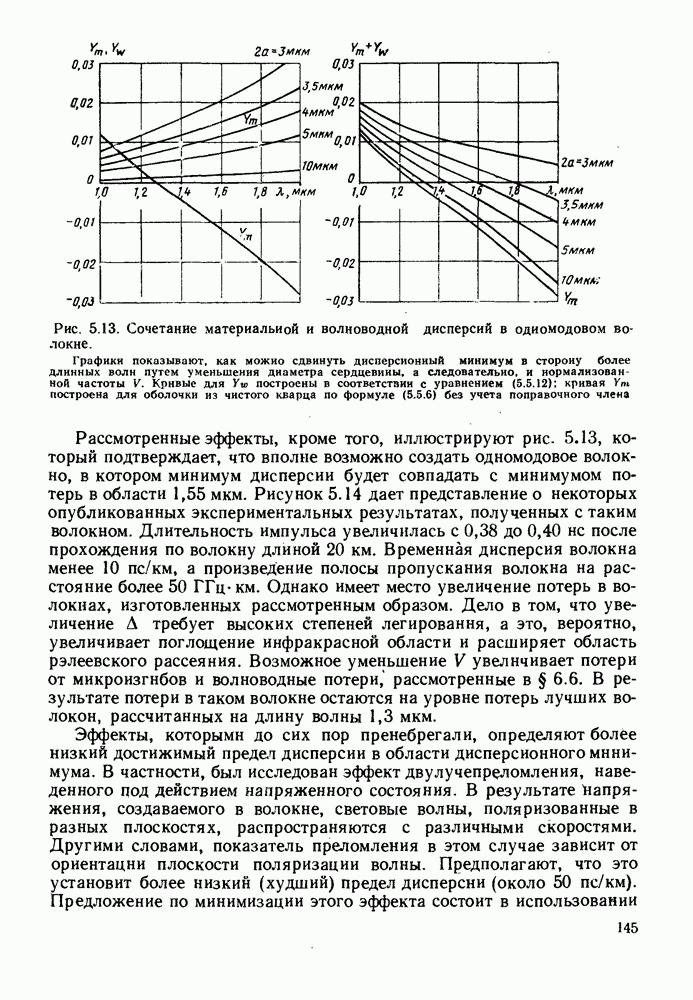
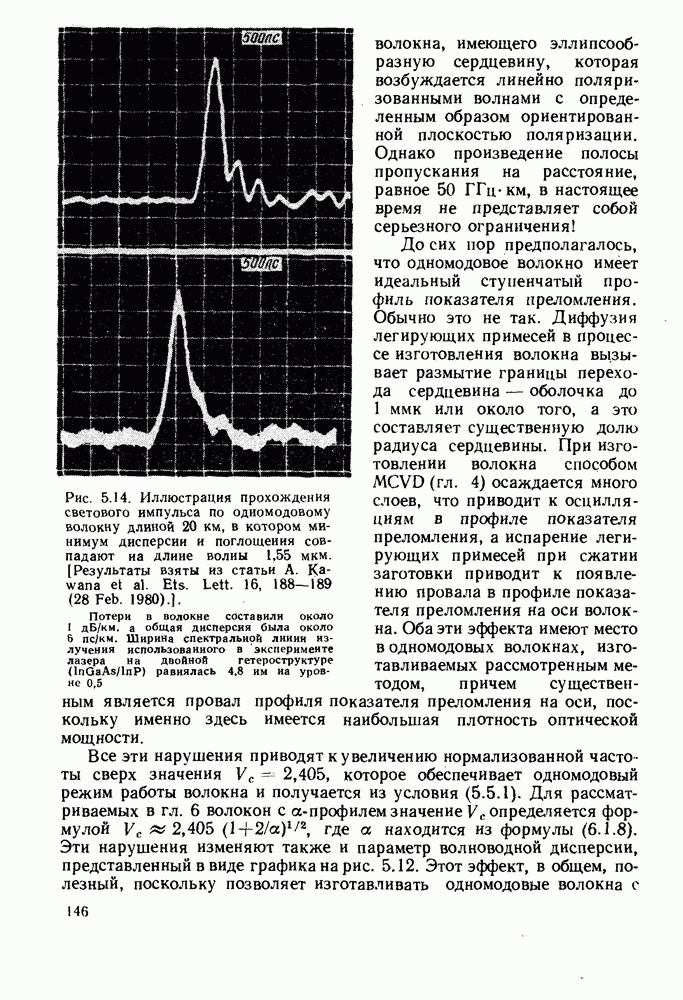
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
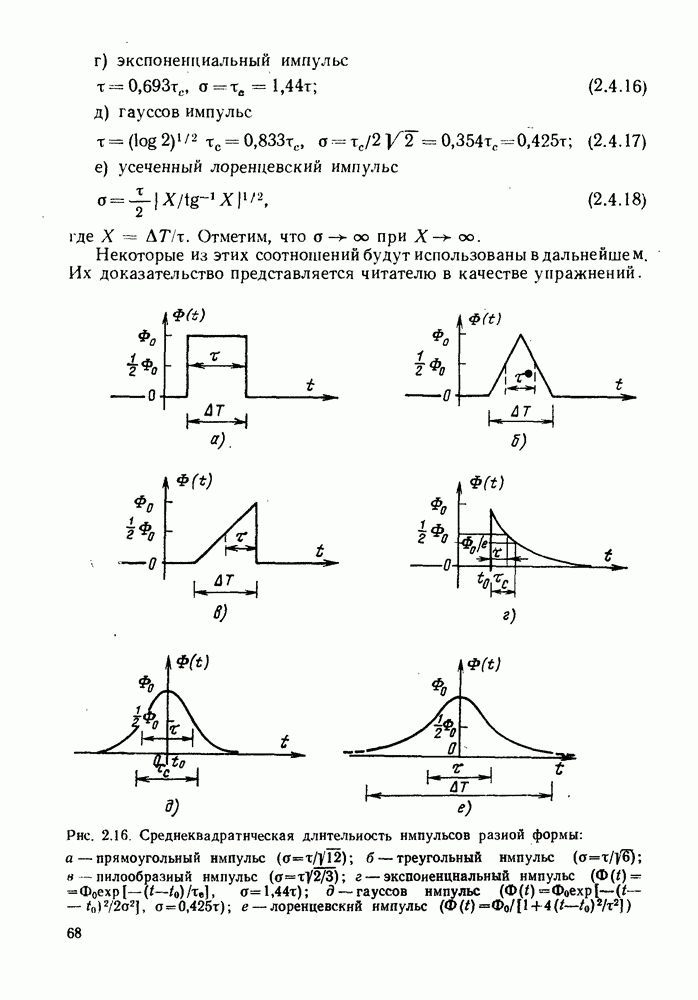
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
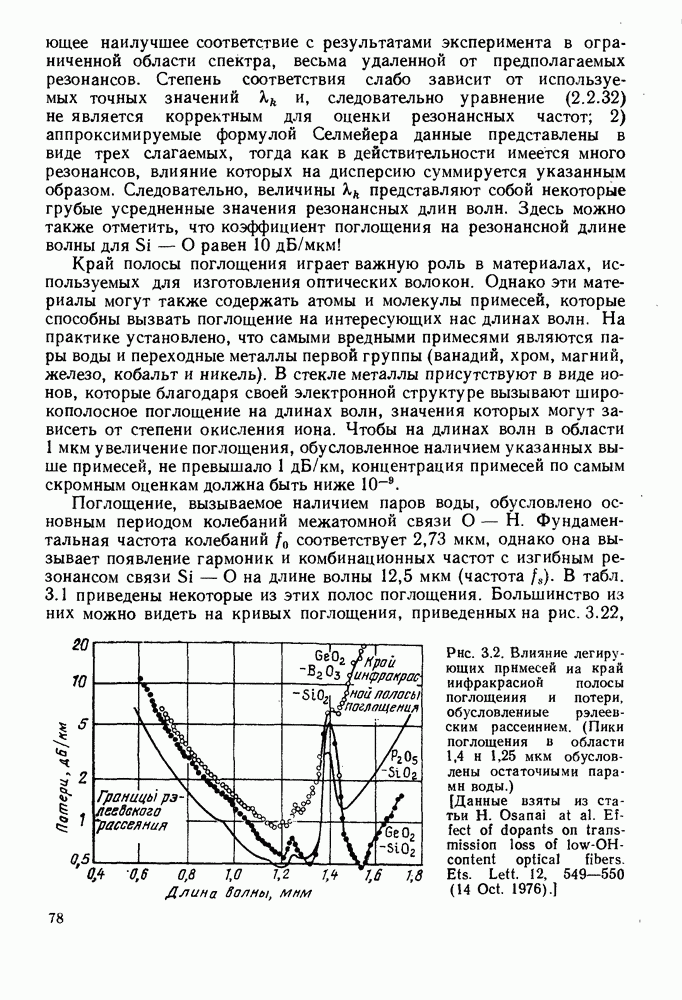
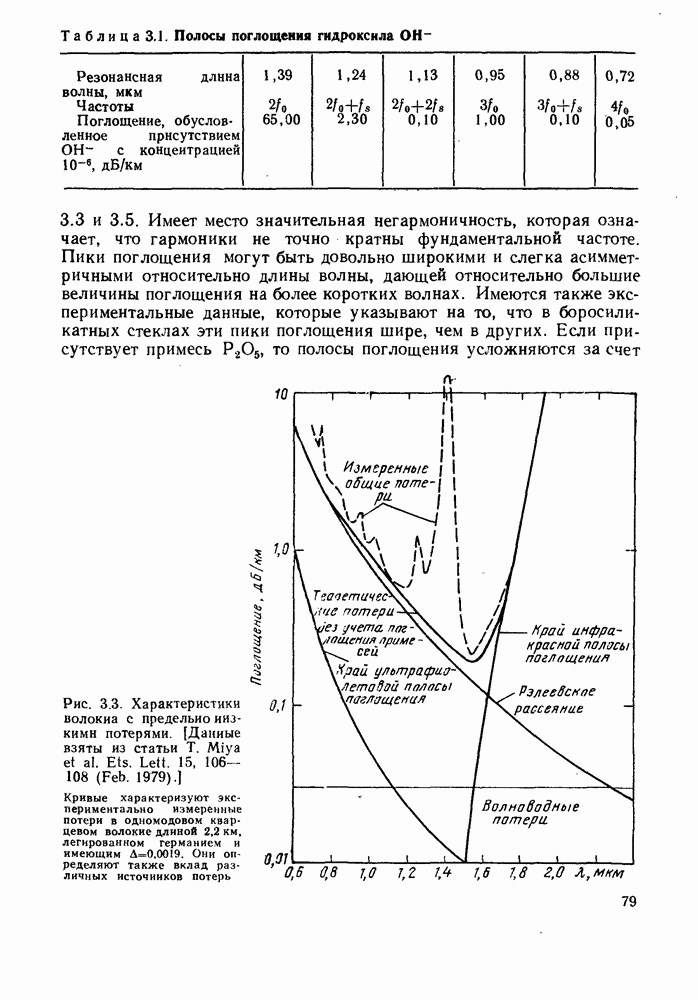
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
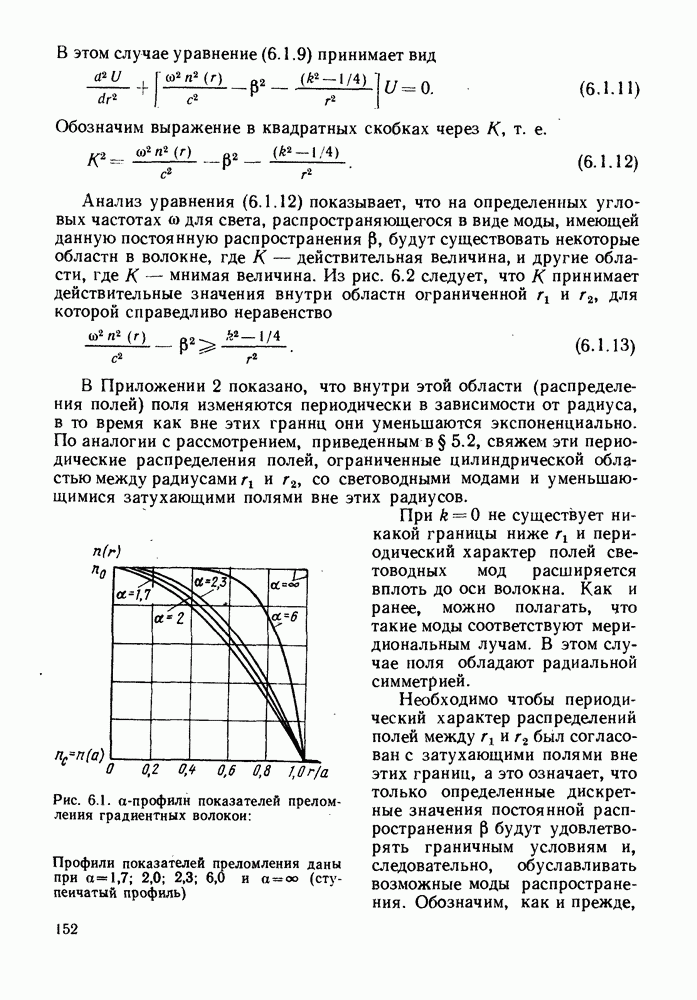
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
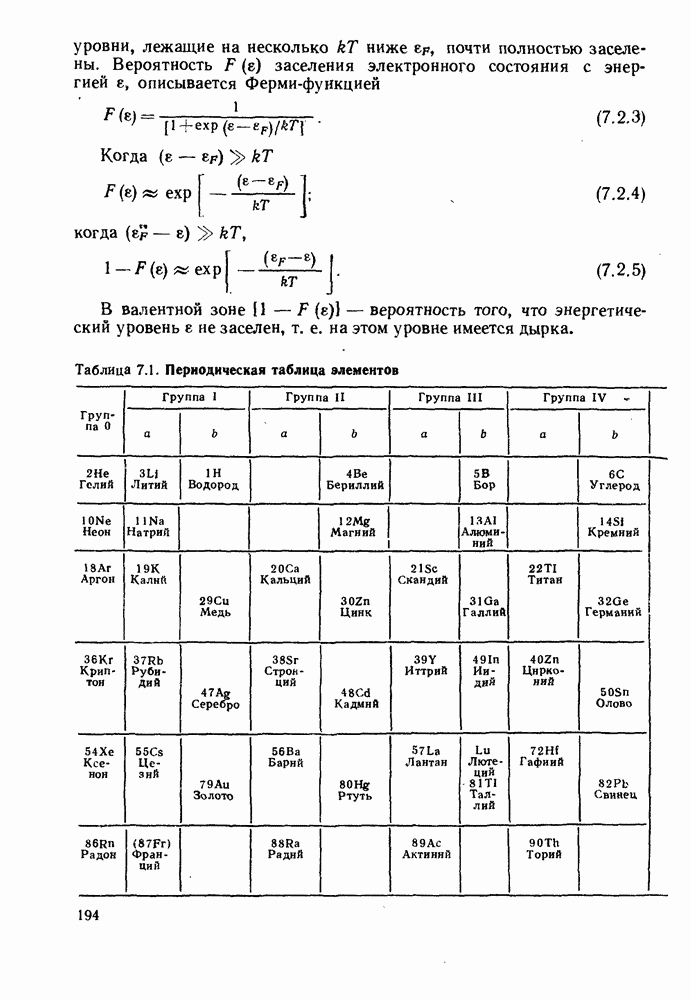
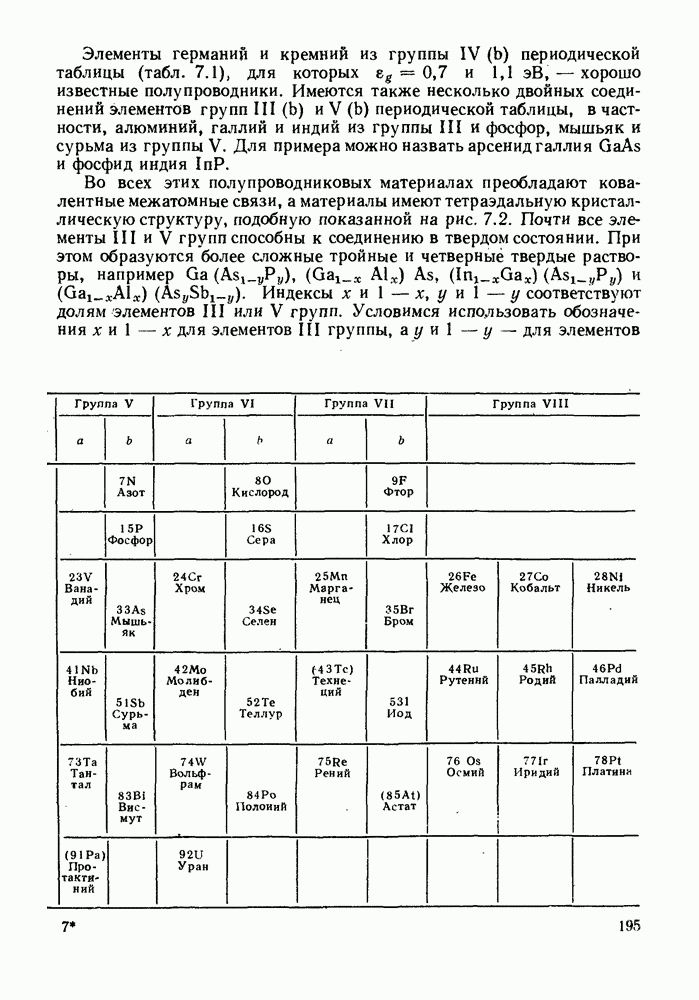
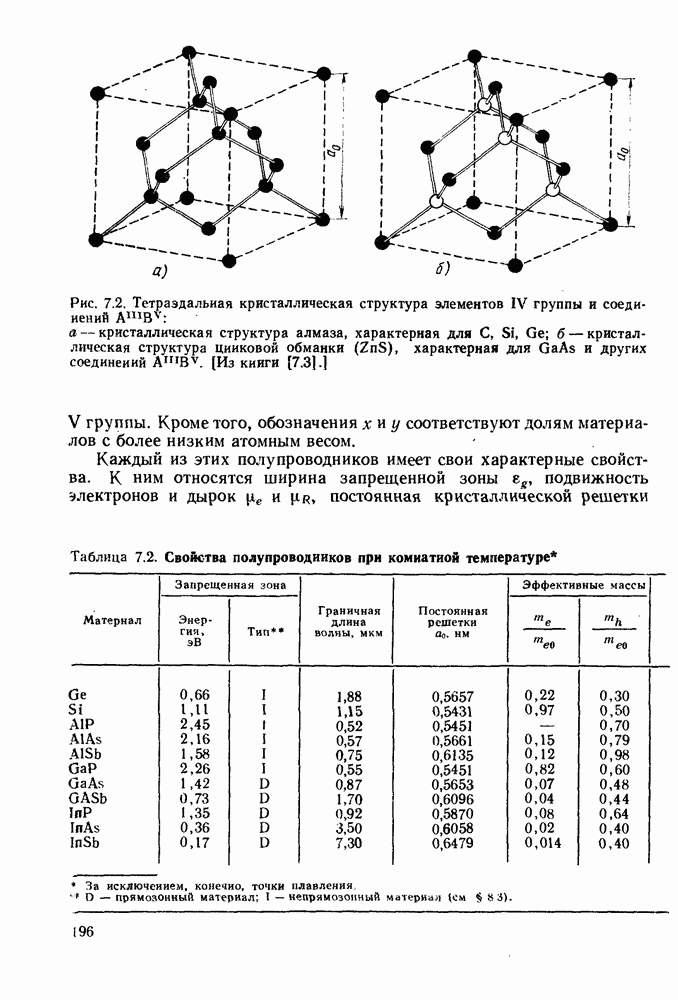
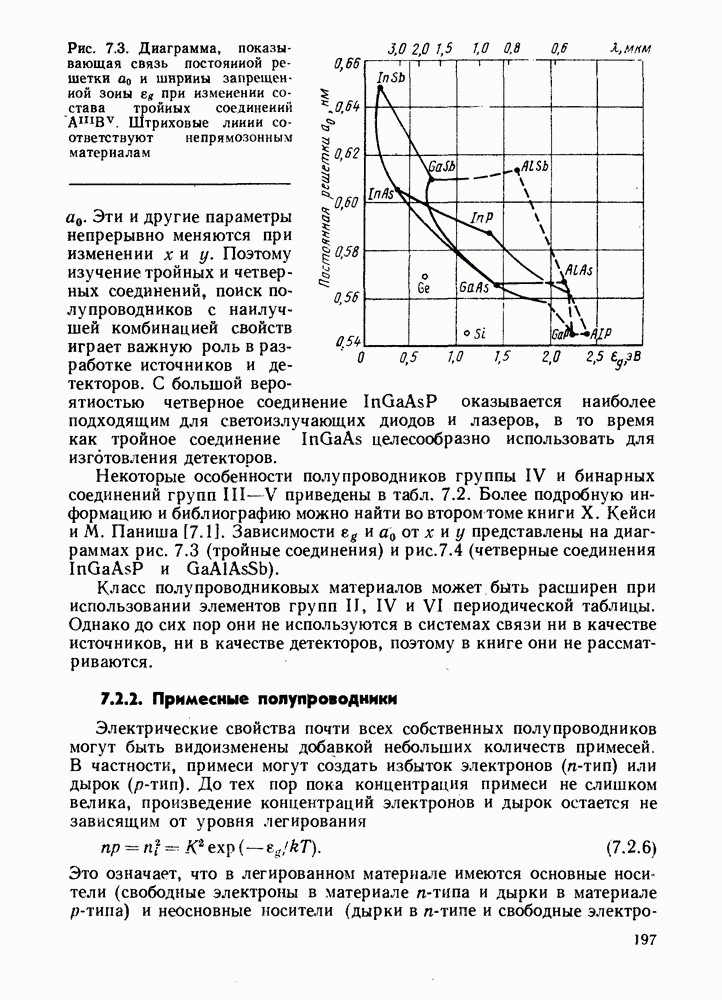
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
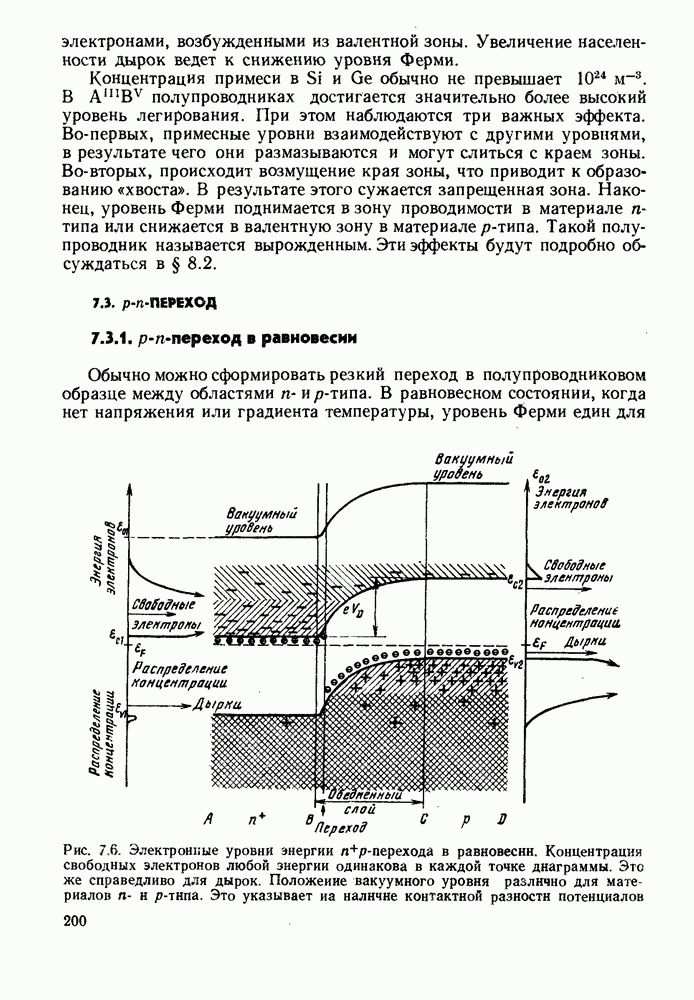
- 7.3.1. p-n-переход в равновесии
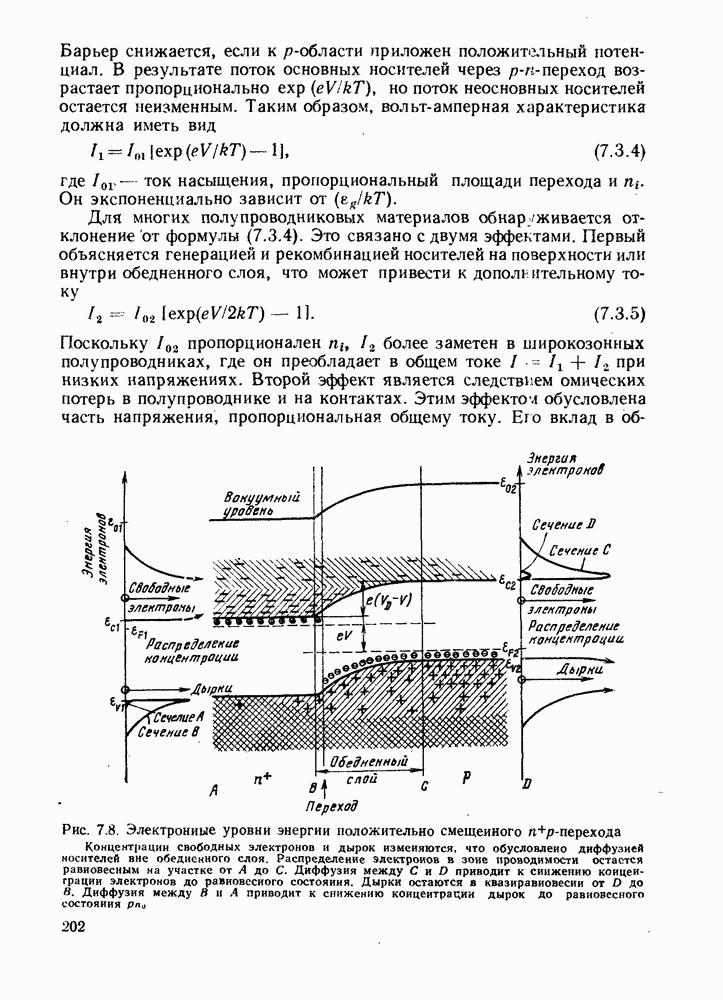
- 7.3.2. Смещенный p-n-переход
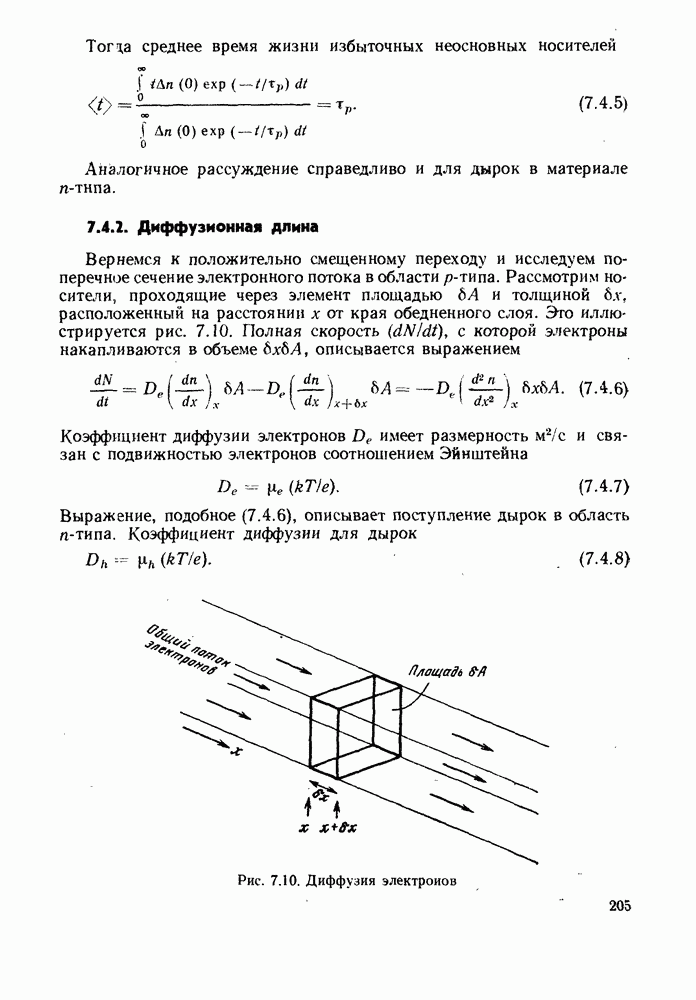
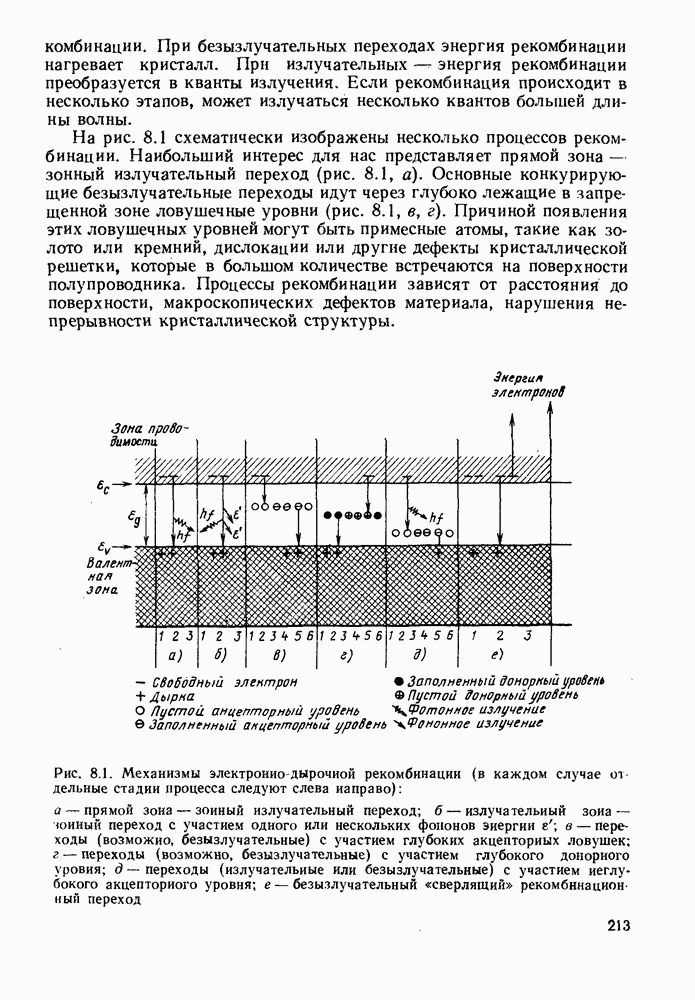
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
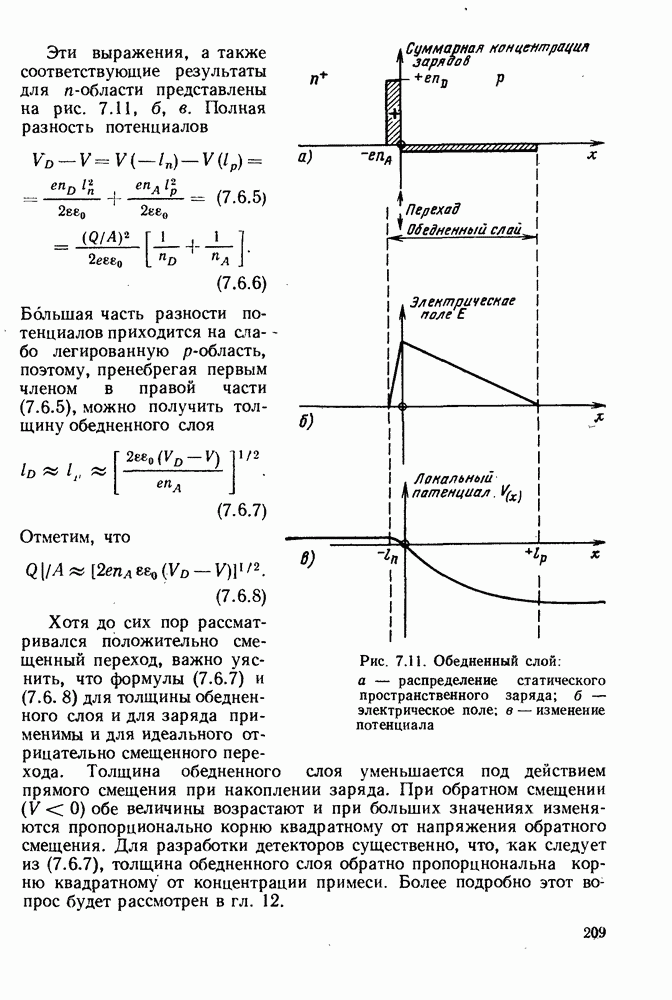
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
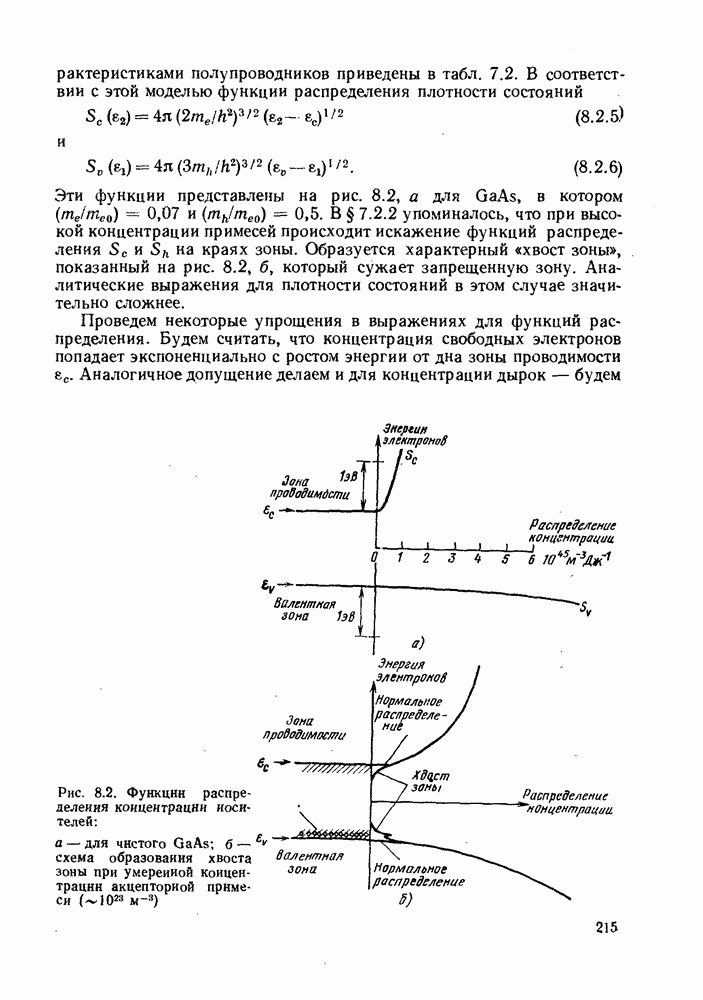
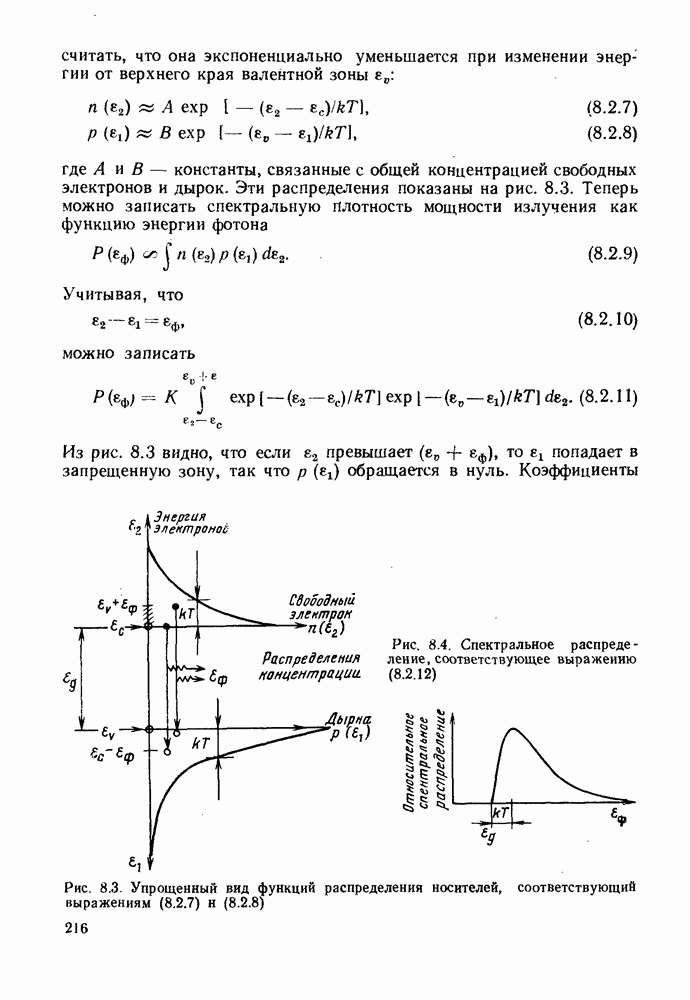
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
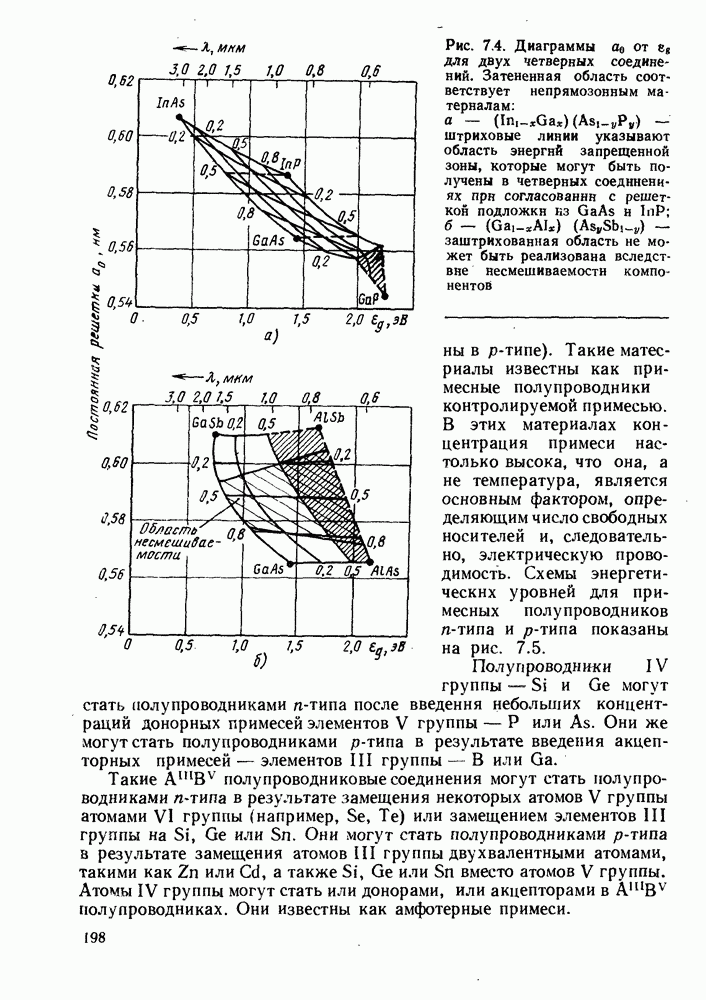
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
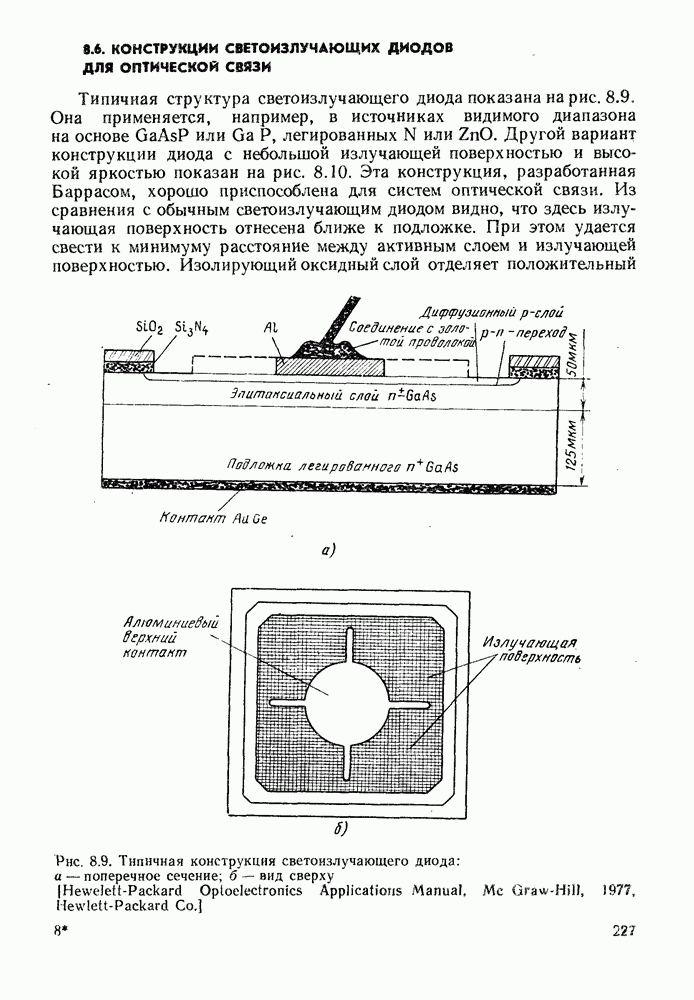
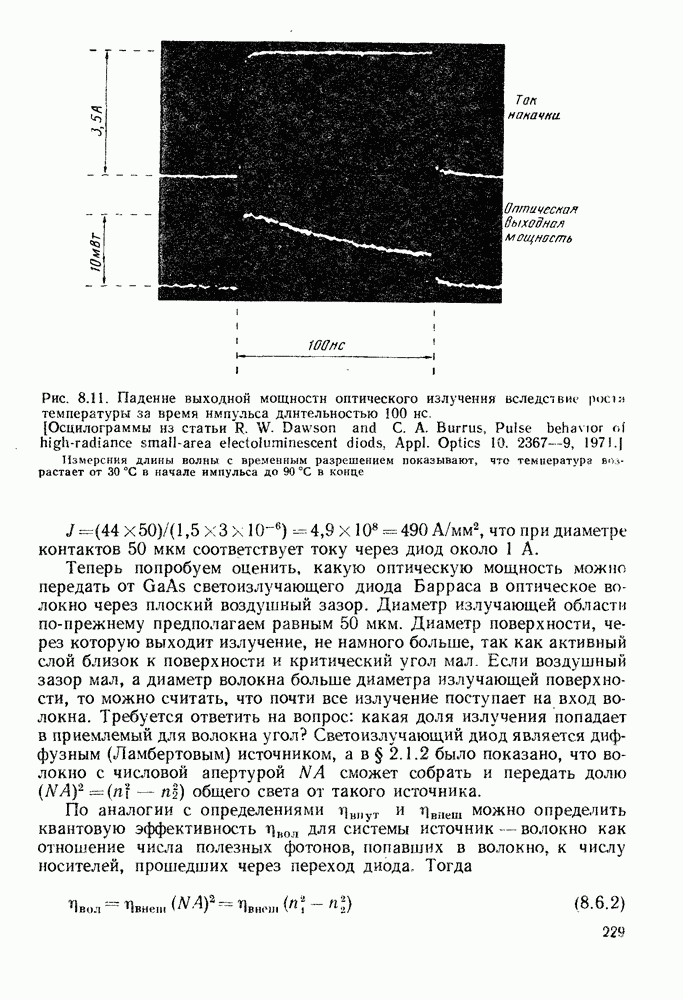
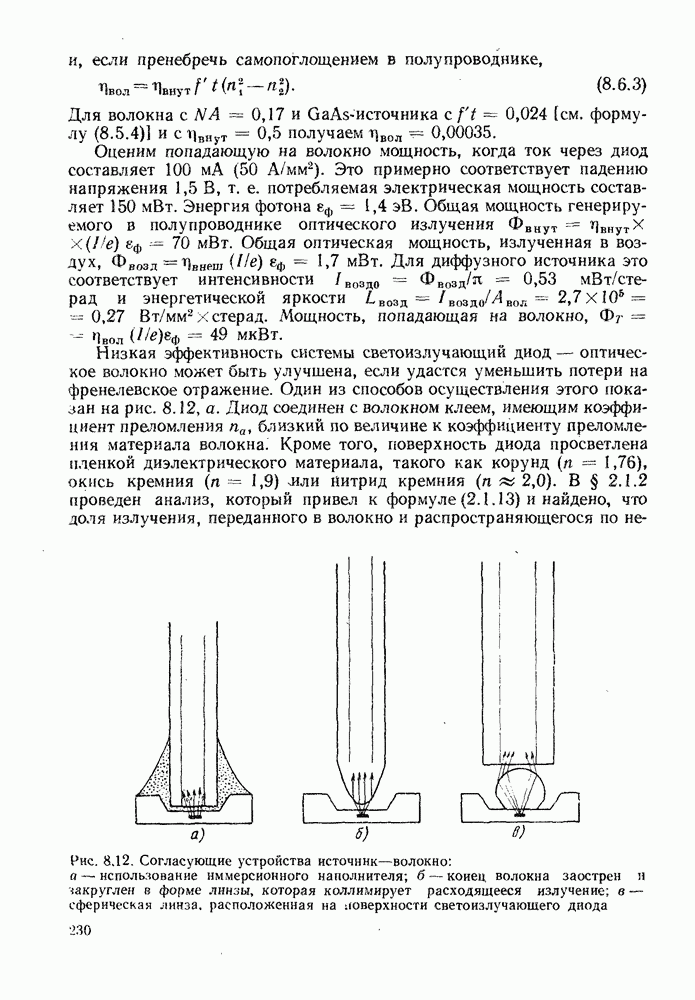
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
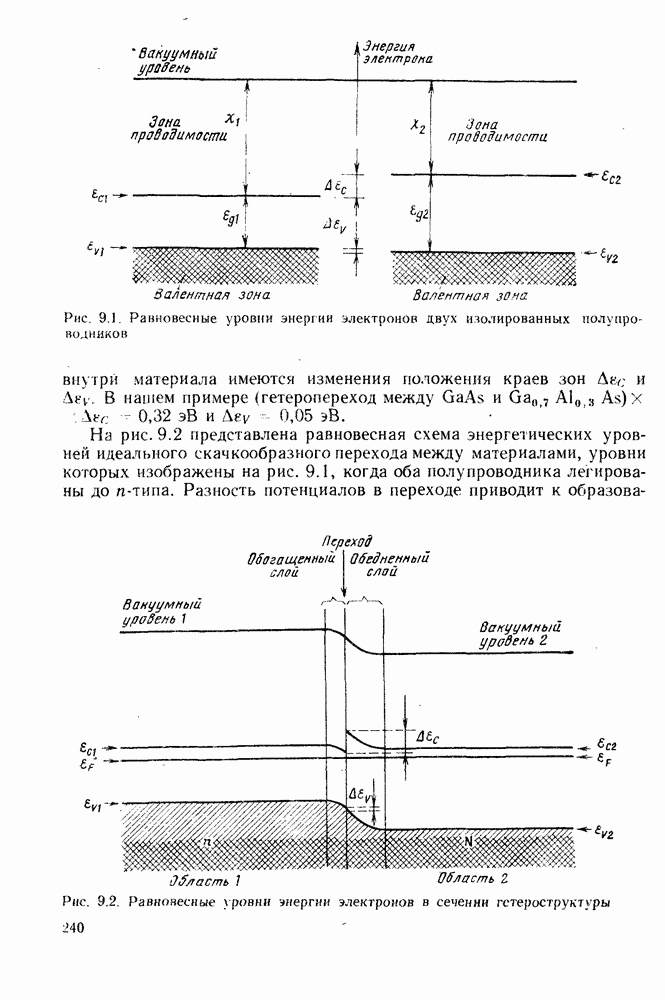
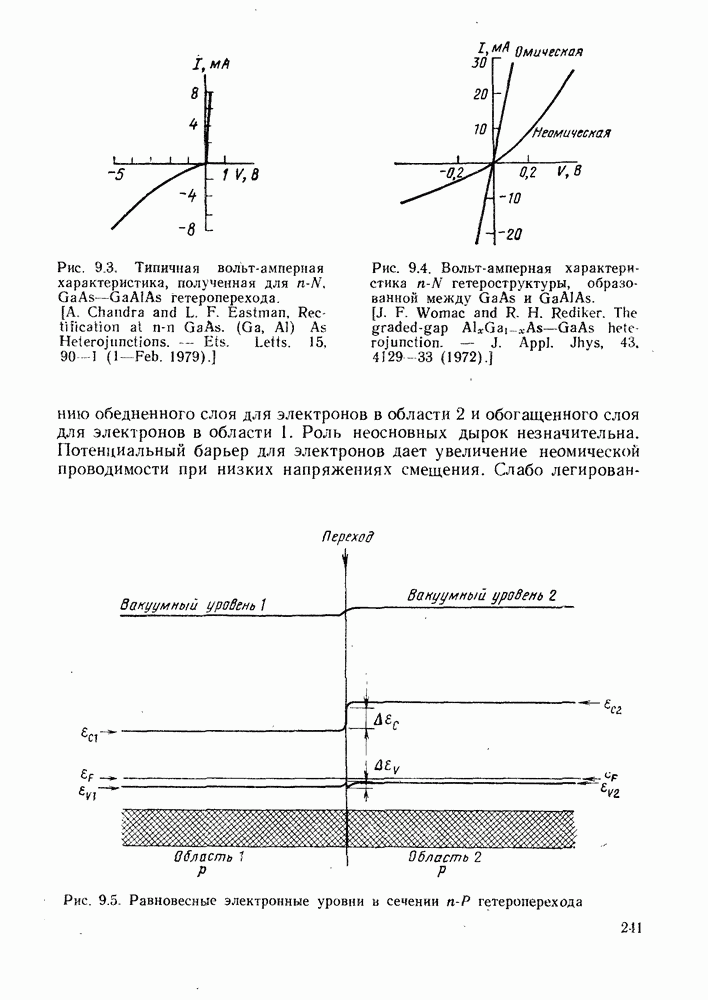
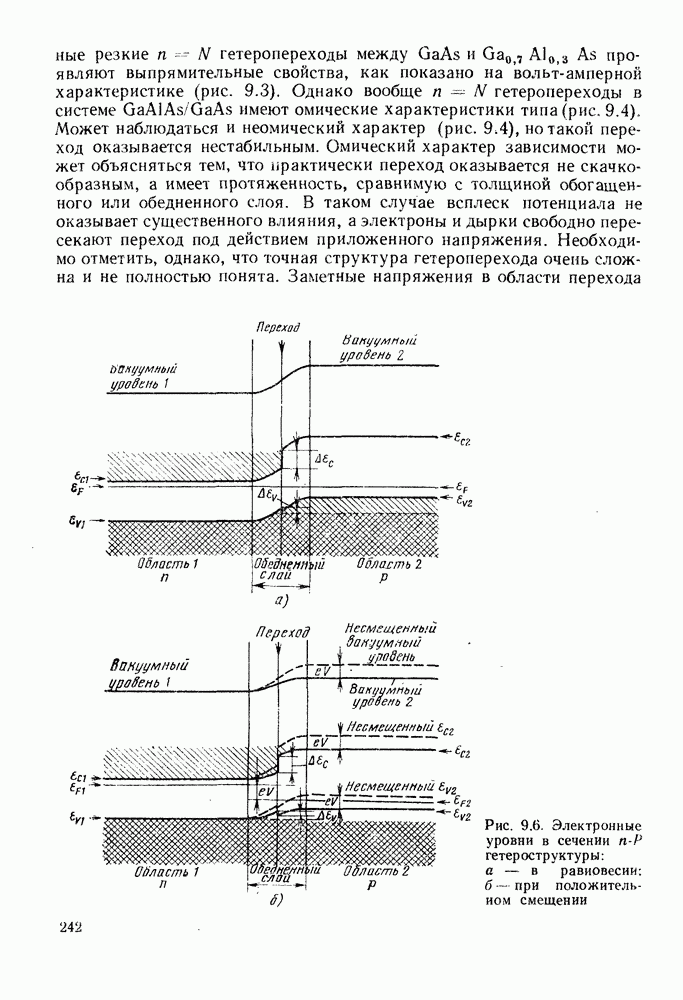
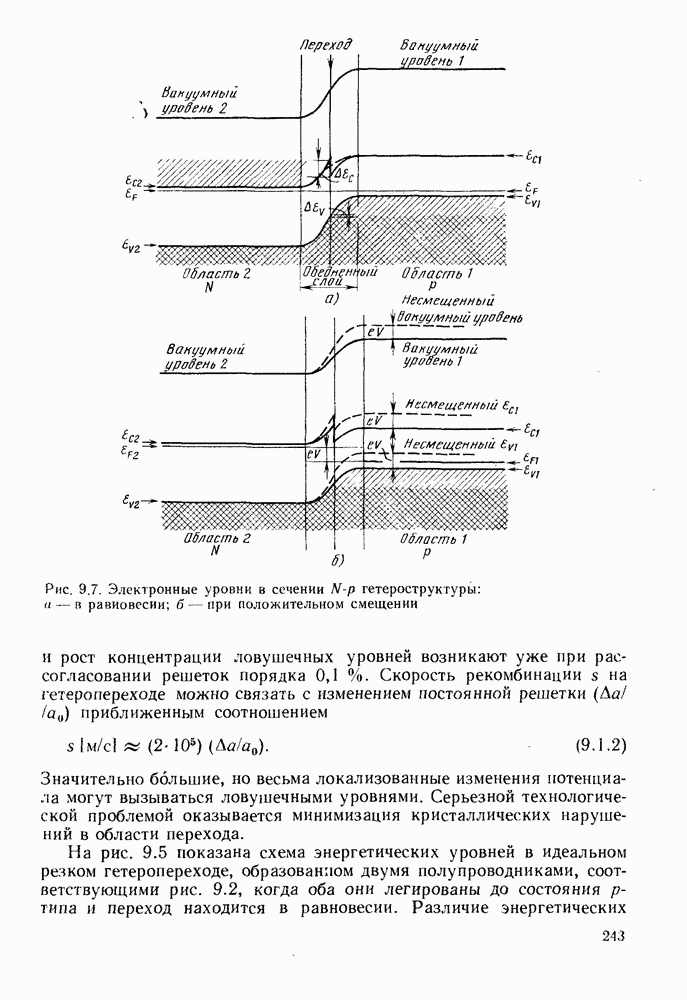
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
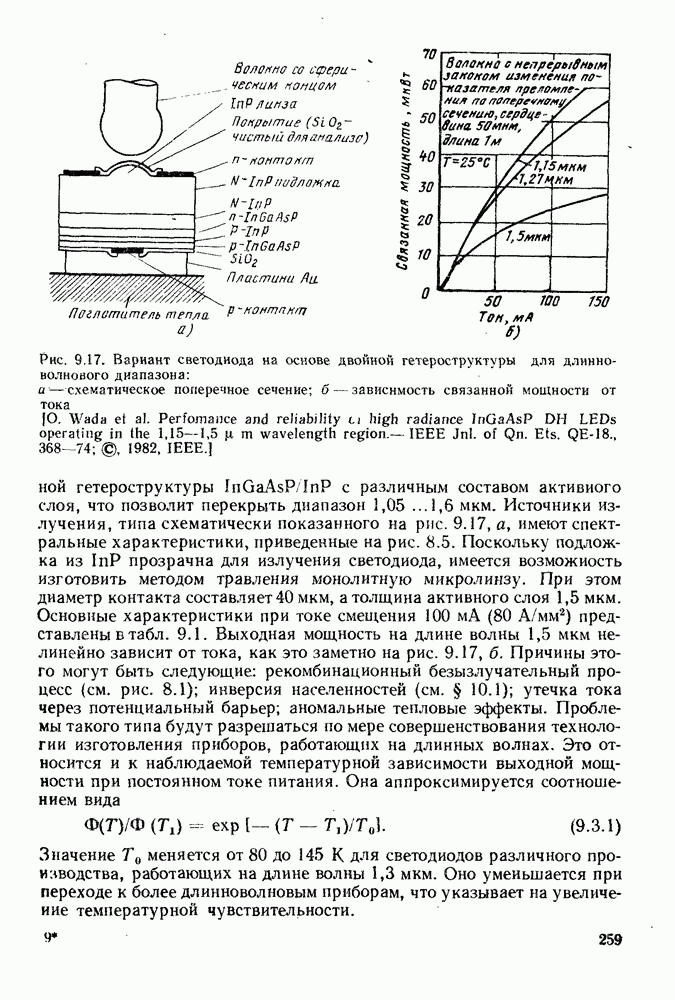
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
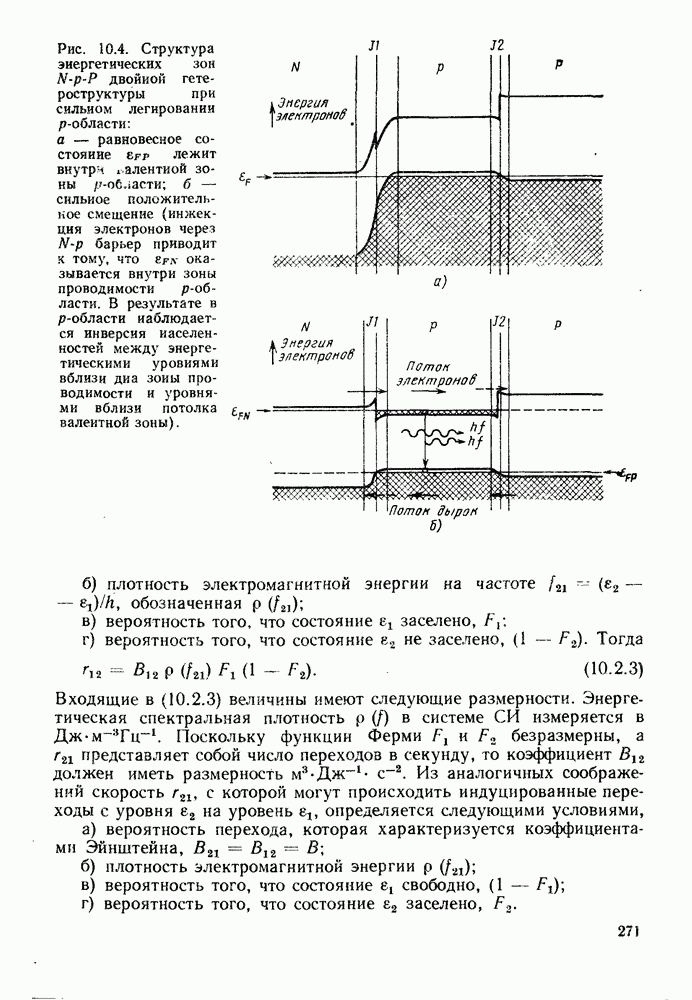
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
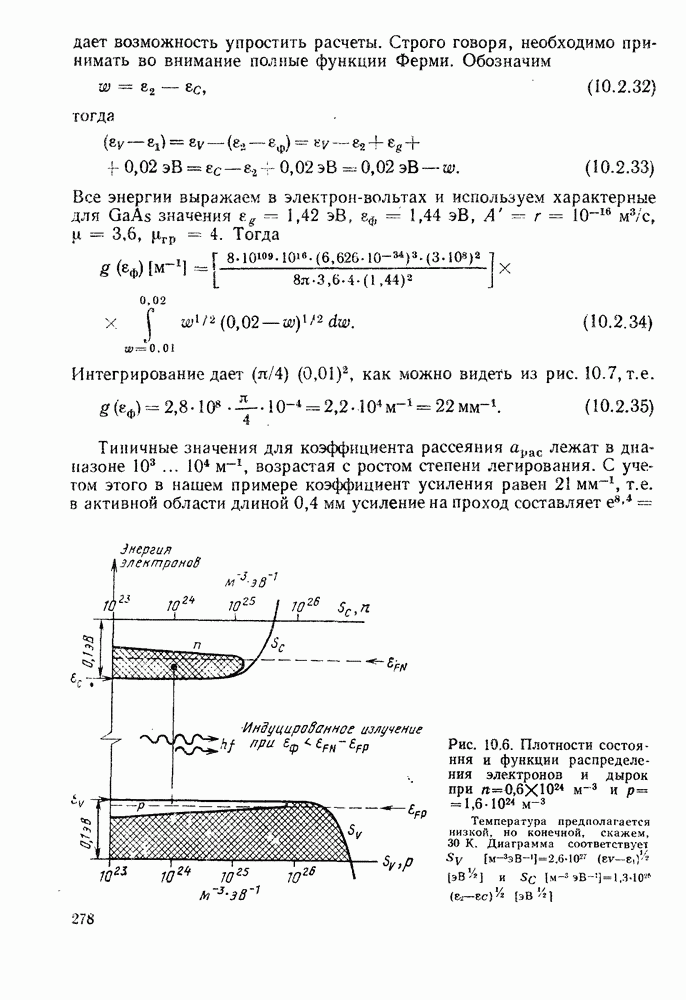
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
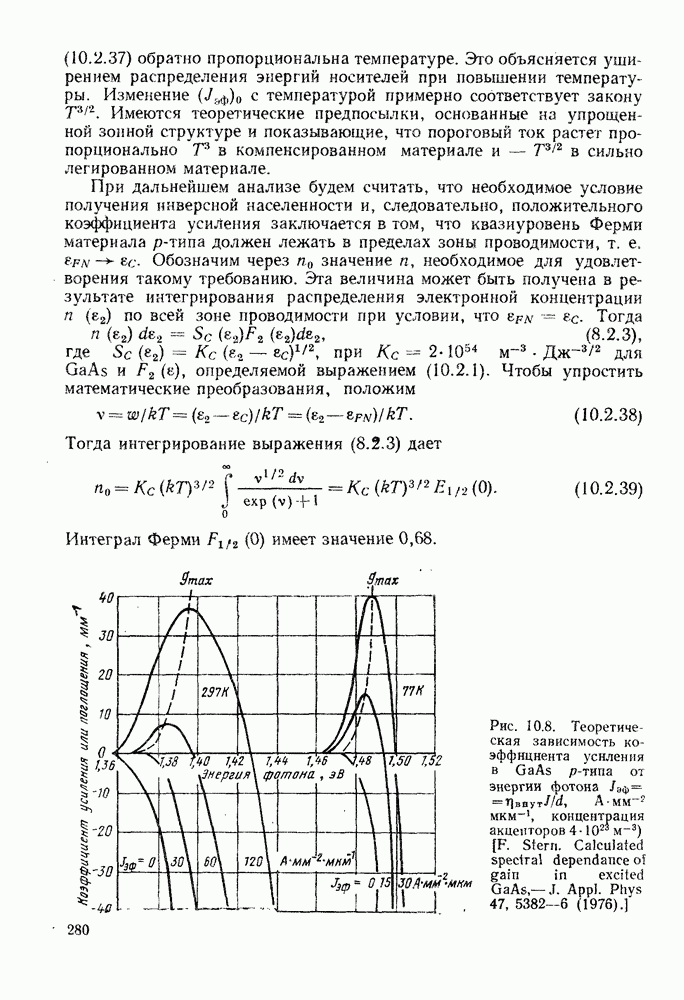
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
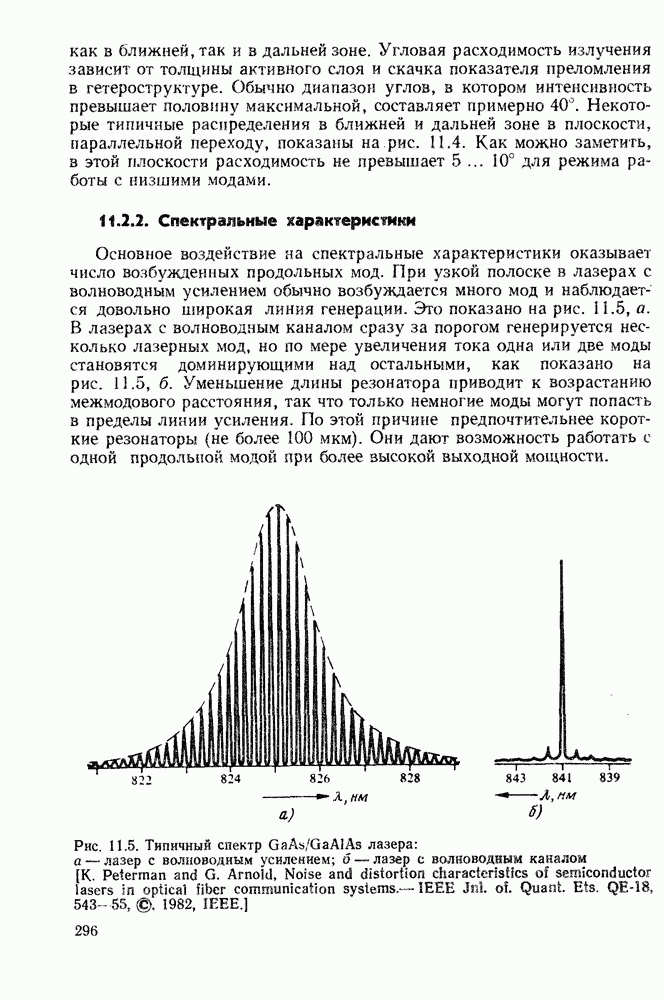
- 11.2.2. Спектральные характеристики
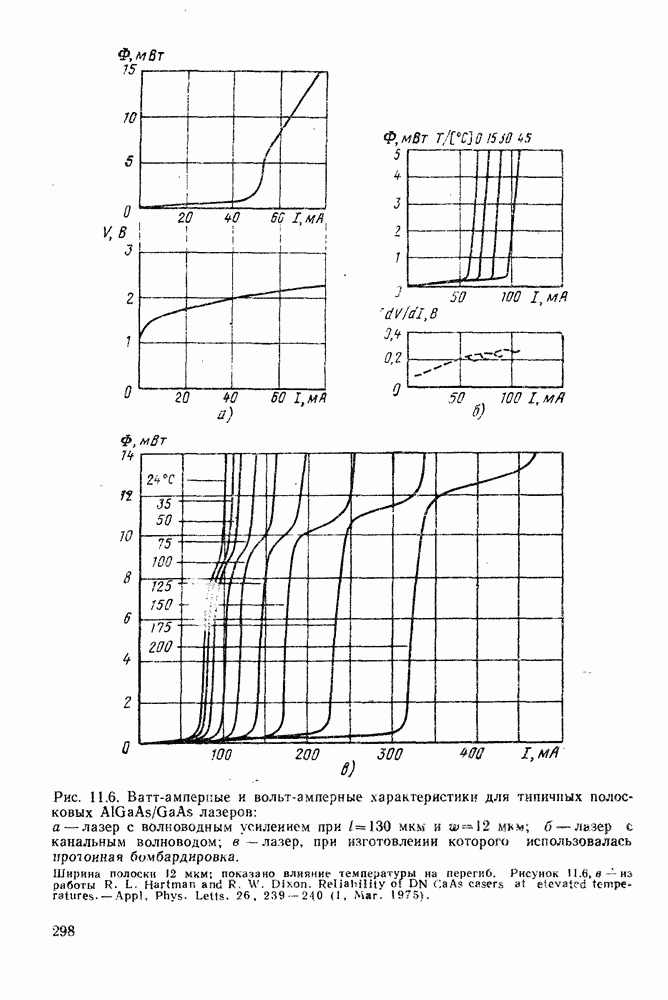
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
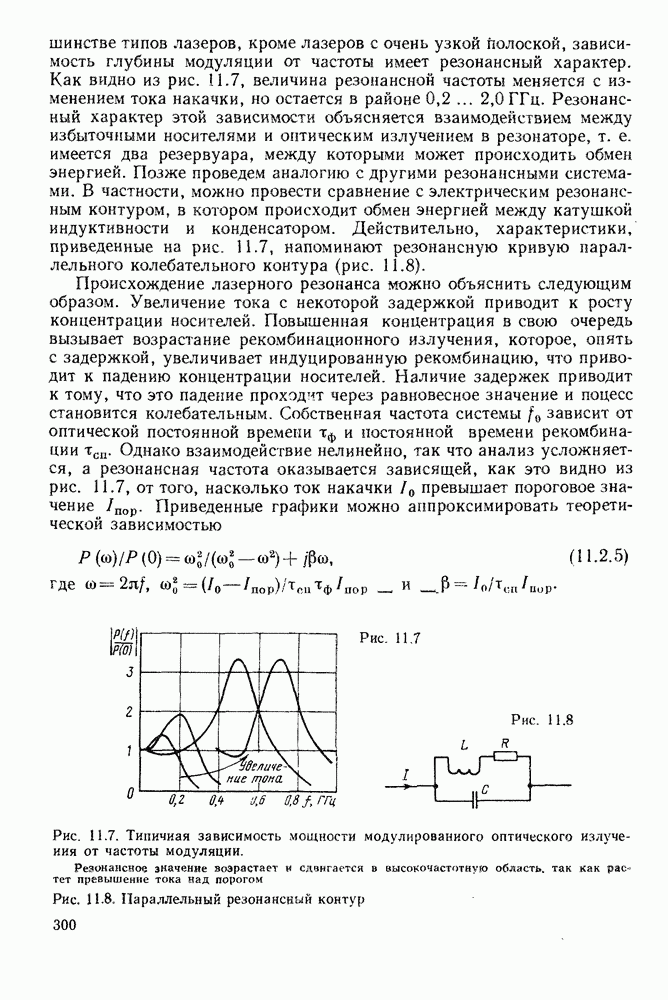
- 11.2.4. Частотные характеристики
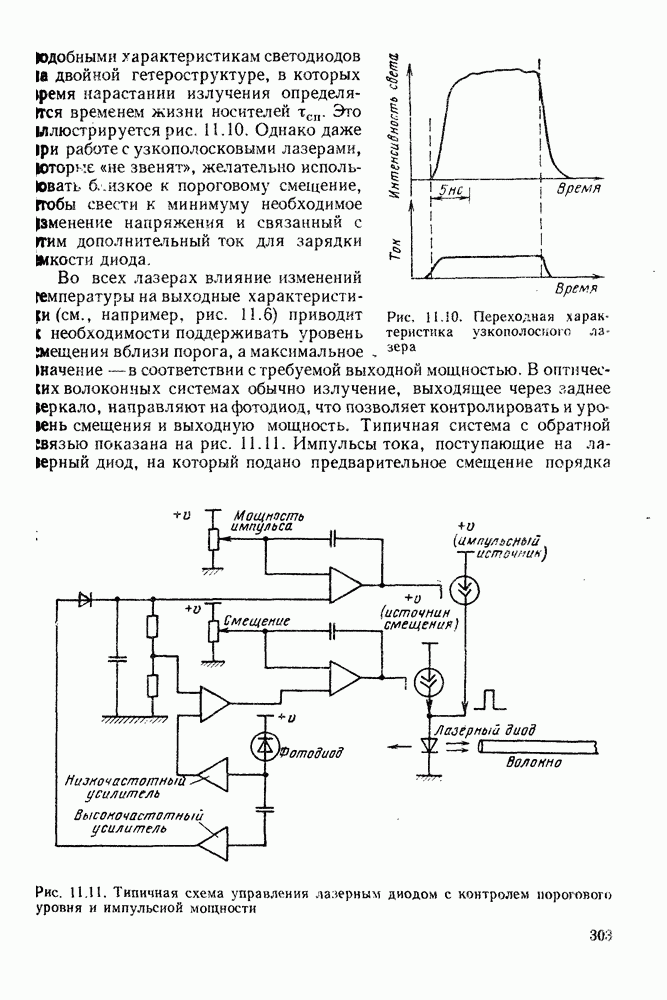
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
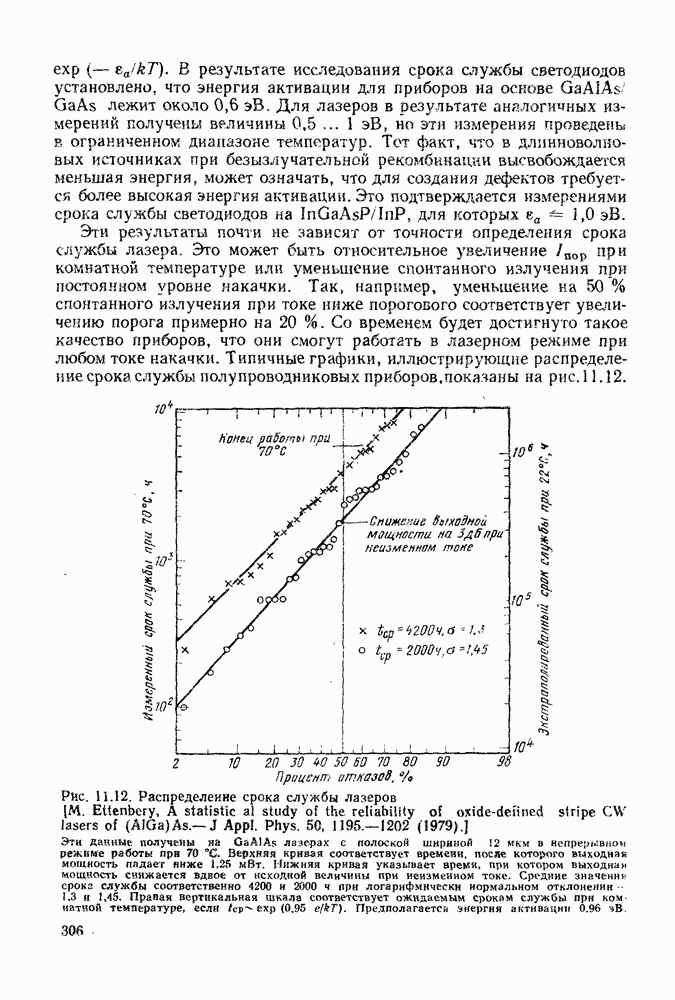
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
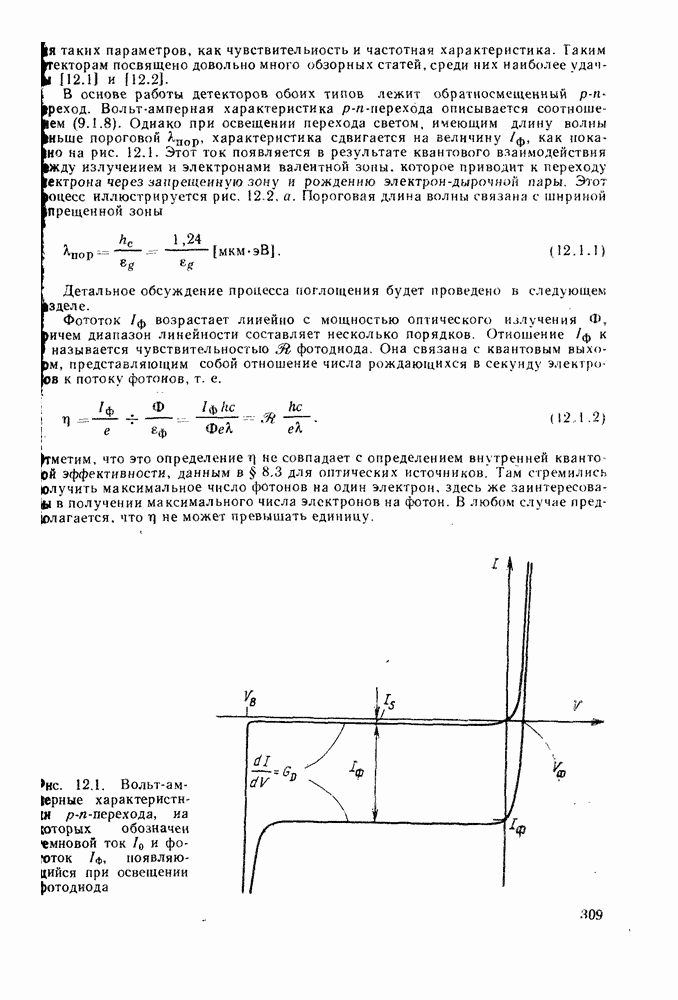
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
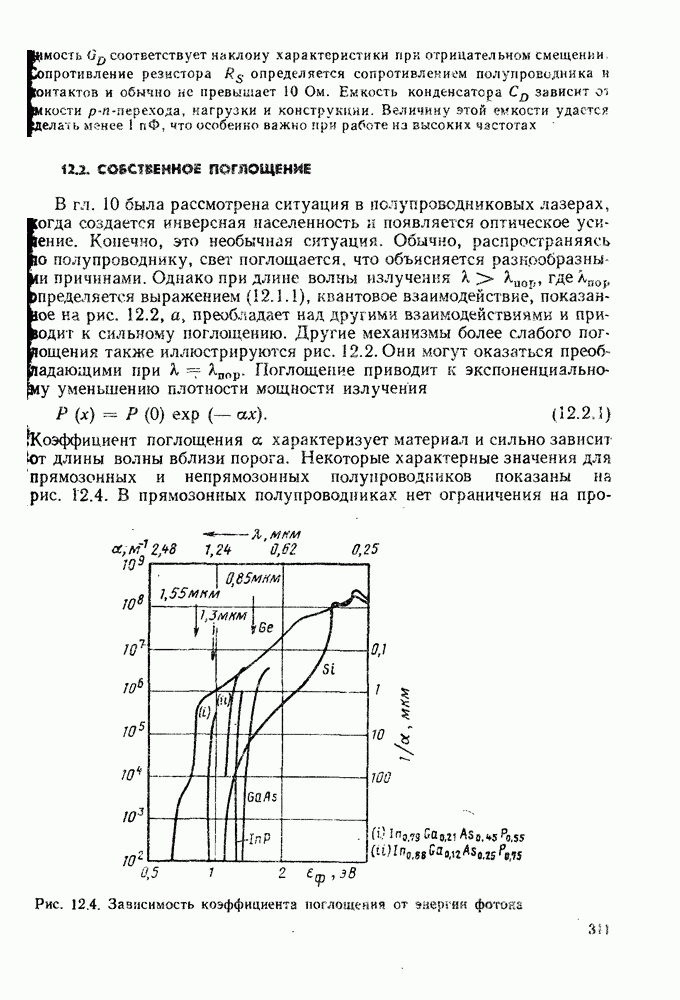
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
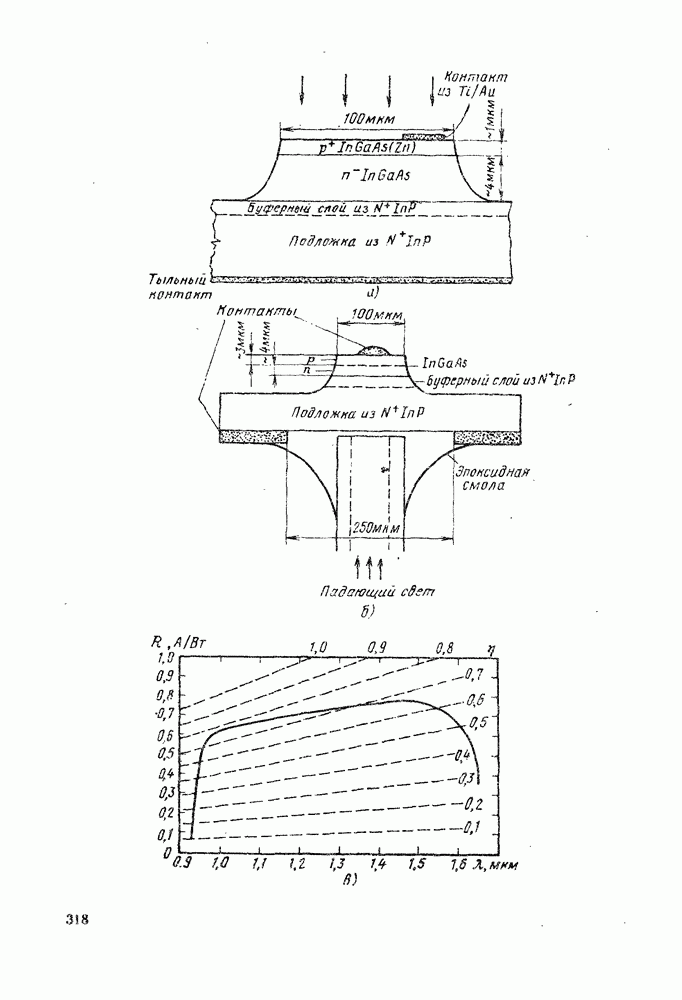
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
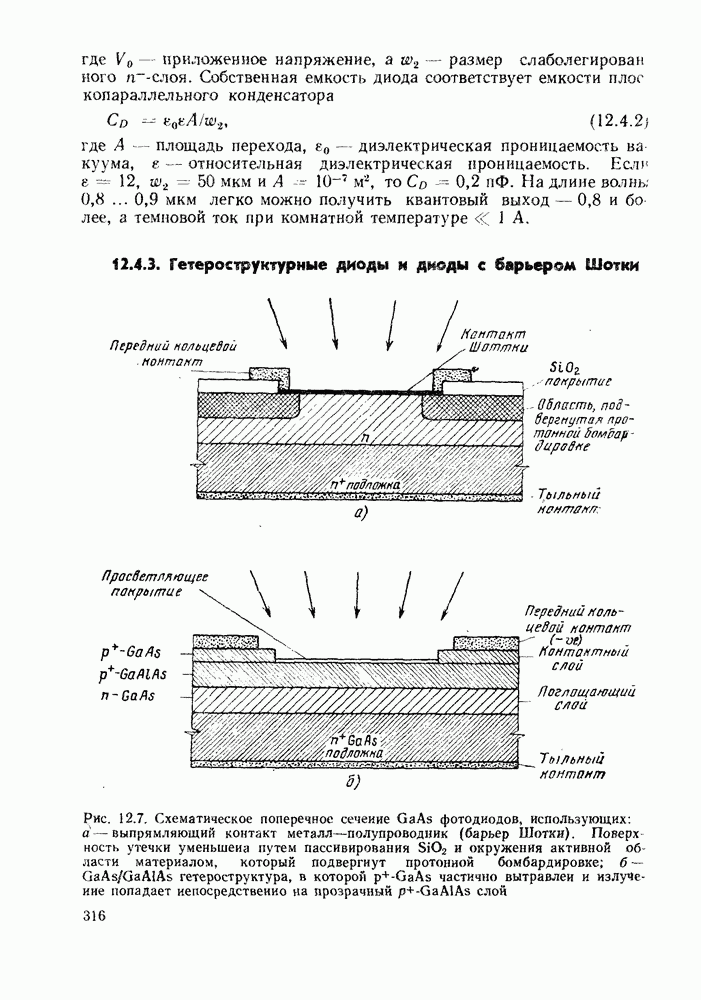
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
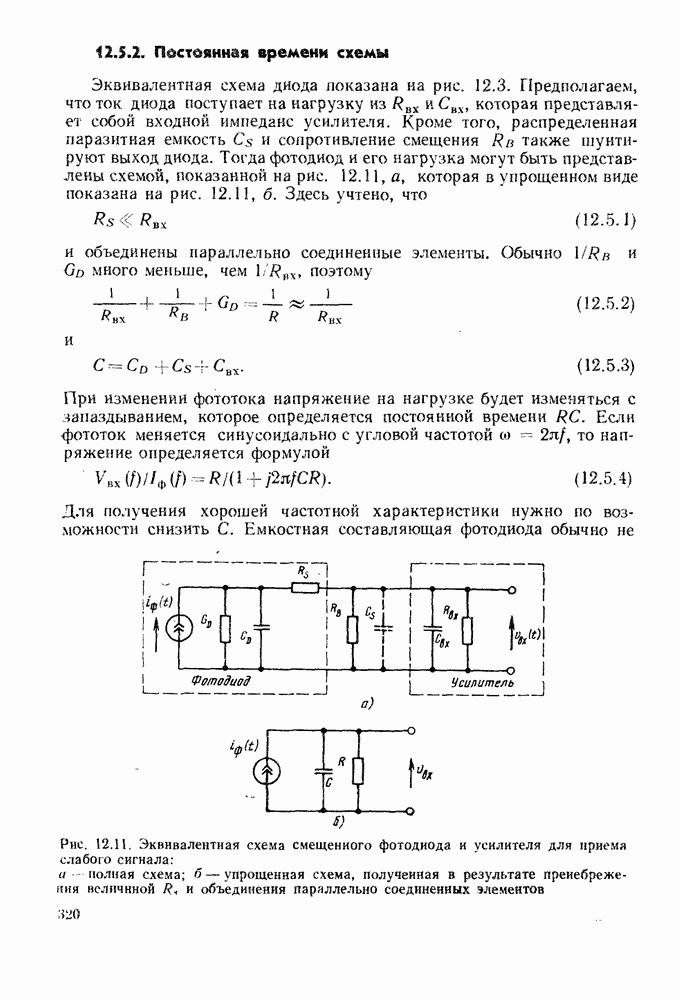
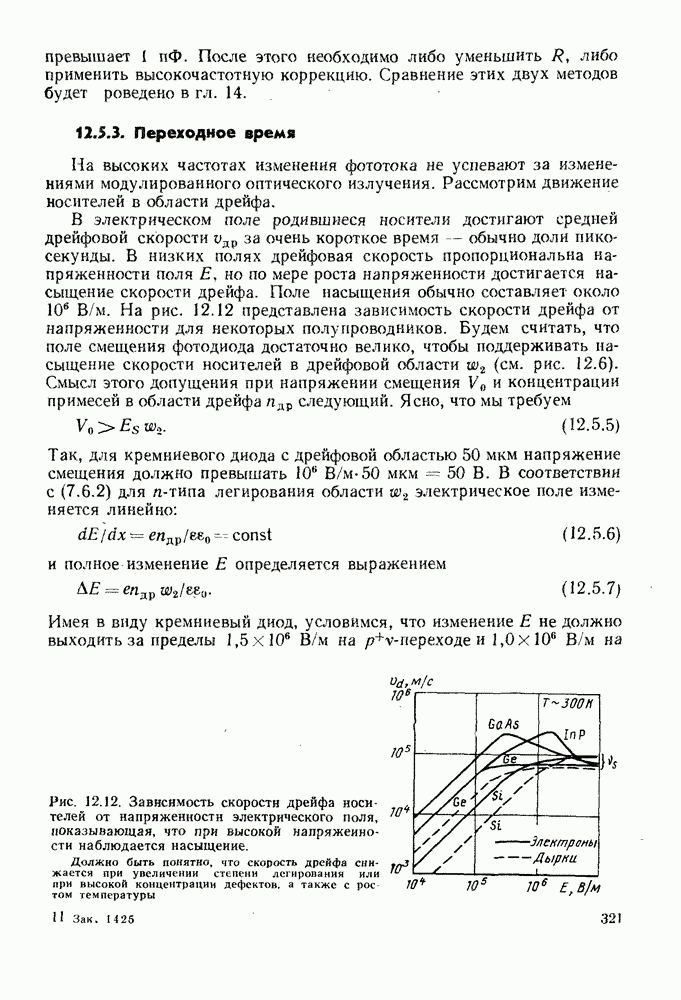
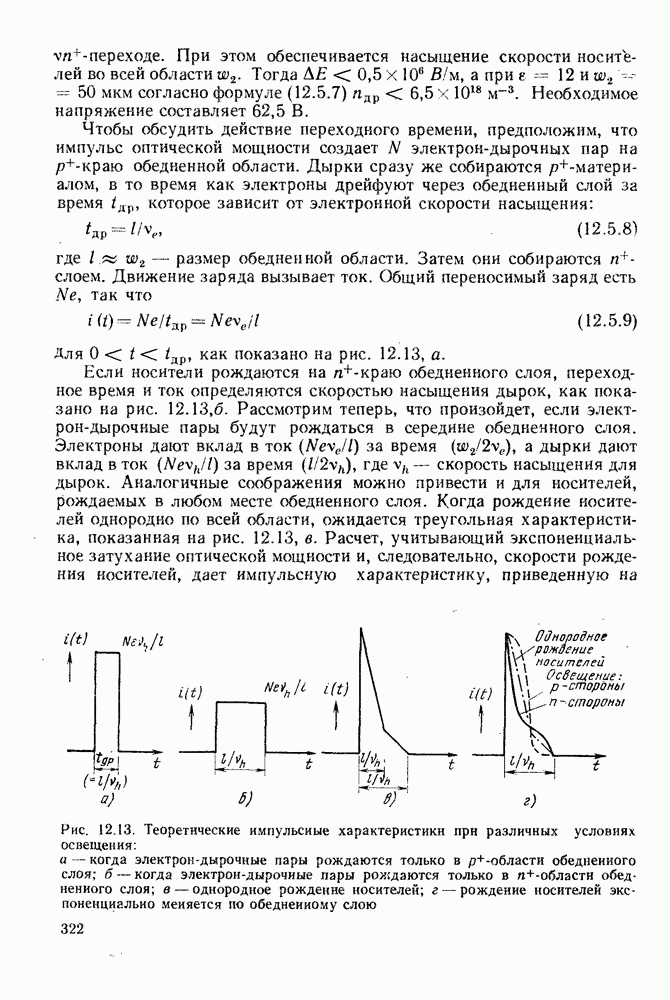
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
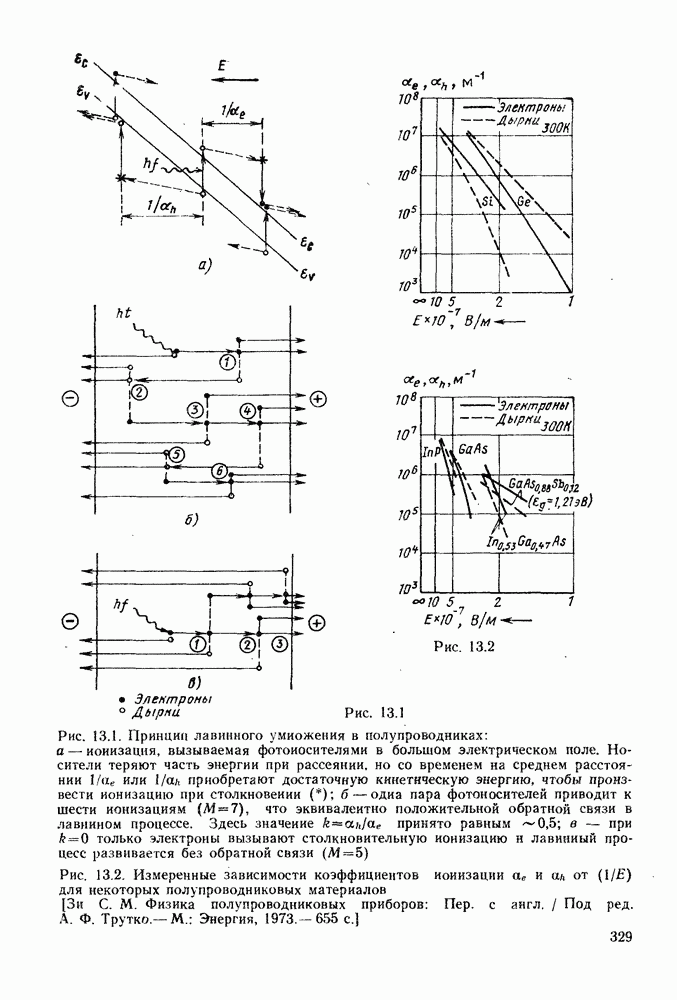
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
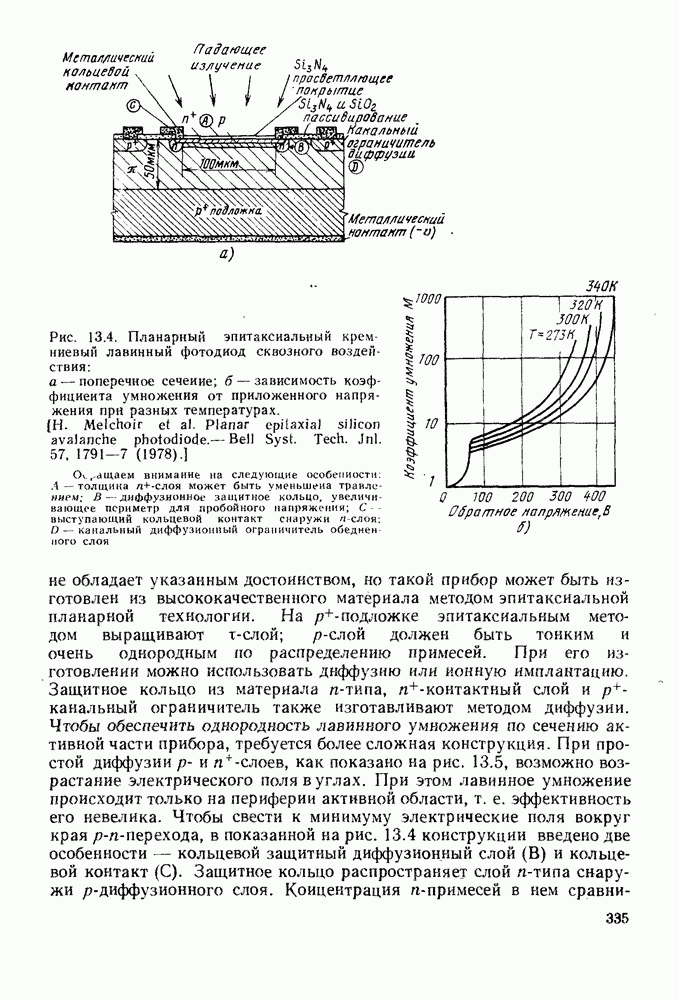
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
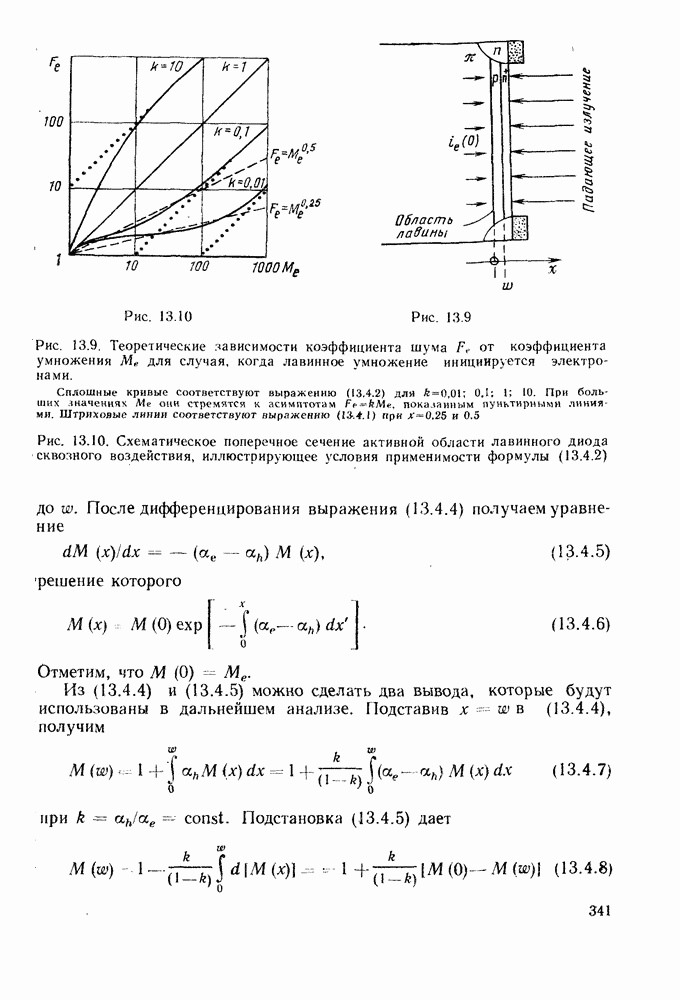
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
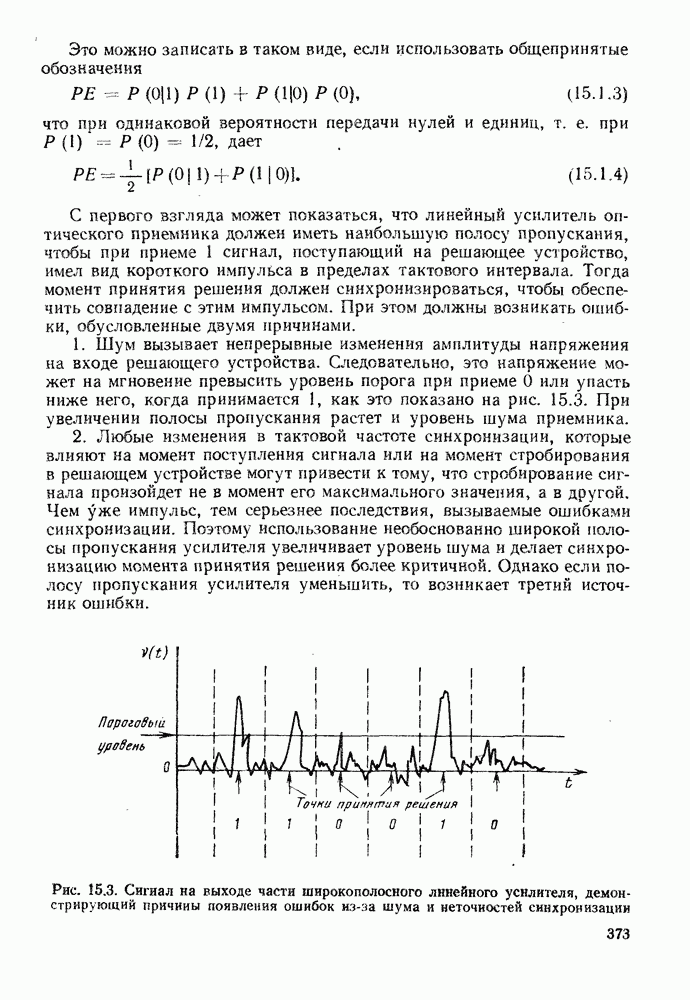
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
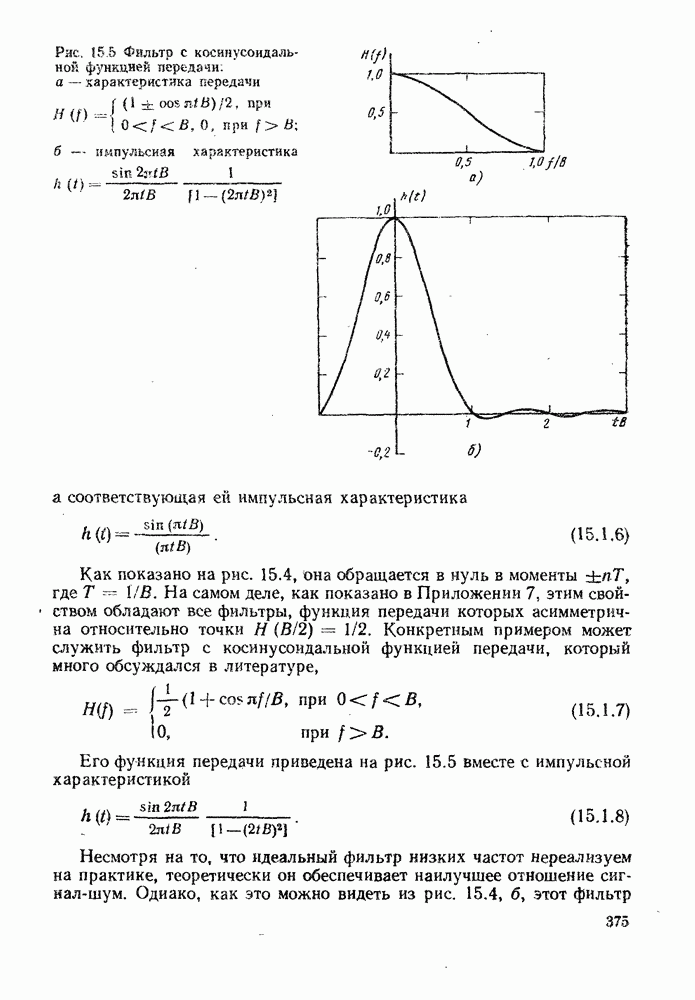
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
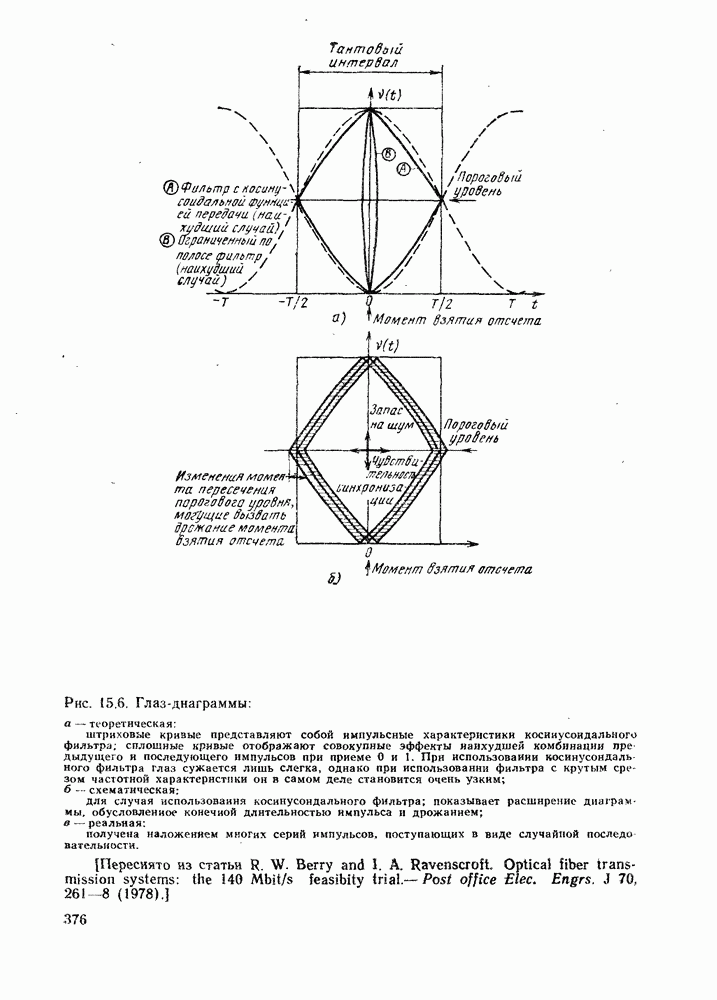
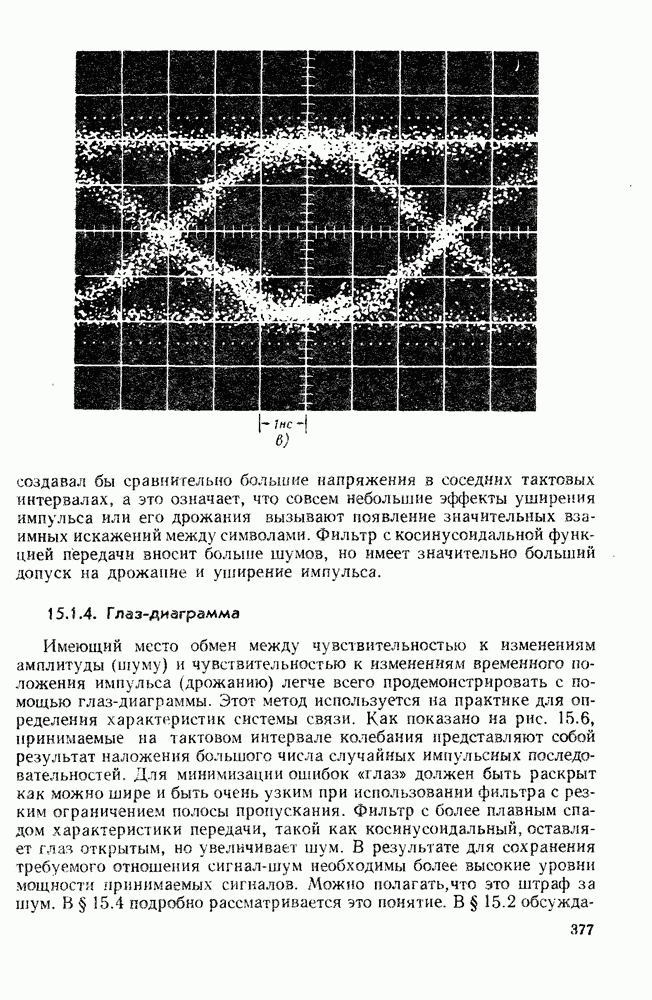
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
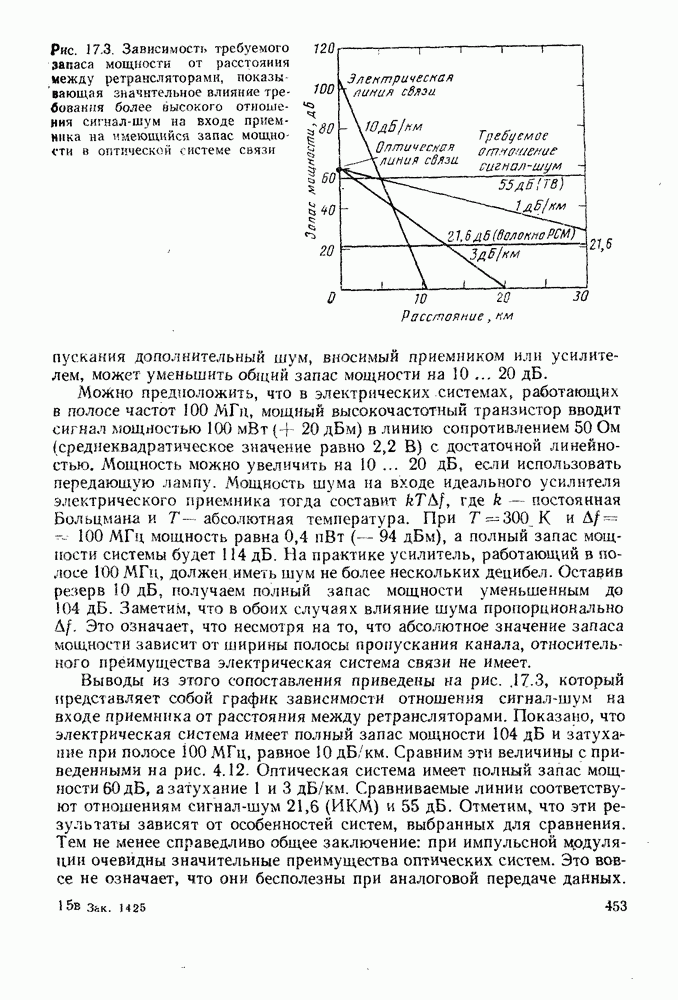
- 15.3.3. Оптимизация оптической системы связи
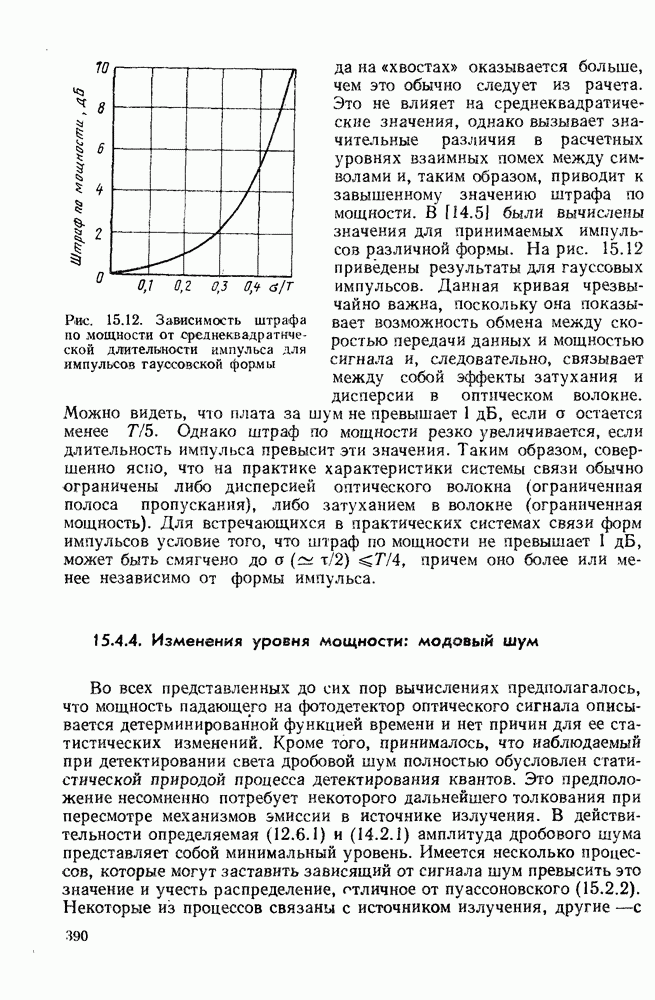
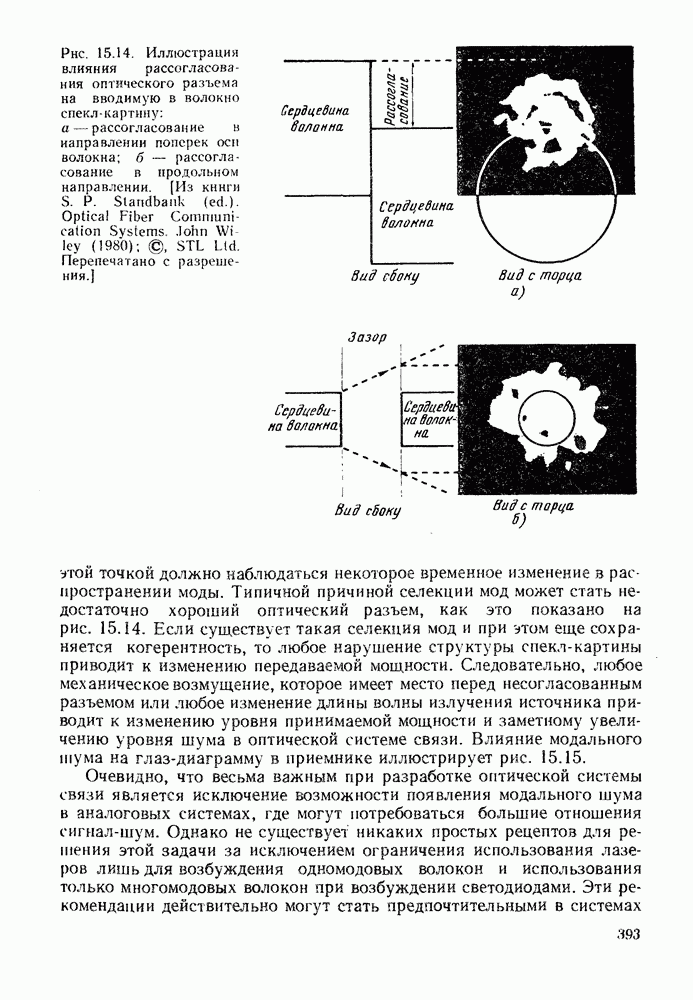
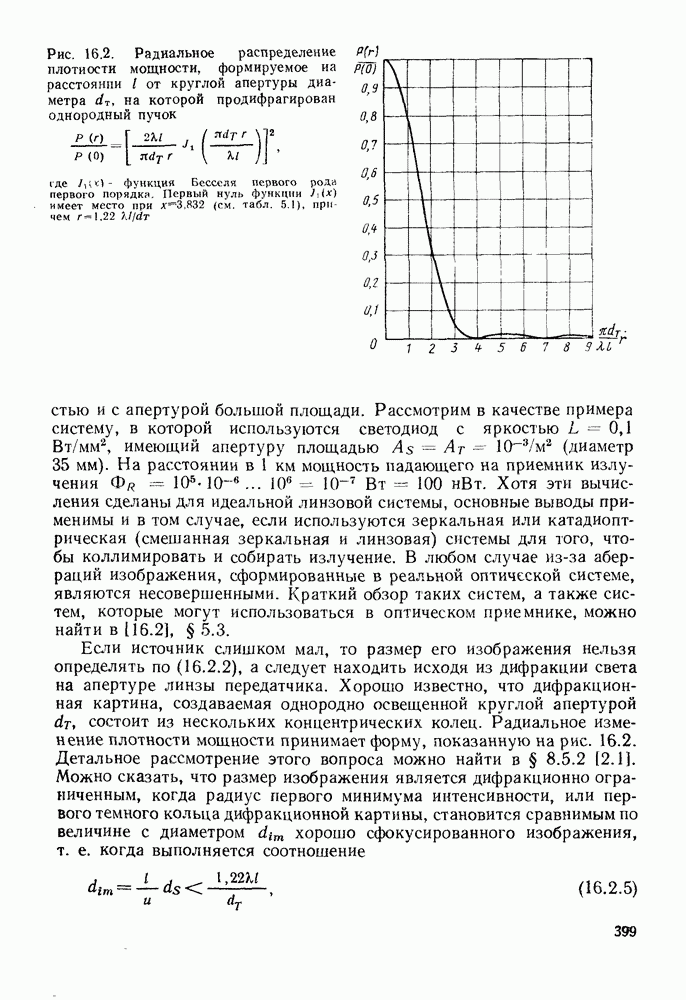
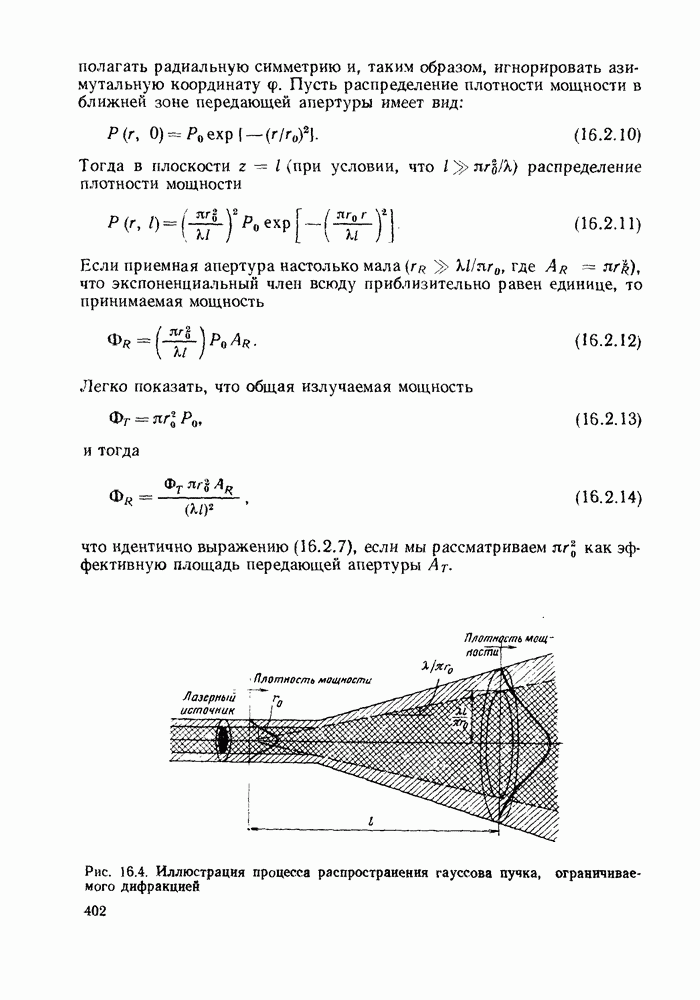
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
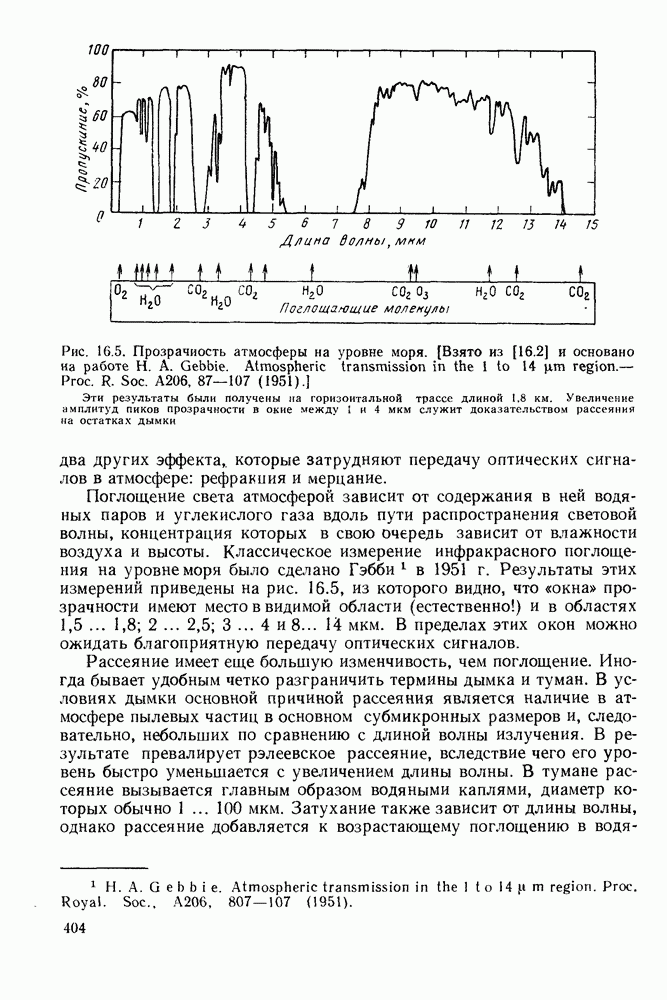
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
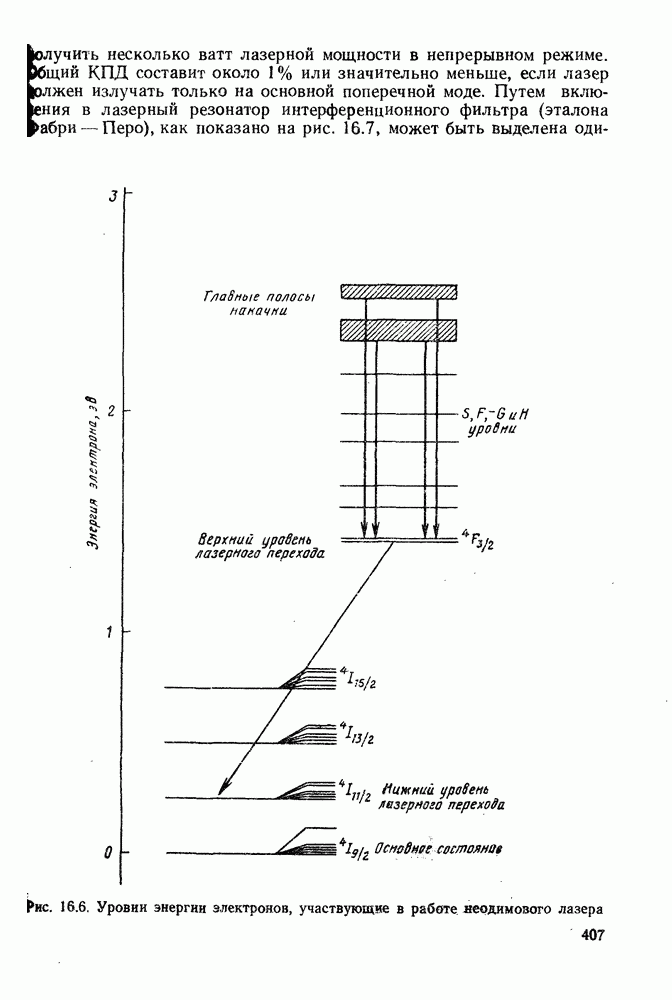
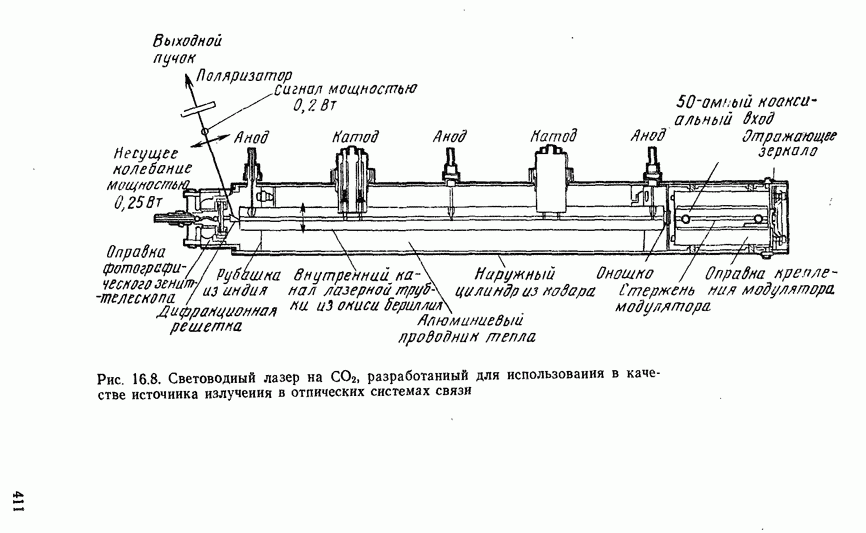
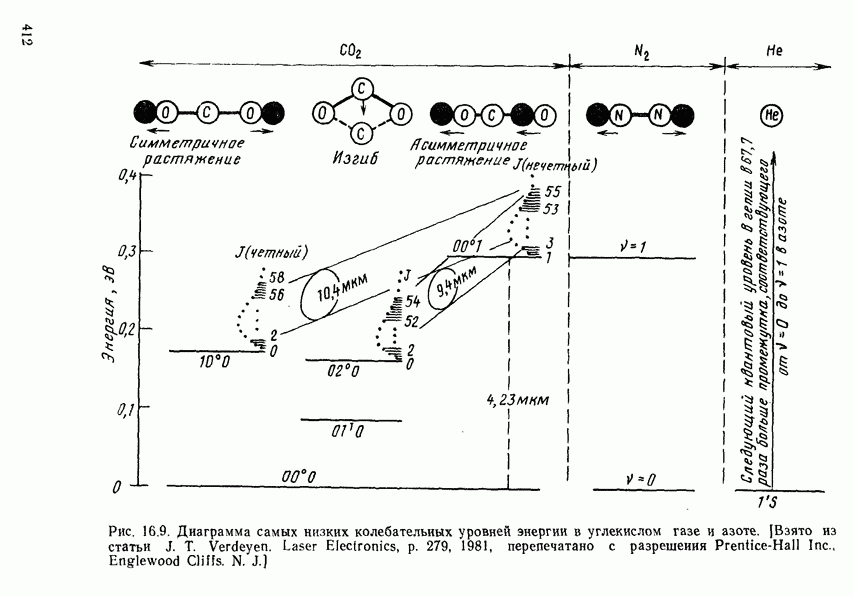
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
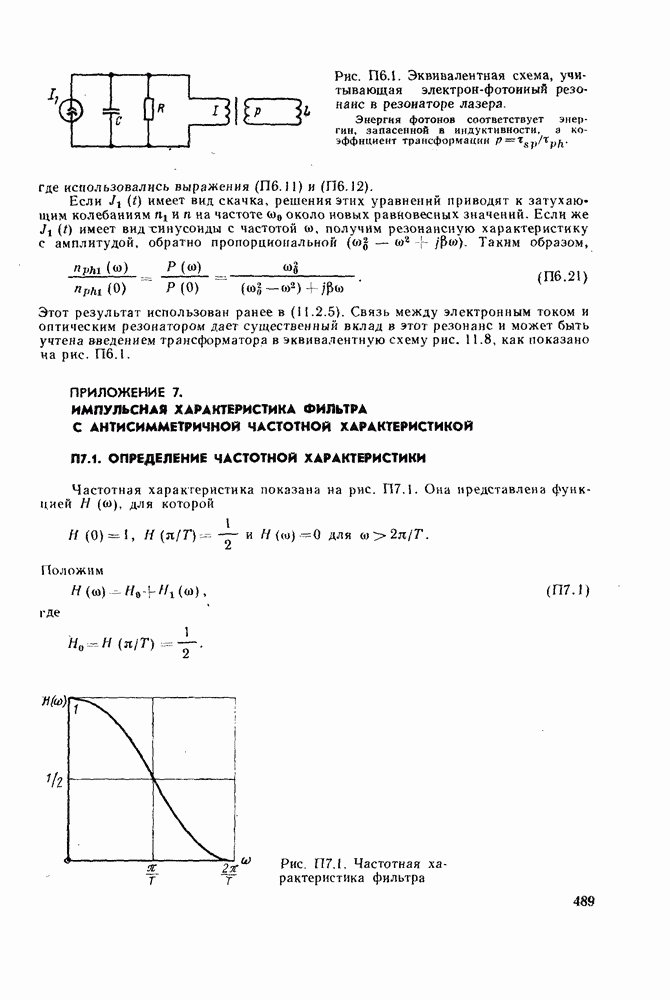
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ