| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
Чтобы получить полезные (применимые) решения волновых уравнений для многомодовых ступенчатых и градиентных волокон, приведенных соответственно в § 5.3 и 6.1, необходимо ограничить рассмотрение тремя случаями. Выше рассматривались только моды высоких порядков на частотах, далеких от частоты отсечки в слабо направляющих волокнах, и обнаружено, что найденные решения являются локальными приближениями к линейно поляризованным плоским поперечным "Электромагнитным волнам. С другой стороны, эти условия именно те, которые необходимы для оптического распространения, описываемого в рамках лучевой модели. Следовательно, можно показать, что эти два по-видимому, очень различных подхода оказываются эквивалентными.
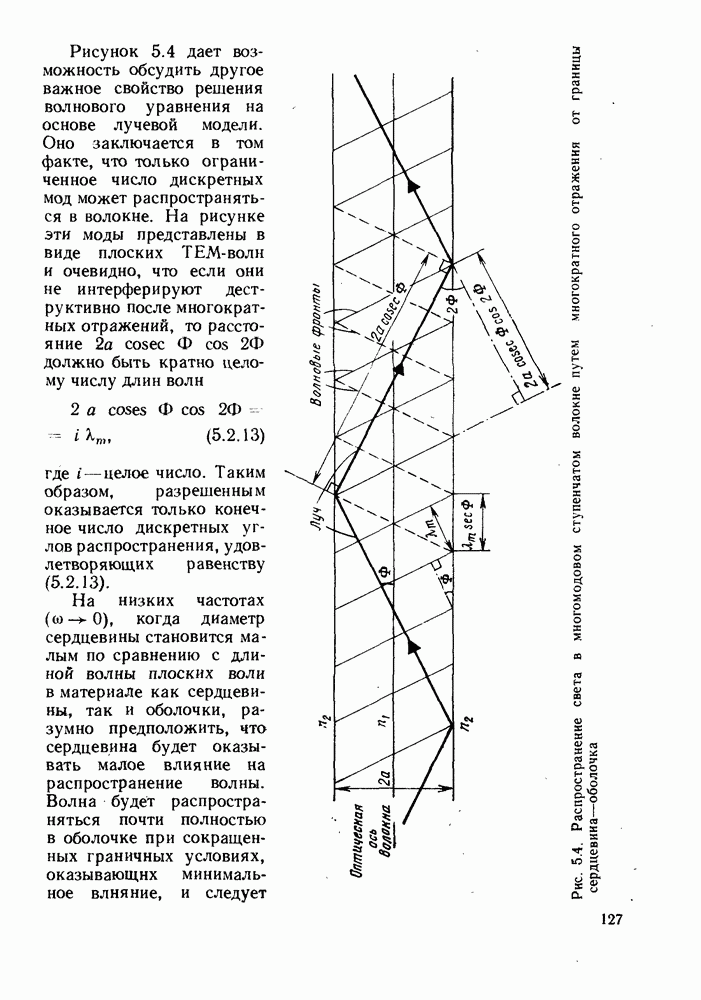
Геометрическое место точек равных фаз в плоской волне ТЕМ образует плоскость, перпендикулярную направлению распространения. Эти плоскости называют волновыми фронтами, а «луч» можно представить в виде траектории, перпендикулярной волновому фронту и передвигающейся в направлении распространения, как это показано на рис. 5.4.
Как уже приводилось ранее, уравнение траектории луча, отображающего волну, распространяющуюся в неоднородной среде с плавно изменяющимся показателем преломления, имеет вид

Здесь  обобщенный вектор положения точки на луче;
обобщенный вектор положения точки на луче;  расстояние до этой точки, измеряемое вдоль траектории луча;
расстояние до этой точки, измеряемое вдоль траектории луча;  показатель преломления среды. Отметим, что производная
показатель преломления среды. Отметим, что производная  это единичный вектор, касательный к лучу в точке, определяемой значением
это единичный вектор, касательный к лучу в точке, определяемой значением  . В данном параграфе это уравнение будет использовано для определения поведения главного косого луча в градиентном волокне, когда
. В данном параграфе это уравнение будет использовано для определения поведения главного косого луча в градиентном волокне, когда  имеет радиальную симметрию. В этом случае для описания вектора положения луча
имеет радиальную симметрию. В этом случае для описания вектора положения луча  удобно использовать цилиндрическую систему координат
удобно использовать цилиндрическую систему координат  с началом на оси волокна.
с началом на оси волокна.
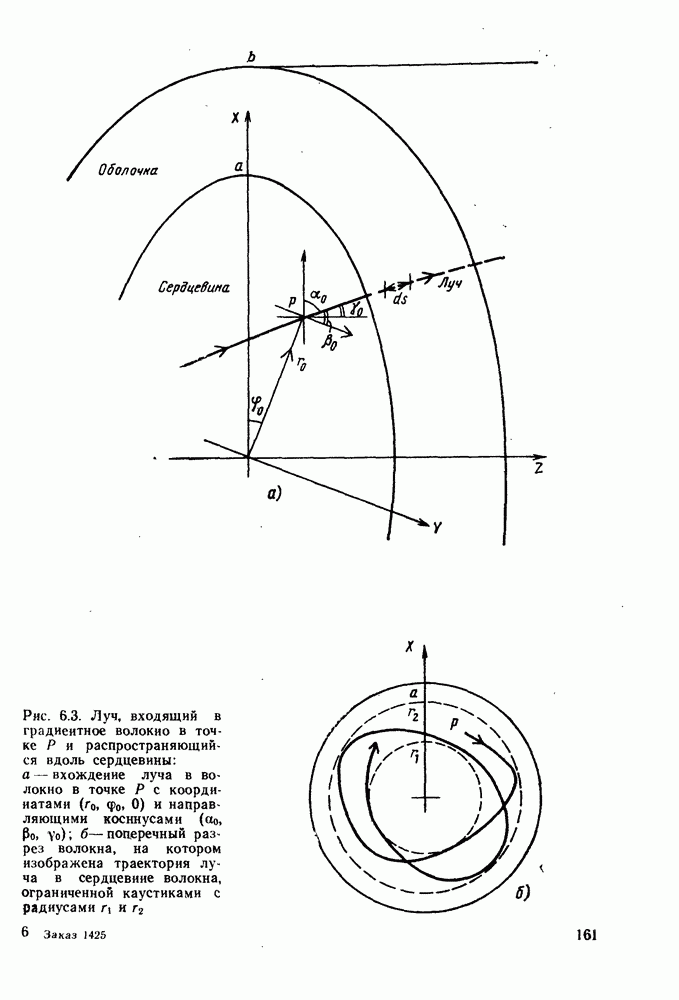
Рассмотрим луч, изображенный на рис. 6.3, а. Он входит в волокно в точке  , а его начальная траектория образует углы
, а его начальная траектория образует углы  с осями координат
с осями координат  соответственно.
соответственно.

(кликните для просмотра скана)
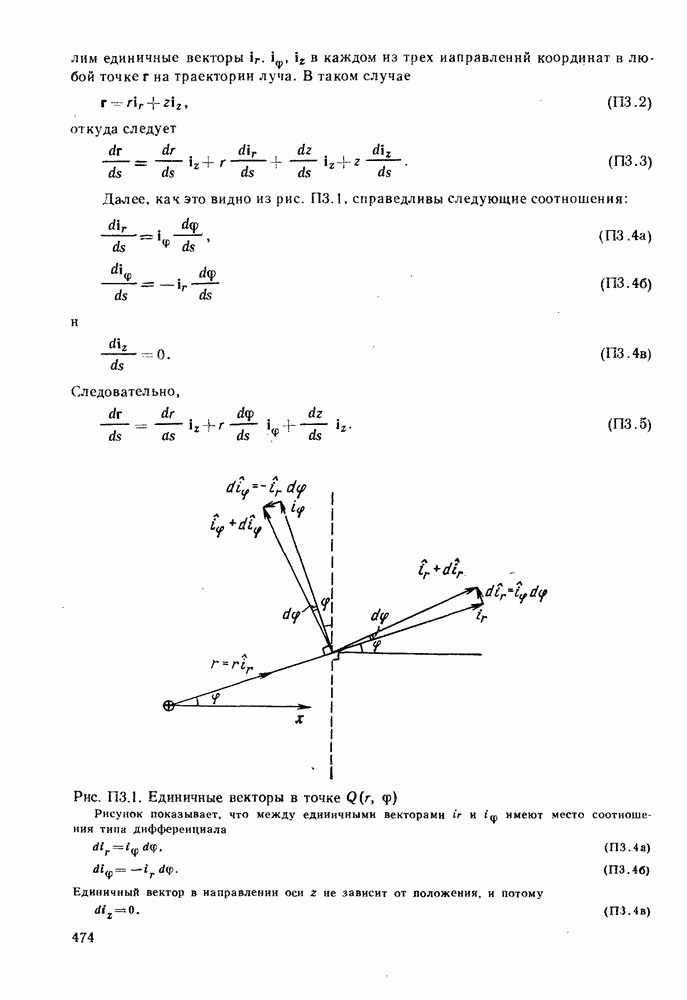
В § П.3.1 Приложения 3 показывается, что векторное уравнение (2.1.21) можно представить в виде следующих трех скалярных дифференциальных уравнений:

и

где

а

— постоянные, которые определяют траекторию луча, распространяющегося в волокне. Они, а следовательно, и траектория данного луча зависят только от начальных условий, т. е. от положения и направления луча при его входе в волокно в плоскости 
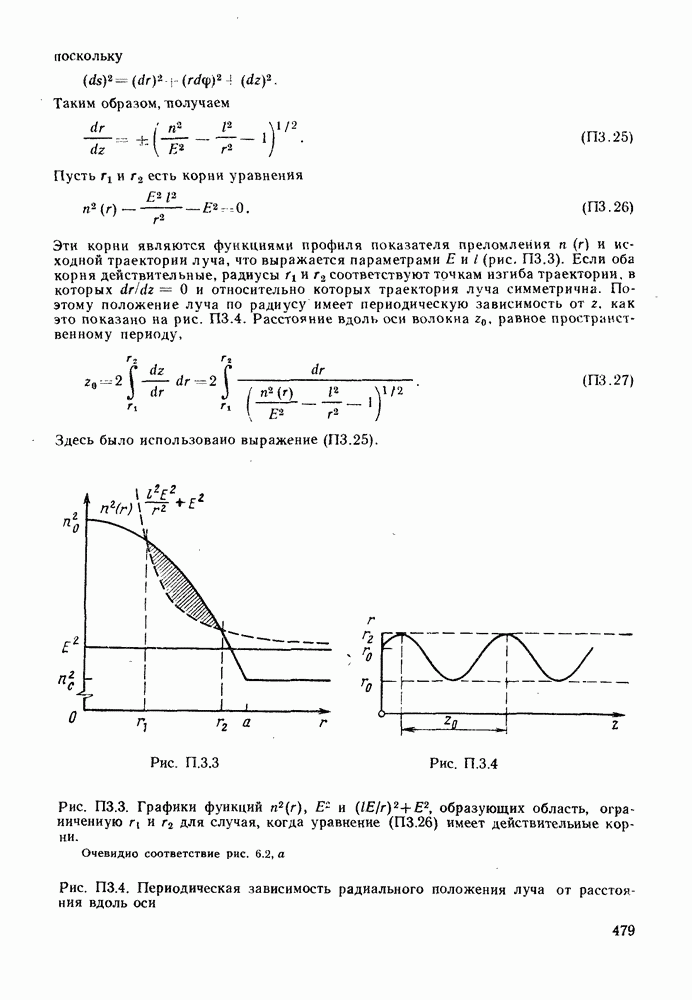
Приложения 3 также показано, каким образом можно проинтегрировать уравнение (6.2.3), чтобы получить

при этом радиусы и  определены как корни следующего уравнения
определены как корни следующего уравнения 

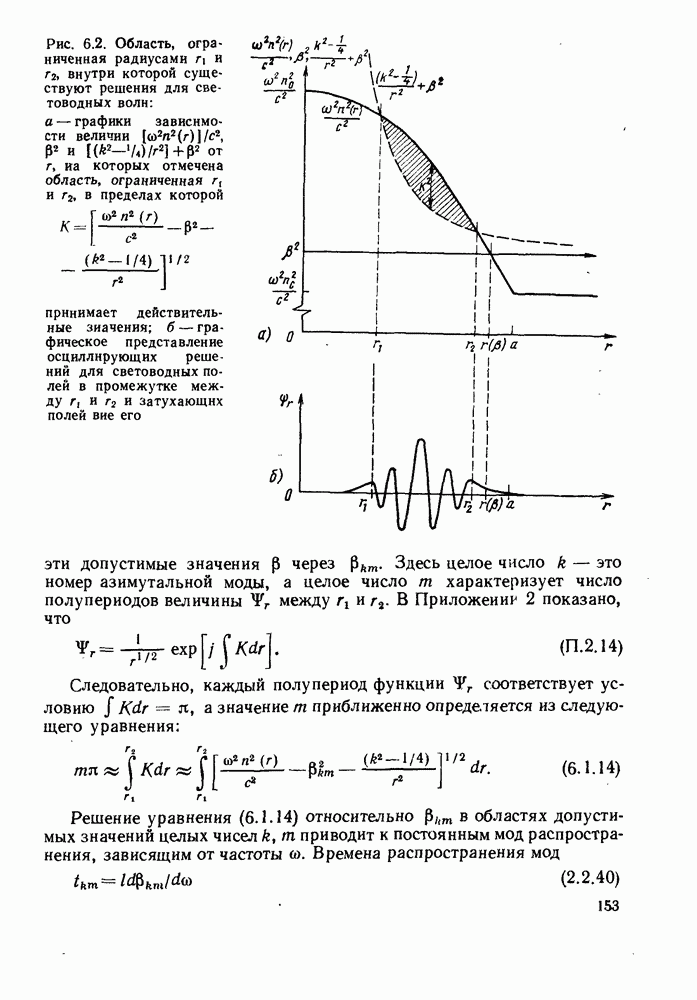
Ряд фактов можно сразу вывести из уравнений (6.2.6) и (6.2.7). Во-первых, величины  зависят от профиля показателя преломления
зависят от профиля показателя преломления  и начальных условий ввода луча в волокно, определяемых
и начальных условий ввода луча в волокно, определяемых  Во-вторых, производная
Во-вторых, производная  принимает вещественное значение только внутри области, ограниченной
принимает вещественное значение только внутри области, ограниченной  В-третьих, радиусы
В-третьих, радиусы  определяют точки поворота, в которых
определяют точки поворота, в которых  а траектория луча не имеет никакой радиальной составляющей. В-четвертых, траектории лучей, для которых уравнение (6.2.7) имеет два вещественных корня, заключены в области между
а траектория луча не имеет никакой радиальной составляющей. В-четвертых, траектории лучей, для которых уравнение (6.2.7) имеет два вещественных корня, заключены в области между  траектории лучей, не удовлетворяющие этому условию, не будут располагаться в волокне. Цилиндрические поверхности радиусов
траектории лучей, не удовлетворяющие этому условию, не будут располагаться в волокне. Цилиндрические поверхности радиусов  ограничивающие траектории лучей, в оптике называются каустиками. В-пятых, можно видеть, что условие прохождения лучей через ось волокна (условие меридиональный лучей) имеет вид
ограничивающие траектории лучей, в оптике называются каустиками. В-пятых, можно видеть, что условие прохождения лучей через ось волокна (условие меридиональный лучей) имеет вид 
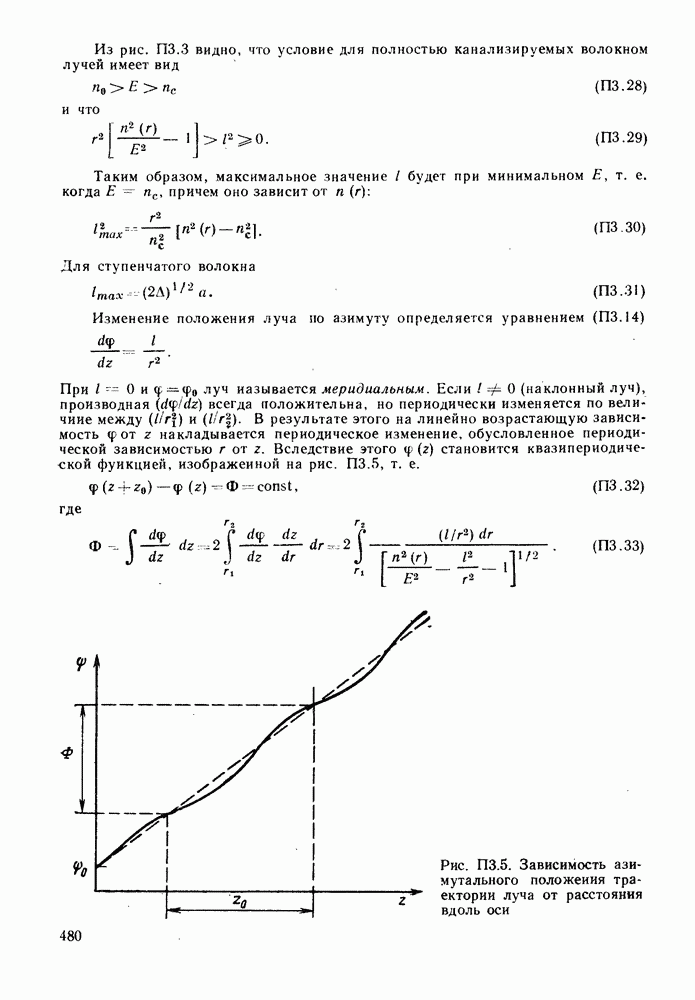
Дальнейшее интегрирование уравнения (6.2.6) показывает, что траектория луча периодически изменяется по  на протяжении
на протяжении 
вдоль оси волокна. В приложении 3 показано, что величину  можно найти по формуле:
можно найти по формуле:

На протяжении расстояния  азимутальное положение луча всегда изменяется на один и тот же угол
азимутальное положение луча всегда изменяется на один и тот же угол  определяемый выражением
определяемый выражением

Таким образом, траектории лучей вдоль волокна имеют вид сложных спиральных линий, как это показано на рис. 6.3, б.
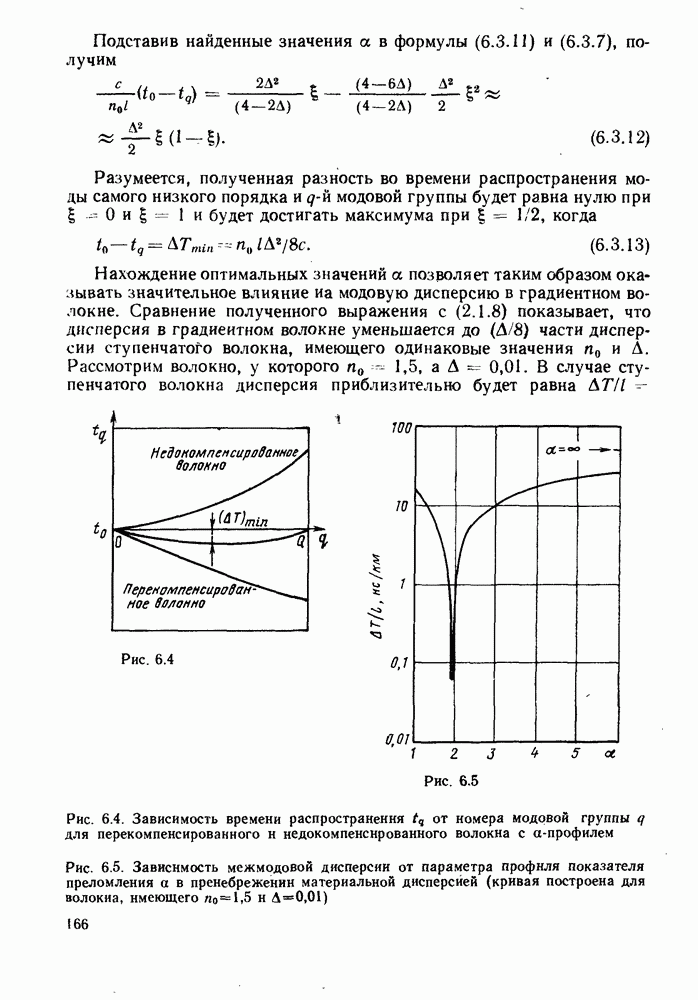
В оптике существует фундаментальный закон, вытекающий из принципа наименьшего времени Ферма, в соответствии с которым в любой среде все лучи, исходящие из точки X и приходящие в другую точку  перемещаются от X до У за одно и то же время, независимо от пройденного пути. Применив его к волокну, можно видеть, что если было бы возможно найти такой профиль показателя преломления сердцевины, который обеспечивал бы постоянство
перемещаются от X до У за одно и то же время, независимо от пройденного пути. Применив его к волокну, можно видеть, что если было бы возможно найти такой профиль показателя преломления сердцевины, который обеспечивал бы постоянство  равенство их для всех значений
равенство их для всех значений  то это означало бы, что волокно с таким профилем было бы свободно от межмодовой дисперсии. Известно, что таких профилей не существует. Однако изменение
то это означало бы, что волокно с таким профилем было бы свободно от межмодовой дисперсии. Известно, что таких профилей не существует. Однако изменение  пределах диапазона значений
пределах диапазона значений  для лучей, распространяющихся в волокне, является мерой дисперсии волокна.
для лучей, распространяющихся в волокне, является мерой дисперсии волокна.
Этим методом была исследована дисперсия волокон с а- профилем, не обладающих материальной дисперсией, и получены результаты, идентичные тем, которые будут представлены в § 6.3 на основе модового анализа. Лучевая модель обеспечивает более простую и физически ясную картину распространения света в оптических волокнах, но она не позволяет определить соотношений, существующих между различными факторами, вызывающими дисперсию, которые будут рассмотрены в § 6.5.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
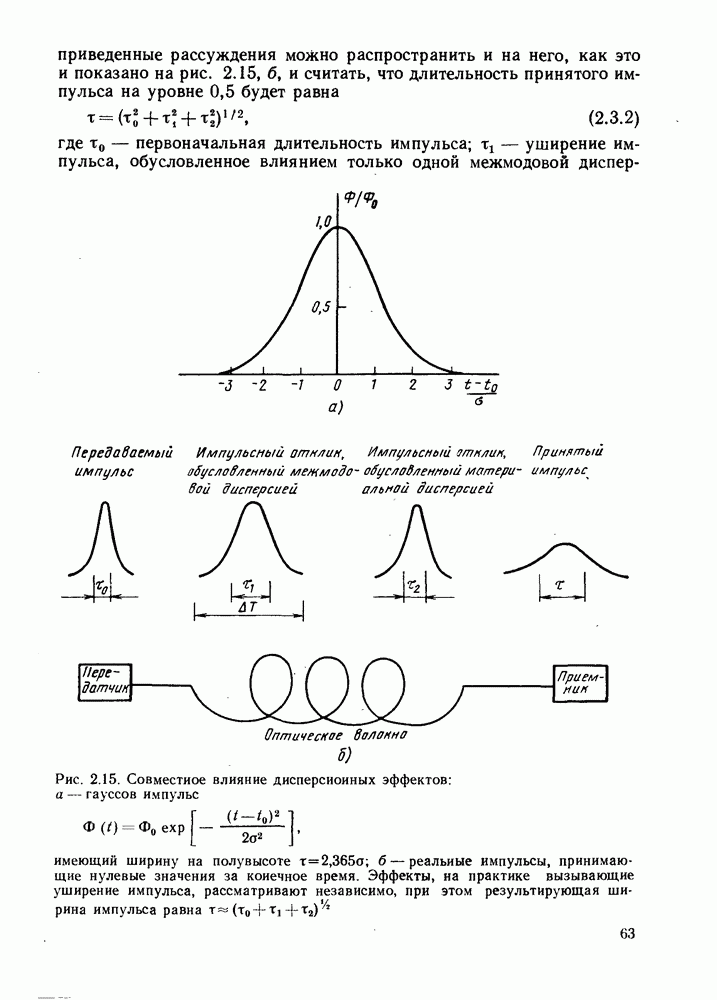
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
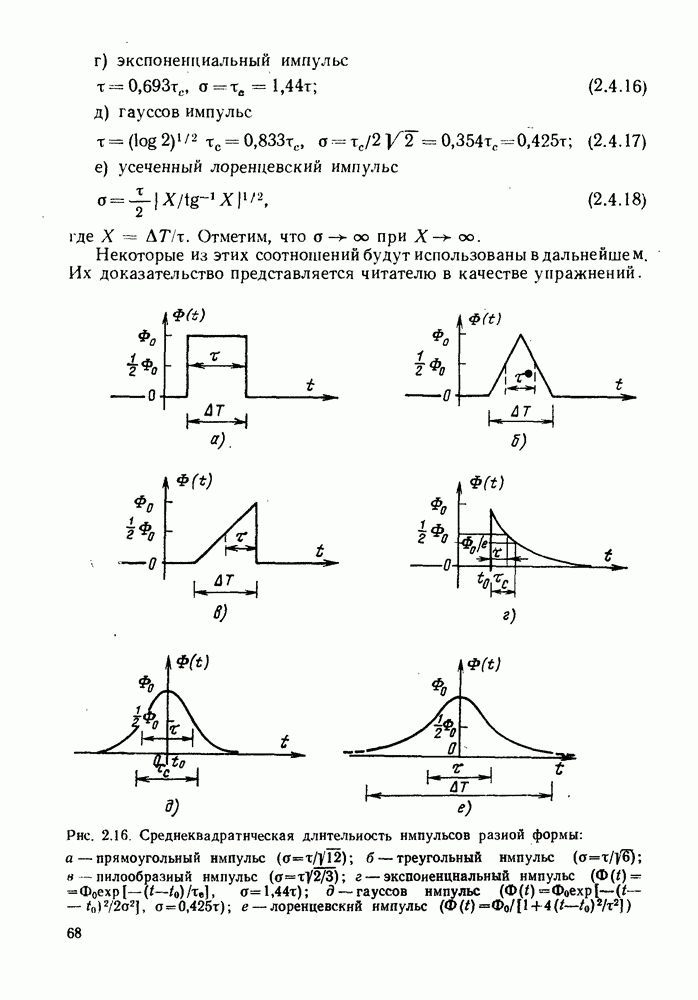
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
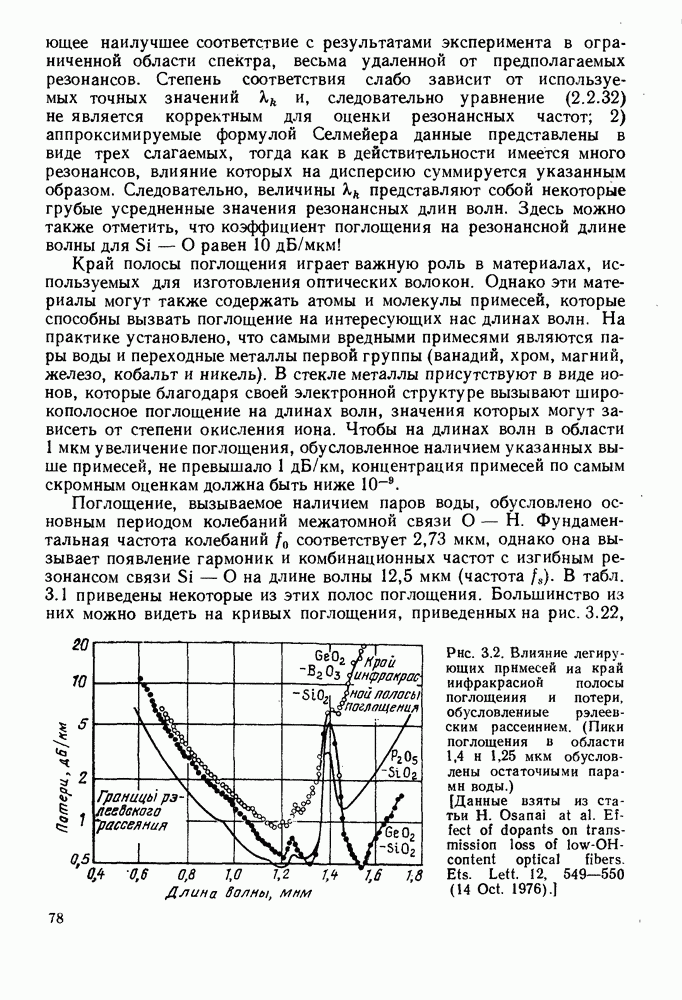
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
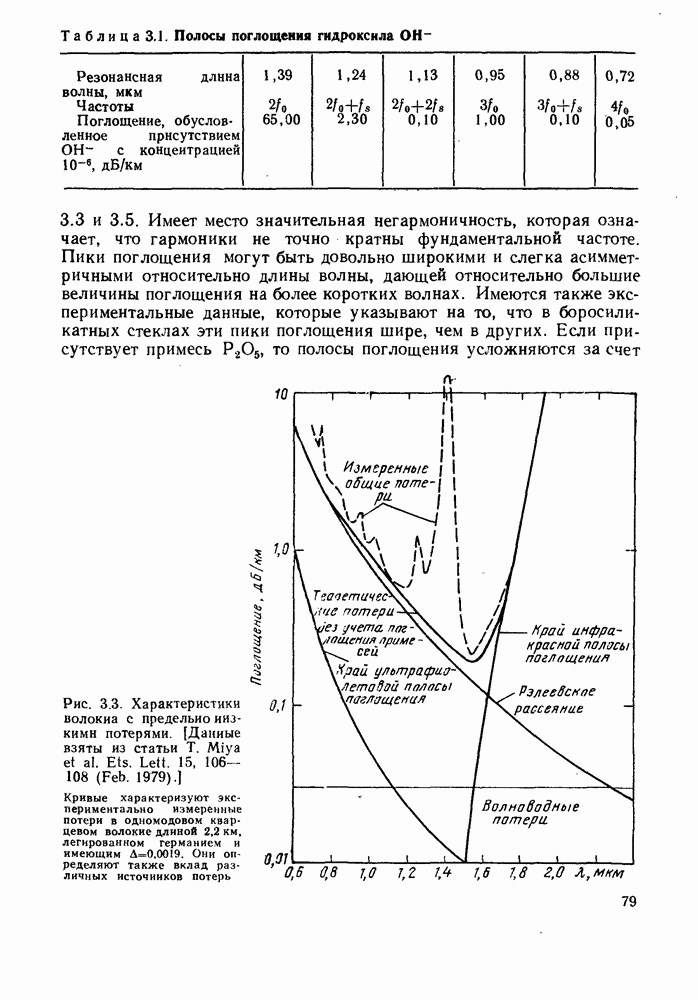
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
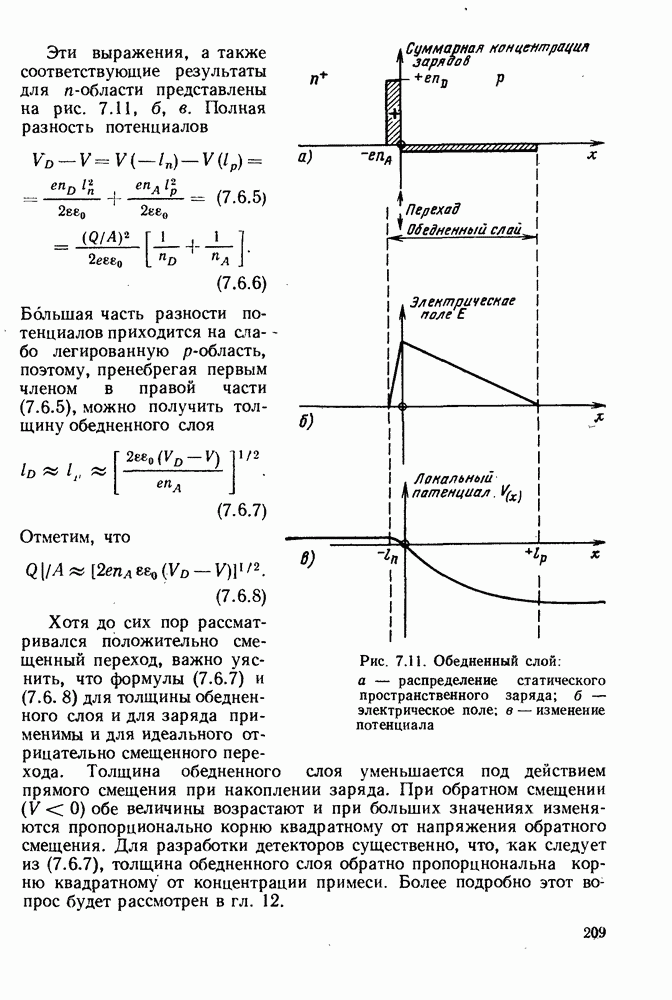
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
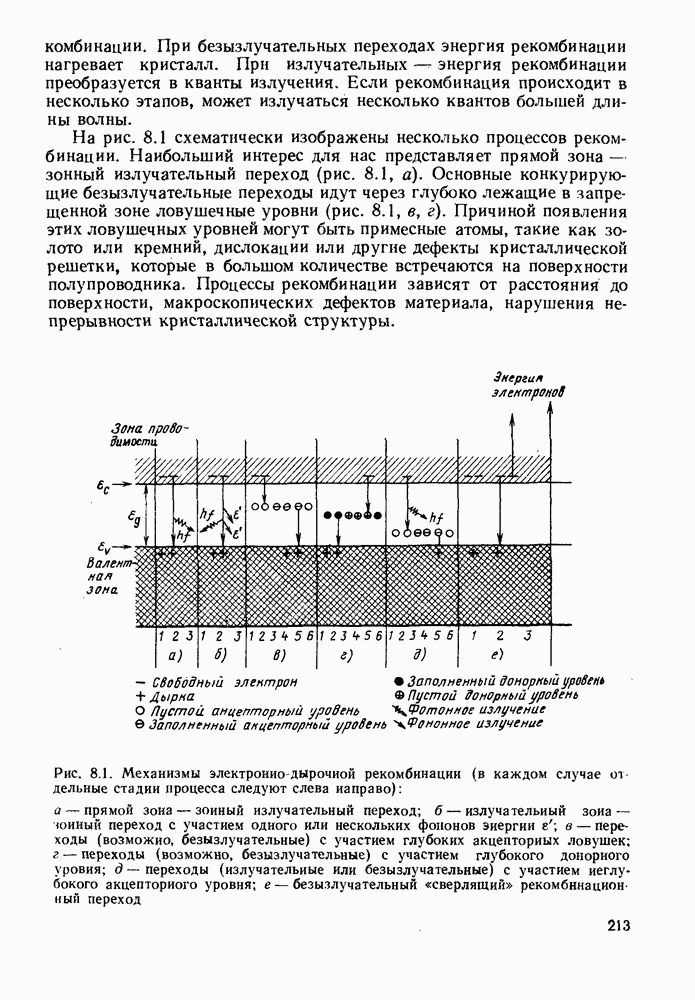
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
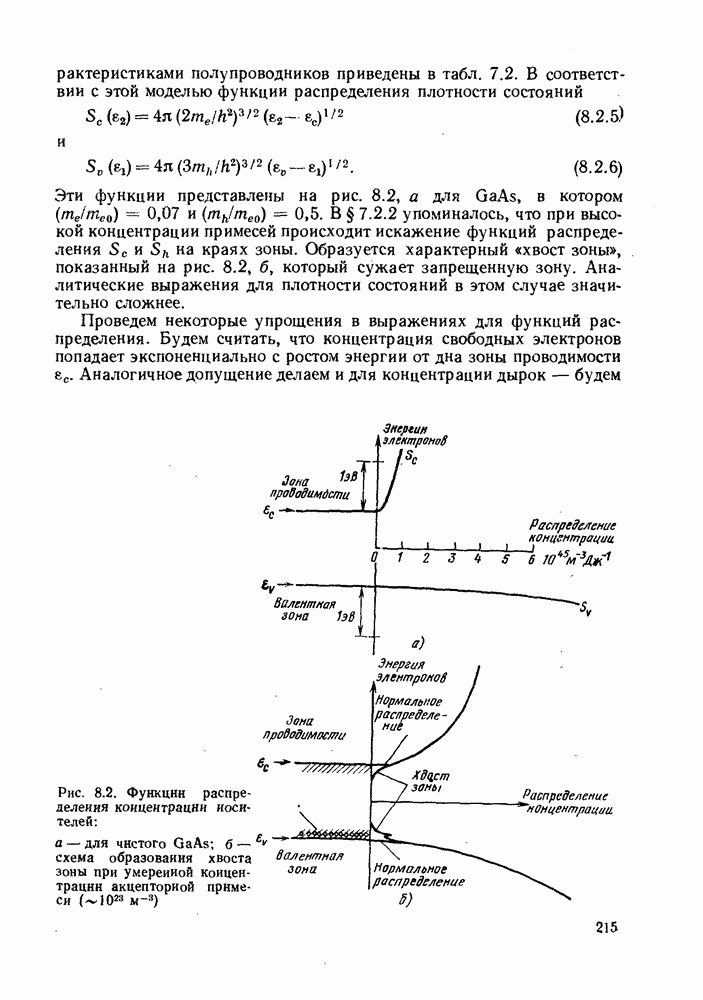
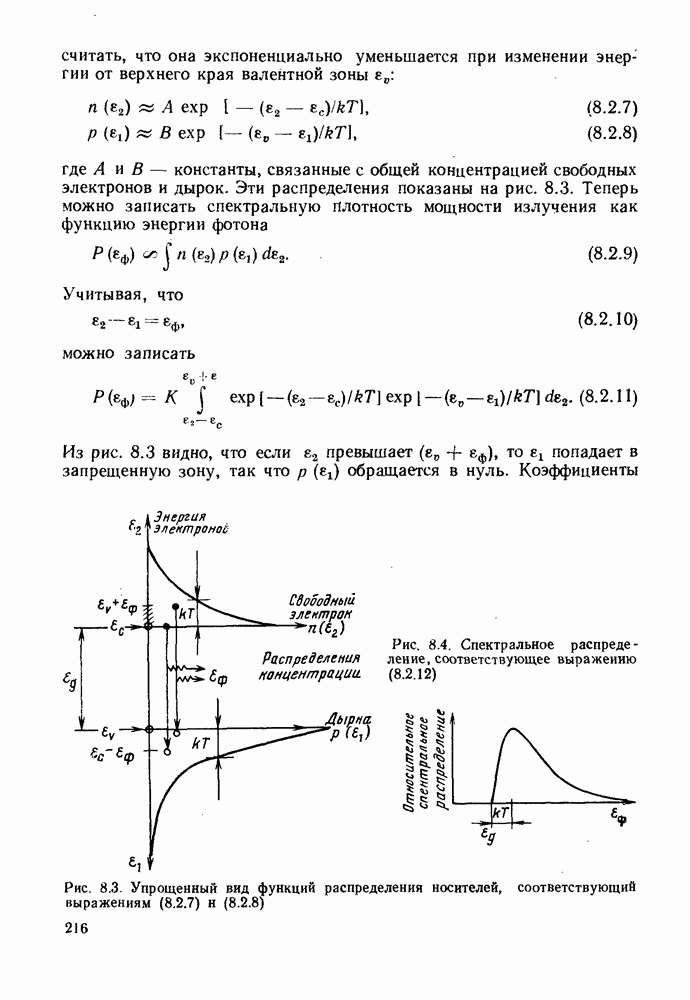
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
- 11.2.2. Спектральные характеристики
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
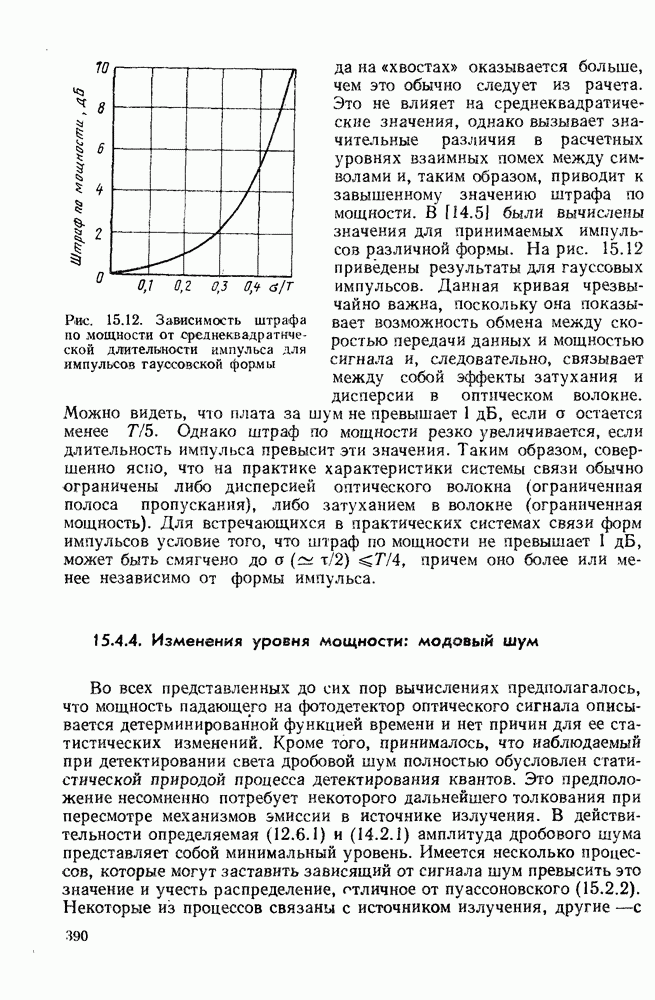
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
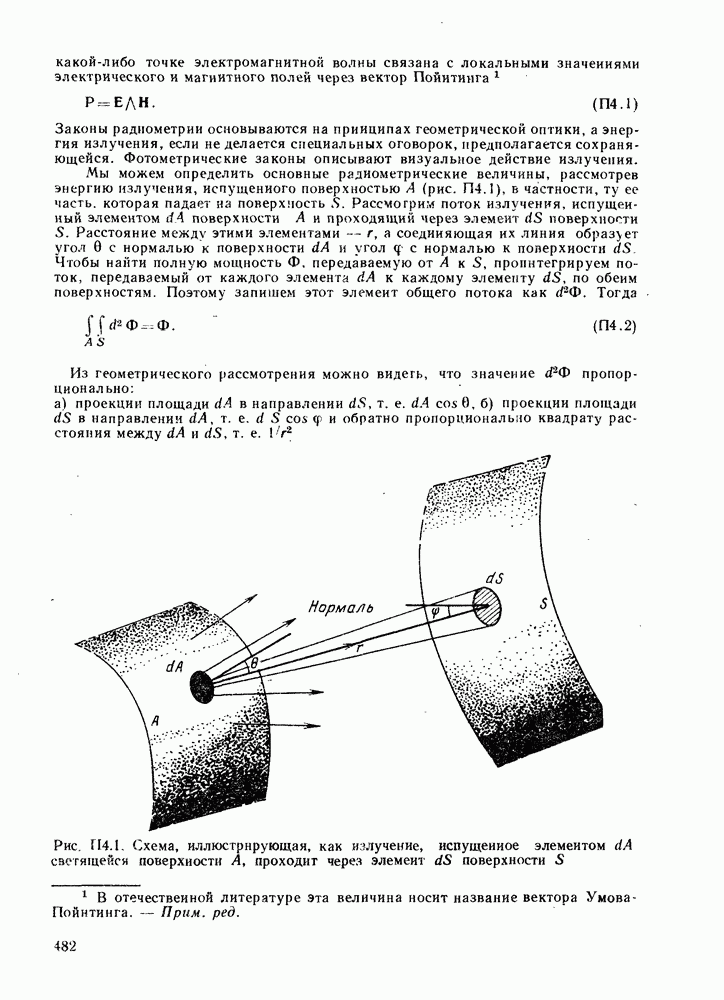
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
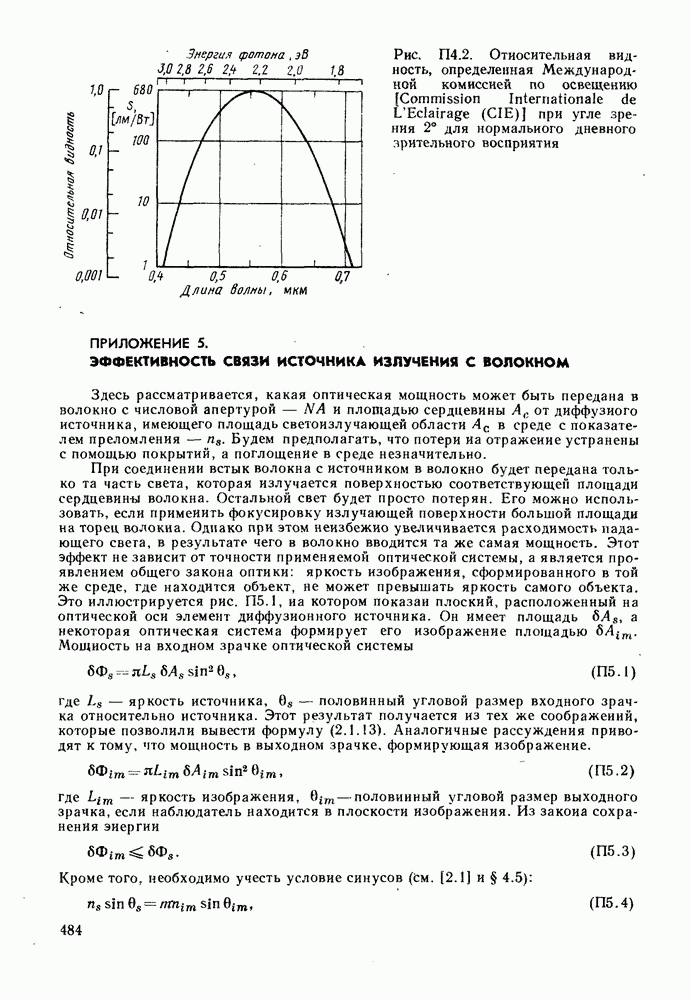
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
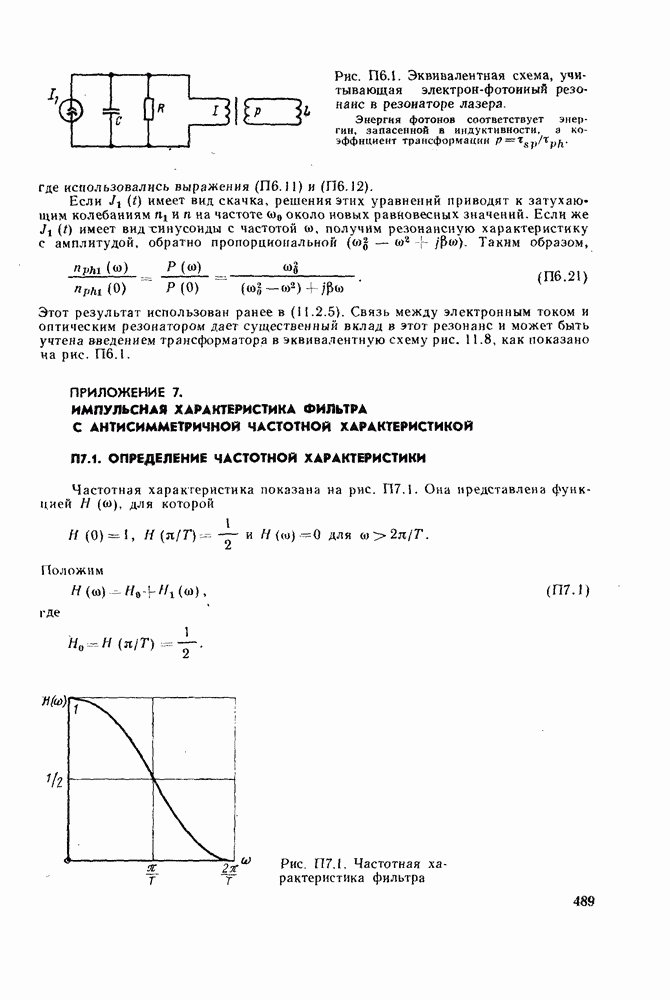
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ