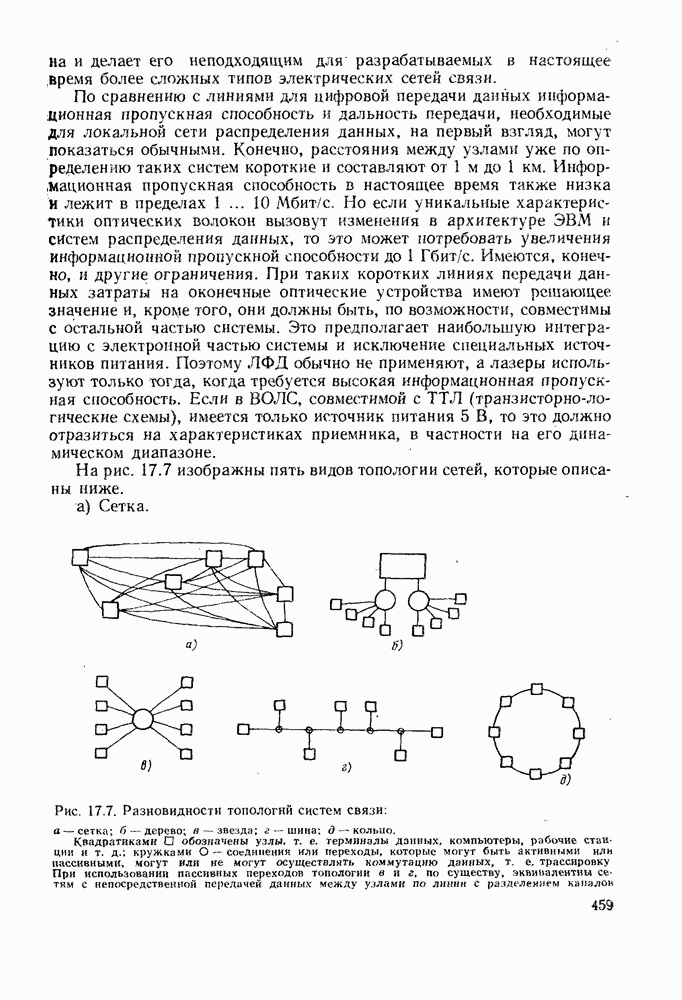
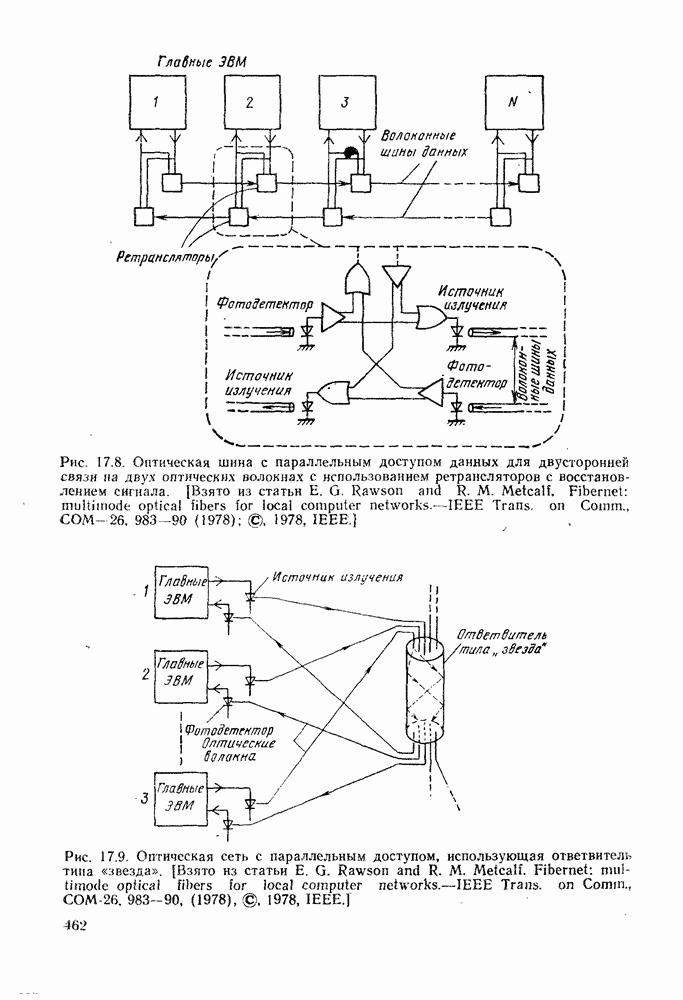
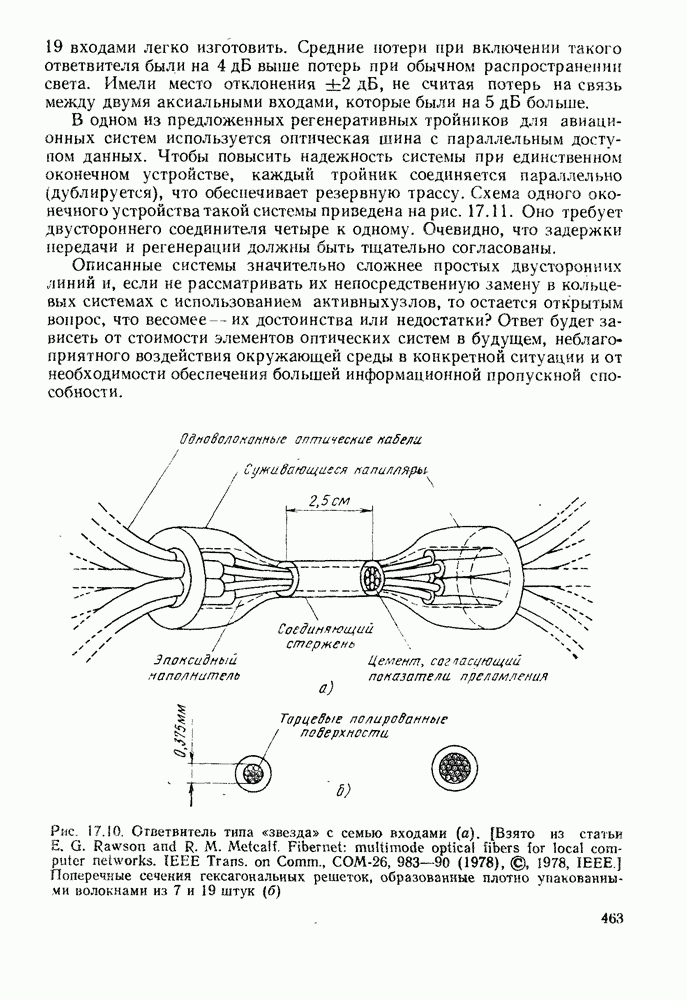
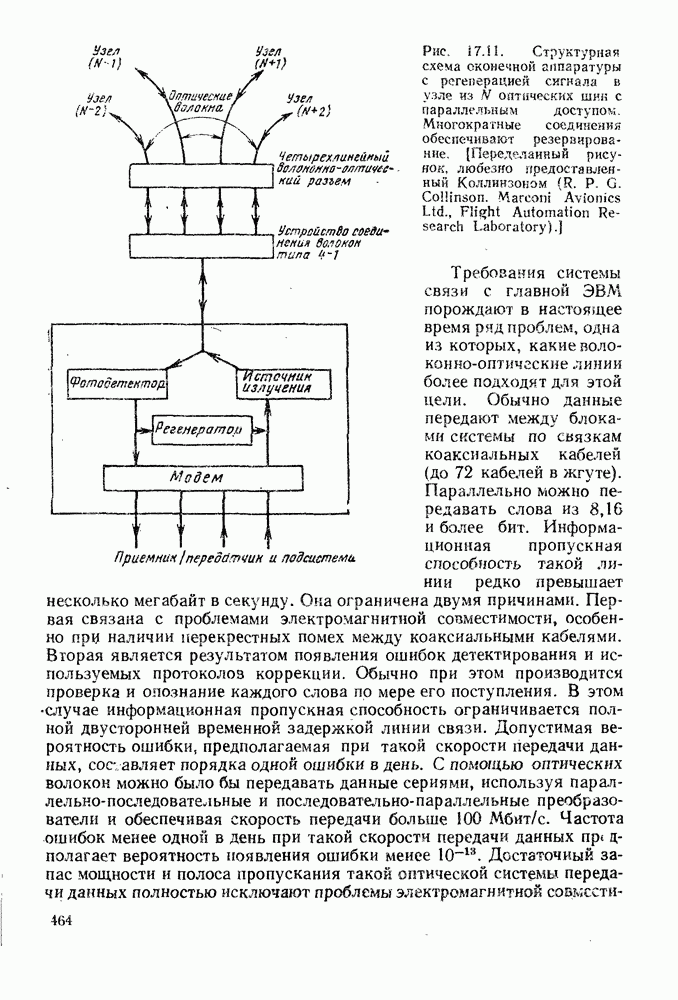
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
В пределах одной или двух инжекционных длин с любой стороны обедненного слоя происходит рекомбинация носителей и рекомбинационное излучение генерируется в этой области. В полупроводниковых источниках света обычно применяют асимметричное легирование, чтобы обеспечить превышение генерации с одной стороны перехода. Обычно материал n-типа легируется значительно сильнее, чем материал  -типа, т. е. формируется
-типа, т. е. формируется  -переход. Значение
-переход. Значение  может составлять
может составлять  тогда как
тогда как  Тогда ток положительного смещения проходит через переход в основном за счет электронов, инжектированных в слабо легированную область
Тогда ток положительного смещения проходит через переход в основном за счет электронов, инжектированных в слабо легированную область  -типа, где и происходит генерация рекомбинационного излучения. В этом случае можно определить эффективность инжекции
-типа, где и происходит генерация рекомбинационного излучения. В этом случае можно определить эффективность инжекции  как отношение электронного тока через переход к общему току. Позже будет показано, как величина
как отношение электронного тока через переход к общему току. Позже будет показано, как величина  определяется из характеристик
определяется из характеристик  и
и  -областей. Плотность электронного тока
-областей. Плотность электронного тока  входящего в область
входящего в область  -типа:
-типа:

где значение  получено в результате дифференцирования уравнения (7.4.12). Отношение концентрации
получено в результате дифференцирования уравнения (7.4.12). Отношение концентрации  при
при  к
к
концентрации электронов в области n-типа по другую сторону потенциального барьера определяется уравнением Больцмана. В равновесии высота потенциального барьера совпадает с величиной диффузионного потенциала  , т. е.
, т. е.

В результате положительного смещения напряжением V потенциальный барьер понижается, тогда

В результате подстановки в (7.5.1)

Аналогичные рассуждения приводят к выражению для плотности дырочного тока, входящего в область  -типа
-типа

Если генерация или рекомбинация носителей в пределах обедненного слоя или на периферии перехода 1/2 в (7.3.5)] оказывается незначительной, то общая плотность тока через переход

и эффективность инжекции

т. е.

При получении этих выражений использованы формулы (7.3.2) и (7.3.3). Ясно, что для получения максимального значения  необходимо обеспечить максимально возможное отношение
необходимо обеспечить максимально возможное отношение  Подставив
Подставив  в (7.5.6) и умножив на площадь перехода А, получим
в (7.5.6) и умножив на площадь перехода А, получим

Таким образом,

или

При этом опять использовались выражения (7.3.2), (7.3.3) и (7.2.6).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
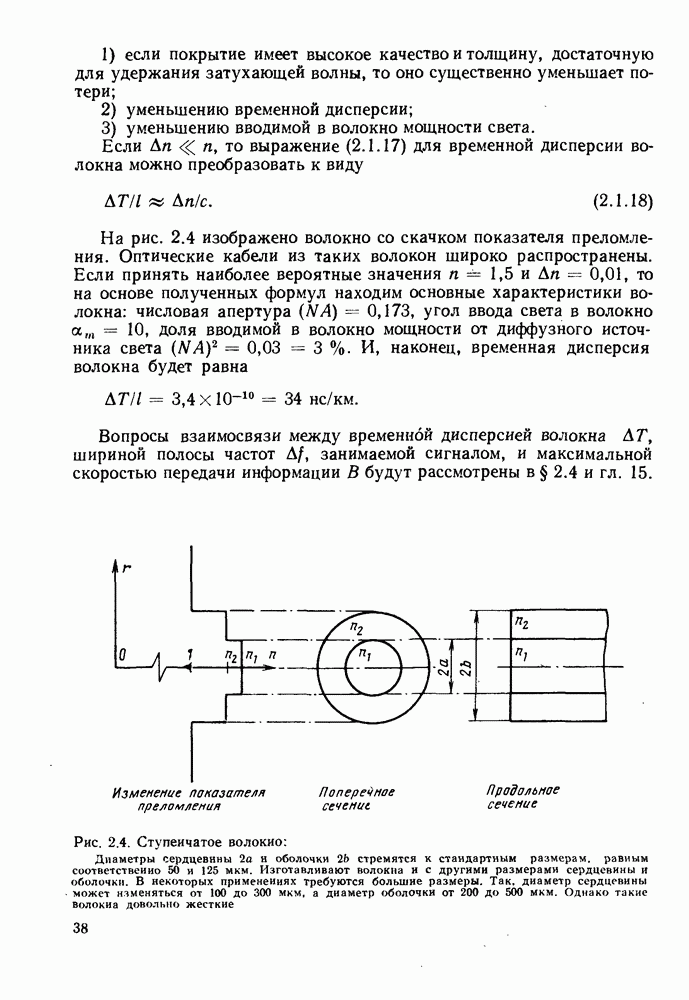
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
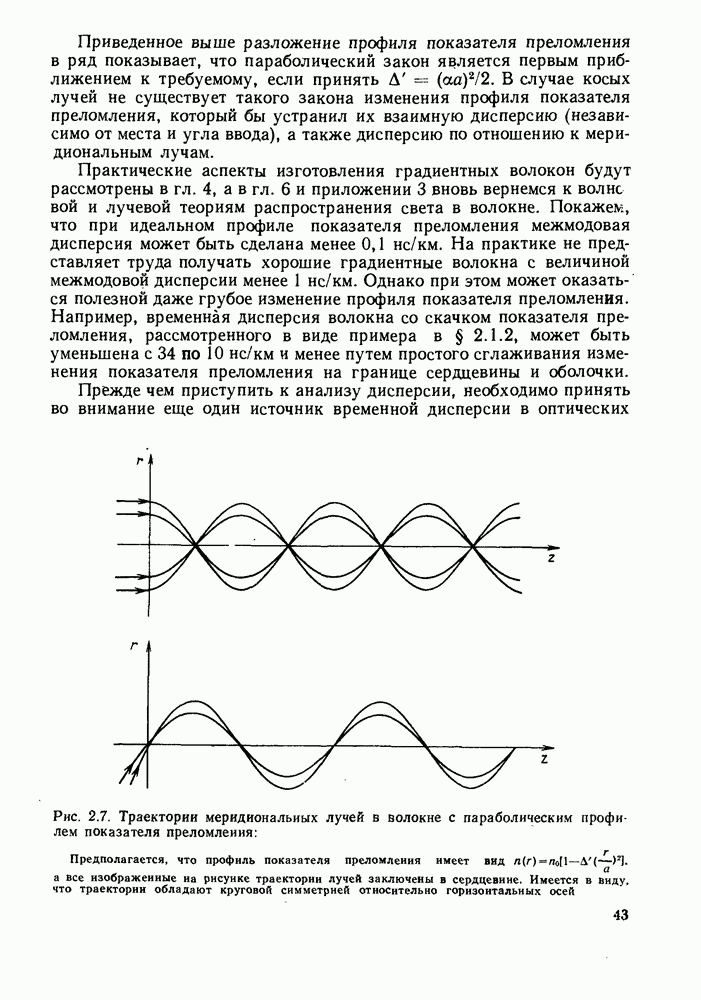
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
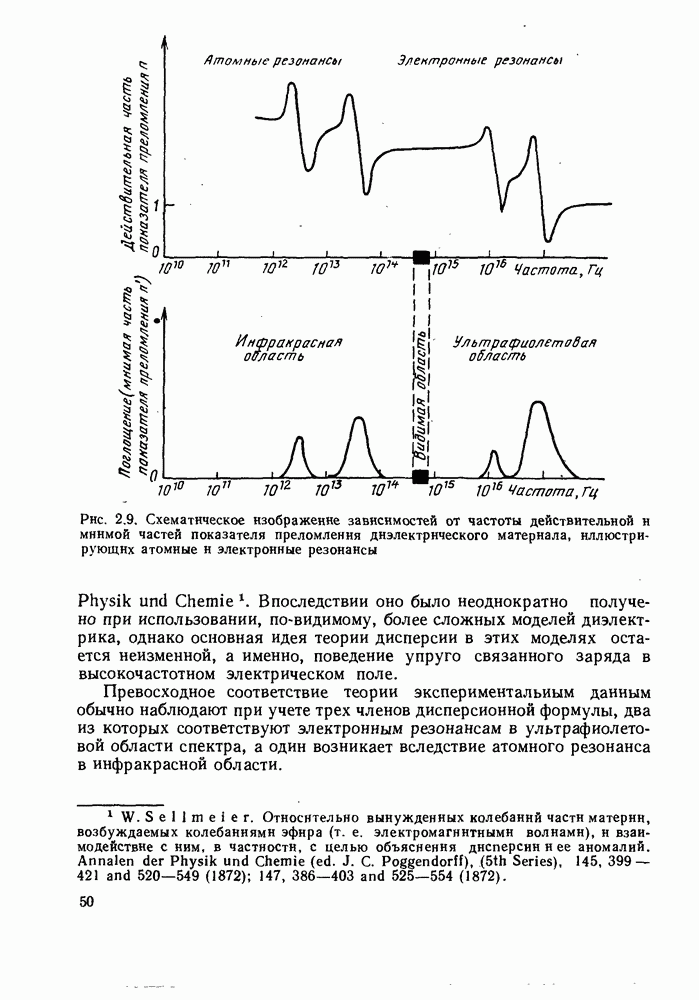
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
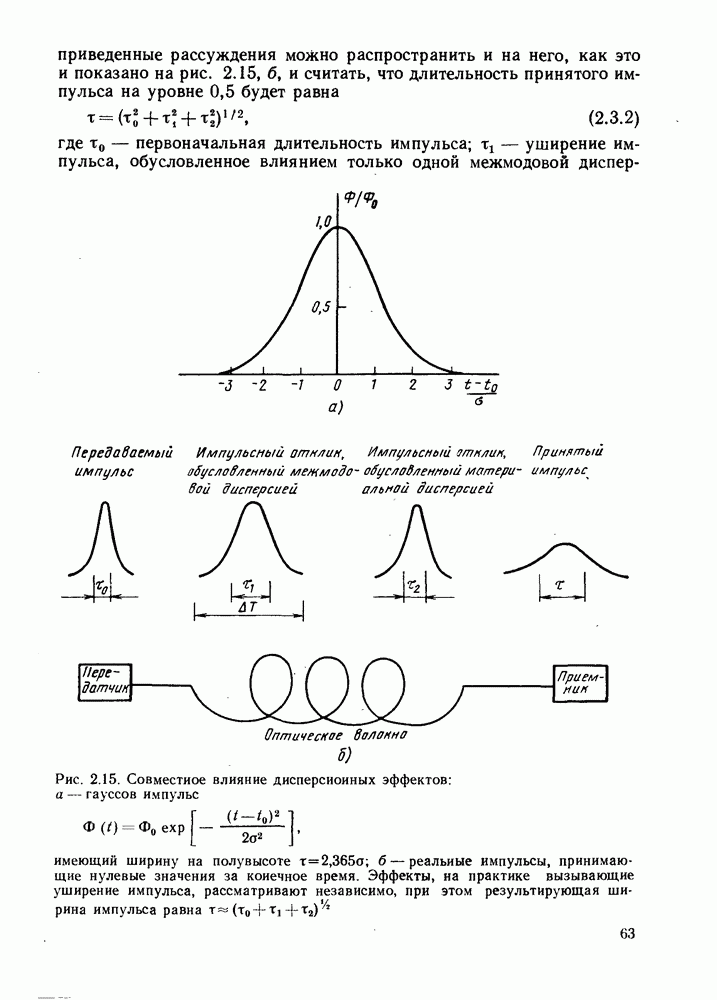
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
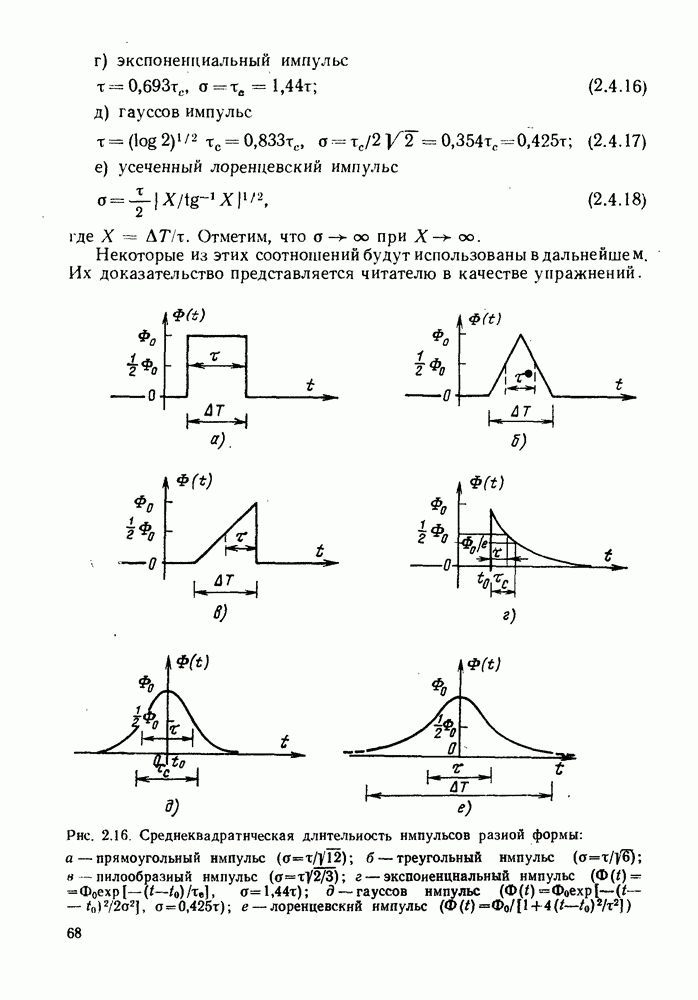
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
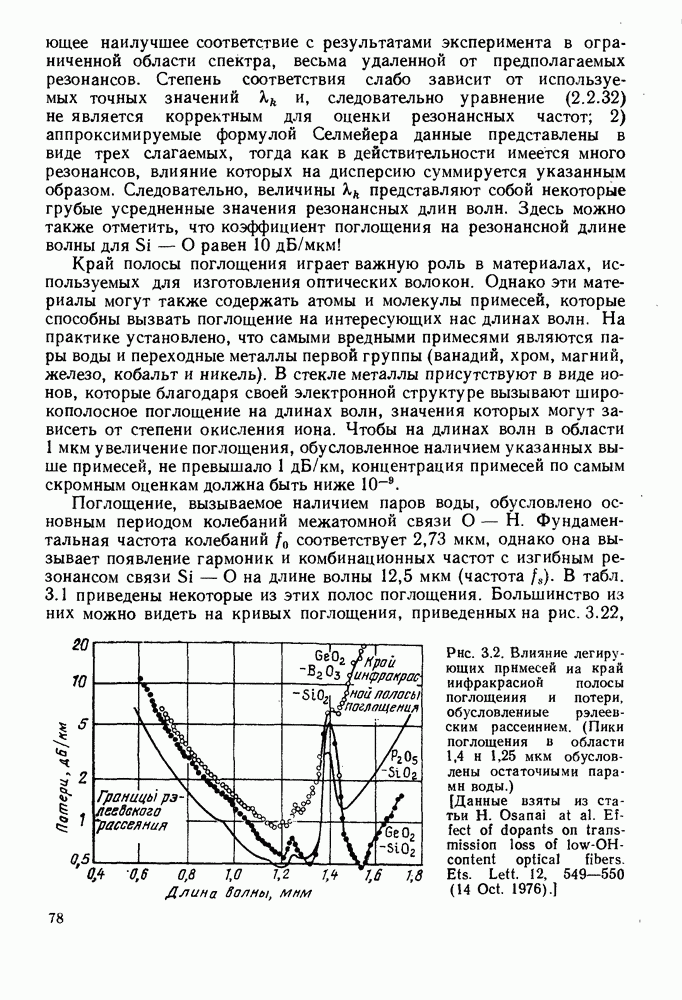
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
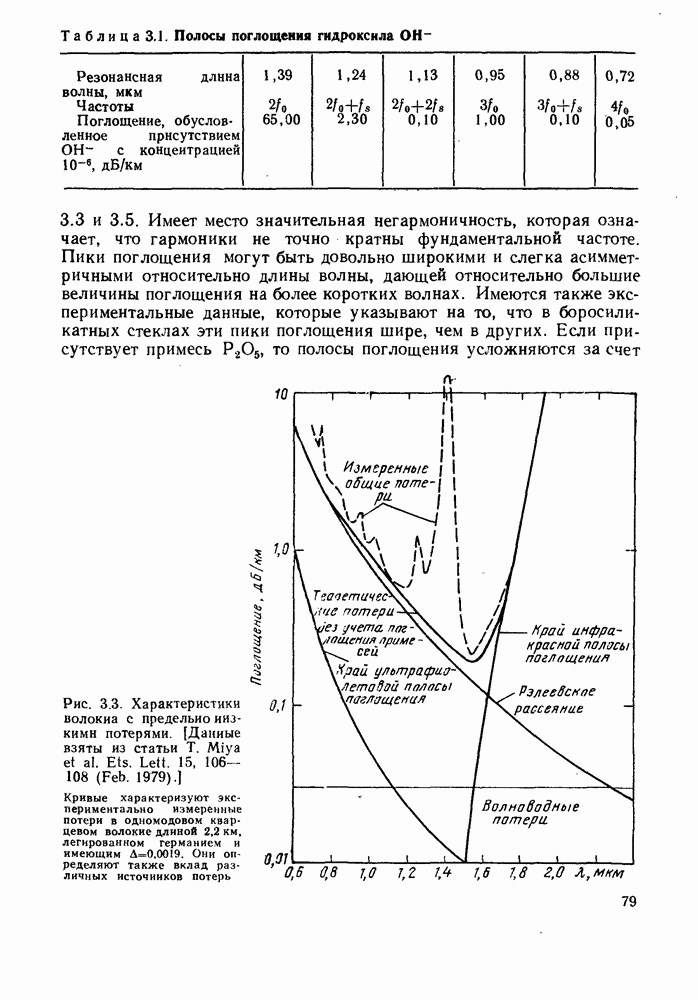
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
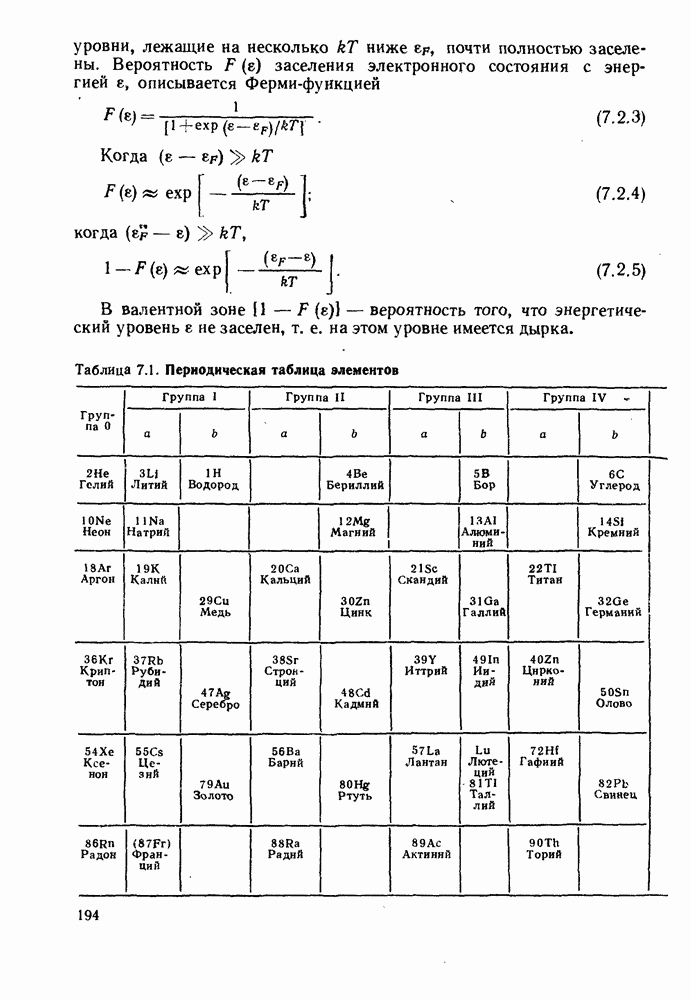
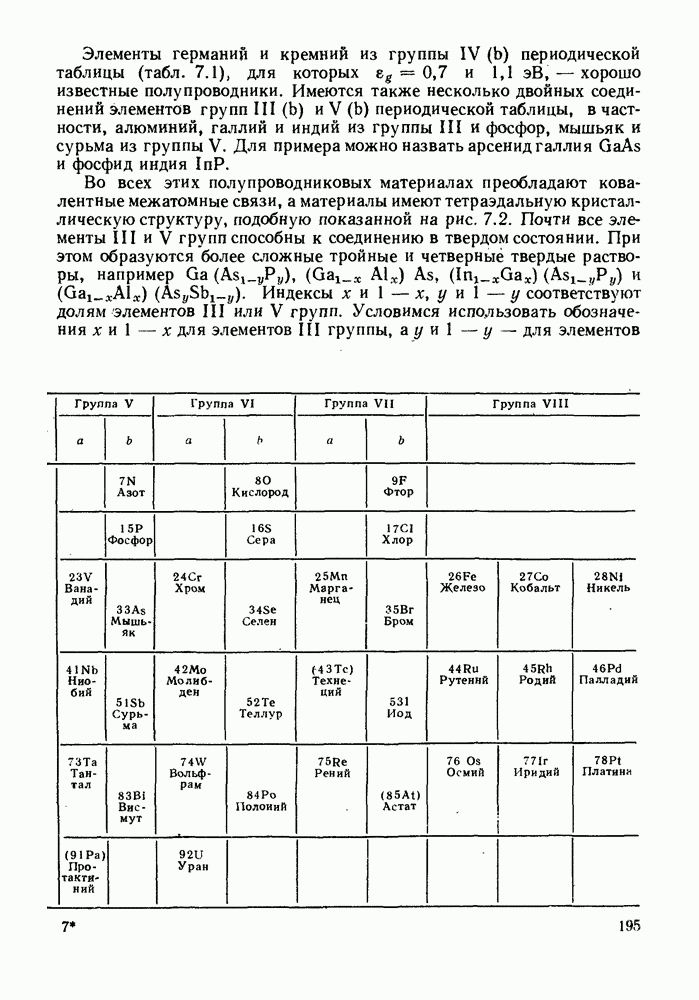
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
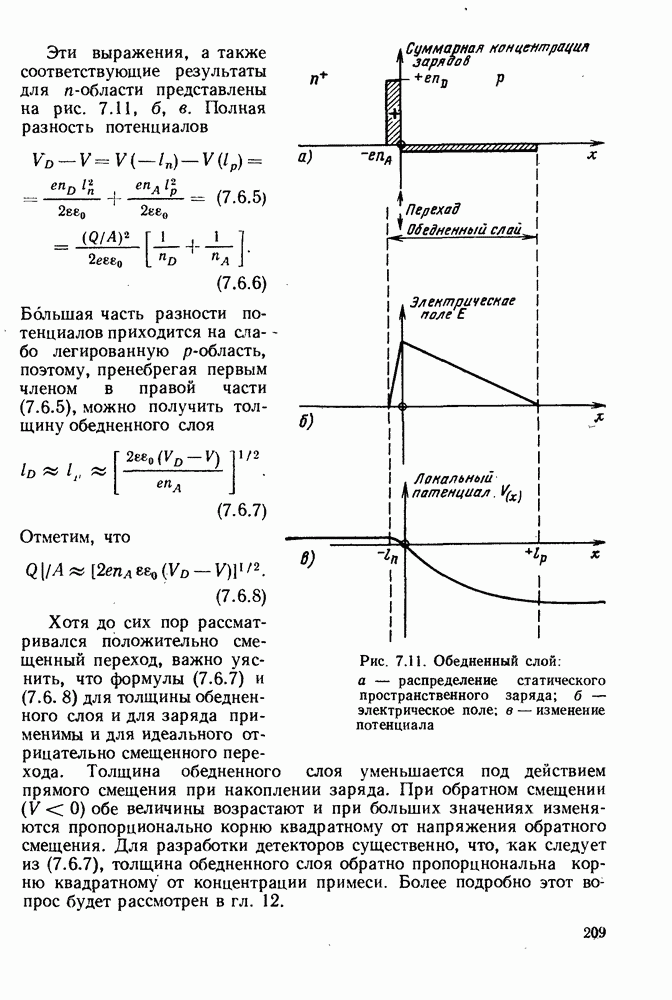
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
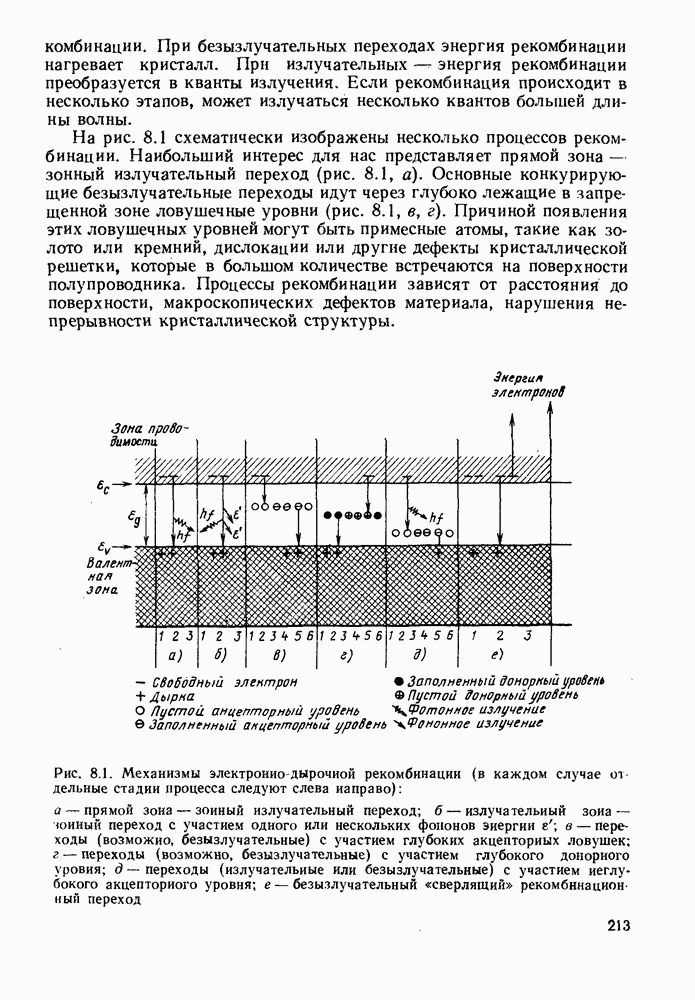
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
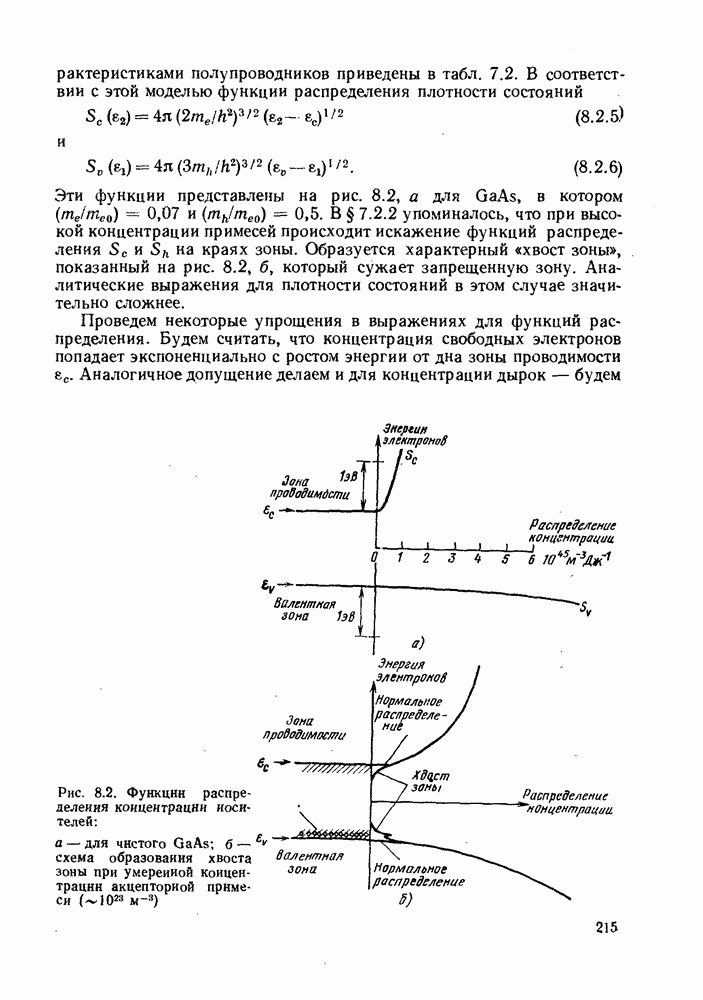
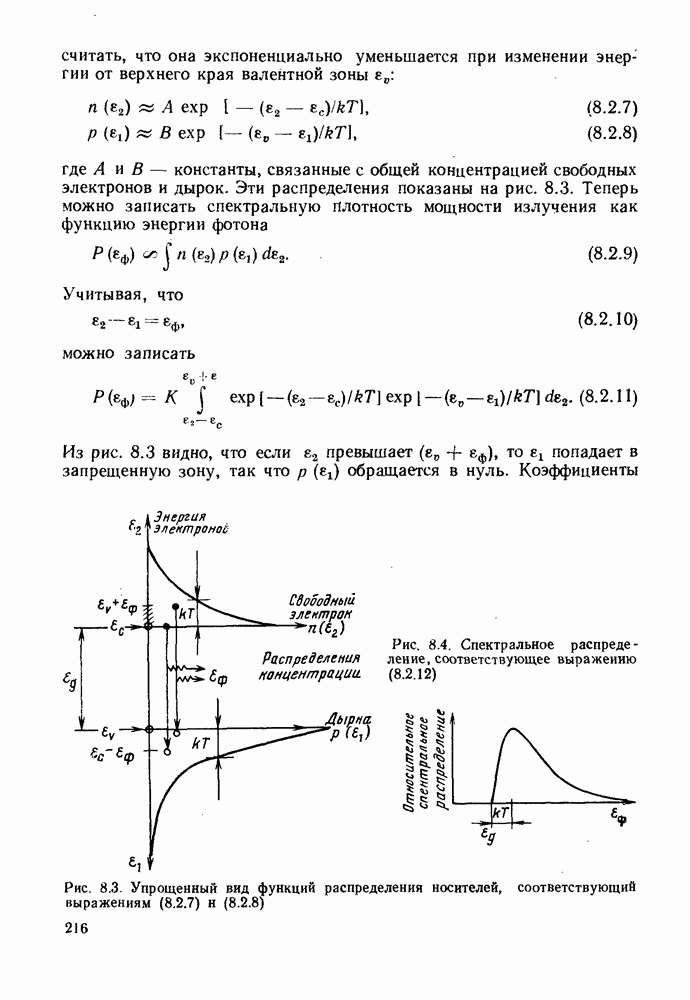
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
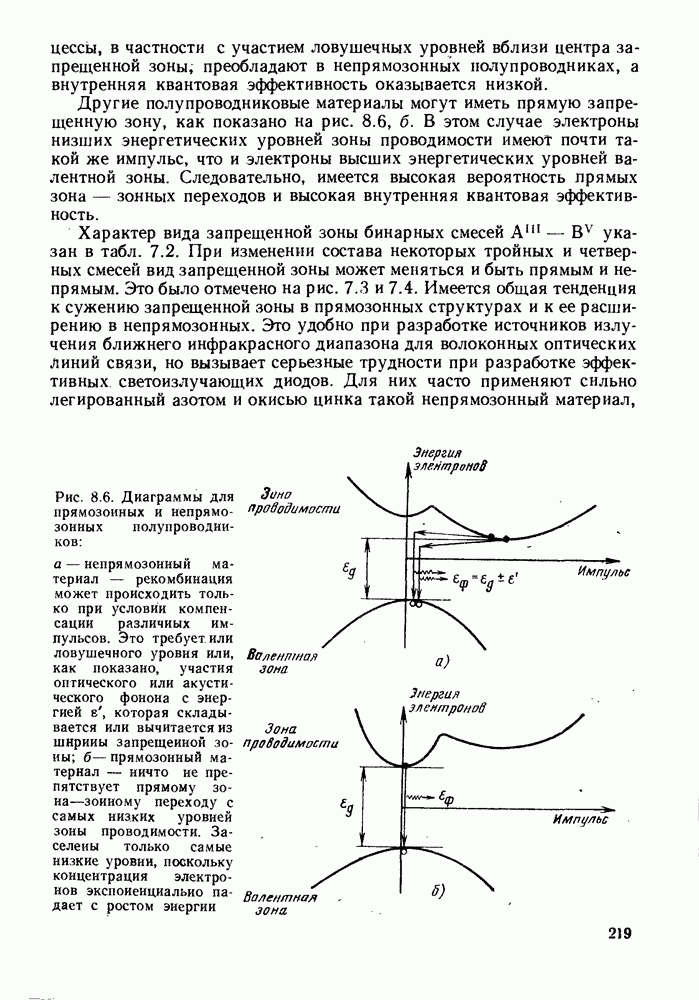
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
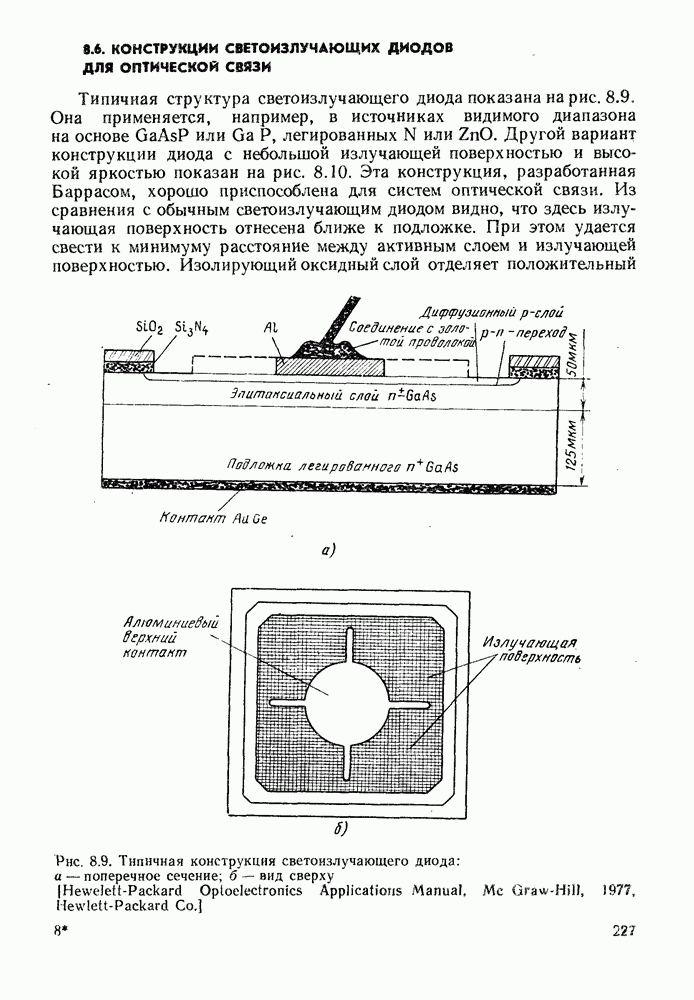
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
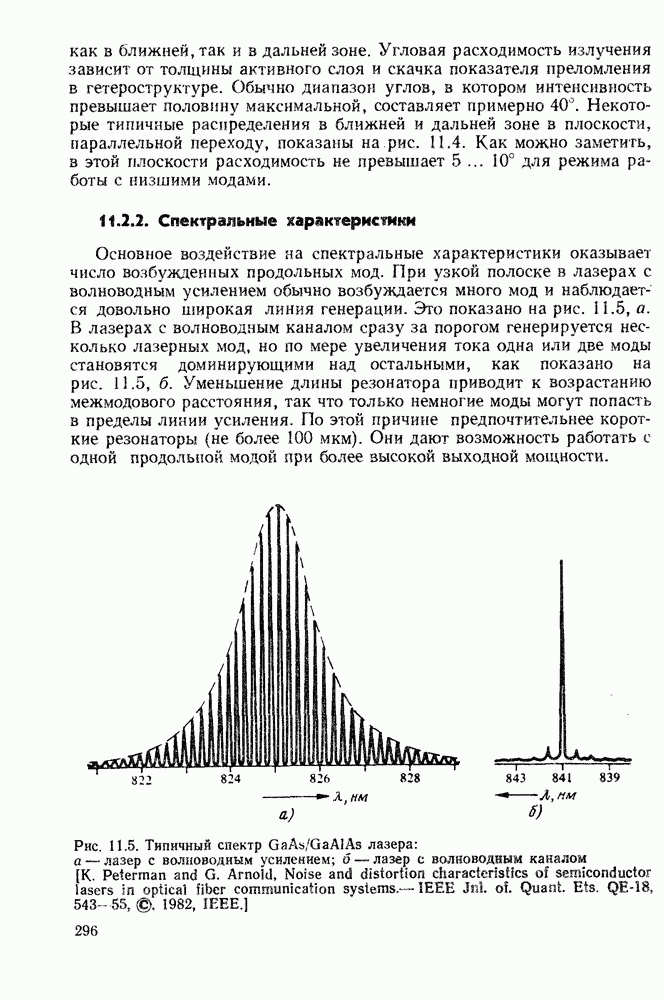
- 11.2.2. Спектральные характеристики
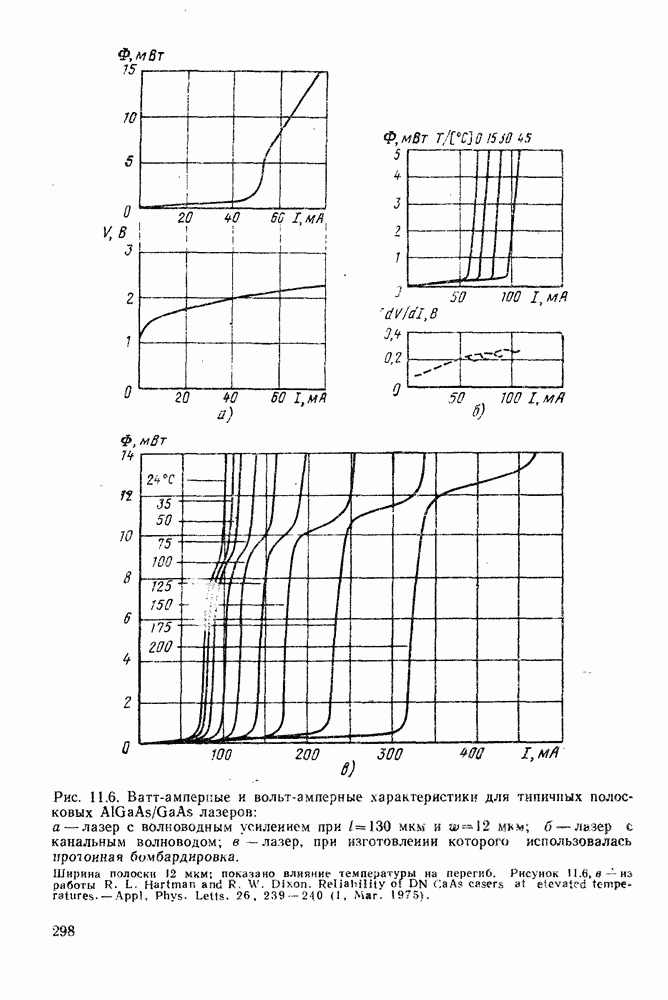
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
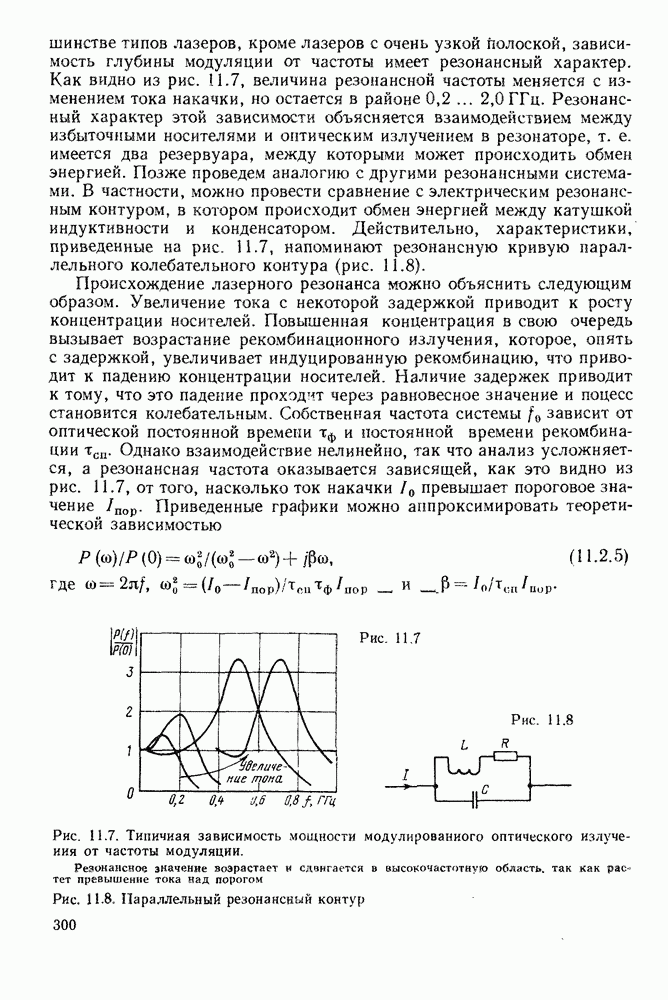
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
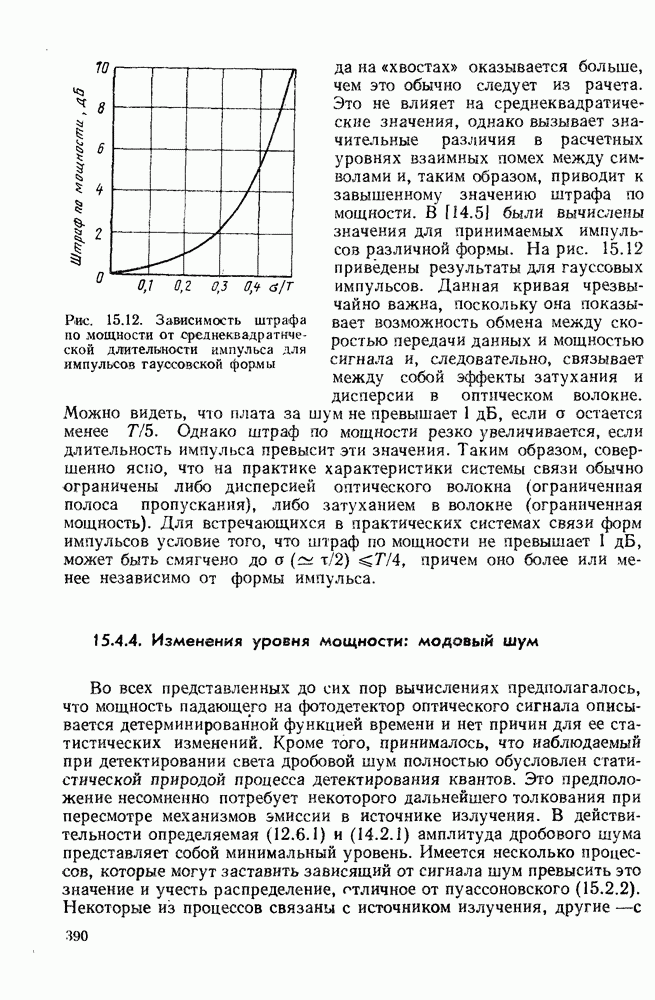
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
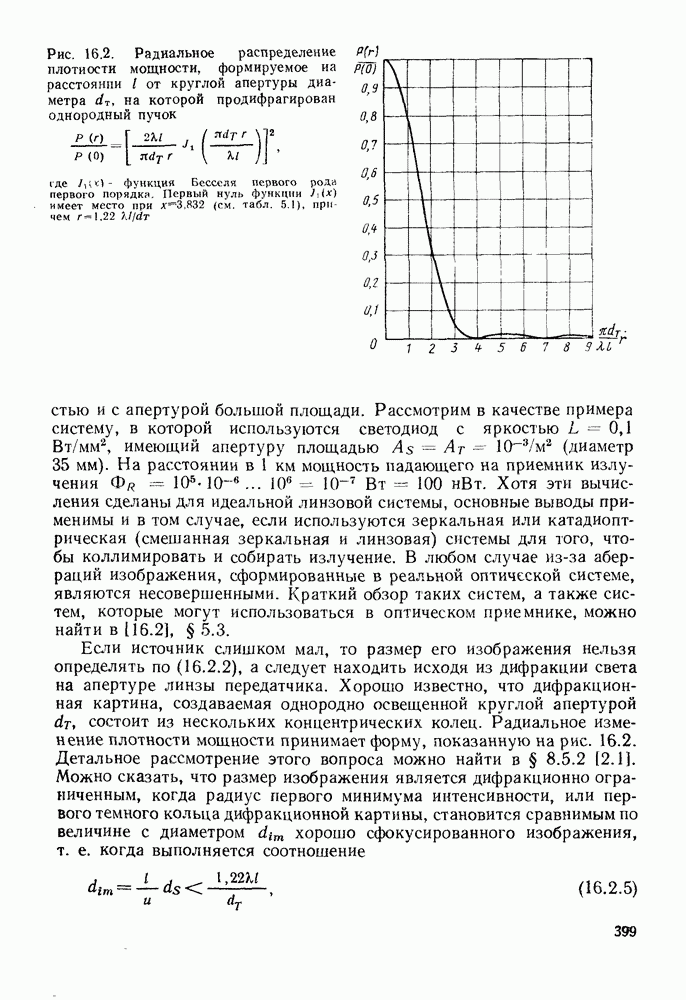
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
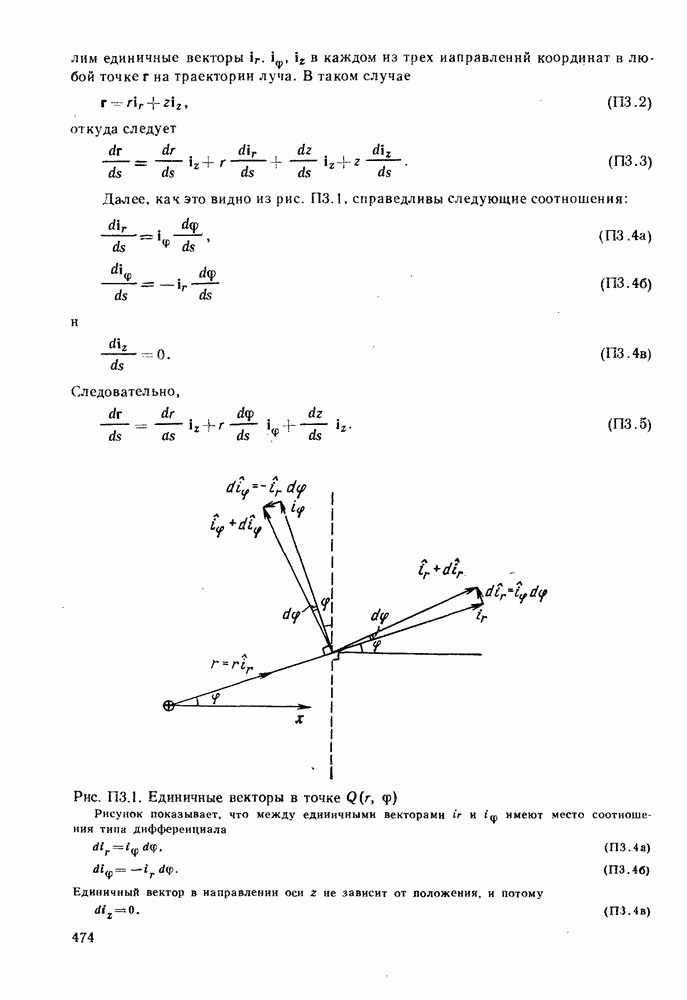
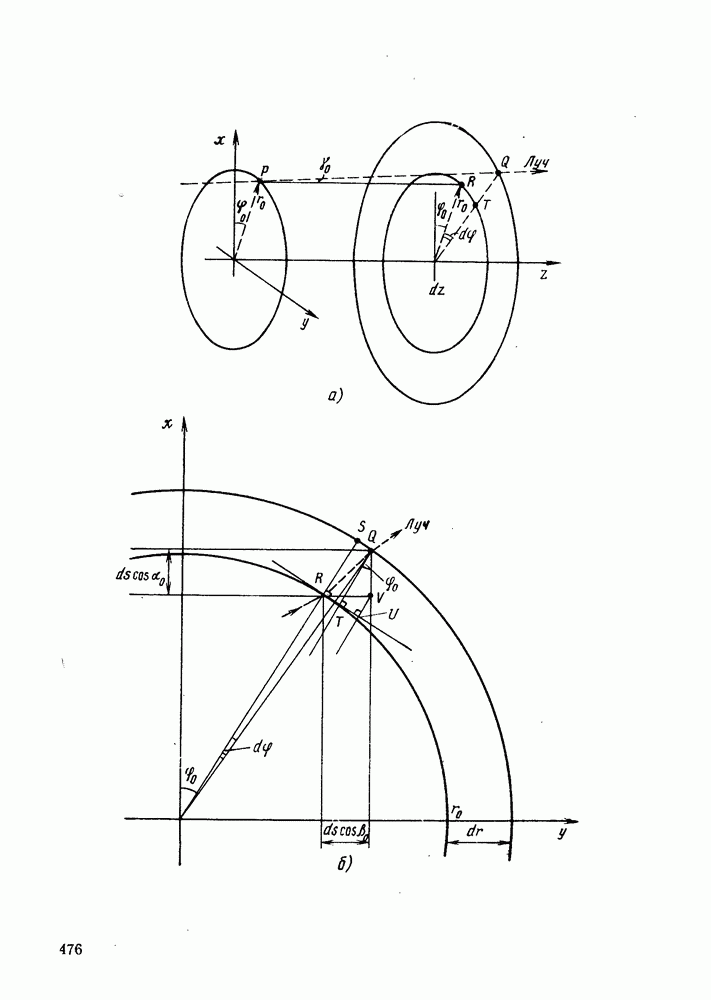
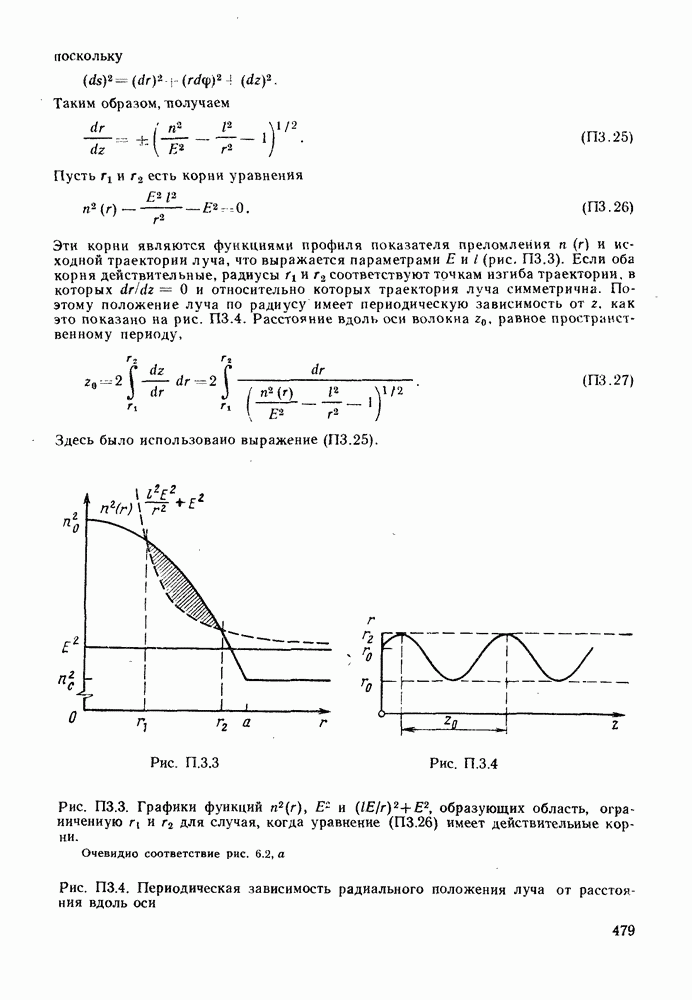
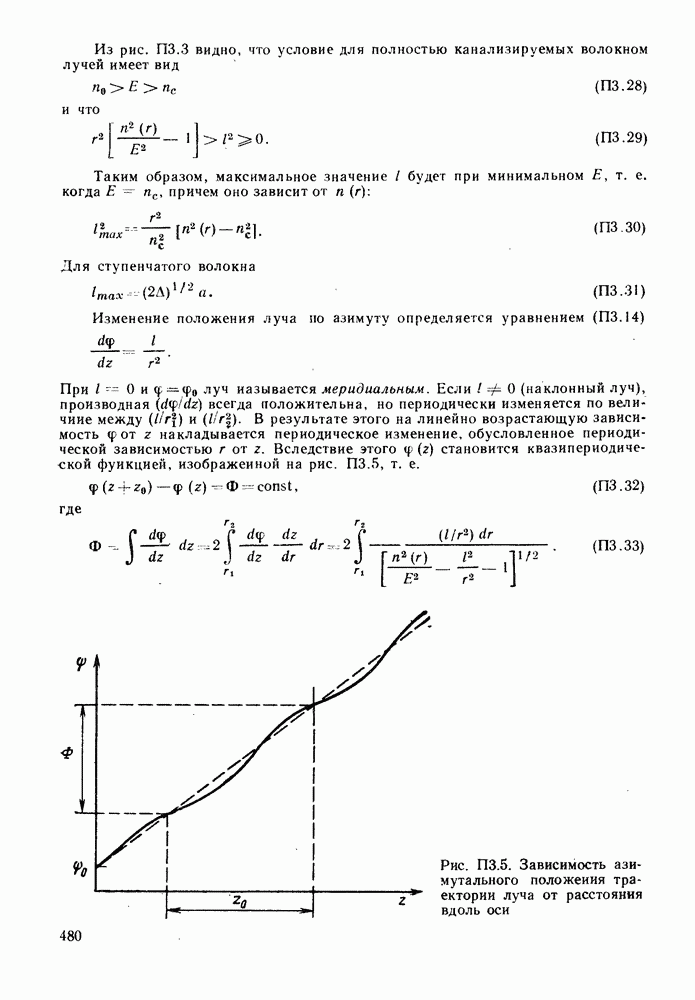
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
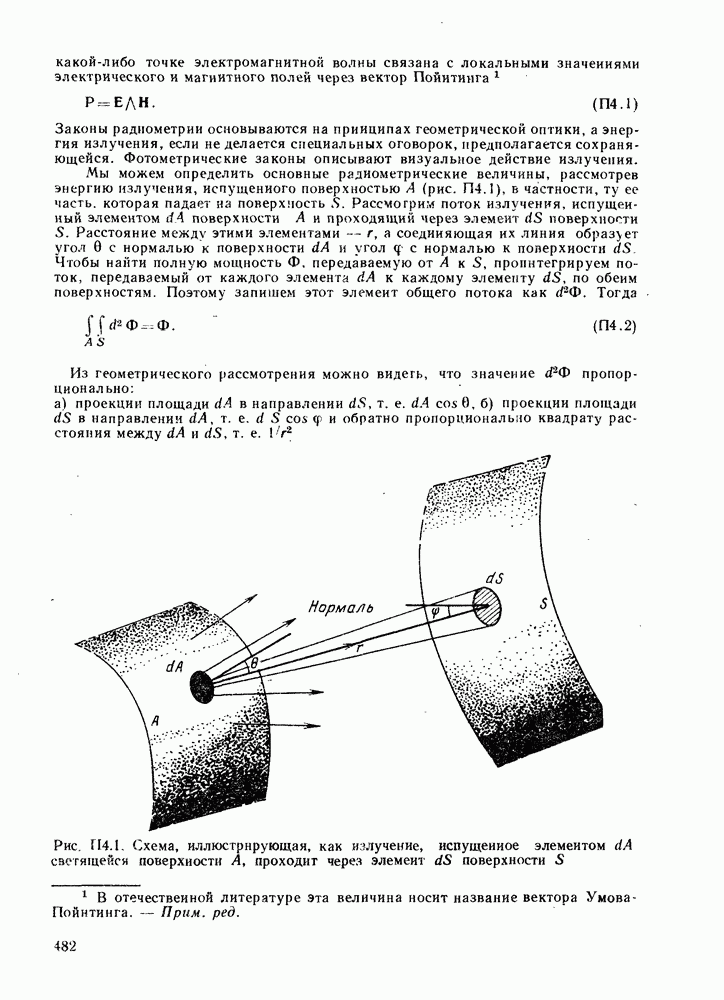
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
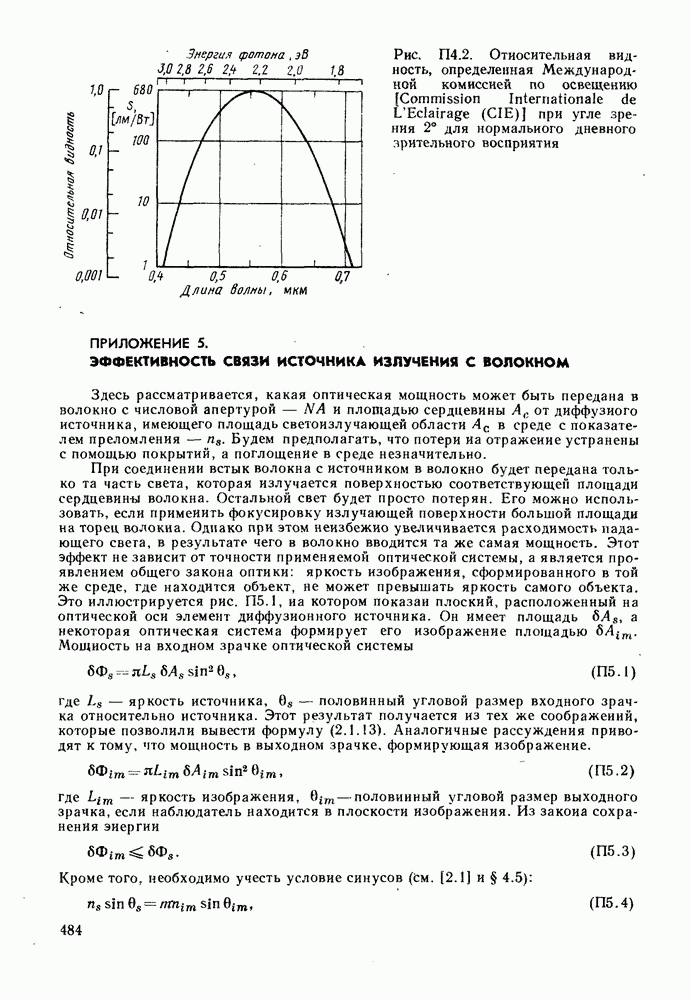
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
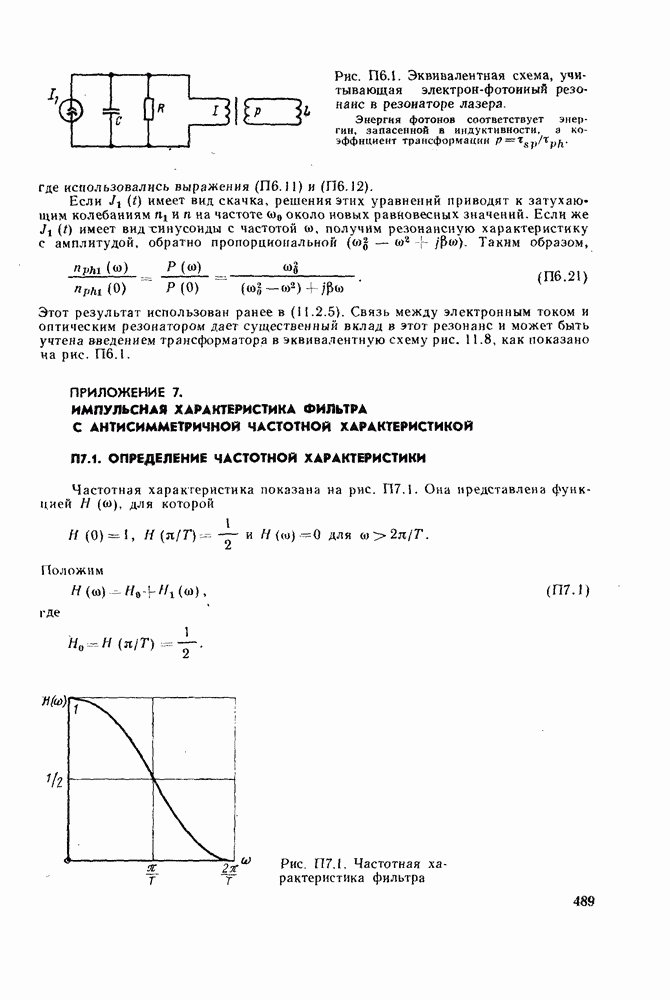
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ