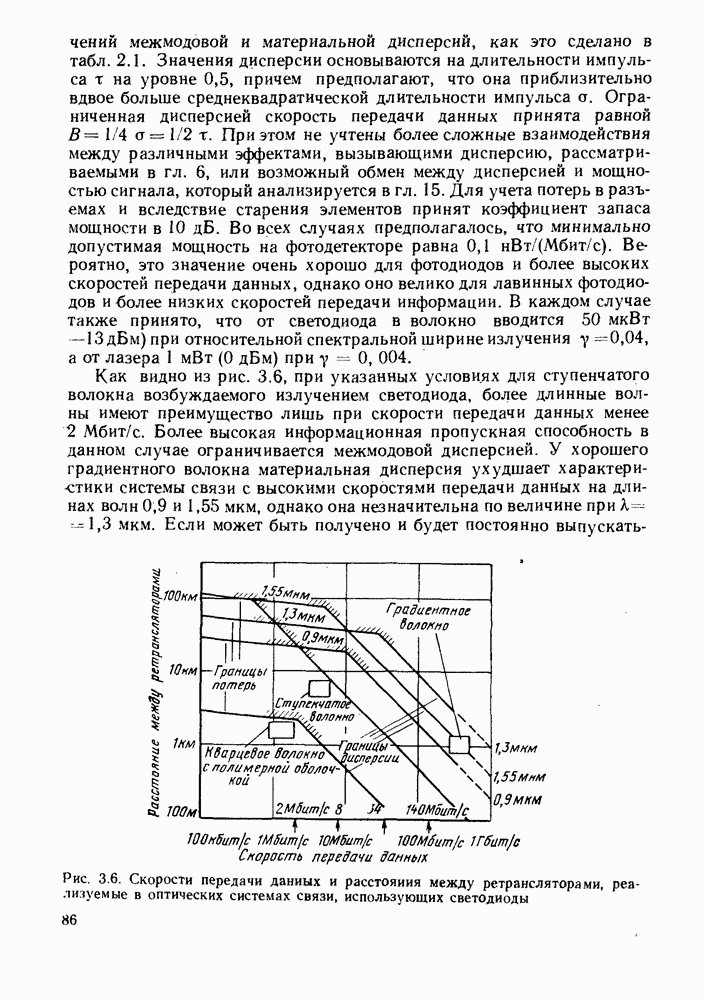
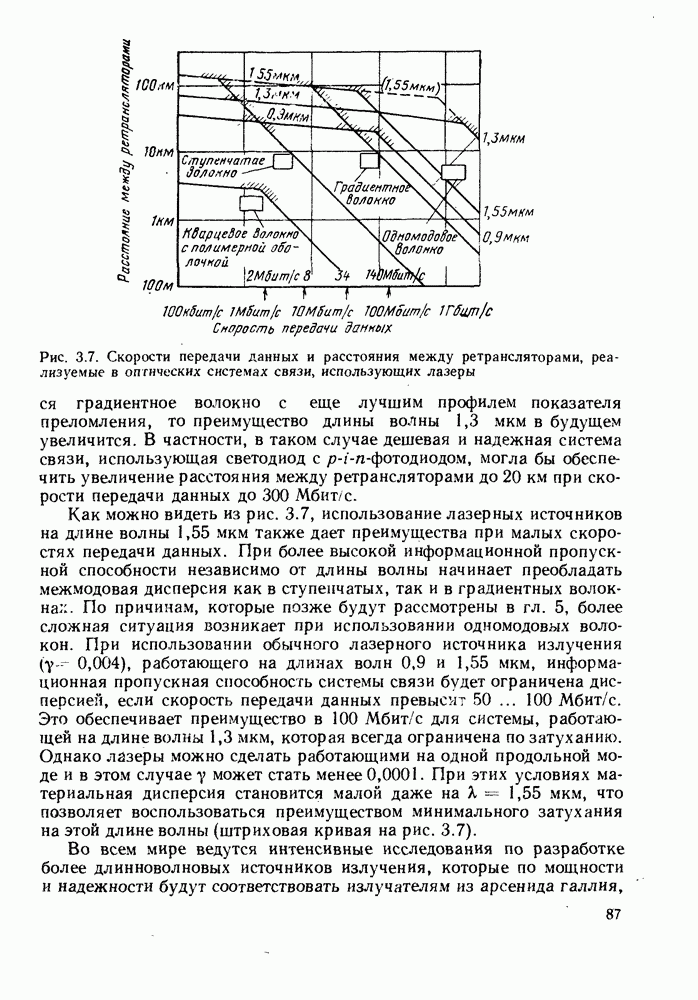
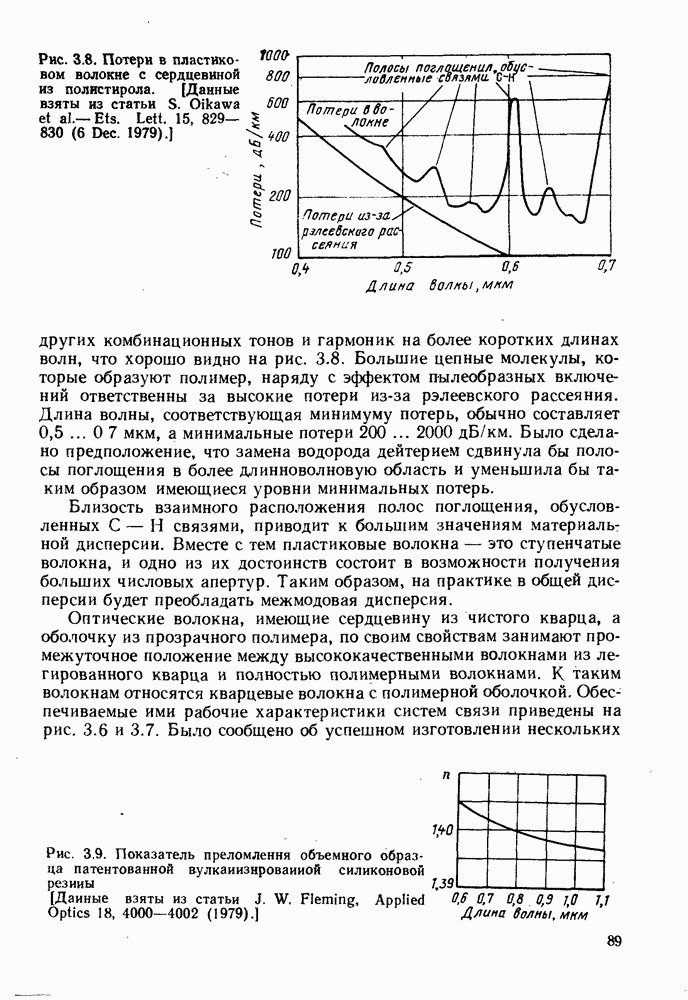
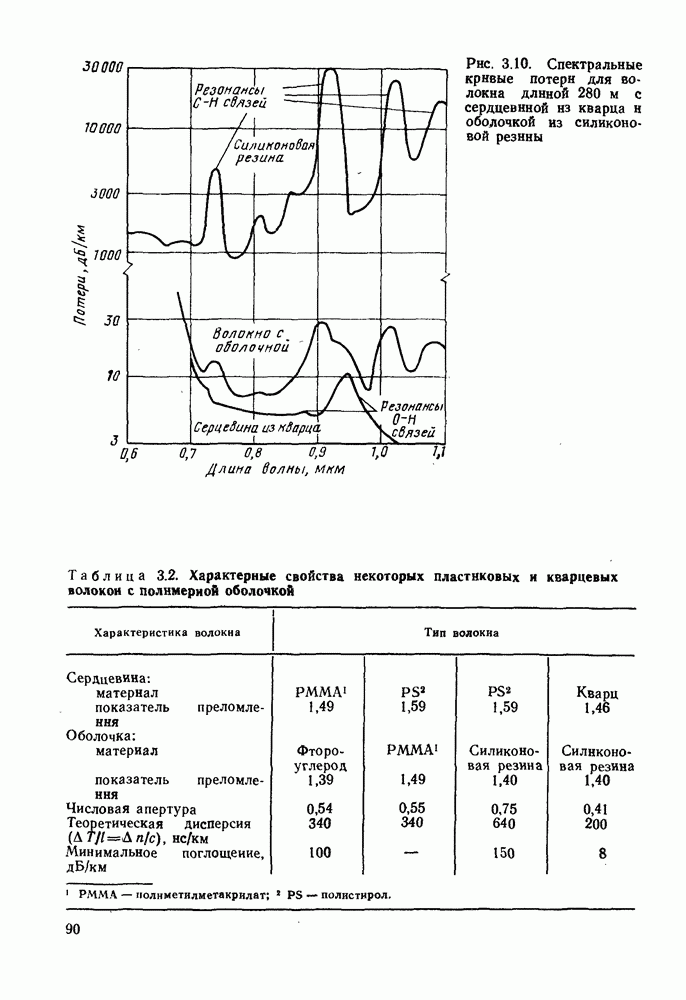
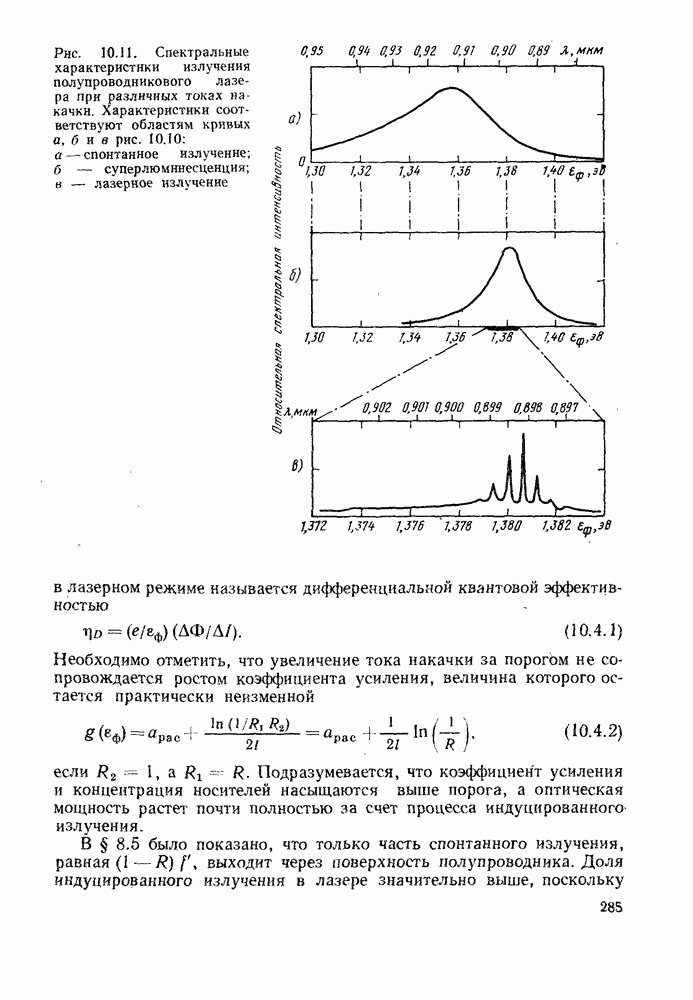
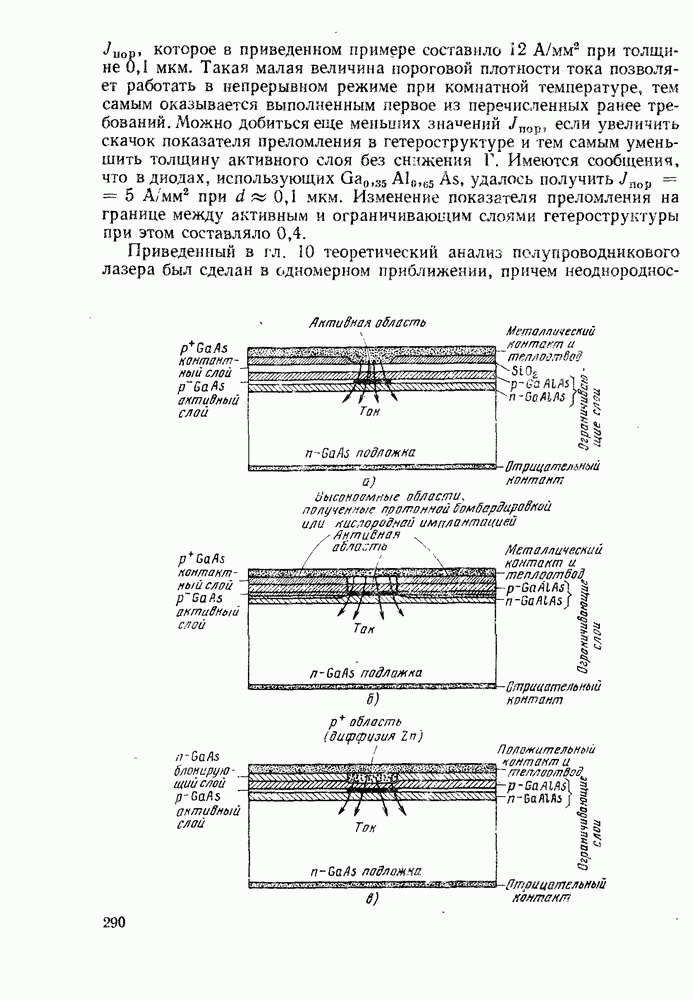
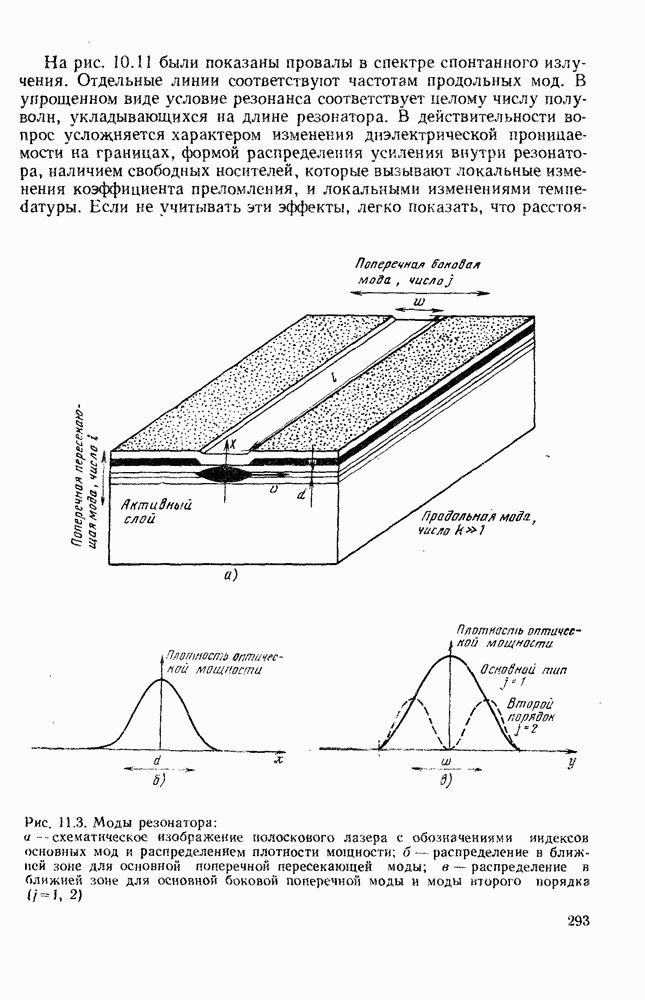
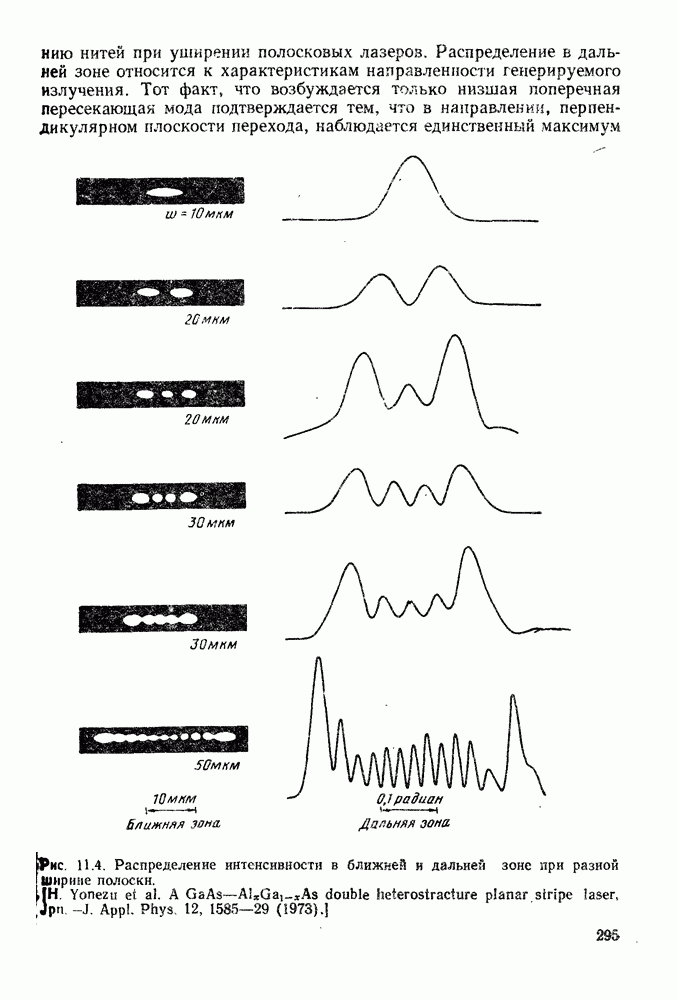
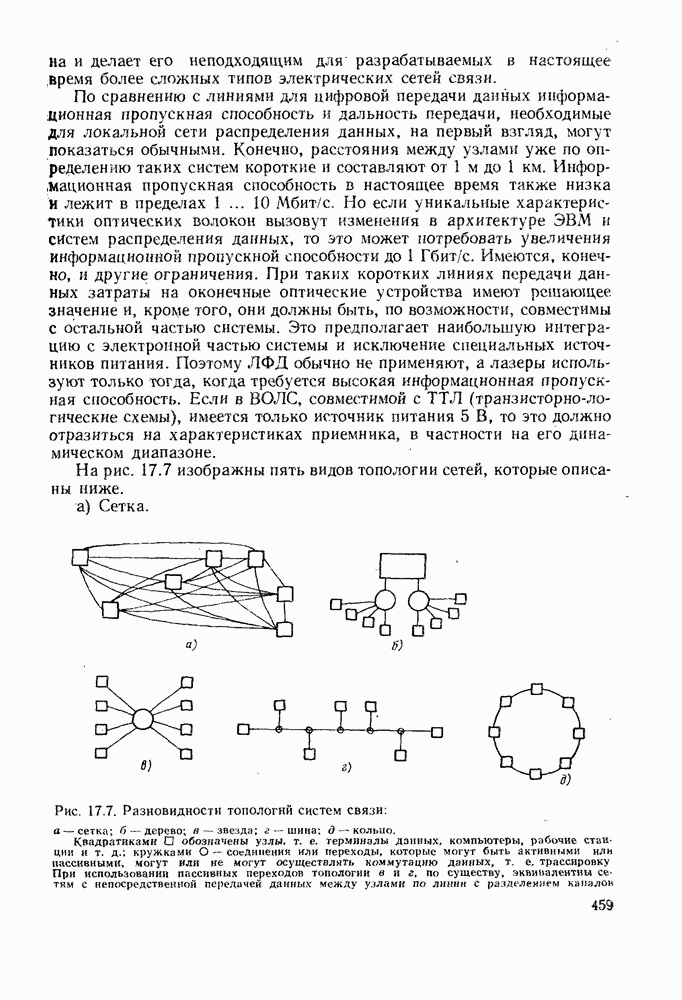
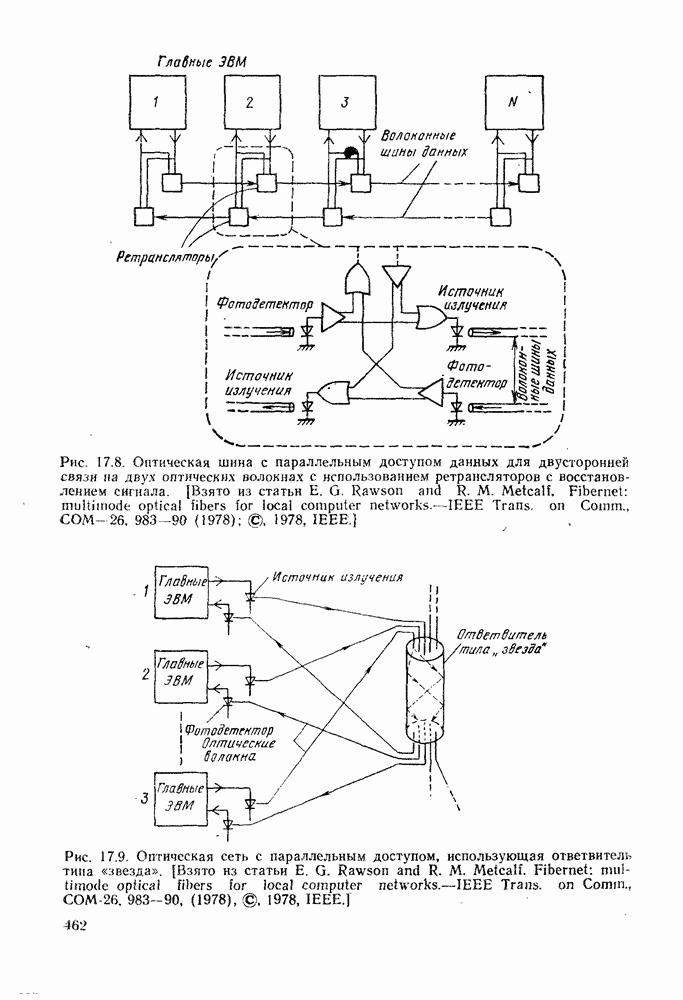
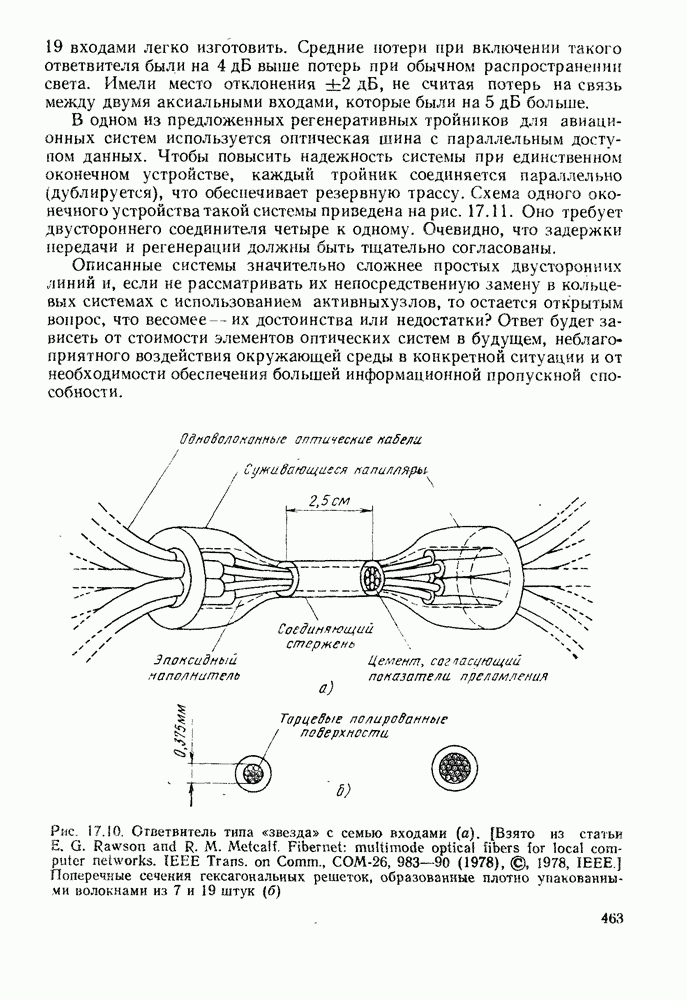
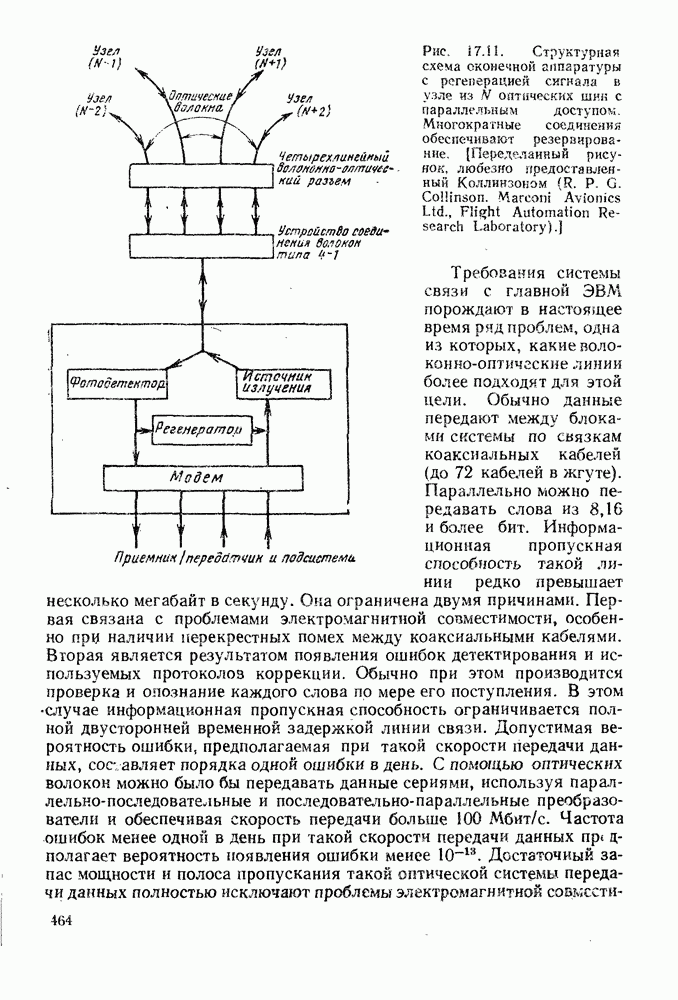
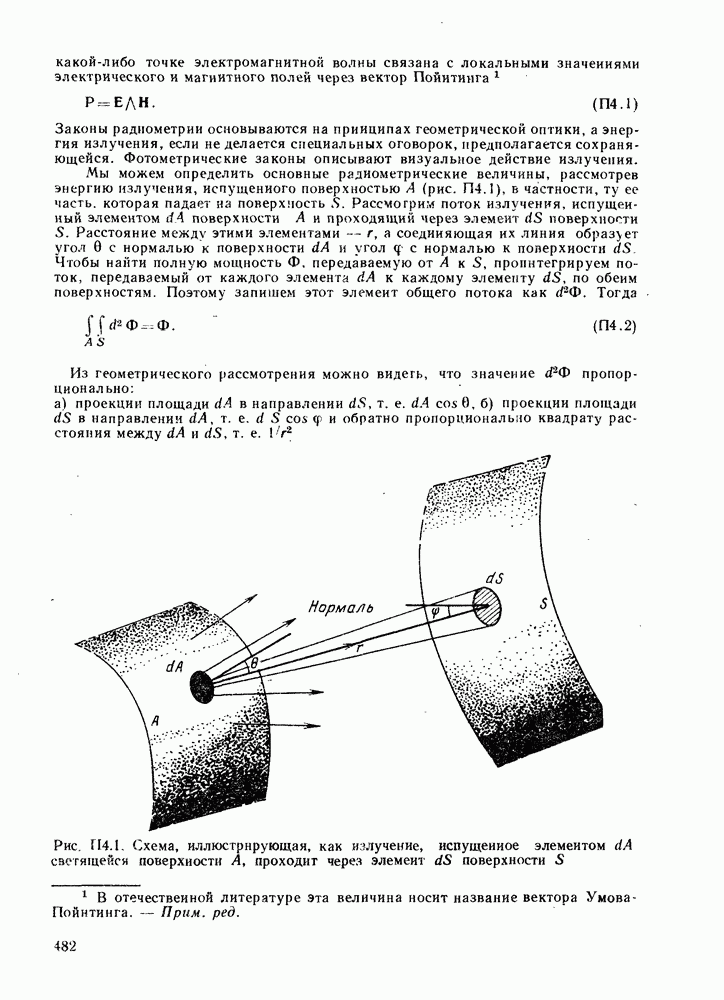
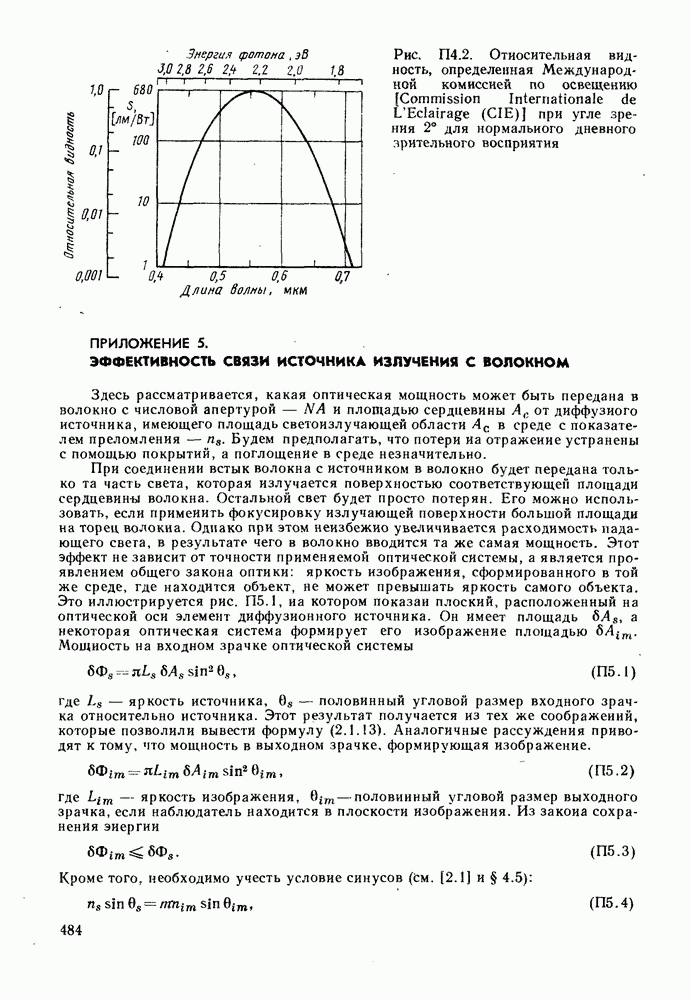
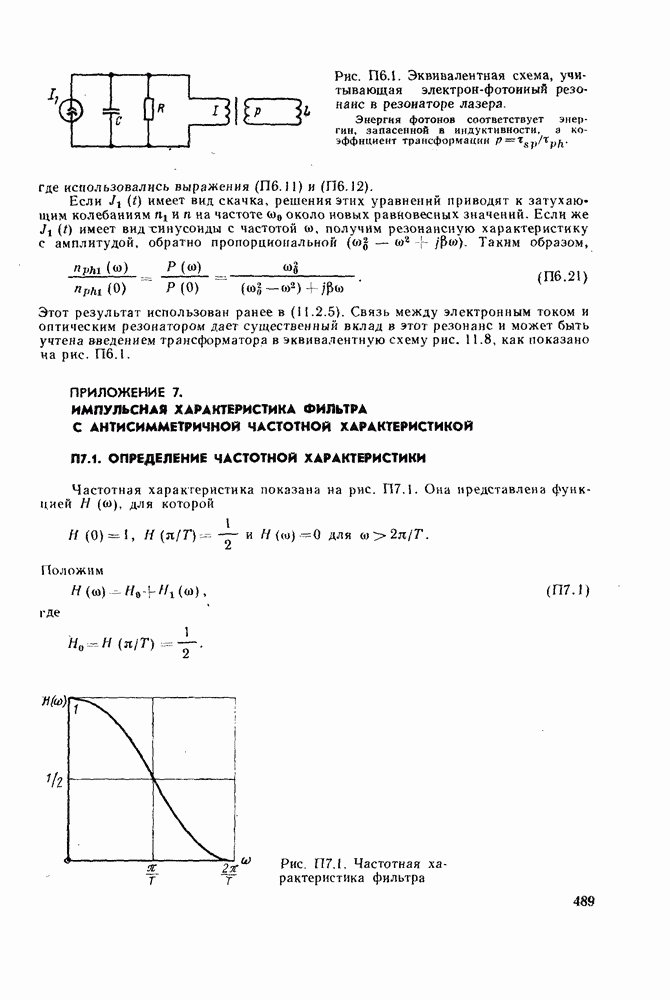
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
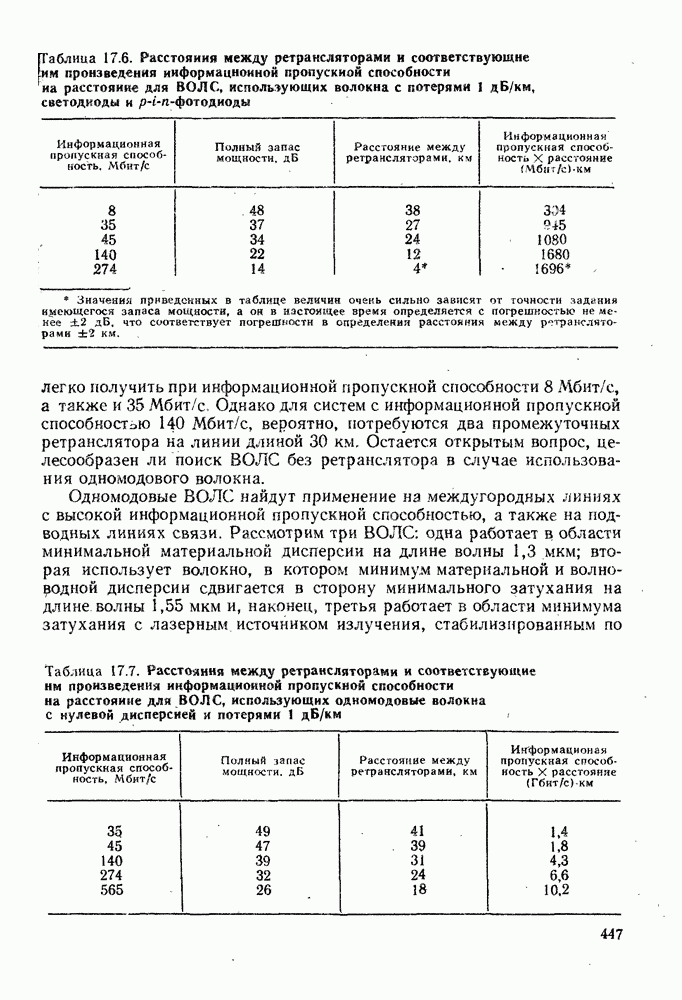
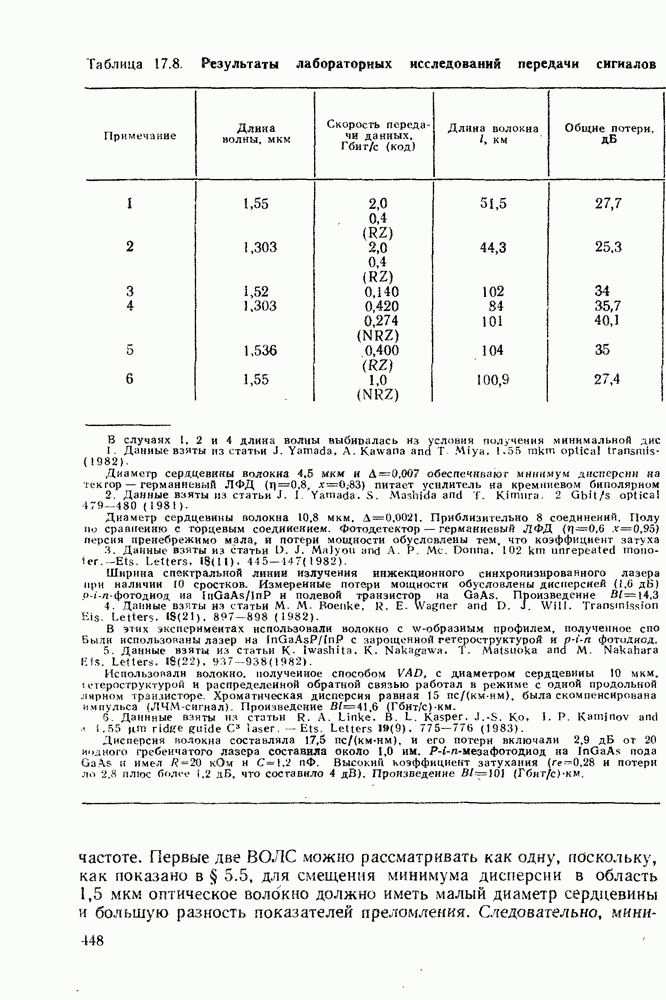
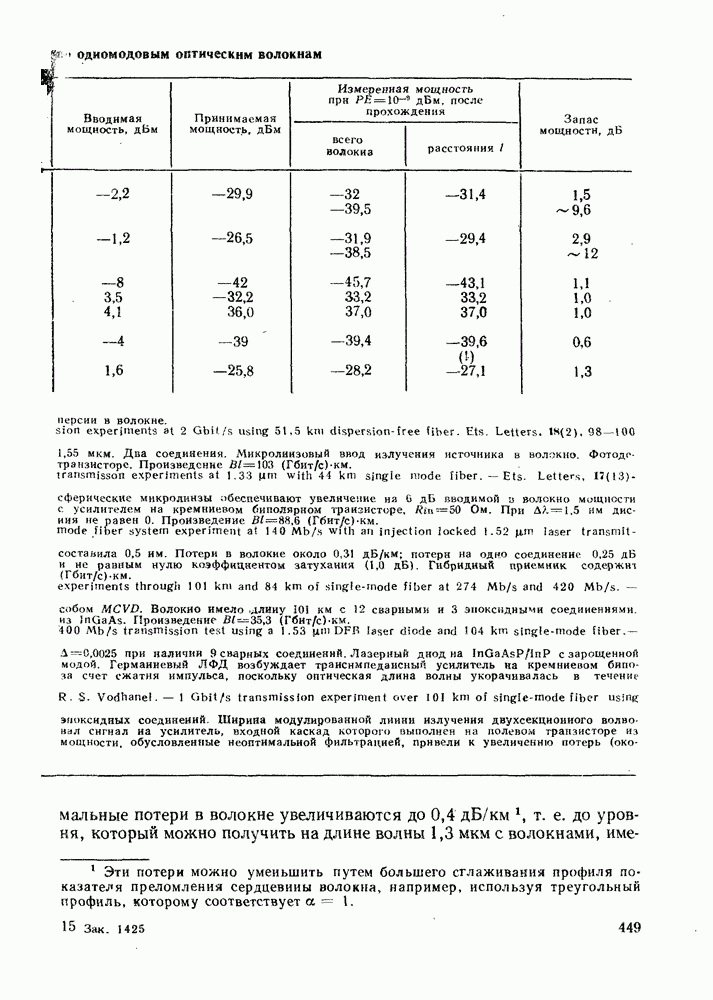
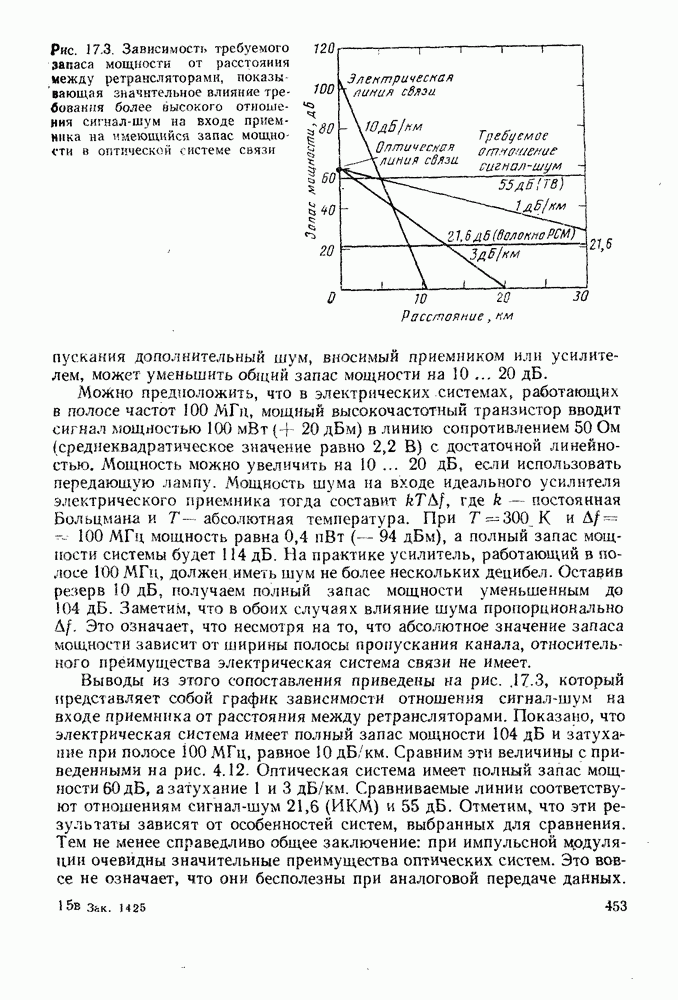
2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
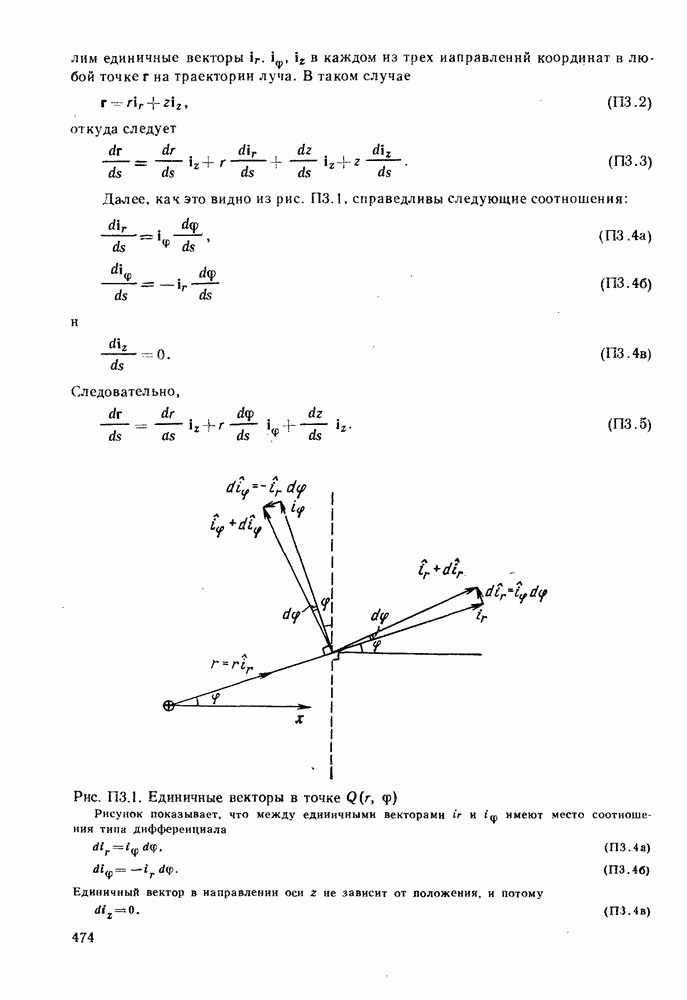
Эффект волноводного распространения света в прозрачной диэлектрической среде, показатель преломления которой больше показателя преломления окружающей среды, был продемонстрирован Тиндаллом на примере водяной струи в 1870 г. во время чтения лекции в Королевском институте.
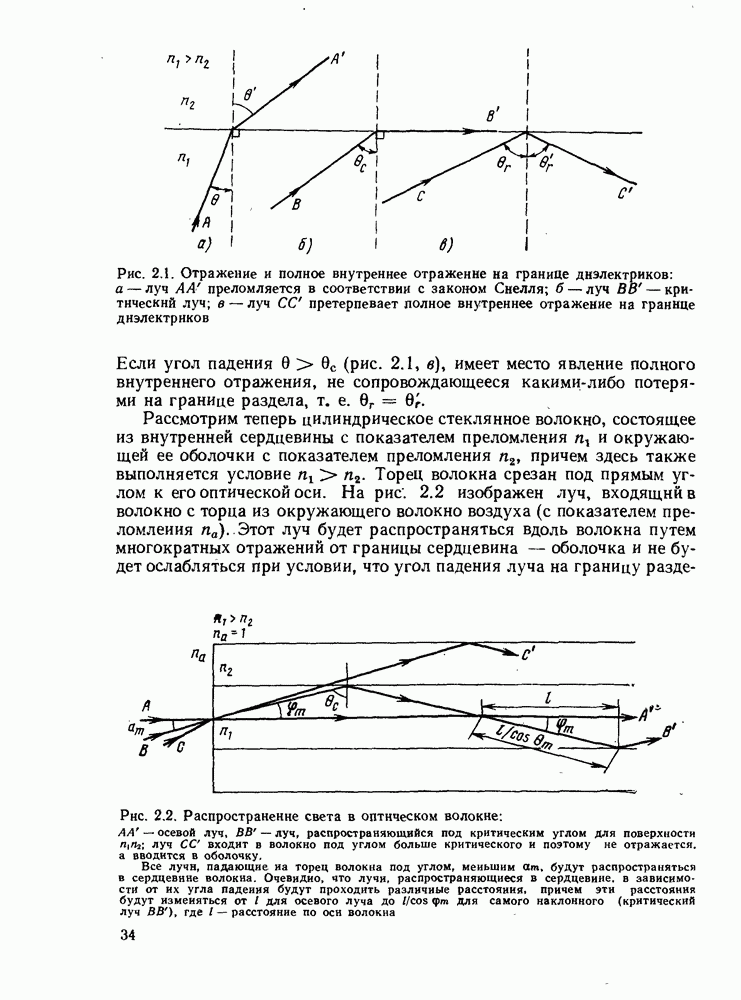
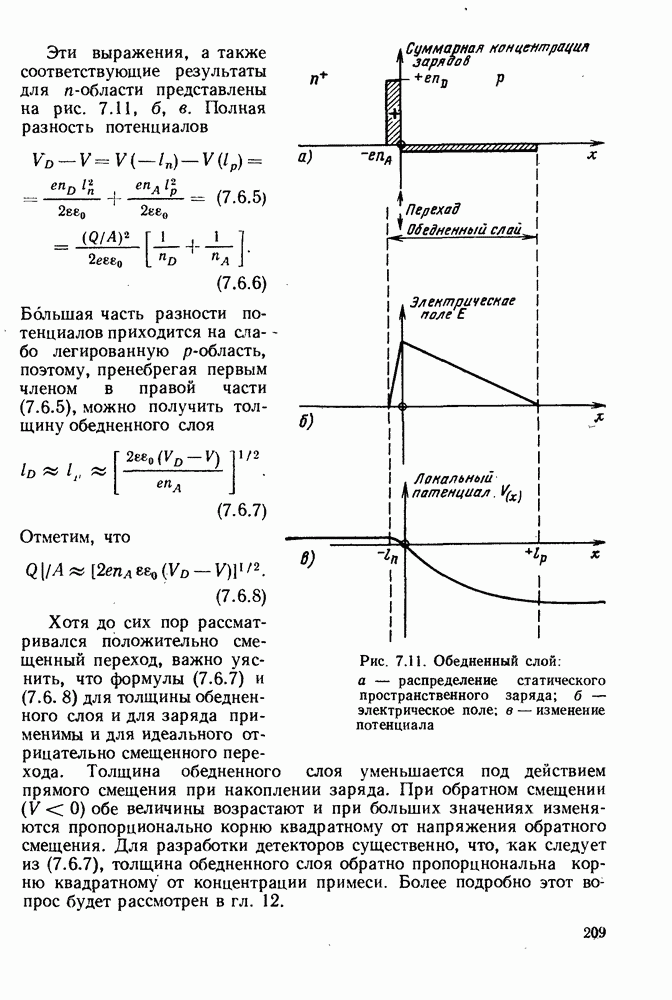
Рисунок 2.1, а иллюстрирует явление преломления света на границе раздела двух сред с разными показателями преломления, которое подчиняется закону Снелля, сформулированному в 1621 г. На рисунке изображен луч света, который проходит сквозь среду с более высоким показателем преломления  и попадает в среду с меньшим показателем преломления
и попадает в среду с меньшим показателем преломления  Если выполняются условия
Если выполняются условия  то справедливо следующее соотношение:
то справедливо следующее соотношение:

где  — соответственно углы падения и преломления.
— соответственно углы падения и преломления.
При называемом критическом угле, т. е. при таком угле падения, при котором угол преломления  (рис. 2.1, б), т. е. при
(рис. 2.1, б), т. е. при 


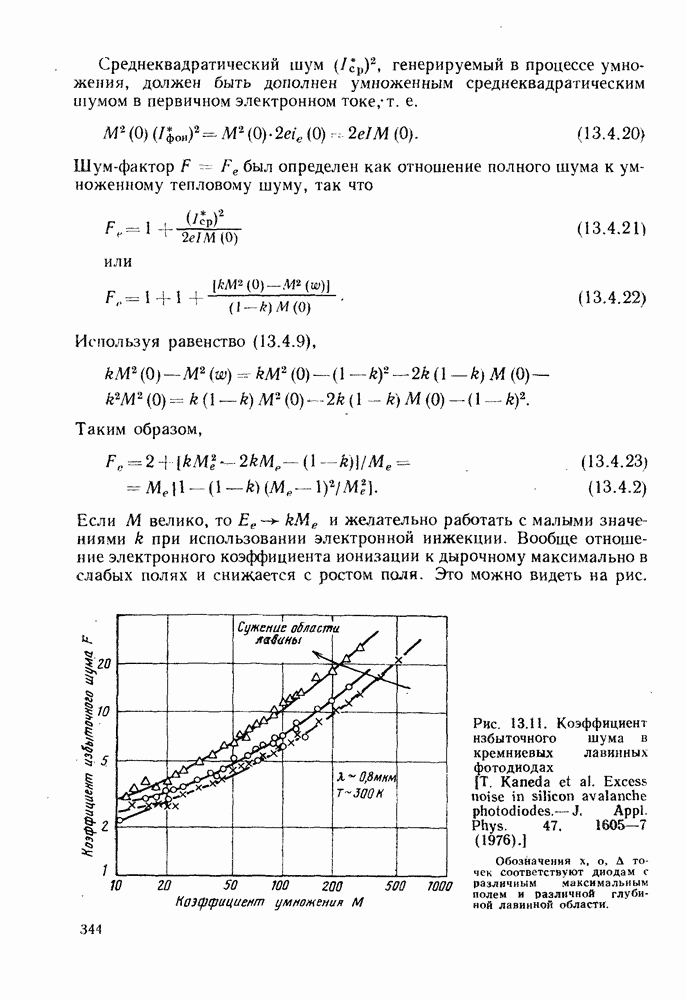
Рис. 2.1. Отражение и полное внутреннее отражение на границе диэлектриков: а — луч  преломляется в соответствии с законом Снелля; б - луч
преломляется в соответствии с законом Снелля; б - луч  критический луч; в — луч
критический луч; в — луч  претерпевает полное внутреннее отражение на границе диэлектриков
претерпевает полное внутреннее отражение на границе диэлектриков
Если угол падения  (рис. 2.1, в), имеет место явление полного внутреннего отражения, не сопровождающееся какими-либо потерями на границе раздела, т. е.
(рис. 2.1, в), имеет место явление полного внутреннего отражения, не сопровождающееся какими-либо потерями на границе раздела, т. е. 
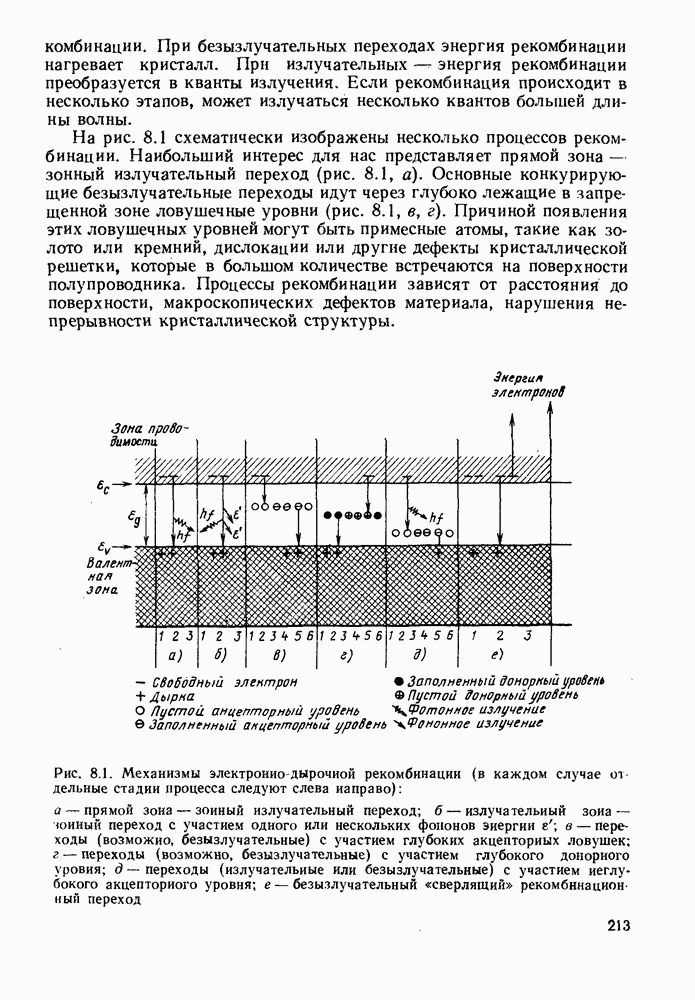
Рассмотрим теперь цилиндрическое стеклянное волокно, состоящее из внутренней сердцевины с показателем преломления  и окружающей ее оболочки с показателем преломления
и окружающей ее оболочки с показателем преломления  причем здесь также выполняется условие
причем здесь также выполняется условие  Торец волокна срезан под прямым углом к его оптической оси. На рис. 2.2 изображен луч, входящий в волокно с торца из окружающего волокно воздуха (с показателем преломления
Торец волокна срезан под прямым углом к его оптической оси. На рис. 2.2 изображен луч, входящий в волокно с торца из окружающего волокно воздуха (с показателем преломления  ). Этот луч будет распространяться вдоль волокна путем многократных отражений от границы сердцевина — оболочка и не будет ослабляться при условии, что угол падения луча на границу разде-
). Этот луч будет распространяться вдоль волокна путем многократных отражений от границы сердцевина — оболочка и не будет ослабляться при условии, что угол падения луча на границу разде-

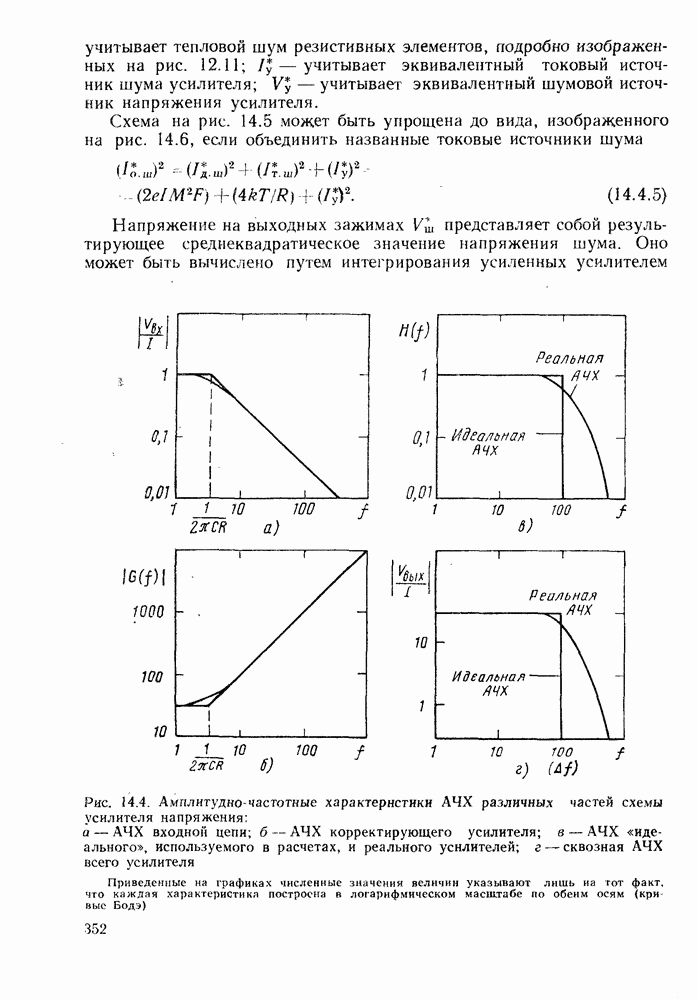
Рис. 2.2. Распространение света в оптическом волокне:  осевой луч,
осевой луч,  луч, распространяющийся под критическим углом для поверхности
луч, распространяющийся под критическим углом для поверхности  луч
луч  входит в волокно под углом больше критического и поэтому не отражается, а вводится в оболочку. Все лучи, падающие на торец волокна под углом, меньшим
входит в волокно под углом больше критического и поэтому не отражается, а вводится в оболочку. Все лучи, падающие на торец волокна под углом, меньшим  будут распространяться в сердцевнне волокна. Очевидно, что лучи, распространяющиеся в сердцевине, в зависимости от
будут распространяться в сердцевнне волокна. Очевидно, что лучи, распространяющиеся в сердцевине, в зависимости от  угла падения будут проходить различные расстояния, причем эти расстояния будут изменяться от I для осевого луча до
угла падения будут проходить различные расстояния, причем эти расстояния будут изменяться от I для осевого луча до  для самого наклонного (критический луч
для самого наклонного (критический луч  где
где  расстояние по осн волокна
расстояние по осн волокна
 будет больше критического угла
будет больше критического угла  Для выполнения этого условия необходимо, чтобы угол наклона луча к оптической оси волокна
Для выполнения этого условия необходимо, чтобы угол наклона луча к оптической оси волокна  был меньше
был меньше  а угол падения а луча на торец волокна был менее определенной величины
а угол падения а луча на торец волокна был менее определенной величины  Для определения величины углов
Для определения величины углов  воспользуемся законом Снелля, приняв
воспользуемся законом Снелля, приняв

При угле падения, равном критическому,

Воспользуемся выражением (2.1.2) и выразим  через показатели преломления сердцевины и оболочки
через показатели преломления сердцевины и оболочки

Введем обозначения

В результате получим

Чем больше угол  тем большая часть падающего на торец волокна света может быть введена в волокно и будет в нем распространяться за счет полного внутреннего отражения. По аналогии с термином, используемым в оптике для определения способности микрообъективов собирать свет, величину
тем большая часть падающего на торец волокна света может быть введена в волокно и будет в нем распространяться за счет полного внутреннего отражения. По аналогии с термином, используемым в оптике для определения способности микрообъективов собирать свет, величину  называют числовой апертурой
называют числовой апертурой  волокна. Таким образом, подставив
волокна. Таким образом, подставив  находим числовую апертуру волокна
находим числовую апертуру волокна

Покажем сначала, что только часть света (пропорциональная  излучаемая малоразмерным диффузным источником, помещенным на оптической оси волокна вблизи его торца, может быть введена в волокно и, следовательно, будет в нем распространяться.
излучаемая малоразмерным диффузным источником, помещенным на оптической оси волокна вблизи его торца, может быть введена в волокно и, следовательно, будет в нем распространяться.
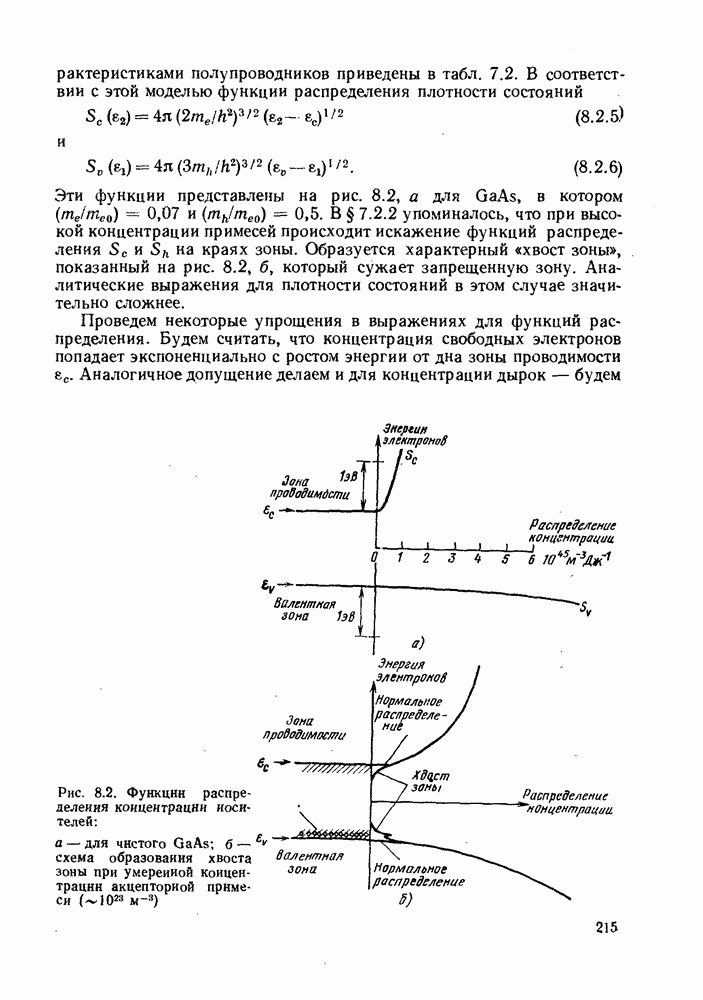
Рассмотрим малоразмерный диффузный источник света, например изотропный (ламбертовский) излучатель, изображенный на рис. 2.3. В этом случае мощность, излучаемая в единицу телесного угла в направлении под углом  к нормали к его поверхности, определяется выражением
к нормали к его поверхности, определяется выражением

Полная мощность  излучаемая таким источником, находится интегрированием
излучаемая таким источником, находится интегрированием  по всем направлениям:
по всем направлениям:

Однако мощность  введенная в волокно, диаметр сердцевины которого больше диаметра источника, определяется следующим интегралом:
введенная в волокно, диаметр сердцевины которого больше диаметра источника, определяется следующим интегралом:

Отсюда ясно, что для того, Чтобы ввести в волокно как можно больше света, необходимо обеспечить большие значения величии  Очевидно, что лучшее, что может быть сделано — это использовать для изготовления волокна стекло с большим показателем преломления и не покрывать его оболочкой. В этом случае полное внутреннее отражение будет происходить на поверхности стекло-воздух совершенно аналогично опыту Тиндалла с водяной струей, где оно наблюдалось на границе вода-воздух. Жгуты из непокрытых оболочкой стеклянных волокон используются в некоторых системах передачи оптической информации на короткие расстояния. При использовании таких жгутов возникают две проблемы. Первая состоит в том, что при полном внутреннем отражении часть волны света проникает сквозь отражающую поверхность. Она называется затухающей волной. Ее амплитуда уменьшается экспоненциально с увеличением расстояния от поверхности волокна и поэтому обычно не может распространяться в
Очевидно, что лучшее, что может быть сделано — это использовать для изготовления волокна стекло с большим показателем преломления и не покрывать его оболочкой. В этом случае полное внутреннее отражение будет происходить на поверхности стекло-воздух совершенно аналогично опыту Тиндалла с водяной струей, где оно наблюдалось на границе вода-воздух. Жгуты из непокрытых оболочкой стеклянных волокон используются в некоторых системах передачи оптической информации на короткие расстояния. При использовании таких жгутов возникают две проблемы. Первая состоит в том, что при полном внутреннем отражении часть волны света проникает сквозь отражающую поверхность. Она называется затухающей волной. Ее амплитуда уменьшается экспоненциально с увеличением расстояния от поверхности волокна и поэтому обычно не может распространяться в

Рис. 2.3. Диффузный источник света:
Мощность, излучаемая в малый телесный угол  в иаправлеиии угла
в иаправлеиии угла  по перпендикуляру к излучающей поверхности, равна
по перпендикуляру к излучающей поверхности, равна  Элементарное угловое кольцо, радиус которого стягивает угол
Элементарное угловое кольцо, радиус которого стягивает угол  ширииа стягивает 60, само кольцо стягивает телесный угол
ширииа стягивает 60, само кольцо стягивает телесный угол 
среде с более низким показателем преломления. Однако наличие всяких неровностей и неоднородностей на отражающей поверхности может привести к преобразованию затухающей волны в волну распространения. В жгуте из волокон без оболочек условия на отражающей поверхности неизбежно и неконтролируемо изменяются, поскольку отдельные волокна входят в контакт друг с другом и окружающей средой. В результате значительная доля распространяющейся в волокнах мощности выводится их них, что и приводит к большим потерям.
Вторая проблема связана с тем, что любой короткий световой импульс, введенный в волокно, состоит из ряда лучей, которые распространяются вдоль оси волокна и по траекториям, очень наклоненным к ней. На рис. 2.2 изображены два крайних луча, образующих конус входных лучей. В данном случае показатель преломления среды можно рассматривать как меру скорости распространения света  в этой среде, т. е.
в этой среде, т. е.

Следовательно, осевой луч будет проходить расстояние вдоль волокна за время  в то время как наиболее наклонный луч, который еще может распространяться в волокне, то же самое расстояние пройдет за время, определяемое соотношением
в то время как наиболее наклонный луч, который еще может распространяться в волокне, то же самое расстояние пройдет за время, определяемое соотношением

Таким образом, если оба эти луча введены в волокно одновременно, то на выходе волокна они окажутся разделенными во времени на интервал  определяемый формулой
определяемый формулой

В результате световой импульс, содержащий лучи под всеми возможными углами, окажется размытым во времени в процессе своего распространения по волокну на величину, определяемую выражением

Это уширение светового импульса при его распространении по волокну известно как межмодовая (многолучевая) временная дисперсия волокна. Для стеклянного волокна без оболочки формула (2.1.17) дает следующее значение этой дисперсии 
В данном случае в волокне будет распространяться свет, падающий на торец волокна под всеми углами.
Покрытие сердцевины волокна стеклянной оболочкой, имеющей немного меньший показатель преломления, приводит к возникновению трех эффектов:
1) если покрытие имеет высокое качество и толщину, достаточную для удержания затухающей волны, то оно существенно уменьшает потери;
2) уменьшению временной дисперсии;
3) уменьшению вводимой в волокно мощности света.
Если  то выражение (2.1.17) для временной дисперсии волокна можно преобразовать к виду
то выражение (2.1.17) для временной дисперсии волокна можно преобразовать к виду

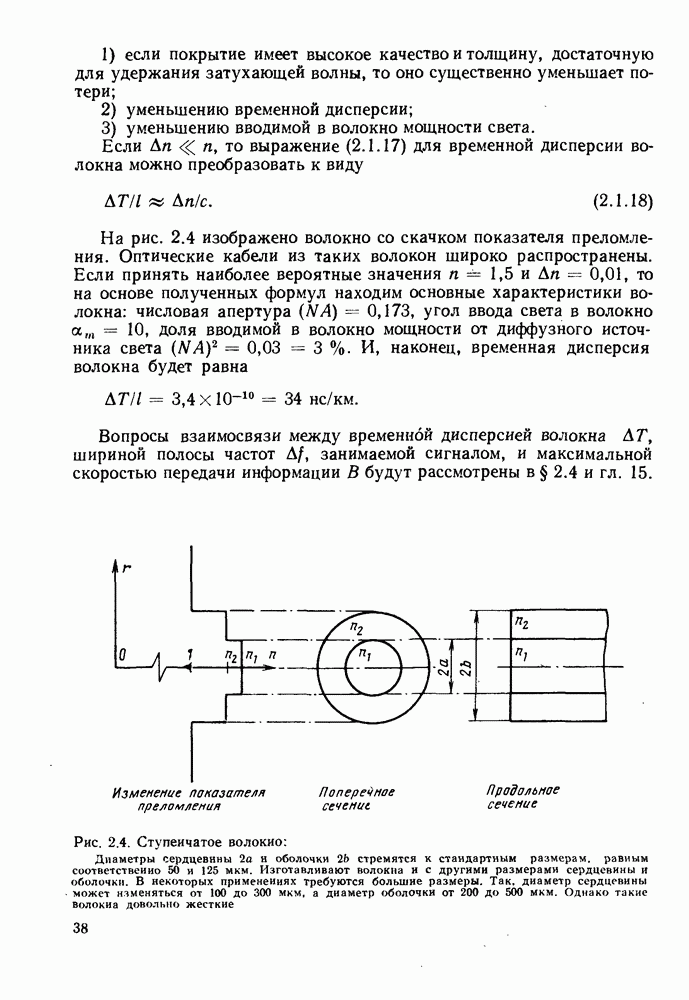
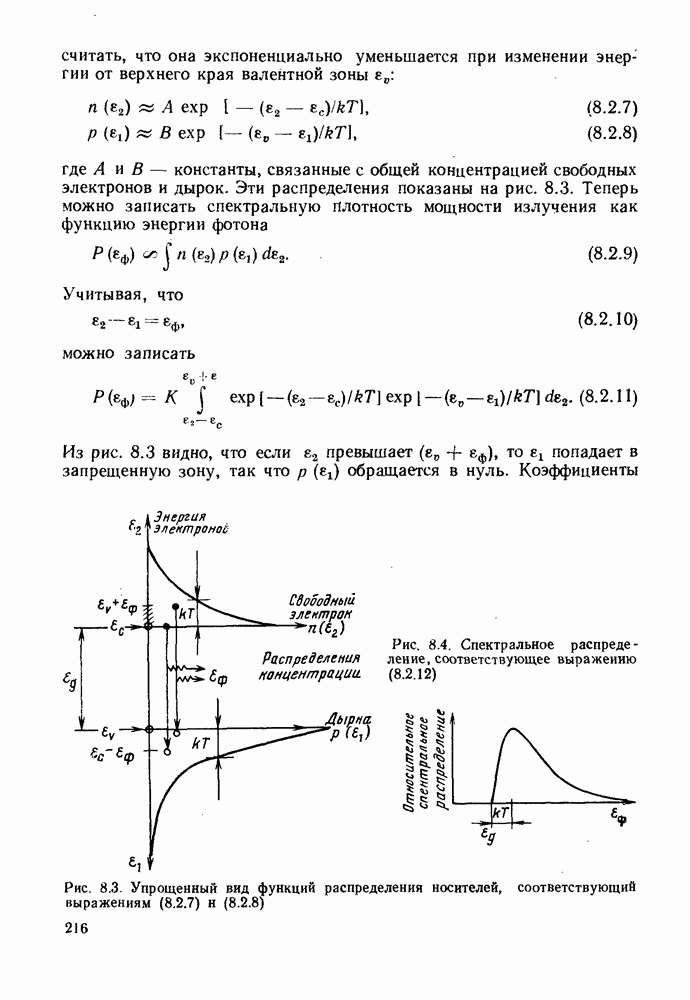
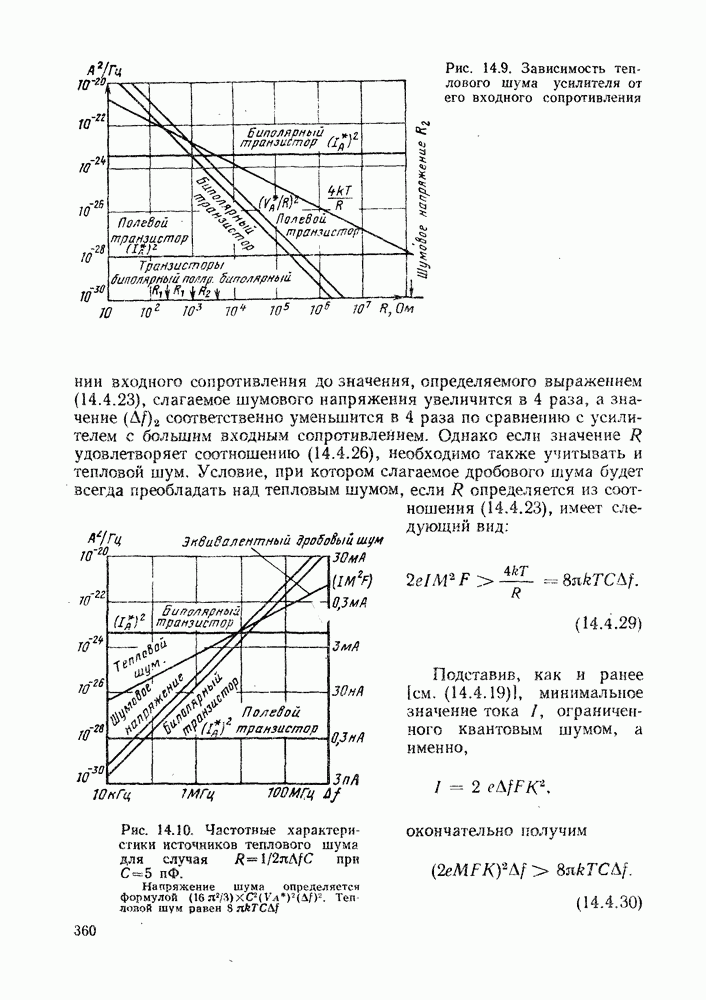
На рис. 2.4 изображено волокно со скачком показателя преломления. Оптические кабели из таких волокон широко распространены. Если принять наиболее вероятные значения  то на основе полученных формул находим основные характеристики волокна: числовая апертура
то на основе полученных формул находим основные характеристики волокна: числовая апертура  угол ввода света в волокно
угол ввода света в волокно  доля вводимой в волокно мощности от диффузного источника света
доля вводимой в волокно мощности от диффузного источника света  наконец, временная дисперсия волокна будет равна
наконец, временная дисперсия волокна будет равна

Вопросы взаимосвязи между временной дисперсией волокна  шириной полосы частот
шириной полосы частот  занимаемой сигналом, и максимальной скоростью передачи информации В будут рассмотрены в § 2.4 и гл. 15.
занимаемой сигналом, и максимальной скоростью передачи информации В будут рассмотрены в § 2.4 и гл. 15.

Рис. 2.4. Ступенчатое волокно: Диаметры сердцевины 2а и оболочки  стремятся к стандартным размерам, равным соответственно 50 и 125 мкм. Изготавливают волокна и с другими размерами сердцевины и оболочки. В некоторых применениях требуются большие размеры. Так, диаметр сердцевины может изменяться от 100 до 300 мкм, а диаметр оболочки от 200 до 500 мкм. Однако такие волокна довольно жесткие
стремятся к стандартным размерам, равным соответственно 50 и 125 мкм. Изготавливают волокна и с другими размерами сердцевины и оболочки. В некоторых применениях требуются большие размеры. Так, диаметр сердцевины может изменяться от 100 до 300 мкм, а диаметр оболочки от 200 до 500 мкм. Однако такие волокна довольно жесткие
Приведем приближенные соотношения между ними, которые, однако, вполне пригодны для большинства применений

откуда

Следовательно, можно сказать, что в рассматриваемом примере произьедение полосы пропускания на расстояние для волокна равно приблизительно 16 МГц-км.
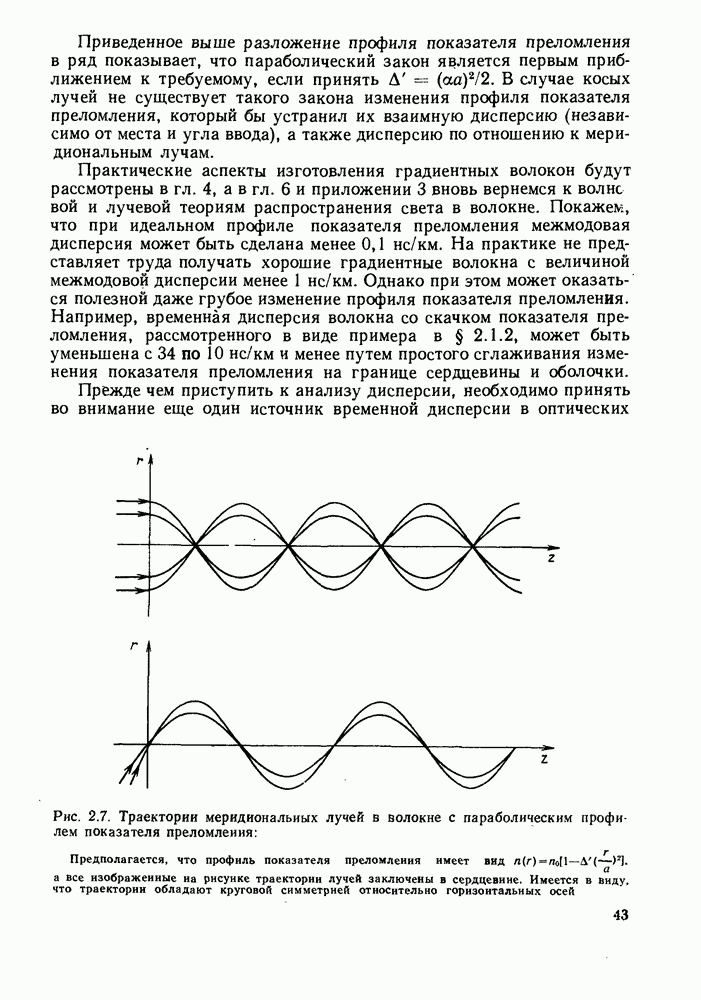
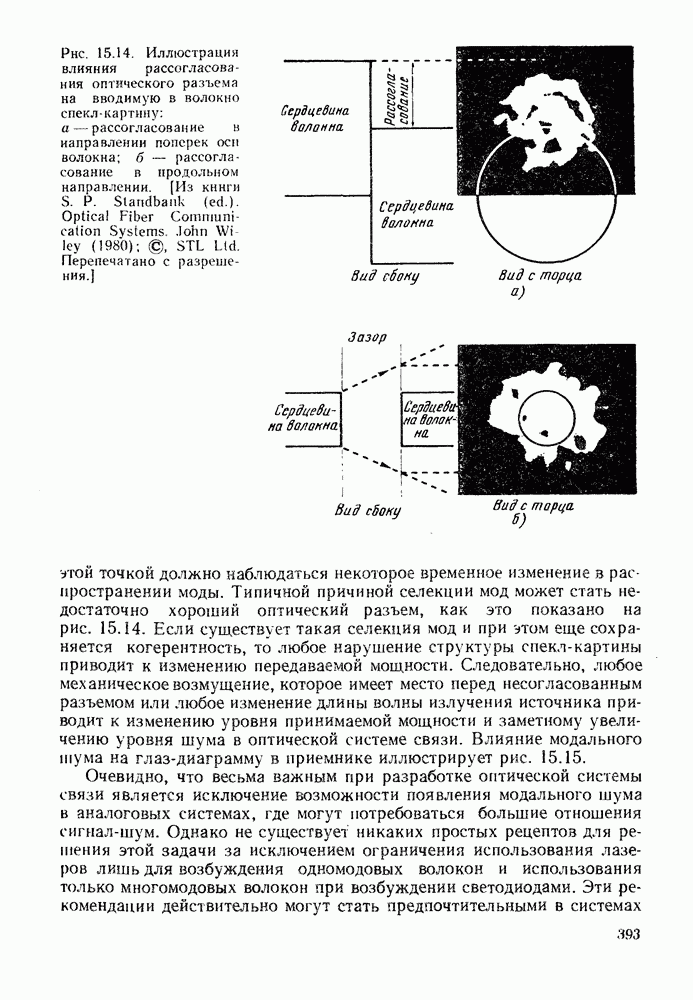
До сих пор рассматривали только такие лучи, которые проходят через ось волокна. Это так называемые меридиональные лучи. Обычно имеются также лучи, которые распространяются в волокне и не удовлетворяют этому условию: они называются косыми лучами. Некоторые из косых лучей сохраняются в сердцевине волокна, даже если они распространяются под очень большими углами к его оси. На практике такие лучи быстро рассеиваются на изгибах и неоднородностях и покидают сердцевину, не внося, таким образом, заметного вклада во временную дисперсию. Однако строгий анализ этого явления сложен.
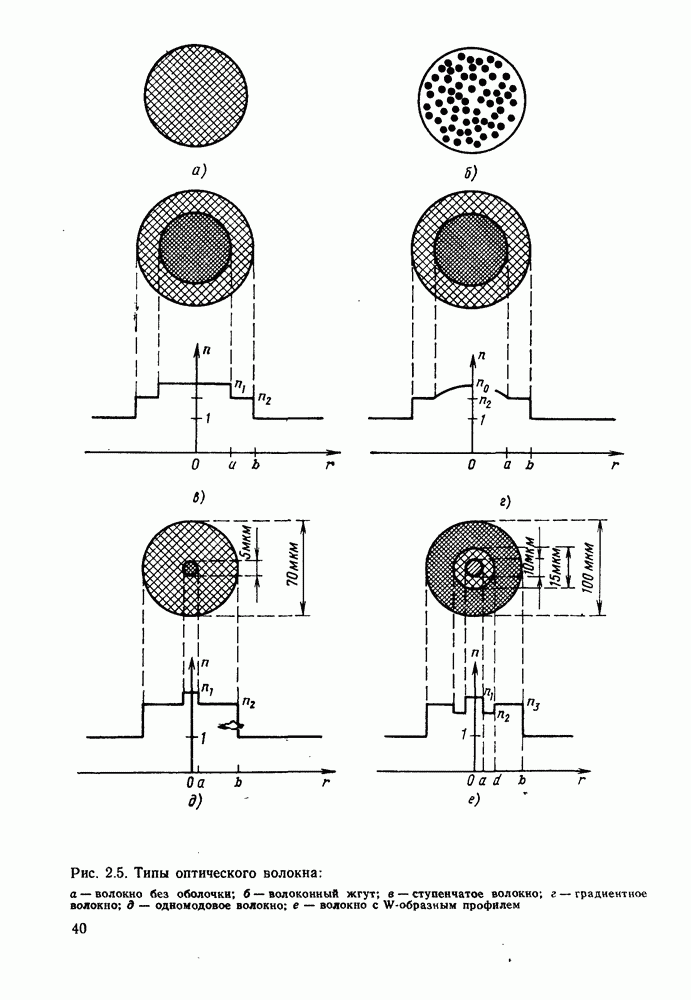
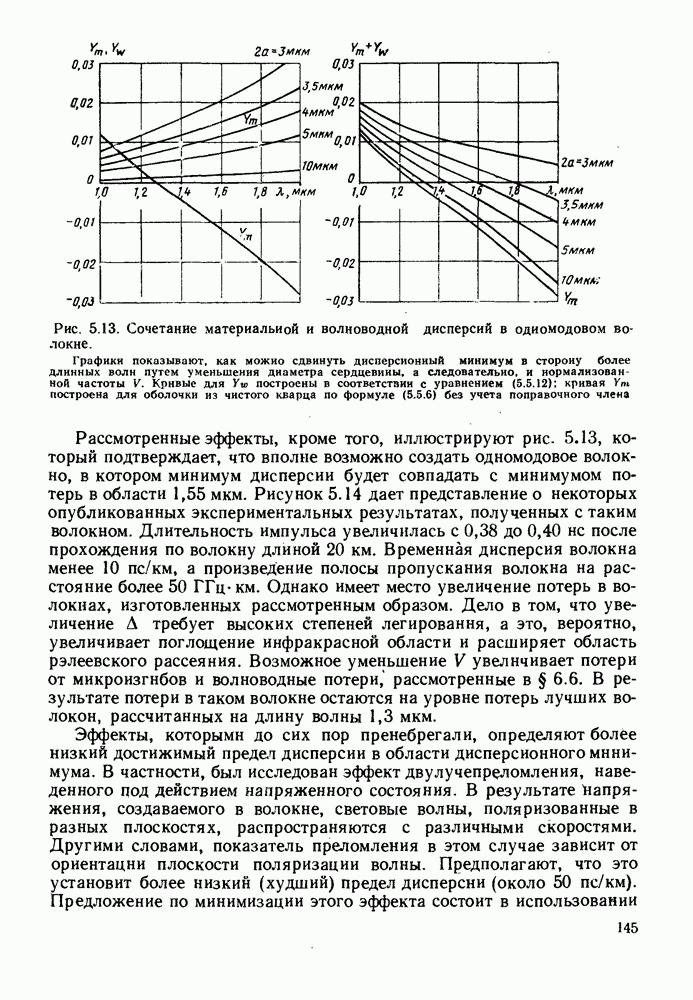
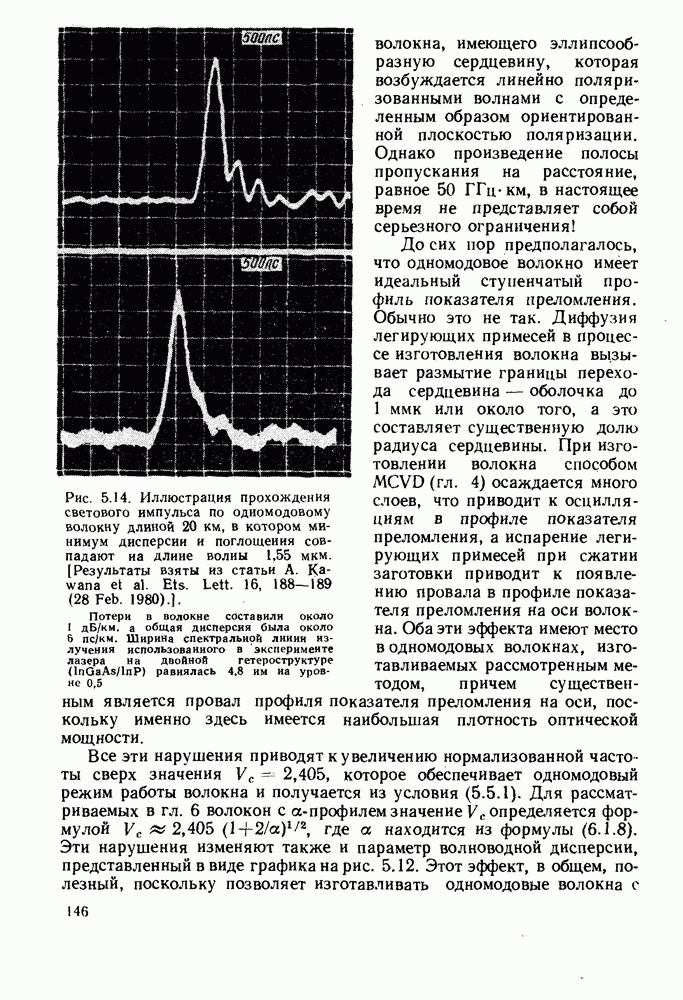
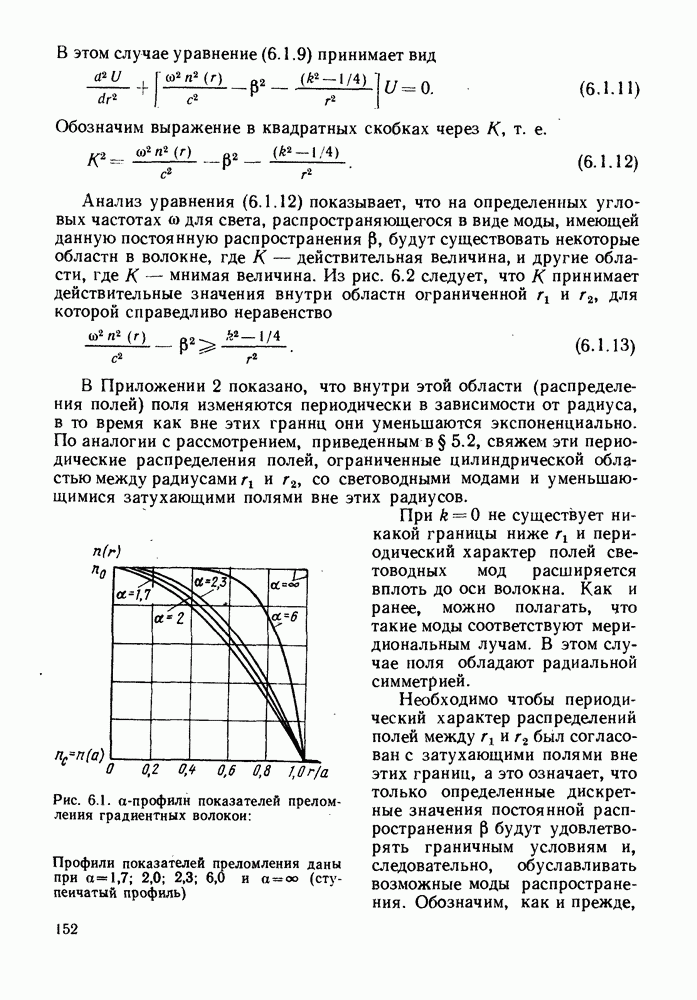
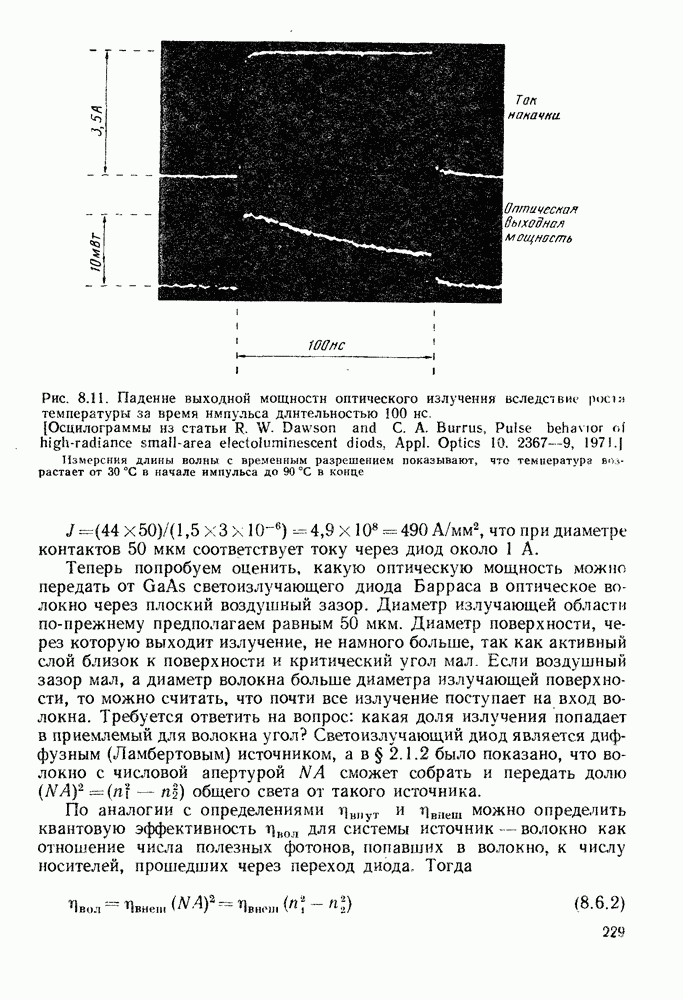
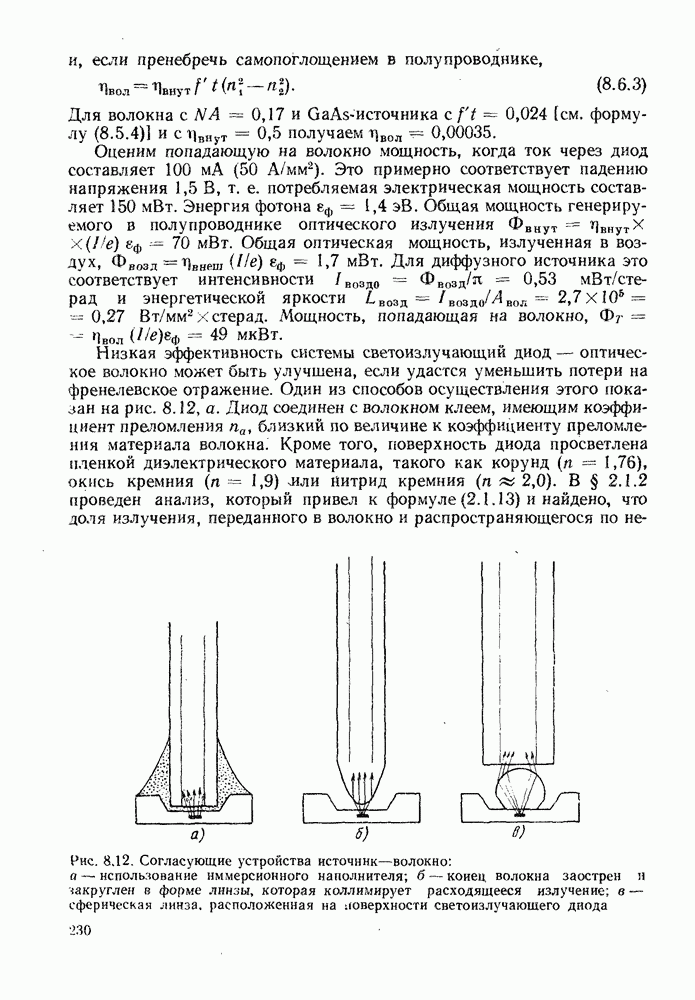
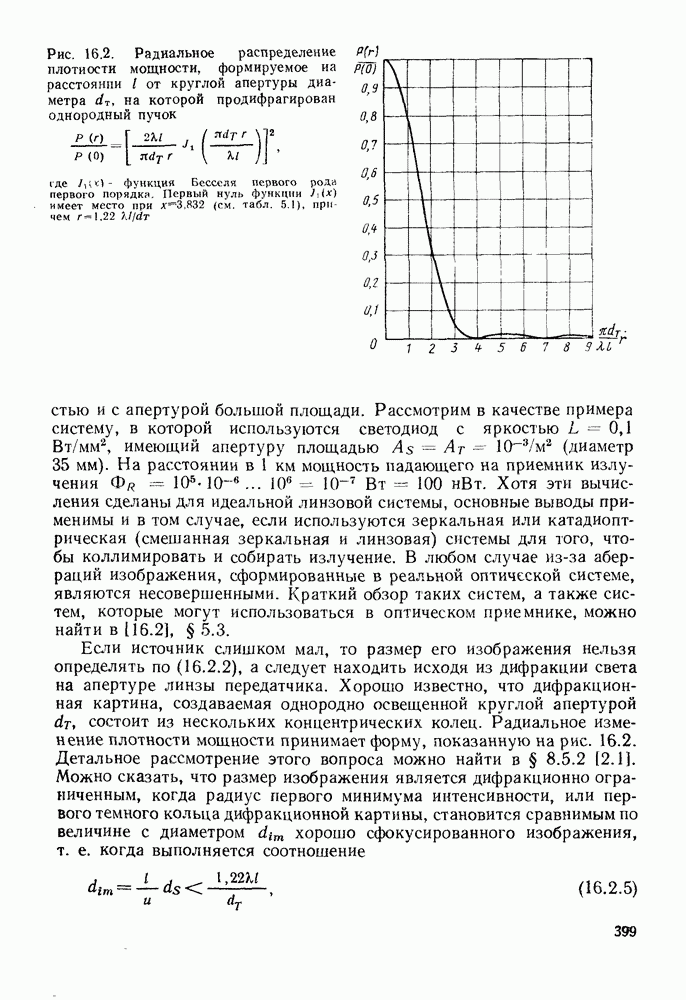
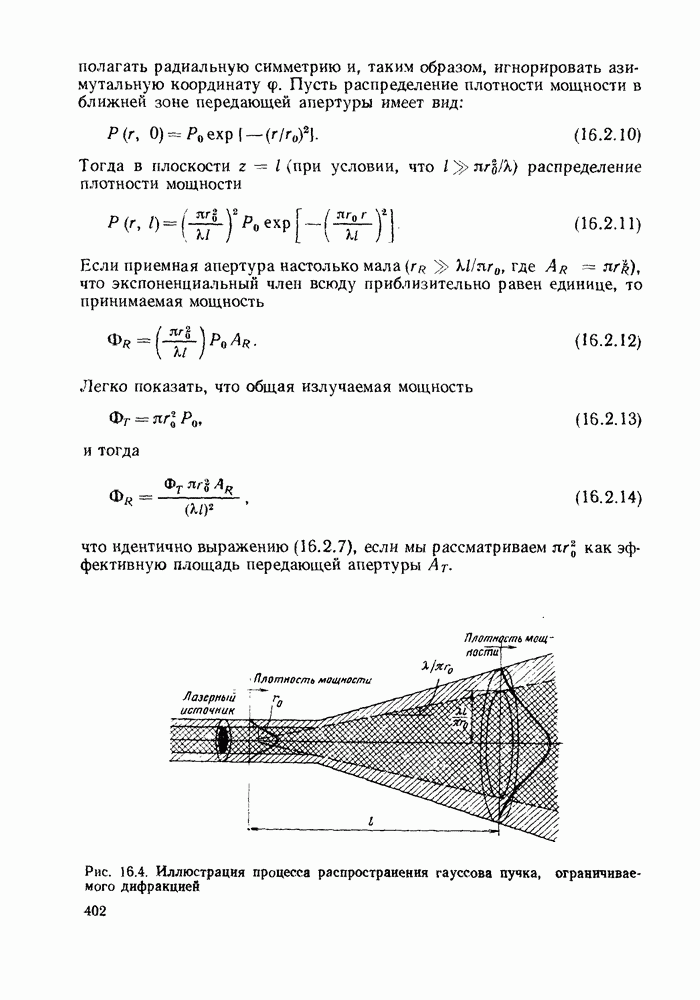
Вопрос о величине оптической мощности, которая может быть эффективно введена в волокно от протяженного источника, рассматривается в гл. 4. Определяемое формулой (2.1.20) произведение полосы пропускания на расстояние на практике оказывается существенно ниже реального. Из-за рассеяния в волокне большинство наклонных лучей испытывают большое затухание и при прохождении большого расстояния имеет место усреднение наклона траекторий, более близких к оси лучей. Происходящие при этом эффекты будут предметом рассмотрения в § 6.6, а здесь отметим, что они приводят к уменьшению дисперсии и в результате в волокнах большой длины она увеличивается пропорционально корню квадратному из длины. Тем не менее дисперсия накладывает строгие ограничения на использование ступенчатых волокон, допуская их применение лишь в сравнительно коротких линиях связи со сравнительно неширокой полосой пропускания. Пример, приведенный в конце гл. 1, подтверждает это. Существует два типа волокон, в которых преодолен этот недостаток (рис. 2.5). Первое из них, так называемое градиентное волокно (рис. 2.5, г), было очень распространено на ранней стадии развития волоконной оптики, и оно будет рассмотрено чуть позже. Изображенное на рис. 2.5, д одномодовое волокно, вероятно, станет основным типом в будущем. Оно будет описано в § 2.3 и гл. 5, где также отмечены и возможные преимущества волокна с W-профилем, изображенного на рис. 2.5, е.

(кликните для просмотра скана)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
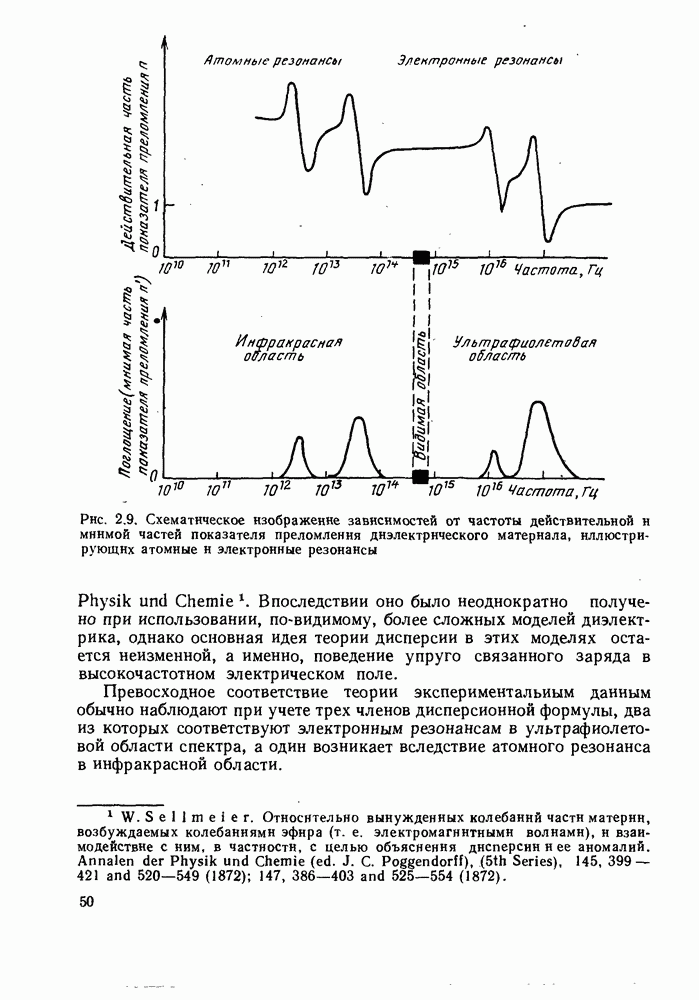
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
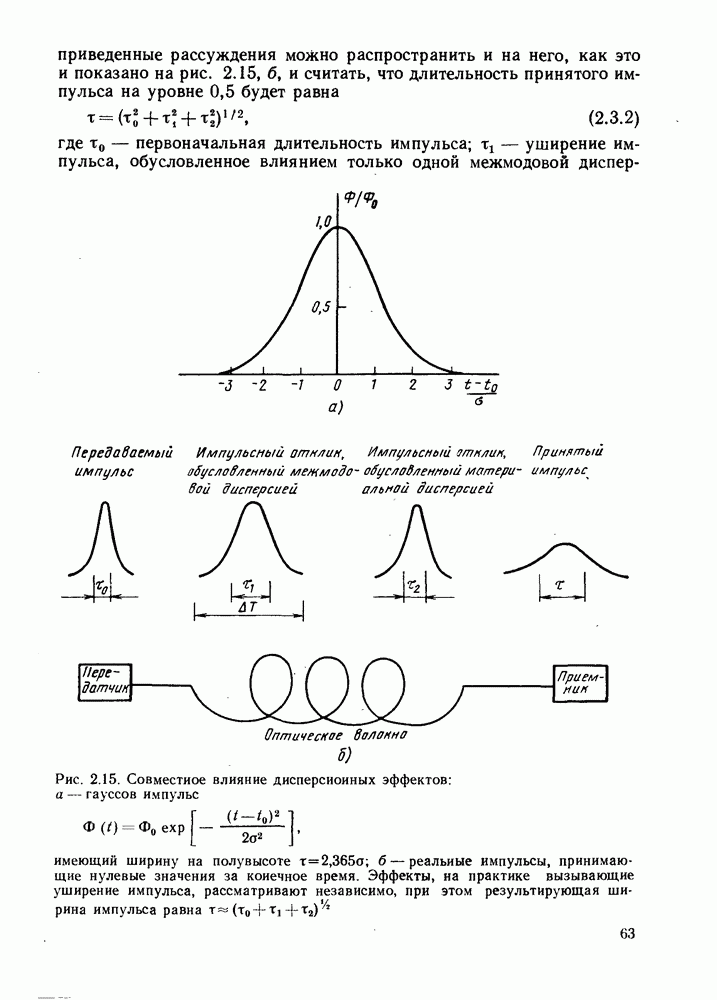
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
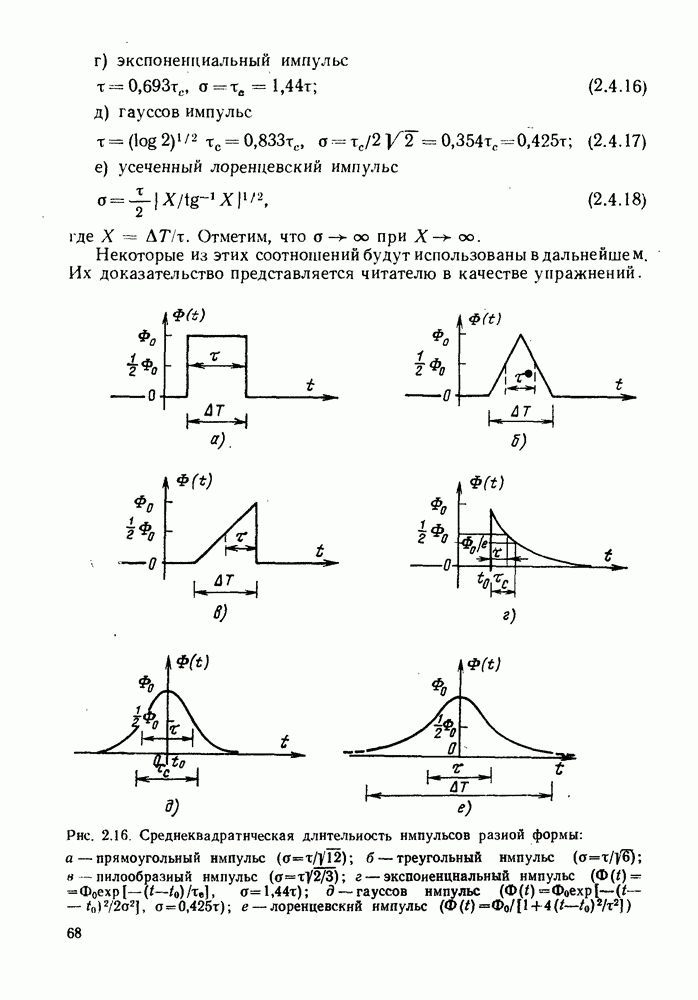
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
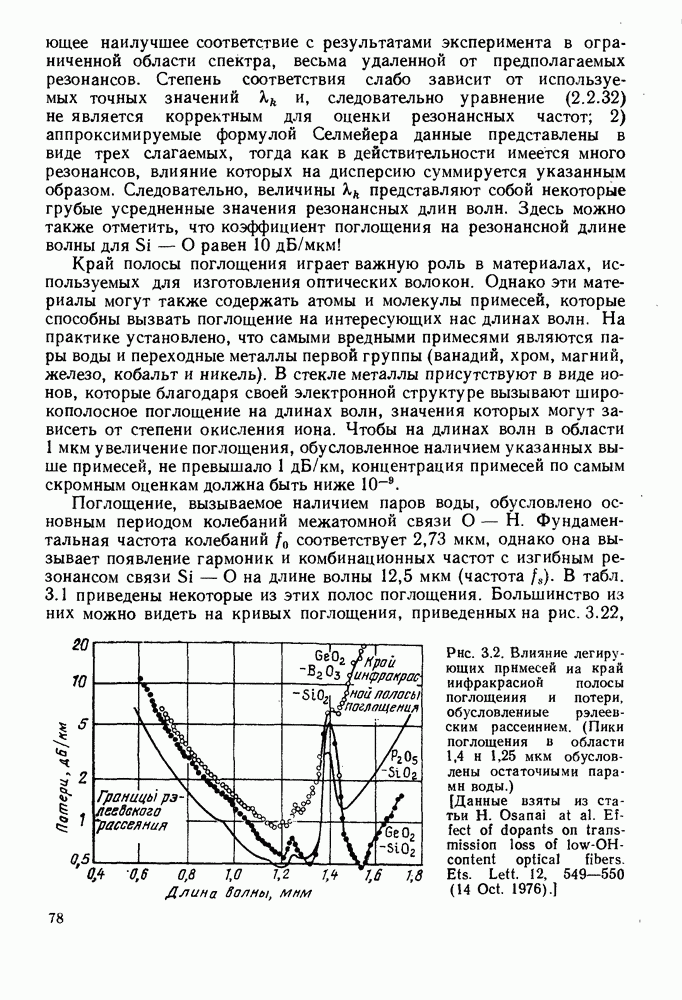
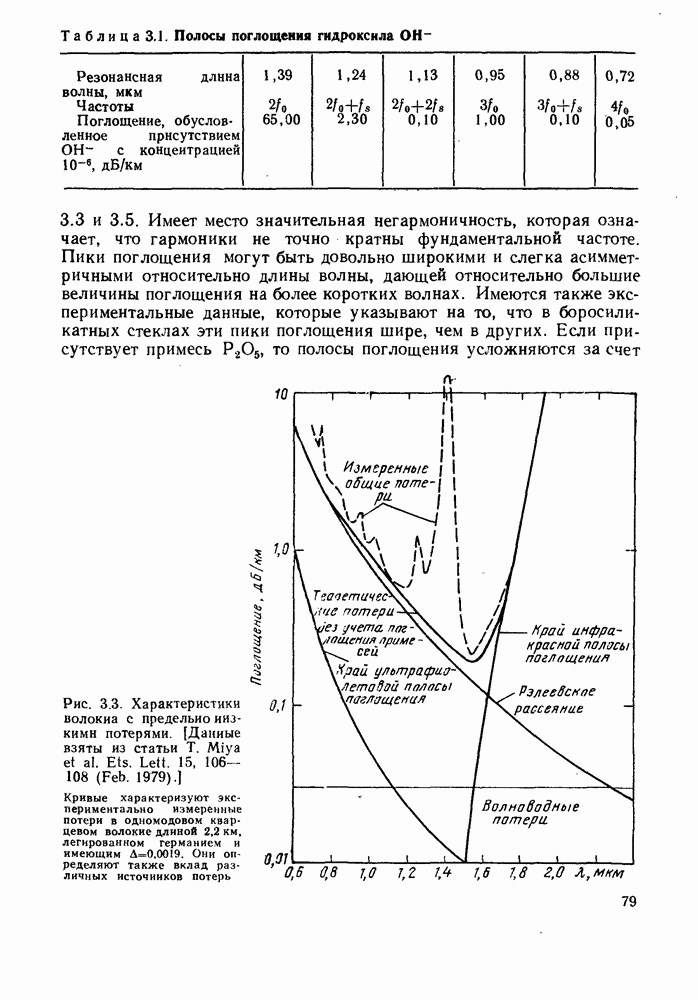
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
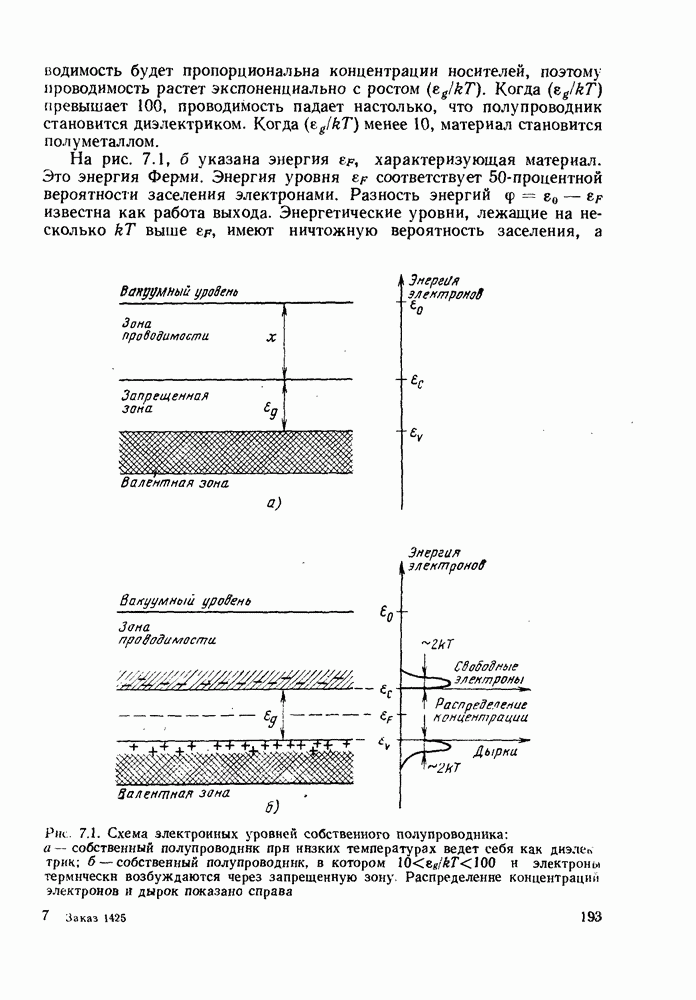
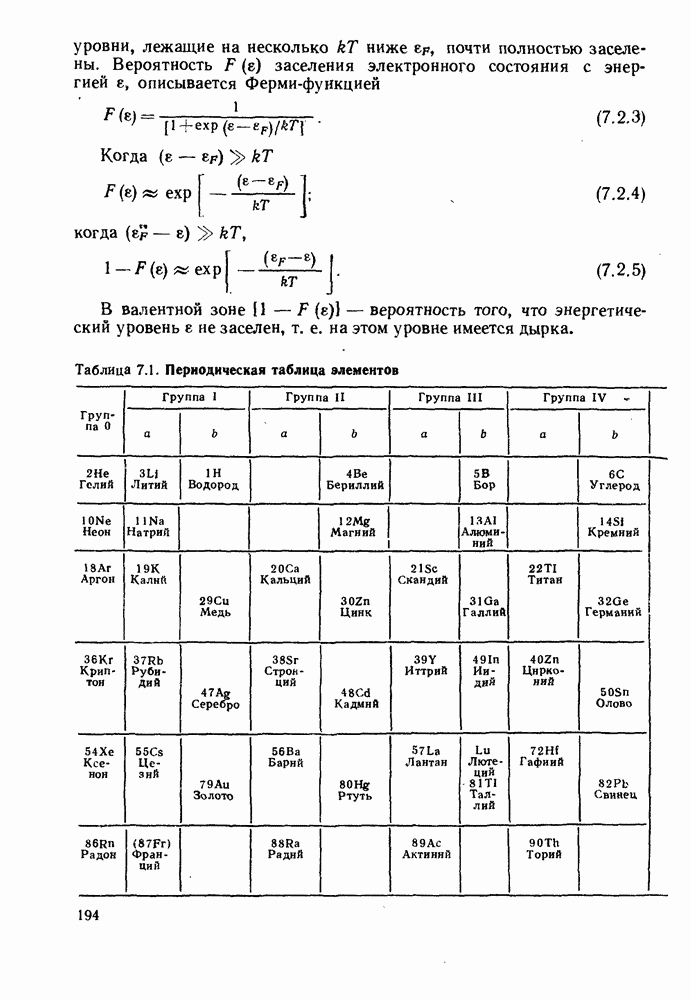
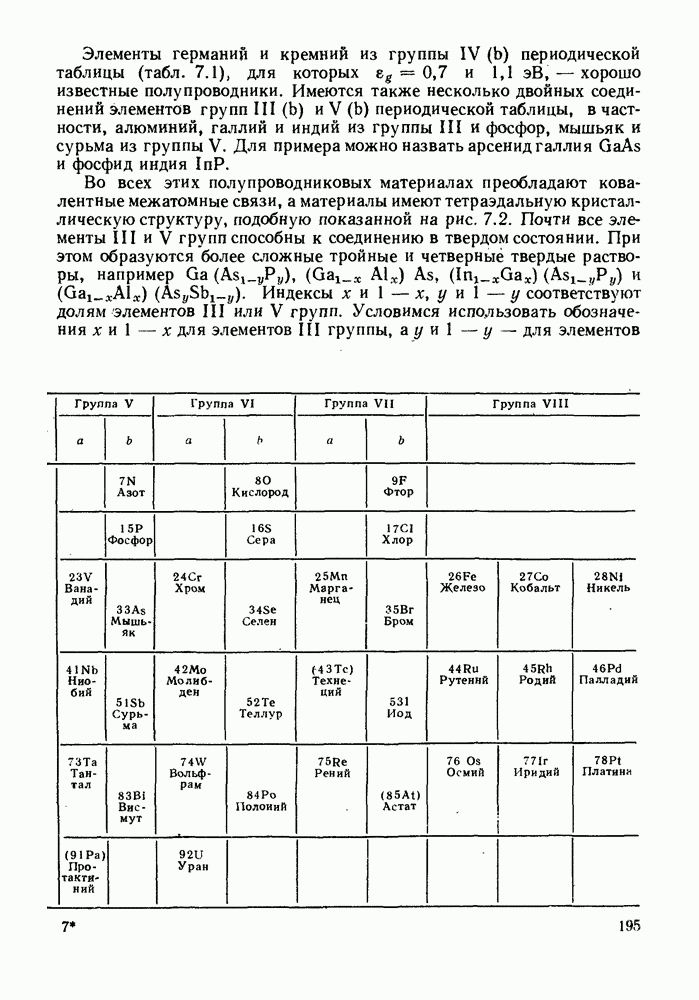
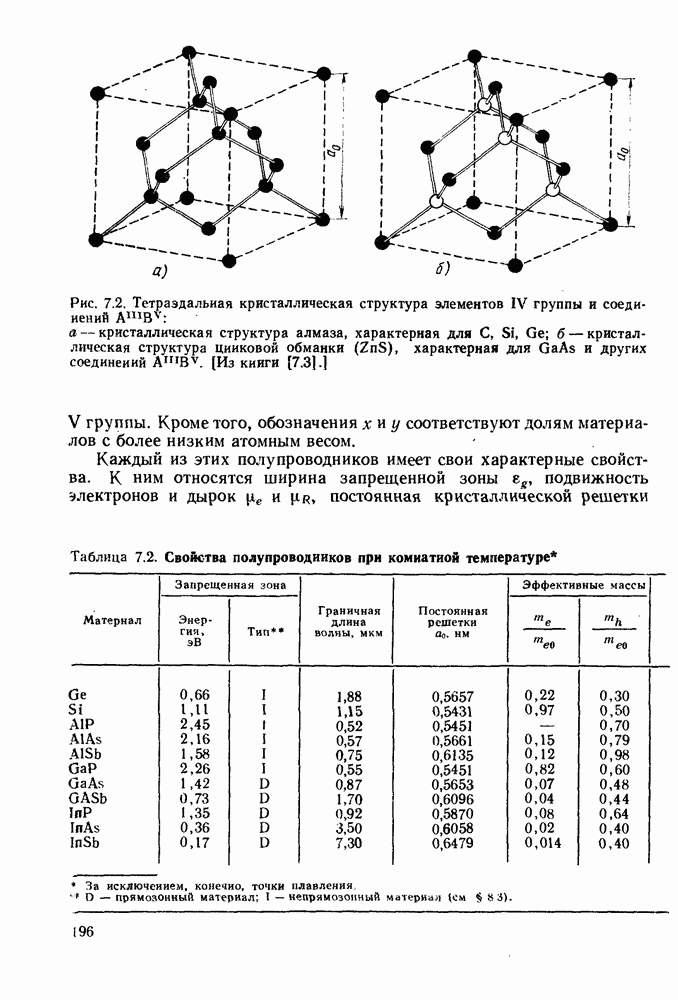
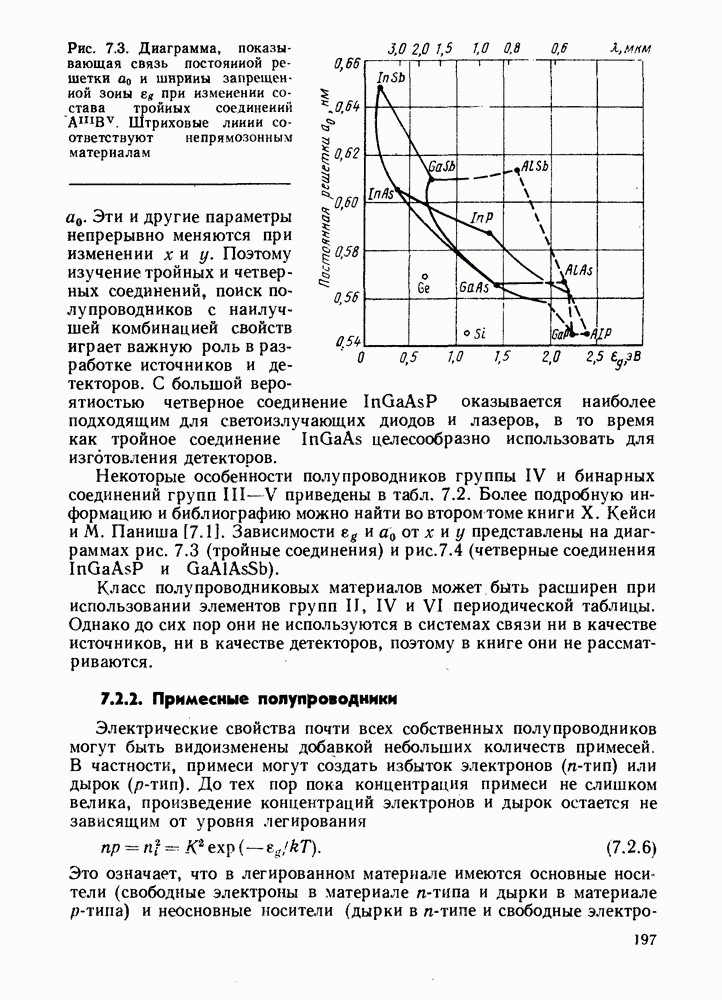
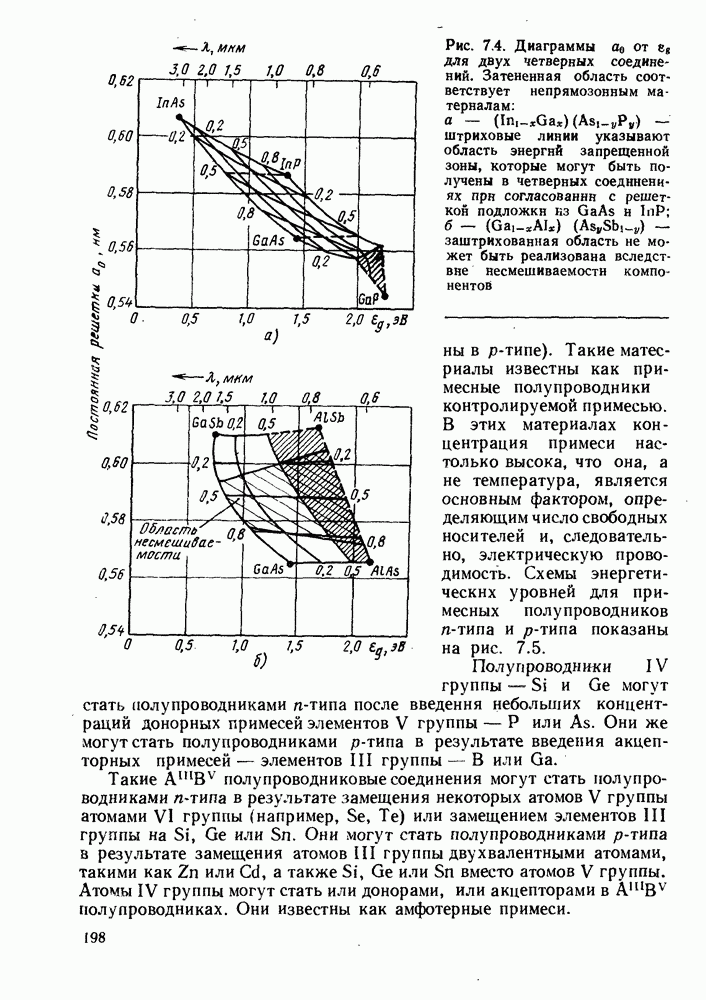
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
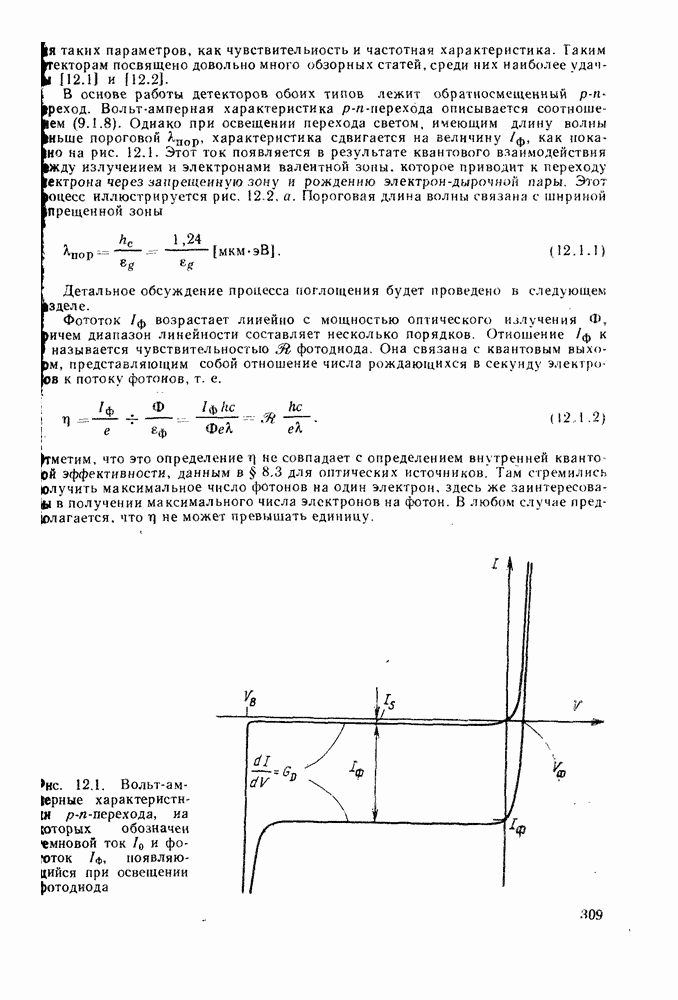
- 7.3. p-n-ПЕРЕХОД
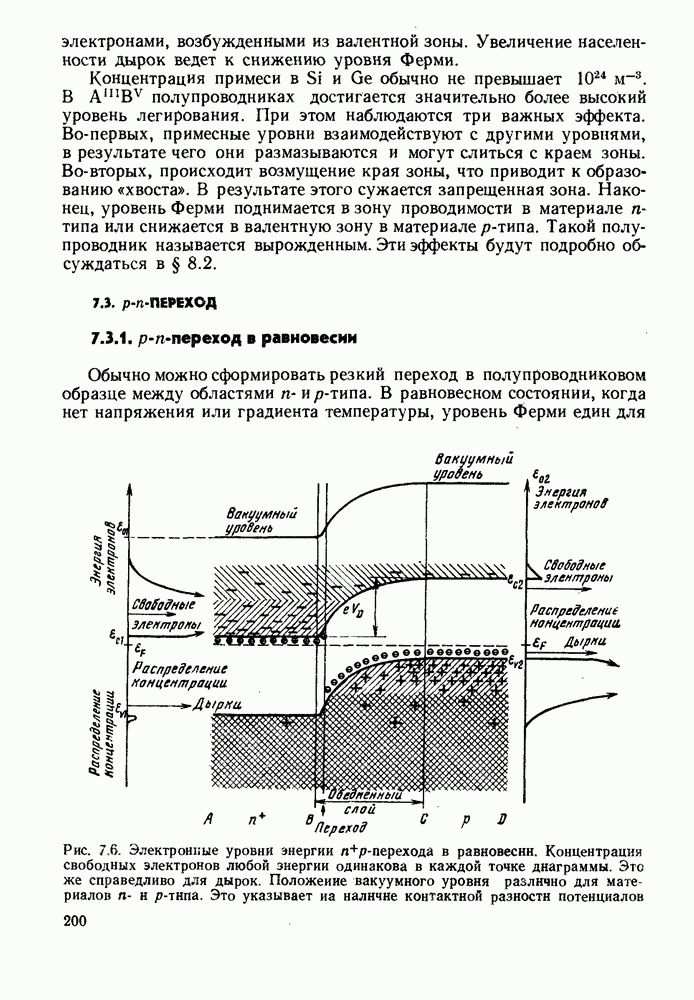
- 7.3.1. p-n-переход в равновесии
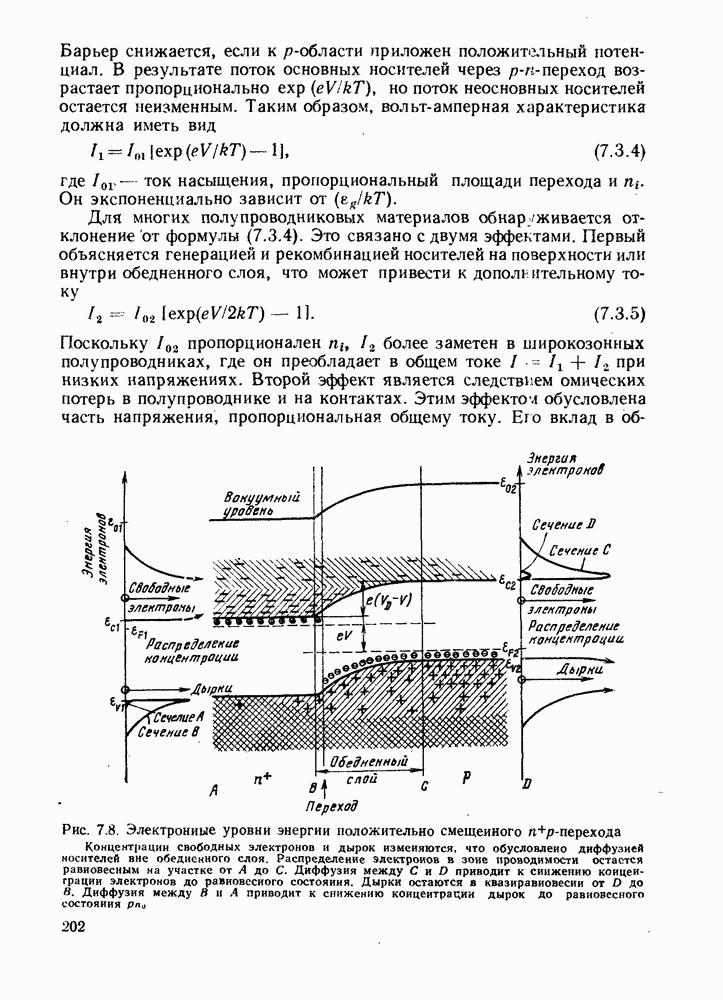
- 7.3.2. Смещенный p-n-переход
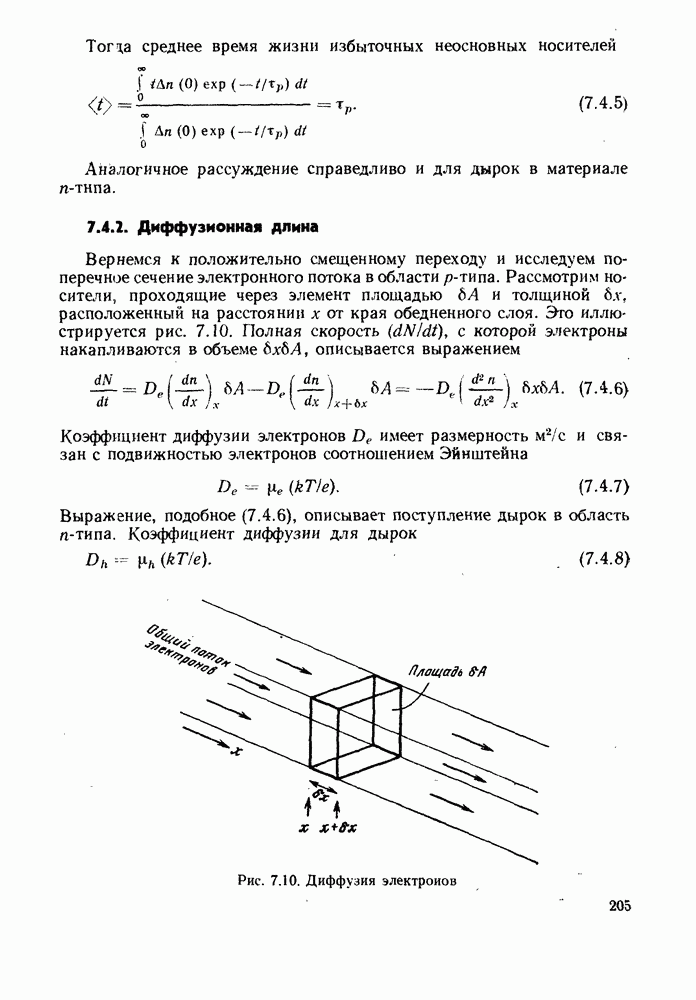
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
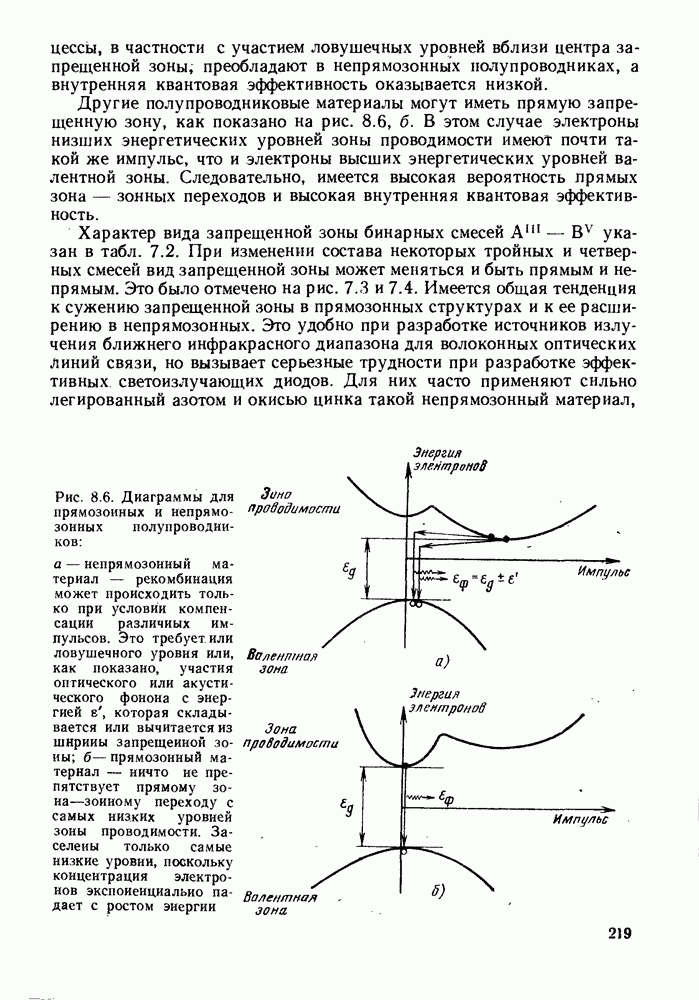
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
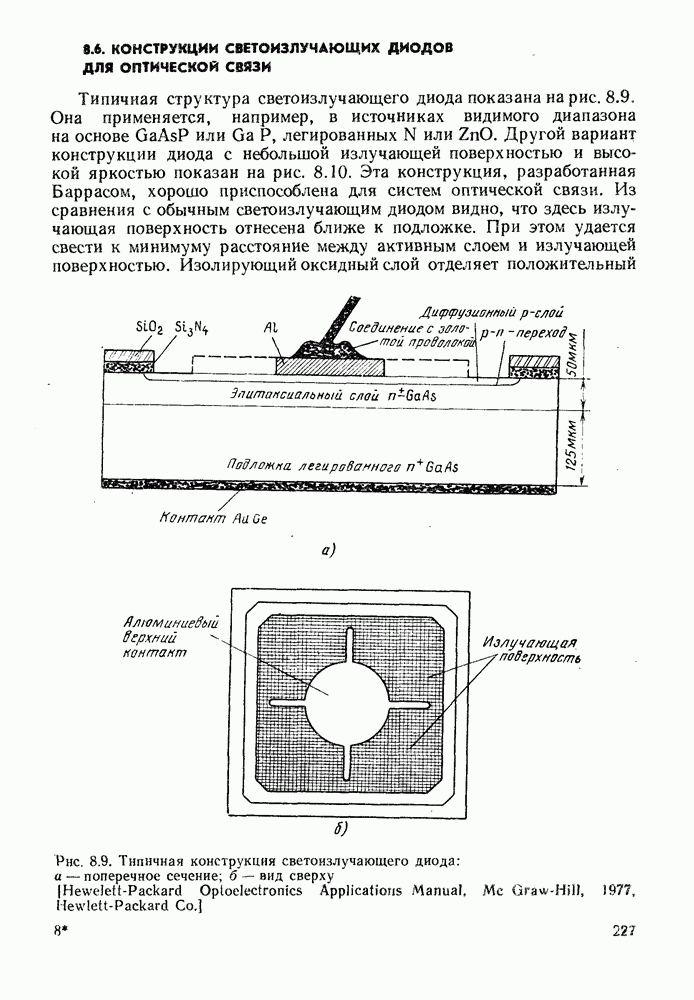
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
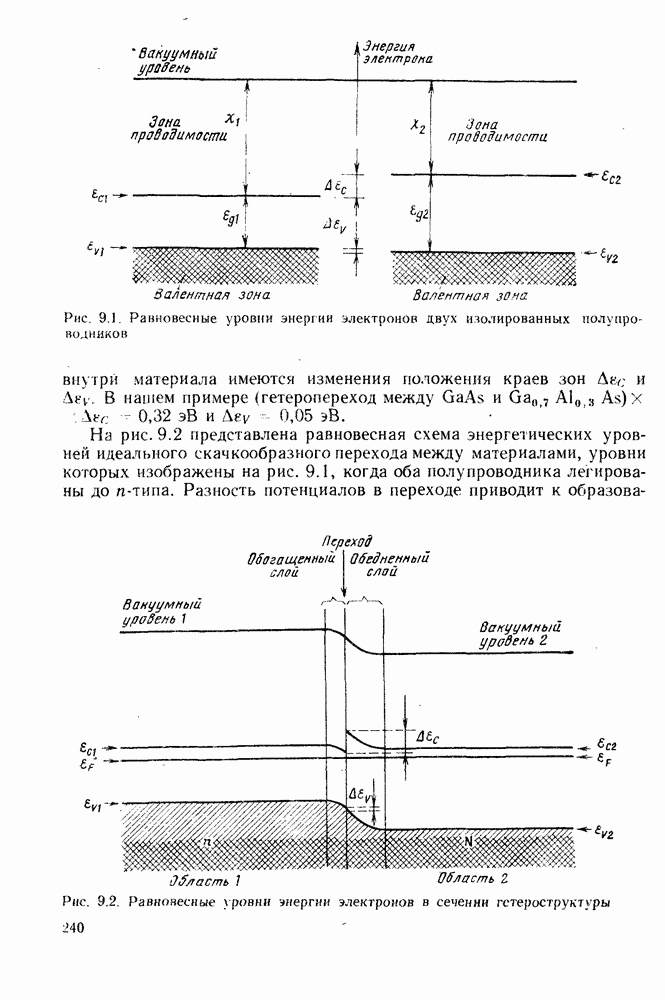
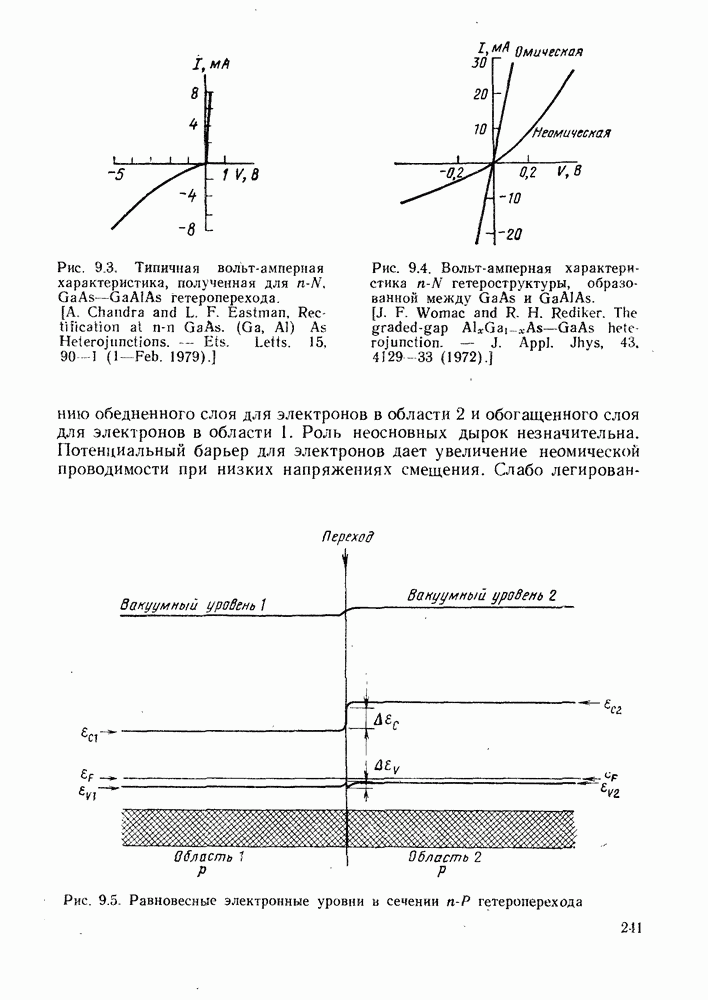
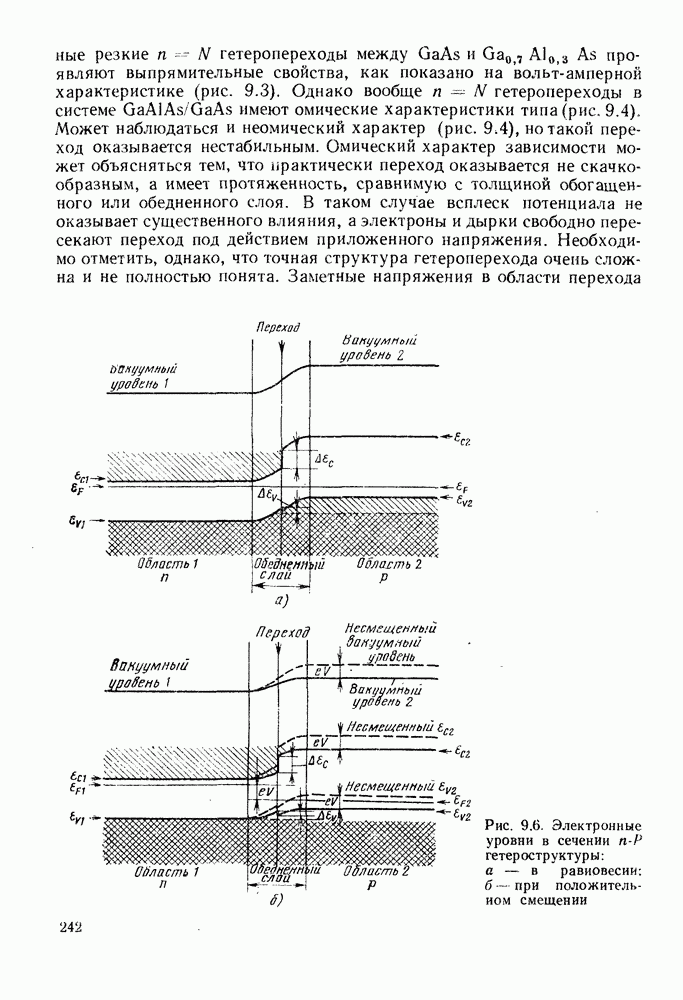
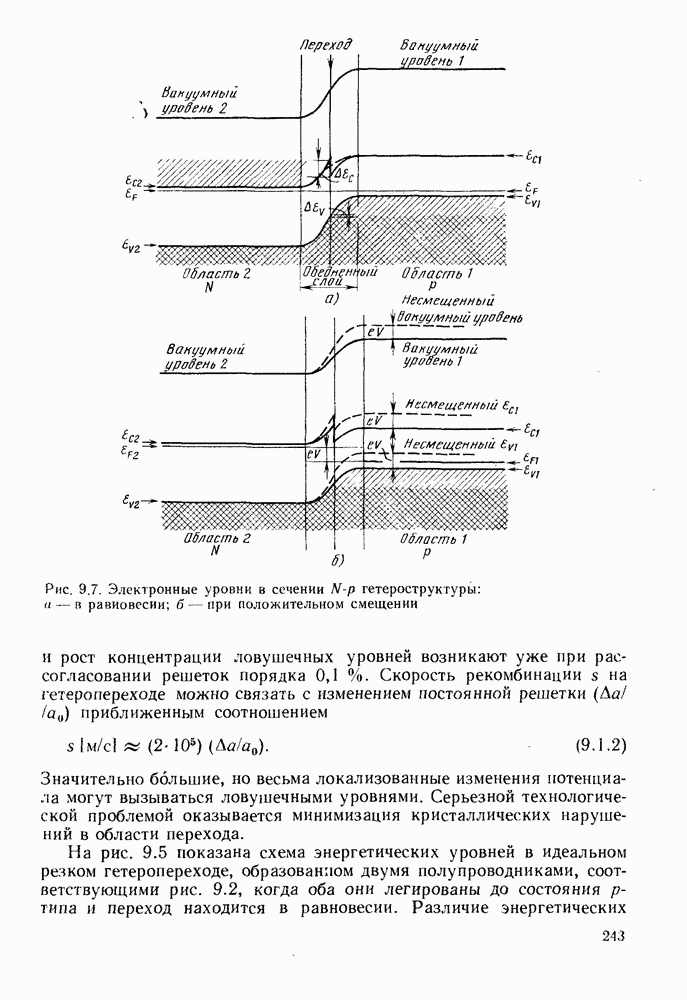
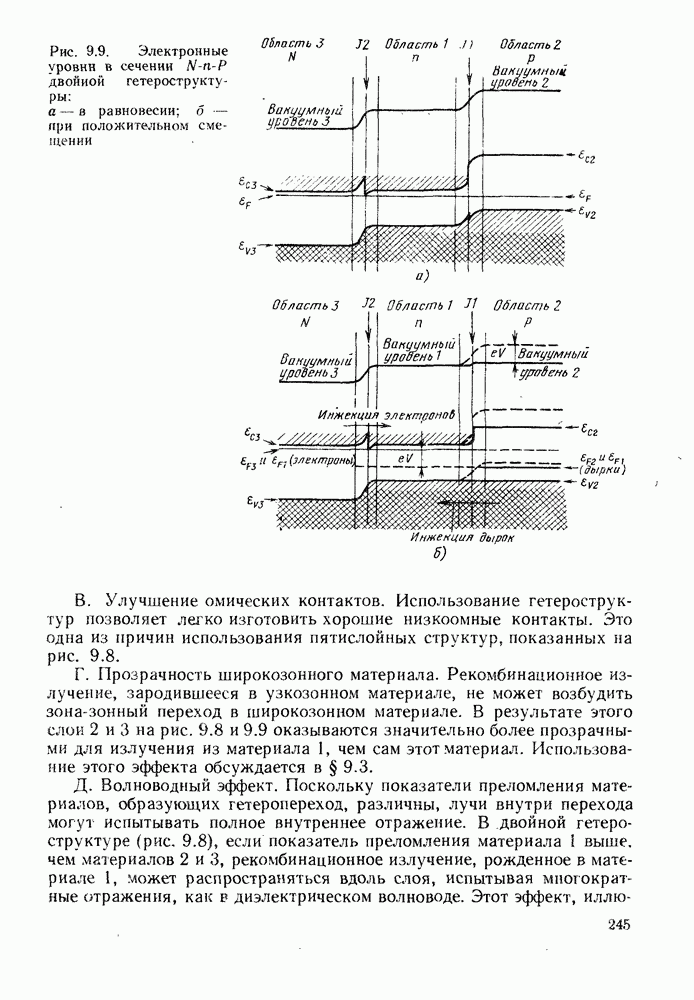
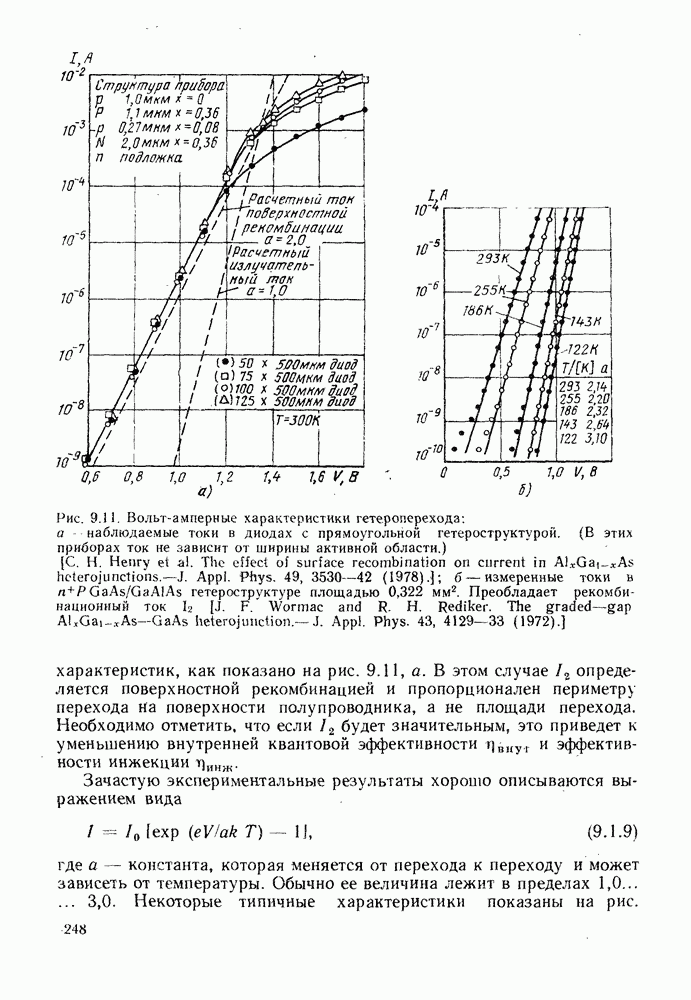
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
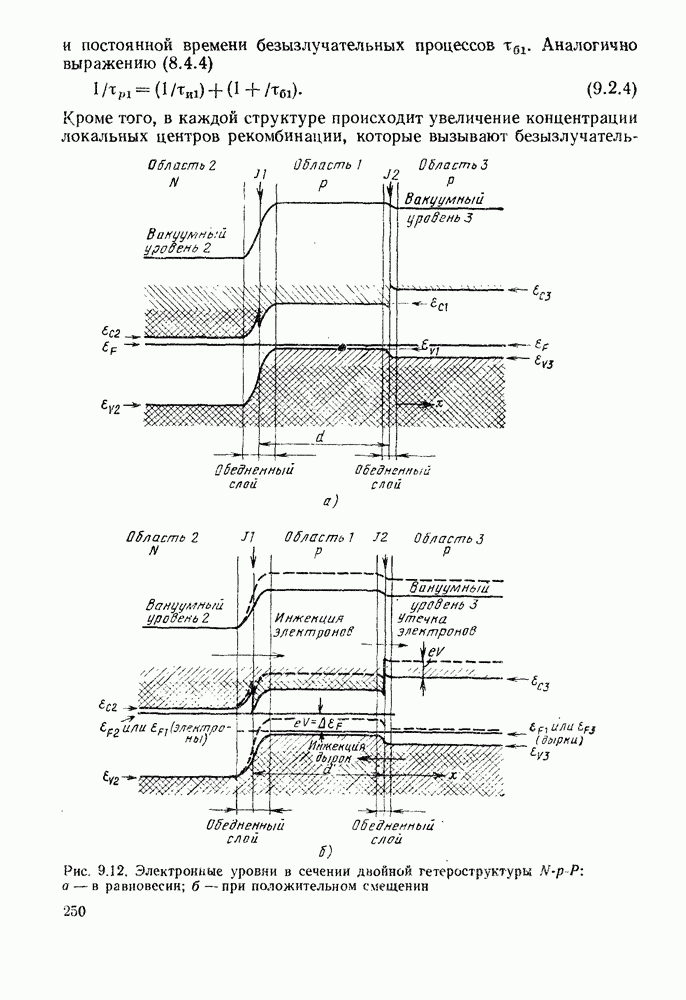
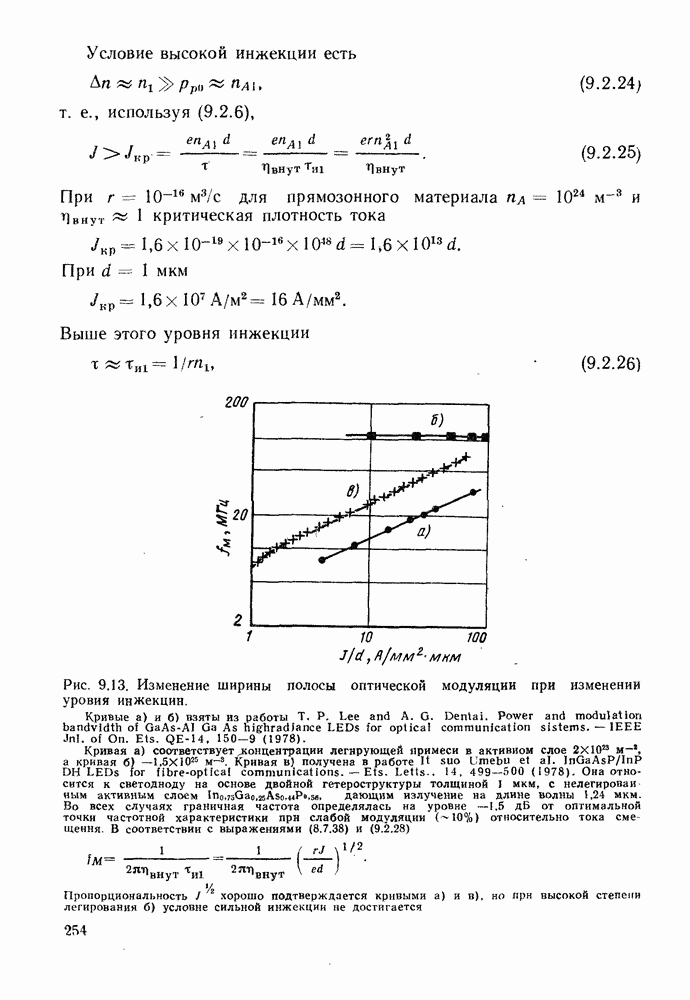
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
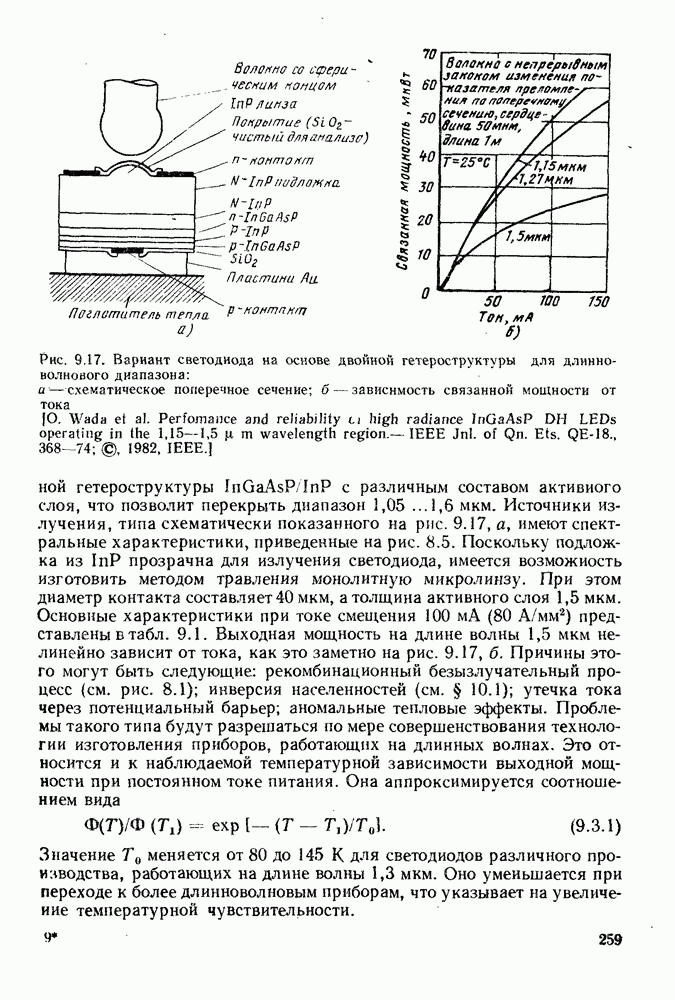
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
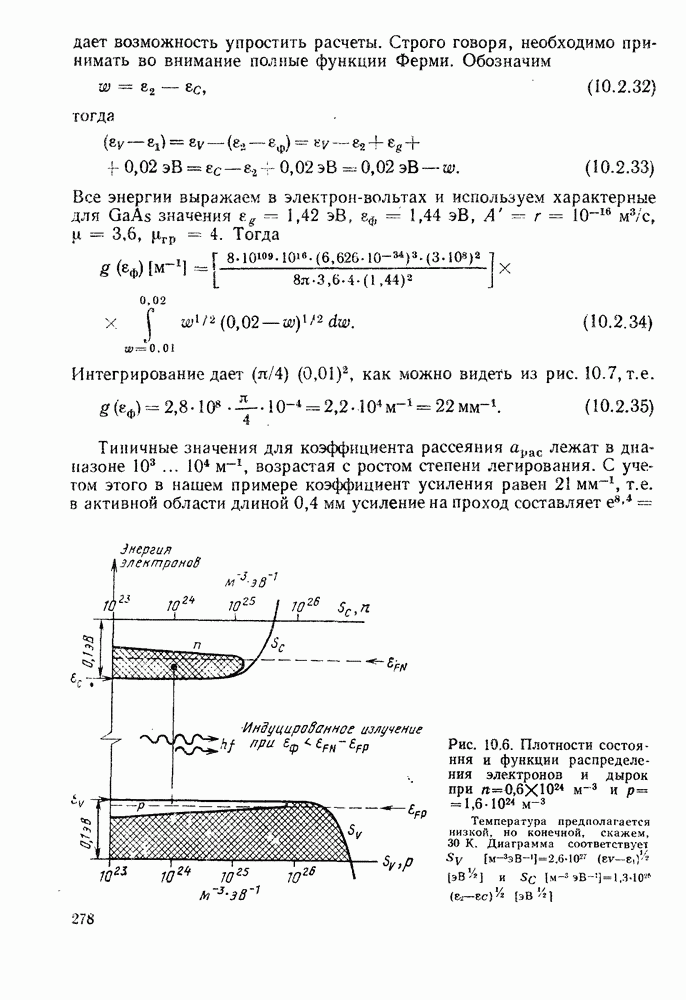
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
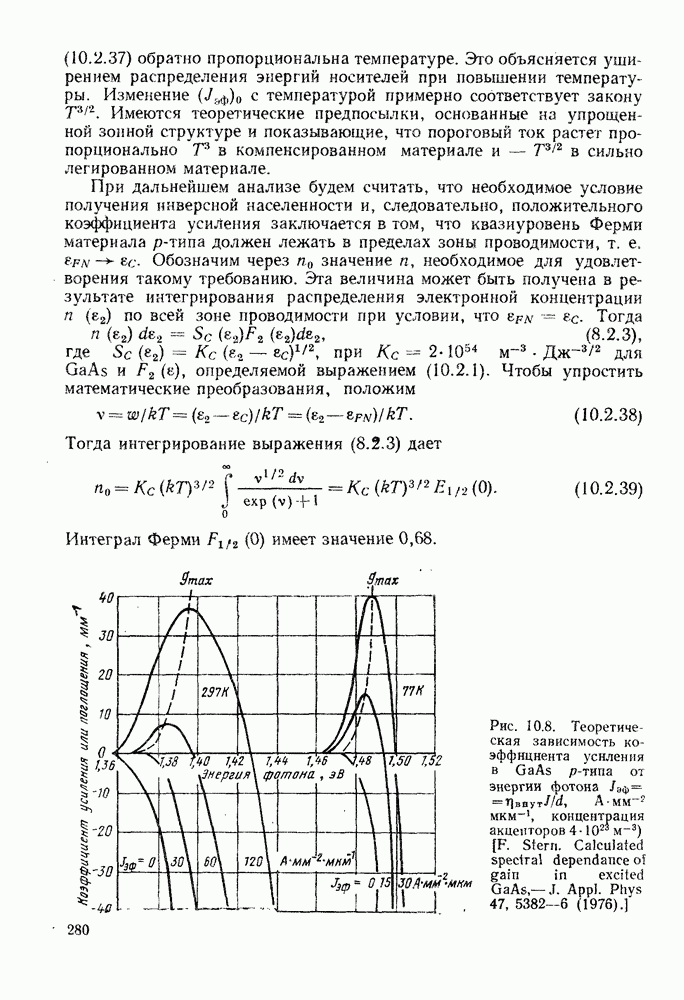
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
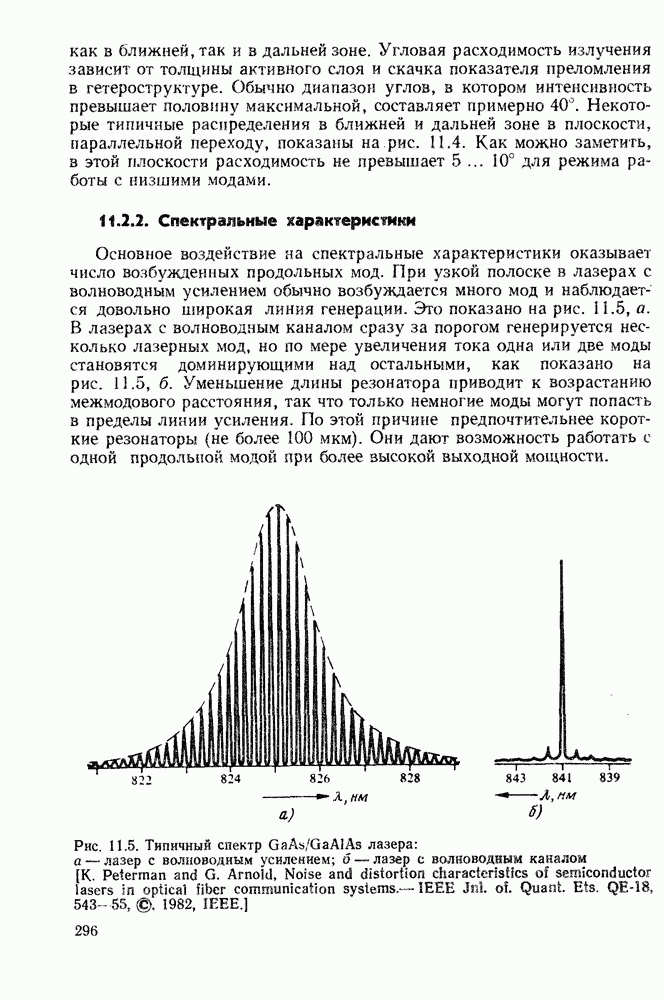
- 11.2.2. Спектральные характеристики
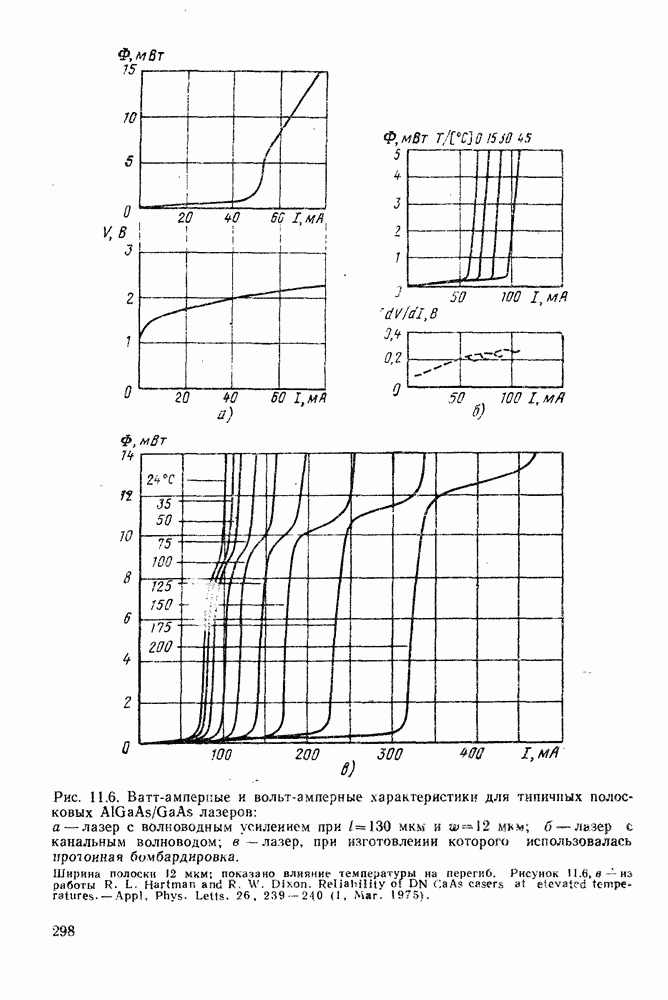
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
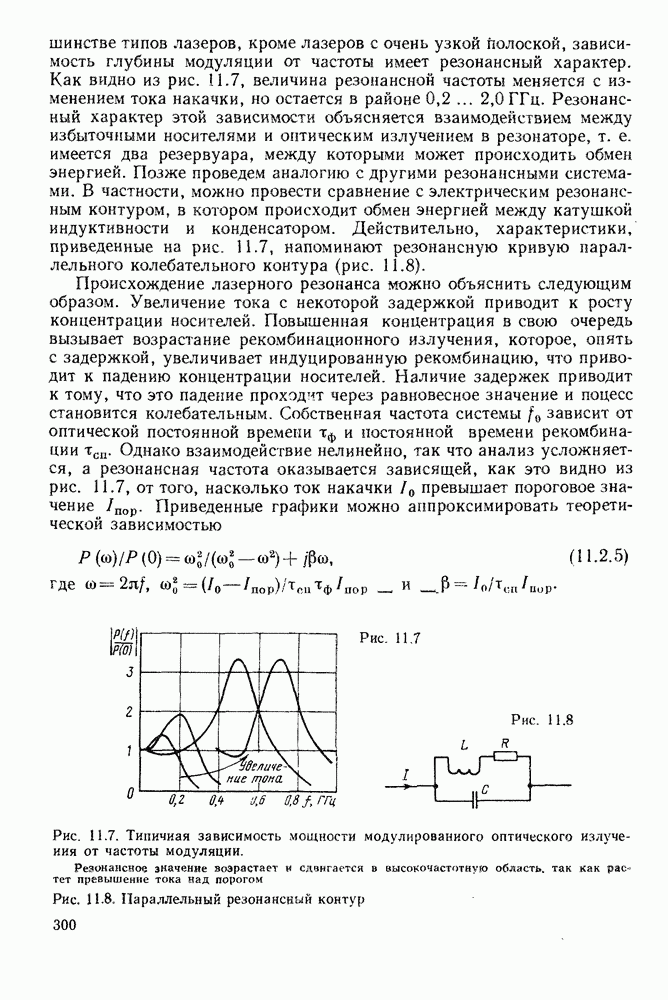
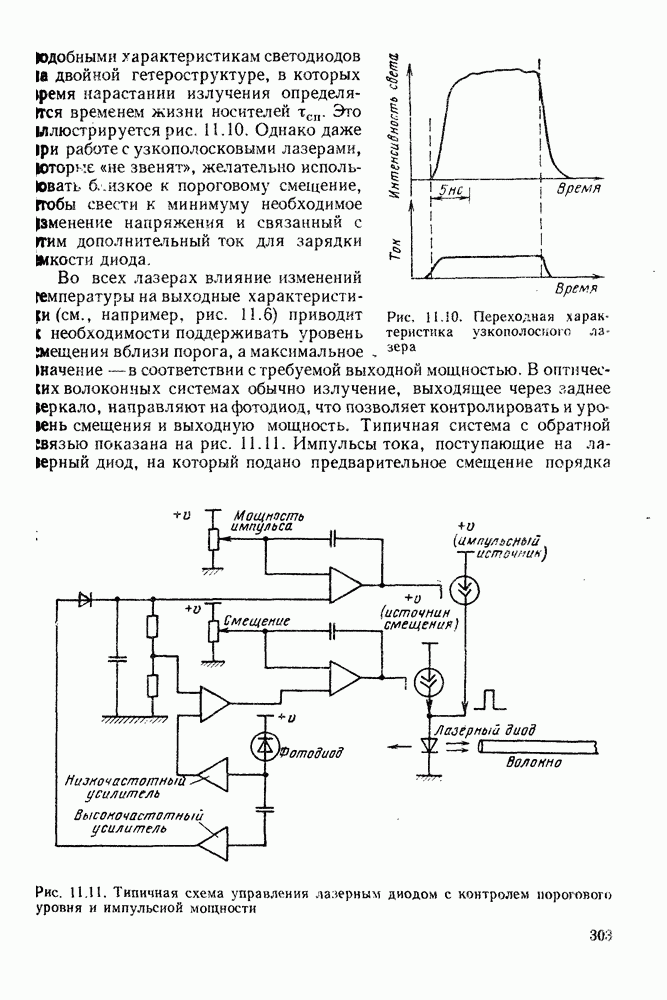
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
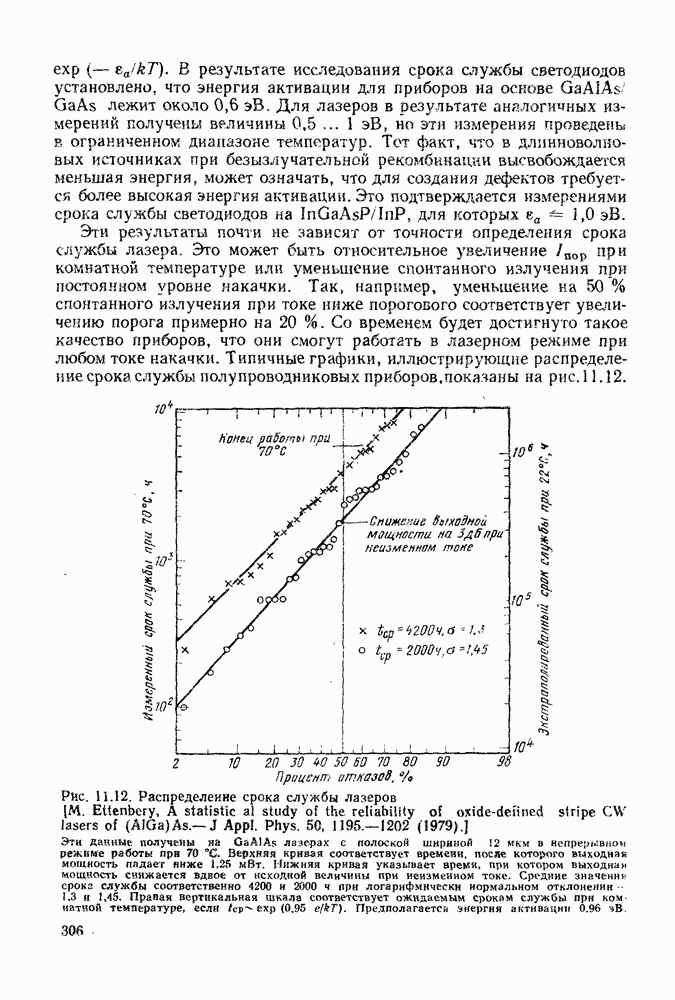
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
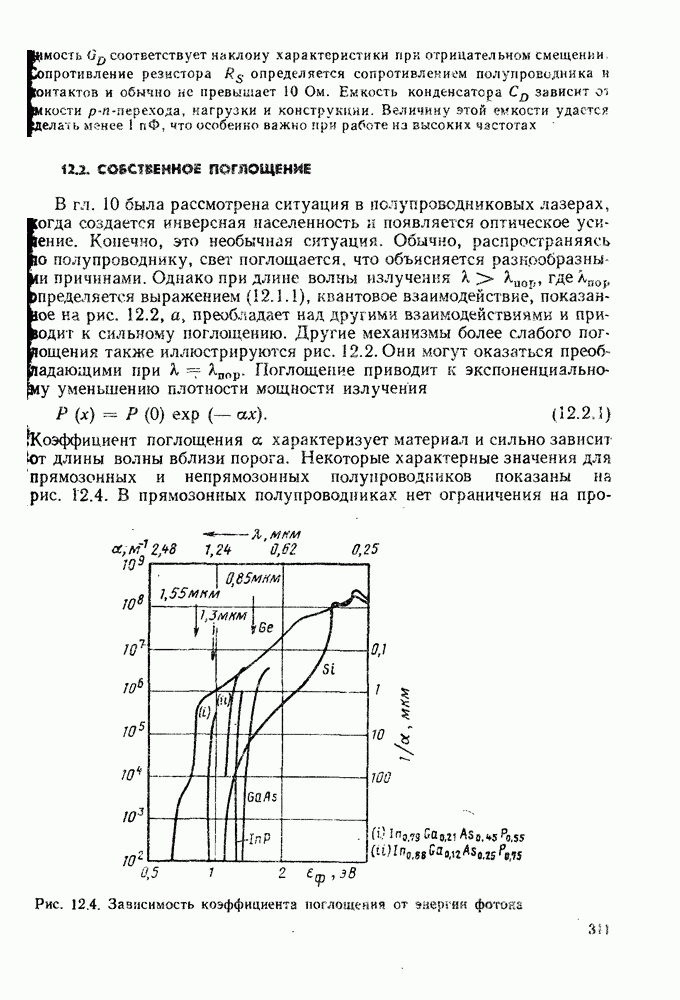
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
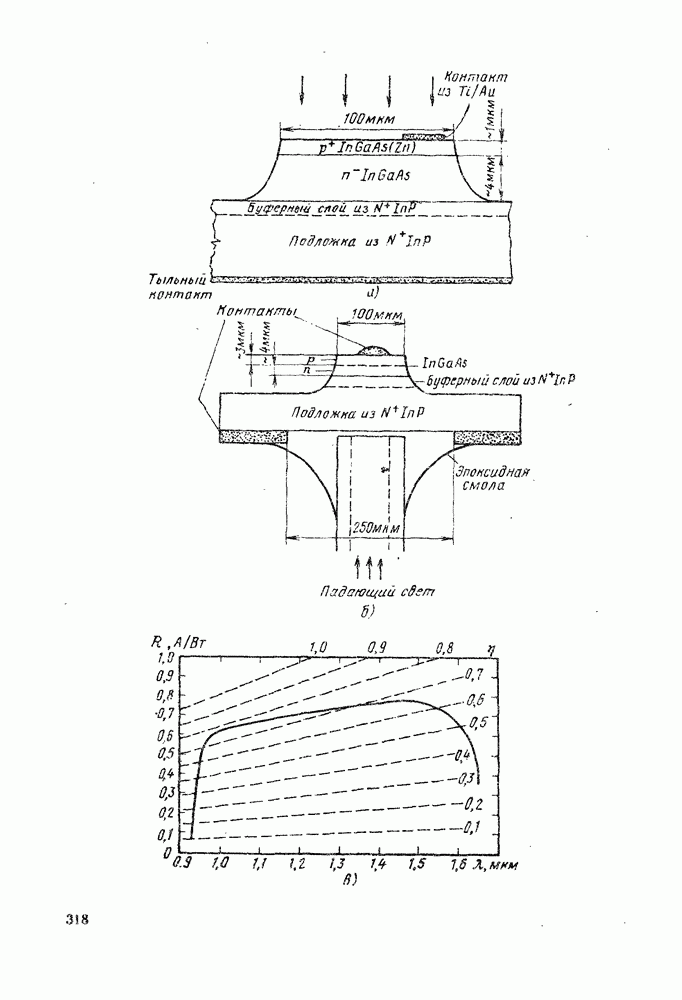
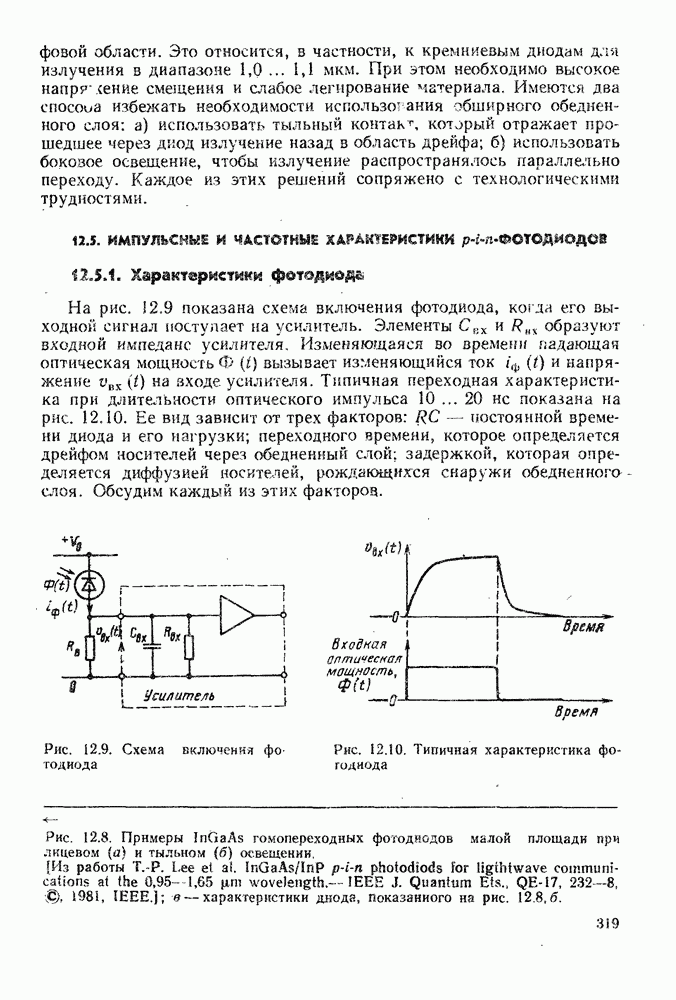
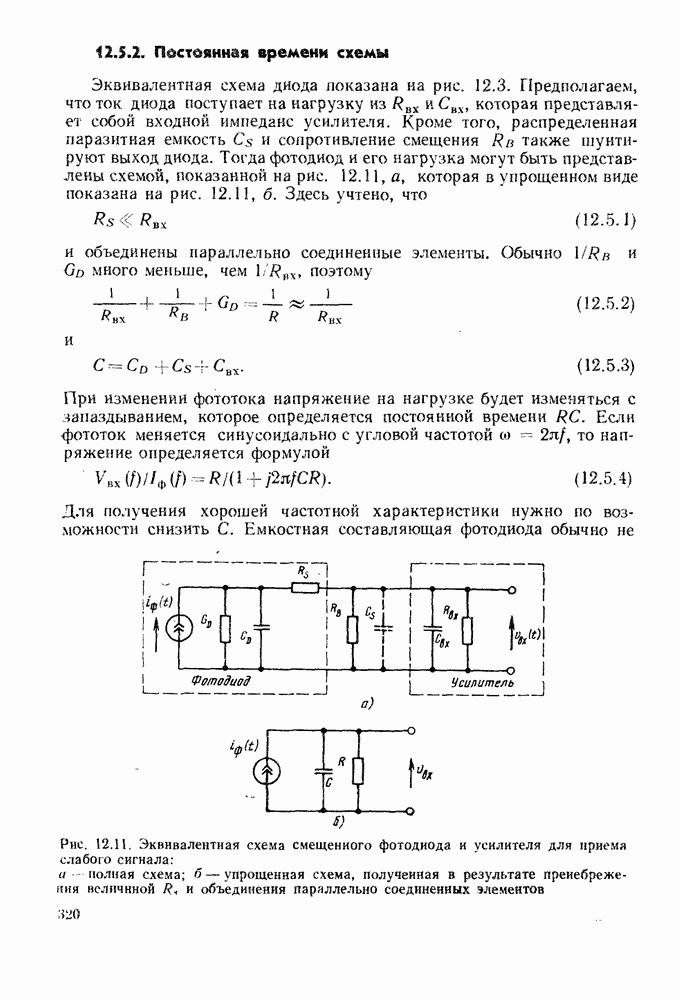
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
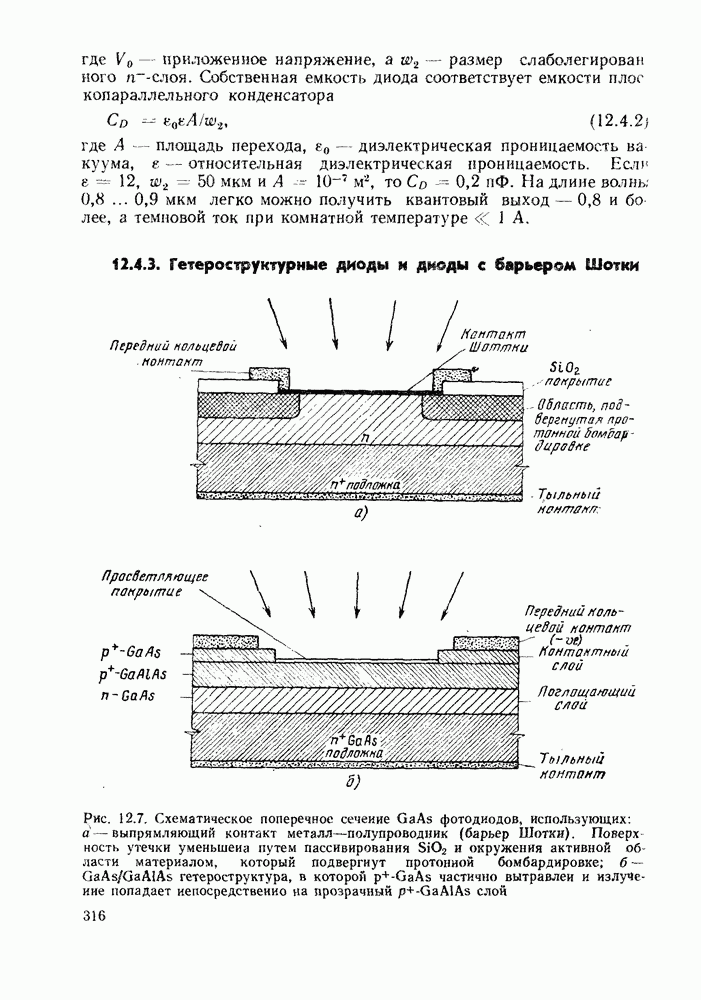
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
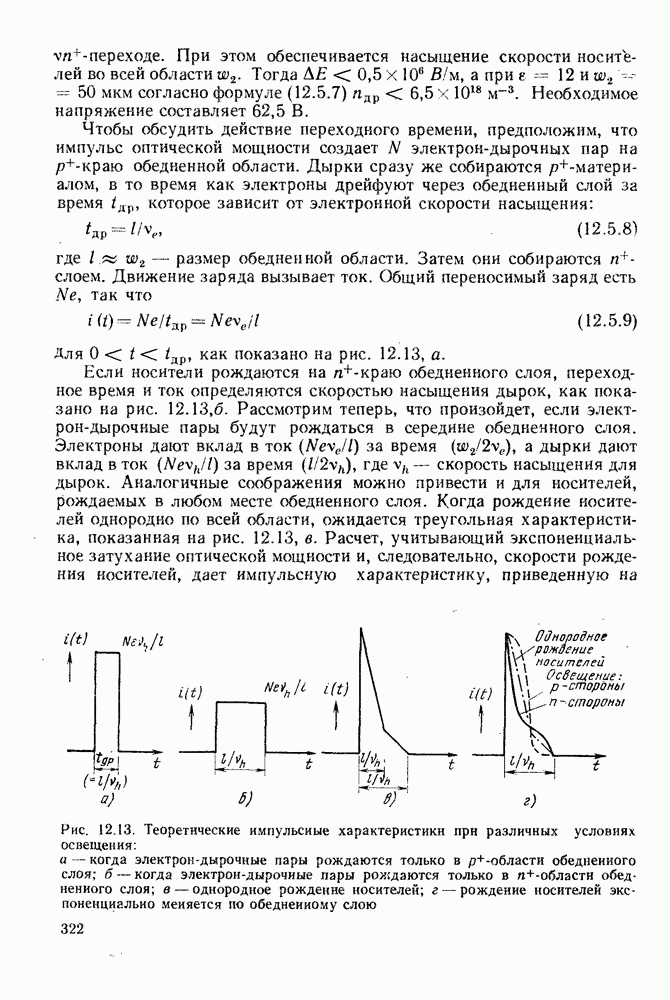
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
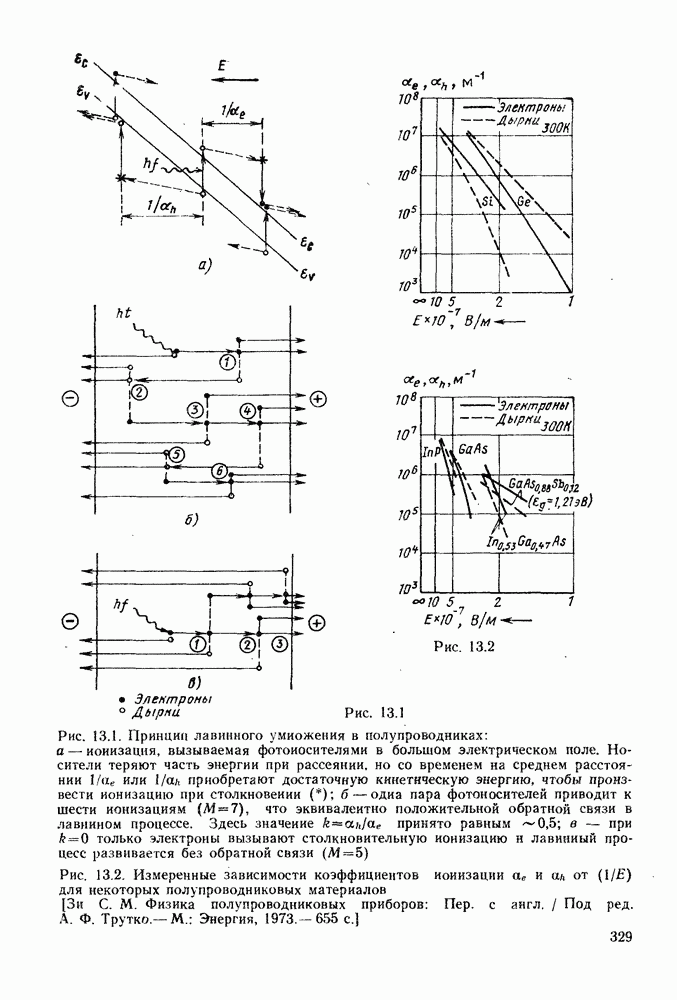
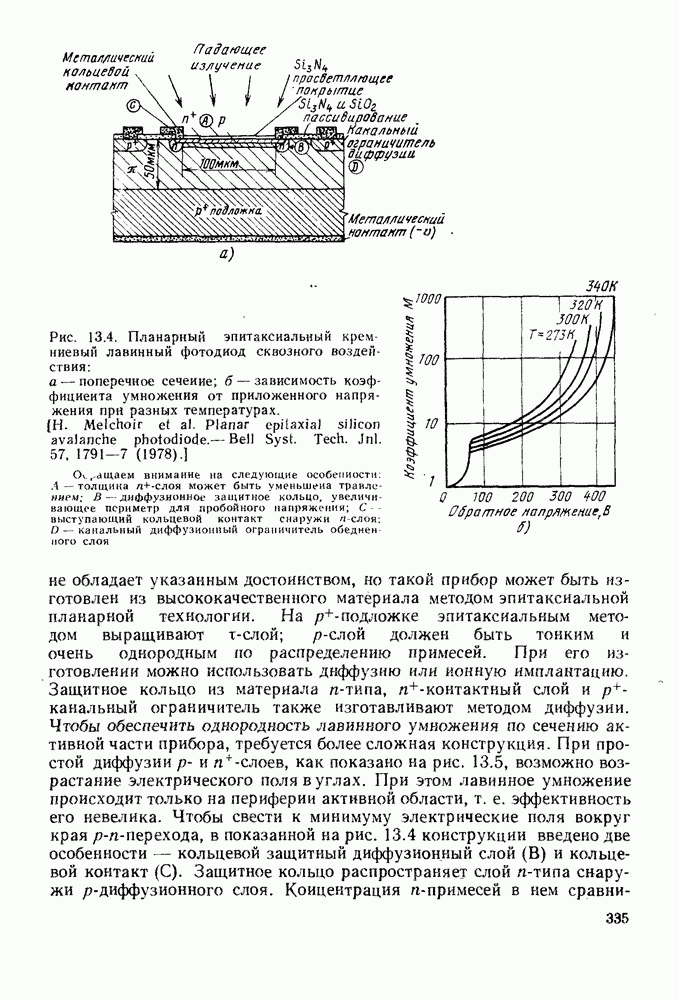
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
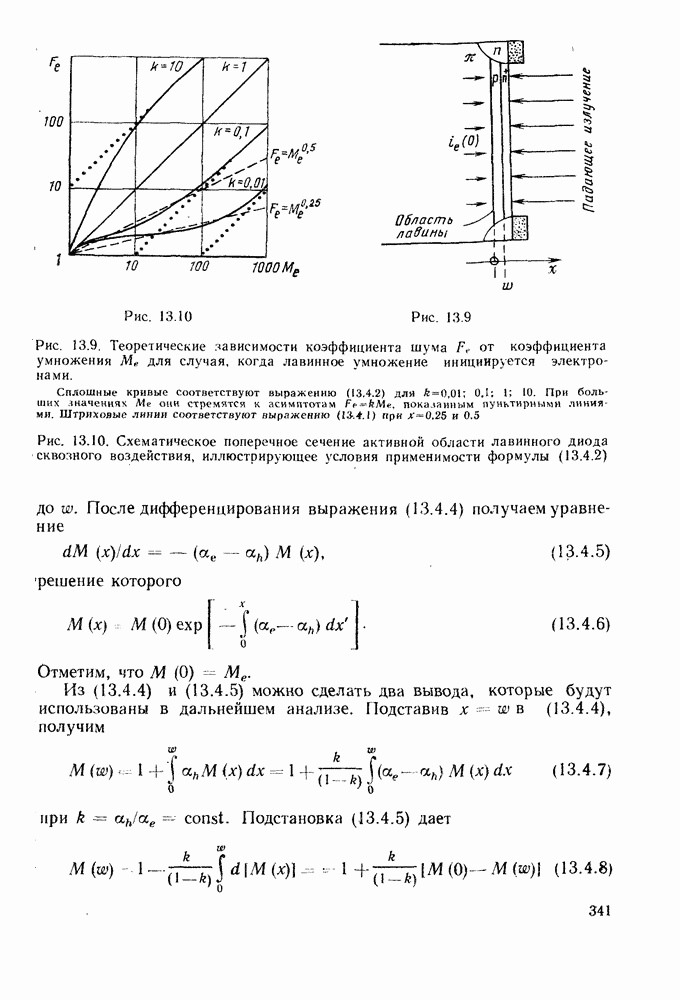
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
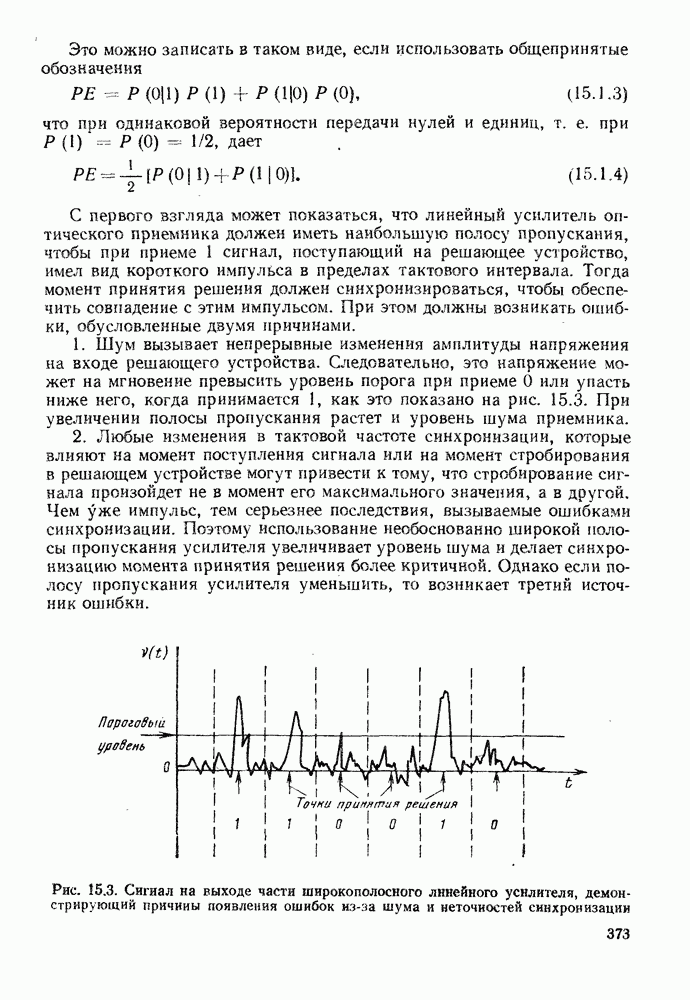
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
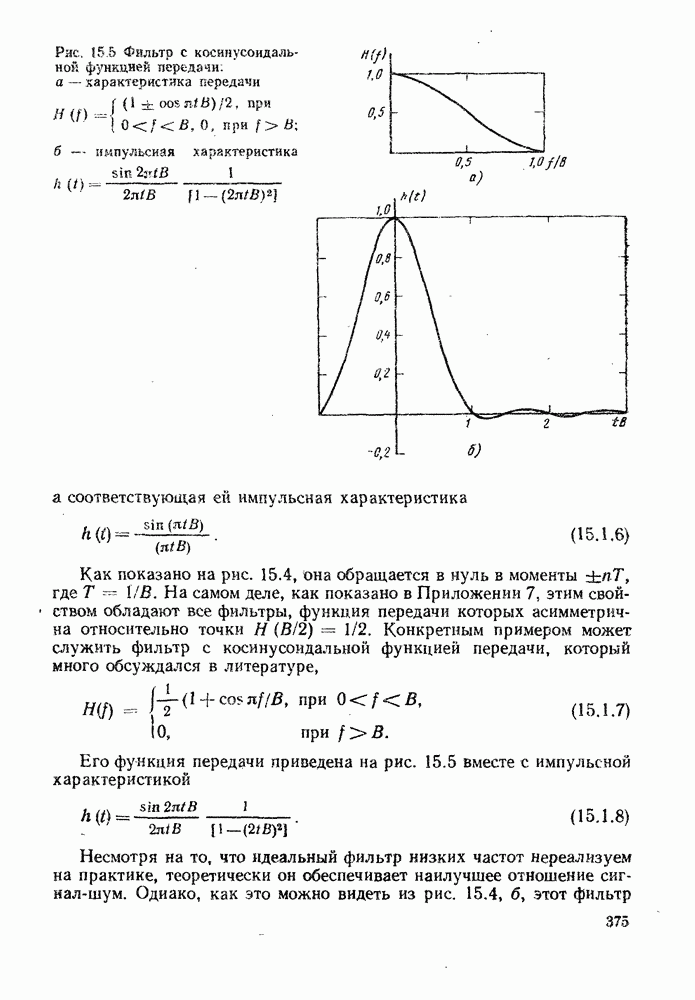
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
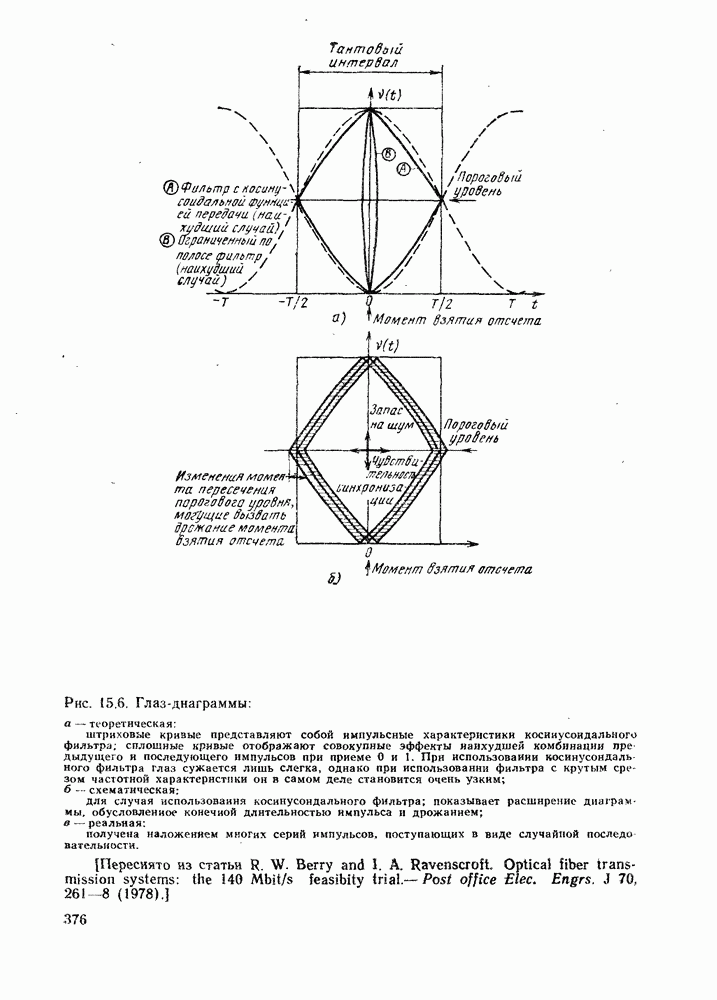
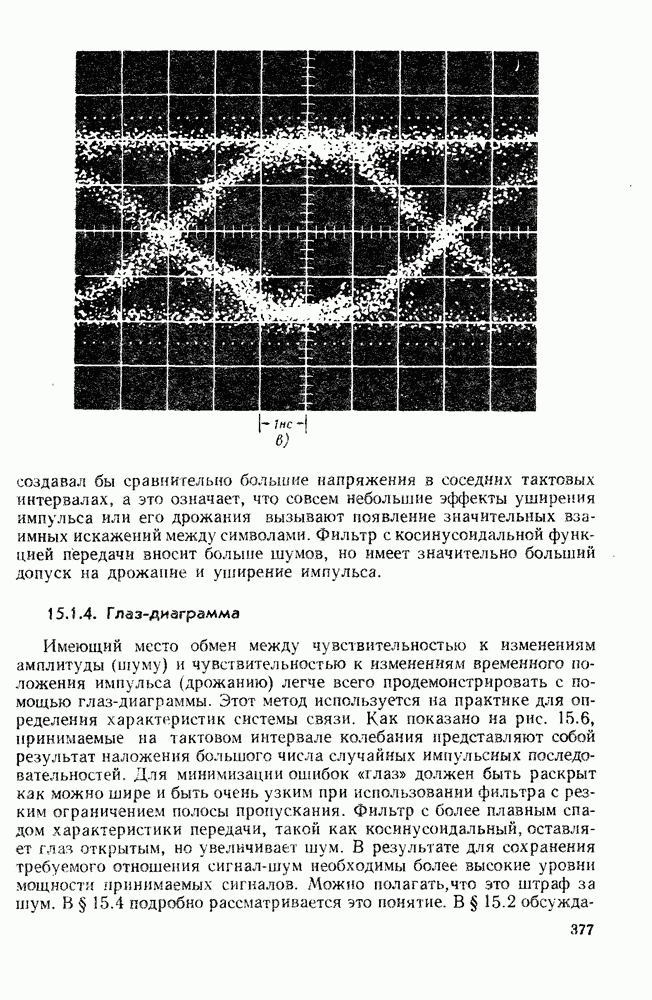
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
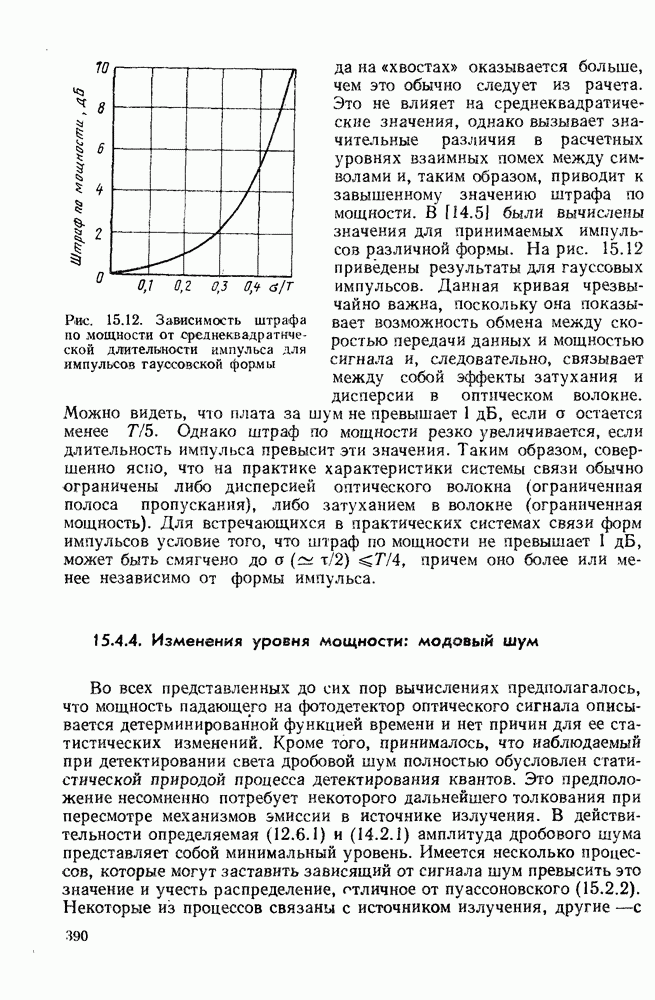
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
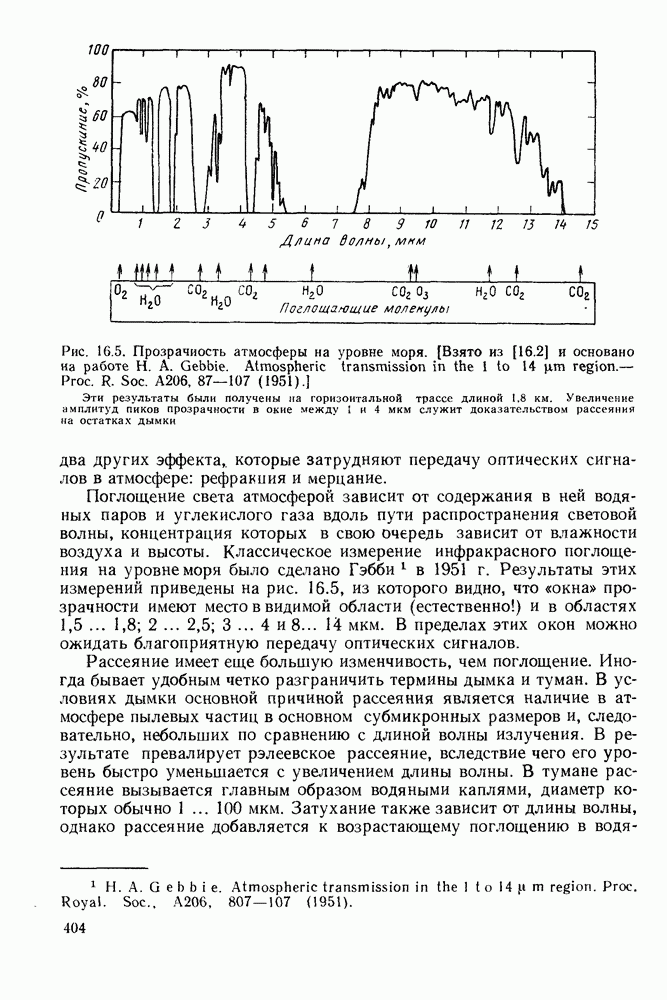
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
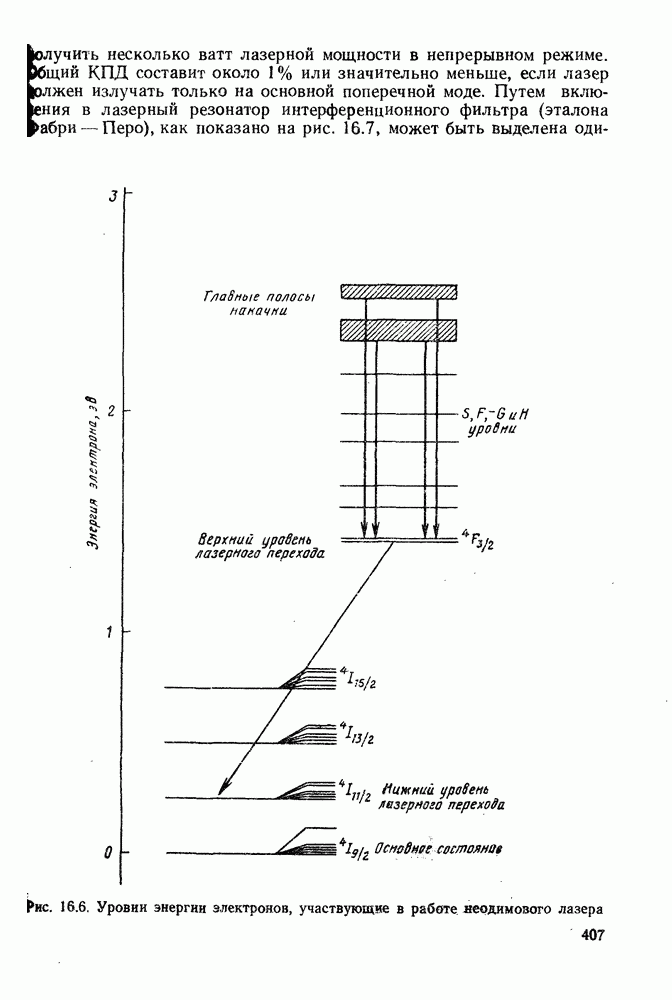
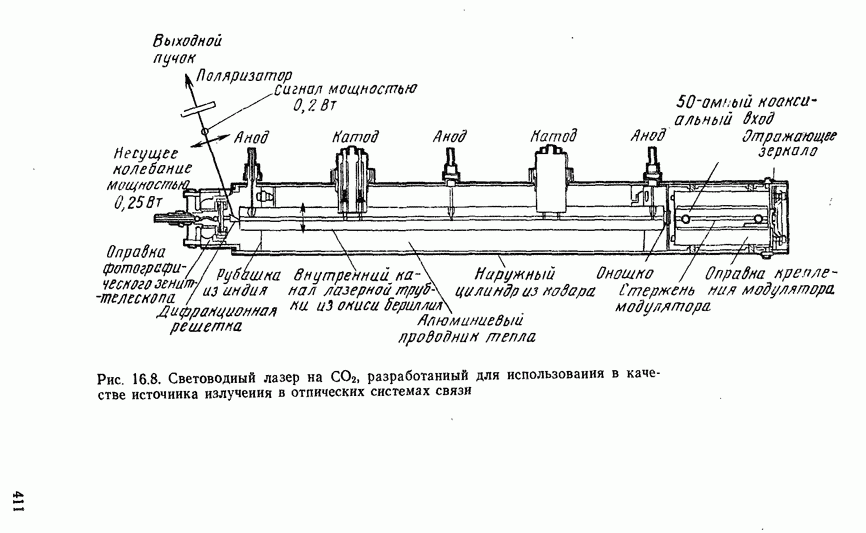
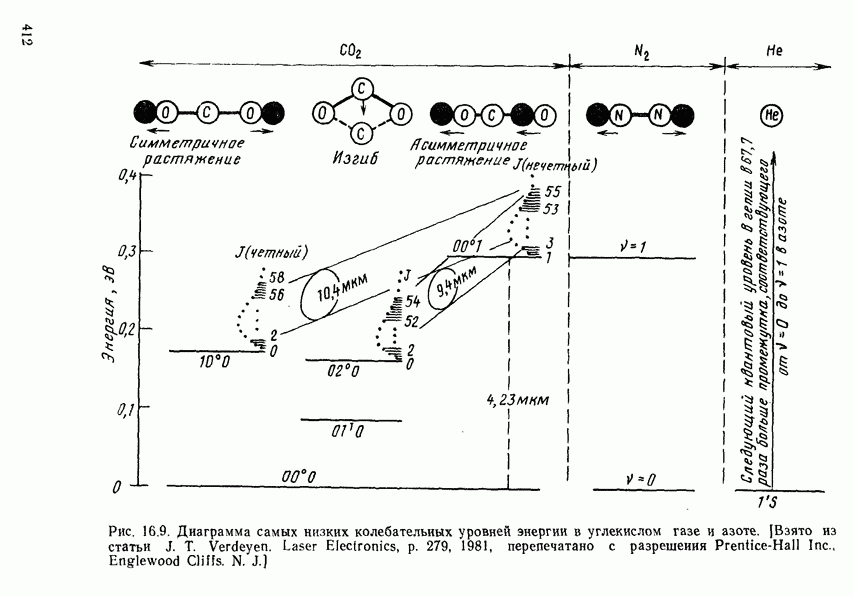
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ