| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
Подчеркнем еще раз, что лежащее в основе анализа дисперсии в градиентных волокнах соотношение (6.1.40) справедливо только для тех мод высоких порядков, распространяющихся в многомодовых волокнах, которые далеки от частоты отсечки. Предположим, что большая часть передаваемой по волокну оптической мощности переносится именно такими модами. В этом параграфе найдем среднеквадратическое отклонение времени распространения, усредненное по всем этим модам. При этом будем предполагать, что свет вводится в волокно от источника, спектральная ширина излучения которого на уровне половинной мощности равна  (или среднеквадратическая ширина равна
(или среднеквадратическая ширина равна  и распределяется равномерно между всеми модами распространения.
и распределяется равномерно между всеми модами распространения.
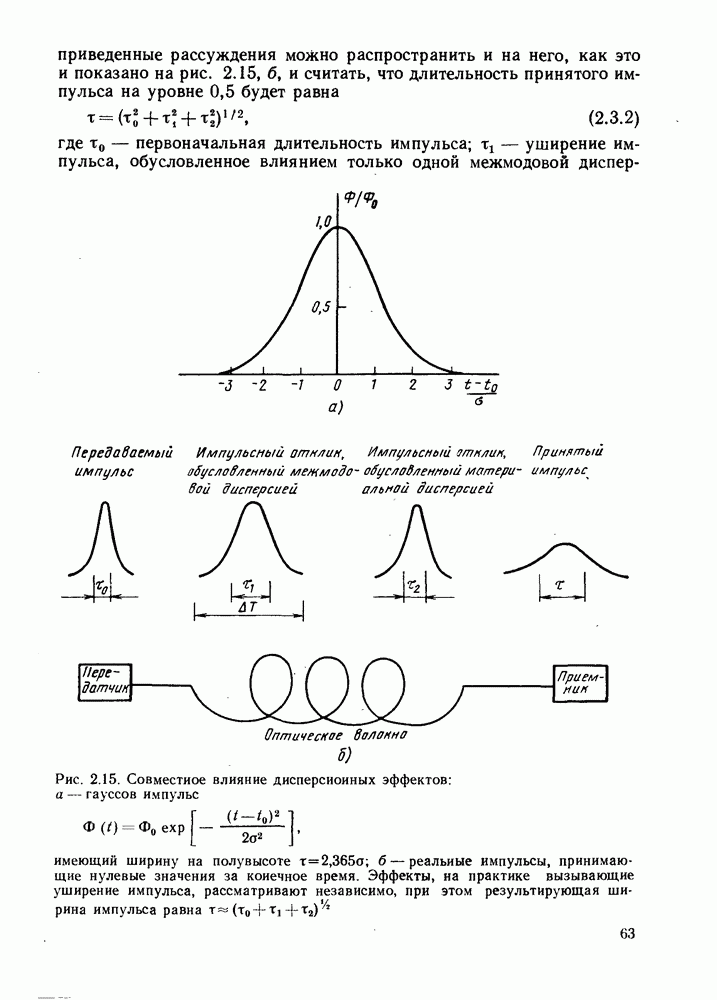
Для определения общей дисперсии необходимо объединить определенным образом эффекты, обусловливающие межмодовую и внутримодовую дисперсии. Из предыдущих параграфов очевидно, что эти эффекты независимы и некоррелированы. По этой причине самым удобным способом их объединения оказывается сложение среднеквадратических длительностей импульсов, независимо создаваемых каждым из эффектов дисперсии в отсутствие другого. Как было показано в § 2.4, в таком случае общая среднещадратическая длительность импульса а, обусловленная влиянием обоих видов дисперсий, определяется соотношением

где  среднеквадратическая длительность импульса, являющаяся результатом одной межмодовой дисперсии, а а2 - среднеквадратическая длительность импульса, обусловленная влиянием только внутримодовой дисперсии.
среднеквадратическая длительность импульса, являющаяся результатом одной межмодовой дисперсии, а а2 - среднеквадратическая длительность импульса, обусловленная влиянием только внутримодовой дисперсии.
В предыдущем параграфе было показано, что межмодовая дисперсия определяется слагаемым, характеризующим материальную дисперсию и одинаковым для всех мод, а также рядом других слагаемых, определяющих волноводную дисперсию, и изменяющихся от моды к моде. Перечисленные слагаемые, как и выражение (6.4.6), содержат параметр ?. Не зависящее от мод слагаемое доминирует над всеми другими за исключением, может быть, случая близости к минимуму материальной дисперсии, поэтому для упрощения выкладок оставим только его. В выражении (6.4.6) внутримодовая дисперсия была представлена в виде длительности импульса на полувысоте  создаваемого каждой модовой группой
создаваемого каждой модовой группой  зависящей от ширины спектральной линии излучения
зависящей от ширины спектральной линии излучения  определяемой по тому же критерию (ширина на полувысоте). Для решения задачи данного параграфа удобнее использовать среднеквадратическую длительность импульса
определяемой по тому же критерию (ширина на полувысоте). Для решения задачи данного параграфа удобнее использовать среднеквадратическую длительность импульса  которую можно непосредственно выразить через среднеквадратическую ширину спектральной линии излучения ом- Таким образом, если ограничиться только одним первым слагаемым, выражение (6.4.6) упрощается по (2.4.12).
которую можно непосредственно выразить через среднеквадратическую ширину спектральной линии излучения ом- Таким образом, если ограничиться только одним первым слагаемым, выражение (6.4.6) упрощается по (2.4.12).

Теперь необходимо определить  — среднеквадратическую длительность импульса, являющегося результатом межмодовой дисперсии, когда величина
— среднеквадратическую длительность импульса, являющегося результатом межмодовой дисперсии, когда величина  очень мала. Для этого необходимо использовать результаты § 6.3, где исследовался общий разброс по времени распространения различных мод. Чтобы найти
очень мала. Для этого необходимо использовать результаты § 6.3, где исследовался общий разброс по времени распространения различных мод. Чтобы найти  нужно оценить соотношение (2.4.3) в предположении, что введенная в волокно в виде импульса единичной энергии оптическая мощность распределена равномерно между распространяющимися в нем модами. В таком случае принимаемая мощность будет поступать в виде последовательности взвешенных импульсов по мере того, как модовые группы будут прибывать после соответствующего времени распространения. Каждая из
нужно оценить соотношение (2.4.3) в предположении, что введенная в волокно в виде импульса единичной энергии оптическая мощность распределена равномерно между распространяющимися в нем модами. В таком случае принимаемая мощность будет поступать в виде последовательности взвешенных импульсов по мере того, как модовые группы будут прибывать после соответствующего времени распространения. Каждая из  модовых групп опознается по параметру модовой группы
модовых групп опознается по параметру модовой группы  и состоит из
и состоит из  независимых мод. Таким образом, энергия, поступающая во время
независимых мод. Таким образом, энергия, поступающая во время  с модовой группой
с модовой группой  пропорциональна индексу
пропорциональна индексу  Общее число отдельных мод будет равно
Общее число отдельных мод будет равно

Поскольку мы используем результаты анализа, полученные в приближении Венцеля — Крамерса — Бриллюэна, необходимо предположить, что  велико и результаты могут быть неточными для мод самых низких и самых высоких порядков, т. е. когда
велико и результаты могут быть неточными для мод самых низких и самых высоких порядков, т. е. когда  мало и когда оно приближается к
мало и когда оно приближается к  При равномерном распределении энергии единичного импульса между модами энергия каждой из мод будет равна
При равномерном распределении энергии единичного импульса между модами энергия каждой из мод будет равна  а энергия каждой модовой группы составит
а энергия каждой модовой группы составит 
Исследуем распределение времени распространения для модовой группы при некоторых типичных значениях параметра а, характеризующего закон изменения показателя преломления. На этой основе можно получить импульсную характеристику волокна, а следовательно, и найти значение  Наш анализ будет основываться на выражении
Наш анализ будет основываться на выражении

Более удобно представить эти времена распространения в нормализованном виде относительно времени распространения моды самого низкого порядка  Момент времени
Момент времени  можно также использовать в качестве начала координат при отсчете времени прихода других мод. Таким образом, нормализованное время распространения
можно также использовать в качестве начала координат при отсчете времени прихода других мод. Таким образом, нормализованное время распространения  будет определяться следующим образом:
будет определяться следующим образом:

или

где

Итак, временной интервал между импульсами определяется значением производной  и поэтому скорость поступления модовых групп будет равна
и поэтому скорость поступления модовых групп будет равна  Средняя мощность, принимаемая в любой момент времени
Средняя мощность, принимаемая в любой момент времени  будет равна
будет равна

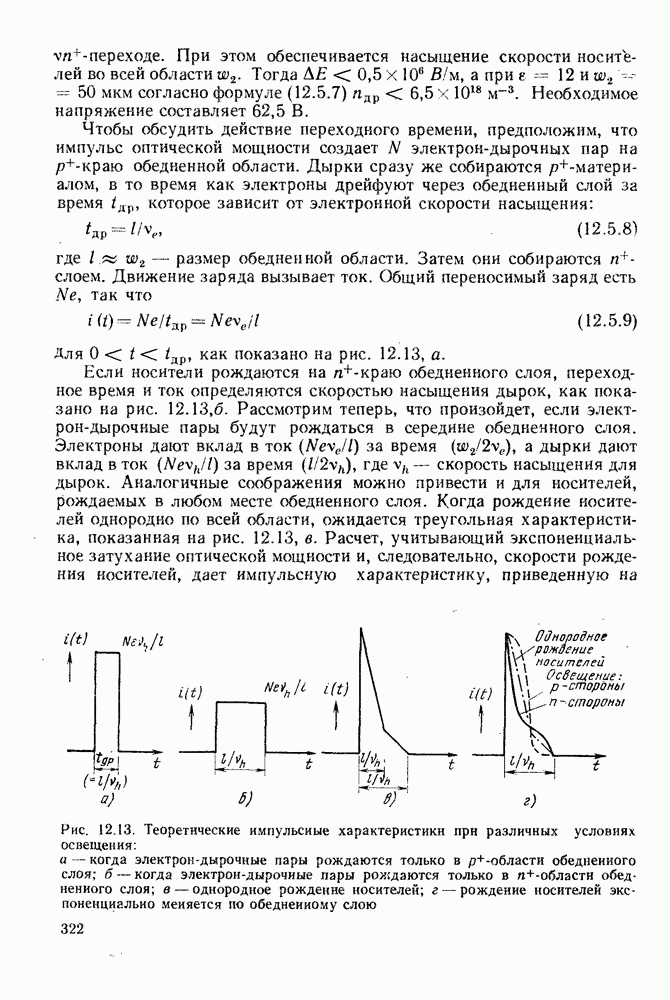
поскольку каждая модовая группа переносит энергию  Полученное выражение представляет собой сглаженную импульсную характеристику волокна. Оно описывает отклик на выходе волокна, когда приемник действует как фильтр низких частот, неспособный различить отдельные импульсы, появляющиеся в момент прихода отдельных модовых групп.
Полученное выражение представляет собой сглаженную импульсную характеристику волокна. Оно описывает отклик на выходе волокна, когда приемник действует как фильтр низких частот, неспособный различить отдельные импульсы, появляющиеся в момент прихода отдельных модовых групп.
Общее выражение для  можно получить, подставив (6.5.6) и (6.5.3) в (2.4.3)
можно получить, подставив (6.5.6) и (6.5.3) в (2.4.3)

что приводит 

Если теперь подставить значение  определяемое (6.5.3), то после ряда простых преобразований
определяемое (6.5.3), то после ряда простых преобразований

Вместо того, чтобы слепо подставить в полученное выражеь не значения а, исследуем сначала импульсные характеристики волокна, получаемые в некоторых специфических случаях, а затем на их основе найдем значения 
Рассмотрим сначала ступенчатое волокно, у которого  . В этом случае только первое слагаемое в (6.5.3) будет существенным и можно написать
. В этом случае только первое слагаемое в (6.5.3) будет существенным и можно написать

Следовательно, мощность принимается в течение промежутка времени  Это нормализованное время, которому соответствует интервал реального времени, равный
Это нормализованное время, которому соответствует интервал реального времени, равный  . В течение этого временного отрезка средняя принимаемая мощность постоянна. Воспользовавшись формулой (6.5.6), находим, что
. В течение этого временного отрезка средняя принимаемая мощность постоянна. Воспользовавшись формулой (6.5.6), находим, что

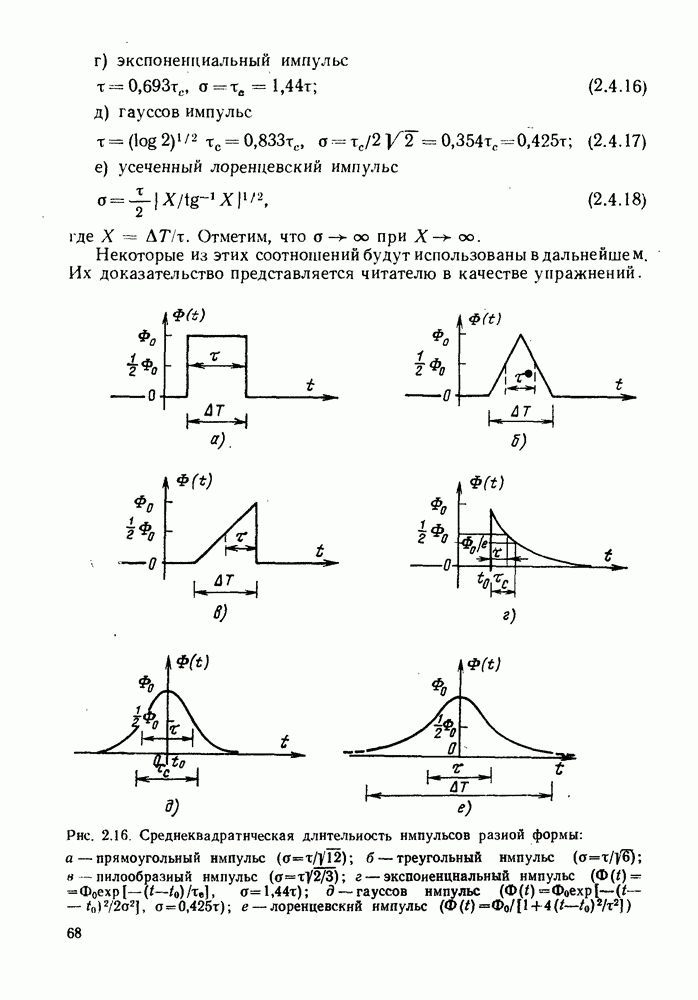
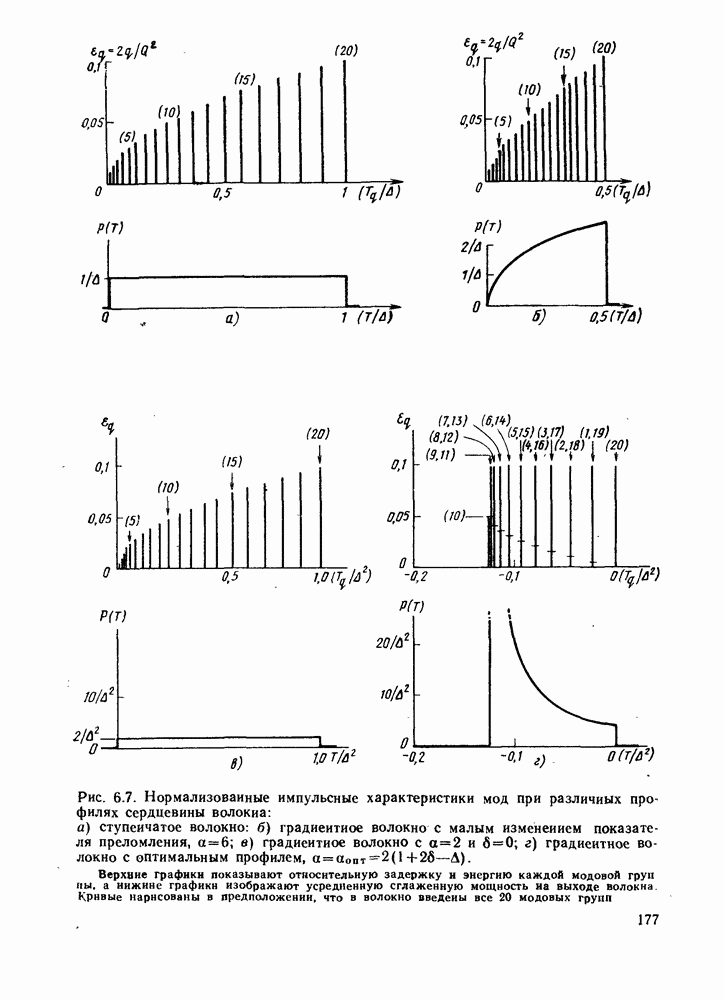
На рис. 6.7, а показаны распределение  и сглаженная импульсная характеристика ступенчатого волокна при
и сглаженная импульсная характеристика ступенчатого волокна при  . В § 2.4 было показано, что среднеквадратическая длительность импульса прямоугольной формы составляет
. В § 2.4 было показано, что среднеквадратическая длительность импульса прямоугольной формы составляет  часть от его длительности [см. формулу (2.4.13)]. Следовательно, среднеквадратическая длительность
часть от его длительности [см. формулу (2.4.13)]. Следовательно, среднеквадратическая длительность

(кликните для просмотра скана)
нормализованной импульсной характеристики ступенчатого волокна будет равна

Подставновка  в первое слагаемое выражения (6.5.9) приводит к тому же результату.
в первое слагаемое выражения (6.5.9) приводит к тому же результату.
Рассмотрим другой частный случай, на этот раз волокно со слабым изменением показателя преломления, имеющее  . В этом случае, снова учитывая только первое слагаемое в (6.5.3) и пренебрегая 6 по сравнению с единицей, получаем
. В этом случае, снова учитывая только первое слагаемое в (6.5.3) и пренебрегая 6 по сравнению с единицей, получаем

Общее расширение импульсной характеристики волокна при этом равно  а распределение мощности примет вид
а распределение мощности примет вид

Модальная и сглаженная импульсные характеристики такого волокна изображены на рис. 6.7, б. Среднеквадратическая длительность в соответствии с первым слагаемым (6.5.9) импульсной характеристики равна

что в 2 с лишним раза меньше, чем в ступенчатом волокне.
В качестве следующего примера рассмотрим волокно с параболическим профилем показателя преломления  у которого дисперсионный коэффициент
у которого дисперсионный коэффициент  таком случае
таком случае

где

Тогда

а

Таким образом, принимаемая мощность остается постоянной в течение длительности импульса  Следовательно, среднеквадратическая длительность импульсной характеристики будет равна
Следовательно, среднеквадратическая длительность импульсной характеристики будет равна

Эта характеристика приведена на рис. 6.7, в. При  достигается весьма существенное уменьшение среднеквадратической длительности
достигается весьма существенное уменьшение среднеквадратической длительности
импульсной характеристики. При  получается результат, аналогичный предписываемому формулой (6.5.19), если выбрать
получается результат, аналогичный предписываемому формулой (6.5.19), если выбрать  Это легко показать, сделав подстановку в формулу (6.5.9).
Это легко показать, сделав подстановку в формулу (6.5.9).
Наконец, рассмотрим волокно с таким значением а, которое, как показано в § 5.4, минимизирует длительность импульсной характеристики по  а именно, когда
а именно, когда  . Снова предполагаем что
. Снова предполагаем что  и
и  Тогда
Тогда

Таким образом,  обращаются в нуль,
обращаются в нуль,  Следовательно,
Следовательно,

а распределение мощности

Теперь необходимо решить уравнение (6.5.20) относительно  и подставить найденное значение в формулу (6.5.22). Введем обозначение
и подставить найденное значение в формулу (6.5.22). Введем обозначение  с тем, чтобы формула (6.5.22) приняла вид
с тем, чтобы формула (6.5.22) приняла вид

Тогда, используя уравнение (6.5.20), можно написать

откуда

Таким образом, для каждого у, а следовательно, и каждого  имеется два решения. Общая мощность определяется арифметической суммой этих двух решений. Чтобы упростить запись полученного результата, введем обозначения
имеется два решения. Общая мощность определяется арифметической суммой этих двух решений. Чтобы упростить запись полученного результата, введем обозначения

Тогда суммирование двух решений дает

Отсюда

Модальная и сглаженная импульсные характеристики рассмотренного волокна приведены на рис. 6.7, г. Вычисления по формуле (2.4.3) с использованием (6.5.26) дают

Прямая подстановка в (6.5.9) значения  в предположении, что
в предположении, что  приводит к такому же результату.
приводит к такому же результату.
Необходимо отметить, что для минимизации общего расширения импульса значение а выбирают из условия а — аопт  Однако при этом не получается наименьшее теоретическое значение для
Однако при этом не получается наименьшее теоретическое значение для  Можно показать, что в соответствии с формулой (6.5.9) минимальные значения для
Можно показать, что в соответствии с формулой (6.5.9) минимальные значения для  достигаются при выборе значения а близким к
достигаются при выборе значения а близким к  Тогда
Тогда  будет равно
будет равно

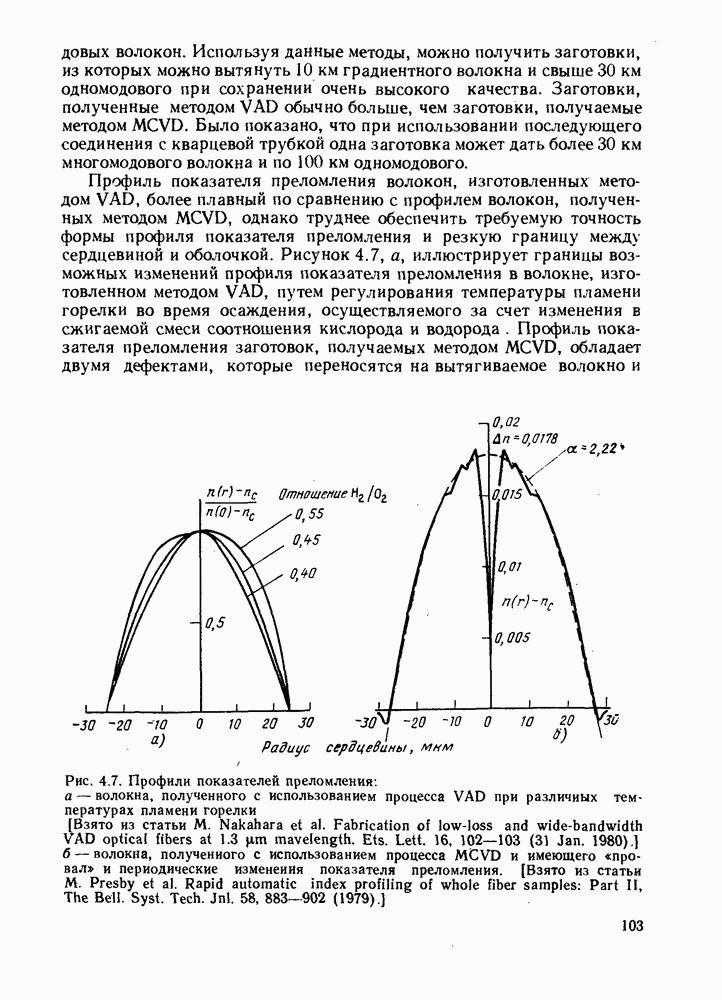
Такие различия, скорее, представляют теоретический интерес и не имеют практического значения. Для изготовителя оптического волокна важно знать, насколько увеличится модовая дисперсия при заданном допустимом отклонении значения а от оптимального. Об этом можно получить некоторое представление на основании вышеизложенного. Были опубликованы и более сложные теории, на основе которых определены влияния на параметры распространения мод статистических отклонений значений а от оптимального и искажений профиля показателя преломления, подобных изображенным на рис. 4.7. Можно только повторить еще раз, что для достижения уровня модовой дисперсии, близкого к теоретическому минимуму, необходимо поддерживать значение а с точностью порядка величины А, т. е. с погрешностью  Однако даже грубое изменение профиля показателя преломления приводит к значительному уменьшению длительности импульса.
Однако даже грубое изменение профиля показателя преломления приводит к значительному уменьшению длительности импульса.
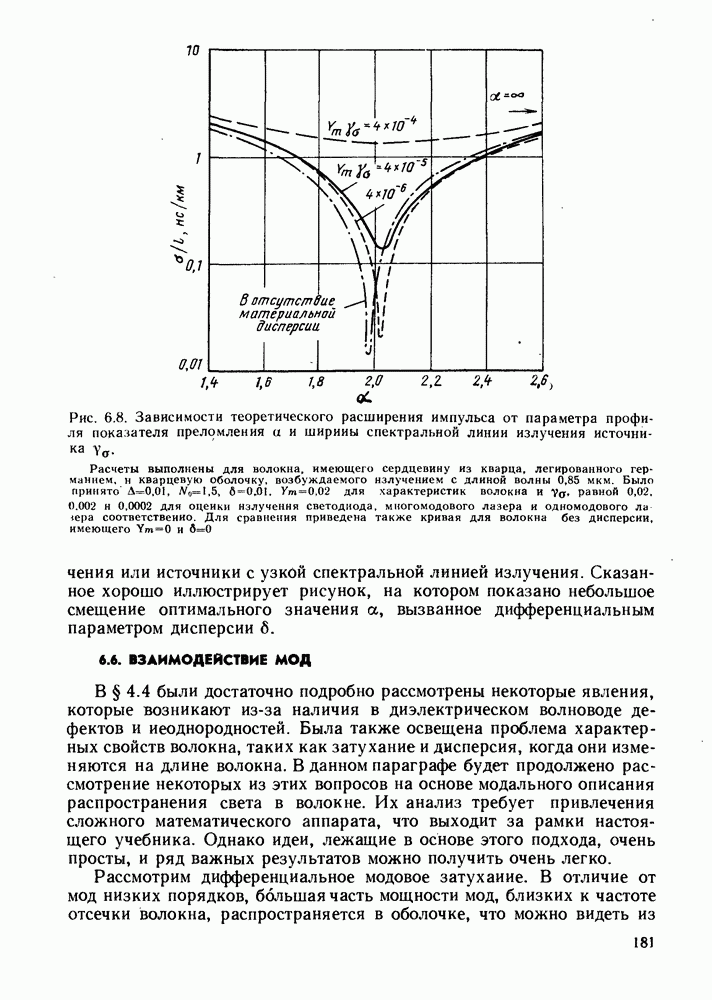
Приступим теперь к определению общего. эффекта, когда модовая и материальная дисперсии присутствуют одновременно. На рис. 6.8 изображена зависимость общей дисперсии от а при наличии изменяющейся по величине материальной дисперсии. Общая дисперсия получается подстановкой выражений (6.5.9) и (6.5.1) в формулу (2.4.10). Для значений а, не очень близких к двум она принимает вид

Если значения  лежат в окрестности 2, для определения
лежат в окрестности 2, для определения  необходимо использовать формулу (6.5.9). В рассматриваемых оптических волокнах с хорошо выполненным профилем показателя преломления материальная дисперсия может легко преобладать над модовой дисперсией, если только не используются длинноволновые источники
необходимо использовать формулу (6.5.9). В рассматриваемых оптических волокнах с хорошо выполненным профилем показателя преломления материальная дисперсия может легко преобладать над модовой дисперсией, если только не используются длинноволновые источники

Рис. 6.8. Зависимости теоретического расширения импульса от параметра профиля показателя преломления а и ширины спектральной линии излучения источника  Расчеты выполнены для волокна, имеющего сердцевину из кварца, легированного германием, и кварцевую оболочку, возбуждаемого излучением с длиной волны 0,85 мкм. Было принято
Расчеты выполнены для волокна, имеющего сердцевину из кварца, легированного германием, и кварцевую оболочку, возбуждаемого излучением с длиной волны 0,85 мкм. Было принято  для характеристик волокна и 70 равной 0,02, 0.002 и 0,0002 для оценки излучения светодиода, многомодового лазера и одномодового лазера соответствеиио. Для сравнения приведена также кривая для волокна без дисперсии, имеющего
для характеристик волокна и 70 равной 0,02, 0.002 и 0,0002 для оценки излучения светодиода, многомодового лазера и одномодового лазера соответствеиио. Для сравнения приведена также кривая для волокна без дисперсии, имеющего 
излучения или источники с узкой спектральной линией излучения. Сказанное хорошо иллюстрирует рисунок, на котором показано небольшое смещение оптимального значения а, вызванное дифференциальным параметром дисперсии 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
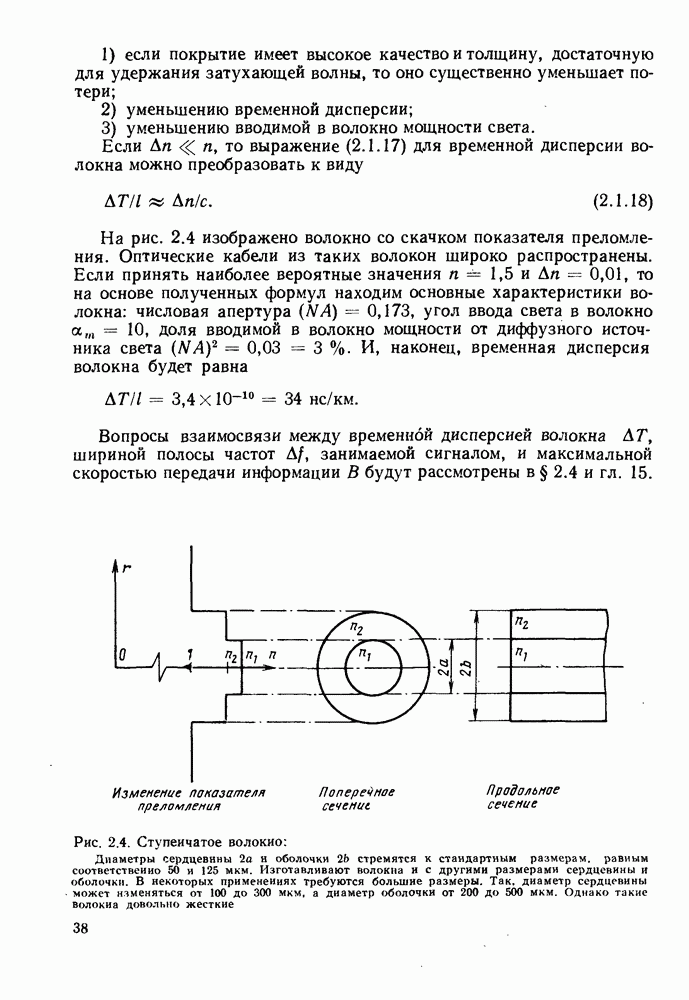
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
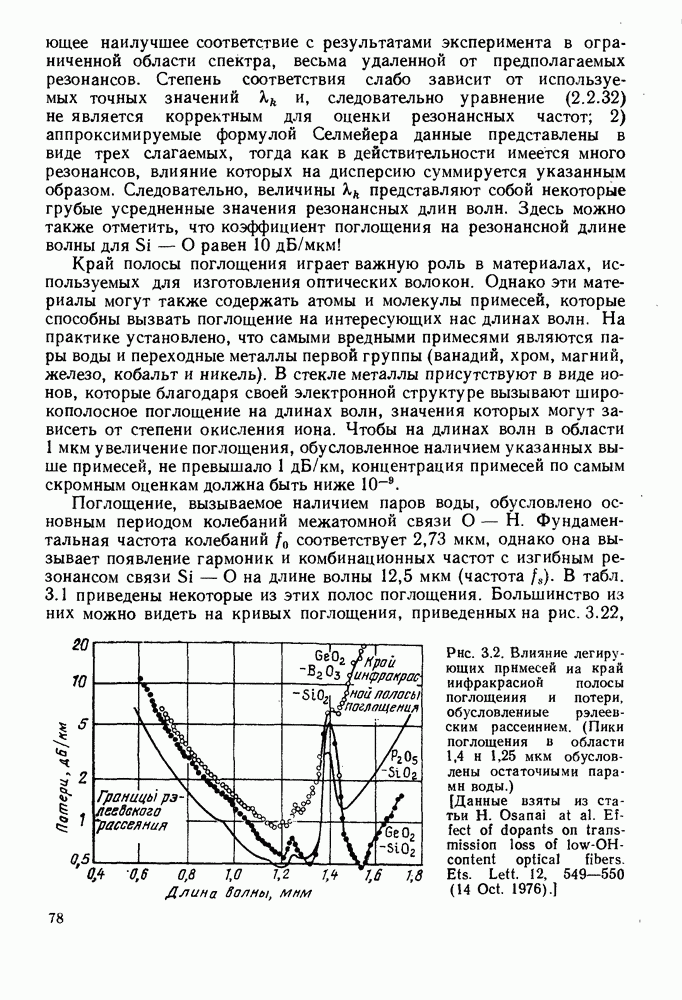
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
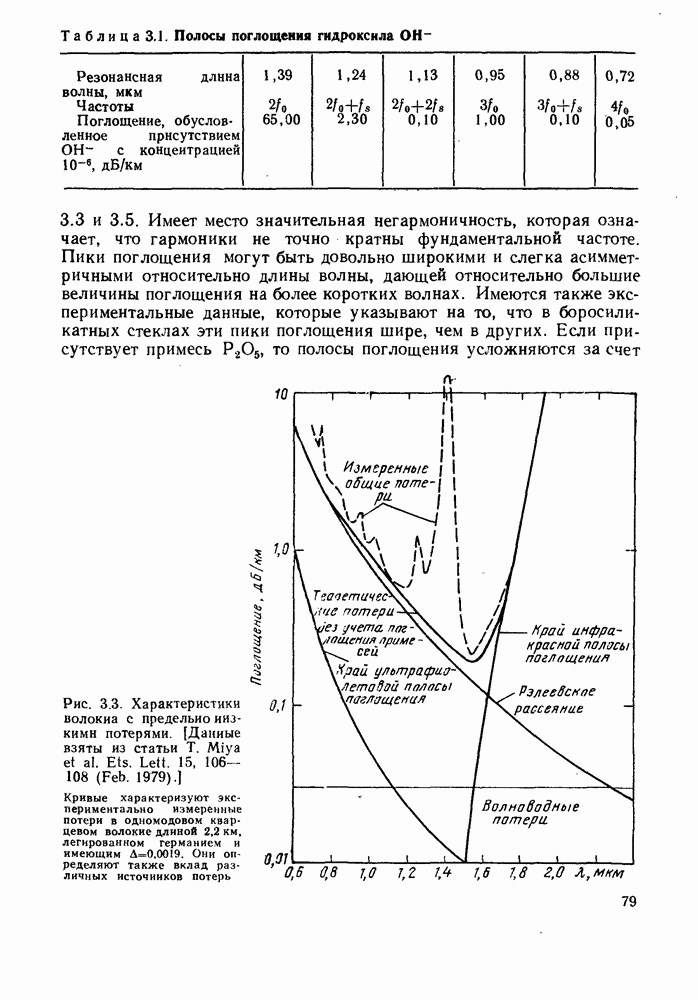
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
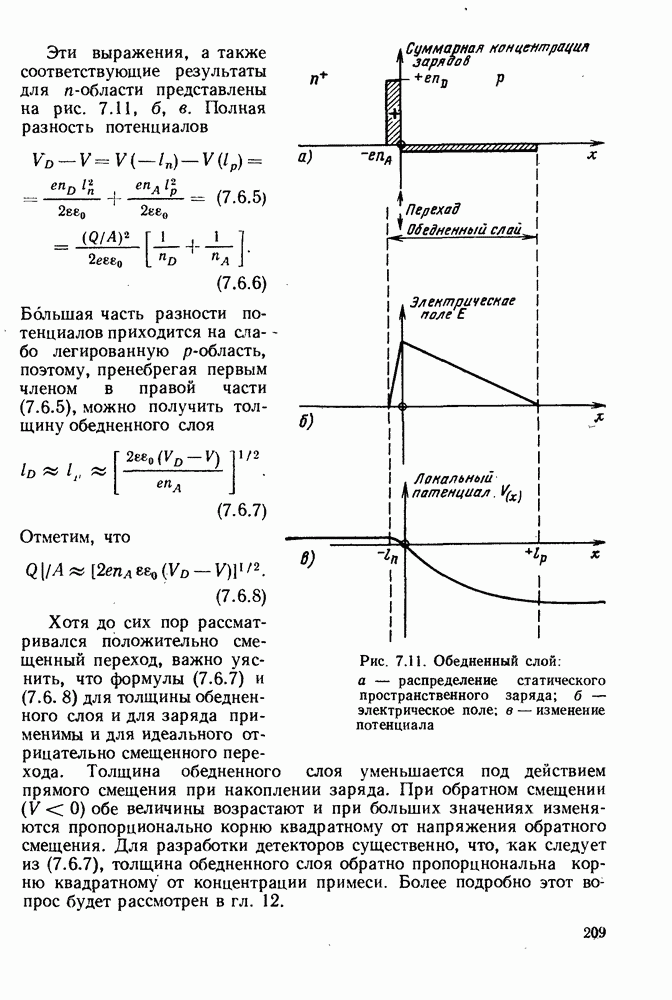
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
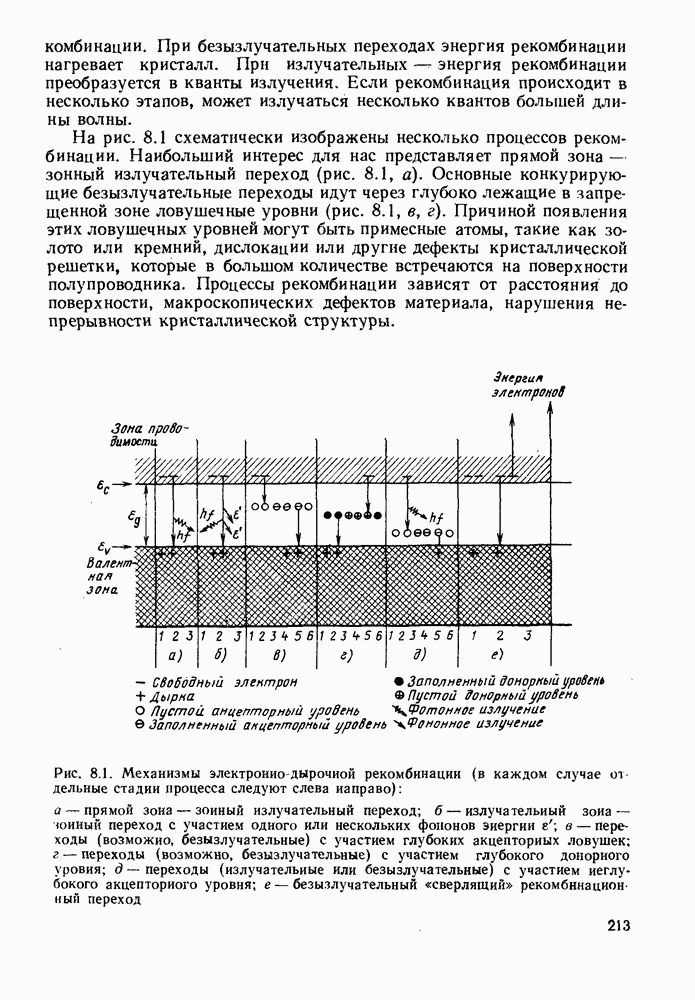
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
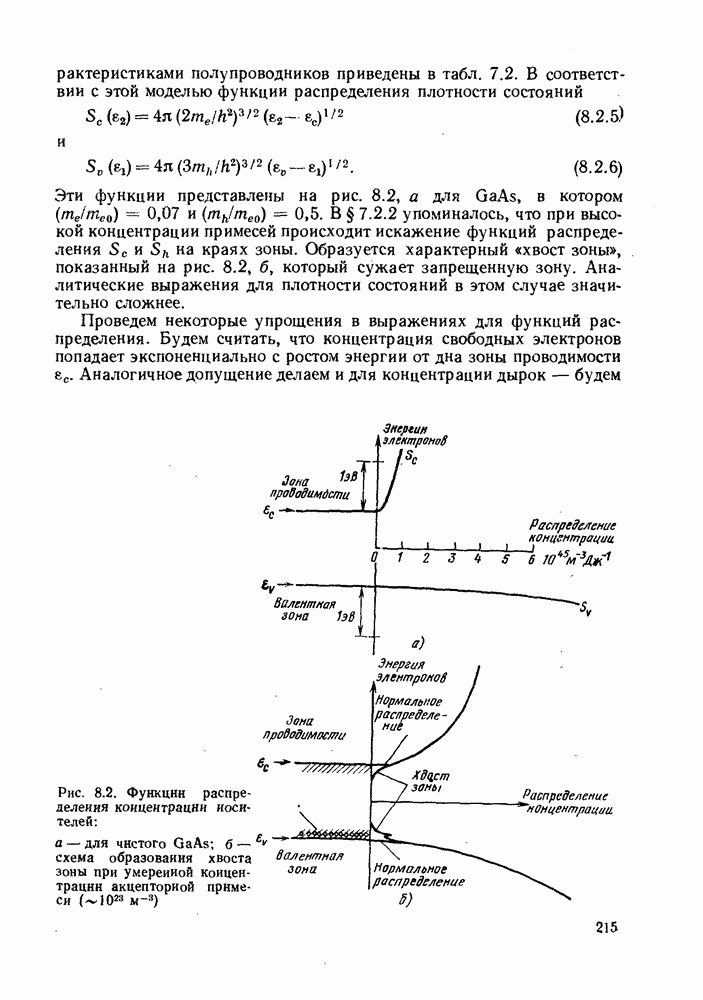
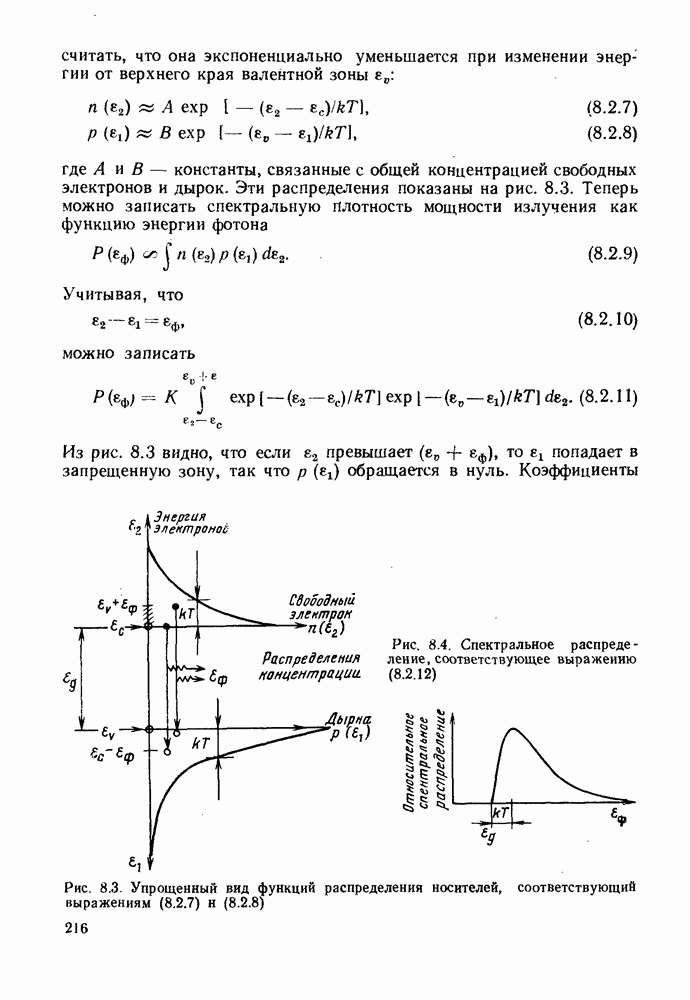
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
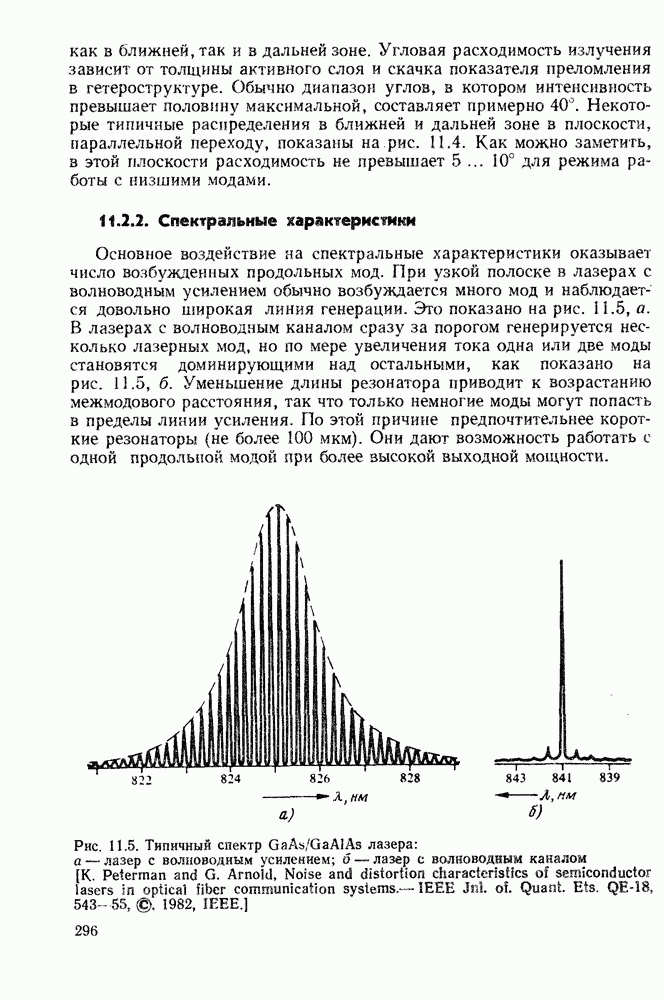
- 11.2.2. Спектральные характеристики
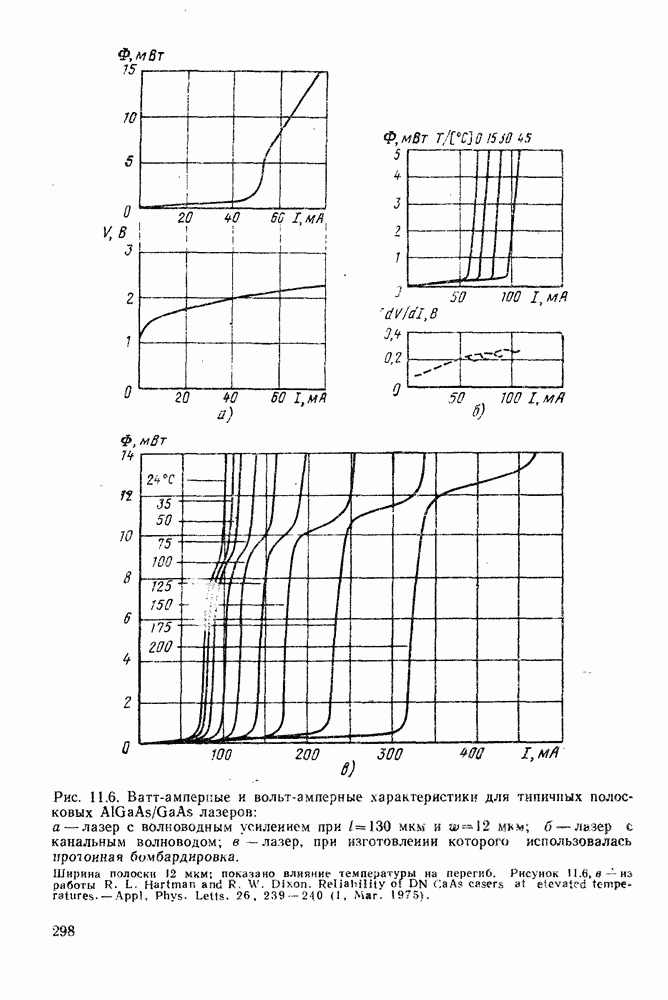
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
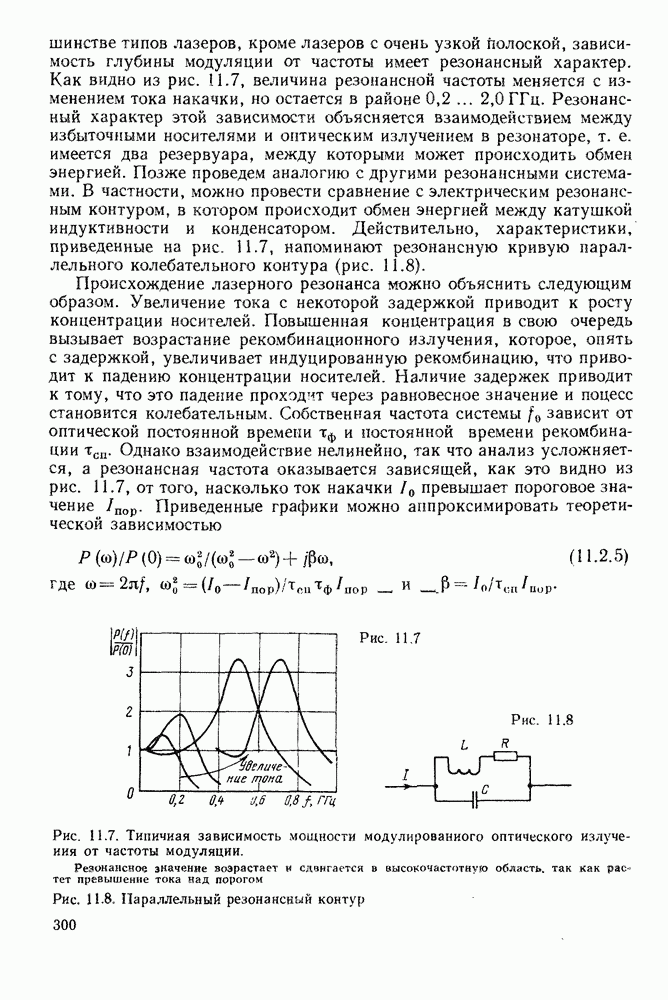
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
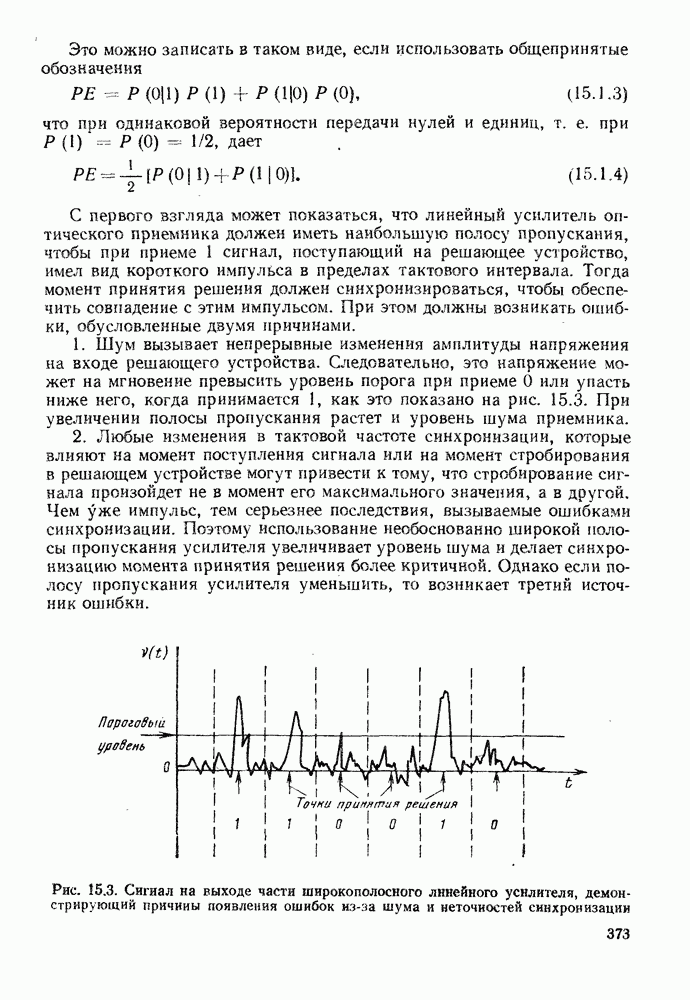
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
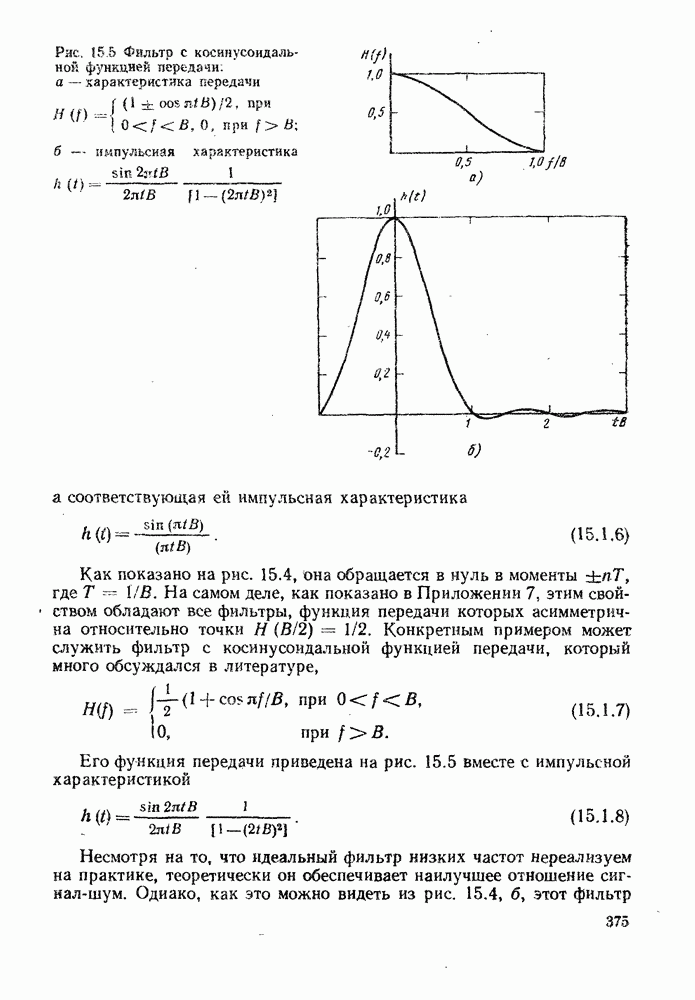
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
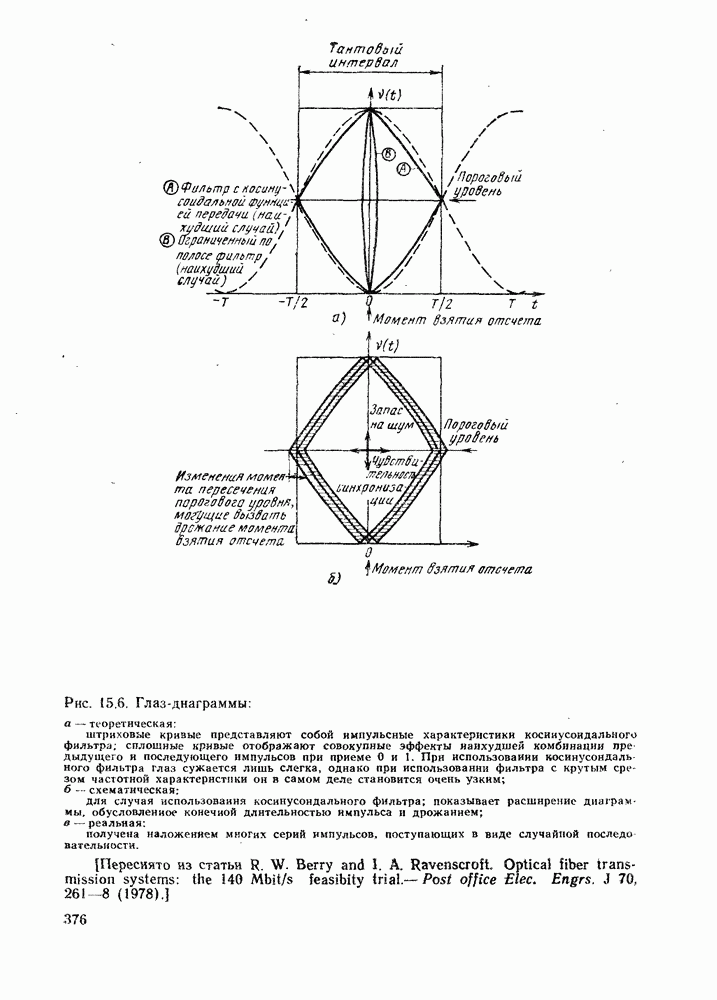
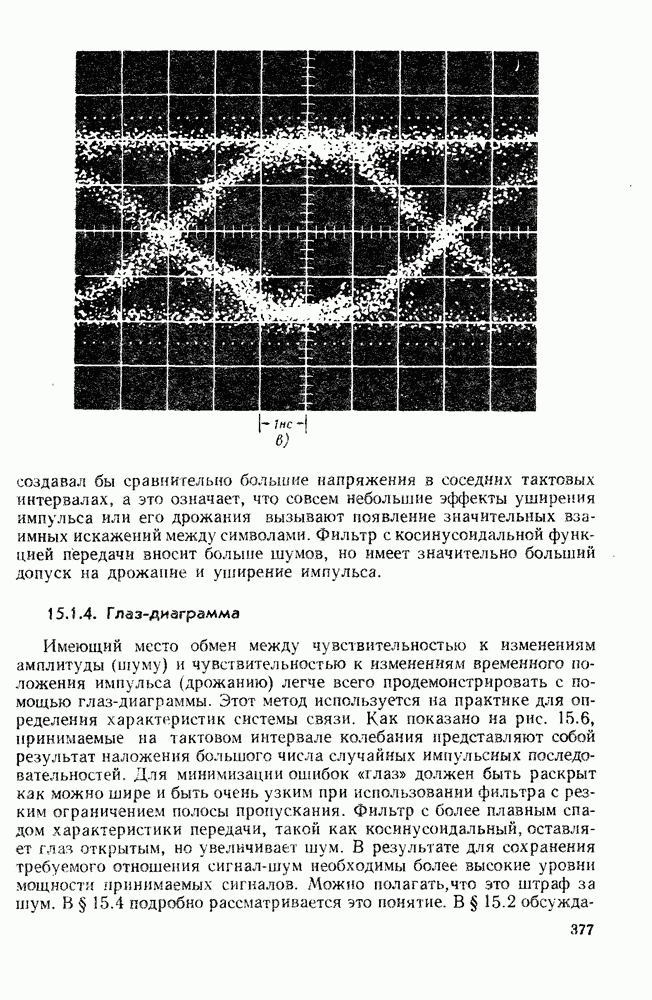
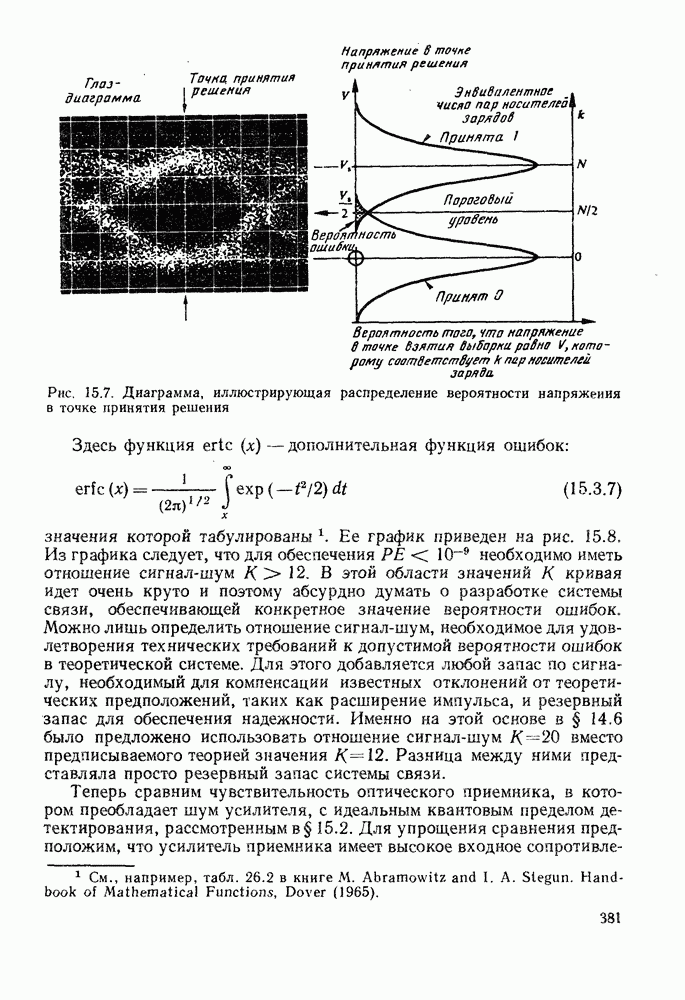
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
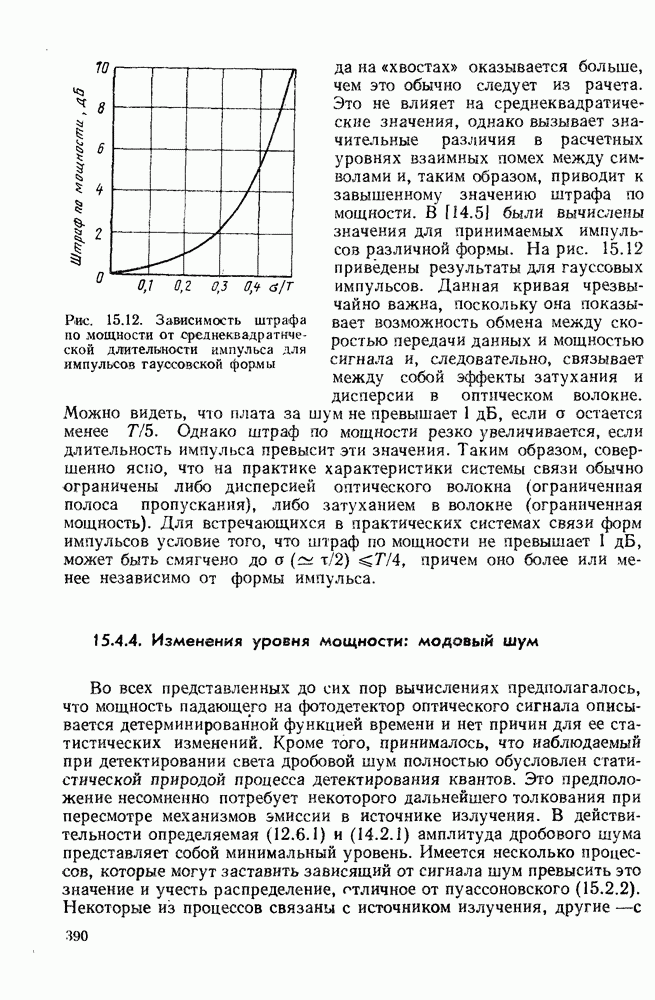
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
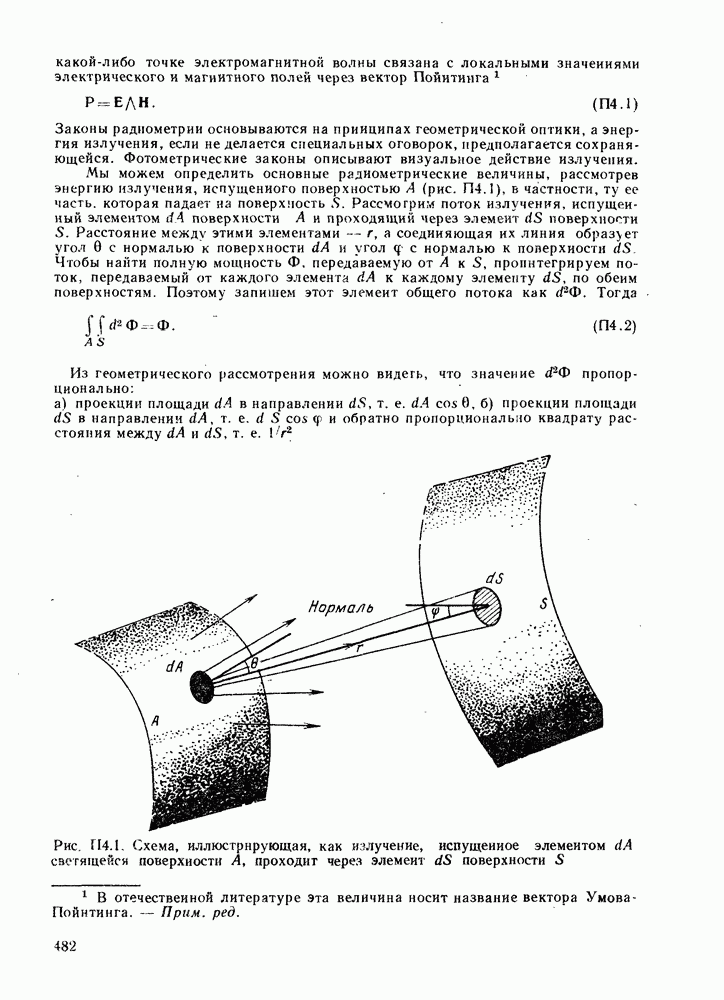
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
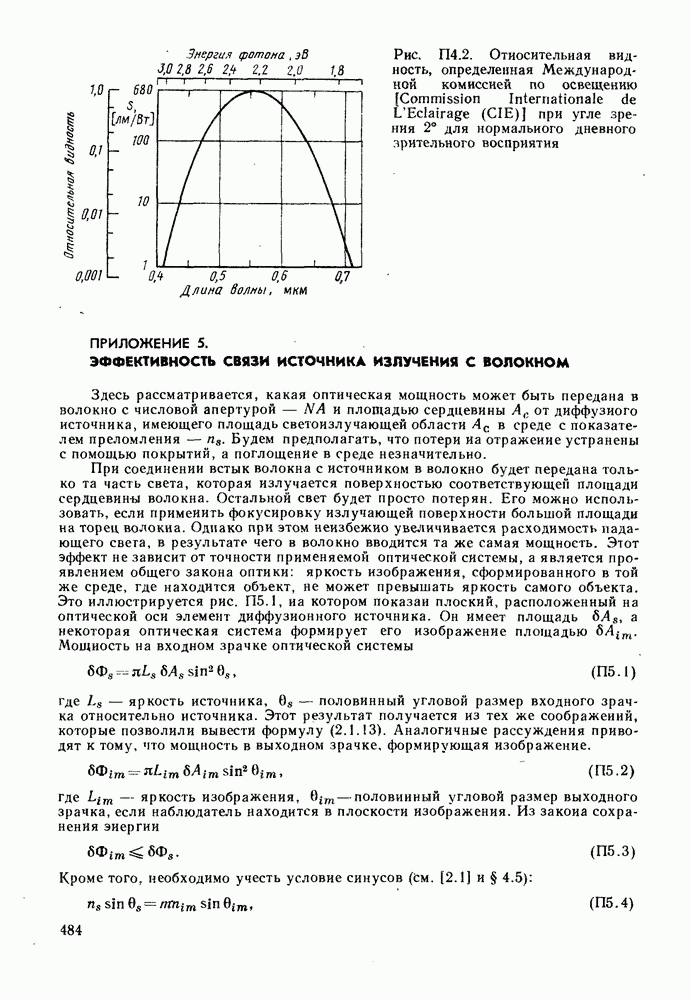
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
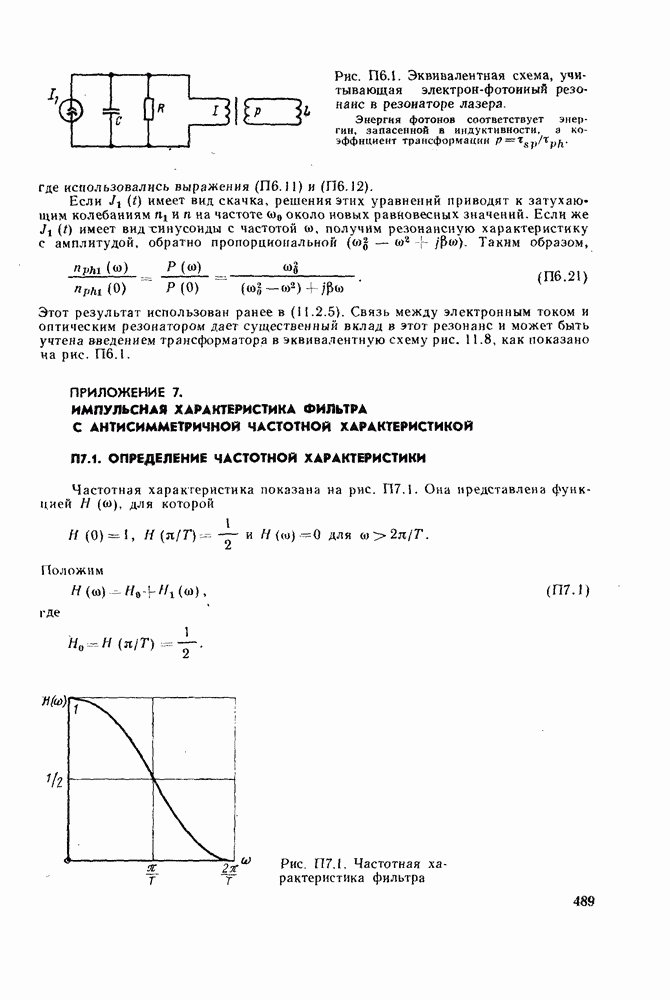
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ