| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
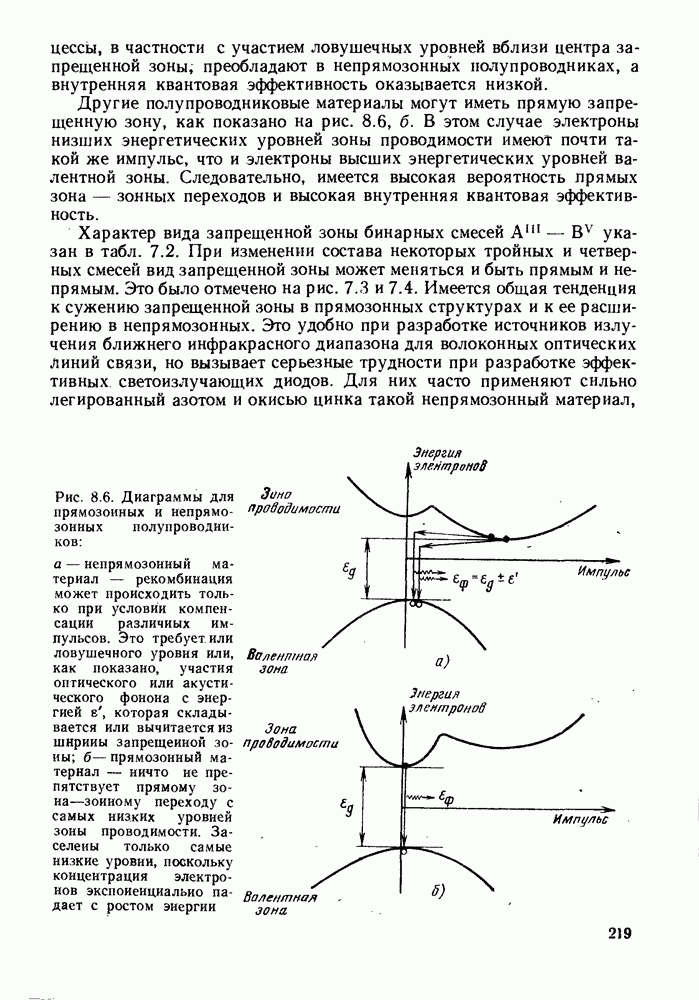
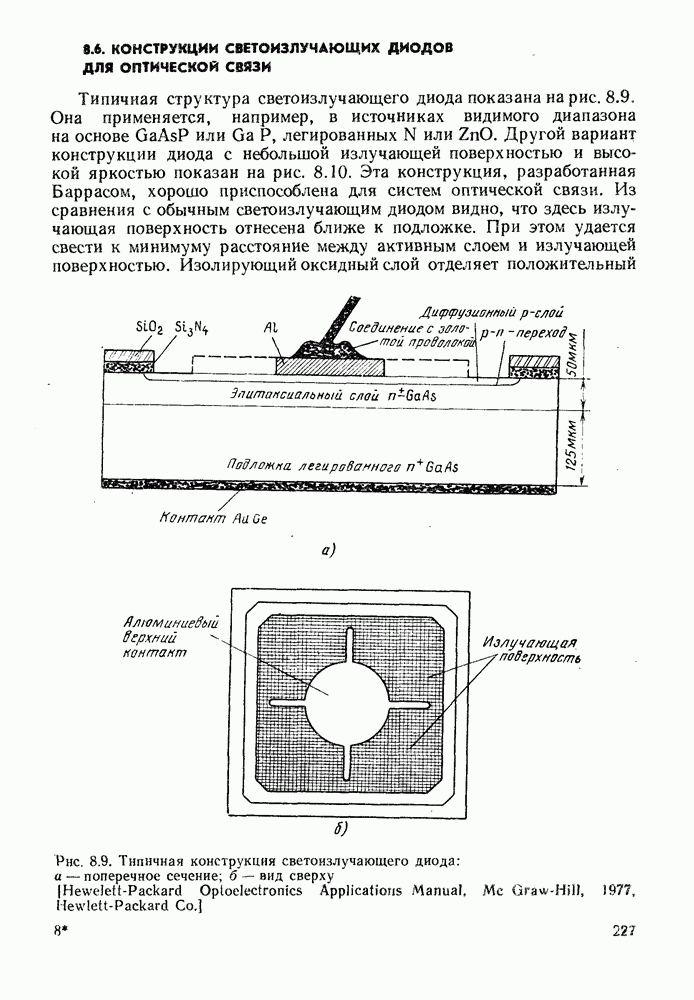
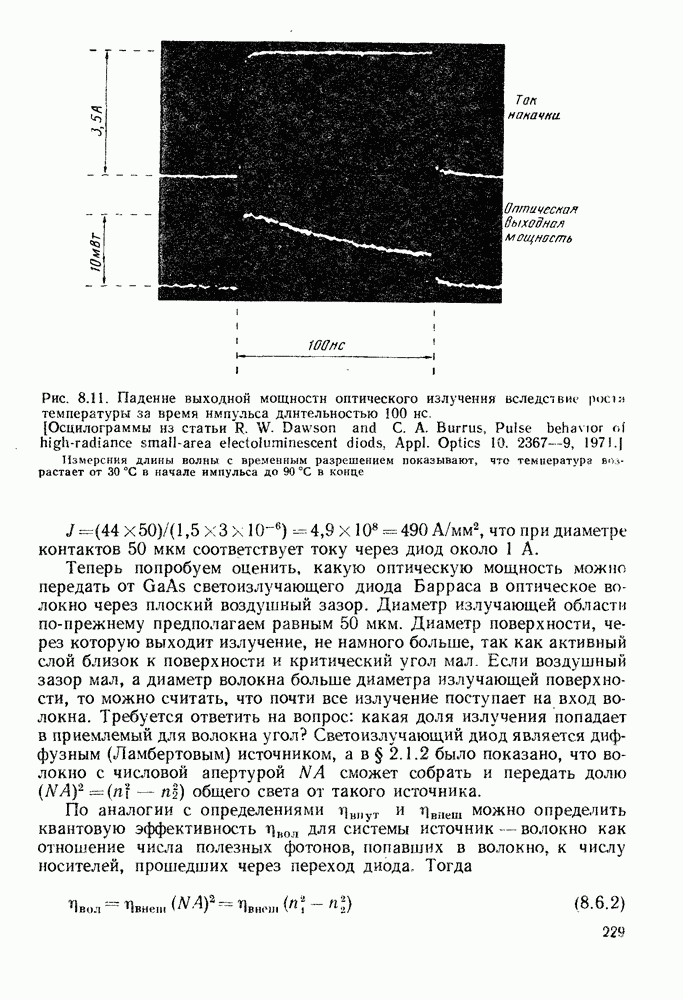
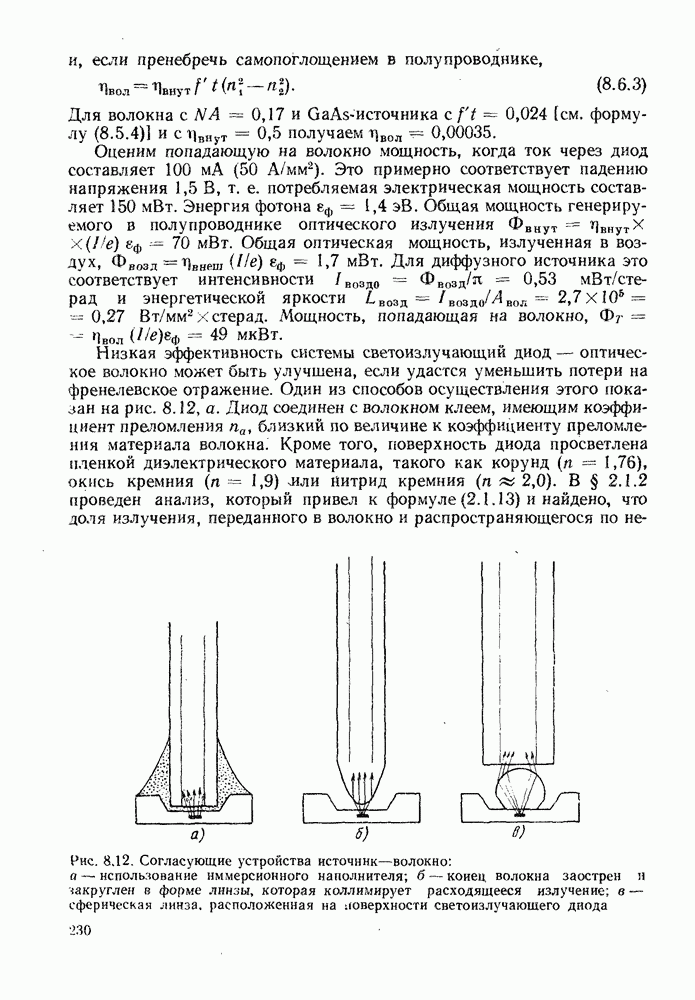
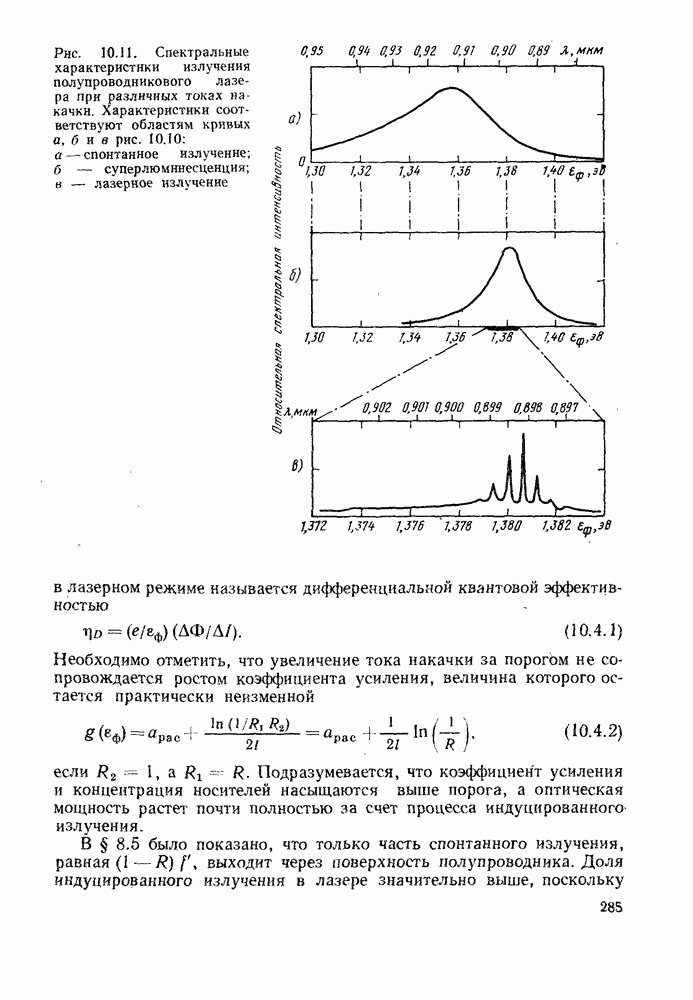
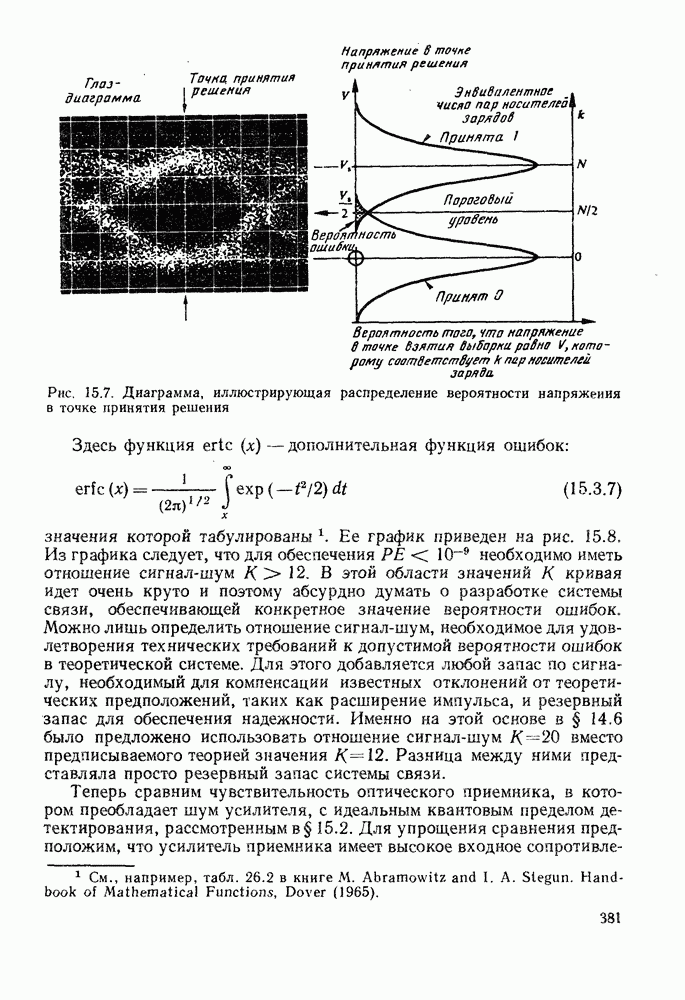
15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
Из приведенного в гл. 14 анализа шумов ясно, что при использовании в качестве фотодетектора  -фотодиода дробовой шум обычно пренебрежимо мал, что предполагалось в предыдущем параграфе. Однако при использовании хороших лавинных фотодиодов, обеспечивающих коэффициент усиления 20 или более, обычно достаточно
-фотодиода дробовой шум обычно пренебрежимо мал, что предполагалось в предыдущем параграфе. Однако при использовании хороших лавинных фотодиодов, обеспечивающих коэффициент усиления 20 или более, обычно достаточно
гарантировать, что относительное влияние шума от других источников уменьшено до уровня, сравнимого или меньше уровня усиленного дробового шума. Эта ситуация исключительно сложна, чтобы ее анализировать на том же уровне строгости, который был возможен до сих пор. Причина состоит в необходимости использования различных функций распределения для дробового шума и шумов других источников, а также в том, что теперь уровень шума может зависеть от величины сигнала.
Было принято, что источники теплового шума и шума усилителя имеют гауссовские распределения амплитуд. Это позволяет выразить общий эффект от ряда независимых и некоррелированных источников шума в виде суммы средних квадратов амплитуд каждого из них. Влияние дробового шума было учтено аналогичным образом. Как было показано в § 15.2. дробовый шум подчиняется пуассоновской статистике. Амплитудное распределение умноженного дробового шума на выходе лавинного фотодиода будет зависеть, кроме того, от статистик процессов генерации носителей заряда при лавинном умножении, которые не достаточно исследованы теоретически. Как указывалось в гл. 14, оправданием такого сложения различных источников шума служит тот факт, что при достаточно большом числе случайных величин, что имеет место в нашем случае, все распределения приближаются к гауссовскому относительно своего среднего значения. Следовательно, полученное таким образом суммарное среднеквадратическое значение шума представляет собой приемлемое приближение. Однако при определении вероятностей ошибок имеем дело с «хвостами» функций распределения и важно помнить, что простое предположение об аппроксимации распределений всех шумов гауссовой функцией может привести к значительным ошибкам. Тем не менее и далее будем использовать эту аппроксимацию.
В случае, когда дробовый шум и шум усилителя значительны по величине, решение для минимального среднего тока можно получить из уравнений (14.4.32) — (14.4.34). Оно имеет вид

где

и

Здесь  представлялось вместо
представлялось вместо  и предполагалось, что R достаточно велико по сравнению со слагаемыми шума а
и предполагалось, что R достаточно велико по сравнению со слагаемыми шума а  чтобы
чтобы  можно было пренебречь. Отметим, что
можно было пренебречь. Отметим, что

Как функция скорости передачи данных, решение для  представленное в виде (15.3.10), распадается на две либо на три части. Этот вопрос уже поднимался в § 14.4.3. При
представленное в виде (15.3.10), распадается на две либо на три части. Этот вопрос уже поднимался в § 14.4.3. При

величина  принимает минимальное значение:
принимает минимальное значение:

При  в правых частях выражений (15.3.12) и (15.3.13) преобладает слагаемое шумового напряжения; если
в правых частях выражений (15.3.12) и (15.3.13) преобладает слагаемое шумового напряжения; если  доминирующим становится слагаемое шумового тока. Если
доминирующим становится слагаемое шумового тока. Если  то при всех скоростях передачи данных дробовой шум пренебрежимо мал и
то при всех скоростях передачи данных дробовой шум пренебрежимо мал и  При
При 

при этом предполагается, что распределения шума - гауссовы и  . При
. При 

Даже когда  слагаемое шумового тока все же доминирует, если скорость передачи данных достаточно мала, чтобы обеспечить
слагаемое шумового тока все же доминирует, если скорость передачи данных достаточно мала, чтобы обеспечить  а слагаемое шумового напряжения доминирует при больших скоростях передач и данных, достаточных для удовлетворения того же самого условия. Таким образом, когда
а слагаемое шумового напряжения доминирует при больших скоростях передач и данных, достаточных для удовлетворения того же самого условия. Таким образом, когда

значение  еще раз определяется (15.3.16), а если
еще раз определяется (15.3.16), а если

значение снова находят по (15.3.17). Теперь может существовать и средняя область значений скоростей передачи данных, а именно,  при
при  Тогда
Тогда

В этом случае преобладающим становится умноженный дробовой шум, который может иметь не гауссово и даже несимметричное распределение. Следовательно, может стать нецелесообразным использовать значение  для поддержания вероятности ошибок ниже уровня
для поддержания вероятности ошибок ниже уровня  Может также стать неуместной установка уровня порога посередине между уровнями сигналов, соответствующих 0 и 1.
Может также стать неуместной установка уровня порога посередине между уровнями сигналов, соответствующих 0 и 1.
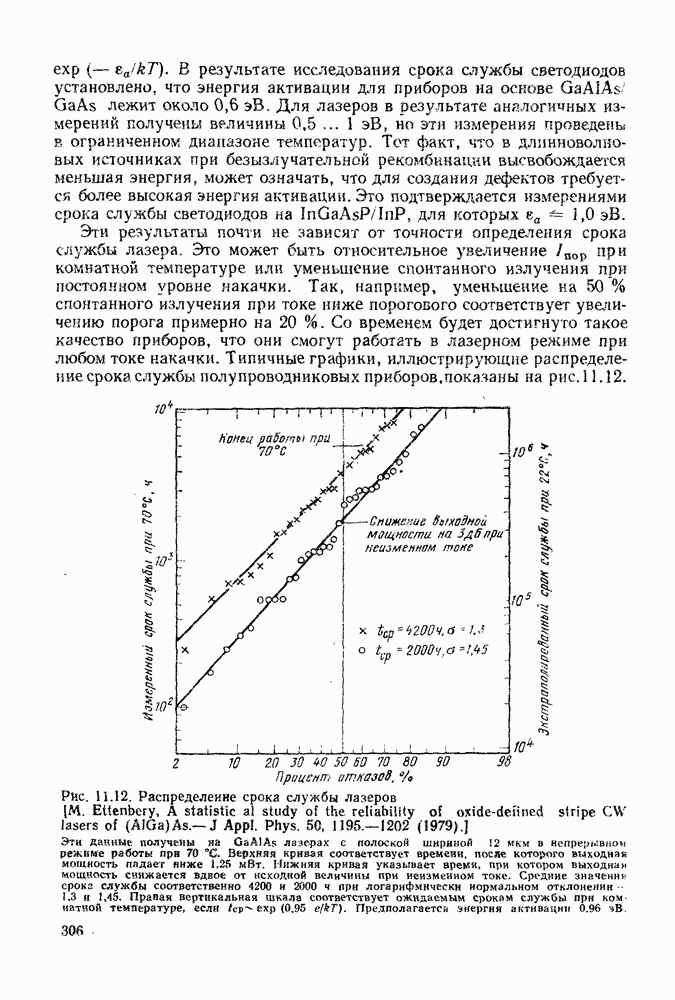
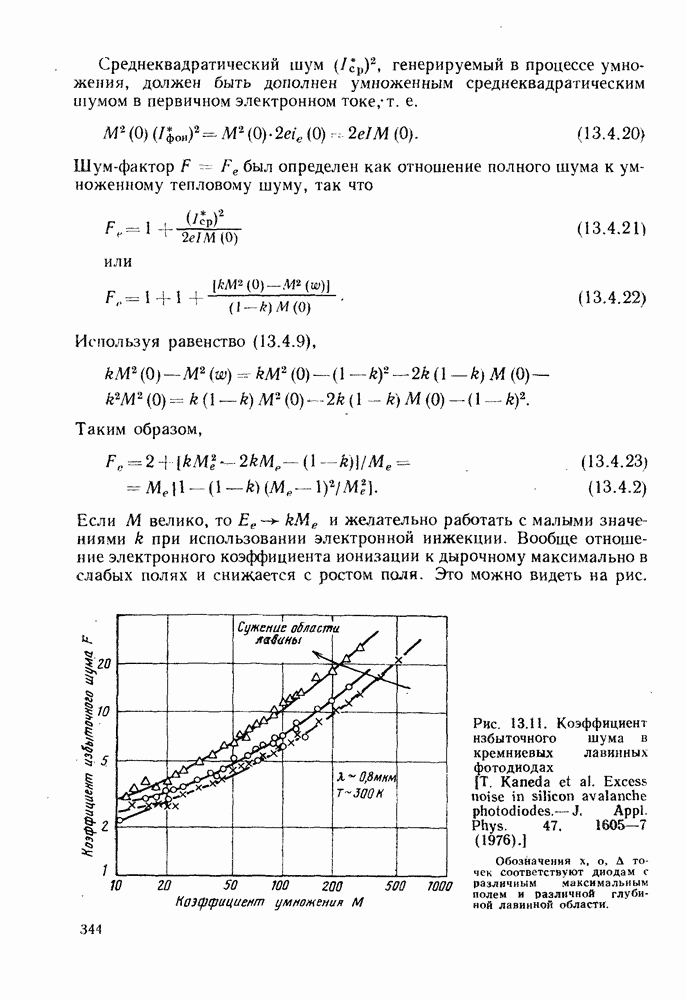
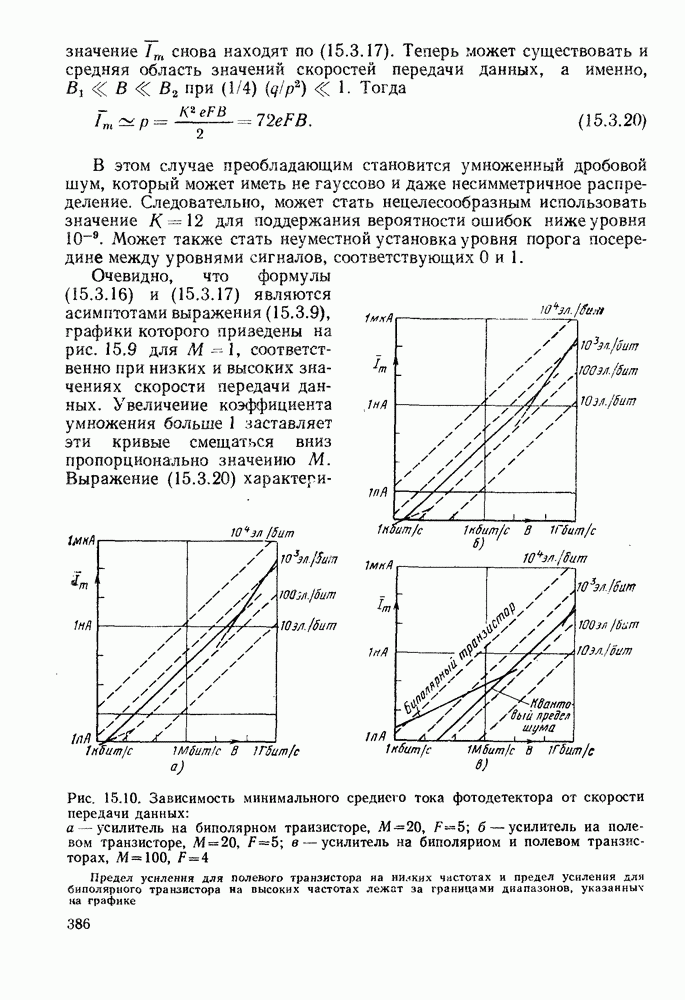
Очевидно, что формулы (15.3.16) и (15.3.17) являются асимптотами выражения (15.3.9), графики которого приведены на рис. 15.9 для  соответственно при низких и высоких значениях скорости передачи данных. Увеличение коэффициента умножения больше 1 заставляет эти кривые смещаться вниз пропорционально значению
соответственно при низких и высоких значениях скорости передачи данных. Увеличение коэффициента умножения больше 1 заставляет эти кривые смещаться вниз пропорционально значению 
Выражение (15.3.20)
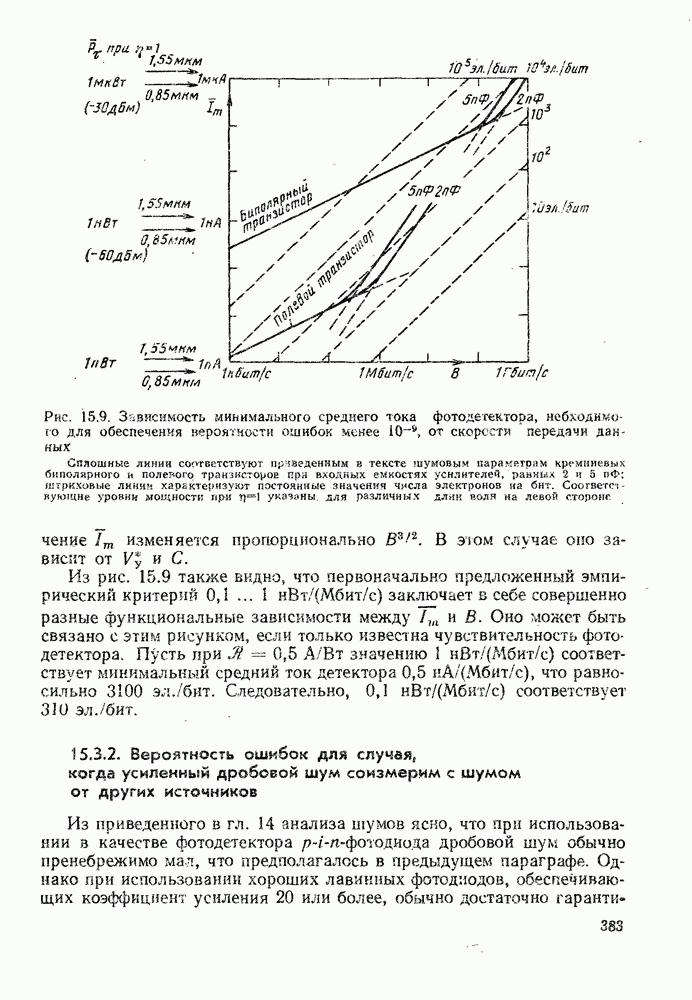
Рис. 15.10. (см. скан) Зависимость минимального среднего тока фотодетектора от скорости передачи данных: а — усилитель на биполярном транзисторе,  усилитель на полевом транзисторе,
усилитель на полевом транзисторе,  в — усилитель на биполярном и полевом транзисторах,
в — усилитель на биполярном и полевом транзисторах,  Предел усиления для полевого транзистора на низких частотах и предел усиления для биполярного транзистора на высоких частотах лежат за границами диапазонов, указанных на графике
Предел усиления для полевого транзистора на низких частотах и предел усиления для биполярного транзистора на высоких частотах лежат за границами диапазонов, указанных на графике
характеризует уменьшение предельной чувствительности, ограниченной квантовым пределом, которая была определена в § 15.2 коэффициентом  Если исходить из числа пар носителей заряда, генерируемых при приеме одного бита, эта чувствительность станет равной
Если исходить из числа пар носителей заряда, генерируемых при приеме одного бита, эта чувствительность станет равной  или
или  носителей заряда/бит. На рис. 15.10 приведены графики этих трех приближенных решений уравнения (15.3.10) для некоторых частных примеров, где учтены шумовые параметры входных каскадов усилителя на кремниевых полевом и биполярном транзисторах с входной емкостью
носителей заряда/бит. На рис. 15.10 приведены графики этих трех приближенных решений уравнения (15.3.10) для некоторых частных примеров, где учтены шумовые параметры входных каскадов усилителя на кремниевых полевом и биполярном транзисторах с входной емкостью  Таким образом, имеем: для полевого транзистора —
Таким образом, имеем: для полевого транзистора —  Гц и
Гц и  для биполярного
для биполярного  Значения коэффициента усиления и коэффициента шума лавинного фотодиода следующее
Значения коэффициента усиления и коэффициента шума лавинного фотодиода следующее  причем более высокий коэффициент, усиления можно ожидать от малошумящих кремниевых ЛФД. Из рисунка видно, что в обоих случаях усилитель на полевом транзисторе оказывается ограниченным дробовым шумом повсюду в наиболее полезной области частот, в то время как усилитель на биполярном транзисторе едва достигает предела дробового шума при невысоких коэффициентах усиления ЛФД. Важно иметь в виду, что все приведенные вычисления предполагали однородную спектральную плотность шума усилителя на всех частотах. Имеются все основания полагать, что на практике величины
причем более высокий коэффициент, усиления можно ожидать от малошумящих кремниевых ЛФД. Из рисунка видно, что в обоих случаях усилитель на полевом транзисторе оказывается ограниченным дробовым шумом повсюду в наиболее полезной области частот, в то время как усилитель на биполярном транзисторе едва достигает предела дробового шума при невысоких коэффициентах усиления ЛФД. Важно иметь в виду, что все приведенные вычисления предполагали однородную спектральную плотность шума усилителя на всех частотах. Имеются все основания полагать, что на практике величины  будут увеличиваться на высоких и низких частотах. Это приведет к уменьшению области частот, в пределах которой можно поддерживать режим детектирования, ограниченный дробовым шумом.
будут увеличиваться на высоких и низких частотах. Это приведет к уменьшению области частот, в пределах которой можно поддерживать режим детектирования, ограниченный дробовым шумом.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
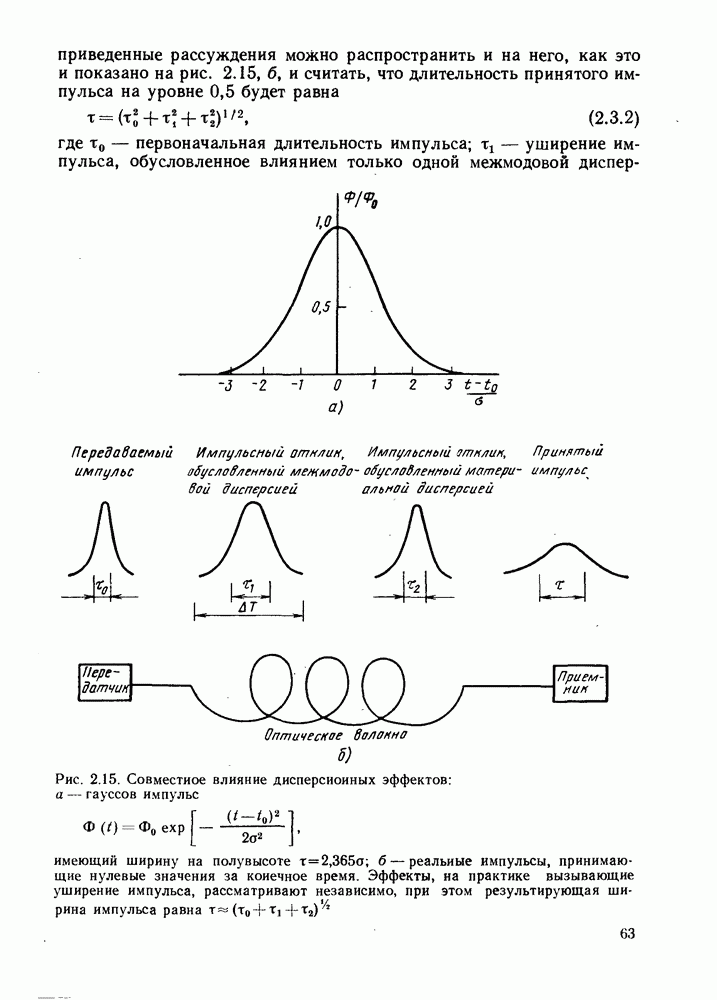
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
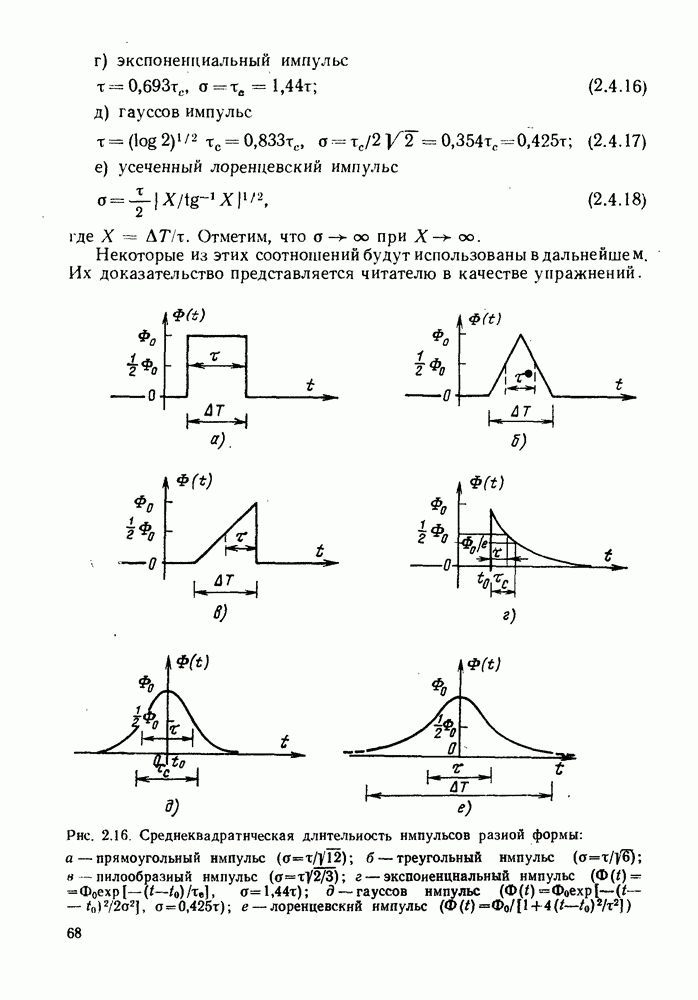
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
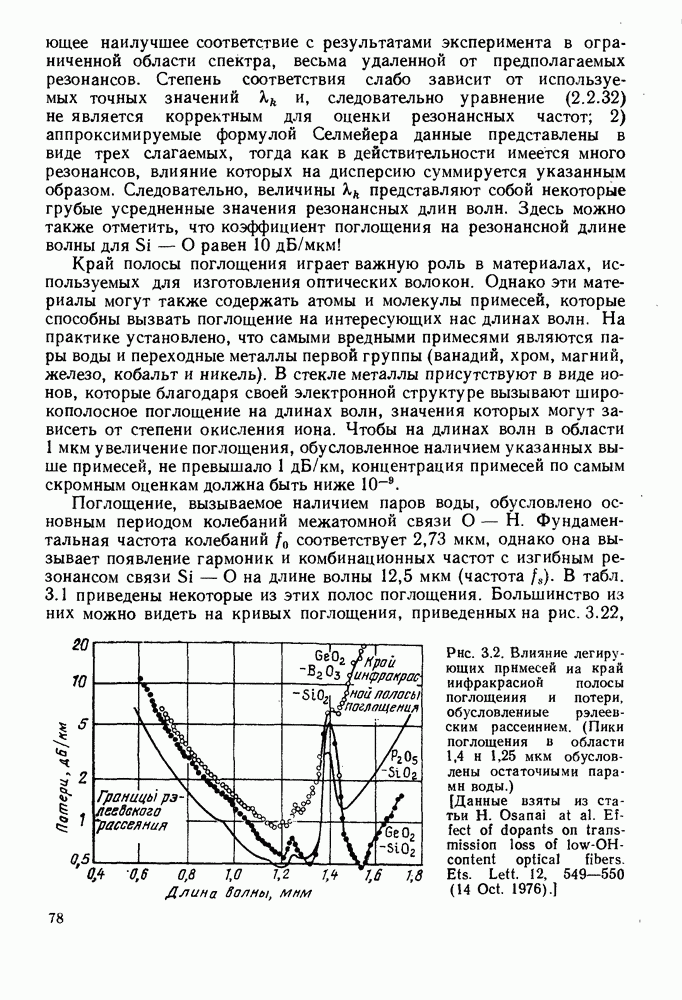
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
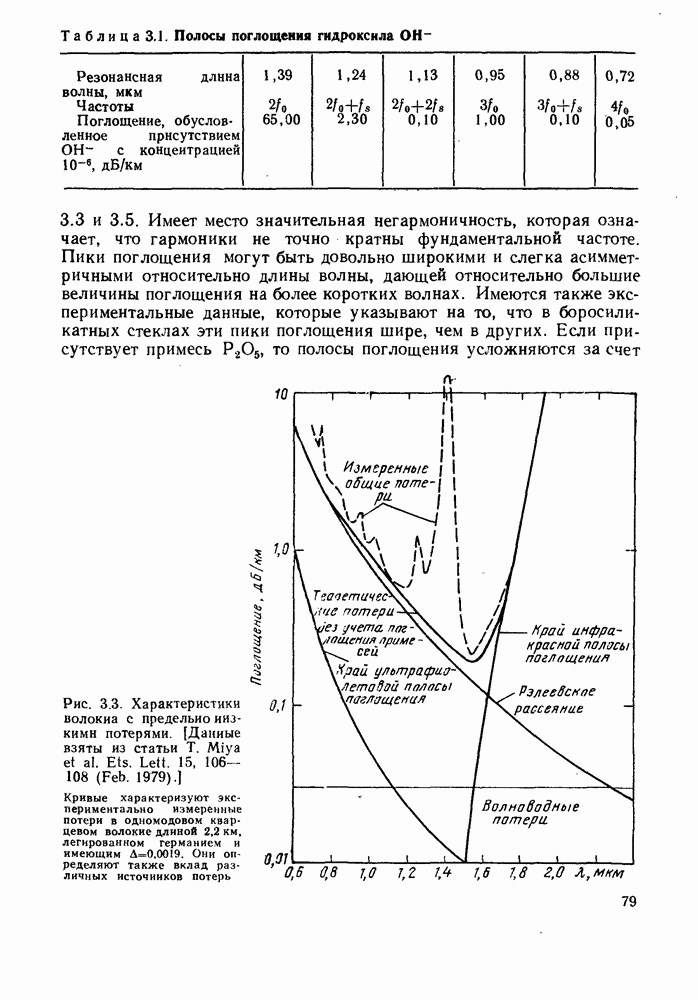
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
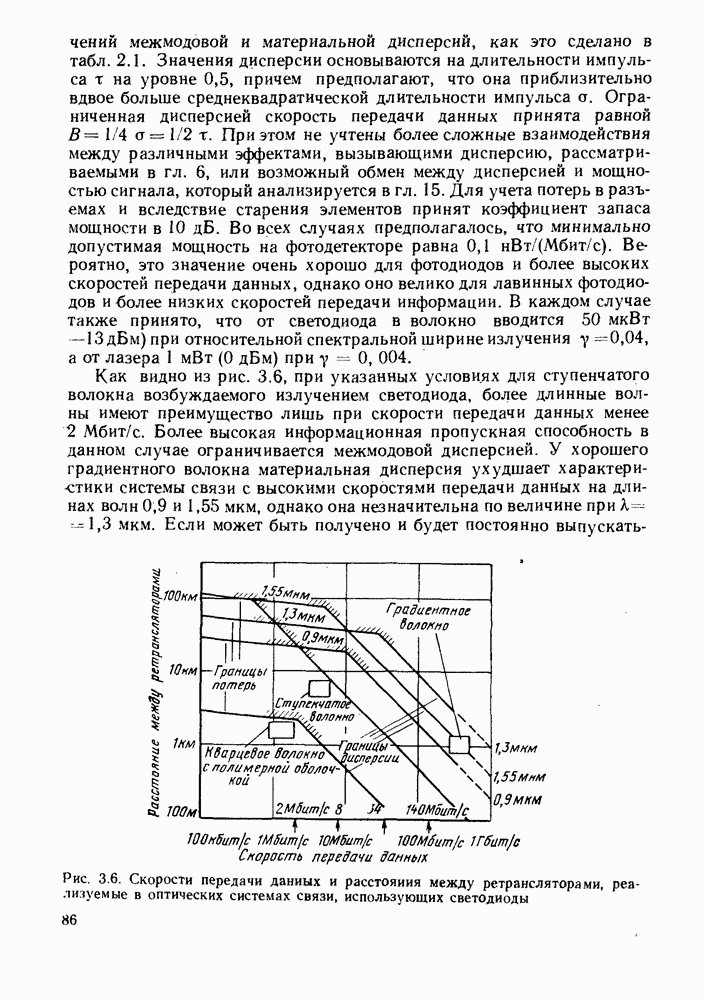
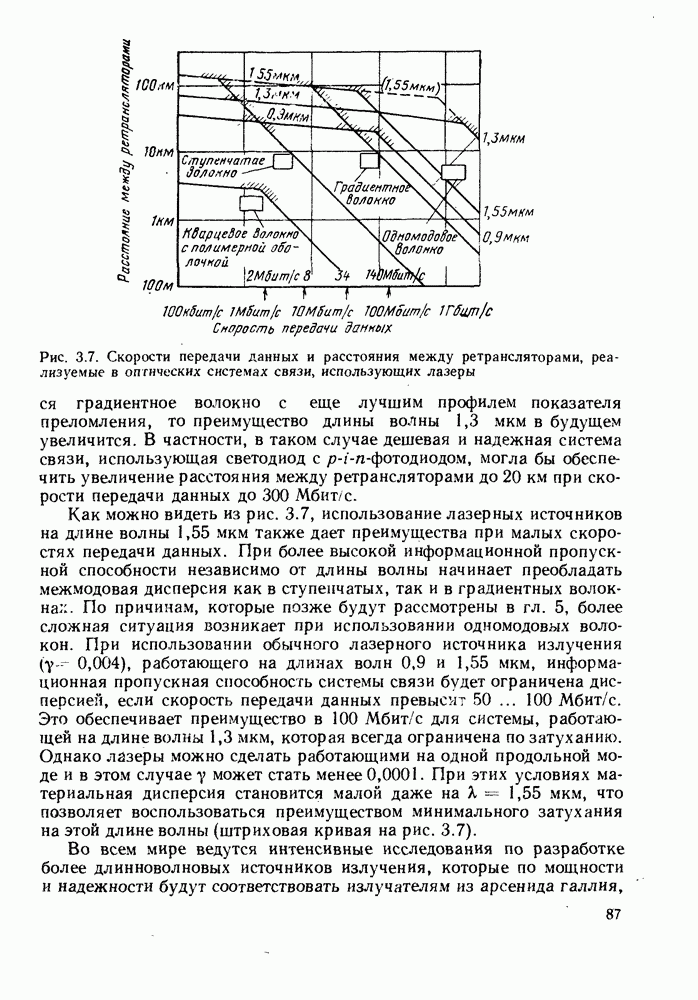
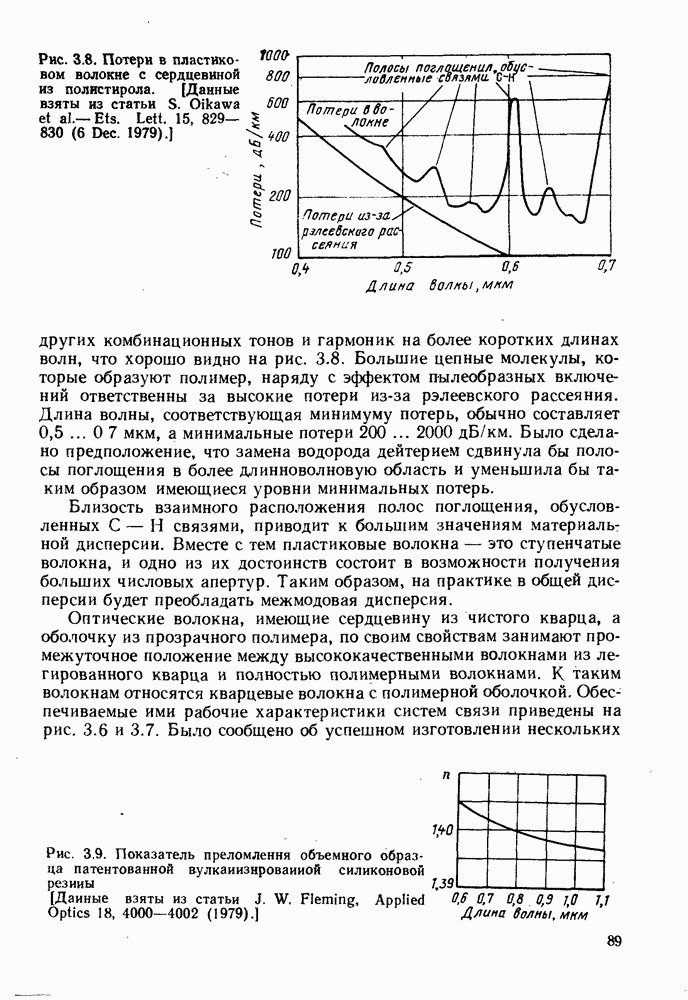
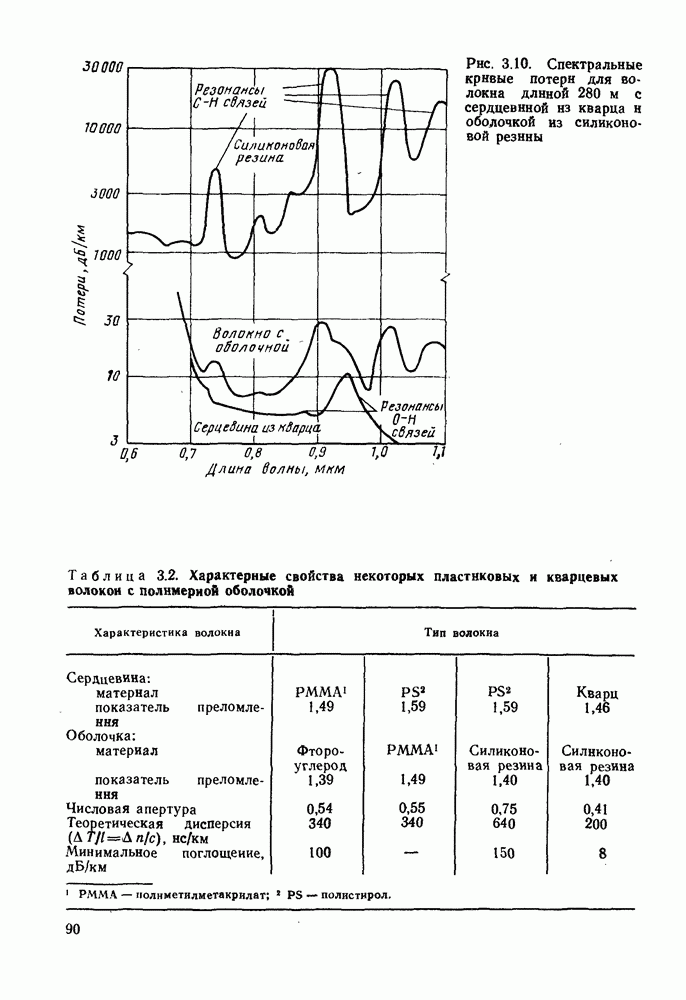
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
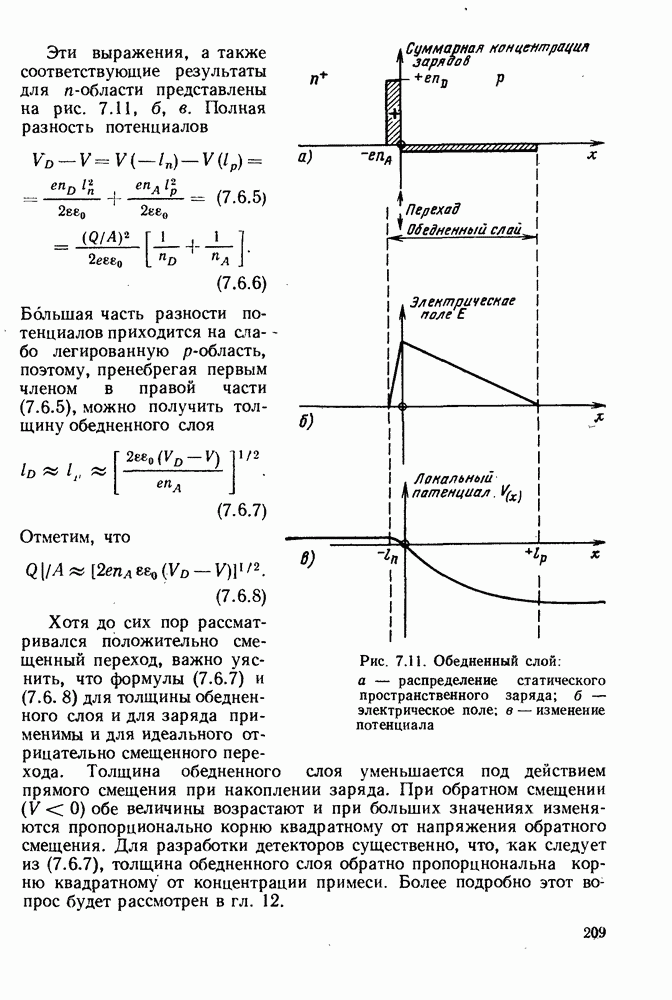
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
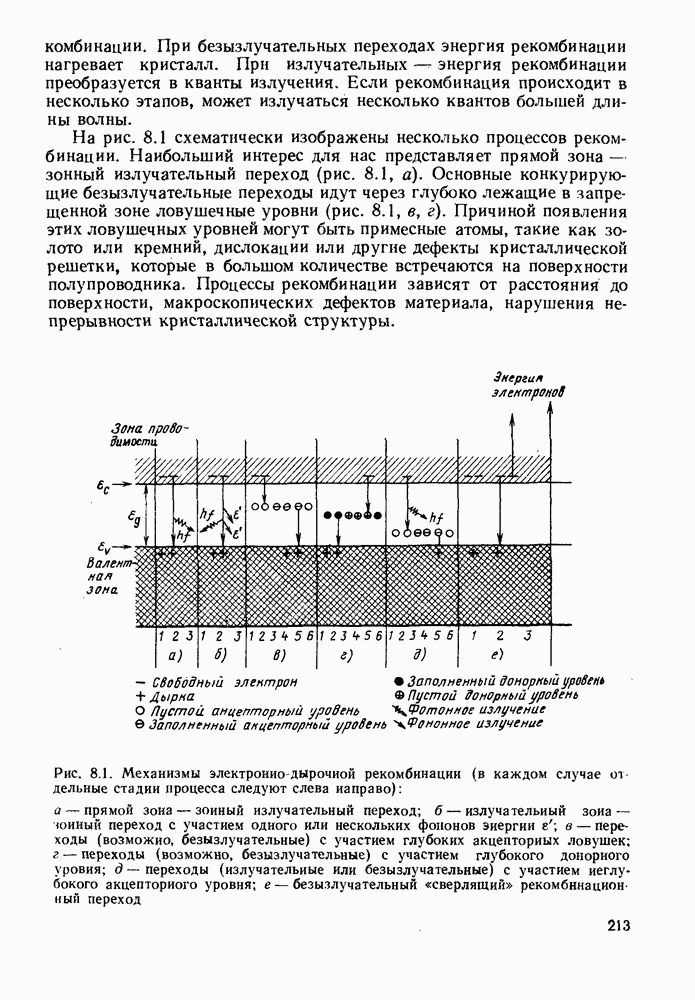
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
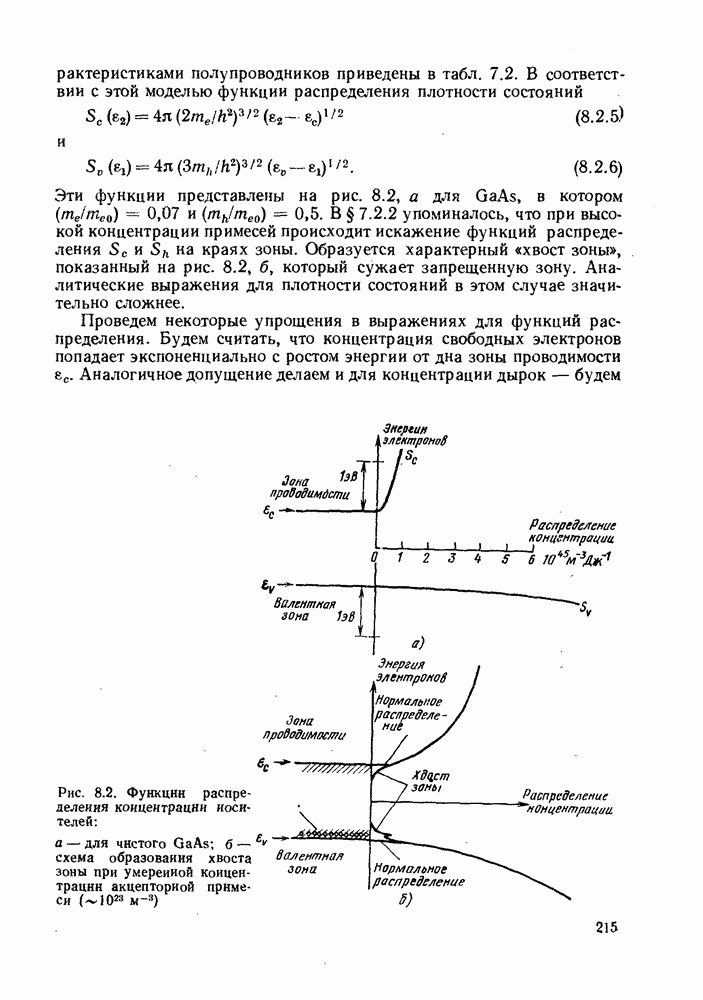
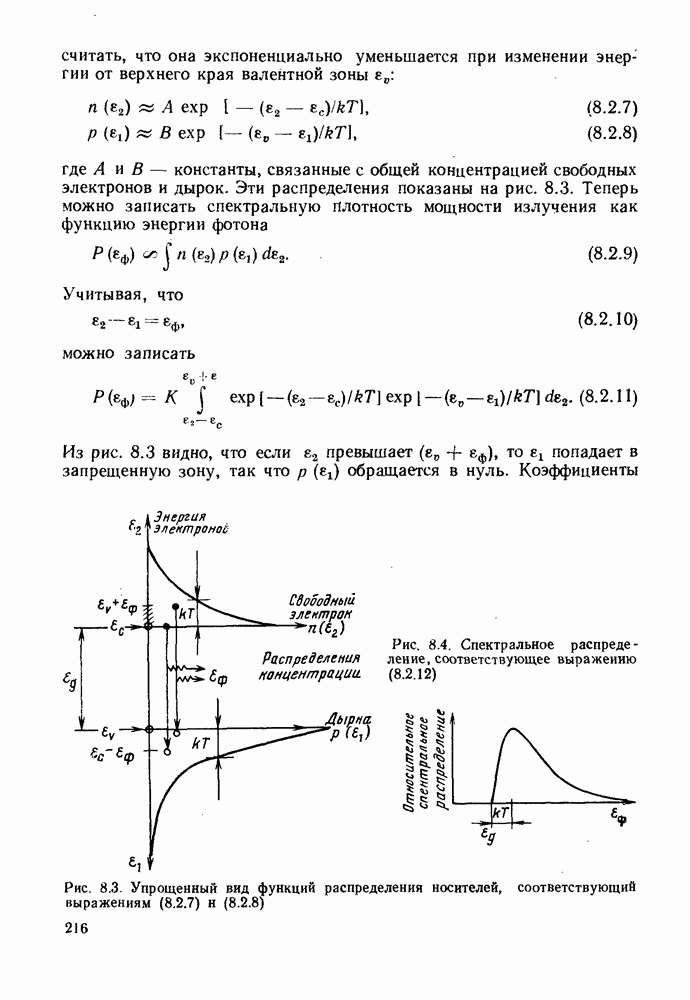
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
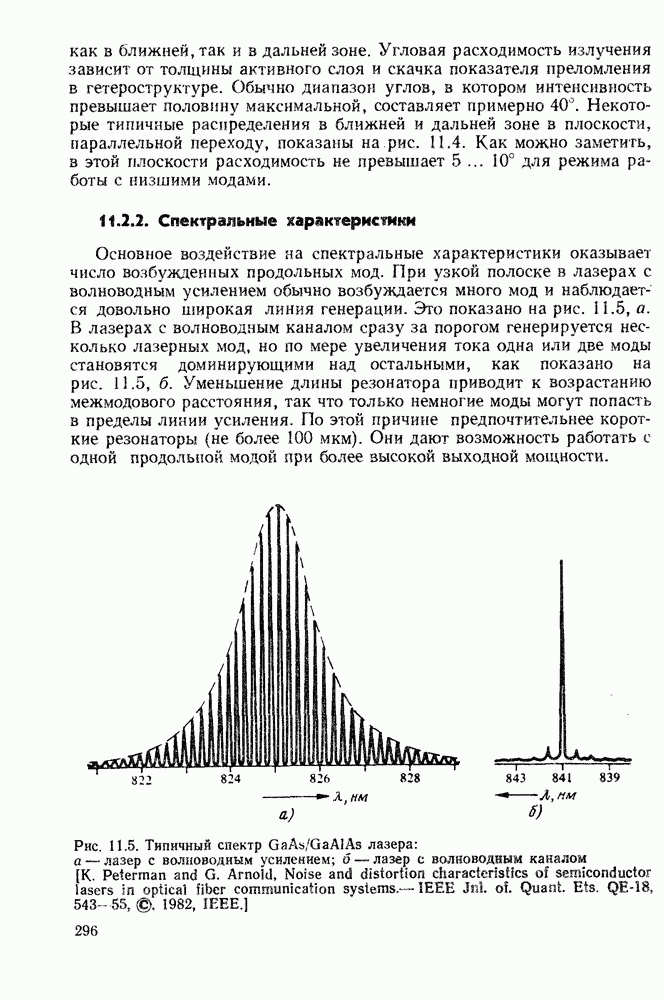
- 11.2.2. Спектральные характеристики
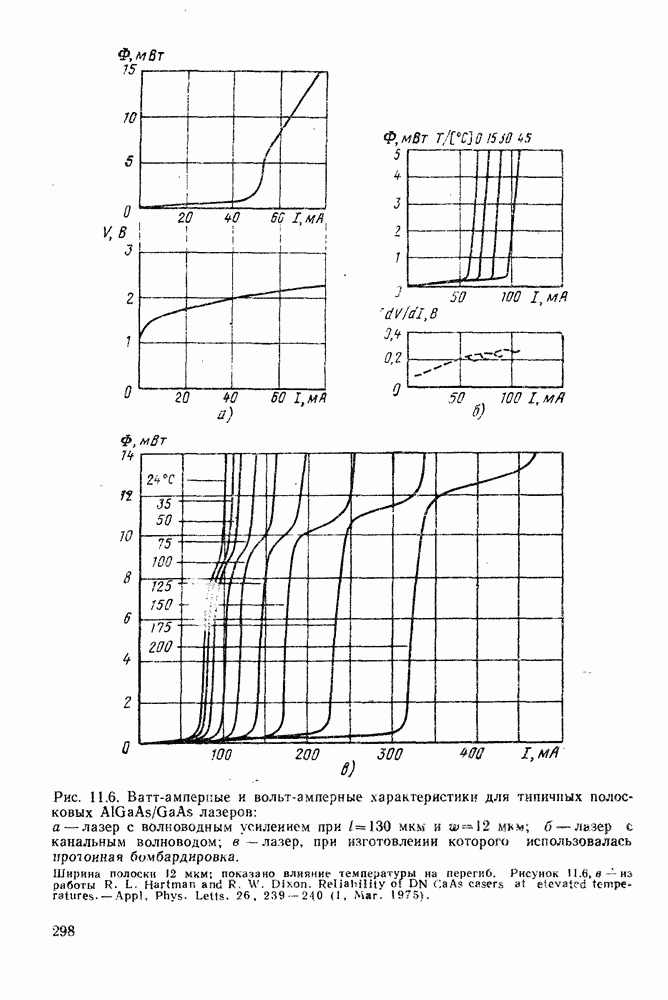
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
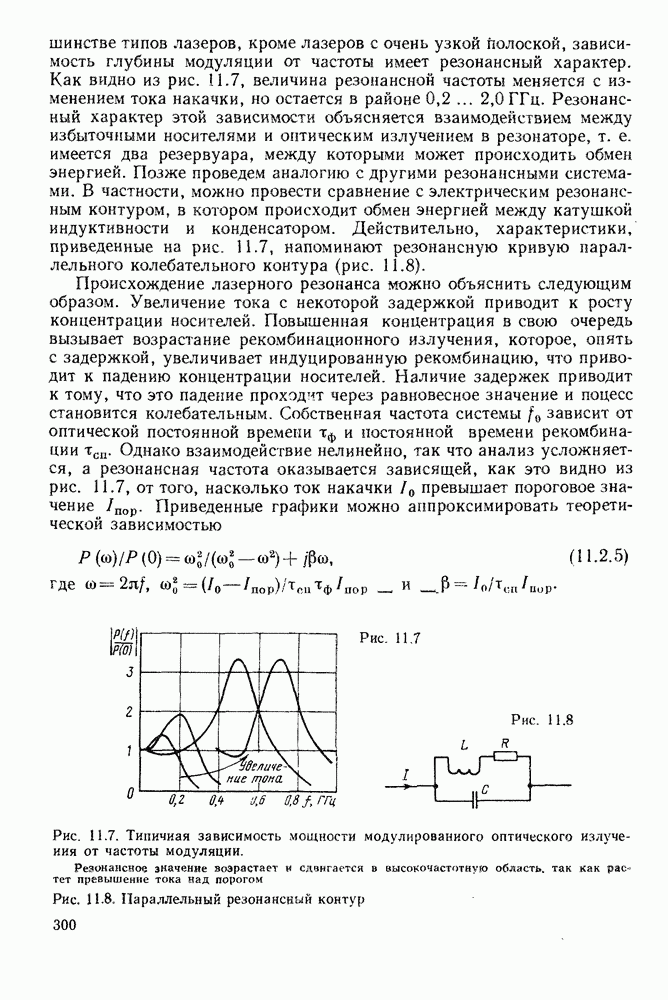
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
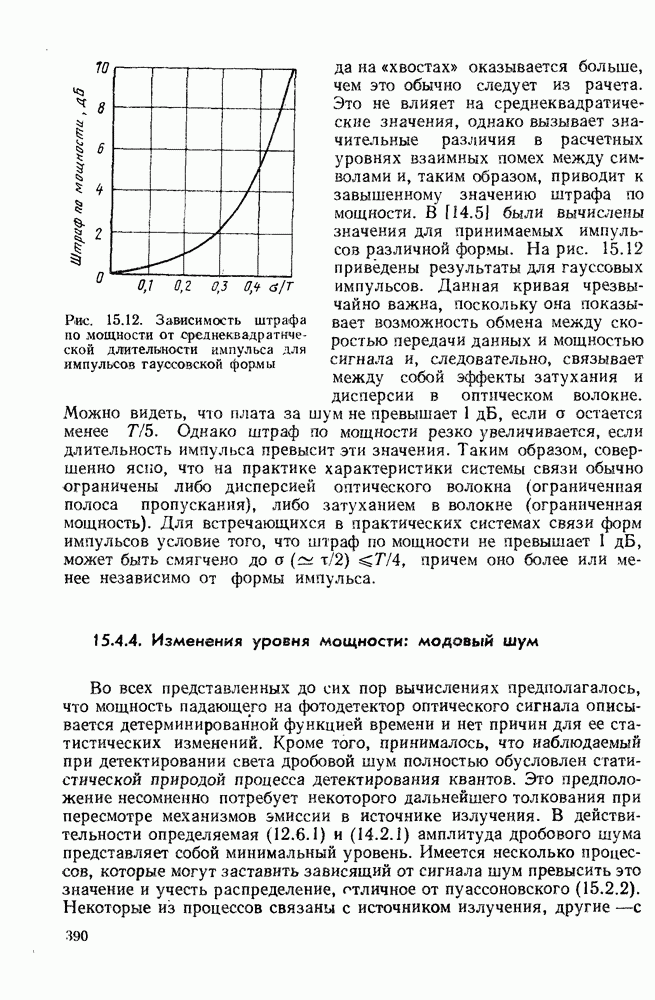
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
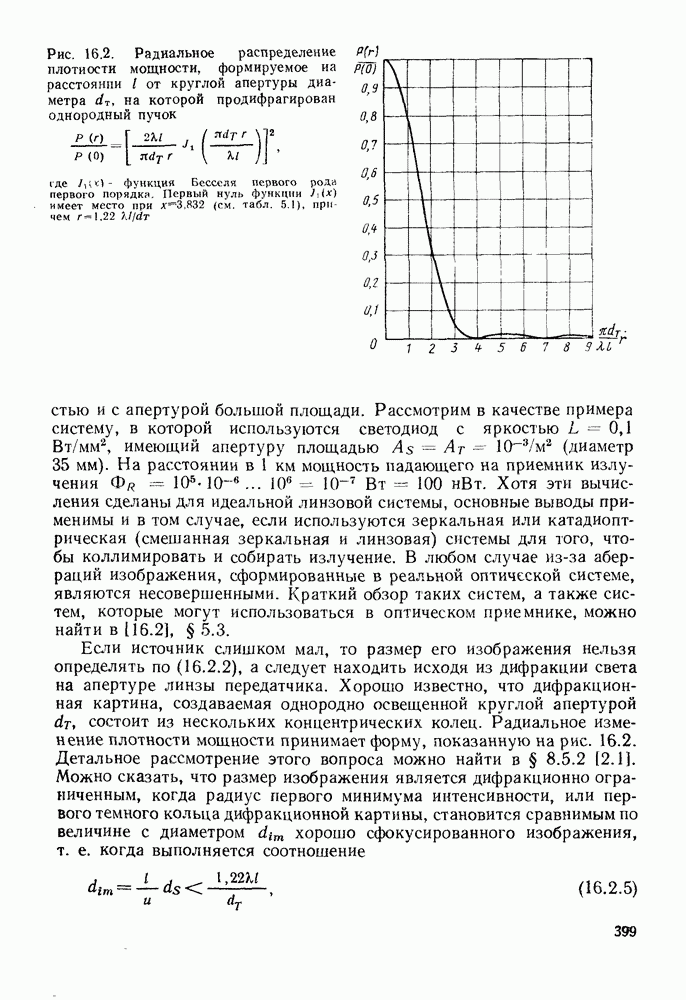
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
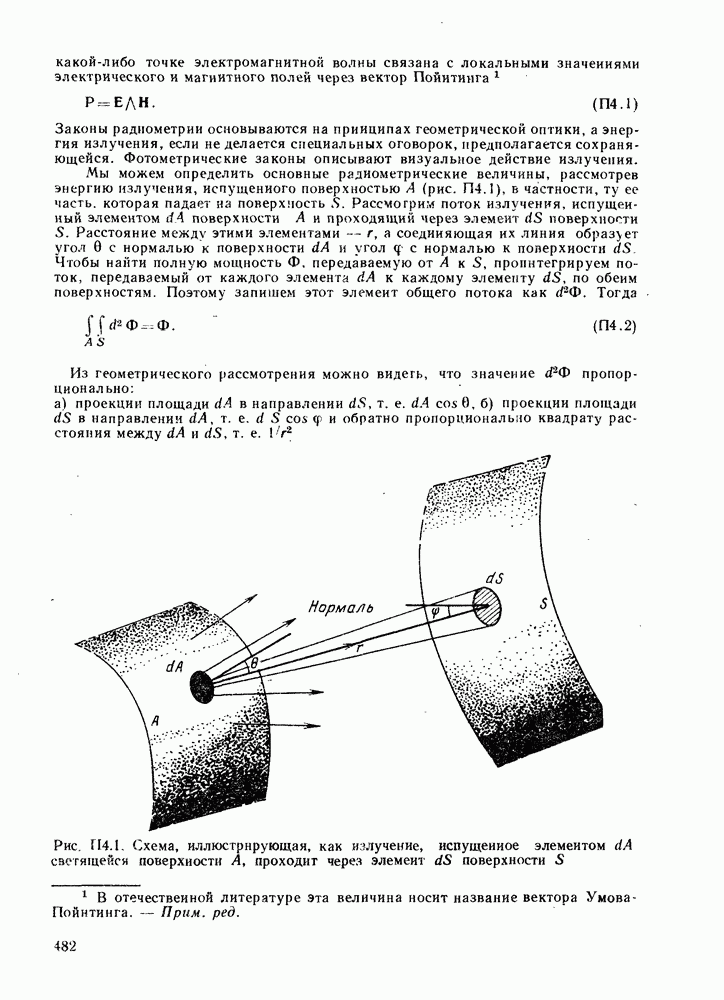
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
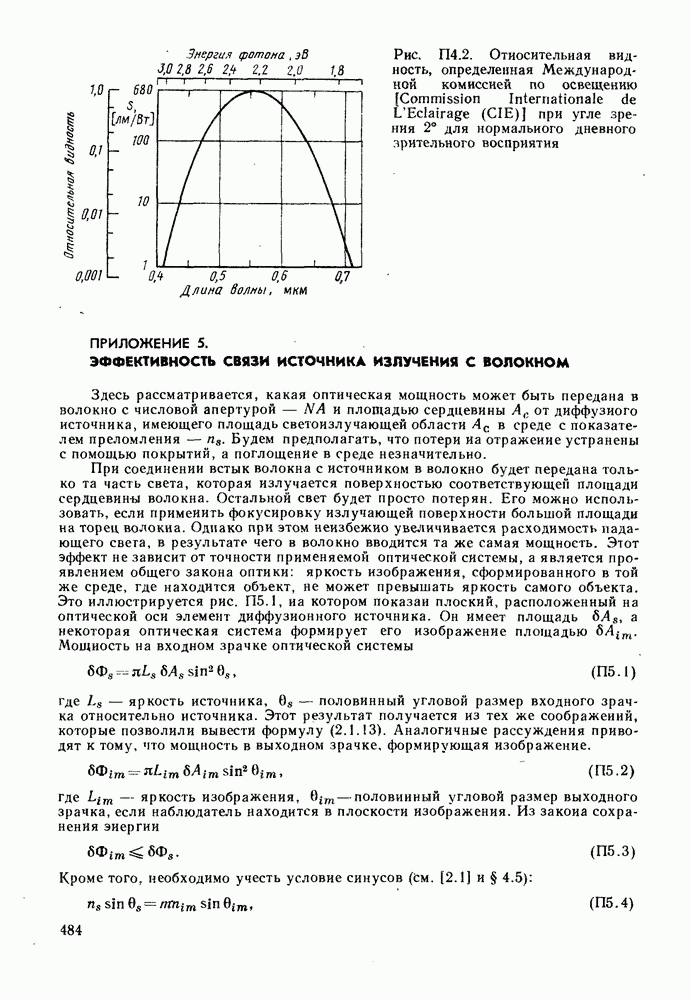
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
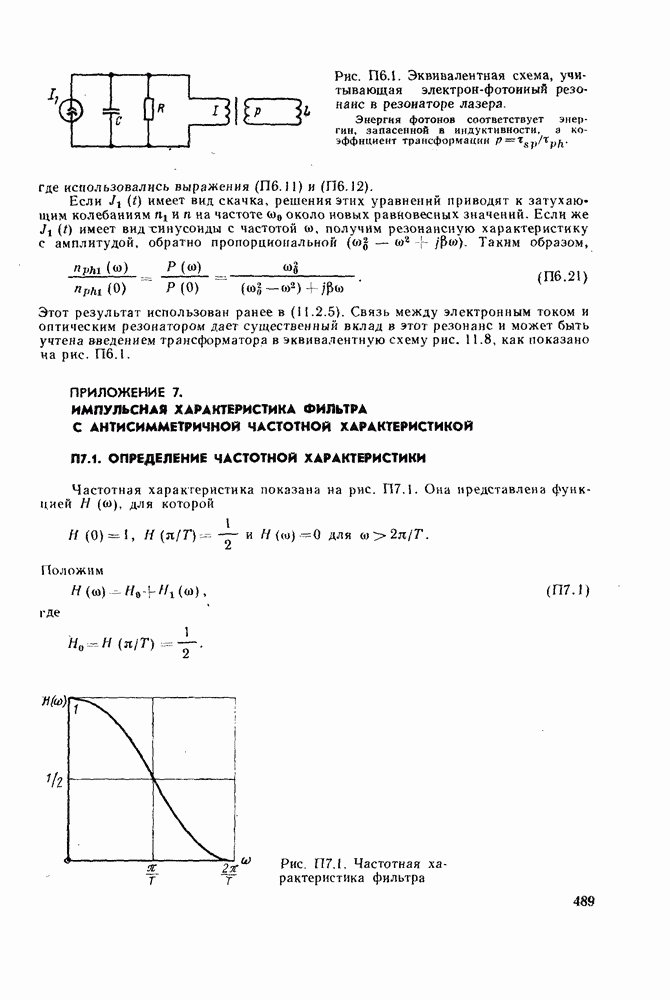
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ