| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
2.2.1. Показатель преломления объемной среды: теория
На распространение электромагнитных волн в прозрачных материалах оказывает влияние их взаимодействие с молекулами среды. Поскольку такое взаимодействие зависит от частоты, то и скорость распространения электромагнитных волн также зависит от частоты: говорят, что материал обладает дисперсией. Одним из проявлений такой дисперсии является уширение коротких световых импульсов при их распространении в диспергирующей среде. Величина уширения пропорциональна ширине спектра импульса и является другим важным фактором, который ограничивает полосу пропускания оптических волокон.
В оптике обычно имеют дело с показателем преломления среды  Он показывает, во сколько раз уменьшается фазовая скорость
Он показывает, во сколько раз уменьшается фазовая скорость  волны, распространяющейся в данной среде, по сравнению с фазовой скоростью с в вакууме
волны, распространяющейся в данной среде, по сравнению с фазовой скоростью с в вакууме

Другая особенность оптики состоит в том, что, начиная с момента зарождения оптики как науки в XVI веке, при описании источников оптического излучения используют не частоту  а длину волны
а длину волны  , излучаемых колебаний. Это приводит к понятию длины волны в свободном пространстве
, излучаемых колебаний. Это приводит к понятию длины волны в свободном пространстве  При распространении колебаний в преломляющей среде длина волны уменьшается до
При распространении колебаний в преломляющей среде длина волны уменьшается до  причем
причем

и

Будем описывать электромагнитную волну частотой  распространяющуюся через преломляющую среду вдоль оси
распространяющуюся через преломляющую среду вдоль оси  в виде проекции амплитуды электрической составляющей поля на ось х, как действительной части
в виде проекции амплитуды электрической составляющей поля на ось х, как действительной части  т. е.
т. е.

где  постоянная поля;
постоянная поля;  коэффициент распространения в среде;
коэффициент распространения в среде;  угловая частота волны,
угловая частота волны, 
Выражение (2.2.4) описывает плоскую волну, распространяющуюся в объемном материале. Будем полагать, что волна линейно
поляризована и вектср электрического поля совмещен с плоскостью  Фазовая скорость такой волны равна
Фазовая скорость такой волны равна  следовательно,
следовательно,

откуда

Если при прохождении через среду волна ослабляется, то это можно учесть введением коэффициента поглощения а, так что

Можно учесть затухание волны путем введения комплексного показателя преломления среды

Таким образом, действительная часть показателя преломления все еще определяется выражением (2.2.6), в то время как мнимая часть становится равной

Ниже будет показано, что те же самые процессы, которые приводят к зависимости показателя преломления среды от частоты, вызывают также и затухание в среде электромагнитных волн. Таким образом, показатель преломления дисперсионной ереды является комплексным и зависит от частоты. Указанные физические процессы легко рассмотреть на примере диэлектриков, однако количественный теоретический анализ для любой, даже простейшей среды становится неимоверно сложным.
Электрическая составляющая поля распространяющейся в диэлектрике оптической электромагнитной волны поляризует его молекулы, в результате чего они или их электронные структуры начинают колебаться с частотой волны. Колеблющиеся заряды излучают новые волны той же частоты, которые интерферируют с породившей их волной таким образом, что результирующая волна получает суммарный фазовый сдвиг относительно исходной волны. Поскольку эти эффекты происходят непрерывно во времени, общий фазовый сдвиг оказывается пропорциональным пройденному волной расстоянию. Это приводит к тому, что волна распространяется в среде с меньшей фазовой скоростью.
Взаимодействие волны с молекулами среды происходит в виде последовательности затухающих гармонических резонансов. На частоте выше резонансной колебание отдельного атомного или электронного
заряда больше не соответствует колебаниям электрического поля. Среда уже не поляризуется описанным образом, в результате чего на частотах выше резонансной показатель преломления уменьшается по сравнению со своим значением при резонансе.
Влияние электрического поля на поляризуемость диэлектрического материала обычно выражают с помощью относительной диэлектрической постоянной или диэлектрической проницаемости среды. Показатель преломления, обусловленный поляризацией материала на высоких частотах, может быть легко связан с диэлектрической проницаемостью материала на этих частотах. Как известно из теории электромагнитных волн, фазовая скорость электромагнитных волн, распространяющихся в среде, имеющей относительную магнитную проницаемость  и относительную диэлектрическую проницаемость
и относительную диэлектрическую проницаемость  определяется выражением
определяется выражением

где  соответственно магнитная и диэлектрическая проницаемости свободного пространства. Следовательно,
соответственно магнитная и диэлектрическая проницаемости свободного пространства. Следовательно,  цгег, а поскольку магнитные эффекты в диэлектриках обычно ничтожно малы, то можно принять
цгег, а поскольку магнитные эффекты в диэлектриках обычно ничтожно малы, то можно принять  и в результате получить следующую практическую формулу
и в результате получить следующую практическую формулу

Более подробно этот вопрос рассмотрен в Приложении 1.
Теперь нам необходима теория, которая описывала бы зависимость  а следовательно, и
а следовательно, и  от частоты в оптическом диапазоне. Рассмотрение такой теории приводится во многих учебниках по электромагнетизму, оптике и физике твердого тела, и они рекомендуются читателю для более глубокого изучения вопроса.
от частоты в оптическом диапазоне. Рассмотрение такой теории приводится во многих учебниках по электромагнетизму, оптике и физике твердого тела, и они рекомендуются читателю для более глубокого изучения вопроса.
При анализе этого вопроса сначала вводят понятие поляризуемости отдельной молекулы материала, обозначаемой а. Это означает, что электрический дипольный момент  возникающий в направлении оси х под действием локального электрического поля
возникающий в направлении оси х под действием локального электрического поля  будет равен
будет равен

В газе, содержащем  молекул в единице объема, объемная поляризация среды
молекул в единице объема, объемная поляризация среды  определяется выражением:
определяется выражением:

Теперь относительную диэлектрическую проницаемость можно определить следующим образом:

Таким образом, окончательно получаем

В случае твердого диэлектрика необходимо учитывать влияние, оказываемое на степень поляризации каждой отдельной молекулы окружающими ее молекулами. При использовании простейшего приближения, которое оказывается точным для идеальной кубической решетки, полагают, что каждая поляризуемая молекула представляет собой сферическую замкнутую полость в однородном диэлектрике. При этом под действием среднего поля  локальное поле увеличится в
локальное поле увеличится в  раз. Следовательно, поляризация диэлектрика будет равна
раз. Следовательно, поляризация диэлектрика будет равна

Результирующую относительную диэлектрическую проницаемость при этом получаем путем подстановки (2.2.16) в (2.2.14):

Этот результат иногда выражают в иной форме, предложенной Моссотти,

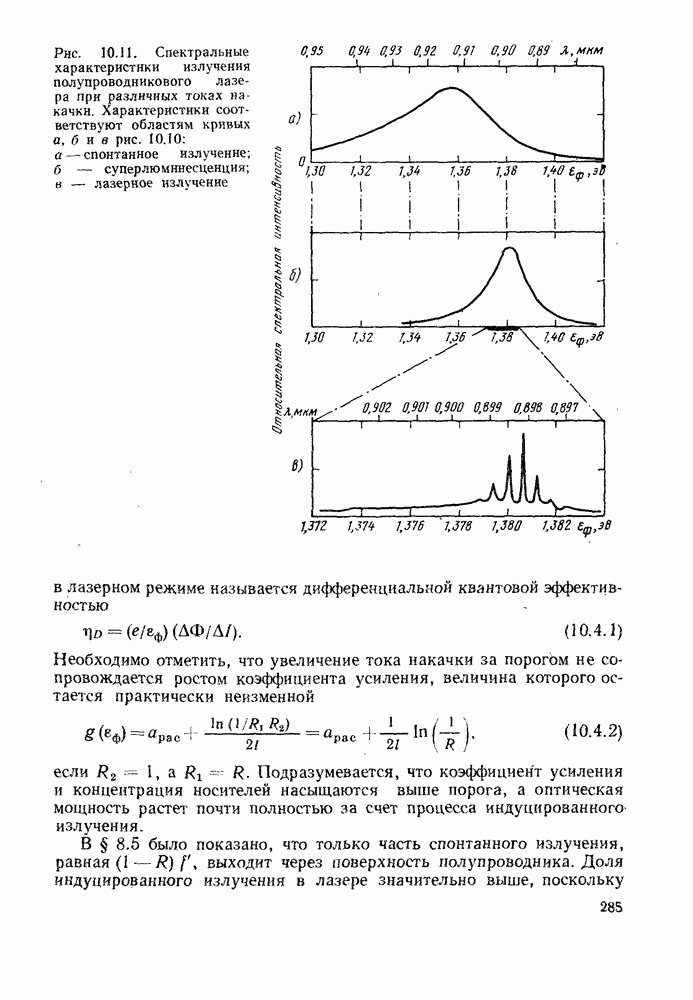
На рис. 2.8 приведена зависимость средней молекулярной поляризуемости а (а следовательно, и средней степени поляризации в единице объема  от частоты возбуждающего электрического поля. Энергетические переходы, соответствующие частотам радиодиапазона, обусловлены быстро затухающими эффектами переориентации молекул и не играют заметной роли в интересующей нас области спектра.
от частоты возбуждающего электрического поля. Энергетические переходы, соответствующие частотам радиодиапазона, обусловлены быстро затухающими эффектами переориентации молекул и не играют заметной роли в интересующей нас области спектра.

Рис. 2.8. Схематическое изображение зависимости поляризации диэлектрического материала от частоты, учитывающее отдельные атомные и электронные резонансы
Другие переходы являются результатом описанных ранее резонансных явлений. При этом высокочастотные эффекты возникают вследствие отклика электронной структуры молекул на поле, частота которого лежит в оптическом диапазоне спектра. На практике наблюдается ряд таких резонансов в ультрафиолетовой части спектра. Выделяемый низкочастотный переход обусловлен движением молекулы в ответ на воздействие оптического поля. Это колебания решетки, возбуждаемые электрическим полем с частотой, соответствующей иноракрасному участку спектра. В рассматриваемых резонансных явлениях смещаемый в процессе взаимодействия с электрическим полем и приводящий к появлению поляризации заряд подвергается воздействию восстанавливающей силы, величина которой пропорциональна смещению заряда. В таком случае движущийся заряд представляет собой гармонический осциллятор. Электрическое поле в направлении оси х, создаваемое электромагнитной волной в данной точке материала, определяется путем подстановки в (2.2.7) значения  и может быть выражено в виде реальной части
и может быть выражено в виде реальной части  где
где  — постоянная поля.
— постоянная поля.
В этом случае дифференциальное уравнение, связывающее смещение х, заряд  и массу
и массу  электрона, находящегося под воздействием электрического поля, имеет вид
электрона, находящегося под воздействием электрического поля, имеет вид

где  резонансная частота данного взаимодействия, а у — коэффициент затухания, учитывающий диссипативные эффекты, связанные с этим взаимодействием и являющиеся результатом излучательных потерь и соударений.
резонансная частота данного взаимодействия, а у — коэффициент затухания, учитывающий диссипативные эффекты, связанные с этим взаимодействием и являющиеся результатом излучательных потерь и соударений.
Решение этого уравнения для случая вынужденных затухающих колебаний имеет вид

Теперь видно, что поляризуемость молекулы становится комплексной функцией частоты. Обозначим ее а, причем

Аналогично этому и относительная диэлектрическая проницаемость  будет комплексной функцией частоты. Она может быть найдена подстановкой выражения (2.2.21), описывающего поляризуемость атома, в (2.2.17)
будет комплексной функцией частоты. Она может быть найдена подстановкой выражения (2.2.21), описывающего поляризуемость атома, в (2.2.17)

Если учесть все возможные резонансы и представить силу (напряженность поля) каждого из них коэффициентом  (который появляется при квантово-механическом подходе к данной проблеме), тогда
(который появляется при квантово-механическом подходе к данной проблеме), тогда  как функция частоты будет равна
как функция частоты будет равна

Ясно, что теперь и показатель преломления тоже становится комплексным

и мы получаем

В интересующих нас материалах затухание должно быть очень малым, поэтому рассмотрим только частоты, далеко отстоящие от резонансных, где справедливо предположение  . В таком случае
. В таком случае

а

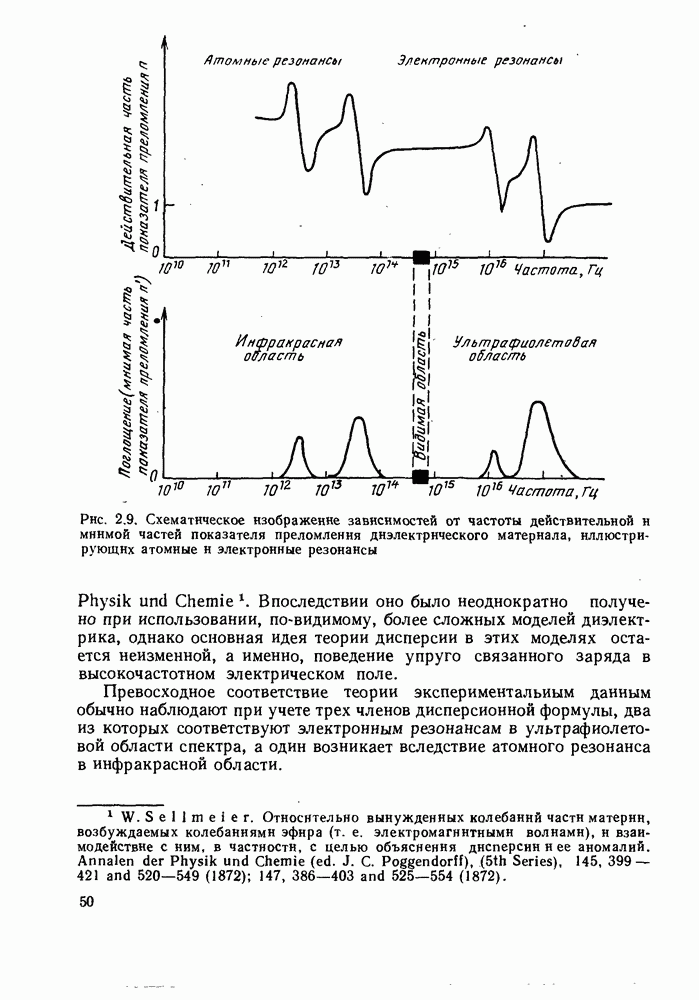
На рис. 2.9 приведены зависимости действительной и мнимой частей  от частоты для случая идеального диэлектрика. Вдали от резонансных частот влияние мнимой части
от частоты для случая идеального диэлектрика. Вдали от резонансных частот влияние мнимой части  может быть незначительным, и тогда показатель преломления можно записать таким образом:
может быть незначительным, и тогда показатель преломления можно записать таким образом:

Обычно изменение показателя преломления оптических материалов выражают в виде (2.2.27), известном как дисперсионная формула Селмейера. Одним из любопытных фактов истории науки является то, что основные идеи приведенного анализа впервые были высказаны Максвеллом в 1869 г. во время сдачи экзамена по математике в Кембридже. Позднее, в 1872 г., независимо пришел к выражению (2.2.27) В. Селмейер в ряде своих статей, опубликованных в Annalen der

Рис. 2.9. Схематическое изображение зависимостей от частоты действительной и мнимой частей показателя преломления диэлектрического материала, иллюстрирующих атомные и электронные резонансы
Physik und Chemie. Впоследствии оно было неоднократно получено при использовании, по-видимому, более сложных моделей диэлектрика, однако основная идея теории дисперсии в этих моделях остается неизменной, а именно, поведение упруго связанного заряда в высокочастотном электрическом поле.
Превосходное соответствие теории экспериментальным данным обычно наблюдают при учете трех членов дисперсионной формулы, два из которых соответствуют электронным резонансам в ультрафиолетовой области спектра, а один возникает вследствие атомного резонанса в инфракрасной области.
Выражение (2.2.27) оказывается слишком громоздким для анализа, а поскольку рассматриваются значения  весьма удаленные от значений
весьма удаленные от значений  то можно аппроксимировать уравнение Селмейера полиномом по степеням
то можно аппроксимировать уравнение Селмейера полиномом по степеням  . В результате получаем
. В результате получаем

Для слагаемых, для которых выполняется условие  подставим
подставим  и предположим, что
и предположим, что  Тогда воспользовавшись биноминальным разложением, находим
Тогда воспользовавшись биноминальным разложением, находим

В те слагаемые, где  подставим
подставим  и предположим
и предположим  Опять используя биноминальное разложение, можно написать
Опять используя биноминальное разложение, можно написать

Таким образом, уравнение (2.2.27) принимает следующий вид:

где 

Как видно из рис. 2.9, в оптических участках спектра, достаточно удаленных от резонансов, следует предполагать, что  будет медленно увеличиваться с ростом частоты электрического поля и, следовательно,
будет медленно увеличиваться с ростом частоты электрического поля и, следовательно,  будет медленно уменьшаться с увеличением его длины волны. Таким образом, в интересующих нас областях спектра производная
будет медленно уменьшаться с увеличением его длины волны. Таким образом, в интересующих нас областях спектра производная  будет малой по величине и отрицательной по знаку. Из рис. 2.9 также видно, что имеет место тесная связь между дисперсией (областями, где
будет малой по величине и отрицательной по знаку. Из рис. 2.9 также видно, что имеет место тесная связь между дисперсией (областями, где  изменяется при изменении частоты поля) и поглощением (областями, где
изменяется при изменении частоты поля) и поглощением (областями, где  становится значительным по величине). Эта связь носит фундаментальный характер. В любой линейной стационарной физически реализуемой системе, в которой ограниченное по величине входное воздействие порождает также ограниченный по величине отклик, мнимая часть передаточной функции может быть всегда однозначно определена по известной реальной части передаточной
становится значительным по величине). Эта связь носит фундаментальный характер. В любой линейной стационарной физически реализуемой системе, в которой ограниченное по величине входное воздействие порождает также ограниченный по величине отклик, мнимая часть передаточной функции может быть всегда однозначно определена по известной реальной части передаточной
функции, и наоборот. В физике эти соотношения известны как соотношения Крамерса-Кронига, в то время как инженерам-электрикам они стали известны из книги Боде.
Этот параграф был посвящен рассмотрению теоретических основ явления дисперсии в диэлектриках. В следующем параграфе будут представлены экспериментальные результаты по изучению дисперсии в материалах, используемых для изготовления оптических волокон, из которых будет видно хорошее соответствие с рассмотренной теорией. В последних параграфах будет исследовано влияние зависимости показателя преломления от частоты на скорость передачи сигналов, достижимую в оптических волокнах при использовании различных частот.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
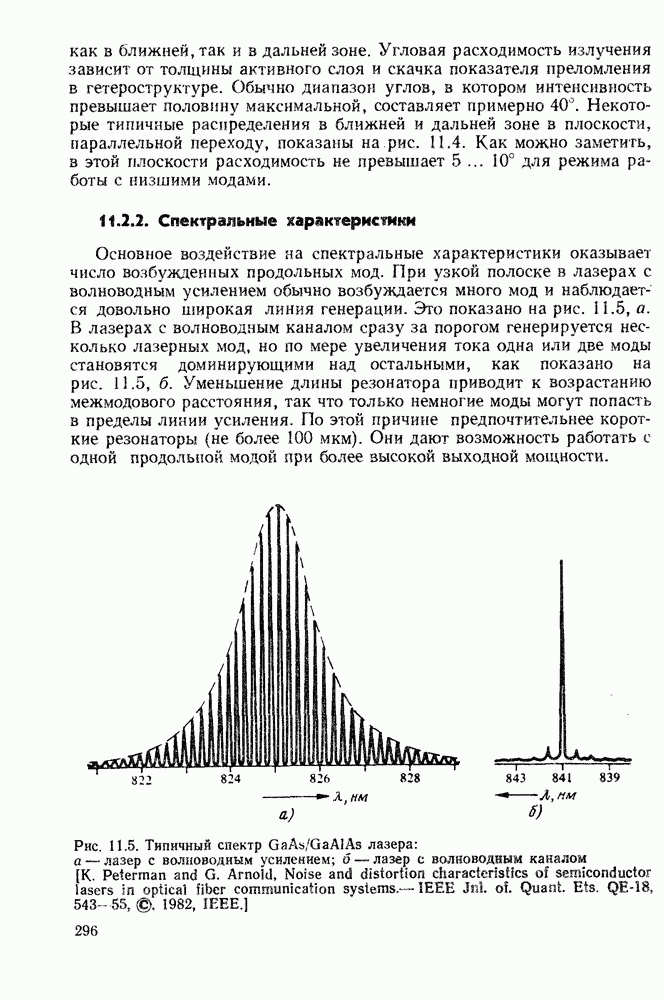
- 11.2.2. Спектральные характеристики
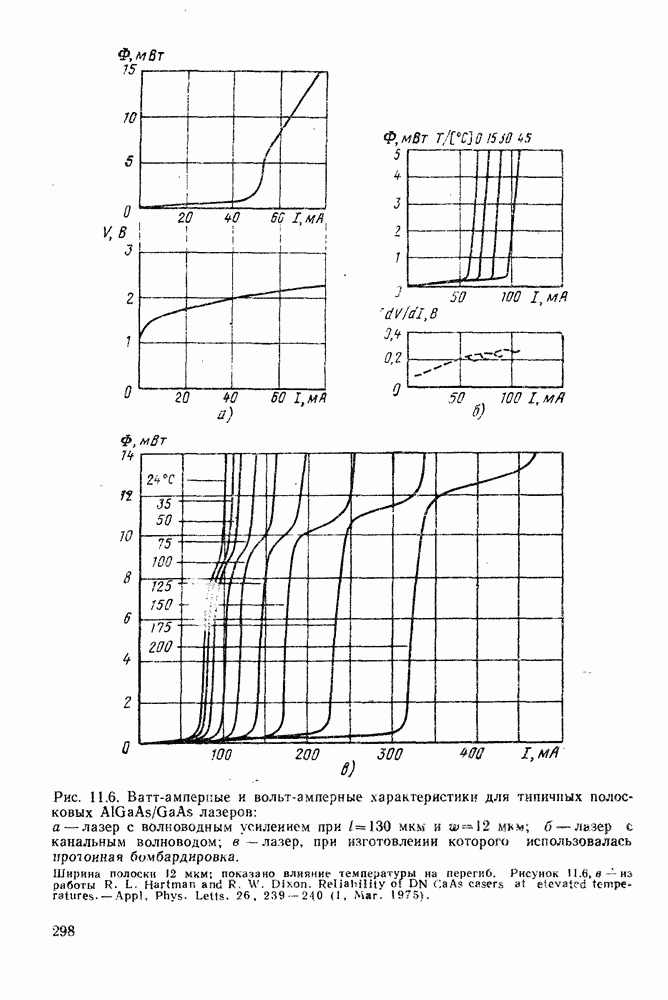
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
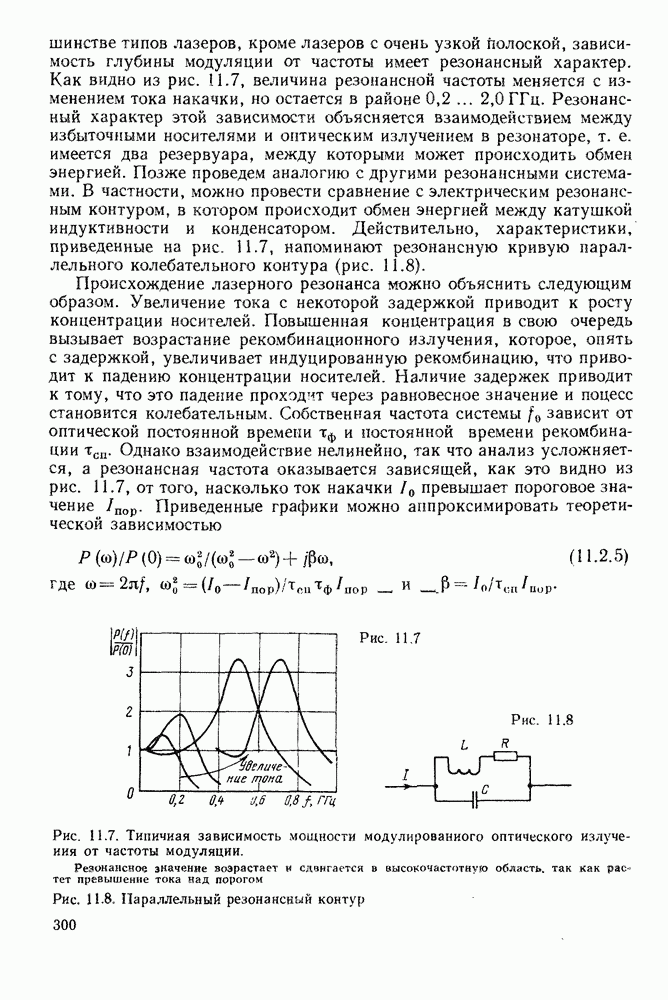
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
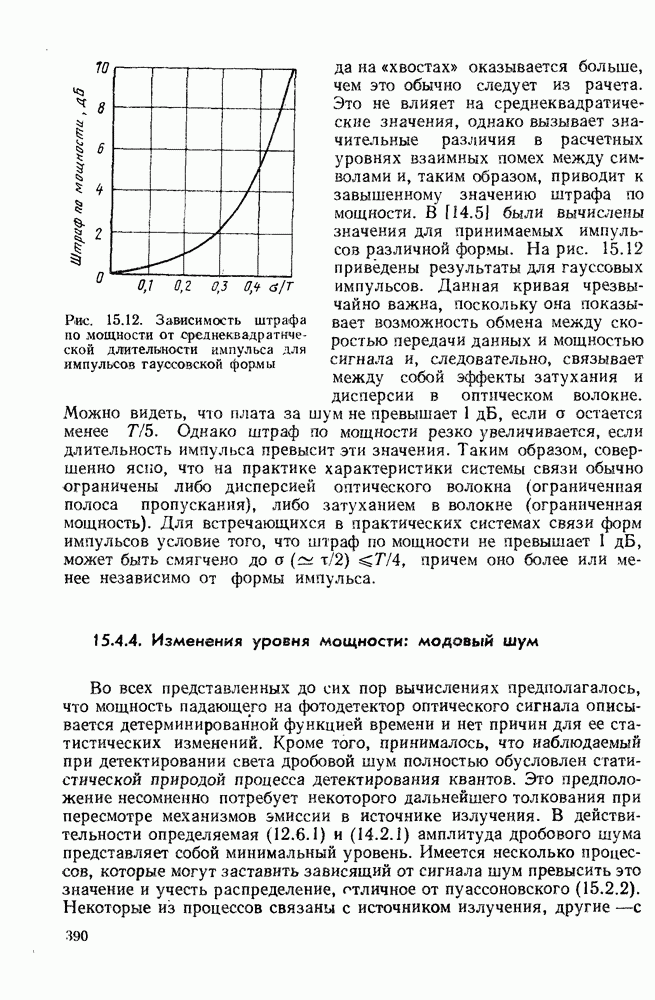
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
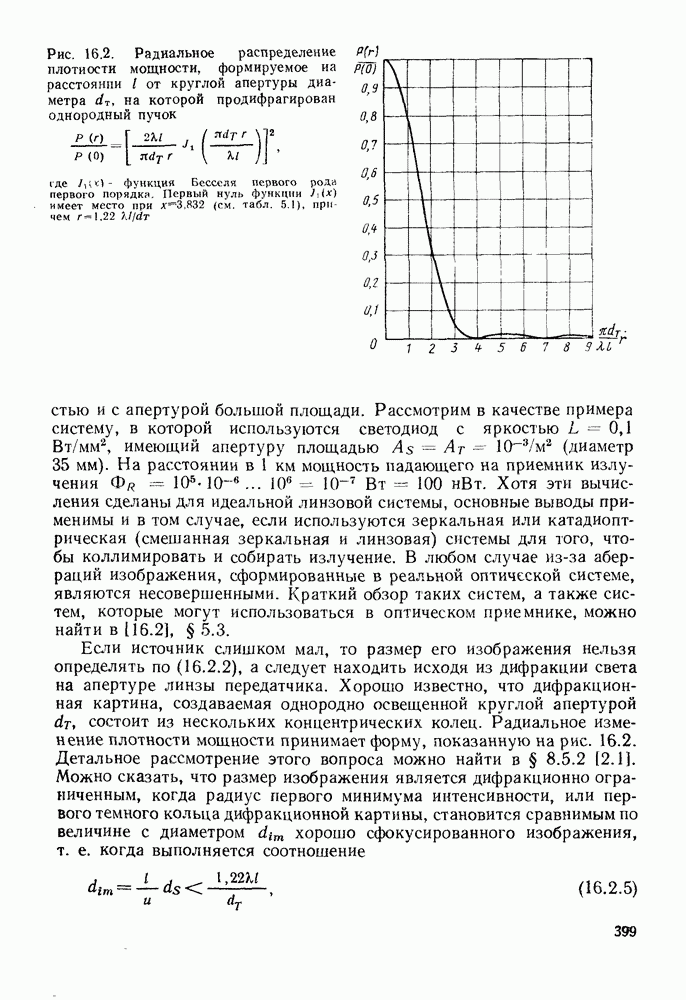
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
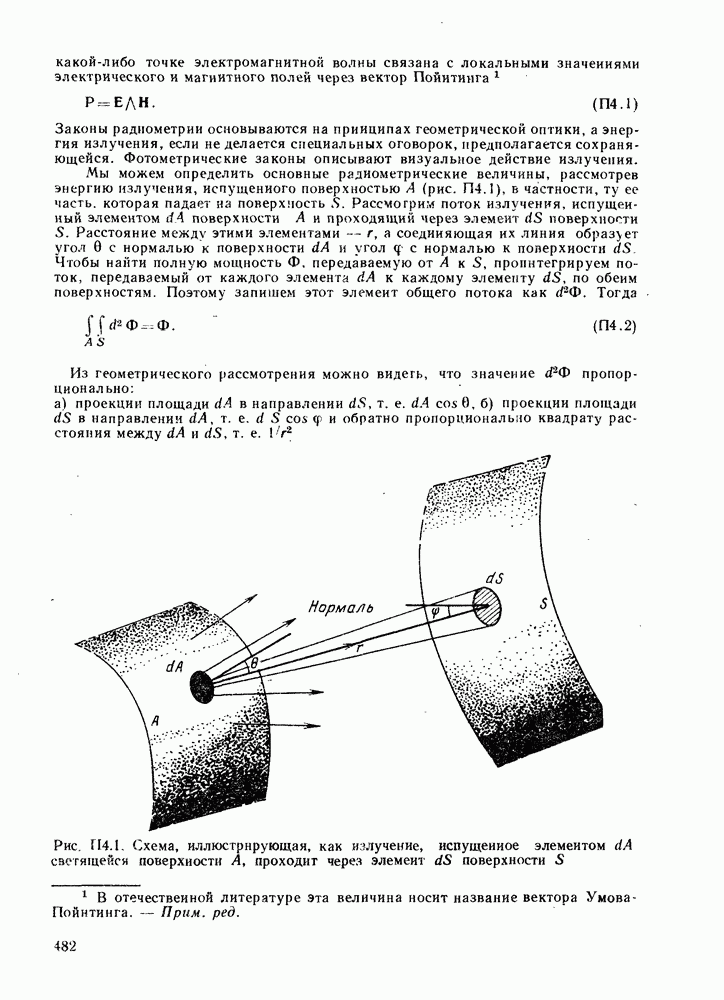
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
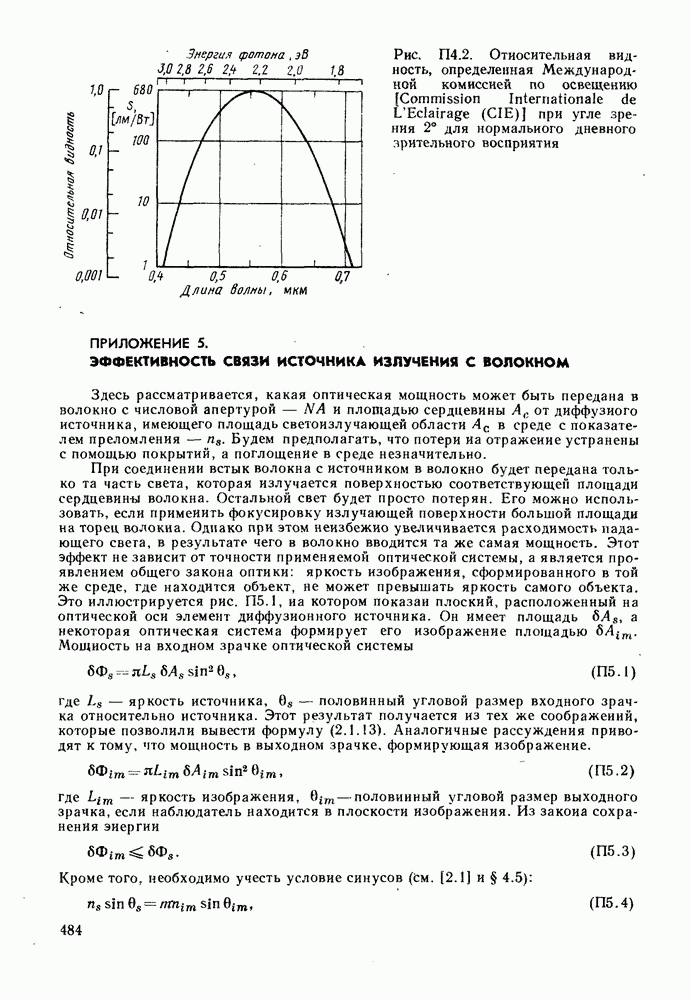
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
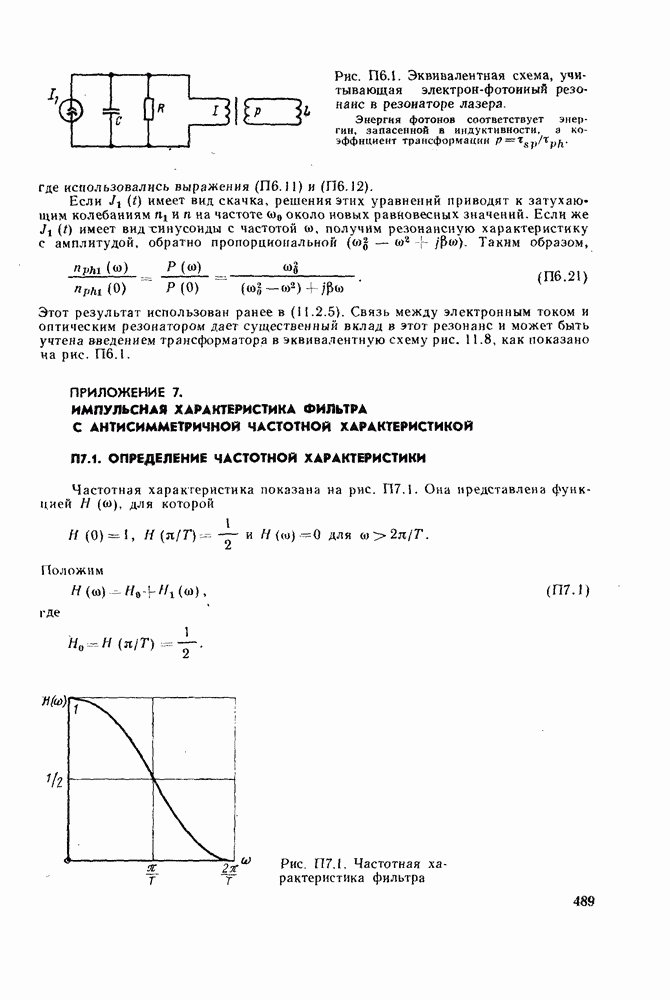
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ