| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
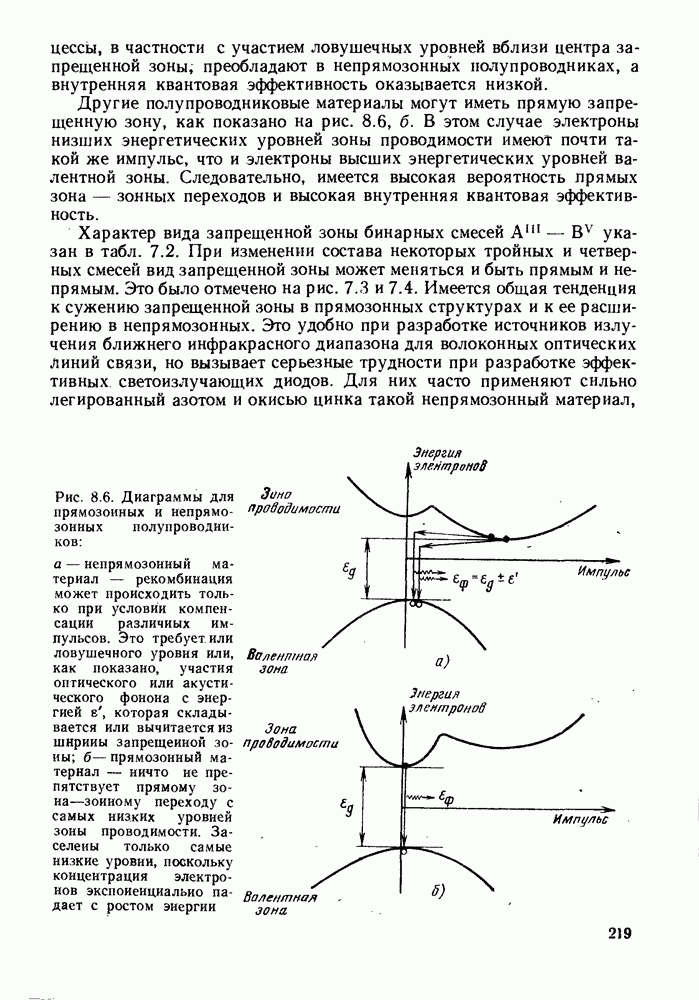
8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
Энергия фотона, рождающегося в результате рекомбинации, определяется законом Планка

где  энергия фотона;
энергия фотона;  частота; X — длина волны излучения в вакууме.
частота; X — длина волны излучения в вакууме.
Чтобы выяснить распределение энергии рекомбинационного излучения по энергиям, проведем следующее рассуждение. Вероятность рекомбинации электрона с энергией  и дырки с энергией
и дырки с энергией  пропорциональна соответствующим концентрациям
пропорциональна соответствующим концентрациям  Вероятность излучения фотона с энергией
Вероятность излучения фотона с энергией  может быть получена в результате интегрирования произведения
может быть получена в результате интегрирования произведения  по всем значениям ел (или
по всем значениям ел (или  Для вычисления этого распределения необходимо знать распределения концентраций носителей в валентной зоне и зоне проводимости
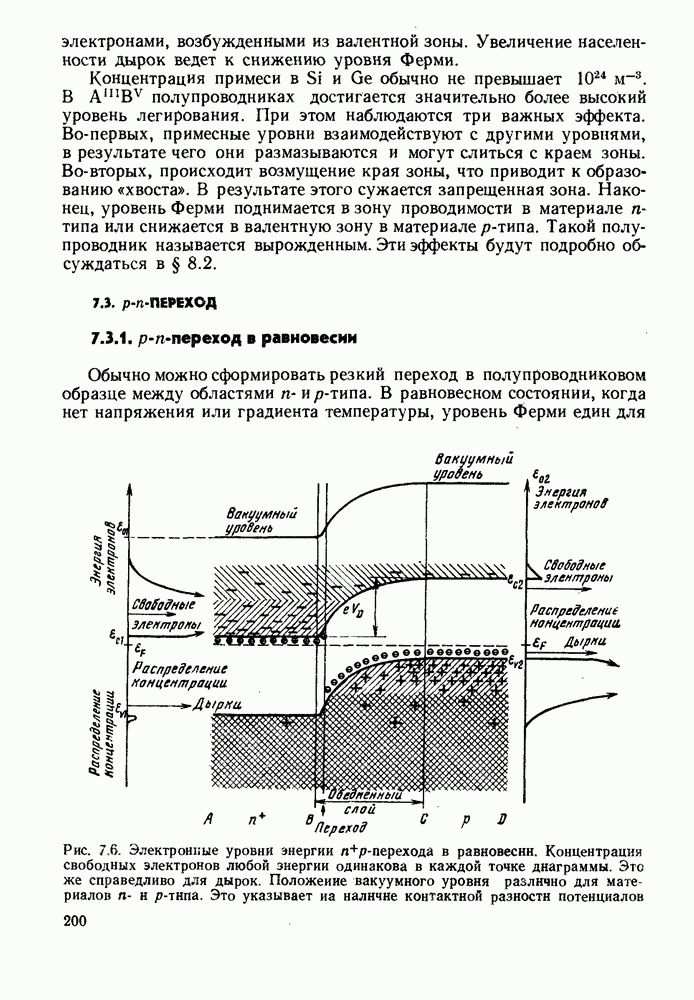
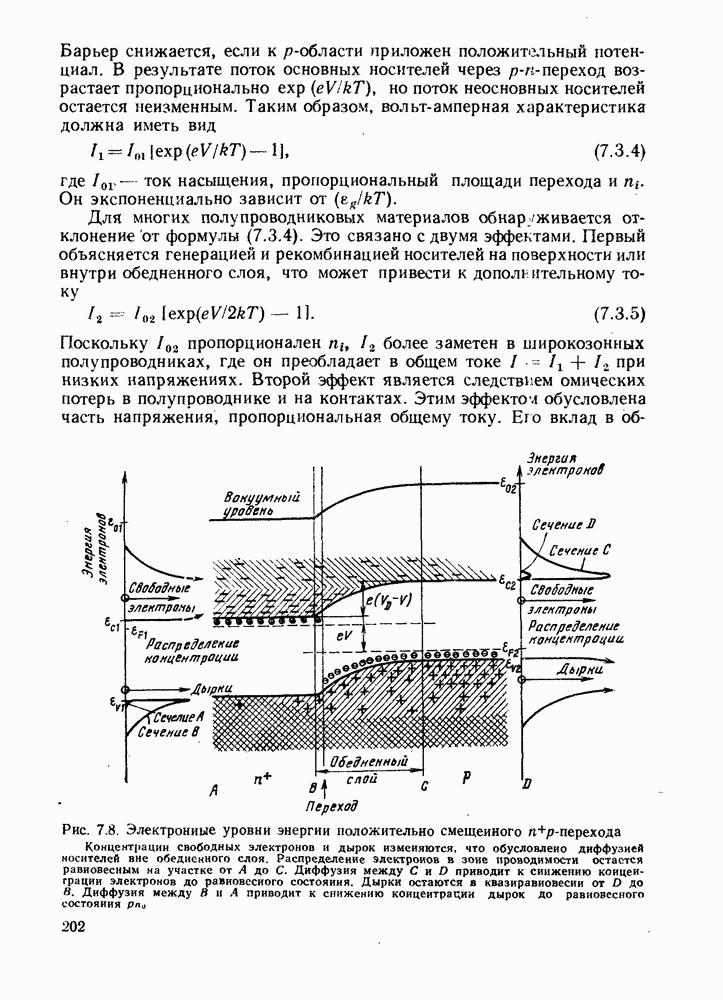
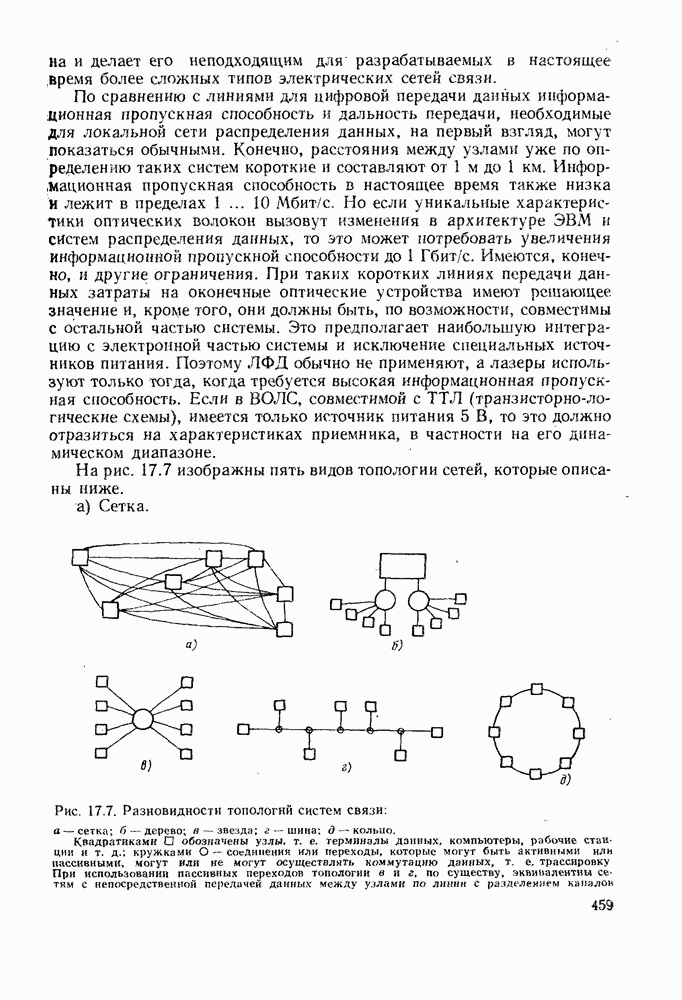
Для вычисления этого распределения необходимо знать распределения концентраций носителей в валентной зоне и зоне проводимости  Общий вид этих распределений для положительно смещенного p-n-перехода представлен на рис. 7.8. В соответствии с принятой при построении этой диаграммы простой моделью распределения быстро растут вблизи границы зоны, сравнительно слабо меняются при энергиях свыше
Общий вид этих распределений для положительно смещенного p-n-перехода представлен на рис. 7.8. В соответствии с принятой при построении этой диаграммы простой моделью распределения быстро растут вблизи границы зоны, сравнительно слабо меняются при энергиях свыше  наконец, падают пропорционально Больцмановской экспоненте
наконец, падают пропорционально Больцмановской экспоненте  Необходимо получить ответ на два вопроса: как получаются такие распределения и в каком виде они должны быть представлены, чтобы получить вид спектра рекомбинационного излучения.
Необходимо получить ответ на два вопроса: как получаются такие распределения и в каком виде они должны быть представлены, чтобы получить вид спектра рекомбинационного излучения.
Распределение концентрации электронов энергии  в зоне проводимости определяется произведением двух членов. Первый
в зоне проводимости определяется произведением двух членов. Первый  представляет распределение разрешенных энергетических состояний. Второй — вероятность того, что это состояние заселено и является функцией Ферми
представляет распределение разрешенных энергетических состояний. Второй — вероятность того, что это состояние заселено и является функцией Ферми  (см. § 7.2.1). Таким образом,
(см. § 7.2.1). Таким образом,

Аналогично можно получить распределение концентрации дырок в валентной зоне

где  распределение разрешенных энергетических состояний.
распределение разрешенных энергетических состояний.
Очень простая модель поведения носителей в полупроводнике позволяет получить выражения для  В этой модели носители предполагаются движущимися внутри полупроводника подобно свободным заряженным частицам. При этом электрону приписывается эффективная масса те, а дырке —
В этой модели носители предполагаются движущимися внутри полупроводника подобно свободным заряженным частицам. При этом электрону приписывается эффективная масса те, а дырке —  причем значения эффективных масс отличаются от истинной массы электрона
причем значения эффективных масс отличаются от истинной массы электрона  Эффективные массы характеризуют материал и наряду с другими
Эффективные массы характеризуют материал и наряду с другими
характеристиками полупроводников приведены в табл. 7.2. В соответствии с этой моделью функции распределения плотности состояний

и

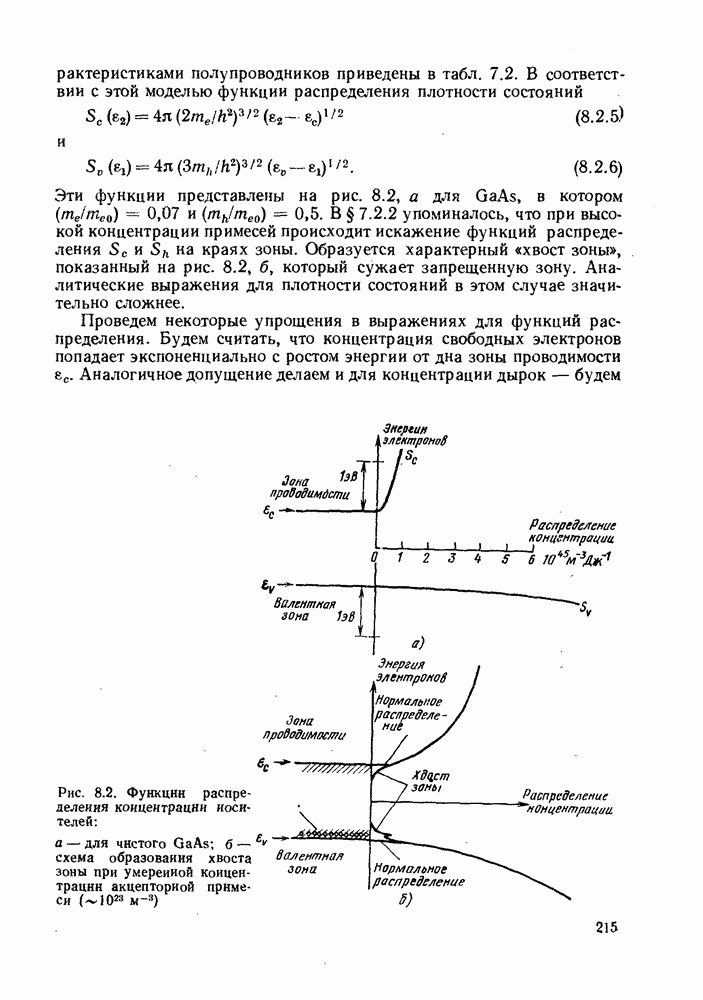
Эти функции представлены на рис. 8.2, а для GaAs, в котором  В § 7.2.2 упоминалось, что при высокой концентрации примесей происходит искажение функций распределения
В § 7.2.2 упоминалось, что при высокой концентрации примесей происходит искажение функций распределения  на краях зоны. Образуется характерный «хвост зоны», показанный на рис. 8.2, б, который сужает запрещенную зону. Аналитические выражения для плотности состояний в этом случае значительно сложнее.
на краях зоны. Образуется характерный «хвост зоны», показанный на рис. 8.2, б, который сужает запрещенную зону. Аналитические выражения для плотности состояний в этом случае значительно сложнее.
Проведем некоторые упрощения в выражениях для функций распределения. Будем считать, что концентрация свободных электронов попадает экспоненциально с ростом энергии от дна зоны проводимости  Аналогичное допущение делаем и для концентрации дырок — будем
Аналогичное допущение делаем и для концентрации дырок — будем

Рис. 8.2. Функции распределения концентрации носителей: а — для чистого GaAs; б - схема образования хвоста зоны при умеренной концентрации акцепторной примеси 
считать, что она экспоненциально уменьшается при изменении энер:  от верхнего края валентной зоны
от верхнего края валентной зоны 

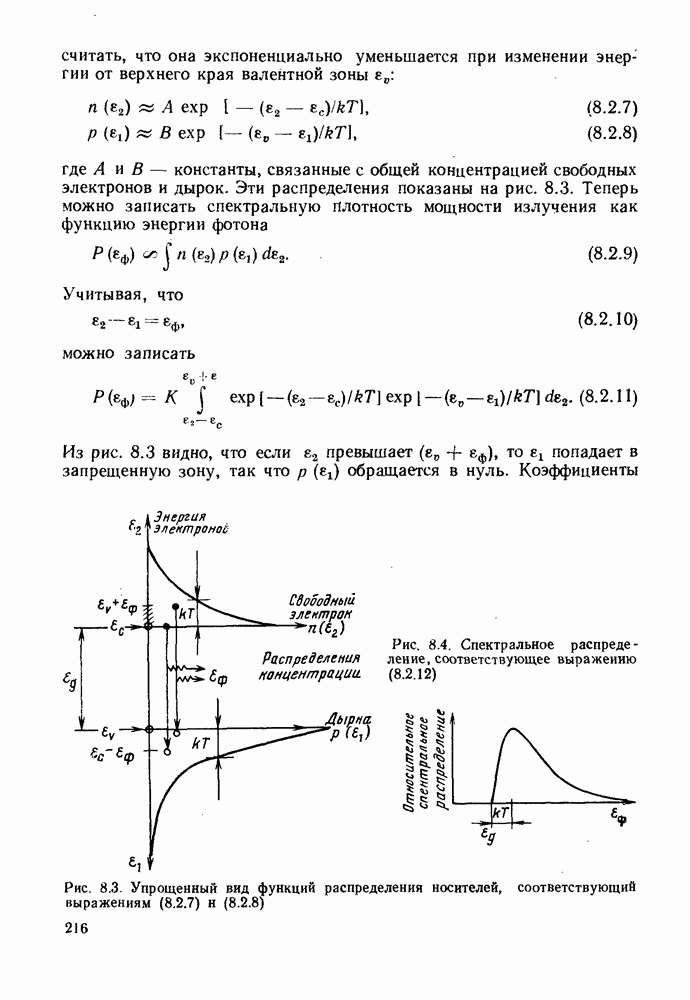
где  константы, связанные с общей концентрацией свободных электронов и дырок. Эти распределения показаны на рис. 8.3. Теперь можно записать спектральную плотность мощности излучения как функцию энергии фотона
константы, связанные с общей концентрацией свободных электронов и дырок. Эти распределения показаны на рис. 8.3. Теперь можно записать спектральную плотность мощности излучения как функцию энергии фотона

Учитывая, что

можно записать

Из рис. 8.3 видно, что если  превышает
превышает  то
то  попадает в запрещенную зону, так что
попадает в запрещенную зону, так что  обращается в нуль. Коэффициенты
обращается в нуль. Коэффициенты

Рис. 8.3. Упрощенный вид функций распределения носителей, соответствующий выражениям (8.2.7) и (8.2.8)

Рис. 8.4. Спектральное распределение, соответствующее выражению 

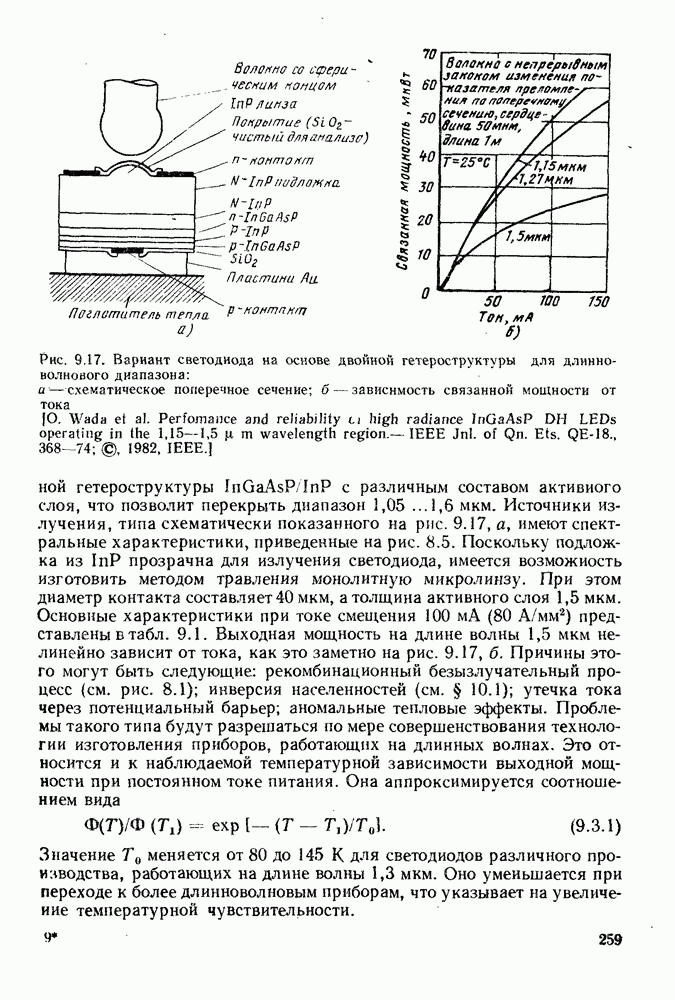
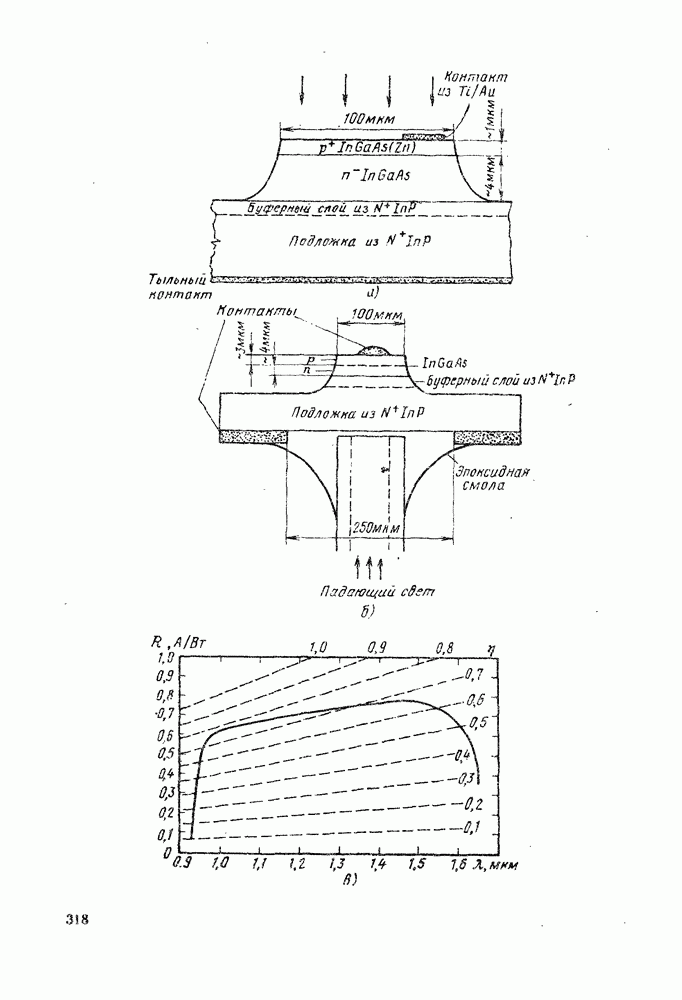
Рис. 8.5. Примеры наблюдаемых спектров светоизлучающих диодов: а — характерный спектр диода на основе GaAs, легированного Si; б - спектры излучения диодов на основе  трех различных составов. В этих приборах
трех различных составов. В этих приборах  . [Взято из работы О. Wada et al. Perfomance and reliability of high radiance In Ga AsP/ln P DH LEDs operating in 1,15-1,5 цш wavelength region,-IEEE Jnl. of Quantum Ets" QE-18, 368-74 (1982).]
. [Взято из работы О. Wada et al. Perfomance and reliability of high radiance In Ga AsP/ln P DH LEDs operating in 1,15-1,5 цш wavelength region,-IEEE Jnl. of Quantum Ets" QE-18, 368-74 (1982).]
 заменены коэффициентом К, в который входят вероятность перехода и радиационное время жизни электронов
заменены коэффициентом К, в который входят вероятность перехода и радиационное время жизни электронов  Тогда
Тогда

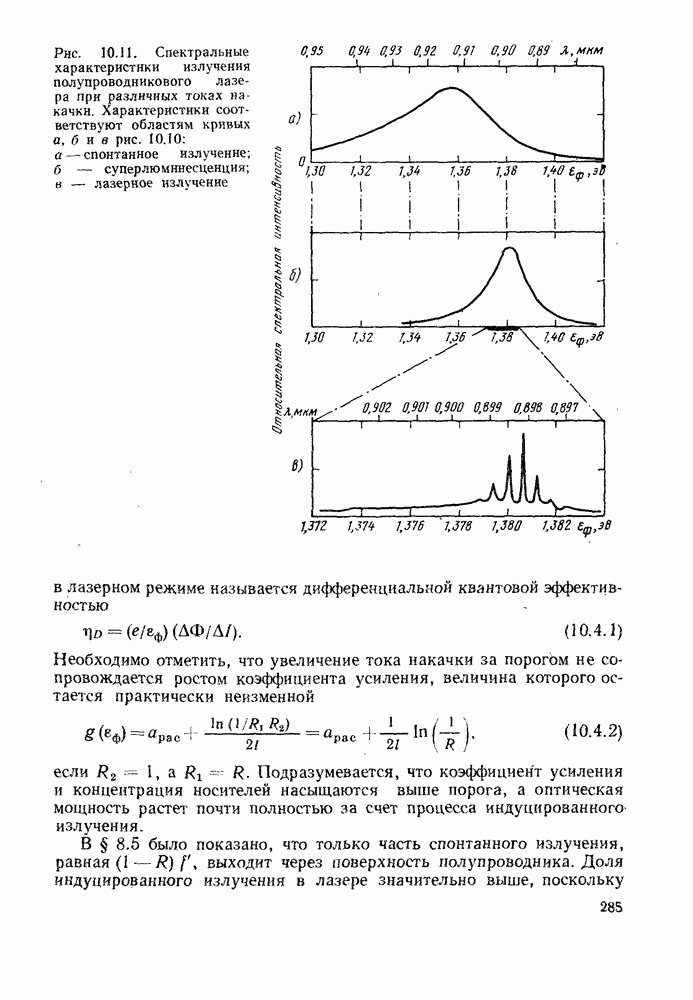
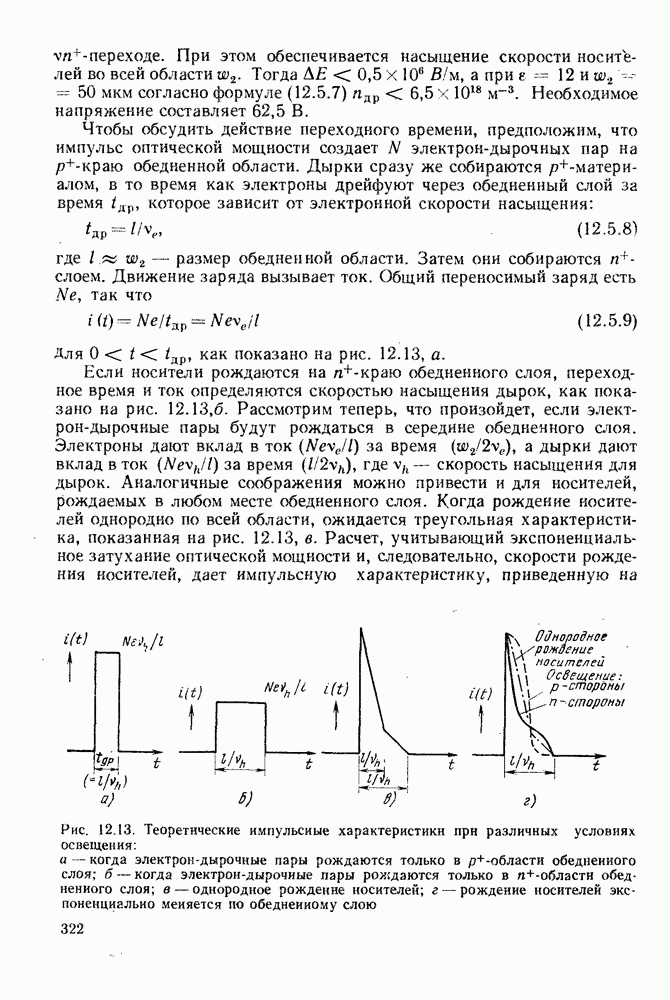
В результате проведенного анализа получаем, что спектральное распределение рекомбинационного излучения (8.2.12) имеет вид рис. 8.4. Наблюдаемый спектр всегда выглядит более симметрично (см. рис. 8.5). Это определяется рядом обстоятельств. Во-первых, в светоизлучающих диодах и лазерах обычно используются высокие концентрации донорных и акцепторных примесей, что вызывает искажение края запрещенной зоны, показанное на рис. 8.2, б. Во-вторых, наряду с излучением фотона может происходить взаимодействие с кристаллической решеткой. В таком случае часть энергии рекомбинационного перехода (примерно  может передаваться колебаниям решетки — оптическому или акустическому фонону, который возбуждается в тот же момент времени. В-третьих, переход может идти в несколько этапов с участием одного из примесных уровней вблизи края зоны. В результате в основном излучательном переходе присутствует энергия, меньшая, чем ширина запрещенной зоны.
может передаваться колебаниям решетки — оптическому или акустическому фонону, который возбуждается в тот же момент времени. В-третьих, переход может идти в несколько этапов с участием одного из примесных уровней вблизи края зоны. В результате в основном излучательном переходе присутствует энергия, меньшая, чем ширина запрещенной зоны.
Из рис. 8.4 видно, что наибольшая интенсивность излучения соответствует энергии  и полуширина линии составляет
и полуширина линии составляет  Упомянутые эффекты приводят к сдвигу максимума интенсивности в длинноволновую область. Обычно полуширина линии лежит в интервале от
Упомянутые эффекты приводят к сдвигу максимума интенсивности в длинноволновую область. Обычно полуширина линии лежит в интервале от  до
до  Основные соотношения с использованием длины волны излучения:
Основные соотношения с использованием длины волны излучения:

При комнатной температуре  т. е. при
т. е. при  при 1,3 мкм при
при 1,3 мкм при  эти значения соответствуют наблюдаемым. Однако необходимо помнить, что они зависят от многих факторов и поэтому могут быть различными для разных типов приборов. В частности, спектр уширяется с ростом температуры и при увеличении концентрации примеси.
эти значения соответствуют наблюдаемым. Однако необходимо помнить, что они зависят от многих факторов и поэтому могут быть различными для разных типов приборов. В частности, спектр уширяется с ростом температуры и при увеличении концентрации примеси.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ОБЩИЕ СВЕДЕНИЯ ОБ ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 1.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ И ИНФОРМАЦИОННАЯ ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ
- 1.3. АРХИТЕКТУРА СИСТЕМ СВЯЗИ
- 1.4. ОСНОВНЫЕ ВИДЫ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 2.1. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ НА ОСНОВЕ ЛУЧЕВОЙ МОДЕЛИ
- 2.1.2. Ступенчатое волокно: числовая апертура и межмодовая дисперсия
- 2.1.3. Распространение света и межмодовая дисперсия в градиентных волокнах
- 2.2. МАТЕРИАЛЬНАЯ ДИСПЕРСИЯ
- 2.2.1. Показатель преломления объемной среды: теория
- 2.2.2. Показатель преломления материала: экспериментальные значения
- 2.2.3. Временная дисперсия в объемной среде
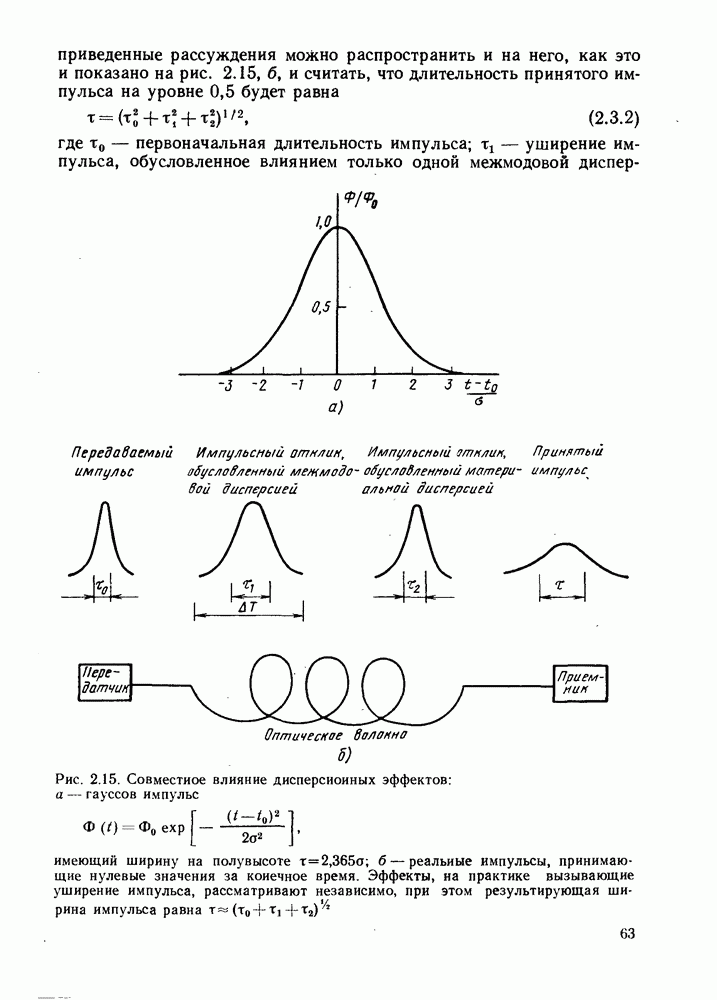
- 2.3. СОВМЕСТНОЕ ВЛИЯНИЕ ДИСПЕРСИИ МАТЕРИАЛА И МЕЖМОДОВОЙ ДИСПЕРСИИ
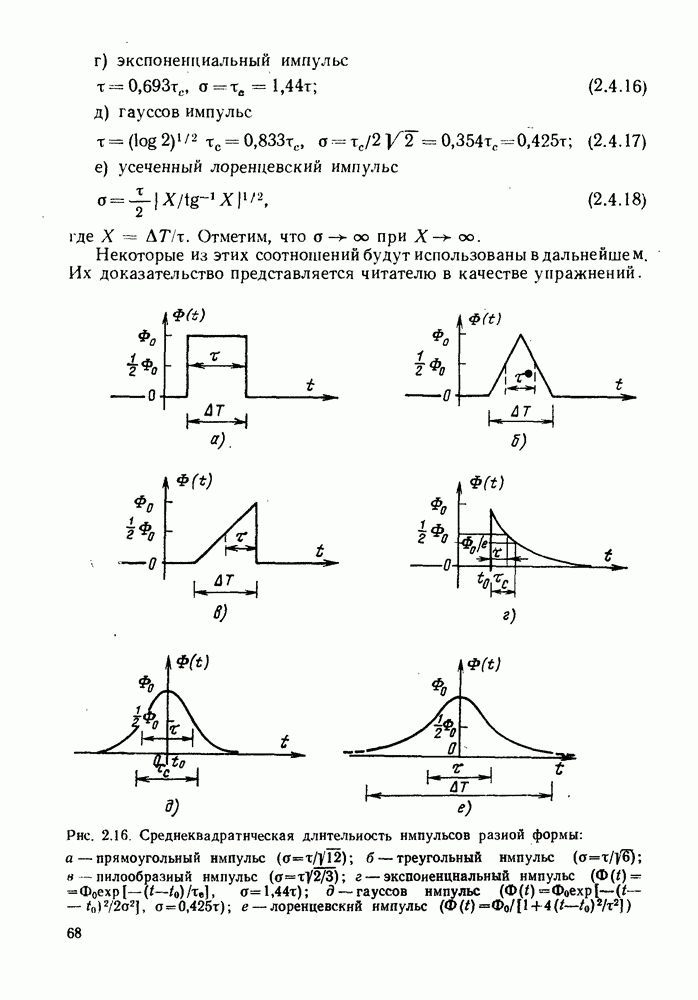
- 2.4. СРЕДНЕКВАДРАТИЧЕСКАЯ ДЛИТЕЛЬНОСТЬ ИМПУЛЬСОВ И ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА ВОЛОКНА
- 2.4.2. Передаточная характеристика волокна
- 2.4.3. Общая среднеквадратическая длительность импульсов
- 3. ПОТЕРИ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 3.1.2. Поглощение
- 3.1.3. Рассеяние
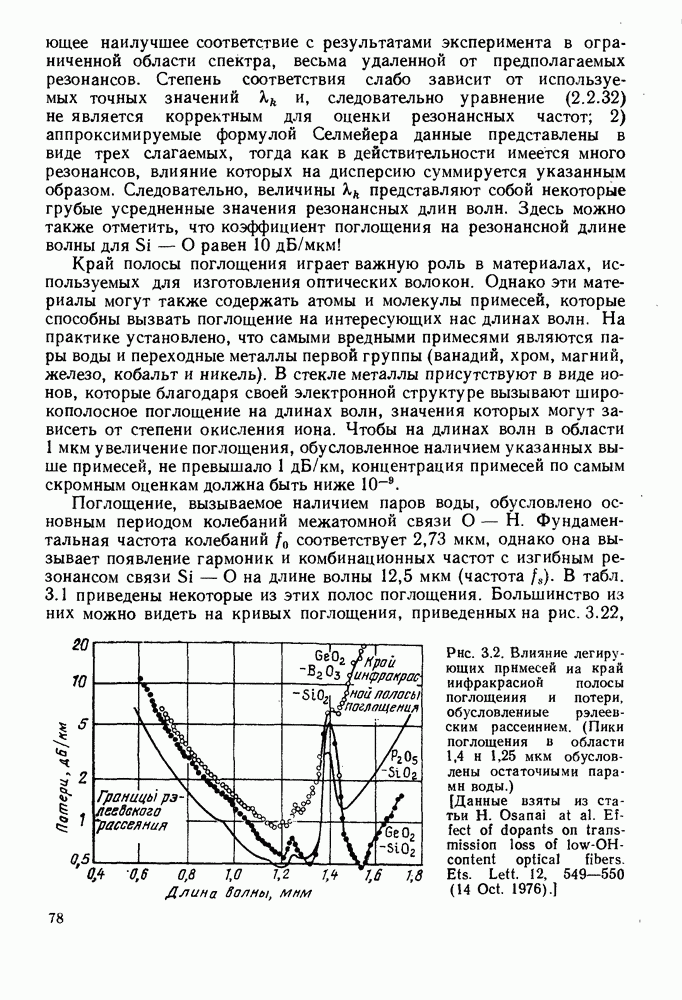
- 3.2. ВЛИЯНИЕ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
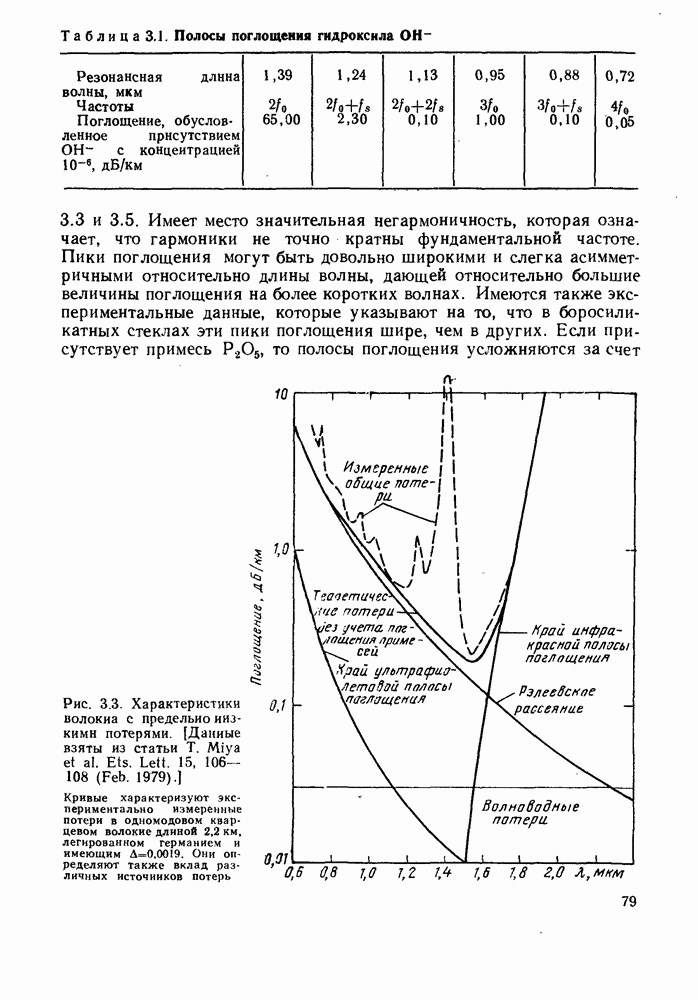
- 3.3. ОПТИМАЛЬНАЯ ДЛИНА ВОЛНЫ ДЛЯ КВАРЦЕВЫХ ОПТИЧЕСКИХ ВОЛОКОН
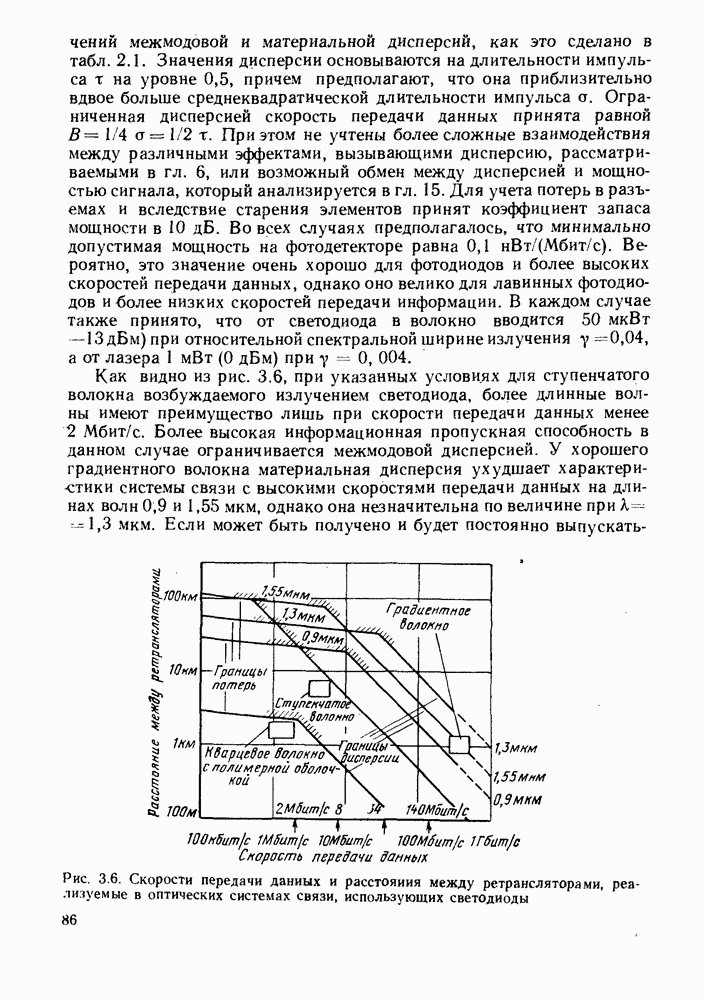
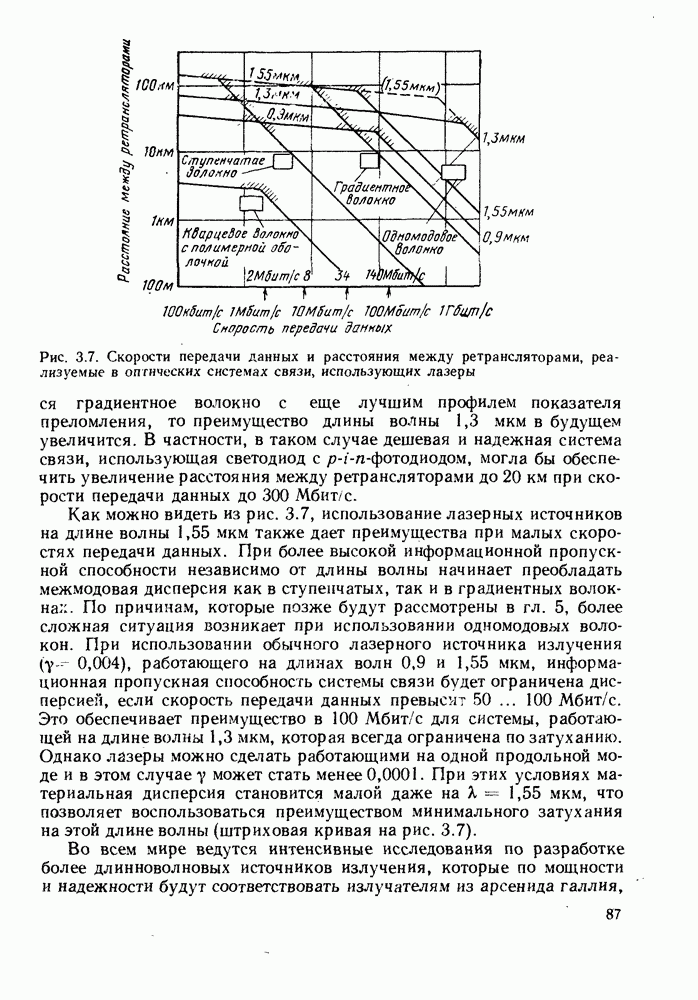
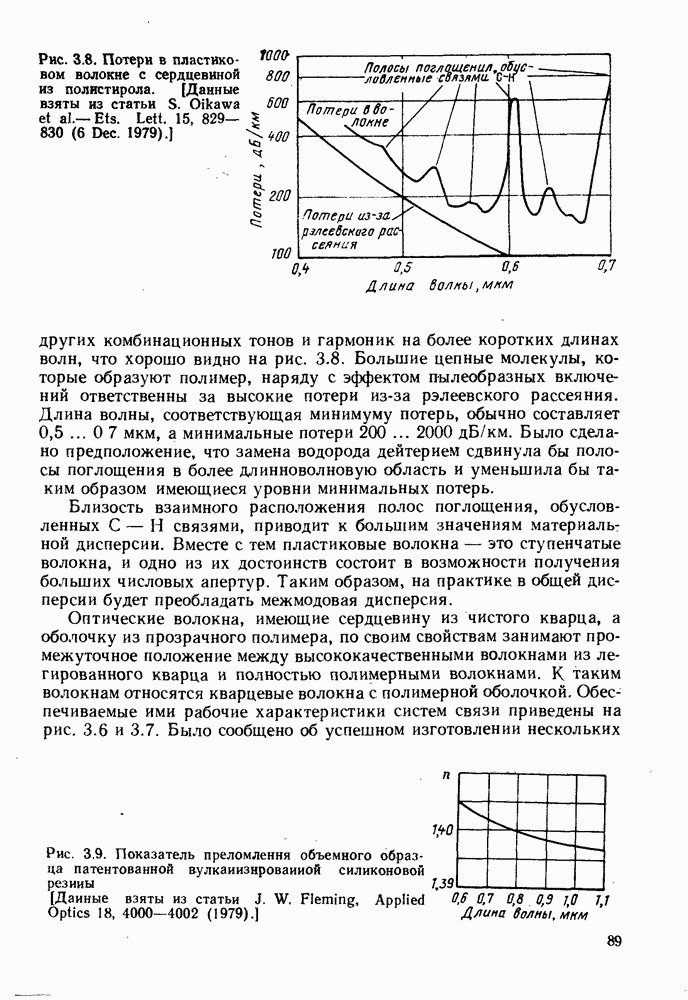
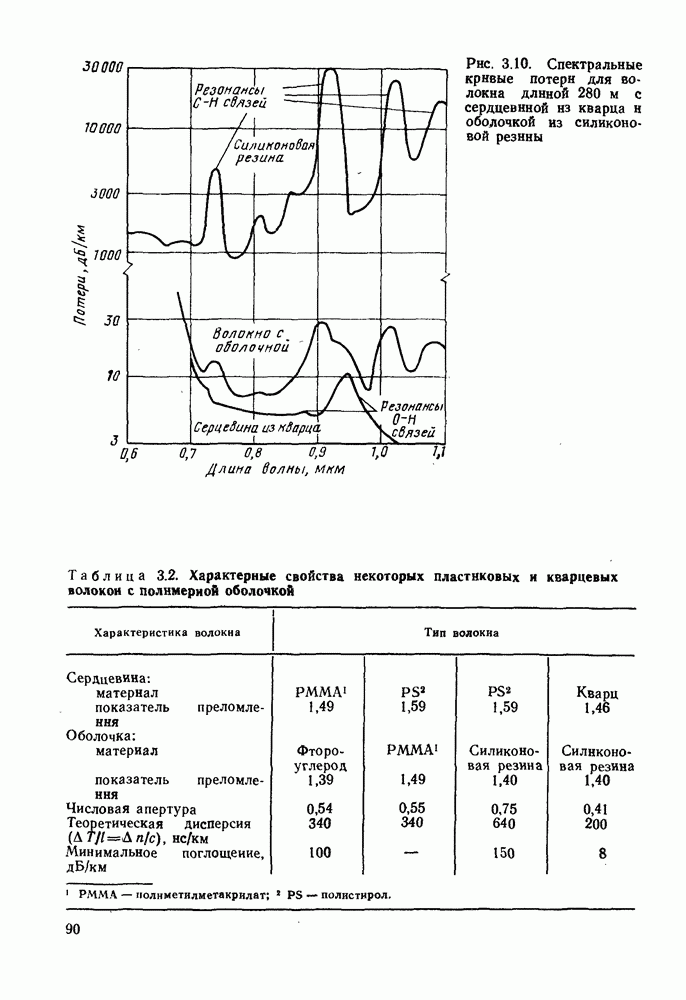
- 3.4. ПЛАСТМАССОВЫЕ ВОЛОКНА И КВАРЦЕВЫЕ ВОЛОКНА С ПОЛИМЕРНОЙ ОБОЛОЧКОЙ
- 4. ИЗГОТОВЛЕНИЕ ОПТИЧЕСКИХ КВАРЦЕВЫХ ВОЛОКОН И КАБЕЛЕЙ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- 4.2. ОПТИЧЕСКИЕ КАБЕЛИ
- 4.3. СОЕДИНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОН И СОЕДИНИТЕЛЬНЫЕ УСТРОЙСТВА
- 4.4. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ОПТИЧЕСКОГО ВОЛОКНА
- 4.5. СРАВНЕНИЕ ОПТИЧЕСКИХ ВОЛОКОННЫХ ЛИНИЙ С ОБЫЧНЫМИ ЭЛЕКТРИЧЕСКИМИ ЛИНИЯМИ ПЕРЕДАЧИ ДАННЫХ
- 5. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В СТУПЕНЧАТЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 5.2. РАСПРОСТРАНЕНИЕ ВОЛНОВОДНЫХ МОД В ИДЕАЛЬНОМ СТУПЕНЧАТОМ ВОЛОКНЕ
- 5.3. СЛАБО НАПРАВЛЯЮЩИЕ ВОЛОКНА
- 5.4. ВРЕМЕННАЯ ДИСПЕРСИЯ В СТУПЕНЧАТЫХ ВОЛОКНАХ
- 5.5. ОДНОМОДОВЫЕ ОПТИЧЕСКИЕ ВОЛОКНА
- 6. РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ГРАДИЕНТНЫХ ОПТИЧЕСКИХ ВОЛОКНАХ
- 6.1.2. Приближенное решение
- 6.1.3. Число мод распространения
- 6.1.4. Изменение постоянной распространения
- 6.2. ЭКВИВАЛЕНТНОСТЬ ПРИБЛИЖЕНИЯ ВЕНЦЕЛЯ — КРАМЕРСА — БРИЛЛЮЭНА И ЛУЧЕВОЙ МОДЕЛИ
- 6.3. МЕЖМОДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.3.2. Межмодовая дисперсия с учетом материальной дисперсии
- 6.4. ВНУТРИАЮДОВАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.5. ОБЩАЯ ДИСПЕРСИЯ В ГРАДИЕНТНЫХ ВОЛОКНАХ
- 6.6. ВЗАИМОДЕЙСТВИЕ МОД
- 7. ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВ
- 7.2. СОБСТВЕННЫЕ И ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ
- 7.2.2. Примесные полупроводники
- 7.3. p-n-ПЕРЕХОД
- 7.3.1. p-n-переход в равновесии
- 7.3.2. Смещенный p-n-переход
- 7.4. РЕКОМБИНАЦИЯ И ДИФФУЗИЯ НОСИТЕЛЕЙ
- 7.5. ЭФФЕКТИВНОСТЬ ИНЖЕКЦИИ
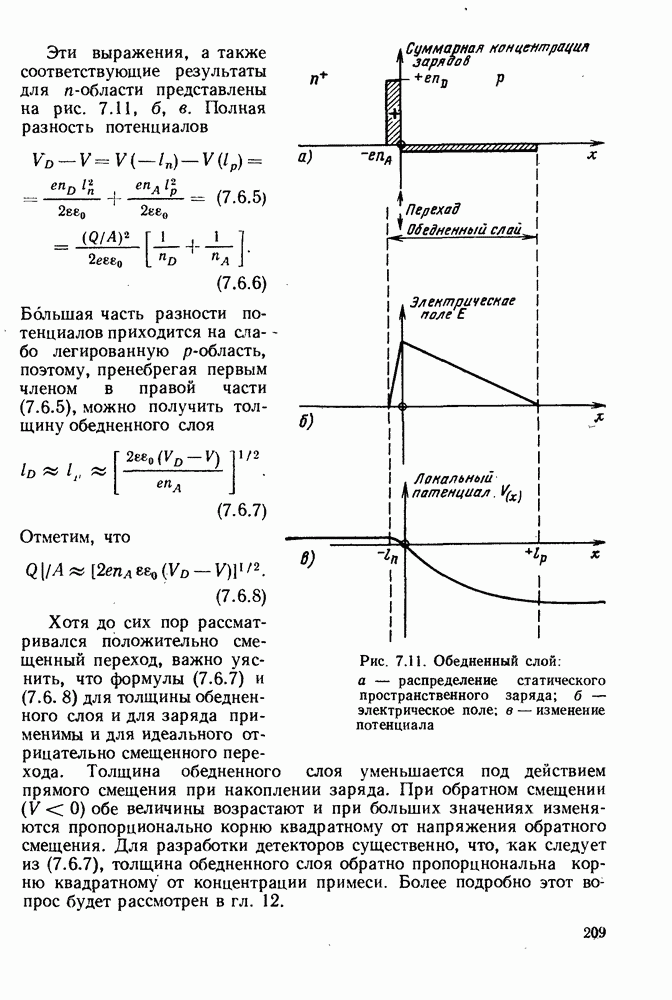
- 7.6. ОБЕДНЕННЫЙ СЛОЙ
- 7.7. ЭКВИВАЛЕНТНАЯ СХЕМА p-n-ПЕРЕХОДА
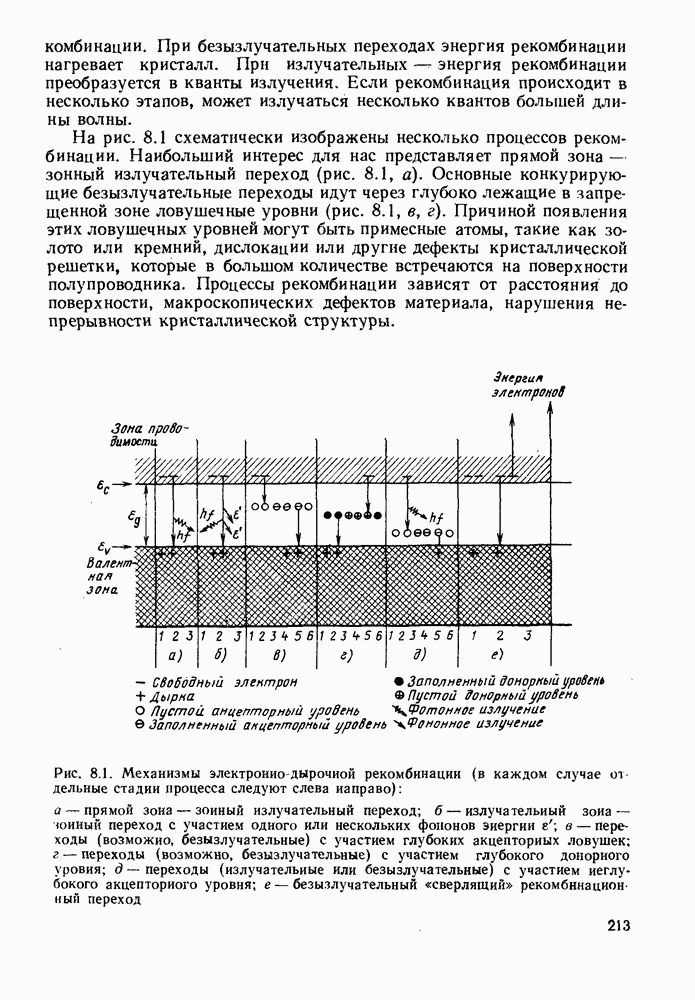
- 8. ИНЖЕКЦИОННАЯ ЛЮМИНЕСЦЕНЦИЯ
- 8.2. СПЕКТРЫ РЕКОМБИНАЦИОННОГО ИЗЛУЧЕНИЯ
- 8.3. ПРЯМОЗОННЫЕ И НЕПРЯМОЗОННЫЕ ПОЛУПРОВОДНИКИ
- 8.4. ВНУТРЕННЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.5. ВНЕШНЯЯ КВАНТОВАЯ ЭФФЕКТИВНОСТЬ
- 8.6. КОНСТРУКЦИИ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 8.7. ВЫСОКОЧАСТОТНЫЕ ОСОБЕННОСТИ
- 9. ИСПОЛЬЗОВАНИЕ ГЕТЕРОСТРУКТУР
- 9.1.2. Полезные свойства гетеропереходов
- 9.1.3. Эффективность инжекции
- 9.1.4. Характеристики гетеропереходов
- 9.2. ДВОЙНАЯ ГЕТЕРОСТРУКТУРА
- 9.2.2. Ширина полосы модуляции
- 9.3. СВЕТОИЗЛУЧАЮЩИЕ ДИОДЫ НА ОСНОВЕ ДВОЙНОЙ ГЕТЕРОСТРУКТУРЫ
- 9.4. ИЗГОТОВЛЕНИЕ ГЕТЕРОСТРУКТУР
- 10. РАБОТА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА
- 10.1.2. Условия работы лазера
- 10.2. ОПТИЧЕСКОЕ УСИЛЕНИЕ В ПОЛУПРОВОДНИКЕ
- 10.2.2. Скорости спонтанного и индуцированного излучения
- 10.2.3. Влияние показателя преломления
- 10.2.4. Расчет коэффициента усиления
- 10.2.5. Отношение коэффициента усиления к плотности тока
- 10.2.6. Конкретизация. Упрощения. Рабочие примеры
- 10.2.7. Полуэмпирический анализ
- 10.3. ЛАЗЕРНЫЙ ПОРОГ
- 10.4. ХАРАКТЕРИСТИКИ ЛАЗЕРОВ
- 11. ПОЛУПРОВОДНИКОВЫЕ ЛАЗЕРЫ ДЛЯ ОПТИЧЕСКОЙ СВЯЗИ
- 11.1. ОПТИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛОСКОВЫХ И ЗАРОЩЕННЫХ ГЕТЕРОСТРУКТУРНЫХ ЛАЗЕРОВ
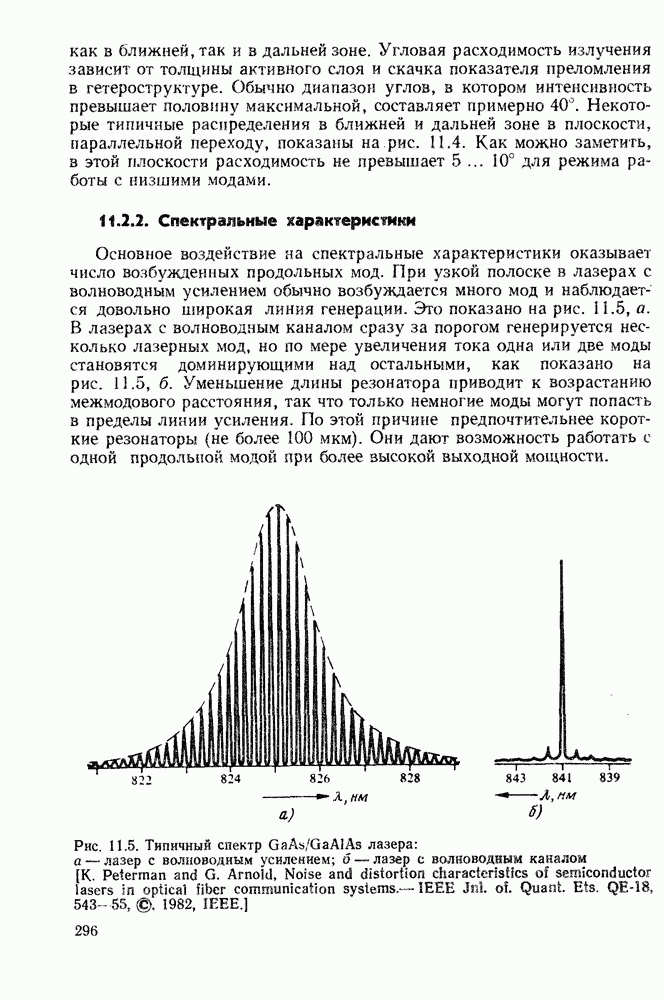
- 11.2.2. Спектральные характеристики
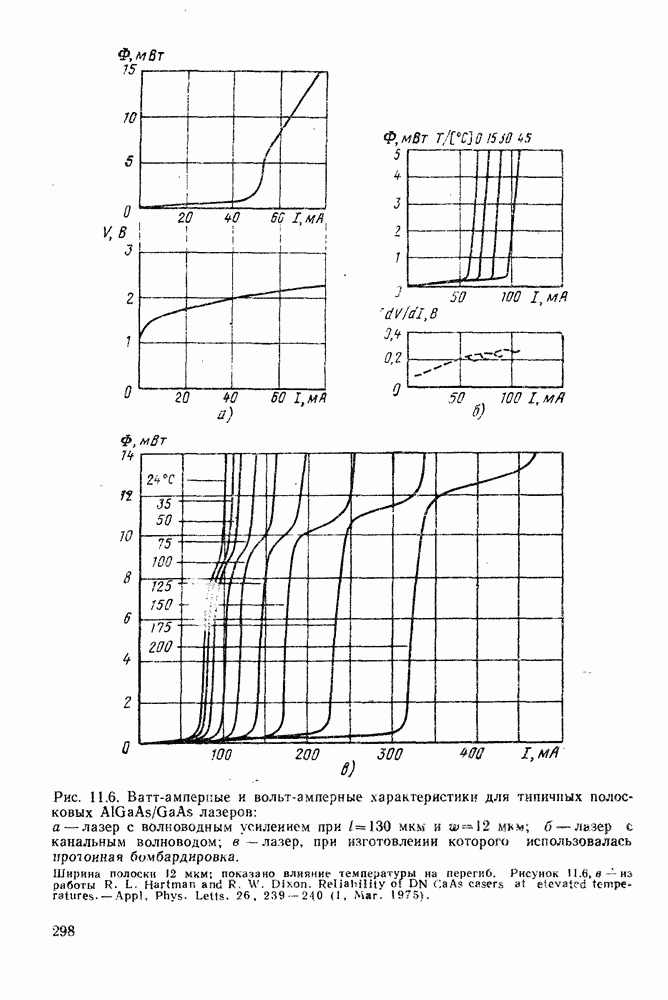
- 11.2.3. Ватт-амперные и вольт-амперные характеристики
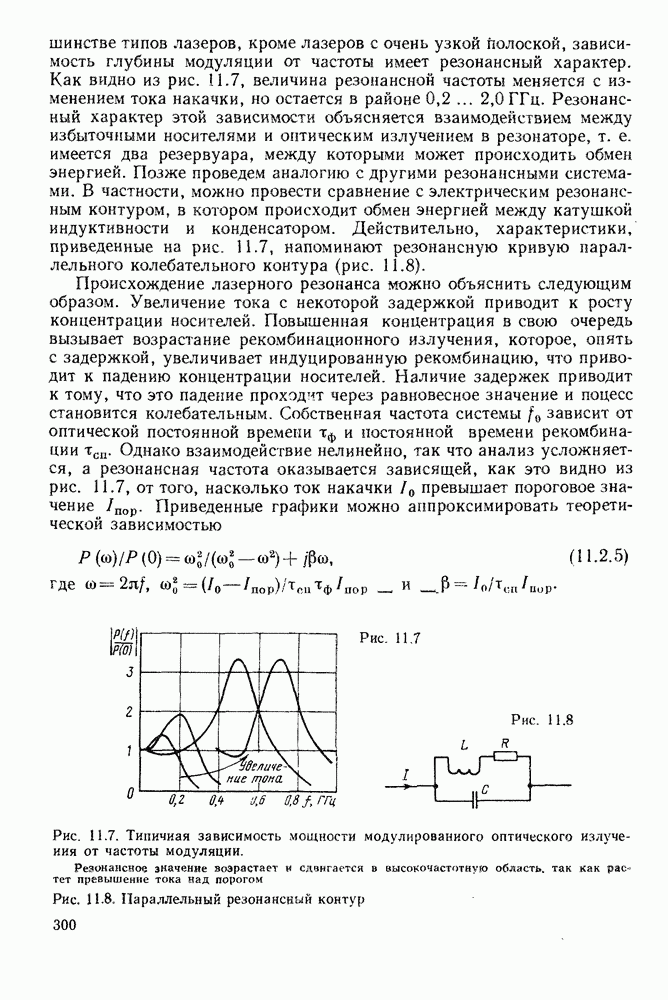
- 11.2.4. Частотные характеристики
- 11.3. ИСТОЧНИКИ ДЛИННОВОЛНОВОГО ИЗЛУЧЕНИЯ
- 11.4. НАДЕЖНОСТЬ СВЕТОДИОДОВ И ЛАЗЕРОВ НА ОСНОВЕ ДВОЙНЫХ ГЕТЕРОСТРУКТУР
- 12. ПОЛУПРОВОДНИКОВЫЕ р-i-n-ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 12.2. СОБСТВЕННОЕ ПОГЛОЩЕНИЕ
- 12.3. КВАНТОВЫЙ ВЫХОД
- 12.4. МАТЕРИАЛЫ И КОНСТРУКЦИИ р-i-n-ФОТОДИОДОВ
- 12.4.3. Гетеростру ктурные диоды и диоды с барьером Шотки
- 12.4.4. Фотодиоды для длинноволнового диапазона
- 12.5. ИМПУЛЬСНЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ p-i-n-ФОТОДИОДОВ
- 12.6. ШУМ p-i-n-ФОТОДИОДОВ
- 13. ЛАВИННЫЕ ФОТОДИОДНЫЕ ДЕТЕКТОРЫ
- 13.2. УСТРОЙСТВО ЛАВИННЫХ ФОТОДИОДОВ
- 13.3. ШИРИНА ПРОПУСКАНИЯ ЛАВИННЫХ ФОТОДИОДОВ
- 13.4. ШУМ ЛАВИННЫХ ФОТОДИОДОВ
- 14. УСИЛИТЕЛЬ ПРИЕМНИКА ОПТИЧЕСКИХ СИГНАЛОВ
- 14.2. ИСТОЧНИКИ ШУМА В ОПТИЧЕСКОМ ПРИЕМНИКЕ
- 14.3. СХЕМЫ УСИЛИТЕЛЕЙ И ИХ ЭЛЕМЕНТНАЯ БАЗА
- 14.4. СХЕМА УСИЛИТЕЛЯ НАПРЯЖЕНИЯ
- 14.4.3. Усилитель с высоким входным сопротивлением, или интегрирующий усилитель
- 14.4.4. Усилитель с низким входным сопротивлением
- 14.4.5. Точное решение для тока фотодиода
- 14.5. УСИЛИТЕЛЬ С ОБРАТНОЙ СВЯЗЬЮ, ИЛИ ТРАНСИМПЕДАНСНЫЙ УСИЛИТЕЛЬ
- 14.6. ПРАКТИЧЕСКИЙ ПРИМЕР
- 15. РЕГЕНЕРАЦИЯ ЦИФРОВЫХ СИГНАЛОВ
- 15.1. ПРИЧИНЫ ПОЯВЛЕНИЯ ОШИБОК ПРИ РЕГЕНЕРАЦИИ ЦИФРОВЫХ СИГНАЛОВ
- 15.1.3. Характеристики фильтра, минимизирующего межсимвольные помехи
- 15.1.4. Глаз-диаграмма
- 15.2. КВАНТОВЫЙ ПРЕДЕЛ ДЕТЕКТИРОВАНИЯ
- 15.3. ВЛИЯНИЕ ШУМОВ УСИЛИТЕЛЯ И ТЕПЛОВЫХ ШУМОВ НА ВЕРОЯТНОСТЬ ОШИБОК
- 15.3.2. Вероятность ошибок для случая, когда усиленный дробовой шум соизмерим с шумом от других источников
- 15.3.3. Оптимизация оптической системы связи
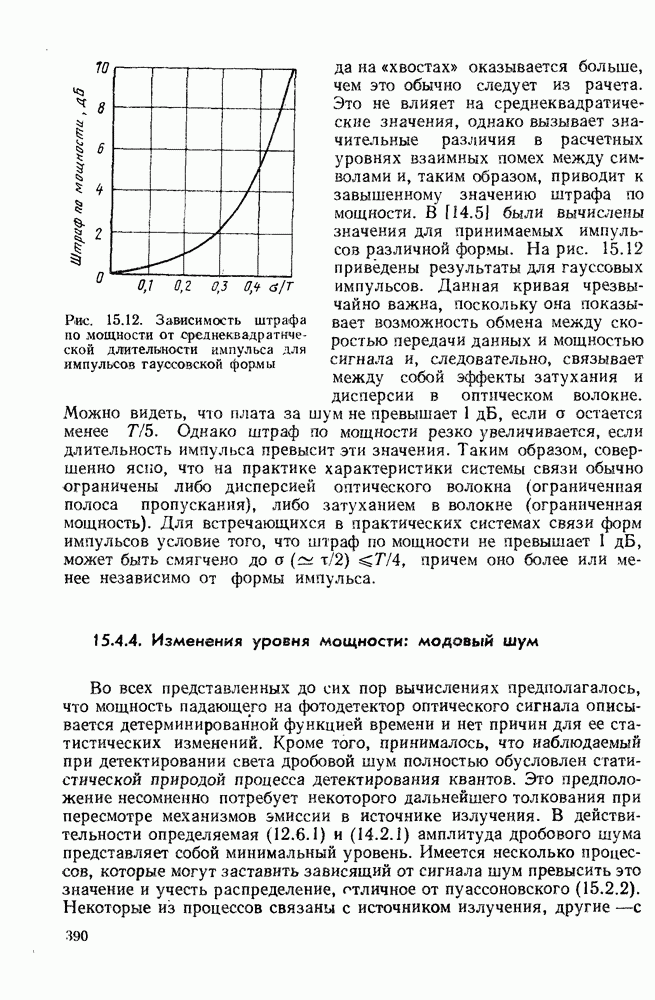
- 15.4. ШТРАФ ЗА ШУМ В ПРАКТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
- 16. ОТКРЫТЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 16.2. ХАРАКТЕРИСТИКИ ПЕРЕДАЧИ
- 16.2.2. Затухание оптического излучения в атмосфере
- 16.3. ИСТОЧНИКИ ИЗЛУЧЕНИЯ
- 16.3.3. Лазерные источники излучения на углекислом газе
- 16.4. ФОТОДЕТЕКТОРЫ
- 16.4.3. Фотодетекторы для более длинных волн
- 16.4.4. Использование гетеродинного детектирования
- 16.5. ПРИМЕРЫ ОТКРЫТЫХ ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 16.5.2. Перспективная оптическая система для связи в ближнем космосе
- 17. ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.2. ЭКОНОМИЧЕСКИЕ ПРЕИМУЩЕСТВА ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ СВЯЗИ
- 17.2.2. Связь на большие расстояния
- 17.2.3. Услуги местного распределения
- 17.2.4. Телеметрия и локальная передача данных
- 17.3. ЦИФРОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4. АНАЛОГОВЫЕ ВОЛОКОННО-ОПТИЧЕСКИЕ СИСТЕМЫ СВЯЗИ
- 17.4.2. Прямая модуляция по интенсивности в полосе спектра модулирующего сигнала
- 17.4.3. Использование частотно-модулированной поднесущей
- 17.5. ПРИМЕНЕНИЕ ВОЛС В ЛОКАЛЬНЫХ СЕТЯХ СВЯЗИ
- 17.6. ГОРОДСКИЕ СЕТИ СВЯЗИ
- ПРИЛОЖЕНИЕ 1. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ИЗОТРОПНОЙ СРЕДЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- ПРИЛОЖЕНИЕ 2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ГРАДИЕНТНОМ ВОЛОКНЕ: ПРИБЛИЖЕНИЕ ВКБ (ВЕНЦЕЛЯ КРАМЕРСА, БРИЛЛЮЭНА)
- ПРИЛОЖЕНИЕ 3. ТРАЕКТОРИИ ЛУЧЕЙ В ГРАДИЕНТНОМ ВОЛОКНЕ
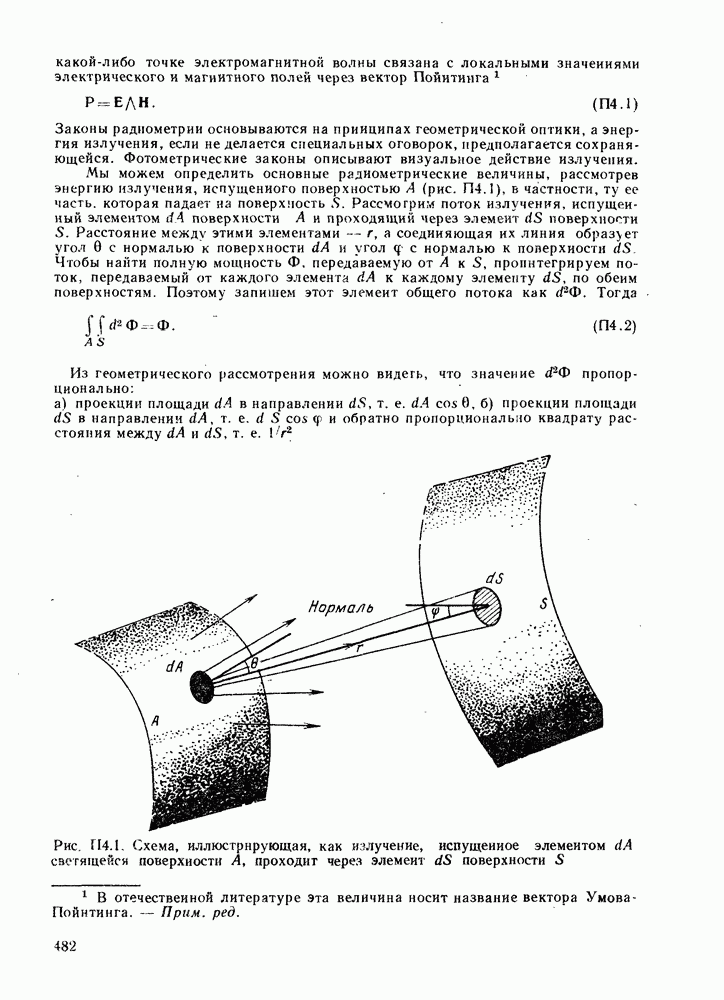
- ПРИЛОЖЕНИЕ 4. РАДИОМЕТРИЯ И ФОТОМЕТРИЯ
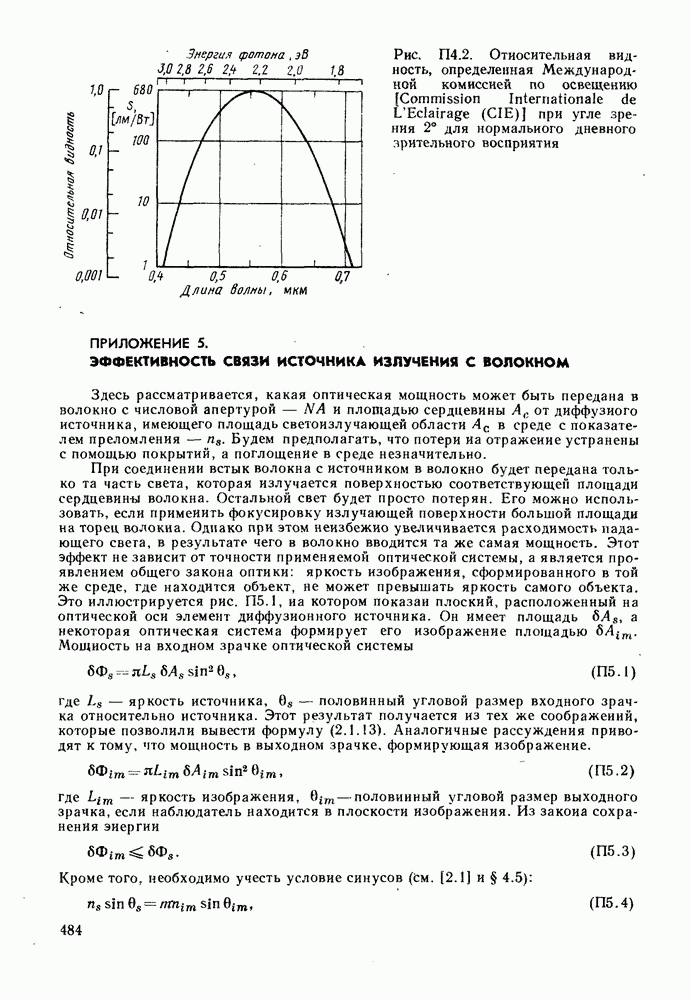
- ПРИЛОЖЕНИЕ 5. ЭФФЕКТИВНОСТЬ СВЯЗИ ИСТОЧНИКА ИЗЛУЧЕНИЯ С ВОЛОКНОМ
- ПРИЛОЖЕНИЕ 6. ВЫВОД ФОРМУЛЫ ДЛЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЛАЗЕРНОГО ДИОДА [ВЫРАЖЕНИЕ (11.2.5)]
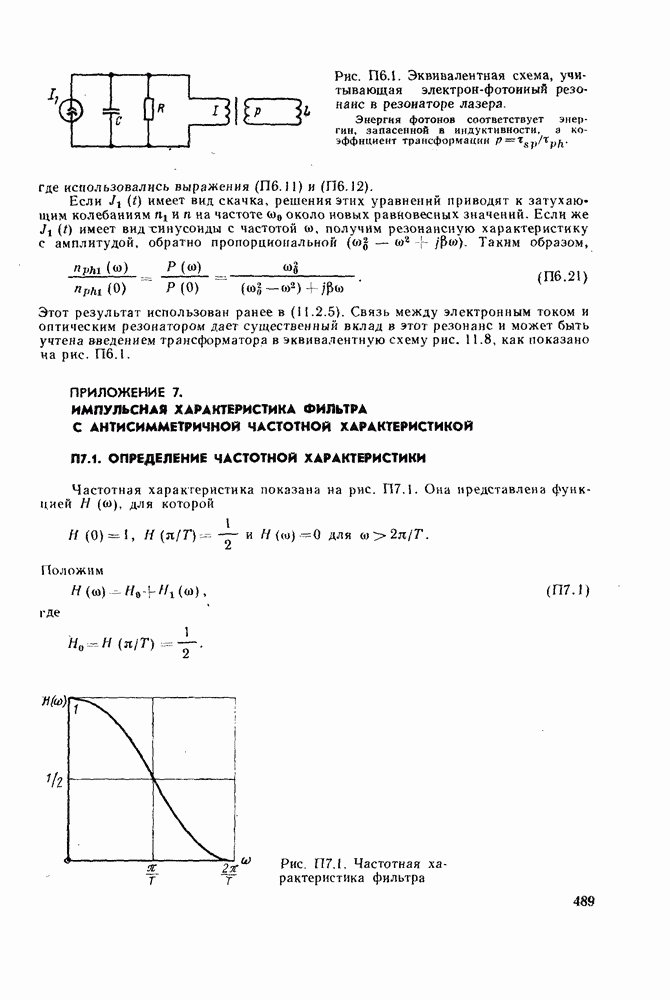
- ПРИЛОЖЕНИЕ 7. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ФИЛЬТРА С АНТИСИММЕТРИЧНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
- СПИСОК ЛИТЕРАТУРЫ