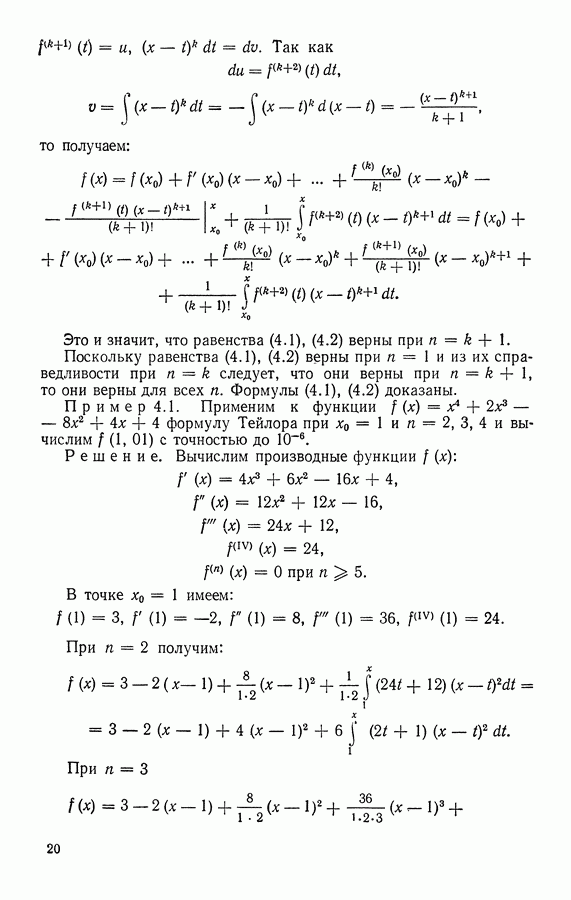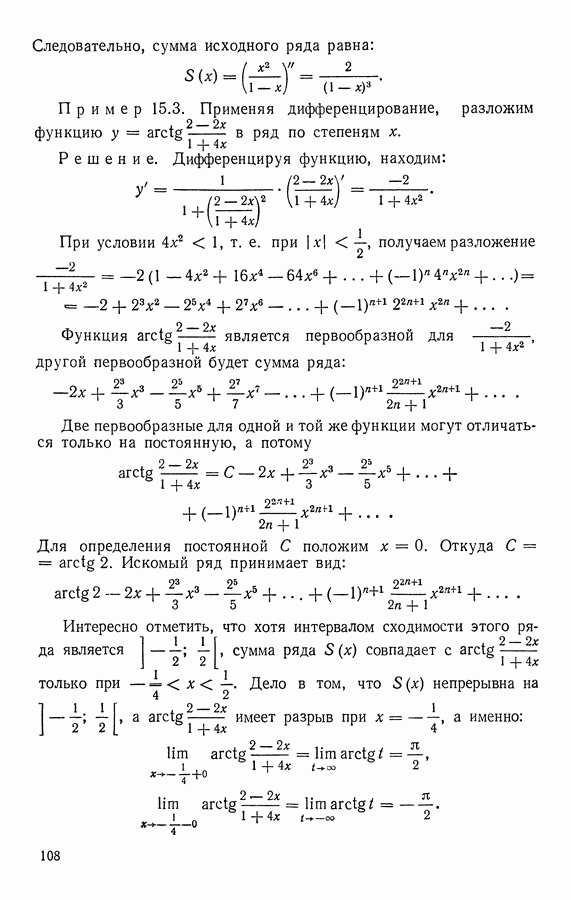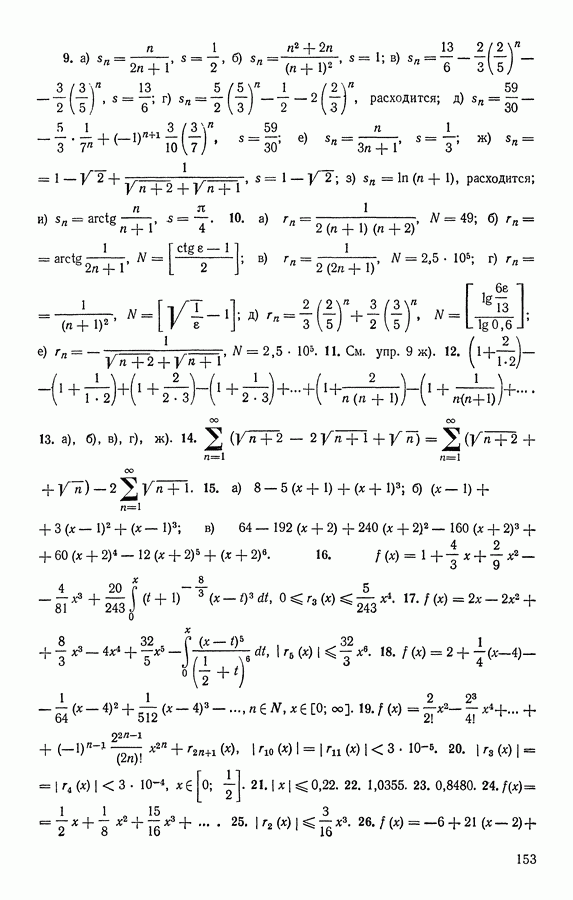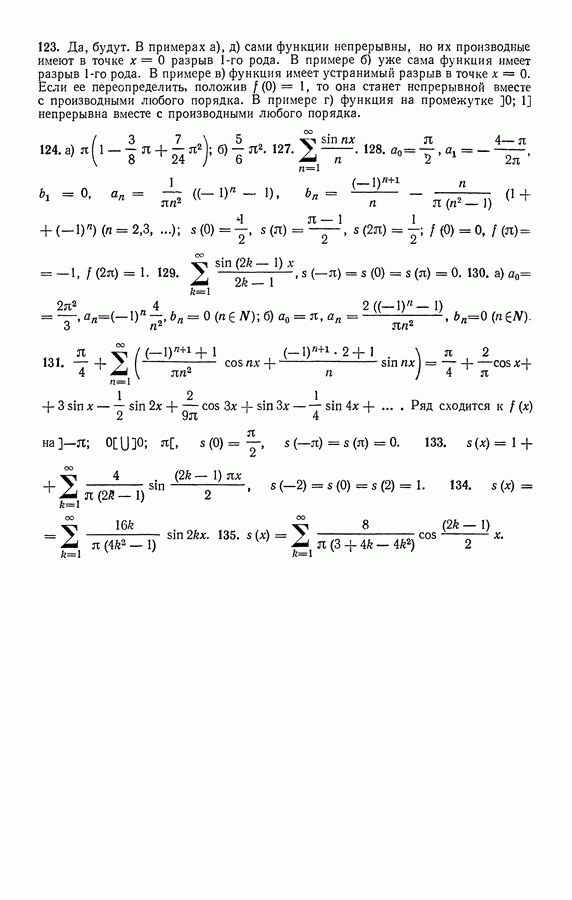| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРЕДИСЛОВИЕ
Предлагаемая вниманию читателя книга является учебным пособием для студентов-заочников физико-математических факультетов пединститутов по разделам «Ряды» и «Ряды Фурье» программы курса «Математический анализ». Мы не сочли целесообразным, в отличие от действующей сейчас программы, отрывать изучение рядов Фурье от изучения функциональных рядов. Кроме того, мы считали полезным до изучения общей теории числовых и функциональных рядов получить разложение в степенные ряды основных элементарных функций — это позволяет студентам заранее приобрести общую ориентировку в вопросах, с которыми им предстоит познакомиться.
Первая глава книги содержит основные понятия о рядах и доказательство свойств сходящихся рядов, а также вывод формул для разложения элементарных функций в степенные ряды.
Вторая глава посвящена числовым рядам. Отметим упрощение доказательств теоремы об умножении рядов и теоремы Лейбница, для последней доказательство непосредственно сводится к теореме о стягивающейся системе отрезков (иной формулировкой, которой она и является). Одновременно рассматриваются числовые ряды в комплексной области.
Третья и четвертая главы посвящены функциональным и, в частности, степенным рядам как в действительной, так и в комплексной областях. Вопрос о равномерной сходимости последовательностей функций изложен на основе понятия о чебышевском расстоянии между функциями, что позволило упростить как формулировку самого понятия равномерной сходимости, так и доказательство основных теорем. Отметим доказательство теоремы о почленном дифференцировании степенного ряда в комплексной области. Ради упрощения курса мы не рассматриваем формулу Коши — Адамара, поскольку формулировка соответствующего утверждения потребовала бы включения в курс понятия верхнего предела последовательности, тогда как сама эта формула практически используется редко.
Последняя глава книги посвящена изучению рядов Фурье, доведенному до теоремы о сходимости ряда Фурье кусочно-гладкой функции. Заключительная часть этого раздела, связанная с
ортонормированными базисами в гильбертовом пространстве, изложена в §20 книги Н. Я. Виленкина, М. Б. Балка и В. А. Петрова «Математический анализ. Мощность, метрика, интеграл», выпущенной издательством «Просвещение» в 1980 г.
Предлагаемая книга входит в серию учебных пособий для студентов-заочников по математическому анализу, выходящих под общим руководством профессора Н. Я. Виленкина (ранее опубликованы книги «Введение в анализ», «Дифференциальное исчисление», «Интегральное исчисление», «Мощность, метрика, интеграл»). В основу книги легли лекции, неоднократно читавшиеся авторами студентам МГЗПИ. Ранее был издан ротапринтный вариант этой книги. Теоретическая .часть настоящего пособия написана Н. Я. Виленкиным и В. В. Цукерманом. Упражнения составлены М. А. Доброхотовой, А. Н. Сафоновым и В. В. Цукерманом.
Книга разбита на главы, параграфы и пункты. Нумерация теорем, лемм, примеров и формул сплошная в пределах каждого параграфа. Почти все параграфы снабжены упражнениями и вопросами для самопроверки.
Авторы выражают глубокую благодарность за тщательное рецензирование, способствовавшее улучшению рукописи, профессору М. И. Граеву и доцентам А. С. Симонову, В. А. Тоняну и П. П. Мосолову (ротапринтный вариант), а также кафедре математического анализа Тульского педагогического института им. Л. Н. Толстого.
Авторы просят присылать отзывы и замечания по адресу: Москва, 129846, 3-й проезд Марьиной рощи, д. 41, издательство «Просвещение», редакция математики.
| Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
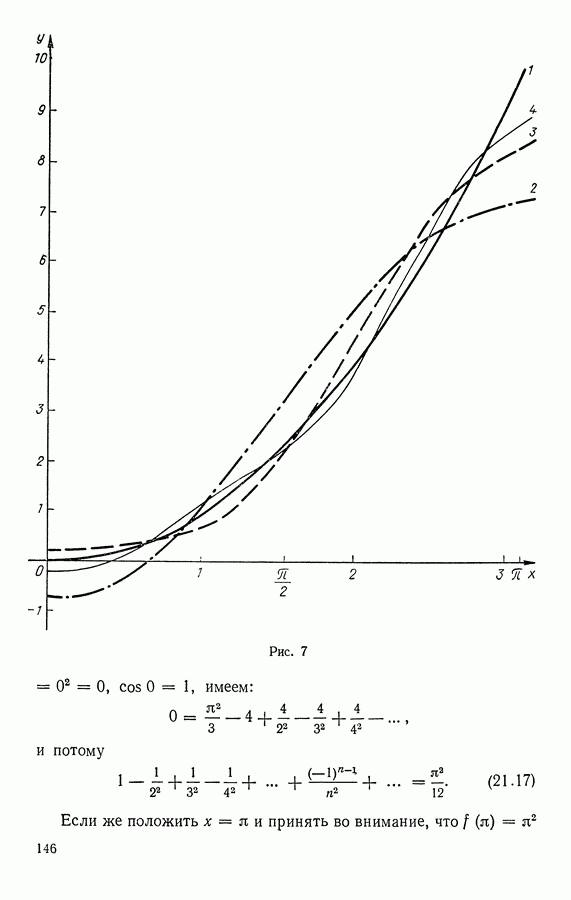
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям