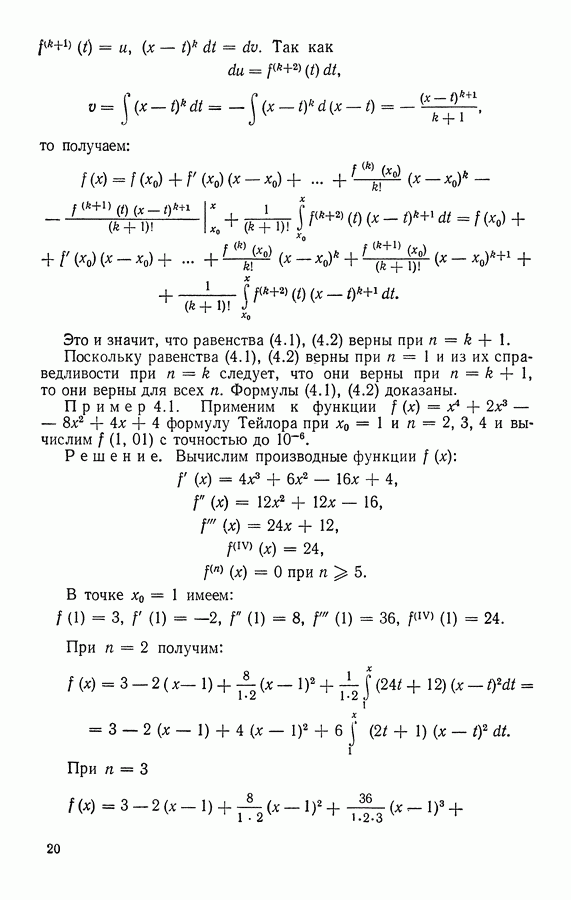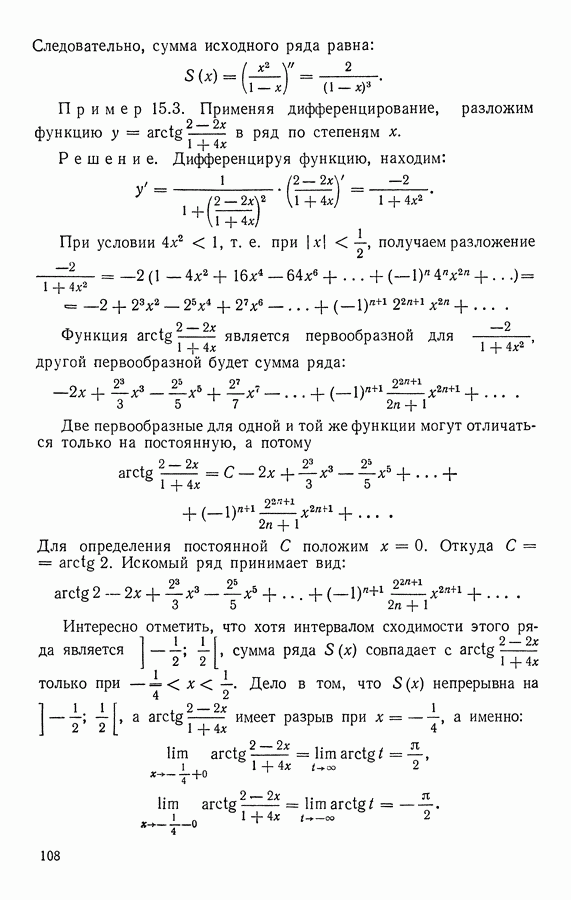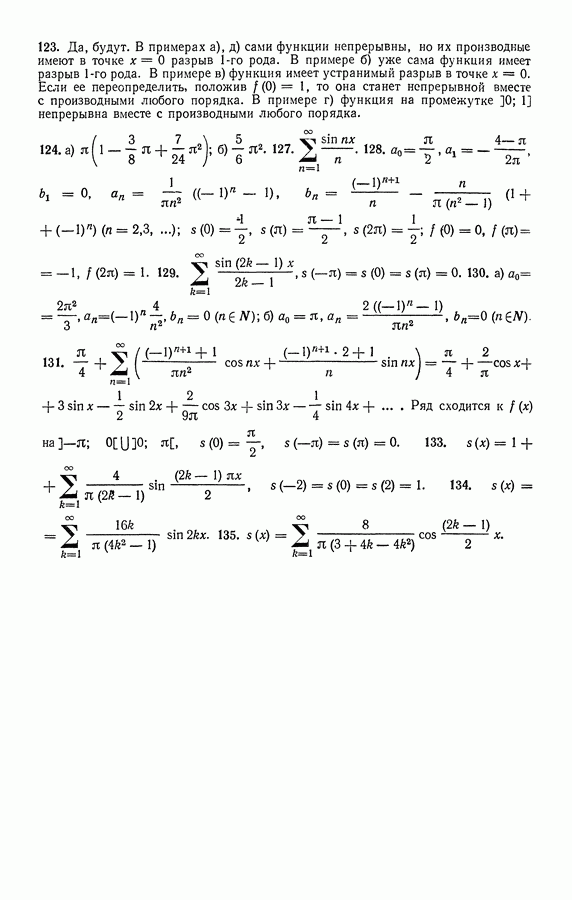| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. ФОРМУЛА ТЕЙЛОРА
Представление функции  в виде суммы ряда вида
в виде суммы ряда вида  называется разложением этой функции в степенной ряд. Для разложения функций в степенные ряды применяется формула Тейлора, которую мы сейчас докажем.
называется разложением этой функции в степенной ряд. Для разложения функций в степенные ряды применяется формула Тейлора, которую мы сейчас докажем.
Теорема 4.1. Пусть функция  имеет на отрезке
имеет на отрезке  производные до
производные до  порядка включительно,
порядка включительно,
причем  непрерывна на этом отрезке. Тогда для любого х из этого отрезка выполняется равенство
непрерывна на этом отрезке. Тогда для любого х из этого отрезка выполняется равенство

где

Равенство (4.1) называют формулой Тейлора,  — остаточным членом этой формулы, а выражение (4.2) — интегральной формой остаточного члена формулы Тейлора. Отметим, что из существования на отрезке
— остаточным членом этой формулы, а выражение (4.2) — интегральной формой остаточного члена формулы Тейлора. Отметим, что из существования на отрезке  производных функции
производных функции  до
до  порядка включительно вытекает непрерывность функций
порядка включительно вытекает непрерывность функций  на этом отрезке.
на этом отрезке.
Доказательство. Из формулы Ньютона — Лейбница следует, что  и потому
и потому

Поскольку переменной интегрирования является  мы считаем значение х постоянным. Но тогда
мы считаем значение х постоянным. Но тогда  Интегрируя по частям в формуле (4.3) и полагая
Интегрируя по частям в формуле (4.3) и полагая  получаем:
получаем:

Но при  выражение
выражение  обращается в нуль, и потому
обращается в нуль, и потому

Полученное выражение совпадает с (4.1), (4.2) при  Предположим теперь, что равенства (4.1), (4.2) доказаны при
Предположим теперь, что равенства (4.1), (4.2) доказаны при  т. е. что доказано соотношение
т. е. что доказано соотношение

Предполагая существование и непрерывность  положим
положим

то получаем:

Это и значит, что равенства (4.1), (4.2) верны при  Поскольку равенства (4.1), (4.2) верны при
Поскольку равенства (4.1), (4.2) верны при  и из их справедливости при
и из их справедливости при  следует, что они верны при
следует, что они верны при  то они верны для всех
то они верны для всех  Формулы (4.1), (4.2) доказаны.
Формулы (4.1), (4.2) доказаны.
Пример 4.1. Применим к функции  формулу Тейлора при
формулу Тейлора при  и вычислим
и вычислим  с точностью до
с точностью до 
Решение. Вычислим производные функции 

В точке  имеем:
имеем:

При  получим:
получим:

При 


При  получаем разложение функции
получаем разложение функции  по степеням
по степеням  поскольку
поскольку  тождественно обращается в нуль:
тождественно обращается в нуль:

Легко непосредственно проверить, что

Последнее слагаемое в разложении  при
при  равно
равно  Предыдущее слагаемое при
Предыдущее слагаемое при  равно
равно  Для вычисления с точностью
Для вычисления с точностью  можно отбросить лишь последнее слагаемое. Имеем:
можно отбросить лишь последнее слагаемое. Имеем:

с точностью до  . В данном примере мы фактически знаем больше: истинное значение
. В данном примере мы фактически знаем больше: истинное значение  превышает найденное на
превышает найденное на  (на величину отброшенного члена).
(на величину отброшенного члена).
Замечание. Использование формулы Тейлора для многочлена  степени при
степени при  дает разложение многочлена по степеням
дает разложение многочлена по степеням  так как
так как  в силу того, что
в силу того, что 
Пример 4.2. Напишем формулу Тейлора при  и выражение остаточного члена для
и выражение остаточного члена для 
Дадим оценку  на отрезке [0; 1].
на отрезке [0; 1].
Решение. Имеем:

Отсюда:

Искомая формула имеет вид:

или

где

Подынтегральная функция положительна и, кроме того,  (так как
(так как  ). Следовательно,
). Следовательно,

Таким образом, вычисление функции  на отрезке [0; 1] по приближенной формуле
на отрезке [0; 1] по приближенной формуле

дает ее значение с избытком и ошибка не превышает величины 
Пример 4.3. Найдем четвертый коэффициент в формуле Тейлора функции  при
при  дадим оценку остаточного члена
дадим оценку остаточного члена  на отрезке
на отрезке 
Решение. Как мы видели (см. пример 4.2), 
Отсюда  и четвертый коэффициент
и четвертый коэффициент
в формуле Тейлора равен:

Для  имеет место выражение
имеет место выражение

(ср. с примером 4.2). Функция  монотонно убывает на отрезке
монотонно убывает на отрезке  и достигает наибольшего значения при
и достигает наибольшего значения при  т. е.
т. е.

Следовательно, имеет место оценка

и поэтому

Пример 4.4. Выясним, при каком наибольшем значении  можно записать формулу Тейлора с остаточным членом в интегральной форме для функции
можно записать формулу Тейлора с остаточным членом в интегральной форме для функции  при
при  и найдем соответствующую формулу Тейлора.
и найдем соответствующую формулу Тейлора.
Решение. В точке  функция имеет производные до
функция имеет производные до  порядка включительно, и все эти производные равны нулю. Производные более высоких порядков в точке
порядка включительно, и все эти производные равны нулю. Производные более высоких порядков в точке  не существуют. Так как значение функции
не существуют. Так как значение функции  в точке
в точке  также равно нулю, то искомая формула Тейлора принимает вид
также равно нулю, то искомая формула Тейлора принимает вид  Пример 4.5. Выясним происхождение формулы
Пример 4.5. Выясним происхождение формулы

и укажем тот промежуток значений х, на котором эта приближенная формула имеет место с точностью до 0,00005.
Решение. Поскольку записанная формула представляет
собой разложение по степеням х, найдем для сравнения с ней формулу Тейлора для функции  при
при 
Имеем:

Отсюда:

Таким образом, часть формулы Тейлора без остаточного члена и при  и при
и при  совпадает с исходной формулой. Мы примем
совпадает с исходной формулой. Мы примем  так как при этом получается лучшая оценка остаточного члена. Итак,
так как при этом получается лучшая оценка остаточного члена. Итак,

где

Таким образом, абсолютная погрешность записанной в условии задачи формулы следует из оценки  Так как
Так как  , то получим:
, то получим:

Чтобы абсолютная погрешность была меньше 0,00005, достаточно потребовать выполнения неравенства

Решая это неравенство, получим  т. е. указанная точность приближения обеспечивается значениями, удовлетворяющими неравенству
т. е. указанная точность приближения обеспечивается значениями, удовлетворяющими неравенству

Замечание. Так как использованная нами оценка остаточного члена дана «с запасом», то мы получили не наибольший промежуток, в котором обеспечивается требуемая точность нашей приближенной формулы для  Эта точность может быть достигнута и в несколько более широком промежутке.
Эта точность может быть достигнута и в несколько более широком промежутке.
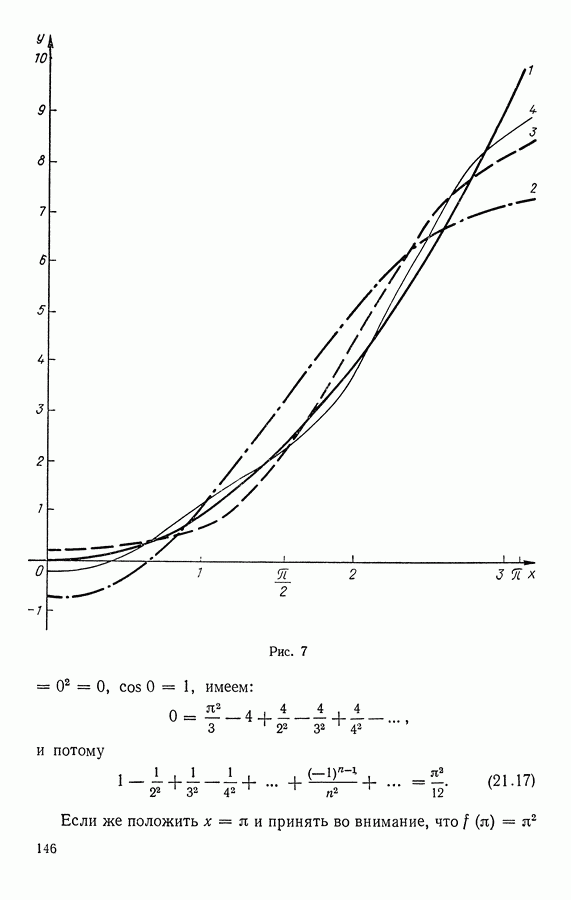
Вопросы для самоконтроля
(см. скан)
Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям