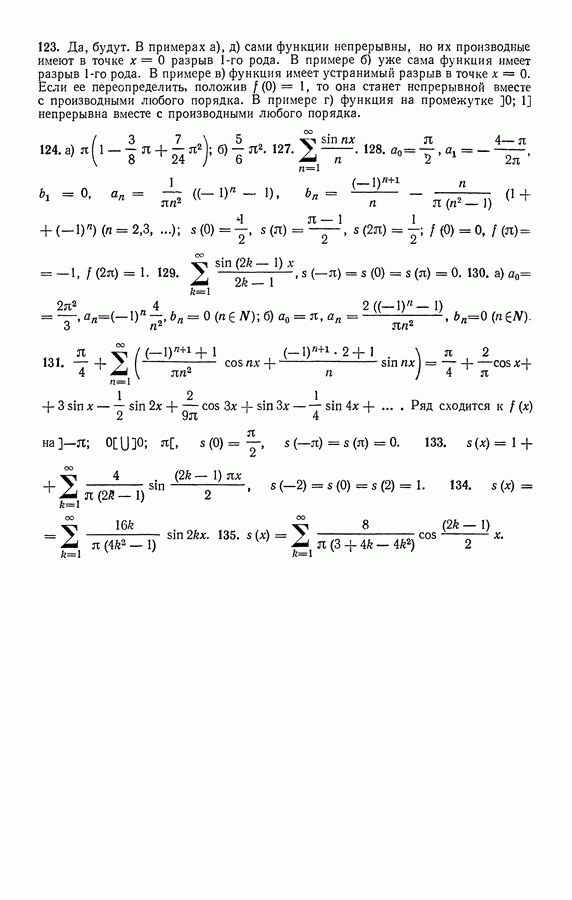| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
1. Ряд Тейлора.
Формула (4.1) дает представление функции  в виде суммы конечного множества слагаемых. Если функция
в виде суммы конечного множества слагаемых. Если функция  имеет на
имеет на  производные любого порядка, причем на этом отрезке выполняется соотношение
производные любого порядка, причем на этом отрезке выполняется соотношение  то можно перейти в формуле Тейлора к пределу при
то можно перейти в формуле Тейлора к пределу при  Мы получим, что
Мы получим, что

т. е. что

Ряд, стоящий в правой части формулы (5.1), называется рядом Тейлора функции  Он зависит не только от этой функции, но и от выбора значения
Он зависит не только от этой функции, но и от выбора значения  Если
Если  то ряд Тейлора принимает вид:
то ряд Тейлора принимает вид:

Непосредственно проверить, что  для всех х из отрезка
для всех х из отрезка  иногда бывает затруднительно. Поэтому нужно вывести признак того, что на нем выполняется равенство (5.1), т. е. что функция равна на нем сумме своего ряда Тейлора. Сначала докажем следующую лемму:
иногда бывает затруднительно. Поэтому нужно вывести признак того, что на нем выполняется равенство (5.1), т. е. что функция равна на нем сумме своего ряда Тейлора. Сначала докажем следующую лемму:
Лемма 5.1. Пусть последовательность  состоит из положительных чисел и пусть существует такое число
состоит из положительных чисел и пусть существует такое число  что
что  и для всех
и для всех  выполняется неравенство
выполняется неравенство  Тогда для всех
Тогда для всех  имеем
имеем 
Доказательство. По условию леммы выполняется неравенство  Предположим теперь, что доказано неравенство
Предположим теперь, что доказано неравенство
ство  Тогда по условию леммы
Тогда по условию леммы  и потому
и потому

Итак, неравенство  выполняется при
выполняется при  и из его выполнения при
и из его выполнения при  следует, что оно выполняется и при
следует, что оно выполняется и при  Значит, это неравенство верно для всех
Значит, это неравенство верно для всех 
Поскольку  то из неравенств
то из неравенств  следует, что
следует, что

и потому 
Утверждение, что  остается справедливым и в случае, когда неравенство
остается справедливым и в случае, когда неравенство  выполняется не для всех
выполняется не для всех  а лишь начиная с некоторого значения
а лишь начиная с некоторого значения  . В самом деле, если от последовательности
. В самом деле, если от последовательности  отбросить первые
отбросить первые  членов, то ее предел не изменится.
членов, то ее предел не изменится.
Пример 5.1. Докажем, что для любого х выполняется равенство

В самом деле, имеем:

Но если  то
то  Значит,
Значит,

Признак сходимости ряда Тейлора к разлагаемой функции формулируется следующим образом:
Теорема 5.1. Пусть функция  бесконечно дифференцируема на
бесконечно дифференцируема на  и пусть существует такое число
и пусть существует такое число  что для всех х из этого отрезка и всех
что для всех х из этого отрезка и всех  выполняется неравенство
выполняется неравенство  . Тогда функция
. Тогда функция  является на
является на  суммой своего ряда Тейлора.
суммой своего ряда Тейлора.
Иными словами, в этом случае  для всех
для всех 
Доказательство. Для любого  и любого
и любого  выполняется равенство
выполняется равенство

Но по условию теоремы имеем  . Поэтому
. Поэтому

Как было показано в примере  следовательно, для любого
следовательно, для любого  имеем
имеем  а это и значит, что функция
а это и значит, что функция  является на
является на  суммой своего ряда Тейлора.
суммой своего ряда Тейлора.
Пример 5.2. Найдем ряд Тейлора  для функции
для функции

Решение. Прежде всего необходимо доказать существование всех производных функции  при
при  и вычислить эти производные. Напомним, что при любом
и вычислить эти производные. Напомним, что при любом 

При  это очевидно, а для
это очевидно, а для  результат устанавливается с помощью правила Лопиталя. Если
результат устанавливается с помощью правила Лопиталя. Если  — натуральное число, то, применяя правило Лопиталя
— натуральное число, то, применяя правило Лопиталя  раз, получим:
раз, получим:

Если  не является целым числом, то правило Лопиталя нужно применить
не является целым числом, то правило Лопиталя нужно применить  раз, где
раз, где  . В этом случае имеем:
. В этом случае имеем:

так как 
Найдем  Имеем:
Имеем:

Если заменить 1 на  то получим
то получим  а потому при
а потому при 

Точно так же

Следовательно, 
С помощью метода математической индукции можно доказать, что при любом  имеем
имеем  Значит, все члены ряда Тейлора равны нулю, и потому он сходится к функции, тождественно равной нулю, а не к в
Значит, все члены ряда Тейлора равны нулю, и потому он сходится к функции, тождественно равной нулю, а не к в 
Этот пример показывает, что даже в случае, когда функция  имеет производные любого порядка в точке
имеет производные любого порядка в точке  сумма ее ряда Тейлора в окрестности этой точки может совпадать с
сумма ее ряда Тейлора в окрестности этой точки может совпадать с  лишь при
лишь при 
В некоторых случаях разложение функции в степенной ряд легче получить не опираясь на теорему о ряде Тейлора.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям