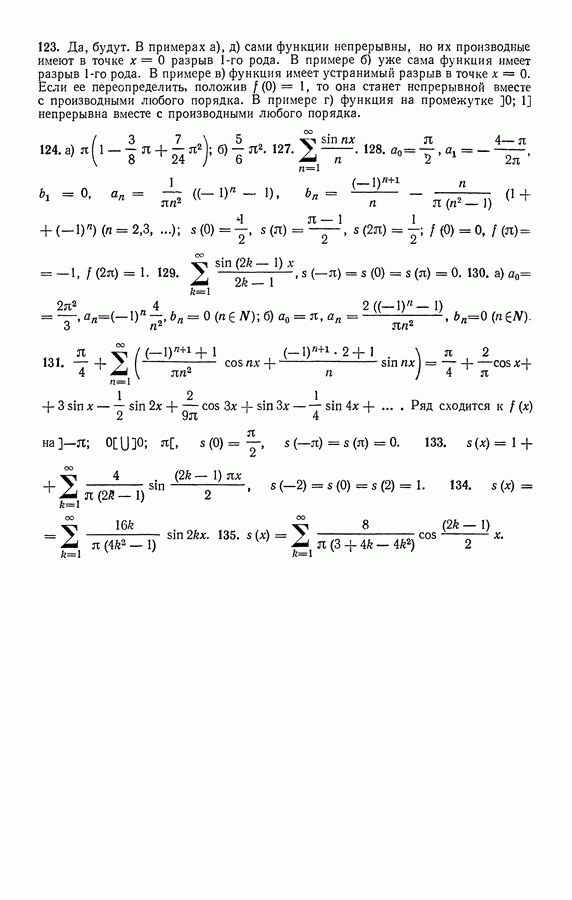| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Примеры исследования рядов на сходимость.
Рассмотрим дальнейшие примеры на все признаки сходимости.
Пример 6.6. Исследуем сходимость ряда:

Решение. Общий член ряда 
Заметим, что

Но ряд с общим членом  сходится (это геометрическая прогрессия со знаменателем
сходится (это геометрическая прогрессия со знаменателем  По первой теореме сравнения заданный ряд сходится.
По первой теореме сравнения заданный ряд сходится.
Пример 6.7. Исследуем сходимость ряда:

Решение. Общий член ряда  а
а

Необходимое условие сходимости ряда выполняется, но ряд расходится. Действительно,

Ряд с общим членом  расходится (это гармонический ряд). Поэтому на основании первой теоремы сравнения и заданный ряд расходится.
расходится (это гармонический ряд). Поэтому на основании первой теоремы сравнения и заданный ряд расходится.
Замечание. Мы использовали неравенство  Для его доказательства рассмотрим функцию
Для его доказательства рассмотрим функцию
 Ее производная
Ее производная  больше нуля при положительных значениях х. Следовательно, на
больше нуля при положительных значениях х. Следовательно, на  функция
функция  монотонно возрастает, а так как
монотонно возрастает, а так как  то она положительна на
то она положительна на  Полагая теперь
Полагая теперь  имеем:
имеем:

Пример 6.8. Исследуем сходимость ряда:

Решение.  Необходимое условие сходимости выполняется. Возьмем гармонический ряд (его общий член
Необходимое условие сходимости выполняется. Возьмем гармонический ряд (его общий член  и рассмотрим предел
и рассмотрим предел

Предел существует и отличен от нуля. Поскольку гармонический ряд расходится, то на основании второй теоремы сравнения заданный ряд также расходится.
Пример 6.9. Оценим остаток  ряда:
ряда:

Решение. Все члены ряда:

начиная со второго, меньше соответствующих членов геометрической прогрессии

Поэтому остаток  меньше суммы этой геометрической прогрессии, которую обозначим
меньше суммы этой геометрической прогрессии, которую обозначим 

Следовательно,  Если, например, взять вместо
Если, например, взять вместо
суммы  данного ряда частичную сумму
данного ряда частичную сумму  то возникающая при этом погрешность
то возникающая при этом погрешность  , таким образом, будет допущена ошибка, меньшая, чем
, таким образом, будет допущена ошибка, меньшая, чем 
Пример 6.10. Исследуем сходимость ряда:

Решение. Воспользуемся признаком Даламбера. Общий член ряда  Поэтому
Поэтому 
Ряд сходится. Заметим, что мы доказали также соотношение 

(общий член сходящегося ряда стремится к нулю).
Пример 6.11. Исследуем сходимость ряда:

Решение. Как и в предыдущем примере, воспользуемся признаком Даламбера:

При  имеем
имеем  , следовательно, ряд сходится. При
, следовательно, ряд сходится. При  ряд расходится, так как
ряд расходится, так как  При
При  имеем
имеем  Признак Даламбера формально не дает ответа на вопрос о сходимости ряда, но поскольку в рассматриваемом случае
Признак Даламбера формально не дает ответа на вопрос о сходимости ряда, но поскольку в рассматриваемом случае

 стремится к пределу
стремится к пределу  монотонно возрастая, то
монотонно возрастая, то  Это означает, что
Это означает, что  и потому
и потому  для
для
каждого  Таким образом, необходимый признак сходимости нарушается и ряд расходится. Итак, заданный ряд сходится при
Таким образом, необходимый признак сходимости нарушается и ряд расходится. Итак, заданный ряд сходится при  и расходится при х е.
и расходится при х е.
Пример 6.12. Исследуем сходимость ряда:

Решение. Общий член ряда  Так как в рассматриваемом случае легко найти
Так как в рассматриваемом случае легко найти  то воспользуемся признаком Коши:
то воспользуемся признаком Коши:

Значит, ряд сходится. Отсюда следует, что, в частности,

Пример 6.13. Докажем сходимость ряда  и оценим погрешность при замене суммы ряда суммой первых десяти членов.
и оценим погрешность при замене суммы ряда суммой первых десяти членов.
Решение. Признаки Даламбера и Коши здесь не дают ответа на вопрос о сходимости ряда. Члены ряда положительны и монотонно убывают. Рассмотрим функцию 
При  она положительна и монотонно убывает. При
она положительна и монотонно убывает. При  ее значения совпадают с соответствующими членами ряда. Согласно интегральному признаку Коши, данный ряд сходится или расходится одновременно с несобственным интегралом
ее значения совпадают с соответствующими членами ряда. Согласно интегральному признаку Коши, данный ряд сходится или расходится одновременно с несобственным интегралом

Подстановка  показывает, что
показывает, что

Поскольку очевидно, что  то интеграл, а
то интеграл, а
следовательно, и ряд сходятся. Для оценки остатка воспользуемся формулой (6.2)

Из нее следует, что

Имеем:

Точно так же получаем:

По таблице логарифмов находим, что 
Пример 6.14. Сколько членов ряда  следует взять, чтобы вычислить сумму ряда с точностью до 0,002?
следует взять, чтобы вычислить сумму ряда с точностью до 0,002?
Решение. Оценим величину  Имеем:
Имеем:

Так как

то

Поэтому нам нужно выбрать такое значение  чтобы выполнялось неравенство
чтобы выполнялось неравенство

Так как  то достаточно решить неравенство
то достаточно решить неравенство  т. е. неравенство
т. е. неравенство  или, иначе,
или, иначе,  Подбором находим
Подбором находим 
Вопросы для самоконтроля
(см. скан)
Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям