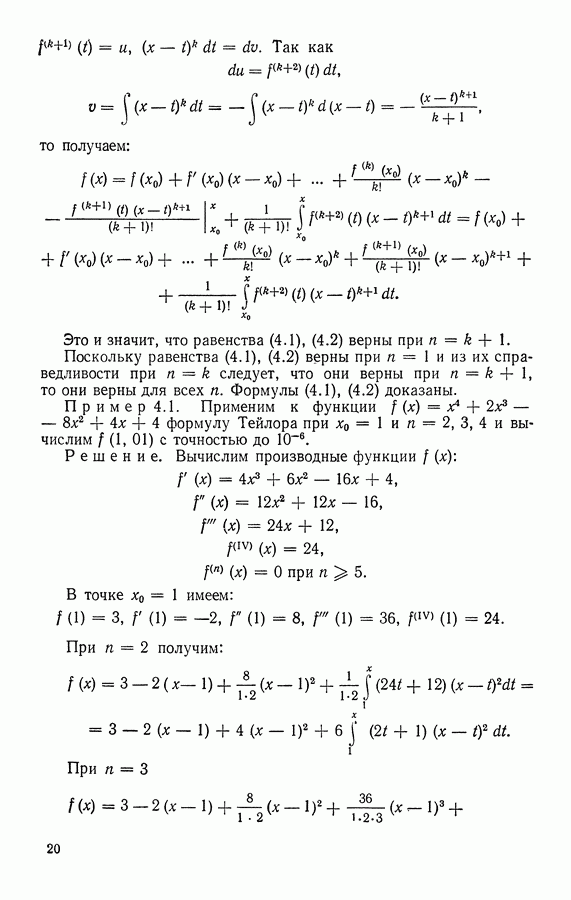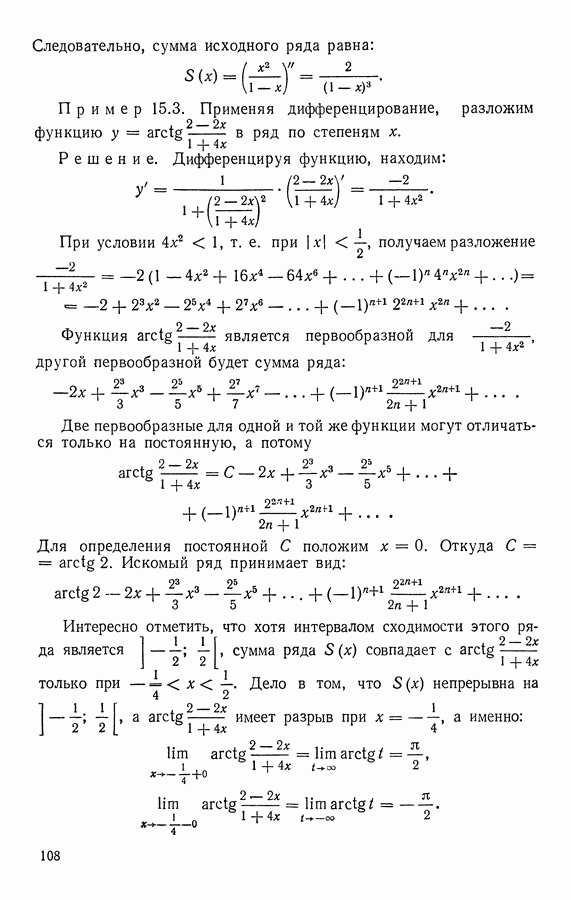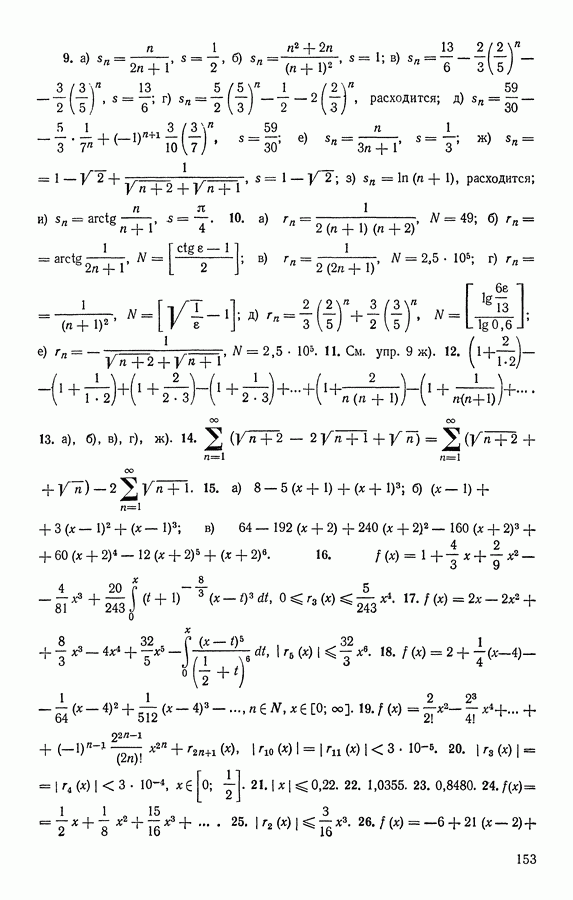| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
1. Теорема Лейбница.
Перейдем теперь к изучению рядов с членами произвольного знака, или, как говорят, знакопеременных рядов. Сначала рассмотрим знакочередующиеся ряды, т. е. ряды 

Рис. 2
у которых знаки соседних членов противоположны. Если положить  то такой ряд записывается при
то такой ряд записывается при  следующим образом:
следующим образом:

где все  Если же
Если же  то знакочередующийся ряд имеет вид:
то знакочередующийся ряд имеет вид:

Имеет место следующий признак Лейбница для сходимости знакочередующихся рядов:
Теорема 8.1 (Лейбница). Если модули членов знакочередующегося ряда монотонно убывают и стремятся к нулю, то этот ряд сходится. Модуль остатка такого ряда не превосходит модуля первого члена остатка ряда и имеет тот же знак, что этот член (иными словами,  ).
).
В частности, сумма ряда положительна, если  и отрицательна, если
и отрицательна, если 
Доказательство. Будем для определенности считать, что  т. е. что ряд имеет вид (8.1). Изобразим частичные суммы ряда (8.1) на числовой прямой (рис. 2). Из условия теоремы видно, что каждая следующая частичная сумма заключена между двумя предыдущими, а потому в системе отрезков
т. е. что ряд имеет вид (8.1). Изобразим частичные суммы ряда (8.1) на числовой прямой (рис. 2). Из условия теоремы видно, что каждая следующая частичная сумма заключена между двумя предыдущими, а потому в системе отрезков

каждый следующий содержится в предыдущем.
При этом  и потому длины этих отрезков стремятся к нулю. Но тогда есть лишь одно число, принадлежащее этим отрезкам, причем отрезки стягиваются к этому числу
и потому длины этих отрезков стремятся к нулю. Но тогда есть лишь одно число, принадлежащее этим отрезкам, причем отрезки стягиваются к этому числу  Отсюда следует, что
Отсюда следует, что  что ряд сходится к числу
что ряд сходится к числу 
Одновременно мы доказала, что при любом  выполняются неравенства
выполняются неравенства  Но тогда
Но тогда  Это значит, что для любого
Это значит, что для любого  имеем
имеем  причем знаки
причем знаки  совпадают.
совпадают.
Случай, когда  сводится к рассмотренному, если вынести минус за скобки.
сводится к рассмотренному, если вынести минус за скобки.
Пример 8.1. Ряд:

сходится при любом  так как
так как  причем
причем 
Пример 8.2. Сколько членов ряда  нужно взять, чтобы вычислить его сумму с точностью до 0,01? до 0,001?
нужно взять, чтобы вычислить его сумму с точностью до 0,01? до 0,001?
Решение. Рассматриваемый ряд удовлетворяет условию теоремы Лейбница. Следовательно, ряд сходится, а модуль разности суммы ряда  и частичной суммы
и частичной суммы  не превышает модуля первого отброшенного члена. Запишем последовательно значения
не превышает модуля первого отброшенного члена. Запишем последовательно значения  пока не превысим числа 1000:
пока не превысим числа 1000:

Следовательно, для вычисления суммы ряда с точностью до 0,01 достаточно вычислить  т. е. ограничиться суммой первых четырех членов. При этом знак погрешности совпадает со знаком
т. е. ограничиться суммой первых четырех членов. При этом знак погрешности совпадает со знаком  Таким образом,
Таким образом,  дает приближенное значение суммы ряда с избытком, не превышающим
дает приближенное значение суммы ряда с избытком, не превышающим 
Точно так же для получения ответа с точностью до 0,001 можно ограничиться суммой первых шести членов ряда. При этом получаем приближенное значение с избытком, не превышающим 
Пример 8.3. Докажем, что знакочередующийся ряд:

расходится, и выясним, почему здесь не применима теорема Лейбница о знакочередующихся рядах.
Решение. Четная частичная сумма  может быть записана в виде:
может быть записана в виде:


Таким образом,  равна удвоенной частичной сумме номера
равна удвоенной частичной сумме номера  для гармонического ряда. Гармонический ряд, как известно, расходится. Следовательно,
для гармонического ряда. Гармонический ряд, как известно, расходится. Следовательно,  Необходимый признак сходимости для рассматриваемого ряда, очевидно, выполнен. В частности,
Необходимый признак сходимости для рассматриваемого ряда, очевидно, выполнен. В частности, 

Следовательно,

Итак, для рассматриваемого ряда предел частичных сумм равен  — ряд расходится.
— ряд расходится.
Теорема Лейбница здесь не применима, так как модуль общего члена стремится к нулю не монотонно. Действительно,

поскольку, как легко проверить, 
Этот пример показывает, что монотонное стремление к нулю модуля общего члена знакочередующегося ряда является существенным условием теоремы Лейбница.
Вопросы для самоконтроля
(см. скан)
Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
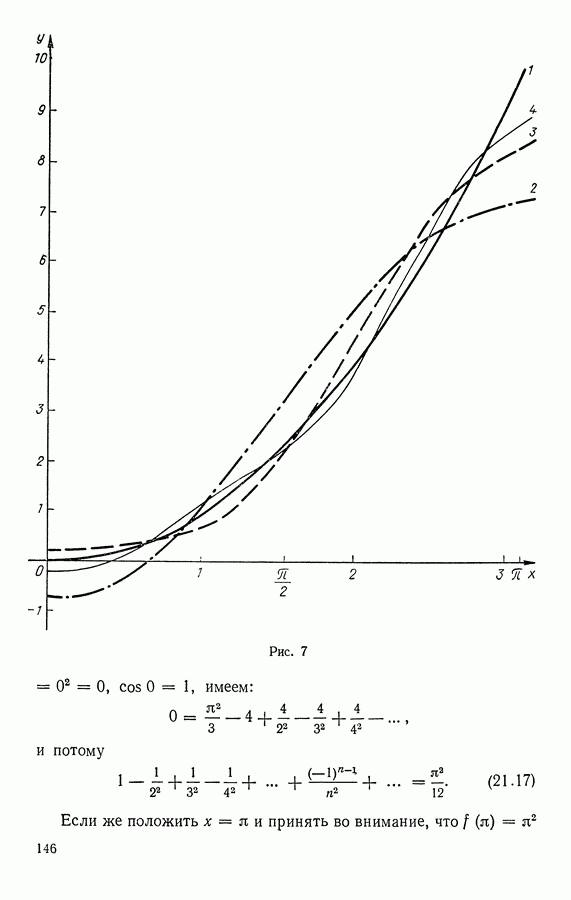
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям