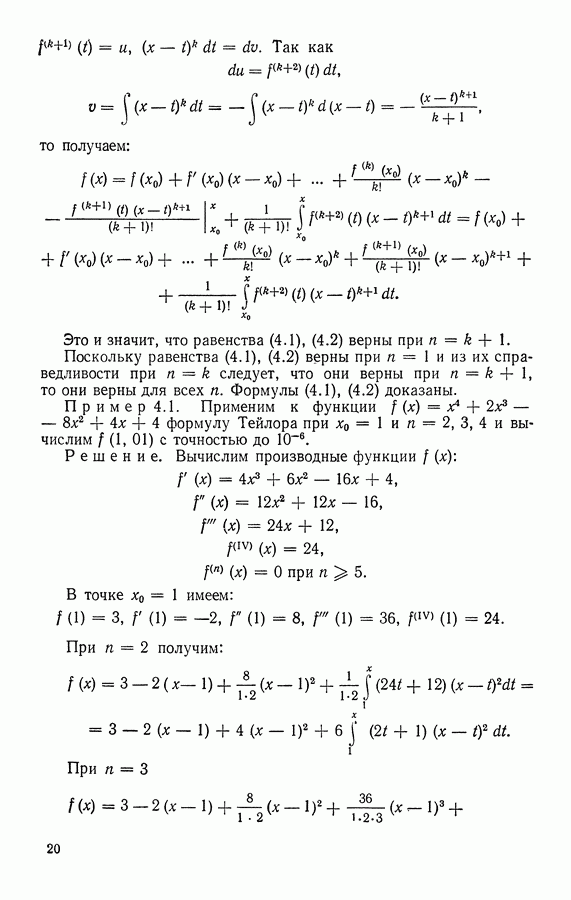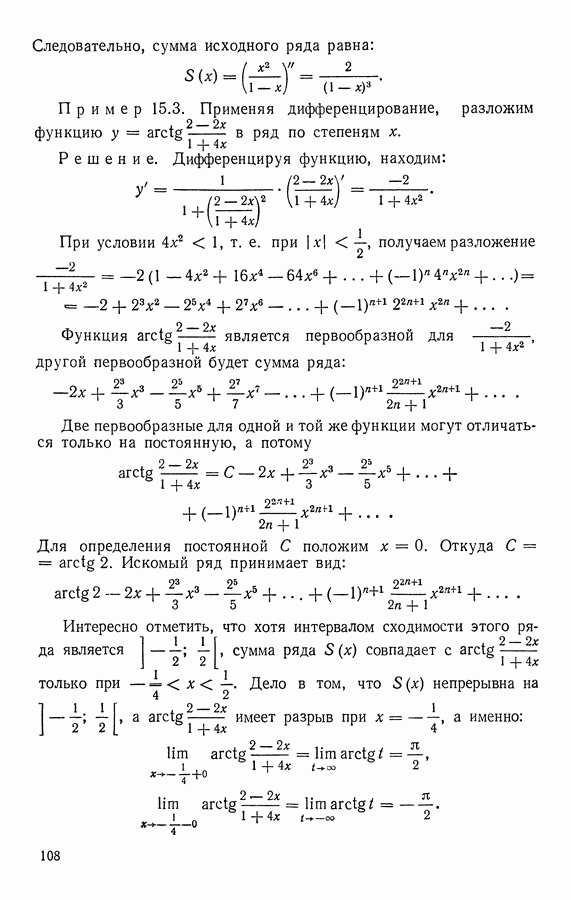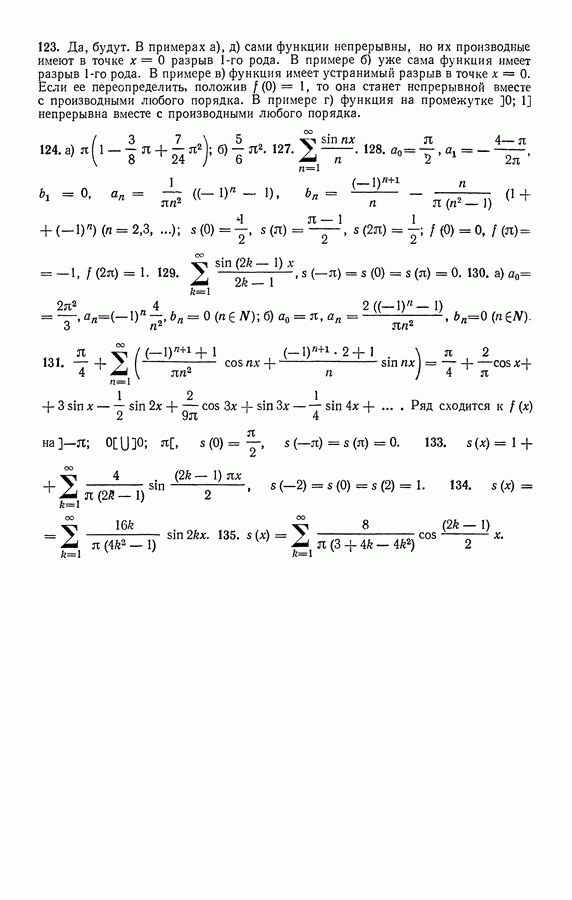| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Примеры разложения функций в ряды Фурье.
Пример 21.1. Разложим в ряд Фурье функцию  имеющую период
имеющую период  и заданную на
и заданную на  выражением
выражением  (рис. 6).
(рис. 6).
Решение. Данная функция является четной. В самом деле, на интервале  имеем
имеем  в силу периодичности. Поэтому разложение в ряд Фурье имеет вид
в силу периодичности. Поэтому разложение в ряд Фурье имеет вид

Рис. 6
(21.8), причем коэффициенты Фурье вычисляются по формулам (21.9)

Имеем:

Далее, используя формулы 120 и 93 Приложения I к «Интегральному исчислению», получаем:

(мы воспользовались тем, что  .
.
Значит, искомое разложение имеет вид:

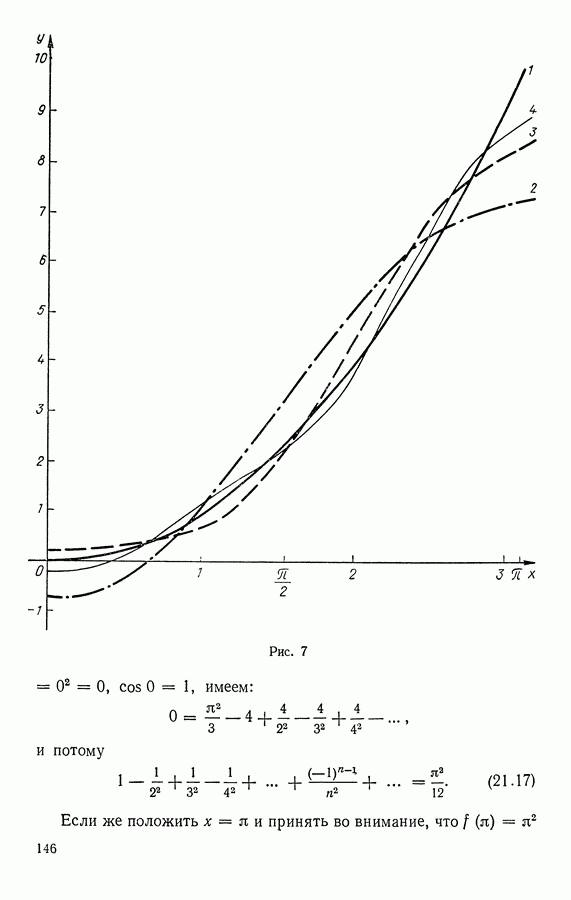
На рисунке 7 изображены графики первых трех частичных сумм ряда (21.16). Мы видим, как они приближаются к графику функции 
Замечание 1. В примере 19.1 было получено разложение в ряд Фурье функции, имеющей период  и заданной на промежутке
и заданной на промежутке  выражением
выражением  Это разложение отлично от полученного в рассматриваемом случае. Дело в том, что разлагаемые функции совпадают на
Это разложение отлично от полученного в рассматриваемом случае. Дело в том, что разлагаемые функции совпадают на  и отличны друг от друга на
и отличны друг от друга на  . А именно функция примера 19.1 при
. А именно функция примера 19.1 при  принимает значения
принимает значения  (поскольку в этом случае
(поскольку в этом случае  а на
а на  функция задана выражением
функция задана выражением  Функция же примера 21.1 при
Функция же примера 21.1 при  принимает значение
принимает значение 
Замечание 2. Тот же ответ (21.16) получился бы, если бы требовалось получить разложение функции  на отрезке
на отрезке  .
.
При частных значениях х из этого разложения получаем любопытные соотношения. Если положить  то, поскольку
то, поскольку 
Рис. 7 (см. скан)
 имеем:
имеем:

и потому

Если же положить  принять во внимание, что
принять во внимание, что 

Рис. 8
 получаем:
получаем:

и потому

Подчеркнем, что при тех значениях х, которые не принадлежат промежутку  сумма ряда (21.16) равна не
сумма ряда (21.16) равна не  а функции, полученной путем периодического продолжения с промежутка
а функции, полученной путем периодического продолжения с промежутка  Эта функция на [я
Эта функция на [я  принимает значение
принимает значение  Поэтому, например, если в ряд (21.16) подставить вместо х значение
Поэтому, например, если в ряд (21.16) подставить вместо х значение  , то получим не
, то получим не 
Пример 21.2. Разложим в ряд Фурье функцию  имеющую период
имеющую период  и заданную на
и заданную на  выражением х (рис. 8).
выражением х (рис. 8).
Решение. Поскольку  то данная функция является нечетной, и потому ее разложение в ряд Фурье имеет вид (21.10), причем ее коэффициенты выражаются следующей формулой
то данная функция является нечетной, и потому ее разложение в ряд Фурье имеет вид (21.10), причем ее коэффициенты выражаются следующей формулой

Используя формулу 93 Приложения I к «Интегральному исчислению», получаем:

Значит,

Если в (21.19) положить  то правая часть ряда обратится в нуль. Поскольку в точке
то правая часть ряда обратится в нуль. Поскольку в точке  функция
функция  имеет разрыв (см. рис. 8), то в соответствии с теоремой 21.1 сумма ряда Фурье должна равняться
имеет разрыв (см. рис. 8), то в соответствии с теоремой 21.1 сумма ряда Фурье должна равняться 
Так как  то
то  в согласии с упомянутой теоремой.
в согласии с упомянутой теоремой.
Пример 21.3. Разложим в ряд Фурье функцию  имеющую период
имеющую период  и заданную на
и заданную на  выражением
выражением 
Решение. Искомое разложение сразу получается из разложений, полученных в предыдущих двух примерах:

Предоставляем читателю найти этот ответ непосредственным вычислением коэффициентов Фурье по формулам (19.12) и (19.14).
Пример 21.4. Разложим в ряд Фурье функцию  имеющую период
имеющую период  и заданную на
и заданную на  следующим образом:
следующим образом:

График этой функции изображен на рисунке 9.
Решение. Так как данная функция задана различными выражениями на участках  то при вычислении ее коэффициентов Фурье надо разбить промежутки интегрирования в формулах (19.12) — (19.14) на указанные участки (то обстоятельство, что получаются интегралы не по отрезкам, а по полуоткрытым промежуткам, роли не играет, так как интеграл функции не изменяется от изменения ее значения в одной точке).
то при вычислении ее коэффициентов Фурье надо разбить промежутки интегрирования в формулах (19.12) — (19.14) на указанные участки (то обстоятельство, что получаются интегралы не по отрезкам, а по полуоткрытым промежуткам, роли не играет, так как интеграл функции не изменяется от изменения ее значения в одной точке).
Итак, имеем:


Рис. 9.

Значит,

Пример 21.5. Разложим в ряд Фурье функцию  имеющую период 6 и заданную на
имеющую период 6 и заданную на  выражением
выражением 
Решение. В данном случае период равен 21, где  Так как заданная функция нечетна, то по формулам (21.14) и (21. 15) получаем, что
Так как заданная функция нечетна, то по формулам (21.14) и (21. 15) получаем, что

где

Значит

Вопросы для самоконтроля
(см. скан)
(см. скан)
Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям