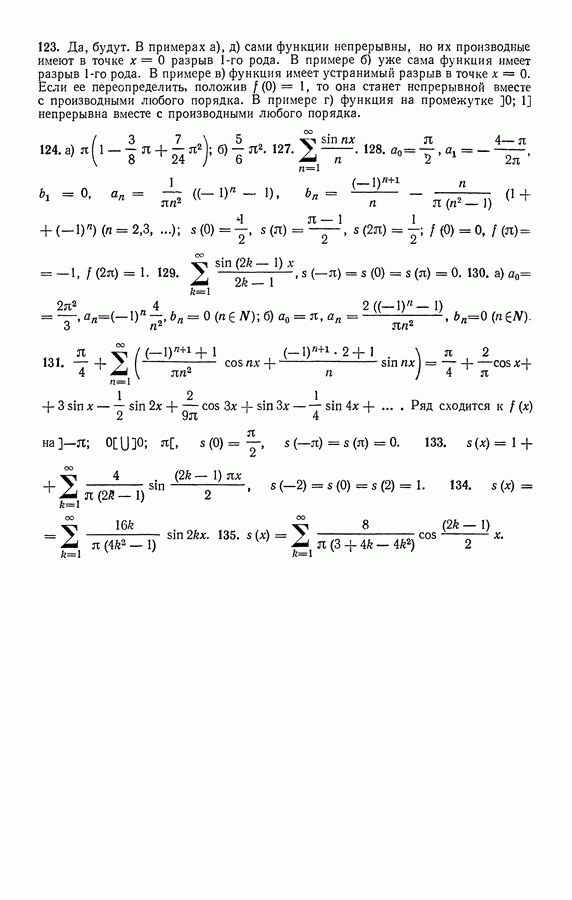| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 20. ЛЕММА РИМАНА
1. Кусочно гладкие функции.
Прежде всего напомним определение кусочно непрерывной функции. Функция  , заданная на
, заданная на  называется кусочно непрерывной, если этот отрезок можно разбить на конечное число отрезков:
называется кусочно непрерывной, если этот отрезок можно разбить на конечное число отрезков: 
 таких, что функция
таких, что функция  непрерывна во всех внутренних точках
непрерывна во всех внутренних точках  и имеет конечные пределы:
и имеет конечные пределы:

Периодическая функция называется кусочно непрерывной, если она кусочно непрерывна на отрезке, длина которого равна периоду.
Будем обозначать через  следующую функцию:
следующую функцию:

Таким образом, все функции  непрерывны на соответствующих отрезках
непрерывны на соответствующих отрезках  Отметим также, что функция
Отметим также, что функция  , кусочно непрерывная на
, кусочно непрерывная на  интегрируема на этом отрезке и
интегрируема на этом отрезке и

Аналогично определяется кусочно непрерывная функция на интервале или полуоткрытом промежутке. Сохраняется формула для вычисления определенного интеграла, поскольку величина правой части написанного выражения не зависит от значений функции в точках 
Существуют примеры непрерывных функций, ряды Фурье которых расходятся на бесконечном множестве точек. Поэтому, чтобы гарантировать сходимость ряда Фурье по тригонометрической системе функций, надо наложить на разлагаемую функцию более сильные ограничительные требования, чем кусочная непрерывность, и тем более — непрерывность.
Определение 20.1. Функция  имеющая период 21, называется кусочно гладкой, если существует такое разбиение отрезка
имеющая период 21, называется кусочно гладкой, если существует такое разбиение отрезка  на отрезки
на отрезки  что каждая из функций
что каждая из функций  имеет на отрезке
имеет на отрезке  непрерывную производную второго порядка (в точках
непрерывную производную второго порядка (в точках  речь идет об односторонних производных).
речь идет об односторонних производных).
Пример 20.1. Функция

является кусочно гладкой. Здесь отрезок  разбивается на отрезки
разбивается на отрезки  При этом
При этом

Рассмотрим функцию  Она определена, непрерывна, имеет непрерывные производные
Она определена, непрерывна, имеет непрерывные производные  на всей числовой оси (существенна лишь непрерывность
на всей числовой оси (существенна лишь непрерывность  и ее производных на каком-либо интервале, содержащем
и ее производных на каком-либо интервале, содержащем  и при
и при  совпадает с
совпадает с  Отсюда и следует, что на
Отсюда и следует, что на  являются сужением
являются сужением  на
на 
Разумеется, при этом сохраняется непрерывность. Откуда 
Мы рассмотрели случай  Точно так же рассматриваются случаи
Точно так же рассматриваются случаи 
Проверка кусочной гладкости функции в этом примере не вызывала затруднений потому, что для каждого  мы могли сразу указать нужную функцию
мы могли сразу указать нужную функцию  заданную на интервале, содержащем
заданную на интервале, содержащем  непрерывную вместе с производными (это легко усматривалось из ее аналитического выражения) и совпадающую с
непрерывную вместе с производными (это легко усматривалось из ее аналитического выражения) и совпадающую с  на отрезке
на отрезке  . В более сложных случаях такая простая проверка кусочной гладкости не удается, и тогда может быть полезно следующее предложение: если существует конечный предел
. В более сложных случаях такая простая проверка кусочной гладкости не удается, и тогда может быть полезно следующее предложение: если существует конечный предел  то он равен
то он равен  , таким образом,
, таким образом,  непрерывна в точке
непрерывна в точке 
В самом деле, 
Но по теореме Лагранжа найдется такое с, что  и потому
и потому 
Аналогично доказывается, что если существует  то он равен
то он равен 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям