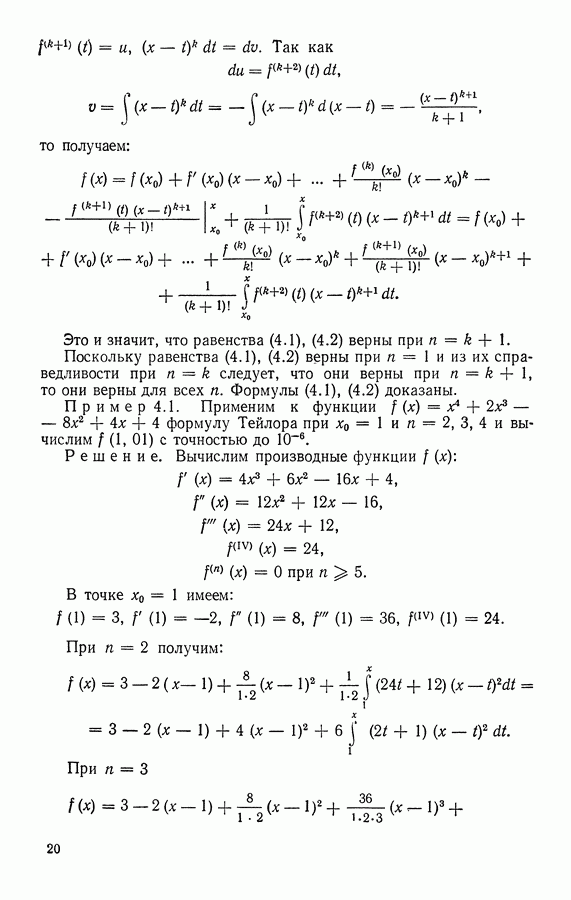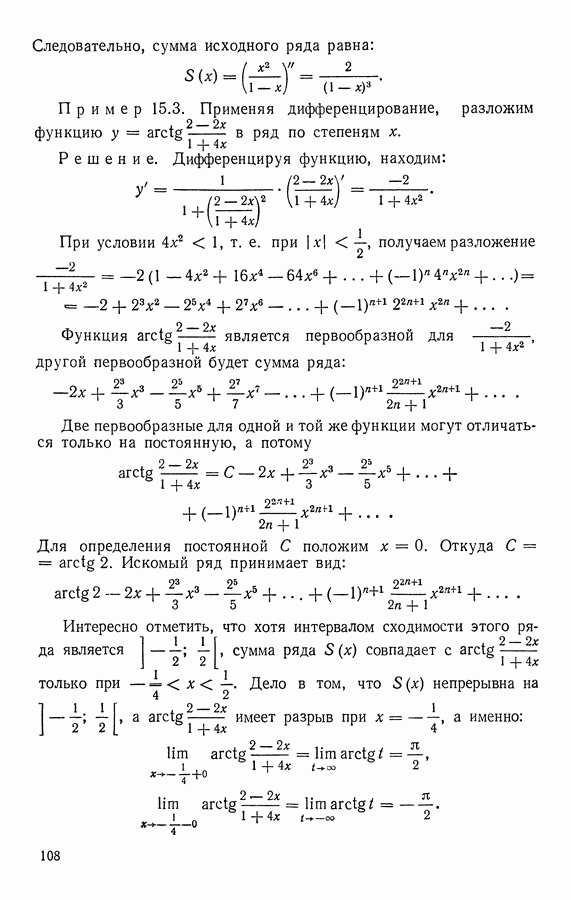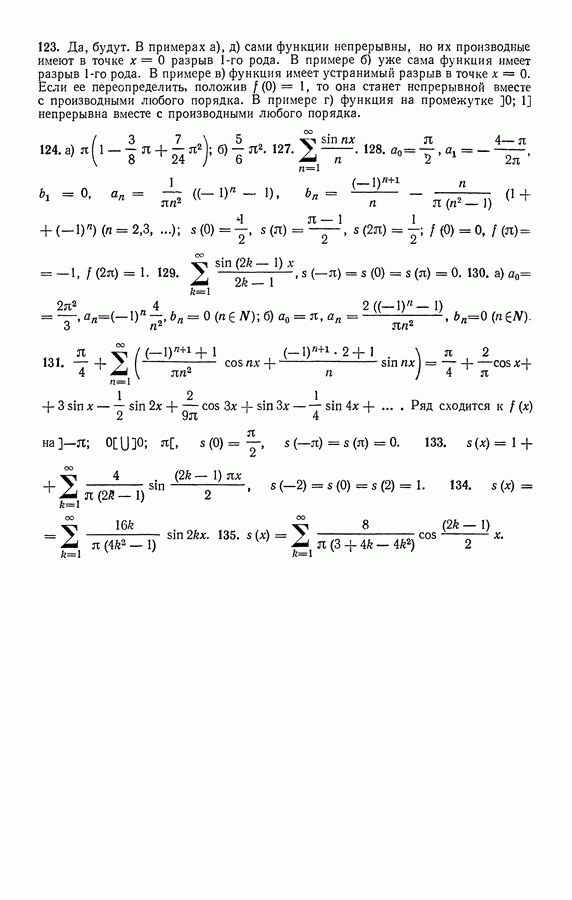| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
§ 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
1. Признаки сравнения.
Начнем с изучения рядов, все члены которых неотрицательны.
Пусть дан ряд вида  где все
где все  Так как
Так как  то
то  Это значит, что последовательность
Это значит, что последовательность  частичных сумм данного ряда неубывающая:
частичных сумм данного ряда неубывающая: 
В курсе «Введение в анализ» доказывается, что для сходимости неубывающей последовательности необходимо и достаточно, чтобы она была ограничена сверху, т. е. необходимо и достаточно, чтобы существовало тацое М, что  для всех
для всех  Значит, в этом и только в этом случае ряд
Значит, в этом и только в этом случае ряд  где
где  сходится.
сходится.
Мы доказали следующее утверждение:
Теорема 6.1. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.
Если последовательность  неубывающая, то ее предел не меньше любого из ее членов, т. е. для всех
неубывающая, то ее предел не меньше любого из ее членов, т. е. для всех  выполняется неравенство
выполняется неравенство  где
где 
Доказанное утверждение позволяет установить следующий признак сходимости рядов с неотрицательными членами:
Теорема 6.2. Пусть даны два ряда  члены которых неотрицательны, причем для всех
члены которых неотрицательны, причем для всех  выполняется неравенство
выполняется неравенство  Тогда если сходится ряд
Тогда если сходится ряд  то сходится и ряд
то сходится и ряд  причем
причем  (из сходимости ряда соответственно с большими членами вытекает сходимость ряда с соответственно мецьщими членами).
(из сходимости ряда соответственно с большими членами вытекает сходимость ряда с соответственно мецьщими членами).
Доказательство. Обозначим частичные суммы ряда  через
через  а ряда
а ряда  — через
— через  По предположению для всех
По предположению для всех  имеем
имеем  т. е.
т. е. 
Далее, так как ряд  сходится, а члены этого ряда неотрицательны, то для всех
сходится, а члены этого ряда неотрицательны, то для всех  имеем
имеем  , где а — сумма этого ряда. Но тогда для всех
, где а — сумма этого ряда. Но тогда для всех  имеем
имеем  а. Это значит, что частичные суммы
а. Это значит, что частичные суммы  ряда
ряда  ограничены сверху числом
ограничены сверху числом  а поскольку члены этого ряда неотрицательны, он по теореме 6.1. сходится.
а поскольку члены этого ряда неотрицательны, он по теореме 6.1. сходится.
Обозначим  через
через  Из неравенства
Из неравенства  вытекает, что
вытекает, что  (это вполне естественно — если для всех
(это вполне естественно — если для всех  имеем
имеем 
Следствие. Если члены рядов  неотрицательны и для всех
неотрицательны и для всех  выполняется неравенство
выполняется неравенство  то
то  расходимости ряда
расходимости ряда  вытекает, что и ряд
вытекает, что и ряд  расходится.
расходится.
В самом деле, если бы ряд  сходился, то по доказанной выше теореме сходился бы и ряд
сходился, то по доказанной выше теореме сходился бы и ряд  вопреки предположению.
вопреки предположению.
Пример 6.1. Выше (см. пример 1.5) было доказано, что ряд  - сходится. Но при любом
- сходится. Но при любом  имеет место неравенство
имеет место неравенство  Значит, ряд
Значит, ряд  тоже сходится.
тоже сходится.
Пример 6.2. Так как ряд  расходится, а при любом
расходится, а при любом  имеем —
имеем —  то ряд
то ряд  тоже расходится.
тоже расходится.
Замечание. Так как сходимость ряда равносильна сходимости любого его остатка, то члены рядов  можно сравнивать и лишь начиная с некоторого места (однако если
можно сравнивать и лишь начиная с некоторого места (однако если  лишь при
лишь при  то, вообще говоря, неравенство
то, вообще говоря, неравенство  может не иметь места).
может не иметь места).
Иногда удобнее применять другую теорему сравнения рядов с неотрицательными членами.
Теорема 6.3 (вторая теорема сравнения рядов с неотрицательными членами). Пусть все члены рядов 
неотрицательны и пусть существует предел  Тогда при
Тогда при  оба ряда либо одновременно сходятся, либо одновременно расходятся. Если же
оба ряда либо одновременно сходятся, либо одновременно расходятся. Если же  то из сходимости ряда
то из сходимости ряда  вытекает сходимость ряда
вытекает сходимость ряда  а из расходимости ряда
а из расходимости ряда  — расходимость ряда
— расходимость ряда 
Доказательство. Пусть  Выберем такую окрестность
Выберем такую окрестность  что
что  (рис. 1). Так как
(рис. 1). Так как  то, начиная с некоторого значения
то, начиная с некоторого значения  все — окажутся в этой окрестности, а тогда для всех
все — окажутся в этой окрестности, а тогда для всех  будут выполняться неравенства
будут выполняться неравенства  где
где  . Но тогда из сходимости ряда
. Но тогда из сходимости ряда  следует сходимость ряда а
следует сходимость ряда а  а тем самым и ряда
а тем самым и ряда  Из сходимости же ряда
Из сходимости же ряда  следует сходимость ряда
следует сходимость ряда  а тогда сходится и ряд
а тогда сходится и ряд  Значит, сходимость одного из рядов (А), (В) влечет за собой сходимость другого ряда.
Значит, сходимость одного из рядов (А), (В) влечет за собой сходимость другого ряда.

Рис. 1.
Если же  то аналогичные рассуждения показывают существование такого
то аналогичные рассуждения показывают существование такого  что при
что при  выполняется неравенство
выполняется неравенство  Но тогда сходимость ряда
Но тогда сходимость ряда  влечет за собой сходимость ряда
влечет за собой сходимость ряда  а из расходимости ряда
а из расходимости ряда  следует расходимость ряда
следует расходимость ряда  Теорема доказана.
Теорема доказана.
Пример 6.3. Мы знаем, что ряд V - сходится. Так как  то и ряд
то и ряд  сходится.
сходится.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
- § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
- 2. Сумма ряда. Сходящиеся и расходящиеся ряды.
- § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
- 1. Необходимый признак сходимости ряда. Остаток ряда.
- § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
- § 4. ФОРМУЛА ТЕЙЛОРА
- § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
- 1. Ряд Тейлора.
- 2. Разложение функции у = ln(1 + х).
- 3. Разложение функции у = arctg х.
- 4. Разложение в степенной ряд функции у = ех.
- 5. Разложение в степенной ряд функций y = sin x и y = cos x.
- 6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
- 7. Разложение других элементарных функций.
- ЗАКЛЮЧЕНИЕ
- ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
- § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сходимости Даламбера и Коши.
- 3. Интегральный признак сходимости Коши.
- 4. Примеры исследования рядов на сходимость.
- § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 1. Перестановка членов ряда с неотрицательными членами.
- 2. Группировка членов и умножение рядов с неотрицательными членами.
- § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- 2. Абсолютно сходящиеся ряды.
- 3. Свойства абсолютно сходящихся рядов.
- 4. Свойства условно сходящихся рядов.
- § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 2. Чебышевское расстояние между функциями.
- 3. Равномерно сходящиеся функциональные последовательности.
- 4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
- 5. Сохранение свойства непрерывности в случае равномерной сходимости.
- § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
- 1. Почленное интегрирование функциональных рядов.
- 2. Почленное дифференцирование функциональных рядов.
- § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Функции комплексного переменного.
- 2. Дифференцирование функций комплексного переменного.
- 3. Функциональные последовательности и ряды в комплексной области.
- ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
- § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
- 2. Область сходимости степенного ряда. Круг и радиус сходимости.
- 3. Равномерная сходимость и непрерывность суммы степенного ряда.
- § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
- 1. Интегрирование и дифференцирование степенных рядов в действительной области.
- 2. Почленное дифференцирование рядов в комплексной области.
- 3. Единственность разложения функции в степенной ряд.
- § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 1. Показательная функция в комплексной области.
- 2. Тригонометрические функции в комплексной области. Формулы Эйлера.
- § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
- 1. Вычисление значений функций и интегралов.
- 2. Вычисление пределов.
- 3. Метод последовательных приближений.
- ГЛАВА V. РЯДЫ ФУРЬЕ
- § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
- 2. Скалярное произведение функций.
- 3. Ортонормированные системы функций.
- § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
- 2. Коэффициенты Фурье для тригонометрических систем функций.
- § 20. ЛЕММА РИМАНА
- 1. Кусочно гладкие функции.
- 2. Лемма Римана.
- § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
- 1. Формула для частичных сумм ряда Фурье.
- 2. Сходимость разложения кусочно гладких функций в ряды Фурье.
- 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
- 4. Разложение четных и нечетных функций в ряды Фурье.
- 5. Примеры разложения функций в ряды Фурье.
- Ответы к упражнениям