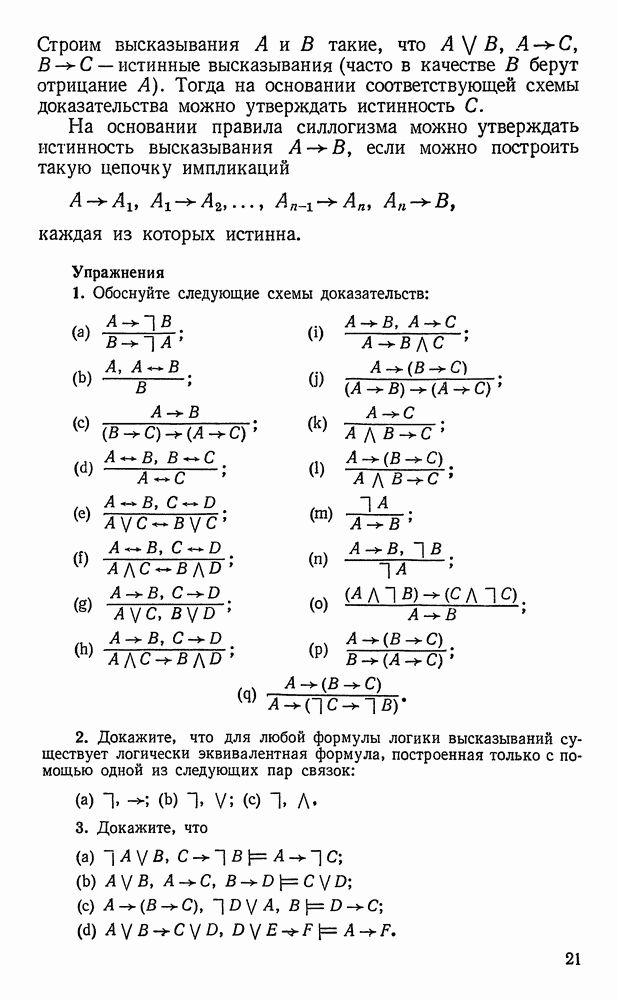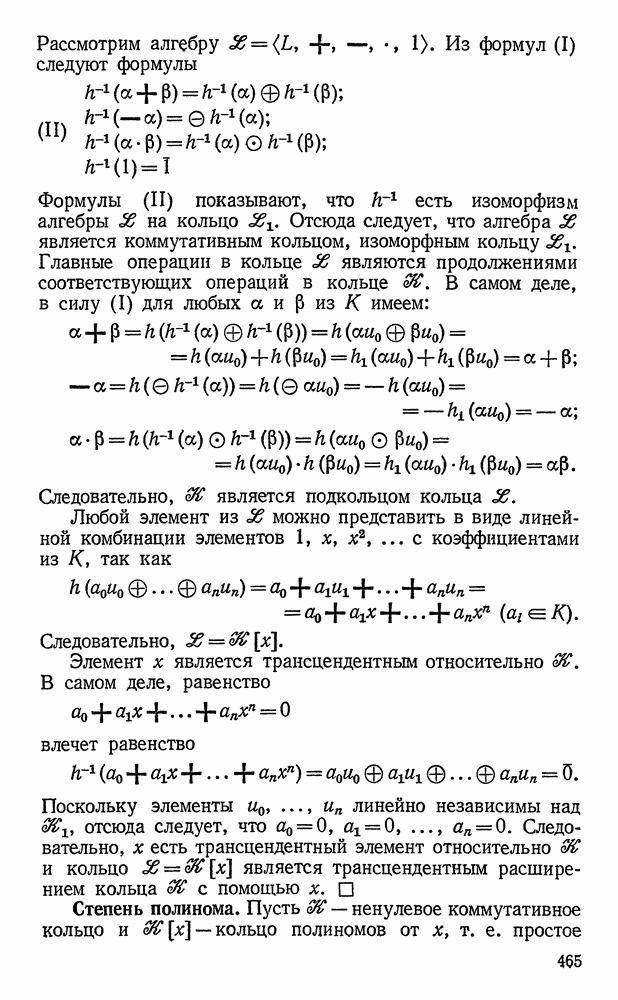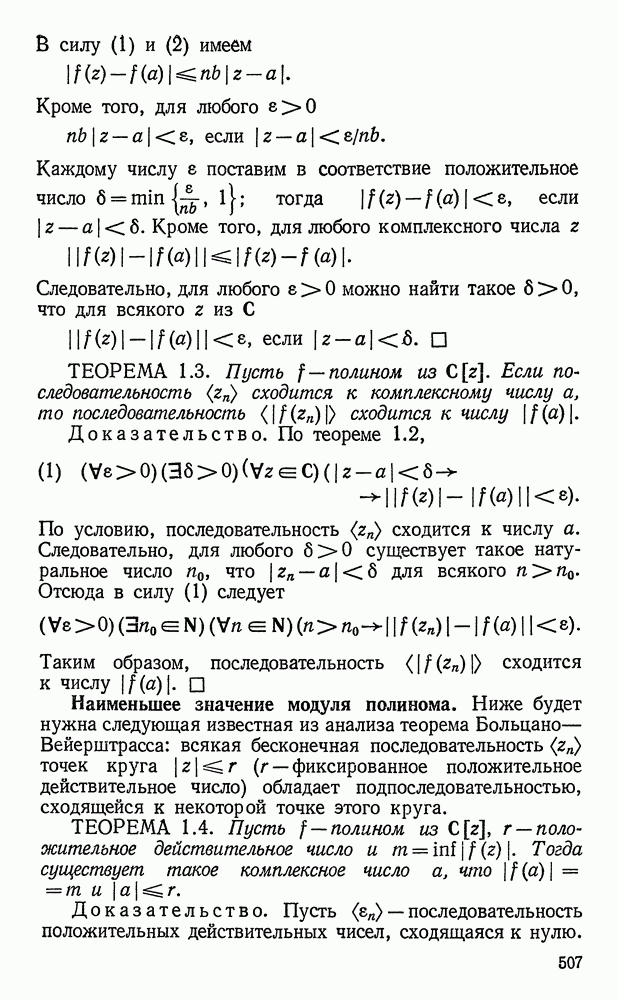| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Следствия однородной системы линейных неравенств.
Для доказательства теоремы Минковского необходимы следующие две леммы.
ЛЕММА 1.4. Если

то неравенство

не является следствием системы

Доказательство. Ранг системы векторов  обозначим через
обозначим через  . Предположим, что выполняется условие (3), тогда
. Предположим, что выполняется условие (3), тогда

Пусть

Рассмотрим систему линейных уравнений 

На основании (4) заключаем, что ранги основной и расширенной матриц системы (5) равны  . Следовательно, система (5) совместна. Поэтому существует вектор
. Следовательно, система (5) совместна. Поэтому существует вектор  такой, что
такой, что

Вектор  является решением системы (1), не удовлетворяющим (2). Таким образом, неравенство (2) не является следствием системы (1).
является решением системы (1), не удовлетворяющим (2). Таким образом, неравенство (2) не является следствием системы (1).
СЛЕДСТВИЕ 1.5. Если неравенство (2) есть следствие системы (1), то

По закону контрапозиции, это утверждение равносильно лемме 1.4.
ЛЕММА 1.6. Пусть неравенство

есть следствие системы

и

Тогда неравенство (2) является следствием системы

Доказательство. Рассмотрим систему

Вектор с в силу (3) есть неотрицательная линейная комбинация векторов 

В силу предложения 1.1 отсюда следует, что (2) является следствием системы (II):

Надо доказать, что любое решение  системы (4) является решением неравенства (2). Возможны два случая:
системы (4) является решением неравенства (2). Возможны два случая:  или
или  . Если 0, то
. Если 0, то  есть решение системы (1) и, следовательно, по условию,
есть решение системы (1) и, следовательно, по условию,  является решением неравенства (2). Если же
является решением неравенства (2). Если же  , то
, то  есть решение системы (1'); следовательно, ввиду (4) является решением и неравенства (2). Итак, любое решение системы (4) является решением неравенства (2).
есть решение системы (1'); следовательно, ввиду (4) является решением и неравенства (2). Итак, любое решение системы (4) является решением неравенства (2).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава первая. ЭЛЕМЕНТЫ ЛОГИКИ
- § 1. ЛОГИКА ВЫСКАЗЫВАНИЙ
- Формулы логики высказываний.
- Законы логики.
- Упражнения
- § 2. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ
- Схемы доказательств.
- § 3. ПРЕДИКАТЫ
- Предикаты.
- Операции над предикатами.
- Упражнения
- § 4. КВАНТОРЫ
- Запись высказываний на языке логики предикатов.
- Упражнения
- § 5. ПРЕДИКАТНЫЕ ФОРМУЛЫ. ЗАКОНЫ ЛОГИКИ
- Предикатные формулы.
- Законы логики предикатов.
- Упражнения
- Глава вторая. МНОЖЕСТВА И ОТНОШЕНИЯ
- § 1. МНОЖЕСТВА
- Подмножества.
- Пустое множество.
- Операции над множествами.
- Основные свойства операций над множествами.
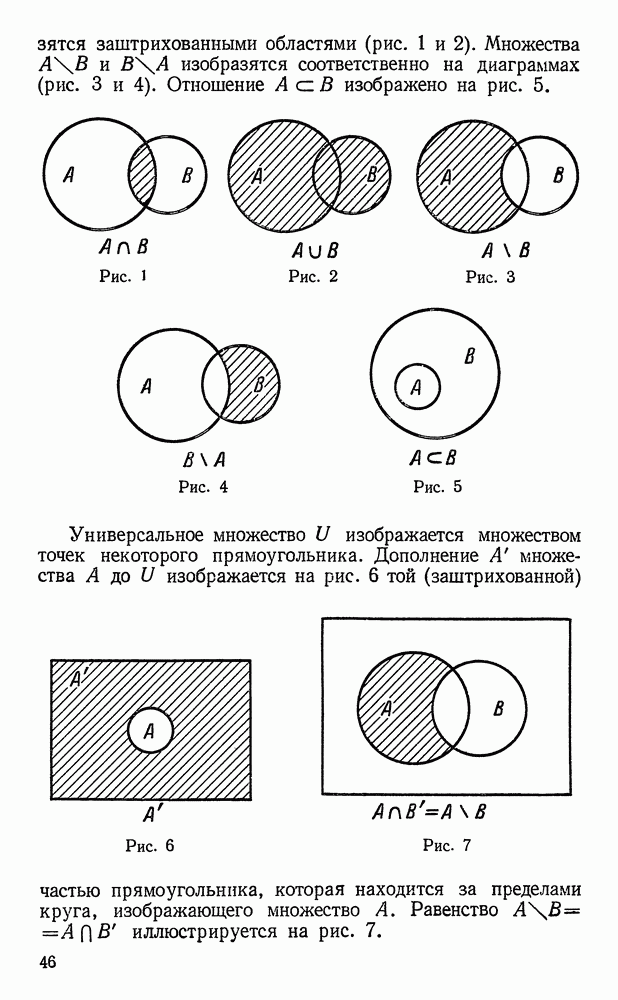
- Универсальное множество. Дополнение множества.
- Диаграммы Эйлера — Венна.
- Упражнения
- § 2. БИНАРНЫЕ ОТНОШЕНИЯ
- Упражнения
- § 3. ФУНКЦИИ
- Композиция функций.
- Инъективные функции.
- Обратимые функции.
- Ограничение функции.
- Упражнения
- § 4. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
- Отношение эквивалентности.
- Фактор-множество.
- Отношение равнообразности отображения.
- Упражнения
- § 5. ОТНОШЕНИЯ ПОРЯДКА
- Упорядоченное множество.
- Упражнения
- Глава третья. АЛГЕБРЫ И АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
- § 1. БИНАРНЫЕ ОПЕРАЦИИ
- Виды бинарных операций.
- Нейтральные элементы.
- Симметричные элементы.
- Подмножества, замкнутые относительно операций.
- Аддитивная и мультипликативная формы записи.
- Конгруэнция.
- Упражнения.
- § 2. АЛГЕБРЫ
- Гомоморфизмы алгебр.
- Подалгебры.
- Фактор-алгебра.
- Упражнения
- § 3. ГРУППЫ
- Примеры групп.
- Простейшие свойства группы.
- Гомоморфизмы групп.
- Подгруппы.
- Упражнения
- § 4. КОЛЬЦА
- Простейшие свойства кольца.
- Гомоморфизмы колец.
- Подкольца.
- Упражнения
- § 5. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
- Изоморфизмы алгебраических систем.
- Подсистемы.
- Упражнения
- Глава четвертая. ОСНОВНЫЕ ЧИСЛОВЫЕ СИСТЕМЫ
- § 1. СИСТЕМА НАТУРАЛЬНЫХ ЧИСЕЛ
- Слова в однобуквенном алфавите.
- Система натуральных чисел.
- Принцип математической индукции.
- Упражнения
- § 2. СВОЙСТВА СЛОЖЕНИЯ И УМНОЖЕНИЯ НАТУРАЛЬНЫХ ЧИСЕЛ
- Свойства умножения.
- § 3. ОТНОШЕНИЕ ПОРЯДКА НА МНОЖЕСТВЕ НАТУРАЛЬНЫХ ЧИСЕЛ
- Полная упорядоченность множества натуральных чисел.
- Упражнения
- § 4. КОЛЬЦО ЦЕЛЫХ ЧИСЕЛ
- Естественное умножение в аддитивной группе целых чисел.
- Кольцо целых чисел.
- Отношение делимости в кольце целых чисел.
- Упражнения
- § 5. ПОЛЯ. ПОЛЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- Поле рациональных чисел.
- Упражнения
- § 6. СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- Система действительных чисел.
- Упражнения
- § 7. ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ
- Поле комплексных чисел.
- Модуль комплексного числа.
- Геометрическое представление комплексных чисел.
- Упражнения
- § 8. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА. ИЗВЛЕЧЕНИЕ КОРНЕЙ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ
- Корни n-й степени из единицы.
- Корни n-й степени из произвольного комплексного числа.
- Упражнения
- Глава пятая. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Линейная зависимость и независимость системы векторов.
- Эквивалентные системы векторов.
- Базис конечной системы векторов.
- Ранг конечной системы векторов.
- Упражнения
- § 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Равносильные системы линейных уравнений и элементарные преобразования системы.
- Равенство строчечного и столбцового рангов матрицы.
- Связь между решениями неоднородной линейной системы и решениями ассоциированной с ней однородной системы.
- Теоремы о следствиях системы линейных уравнений.
- Упражнения.
- § 3. СТУПЕНЧАТЫЕ МАТРИЦЫ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Приведенные ступенчатые матрицы.
- Однородные системы линейных уравнений.
- Фундаментальная система решений.
- Решение системы линейных уравнений методом последовательного исключения переменных.
- Упражнения
- Глава шестая. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- § 1. ОПЕРАЦИИ НАД МАТРИЦАМИ И ИХ СВОЙСТВА
- Транспонирование произведения матриц.
- Упражнения
- § 2. ОБРАТИМЫЕ МАТРИЦЫ
- Элементарные матрицы.
- Вычисление обратной матрицы.
- Запись и решение системы n линейных уравнений с n переменными в матричной форме.
- Упражнения
- § 3. ПОДСТАНОВКИ
- Четные и нечетные подстановки.
- Знак подстановки.
- Упражнения
- § 4. ОПРЕДЕЛИТЕЛИ
- Основные свойства определителей.
- Упражнения
- § 5. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ. ТЕОРЕМЫ ОБ ОПРЕДЕЛИТЕЛЯХ
- Разложение определителя по строке или столбцу.
- Определитель произведения матриц.
- Необходимые и достаточные условия равенства нулю определителя.
- § 6. ТЕОРЕМЫ О МАТРИЦАХ. ПРАВИЛО КРАМЕРА
- Правило Крамера.
- Условия, при которых система n линейных однородных уравнений с n переменными имеет ненулевые решения.
- Упражнения
- Глава седьмая. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- § 1. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Простейшие свойства векторных пространств.
- Линейная зависимость и независимость системы векторов.
- Упражнения
- § 2. ПОДПРОСТРАНСТВА ВЕКТОРНОГО ПРОСТРАНСТВА
- Линейная оболочка множества векторов.
- Сумма подпространств.
- Линейные многообразия.
- Упражнения
- § 3. БАЗИС И РАЗМЕРНОСТЬ ВЕКТОРНОГО ПРОСТРАНСТВА
- Дополнение независимой системы векторов до базиса.
- Размерность векторного пространства.
- Упражнения.
- § 4. ИЗОМОРФИЗМЫ ВЕКТОРНЫХ ПРОСТРАНСТВ
- Изоморфизм векторных пространств.
- Упражнения
- § 5. ВЕКТОРНЫЕ ПРОСТРАНСТВА СО СКАЛЯРНЫМ УМНОЖЕНИЕМ
- Ортогональная система векторов.
- Процесс ортогонализации.
- Упражнения.
- § 6. ЕВКЛИДОВЫ ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Норма вектора.
- Ортонормированный базис евклидова пространства.
- Изоморфизмы евклидовых пространств.
- Упражнения.
- Глава восьмая. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- Ядро и образ линейного оператора.
- Операции над линейными отображениями.
- Упражнения
- § 2. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ МАТРИЦАМИ
- Связь между координатными столбцами векторов х и ф(x).
- Ранг линейного оператора.
- Связь между координатными столбцами вектора относительно различных базисов.
- Связь между матрицами линейного оператора относительно различных базисов.
- Упражнения
- § 3. ЛИНЕЙНЫЕ АЛГЕБРЫ
- Алгебра линейных операторов векторного пространства
- Изоморфизм алгебры линейных операторов и полной матричной алгебры.
- Упражнения
- § 4. ОБРАТИМЫЕ ОПЕРАТОРЫ
- Полная линейная группа.
- Упражнения
- § 5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ. ХАРАКТЕРИСТИЧЕСКИЕ УРАВНЕНИЯ
- Нахождение собственных векторов линейного оператора.
- Характеристическое уравнение.
- Линейные операторы с простым спектром.
- Условия, при которых матрица подобна диагональной матрице.
- Упражнения
- Глава девятая. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- § 1. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- Однородные системы линейных неравенств и выпуклые конусы.
- Следствия однородной системы линейных неравенств.
- Теорема Минковского.
- Критерий несовместности системы линейных неравенств.
- Неотрицательные решения системы линейных уравнений и системы линейных неравенств.
- Упражнения
- § 2. СТАНДАРТНЫЕ И КАНОНИЧЕСКИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ТЕОРЕМЫ ДВОЙСТВЕННОСТИ
- Допустимые и оптимальные векторы.
- Теорема двойственности для стандартных задач.
- Теорема двойственности для канонических задач.
- Теорема равновесия.
- Упражнения
- § 3. СИМПЛЕКС-МЕТОД
- Упражнения
- Глава десятая. ГРУППЫ
- § 1. ПОЛУГРУППЫ И МОНОИДЫ
- Моноиды.
- Обобщенный закон ассоциативности.
- Упражнения
- § 2. ПОДГРУППЫ И СМЕЖНЫЕ КЛАССЫ
- Смежные классы.
- Теорема Лагранжа.
- Упражнения
- § 3. ЦИКЛИЧЕСКИЕ ГРУППЫ
- Циклические группы.
- Подгруппы циклической группы.
- Упражнения
- § 4. НОРМАЛЬНЫЕ ДЕЛИТЕЛИ И ФАКТОР-ГРУППЫ
- Фактор-группа.
- Ядро гомоморфизма.
- Упражнения
- Глава одиннадцатая. ТЕОРИЯ ДЕЛИМОСТИ В КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- § 1. РАЗЛОЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ
- Простые числа.
- Разложение целых чисел на простые множители.
- Делители целого числа.
- Число и сумма натуральных делителей числа.
- Бесконечность множества простых чисел.
- Решето Эратосфена.
- Упражнения
- § 2. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Взаимно простые числа.
- Наименьшее общее кратное.
- Упражнения
- § 3. АЛГОРИТМ ЕВКЛИДА И КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
- Конечные цепные дроби.
- Подходящие дроби.
- Упражнения.
- § 4. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА
- Арифметические операции над целыми систематическими числами
- Перевод чисел из одной системы счисления в другую.
- Упражнения
- § 5. РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ
- Функции T(х) и Л(х).
- Неравенства для функции Т(х).
- Неравенства Чебышева.
- Простые числа в арифметических прогрессиях.
- Упражнения
- Глава двенадцатая. ТЕОРИЯ СРАВНЕНИЙ С АРИФМЕТИЧЕСКИМИ ПРИЛОЖЕНИЯМИ
- § 1. СРАВНЕНИЯ И ИХ СВОЙСТВА
- Упражнения
- § 2. ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ
- Упражнения
- § 3. ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ
- Мультипликативная группа классов вычетов, взаимно простых с модулем.
- Функция Эйлера.
- Теоремы Эйлера и Ферма.
- Упражнения
- § 4. СРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ. СРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ ПО ПРОСТОМУ МОДУЛЮ
- Сравнения первой степени.
- Сравнения высших степеней по простому модулю.
- Упражнения
- § 5. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- Первообразные корни по простому модулю.
- Индексы по простому модулю.
- Двучленные сравнения.
- Упражнения
- § 6. ОБРАЩЕНИЕ ОБЫКНОВЕННОЙ ДРОБИ В СИСТЕМАТИЧЕСКУЮ И ОПРЕДЕЛЕНИЕ ДЛИНЫ ПЕРИОДА СИСТЕМАТИЧЕСКОЙ ДРОБИ
- Упражнения
- Глава тринадцатая. КОЛЬЦА
- § 1. ИДЕАЛЫ КОЛЬЦА. ФАКТОР-КОЛЬЦО
- Сравнения и классы вычетов по идеалу.
- Фактор-кольцо.
- Теорема об эпиморфизмах колец.
- Характеристика кольца.
- Наименьшее подкольцо кольца.
- Упражнения
- § 2. ПОЛЕ ЧАСТНЫХ ОБЛАСТИ ЦЕЛОСТНОСТИ
- Изоморфизм полей частных.
- Упражнения
- § 3. КОЛЬЦА ГЛАВНЫХ ИДЕАЛОВ
- Простые и составные элементы области целостности.
- Кольца главных идеалов.
- Факториальность кольца главных идеалов.
- Евклидовы кольца.
- Упражнения
- § 4. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Наименьшее общее кратное.
- Упражнения
- Глава четырнадцатая. ПОЛИНОМЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. КОЛЬЦО ПОЛИНОМОВ
- Теорема о существовании простого трансцендентного расширения коммутативного кольца.
- Степень полинома.
- Деление полинома на двучлен и корни полинома.
- Теорема о наибольшем возможном числе корней полинома в области целостности.
- Алгебраическое и функциональное равенства полиномов.
- Упражнения
- § 2. ПОЛИНОМЫ НАД ПОЛЕМ
- Алгоритм Евклида.
- Неприводимые над данным полем полиномы.
- Разложение полинома в произведение нормированных неприводимых множителей.
- Упражнения
- § 3. ФАКТОРИАЛЬНОСТЬ КОЛЬЦА ПОЛИНОМОВ НАД ФАКТОРИАЛЬНЫМ КОЛЬЦОМ
- Факториальность кольца полиномов.
- § 4. ФОРМАЛЬНАЯ ПРОИЗВОДНАЯ ПОЛИНОМА. НЕПРИВОДИМЫЕ КРАТНЫЕ МНОЖИТЕЛИ
- Разложение полинома по степеням разности х — с.
- Неприводимые кратные множители полинома.
- Кратные корни полинома.
- Упражнения
- Глава пятнадцатая. ПОЛИНОМЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. КОЛЬЦО ПОЛИНОМОВ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- Кольцо полиномов от нескольких переменных.
- Изоморфизм колец полиномов.
- Нормальное представление полинома и степень полинома.
- Факториалыюсть кольца полиномов.
- § 2. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ
- Лемма о высшем члене произведения двух полиномов.
- Симметрические полиномы.
- Леммы о симметрических полиномах.
- Основная теорема о симметрических полиномах.
- Упражнения
- 3. РЕЗУЛЬТАНТ ПОЛИНОМОВ И ИСКЛЮЧЕНИЕ ПЕРЕМЕННЫХ
- Исключение переменных.
- Глава шестнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ КОМПЛЕКСНЫХ ЧИСЕЛ И НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 1. АЛГЕБРАИЧЕСКАЯ ЗАМКНУТОСТЬ ПОЛЯ КОМПЛЕКСНЫХ ЧИСЕЛ
- Непрерывность модуля полинома.
- Наименьшее значение модуля полинома.
- Лемма Даламбера.
- Алгебраическая замкнутость поля комплексных чисел.
- Формулы Виета.
- Упражнения
- § 2. ПОЛИНОМЫ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. УРАВНЕНИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ СТЕПЕНИ
- Исследование корней уравнения третьей степени с действительными коэффициентами.
- Уравнения четвертой степени.
- § 4. ОТДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ ПОЛИНОМА
- Теорема Штурма.
- Глава семнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ЧИСЕЛ И АЛГЕБРАИЧЕСКИЕ ЧИСЛА
- § 1. ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ КОРНИ ПОЛИНОМА. КРИТЕРИЙ НЕПРИВОДИМОСТИ
- § 2. ПРОСТОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
- § 3. СОСТАВНОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
- § 4. УСЛОВИЯ РАЗРЕШИМОСТИ УРАВНЕНИЯ ТРЕТЬЕЙ СТЕПЕНИ В КВАДРАТНЫХ РАДИКАЛАХ
- ЛИТЕРАТУРА