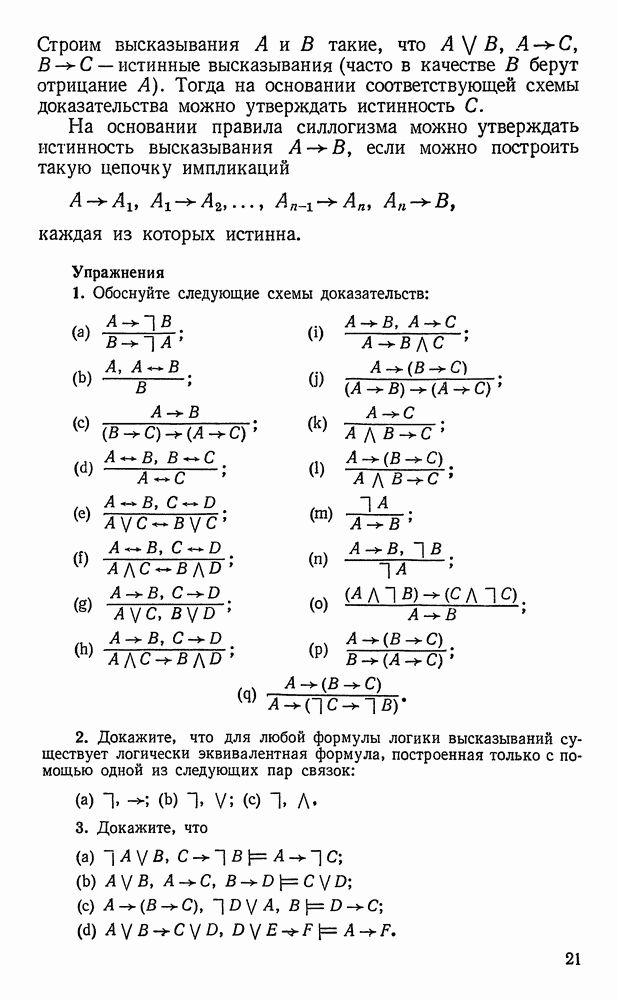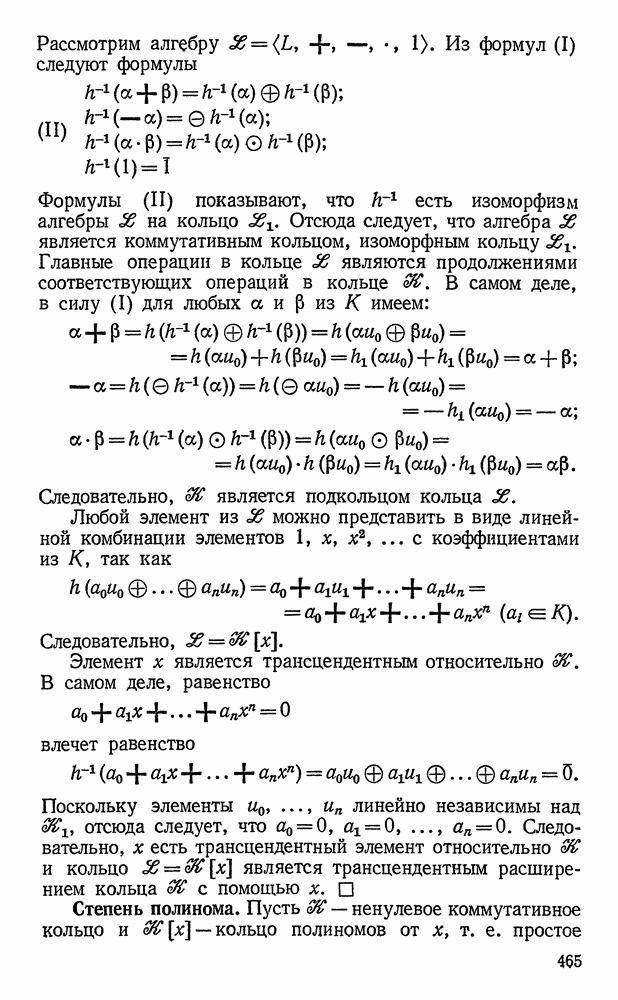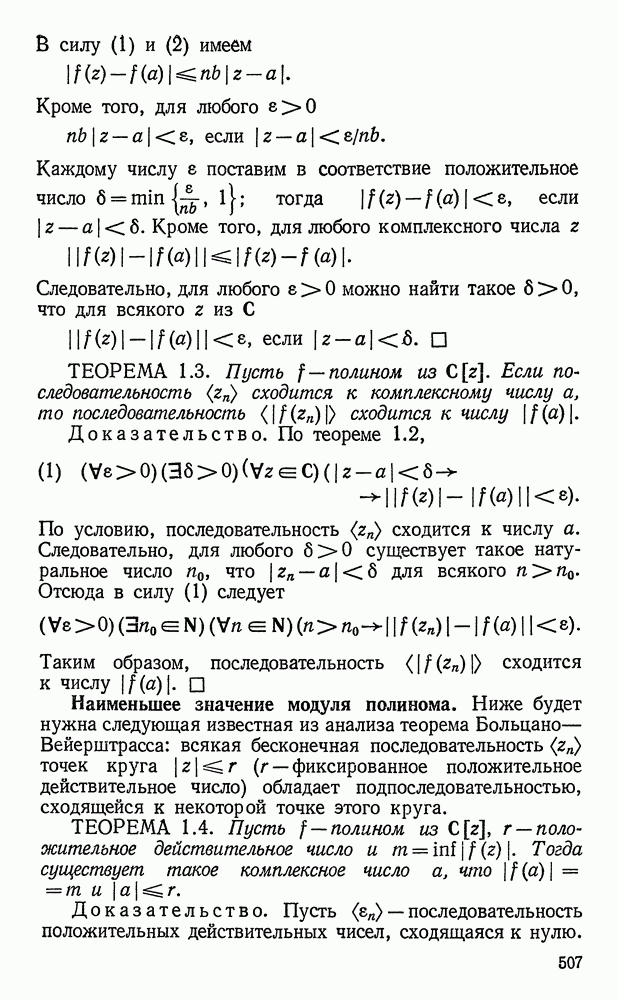| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. ЕВКЛИДОВЫ ВЕКТОРНЫЕ ПРОСТРАНСТВА
Евклидово векторное пространство.
Пусть — векторное пространство со скалярным умножением над полем <М действительных чисел. Такое пространство называют также действительным векторным пространством.
ОПРЕДЕЛЕНИЕ. Векторное пространство над полем <М с положительно определенным скалярным умножением (т. е. а  для любого
для любого  ) называется евклидовым векторным пространством.
) называется евклидовым векторным пространством.
ТЕОРЕМА 6.1. Арифметическое векторное пространство над полем  со стандартным скалярным умножением является евклидовым.
со стандартным скалярным умножением является евклидовым.
Доказательство.  -арифметическое векторное пространство со стандартным скалярным умножением и
-арифметическое векторное пространство со стандартным скалярным умножением и  — векторы этого пространства. По определению стандартного скалярного умножения,
— векторы этого пространства. По определению стандартного скалярного умножения,  Следовательно,
Следовательно,  . А так как
. А так как  -действительные числа, то
-действительные числа, то  для любого ненулевого вектора а пространства
для любого ненулевого вектора а пространства  .
.
ОПРЕДЕЛЕНИЕ. Арифметическое векторное пространство  со стандартным скалярным умножением называется
со стандартным скалярным умножением называется  -мерным стандартным евклидовым пространством и обозначается через
-мерным стандартным евклидовым пространством и обозначается через 
Пример. Рассмотрим множество V всех действительных функций одной действительной переменной  непрерывных на отрезке [0, 1]. Множество V относительно сложения и умножений на действительные числа является (бесконечномерным) векторным пространством над
непрерывных на отрезке [0, 1]. Множество V относительно сложения и умножений на действительные числа является (бесконечномерным) векторным пространством над  Формула
Формула  определяет в V скалярное умножение. Таким образом, получаем евклидово векторное пространство со скалярным умножением.
определяет в V скалярное умножение. Таким образом, получаем евклидово векторное пространство со скалярным умножением.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава первая. ЭЛЕМЕНТЫ ЛОГИКИ
- § 1. ЛОГИКА ВЫСКАЗЫВАНИЙ
- Формулы логики высказываний.
- Законы логики.
- Упражнения
- § 2. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ
- Схемы доказательств.
- § 3. ПРЕДИКАТЫ
- Предикаты.
- Операции над предикатами.
- Упражнения
- § 4. КВАНТОРЫ
- Запись высказываний на языке логики предикатов.
- Упражнения
- § 5. ПРЕДИКАТНЫЕ ФОРМУЛЫ. ЗАКОНЫ ЛОГИКИ
- Предикатные формулы.
- Законы логики предикатов.
- Упражнения
- Глава вторая. МНОЖЕСТВА И ОТНОШЕНИЯ
- § 1. МНОЖЕСТВА
- Подмножества.
- Пустое множество.
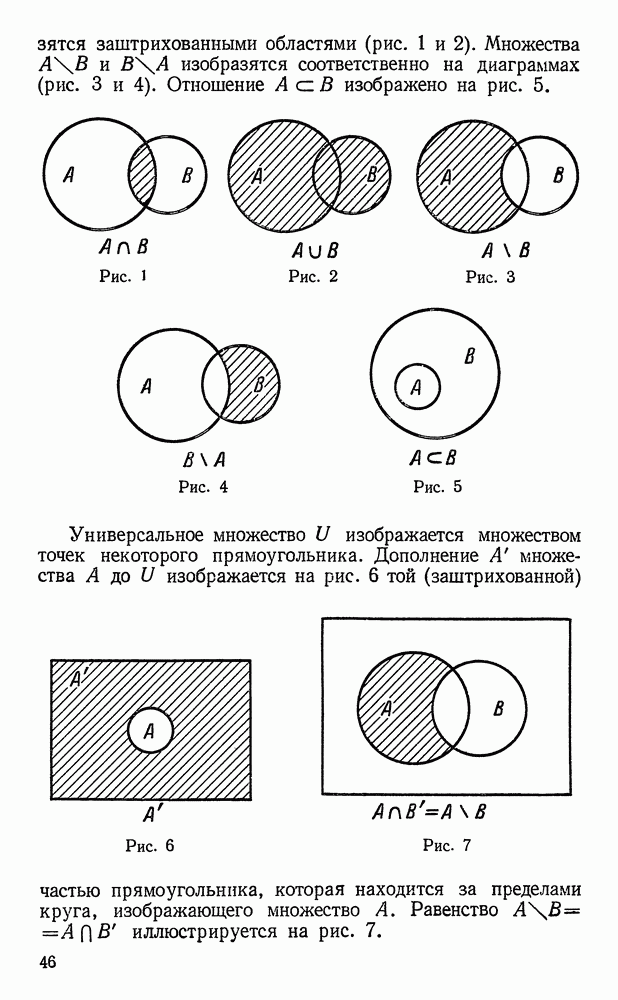
- Операции над множествами.
- Основные свойства операций над множествами.
- Универсальное множество. Дополнение множества.
- Диаграммы Эйлера — Венна.
- Упражнения
- § 2. БИНАРНЫЕ ОТНОШЕНИЯ
- Упражнения
- § 3. ФУНКЦИИ
- Композиция функций.
- Инъективные функции.
- Обратимые функции.
- Ограничение функции.
- Упражнения
- § 4. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
- Отношение эквивалентности.
- Фактор-множество.
- Отношение равнообразности отображения.
- Упражнения
- § 5. ОТНОШЕНИЯ ПОРЯДКА
- Упорядоченное множество.
- Упражнения
- Глава третья. АЛГЕБРЫ И АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
- § 1. БИНАРНЫЕ ОПЕРАЦИИ
- Виды бинарных операций.
- Нейтральные элементы.
- Симметричные элементы.
- Подмножества, замкнутые относительно операций.
- Аддитивная и мультипликативная формы записи.
- Конгруэнция.
- Упражнения.
- § 2. АЛГЕБРЫ
- Гомоморфизмы алгебр.
- Подалгебры.
- Фактор-алгебра.
- Упражнения
- § 3. ГРУППЫ
- Примеры групп.
- Простейшие свойства группы.
- Гомоморфизмы групп.
- Подгруппы.
- Упражнения
- § 4. КОЛЬЦА
- Простейшие свойства кольца.
- Гомоморфизмы колец.
- Подкольца.
- Упражнения
- § 5. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
- Изоморфизмы алгебраических систем.
- Подсистемы.
- Упражнения
- Глава четвертая. ОСНОВНЫЕ ЧИСЛОВЫЕ СИСТЕМЫ
- § 1. СИСТЕМА НАТУРАЛЬНЫХ ЧИСЕЛ
- Слова в однобуквенном алфавите.
- Система натуральных чисел.
- Принцип математической индукции.
- Упражнения
- § 2. СВОЙСТВА СЛОЖЕНИЯ И УМНОЖЕНИЯ НАТУРАЛЬНЫХ ЧИСЕЛ
- Свойства умножения.
- § 3. ОТНОШЕНИЕ ПОРЯДКА НА МНОЖЕСТВЕ НАТУРАЛЬНЫХ ЧИСЕЛ
- Полная упорядоченность множества натуральных чисел.
- Упражнения
- § 4. КОЛЬЦО ЦЕЛЫХ ЧИСЕЛ
- Естественное умножение в аддитивной группе целых чисел.
- Кольцо целых чисел.
- Отношение делимости в кольце целых чисел.
- Упражнения
- § 5. ПОЛЯ. ПОЛЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
- Поле рациональных чисел.
- Упражнения
- § 6. СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- Система действительных чисел.
- Упражнения
- § 7. ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ
- Поле комплексных чисел.
- Модуль комплексного числа.
- Геометрическое представление комплексных чисел.
- Упражнения
- § 8. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА. ИЗВЛЕЧЕНИЕ КОРНЕЙ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ
- Корни n-й степени из единицы.
- Корни n-й степени из произвольного комплексного числа.
- Упражнения
- Глава пятая. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Линейная зависимость и независимость системы векторов.
- Эквивалентные системы векторов.
- Базис конечной системы векторов.
- Ранг конечной системы векторов.
- Упражнения
- § 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Равносильные системы линейных уравнений и элементарные преобразования системы.
- Равенство строчечного и столбцового рангов матрицы.
- Связь между решениями неоднородной линейной системы и решениями ассоциированной с ней однородной системы.
- Теоремы о следствиях системы линейных уравнений.
- Упражнения.
- § 3. СТУПЕНЧАТЫЕ МАТРИЦЫ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Приведенные ступенчатые матрицы.
- Однородные системы линейных уравнений.
- Фундаментальная система решений.
- Решение системы линейных уравнений методом последовательного исключения переменных.
- Упражнения
- Глава шестая. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- § 1. ОПЕРАЦИИ НАД МАТРИЦАМИ И ИХ СВОЙСТВА
- Транспонирование произведения матриц.
- Упражнения
- § 2. ОБРАТИМЫЕ МАТРИЦЫ
- Элементарные матрицы.
- Вычисление обратной матрицы.
- Запись и решение системы n линейных уравнений с n переменными в матричной форме.
- Упражнения
- § 3. ПОДСТАНОВКИ
- Четные и нечетные подстановки.
- Знак подстановки.
- Упражнения
- § 4. ОПРЕДЕЛИТЕЛИ
- Основные свойства определителей.
- Упражнения
- § 5. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ. ТЕОРЕМЫ ОБ ОПРЕДЕЛИТЕЛЯХ
- Разложение определителя по строке или столбцу.
- Определитель произведения матриц.
- Необходимые и достаточные условия равенства нулю определителя.
- § 6. ТЕОРЕМЫ О МАТРИЦАХ. ПРАВИЛО КРАМЕРА
- Правило Крамера.
- Условия, при которых система n линейных однородных уравнений с n переменными имеет ненулевые решения.
- Упражнения
- Глава седьмая. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- § 1. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Простейшие свойства векторных пространств.
- Линейная зависимость и независимость системы векторов.
- Упражнения
- § 2. ПОДПРОСТРАНСТВА ВЕКТОРНОГО ПРОСТРАНСТВА
- Линейная оболочка множества векторов.
- Сумма подпространств.
- Линейные многообразия.
- Упражнения
- § 3. БАЗИС И РАЗМЕРНОСТЬ ВЕКТОРНОГО ПРОСТРАНСТВА
- Дополнение независимой системы векторов до базиса.
- Размерность векторного пространства.
- Упражнения.
- § 4. ИЗОМОРФИЗМЫ ВЕКТОРНЫХ ПРОСТРАНСТВ
- Изоморфизм векторных пространств.
- Упражнения
- § 5. ВЕКТОРНЫЕ ПРОСТРАНСТВА СО СКАЛЯРНЫМ УМНОЖЕНИЕМ
- Ортогональная система векторов.
- Процесс ортогонализации.
- Упражнения.
- § 6. ЕВКЛИДОВЫ ВЕКТОРНЫЕ ПРОСТРАНСТВА
- Норма вектора.
- Ортонормированный базис евклидова пространства.
- Изоморфизмы евклидовых пространств.
- Упражнения.
- Глава восьмая. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- Ядро и образ линейного оператора.
- Операции над линейными отображениями.
- Упражнения
- § 2. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ МАТРИЦАМИ
- Связь между координатными столбцами векторов х и ф(x).
- Ранг линейного оператора.
- Связь между координатными столбцами вектора относительно различных базисов.
- Связь между матрицами линейного оператора относительно различных базисов.
- Упражнения
- § 3. ЛИНЕЙНЫЕ АЛГЕБРЫ
- Алгебра линейных операторов векторного пространства
- Изоморфизм алгебры линейных операторов и полной матричной алгебры.
- Упражнения
- § 4. ОБРАТИМЫЕ ОПЕРАТОРЫ
- Полная линейная группа.
- Упражнения
- § 5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ. ХАРАКТЕРИСТИЧЕСКИЕ УРАВНЕНИЯ
- Нахождение собственных векторов линейного оператора.
- Характеристическое уравнение.
- Линейные операторы с простым спектром.
- Условия, при которых матрица подобна диагональной матрице.
- Упражнения
- Глава девятая. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- § 1. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- Однородные системы линейных неравенств и выпуклые конусы.
- Следствия однородной системы линейных неравенств.
- Теорема Минковского.
- Критерий несовместности системы линейных неравенств.
- Неотрицательные решения системы линейных уравнений и системы линейных неравенств.
- Упражнения
- § 2. СТАНДАРТНЫЕ И КАНОНИЧЕСКИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ТЕОРЕМЫ ДВОЙСТВЕННОСТИ
- Допустимые и оптимальные векторы.
- Теорема двойственности для стандартных задач.
- Теорема двойственности для канонических задач.
- Теорема равновесия.
- Упражнения
- § 3. СИМПЛЕКС-МЕТОД
- Упражнения
- Глава десятая. ГРУППЫ
- § 1. ПОЛУГРУППЫ И МОНОИДЫ
- Моноиды.
- Обобщенный закон ассоциативности.
- Упражнения
- § 2. ПОДГРУППЫ И СМЕЖНЫЕ КЛАССЫ
- Смежные классы.
- Теорема Лагранжа.
- Упражнения
- § 3. ЦИКЛИЧЕСКИЕ ГРУППЫ
- Циклические группы.
- Подгруппы циклической группы.
- Упражнения
- § 4. НОРМАЛЬНЫЕ ДЕЛИТЕЛИ И ФАКТОР-ГРУППЫ
- Фактор-группа.
- Ядро гомоморфизма.
- Упражнения
- Глава одиннадцатая. ТЕОРИЯ ДЕЛИМОСТИ В КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- § 1. РАЗЛОЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ
- Простые числа.
- Разложение целых чисел на простые множители.
- Делители целого числа.
- Число и сумма натуральных делителей числа.
- Бесконечность множества простых чисел.
- Решето Эратосфена.
- Упражнения
- § 2. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Взаимно простые числа.
- Наименьшее общее кратное.
- Упражнения
- § 3. АЛГОРИТМ ЕВКЛИДА И КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
- Конечные цепные дроби.
- Подходящие дроби.
- Упражнения.
- § 4. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА
- Арифметические операции над целыми систематическими числами
- Перевод чисел из одной системы счисления в другую.
- Упражнения
- § 5. РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ
- Функции T(х) и Л(х).
- Неравенства для функции Т(х).
- Неравенства Чебышева.
- Простые числа в арифметических прогрессиях.
- Упражнения
- Глава двенадцатая. ТЕОРИЯ СРАВНЕНИЙ С АРИФМЕТИЧЕСКИМИ ПРИЛОЖЕНИЯМИ
- § 1. СРАВНЕНИЯ И ИХ СВОЙСТВА
- Упражнения
- § 2. ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ
- Упражнения
- § 3. ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ
- Мультипликативная группа классов вычетов, взаимно простых с модулем.
- Функция Эйлера.
- Теоремы Эйлера и Ферма.
- Упражнения
- § 4. СРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ. СРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ ПО ПРОСТОМУ МОДУЛЮ
- Сравнения первой степени.
- Сравнения высших степеней по простому модулю.
- Упражнения
- § 5. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- Первообразные корни по простому модулю.
- Индексы по простому модулю.
- Двучленные сравнения.
- Упражнения
- § 6. ОБРАЩЕНИЕ ОБЫКНОВЕННОЙ ДРОБИ В СИСТЕМАТИЧЕСКУЮ И ОПРЕДЕЛЕНИЕ ДЛИНЫ ПЕРИОДА СИСТЕМАТИЧЕСКОЙ ДРОБИ
- Упражнения
- Глава тринадцатая. КОЛЬЦА
- § 1. ИДЕАЛЫ КОЛЬЦА. ФАКТОР-КОЛЬЦО
- Сравнения и классы вычетов по идеалу.
- Фактор-кольцо.
- Теорема об эпиморфизмах колец.
- Характеристика кольца.
- Наименьшее подкольцо кольца.
- Упражнения
- § 2. ПОЛЕ ЧАСТНЫХ ОБЛАСТИ ЦЕЛОСТНОСТИ
- Изоморфизм полей частных.
- Упражнения
- § 3. КОЛЬЦА ГЛАВНЫХ ИДЕАЛОВ
- Простые и составные элементы области целостности.
- Кольца главных идеалов.
- Факториальность кольца главных идеалов.
- Евклидовы кольца.
- Упражнения
- § 4. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
- Наименьшее общее кратное.
- Упражнения
- Глава четырнадцатая. ПОЛИНОМЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. КОЛЬЦО ПОЛИНОМОВ
- Теорема о существовании простого трансцендентного расширения коммутативного кольца.
- Степень полинома.
- Деление полинома на двучлен и корни полинома.
- Теорема о наибольшем возможном числе корней полинома в области целостности.
- Алгебраическое и функциональное равенства полиномов.
- Упражнения
- § 2. ПОЛИНОМЫ НАД ПОЛЕМ
- Алгоритм Евклида.
- Неприводимые над данным полем полиномы.
- Разложение полинома в произведение нормированных неприводимых множителей.
- Упражнения
- § 3. ФАКТОРИАЛЬНОСТЬ КОЛЬЦА ПОЛИНОМОВ НАД ФАКТОРИАЛЬНЫМ КОЛЬЦОМ
- Факториальность кольца полиномов.
- § 4. ФОРМАЛЬНАЯ ПРОИЗВОДНАЯ ПОЛИНОМА. НЕПРИВОДИМЫЕ КРАТНЫЕ МНОЖИТЕЛИ
- Разложение полинома по степеням разности х — с.
- Неприводимые кратные множители полинома.
- Кратные корни полинома.
- Упражнения
- Глава пятнадцатая. ПОЛИНОМЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. КОЛЬЦО ПОЛИНОМОВ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- Кольцо полиномов от нескольких переменных.
- Изоморфизм колец полиномов.
- Нормальное представление полинома и степень полинома.
- Факториалыюсть кольца полиномов.
- § 2. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ
- Лемма о высшем члене произведения двух полиномов.
- Симметрические полиномы.
- Леммы о симметрических полиномах.
- Основная теорема о симметрических полиномах.
- Упражнения
- 3. РЕЗУЛЬТАНТ ПОЛИНОМОВ И ИСКЛЮЧЕНИЕ ПЕРЕМЕННЫХ
- Исключение переменных.
- Глава шестнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ КОМПЛЕКСНЫХ ЧИСЕЛ И НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 1. АЛГЕБРАИЧЕСКАЯ ЗАМКНУТОСТЬ ПОЛЯ КОМПЛЕКСНЫХ ЧИСЕЛ
- Непрерывность модуля полинома.
- Наименьшее значение модуля полинома.
- Лемма Даламбера.
- Алгебраическая замкнутость поля комплексных чисел.
- Формулы Виета.
- Упражнения
- § 2. ПОЛИНОМЫ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 3. УРАВНЕНИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ СТЕПЕНИ
- Исследование корней уравнения третьей степени с действительными коэффициентами.
- Уравнения четвертой степени.
- § 4. ОТДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ ПОЛИНОМА
- Теорема Штурма.
- Глава семнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ЧИСЕЛ И АЛГЕБРАИЧЕСКИЕ ЧИСЛА
- § 1. ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ КОРНИ ПОЛИНОМА. КРИТЕРИЙ НЕПРИВОДИМОСТИ
- § 2. ПРОСТОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
- § 3. СОСТАВНОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ
- § 4. УСЛОВИЯ РАЗРЕШИМОСТИ УРАВНЕНИЯ ТРЕТЬЕЙ СТЕПЕНИ В КВАДРАТНЫХ РАДИКАЛАХ
- ЛИТЕРАТУРА