| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 16. Отношение теплоемкостей
Численное значение к может быть определено путем адиабатического расширения газа. Возьмем баллон шарообразной формы, наполненный газом при давлении  превосходящем атмосферное давление
превосходящем атмосферное давление  , и температуре Т, равной температуре окружающей среды. Баллон сообщается с трубкой с широким краном на конце. Откроем кран, тогда газ быстро, а следовательно, и адиабатически, расширится, пока давление в баллоне не сравняется с
, и температуре Т, равной температуре окружающей среды. Баллон сообщается с трубкой с широким краном на конце. Откроем кран, тогда газ быстро, а следовательно, и адиабатически, расширится, пока давление в баллоне не сравняется с  Температура газа упадет при этом до Т. Как только газ расширился таким образом, кран снова закрывается. Через некоторое время температура газа в баллоне возвратится к своему начальному значению Т, а давление возрастет до
Температура газа упадет при этом до Т. Как только газ расширился таким образом, кран снова закрывается. Через некоторое время температура газа в баллоне возвратится к своему начальному значению Т, а давление возрастет до  при этом
при этом 
Последний процесс произойдет при постоянном объеме, так что

Первый процесс — адиабатический; применив к нему формулу Пуассона, получим:

откуда

или

и окончательно

Так как 
Если давления мало отличаются друг от друга, то разности их логарифмов приблизительно пропорциональны разностям самих давлений, и формула получает вид

Лучшее определение к по этому методу принадлежит Рентгену (Pugg. Ann., CXLI, 1870). Рентген работал с большим шарообразным баллоном емкостью в 70 литров. Давления измерялись металлическим манометром — волнистой пластинкой германского серебра [german silver], укрепленной в одном из отверстий баллона. Малейшее движение пластинки, обусловленное изменением давления в баллоне, сообщалось одновременно и зеркальцу, связанному с пластинкой. Угол отклонения зеркала можно было измерять с помощью оптической трубы и шкалы. Так как деления линейки были прокалиброваны уже заранее, то по линейке можно было прямо отсчитывать миллиметры ртутного столба.
Во время этих опытов возник ряд вопросов. Оказывала ли влияние быстрота истечения? Действительно ли процесс был адиабатическим? Можно ли применять здесь формулы, справедливые для идеальных газов? Рентген исследовал даже упругое последействие металлической пластинки — манометра.
Рентген получил следующие значения для к при опытах с сухим атмосферным воздухом при 17°:

где среднее  , причем третья цифра еще достоверна: вероятная ошибка равна 0,00027.
, причем третья цифра еще достоверна: вероятная ошибка равна 0,00027.
Реньо получил для воздуха  . Тогда можно вычислить
. Тогда можно вычислить  , затем и
, затем и  .
.
Но R можно вычислить и в единицах механической работы, пользуясь равенством  , где
, где  и Т получаем, зная удельный вес воздуха при 0° С и давлении в 760 мм; литр воздуха при этих условиях весит 1,293 г. Если
и Т получаем, зная удельный вес воздуха при 0° С и давлении в 760 мм; литр воздуха при этих условиях весит 1,293 г. Если  выражены в единицах системы CGS, то R выразится в эргах. Таким образом находим механический эквивалент теплоты. Одна малая калория эквивалентна
выражены в единицах системы CGS, то R выразится в эргах. Таким образом находим механический эквивалент теплоты. Одна малая калория эквивалентна  эргов.
эргов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора к первому изданию
- § 1. Основные понятия термодинамики
- § 2. Первое начало термодинамики
- § 3. Другой пример вычисления работы
- § 4. Приложение к идеальным газам
- § 5. Стационарный ток жидкости через трубу с переменным сечением
- § 6. Однородное тело
- § 7. Применение первого начала к химии: теплота реакции и температура
- § 8. Второе начало термодинамики
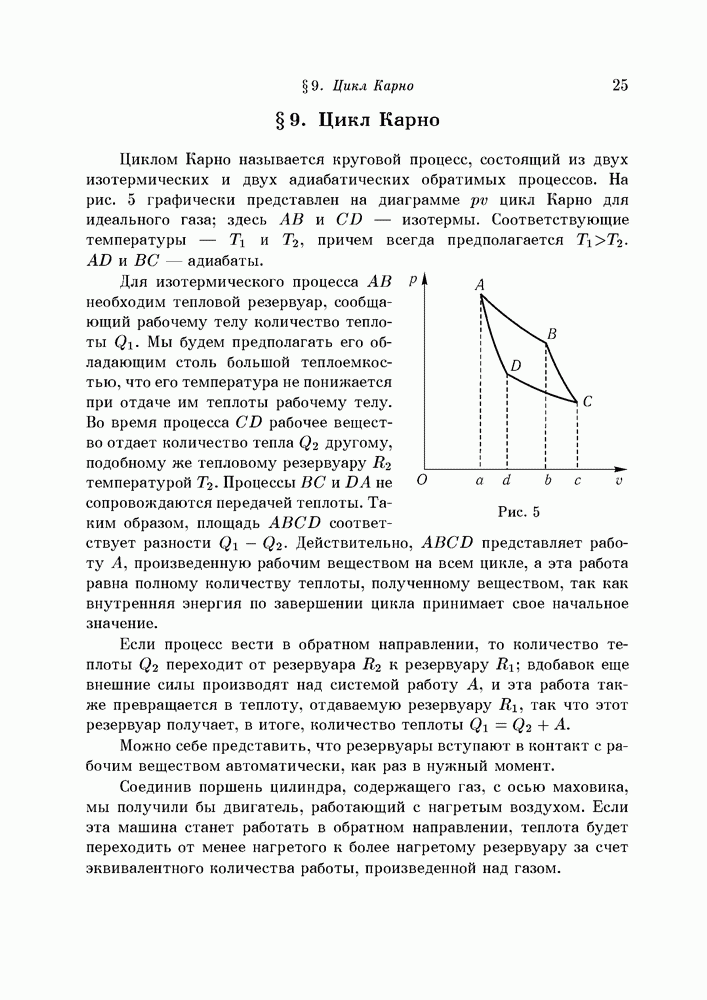
- § 9. Цикл Карно
- § 10. Коэффициент полезного действия. Универсальная функция температуры
- § 11. Другой способ определения универсальной функции температуры
- § 12. Второе начало для обратимых процессов
- § 13. Второе начало для обратимых процессов [общий случай]
- § 14. Различные обратимые пути между двумя состояниями. Энтропия
- § 15. Несколько простейших приложений
- § 16. Отношение теплоемкостей
- § 17. Система с произвольным числом параметров
- § 18. Значение полученных общих формул
- § 19. Значение второго начала
- § 20. Приложения второго начала к адиабатическим процессам
- § 21. Сжатие жидкостей
- § 22. Опыты по адиабатическому растяжению проволок
- § 23. Непосредственный вывод уравнения адиабатических процессов
- § 24. Применение к жидким пленкам
- § 25. Применение к гальваническому элементу
- § 26. Уравнение Клапейрона
- § 27. Опытная проверка уравнения Клапейрона (Клаузиус)
- § 28. Опыты де-Виссера с уксусной кислотой
- § 29. Режеляция льда
- § 30. Закон Стефана-Больцмана
- § 31. Другие выражения второго начала
- § 32. Свойства энтропии
- § 33. Свободная энергия
- § 34. Термодинамический потенциал
- § 35. Свободная энергия идеального газа
- § 36. Неравновесные состояния
- § 37. Необратимые процессы
- § 38. Изотермический процесс
- § 39. Свободная энергия и работа
- § 40. Обобщенные силы
- § 41. Условия равновесия
- § 42. Система в поле консервативных сил
- § 43. Газ или жидкость в поле силы тяжести
- § 44. Решение того же вопроса с помощью энтропии
- § 45. Система жидкость-пар
- § 46. Равновесие трехфазной системы
- § 47. Упругость пара над разбавленным раствором
- § 48. Различие в давлении пара над чистой водой и над раствором
- § 49. Смеси
- § 50. Двухкомпонентная система
- § 51. Устойчивые и неустойчивые жидкие фазы; равновесие между двумя жидкими фазами
- § 52. Равновесие между твердой и жидкой фазами; переохлаждение
- § 53. Равновесие трехфазной системы, состоящей из двух компонент
- § 54. Равновесие раствора соли с ее твердым гидратом
- § 55. Равновесие между двумя растворами различной концентрации
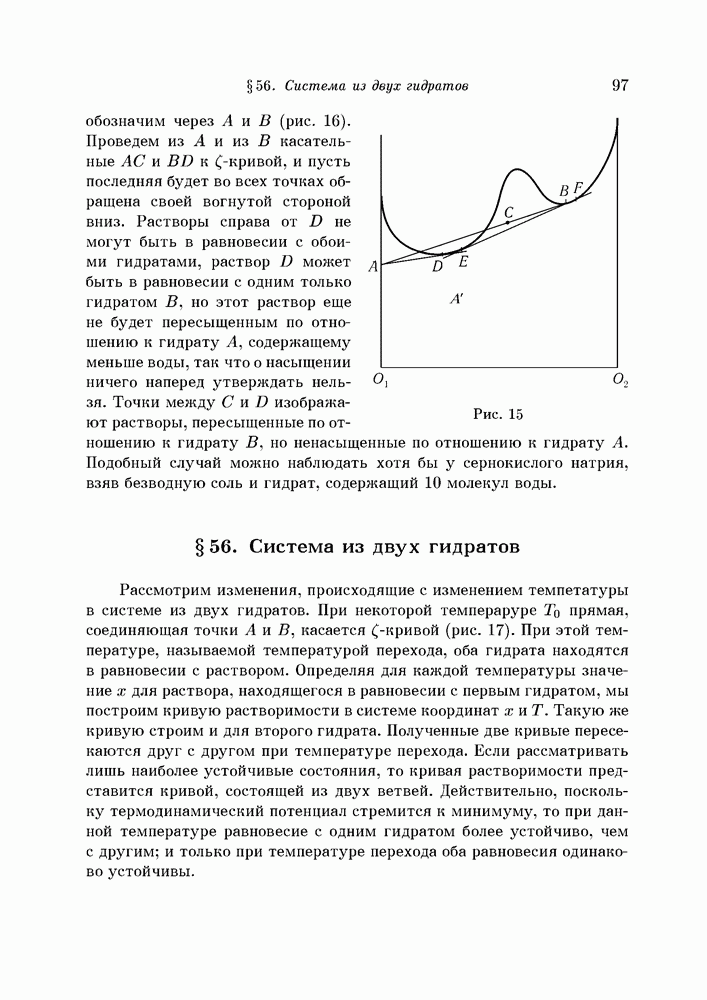
- § 56. Система из двух гидратов
- § 57. Другой способ построения кривой
- § 58. Трехкомпонентные системы
- § 59. Трехфазная система из трех компонент
- § 60. Форма поверхности
- § 61. Условия равновесия между твердой и жидкой фазами
- § 62. Равновесие двух твердых фаз с жидкими фазами
- § 63. Равновесие между двумя жидкими фазами
- § 64. Другие способы построения поверхности
- § 65. Смешанные кристаллы
- § 66. Равновесие между смесями и растворами
- § 67. Неопределенность в выражении термодинамического потенциала
- § 68. Смесь газов в поле силы тяжести
- § 69. Смешение и разделение двух газов
- § 70. Парадокс Гиббса
- § 71. Обобщение теоремы Гиббса на случай трех и более газов
- § 72. Уменьшение свободной энергии при смешении двух газов
- § 73. Свободная энергия жидкой смеси
- § 74. Общее выражение для свободной энергии смеси
- § 75. Случай, когда одна из компонент присутствует в весьма малом количестве
- § 76. Равновесие двух фаз, каждая из которых состоит из двух компонент
- § 77. Смесь под действием внешних сил
- § 78. Вывод уравнений равновесия
- § 79. Второй пример системы под действием внешних сил
- § 80. Осмотическое давление. Закон вант-Гоффа
- § 81. Другой вывод закона вант-Гоффа
- § 82. Общие условия равновесия многофазных систем
- § 83. Равновесие трех фаз
- § 84. Вывод условий равновесия с помощью термодинамического потенциала
- § 85. Число независимых условий равновесия
- § 86. Сравнение между собой двух состояний равновесия
- § 87. Общее соотношение между двумя состояниями равновесия
- § 88. Смысл полученного соотношения
- § 89. Добавление некоторого весьма малого количества новой компоненты
- § 90. Несколько заключительных замечаний
- § 91. Диссоциация газа
- § 92. поверхности ван-дер-Ваальса
- § 93. Изменение формы поверхности с температурой
- § 94. Сечения Ф-поверхности
- § 95. Условия равновесия
- § 96. Сосуществующие фазы
- § 97. Математическая теория конечных точек складки
- § 98. Исследование Ф-поверхности в окрестности конечной точки складки
- § 99. Конечная точка складки первого рода
- § 100. Индикатриса, бинодаль и спинодаль
- § 101. Определение координат конечной точки складки непосредственно из самого уравнения Ф-поверхности
- § 102. Кривая конечных точек складки
- § 103. Изменение давления при бесконечно малом изменении состояния
- § 104. Зависимость давления от состава смеси
- § 105. Изобары
- § 106. Изотермическое сжатие смесей
- § 107. Обратная конденсация