| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 78. Вывод уравнений равновесия
Зависимые вариации можно исключить тем же способом, что и в предшествовавших случаях. Именно, умножим равенства (88) и (89) на постоянные множители  и прибавим их к уравнению
и прибавим их к уравнению

записанному в развернутом виде; при этом значение  дается формулой (87). Тогда производные по х и по v от
дается формулой (87). Тогда производные по х и по v от  , т. е. интеграла
, т. е. интеграла

должны равняться нулю при всяком z.
Дифференцирование состоит здесь в следующем: мы считаем х и v в окрестности данного z переменными, а при всяком другом z — постоянными. Тогда знак интеграла можно опустить, и условия равновесия запишутся в виде

и
 (93)
(93)
где  — некоторые постоянные.
— некоторые постоянные.
Разрешая уравнения (92) и (93) относительно  находим окончательно условия равновесия в виде равенства двух функций от
находим окончательно условия равновесия в виде равенства двух функций от  некоторым постоянным, скажем,
некоторым постоянным, скажем,  Зная
Зная  и v на некоторой высоте
и v на некоторой высоте  , можно определить значения
, можно определить значения 
Если  очень мало, то в выражении для производной (см. § 75) главную роль играет член, содержащим
очень мало, то в выражении для производной (см. § 75) главную роль играет член, содержащим  так что сводится к одному члену
так что сводится к одному члену  Уравнение (93) примет тогда следующий вид:
Уравнение (93) примет тогда следующий вид:

или

Окончательно,

где  / Значение
/ Значение  будет с высотой или увеличиваться или уменьшаться, смотря по знаку разности
будет с высотой или увеличиваться или уменьшаться, смотря по знаку разности  Так, в разбавленном водном растворе соли (первая компонента) с большим, чем у воды молекулярным весом, концентрация с высотой понижается, ибо
Так, в разбавленном водном растворе соли (первая компонента) с большим, чем у воды молекулярным весом, концентрация с высотой понижается, ибо  отрицательно. Для соли с меньшим молекулярным весом, чем у растворителя, концентрация раствора с высотой растет. При
отрицательно. Для соли с меньшим молекулярным весом, чем у растворителя, концентрация раствора с высотой растет. При  концентрация раствора одна и та же на любой высоте.
концентрация раствора одна и та же на любой высоте.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора к первому изданию
- § 1. Основные понятия термодинамики
- § 2. Первое начало термодинамики
- § 3. Другой пример вычисления работы
- § 4. Приложение к идеальным газам
- § 5. Стационарный ток жидкости через трубу с переменным сечением
- § 6. Однородное тело
- § 7. Применение первого начала к химии: теплота реакции и температура
- § 8. Второе начало термодинамики
- § 9. Цикл Карно
- § 10. Коэффициент полезного действия. Универсальная функция температуры
- § 11. Другой способ определения универсальной функции температуры
- § 12. Второе начало для обратимых процессов
- § 13. Второе начало для обратимых процессов [общий случай]
- § 14. Различные обратимые пути между двумя состояниями. Энтропия
- § 15. Несколько простейших приложений
- § 16. Отношение теплоемкостей
- § 17. Система с произвольным числом параметров
- § 18. Значение полученных общих формул
- § 19. Значение второго начала
- § 20. Приложения второго начала к адиабатическим процессам
- § 21. Сжатие жидкостей
- § 22. Опыты по адиабатическому растяжению проволок
- § 23. Непосредственный вывод уравнения адиабатических процессов
- § 24. Применение к жидким пленкам
- § 25. Применение к гальваническому элементу
- § 26. Уравнение Клапейрона
- § 27. Опытная проверка уравнения Клапейрона (Клаузиус)
- § 28. Опыты де-Виссера с уксусной кислотой
- § 29. Режеляция льда
- § 30. Закон Стефана-Больцмана
- § 31. Другие выражения второго начала
- § 32. Свойства энтропии
- § 33. Свободная энергия
- § 34. Термодинамический потенциал
- § 35. Свободная энергия идеального газа
- § 36. Неравновесные состояния
- § 37. Необратимые процессы
- § 38. Изотермический процесс
- § 39. Свободная энергия и работа
- § 40. Обобщенные силы
- § 41. Условия равновесия
- § 42. Система в поле консервативных сил
- § 43. Газ или жидкость в поле силы тяжести
- § 44. Решение того же вопроса с помощью энтропии
- § 45. Система жидкость-пар
- § 46. Равновесие трехфазной системы
- § 47. Упругость пара над разбавленным раствором
- § 48. Различие в давлении пара над чистой водой и над раствором
- § 49. Смеси
- § 50. Двухкомпонентная система
- § 51. Устойчивые и неустойчивые жидкие фазы; равновесие между двумя жидкими фазами
- § 52. Равновесие между твердой и жидкой фазами; переохлаждение
- § 53. Равновесие трехфазной системы, состоящей из двух компонент
- § 54. Равновесие раствора соли с ее твердым гидратом
- § 55. Равновесие между двумя растворами различной концентрации
- § 56. Система из двух гидратов
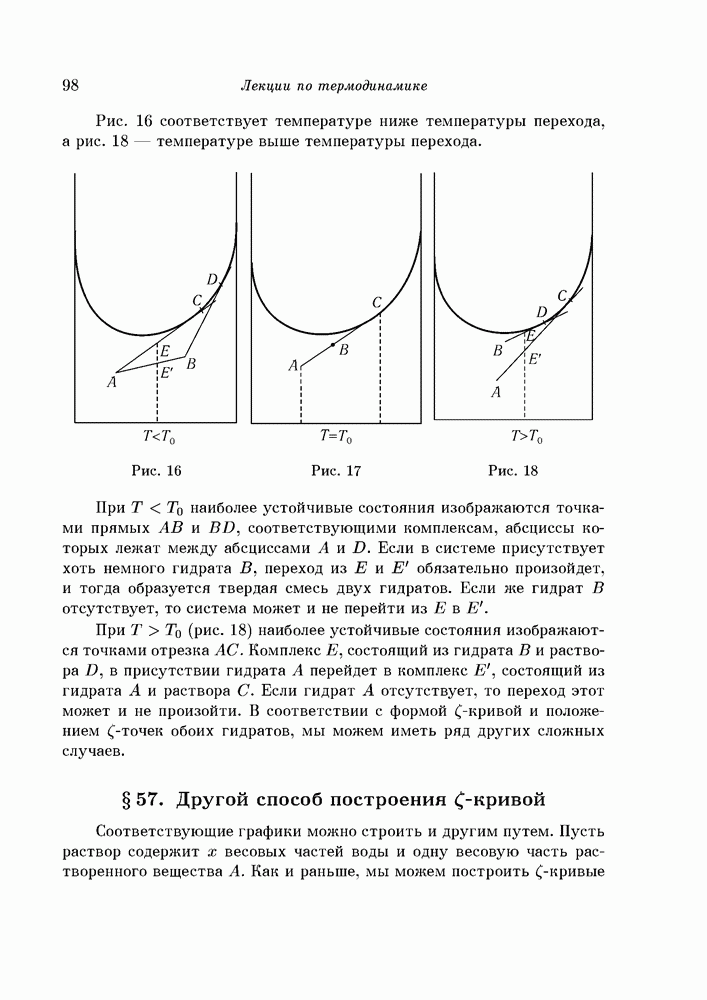
- § 57. Другой способ построения кривой
- § 58. Трехкомпонентные системы
- § 59. Трехфазная система из трех компонент
- § 60. Форма поверхности
- § 61. Условия равновесия между твердой и жидкой фазами
- § 62. Равновесие двух твердых фаз с жидкими фазами
- § 63. Равновесие между двумя жидкими фазами
- § 64. Другие способы построения поверхности
- § 65. Смешанные кристаллы
- § 66. Равновесие между смесями и растворами
- § 67. Неопределенность в выражении термодинамического потенциала
- § 68. Смесь газов в поле силы тяжести
- § 69. Смешение и разделение двух газов
- § 70. Парадокс Гиббса
- § 71. Обобщение теоремы Гиббса на случай трех и более газов
- § 72. Уменьшение свободной энергии при смешении двух газов
- § 73. Свободная энергия жидкой смеси
- § 74. Общее выражение для свободной энергии смеси
- § 75. Случай, когда одна из компонент присутствует в весьма малом количестве
- § 76. Равновесие двух фаз, каждая из которых состоит из двух компонент
- § 77. Смесь под действием внешних сил
- § 78. Вывод уравнений равновесия
- § 79. Второй пример системы под действием внешних сил
- § 80. Осмотическое давление. Закон вант-Гоффа
- § 81. Другой вывод закона вант-Гоффа
- § 82. Общие условия равновесия многофазных систем
- § 83. Равновесие трех фаз
- § 84. Вывод условий равновесия с помощью термодинамического потенциала
- § 85. Число независимых условий равновесия
- § 86. Сравнение между собой двух состояний равновесия
- § 87. Общее соотношение между двумя состояниями равновесия
- § 88. Смысл полученного соотношения
- § 89. Добавление некоторого весьма малого количества новой компоненты
- § 90. Несколько заключительных замечаний
- § 91. Диссоциация газа
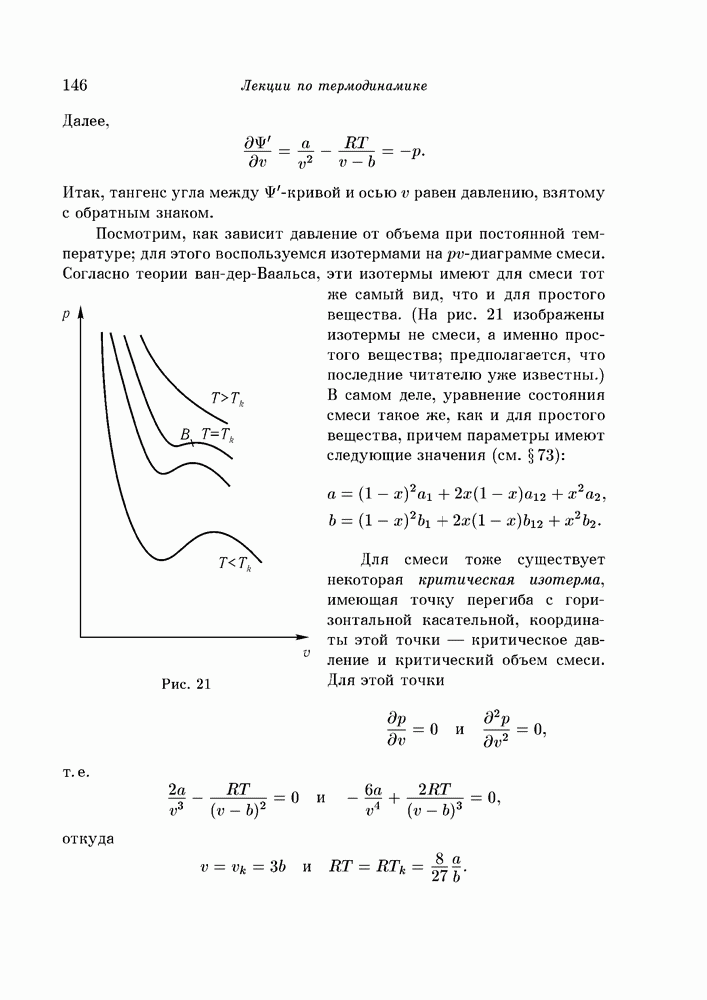
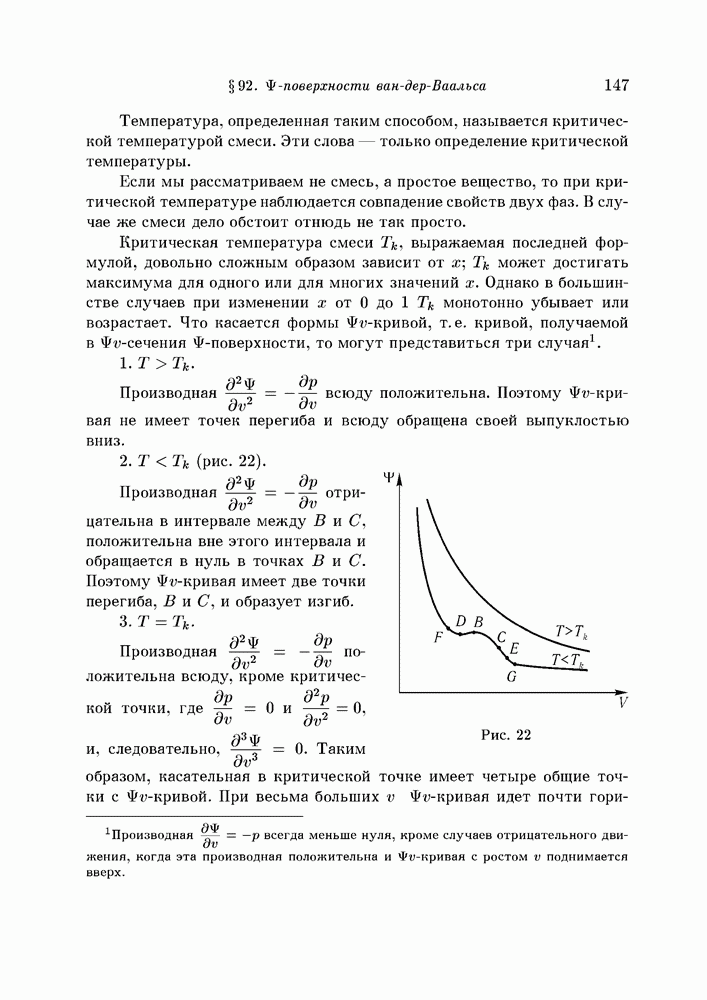
- § 92. поверхности ван-дер-Ваальса
- § 93. Изменение формы поверхности с температурой
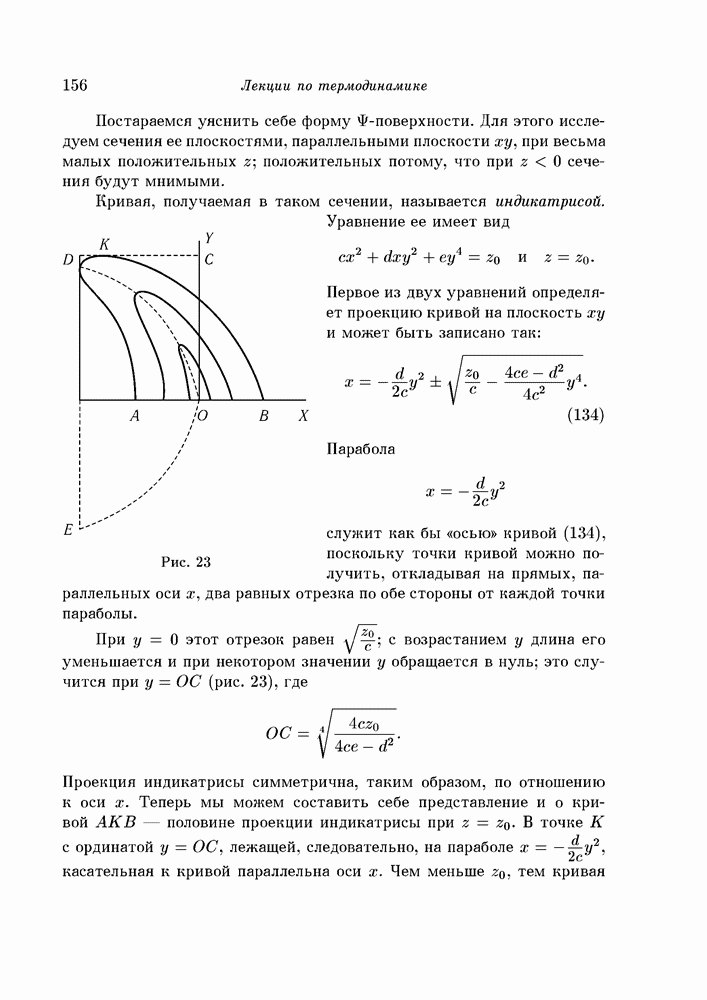
- § 94. Сечения Ф-поверхности
- § 95. Условия равновесия
- § 96. Сосуществующие фазы
- § 97. Математическая теория конечных точек складки
- § 98. Исследование Ф-поверхности в окрестности конечной точки складки
- § 99. Конечная точка складки первого рода
- § 100. Индикатриса, бинодаль и спинодаль
- § 101. Определение координат конечной точки складки непосредственно из самого уравнения Ф-поверхности
- § 102. Кривая конечных точек складки
- § 103. Изменение давления при бесконечно малом изменении состояния
- § 104. Зависимость давления от состава смеси
- § 105. Изобары
- § 106. Изотермическое сжатие смесей
- § 107. Обратная конденсация