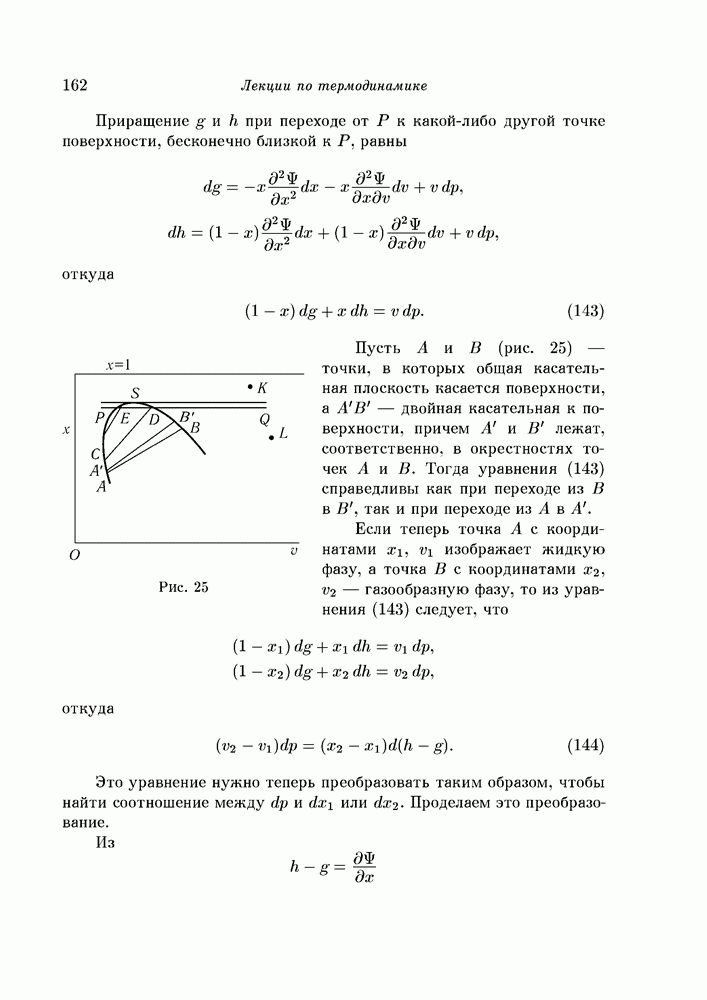
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 32. Свойства энтропии
Докажем следующую теорему:
Энтропия всякой изолированной системы тел не может уменьшаться, а может только оставаться постоянной или увеличиваться.
Если система состоит из нескольких тел, то это положение справедливо для полной энтропии всех этих тел. Энтропия системы из двух тел есть сумма энтропий этих тел.
Как пример, возьмем два тела с температурами  одно из которых отдает другому теплоту путем теплопроводности. Пусть, далее,
одно из которых отдает другому теплоту путем теплопроводности. Пусть, далее,  . Если путем теплопроводности или лучеиспускания от первого тела ко второму перейдет некоторое количество тепла
. Если путем теплопроводности или лучеиспускания от первого тела ко второму перейдет некоторое количество тепла  то энтропия первого тела уменьшится на
то энтропия первого тела уменьшится на  , а энтропия второго — увеличится на
, а энтропия второго — увеличится на  , так что общая энтропия системы возрастет на положительную величину
, так что общая энтропия системы возрастет на положительную величину 
Чтобы перейти к доказательству в общем случае, напомним, что (см. § 13) для произвольного цикла  , а для обратимого цикла всегда
, а для обратимого цикла всегда  . Для необратимого цикла, однако,
. Для необратимого цикла, однако,  .
.
Представим себе, что некоторая произвольная система переходит каким-либо образом из состояния А в состояние В, причем температуру в любой момент времени предположим одинаковой во всех точках тела. Если теперь вернуть систему из состояния В в состояние А по какому-либо обратимому пути, мы получим замкнутый цикл, к которому применима только что упомянутая общая теорема. Нельзя забывать при этом, что переход из А в В следует рассматривать как реальный процесс, о котором мы хотим что-то узнать, а переход из В в А — как фиктивный. Раз переход из В в А обратим, то для него интеграл  равен
равен  и для всего цикла
и для всего цикла

а для перехода из А в В

(о вспомогательном обратимом переходе из В в А мы в дальнейшем упоминать не будем).
Для адиабатического процесса  , и формула (37) примет вид
, и формула (37) примет вид

Таким образом, при адиабатическом процессе энтропия не может убывать; она остается неизменной, если процесс обратим.
Итак, мы доказали, что энтропия изолированной системы, т. е. системы, не обменивающейся теплотой с окружающей средой, не может убывать. Но тогда и энтропия всей вселенной не может убывать, ибо вселенная представляет собой изолированную систему.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора к первому изданию
- § 1. Основные понятия термодинамики
- § 2. Первое начало термодинамики
- § 3. Другой пример вычисления работы
- § 4. Приложение к идеальным газам
- § 5. Стационарный ток жидкости через трубу с переменным сечением
- § 6. Однородное тело
- § 7. Применение первого начала к химии: теплота реакции и температура
- § 8. Второе начало термодинамики
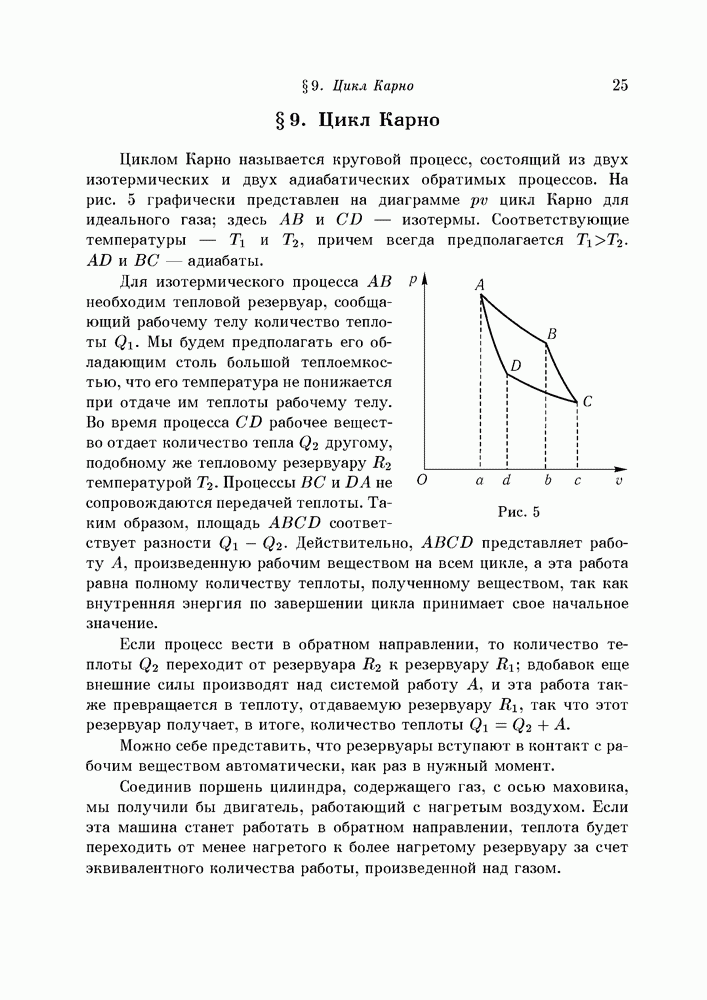
- § 9. Цикл Карно
- § 10. Коэффициент полезного действия. Универсальная функция температуры
- § 11. Другой способ определения универсальной функции температуры
- § 12. Второе начало для обратимых процессов
- § 13. Второе начало для обратимых процессов [общий случай]
- § 14. Различные обратимые пути между двумя состояниями. Энтропия
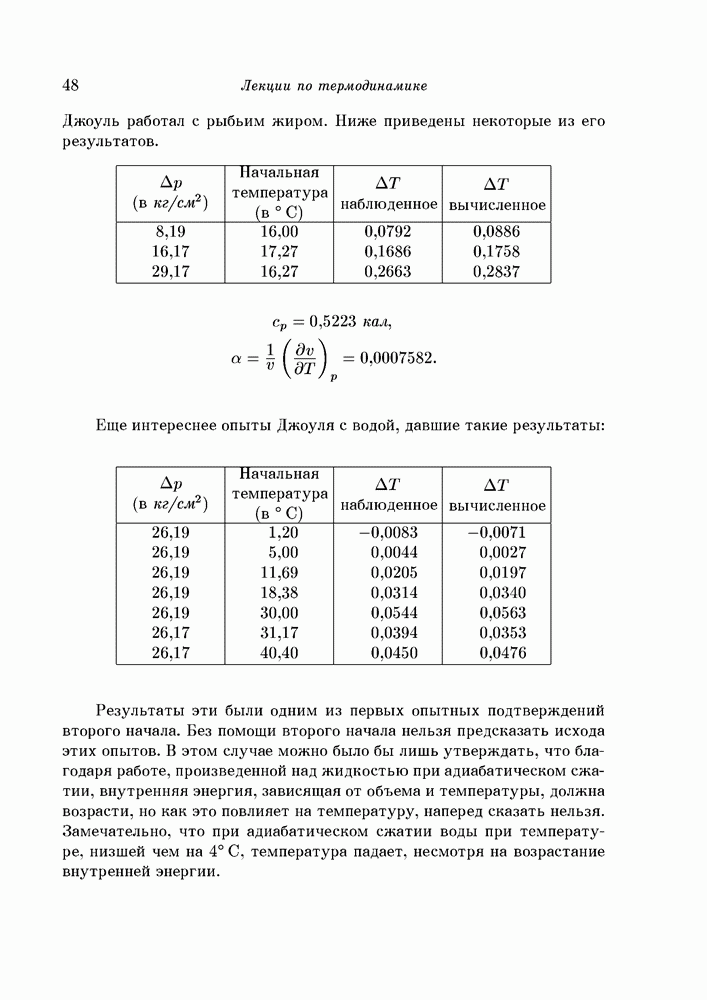
- § 15. Несколько простейших приложений
- § 16. Отношение теплоемкостей
- § 17. Система с произвольным числом параметров
- § 18. Значение полученных общих формул
- § 19. Значение второго начала
- § 20. Приложения второго начала к адиабатическим процессам
- § 21. Сжатие жидкостей
- § 22. Опыты по адиабатическому растяжению проволок
- § 23. Непосредственный вывод уравнения адиабатических процессов
- § 24. Применение к жидким пленкам
- § 25. Применение к гальваническому элементу
- § 26. Уравнение Клапейрона
- § 27. Опытная проверка уравнения Клапейрона (Клаузиус)
- § 28. Опыты де-Виссера с уксусной кислотой
- § 29. Режеляция льда
- § 30. Закон Стефана-Больцмана
- § 31. Другие выражения второго начала
- § 32. Свойства энтропии
- § 33. Свободная энергия
- § 34. Термодинамический потенциал
- § 35. Свободная энергия идеального газа
- § 36. Неравновесные состояния
- § 37. Необратимые процессы
- § 38. Изотермический процесс
- § 39. Свободная энергия и работа
- § 40. Обобщенные силы
- § 41. Условия равновесия
- § 42. Система в поле консервативных сил
- § 43. Газ или жидкость в поле силы тяжести
- § 44. Решение того же вопроса с помощью энтропии
- § 45. Система жидкость-пар
- § 46. Равновесие трехфазной системы
- § 47. Упругость пара над разбавленным раствором
- § 48. Различие в давлении пара над чистой водой и над раствором
- § 49. Смеси
- § 50. Двухкомпонентная система
- § 51. Устойчивые и неустойчивые жидкие фазы; равновесие между двумя жидкими фазами
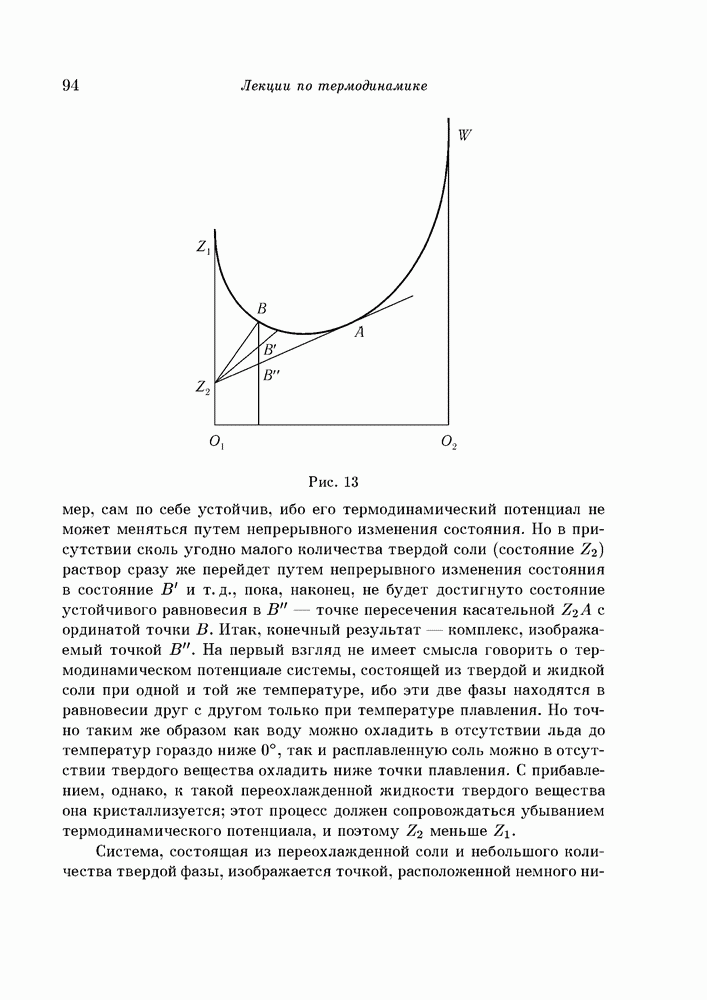
- § 52. Равновесие между твердой и жидкой фазами; переохлаждение
- § 53. Равновесие трехфазной системы, состоящей из двух компонент
- § 54. Равновесие раствора соли с ее твердым гидратом
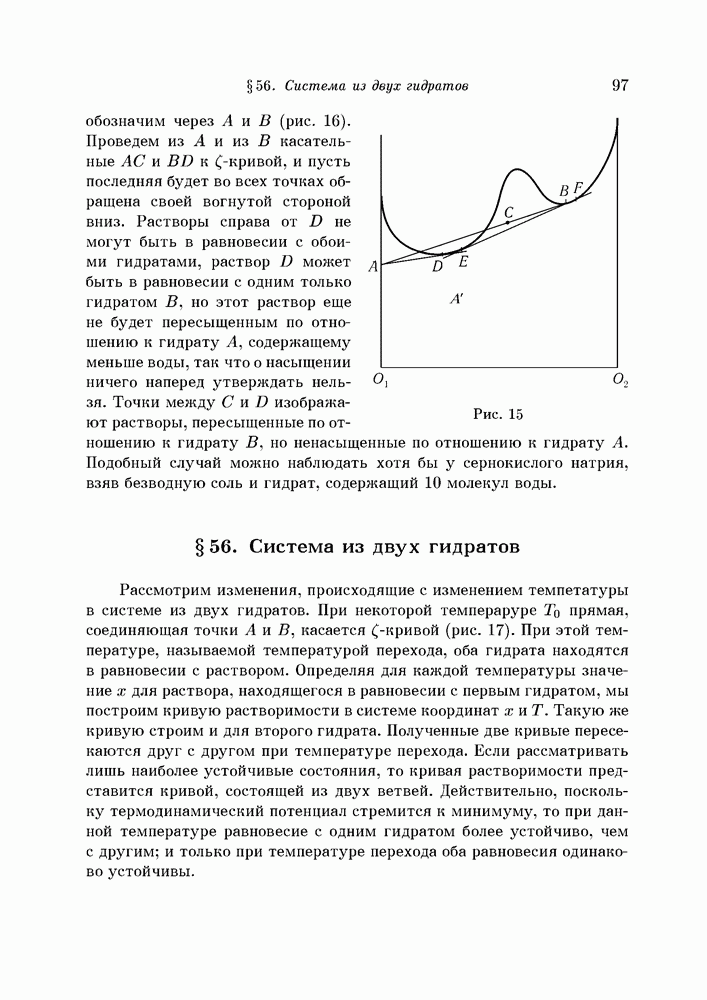
- § 55. Равновесие между двумя растворами различной концентрации
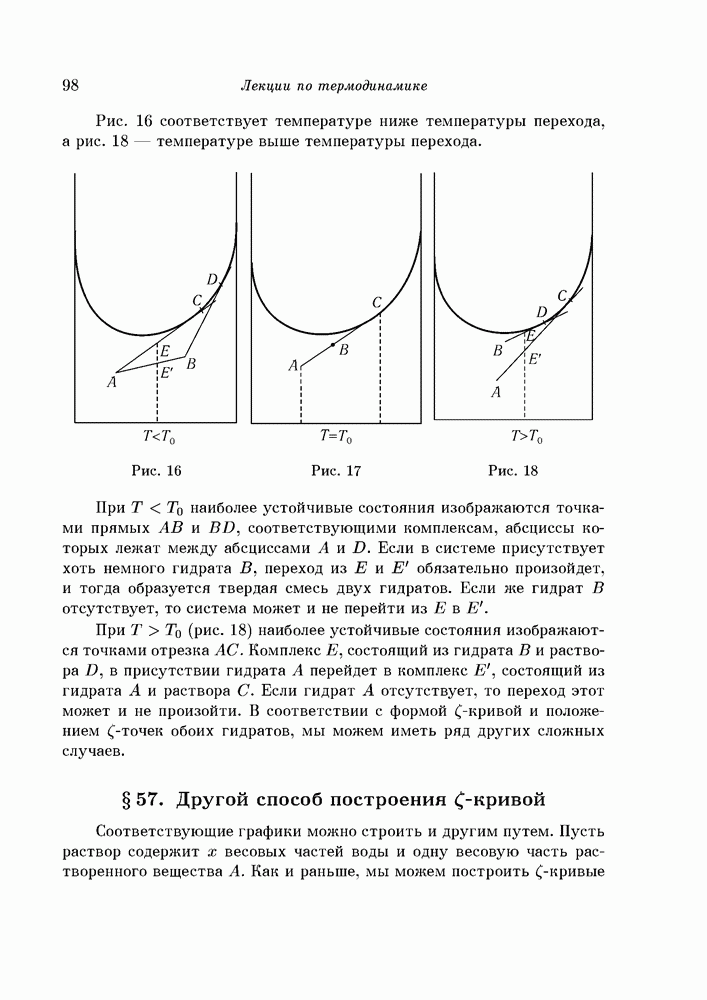
- § 56. Система из двух гидратов
- § 57. Другой способ построения кривой
- § 58. Трехкомпонентные системы
- § 59. Трехфазная система из трех компонент
- § 60. Форма поверхности
- § 61. Условия равновесия между твердой и жидкой фазами
- § 62. Равновесие двух твердых фаз с жидкими фазами
- § 63. Равновесие между двумя жидкими фазами
- § 64. Другие способы построения поверхности
- § 65. Смешанные кристаллы
- § 66. Равновесие между смесями и растворами
- § 67. Неопределенность в выражении термодинамического потенциала
- § 68. Смесь газов в поле силы тяжести
- § 69. Смешение и разделение двух газов
- § 70. Парадокс Гиббса
- § 71. Обобщение теоремы Гиббса на случай трех и более газов
- § 72. Уменьшение свободной энергии при смешении двух газов
- § 73. Свободная энергия жидкой смеси
- § 74. Общее выражение для свободной энергии смеси
- § 75. Случай, когда одна из компонент присутствует в весьма малом количестве
- § 76. Равновесие двух фаз, каждая из которых состоит из двух компонент
- § 77. Смесь под действием внешних сил
- § 78. Вывод уравнений равновесия
- § 79. Второй пример системы под действием внешних сил
- § 80. Осмотическое давление. Закон вант-Гоффа
- § 81. Другой вывод закона вант-Гоффа
- § 82. Общие условия равновесия многофазных систем
- § 83. Равновесие трех фаз
- § 84. Вывод условий равновесия с помощью термодинамического потенциала
- § 85. Число независимых условий равновесия
- § 86. Сравнение между собой двух состояний равновесия
- § 87. Общее соотношение между двумя состояниями равновесия
- § 88. Смысл полученного соотношения
- § 89. Добавление некоторого весьма малого количества новой компоненты
- § 90. Несколько заключительных замечаний
- § 91. Диссоциация газа
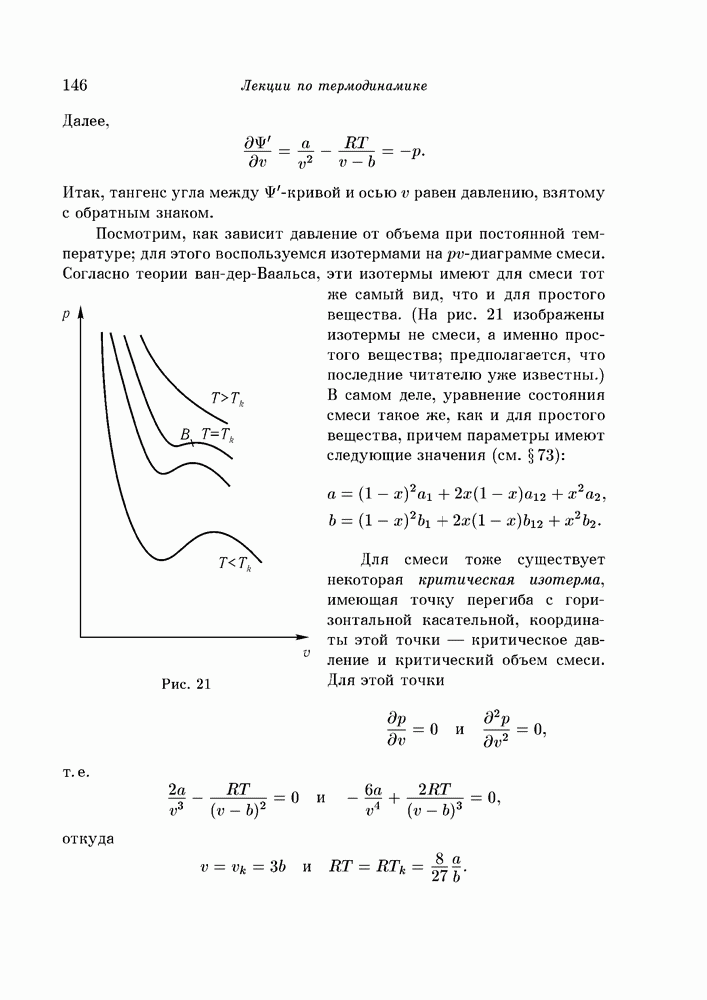
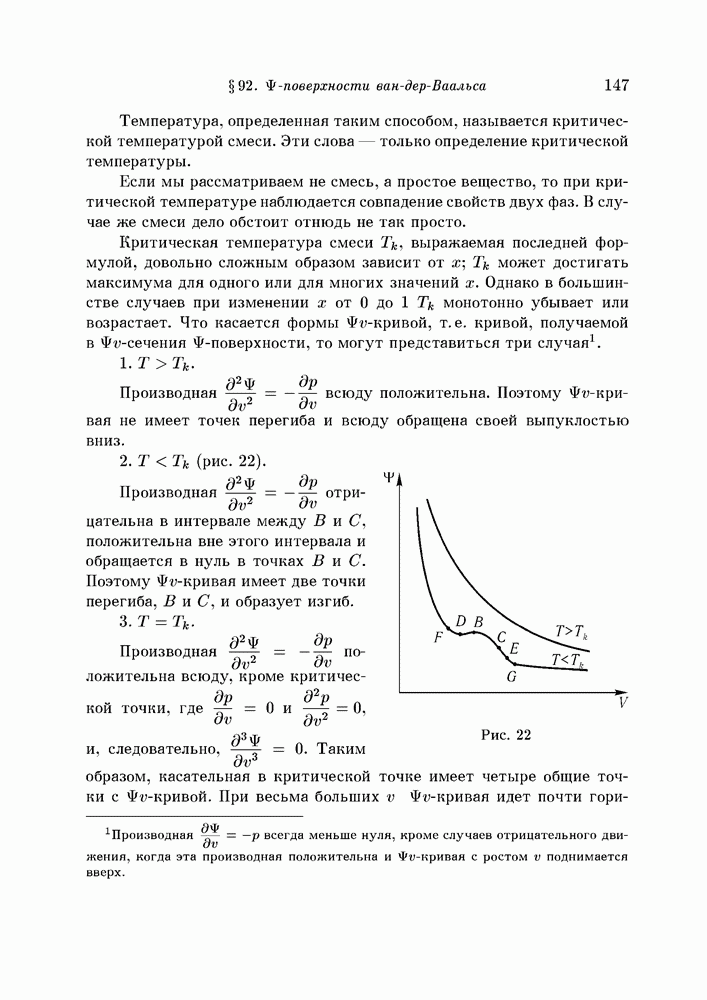
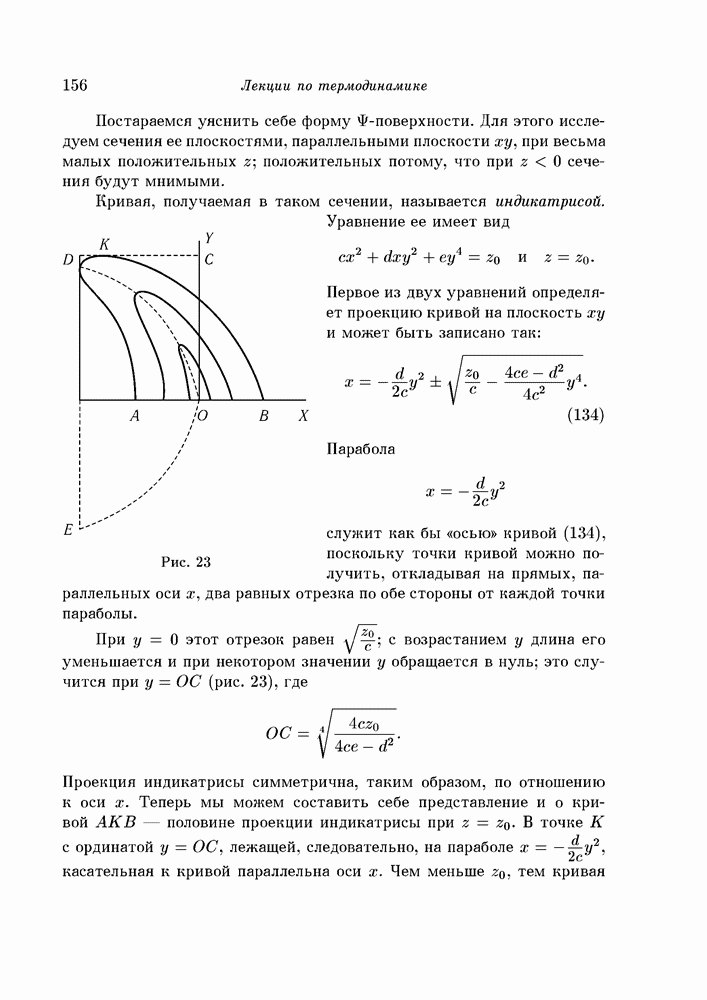
- § 92. поверхности ван-дер-Ваальса
- § 93. Изменение формы поверхности с температурой
- § 94. Сечения Ф-поверхности
- § 95. Условия равновесия
- § 96. Сосуществующие фазы
- § 97. Математическая теория конечных точек складки
- § 98. Исследование Ф-поверхности в окрестности конечной точки складки
- § 99. Конечная точка складки первого рода
- § 100. Индикатриса, бинодаль и спинодаль
- § 101. Определение координат конечной точки складки непосредственно из самого уравнения Ф-поверхности
- § 102. Кривая конечных точек складки
- § 103. Изменение давления при бесконечно малом изменении состояния
- § 104. Зависимость давления от состава смеси
- § 105. Изобары
- § 106. Изотермическое сжатие смесей
- § 107. Обратная конденсация