| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 86. Сравнение между собой двух состояний равновесия
Решить выведенные выше уравнения мы, вообще говоря, не можем, ибо не знаем вида функций  . Но сравнивая два весьма близких между собой состояния равновесия, можно получить количественные результаты, поддающиеся проверке на опыте. В одном из этих состояний (назовем его первым) система, в которой
. Но сравнивая два весьма близких между собой состояния равновесия, можно получить количественные результаты, поддающиеся проверке на опыте. В одном из этих состояний (назовем его первым) система, в которой  фаз и
фаз и  компонент А, находится в равновесии при температуре Т и давлении
компонент А, находится в равновесии при температуре Т и давлении  . Второе состояние отличается от первого тем, что, во-первых, температура и давление равны
. Второе состояние отличается от первого тем, что, во-первых, температура и давление равны  , а во-вторых, в систему введено небольшое количество новой компоненты С. Количество компоненты С в каждой из фаз обозначим через
, а во-вторых, в систему введено небольшое количество новой компоненты С. Количество компоненты С в каждой из фаз обозначим через  . Все с, а также
. Все с, а также  будем считать бесконечно малыми одного и того же порядка.
будем считать бесконечно малыми одного и того же порядка.
Начнем с первого состояния. Здесь можно указать  чисел
чисел  отношения которых определяются уравнениями
отношения которых определяются уравнениями

где некоторые коэффициенты могут быть нулями. Одни из этих чисел а будут, конечно, отрицательными, а другие положительными. Допустим, что  из чисел а положительны, а остальные — отрицательны. Тогда возможно, как это следует из уравнений (114), такое изменение состояния системы, при котором температура, давление, плотность и состав каждой фазы остаются постоянными, а массы первых
из чисел а положительны, а остальные — отрицательны. Тогда возможно, как это следует из уравнений (114), такое изменение состояния системы, при котором температура, давление, плотность и состав каждой фазы остаются постоянными, а массы первых  фаз возрастают за счет остальных
фаз возрастают за счет остальных  . Мы определим такое изменение состояния тем, что потребуем приращения массы каждой фазы в отношении 1 к
. Мы определим такое изменение состояния тем, что потребуем приращения массы каждой фазы в отношении 1 к  , где а — число, соответствующее данной фазе,
, где а — число, соответствующее данной фазе,  — некоторая бесконечно малая постоянная.
— некоторая бесконечно малая постоянная.
Так же изменится и термодинамический потенциал каждой фазы. Полный термодинамический потенциал получит приращение

Но приращение термодинамического потенциала должно равняться нулю, поэтому

Уравнение (115) можно с легкостью вывести из условий равновесия, приведенных в § 84, в сочетании с уравнениями (114). Для этого достаточно заметить, что, согласно § 85, термодинамический потенциал представляет собой однородную функцию первого порядка от аргументов  поэтому для каждой фазы справедливо соотношение
поэтому для каждой фазы справедливо соотношение

Рассмотрим второе состояние. Величины  бесконечно мало отличающиеся от
бесконечно мало отличающиеся от  обозначают массы компонент А в отдельных фазах;
обозначают массы компонент А в отдельных фазах;  обозначают
обозначают  чисел, бесконечно близких к
чисел, бесконечно близких к  и удовлетворяющих уравнениям
и удовлетворяющих уравнениям

Подвергнем систему и во втором состоянии бесконечно малому изменению при постоянстве температуры и объема и приравняем нулю соответствующую вариацию термодинамического потенциала. Пусть этот процесс состоит в изменении массы каждой компоненты А в каждой фазе в отношении  причем масса компоненты С не меняется.
причем масса компоненты С не меняется.
Тогда массы первых  компонент
компонент  возрастут в каждой фазе на
возрастут в каждой фазе на  ; соответствующее приращение
; соответствующее приращение  термодинамического потенциала будет равно
термодинамического потенциала будет равно

Но  — однородная функция первого порядка от аргументов
— однородная функция первого порядка от аргументов  , поэтому
, поэтому

и выражение (117) можно переписать в виде

Так как

то ясно, что доказанное в § 74 для Ф справедливо и для переменная  — в данном случае с — встречается явно лишь в члене
— в данном случае с — встречается явно лишь в члене

с по условию весьма мало, поэтому

где  — значение
— значение  при
при  . Итак,
. Итак,

и, окончательно, выражение (117) запишется в виде

Составив подобные выражения для каждой фазы и приравняв нулю вариацию термодинамического потенциала всей системы, мы находим

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора к первому изданию
- § 1. Основные понятия термодинамики
- § 2. Первое начало термодинамики
- § 3. Другой пример вычисления работы
- § 4. Приложение к идеальным газам
- § 5. Стационарный ток жидкости через трубу с переменным сечением
- § 6. Однородное тело
- § 7. Применение первого начала к химии: теплота реакции и температура
- § 8. Второе начало термодинамики
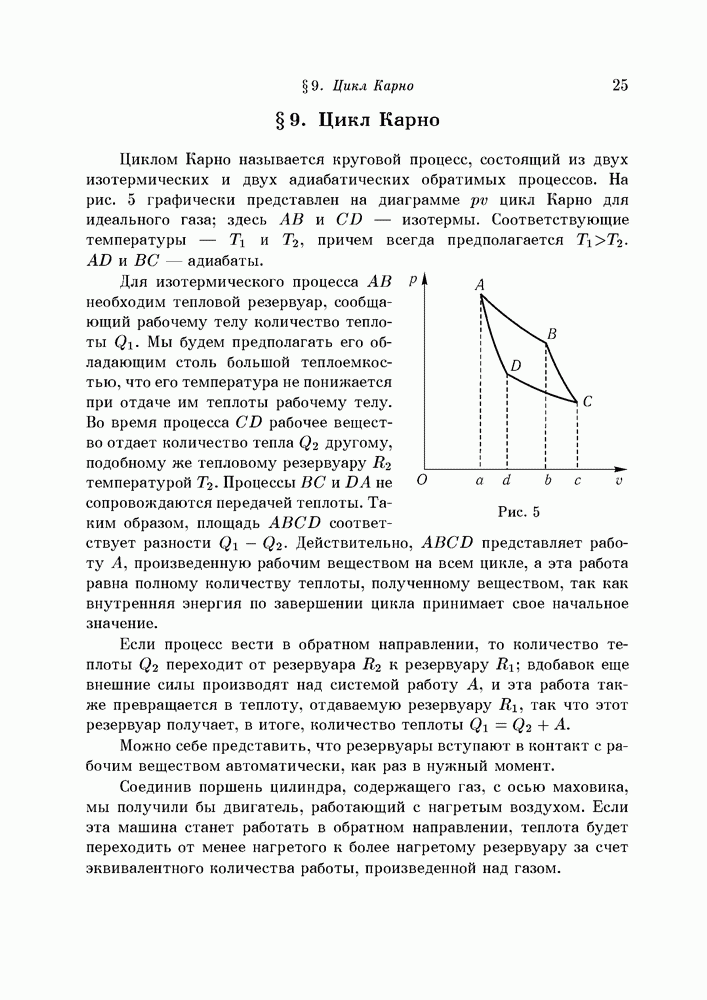
- § 9. Цикл Карно
- § 10. Коэффициент полезного действия. Универсальная функция температуры
- § 11. Другой способ определения универсальной функции температуры
- § 12. Второе начало для обратимых процессов
- § 13. Второе начало для обратимых процессов [общий случай]
- § 14. Различные обратимые пути между двумя состояниями. Энтропия
- § 15. Несколько простейших приложений
- § 16. Отношение теплоемкостей
- § 17. Система с произвольным числом параметров
- § 18. Значение полученных общих формул
- § 19. Значение второго начала
- § 20. Приложения второго начала к адиабатическим процессам
- § 21. Сжатие жидкостей
- § 22. Опыты по адиабатическому растяжению проволок
- § 23. Непосредственный вывод уравнения адиабатических процессов
- § 24. Применение к жидким пленкам
- § 25. Применение к гальваническому элементу
- § 26. Уравнение Клапейрона
- § 27. Опытная проверка уравнения Клапейрона (Клаузиус)
- § 28. Опыты де-Виссера с уксусной кислотой
- § 29. Режеляция льда
- § 30. Закон Стефана-Больцмана
- § 31. Другие выражения второго начала
- § 32. Свойства энтропии
- § 33. Свободная энергия
- § 34. Термодинамический потенциал
- § 35. Свободная энергия идеального газа
- § 36. Неравновесные состояния
- § 37. Необратимые процессы
- § 38. Изотермический процесс
- § 39. Свободная энергия и работа
- § 40. Обобщенные силы
- § 41. Условия равновесия
- § 42. Система в поле консервативных сил
- § 43. Газ или жидкость в поле силы тяжести
- § 44. Решение того же вопроса с помощью энтропии
- § 45. Система жидкость-пар
- § 46. Равновесие трехфазной системы
- § 47. Упругость пара над разбавленным раствором
- § 48. Различие в давлении пара над чистой водой и над раствором
- § 49. Смеси
- § 50. Двухкомпонентная система
- § 51. Устойчивые и неустойчивые жидкие фазы; равновесие между двумя жидкими фазами
- § 52. Равновесие между твердой и жидкой фазами; переохлаждение
- § 53. Равновесие трехфазной системы, состоящей из двух компонент
- § 54. Равновесие раствора соли с ее твердым гидратом
- § 55. Равновесие между двумя растворами различной концентрации
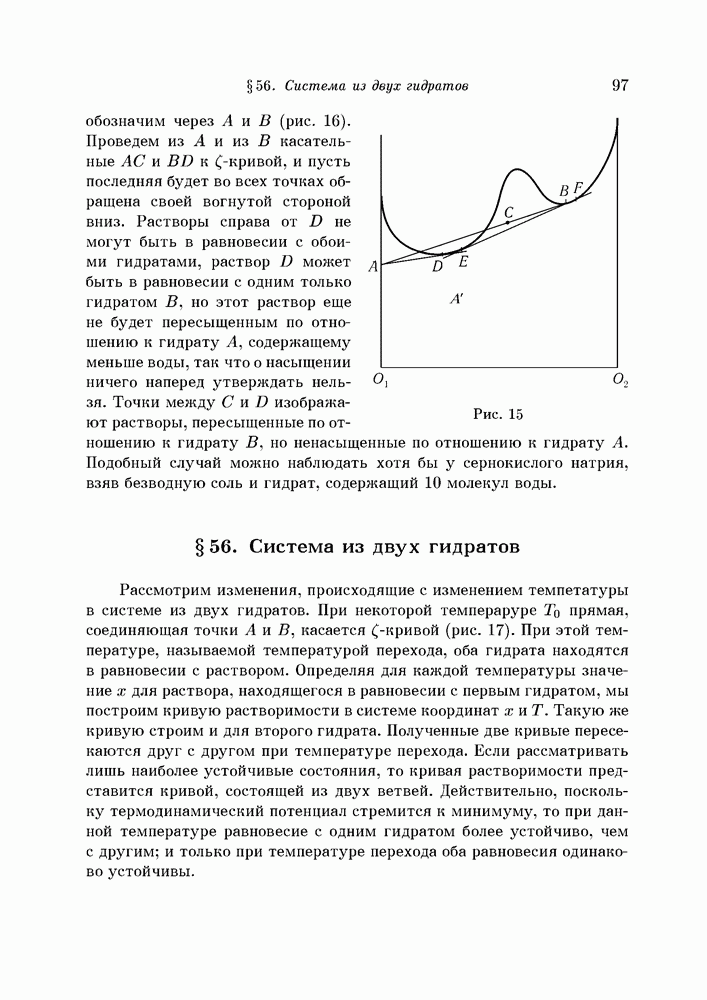
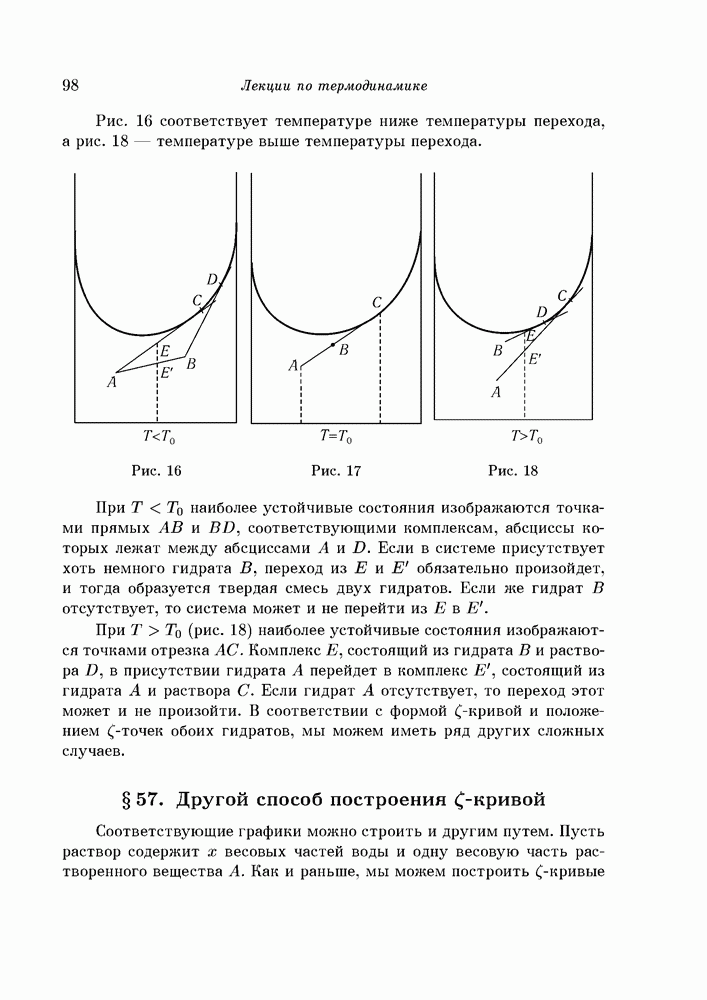
- § 56. Система из двух гидратов
- § 57. Другой способ построения кривой
- § 58. Трехкомпонентные системы
- § 59. Трехфазная система из трех компонент
- § 60. Форма поверхности
- § 61. Условия равновесия между твердой и жидкой фазами
- § 62. Равновесие двух твердых фаз с жидкими фазами
- § 63. Равновесие между двумя жидкими фазами
- § 64. Другие способы построения поверхности
- § 65. Смешанные кристаллы
- § 66. Равновесие между смесями и растворами
- § 67. Неопределенность в выражении термодинамического потенциала
- § 68. Смесь газов в поле силы тяжести
- § 69. Смешение и разделение двух газов
- § 70. Парадокс Гиббса
- § 71. Обобщение теоремы Гиббса на случай трех и более газов
- § 72. Уменьшение свободной энергии при смешении двух газов
- § 73. Свободная энергия жидкой смеси
- § 74. Общее выражение для свободной энергии смеси
- § 75. Случай, когда одна из компонент присутствует в весьма малом количестве
- § 76. Равновесие двух фаз, каждая из которых состоит из двух компонент
- § 77. Смесь под действием внешних сил
- § 78. Вывод уравнений равновесия
- § 79. Второй пример системы под действием внешних сил
- § 80. Осмотическое давление. Закон вант-Гоффа
- § 81. Другой вывод закона вант-Гоффа
- § 82. Общие условия равновесия многофазных систем
- § 83. Равновесие трех фаз
- § 84. Вывод условий равновесия с помощью термодинамического потенциала
- § 85. Число независимых условий равновесия
- § 86. Сравнение между собой двух состояний равновесия
- § 87. Общее соотношение между двумя состояниями равновесия
- § 88. Смысл полученного соотношения
- § 89. Добавление некоторого весьма малого количества новой компоненты
- § 90. Несколько заключительных замечаний
- § 91. Диссоциация газа
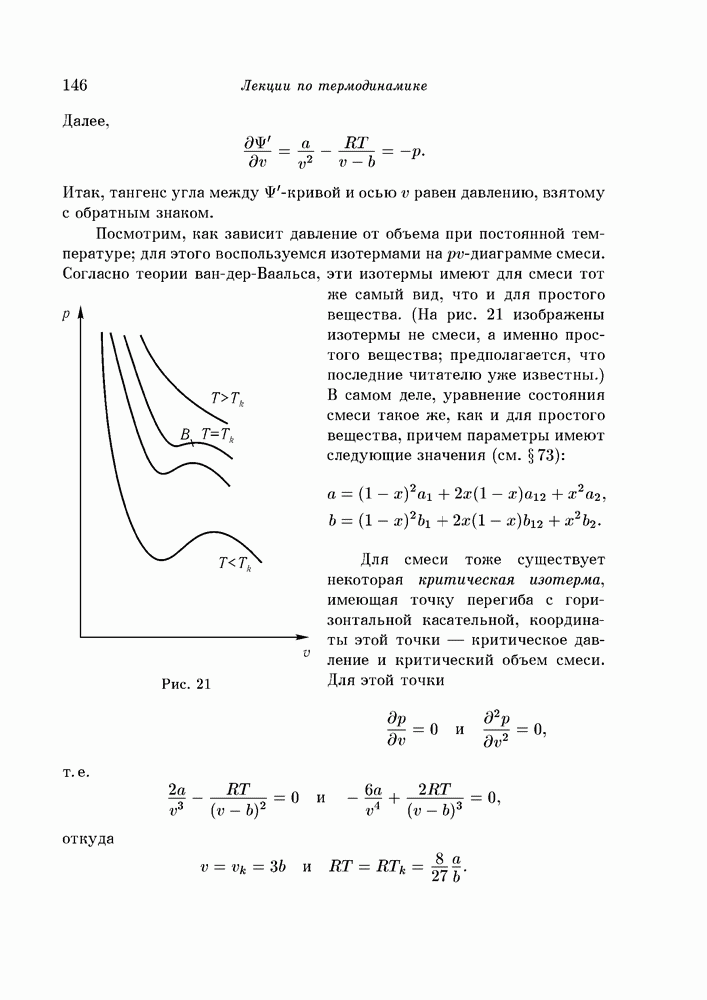
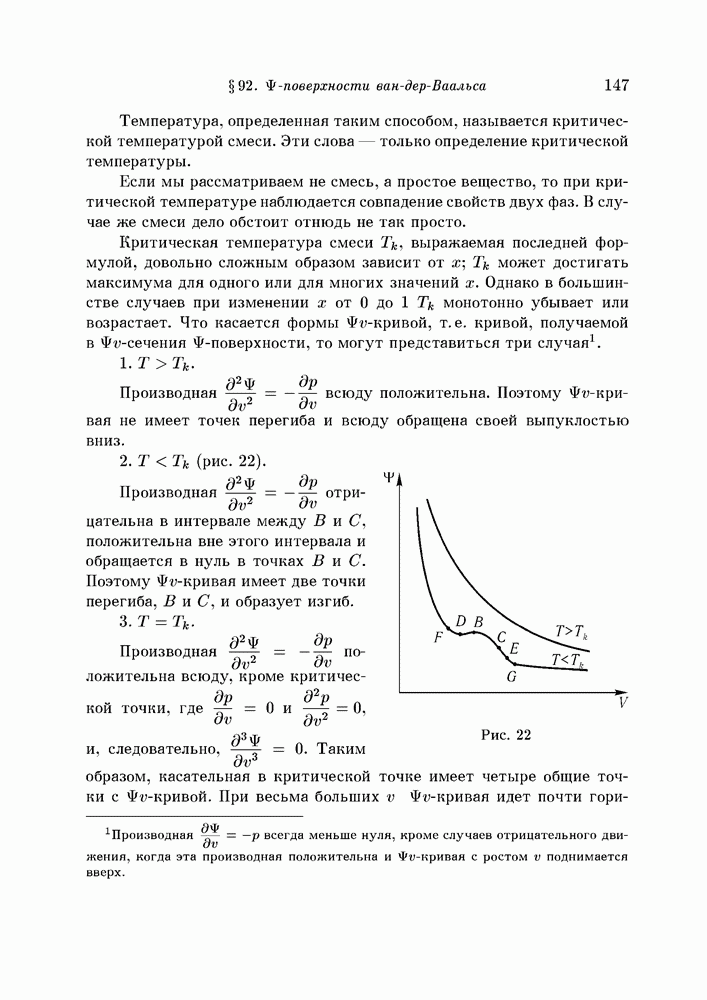
- § 92. поверхности ван-дер-Ваальса
- § 93. Изменение формы поверхности с температурой
- § 94. Сечения Ф-поверхности
- § 95. Условия равновесия
- § 96. Сосуществующие фазы
- § 97. Математическая теория конечных точек складки
- § 98. Исследование Ф-поверхности в окрестности конечной точки складки
- § 99. Конечная точка складки первого рода
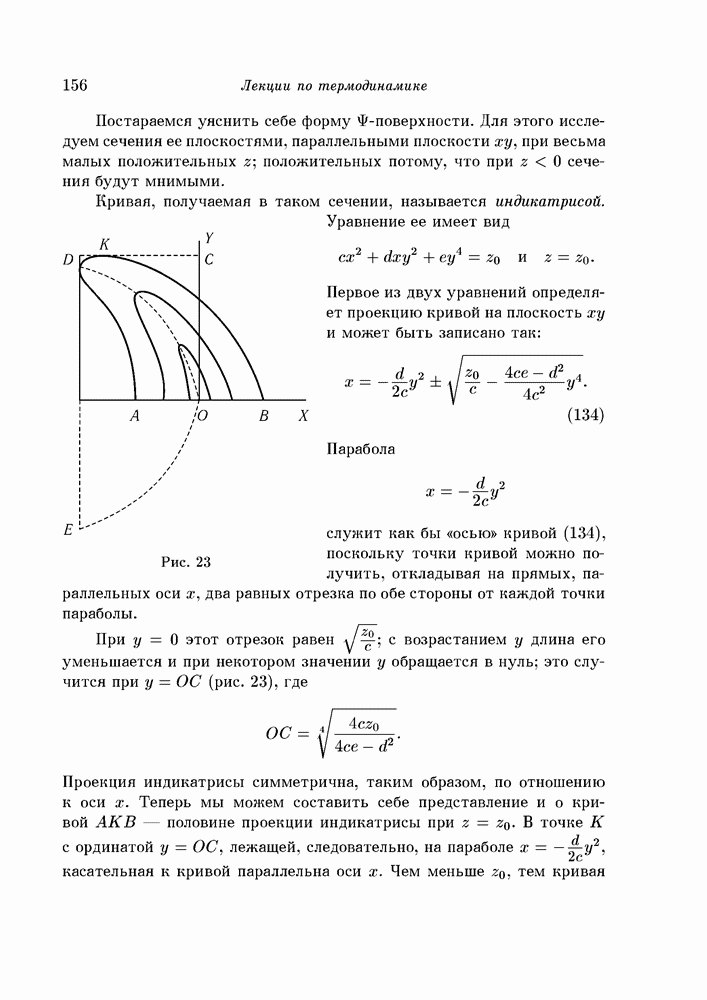
- § 100. Индикатриса, бинодаль и спинодаль
- § 101. Определение координат конечной точки складки непосредственно из самого уравнения Ф-поверхности
- § 102. Кривая конечных точек складки
- § 103. Изменение давления при бесконечно малом изменении состояния
- § 104. Зависимость давления от состава смеси
- § 105. Изобары
- § 106. Изотермическое сжатие смесей
- § 107. Обратная конденсация