| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.2. Оже-переходы
11.2.1. Система обозначений
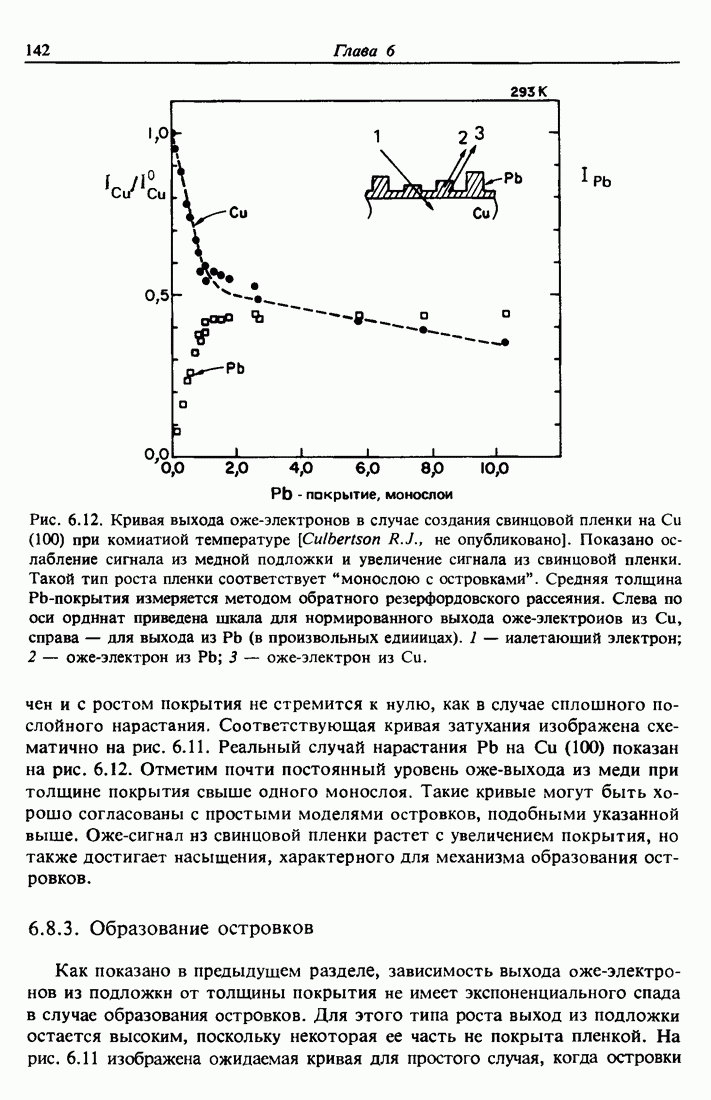
Обозначения, используемые при описании оже-процессов, показаны на рис. 11.1. В случае вакансий в  -оболочке оже-процесс начинается, когда электрон с более удаленной оболочки, например
-оболочке оже-процесс начинается, когда электрон с более удаленной оболочки, например  (дипольные правила отбора
(дипольные правила отбора

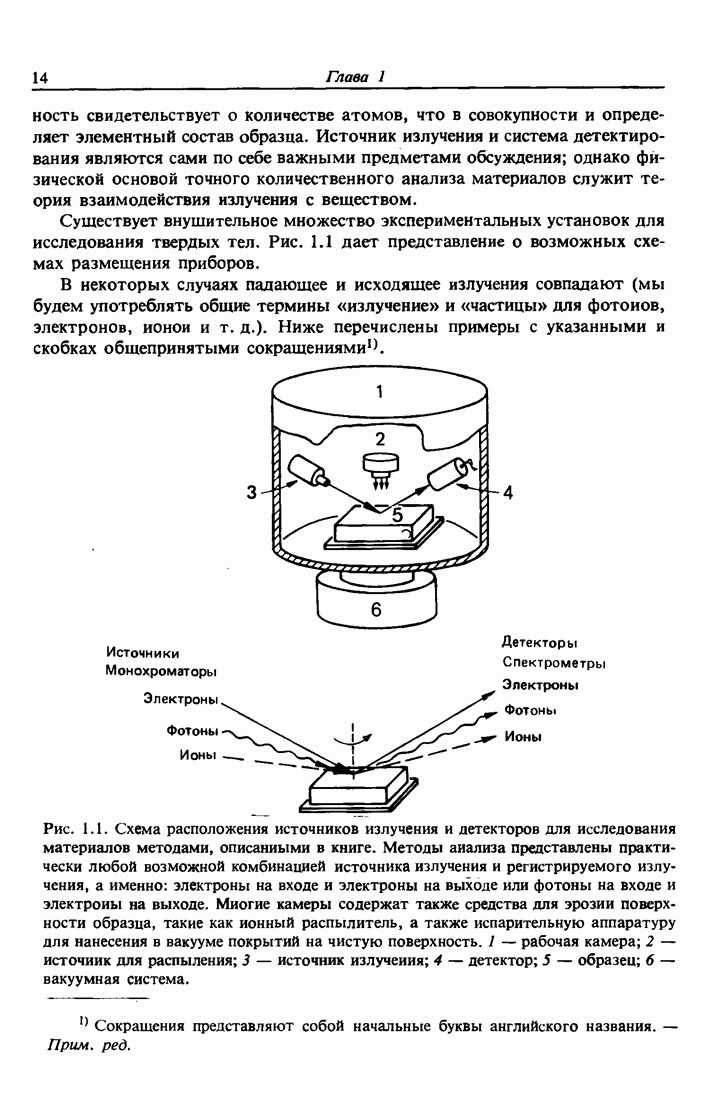
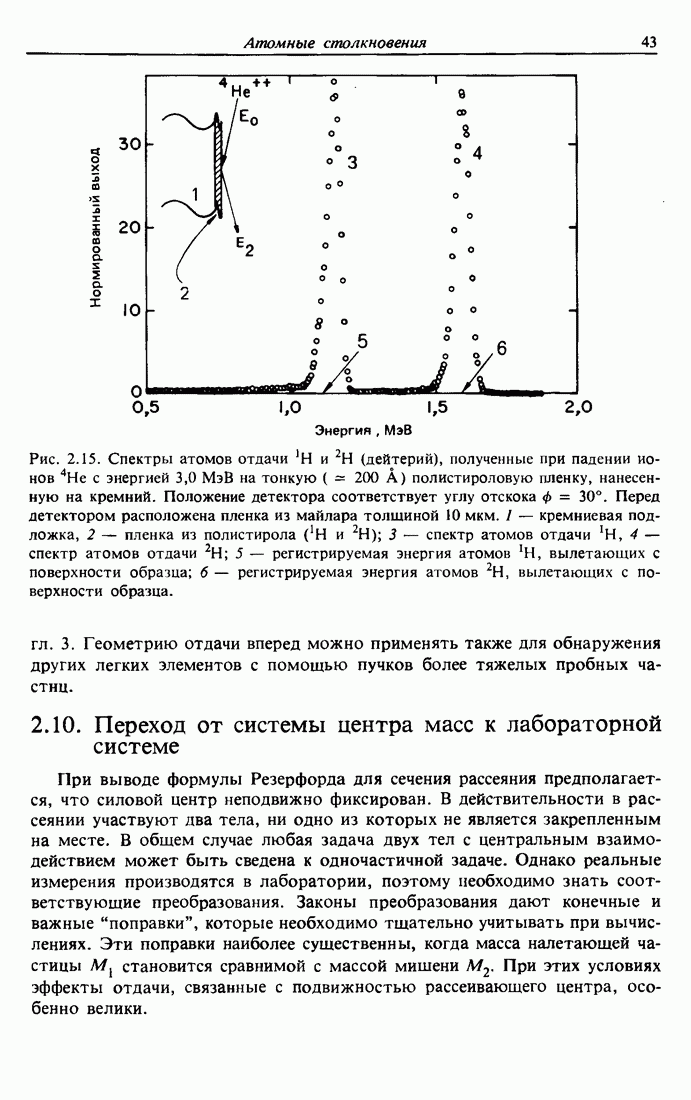
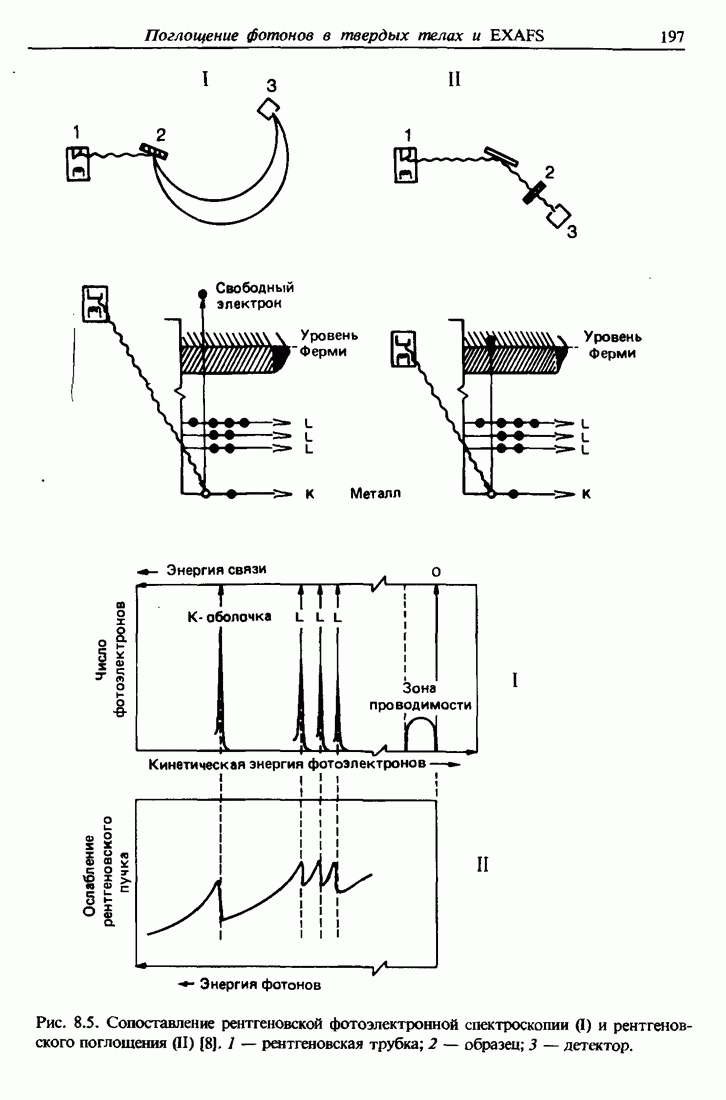
Рис. 11.1. Схематическое представление различных двухэлектронных процессов снятия возбуждения. Оже-переход  соответствует первоначальной дырке в К-оболочке, которая заполняется электроном с
соответствует первоначальной дырке в К-оболочке, которая заполняется электроном с  -оболочки, и одновременно другой
-оболочки, и одновременно другой  -электрон выбрасывается в вакуум. Оже-переход LMXMX соответствует процессу с первоначальной 2 s-вакаисией. Переход Костера — Кронига
-электрон выбрасывается в вакуум. Оже-переход LMXMX соответствует процессу с первоначальной 2 s-вакаисией. Переход Костера — Кронига  отвечает первоначальной дырке в
отвечает первоначальной дырке в  -оболочке, которая заполняется электроном с той же самой оболочке (но другой подоболочки
-оболочке, которая заполняется электроном с той же самой оболочке (но другой подоболочки  ).
).
не работают), заполняет дырку. Высвободившаяся энергия может быть передана другому электрону, например другому или  электрону, который при этом выбрасывается из атома. Энергия вылетающего электрона равна
электрону, который при этом выбрасывается из атома. Энергия вылетающего электрона равна  . Описываемый процесс называют KLL оже-переходом, или, более подробно,
. Описываемый процесс называют KLL оже-переходом, или, более подробно,  или
или  . Если вакансии содержатся в
. Если вакансии содержатся в  -оболочке, то имеют место процессы, при которых электрон М-оболочки (
-оболочке, то имеют место процессы, при которых электрон М-оболочки ( -электрон) заполняет
-электрон) заполняет  -дырку, а другой электрон
-дырку, а другой электрон  -оболочки (например,
-оболочки (например,  -электрон) выбрасывается; такой переход называется переходом
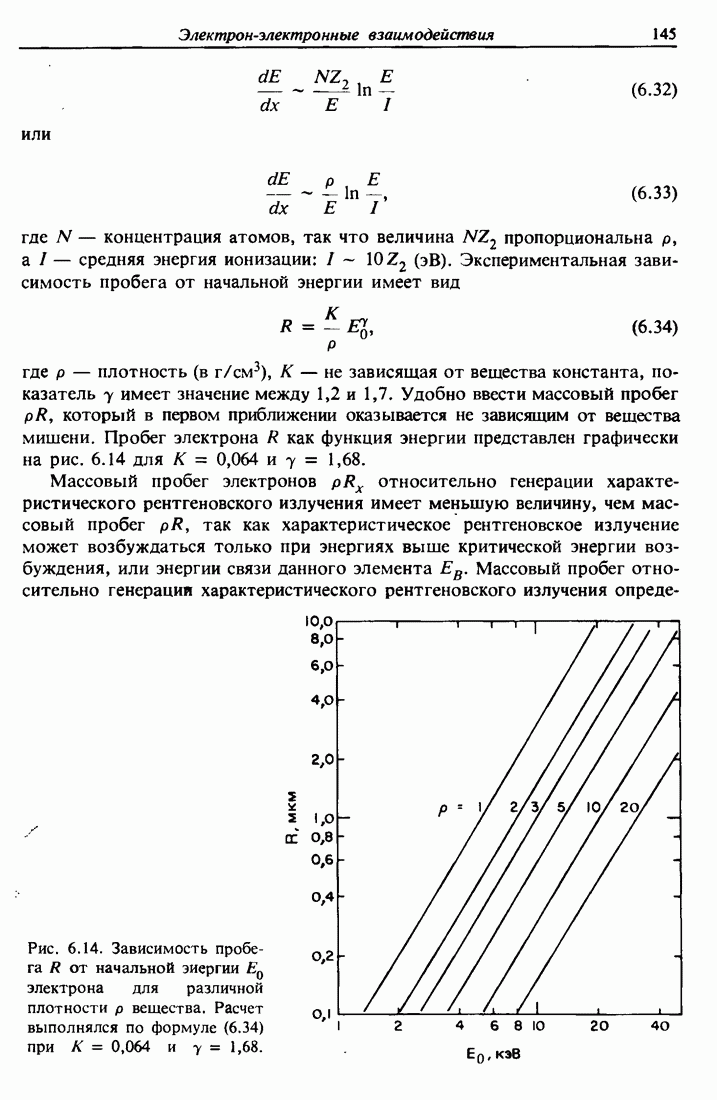
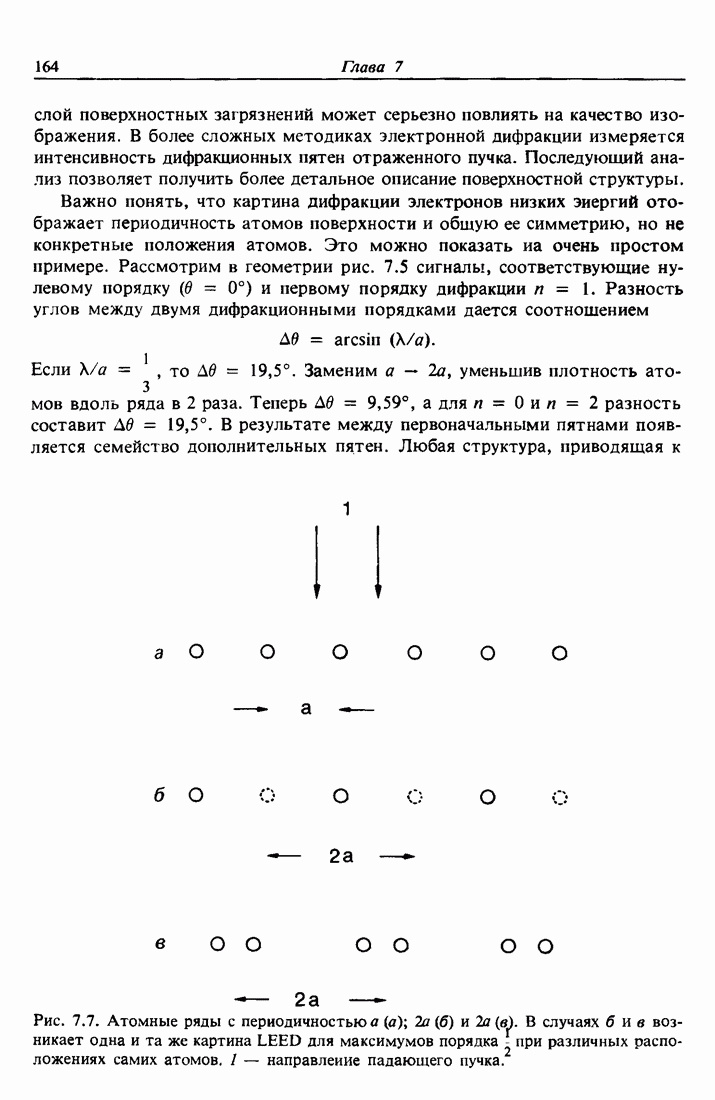
-электрон) выбрасывается; такой переход называется переходом  Поскольку электрон-электронные взаимодействия наиболее сильны между электронами, орбитали которых ближе расположены друг к другу, наиболее сильными оже-переходами являются переходы типа KLL или LMM. При переходах Костера — Кронига вакансия заполняется электронами, приходящими с той же самой оболочки, поэтому они обозначаются, например, LLM. Оже-переходы, вовлекающие самые отдаленные орбитали, валентную зону, имеют энергетическую ширину, примерно в два раза превышающую ширину валентной зоны. На рис. 11.2 показаны оже-переходы
Поскольку электрон-электронные взаимодействия наиболее сильны между электронами, орбитали которых ближе расположены друг к другу, наиболее сильными оже-переходами являются переходы типа KLL или LMM. При переходах Костера — Кронига вакансия заполняется электронами, приходящими с той же самой оболочки, поэтому они обозначаются, например, LLM. Оже-переходы, вовлекающие самые отдаленные орбитали, валентную зону, имеют энергетическую ширину, примерно в два раза превышающую ширину валентной зоны. На рис. 11.2 показаны оже-переходы  (или LVV), где -
(или LVV), где - 

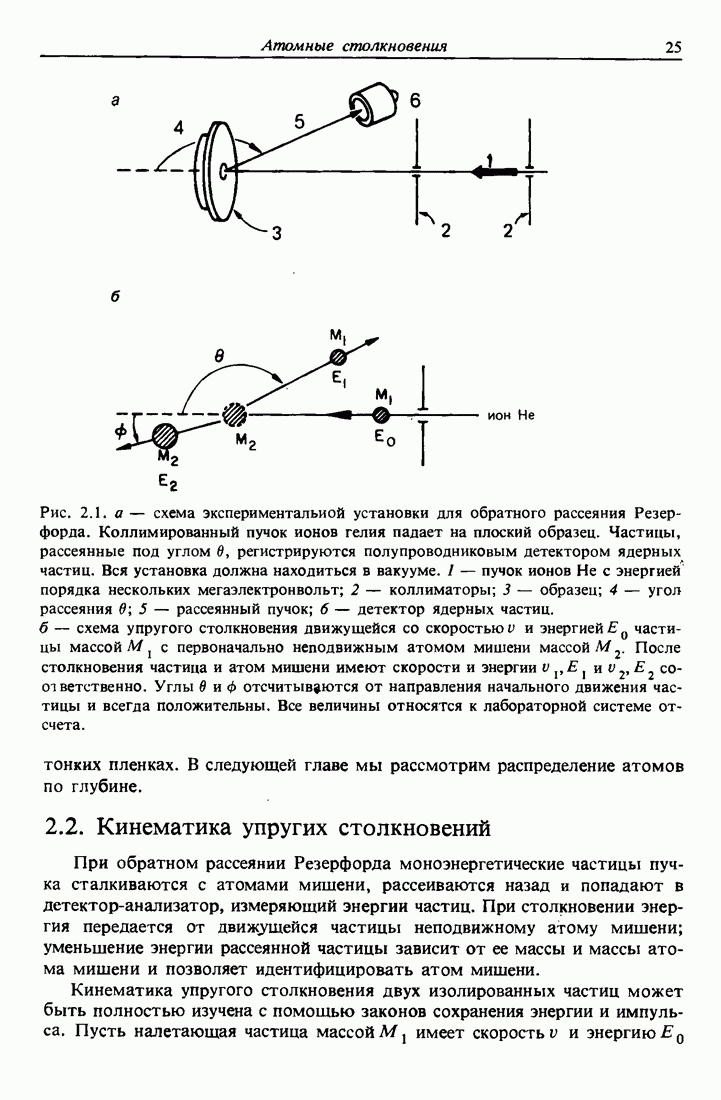
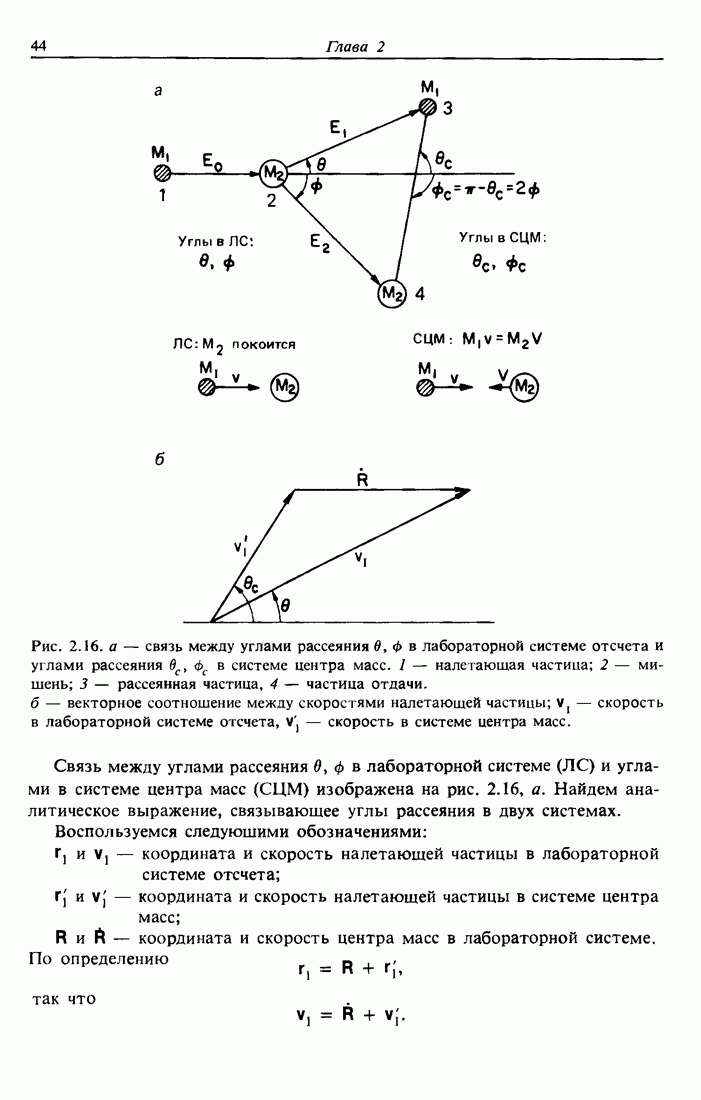
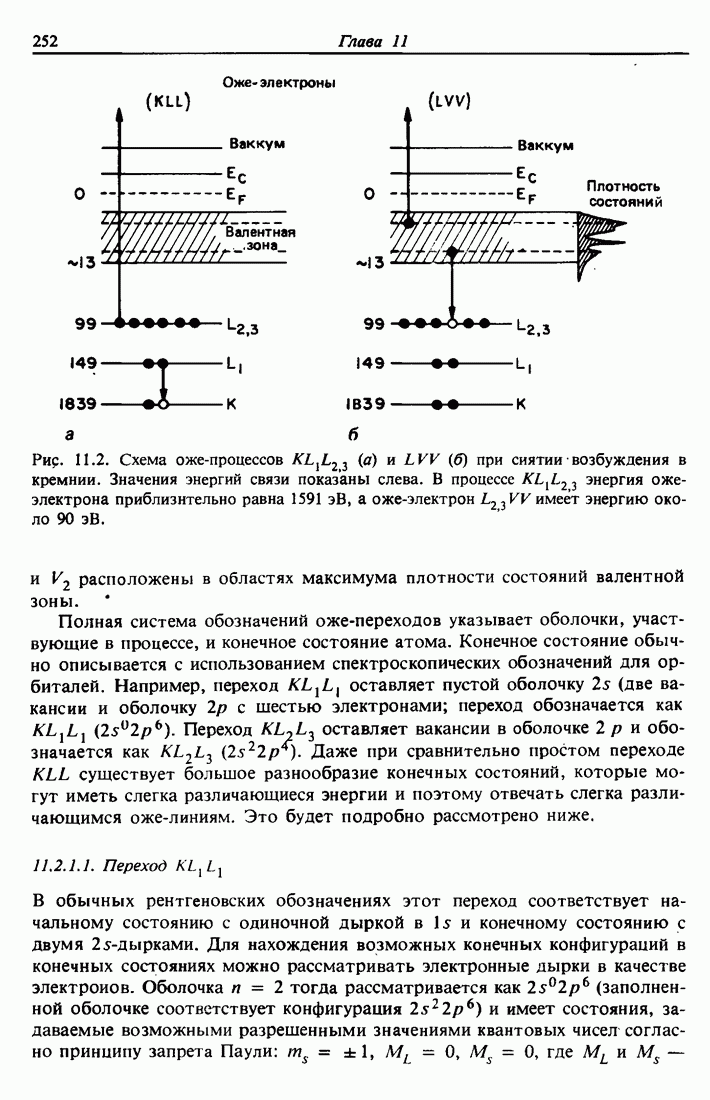
Рис. 11.2. Схема оже-процессов  (а) и LVV (б) при снятии возбуждения в кремнии. Значения энергий связи показаны слева. В процессе
(а) и LVV (б) при снятии возбуждения в кремнии. Значения энергий связи показаны слева. В процессе  энергия оже-электрона приблизительно равна 1591 эВ, а оже-электрон
энергия оже-электрона приблизительно равна 1591 эВ, а оже-электрон  имеет энергию около 90 эВ.
имеет энергию около 90 эВ.
и  расположены в областях максимума плотности состояний валентной зоны.
расположены в областях максимума плотности состояний валентной зоны.
Полная система обозначений оже-переходов указывает оболочки, участвующие в процессе, и конечное состояние атома. Конечное состояние обычно описывается с использованием спектроскопических обозначений для орбиталей. Например, переход KLXLX оставляет пустой оболочку  (две вакансии и оболочку 2р с шестью электронами; переход обозначается как KLXLX (
(две вакансии и оболочку 2р с шестью электронами; переход обозначается как KLXLX ( ). Переход
). Переход  оставляет вакансии в оболочке 2р и обозначается как
оставляет вакансии в оболочке 2р и обозначается как  . Даже при сравнительно простом переходе KLL существует большое разнообразие конечных состояний, которые могут иметь слегка различающиеся энергии и поэтому отвечать слегка различающимся оже-линиям. Это будет подробно рассмотрено ниже.
. Даже при сравнительно простом переходе KLL существует большое разнообразие конечных состояний, которые могут иметь слегка различающиеся энергии и поэтому отвечать слегка различающимся оже-линиям. Это будет подробно рассмотрено ниже.
11.2.1.1. Переход KLXLX
В обычных рентгеновских обозначениях этот переход соответствует начальному состоянию с одиночной дыркой в  и конечному состоянию с двумя
и конечному состоянию с двумя  -дырками. Для нахождения возможных конечных конфигураций в конечных состояниях можно рассматривать электронные дырки в качестве электронов. Оболочка
-дырками. Для нахождения возможных конечных конфигураций в конечных состояниях можно рассматривать электронные дырки в качестве электронов. Оболочка  тогда рассматривается как
тогда рассматривается как  (заполненной оболочке соответствует конфигурация
(заполненной оболочке соответствует конфигурация  ) и имеет состояния, задаваемые возможными разрешенными значениями квантовых чисел согласно принципу запрета Паули:
) и имеет состояния, задаваемые возможными разрешенными значениями квантовых чисел согласно принципу запрета Паули:  где
где  и
и  —
—
полный орбитальный и спиновый моменты соответственно. Обозначение  указывает на состояние с нулевым полным орбитальным моментом (S). Подходящая запись для этого перехода
указывает на состояние с нулевым полным орбитальным моментом (S). Подходящая запись для этого перехода  хотя конечное состояние
хотя конечное состояние  является единственно возможным и в этом случае обозначение несколько излишне.
является единственно возможным и в этом случае обозначение несколько излишне.
11.2.1.2. Переходы
В этом случае конфигурация конечного электронного состояния записывается как  Возможными квантовыми состояниями являются
Возможными квантовыми состояниями являются  где Р обозначает полный орбитальный момент. Они соответствуют двум состояниям с полным угловым моментом
где Р обозначает полный орбитальный момент. Они соответствуют двум состояниям с полным угловым моментом  , т. е. Р-состоянию с параллельным спином
, т. е. Р-состоянию с параллельным спином  и антипараллельным спином
и антипараллельным спином  .
.
11.2.1.3. Переходы
Конечные состояния в этом случае могут получаться в результате связи полных орбитальных моментов  с различными возможными ориентациями спина, которая приводит к состояниям
с различными возможными ориентациями спина, которая приводит к состояниям  .
.
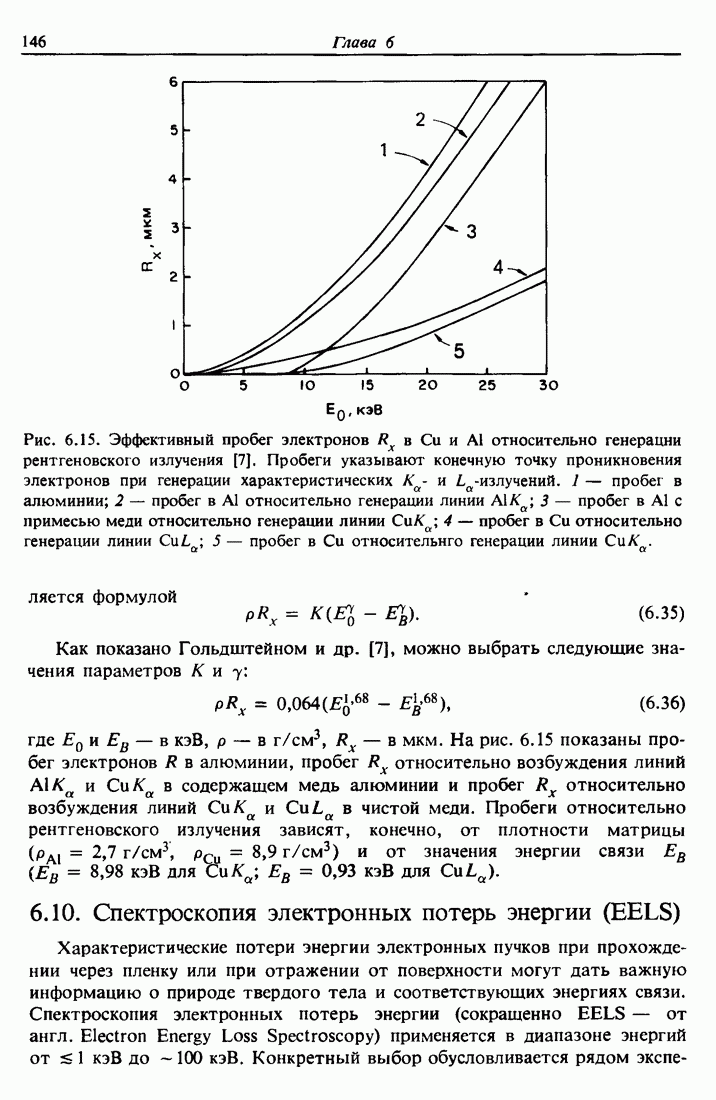
Таким образом, в переходах типа KLL могут быть шесть конечных состояний:

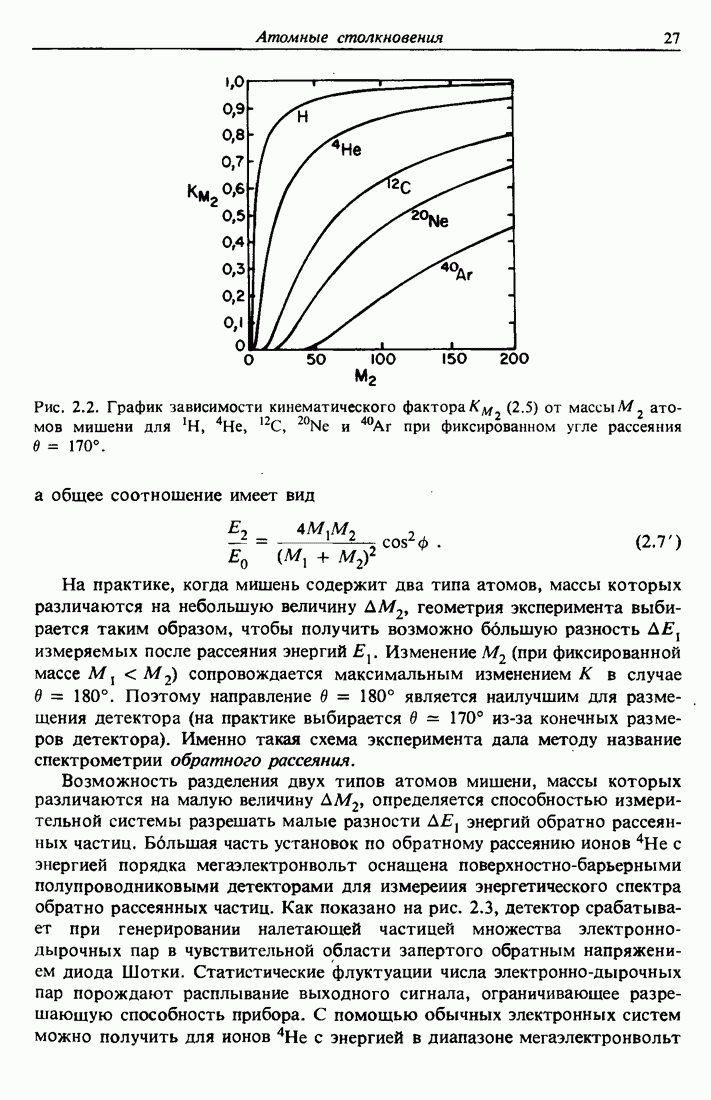
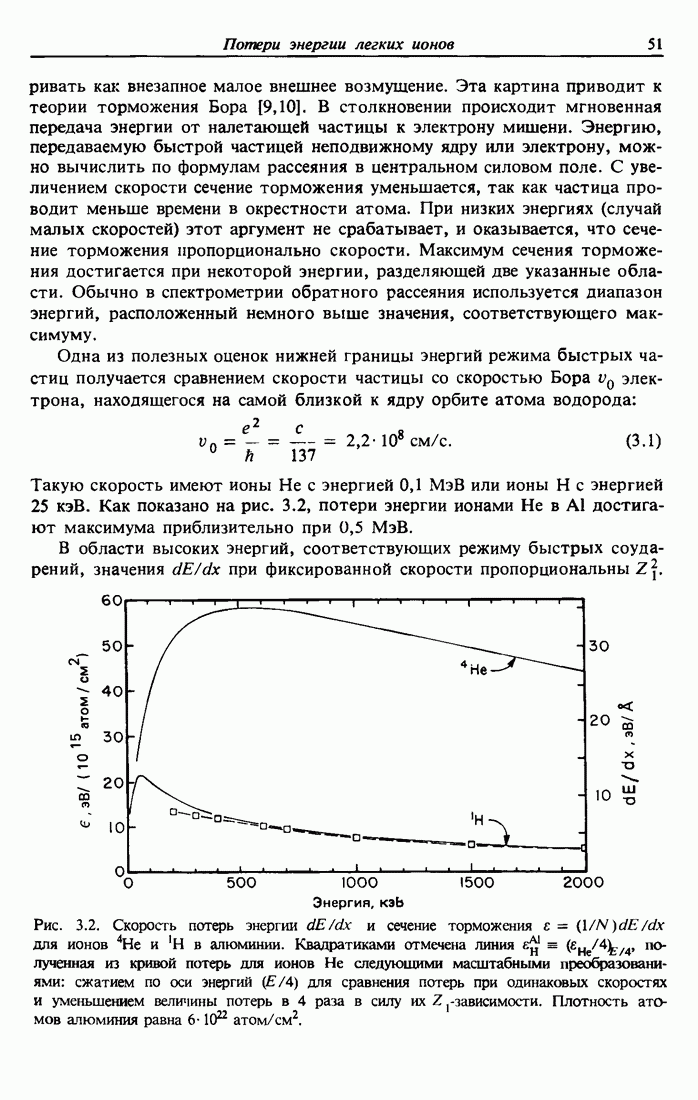
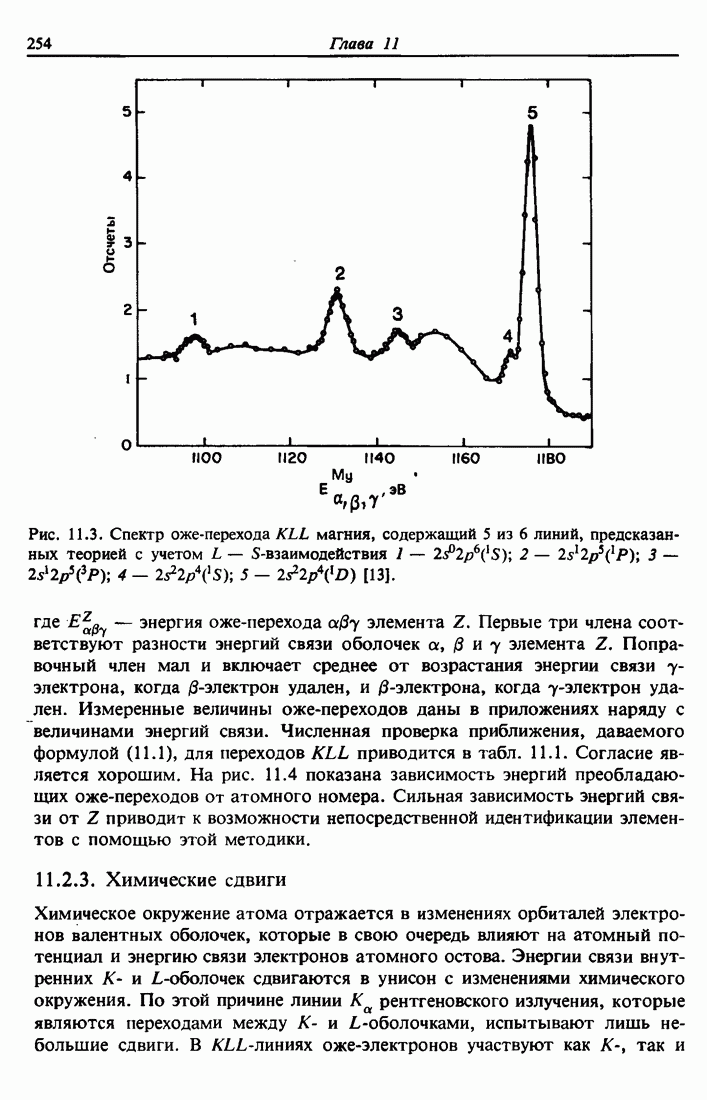
Экспериментальные результаты для магния, где показаны эти конечные состояния, приведены на рис. 11.3. [Фактически состояние  не наблюдается из-за недостаточной интенсивности.]
не наблюдается из-за недостаточной интенсивности.]
11.2.2. Энергии
Энергия оже-электронов в принципе может быть определена таким же способом, как и для рентгеновского излучения: по разности полный энергий до и после перехода. Эмпирически это можно сделать, например, с помощью соотношения


Рис. 11.3. Спектр оже-перехода KLL магния, содержащий 5 из 6 линий, предсказанных теорией с учетом L — S-взаимодействия 1 —  [13].
[13].
где  — энергия оже-перехода
— энергия оже-перехода  элемента Z. Первые три члена соответствуют разности энергий связи оболочек а,
элемента Z. Первые три члена соответствуют разности энергий связи оболочек а,  и
и  элемента Z. Поправочный член мал и включает среднее от возрастания энергии связи
элемента Z. Поправочный член мал и включает среднее от возрастания энергии связи  -электрона, когда
-электрона, когда  -электрон удален, и
-электрон удален, и  -электрона, когда
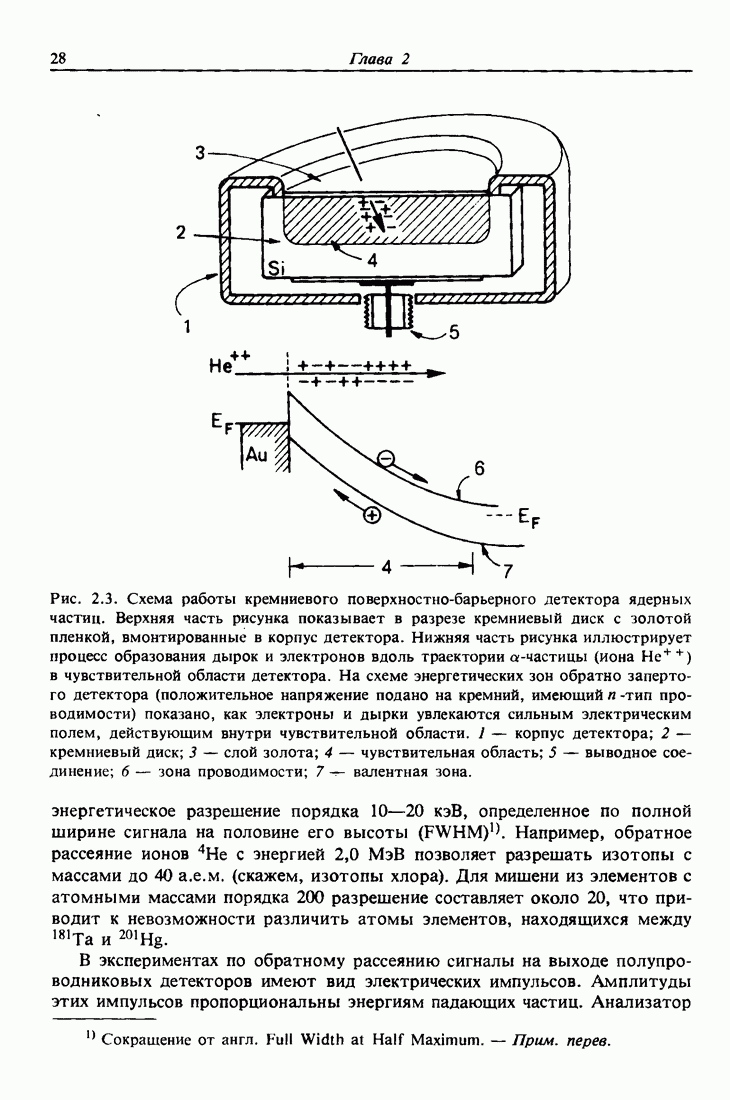
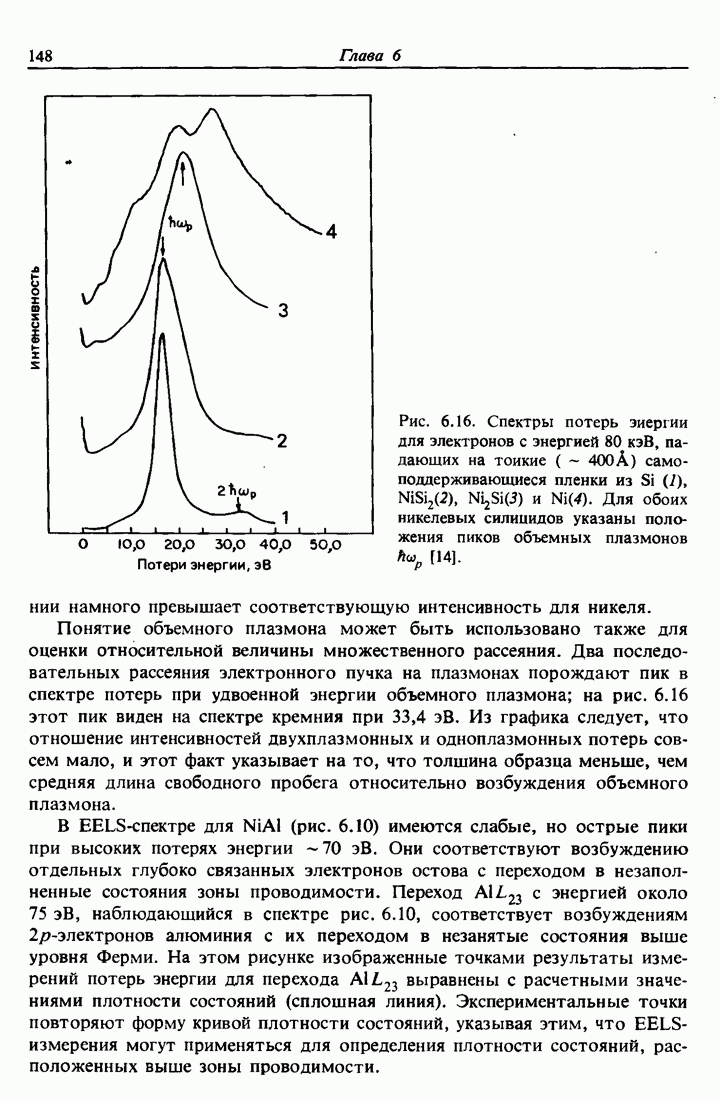
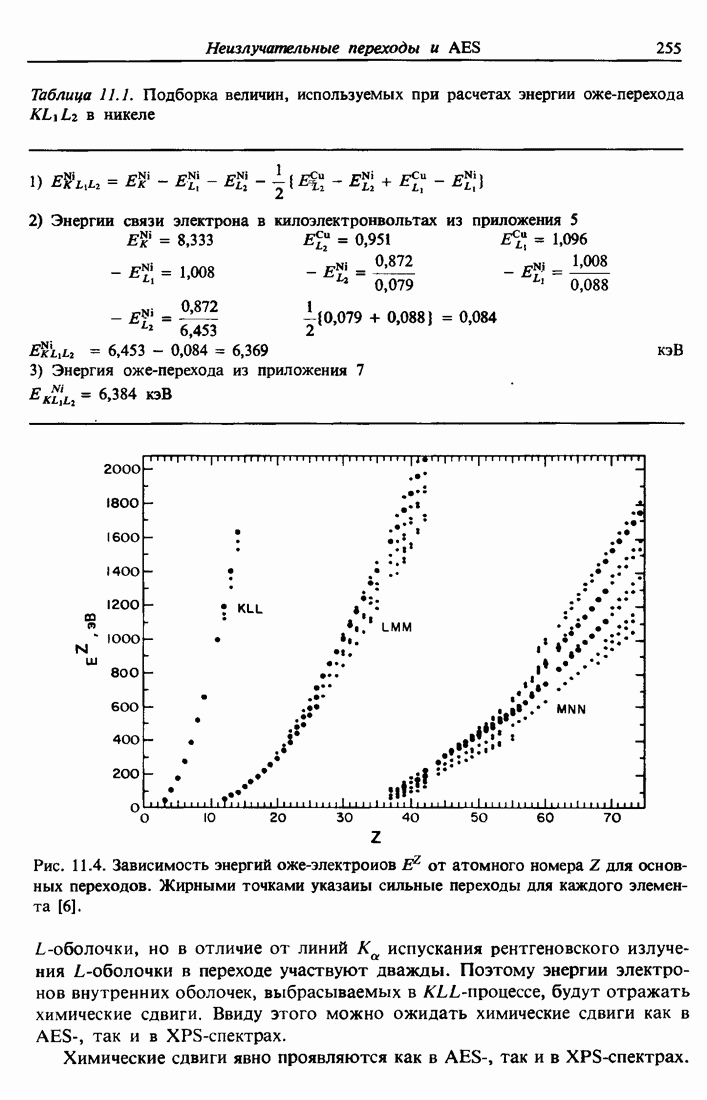
-электрона, когда  -электрон удален. Измеренные величины оже-переходов даны в приложениях наряду с величинами энергий связи. Численная проверка приближения, даваемого формулой (11.1), для переходов KLL приводится в табл. 11.1. Согласие является хорошим. На рис. 11.4 показана зависимость энергий преобладающих оже-переходов от атомного номера. Сильная зависимость энергий связи от Z приводит к возможности непосредственной идентификации элементов с помощью этой методики.
-электрон удален. Измеренные величины оже-переходов даны в приложениях наряду с величинами энергий связи. Численная проверка приближения, даваемого формулой (11.1), для переходов KLL приводится в табл. 11.1. Согласие является хорошим. На рис. 11.4 показана зависимость энергий преобладающих оже-переходов от атомного номера. Сильная зависимость энергий связи от Z приводит к возможности непосредственной идентификации элементов с помощью этой методики.
11.2.3. Химические сдвиги
Химическое окружение атома отражается в изменениях орбиталей электронов валентных оболочек, которые в свою очередь влияют на атомный потенциал и энергию связи электронов атомного остова. Энергии связи внутренних К- и L-оболочек сдвигаются в унисон с изменениями химического окружения. По этой причине линии К рентгеновского излучения, которые являются переходами между К- и L-оболочками, испытывают лишь небольшие сдвиги. В KLL-линиях оже-электронов участвуют как  так и
так и
Таблица 11.1. Подборка величин, используемых при расчетах энергии оже-перехода  в никеле
в никеле


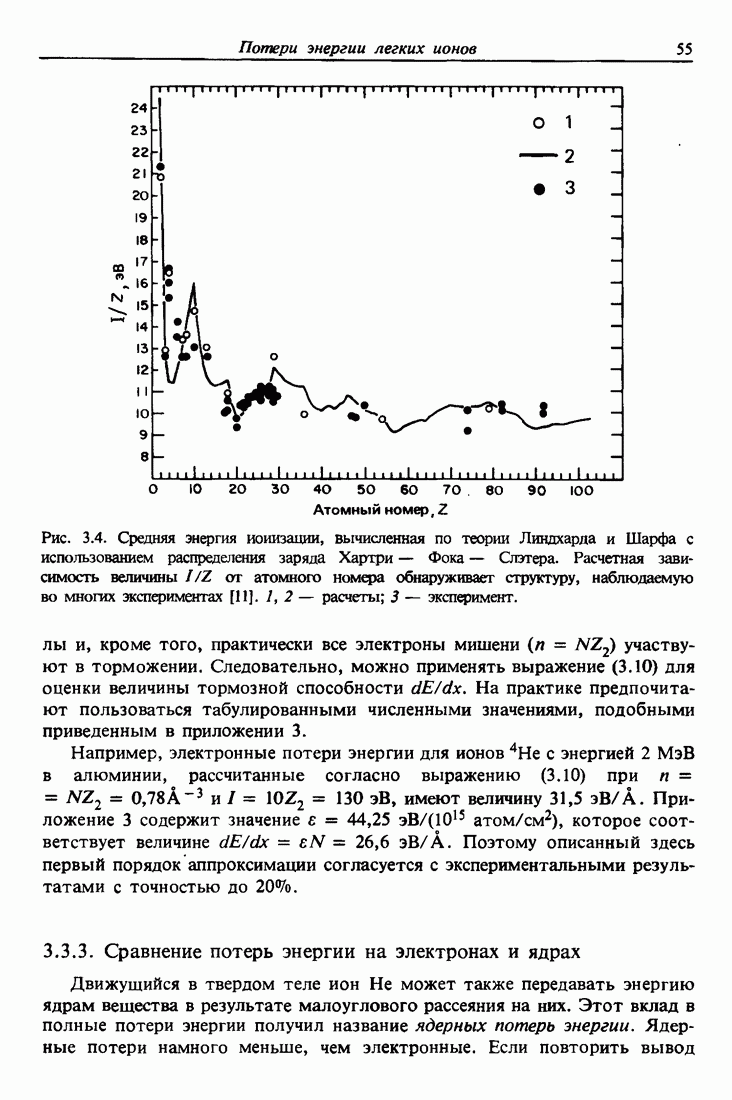
Рис. 11.4. Зависимость энергий оже-электронов  от атомного номера Z для основных переходов. Жирными точками указаны сильные переходы для каждого элемента [6].
от атомного номера Z для основных переходов. Жирными точками указаны сильные переходы для каждого элемента [6].
L-оболочки, но в отличие от линий  испускания рентгеновского излучения
испускания рентгеновского излучения  -оболочки в переходе участвуют дважды. Поэтому энергии электронов внутренних оболочек, выбрасываемых в
-оболочки в переходе участвуют дважды. Поэтому энергии электронов внутренних оболочек, выбрасываемых в  -процессе, будут отражать химические сдвиги. Ввиду этого можно ожидать химические сдвиги как в
-процессе, будут отражать химические сдвиги. Ввиду этого можно ожидать химические сдвиги как в  так и в
так и в  -спектрах.
-спектрах.
Химические сдвиги явно проявляются как в  так и в XPS-спектрах.
так и в XPS-спектрах.
Однако в двухэлектронных оже-процессах химические сдвиги интерпретировать немного труднее, чем в одноэлектронных фотоэлектрических процессах. Кроме того, оже-линии более широки, чем XPS-линии. В результате этого именно последняя методика обычно используется для исследования изменений в химических связях.
11.2.4. Расчет вероятности KLL-переходов в водородоподобном атоме
Вероятность перехода  для эффекта Оже может быть записана известным образом:
для эффекта Оже может быть записана известным образом:

где  — плотность состояний с нормировкой в ящике объемом V. Состояния водородоподобного атома для оже-переходов KLL имеют вид
— плотность состояний с нормировкой в ящике объемом V. Состояния водородоподобного атома для оже-переходов KLL имеют вид

Эти волновые функции описывают соответственно электроны в состояниях 2 р, 1 s, 2 р и свободный электрон, где  — боровский радиус. Для удобства эти выражения можно переписать в виде функции от
— боровский радиус. Для удобства эти выражения можно переписать в виде функции от  :
:


а потенциал в виде
 (11.7)
(11.7)
В данном расчете мы рассматриваем оже-переход  переход электрона 2 р-оболочки
переход электрона 2 р-оболочки  в состояние
в состояние  и последующее испускание другого 2 р-электрона
и последующее испускание другого 2 р-электрона  в свободное состояние. В этой водородоподобной модели энергия оже-электрона
в свободное состояние. В этой водородоподобной модели энергия оже-электрона  равна
равна

где  — энергии связи соответственно К- и
— энергии связи соответственно К- и  -оболочек, причем
-оболочек, причем  в боровской модели. В водородоподобной модели
в боровской модели. В водородоподобной модели

и

поэтому

где было использовано соотношение Бора  . Отсюда
. Отсюда

В этом выражении можно выделить общую зависимость вероятности перехода от атомных параметров, например от атомного номера Z. Подставляя  (в измененном виде) в формулу для вероятности перехода, находим
(в измененном виде) в формулу для вероятности перехода, находим

где  , и
, и

Величина F — это интеграл по всему пространству для  который представляет собой матричный элемент потенциального множителя
который представляет собой матричный элемент потенциального множителя  .
.
Вспомнив, что  и полагая
и полагая  можно записать вероятность перехода в виде
можно записать вероятность перехода в виде

где С — числовая постоянная, зависящая от различных факторов, влияющих на  и F. Замечая, что
и F. Замечая, что  получаем простое соотношение
получаем простое соотношение

где  — боровская скорость;
— боровская скорость;  — боровский радиус,
— боровский радиус,  — характерное атомное время. Интеграл F
— характерное атомное время. Интеграл F
Таблица 11.2. Сравнение скоростей оже-переходов и скоростей испускания рентегновского излучения К-линии

можно вычислить для грубого приближения  так что
так что  где
где  Данное приближение основано на том, что радиальная протяженность волновой функции
Данное приближение основано на том, что радиальная протяженность волновой функции  мала по сравнению с функцией
мала по сравнению с функцией  . Расчет величины С трудоемок, однако может быть выполнен непосредственно, что дает
. Расчет величины С трудоемок, однако может быть выполнен непосредственно, что дает  . Как следует из табл. 11.2, результат для
. Как следует из табл. 11.2, результат для  [формула (11.9)] не зависит от Z. В более полном расчете необходимо должным образом описать все различные пары эквивалентных электронов, участвующие в оже-процессе. Более точные расчеты могут быть выполнены численными методами с использованием более совершенных волновых функций и лучшего описания потенциала взаимодействия [1]. Главной особенностью вероятности оже-переходов является то, что они почти не зависят от Z в противоположность сильной зависимости от Z излучательных переходов.
[формула (11.9)] не зависит от Z. В более полном расчете необходимо должным образом описать все различные пары эквивалентных электронов, участвующие в оже-процессе. Более точные расчеты могут быть выполнены численными методами с использованием более совершенных волновых функций и лучшего описания потенциала взаимодействия [1]. Главной особенностью вероятности оже-переходов является то, что они почти не зависят от Z в противоположность сильной зависимости от Z излучательных переходов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
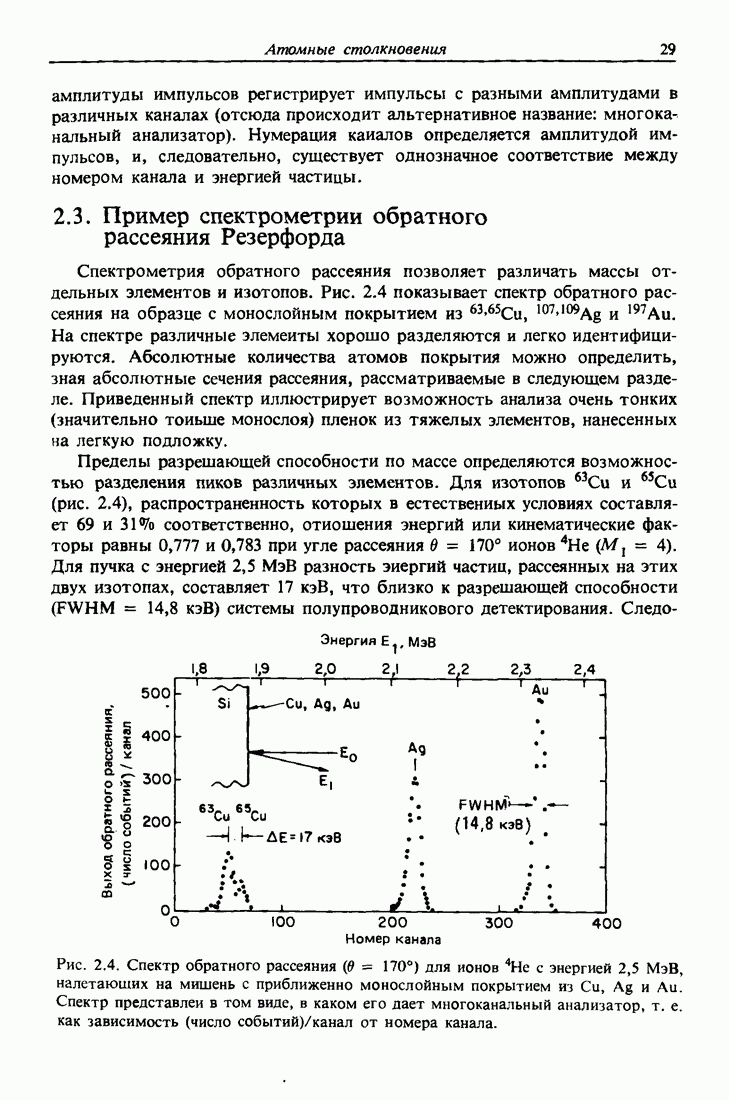
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
- 2.4. Сечение рассеяния и прицельный параметр
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
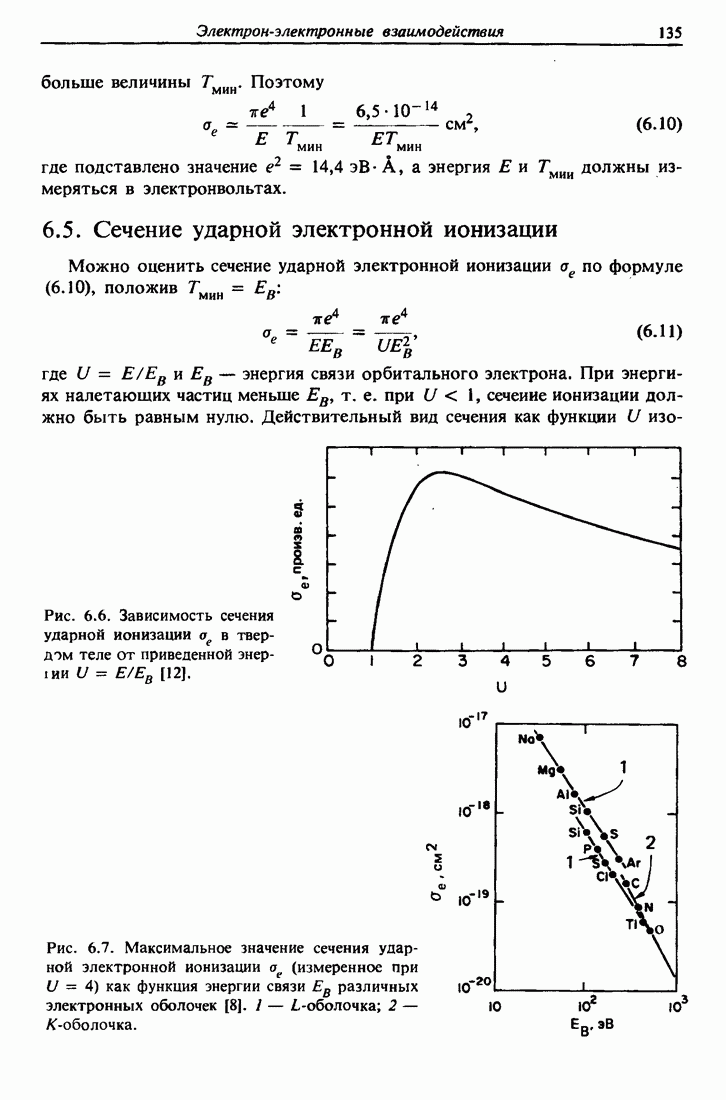
- 6.5. Сечение ударной электронной ионизации
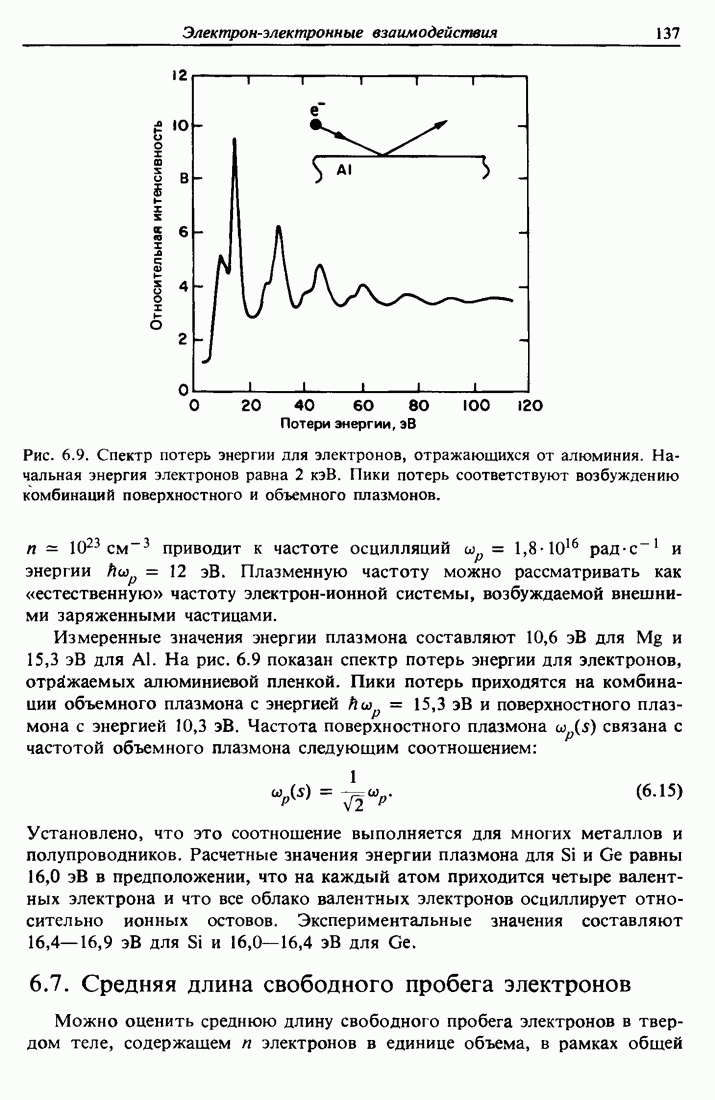
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
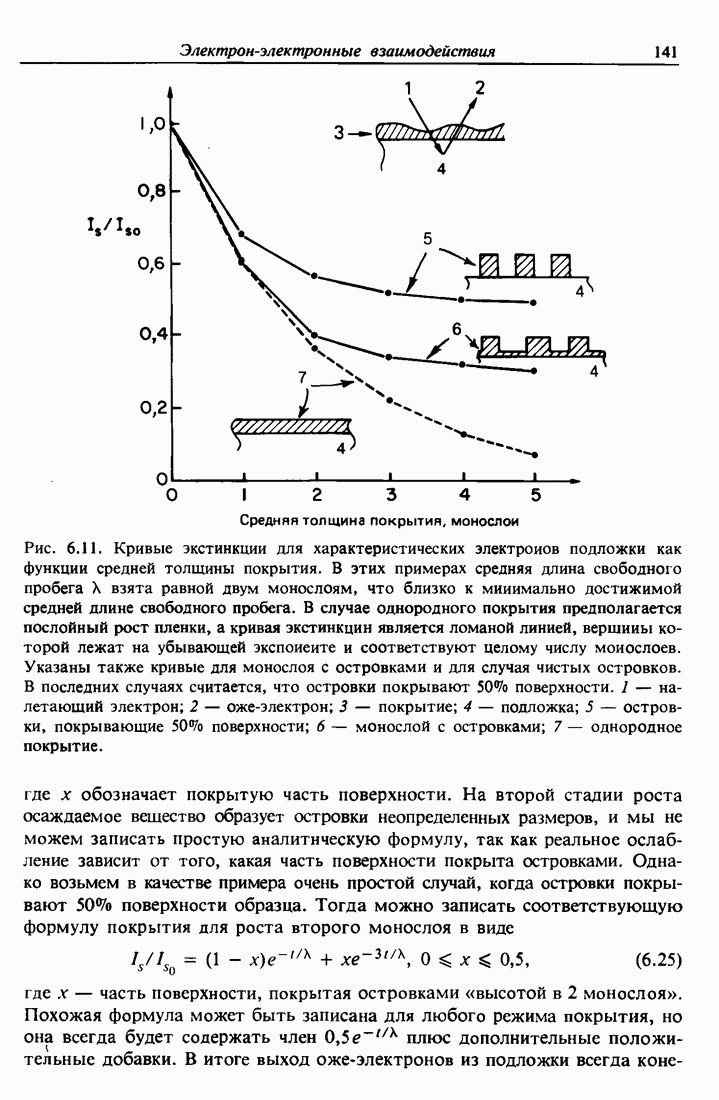
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
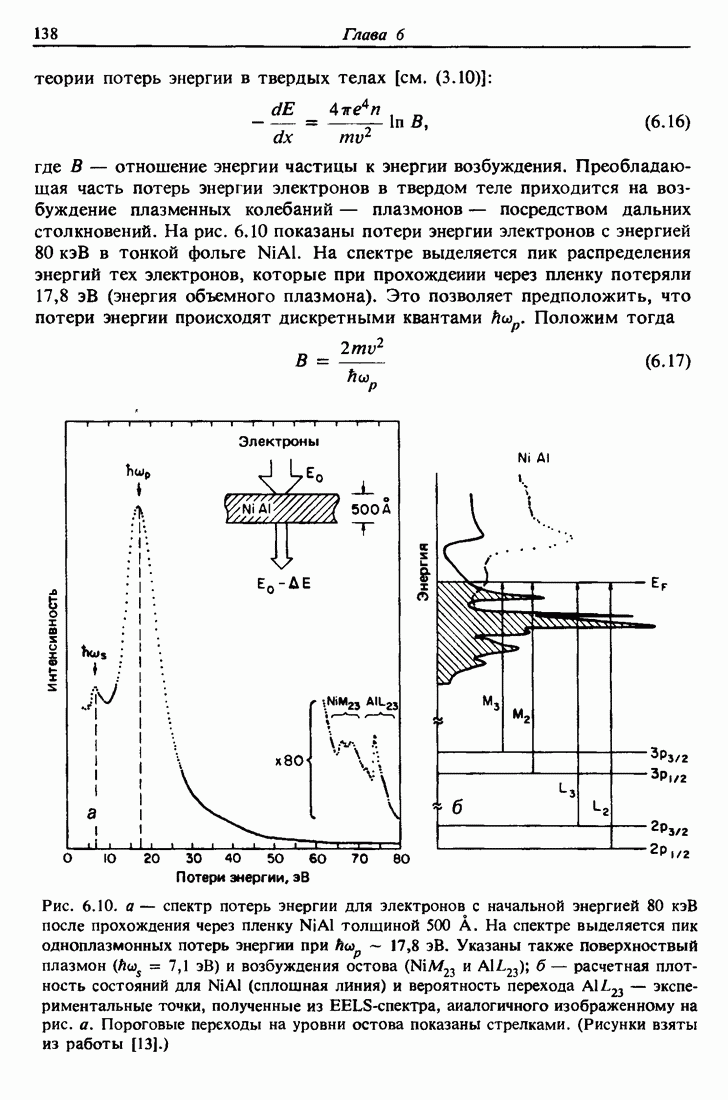
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
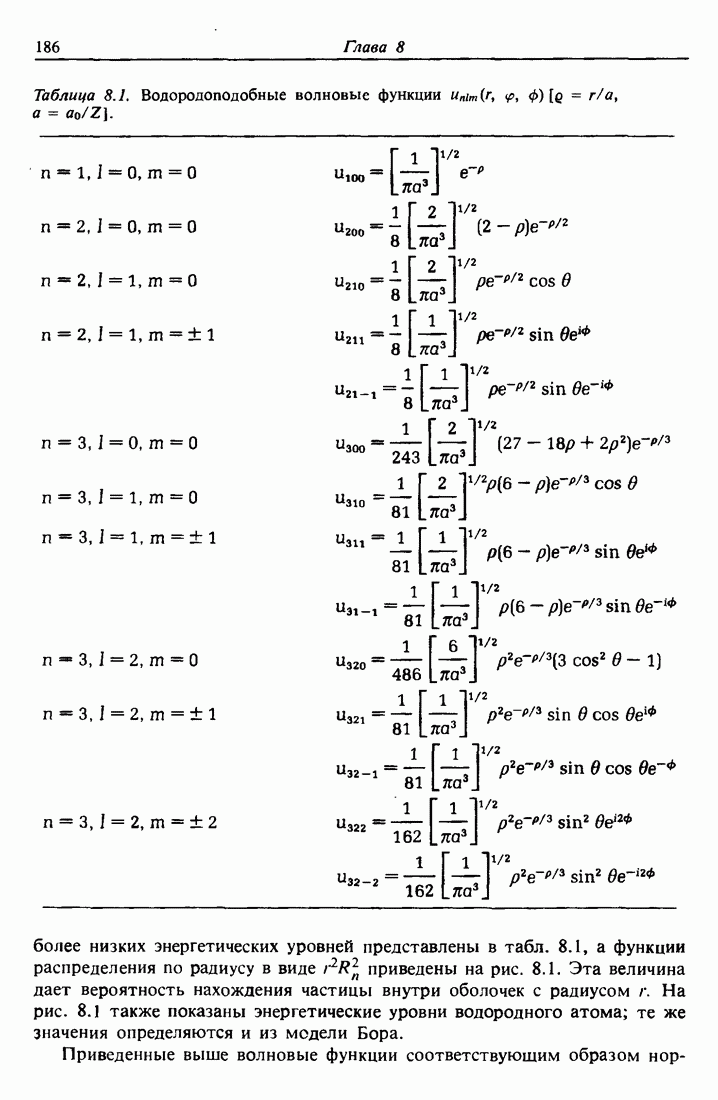
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
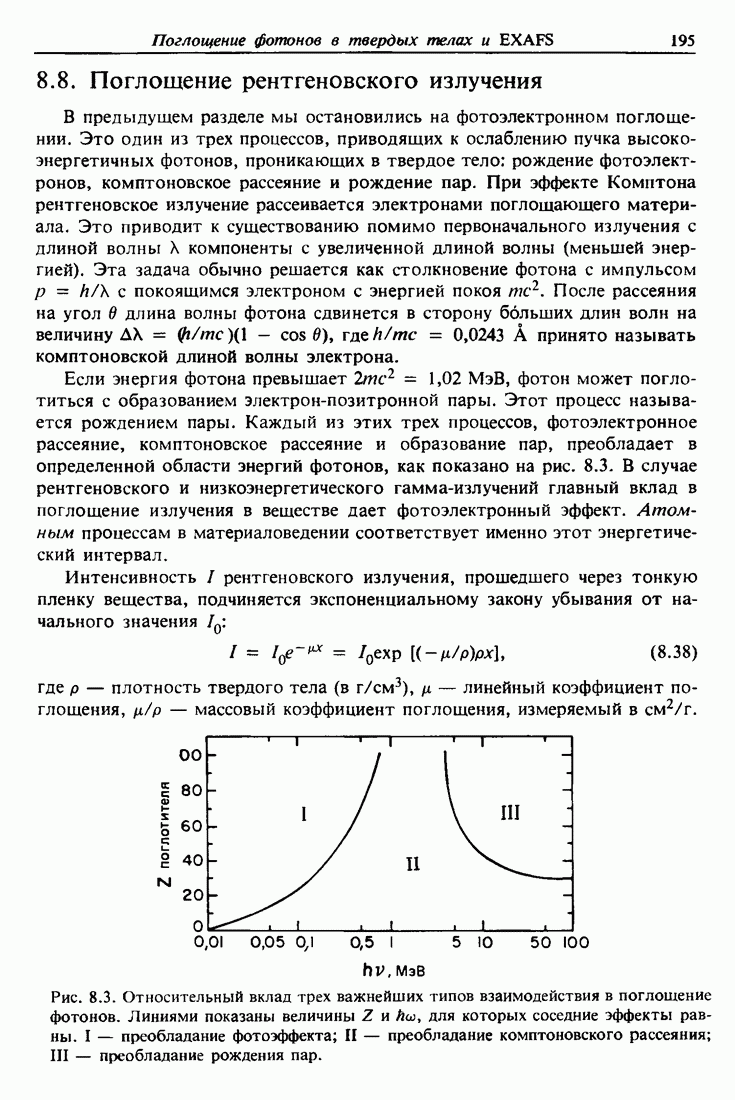
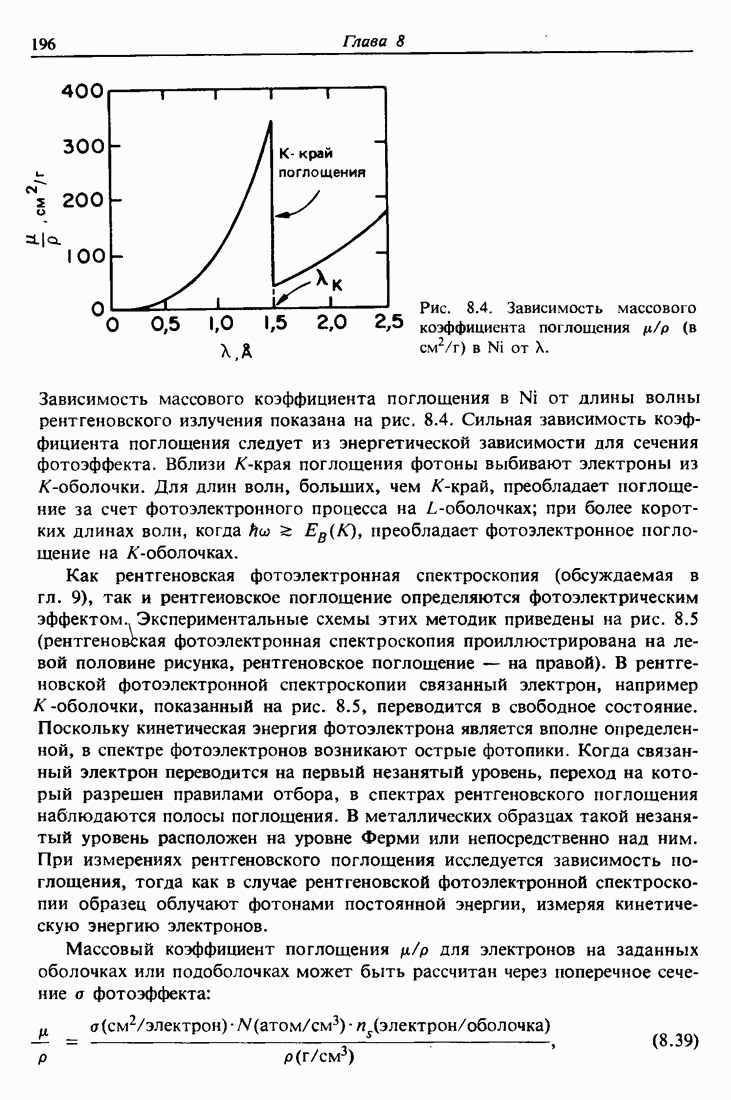
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
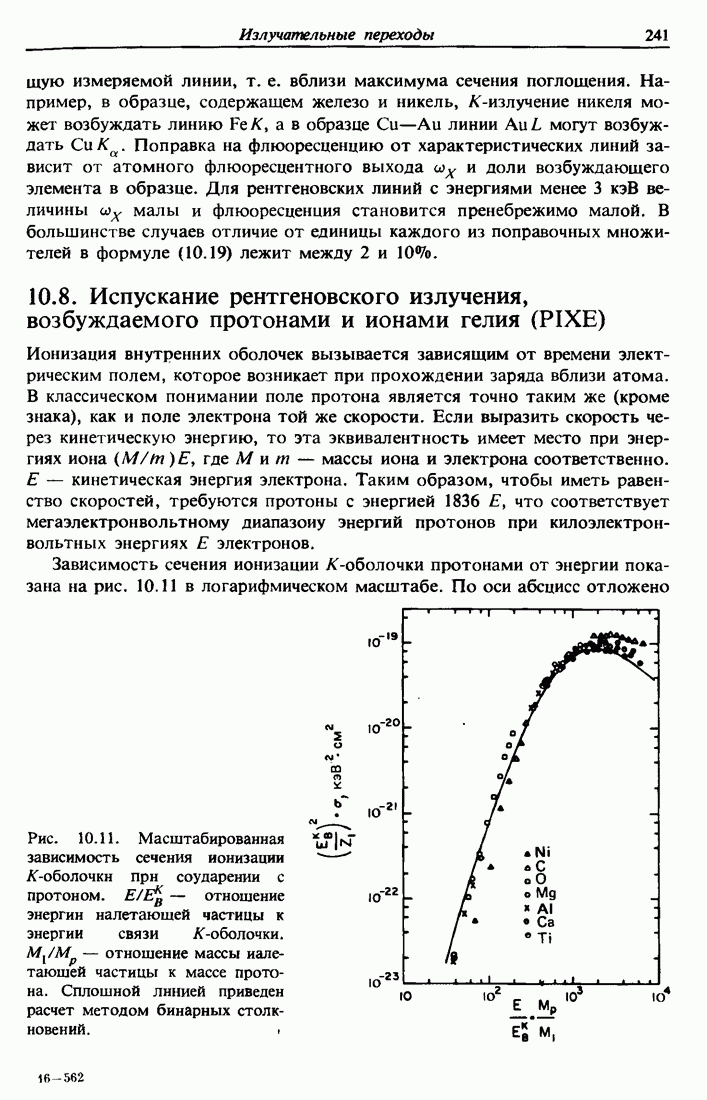
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
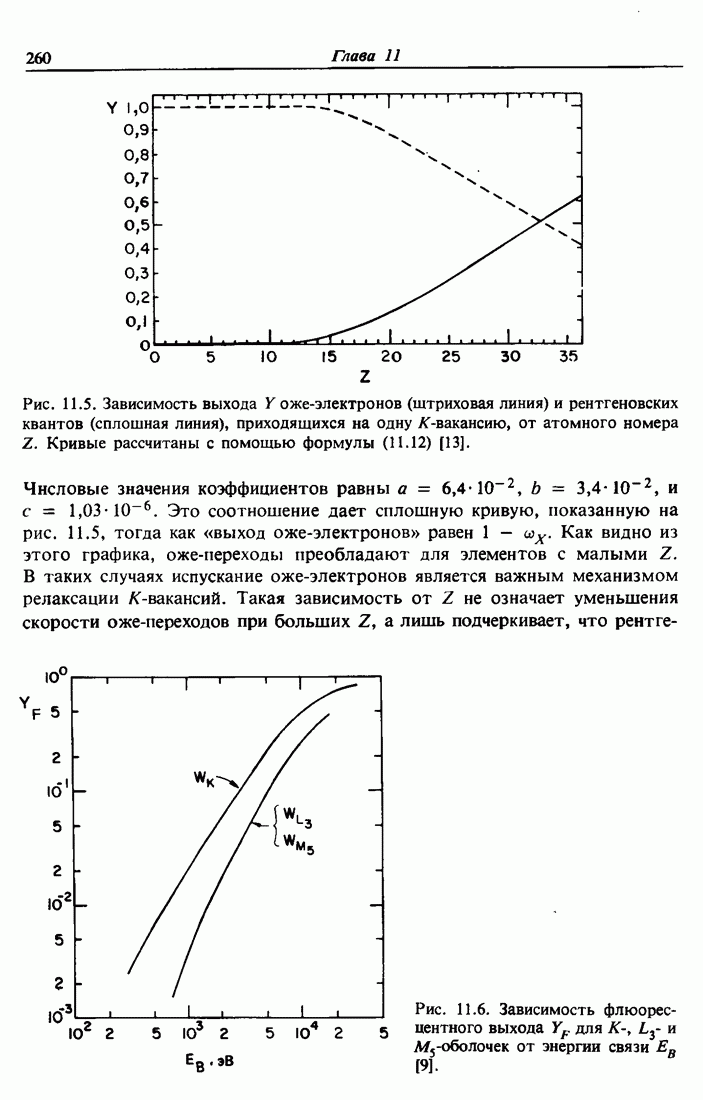
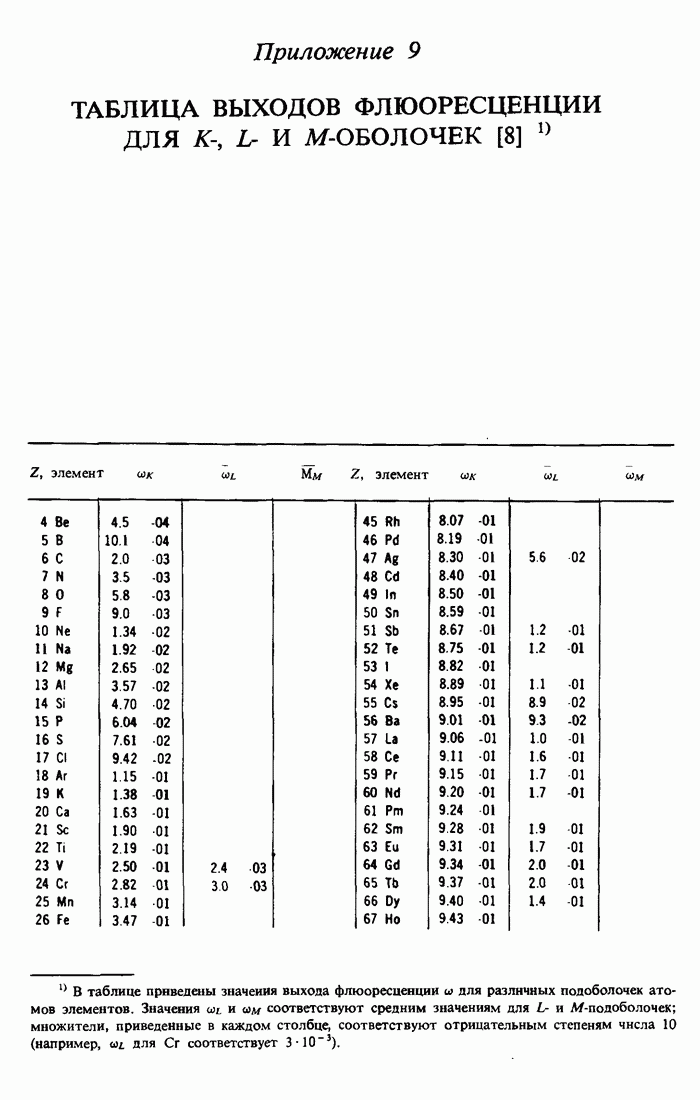
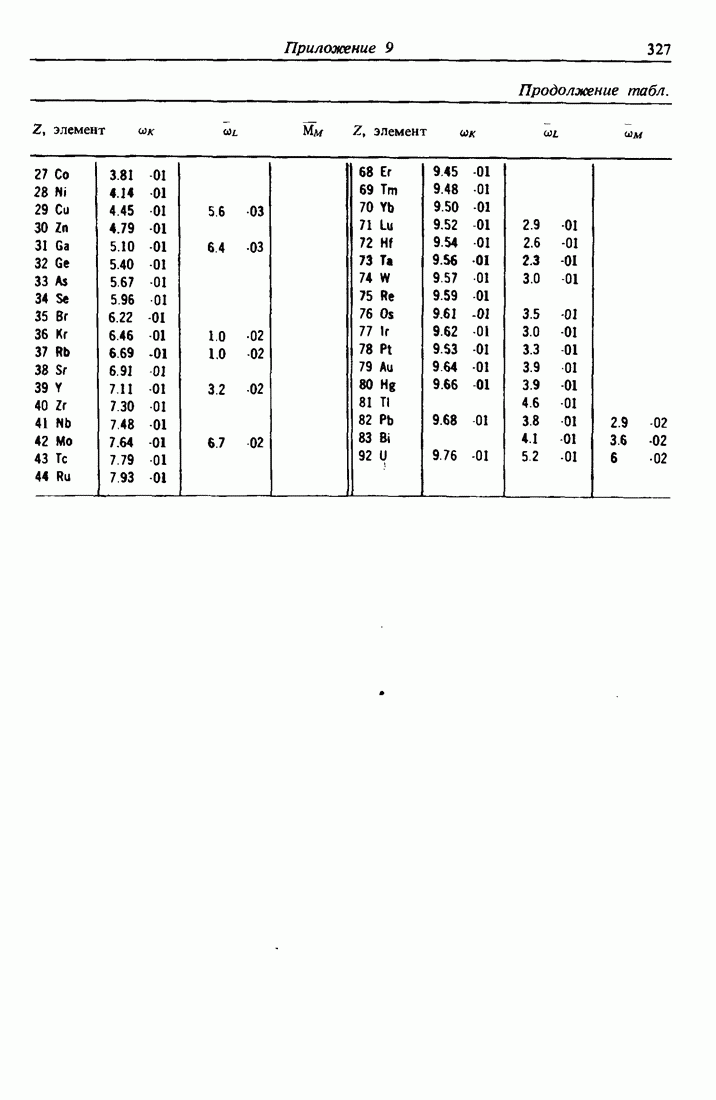
- 11.3. Выход оже-электронов и флюоресценция
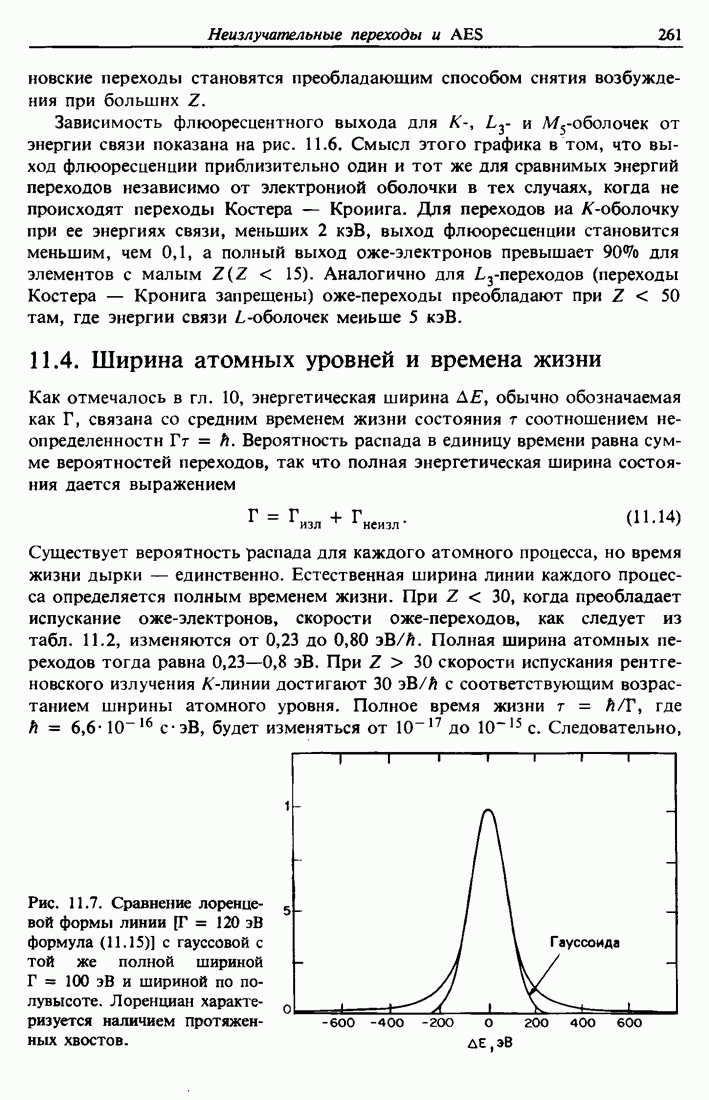
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
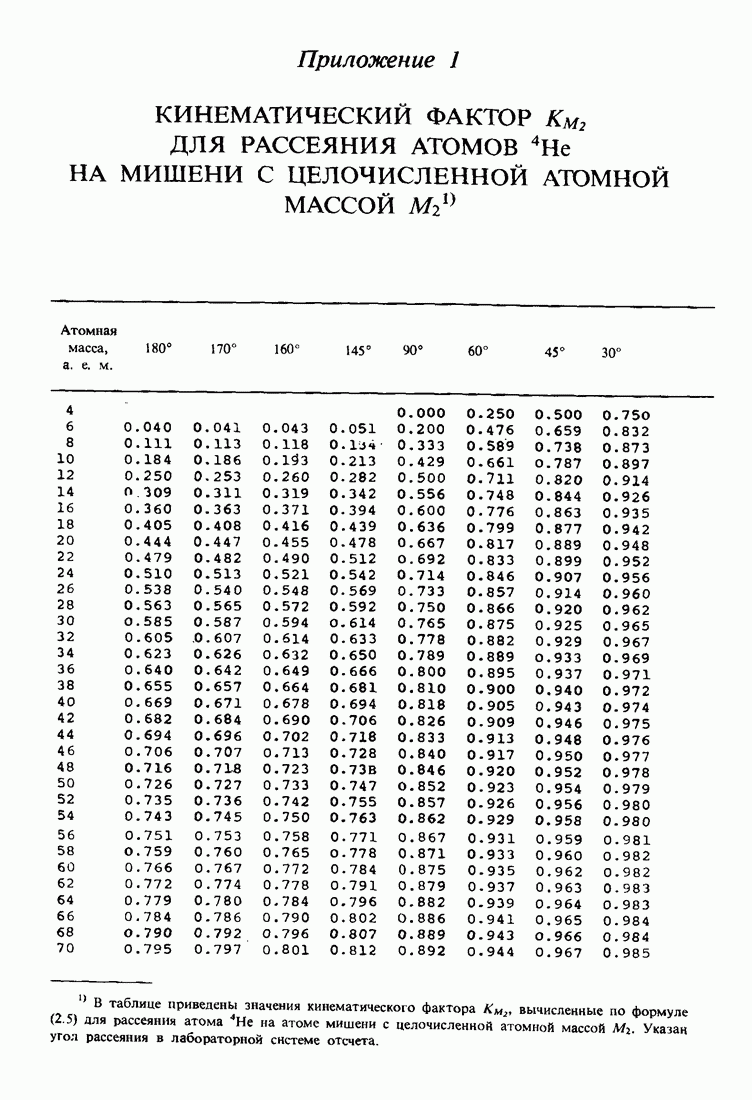
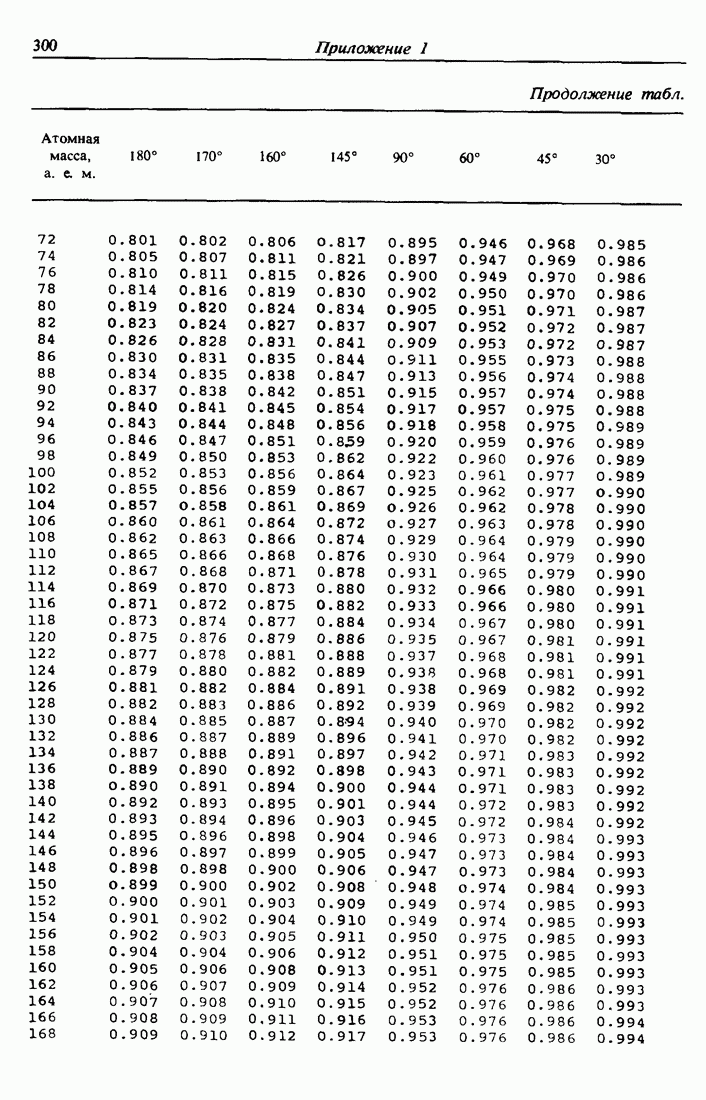
- ПРИЛОЖЕНИЕ 1.
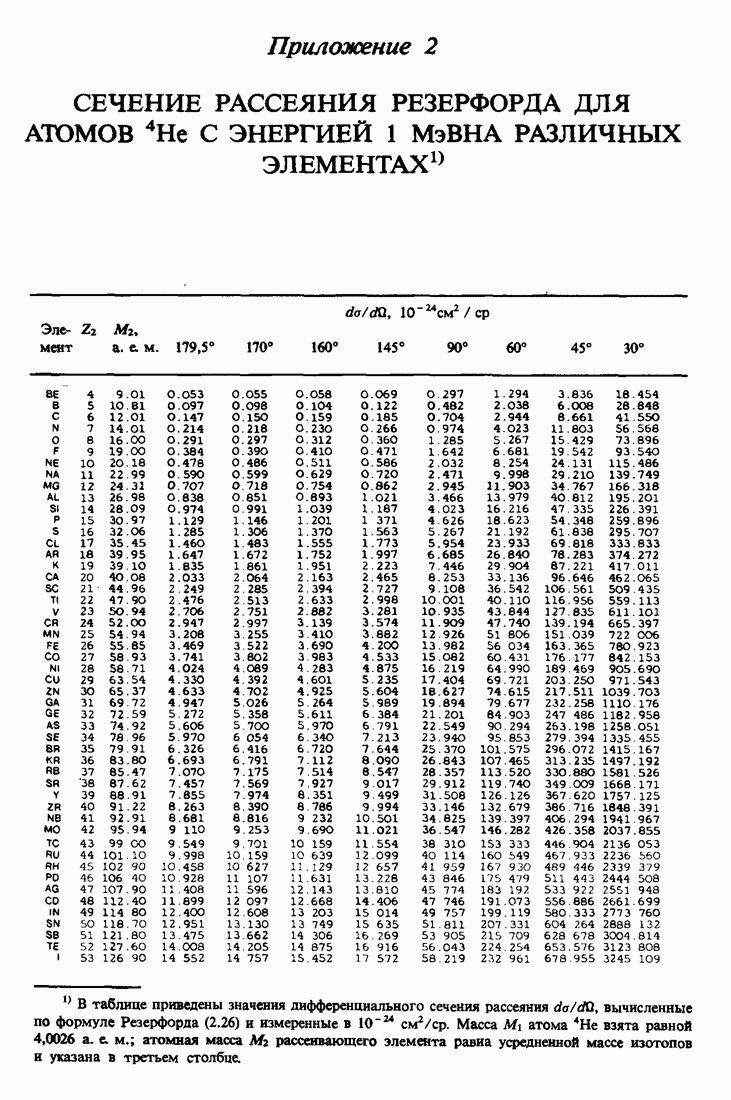
- ПРИЛОЖЕНИЕ 2.
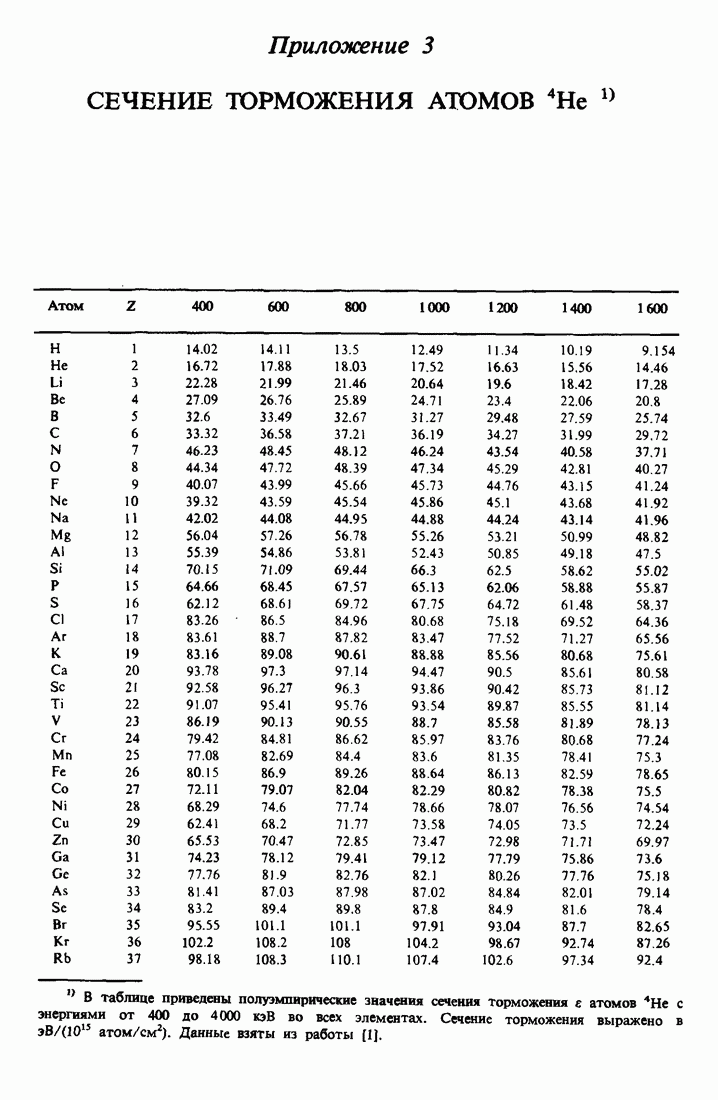
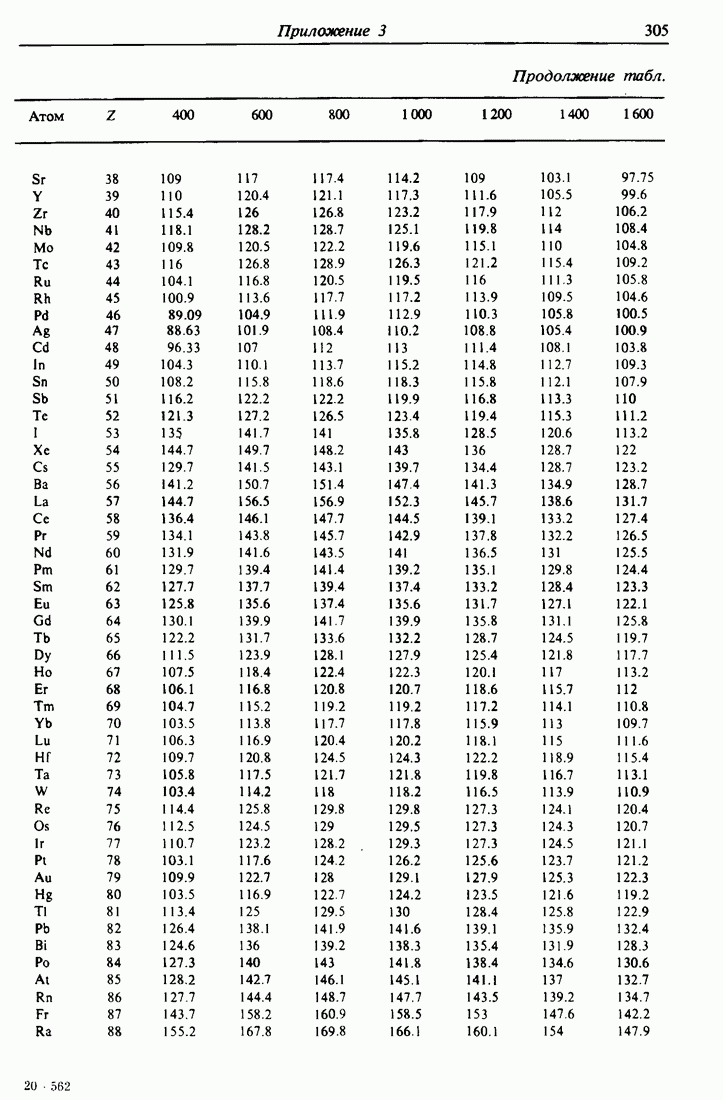
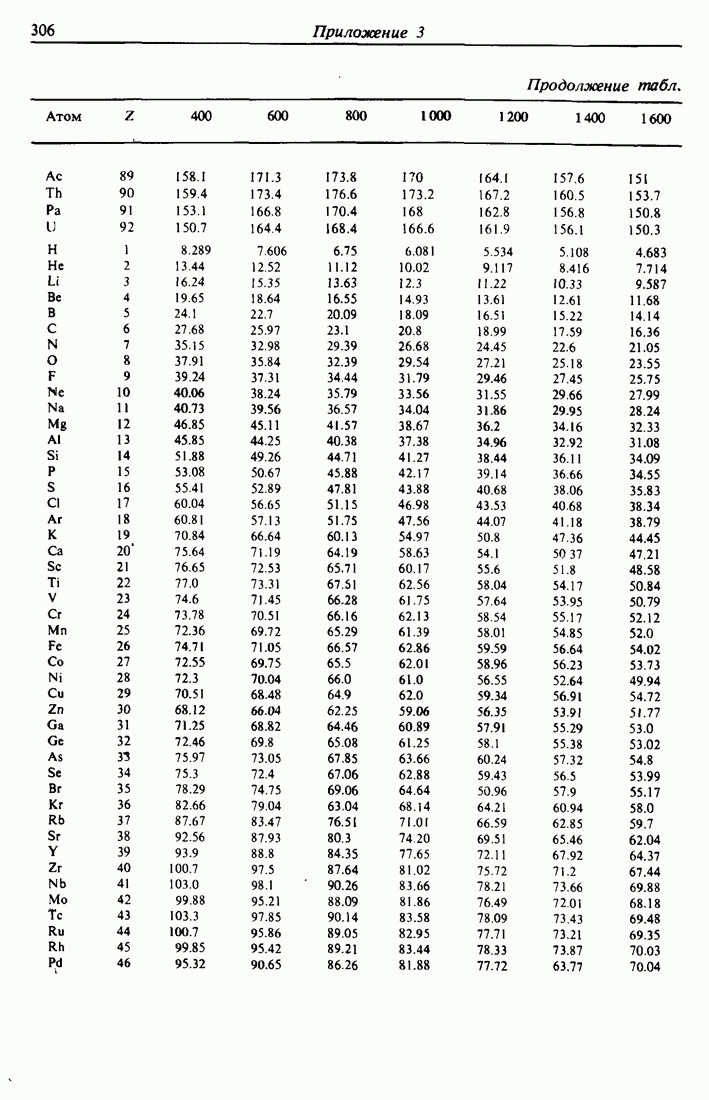
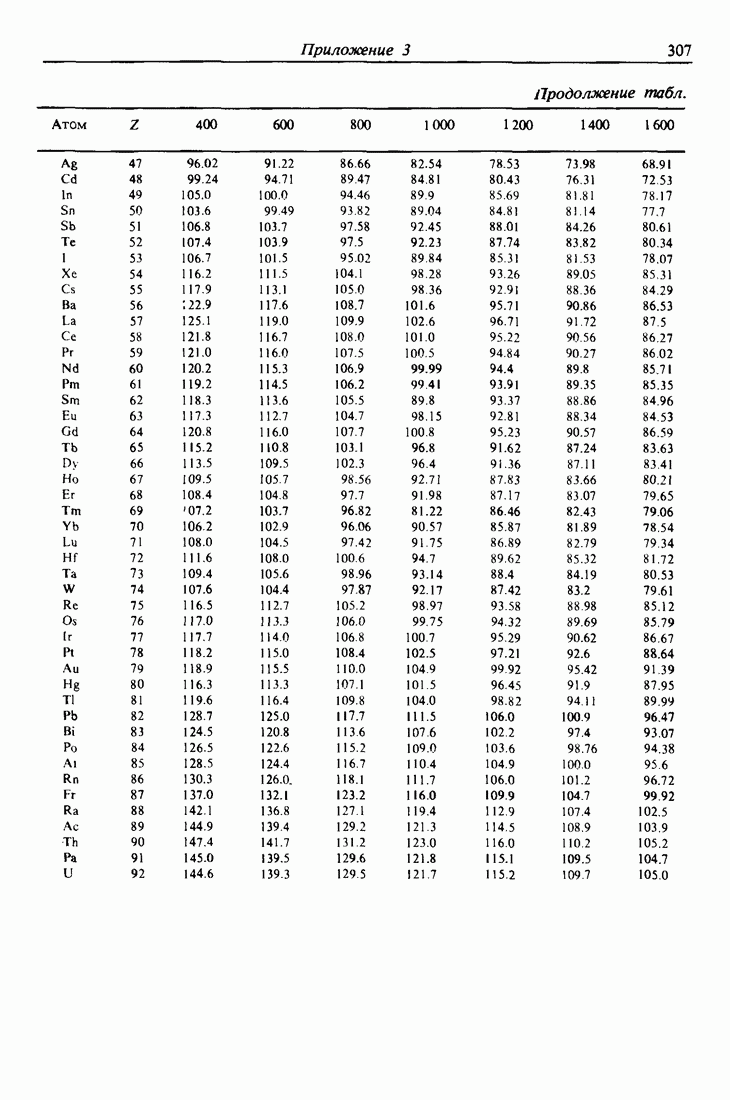
- ПРИЛОЖЕНИЕ 3.
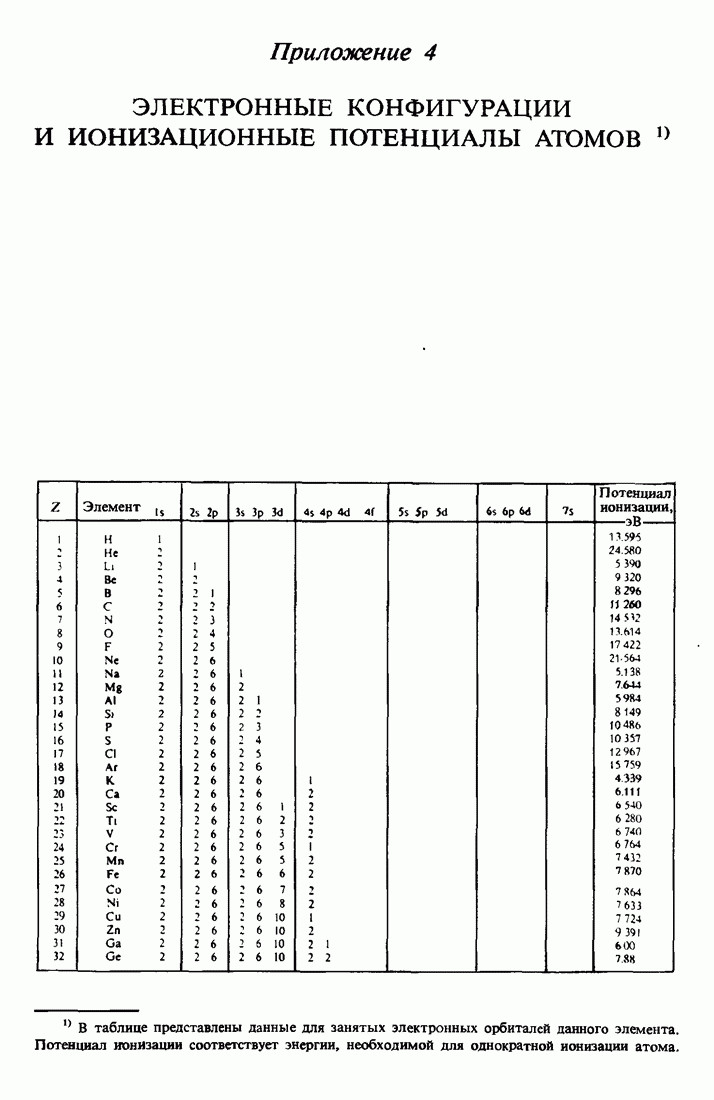
- ПРИЛОЖЕНИЕ 4.
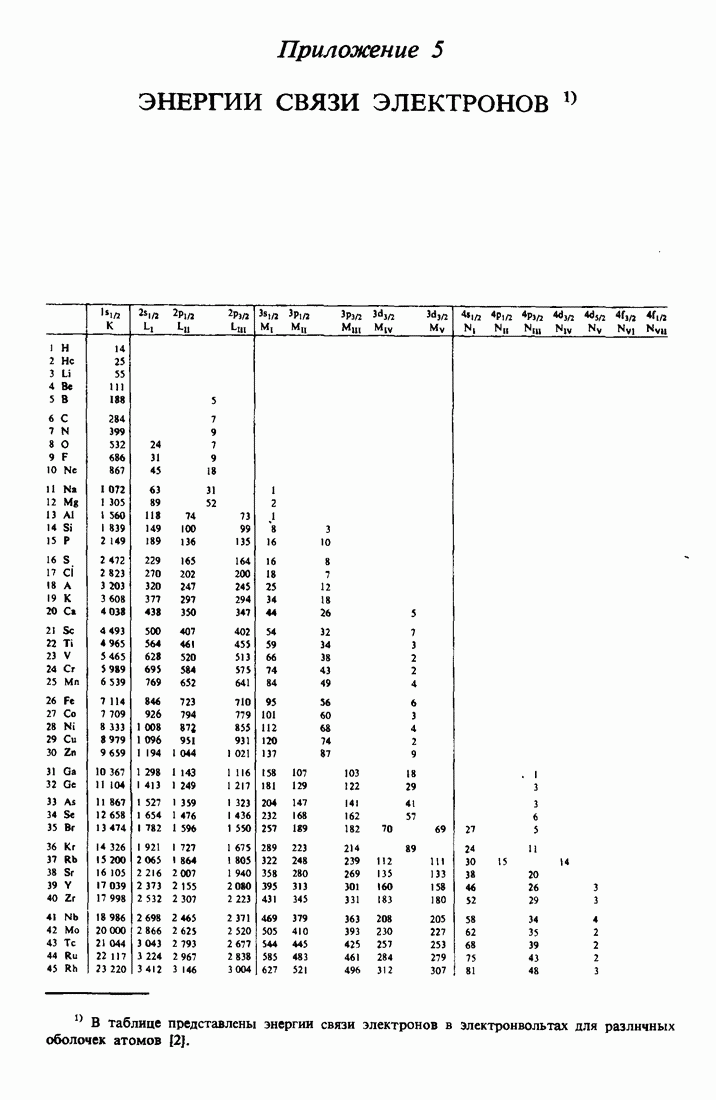
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
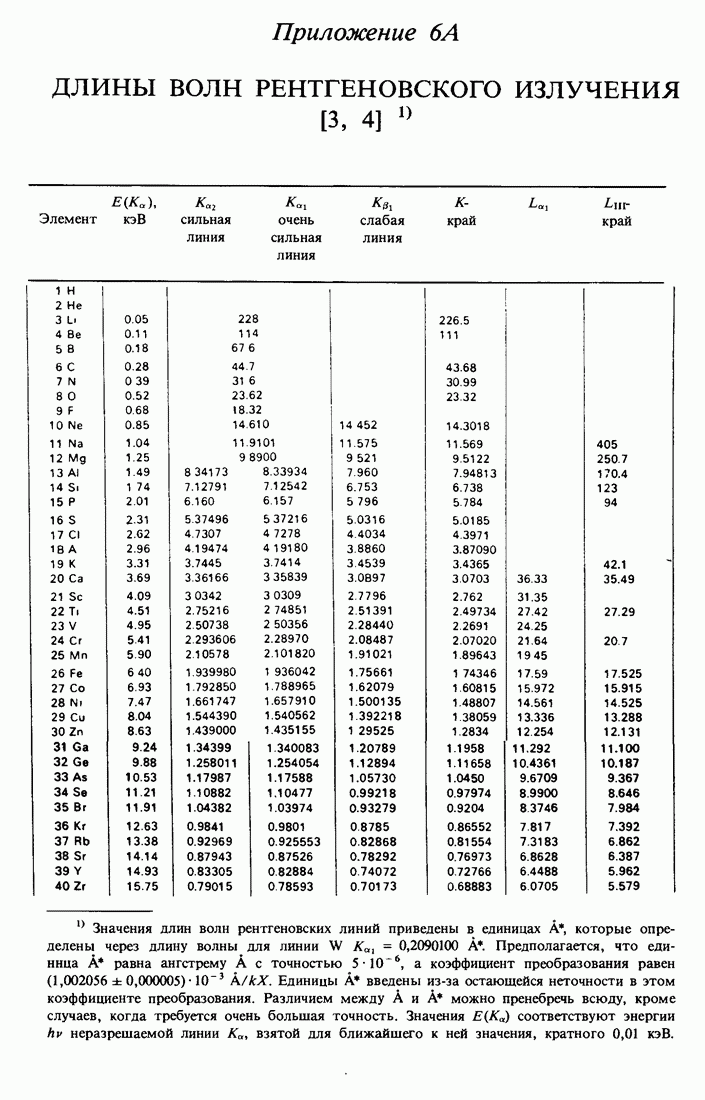
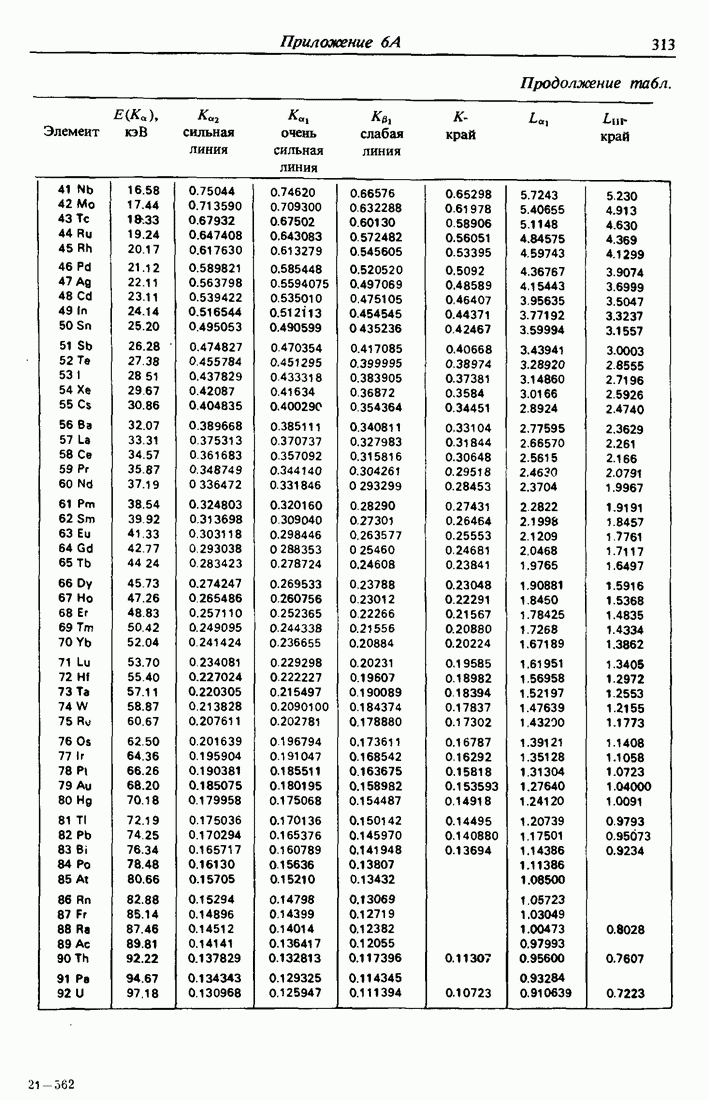
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
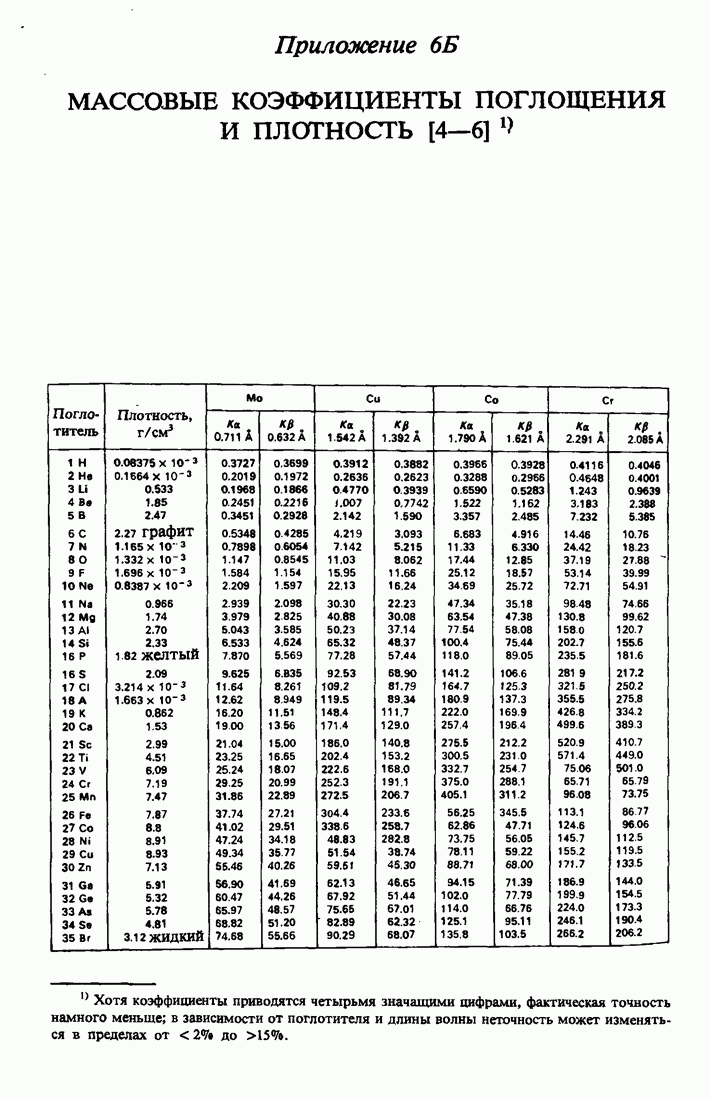
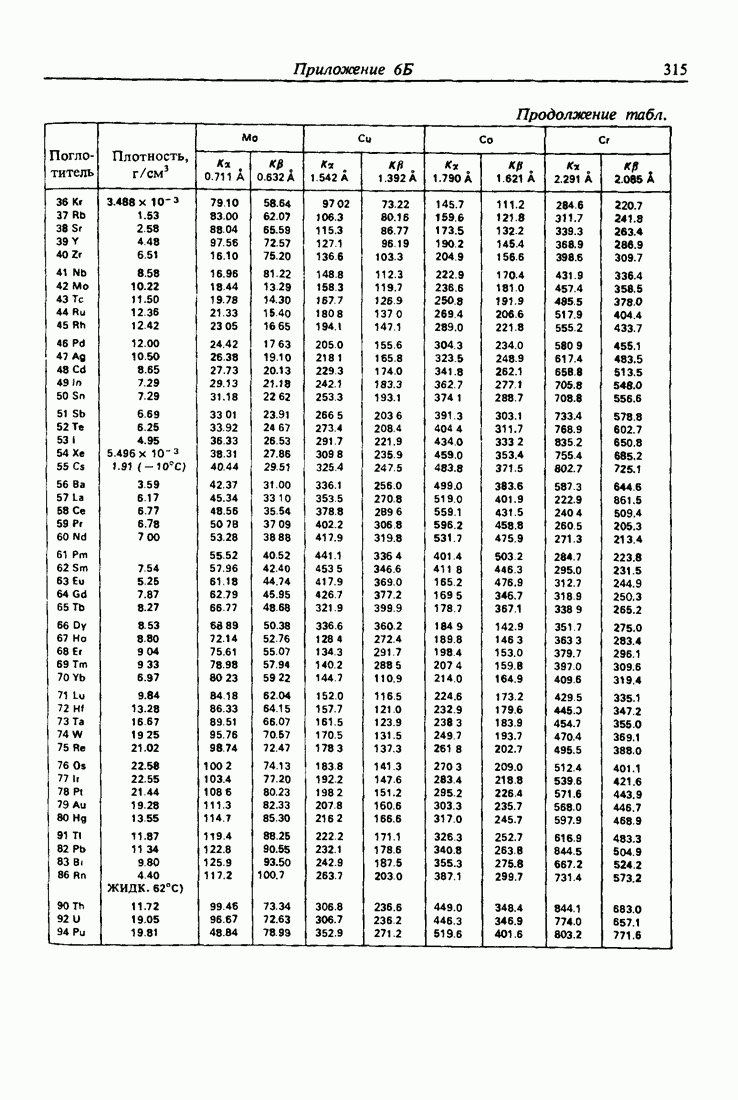
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
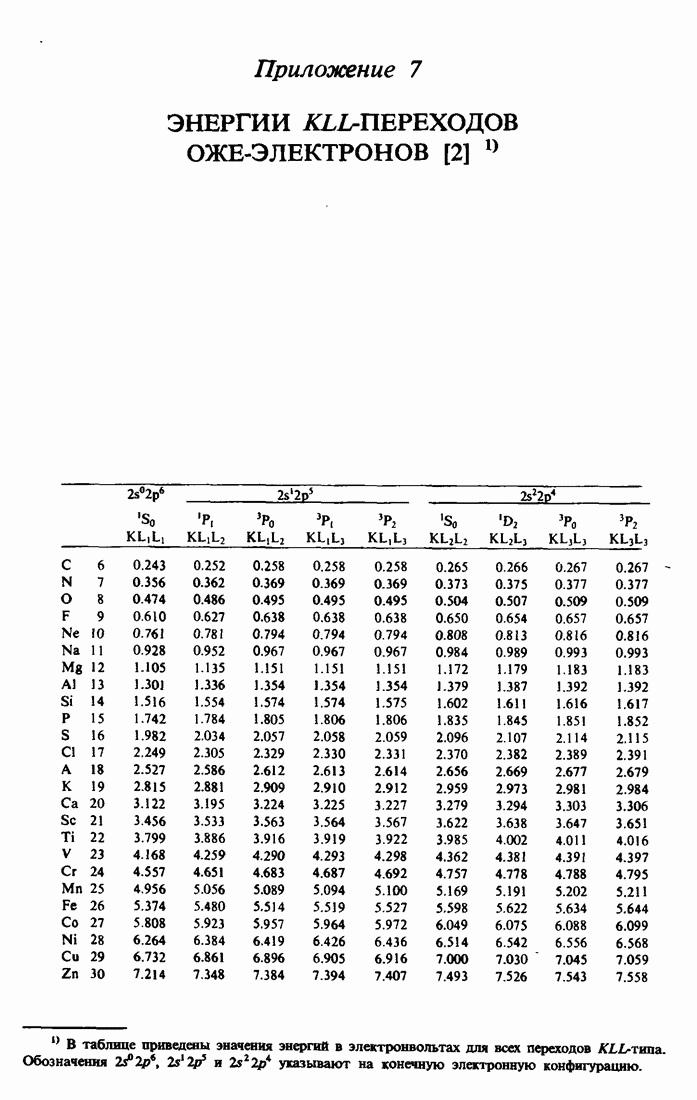
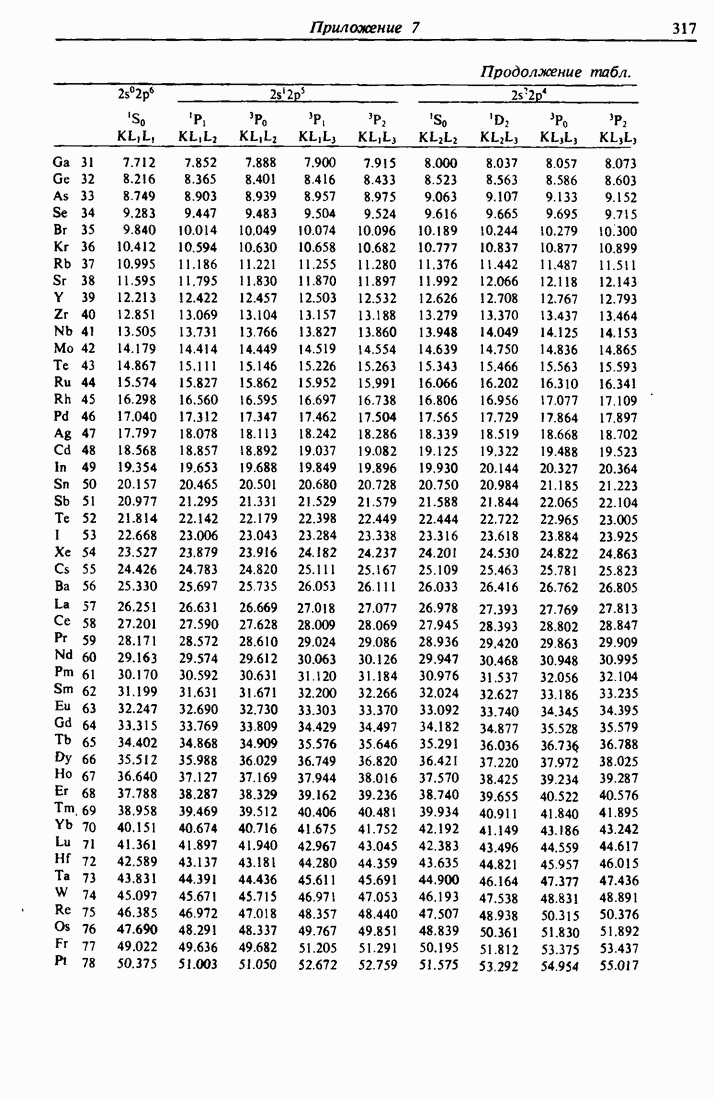
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
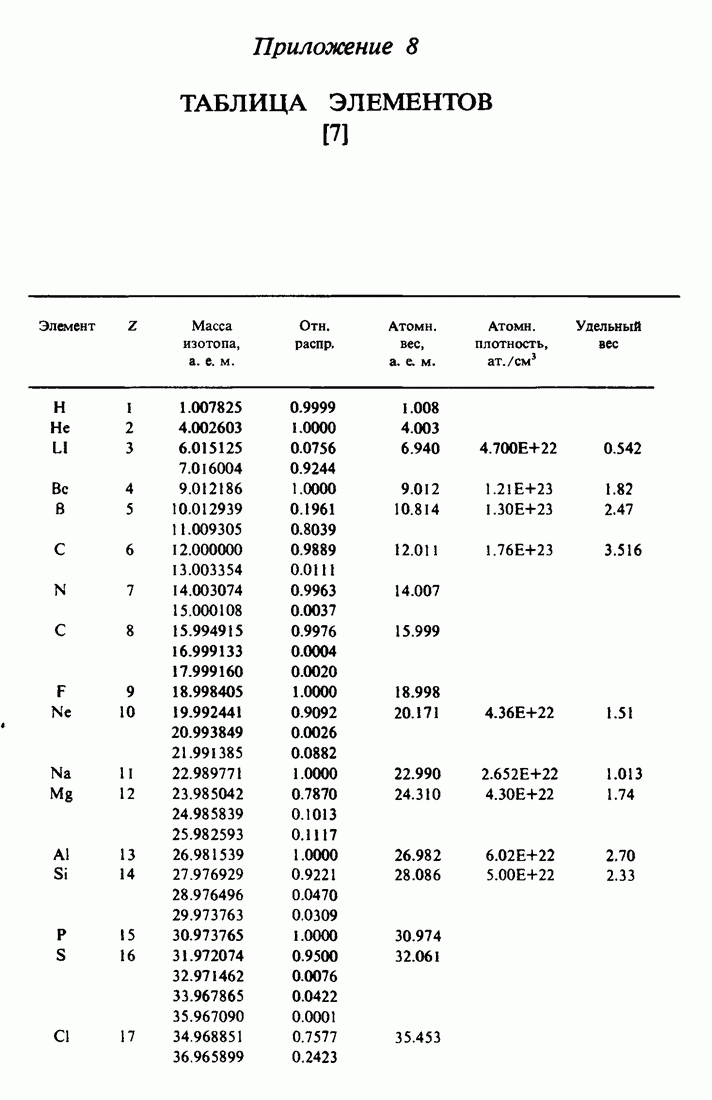
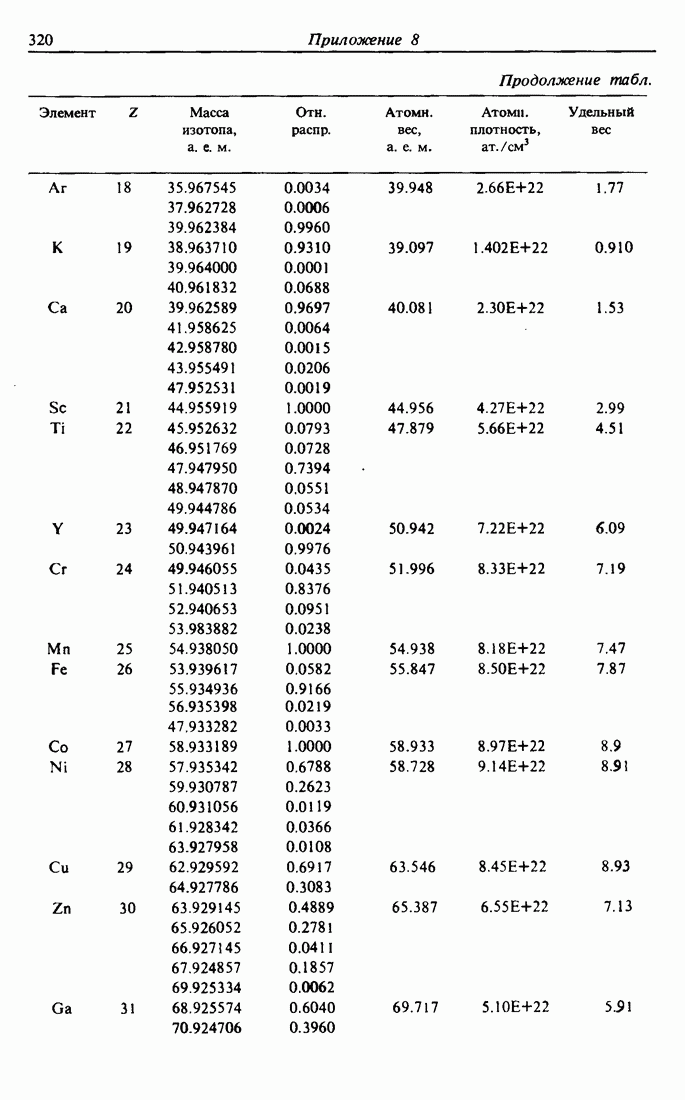
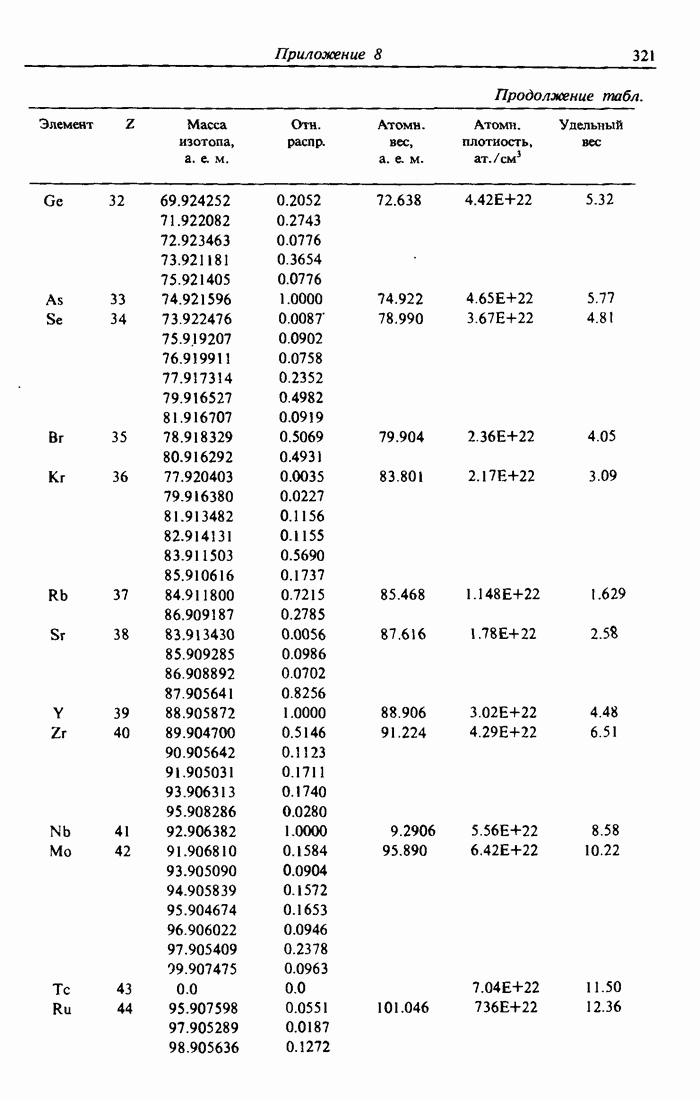
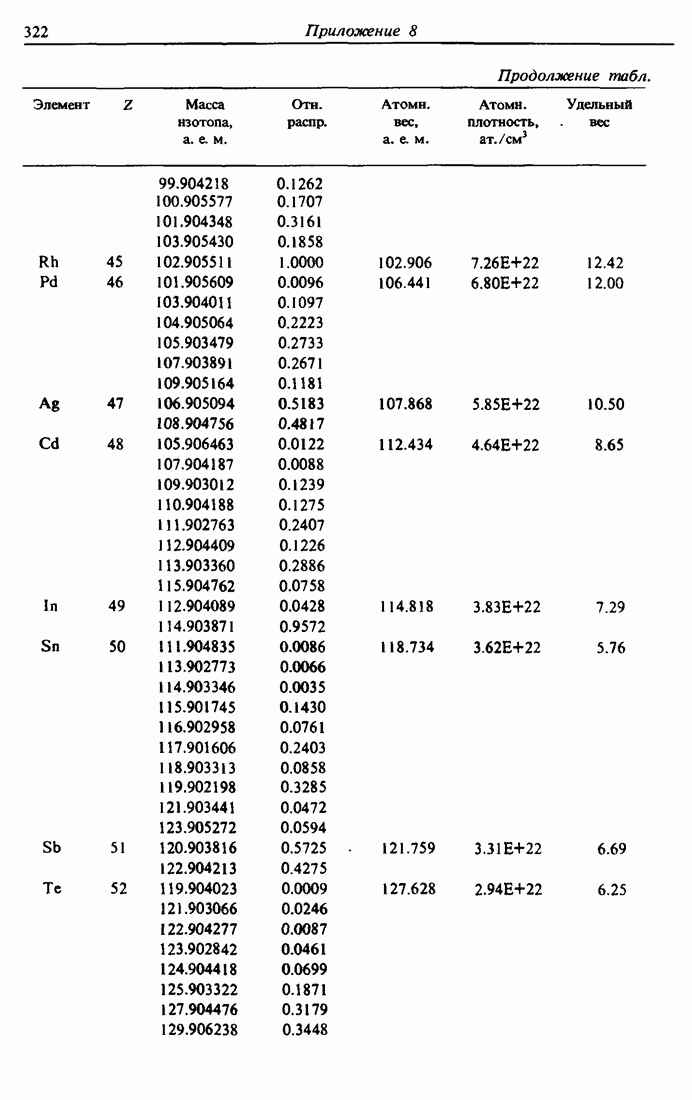
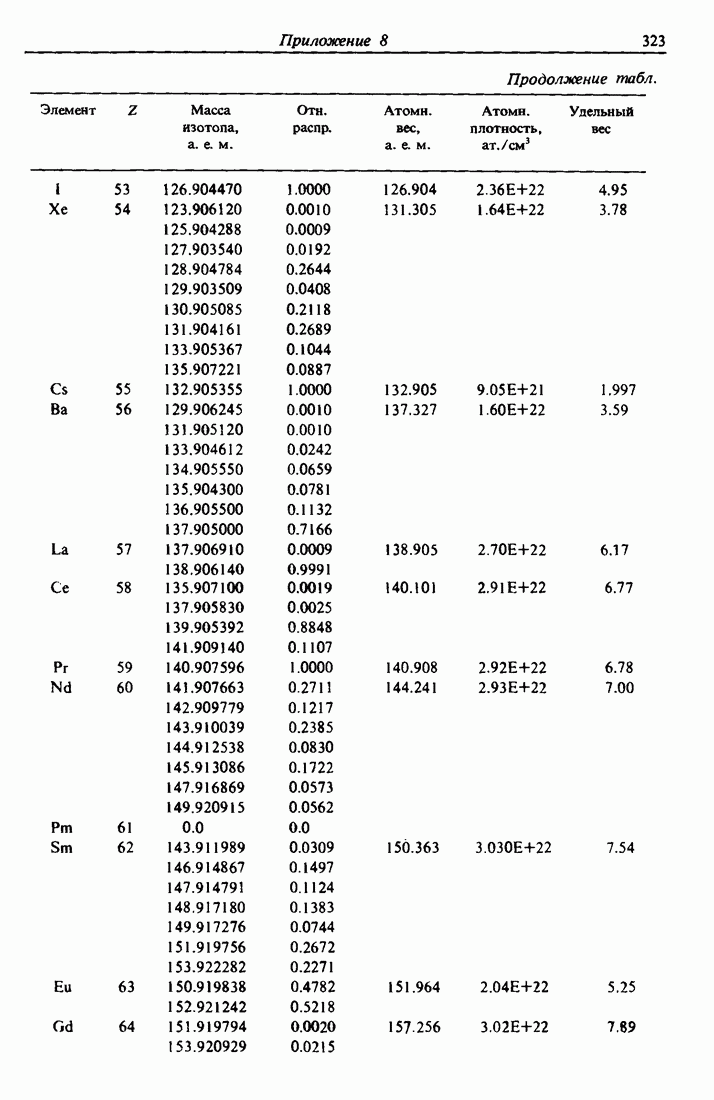
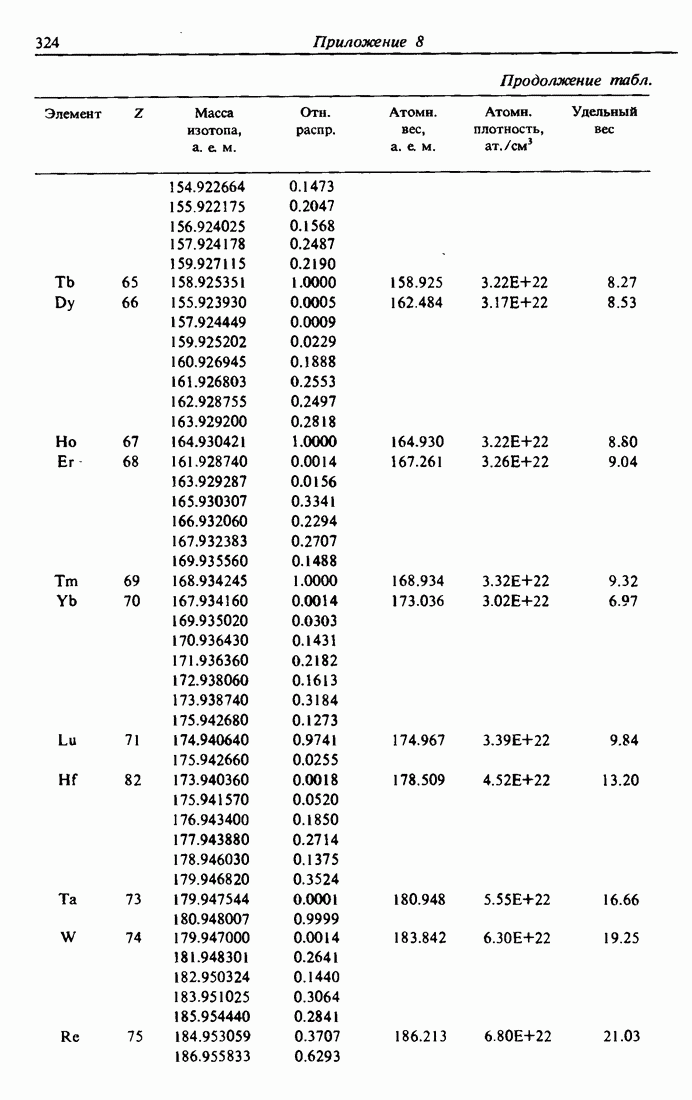
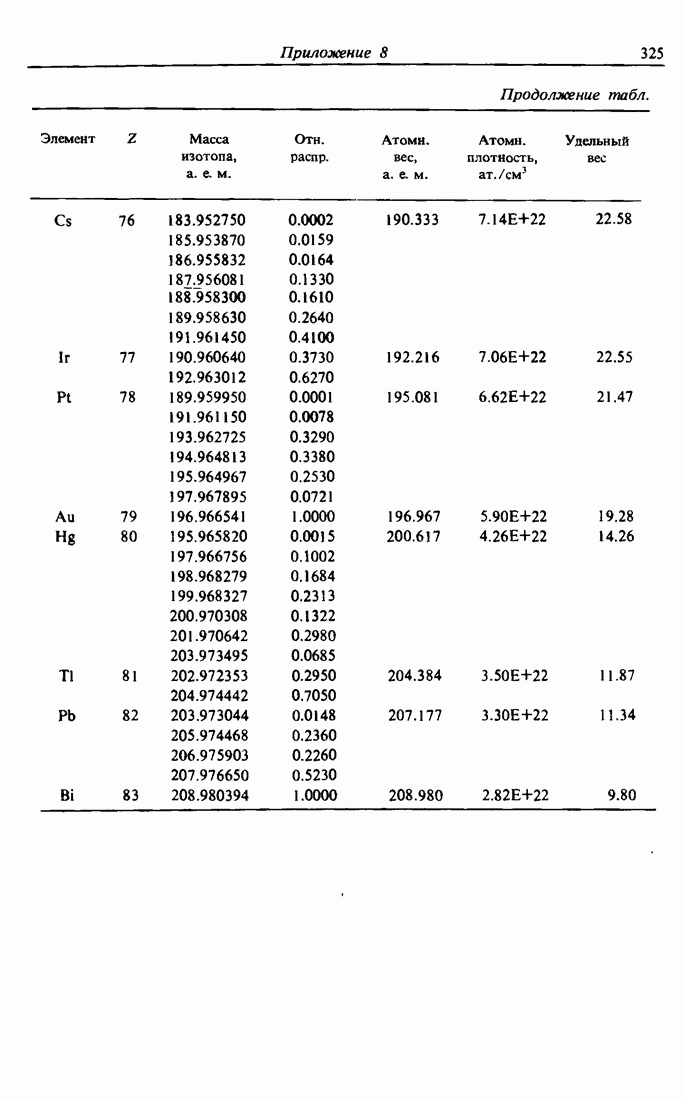
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ