| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Каналирование в монокристаллах
Каналирование движущихся ионов возникает, когда направление распространения пучка устанавливается точно по направлению главной симметрии кристалла [7]. Под направлением главной симметрии мы понимаем одно из свободных от атомов направлений в монокристалле вдоль атомной цепочки. На рис. 5.1 изображен вид сбоку на процесс, в котором большая часть ионов пучка направляется по каналам, образованным рядами атомов (каналируется). Каналированные частицы не могут подойти достаточно близко к атомным ядрам и подвергнуться резерфордовскому рассеянию на большой угол, поэтому выход обратного рассеяния резко уменьшается примерно на два порядка. В результате повышается чувствительность рассеяния к незначительным содержаниям примеси на поверхности. Очень важно, что происходит полное взаимодействие пучка с первыми монослоями твердого тела. Это «поверхностное взаимодействие» приводит к улучшению «разрешения по глубине» в таких экспериментах.
Траектория каналированного иона такова, что ион испытывает скользящие столкновения с осями (аксиальное каналирование) или плоскостями

Рис. 5.1. Траектории частнц, рассеивающихся на поверхности и каналируемых в кристалле. Для наглядности масштаб глубины уменьшен по отношению к ширине канала.
(плоскостное каналнрованне) кристалла и направляется посредством малоугловых рассеяний, не приближаясь к атомным ядрам ближе, чем на 0,1 А. Поскольку траектория каналированной частицы формируется в результате столкновений с большим числом атомов, можно рассмотреть непрерывную модель, в которой заряд атомных ядер в цепочке (или плоскости) равномерно распределен вдоль цепочки (или плоскости). Взаимодействие каналированной частицы с атомной цепочкой описывается в этой модели непрерывным потенциалом  , где r — расстояние по перпендикуляру от цепочки. Потенциал
, где r — расстояние по перпендикуляру от цепочки. Потенциал  получается усреднением атомного потенциала вдоль цепочки атомов, расположенных с шагом d:
получается усреднением атомного потенциала вдоль цепочки атомов, расположенных с шагом d:

где  — экранированный кулоновский потенциал,
— экранированный кулоновский потенциал,  — радиальная сферическая координата. В качестве экранированного кулоновского потенциала мы возьмем не потенциал Мольера, а другую, более удобную аппроксимацию, которая широко используется в теории каналирования, так как позволяет получать явные выражения для параметров каналирования без большой потери точности. Этот «стандартный потенциал» определяется формулой
— радиальная сферическая координата. В качестве экранированного кулоновского потенциала мы возьмем не потенциал Мольера, а другую, более удобную аппроксимацию, которая широко используется в теории каналирования, так как позволяет получать явные выражения для параметров каналирования без большой потери точности. Этот «стандартный потенциал» определяется формулой 

где  обычно выбирается равным 3, а — расстояние экранировки Томаса — Ферми (4.5). Тогда для непрерывного потенциала оси получаем выражение
обычно выбирается равным 3, а — расстояние экранировки Томаса — Ферми (4.5). Тогда для непрерывного потенциала оси получаем выражение

где d — среднее расстояние между атомами цепочки. Этот потенциал сравним по величине с атомными потенциалами; например, для аксиального каналирования ионов гелия вдоль направления  в кремнии
в кремнии  его значение при
его значение при  равно 223 эВ.
равно 223 эВ.
Использование непрерывного потенциала и закона сохранения энергии позволяет найти критический угол каналирования. Полная энергия Е частицы в кристалле равна

где  — компоненты импульса, параллельные и перпендикулярные цепочке (рис. 5.2). Тогда
— компоненты импульса, параллельные и перпендикулярные цепочке (рис. 5.2). Тогда

и

Углы каналирования малы, поэтому мы воспользуемся малоугловым приближением, а последние два члена в (5.5) приравняем поперечной энергии

равной сумме кинетической и потенциальной энергий. Полная энергия частицы сохраняется, а в нашем приближении сохраняется и поперечная энергия. Тогда критический угол  определяется приравниванием поперечной энергии
определяется приравниванием поперечной энергии  в точке поворота и поперечной энергии в средней точке:
в точке поворота и поперечной энергии в средней точке:

или

«Размазанность» положений атомов вследствие тепловых колебаний ограничивает снизу минимальное расстояние гмии, при котором может возникнуть коррелированная последовательность рассеяний, необходимая для выполнения условий каналирования. Наиболее полезное первое приближение

Рис. 5.2. Компоненты начального импульса частицы, падающей под углом скольжения  на атомную цепочку.
на атомную цепочку.
для критического угла получается подстановкой  в соотношения (5.3) и (5.8), где
в соотношения (5.3) и (5.8), где  равно 2/3 среднеквадратичной амплитуды тепловых колебаний [см. (7.5)]:
равно 2/3 среднеквадратичной амплитуды тепловых колебаний [см. (7.5)]:

причем

(Тепловые колебания и определение р обсуждаются в разд. 7.3.)
Значения  согласуются с результатами измерений в пределах 20%-ной точности и имеют температурную зависимость, подтверждаемую экспериментами. Для ионов Не с энергией 1,0 МэВ, падающих на кремний при комнатной температуре вдоль оси
согласуются с результатами измерений в пределах 20%-ной точности и имеют температурную зависимость, подтверждаемую экспериментами. Для ионов Не с энергией 1,0 МэВ, падающих на кремний при комнатной температуре вдоль оси  , расчетное значение критического угла
, расчетное значение критического угла  равно 0,65°, а экспериментальное значение составляет 0,55°.
равно 0,65°, а экспериментальное значение составляет 0,55°.
Понятие расстояния наибольшего сближения гмнн позволяет получить простой геометрический вывод доли частиц, перешедших в режим каналирования при падении пучка параллельно оси кристалла  . На рис. 5.3 изображен вид спереди на кристалл. Каждая цепочка атомов окружена площадью
. На рис. 5.3 изображен вид спереди на кристалл. Каждая цепочка атомов окружена площадью  в пределах которой каналирование отсутствует; частицы с
в пределах которой каналирование отсутствует; частицы с  лмин могут канапироваться. Поэтому доля неканалированных частиц равна просто отношению площадей
лмин могут канапироваться. Поэтому доля неканалированных частиц равна просто отношению площадей  где
где  — радиус круга, приходящегося на одну цепочку:
— радиус круга, приходящегося на одну цепочку:

Здесь N — концентрация атомов, d — период расположения атомов вдоль цепочки. В литературе отношение  обычно называется минимальным выходом
обычно называется минимальным выходом  . Например, в эксперименте по обратному рассеянию Хмин определяет выход частиц, испытавших близкие столкновения в процессе
. Например, в эксперименте по обратному рассеянию Хмин определяет выход частиц, испытавших близкие столкновения в процессе

Рис. 5.3. Вид спереди на идеальный кристалл с непрерывными рядами атомов. На каждый ряд приходится площадь  , а наибольшему сближению каналированной частицы с атомной цепочкой соответствует площадь
, а наибольшему сближению каналированной частицы с атомной цепочкой соответствует площадь
каналирования. Поскольку лмин — 0,1 А, минимальный выход составляет порядка 1%, а доля каналированных частиц достигает  .
.
Непрерывное описание может быть применено не только к аксиальному, но и к плоскостному каналированию. В этом случае двумерное усреднение атомного потенциала соответствует однородному распределению заряда по плоскости и приводит к следующему определению непрерывного потенциала плоскости  :
:

где  — среднее число атомов плоскости на единицу площади,
— среднее число атомов плоскости на единицу площади,  — расстояние между плоскостями, у — расстояние от плоскости. Для стандартного потенциала
— расстояние между плоскостями, у — расстояние от плоскости. Для стандартного потенциала  имеет вид
имеет вид

Аналогично аксиальному случаю можно ввести критический угол плоскостного каналирования, равный

где  — амплитуда одномерных колебаний. Следуя Линдхарду [7], приведем также другое определение критического угла плоскостного канал ипования:
— амплитуда одномерных колебаний. Следуя Линдхарду [7], приведем также другое определение критического угла плоскостного канал ипования:

который имеет тот же порядок величины, что и введенный выше критический угол (5.14). Экспериментально установлено, что критические углы плоскостного каналирования в 2—4 раза меньше, чем характерные критические углы аксиального каналирования.
Согласно геометрической картине плоскостного каналирования минимальный выход  приближенно равен
приближенно равен

что значительно больше соответствующего выхода хмин в аксиальном случае. Значение минимального выхода для хороших направлений плоскостного каналирования обычно имеет порядок 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
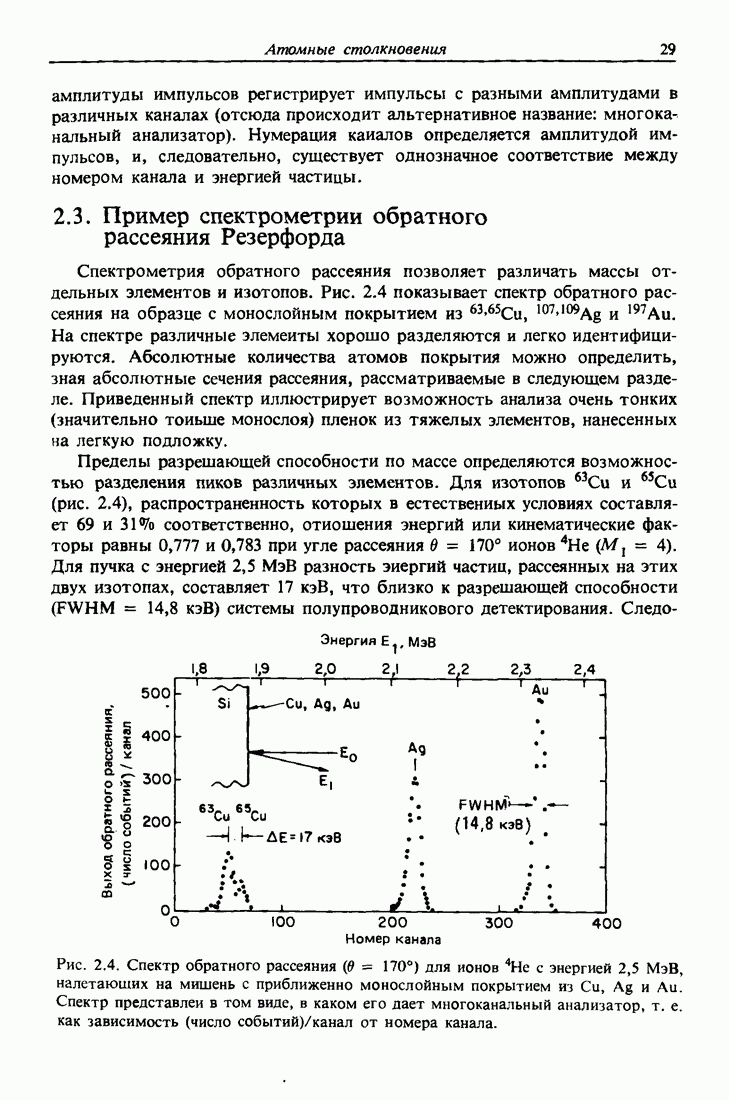
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
- 2.4. Сечение рассеяния и прицельный параметр
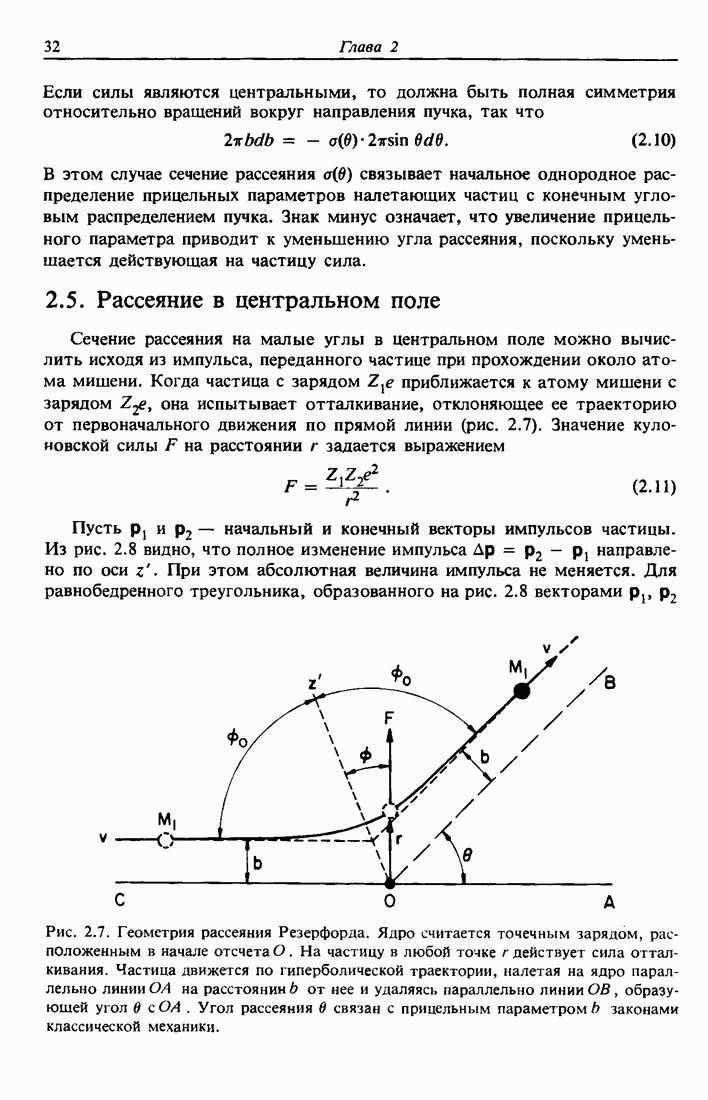
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
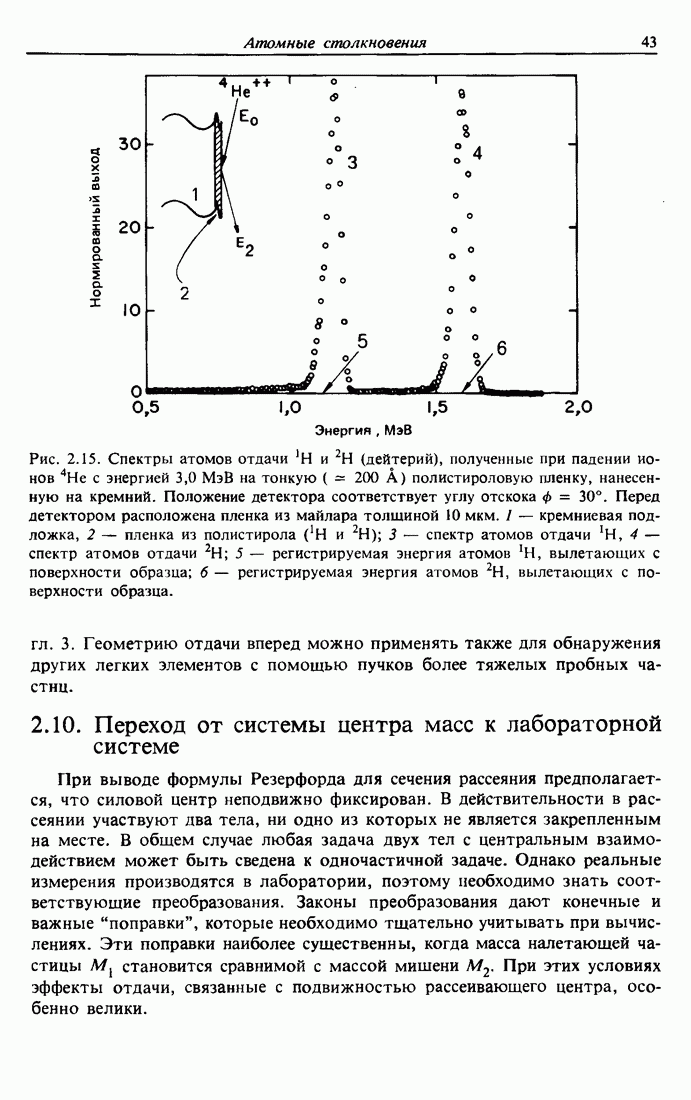
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
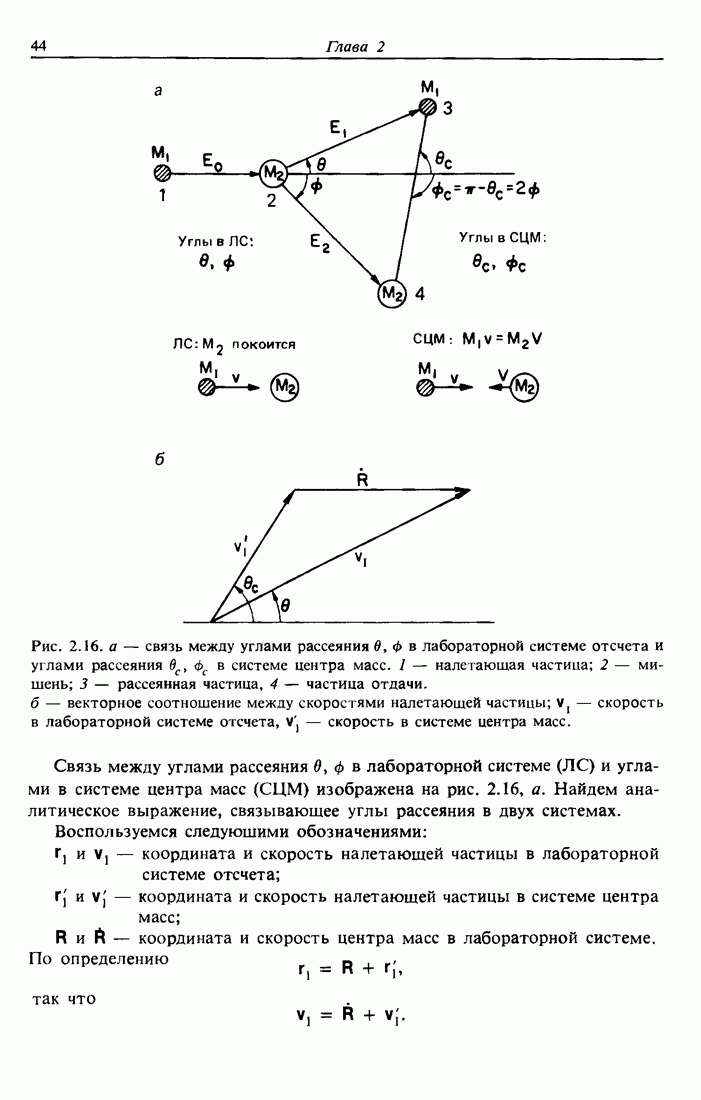
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
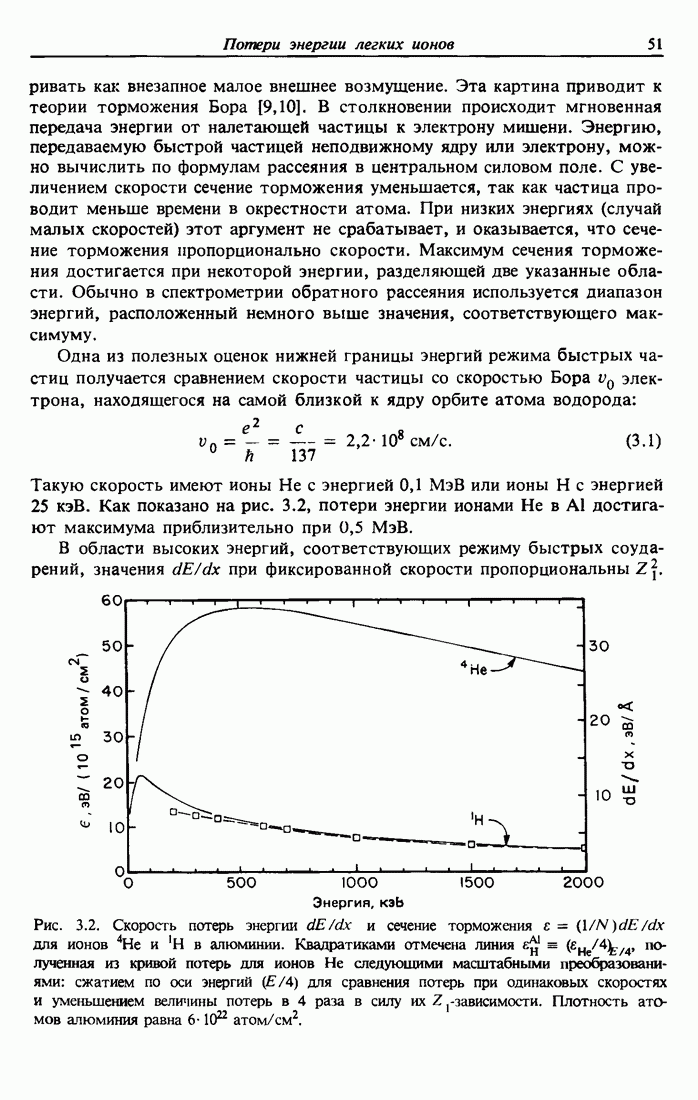
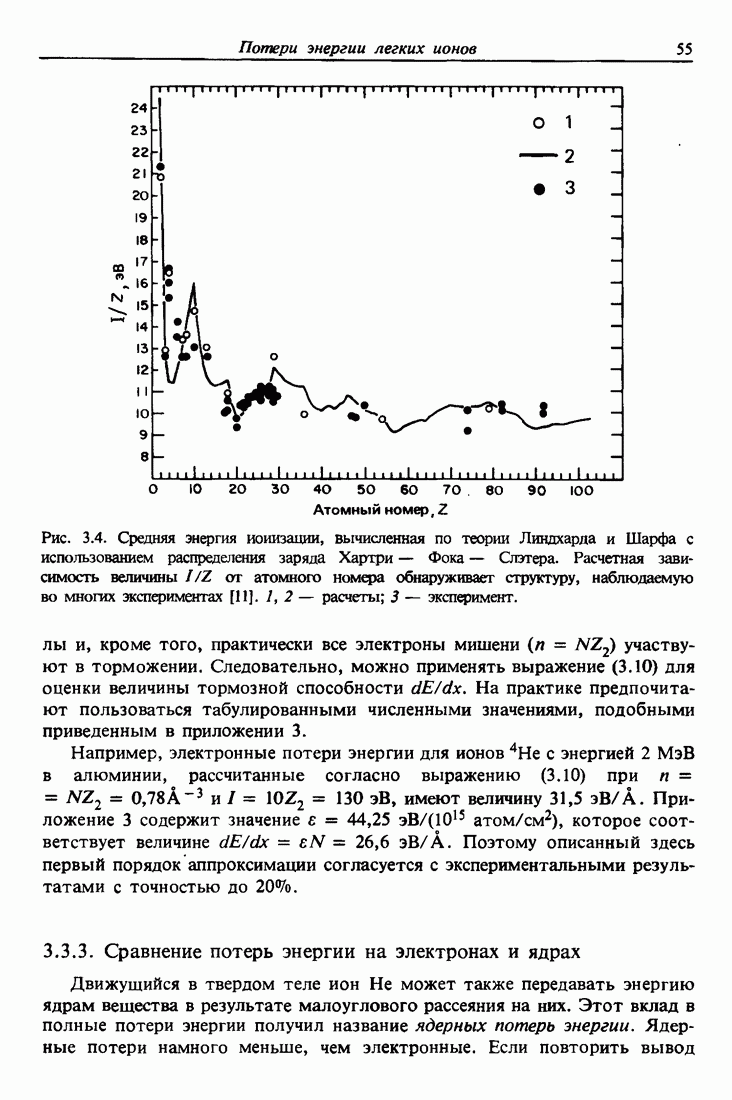
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
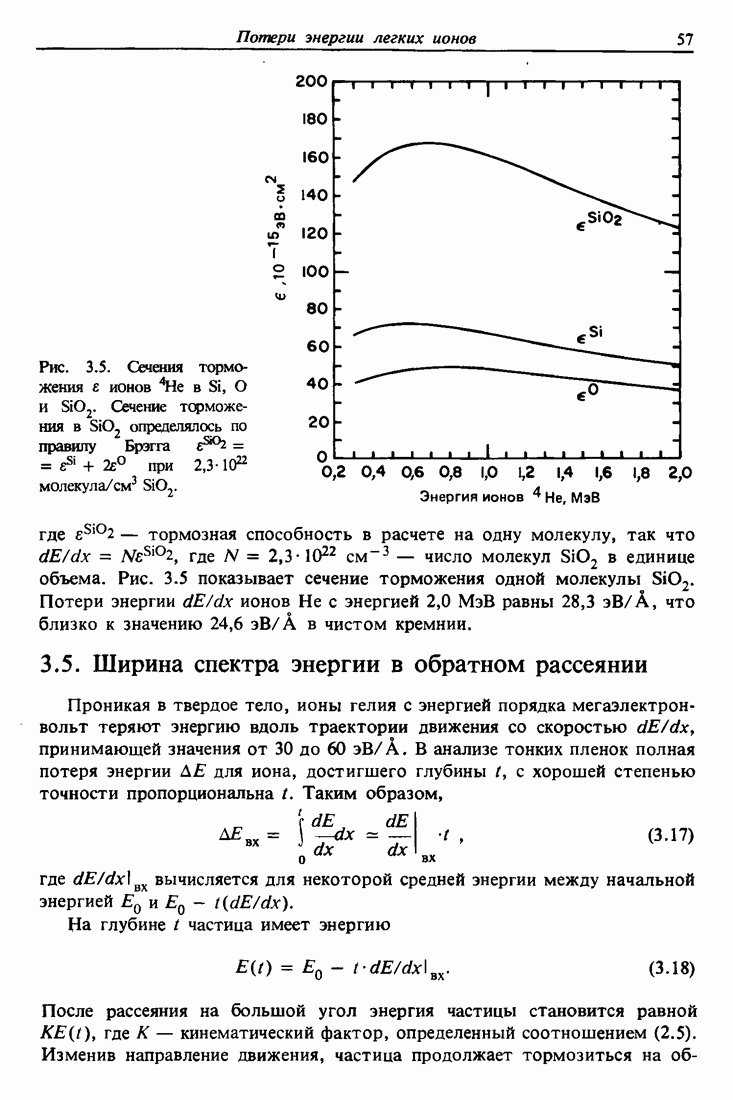
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
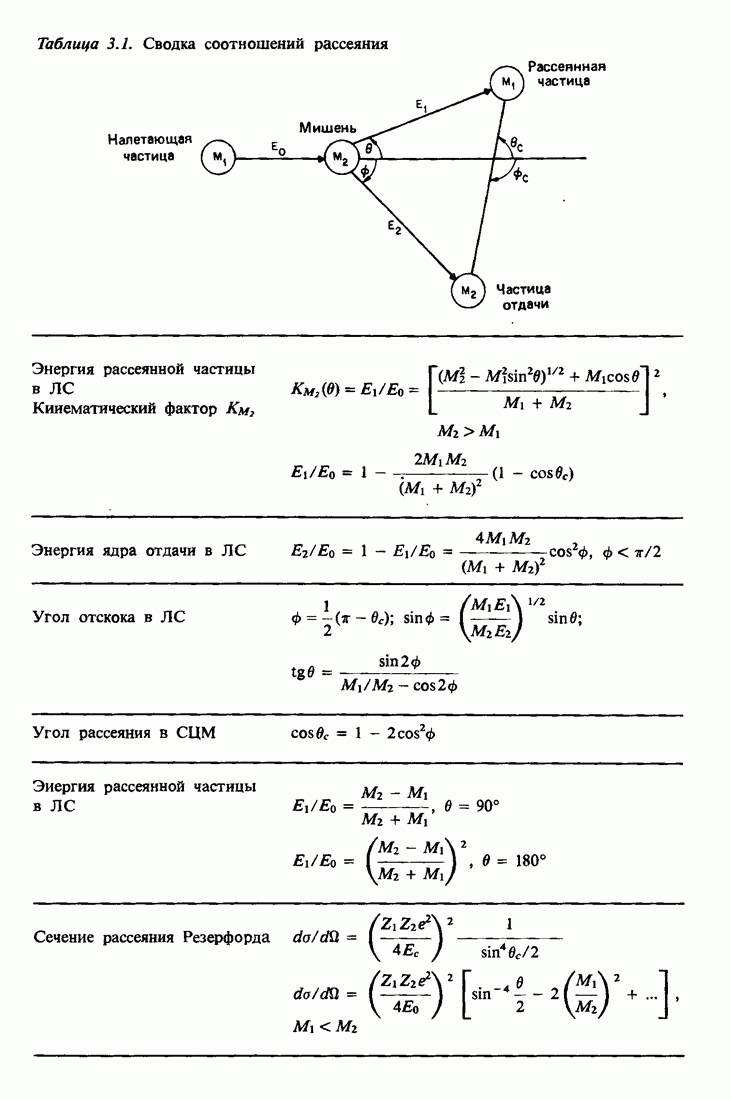
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
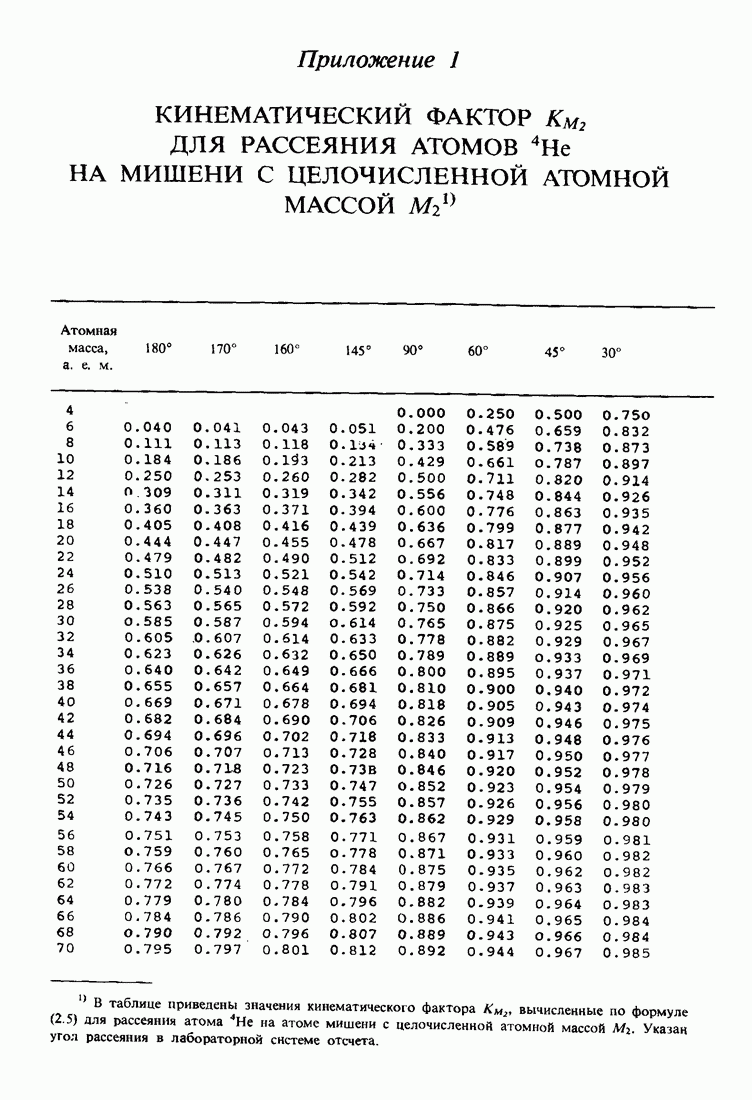
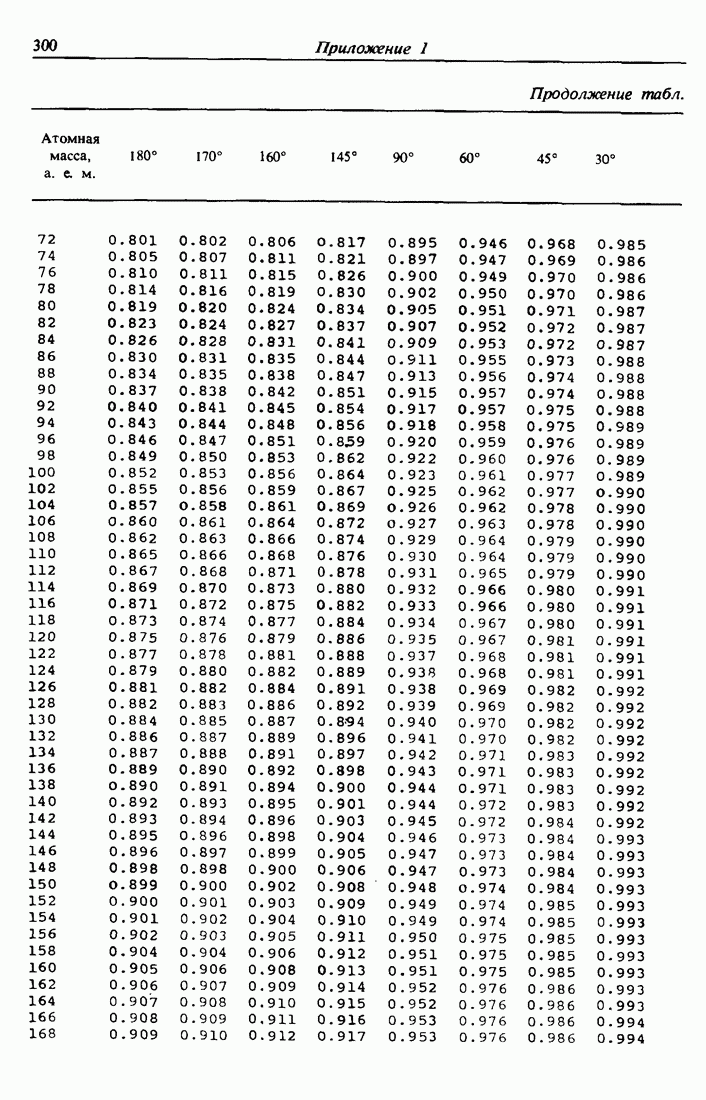
- ПРИЛОЖЕНИЕ 1.
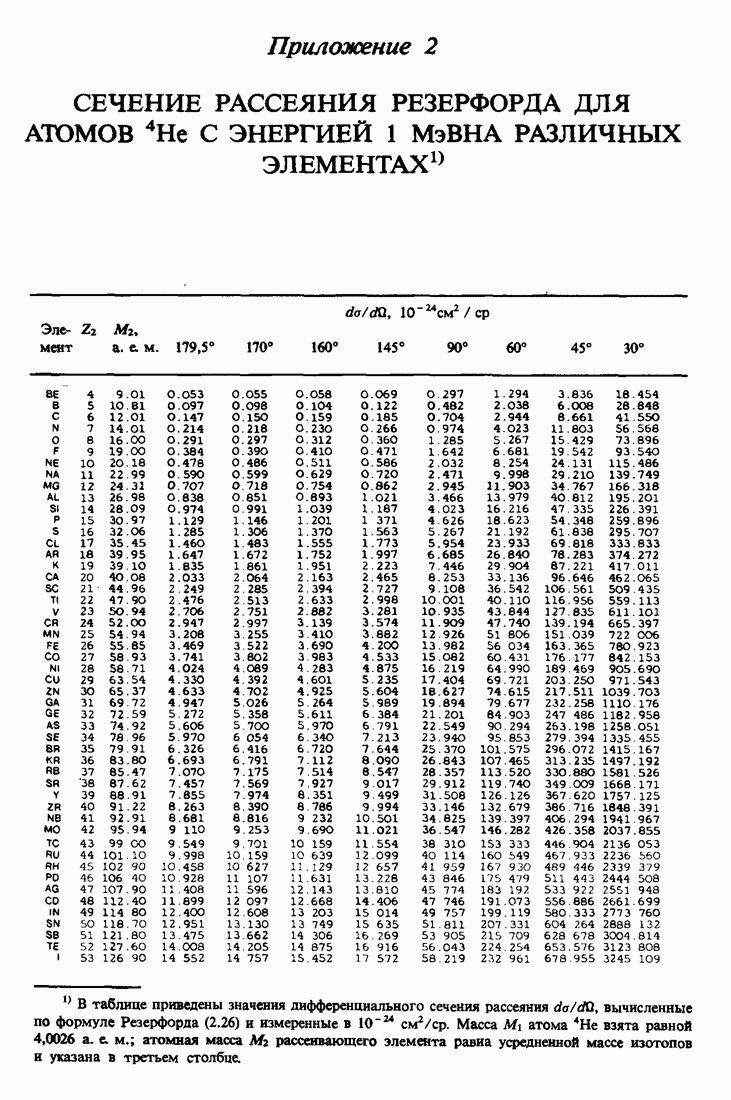
- ПРИЛОЖЕНИЕ 2.
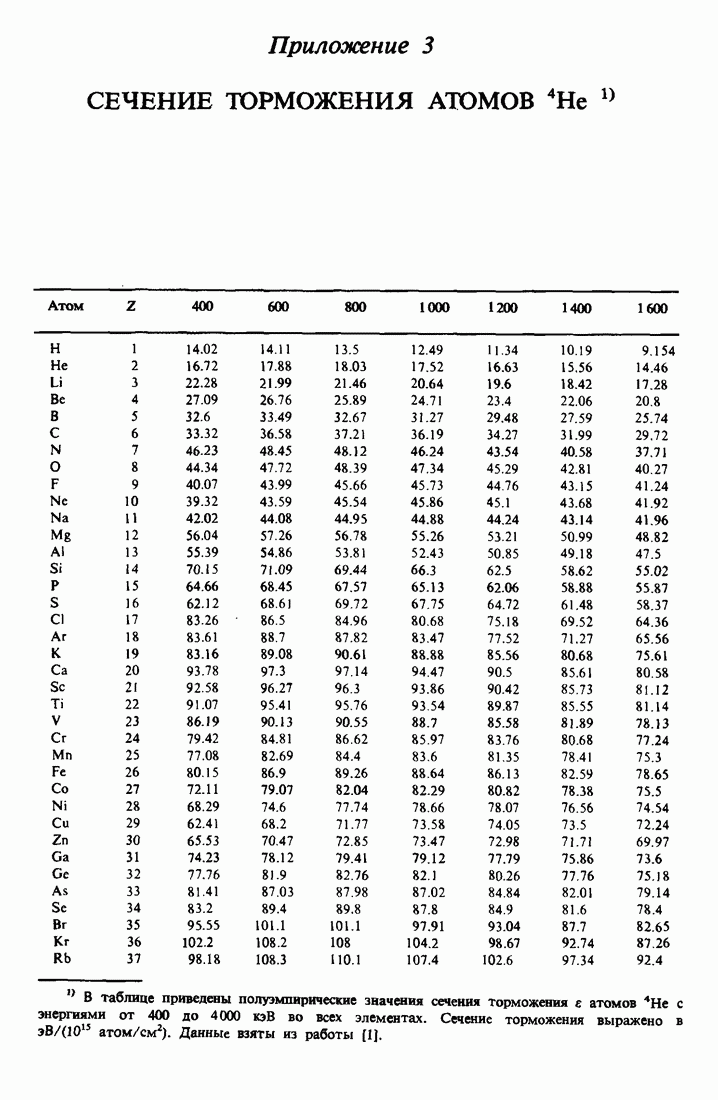
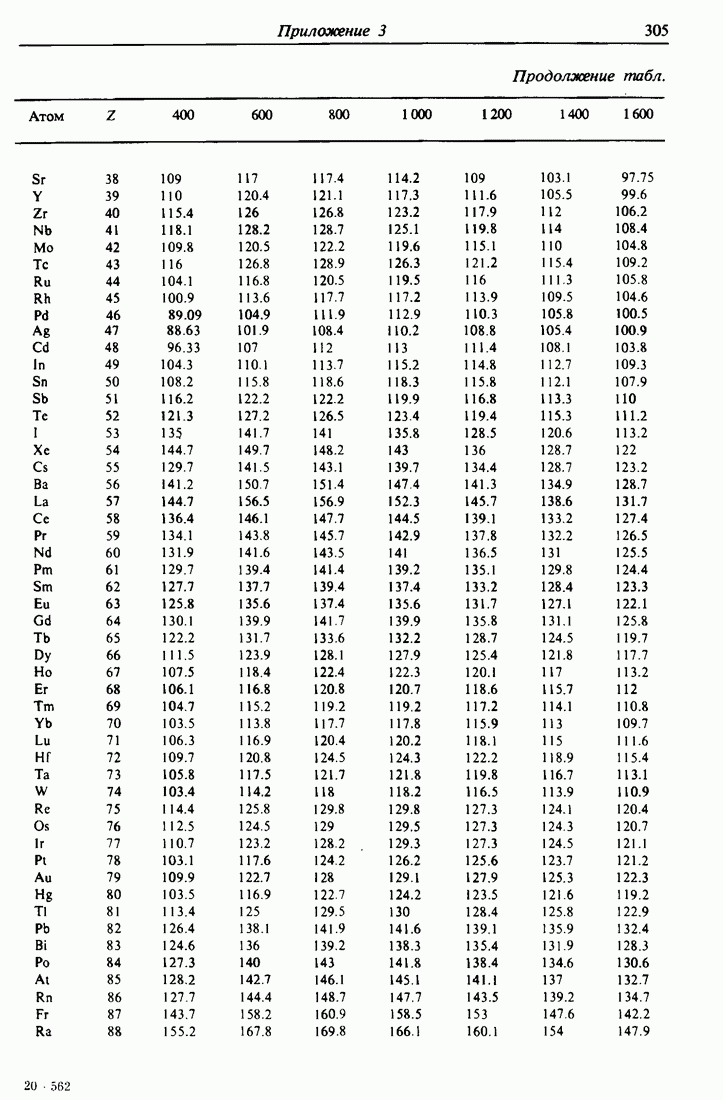
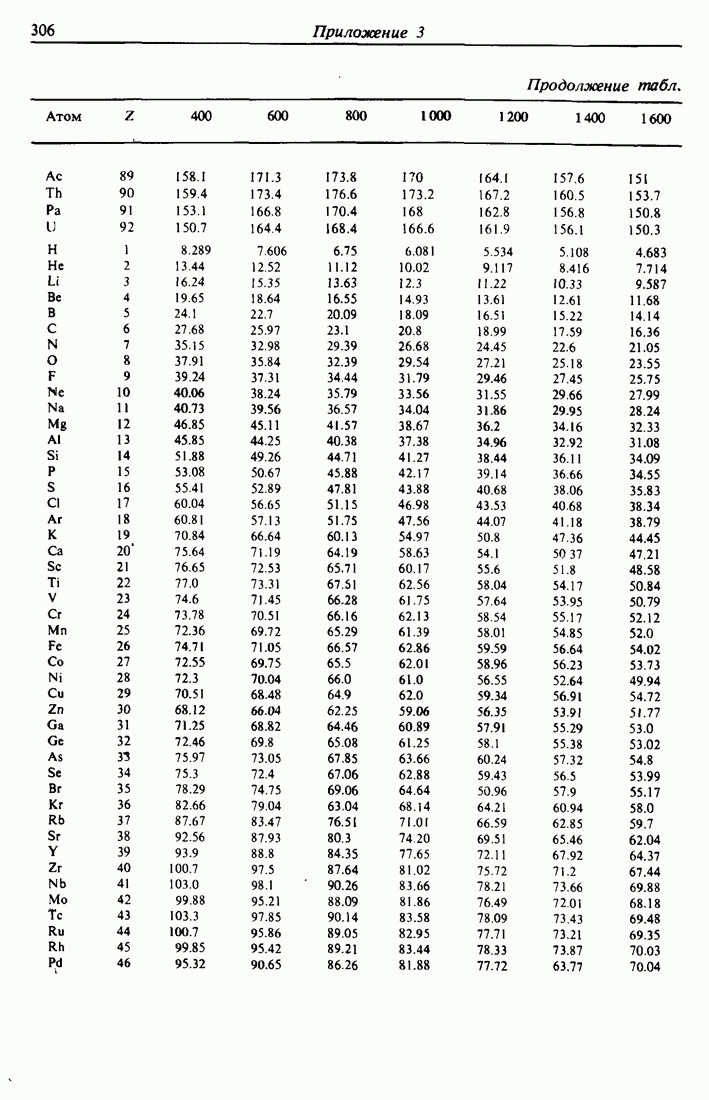
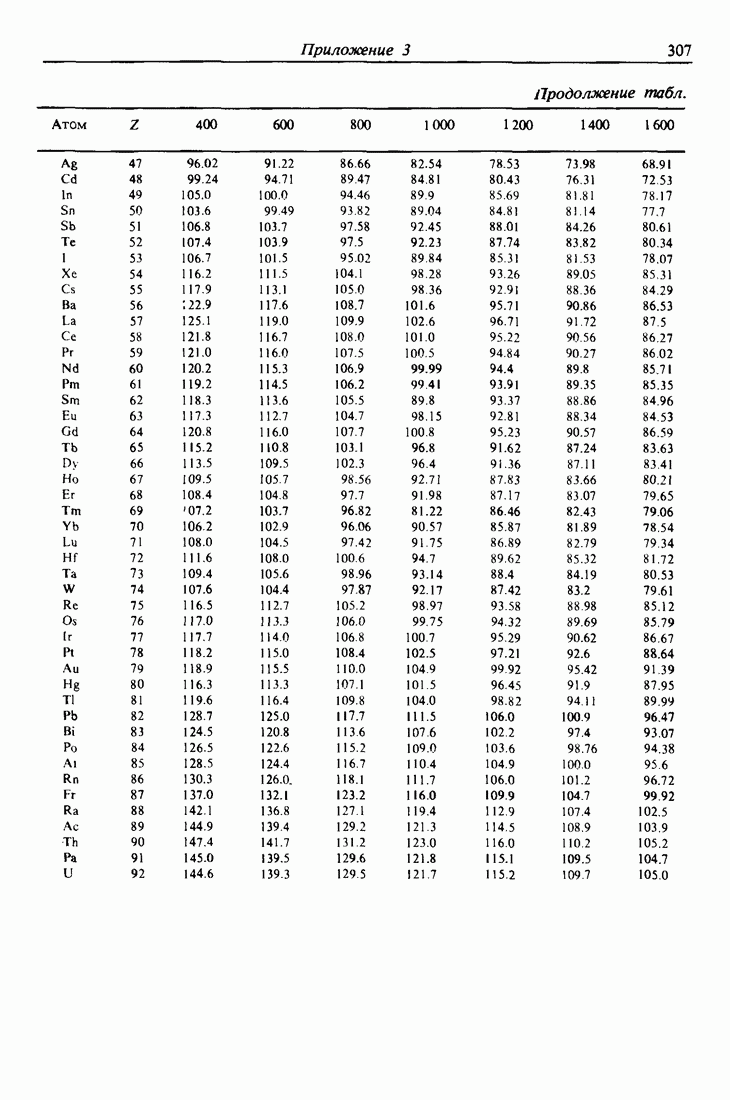
- ПРИЛОЖЕНИЕ 3.
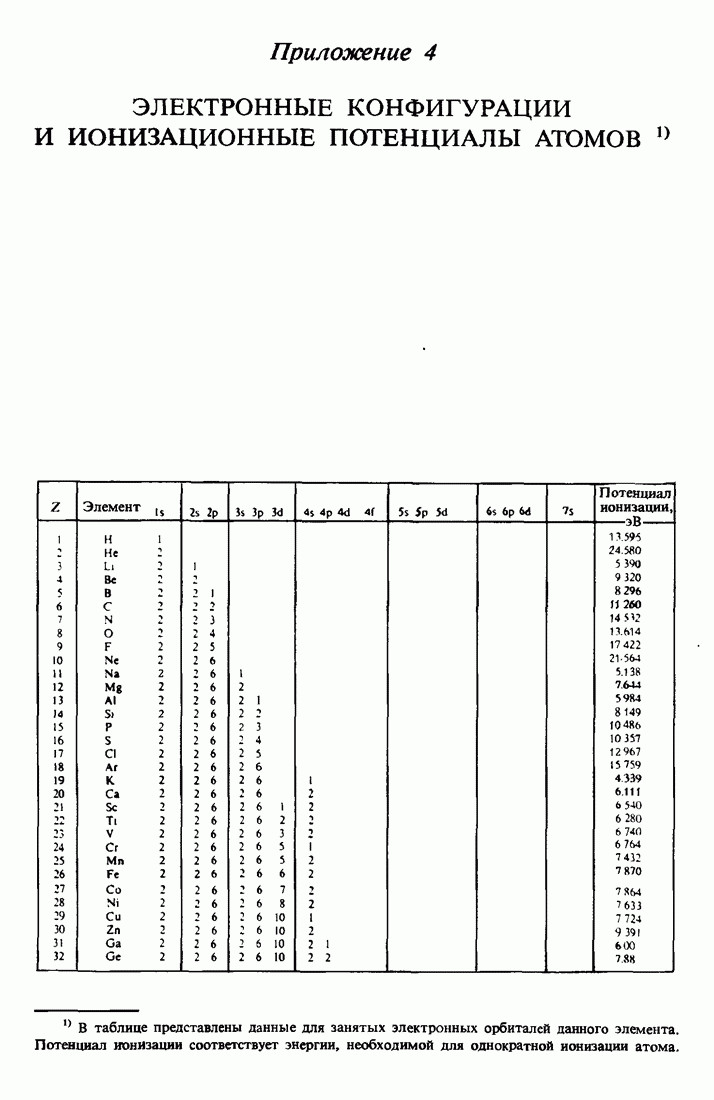
- ПРИЛОЖЕНИЕ 4.
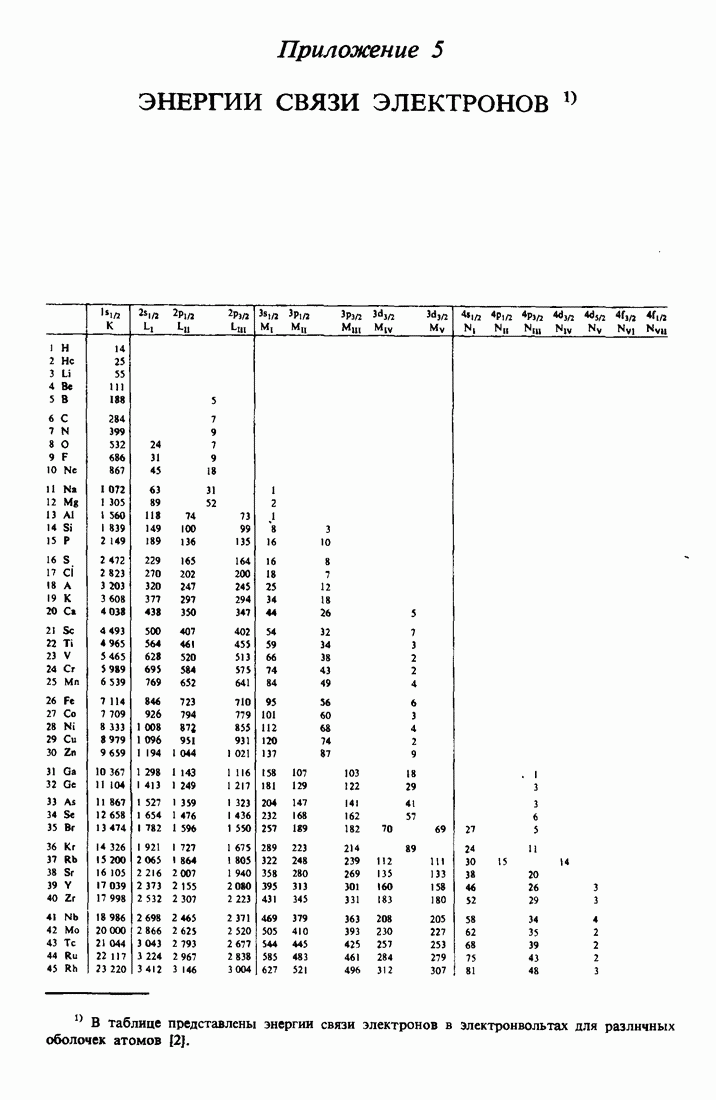
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
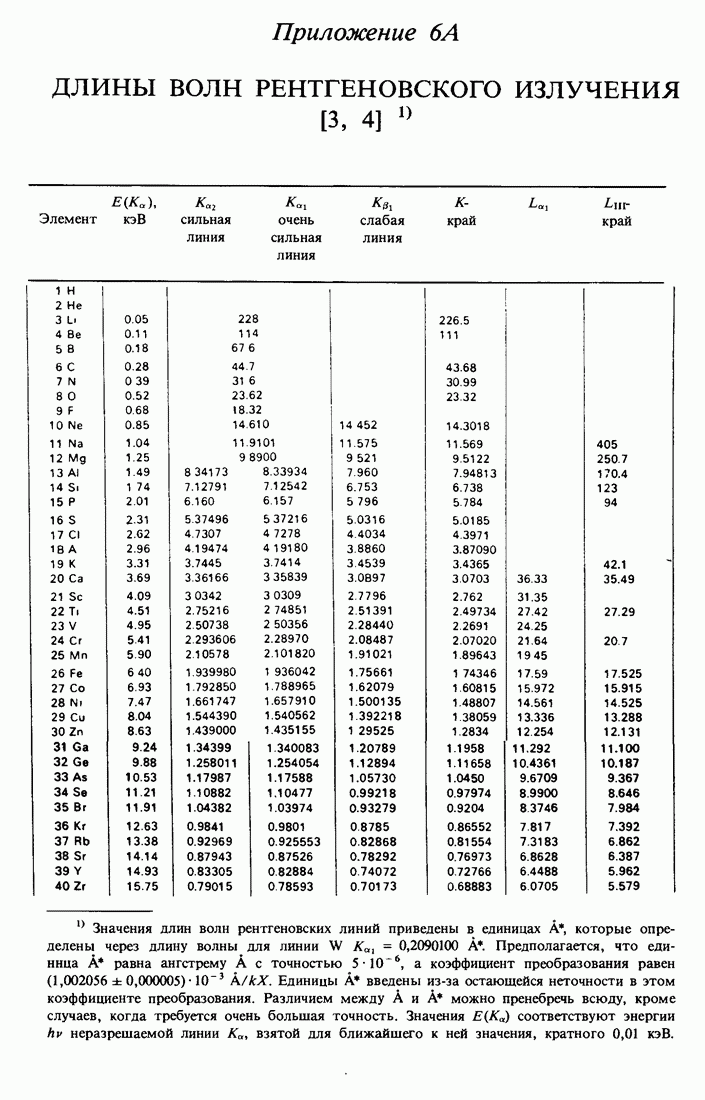
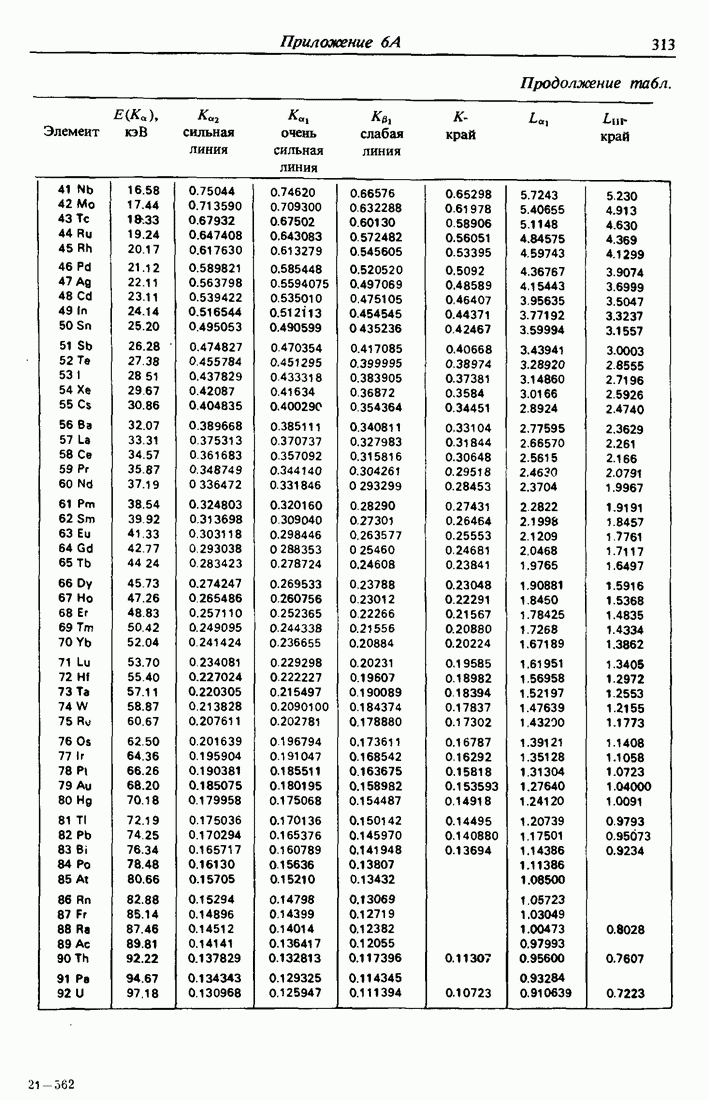
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
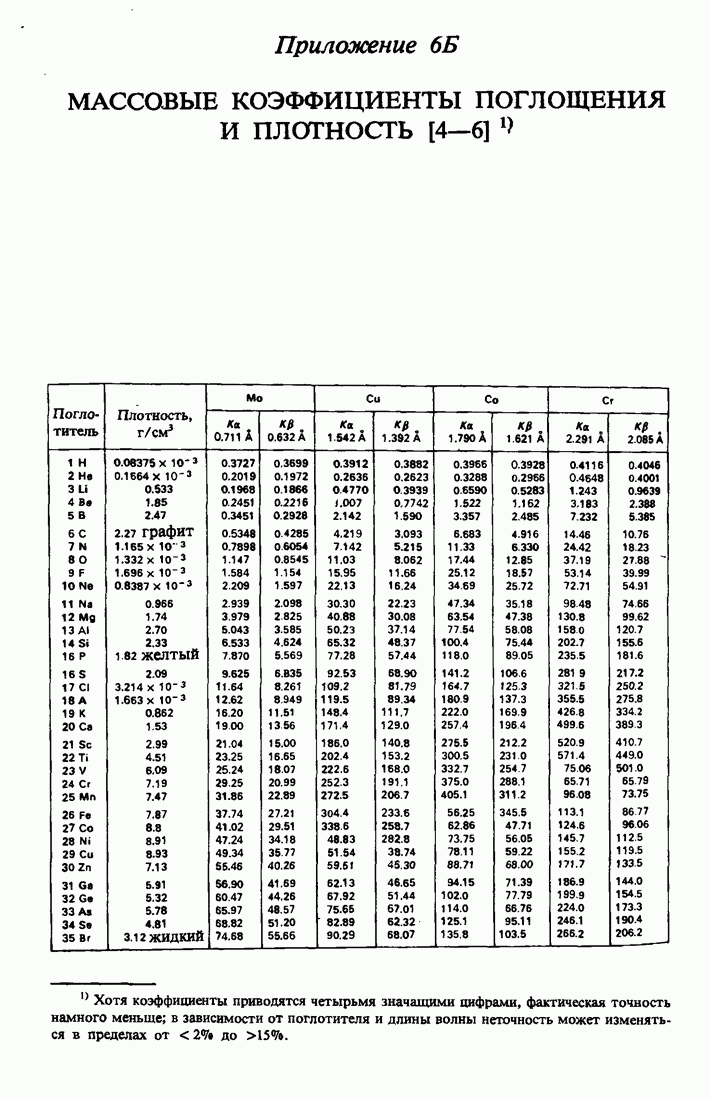
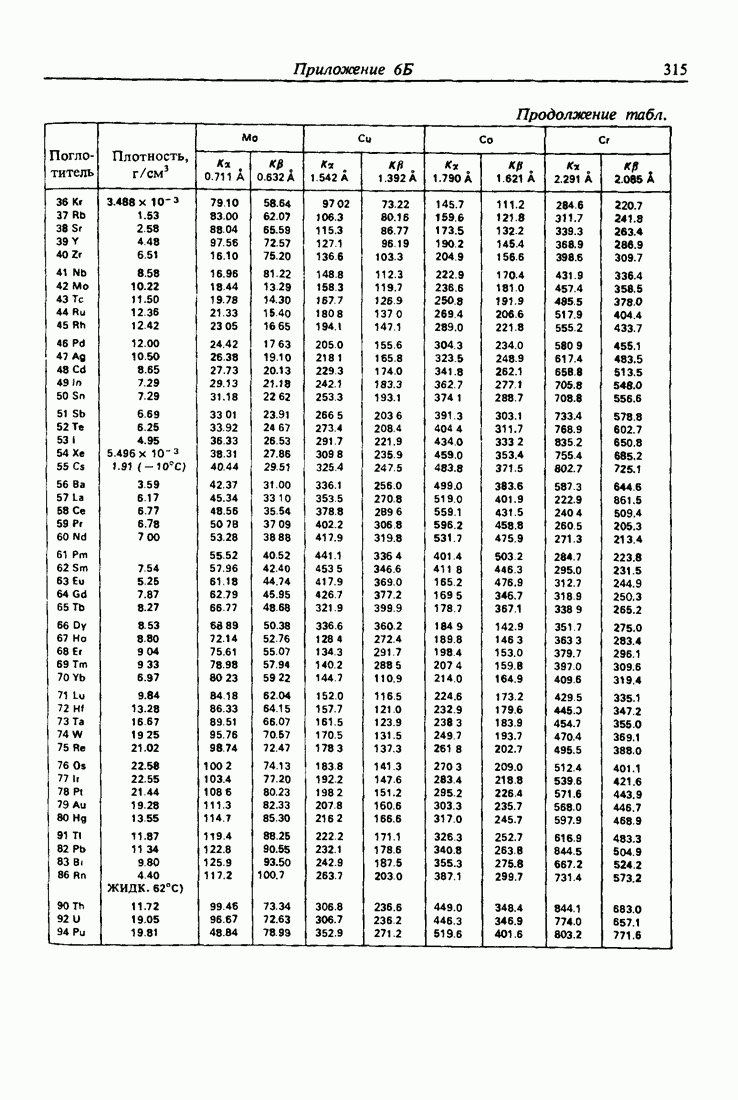
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
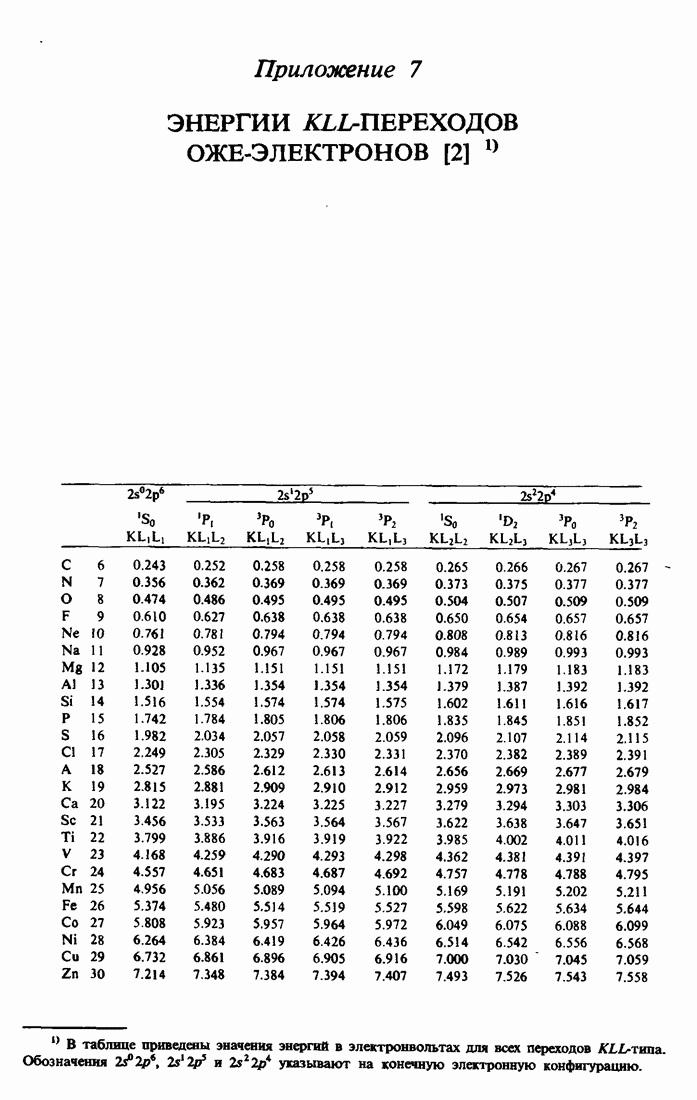
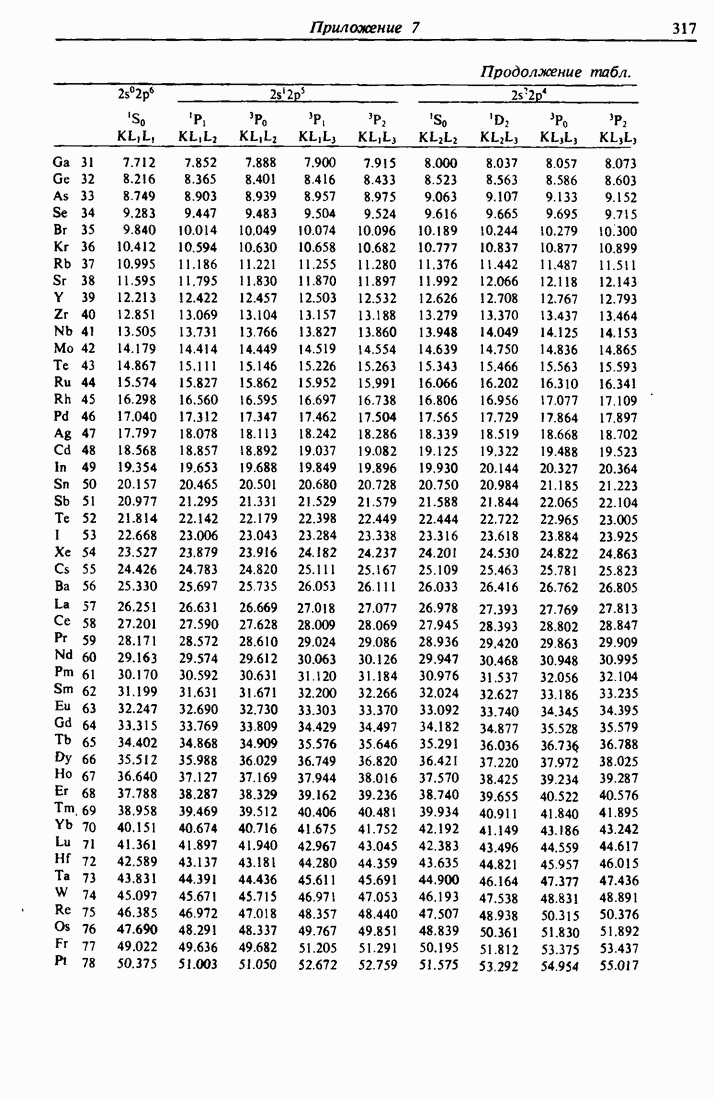
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
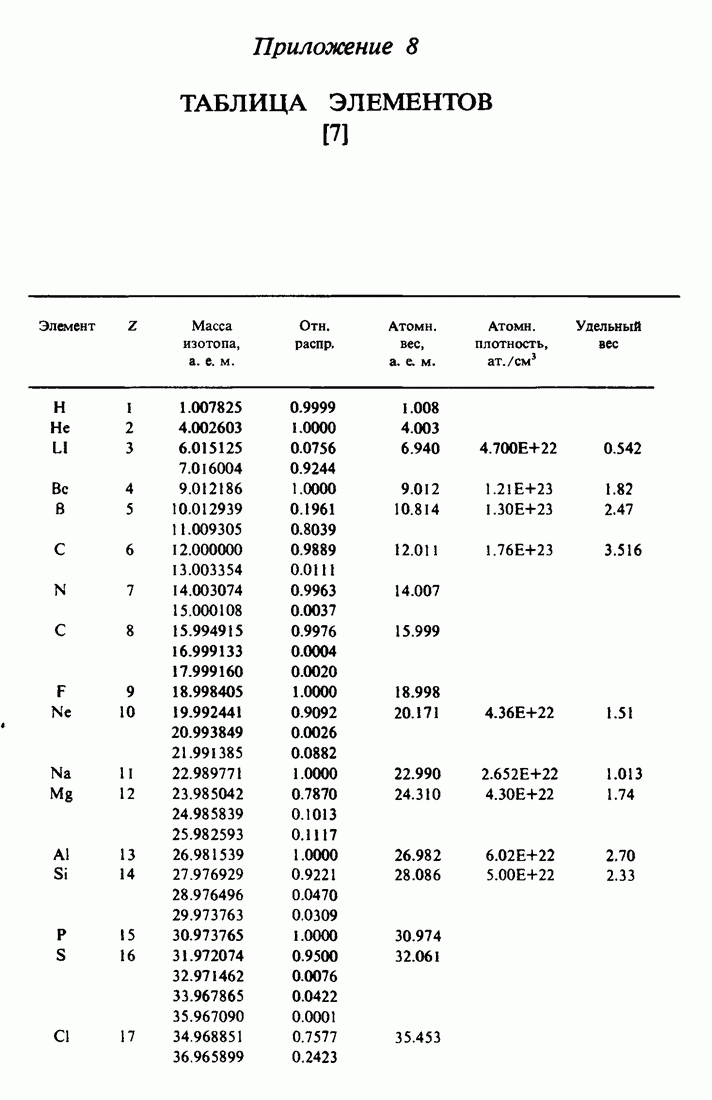
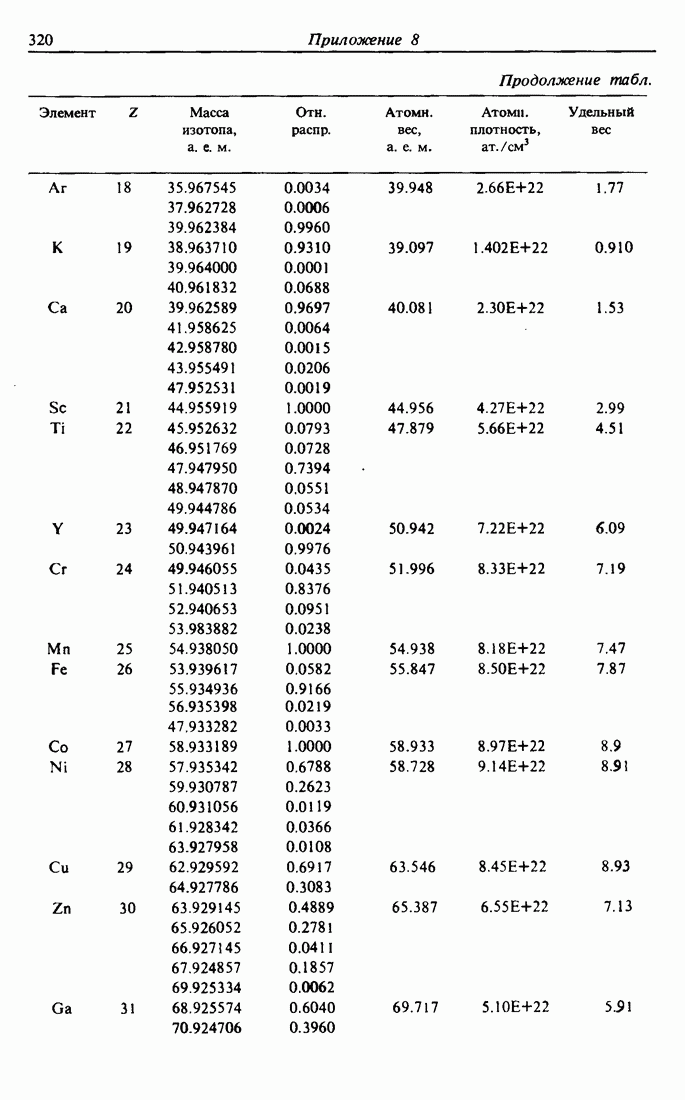
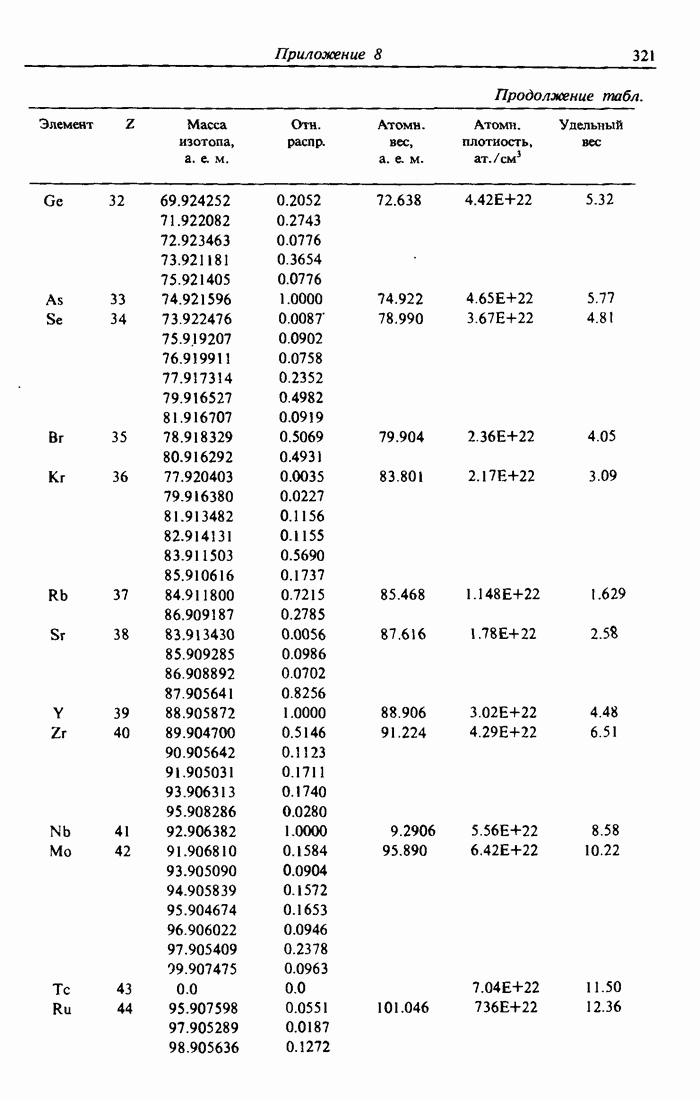
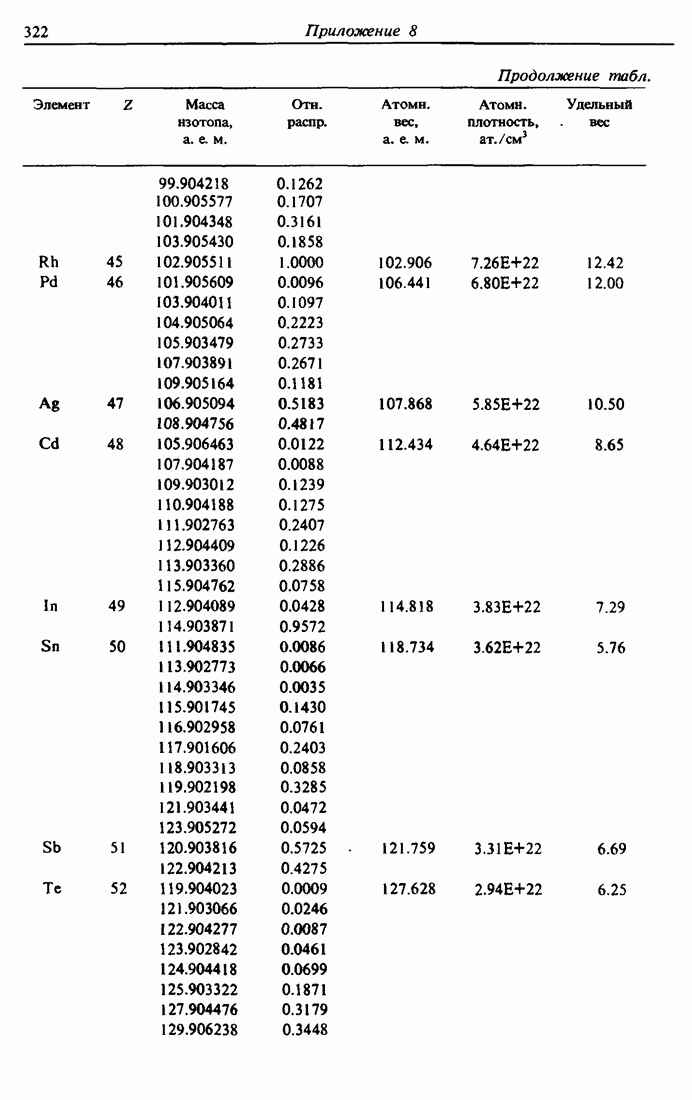
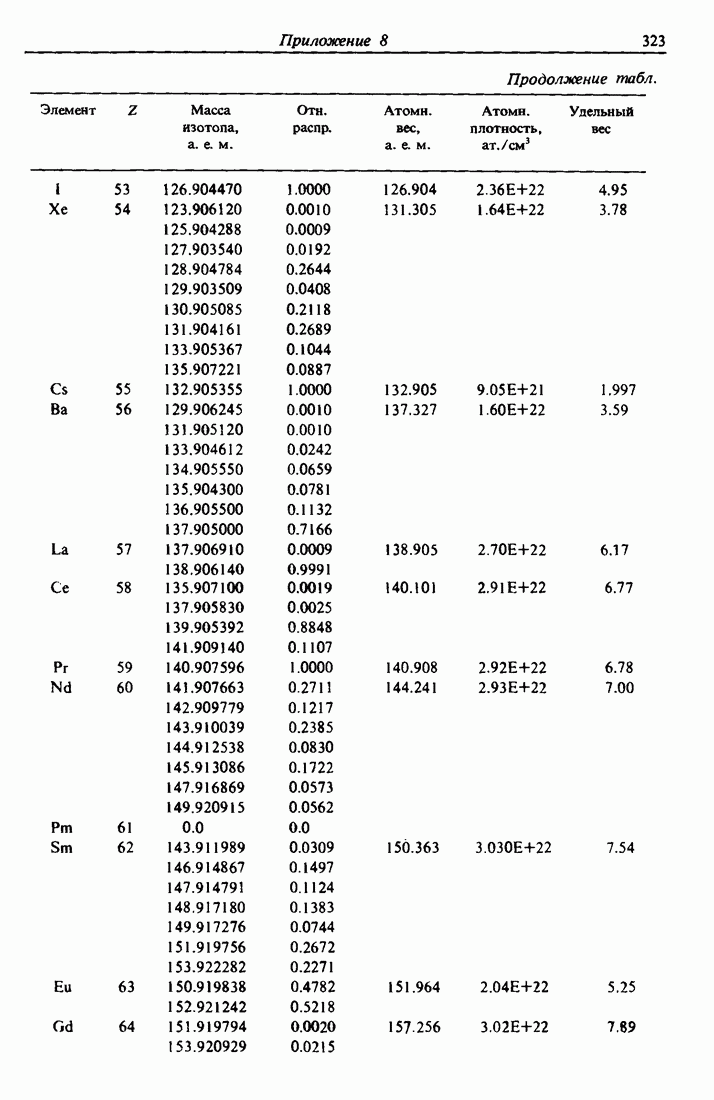
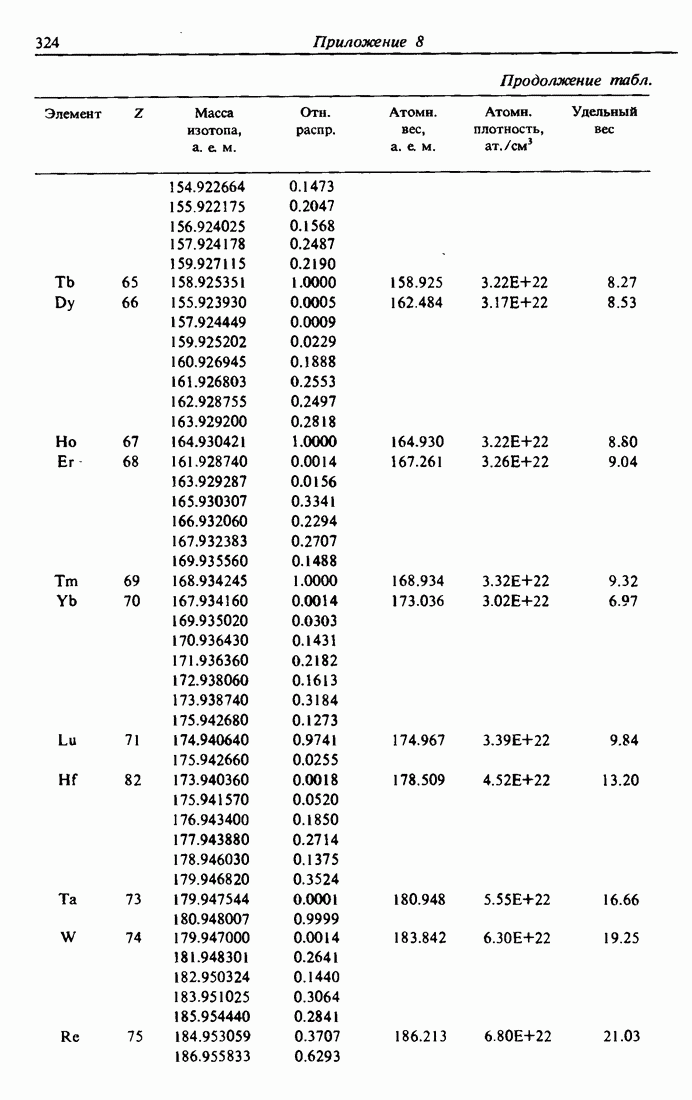
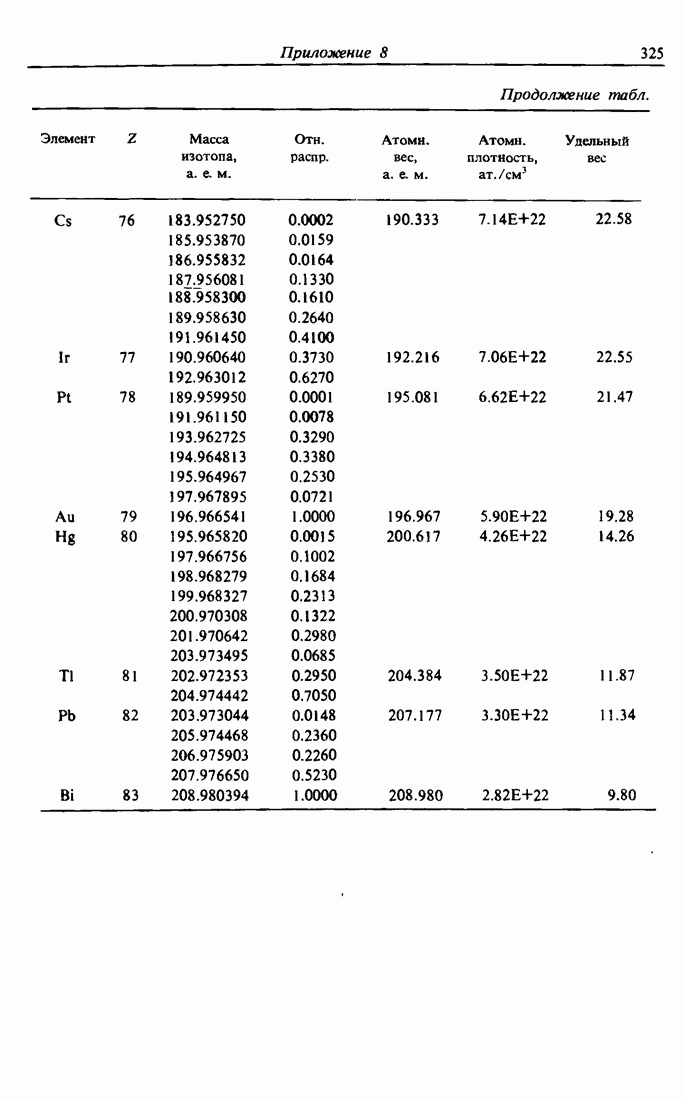
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
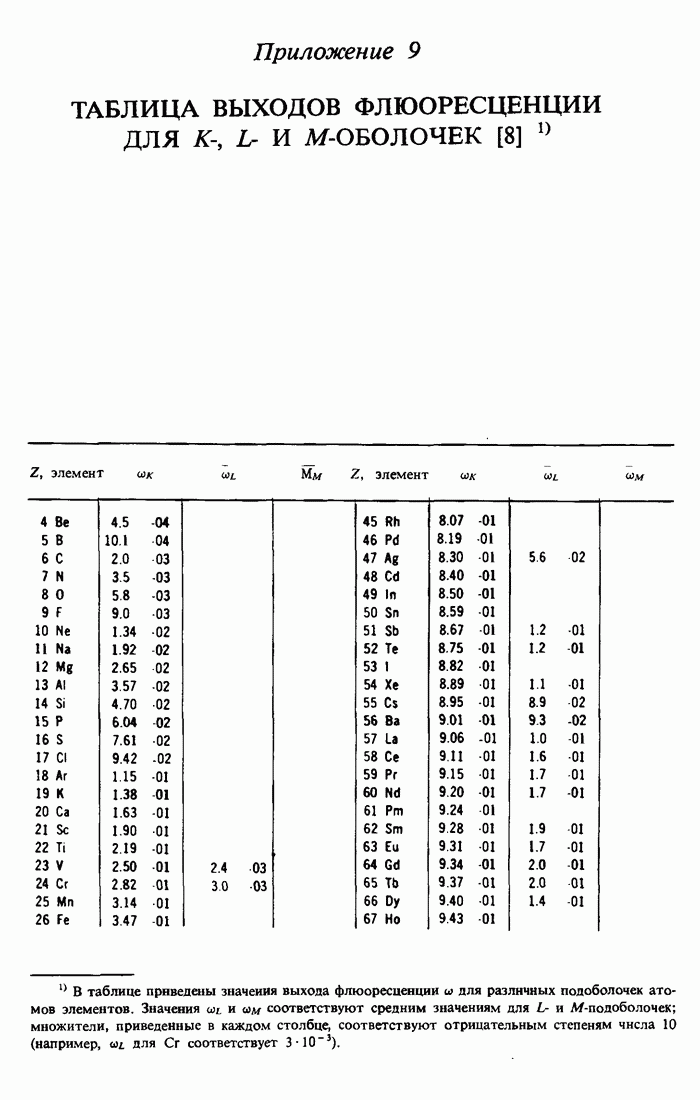
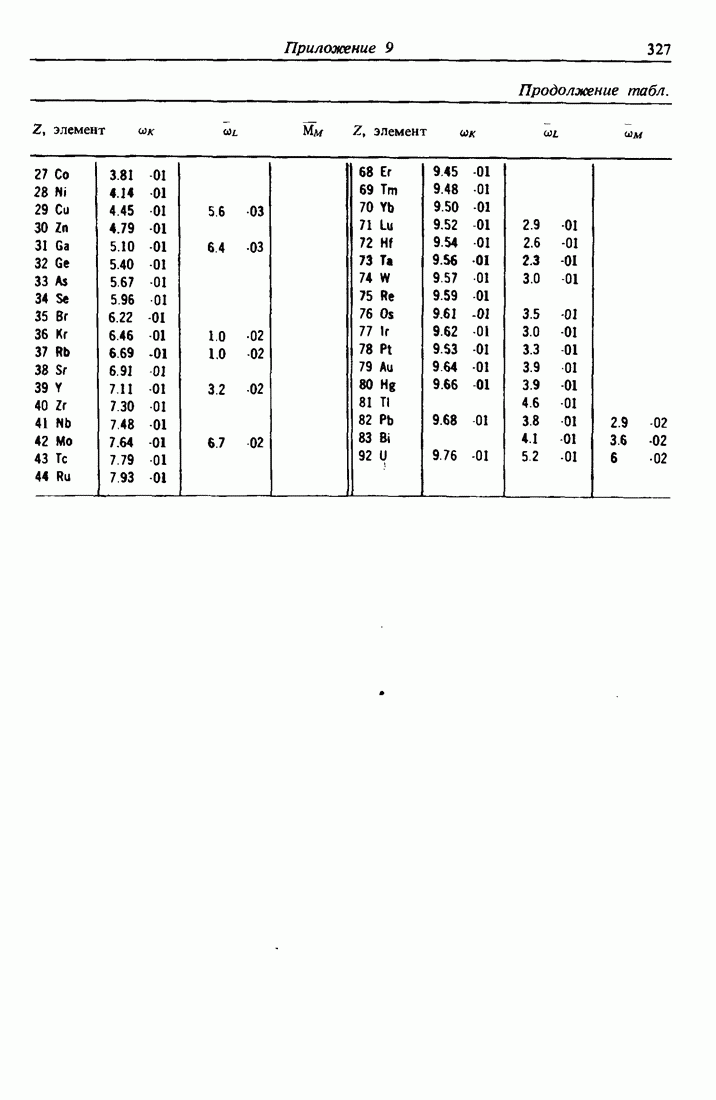
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ