| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.6. Поверхностный пик
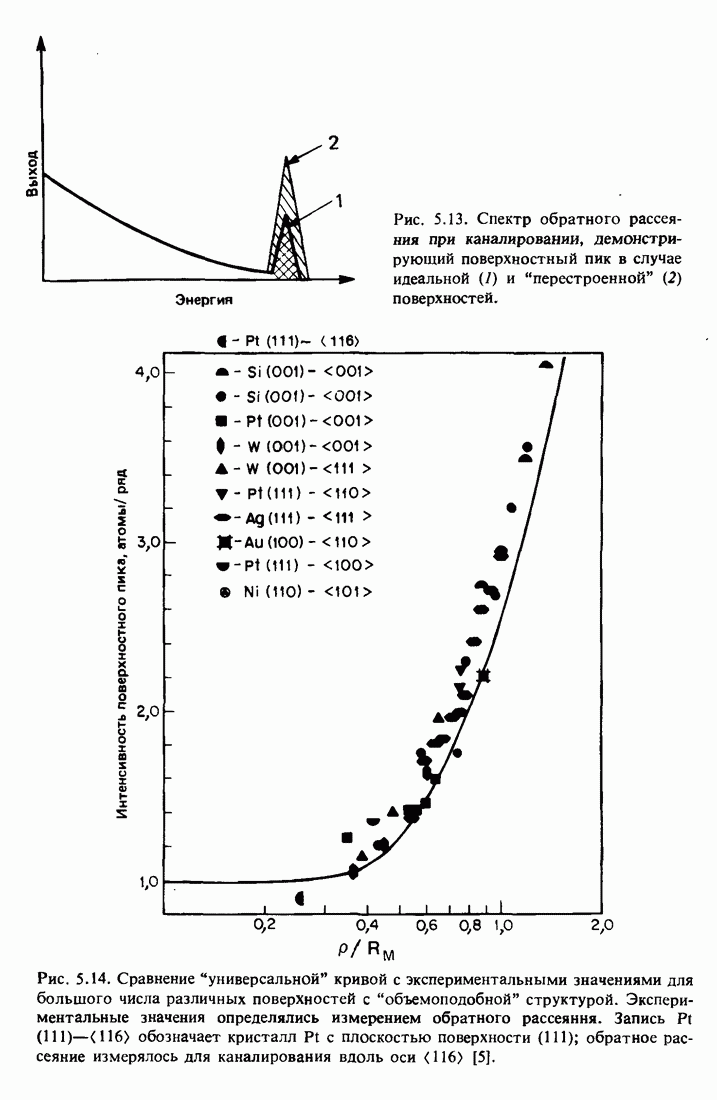
Применение ионных пучков для исследования структуры поверхности основано на 1) точном измерении поверхностного пика монослоев и 2) возможности предсказания поверхностного пика для заданной поверхностной структуры. Например, изображенные на рис. 5.13 спектры от ориентированного кристалла различаются интенсивностями поверхностных пиков, соответствующих разным поверхностным структурам. Из-за поверхностных смещений перестроенная поверхность дает более высокий выход обратного рассеяния, чем идеальная поверхность.

Рис. 5.13. Спектр обратного рассеяния при каналировании, демонстрирующий поверхностный пик в случае идеальной (1) и "перестроенной" (2) поверхностей.

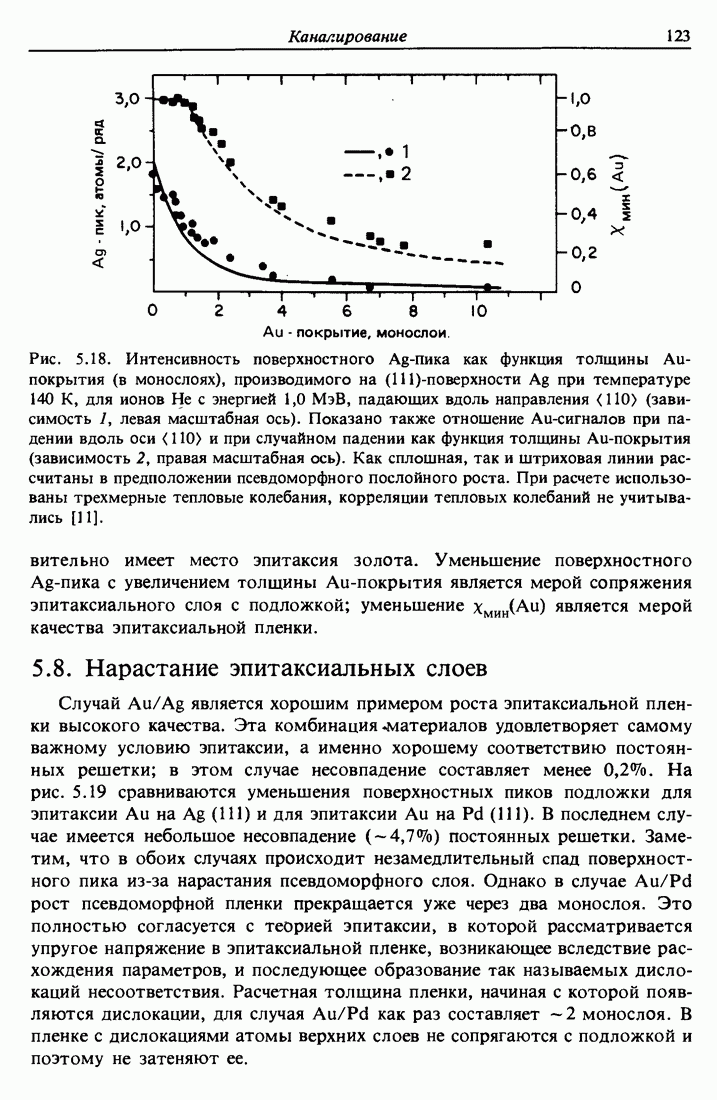
Рис. 5.14. Сравнение "универсальной" кривой с экспериментальными значениями для большого числа различных поверхностей с "объемоподобной" структурой. Экспериментальные значения определялись измерением обратного рассеяния. Запись  обозначает кристалл
обозначает кристалл  с плоскостью поверхности (111); обратное рассеяние измерялось для каналирования вдоль оси (116) [5].
с плоскостью поверхности (111); обратное рассеяние измерялось для каналирования вдоль оси (116) [5].
Более утонченное рассмотрение поверхностного пика принимает в расчет тот факт, что в его формирование дают вклад не два атома, а больше, и что потенциал взаимодействия является не чисто кулоновским, а экранированным (например, потенциалом Мольера). Интенсивность поверхностного пика устанавливается расчетами. Результаты большого числа вычислений показывают, что для поверхностного пика по-прежнему имеет место скейлинг, причем параметром скейлинга является отношение  , где
, где  — радиус конуса тени, соответствующий потенциалу Мольера, и выполняется грубая оценка
— радиус конуса тени, соответствующий потенциалу Мольера, и выполняется грубая оценка 
Амплитуда поверхностного пика в единицах (число атомов)/цепочка была вычислена для широкого набора случаев в предположении, что поверхность идеальна и обладает «объемоподобной» структурой. Результаты изображены на рис. 5.14 в виде «универсальной кривой» для интенсивности

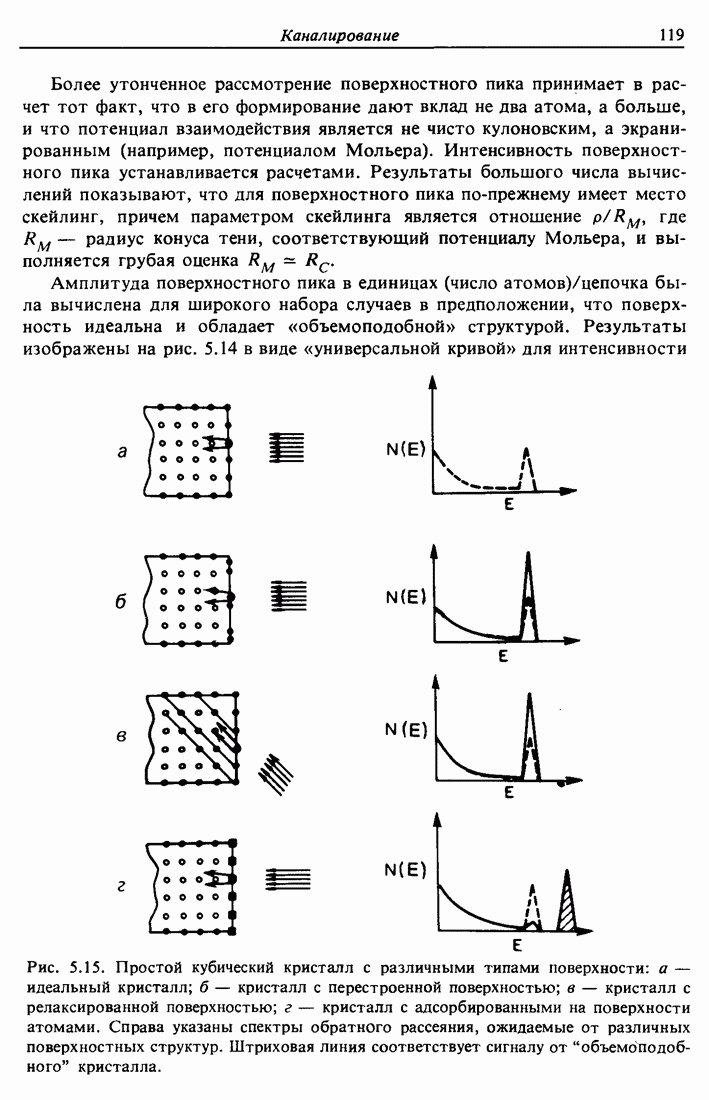
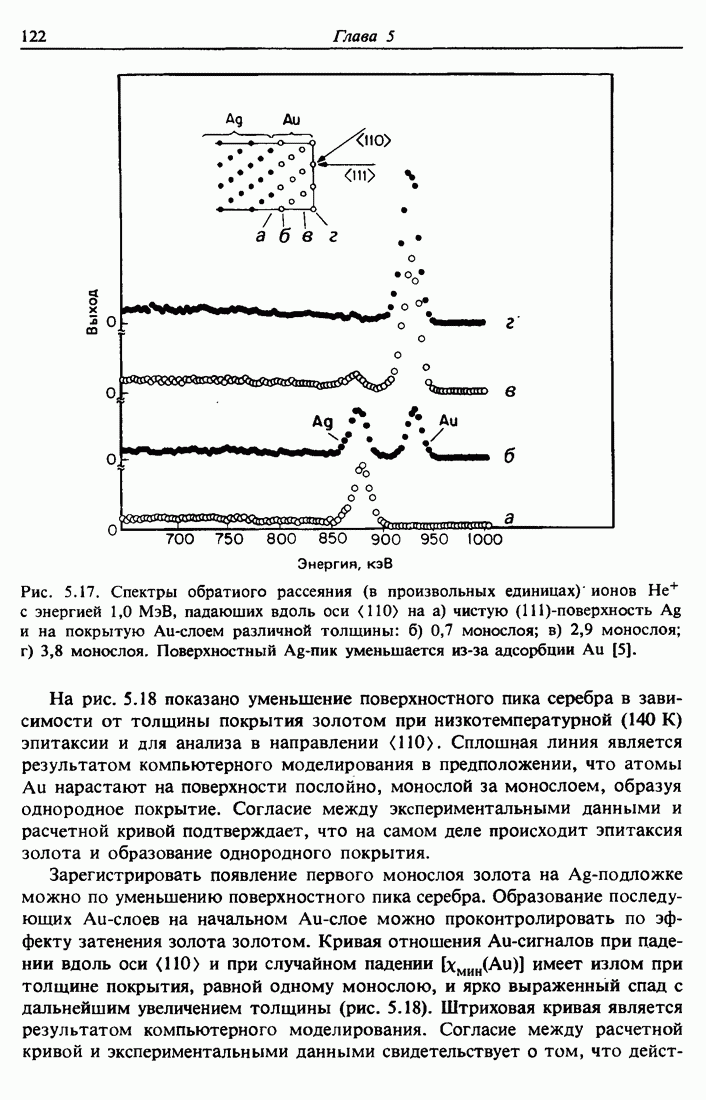
Рис. 5.15. Простой кубический кристалл с различными типами поверхности: а — идеальный кристалл; б — кристалл с перестроенной поверхностью; в — кристалл с релаксированной поверхностью; г — кристалл с адсорбированными на поверхности атомами. Справа указаны спектры обратного рассеяния, ожидаемые от различных поверхностных структур. Штриховая линия соответствует сигналу от "объемоподоб-ного" кристалла.
поверхностного пика как функции переменной p/RM, где р — амплитуда двумерных колебаний. Значения RM можно найти в монографии [5], где приводится также большое число экспериментальных данных. Согласие между "экспериментом и теорией является чрезвычайно хорошим.
На рис. 5.15 изображены четыре простых вида поверхностной структуры и соответствующие им спектры с поверхностными пиками. Пунктиром указаны выходы рассеяния на кристалле с идеальной поверхностью в случае, когда амплитуда тепловых колебаний р намного меньше радиуса конуса тени RM (рис. 5.15, а). Это условие гарантирует, что интенсивность поверхностного пика соответствует одному атому на цепочку. Кристалл с поверхностью, перестроенной таким образом, что поверхностные атомы смещены в плоскости поверхности (рис. 5.15, б), представляет ситуацию, в которой второй атом не затеняется. В этом случае интенсивность поверхностного пика в два раза больше, чем для идеального кристалла. Чтобы обнаружить релаксацию, вызванную смещением поверхностных атомов перпендикулярно поверхности (рис. 5.15, в), необходимо использовать наклонное падение пучка, при котором ряды атомов в объеме образца не попадают в конусы тени от атомов поверхности. Нормальное падение привело бы в этом случае к интенсивности поверхностного пика, эквивалентной одному монослою. Поэтому сравнение двух измерений — при нормальном и наклонном падении — позволяет обнаружить наличие растяжения. Поверхностный атом-адсорбат может затенять атомы подложки, если  . Чувствительность ионного рассеяния к массам атомов-рассеивателей позволяет отличить подложку от адсорбата. На рис. 5.15, г адсорбированные атомы расположены точно над атомами поверхности и поэтому снижают амплитуду поверхностного пика подложки.
. Чувствительность ионного рассеяния к массам атомов-рассеивателей позволяет отличить подложку от адсорбата. На рис. 5.15, г адсорбированные атомы расположены точно над атомами поверхности и поэтому снижают амплитуду поверхностного пика подложки.
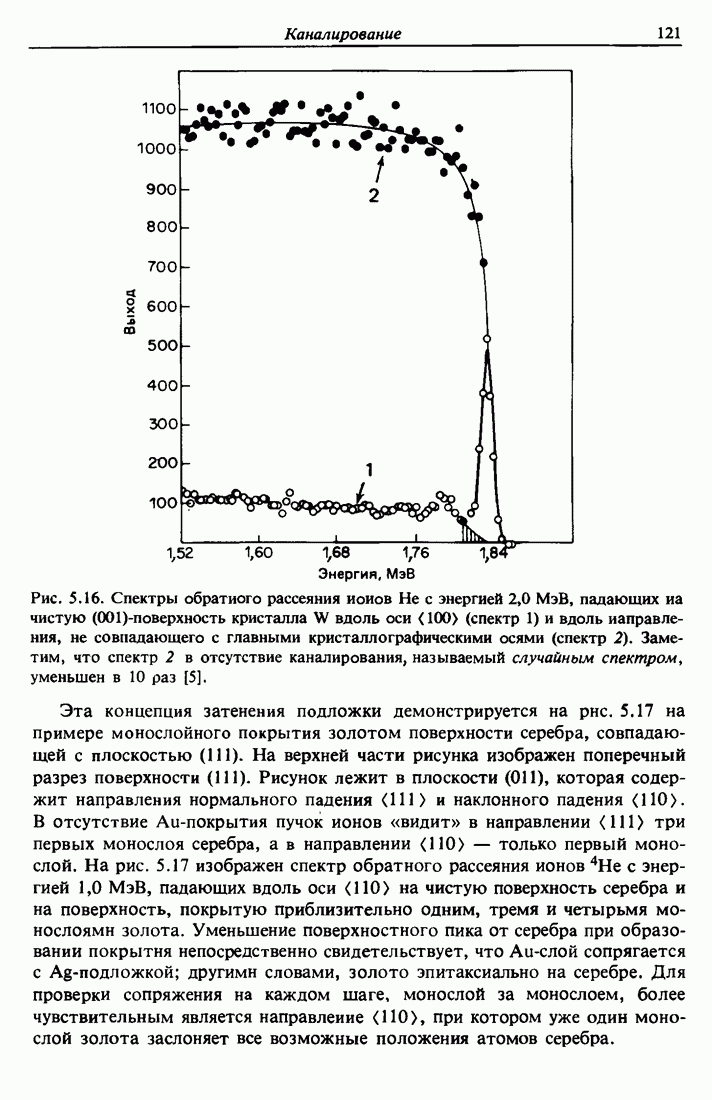
На рис. 5.16 проведено сравнение спектра, который получен с помощью пучка, направленного вдоль оси  вольфраме (спектр от ориентированного кристалла), и спектра, который получен в разориентированном кристалле (случайный спектр). На рисунке отчетливо виден поверхностный пик, соответствующий примерно двум атомам на цепочку
вольфраме (спектр от ориентированного кристалла), и спектра, который получен в разориентированном кристалле (случайный спектр). На рисунке отчетливо виден поверхностный пик, соответствующий примерно двум атомам на цепочку  . Эффект каналирования приводит к уменьшению на два порядка выхода рассеяния в объеме кристалла при использовании геометрии каналирования по сравнению с выходом рассеяния при случайном падении. Именно подавление рассеяния в объеме образца, которое наблюдается в спектре от ориентированного кристалла, позволяет выполнить измерения поверхностного пика.
. Эффект каналирования приводит к уменьшению на два порядка выхода рассеяния в объеме кристалла при использовании геометрии каналирования по сравнению с выходом рассеяния при случайном падении. Именно подавление рассеяния в объеме образца, которое наблюдается в спектре от ориентированного кристалла, позволяет выполнить измерения поверхностного пика.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
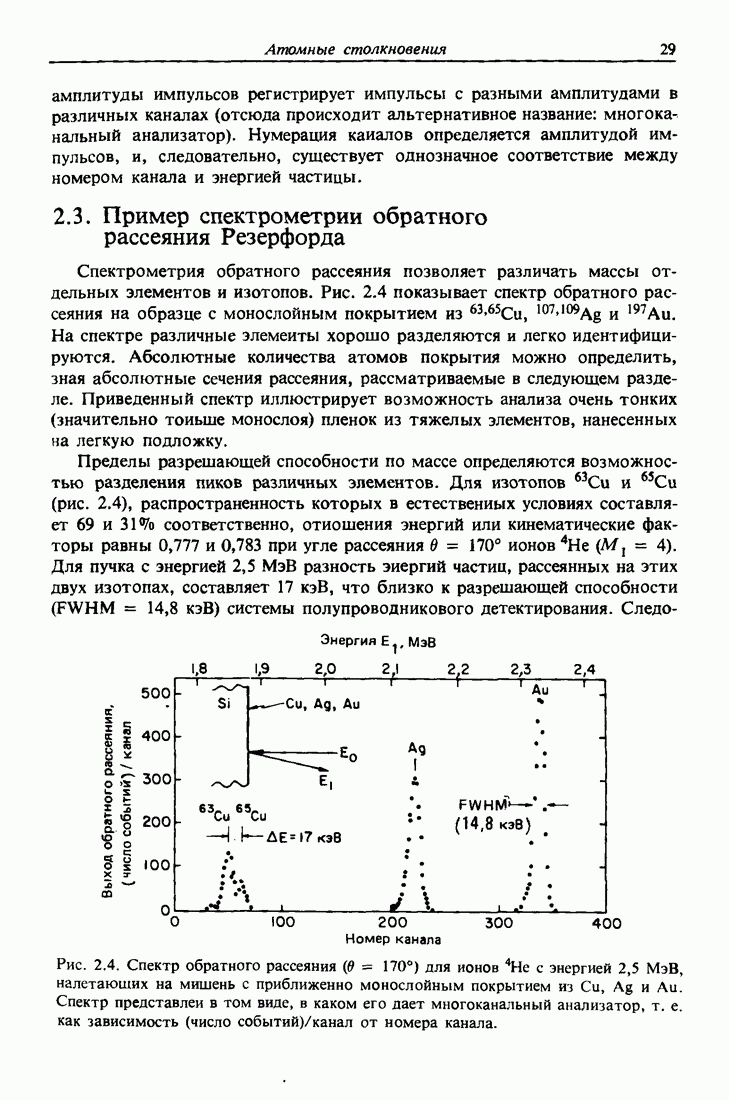
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
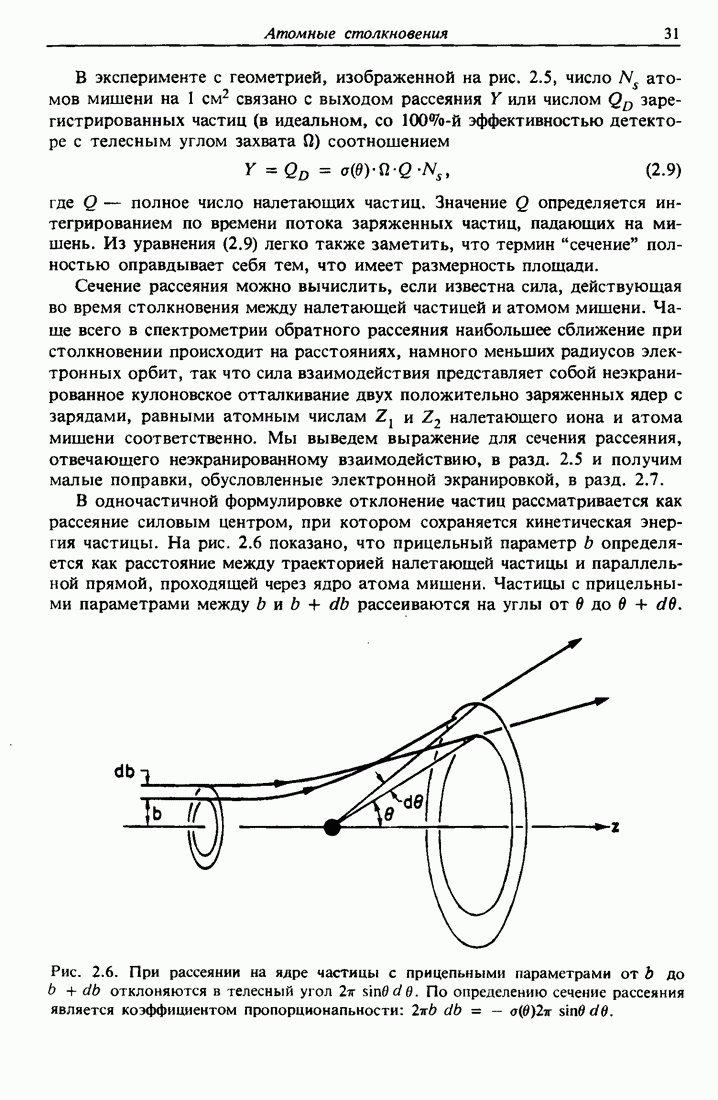
- 2.4. Сечение рассеяния и прицельный параметр
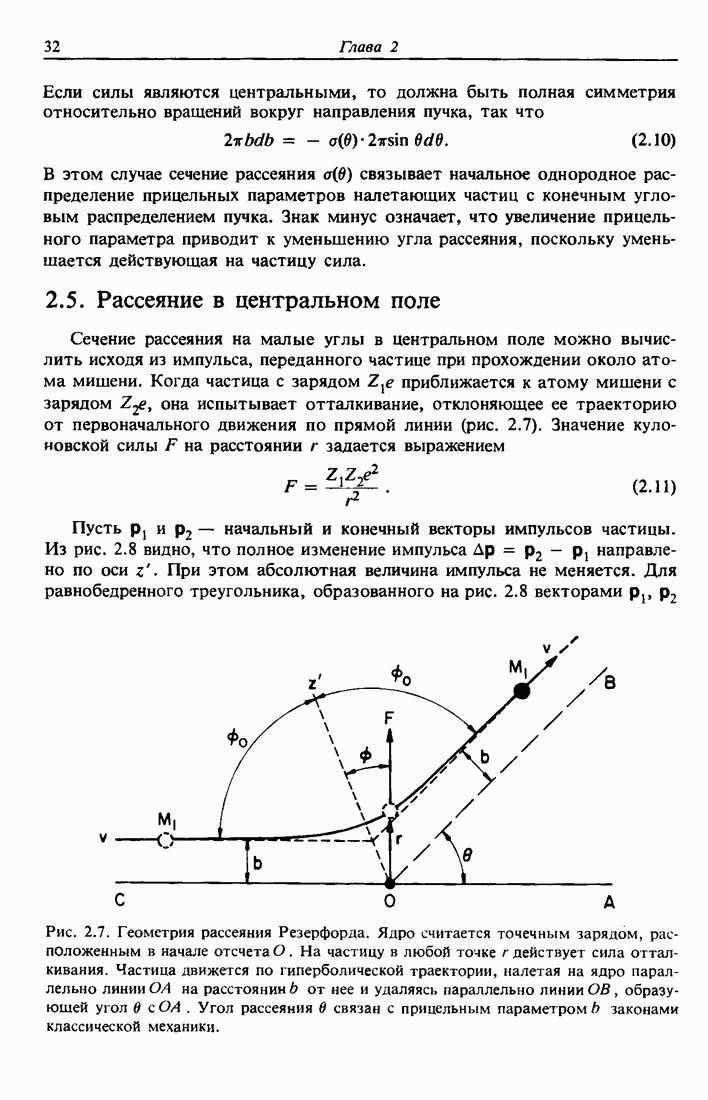
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
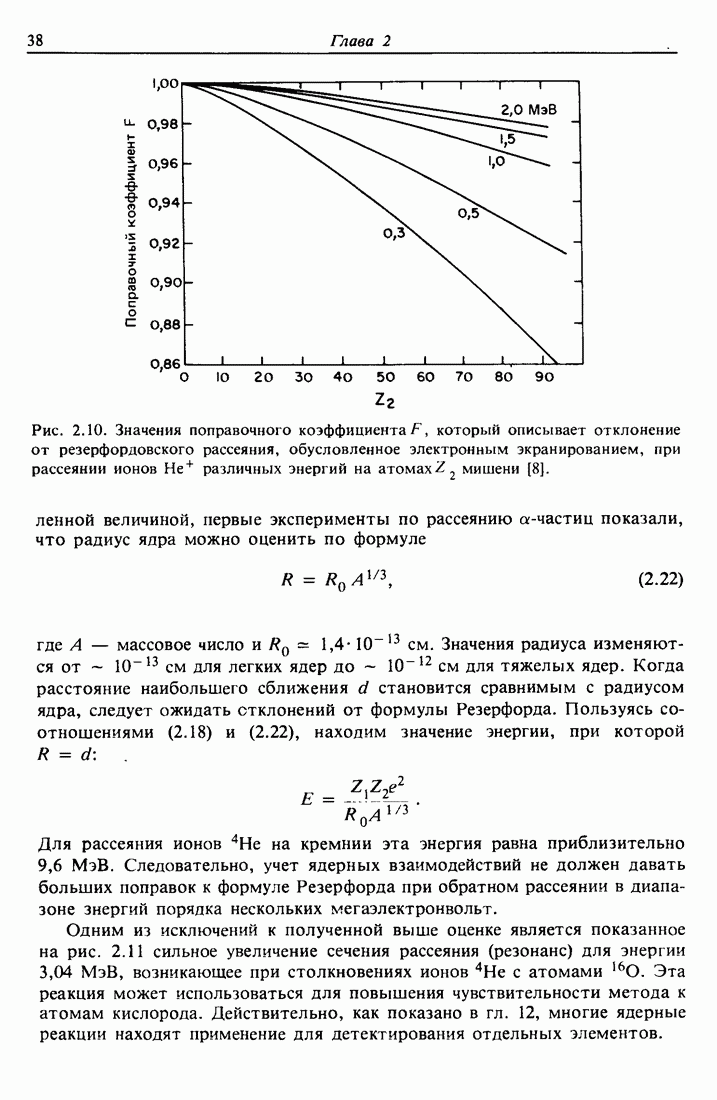
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
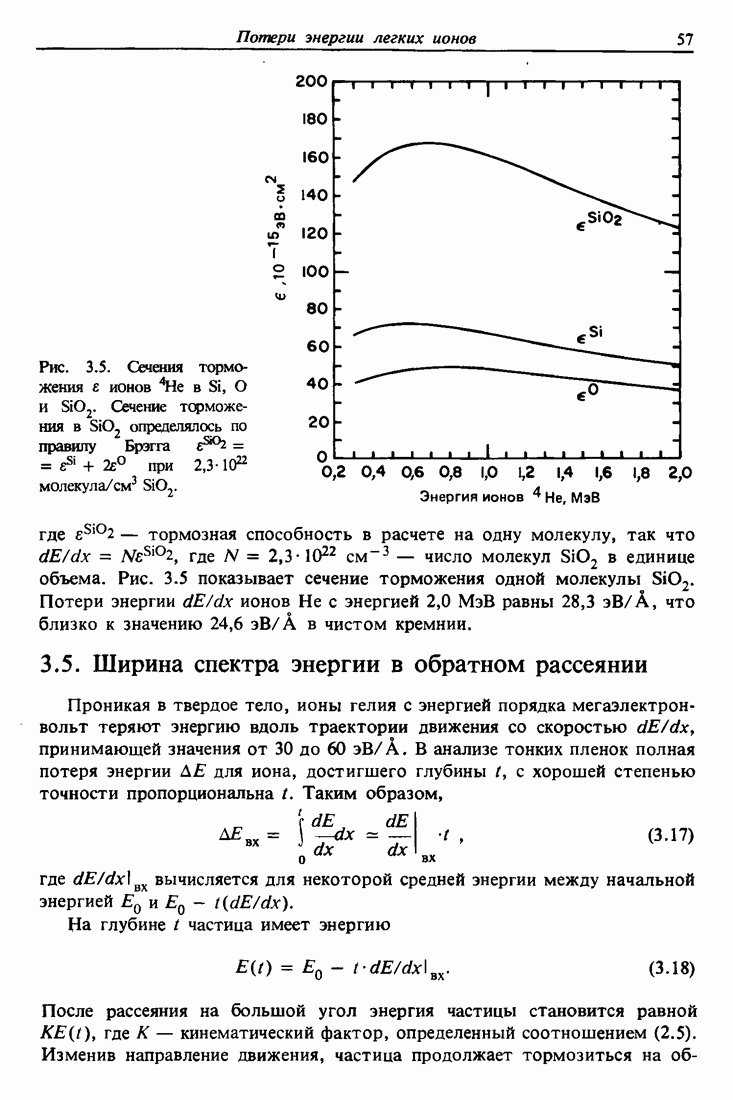
- 3.4. Потери энергии в химических соединениях и правило Брэгга
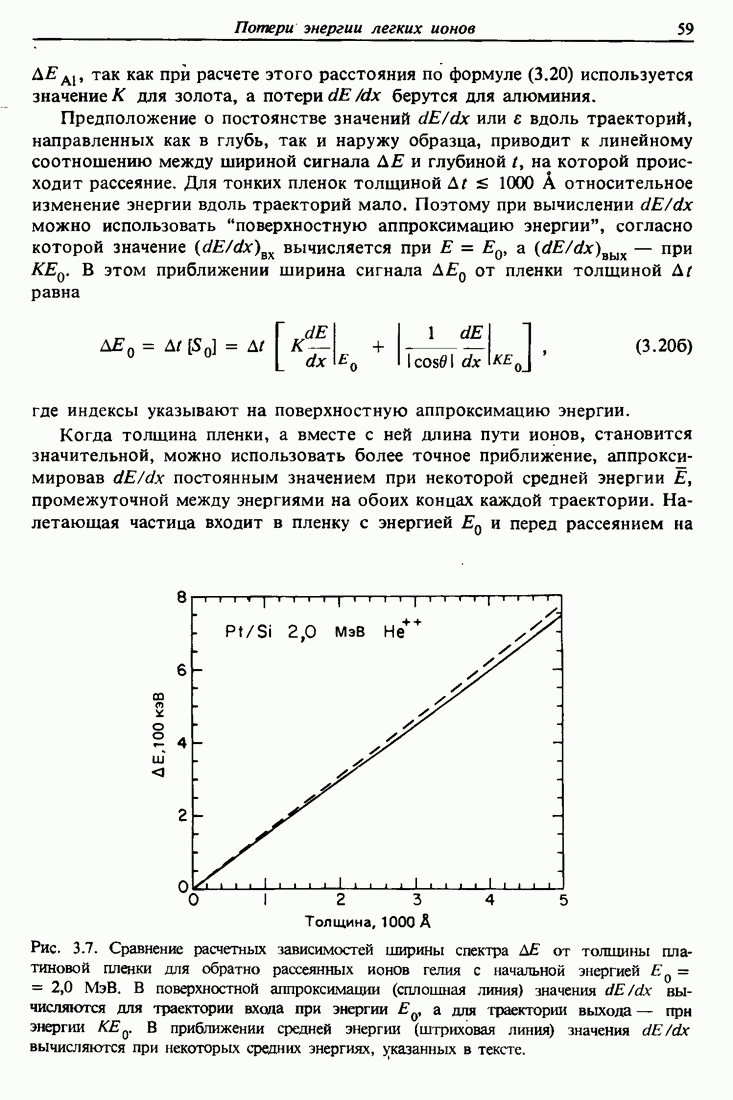
- 3.5. Ширина спектра энергии в обратном рассеянии
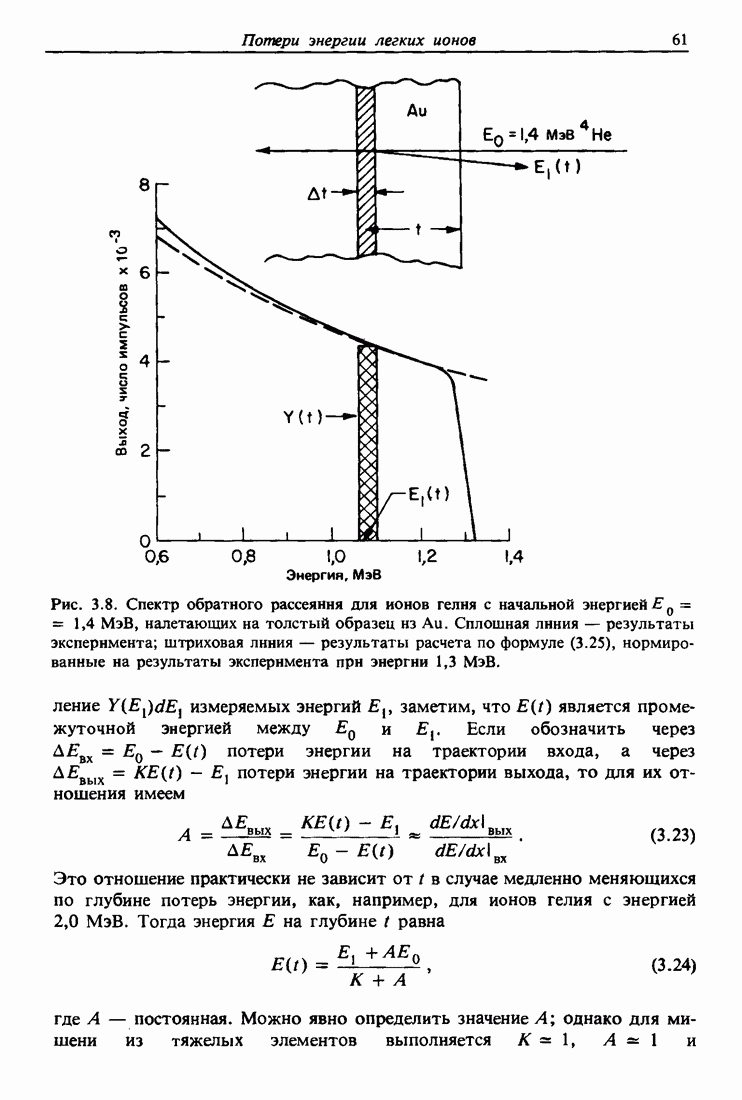
- 3.6. Форма спектра обратного рассеяния
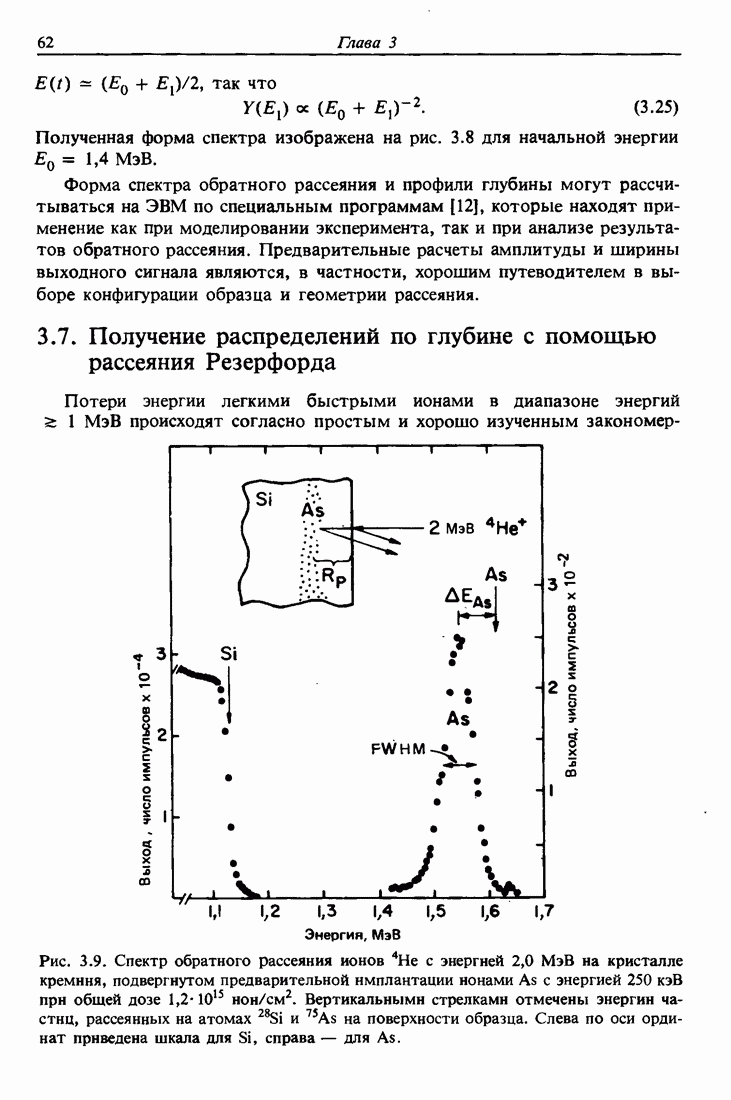
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
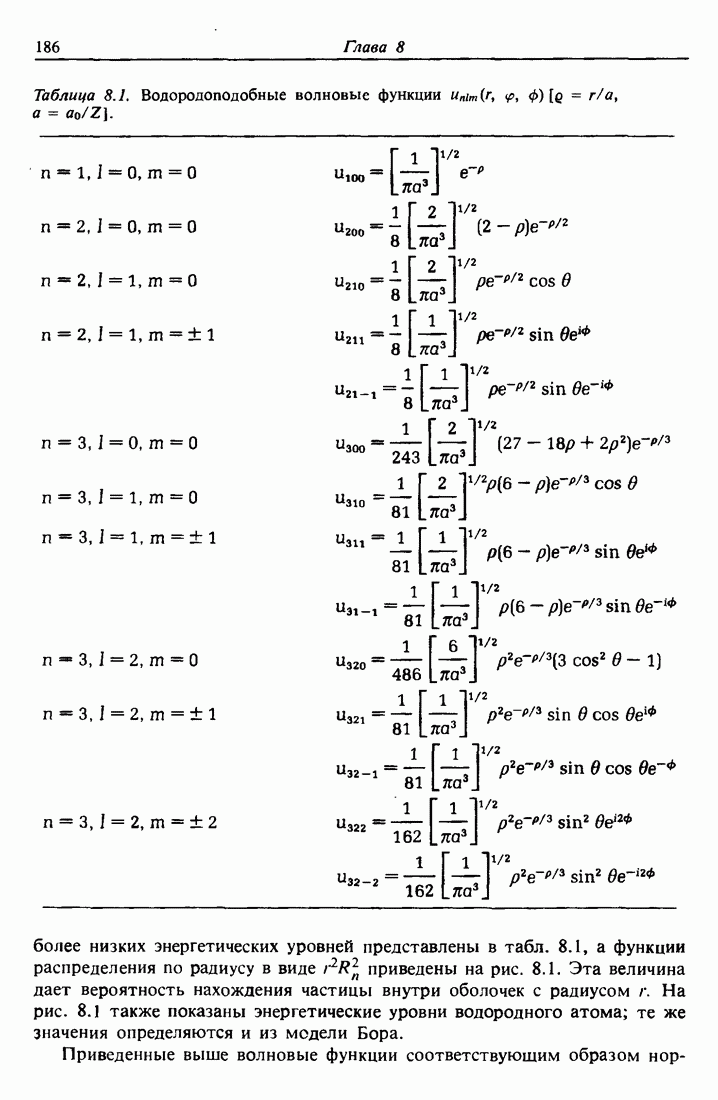
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
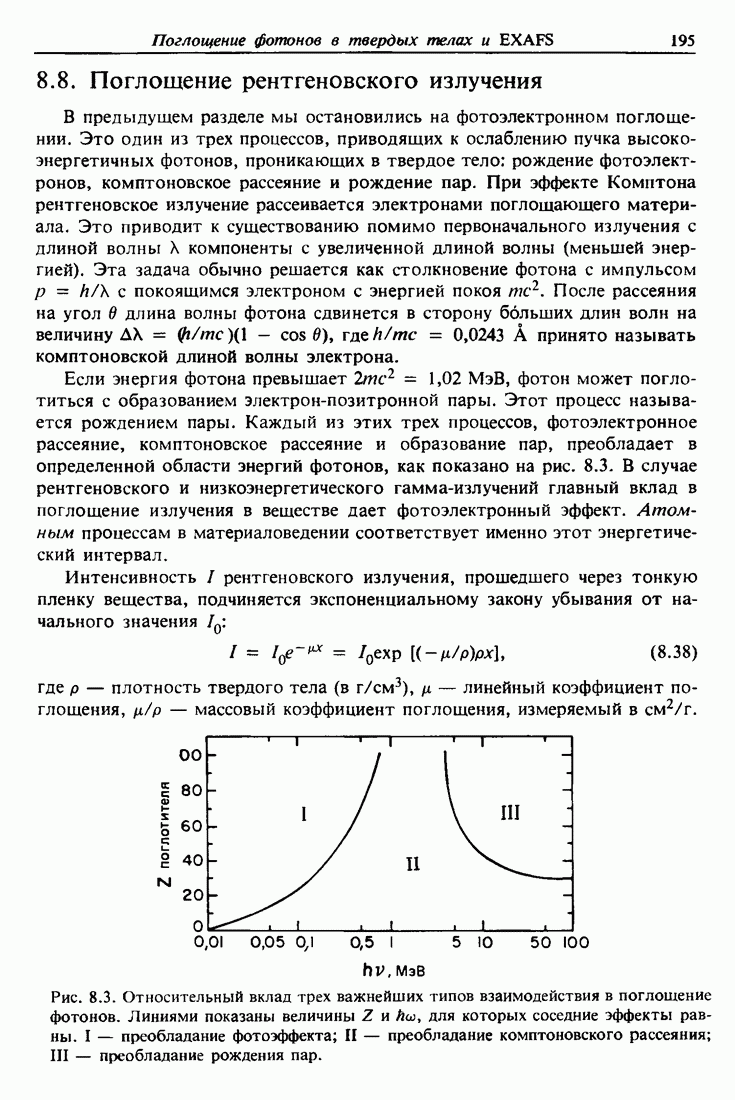
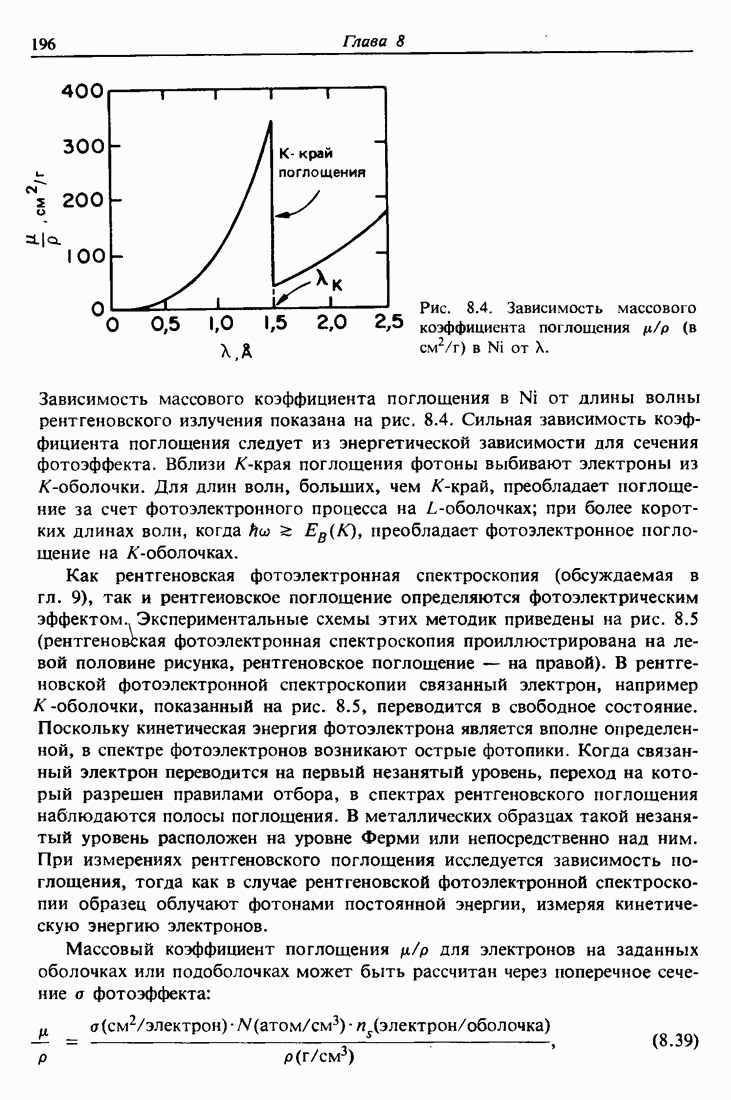
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
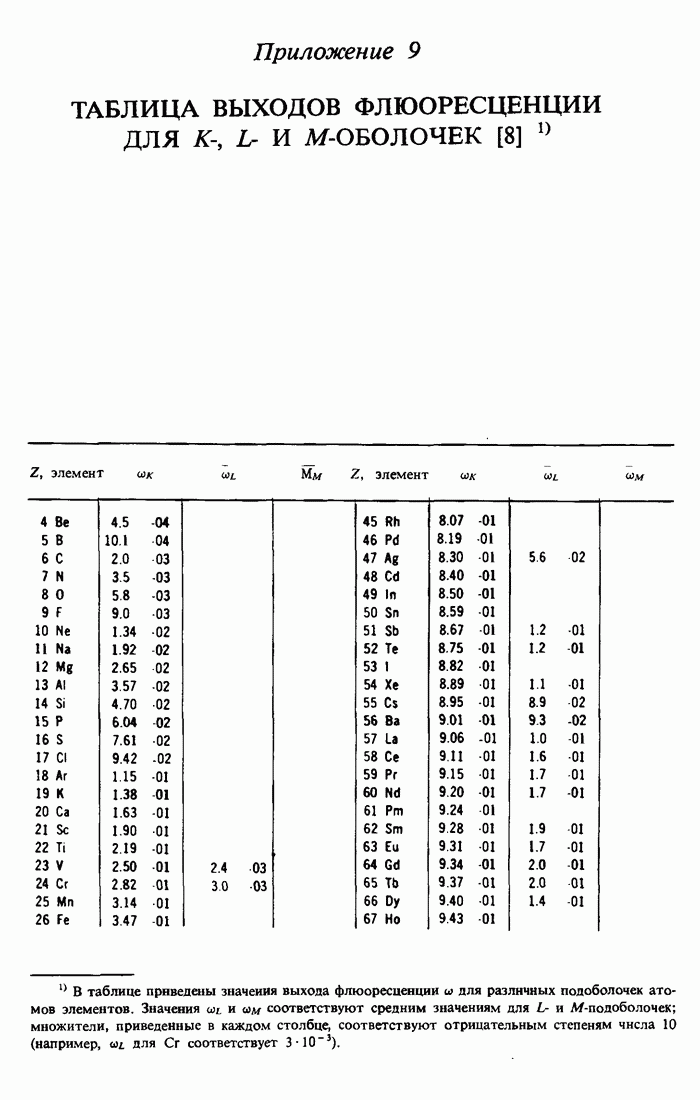
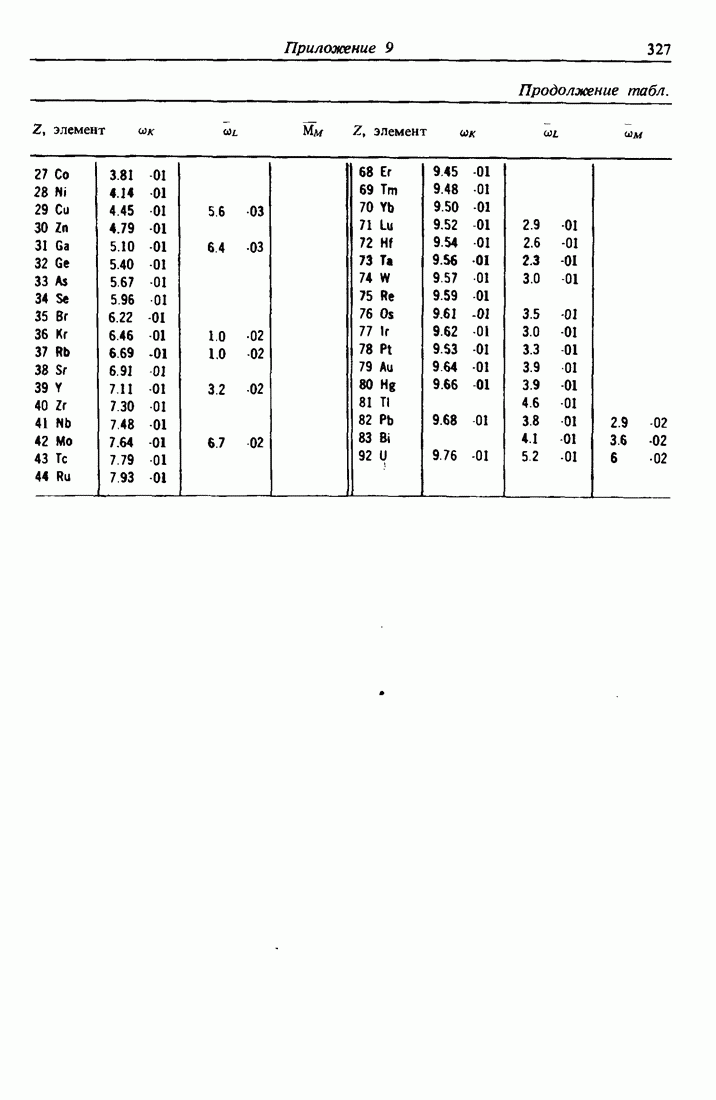
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
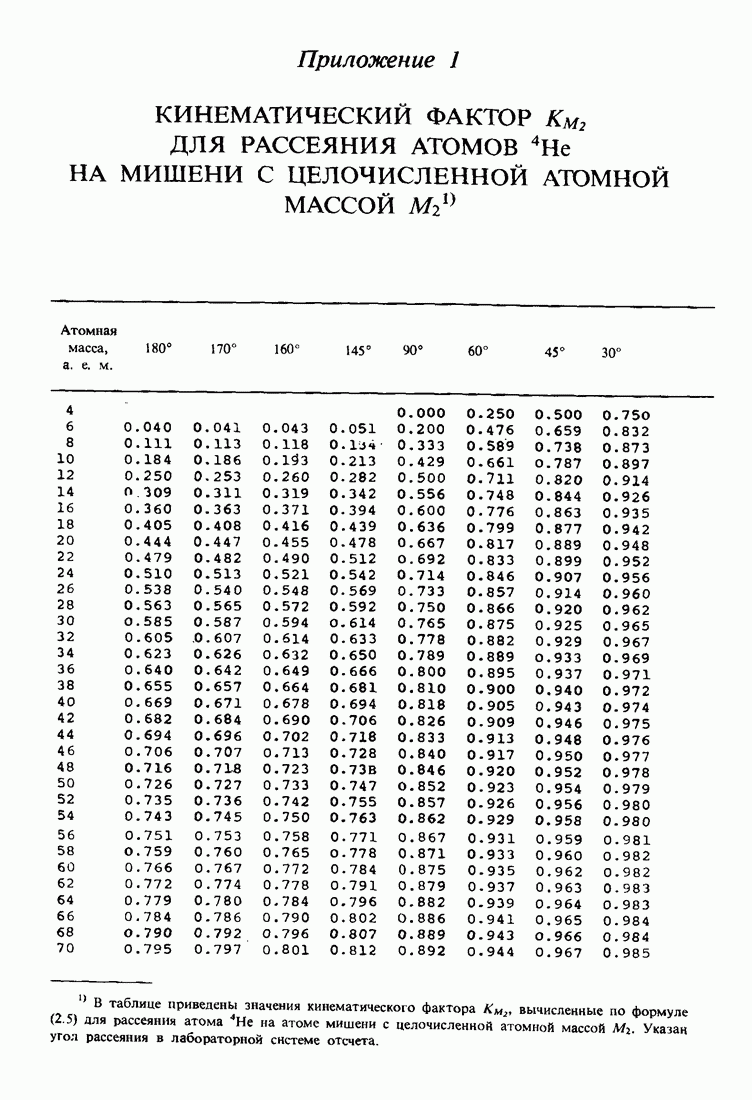
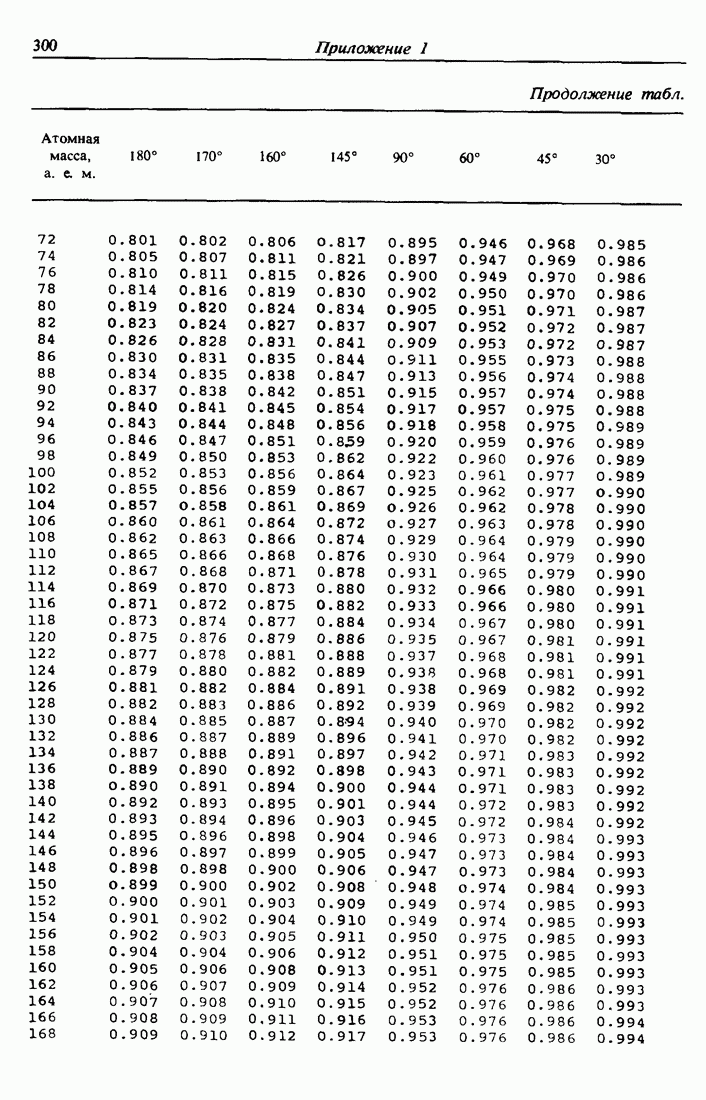
- ПРИЛОЖЕНИЕ 1.
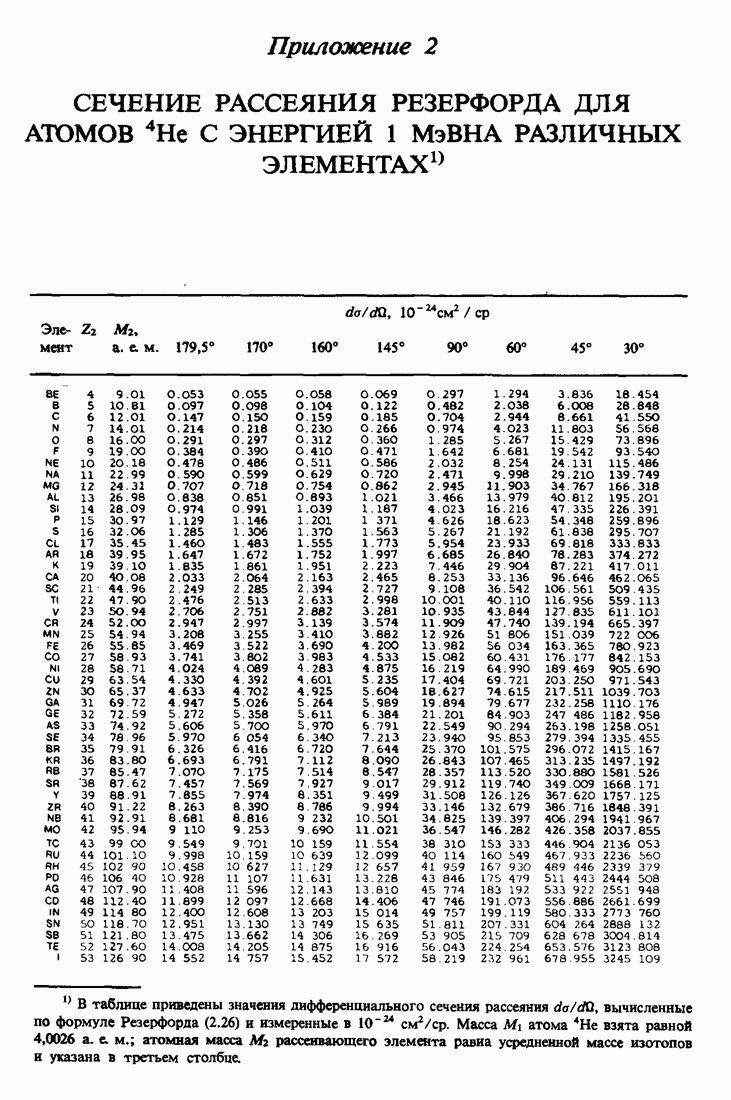
- ПРИЛОЖЕНИЕ 2.
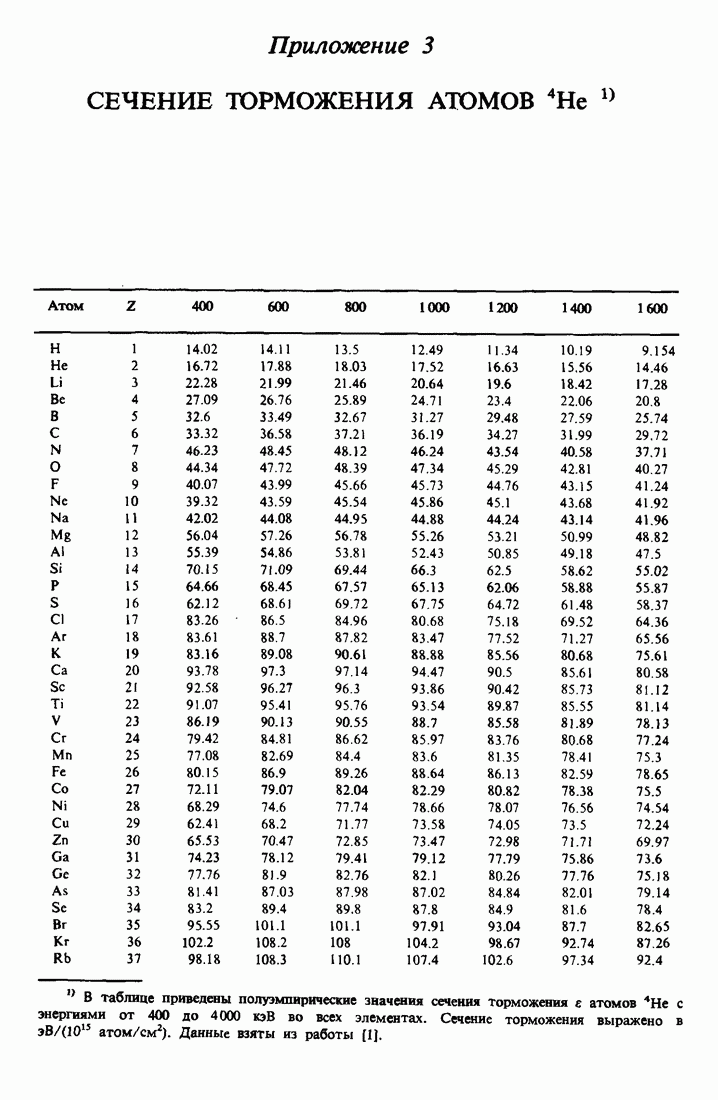
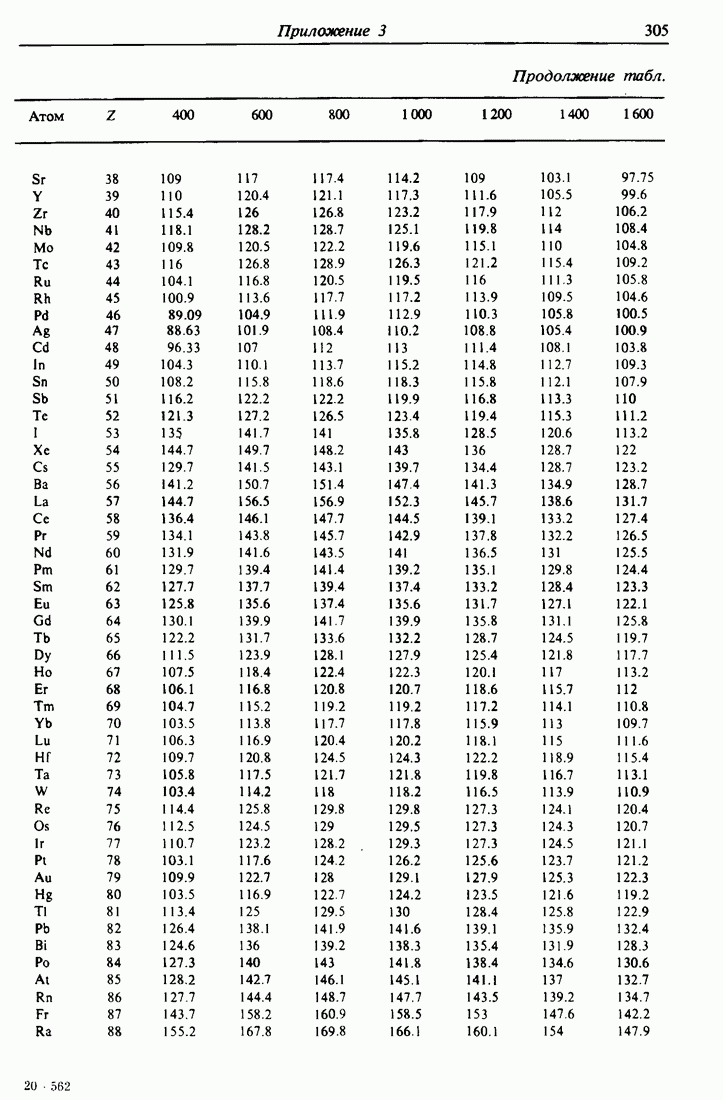
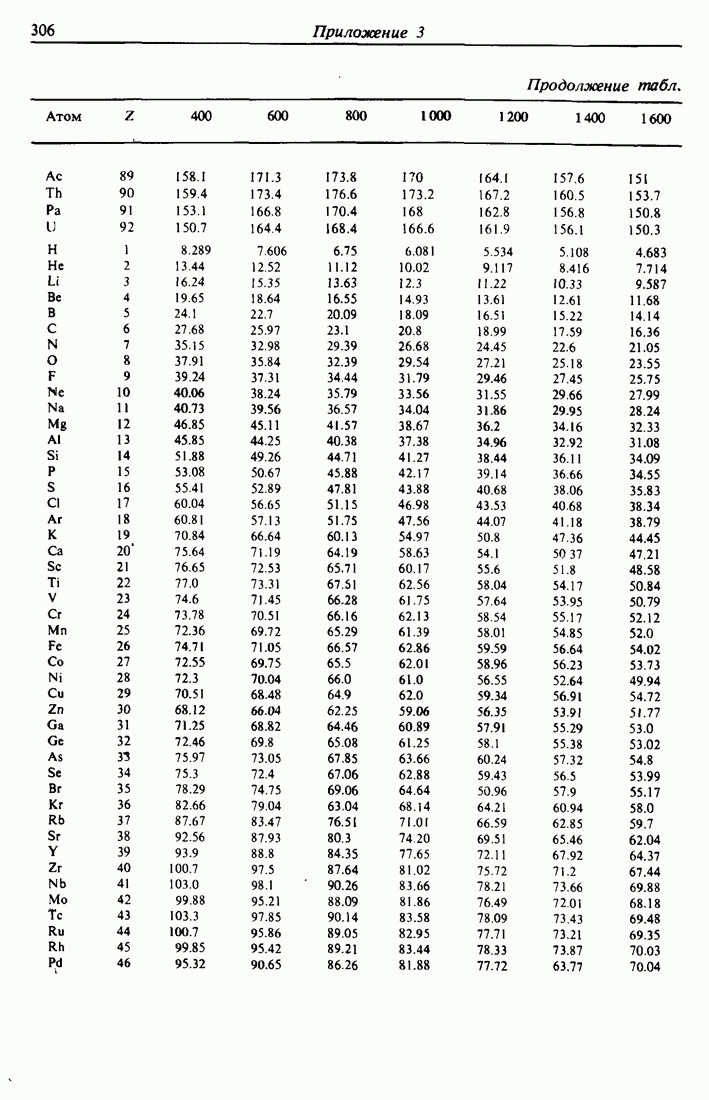
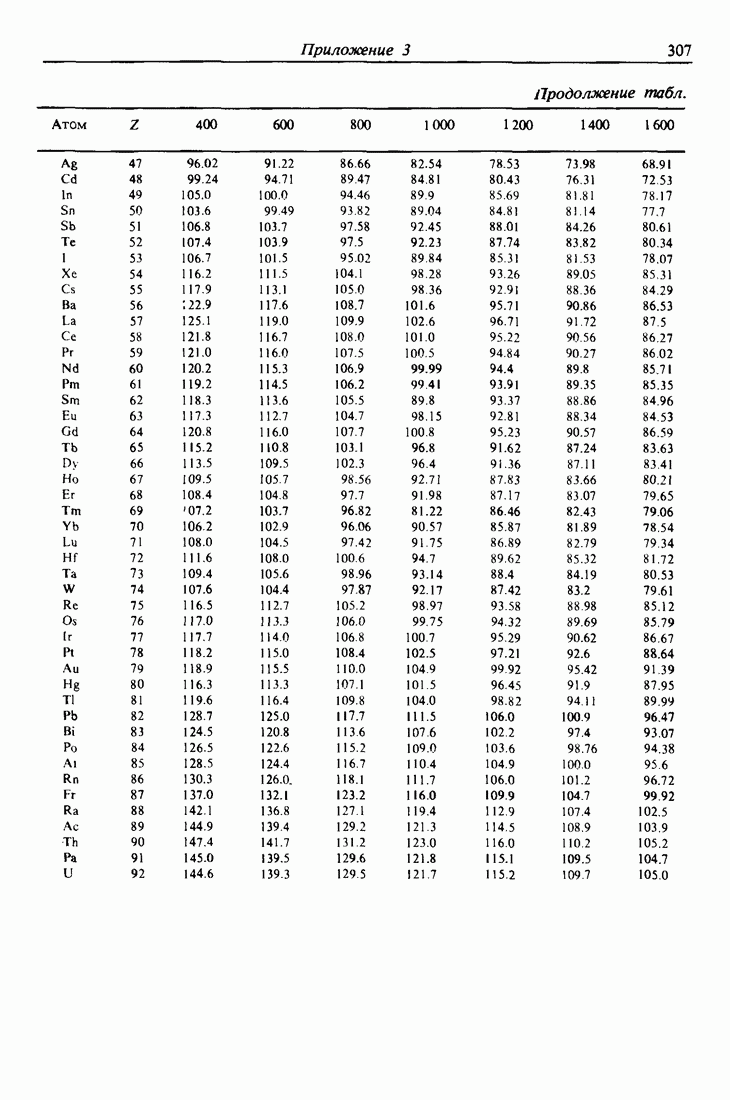
- ПРИЛОЖЕНИЕ 3.
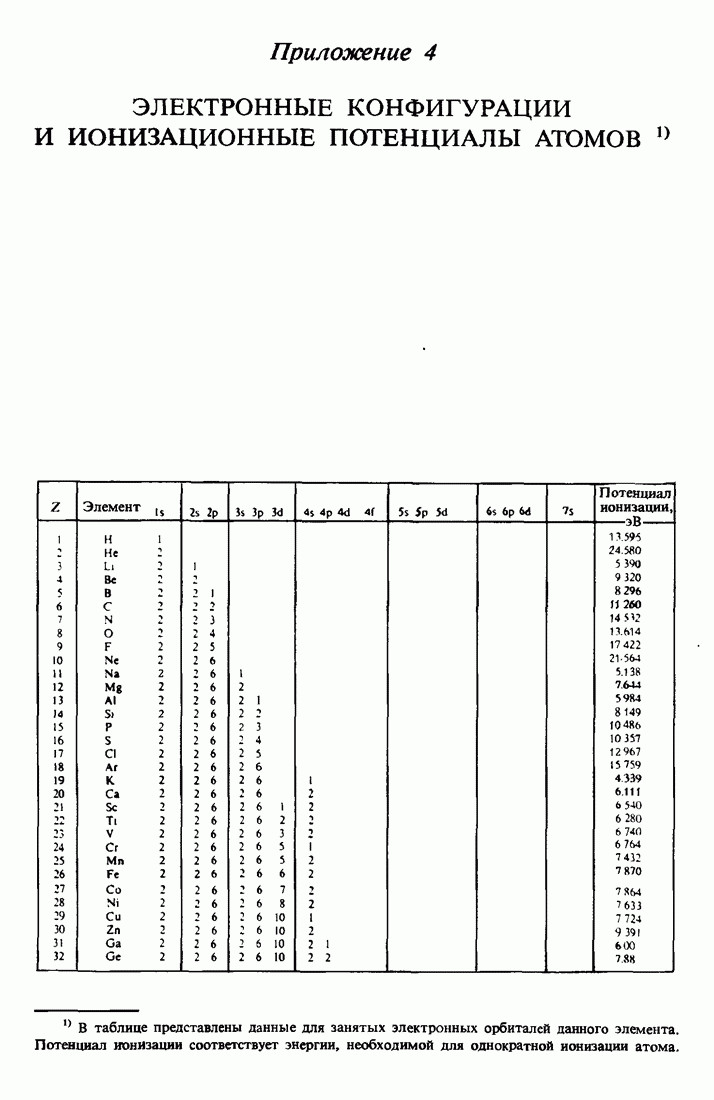
- ПРИЛОЖЕНИЕ 4.
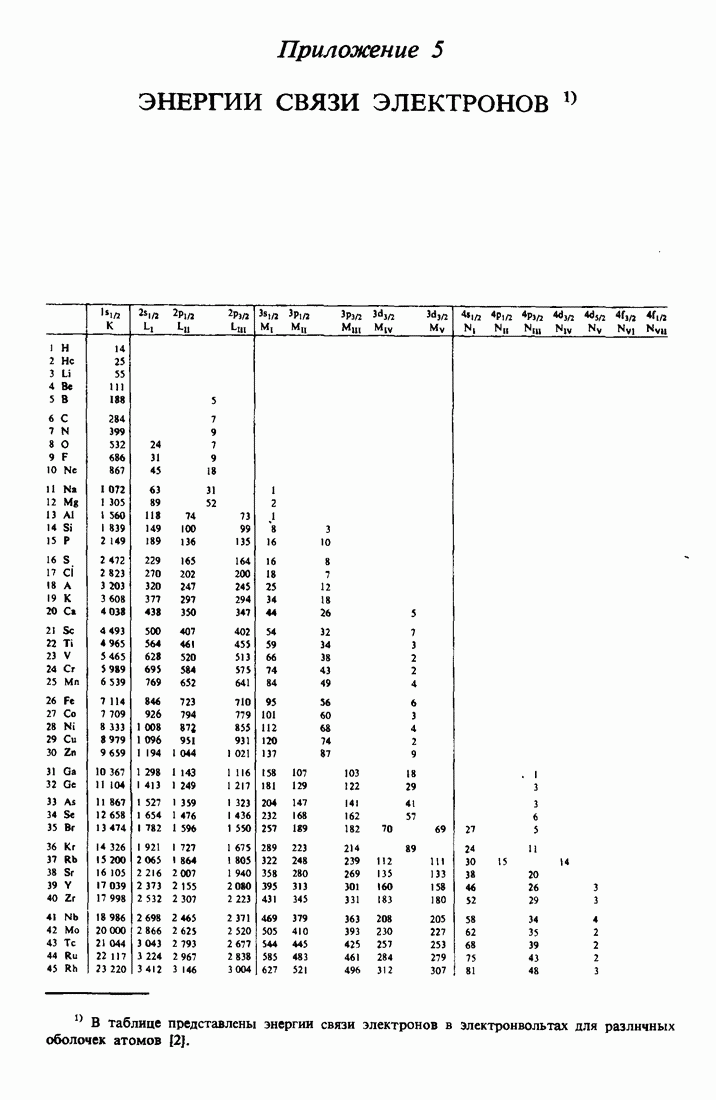
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
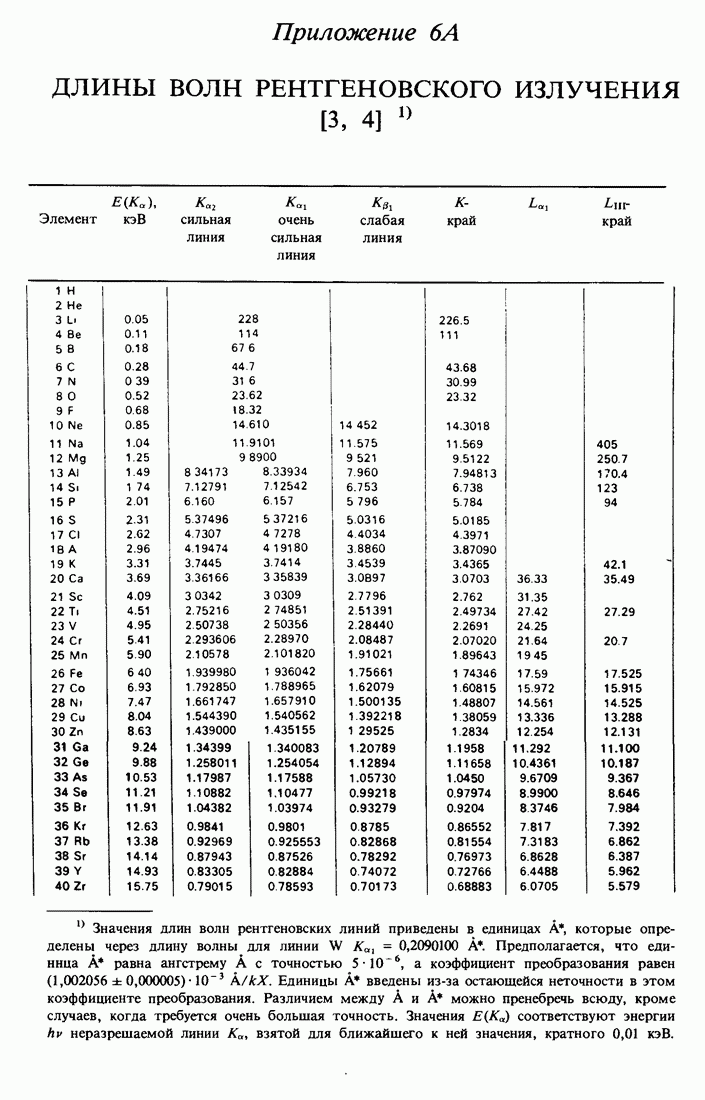
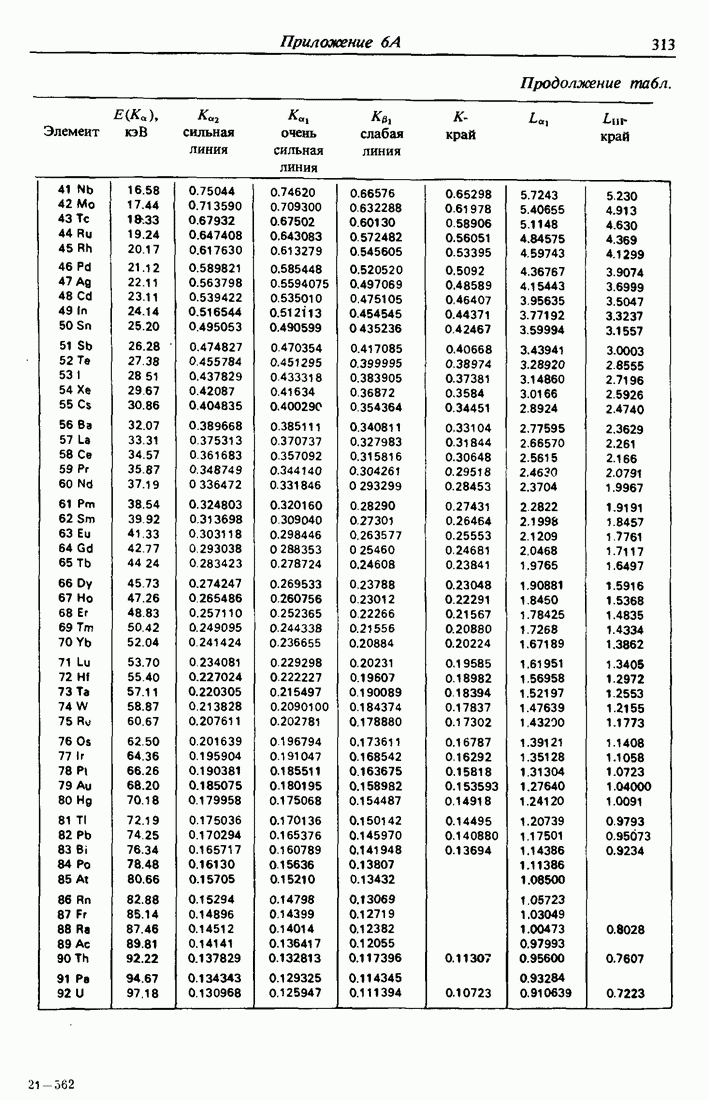
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
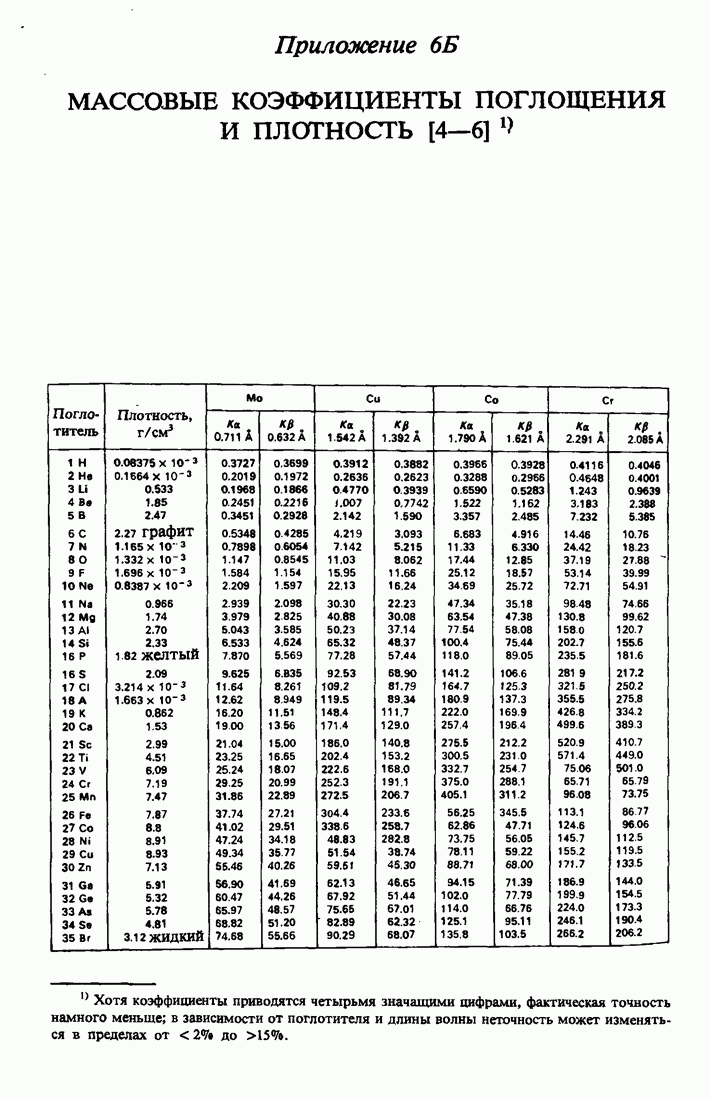
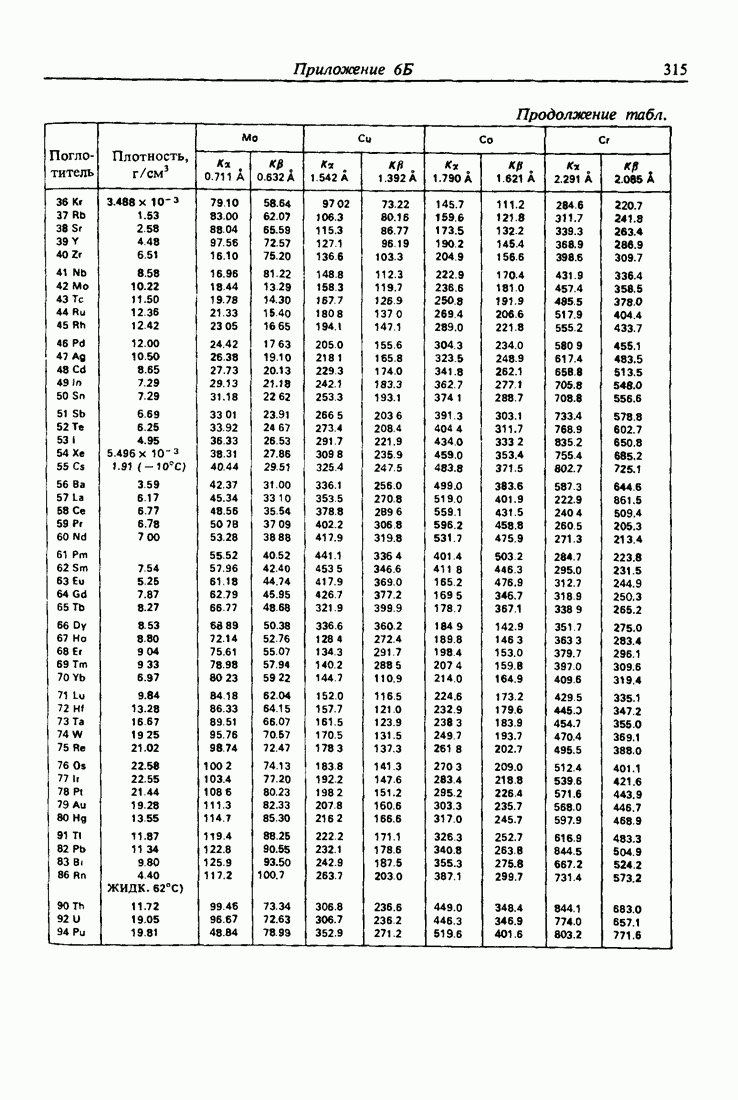
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
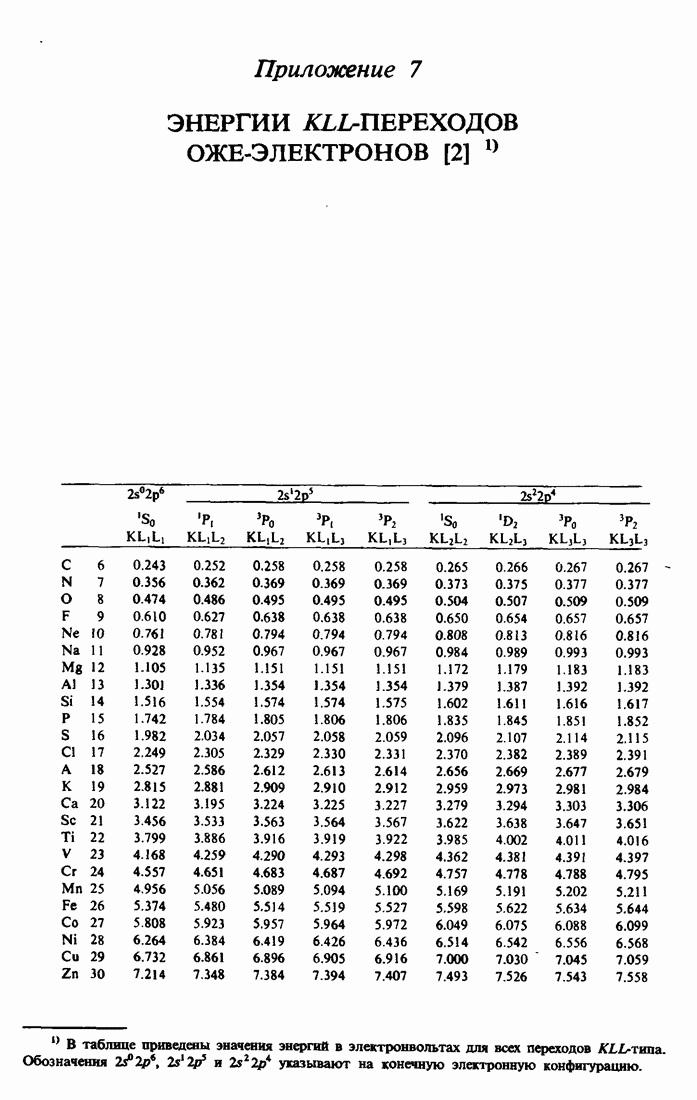
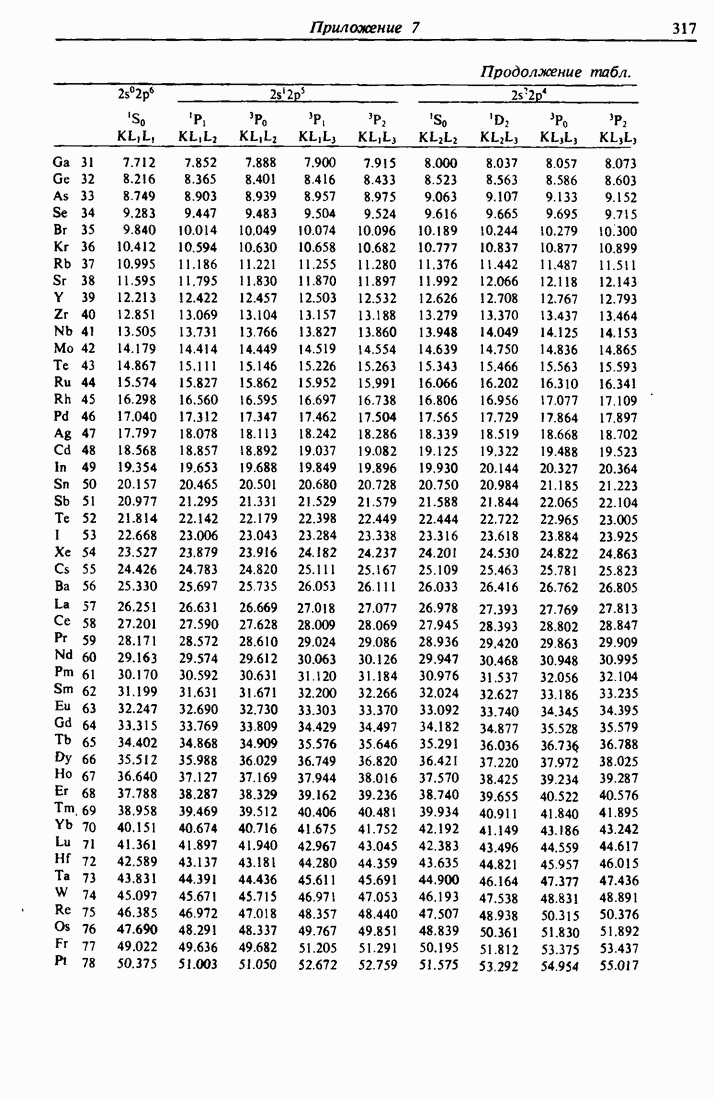
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
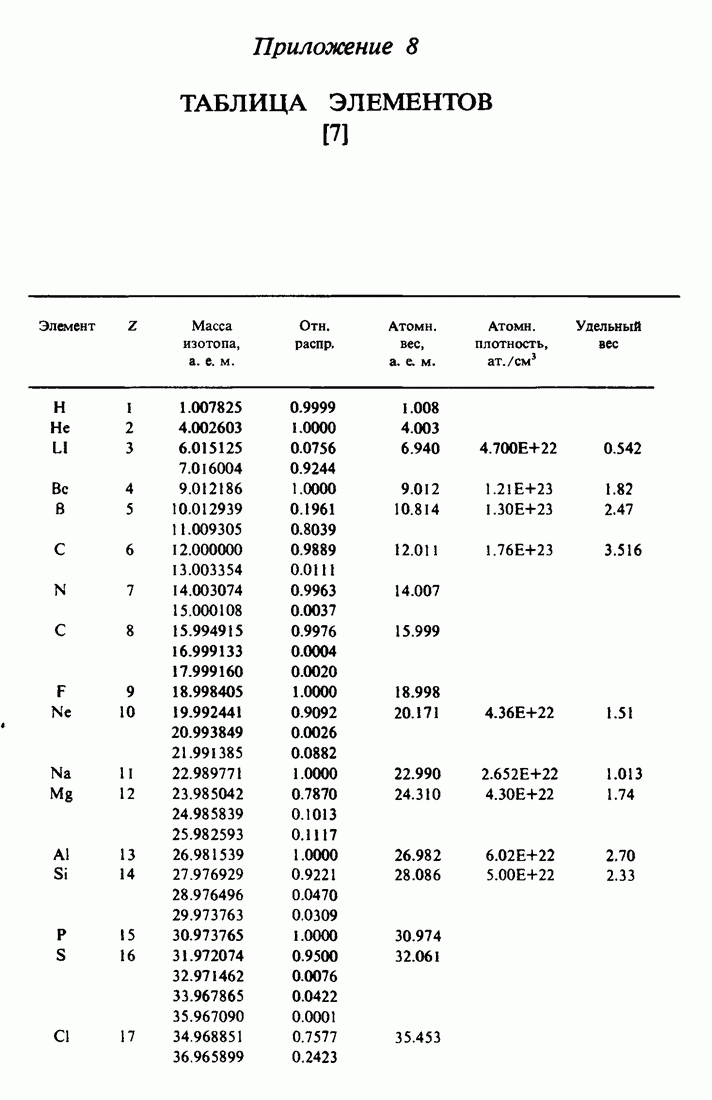
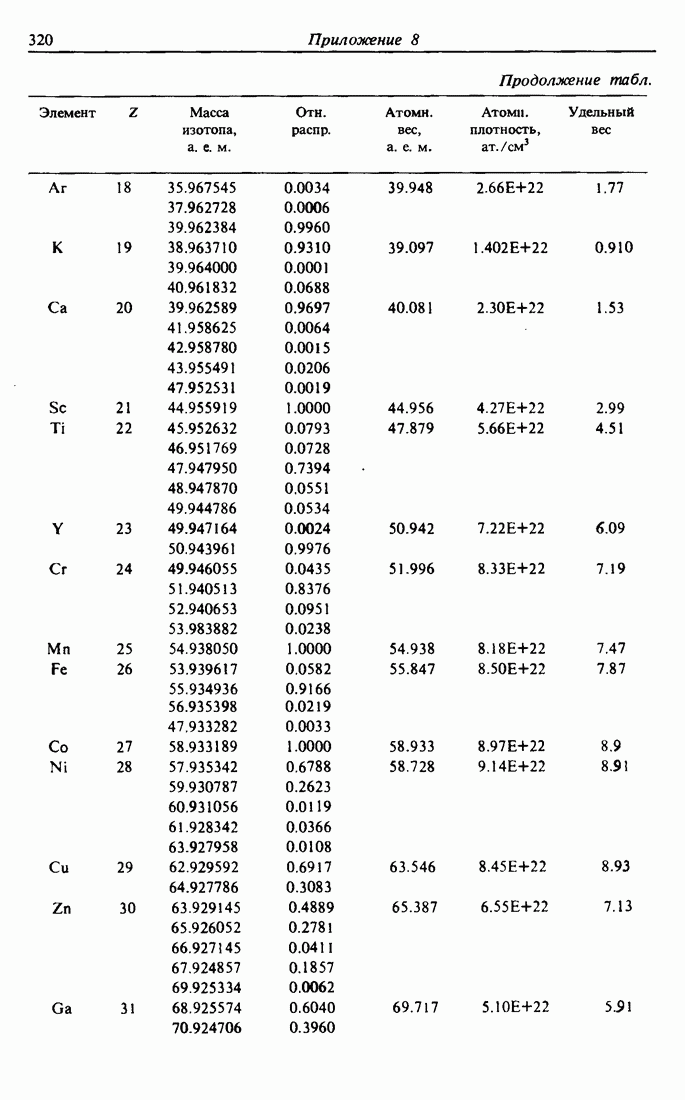
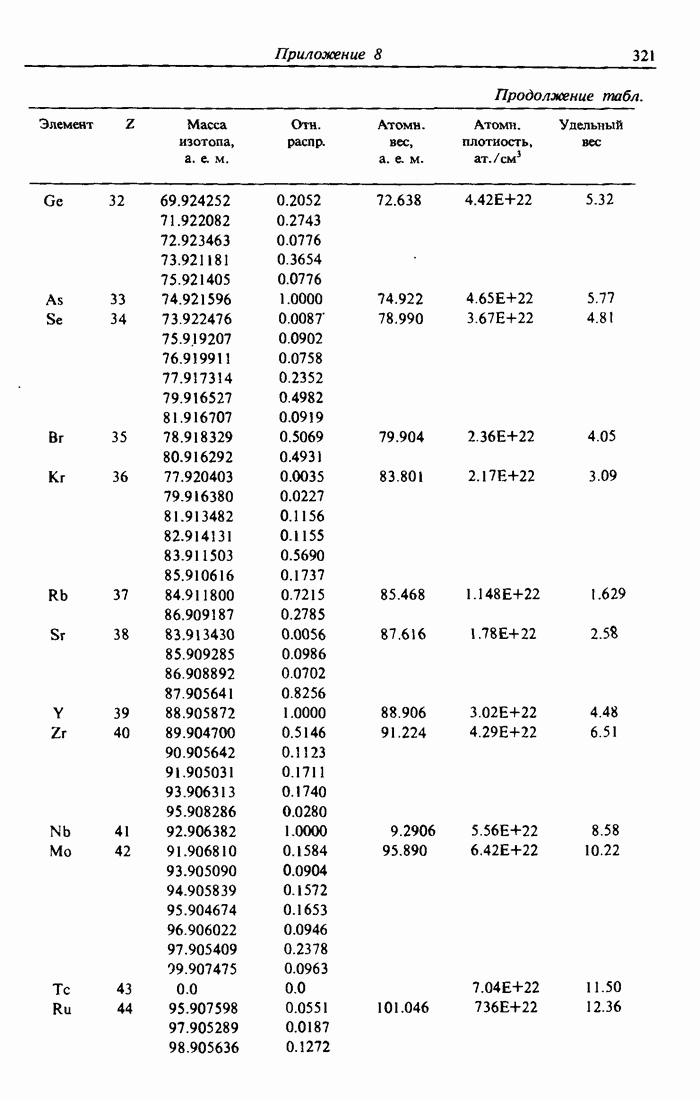
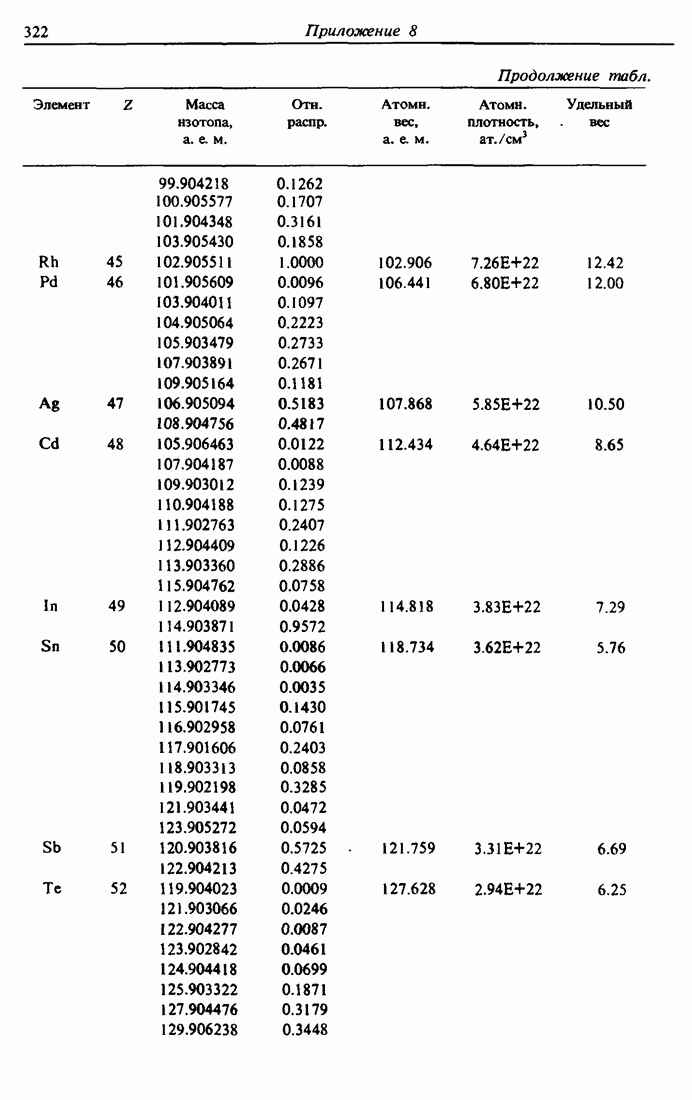
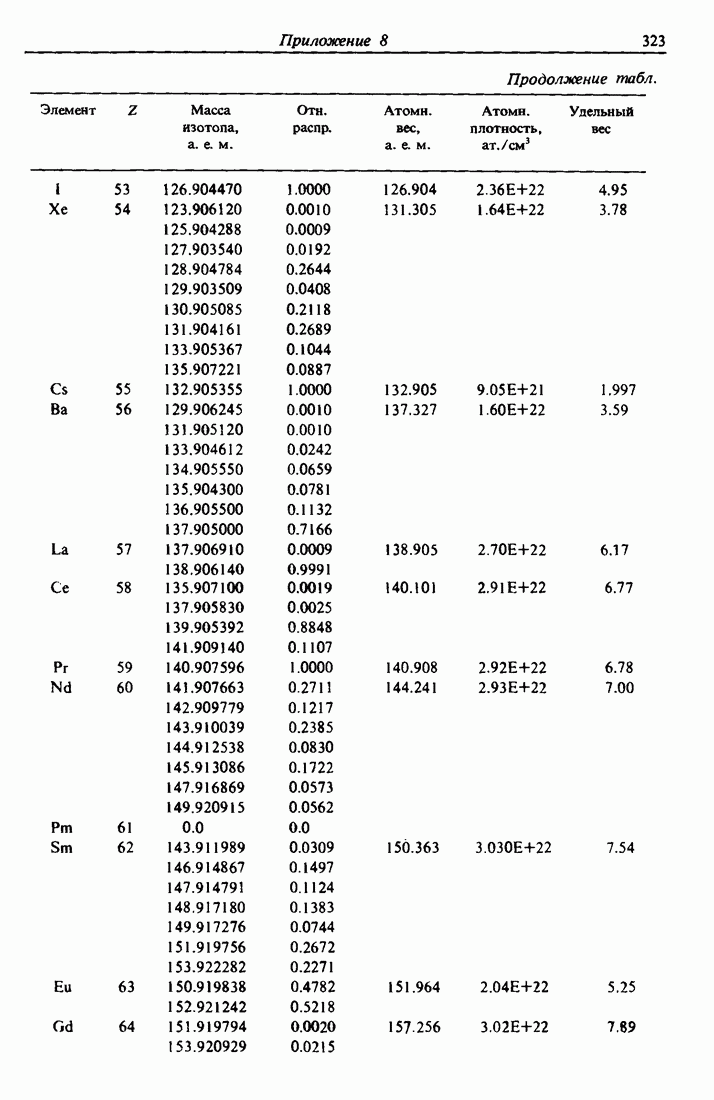
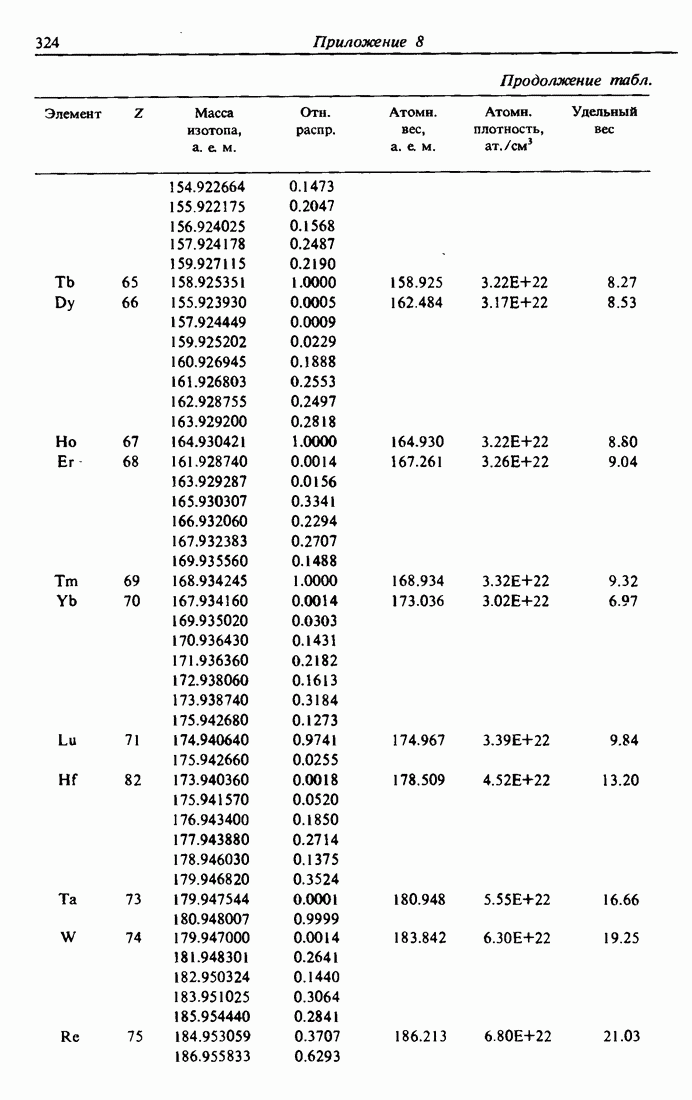
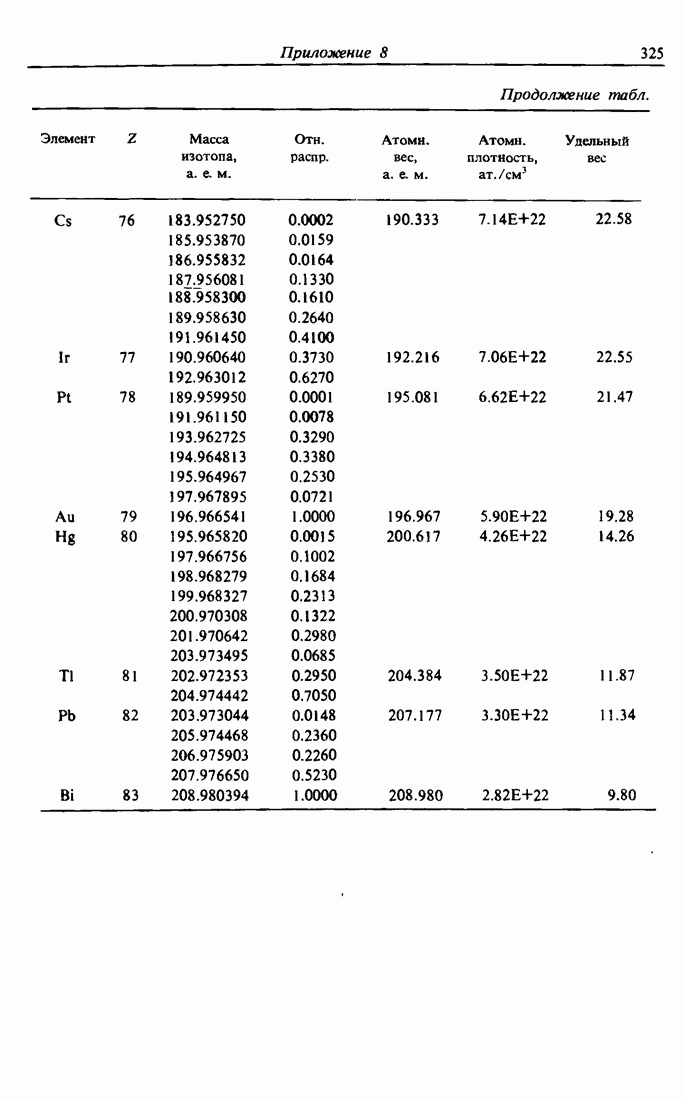
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ