| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
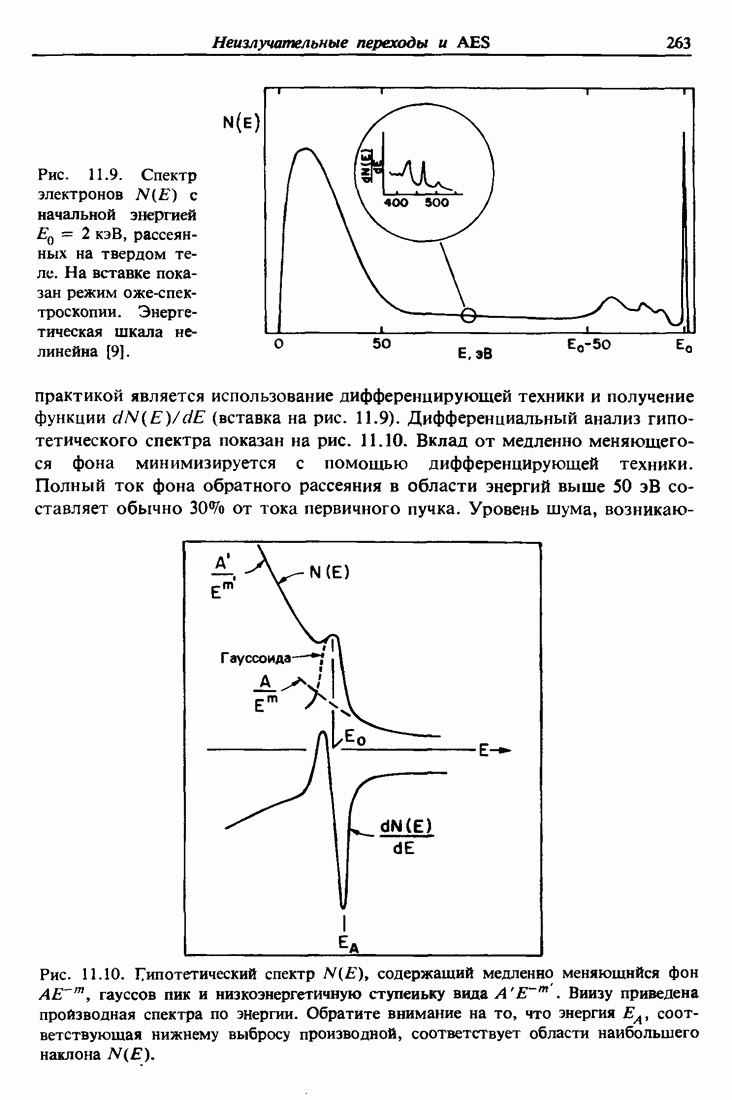
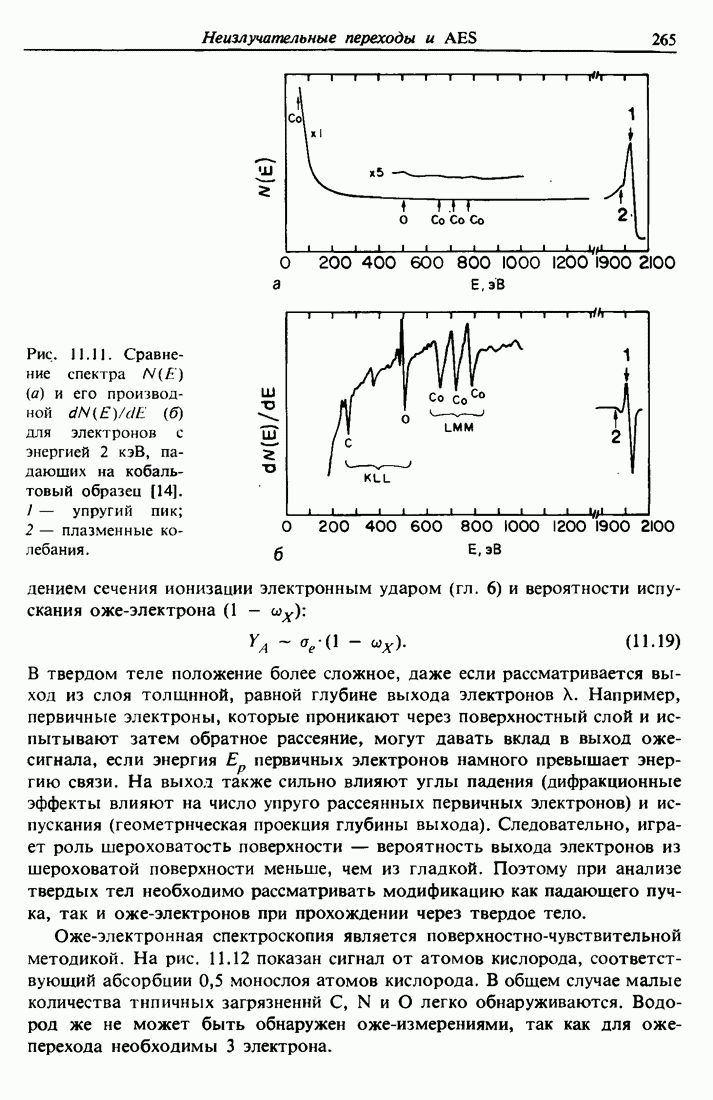
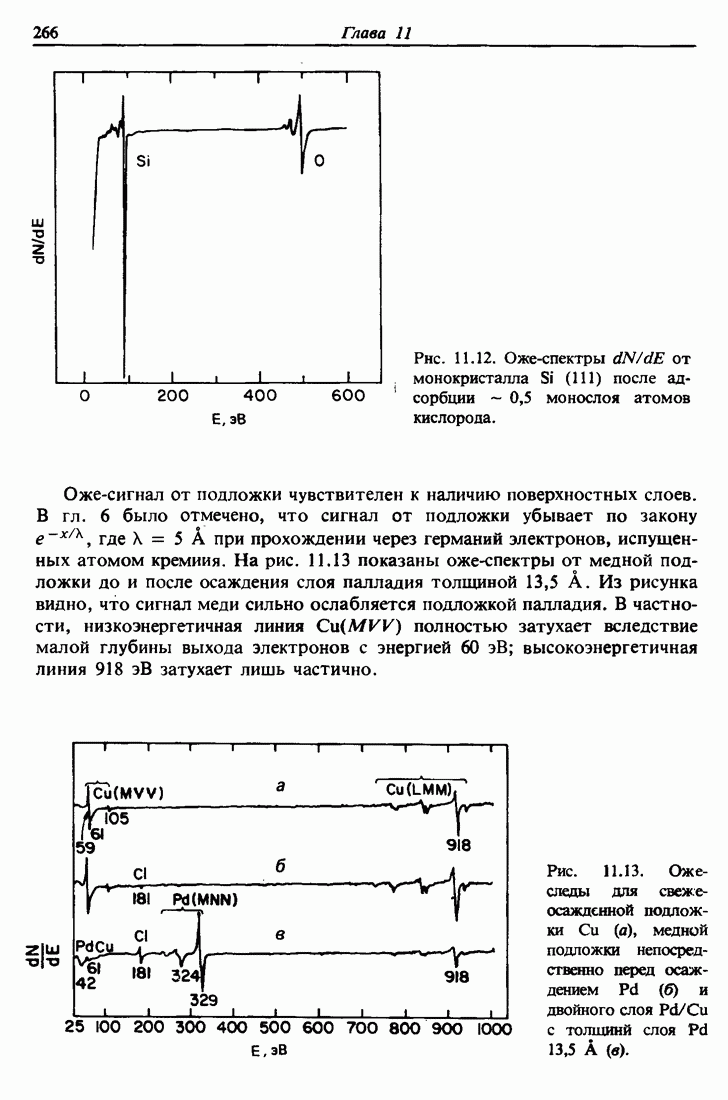
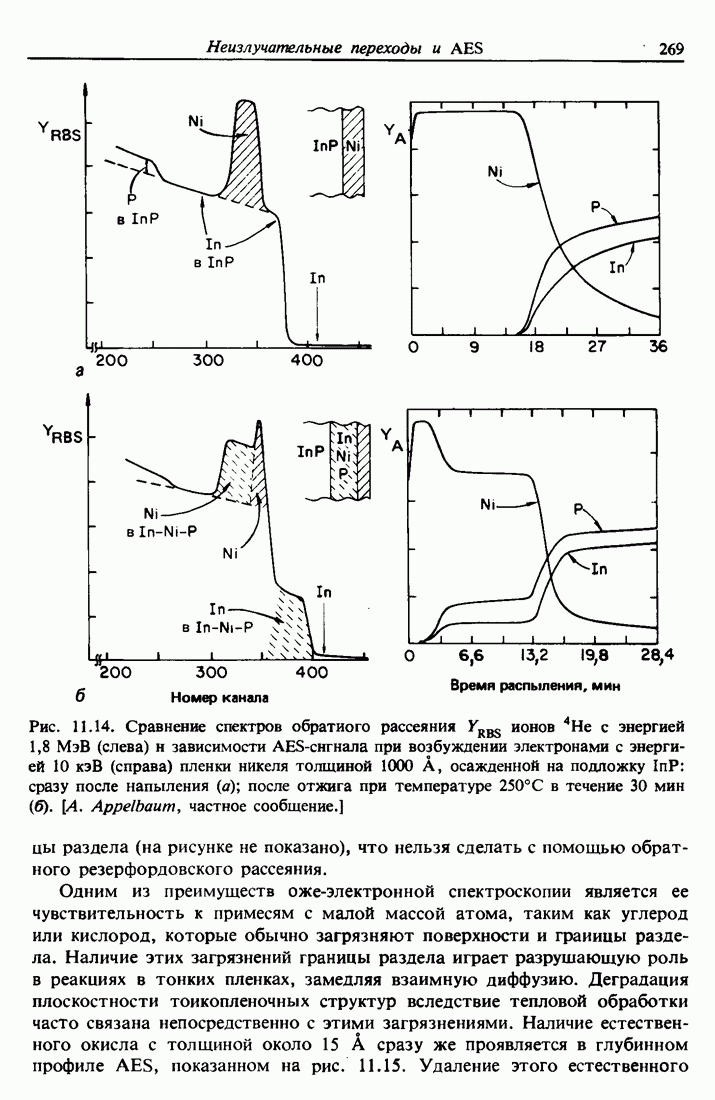
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
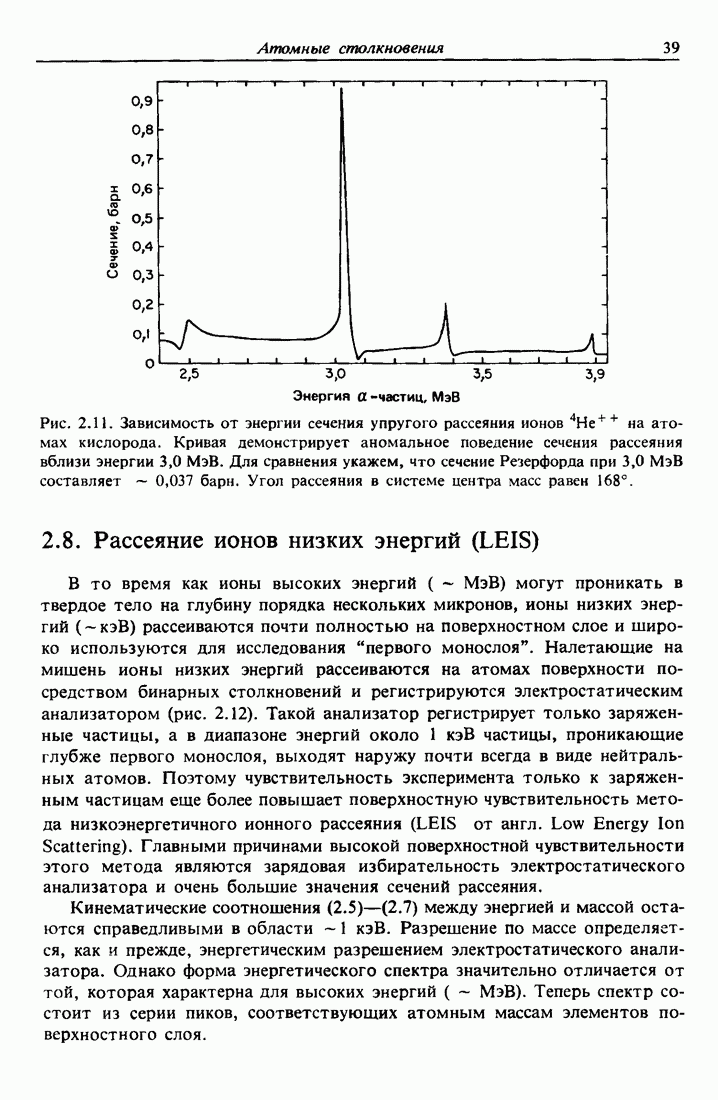
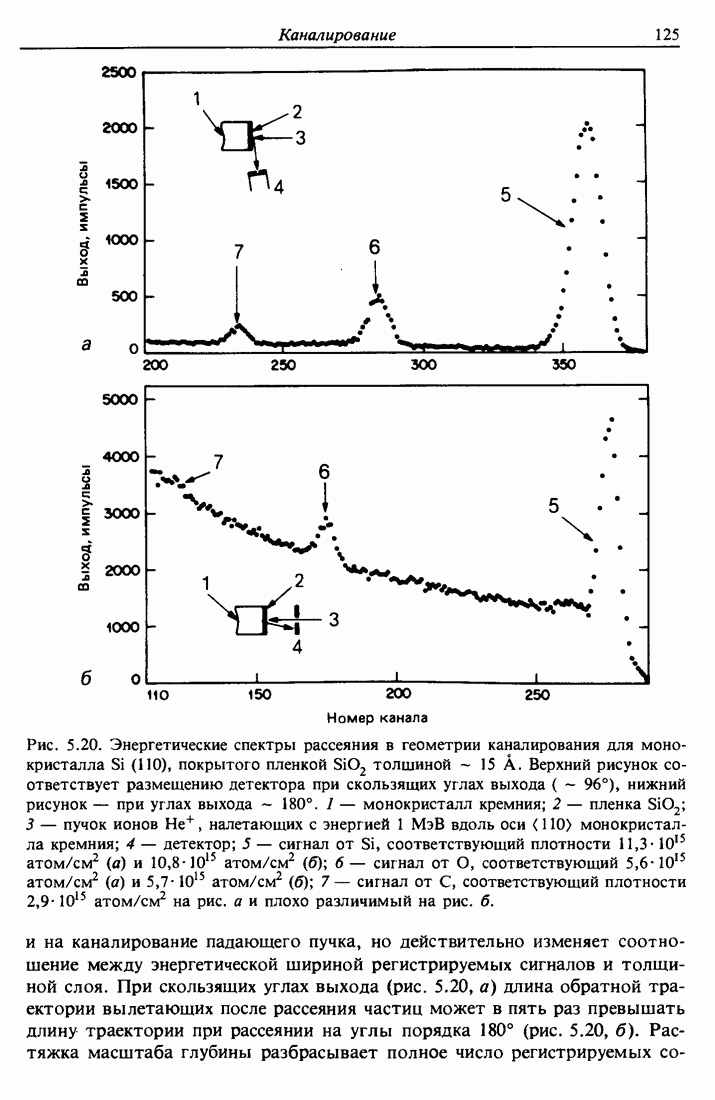
5.4. Распределение потока каналированных частиц
Поперечное движение каналированной частицы ограничено линиями равного потенциала  , подобными замкнутым контурам на рис. 5.5. Здесь
, подобными замкнутым контурам на рис. 5.5. Здесь  — сумма отдельных потенциалов
— сумма отдельных потенциалов  близлежащих рядов или плоскостей. Таким образом, частица с заданной поперечной энергией
близлежащих рядов или плоскостей. Таким образом, частица с заданной поперечной энергией  должна всегда оставаться в области, определяемой неравенством
должна всегда оставаться в области, определяемой неравенством  .
.
В кремнии эквипотенциальный контур, соответствующий значению 3 эВ, замыкается вокруг центра канала (рис. 5.5). Поэтому частицы с поперечной энергией менее 3 эВ оказываются запертыми внутри одного из каналов. Каналированные частицы с более высокой поперечной энергией  эВ не привязаны к одному каналу, а движутся под действием цилиндрически симметричных потенциалов вокруг атомных цепочек (рис. 5.5).
эВ не привязаны к одному каналу, а движутся под действием цилиндрически симметричных потенциалов вокруг атомных цепочек (рис. 5.5).
Нормируем на единицу вероятность обнаружения частицы с поперечной энергией  где-нибудь в допустимой области
где-нибудь в допустимой области  . Тогда вероятность нахождения частицы в произвольной точке
. Тогда вероятность нахождения частицы в произвольной точке  равна
равна

Область  ограничена эквипотенциальным контуром, подобным изображенным на рис. 5.5. Например, частицы с поперечной энергией 10 эВ (в частности, это могут быть частицы с энергией 1 МэВ, входящие в центр
ограничена эквипотенциальным контуром, подобным изображенным на рис. 5.5. Например, частицы с поперечной энергией 10 эВ (в частности, это могут быть частицы с энергией 1 МэВ, входящие в центр

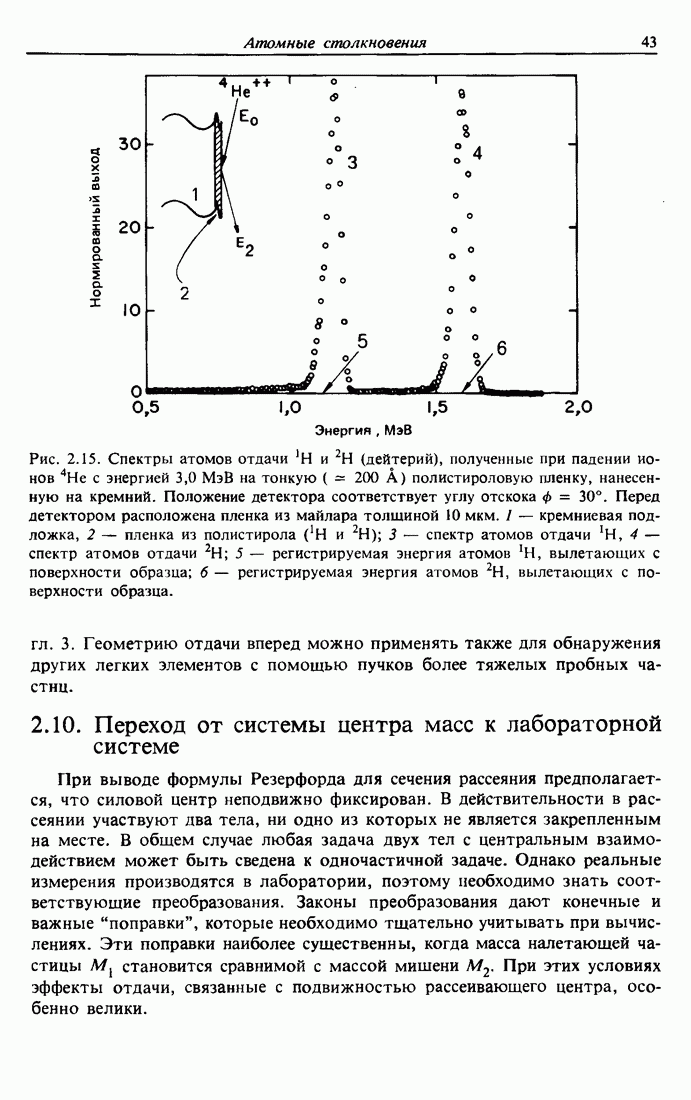
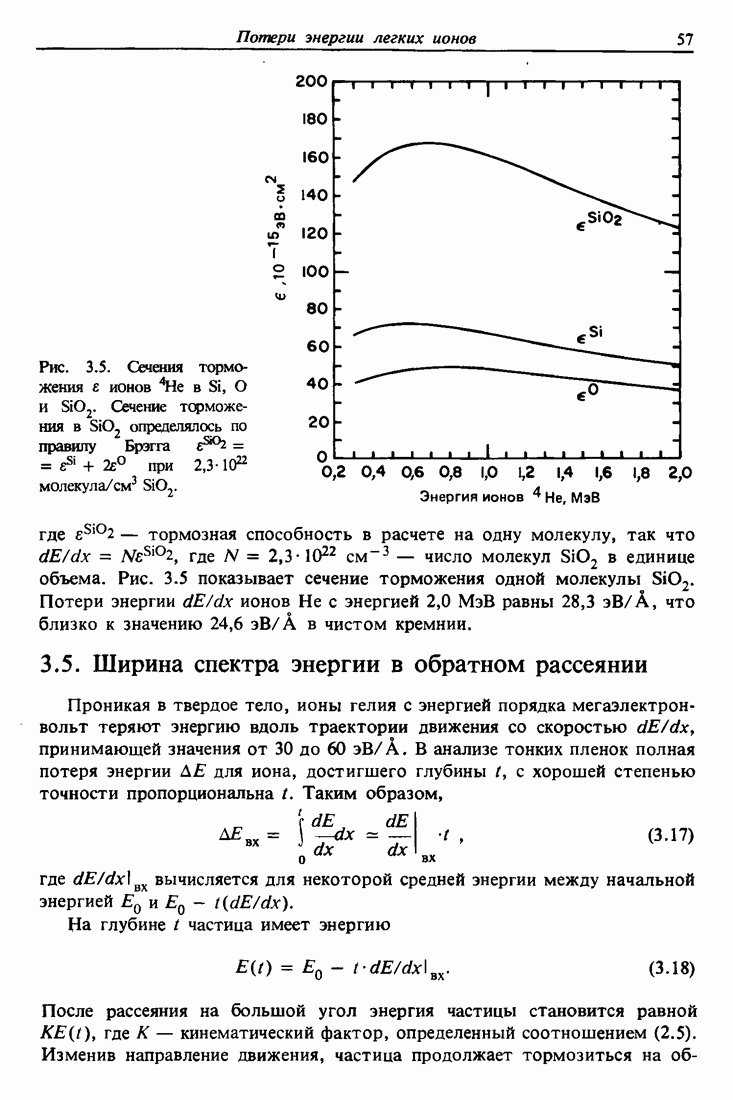
Рис. 5.5. а — эквипотенциальные контуры непрерывного потенциала оси  для ионов Не в кремнии. Отметим изменение формы контуров в соответствии с геометрией канала; б — эквипотенциальные контуры изображенного на рис. 5.5, а типа для большого числа каналов.
для ионов Не в кремнии. Отметим изменение формы контуров в соответствии с геометрией канала; б — эквипотенциальные контуры изображенного на рис. 5.5, а типа для большого числа каналов.
канала под углом 0,18°) обладают равной вероятностью обнаружения в любой точке области, ограниченной эквипотенциальным контуром  эВ.
эВ.
В дальнейшем мы вычисляем распределение потока ионов для каналированного пучка  при следующих предположениях.
при следующих предположениях.
1. Сохраняется поперечная энергия: частица, входящая в канал на расстоянии  от цепочки, не может подойти к ней на более близкое расстояние.
от цепочки, не может подойти к ней на более близкое расстояние.
2. Для двумерного аксиального каналирования частица имеет однородную вероятность обнаружения в своей «разрешенной» области; при цилиндрической симметрии площадь разрешенной области равна  , где
, где  — начальное расстояние от частицы до цепочки на поверхности кристалла, т. е.
— начальное расстояние от частицы до цепочки на поверхности кристалла, т. е.

3. Для простоты мы предполагаем, что имеет место цилиндрическая симметрия (рис. 5.6).
Тогда распределение потока в кристалле  получается интегрированием по всем значениям начального прицельного параметра:
получается интегрированием по всем значениям начального прицельного параметра:

Эффект каналирования состоит в преобразовании пространственно однородного распределения к сильно неоднородному распределению, изображенному на рис. 5.7. Это распределение потока демонстрирует самую отличительную черту каналирования, а именно: интенсивность потока и,

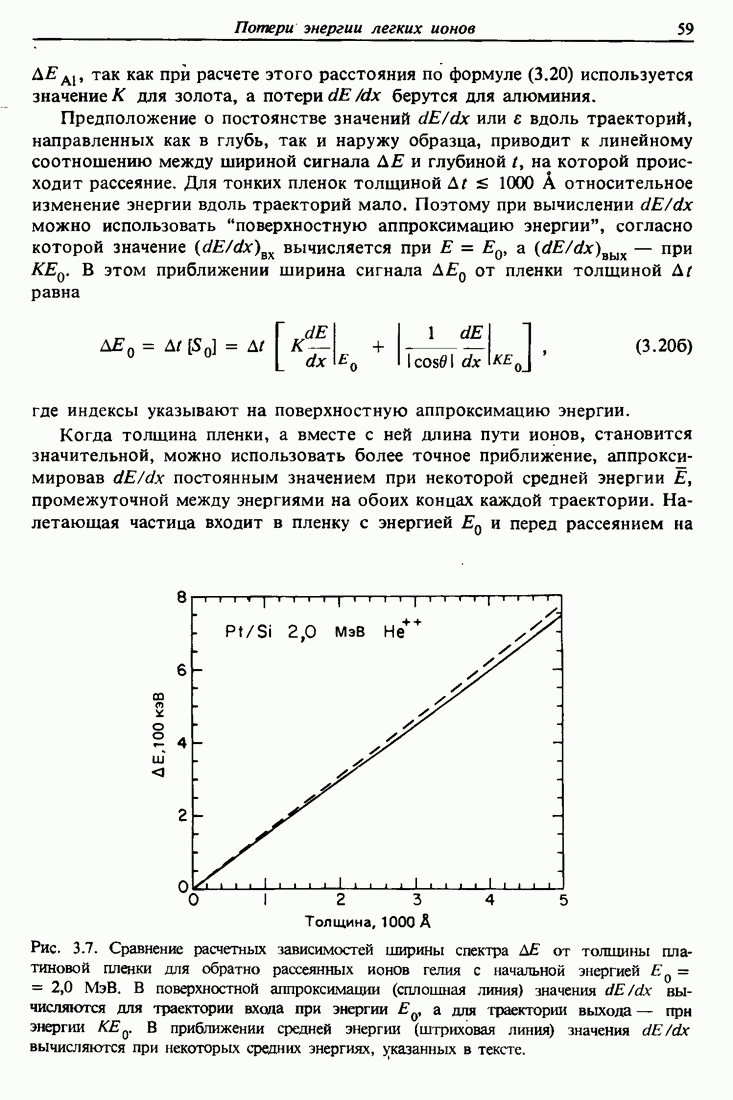
Рис. 5.6. Иллюстрация понятий "цилиндрической симметрии" и "разрешенной области", используемых при выводе распределения каналированного потока.

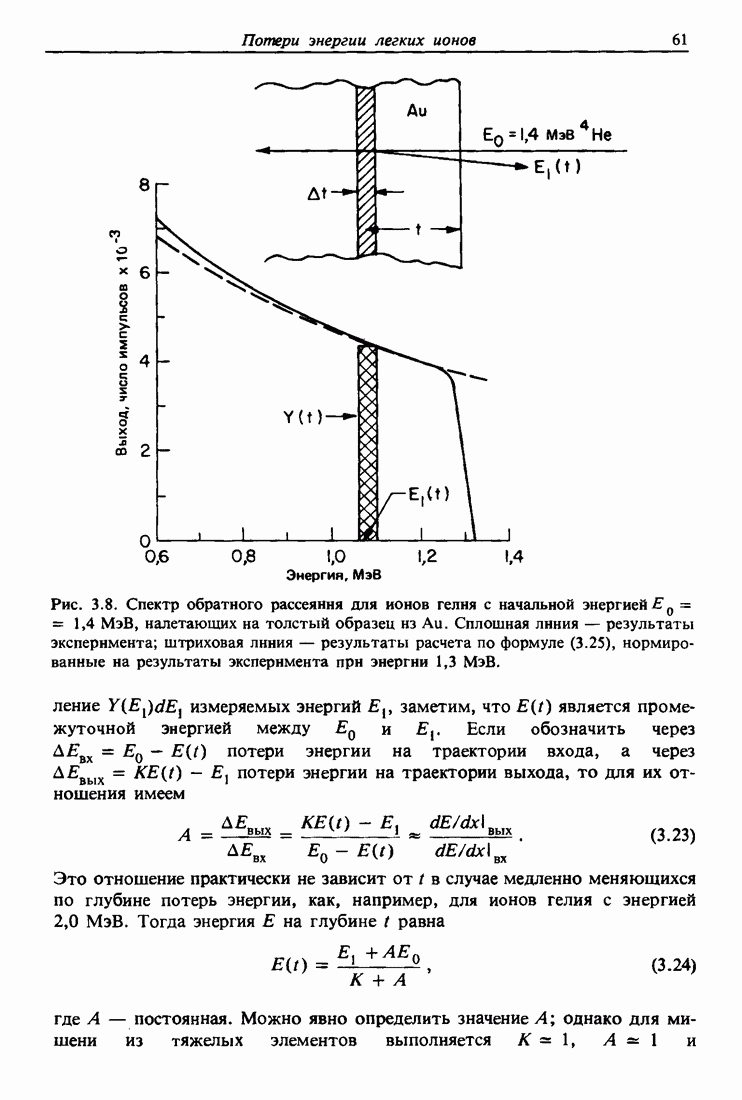
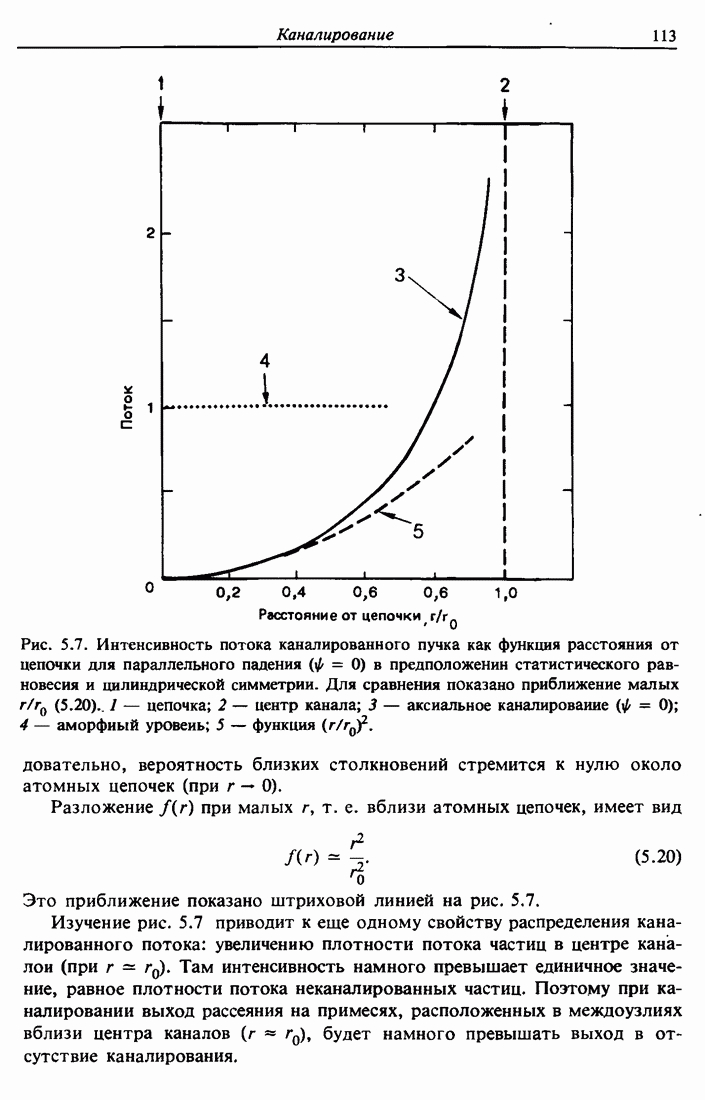
Рис. 5.7. Интенсивность потока каналированного пучка как функция расстояния от цепочки для параллельного падения  в предположении статистического равновесия и цилиндрической симметрии. Для сравнения показано приближение малых
в предположении статистического равновесия и цилиндрической симметрии. Для сравнения показано приближение малых  . 1 — цепочка; 2 — центр канала; 3 — аксиальное каналироваиие
. 1 — цепочка; 2 — центр канала; 3 — аксиальное каналироваиие  ; 4 — аморфный уровень; 5 — функция
; 4 — аморфный уровень; 5 — функция  .
.
следовательно, вероятность близких столкновений стремится к нулю около атомных цепочек (при  ).
).
Разложение  при малых
при малых  , т. е. вблизи атомных цепочек, имеет вид
, т. е. вблизи атомных цепочек, имеет вид

Это приближение показано штриховой линией на рис. 5.7.
Изучение рис. 5.7 приводит к еще одному свойству распределения каналированного потока: увеличению плотности потока частиц в центре каналои (при  ). Там интенсивность намного превышает единичное значение, равное плотности потока неканалированных частиц. Поэтому при каналировании выход рассеяния на примесях, расположенных в междоузлиях вблизи центра каналов
). Там интенсивность намного превышает единичное значение, равное плотности потока неканалированных частиц. Поэтому при каналировании выход рассеяния на примесях, расположенных в междоузлиях вблизи центра каналов  , будет намного превышать выход в отсутствие каналирования.
, будет намного превышать выход в отсутствие каналирования.

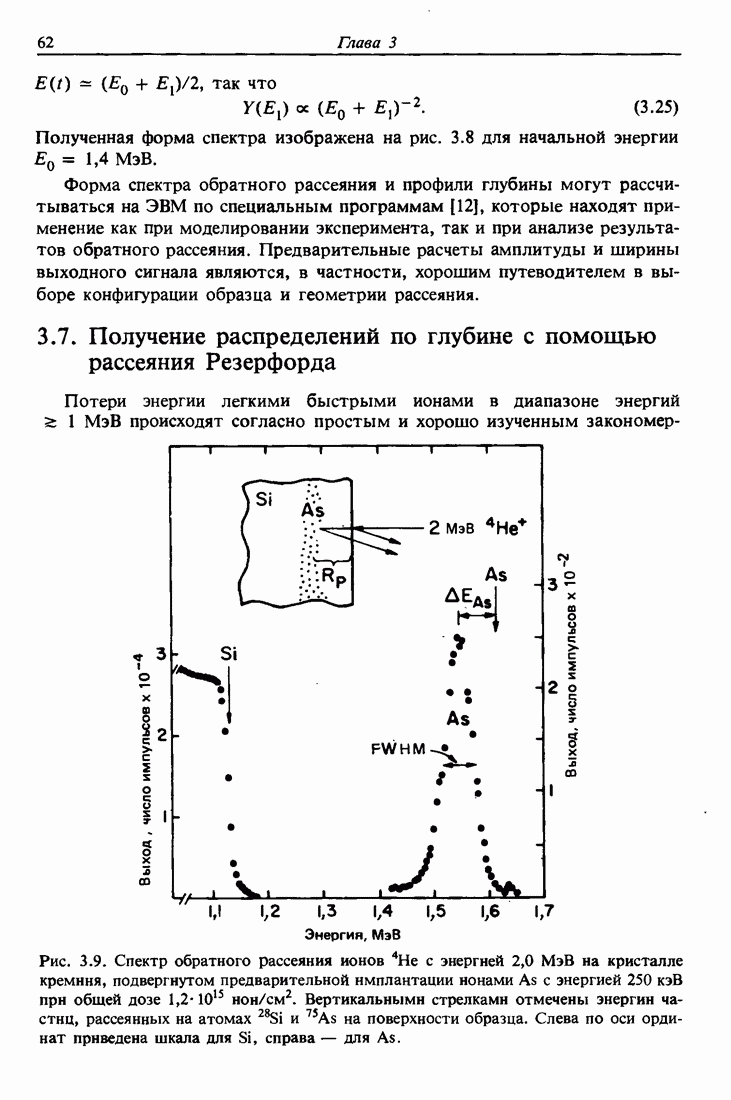
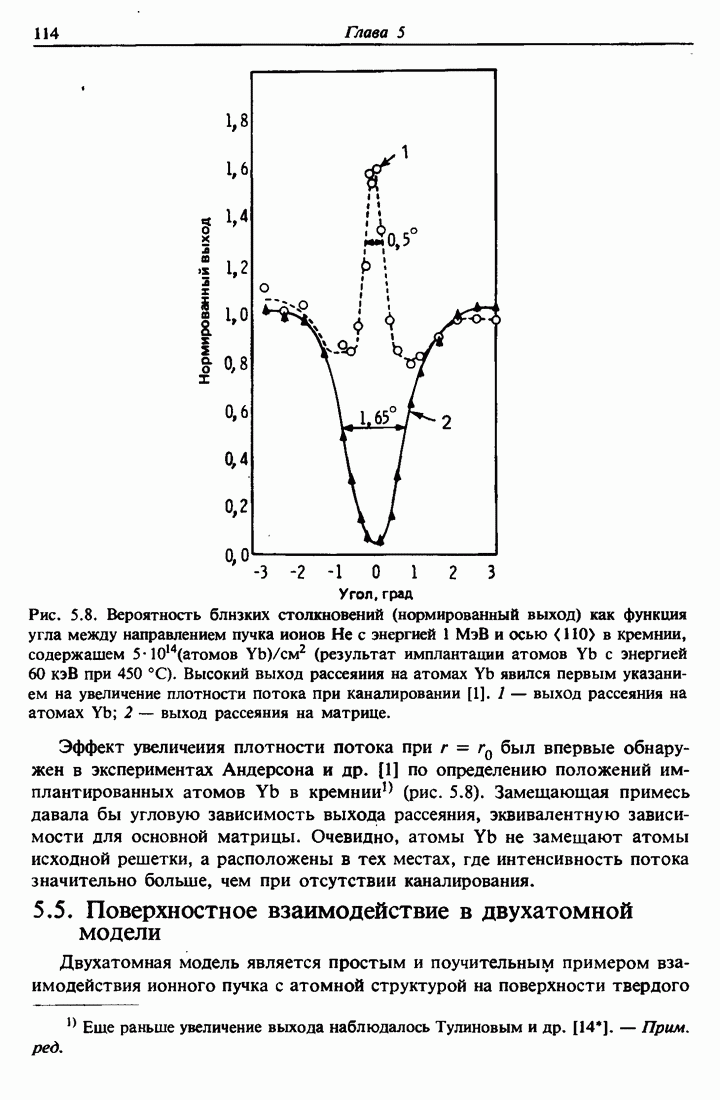
Рис. 5.8. Вероятность близких столкновений (нормированный выход) как функция угла между направлением пучка иоиов Не с энергией 1 МэВ и осью  в кремнии, содержащем
в кремнии, содержащем  (результат имплантации атомов
(результат имплантации атомов  с энергией
с энергией  при 450 °С). Высокий выход рассеяния на атомах
при 450 °С). Высокий выход рассеяния на атомах  явился первым указанием на увеличение плотности потока при каналировании [1]. 1 — выход рассеяния на атомах
явился первым указанием на увеличение плотности потока при каналировании [1]. 1 — выход рассеяния на атомах  — выход рассеяния на матрице.
— выход рассеяния на матрице.
Эффект увеличения плотности потока при  был впервые обнаружен в экспериментах Андерсона и др. [1] по определению положений имплантированных атомов
был впервые обнаружен в экспериментах Андерсона и др. [1] по определению положений имплантированных атомов  в кремнии (рис. 5.8). Замещающая примесь давала бы угловую зависимость выхода рассеяния, эквивалентную зависимости для основной матрицы. Очевидно, атомы
в кремнии (рис. 5.8). Замещающая примесь давала бы угловую зависимость выхода рассеяния, эквивалентную зависимости для основной матрицы. Очевидно, атомы  не замещают атомы исходной решетки, а расположены в тех местах, где интенсивность потока значительно больше, чем при отсутствии каналирования.
не замещают атомы исходной решетки, а расположены в тех местах, где интенсивность потока значительно больше, чем при отсутствии каналирования.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
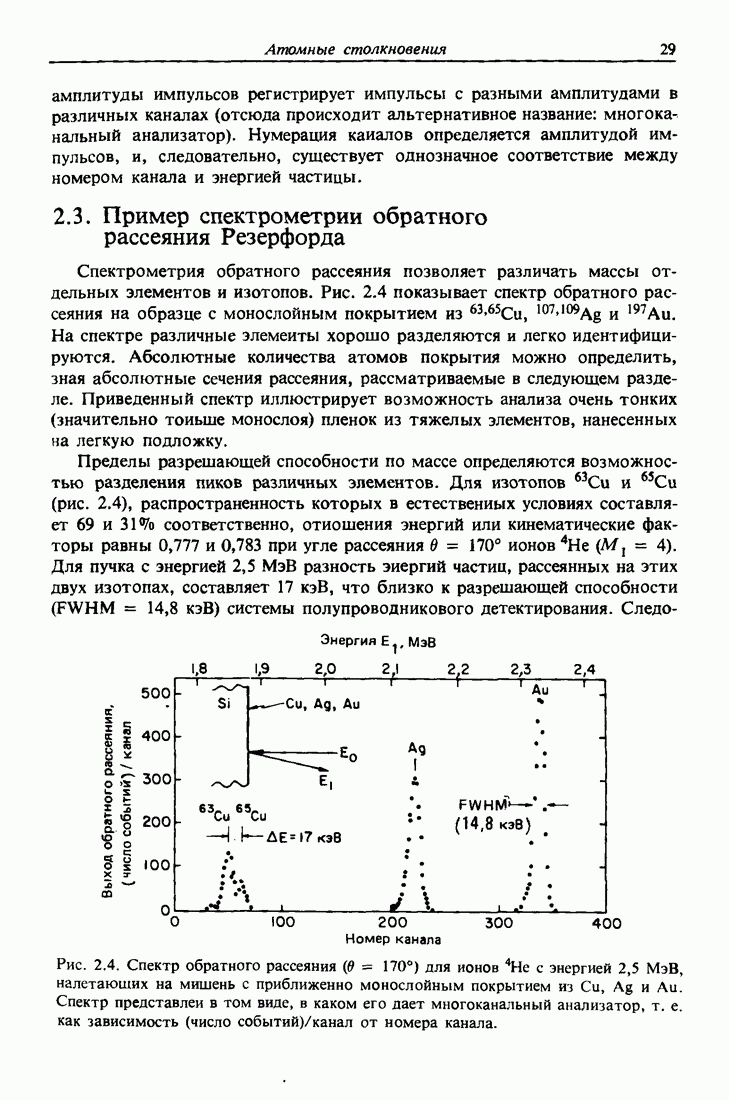
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
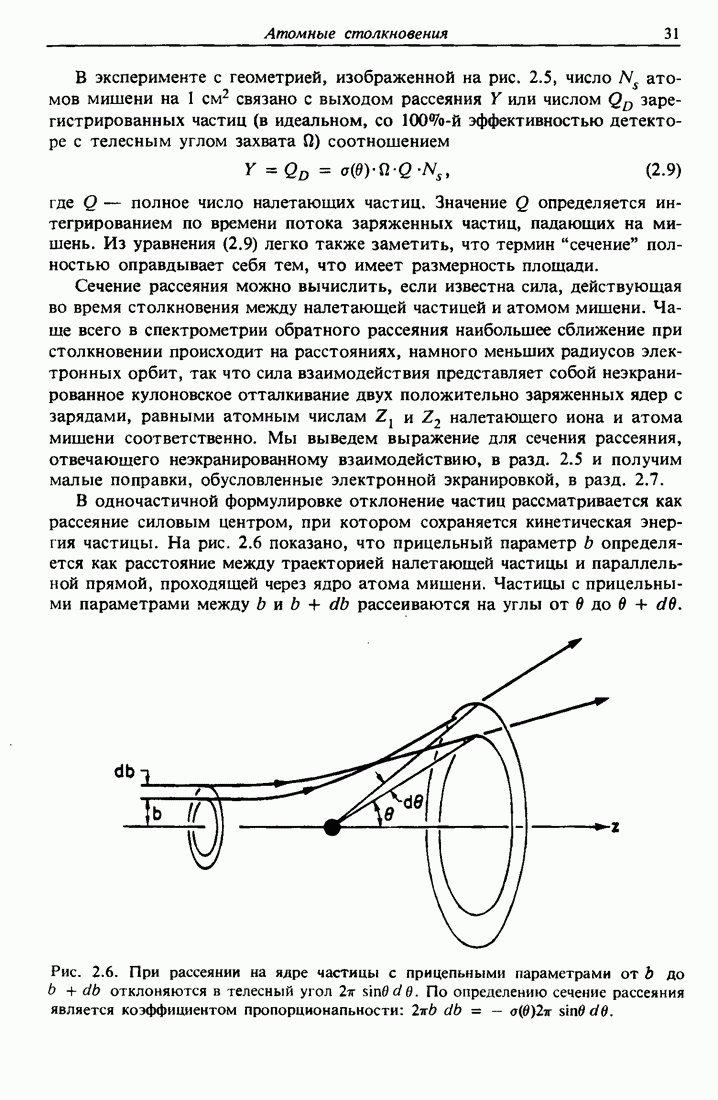
- 2.4. Сечение рассеяния и прицельный параметр
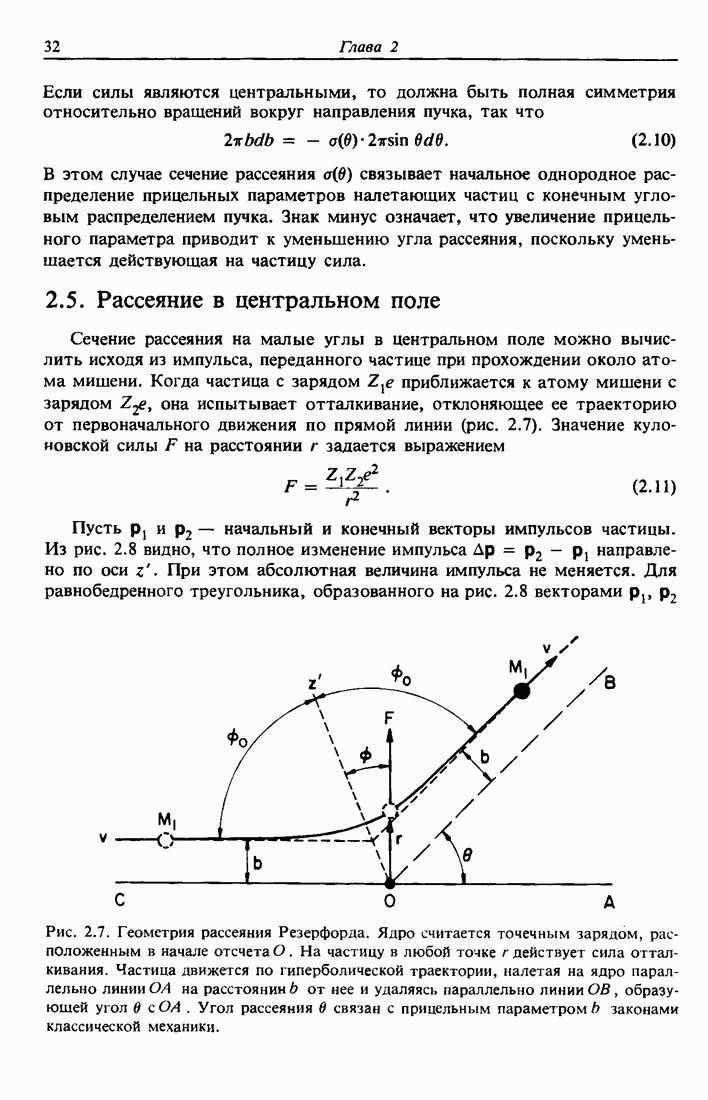
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
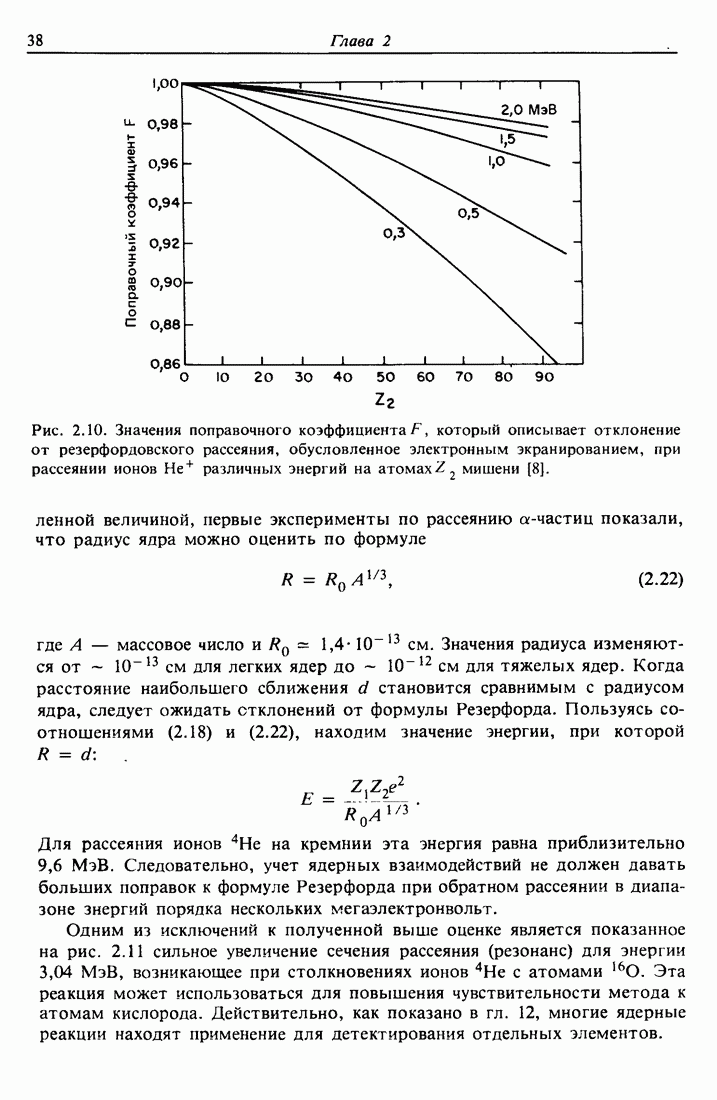
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
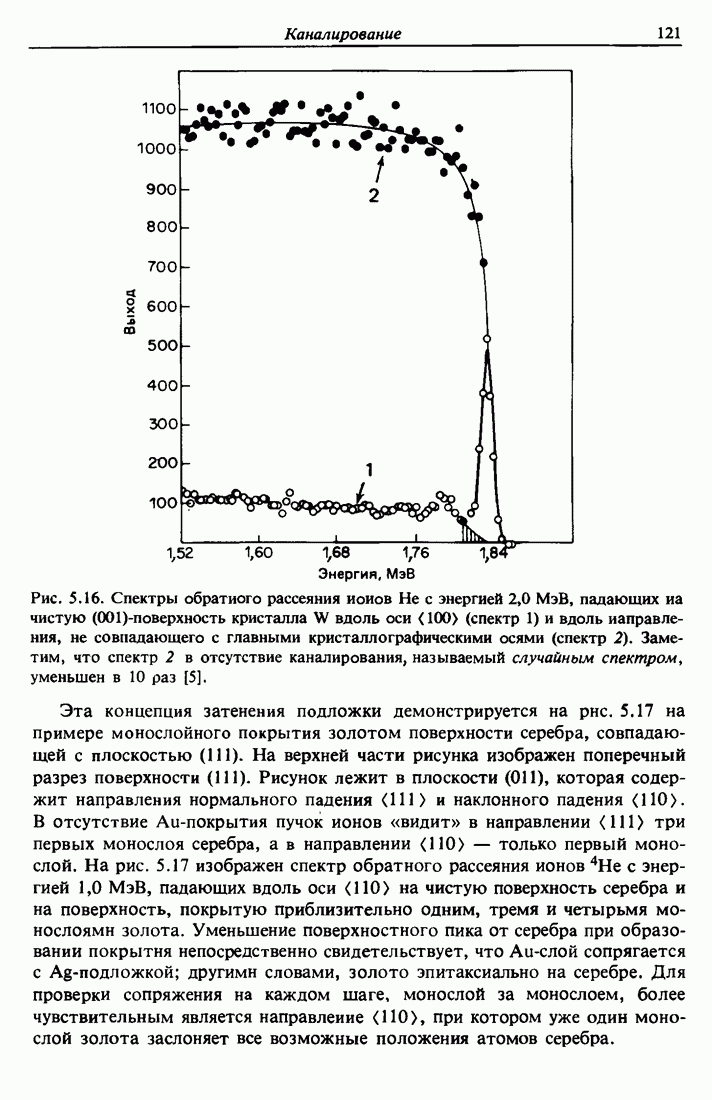
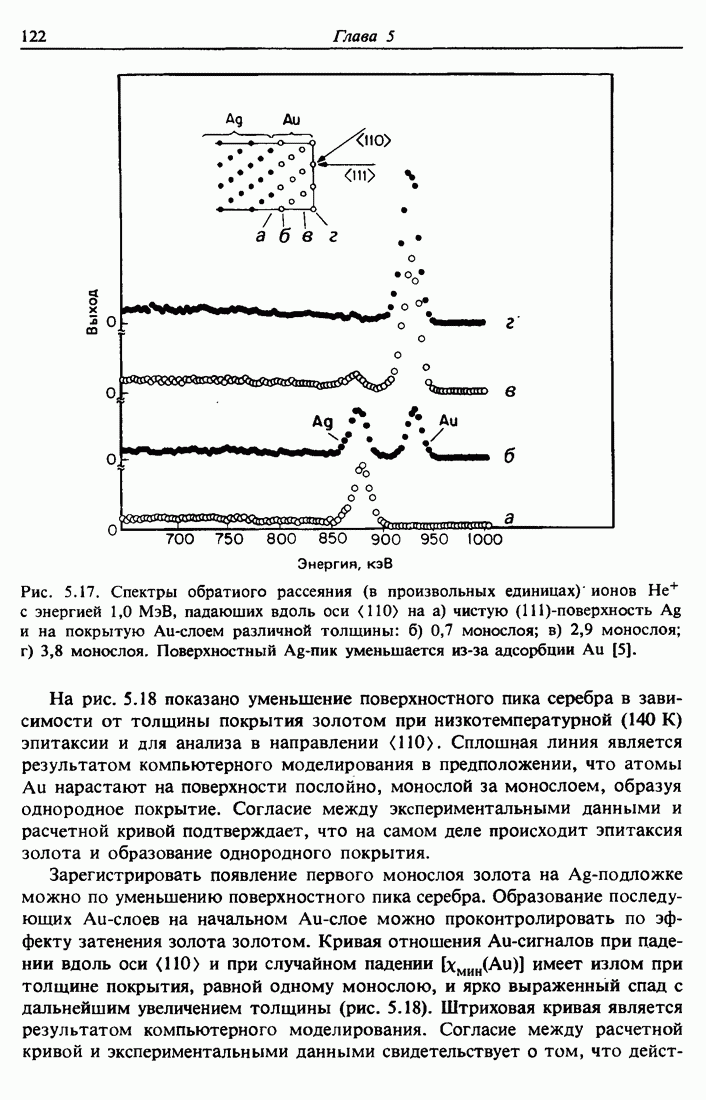
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
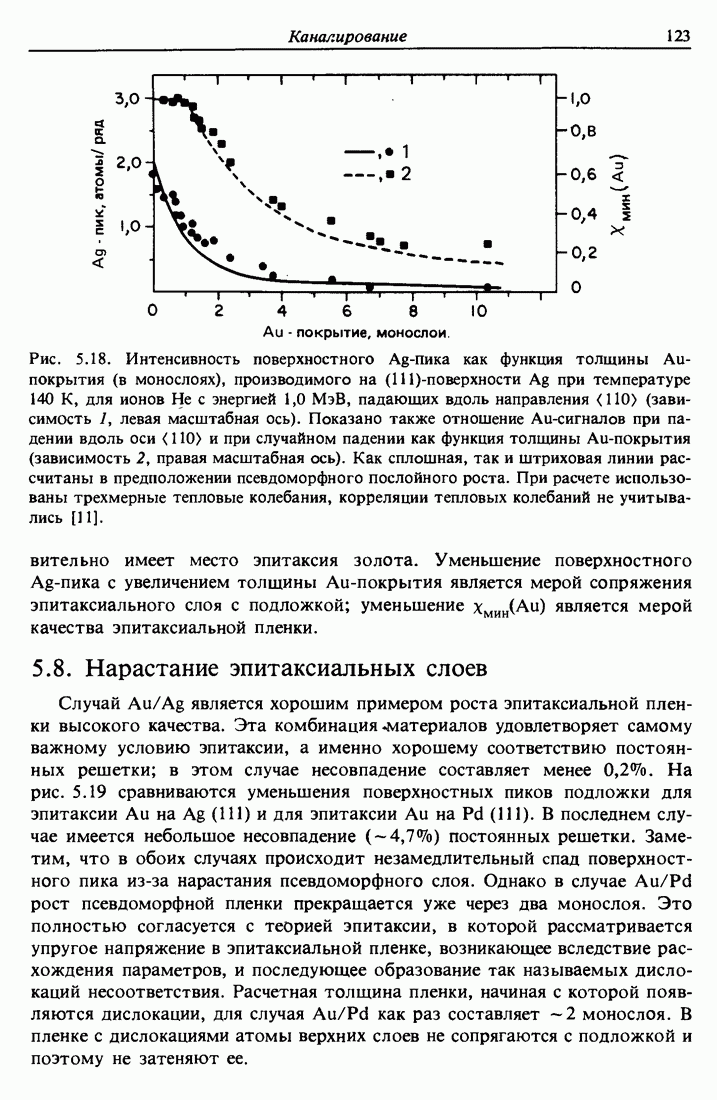
- 5.8. Нарастание эпитаксиальных слоев
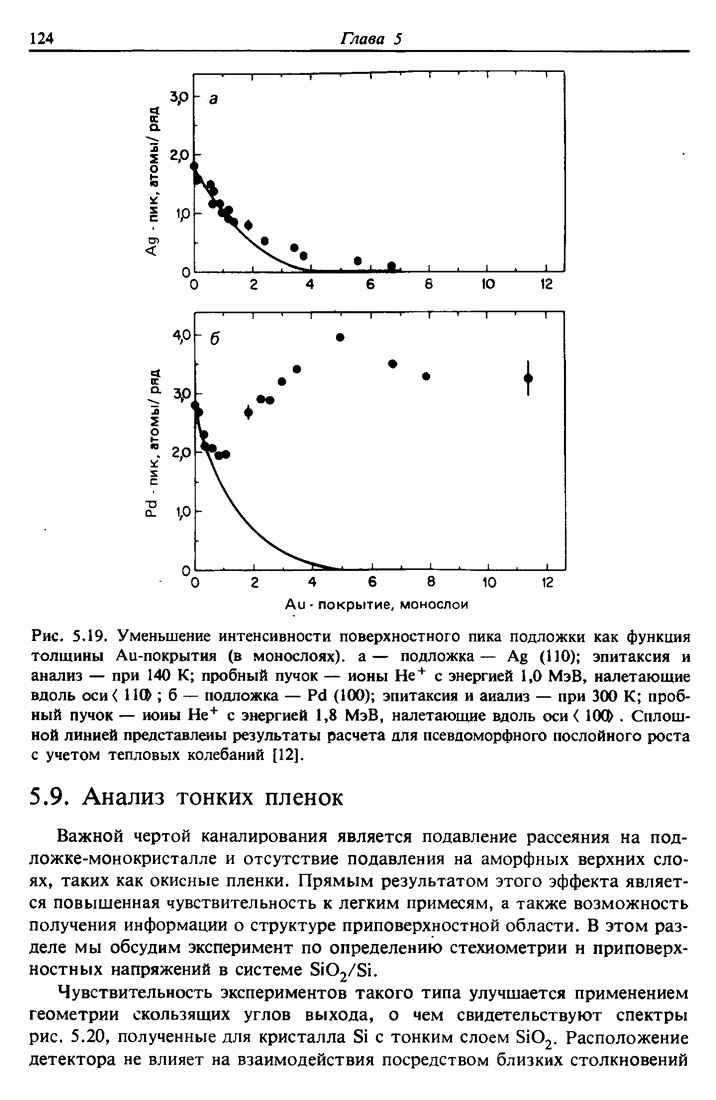
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
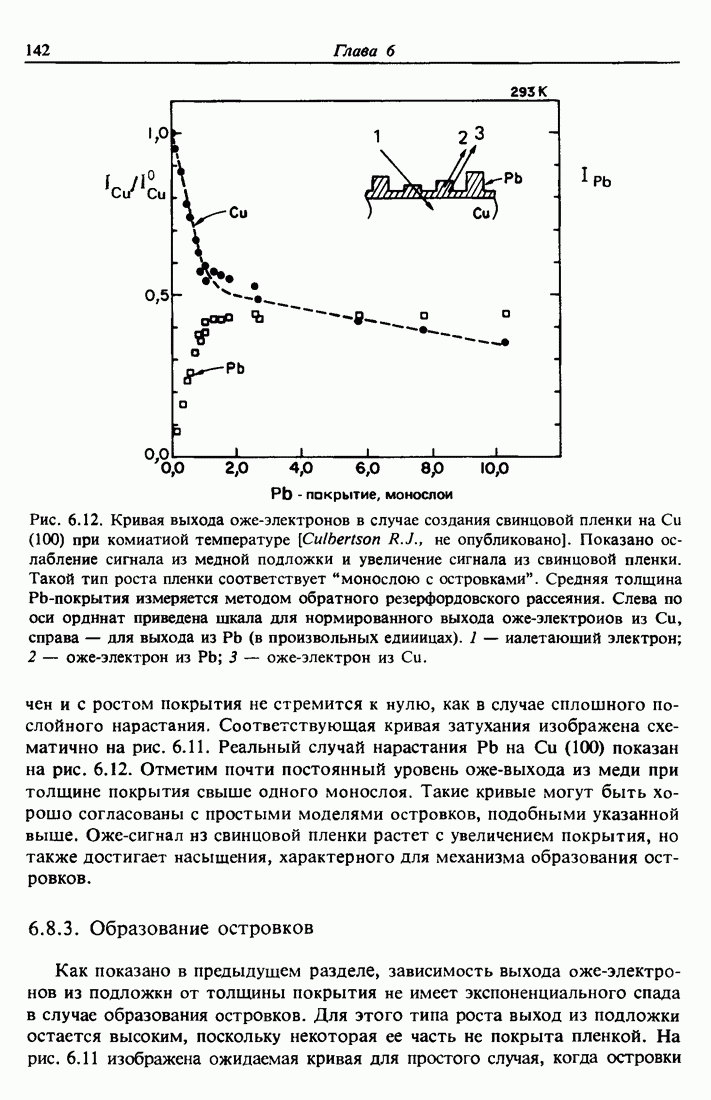
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
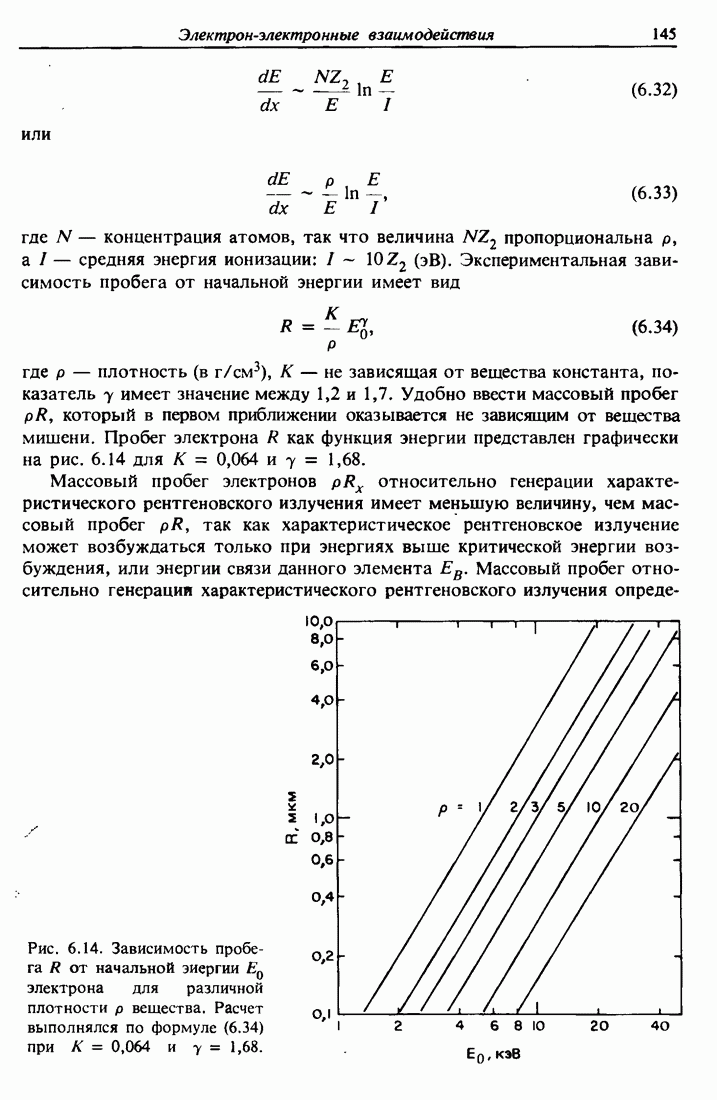
- 6.9. Пробеги электронов в твердых телах
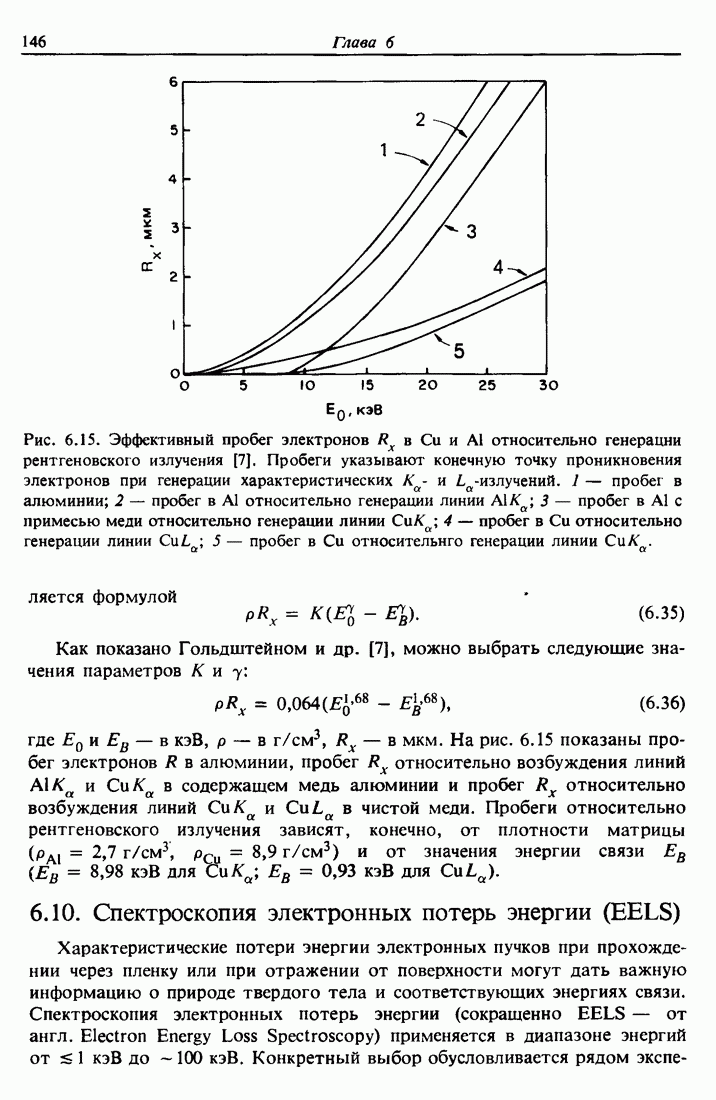
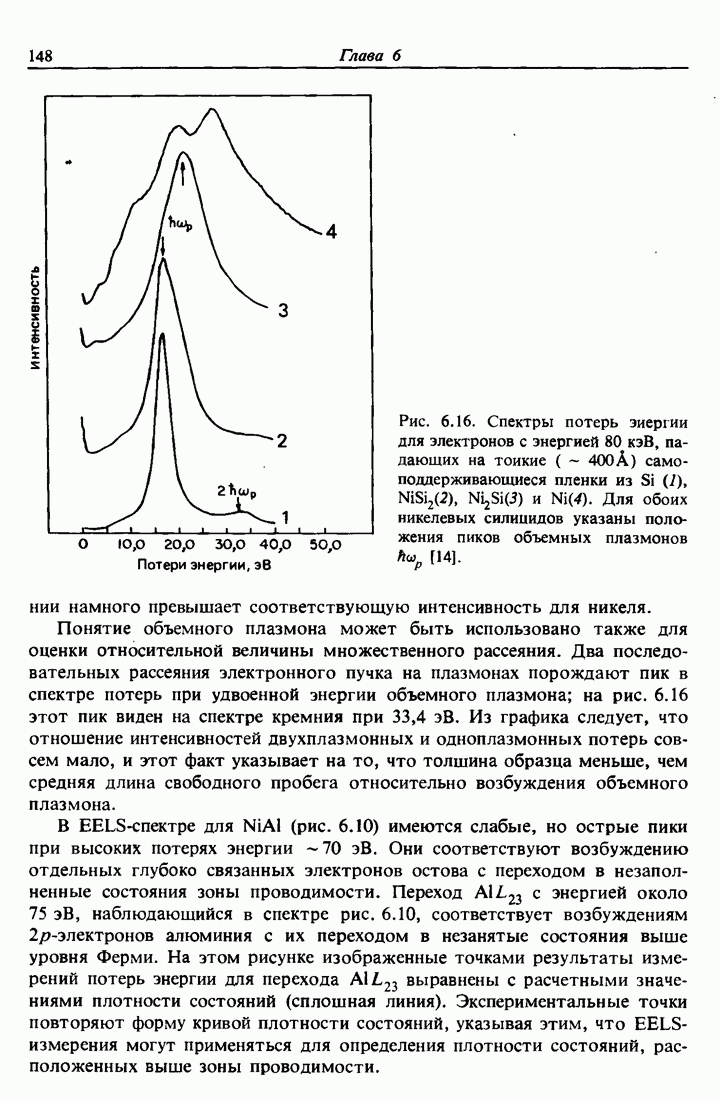
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
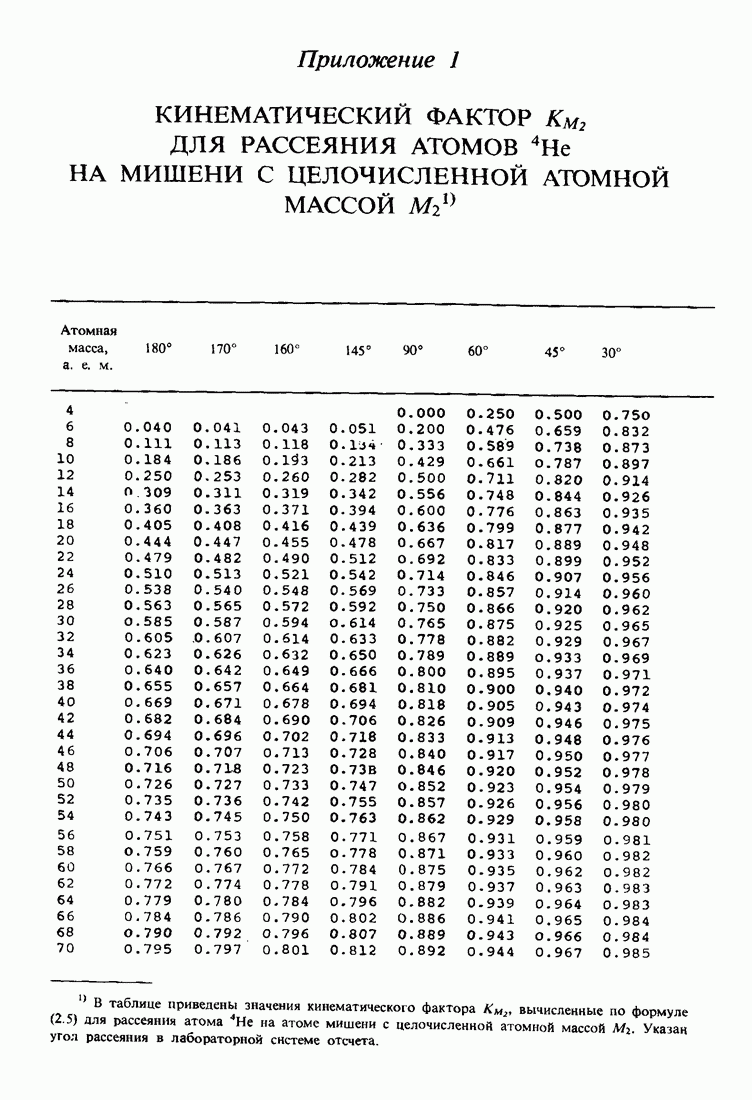
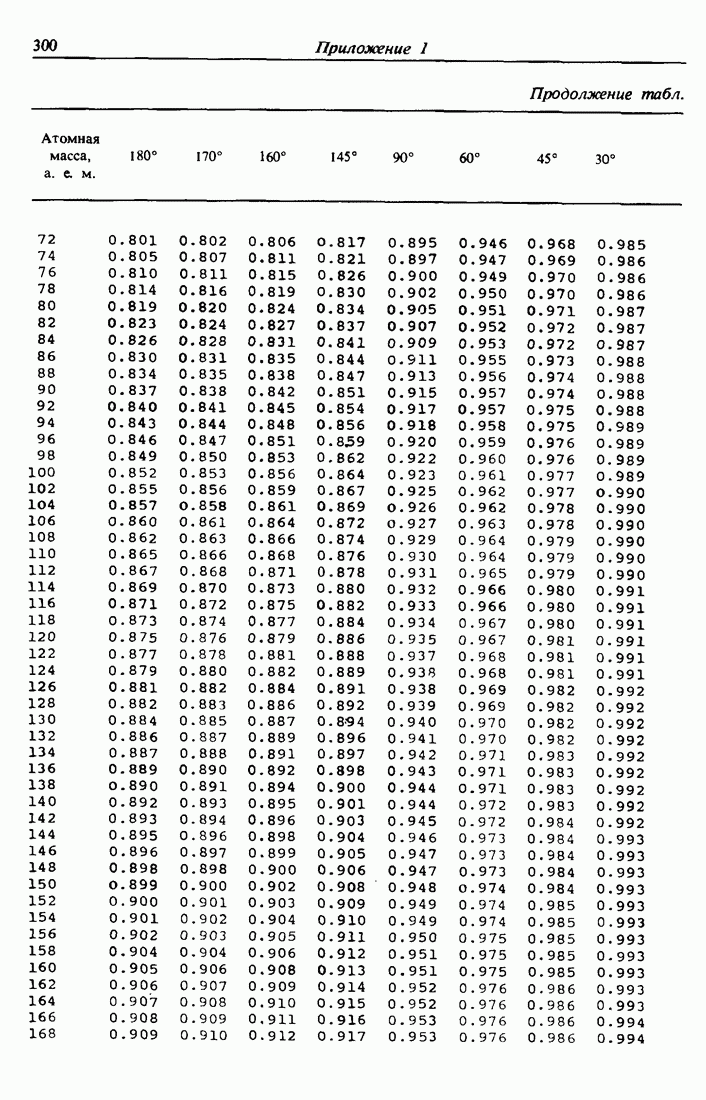
- ПРИЛОЖЕНИЕ 1.
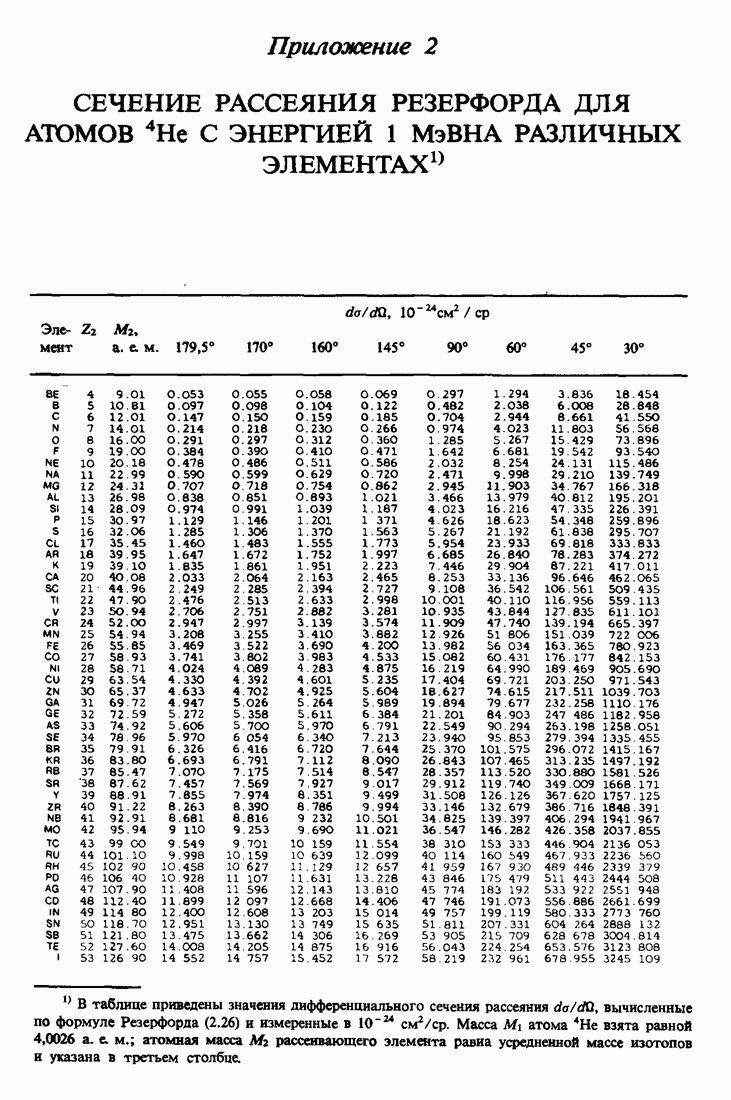
- ПРИЛОЖЕНИЕ 2.
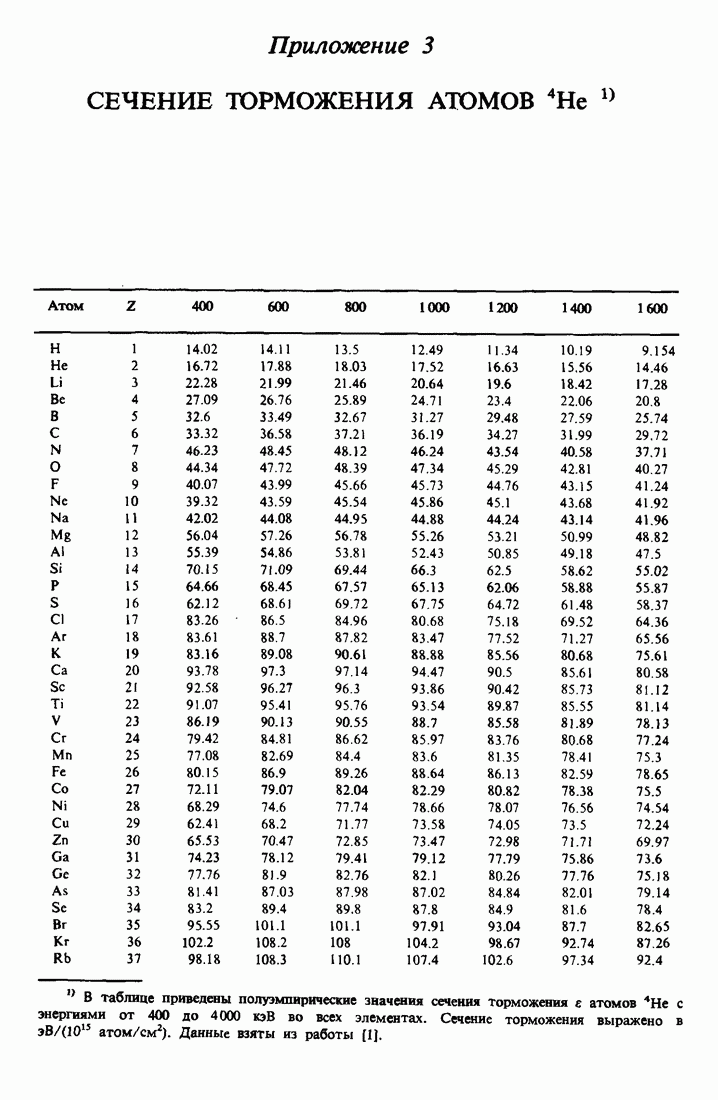
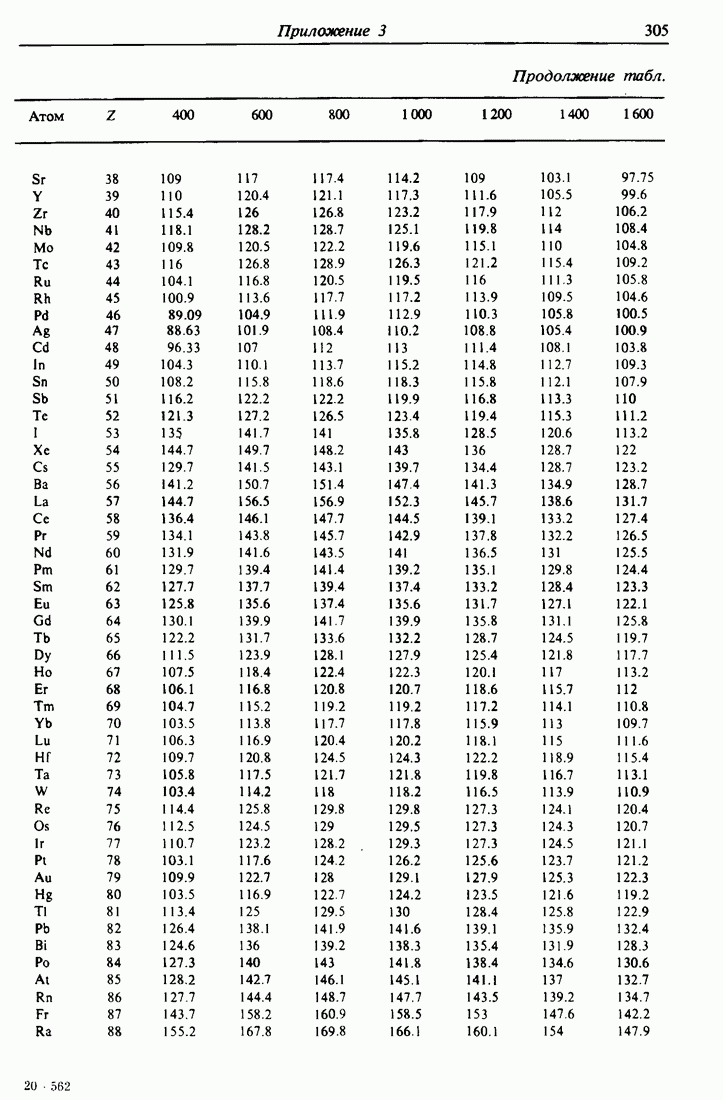
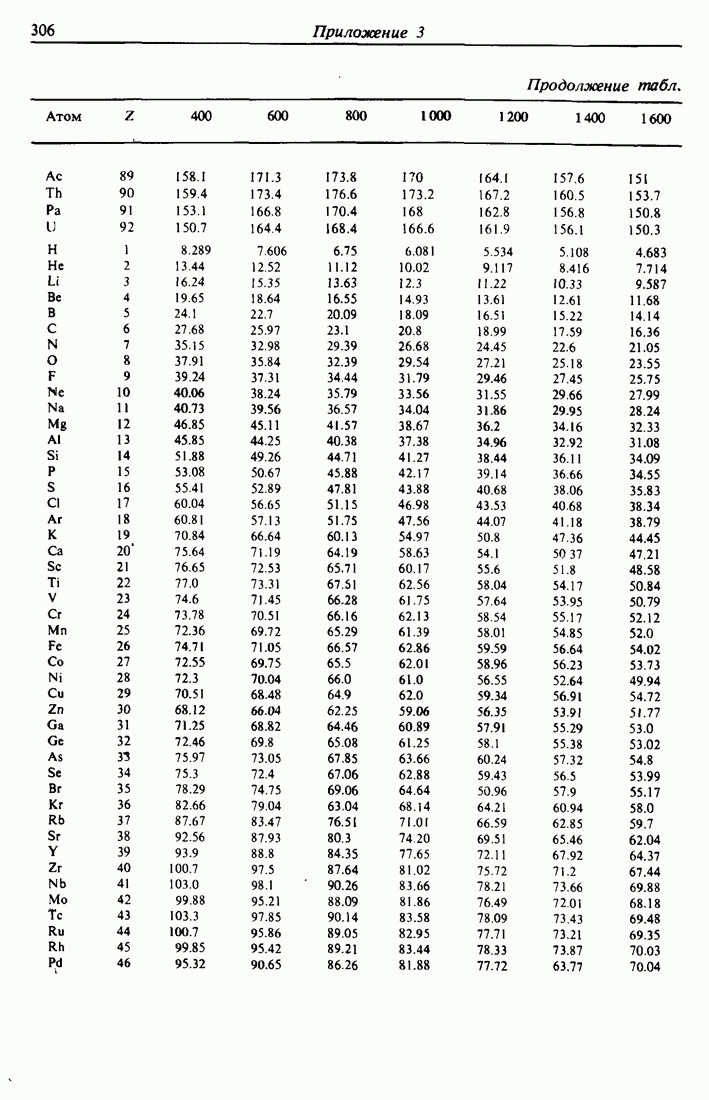
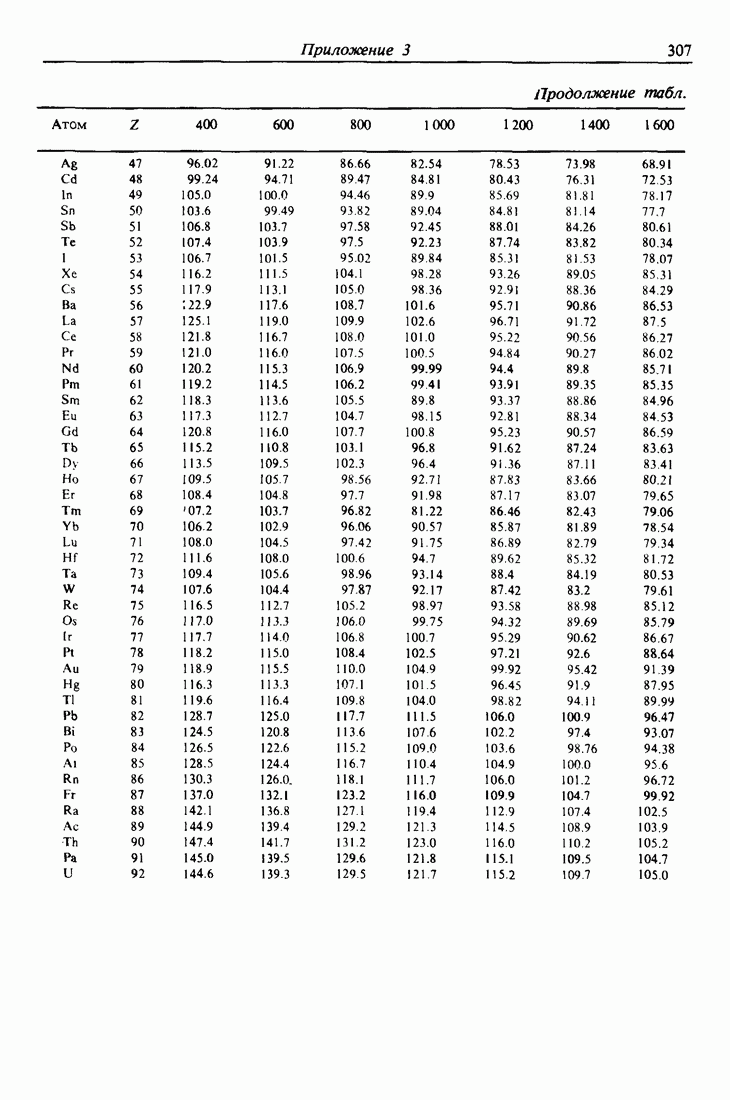
- ПРИЛОЖЕНИЕ 3.
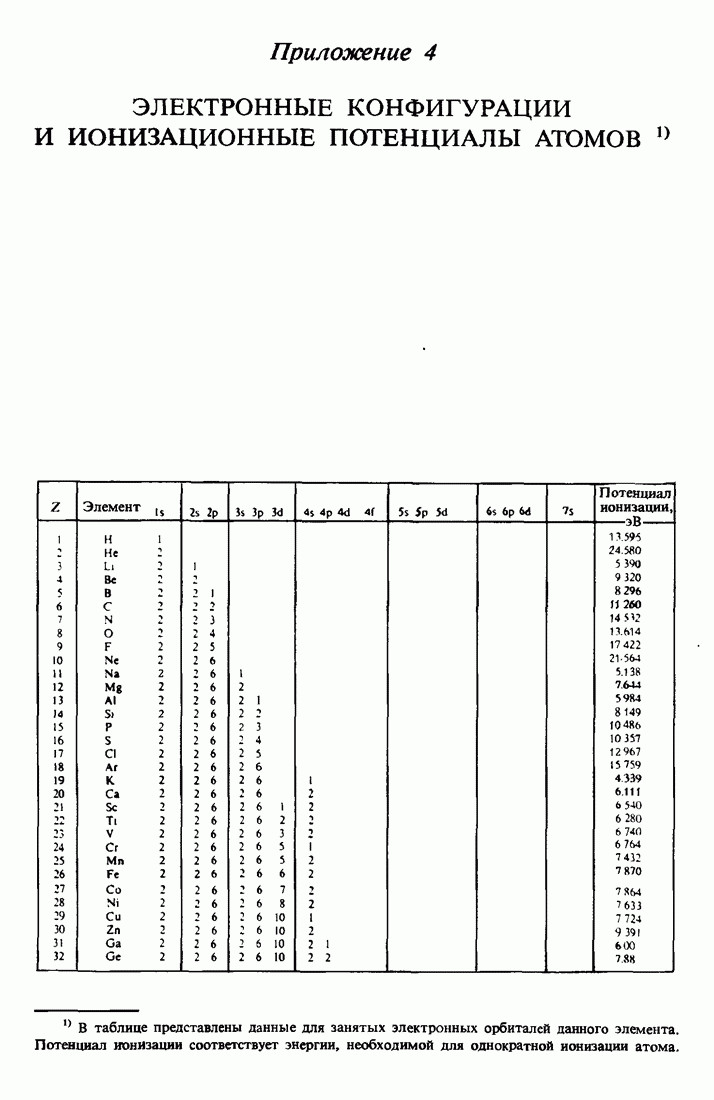
- ПРИЛОЖЕНИЕ 4.
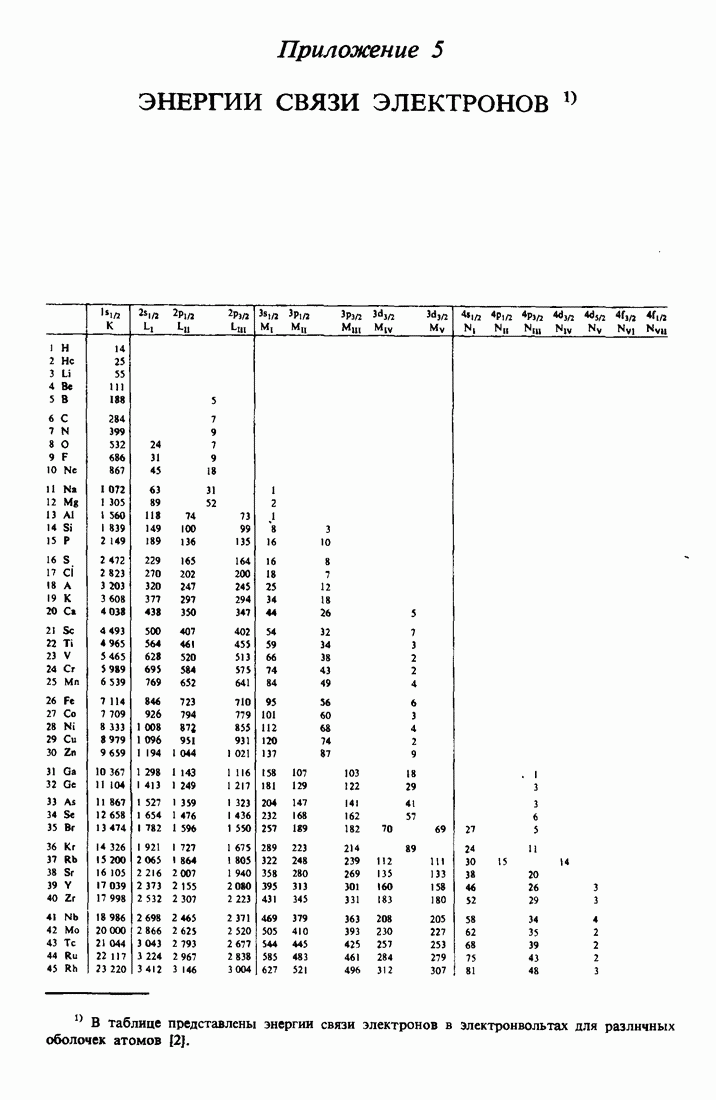
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
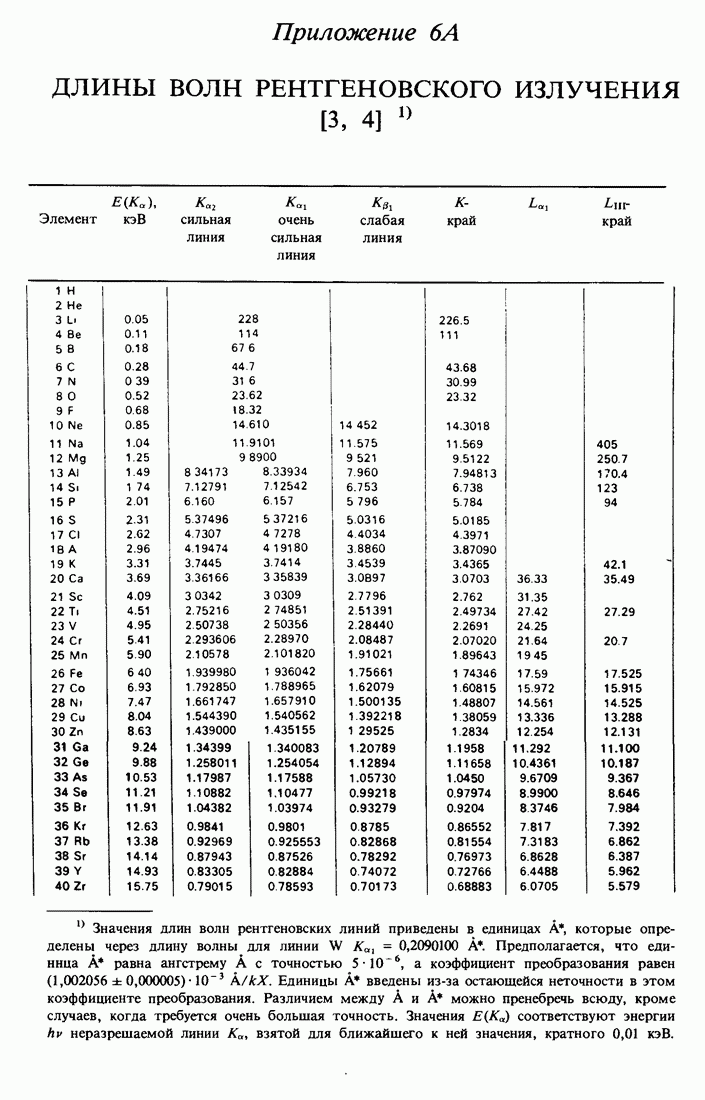
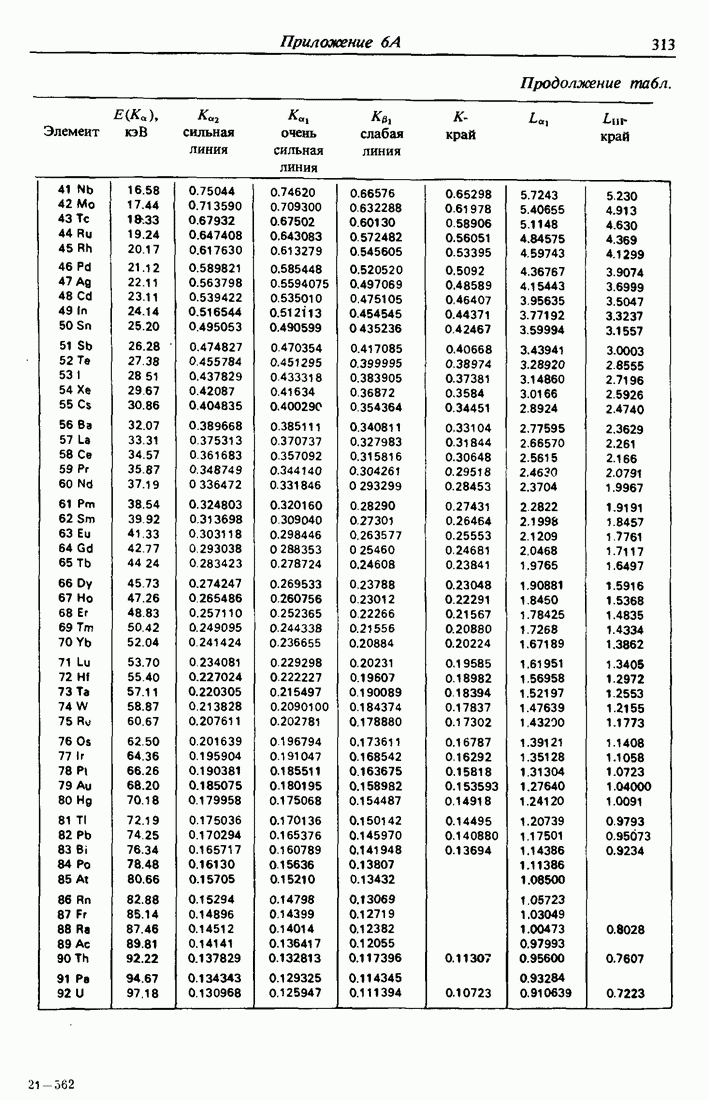
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
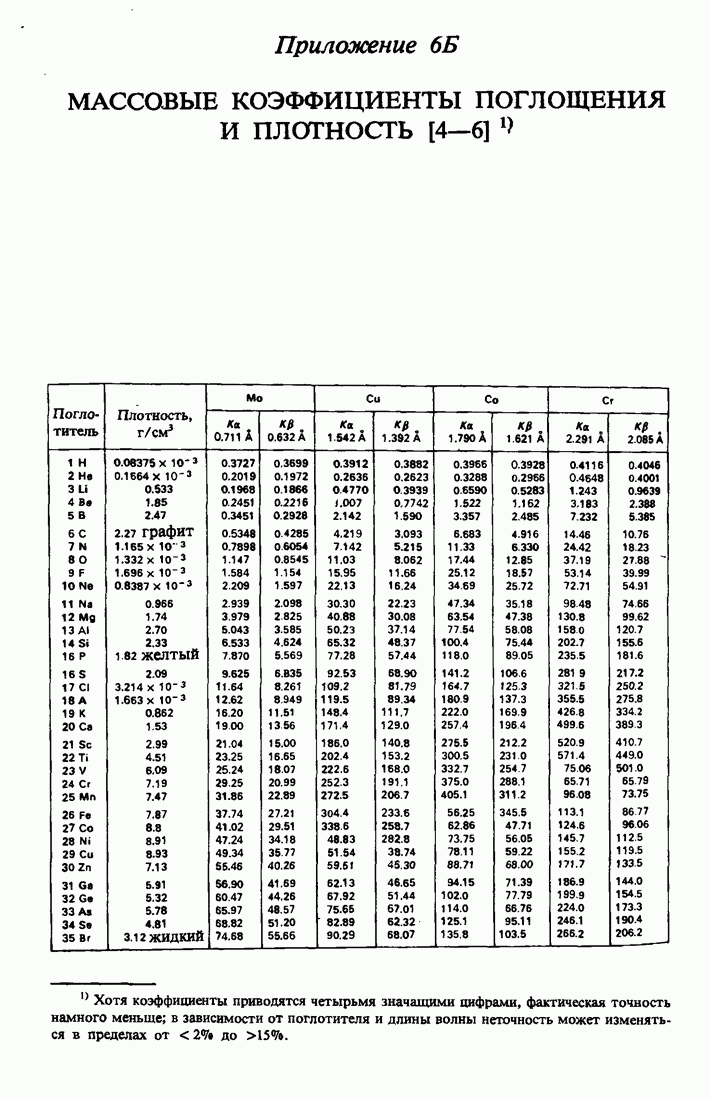
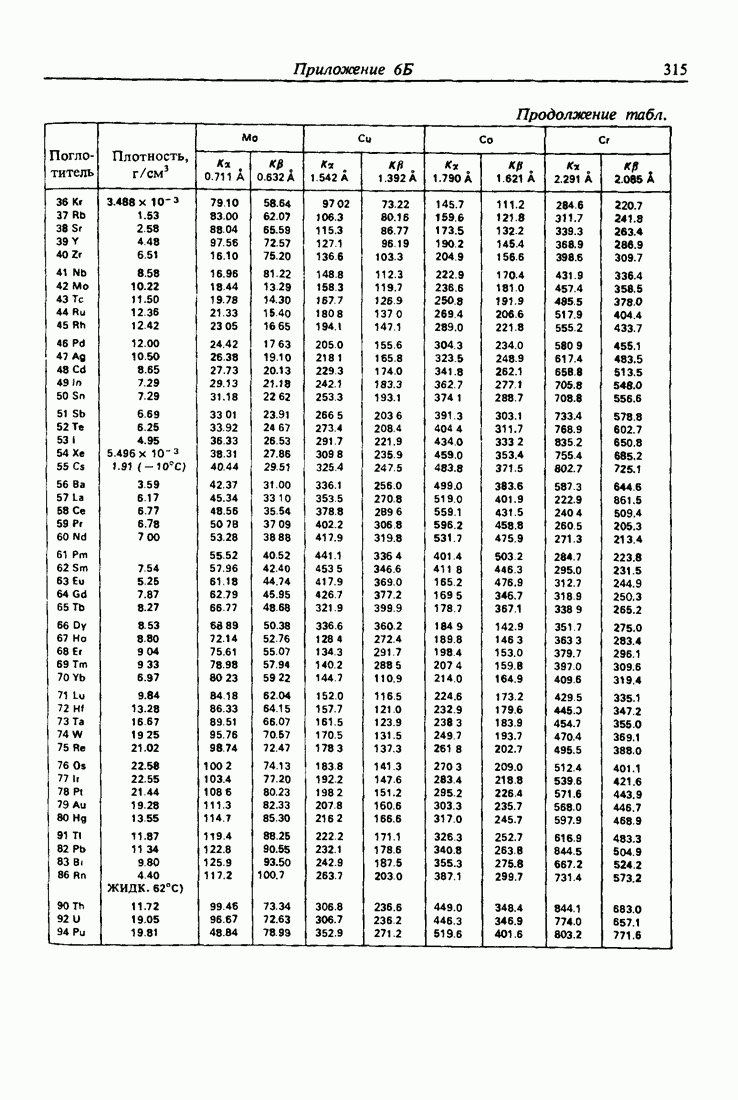
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
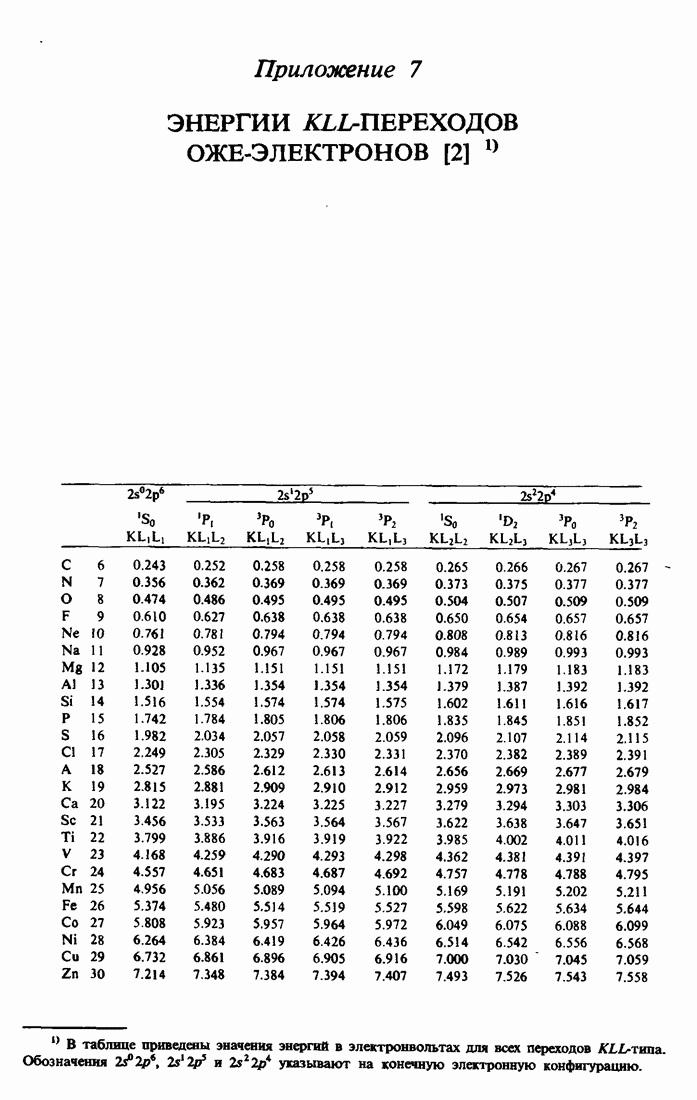
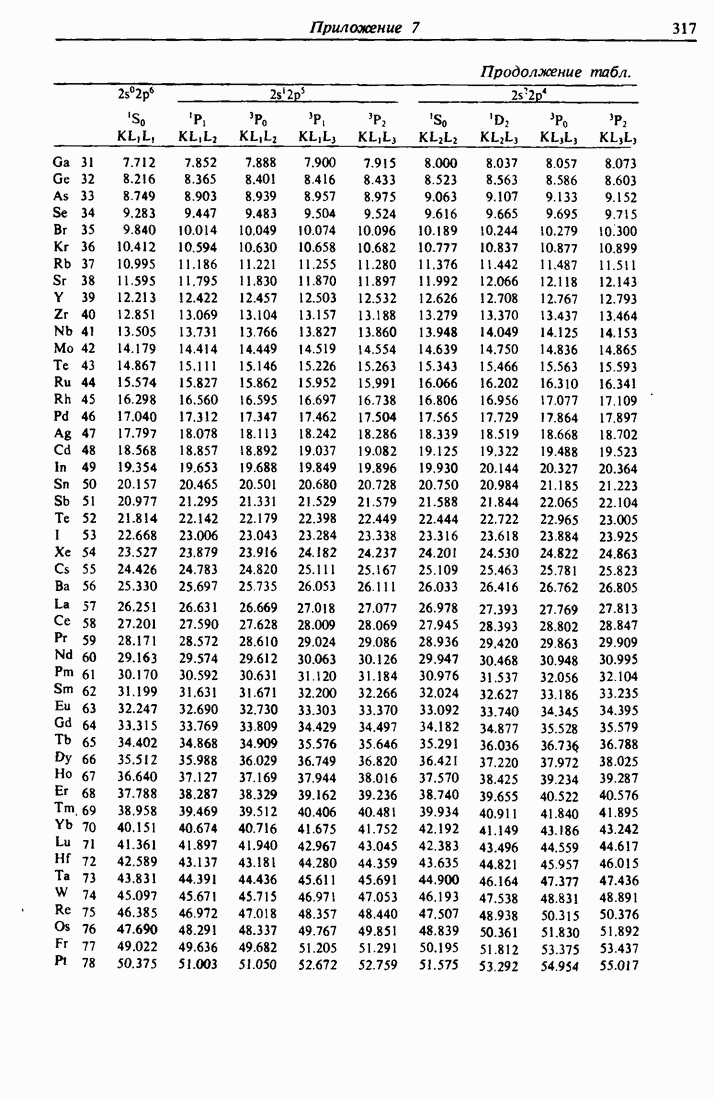
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
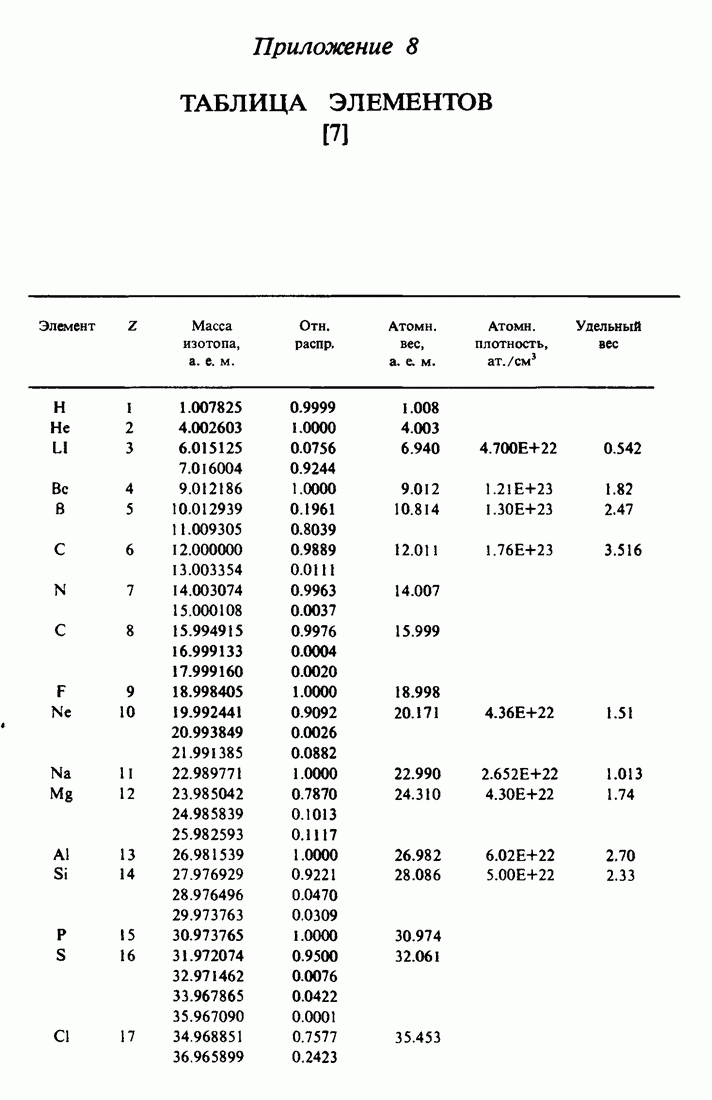
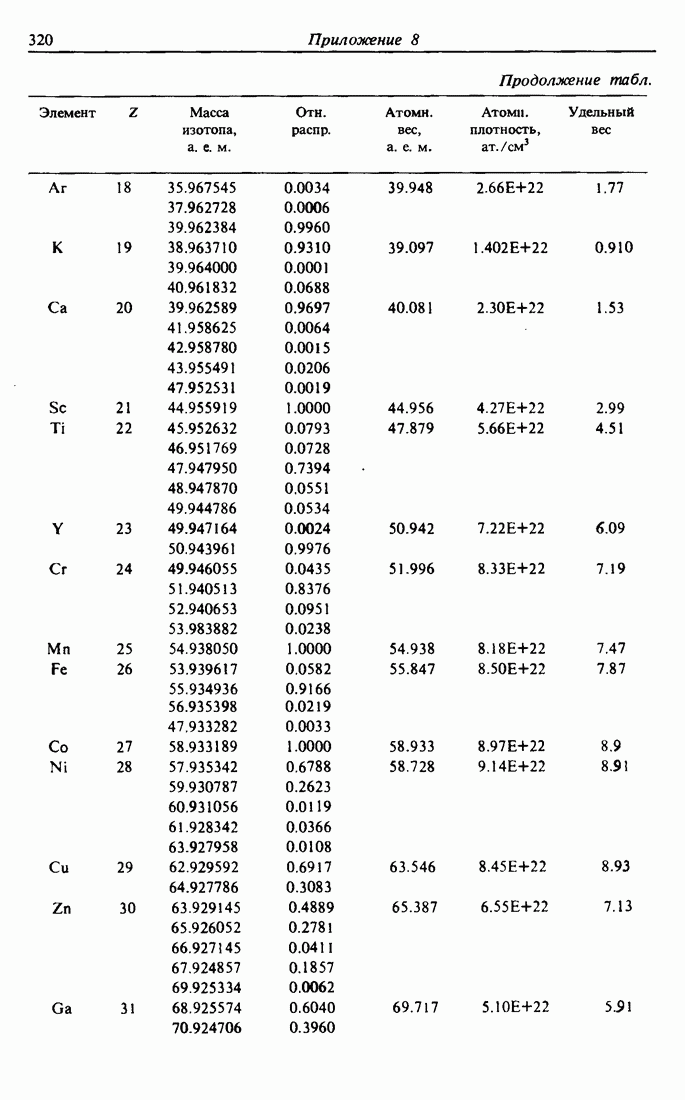
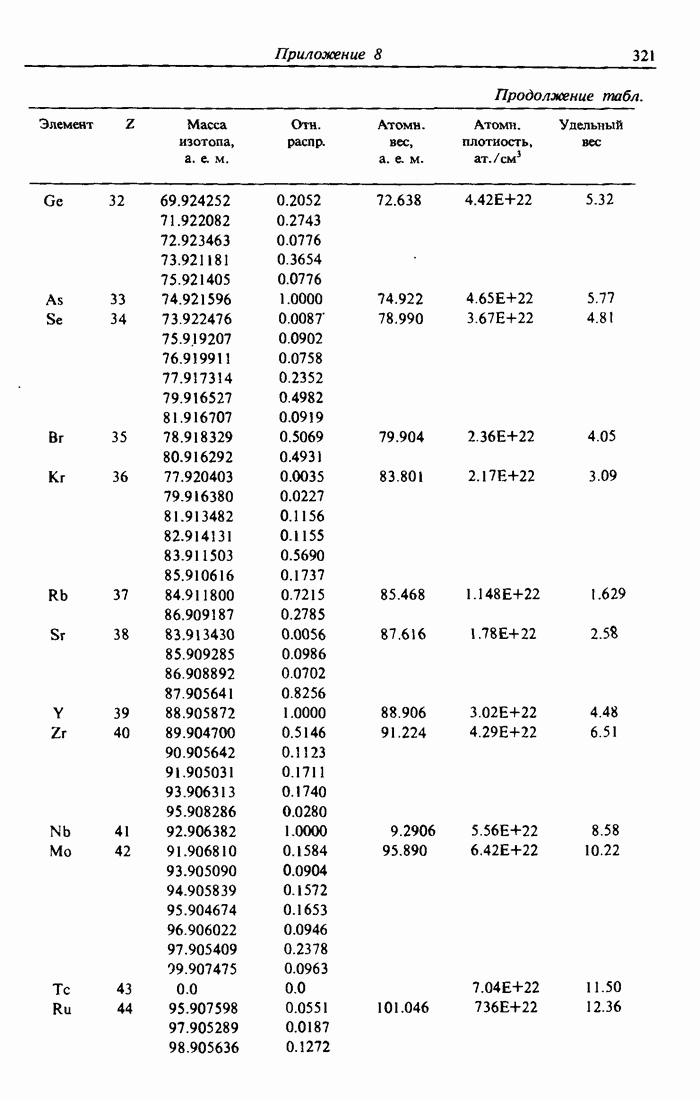
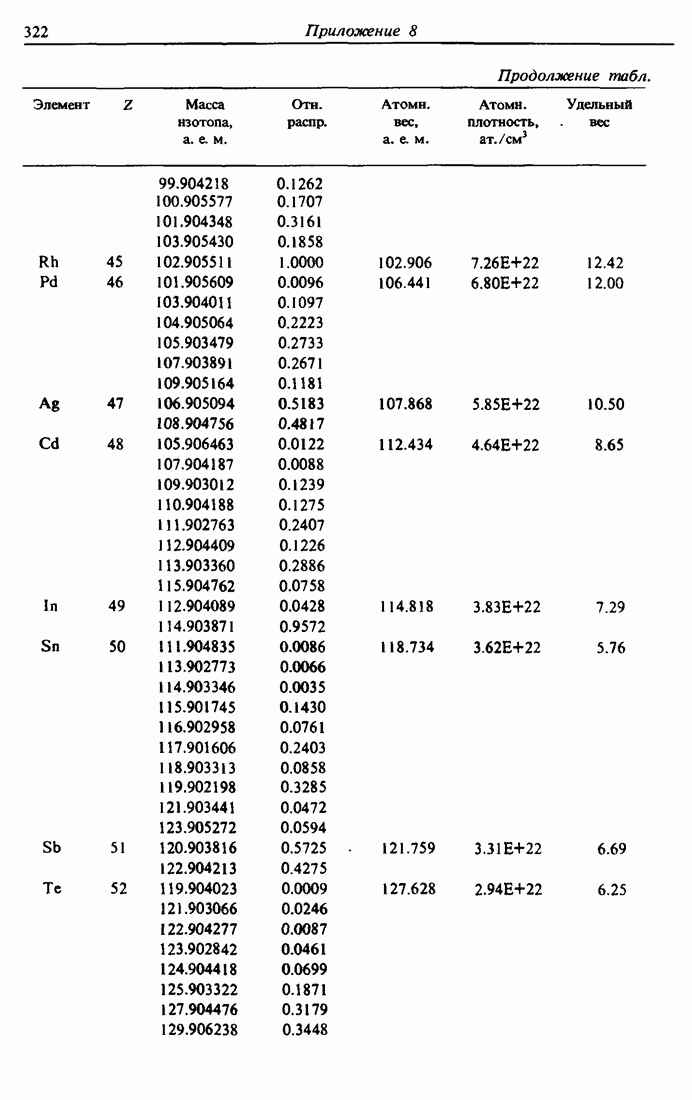
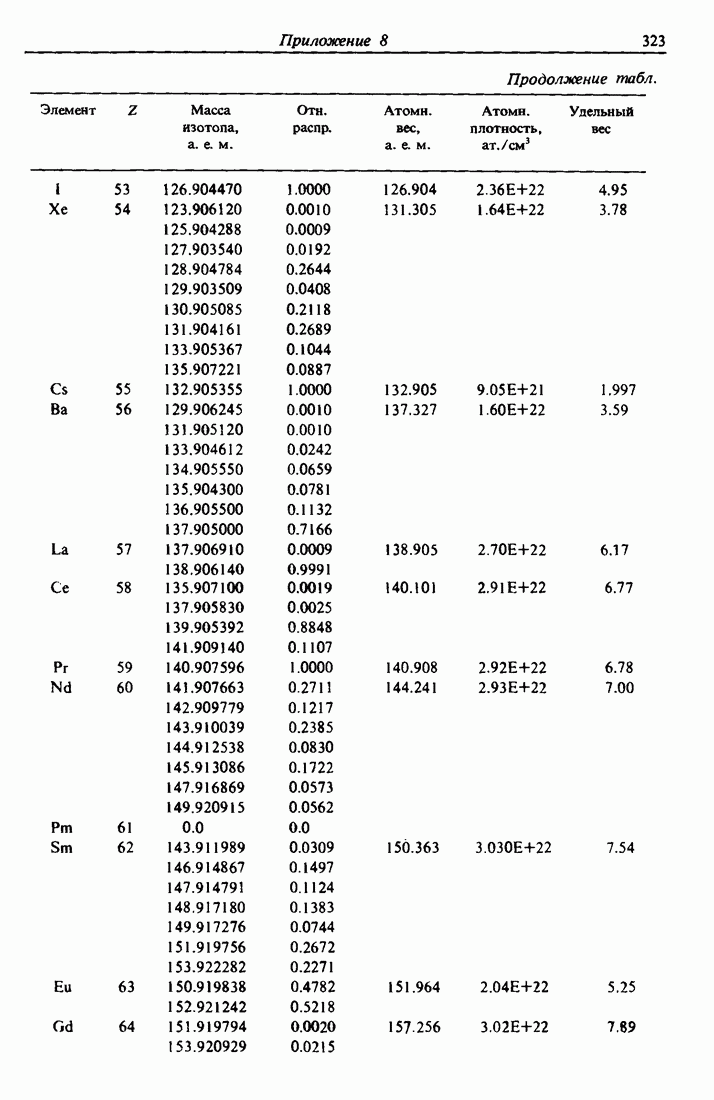
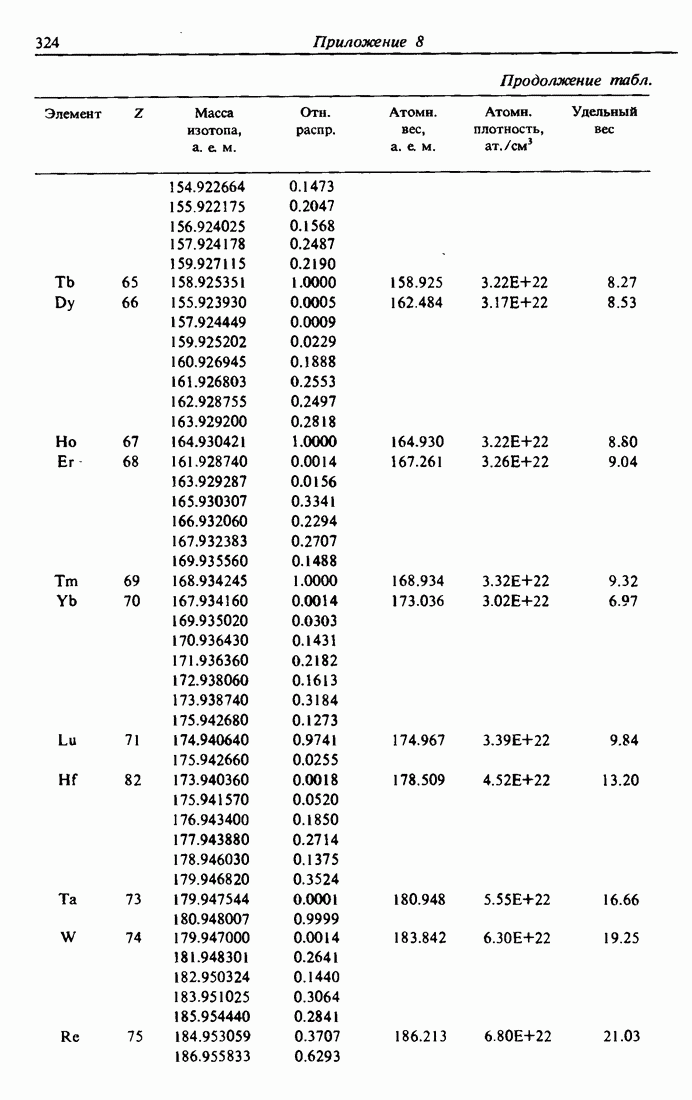
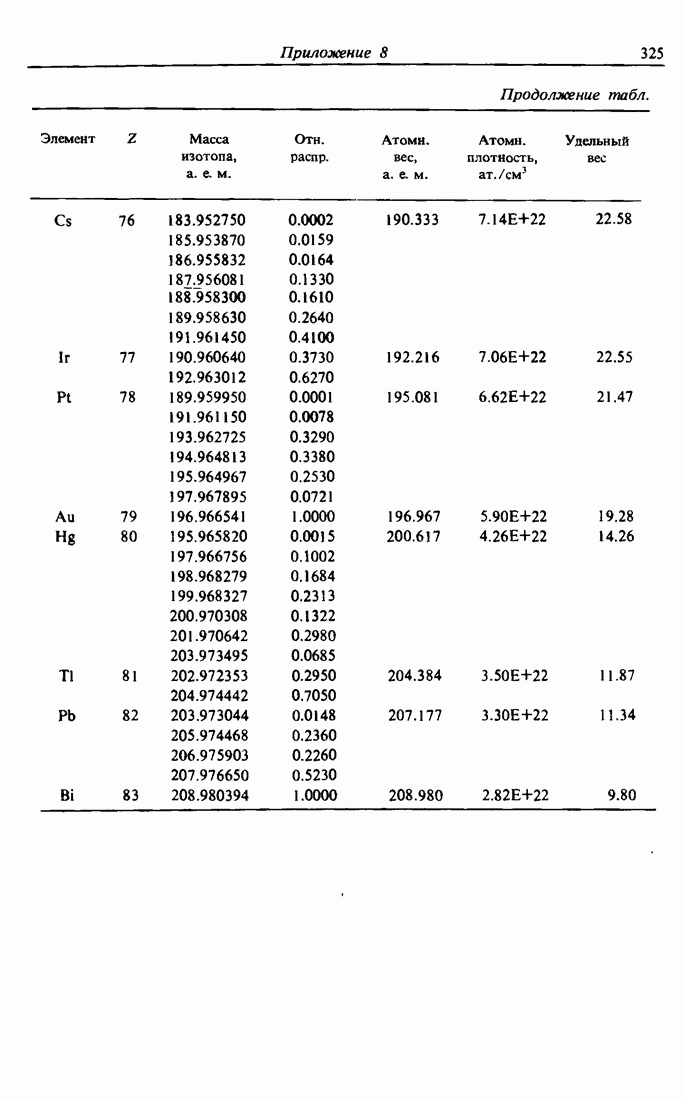
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
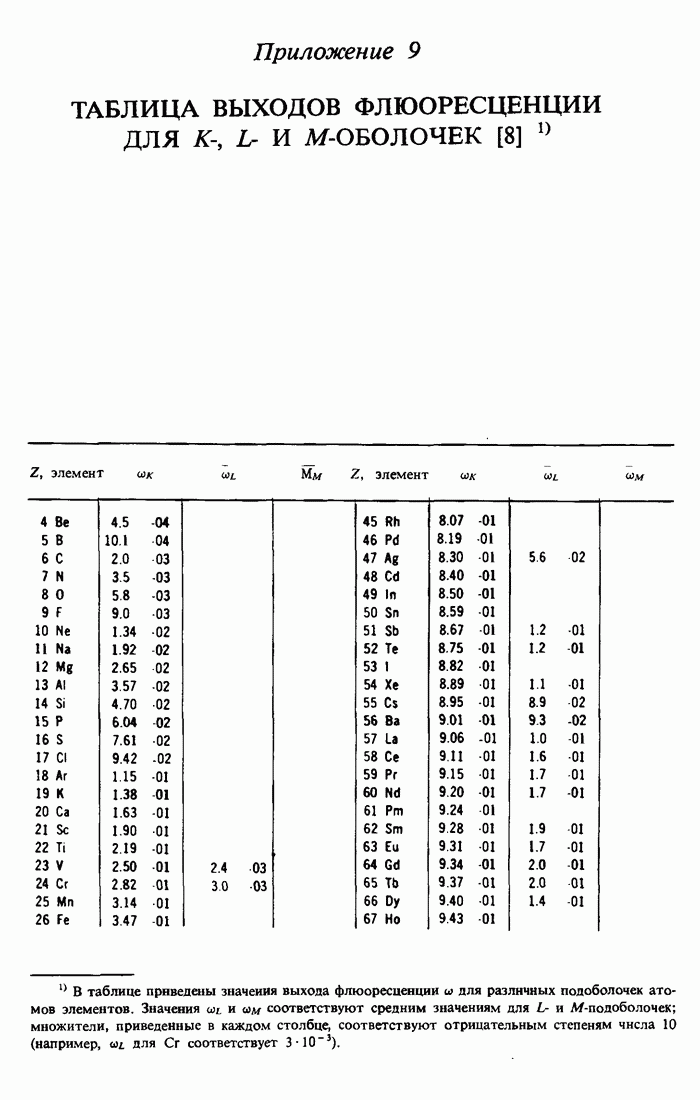
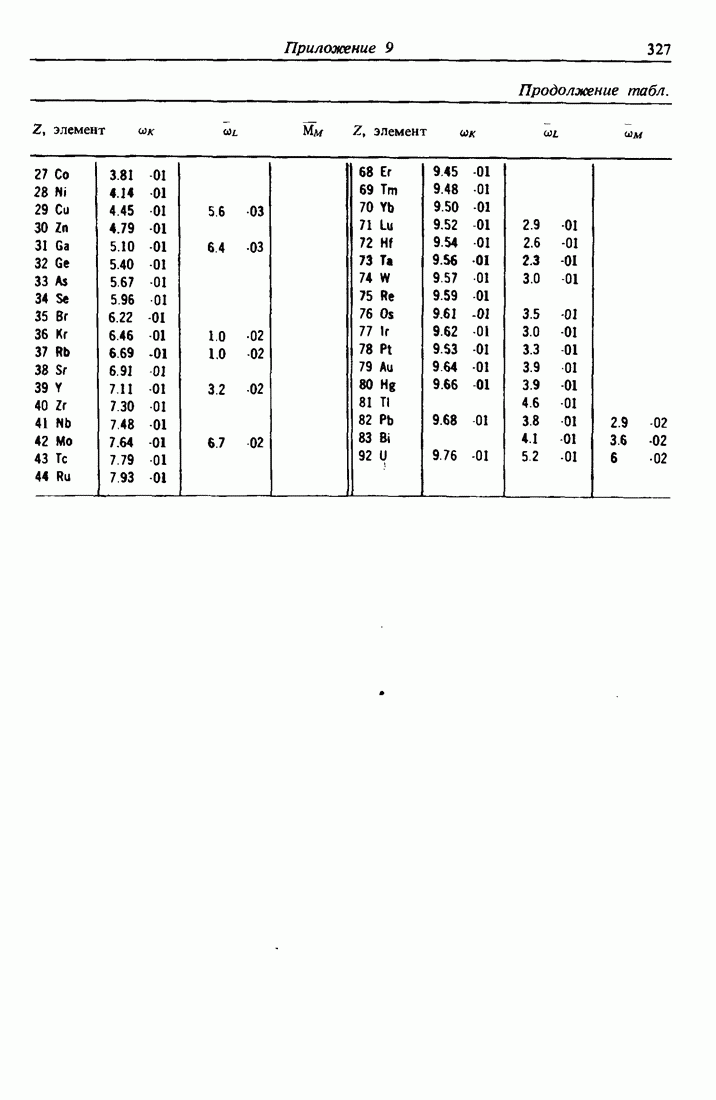
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ