| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
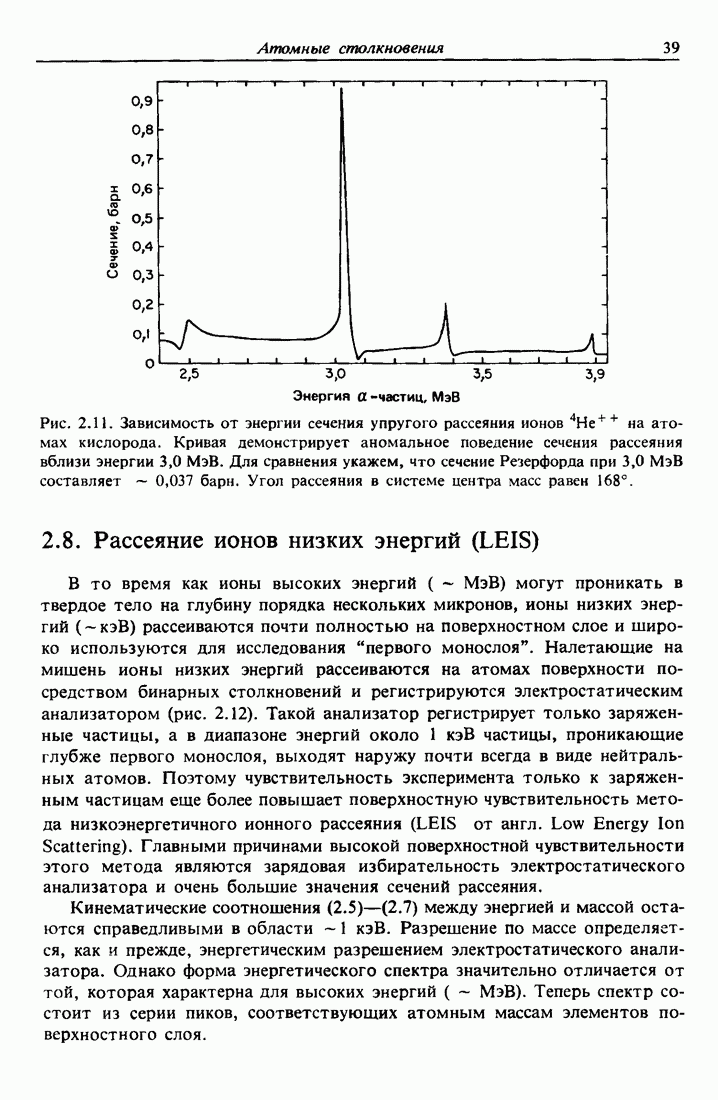
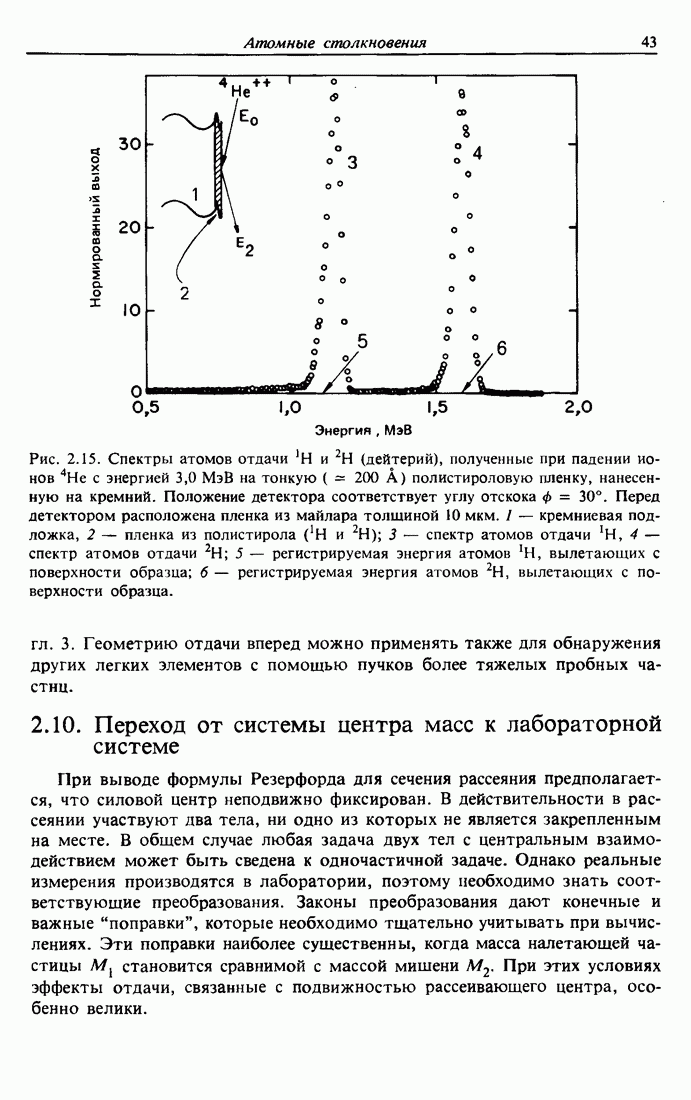
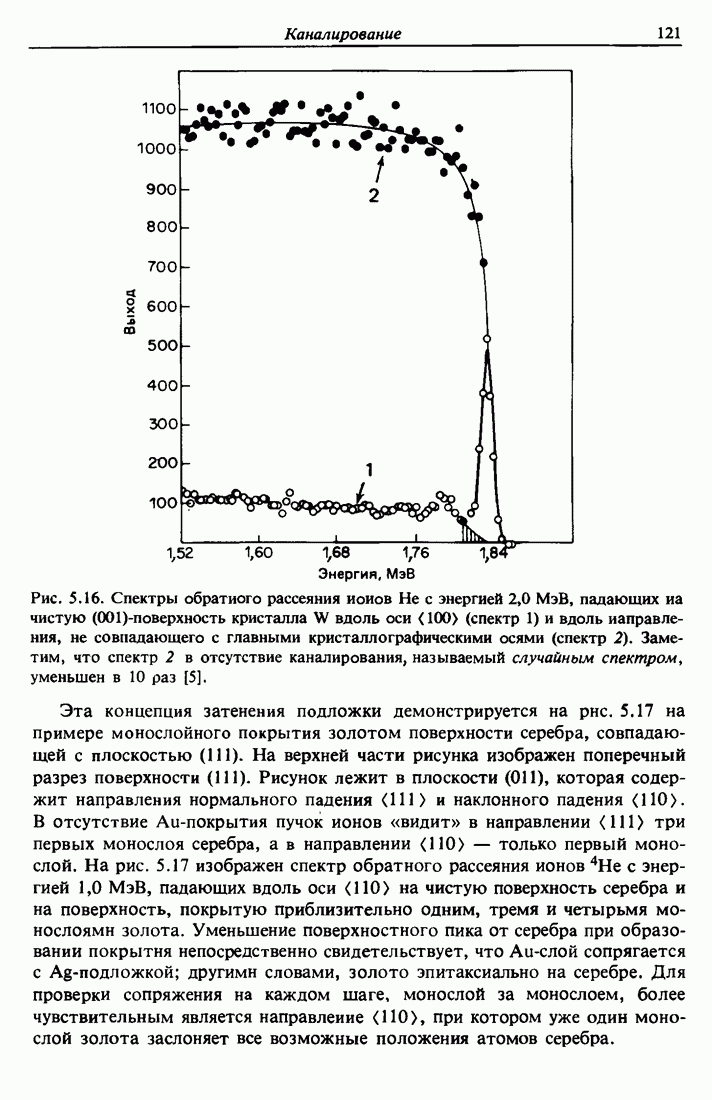
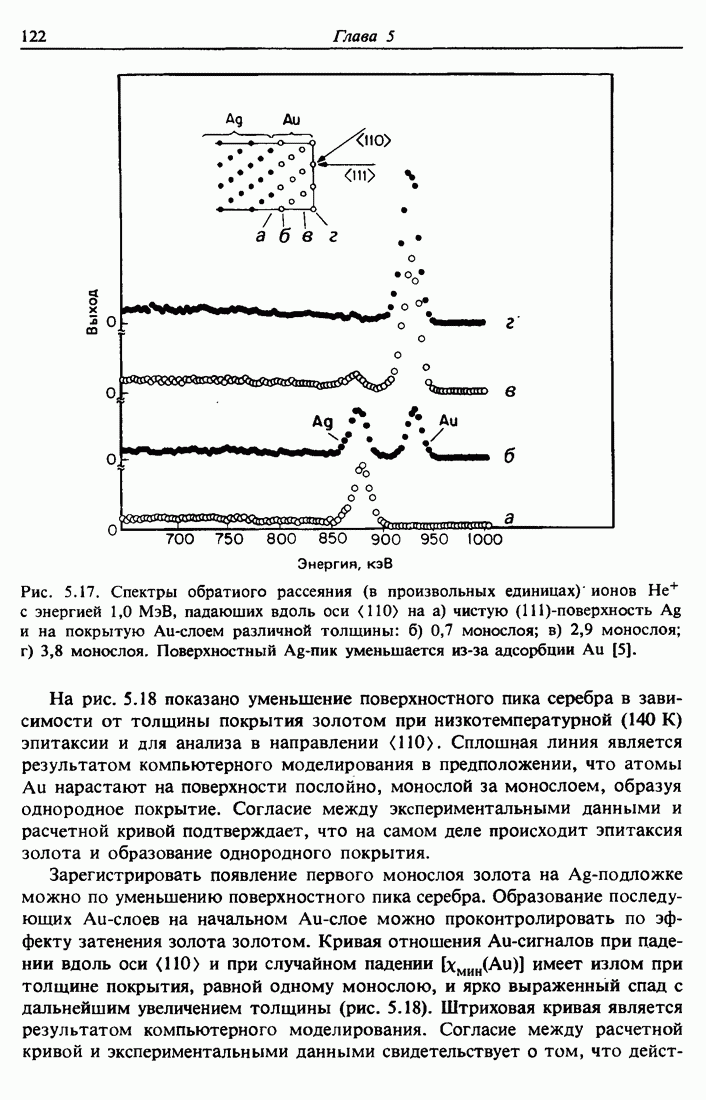
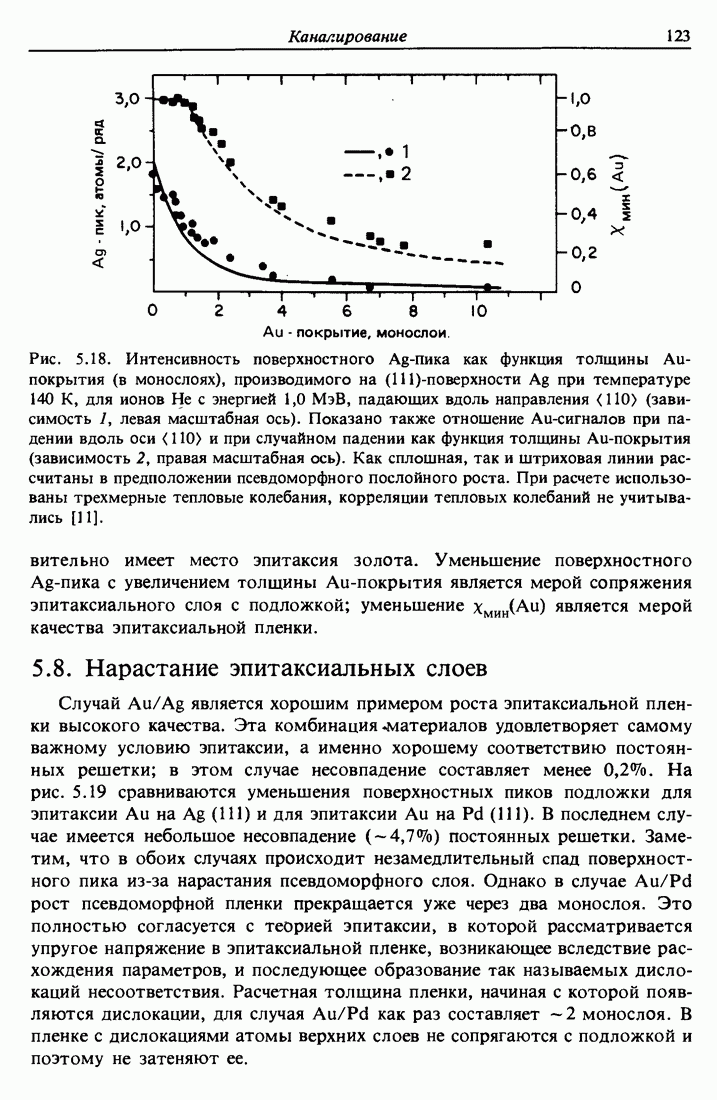
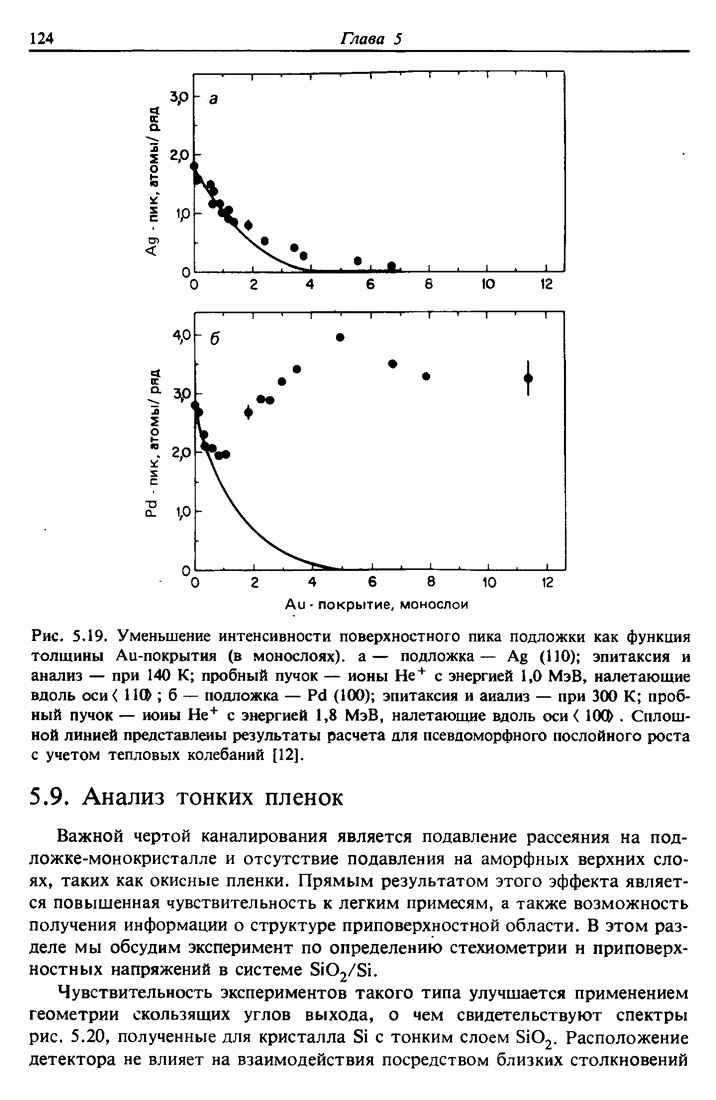
3.5. Ширина спектра энергии в обратном рассеянии
Проникая в твердое тело, ионы гелия с энергией порядка мегаэлектронвольт теряют энергию вдоль траектории движения со скоростью dE/dx, принимающей значения от 30 до 60 эВ/А. В анализе тонких пленок полная потеря энергии АЕ для иона, достигшего глубины  , с хорошей степенью точности пропорциональна t. Таким образом,
, с хорошей степенью точности пропорциональна t. Таким образом,

где  вычисляется для некоторой средней энергии между начальной энергией
вычисляется для некоторой средней энергии между начальной энергией  .
.
На глубине t частица имеет энергию

После рассеяния на большой угол энергия частицы становится равной  где K — кинематический фактор, определенный соотношением (2.5). Изменив направление движения, частица продолжает тормозиться на обратном
где K — кинематический фактор, определенный соотношением (2.5). Изменив направление движения, частица продолжает тормозиться на обратном
пути и появляется на наружной поверхности, обладая энергией

где  — угол рассеяния. Таким образом, ширина
— угол рассеяния. Таким образом, ширина  энергетического спектра частиц, обратно рассеянных пленкой толщиной
энергетического спектра частиц, обратно рассеянных пленкой толщиной  , равна
, равна

Индексы  указывают энергии, при которых вычисляется производная
указывают энергии, при которых вычисляется производная  , а величину
, а величину  часто называют коэффициентом энергетических потерь обратного рассеяния.
часто называют коэффициентом энергетических потерь обратного рассеяния.
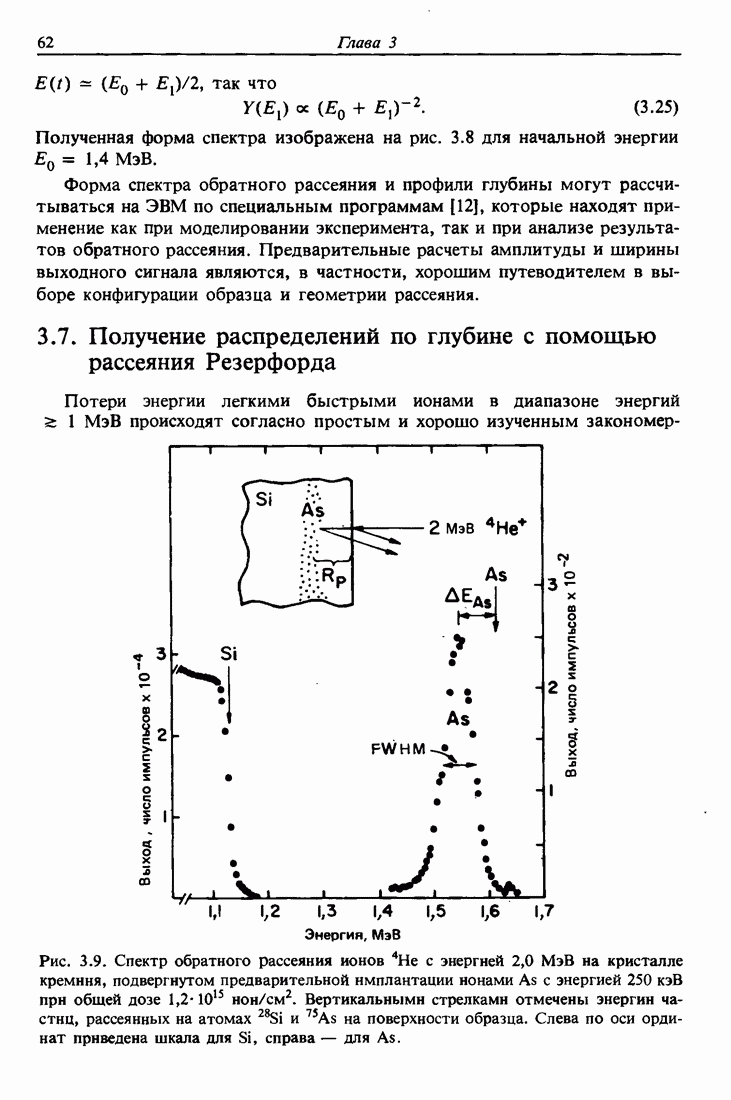
На рис. 3.6 показан спектр обратного рассеяния при  для ионов
для ионов  с энергией 3 МэВ, падающих на алюминиевую пленку толщиной 4000 А, покрытую с обеих сторон тонкими золотыми маркерами
с энергией 3 МэВ, падающих на алюминиевую пленку толщиной 4000 А, покрытую с обеих сторон тонкими золотыми маркерами  монослоя
монослоя  . В алюминии скорость потерь энергии
. В алюминии скорость потерь энергии  вдоль траектории, направленной в глубь пленки, равна приблизительно
вдоль траектории, направленной в глубь пленки, равна приблизительно  при энергиях ионов около 3 МэВ, а вдоль траектории обратного движения эта скорость составляет примерно
при энергиях ионов около 3 МэВ, а вдоль траектории обратного движения эта скорость составляет примерно  при энергиях ионов около 1,5 МэВ
при энергиях ионов около 1,5 МэВ  Подставляя эти величины в выражение (3.20), получаем для ширины сигнала
Подставляя эти величины в выражение (3.20), получаем для ширины сигнала  значение
значение  Расстояние между двумя
Расстояние между двумя  -пиками в спектре составляет
-пиками в спектре составляет  что немного больше ширины
что немного больше ширины

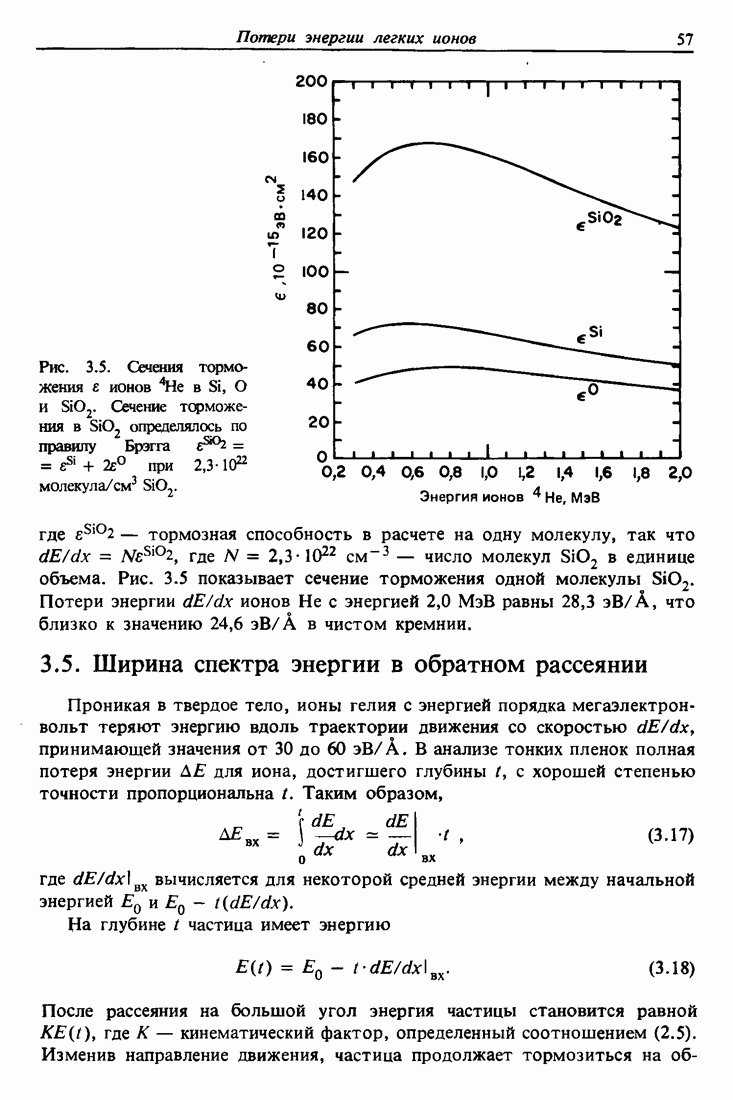
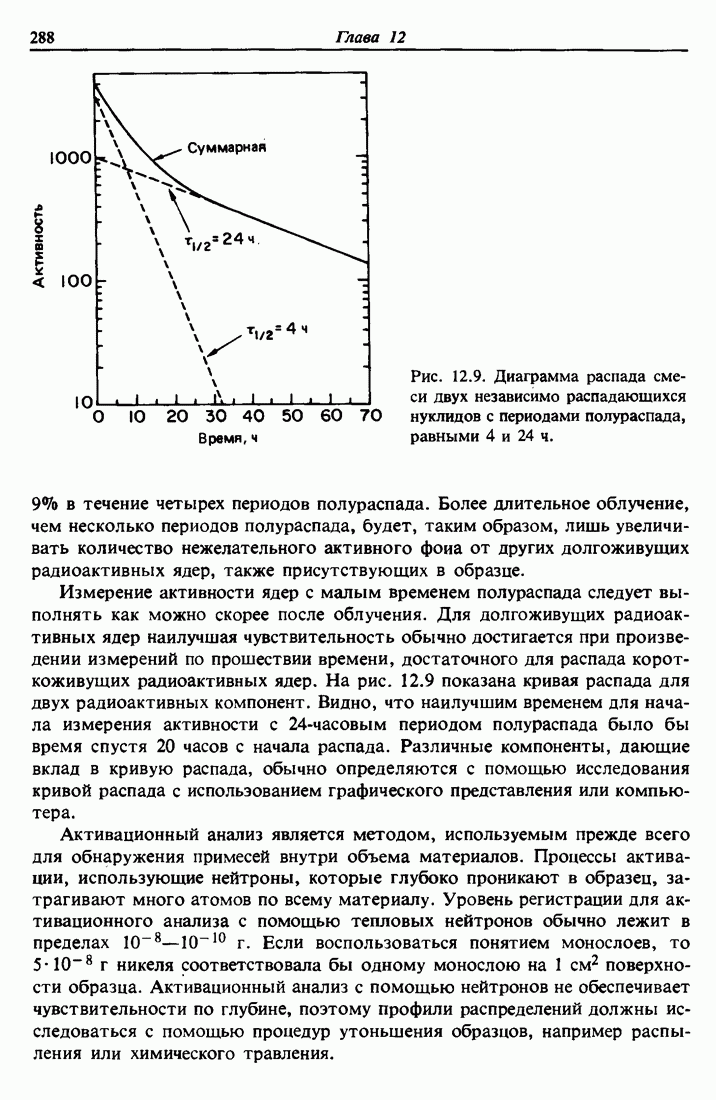
Рис. 3.6. Спектр обратного рассеяния  ионов гелия с энергией 3,0 МэВ, падающих на алюминиевую пленку толщиной 4000 А, покрытую с обеих сторон тонкими золотыми маркерами.
ионов гелия с энергией 3,0 МэВ, падающих на алюминиевую пленку толщиной 4000 А, покрытую с обеих сторон тонкими золотыми маркерами.
 , так как при расчете этого расстояния по формуле (3.20) используется значение К для золота, а потери dE/dx берутся для алюминия.
, так как при расчете этого расстояния по формуле (3.20) используется значение К для золота, а потери dE/dx берутся для алюминия.
Предположение о постоянстве значений  или е вдоль траекторий, направленных как в глубь, так и наружу образца, приводит к линейному соотношению между шириной сигнала
или е вдоль траекторий, направленных как в глубь, так и наружу образца, приводит к линейному соотношению между шириной сигнала  и глубиной
и глубиной  на которой происходит рассеяние. Для тонких пленок толщиной
на которой происходит рассеяние. Для тонких пленок толщиной  относительное изменение энергии вдоль траекторий мало. Поэтому при вычислении
относительное изменение энергии вдоль траекторий мало. Поэтому при вычислении  можно использовать "поверхностную аппроксимацию
можно использовать "поверхностную аппроксимацию  согласно которой значение
согласно которой значение  вычисляется при
вычисляется при  — при
— при  . В этом приближении ширина сигнала
. В этом приближении ширина сигнала  от пленки толщиной
от пленки толщиной  равна
равна
 (3.20б)
(3.20б)
где индексы указывают на поверхностную аппроксимацию энергии.
Когда толщина пленки, а вместе с ней длина пути ионов, становится значительной, можно использовать более точное приближение, аппроксимировав  постоянным значением при некоторой средней энергии Е, промежуточной между энергиями на обоих концах каждой траектории. Налетающая частица входит в пленку с энергией
постоянным значением при некоторой средней энергии Е, промежуточной между энергиями на обоих концах каждой траектории. Налетающая частица входит в пленку с энергией  и перед рассеянием на
и перед рассеянием на

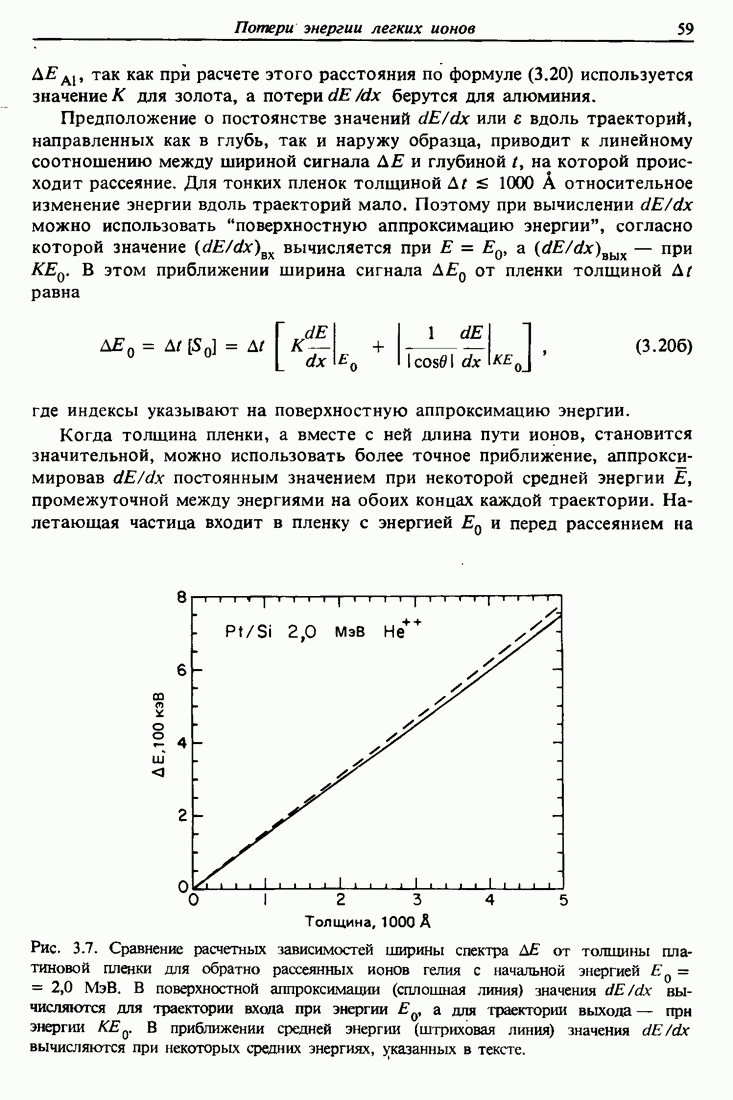
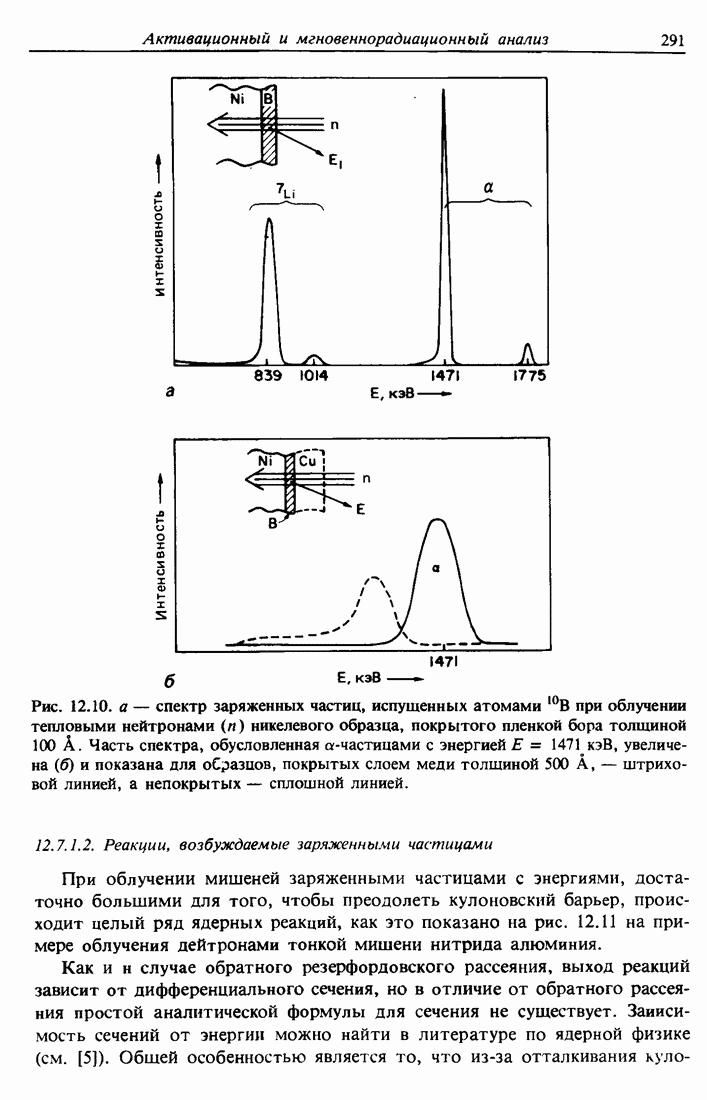
Рис. 3.7. Сравнение расчетных зависимостей ширины спектра  от толщины платиновой пленки для обратно рассеянных ионов гелия с начальной энергией
от толщины платиновой пленки для обратно рассеянных ионов гелия с начальной энергией  МэВ. В поверхностной аппроксимации (сплошная линия) значения dE/dx вычисляются для траектории входа при энергии
МэВ. В поверхностной аппроксимации (сплошная линия) значения dE/dx вычисляются для траектории входа при энергии  а для траектории выхода — при энергии
а для траектории выхода — при энергии  . В приближении средней энергии (штриховая линия) значения
. В приближении средней энергии (штриховая линия) значения  вычисляются при некоторых средних энергиях, указанных в тексте.
вычисляются при некоторых средних энергиях, указанных в тексте.
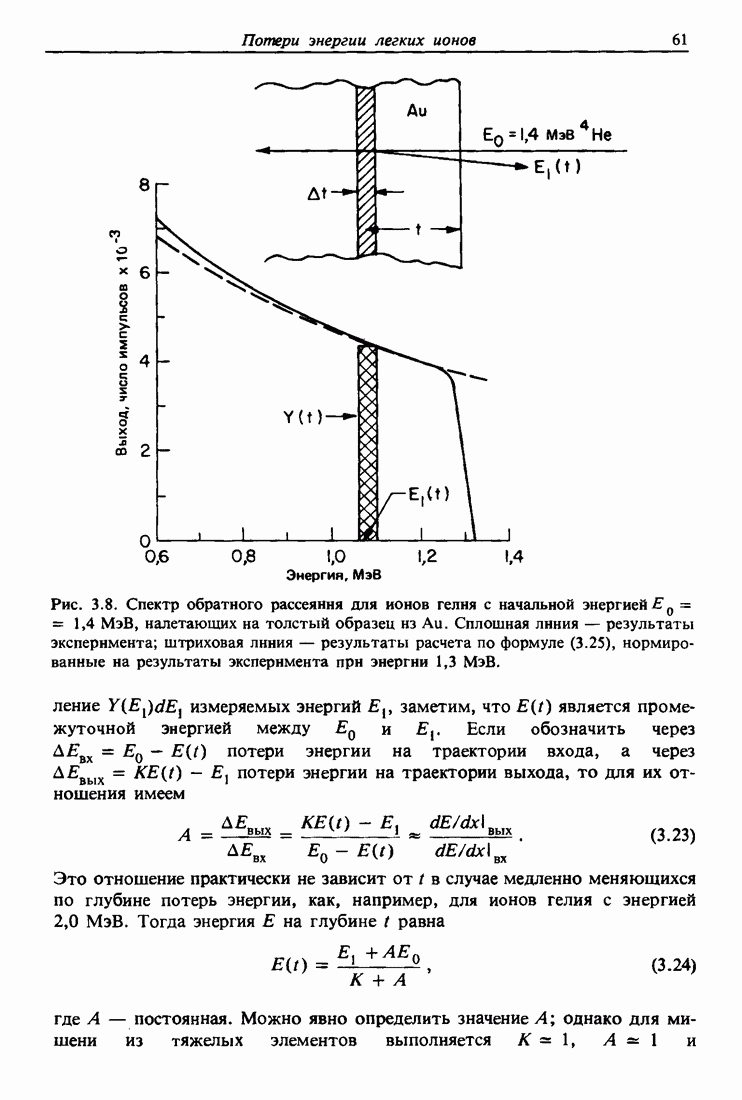
глубине  имеет энергию
имеет энергию  так что
так что  После
После  сеяния частица имеет энергию
сеяния частица имеет энергию  так что на траектории выхода
так что на траектории выхода  . В этой "аппроксимации средней энергией" энергию
. В этой "аппроксимации средней энергией" энергию  перед рассеянием можно вычислить по значениям производной
перед рассеянием можно вычислить по значениям производной  или в свою очередь аппроксимировать, предположив, что разность энергий
или в свою очередь аппроксимировать, предположив, что разность энергий  на выходе измерена или известна и что потери распределяются поровну между прямой и обратной траекториями, так что
на выходе измерена или известна и что потери распределяются поровну между прямой и обратной траекториями, так что  приближенно равно
приближенно равно  . Тогда
. Тогда  и
и 
Сравнение двух описанных аппроксимаций проведено на рис. 3.7 для ионов Не с энергией 2,0 МэВ, рассеянных пленкой из  . В поверхностной аппроксимации ширина спектра АЕ пропорциональна толщине слоя
. В поверхностной аппроксимации ширина спектра АЕ пропорциональна толщине слоя  с коэффициентом пропорциональности
с коэффициентом пропорциональности  . В аппроксимации средней энергией зависимость
. В аппроксимации средней энергией зависимость  от
от  отклоняется от линейной и значение
отклоняется от линейной и значение  для пленки толщиной 5000 А превышает на 3% значение
для пленки толщиной 5000 А превышает на 3% значение  , полученное в рамках поверхностной аппроксимации. Сравнение двух аппроксимаций дает быструю оценку возможных ошибок, вносимых поверхностной аппроксимацией. Главное, о чем здесь идет речь, — это то, что спектр обратного рассеяния можно рассматривать как линейный профиль глубины для элементов, входящих в состав образца.
, полученное в рамках поверхностной аппроксимации. Сравнение двух аппроксимаций дает быструю оценку возможных ошибок, вносимых поверхностной аппроксимацией. Главное, о чем здесь идет речь, — это то, что спектр обратного рассеяния можно рассматривать как линейный профиль глубины для элементов, входящих в состав образца.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
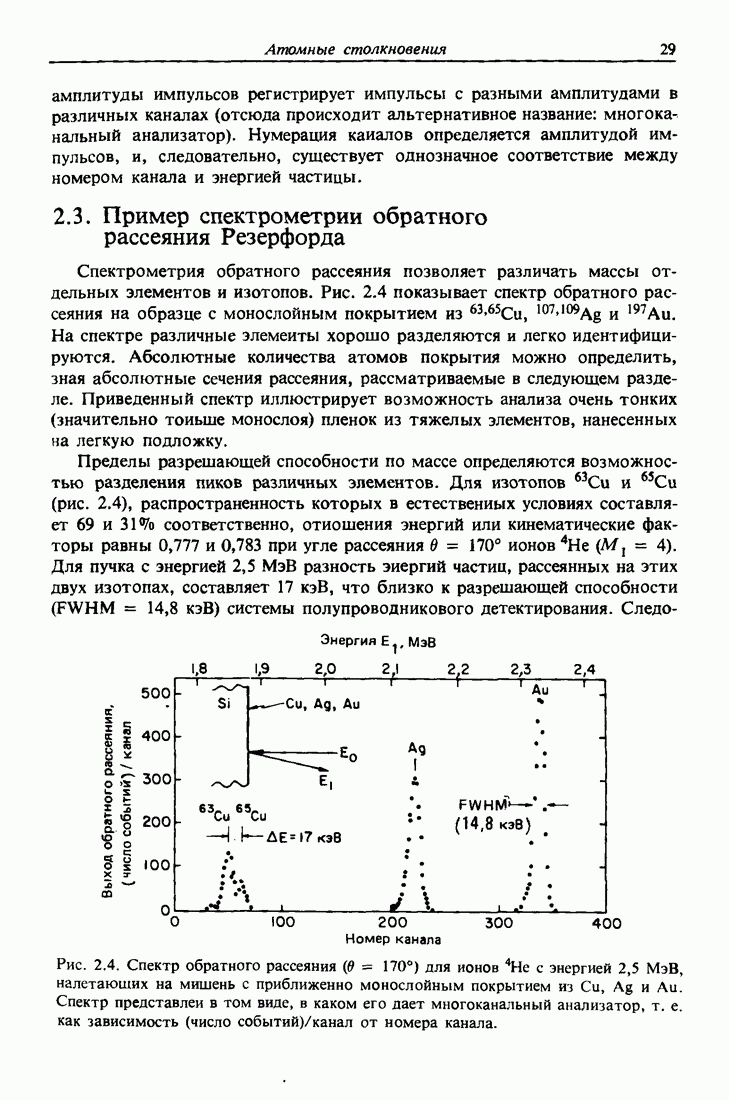
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
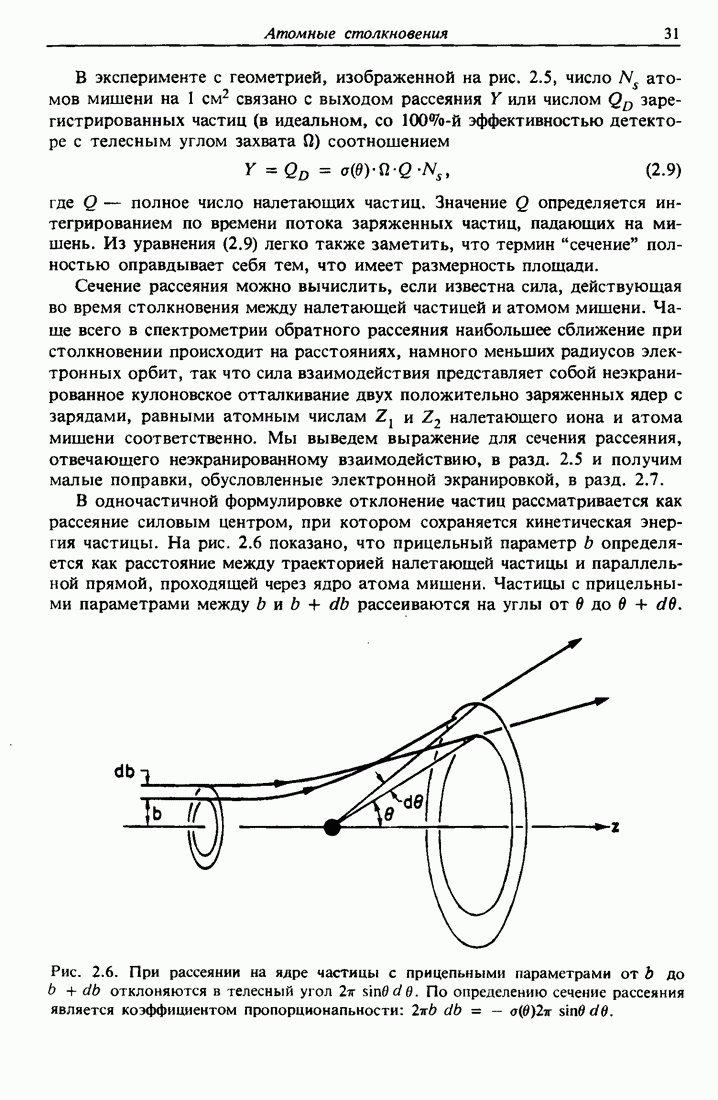
- 2.4. Сечение рассеяния и прицельный параметр
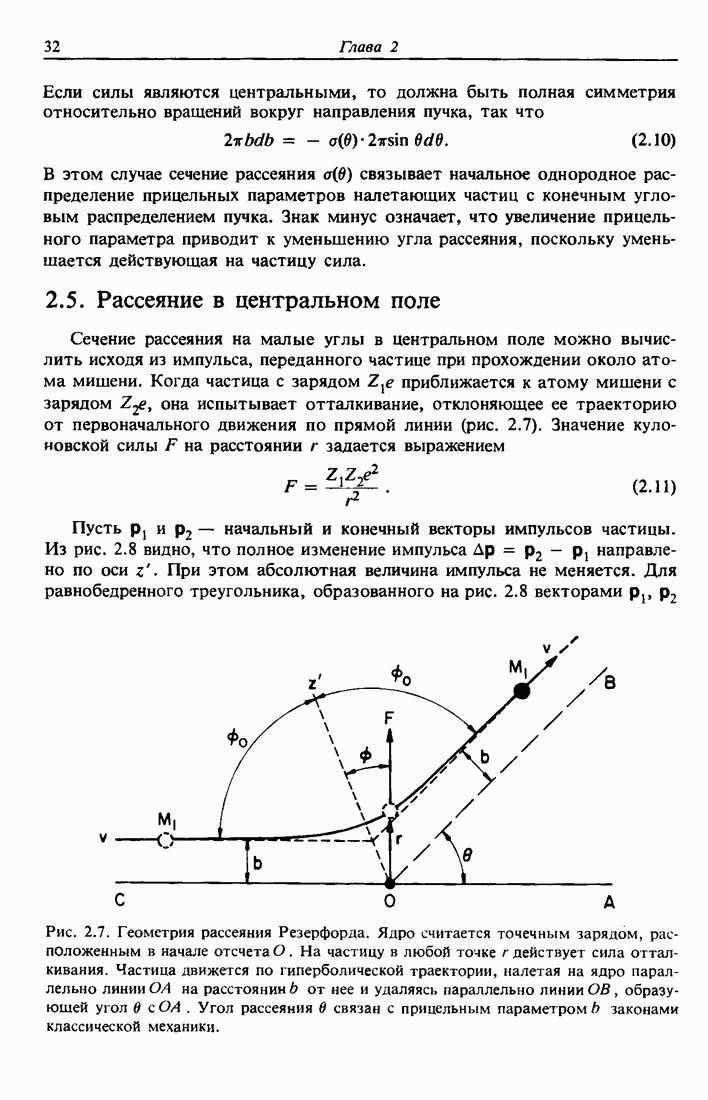
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
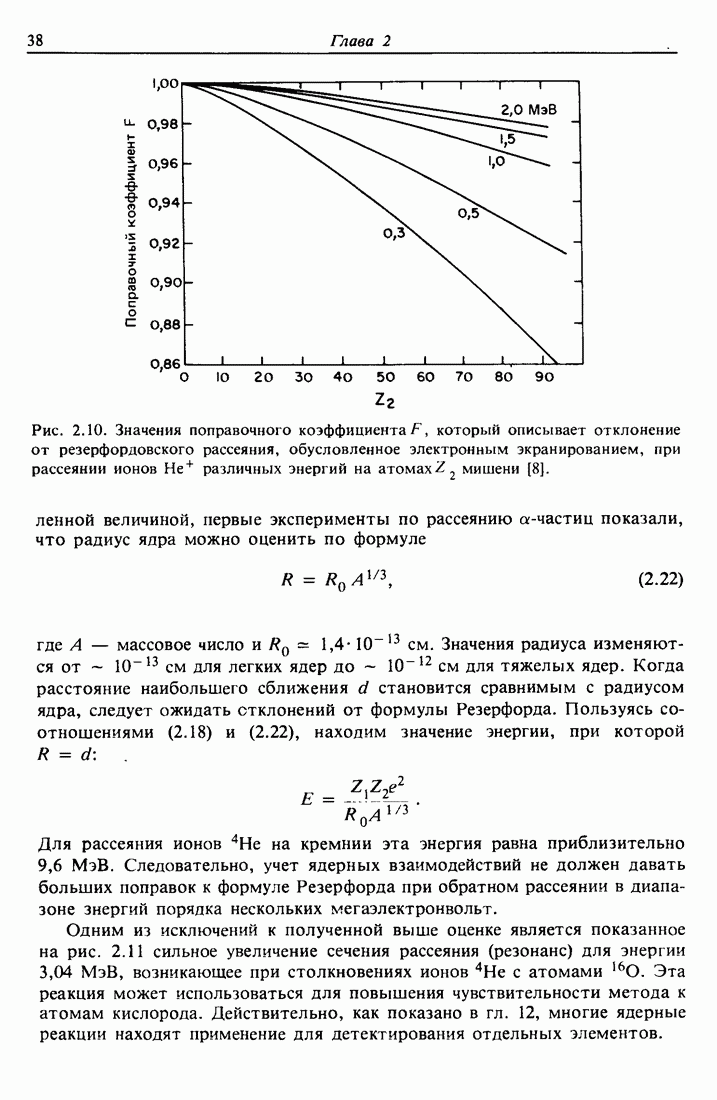
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
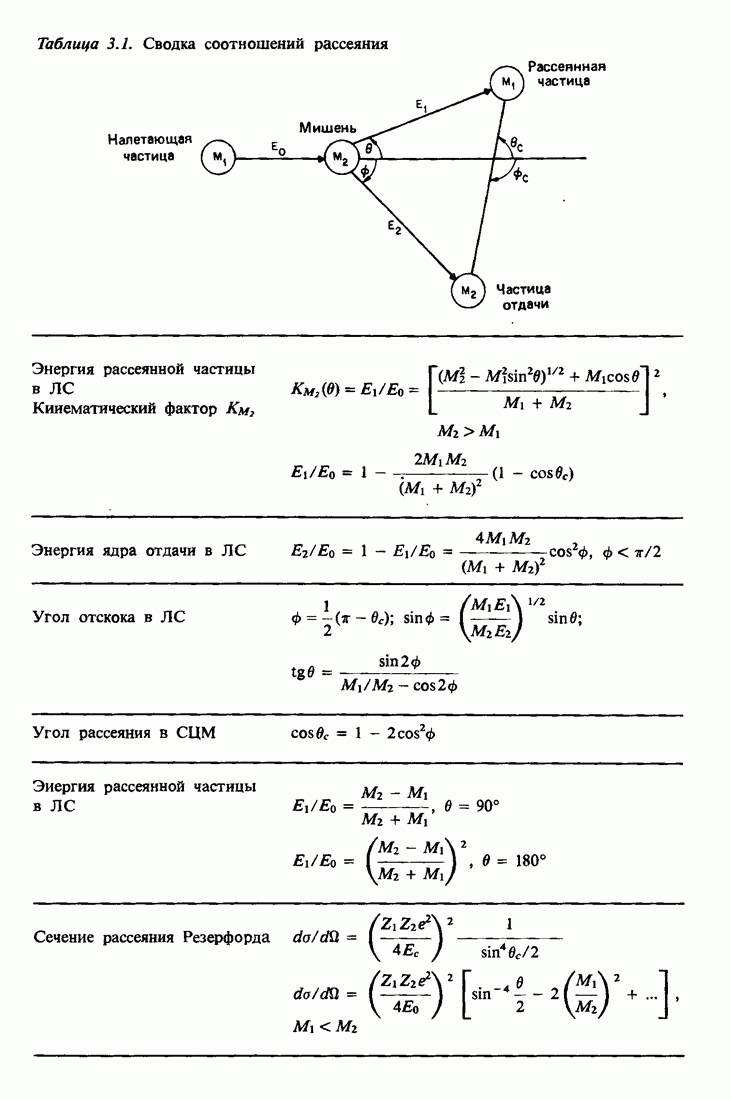
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
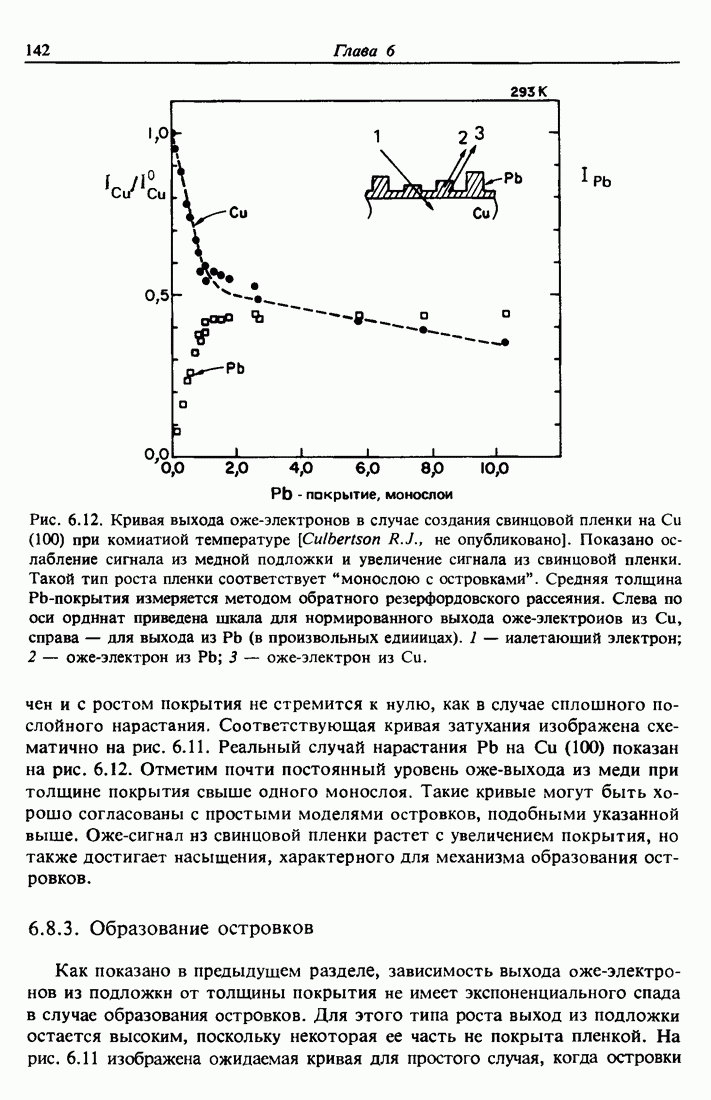
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
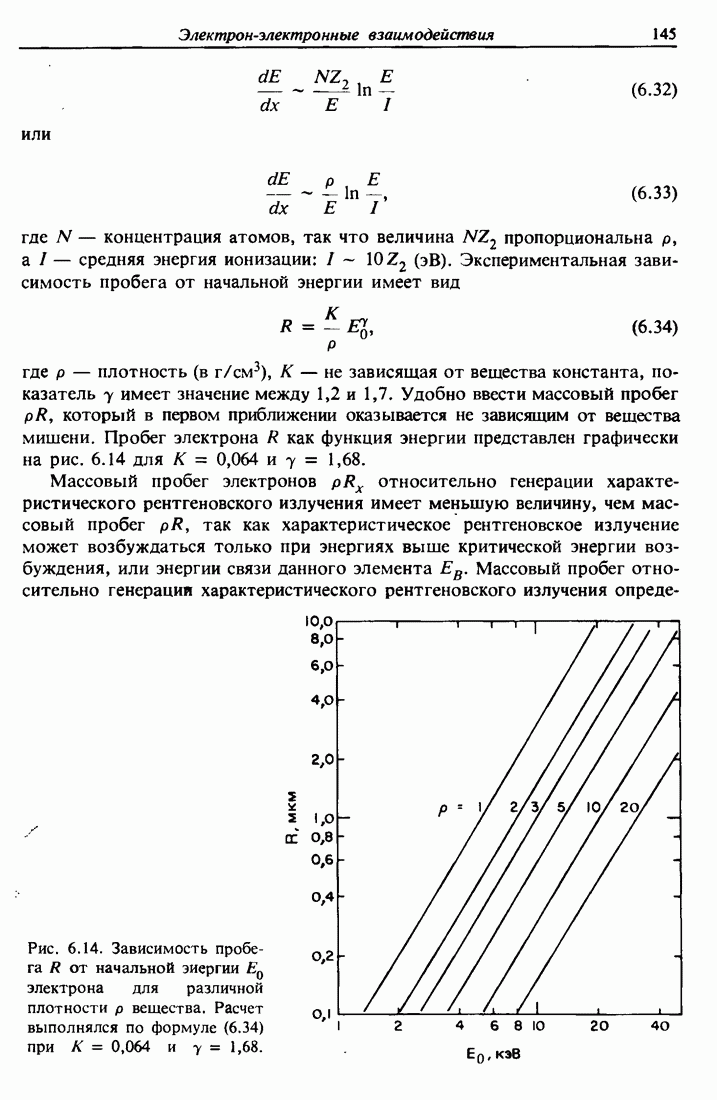
- 6.9. Пробеги электронов в твердых телах
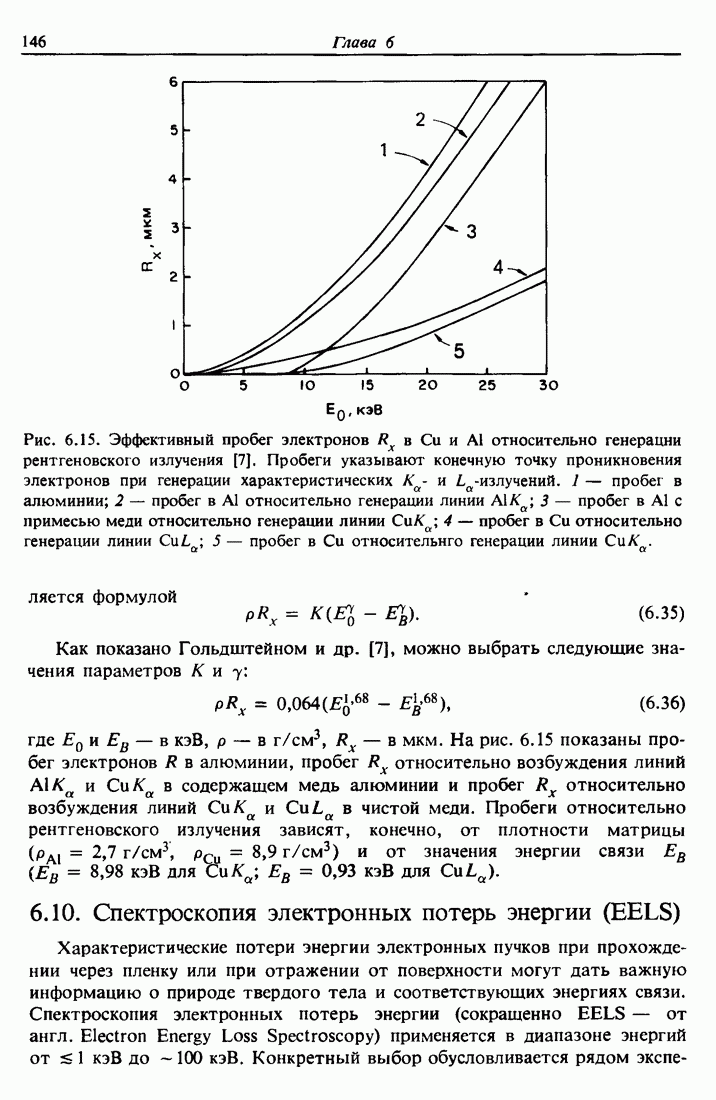
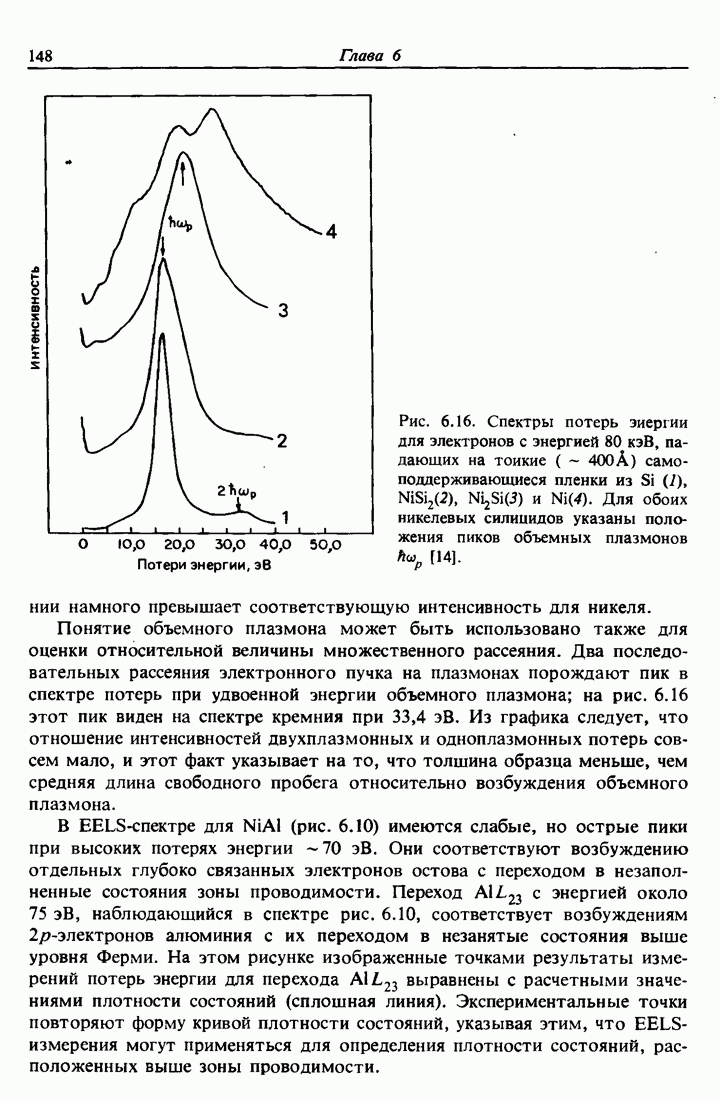
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
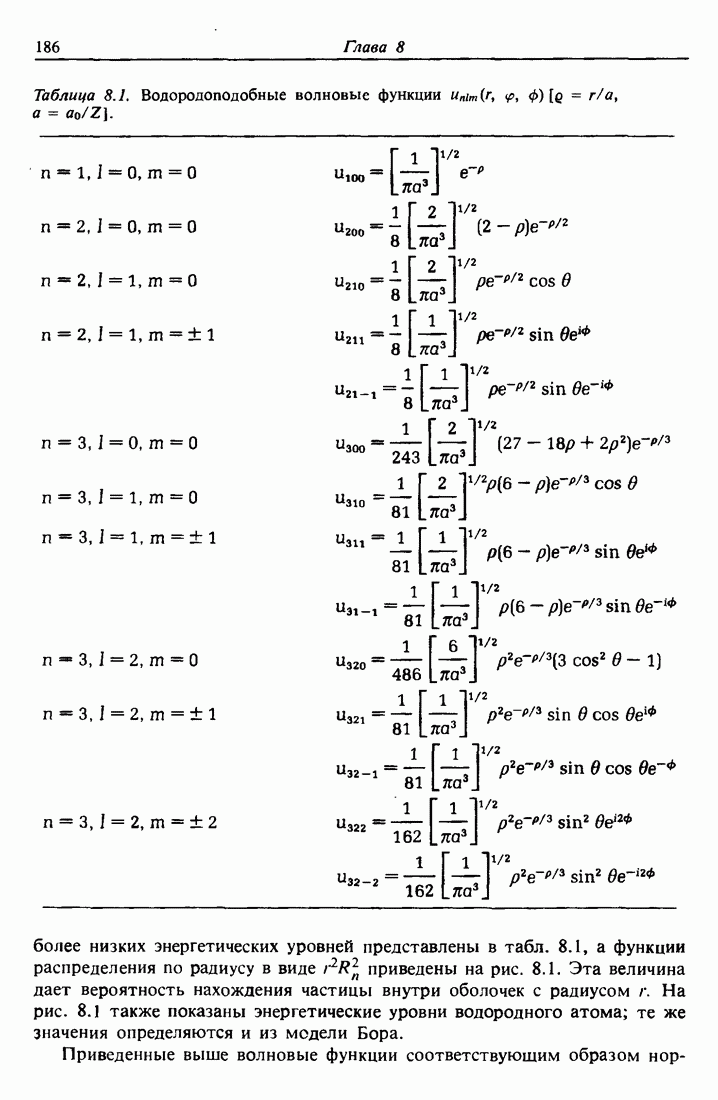
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
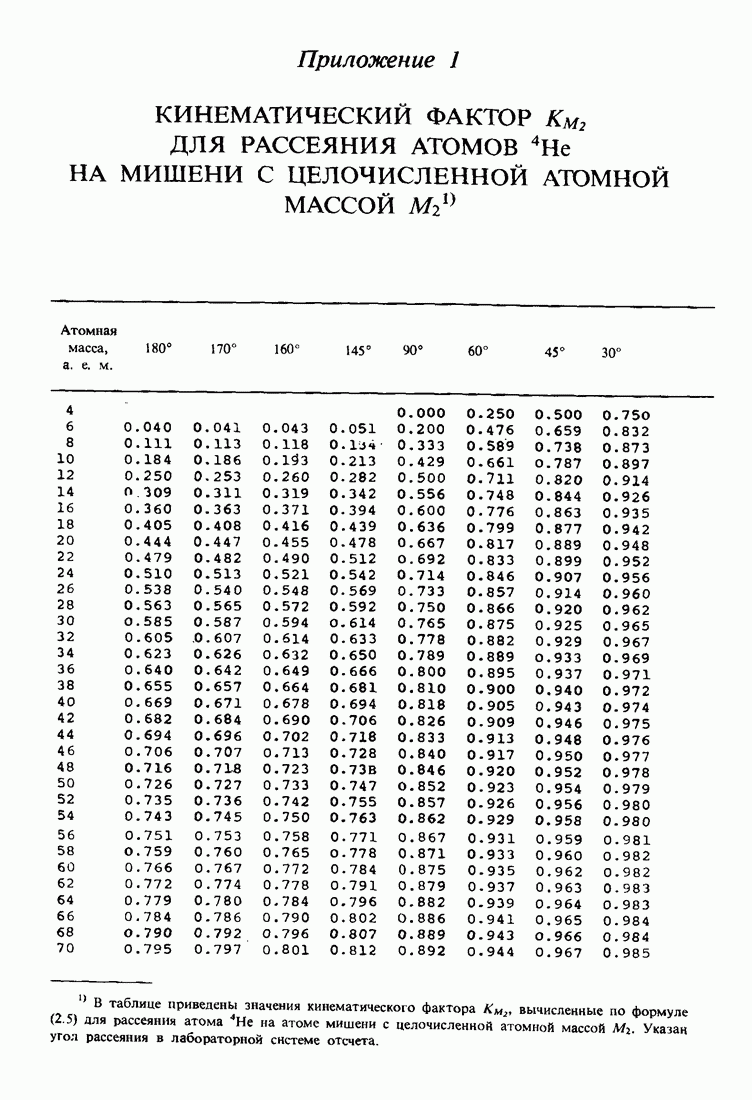
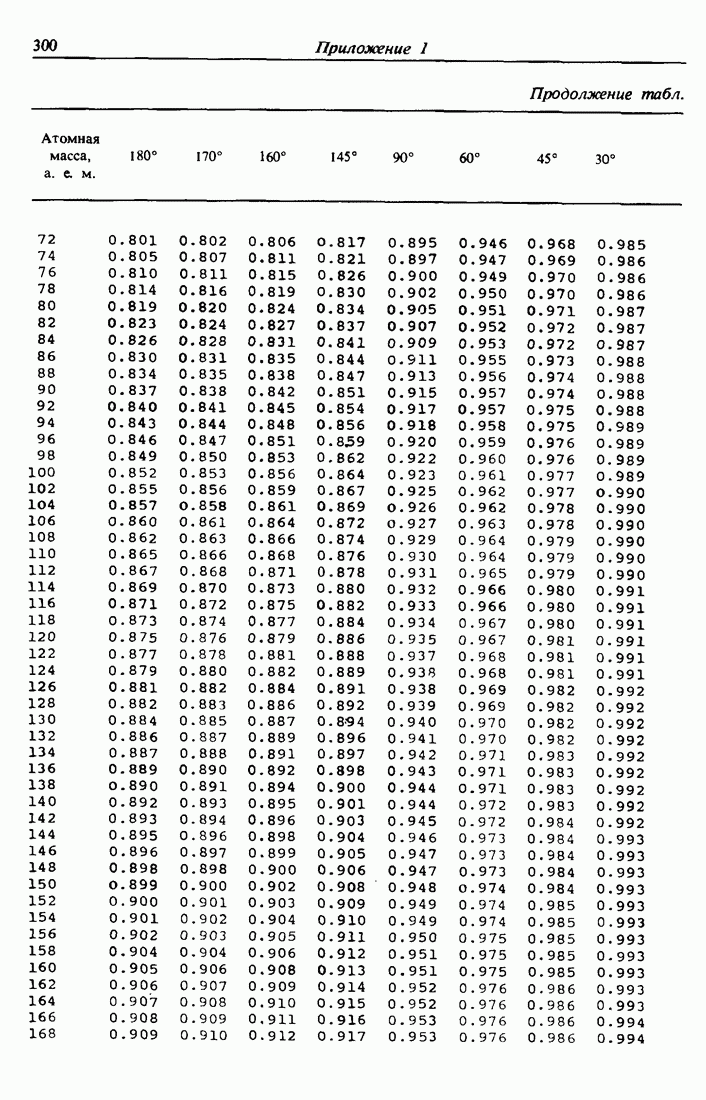
- ПРИЛОЖЕНИЕ 1.
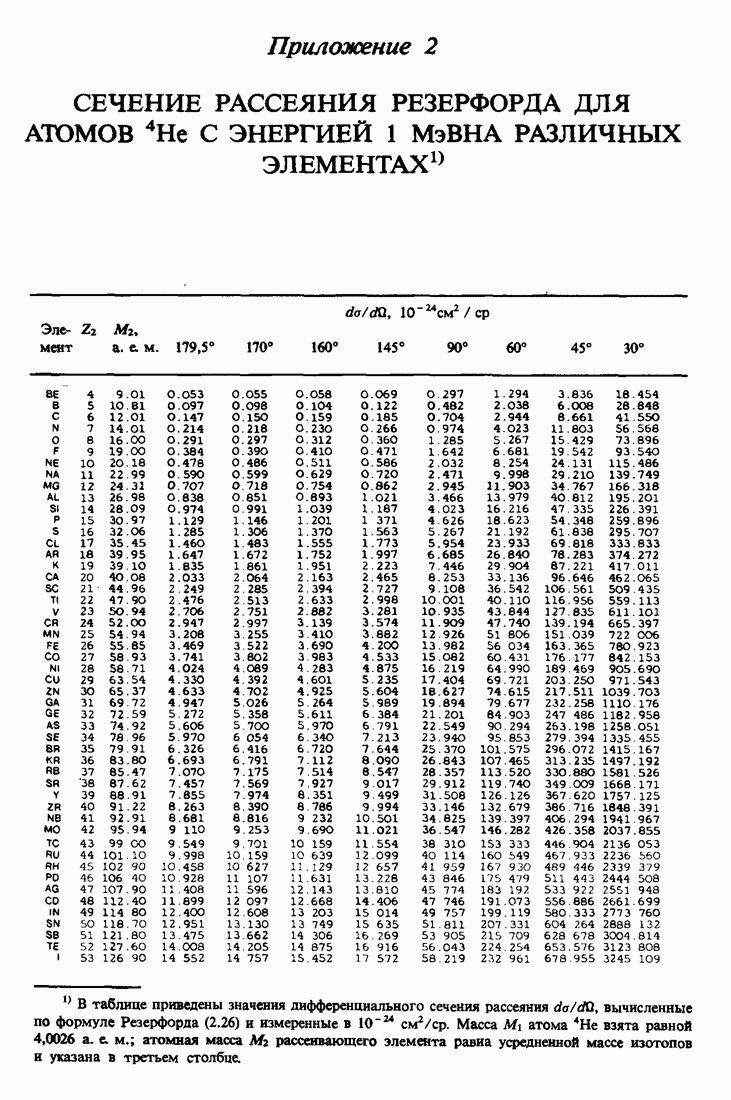
- ПРИЛОЖЕНИЕ 2.
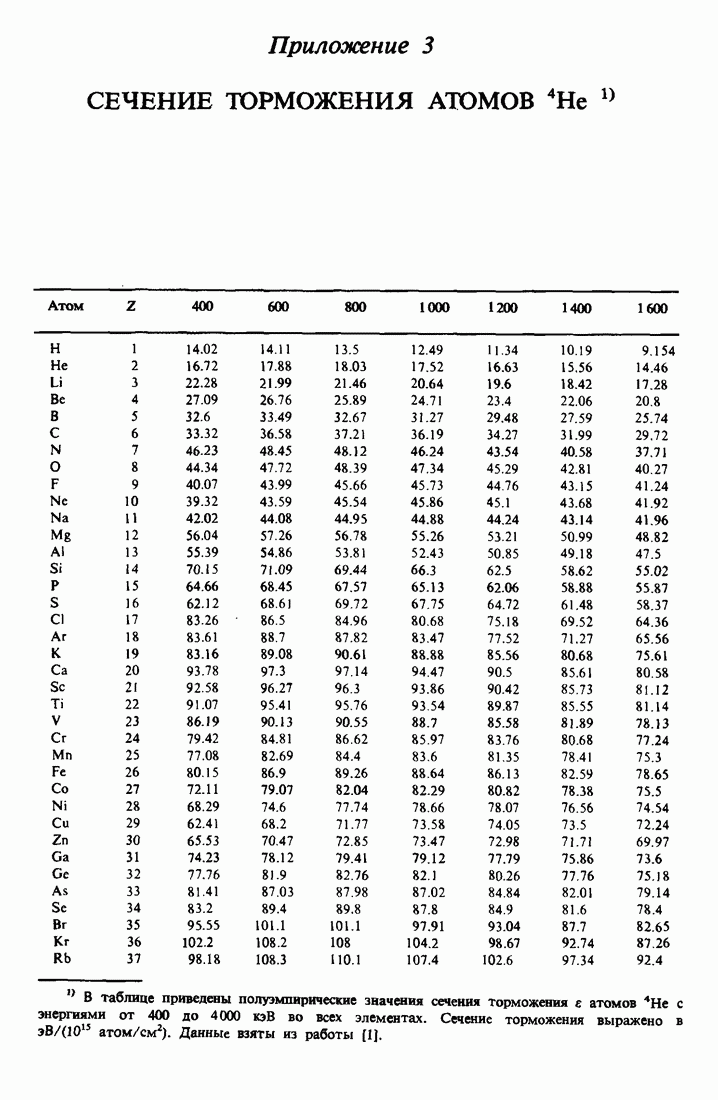
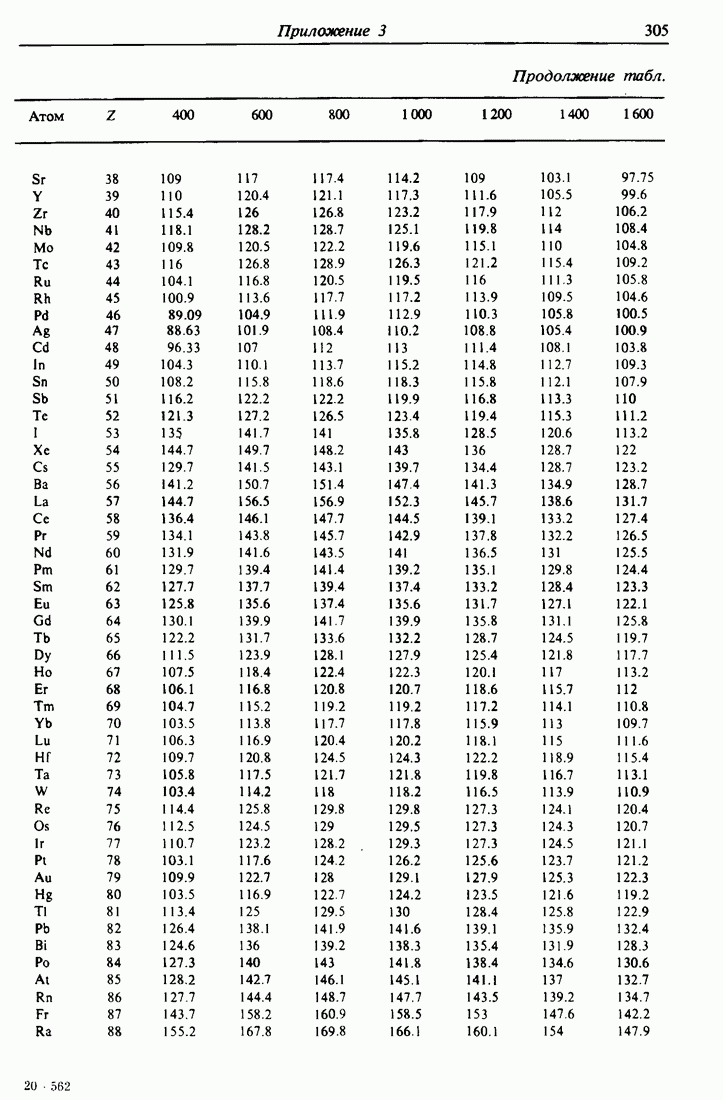
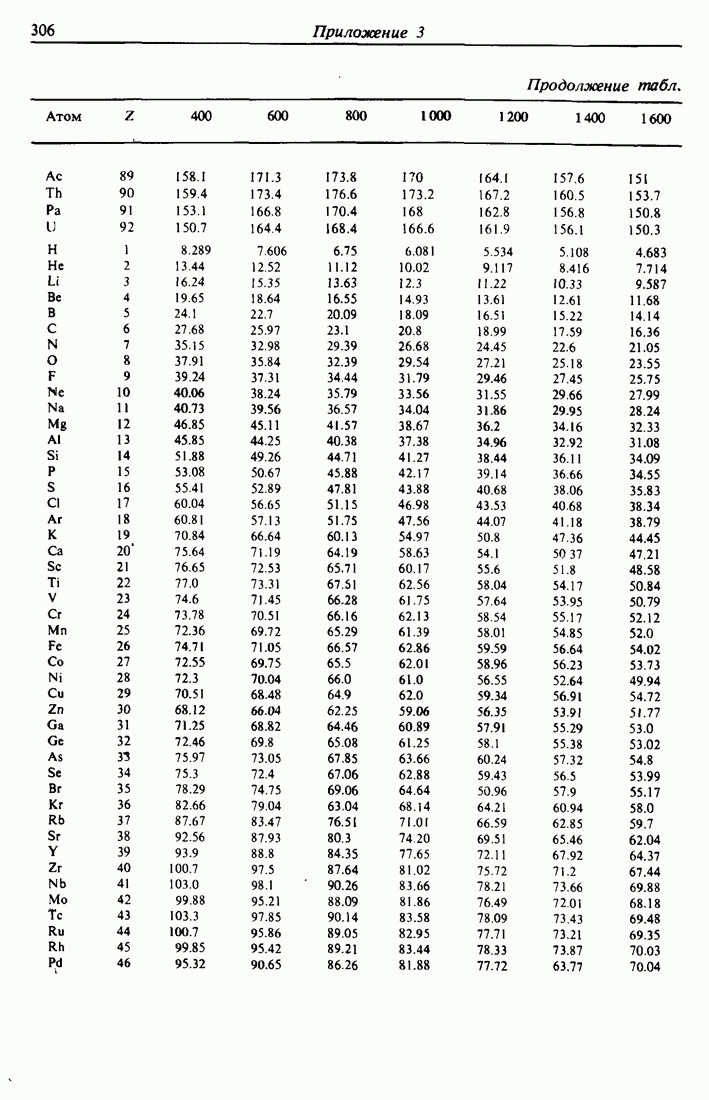
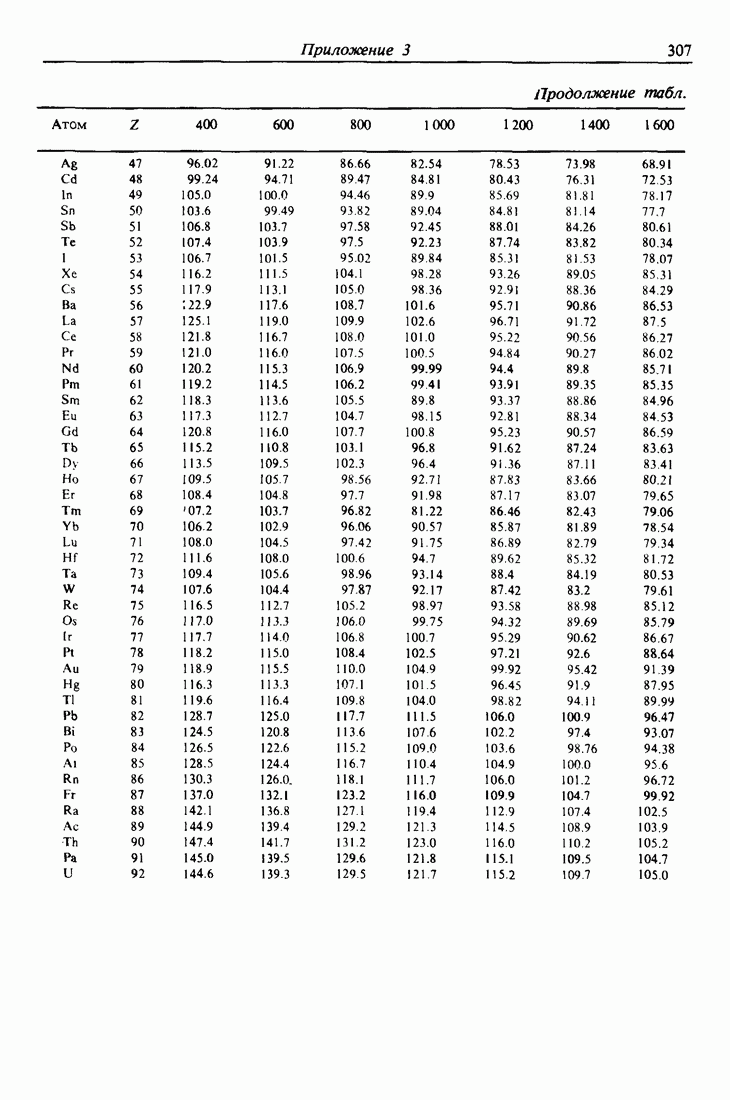
- ПРИЛОЖЕНИЕ 3.
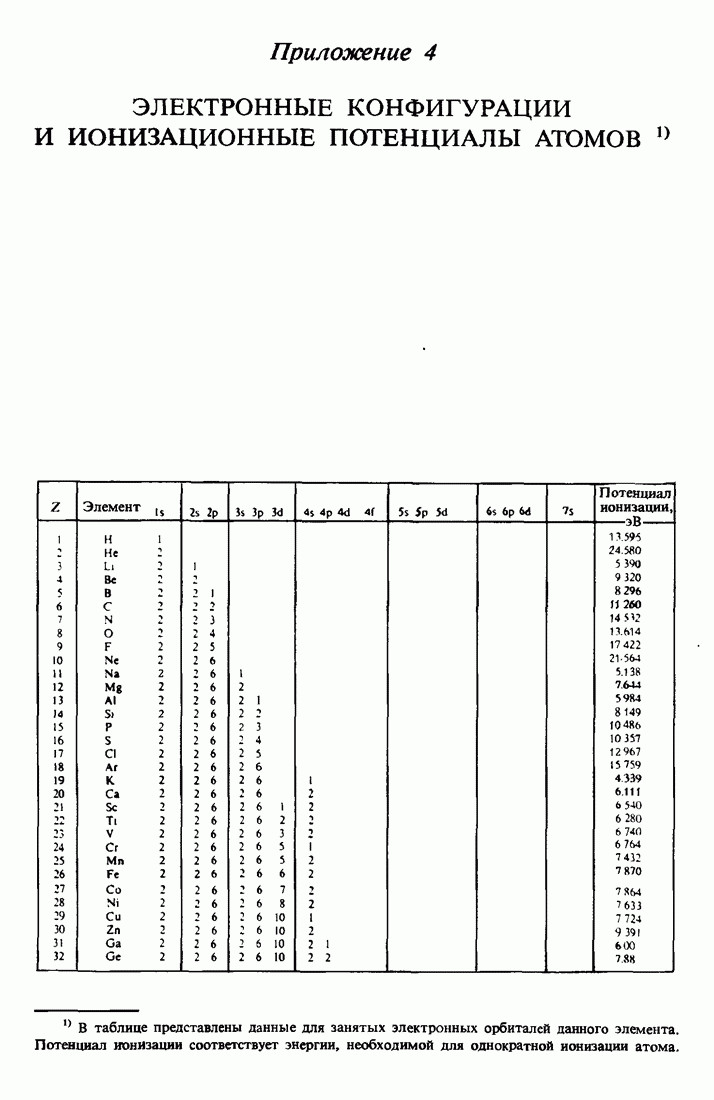
- ПРИЛОЖЕНИЕ 4.
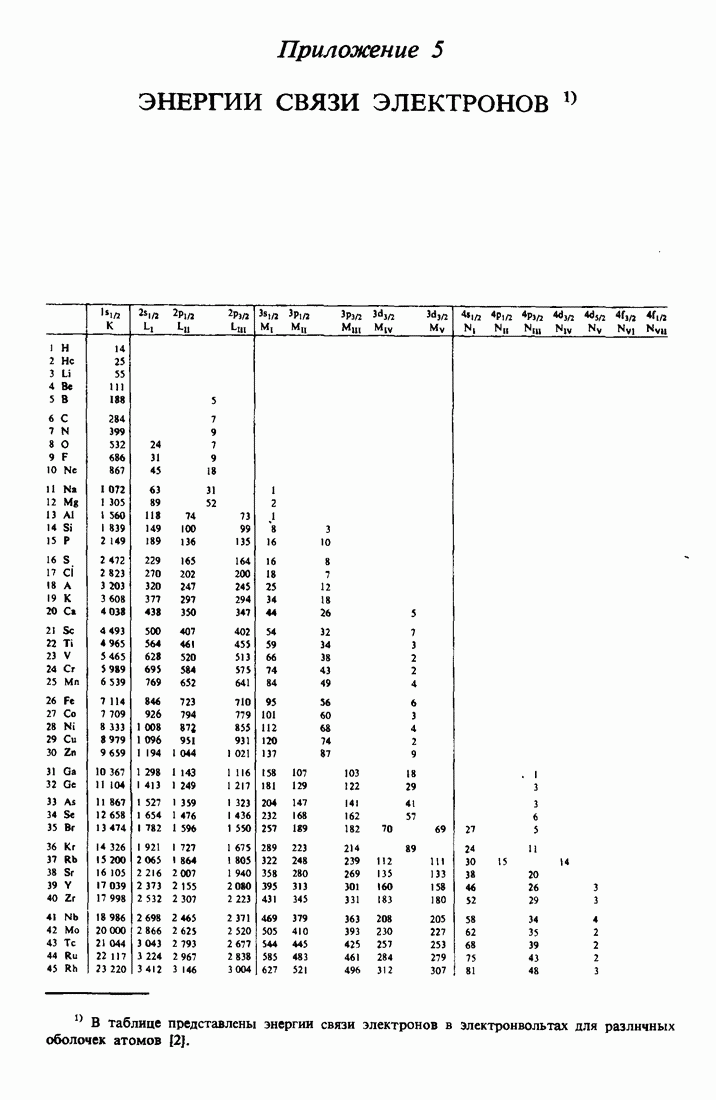
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
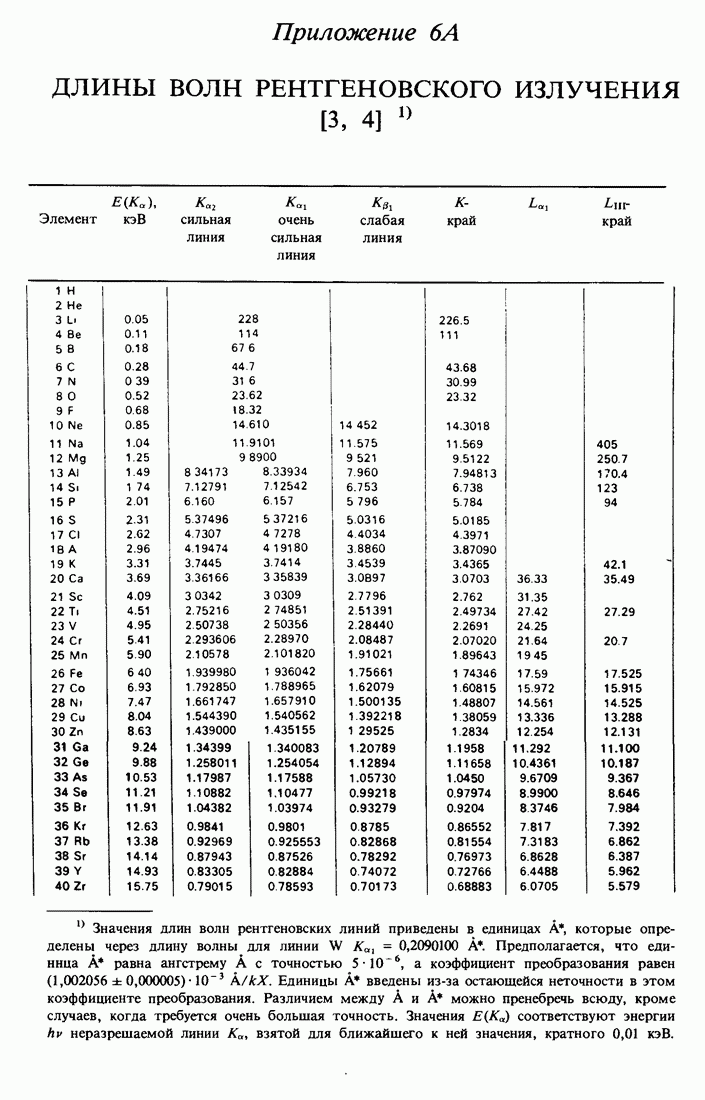
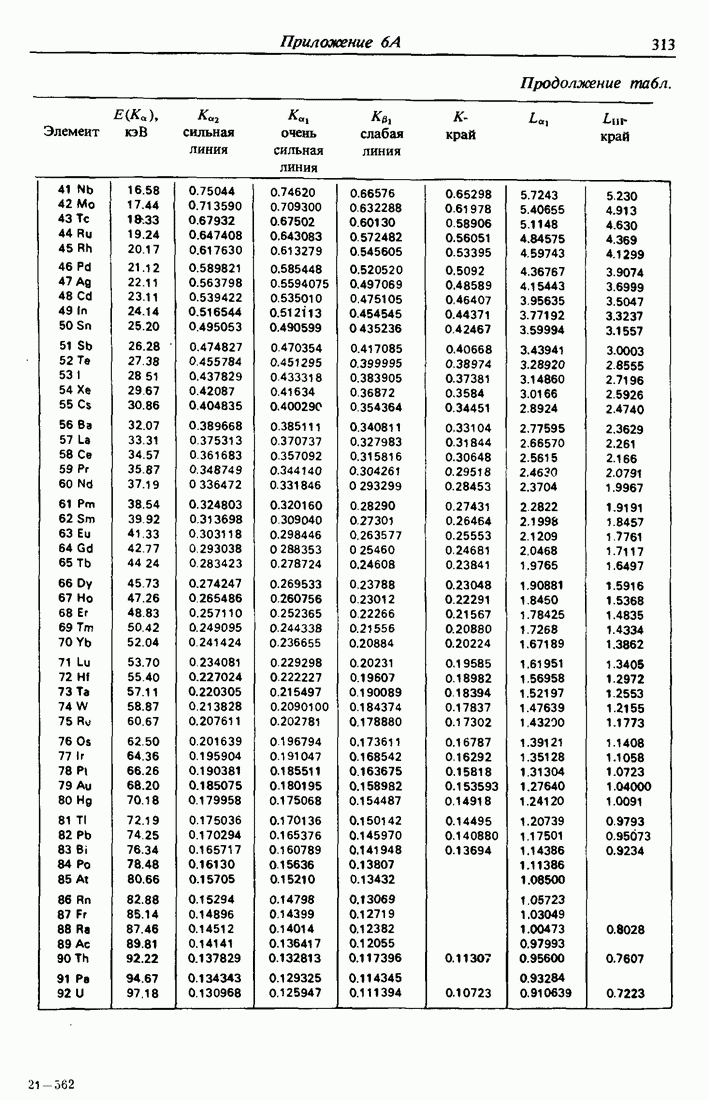
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
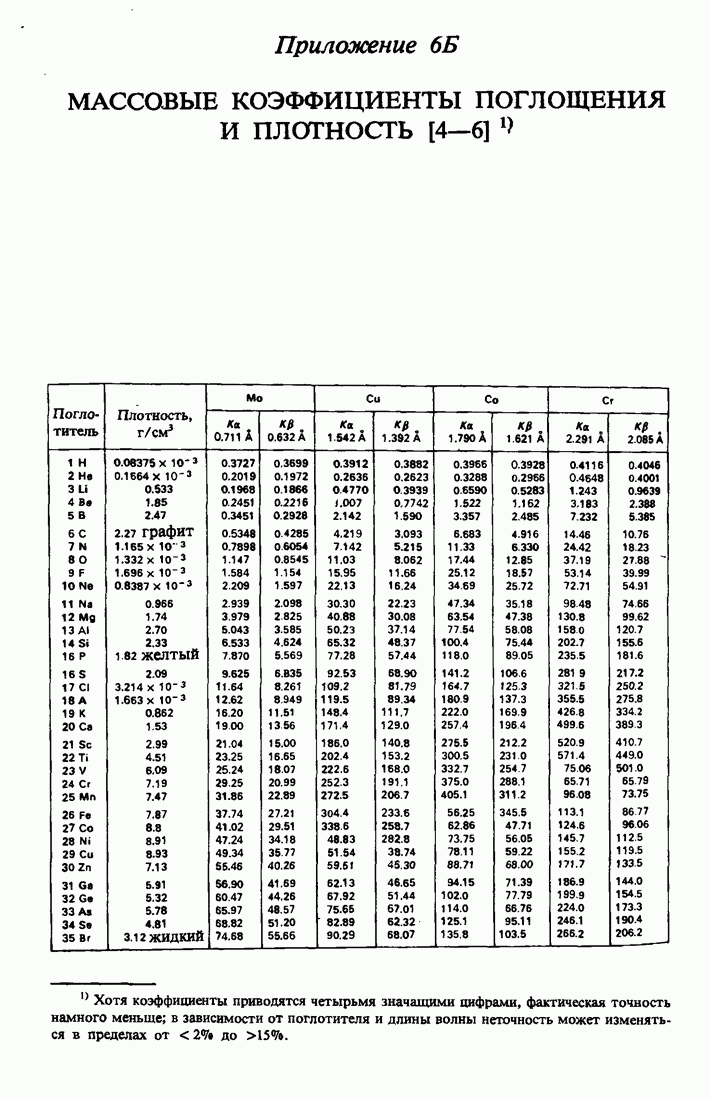
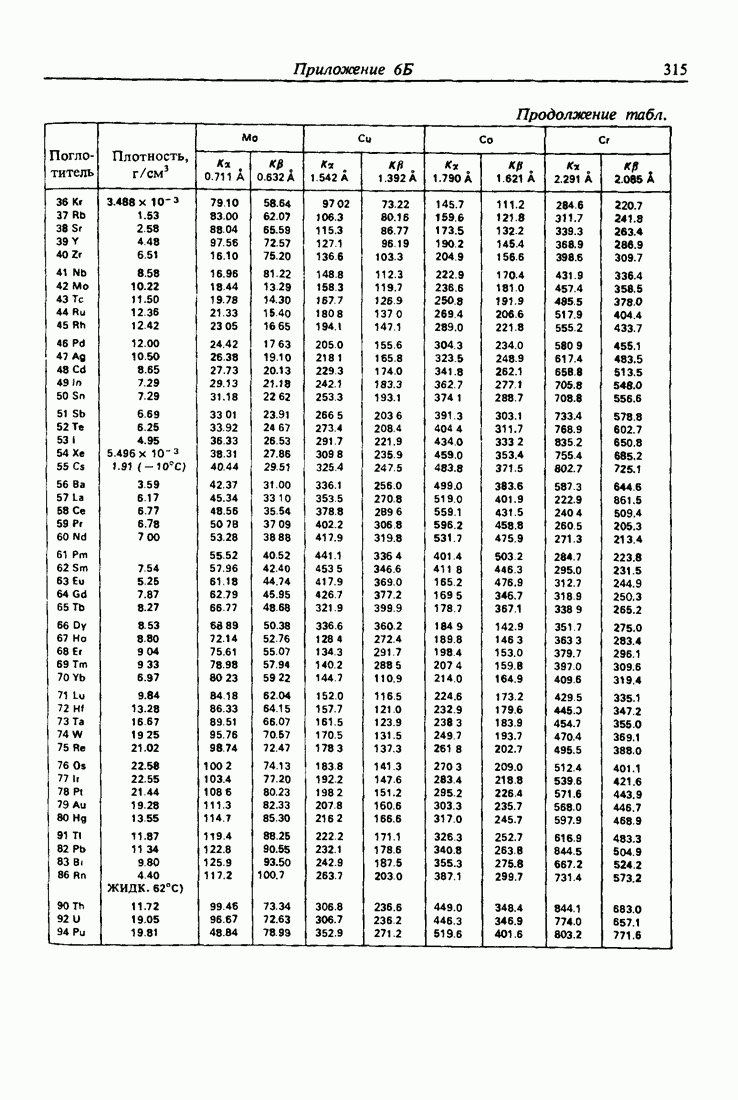
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
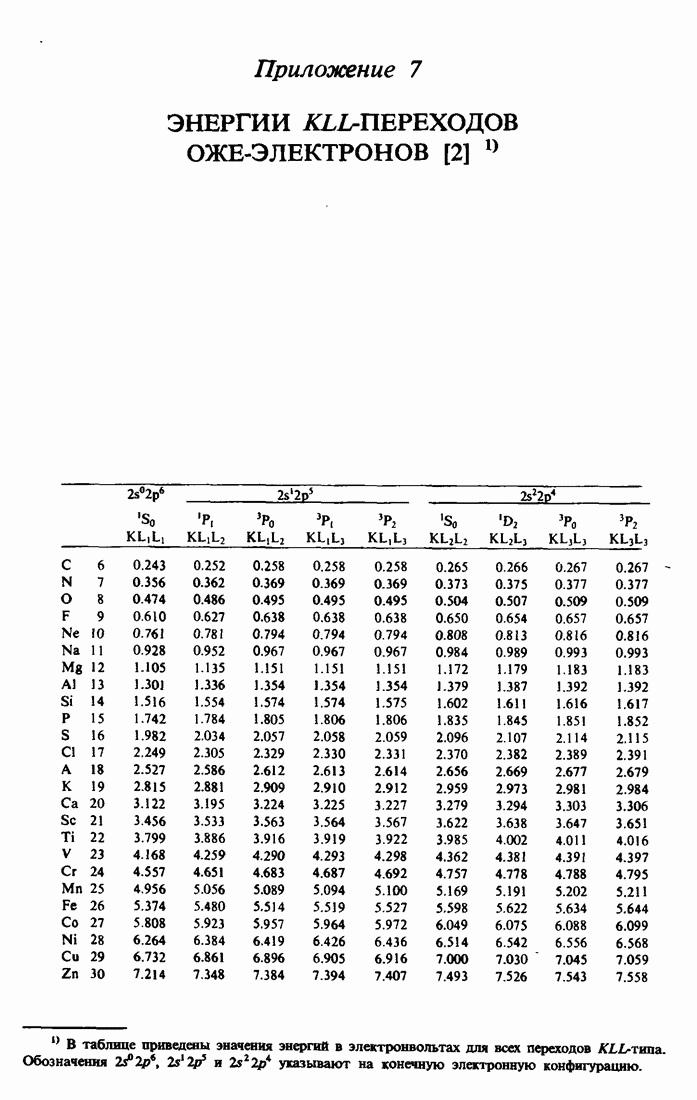
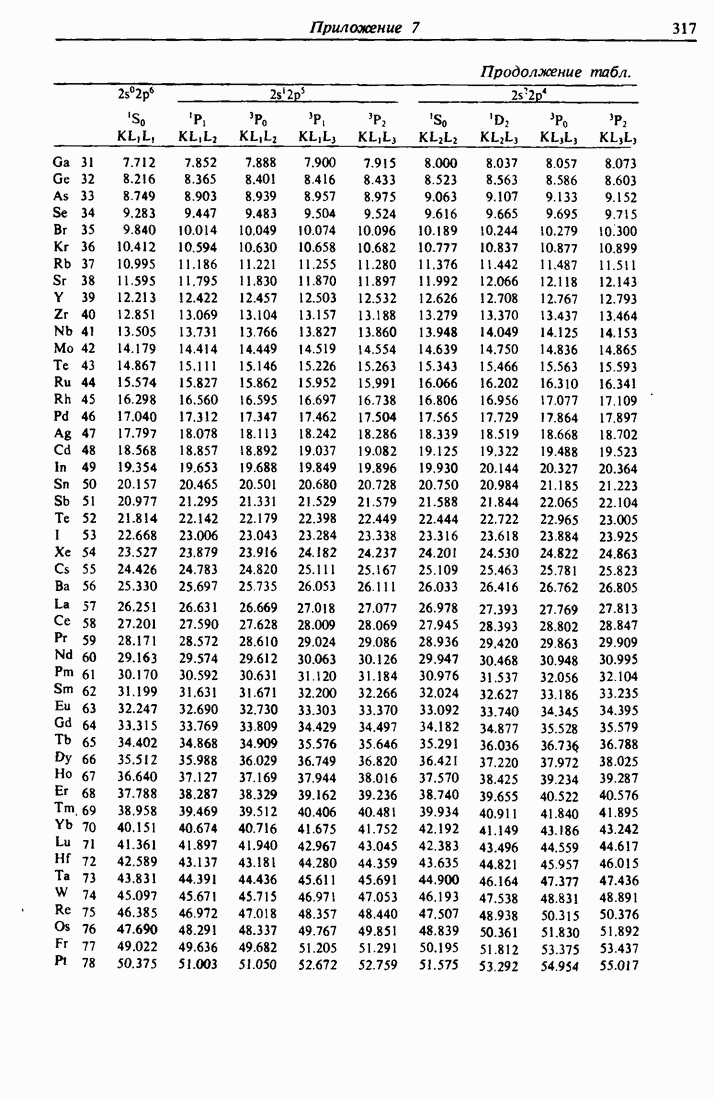
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
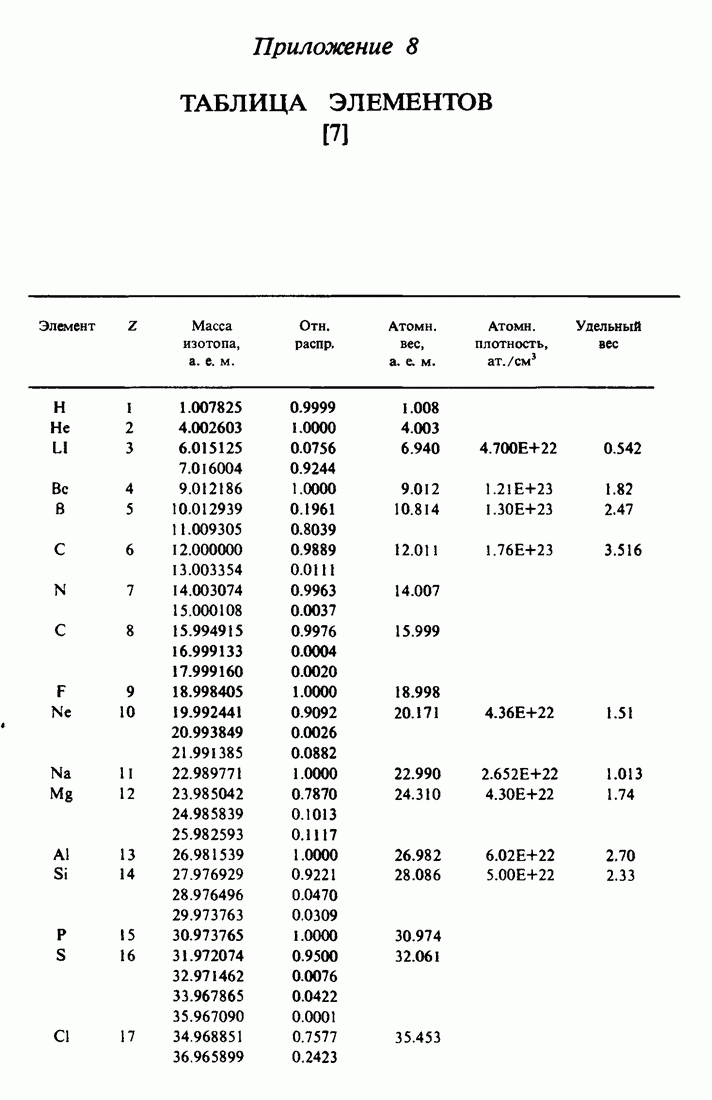
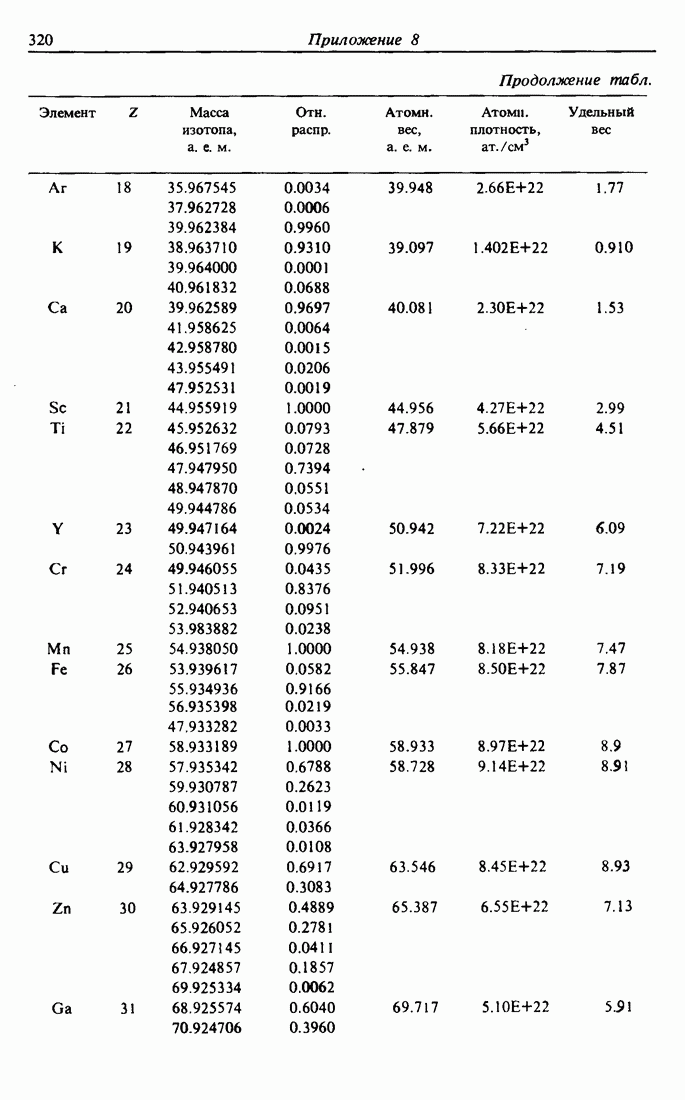
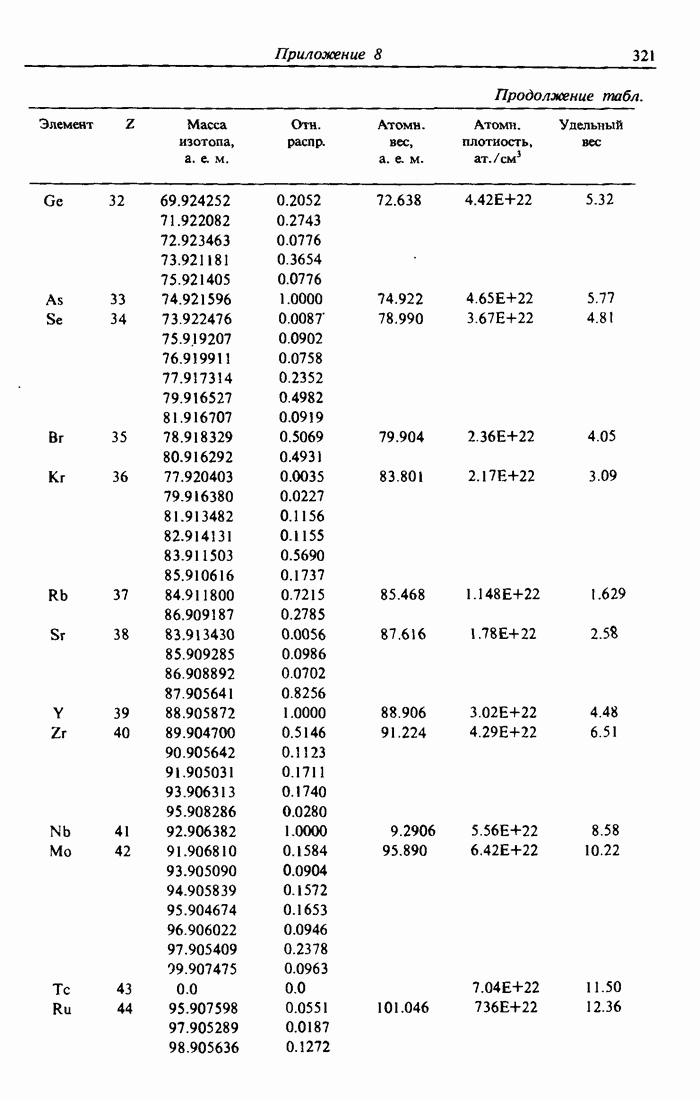
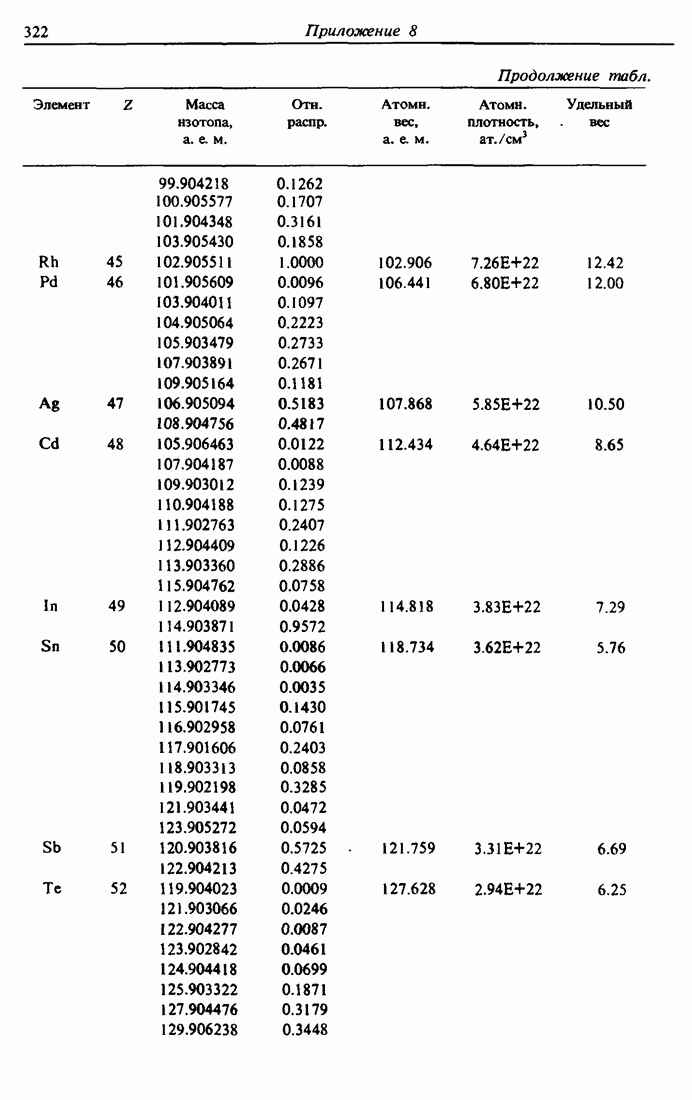
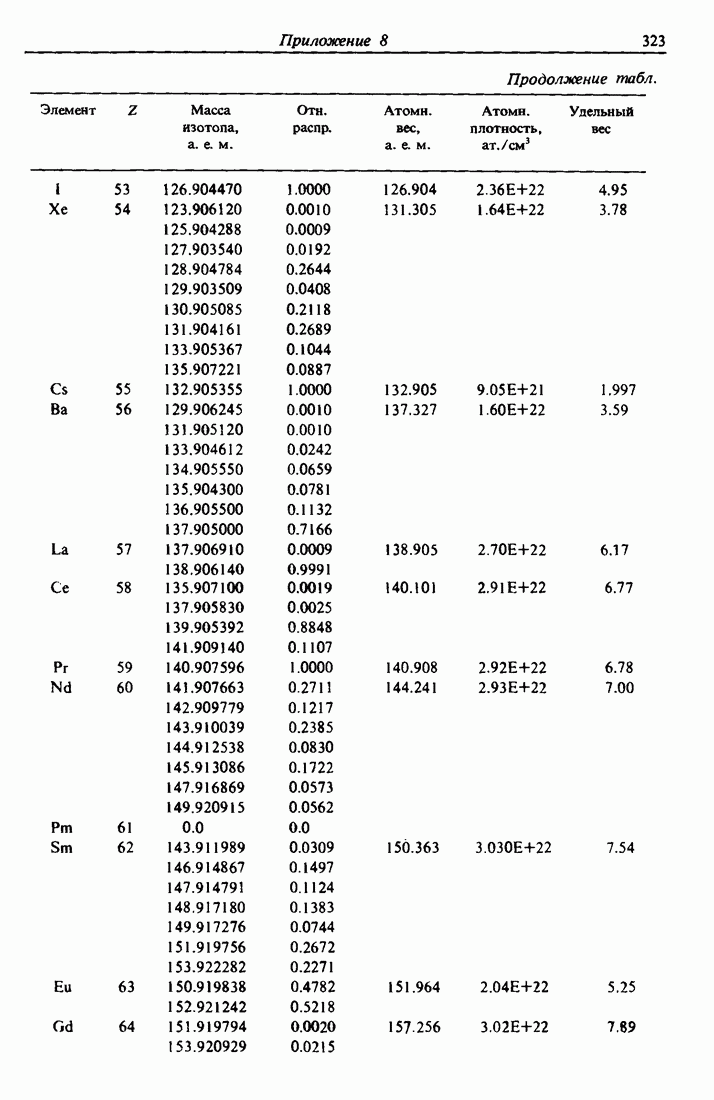
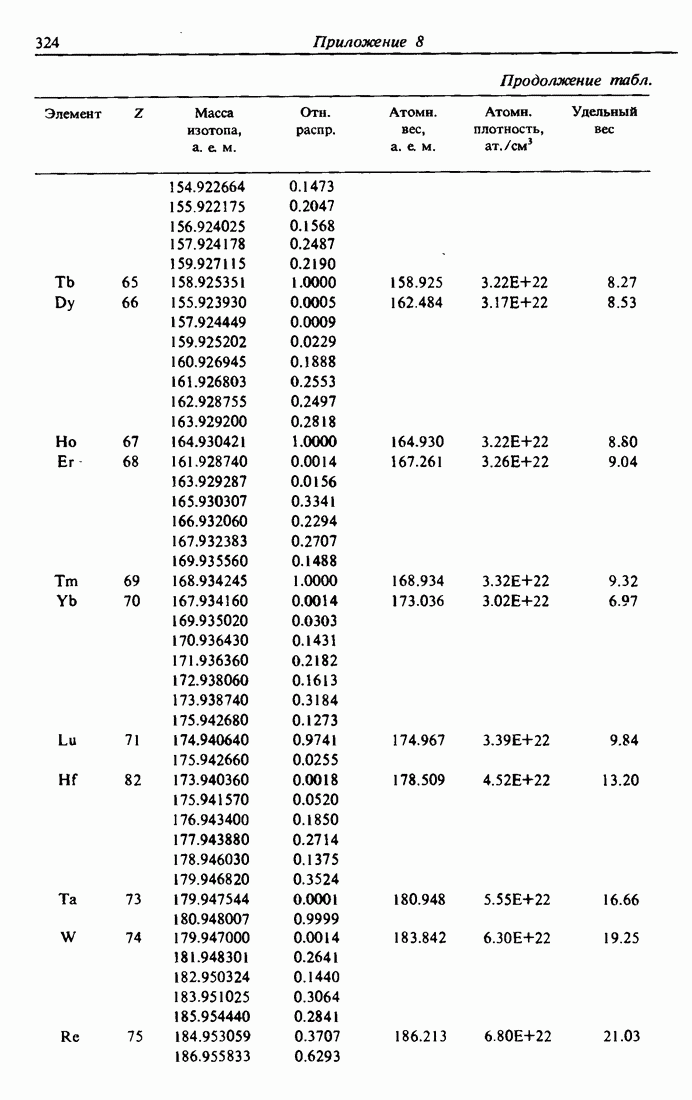
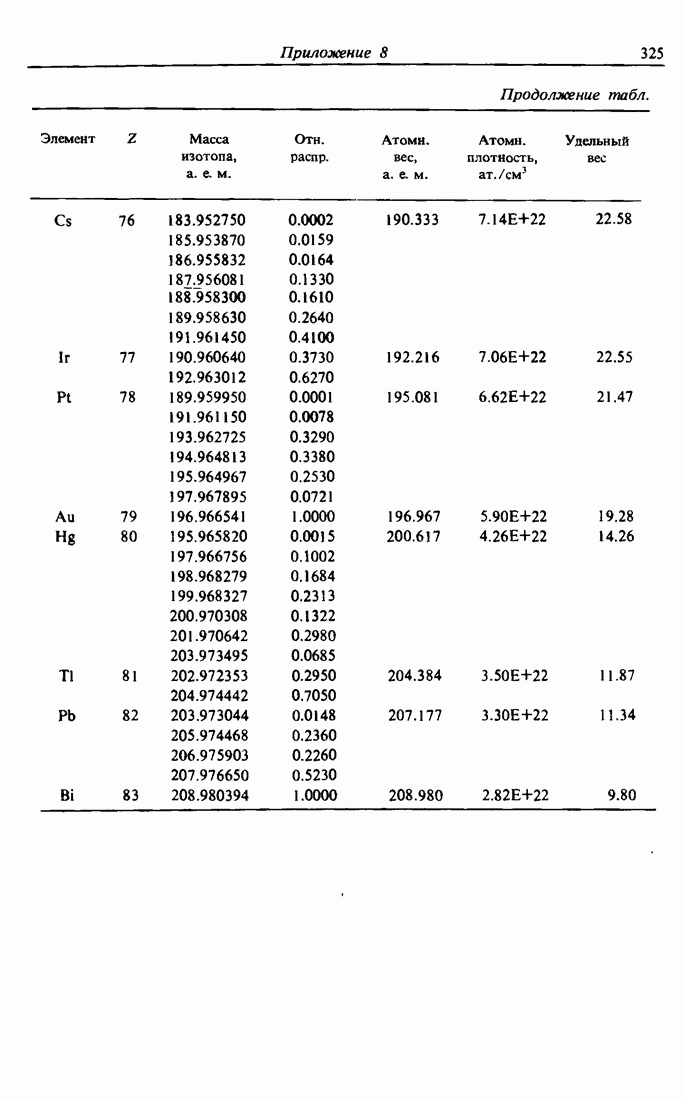
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
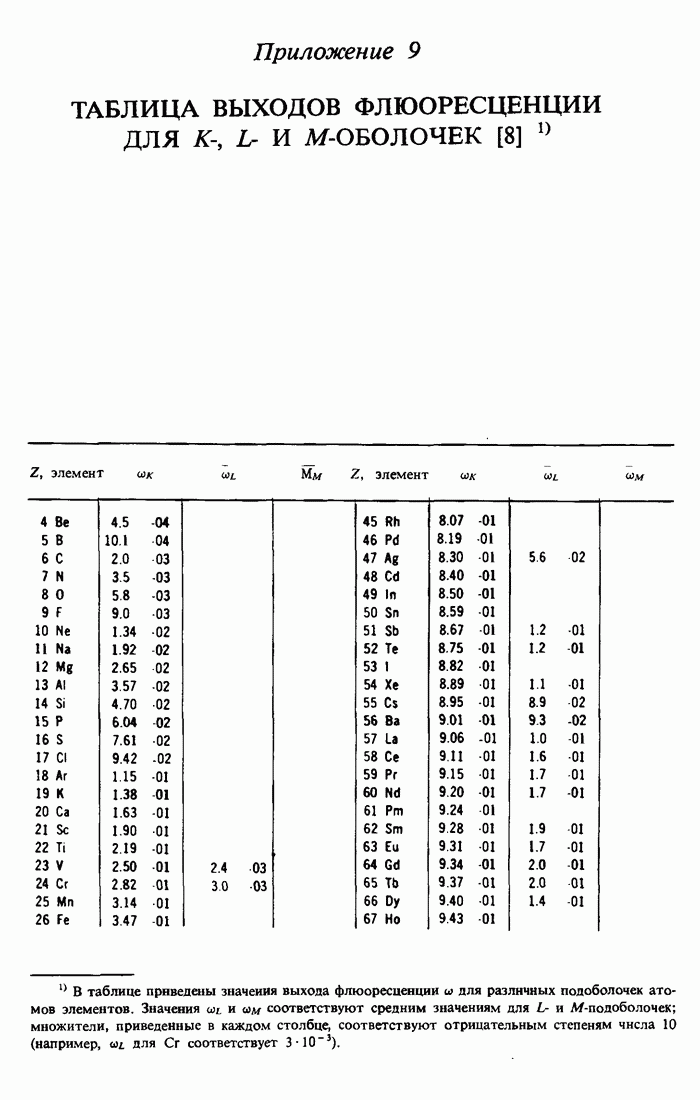
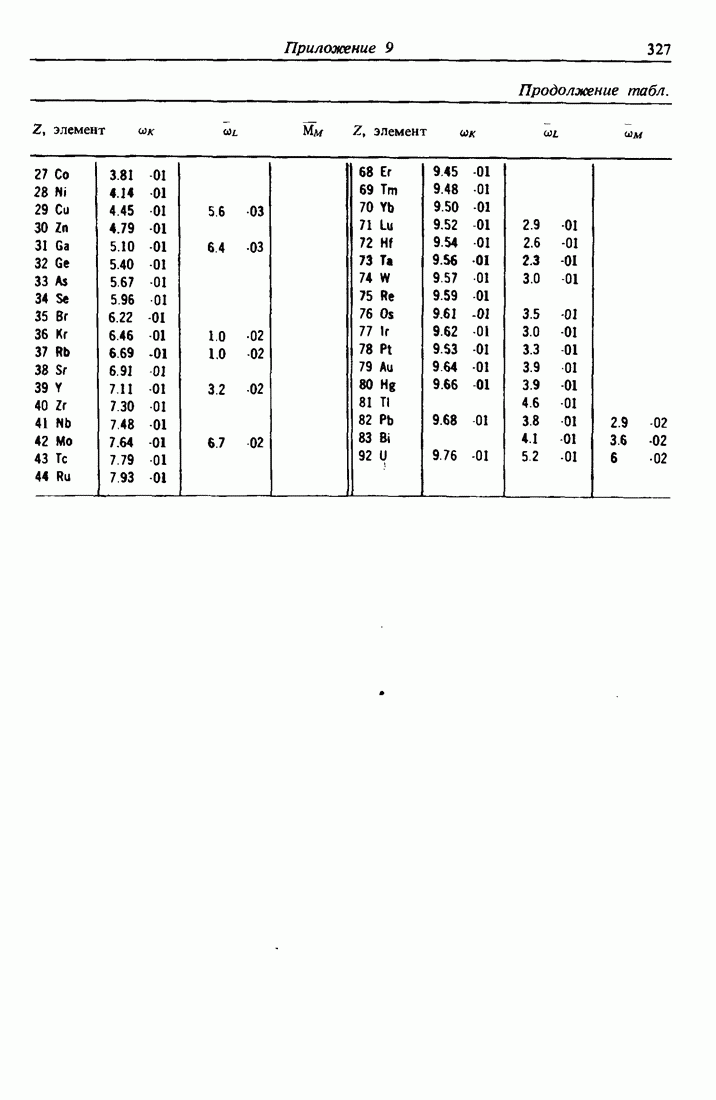
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ