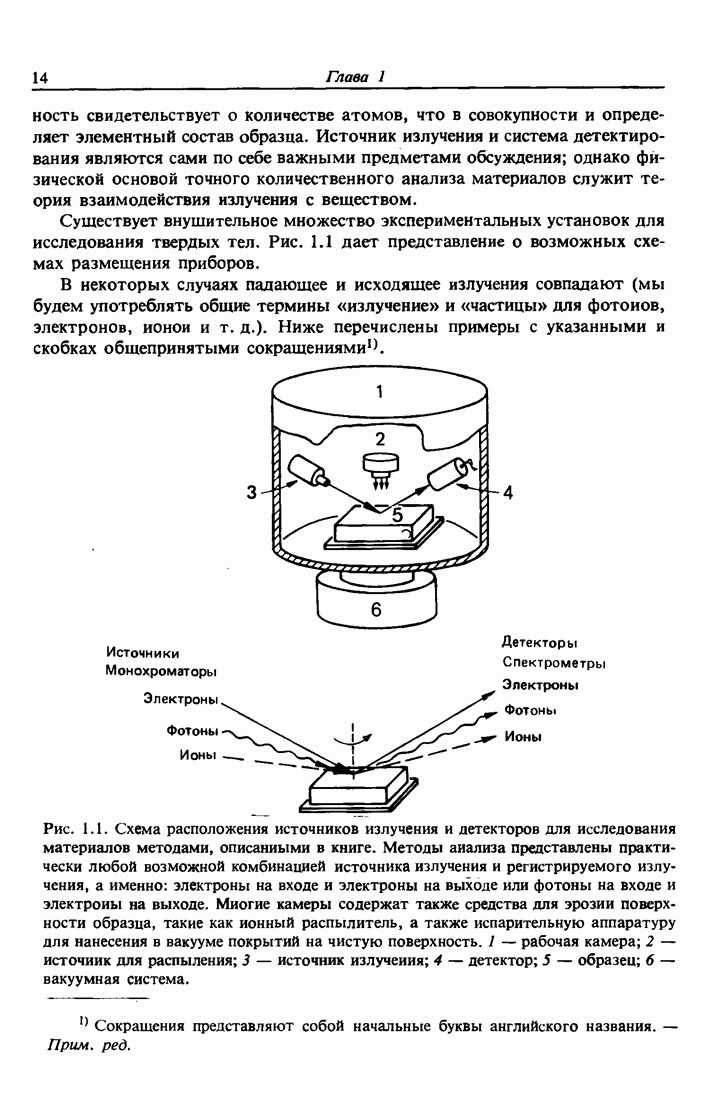
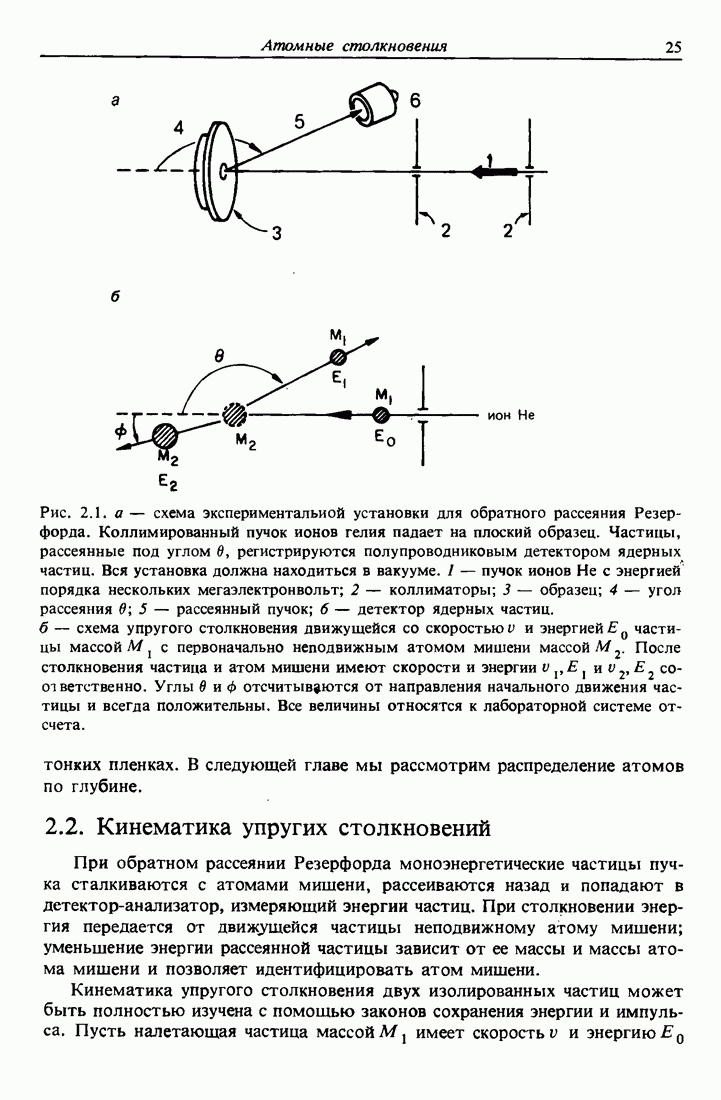
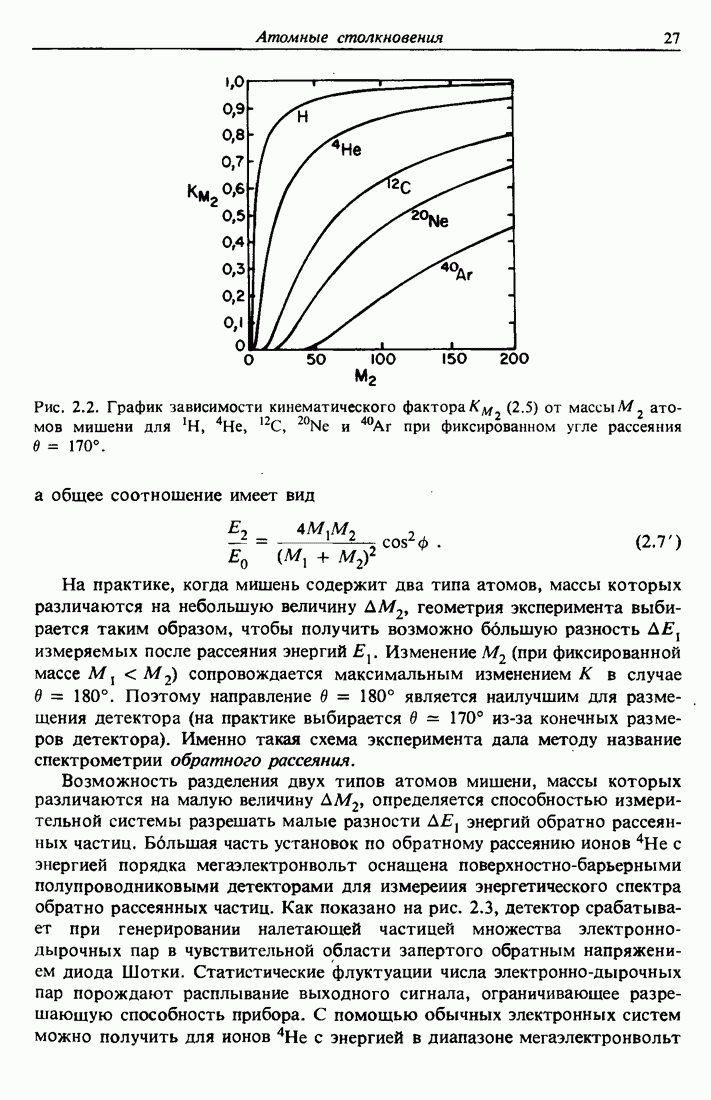
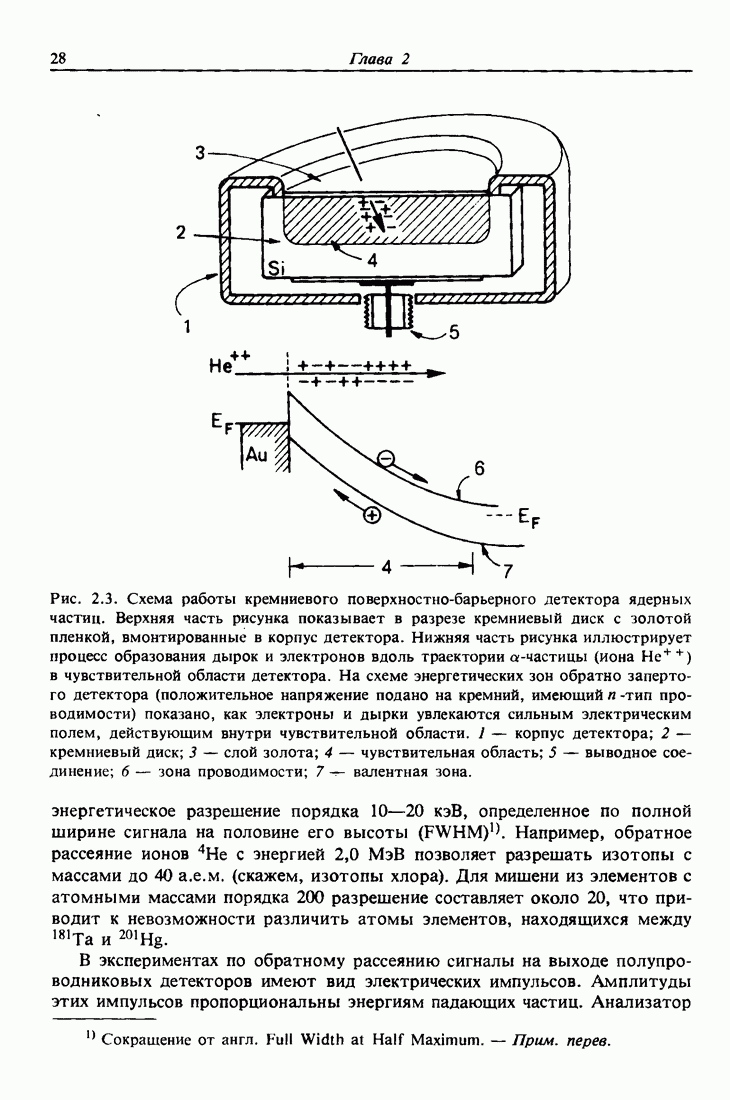
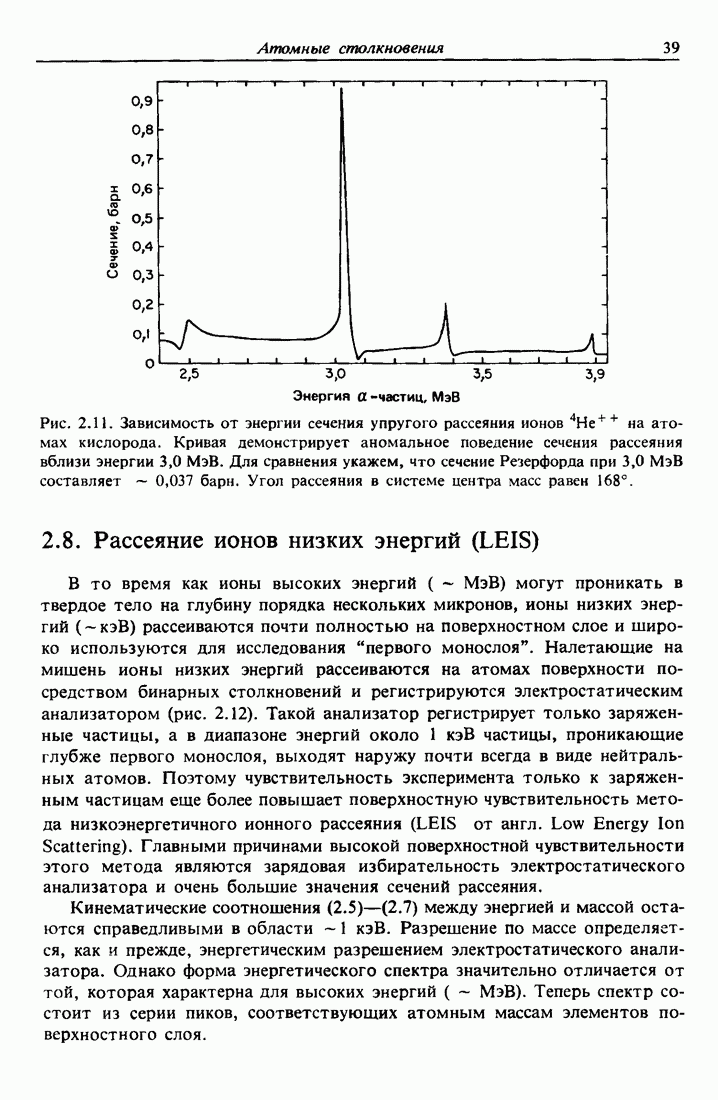
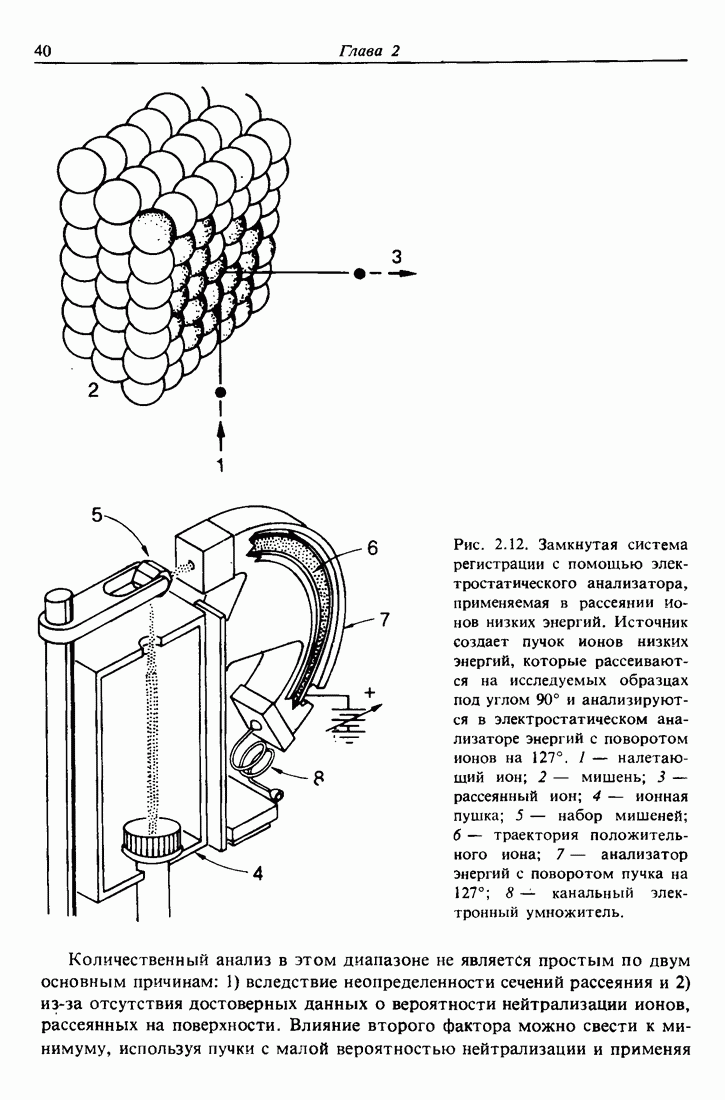
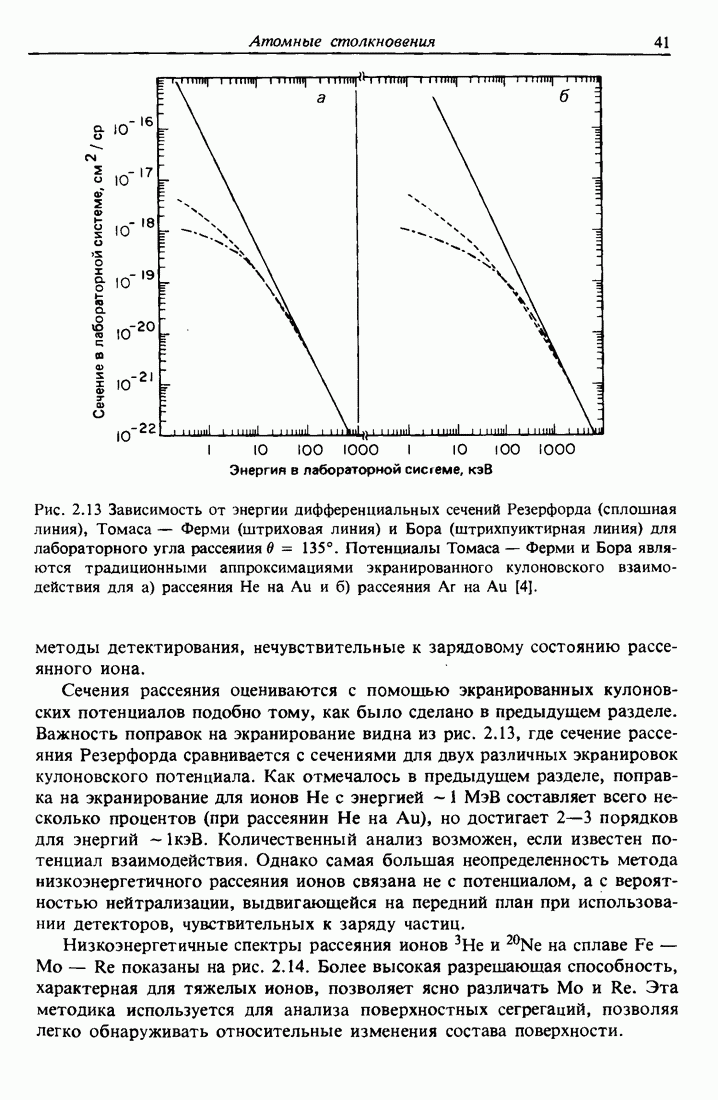
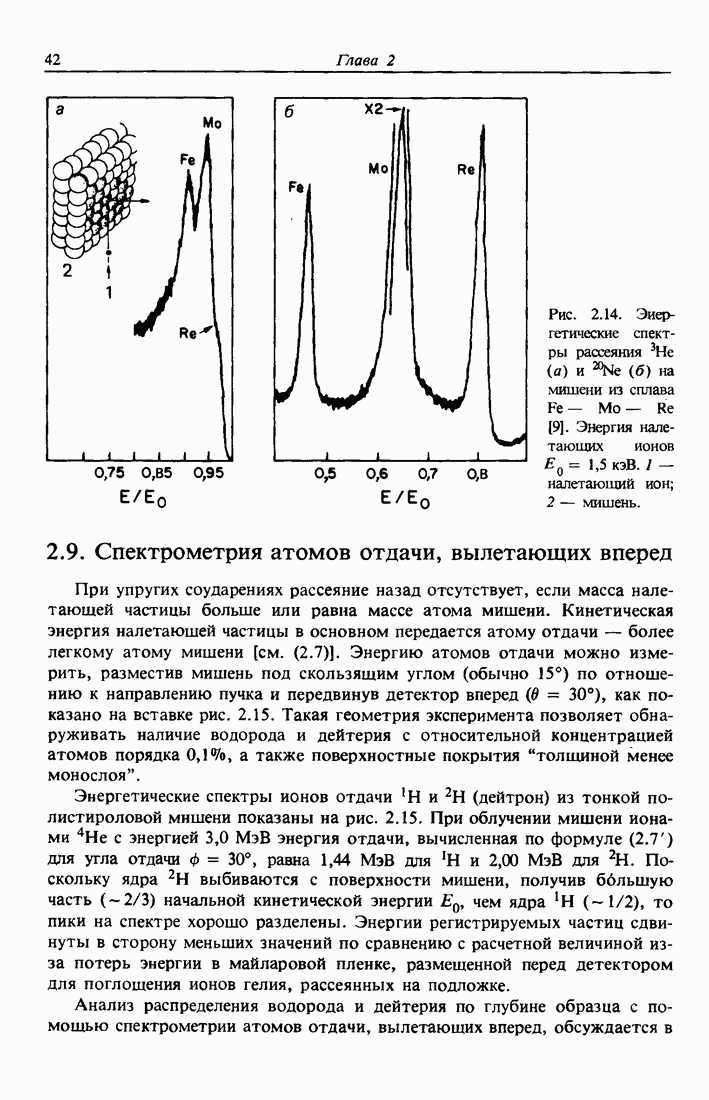
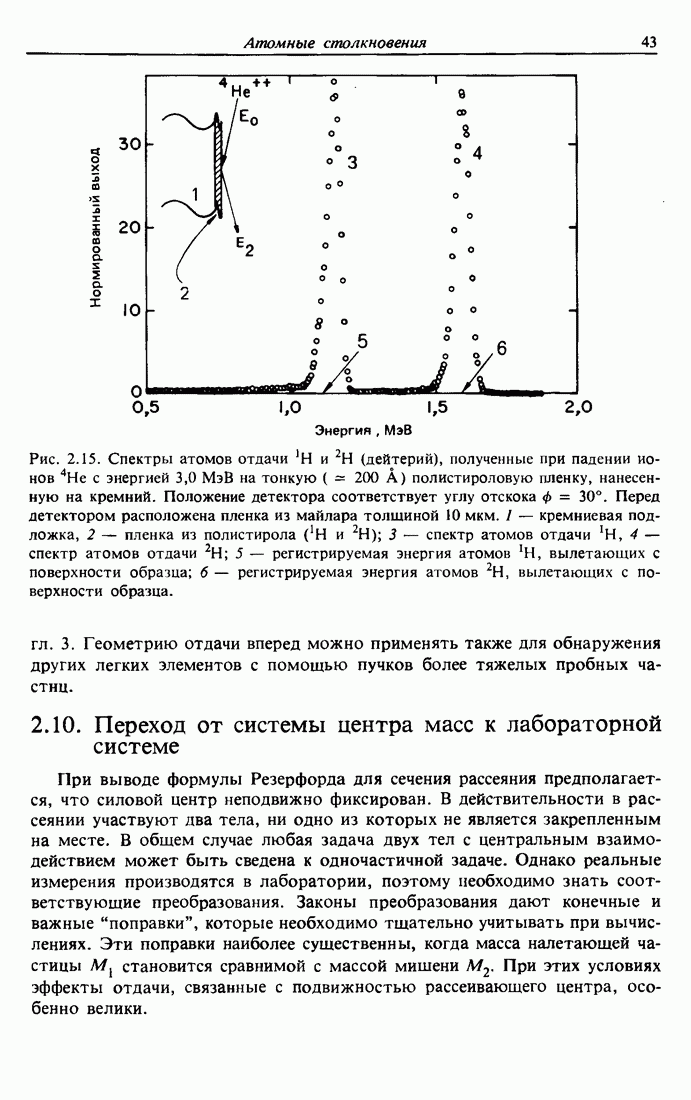
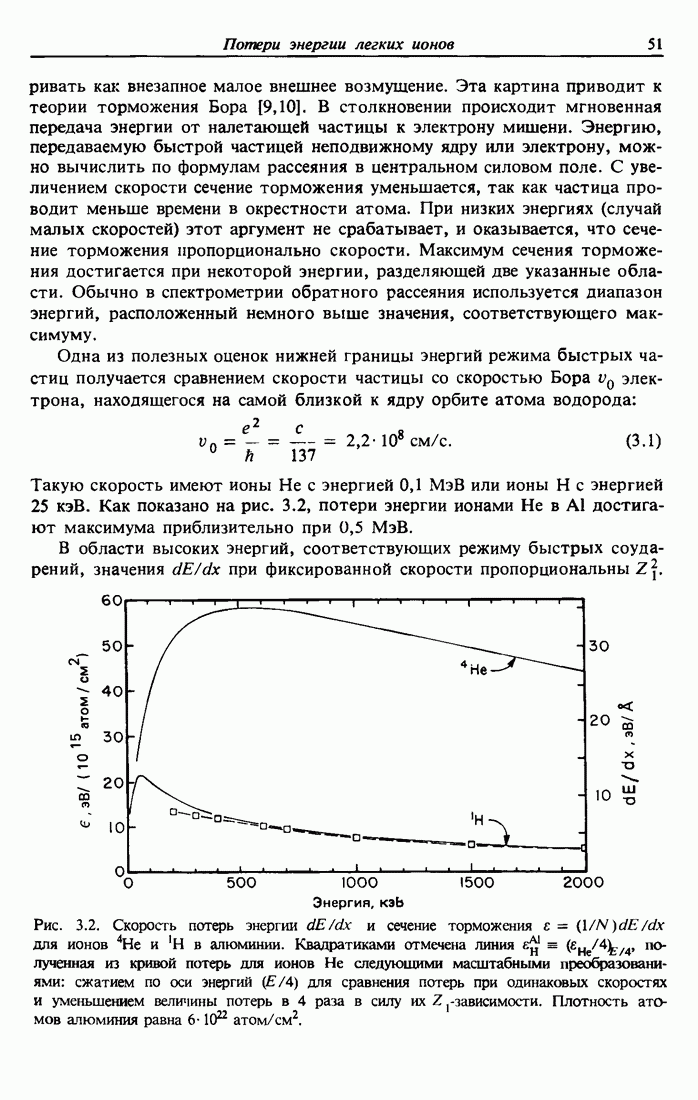
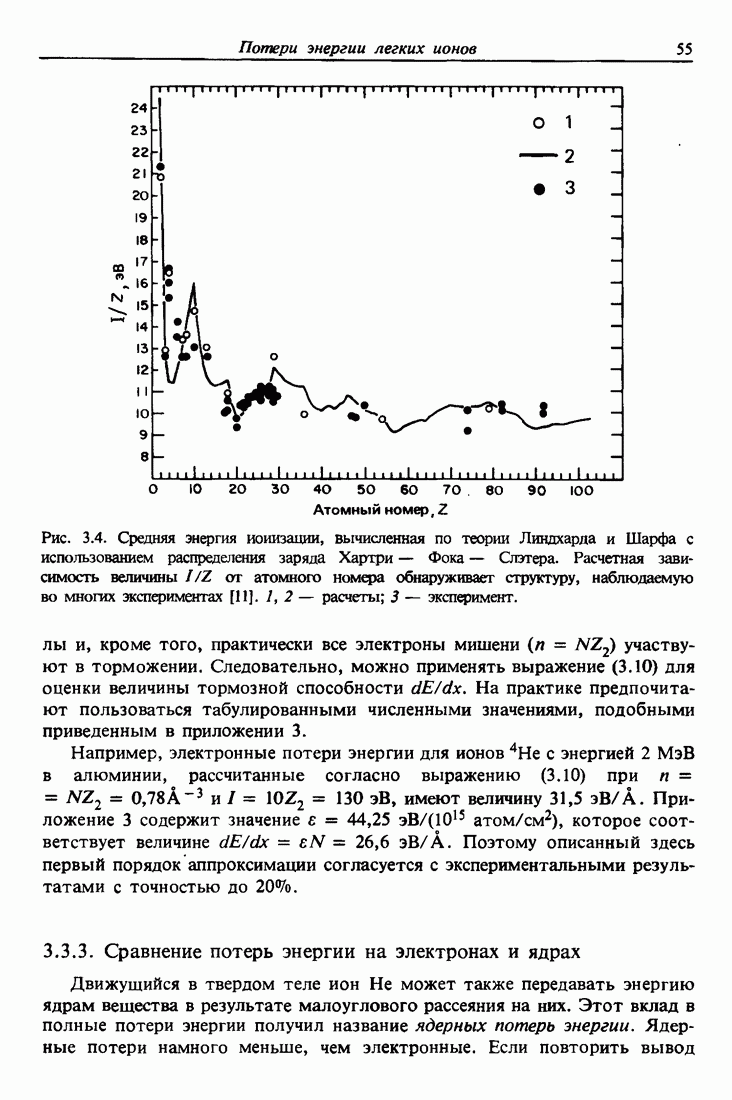
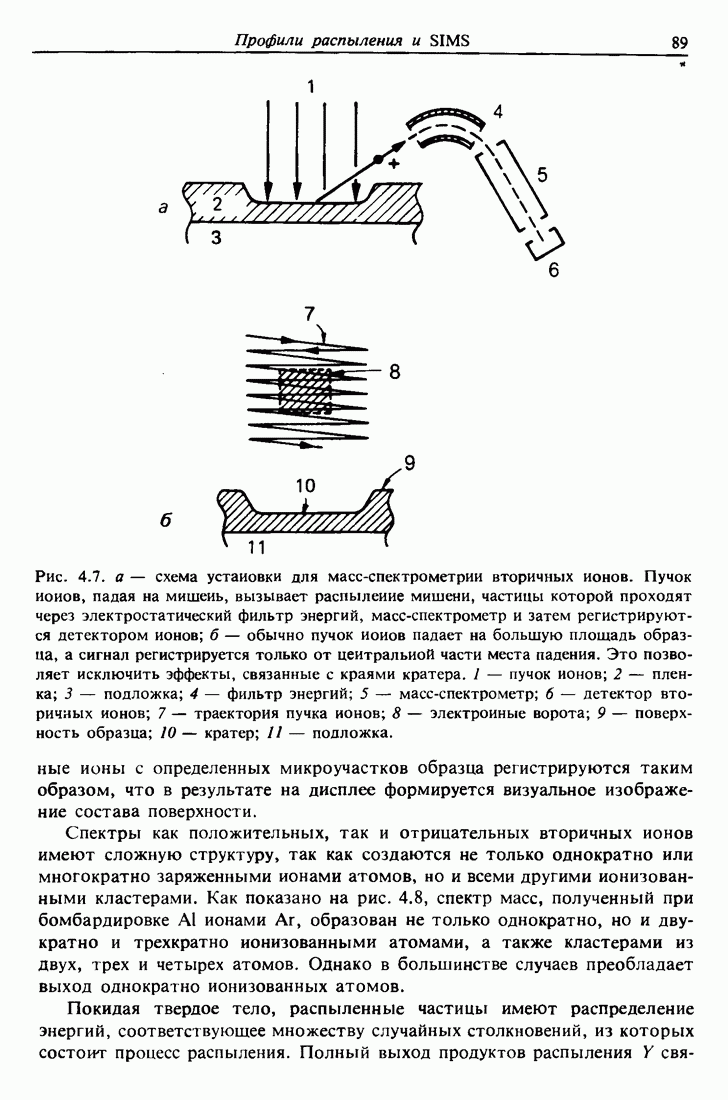
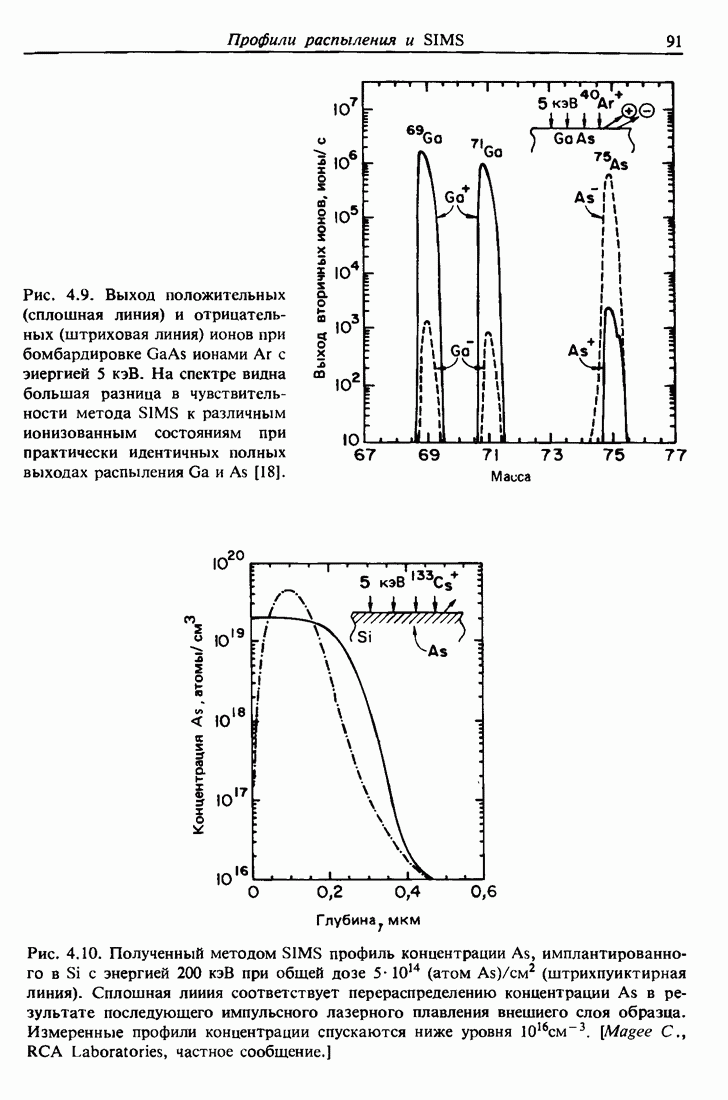
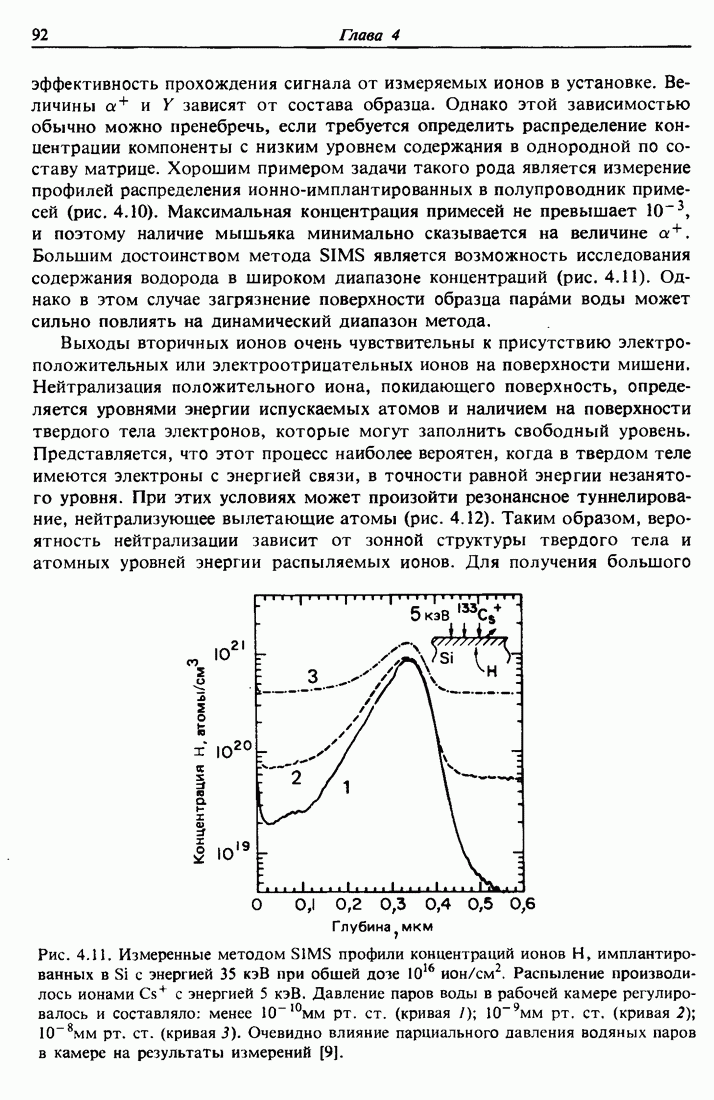
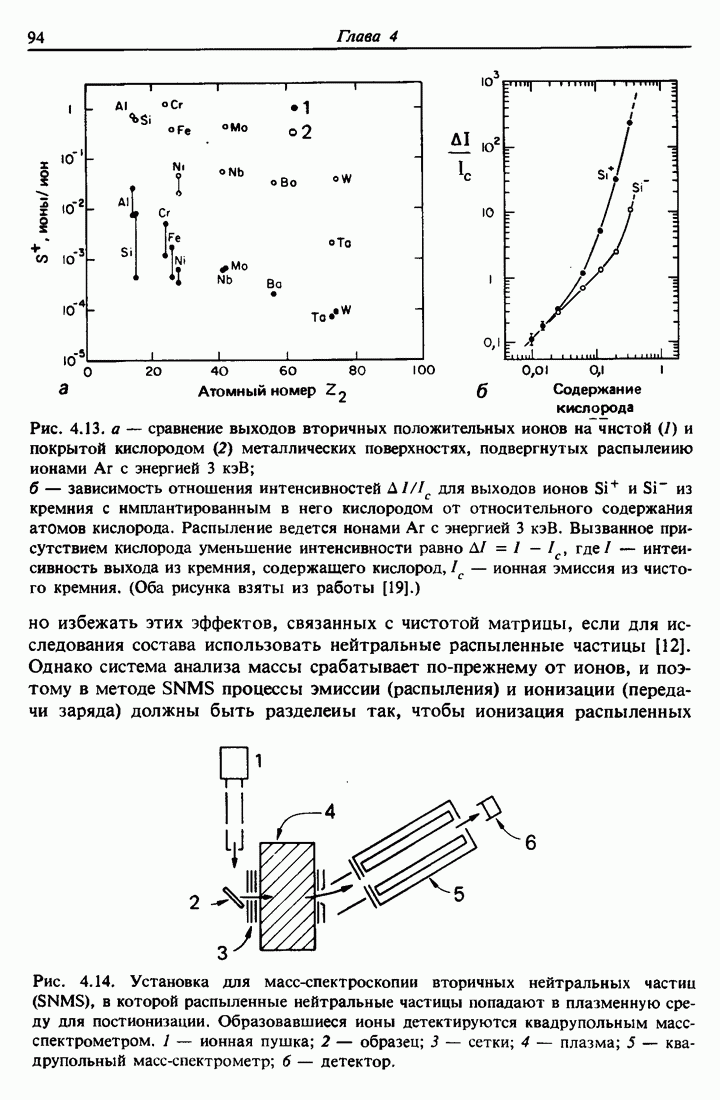
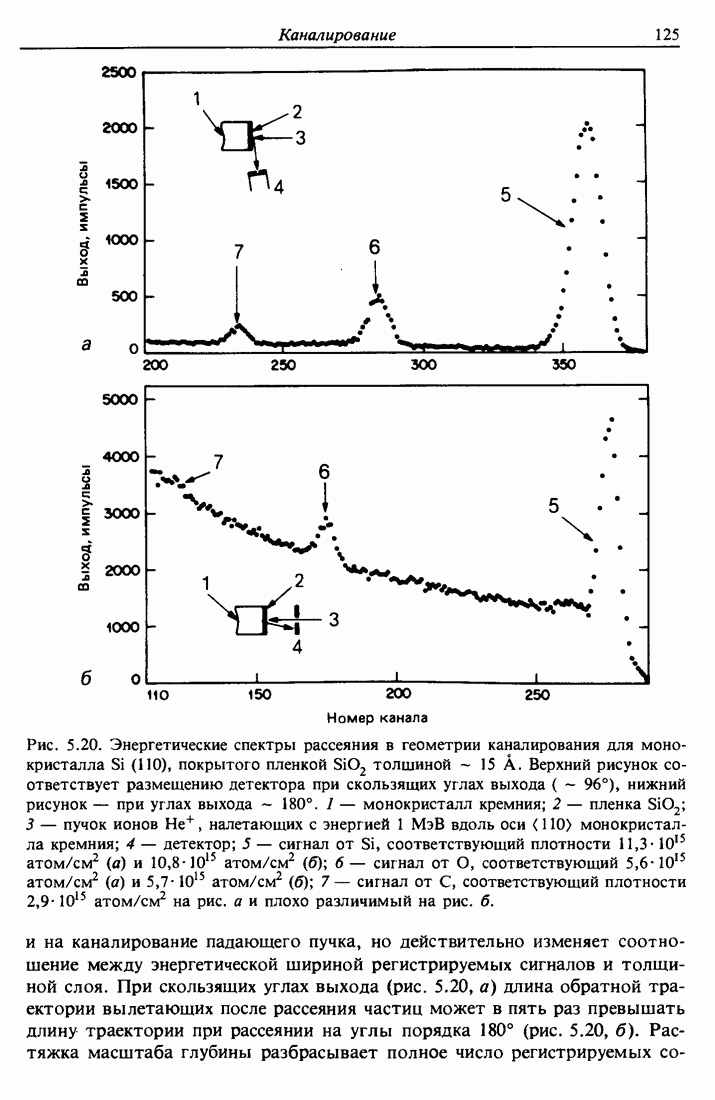
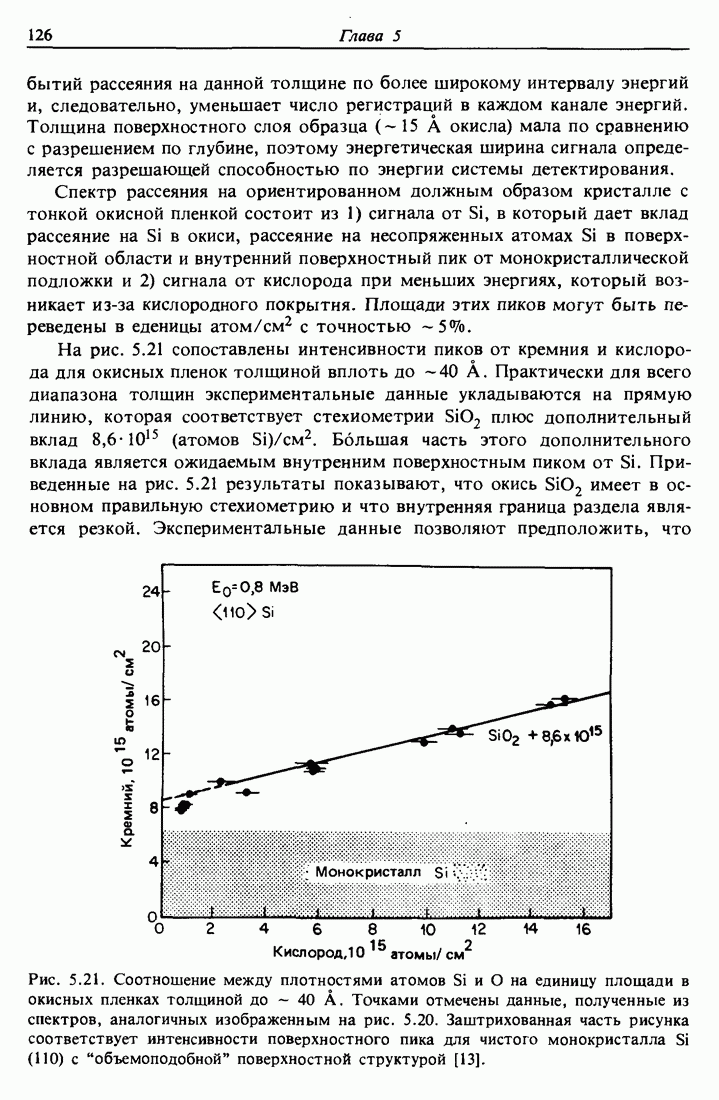
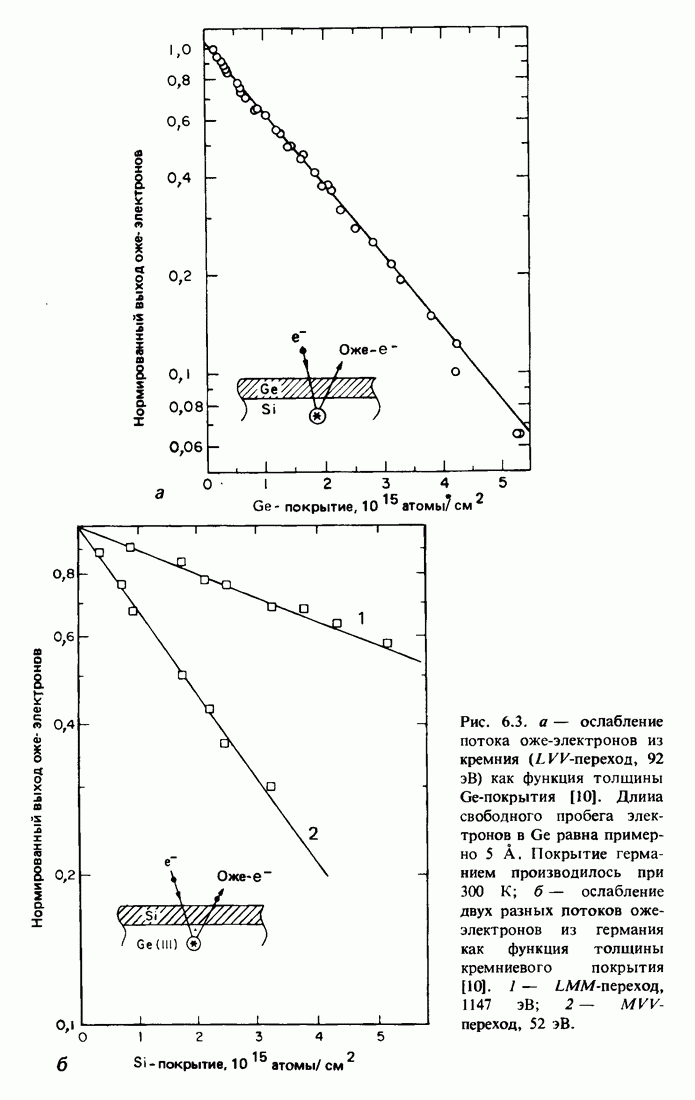
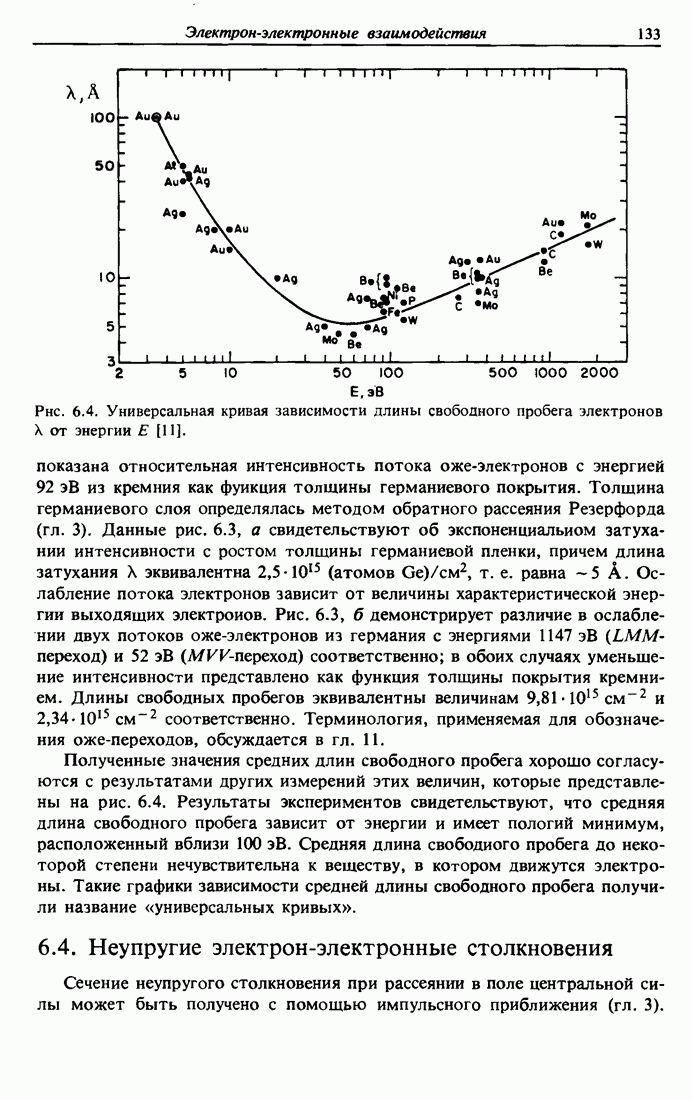
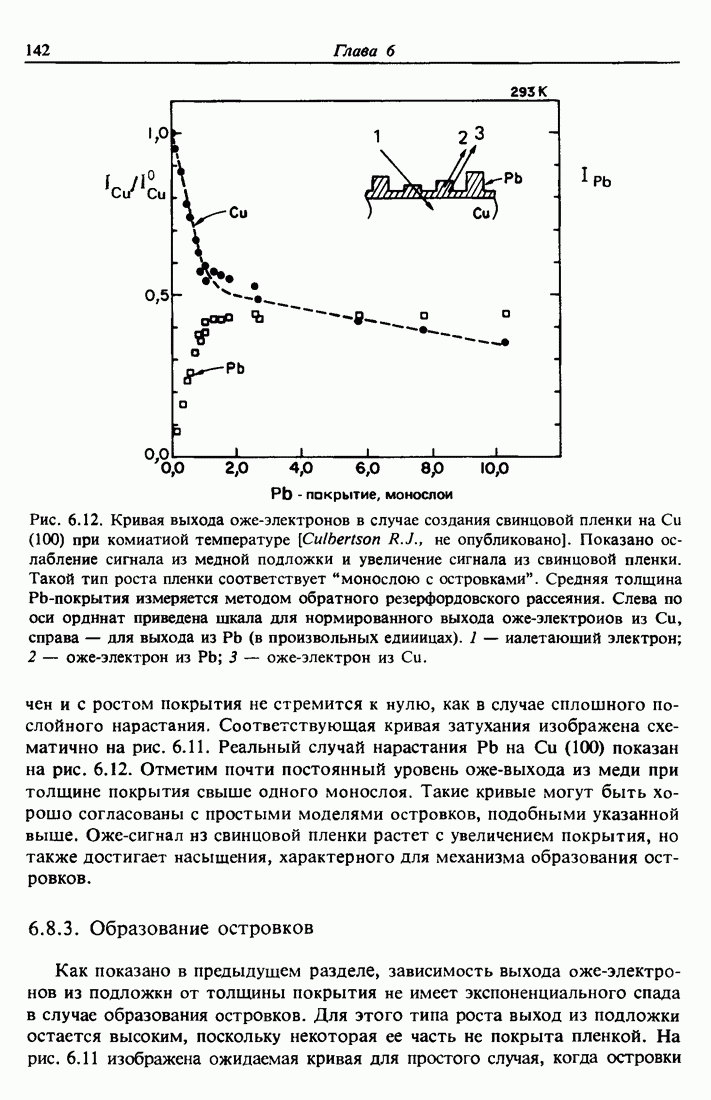
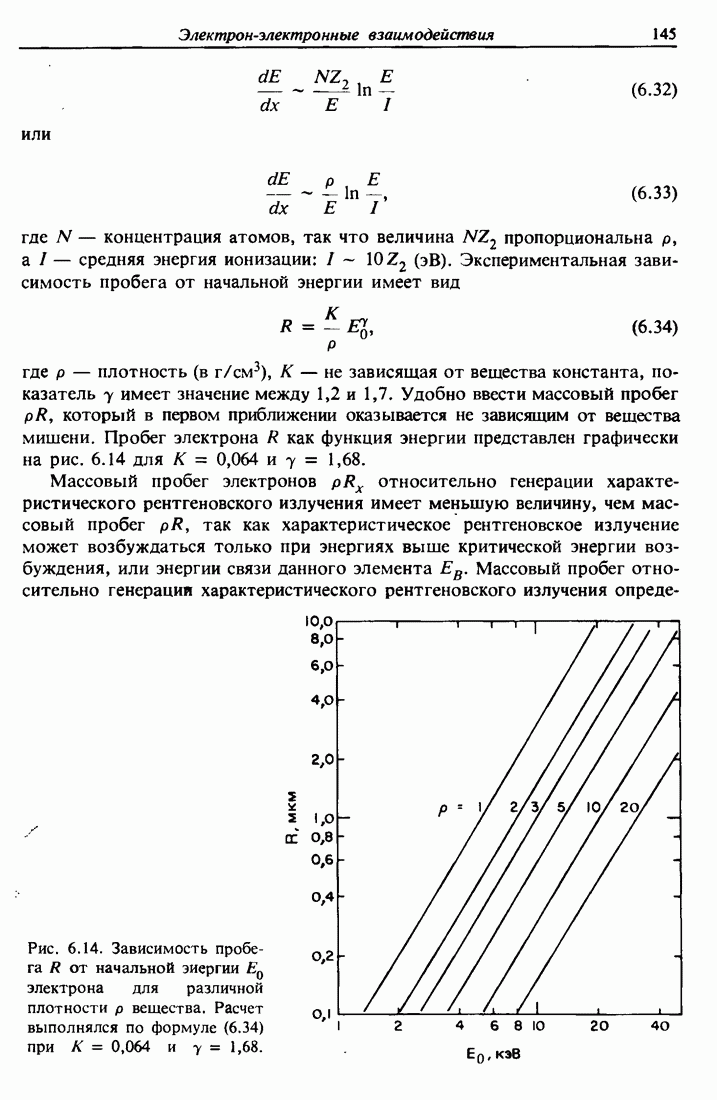
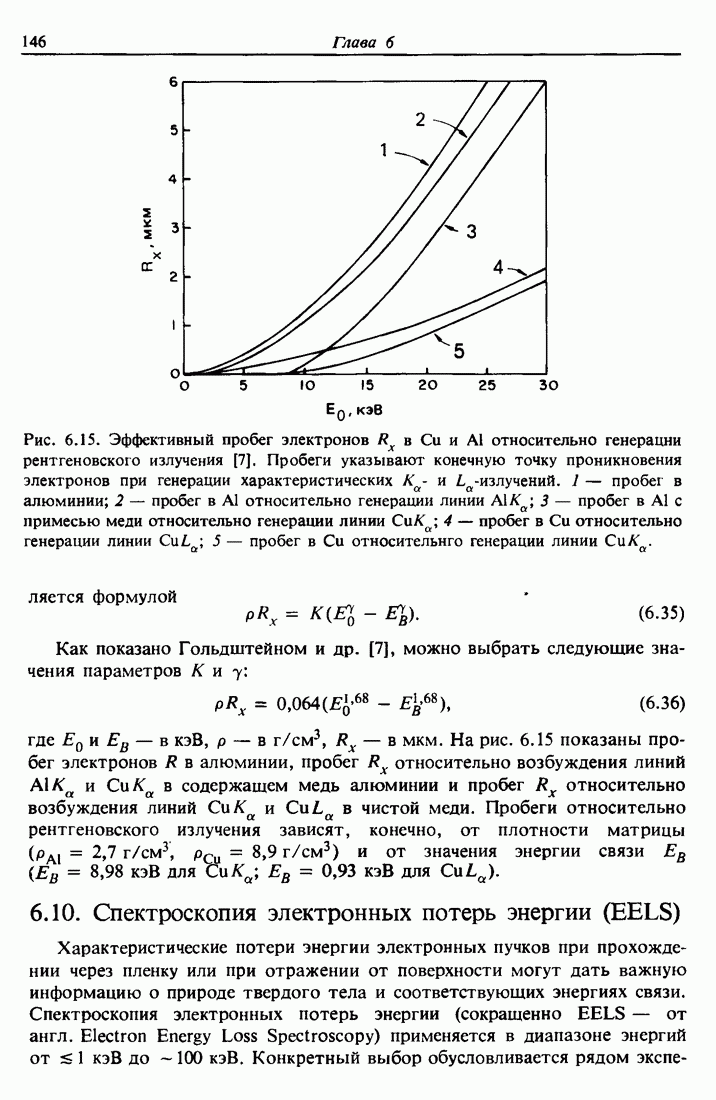
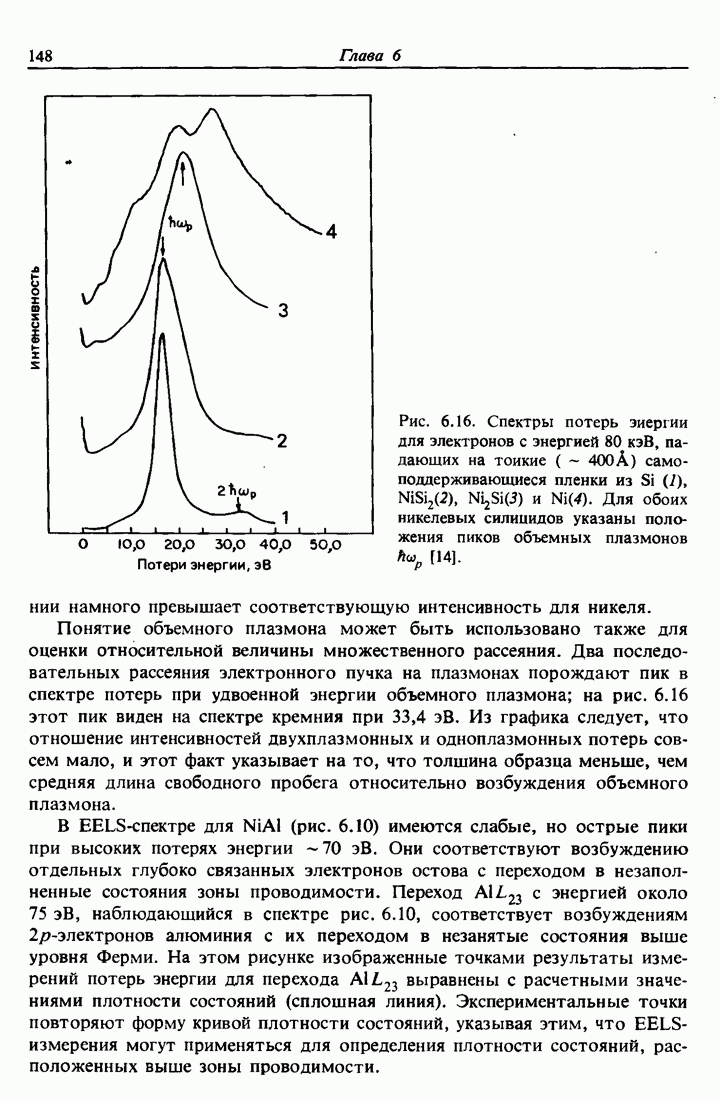
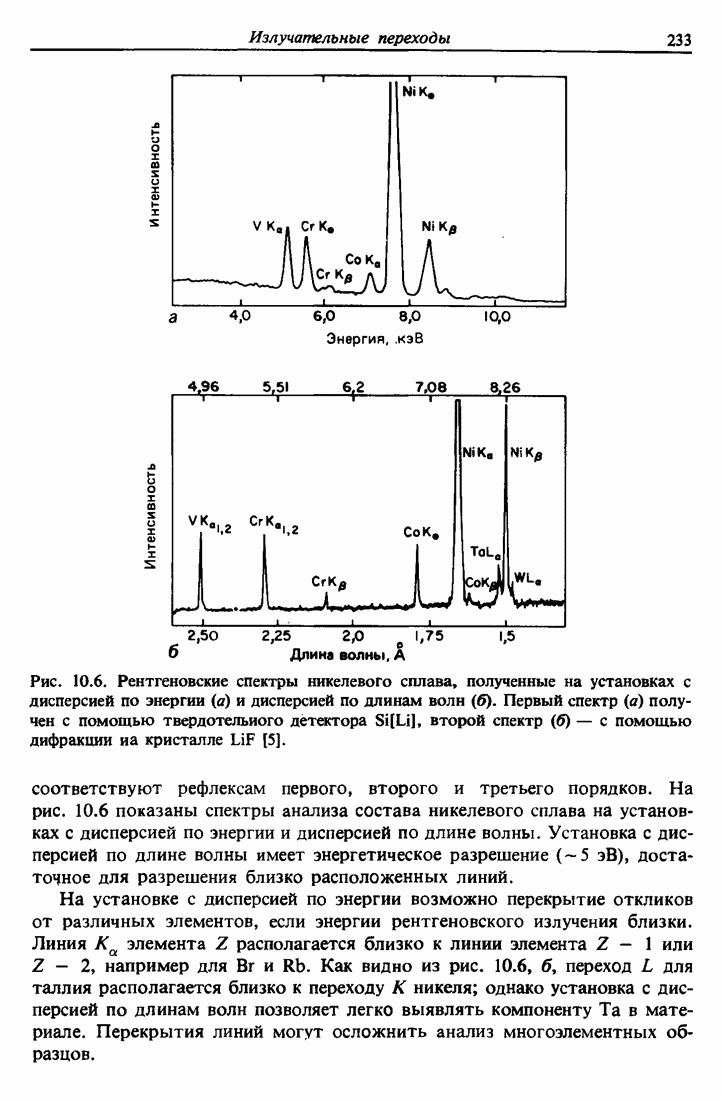
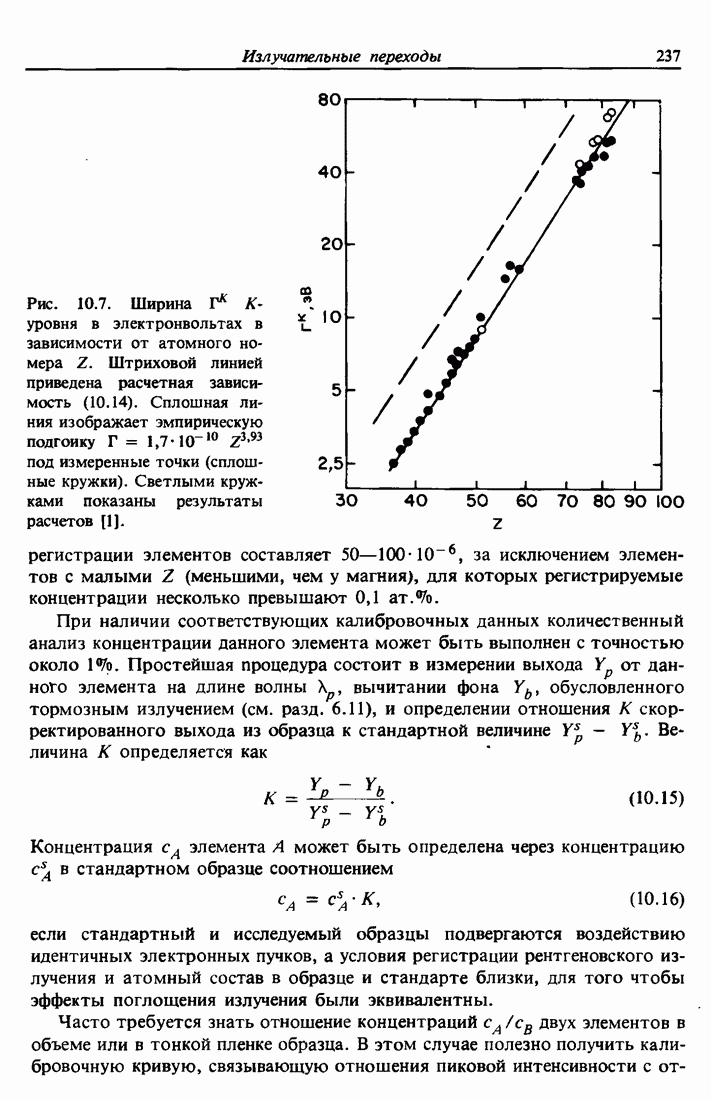
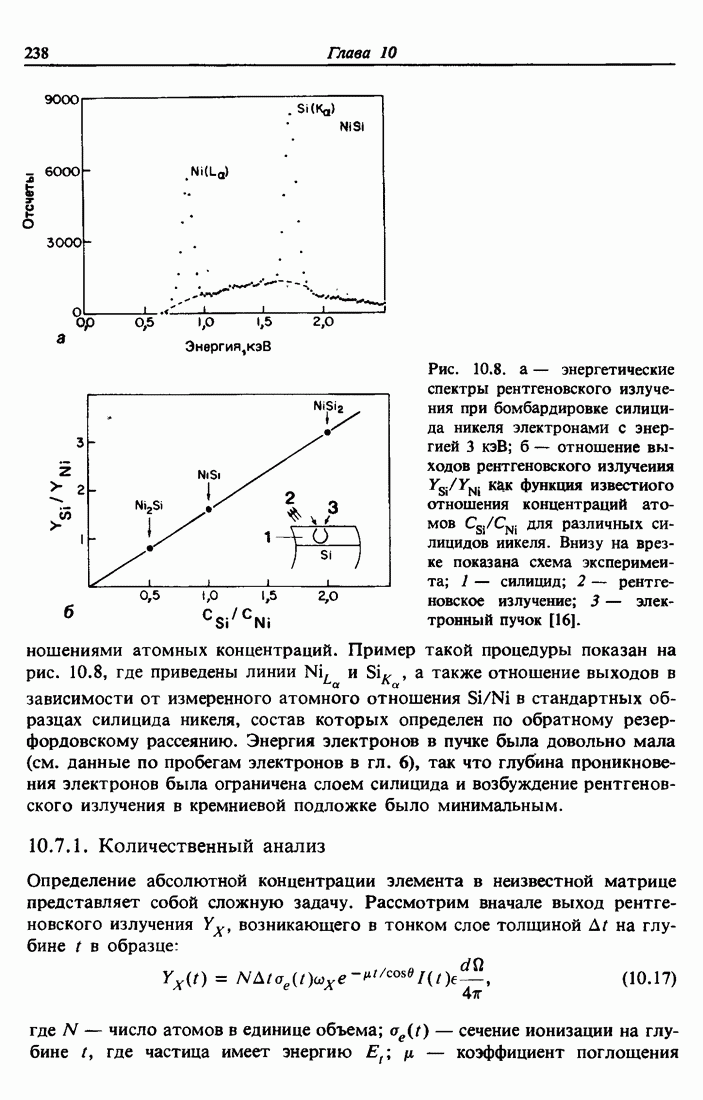
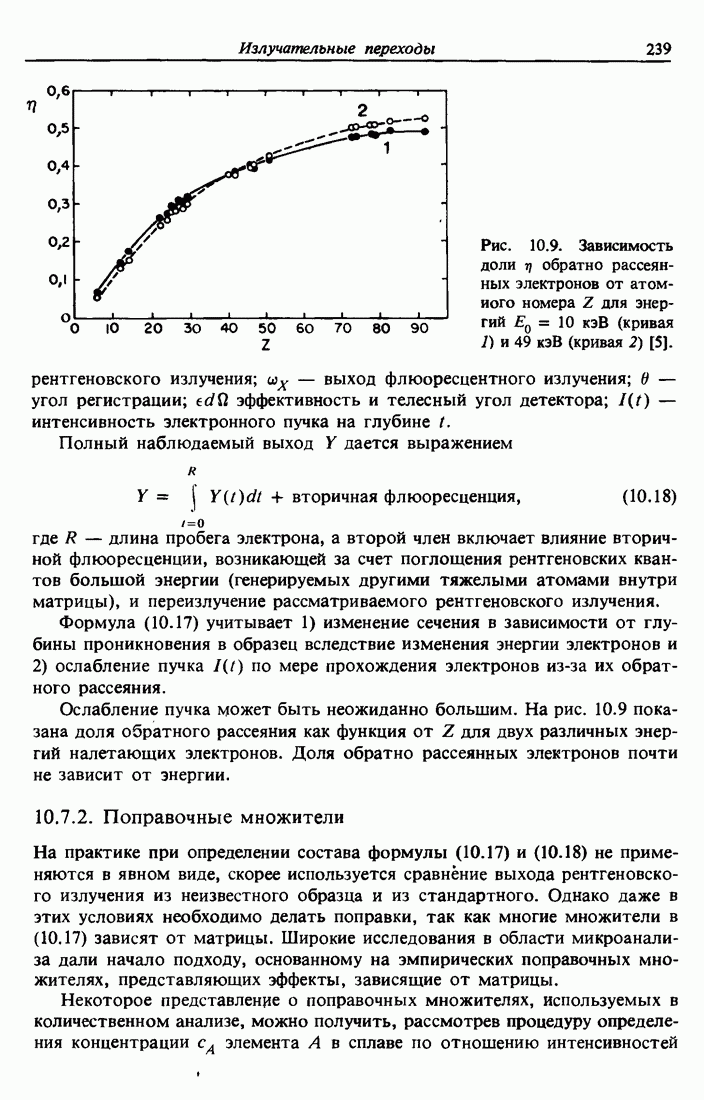
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
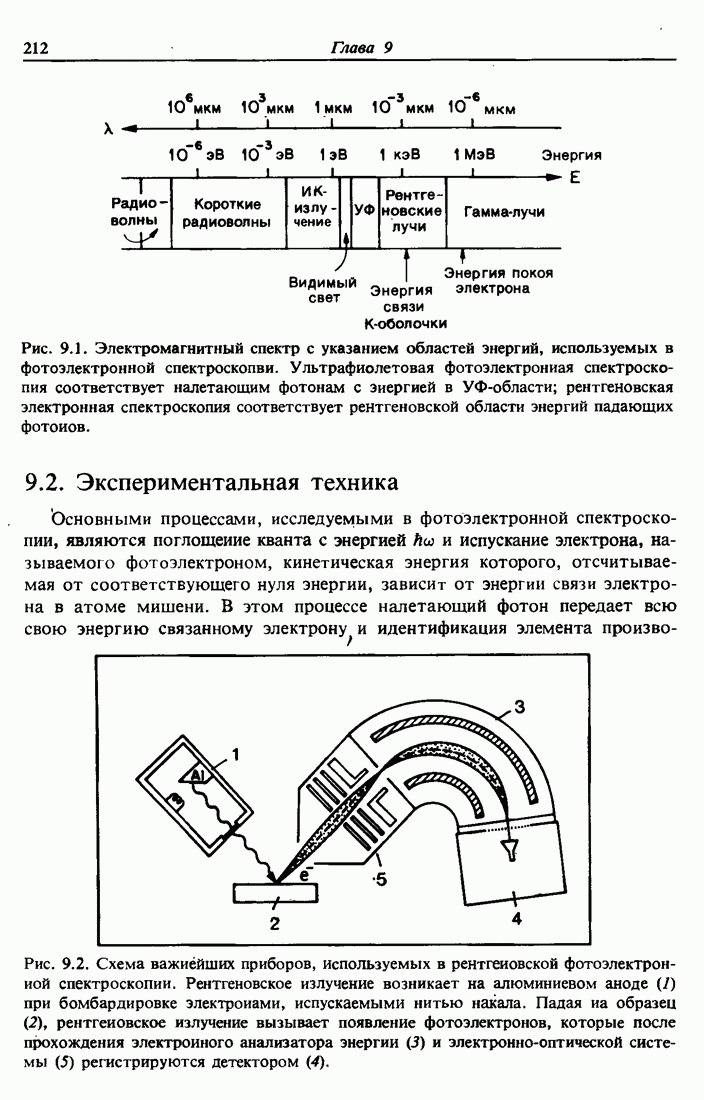
4.9. Статистическая модель атома Томаса — Ферми
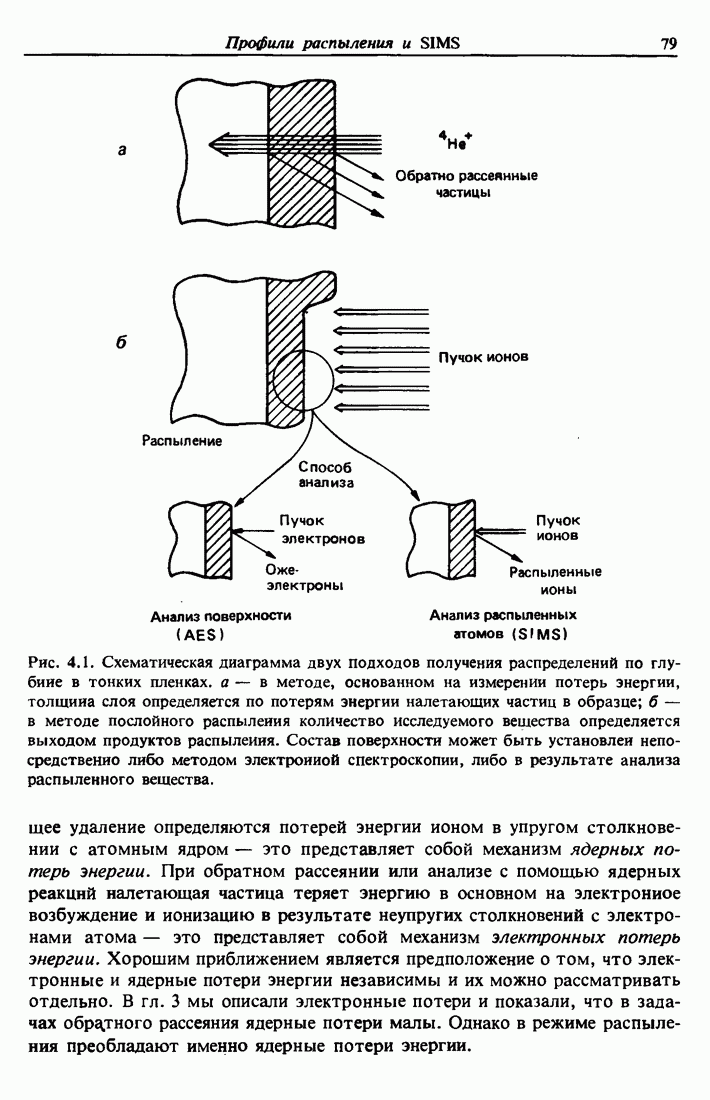
При столкновениях с малыми скоростями заряд ядра экранируется электронами, так как расстояние между налетающей частицей и атомом среды остается достаточно большим. Это приводит к отклонению потенциала рассеяния от чисто кулоновского вида  . Модифицированный потенциал определяется из теории Томаса — Ферми, которая единообразно
. Модифицированный потенциал определяется из теории Томаса — Ферми, которая единообразно
описывает все атомы и отличие состоит лишь в значениях масштабных множителей.
В модели Томаса — Ферми предполагается, что к электронам применимо статистическое описание, а именно статистика Ферми — Дирака, в рамках которой они ведут себя как идеальный газ частиц, заполняющих потенциальную яму вокруг положительно заряженного остова. Плотность состояний  свободного электронного газа можно определить, выбрав элемент объема V в виде куба со стороной L и наложив периодические граничные условия:
свободного электронного газа можно определить, выбрав элемент объема V в виде куба со стороной L и наложив периодические граничные условия:

Энергия электронного газа растет с увеличением числа электронов. Число электронов  в элементе объема V, расположенном в окрестности точки r, получается интегрированием плотности состояний:
в элементе объема V, расположенном в окрестности точки r, получается интегрированием плотности состояний:

где  — энергия Ферми, определяемая как максимальная кинетическая энергия ансамбля электронов в окрестности точки r.
— энергия Ферми, определяемая как максимальная кинетическая энергия ансамбля электронов в окрестности точки r.
В рассматриваемых нами многоэлектронных атомах полная энергия электрона в точке г равна  , где
, где  — его кинетическая энергия. Для электрона в связанном состоянии
— его кинетическая энергия. Для электрона в связанном состоянии  и поэтому максимальная кинетическая энергия связанного электрона есть
и поэтому максимальная кинетическая энергия связанного электрона есть  Из формулы (4.37) получаем плотность электронов в точке r.
Из формулы (4.37) получаем плотность электронов в точке r.

Условие самосогласованности состоит в том, что потенциал, порождаемый распределением электронов с плотностью (4.38) и зарядом ядра, должен правильно воспроизводить потенциальную энергию  Следовательно, плотность заряда —
Следовательно, плотность заряда —  и электростатический потенциал —
и электростатический потенциал —  удовлетворяют уравнению Пуассона
удовлетворяют уравнению Пуассона

или

Уравнения (4.38) и (4.39) должны решаться одновременно для  и
и  со следующими граничными условиями: при
со следующими граничными условиями: при  потенциальная энергия определяется ядром, т. е.
потенциальная энергия определяется ядром, т. е.  при
при  заряд вне сферы радиусом r равен нулю и поэтому
заряд вне сферы радиусом r равен нулю и поэтому  убывает быстрее
убывает быстрее 
Уравнение (4.39) и указанные граничные условия удобно выразить в безразмерной форме, в которой величины Z, Е, m и  входят только через посредство
входят только через посредство
масштабных единиц. Положим

и

где  — радиус Бора. Соотношение (4.40) указывает, что единица масштаба а, описывающая размер атома, обратно пропорциональна кубическому корню из атомного номера. (В электронной спектроскопии, использующей переходы между уровнями остова, радиус орбиты состояния
— радиус Бора. Соотношение (4.40) указывает, что единица масштаба а, описывающая размер атома, обратно пропорциональна кубическому корню из атомного номера. (В электронной спектроскопии, использующей переходы между уровнями остова, радиус орбиты состояния  аппроксимируется величиной
аппроксимируется величиной  .) После указанных подстановок уравнение (4.38) принимает вид
.) После указанных подстановок уравнение (4.38) принимает вид

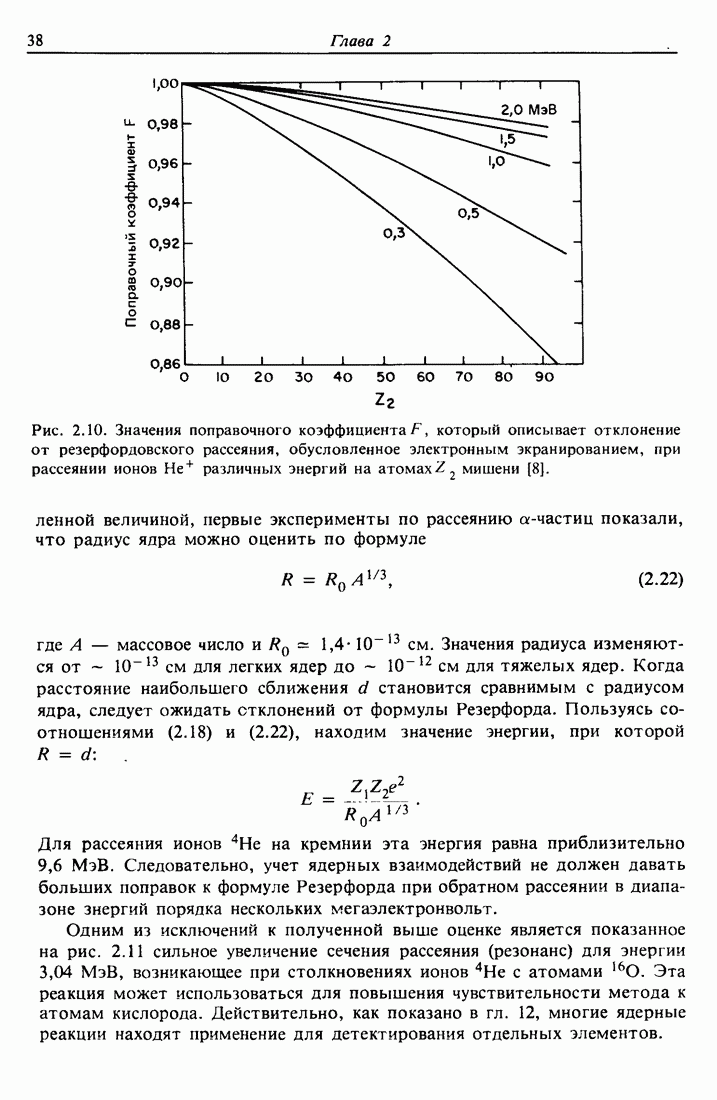
Потенциал этого безразмерного уравнения Томаса — Ферми обладает кулоновским поведением в пределе  . Точное решение уравнения (4.41) находится численными методами. Существуют также аналитические аппроксимации решения в виде экспонент или степенных разложений. Наиболее часто в компьютерных вычислениях для функции экранирования Томаса — Ферми используется аппроксимация Мольера, показанная на рис. 4.4 и задаваемая выражением
. Точное решение уравнения (4.41) находится численными методами. Существуют также аналитические аппроксимации решения в виде экспонент или степенных разложений. Наиболее часто в компьютерных вычислениях для функции экранирования Томаса — Ферми используется аппроксимация Мольера, показанная на рис. 4.4 и задаваемая выражением

где  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
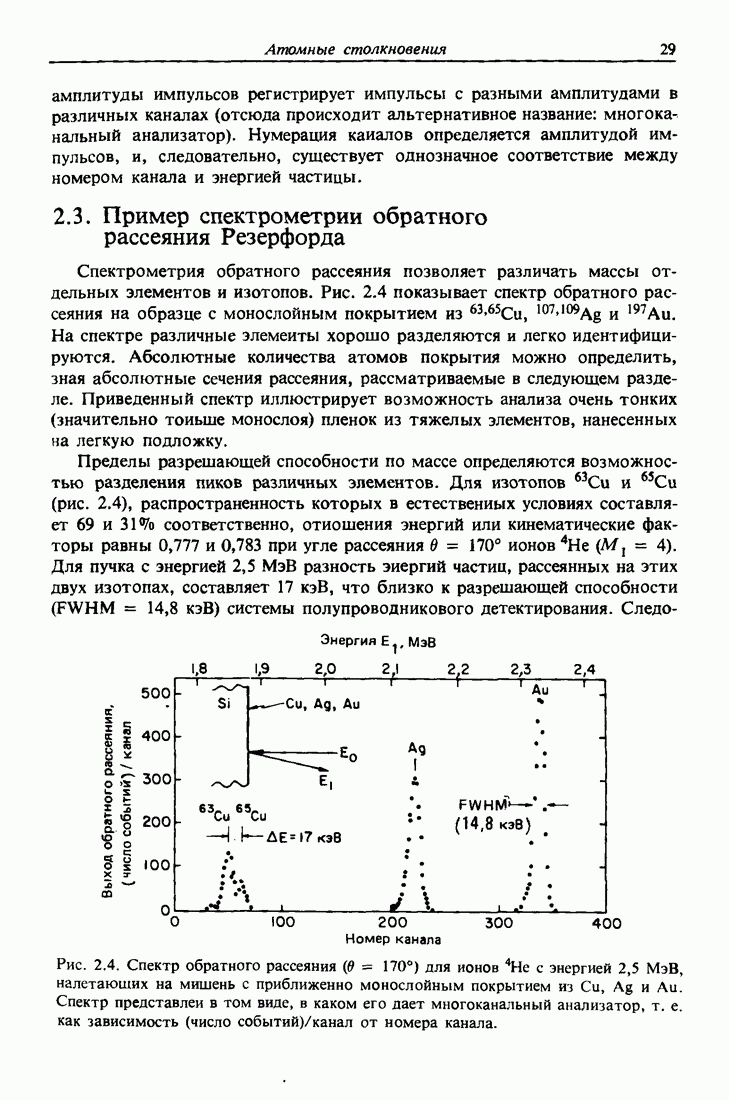
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
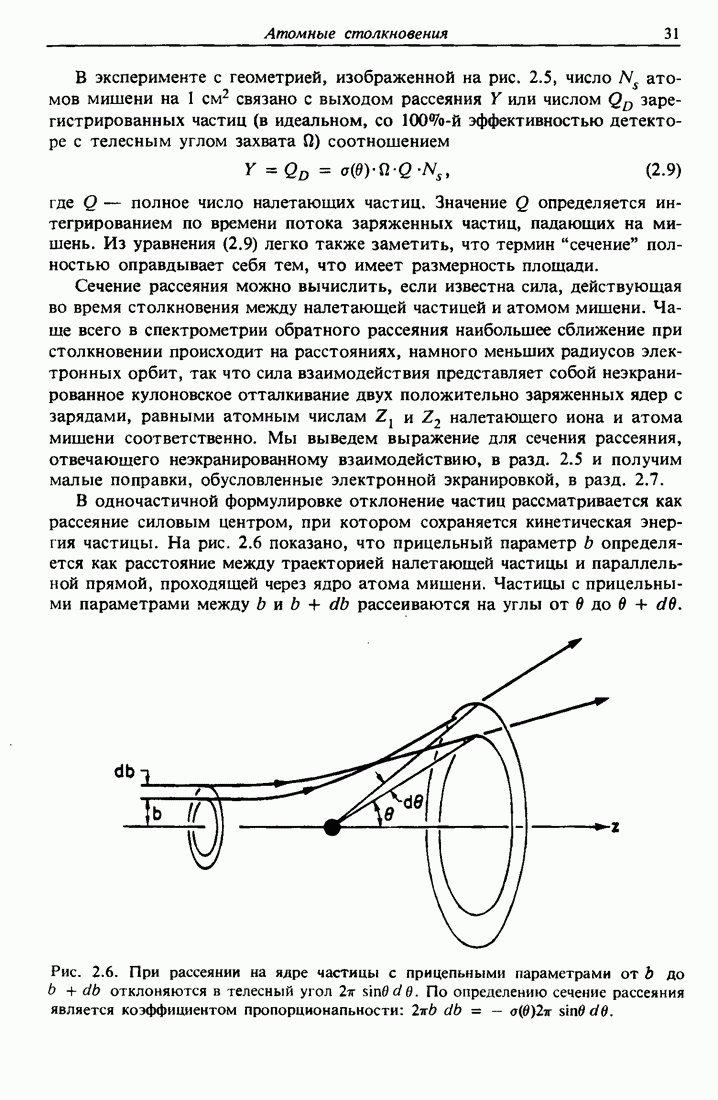
- 2.4. Сечение рассеяния и прицельный параметр
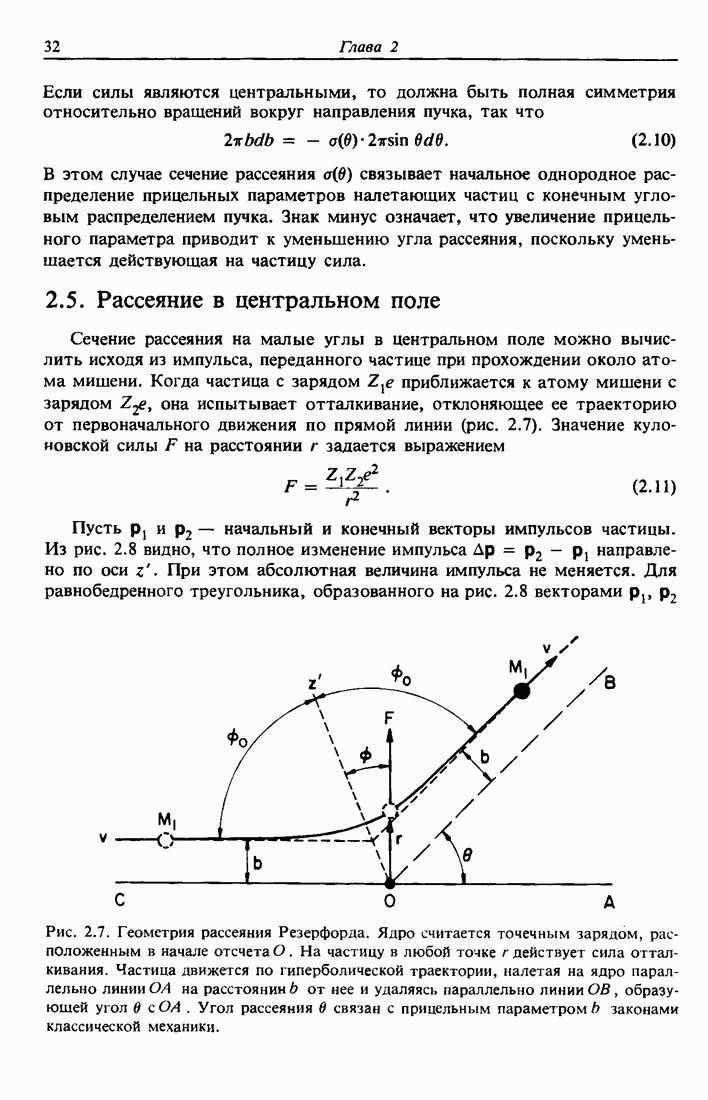
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
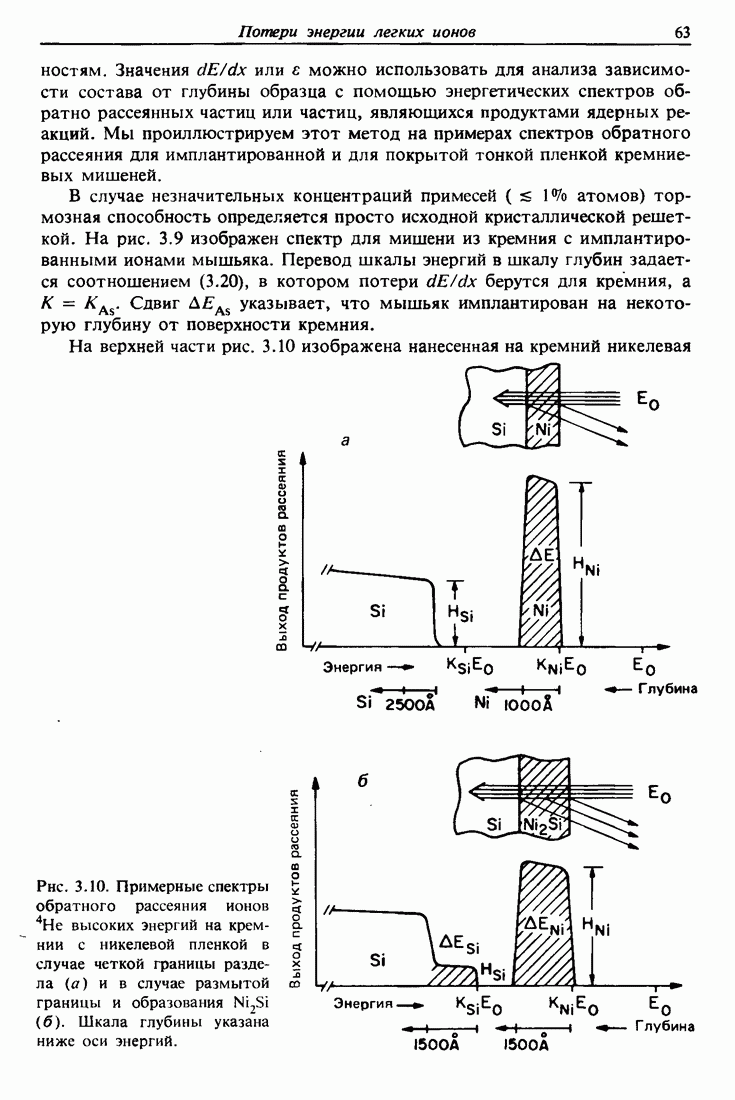
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
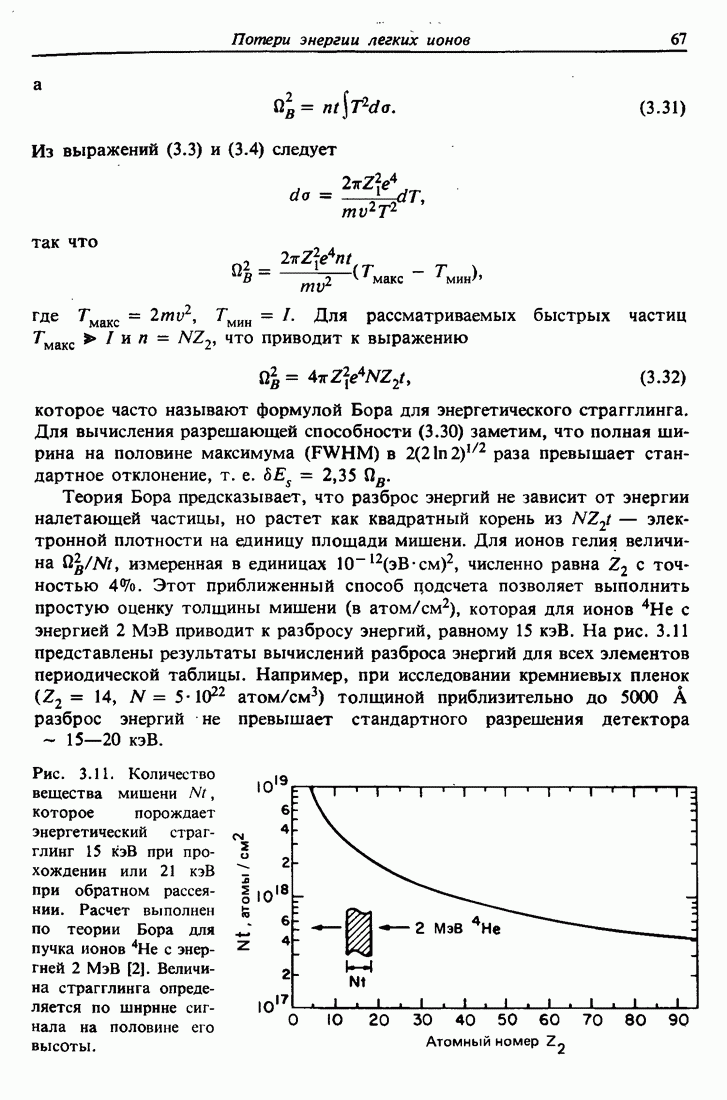
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
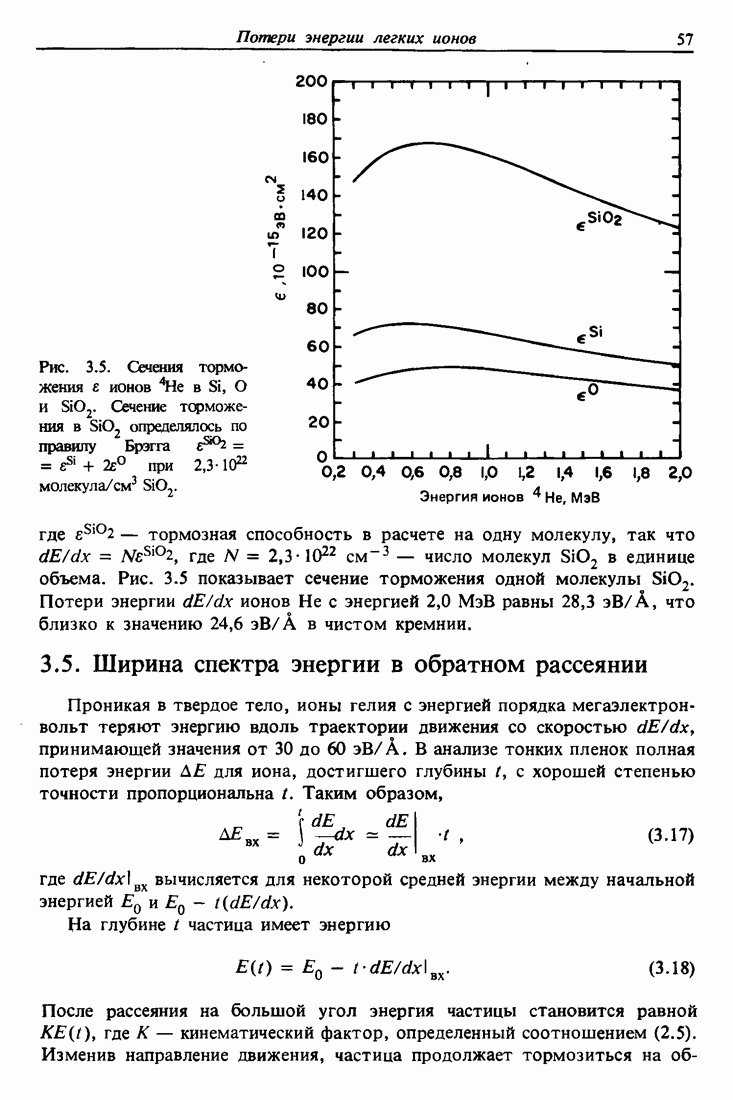
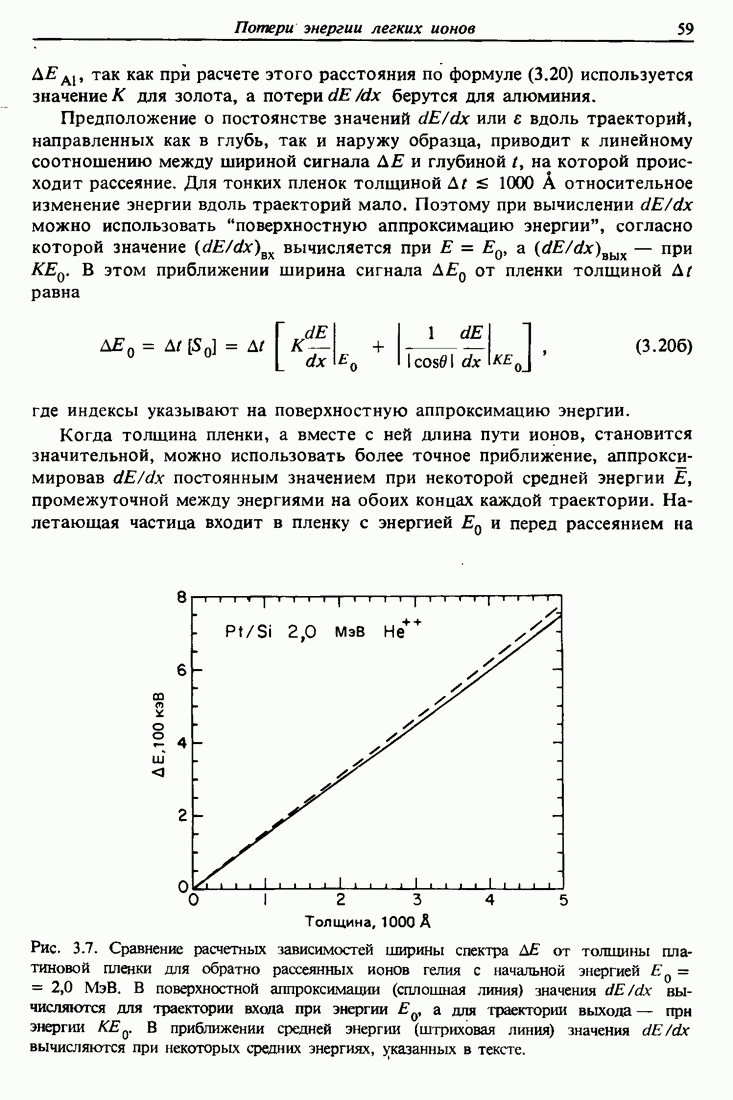
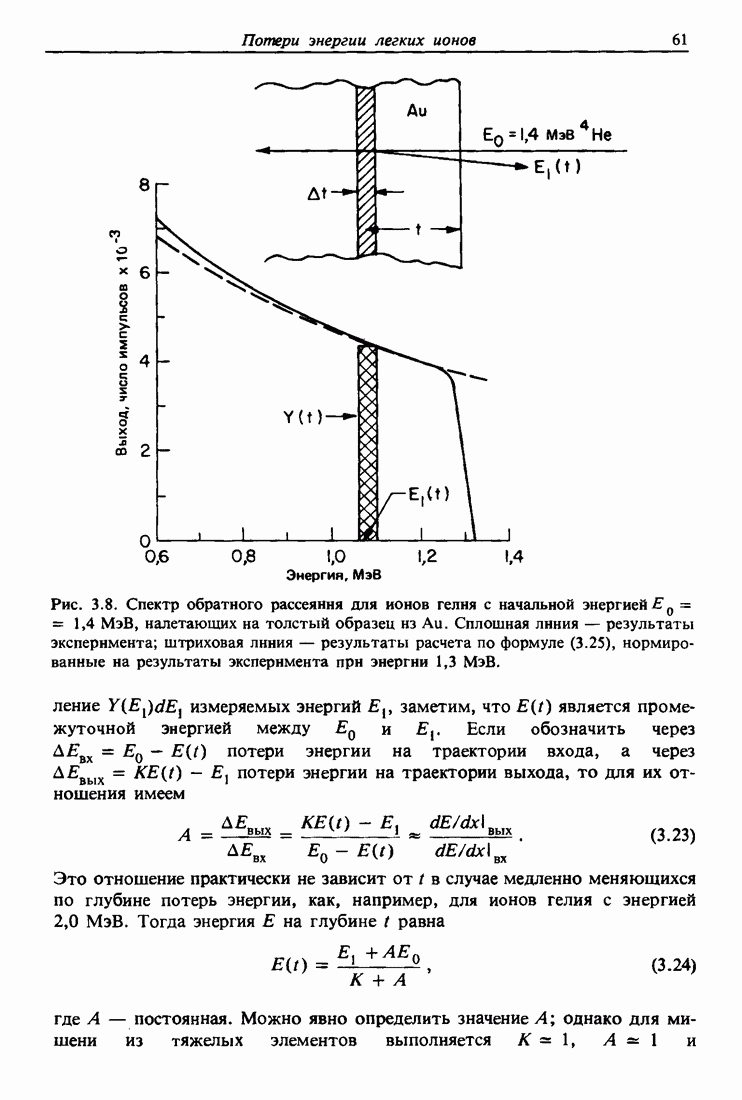
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
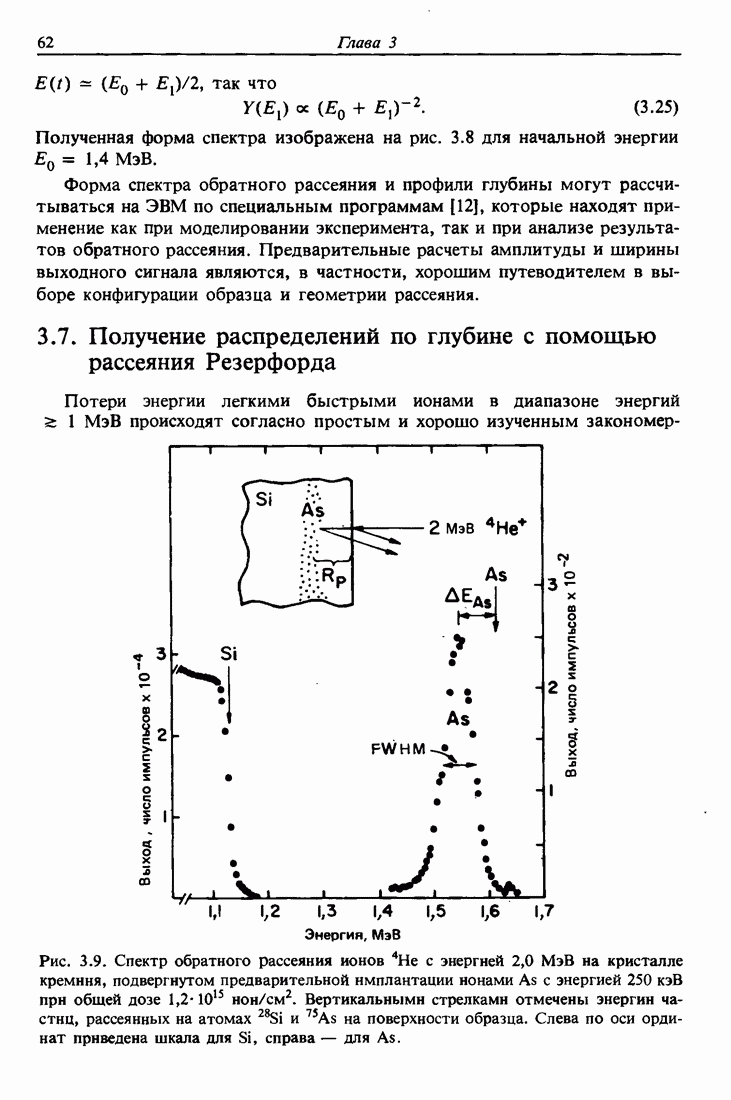
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
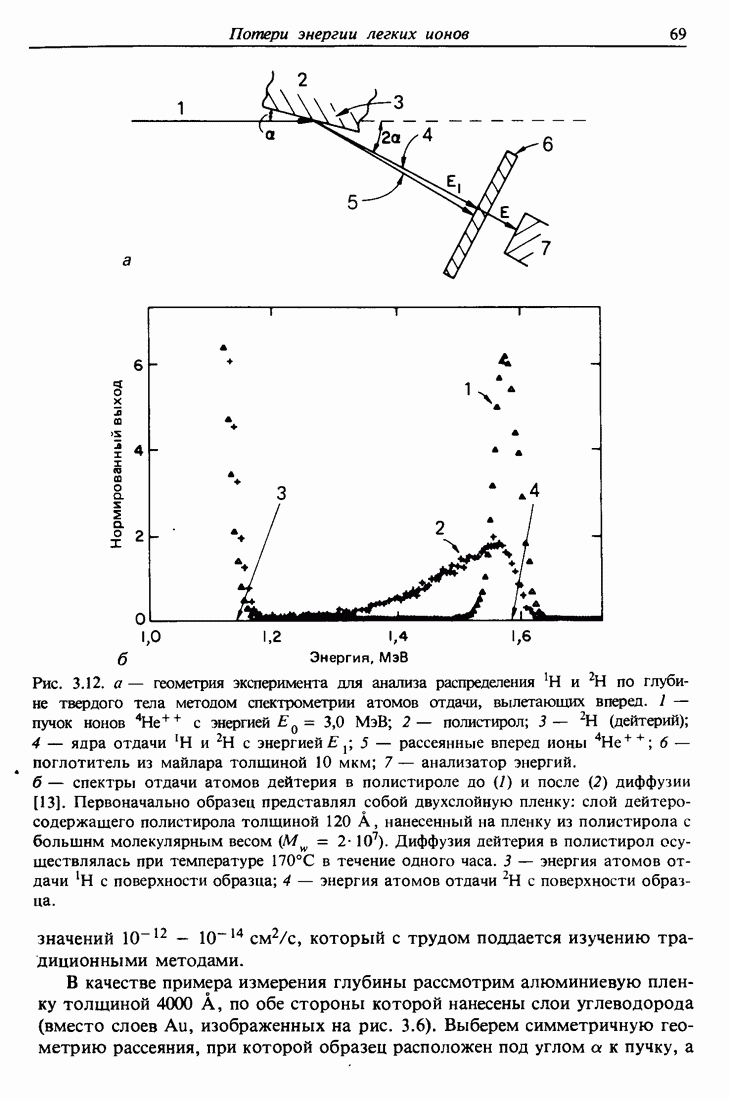
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
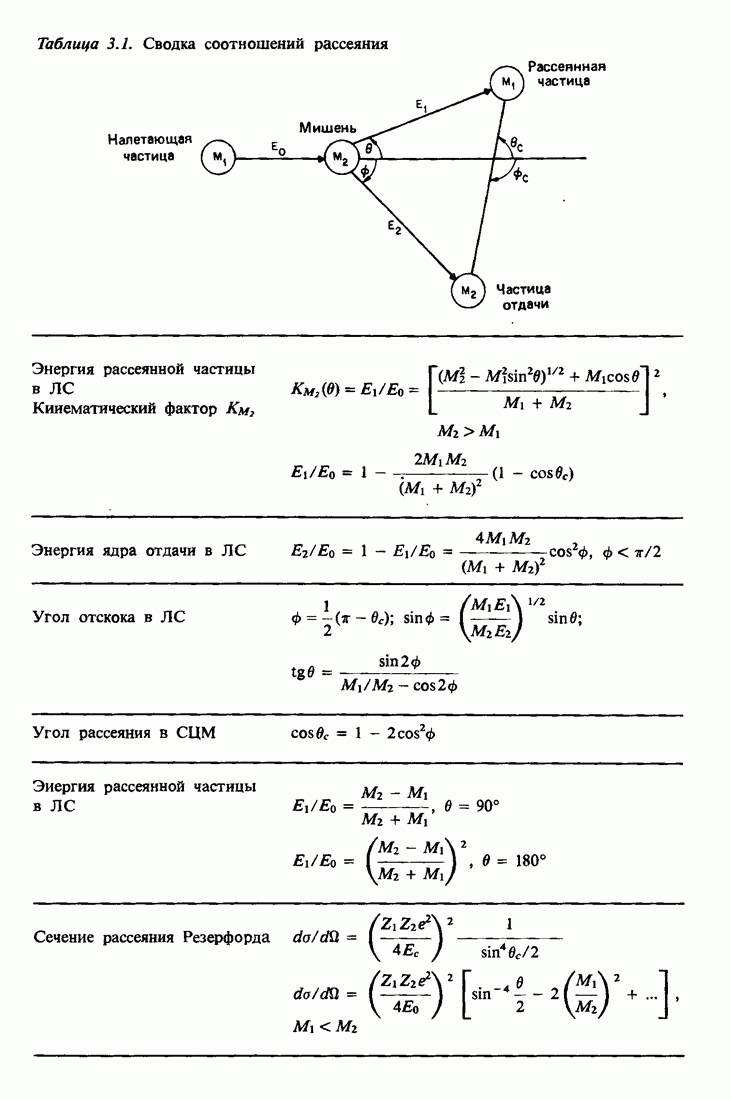
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
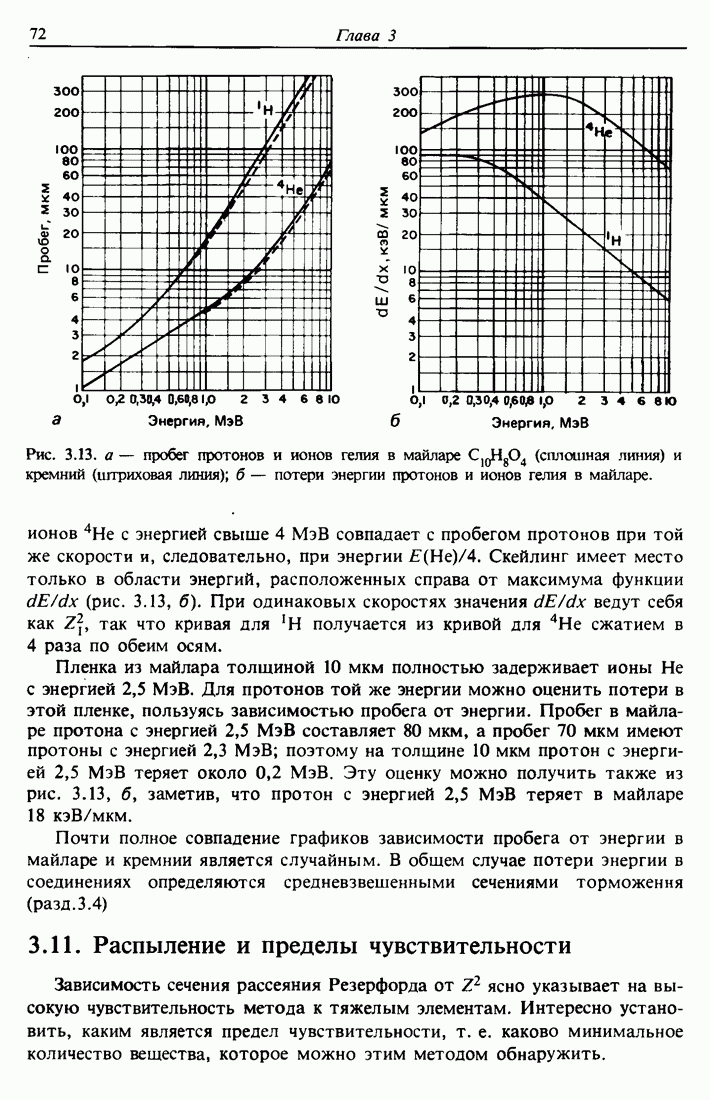
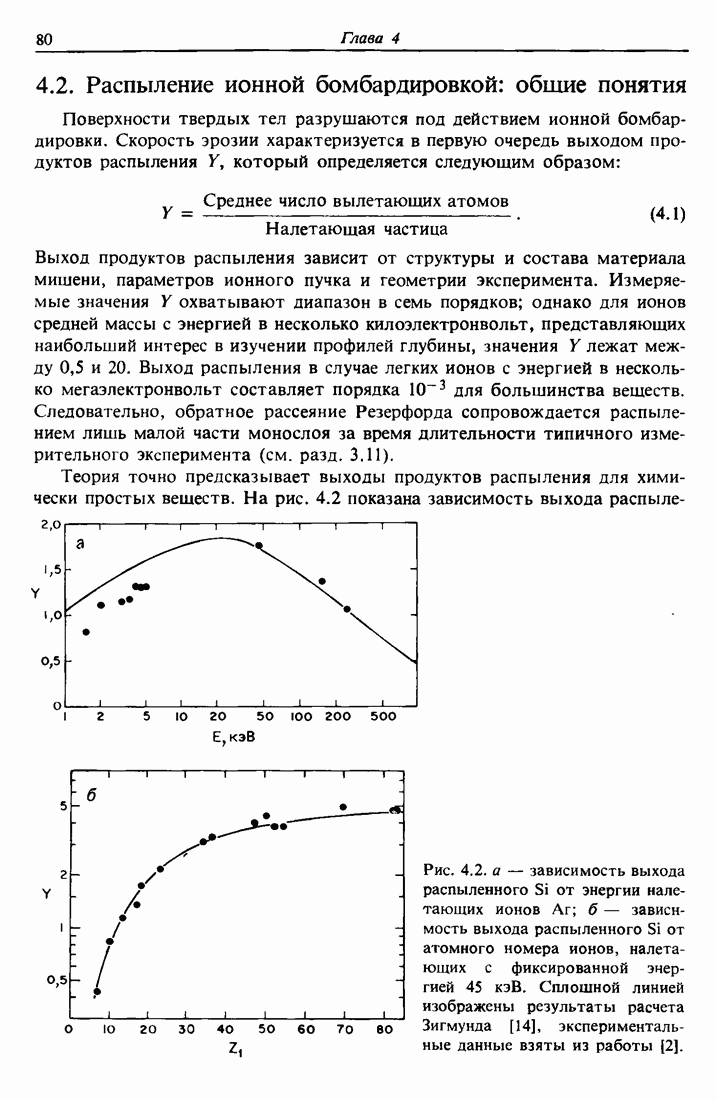
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
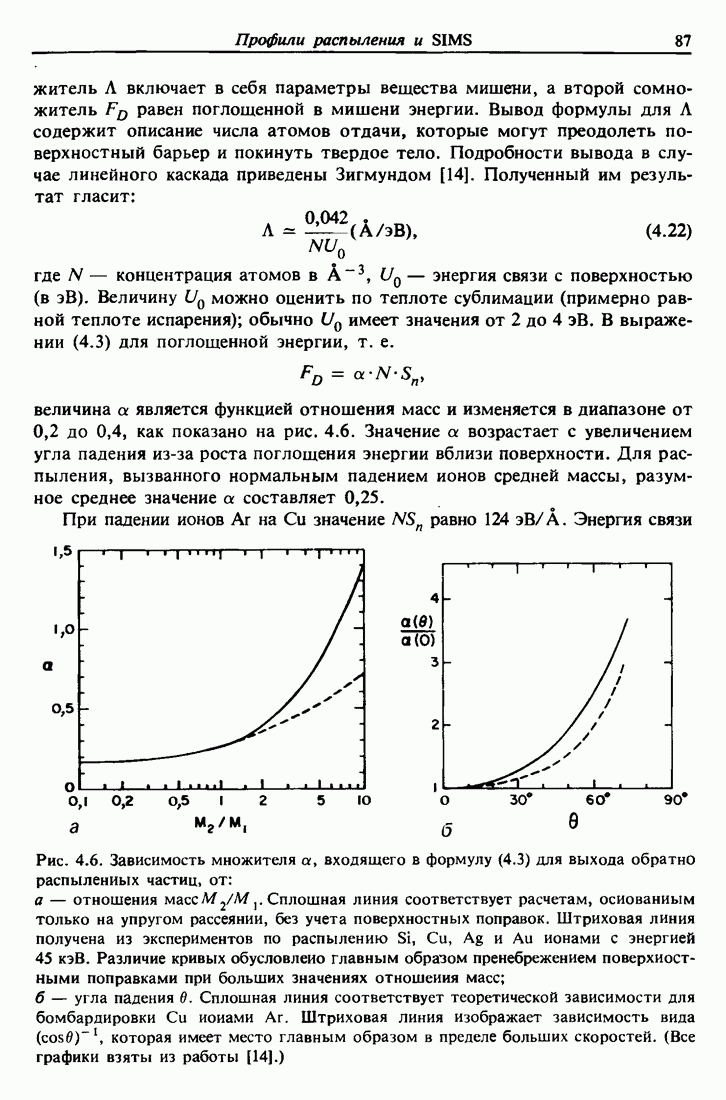
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
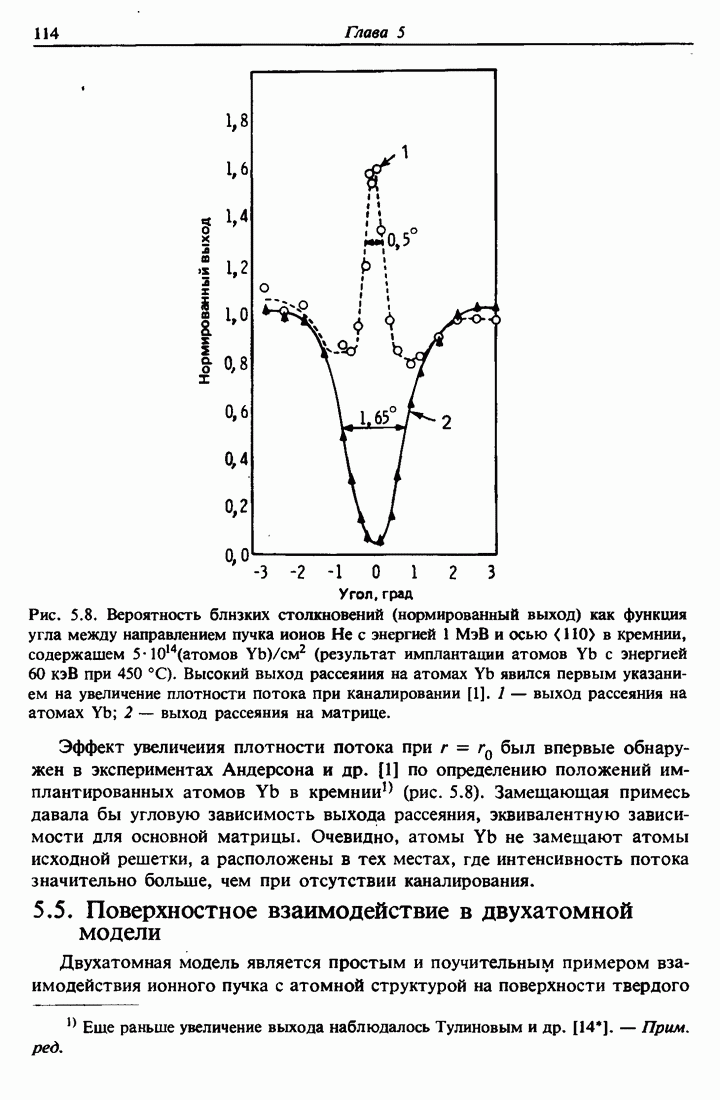
- 5.3. Определение месторасположения примесей в кристаллах
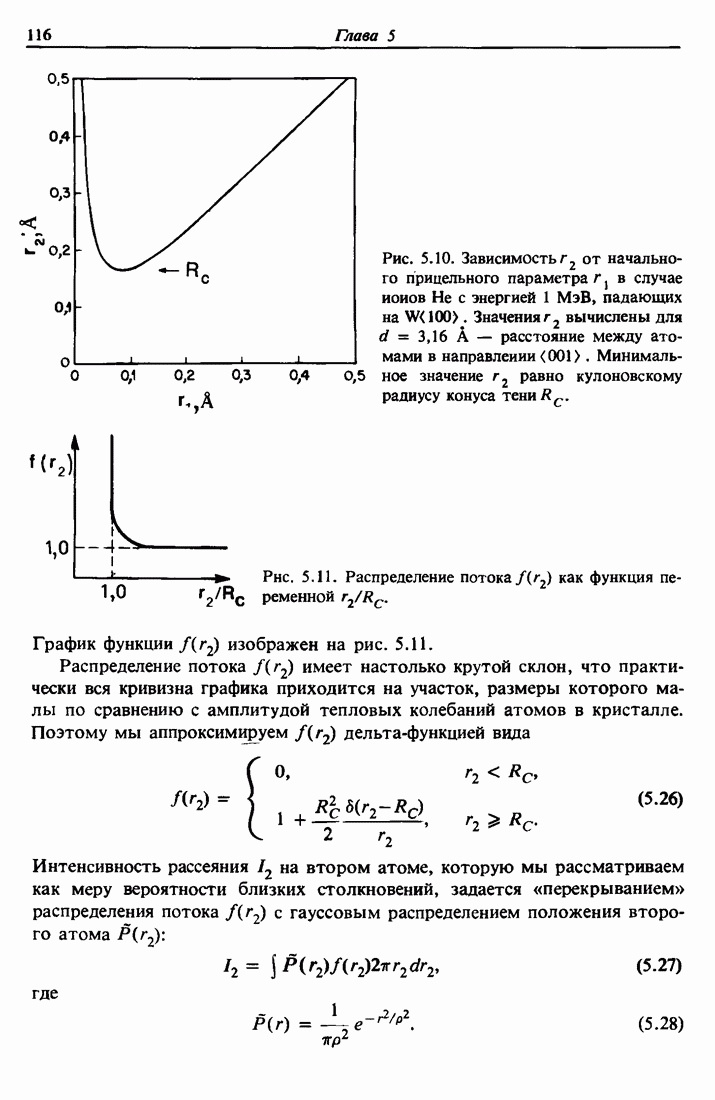
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
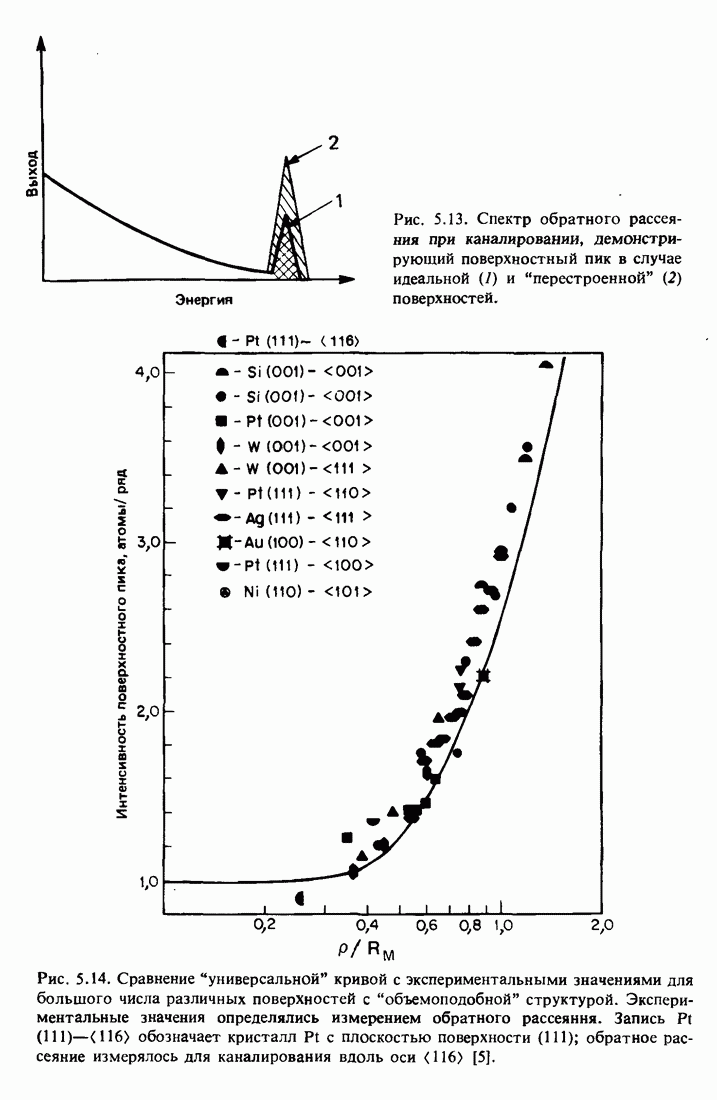
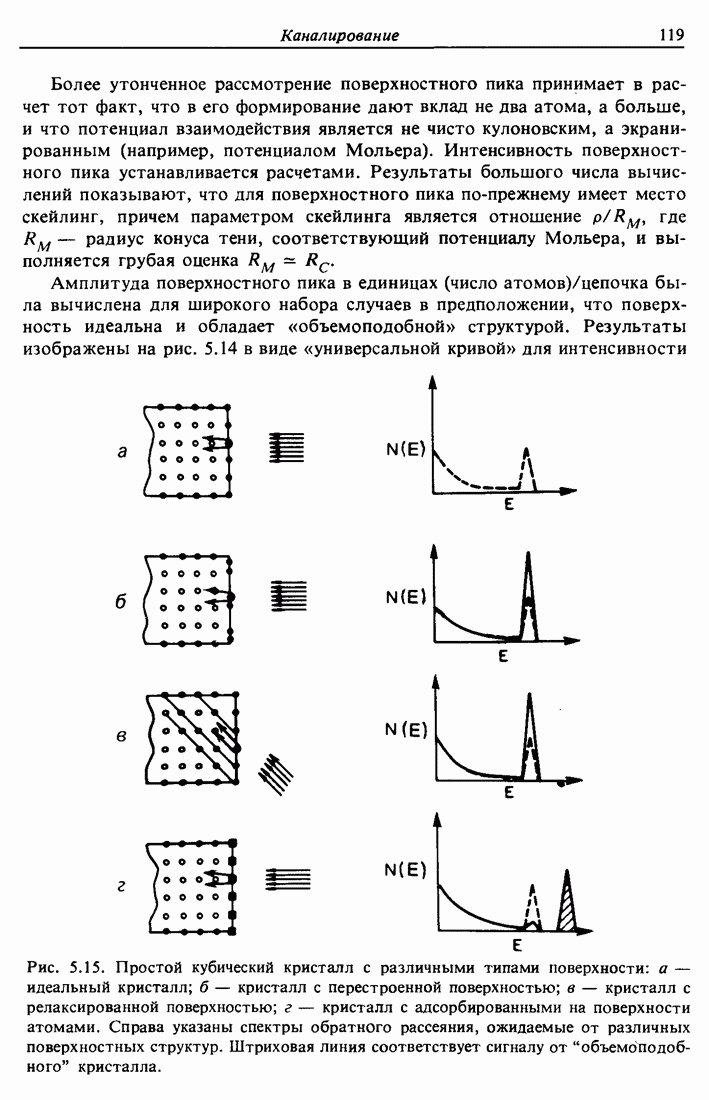
- 5.6. Поверхностный пик
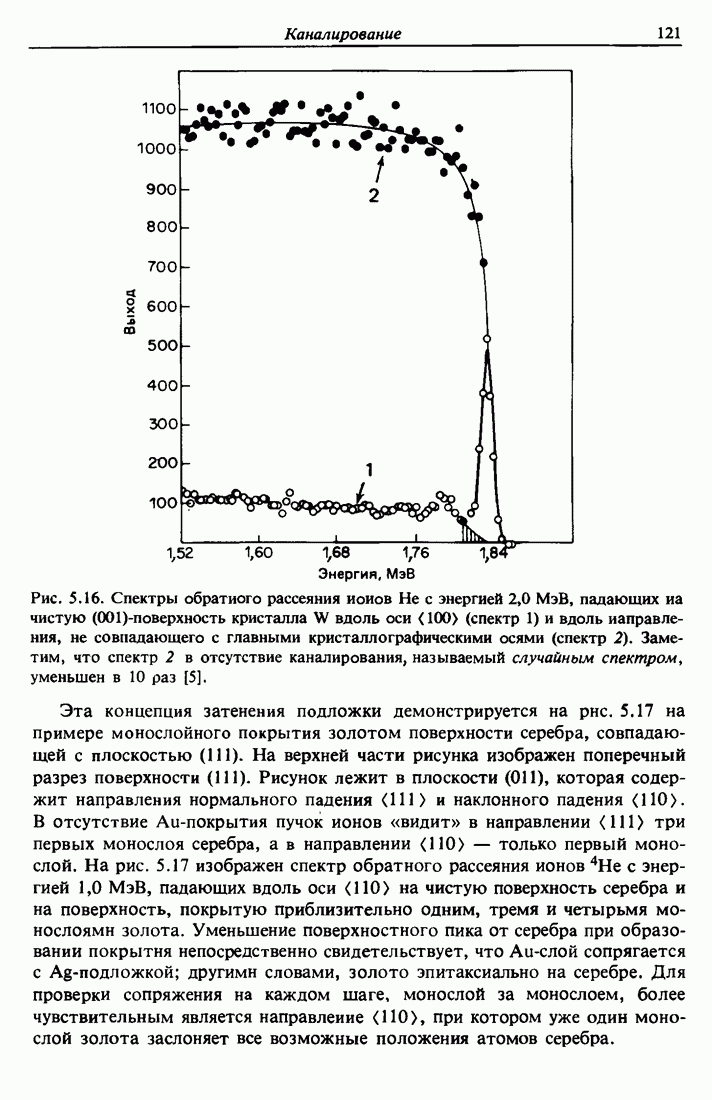
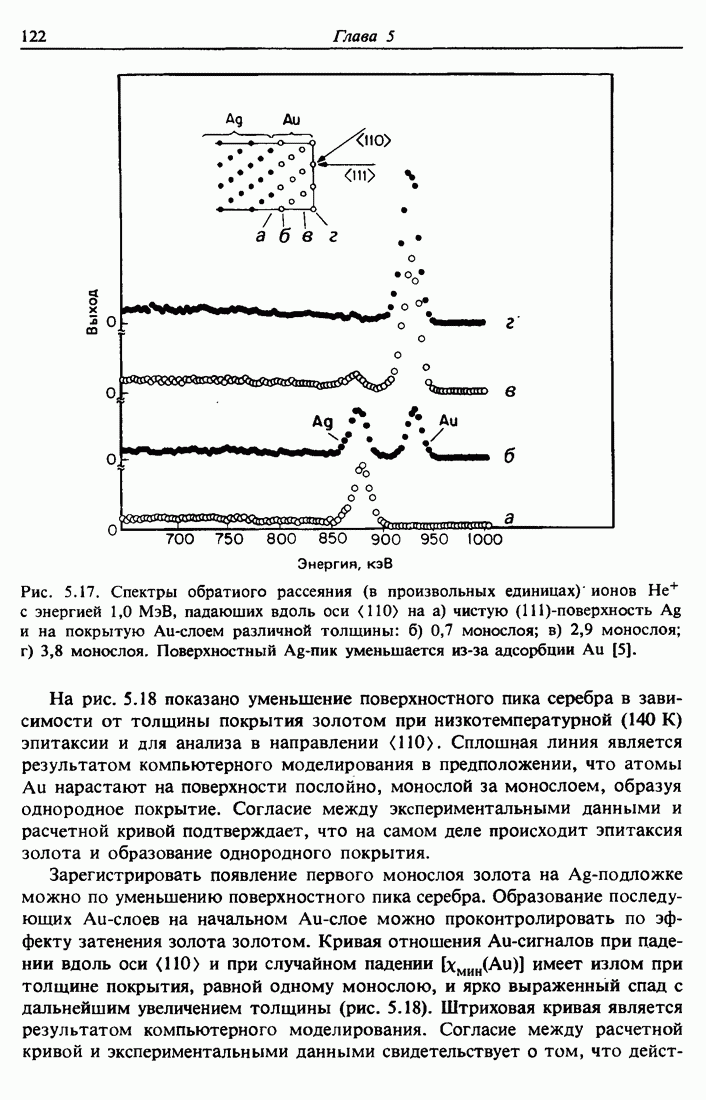
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
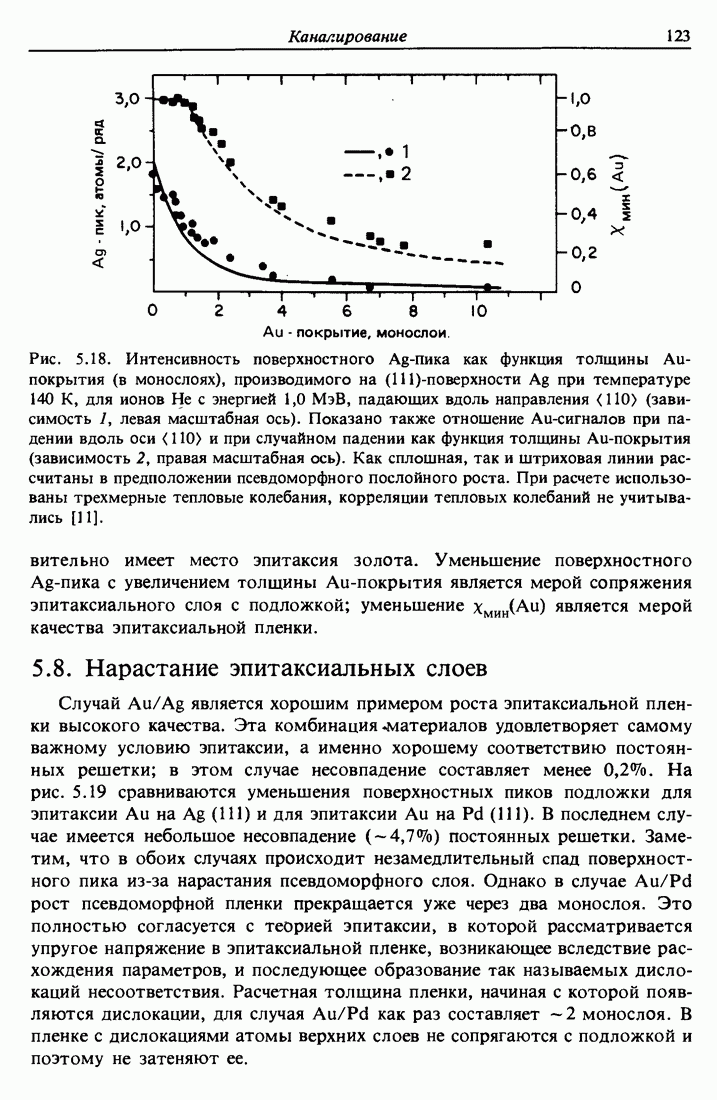
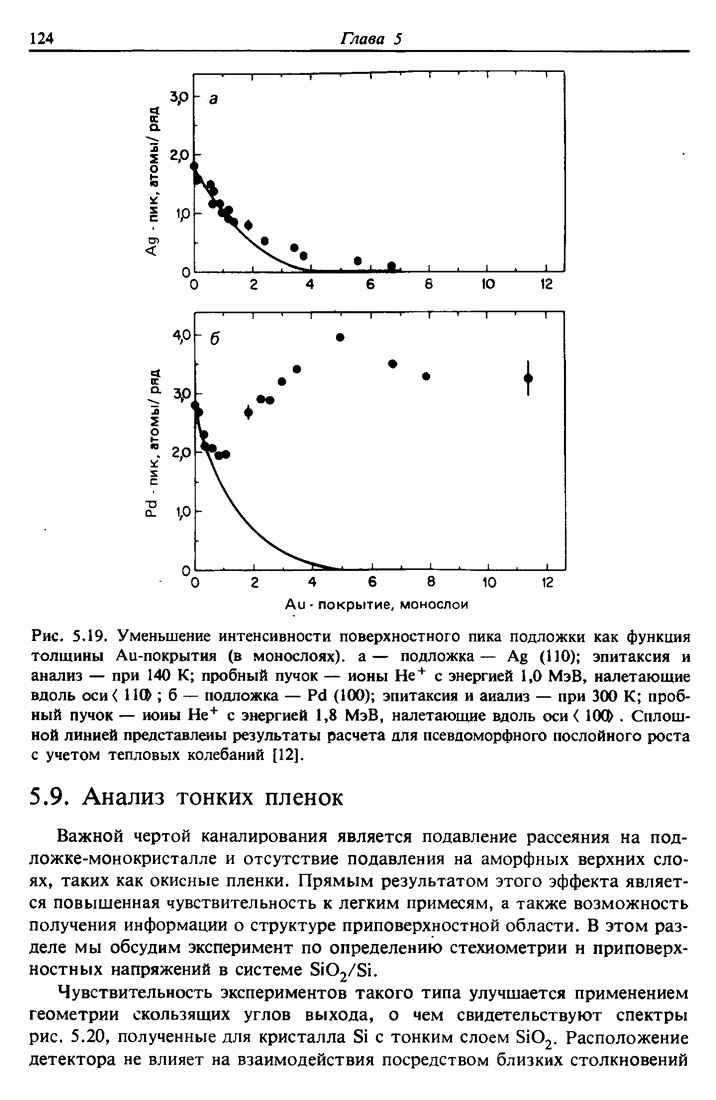
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
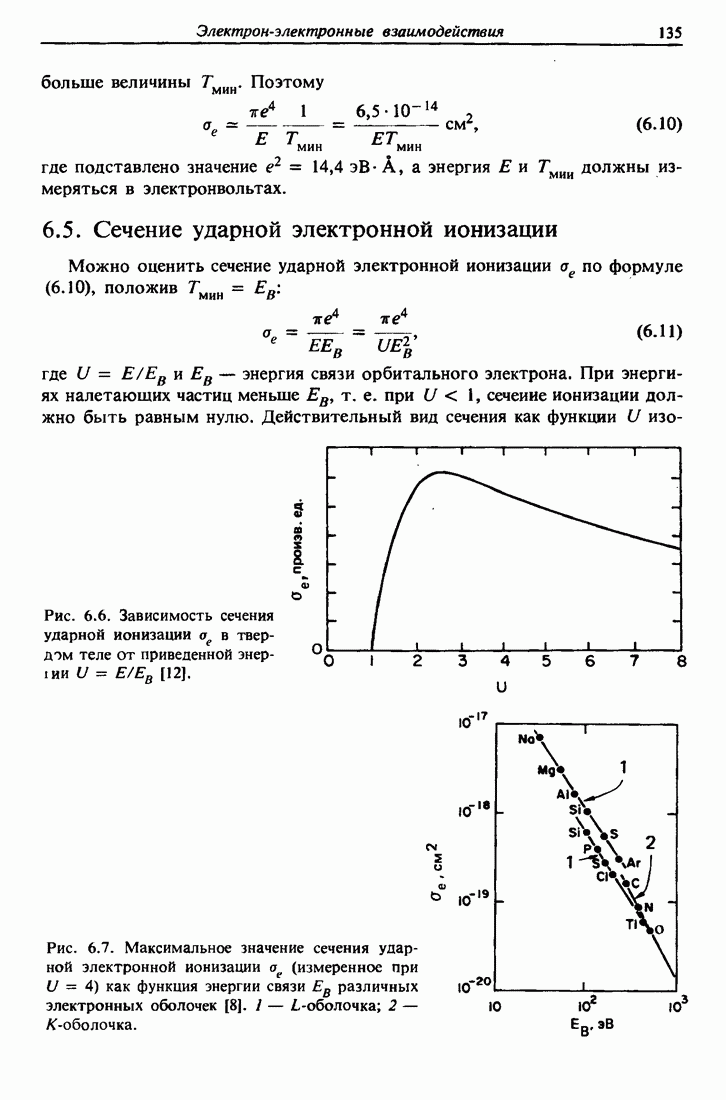
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
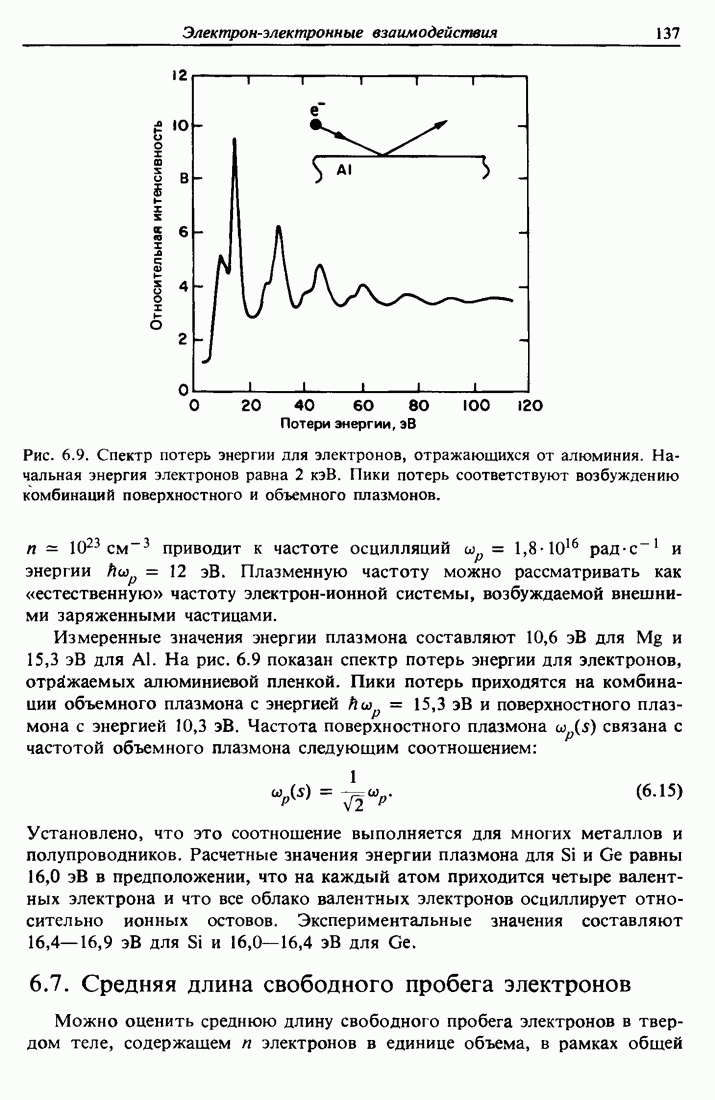
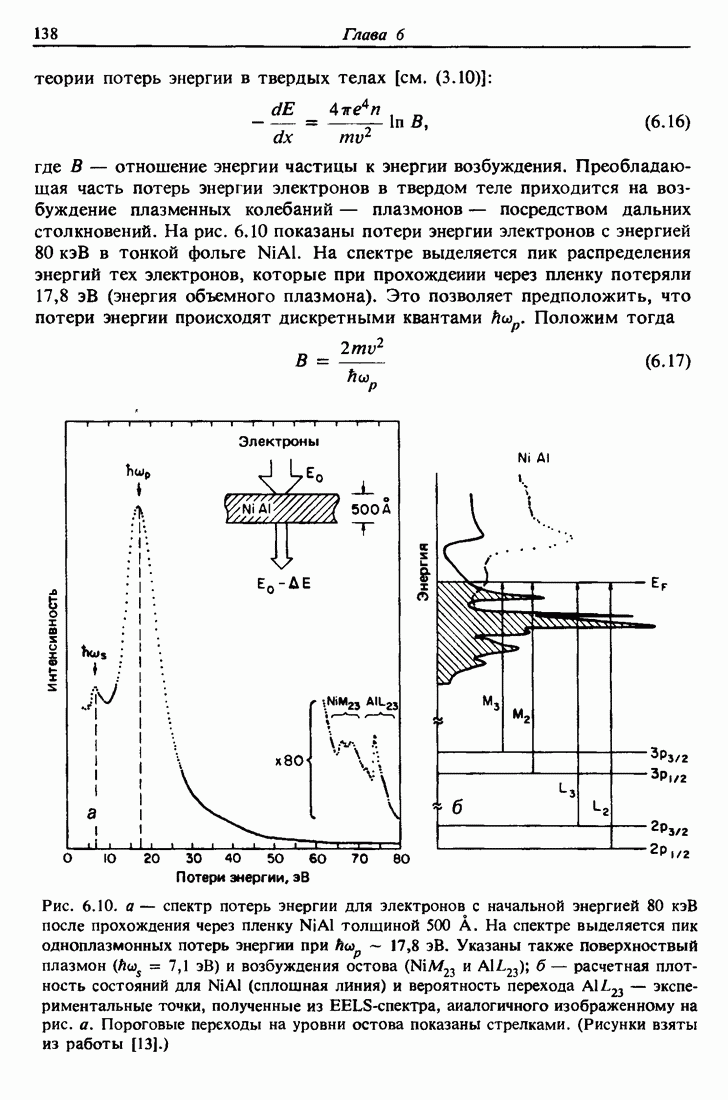
- 6.7. Средняя длина свободного пробега электронов
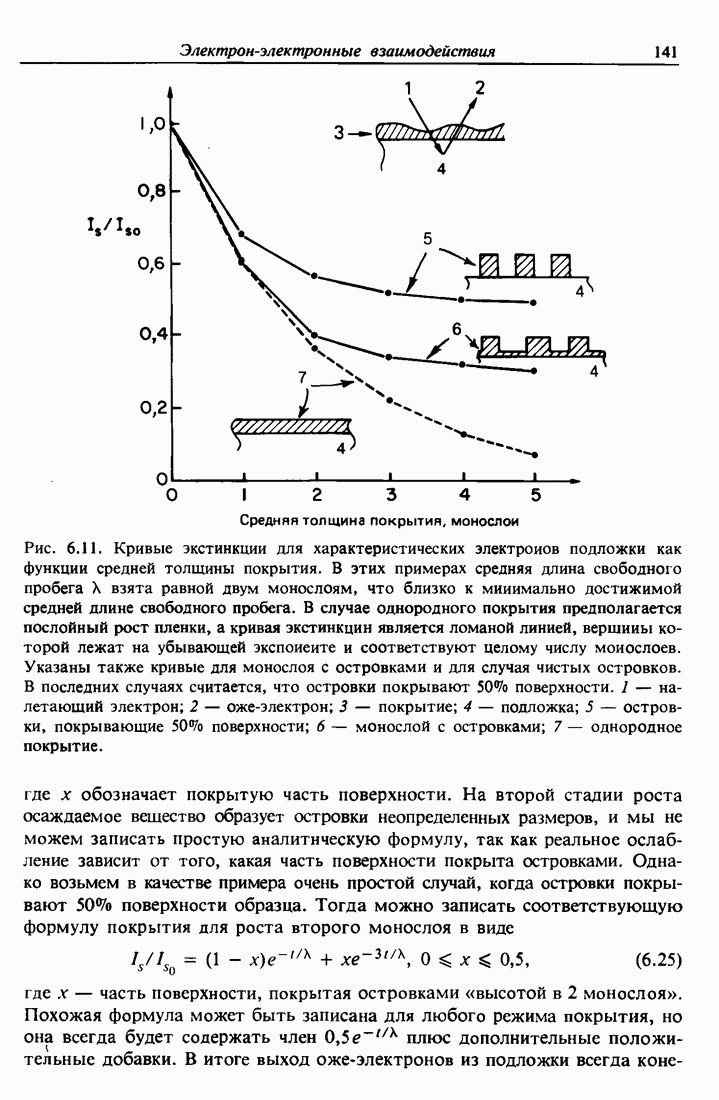
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
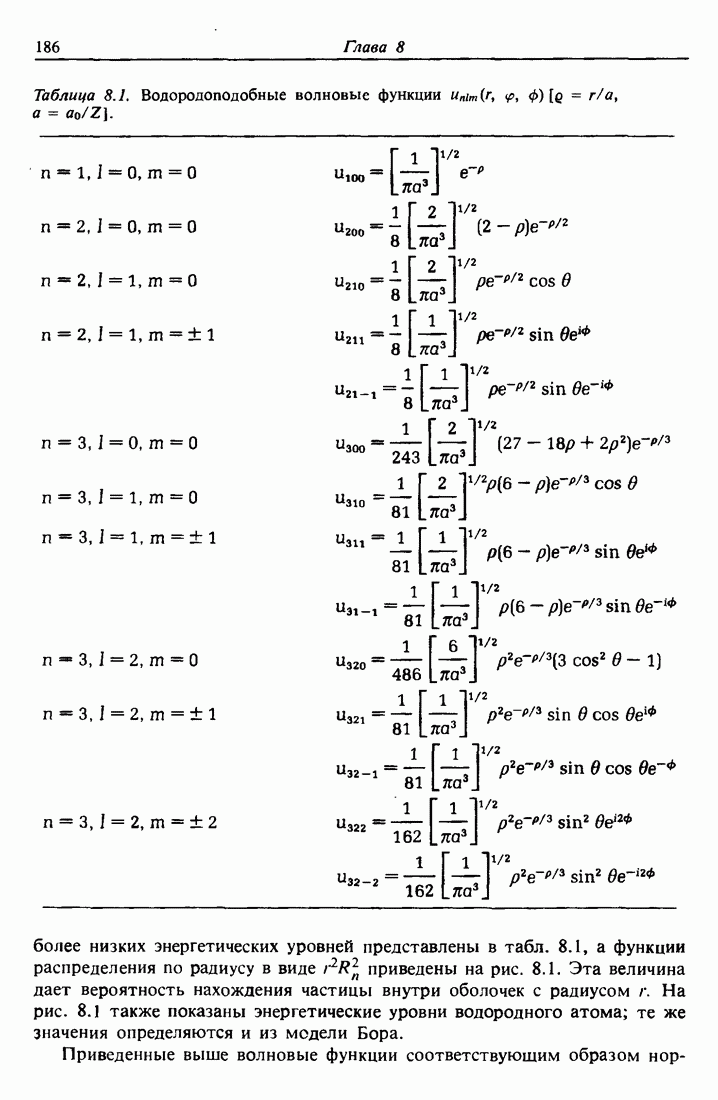
- 8.3. Волновые функции
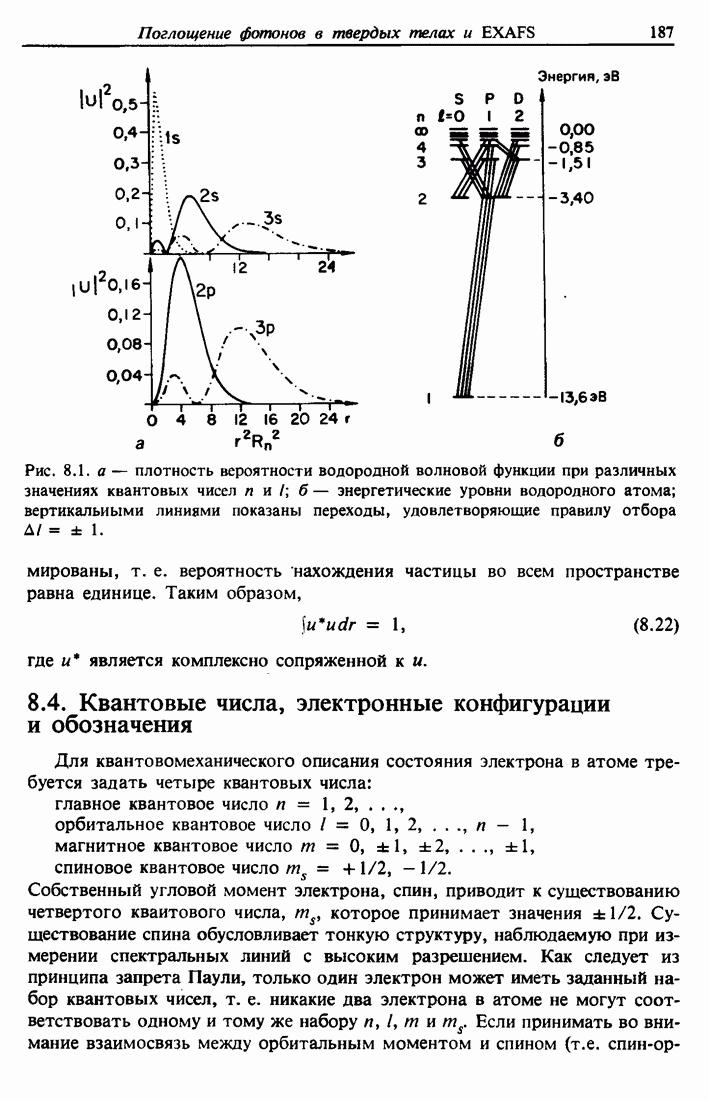
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
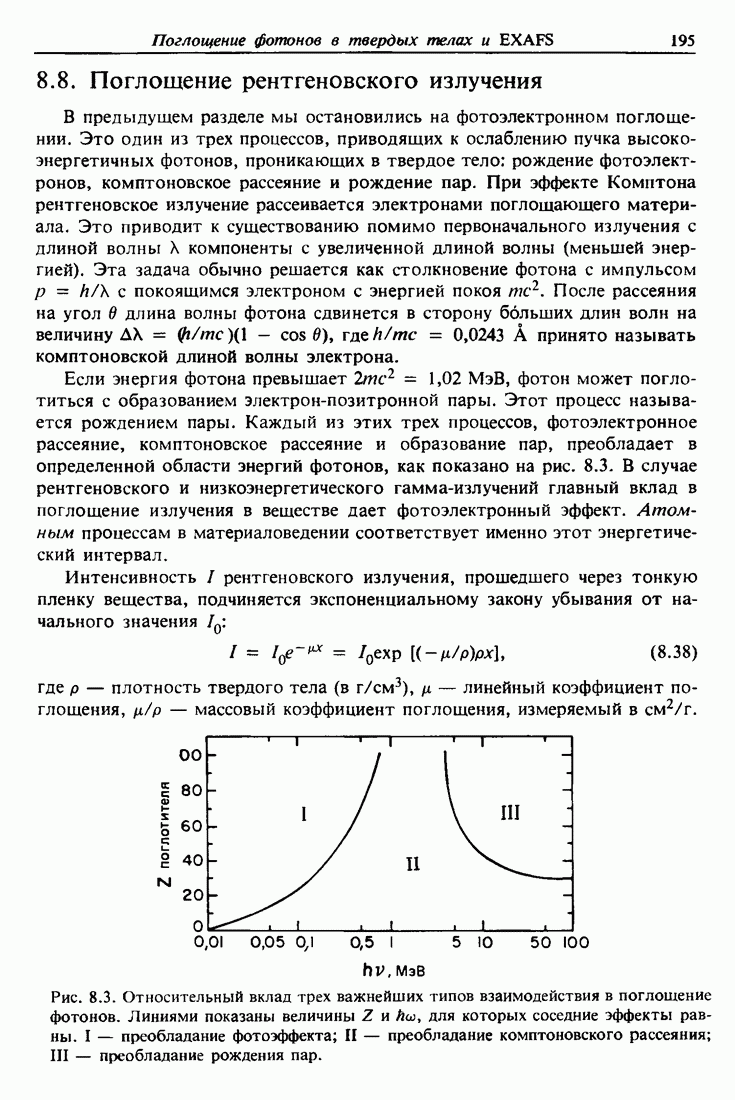
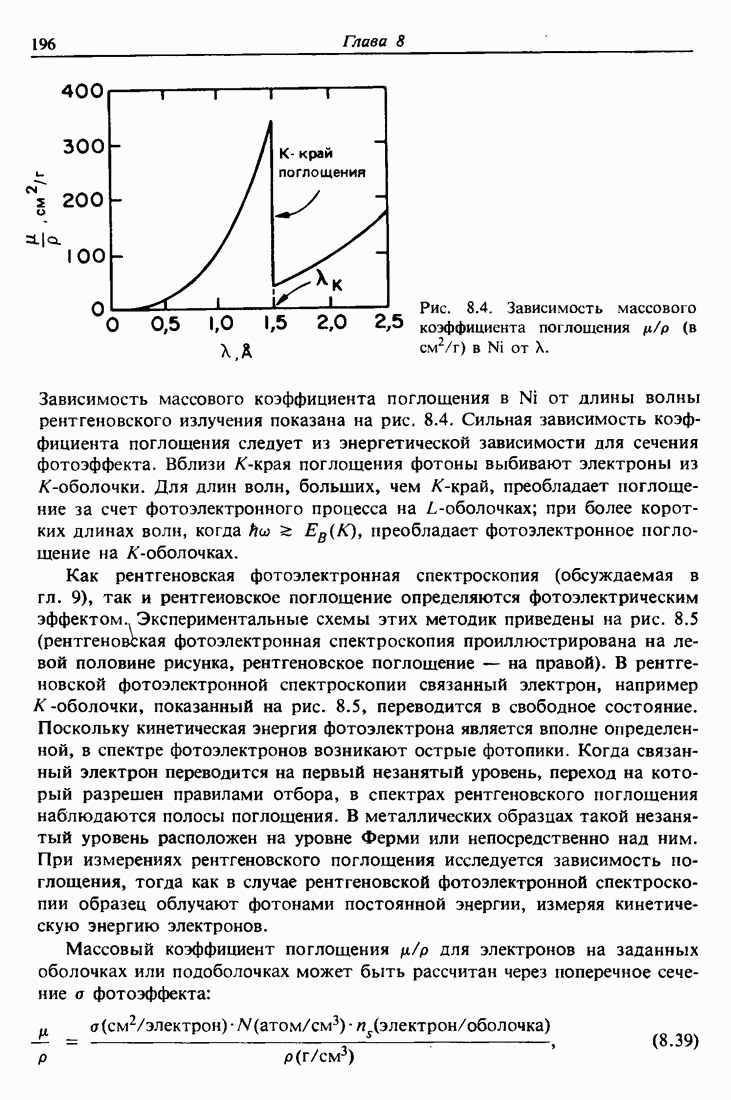
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
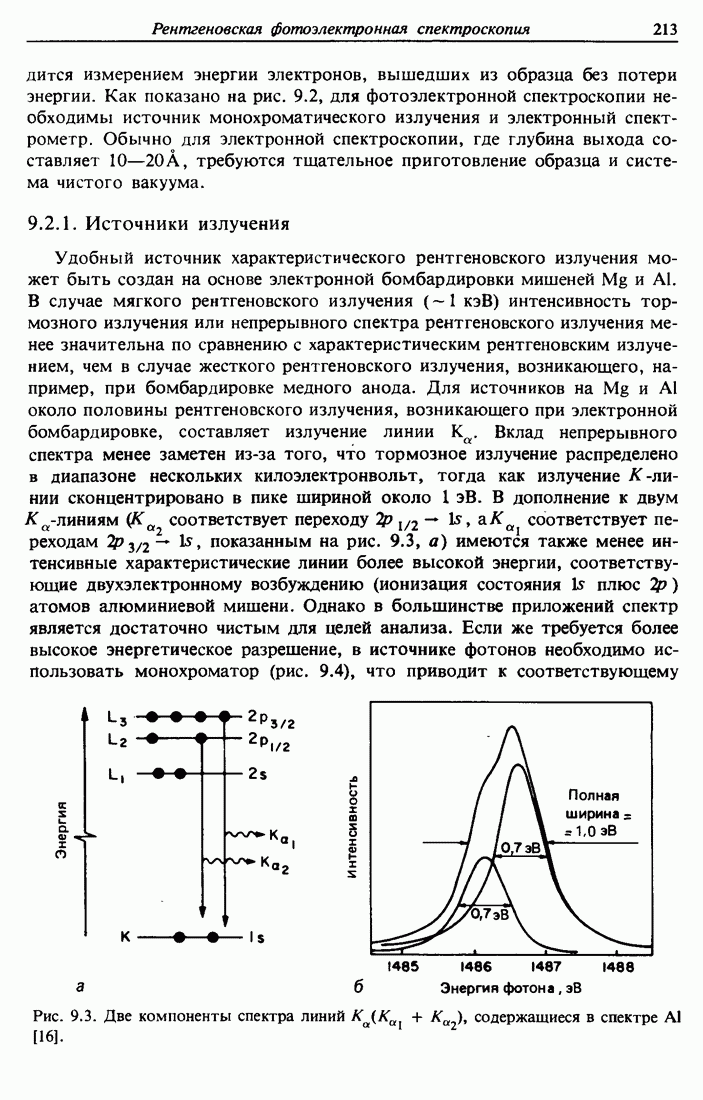
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
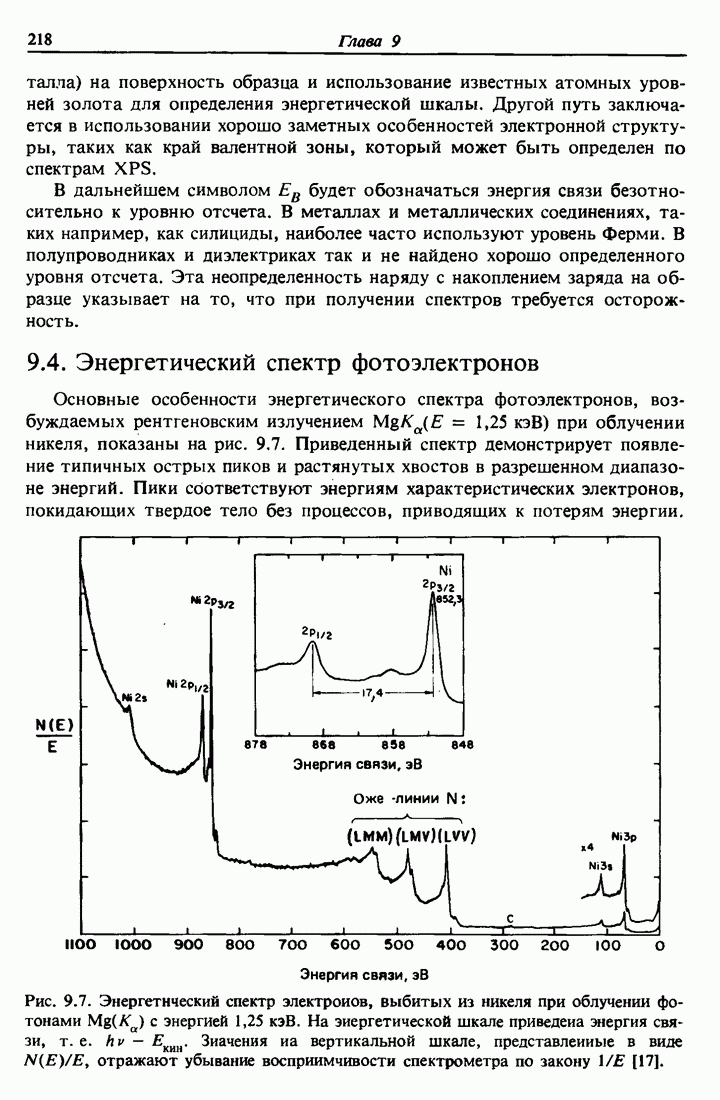
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
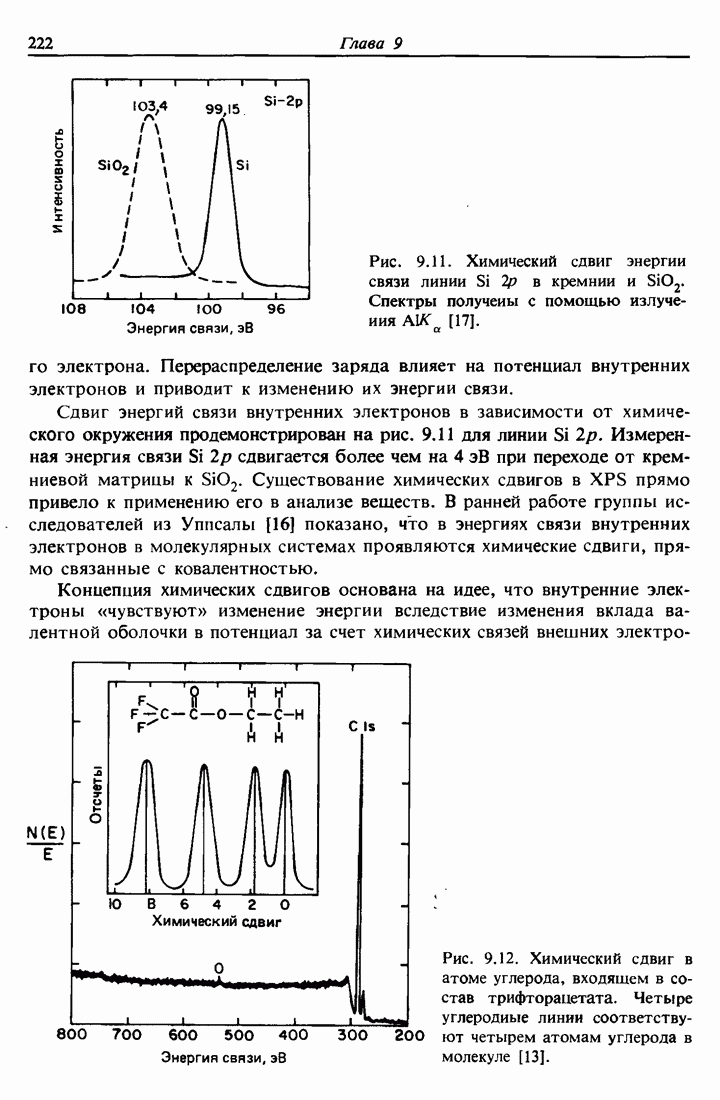
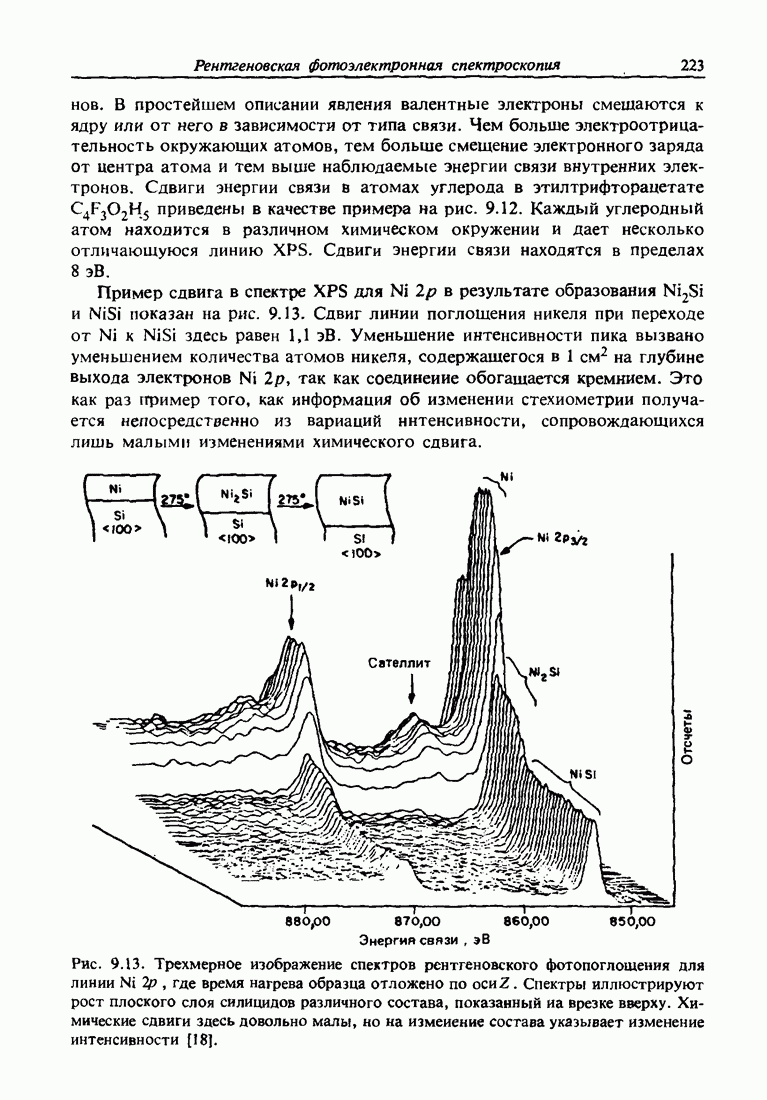
- 9.6. Сдвиги энергии связи; химические сдвиги
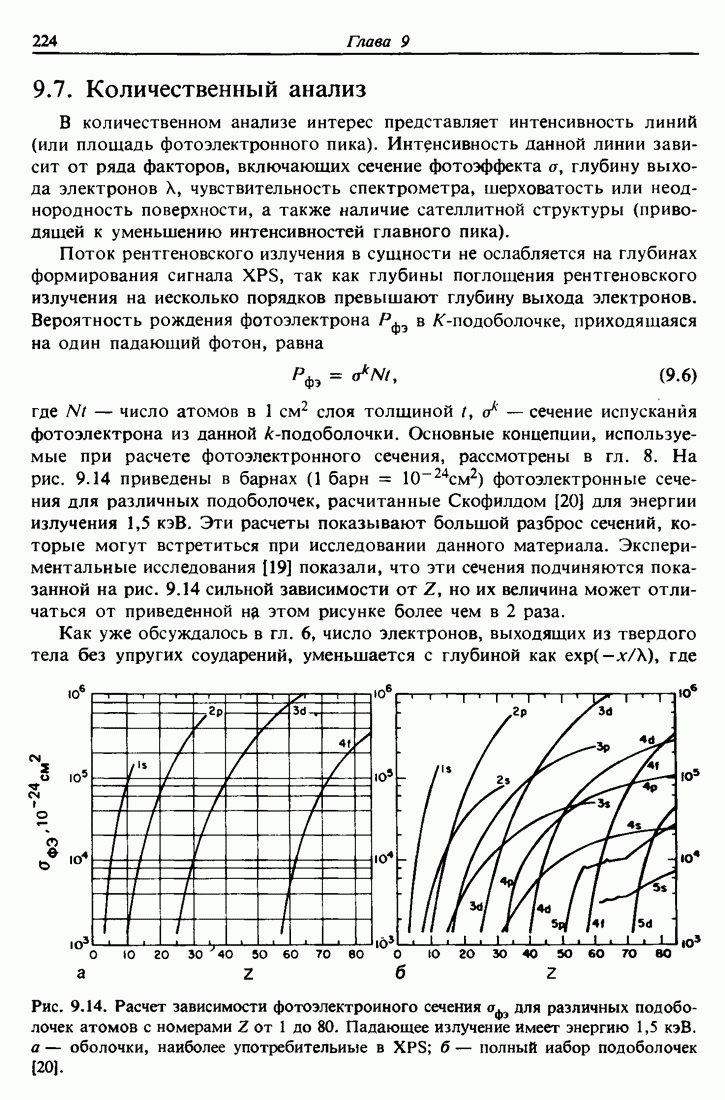
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
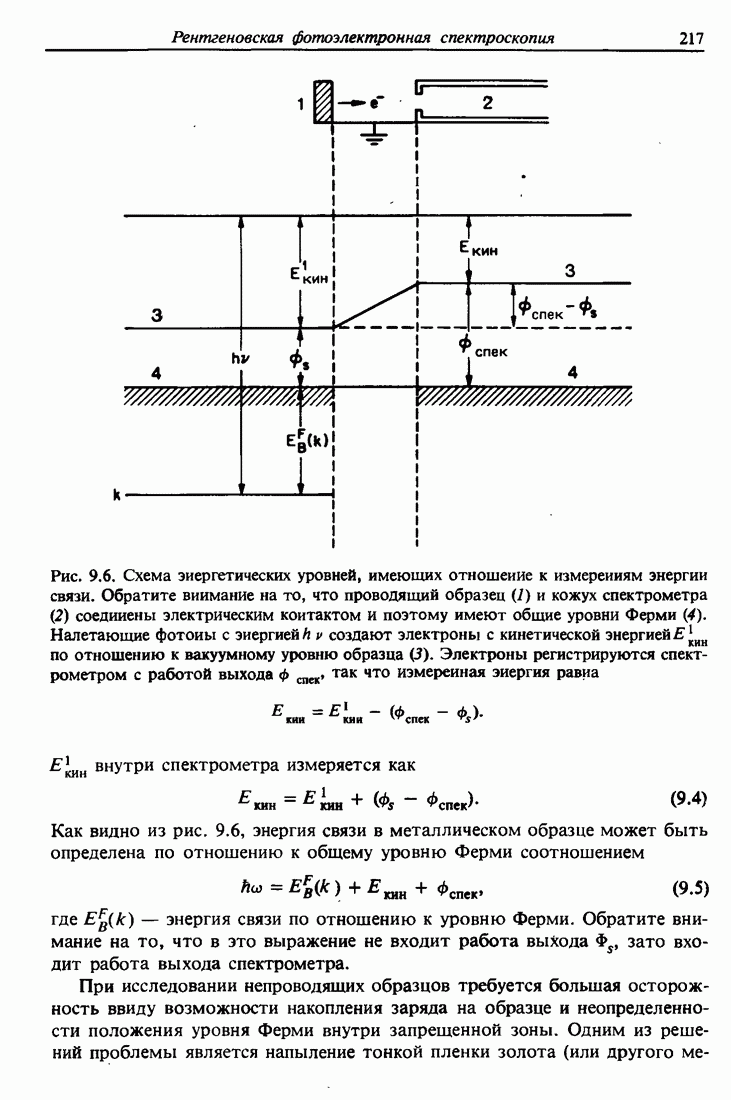
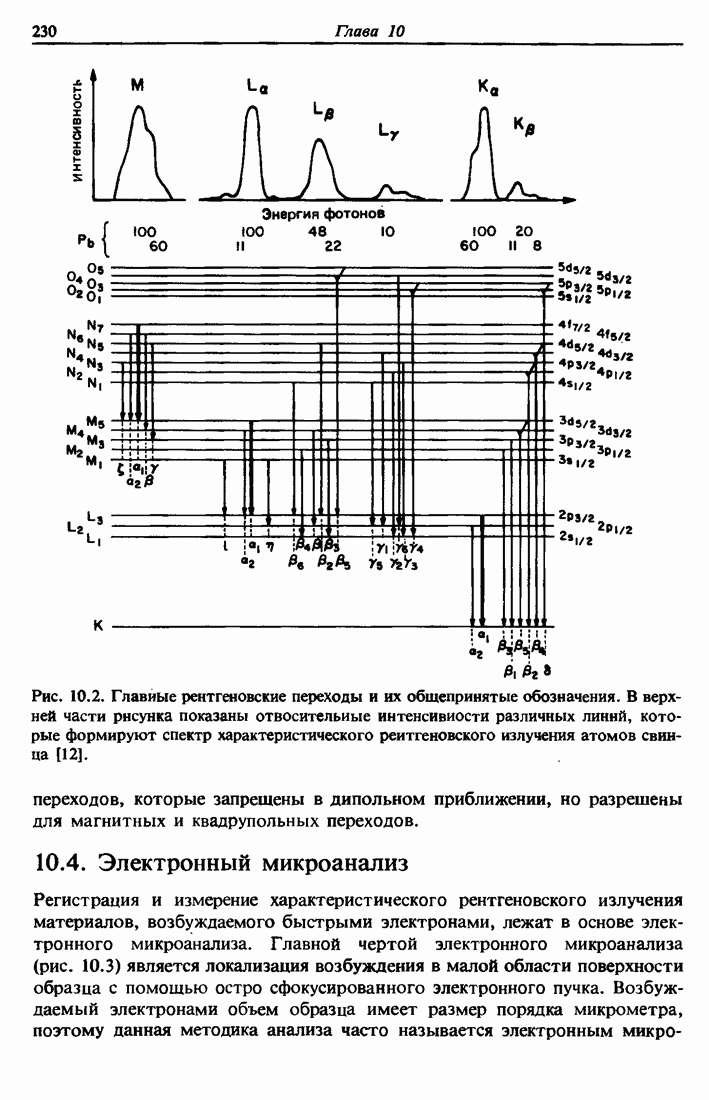
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
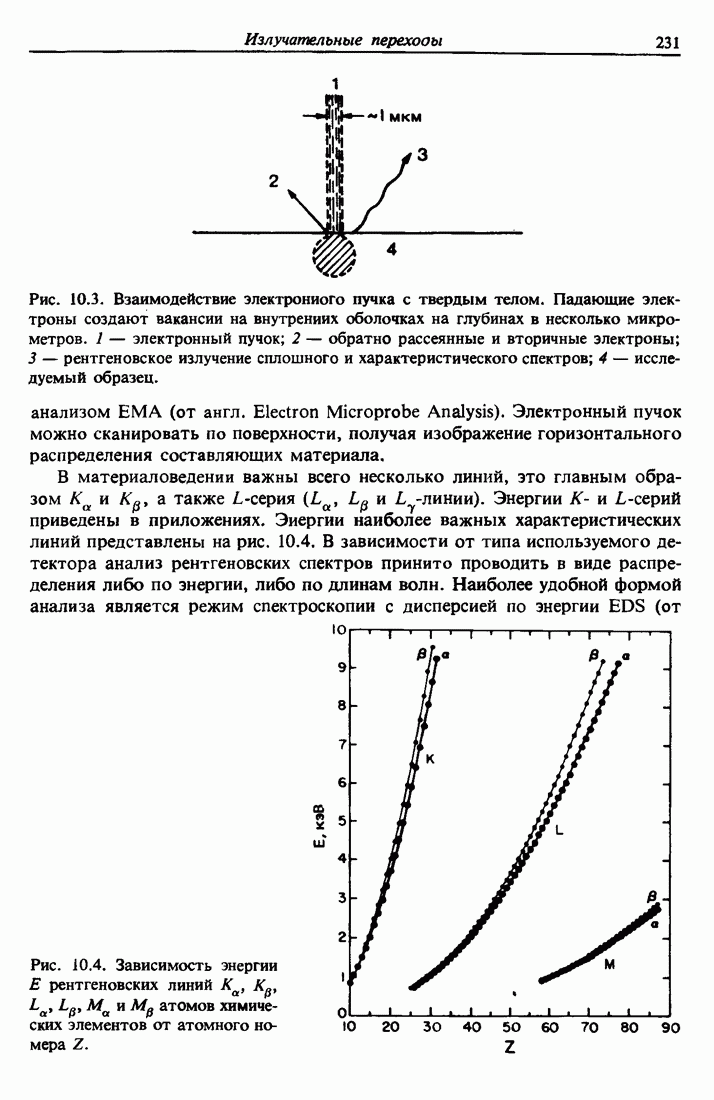
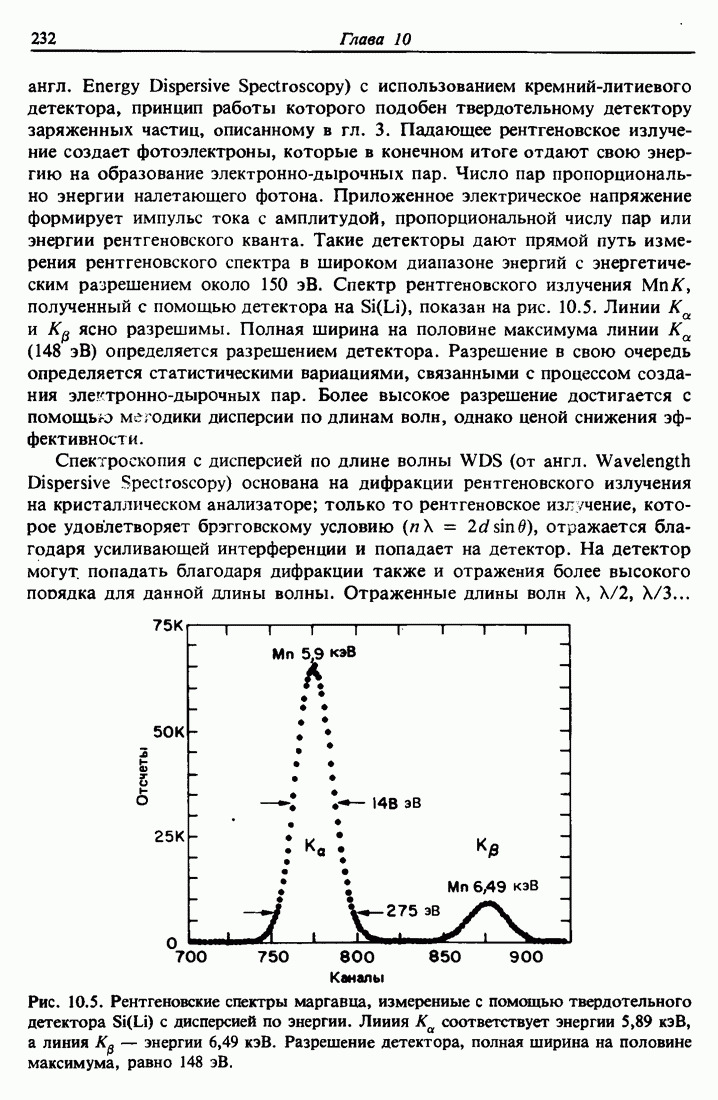
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
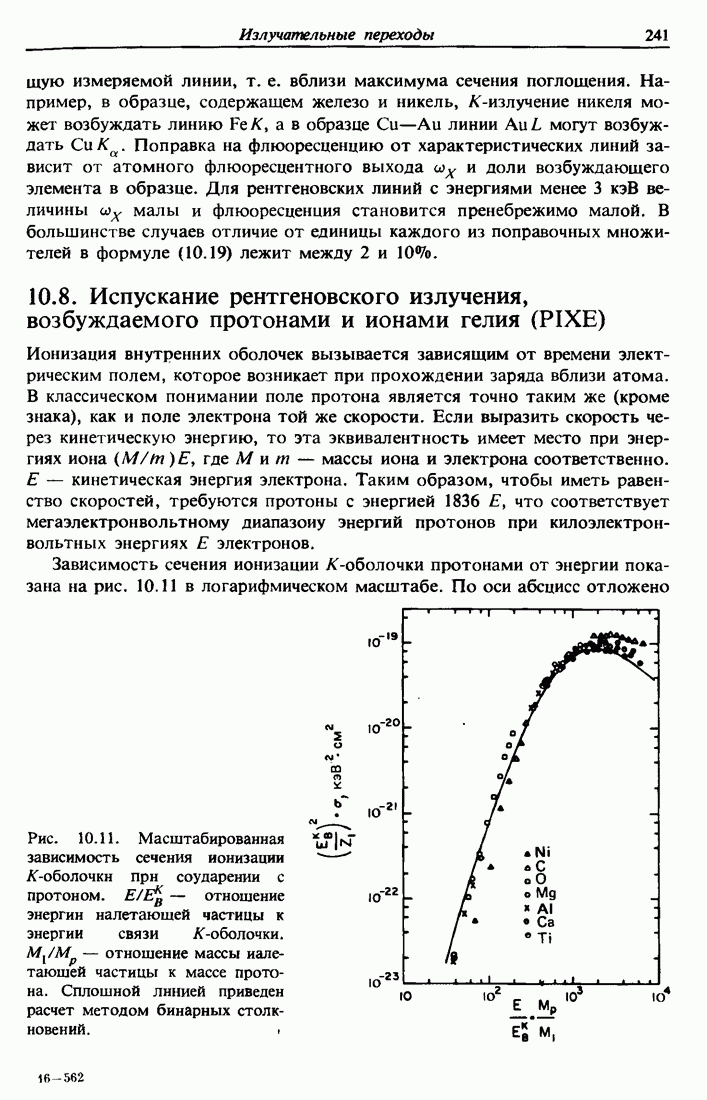
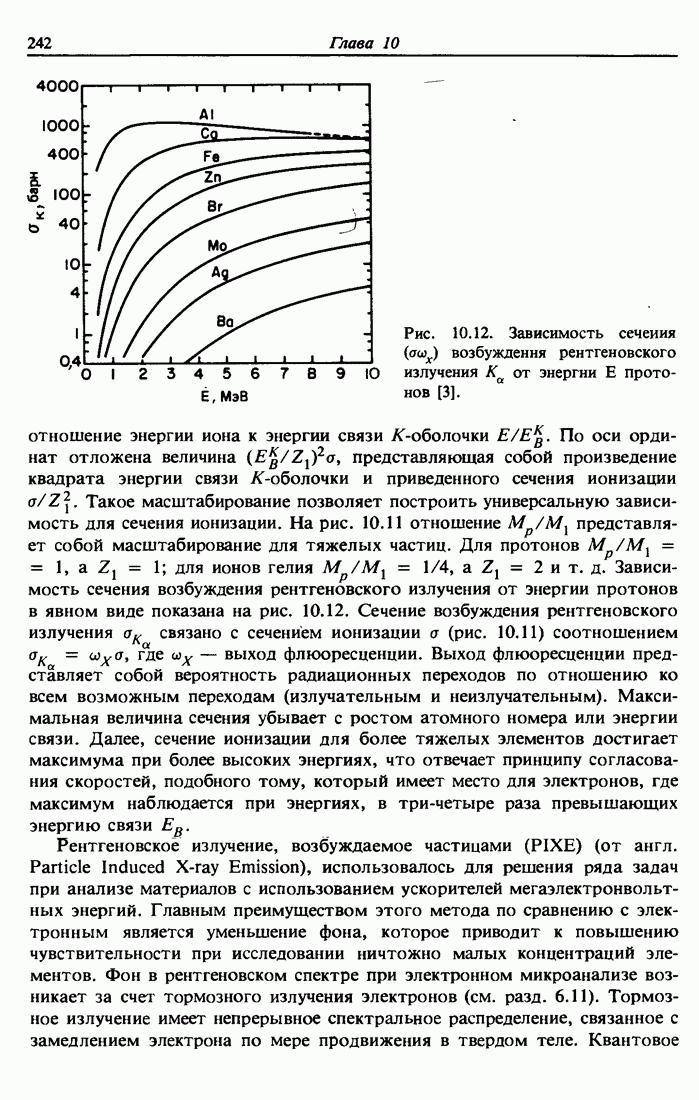
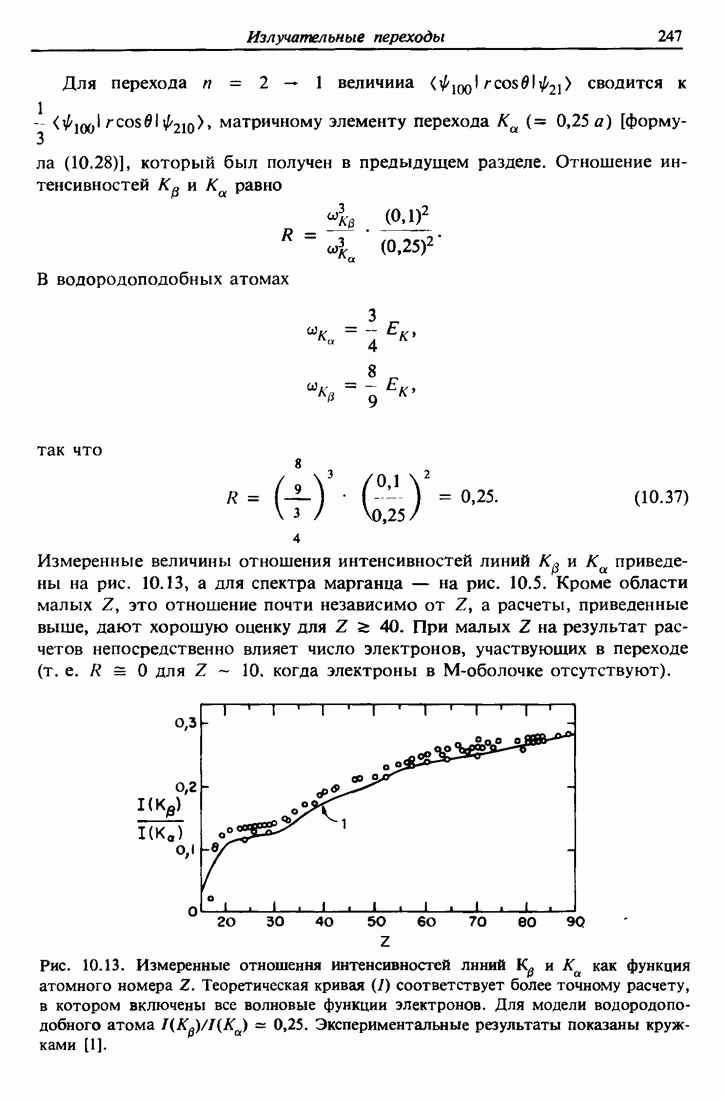
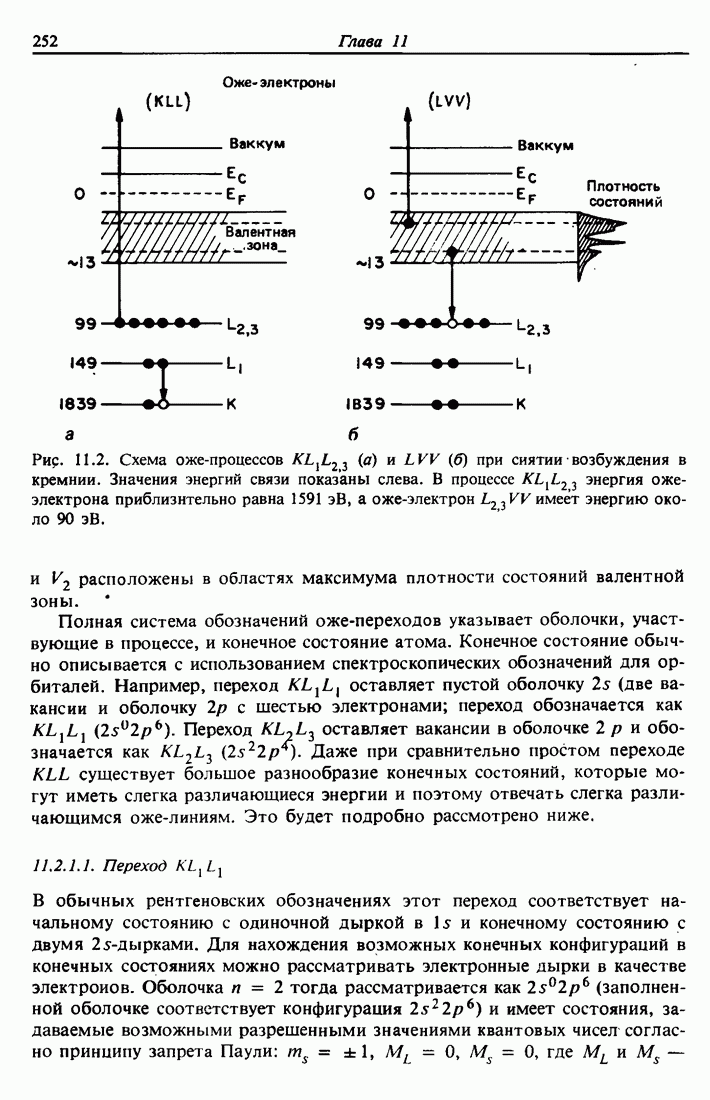
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
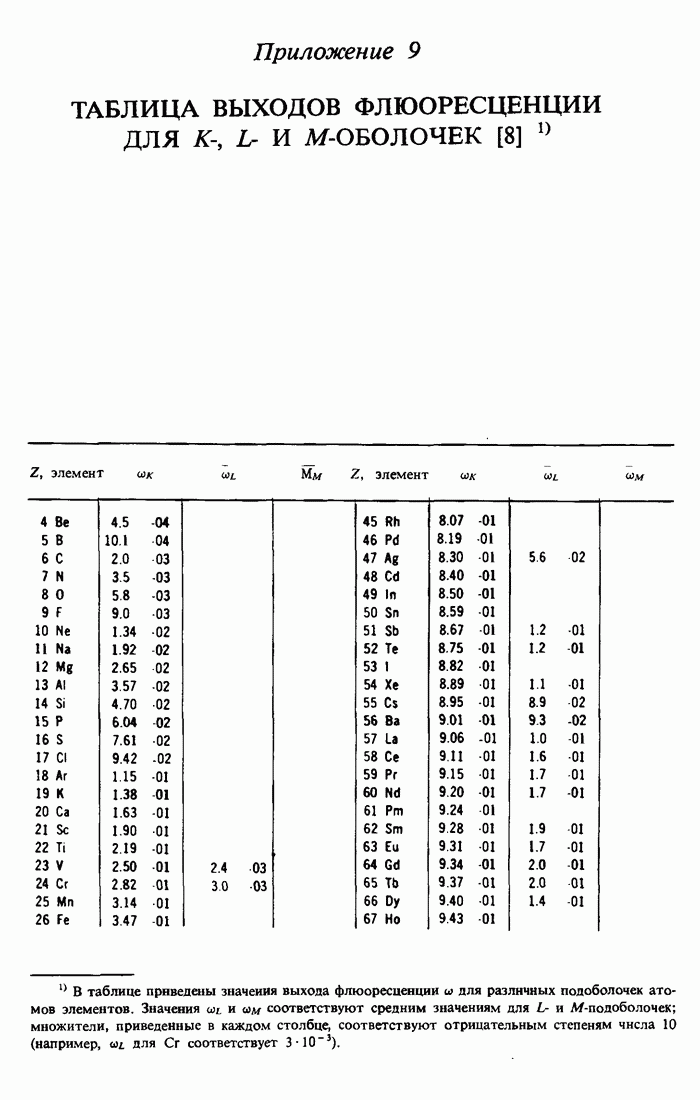
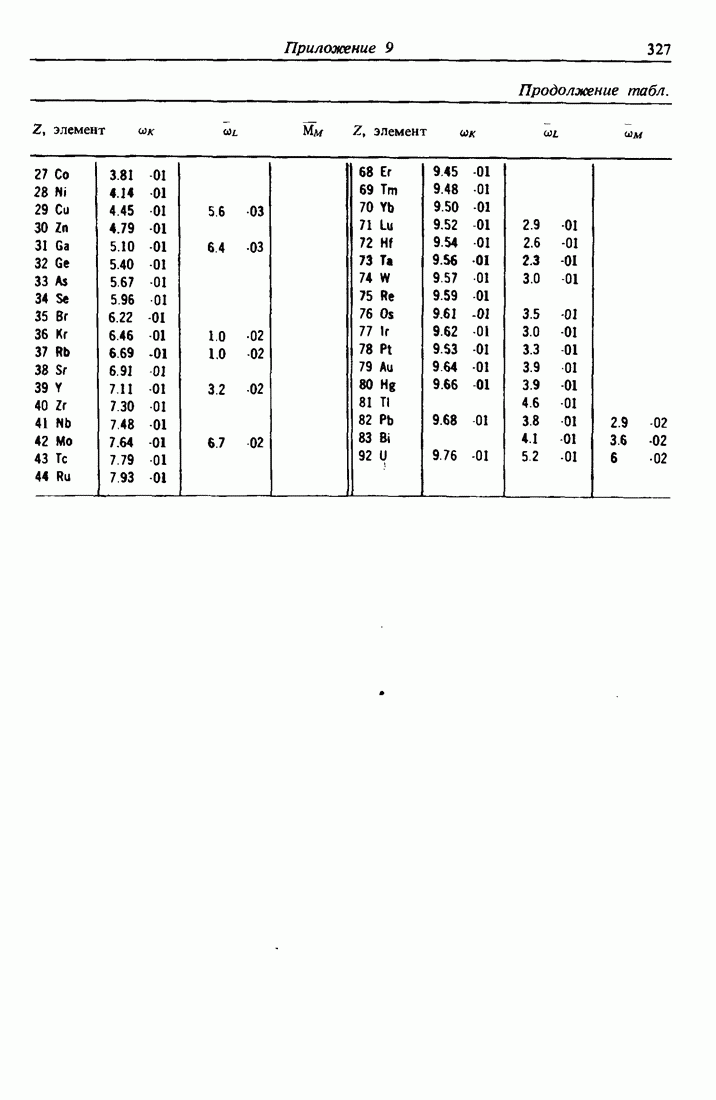
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
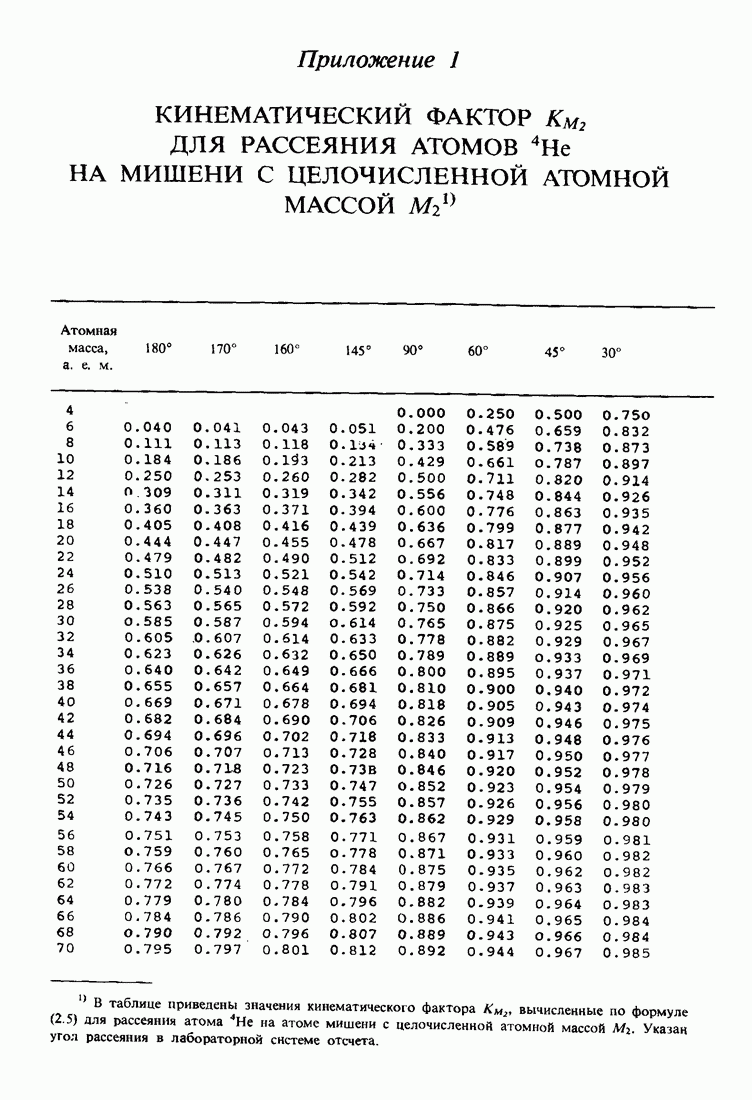
- ПРИЛОЖЕНИЕ 1.
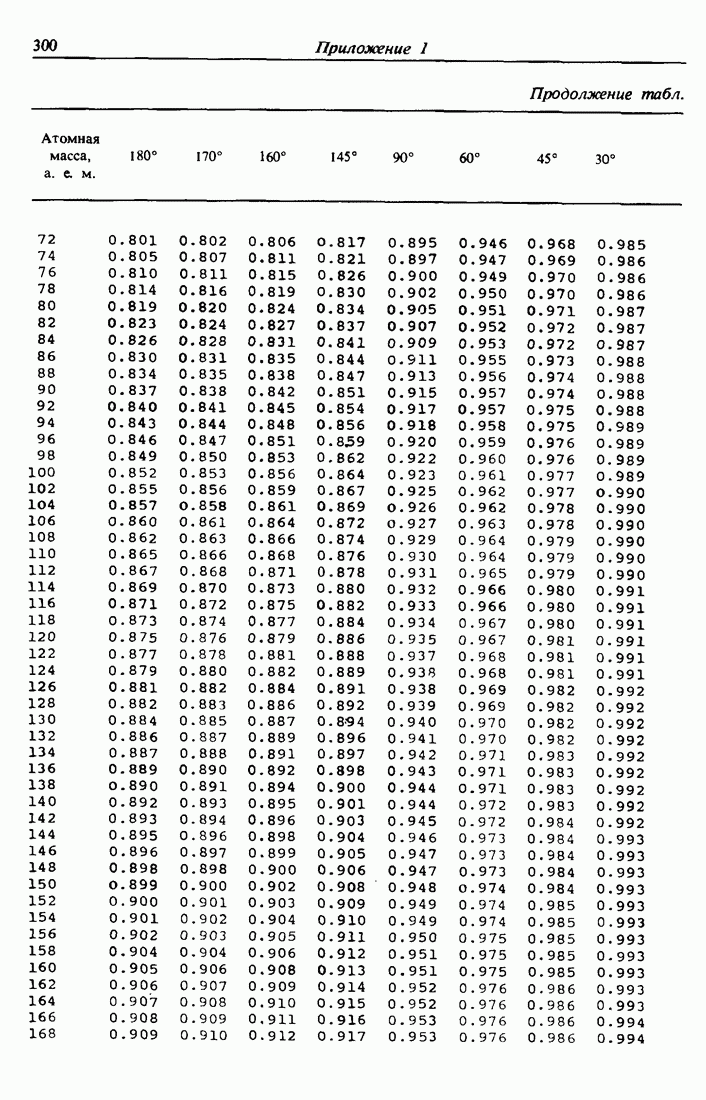
- ПРИЛОЖЕНИЕ 2.
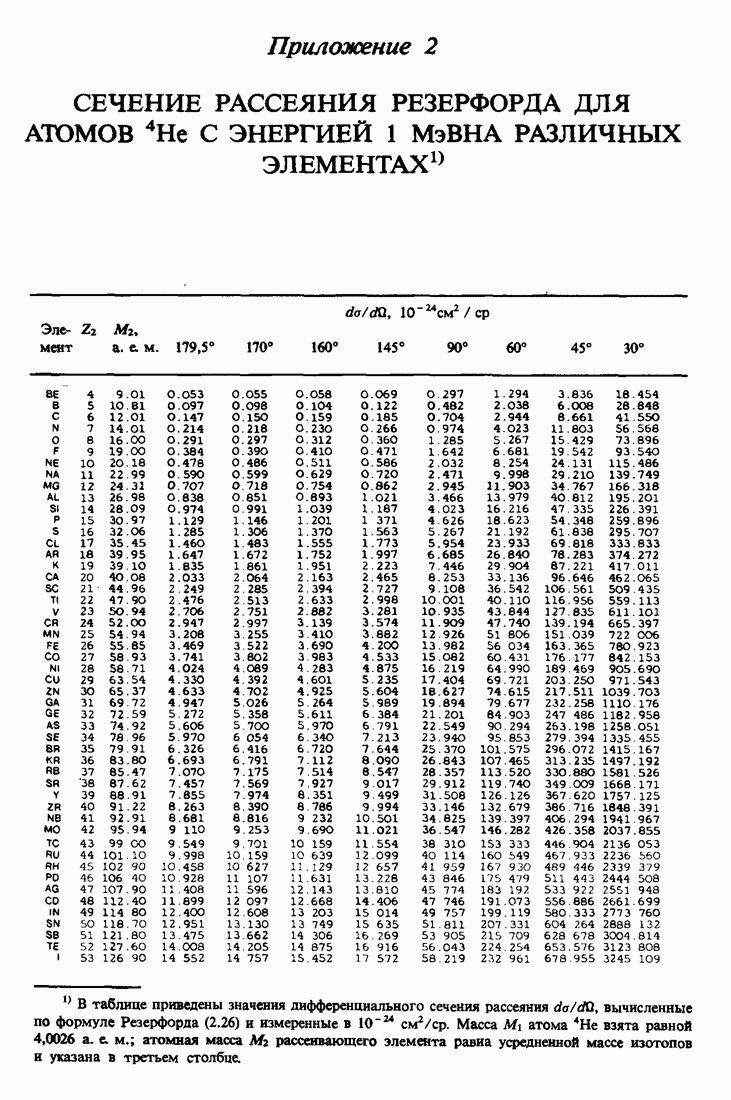
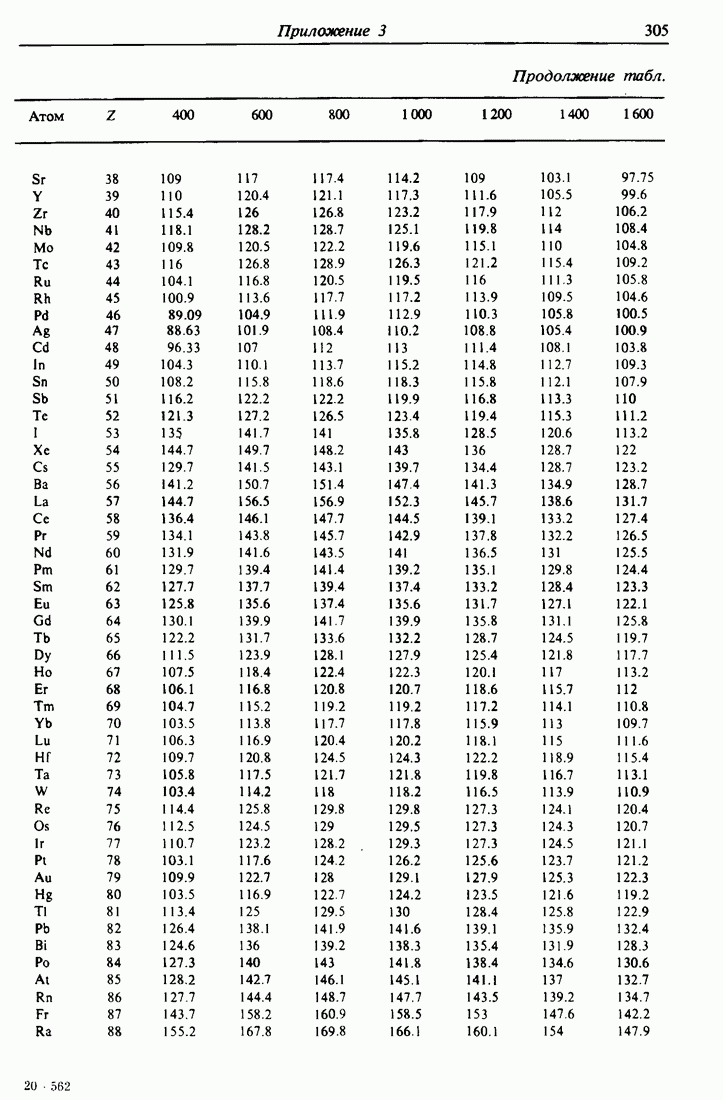
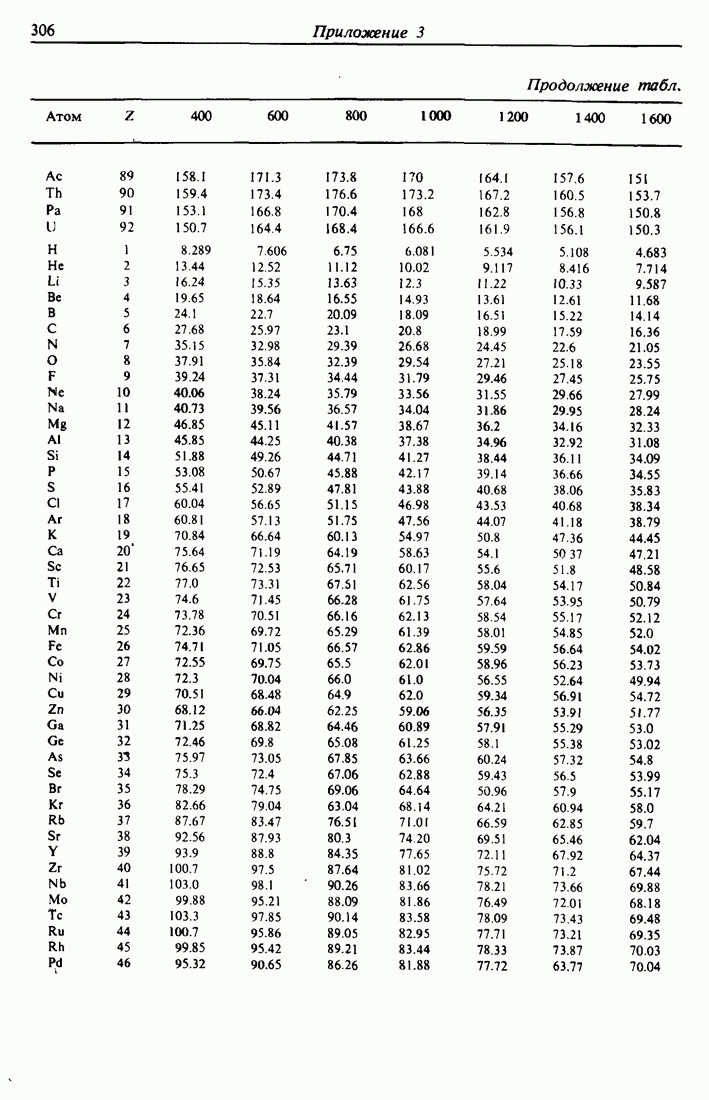
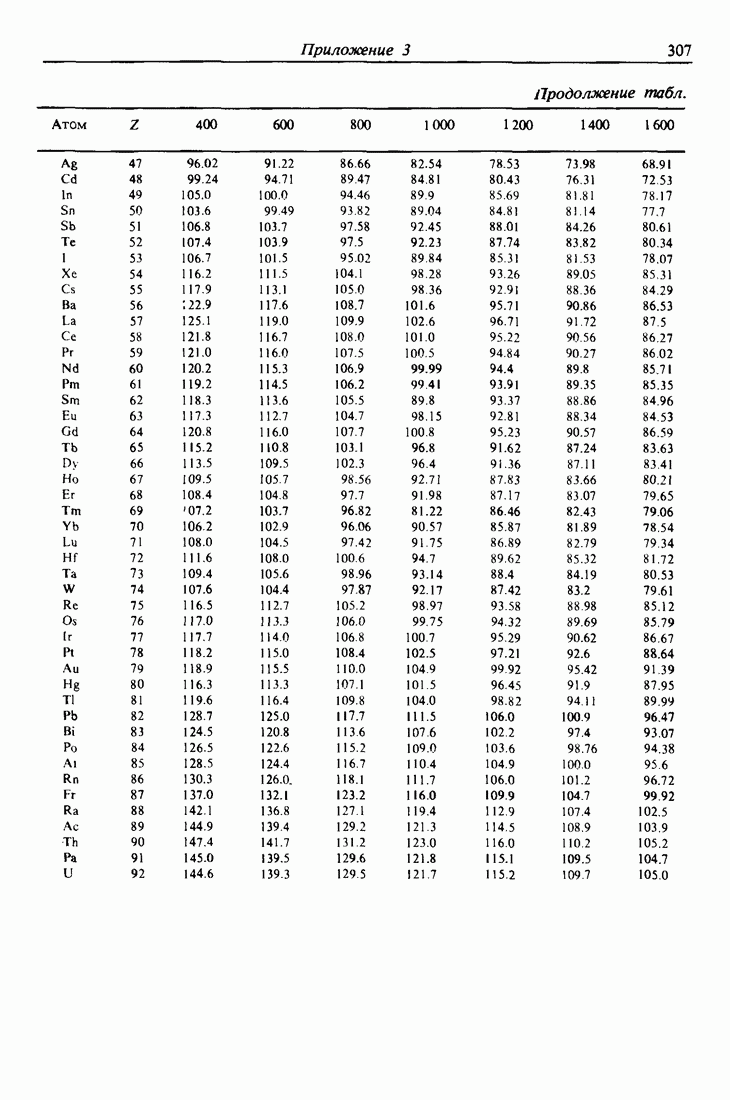
- ПРИЛОЖЕНИЕ 3.
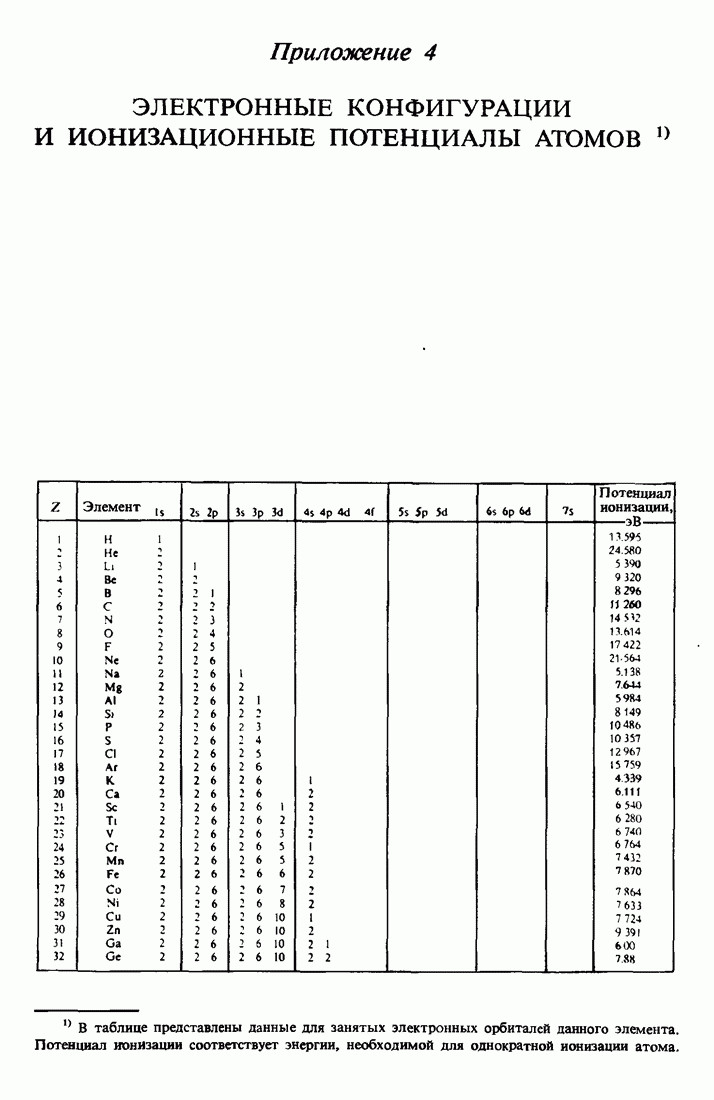
- ПРИЛОЖЕНИЕ 4.
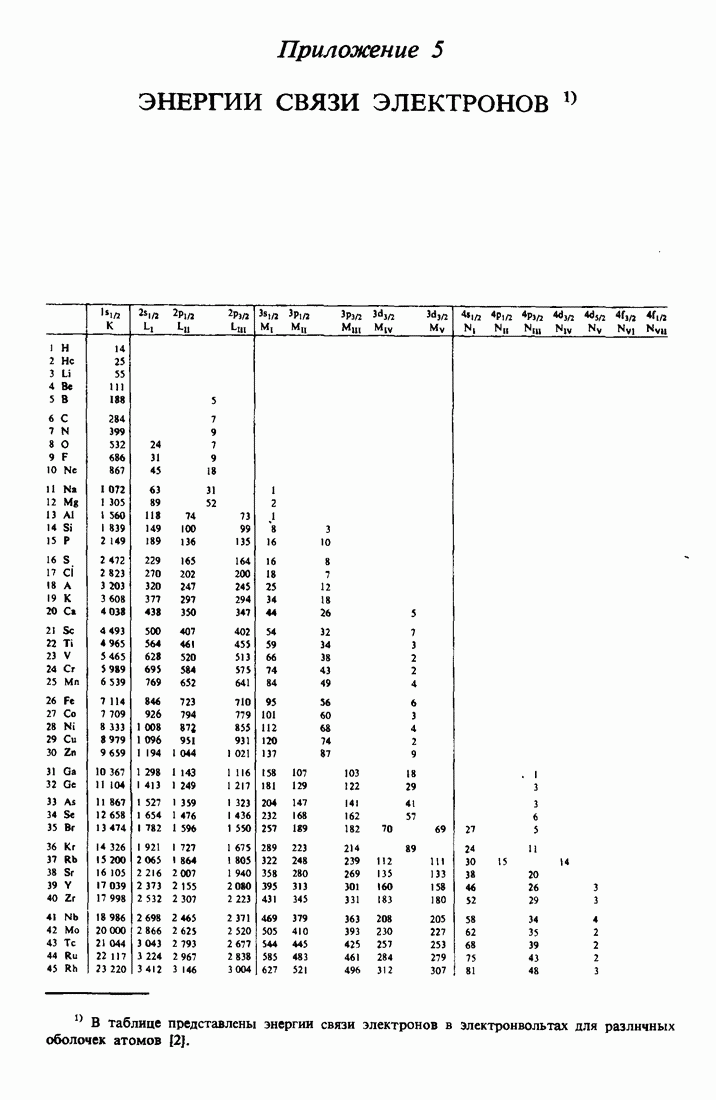
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
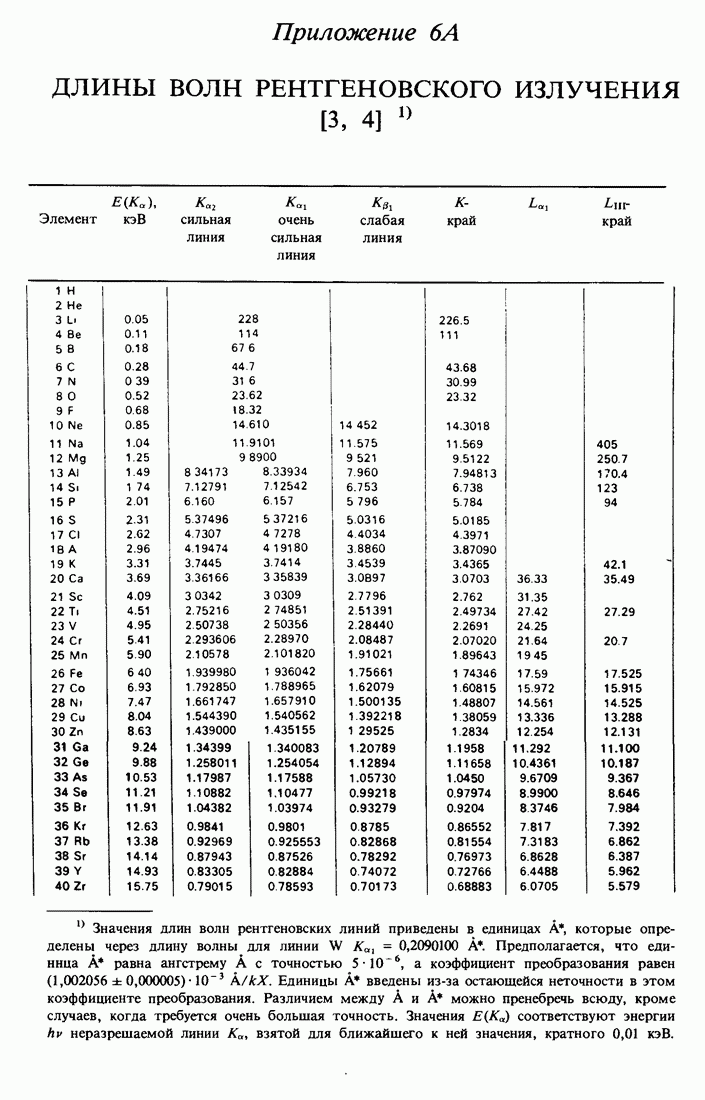
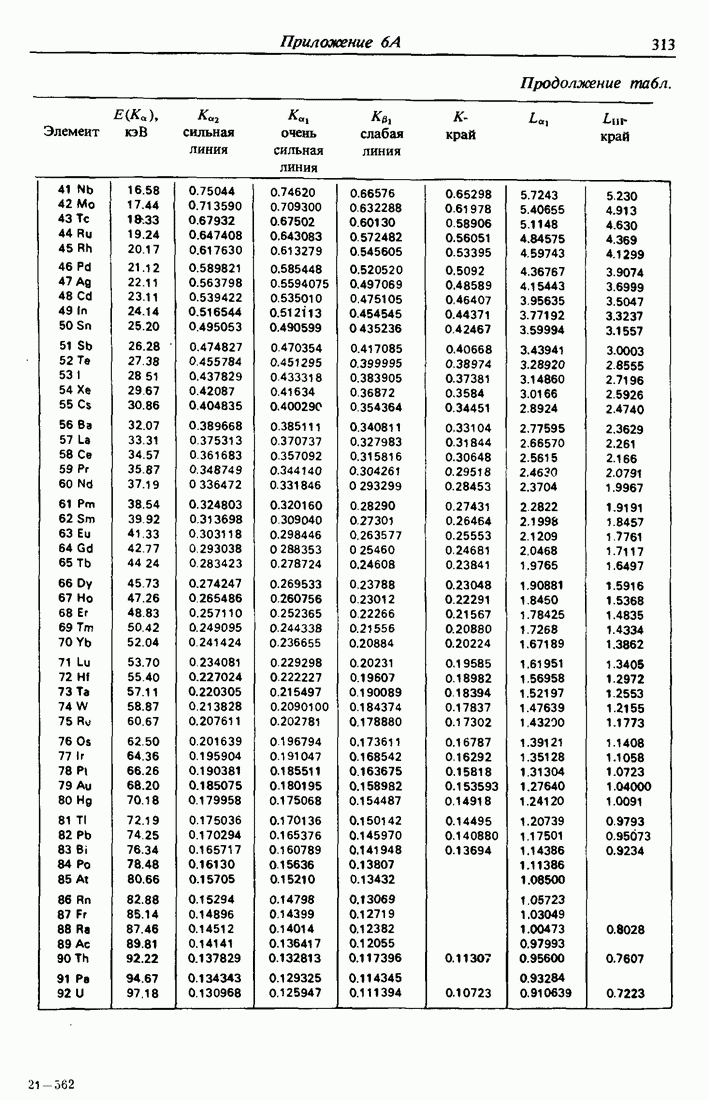
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
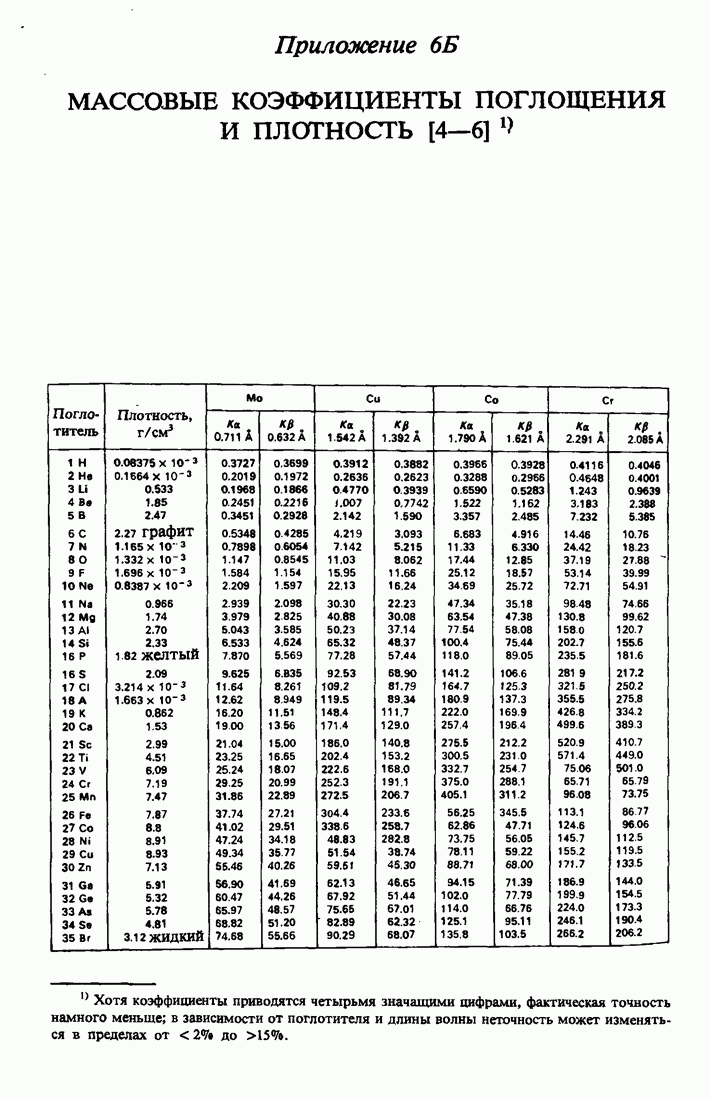
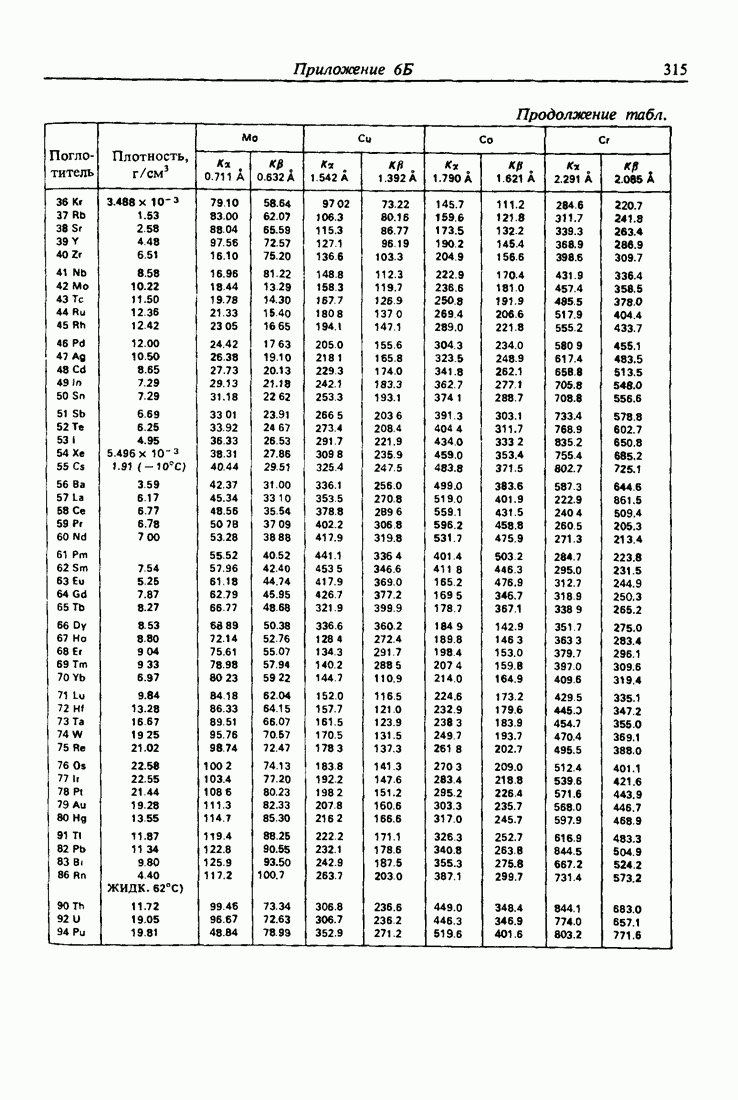
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
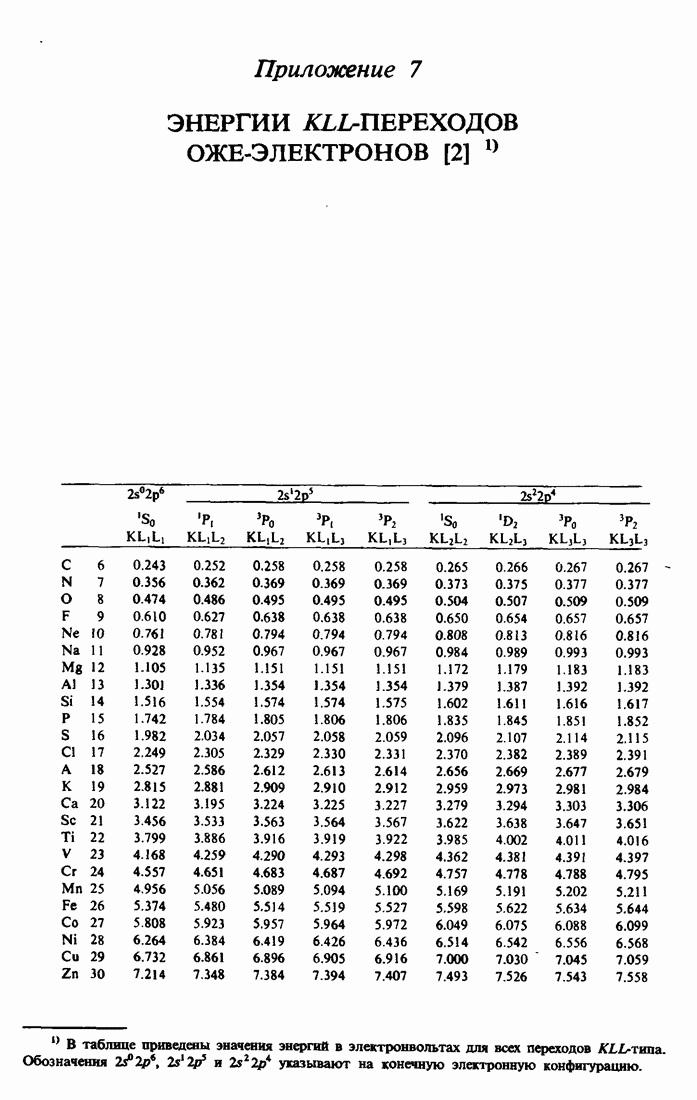
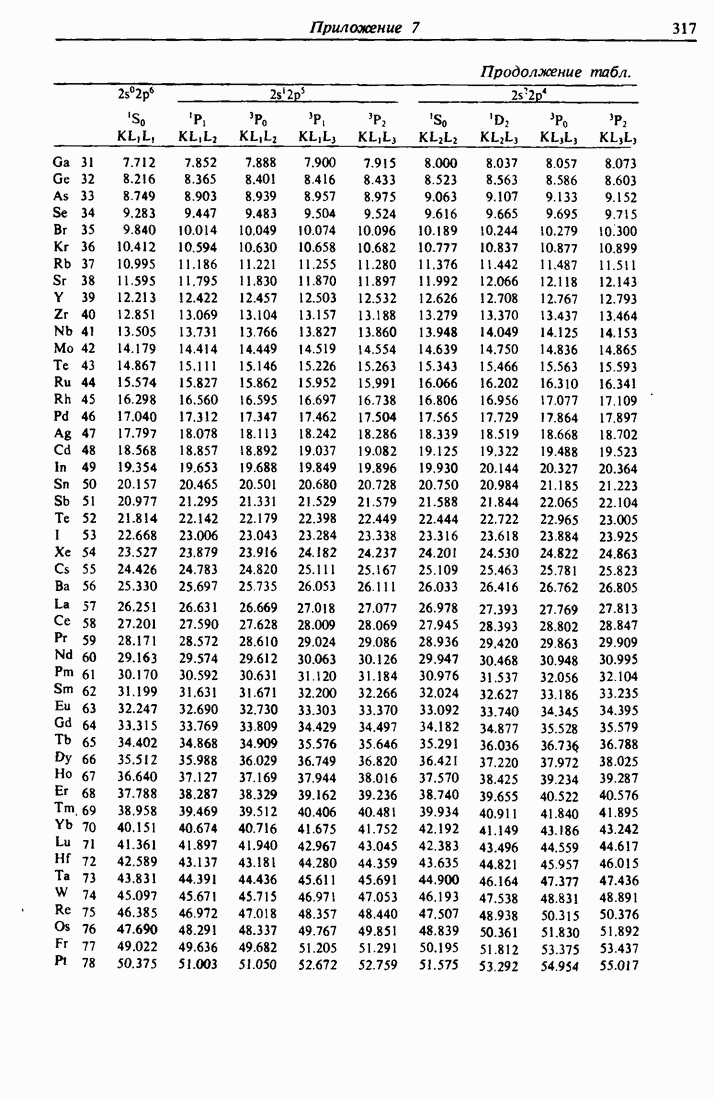
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
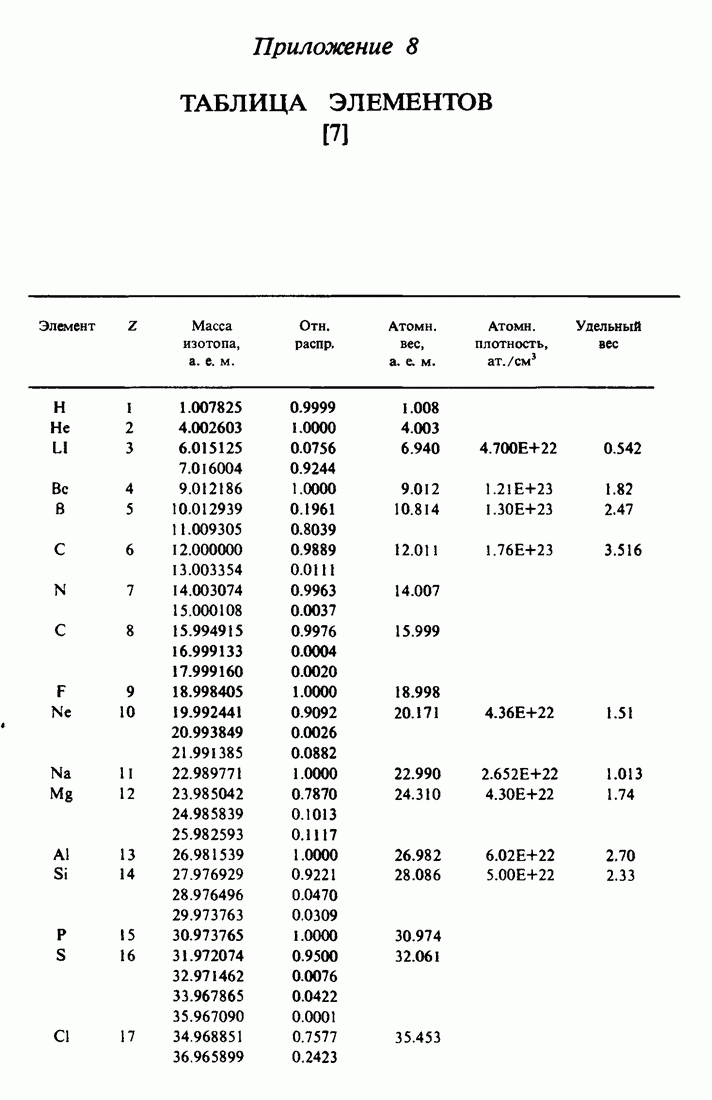
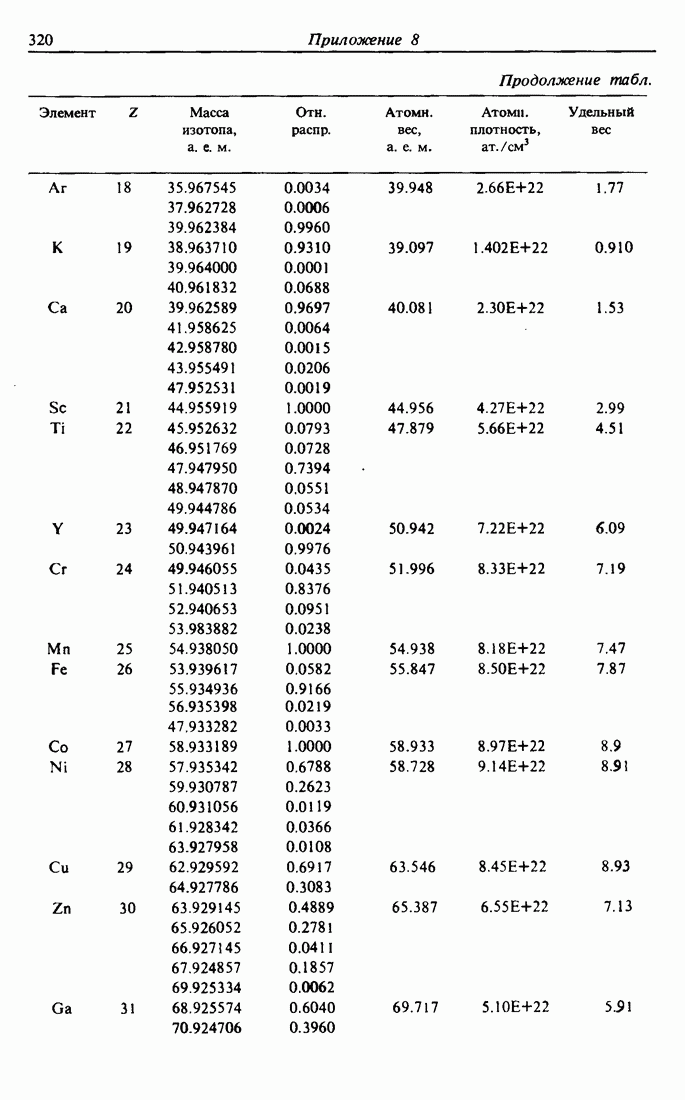
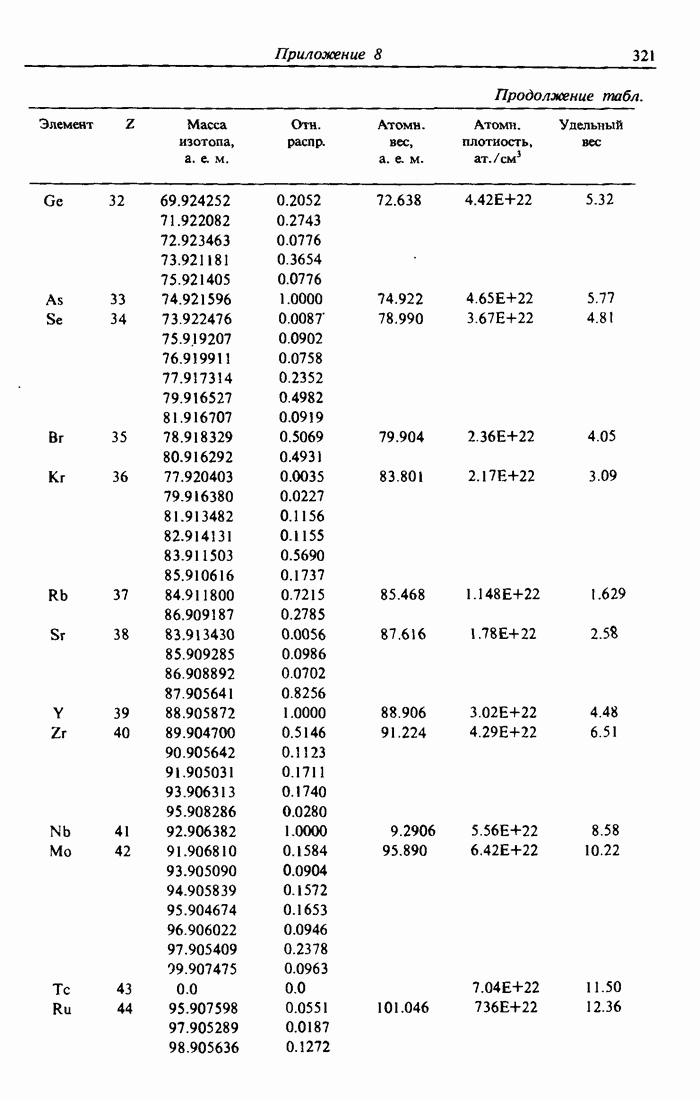
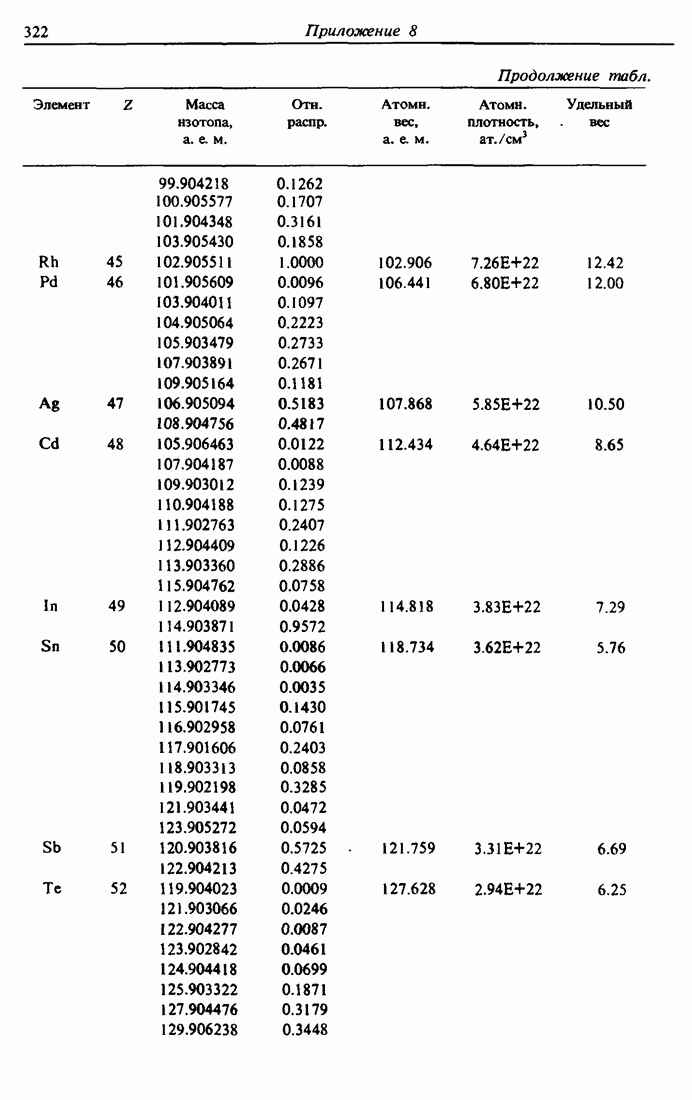
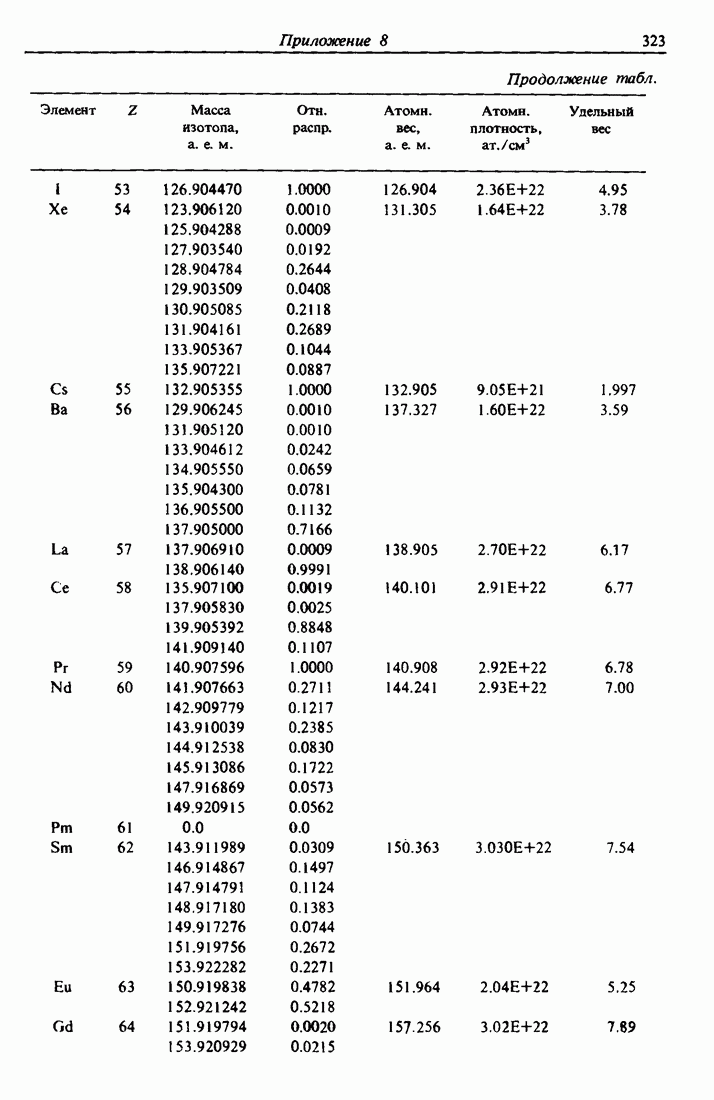
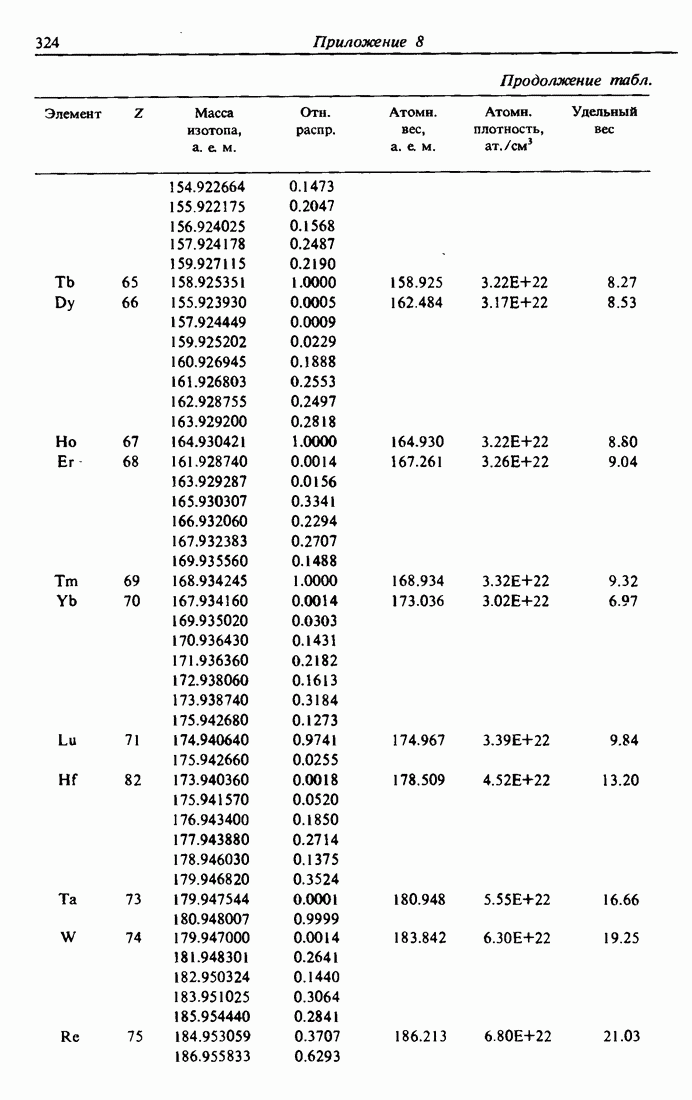
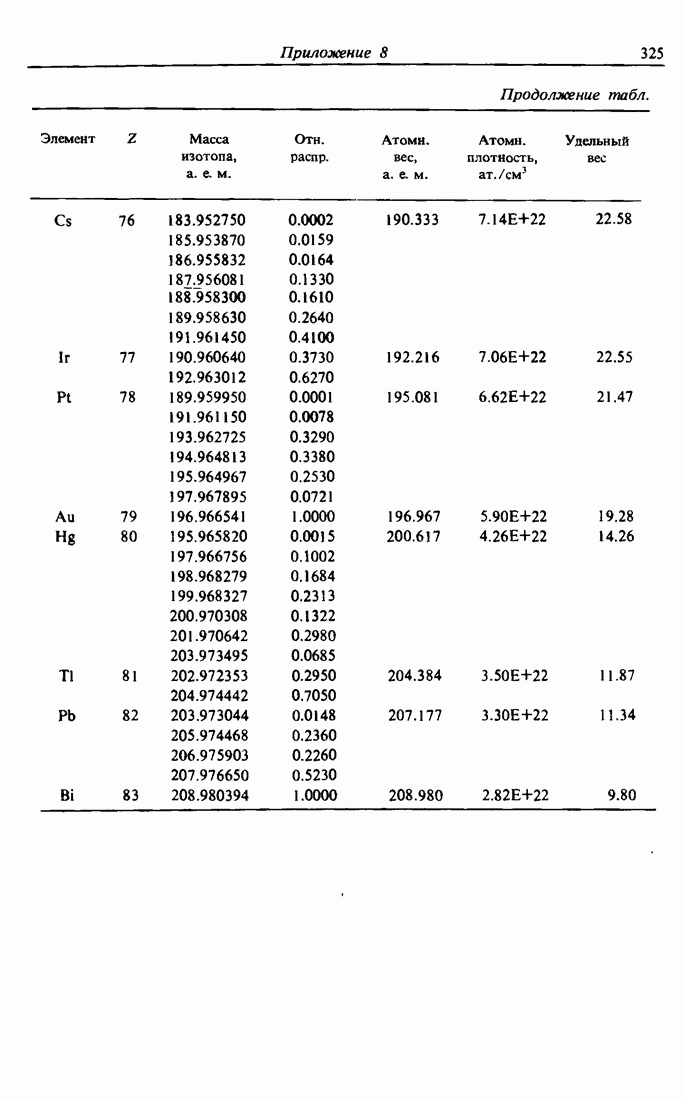
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ