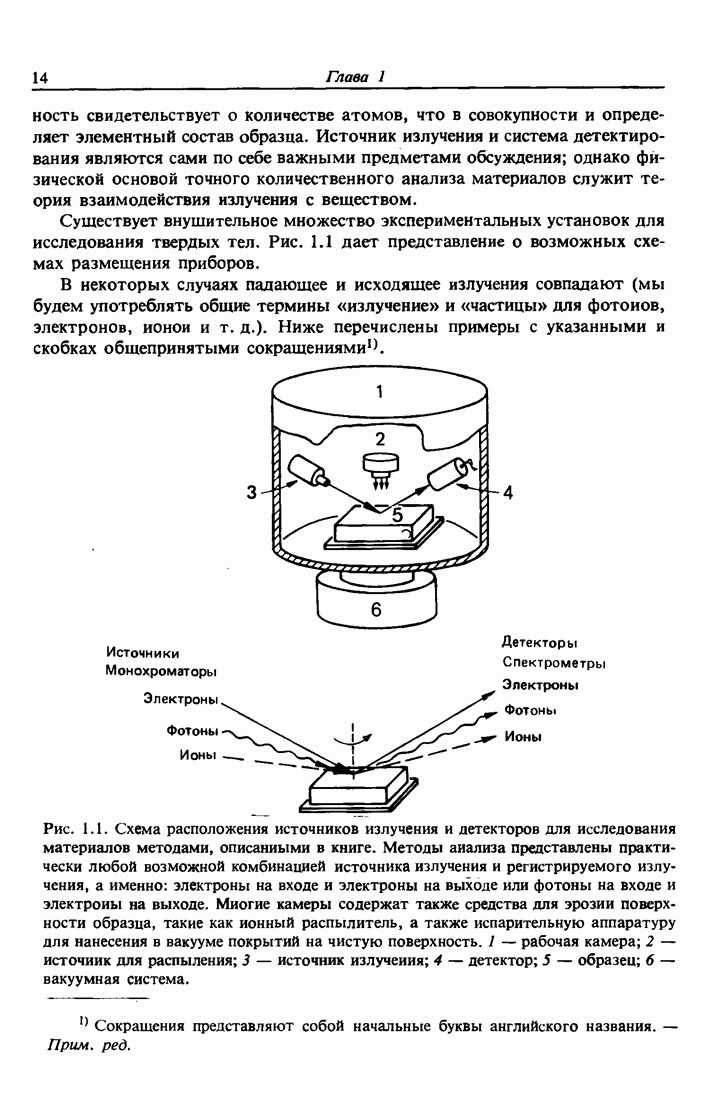
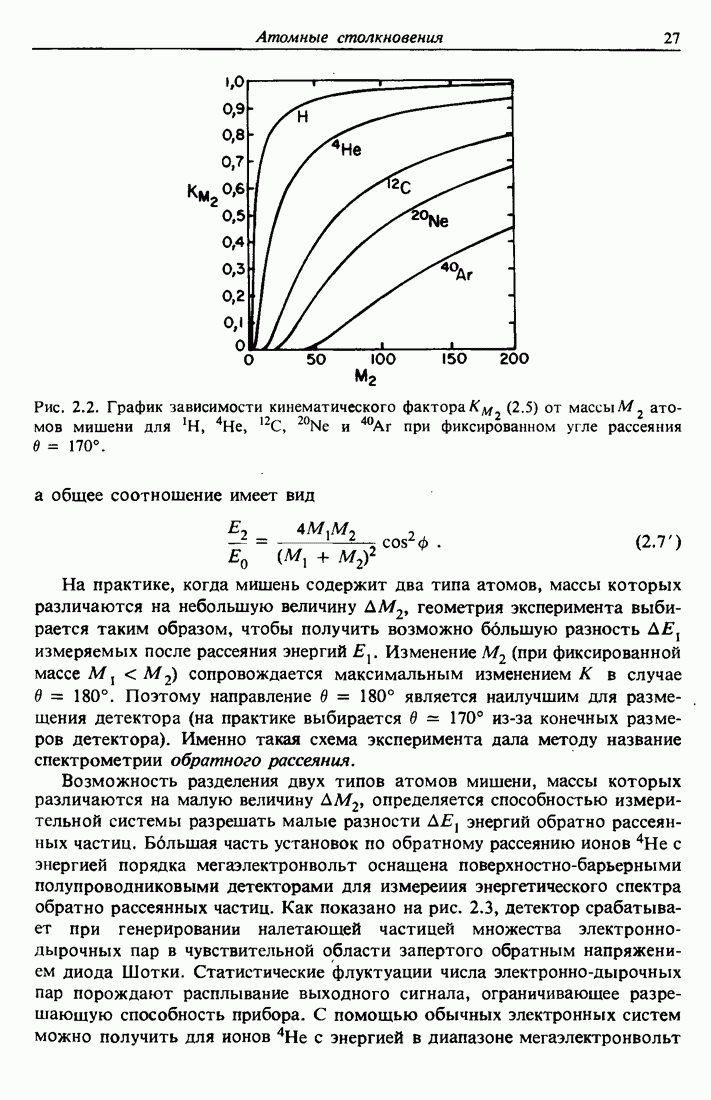
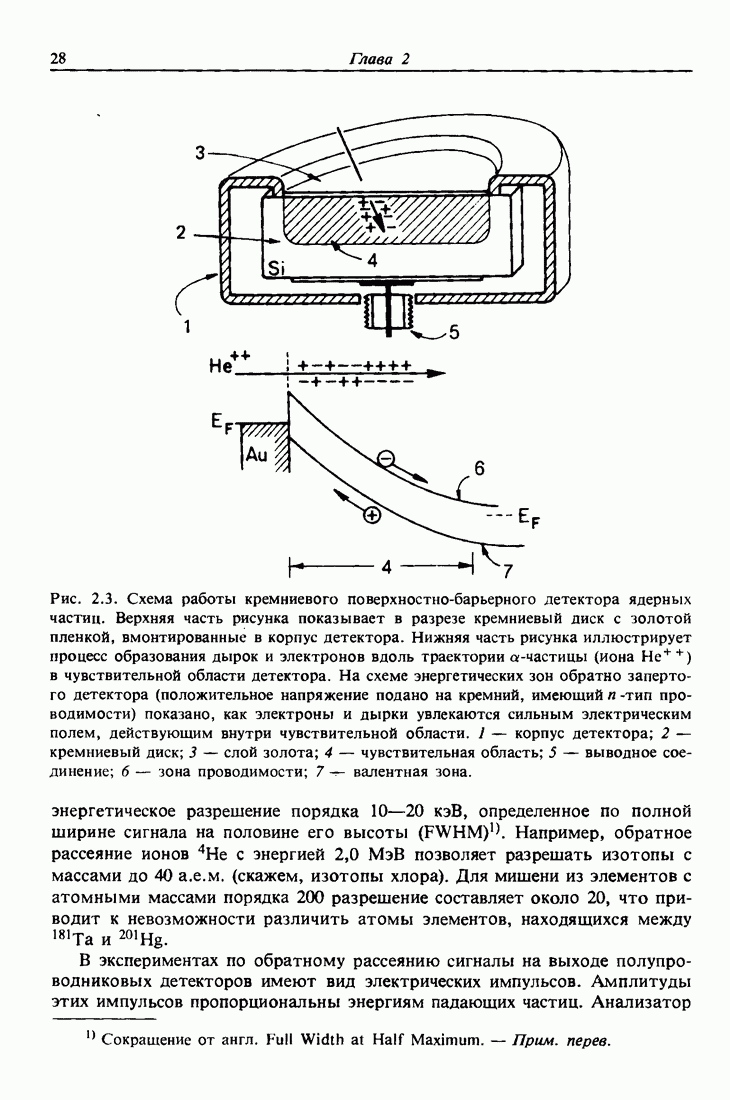
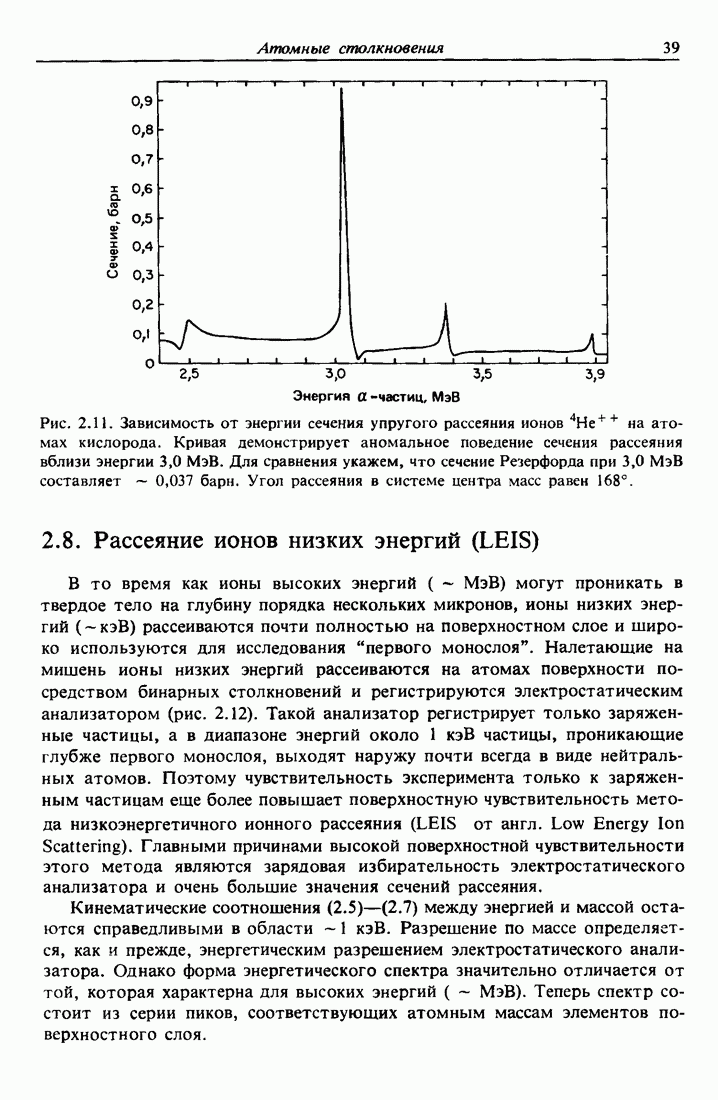
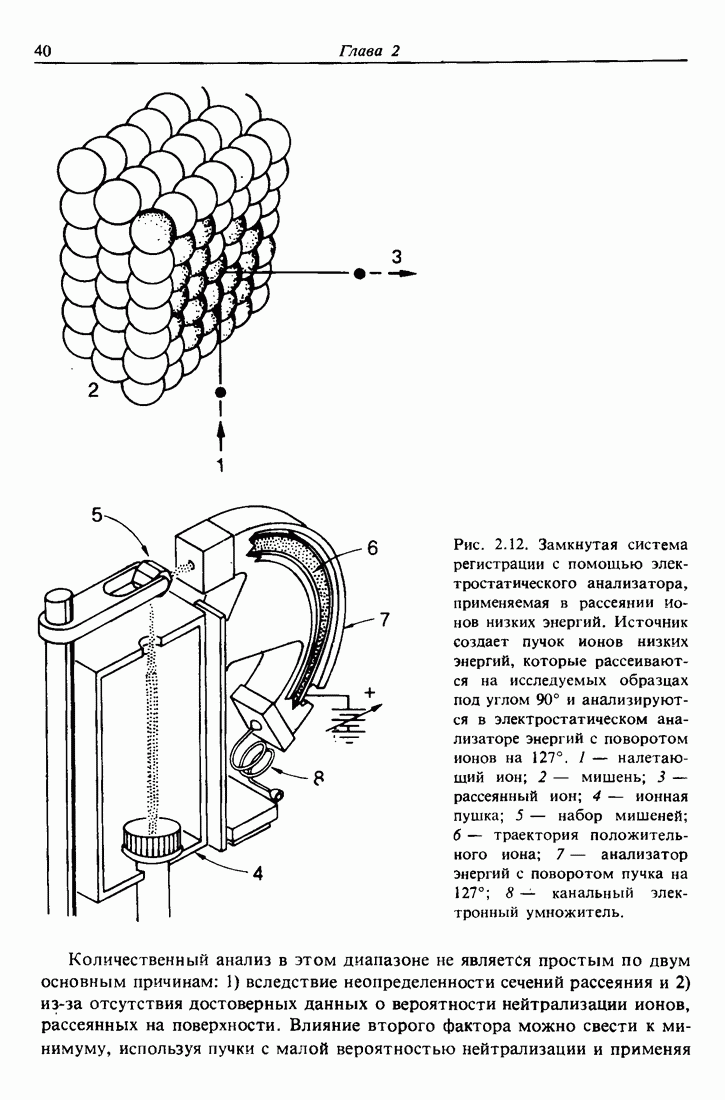
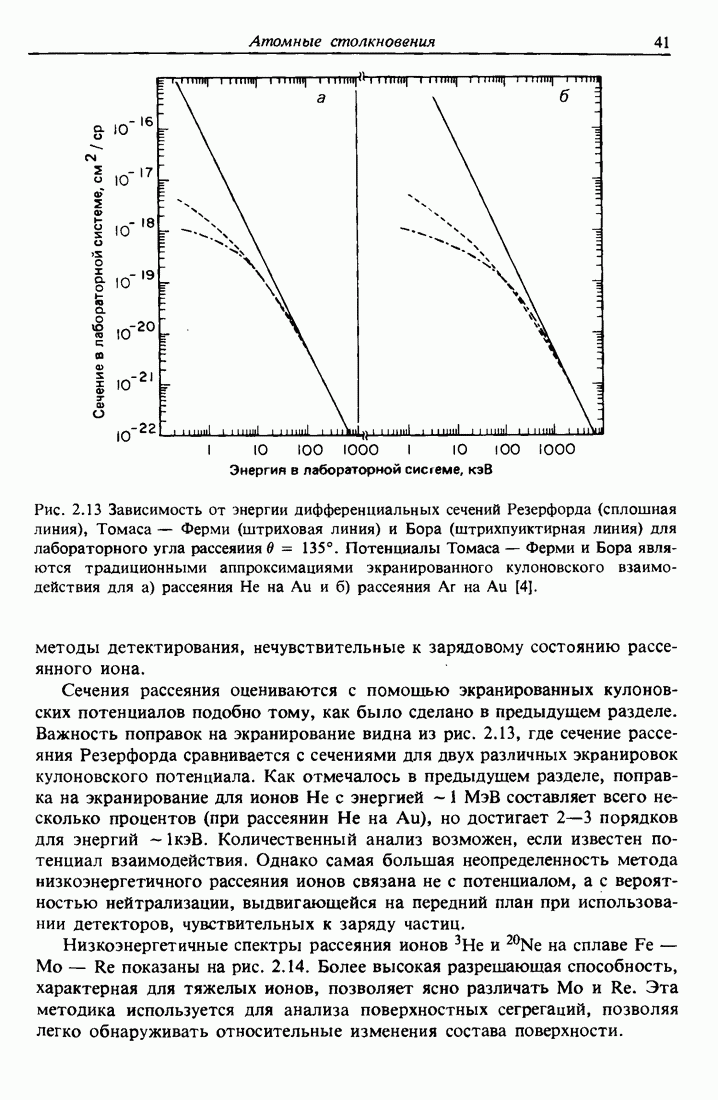
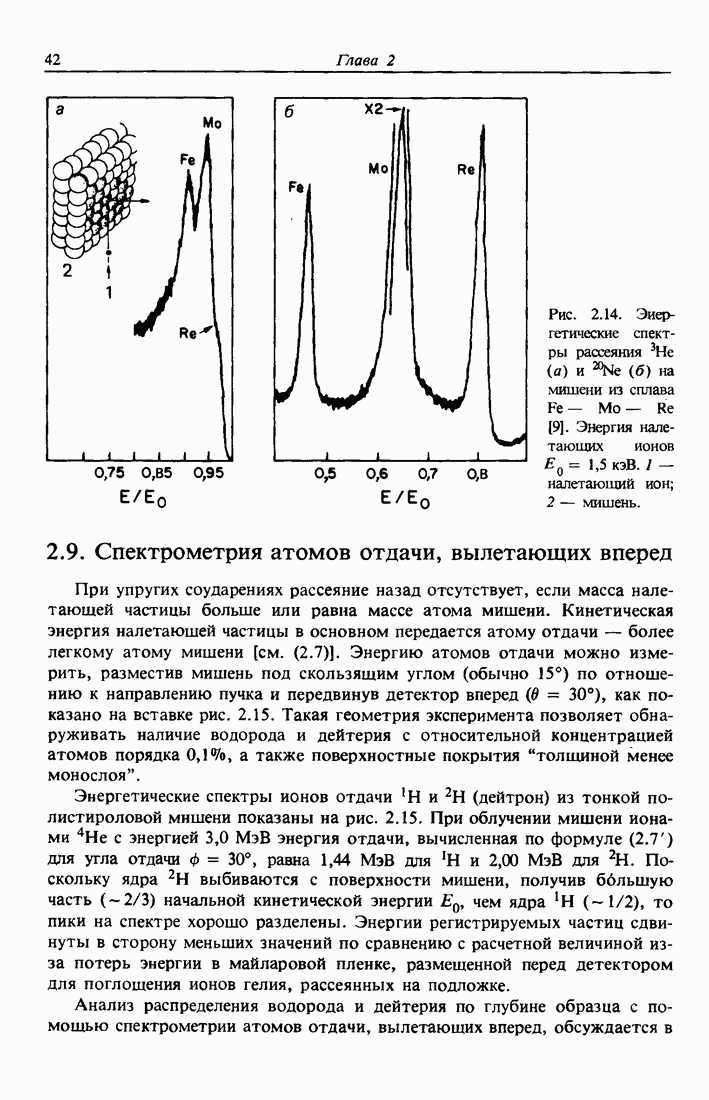
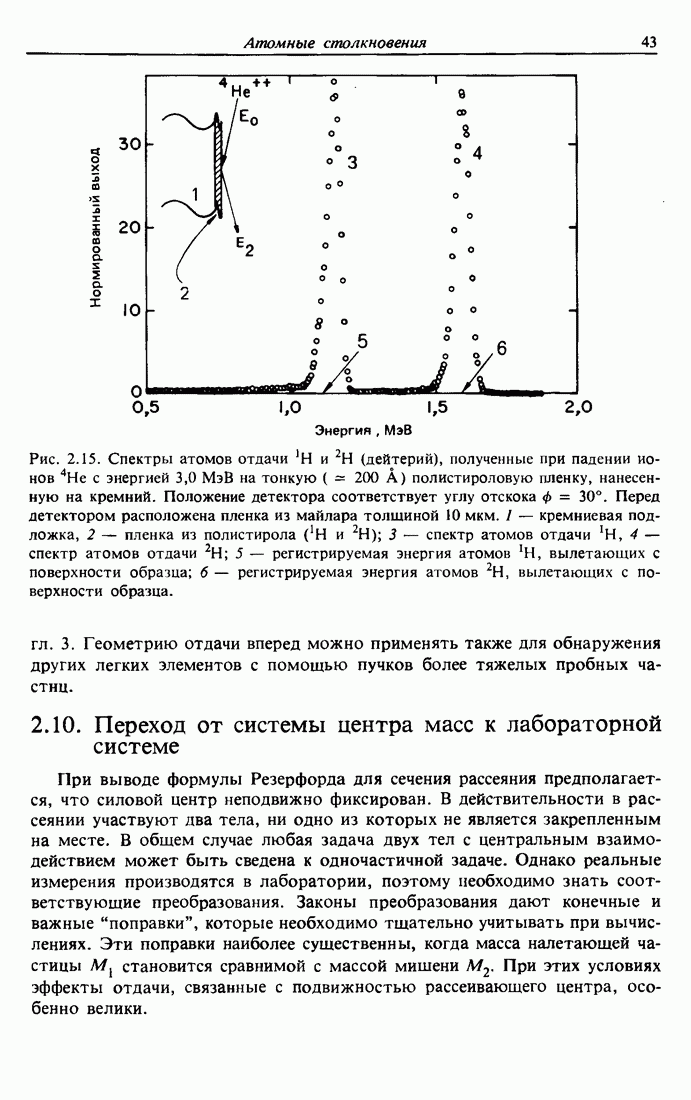
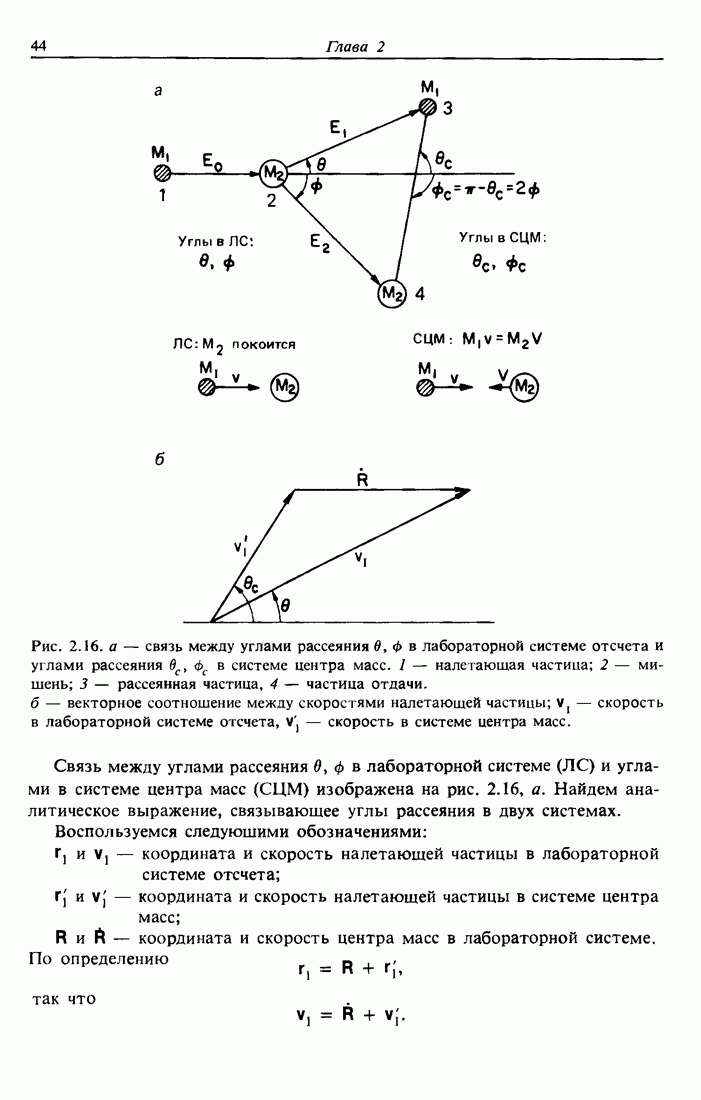
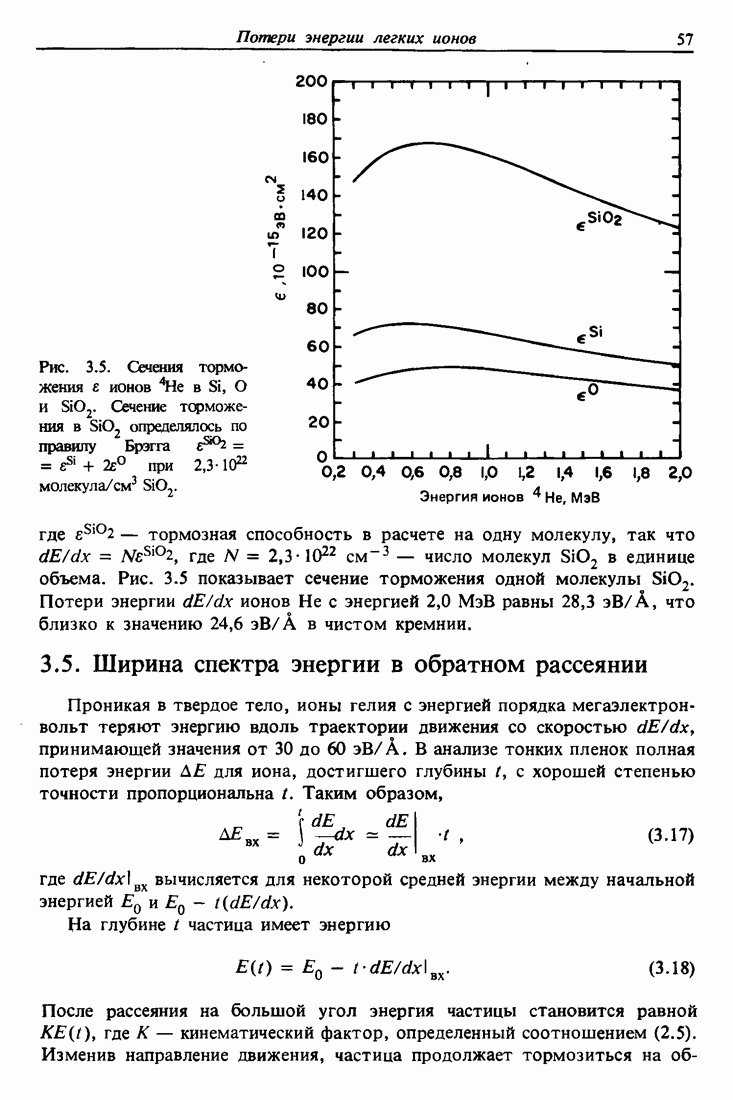
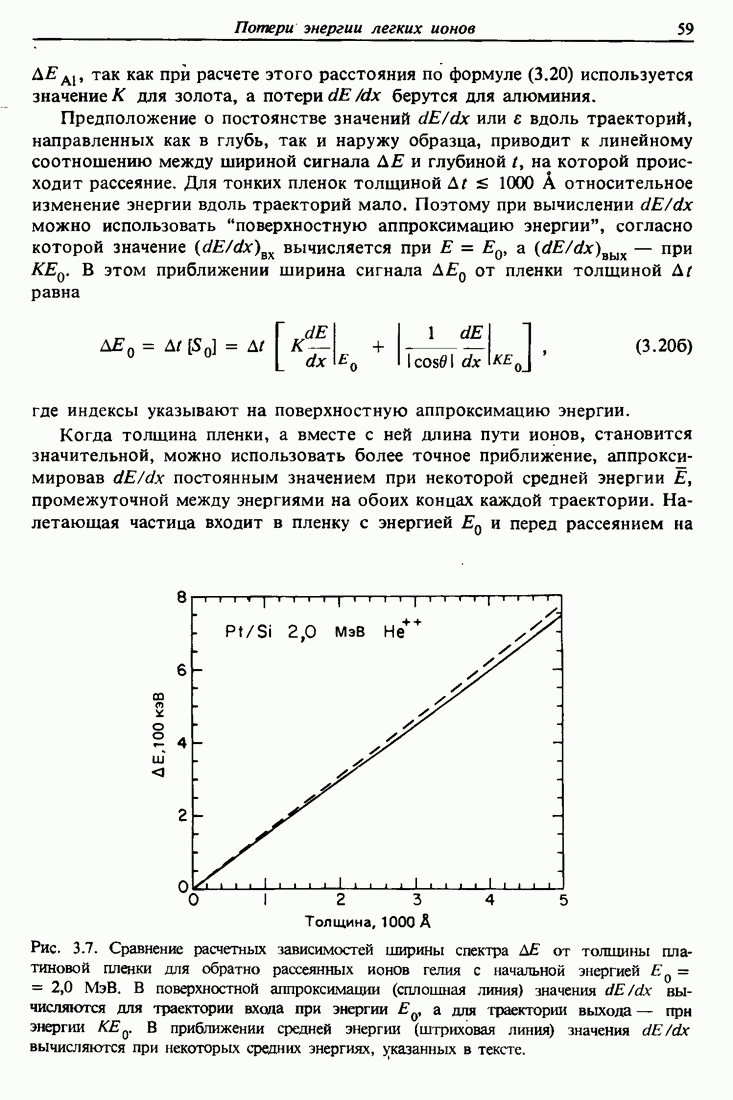
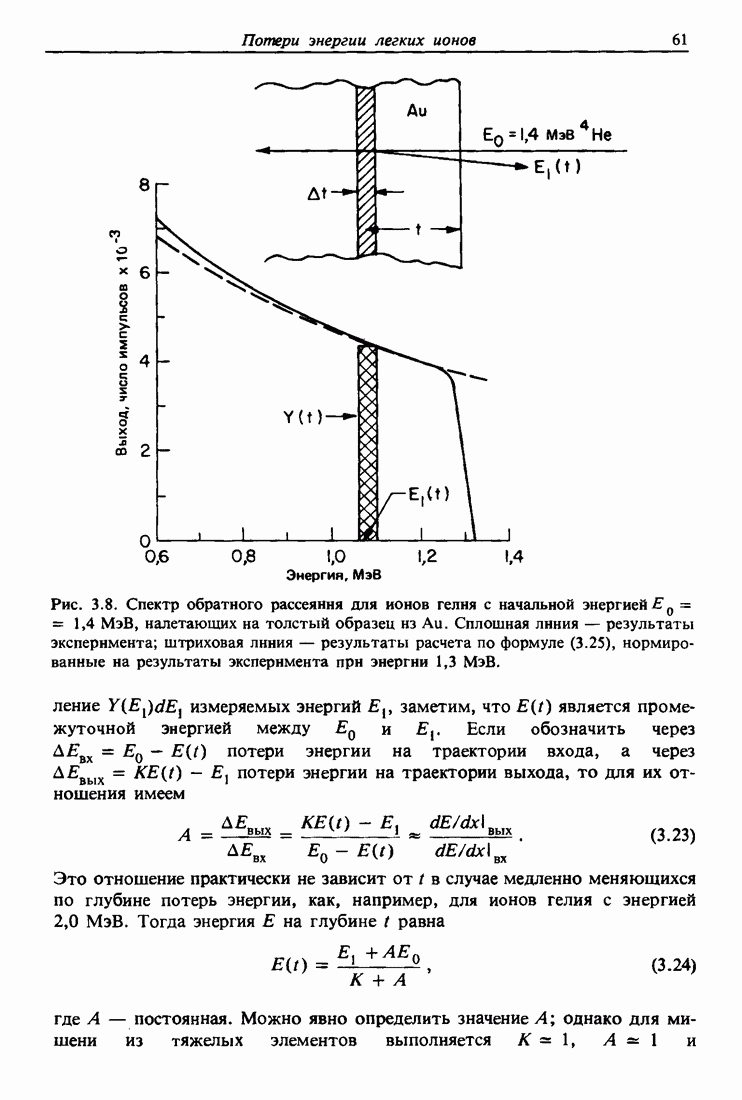
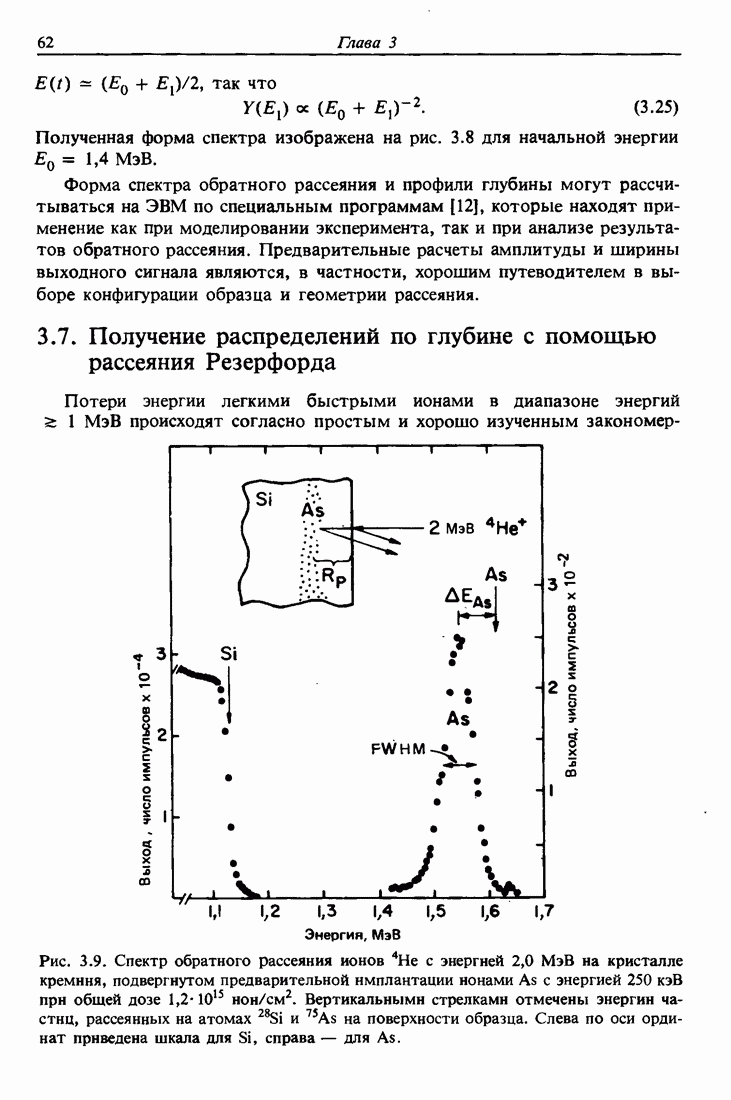
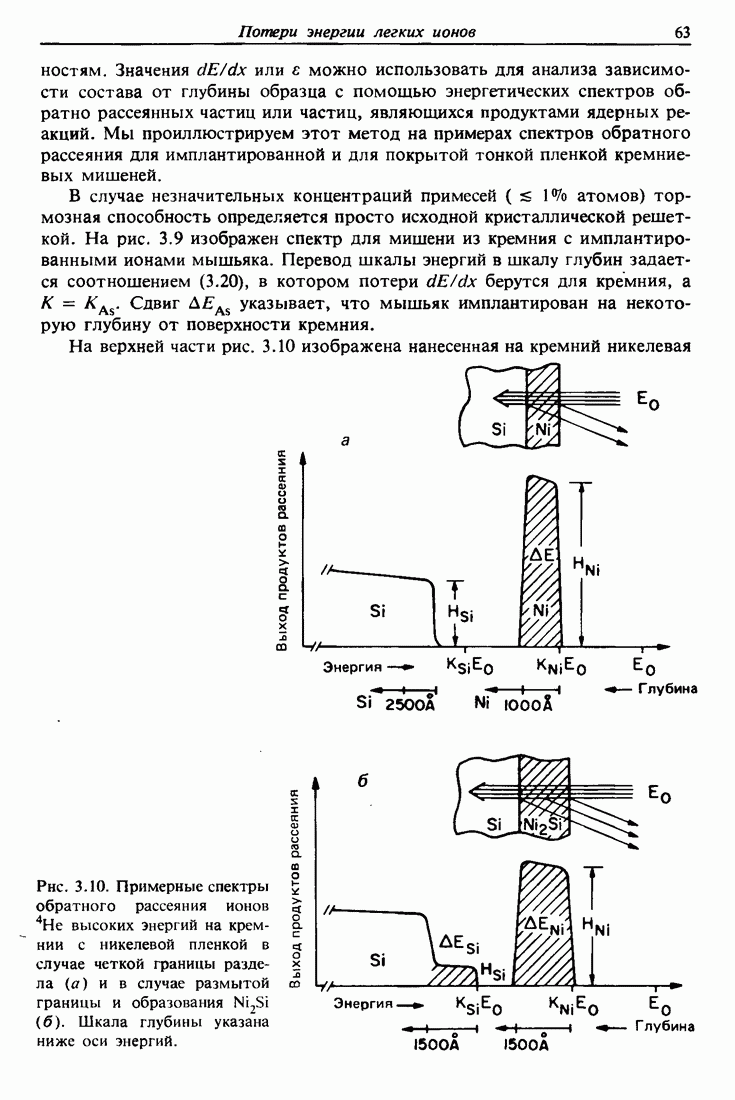
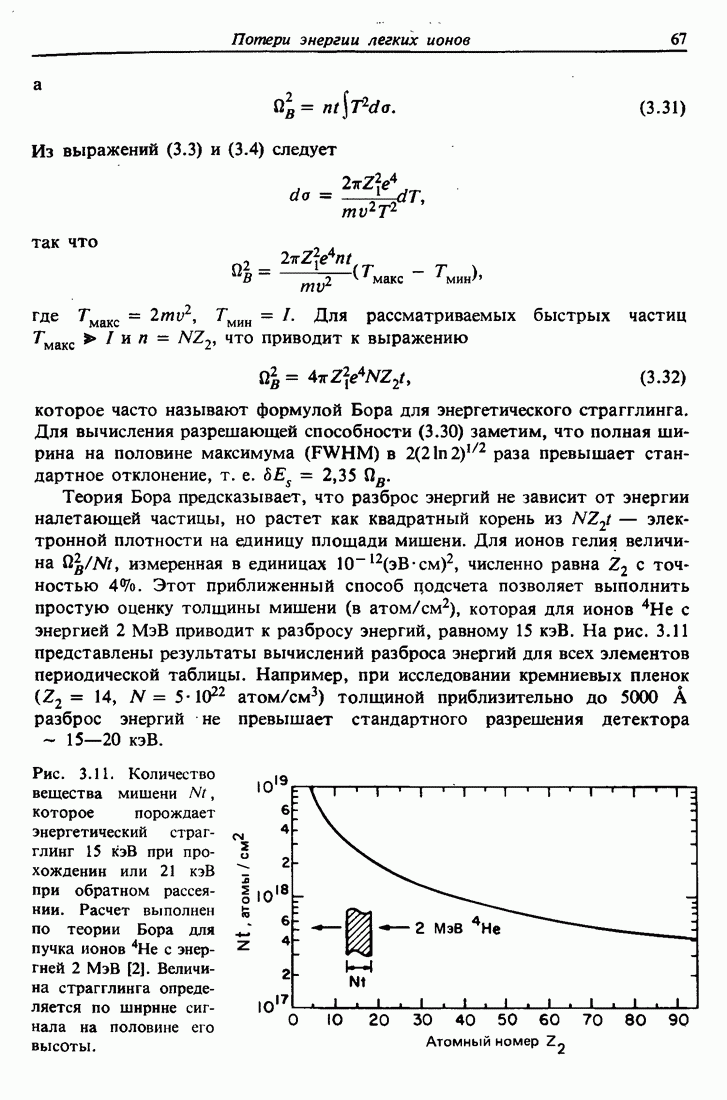
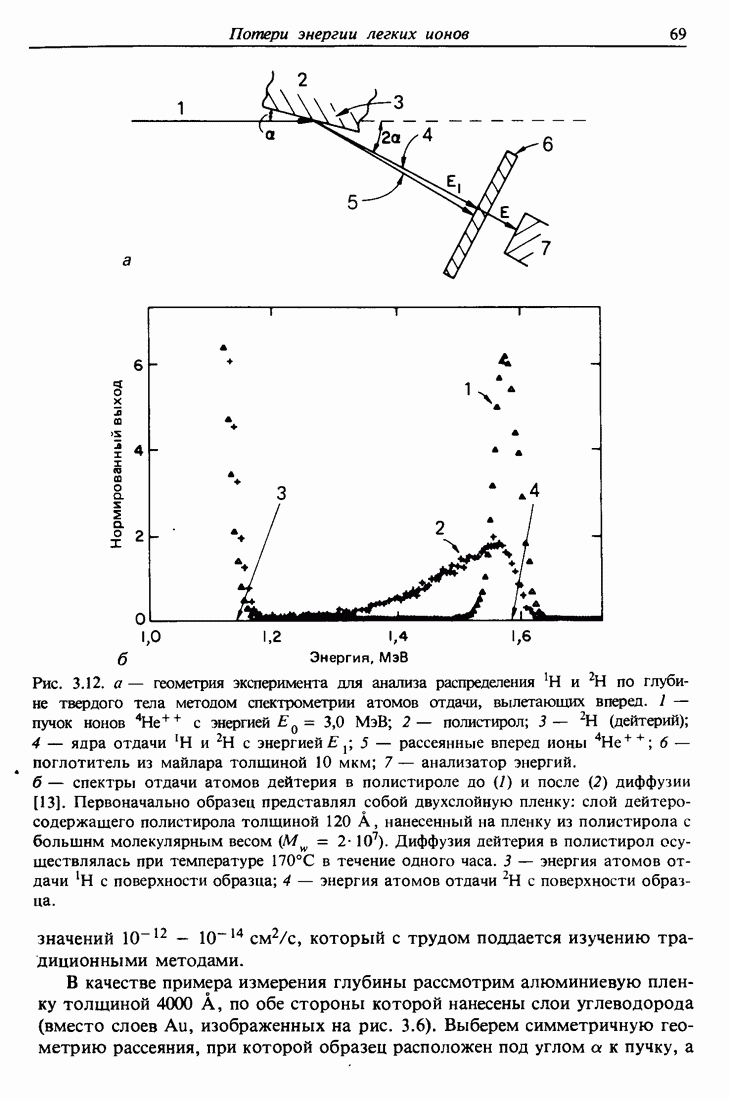
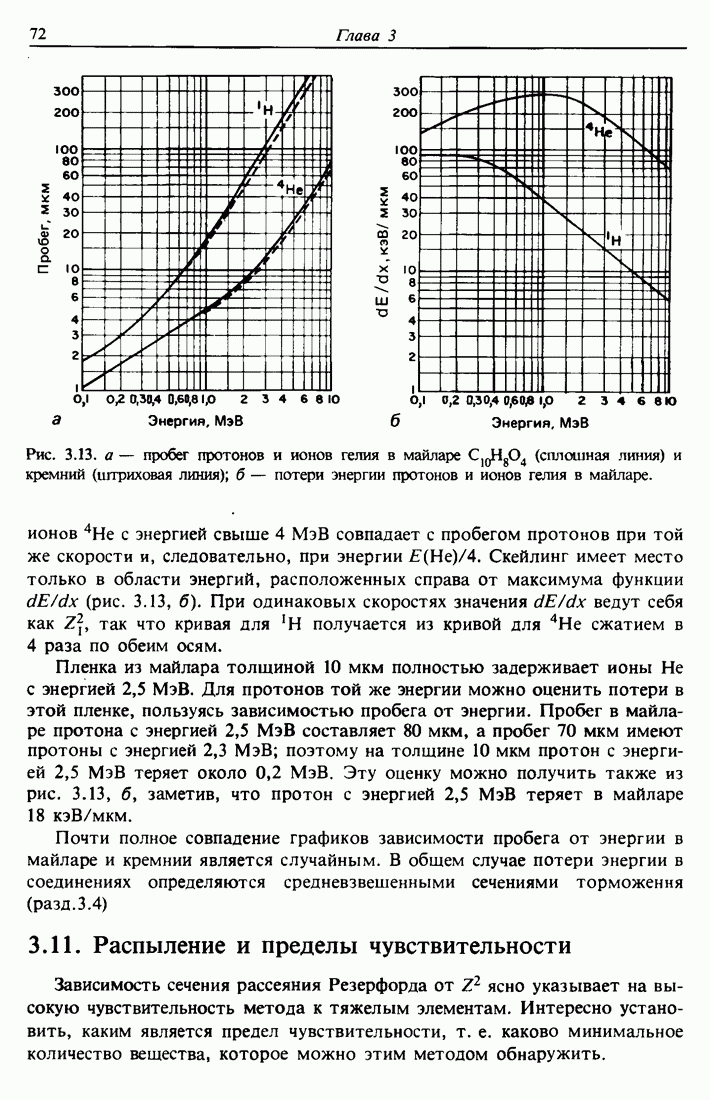
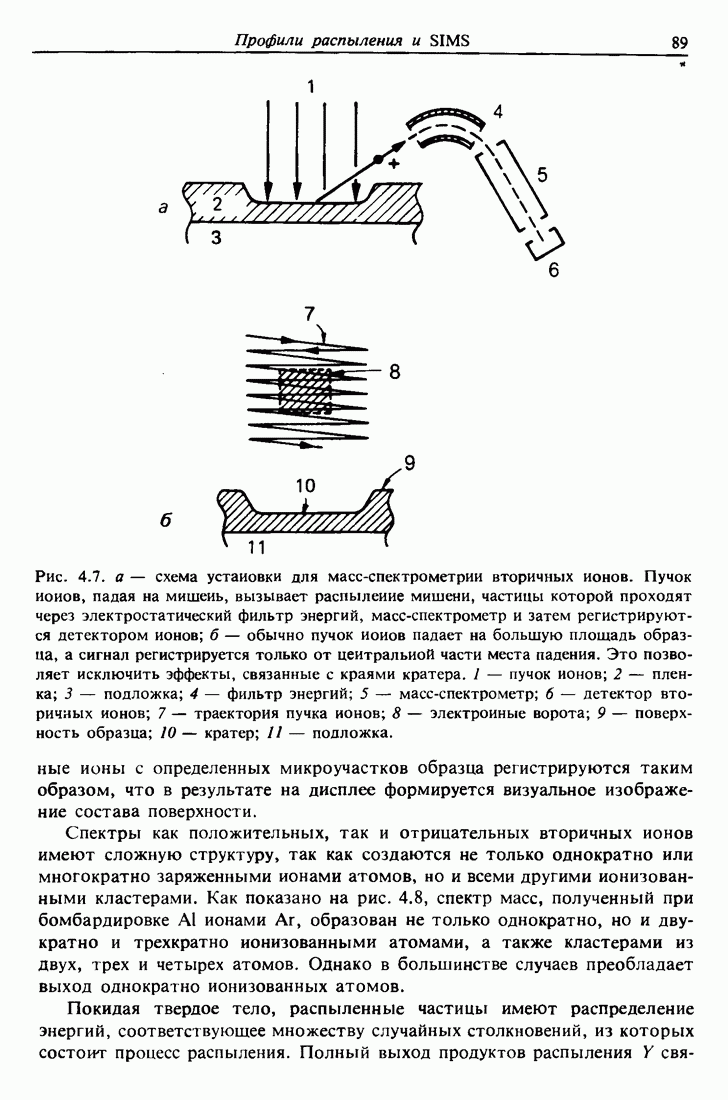
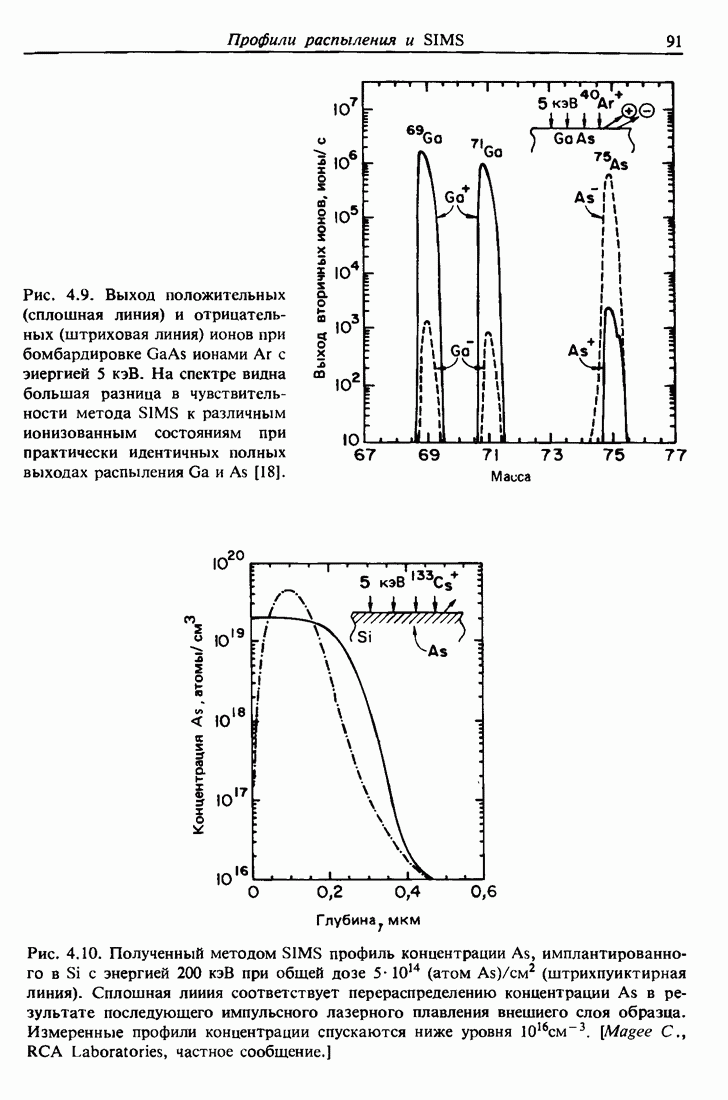
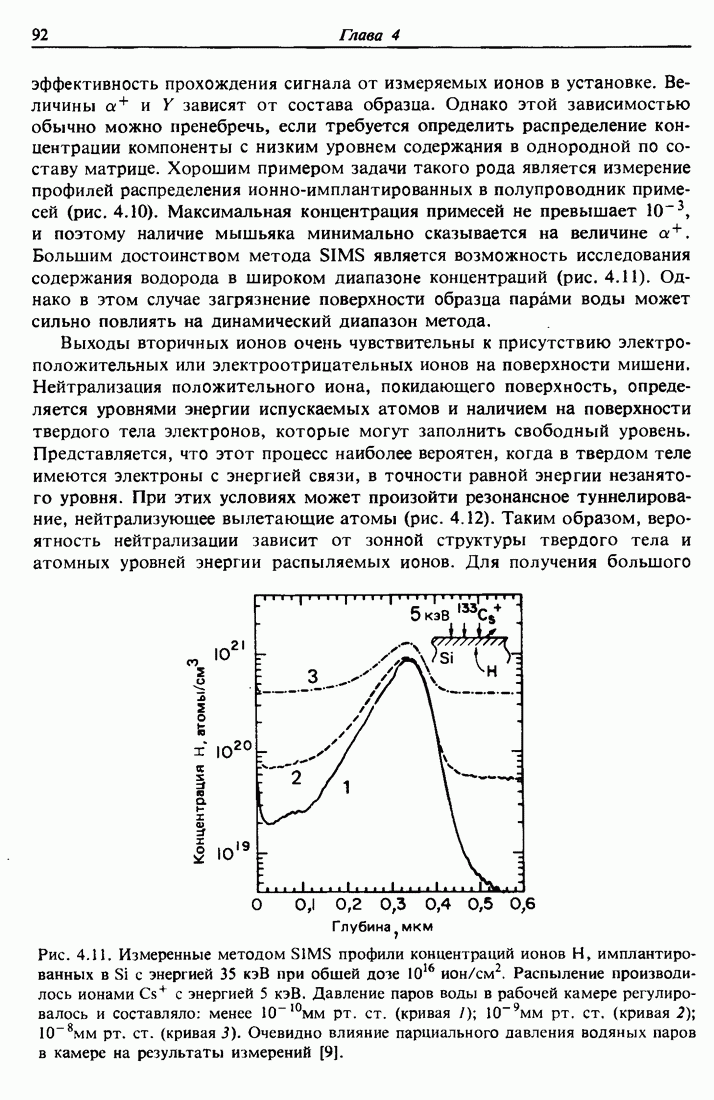
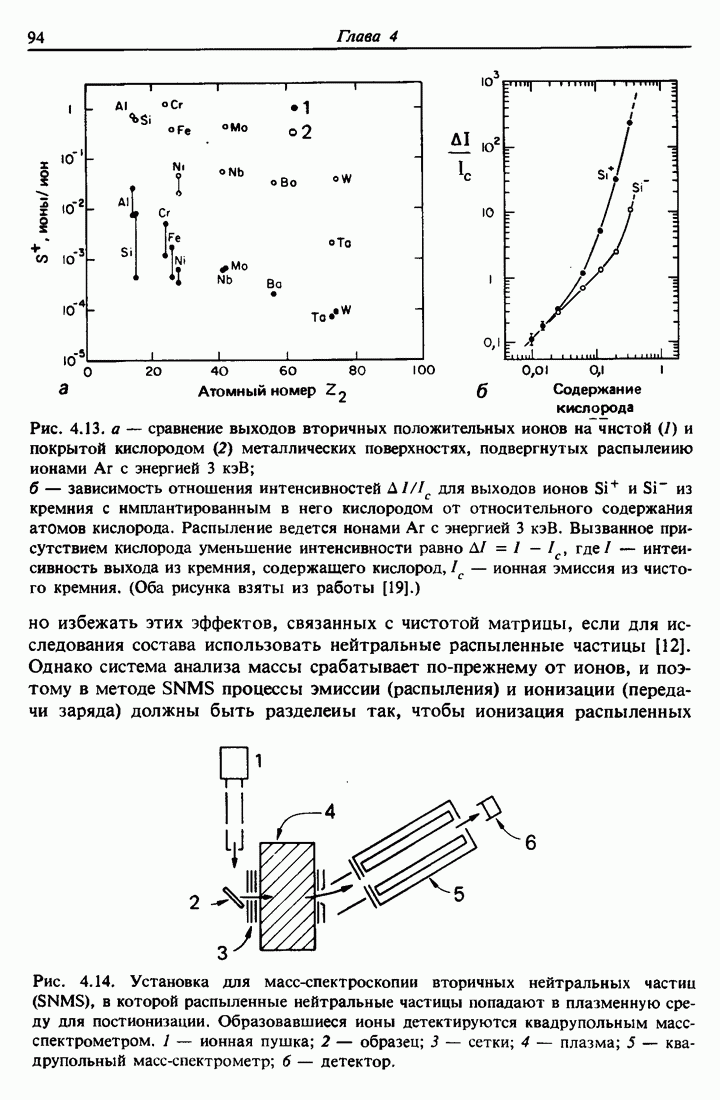
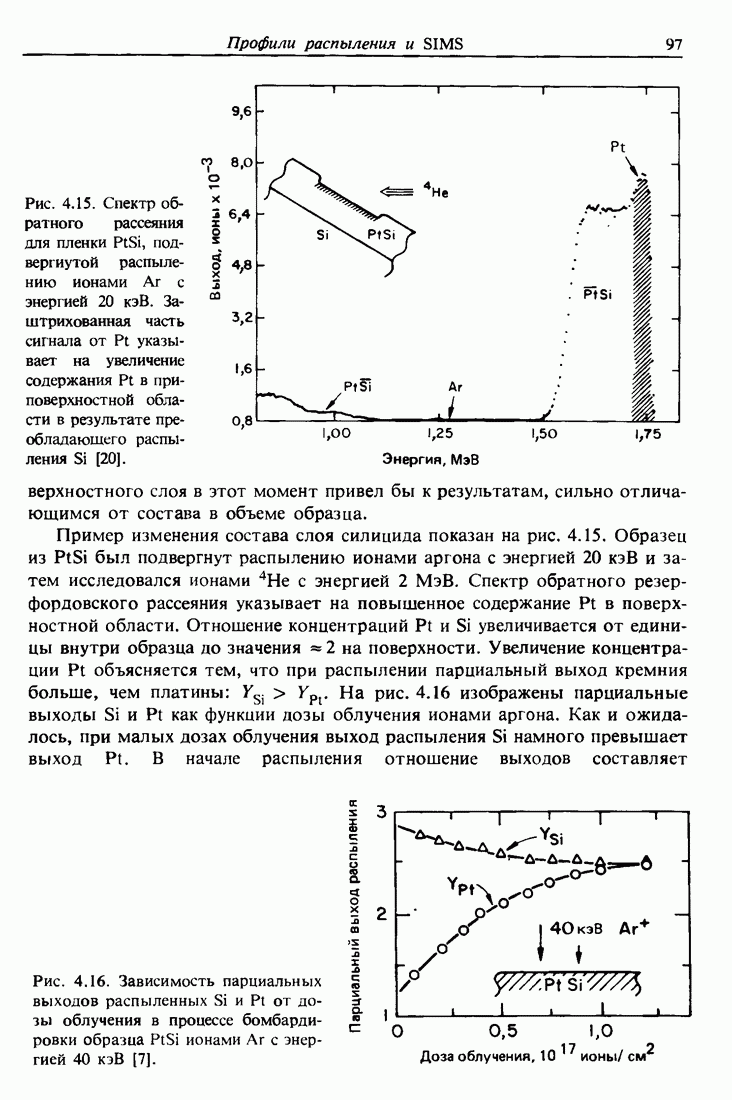
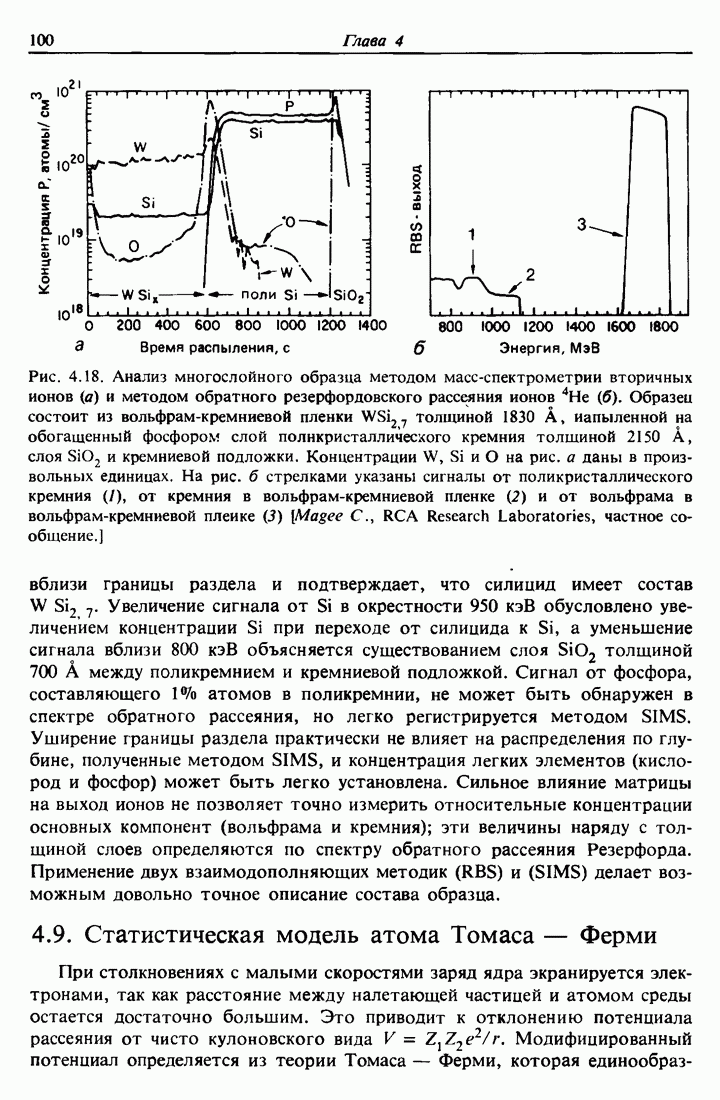
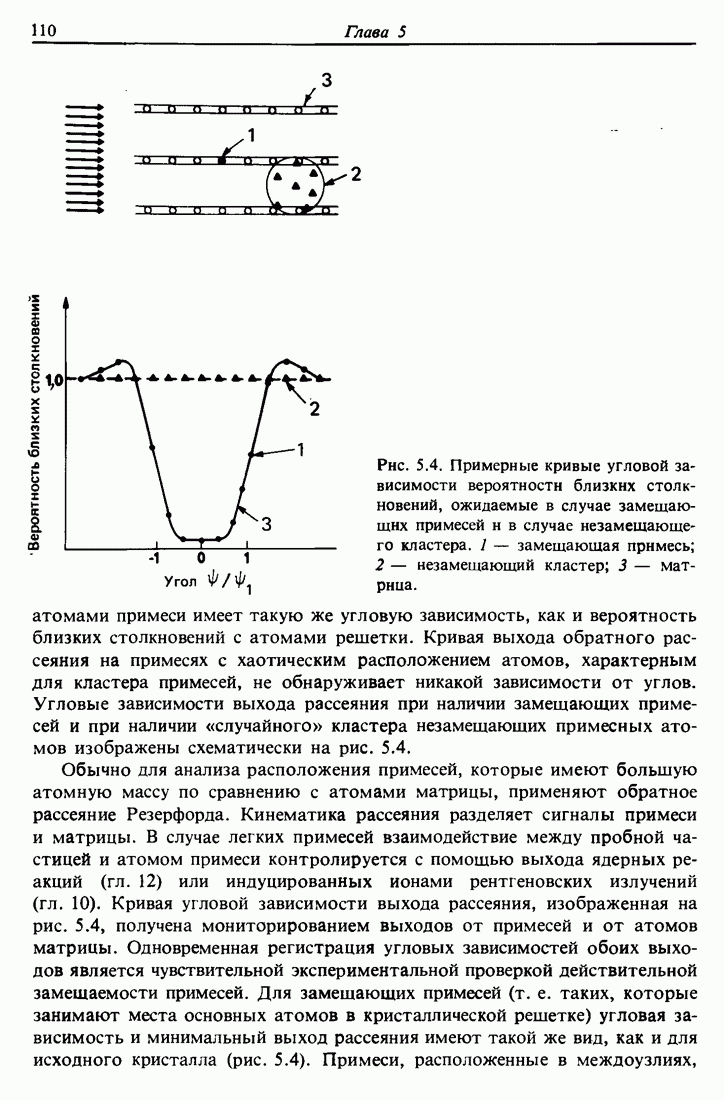
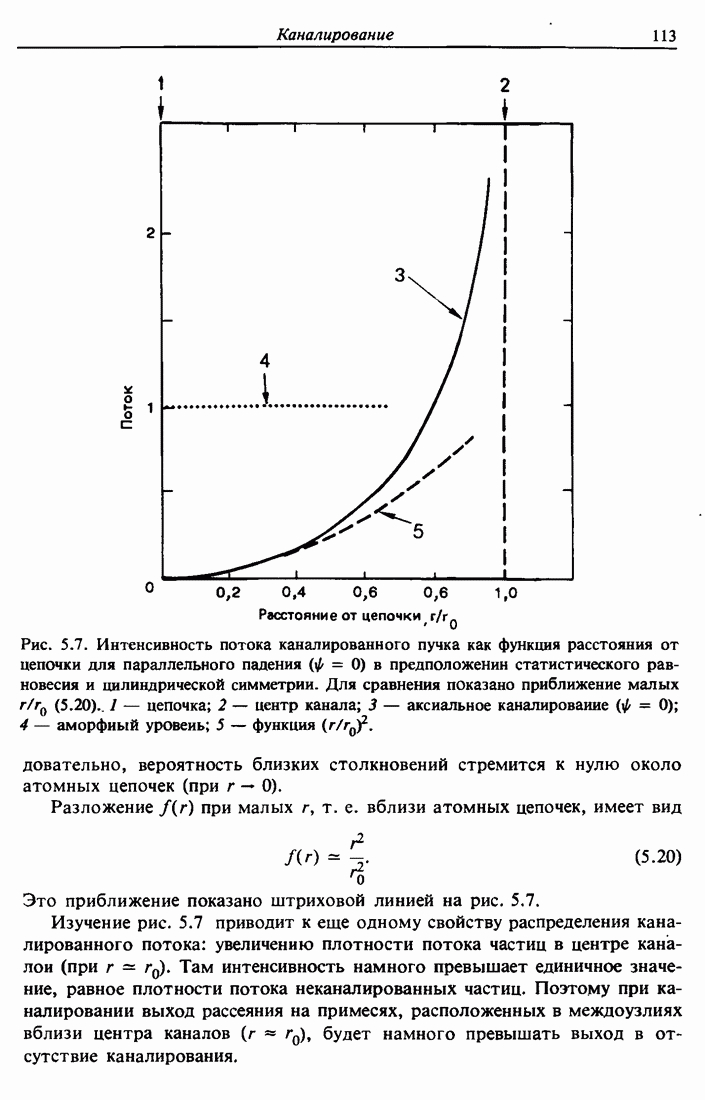
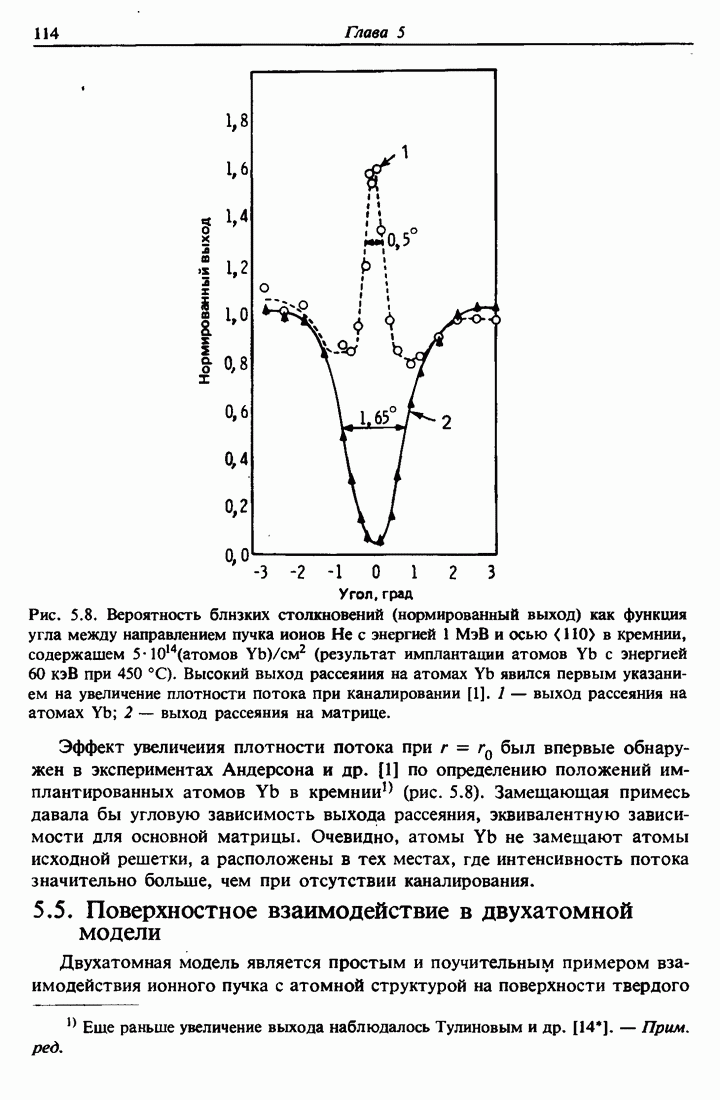
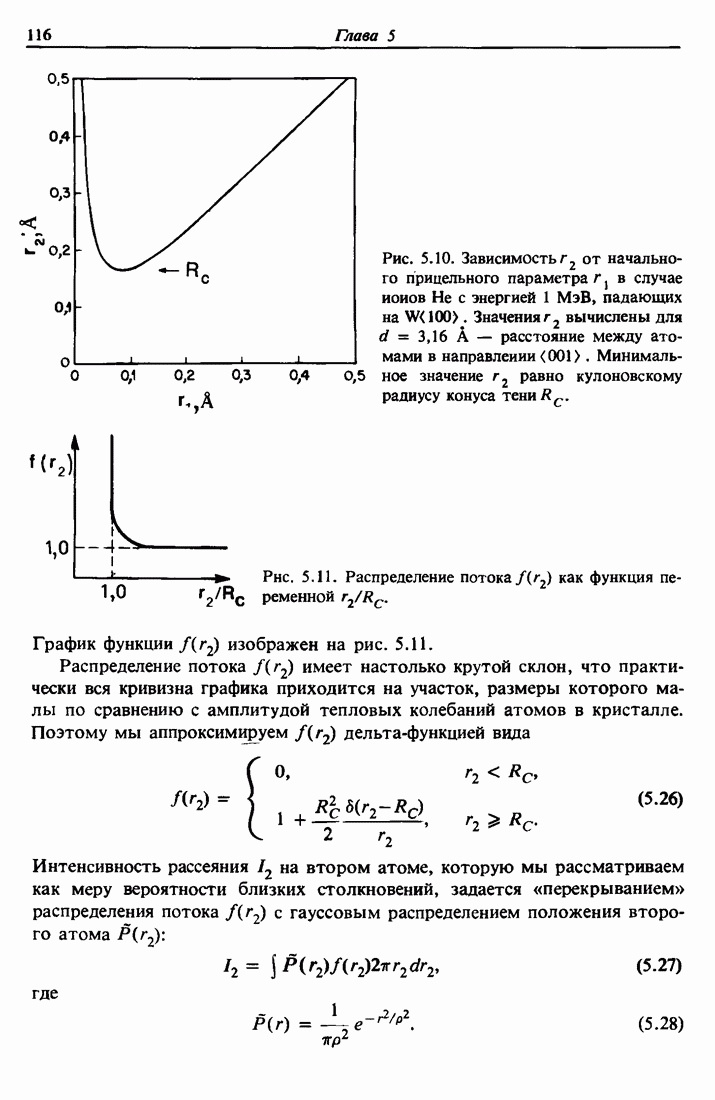
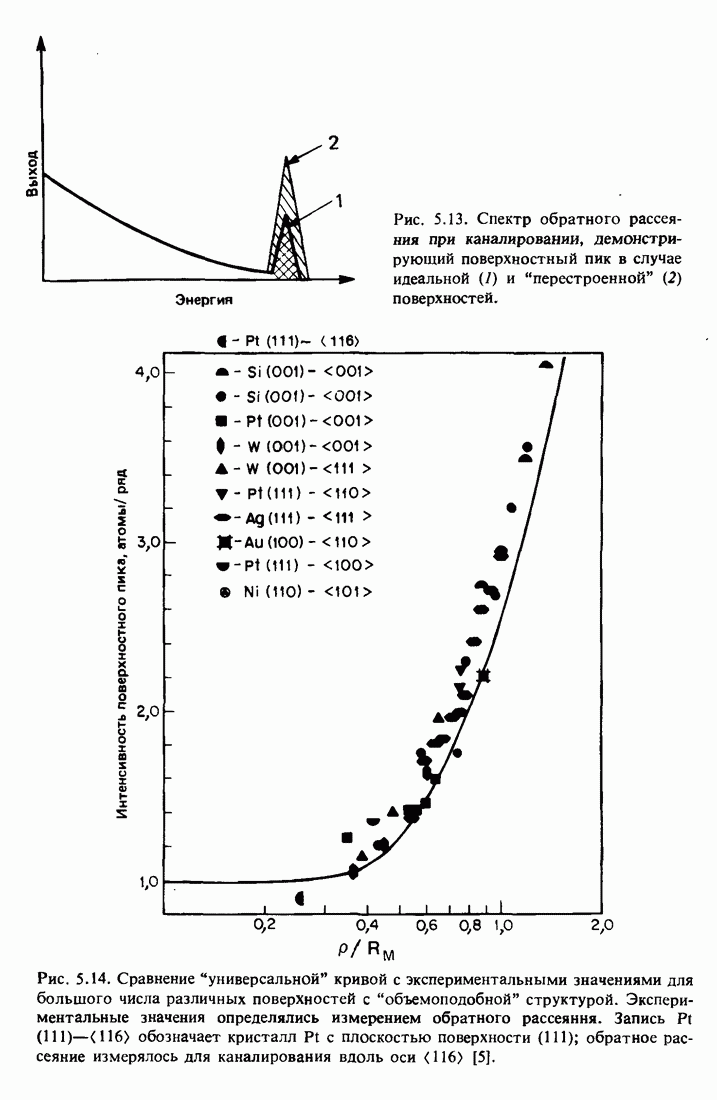
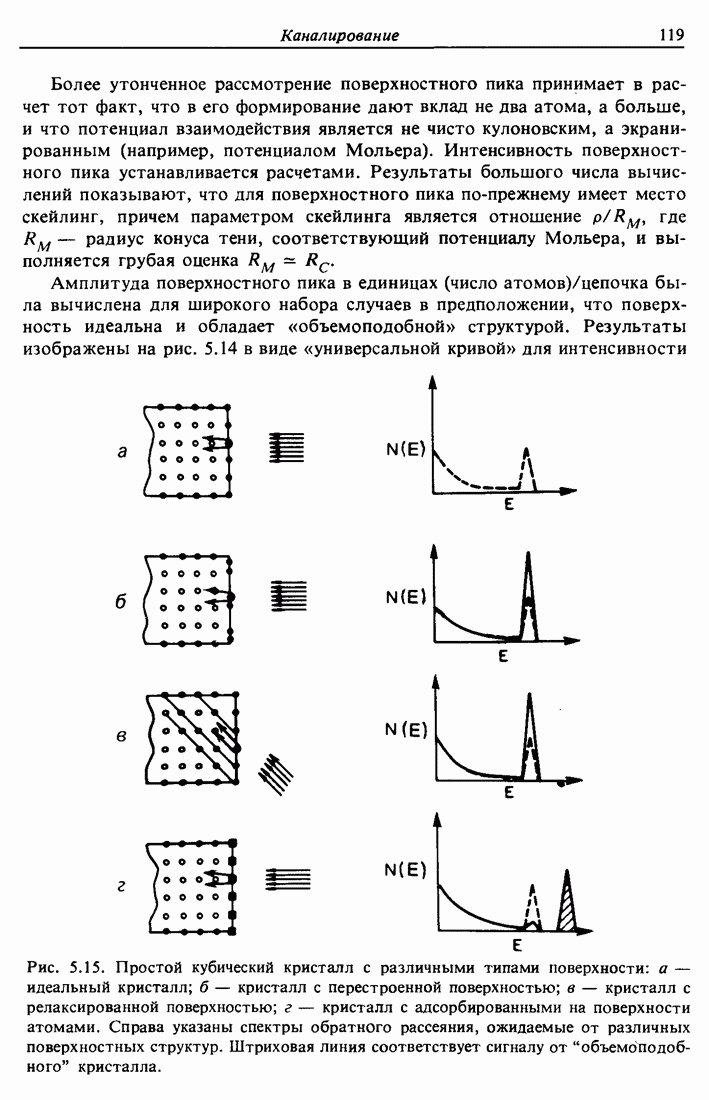
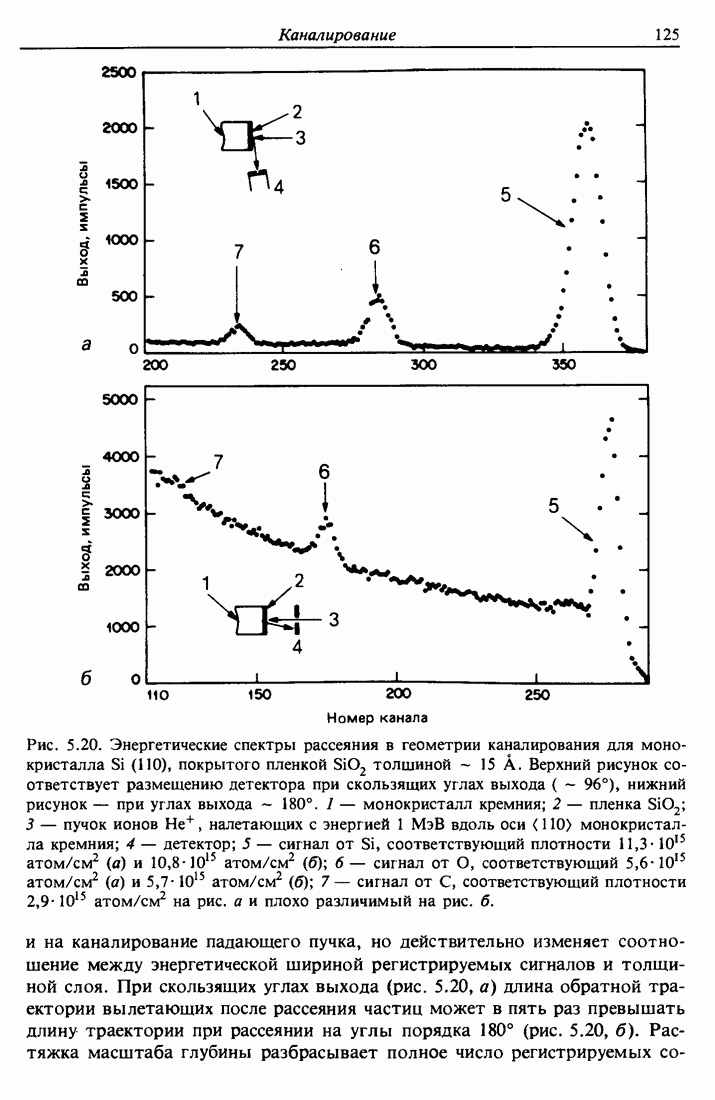
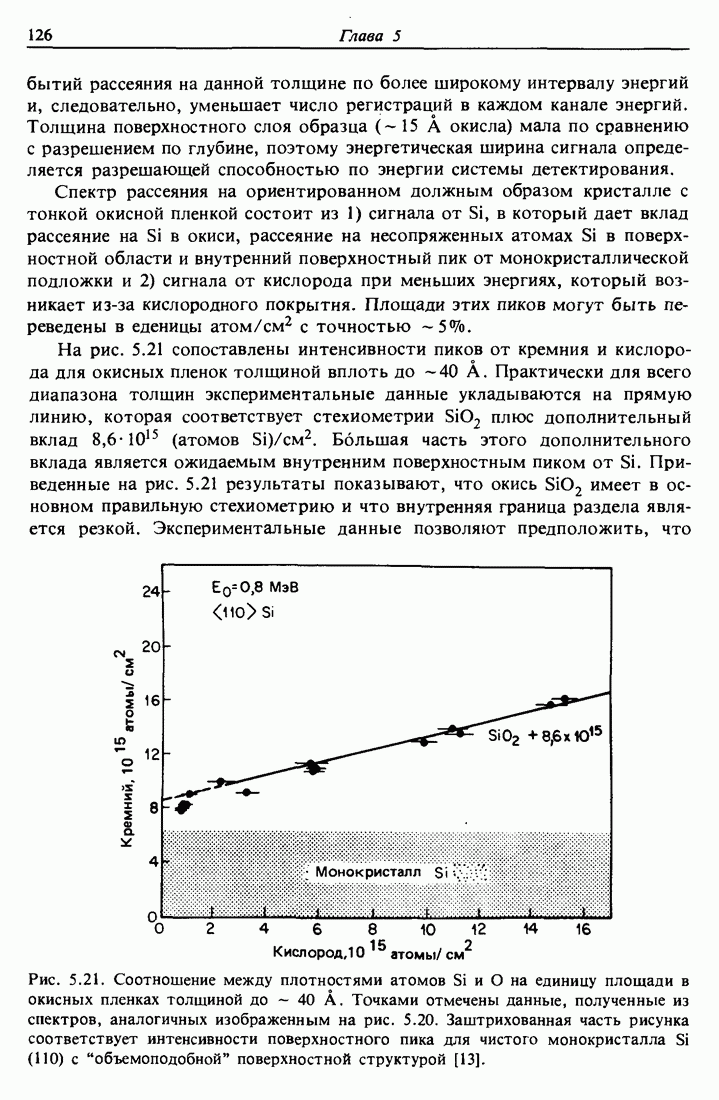
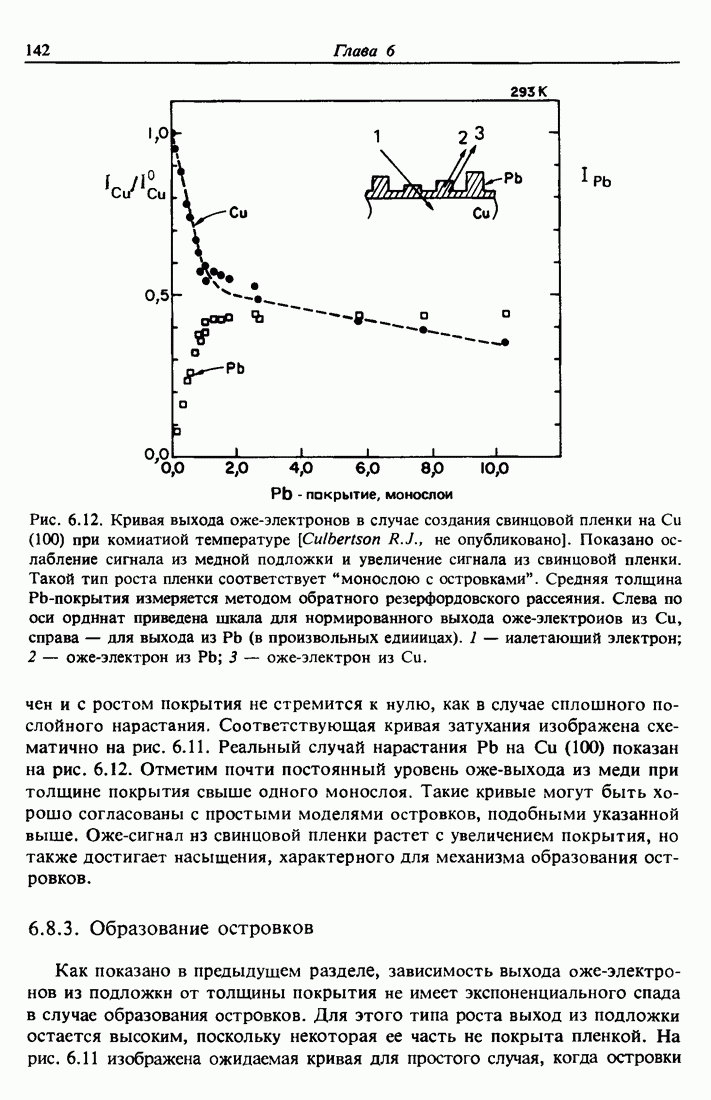
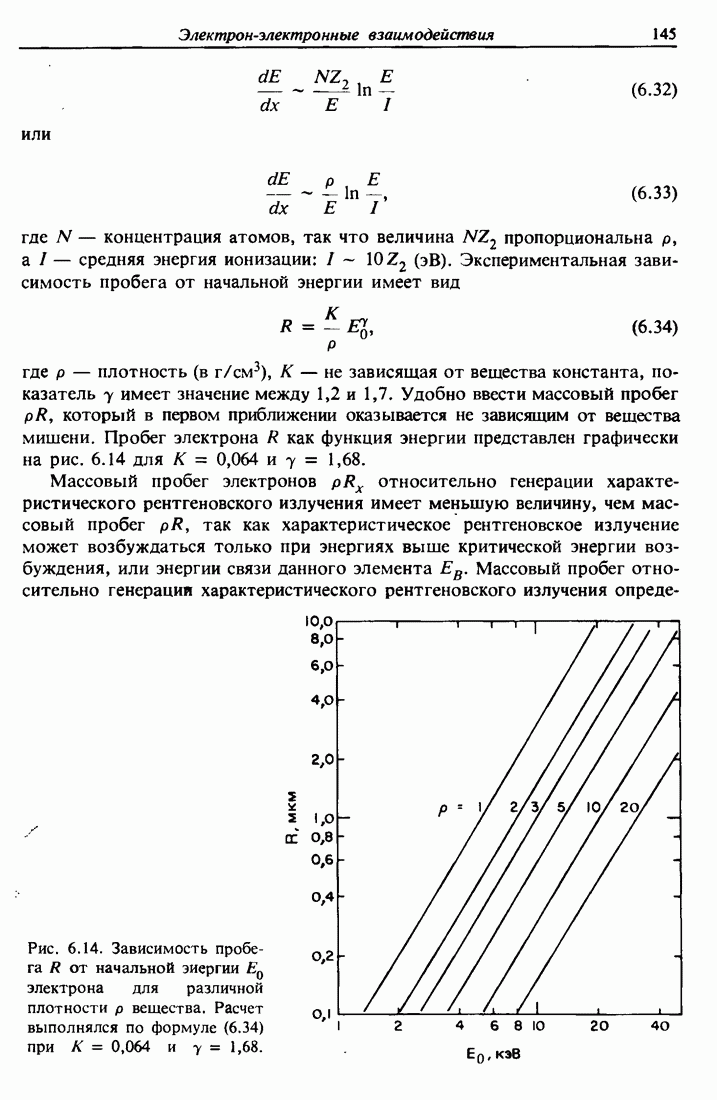
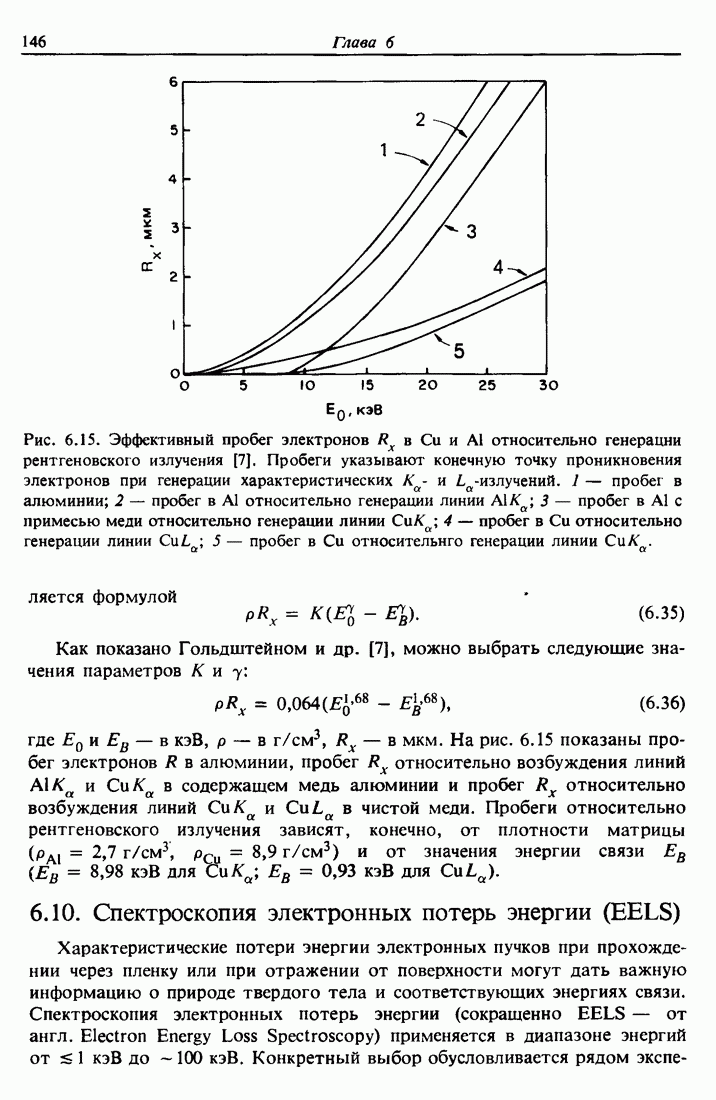
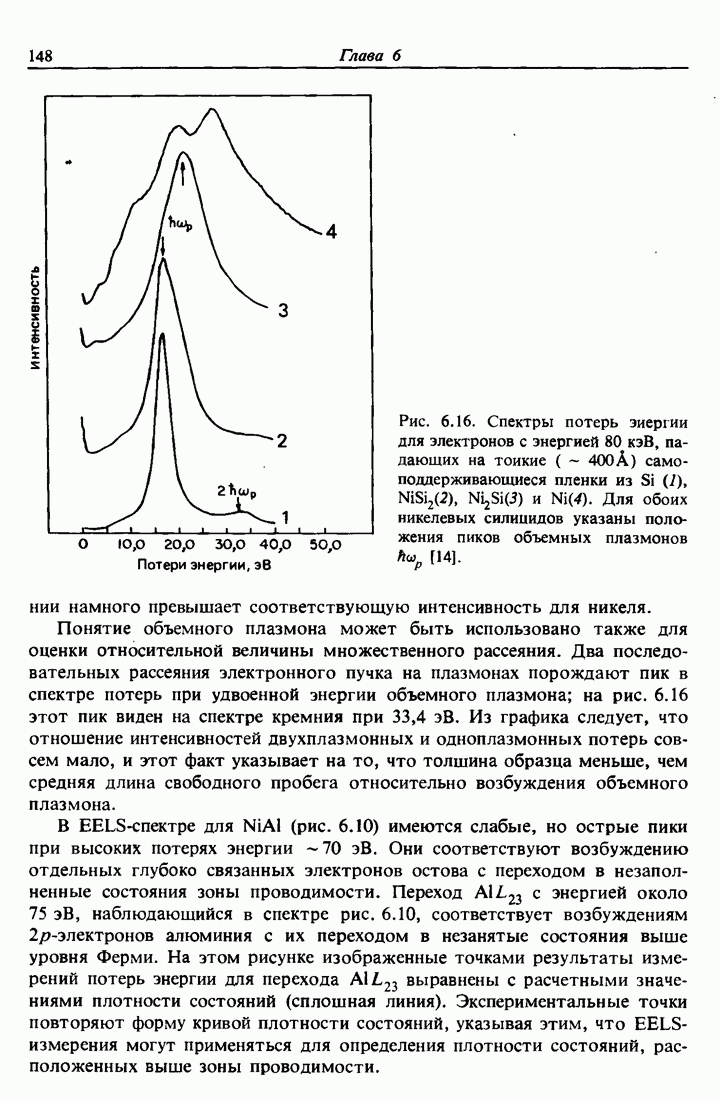
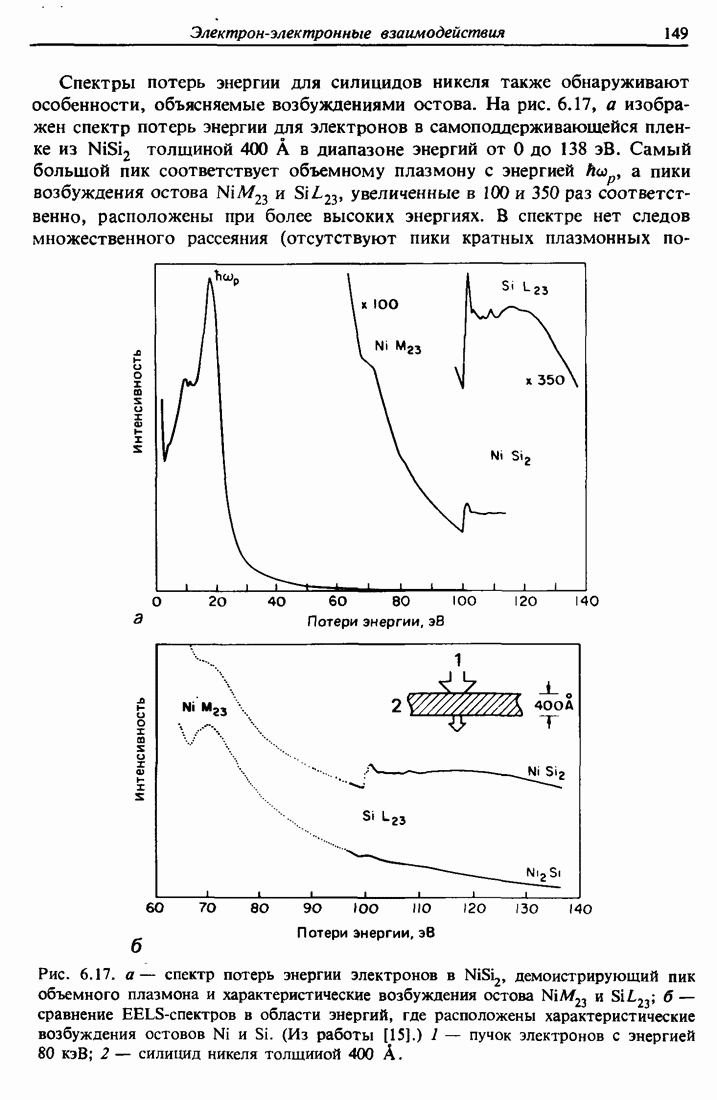
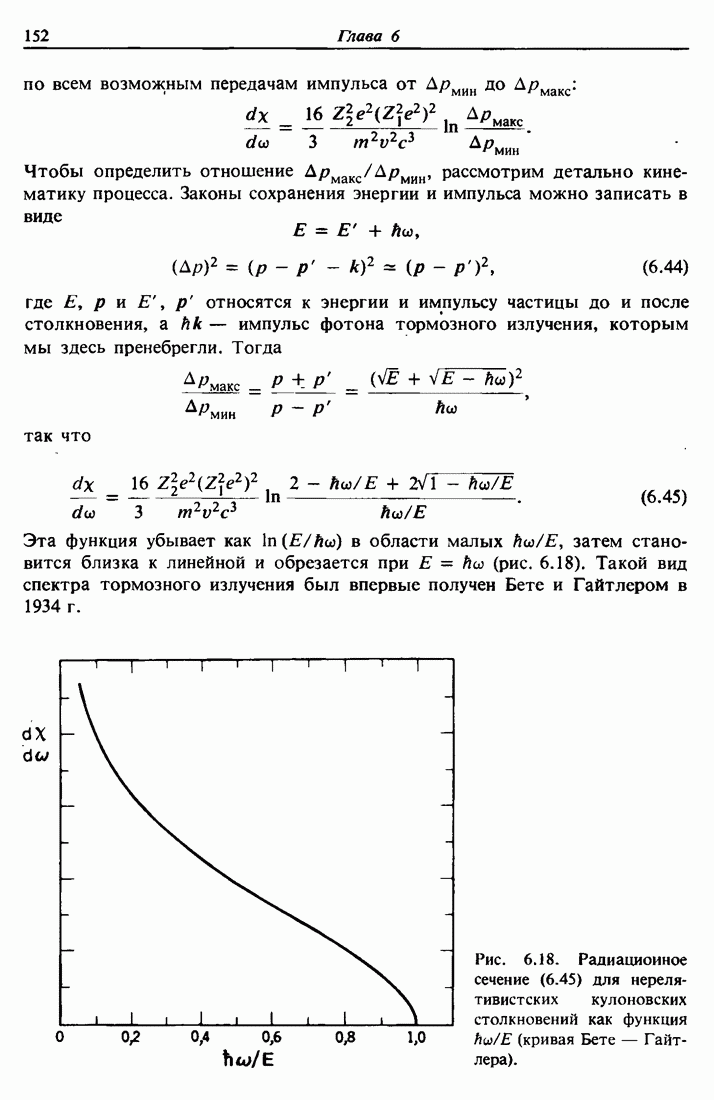
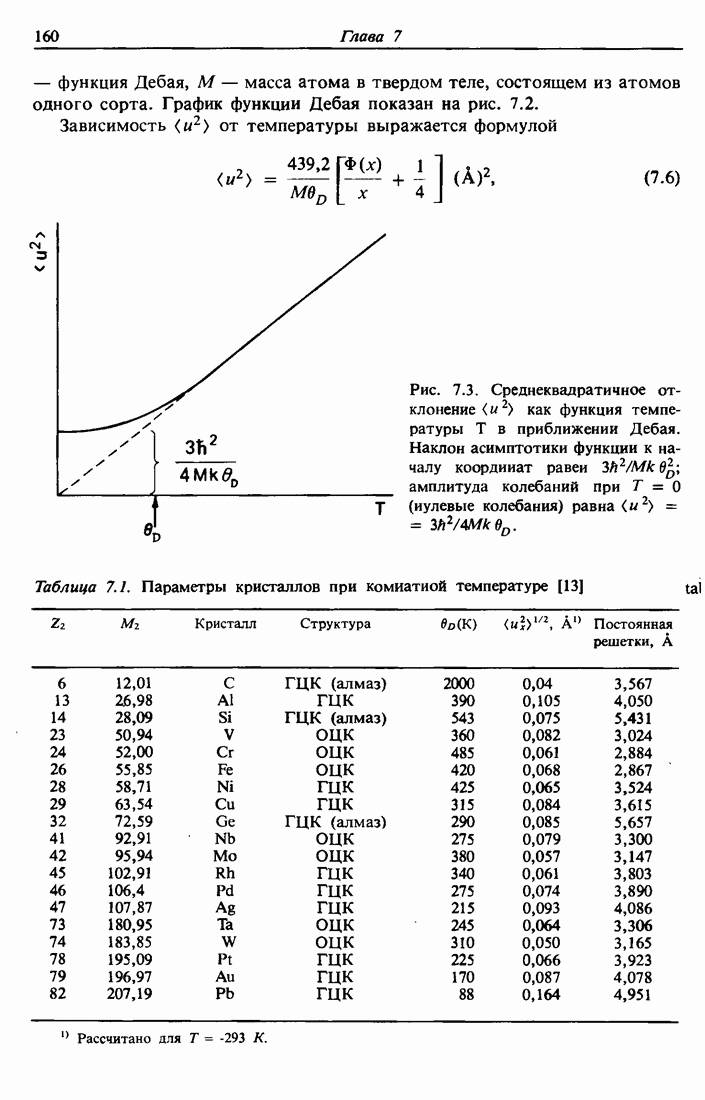
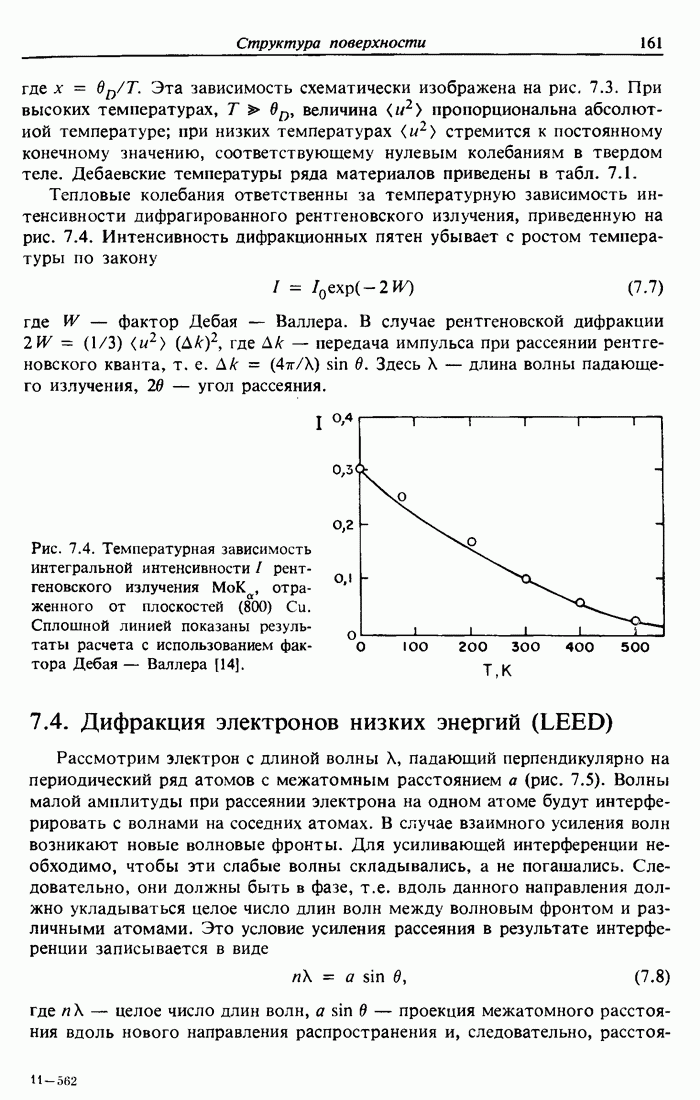
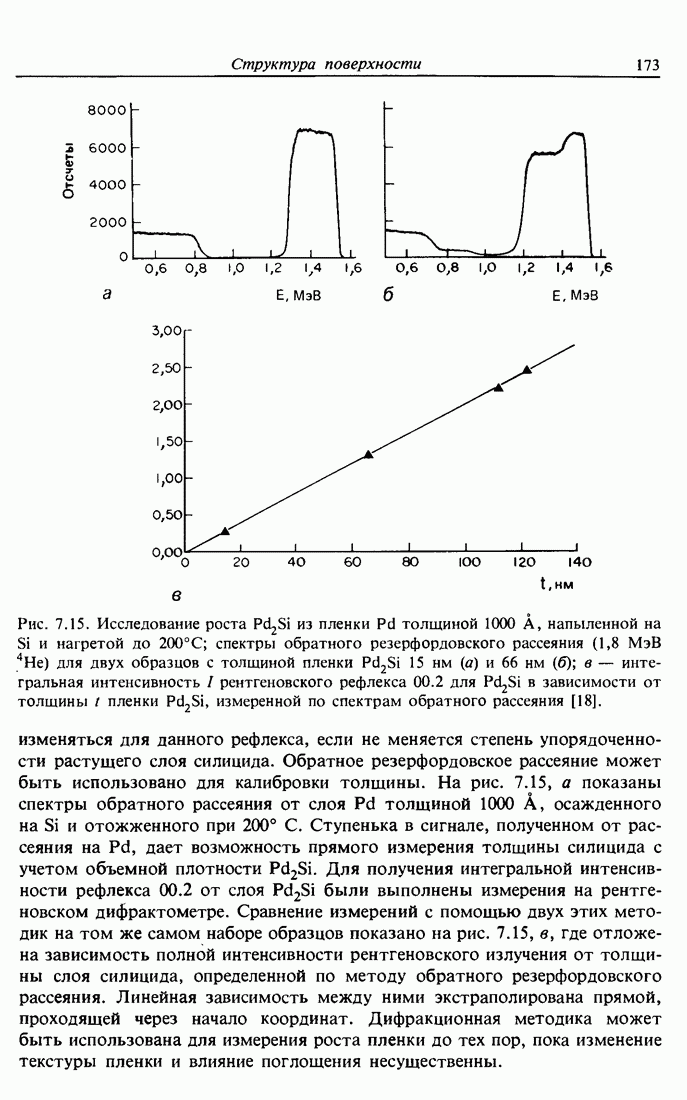
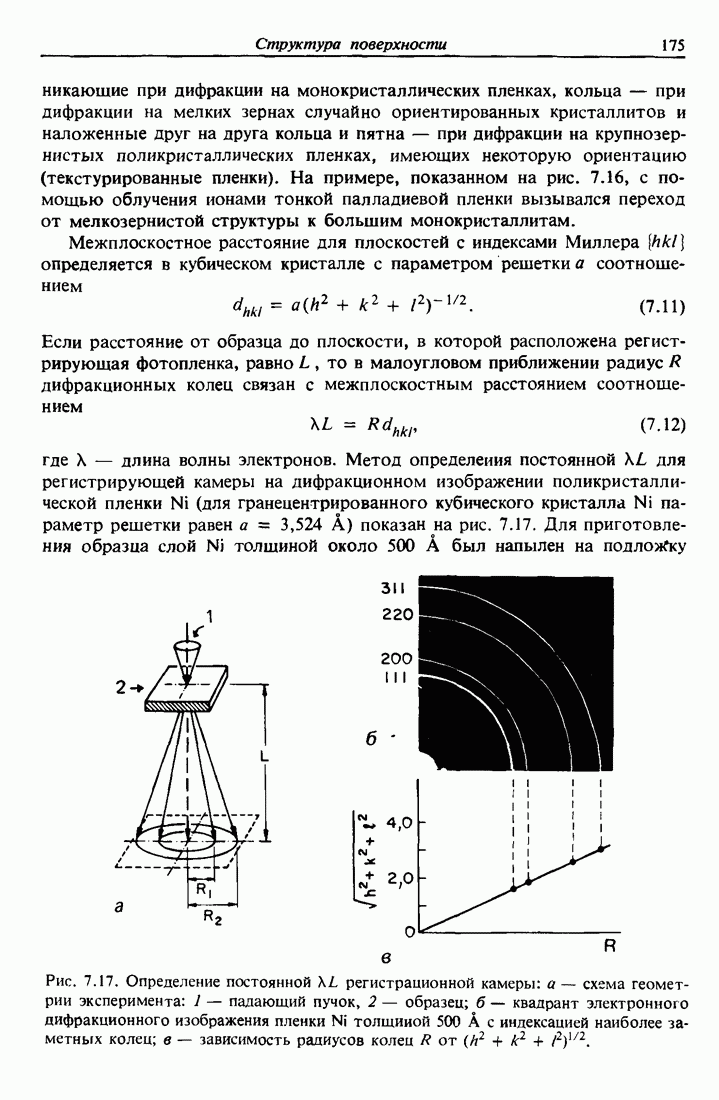
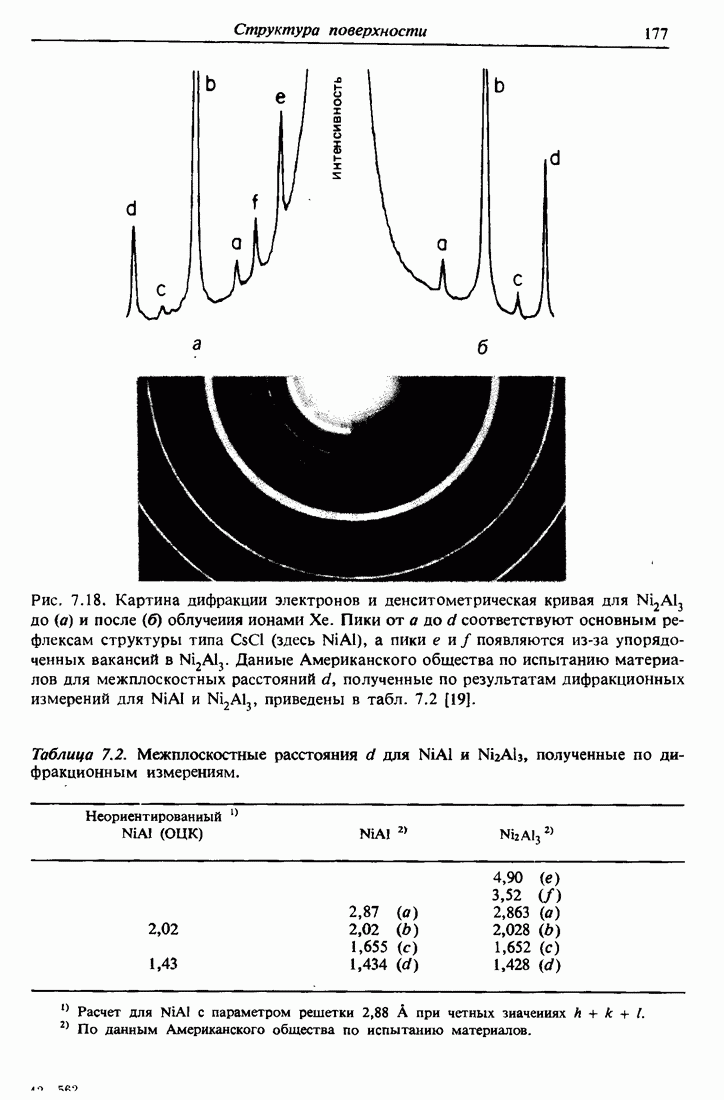
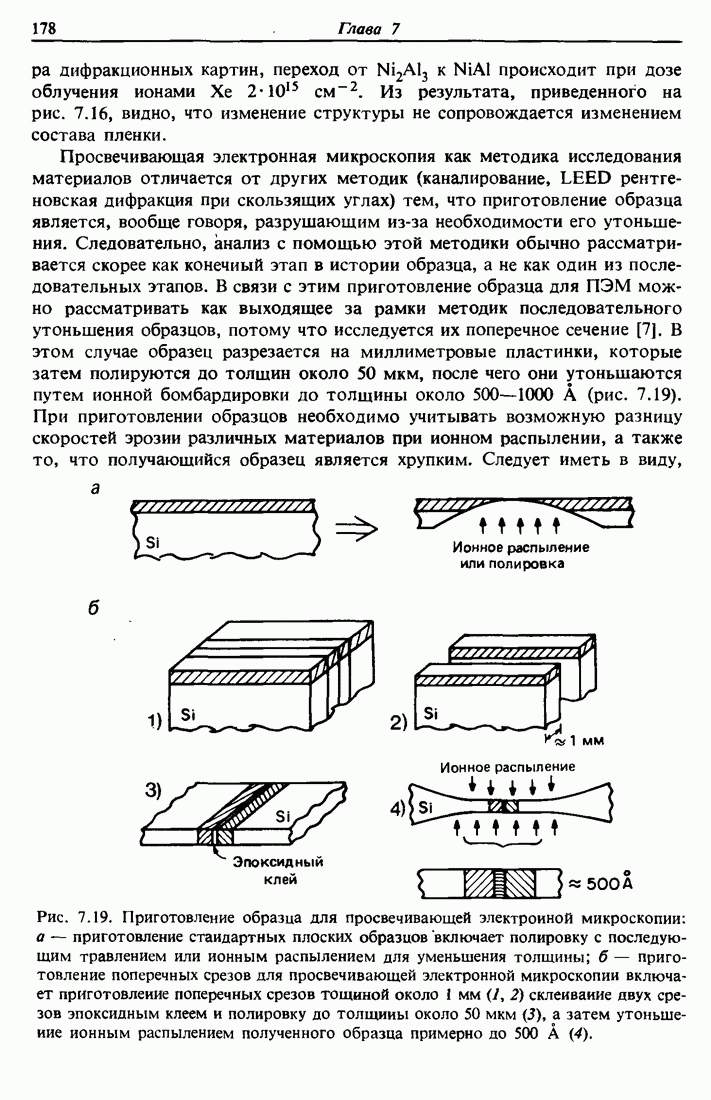
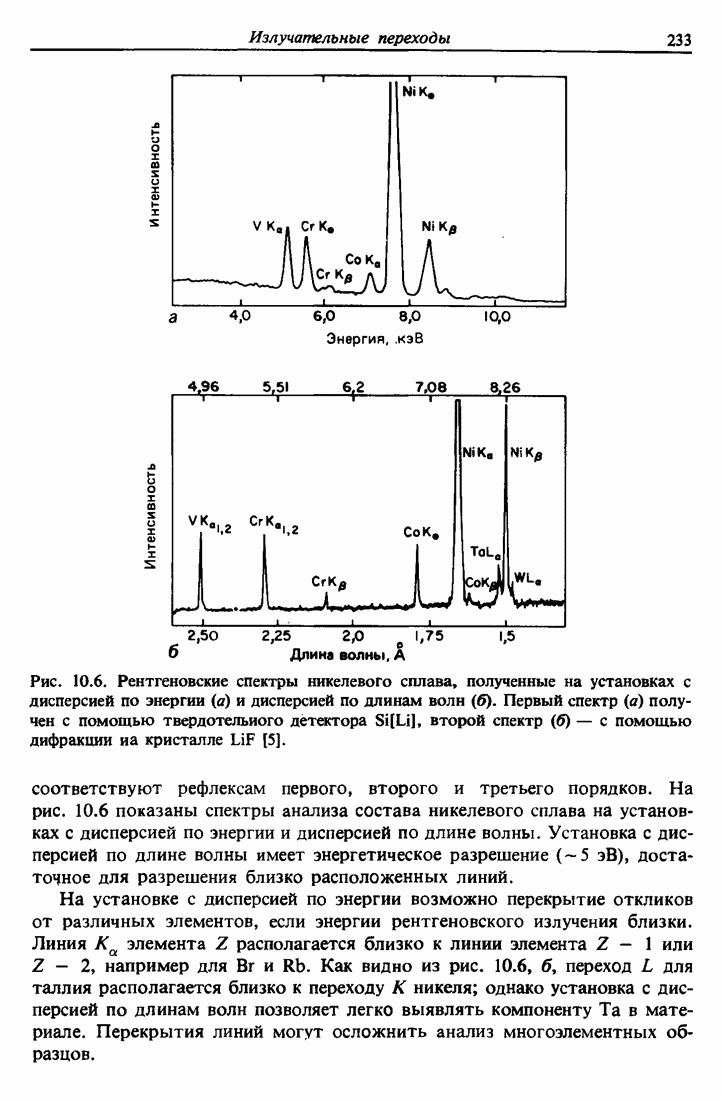
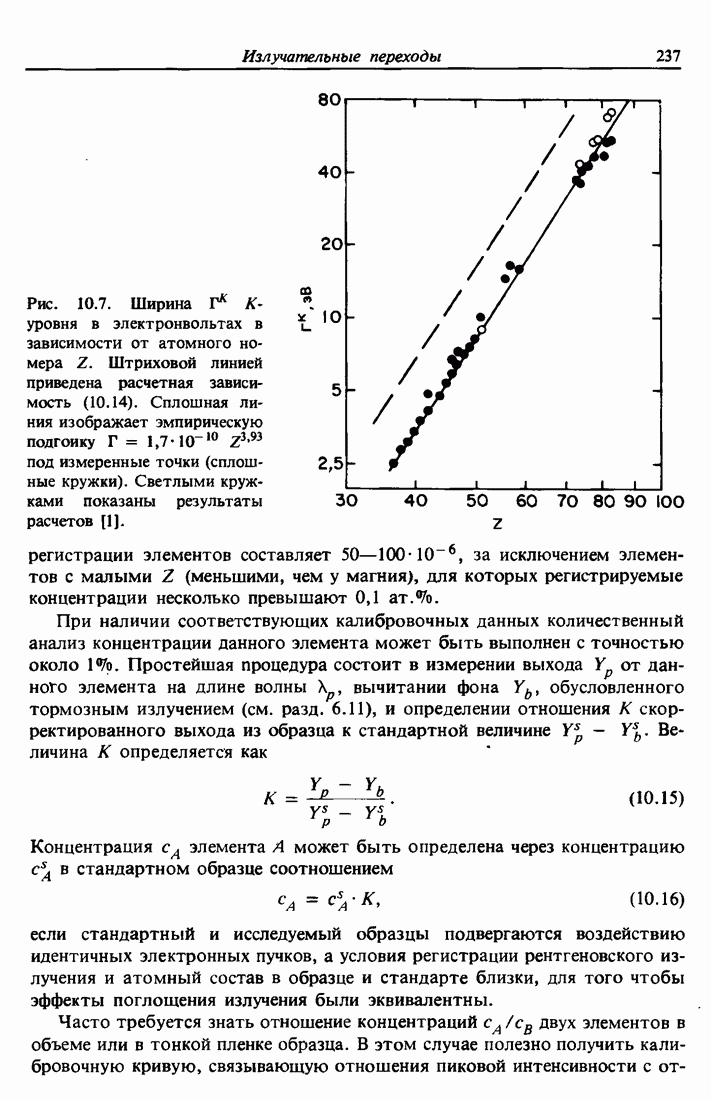
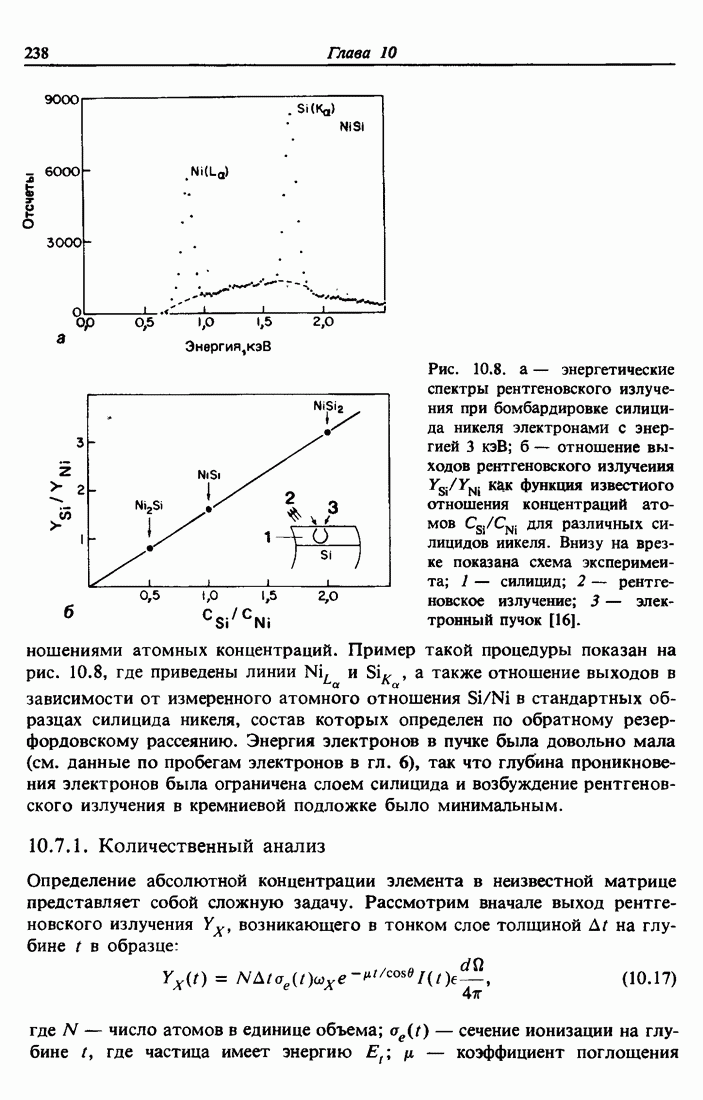
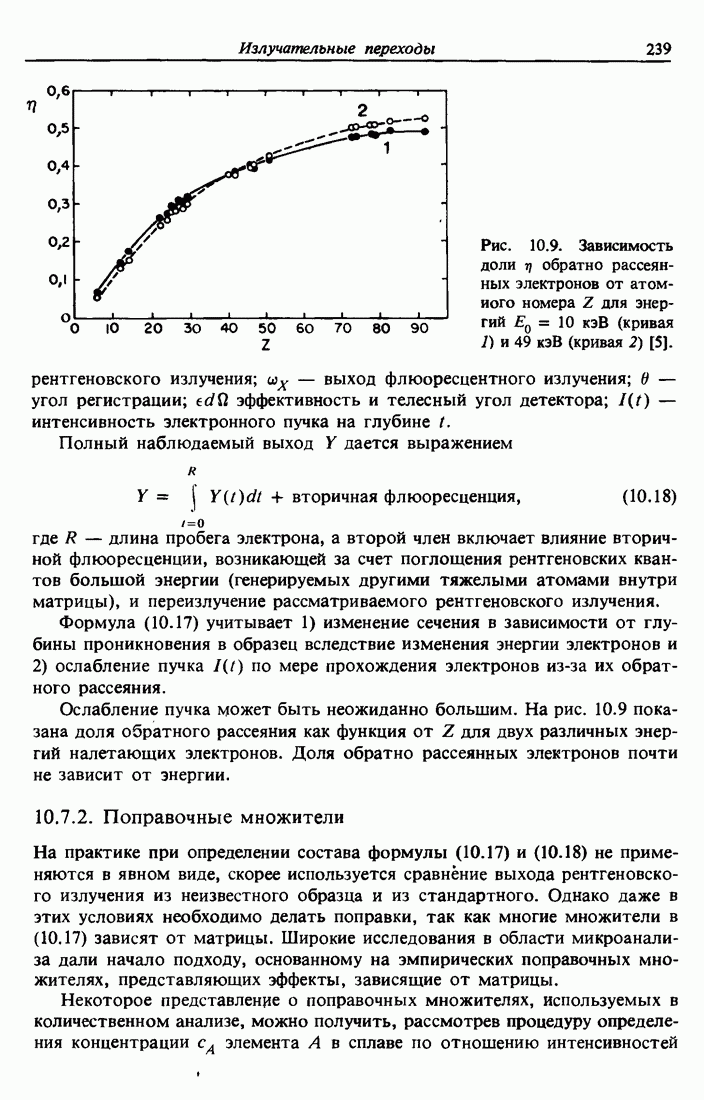
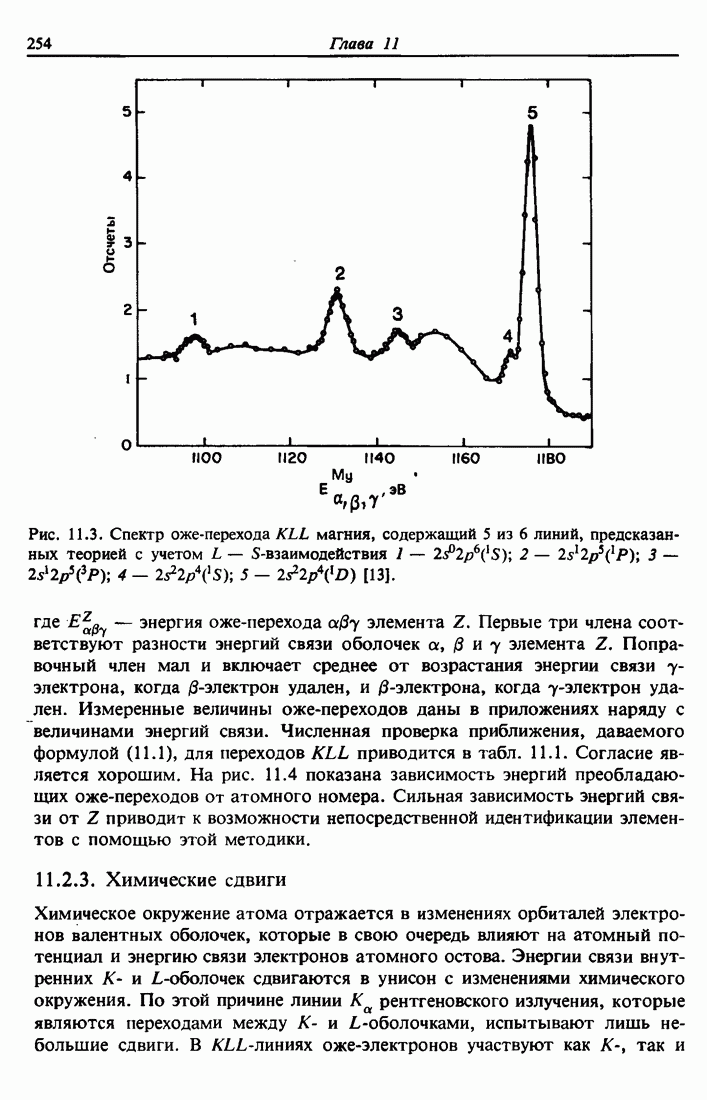
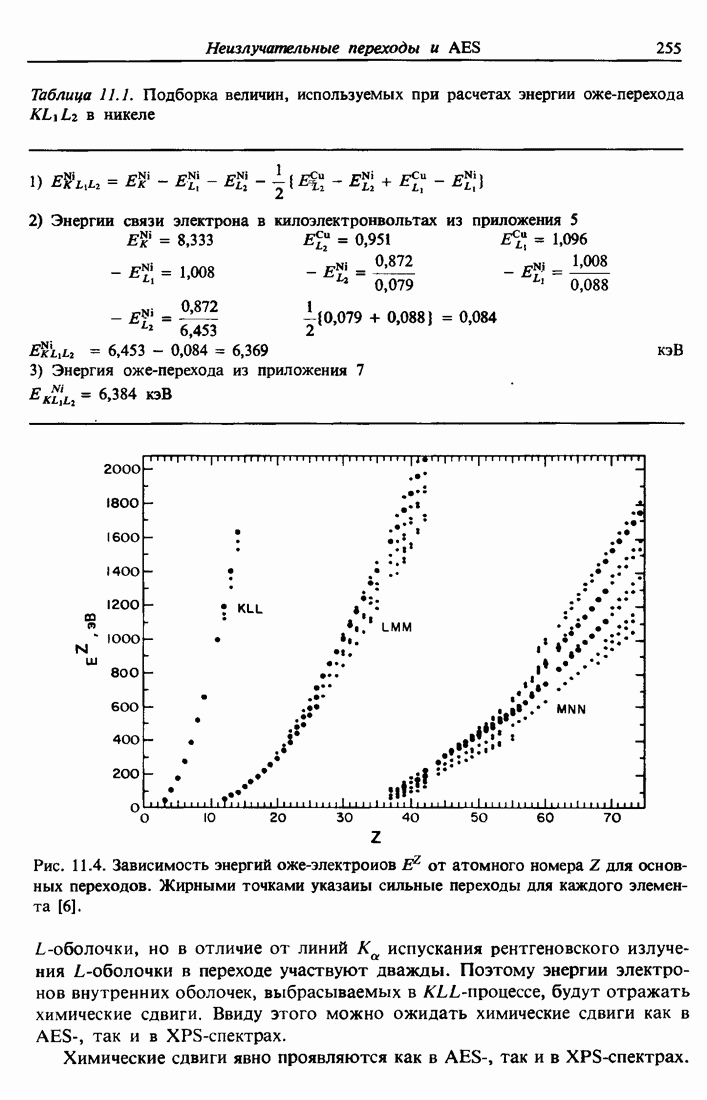
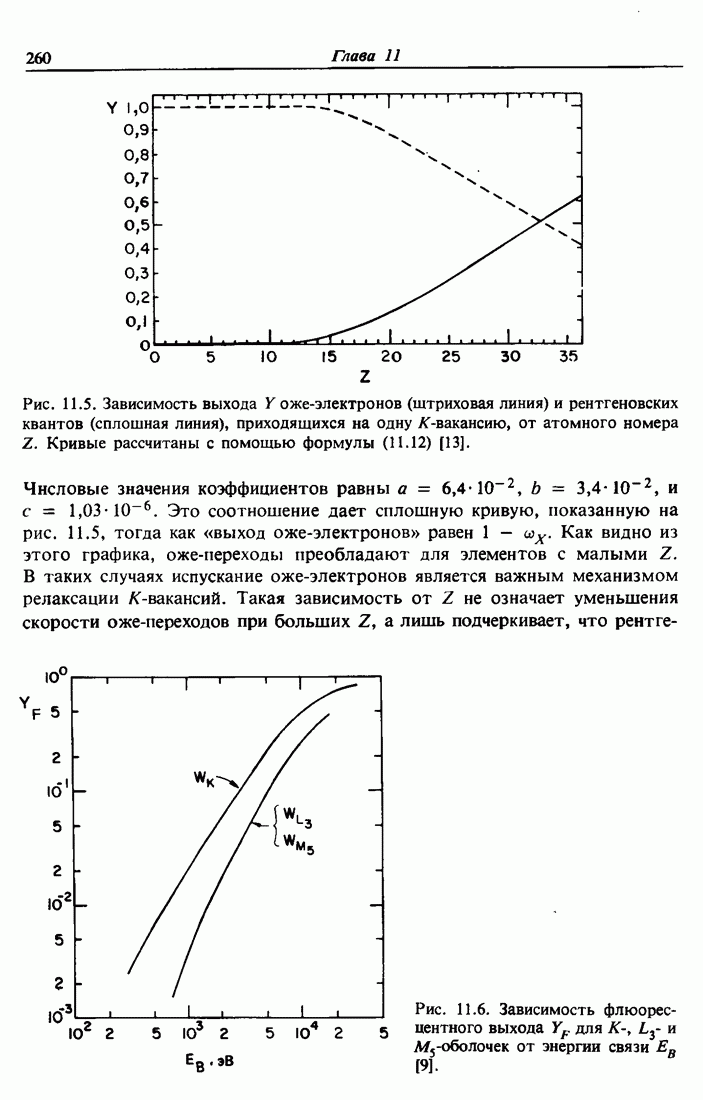
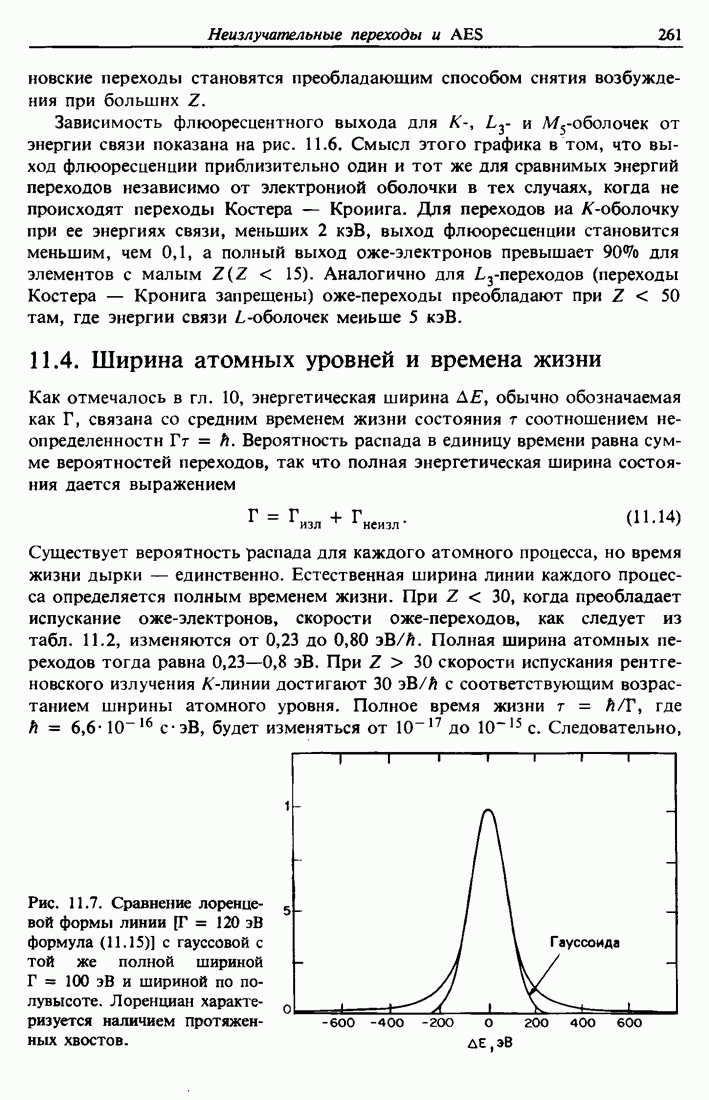
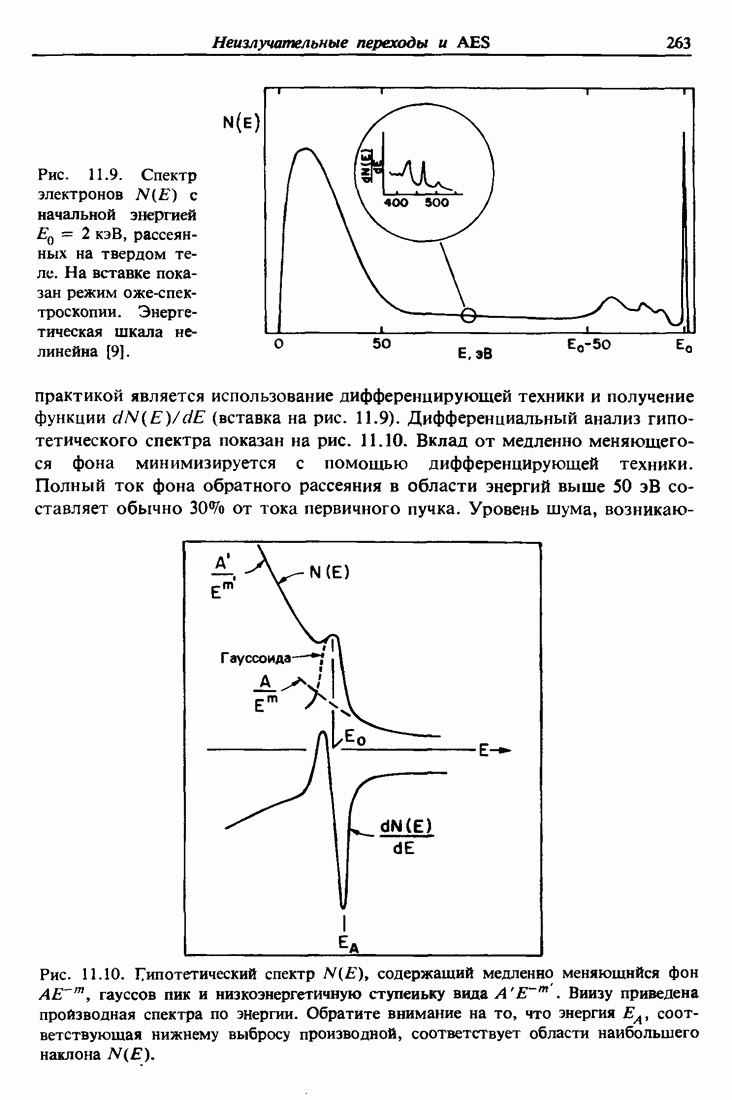
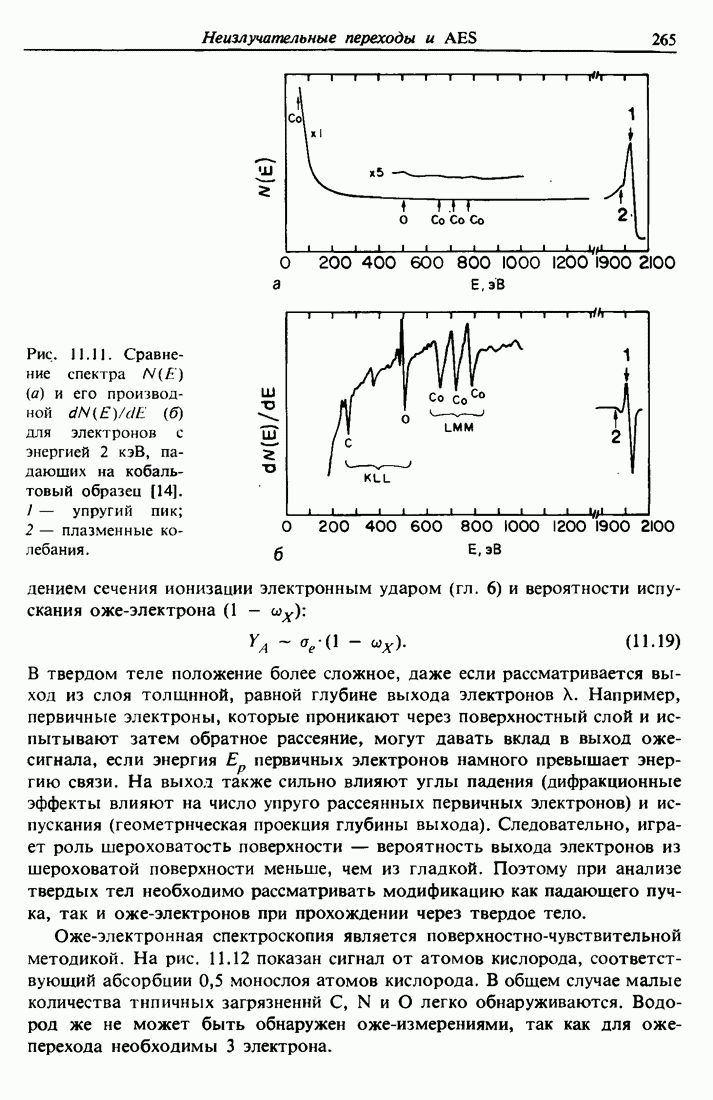
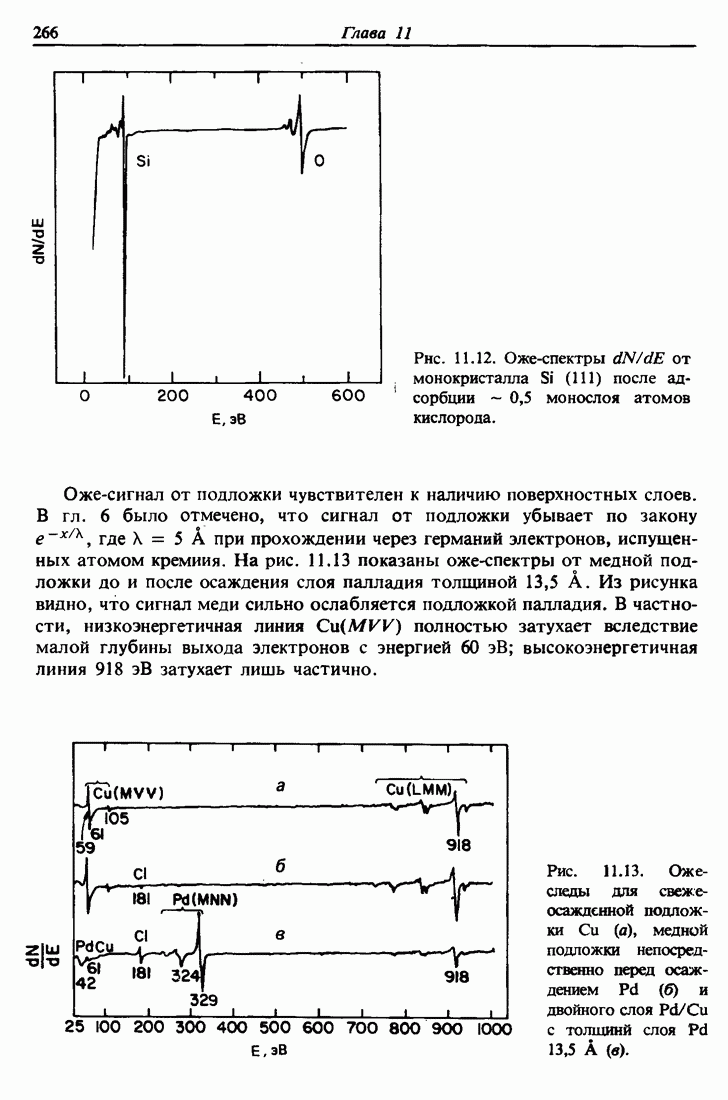
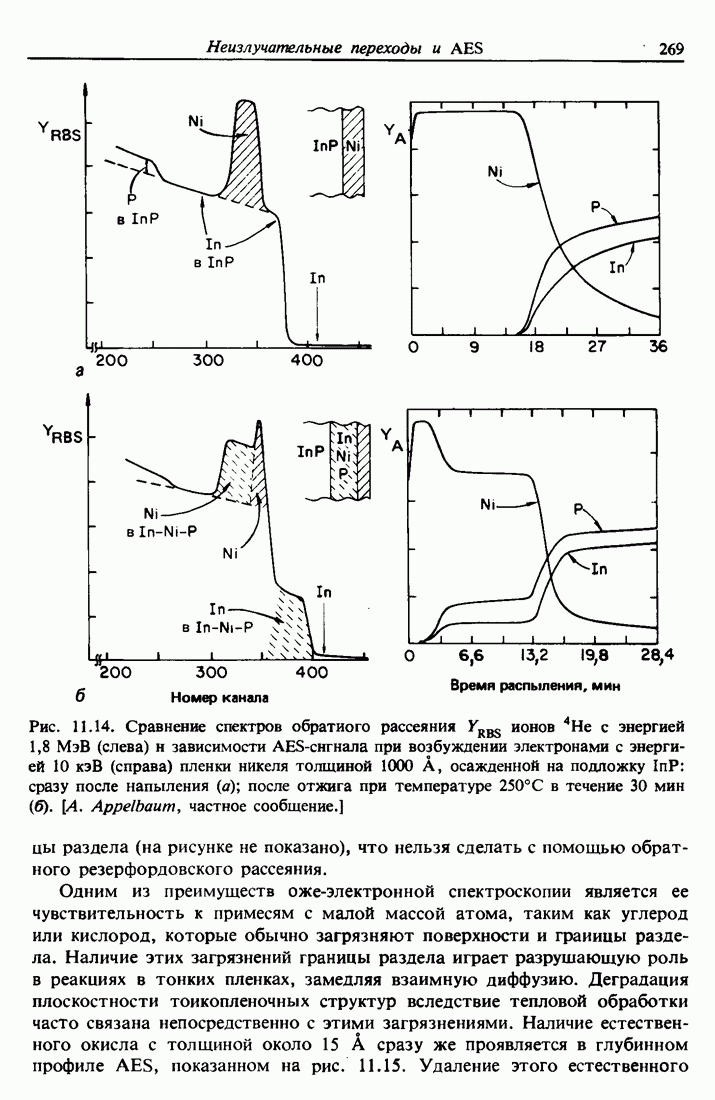
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. Потери энергии легких ионов высоких энергий в твердых телах
3.3.1. Оптимальный диапазон энергий
При движении в веществе ион гелия или водорода теряет энергию в результате взаимодействий с электронами, которые переходят в возбужденные состояния или покидают атом. Рассеяние на ядрах происходит значительно реже, чем взаимодействия с электронами, так как ядра атомов имеют ничтожно малые по сравнению с самими атомами размеры; поэтому, описывая торможение частицы, в первом приближении можно пренебречь ядерными взаимодействиями.
В теории неупругих столкновений заряженных частиц с атомами или молекулами мишени рассматриваются отдельно случаи быстрых и медленных соударений. Критерием является отношение скорости налетающей частицы к средней орбитальной скорости атомных или молекулярных электронов в данной оболочке или подоболочке атома мишени. Когда скорость v налетающей частицы намного превышает скорость орбитального электрона (случай быстрых частиц), влияние частицы на атом можно рассматривать
как внезапное малое внешнее возмущение. Эта картина приводит к теории торможения Бора [9,10]. В столкновении происходит мгновенная передача энергии от налетающей частицы к электрону мишени. Энергию, передаваемую быстрой частицей неподвижному ядру или электрону, можно вычислить по формулам рассеяния в центральном силовом поле. С увеличением скорости сечение торможения уменьшается, так как частица проводит меньше времени в окрестности атома. При низких энергиях (случай малых скоростей) этот аргумент не срабатывает, и оказывается, что сечение торможения пропорционально скорости. Максимум сечения торможения достигается при некоторой энергии, разделяющей две указанные области. Обычно в спектрометрии обратного рассеяния используется диапазон энергий, расположенный немного выше значения, соответствующего максимуму.
Одна из полезных оценок нижней границы энергий режима быстрых частиц получается сравнением скорости частицы со скоростью Бора  электрона, находящегося на самой близкой к ядру орбите атома водорода:
электрона, находящегося на самой близкой к ядру орбите атома водорода:

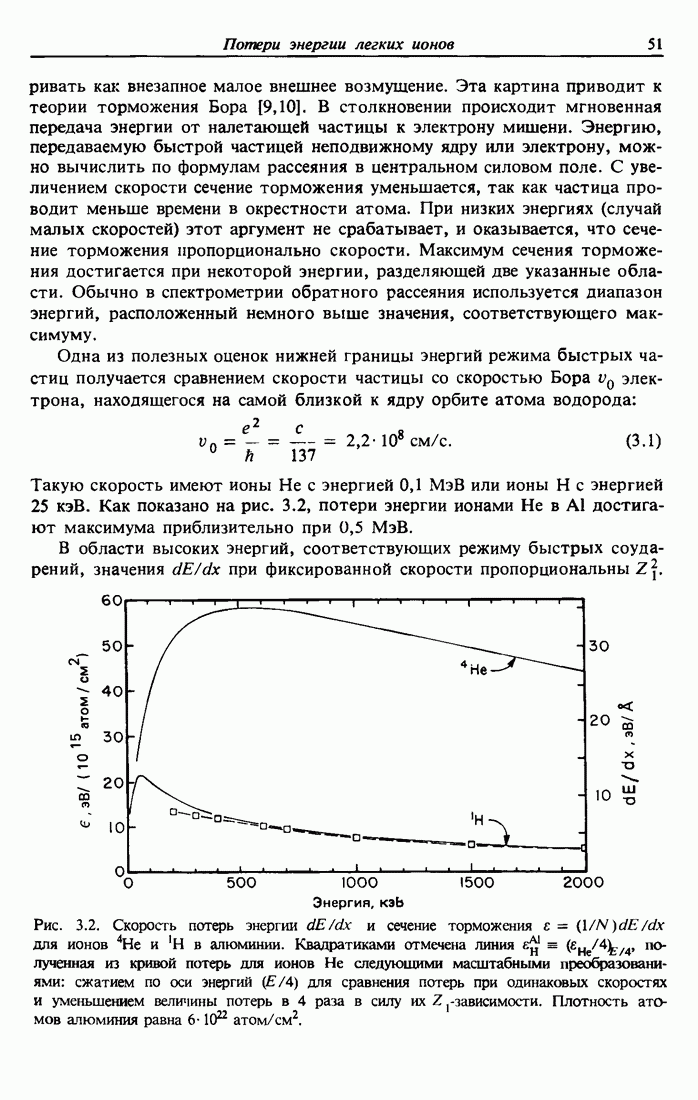
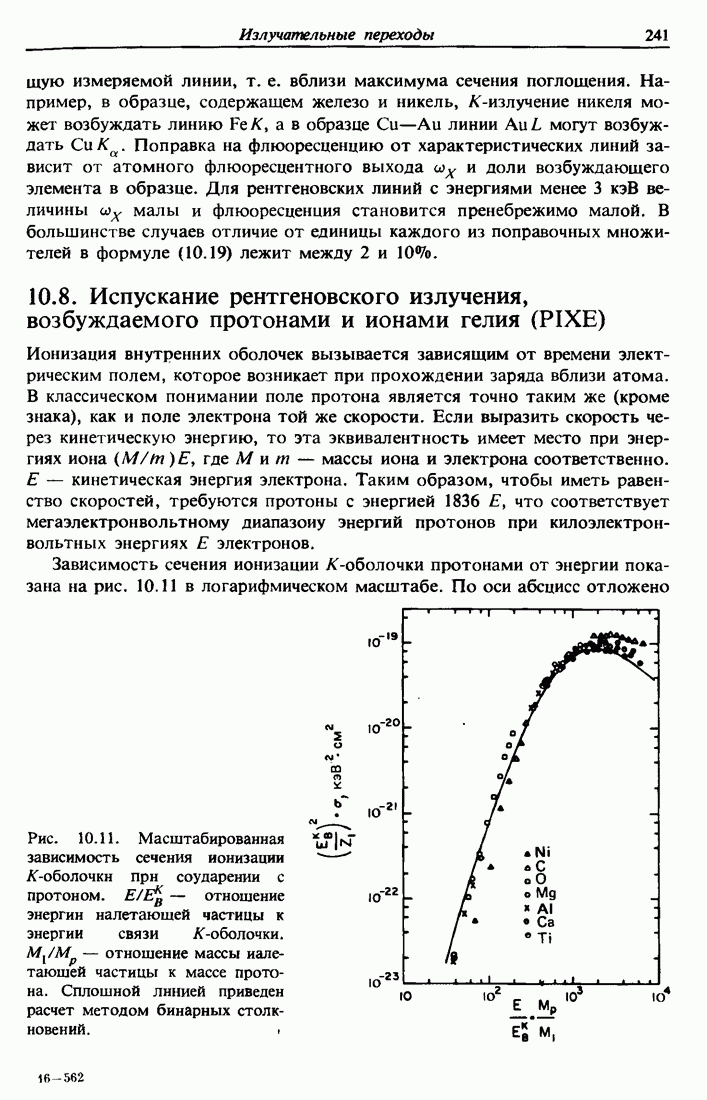
Такую скорость имеют ионы Не с энергией 0,1 МэВ или ионы Н с энергией 25 кэВ. Как показано на рис. 3.2, потери энергии ионами Не в  достигают максимума приблизительно при 0,5 МэВ.
достигают максимума приблизительно при 0,5 МэВ.
В области высоких энергий, соответствующих режиму быстрых соударений, значения  при фиксированной скорости пропорциональны
при фиксированной скорости пропорциональны 

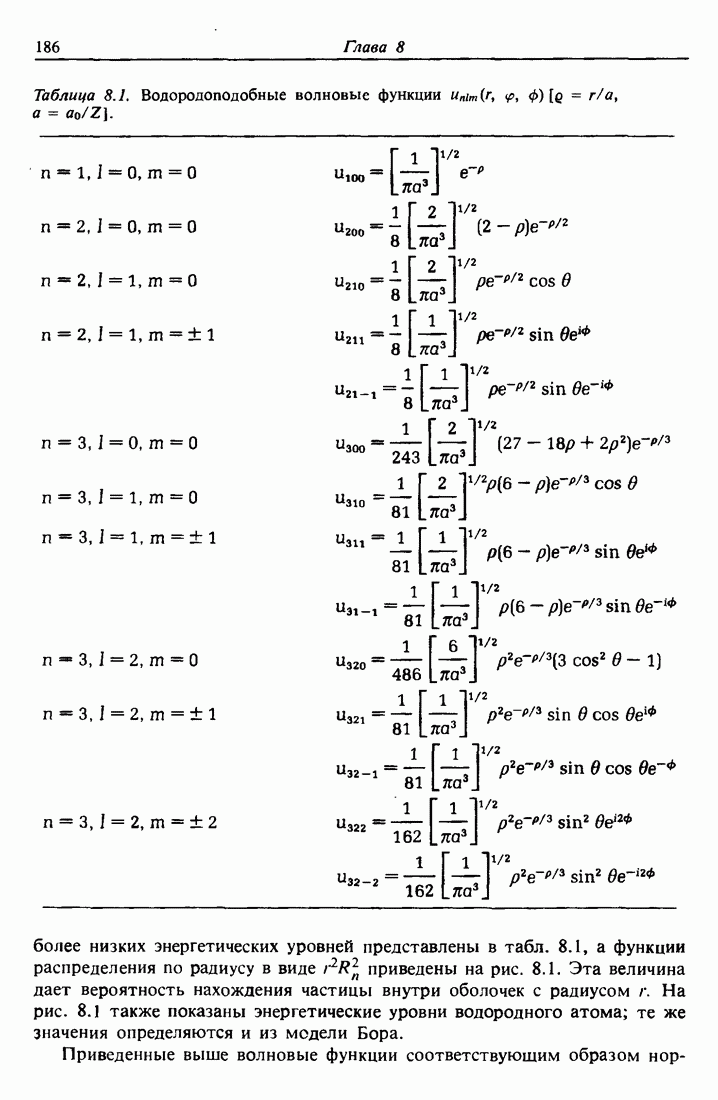
Рис. 3.2. Скорость потерь энергии  и сечение торможения
и сечение торможения  для ионов
для ионов  и Н в алюминии. Квадратиками отмечена линия
и Н в алюминии. Квадратиками отмечена линия  полученная из кривой потерь для ионов Не следующими масштабными преобразованиями: сжатием по оси энергий
полученная из кривой потерь для ионов Не следующими масштабными преобразованиями: сжатием по оси энергий  для сравнения потерь при одинаковых скоростях и уменьшением величины потерь в 4 раза в силу их Z зависимости. Плотность атомов алюминия равна
для сравнения потерь при одинаковых скоростях и уменьшением величины потерь в 4 раза в силу их Z зависимости. Плотность атомов алюминия равна  атом/см2.
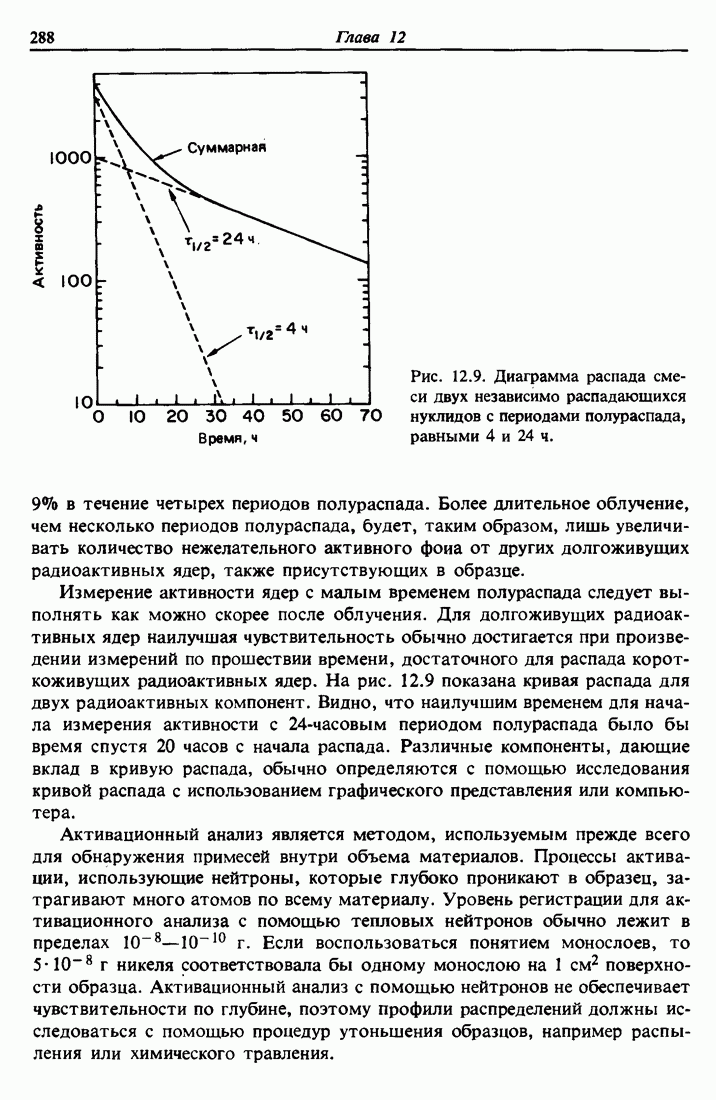
атом/см2.
Штриховая кривая и квадратики на рис. 3.2 показывают значения потерь энергий для ионов  уменьшенные в четыре раза
уменьшенные в четыре раза  и отнесенные к величине энергии, в четыре раза меньшей, чем на графике для Не
и отнесенные к величине энергии, в четыре раза меньшей, чем на графике для Не  , т. е. при одинаковых скоростях. При прохождении через вещество атомы Не или Н считаются полностью ионизованными (
, т. е. при одинаковых скоростях. При прохождении через вещество атомы Не или Н считаются полностью ионизованными ( или а-частица,
или а-частица,  или протон), так как скорость движения атомов настолько велика, что они теряют все свои электроны. С уменьшением скорости средний заряд налетающей частицы уменьшается, и число электронов среды, которые могут быть возбуждены взаимодействием, также становится меньше; поэтому потери энергии падают.
или протон), так как скорость движения атомов настолько велика, что они теряют все свои электроны. С уменьшением скорости средний заряд налетающей частицы уменьшается, и число электронов среды, которые могут быть возбуждены взаимодействием, также становится меньше; поэтому потери энергии падают.
3.3.2. Вывод выражения для dE/dx
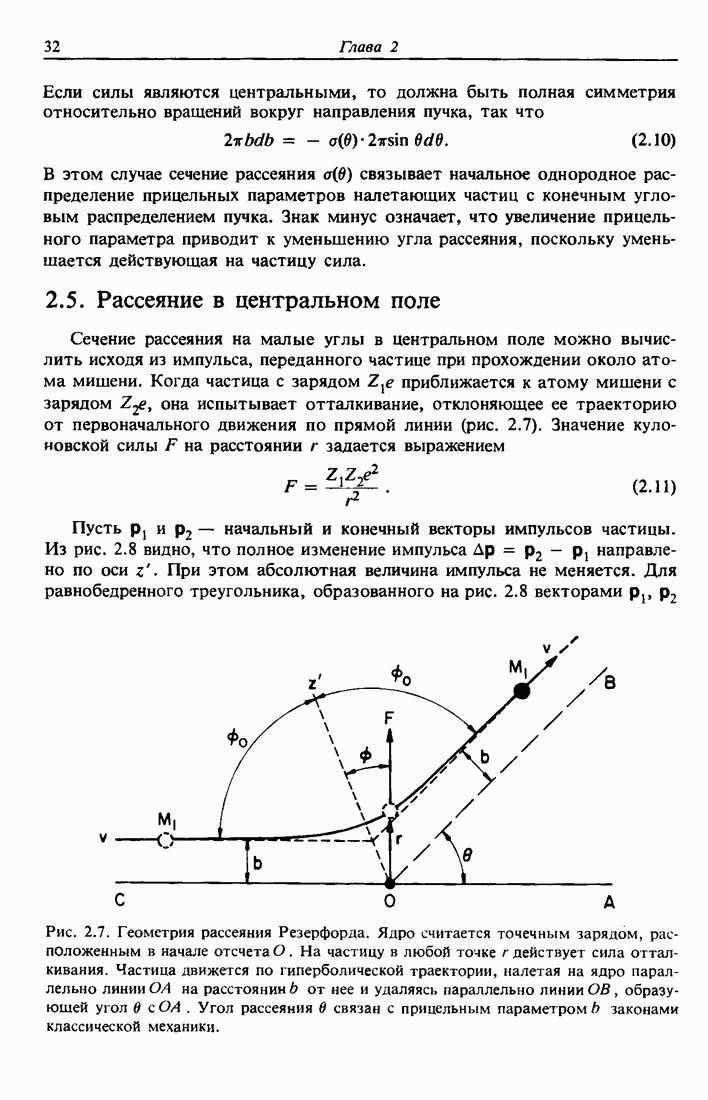
В 1913 г. Бор получил выражение для скорости потерь энергии заряженной частицы на основании классических представлений. Он рассмотрел тяжелую частицу, такую как а-частица или протон, с зарядом  массой
массой  и скоростью у, проходящую на расстоянии b от принадлежащего атому электрона массой
и скоростью у, проходящую на расстоянии b от принадлежащего атому электрона массой  (рис. 3.3). При движении тяжелой частицы кулоновская сила, действующая на электрон, непрерывно меняет направление. Если смещением электрона во время пролета тяжелой частицы можно пренебречь, то составляющая импульса силы
(рис. 3.3). При движении тяжелой частицы кулоновская сила, действующая на электрон, непрерывно меняет направление. Если смещением электрона во время пролета тяжелой частицы можно пренебречь, то составляющая импульса силы  вдоль направления движения частицы равна нулю в силу симметрии, так как каждому положению —
вдоль направления движения частицы равна нулю в силу симметрии, так как каждому положению —  на траектории соответствует положение
на траектории соответствует положение  которое дает противоположный вклад в
которое дает противоположный вклад в  -компоненту импульса. Однако на протяжении всего столкновения электрон подвергается действию силы в
-компоненту импульса. Однако на протяжении всего столкновения электрон подвергается действию силы в  -направлении и ему передается импульс
-направлении и ему передается импульс  Задача вычисления переданной энергии становится аналогичной изложенному в
Задача вычисления переданной энергии становится аналогичной изложенному в  выводу формулы рассеяния Резерфорда в кулоновском поле сил, если мы перейдем в систему отсчета, в которой электрон движется со скоростью v навстречу неподвижному ядру. Тогда импульс, полученный электроном во время столкновения, равен
выводу формулы рассеяния Резерфорда в кулоновском поле сил, если мы перейдем в систему отсчета, в которой электрон движется со скоростью v навстречу неподвижному ядру. Тогда импульс, полученный электроном во время столкновения, равен


Рис. 3.3. а — схема пролета тяжелой частицы с зарядом  на расстоянии b от электрона; б — цилиндрический слой радиусом b и толщиной
на расстоянии b от электрона; б — цилиндрический слой радиусом b и толщиной  , ось которого совпадает с траекторией движения тяжелой заряженной частицы.
, ось которого совпадает с траекторией движения тяжелой заряженной частицы.
где мы использовали выражение (2.15а) при  т. е. в рамках малоуглового приближения. Если электрон в результате столкновения не разгоняется до релятивистских скоростей, то его энергия становится равной
т. е. в рамках малоуглового приближения. Если электрон в результате столкновения не разгоняется до релятивистских скоростей, то его энергия становится равной

где Т — переданная в столкновении энергия.
Дифференциальное сечение  передачи энергии в интервале от Т до
передачи энергии в интервале от Т до  равно
равно
 (3.4)
(3.4)
а потери энергии на единицу длины  определяются выражением
определяются выражением

где n — число электронов в единице объема. Переходя к прицельному параметру b, получим

что с учетом (3.3) сводится к выражению

Чтобы выбрать разумное значение для  заметим, что неподвижный электрон приобретает максимальную скорость
заметим, что неподвижный электрон приобретает максимальную скорость  при лобовом попадании в него тяжелой частицы. Соответствующая максимальная кинетическая энергия (в нерелятивистском случае) равна
при лобовом попадании в него тяжелой частицы. Соответствующая максимальная кинетическая энергия (в нерелятивистском случае) равна  После подстановки этого значения
После подстановки этого значения  в соотношение (3.3) получаем выражение для
в соотношение (3.3) получаем выражение для 

Если  положить равным бесконечности, то —
положить равным бесконечности, то —  также стремится к бесконечности, поскольку неограниченный вклад дают малые передачи энергии большому числу удаленных электронов. Однако минимальная энергия, которую может получить электрон атома, должна быть достаточной для перевода электрона в разрешенное возбужденное состояние. Мы выбираем
также стремится к бесконечности, поскольку неограниченный вклад дают малые передачи энергии большому числу удаленных электронов. Однако минимальная энергия, которую может получить электрон атома, должна быть достаточной для перевода электрона в разрешенное возбужденное состояние. Мы выбираем  , где
, где  — средняя энергия возбуждения электрона, и находим
— средняя энергия возбуждения электрона, и находим

После подстановки выражений (3.8) и (3.9) в равенство (3.7) получаем

Проведенные вычисления учитывают прямые столкновения с электронами в твердом теле. Существует, однако, еще одно слагаемое того же порядка, обусловленное резонансной передачей энергии при взаимодействии на большом расстоянии. Подробный вывод этого слагаемого выходит за рамки книги, но можно показать, что с его учетом полная тормозная способность должна быть в два раза больше полученного выше результата, т. е.

или

где  есть концентрация атомов в тормозящей среде.
есть концентрация атомов в тормозящей среде.
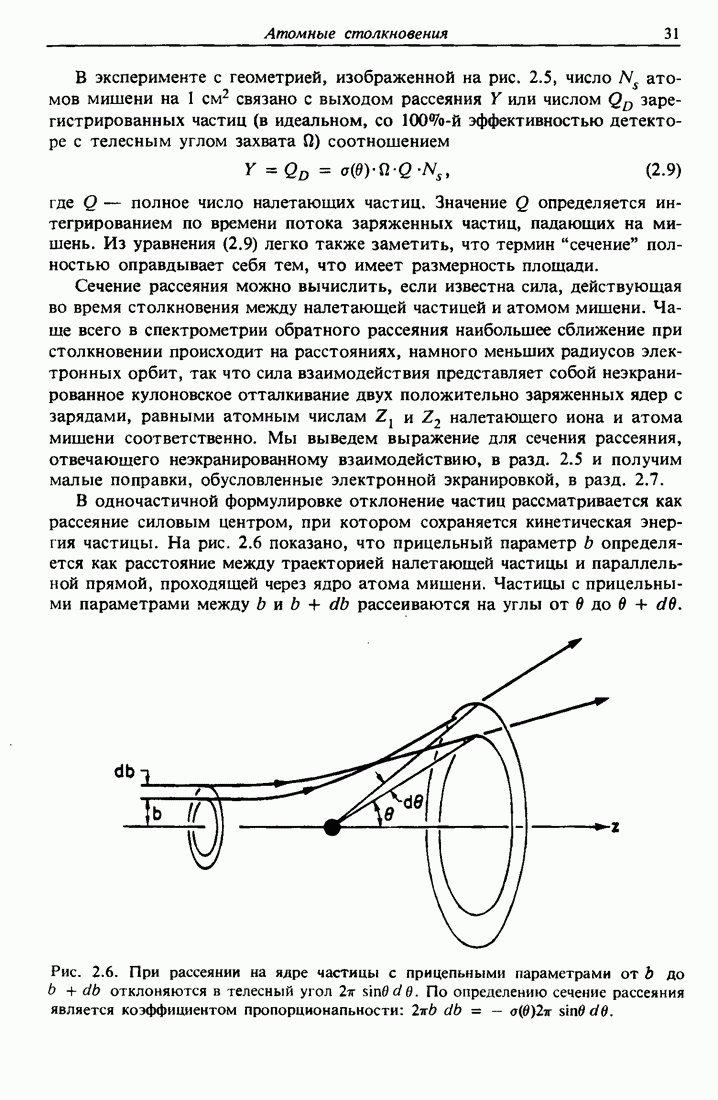
Таким образом, можно считать, что два вида процессов дают вклад во взаимодействие движущегося иона с электронами твердого тела: 1) столкновения с малыми прицельными параметрами и большими передачами импульса, когда траектория частицы пересекает орбиты электронов, и 2) столкновения с большими прицельными параметрами и малыми передачами импульса, когда частица пролетает вне электронных орбит. Оба вклада примерно равны (правило равнораспределения) для скоростей частиц, использующихся в обратном резерфордовском рассеянии.
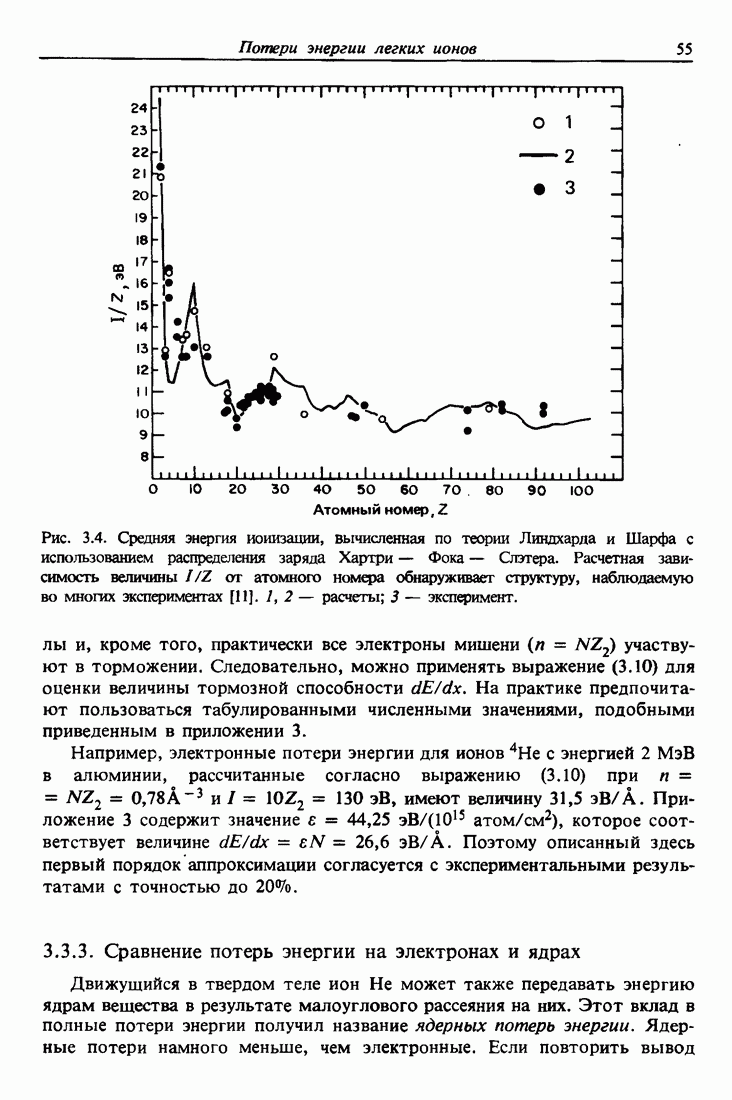
Средняя энергия возбуждения  для большинства элементов примерно равна
для большинства элементов примерно равна  , где
, где  — атомный номер атомов мишени. Экспериментальные и расчетные значения
— атомный номер атомов мишени. Экспериментальные и расчетные значения  представлены на рис. 3.4. До сих пор при описании тормозной способности мы пренебрегали структурой электронных оболочек атома и различиями в энергиях связи электронов. Как показано на рис. 3.4, в эксперименте эти эффекты проявляют себя в виде малых отклонений от аппроксимации
представлены на рис. 3.4. До сих пор при описании тормозной способности мы пренебрегали структурой электронных оболочек атома и различиями в энергиях связи электронов. Как показано на рис. 3.4, в эксперименте эти эффекты проявляют себя в виде малых отклонений от аппроксимации  (за исключением самых легких элементов).
(за исключением самых легких элементов).
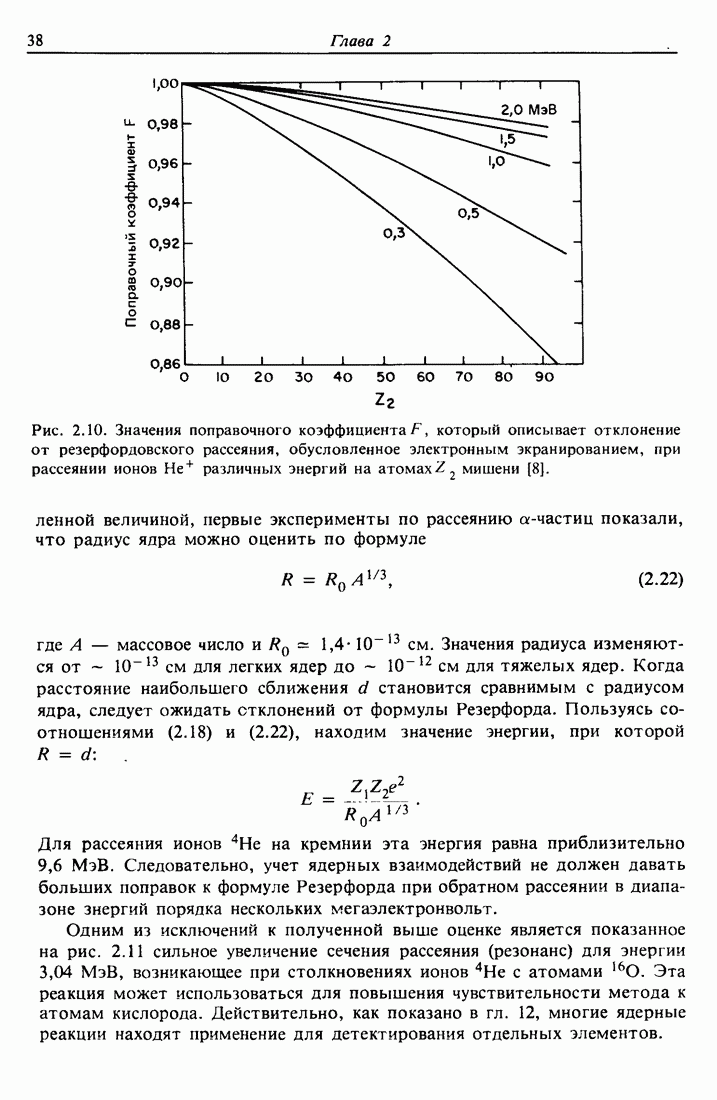
Полная формула энергетических потерь, часто называемая формулой Бете, содержит релятивистские поправки при больших скоростях и учитывает тот факт, что сильно связанные электроны внутренних оболочек не дают вклада в торможение. Для ионов гелия в диапазоне энергий порядка нескольких мегаэлектронвольт релятивистские эффекты пренебрежимо

Рис. 3.4. Средняя энергия ионизации, вычисленная по теории Линдхарда и Шарфа с использованием распределения заряда Хартри — Фока — Слэтера. Расчетная зависимость величины  от атомного номера обнаруживает структуру, наблюдаемую во многих экспериментах [11]. 1,2 — расчеты; 3 — эксперимент.
от атомного номера обнаруживает структуру, наблюдаемую во многих экспериментах [11]. 1,2 — расчеты; 3 — эксперимент.
малы и, кроме того, практически все электроны мишени  участвуют в торможении. Следовательно, можно применять выражение (3.10) для оценки величины тормозной способности
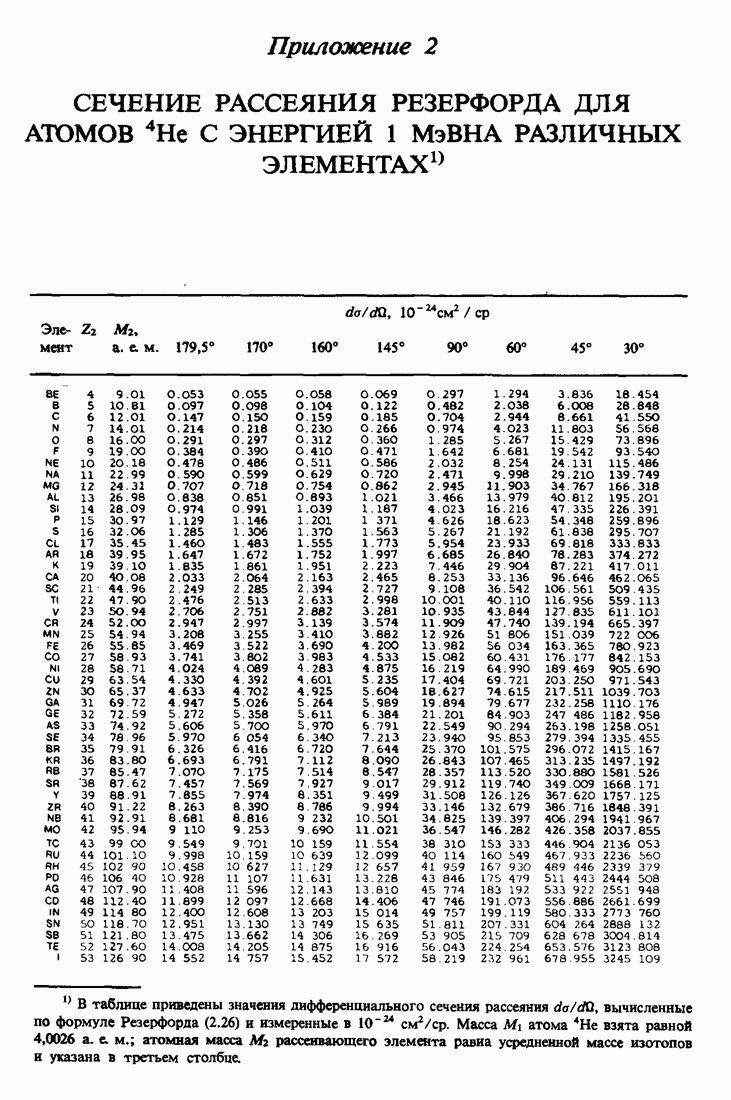
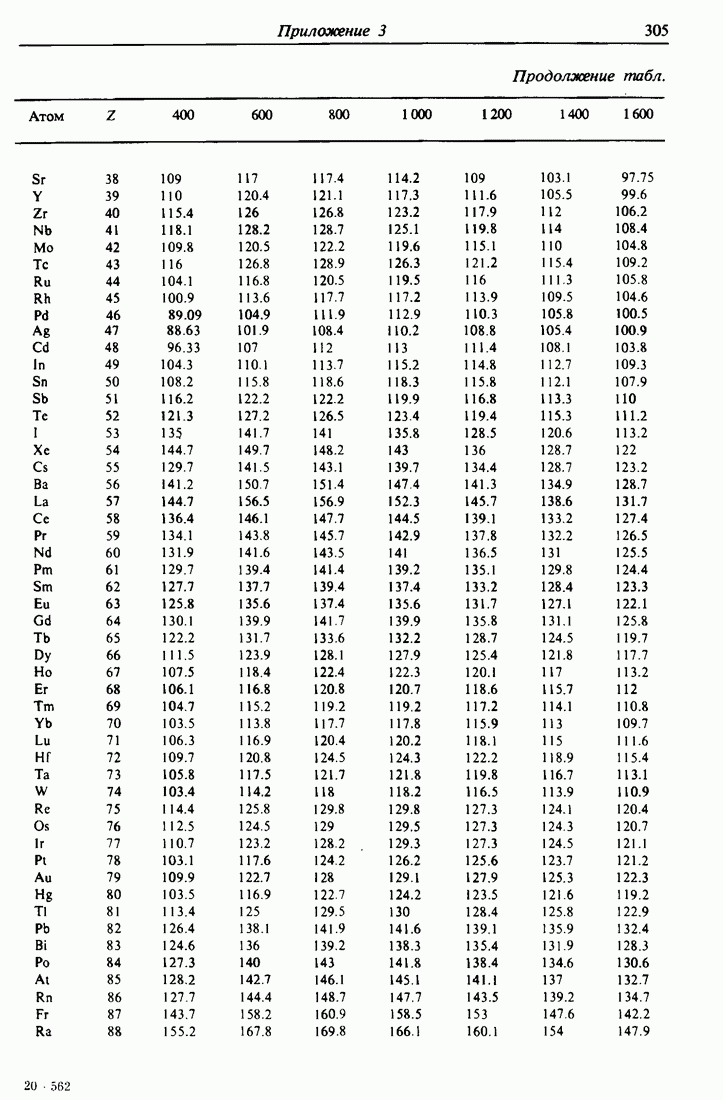
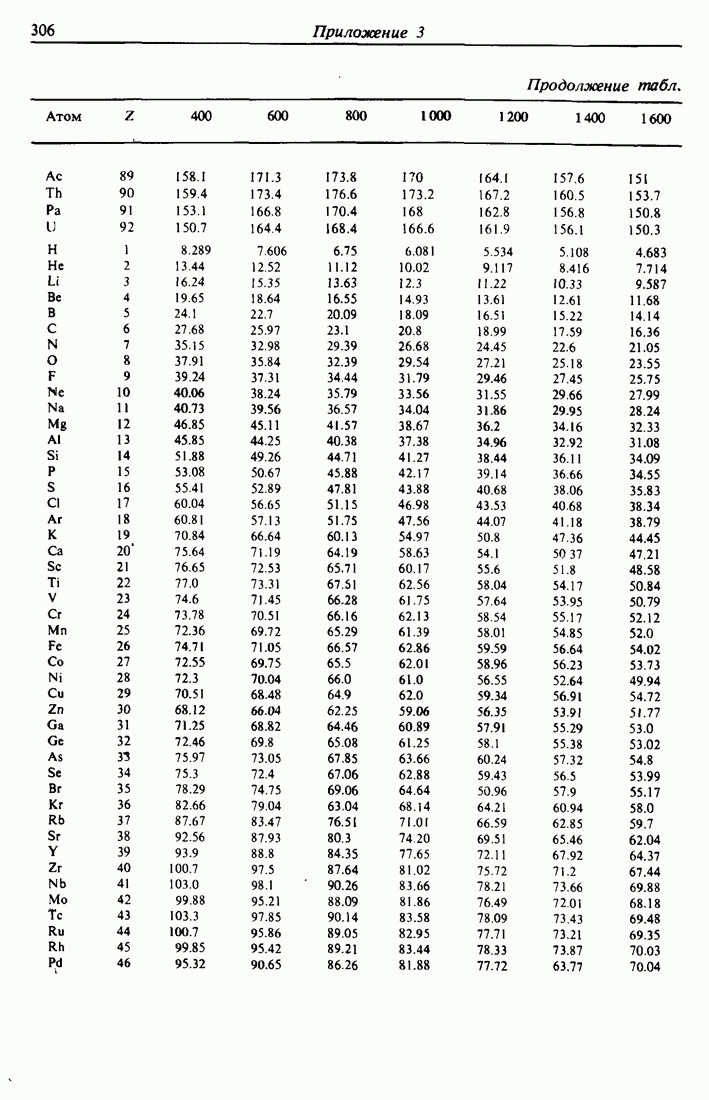
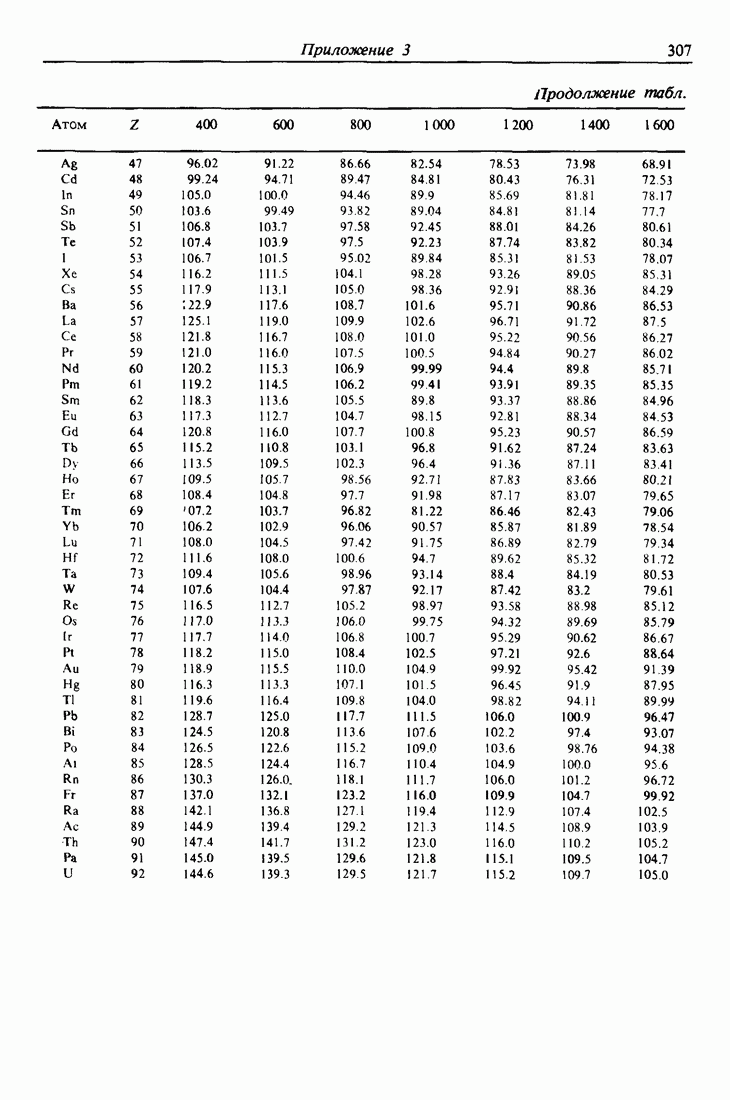
участвуют в торможении. Следовательно, можно применять выражение (3.10) для оценки величины тормозной способности  . На практике предпочитают пользоваться табулированными численными значениями, подобными приведенным в приложении 3.
. На практике предпочитают пользоваться табулированными численными значениями, подобными приведенным в приложении 3.
Например, электронные потери энергии для ионов  с энергией 2 МэВ в алюминии, рассчитанные согласно выражению (3.10) при
с энергией 2 МэВ в алюминии, рассчитанные согласно выражению (3.10) при  эВ, имеют величину
эВ, имеют величину  . Приложение 3 содержит значение
. Приложение 3 содержит значение  , которое соответствует величине
, которое соответствует величине  Поэтому описанный здесь первый порядок аппроксимации согласуется с экспериментальными результатами с точностью до 20976.
Поэтому описанный здесь первый порядок аппроксимации согласуется с экспериментальными результатами с точностью до 20976.
3.3.3. Сравнение потерь энергии на электронах и ядрах
Движущийся в твердом теле ион Не может также передавать энергию ядрам вещества в результате малоуглового рассеяния на них. Этот вклад в полные потери энергии получил название ядерных потерь энергии. Ядерные потери намного меньше, чем электронные. Если повторить вывод
формулы (3.7) для столкновений с атомами мишени, имеющими массу  , получим
, получим

где  соответствует максимальной энергии
соответствует максимальной энергии

передаваемой атому мишени при лобовом столкновении, так что  в рассматриваемом случае имеет вид
в рассматриваемом случае имеет вид

а Ьмакс можно аппроксимировать выражением (3.9), где I теперь представляет энергию смещения атома в твердом теле.
Главное различие формул (3.7) и (3.11) состоит в величине массы ( или
или  ), входящей в знаменатель, и в появлении заряда
), входящей в знаменатель, и в появлении заряда  ядра мишени в числителе (3.11). Пренебрегая отношением логарифмических членов, получаем, что для протонов отношение ядерных и электронных потерь энергии в расчете на 1 атом составляет
ядра мишени в числителе (3.11). Пренебрегая отношением логарифмических членов, получаем, что для протонов отношение ядерных и электронных потерь энергии в расчете на 1 атом составляет

где число электронов в единице объема равно  масса атома мишени
масса атома мишени  и масса протона
и масса протона  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
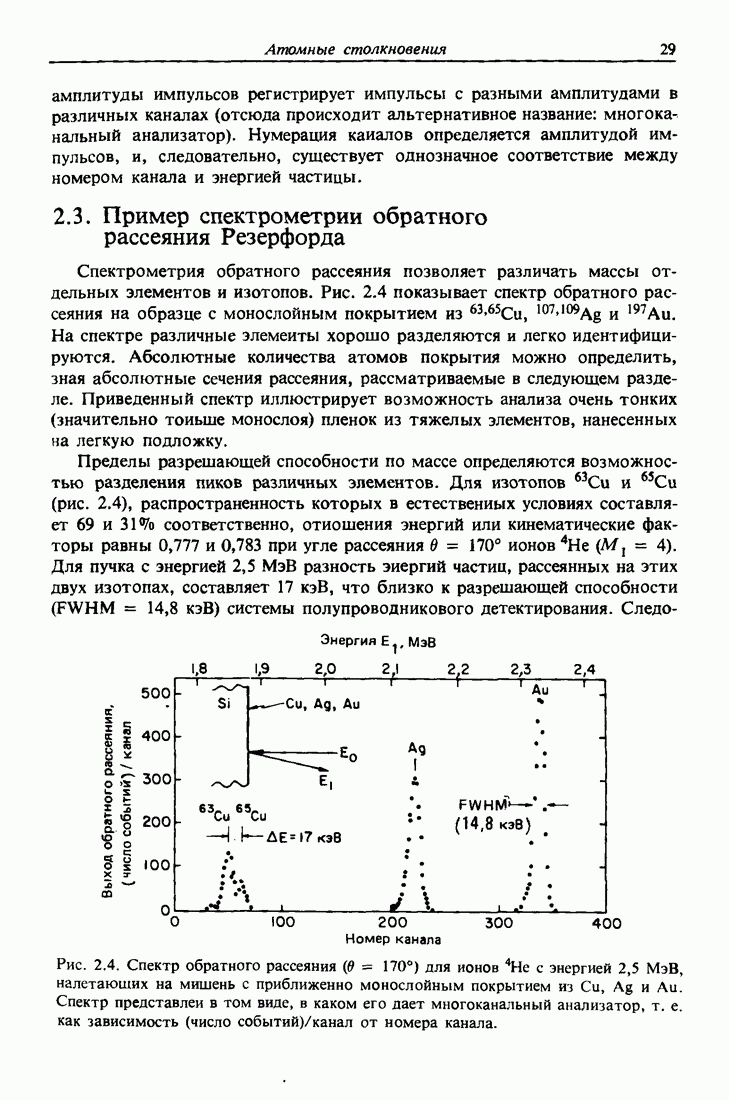
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
- 2.4. Сечение рассеяния и прицельный параметр
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
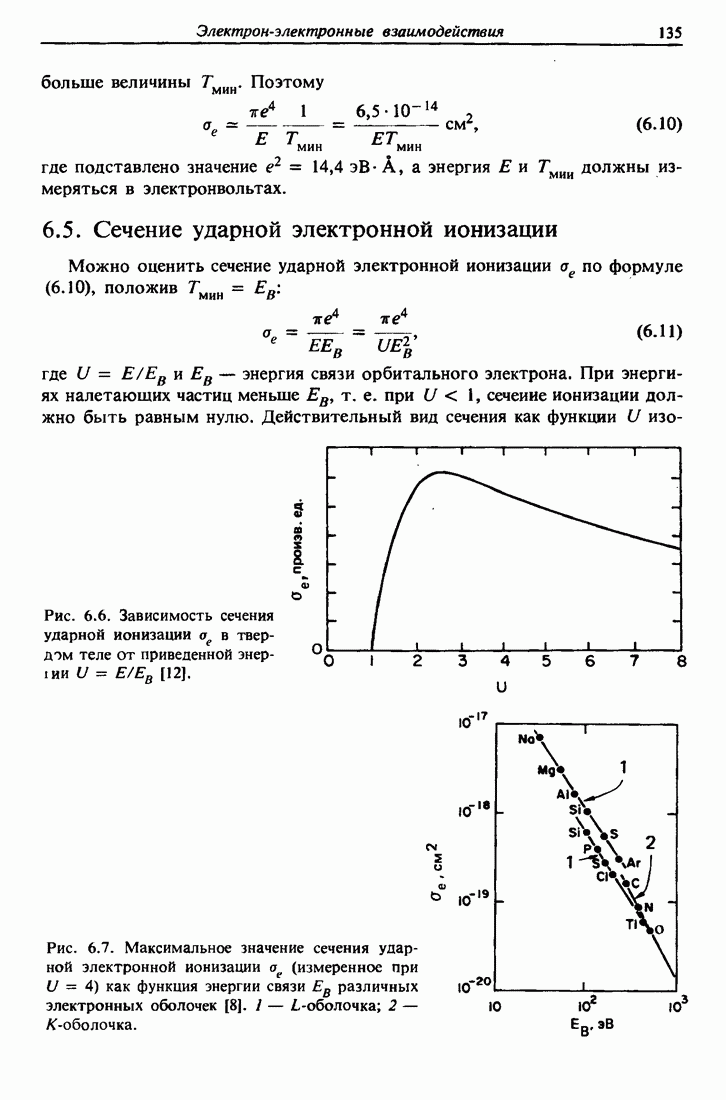
- 6.5. Сечение ударной электронной ионизации
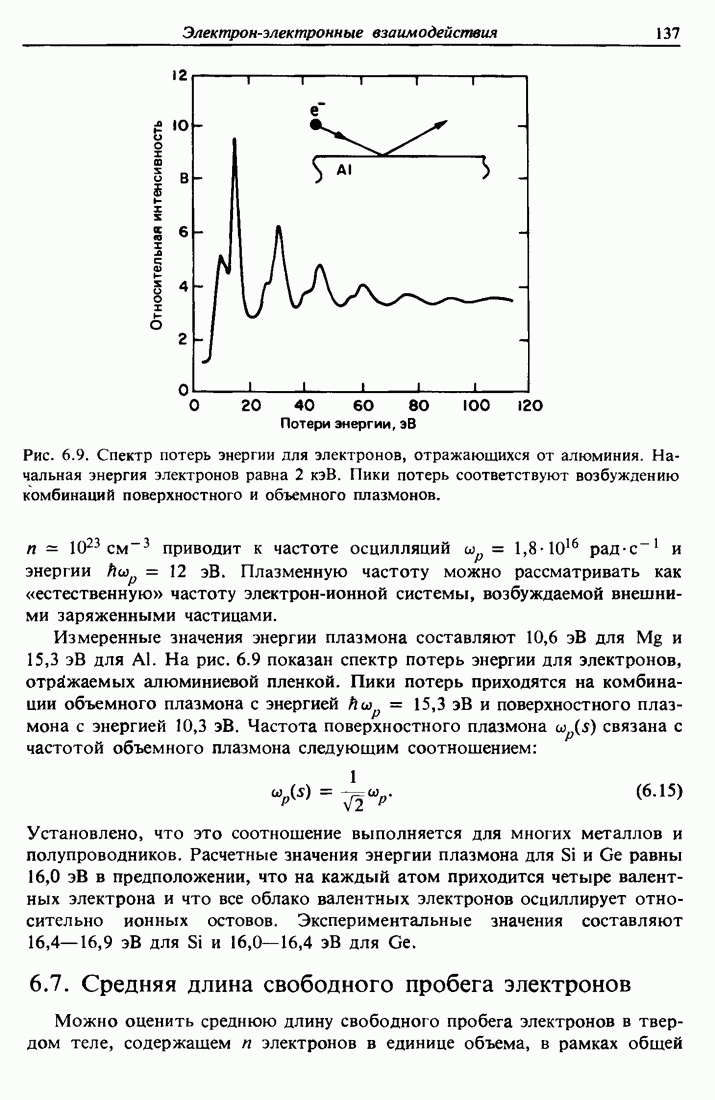
- 6.6. Плазмоны
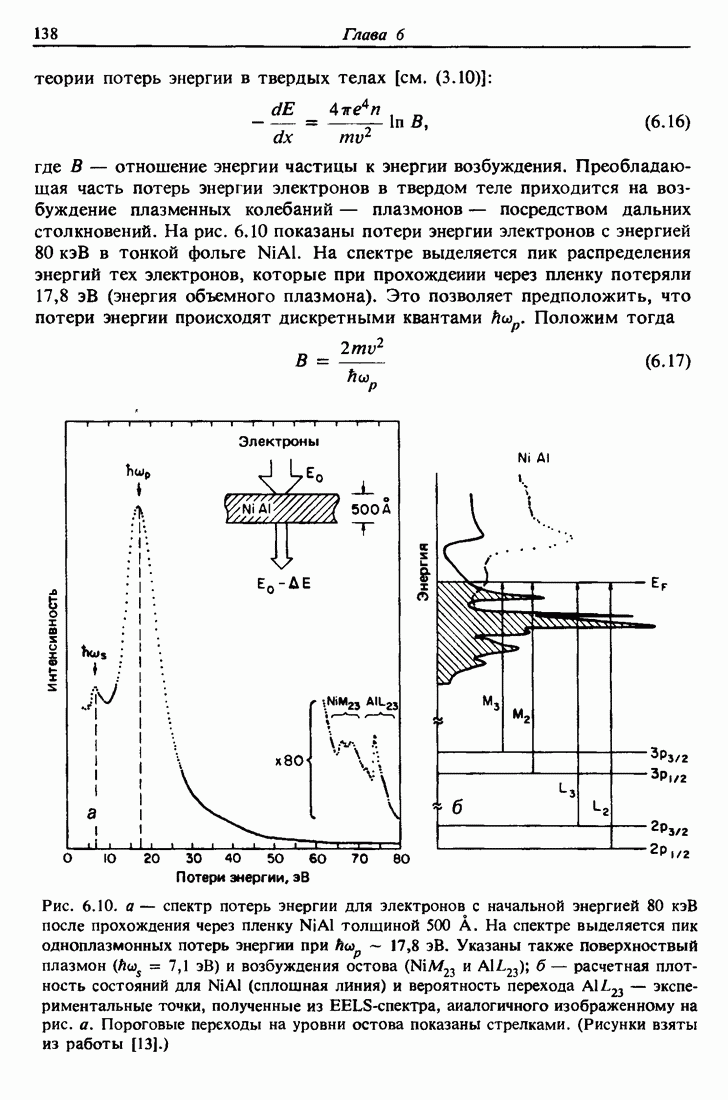
- 6.7. Средняя длина свободного пробега электронов
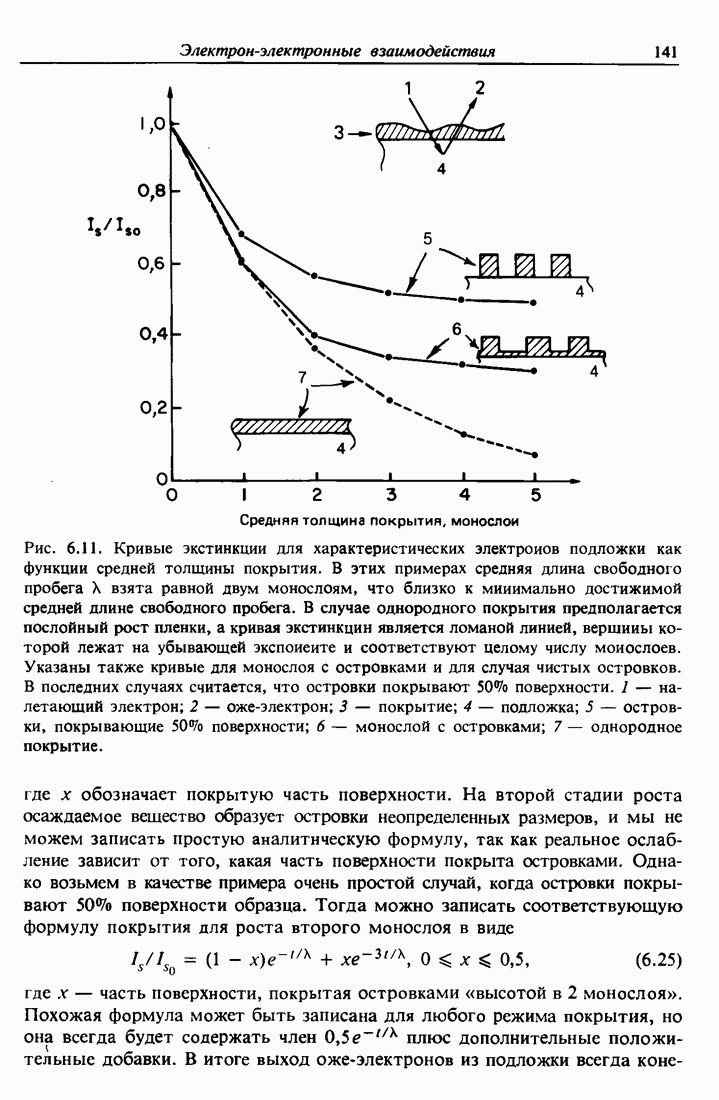
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
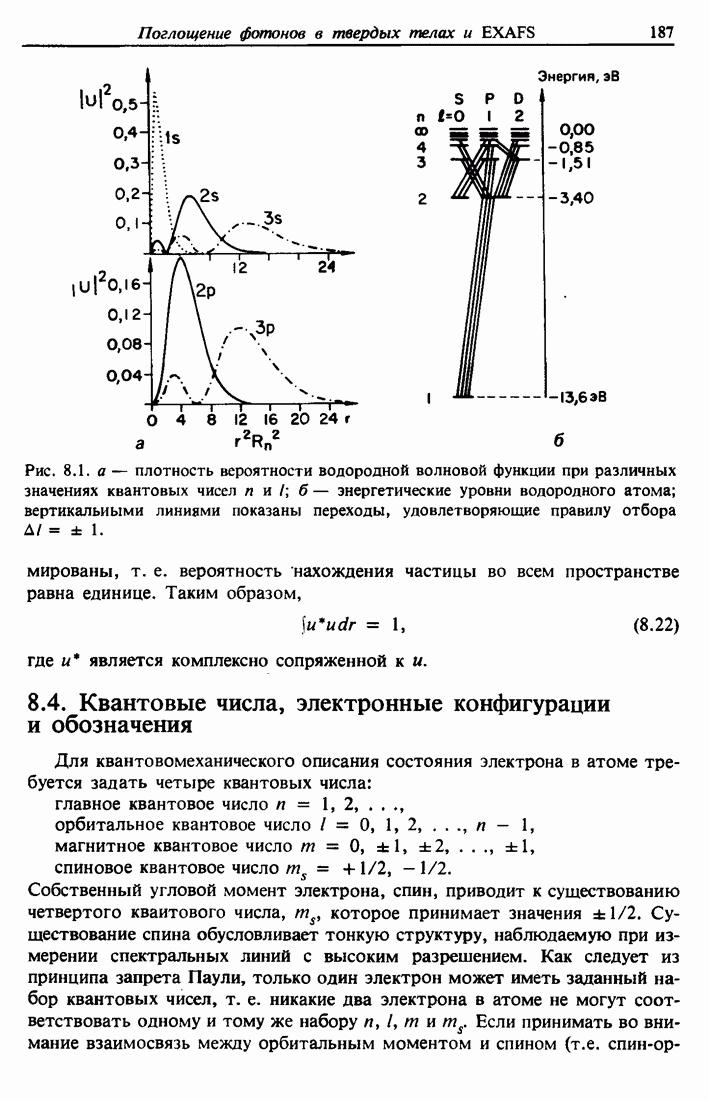
- 8.3. Волновые функции
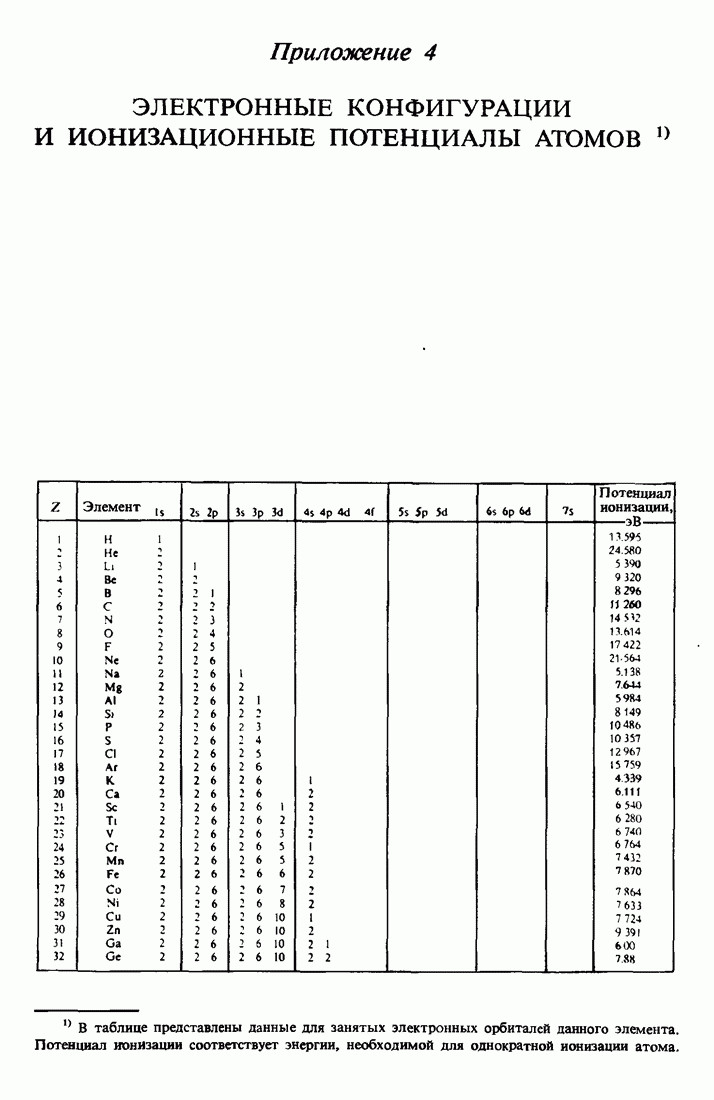
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
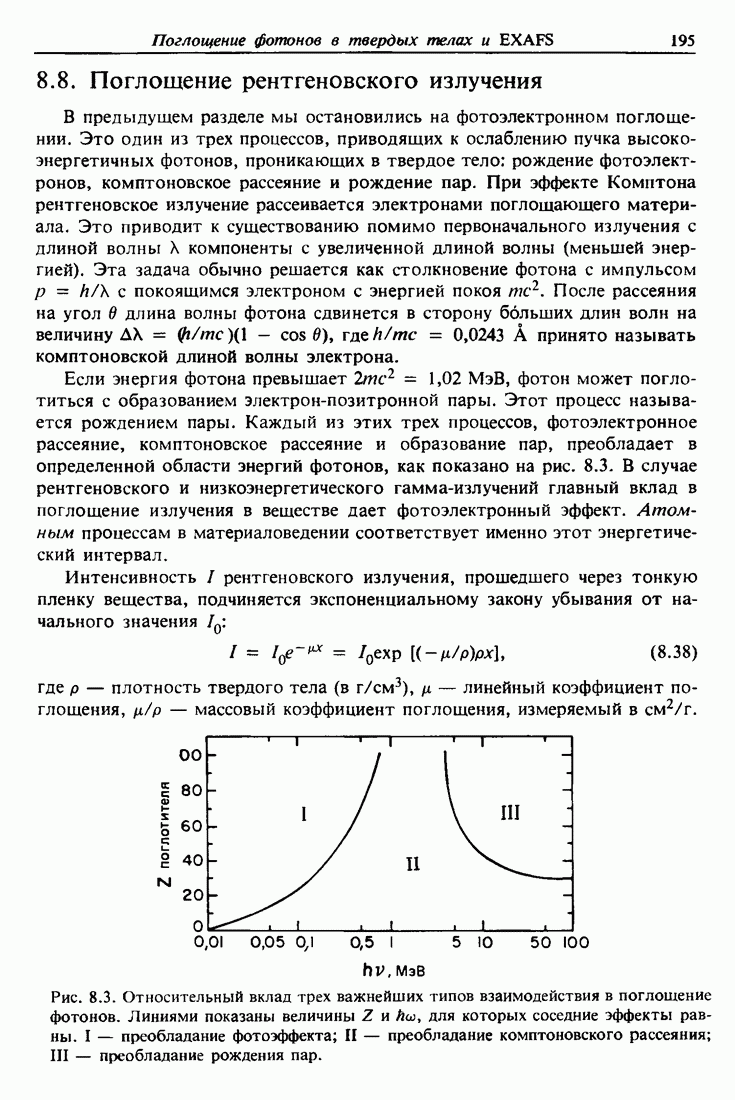
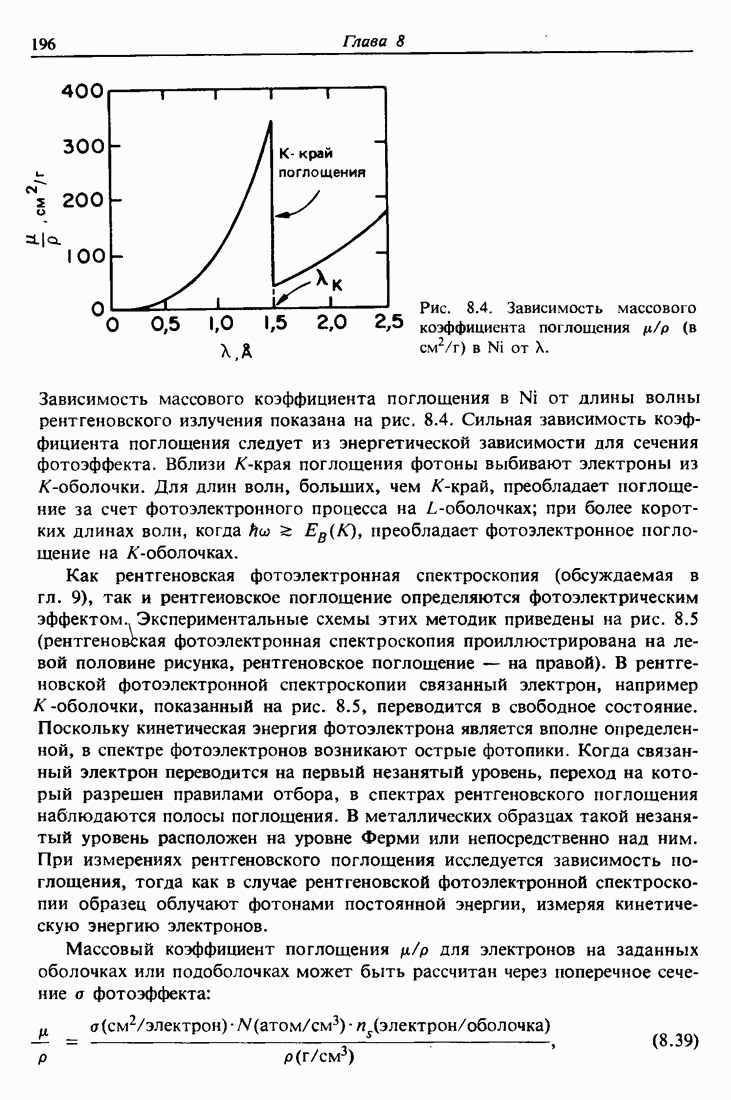
- 8.8. Поглощение рентгеновского излучения
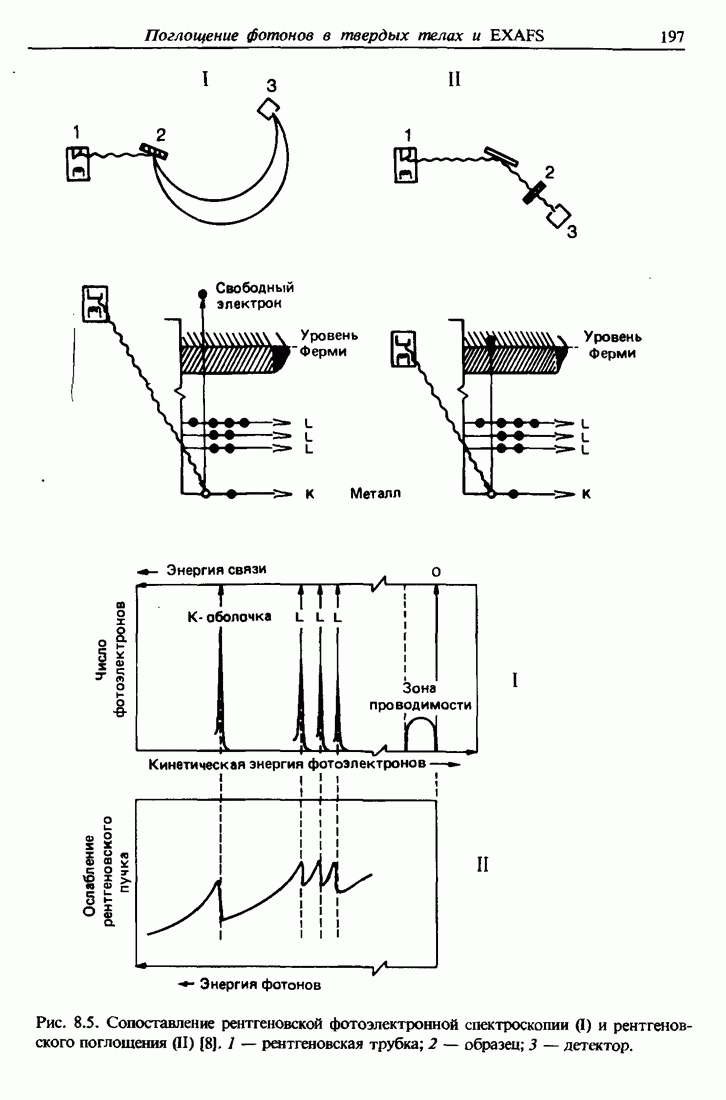
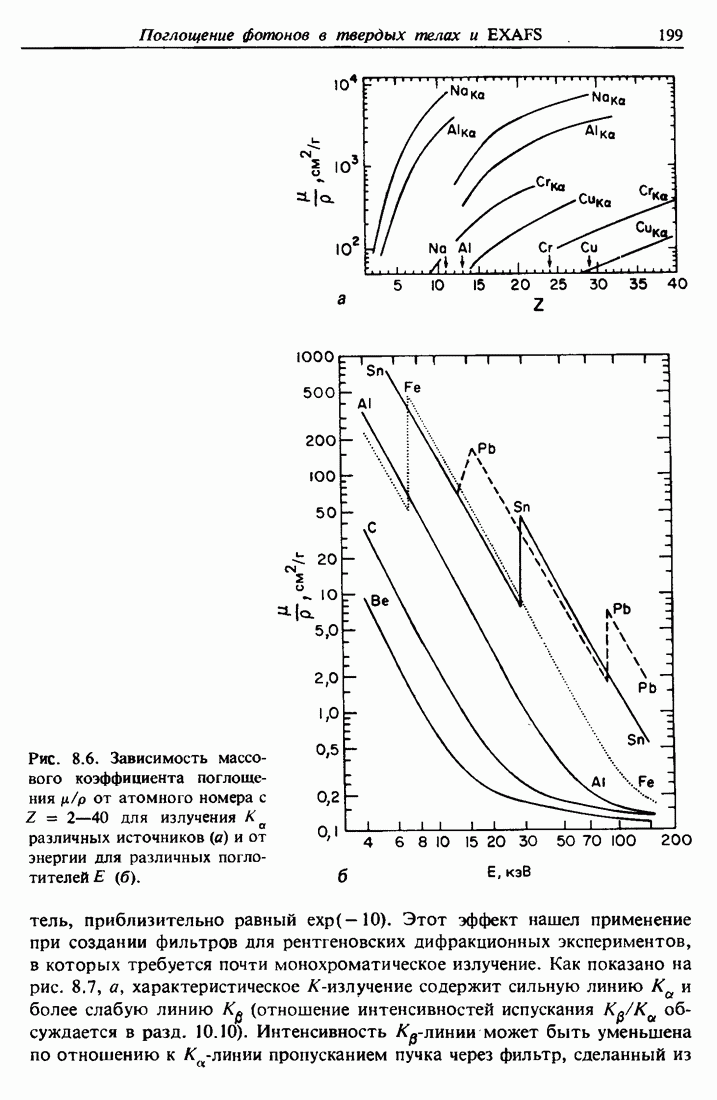
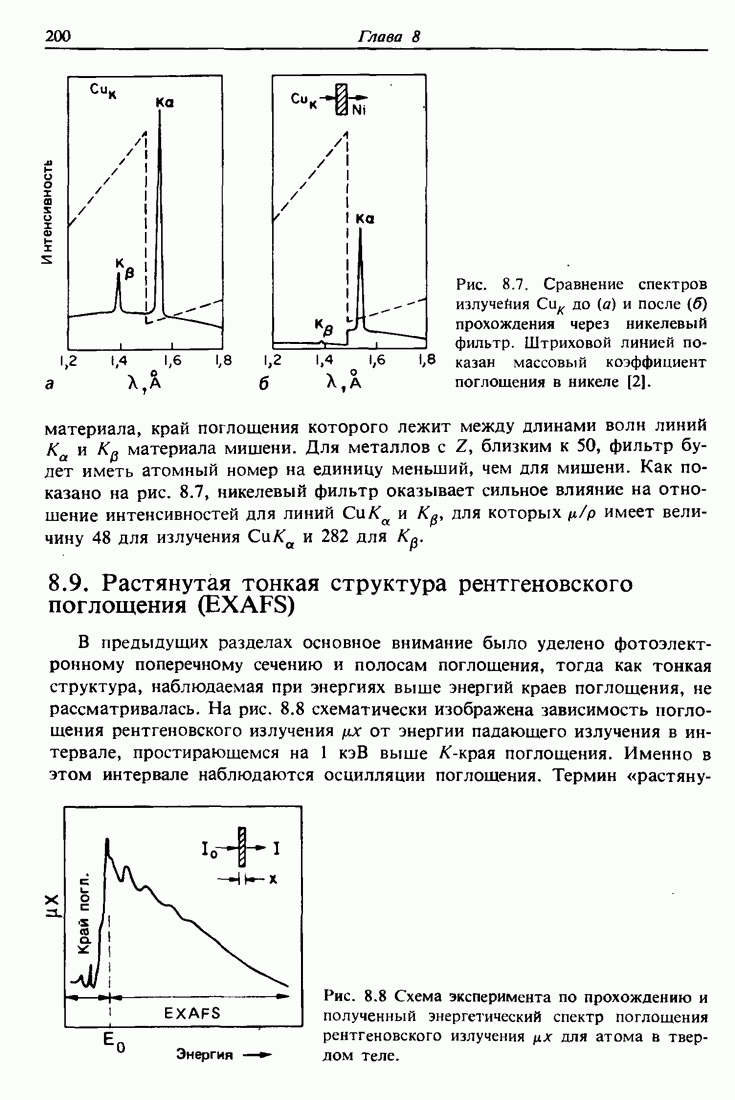
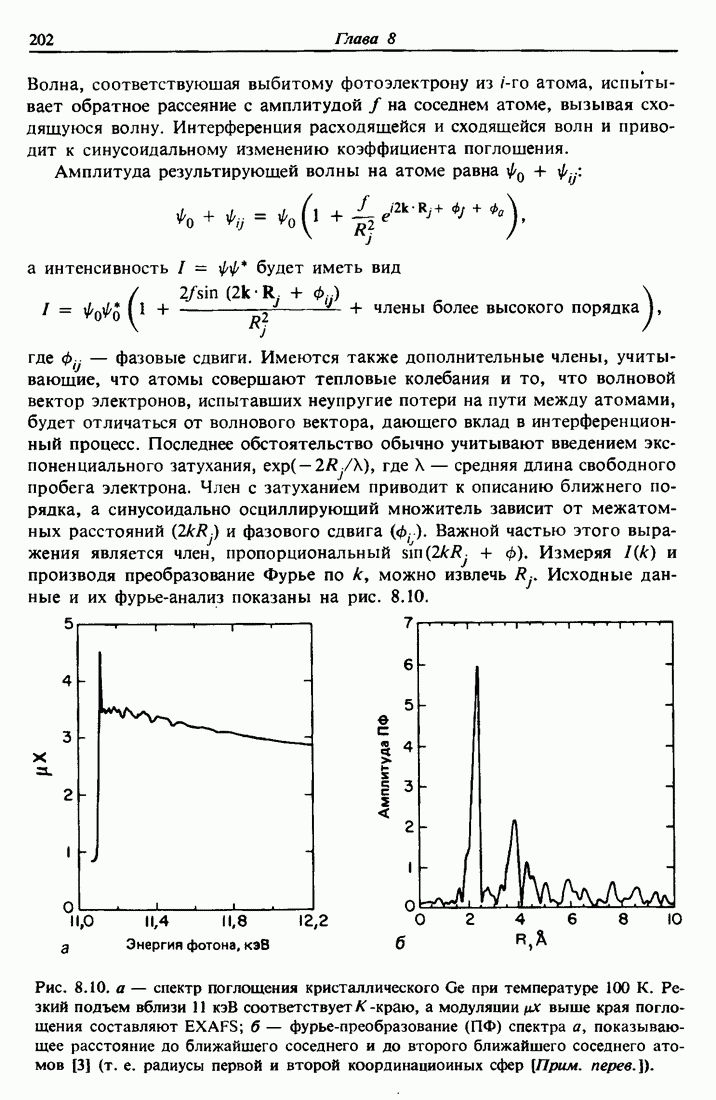
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
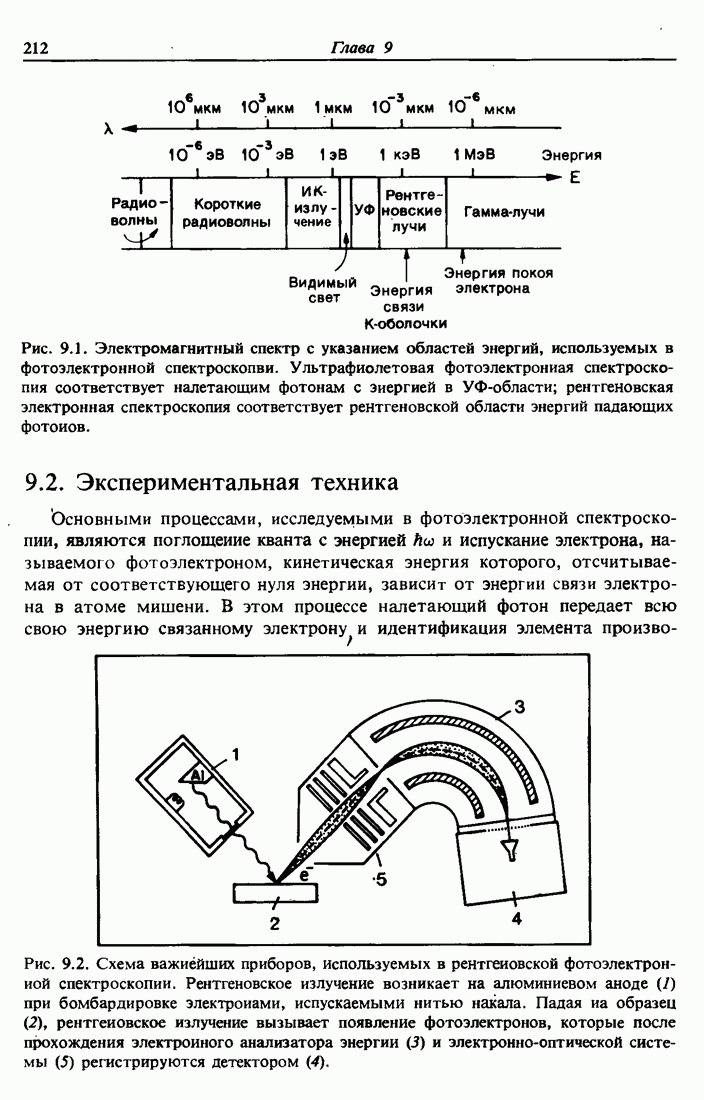
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
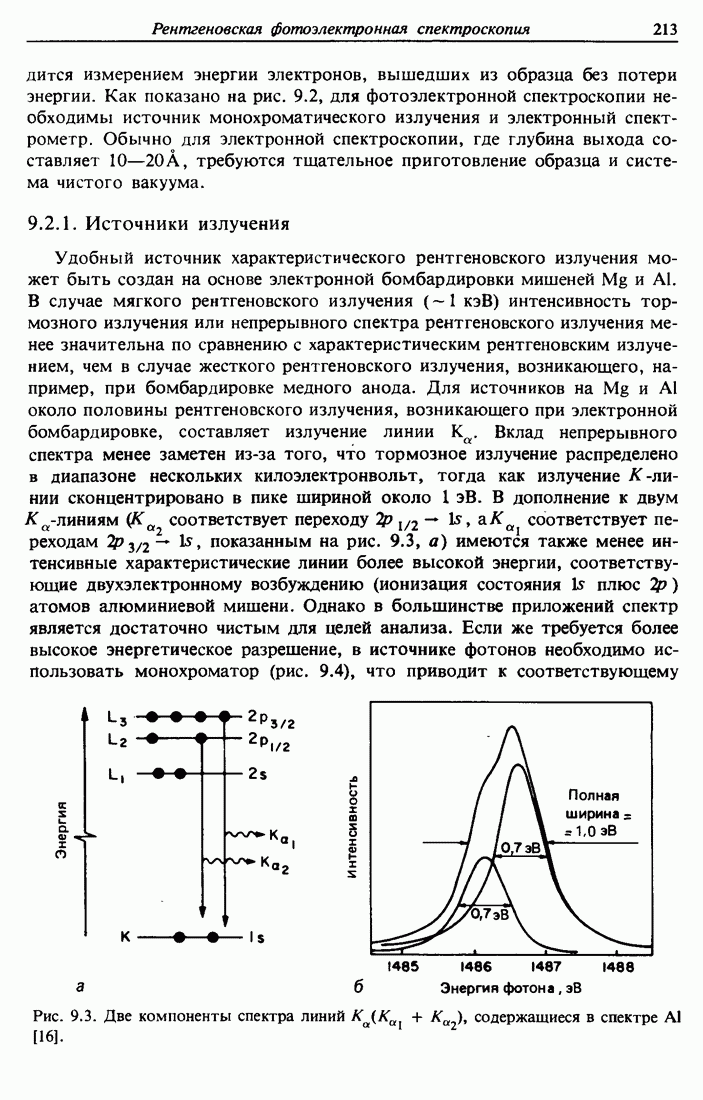
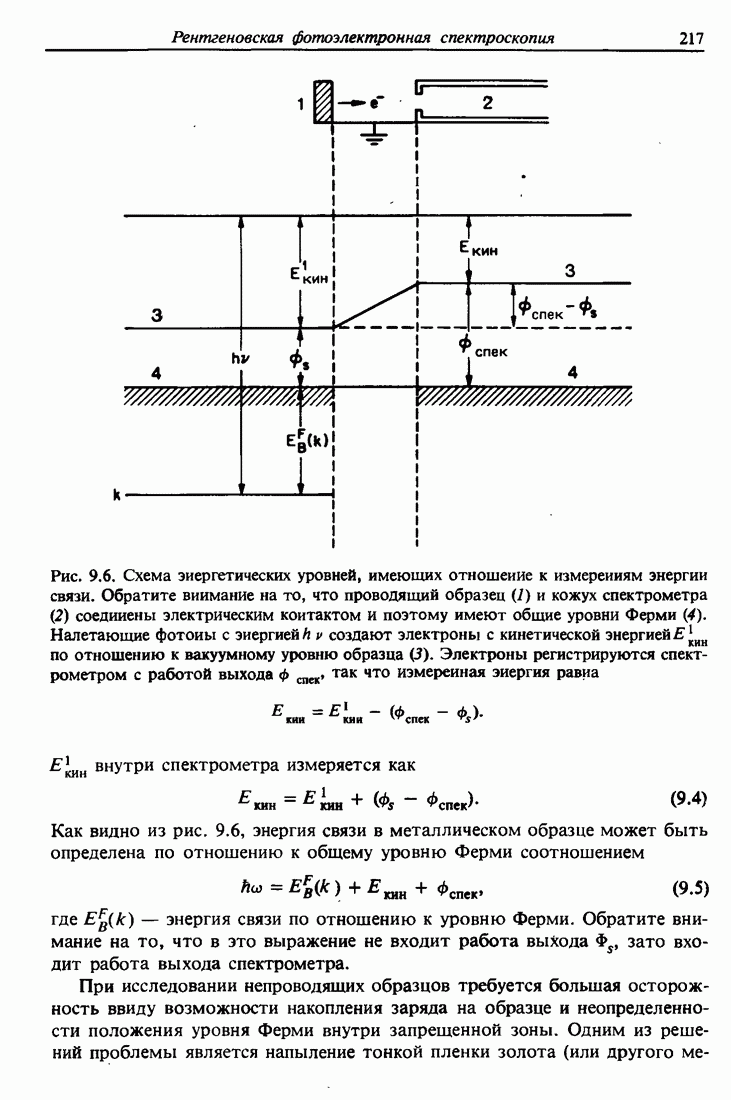
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
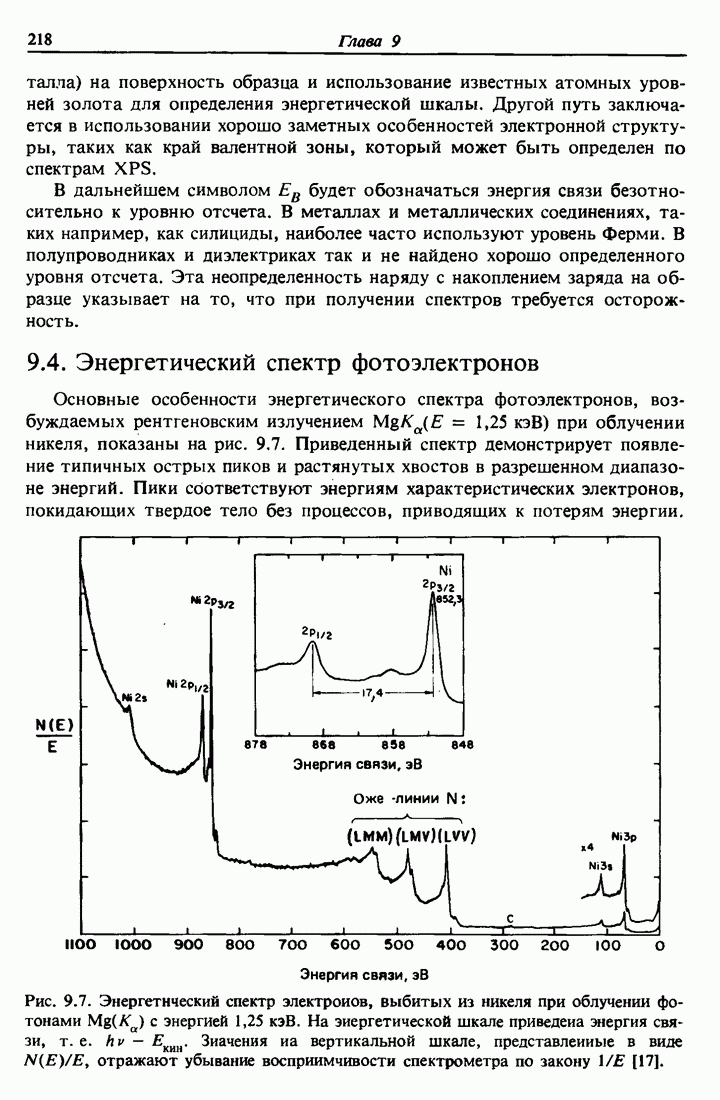
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
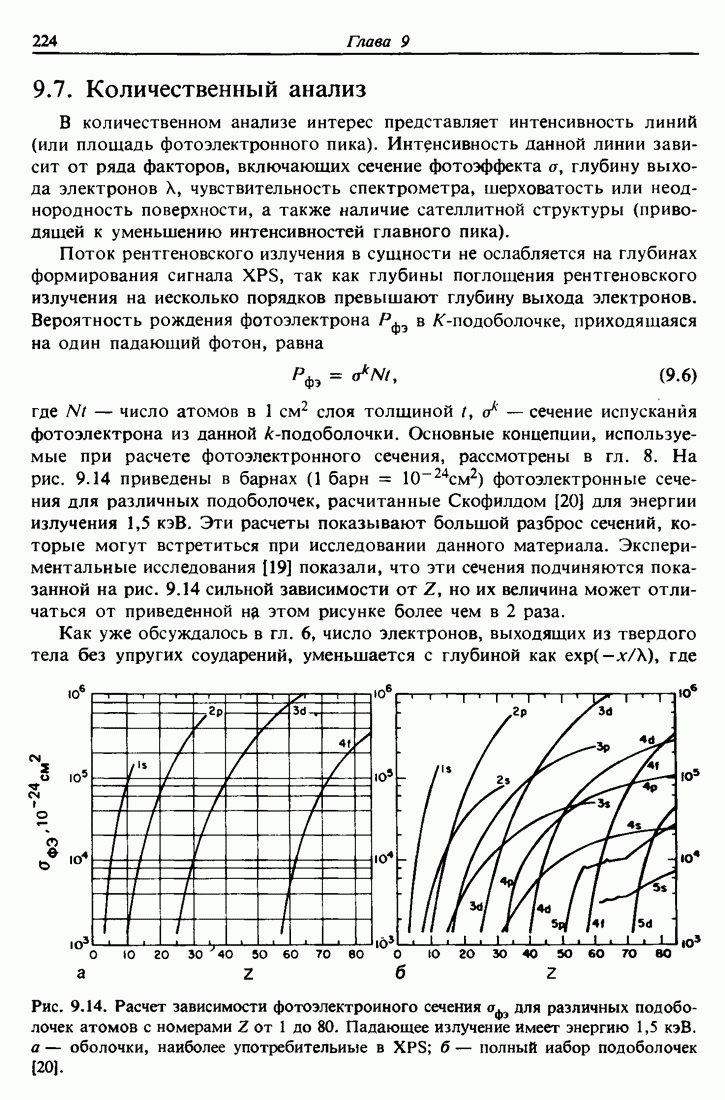
- 9.7. Количественный анализ
- Задачи
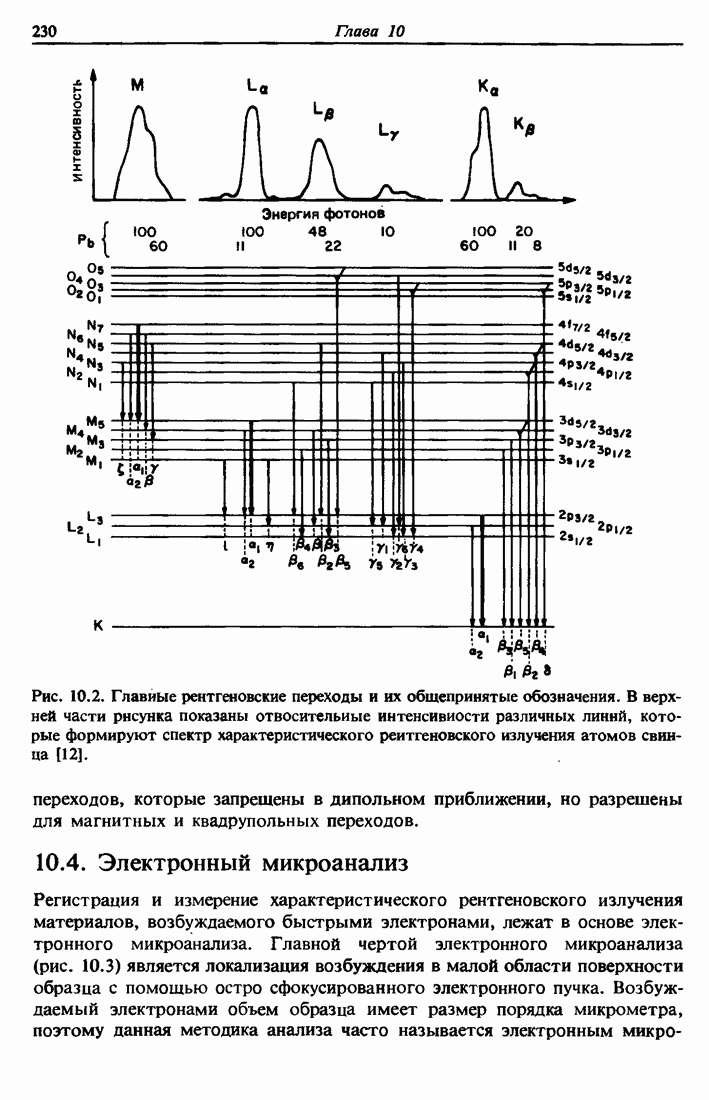
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
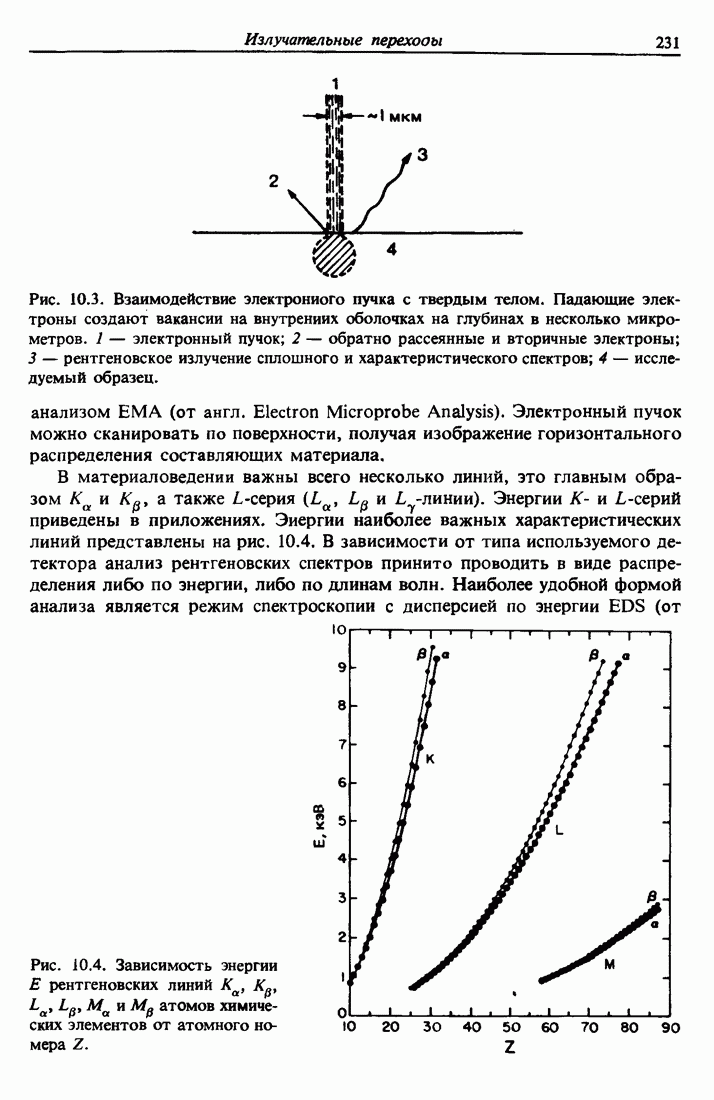
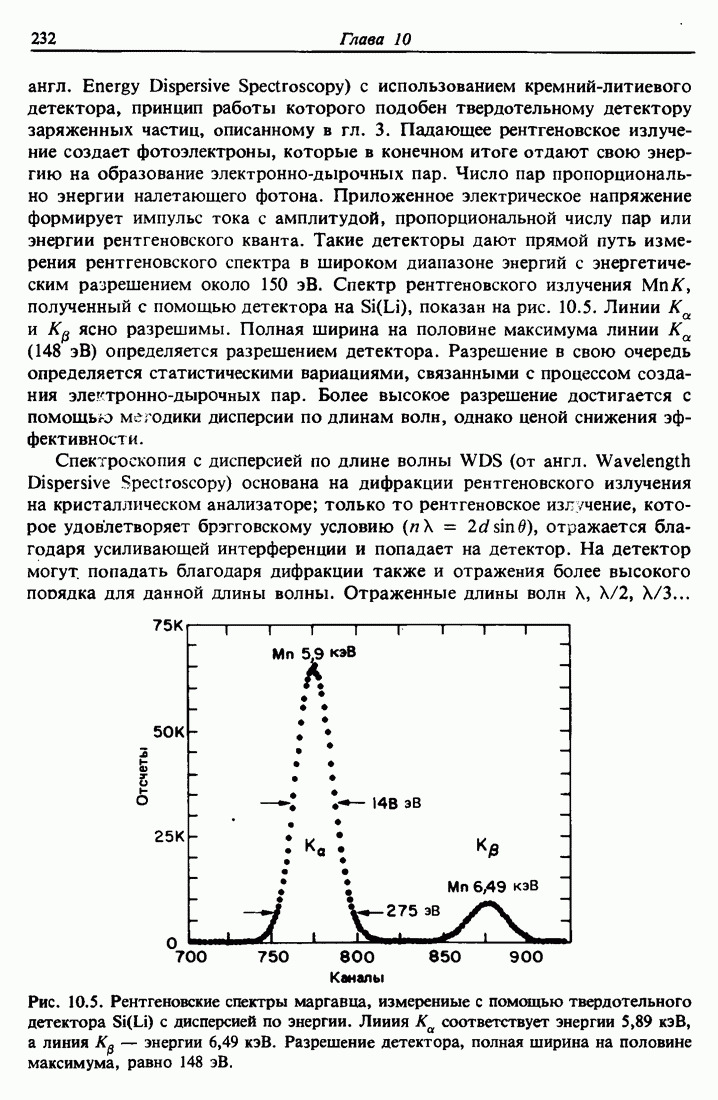
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
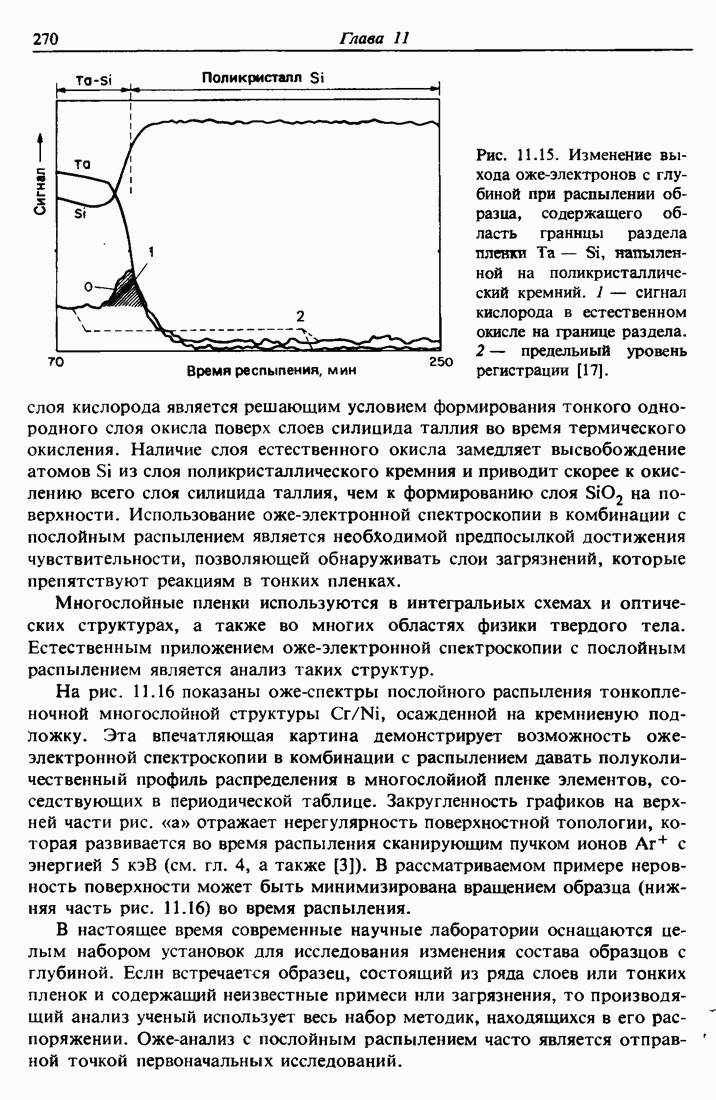
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
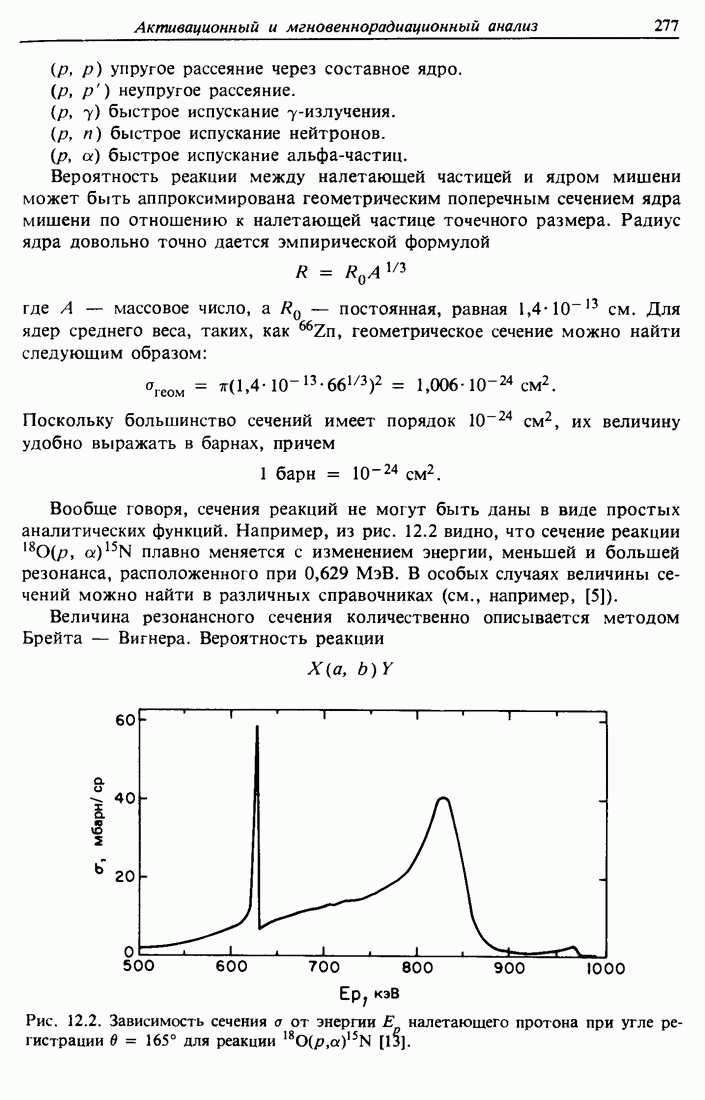
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
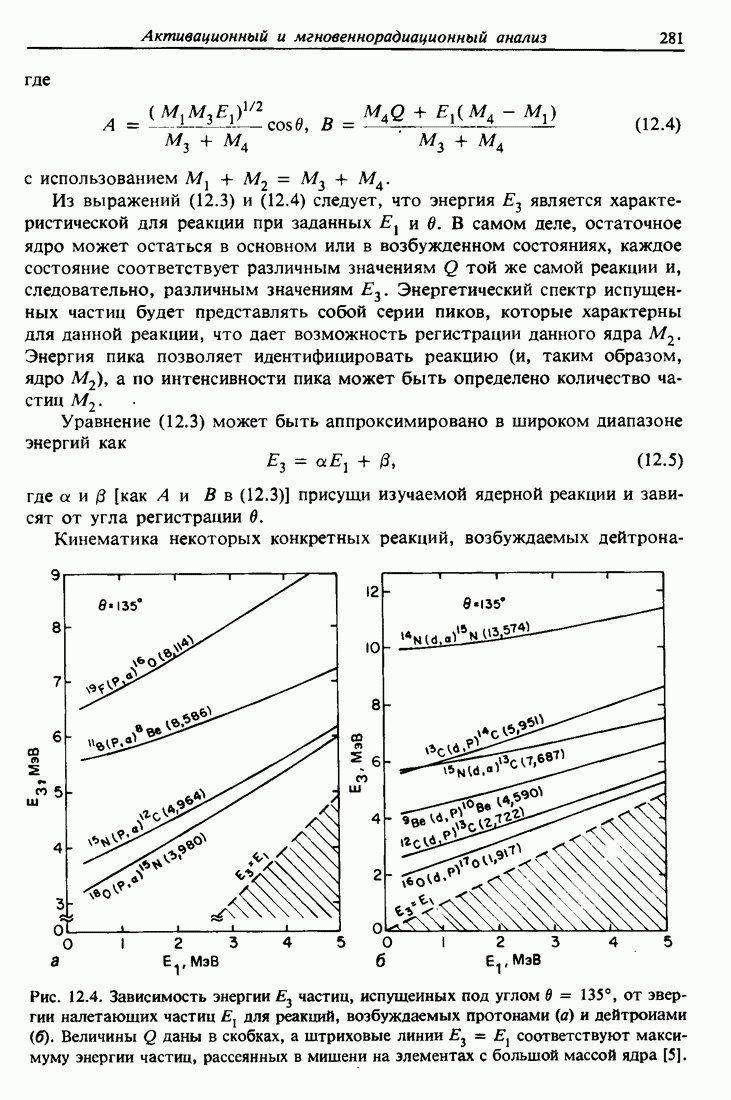
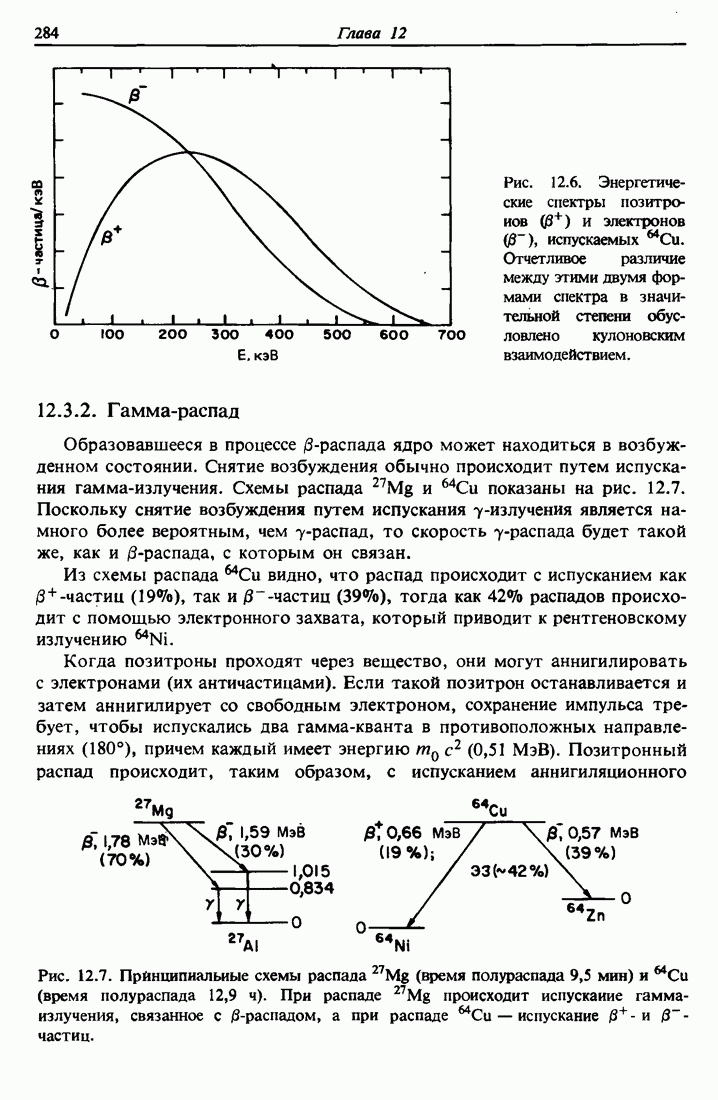
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
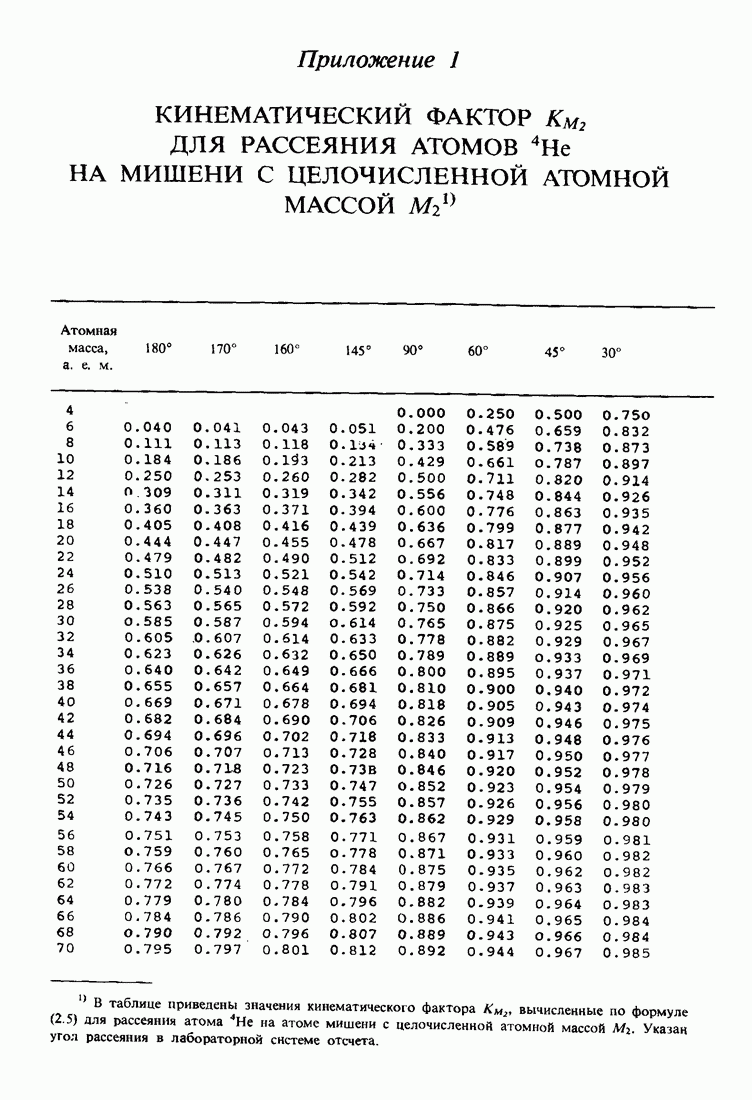
- ПРИЛОЖЕНИЕ 1.
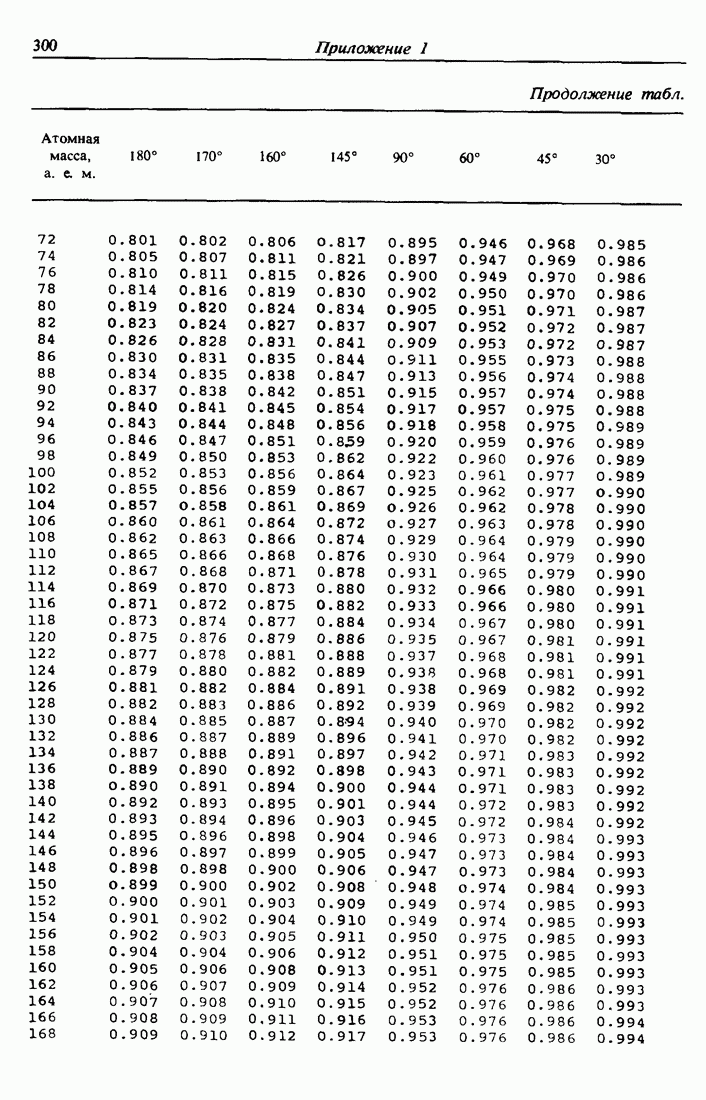
- ПРИЛОЖЕНИЕ 2.
- ПРИЛОЖЕНИЕ 3.
- ПРИЛОЖЕНИЕ 4.
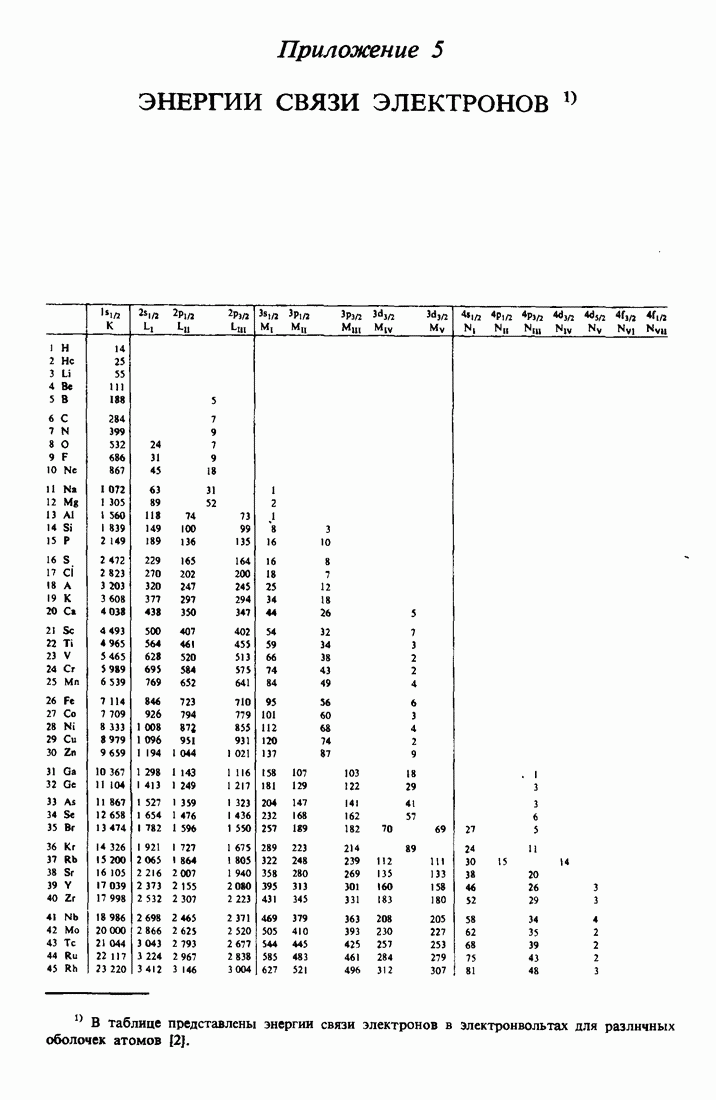
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
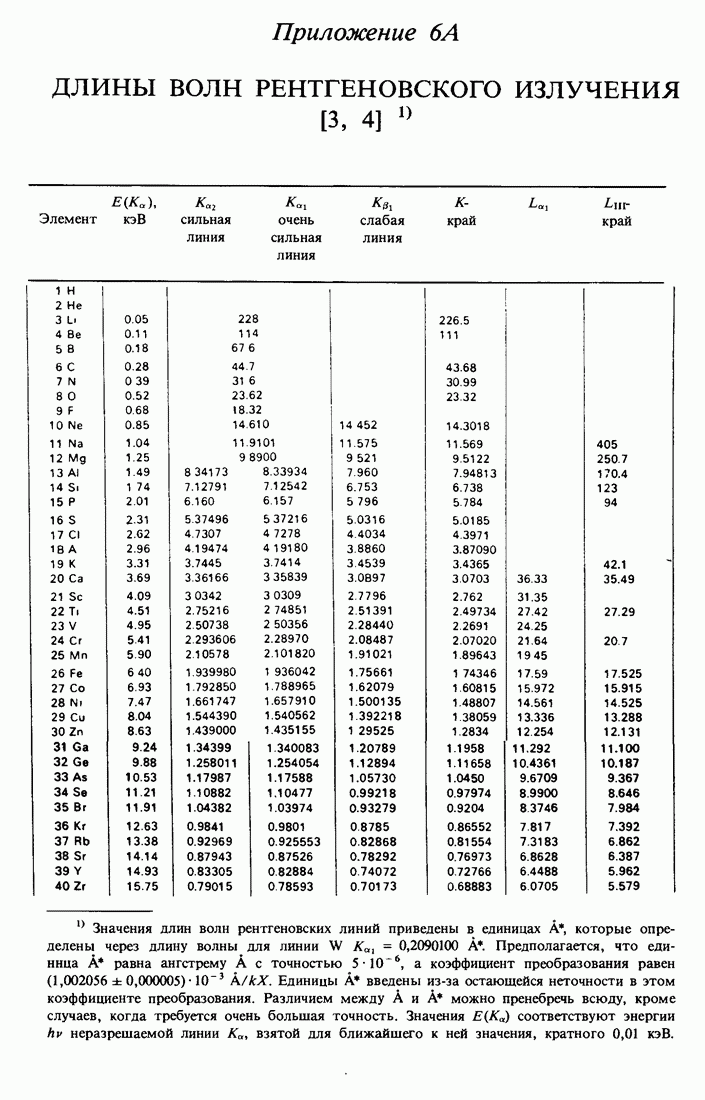
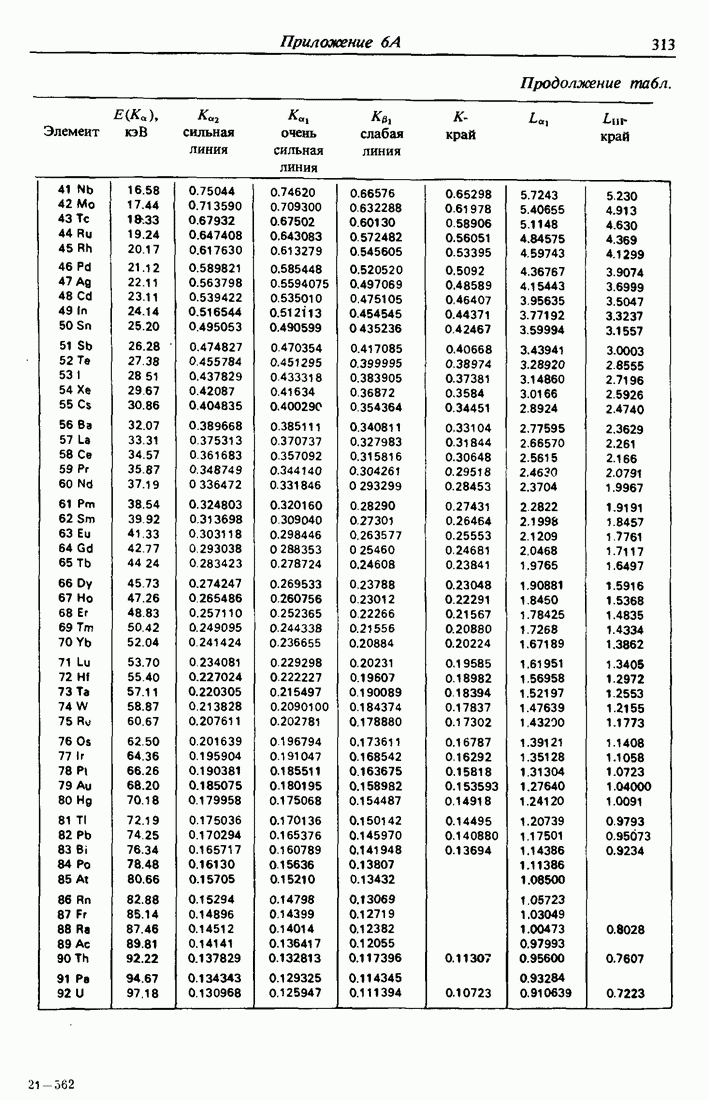
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
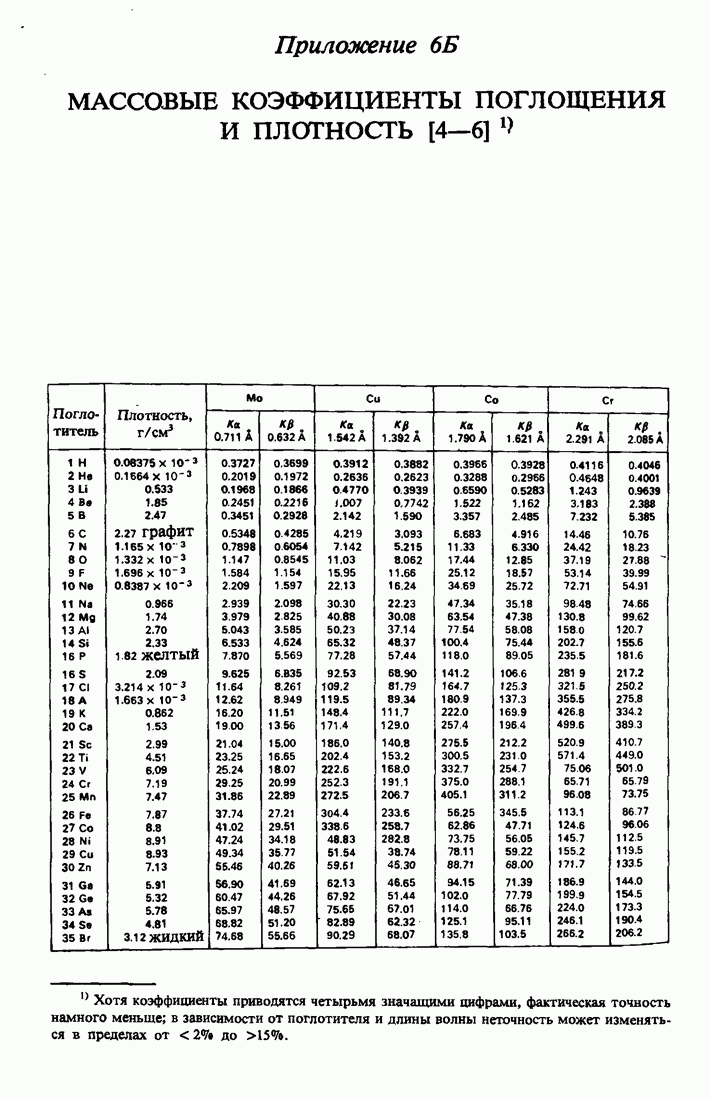
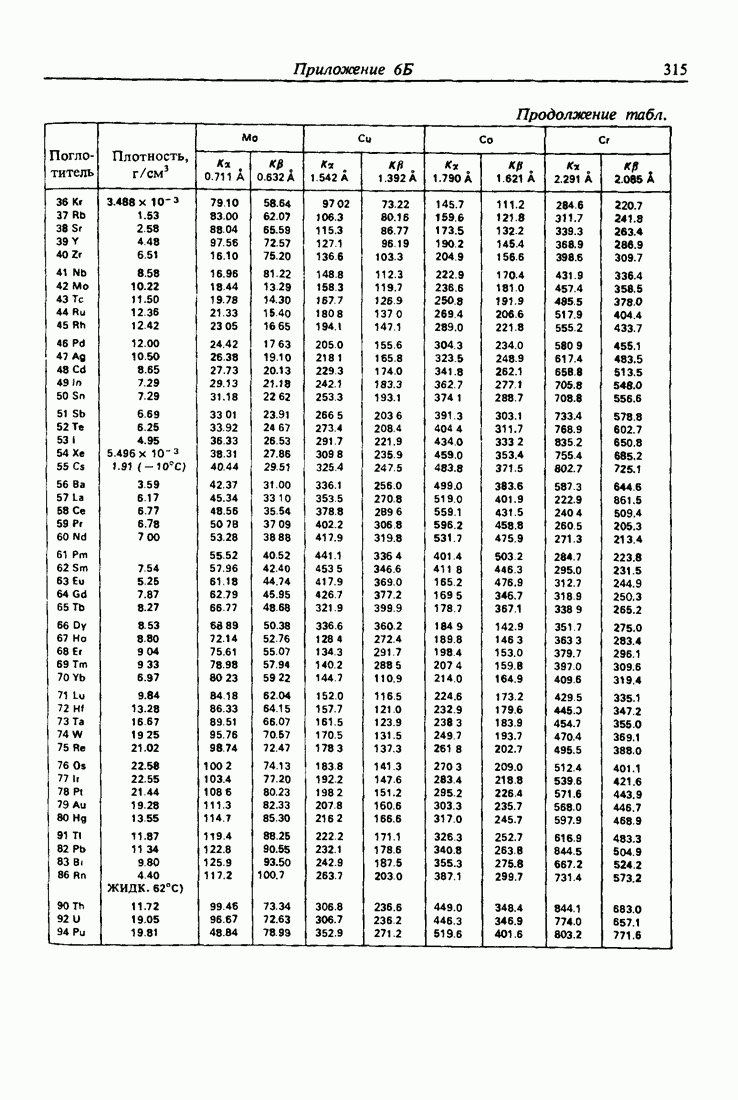
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
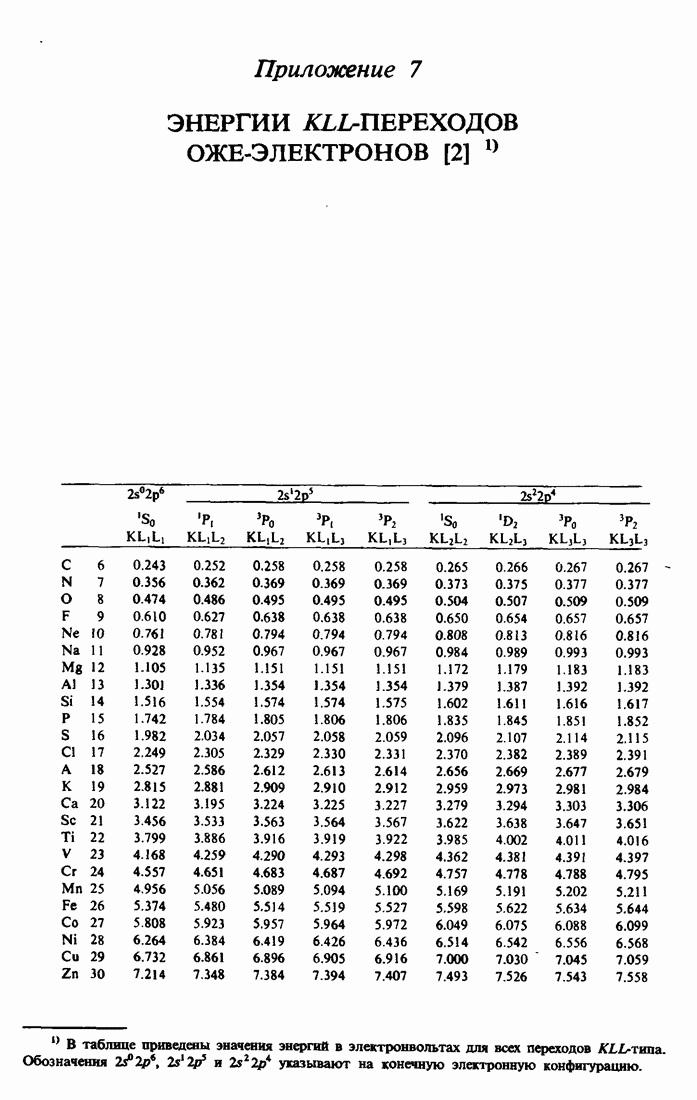
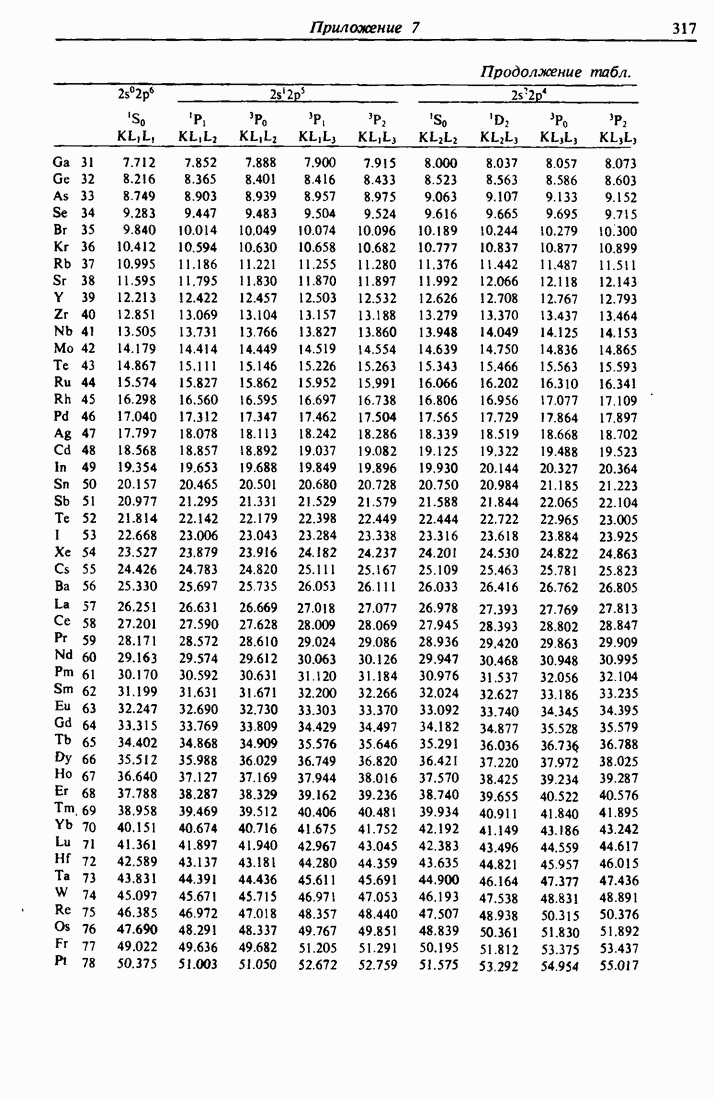
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
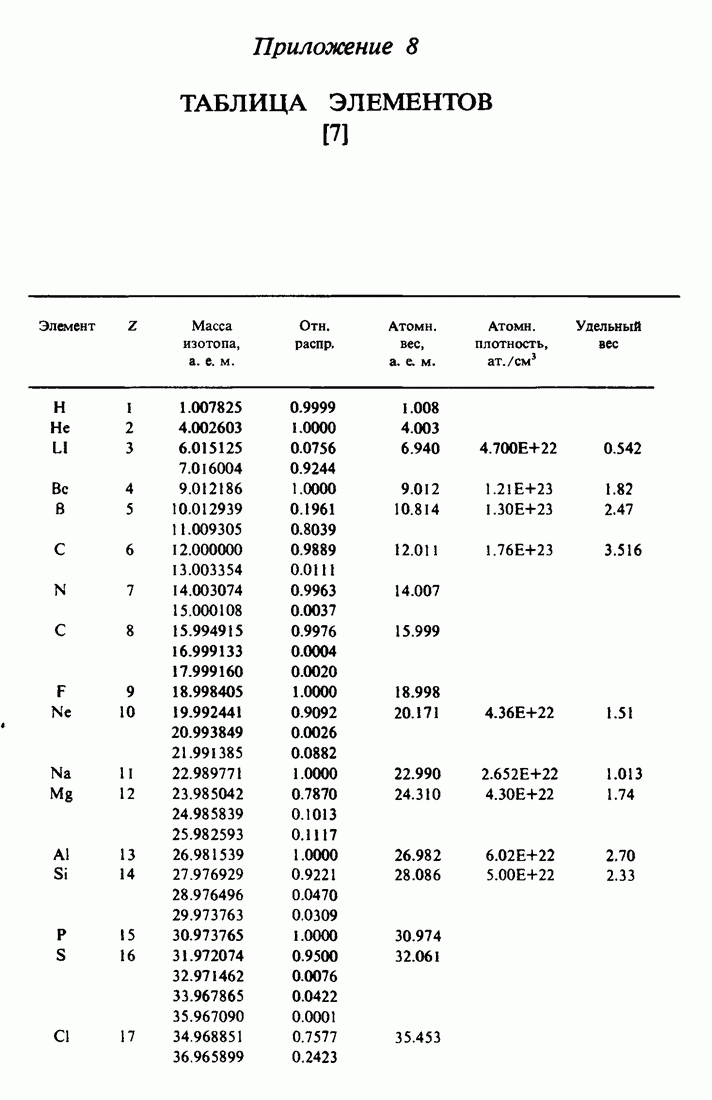
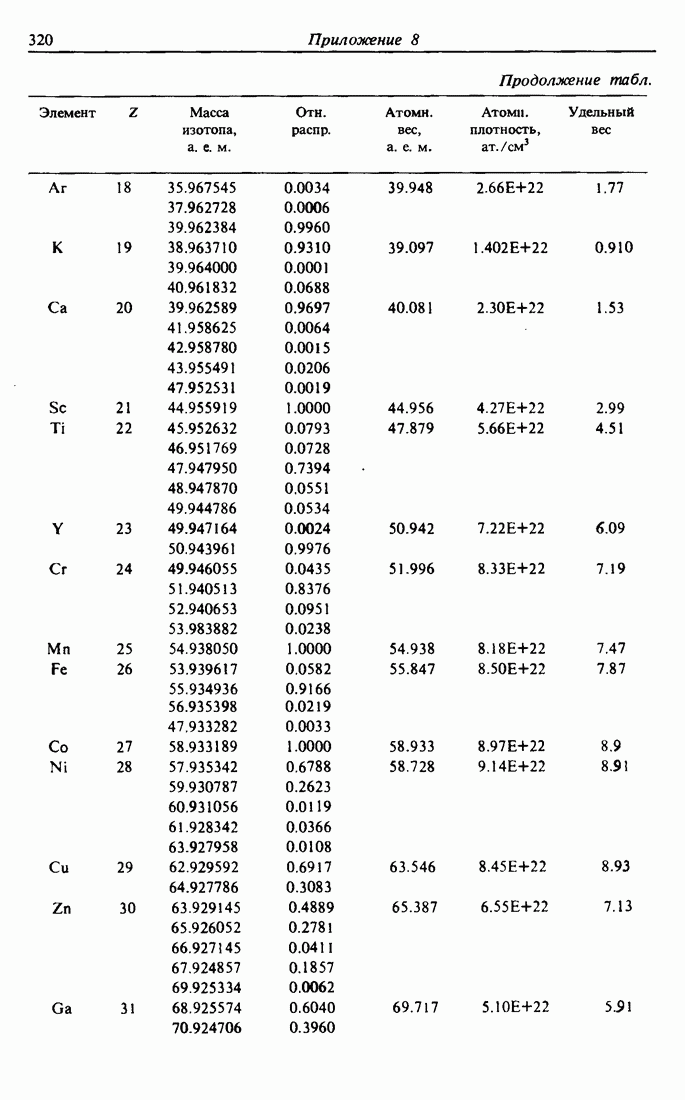
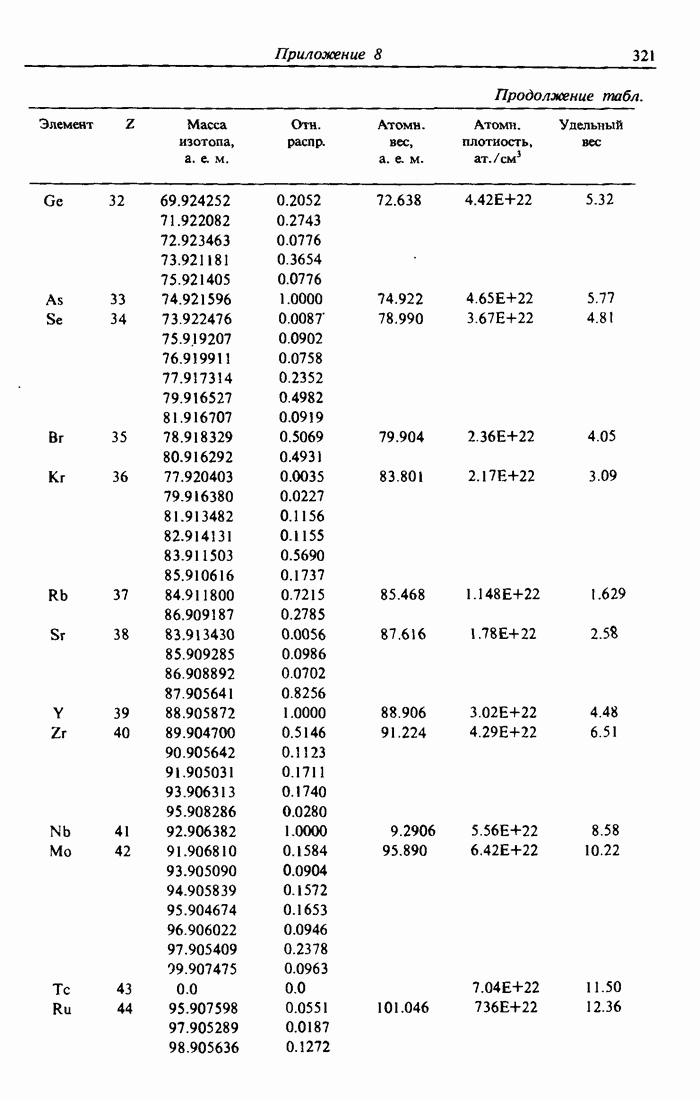
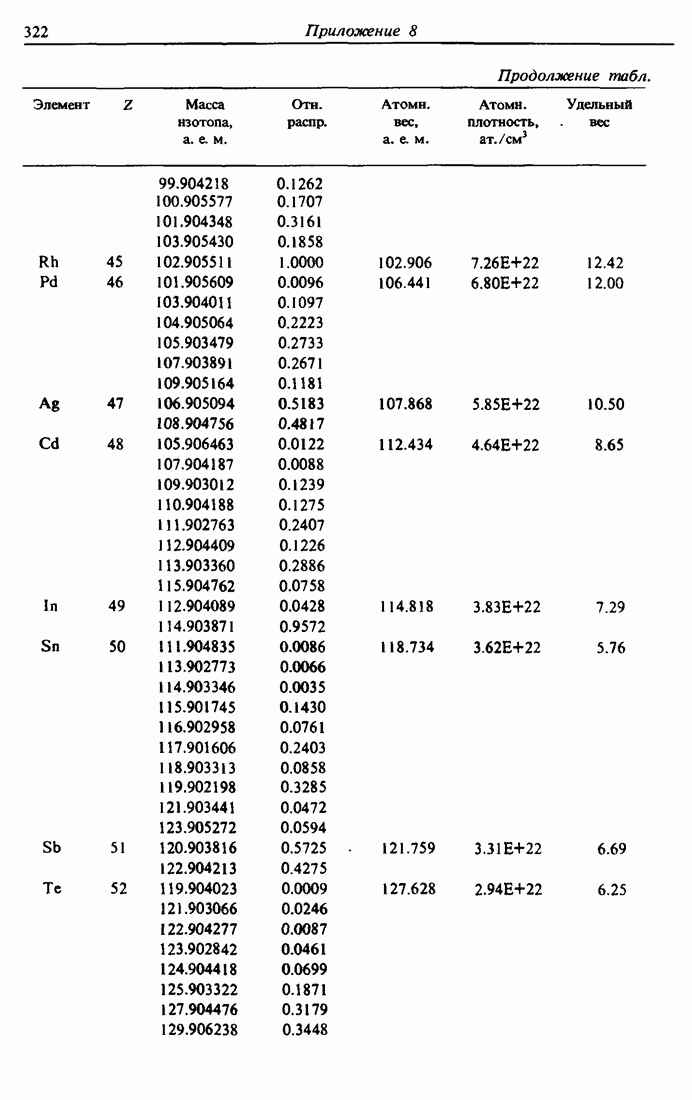
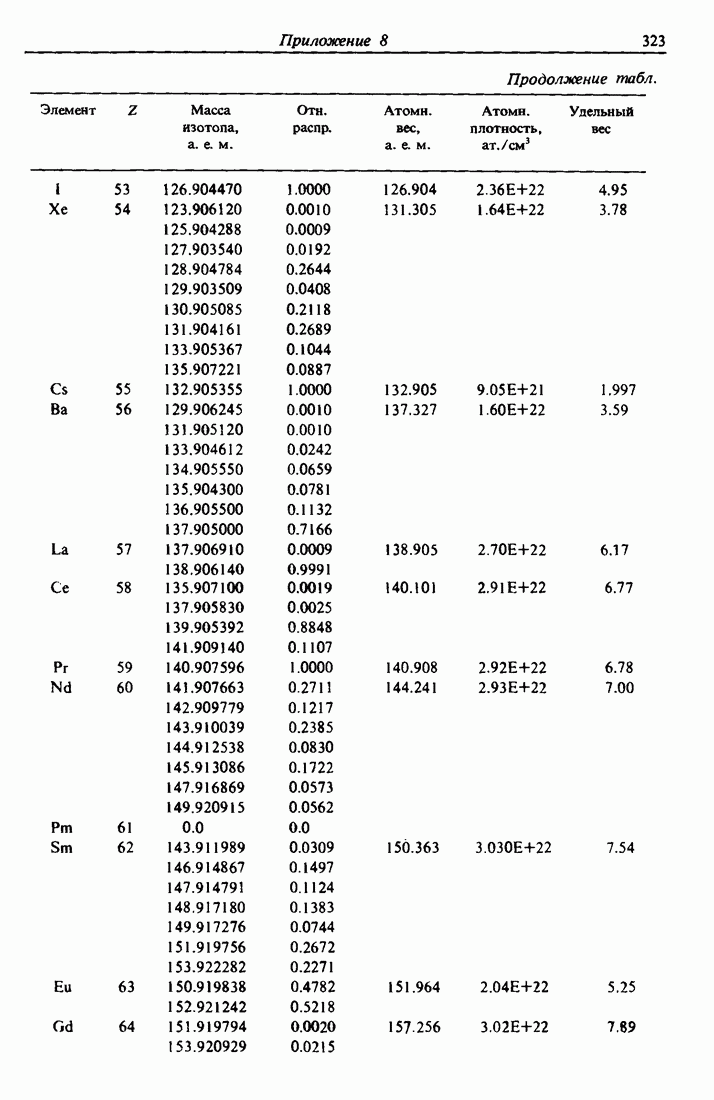
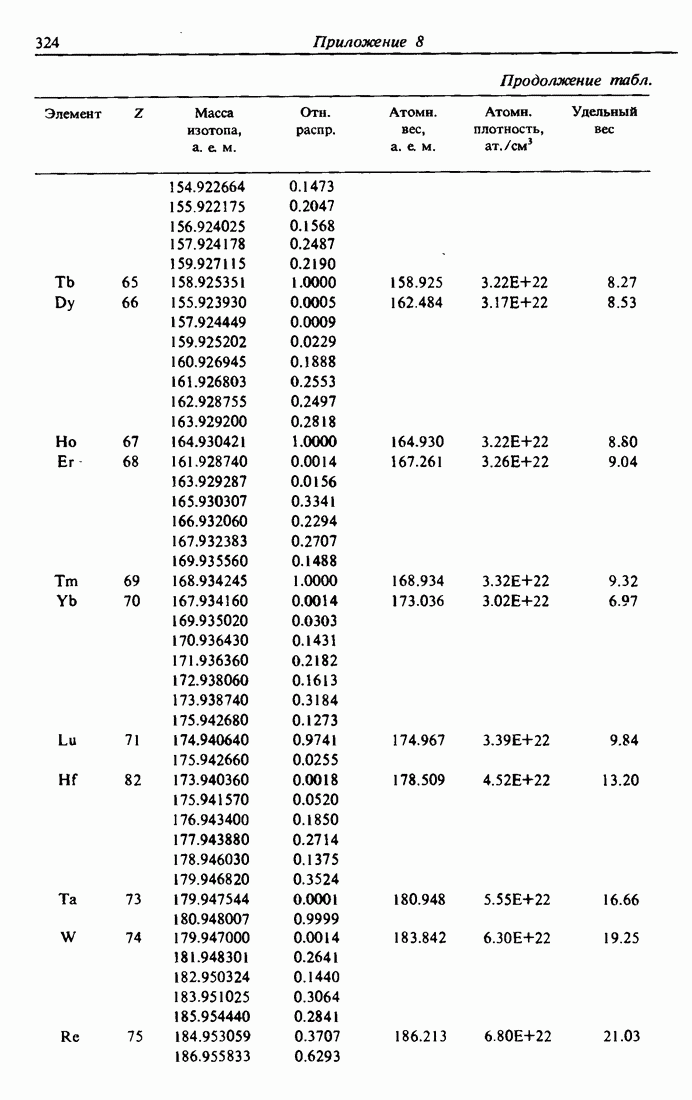
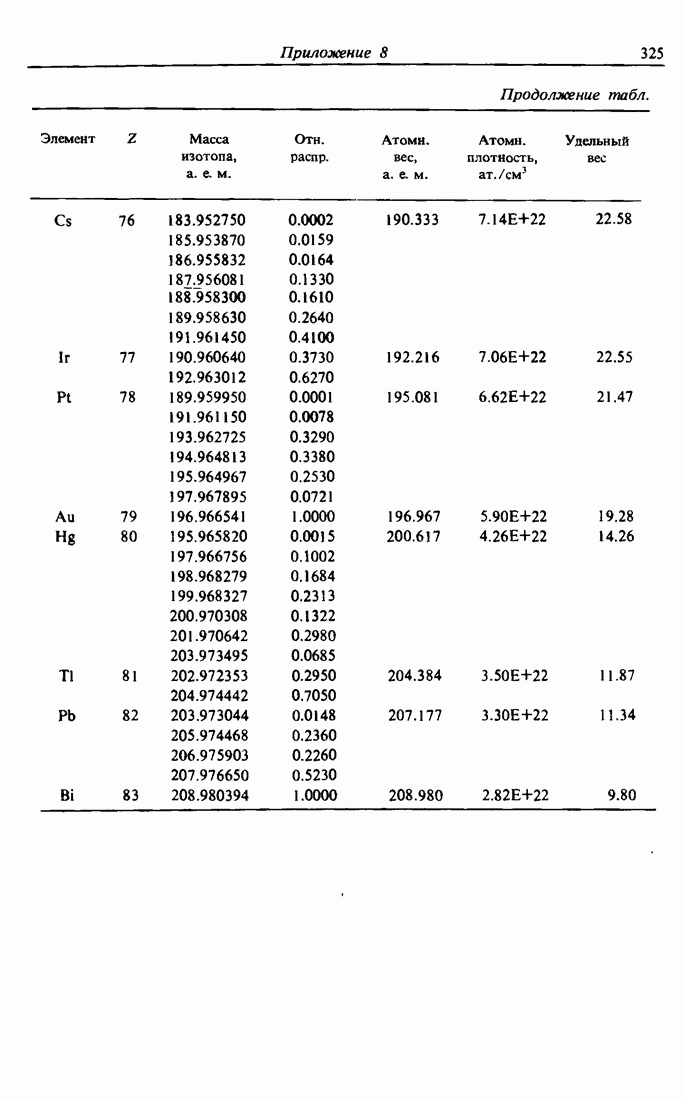
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
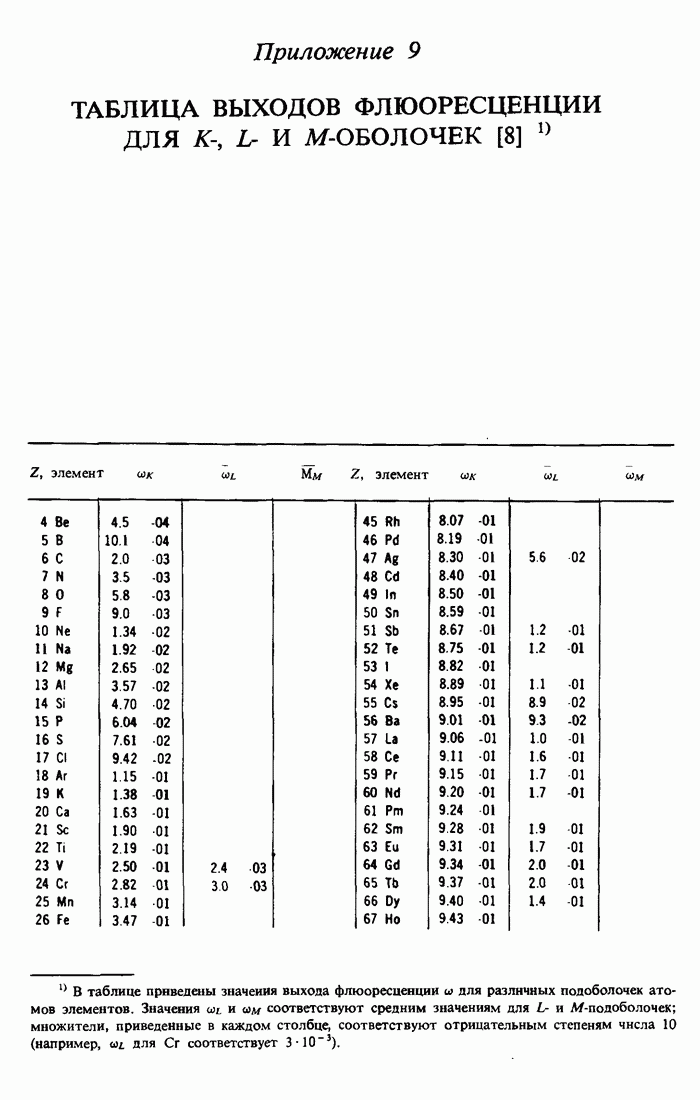
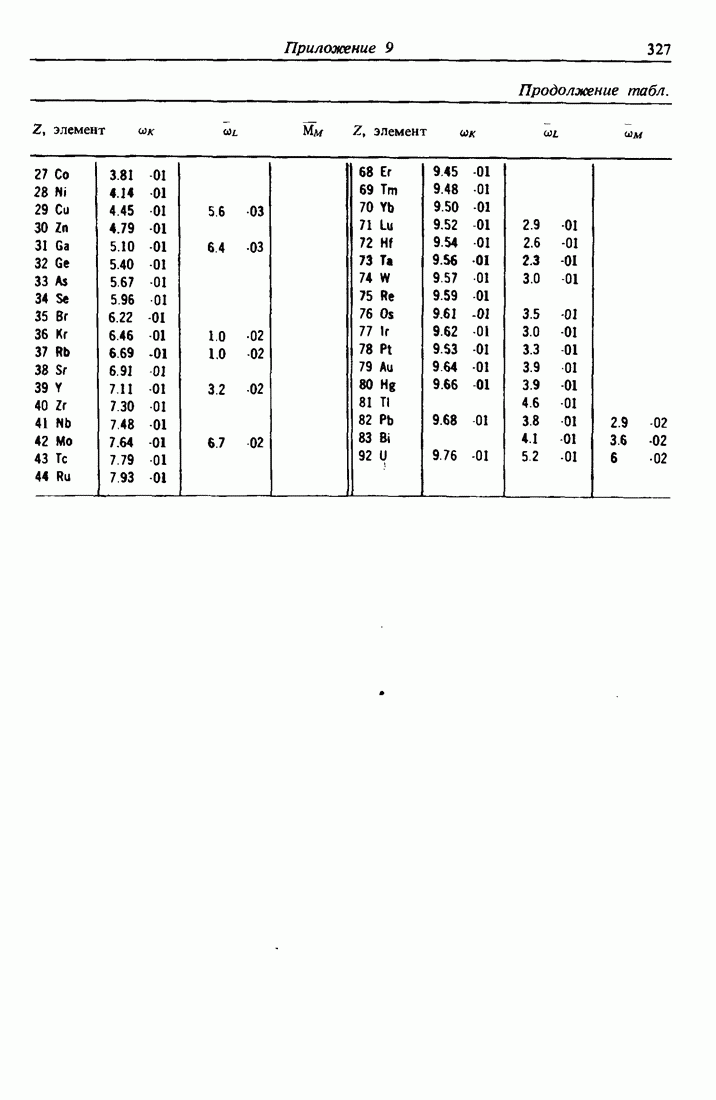
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ