| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Ядерные потери энергии
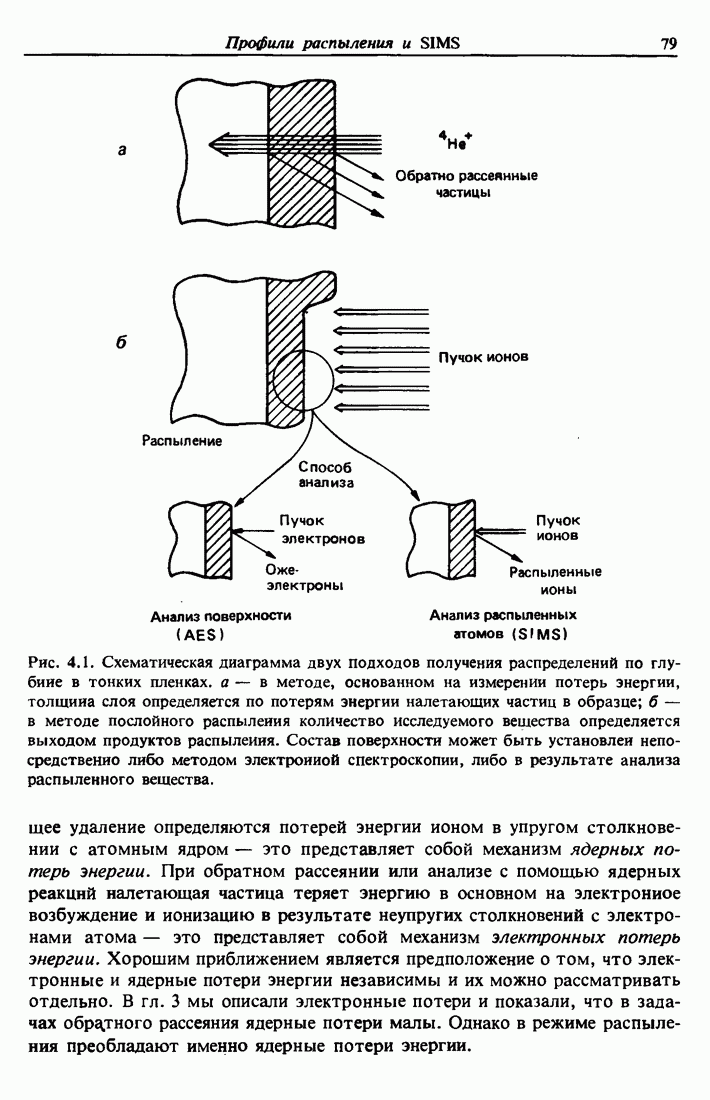
При движении в твердом теле заряженная частица теряет энергию в результате двух процессов: 1) передачи энергии электронам — электронные потери энергии и 2) передачи энергии атомам среды — ядерные потери энергии. В обоих случаях взаимодействие является в своей основе кулоновским; в электронном случае оно чисто кулоновское (см. гл. 3), а в ядерном оно описывается экранированным кулоновским потенциалом. Эти два механизма потерь различаются своей зависимостью от энергии: для легких налетающих частиц сечение электронных потерь имеет пик при энергиях порядка 0,1 — 1,0 МэВ, а пик сечения ядерных потерь приходится на значительно меньшие энергии порядка 0,1 — 10 кэВ. В теории проникновения частиц в вещество электронные и ядерные потери обычно рассматриваются как независимые и просто суммируются. Во многих случаях один из этих вкладов пренебрежимо мал и поэтому игнорируется. Распыление определяется количеством энергии, поглощаемой на поверхности твердого тела посредством
механизма ядерных потерь. Именно этот механизм передачи импульса и энергии атомам твердого тела приводит к образованию вторичных частиц высоких энергий и распылению. В этом разделе мы дадим простое описание ядерных потерь энергии и сравним его с более сложными рассмотрениями. Как и в других разделах этой книги, нашей целью является простое математическое описание процесса, позволяющее создать количественные представления о физике явления.
Вывод формулы для ядерных потерь энергии использует два главных допущения: 1) введение экранированного кулоновского потенциала простого вида и 2) применение импульсного приближения.
Взаимодействие двух атомов  можно описать экранированным кулоновским потенциалом (разд. 4.9) с некоторой функцией экранирования
можно описать экранированным кулоновским потенциалом (разд. 4.9) с некоторой функцией экранирования 

где а — радиус экранирования Томаса — Ферми:

Для большинства взаимодействий значение а лежит между 0,1 и 0,2 А. В качестве функции экранирования возьмем

что приводит к потенциалу вида

Функции экранирования  изображены на рис. 4.4, причем последняя из них в области
изображены на рис. 4.4, причем последняя из них в области  близка к более точному потенциалу Мольера. При
близка к более точному потенциалу Мольера. При  потенциал вида
потенциал вида  вообще не является хорошей аппроксимацией,
вообще не является хорошей аппроксимацией,

Рис. 4.4. Функция экранирования  в приближении Мольера (кривая
в приближении Мольера (кривая  ). При
). При  значение функции уменьшается приблизительно до 0,4, подтверждая этим, что а выбирается как векоторая аппроксимация размера атома. Показаны также функции экранирования
значение функции уменьшается приблизительно до 0,4, подтверждая этим, что а выбирается как векоторая аппроксимация размера атома. Показаны также функции экранирования  (кривая 2) и
(кривая 2) и  (кривая 3).
(кривая 3).
поскольку он не переходит в чисто кулоновское выражение при  . Однако это не приводит к серьезным затруднениям, поскольку для распыления применяются частицы низких энергий, у которых расстояние наибольшего сближения с атомом достаточно велико, что исключает взаимодействия при малых r.
. Однако это не приводит к серьезным затруднениям, поскольку для распыления применяются частицы низких энергий, у которых расстояние наибольшего сближения с атомом достаточно велико, что исключает взаимодействия при малых r.
Импульсное приближение вполне подходит для описания столкновений с большими прицельными параметрами и малыми углами рассеяния. В основном именно такие столкновения образуют последовательность событий рассеяния, которая определяет траекторию заряженной частицы. Мы уже использовали импульсную аппроксимацию для вывода сечения электронного торможения в гл. 3. В этом приближении изменение импульса задается выражением

или

где  — компонента силы, действующая на ион перпендикулярно направлению его падения. Пользуясь геометрией рис. 3.3, перепишем силу
— компонента силы, действующая на ион перпендикулярно направлению его падения. Пользуясь геометрией рис. 3.3, перепишем силу  в виде
в виде

где  Тогда
Тогда

или в силу (4.7)

что сводится к выражению

Переданная атому энергия Т равна

Сечение  передачи энергии в интервале от Т до T+dT есть
передачи энергии в интервале от Т до T+dT есть

где  .
.
Удобно выразить этот результат в терминах максимальной передачи энергии  , которая равна
, которая равна

Тогда

Сечение  ядерного торможения определяется по формуле
ядерного торможения определяется по формуле

что после вычислений дает

Ядерные потери энергии задаются выражением

где N — число атомов в единице объема твердого тела. Заметим, что в полученном приближении значение  не зависит от энергии:
не зависит от энергии:

На рис. 4.5 это значение сравнивается с величиной ядерных потерь энергии для потенциала Томаса — Ферми.
Рис. 4.5 построен согласно методу Линдхарда, в котором ядерные потери энергии выражаются в единицах приведенной энергии  , представляющей
, представляющей

Рис. 4.5. Зависимость приведенного сечения ядерного торможения  от приведенной энергии
от приведенной энергии  . Кривая 1 соответствует потенциалу Томаса — Ферми и дает наиболее точные значения
. Кривая 1 соответствует потенциалу Томаса — Ферми и дает наиболее точные значения  горизонтальная линия 2 изображает результат (4.17) для потенциала
горизонтальная линия 2 изображает результат (4.17) для потенциала 
отношение параметра экранирования Томаса — Ферми к расстоянию наибольшего сближения:
 (4.20а)
(4.20а)
и приведенной длины р, определяемой через поперечное сечение  и отношение энергий
и отношение энергий  в виде
в виде
 (4.206)
(4.206)
Такое представление полезно тем, что позволяет определить тормозную способность для любой комбинации мишени и налетающей частицы произвольной энергии. В этом формализме  так что из определений (4.20а) и (4.206) следует
так что из определений (4.20а) и (4.206) следует

где  зависит от вида потенциала
зависит от вида потенциала  . В приведенных единицах энергии и длины не зависящая от энергии величина (4.19) ядерных потерь
. В приведенных единицах энергии и длины не зависящая от энергии величина (4.19) ядерных потерь  принимает значение 0,393. Это несколько отличается от значения, полученного Линдхардом и др. [8], так как мы воспользовались импульсным приближением, в то время как в работе [8] интеграл рассеяния вычисляется более точно.
принимает значение 0,393. Это несколько отличается от значения, полученного Линдхардом и др. [8], так как мы воспользовались импульсным приближением, в то время как в работе [8] интеграл рассеяния вычисляется более точно.
Заметим, что наше приближенное выражение (4.19) дает правильный порядок величины тормозной способности, но не воспроизводит зависимость от энергии. Наиболее существенным недостатком является то, что при высоких энергиях это выражение не имеет поведения  . Это вызвано использованием потенциала
. Это вызвано использованием потенциала  вместо
вместо  Очевидно, что приближение вида
Очевидно, что приближение вида  хуже всего работает при высоких энергиях, где важны близкие соударения. Точные значения ядерных потерь энергии
хуже всего работает при высоких энергиях, где важны близкие соударения. Точные значения ядерных потерь энергии  можно получить по формуле (4.21) и из рис. 4.5, на котором кривая
можно получить по формуле (4.21) и из рис. 4.5, на котором кривая  вычислена согласно более точному потенциалу Томаса — Ферми (разд. 4.9).
вычислена согласно более точному потенциалу Томаса — Ферми (разд. 4.9).
Для ионов  с энергией
с энергией  падающих на мишень из
падающих на мишень из  ,
,  а для ионов О с энергией
а для ионов О с энергией  и той же мишени
и той же мишени  (Аргон и кислород наиболее широко используются при изучении распределений по глубине методом распыления.) Таким образом, для энергий ионов от 1 до
(Аргон и кислород наиболее широко используются при изучении распределений по глубине методом распыления.) Таким образом, для энергий ионов от 1 до  значения
значения  лежат в диапазоне 0,01 — 0,3; этот интервал расположен слева от плато, образованного максимумом функции
лежат в диапазоне 0,01 — 0,3; этот интервал расположен слева от плато, образованного максимумом функции  . В этом случае для грубых оценок величины
. В этом случае для грубых оценок величины  можно использовать не зависящее от энергии значение
можно использовать не зависящее от энергии значение  являющееся средним для рассматриваемого диапазона. Для ионов
являющееся средним для рассматриваемого диапазона. Для ионов  в
в  величина
величина  составляет примерно
составляет примерно  а для ионов
а для ионов  в
в 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
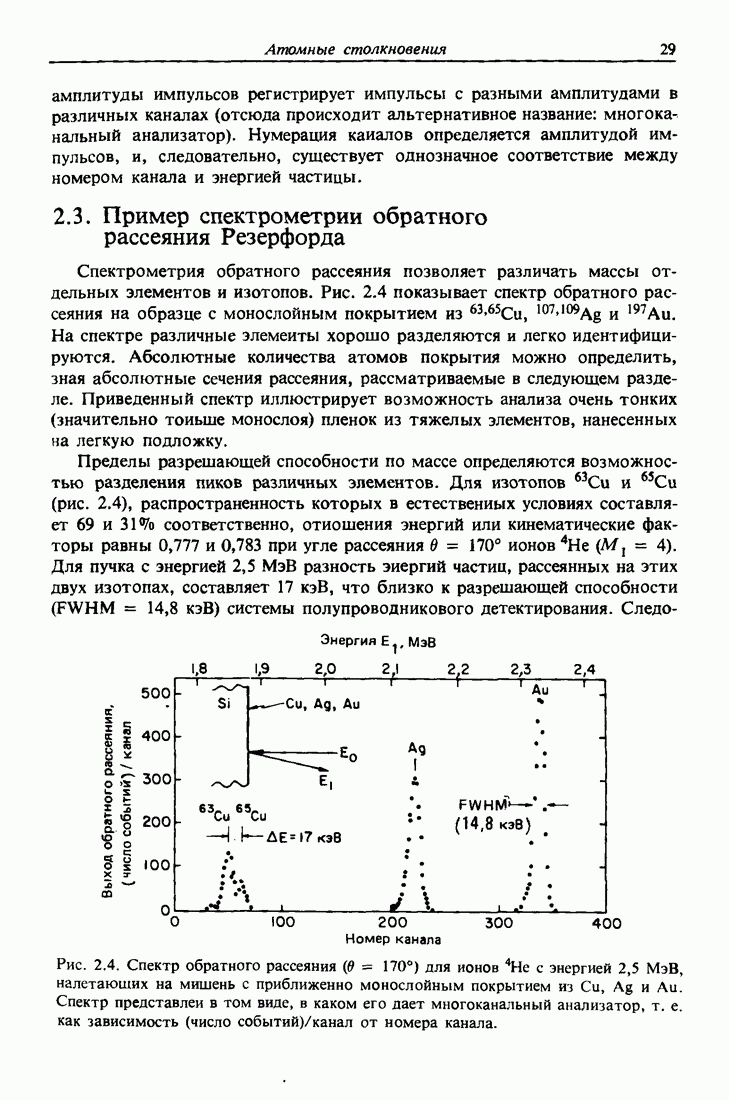
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
- 2.4. Сечение рассеяния и прицельный параметр
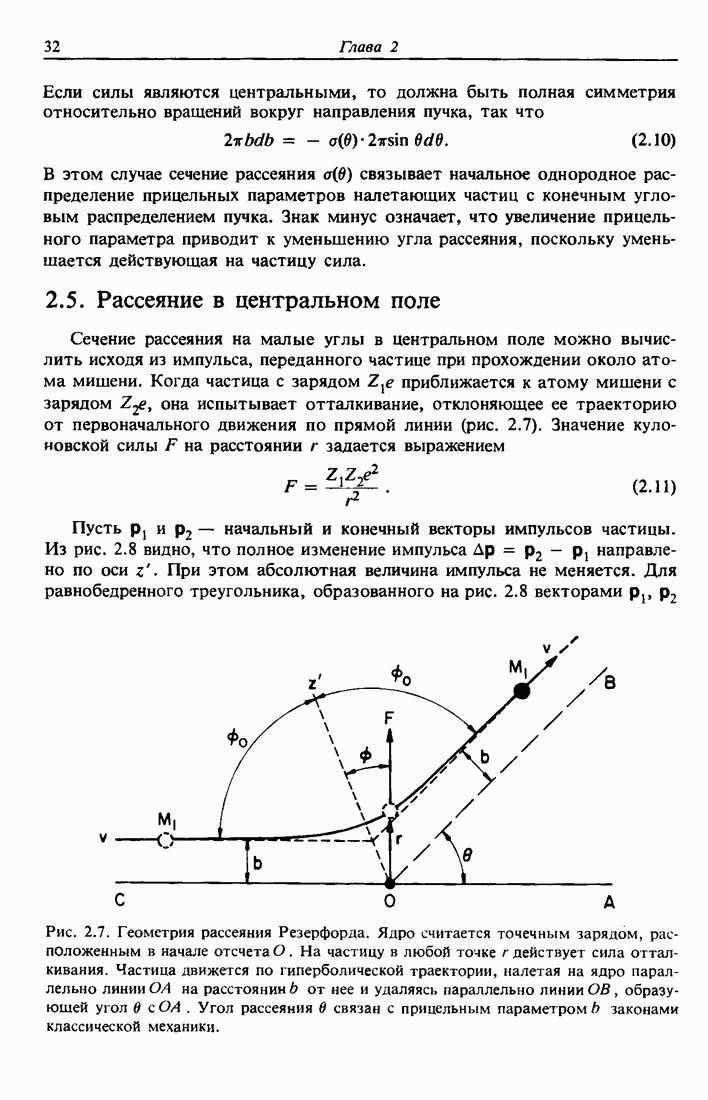
- 2.5. Рассеяние в центральном поле
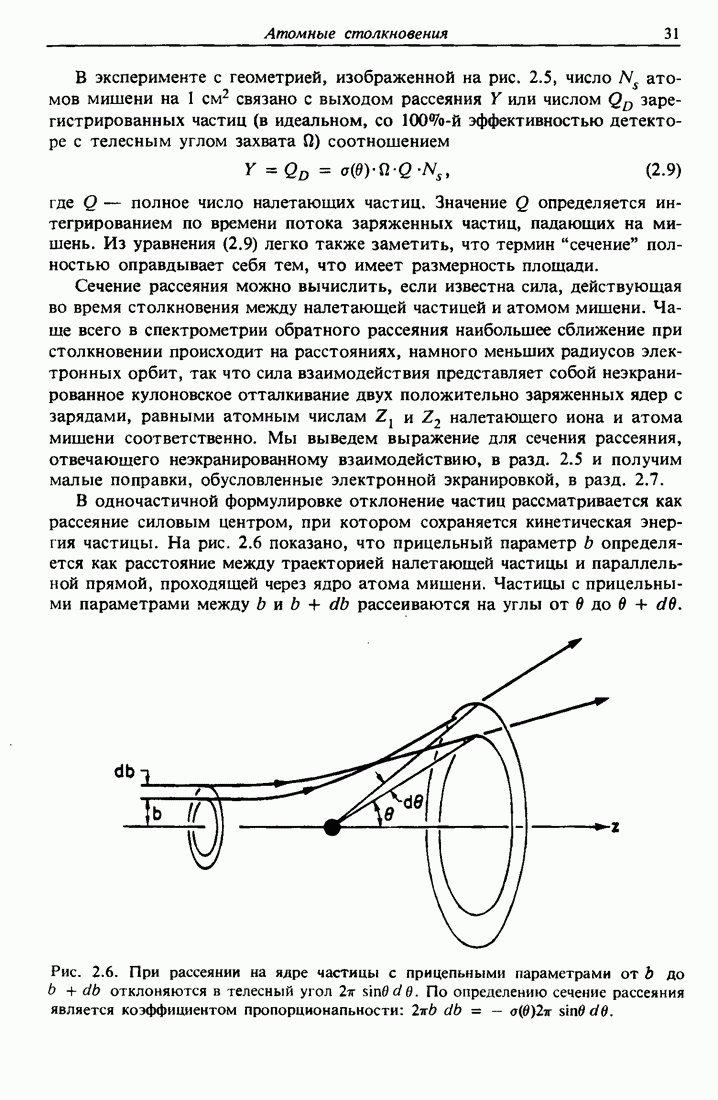
- 2.6. Сечение рассеяния в задаче двух тел
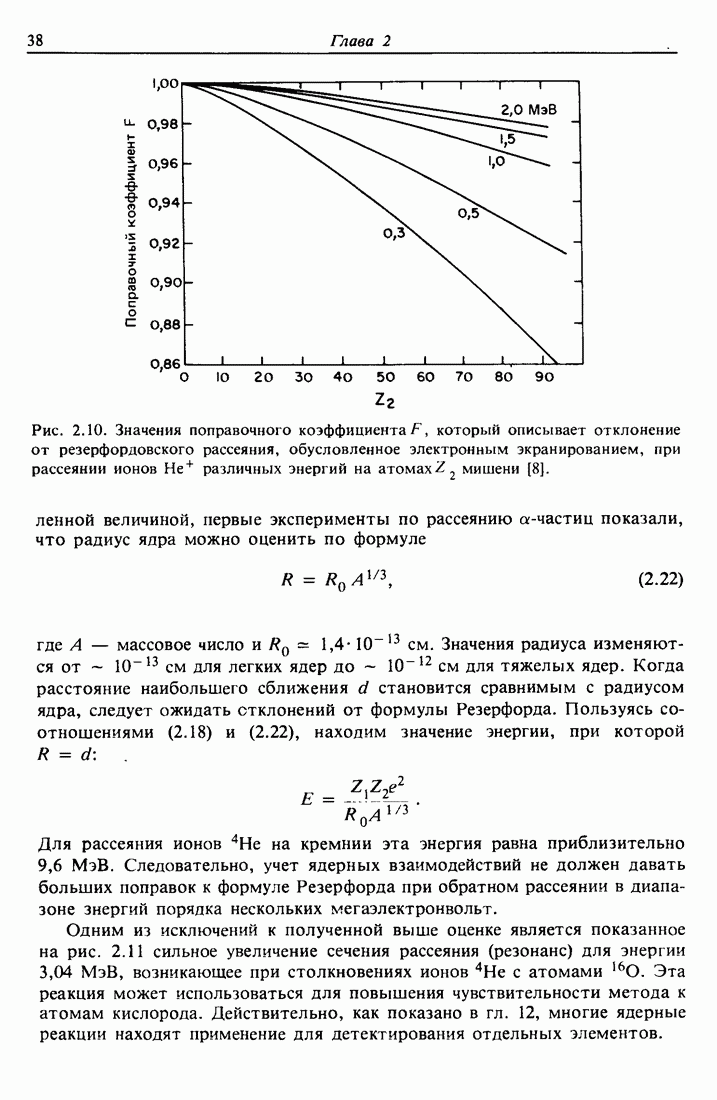
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
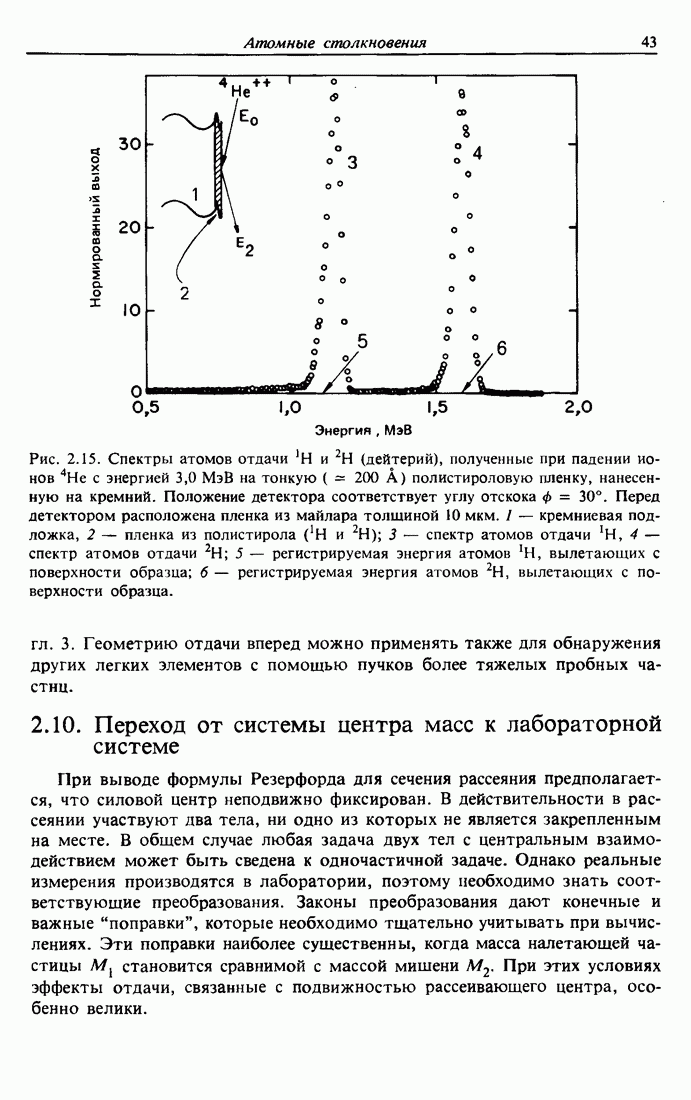
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
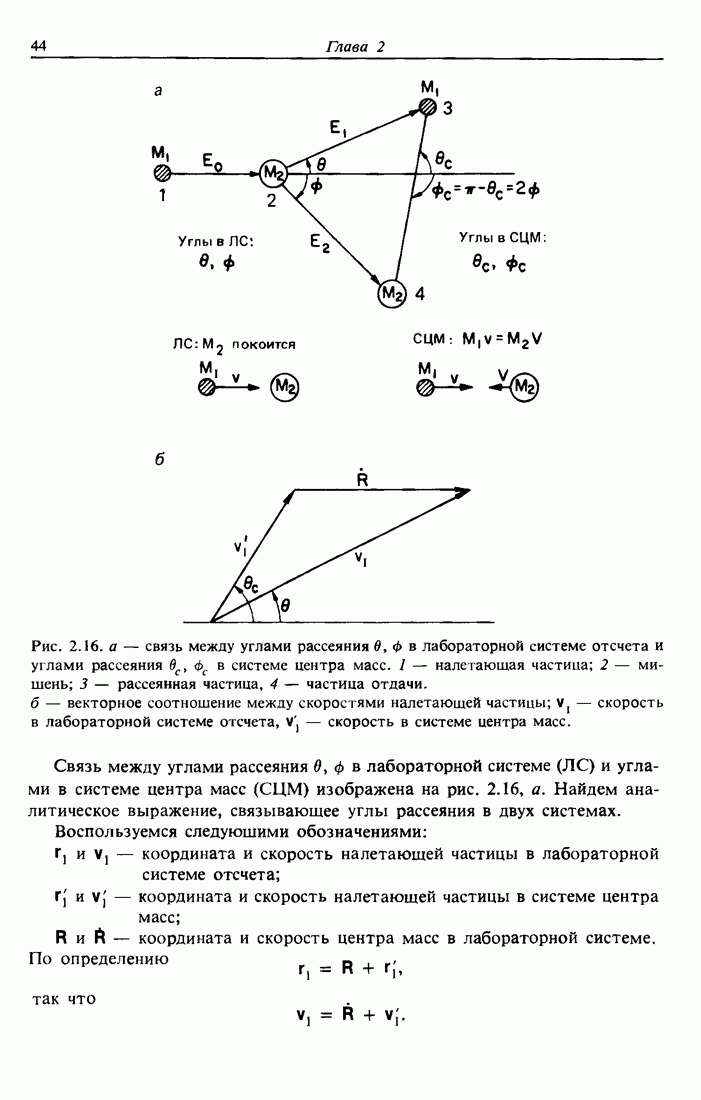
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
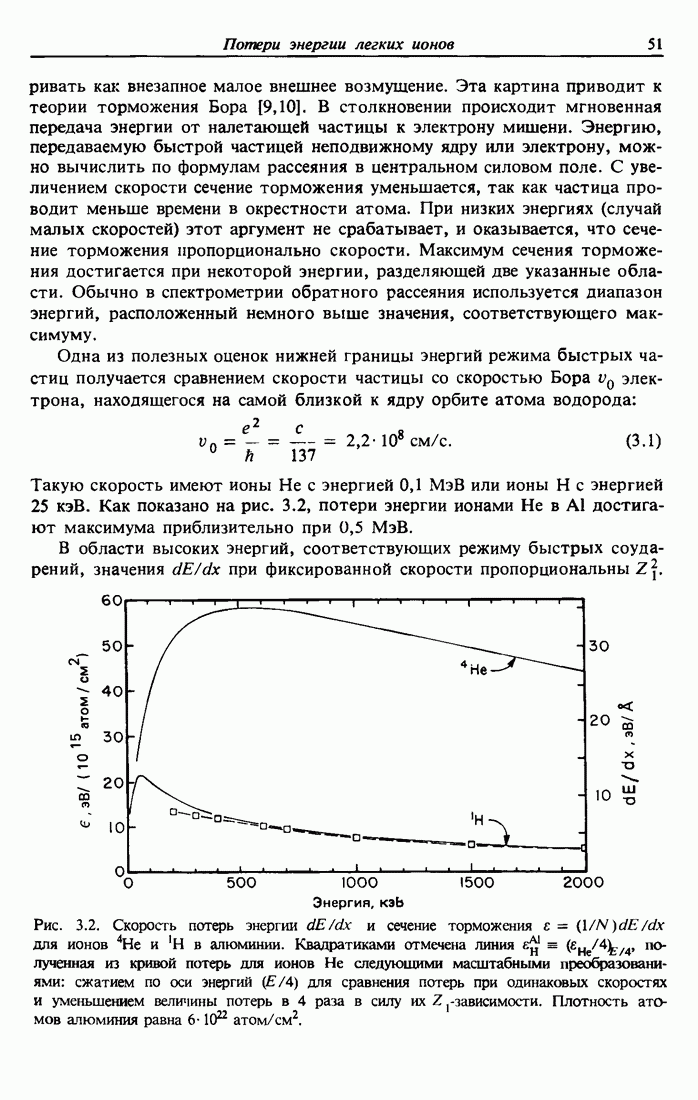
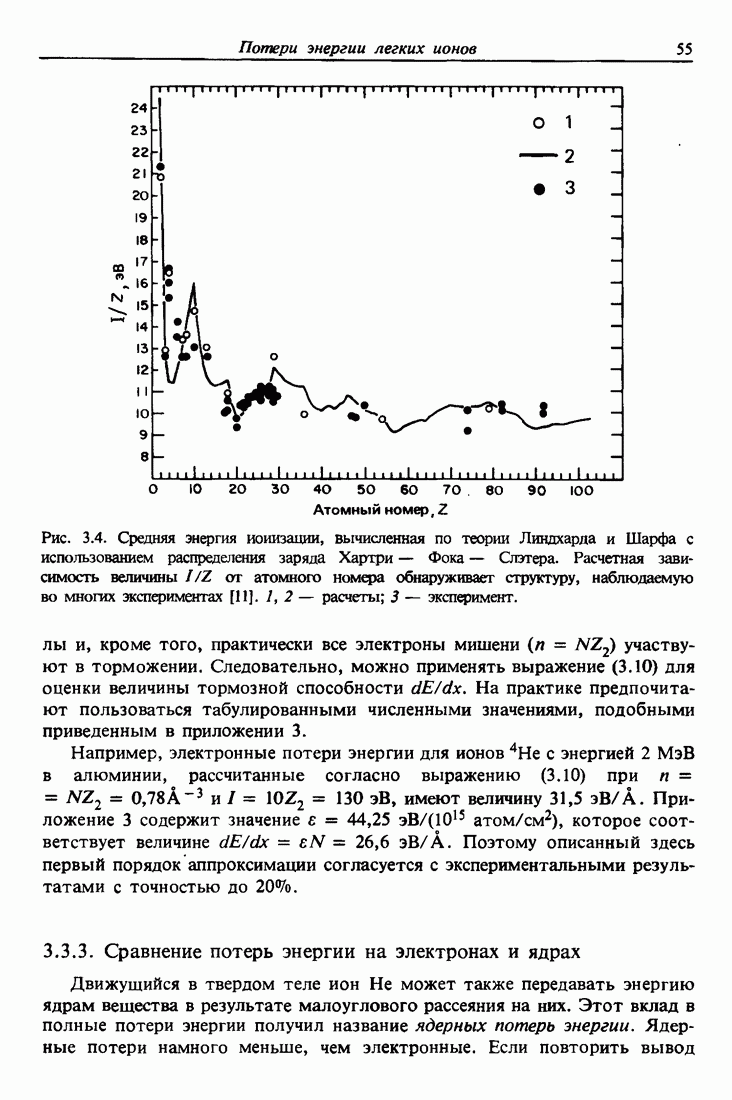
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
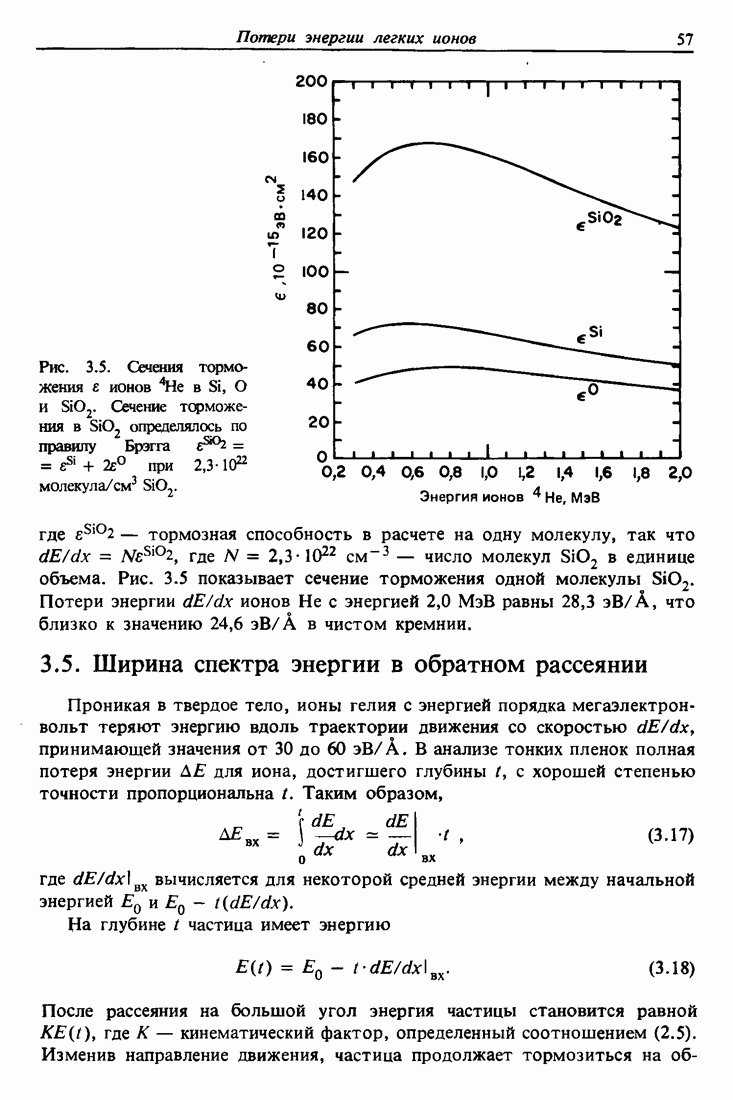
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
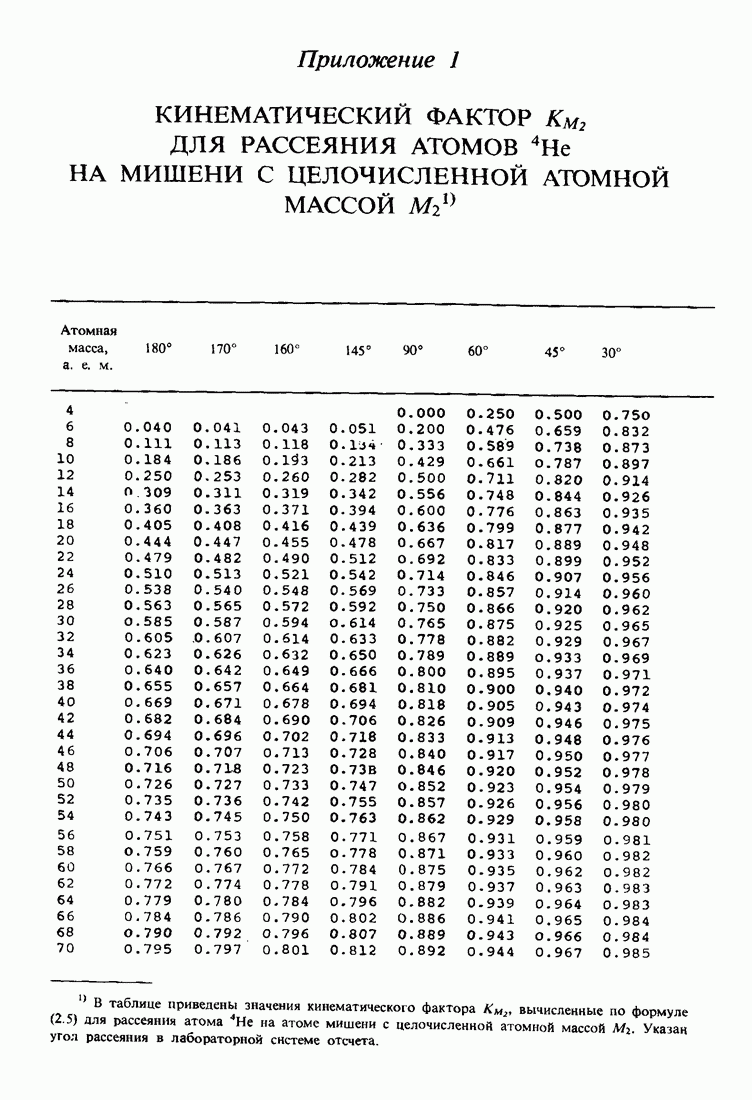
- ПРИЛОЖЕНИЕ 1.
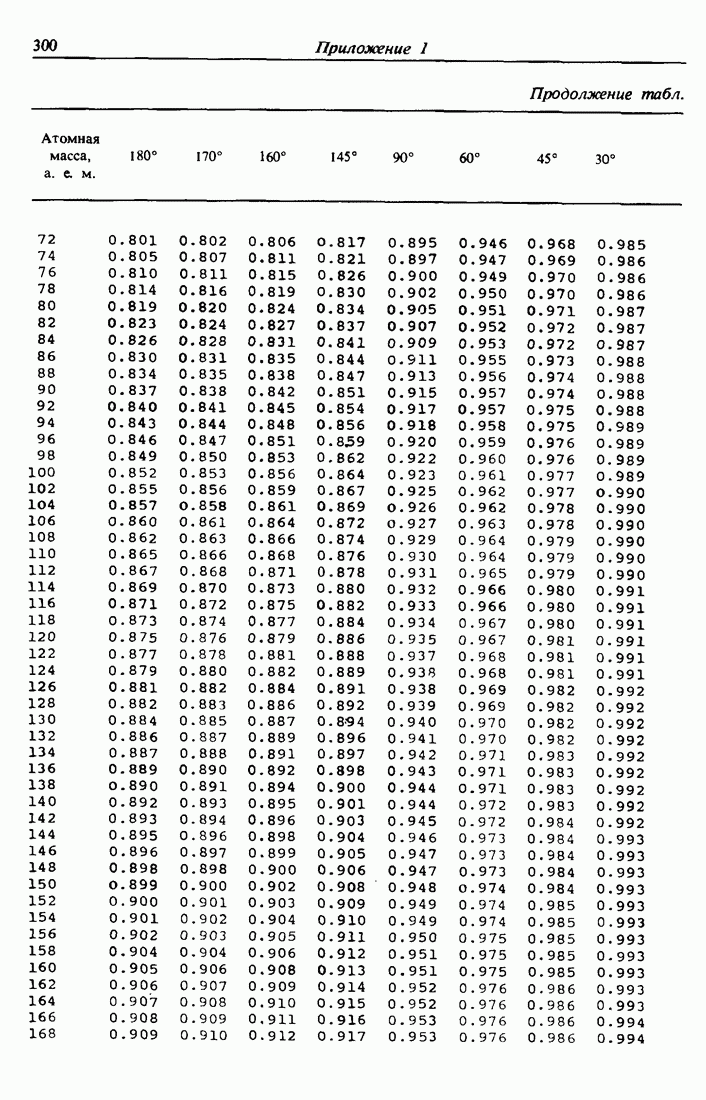
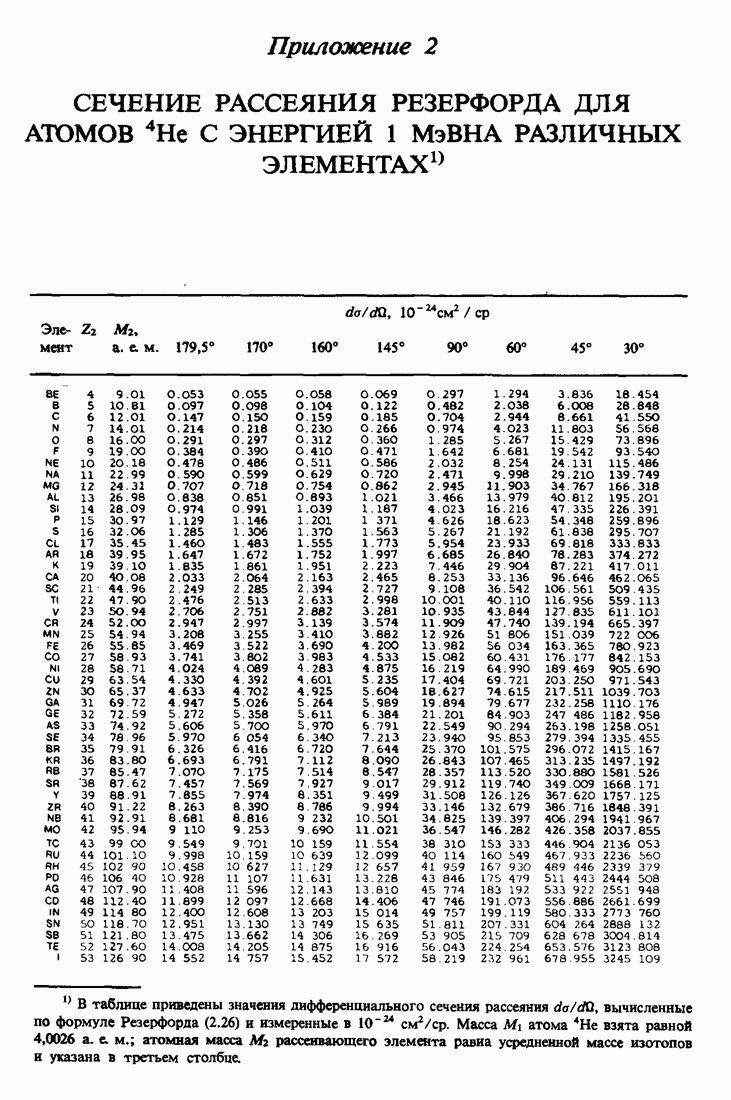
- ПРИЛОЖЕНИЕ 2.
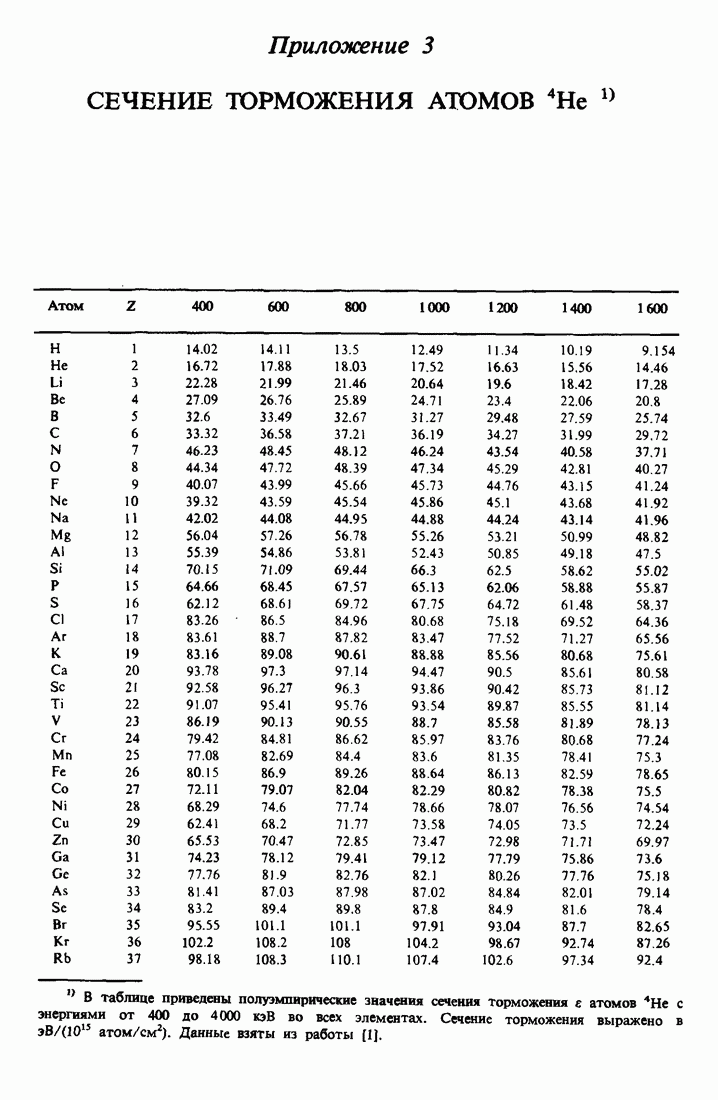
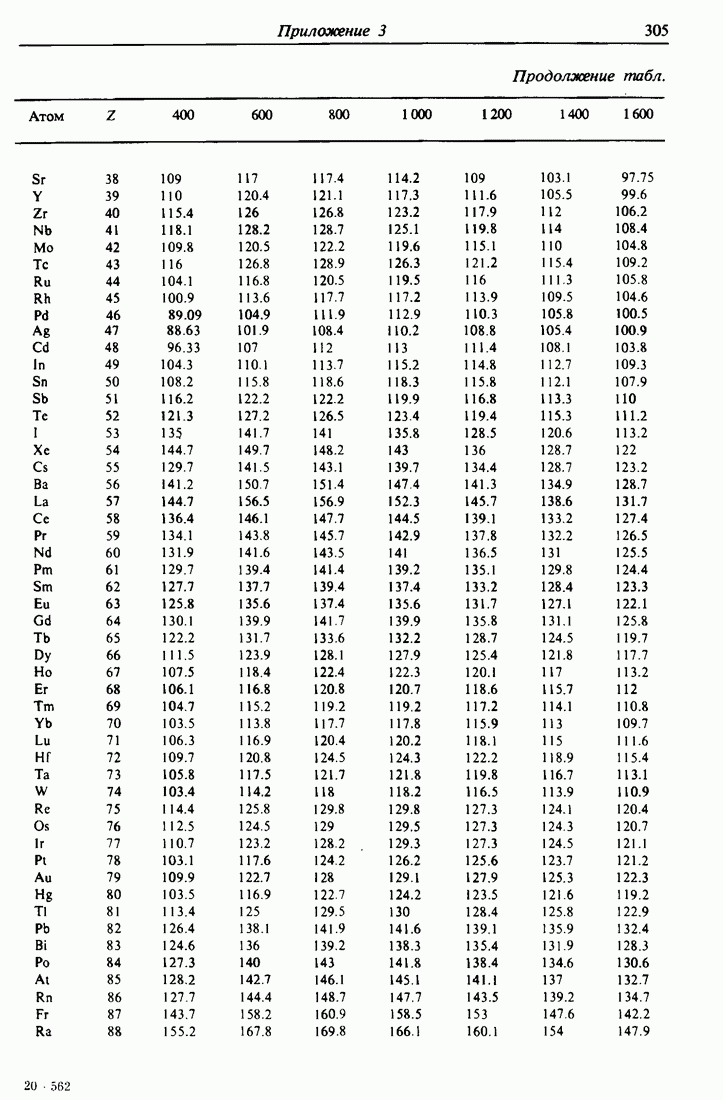
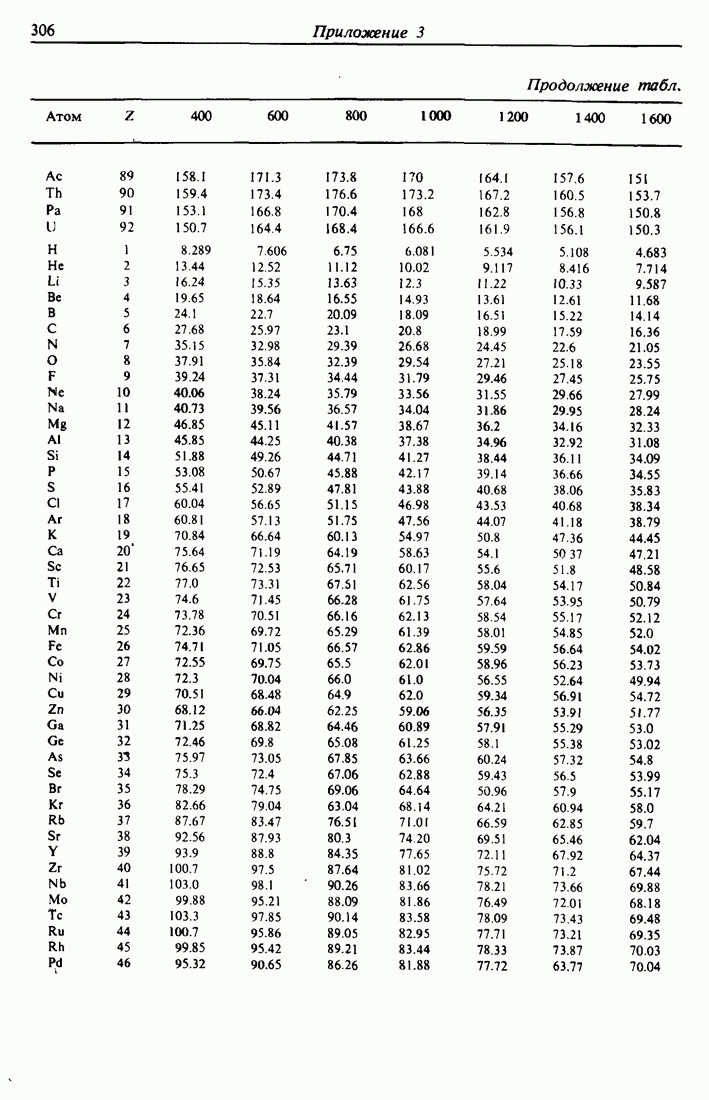
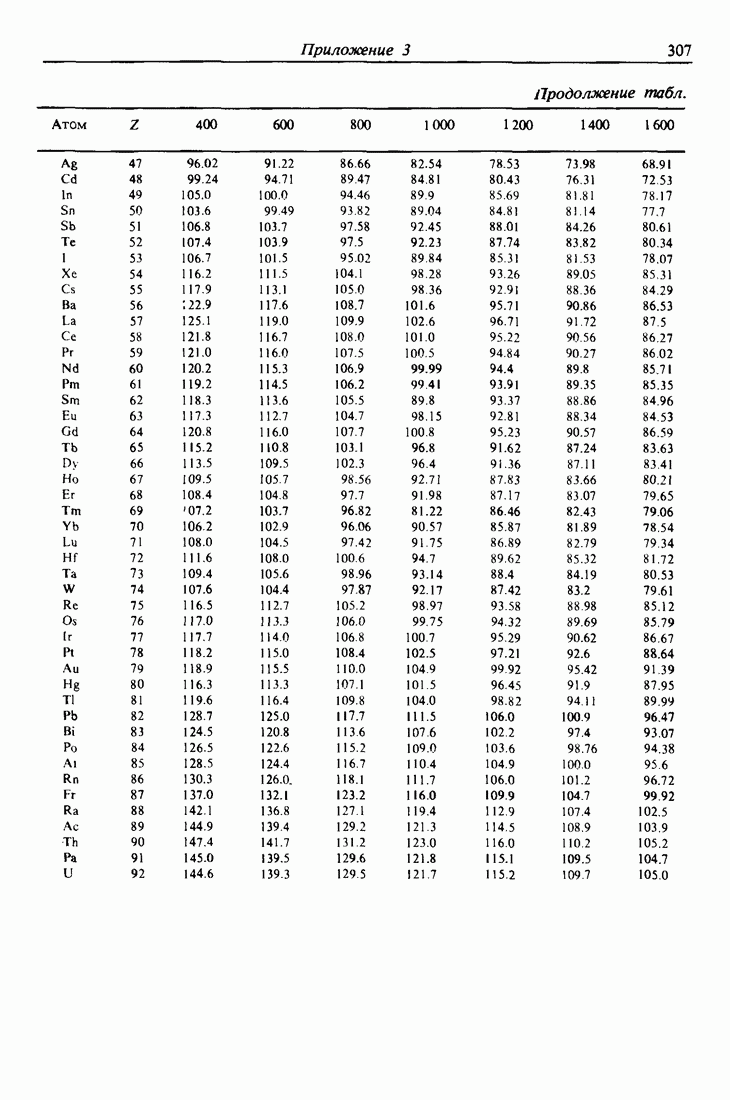
- ПРИЛОЖЕНИЕ 3.
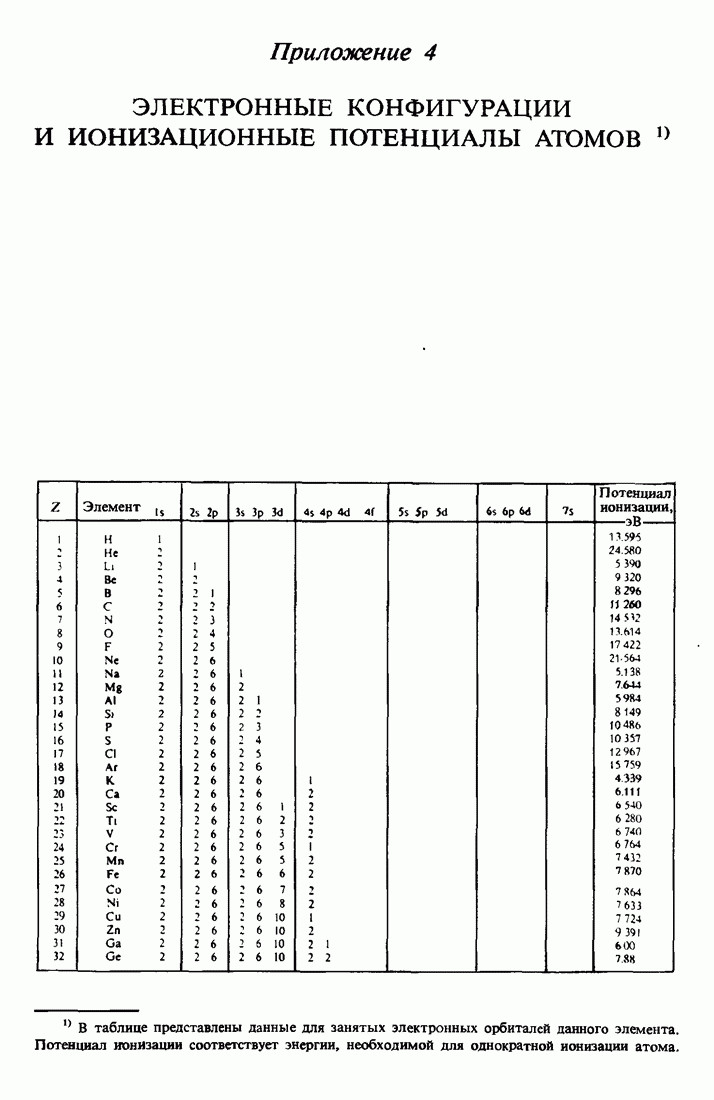
- ПРИЛОЖЕНИЕ 4.
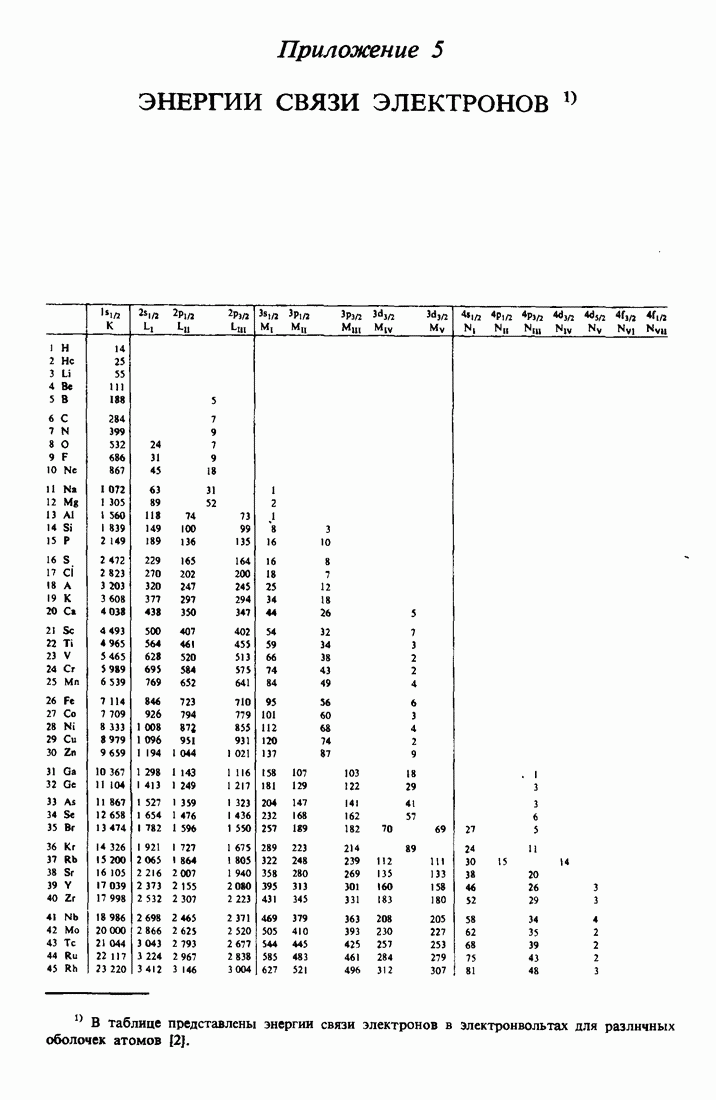
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
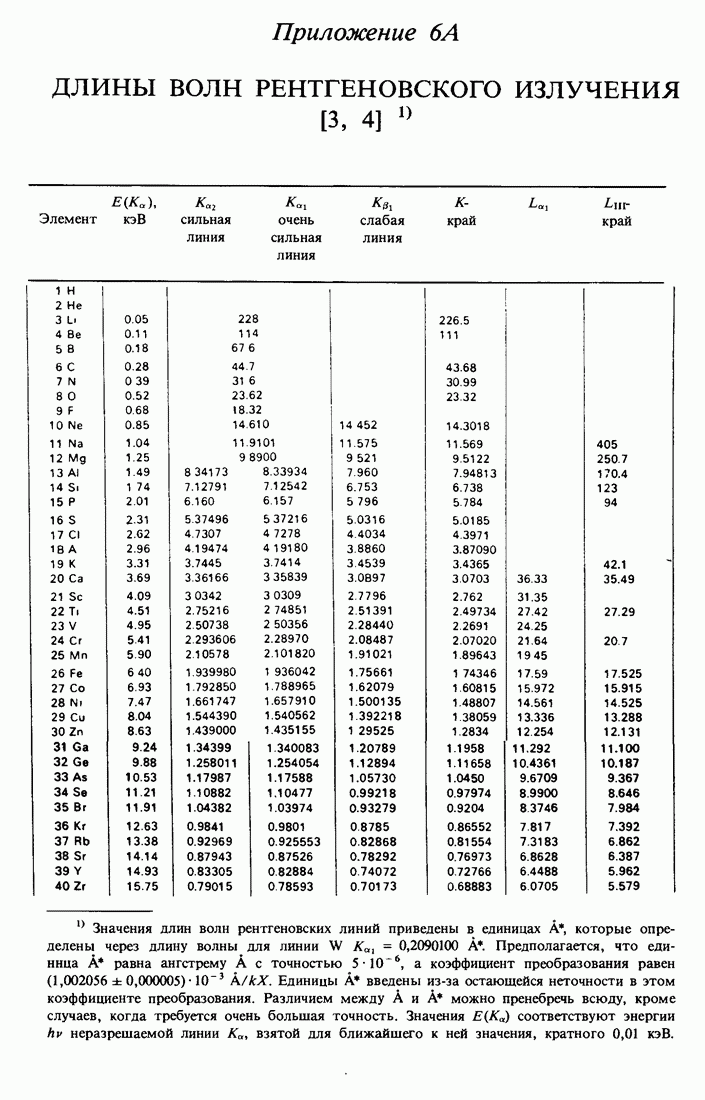
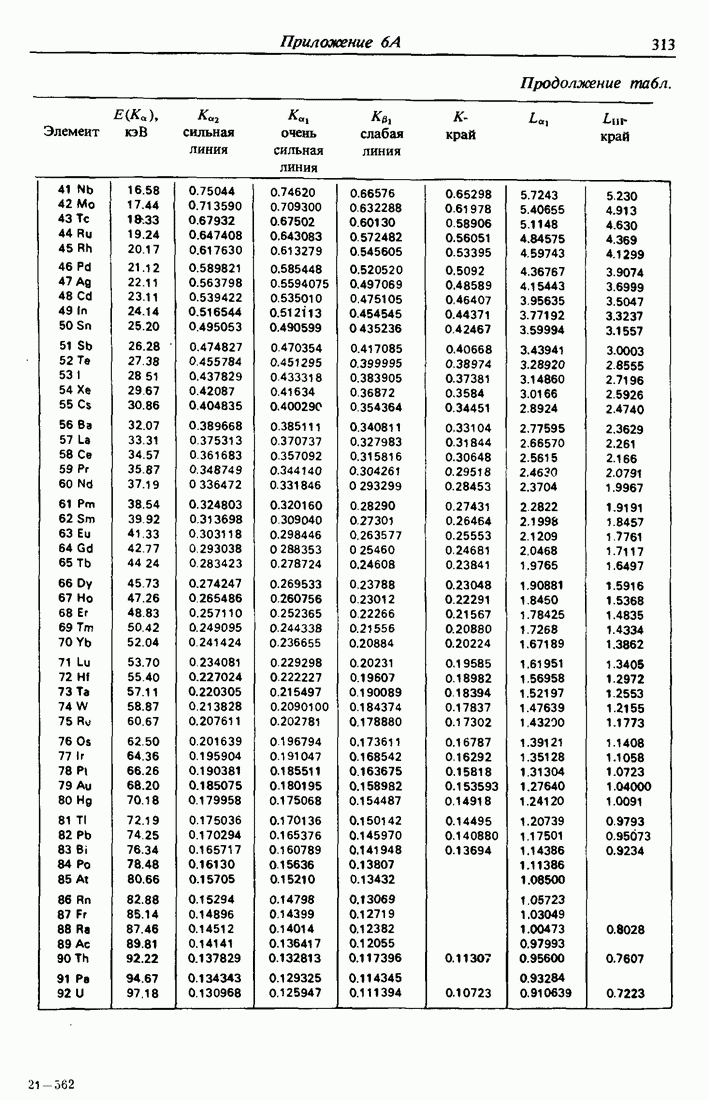
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
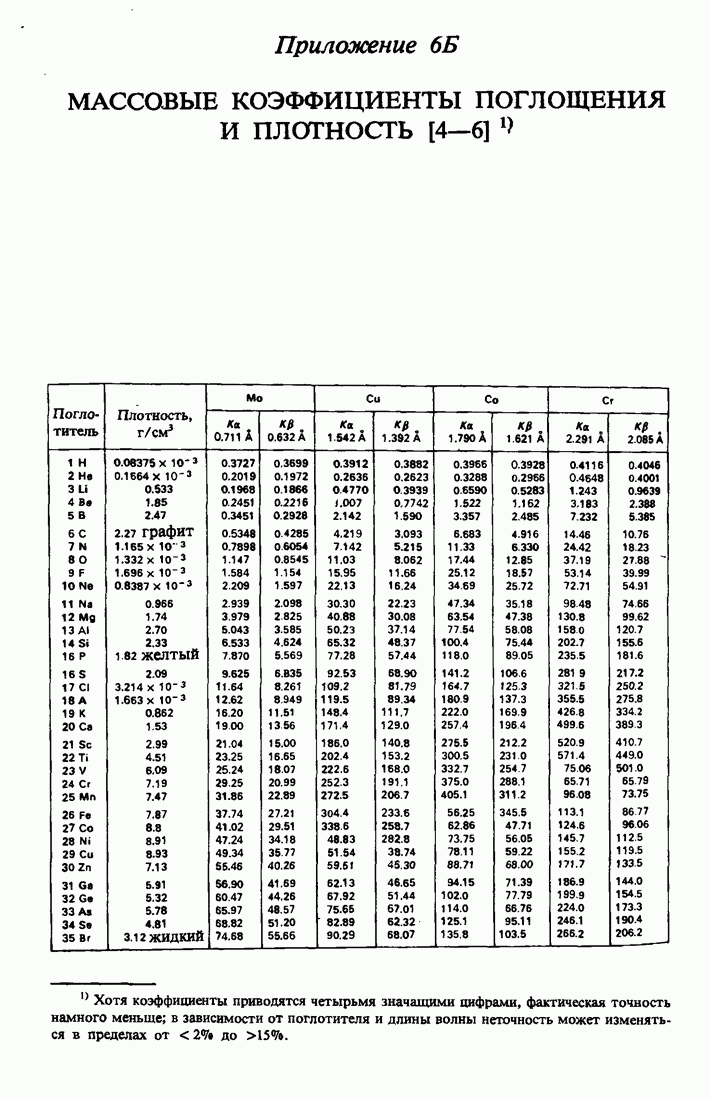
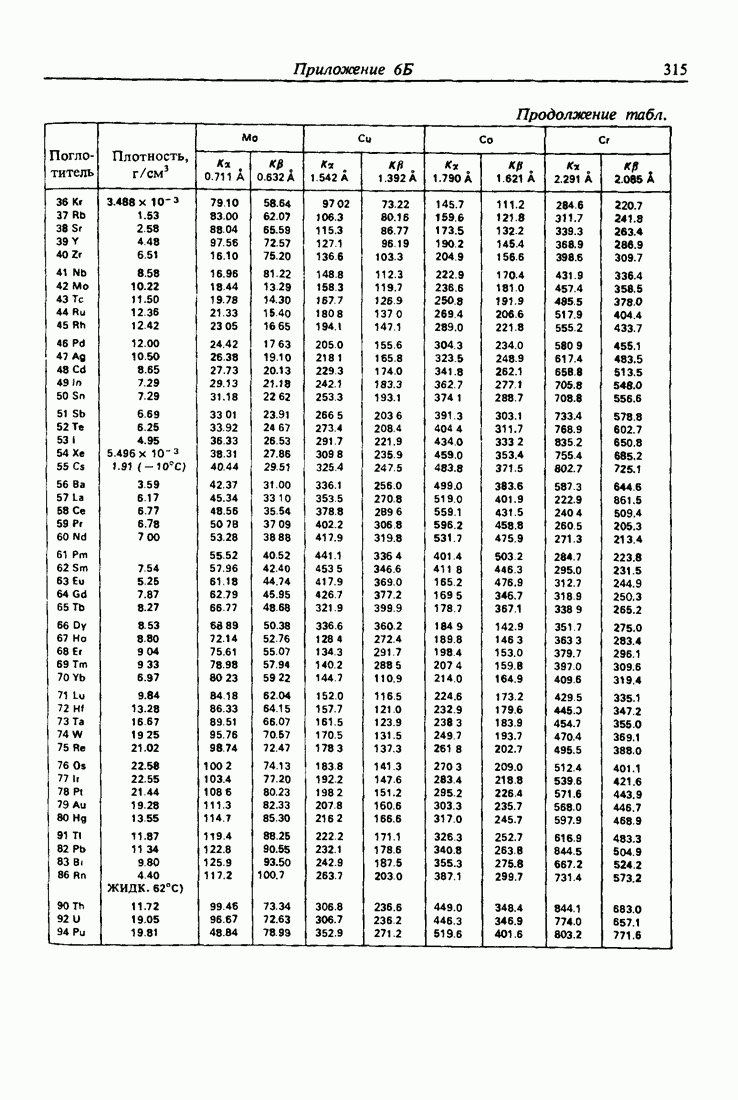
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
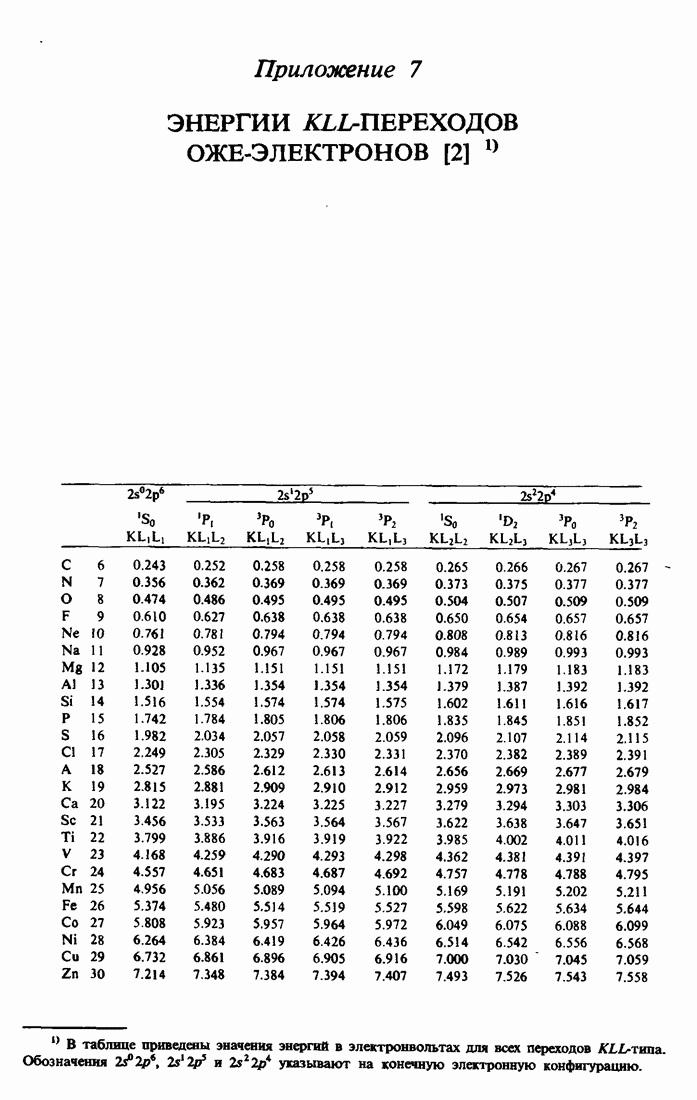
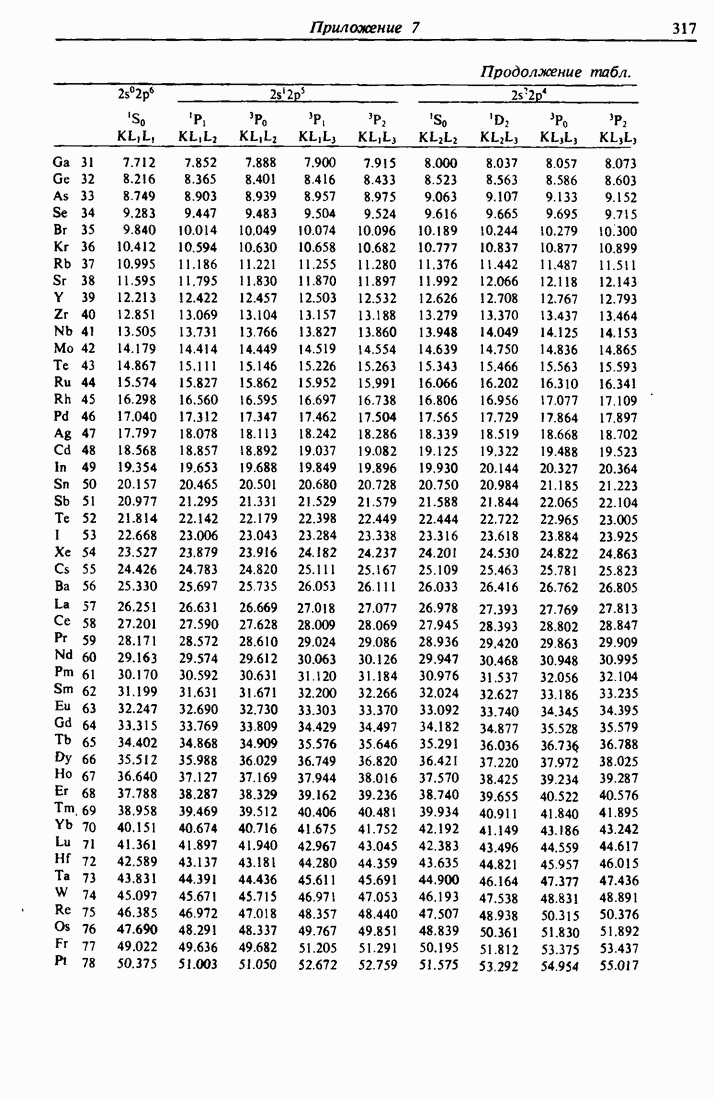
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
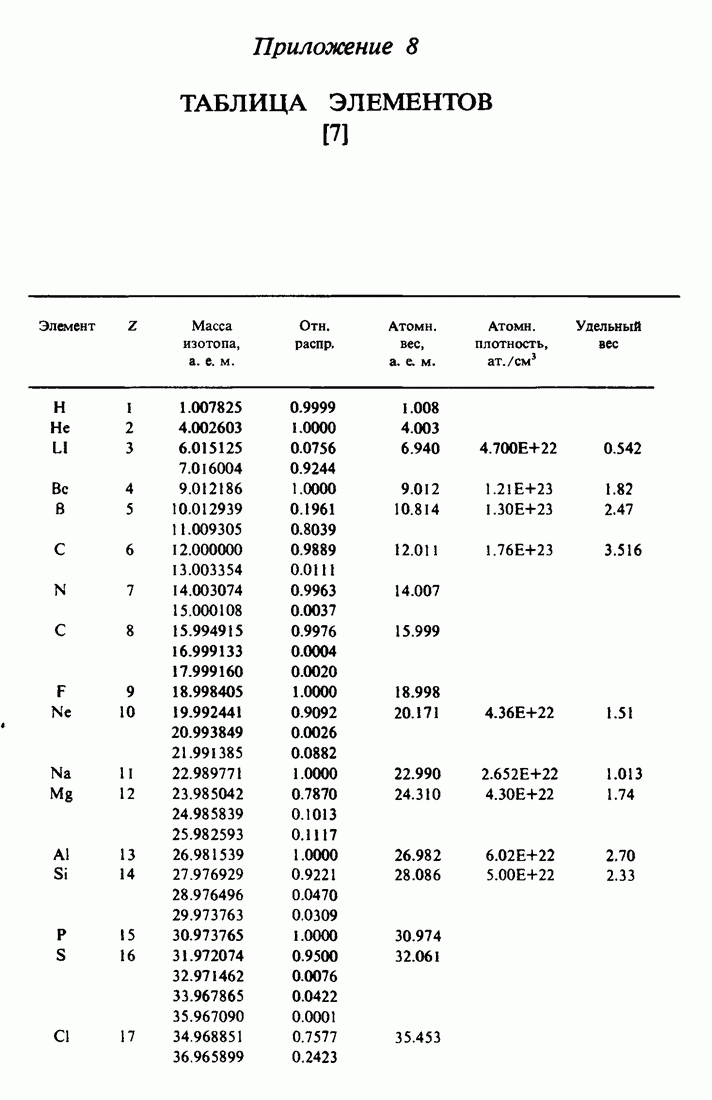
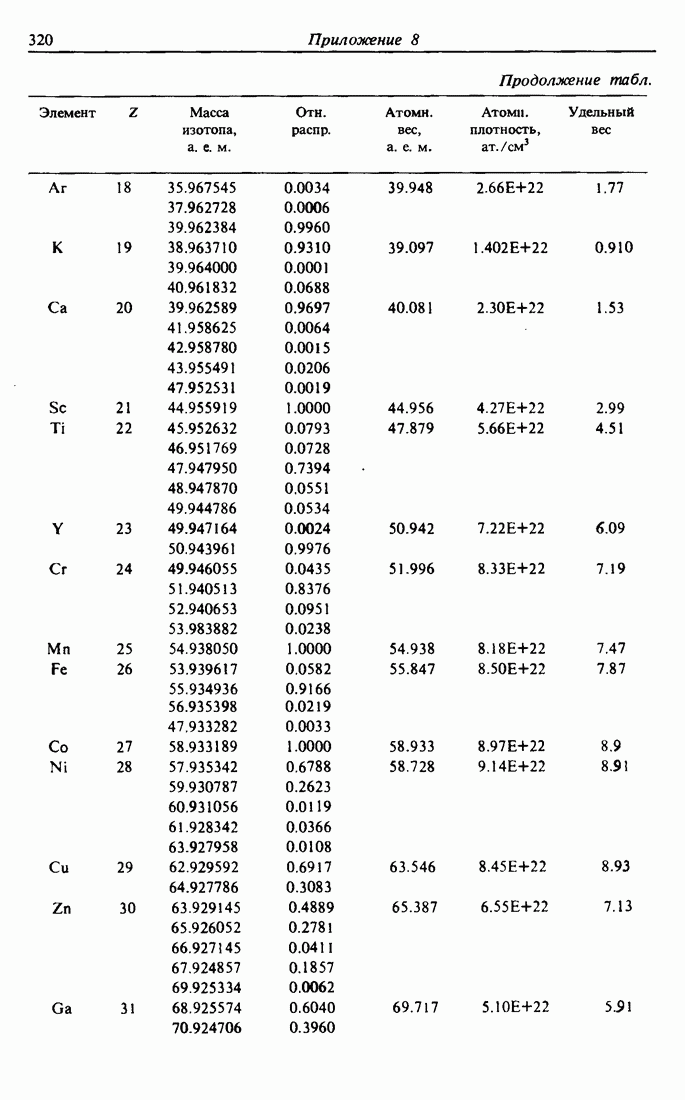
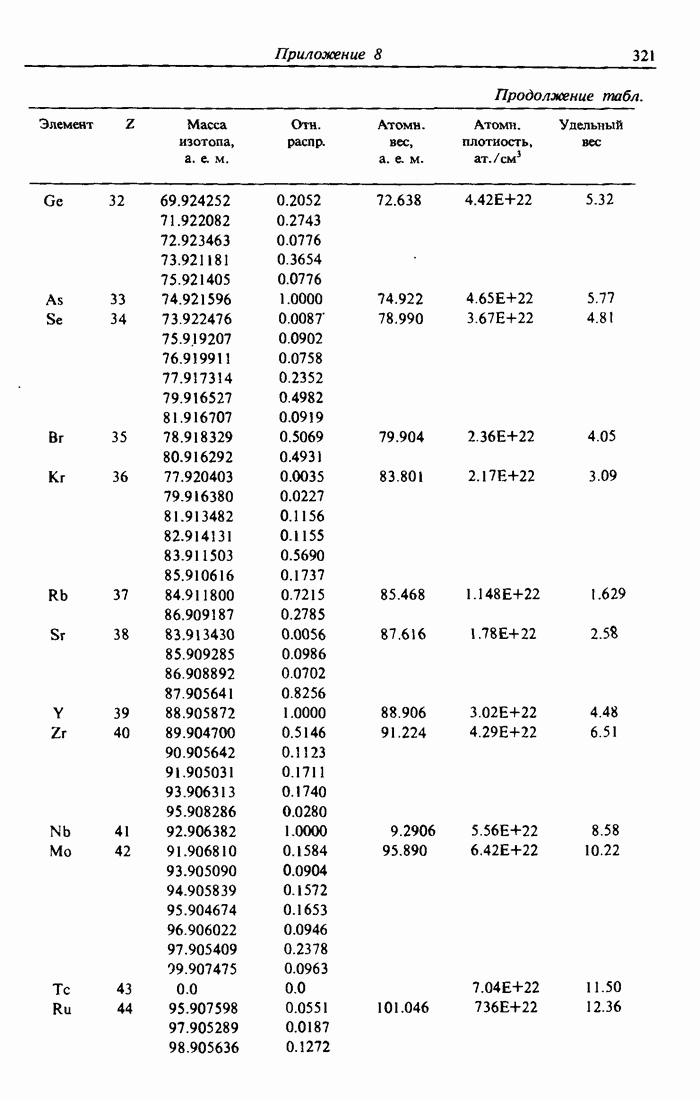
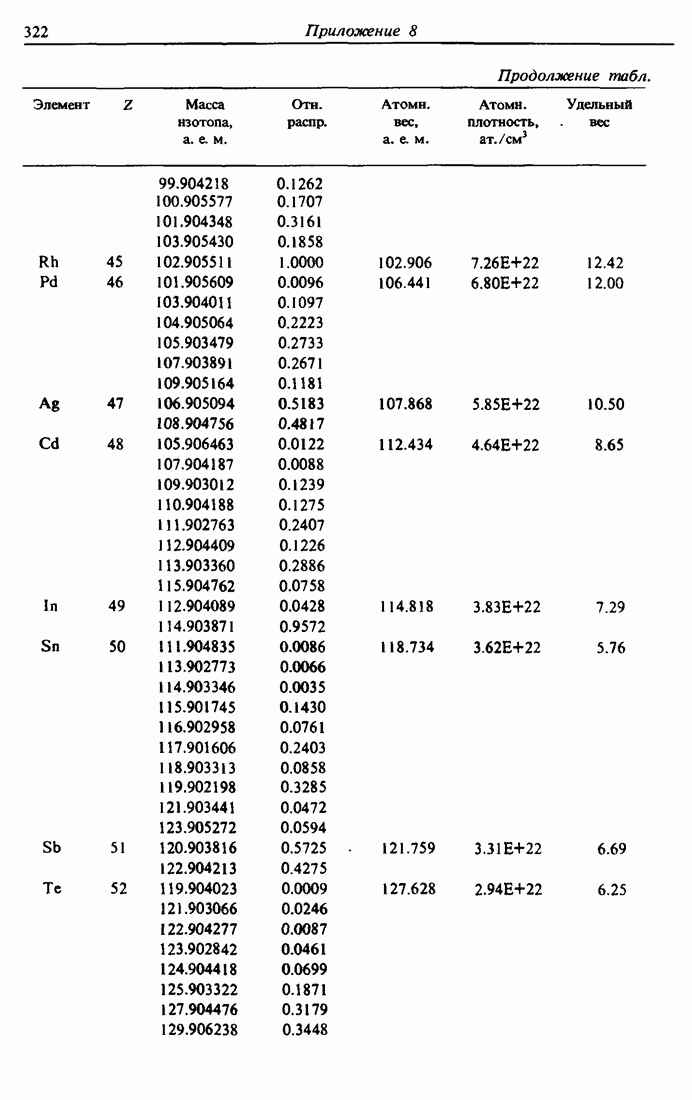
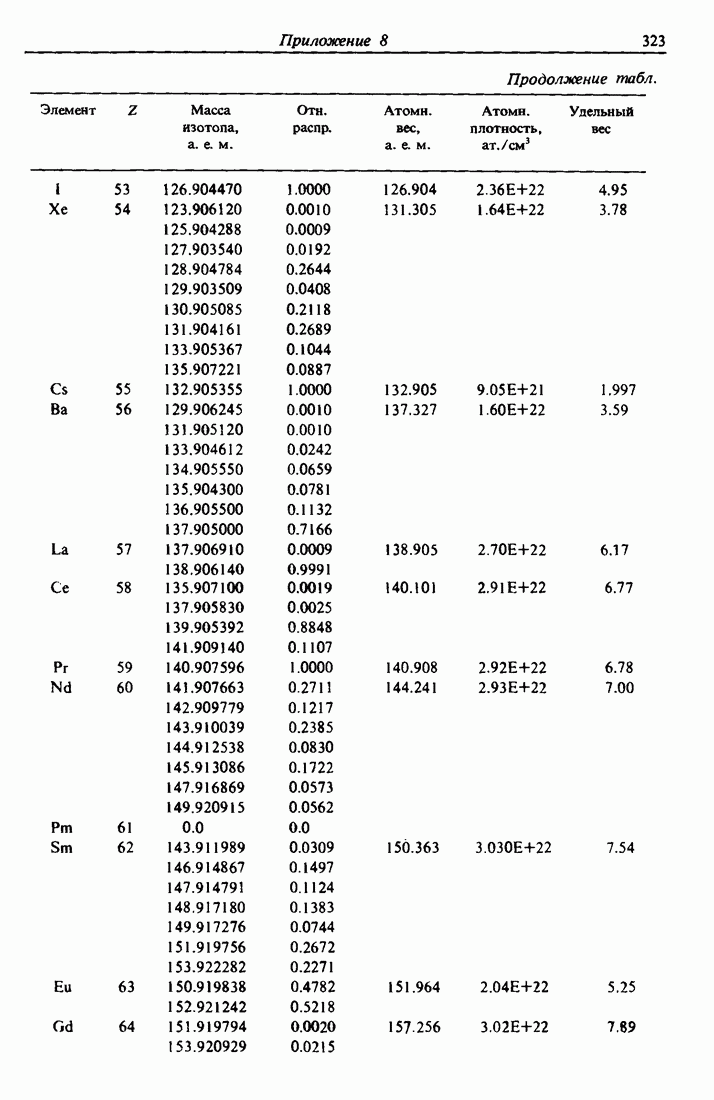
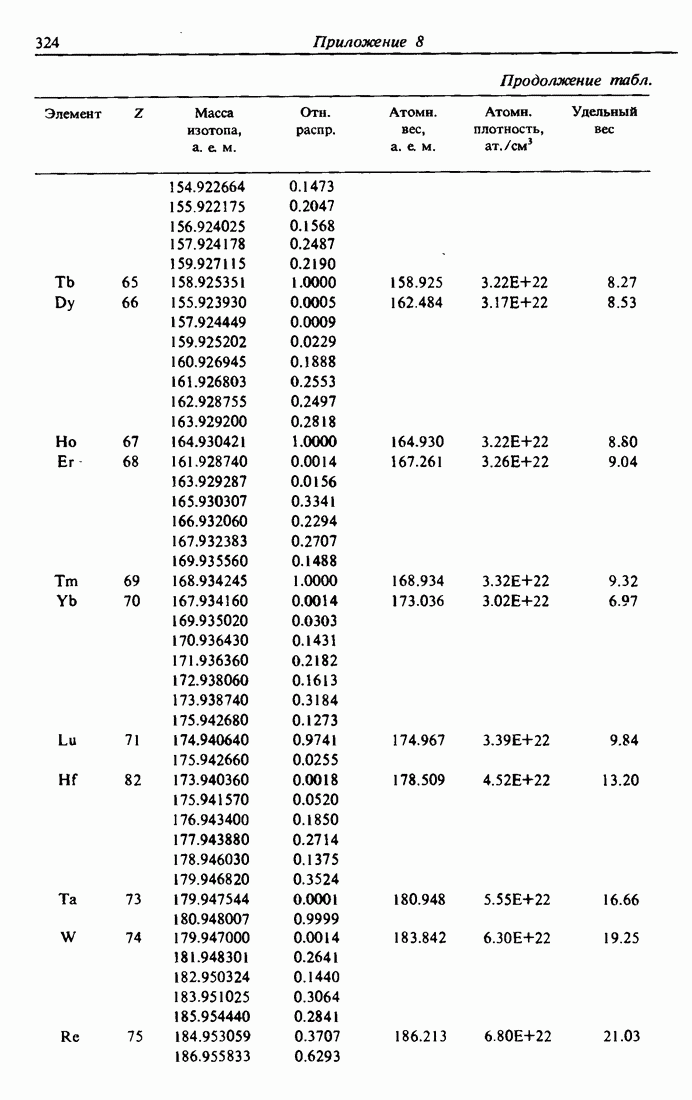
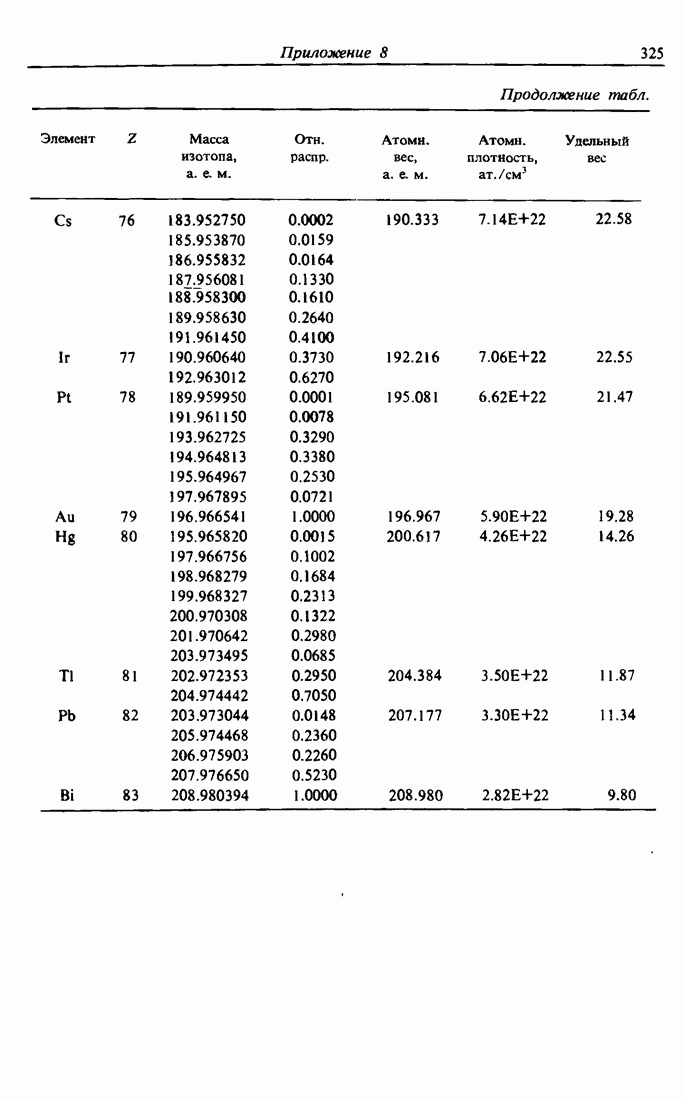
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
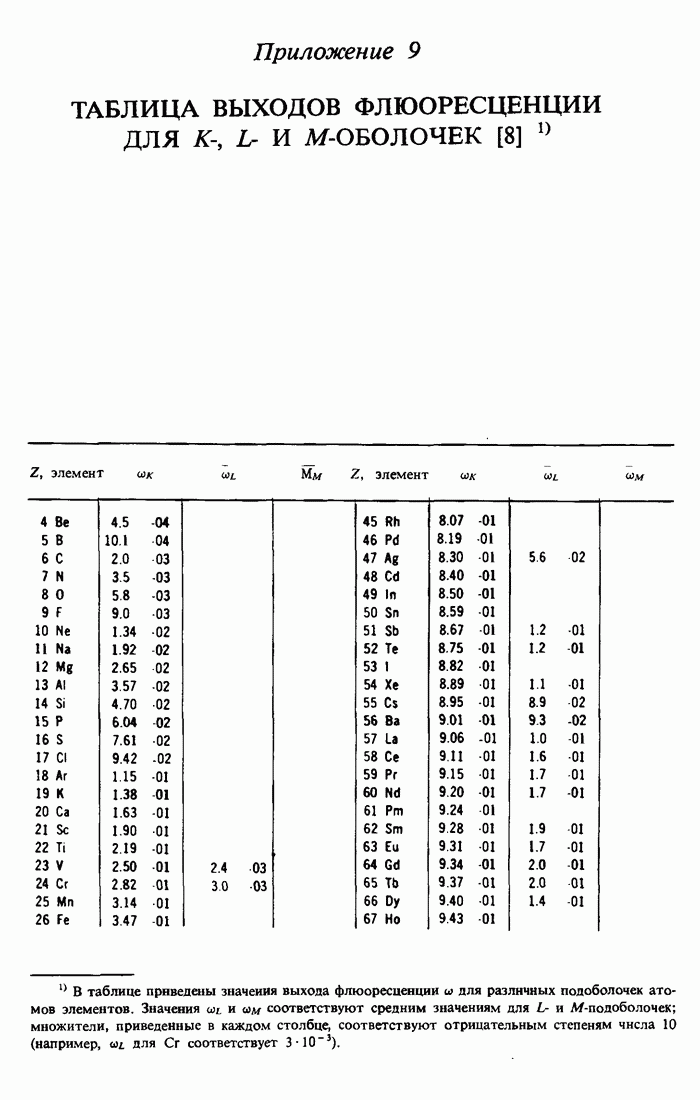
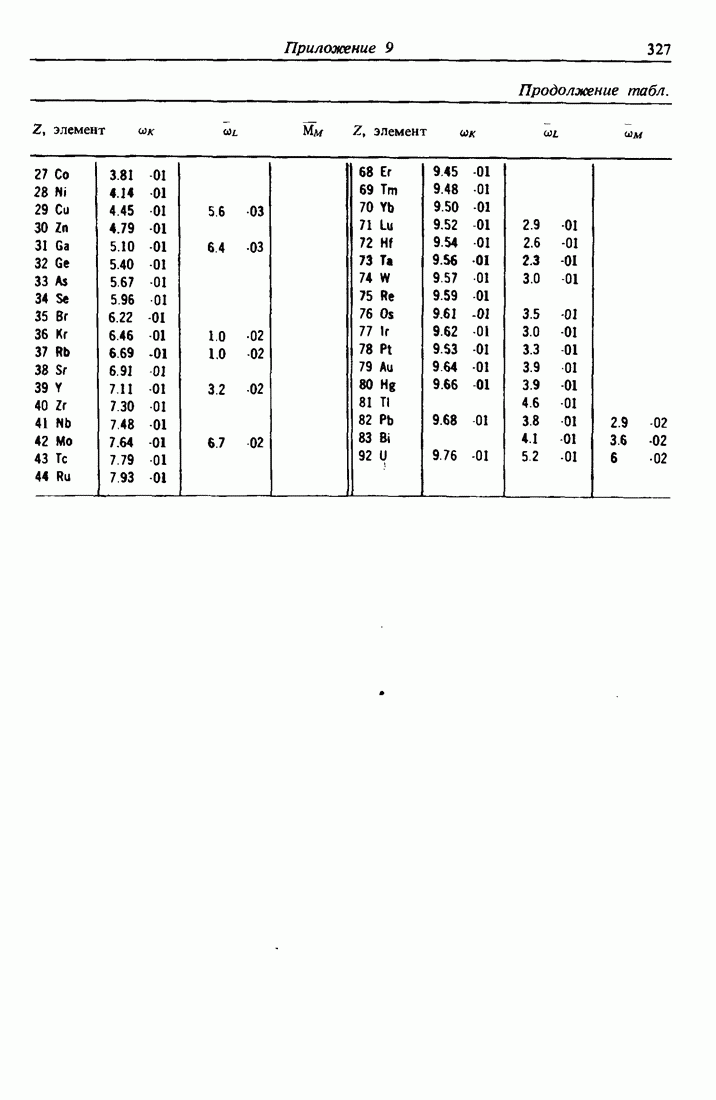
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ