| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.5. Дифракция рентгеновских лучей при скользящем падении
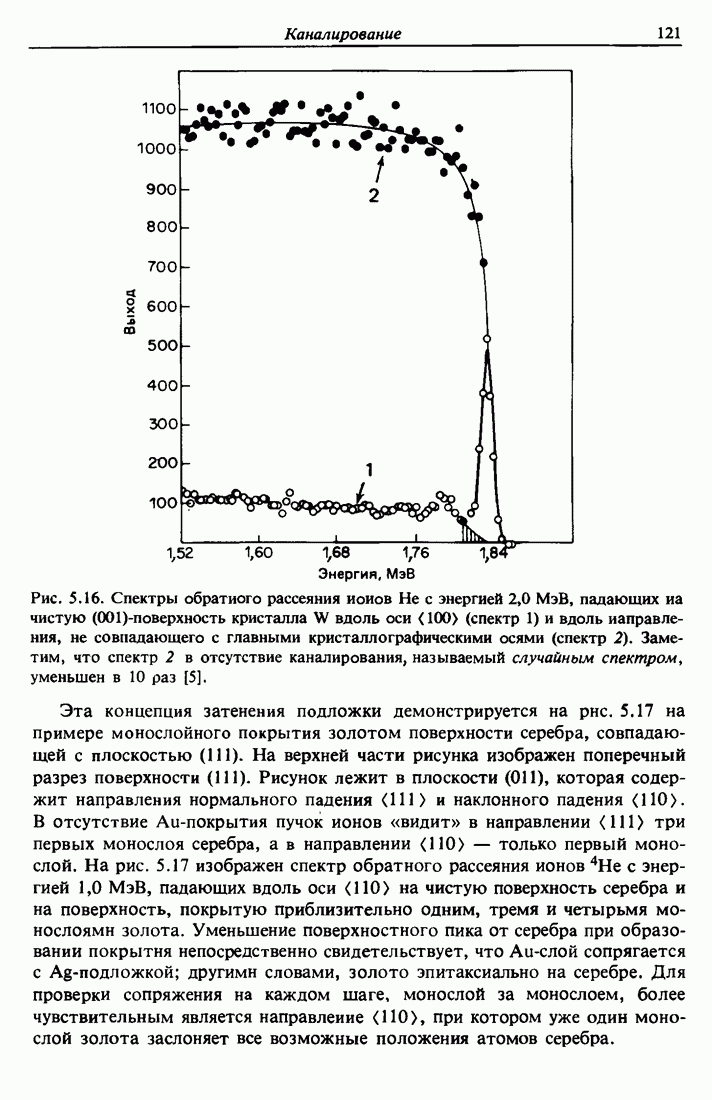
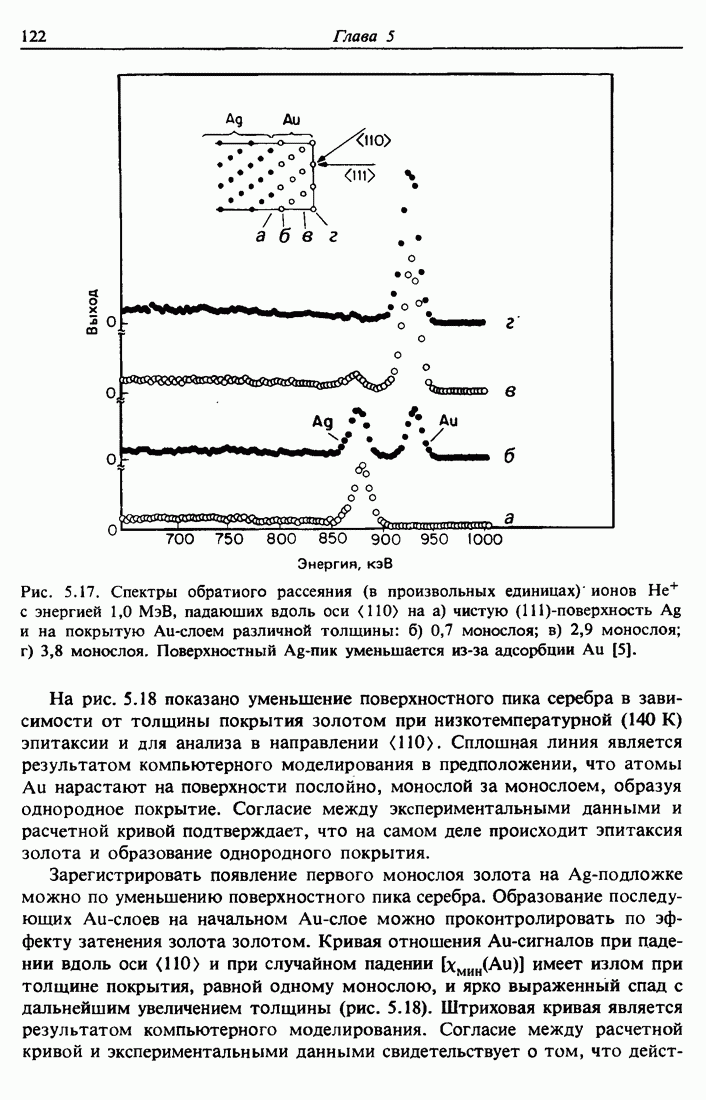
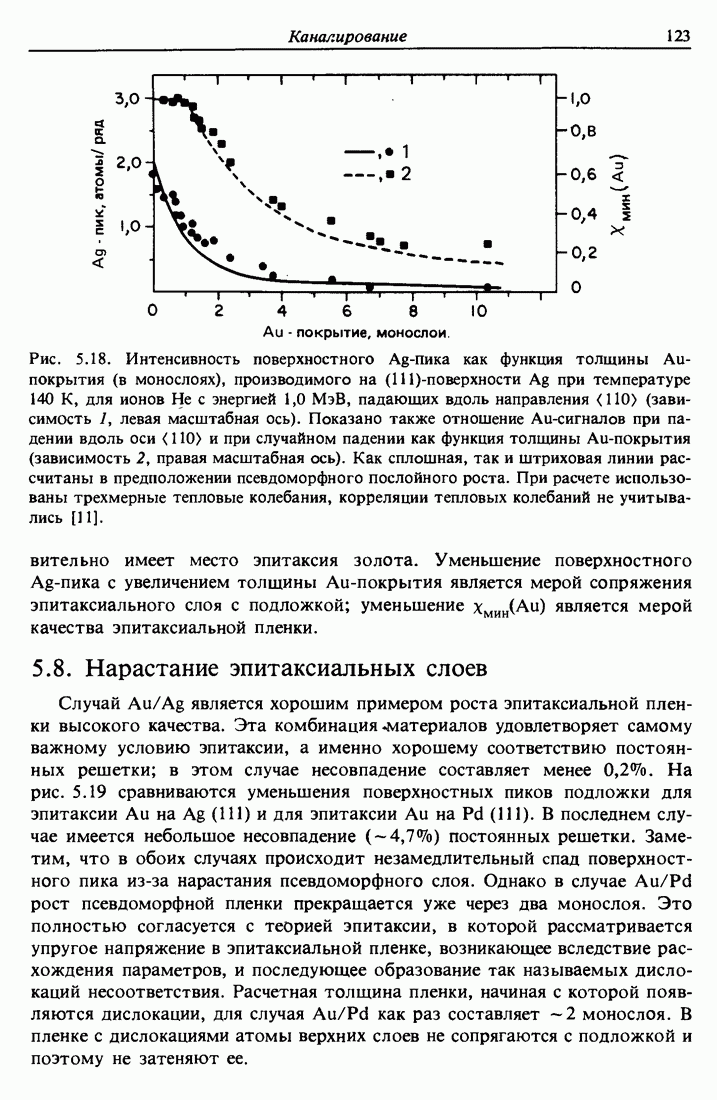
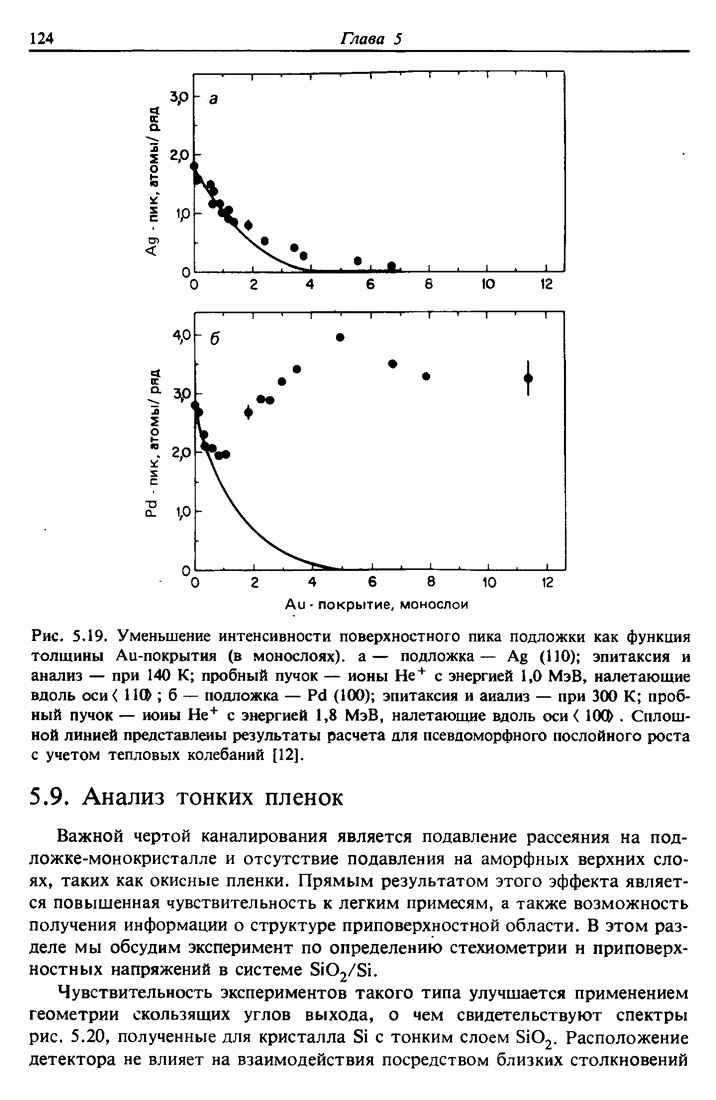
Анализ элементного состава тонких пленок часто производится дифракционными методами, позволяющими однозначно идентифицировать кристаллические фазы вблизи поверхности твердого тела. Дифракция рентгеновских лучей наиболее удобна для пленок толщиной свыше нескольких сотен ангстрем. Для уменьшения проникновения пучка в глубь вещества и увеличения контрастности дифракционной картины используется геометрия скользящего падения. Отдельные кристаллические фазы идентифицируются по характерным дифракционным картинам. Такие рентгеновские дифракционные картины содержат также информацию о распределении ориентации и размеров кристаллитов.
Рентгеновские методы обладают высоким угловым разрешением и позволяют получить более точные структурные данные по сравнению с дифракцией электронов. С другой стороны, в случае рентгеновских лучей интенсивности дифрагированных пучков могут быть значительно меньше, чем для электронов, что приводит к необходимости длительных экспозиций. Главное преимущество электронной дифракции состоит в возможности использования электронных микроскопов, позволяющих производить дифракционный анализ малых участков образца.
Теория дифракции рентгеновских лучей, основывается на уравнении Брэгга, которое описывает условие усиления рентгеновских лучей, рассеянных на атомных плоскостях кристалла, в результате их интерференции. Это условие усиления рассеяния в результате интерференции имеет вид

где  — длина волны падающего излучения.
— длина волны падающего излучения.
Чтобы дифракция имела место, величины в и А должны быть связаны между собой согласно закону Брэгга. Этому условию можно удовлетворить, меняя либо длину волны либо ориентацию монокристалла. В тонких пленках ориентации кристаллов распределены практически непрерывно. Дифракция возникает на тех кристаллитах, которые ориентированы под углом, удовлетворяющим условию Брэгга.
При анализе образцов тонких пленок (толщиной 200—1000  ) обычно используются рентгеновский дифрактометр Зеемана — Болина или камера Рида. Обе установки являются в своей основе рентгеновскими дифракционными устройствами скользящего падения с фиксированным углом скольжения. Использование малых углов скольжения позволяет исследовать относительно большие объемы даже в образцах тонких пленок. Например, при угле скольжения 6,4° длина траектории рентгеновских лучей в тонкой пленке почти в девять раз превышает толщину самой пленки.
) обычно используются рентгеновский дифрактометр Зеемана — Болина или камера Рида. Обе установки являются в своей основе рентгеновскими дифракционными устройствами скользящего падения с фиксированным углом скольжения. Использование малых углов скольжения позволяет исследовать относительно большие объемы даже в образцах тонких пленок. Например, при угле скольжения 6,4° длина траектории рентгеновских лучей в тонкой пленке почти в девять раз превышает толщину самой пленки.
Геометрии экспериментов на двух установках показаны на рис. 7.10. В обоих случаях рентгеновские дифракционные картины получаются с помощью монохроматического пучка (например,  -линии), падающего под углом 6—14° к поверхности исследуемого образца. В установке Зеемана — Болина пучок сфокусирован таким образом, что фокусы падающего и дифрагированного пучков лежат на границе дифракционного круга. Детектор перемещается по дифракционному кругу диаметром 50 см с шагом 0,15° (40) и с временем счета 30 с на каждом шаге. В камере Рида падающий пучок коллимируется посредством двух малых отверстий, а все дифракционные
-линии), падающего под углом 6—14° к поверхности исследуемого образца. В установке Зеемана — Болина пучок сфокусирован таким образом, что фокусы падающего и дифрагированного пучков лежат на границе дифракционного круга. Детектор перемещается по дифракционному кругу диаметром 50 см с шагом 0,15° (40) и с временем счета 30 с на каждом шаге. В камере Рида падающий пучок коллимируется посредством двух малых отверстий, а все дифракционные

Рис. 7.10. Схематическое изображение геометрии камеры Рида (а) и конфигурации Зеемана — Болина (б); 1 — образец; 2 — пучок рентгеновского излучения; 3 — коллиматор; 4 — дифрагированный пучок; 5 — фотопленка; 6 — ограничитель пучка; 7 — счетчик.

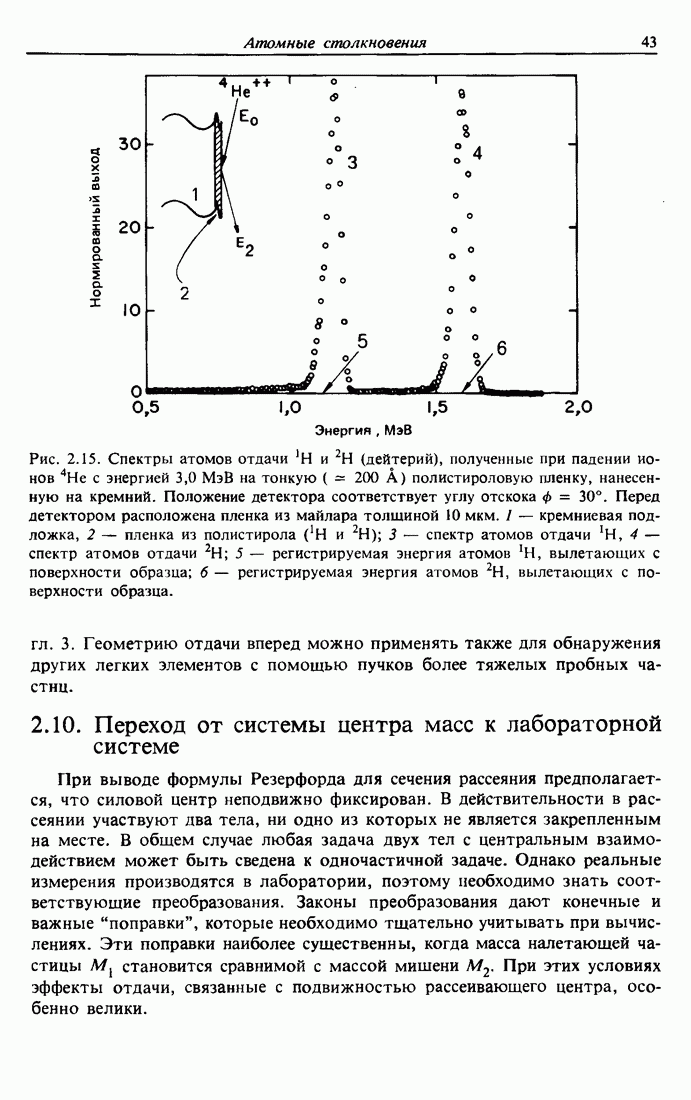
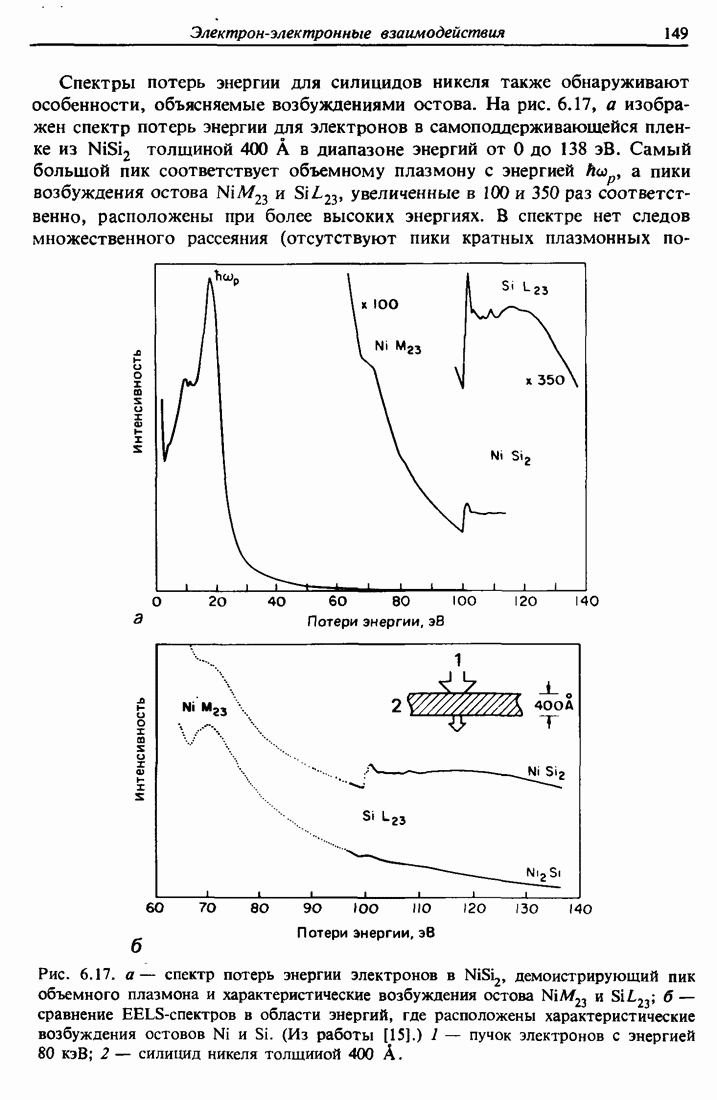
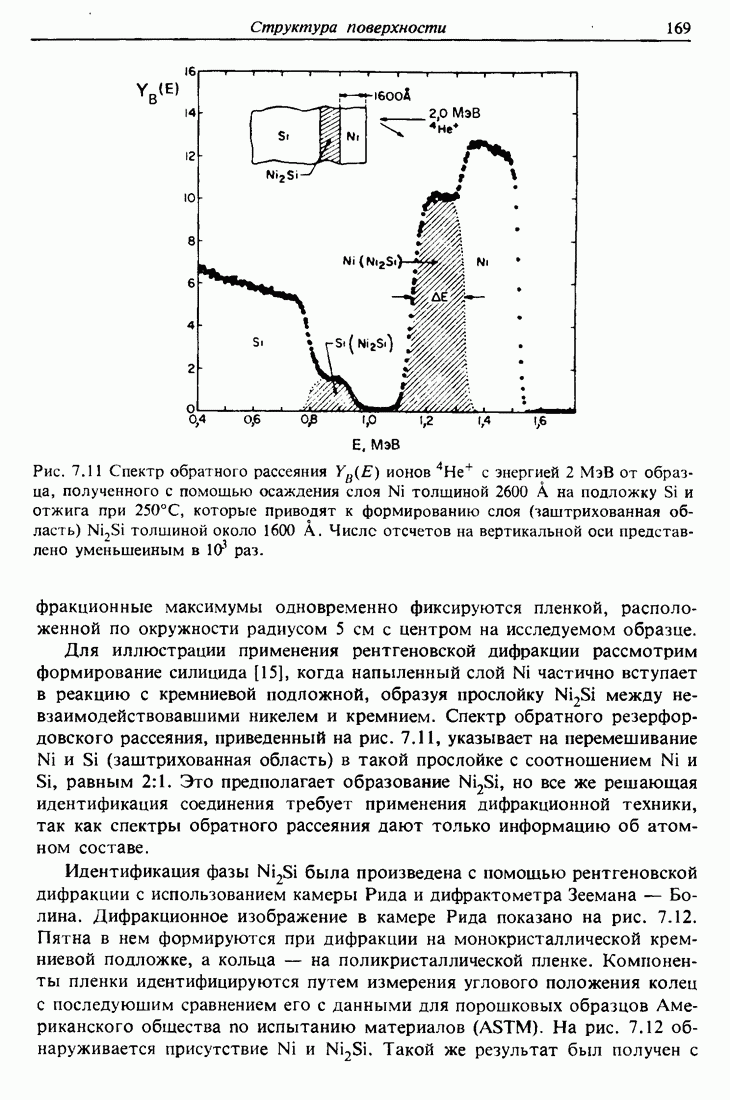
Рис. 7.11 Спектр обратного рассеяния  ионов
ионов  с энергией 2 МэВ от образца, полученного с помощью осаждения слоя
с энергией 2 МэВ от образца, полученного с помощью осаждения слоя  толщиной 2600 А на подложку
толщиной 2600 А на подложку  и отжига при 250°С, которые приводят к формированию слоя (заштрихованная область)
и отжига при 250°С, которые приводят к формированию слоя (заштрихованная область)  толщиной около 1600 А. Числе отсчетов на вертикальной оси представлено уменьшенным в
толщиной около 1600 А. Числе отсчетов на вертикальной оси представлено уменьшенным в  раз.
раз.
максимумы одновременно фиксируются пленкой, расположенной по окружности радиусом 5 см с центром на исследуемом образце.
Для иллюстрации применения рентгеновской дифракции рассмотрим формирование силицида [15], когда напыленный слой  частично вступает в реакцию с кремниевой подложной, образуя прослойку
частично вступает в реакцию с кремниевой подложной, образуя прослойку  между невзаимодействовавшими никелем и кремнием. Спектр обратного резерфордовского рассеяния, приведенный на рис. 7.11, указывает на перемешивание
между невзаимодействовавшими никелем и кремнием. Спектр обратного резерфордовского рассеяния, приведенный на рис. 7.11, указывает на перемешивание  (заштрихованная область) в такой прослойке с соотношением
(заштрихованная область) в такой прослойке с соотношением  равным 2:1. Это предполагает образование
равным 2:1. Это предполагает образование  , но все же решающая идентификация соединения требует применения дифракционной техники, так как спектры обратного рассеяния дают только информацию об атомном составе.
, но все же решающая идентификация соединения требует применения дифракционной техники, так как спектры обратного рассеяния дают только информацию об атомном составе.
Идентификация фазы  была произведена с помощью рентгеновской дифракции с использованием камеры Рида и дифрактометра Зеемана — Болина. Дифракционное изображение в камере Рида показано на рис. 7.12. Пятна в нем формируются при дифракции на монокристаллической кремниевой подложке, а кольца — на поликристаллической пленке. Компоненты пленки идентифицируются путем измерения углового положения колец с последующим сравнением его с данными для порошковых образцов Американского общества по испытанию материалов (ASTM). На рис. 7.12 обнаруживается присутствие
была произведена с помощью рентгеновской дифракции с использованием камеры Рида и дифрактометра Зеемана — Болина. Дифракционное изображение в камере Рида показано на рис. 7.12. Пятна в нем формируются при дифракции на монокристаллической кремниевой подложке, а кольца — на поликристаллической пленке. Компоненты пленки идентифицируются путем измерения углового положения колец с последующим сравнением его с данными для порошковых образцов Американского общества по испытанию материалов (ASTM). На рис. 7.12 обнаруживается присутствие  . Такой же результат был получен с
. Такой же результат был получен с

Рис. 7.12. Рентгеновская дифракционная картина в камере Рида, полученная для образца, показанного на рис. 7.11. Пятнистое изображение обусловлено кремниевой подложкой, а линии, отмеченные индексами, возникают за счет дифракции на  . Остальные линии соответствуют
. Остальные линии соответствуют  .
.
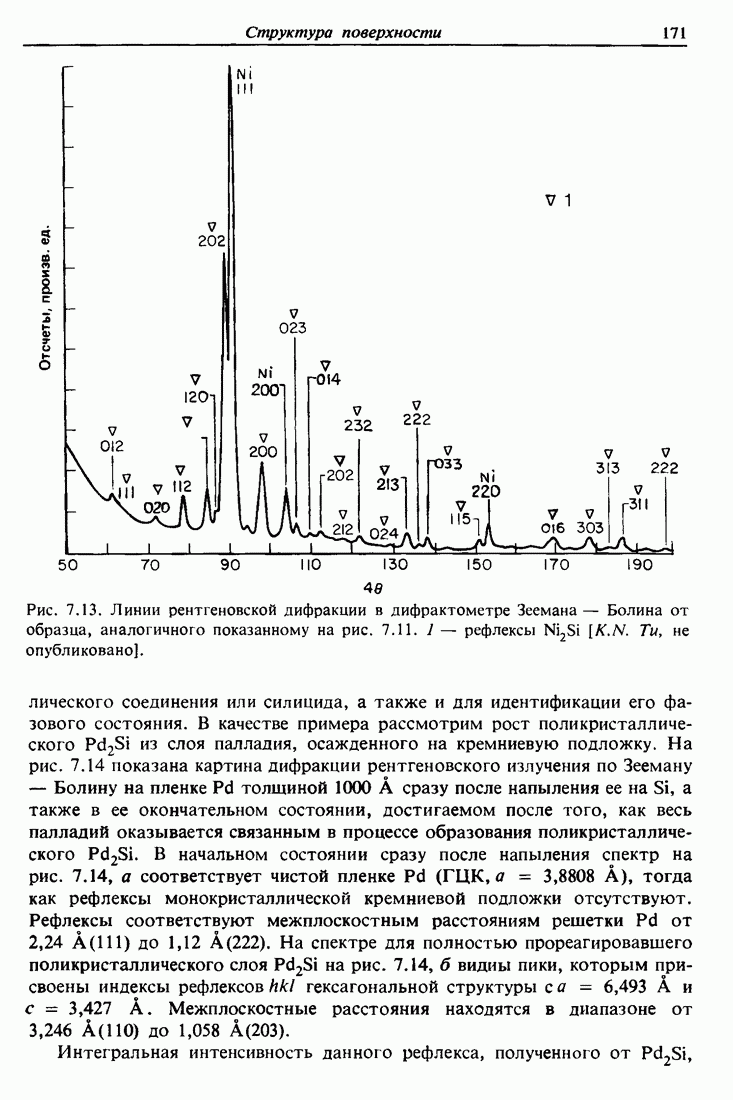
помощью методики Зеемана — Болина, как это видно из рис. 7.13. На этом рисунке интенсивность дифракции представлена в виде функции от 40. Эта дифракционная картина в принципе подобна сканированию вдоль плоскости экватора АВ на рис. 7.12. Рефлексы от монокристаллической кремниевой подложки (пятнистая структура на рис. 7.12) не видны. Это является следствием геометрии в дифрактометре Зеемана — Болина, который нечувствителен к брэгговским отражениям от монокристалла, так как фиксирован угол падения монохроматического излучения  . Следовательно, с помощью этой методики трудно исследовать два крайних случая — как монокристаллические эпитаксиальные слои, так и аморфные слои, дающие скорее широкие гало, чем узкие брэгговские рефлексы.
. Следовательно, с помощью этой методики трудно исследовать два крайних случая — как монокристаллические эпитаксиальные слои, так и аморфные слои, дающие скорее широкие гало, чем узкие брэгговские рефлексы.
В геометрии Зеемана — Болииа, где интенсивность дифракции зависит от угла 40 (рис. 7.13), вектор  на рис. 7.10 представляет собой вектор обратной решетки для плоскости
на рис. 7.10 представляет собой вектор обратной решетки для плоскости  для которой выполняется условие брэгговской дифракции. При фиксированном угле падения у разностный угол
для которой выполняется условие брэгговской дифракции. При фиксированном угле падения у разностный угол  между
между  и нормалью к поверхности n возрастает с ростом брэгговского угла. Направление
и нормалью к поверхности n возрастает с ростом брэгговского угла. Направление  по отношению к n меняется с каждым рефлексом
по отношению к n меняется с каждым рефлексом  таким образом, что каждый пик интенсивности на спектрограммах отраженных лучей дает величину параметра решетки в различных направлениях.
таким образом, что каждый пик интенсивности на спектрограммах отраженных лучей дает величину параметра решетки в различных направлениях.
Методика рентгеновской дифракции при скользящих углах может быть использована для определения толщины (16] выращиваемого иитерметаллического

Рис. 7.13. Линии рентгеновской дифракции в дифрактометре Зеемана—Болина от образца, аналогичного показанному на рис. 7.11. 1 — рефлексы  [K.N. Тu, не опубликовано].
[K.N. Тu, не опубликовано].
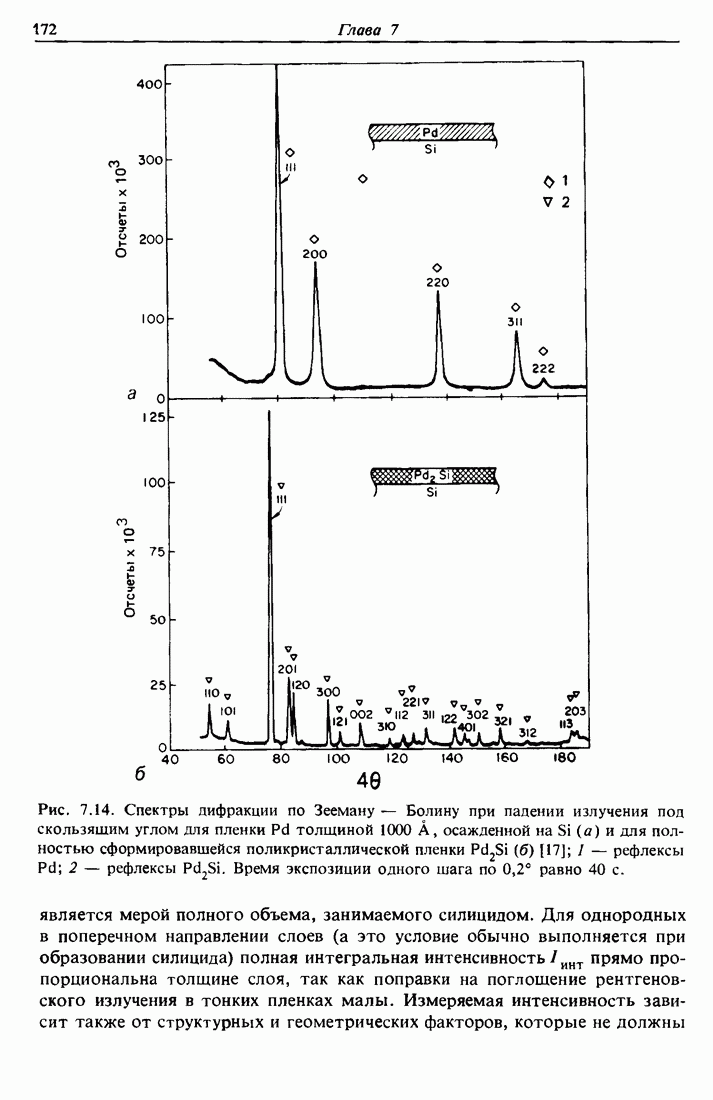
соединения или силицида, а также и для идентификации его фазового состояния. В качестве примера рассмотрим рост поликристаллического  из слоя палладия, осажденного на кремниевую подложку. На рис. 7.14 показана картина дифракции рентгеновского излучения по Зееману — Болину на пленке
из слоя палладия, осажденного на кремниевую подложку. На рис. 7.14 показана картина дифракции рентгеновского излучения по Зееману — Болину на пленке  толщиной 1000 А сразу после напыления ее на
толщиной 1000 А сразу после напыления ее на  , а также в ее окончательном состоянии, достигаемом после того, как весь палладий оказывается связанным в процессе образования поликристаллического
, а также в ее окончательном состоянии, достигаемом после того, как весь палладий оказывается связанным в процессе образования поликристаллического  . В начальном состоянии сразу после напыления спектр на рис. 7.14, а соответствует чистой пленке
. В начальном состоянии сразу после напыления спектр на рис. 7.14, а соответствует чистой пленке  , тогда как рефлексы монокристаллической кремниевой подложки отсутствуют. Рефлексы соответствуют межплоскостным расстояниям решетки
, тогда как рефлексы монокристаллической кремниевой подложки отсутствуют. Рефлексы соответствуют межплоскостным расстояниям решетки  от
от  до
до  . На спектре для полностью прореагировавшего поликристаллического слоя
. На спектре для полностью прореагировавшего поликристаллического слоя  на рис. 7.14, б видны пики, которым присвоены индексы рефлексов
на рис. 7.14, б видны пики, которым присвоены индексы рефлексов  гексагональной структуры с
гексагональной структуры с  . Межплоскостные расстояния находятся в диапазоне от
. Межплоскостные расстояния находятся в диапазоне от  до
до  .
.
Интегральная интенсивность данного рефлекса, полученного от  ,
,

Рис. 7.14. Спектры дифракции по Зееману — Болину при падении излучения под скользящим углом для пленки  толщиной 1000 А, осажденной на
толщиной 1000 А, осажденной на  (а) и для полностью сформировавшейся поликристаллической пленки
(а) и для полностью сформировавшейся поликристаллической пленки  — рефлексы Pd; 2 — рефлексы
— рефлексы Pd; 2 — рефлексы  . Время экспозиции одного шага по 0,2° равно 40 с.
. Время экспозиции одного шага по 0,2° равно 40 с.
является мерой полного объема, занимаемого силицидом. Для однородных в поперечном направлении слоев (а это условие обычно выполняется при образовании силицида) полная интегральная интенсивность  прямо пропорциональна толщине слоя, так как поправки на поглощение рентгеновского излучения в тонких пленках малы. Измеряемая интенсивность зависит также от структурных и геометрических факторов, которые не должны
прямо пропорциональна толщине слоя, так как поправки на поглощение рентгеновского излучения в тонких пленках малы. Измеряемая интенсивность зависит также от структурных и геометрических факторов, которые не должны

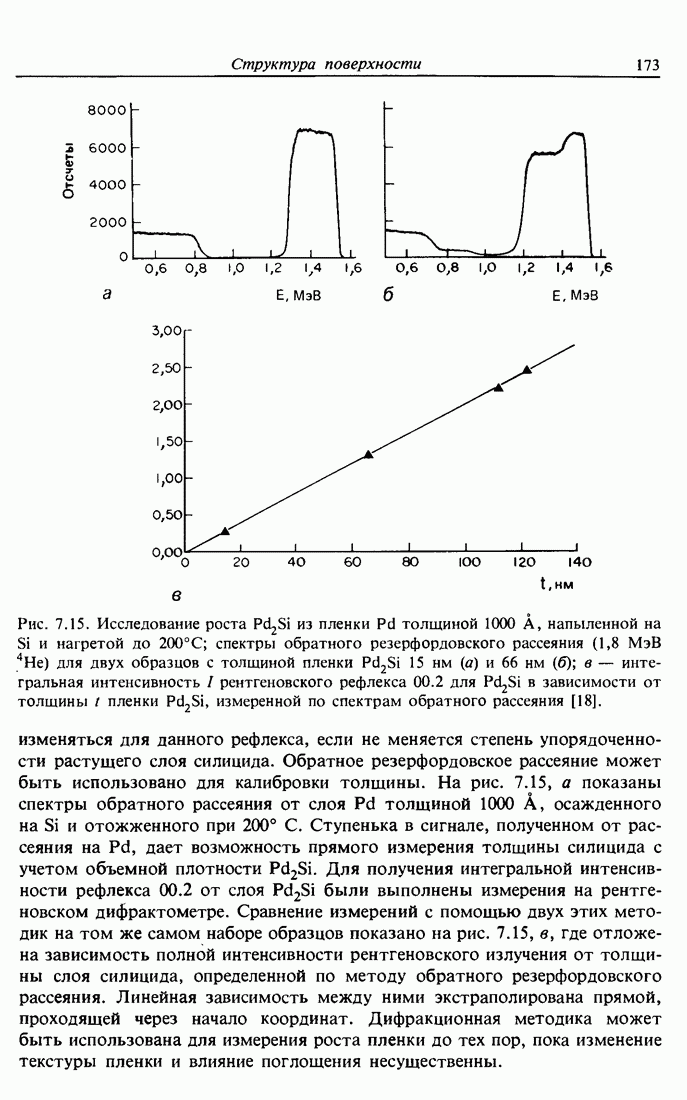
Рис. 7.15. Исследование роста  из пленки Pd толщиной 1000 А, напыленной на Si и нагретой до 200°С; спектры обратного резерфордовского рассеяния (1,8 МэВ
из пленки Pd толщиной 1000 А, напыленной на Si и нагретой до 200°С; спектры обратного резерфордовского рассеяния (1,8 МэВ  ) для двух образцов с толщиной пленки
) для двух образцов с толщиной пленки  15 нм (а) и 66 нм (б); в — интегральная интенсивность
15 нм (а) и 66 нм (б); в — интегральная интенсивность  рентгеновского рефлекса 00.2 для
рентгеновского рефлекса 00.2 для  в зависимости от толщины t пленки
в зависимости от толщины t пленки  , измеренной по спектрам обратного рассеяния [18].
, измеренной по спектрам обратного рассеяния [18].
изменяться для данного рефлекса, если не меняется степень упорядоченности растущего слоя силицида. Обратное резерфордовское рассеяние может быть использовано для калибровки толщины. На рис. 7.15, а показаны спектры обратного рассеяния от слоя  толщиной 1000 А, осажденного на
толщиной 1000 А, осажденного на  и отожженного при 200° С. Ступенька в сигнале, полученном от рассеяния на Pd, дает возможность прямого измерения толщины силицида с учетом объемной плотности
и отожженного при 200° С. Ступенька в сигнале, полученном от рассеяния на Pd, дает возможность прямого измерения толщины силицида с учетом объемной плотности  . Для получения интегральной интенсивности рефлекса 00.2 от слоя
. Для получения интегральной интенсивности рефлекса 00.2 от слоя  были выполнены измерения на рентгеновском дифрактометре. Сравнение измерений с помощью двух этих методик на том же самом наборе образцов показано на рис. 7.15, в, где отложена зависимость полной интенсивности рентгеновского излучения от толщины слоя силицида, определенной по методу обратного резерфордовского рассеяния. Линейная зависимость между ними экстраполирована прямой, проходящей через начало координат. Дифракционная методика может быть использована для измерения роста пленки до тех пор, пока изменение текстуры пленки и влияние поглощения несущественны.
были выполнены измерения на рентгеновском дифрактометре. Сравнение измерений с помощью двух этих методик на том же самом наборе образцов показано на рис. 7.15, в, где отложена зависимость полной интенсивности рентгеновского излучения от толщины слоя силицида, определенной по методу обратного резерфордовского рассеяния. Линейная зависимость между ними экстраполирована прямой, проходящей через начало координат. Дифракционная методика может быть использована для измерения роста пленки до тех пор, пока изменение текстуры пленки и влияние поглощения несущественны.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
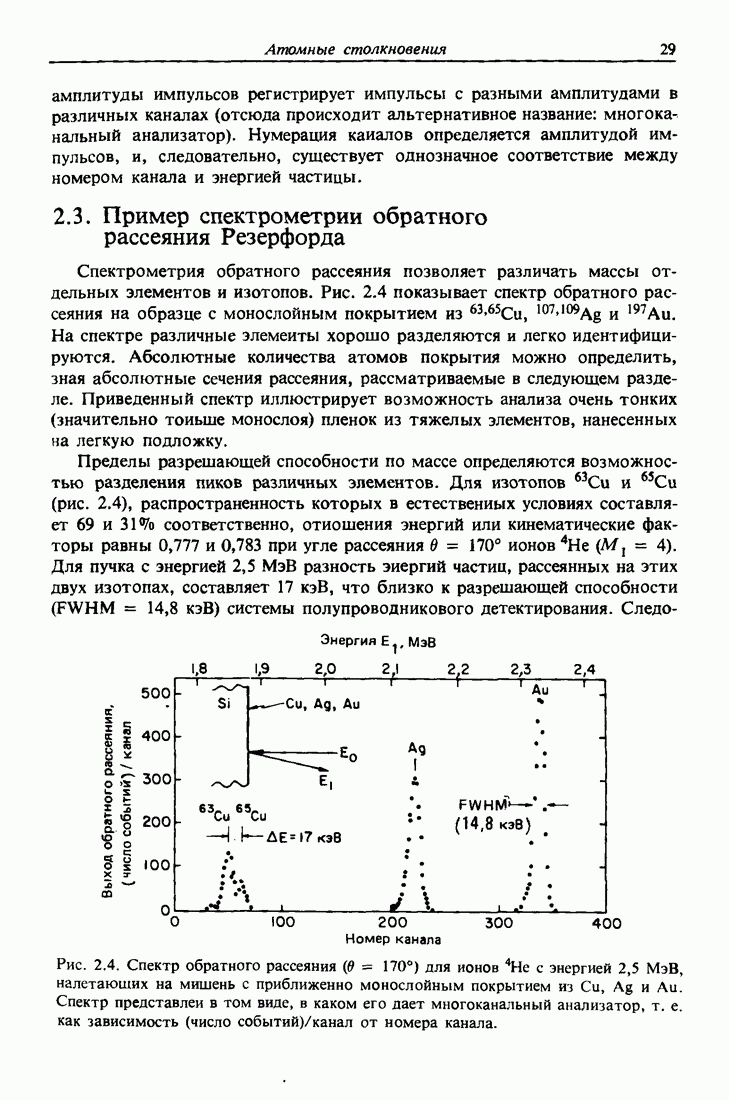
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
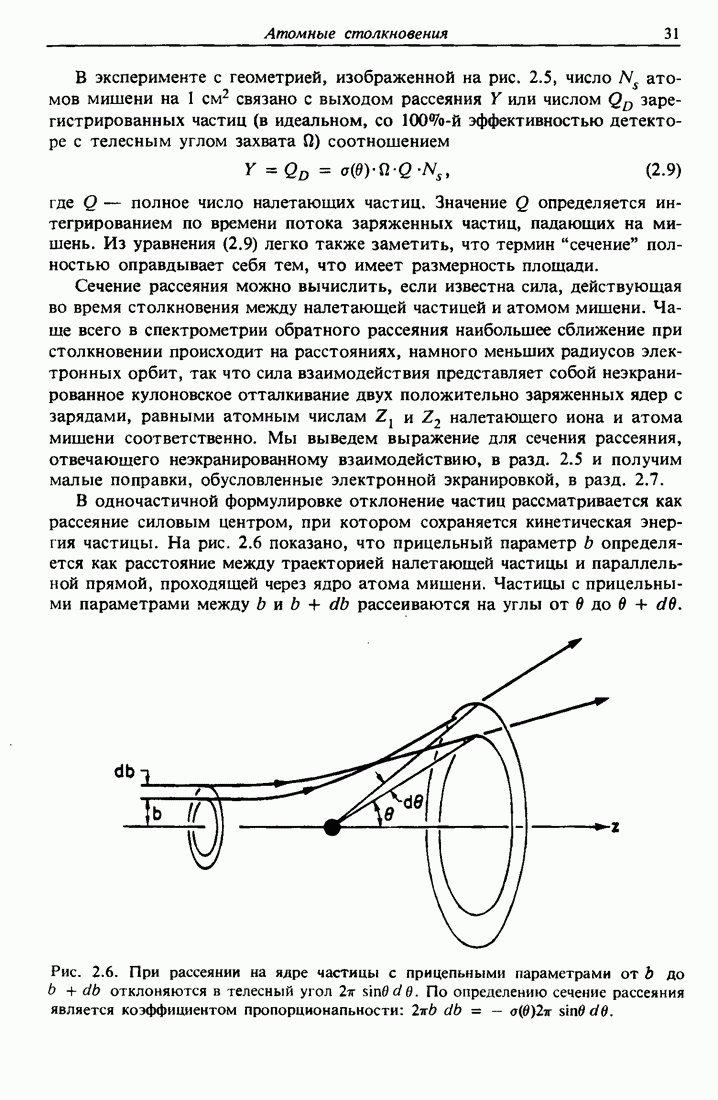
- 2.4. Сечение рассеяния и прицельный параметр
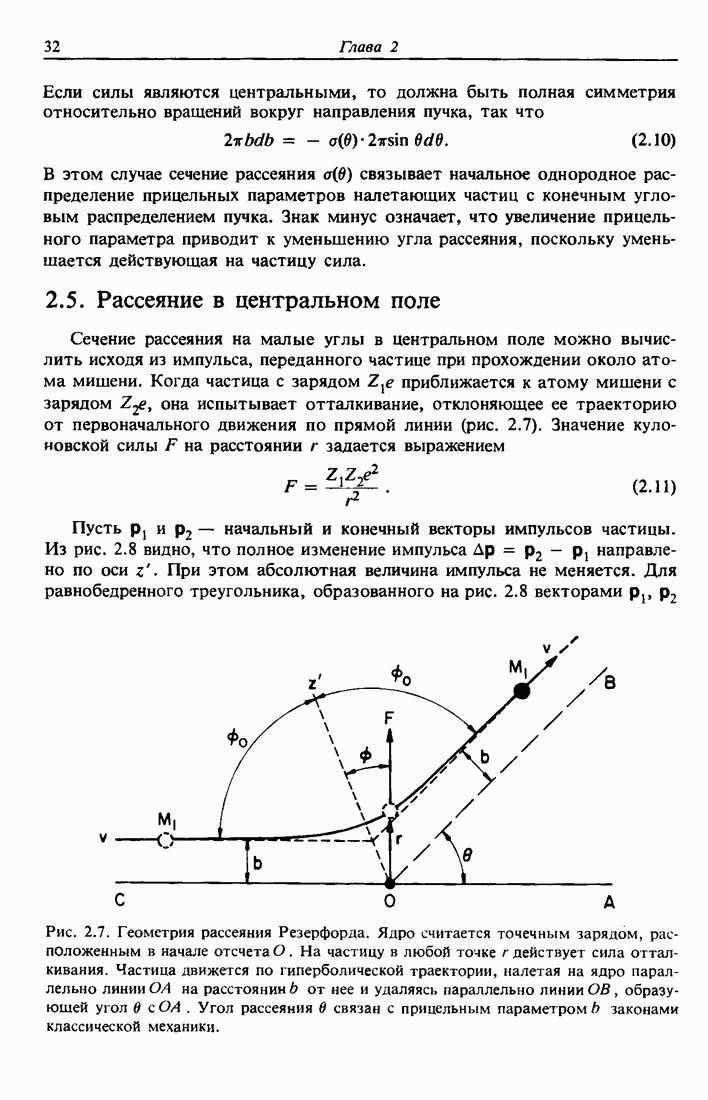
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
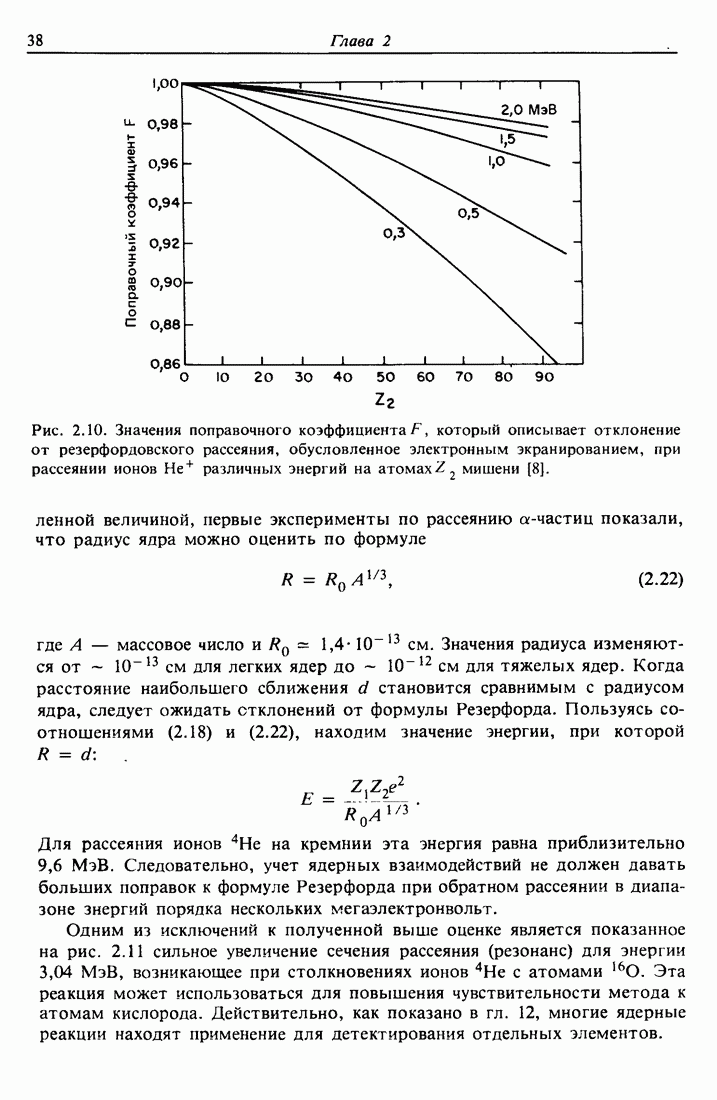
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
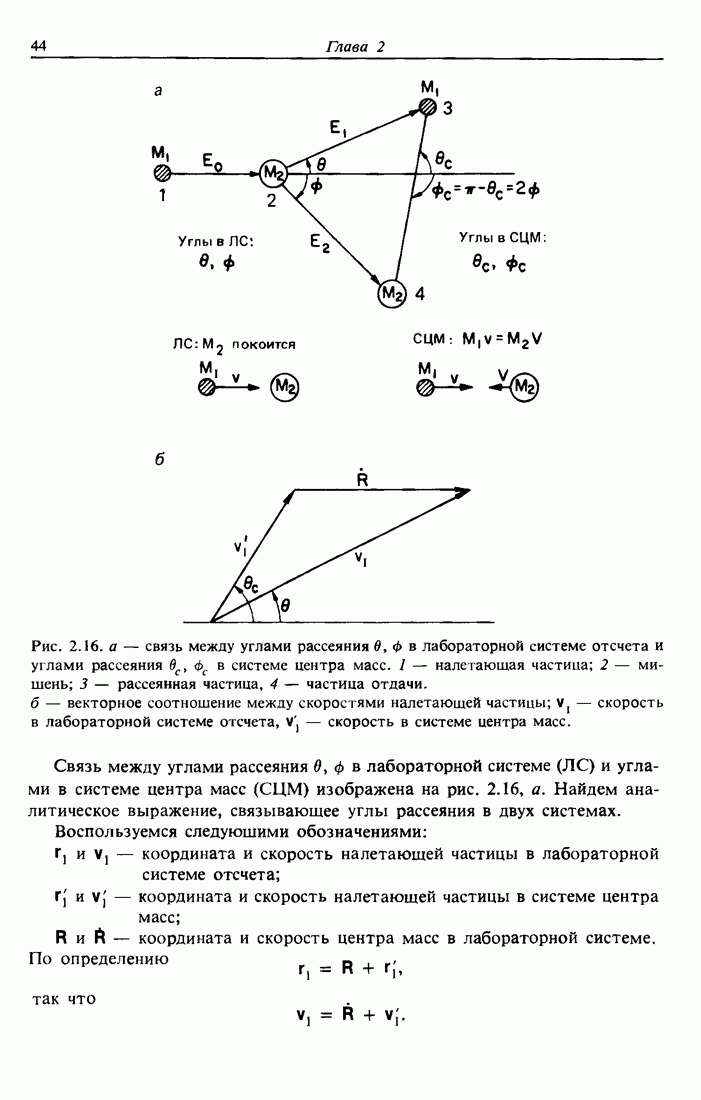
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
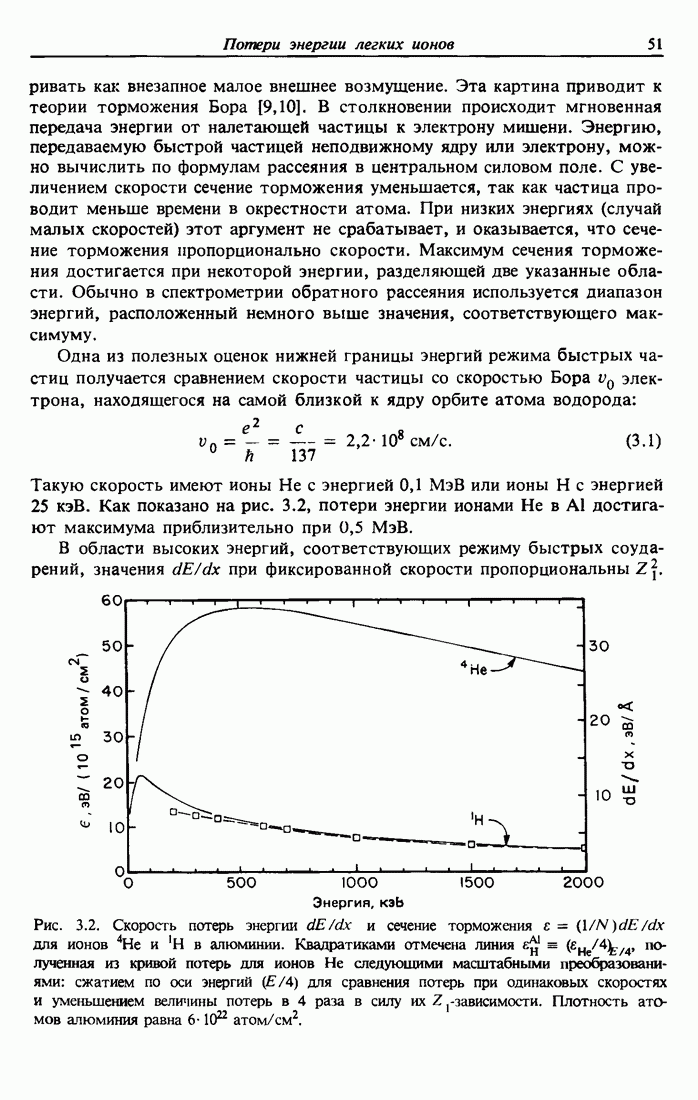
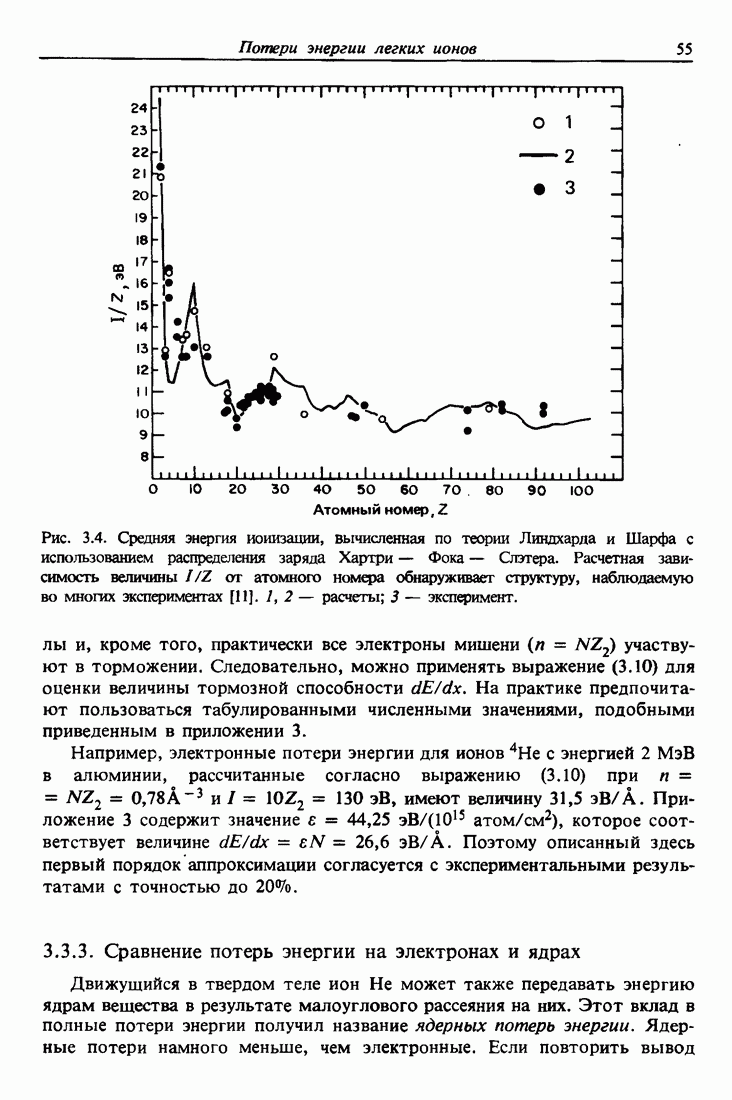
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
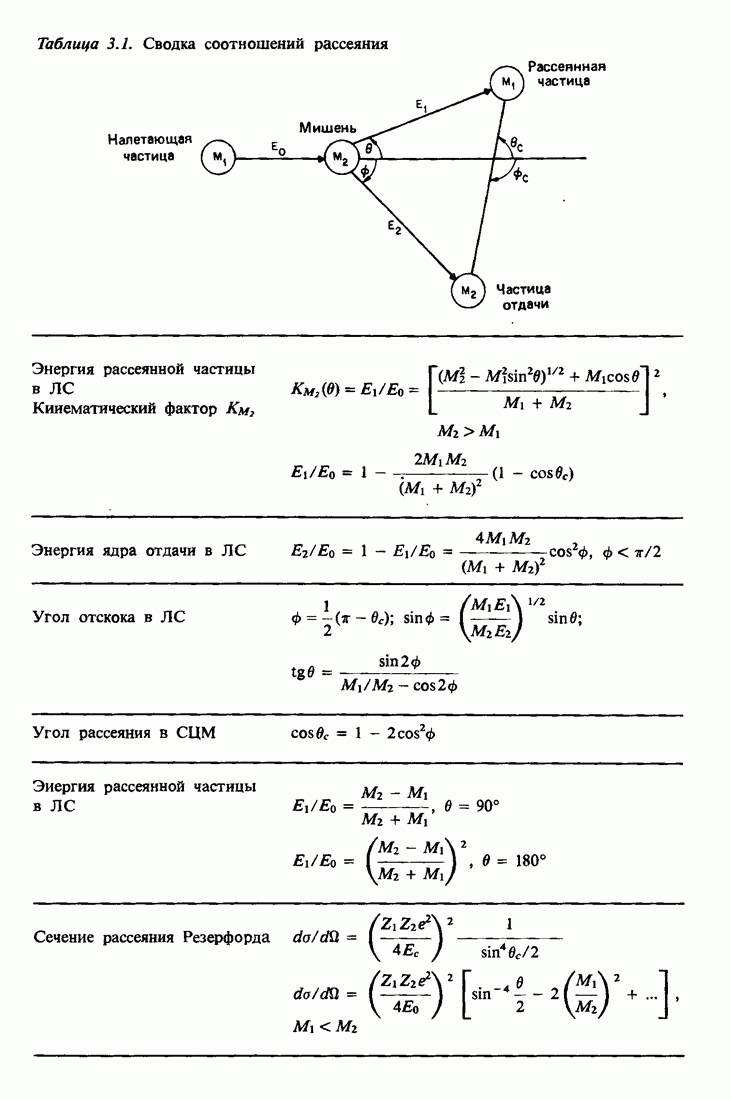
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
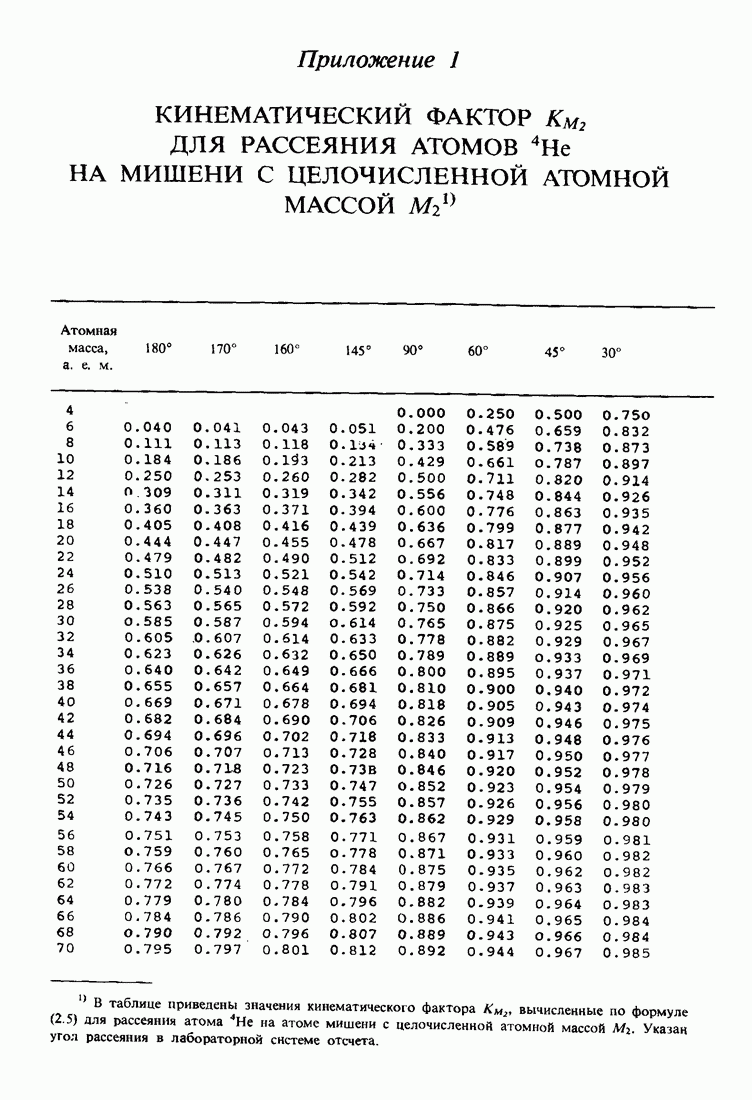
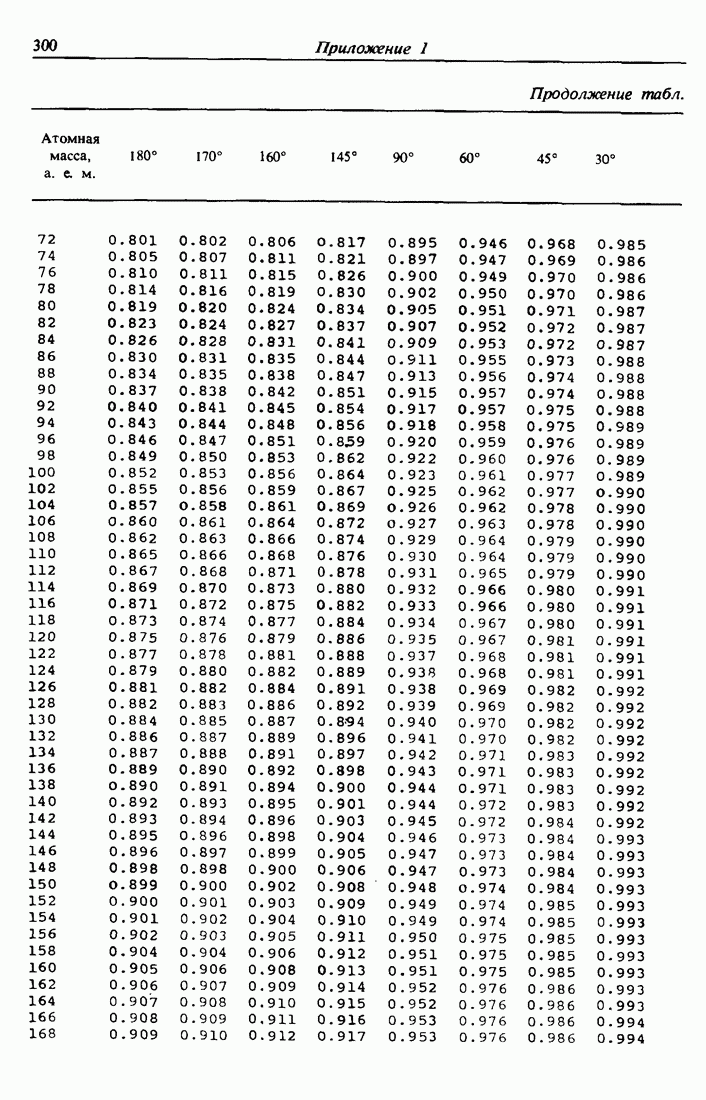
- ПРИЛОЖЕНИЕ 1.
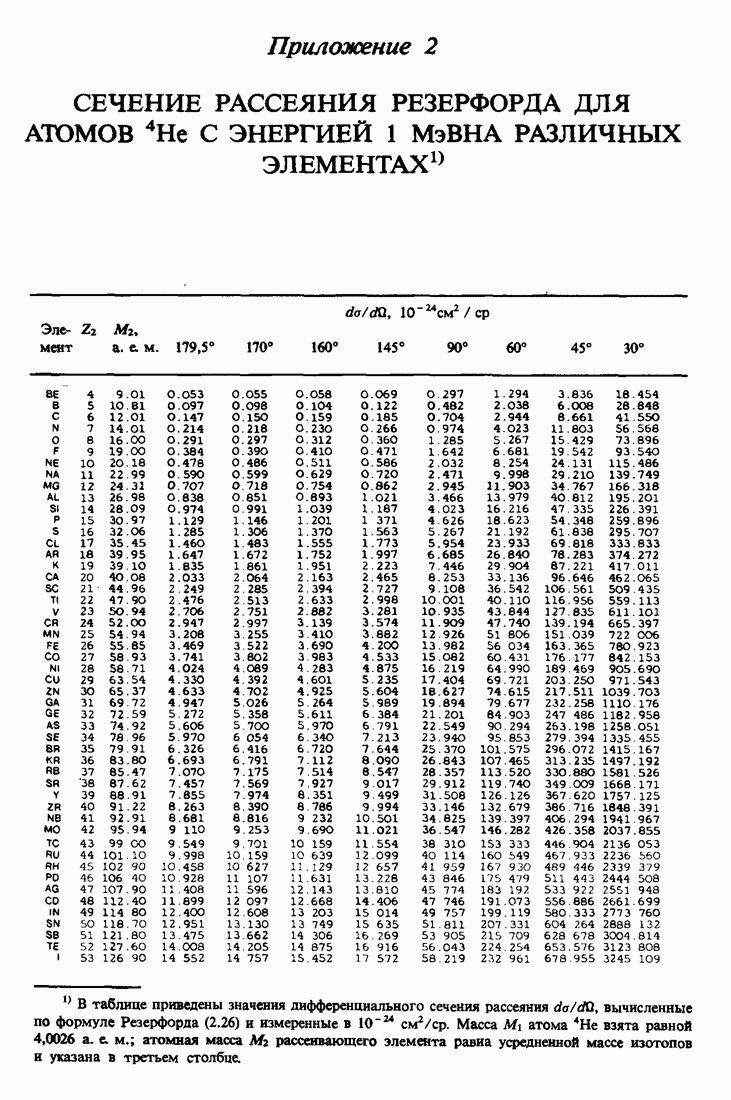
- ПРИЛОЖЕНИЕ 2.
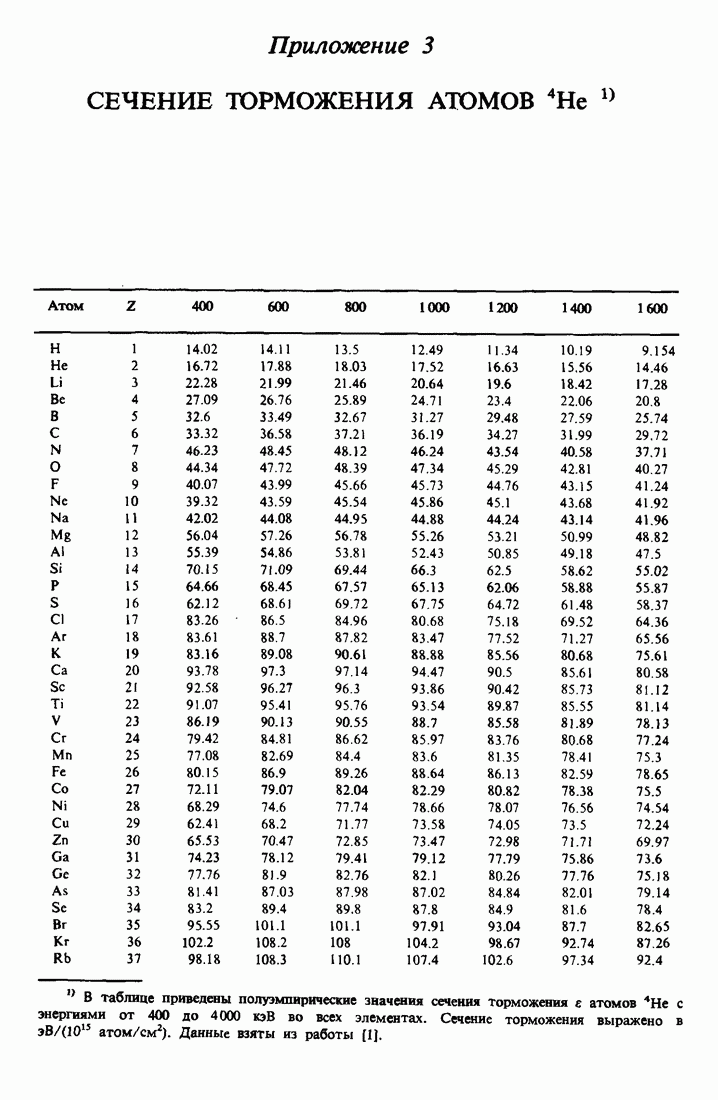
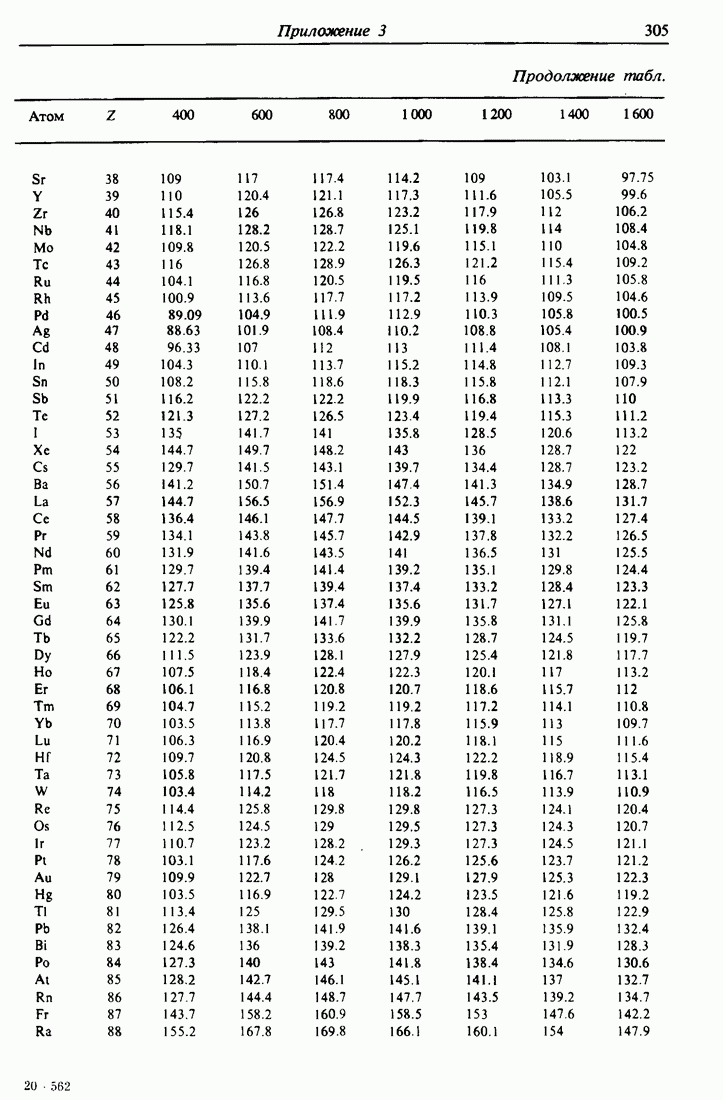
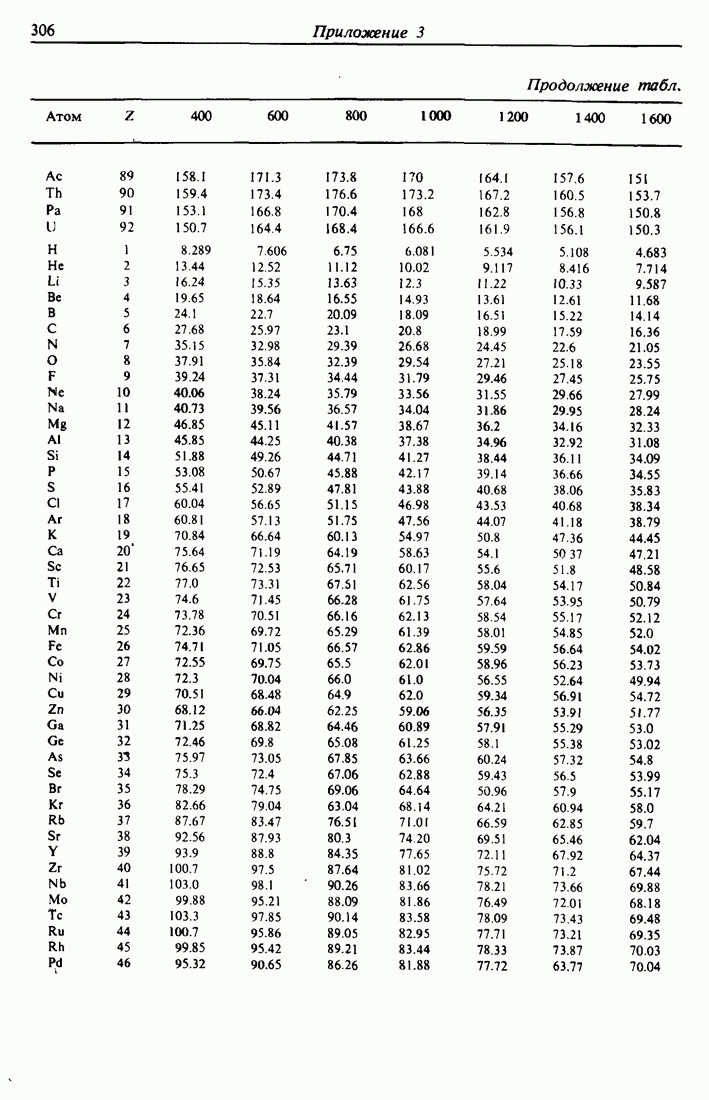
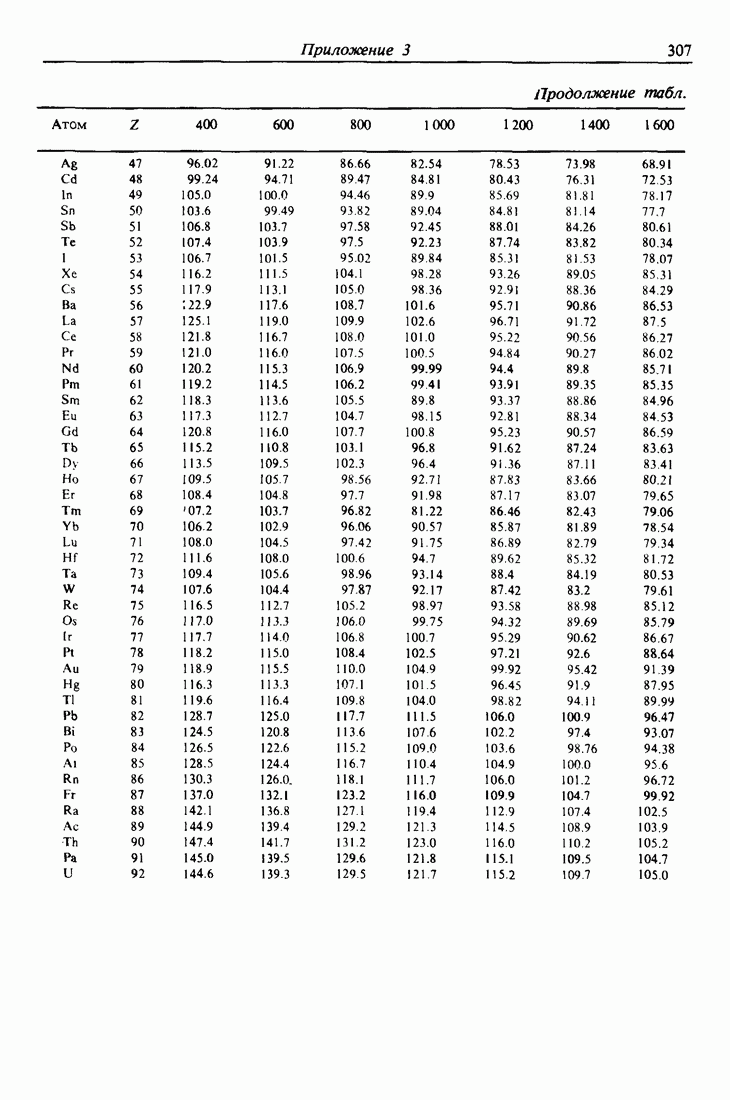
- ПРИЛОЖЕНИЕ 3.
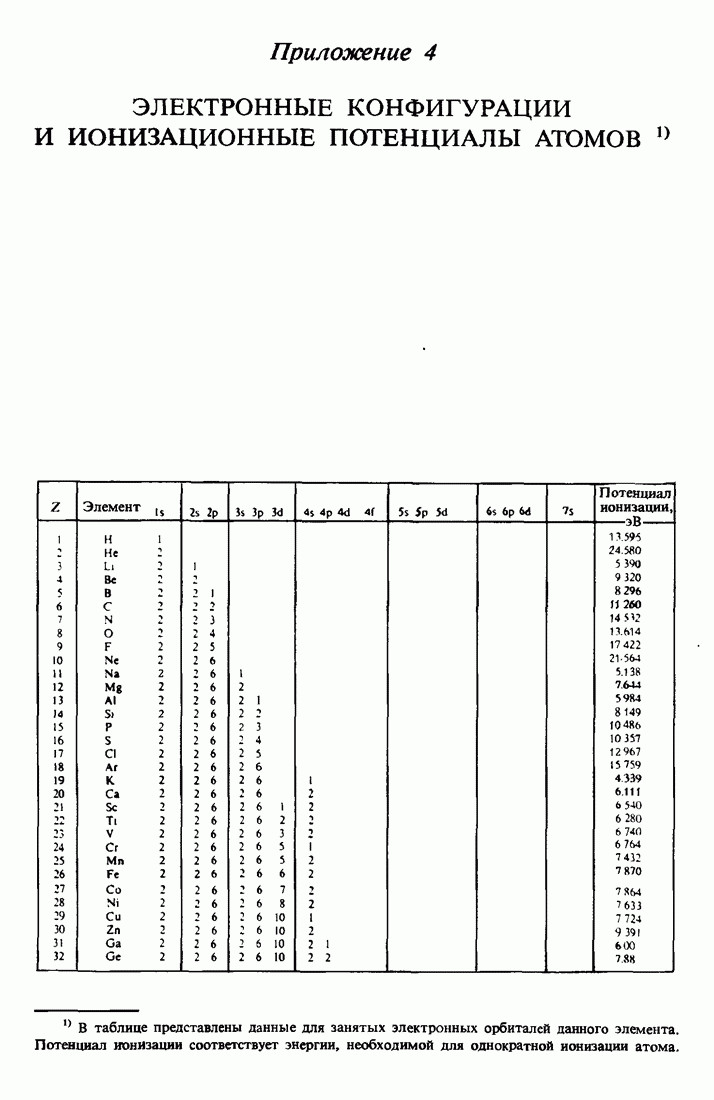
- ПРИЛОЖЕНИЕ 4.
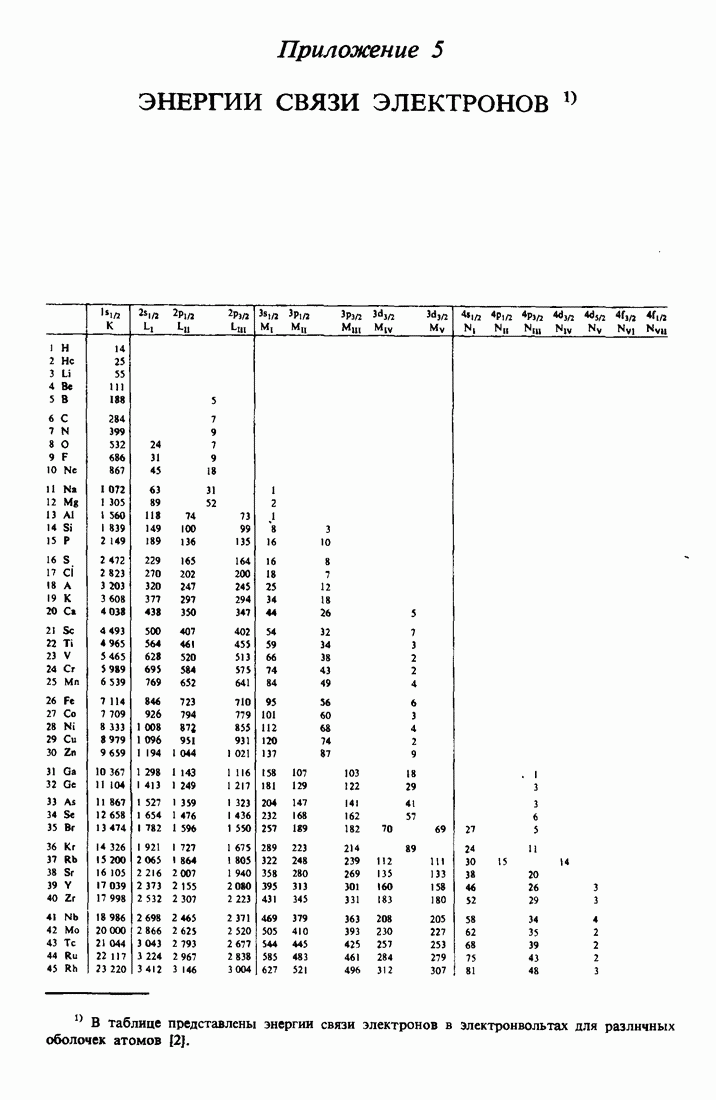
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
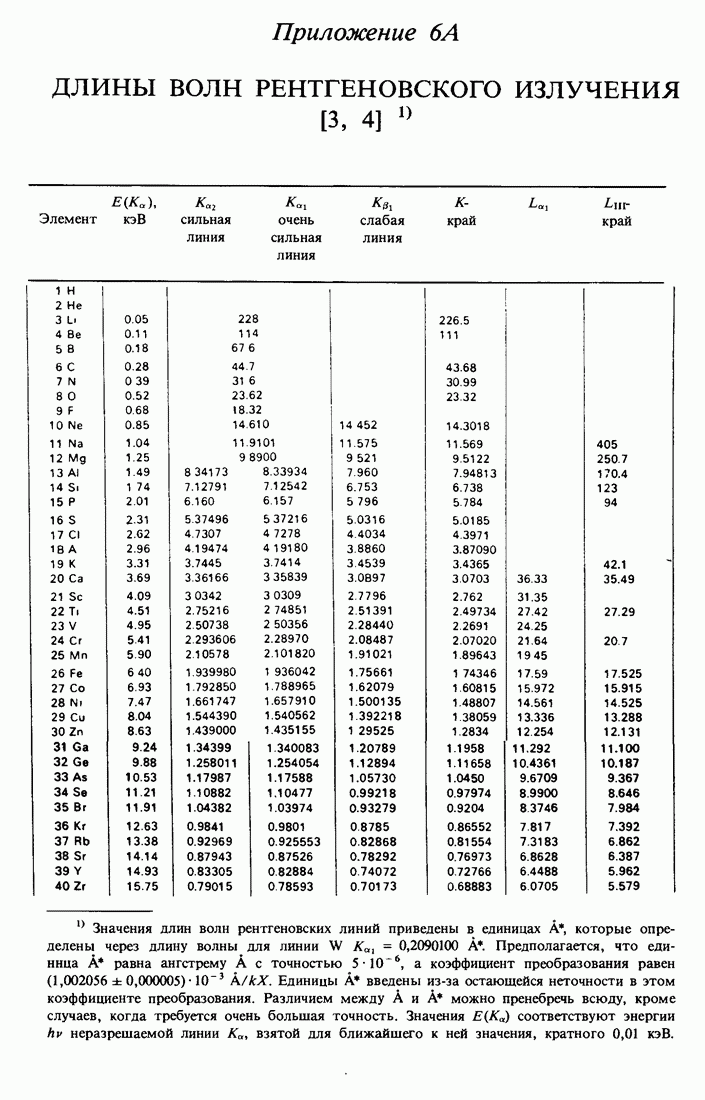
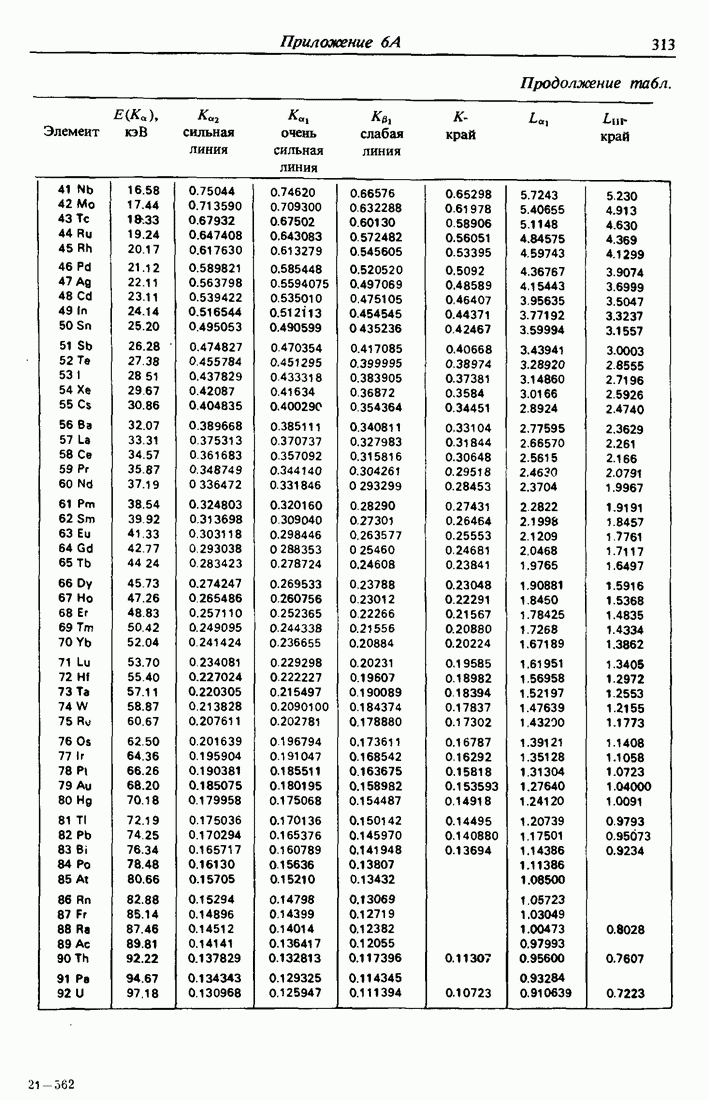
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
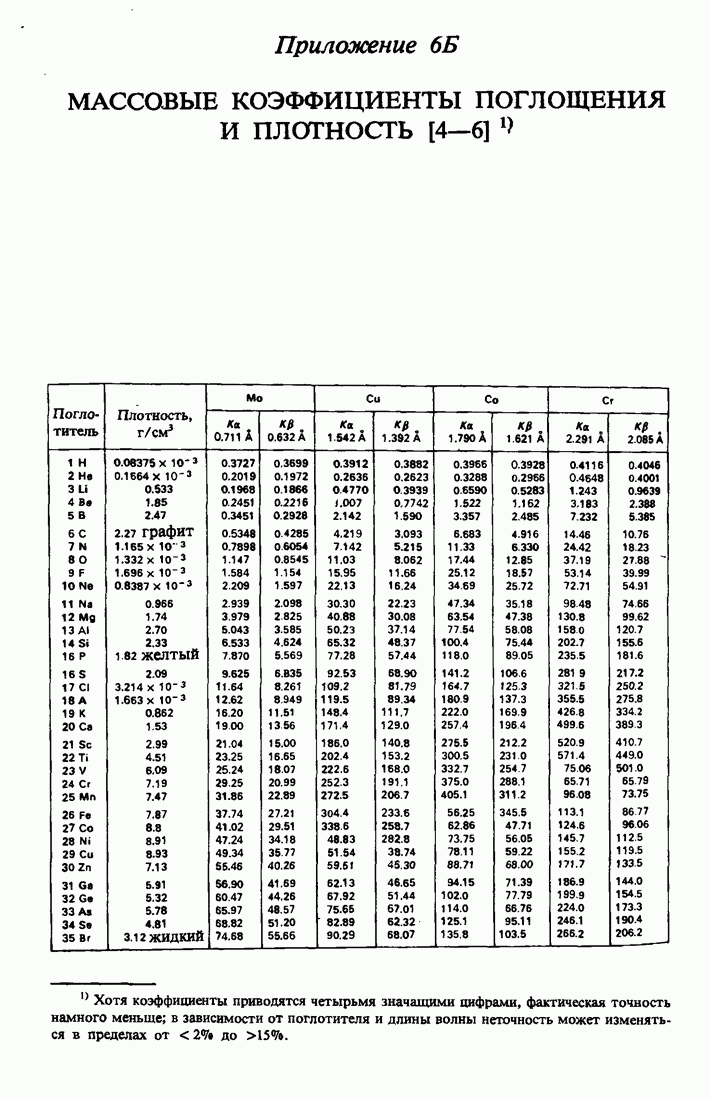
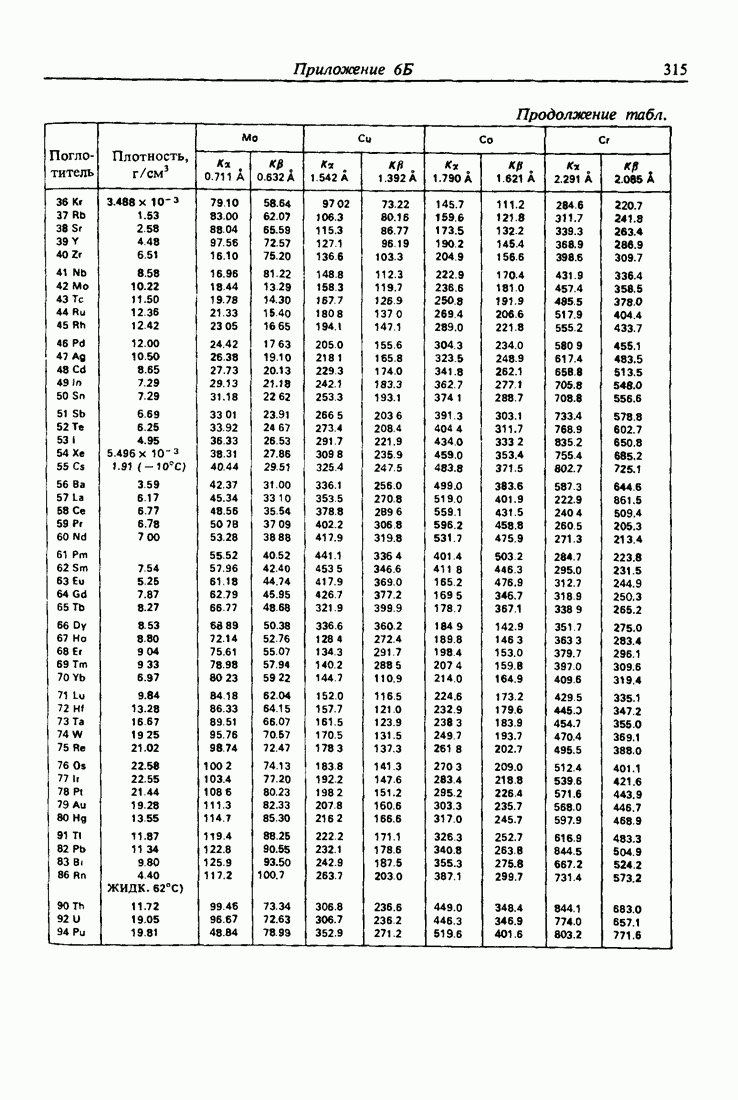
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
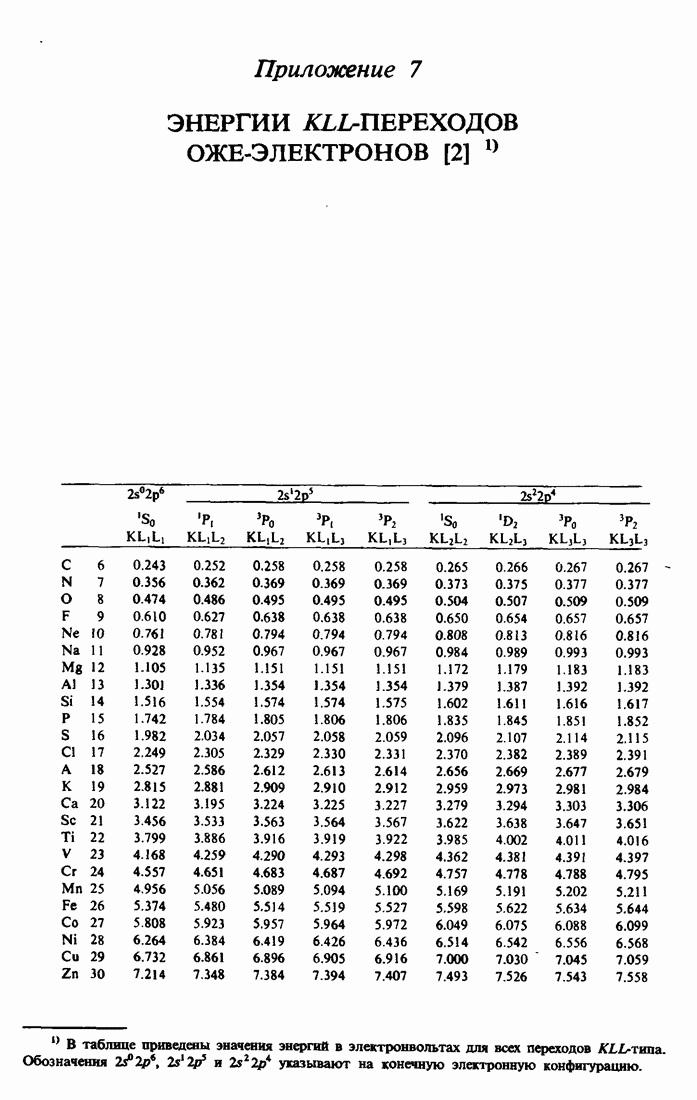
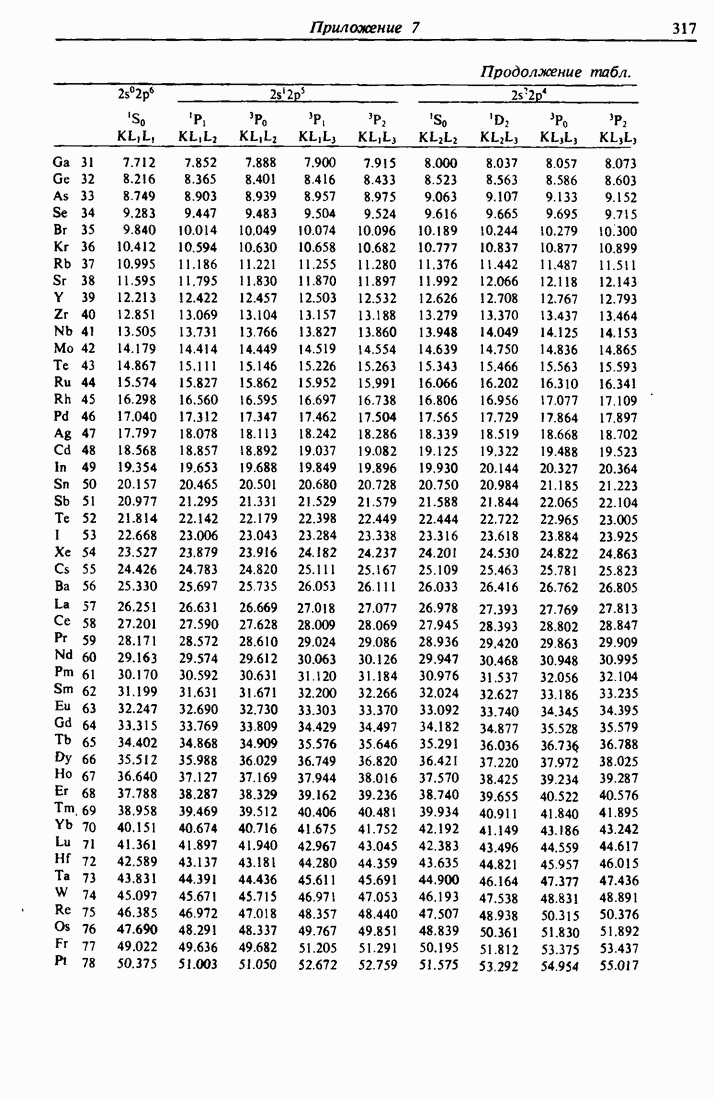
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
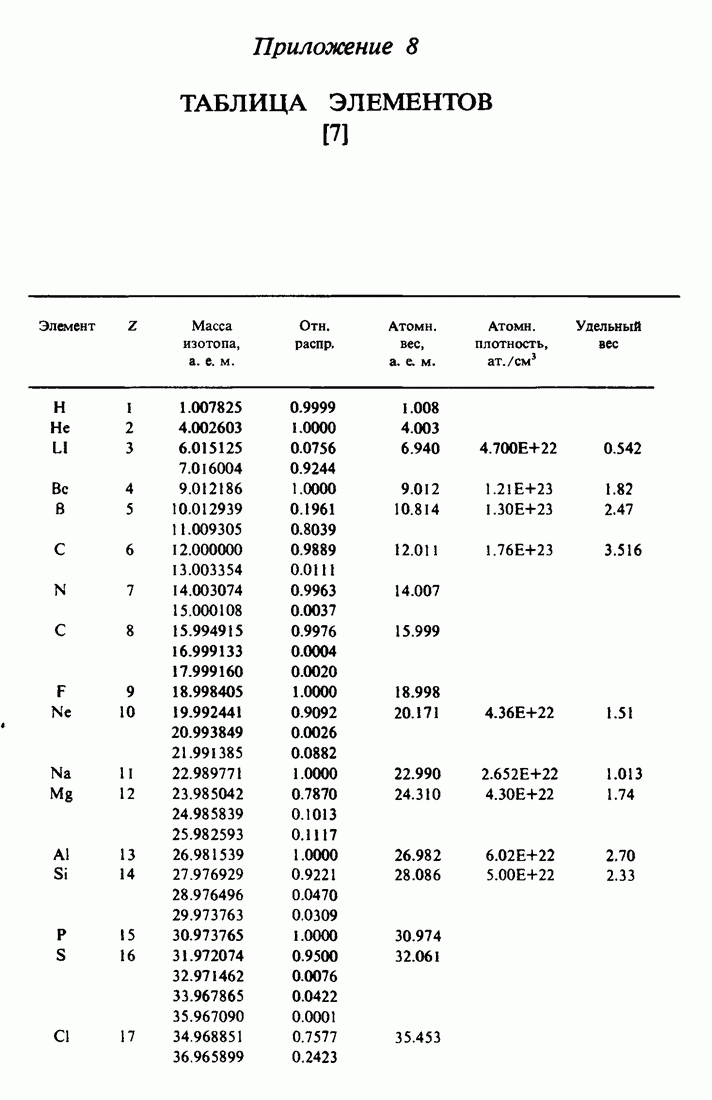
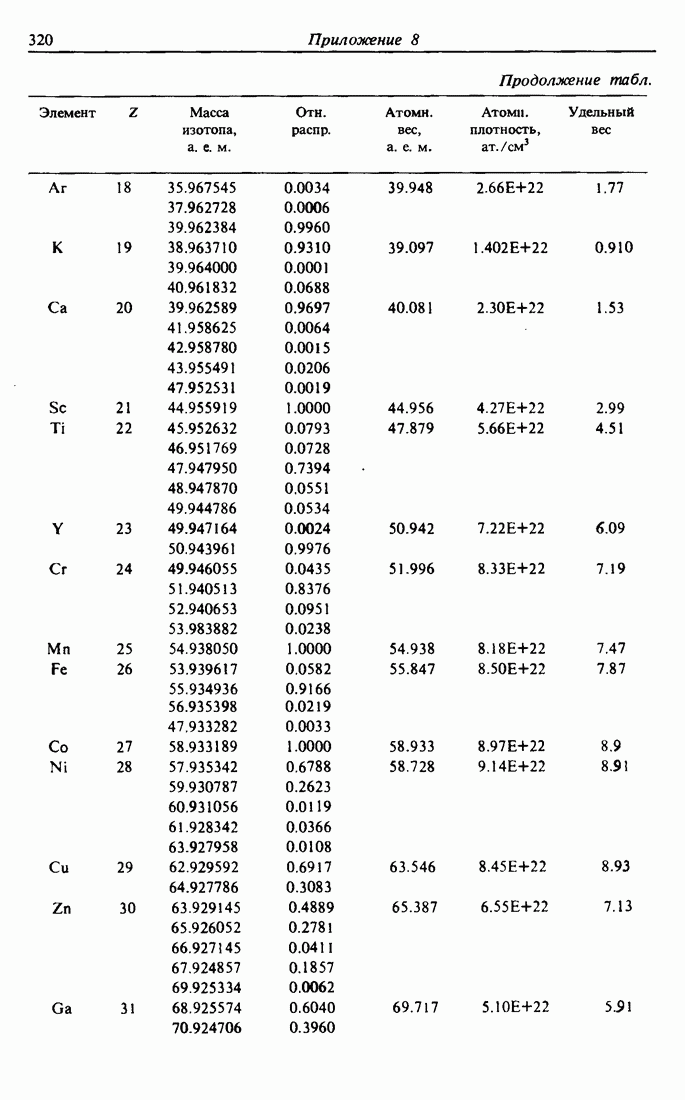
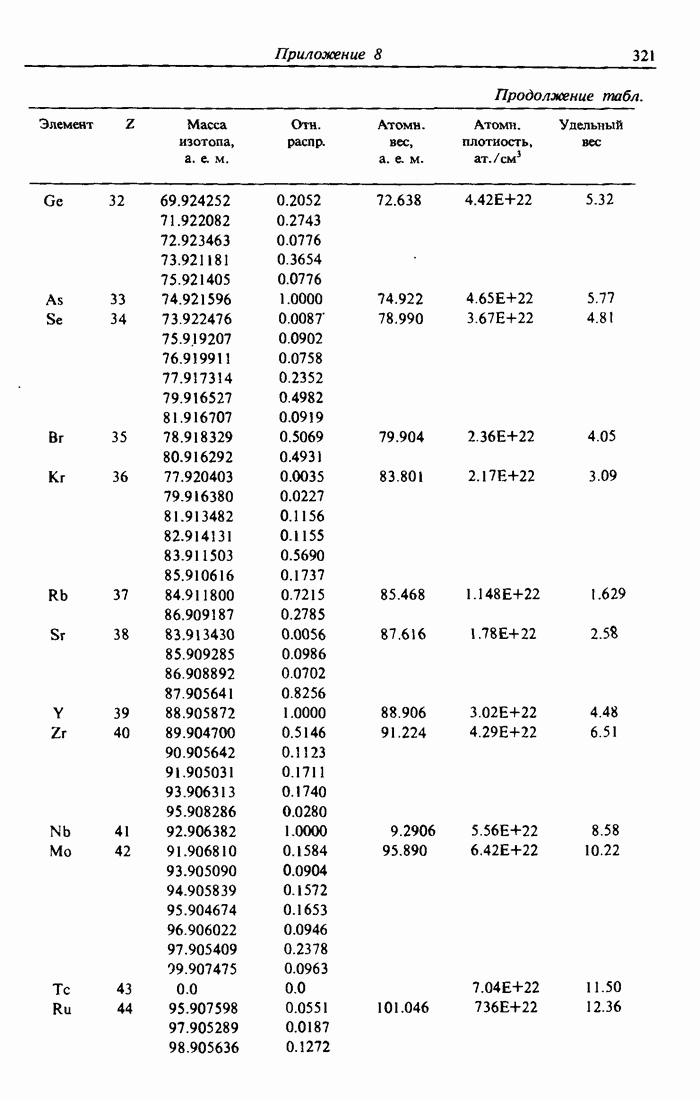
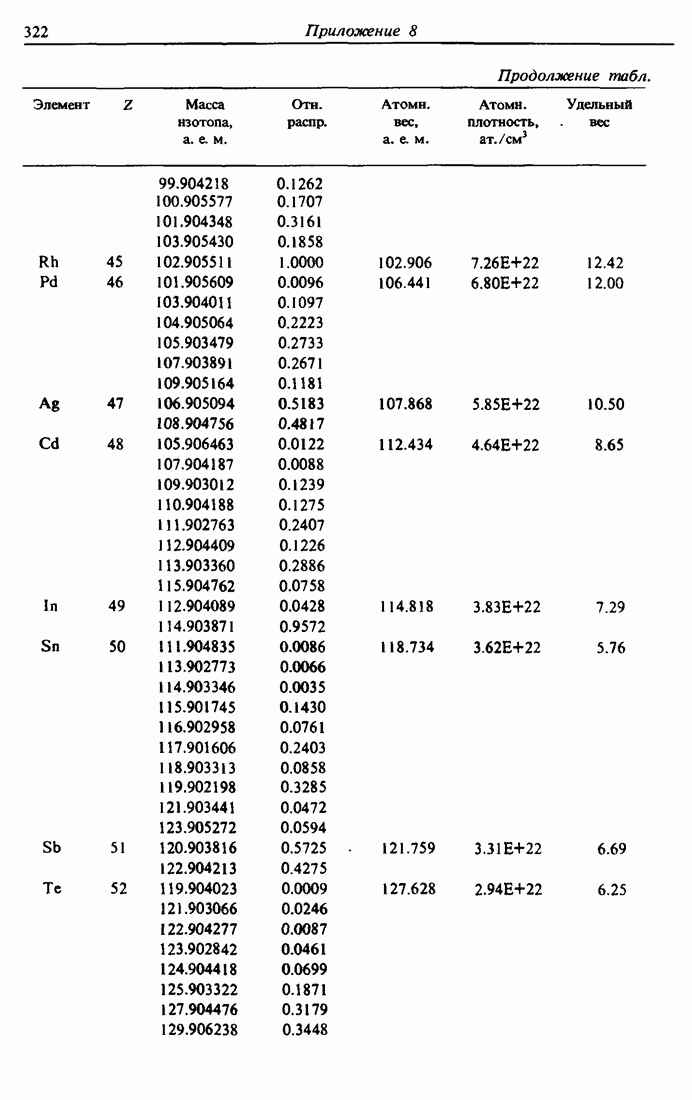
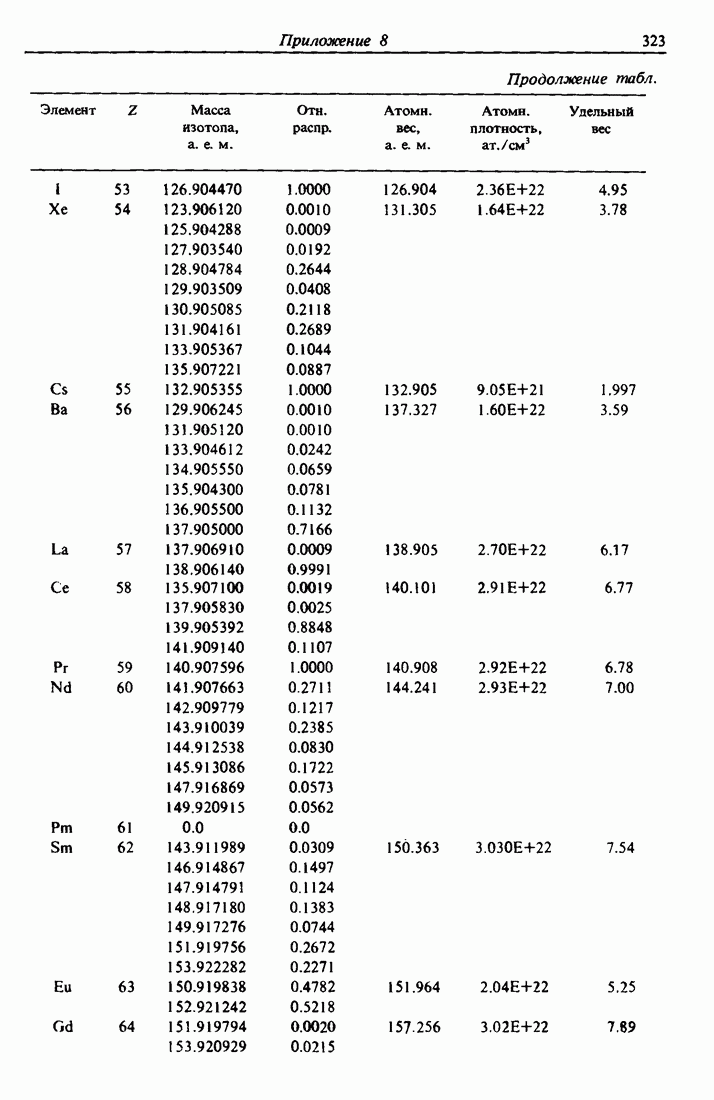
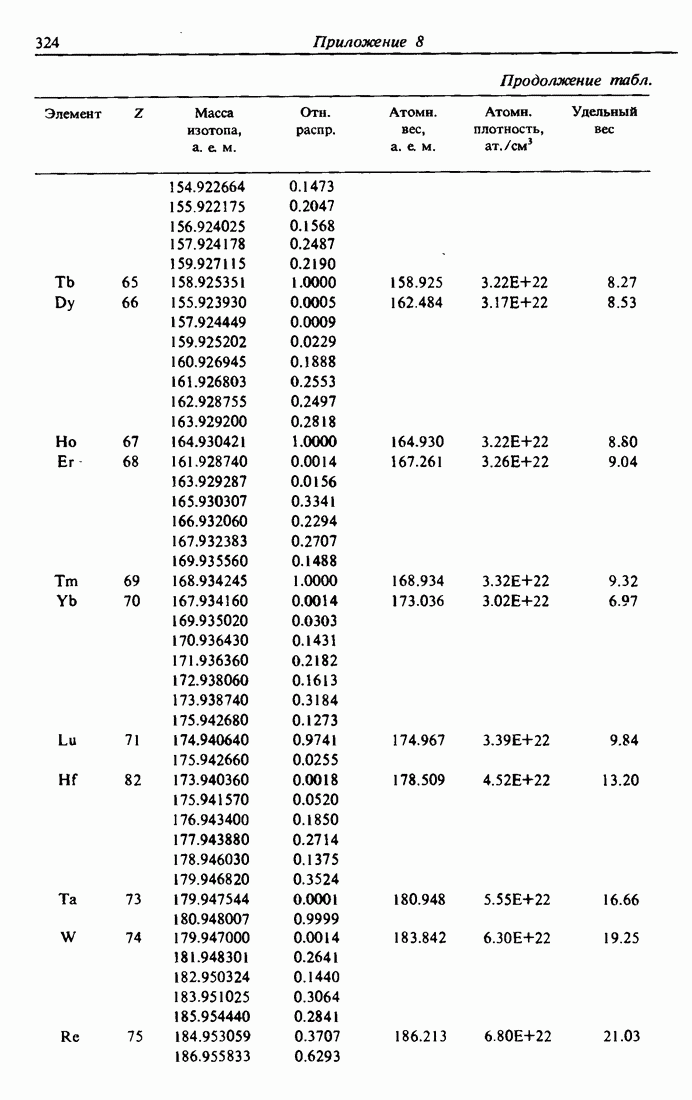
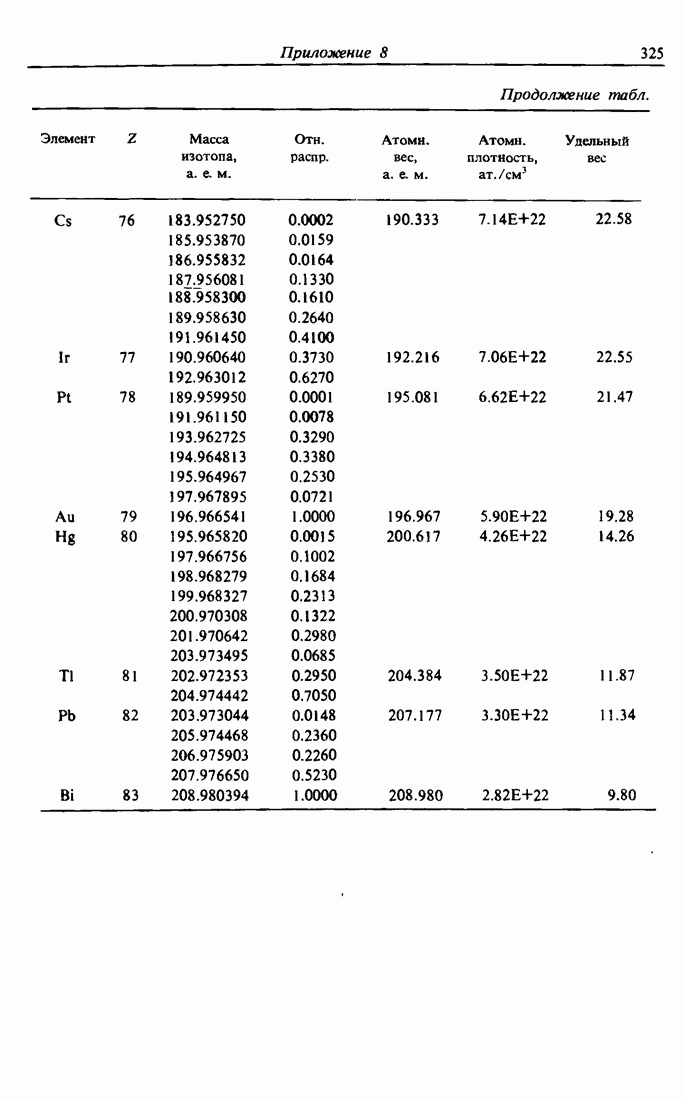
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
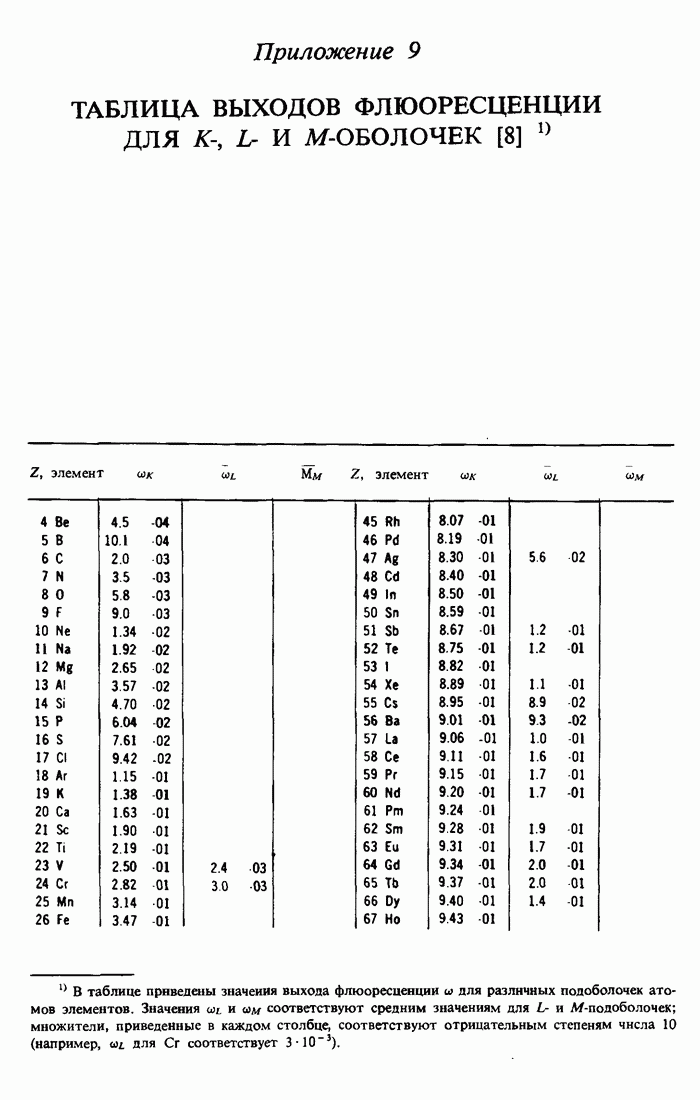
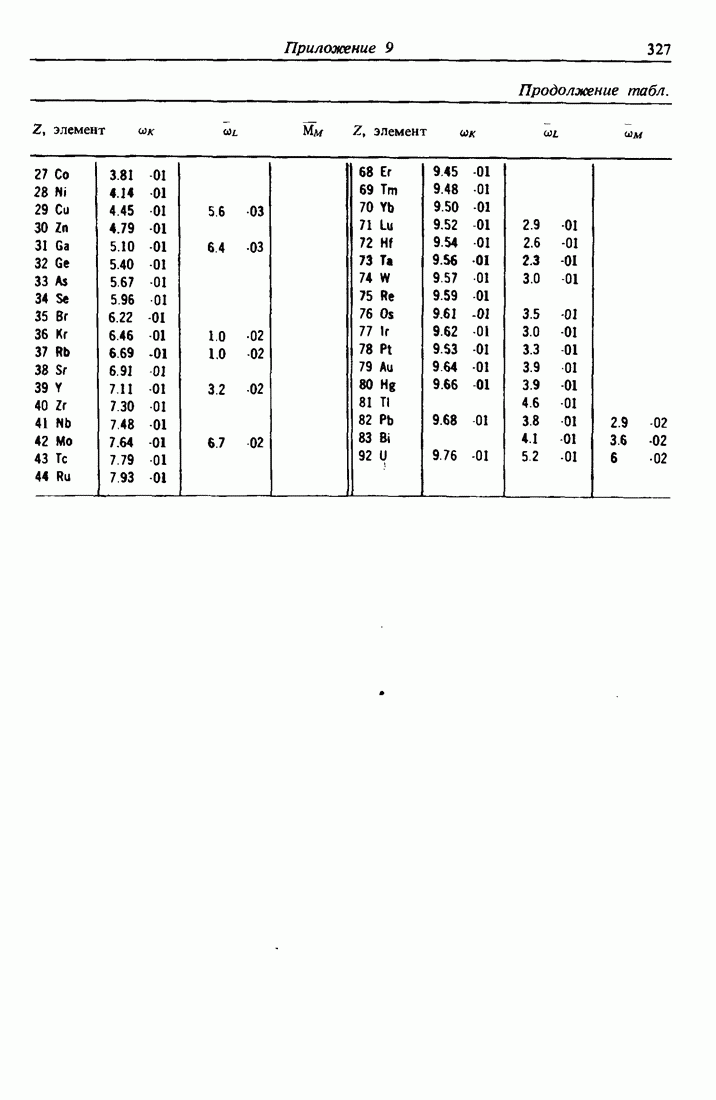
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ