| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.10. Нестационарная теория возмущений
8.10.1. Золотое правило Ферми
В этом разделе мы кратко осветим теорию возмущений, приводящую к основной формуле для вероятности перехода в квантовой системе. Эта формула является отправной точкой при нахождении поперечных сечений процессов, приводимых в книге.
Рассмотрим систему с гамильтонианом Н, определяемым выражением

где  — оператор, не зависящий от времени, с собственной функцией
— оператор, не зависящий от времени, с собственной функцией  . Гамильтониан
. Гамильтониан  может, например, описывать водородоподобный атом, а Н — зависящее от времени возмущение, т.е. осциллирующее электрическое поле. Волновая функция
может, например, описывать водородоподобный атом, а Н — зависящее от времени возмущение, т.е. осциллирующее электрическое поле. Волновая функция  удовлетворяет уравнению Шредингера
удовлетворяет уравнению Шредингера

Поскольку  не зависит от времени, то можно положить
не зависит от времени, то можно положить

или

где  — ортонормированные собственные векторы, удовлетворяющие уравнению
— ортонормированные собственные векторы, удовлетворяющие уравнению

 — постоянные, не зависящие от времени.
— постоянные, не зависящие от времени.
Для возмущенного гамильтониана запишем

и

где коэффициенты  теперь зависят от времени.
теперь зависят от времени.
Подставляя (8.48) в (8.47) и умножая на комплексно сопряженную функцию  , с учетом ортонормированности получаем
, с учетом ортонормированности получаем

где

— интеграл по всему пространству. Можно отметить, что при слабом возмущении изменение  во времени является медленным. В этом случае можно получить приближенное решение, полагая
во времени является медленным. В этом случае можно получить приближенное решение, полагая 

где  .
.
Особым является случай, когда в момент времени  система находится в состоянии
система находится в состоянии  , а значения других коэффициентов равны нулю. Тогда для
, а значения других коэффициентов равны нулю. Тогда для  выражение (8.50) переходит в
выражение (8.50) переходит в

Возмущение  может вызывать переходы из состояния n в любое другое состоянием. Вероятность нахождения системы в
может вызывать переходы из состояния n в любое другое состоянием. Вероятность нахождения системы в  в момент времени равна
в момент времени равна  .
.
Еслн Н не зависит от времени, то

и

что справедливо, пока  .
.
Во многих практических задачах в результате возмущения частица переходит в континуум состояний, т. е. становится свободной частицей. В этом случае вместо точно заданного конечного состояния уместно рассматривать плотность конечных состояний. Будем называть  плотностью конечных состояний (число энергетических уровней на единичный энергетический интервал), полагая, что
плотностью конечных состояний (число энергетических уровней на единичный энергетический интервал), полагая, что  одинаково для всех конечных состояний.
одинаково для всех конечных состояний.
Вероятность перехода  тогда дается выражением
тогда дается выражением

В случае континуума заменяем сумму интегралом, учитывая, что число состояний в энергетическом интервале  равно
равно  откуда
откуда

Главный вклад в интеграл делается при  (это слегка похоже на
(это слегка похоже на  -функцию), поэтому, замечая, что
-функцию), поэтому, замечая, что  получаем
получаем

так что скорость перехода W равна

Это и есть широко известная формула, называемая «золотым правилом» Ферми.
8.10.2. Вероятность переходов в осциллирующем электрическом поле
Другим важным приложением теории возмущений является случай возмущающего поля, имеющего временную зависимость в виде  Рассмотрим в качестве примера осциллирующее электрическое поле, направленное вдоль оси х:
Рассмотрим в качестве примера осциллирующее электрическое поле, направленное вдоль оси х:

и

Подстановка  в (8.51) дает
в (8.51) дает

При  среднее значение интеграла равно нулю. Если
среднее значение интеграла равно нулю. Если  получаем
получаем

где  Поскольку
Поскольку  есть не что иное, как плотность энергии электрического поля, которую обозначим
есть не что иное, как плотность энергии электрического поля, которую обозначим  то вероятность перехода равна
то вероятность перехода равна

Будем предполагать, что спектральное распределение  изменяется намного медленнее, чем имеющая острый пик функция в подынтегральном выражении, на которую умножена
изменяется намного медленнее, чем имеющая острый пик функция в подынтегральном выражении, на которую умножена  . В узком интервале значений
. В узком интервале значений  для которых подынтегральное выражение отлично от нуля,
для которых подынтегральное выражение отлично от нуля,  является почти постоянной величиной, так что
является почти постоянной величиной, так что  можно заменить его значением при
можно заменить его значением при  и вынести за знак интеграла без существенной потери точности. Далее, используя подстановкуг
и вынести за знак интеграла без существенной потери точности. Далее, используя подстановкуг  выражение перепишем в виде и
выражение перепишем в виде и

С учетом

вероятность перехода равна

где  . Выражение (8.63) справедливо для излучения, поляризованного вдоль оси
. Выражение (8.63) справедливо для излучения, поляризованного вдоль оси  . В общем случае, когда излучение падает на атом со всех направлений со случайной поляризацией,
. В общем случае, когда излучение падает на атом со всех направлений со случайной поляризацией,  должно включать равные вклады
должно включать равные вклады  так, что
так, что

где множитель 3 введен в знаменатель потому, что каждое направление поляризации дает вклад в интенсивность. Выражение

называется днпольным матричным элементом, а (8.64) — дипольным приближением для вероятности перехода.
8.10.3. Спонтанные переходы
Переходы, происходящие в отсутствие внешнего поля, называются спонтанными. Примером может служить переход из возбужденного в основное состояние. Для расчета этих явлений мы будем основываться на методе, развитом Эйнштейном в 1917 г., позволяющем рассчитывать скорости спонтанных переходов по известным скоростям вынужденных переходов, рассчитанным в разд. 8.10.2.
Рассмотрим группу атомов в тепловом равновесии; каждый атом может излучать и поглощать излучение с одинаковой скоростью. Пусть  — вероятность того, что данный атом переходит из
— вероятность того, что данный атом переходит из  состояния в 5-е состояние за малое время
состояния в 5-е состояние за малое время  Эта вероятность
Эта вероятность  должна быть пропорциональна вероятности
должна быть пропорциональна вероятности  нахождения атома в
нахождения атома в  начальном состоянии, умноженной на вероятность перехода из
начальном состоянии, умноженной на вероятность перехода из  состояния
состояния  состояние
состояние  [даваемую выражением (8.64)]:
[даваемую выражением (8.64)]:

С учетом (8.64) можно переписать это выражение как

где  было определено ранее,
было определено ранее,  заменяет t в качестве временного интервала, a А соответствует оставшемуся множителю в выражении (8.64).
заменяет t в качестве временного интервала, a А соответствует оставшемуся множителю в выражении (8.64).
Вероятность перехода из верхнего состояния s в нижнее состояние n может быть переписана в виде

причем из симметрии выражений, приводящих к (8.64), мы знаем, что  поэтому
поэтому

Отметим, что  не равно
не равно  , потому что
, потому что  уровень, обладающий меньшей энергией, имеет большую заселенность в соответствии с законом Больцмана.
уровень, обладающий меньшей энергией, имеет большую заселенность в соответствии с законом Больцмана.
Поскольку система находится в равновесии, полное число переходов из n в s должно быть равно полному числу переходов из s в n. Так как вероятности вынужденных переходов не равны  должны существовать дополнительные переходы из состояния j в состояние n, которые являются спонтанными. Вероятность спонтанных переходов по определению не зависит от плотности энергии внешнего поля; эта вероятность может быть записана как
должны существовать дополнительные переходы из состояния j в состояние n, которые являются спонтанными. Вероятность спонтанных переходов по определению не зависит от плотности энергии внешнего поля; эта вероятность может быть записана как  , где
, где  — вероятность спонтанного перехода. Коэффициенты А и В называются коэффициентами Эйнштейна.
— вероятность спонтанного перехода. Коэффициенты А и В называются коэффициентами Эйнштейна.
Следовательно, полная вероятность перехода из s в n равна 
Эта же величина должна равняться вероятности перехода  . Таким образом, из уравнений (8.65) и (8.66) получаем
. Таким образом, из уравнений (8.65) и (8.66) получаем

или

Но заселенность состояния с энергией Е пропорциональна больцмановскому фактору  так что отношение
так что отношение  может быть переписано как
может быть переписано как

Отсюда

Наличие множителя  в уравнении (8.67) может привести в недоумение, так как
в уравнении (8.67) может привести в недоумение, так как  по определению не зависит от плотности энергии поля излучения. Однако этот множитель можно устранить, используя выражение для плотности энергии внутри полости. Закон Планка для теплового излучения приводит к зависимости
по определению не зависит от плотности энергии поля излучения. Однако этот множитель можно устранить, используя выражение для плотности энергии внутри полости. Закон Планка для теплового излучения приводит к зависимости

Подстановка этого выражения в уравнение (8.67) дает выражение для  содержащее только А и известные постоянные:
содержащее только А и известные постоянные:

Итак, скорость спонтанного перехода из заполненного состояния в незаселенное состояние равна

где  . Это выражение можно также записать, как
. Это выражение можно также записать, как

где  выражается в электронвольтах, а матричный элемент имеет размерность
выражается в электронвольтах, а матричный элемент имеет размерность  . Типичная величина W равна
. Типичная величина W равна  для элементов в середине периодической таблицы. В итоге
для элементов в середине периодической таблицы. В итоге

для стационарного возмущения [уравнения (8.24) и (8.57)].

для возмущения с зависимостью от времени  [уравнение (8.64)]
[уравнение (8.64)]

для спонтанных переходов [уравнение (8.70)]
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
- 2.4. Сечение рассеяния и прицельный параметр
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
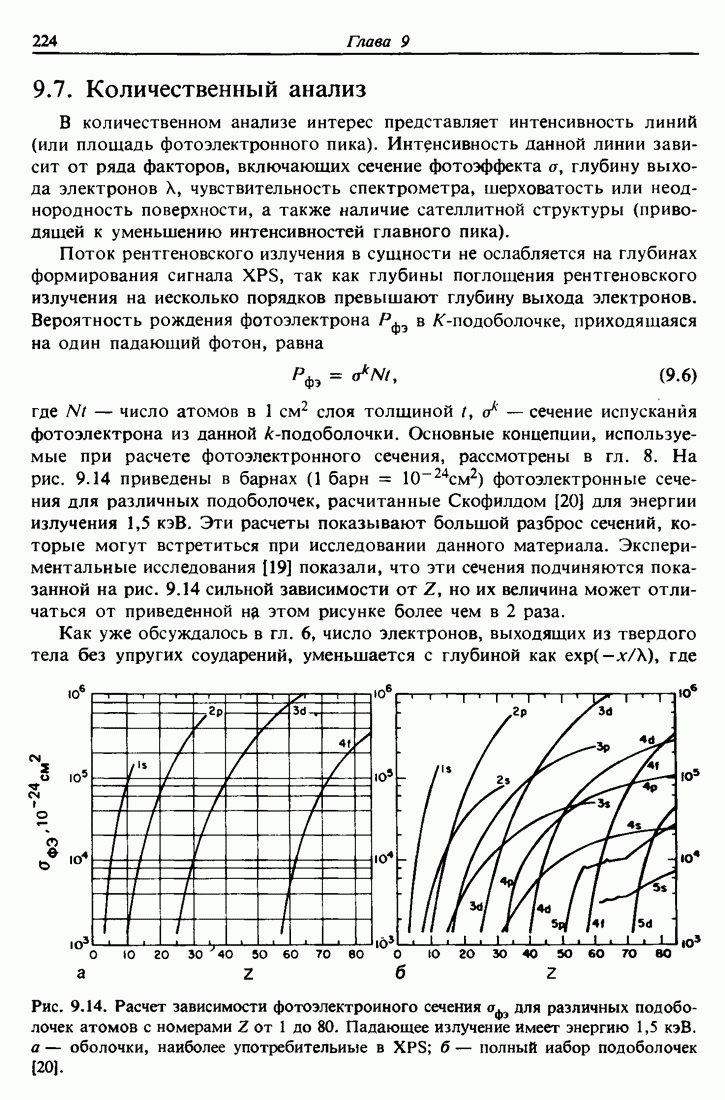
- 9.7. Количественный анализ
- Задачи
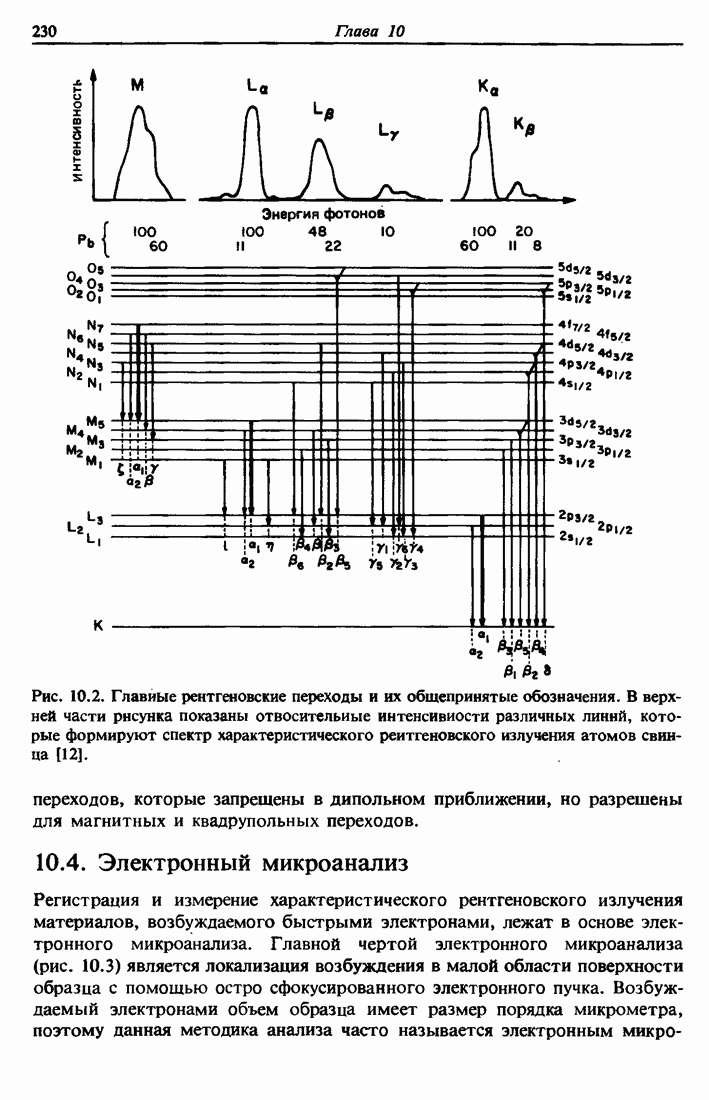
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
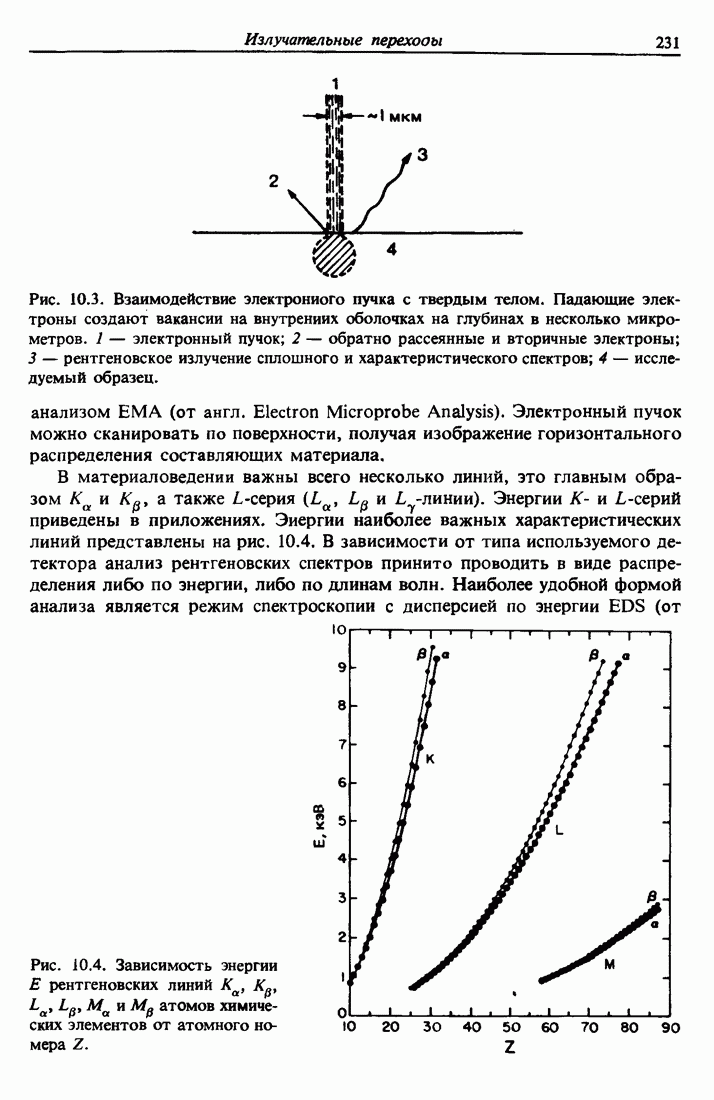
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
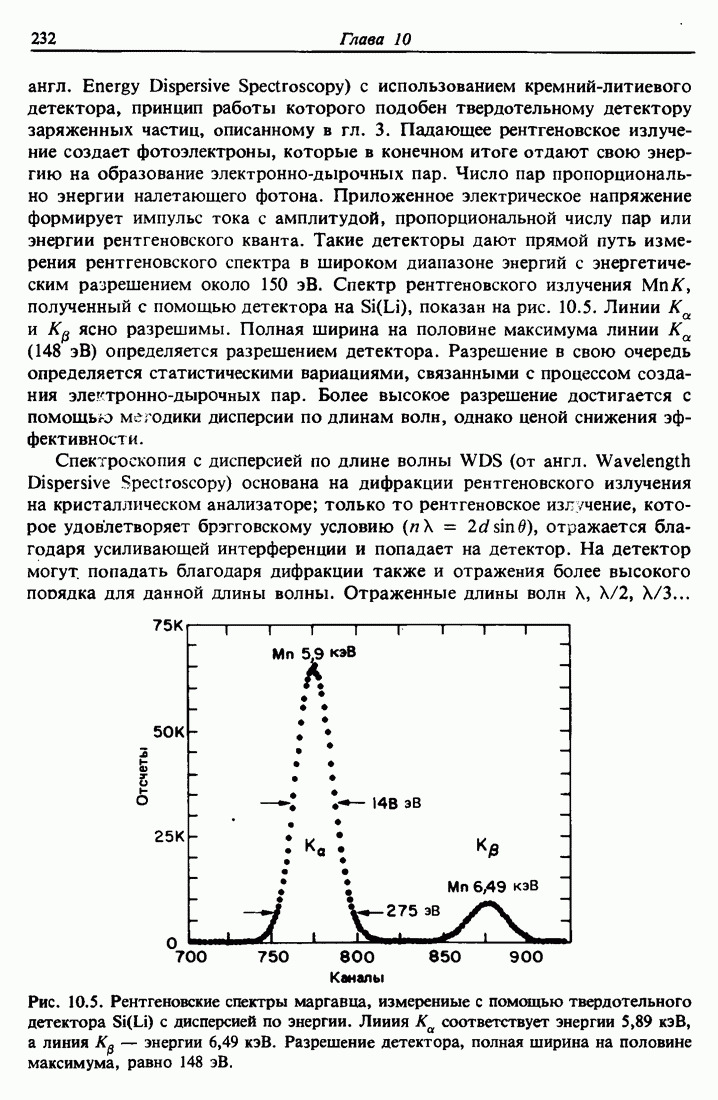
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
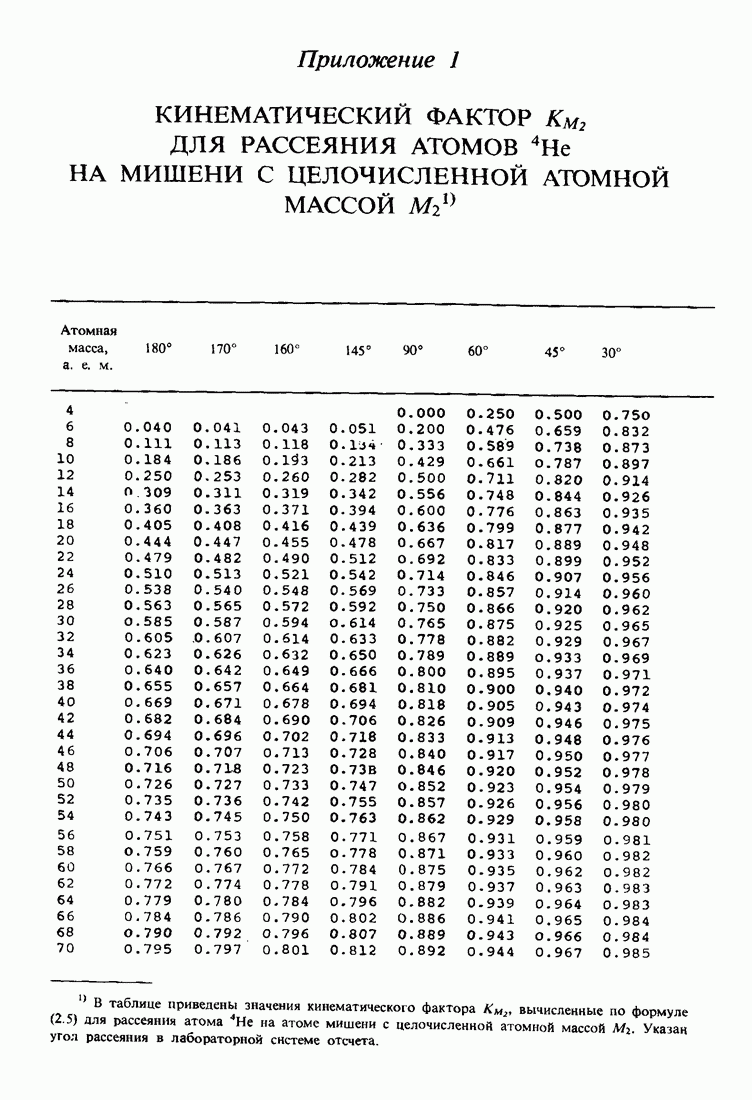
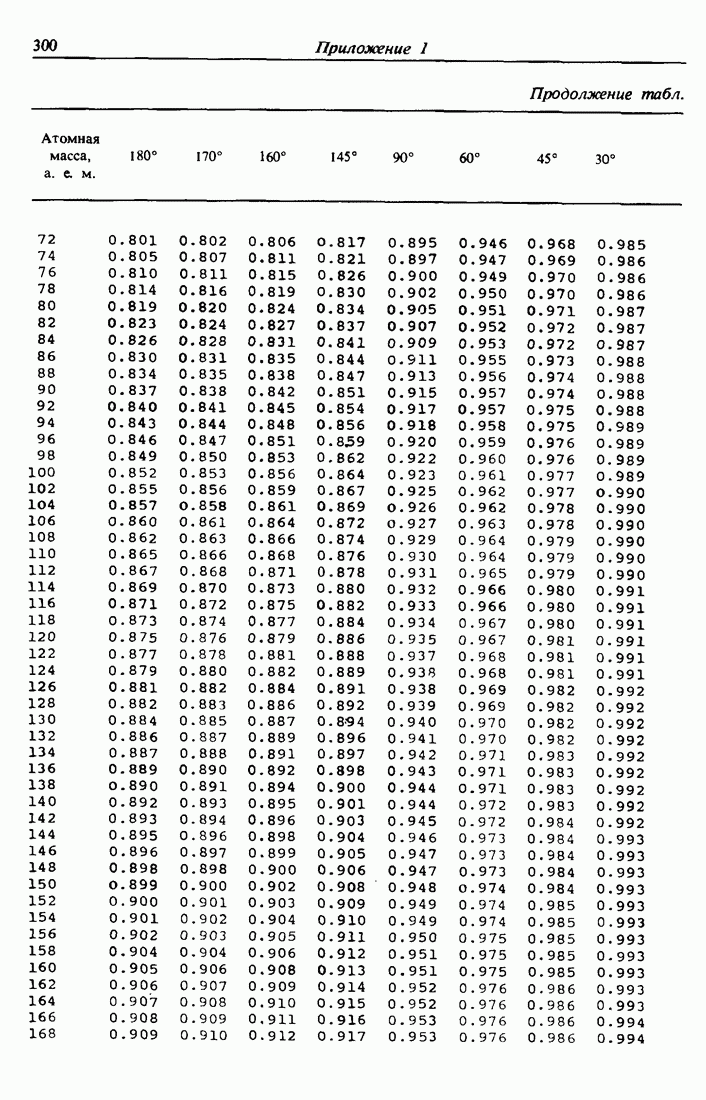
- ПРИЛОЖЕНИЕ 1.
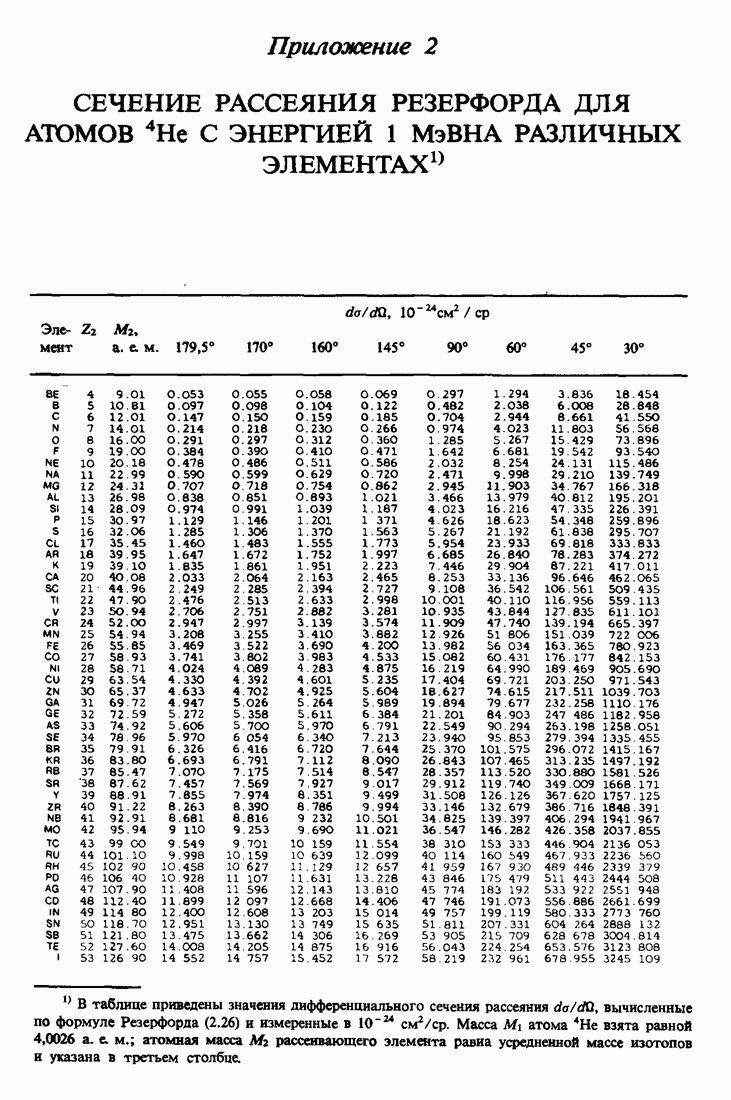
- ПРИЛОЖЕНИЕ 2.
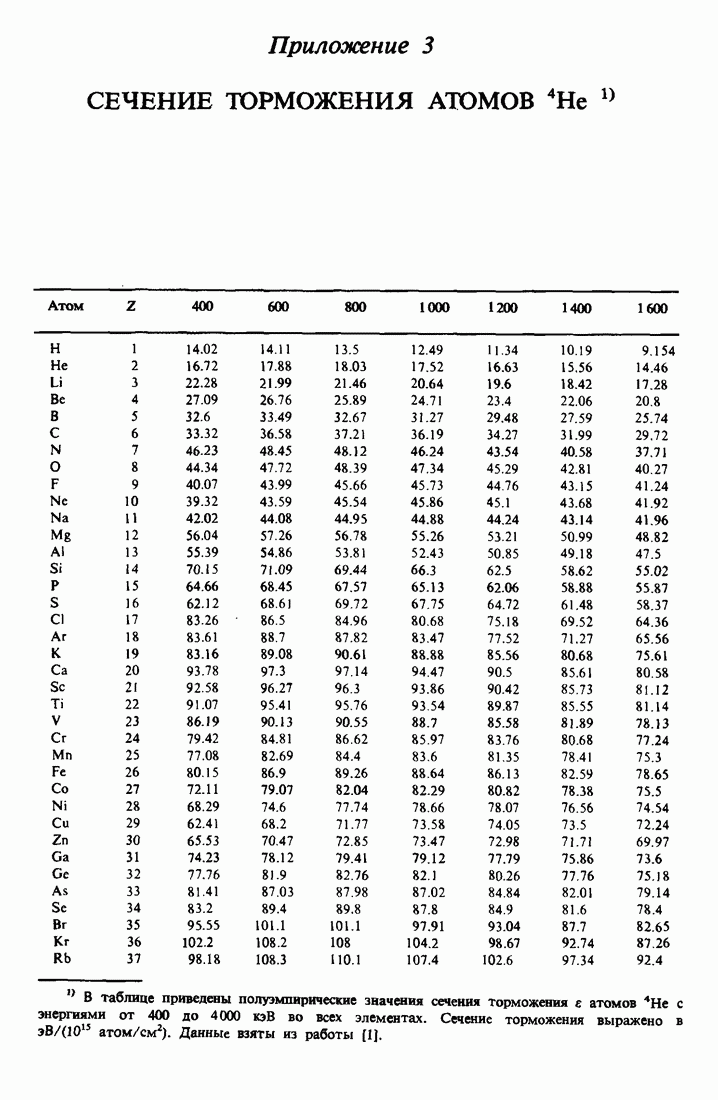
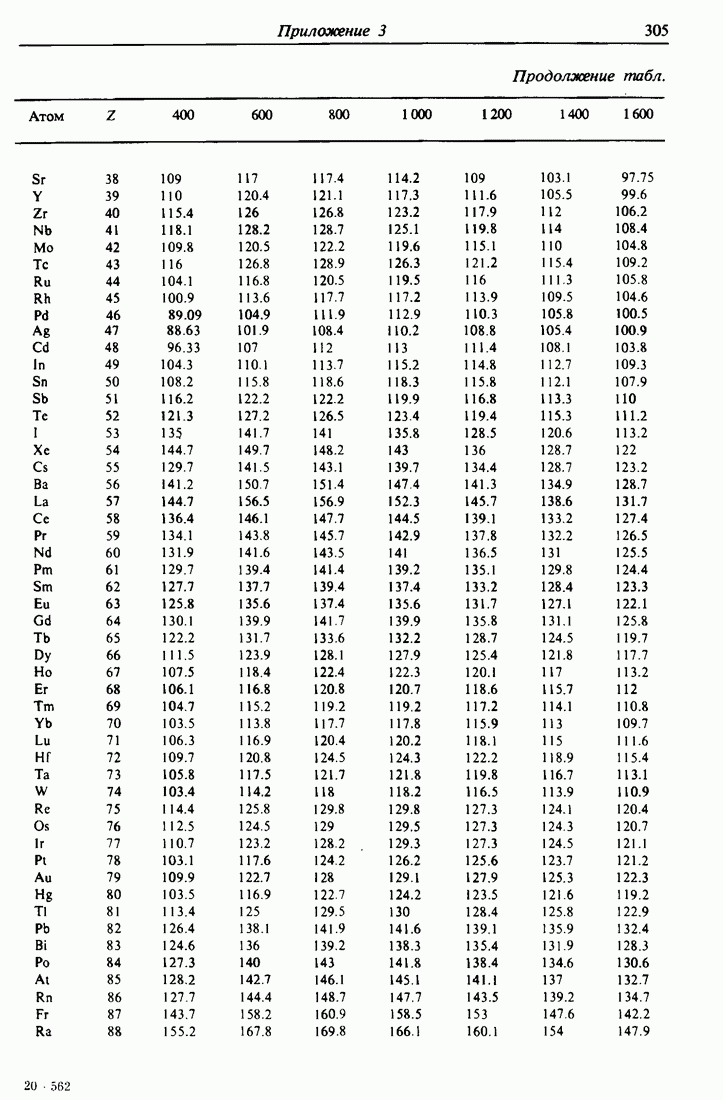
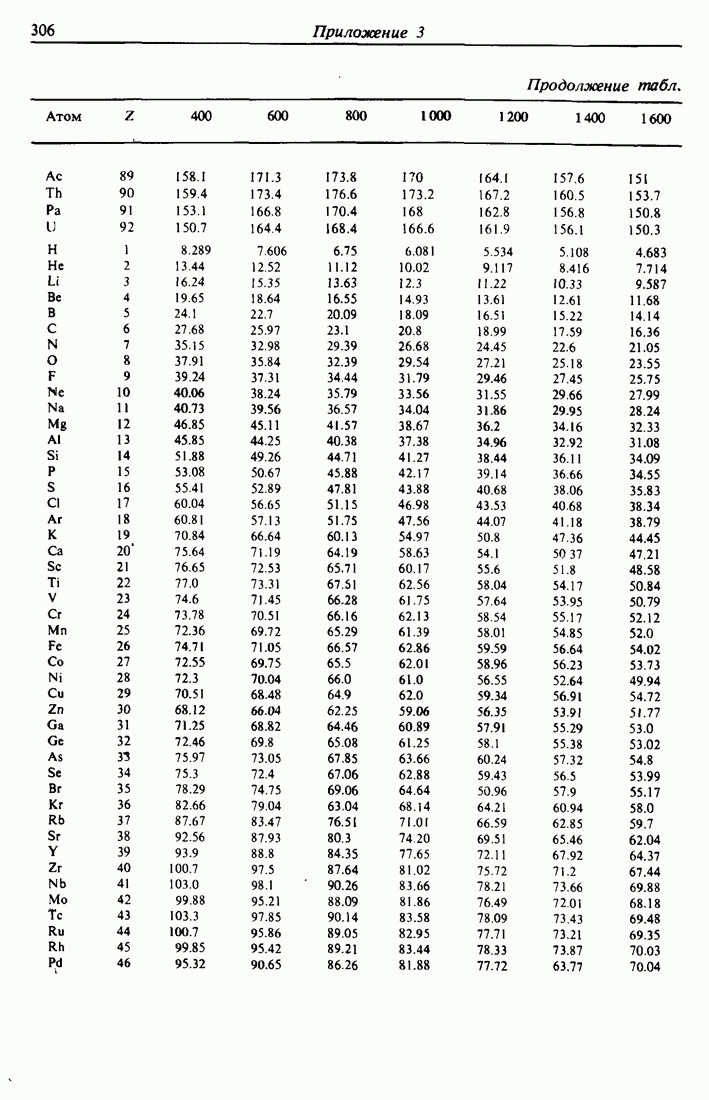
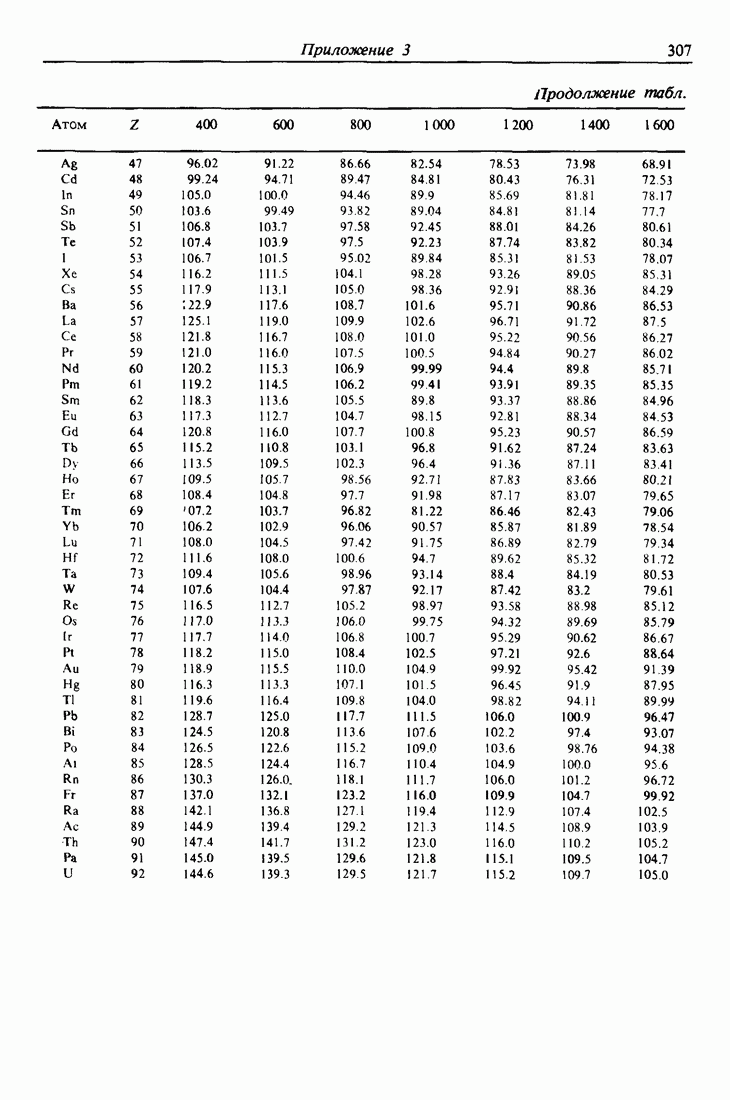
- ПРИЛОЖЕНИЕ 3.
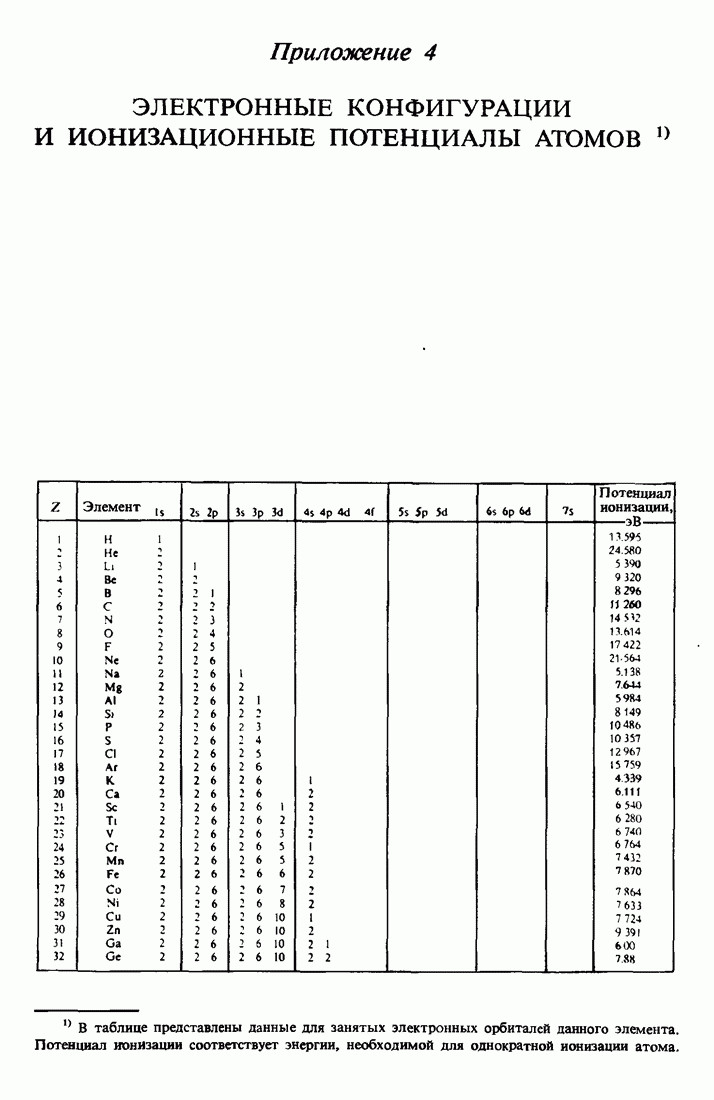
- ПРИЛОЖЕНИЕ 4.
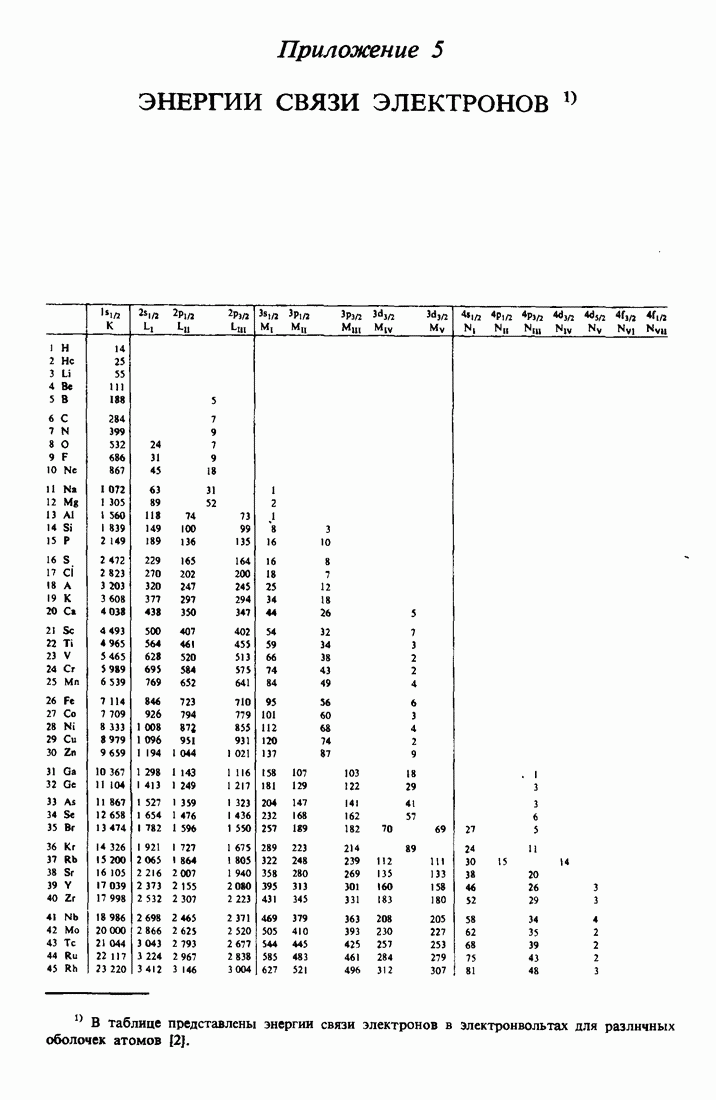
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
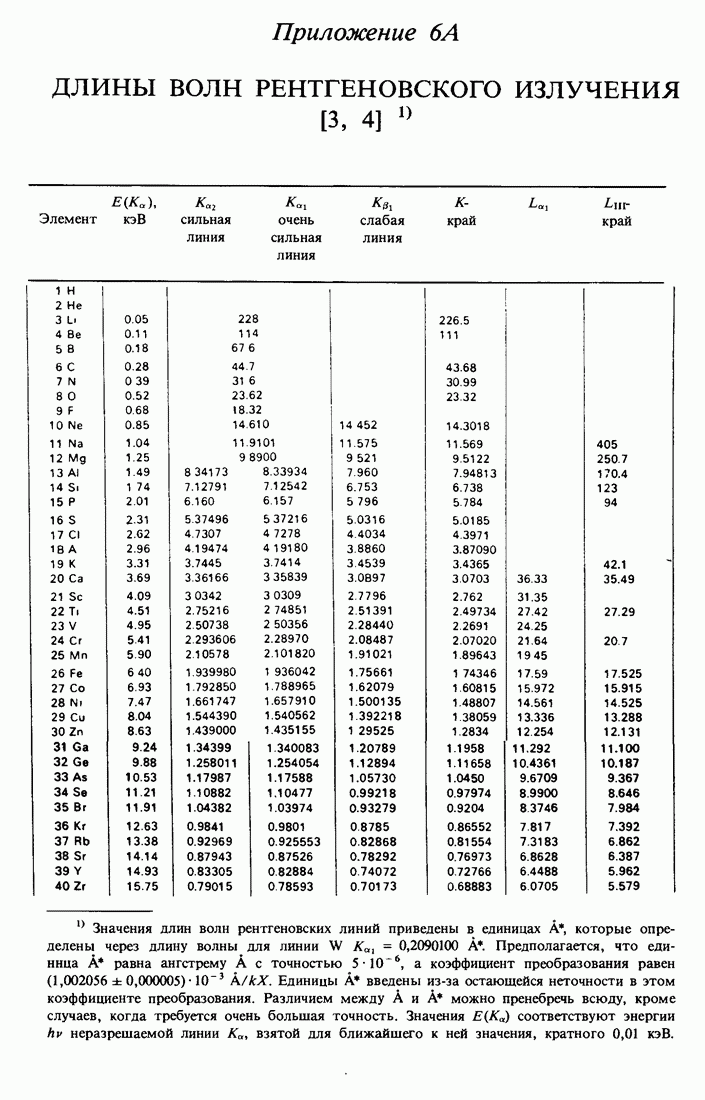
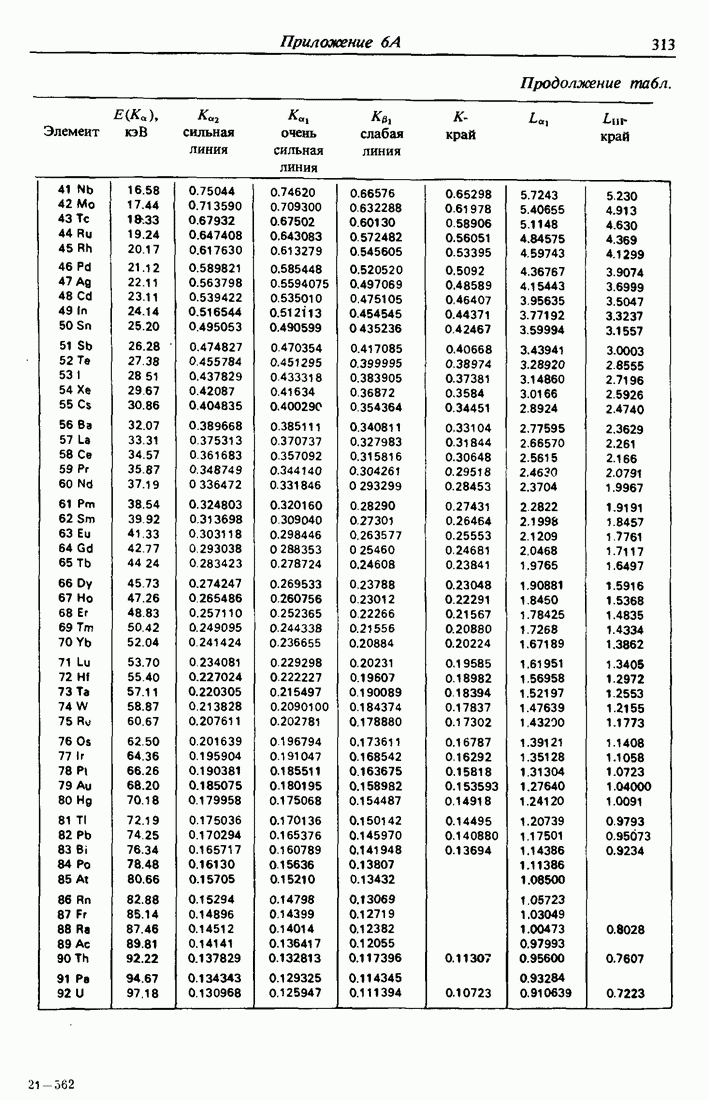
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
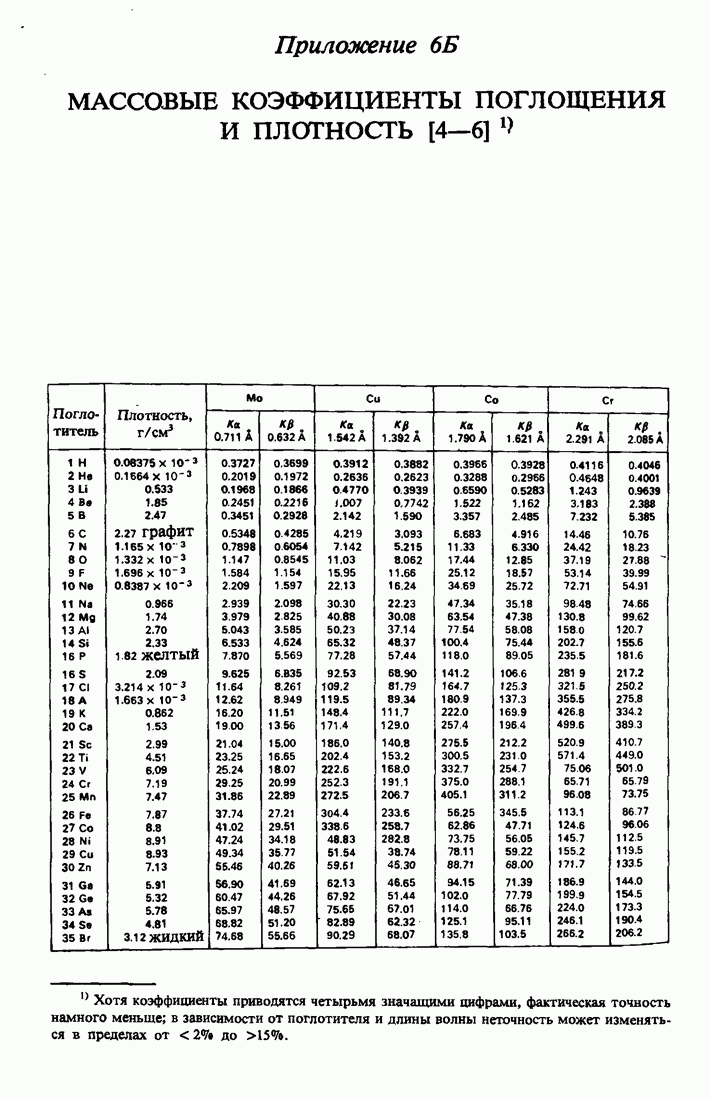
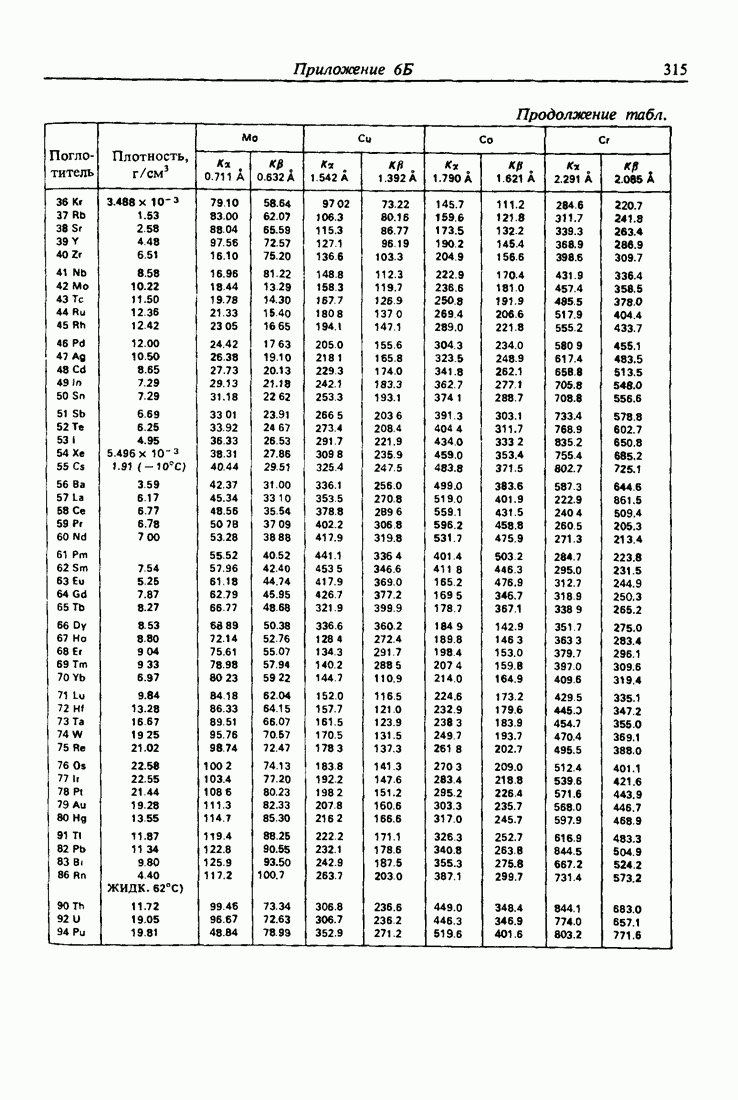
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
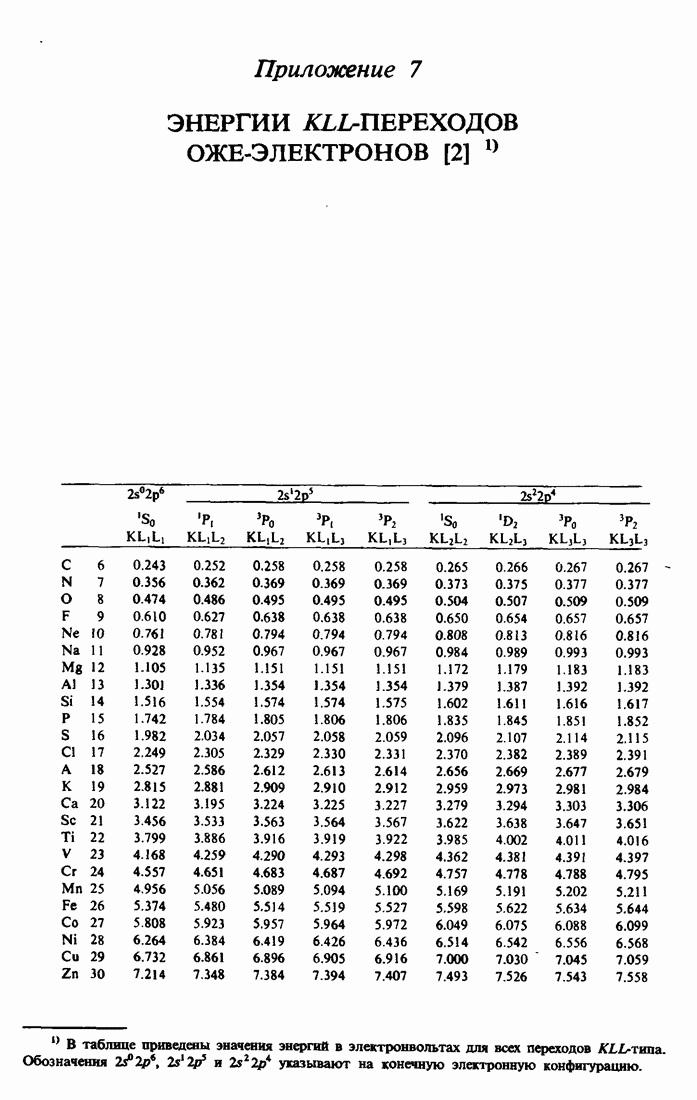
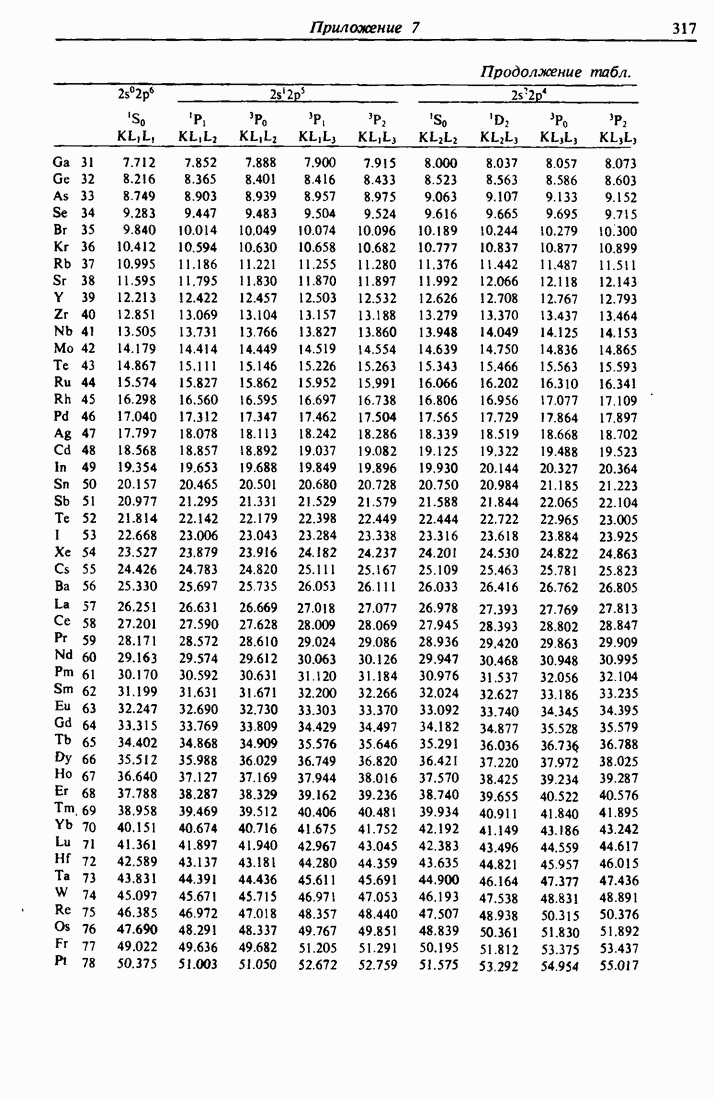
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
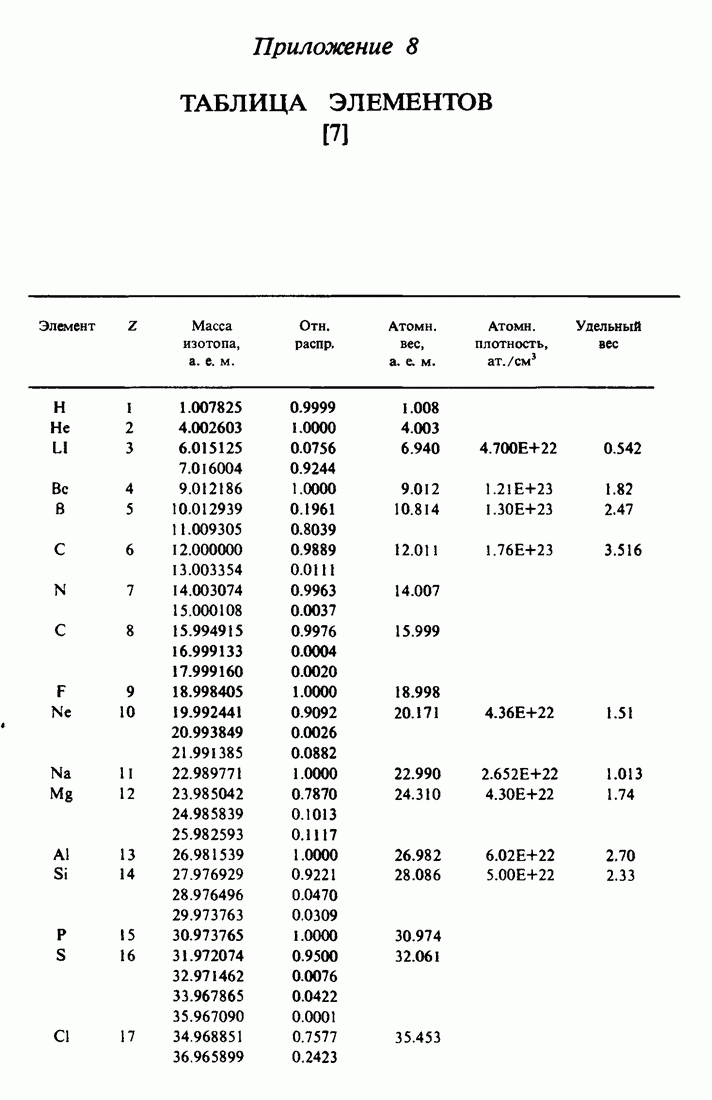
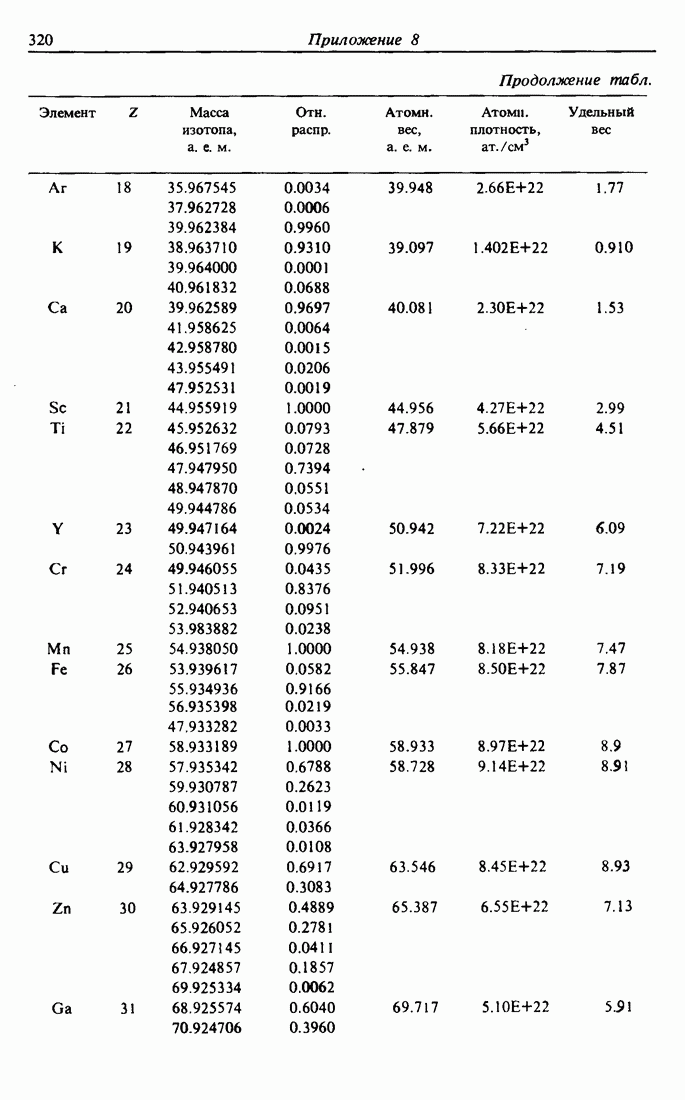
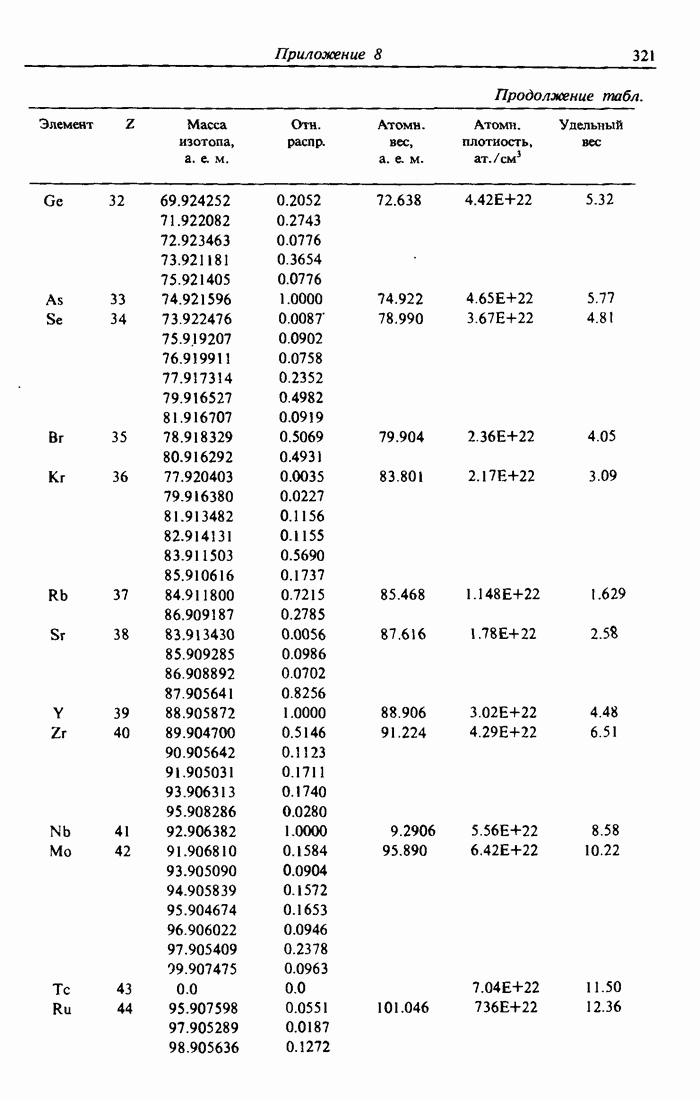
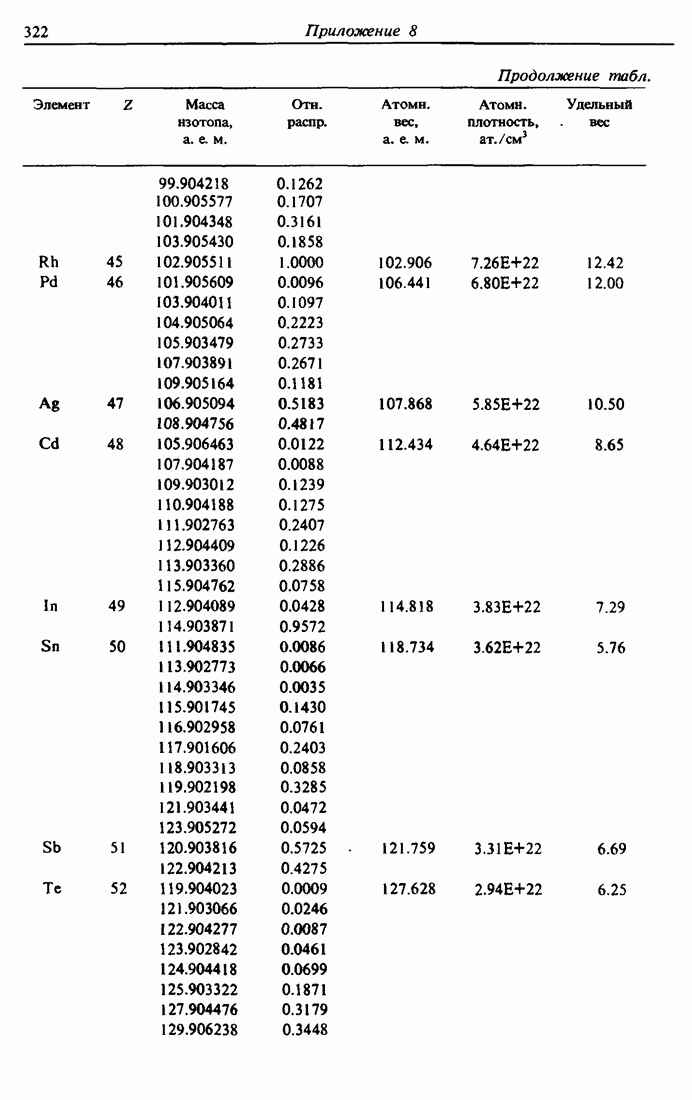
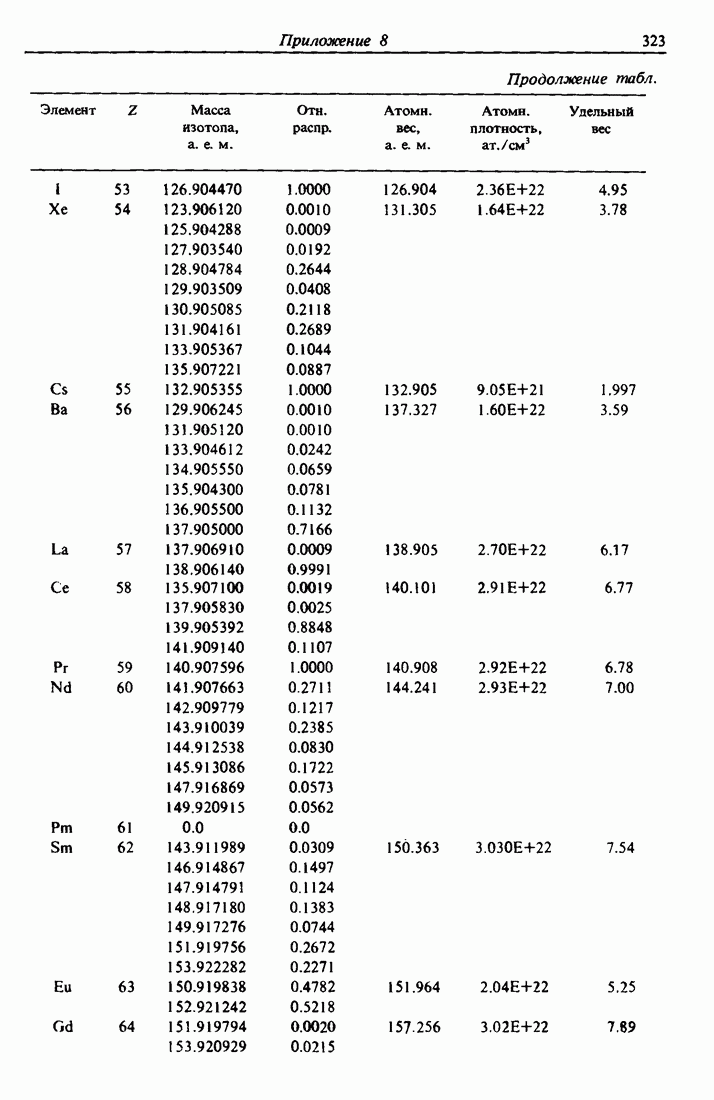
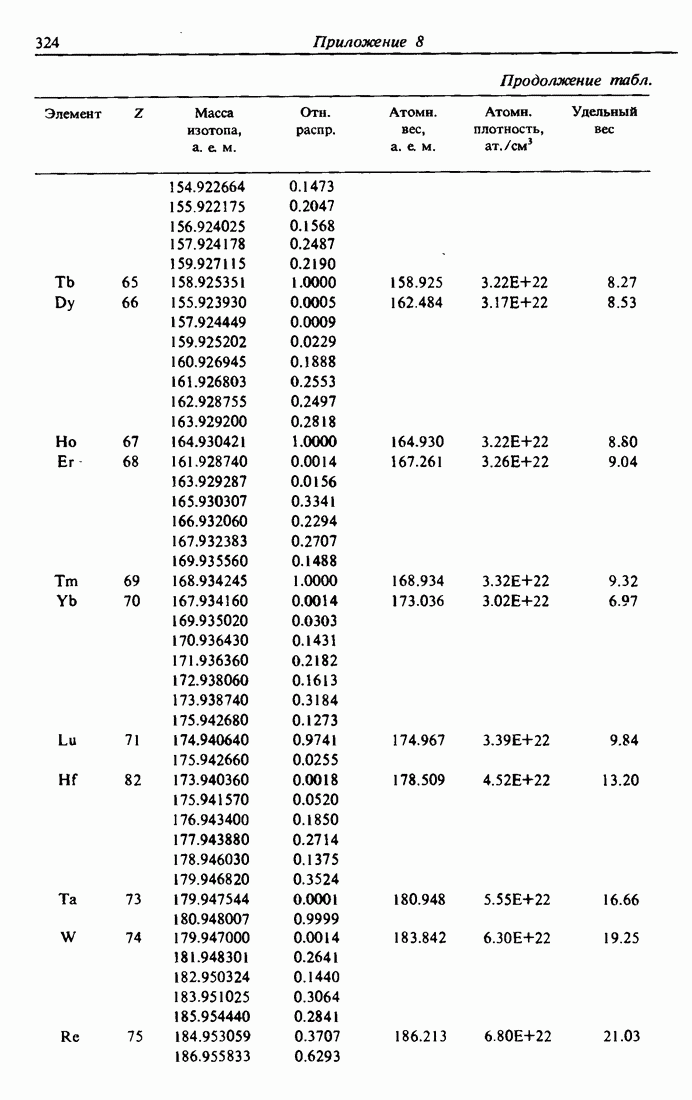
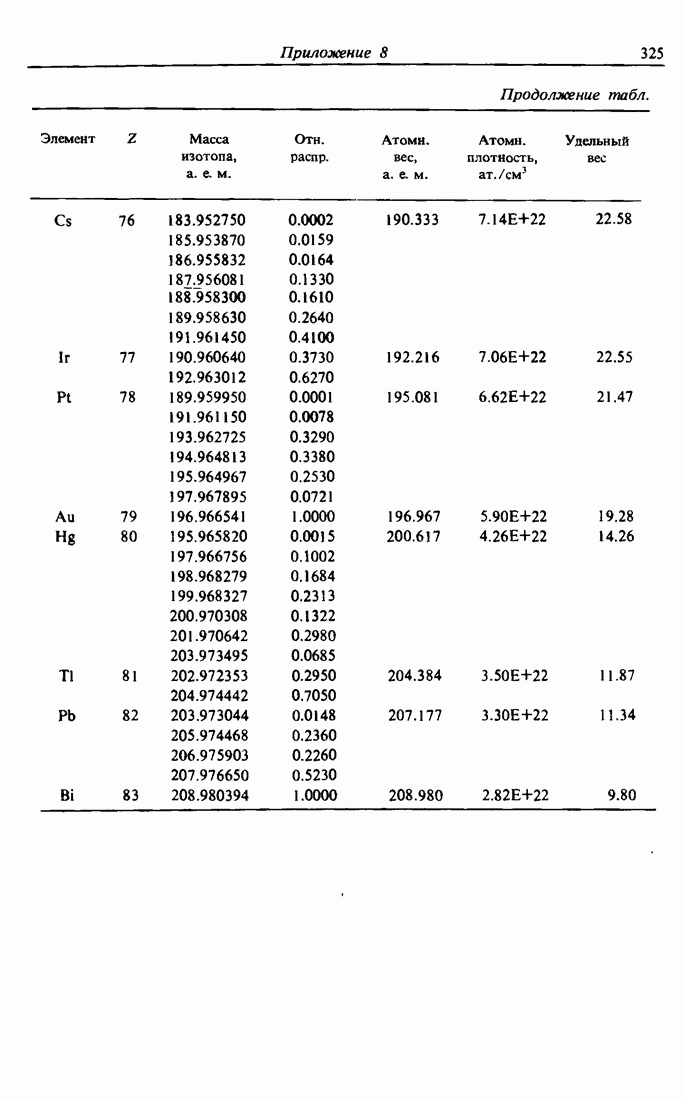
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
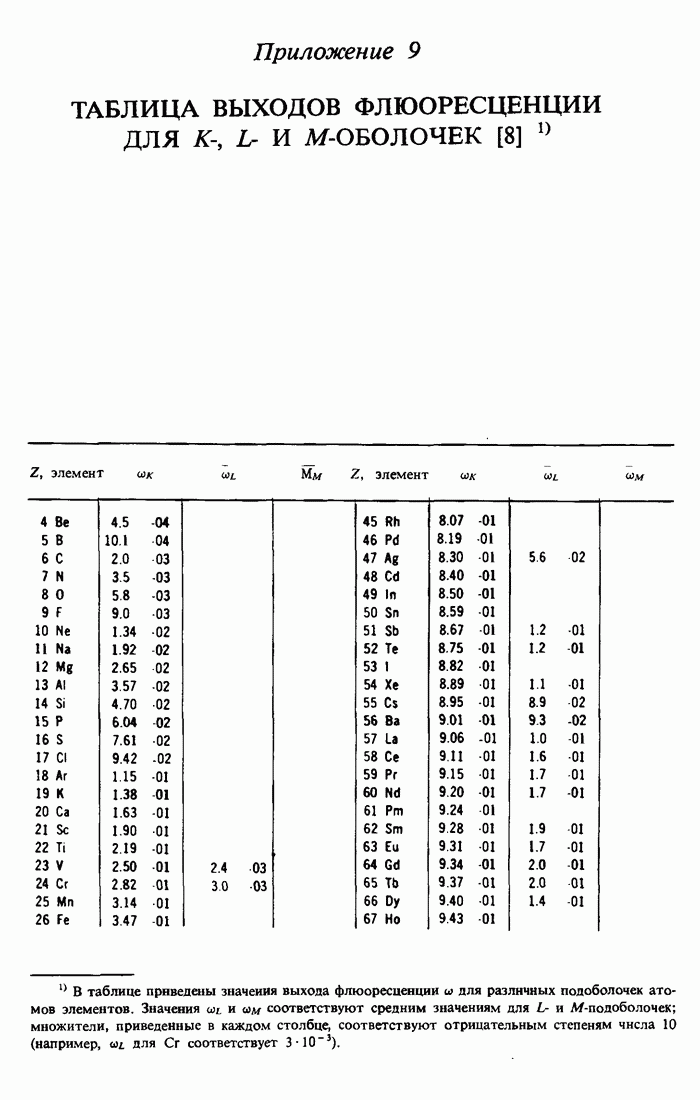
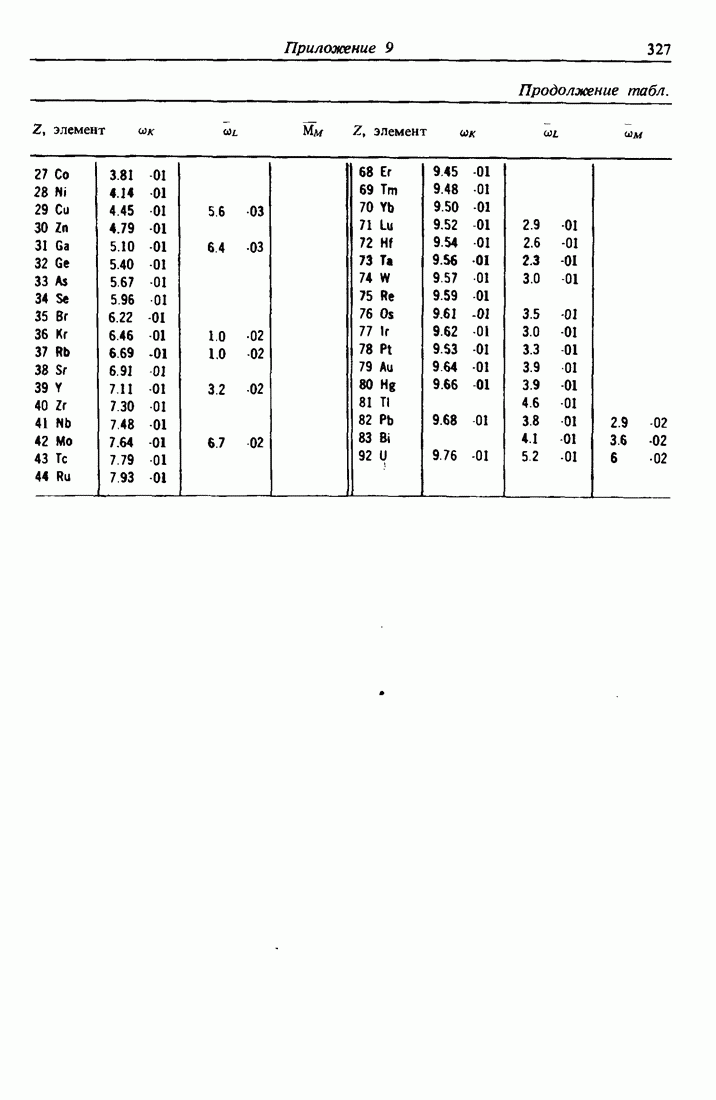
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ