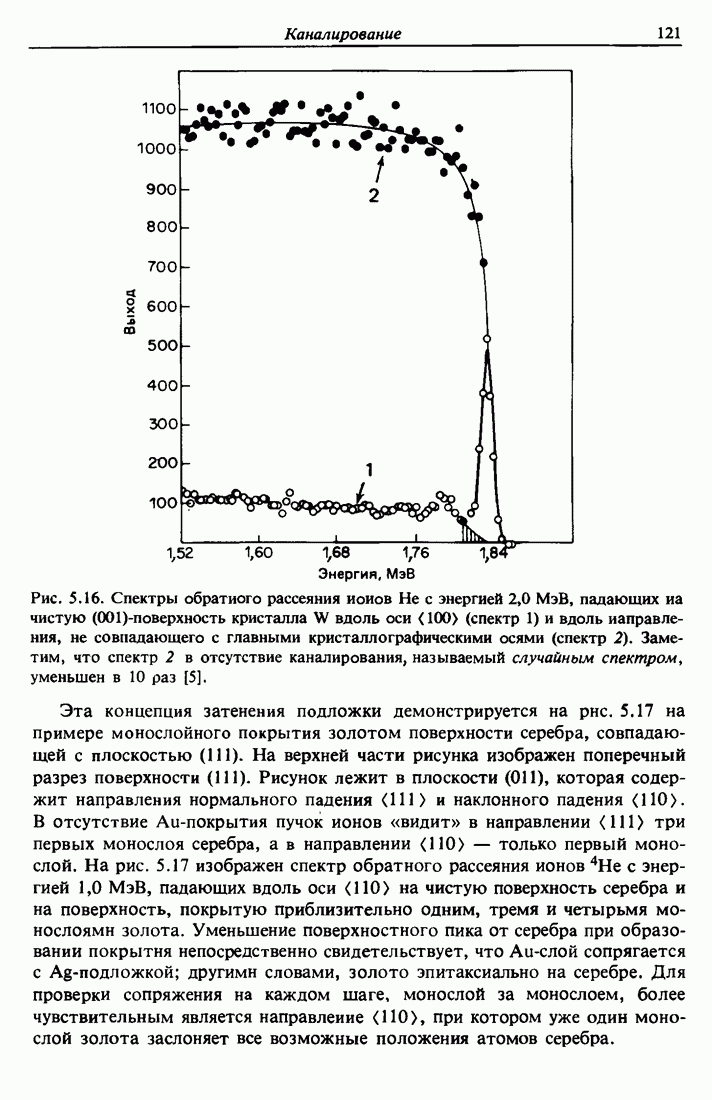
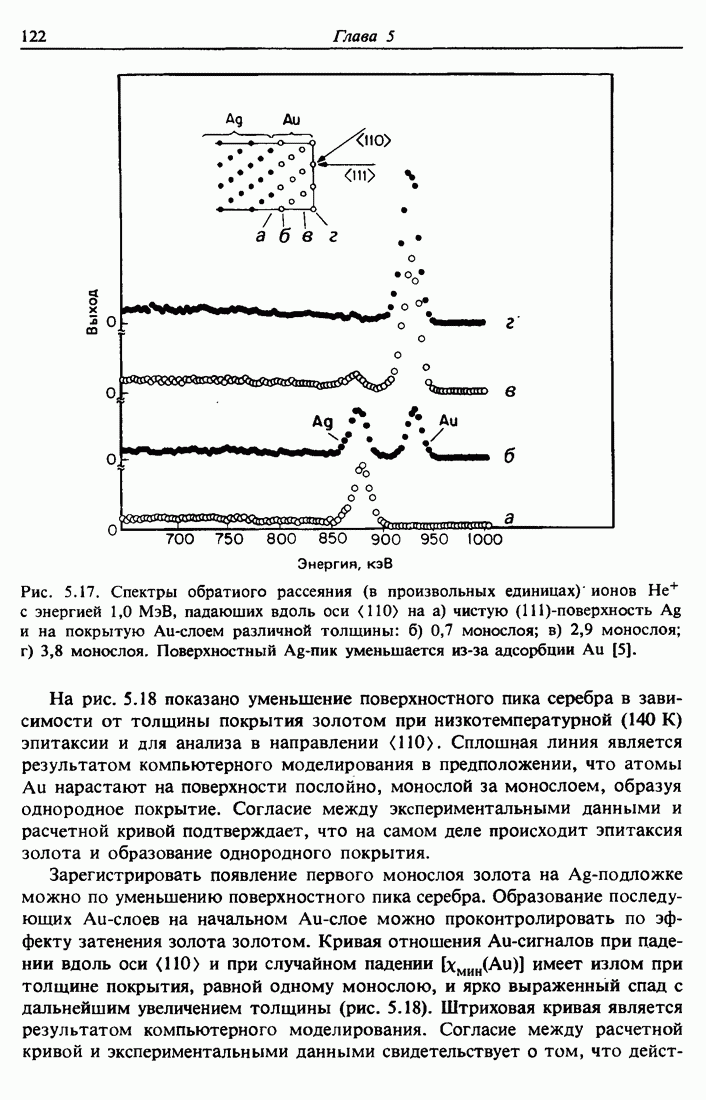
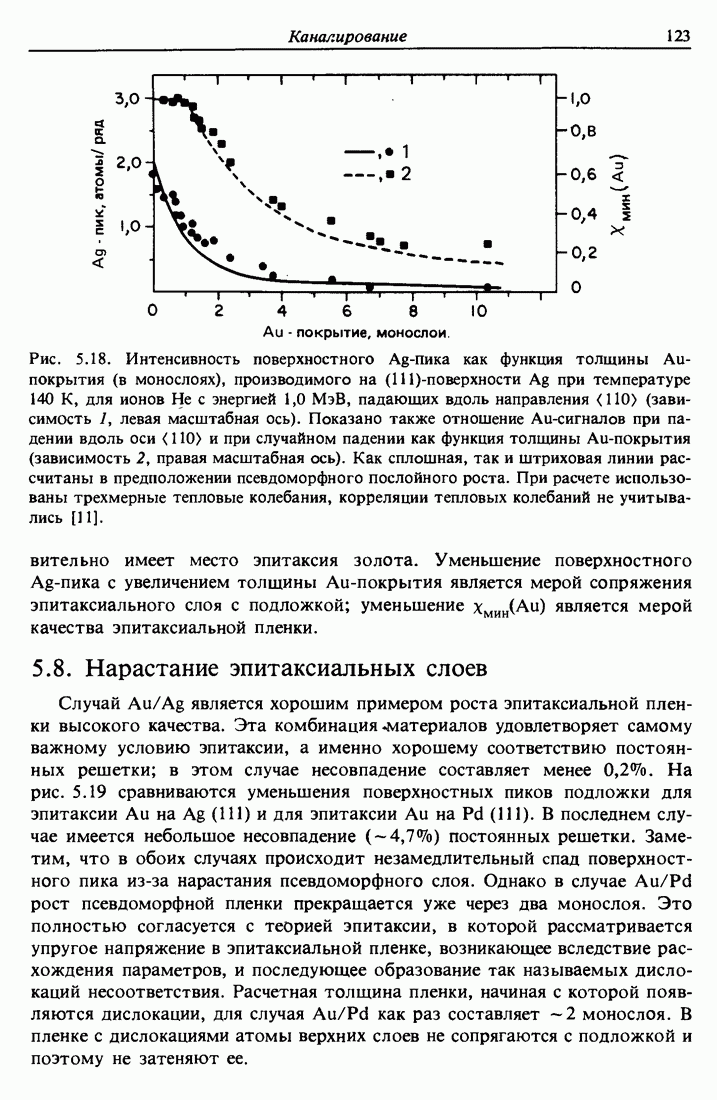
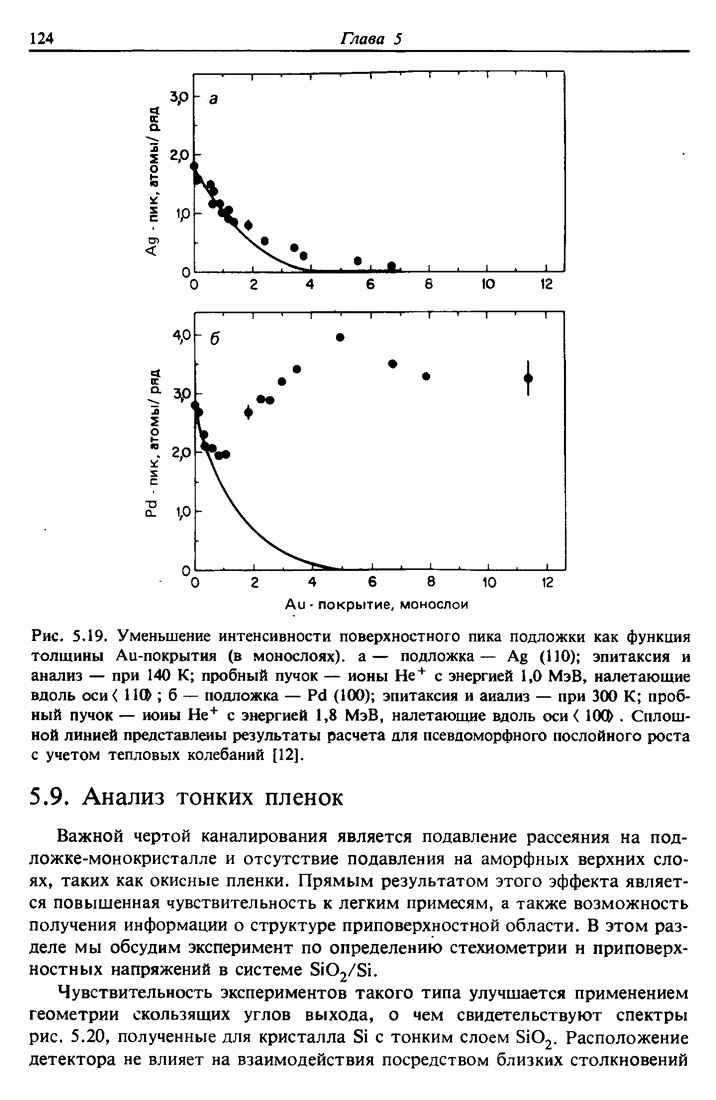
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
2.1. Введение
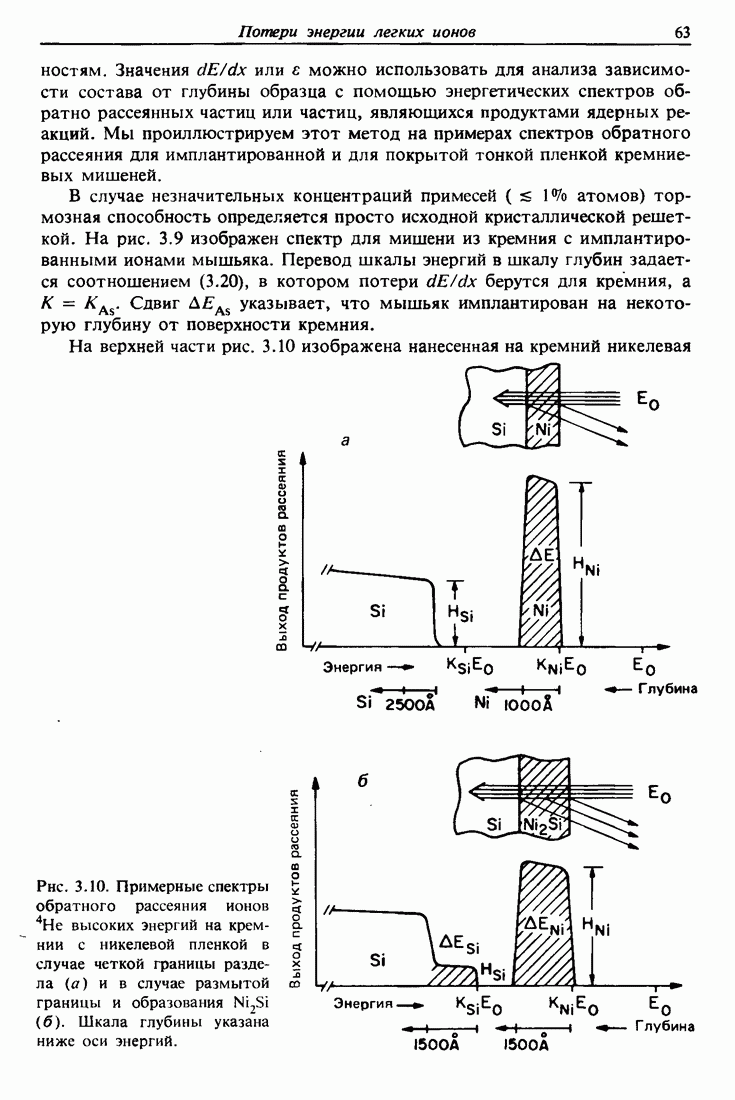
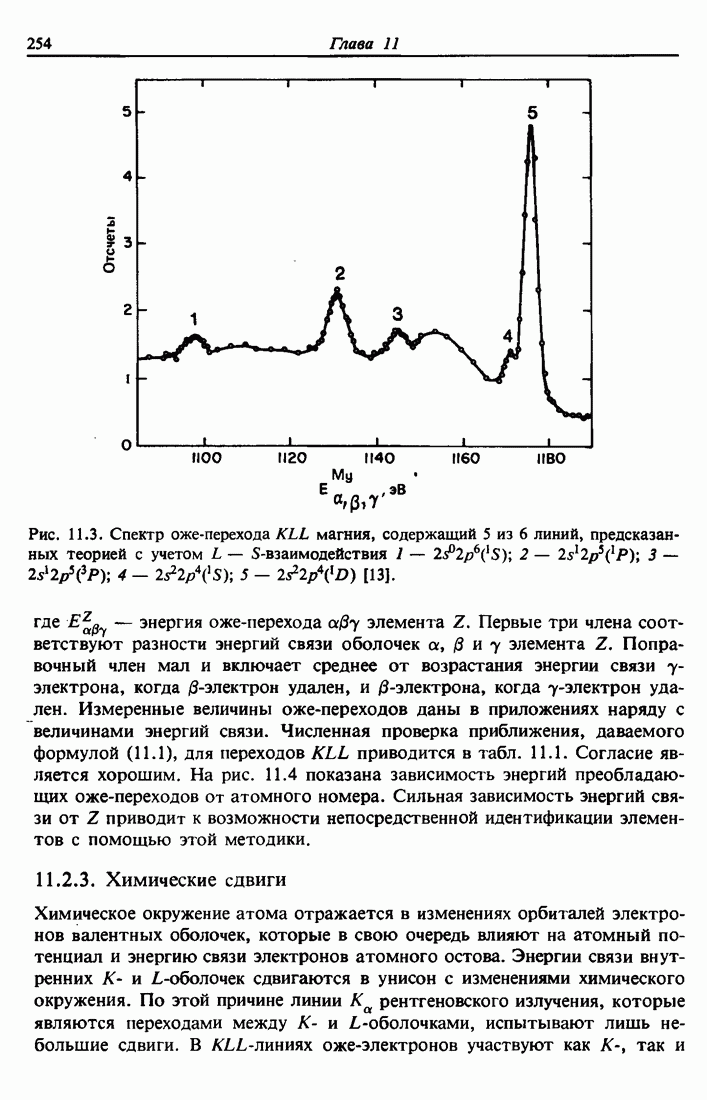
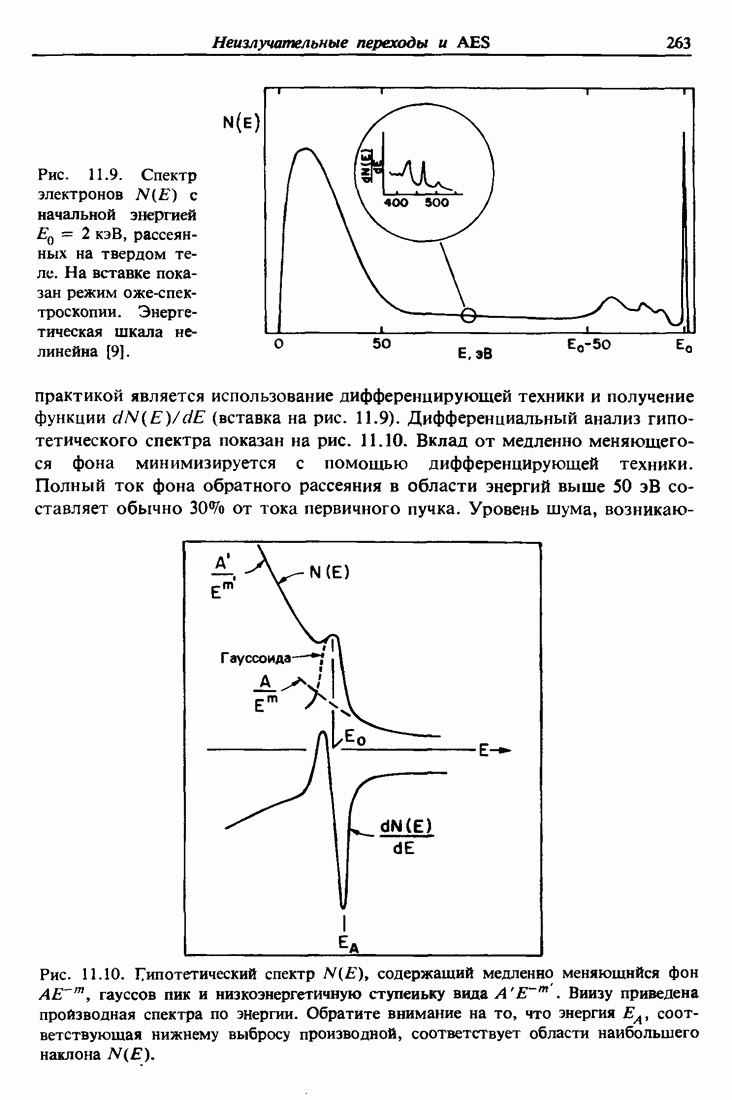
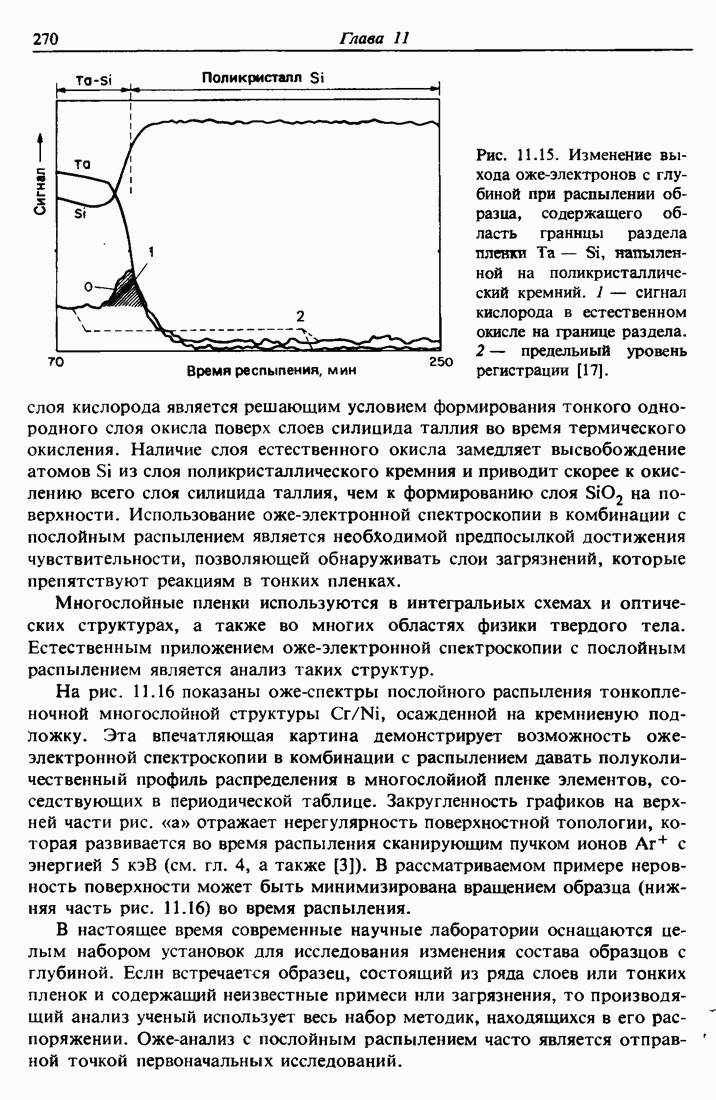
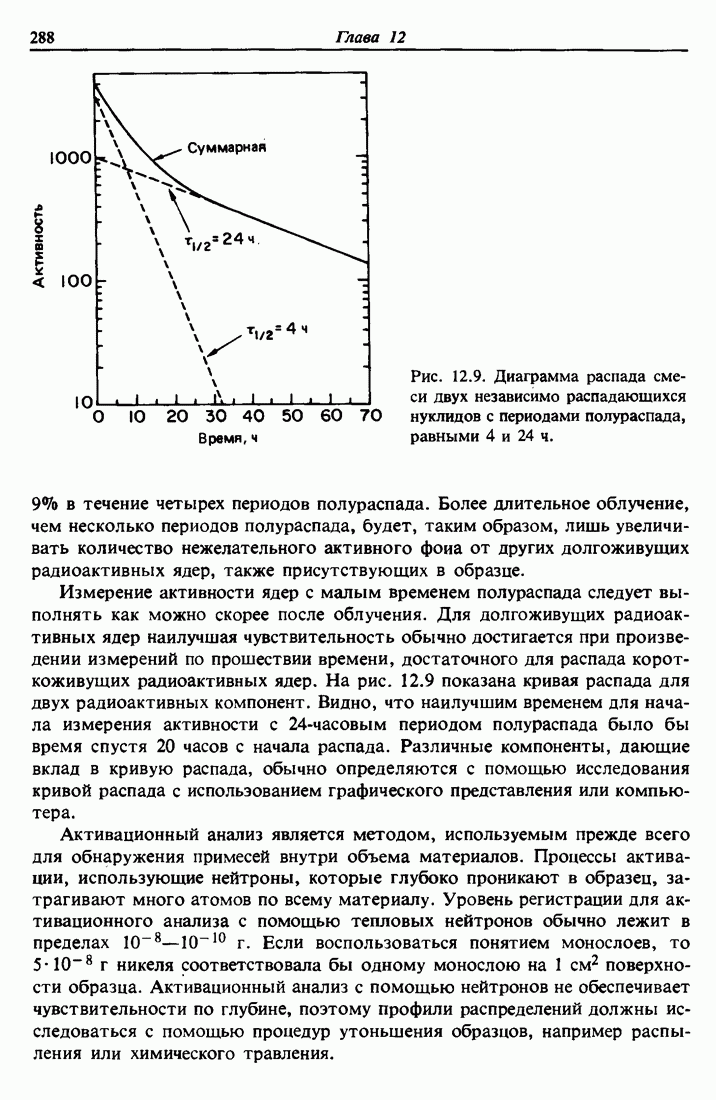
Рассмотрим модель атома в виде облака электронов вокруг положительно заряженного центра — ядра, содержащего Z протонов и А — Z нейтронов, где Z — атомный номер и А — массовое число. Однократное рассеяние а-частиц на большие утлы положительно заряженным ядром не только подтвердило правильность этой модели, но и лежит в основе одного современного метода исследования материалов — спектрометрии обратного рассеяния Резерфорда. В этой главе мы обсудим физические понятия, относящиеся к кулоновскому рассеянию быстрого легкого иона на более тяжелом неподвижном атоме.
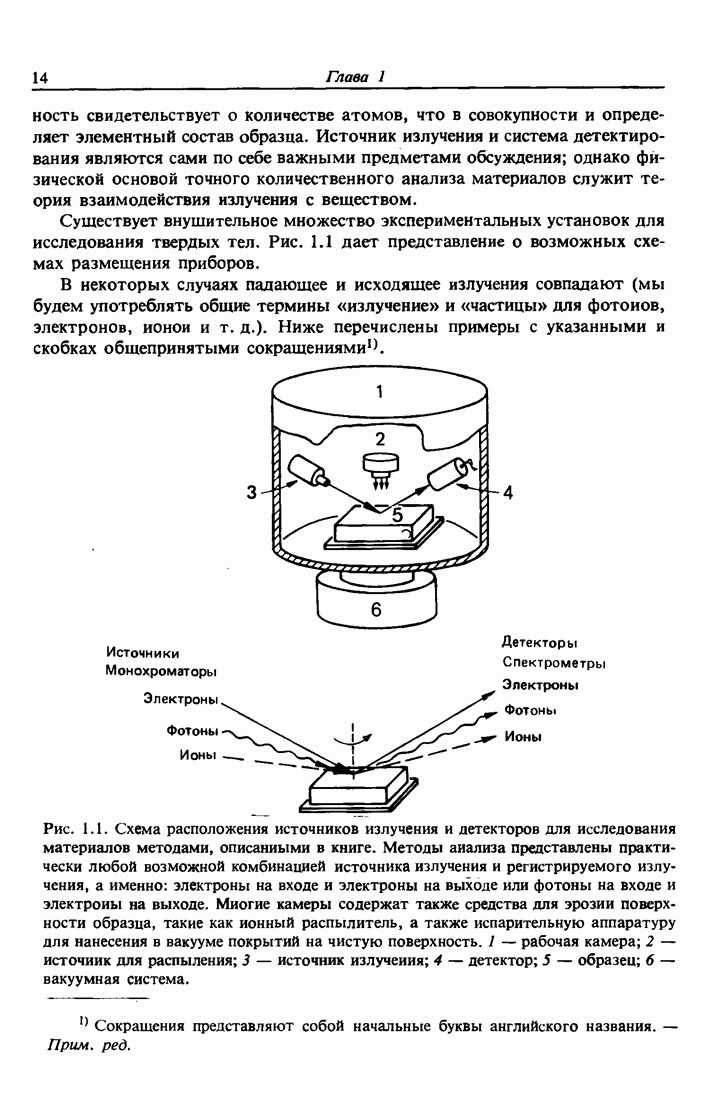
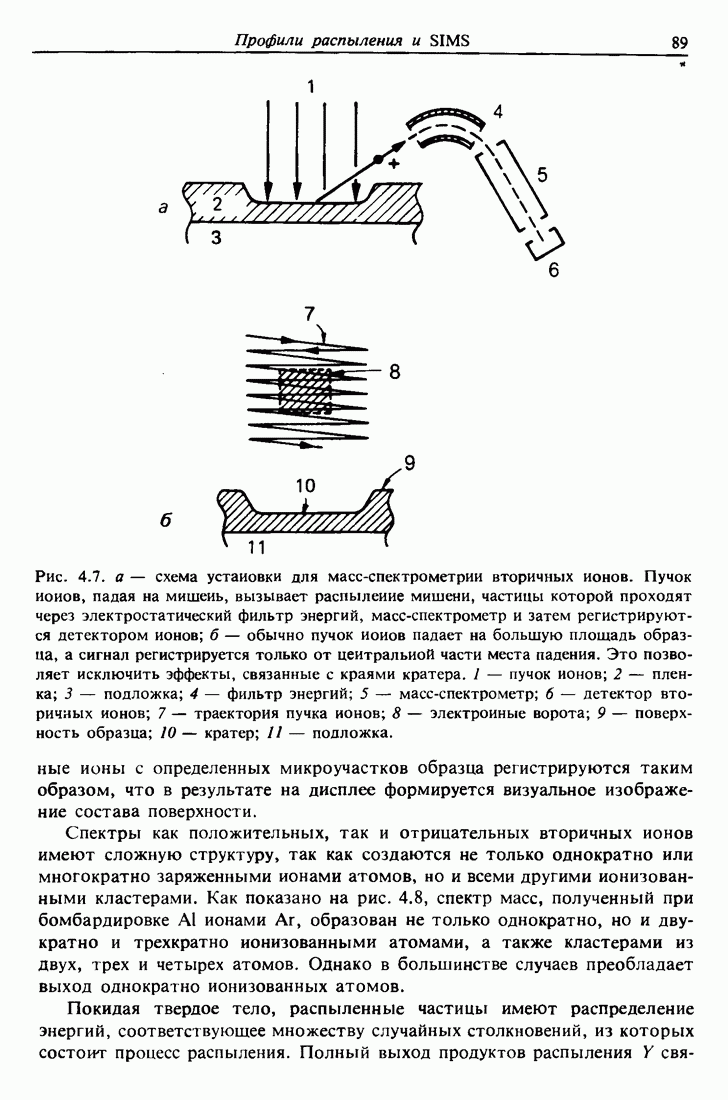
Из всех методов исследования обратное рассеяние Резерфорда является самым простым для понимания и применения, поскольку основывается на классическом рассеянии в поле центральных сил. За исключением ускорителя, обеспечивающего коллимированный пучок частиц с энергиями порядка нескольких мегаэлектронвольт (обычно это ионы  ), вся установка чрезвычайно проста (рис. 2.1, а). Для регистрации частиц используются полупроводниковые детекторы, которые формируют на выходе электрический импульс, пропорциональный энергии частиц, рассеянных образцом в направлении детектора. Этот метод анализа является наиболее точным, так как ионы Не с энергией в несколько мегаэлектронвольт испытывают столкновения при малых значениях прицельного параметра и отклоняются хорошо известными силами кулоновского отталкивания, действующими между положительно заряженными ядрами налетающих частиц и атомов мишени. Кинематика столкновения и сечение рассеяния не зависят от химических связей, поэтому измеренные характеристики обратного рассеяния нечувствительны к электронной конфигурации и химическим связям внутри мишени. Для получения информации об электронной конфигурации необходимо использовать другие методы анализа, такие как фотоэлектронная спектроскопия, основанная на переходах в электронной оболочке.
), вся установка чрезвычайно проста (рис. 2.1, а). Для регистрации частиц используются полупроводниковые детекторы, которые формируют на выходе электрический импульс, пропорциональный энергии частиц, рассеянных образцом в направлении детектора. Этот метод анализа является наиболее точным, так как ионы Не с энергией в несколько мегаэлектронвольт испытывают столкновения при малых значениях прицельного параметра и отклоняются хорошо известными силами кулоновского отталкивания, действующими между положительно заряженными ядрами налетающих частиц и атомов мишени. Кинематика столкновения и сечение рассеяния не зависят от химических связей, поэтому измеренные характеристики обратного рассеяния нечувствительны к электронной конфигурации и химическим связям внутри мишени. Для получения информации об электронной конфигурации необходимо использовать другие методы анализа, такие как фотоэлектронная спектроскопия, основанная на переходах в электронной оболочке.
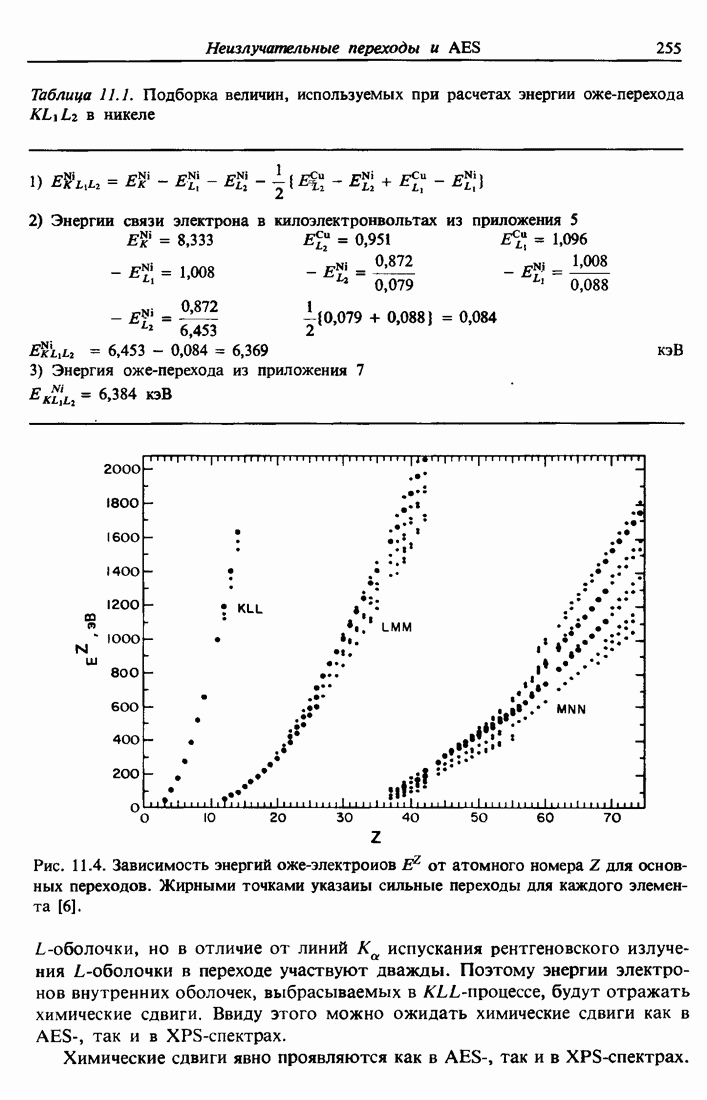
В этой главе мы рассмотрим столкновение двух положительно заряженных ядер с атомными номерами  . Индекс 1 относится везде к налетающей частице, а индекс 2 — к атому мишени. Сначала найдем переданную при столкновении энергию, так как эта величина позволяет идентифицировать атом мишени. Затем вычислим сечение рассеяния, которое является основой количественной теории рассеяния Резерфорда. В этой главе мы имеем дело с рассеянием только на атомах поверхности образца или на тонких пленках.
. Индекс 1 относится везде к налетающей частице, а индекс 2 — к атому мишени. Сначала найдем переданную при столкновении энергию, так как эта величина позволяет идентифицировать атом мишени. Затем вычислим сечение рассеяния, которое является основой количественной теории рассеяния Резерфорда. В этой главе мы имеем дело с рассеянием только на атомах поверхности образца или на тонких пленках.

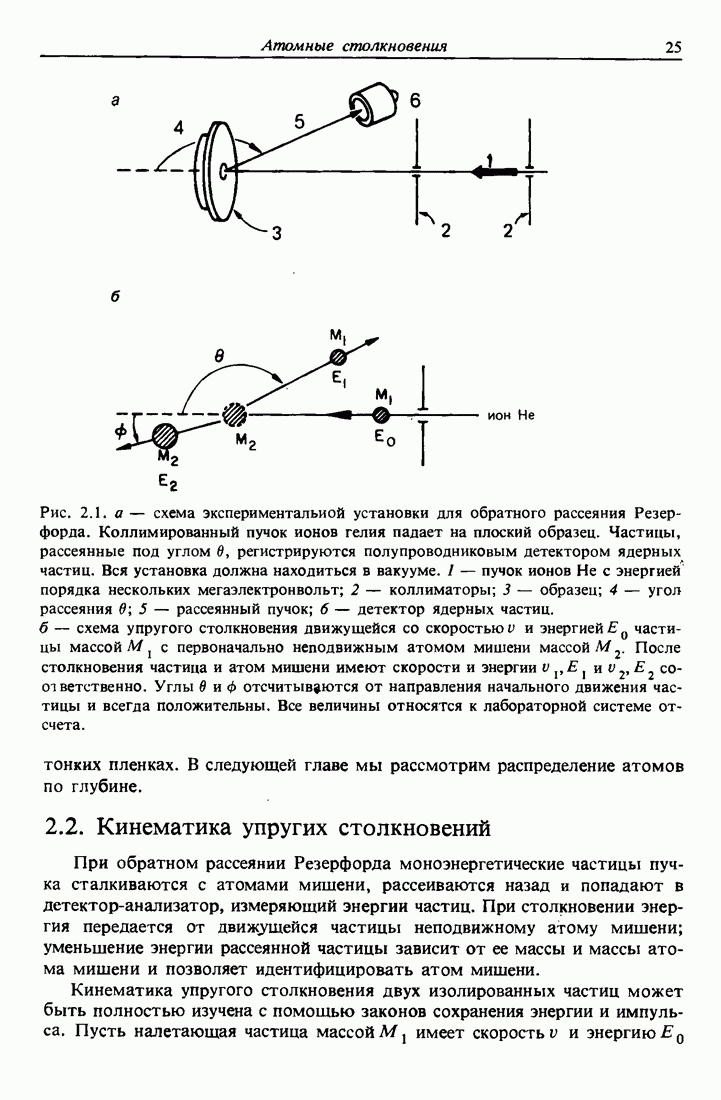
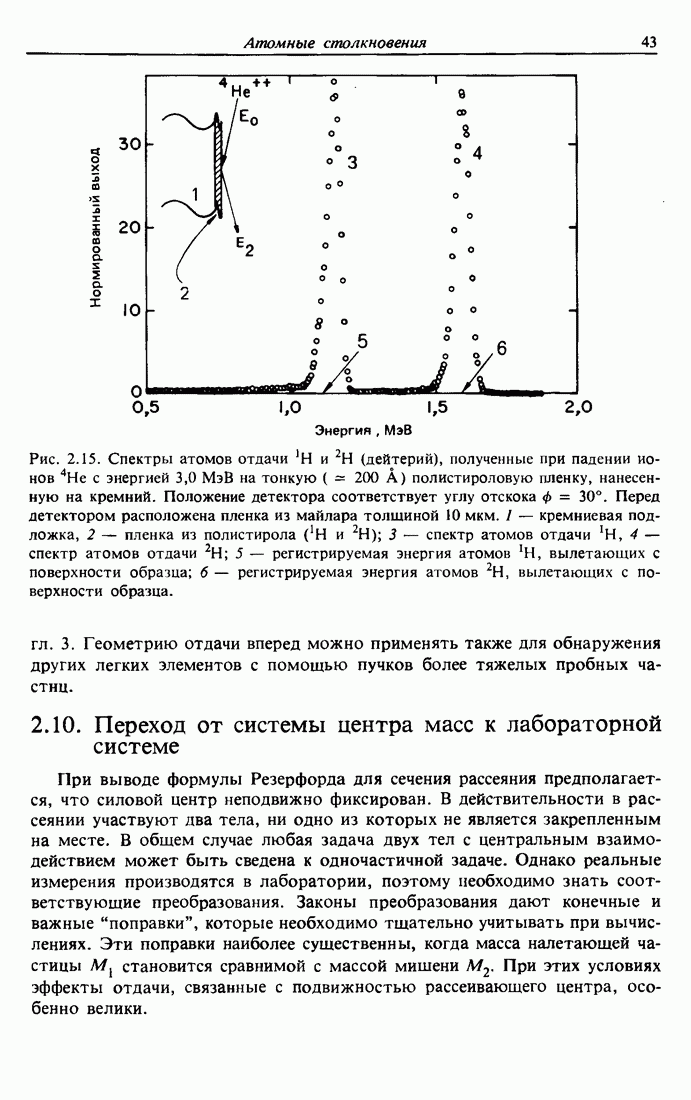
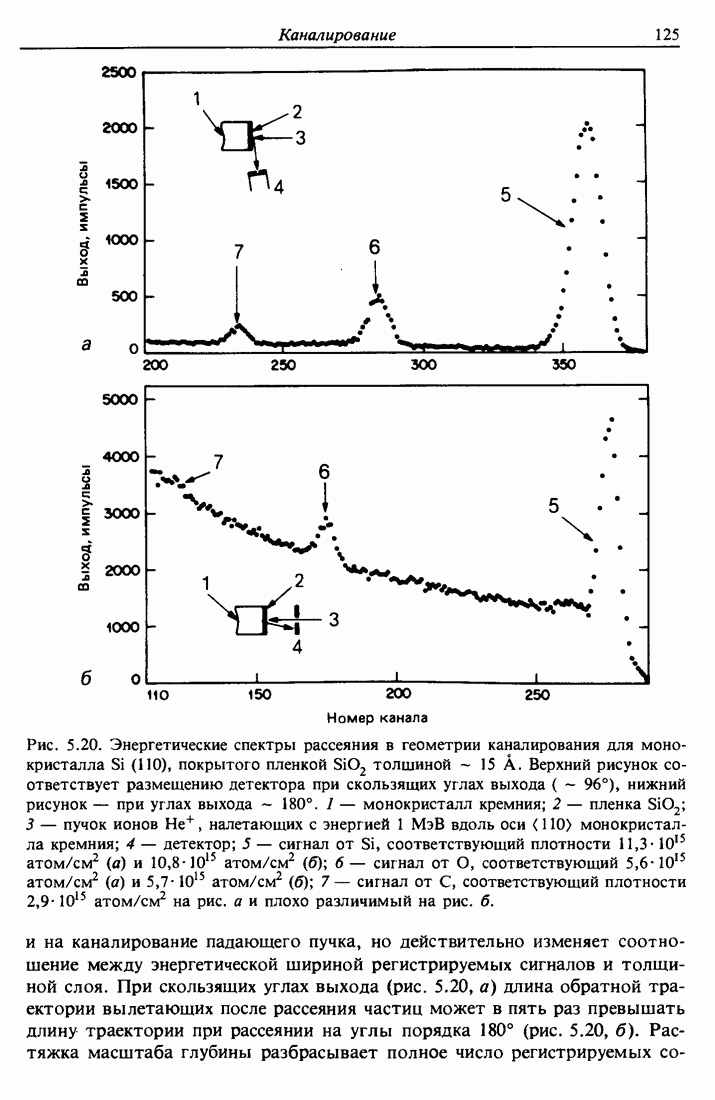
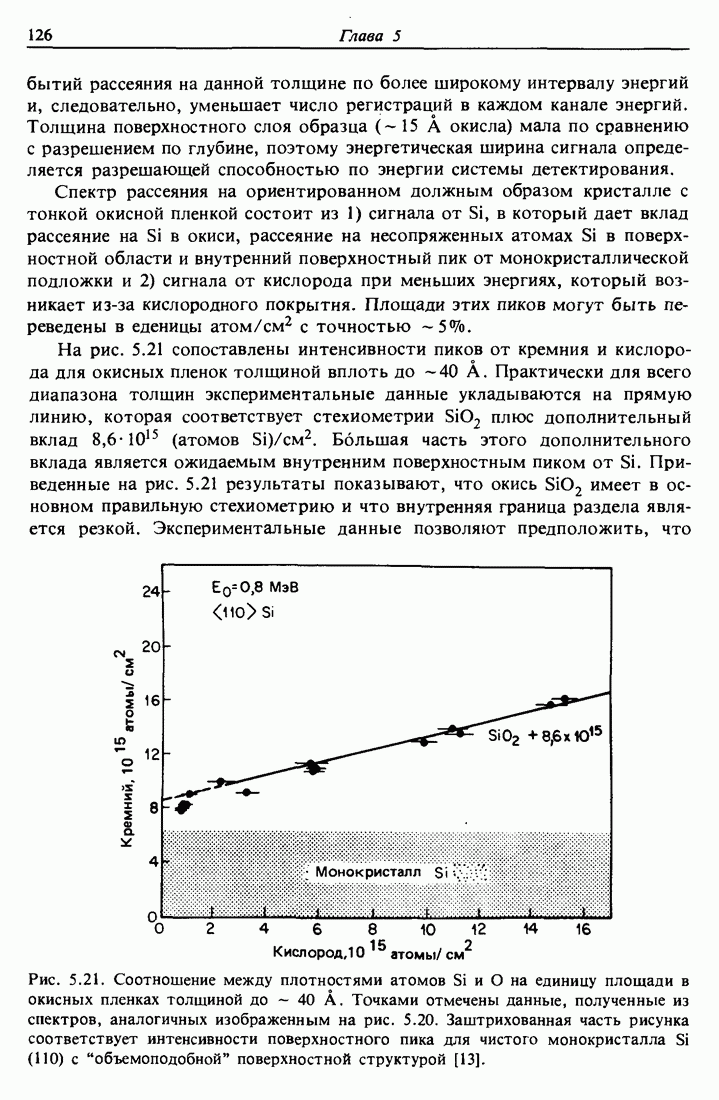
Рис. 2.1. а — схема экспериментальной установки для обратного рассеяния Резерфорда. Коллимированный пучок ионов гелия падает на плоский образец. Частицы, рассеянные под углом  , регистрируются полупроводниковым детектором ядерных частиц. Вся установка должна находиться в вакууме. 1 — пучок ионов Не с энергией порядка нескольких мегаэлектронвольт; 2 — коллиматоры; 3 — образец; 4 — угол рассеяния
, регистрируются полупроводниковым детектором ядерных частиц. Вся установка должна находиться в вакууме. 1 — пучок ионов Не с энергией порядка нескольких мегаэлектронвольт; 2 — коллиматоры; 3 — образец; 4 — угол рассеяния  ; 5 — рассеянный пучок; 6 — детектор ядерных частиц. б — схема упругого столкновения движущейся со скоростью
; 5 — рассеянный пучок; 6 — детектор ядерных частиц. б — схема упругого столкновения движущейся со скоростью  и энергией
и энергией  частицы массой М с первоначально неподвижным атомом мишени массой М После столкновения частица и атом мишени имеют скорости и энергии
частицы массой М с первоначально неподвижным атомом мишени массой М После столкновения частица и атом мишени имеют скорости и энергии  соответственно. Углы
соответственно. Углы  и
и  отсчитывются от направления начального движения частицы и всегда положительны. Все величины относятся к лабораторной системе отсчета.
отсчитывются от направления начального движения частицы и всегда положительны. Все величины относятся к лабораторной системе отсчета.
В следующей главе мы рассмотрим распределение атомов по глубине.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
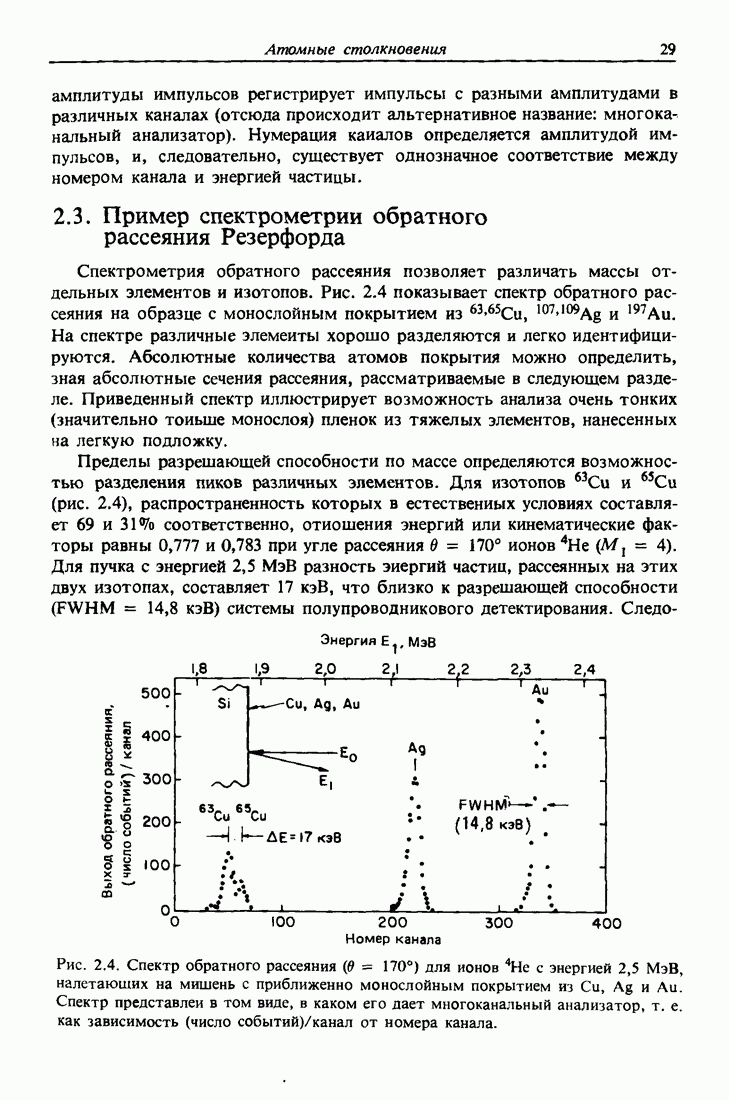
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
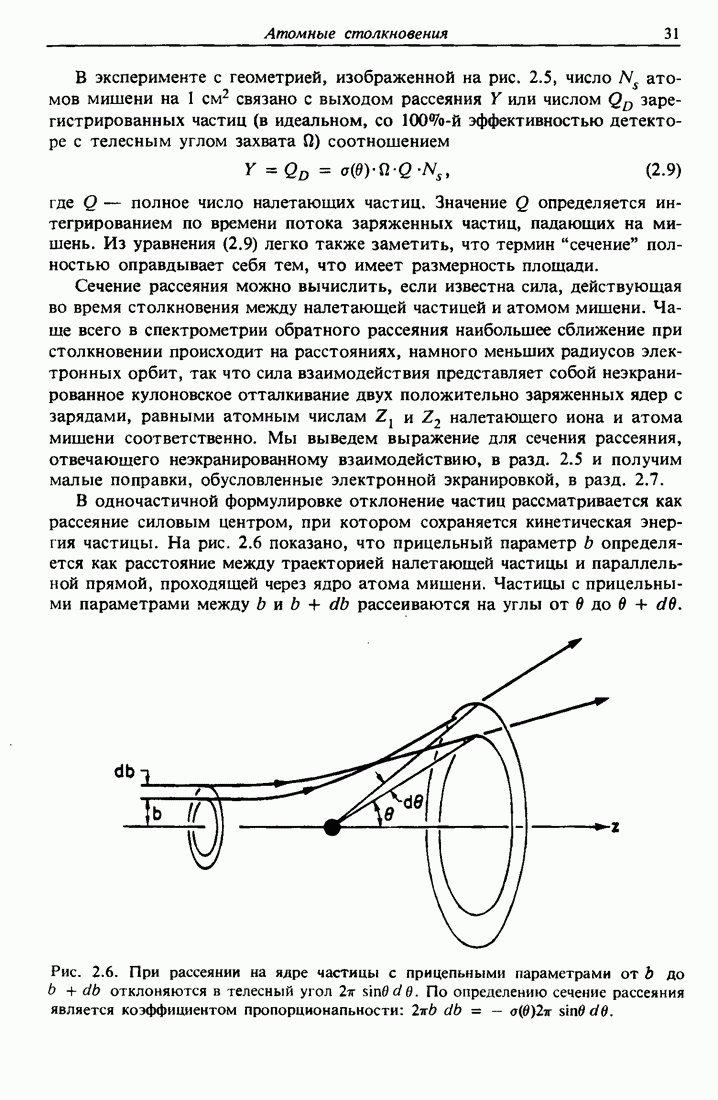
- 2.4. Сечение рассеяния и прицельный параметр
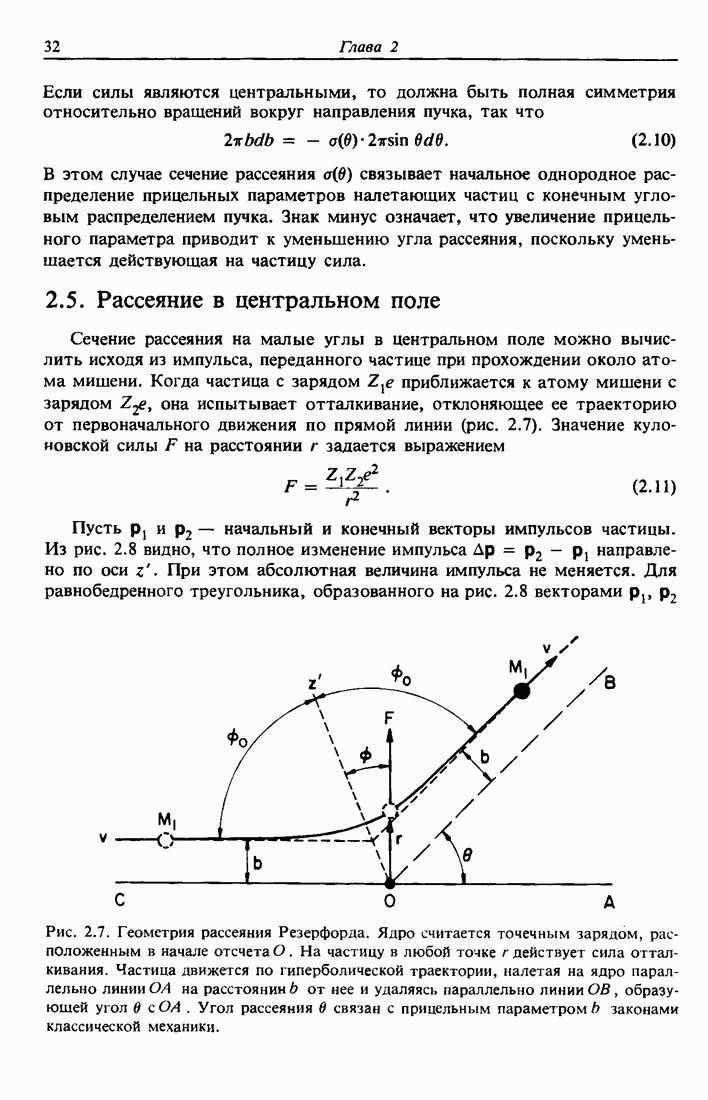
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
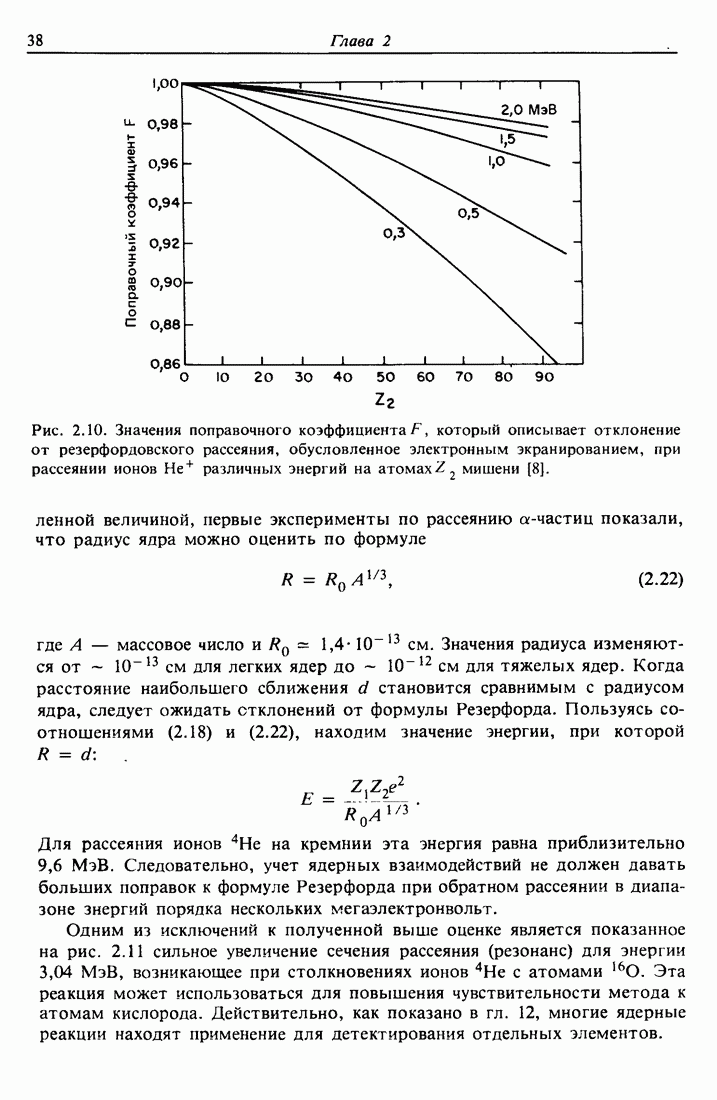
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
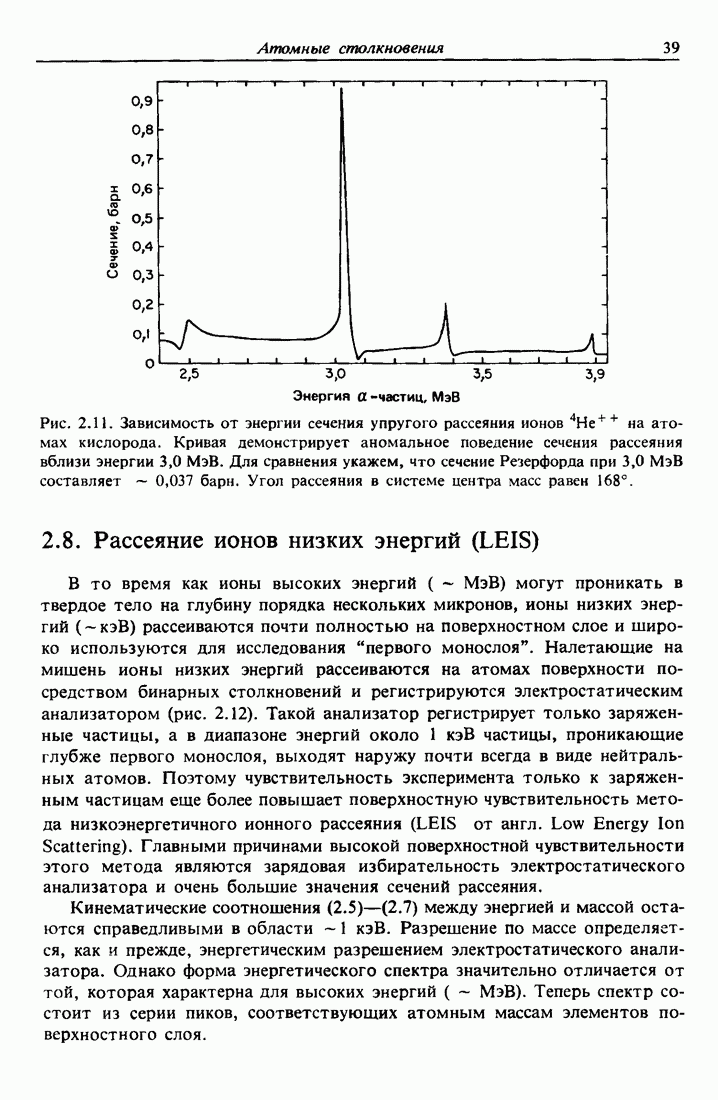
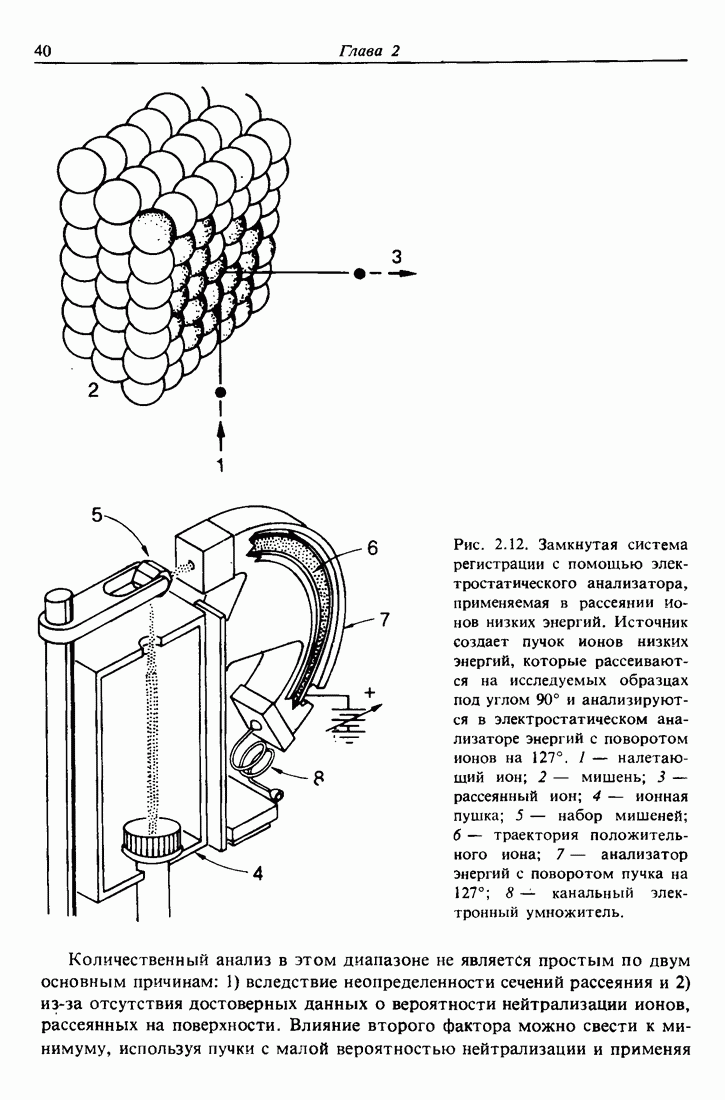
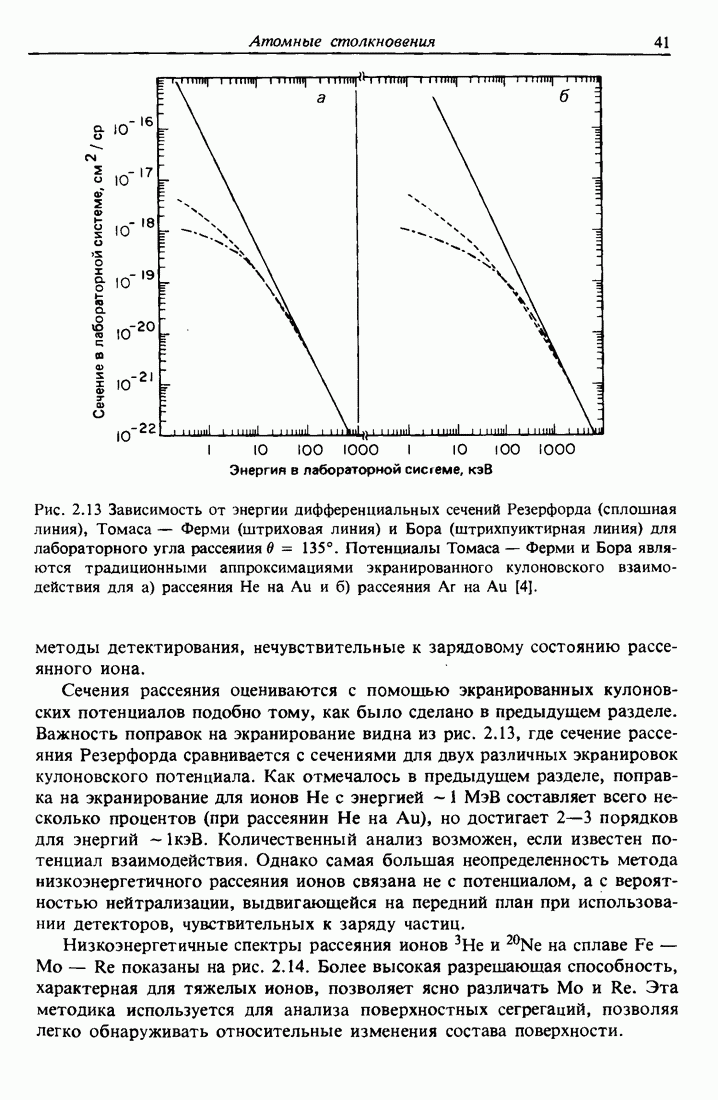
- 2.8. Рассеяние ионов низких энергий (LEIS)
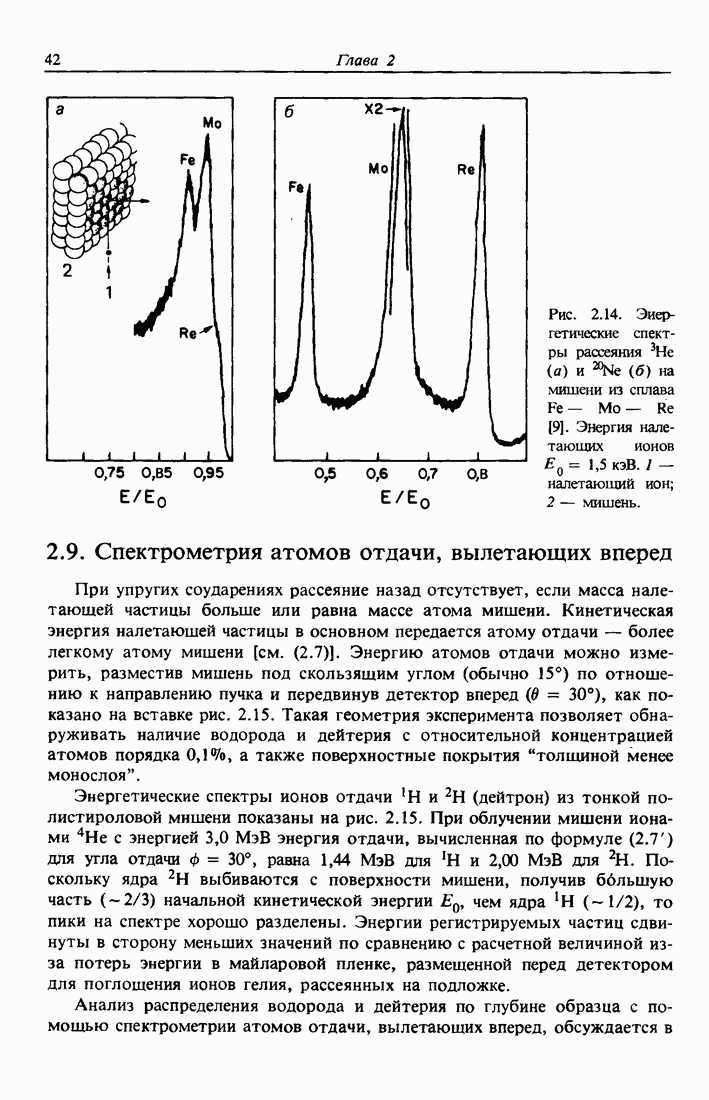
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
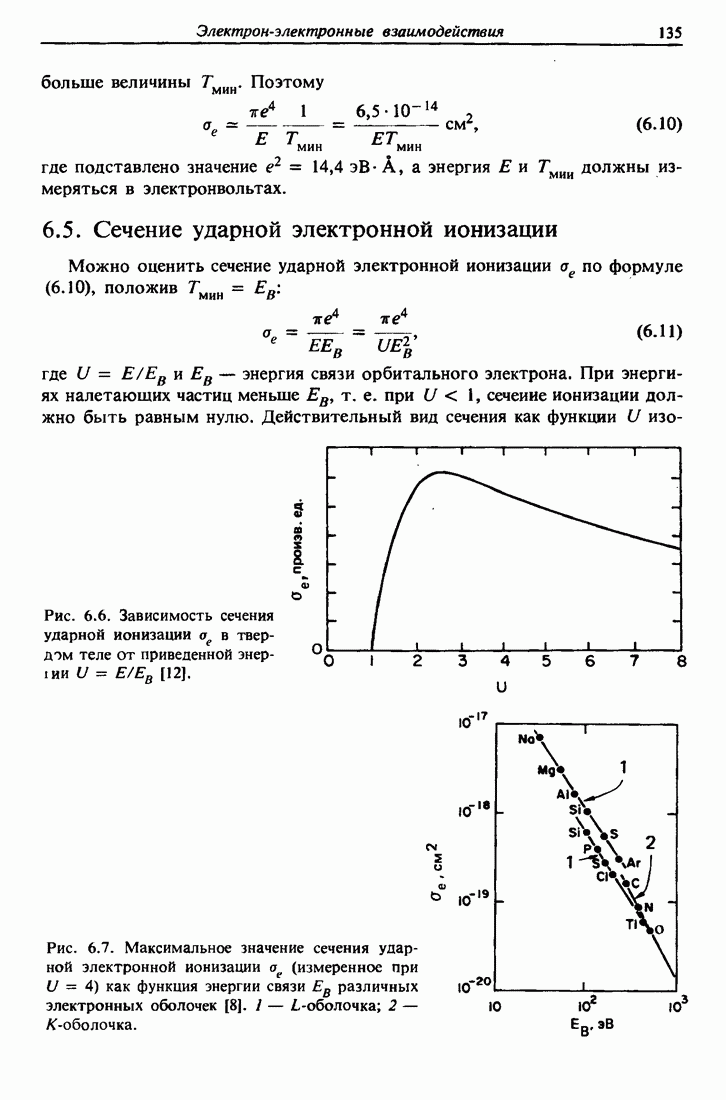
- 6.5. Сечение ударной электронной ионизации
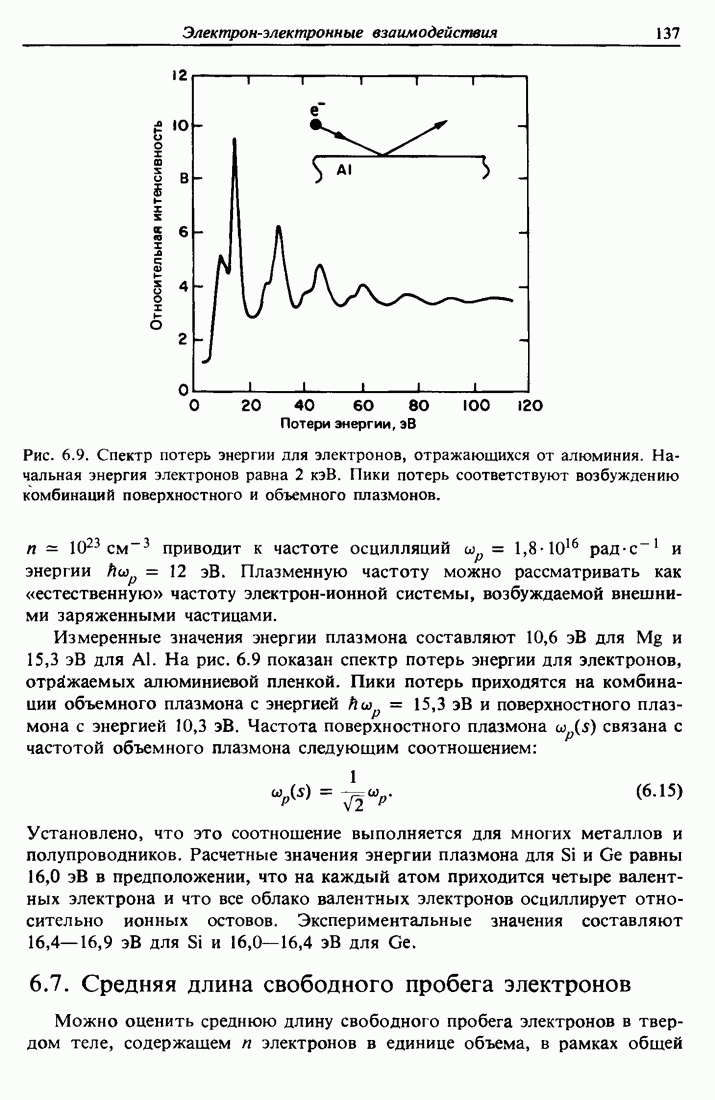
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
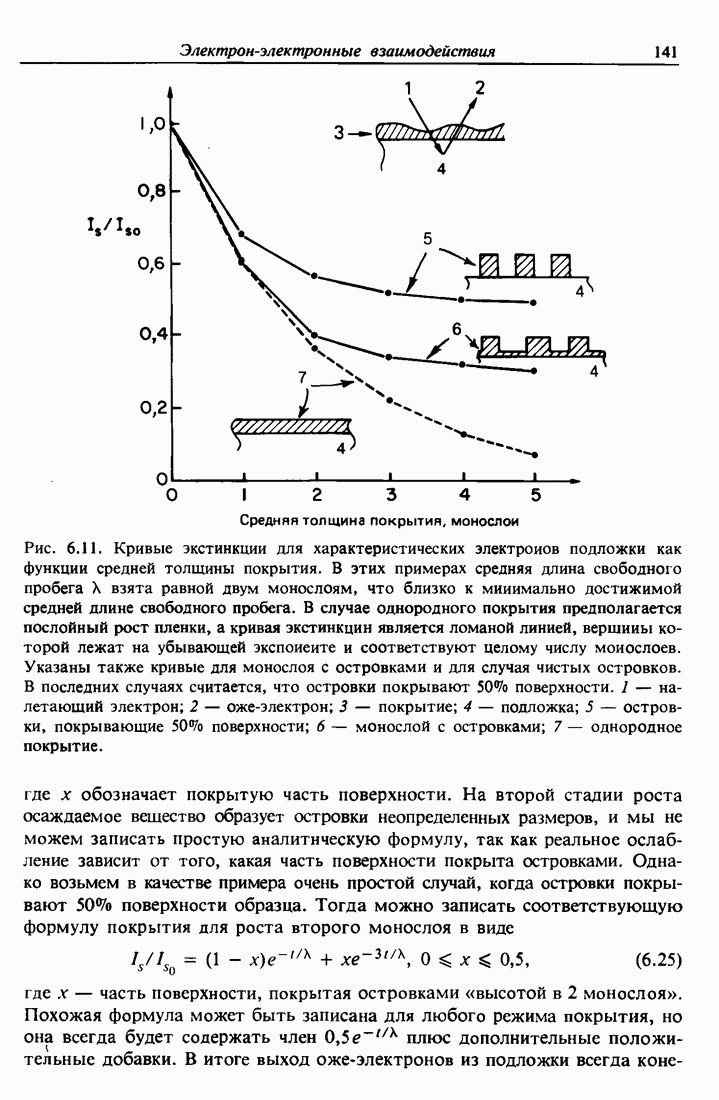
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
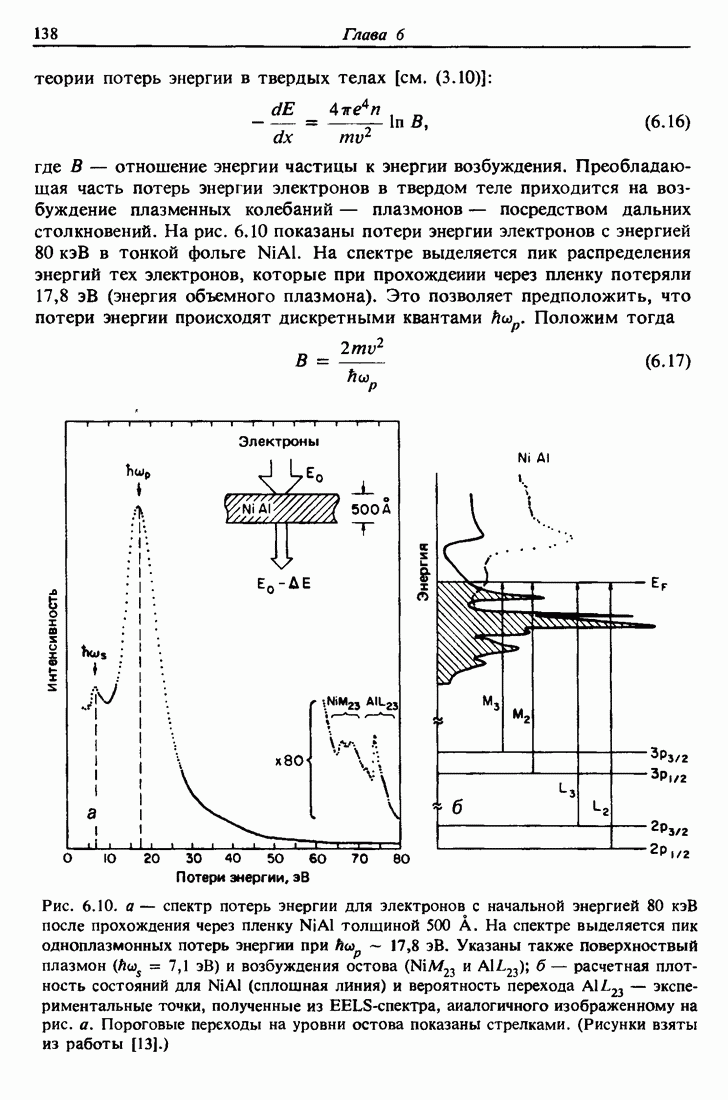
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
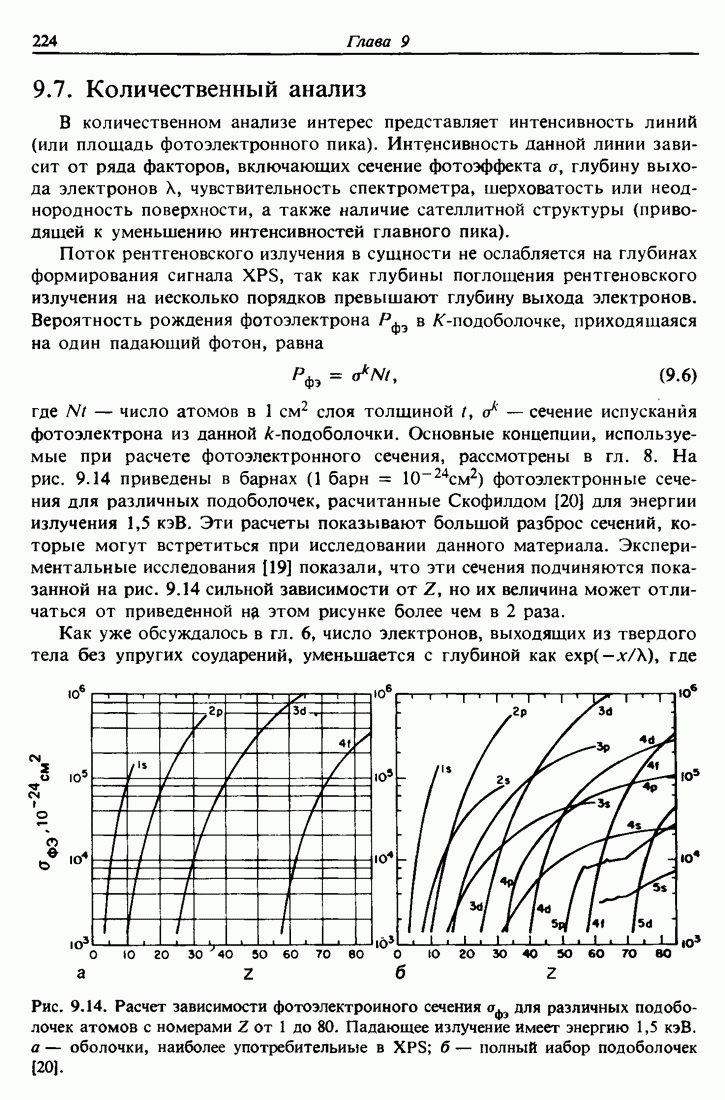
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
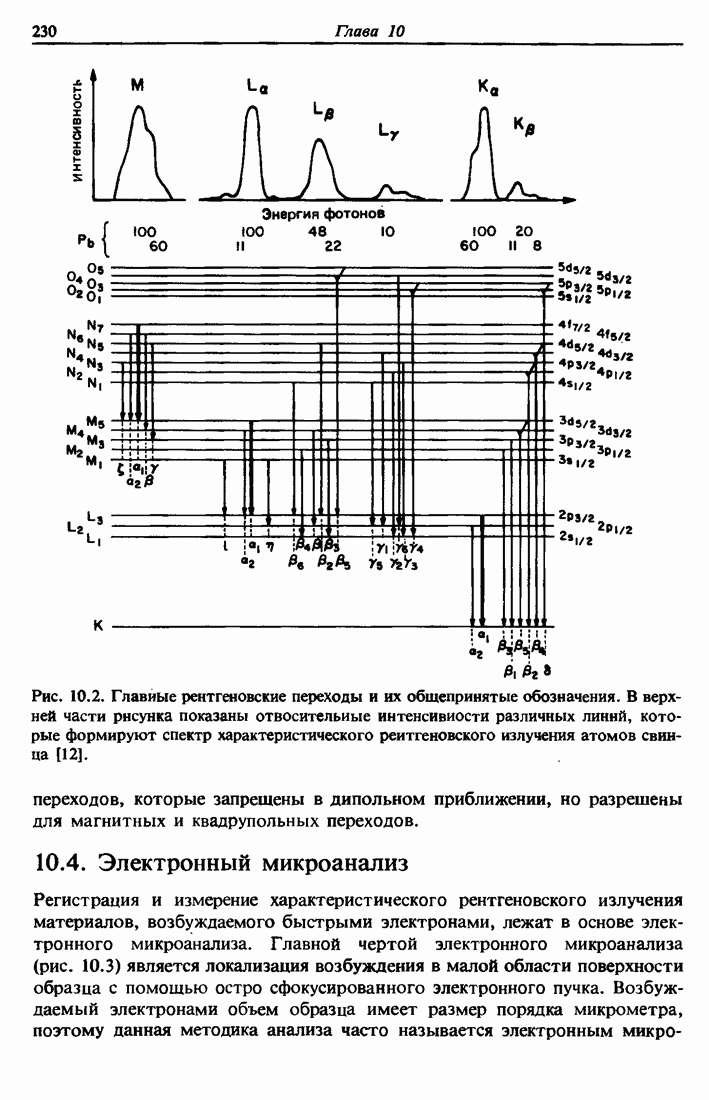
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
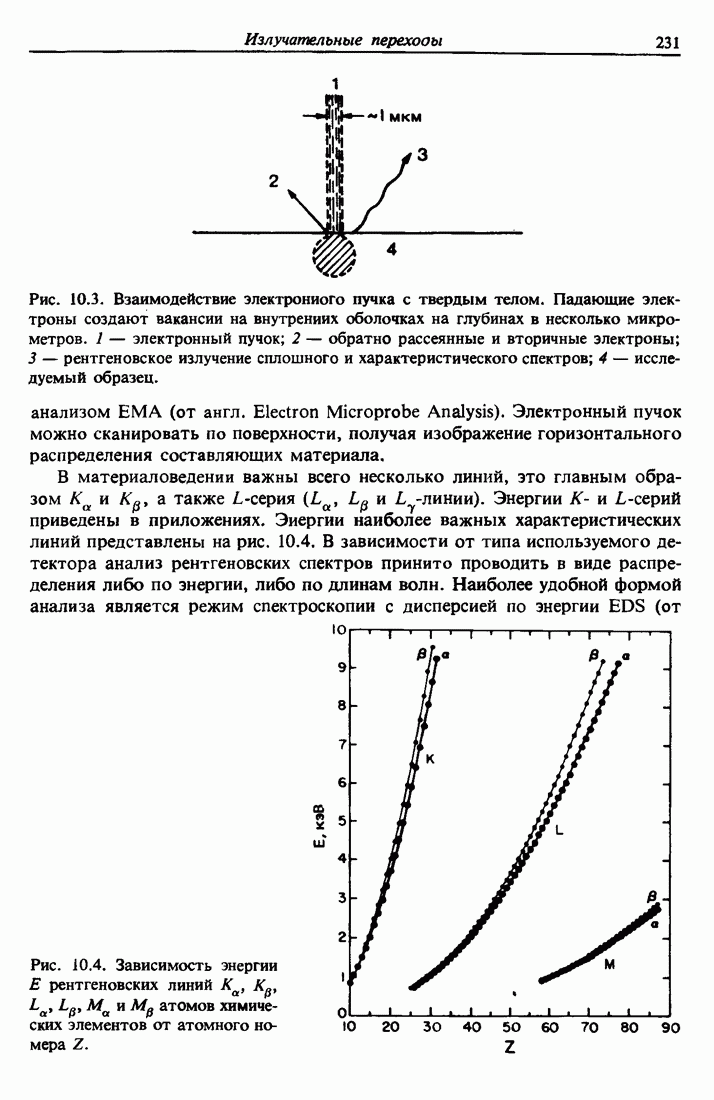
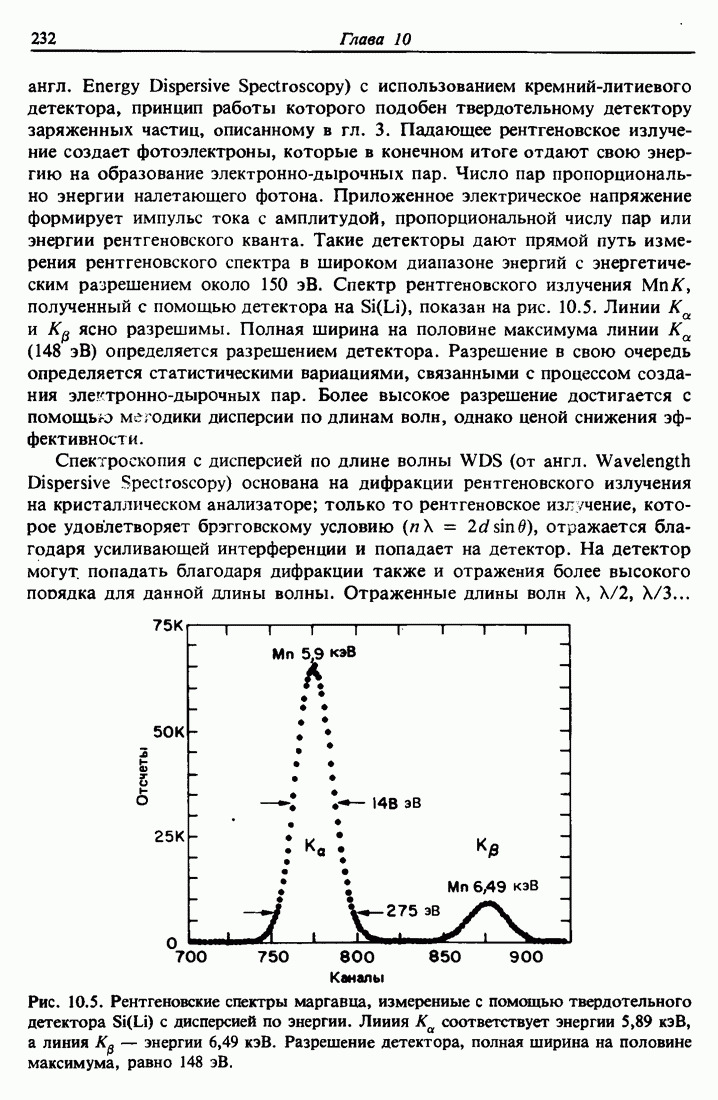
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
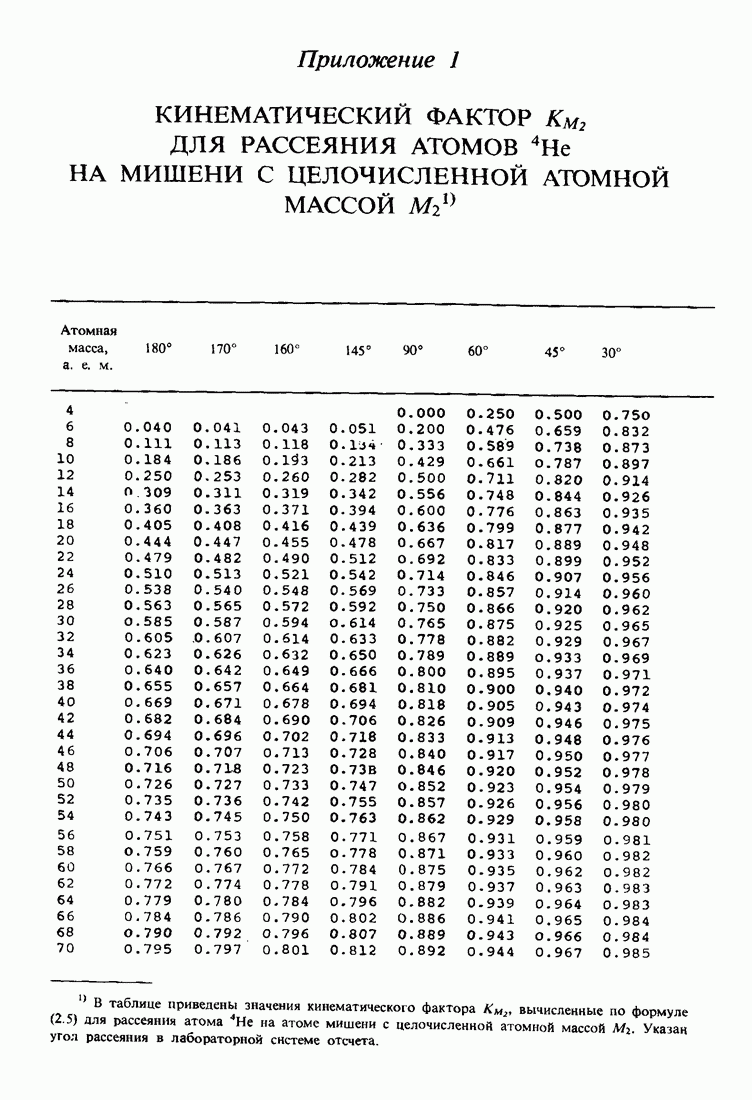
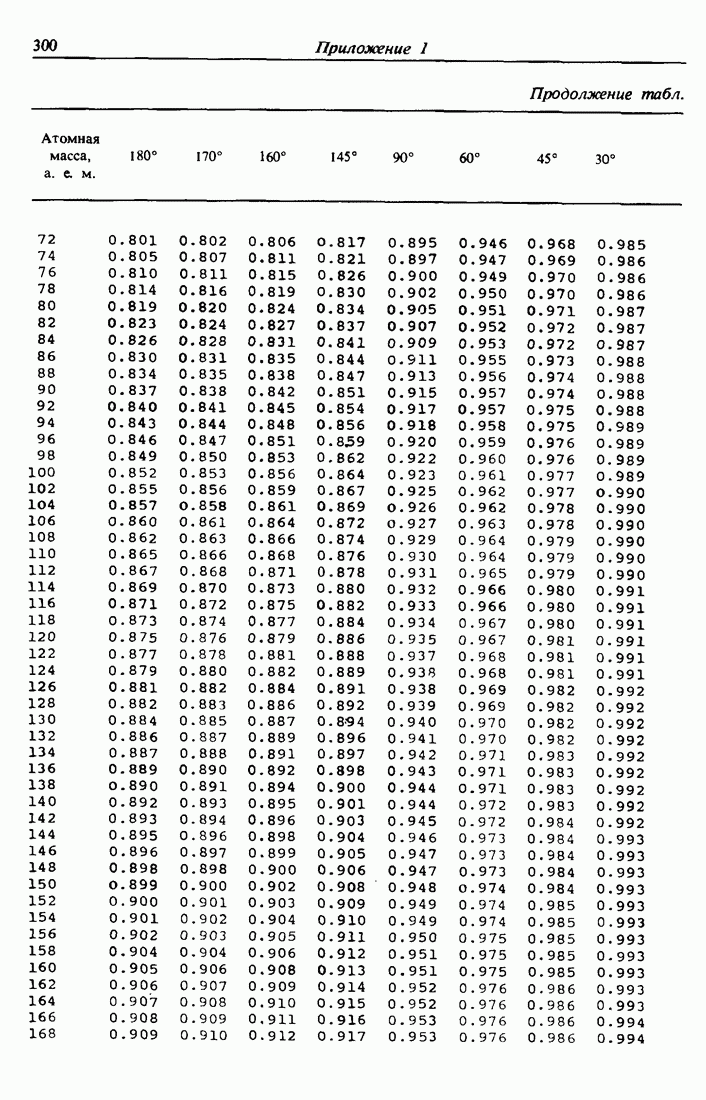
- ПРИЛОЖЕНИЕ 1.
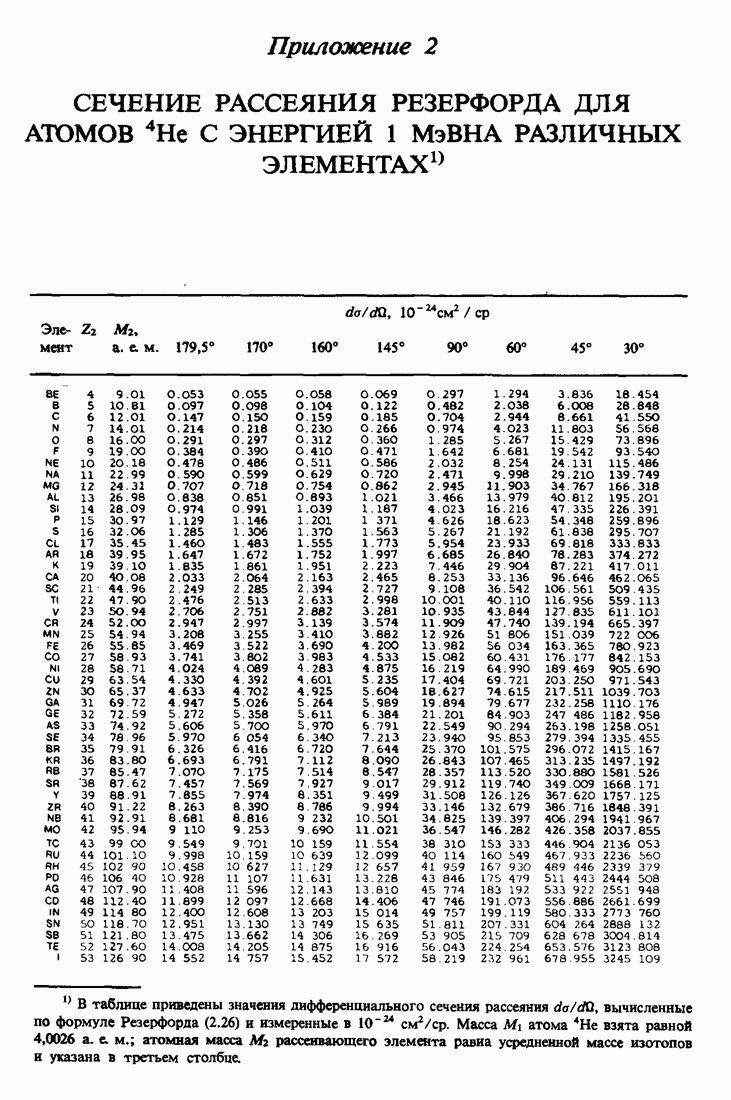
- ПРИЛОЖЕНИЕ 2.
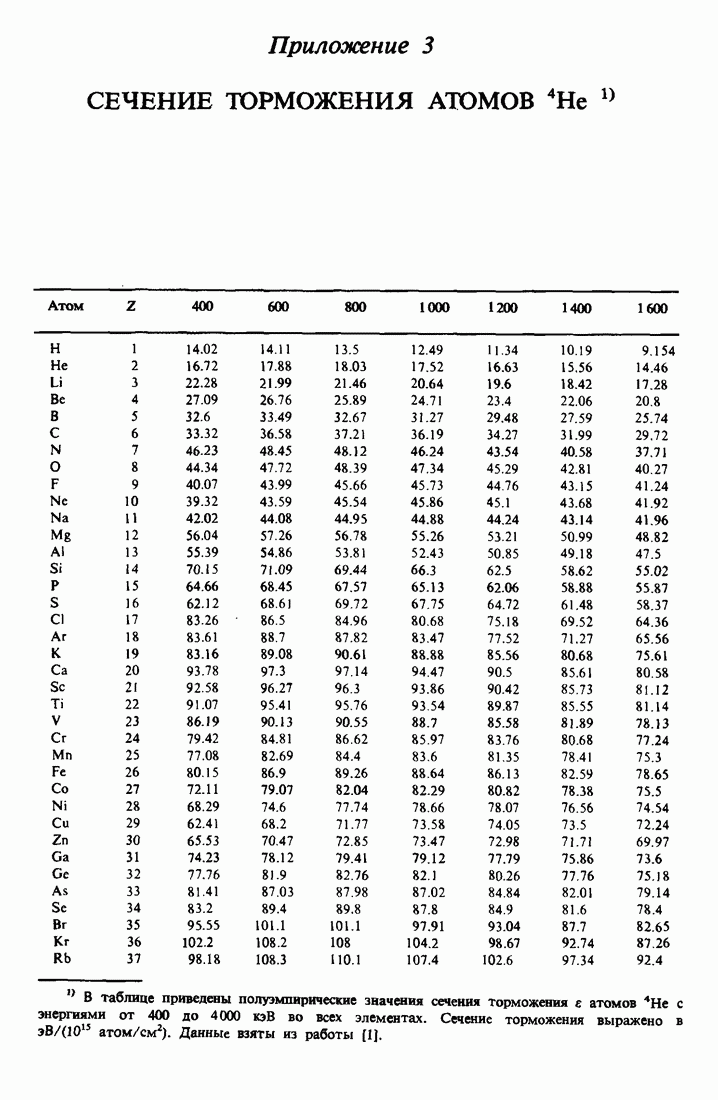
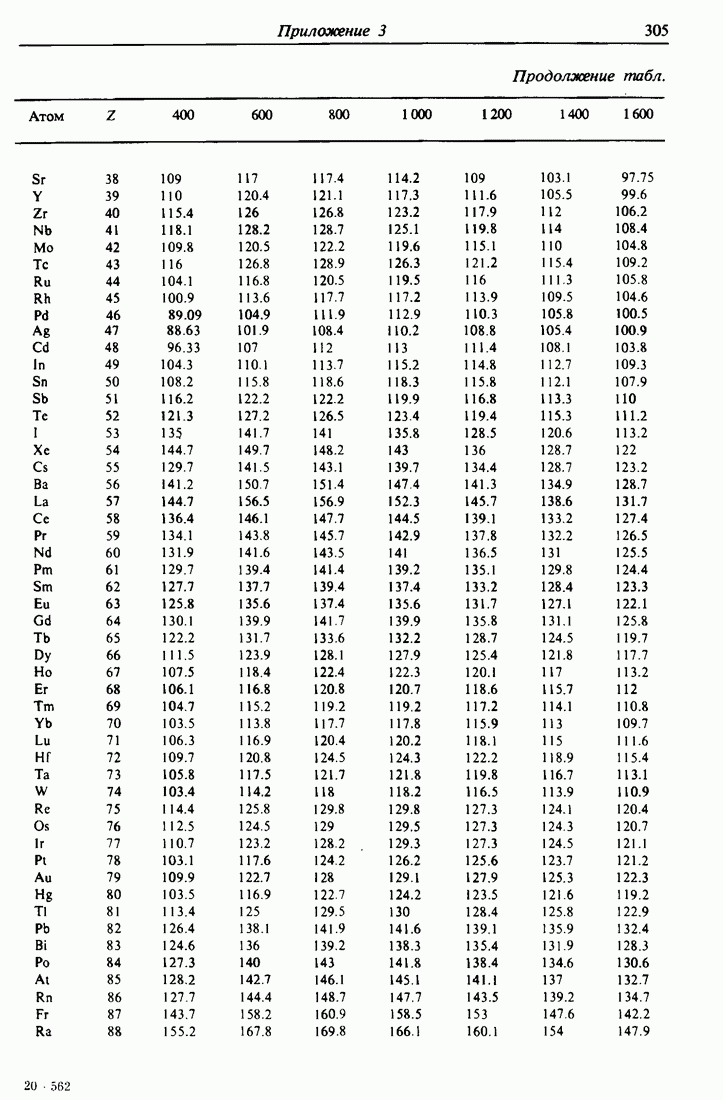
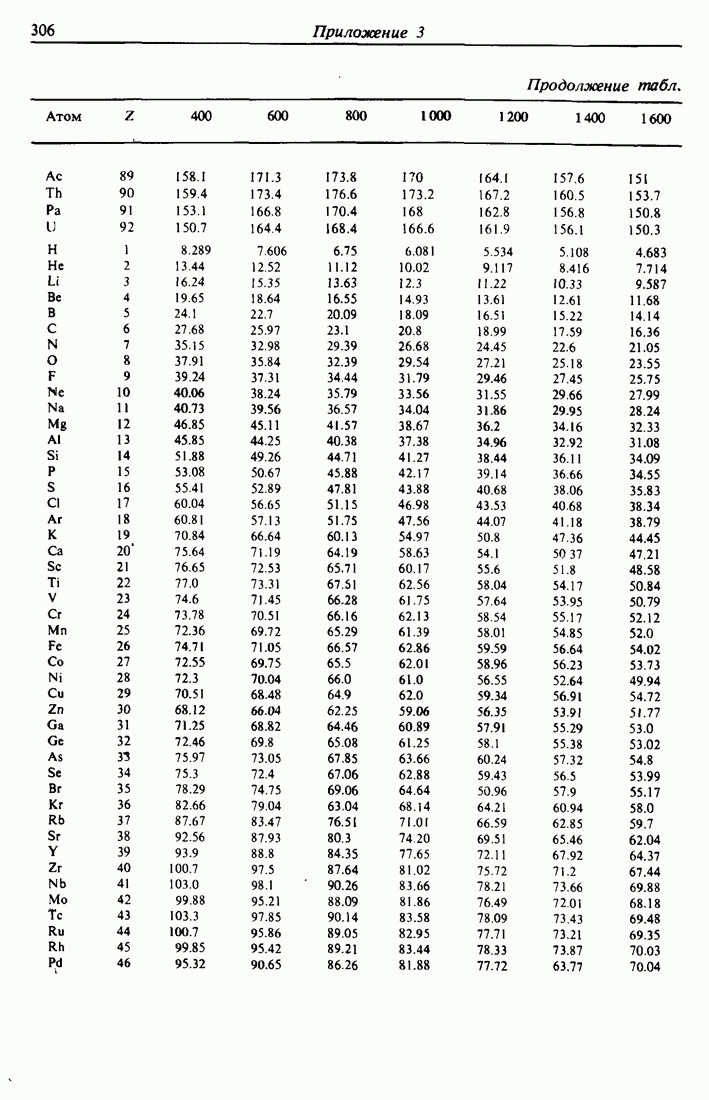
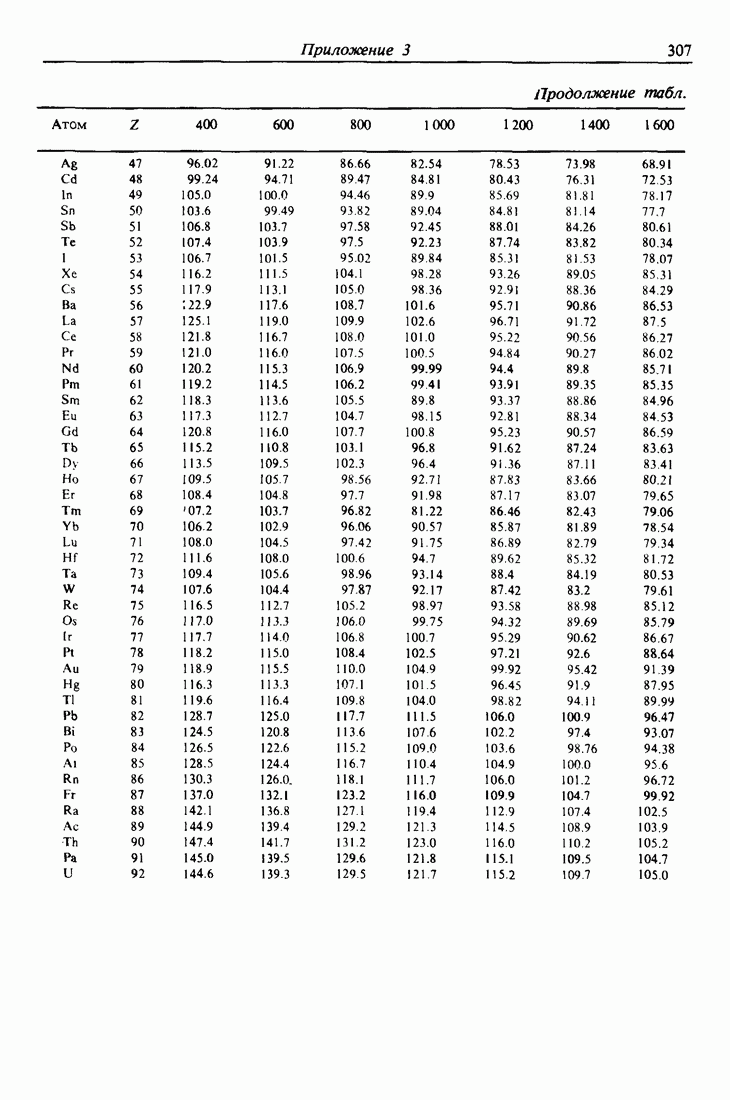
- ПРИЛОЖЕНИЕ 3.
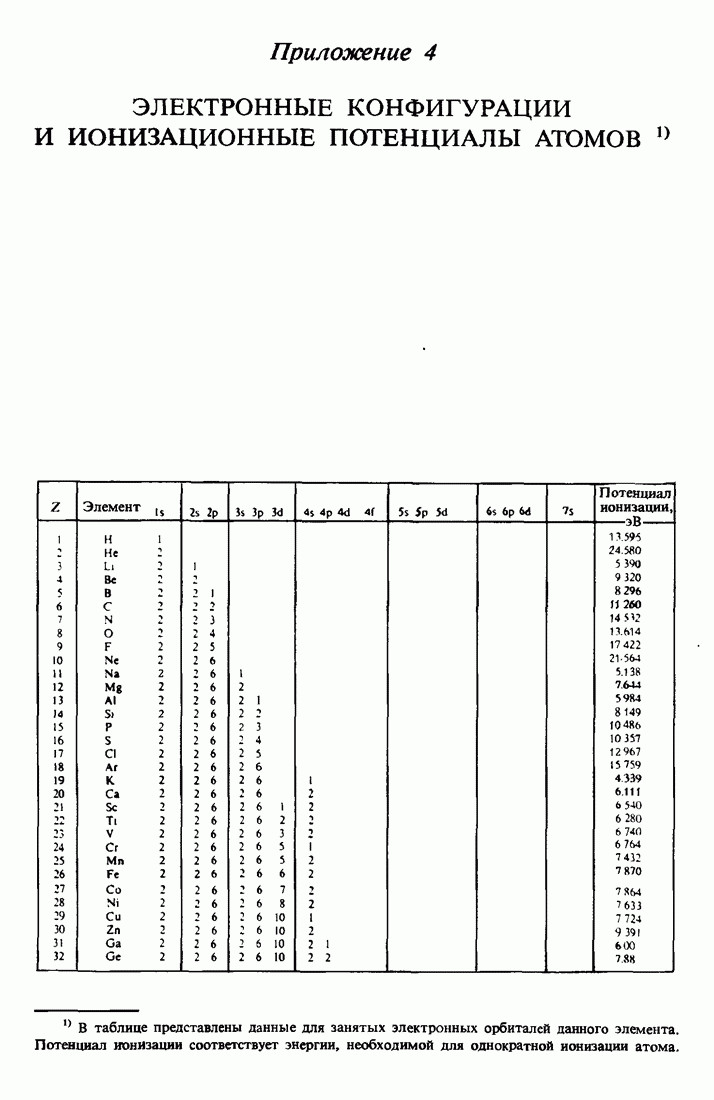
- ПРИЛОЖЕНИЕ 4.
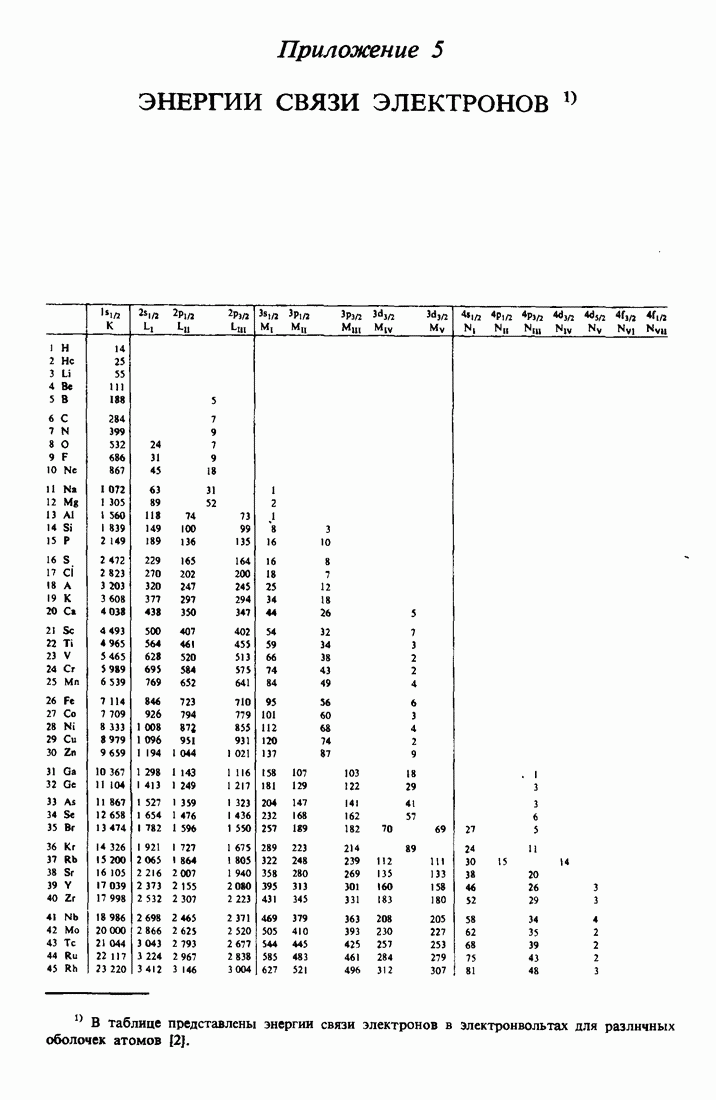
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
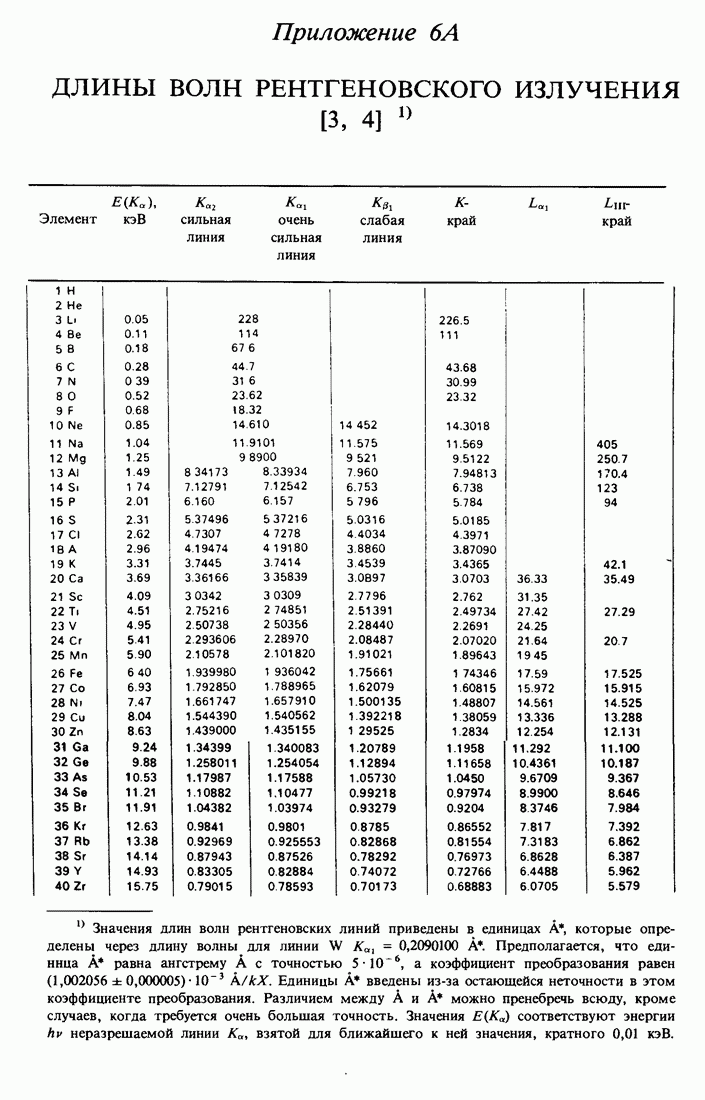
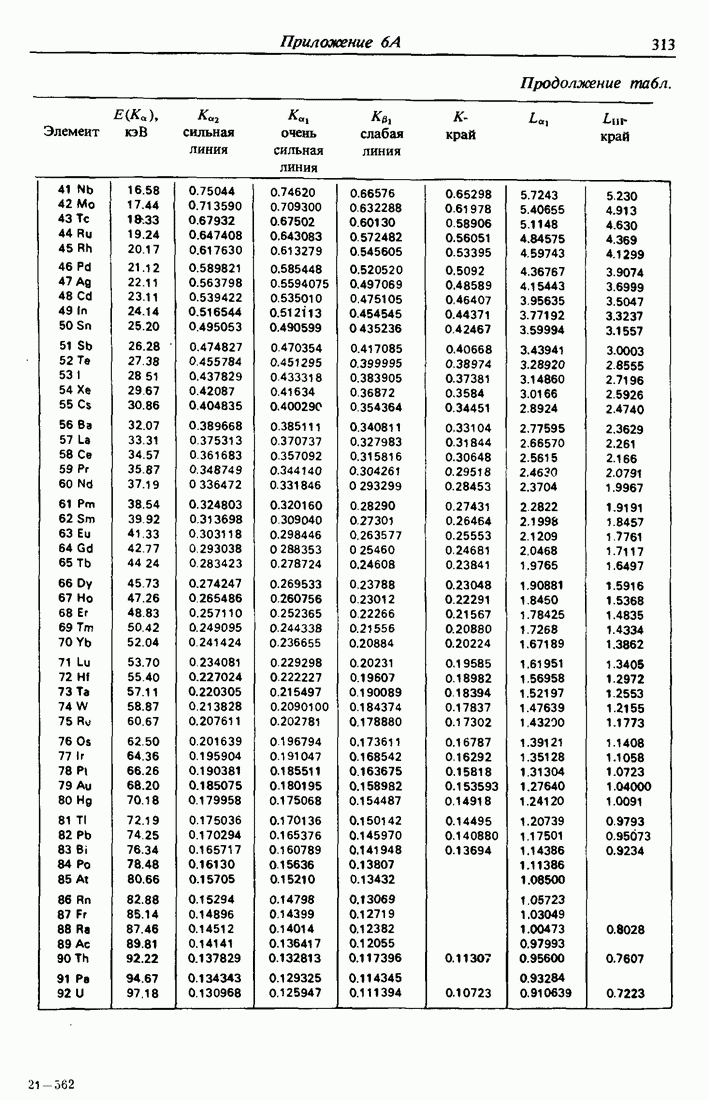
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
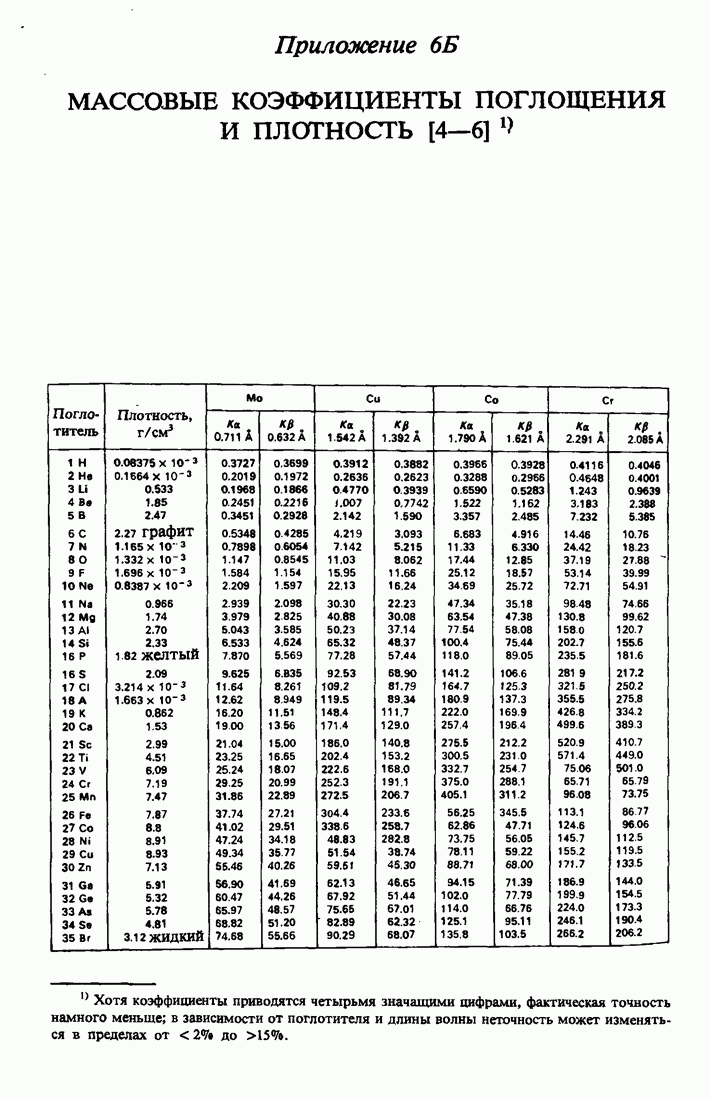
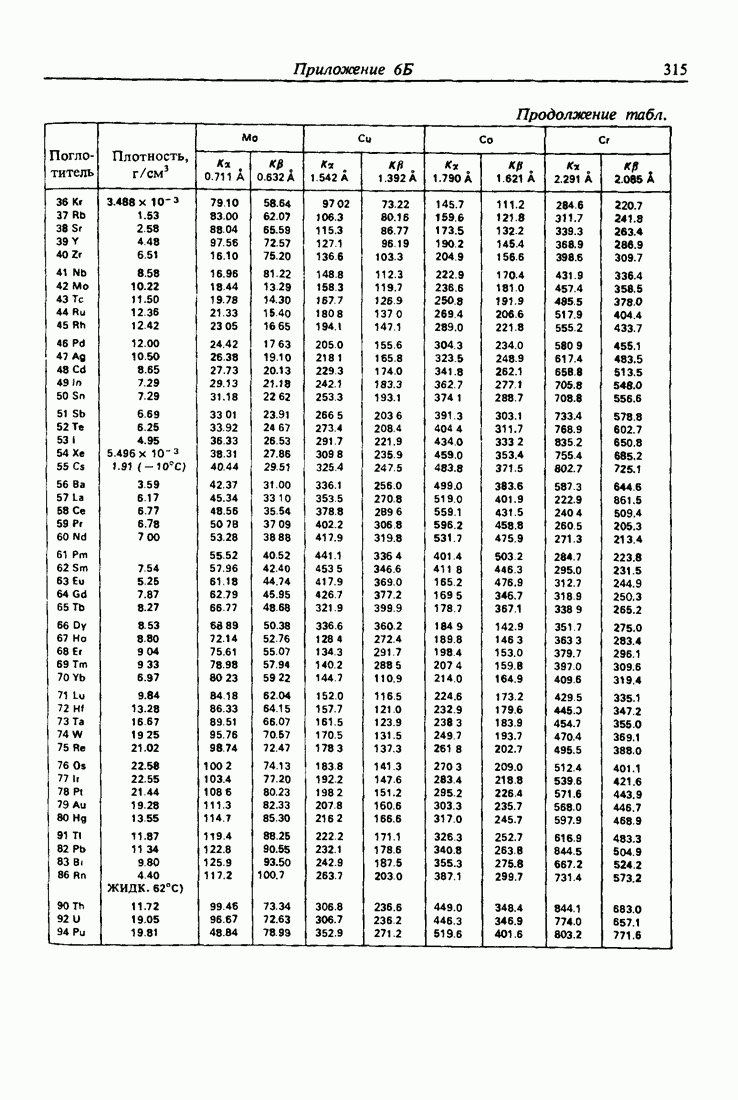
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
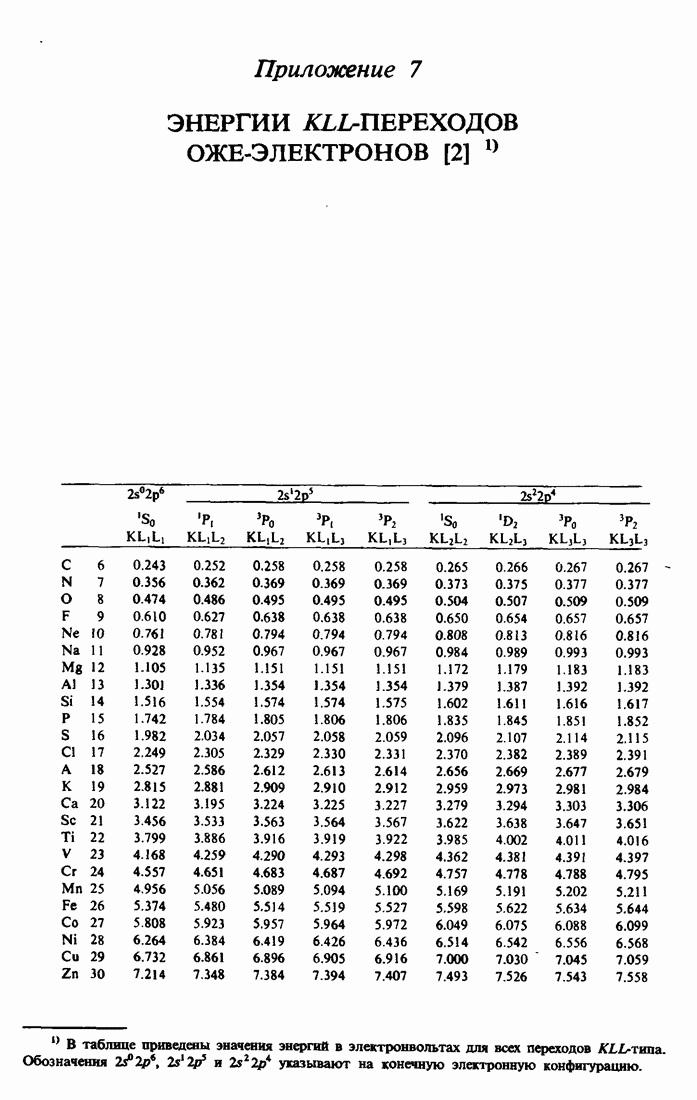
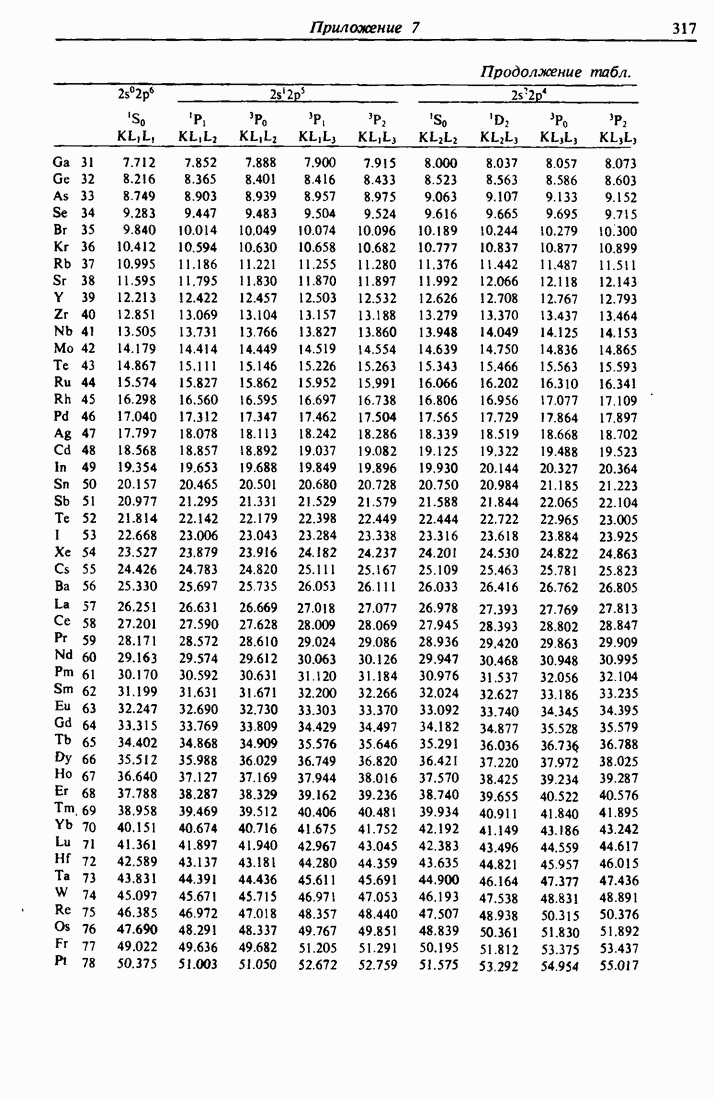
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
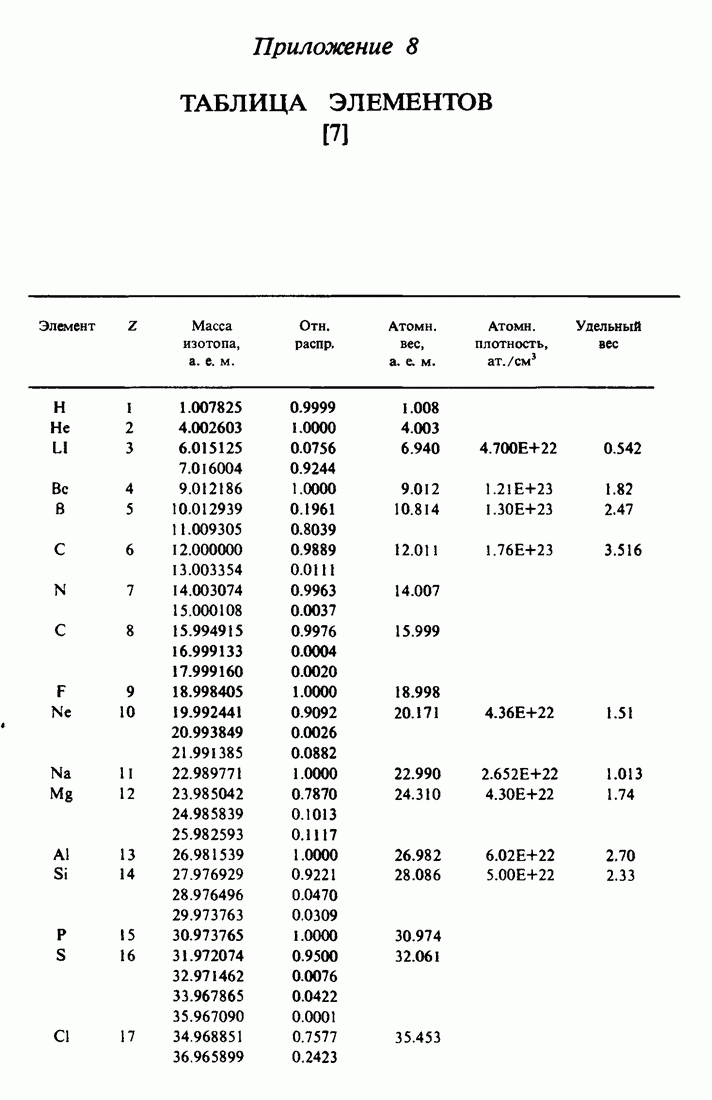
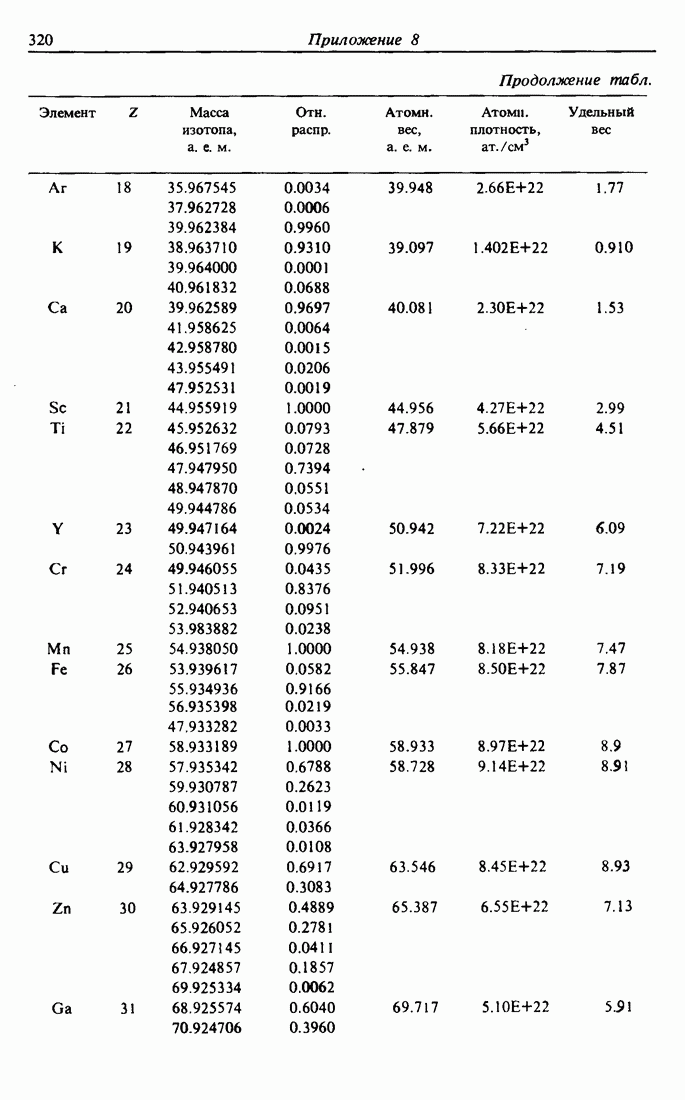
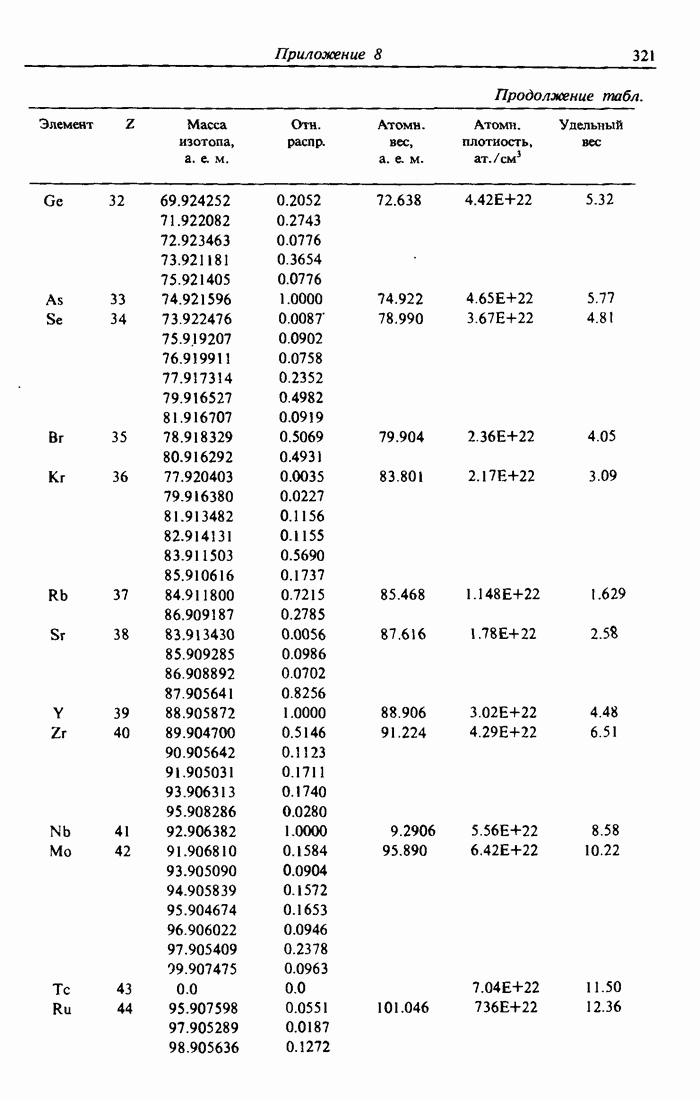
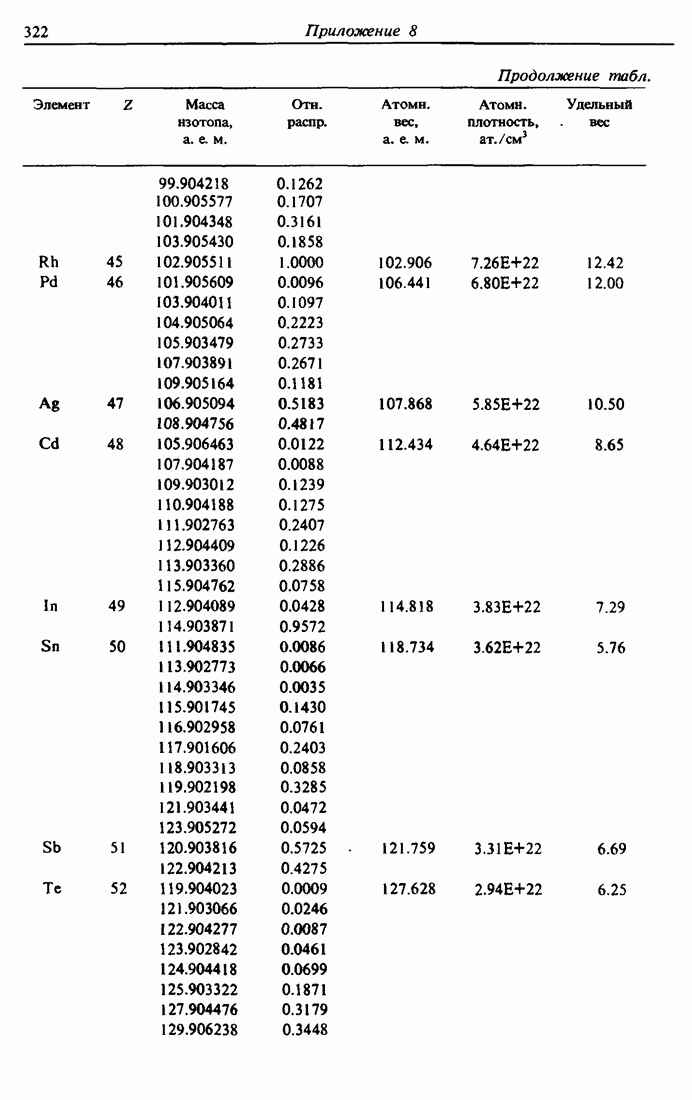
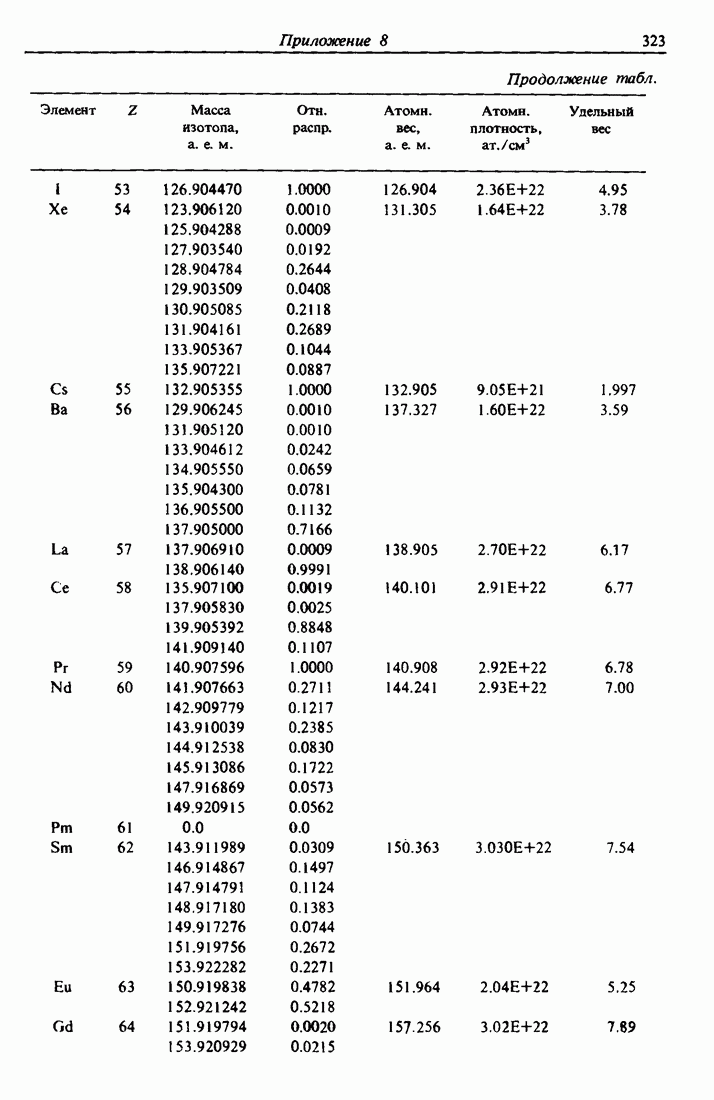
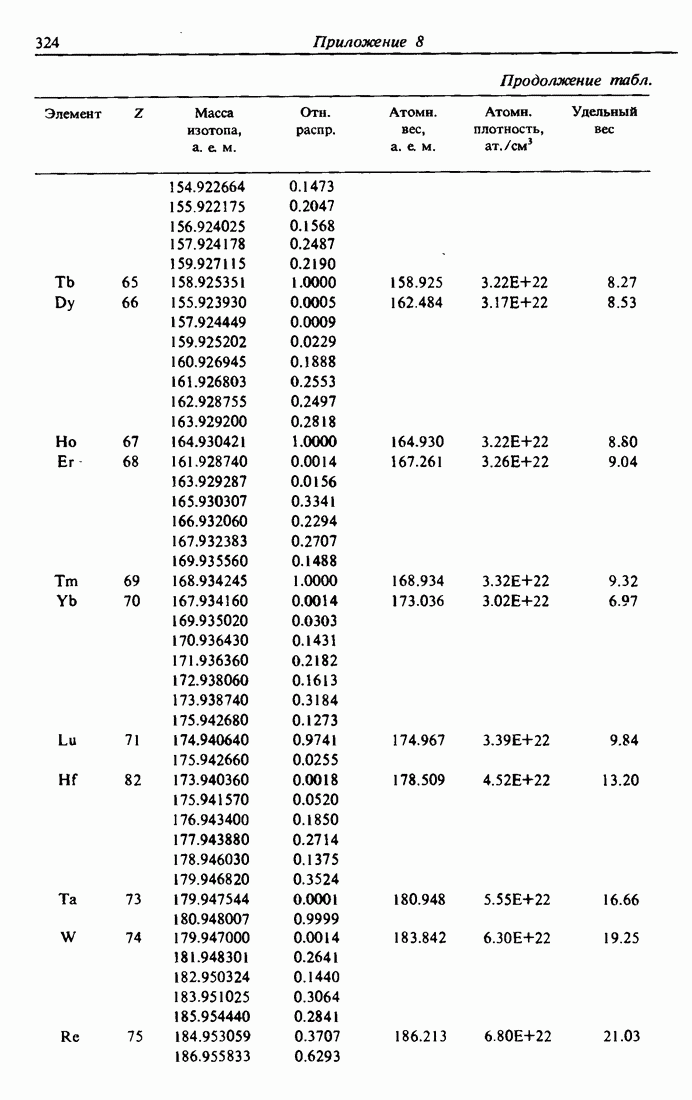
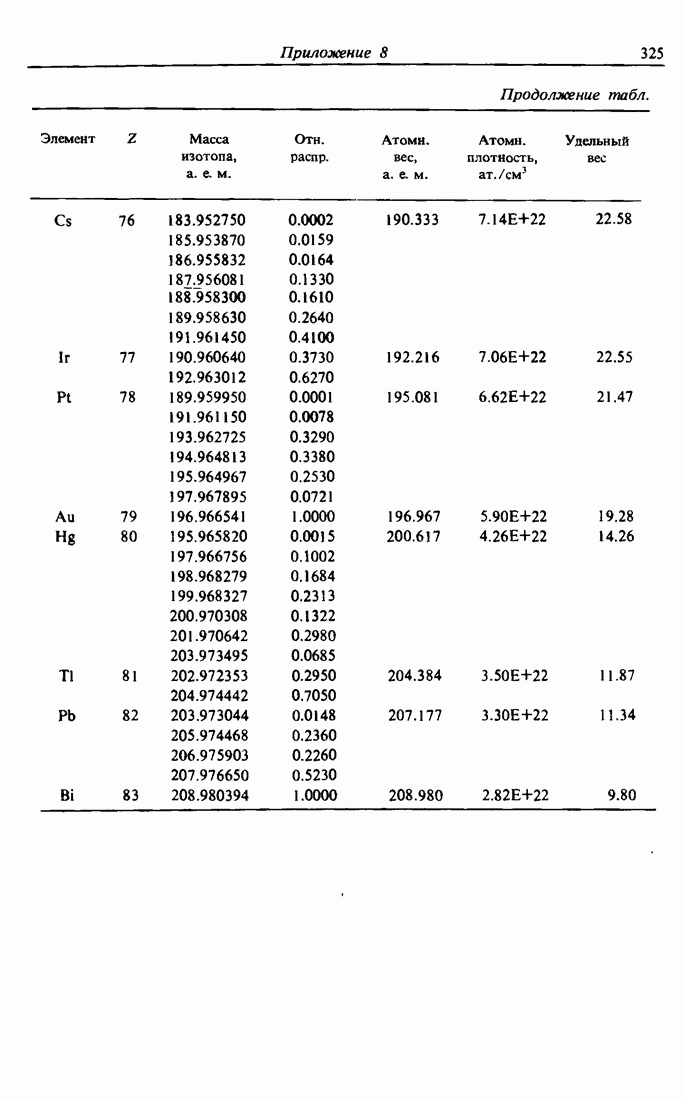
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
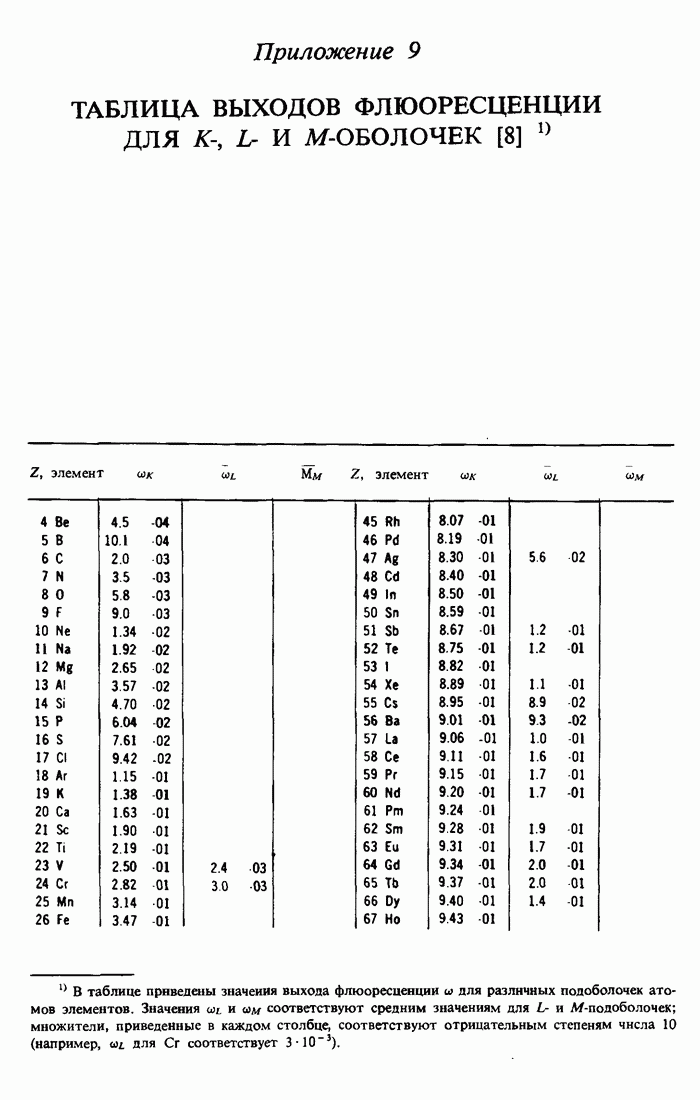
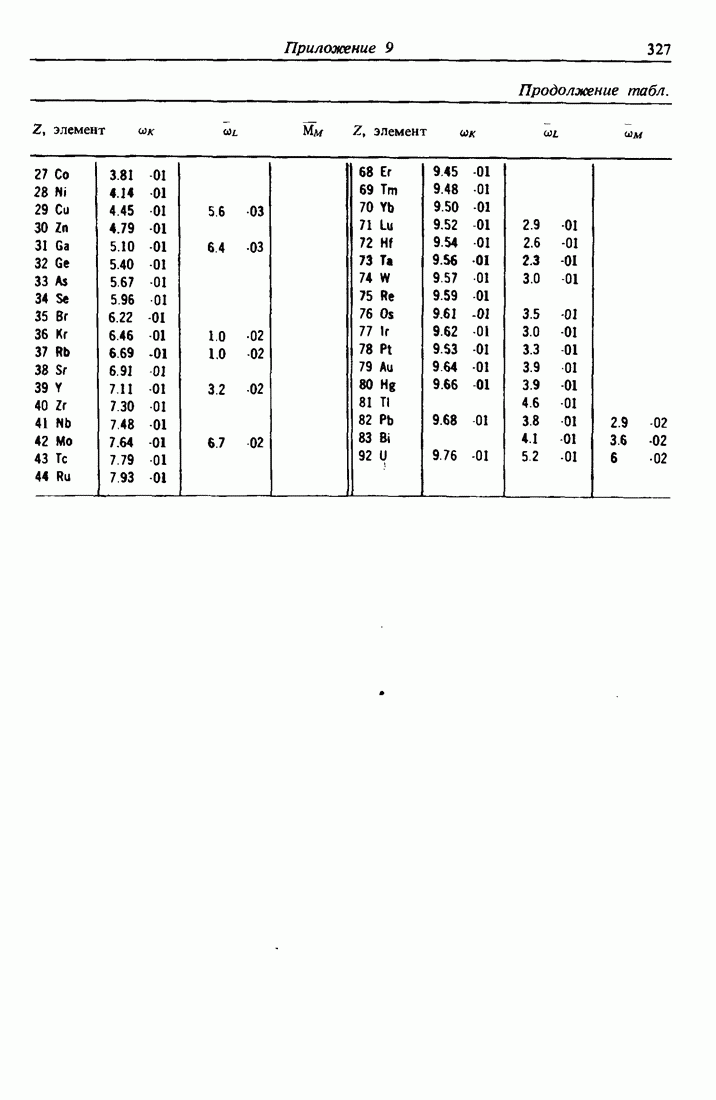
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ