| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.8. Разрешение по глубине и флуктуации потерь энергии
Спектрометрия обратного рассеяния позволяет определять изменение состава с глубиной. В этом разделе мы рассмотрим пределы dt разрешающей способности по глубине, характерные для спектрометрии обратного рассеяния. Связь между разрешением энергии  и разрешением глубины
и разрешением глубины  задается соотношением (3.20) в виде
задается соотношением (3.20) в виде

3.8.1. Метод скользящих углов
Уравнения (3.20а) и (3.28) приводят к следующему выражению для разрешающей способности по глубине:

Это выражение соответствует случаю нормального падения пучка на идеально плоскую поверхность образца и последующего рассеяния под углом в. Для заданной разрешающей способности детектора по энергии наилучшая чувствительность по глубине имеет место в том случае, когда максимальны потери энергии, сопутствующие рассеянию в глубине образца. Обычно это достигается применением скользящих углов регистрации пучка, что увеличивает длину пути частицы и, следовательно, ее потери энергии. В самом деле, из формулы (3.29) следует, что разрешение глубины улучшается, если регистрировать рассеяние на углы, близкие к 90°, поскольку в этом случае  стремится к нулю. Такая геометрия позволяет получить с помощью стандартных полупроводниковых детекторов разрешение по глубине вплоть до 20 А. При этом необходимо учитывать три фактора, влияющих на возможность повышения разрешающей способности с помощью метода скользящих углов.
стремится к нулю. Такая геометрия позволяет получить с помощью стандартных полупроводниковых детекторов разрешение по глубине вплоть до 20 А. При этом необходимо учитывать три фактора, влияющих на возможность повышения разрешающей способности с помощью метода скользящих углов.
1. Конечный угол захвата детектора. Любой детектор обладает конечным углом захвата, что приводит к уширению угла рассеяния, фиксируемого геометрией. Обычно в установках с применением скользящих углов регистрации вход детектора ограничен щелевидной диафрагмой, имеющей ширину 1 мм в плоскости рассеяния и длину  см в перпендикулярной плоскости, т. е. с общей площадью
см в перпендикулярной плоскости, т. е. с общей площадью  Если такой детектор расположен на расстоянии 6 см от мишени, то возникает неопределенность угла рассеяния, равная приблизительно 1°. Этот разброс углов рассеяния является весьма заметным, так как скользящий угол обычно выбирается значительно меньше 5°. Уменьшение угла захвата детектора практически неосуществимо, если принять во внимание величину суммарного заряда (или времени), необходимую для проведения эксперимента.
Если такой детектор расположен на расстоянии 6 см от мишени, то возникает неопределенность угла рассеяния, равная приблизительно 1°. Этот разброс углов рассеяния является весьма заметным, так как скользящий угол обычно выбирается значительно меньше 5°. Уменьшение угла захвата детектора практически неосуществимо, если принять во внимание величину суммарного заряда (или времени), необходимую для проведения эксперимента.
2. Шероховатость поверхности. Одним из наиболее трудных для учета при элементном анализе факторов является поверхностная шероховатость
неизвестного образца. Ясно, однако, что неровность поверхности ограничивает возможности любого метода скользящих углов. Заметим, что хорошо полированный образец из полупроводника является в высшей степени гладким для углов скольжения в несколько градусов и вполне поддается исследованию этими методами. В общем случае именно шероховатость поверхности накладывает окончательные ограничения на разрешающую способность по глубине, даже если углы захвата выбраны чрезвычайно малыми. 3. Флуктуации потерь энергии (страгглинг). Этот фактор обсуждается в следующем разделе.
3.8.2. Страгглинг
Обычно предел разрешения энергии устанавливается двумя факторами: разрешением детектора  и страгглингом
и страгглингом  . Если предположить, что оба вклада независимы друг от друга и удовлетворяют распределению Пуассона, то полное разрешение
. Если предположить, что оба вклада независимы друг от друга и удовлетворяют распределению Пуассона, то полное разрешение  задается выражением
задается выражением

При движении в среде быстрая частица теряет энергию, испытывая множество отдельных столкновений. Этот дискретный процесс подвержен статистическим флуктуациям. В результате одинаковые частицы с одной и той же начальной скоростью после прохождения в однородной среде слоя толщиной  не могут обладать в точности равными энергиями. Потери энергии
не могут обладать в точности равными энергиями. Потери энергии  испытывают флуктуации. Это явление получило название разброса энергий, или энергетического страгглинга. Страгглинг устанавливает конечный предел точности определения потерь энергии и, следовательно, разрешения по глубине.
испытывают флуктуации. Это явление получило название разброса энергий, или энергетического страгглинга. Страгглинг устанавливает конечный предел точности определения потерь энергии и, следовательно, разрешения по глубине.
Легкие частицы, такие как Н или  в диапазоне энергий порядка нескольких мегаэлектронвольт теряют энергию преимущественно в столкновениях с электронами мишени, и главный вклад в разброс энергий дают статистические флуктуации, присущие этим электронным взаимодействиям. Распределение потерь энергии
в диапазоне энергий порядка нескольких мегаэлектронвольт теряют энергию преимущественно в столкновениях с электронами мишени, и главный вклад в разброс энергий дают статистические флуктуации, присущие этим электронным взаимодействиям. Распределение потерь энергии  для пучка частиц, проходящих через фольгу, является приближенно гауссовым, если величина
для пучка частиц, проходящих через фольгу, является приближенно гауссовым, если величина  мала по сравнению с начальной энергией
мала по сравнению с начальной энергией  . Для распределения Гаусса вероятность того, что потери энергии принадлежат интервалу от
. Для распределения Гаусса вероятность того, что потери энергии принадлежат интервалу от  до
до  равна
равна

где  — среднеквадратичное отклонение. Если
— среднеквадратичное отклонение. Если  есть сечение передачи энергии Т, то для фольги толщиной t, содержащей n электронов в
есть сечение передачи энергии Т, то для фольги толщиной t, содержащей n электронов в  аналогично (3.5) выполняется
аналогично (3.5) выполняется


Из выражений (3.3) и (3.4) следует

так что

где  . Для рассматриваемых быстрых частиц
. Для рассматриваемых быстрых частиц  что приводит к выражению
что приводит к выражению

которое часто называют формулой Бора для энергетического страгглинга. Для вычисления разрешающей способности (3.30) заметим, что полная ширина на половине максимума (FWHM) в  раза превышает стандартное отклонение, т. е.
раза превышает стандартное отклонение, т. е.  .
.
Теория Бора предсказывает, что разброс энергий не зависит от энергии налетающей частицы, но растет как квадратный корень из  — электронной плотности на единицу площади мишени. Для ионов гелия величина
— электронной плотности на единицу площади мишени. Для ионов гелия величина  измеренная в единицах
измеренная в единицах  численно равна
численно равна  с точностью 4%. Этот приближенный способ цодсчета позволяет выполнить простую оценку толщины мишени (в атом/см2), которая для ионов
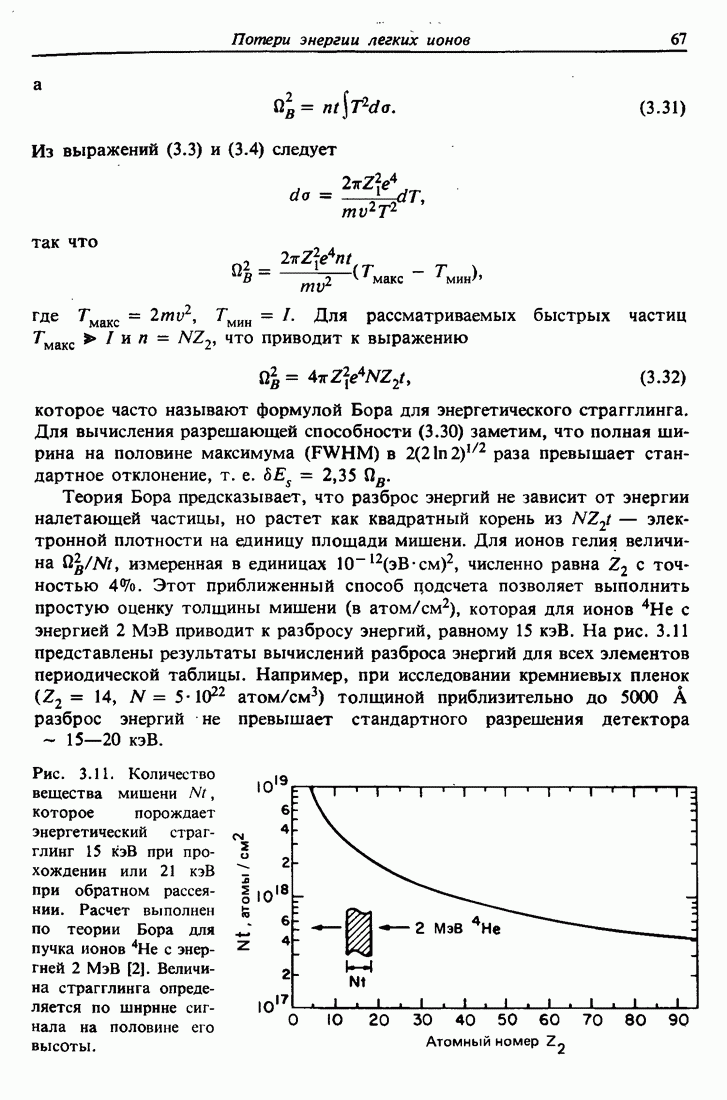
с точностью 4%. Этот приближенный способ цодсчета позволяет выполнить простую оценку толщины мишени (в атом/см2), которая для ионов  с энергией 2 МэВ приводит к разбросу энергий, равному 15 кэВ. На рис. 3.11 представлены результаты вычислений разброса энергий для всех элементов периодической таблицы. Например, при исследовании кремниевых пленок (
с энергией 2 МэВ приводит к разбросу энергий, равному 15 кэВ. На рис. 3.11 представлены результаты вычислений разброса энергий для всех элементов периодической таблицы. Например, при исследовании кремниевых пленок ( атом/см3) толщиной приблизительно до 5000 А разброс энергий не превышает стандартного разрешения детектора ~ 15-20 кэВ.
атом/см3) толщиной приблизительно до 5000 А разброс энергий не превышает стандартного разрешения детектора ~ 15-20 кэВ.

Рис. 3.11. Количество вещества мишени  , которое порождает энергетический страгглинг 15 кэВ при прохождении или 21 кэВ при обратном рассеянии. Расчет выполнен по теории Бора для пучка ионов
, которое порождает энергетический страгглинг 15 кэВ при прохождении или 21 кэВ при обратном рассеянии. Расчет выполнен по теории Бора для пучка ионов  с энергией 2 МэВ [2]. Величина страгглинга определяется по шнрнне сигнала на половине его высоты.
с энергией 2 МэВ [2]. Величина страгглинга определяется по шнрнне сигнала на половине его высоты.
Страгглинг накладывает фундаментальное ограничение на разрешение глубины, достижимое с помощью измерения потерь энергии ионных пучков. Разброс энергий является функцией глубины проникновения, так как Q пропорционально t. Для ионов гелия, падающих на слой толщиной  , разброс энергий мал по сравнению с разрешающей способностью детектора и, следовательно, не влияет на разрешение по глубине. Для толщин свыше 2000 А разброс потерь энергий становится заметным и ограничивает разрешение по глубине. Если частица рассеивается на глубине t под углом 95°, т. е. угол вылета составляет 5° относительно поверхности образца, то длина пути частицы в веществе достигает
, разброс энергий мал по сравнению с разрешающей способностью детектора и, следовательно, не влияет на разрешение по глубине. Для толщин свыше 2000 А разброс потерь энергий становится заметным и ограничивает разрешение по глубине. Если частица рассеивается на глубине t под углом 95°, т. е. угол вылета составляет 5° относительно поверхности образца, то длина пути частицы в веществе достигает  . Поэтому страгглинг, который в традиционной схеме обратного рассеяния влиял на энергетическое разрешение только при глубинах порядка 2000 А, в этом случае становится существенным уже на глубинах примерно 200 А. Таким образом, применение скользящих углов выхода позволяет повысить разрешающую способность по глубине только в достаточно тонком приповерхностном слое.
. Поэтому страгглинг, который в традиционной схеме обратного рассеяния влиял на энергетическое разрешение только при глубинах порядка 2000 А, в этом случае становится существенным уже на глубинах примерно 200 А. Таким образом, применение скользящих углов выхода позволяет повысить разрешающую способность по глубине только в достаточно тонком приповерхностном слое.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
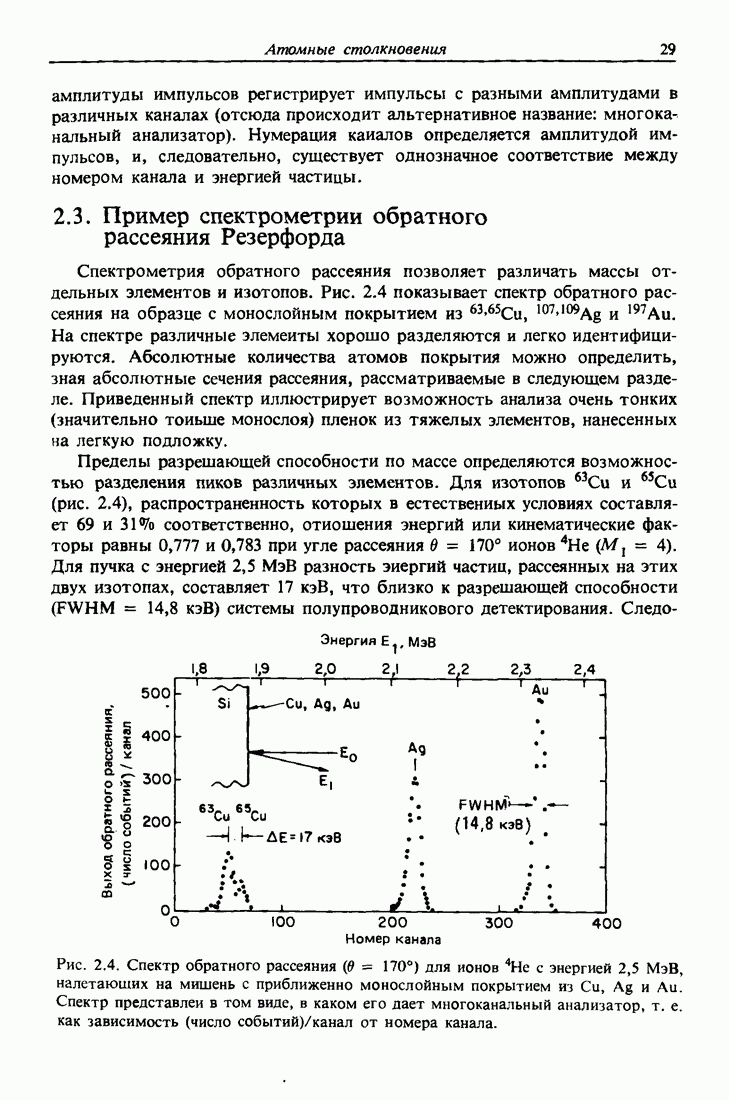
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
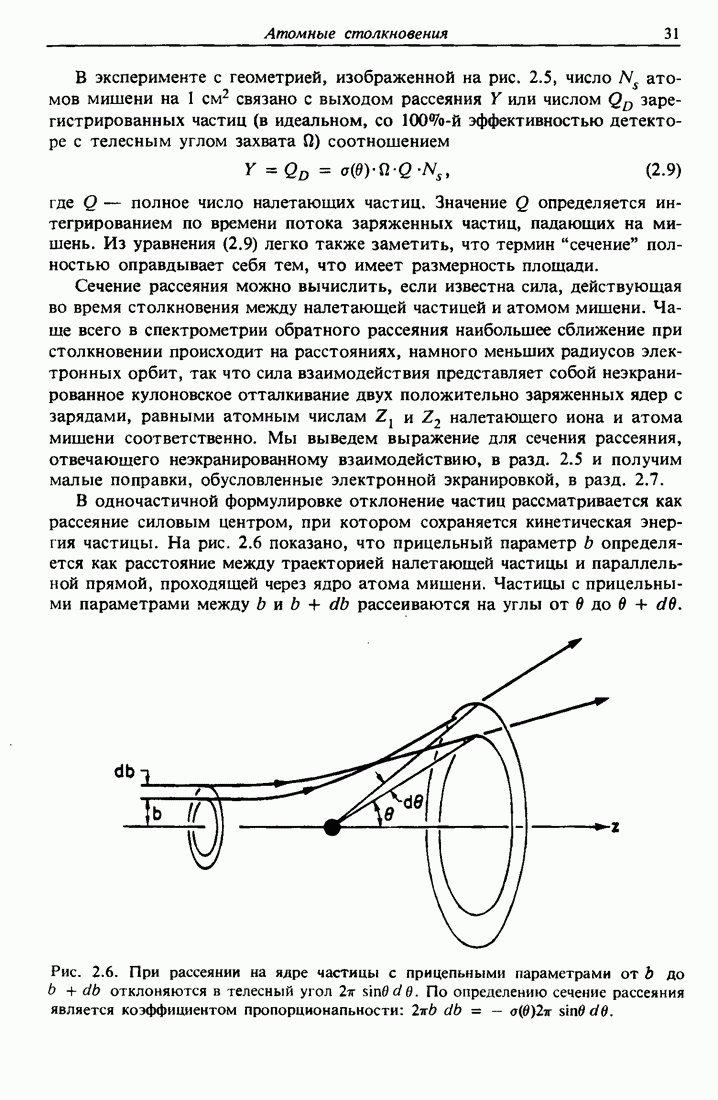
- 2.4. Сечение рассеяния и прицельный параметр
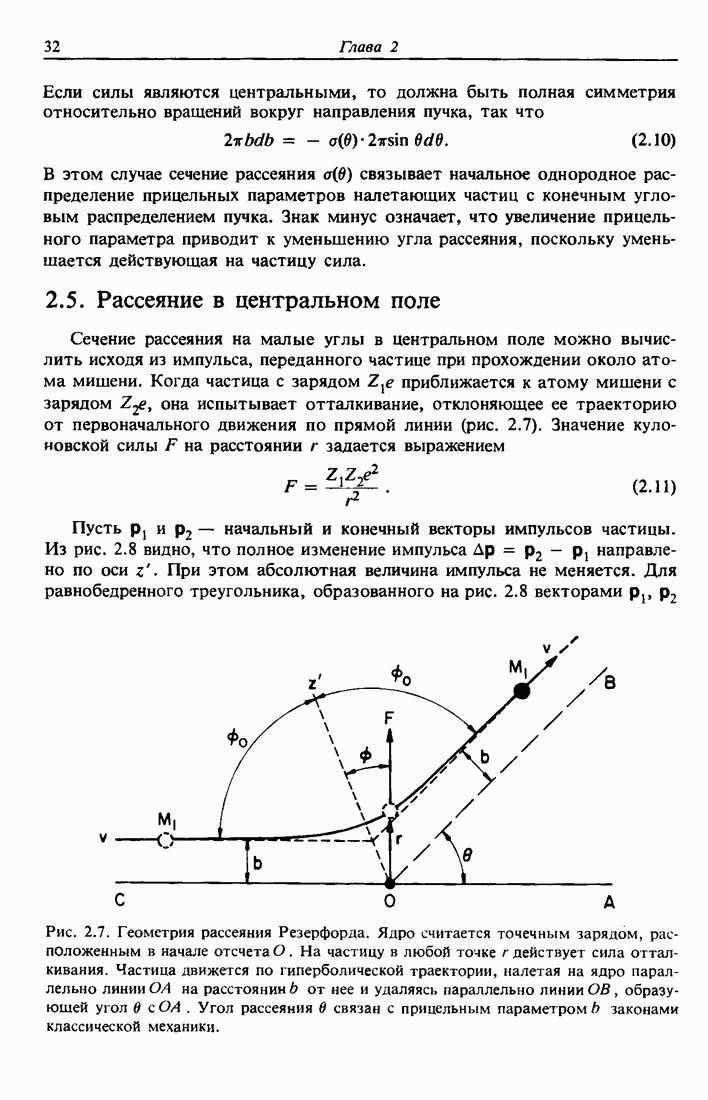
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
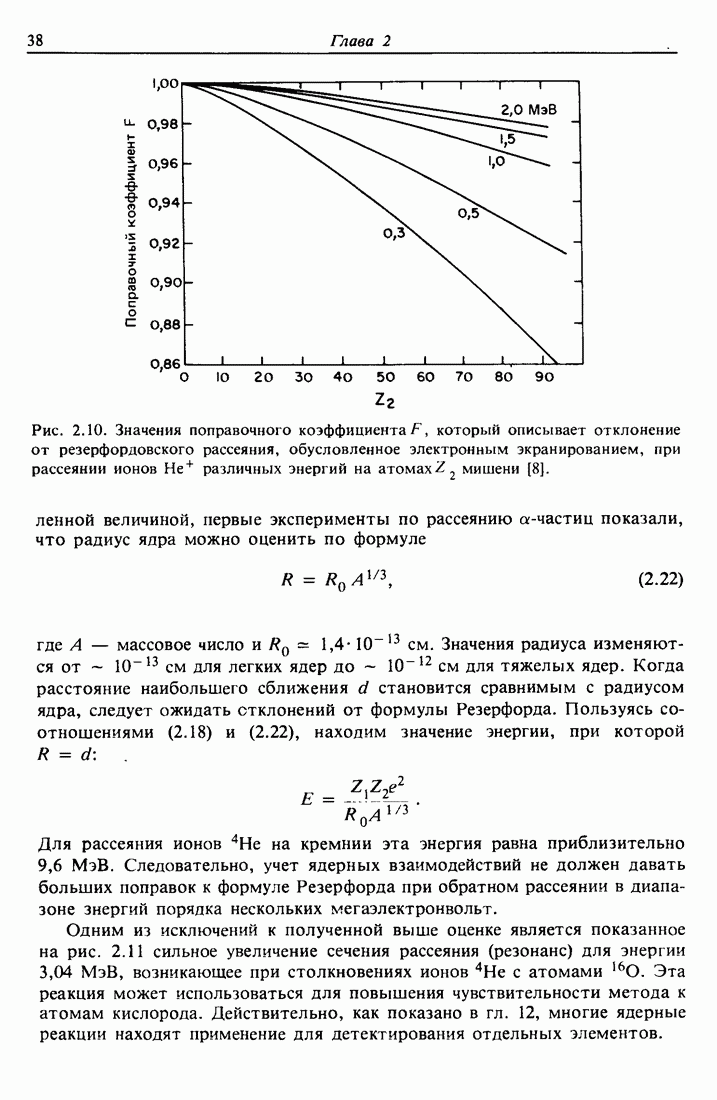
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
- 3.5. Ширина спектра энергии в обратном рассеянии
- 3.6. Форма спектра обратного рассеяния
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
- 6.5. Сечение ударной электронной ионизации
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
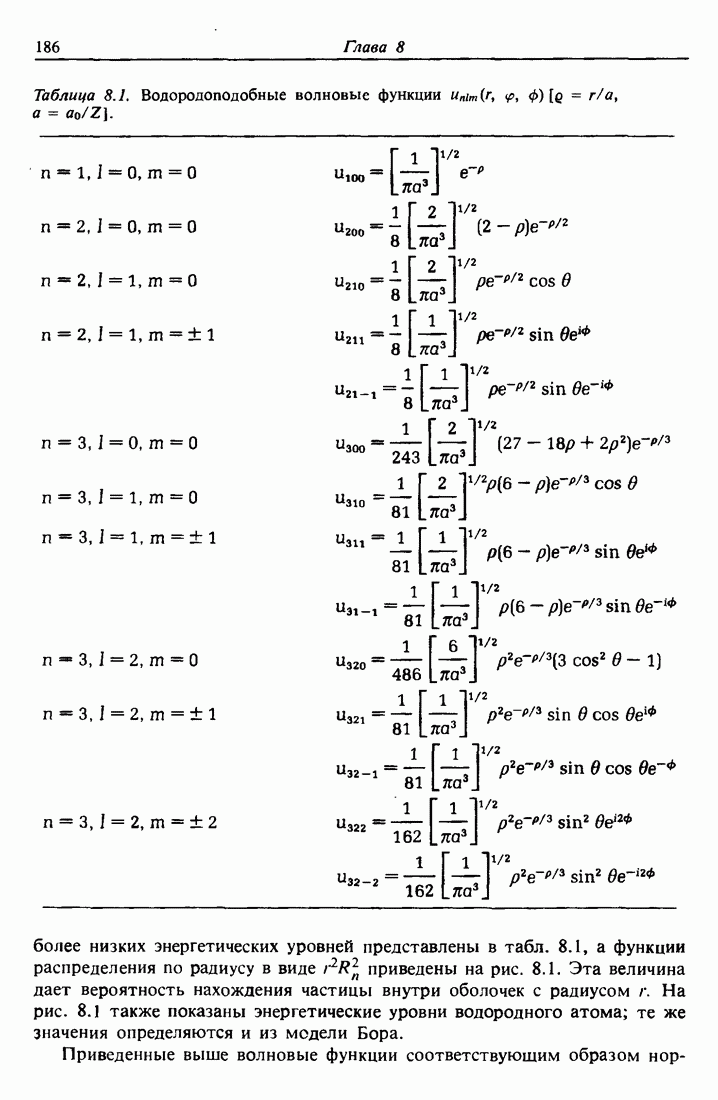
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
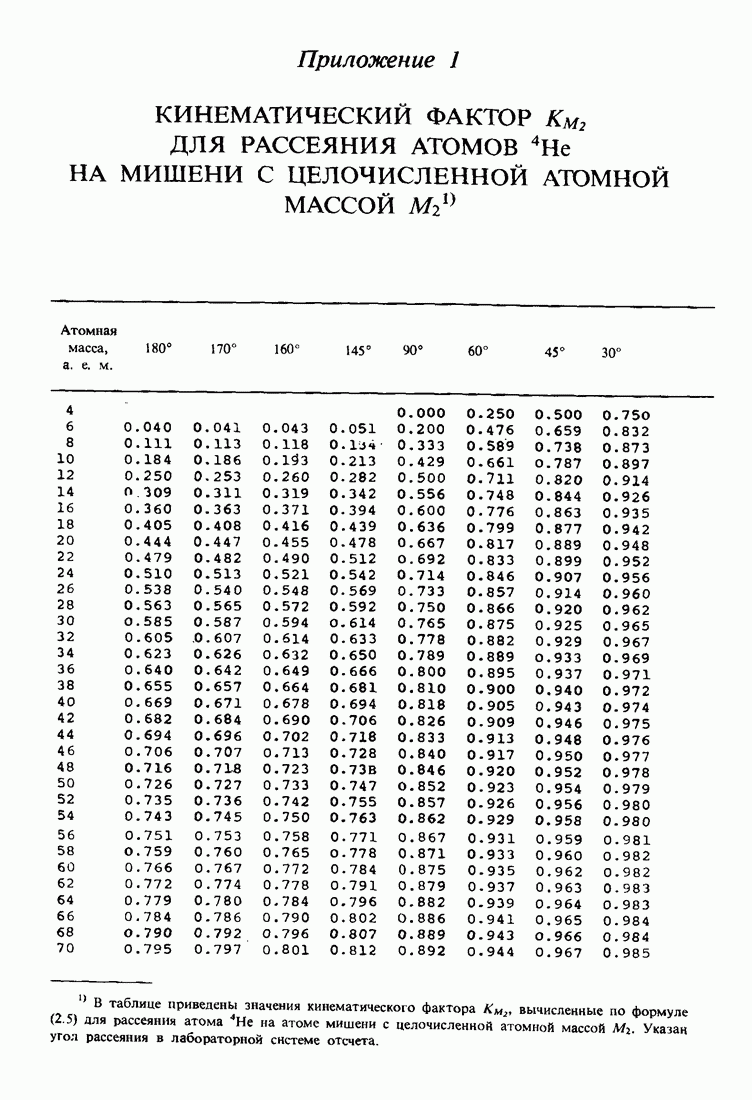
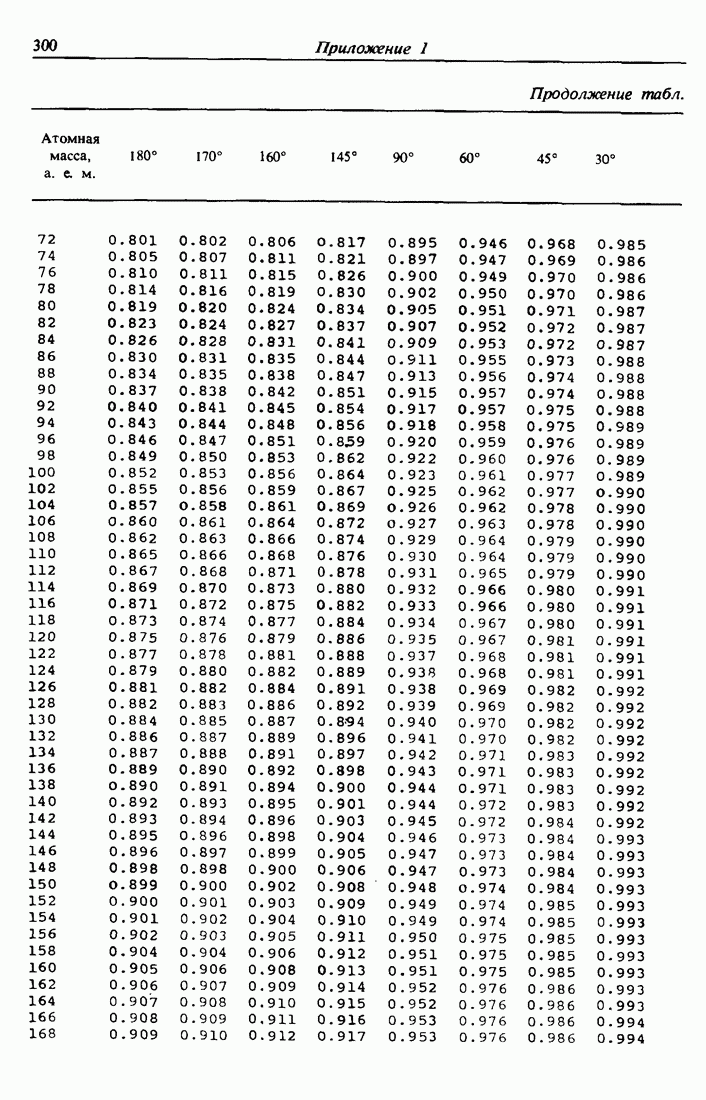
- ПРИЛОЖЕНИЕ 1.
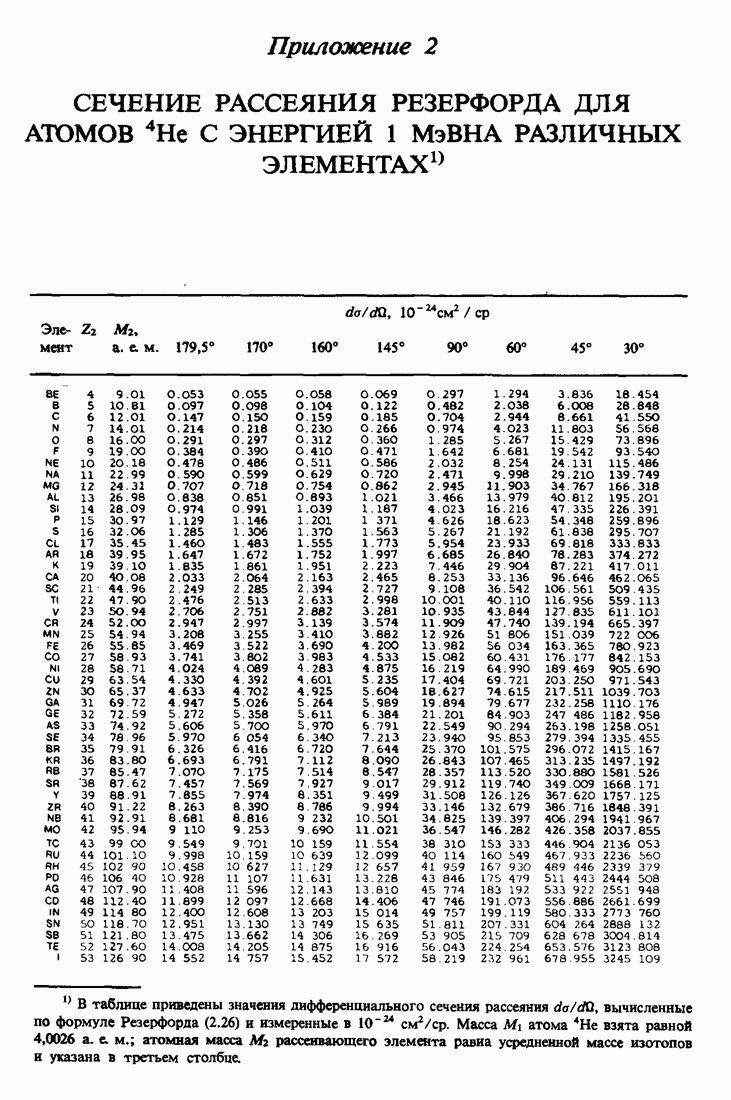
- ПРИЛОЖЕНИЕ 2.
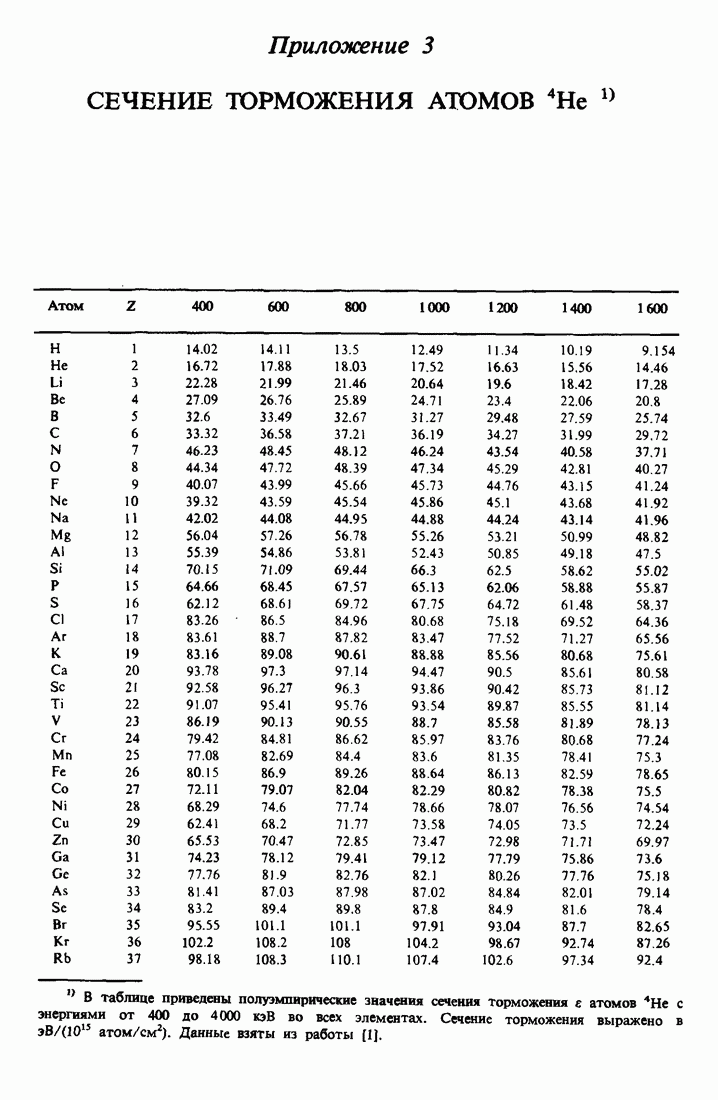
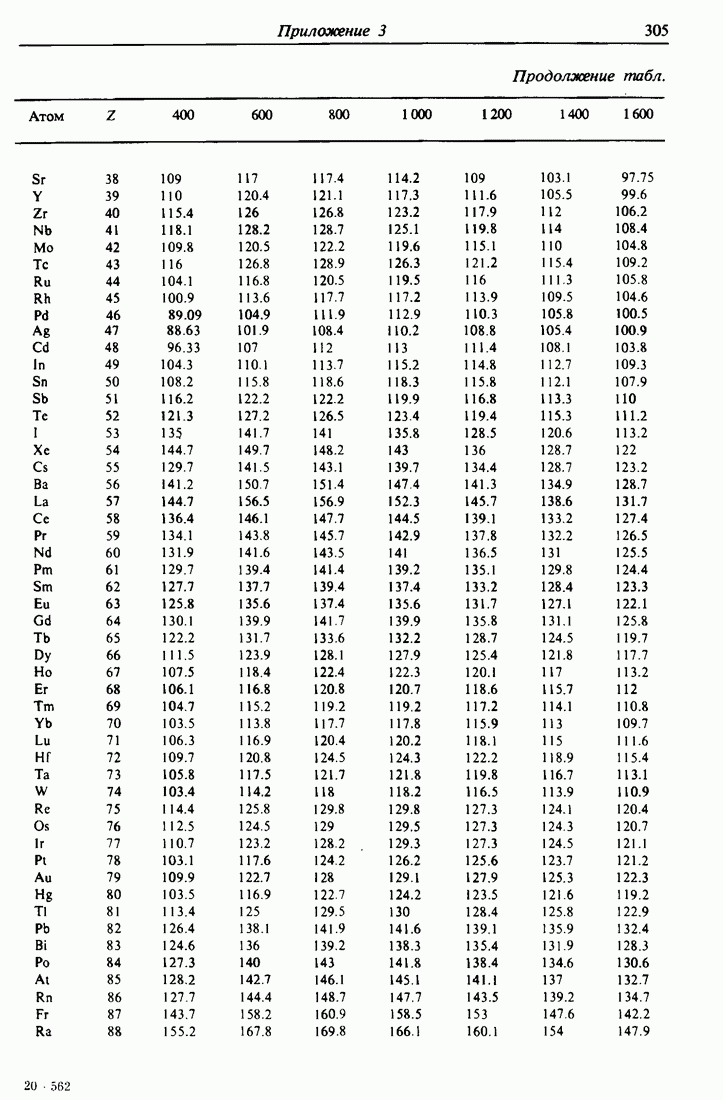
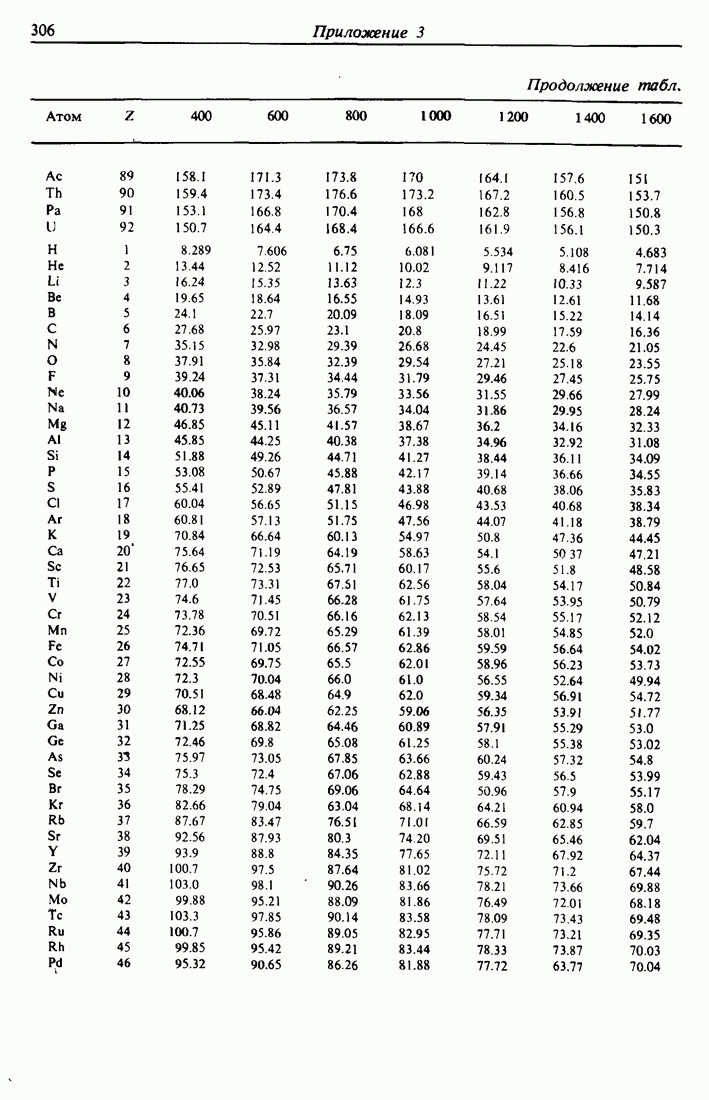
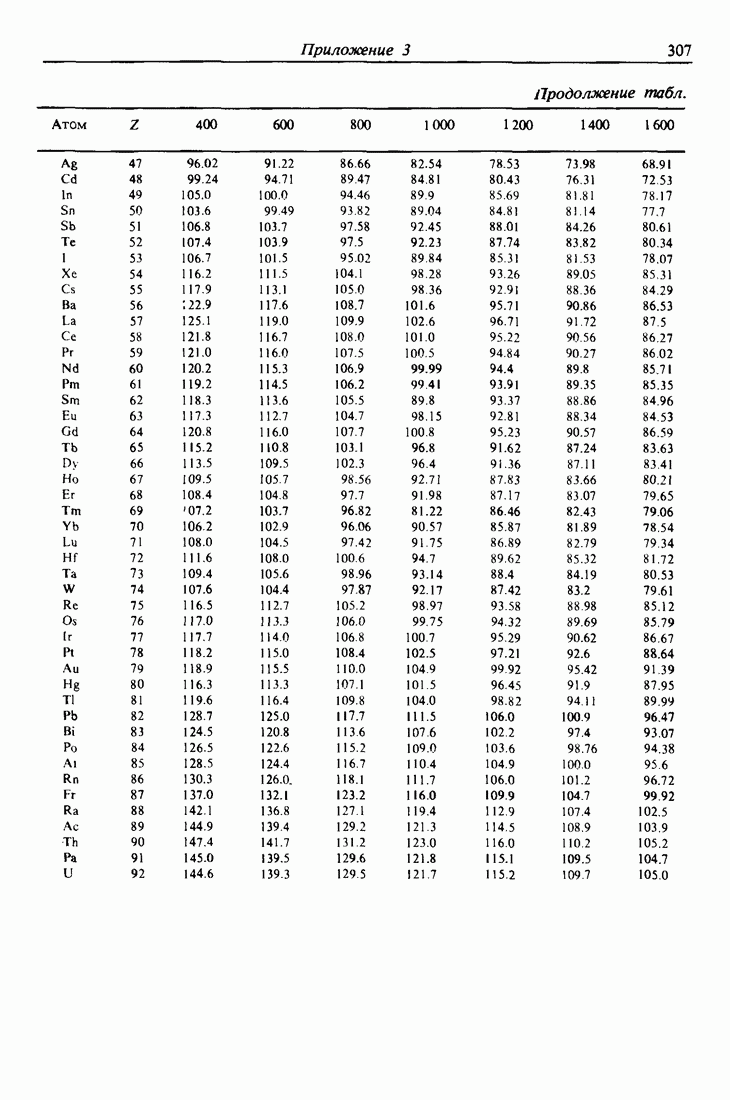
- ПРИЛОЖЕНИЕ 3.
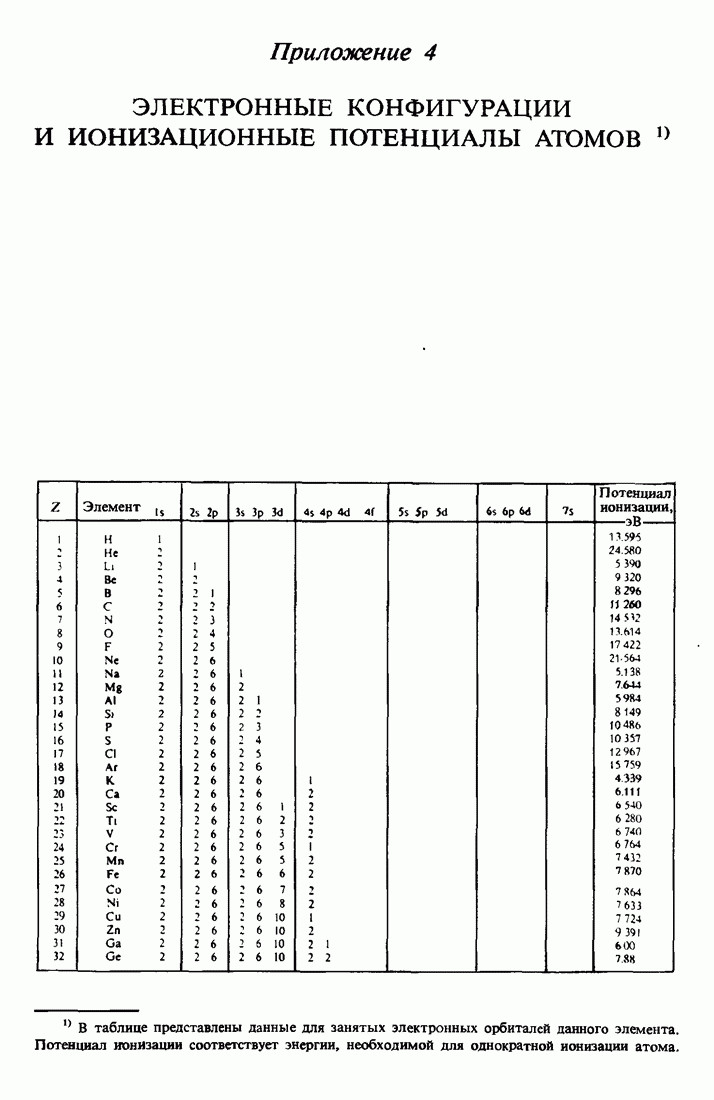
- ПРИЛОЖЕНИЕ 4.
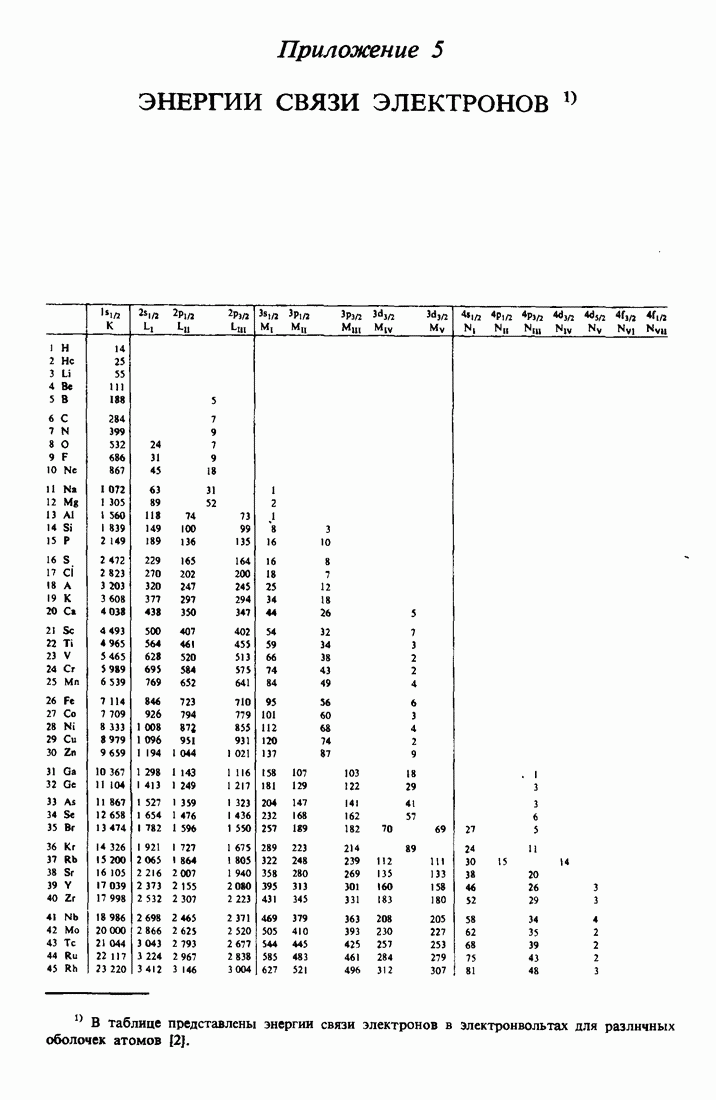
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
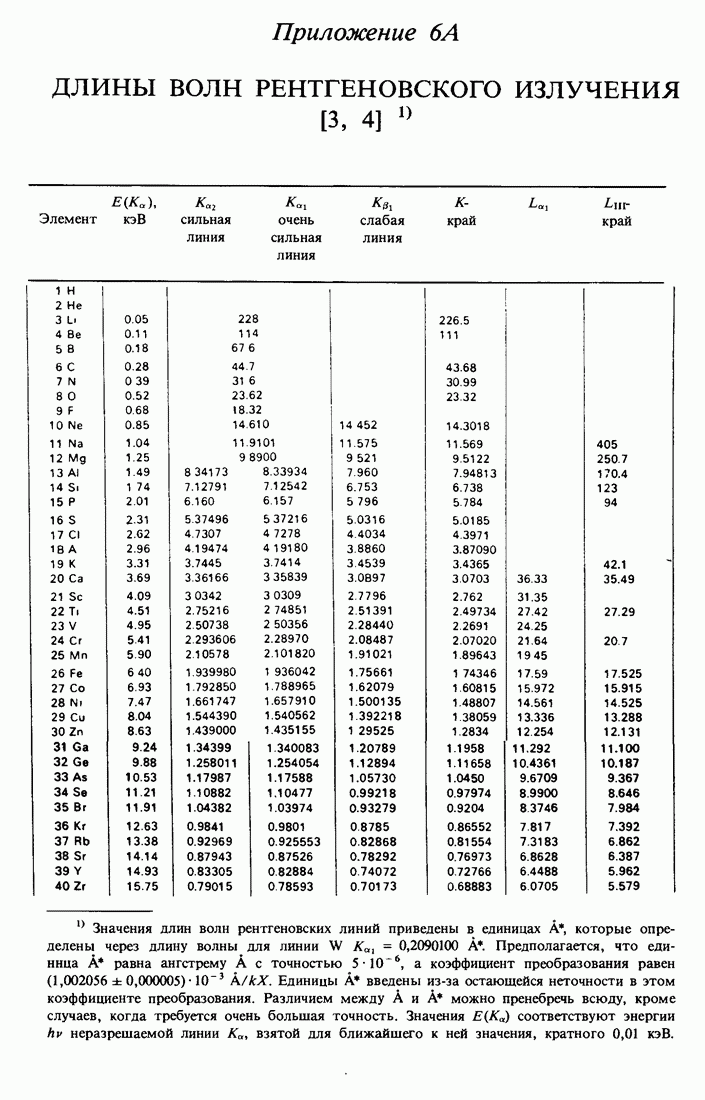
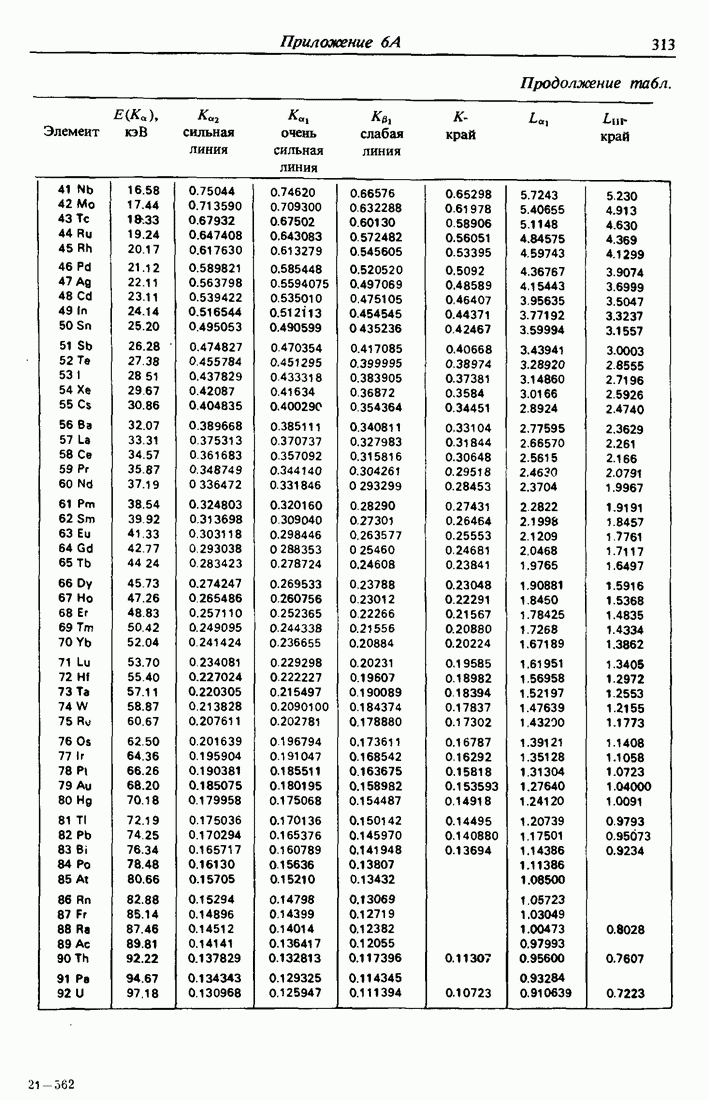
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
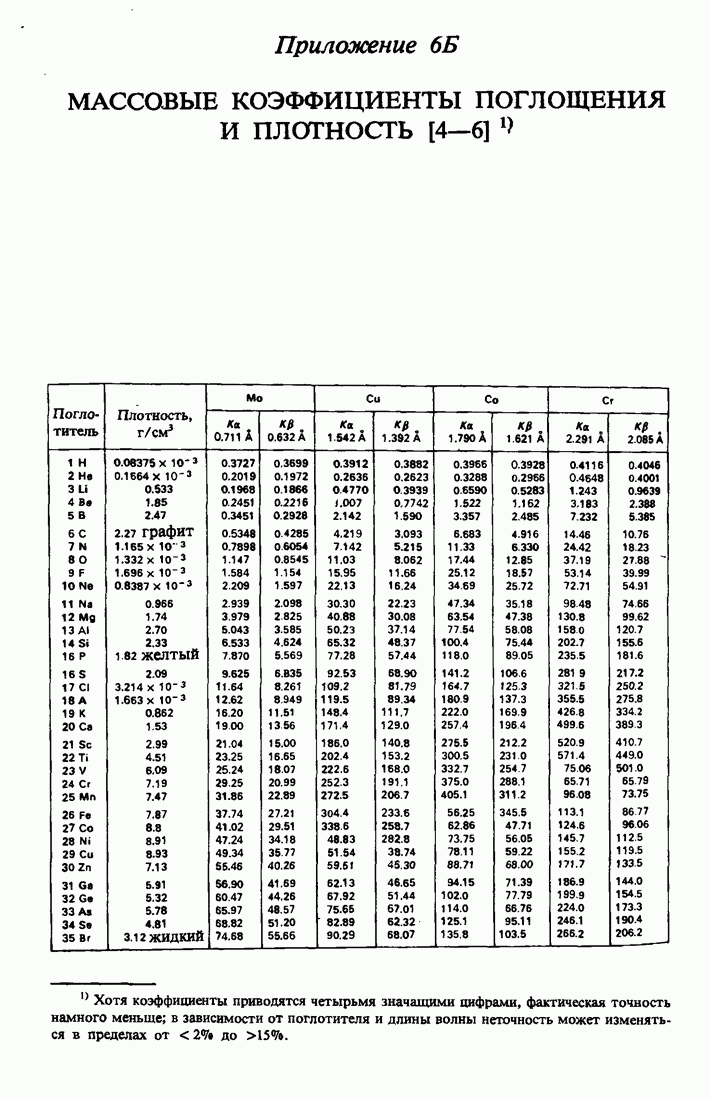
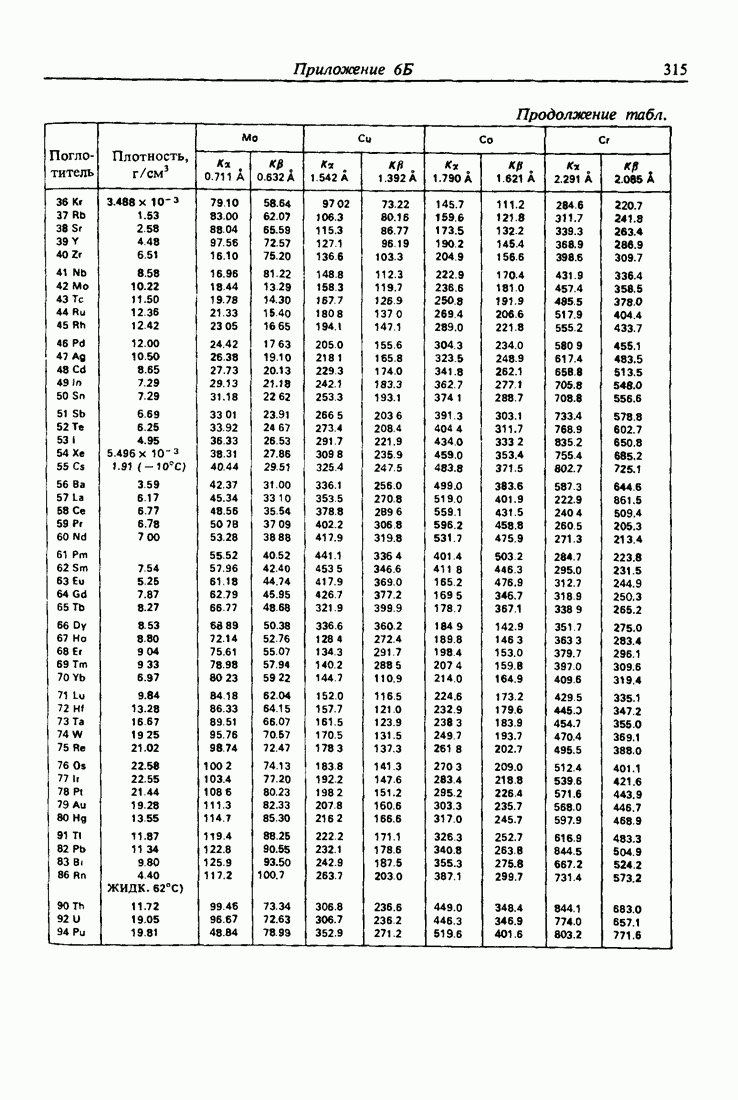
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
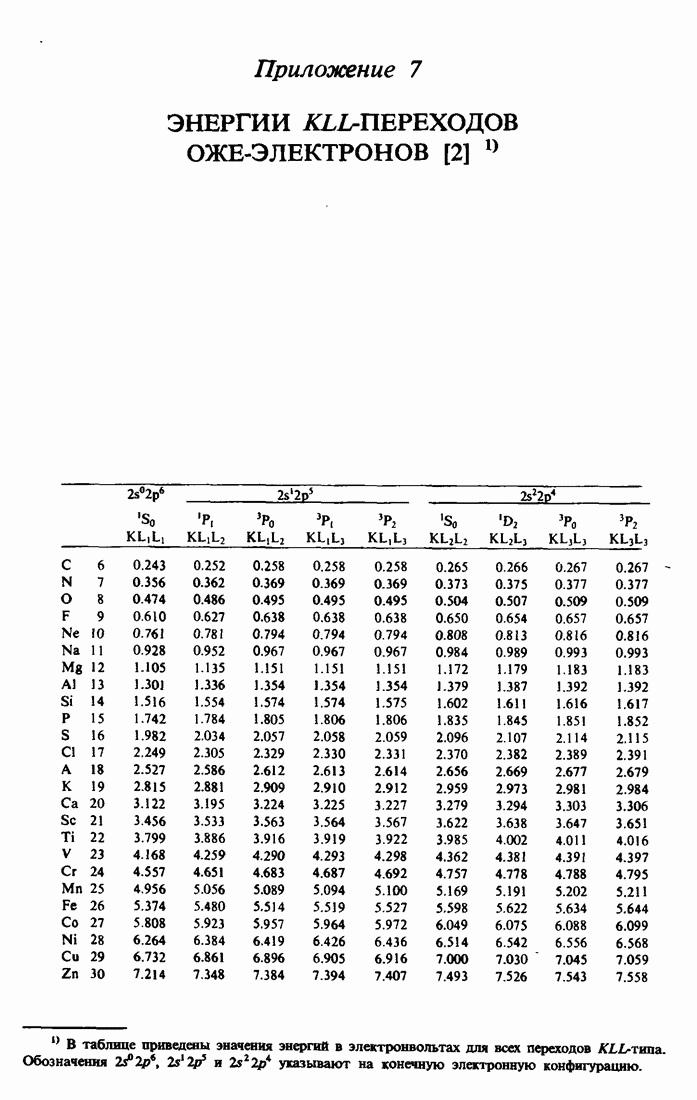
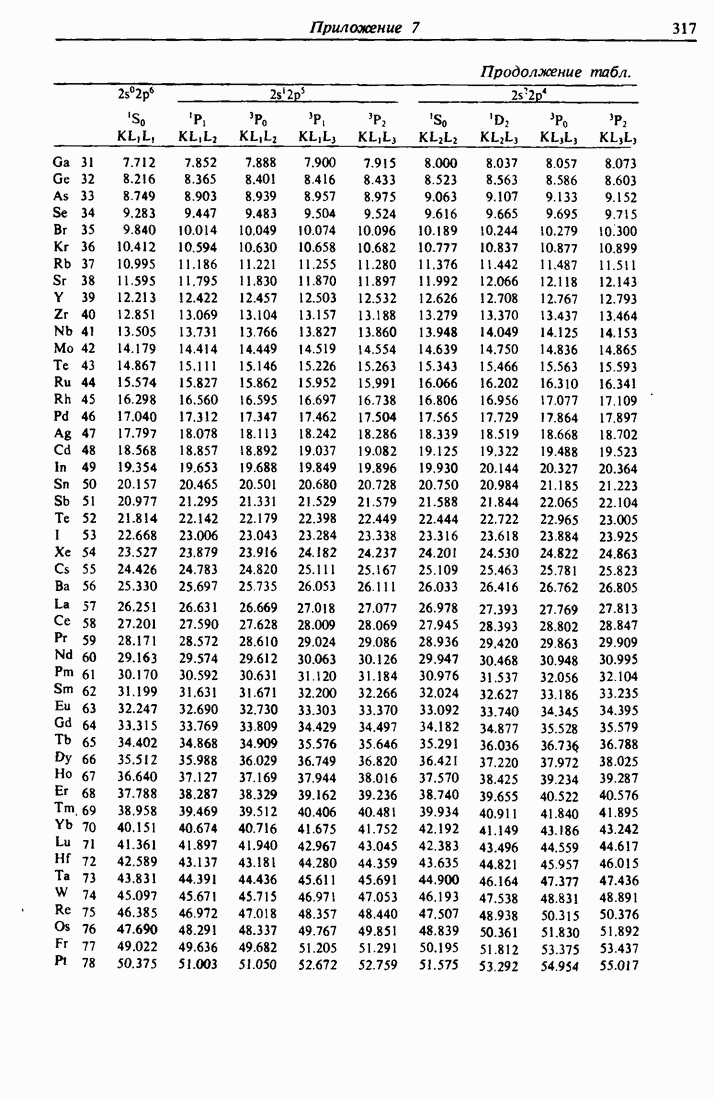
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
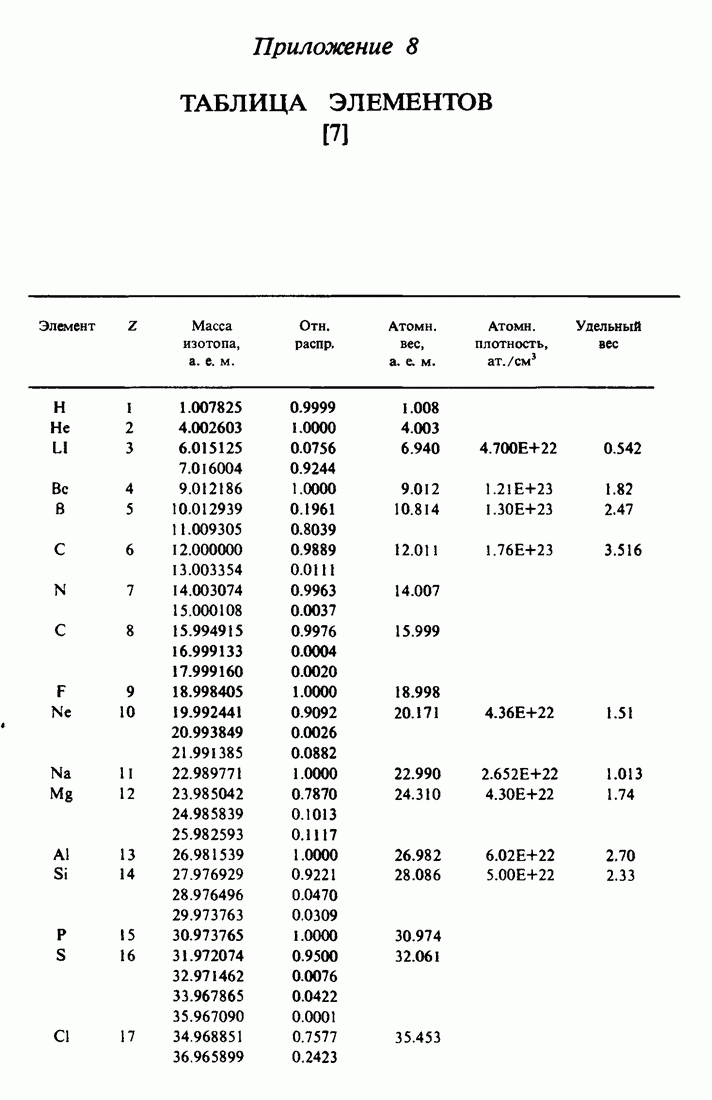
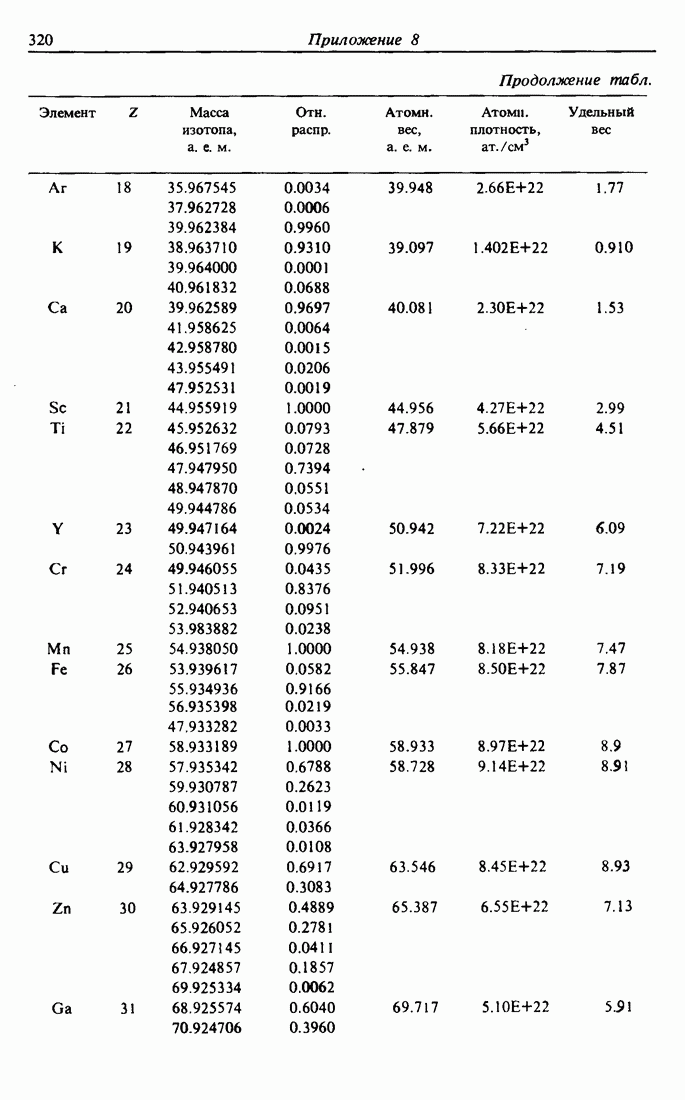
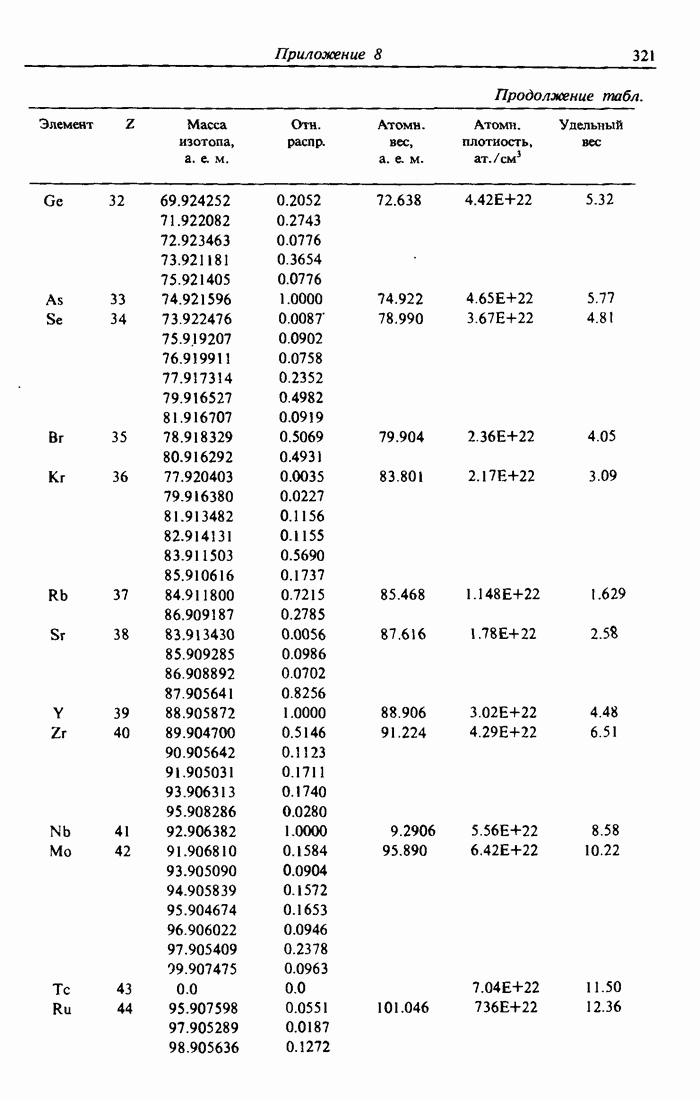
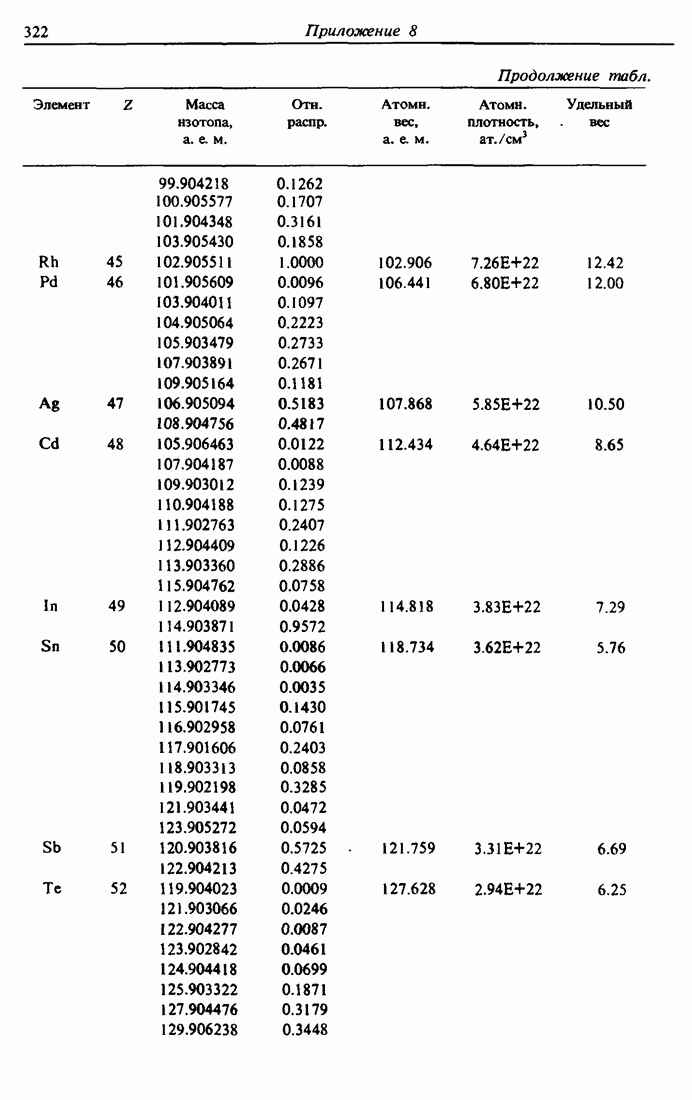
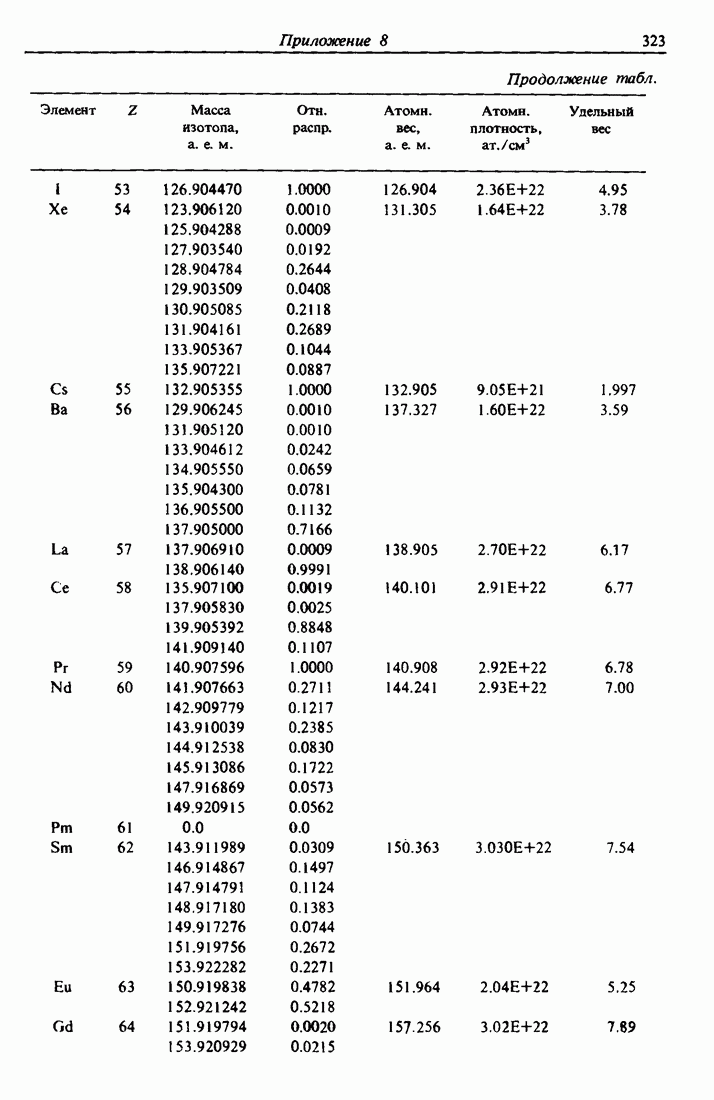
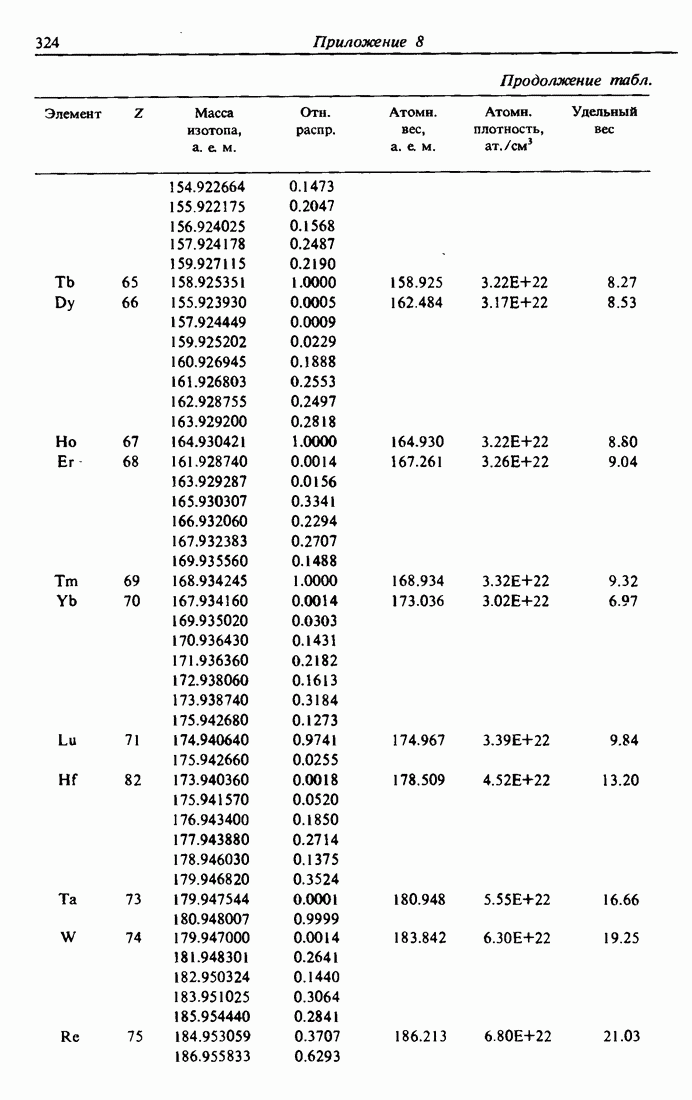
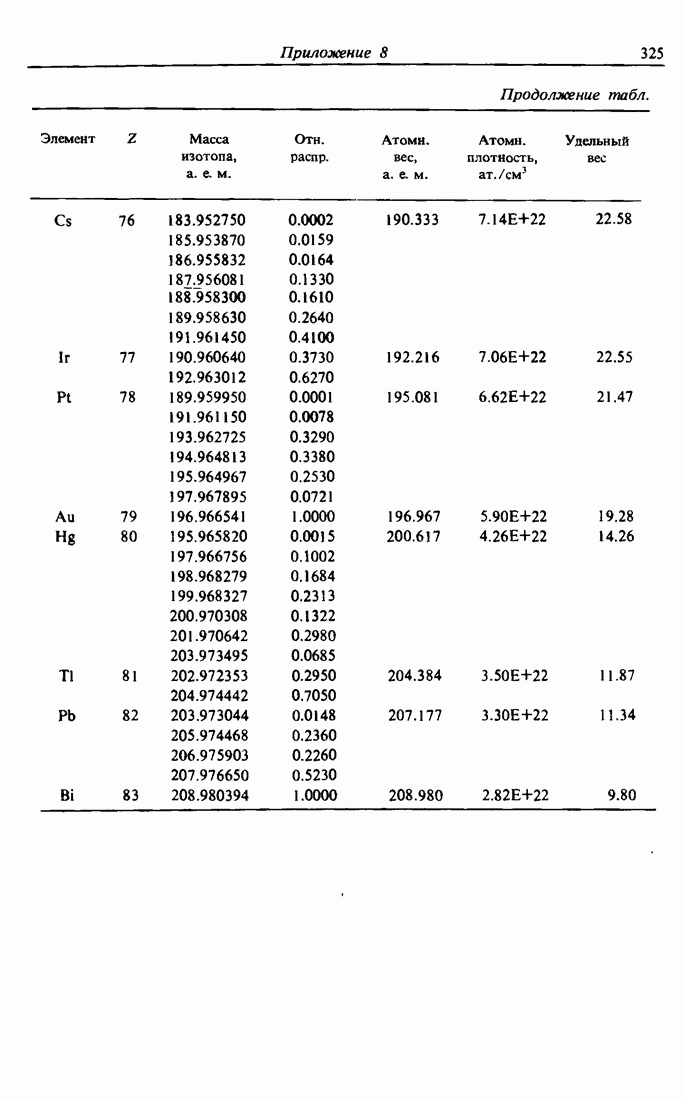
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
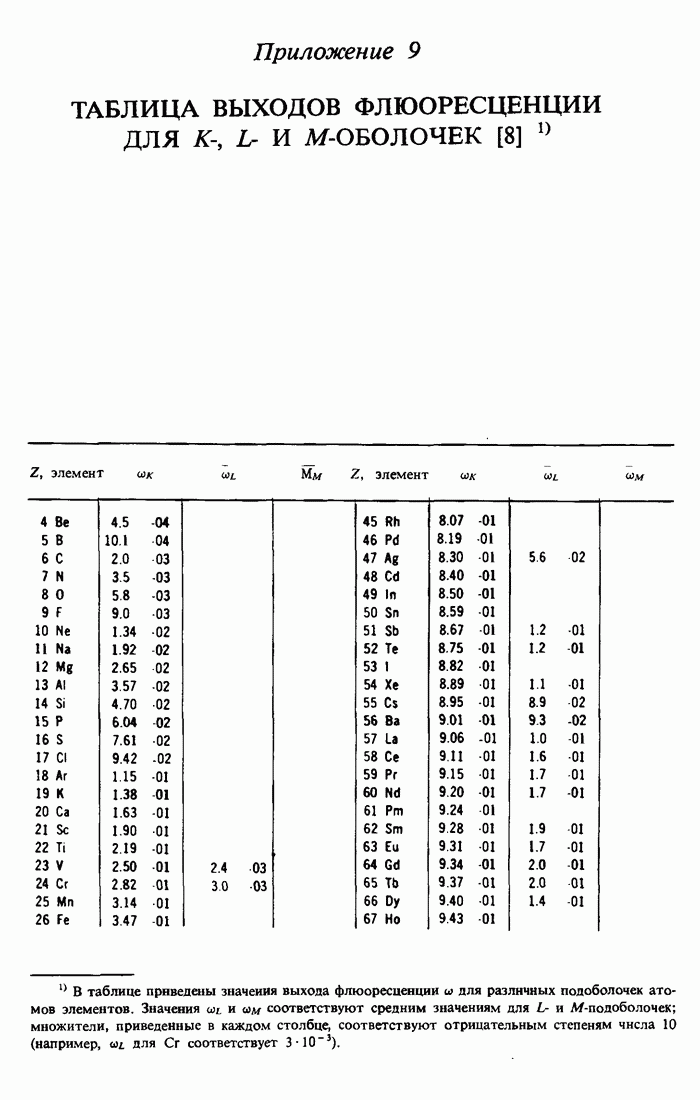
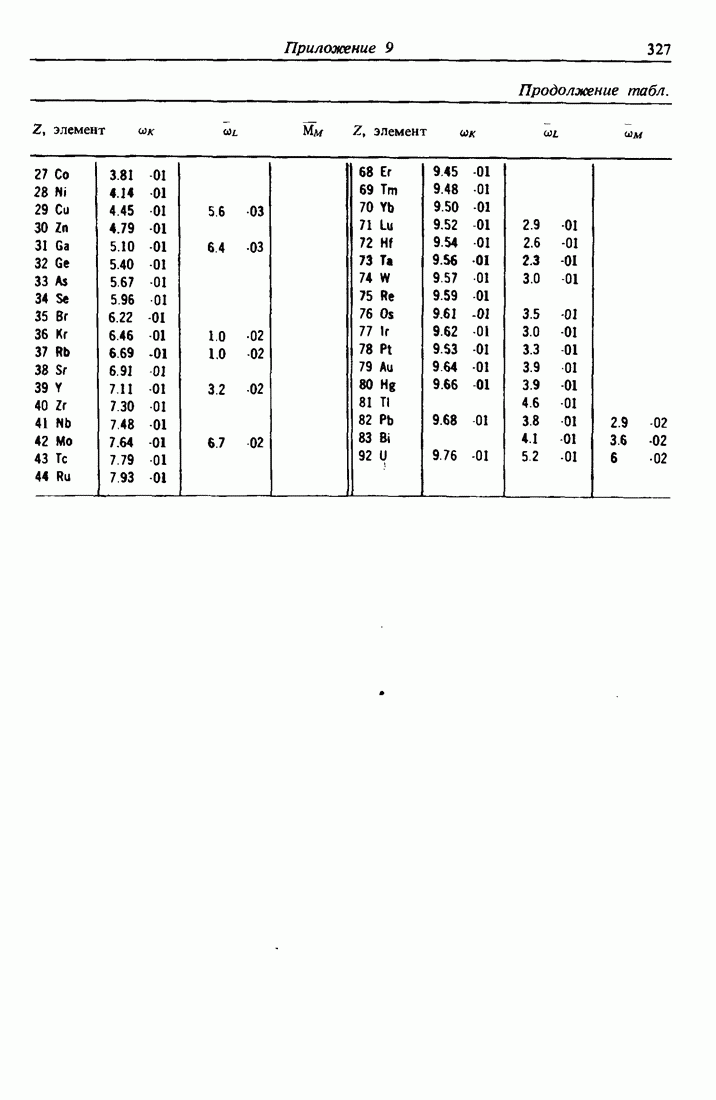
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ