| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8.2. Уравнение Шредингера
Корпускулярно-волновой дуализм материи математически выражается уравнением Шредингера

где  — «волновая функция», которая описывает движение частицы под влиянием потенциала
— «волновая функция», которая описывает движение частицы под влиянием потенциала  . В классической механике физическая проблема «решена», если при заданном потенциале координаты частицы выражаются в виде функций от времени. В квантовой механике задача решена,
. В классической механике физическая проблема «решена», если при заданном потенциале координаты частицы выражаются в виде функций от времени. В квантовой механике задача решена,
если  известна как функция от r и t. Число полностью разрешимых задач, имеющих физический смысл, невелико. Почти все процессы, имеющие отношение к материаловедению, описываются как приближенные решения уравнения Шредингера, полученные с помощью «теории возмущений».
известна как функция от r и t. Число полностью разрешимых задач, имеющих физический смысл, невелико. Почти все процессы, имеющие отношение к материаловедению, описываются как приближенные решения уравнения Шредингера, полученные с помощью «теории возмущений».
В прямоугольных координатах уравнение Шредингера записывается в виде

где  является функцией от х, у, z и t.
является функцией от х, у, z и t.
Во многих случаях достаточно рассмотреть одномерное уравнение Шредингера

Запишем  в виде произведения двух функций
в виде произведения двух функций  :
:

При подстановке в (8.3) это приводит к уравнению

Используя математический метод разделения переменных, замечаем, что левая часть зависит только от х, а правая часть только от f, поэтому обе части пропорциональны константе разделения Е. Итак,

где С — произвольная постоянная, а уравнение для  принимает вид
принимает вид

Полное решение имеет вид

где А — постоянная, определяемая из условия нормировки. Уравнение (8.7) известно как уравнение Шредингера, не зависящее от времени. Разделение переменных может быть выполнено в том случае, когда V не является функцией времени.
Физический смысл уравнения Шредингера подробно обсуждается в ряде книг. Здесь же мы отметим только, что —  соответствует кинетической энергии, V — потенциальной энергии, а уравнение (8.7) часто записывают в кратком виде
соответствует кинетической энергии, V — потенциальной энергии, а уравнение (8.7) часто записывают в кратком виде

где  кинетическая энергия
кинетическая энергия  потенциальная энергия) соответствует классическому гамильтониану. Физический смысл функции
потенциальная энергия) соответствует классическому гамильтониану. Физический смысл функции  может быть понят, если учесть, что
может быть понят, если учесть, что  определяет вероятность нахождения частицы в точке r во время t. Уравнение (8.7) является примером «уравнения на собственные значения», в котором u — собственные функции оператора
определяет вероятность нахождения частицы в точке r во время t. Уравнение (8.7) является примером «уравнения на собственные значения», в котором u — собственные функции оператора  , а Е — собственное значение. Для многих реалистических потенциалов решение уравнения (8.7) включает лишь дискретные значенйя Е, оправдывая, таким образом, предположение о квантовании в теории Бора, рассмотренной в гл. 1.
, а Е — собственное значение. Для многих реалистических потенциалов решение уравнения (8.7) включает лишь дискретные значенйя Е, оправдывая, таким образом, предположение о квантовании в теории Бора, рассмотренной в гл. 1.
В задачах с центральной силой потенциал  , а уравнение Шредингера в сферических координатах
, а уравнение Шредингера в сферических координатах  перепишется в виде
перепишется в виде

Используя вновь разделение переменных

для радиальной части получаем

где  — «орбитальное» квантовое число.
— «орбитальное» квантовое число.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
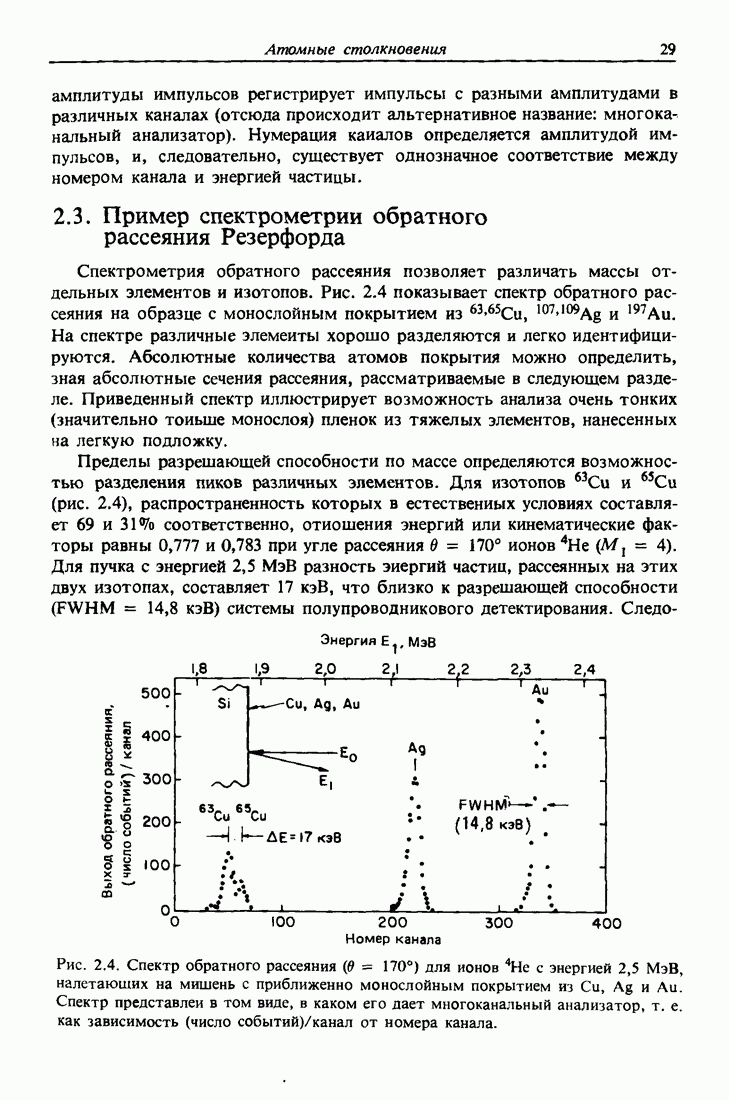
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
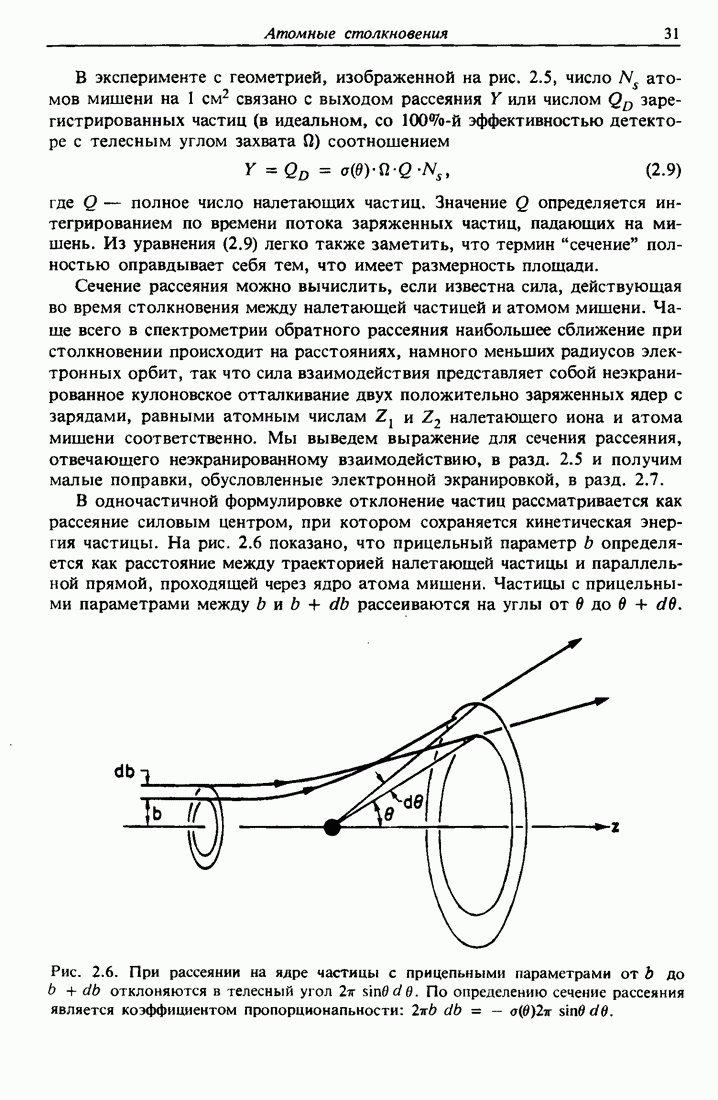
- 2.4. Сечение рассеяния и прицельный параметр
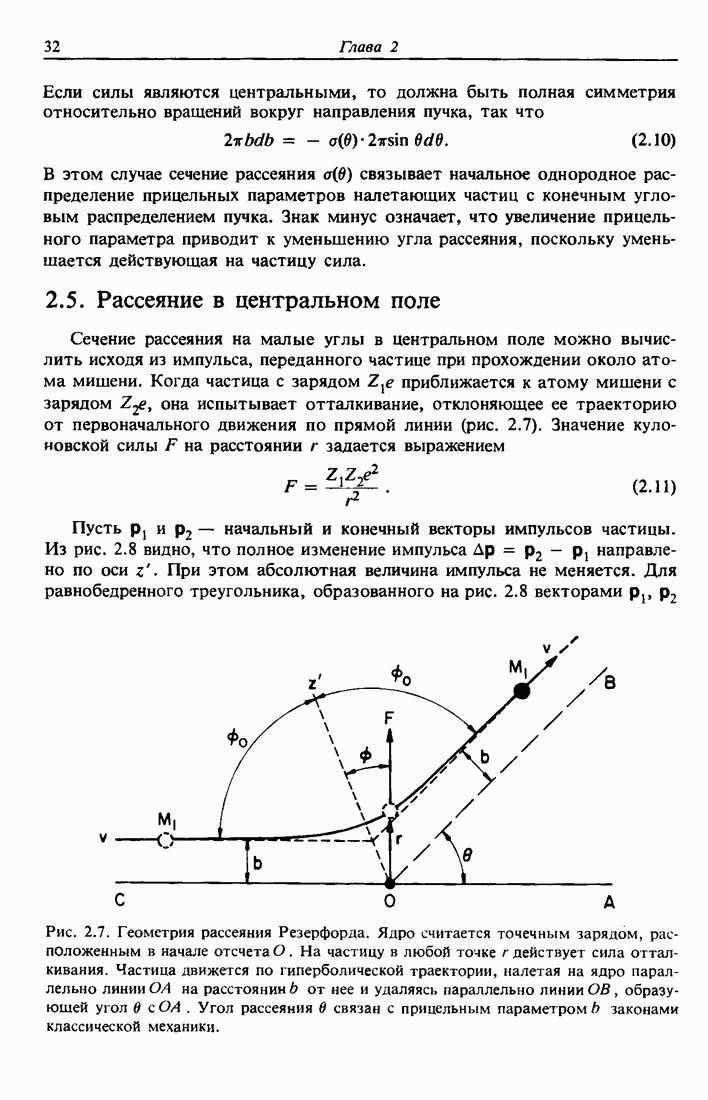
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
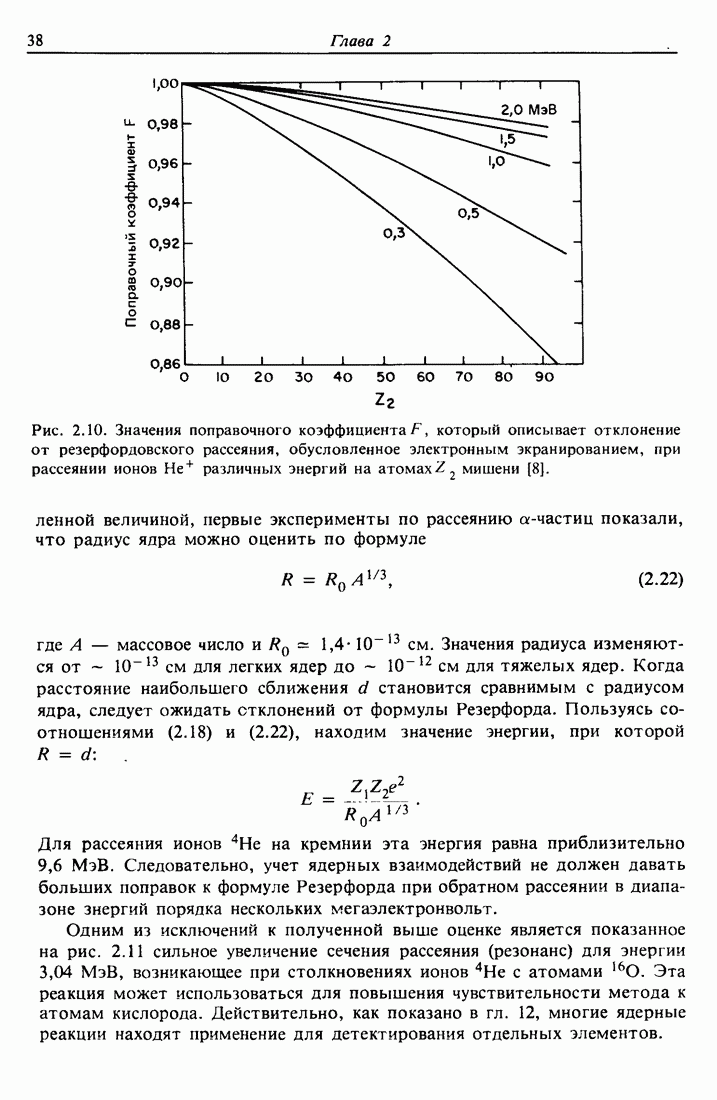
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
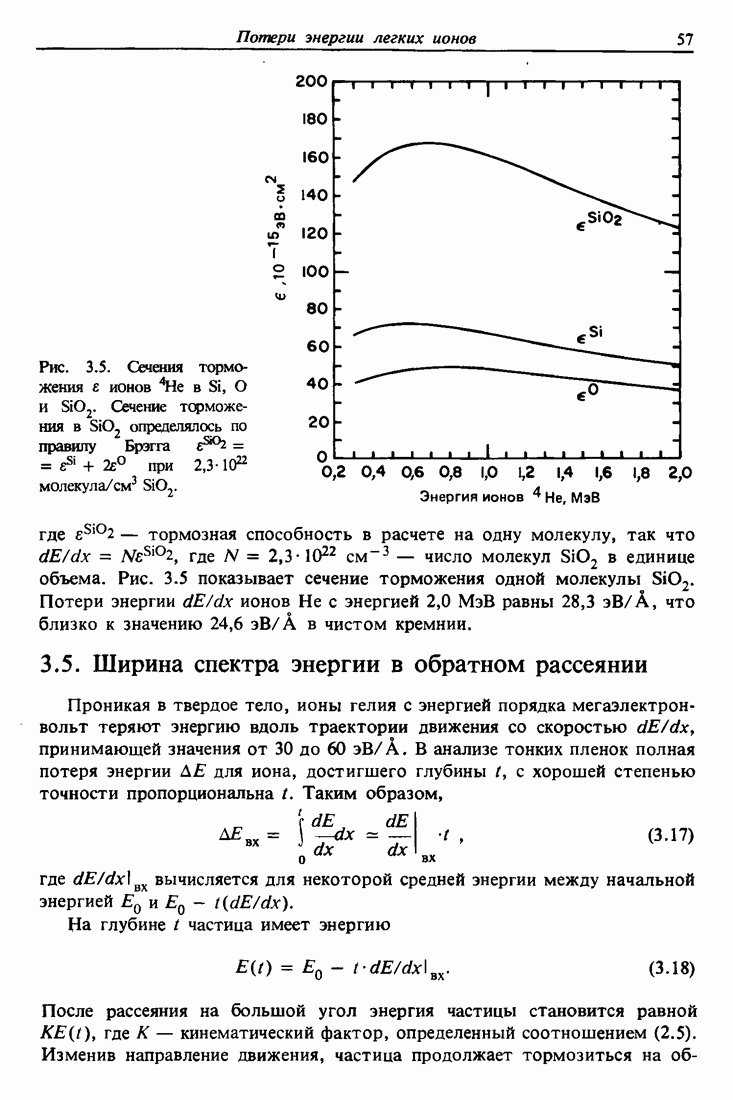
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
- 3.4. Потери энергии в химических соединениях и правило Брэгга
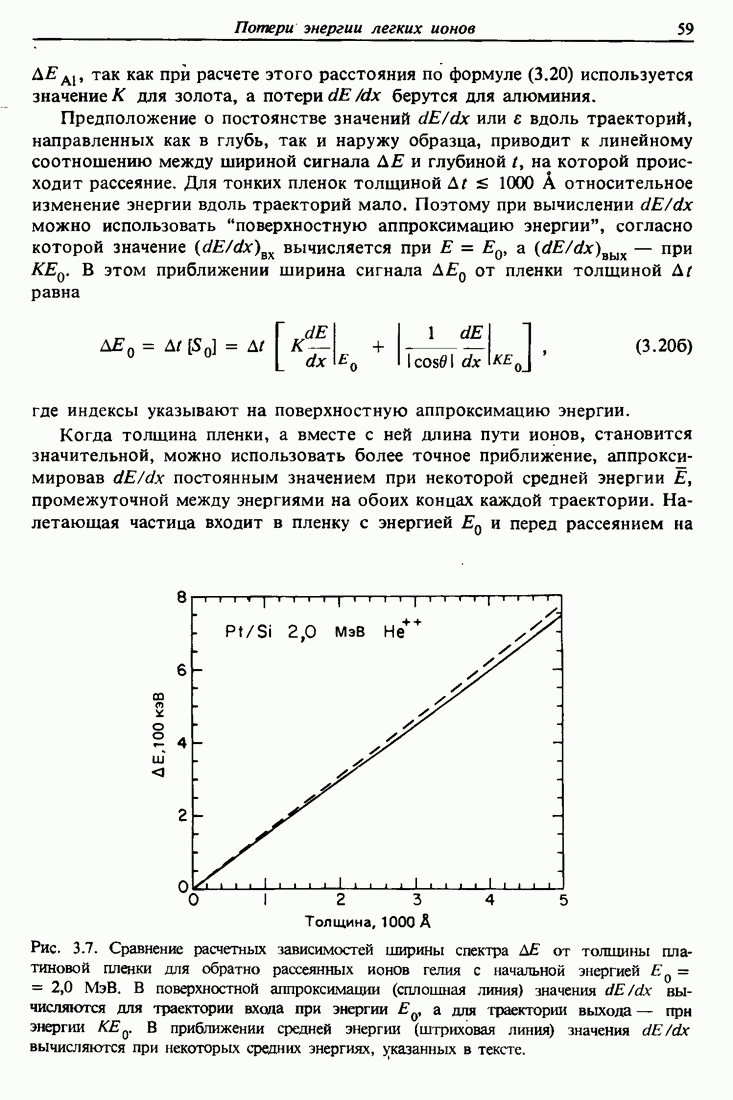
- 3.5. Ширина спектра энергии в обратном рассеянии
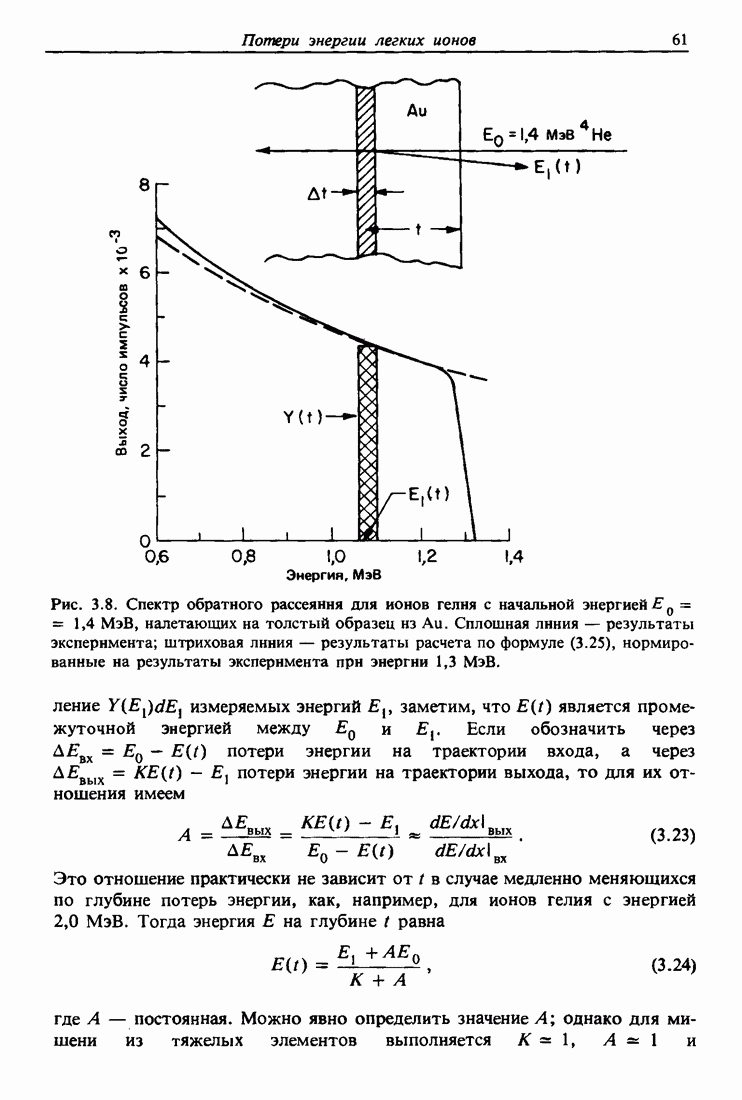
- 3.6. Форма спектра обратного рассеяния
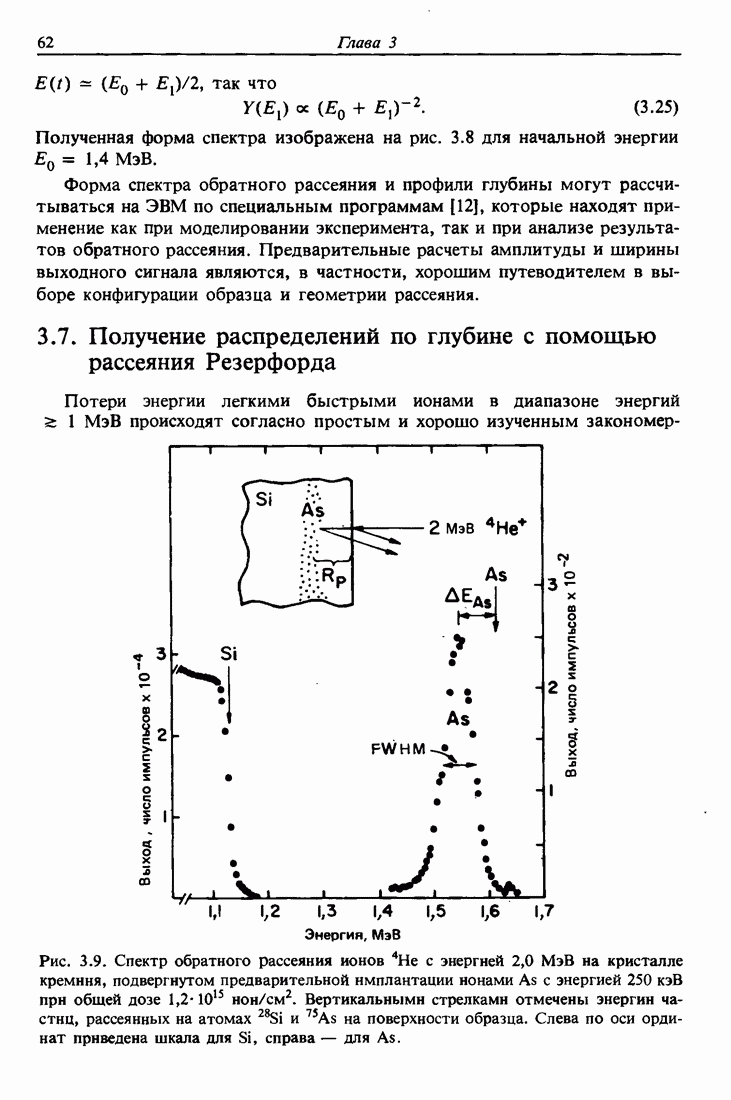
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
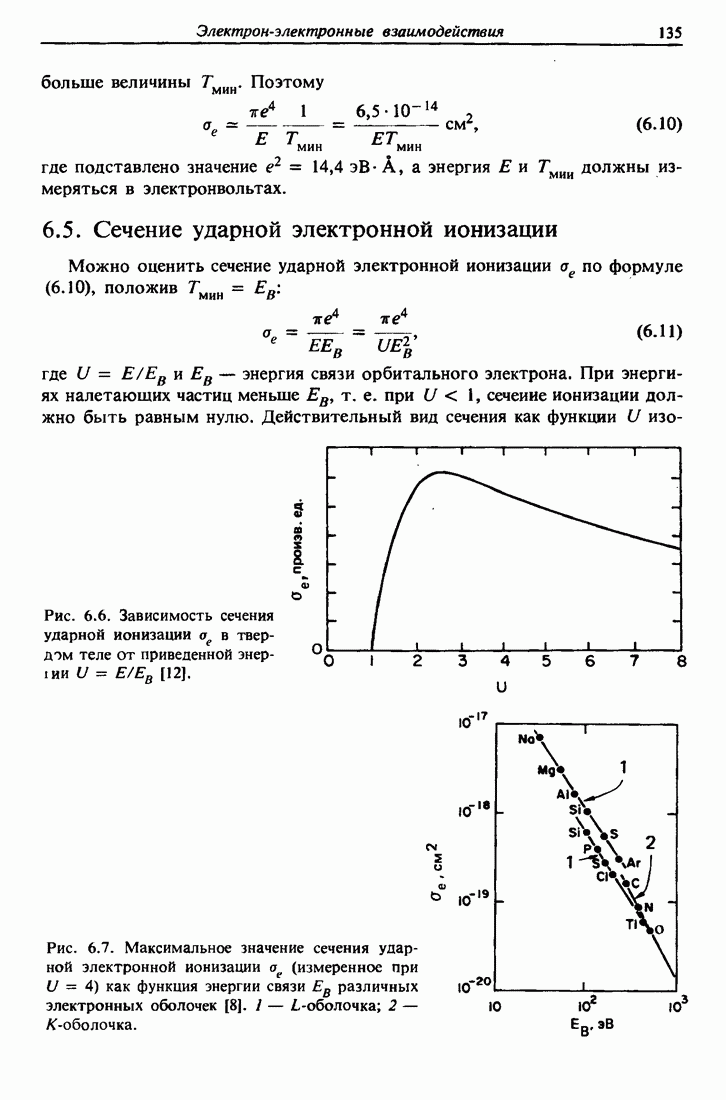
- 6.5. Сечение ударной электронной ионизации
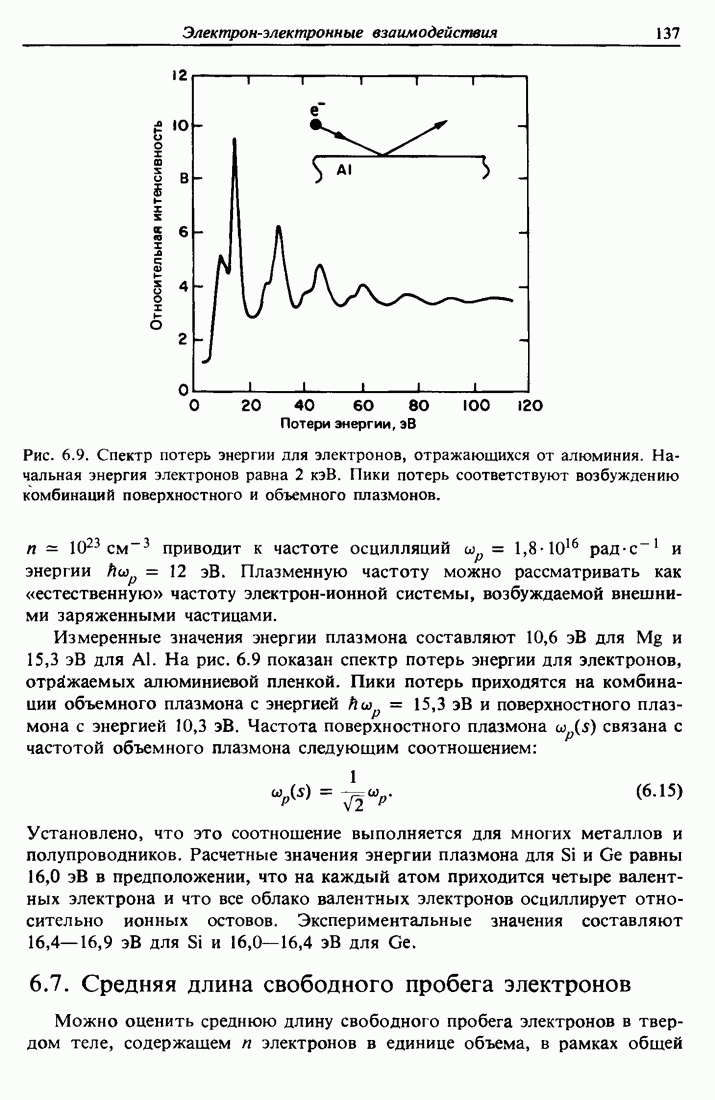
- 6.6. Плазмоны
- 6.7. Средняя длина свободного пробега электронов
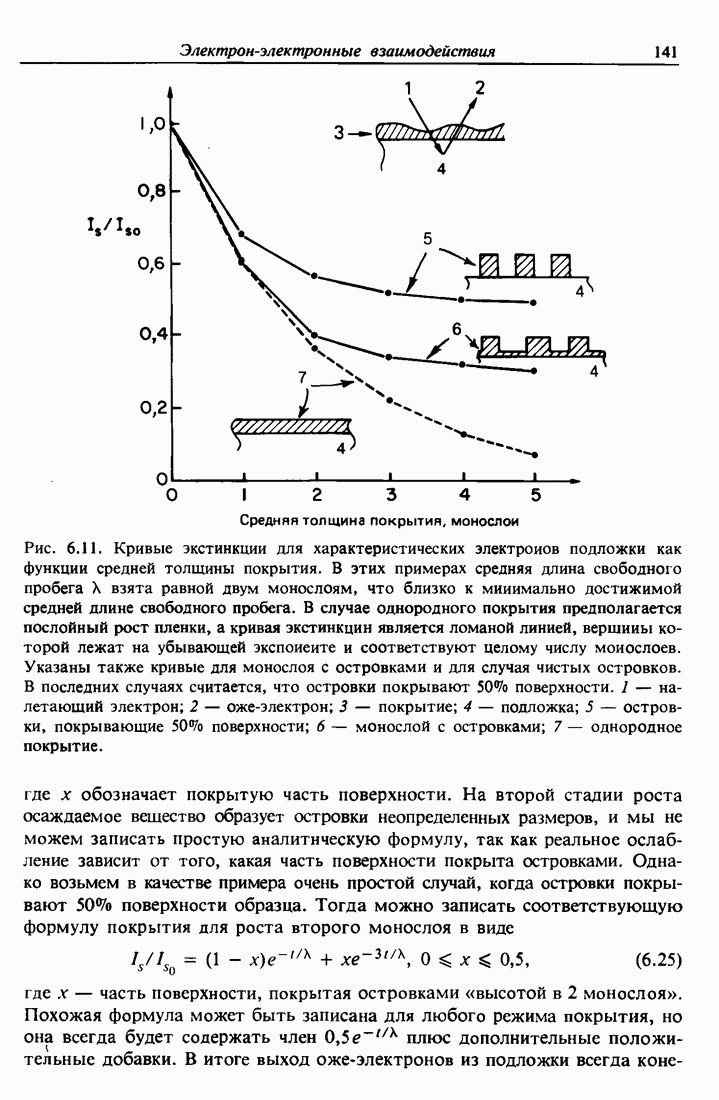
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
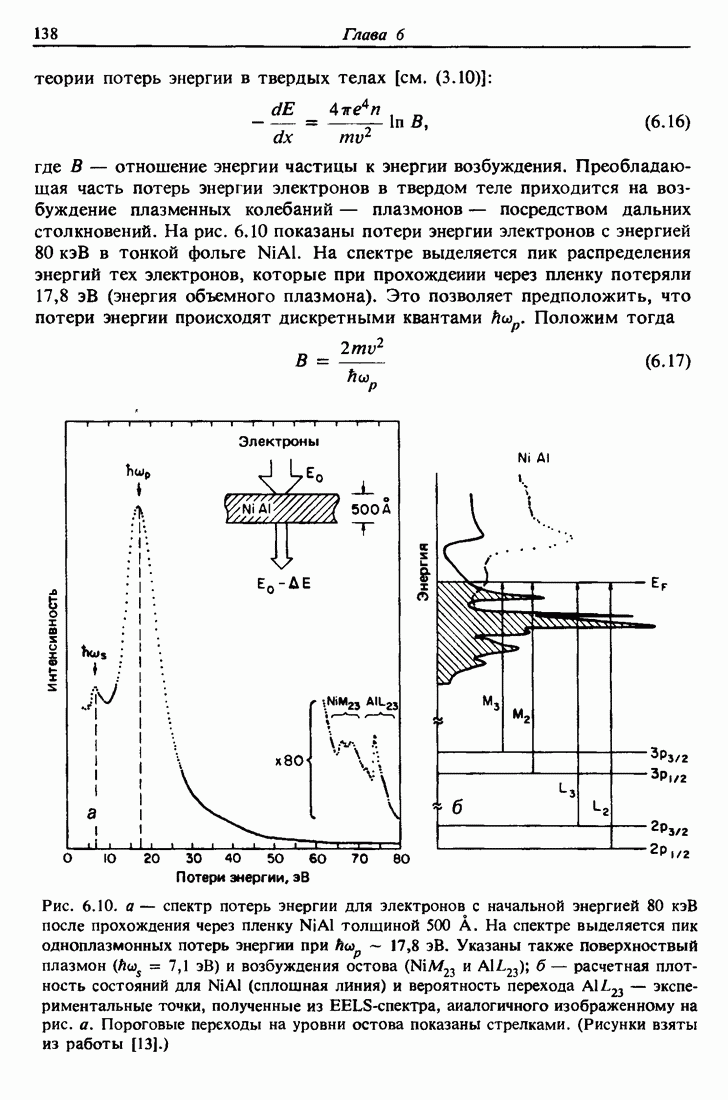
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
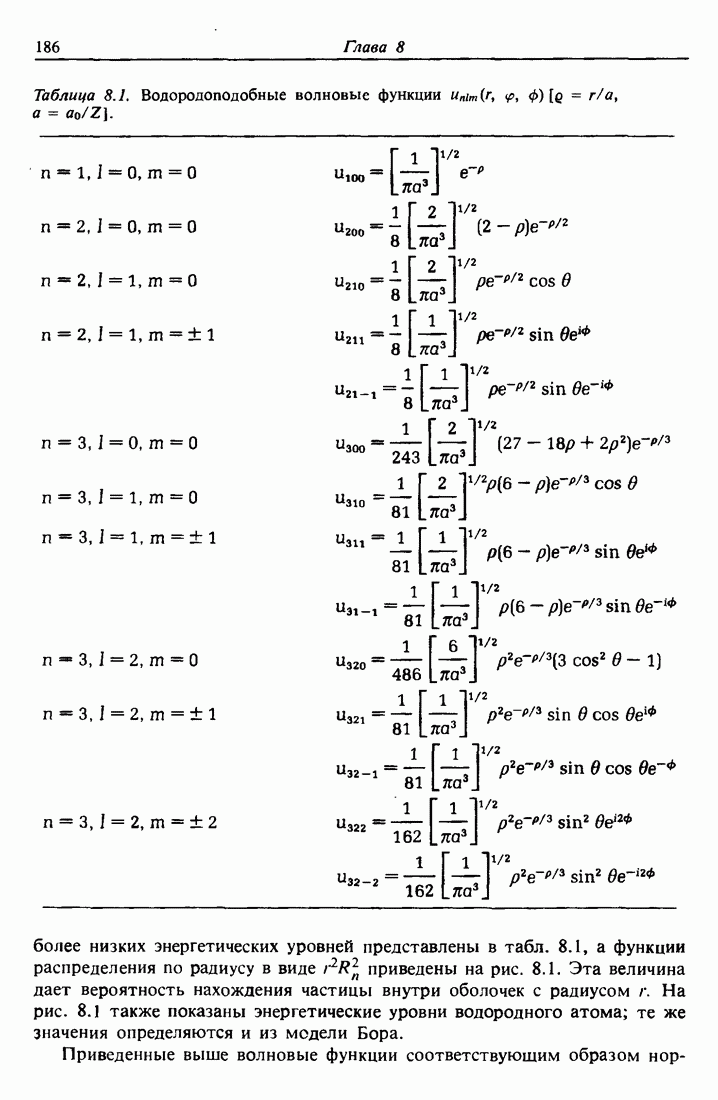
- 8.3. Волновые функции
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
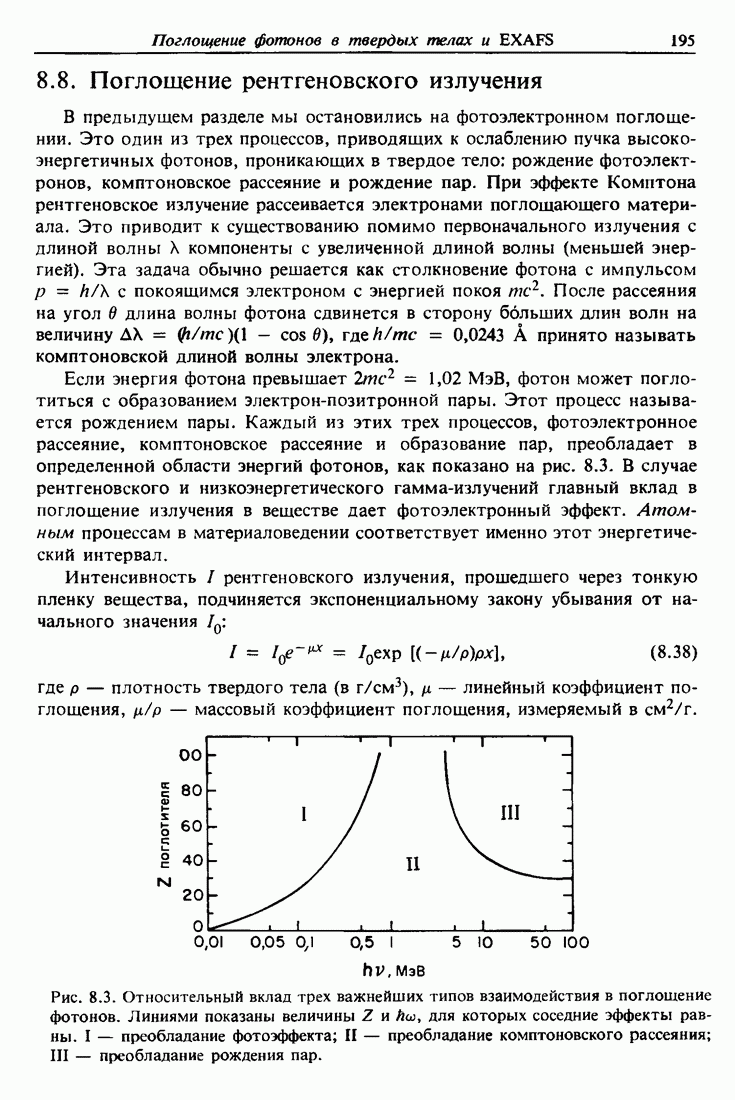
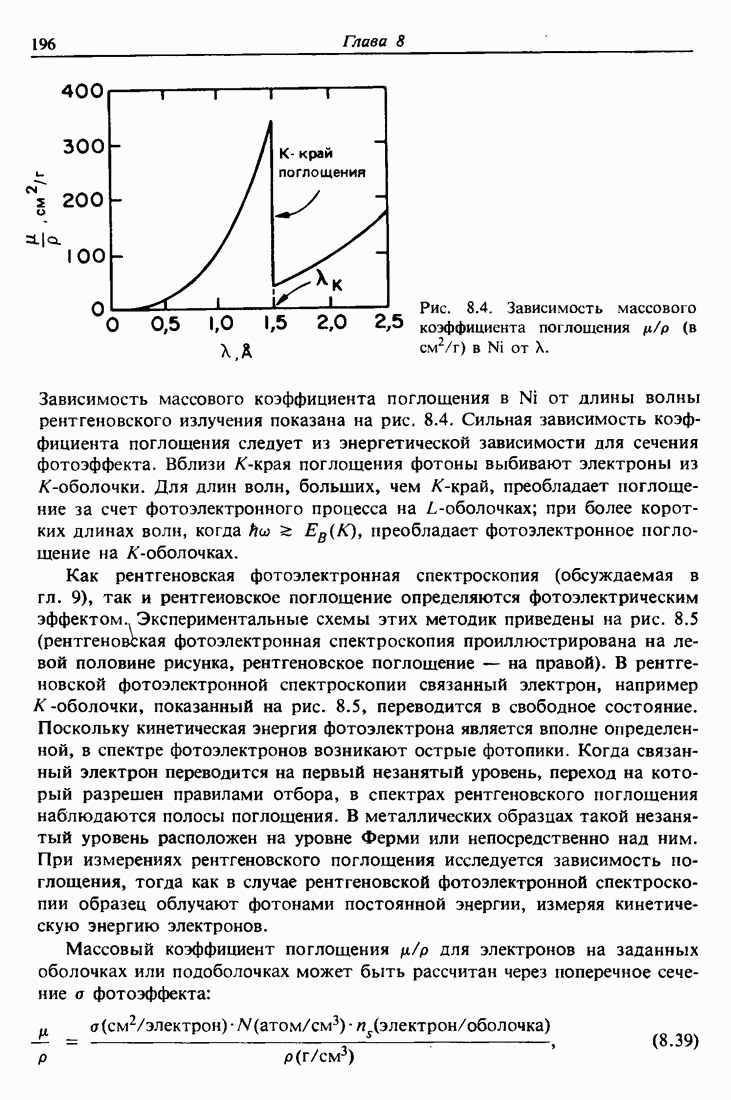
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
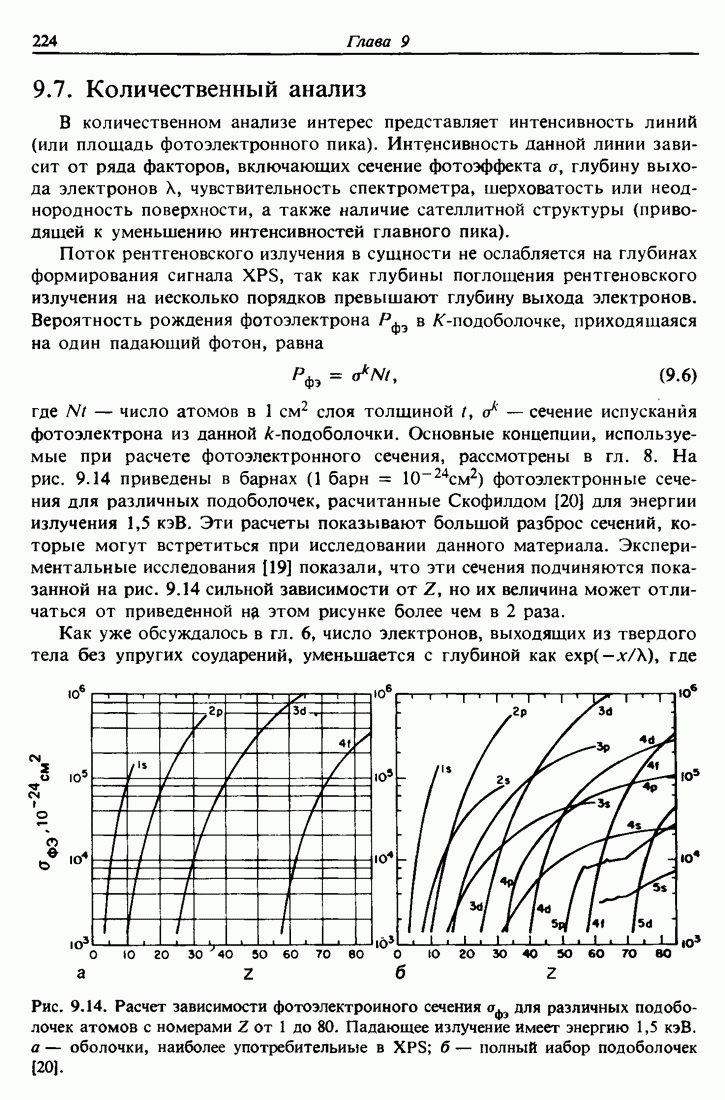
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
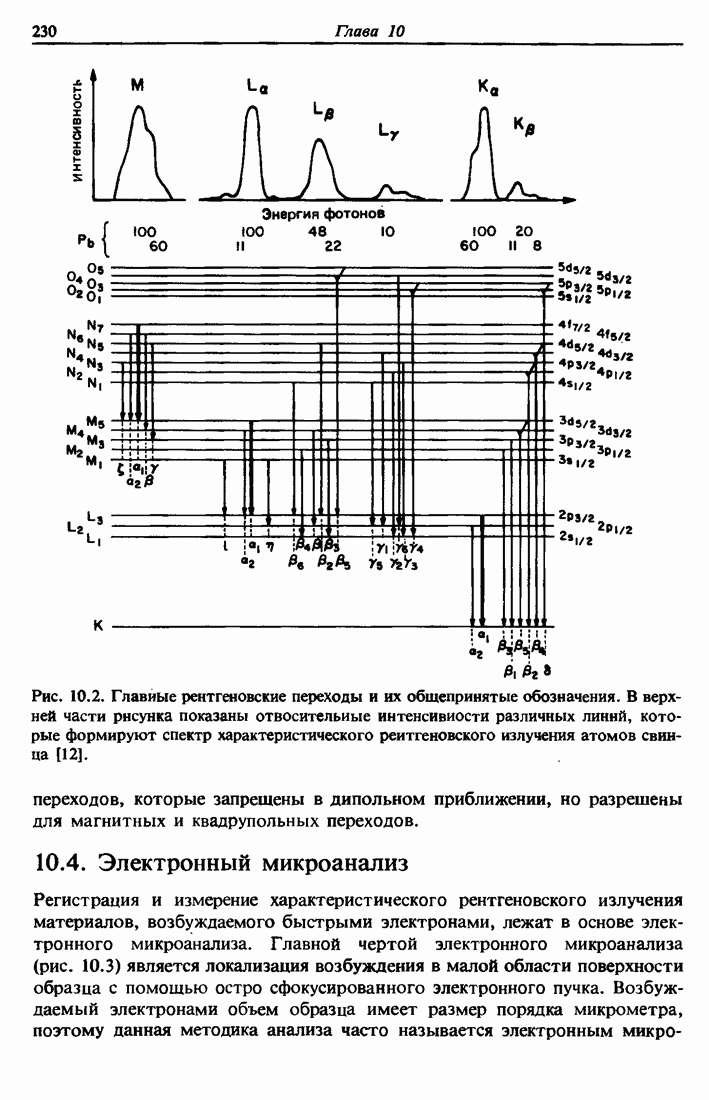
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
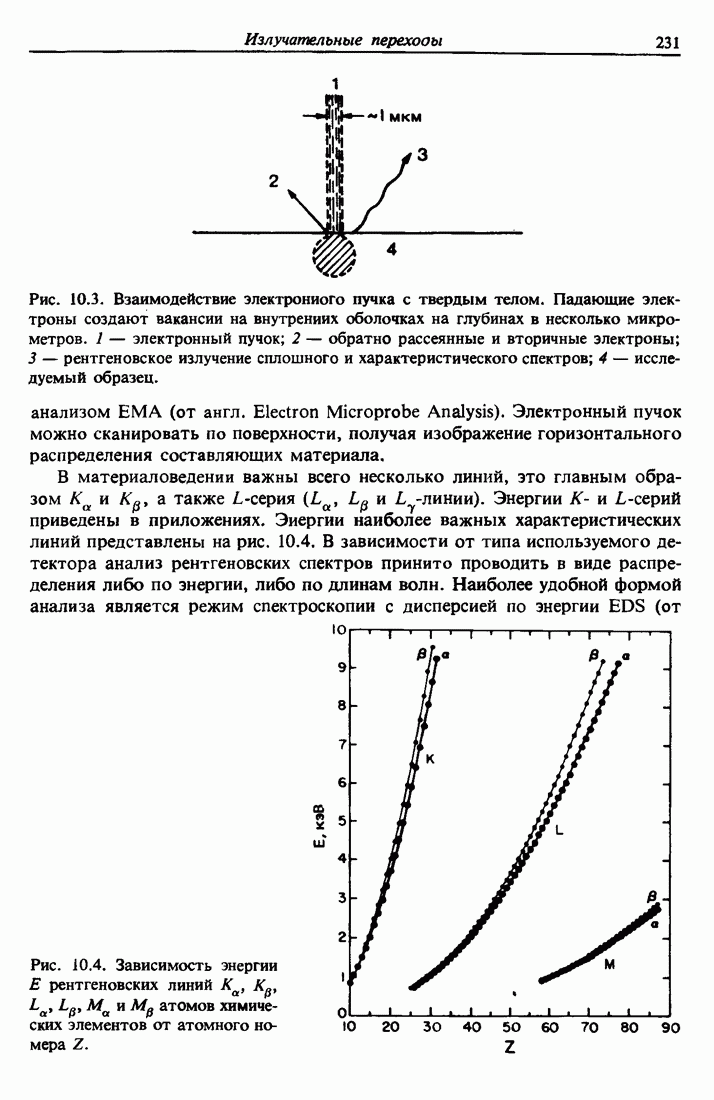
- 10.4. Электронный микроанализ
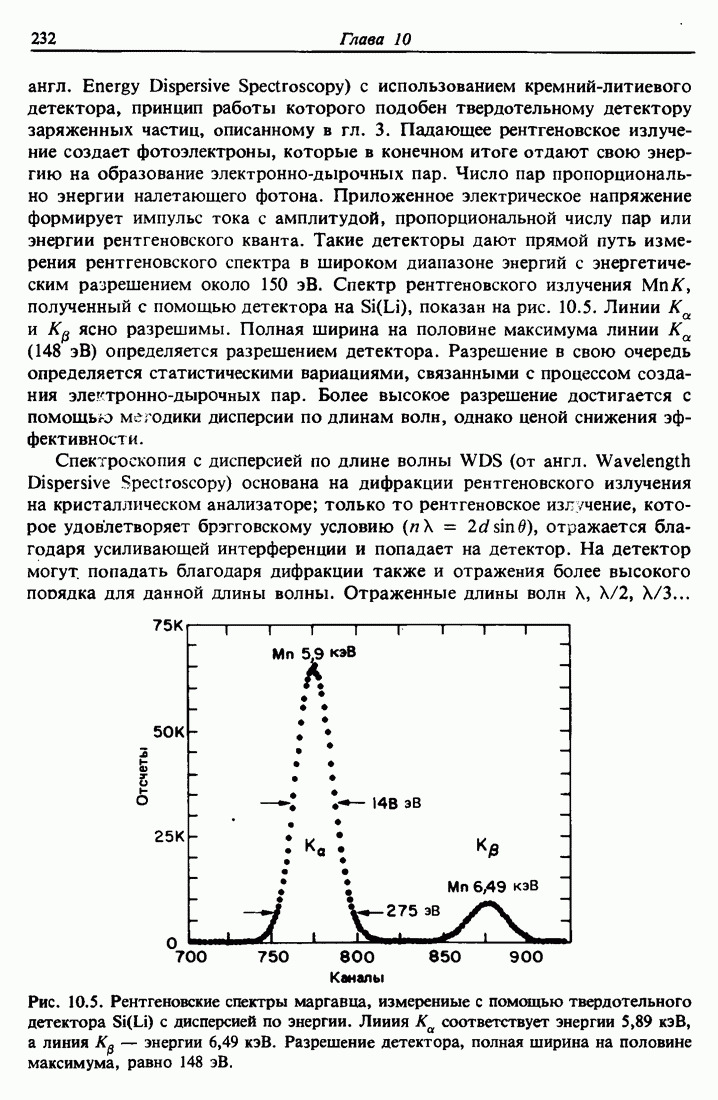
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
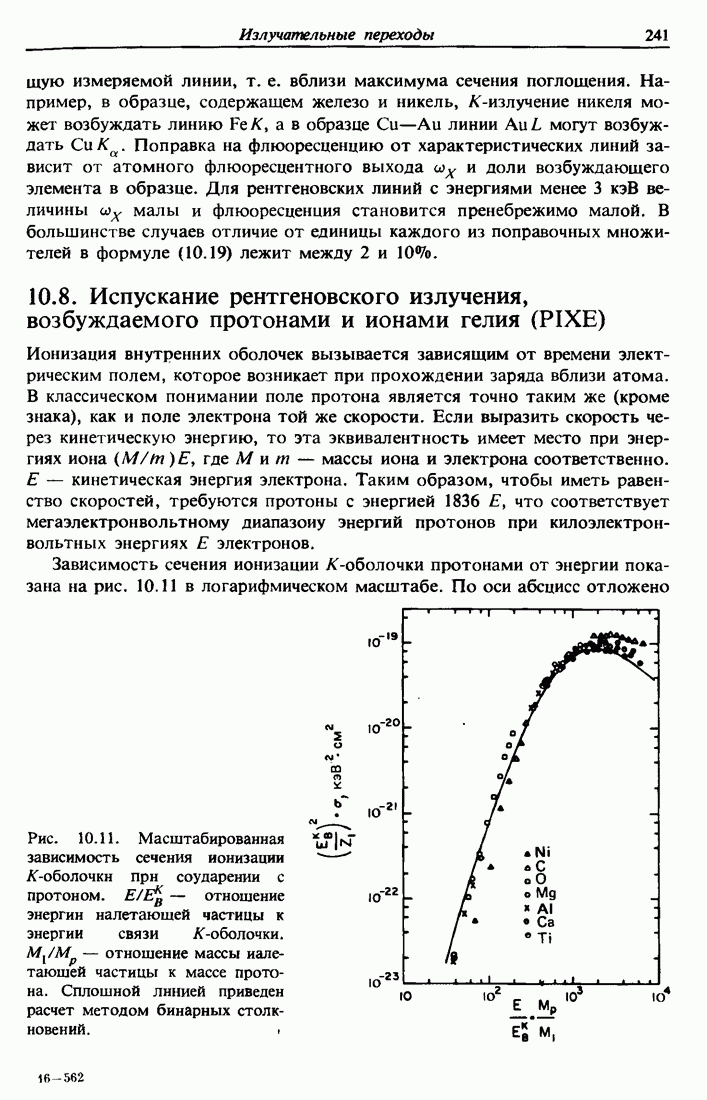
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
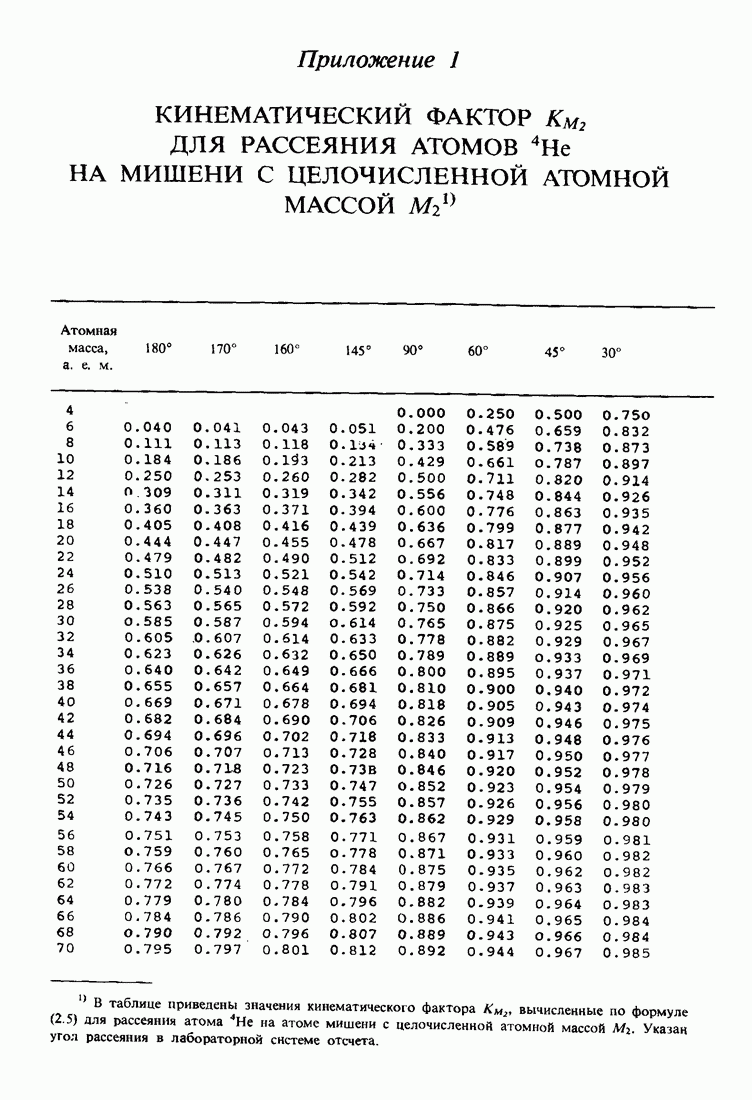
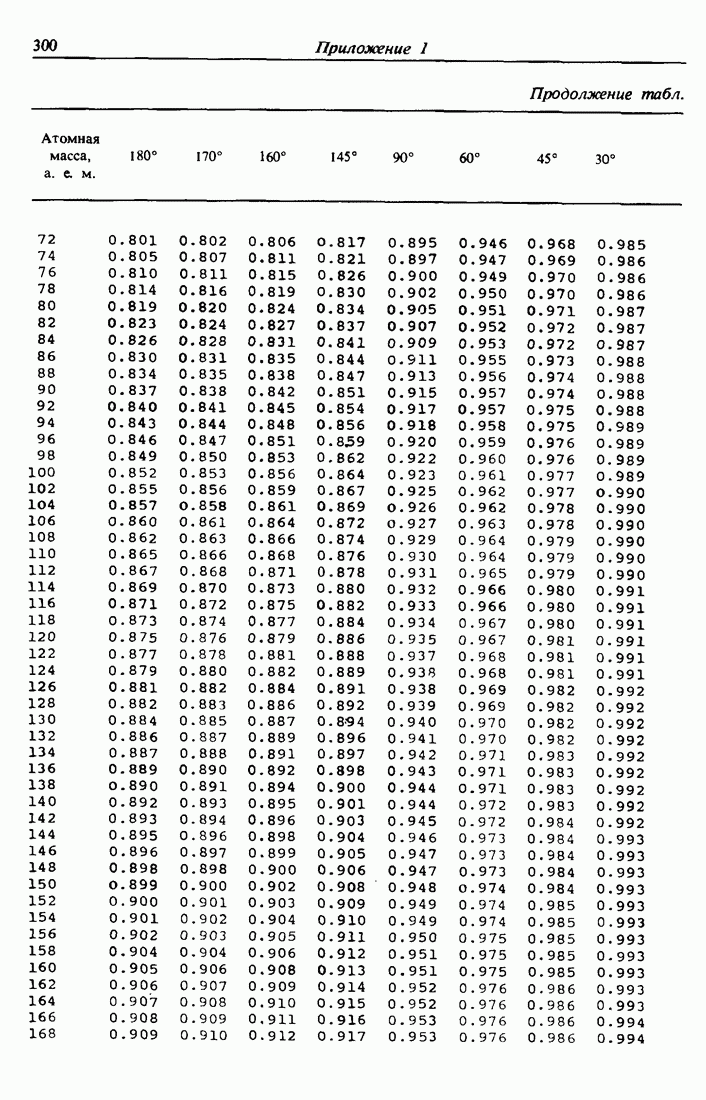
- ПРИЛОЖЕНИЕ 1.
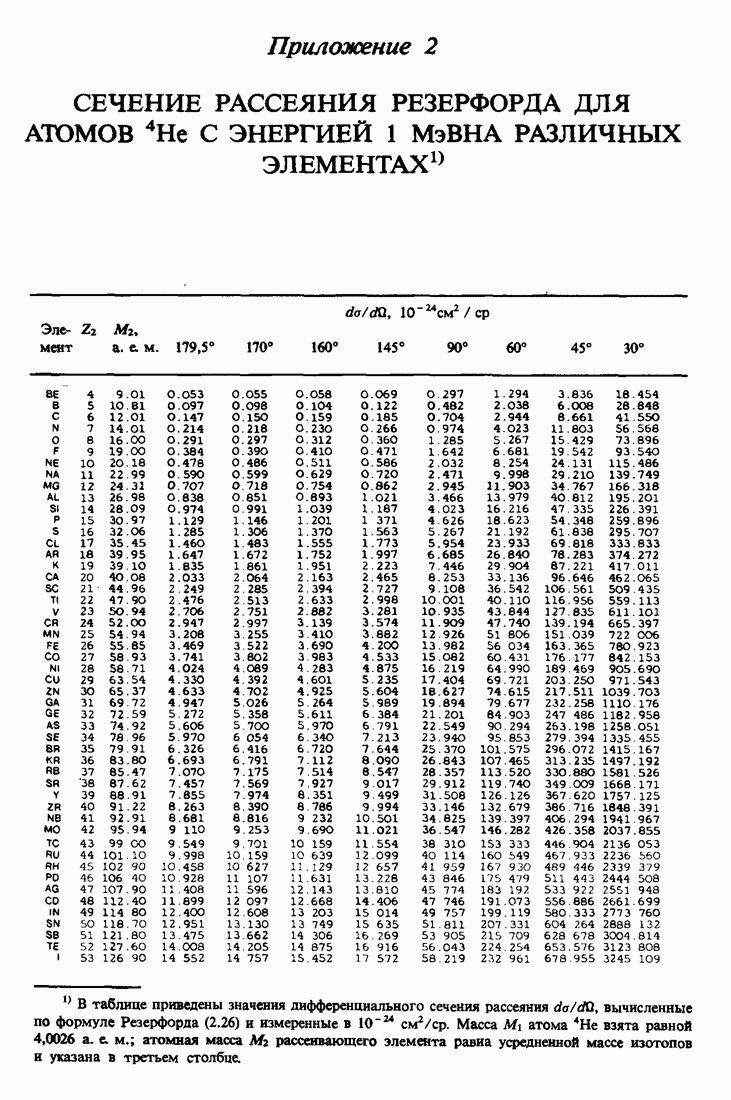
- ПРИЛОЖЕНИЕ 2.
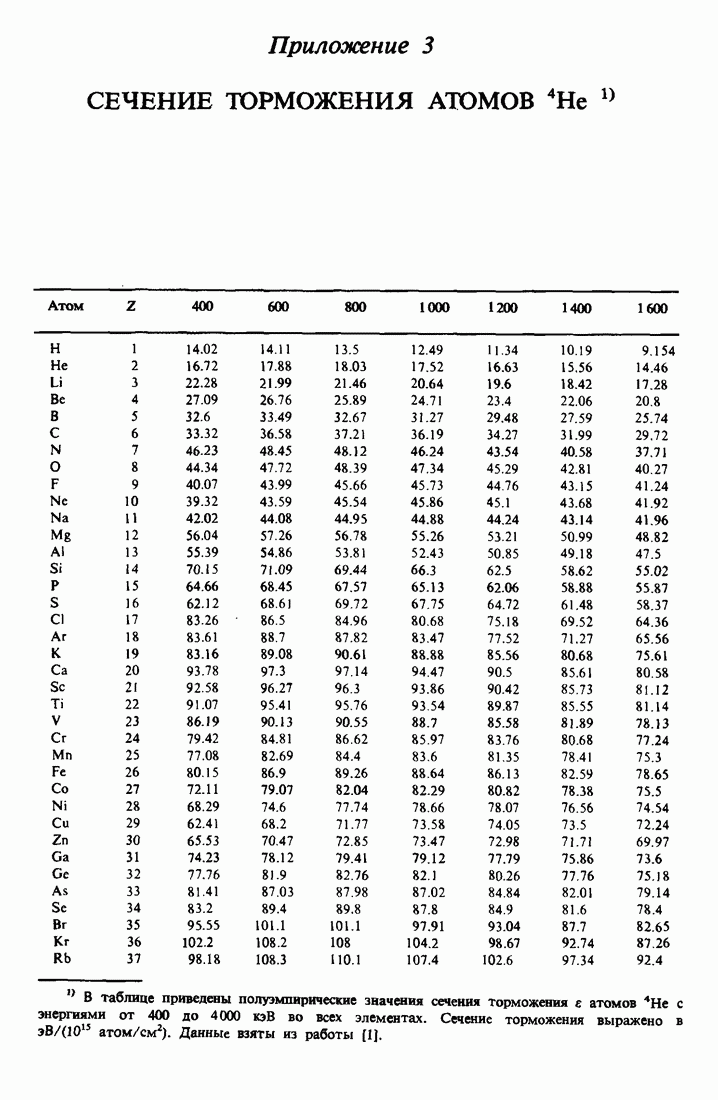
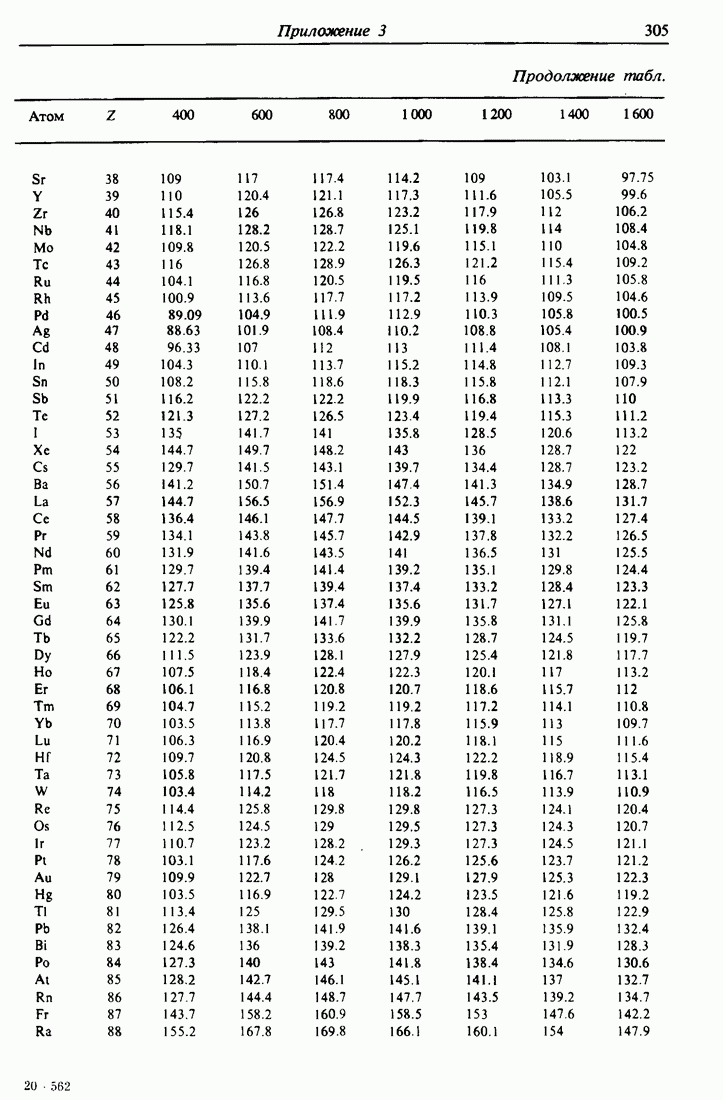
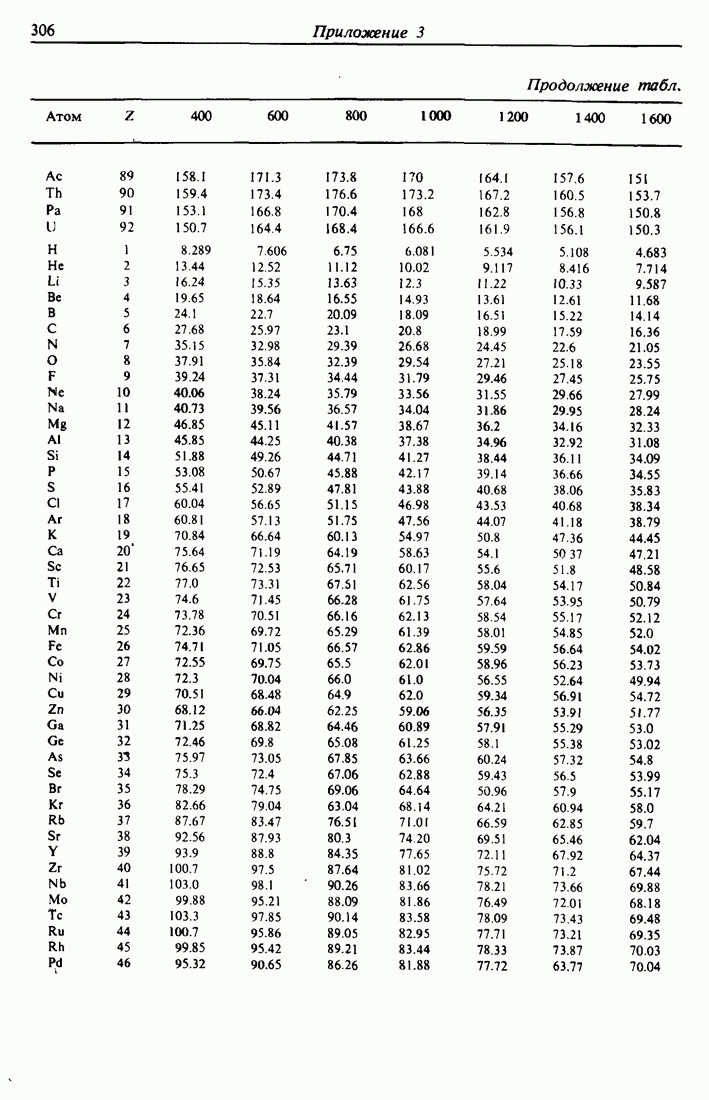
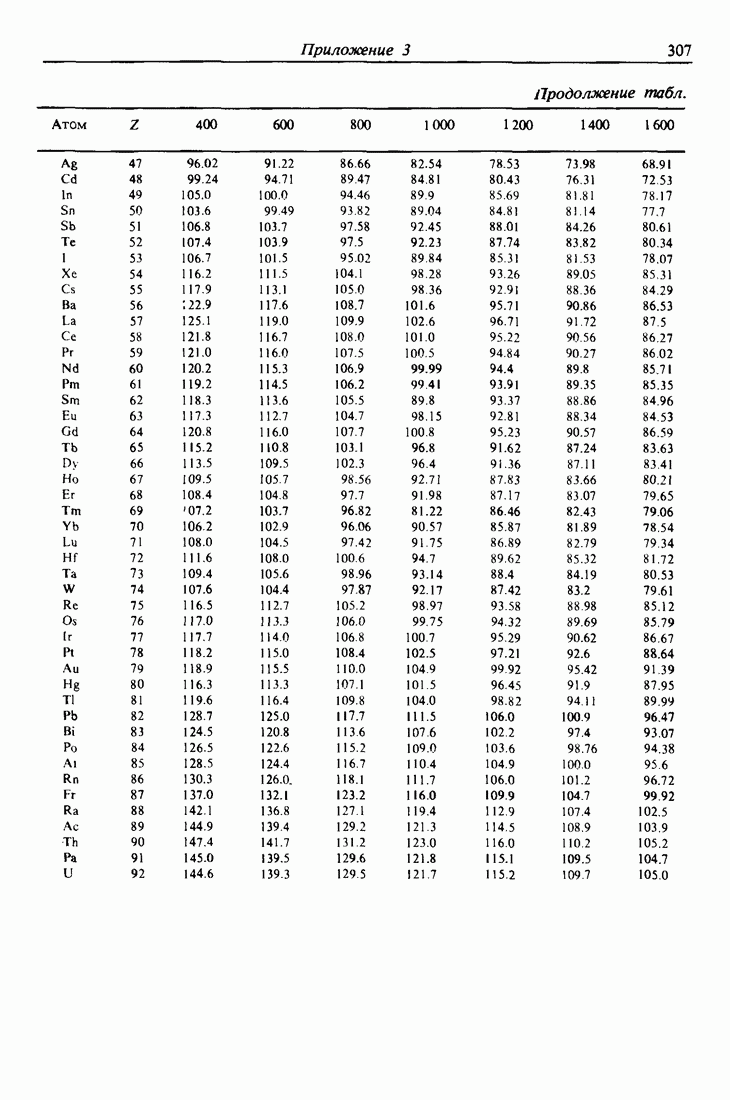
- ПРИЛОЖЕНИЕ 3.
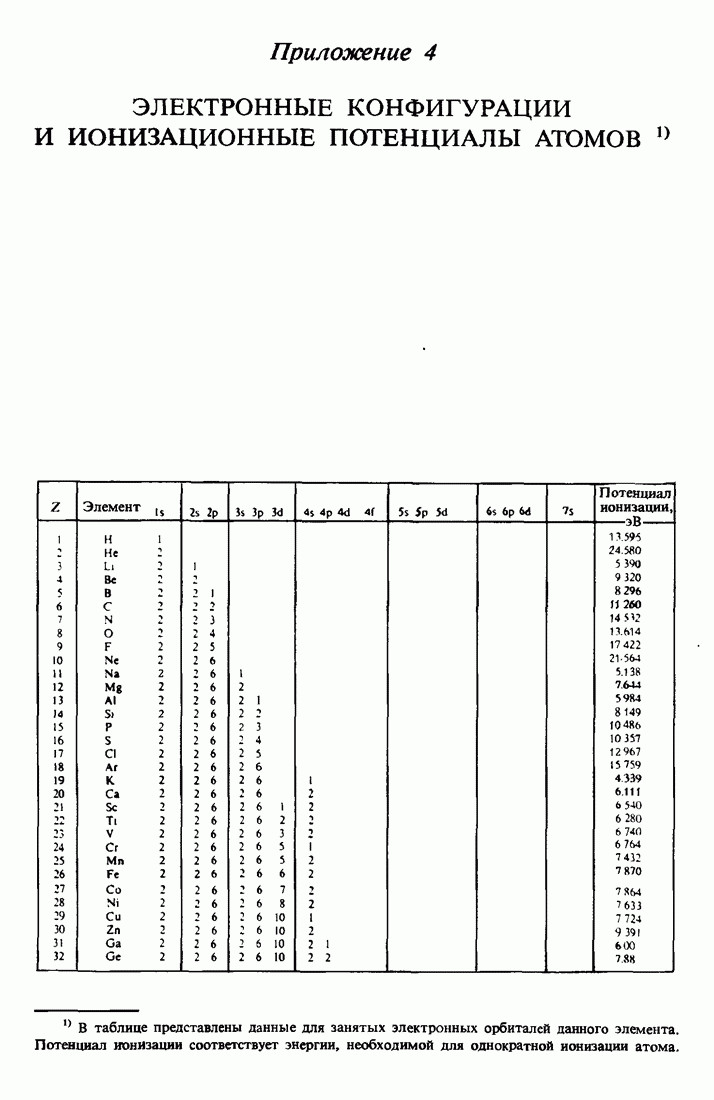
- ПРИЛОЖЕНИЕ 4.
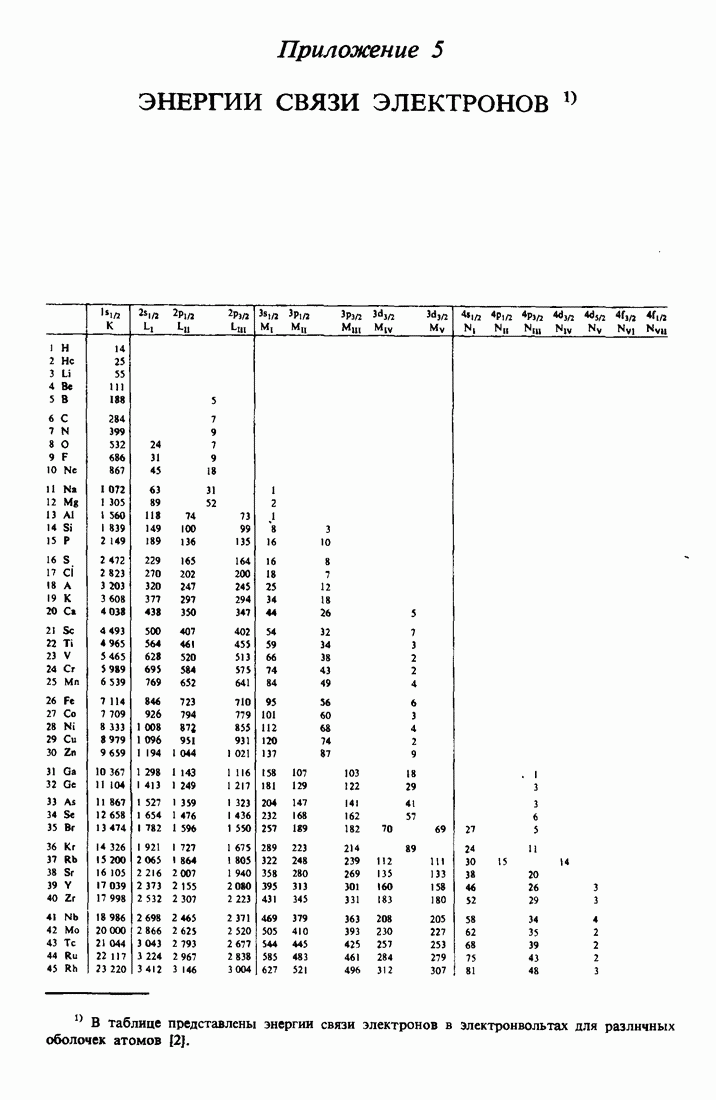
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
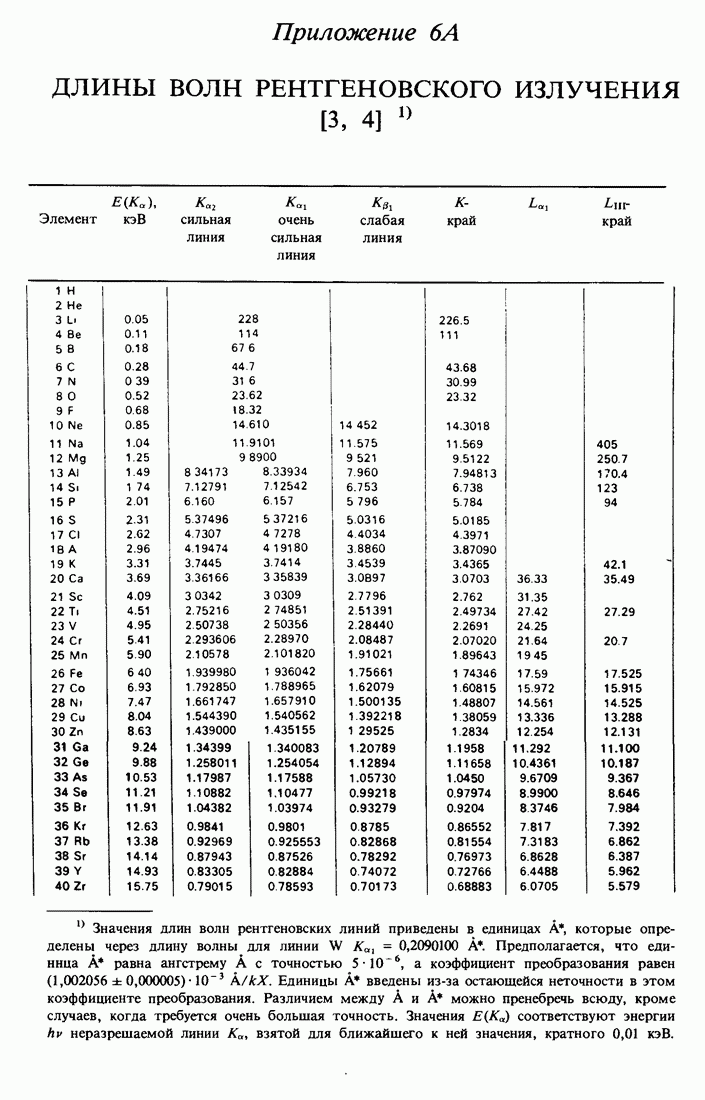
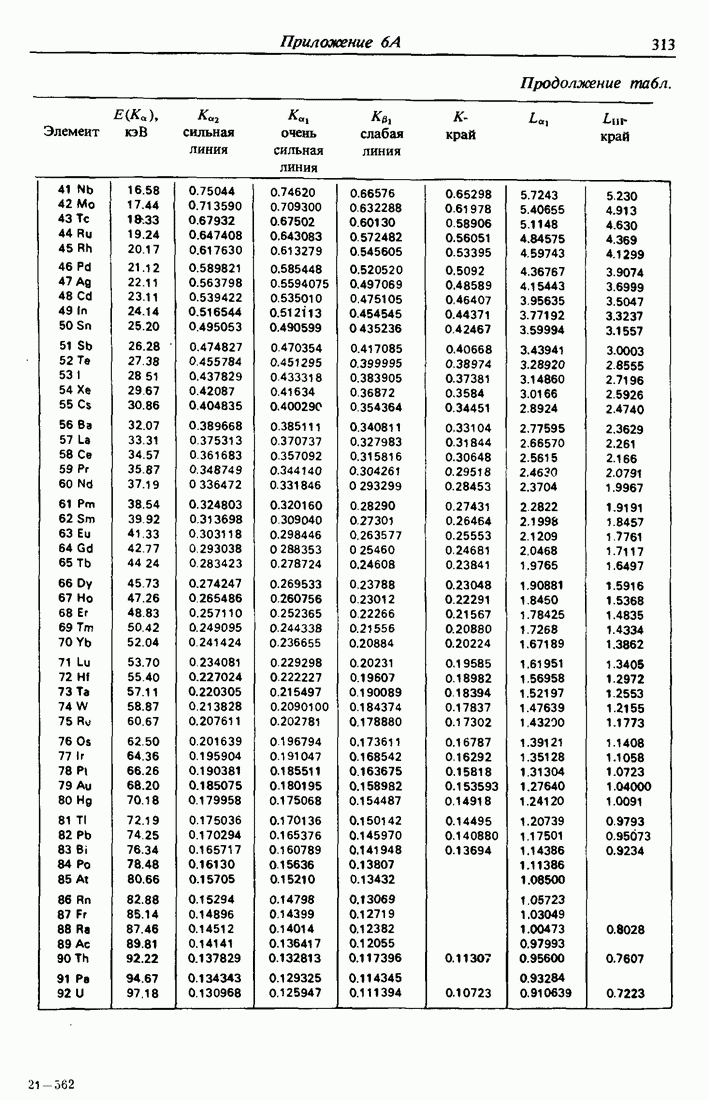
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
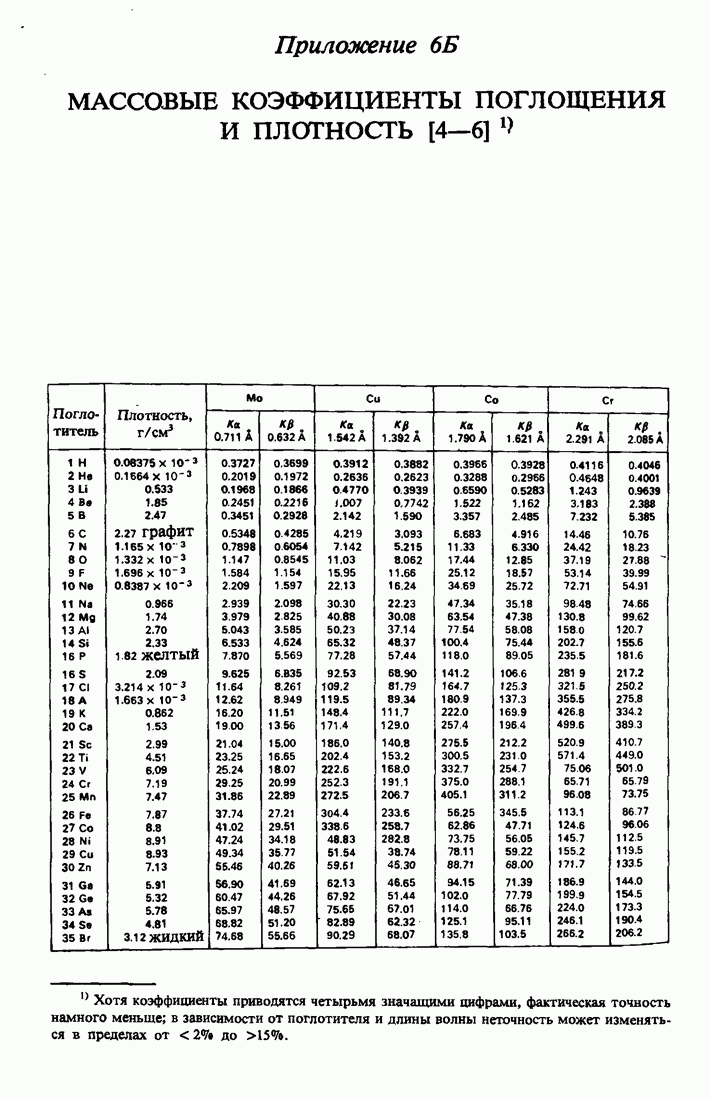
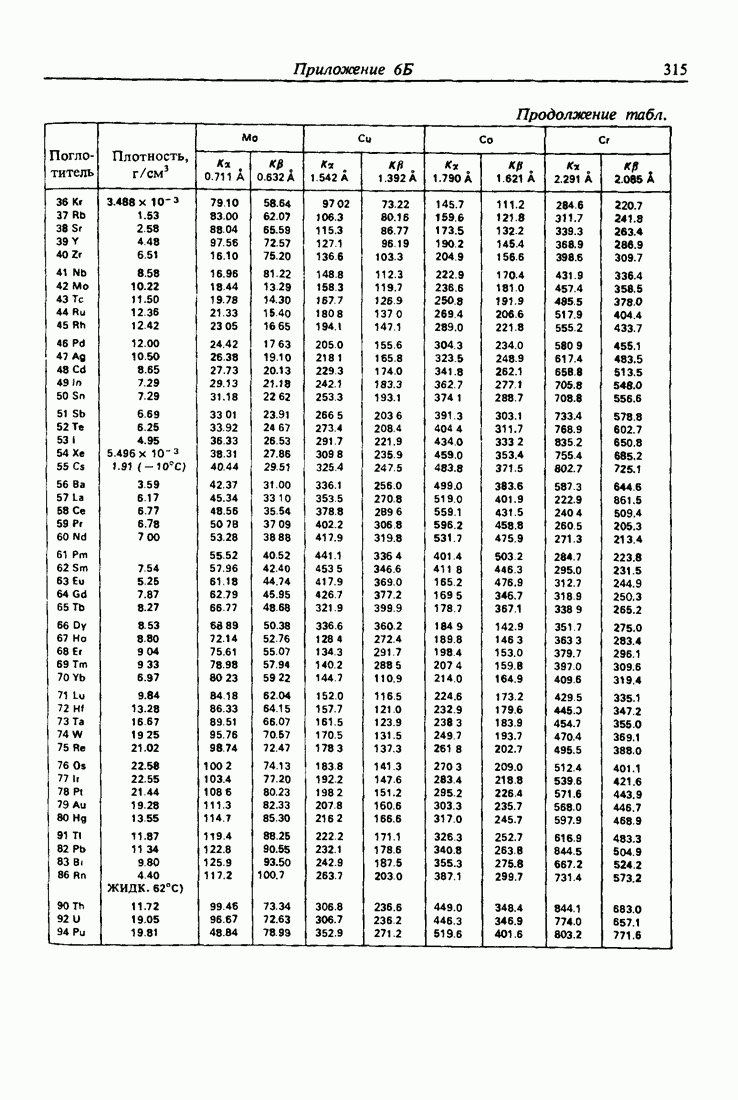
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
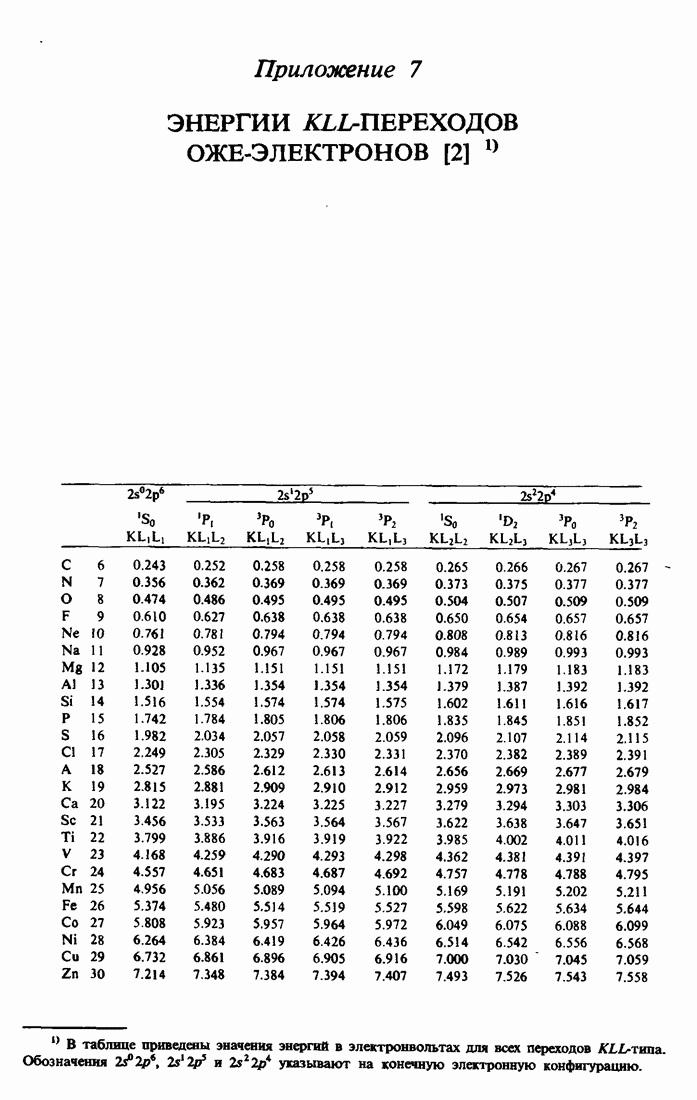
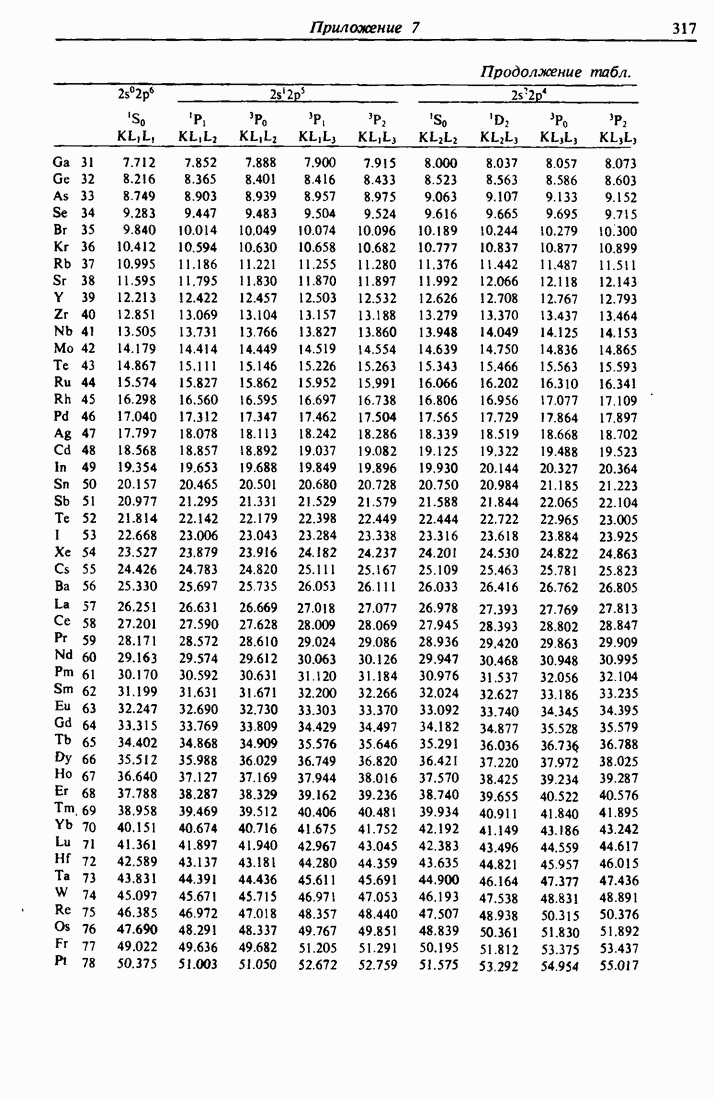
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
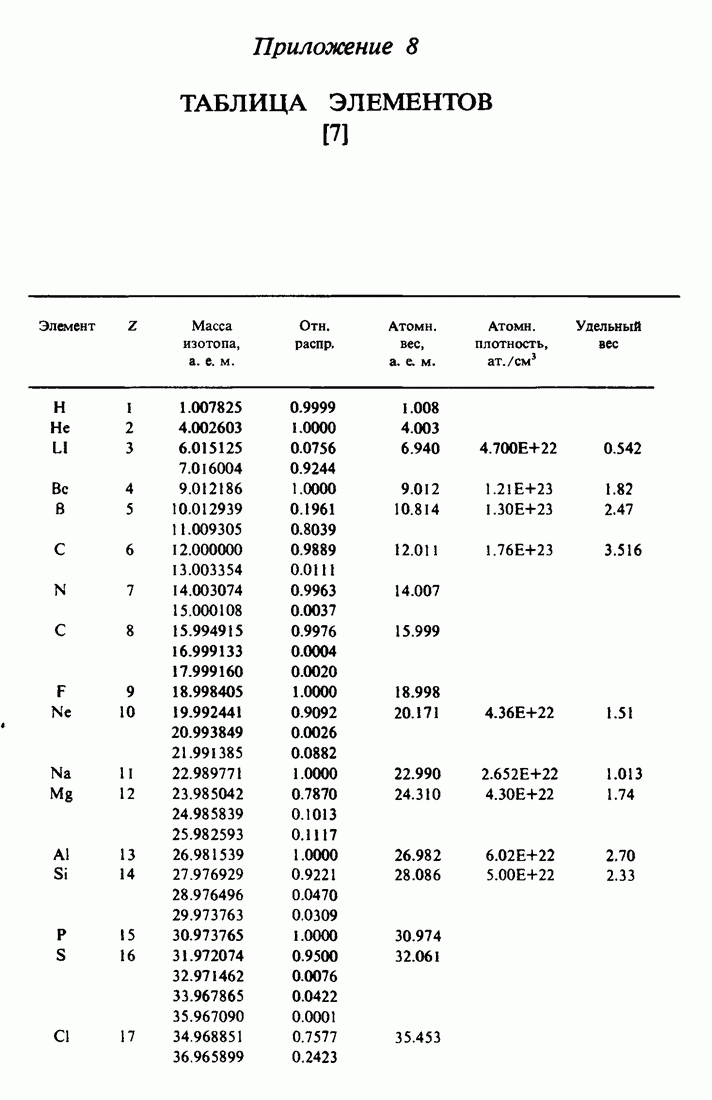
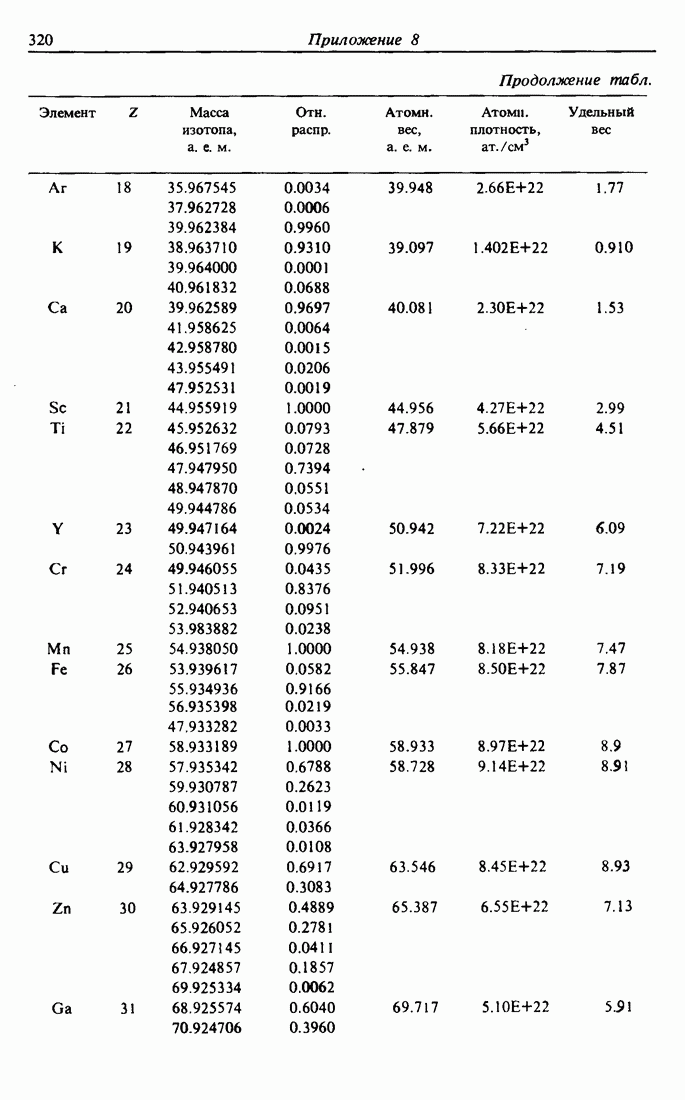
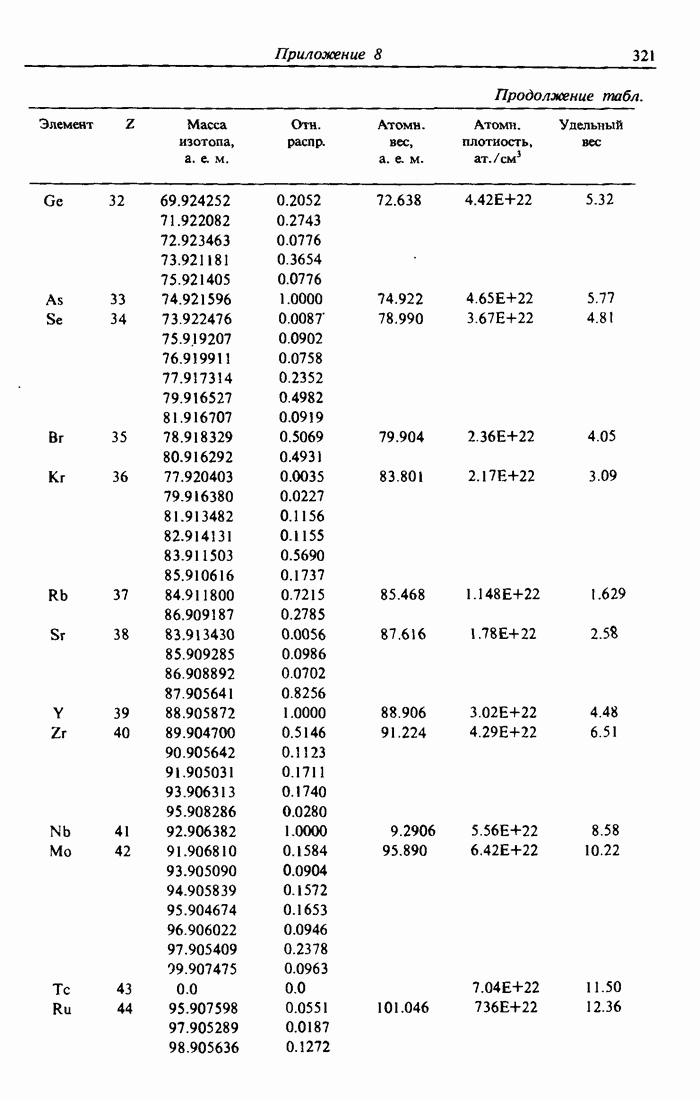
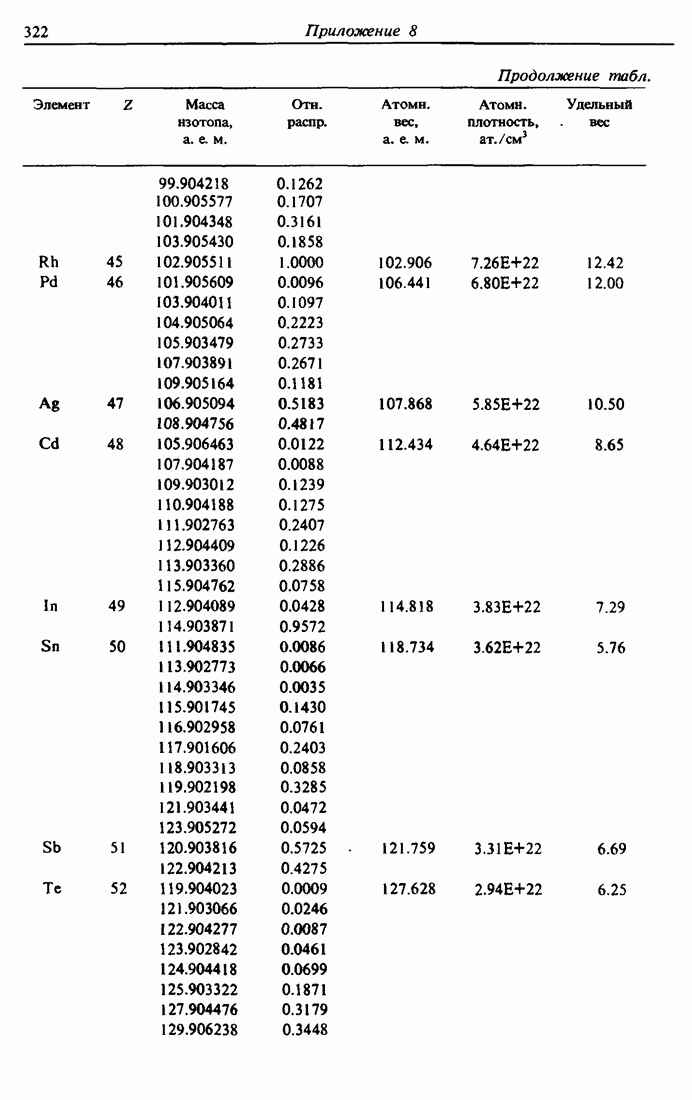
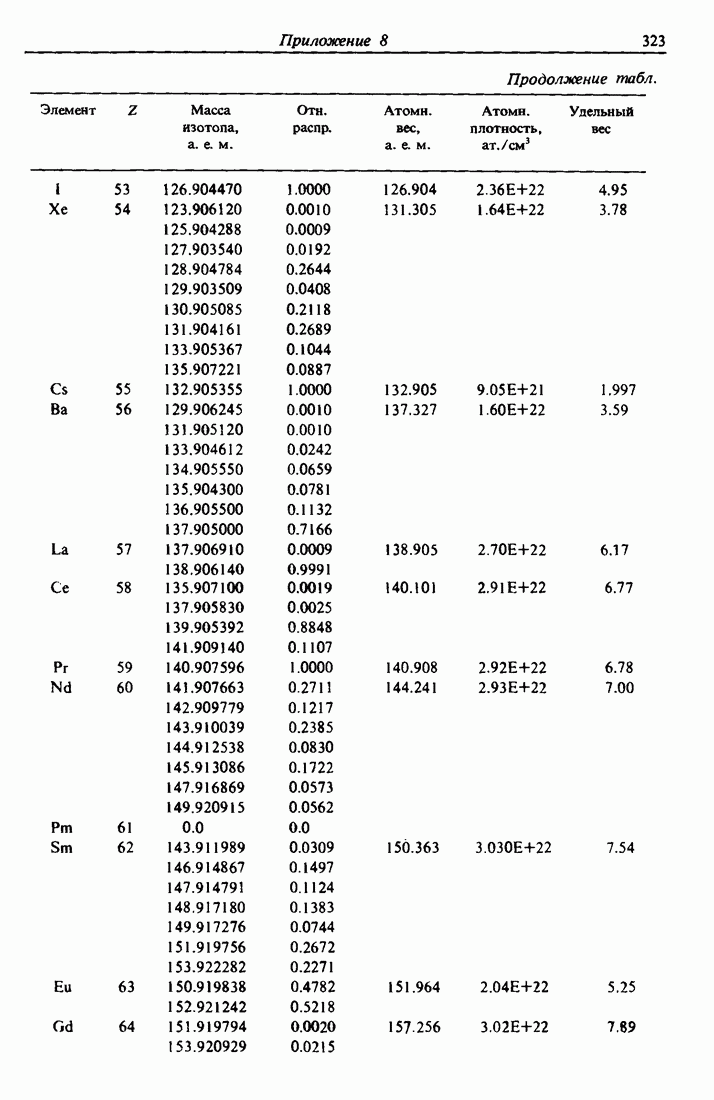
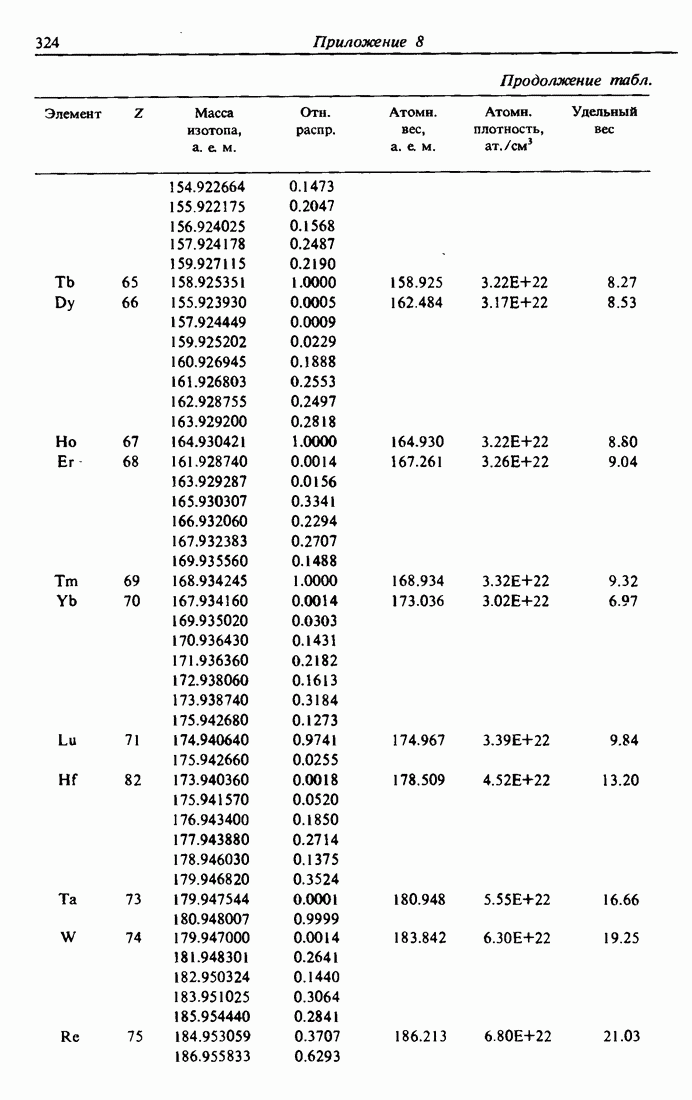
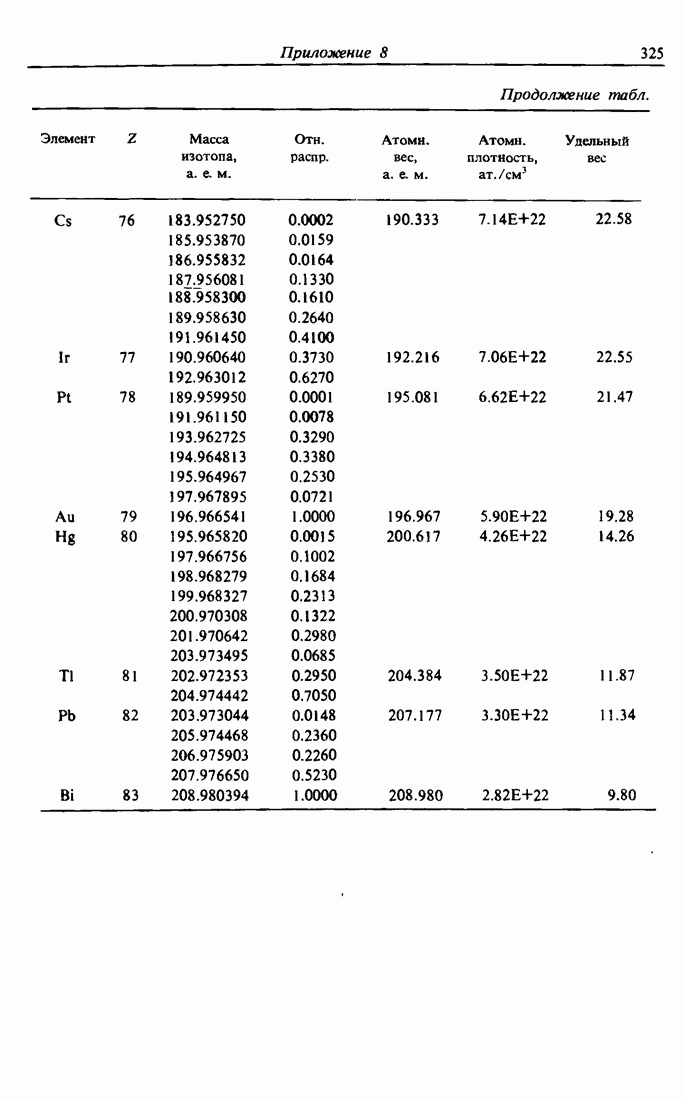
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
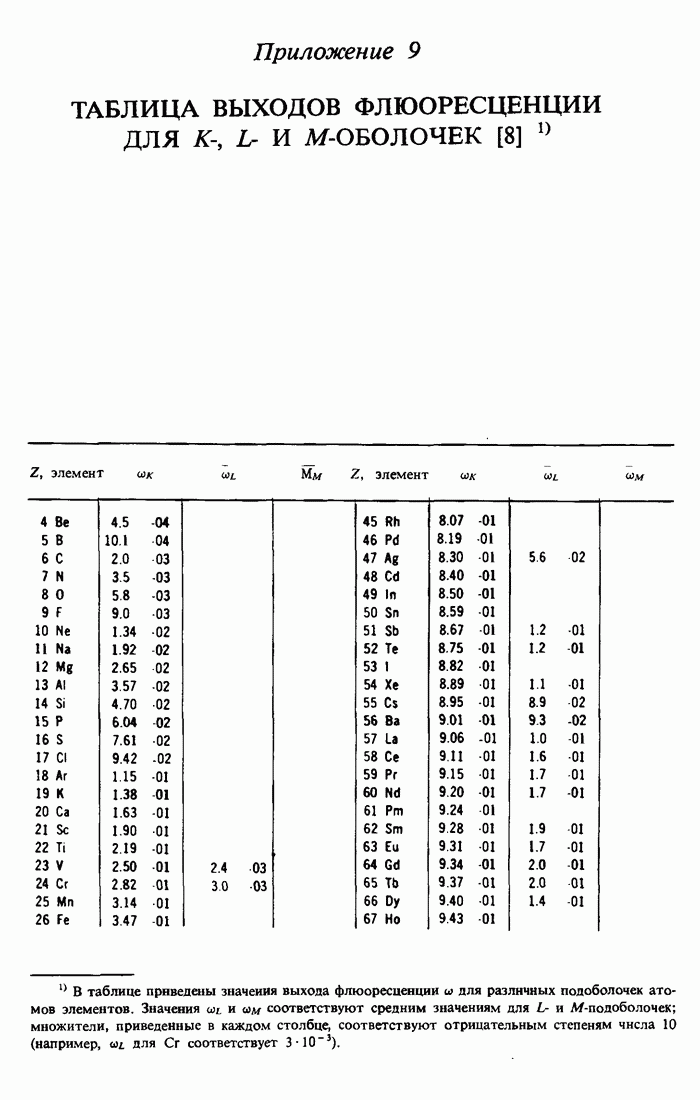
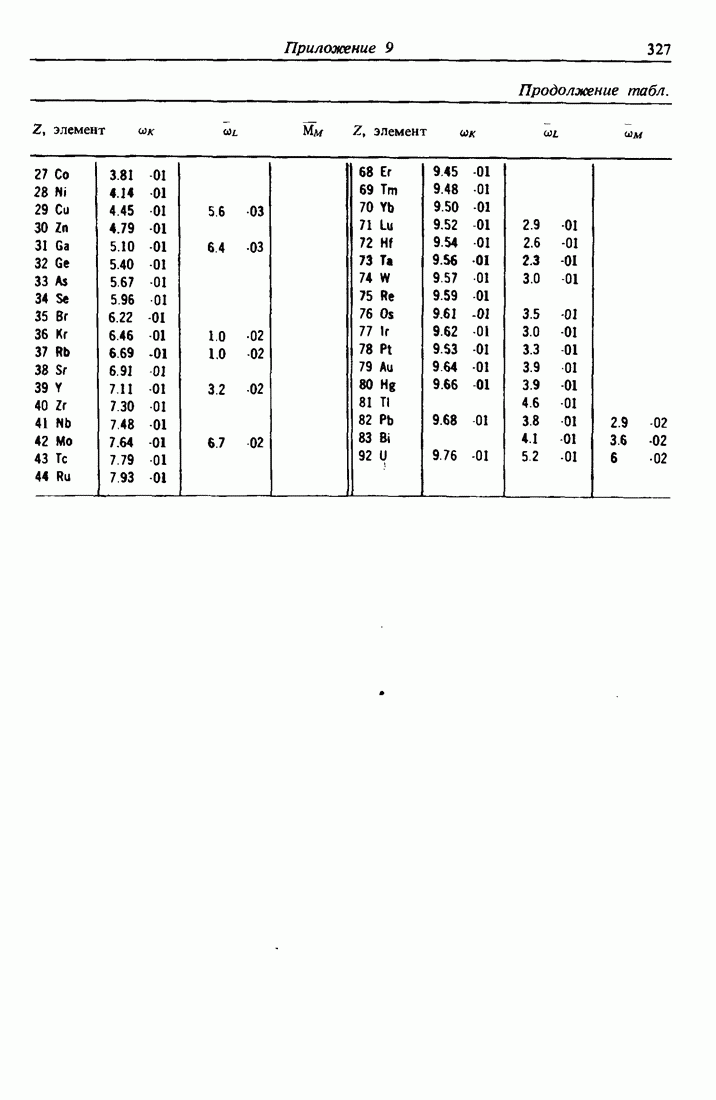
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ