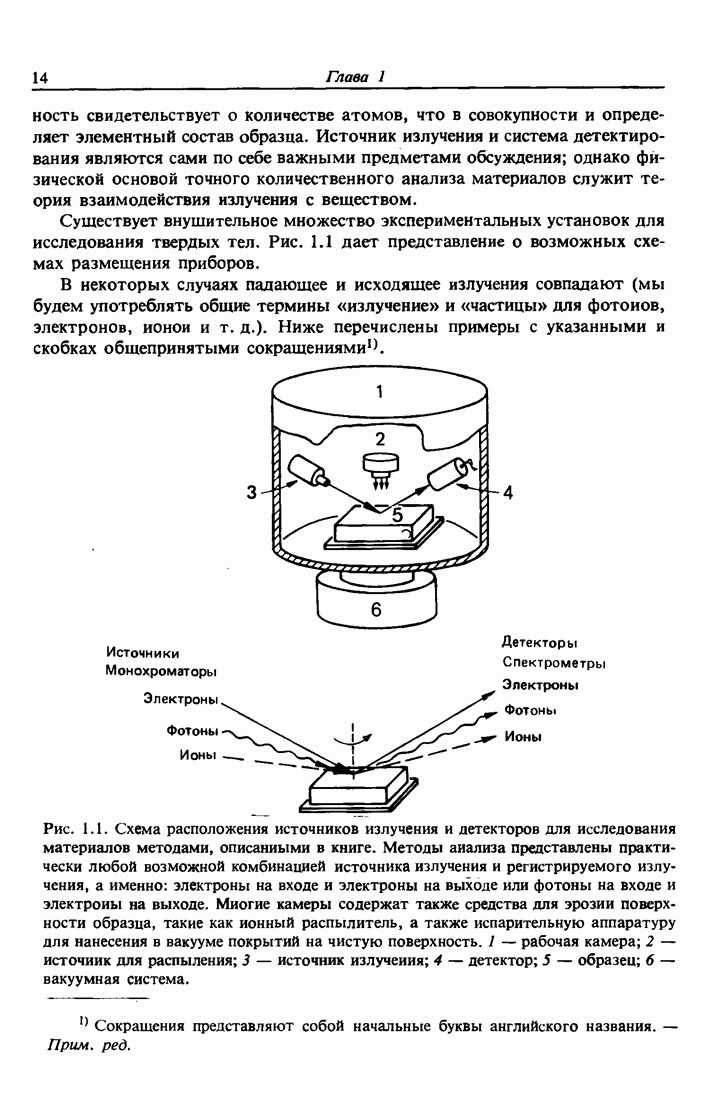
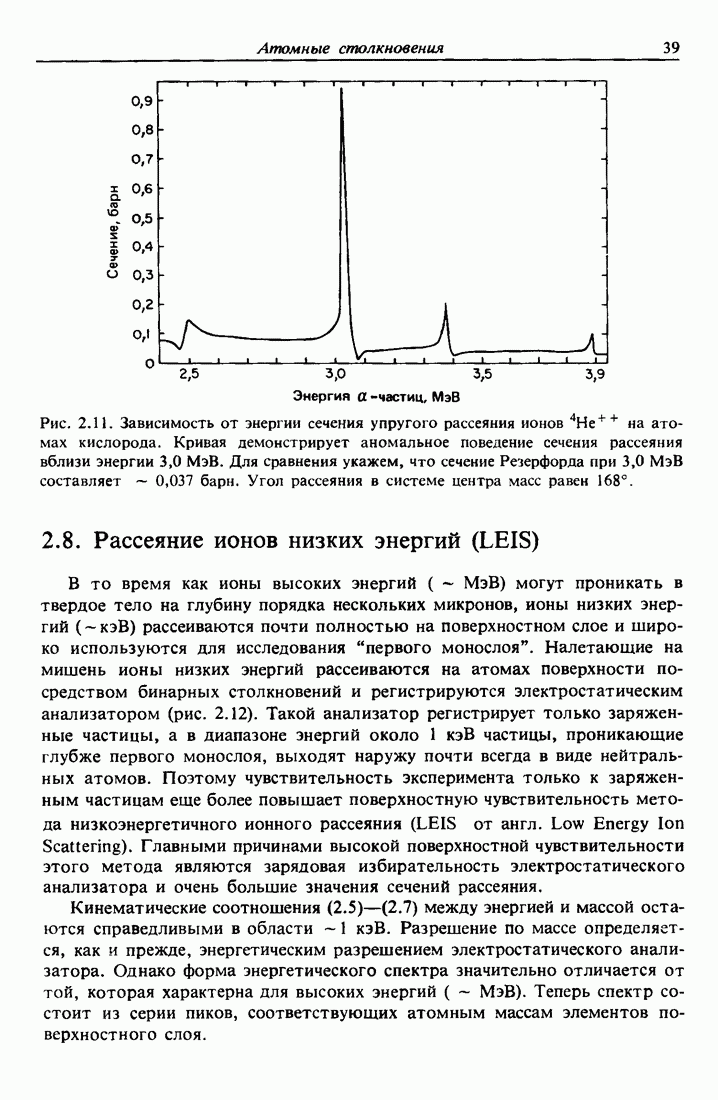
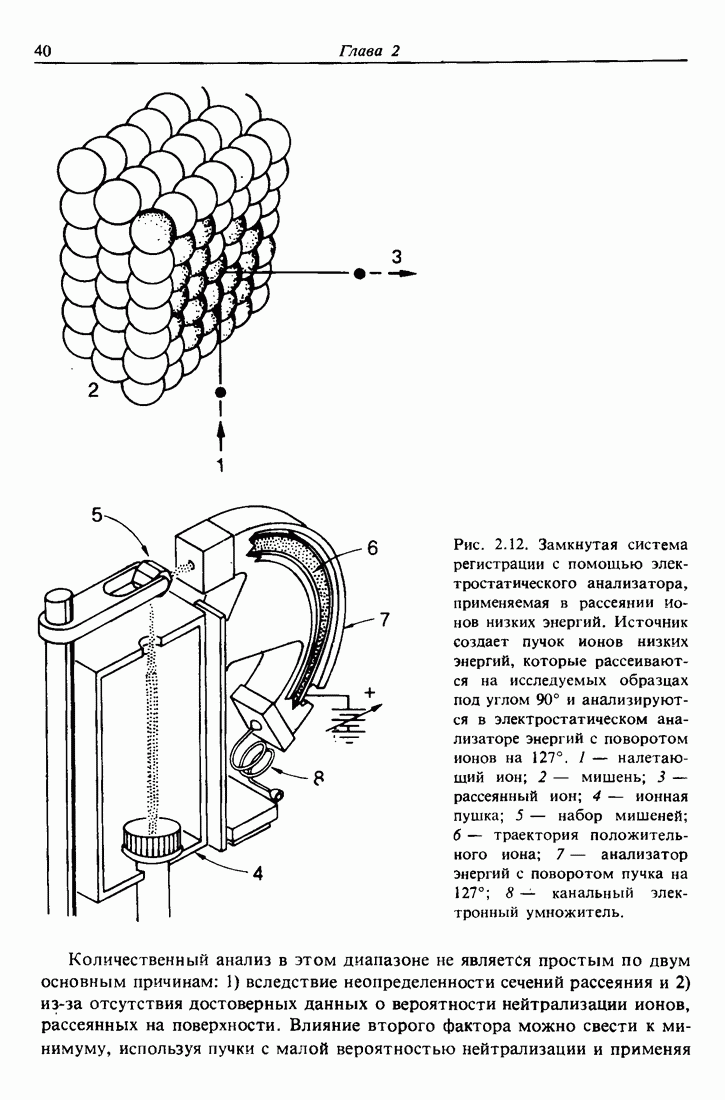
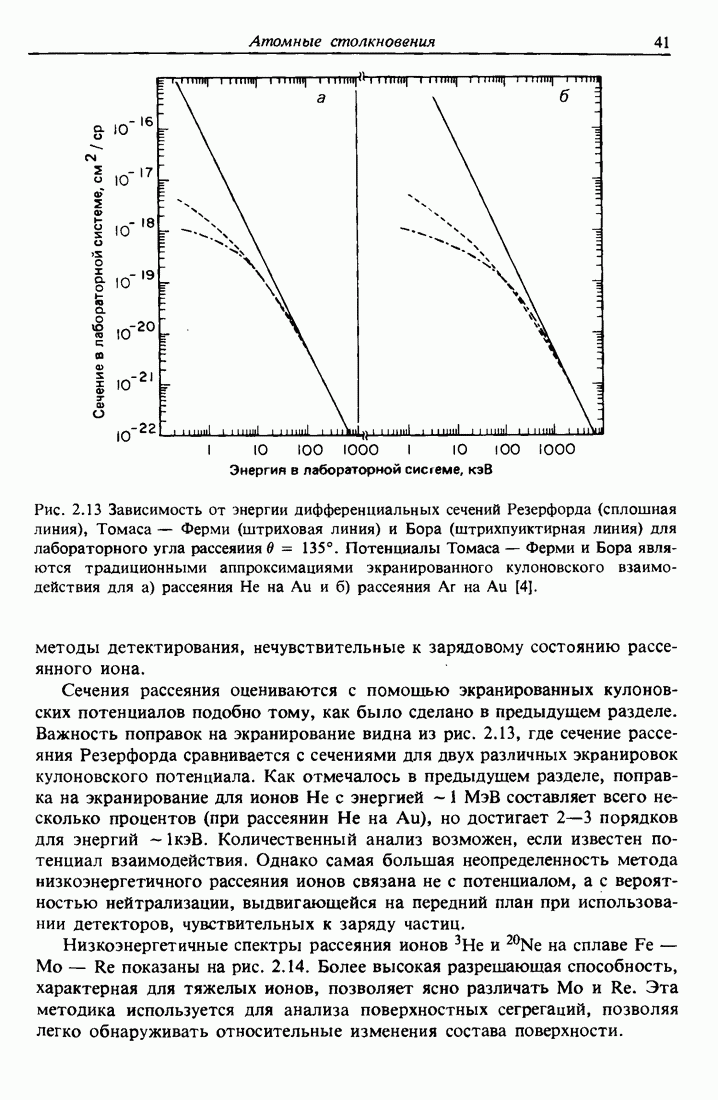
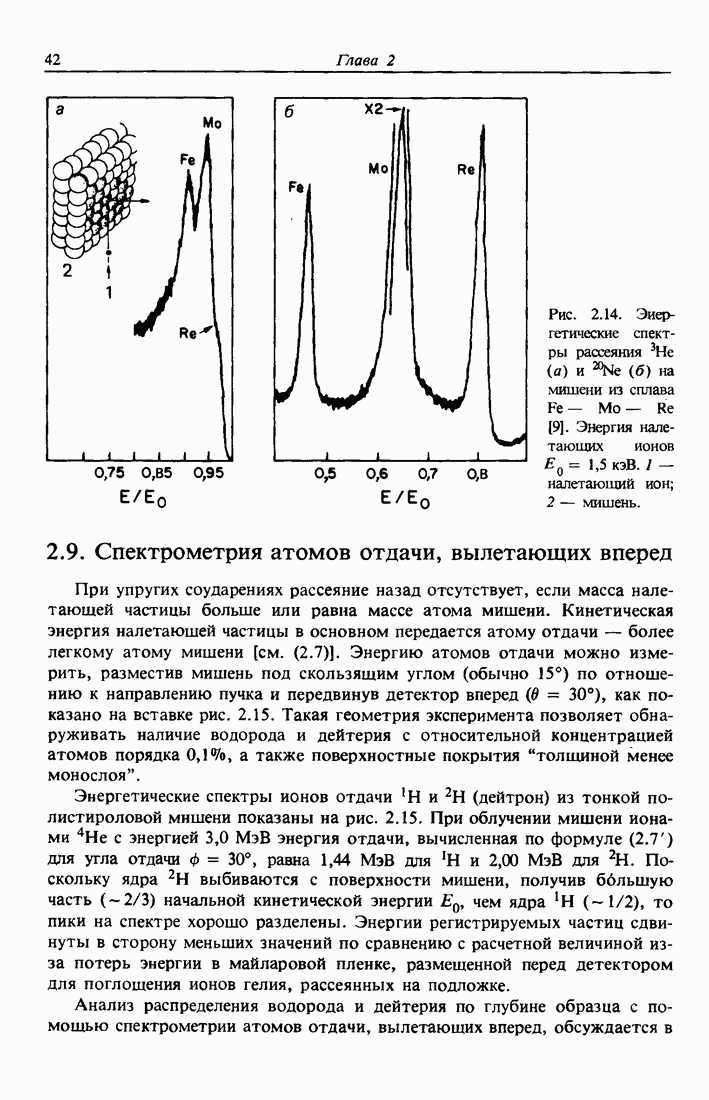
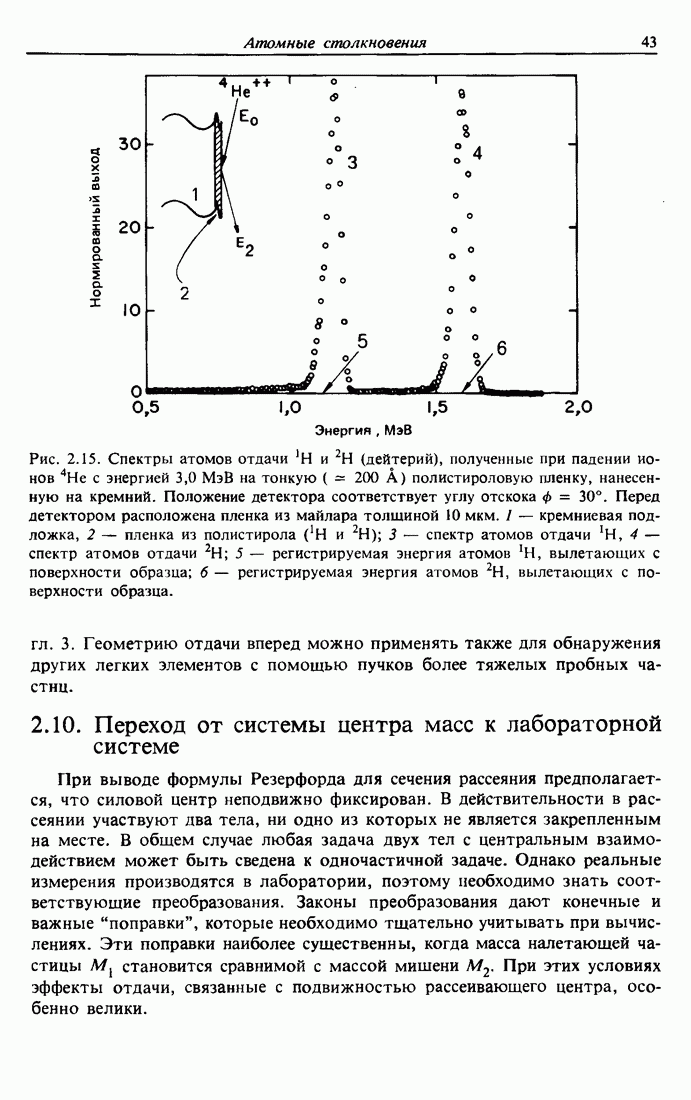
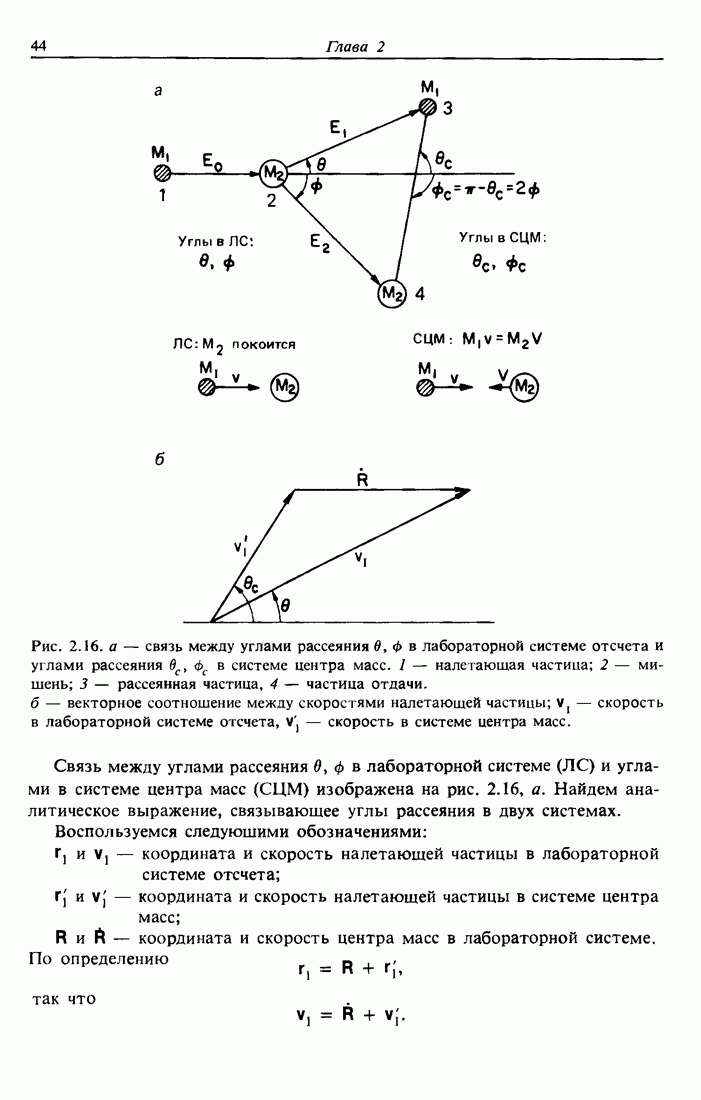
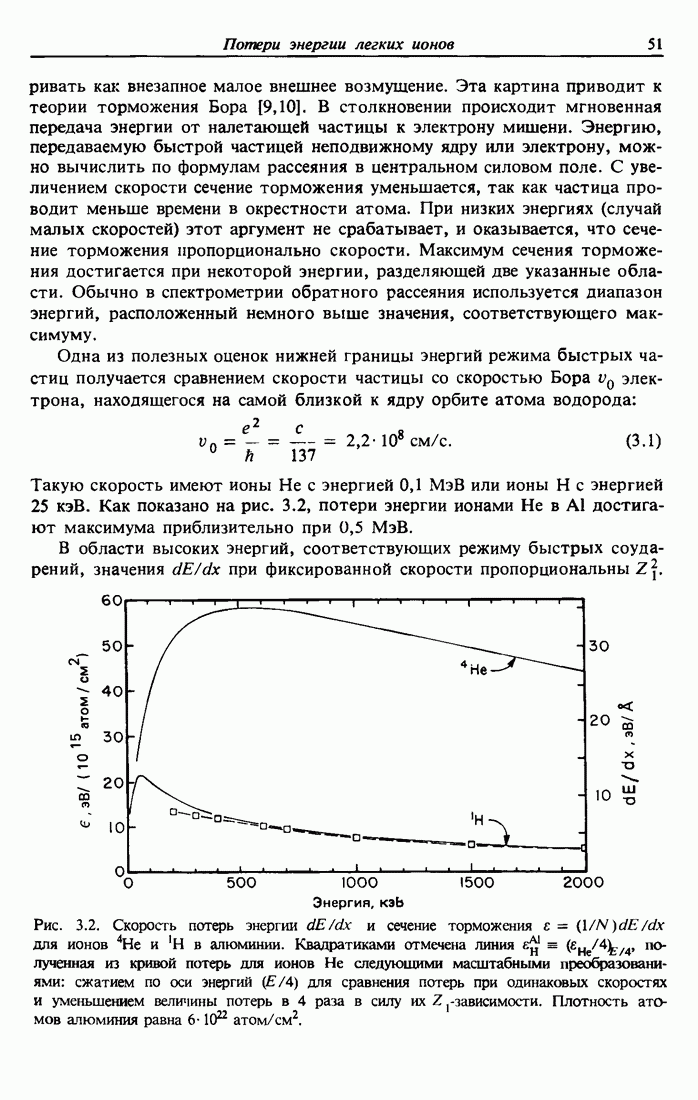
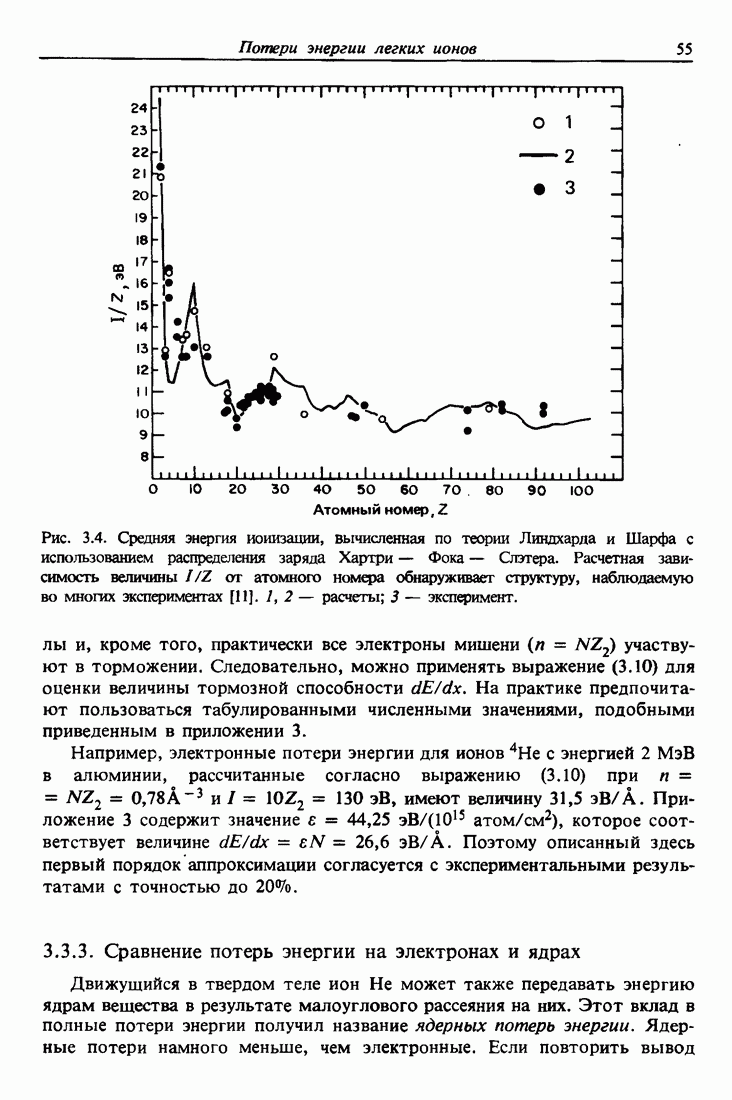
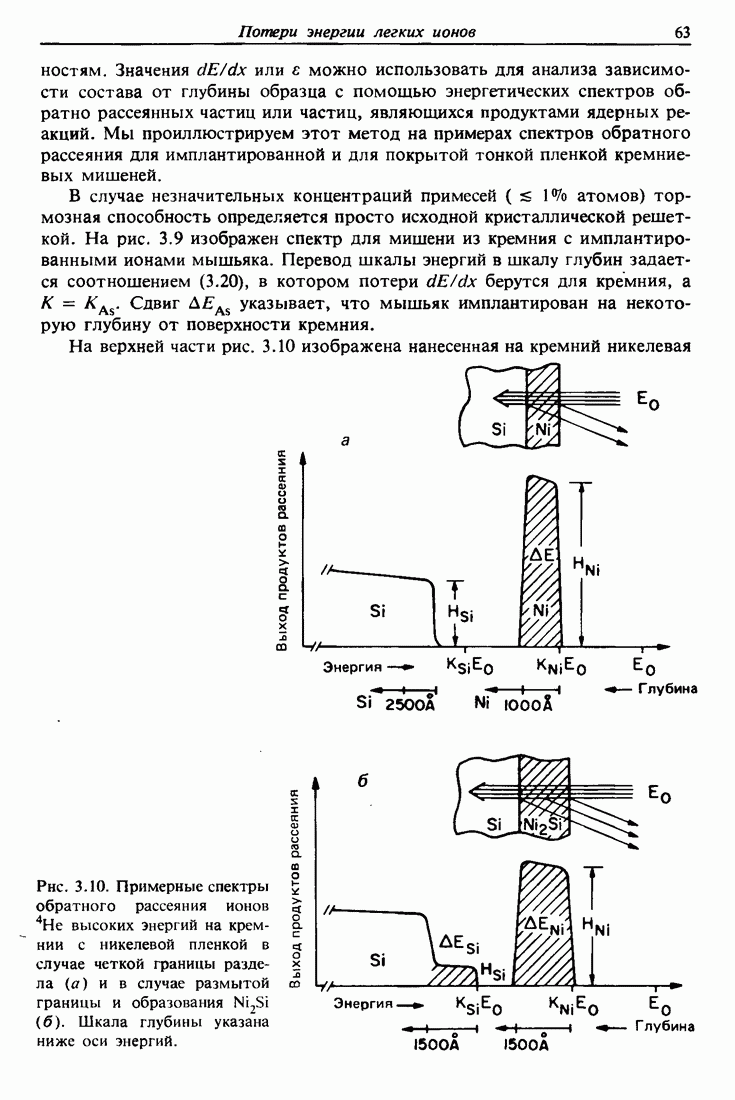
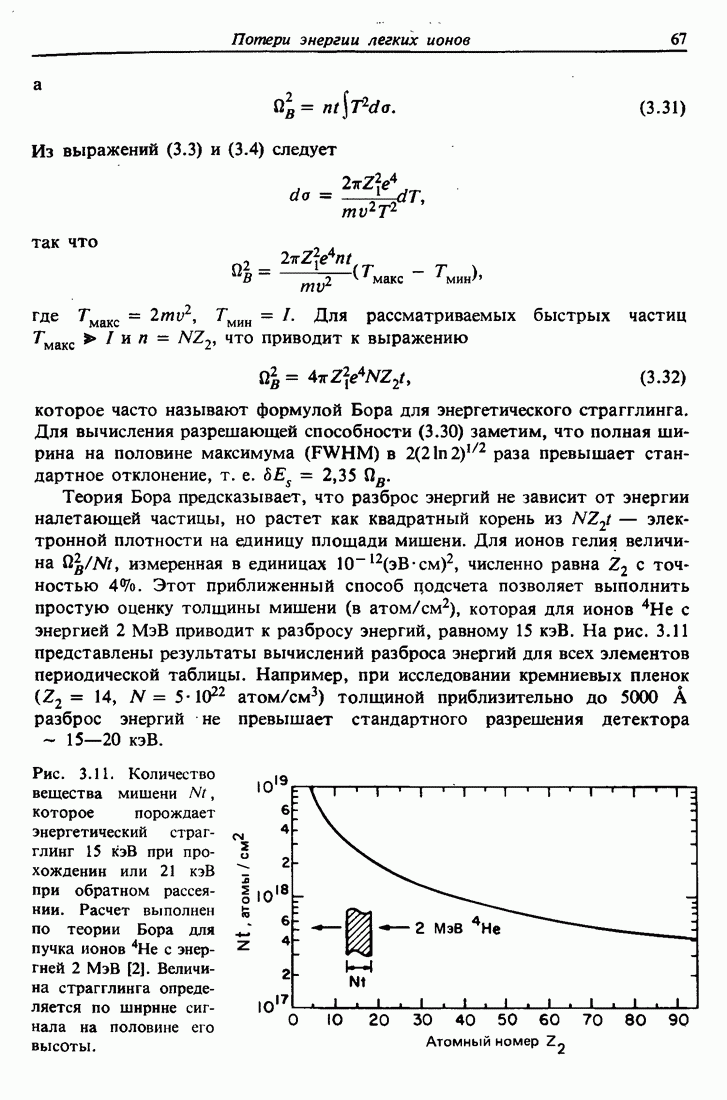
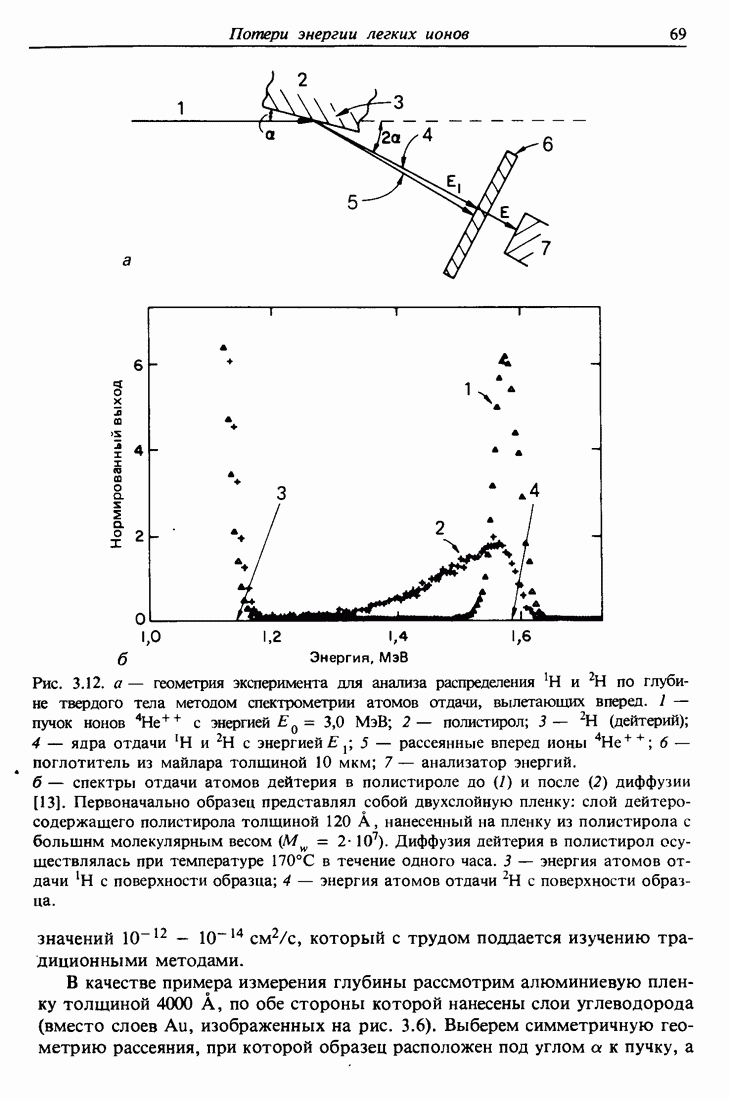
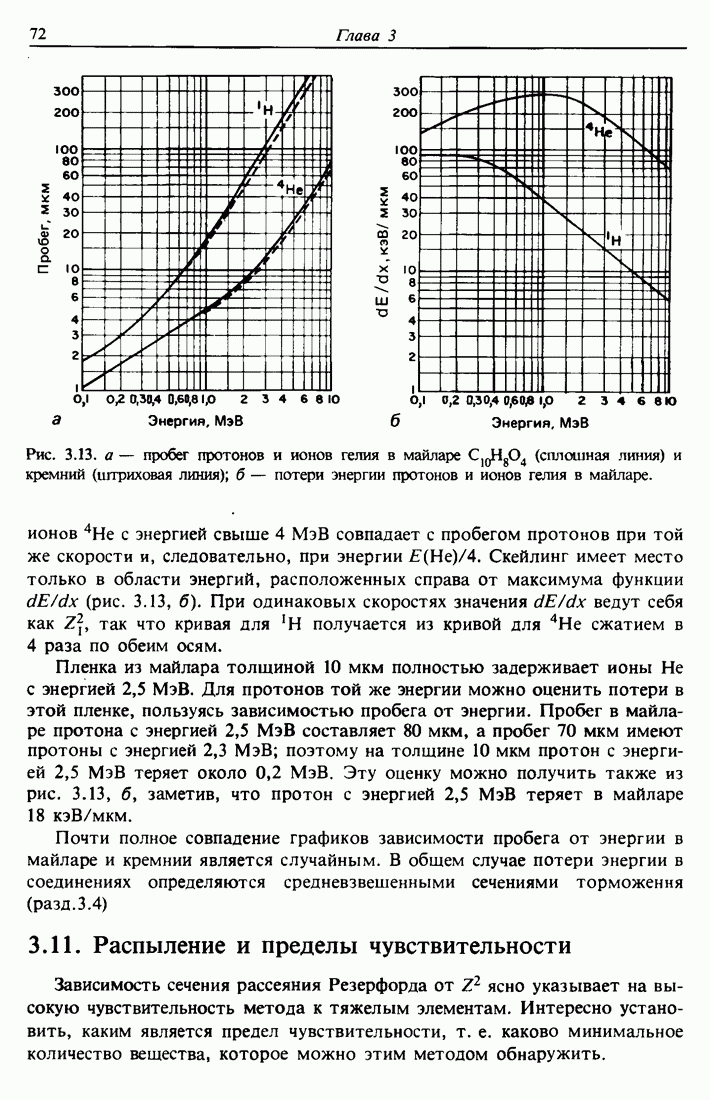
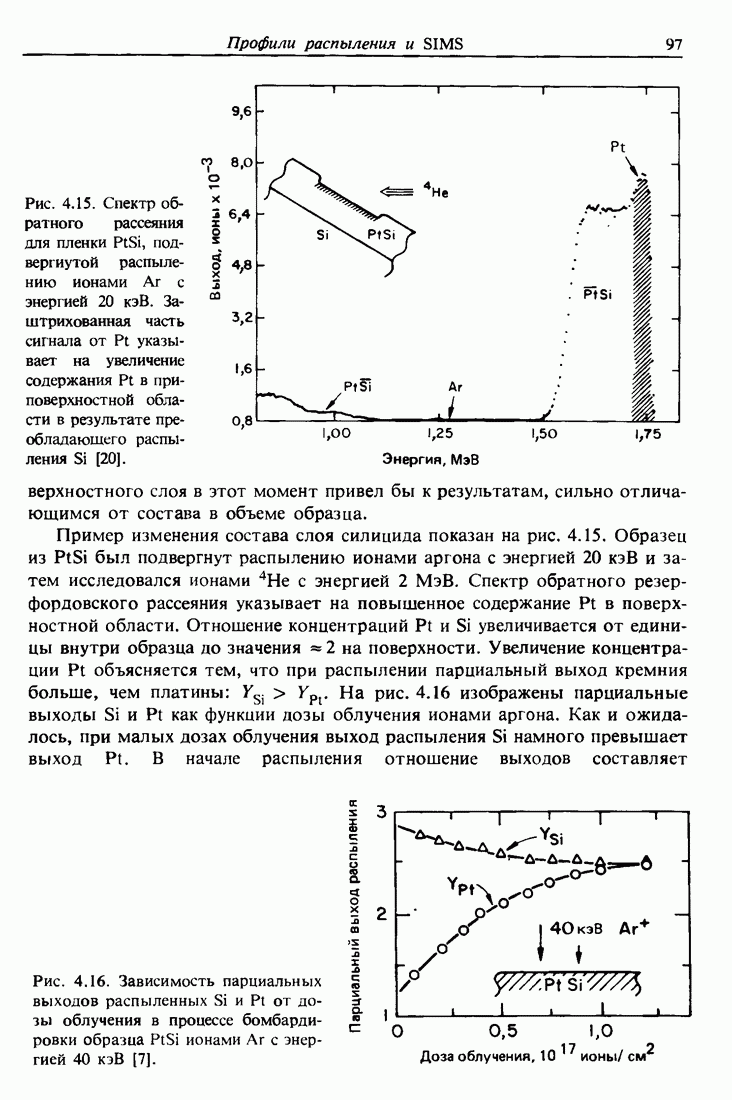
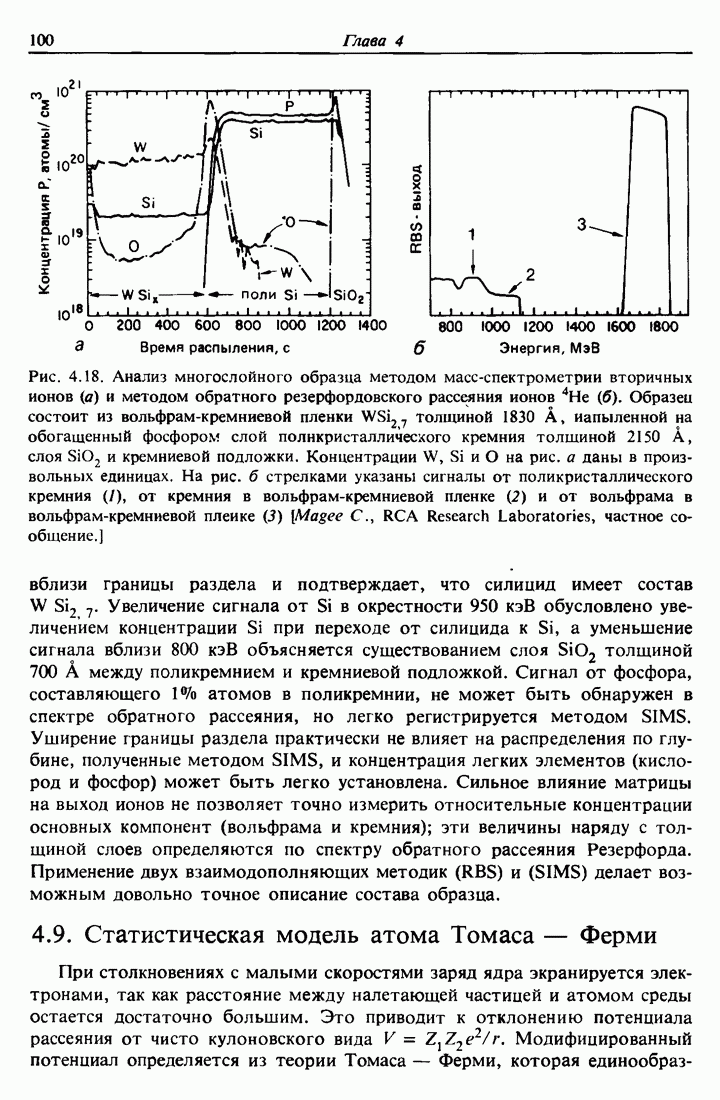
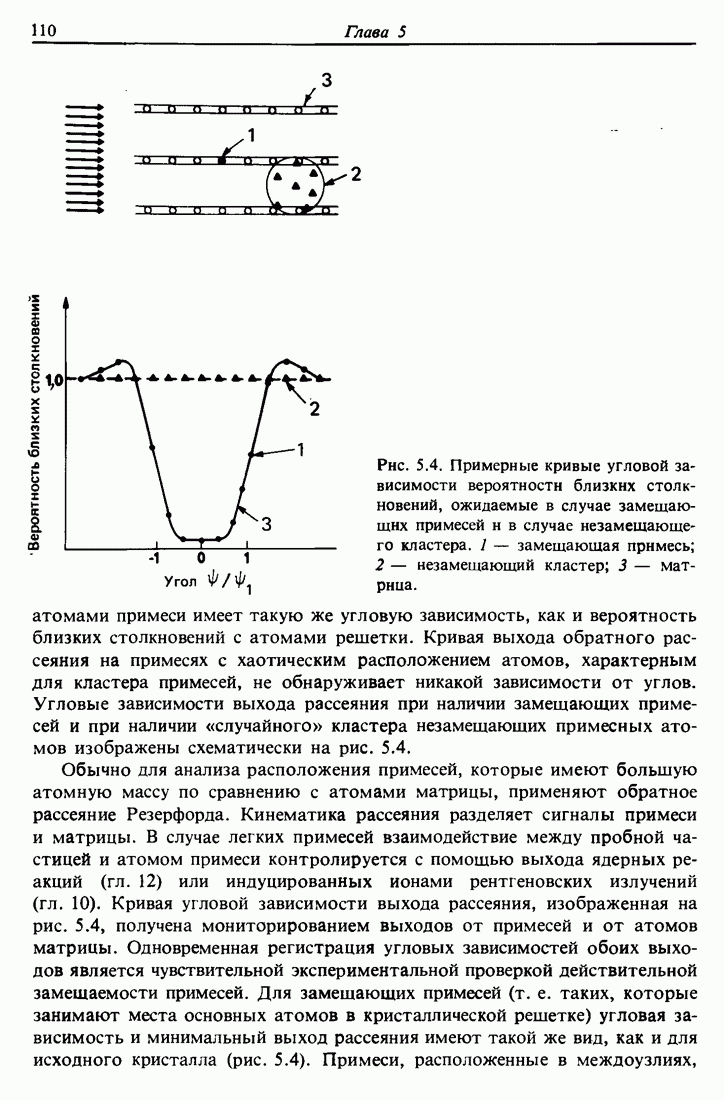
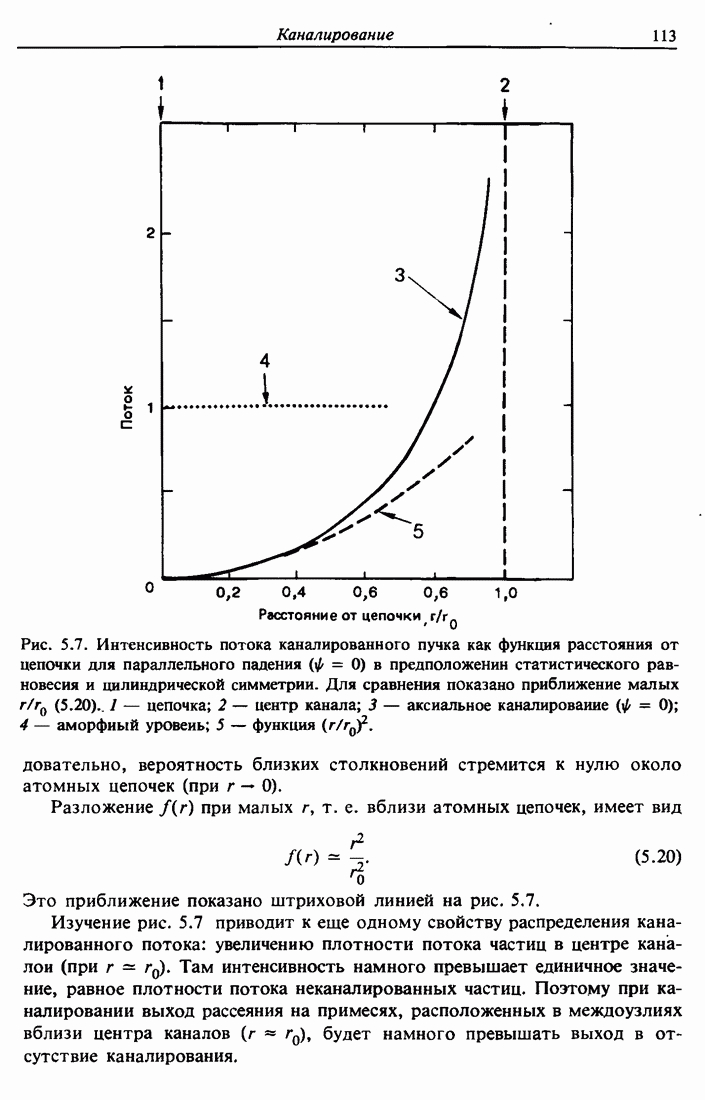
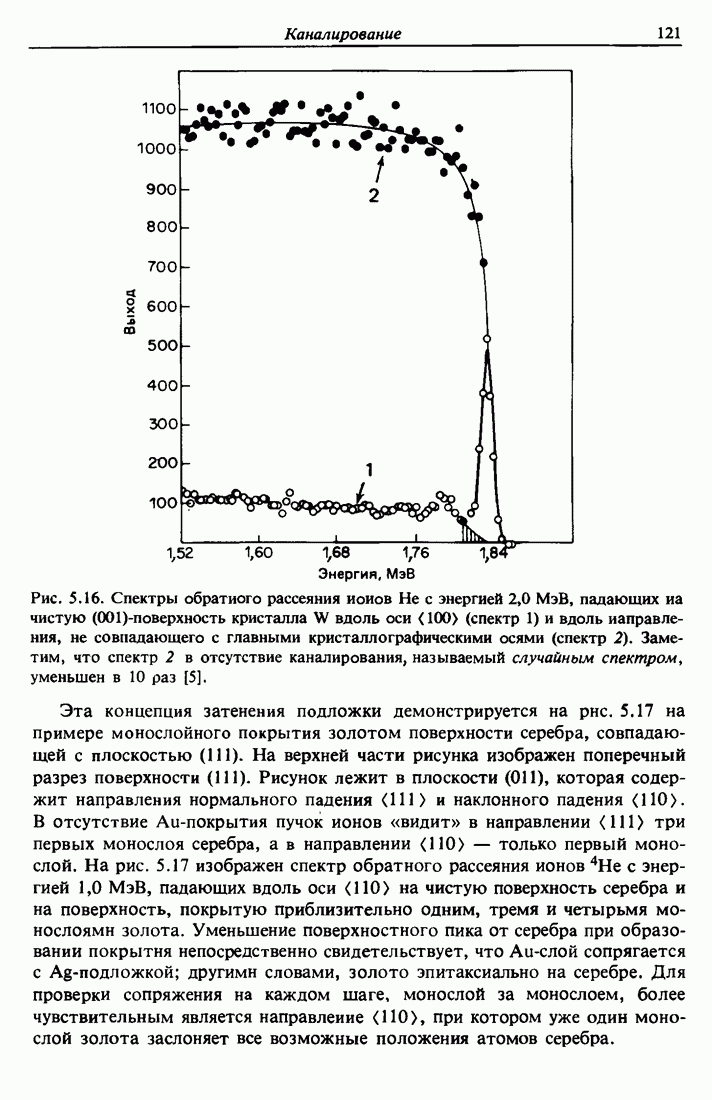
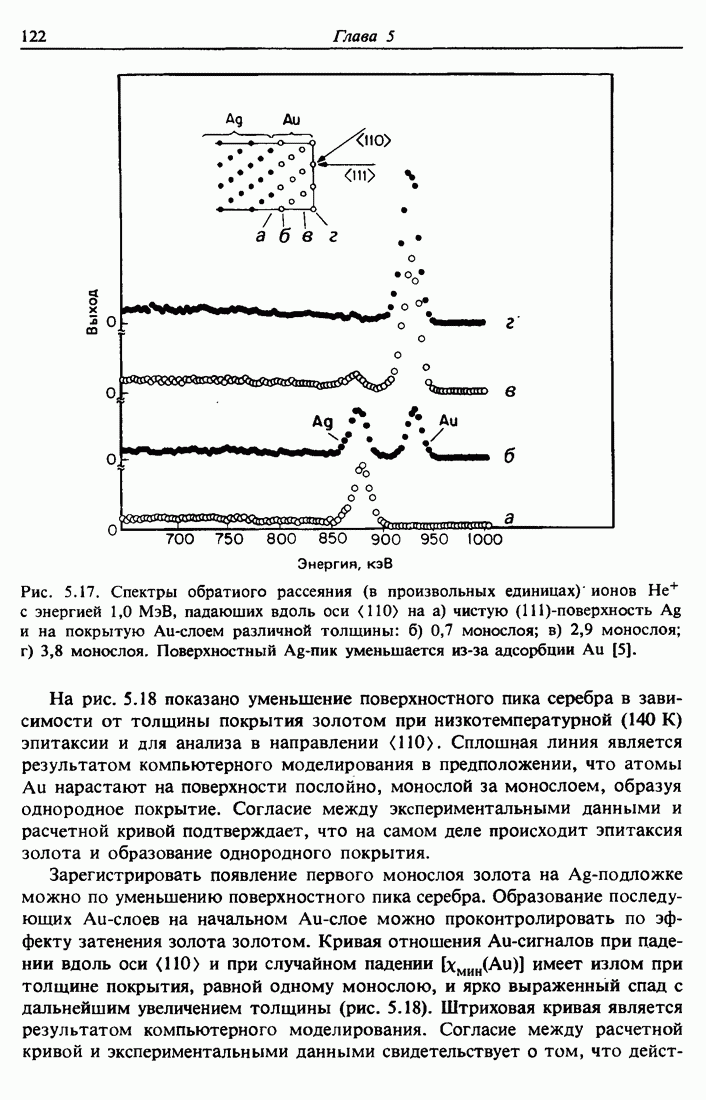
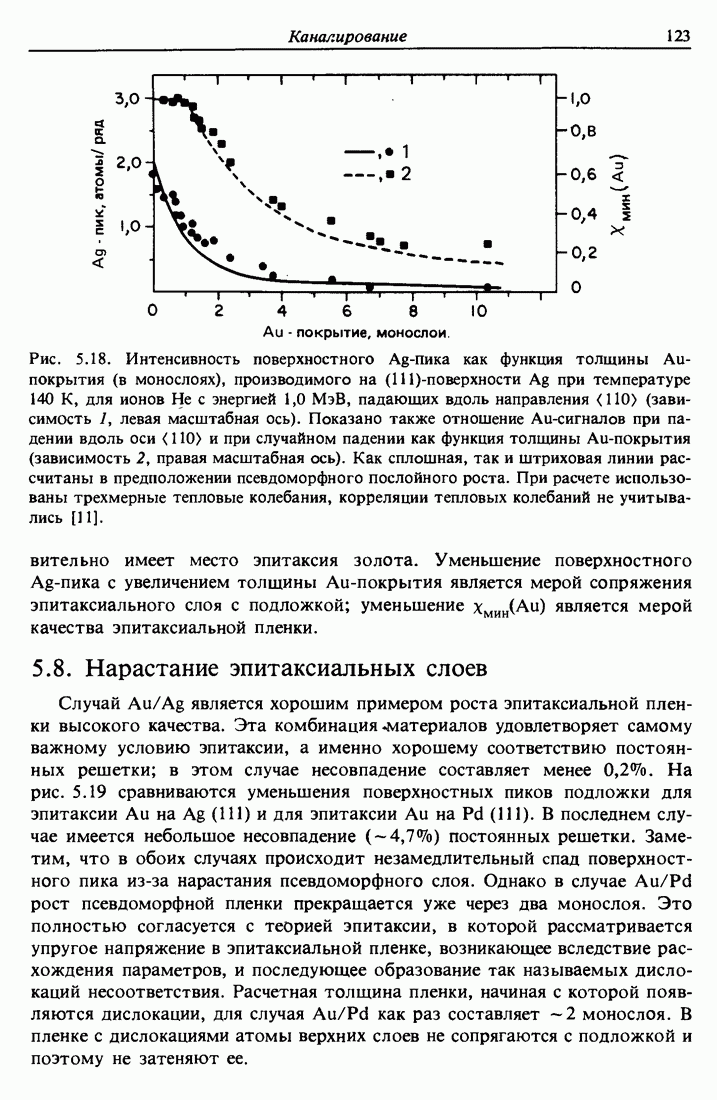
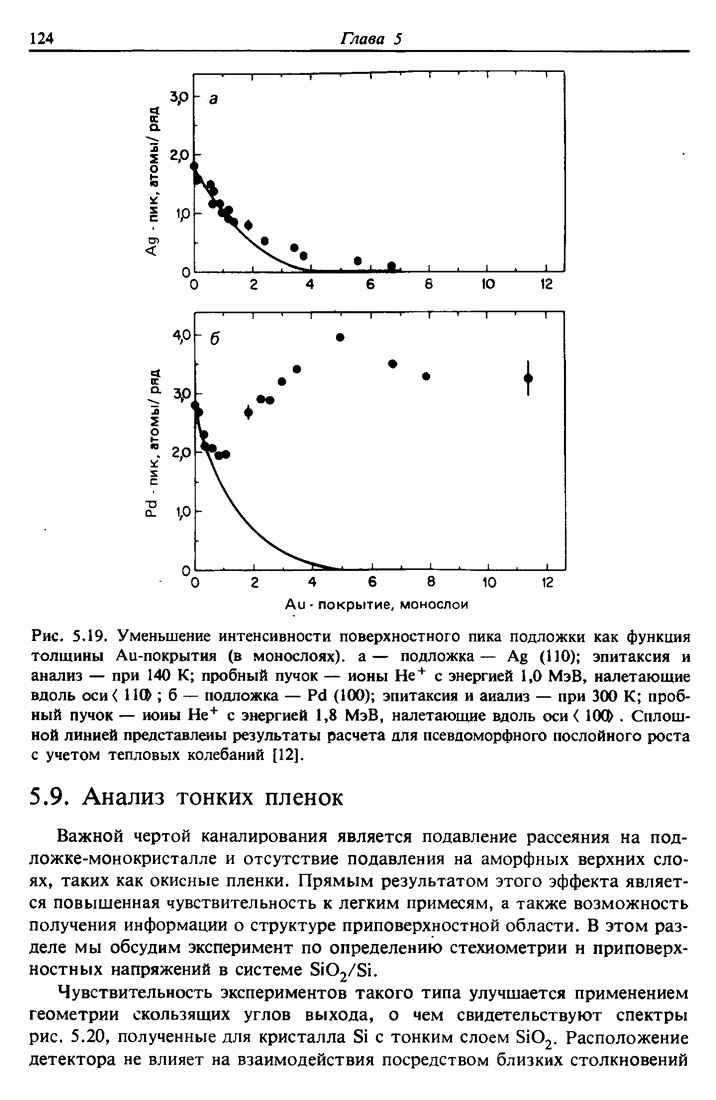
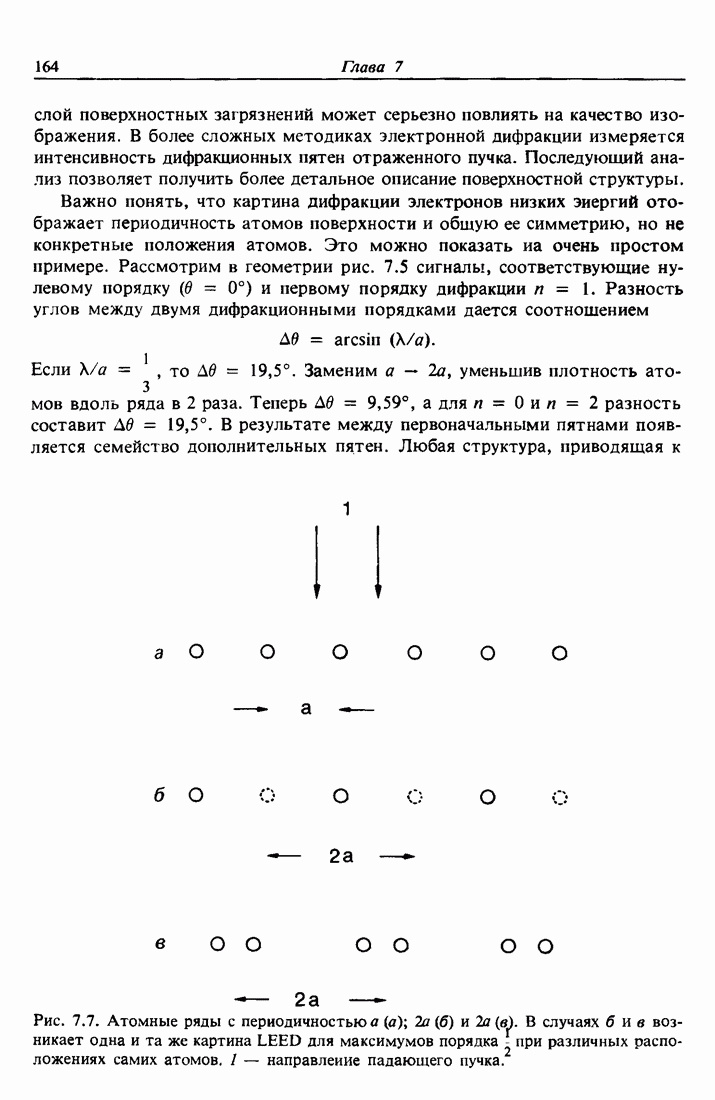
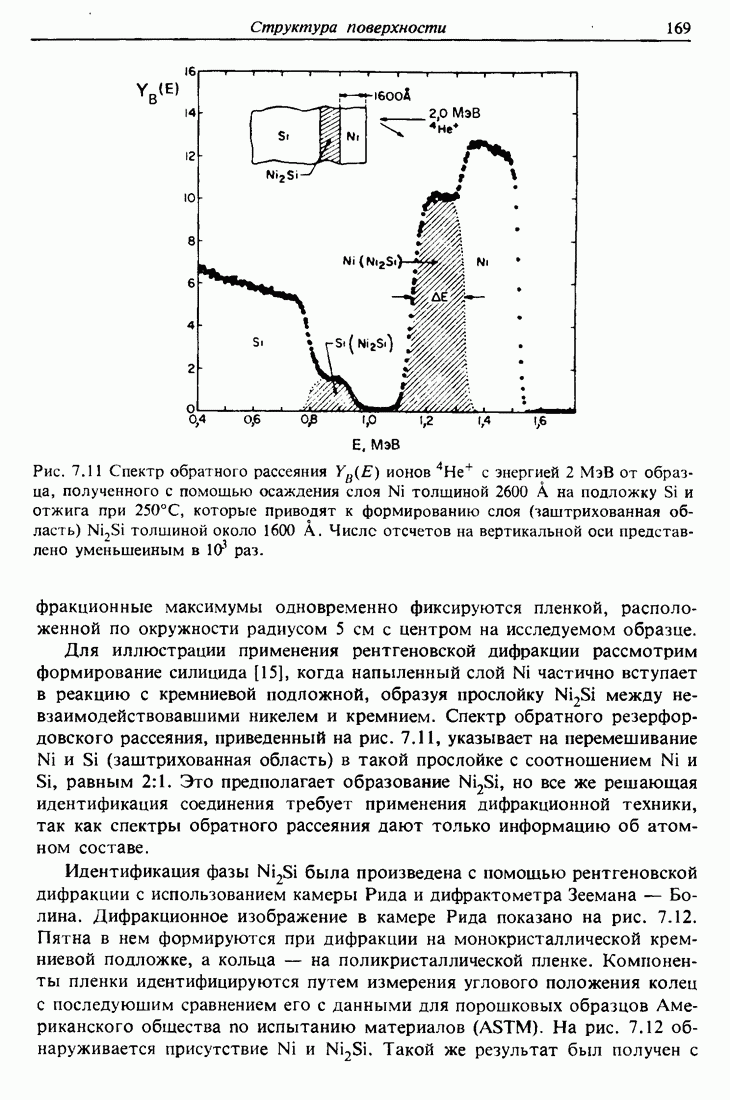
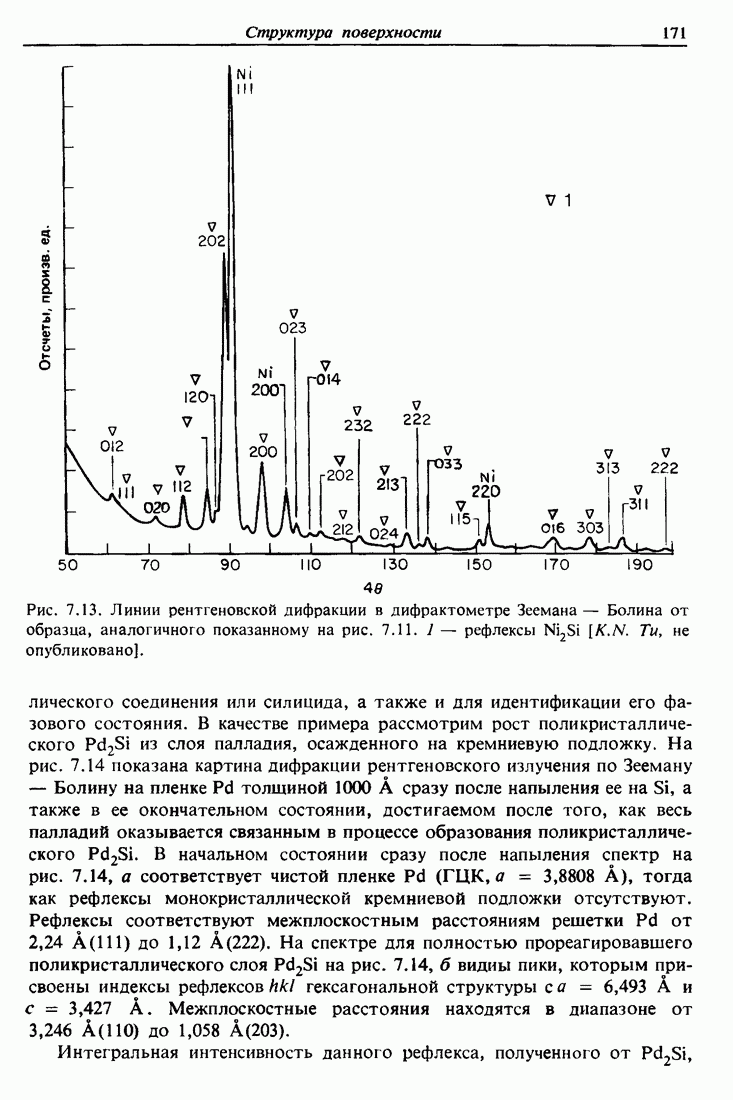
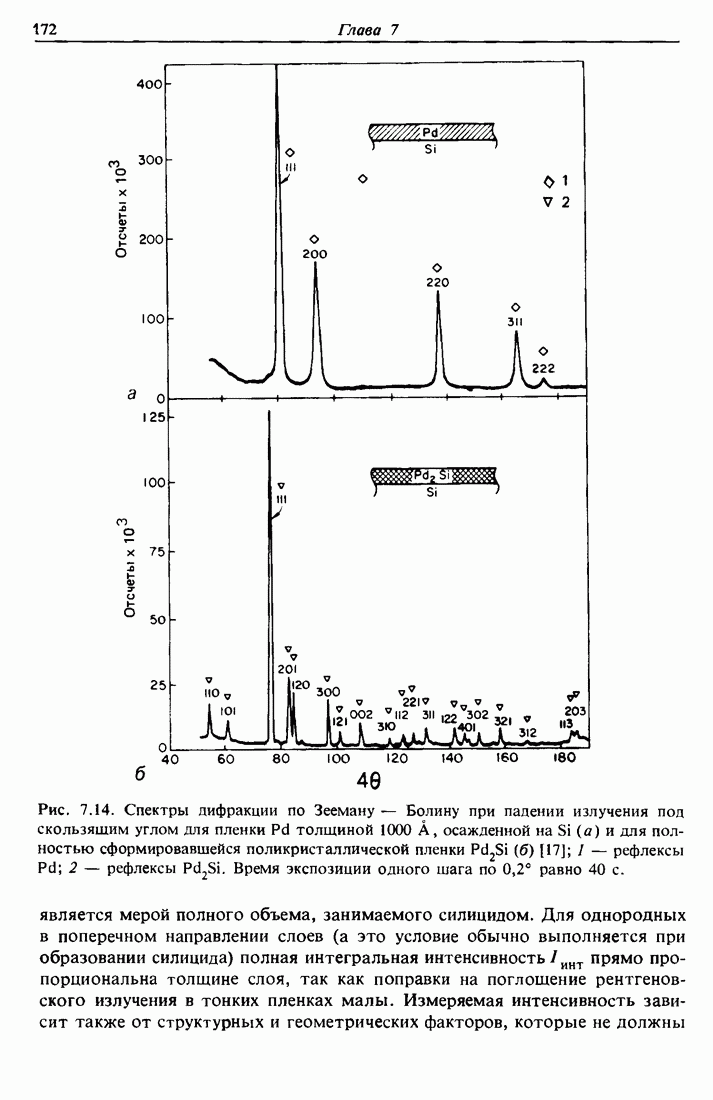
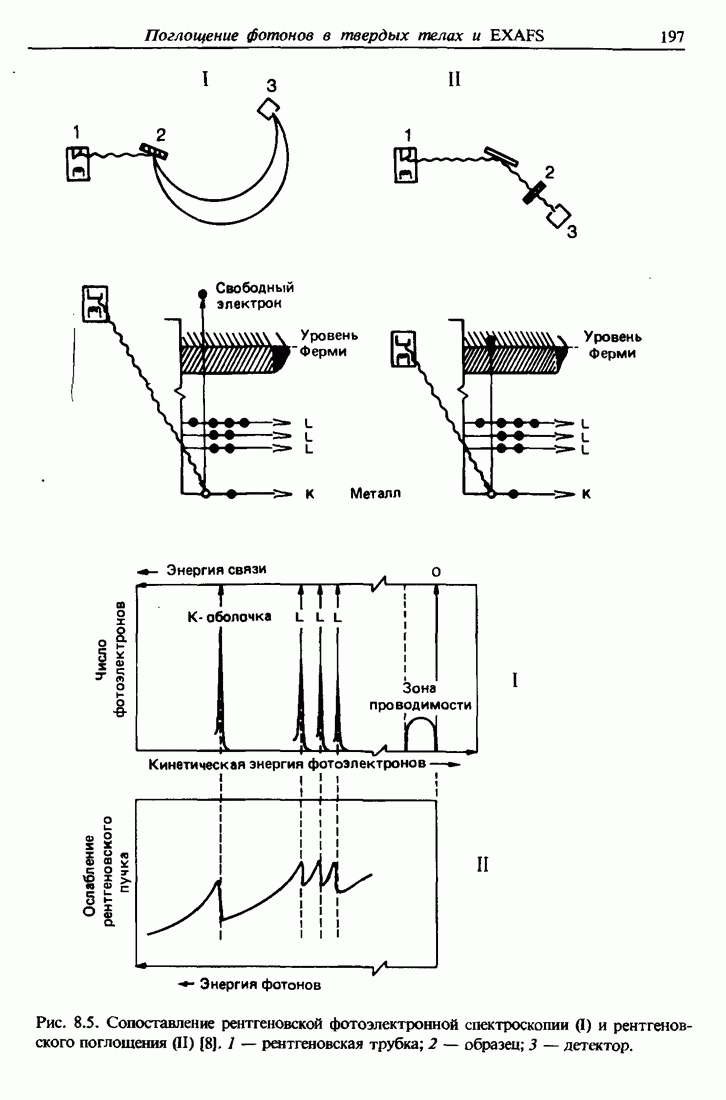
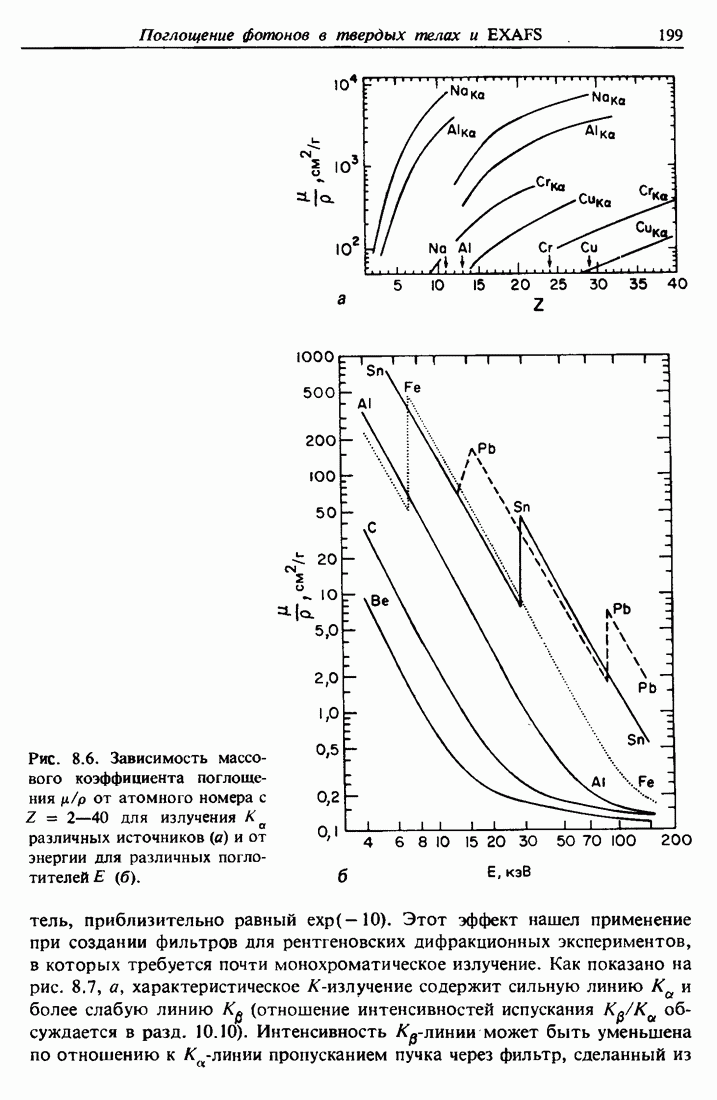
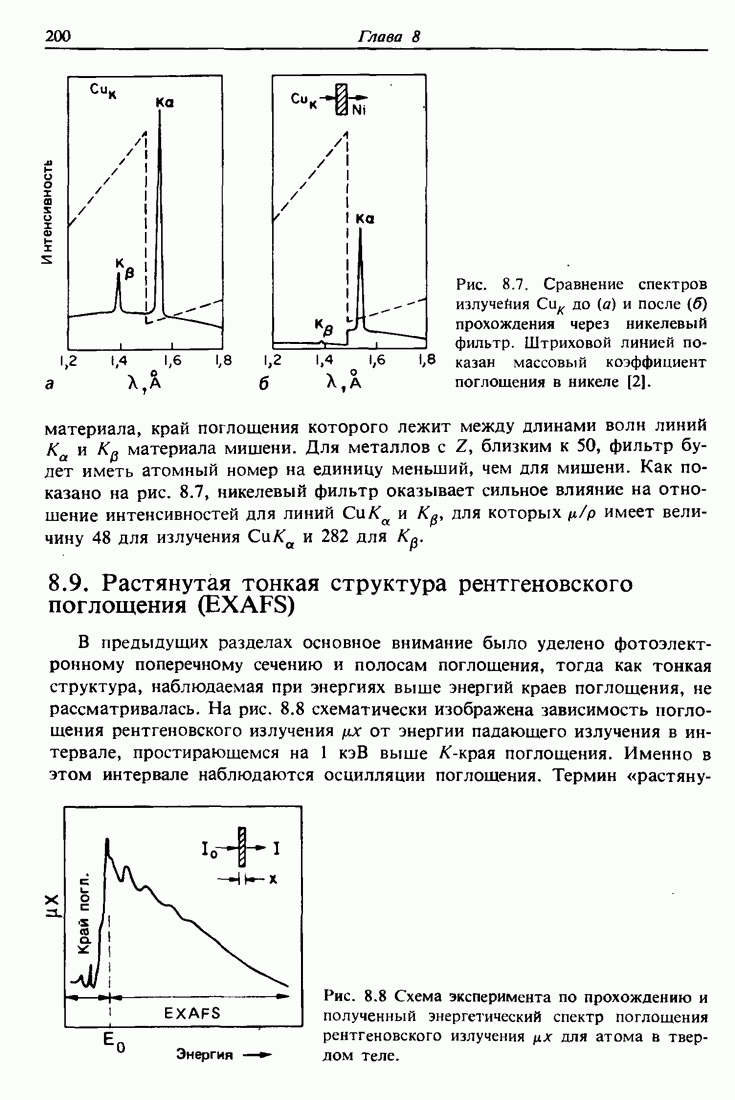
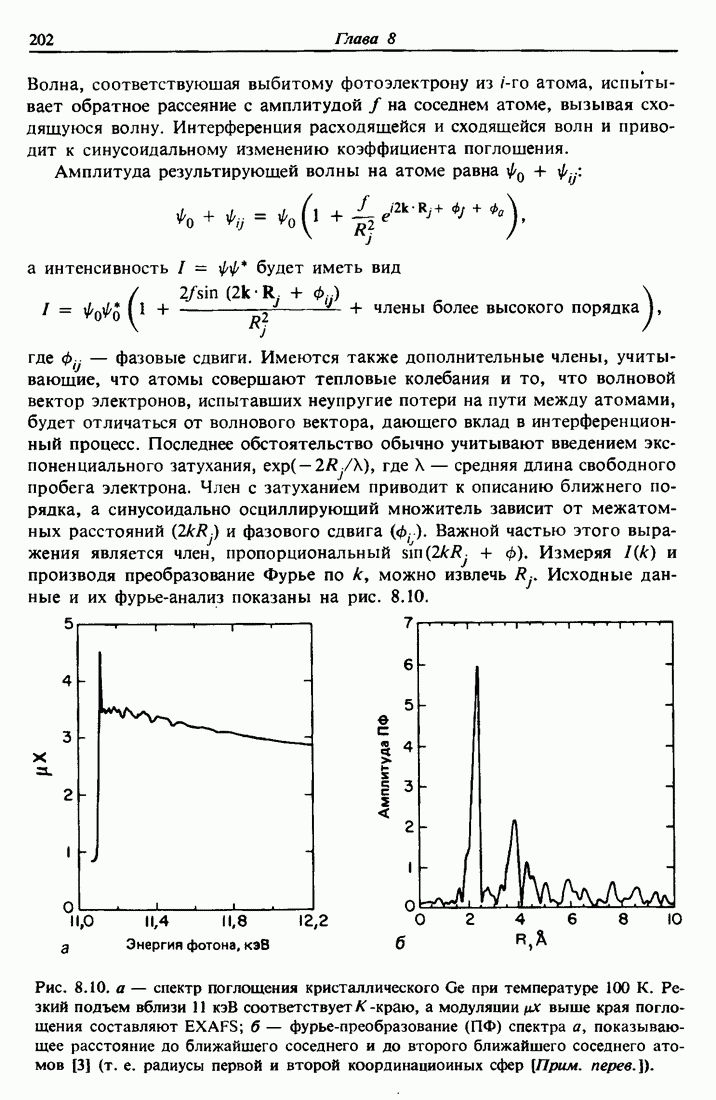
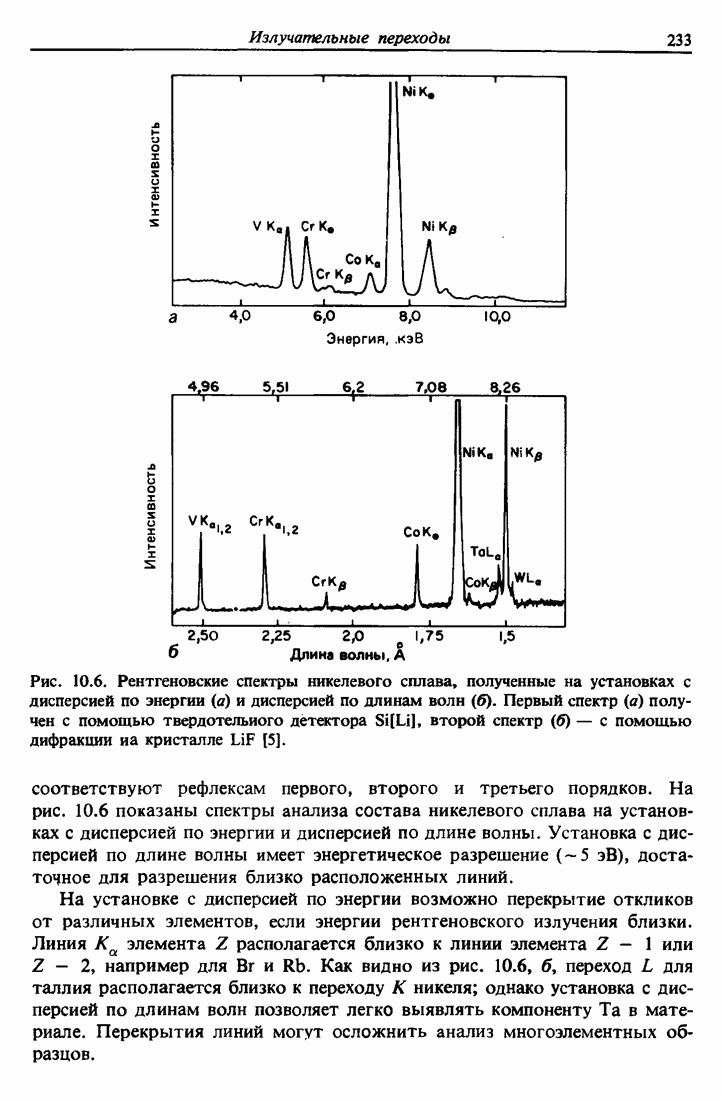
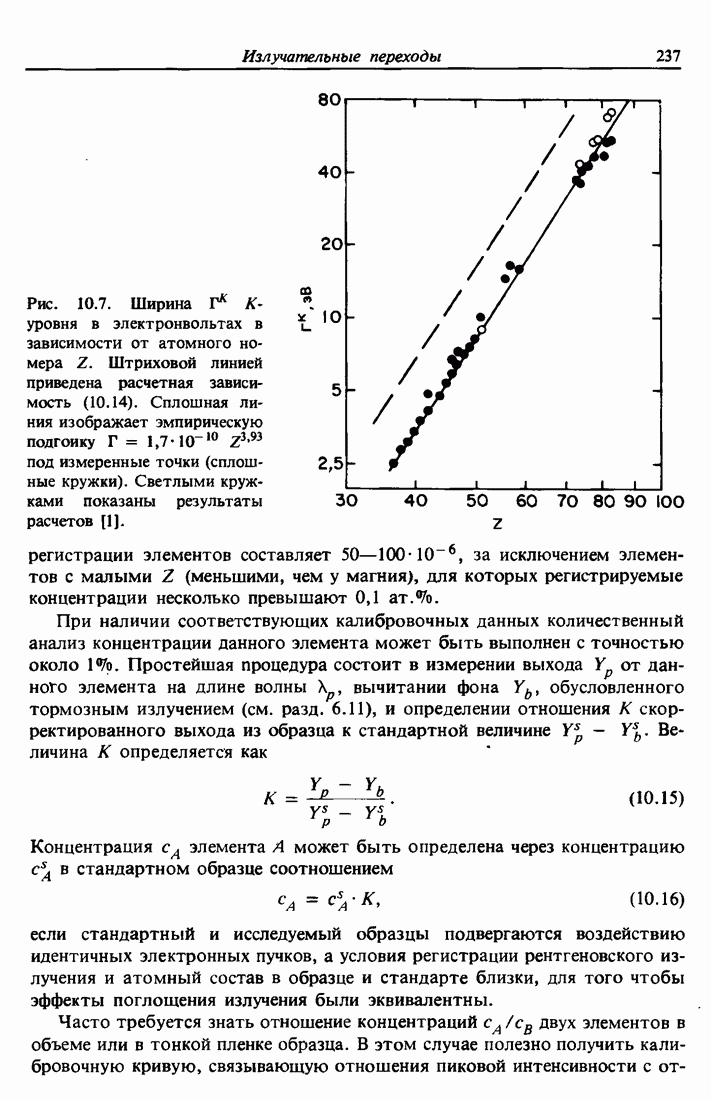
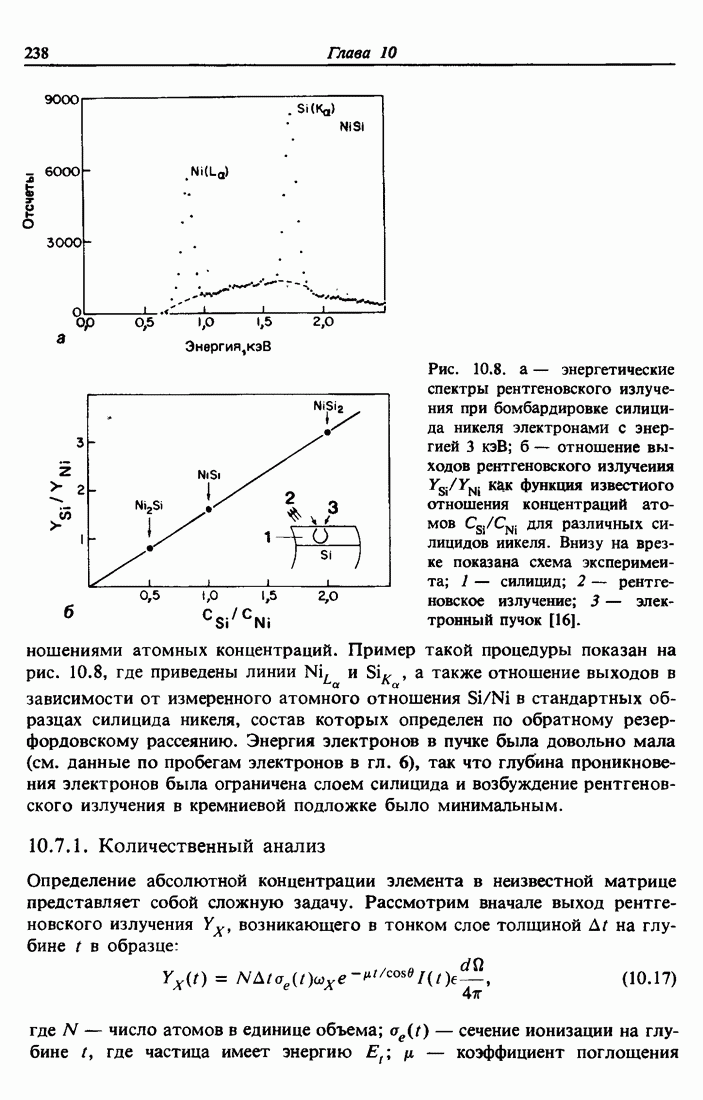
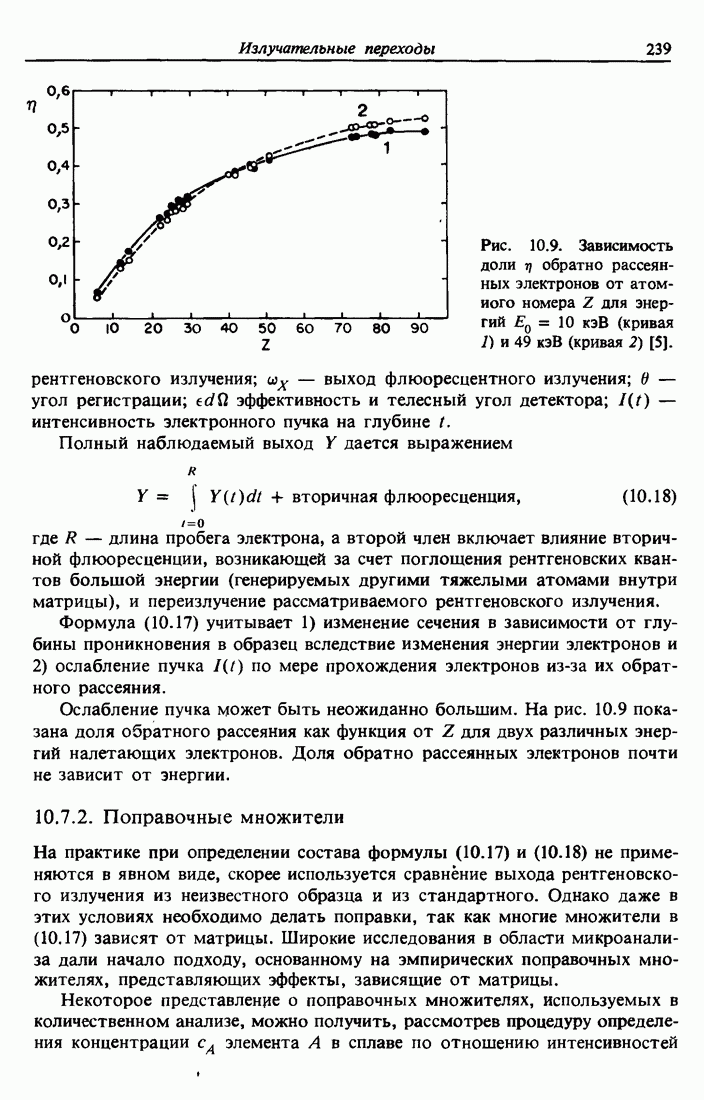
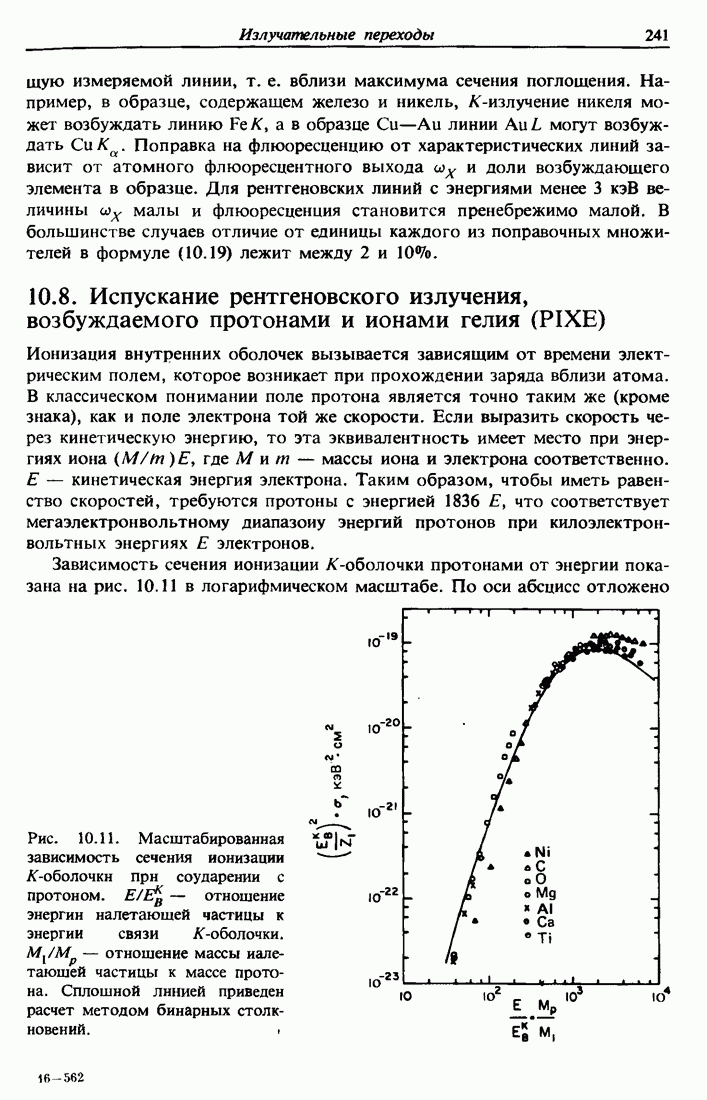
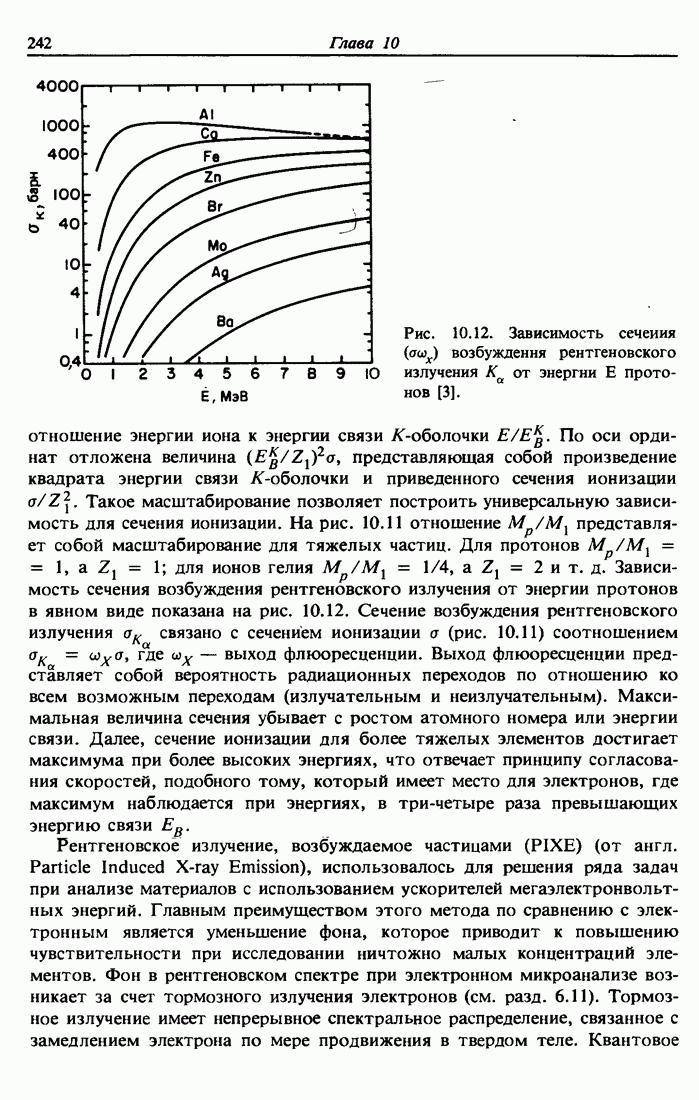
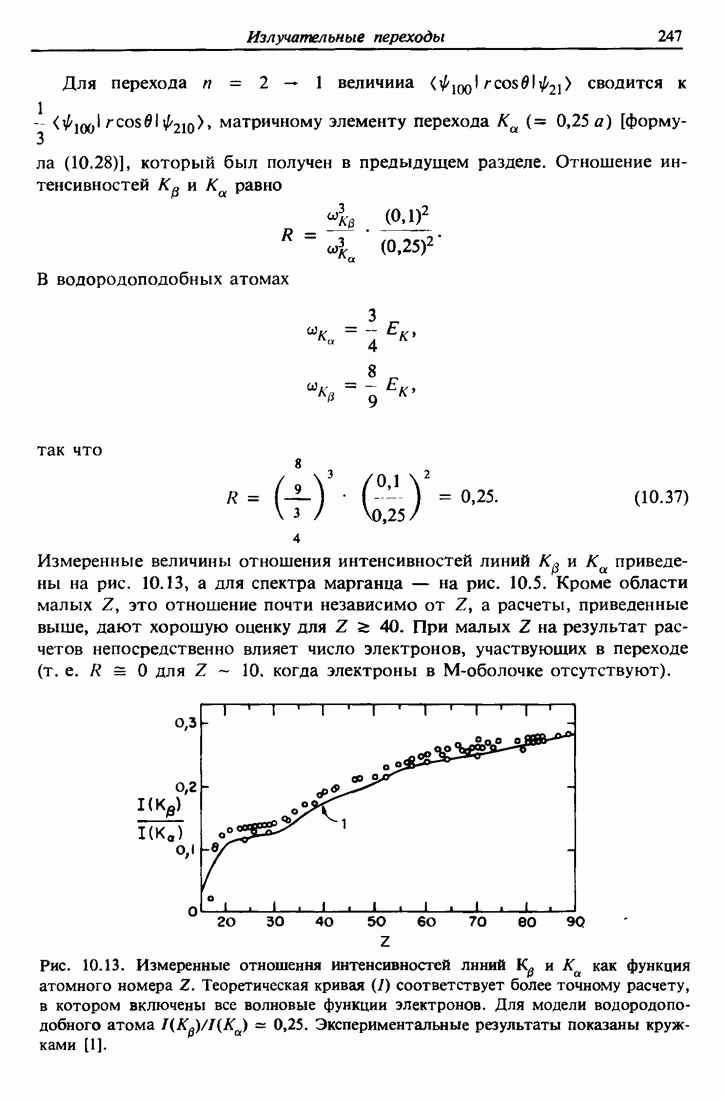
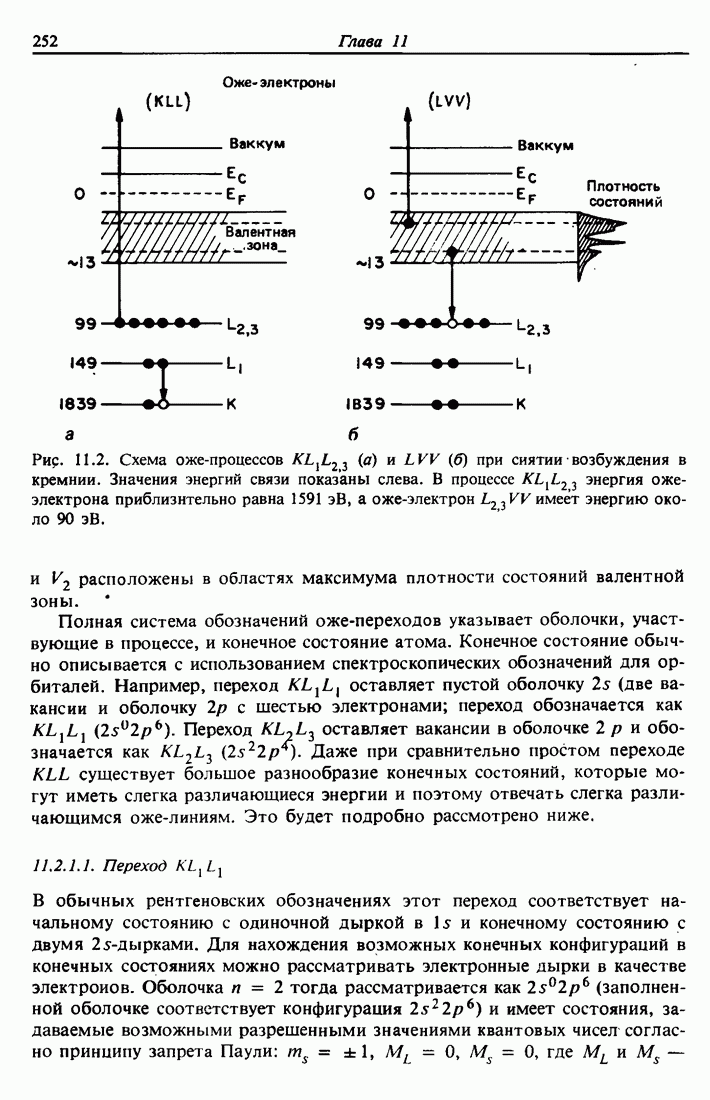
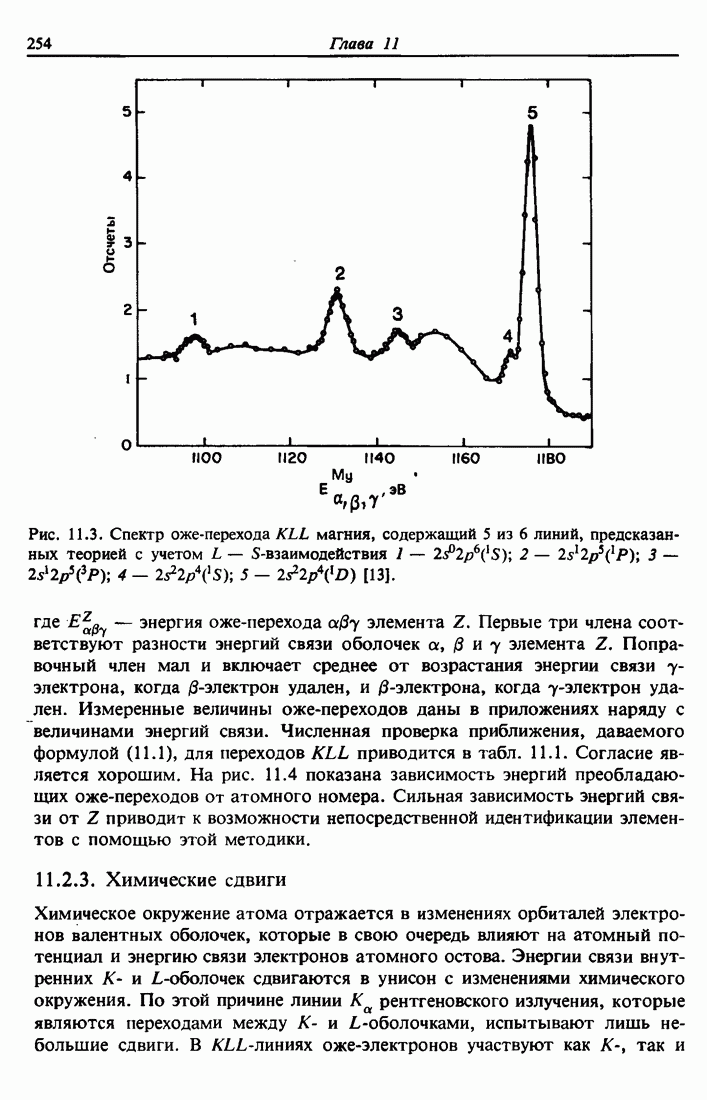
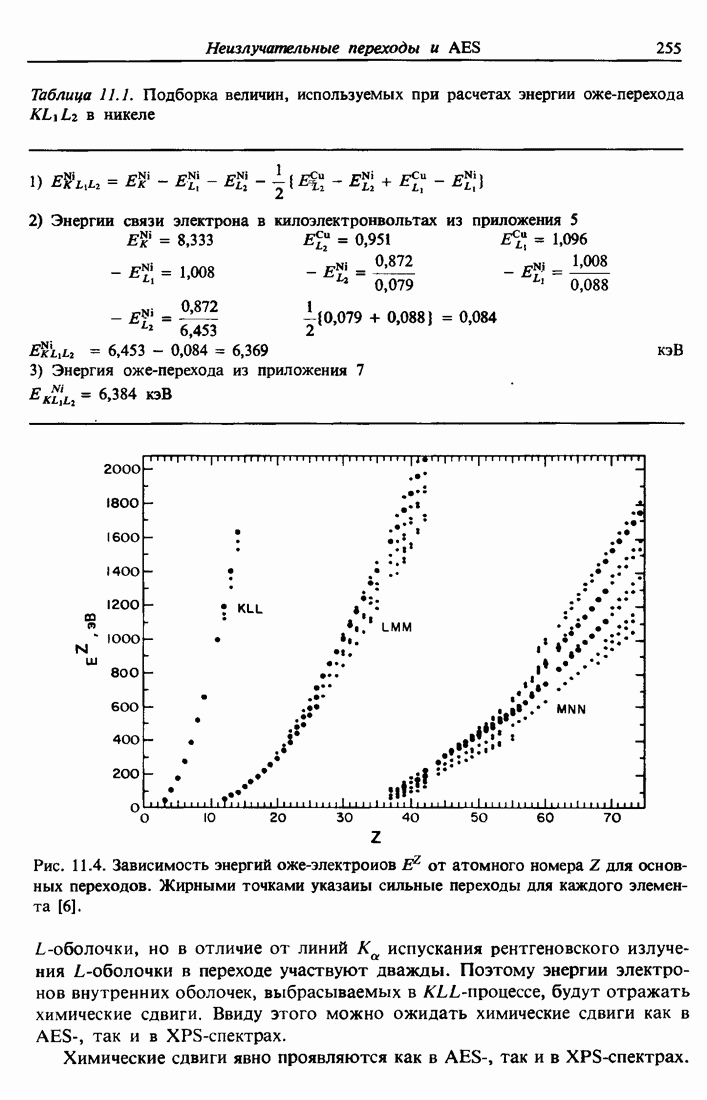
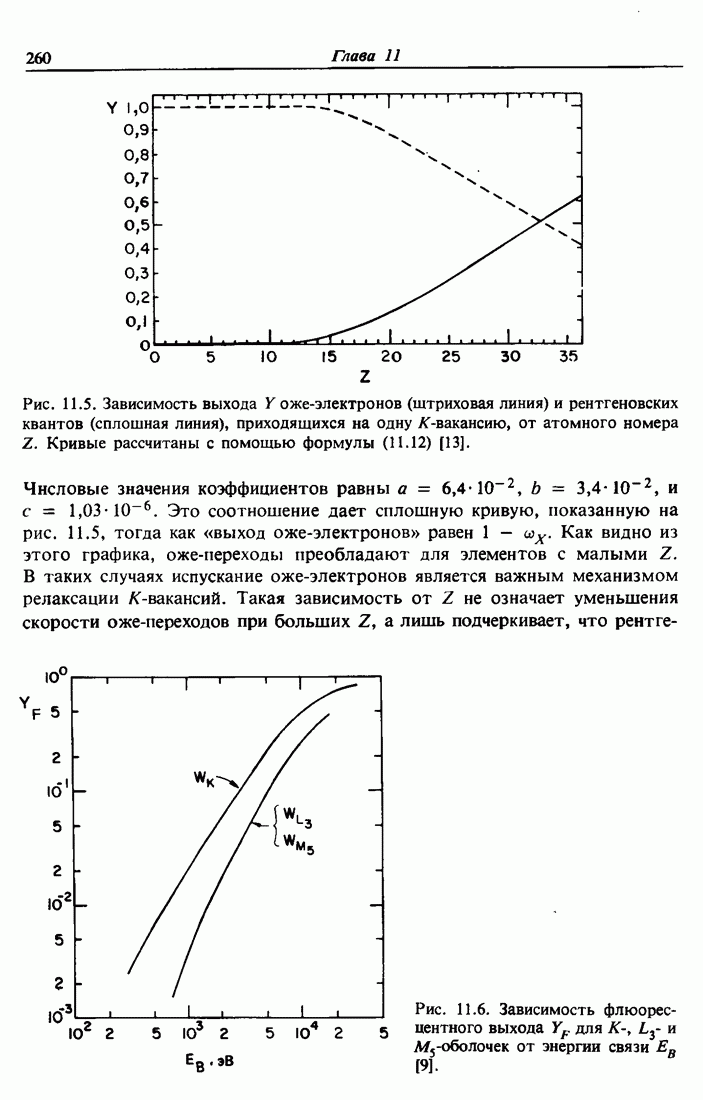
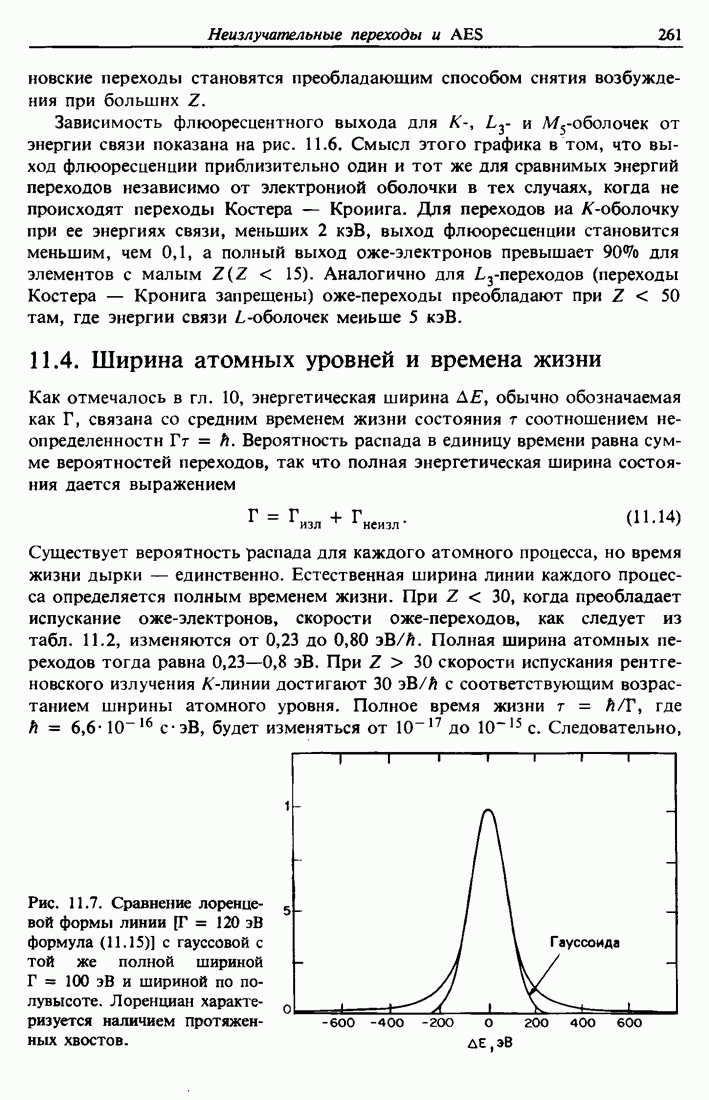
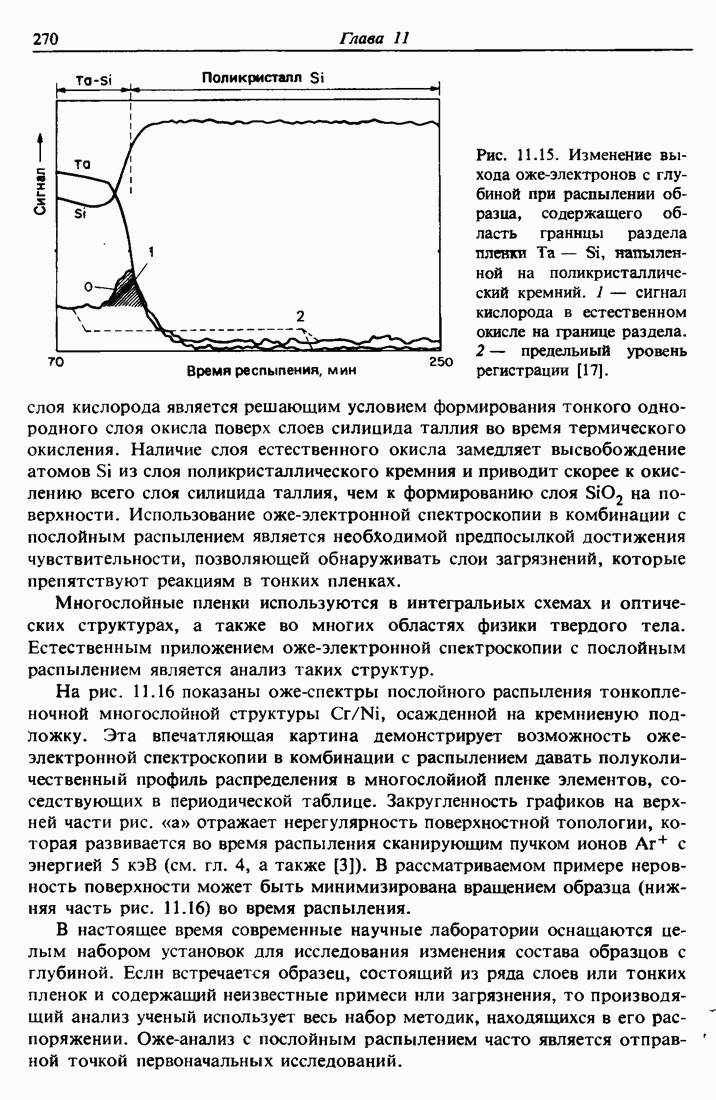
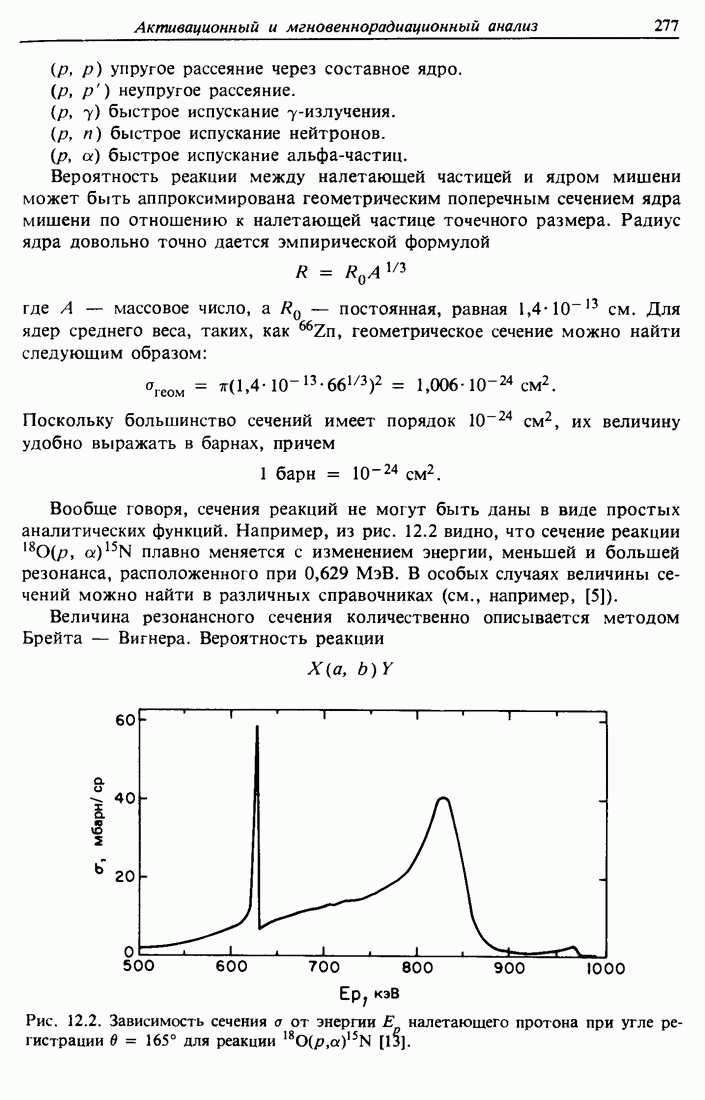
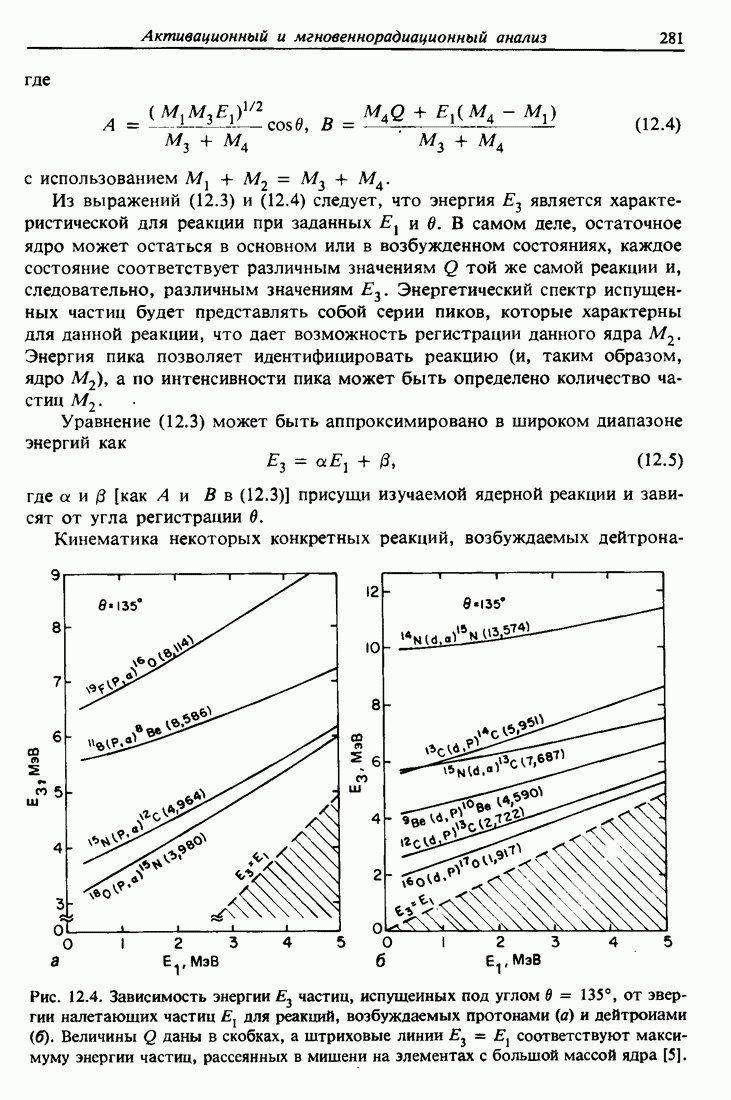
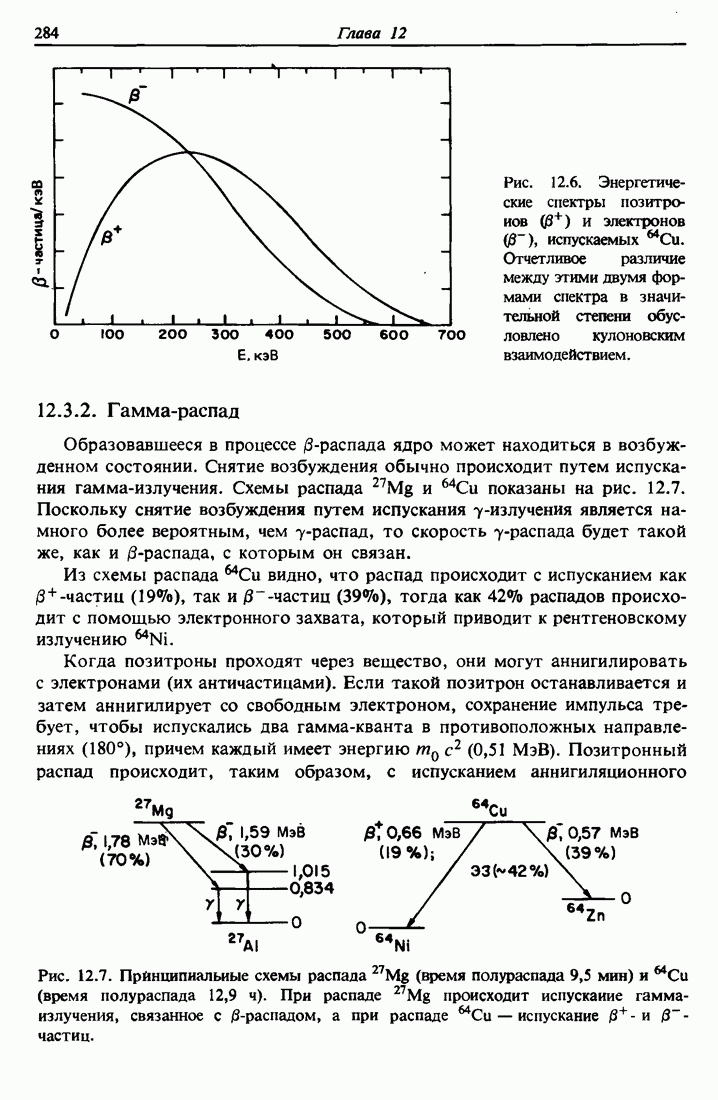
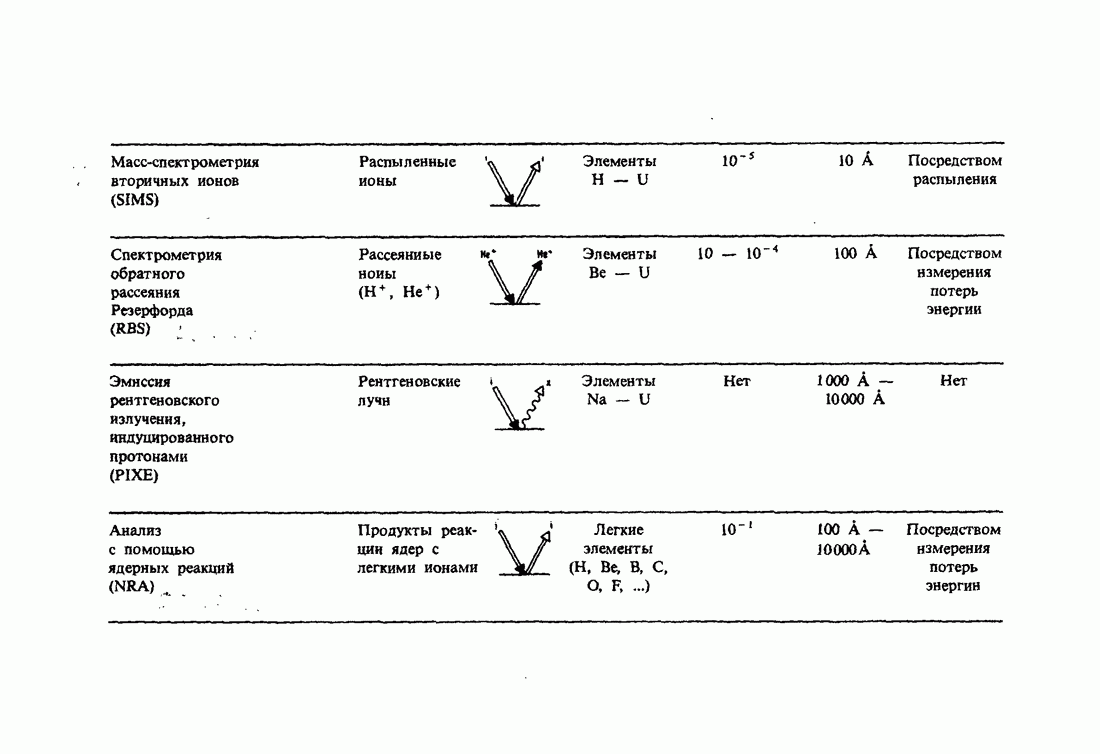
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Кинематика упругих столкновений
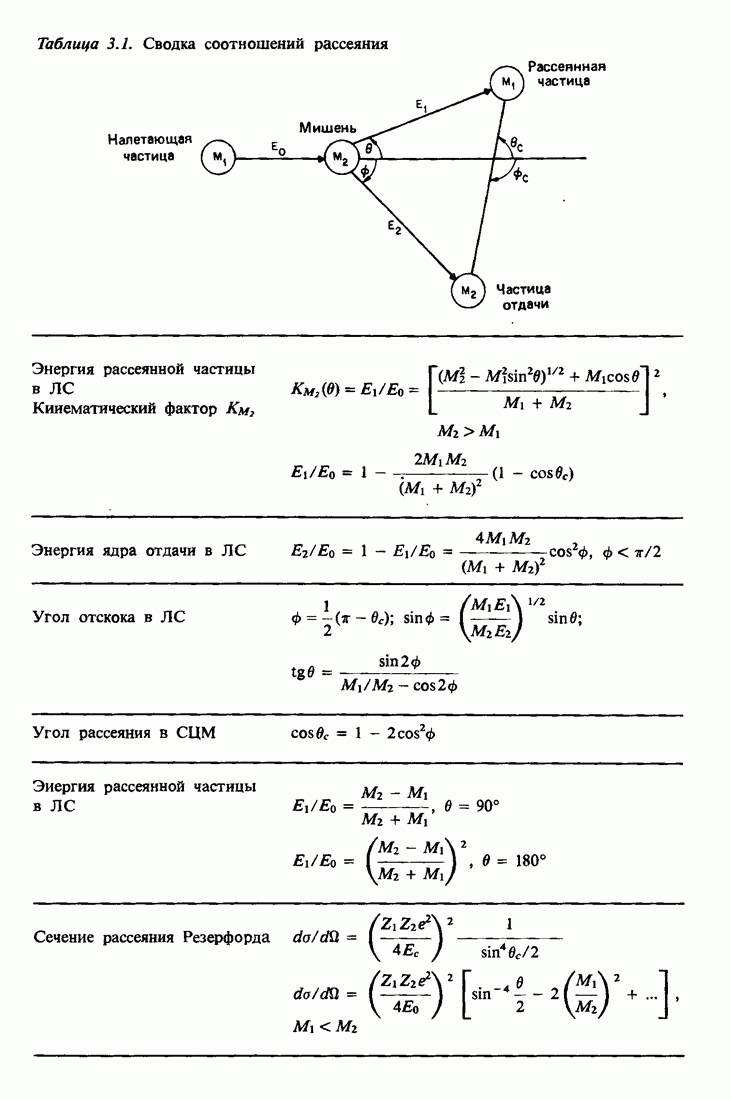
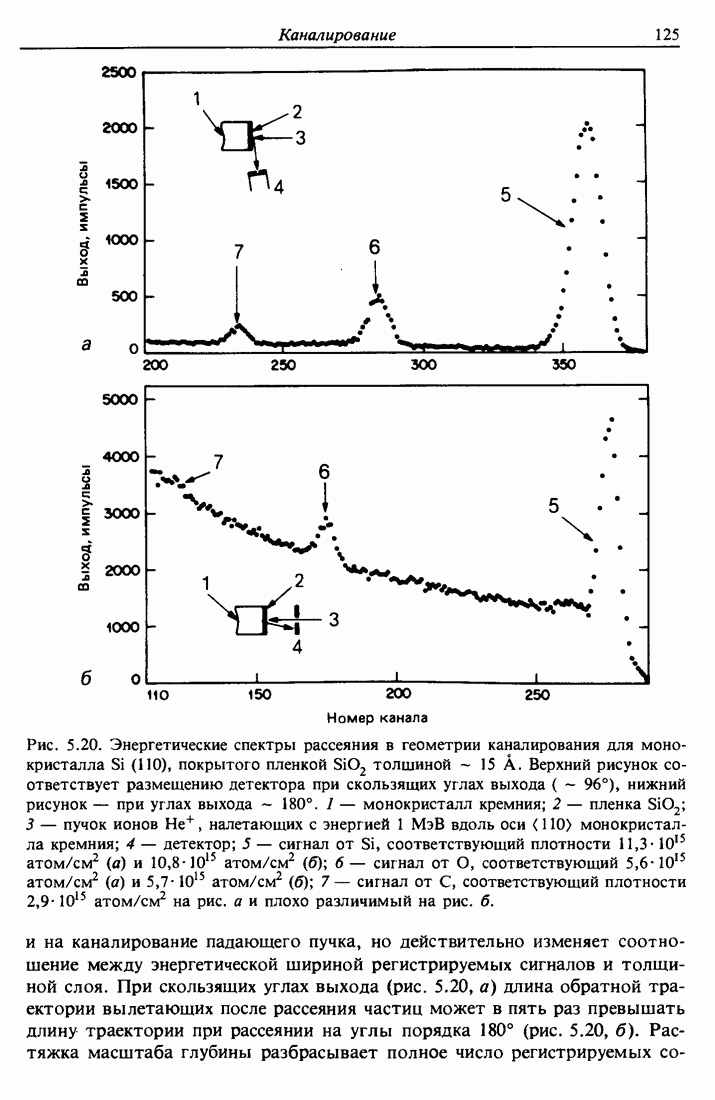
При обратном рассеянии Резерфорда моноэнергетические частицы пучка сталкиваются с атомами мишени, рассеиваются назад и попадают в детектор-анализатор, измеряющий энергии частиц. При столкновении энергия передается от движущейся частицы неподвижному атому мишени; уменьшение энергии рассеянной частицы зависит от ее массы и массы атома мишени и позволяет идентифицировать атом мишени.
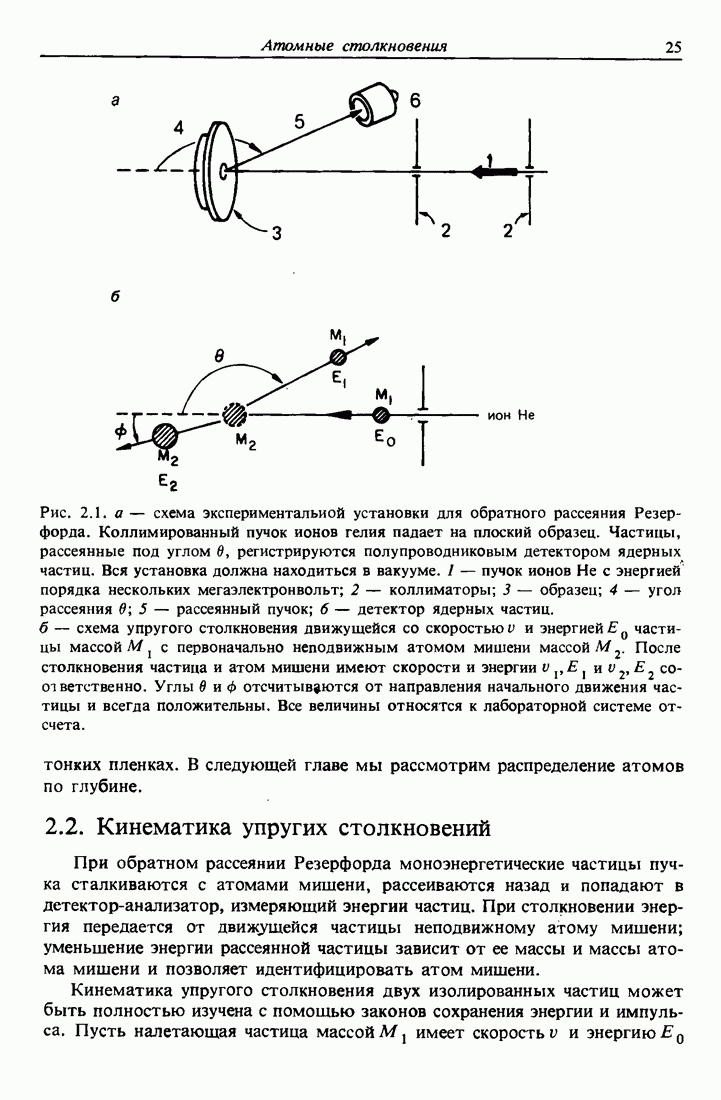
Кинематика упругого столкновения двух изолированных частиц может быть полностью изучена с помощью законов сохранения энергии и импульса. Пусть налетающая частица массой  имеет скоростью и энергию
имеет скоростью и энергию 
 , а атом мишени с массой
, а атом мишени с массой  покоится. После столкновения значения скоростей
покоится. После столкновения значения скоростей  и
и  энергий
энергий  налетающей частицы и атома мишени определяются углом рассеяния в и углом отдачи
налетающей частицы и атома мишени определяются углом рассеяния в и углом отдачи  . Обозначения и геометрия рассеяния в лабораторной системе координат приведены на рис. 2.1, б.
. Обозначения и геометрия рассеяния в лабораторной системе координат приведены на рис. 2.1, б.
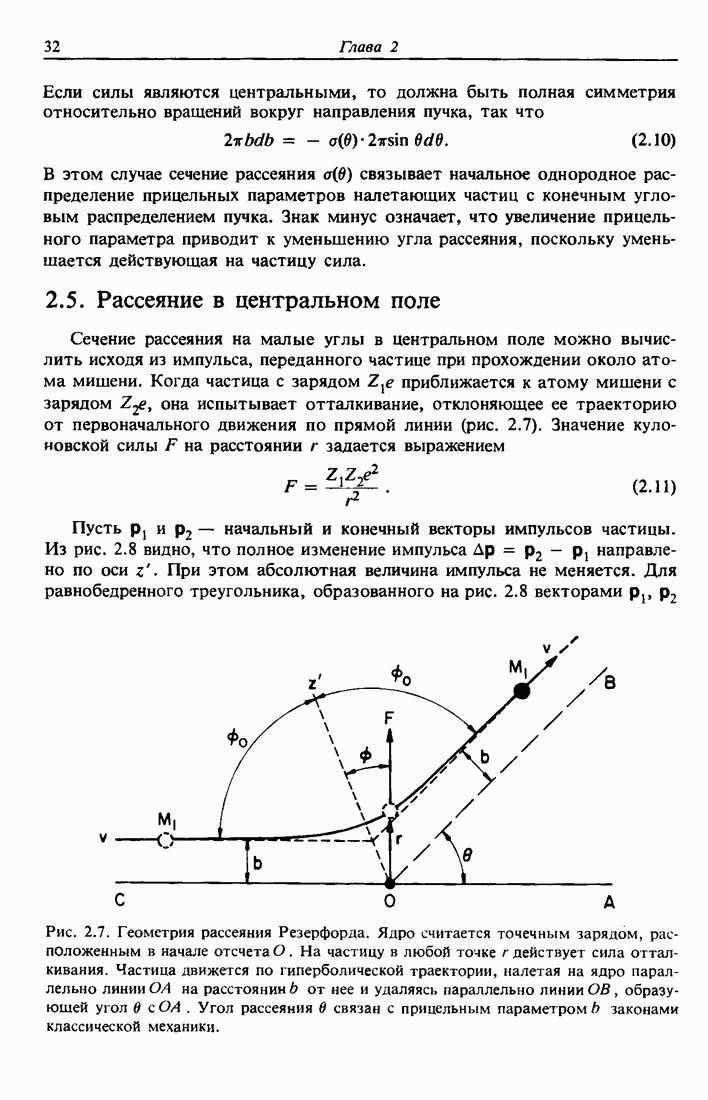
Законы сохранения энергии и компонент импульса, параллельных и перпендикулярных направлению движения налетающей частицы, выражаются уравнениями
 (2.2)
(2.2)
Исключая сначала  , а затем
, а затем  , находим отношение скоростей частицы
, находим отношение скоростей частицы 
Отношение энергий налетающей частицы в случае  когда в (2.4) имеет место знак плюс, определяется выражением
когда в (2.4) имеет место знак плюс, определяется выражением

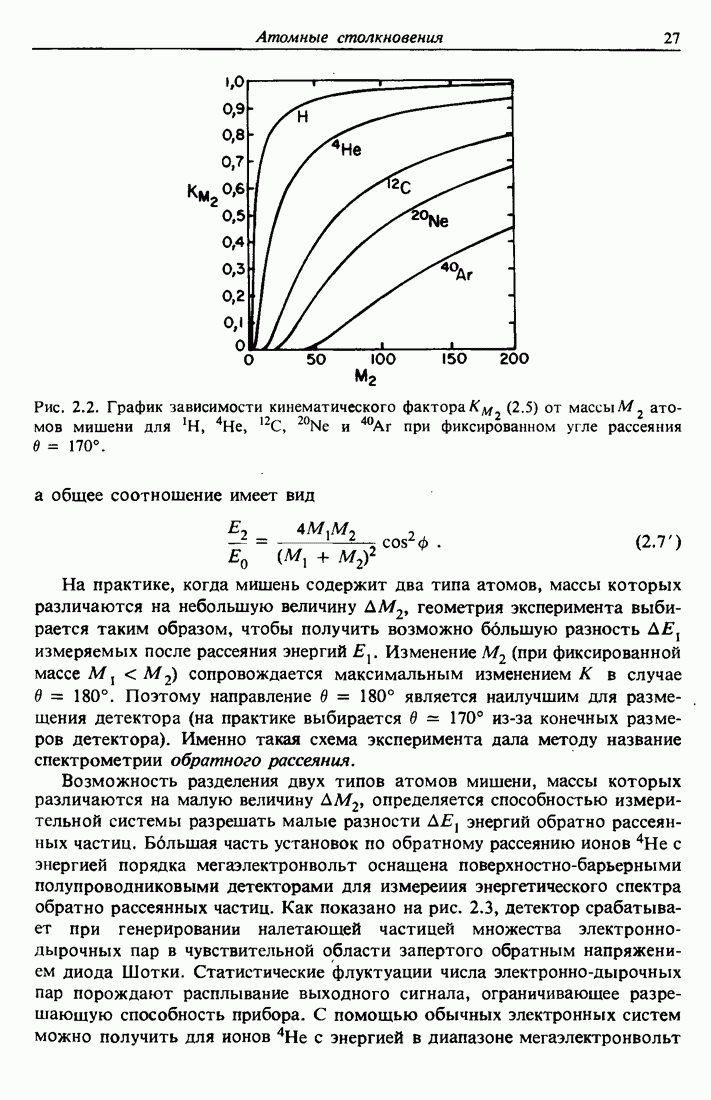
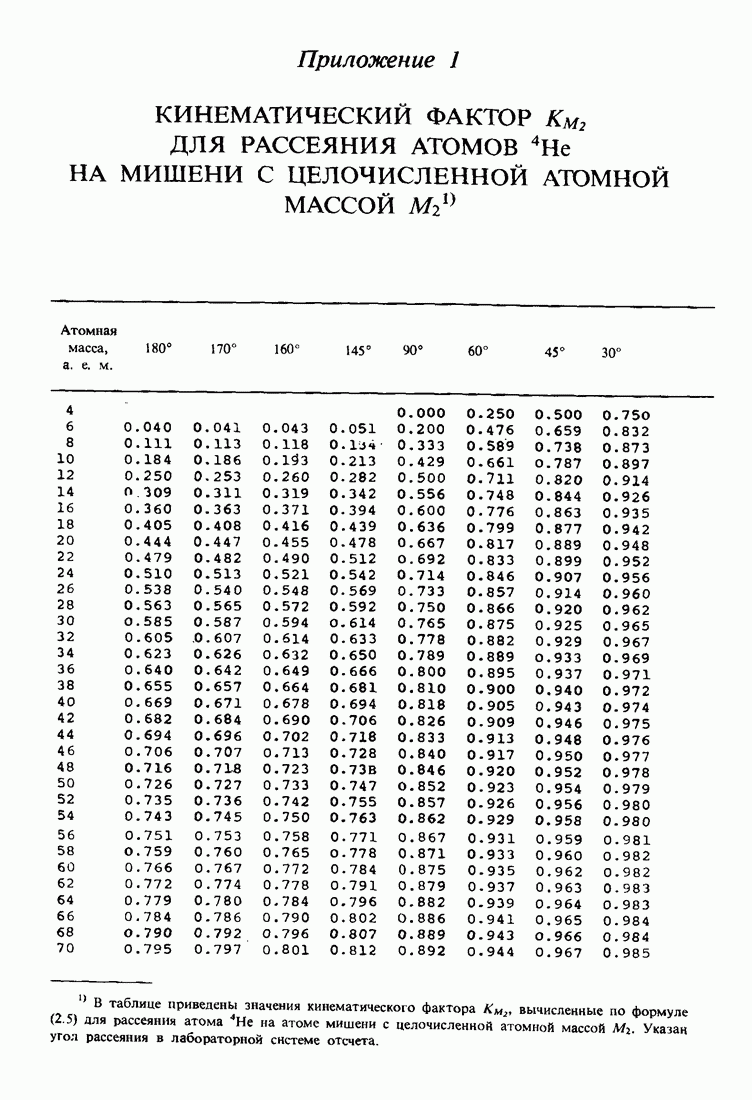
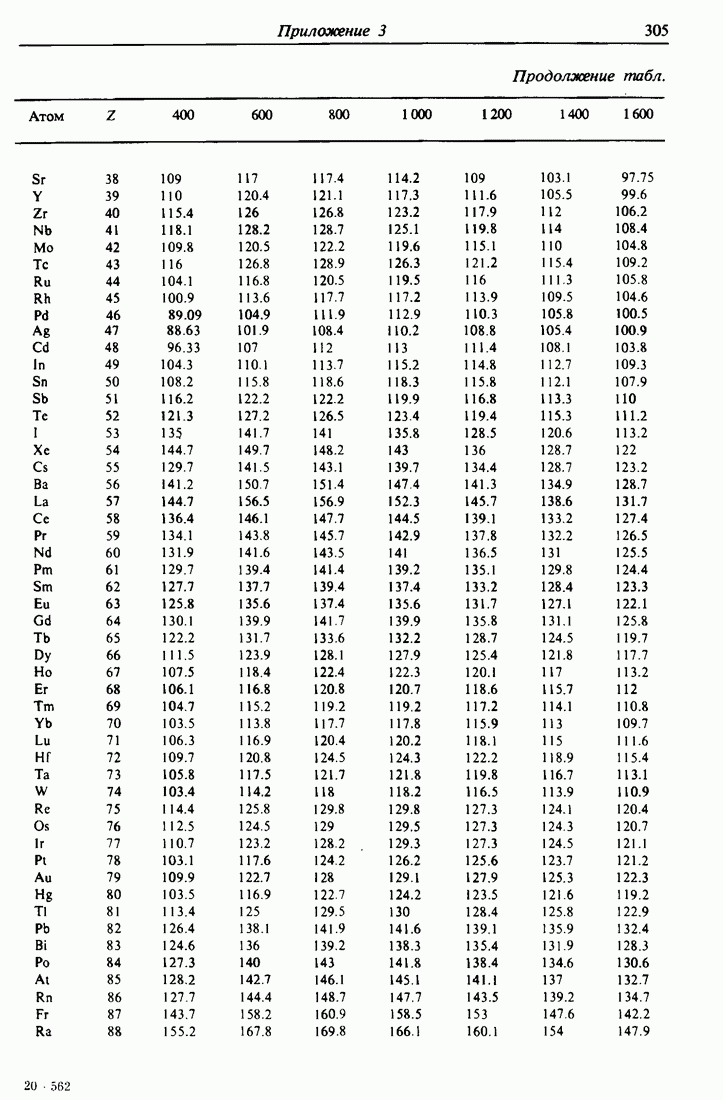
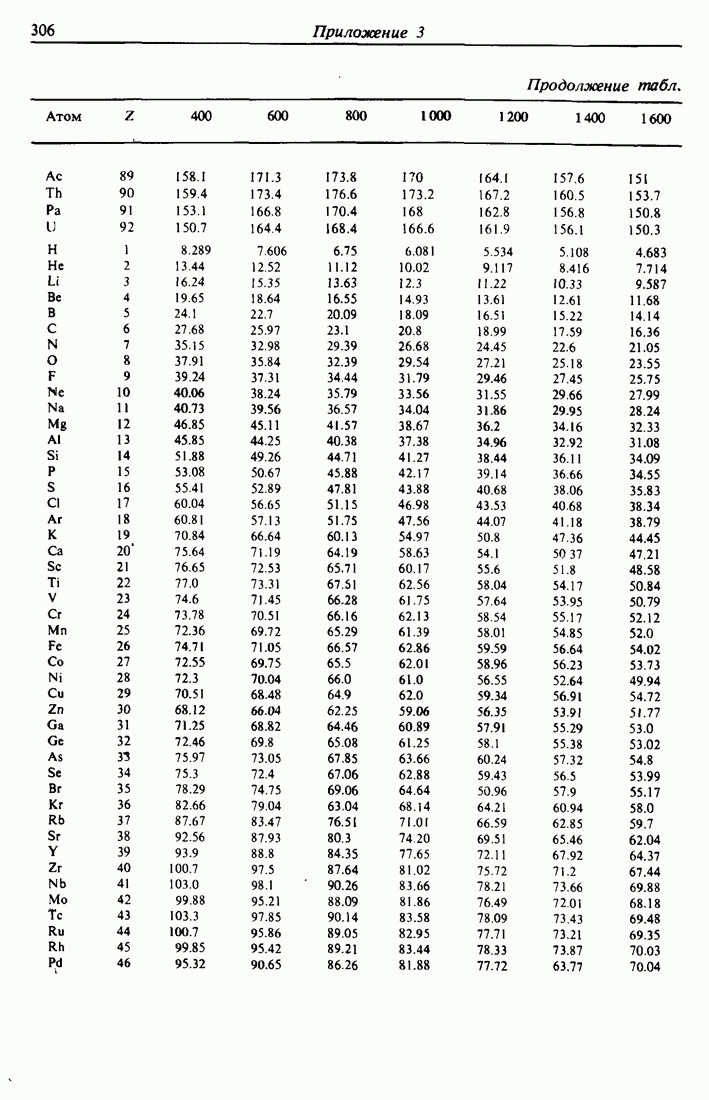
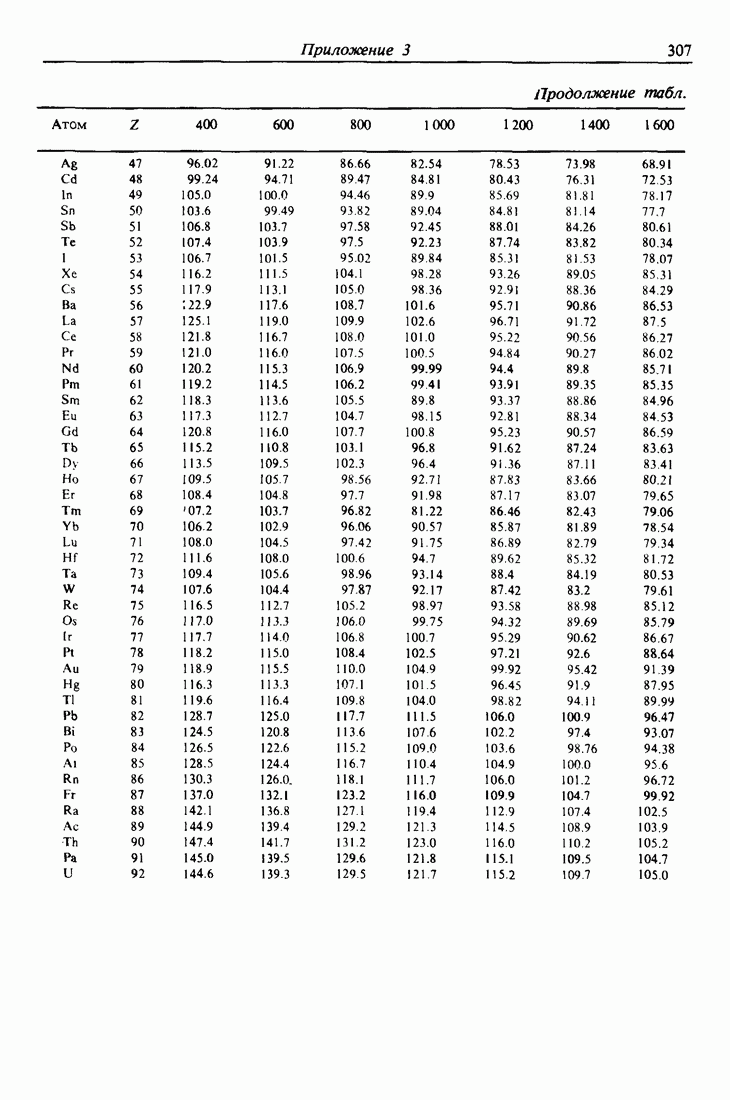
Это отношение энергий  , называемое кинематическим фактором, показывает, что энергия после соударения определяется только массами частиц и углом рассеяния. Чтобы подчеркнуть зависимость К от массы атома мишени, обычно добавляется индекс:
, называемое кинематическим фактором, показывает, что энергия после соударения определяется только массами частиц и углом рассеяния. Чтобы подчеркнуть зависимость К от массы атома мишени, обычно добавляется индекс:  . Таблицы значений К для различных
. Таблицы значений К для различных  и в приведены в приложении 1, а зависимость К от
и в приведены в приложении 1, а зависимость К от  при фиксированном угле
при фиксированном угле  изображена на рис. 2.2. Такие таблицы и графики постоянно используются в экспериментах по обратному рассеянию. Сводка основных соотношений рассеяния содержится в табл. 3.1.
изображена на рис. 2.2. Такие таблицы и графики постоянно используются в экспериментах по обратному рассеянию. Сводка основных соотношений рассеяния содержится в табл. 3.1.
При обратном рассеянии на угол 180° отношение энергий достигает своего минимального значения, равного

а при угле 90°

При равенстве масс  налетающая частица останавливается после столкновения, передав всю энергию атому мишени, — случай, хорошо известный в бильярде. Для
налетающая частица останавливается после столкновения, передав всю энергию атому мишени, — случай, хорошо известный в бильярде. Для  энергия
энергия  переданная атому мишени, достигает своего максимального значения, равного
переданная атому мишени, достигает своего максимального значения, равного


Рис. 2.2. График зависимости кинематического фактора (2.5) от массы  атомов мишени для
атомов мишени для  при фиксированном угле рассеяния
при фиксированном угле рассеяния  .
.
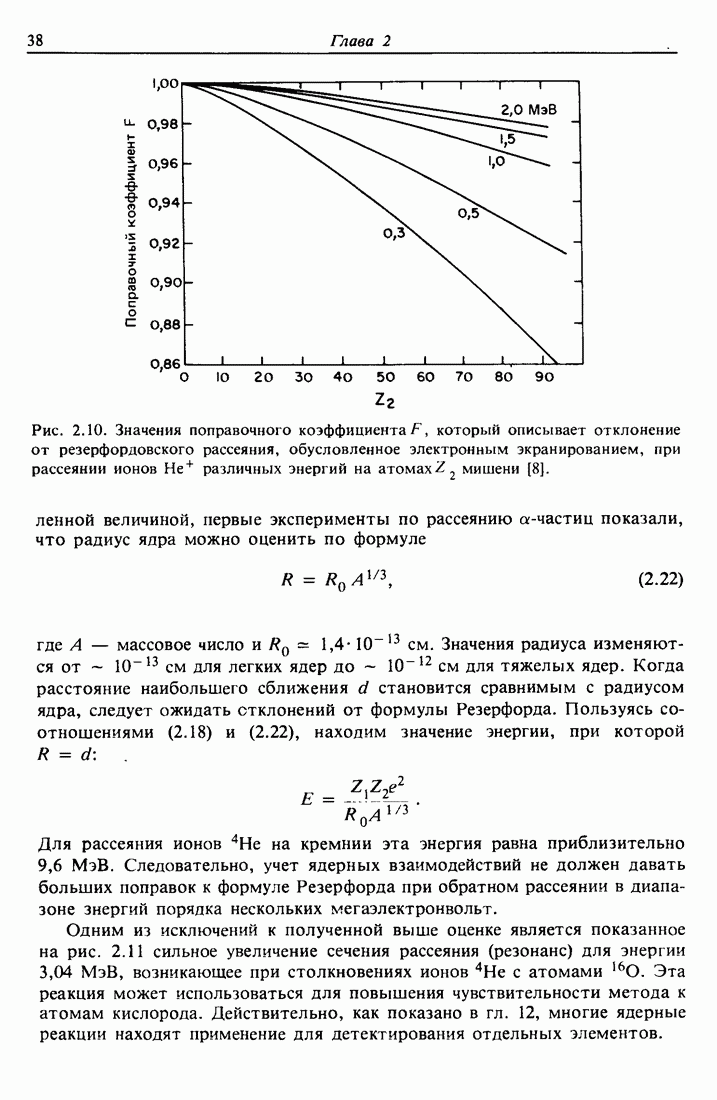
а общее соотношение имеет вид

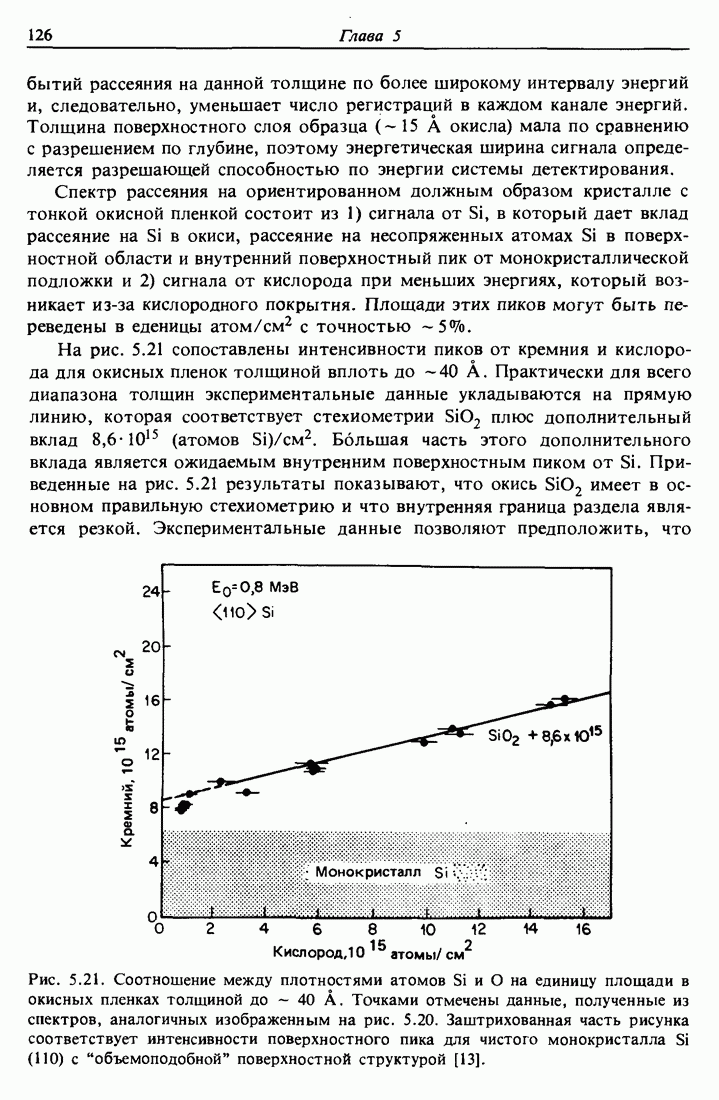
На практике, когда мишень содержит два типа атомов, массы которых различаются на небольшую величину  геометрия эксперимента выбирается таким образом, чтобы получить возможно большую разность
геометрия эксперимента выбирается таким образом, чтобы получить возможно большую разность  измеряемых после рассеяния энергий
измеряемых после рассеяния энергий  . Изменение
. Изменение  (при фиксированной массе
(при фиксированной массе  ) сопровождается максимальным изменением К в случае
) сопровождается максимальным изменением К в случае  . Поэтому направление
. Поэтому направление  является наилучшим для размещения детектора (на практике выбирается
является наилучшим для размещения детектора (на практике выбирается  из-за конечных размеров детектора). Именно такая схема эксперимента дала методу название спектрометрии обратного рассеяния.
из-за конечных размеров детектора). Именно такая схема эксперимента дала методу название спектрометрии обратного рассеяния.
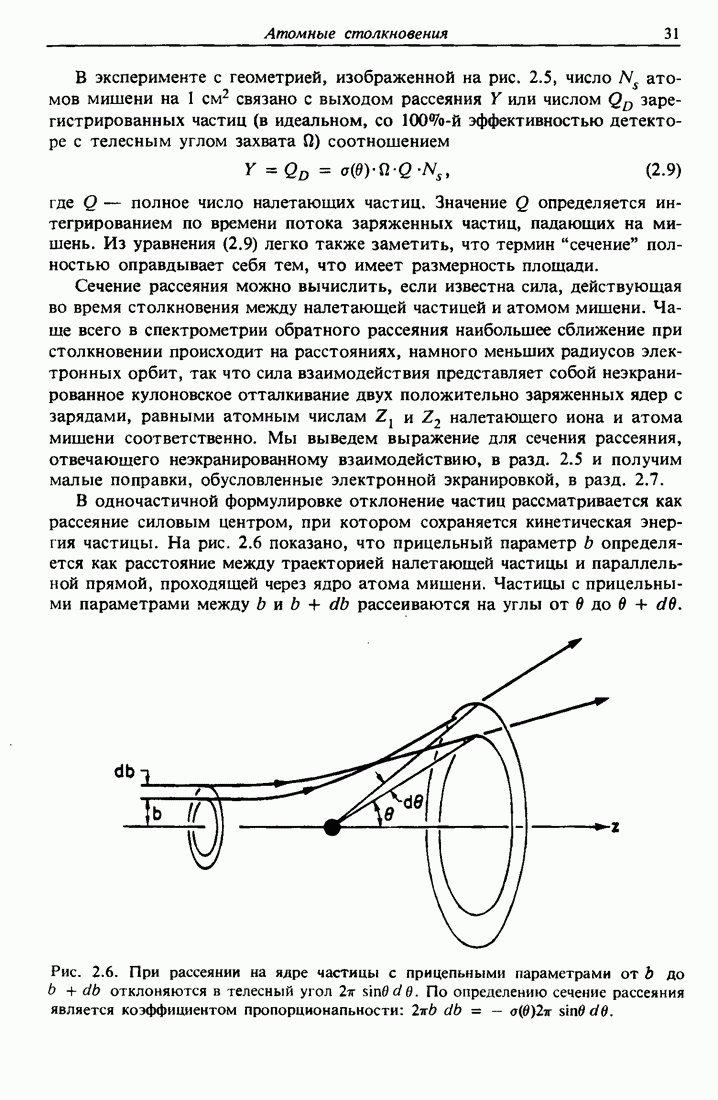
Возможность разделения двух типов атомов мишени, массы которых различаются на малую величину  определяется способностью измерительной системы разрешать малые разности
определяется способностью измерительной системы разрешать малые разности  энергий обратно рассеянных частиц. Большая часть установок по обратному рассеянию ионов
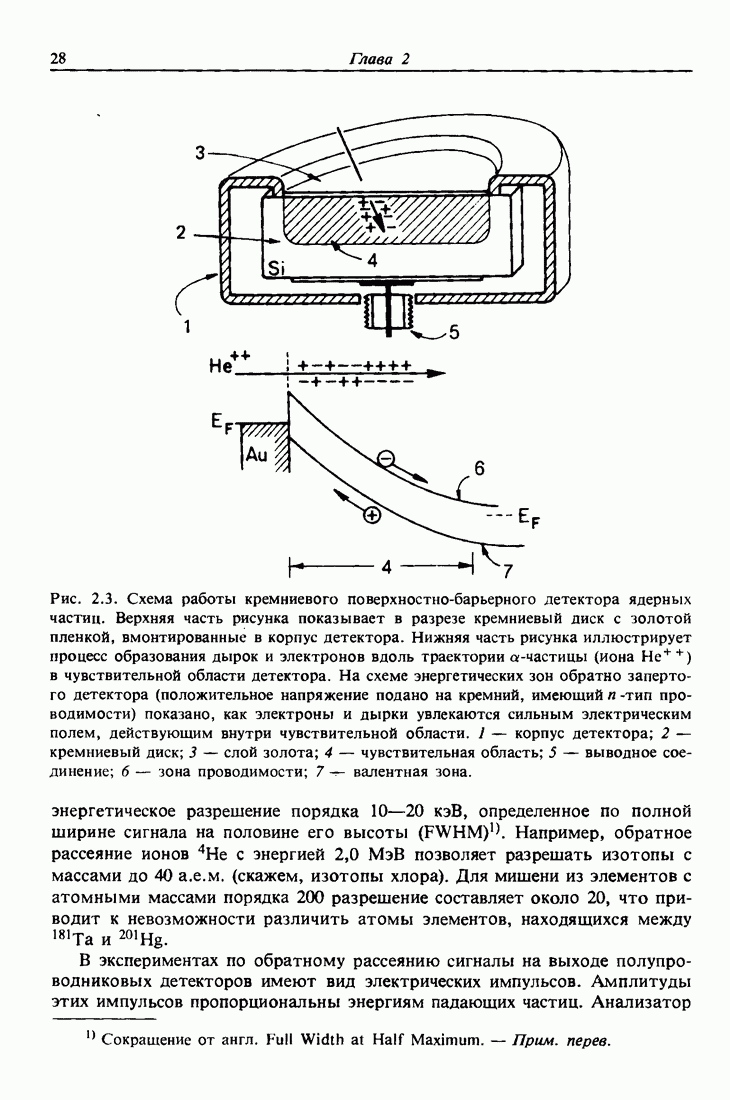
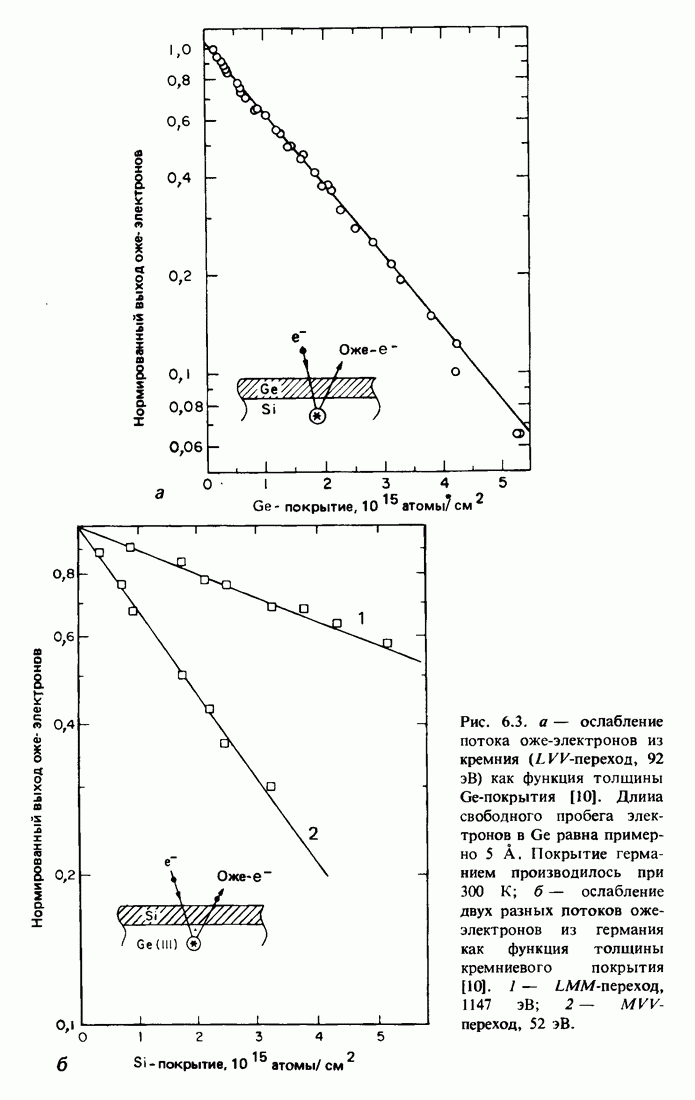
энергий обратно рассеянных частиц. Большая часть установок по обратному рассеянию ионов  с энергией порядка мегаэлектронвольт оснащена поверхностно-барьерными полупроводниковыми детекторами для измерения энергетического спектра обратно рассеянных частиц. Как показано на рис. 2.3, детектор срабатывает при генерировании налетающей частицей множества электронно-дырочных пар в чувствительной области запертого обратным напряжением диода Шотки. Статистические флуктуации числа электронно-дырочных пар порождают расплывание выходного сигнала, ограничивающее разрешающую способность прибора. С помощью обычных электронных систем можно получить для ионов
с энергией порядка мегаэлектронвольт оснащена поверхностно-барьерными полупроводниковыми детекторами для измерения энергетического спектра обратно рассеянных частиц. Как показано на рис. 2.3, детектор срабатывает при генерировании налетающей частицей множества электронно-дырочных пар в чувствительной области запертого обратным напряжением диода Шотки. Статистические флуктуации числа электронно-дырочных пар порождают расплывание выходного сигнала, ограничивающее разрешающую способность прибора. С помощью обычных электронных систем можно получить для ионов  с энергией в диапазоне мегаэлектронвольт
с энергией в диапазоне мегаэлектронвольт

Рис. 2.3. Схема работы кремниевого поверхностно-барьерного детектора ядерных частиц. Верхняя часть рисунка показывает в разрезе кремниевый диск с золотой пленкой, вмонтированные в корпус детектора. Нижняя часть рисунка иллюстрирует процесс образования дырок и электронов вдоль траектории а-частицы (иона  ) в чувствительной области детектора. На схеме энергетических зон обратно запертого детектора (положительное напряжение подано на кремний, имеющий и
) в чувствительной области детектора. На схеме энергетических зон обратно запертого детектора (положительное напряжение подано на кремний, имеющий и  -тип проводимости) показано, как электроны и дырки увлекаются сильным электрическим полем, действующим внутри чувствительной области. 1 — корпус детектора; 2 — кремниевый диск; 3 — слой золота; 4 — чувствительная область; 5 — выводное соединение; 6 — зона проводимости; 7 — валентная зона.
-тип проводимости) показано, как электроны и дырки увлекаются сильным электрическим полем, действующим внутри чувствительной области. 1 — корпус детектора; 2 — кремниевый диск; 3 — слой золота; 4 — чувствительная область; 5 — выводное соединение; 6 — зона проводимости; 7 — валентная зона.
энергетическое разрешение порядка 10-20 кэВ, определенное по полной ширине сигнала на половине его высоты  Например, обратное рассеяние ионов
Например, обратное рассеяние ионов  с энергией 2,0 МэВ позволяет разрешать изотопы с массами до 40 а.е.м. (скажем, изотопы хлора). Для мишени из элементов с атомными массами порядка 200 разрешение составляет около 20, что приводит к невозможности различить атомы элементов, находящихся между
с энергией 2,0 МэВ позволяет разрешать изотопы с массами до 40 а.е.м. (скажем, изотопы хлора). Для мишени из элементов с атомными массами порядка 200 разрешение составляет около 20, что приводит к невозможности различить атомы элементов, находящихся между  .
.
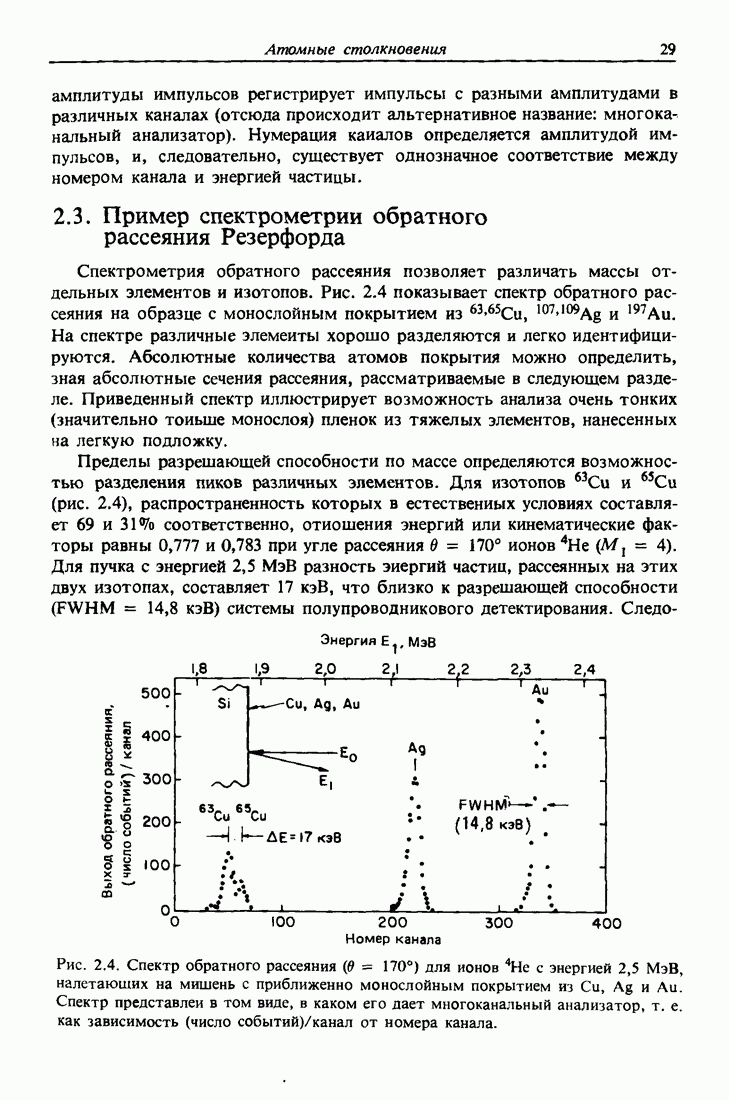
В экспериментах по обратному рассеянию сигналы на выходе полупроводниковых детекторов имеют вид электрических импульсов. Амплитуды этих импульсов пропорциональны энергиям падающих частиц. Анализатор
амплитуды импульсов регистрирует импульсы с разными амплитудами в различных каналах (отсюда происходит альтернативное название: многоканальный анализатор). Нумерация каналов определяется амплитудой импульсов, и, следовательно, существует однозначное соответствие между номером канала и энергией частицы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ, АТОМ БОРА
- 1.2. Единицы измерения физических величин
- 1.3. Корпускулярно-волновой дуализм и кристаллическая структура
- 1.4. Модель Бора
- Задачи
- Глава 2. АТОМНЫЕ СТОЛКНОВЕНИЯ И СПЕКТРОМЕТРИЯ ОБРАТНОГО РАССЕЯНИЯ
- 2.2. Кинематика упругих столкновений
- 2.3. Пример спектрометрии обратного рассеяния Резерфорда
- 2.4. Сечение рассеяния и прицельный параметр
- 2.5. Рассеяние в центральном поле
- 2.6. Сечение рассеяния в задаче двух тел
- 2.7. Отклонения от формулы Резерфорда при низких и высоких энергиях
- 2.8. Рассеяние ионов низких энергий (LEIS)
- 2.9. Спектрометрия атомов отдачи, вылетающих вперед
- 2.10. Переход от системы центра масс к лабораторной системе
- Задачи
- Глава 3. ПОТЕРИ ЭНЕРГИИ ЛЕГКИХ ИОНОВ И ПОЛУЧЕНИЕ РАСПРЕДЕЛЕНИЙ ПО ГЛУБИНЕ С ПОМОЩЬЮ ОБРАТНОГО РАССЕЯНИЯ
- 3.2. Общая картина потерь энергии и единицы их измерения
- 3.3. Потери энергии легких ионов высоких энергий в твердых телах
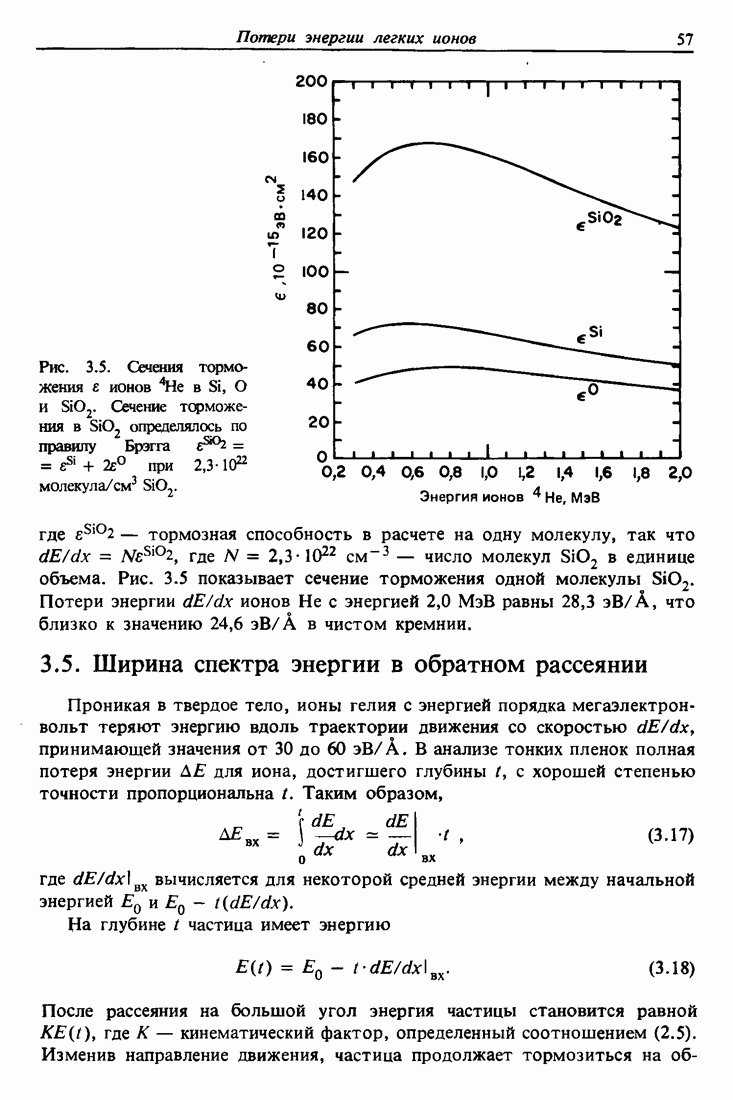
- 3.4. Потери энергии в химических соединениях и правило Брэгга
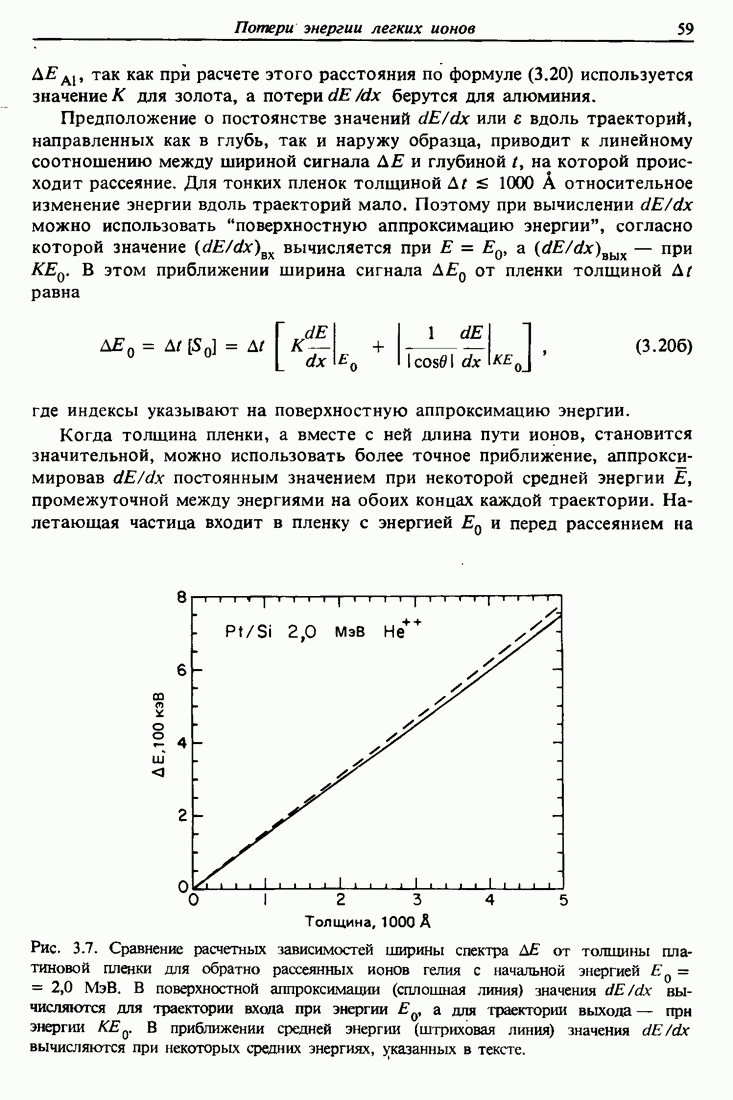
- 3.5. Ширина спектра энергии в обратном рассеянии
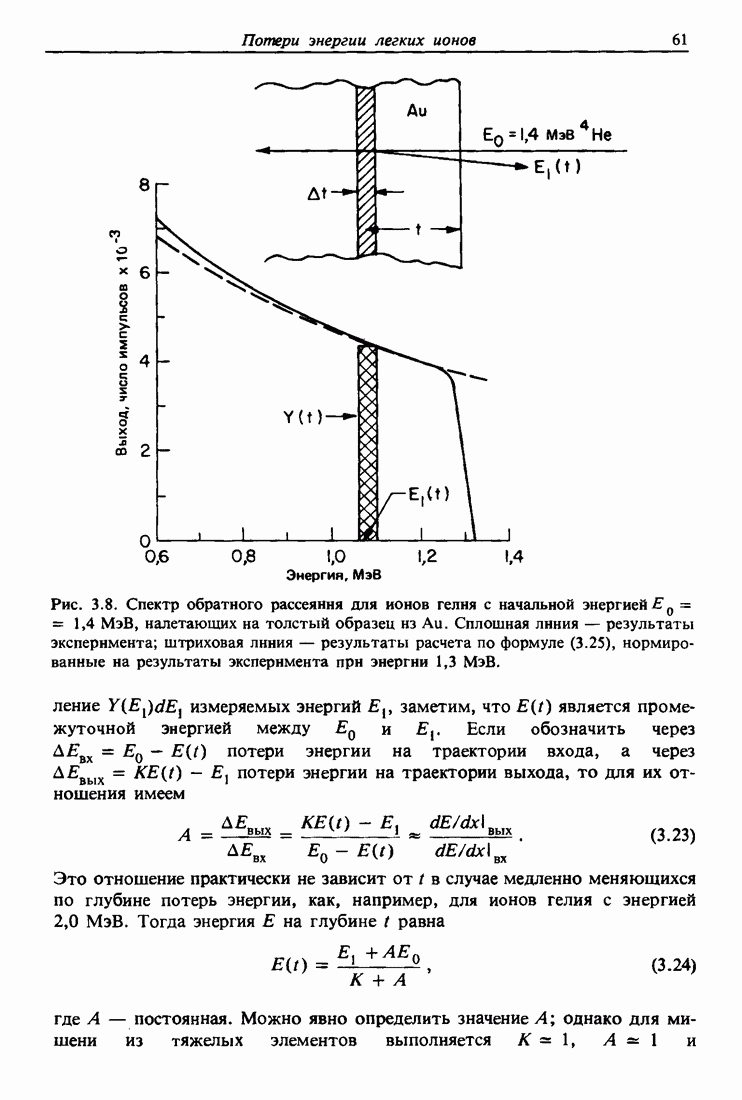
- 3.6. Форма спектра обратного рассеяния
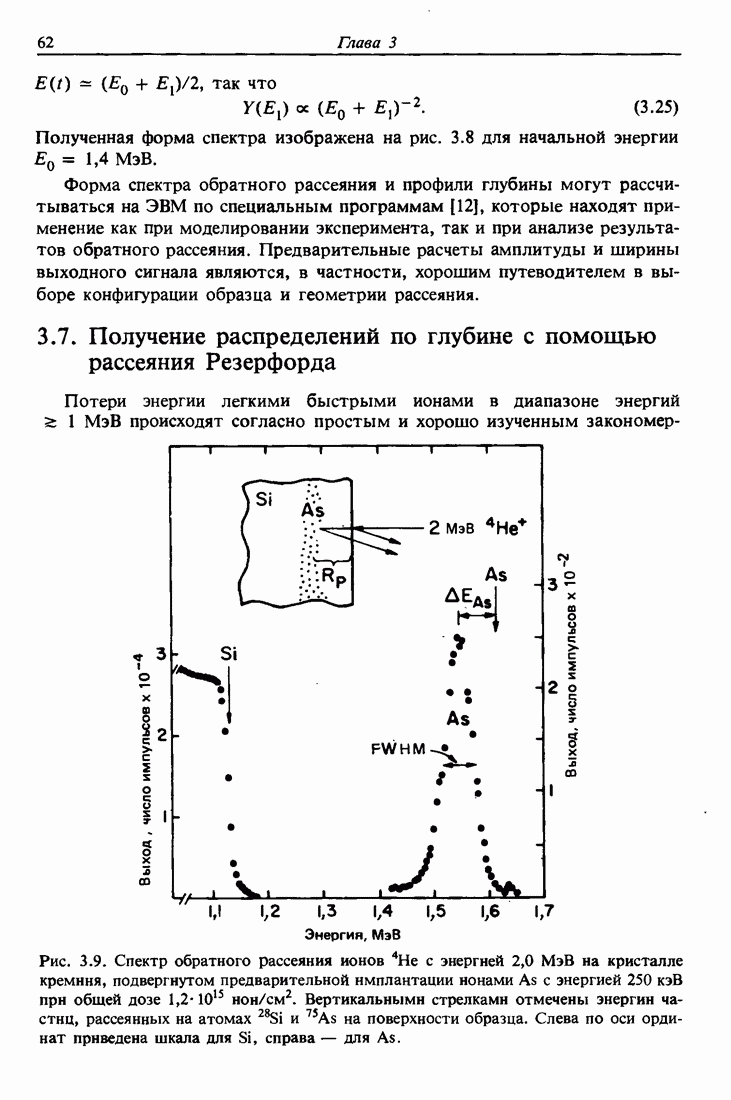
- 3.7. Получение распределений по глубине с помощью рассеяния Резерфорда
- 3.8. Разрешение по глубине и флуктуации потерь энергии
- 3.9. Анализ распределения водорода и дейтерия по глубине
- 3.10. Пробеги ионов Н и Не
- 3.11. Распыление и пределы чувствительности
- 3.12. Сводка соотношений рассеяния
- Задачи
- Глава 4. ПРОФИЛИ РАСПЫЛЕНИЯ И МАСС-СПЕКТРОМЕТРИЯ ВТОРИЧНЫХ ИОНОВ
- 4.2. Распыление ионной бомбардировкой: общие понятия
- 4.3. Ядерные потери энергии
- 4.4. Выход продуктов распыления
- 4.5. Масс-спектрометрия вторичных ионов (SIMS)
- 4.6. Масс-спектрометрия вторичных нейтральных частиц (SNMS)
- 4.7. Избирательное распыление элементов и анализ их распределения по глубине
- 4.8. Уширение внутренней границы раздела и ионное перемешивание
- 4.9. Статистическая модель атома Томаса — Ферми
- Задачи
- Глава 5. КАНАЛИРОВАНИЕ
- 5.2. Каналирование в монокристаллах
- 5.3. Определение месторасположения примесей в кристаллах
- 5.4. Распределение потока каналированных частиц
- 5.5. Поверхностное взаимодействие в двухатомной модели
- 5.6. Поверхностный пик
- 5.7. Затенение подложки Ag (111) эпитаксиальным Au
- 5.8. Нарастание эпитаксиальных слоев
- 5.9. Анализ тонких пленок
- Задачи
- Глава 6. ЭЛЕКТРОН-ЭЛЕКТРОННЫЕ ВЗАИМОДЕЙСТВИЯ И ЧУВСТВИТЕЛЬНОСТЬ К ГЛУБИНЕ В ЭЛЕКТРОННОЙ СПЕКТРОСКОПИИ
- 6.2. Анализ энергии в электронной спектроскопии
- 6.3. Глубина выхода электронов и исследуемый объем вещества
- 6.4. Неупругие электрон-электронные столкновения
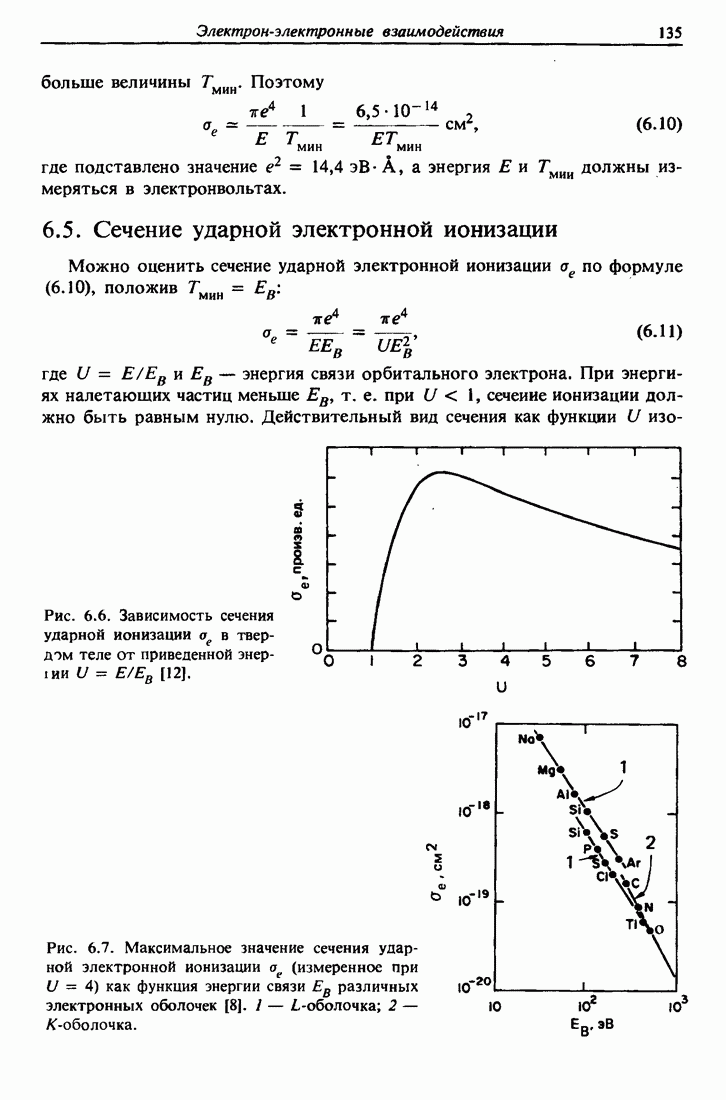
- 6.5. Сечение ударной электронной ионизации
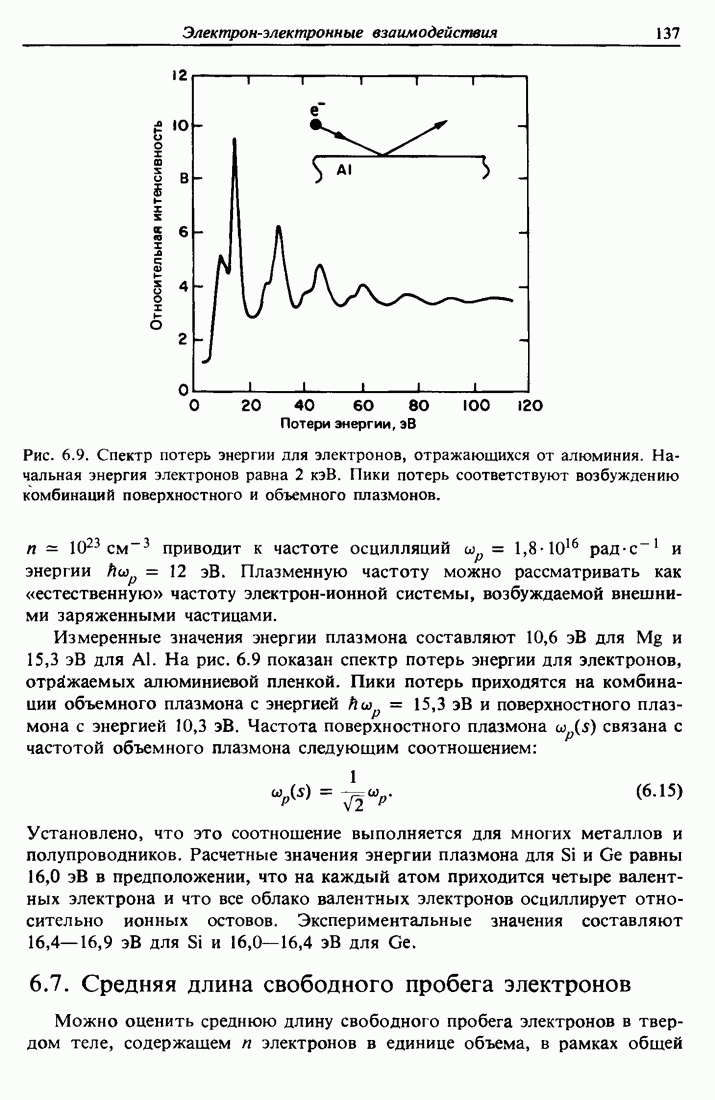
- 6.6. Плазмоны
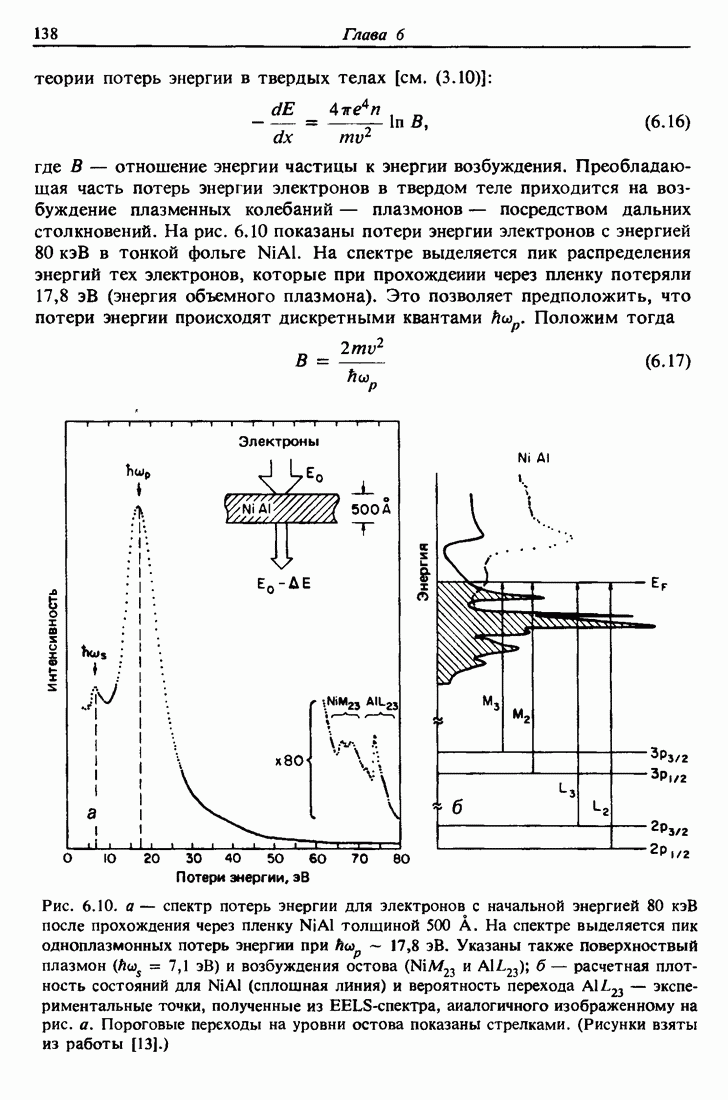
- 6.7. Средняя длина свободного пробега электронов
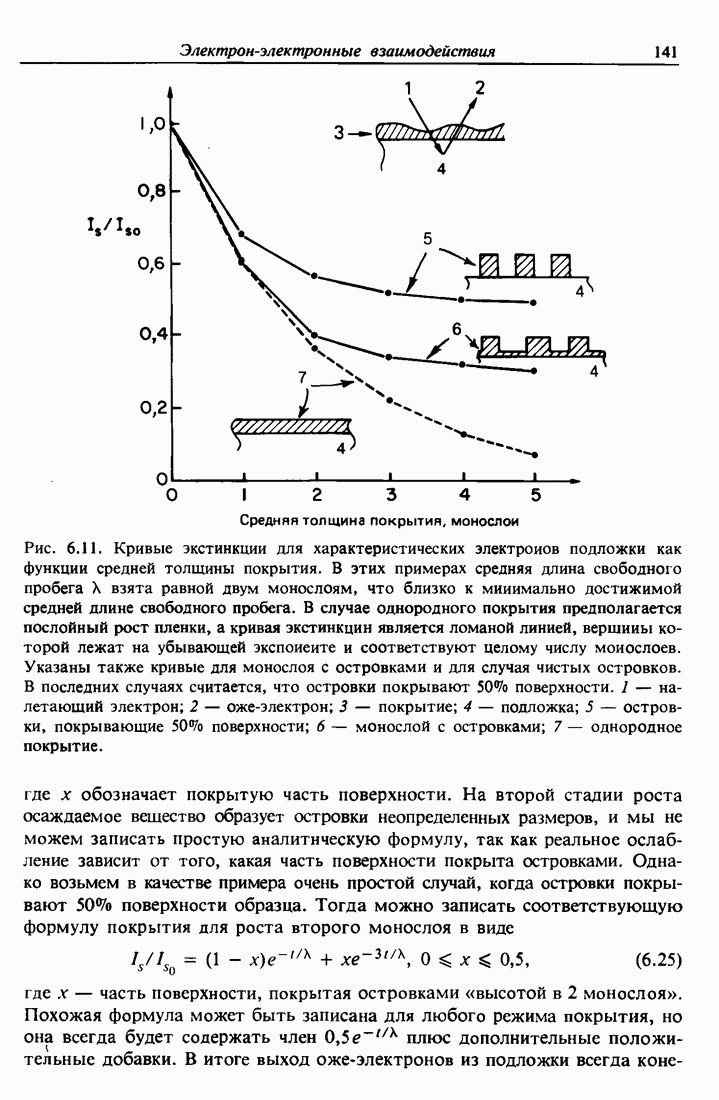
- 6.8. Влияние морфологии тонких пленок на уменьшение выхода электронов
- 6.9. Пробеги электронов в твердых телах
- 6.10. Спектроскопия электронных потерь энергии (EELS)
- 6.11. Тормозное излучение
- Задачи
- Глава 7. СТРУКТУРА ПОВЕРХНОСТИ
- 7.2. Параметры дифракции
- 7.3. Тепловые колебания и фактор Дебая — Валлера
- 7.4. Дифракция электронов низких энергий (LEED)
- 7.5. Дифракция рентгеновских лучей при скользящем падении
- 7.6. Просвечивающая электронная микроскопия
- Задачи
- Глава 8. ПОГЛОЩЕНИЕ ФОТОНОВ В ТВЕРДЫХ ТЕЛАХ И EXAFS
- 8.2. Уравнение Шредингера
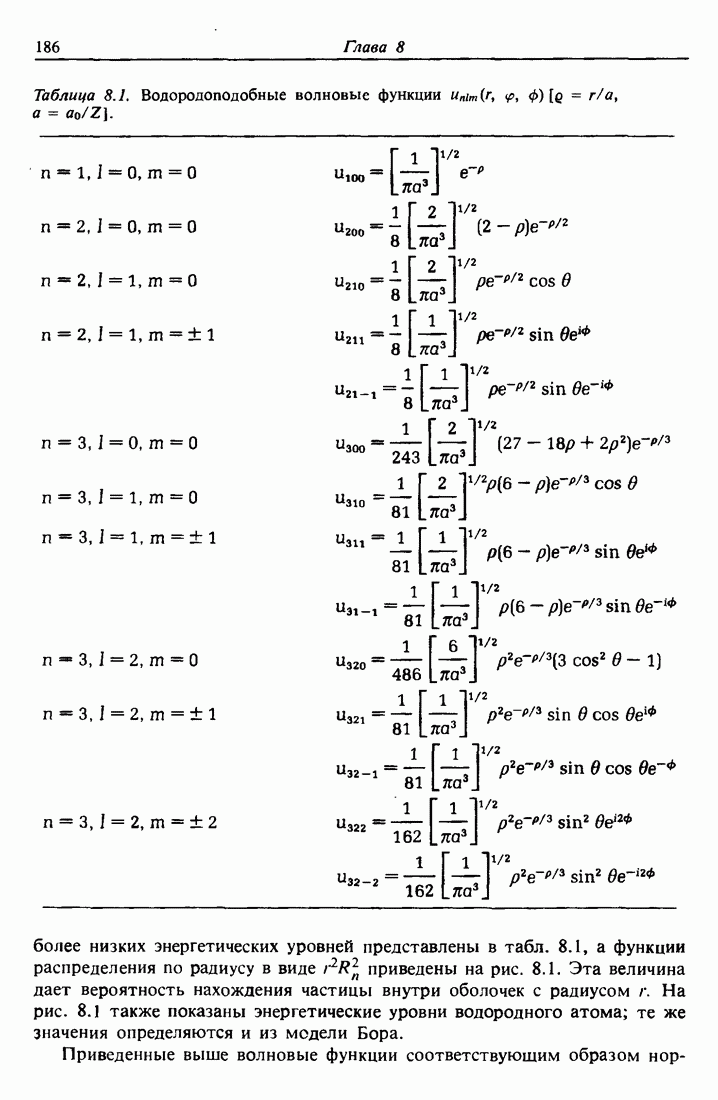
- 8.3. Волновые функции
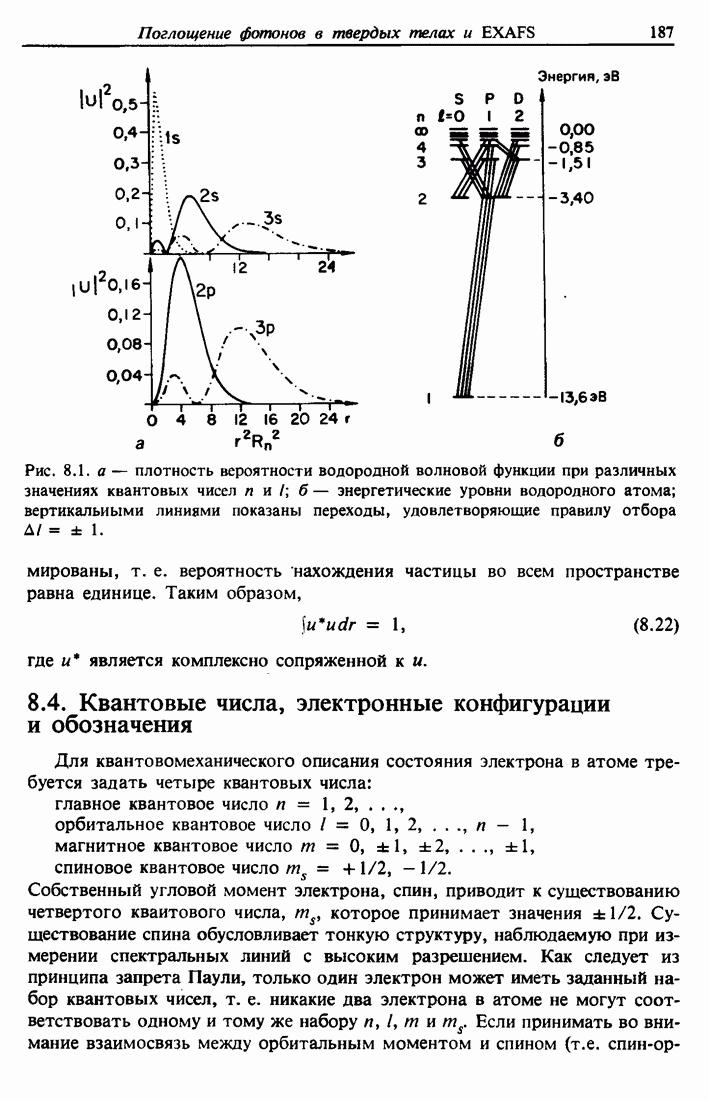
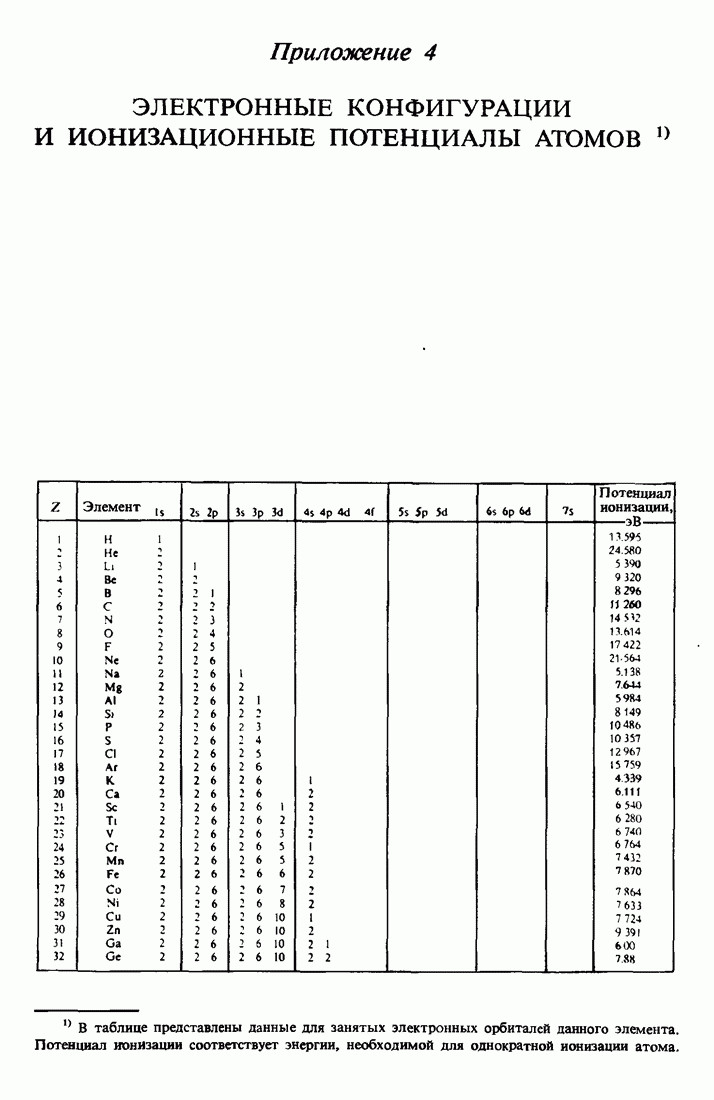
- 8.4. Квантовые числа, электронные конфигурации и обозначения
- 8.5. Вероятность переходов
- 8.6. Фотоэлектрический эффект в приближении прямоугольной ямы
- 8.7. Вероятность фотоэлектронных переходов для водородоподобного атома
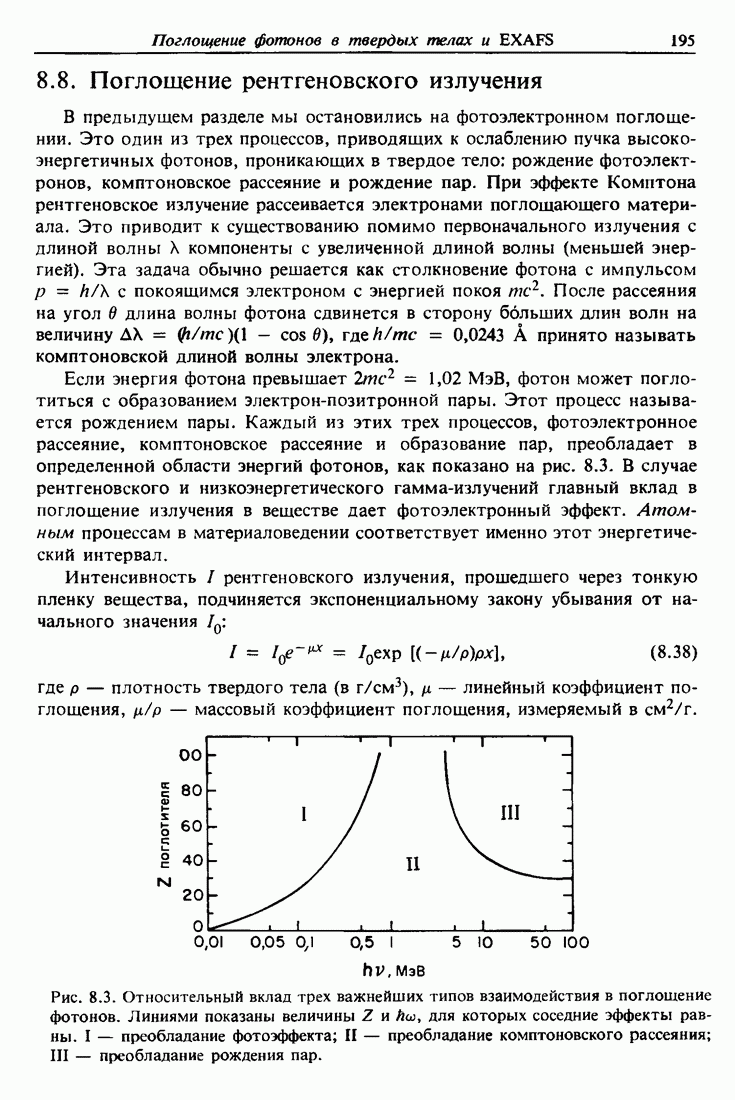
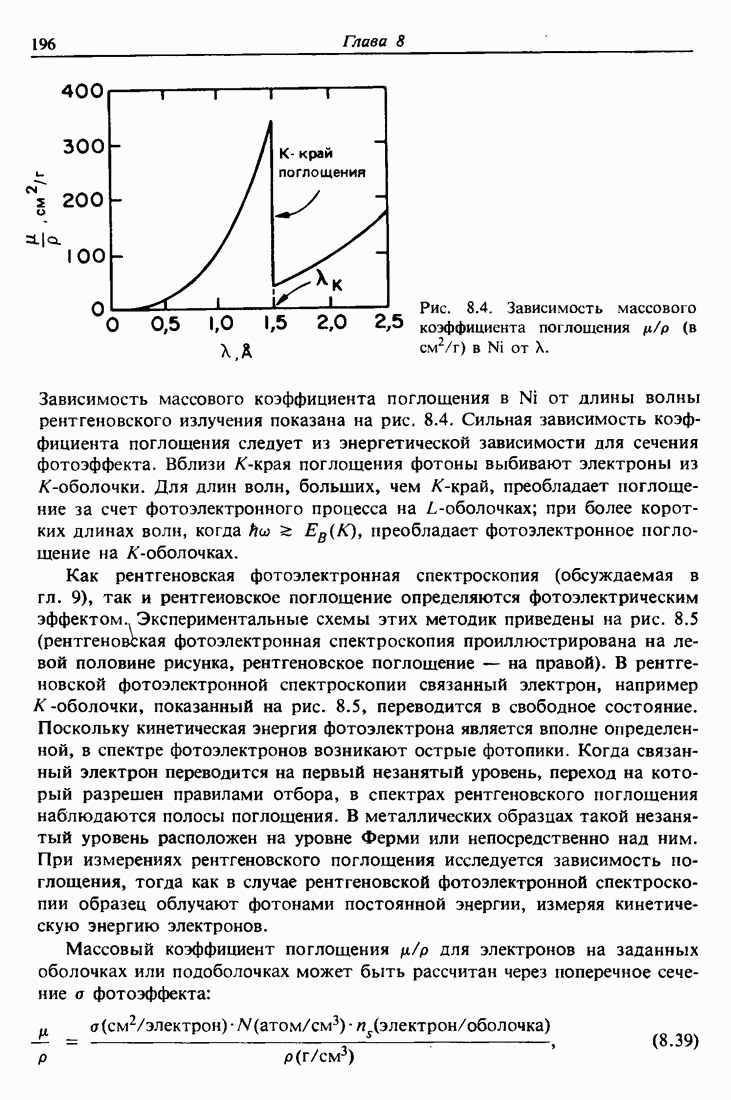
- 8.8. Поглощение рентгеновского излучения
- 8.9. Растянутая тонкая структура рентгеновского поглощения (EXAFS)
- 8.10. Нестационарная теория возмущений
- Задачи
- Глава 9. РЕНТГЕНОВСКАЯ ФОТОЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ (XPS)
- 9.2. Экспериментальная техника
- 9.3. Кинетическая энергия фотоэлектронов
- 9.4. Энергетический спектр фотоэлектронов
- 9.5. Энергия связи и влияние конечных состояний
- 9.6. Сдвиги энергии связи; химические сдвиги
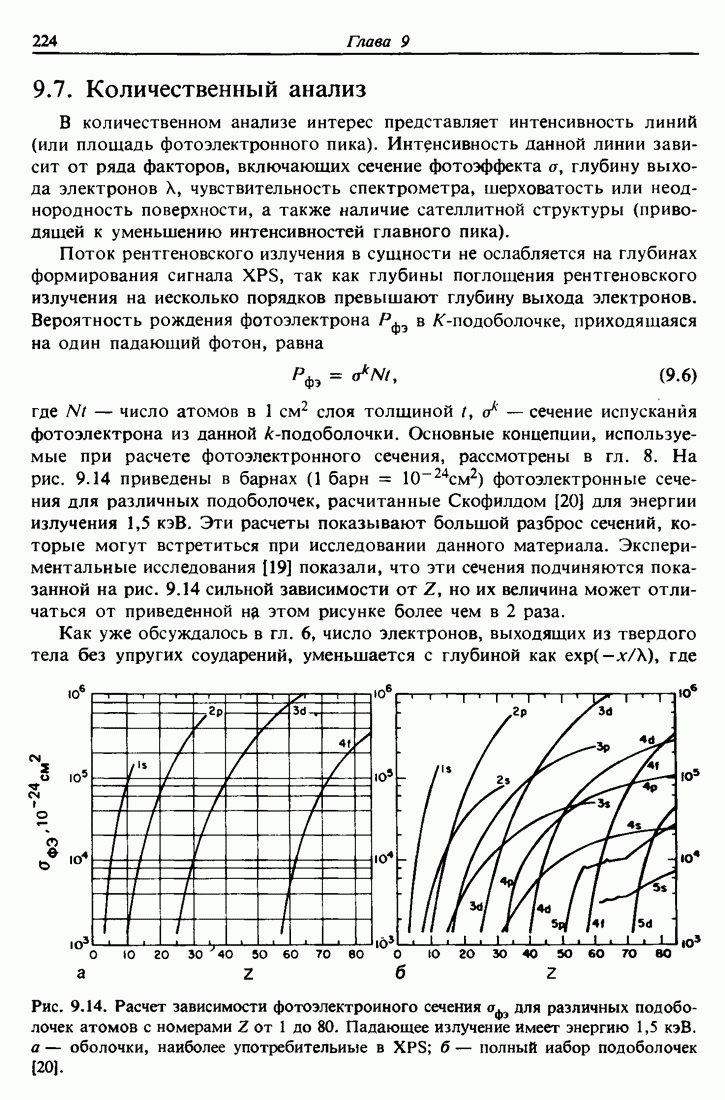
- 9.7. Количественный анализ
- Задачи
- Глава 10. ИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ЭЛЕКТРОННЫЙ МИКРОАНАЛИЗ
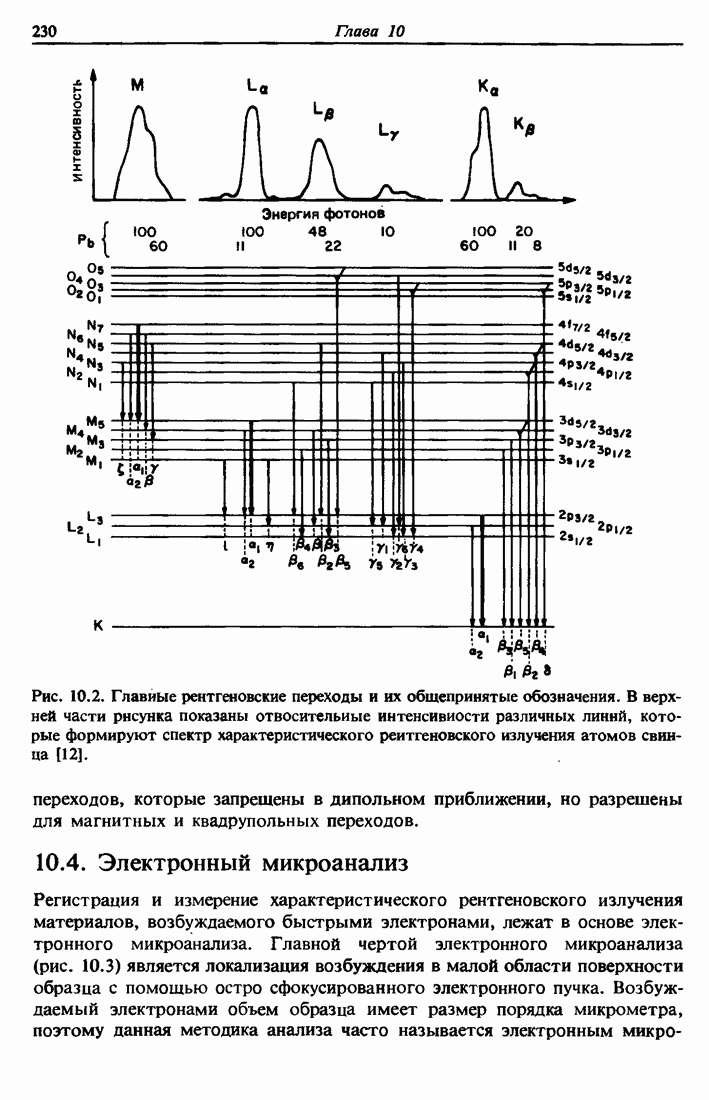
- 10.2. Обозначения в рентгеновской спектроскопии
- 10.3. Дипольные правила отбора
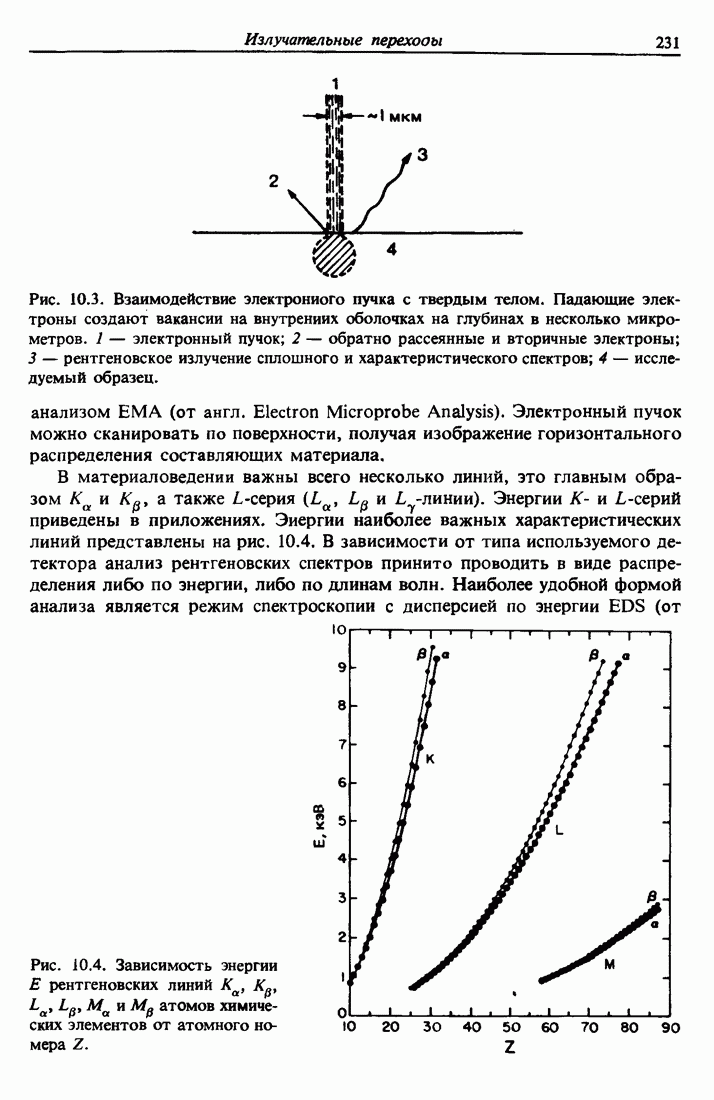
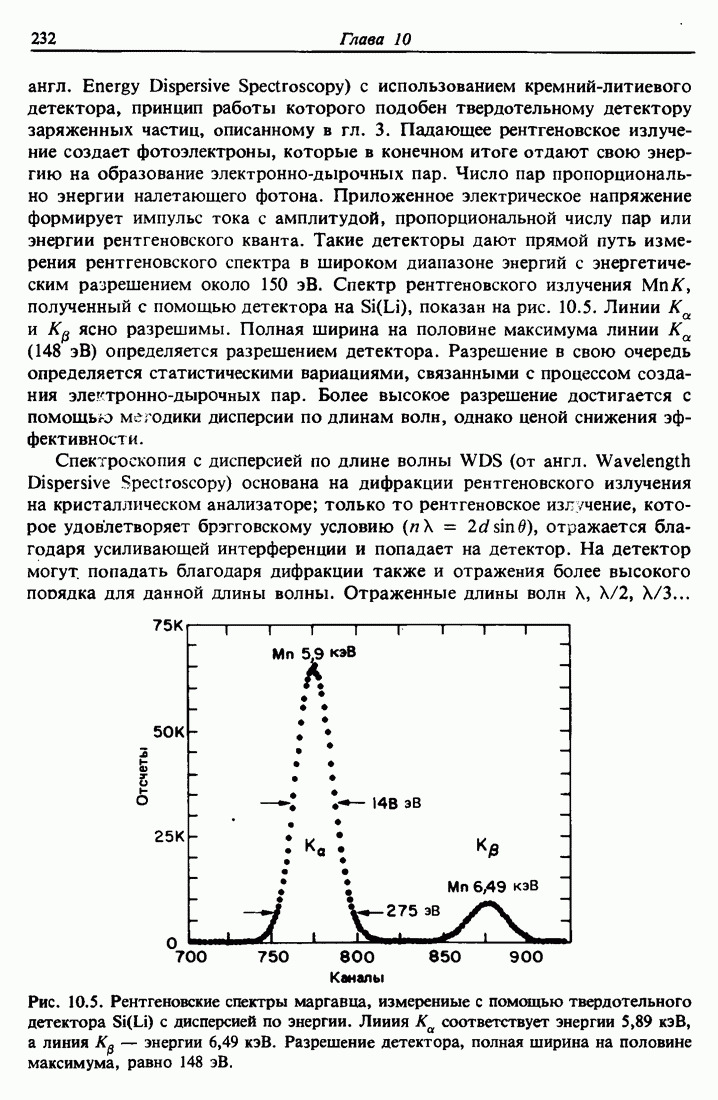
- 10.4. Электронный микроанализ
- 10.5. Скорости переходов при спонтанном излучении
- 10.6. Скорость перехода для излучения Ка в никеле
- 10.7. Электронный микроанализ: количественные результаты
- 10.8. Испускание рентгеновского излучения, возбуждаемого протонами и ионами гелия (PIXE)
- 10.9. Расчет вероятности излучательных переходов
- 10.10. Расчет отношения интенсивностей линий
- Задачи
- Глава 11. НЕИЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ И ОЖЕ-ЭЛЕКТРОННАЯ СПЕКТРОСКОПИЯ
- 11.2. Оже-переходы
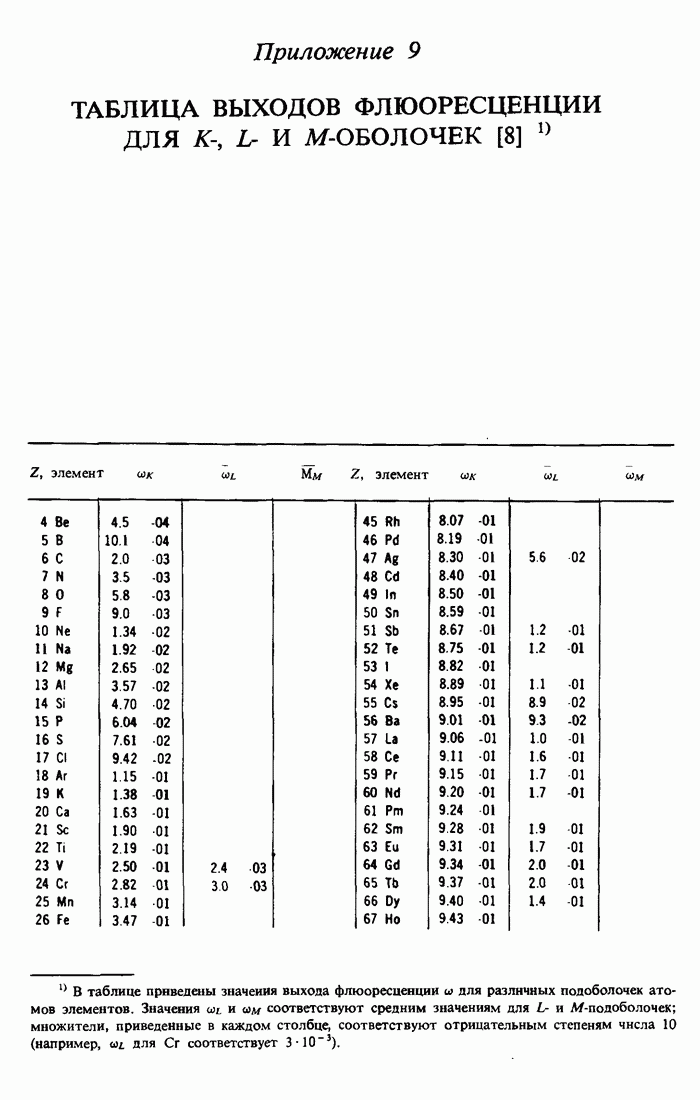
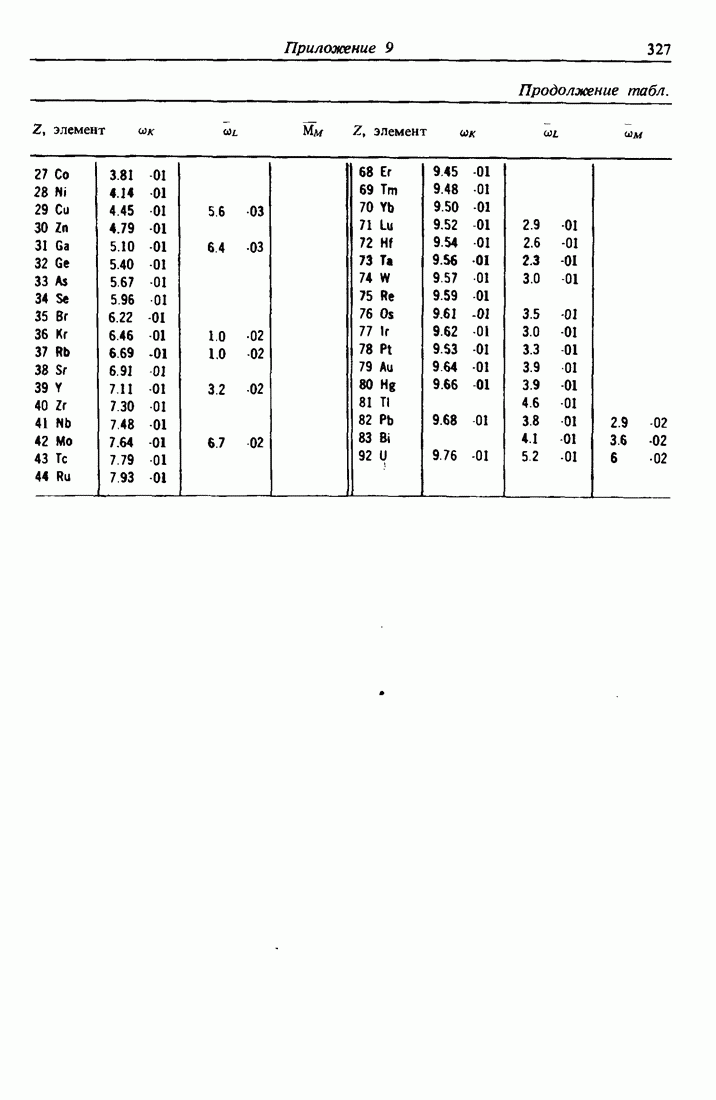
- 11.3. Выход оже-электронов и флюоресценция
- 11.4. Ширина атомных уровней и времена жизни
- 11.5. Оже-электронная спектроскопия
- 11.6. Количественный анализ
- 11.7. Получение профилей концентрации с помощью оже-спектроскопии
- Задачи
- Глава 12. АКТИВАЦИОННЫЙ И МГНОВЕННОРАДИАЦИОННЫЙ ЯДЕРНЫЕ МЕТОДЫ АНАЛИЗА
- 12.2. Значения Q и кинетические энергии
- 12.3. Радиоактивный распад
- 12.4. Закон радиоактивного распада
- 12.5. Получение радионуклидов
- 12.6. Активационный анализ
- 12.7. Мгновеннорадиационный анализ
- Задачи
- ПРИЛОЖЕНИЕ 1.
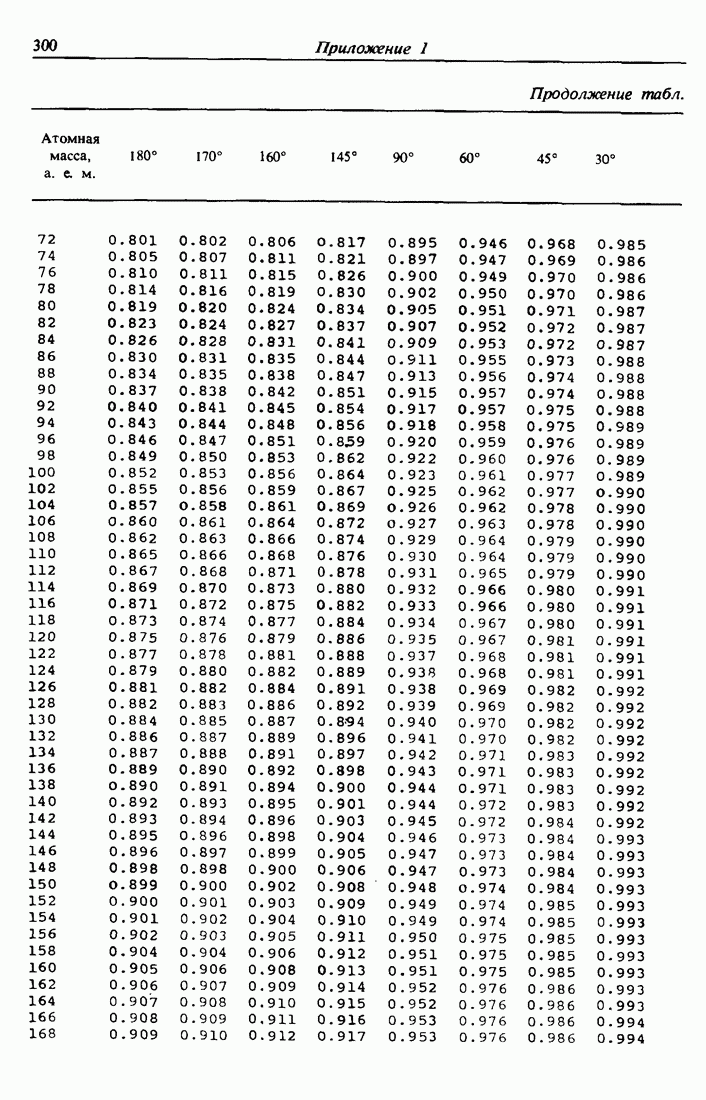
- ПРИЛОЖЕНИЕ 2.
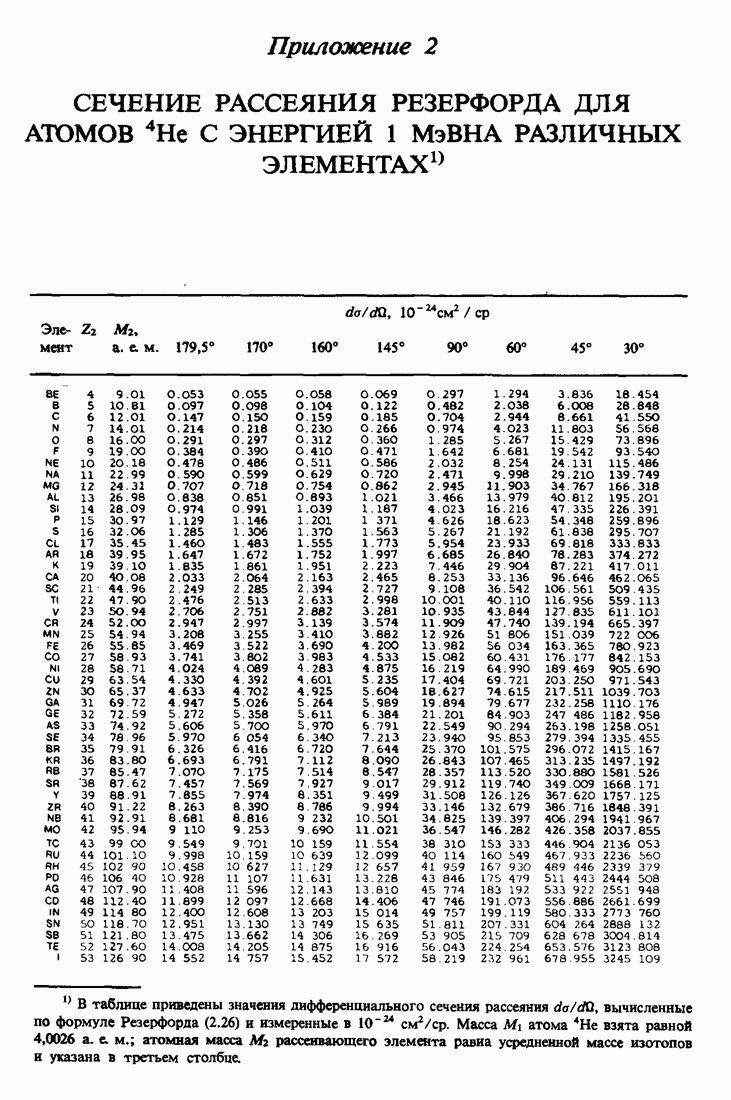
- ПРИЛОЖЕНИЕ 3.
- ПРИЛОЖЕНИЕ 4.
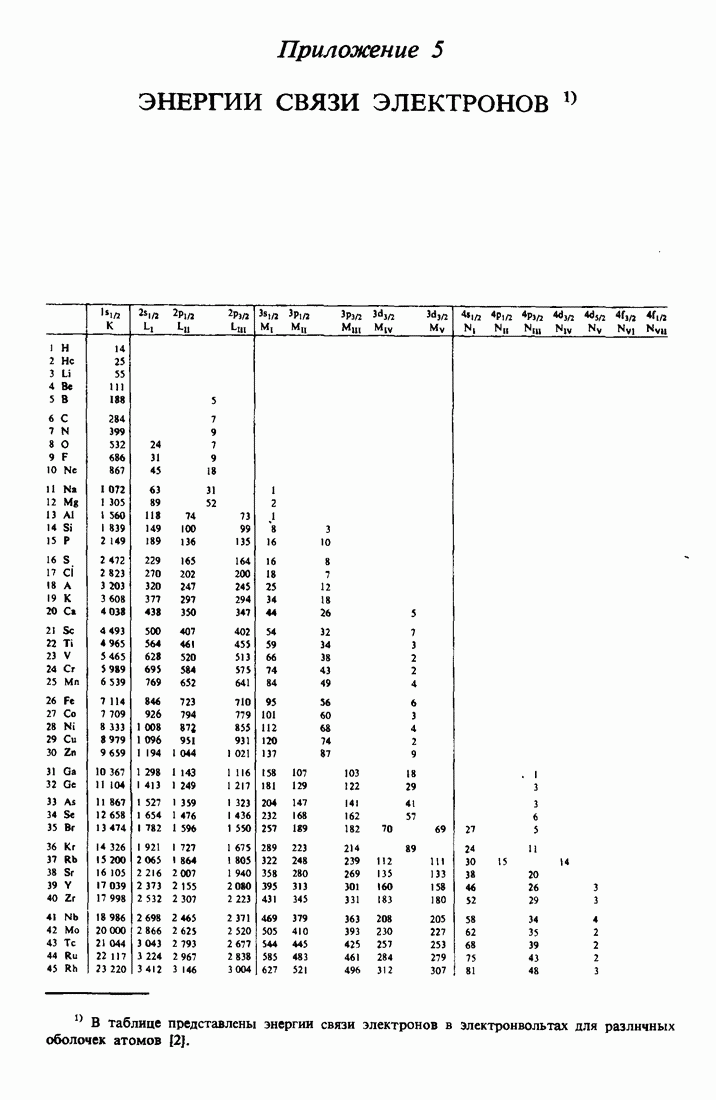
- ПРИЛОЖЕНИЕ 5. ЭНЕРГИИ СВЯЗИ ЭЛЕКТРОНОВ
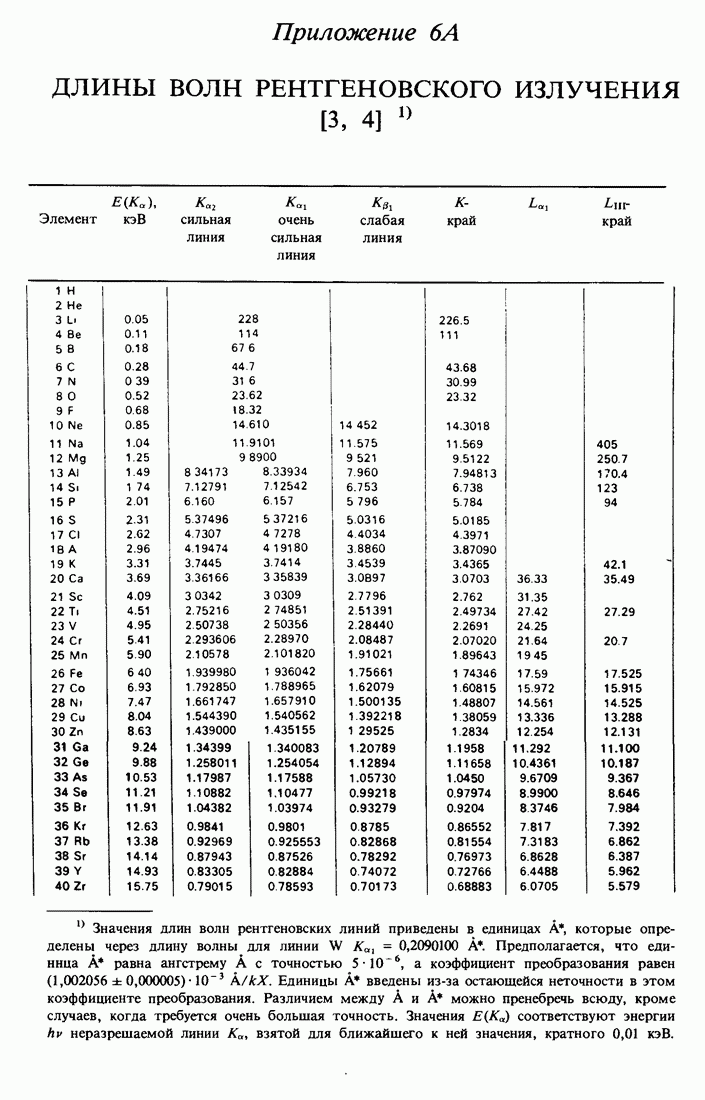
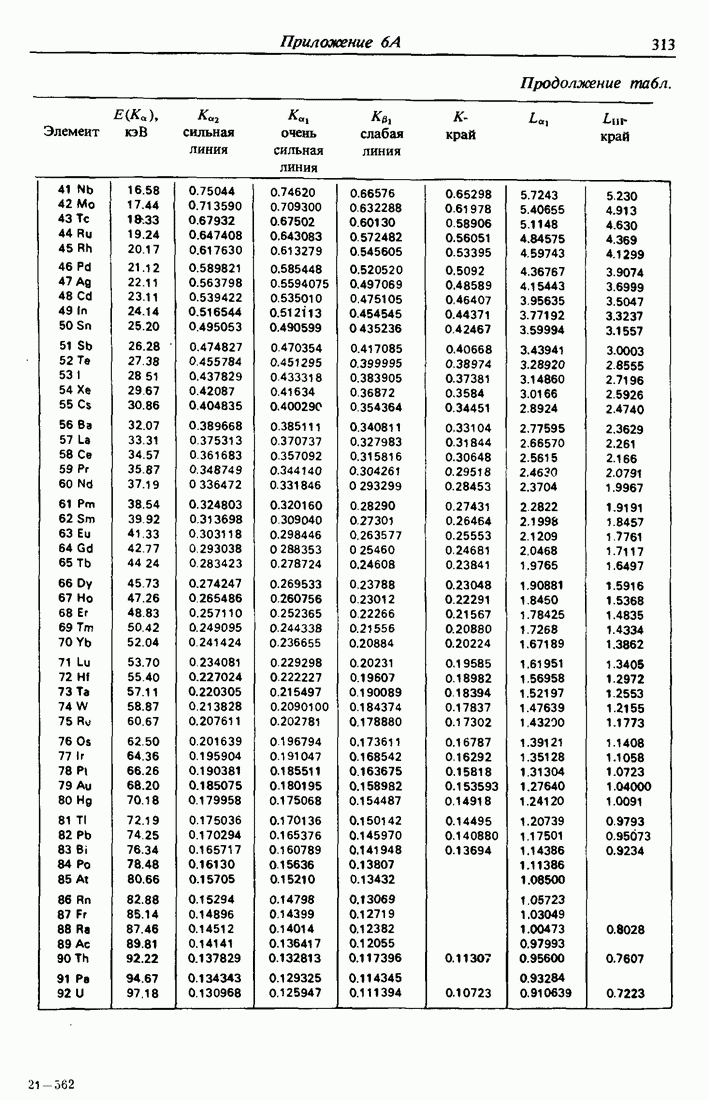
- ПРИЛОЖЕНИЕ 6А. ВОЛН РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ [3,4]
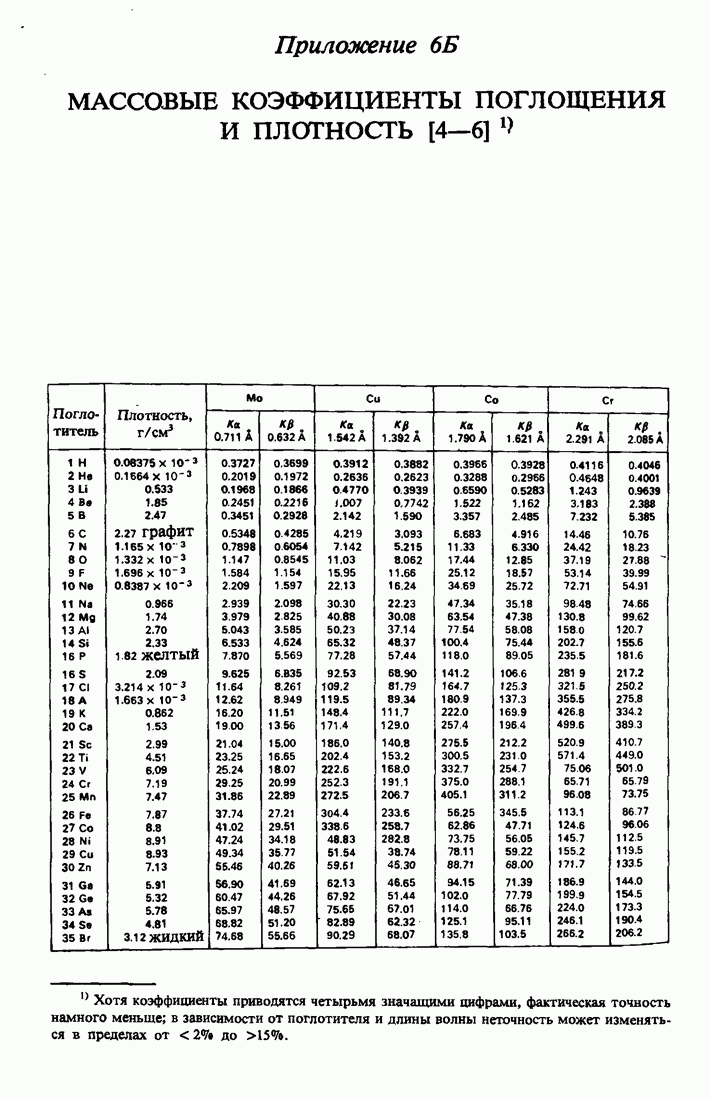
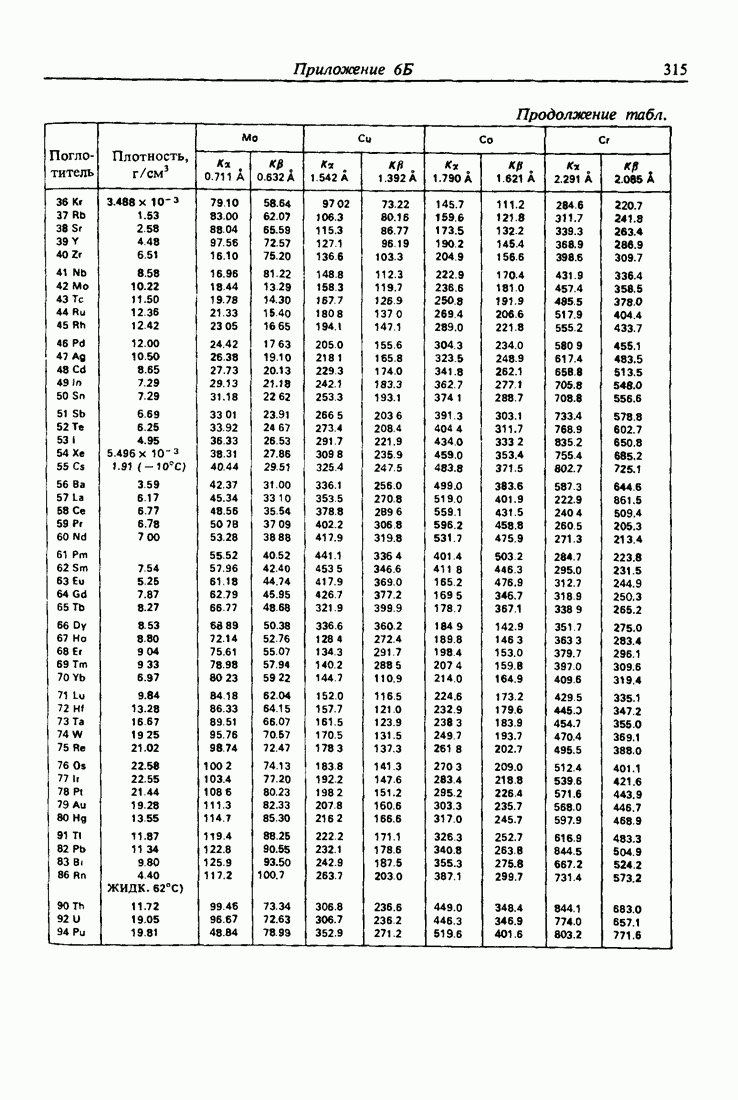
- ПРИЛОЖЕНИЕ 6б. МАССОВЫЕ КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И ПЛОТНОСТЬ [4—6]
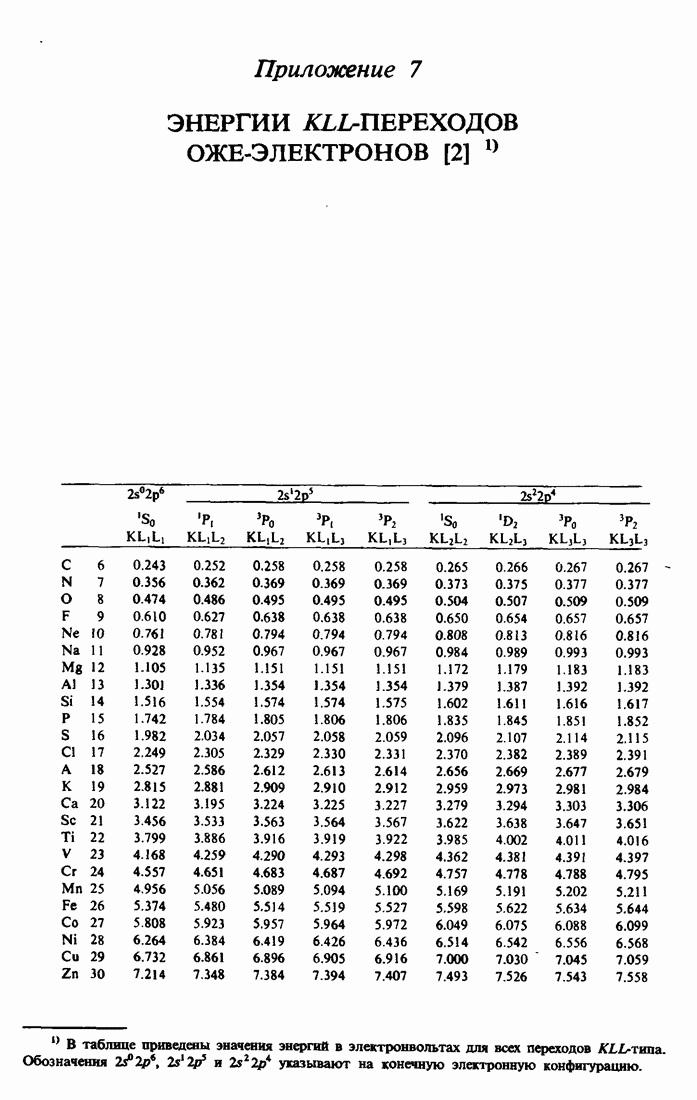
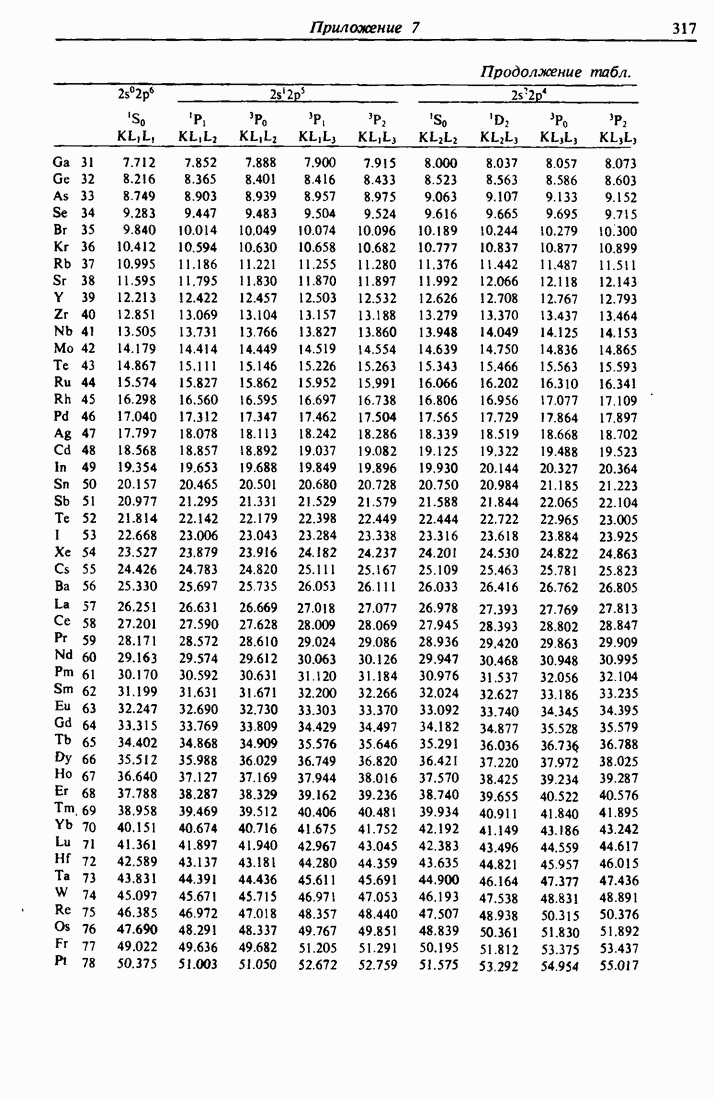
- ПРИЛОЖЕНИЕ 7. ЭНЕРГИИ KLL-ПЕРЕХОДОВ ОЖЕ-ЭЛЕКТРОНОВ [2]
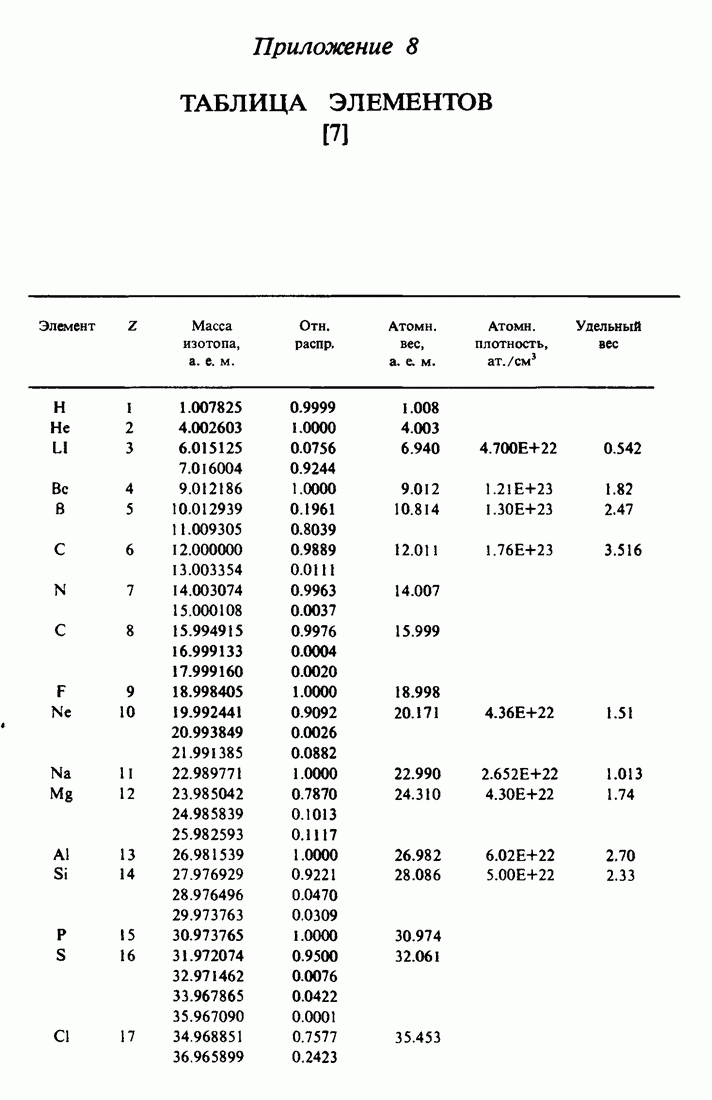
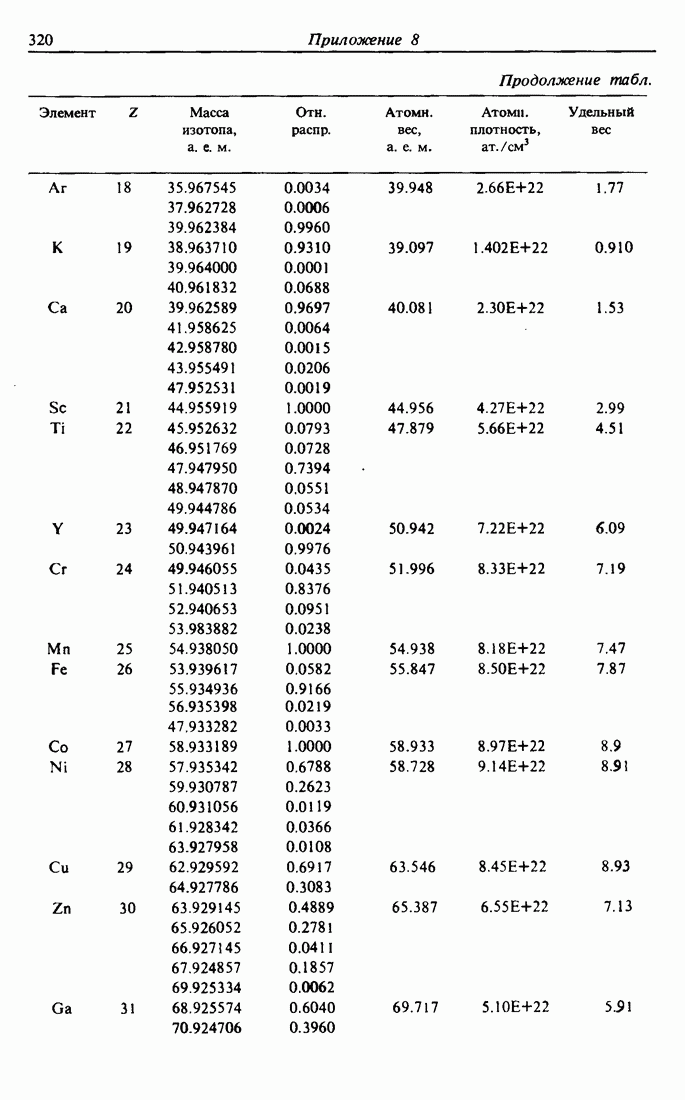
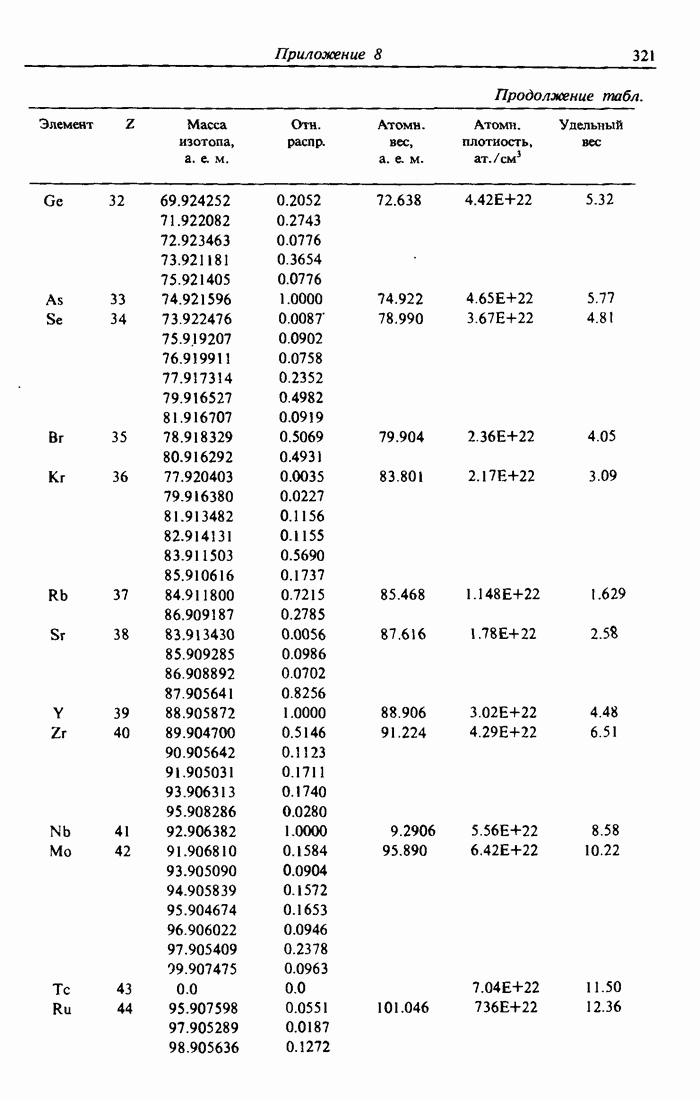
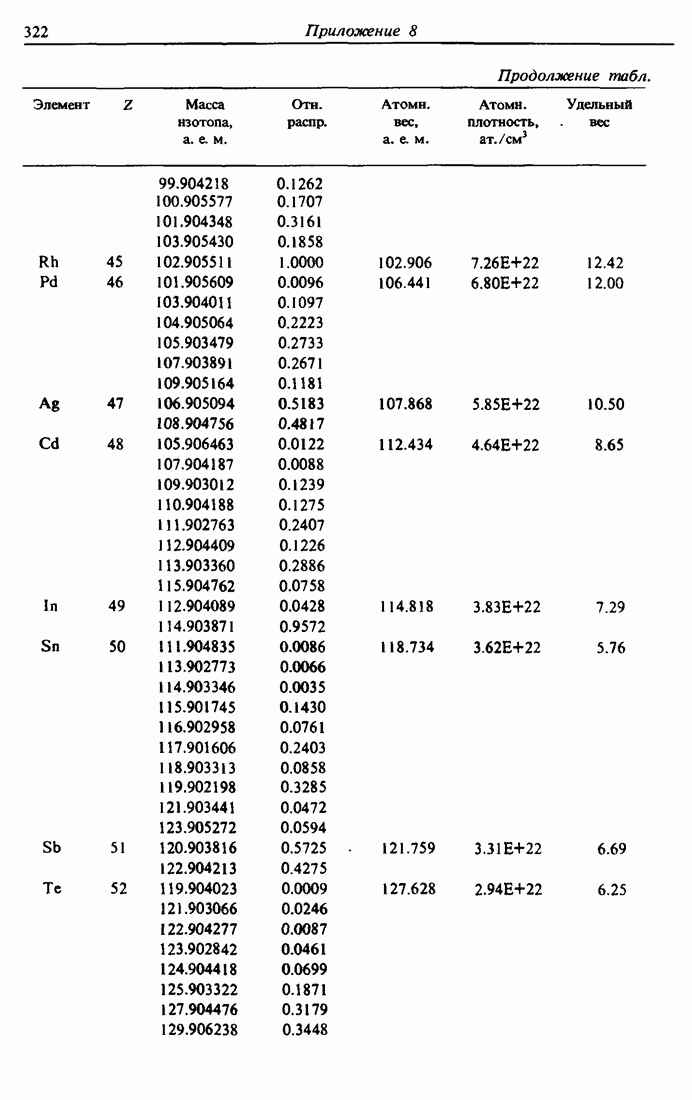
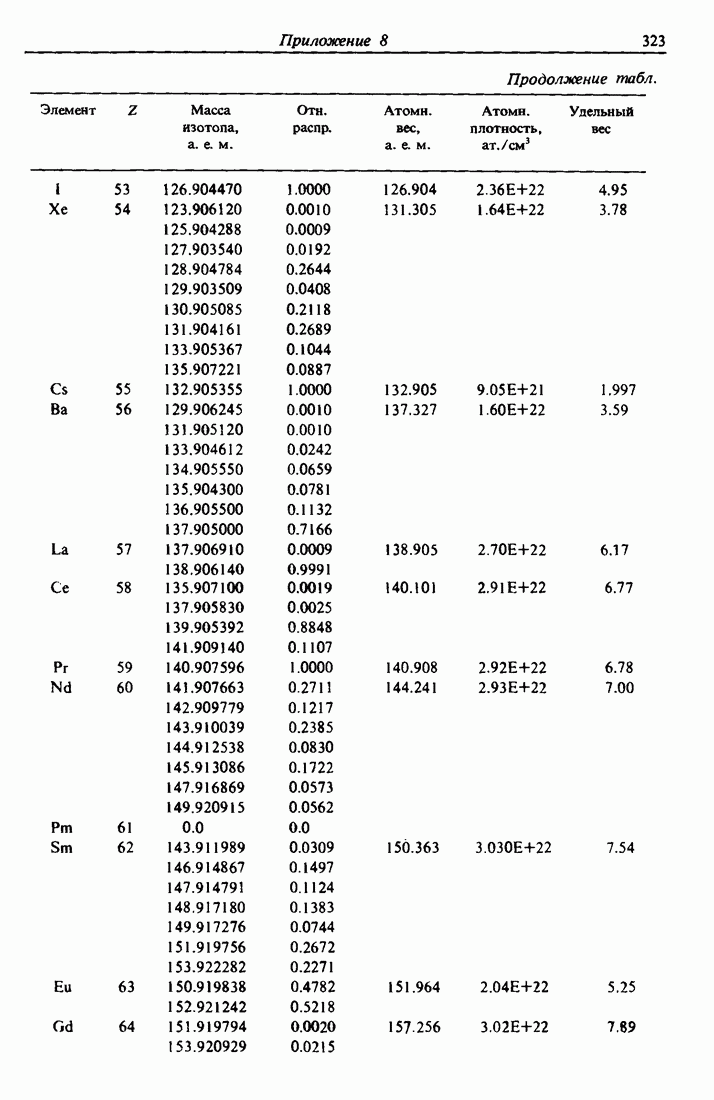
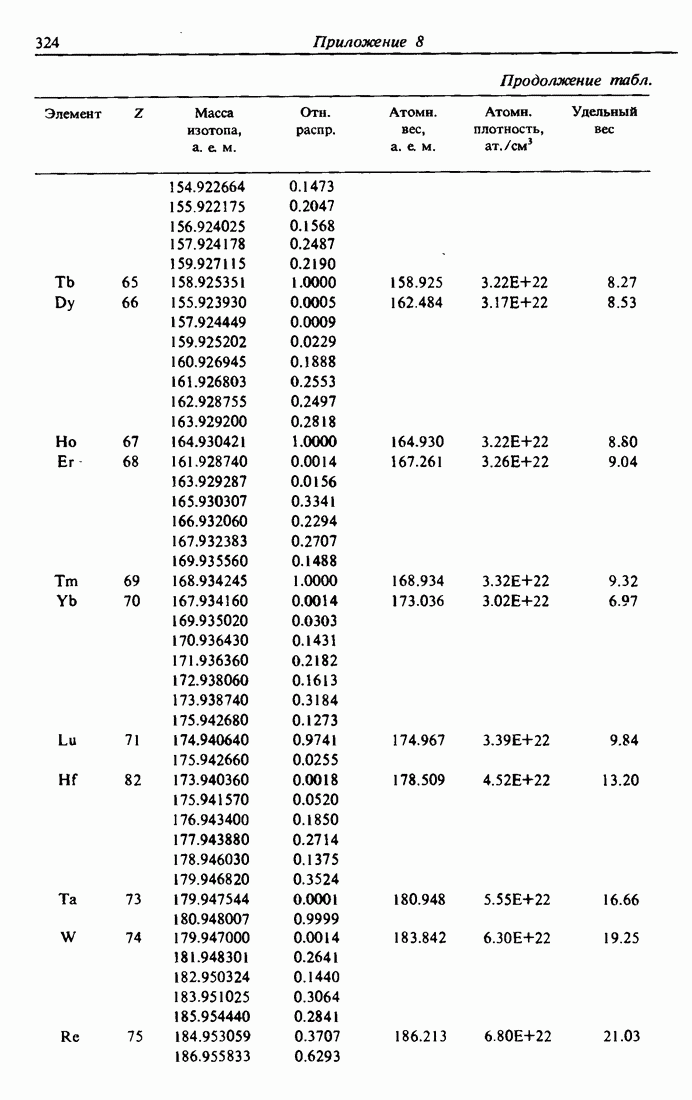
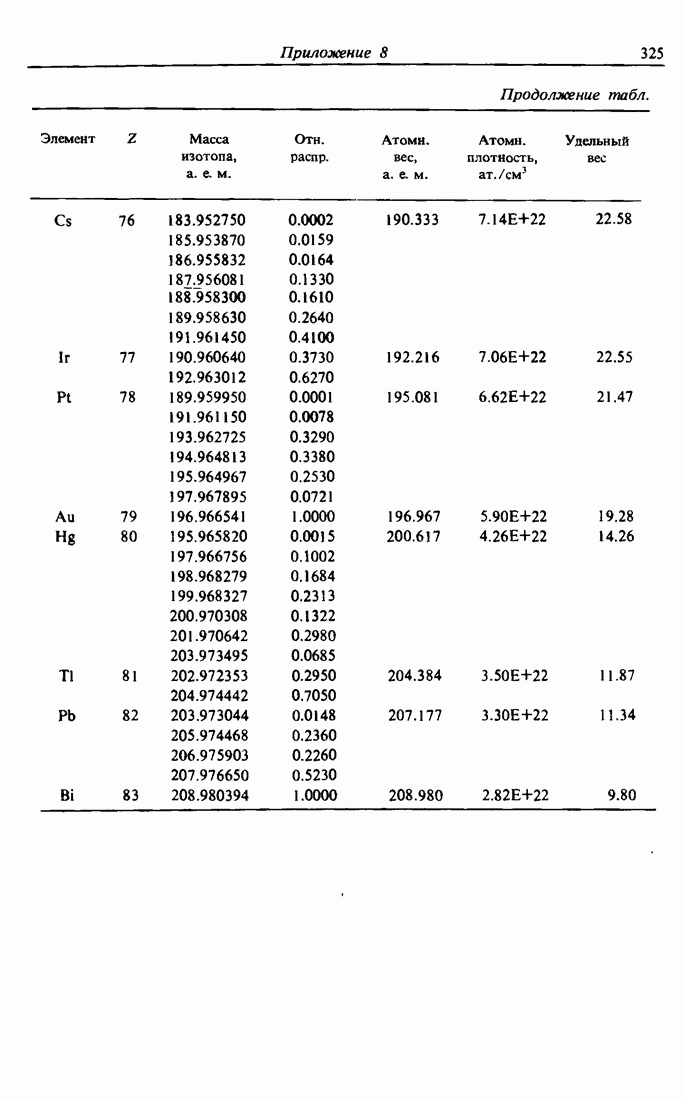
- ПРИЛОЖЕНИЕ 8. ТАБЛИЦА ЭЛЕМЕНТОВ [7]
- ПРИЛОЖЕНИЕ 9.
- ПРИЛОЖЕНИЕ 10. ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ, ПОЛЕЗНЫЕ КОМБИНАЦИИ И СООТНОШЕНИЯ ЕДИНИЦ