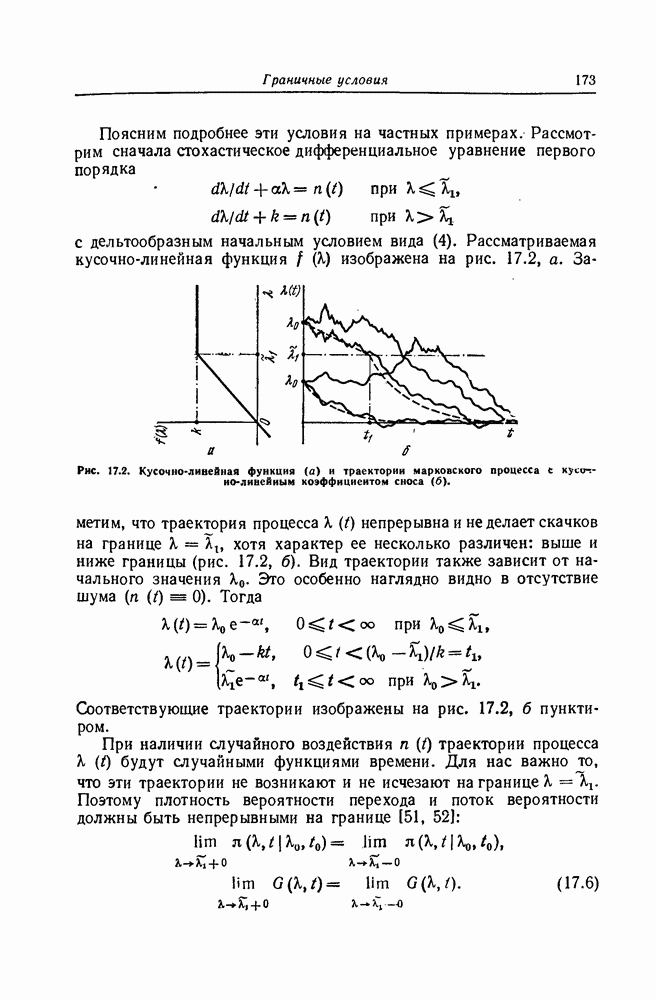
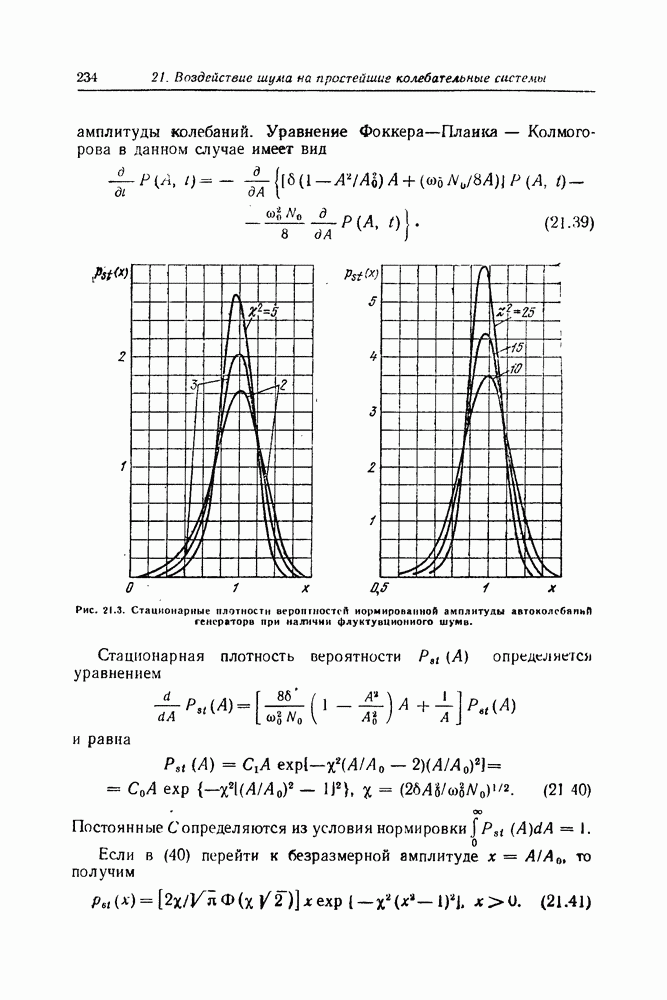
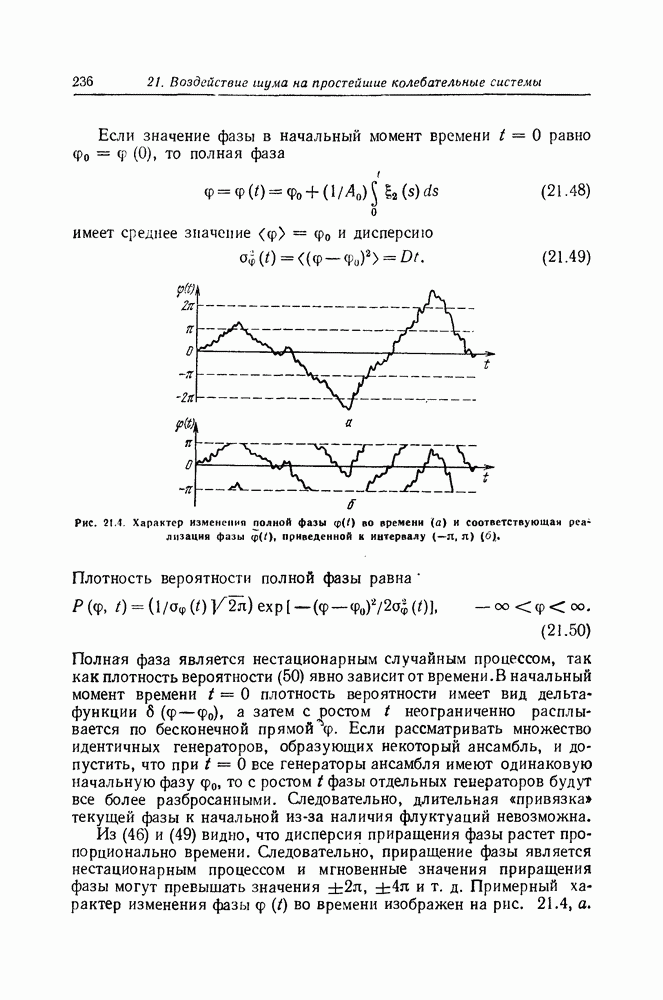
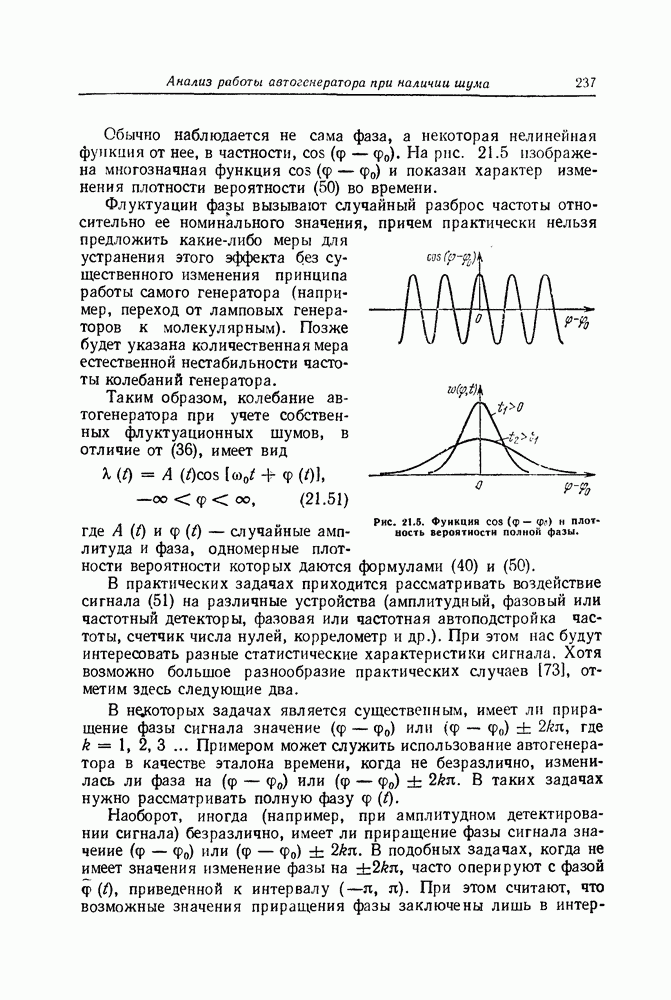
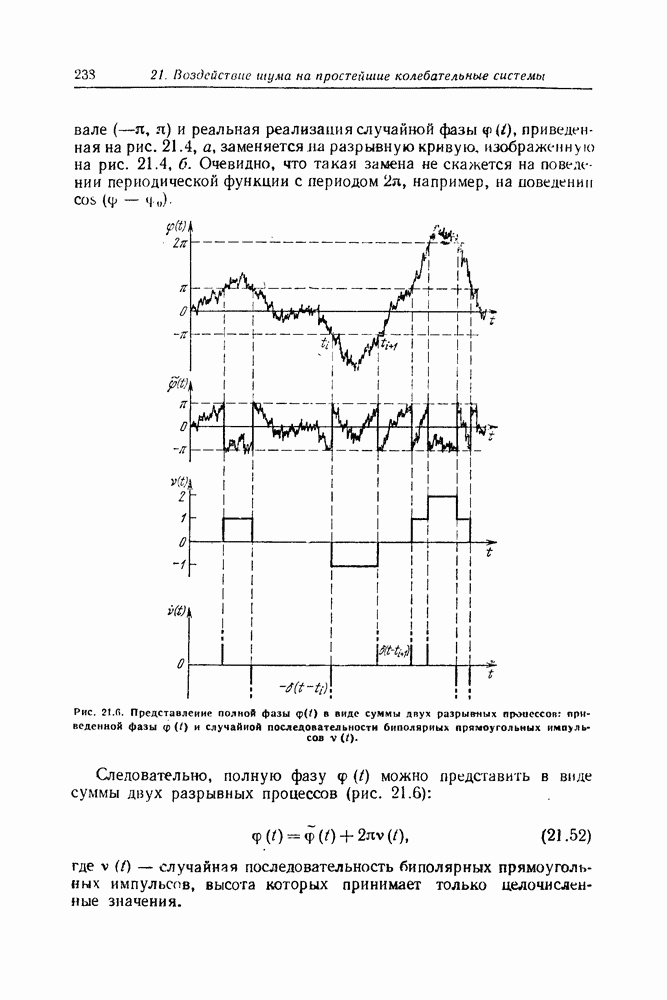
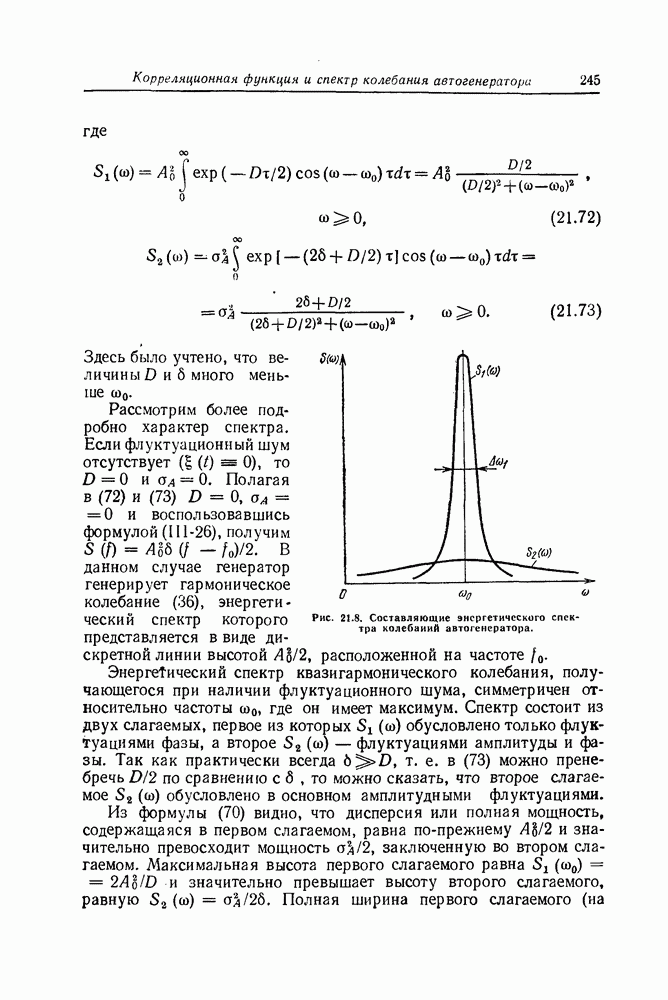
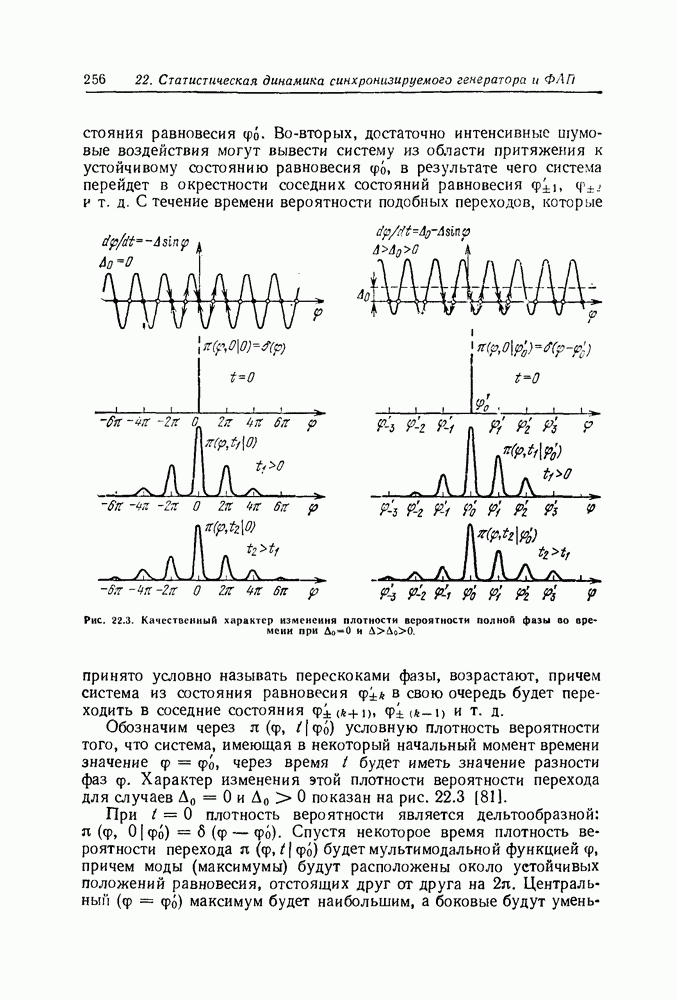
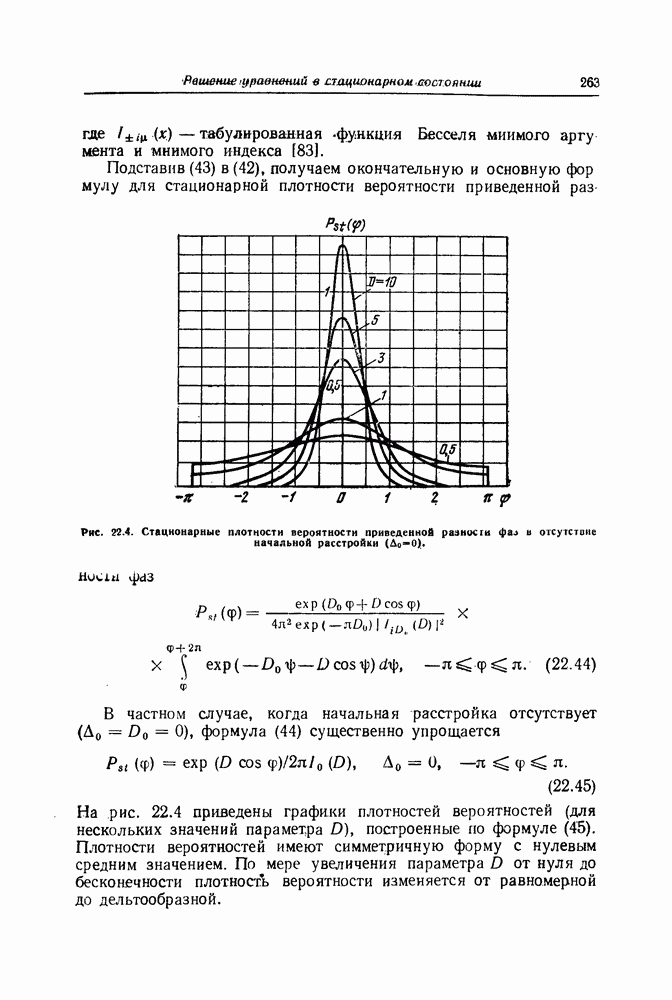
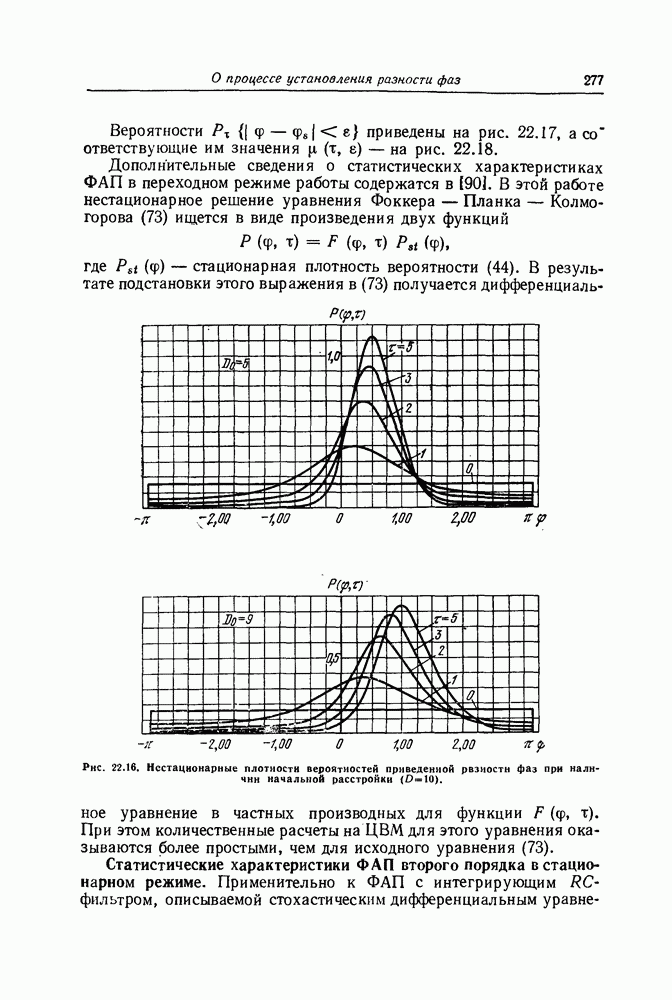
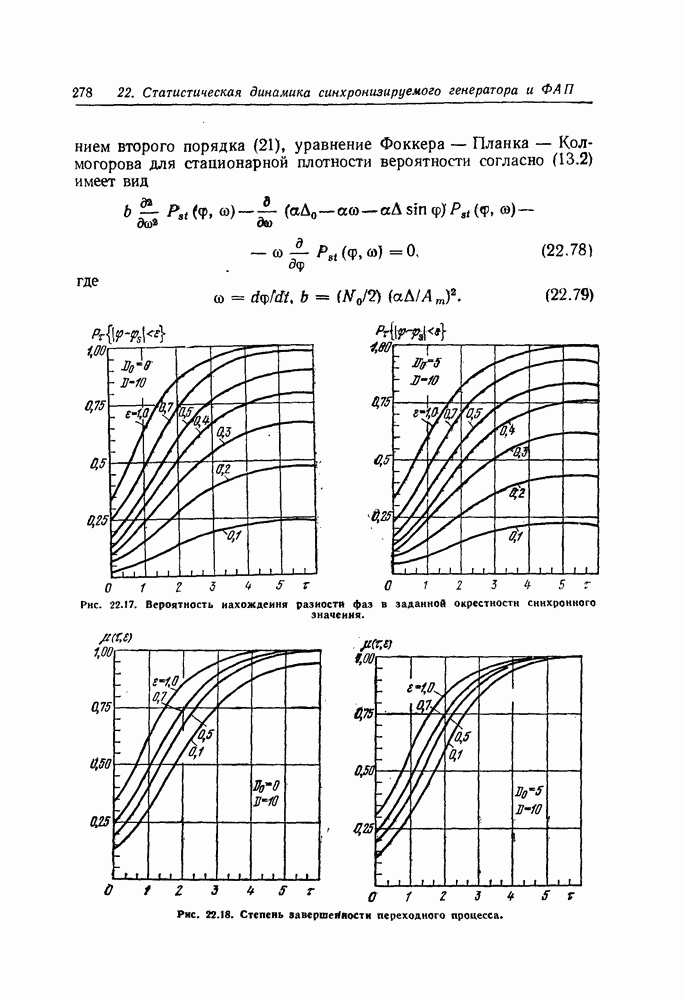
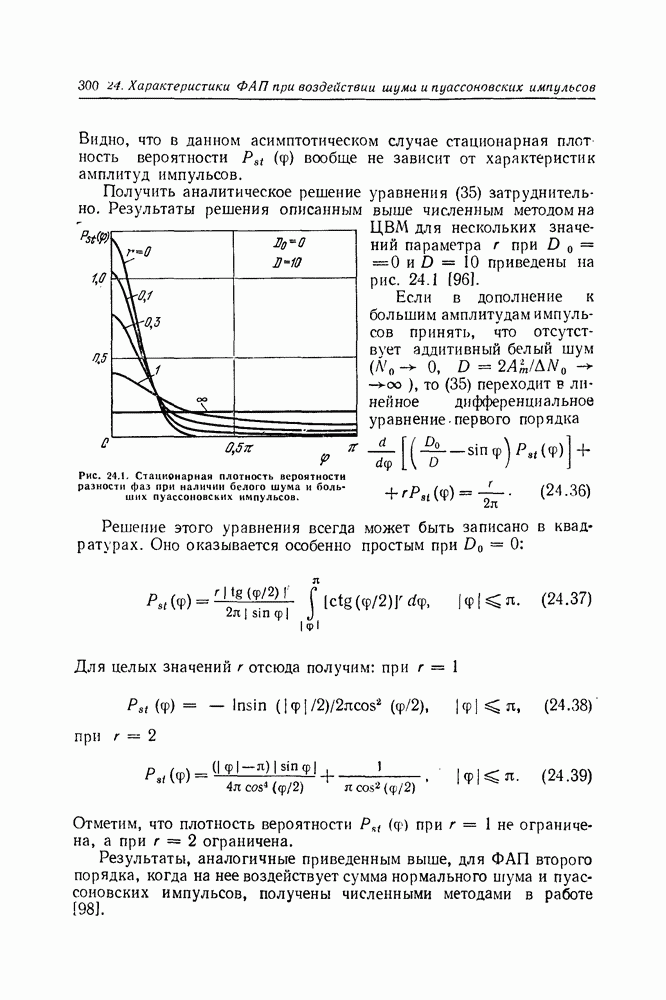
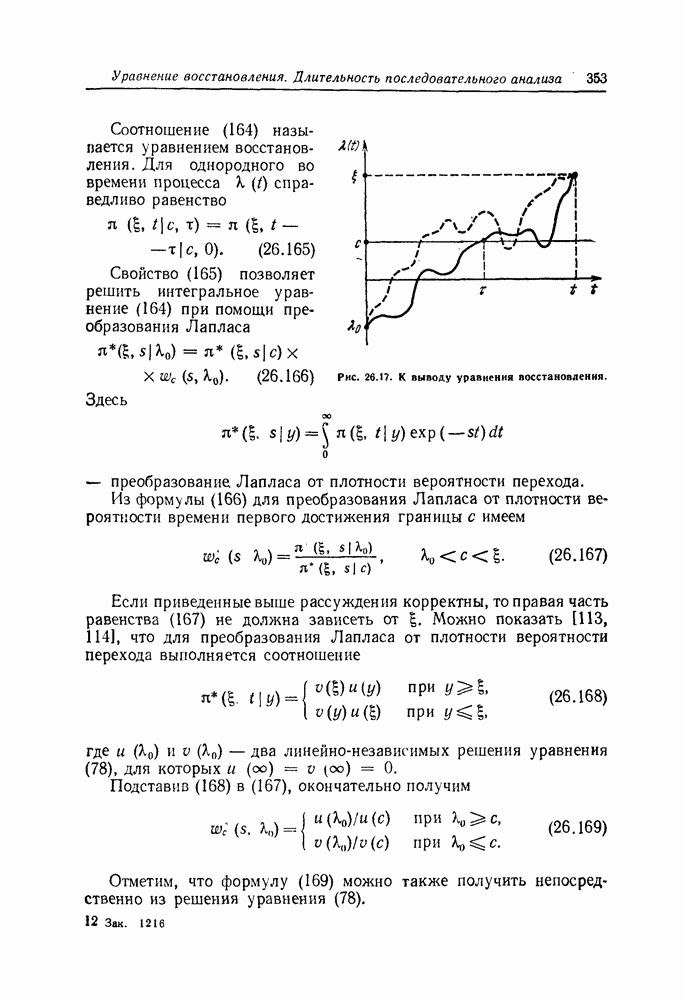
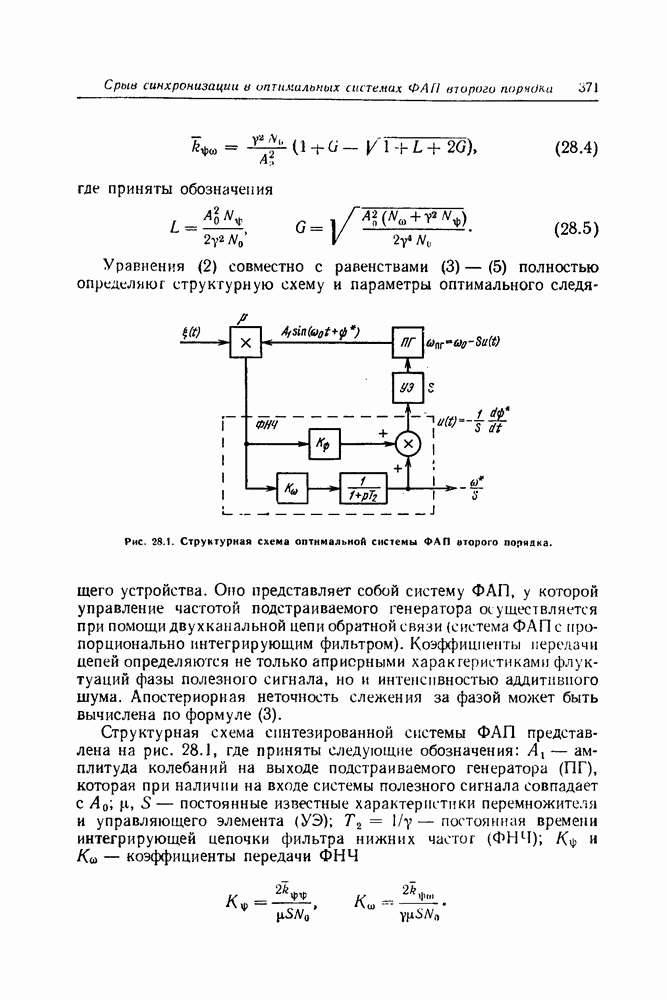
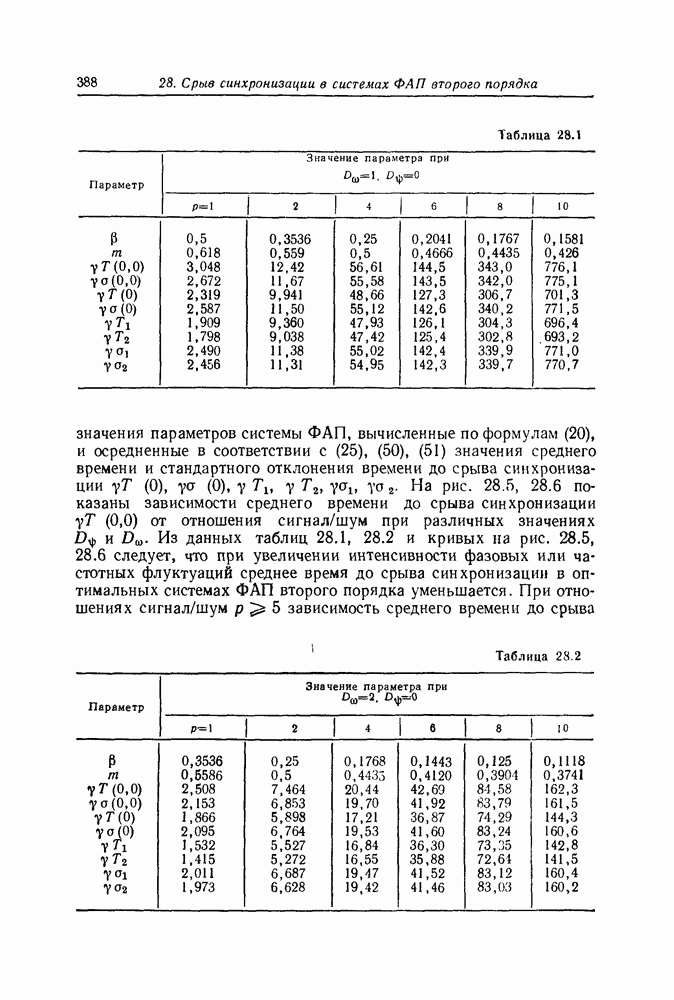
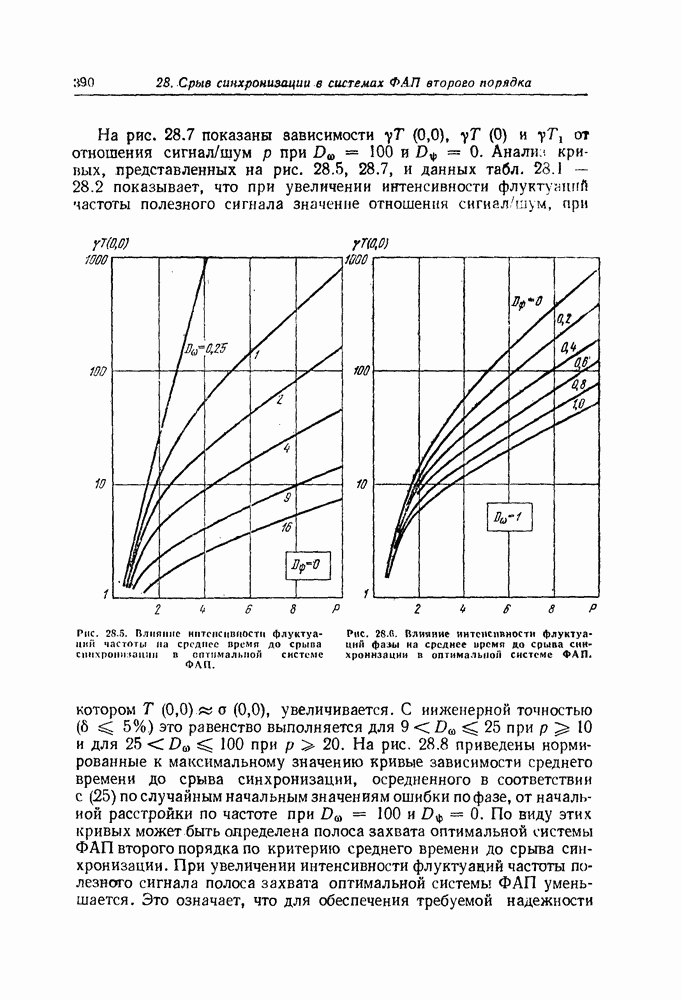
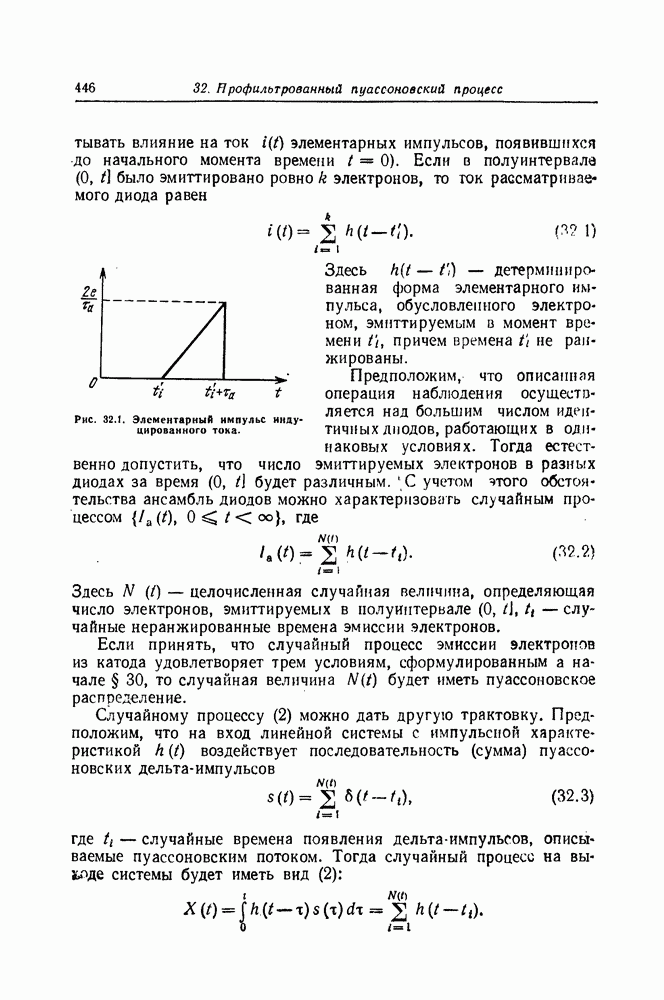
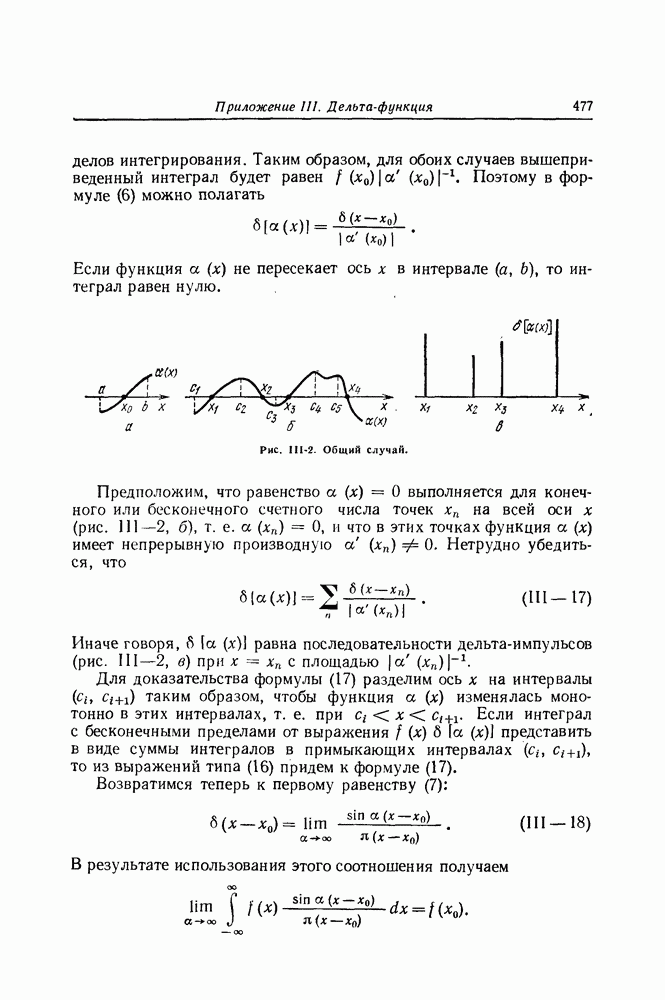
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
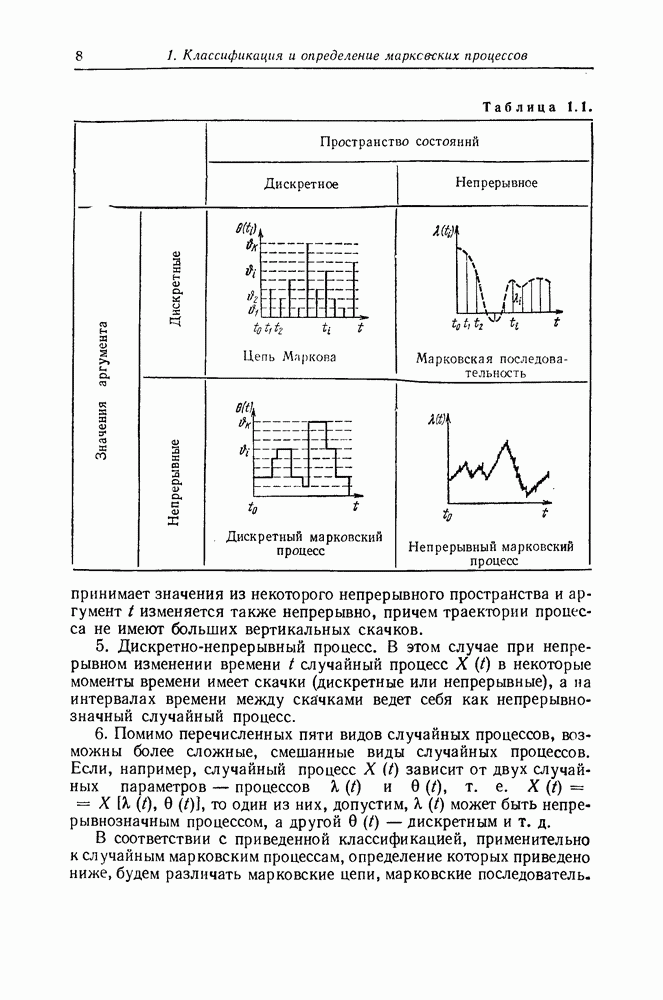
12. Методы решения уравнений Фоккера—Планка — Колмогорова
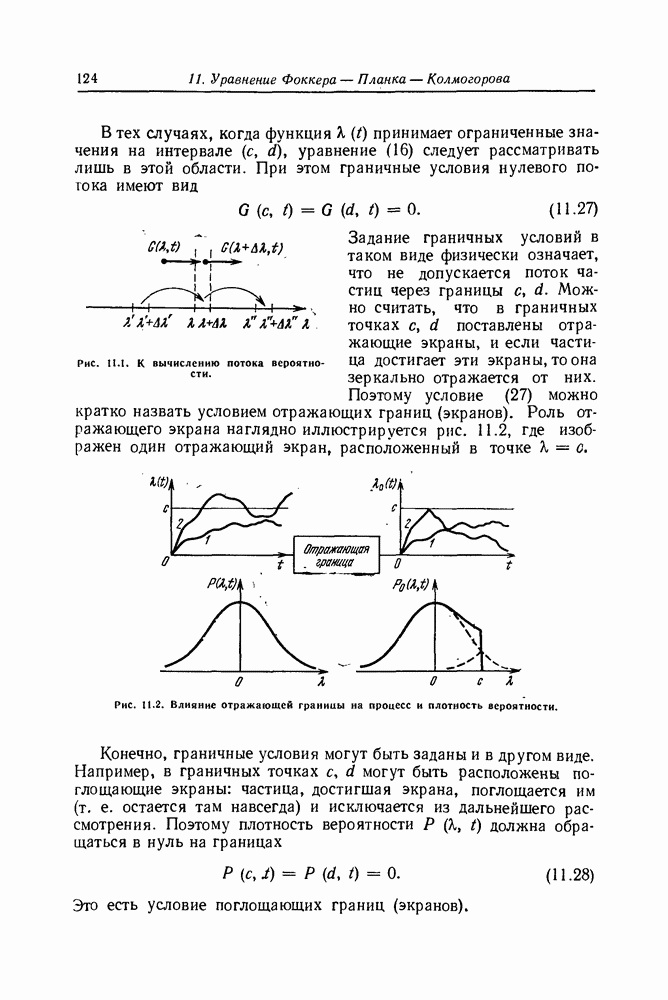
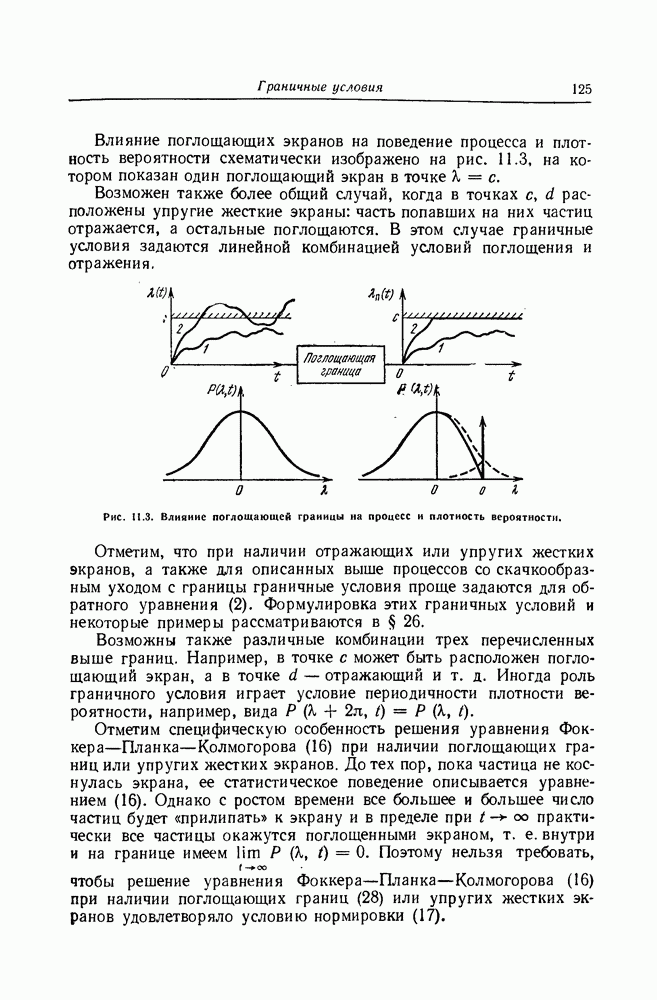
Так как уравнение Фоккера—Планка—Колмогорова принадлежит к уравнениям параболического типа, то для решения его можно применять известные методы решения уравнений этого типа [37]. В дальнейшем мы не будем касаться так называемых сингулярных (вырожденных) диффузионных марковских процессов, требующих специального рассмотрения. Для таких процессов коэффициент  исчезает около одной (возможно двух) из границ или же один из коэффициентов
исчезает около одной (возможно двух) из границ или же один из коэффициентов  или
или  при
при  растет слишком быстро (см. §19).
растет слишком быстро (см. §19).
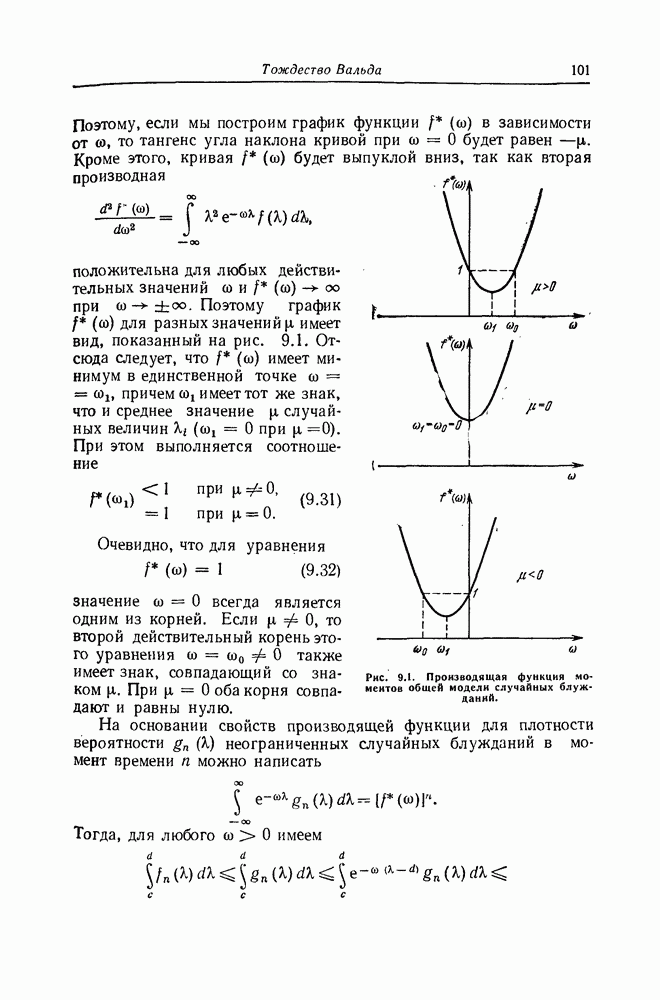
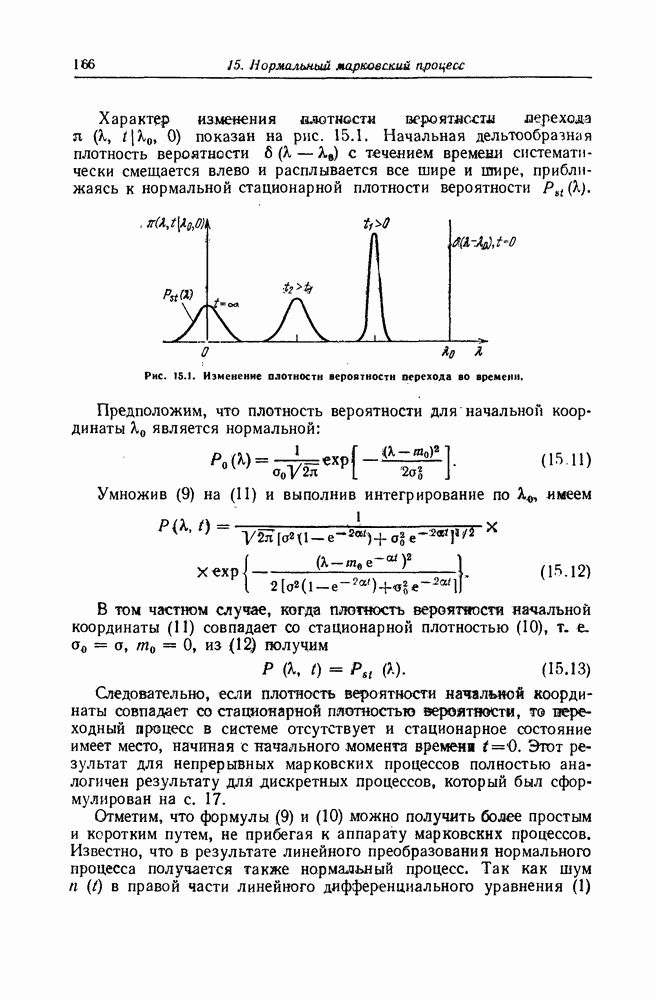
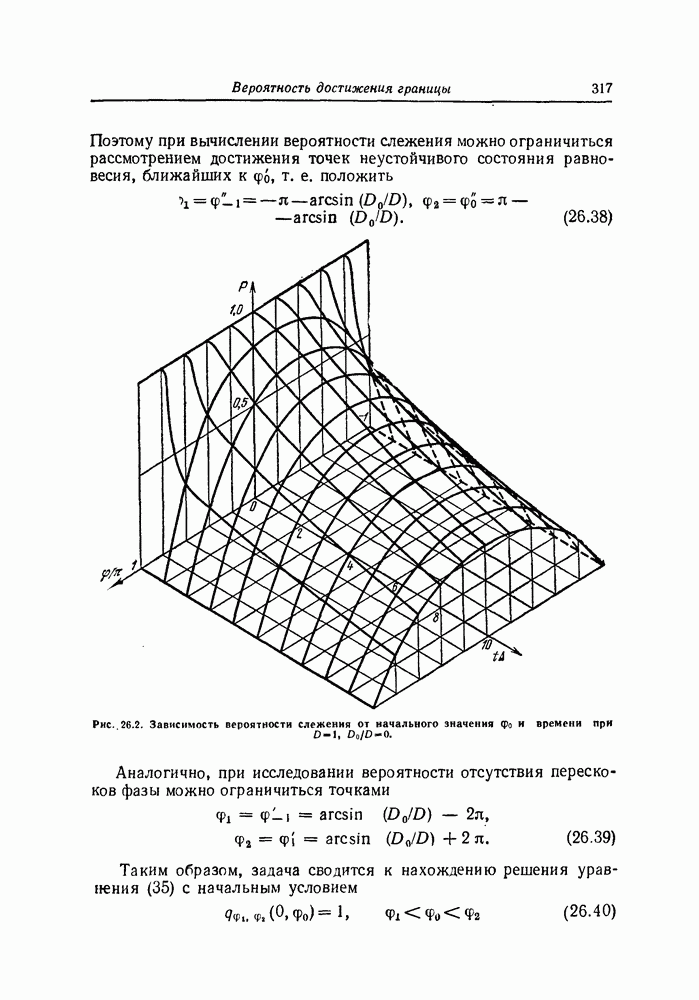
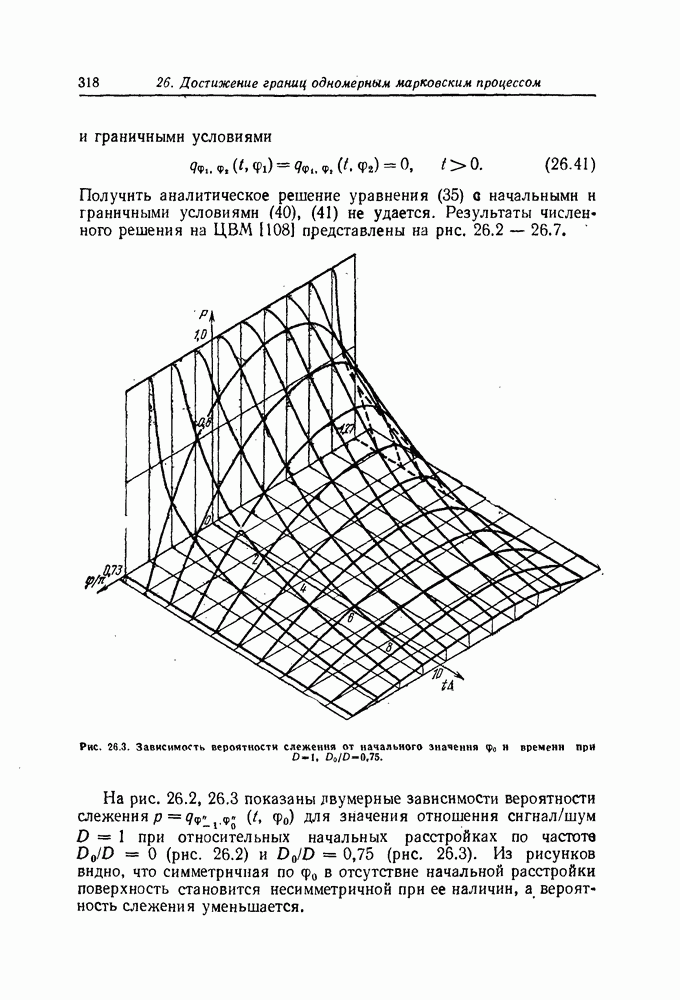
Применительно к одномерным марковским процессам во многих случаях просто находится стационарная плотность вероятности. Для стационарного состояния плотность вероятности перехода (10.10) зависит только от разности рассматриваемых моментов времени, а коэффициенты  и
и  , определенные формулами (11.10) и (11.11), не зависят от времени
, определенные формулами (11.10) и (11.11), не зависят от времени  . Одномерная стационарная плотность вероятности
. Одномерная стационарная плотность вероятности  , если она существует, вообще не зависит от времени
, если она существует, вообще не зависит от времени  и от начального распределения
и от начального распределения  . Поэтому в стационарном состоянии
. Поэтому в стационарном состоянии  и, следовательно,
и, следовательно,  . При этом уравнение Фоккера— Планка —Колмогорова (11.16) переходит в линейное дифференциальное уравнение для
. При этом уравнение Фоккера— Планка —Колмогорова (11.16) переходит в линейное дифференциальное уравнение для  :
:

для которого хорошо известно общее решение [39]:

Здесь произвольная постоянная  определяется из условия нормировки (11,17), а величина потока
определяется из условия нормировки (11,17), а величина потока  находится из граничных условий. В качестве нижнего предела интегрирования
находится из граничных условий. В качестве нижнего предела интегрирования  можно взять любую точку интервала, в котором определен процесс
можно взять любую точку интервала, в котором определен процесс  .
.
При нулевых граничных условиях для потока  уравнение упрощается
уравнение упрощается

Общее решение этого уравнения дается выражением

где постоянная С определяется из условия нормировки (11.17). Этой формулой часто пользуются при решении конкретных задач.
Таким образом, определив из уравнения, описывающего поведение системы, коэффициенты  и
и  по формулам (11.10) и (11.11), в некоторых случаях можно сразу написать выражение для одномерной стационарной плотности вероятности. Это показывает эффективность использования уравнения Фоккера—Планка—Колмогорова.
по формулам (11.10) и (11.11), в некоторых случаях можно сразу написать выражение для одномерной стационарной плотности вероятности. Это показывает эффективность использования уравнения Фоккера—Планка—Колмогорова.
К сожалению, полное исследование переходных процессов, связанное с решением нестационарного уравнения (11.16), является довольно сложной задачей. Аналитическое решение нестационарного уравнения не удается получить в общем виде, кроме некоторых частных случаев, например, когда

Такое задание коэффициентов сноса и диффузии соответствует исходному стохастическому дифференциальному уравнению (см. § 19):

Здесь  — нормальный белый шум с нулевым средним значением и корреляционной функцией
— нормальный белый шум с нулевым средним значением и корреляционной функцией  ,
,  — дельта-функция (см. Приложение III). Отсюда видно, что случайный процесс
— дельта-функция (см. Приложение III). Отсюда видно, что случайный процесс  является нормальным и может быть исследован другими методами.
является нормальным и может быть исследован другими методами.
Если коэффициенты сноса и диффузии имеют вид

то решениями уравнения (11.16) при нулевых граничных условиях для потока и различных значениях отдельных постоянных коэффициентов являются плотности вероятности Пирсона (см. § 16).
Приведем теперь шесть наиболее часто применяемых методов получения нестационарного решения уравнения Фоккера—Планка-Колмогорова (11.16). Такими методами являются: 1) метод разделения переменных, 2) метод преобразования Лапласа, 3) метод характеристической функции, 4) метод замены независимых переменных, 5) метод гауссова приближения и 6) численные методы.
1. Метод разделения переменных. Его целесообразно применять в тех случаях, когда коэффициенты сноса и диффузии не зависят от времени (однородный во времени процесс) и уравнение (11.16) принимает вид

Будем искать решение в виде произведения двух функций

где  и
и  являются функциями только
являются функциями только  и
и  соответственно.
соответственно.
Поделив обе части уравнения (7) на (8), будем иметь

Левая часть равенства (9) зависит только от в то время как правая часть зависит только от  . Поэтому обе части равны одной и той же константе, которую обозначим через
. Поэтому обе части равны одной и той же константе, которую обозначим через  . Следовательно, из (9) получаем два обыкновенных дифференциальных уравнения
. Следовательно, из (9) получаем два обыкновенных дифференциальных уравнения

Простое уравнение первого порядка (10) имеет решение
 (12.12)
(12.12)
а решение линейного уравнения второго порядка (11) может быть найдено известными методами решения обыкновенных дифференциальных уравнений с переменными коэффициентами. Это решение  зависит от двух произвольных постоянных
зависит от двух произвольных постоянных  и
и  . Так как уравнение (7) линейное, то общее решение имеет вид
. Так как уравнение (7) линейное, то общее решение имеет вид
 (12.13)
(12.13)
где постоянные  и
и  определяются граничными и начальными условиями, которые должны быть заданы для любой рассматриваемой задачи.
определяются граничными и начальными условиями, которые должны быть заданы для любой рассматриваемой задачи.
Можно показать [2], что если разность потоков  через границы равна нулю, то решение (13) можно представить в виде
через границы равна нулю, то решение (13) можно представить в виде

где  — собственные функции уравнения (11), соответствующие собственным значениям
— собственные функции уравнения (11), соответствующие собственным значениям  ,
,  — постоянные коэффициенты.
— постоянные коэффициенты.
Функции  ортонормированы с весом
ортонормированы с весом  :
:

При заданной начальной плотности вероятности  коэффициенты
коэффициенты  определяются выражением
определяются выражением

Если начальная плотность вероятности является дельтообразной:  , то решение (13) имеет вид
, то решение (13) имеет вид

где  .
.
2. Метод преобразования Лапласа. Смысл применения преобразования Лапласа к уравнению Фоккера—Планка—Колмогорова состоит в том, что при этом «устраняется» временная переменная  и уравнение в частных производных сводится к обыкновенному дифференциальному уравнению. Проиллюстрируем это на примере уравнения (7), предварительно записав его в развернутом виде
и уравнение в частных производных сводится к обыкновенному дифференциальному уравнению. Проиллюстрируем это на примере уравнения (7), предварительно записав его в развернутом виде
 (12.18)
(12.18)
Здесь штрихи обозначают дифференцирование по  .
.
Обозначим преобразование Лапласа функции  через
через

Применяя правила преобразования Лапласа к уравнению (18), получим

или
 (12.20)
(12.20)
Здесь  — начальное значение плотности вероятности (11.14).
— начальное значение плотности вероятности (11.14).
Уравнение (20) для определения преобразования Лапласа плотности вероятности является неоднородным обыкновенным дифференциальным уравнением второго порядка. Начальное условие, которому должна удовлетворять плотность вероятности  , входит в уравнение. Граничные условия для функции
, входит в уравнение. Граничные условия для функции  перейдут в соответствующие условия для функции
перейдут в соответствующие условия для функции  , которые нужно учитывать при решении уравнения (20).
, которые нужно учитывать при решении уравнения (20).
После того как решение уравнения (20) найдено, функцию  можно получить согласно теореме обращения, а в некоторых случаях можно воспользоваться таблицами преобразовании Лапласа.
можно получить согласно теореме обращения, а в некоторых случаях можно воспользоваться таблицами преобразовании Лапласа.
Укажем, что в некоторых случаях (например, когда коэффициенты сноса и диффузии имеют вид  ) целесообразно применять к уравнению Фоккера—Планка—Колмогорова (11.16) преобразование Лапласа по переменной
) целесообразно применять к уравнению Фоккера—Планка—Колмогорова (11.16) преобразование Лапласа по переменной  .
.
3. Метод характеристической функции. В некоторых случаях (например, при нахождении фундаментального решения) удается получить упрощение путем перехода в уравнении (11.16) от плотности вероятности  к характеристической функции
к характеристической функции

Обычно это делается следующим образом. После подстановки конкретных значений коэффициентов  и
и  обе части уравнения (11.16) сначала умножаются на
обе части уравнения (11.16) сначала умножаются на  , а затем интегрируются по
, а затем интегрируются по  в соответствующих пределах или же используют сразу известные правила преобразования Фурье и записывают уравнение (11.16) для характеристической функции. Начальное значение характеристической функции находится подстановкой в (21) вместо
в соответствующих пределах или же используют сразу известные правила преобразования Фурье и записывают уравнение (11.16) для характеристической функции. Начальное значение характеристической функции находится подстановкой в (21) вместо  начальной плотности вероятности (11.14). Такой прием выше был назван методом характеристической функции.
начальной плотности вероятности (11.14). Такой прием выше был назван методом характеристической функции.
4. Метод замены независимых переменных. Целевое назначение замены независимых переменных заключается в том, что в ряде случаев удается существенно упростить уравнение Фоккера—Планка—Колмогорова, а иногда свести его к простейшему уравнению диффузии (см. § 14)
 (12.22)
(12.22)
При замене независимых переменных затруднительно указать какую-либо единую рецептуру. Рассмотрим два частных случая.
Преобразование координаты фазового пространства. Взаимно-однозначным преобразованием
 (12.23)
(12.23)
фазового пространства марковский процесс  с плотностью вероятности
с плотностью вероятности  может быть преобразован в случайный процесс и
может быть преобразован в случайный процесс и  и
и  который также будет марковским процессом с плотностью вероятности
который также будет марковским процессом с плотностью вероятности  , причем
, причем
 (12.24)
(12.24)
В однородном случае, когда коэффициенты сноса  и диффузии
и диффузии  не зависят от времени, при помощи такого преобразования можно перейти от марковского процесса
не зависят от времени, при помощи такого преобразования можно перейти от марковского процесса  с произвольными коэффициентами
с произвольными коэффициентами  и
и  к марковскому процессу и
к марковскому процессу и  с соответствующими коэффициентами сноса
с соответствующими коэффициентами сноса  или диффузии
или диффузии  имеющими очень простой вид.
имеющими очень простой вид.
В результате перехода к новой переменной уравнение (7) заменится аналогичным уравнением для плотности вероятности  с коэффициентами
с коэффициентами  и
и  , которые как функции старой переменной имеют вид
, которые как функции старой переменной имеют вид
 (12.25)
(12.25)
Из первого соотношения (25) следует, что если мы хотим получить процесс с нулевым коэффициентом сноса  , то преобразование (23) должно быть таким, чтобы выполнялось равенство
, то преобразование (23) должно быть таким, чтобы выполнялось равенство
 (12.26)
(12.26)
Выбирая

получаем процесс  с единичным коэффициентом диффузии
с единичным коэффициентом диффузии  .
.
Итак, однородный марковский процесс при помощи преобразования (26) всегда можно свести к процессу с нулевым коэффицнентом сноса, а при помощи преобразования (27) — к процессу с единичным коэффициентом диффузии.
б) Преобразование ксординатов и времени. Естественно, что при одновременной замене координаты и времени иногда можно добиться упрощения уравнения Фоккера—Планка—Колмогорова общего вида (11.16). Такая возможность была впервые подмечена и применялась А. Н. Колмогоровым [1].
Перейдем в (11.16) от независимых переменных  и
и  к новым переменным
к новым переменным  и путем взаимно-однозначного преобразования
и путем взаимно-однозначного преобразования
 (12.28)
(12.28)
где  — непрерывная и нигде не убывающая функция,
— непрерывная и нигде не убывающая функция,  — относительно
— относительно  произвольна, а по
произвольна, а по  допускает непрерывную производную. При этом
допускает непрерывную производную. При этом
 (12.29)
(12.29)
В результате перехода к новым переменным для плотности вероятности  получим уравнение, аналогичное (11.16):
получим уравнение, аналогичное (11.16):

Здесь коэффициенты сноса  и диффузии
и диффузии  определяются равенствами
определяются равенствами
 (12.31)
(12.31)
где  и
и  в правых частях написанных формул предполагаются выраженными через
в правых частях написанных формул предполагаются выраженными через  и
и  .
.
В зависимости от конкретного вида коэффициентов  и
и  путем подбора соответствующих преобразований (28) можно получить разные упрощения. Укажем одну замечательную возможность, когда уравнение (11.16) может быть сведено к уравнению чистой диффузии вида (22). Введем обозначения
путем подбора соответствующих преобразований (28) можно получить разные упрощения. Укажем одну замечательную возможность, когда уравнение (11.16) может быть сведено к уравнению чистой диффузии вида (22). Введем обозначения

 (12.32)
(12.32)
В приводимых выражениях индекс обозначает дифференцирование по указанной переменной.
Справедлива следующая теорема, доказанная И. Д. Черкасовым [40]. Пусть существуют непрерывные производные  на всей оси
на всей оси  и функции
и функции  ограничены. Тогда необходимым и достаточным условием существования преобразования типа (28), переводящего уравнение (11.16) взаимно-однозначно в уравнение (22), является тождественное выполнение равенства
ограничены. Тогда необходимым и достаточным условием существования преобразования типа (28), переводящего уравнение (11.16) взаимно-однозначно в уравнение (22), является тождественное выполнение равенства  , где
, где

При выполнении этого тождества искомое преобразование дается формулами

Нетрудно, например, убедиться, что условия теоремы выполняются в частном случае, рассмотренном в [1], когда

При этом преобразования (28) должны иметь вид
 (12.36)
(12.36)
Полагая в (35) коэффициент  , из (36) получаем формулы преобразования, позволяющего свести уравнение Фоккера — Планка—Колмогорова к чисто диффузионному уравнению (22) для однородных по координате процессов, коэффициенты сноса и диффузии которых зависят только от времени (процессы типа Башелье).
, из (36) получаем формулы преобразования, позволяющего свести уравнение Фоккера — Планка—Колмогорова к чисто диффузионному уравнению (22) для однородных по координате процессов, коэффициенты сноса и диффузии которых зависят только от времени (процессы типа Башелье).
Можно убедиться [1], что при

формулы перехода к новым переменным будут иметь вид
 (12.38)
(12.38)
В некоторых случаях оказывается полезной замена самой искомой функции, т. е. переход в уравнении (7) от  к другой функции, например,
к другой функции, например,  (см. § 18).
(см. § 18).
5. Гауссово приближение. Кроме перечисленных четырех строгих методов решения уравнения Фоккера—Планка—Колмогорова, применяются различные приближенные приемы. Укажем здесь один из таких приближенных способов решения. В некоторых задачах на основании физических соображений можно заранее ожидать определенный вид плотности вероятности  . При некоторых условиях плотность вероятности
. При некоторых условиях плотность вероятности  , являющаяся решением уравнения (11.16), является нормальной или близкой к ней.
, являющаяся решением уравнения (11.16), является нормальной или близкой к ней.
Нормальная плотность вероятности

определяется двумя параметрами: математическим ожиданием  и дисперсией
и дисперсией  .
.
При выполнении условий (5) нормальная плотность вероятности является точным решением уравнения (11.16) для неограниченного пространства.
С учетом сказанного иногда применяется следующий способ (так называемое гауссово приближение). Разложим коэффициенты  и
и  в ряд Тейлора в окрестности точки тк и ограничимся первыми членами разложения
в ряд Тейлора в окрестности точки тк и ограничимся первыми членами разложения

Подставив выражения (39) и (40) в уравнение (11.16) и приравняв члены при одинаковых степенях разности  , получим систему из двух обыкновенных дифференциальных уравнений для определения параметров
, получим систему из двух обыкновенных дифференциальных уравнений для определения параметров  и
и  :
:

Начальные значения  и
и  , необходимые для решения системы, легко вычисляются по заданной начальной плотности вероятности
, необходимые для решения системы, легко вычисляются по заданной начальной плотности вероятности  . Найдя
. Найдя  и
и  из этой системы и подставив их в (39), получим решение уравнения (11.16) в гауссовом приближении.
из этой системы и подставив их в (39), получим решение уравнения (11.16) в гауссовом приближении.
Отметим, что описанное гауссово приближение следует рассматривать как один из приемов, позволяющих получить из основного сложного дифференциального уравнения в частных производных (11.16) систему из двух сравнительно простых обыкновенных дифференциальных уравнений (41). Разумеется, что вместо гауссовой плотности вероятности (39) можно задаваться и другими видами плотностей вероятностей, соответствующих ожидаемому физическому результату.
В заключение получим более точные уравнения, чем (41), для определения математического ожидания  и дисперсии
и дисперсии  марковского диффузионного процесса
марковского диффузионного процесса  , заданного уравнением (11.16) [41]. Вычисление этих характеристик на выходе нелинейных инерционных систем представляет самостоятельный интерес вне связи с гауссовым приближением.
, заданного уравнением (11.16) [41]. Вычисление этих характеристик на выходе нелинейных инерционных систем представляет самостоятельный интерес вне связи с гауссовым приближением.
По определению,
 (12.42)
(12.42)
Умножая обе части уравнения (11.16) на  и интегрируя результат по
и интегрируя результат по  , можем написать
, можем написать

Считая, что в левой части этого равенства допустима перемена порядка интегрирования и дифференцирования, имеем

Интегралы в правой части равенства (43) находим интегрированием по частям


Предположим, что выполняются следующие граничные условия:

Тогда из (43) получим

Данное уравнение при выполнении условий (45) является точным. К сожалению, этим уравнением невозможно пока воспользоваться, так как неизвестна плотность вероятности  и поэтому нельзя найти среднее значение коэффициента сноса
и поэтому нельзя найти среднее значение коэффициента сноса  . Можно получить приближенное выражение, раскладывая
. Можно получить приближенное выражение, раскладывая  в ряд Тейлора в окрестности значения
в ряд Тейлора в окрестности значения  и ограничиваясь членами до второго порядка включительно:
и ограничиваясь членами до второго порядка включительно:
 (12.47)
(12.47)
Беря математическое ожидание от обеих частей этого равенства, получим

Отметим, что если в разложении (47) учитывать члены более высокого порядка, то в правую часть (48) войдут третий, четвертый и другие центральные моменты.
Подставив (48) в (46), приходим к окончательному приближенному дифференциальному уравнению для математического ожидания
 (12.49)
(12.49)
Если в правой части разложения (47) учесть только первые два члена (линейная аппроксимация), то для математического ожидании можно получить уравнение
 (12.50)
(12.50)
совпадающее с первым уравнением системы (41). Если коэффициент сноса имеет вид  (система линейная), то уравнение (50) является точным. Естественно, что для линейной системы математическое ожидание процесса не зависит от его дисперсии.
(система линейная), то уравнение (50) является точным. Естественно, что для линейной системы математическое ожидание процесса не зависит от его дисперсии.
Возвратимся к основному уравнению (49). В него входит неизвестная пока дисперсия процесса  . Чтобы получить уравнения для дисперсии, умножим обе части уравнения (11.16) на
. Чтобы получить уравнения для дисперсии, умножим обе части уравнения (11.16) на  и затем проинтегрируем по
и затем проинтегрируем по  :
:
 (12.51)
(12.51)
Влевой части этого равенства «поменяем местами» порядок интегрирования и дифференцирования, а в правой части применим интегрирование по частям к первому интегралу один раз, а ко второму дважды. В результате получим

Предположим, как и ранее, что три явных слагаемых в правой части этого равенства при  обращаются в нуль. Тогда можем написать
обращаются в нуль. Тогда можем написать
 (12.52)
(12.52)
или

Хотя это дифференциальное уравнение является точным, однако им практически нельзя воспользоваться, так как неизвестны средние значения, входящие в правую часть (53). Для получения замкнутой системы дифференциальных уравнений применим следующие разложения коэффициентов сноса и диффузии в ряд Тейлора в окрестности  :
:

Подстановка этих выражений в (53) приводит к следующему окончательному результату:
 (12.54)
(12.54)
Отметим, что если в разложении коэффициента диффузии отбросить квадратичный член, то вместе (54) получим уравнение
 (12.55)
(12.55)
совпадающее со вторым уравнением системы (41).
Следовательно, система дифференциальных уравнений (41) получается из уравнения Фоккера— Планка—Колмогорова (11.16) при линейной аппроксимации коэффициентов сноса и диффузии в окрестности текущего значения математического ожидания  .
.
Очевидно, что система уравнений (41) является точной лишь для линейного стохастического дифференциального уравнения вида

где  — нормальный белый шум (см. § 14).
— нормальный белый шум (см. § 14).
Замкнутая система из двух обыкновенных дифференциальных уравнений первого порядка (49), (54):
 (12.56)
(12.56)
получается из уравнения (11.16) при аппроксимации коэффициентов сноса и диффузии с учетом не только линейных, но и квадратичных членов разложения и поэтому является более точной, чем (41).
Система уравнений (56) должна решаться при начальных условиях
 (12.57)
(12.57)
6. Численные методы. В тех случаях, когда перечисленные пять методов не позволяют решить уравнение (11.16) с соответствующими начальными и граничными условиями, для получения решения можно воспользоваться численными методами, которые достаточно просто реализуются на современных ЦВМ [42—44].
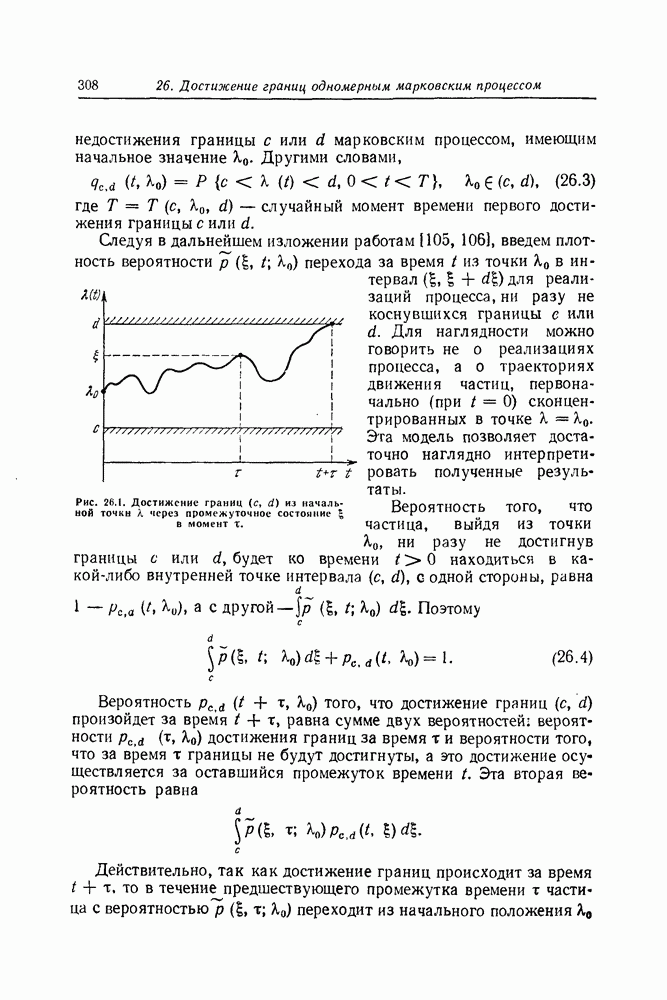
Пусть требуется найти решение уравнения (11.16) с начальным условием (11.14) и граничными условиями (11.28). Для получения приближенного решения этой задачи численными методами рассмотрим прямоугольную сетку узлов, образуемую точками пересечения прямых:

Узлы, лежащие на прямых  , будем называть граничными узлами, все остальные — внутренними. Для каждого внутреннего узла
, будем называть граничными узлами, все остальные — внутренними. Для каждого внутреннего узла  запишем разностное уравнение, аппроксимирующее с некоторой точностью уравнение (11.16). Предварительно заметим, что уравнение (11.16) можно записать в виде
запишем разностное уравнение, аппроксимирующее с некоторой точностью уравнение (11.16). Предварительно заметим, что уравнение (11.16) можно записать в виде

При построении конечно-разностной аппроксимации производные в уравнении (58) можно заменить разностными отношениями различным образом и возможные комбинации этих способов весьма многочисленны (44). Ограничимся случаем, когда производные  и
и  в узле
в узле  заменяются центральными разностными отношениями
заменяются центральными разностными отношениями

где  .
.
Производную заменим разностным отношением вперед
 (12.60)
(12.60)
Подставив (59) и (60) в (58), получим

где

Разностное уравнение (61) содержит значения решения в четырех узлах, изображенных на рис. 12.1, и аппроксимирует уравнение (58) с точностью до  .
.
Из начального условия (11.14) и граничных условий (11.28) следует

Соотношения (61)-(64) в совокупности образуют явную разностную схему, которая очень удобна для выполнения вычислений на ЦВМ. Действительно, так как из начальных условий (63) известны значения решения в узлах начального слоя  , то по ним из (61) легко находятся значения решения во внутренних узлах первого слоя
, то по ним из (61) легко находятся значения решения во внутренних узлах первого слоя  , затем с учетом (64) второго слоя
, затем с учетом (64) второго слоя  и т. д.
и т. д.

Рис. 12.1. Явная разностная схема для шаблона ИЭ четырех узлов.

Рис. 12.2. Неявная разностная схема для шаблона из четырех узлов.
Следовательно, соотношение (61) дает явное выражение решения в слое  через найденные значения решения в слое
через найденные значения решения в слое  .
.
Практическое применение явных разностных схем наталкивается на необходимость выполнения специальных условий устойчивости. Для определения понятия устойчивости разностной схемы предположим, что значения функций в граничных узлах вычислены точно. Предположим далее, что при отыскании решения разностных уравнений (61) погрешность допущена на  слое, а до этого слоя и дальше вычисления проводились точно. За счет погрешности на
слое, а до этого слоя и дальше вычисления проводились точно. За счет погрешности на  слое мы получим добавок
слое мы получим добавок  к точному решению разностной схемы. Без ограничения общности можно считать, что погрешность допущена на начальном слое. Тогда ошибки
к точному решению разностной схемы. Без ограничения общности можно считать, что погрешность допущена на начальном слое. Тогда ошибки  будут являться решением той же самой системы уранений, причем значения их в граничных узлах, лежащих на прямых
будут являться решением той же самой системы уранений, причем значения их в граничных узлах, лежащих на прямых  и
и  равны нулю, а значения в граничных узлах начального слоя равны допущенным погрешностям. Разностная схема называется устойчивой, если для всякого
равны нулю, а значения в граничных узлах начального слоя равны допущенным погрешностям. Разностная схема называется устойчивой, если для всякого  найдется такое
найдется такое  , что как только
, что как только

то будет иметь место неравенство

для любого  , причем
, причем  не зависит от
не зависит от  и
и  . Фактически устойчивость характеризует непрерывную зависимость решения разностной схемы от начальных значений, которая обеспечивает убывание случайно допущенной погрешности при проведении дальнейших расчетов. Поэтому этот тип устойчивости еще называют устойчивостью по начальным значениям.
. Фактически устойчивость характеризует непрерывную зависимость решения разностной схемы от начальных значений, которая обеспечивает убывание случайно допущенной погрешности при проведении дальнейших расчетов. Поэтому этот тип устойчивости еще называют устойчивостью по начальным значениям.
Можно показать [43, 44]. что явная разностная схема (61)-(64) устойчива, если в рассматриваемой области выполняются неравенства
 (12.65)
(12.65)
Из второго неравенства (65) следует, что явная разностная схема требует применения очень мелкого шага  по времени, т. е. если нужно найти решение на конечном отрезке изменения то количество слоев
по времени, т. е. если нужно найти решение на конечном отрезке изменения то количество слоев  должно быть достаточно большим. Кроме этого, если в процессе вычислений нужно уменьшить шаг
должно быть достаточно большим. Кроме этого, если в процессе вычислений нужно уменьшить шаг  по координате
по координате  , то нельзя этого сделать, не уменьшая
, то нельзя этого сделать, не уменьшая  .
.
От этого недостатка свободны неявные разностные схемы, одна из которых получится, если вместо (60) для аппроксимации  воспользоваться разностным отношением назад
воспользоваться разностным отношением назад
 (12.66)
(12.66)
В этом случае аналогично (61) получим

где
 (12.68)
(12.68)
Разностное уравнение (67) содержит значения решения в четырех узлах, изображенных на рис. 12.2, и также аппроксимирует уравнение (58) с точностью до  . Для отыскания значений решения в узлах р-го слоя при известных значениях в узлах предыдущего слоя в этом случае приходится решать систему алгебраических уравнений (67) при
. Для отыскания значений решения в узлах р-го слоя при известных значениях в узлах предыдущего слоя в этом случае приходится решать систему алгебраических уравнений (67) при  с большим числом неизвестных. Широкое применение неявных разностных схем на практике оправдывается тем, что они всегда устойчивы [42—44]. Поэтому выбор значений шагов
с большим числом неизвестных. Широкое применение неявных разностных схем на практике оправдывается тем, что они всегда устойчивы [42—44]. Поэтому выбор значений шагов  и
и  определяется лишь необходимой точностью вычислений и способом решения системы алгебраических уравнений.
определяется лишь необходимой точностью вычислений и способом решения системы алгебраических уравнений.
Для решения разностных уравнений (67) с граничными условиями (64) можно воспользоваться методом прогонки [42]. Суть этого метода состоит в следующем.
Рассмотрим трехточечное разностное уравнение

с граничными условиями
 (12.70)
(12.70)
Здесь  — известные числа,
— известные числа,  — неизвестные значения искомого решения. Очевидно, что разностное уравнение (67) с граничными условиями (64) при фиксированном
— неизвестные значения искомого решения. Очевидно, что разностное уравнение (67) с граничными условиями (64) при фиксированном  является частным случаем (69) и (70).
является частным случаем (69) и (70).
Будем искать решение уравнения (69) в том же виде, в котором заданы граничные условия (70), т. е. в виде
 (12.71)
(12.71)
где  — неизвестные пока коэффициенты. Подставляя (71) и следующее из (71) соотношение
— неизвестные пока коэффициенты. Подставляя (71) и следующее из (71) соотношение

в уравнение (69), получаем

Отсюда видно, что равенство (69) будет выполнено, если потребовать

Таким образом мы получим рекуррентные соотношения для определения прогоночных коэффициентов  и
и  :
:

Величины  и
и  определяются из (71) и граничного условия (70) при
определяются из (71) и граничного условия (70) при  :
:

Значение  , необходимое для начала счета по формулам (71), получается из (71) и граничного условия (70) при
, необходимое для начала счета по формулам (71), получается из (71) и граничного условия (70) при  :
:

Итак, решение краевой задачи (69), (70) может быть получено при помощи алгоритма
 (12.72)
(12.72)
Этот способ решения разностных уравнений (69) получил название метода прогонки. Согласно алгоритму (72) сначала определяются значения коэффициентов  , т. е. совершается прогонка вперед, а затем находятся значения
, т. е. совершается прогонка вперед, а затем находятся значения  при
при  .
.
Формулы прогонки (72) называются устойчивыми, если коэффициенты  , не превосходят по абсолютной величине единицы. В этом случае ошибки округления, возникающие в процессе вычислений по формуле (71), не будут возрастать.
, не превосходят по абсолютной величине единицы. В этом случае ошибки округления, возникающие в процессе вычислений по формуле (71), не будут возрастать.
Условия
 (12.73)
(12.73)
обеспечивают устойчивость формул прогонки (72).
Действительно, если  и
и  , то
, то

Возвращаясь к неявной разностной схеме (67), (63) и (64), на основании (62) и (68) можно показать, что выбором достаточно малых значений  и
и  условия (73) всегда могут быть выполнены при
условия (73) всегда могут быть выполнены при  . В том случае, когда выполнение условий (73) потребует меньших значений шагов, чем выполнение неравенств (65), для решения линейной системы алгебраических уравнений (67) при
. В том случае, когда выполнение условий (73) потребует меньших значений шагов, чем выполнение неравенств (65), для решения линейной системы алгебраических уравнений (67) при  можно воспользоваться каким-либо другим методом [42].
можно воспользоваться каким-либо другим методом [42].
Если требуется найти решение уравнения (11.16) с другими граничными условиями, то в приведенных разностных схемах изменится только (64). Так, например, при решении (11.16) с граничными условиями (11.27) они сами должны быть аппроксимированы разностными соотношениями. При этом следует стремиться использовать аппроксимации, которые не ухудшают общей точности разностной схемы.
Отметим, что замена точных значений решения в граничных узлах приближенными приводит к проблеме обеспечения устойчивости по граничным значениям  . Для повышения устойчивости счета во всех случаях целесообразно использовать выполнение условия нормировки в каждом слое, если оно имеет место в рассматриваемой задаче.
. Для повышения устойчивости счета во всех случаях целесообразно использовать выполнение условия нормировки в каждом слое, если оно имеет место в рассматриваемой задаче.
Использование численных методов для нахождения плотности вероятности перехода, т. е. для решения уравнения (11.12) с начальным условием (11.13) и соответствующими граничными условиями, имеет специфические особенности, связанные с заданием значений решения на начальном слое. В этом случае решение уравнения (11.12) методом сеток начинают со слоя, отстоящего от начального на некотором расстоянии  . На интервале
. На интервале  используется гауссово приближение, которое при малых
используется гауссово приближение, которое при малых  согласно асимптотическому представлению
согласно асимптотическому представлению  -функции (см. (III-7)) выполняется достаточно точно. Таким образом, вместо (11.13) будем иметь
-функции (см. (III-7)) выполняется достаточно точно. Таким образом, вместо (11.13) будем иметь

Значения  и
и  находятся из решения уравнений (56) с начальными условиями
находятся из решения уравнений (56) с начальными условиями  и
и  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
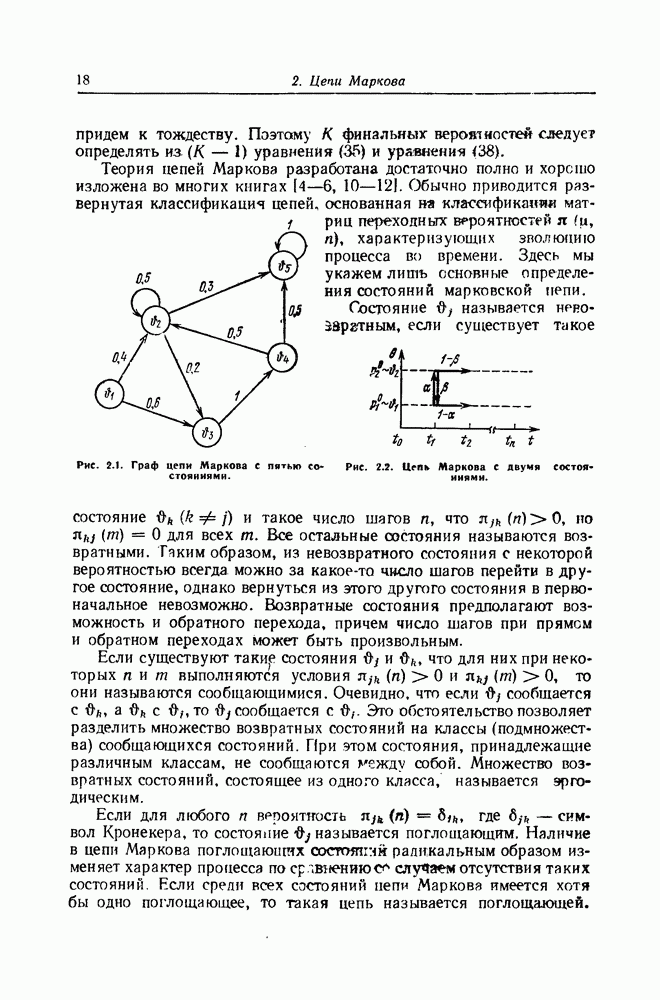
- 1. Классификация и определение марковских процессов
- 2. Цепи Маркова
- Уравнение Маркова
- Цепь Маркова с двумя состояниями
- 3. Энергетические спектры марковских сообщений
- 4. Одномерные дискретные блуждания
- Неограниченные блуждания
- Один поглощающий и один упругий жесткий экраны
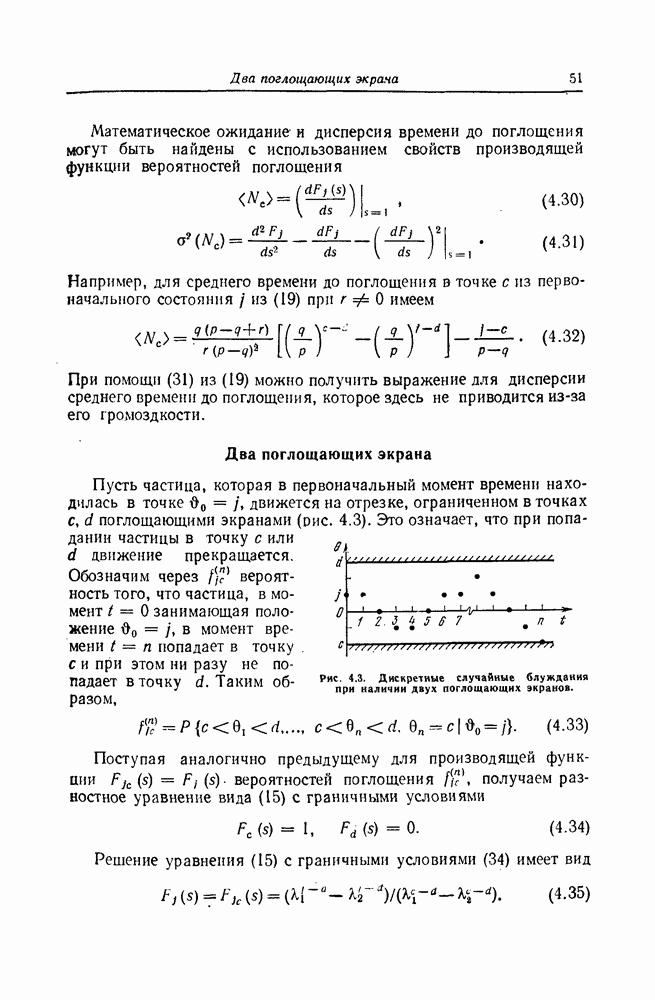
- Два поглощающих экрана
- Один поглощающий экран
- Два отражающих экрана
- Один отражающий экран
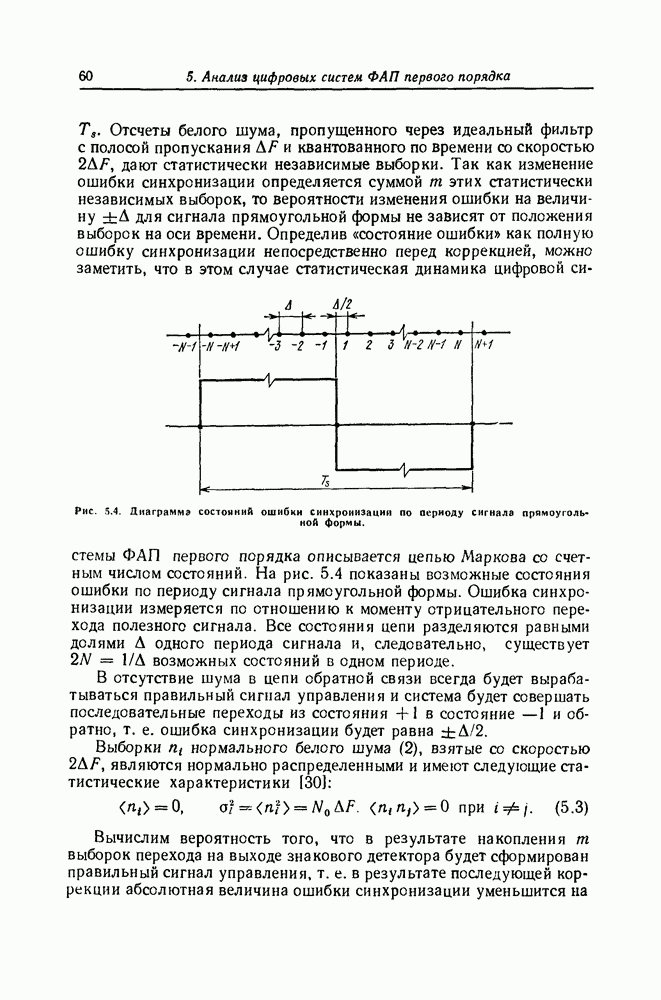
- 5. Анализ цифровых систем ФАП первого порядка
- Средний квадрат ошибки синхронизации
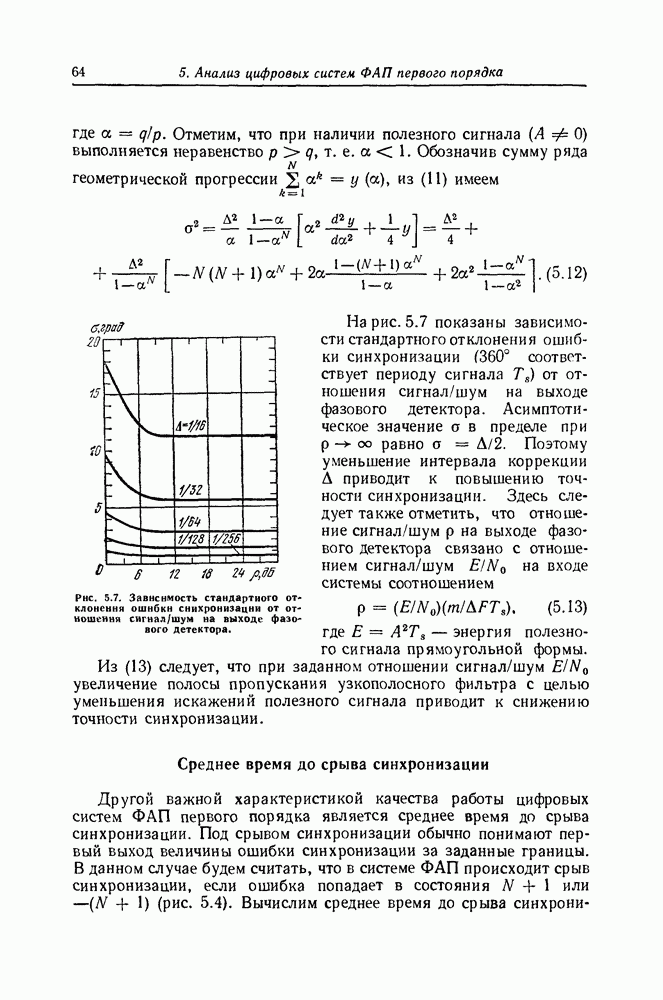
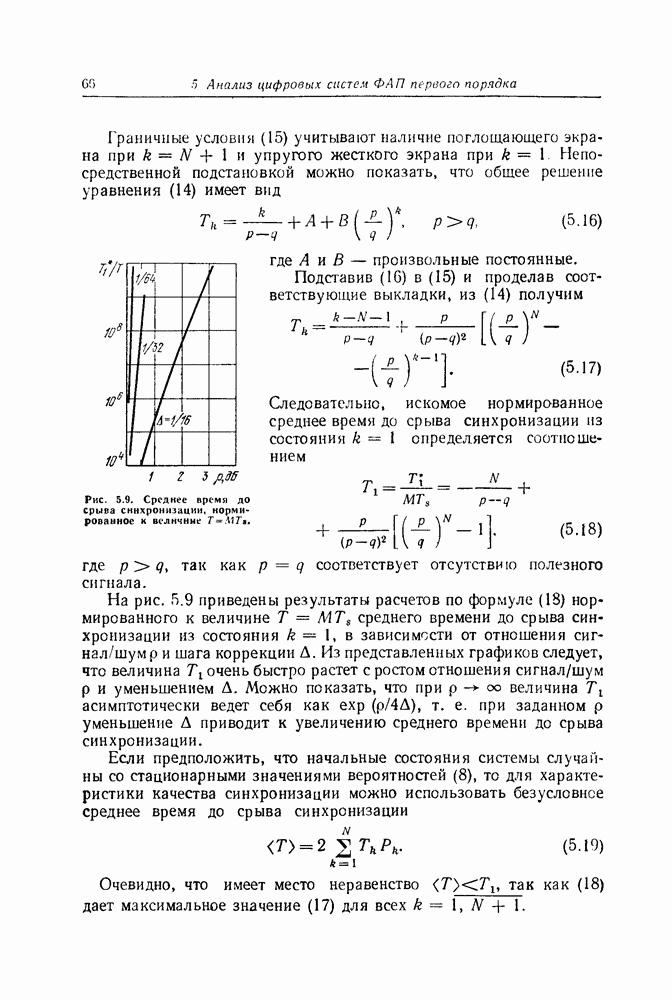
- Среднее время до срыва синхронизации
- Обобщение на случай сигналов более сложной формы
- 6. Дискретный марковской процесс
- 7. Типовые разрывные марковские процессы
- Пуассоновский процесс
- Процесс рождения и гибели
- 8. Полумарковские процессы
- 9. Марковские последовательности
- Общая модель одномерных случайных блужданий
- Случайные блуждания между поглощающими экранами
- Тождество Вальд
- Случайные блуждания между отражающими экранами
- 10. Непрерывный марковский процесс
- Дискретная модель непрерывного процесса
- 11. Уравнение Фоккера—Планка—Колмогорова
- Граничные условия
- 12. Методы решения уравнений Фоккера—Планка — Колмогорова
- 13. Многомерные марковские процессы
- Граничные условия
- 14. Чисто диффузионный процесс
- 15. Нормальный марковский процесс
- 16. Процессы с распределениями Пирсона
- 17. Процессы с кусочно-линейными коэффициентами сноса
- 18. Многомерные пормальные марковские процессы
- 19. Стохастические дифференциальные уравнения
- Стохастические интегралы и дифференциалы
- Теорема Дуба и вычисление локальных характеристик марковского процесса
- Численные методы решения стохастических дифференциальных уравнений
- 20. Область применения аппарата марковских процессов
- О коррелированности случайного воздействия
- Другие отклонения от теоремы Дуба
- Понижение порядка стохастических дифференциальных уравнений с малым параметром
- 21. Воздействие шума на простейшие колебательные системы
- Воздействие шума на колебательный контур
- Анализ работы автогенератора при наличии шума
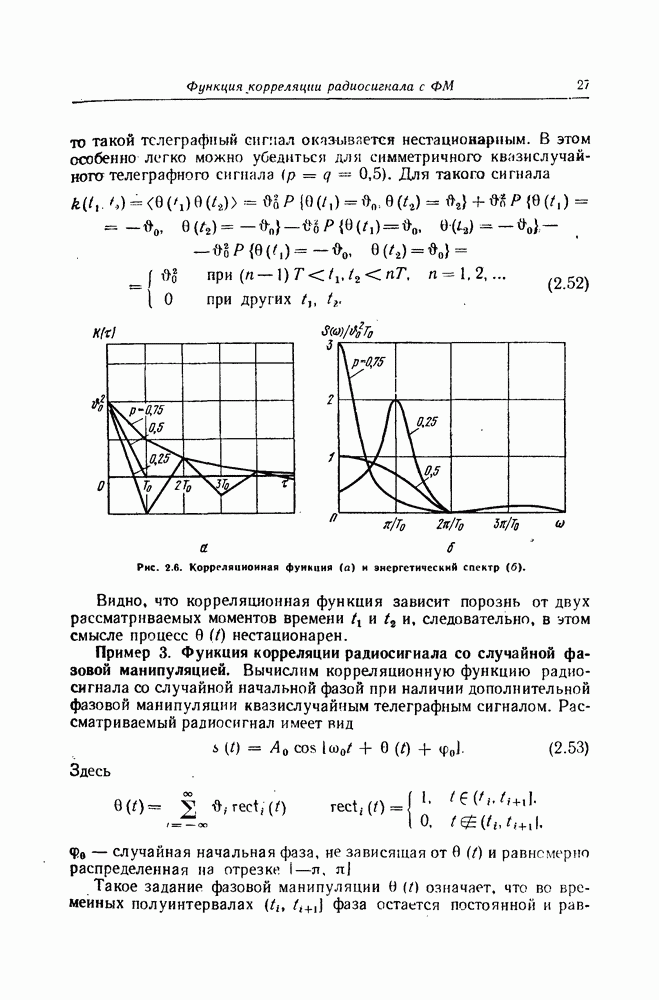
- Корреляционная функция радиосигнала со случайной фазовой манипуляцией
- 22. Статистическая динамика синхронизируемого генератора и фазовой автоподстройки частоты
- 23. Интегродифференциальные уравнении Колмогорова—Феллера
- 24. Статистические характеристики ФАП при воздействии нормального шума и пуассоновских импульсов
- 25. Обобщенные уравнения Фоккера—Планка—Колмогорова для смешанных процессов
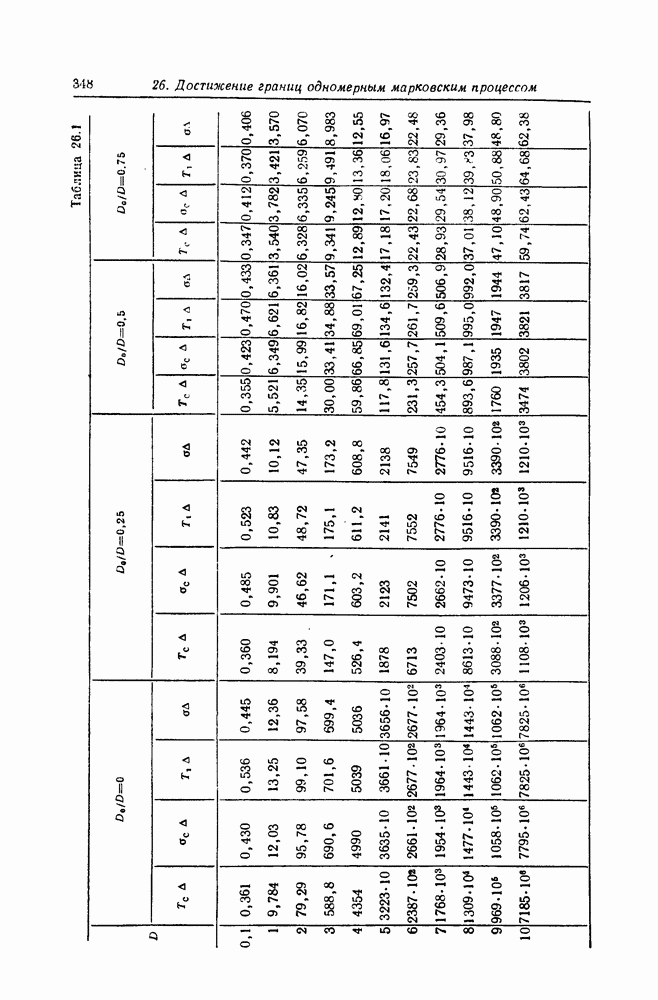
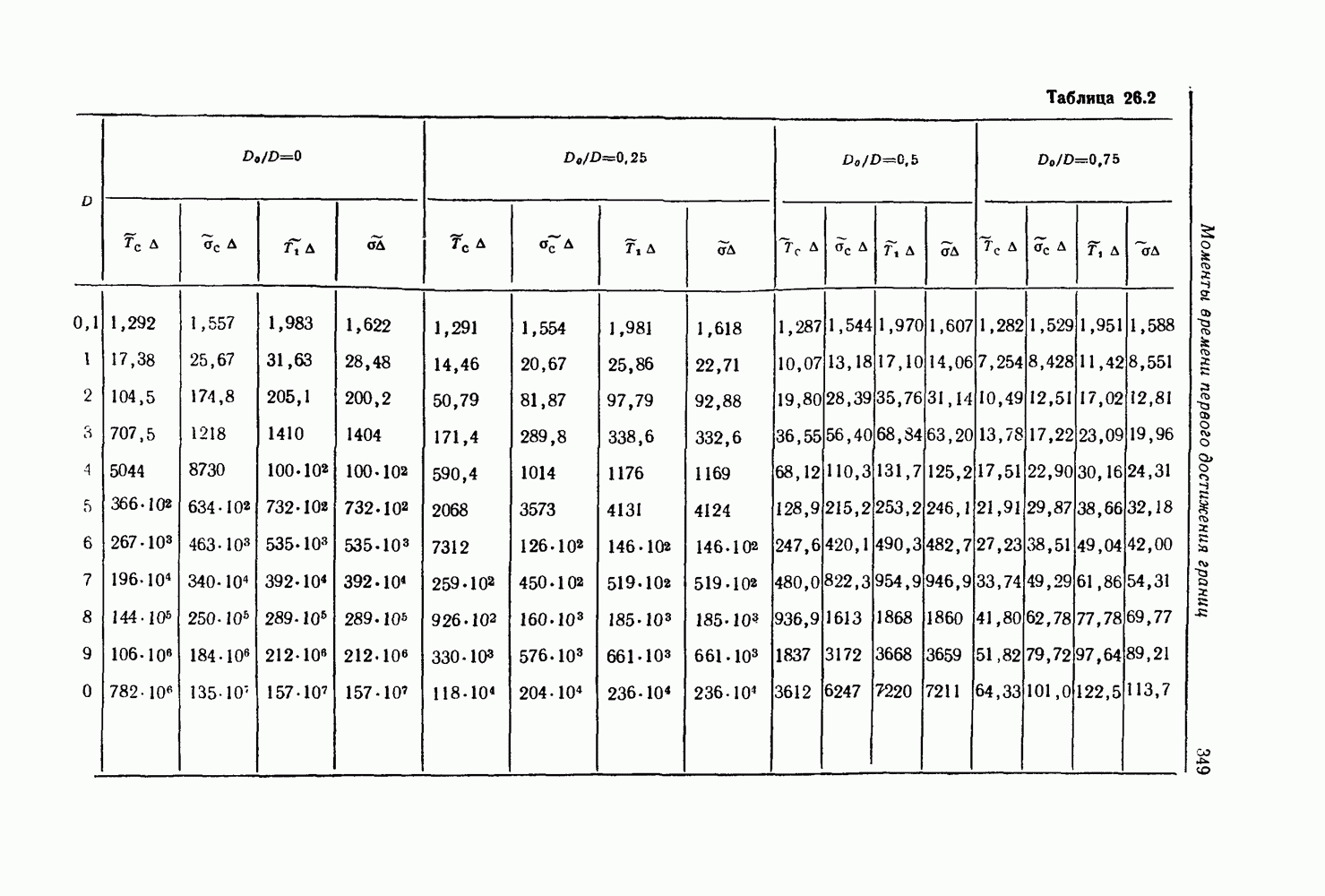
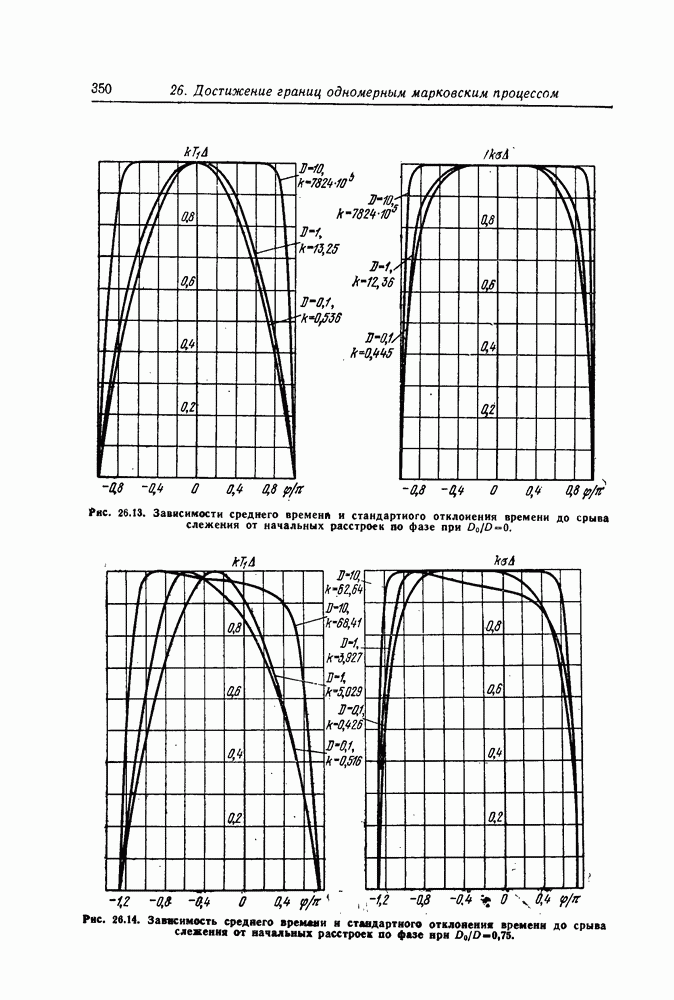
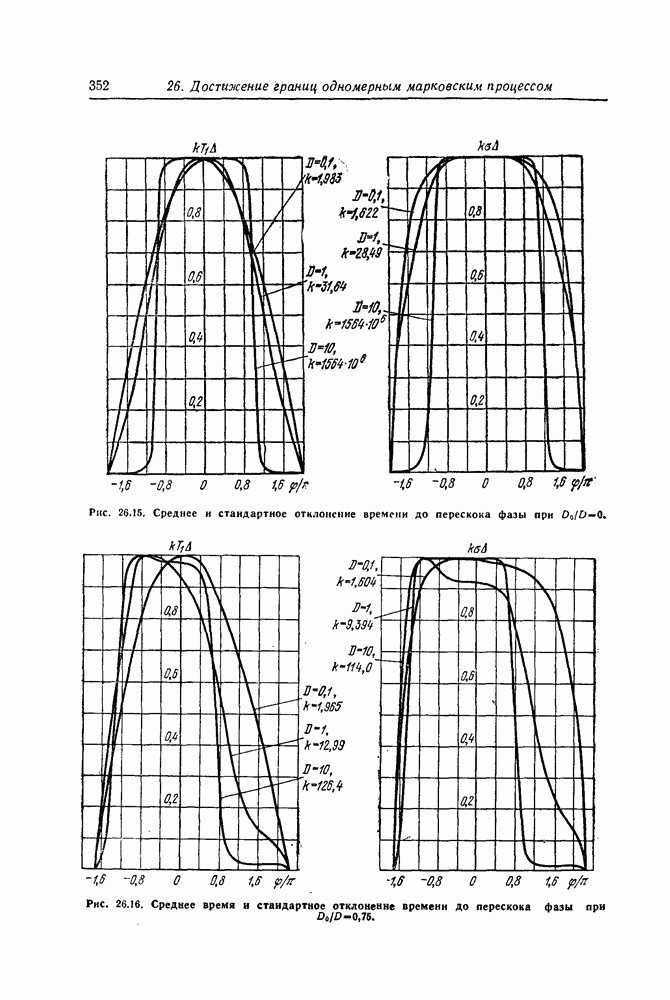
- 26. Достижение границ одномерным марковским процессом
- Вероятность достижения границы одномерным марковским процессом
- Связь уравнения Понтрягина с уравнением Фоккера — Планка — Колмогорова
- Плотность вероятности времени первого достижения границ
- Моменты времени первого достижения границ
- Уравнение восстановления. Определение длительности процедуры последовательного анализа
- Некоторые смежные вопросы
- 27. Достижение границ многомерным марковским процессом
- Уравнения Понтрягина
- Связь с уравнением Фоккера — Планка — Колмогорова
- 28. Срыв синхронизации в системах ФАП второго порядка
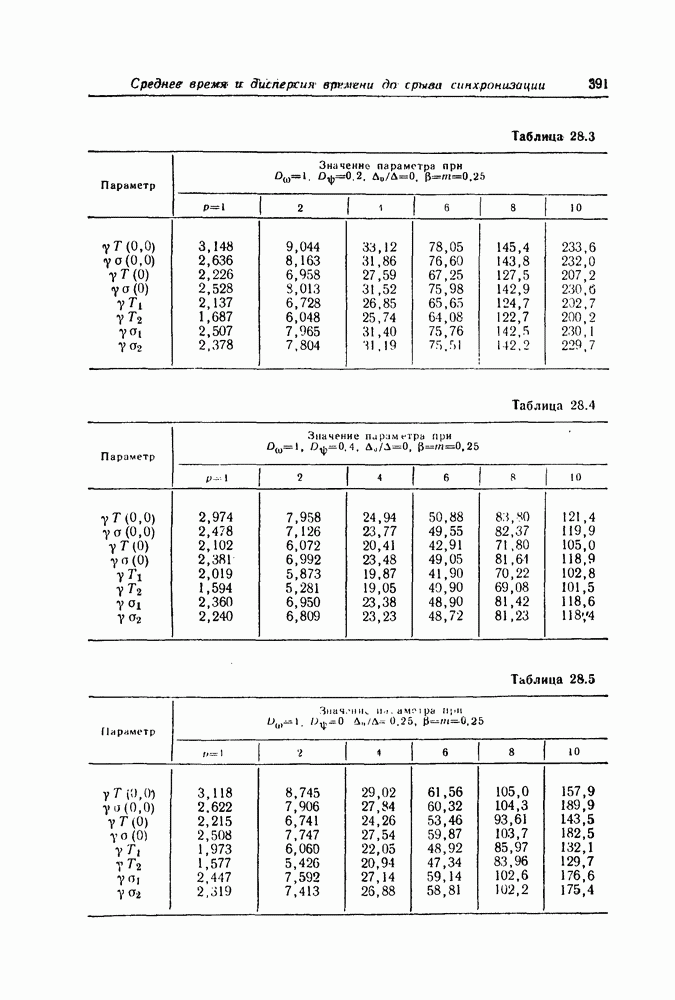
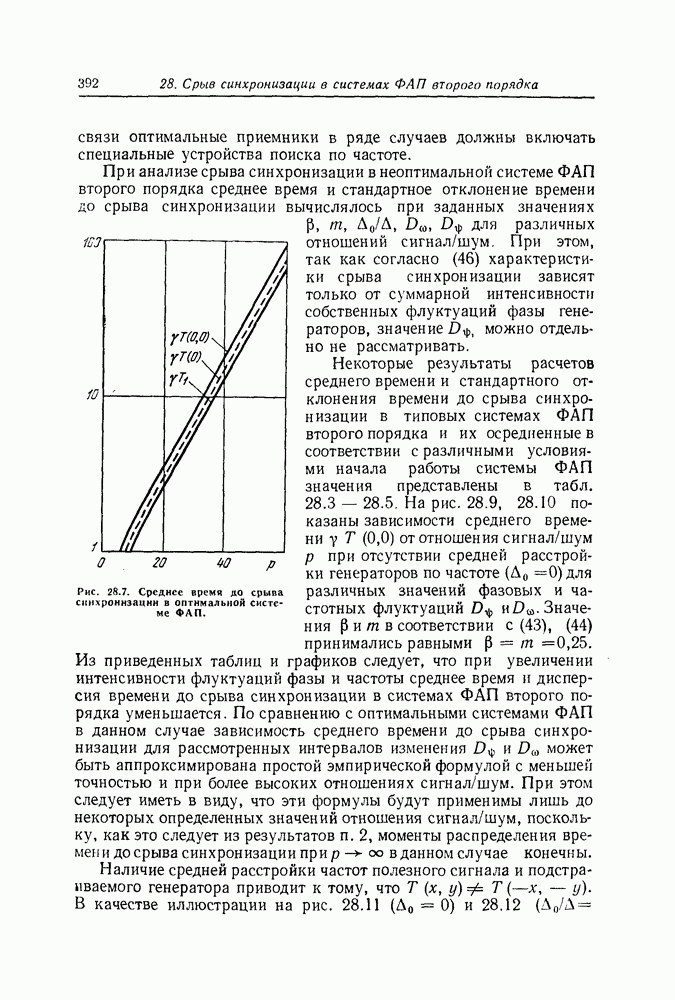
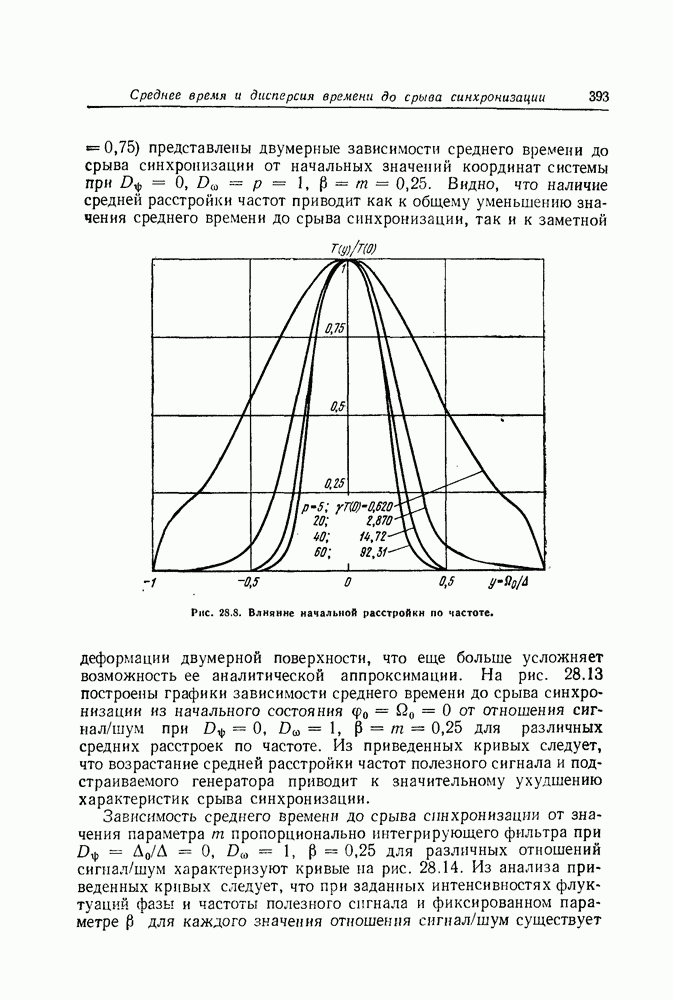
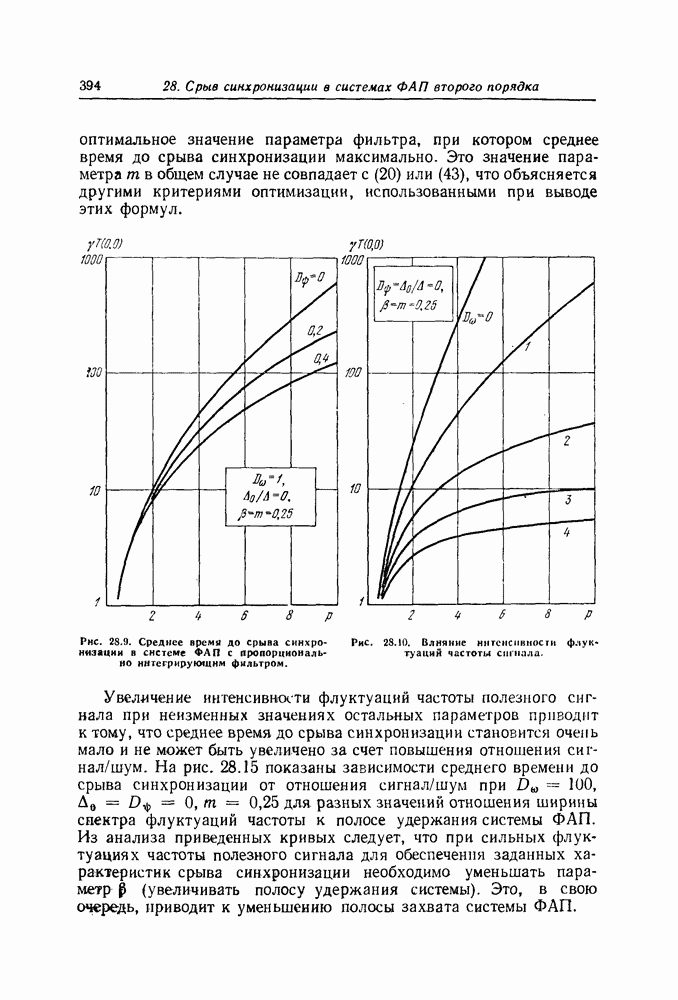
- Уравнение для моментов распределения времени до срыва синхронизации в оптимальных системах ФАП второго порядка
- Уравнение для моментов распределения времени до срыва синхронизации в обычных системах ФАП второго порядка
- Численный метод решения дифференциального уравнения в частных производных эллиптического типа
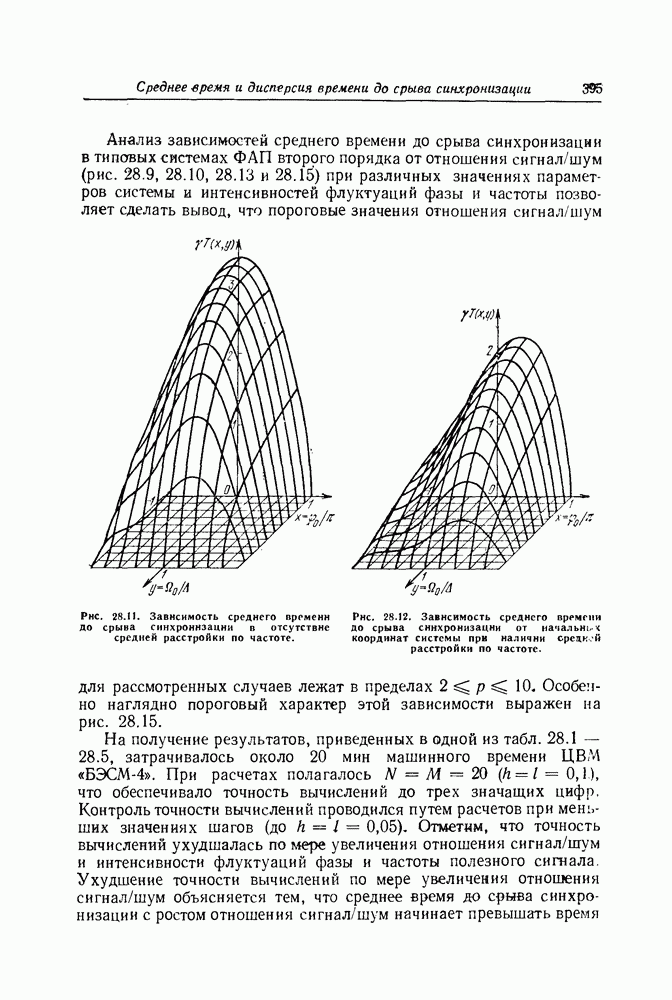
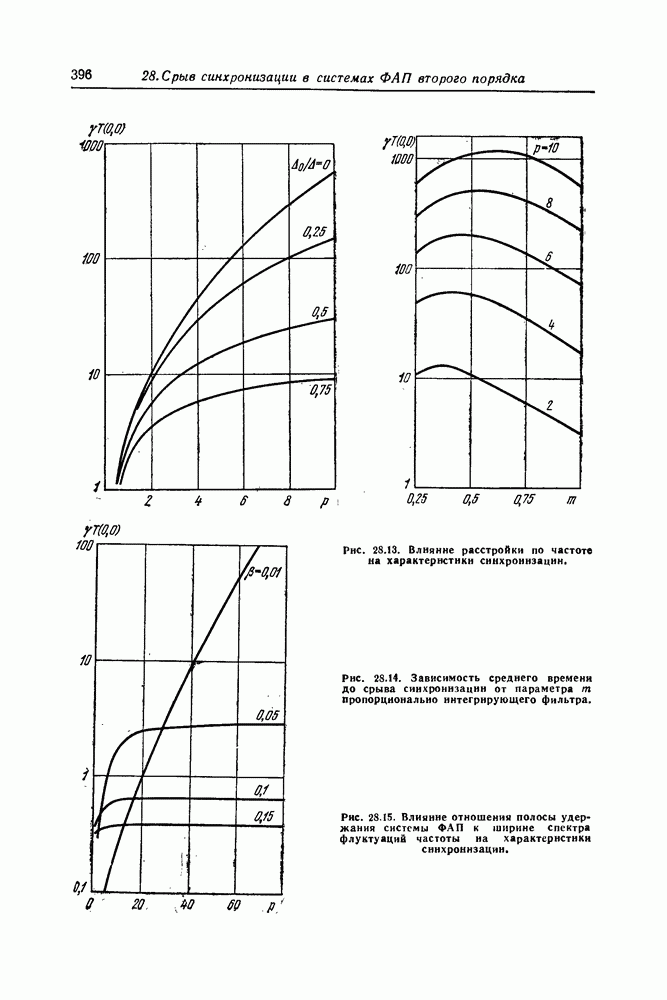
- Среднее время и дисперсия времени до срыва синхронизации в системах ФАП второго порядка
- 29. Общие сведения о случайных точечных процессах
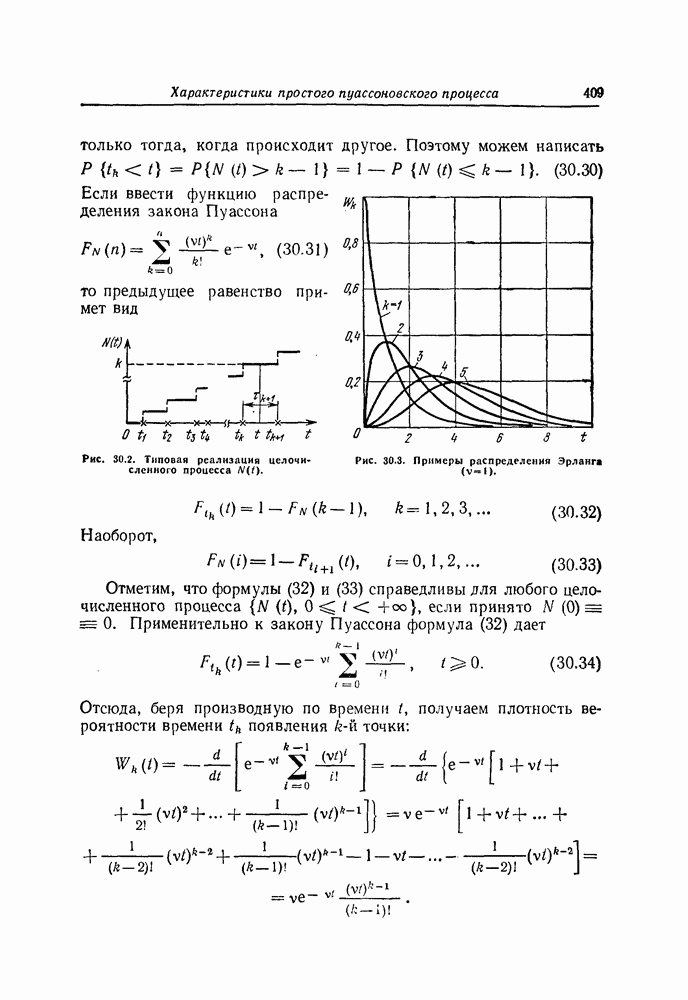
- 30. Пуассоновские процессы
- Обобщения процесса Пуассона
- Простейшие операции над пуассоновским процессом
- 31. Процессы восстановления
- Определение и классификация процессов восстановления
- Основные соотношения
- Функция восстановления
- Плотность восстановления
- Времена возвращения
- Наложение процессов восстановления
- 32. Профильтрованный пуассоповский процесс
- Приложение I. Сведения из теории матриц
- Приложение II. Основные теоремы о производящей функции
- Приложение III. Дельта-функция
- Список литературы