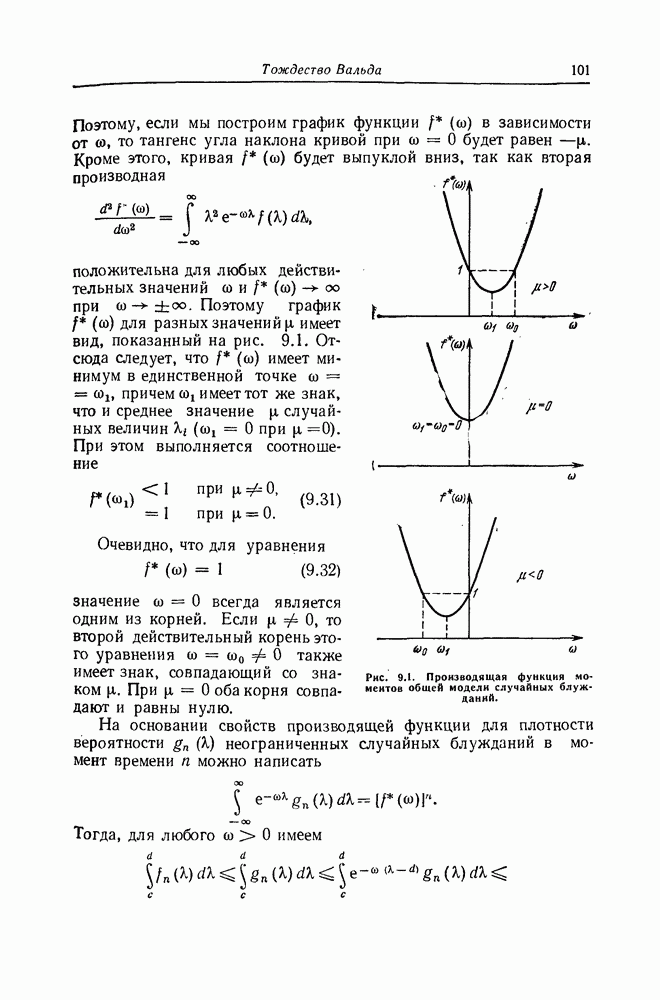
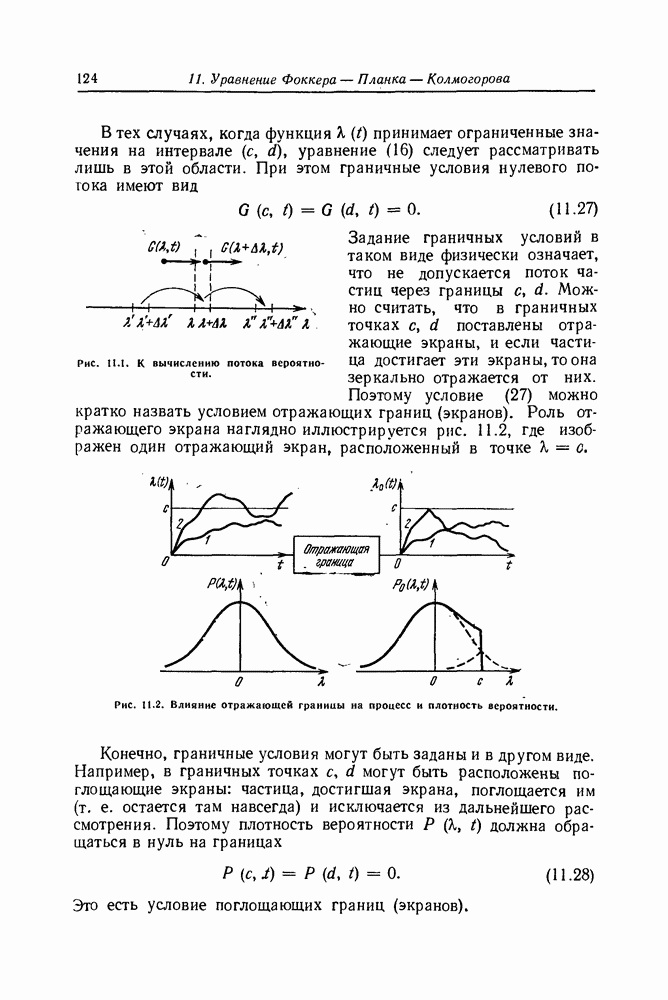
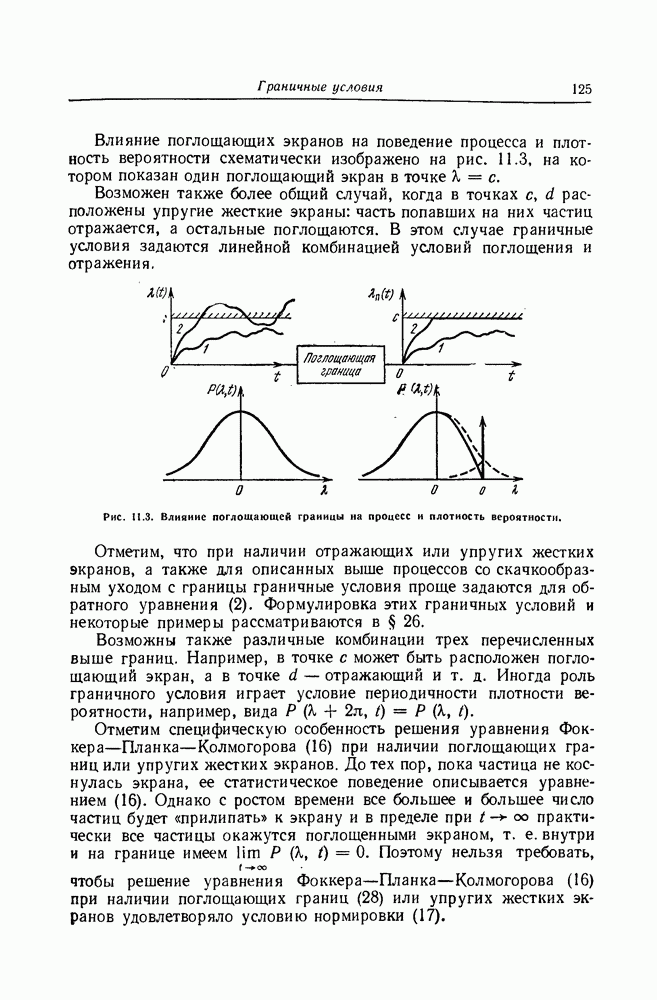
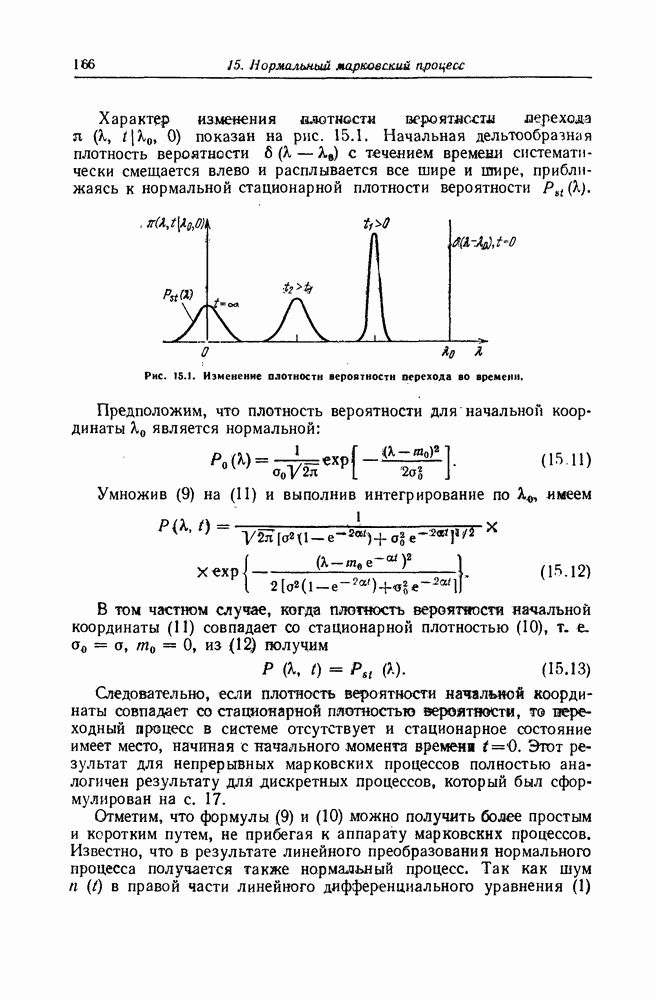
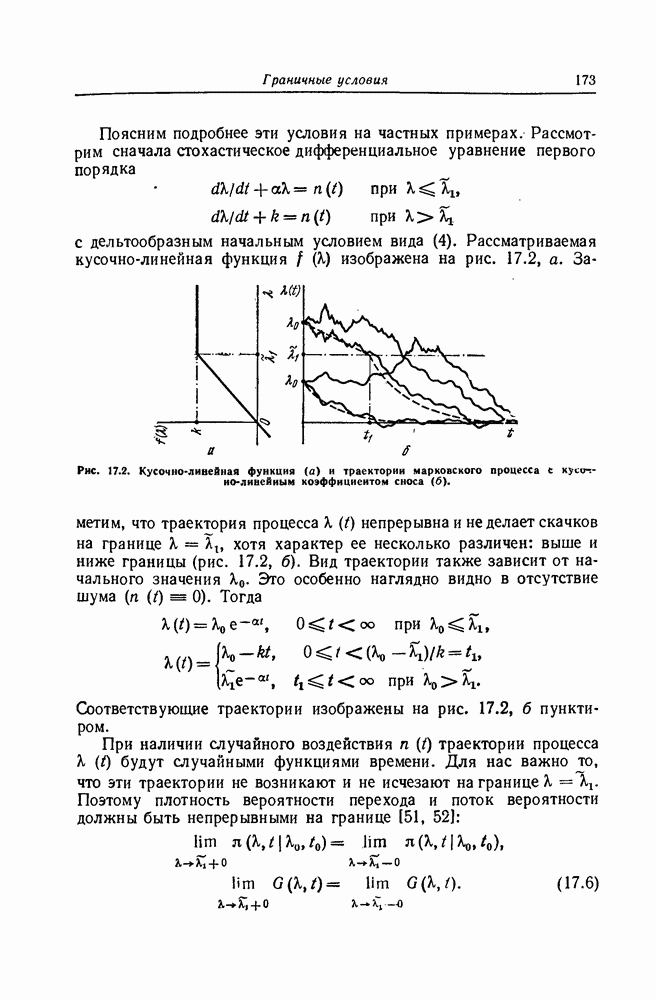
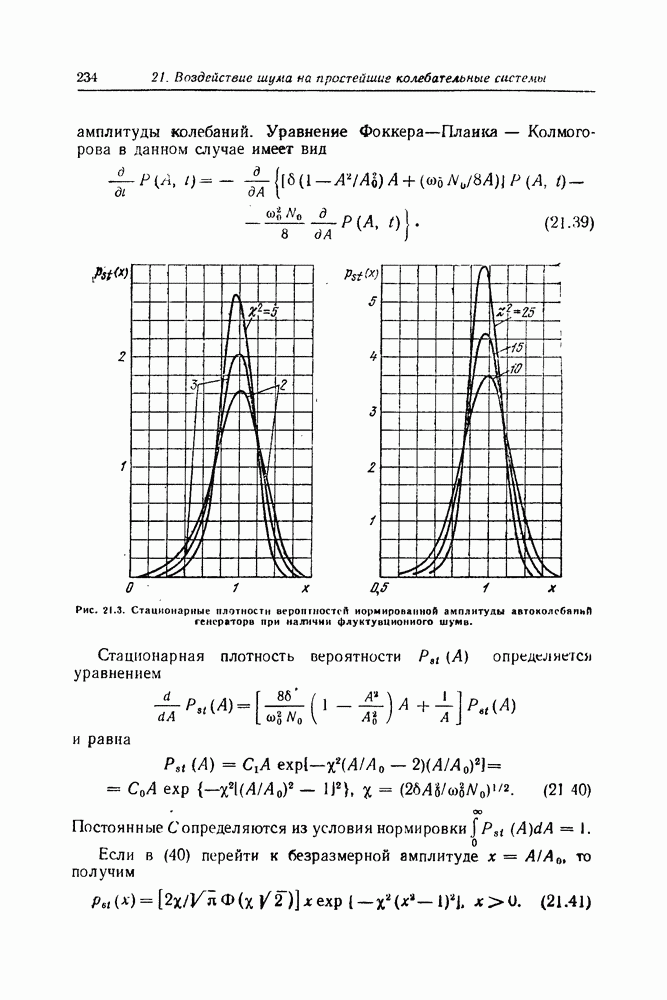
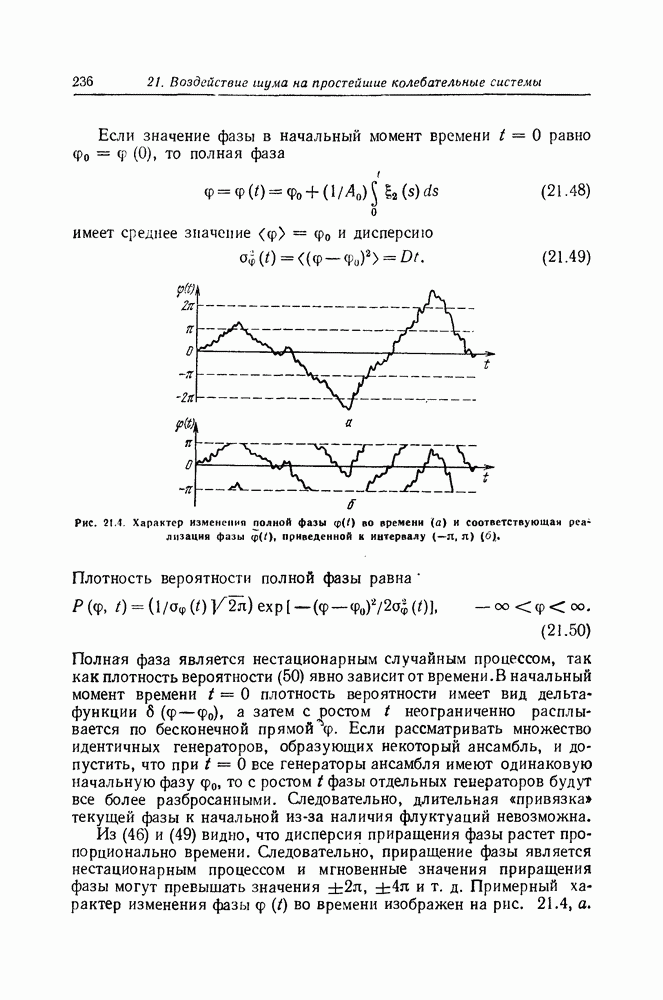
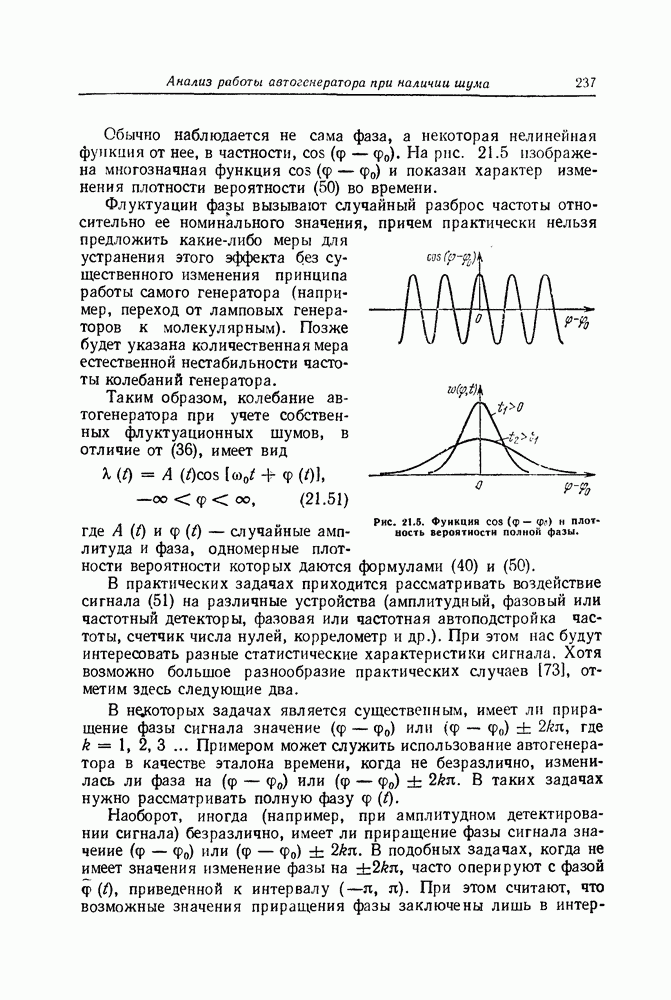
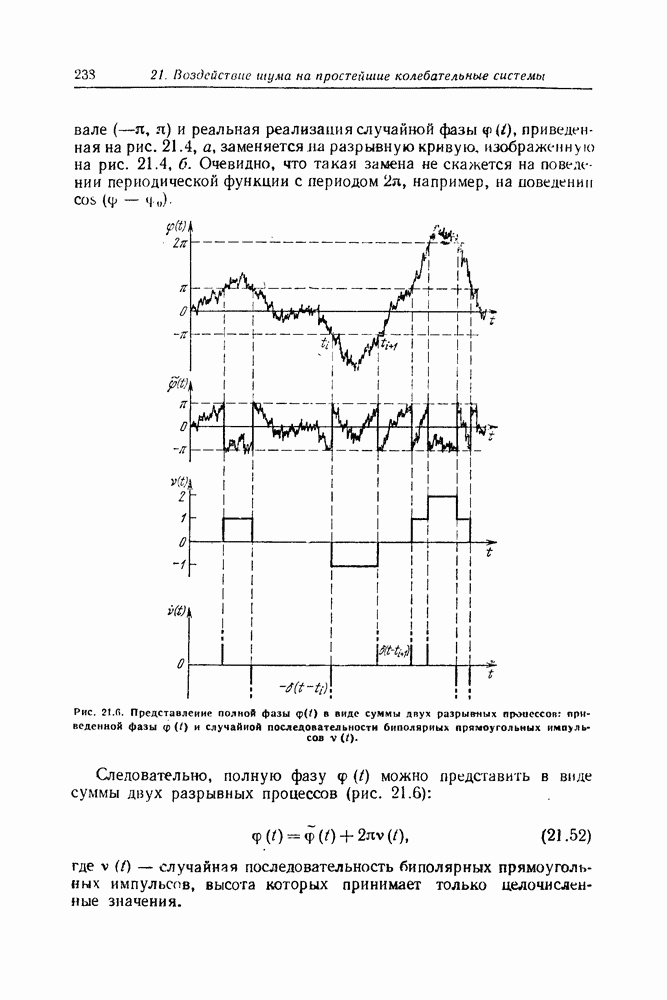
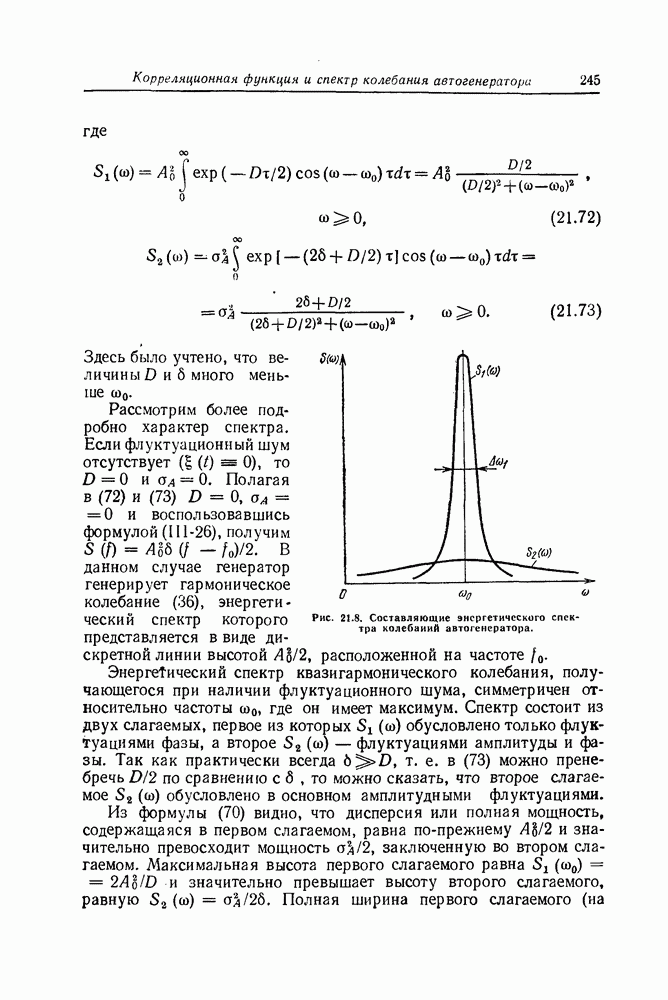
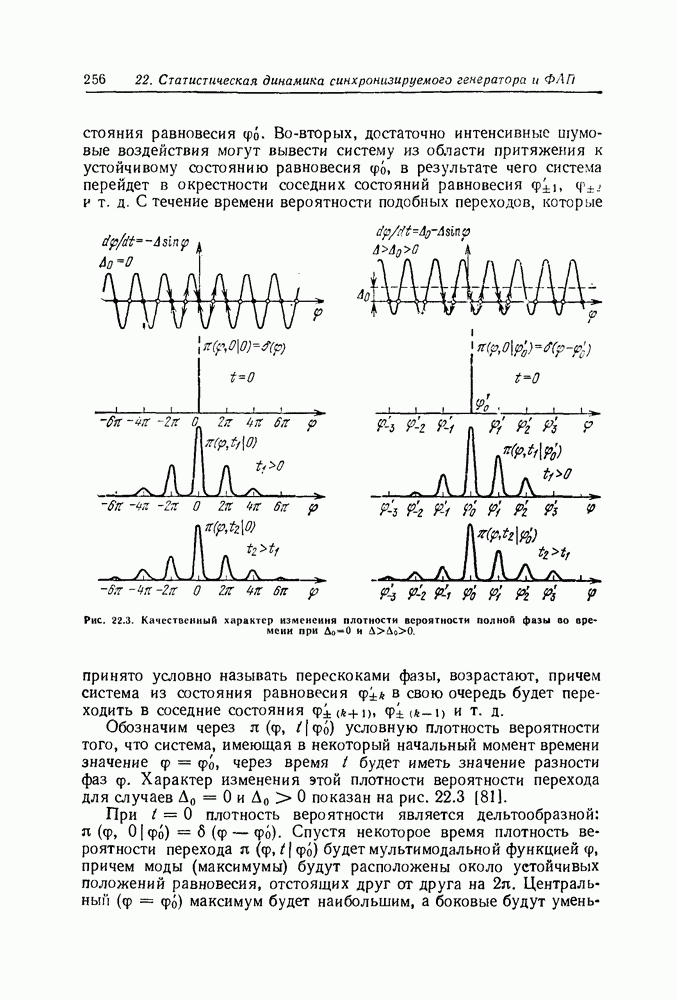
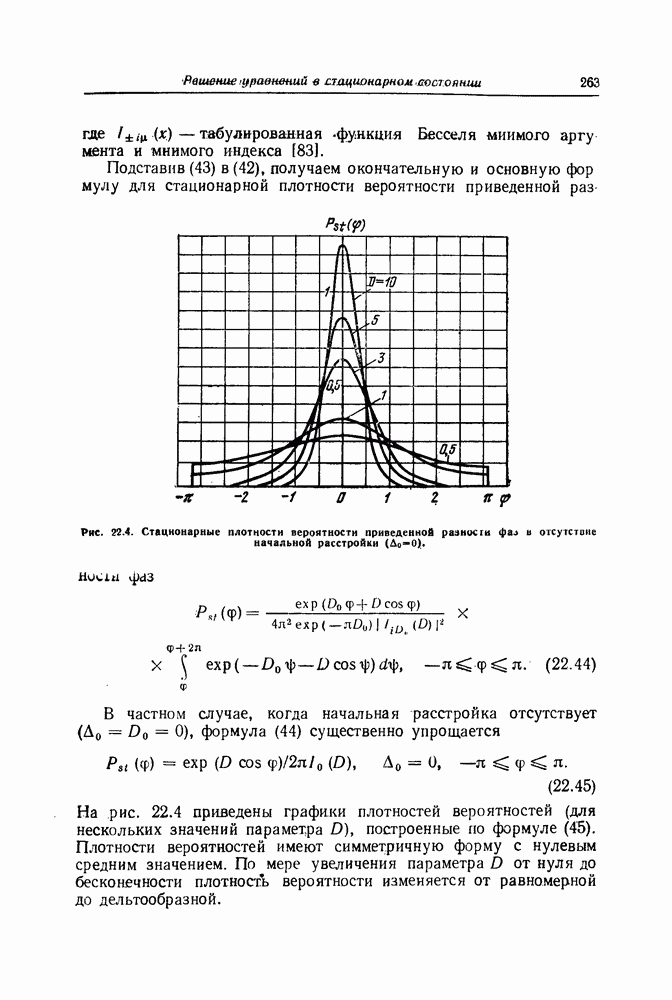
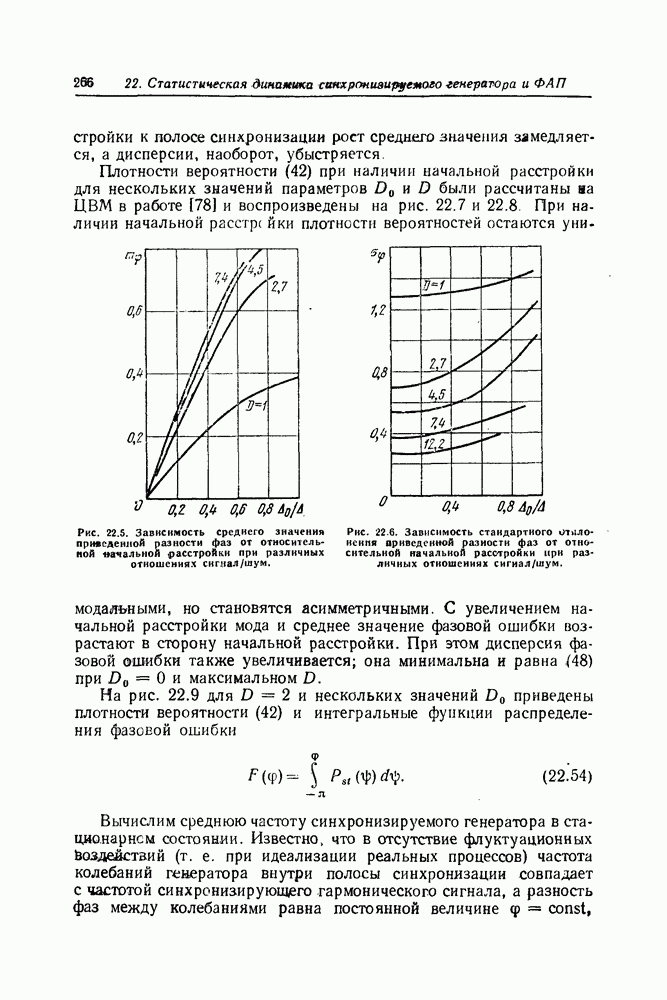
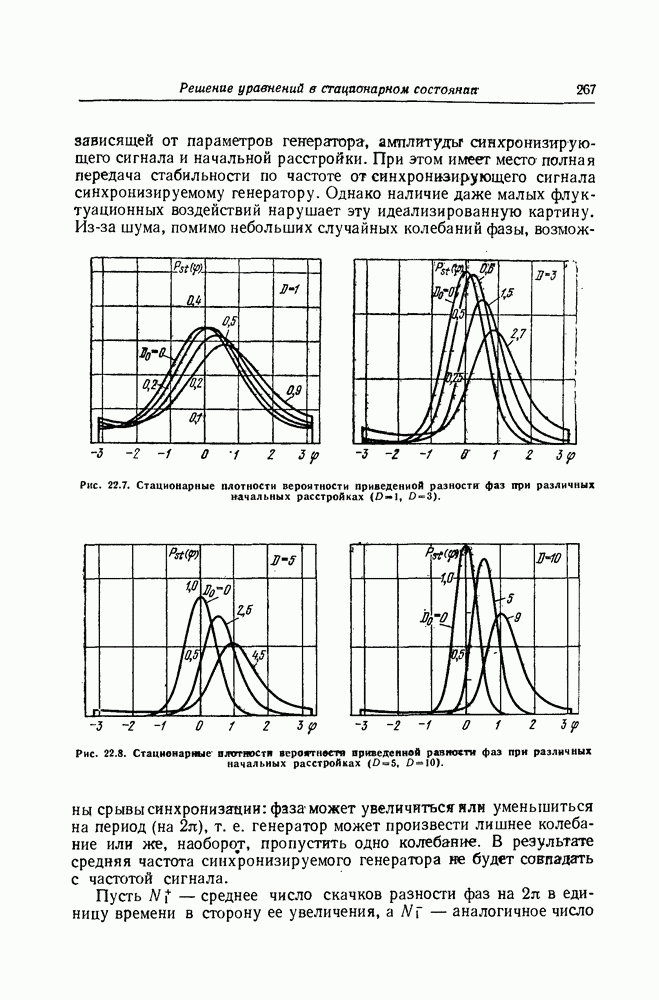
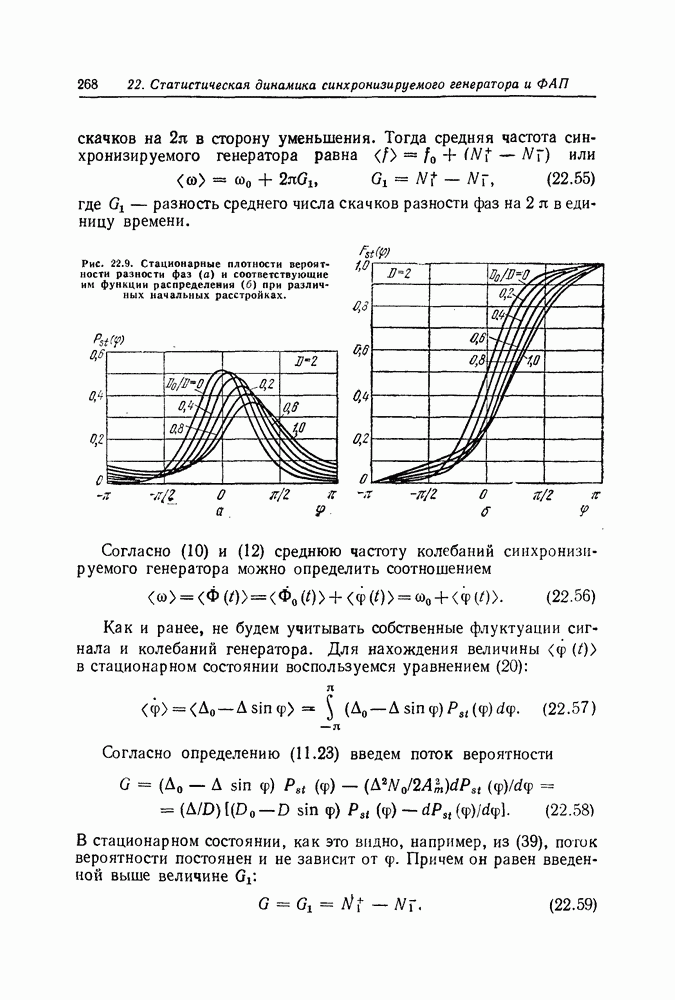
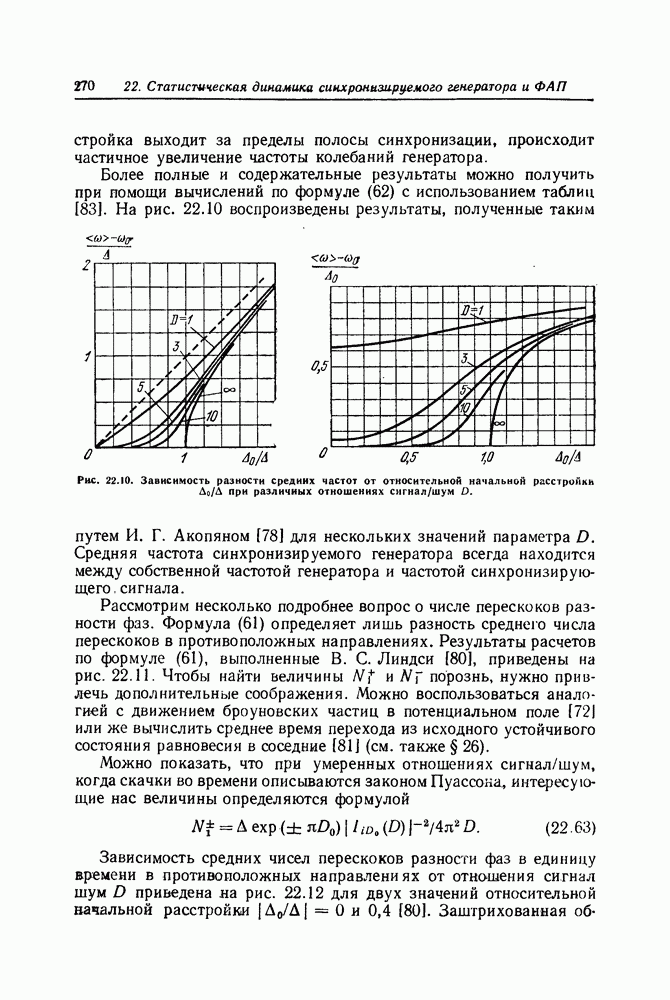
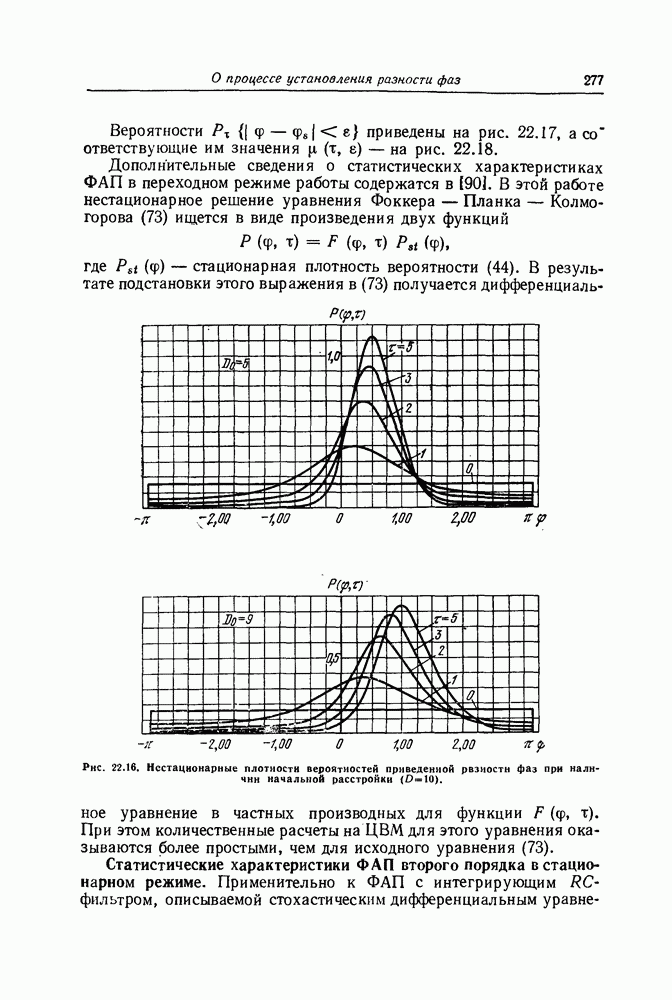
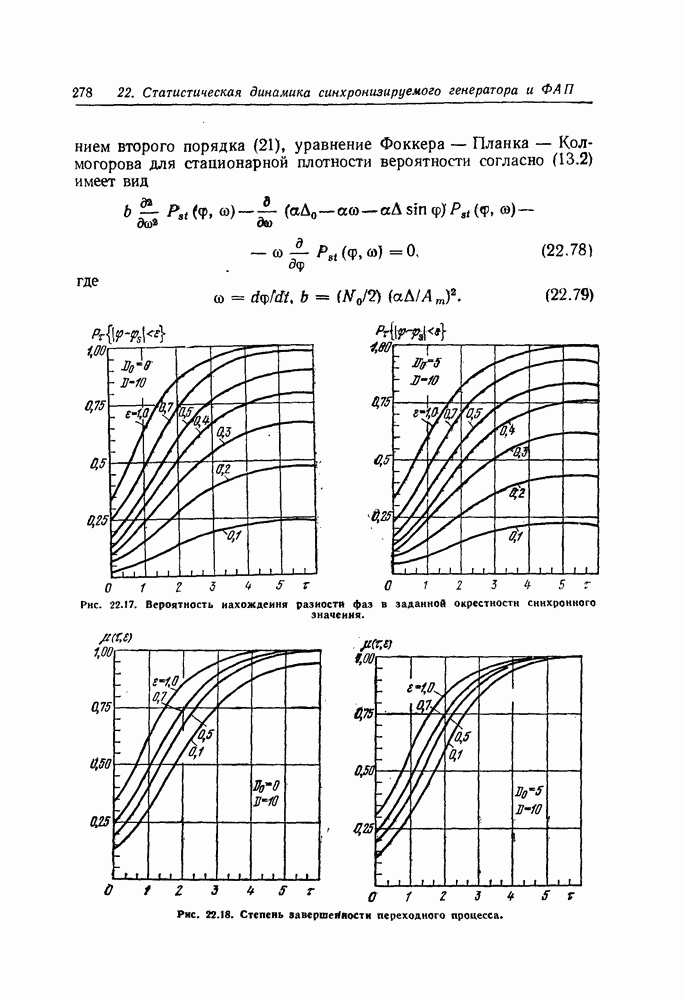
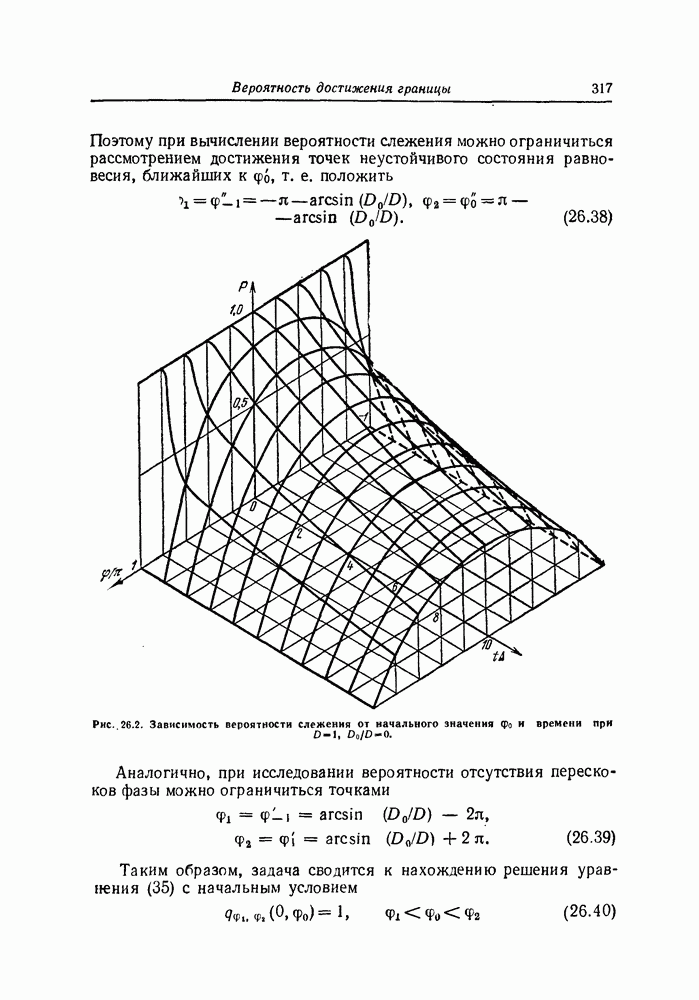
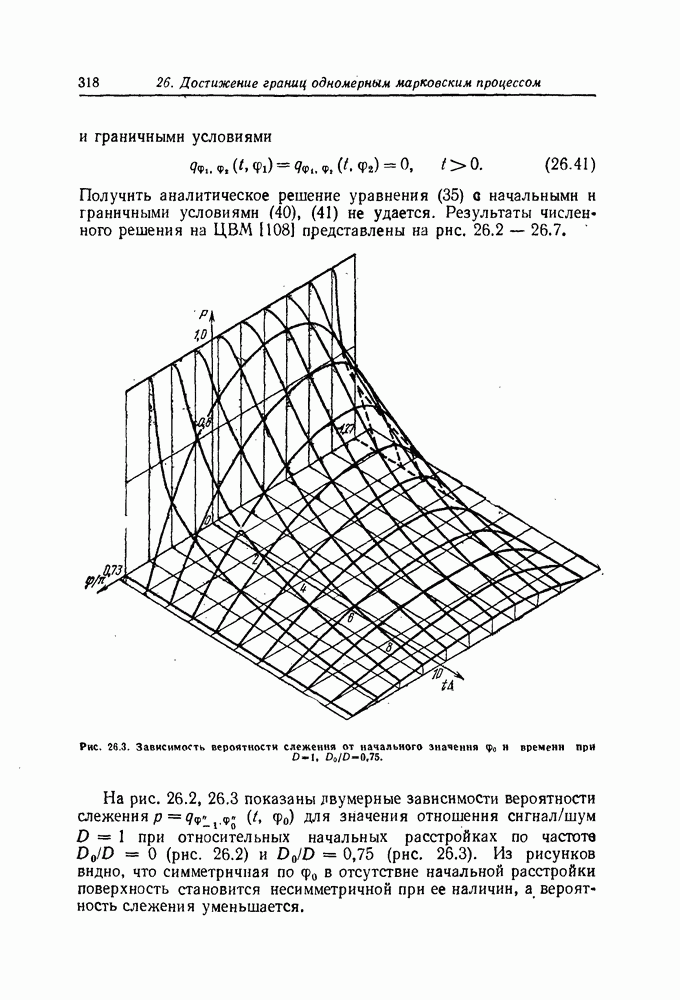
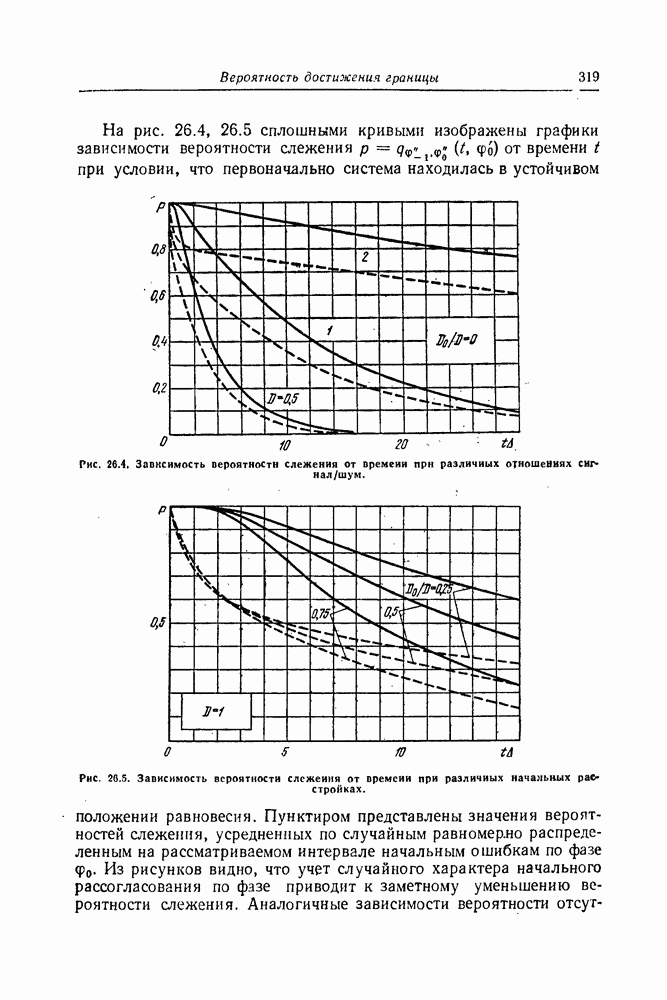
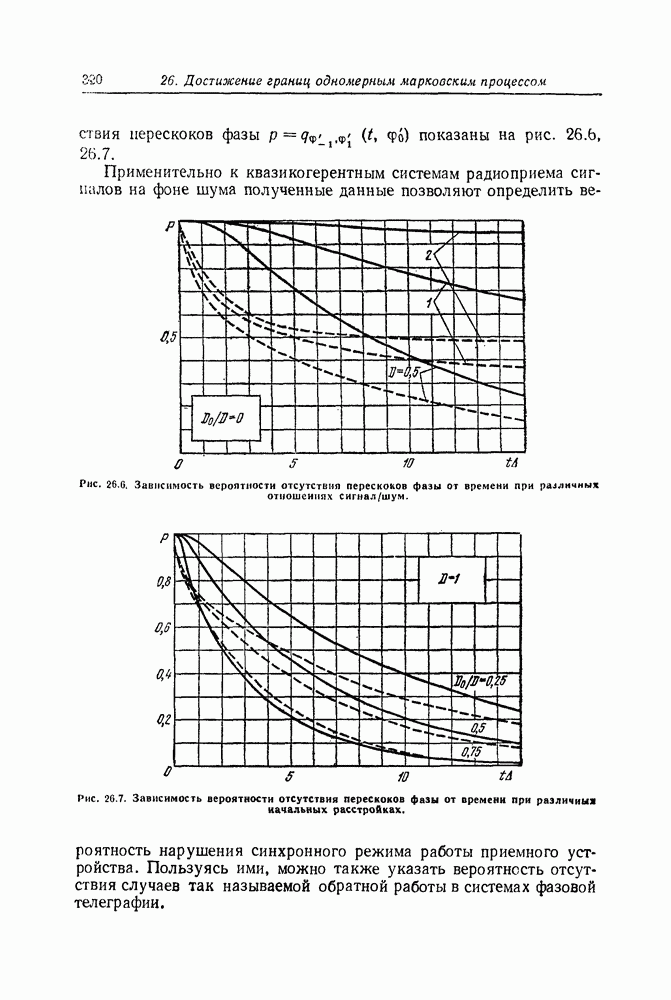
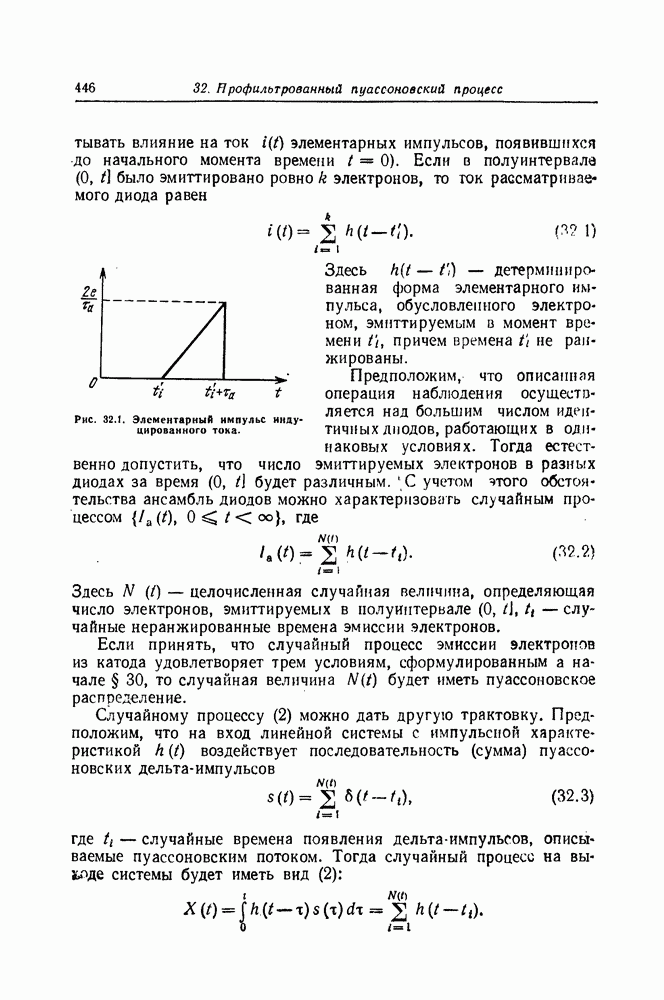
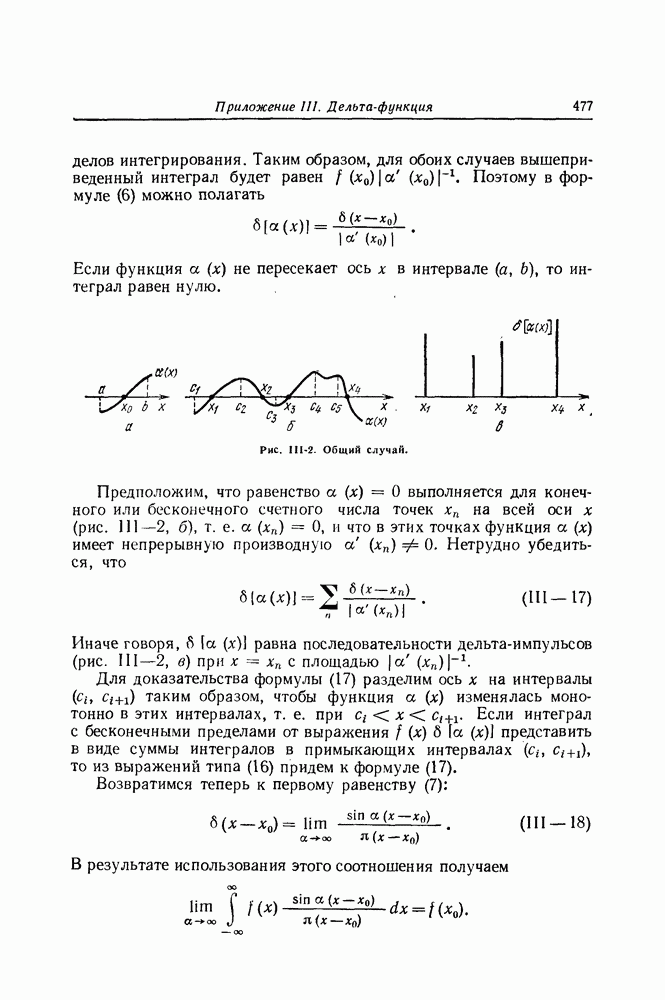
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Теорема Дуба и вычисление локальных характеристик марковского процесса
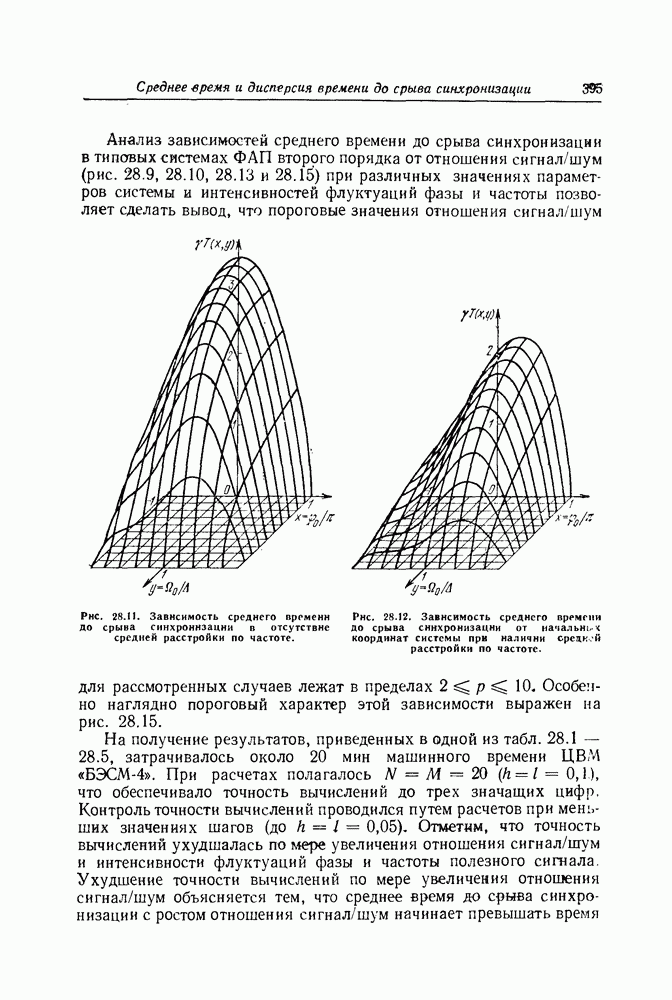
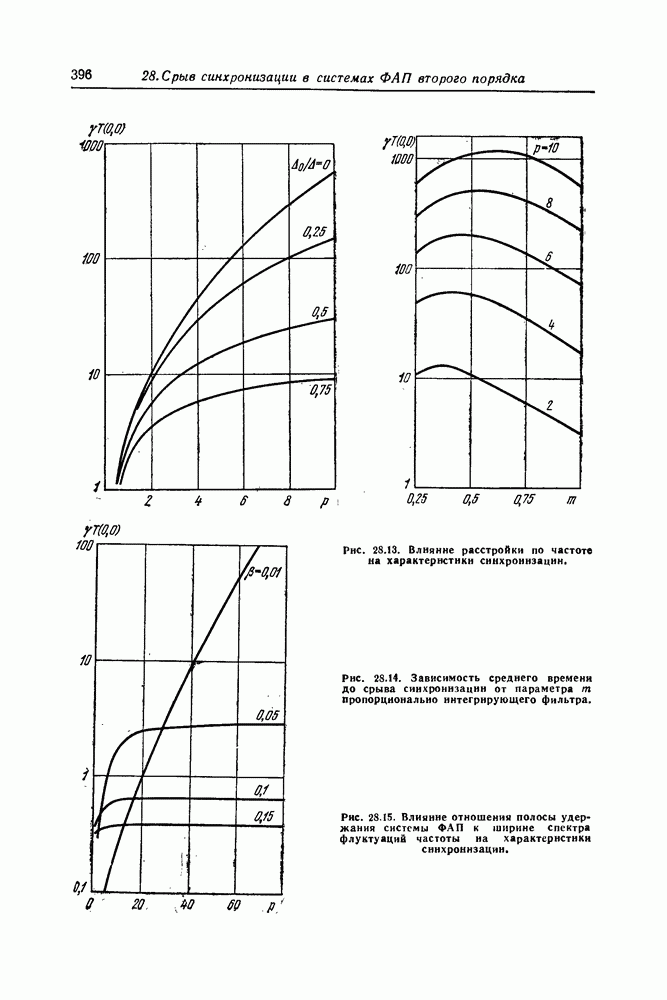
Из приведенных определений и свойств стохастических интегралов и дифференциалов следует, что при задании стохастических дифференциальных уравнений обязательно нужно указывать, в каком смысле понимаются соответствующие интегральные соотношения. В принятых обозначениях под обобщенным стохастическим дифференциальным уравнением для одномерного процесса  будем понимать уравнение вида
будем понимать уравнение вида

Для уравнения (31) можно указать еще две эквивалентные формы записи

При  из (31) следуют симметризованные стохастические уравнения (1), (3), (4), а при
из (31) следуют симметризованные стохастические уравнения (1), (3), (4), а при  стохастическое дифференциальное уравнение Ито (12) и соответствующие ему эквивалентные формы записи.
стохастическое дифференциальное уравнение Ито (12) и соответствующие ему эквивалентные формы записи.
Большой класс одномерных систем, выходные процессы которых являются марковскими диффузионными, определяются следующей теоремой Дуба [3].
Теорема 1. Случайный процесс  , заданный обобщенным стохастическим дифференциальным уравнением (37), является марковским.
, заданный обобщенным стохастическим дифференциальным уравнением (37), является марковским.
Строгое доказательство этой теоремы связано с некоторыми математическими тонкостями. Ограничимся формальным пояснением процедуры доказательства.
Возьмем три момента времени  и воспользуемся интегральной формой записи обобщенного стохастического дифференциального уравнения (31). Тогда можно написать
и воспользуемся интегральной формой записи обобщенного стохастического дифференциального уравнения (31). Тогда можно написать

Воспользовавшись свойством (28) стохастических интегралов, это равенство можно записать иначе:

Пользуясь независимостью приращений винеровского процесса, можно показать, что  при фиксированном
при фиксированном  не зависит от
не зависит от  и, следовательно, для плотности вероятности перехода будет выполняться равенство
и, следовательно, для плотности вероятности перехода будет выполняться равенство

Нетрудно убедиться в выполнении аналогичных равенств не только для трех, а для большего числа рассматриваемых моментов времени и прийти к окончательному заключению, что процесс  — марковский.
— марковский.
Известно, что всякий марковский процесс полностью описывается своими локальными характеристиками (см. § 11). Поэтому нужно знать правила вычисления этих характеристик по исходному стохастическому дифференциальному уравнению.
Из стохастического дифферециального уравнения Ито (12) и определения (11) следует
 (19.32)
(19.32)
Подставляя (32) в (11.10) и (11.11), усредняя полученные выражения при условии  с учетом (14.9) и переходя к пределу при
с учетом (14.9) и переходя к пределу при  , получим, что коэффициенты сноса и диффузии при задании стохастического дифференциального уравнения
, получим, что коэффициенты сноса и диффузии при задании стохастического дифференциального уравнения  определяются соотношениями
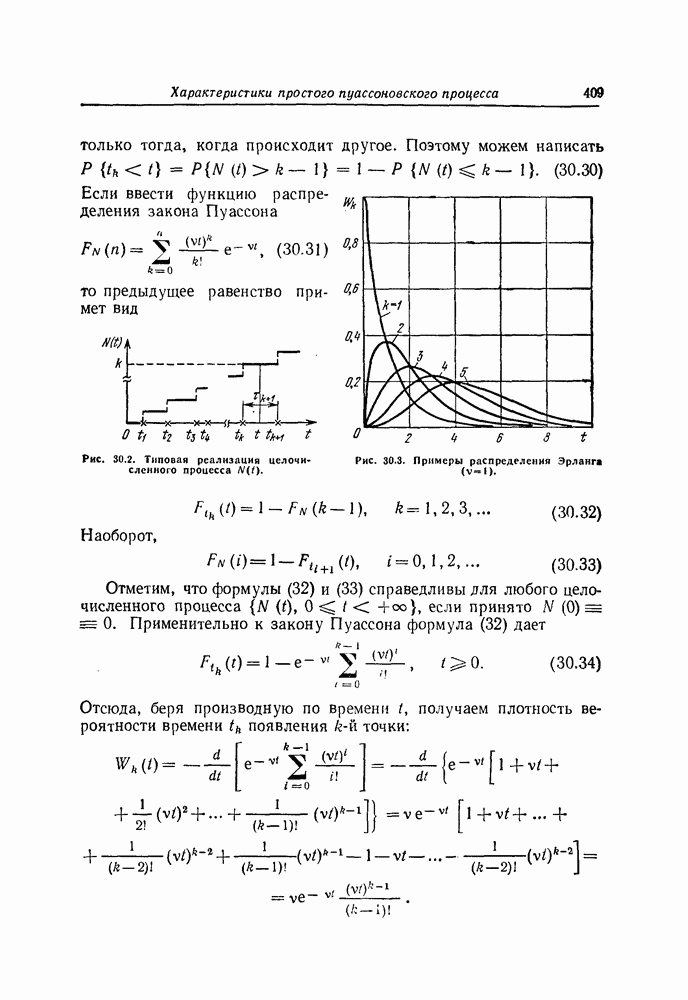
определяются соотношениями
 (19.33)
(19.33)
Для обобщенного стохастического дифференциального уравнения (31), воспользовавшись (26), можно написать

Аналогично (33), отсюда следует, что для обобщенного стохастического дифференциального уравнения (31) локальные характеристики марковского процесса  имеют вид
имеют вид
 (19.34)
(19.34)
Сравнивая (33) и (34), можно заметить, что от того, в каком смысле понимается стохастическое дифференциальное уравнение, зависит только коэффициент сноса  .
.
Следующая основная теорема Дуба [3] определяет важный класс многомерных систем, процессы в которых являются диффузионными марковскими.
Теорема 2. Пусть векторный случайный процесс  задан системой обобщенных стохастических дифференциальных уравнений
задан системой обобщенных стохастических дифференциальных уравнений

где  и
и  — непрерывно дифференцируемые детерминированные функции, удовлетворяющие условию Липшица,
— непрерывно дифференцируемые детерминированные функции, удовлетворяющие условию Липшица,  — независимые винеровские процессы с известными статистическими характеристиками
— независимые винеровские процессы с известными статистическими характеристиками

 — символ Кронекера.
— символ Кронекера.
Тогда многомерный случайный процесс  является марковским.
является марковским.
Формальное доказательство этой, теоремы полностью аналогично одномерному случаю, рассмотренному выше.
Заметим, что задание статистических характеристик винеровских процессов (36) эквивалентно заданию вектора белого шума с нулевым средним значением и корреляционными функциями

Повторяя рассуждения, использованные при выводе (33) и (34), можно показать, что для локальных характеристик многомерного марковского процесса  , заданного обобщенными стохастическими дифференциальными уравнениями (35), имеют место равенства
, заданного обобщенными стохастическими дифференциальными уравнениями (35), имеют место равенства
 (19.37)
(19.37)
В частности, для симметриэованных стохастических дифференциальных уравнений

из (37) следует

Для стохастических дифференциальных уравнений Ито

локальные характеристики марковского процесса  определяются соотношениями
определяются соотношениями
 (19.41)
(19.41)
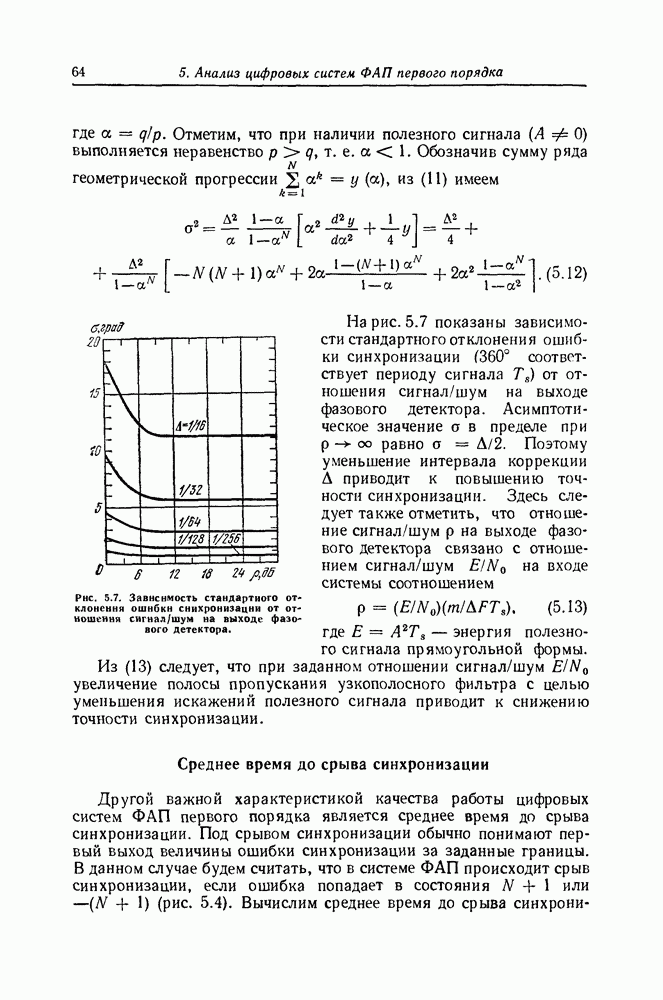
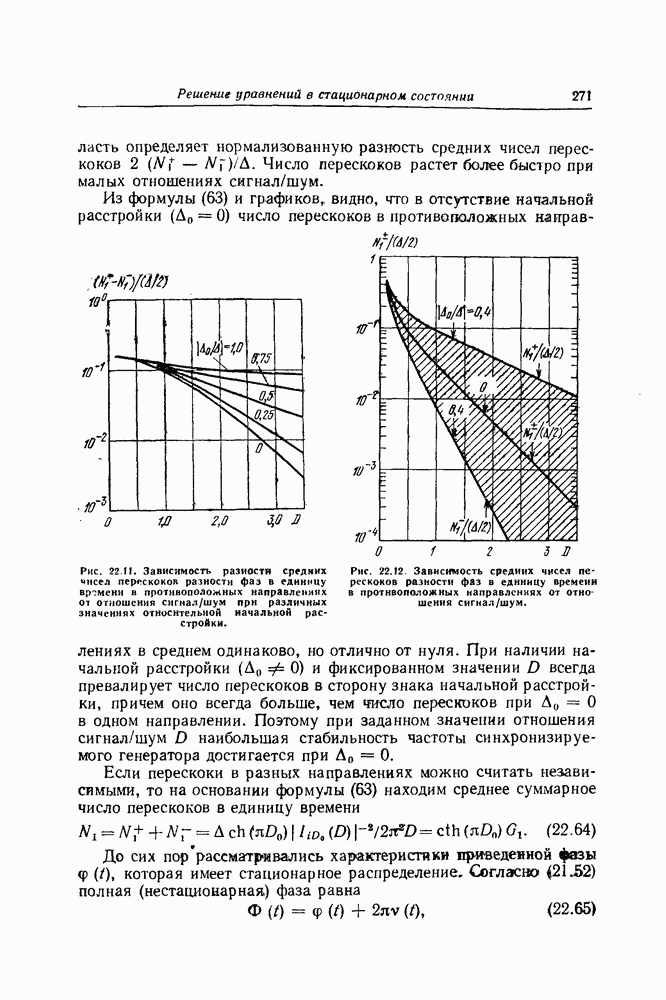
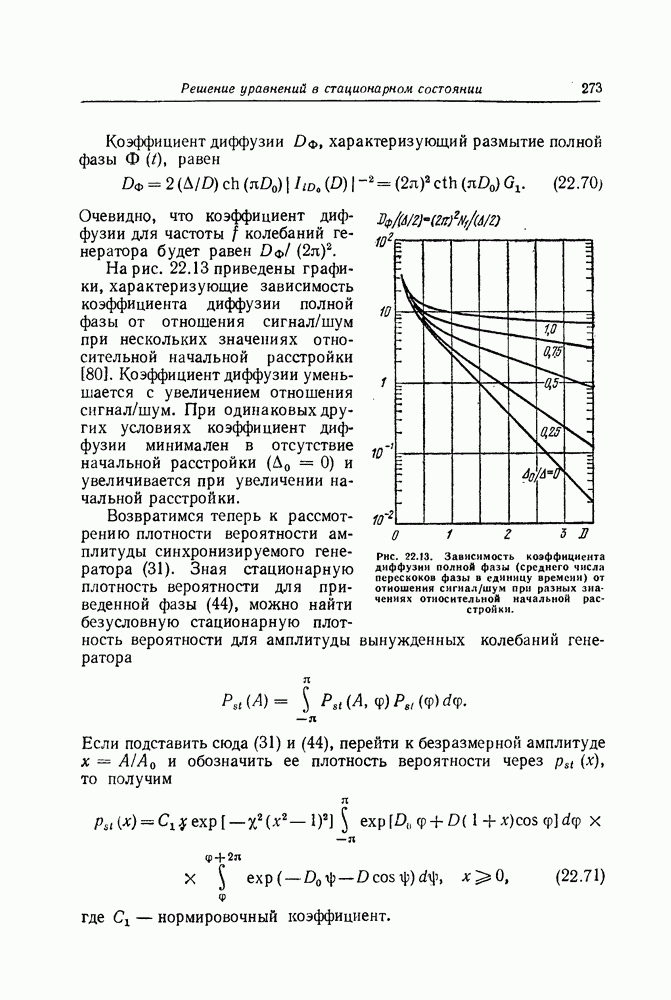
Стохастические дифференциальные уравнения, записанные в симметризованной форме, можно интерпретировать как предел уравнений, записанных для иемарковскнх (но близких к марковским) процессов [57]. В технических задачах входные воздействия обычно представляют собой достаточно гладкие (дифференцируемые) случайные процессы с ограниченной дисперсией. При описании статистической динамики систем, на вход которых действует широкополосный процесс, он приближенно заменяется нормальным белым шумом (см. § 20). Это означает, что стохастические дифференциальные уравнения, описывающие поведение подобных систем, должны пониматься в симметризованном смысле, так как они должны быть устойчивы к такому предельному переходу. При необходимости использования другой формы записи этих уравнений переход к этой форме записи осуществляется следующим образом: сначала по виду (38) при помощи (39) вычисляются локальные характеристики марковского процесса  ; после этого по формулам (37) или (41) определяются значения коэффициентов уравнений (35) или (40). Обратно, если необходимо практически реализовать динамическую систему, описываемую уравнением (35) или (40), сначала необходимо записать эти уравнения в симметризованной форме. Имея это в виду, будем в дальнейшем оперировать, как правило, только с симметрнзованными стохастическими дифференциальными уравнениями и называть их просто стохастическими дифференциальными уравнениями.
; после этого по формулам (37) или (41) определяются значения коэффициентов уравнений (35) или (40). Обратно, если необходимо практически реализовать динамическую систему, описываемую уравнением (35) или (40), сначала необходимо записать эти уравнения в симметризованной форме. Имея это в виду, будем в дальнейшем оперировать, как правило, только с симметрнзованными стохастическими дифференциальными уравнениями и называть их просто стохастическими дифференциальными уравнениями.
Применительно к стохастическому дифференциальному уравнению (1) по формулам (34) находим коэффициенты сноса и диффузии
 (19.42)
(19.42)
При этом уравнение Фоккера—Планка—Колмогорова (11.16) принимает вид

Если коэффициенты  и
и  не зависят от времени, причем
не зависят от времени, причем  , то при граничных условиях нулевого потока вида (11.26) стационарная плотность вероятности
, то при граничных условиях нулевого потока вида (11.26) стационарная плотность вероятности  определяется обыкновенным линейным дифференциальным уравнением первого порядка
определяется обыкновенным линейным дифференциальным уравнением первого порядка

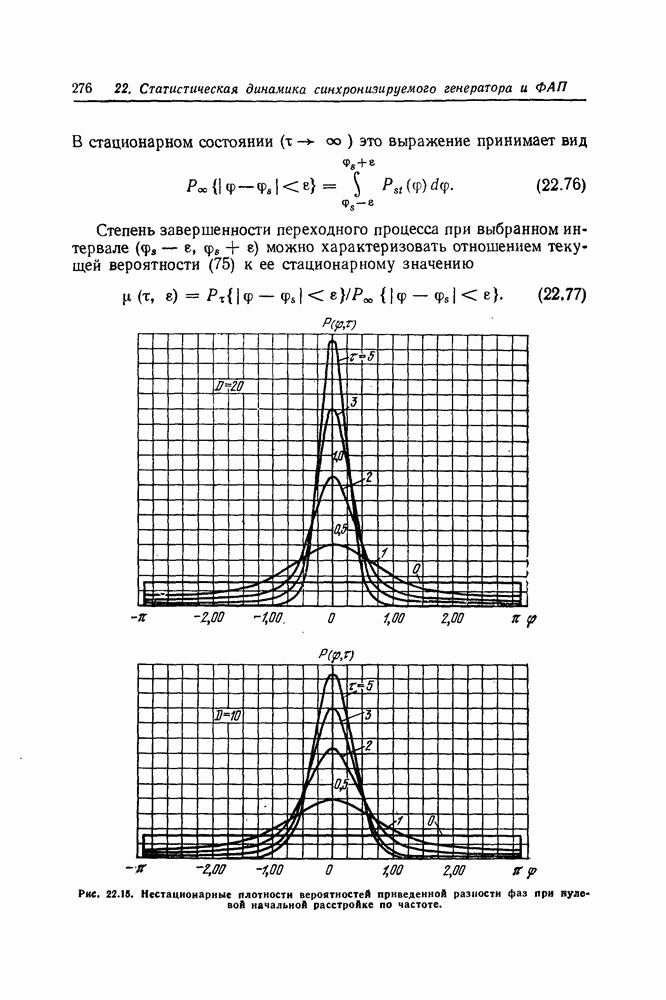
Решение этого уравнения дается выражением
 (19.45)
(19.45)
Такой же результат следует непосредственно из формулы (12.4).
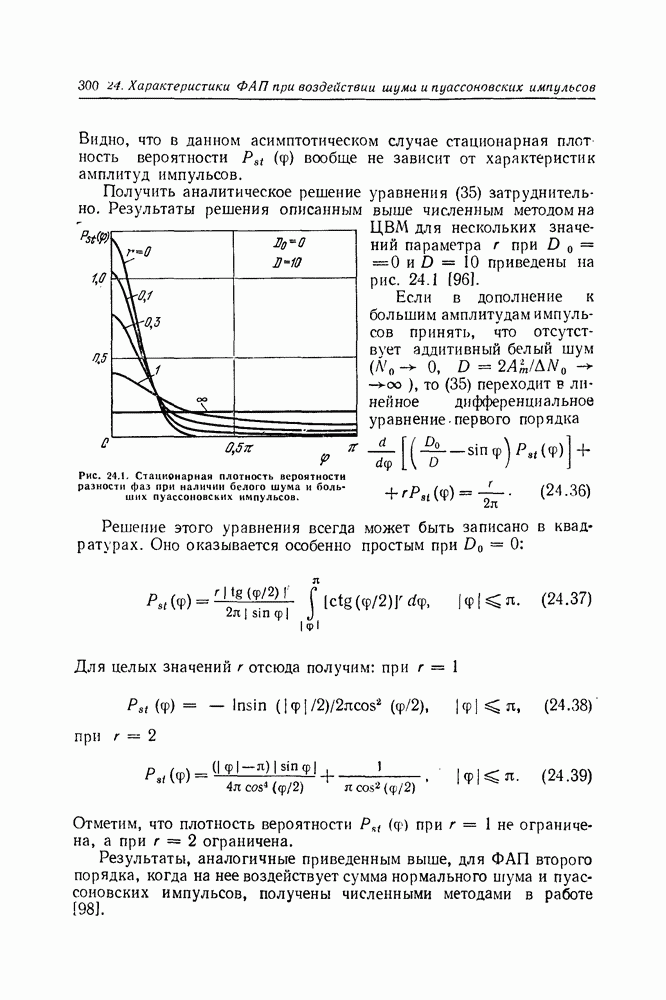
Отметим, что если ограничиться стохастическими уранениями типа  можно решить обратную задачу: по заданному уравнению Фоккера—Планка—Колмогорова (43) можно найти исходное стохастическое дифференциальное уравнение для процесса
можно решить обратную задачу: по заданному уравнению Фоккера—Планка—Колмогорова (43) можно найти исходное стохастическое дифференциальное уравнение для процесса  [2]. В этом смысле стохастическое уравнение (1) и уравнение Фоккера—Планка—Колмогорова (43) можно назвать статистически эквивалентными.
[2]. В этом смысле стохастическое уравнение (1) и уравнение Фоккера—Планка—Колмогорова (43) можно назвать статистически эквивалентными.
Действительно, разрешая соотношения (42) относительно  и
и  , находим
, находим
 (19.46)
(19.46)
Поэтому исходное дифференциальное уравнение можно записать через коэффициенты сноса и диффузии

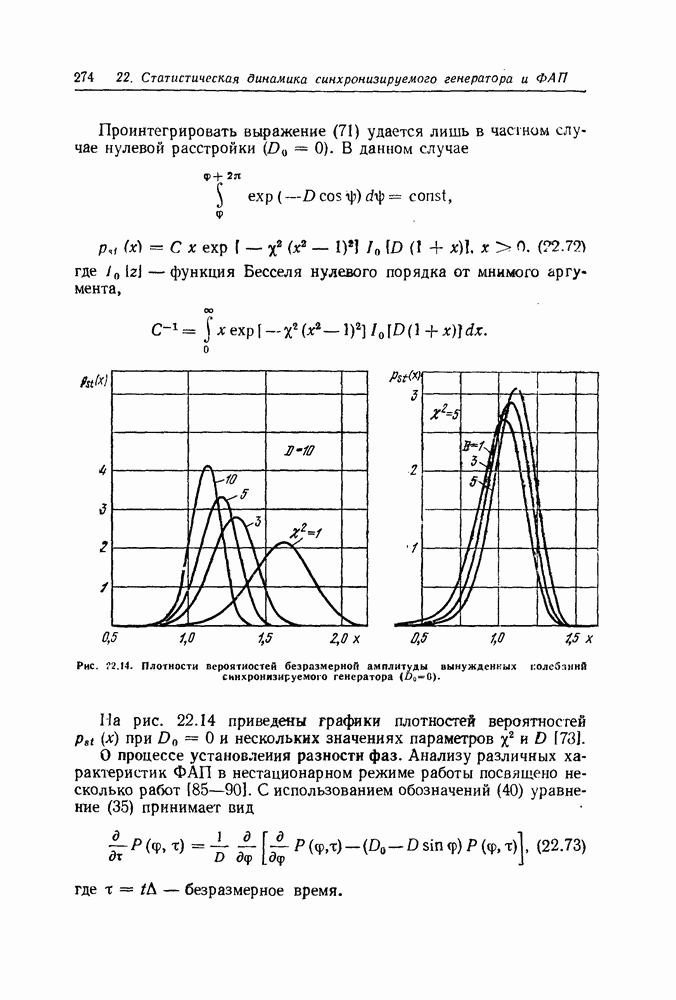
Пример 2. Плотность вероятности Накагами [30]. Рассмотрим нелинейное стохастическое дифференциальное уравнение
 (19.48)
(19.48)
где m и  - постоянные параметры.
- постоянные параметры.
Из сопоставления (48) с (1) следует, что

Подстановка этих выражений в формулу (45) дает

Воспользовавшись известным интегралом [19]

где  — гамма-функция, из условия нормировки определяем постоянную С:
— гамма-функция, из условия нормировки определяем постоянную С:

Теперь записываем окончательное выражение для плотности вероятности Накагами
 (19.49)
(19.49)
Плотность вероятности Накатами (49) часто используется для описания амплитудных замираний радиосигнала, прошедшего через турбулентную среду.
Пример 3. Релеевская плотность вероятности. Пусть задано нелинейное стохастическое дифференциальное уравнение
 (19.50)
(19.50)
В частности, таким уравнением описывается огибающая случайного процесса на выходе колебательного контура, когда на него воздействует белый шум, причем в этом случае  есть затухание контура [64].
есть затухание контура [64].
Согласно (42) имеем

и уравнение (43) принимает вид

Из (45) получаем стационарную плотность вероятности

Плотность вероятности (51) называется релеевской. Она часто применяется для моделирования амплитудных флуктуации отраженных сигналов в радиолокации.
Пример 4. Рассмотрим подробно нелинейное стохастическое дифференциальное уравнение первого порядка более общее, чем (50) [2,65].

Это уравнение переходит в (50) при частном значении  . В данном случае коэффициенты сноса и диффузии
. В данном случае коэффициенты сноса и диффузии

не зависят от времени. Обозначив согласно (10.10) плотность вероятности перехода из точки  в точку
в точку  за время
за время  через
через  , запишем прямое уравнение (11.1):
, запишем прямое уравнение (11.1):

Решим это уравнение методом разделения переменных при дельтообразном начальном и поглощающих граничных условиях:
 (19.54)
(19.54)
 (19.55)
(19.55)
На основании формулы (45) записываем стационарную плотность вероятности

где
 (19.56)
(19.56)
Воспользовавшись значениями гамма-функции  , нетрудно проверить, что из (56) при
, нетрудно проверить, что из (56) при  получаем одностороннюю нормальную плотность вероятности, а при
получаем одностороннюю нормальную плотность вероятности, а при  — плотность вероятности Релея (51).
— плотность вероятности Релея (51).
Если в (53) положить  (см. (12.8) и далее), то получим
(см. (12.8) и далее), то получим
 (19.58)
(19.58)
Обозначив собственные функции уравнения (59), соответствующие собственным значениям  через
через  , запишем решение в виде (12.17)
, запишем решение в виде (12.17)

Предполагается, что собственные функции ортонормированы, т. е. удовлетворяют условию (12.15).
Перейдем в уравнении (59) к новым переменным

В результате получим уравнение гипергеометрического типа

Собственным значениям  этого уравнения соответствуют собственные функции
этого уравнения соответствуют собственные функции

где

— полиномы Лагерра.
Возвращаясь к первоначальным переменным и используя условие (12.15), получим следующее выражение для ортонормированных собственных функций

Окончательное выражение для плотности вероятности перехода получаем подстановкой (61) в (60):

Учитывая равенство  , отсюда находим стационарную плотность вероятности (56):
, отсюда находим стационарную плотность вероятности (56):

Используя известные интегралы [19]

нетрудно показать, что

Воспользовавшись этим интегралом, находим условное математическое ожидание

При  отсюда получаем безусловное математическое ожидание в стационарном состоянии
отсюда получаем безусловное математическое ожидание в стационарном состоянии

Зная одномерную стационарную плотность вероятности и плотность вероятности перехода, по формуле (10.14) находим двумерную плотность вероятности

где
 (19.67)
(19.67)
Учитывая выражение (63), получаем формулу для корреляционной функции

Спектральная плотность марковского процесса  равна
равна
 (19.69)
(19.69)
Применительно к релеевскому случайному процессу  формулы (66), (68) и (69) упрощаются. Так, например, формула (66) принимает вид
формулы (66), (68) и (69) упрощаются. Так, например, формула (66) принимает вид

Применяя известное соотношение [19]
 (19.71)
(19.71)
получаем двумерную релеевскую плотность вероятности [30]

Приведем также формулу для функции корреляции в этом частном случае

Пример 5. Логарифмически-нормальная плотность вероятности. Для стохастического дифференциального уравнения

уравнение Фоккера—Планка—Колмогорова (43) примет вид

Воспользовавшись формулой (45), находим стационарное решение
 (19.73)
(19.73)
Логарифмически-нормальная плотность вероятности (73) широко используется в теории распространения радиоволн и в теории надежности. Свойства и разнообразные приложения этого закона рассмотрены в ряде работ.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
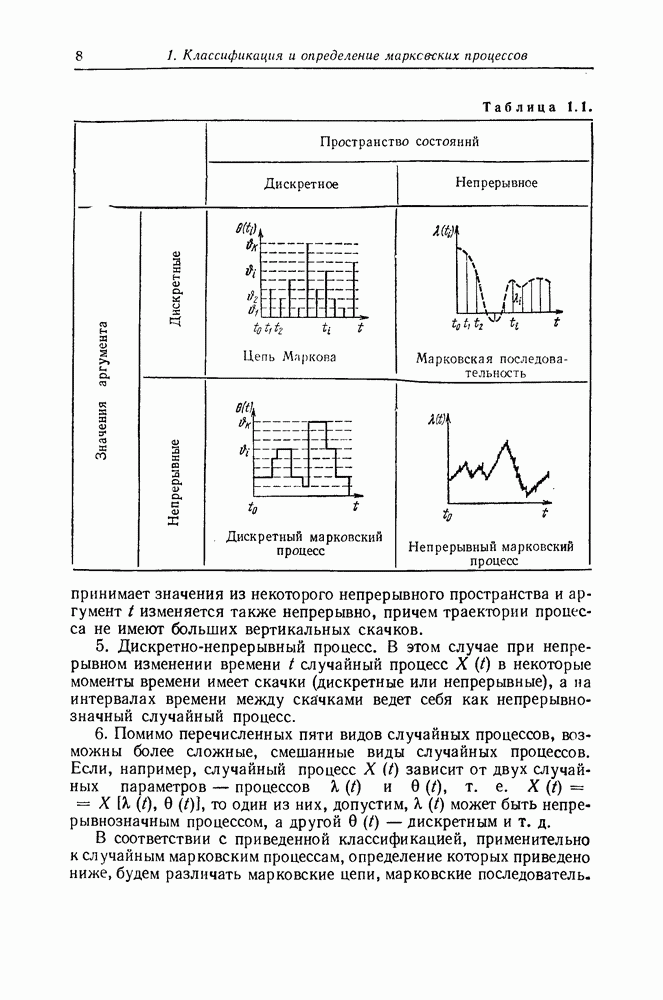
- 1. Классификация и определение марковских процессов
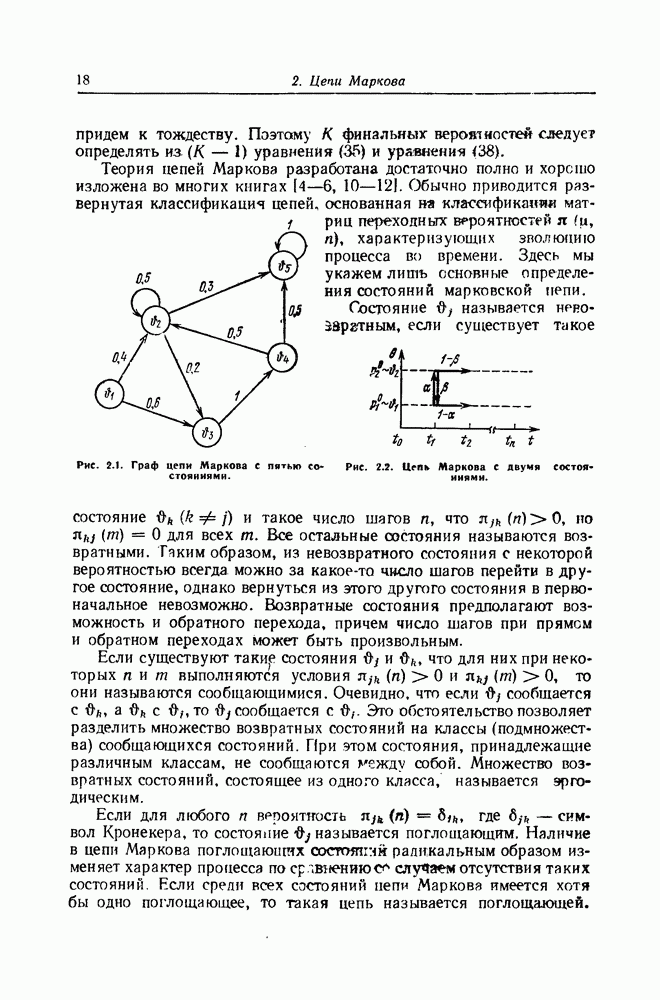
- 2. Цепи Маркова
- Уравнение Маркова
- Цепь Маркова с двумя состояниями
- 3. Энергетические спектры марковских сообщений
- 4. Одномерные дискретные блуждания
- Неограниченные блуждания
- Один поглощающий и один упругий жесткий экраны
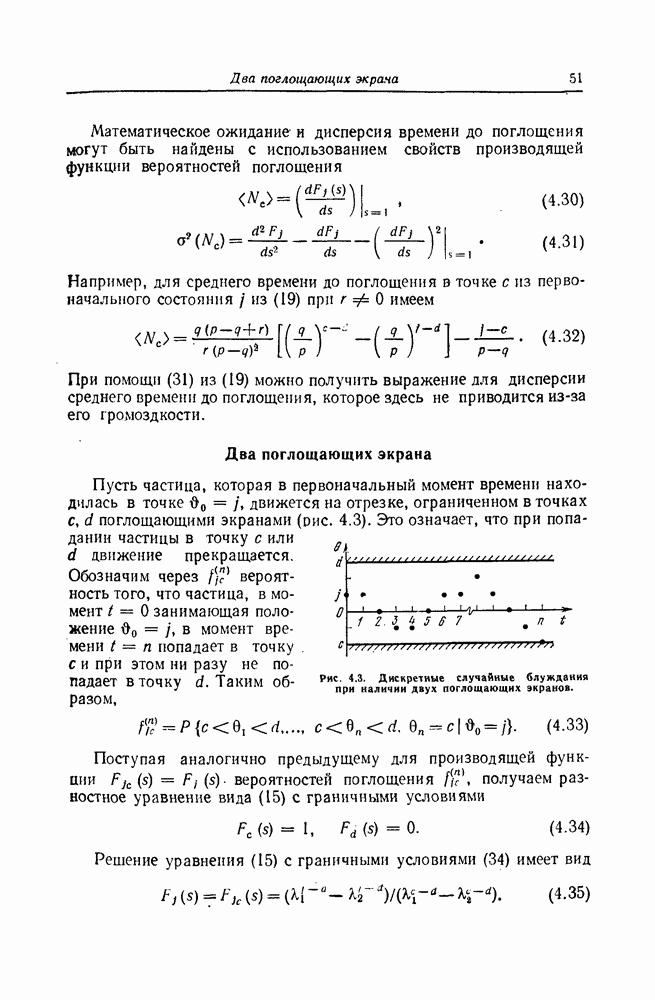
- Два поглощающих экрана
- Один поглощающий экран
- Два отражающих экрана
- Один отражающий экран
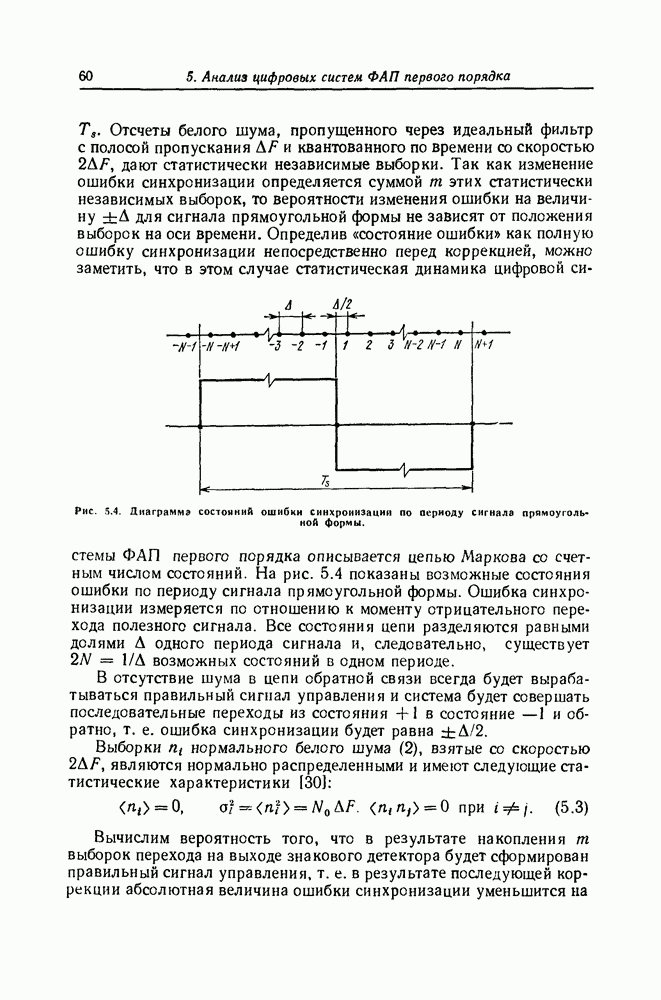
- 5. Анализ цифровых систем ФАП первого порядка
- Средний квадрат ошибки синхронизации
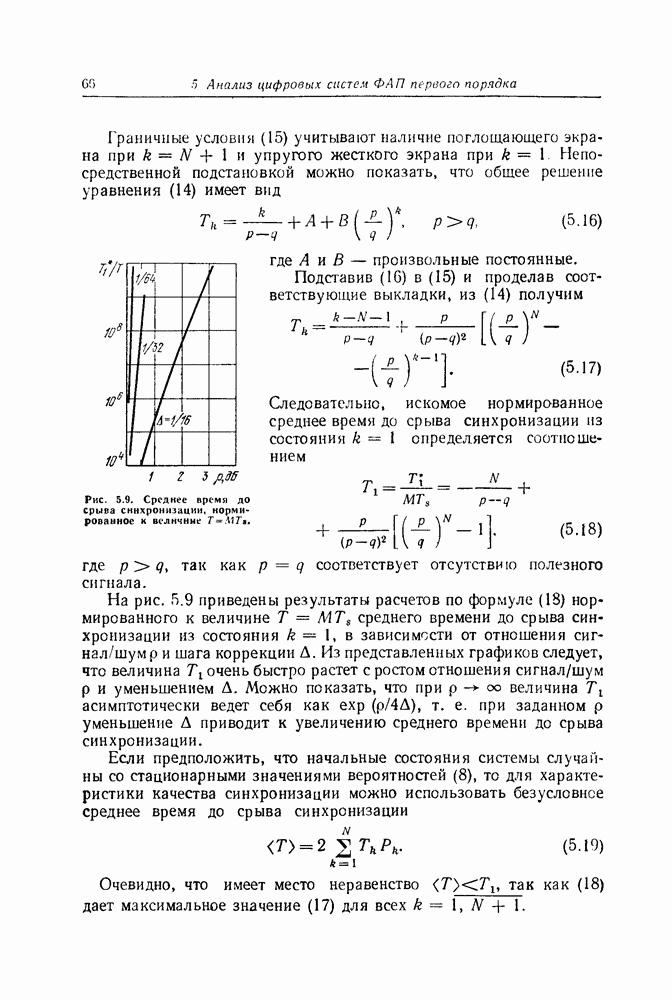
- Среднее время до срыва синхронизации
- Обобщение на случай сигналов более сложной формы
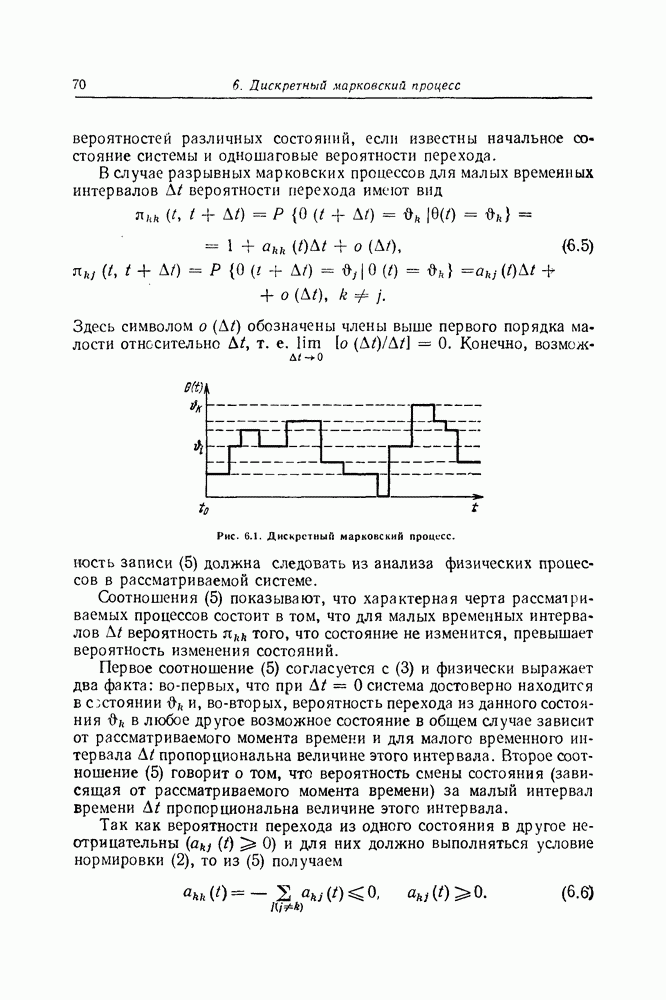
- 6. Дискретный марковской процесс
- 7. Типовые разрывные марковские процессы
- Пуассоновский процесс
- Процесс рождения и гибели
- 8. Полумарковские процессы
- 9. Марковские последовательности
- Общая модель одномерных случайных блужданий
- Случайные блуждания между поглощающими экранами
- Тождество Вальд
- Случайные блуждания между отражающими экранами
- 10. Непрерывный марковский процесс
- Дискретная модель непрерывного процесса
- 11. Уравнение Фоккера—Планка—Колмогорова
- Граничные условия
- 12. Методы решения уравнений Фоккера—Планка — Колмогорова
- 13. Многомерные марковские процессы
- Граничные условия
- 14. Чисто диффузионный процесс
- 15. Нормальный марковский процесс
- 16. Процессы с распределениями Пирсона
- 17. Процессы с кусочно-линейными коэффициентами сноса
- 18. Многомерные пормальные марковские процессы
- 19. Стохастические дифференциальные уравнения
- Стохастические интегралы и дифференциалы
- Теорема Дуба и вычисление локальных характеристик марковского процесса
- Численные методы решения стохастических дифференциальных уравнений
- 20. Область применения аппарата марковских процессов
- О коррелированности случайного воздействия
- Другие отклонения от теоремы Дуба
- Понижение порядка стохастических дифференциальных уравнений с малым параметром
- 21. Воздействие шума на простейшие колебательные системы
- Воздействие шума на колебательный контур
- Анализ работы автогенератора при наличии шума
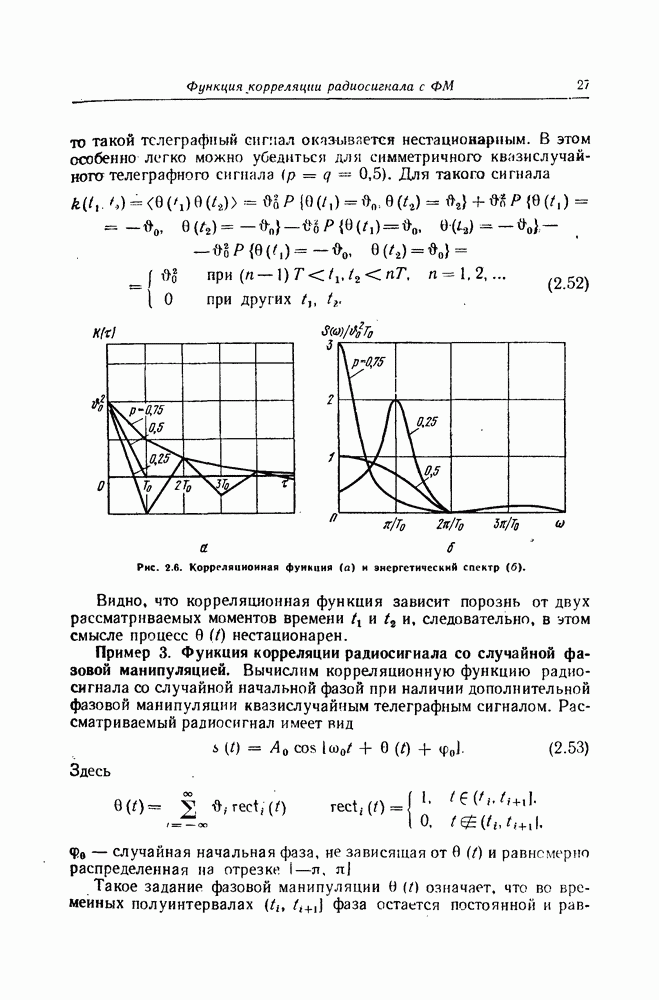
- Корреляционная функция радиосигнала со случайной фазовой манипуляцией
- 22. Статистическая динамика синхронизируемого генератора и фазовой автоподстройки частоты
- 23. Интегродифференциальные уравнении Колмогорова—Феллера
- 24. Статистические характеристики ФАП при воздействии нормального шума и пуассоновских импульсов
- 25. Обобщенные уравнения Фоккера—Планка—Колмогорова для смешанных процессов
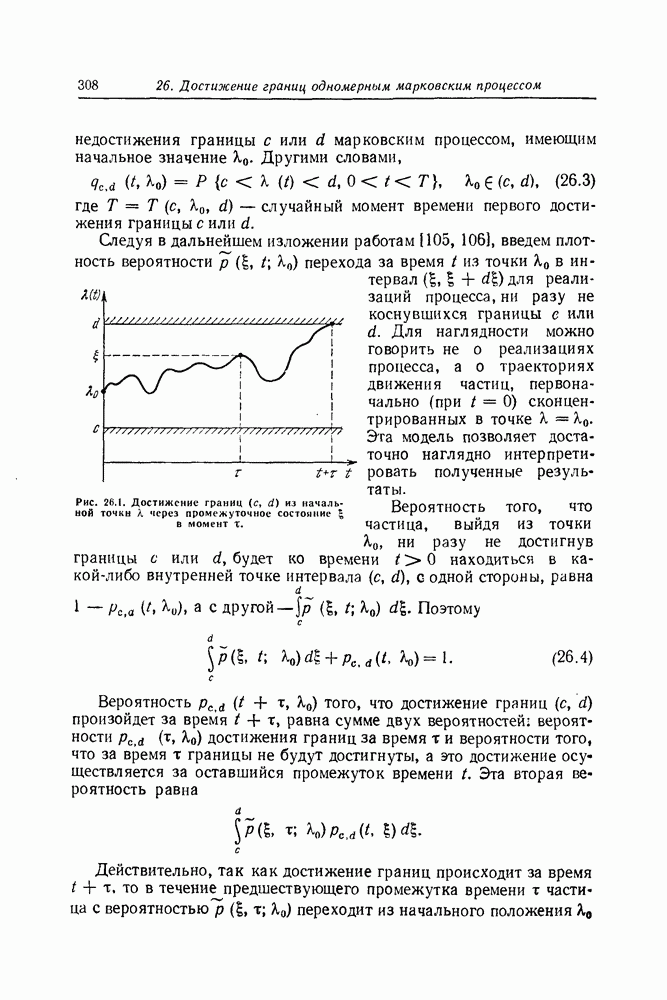
- 26. Достижение границ одномерным марковским процессом
- Вероятность достижения границы одномерным марковским процессом
- Связь уравнения Понтрягина с уравнением Фоккера — Планка — Колмогорова
- Плотность вероятности времени первого достижения границ
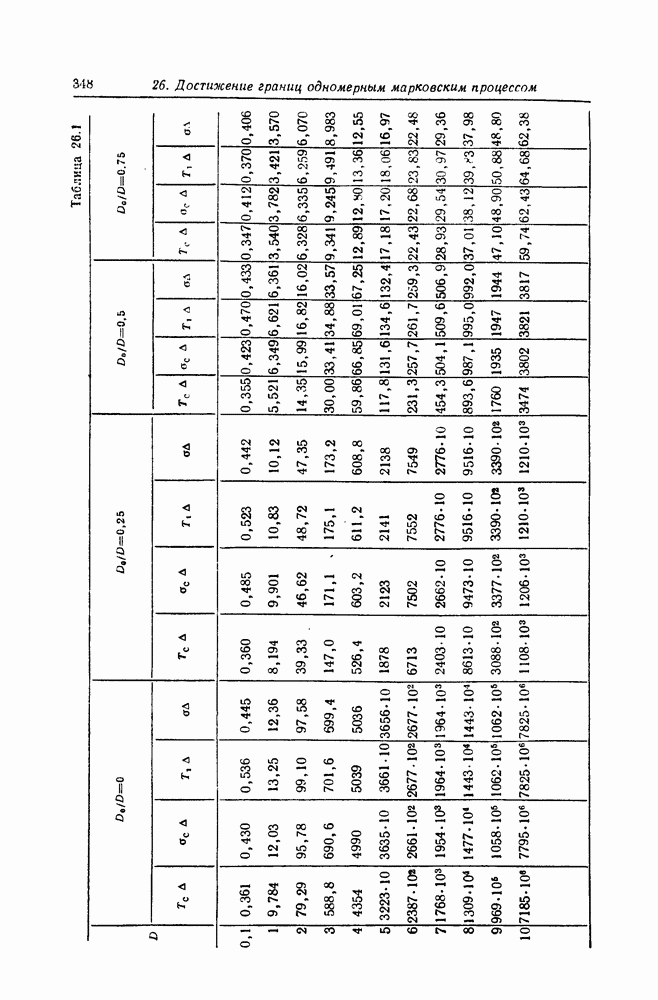
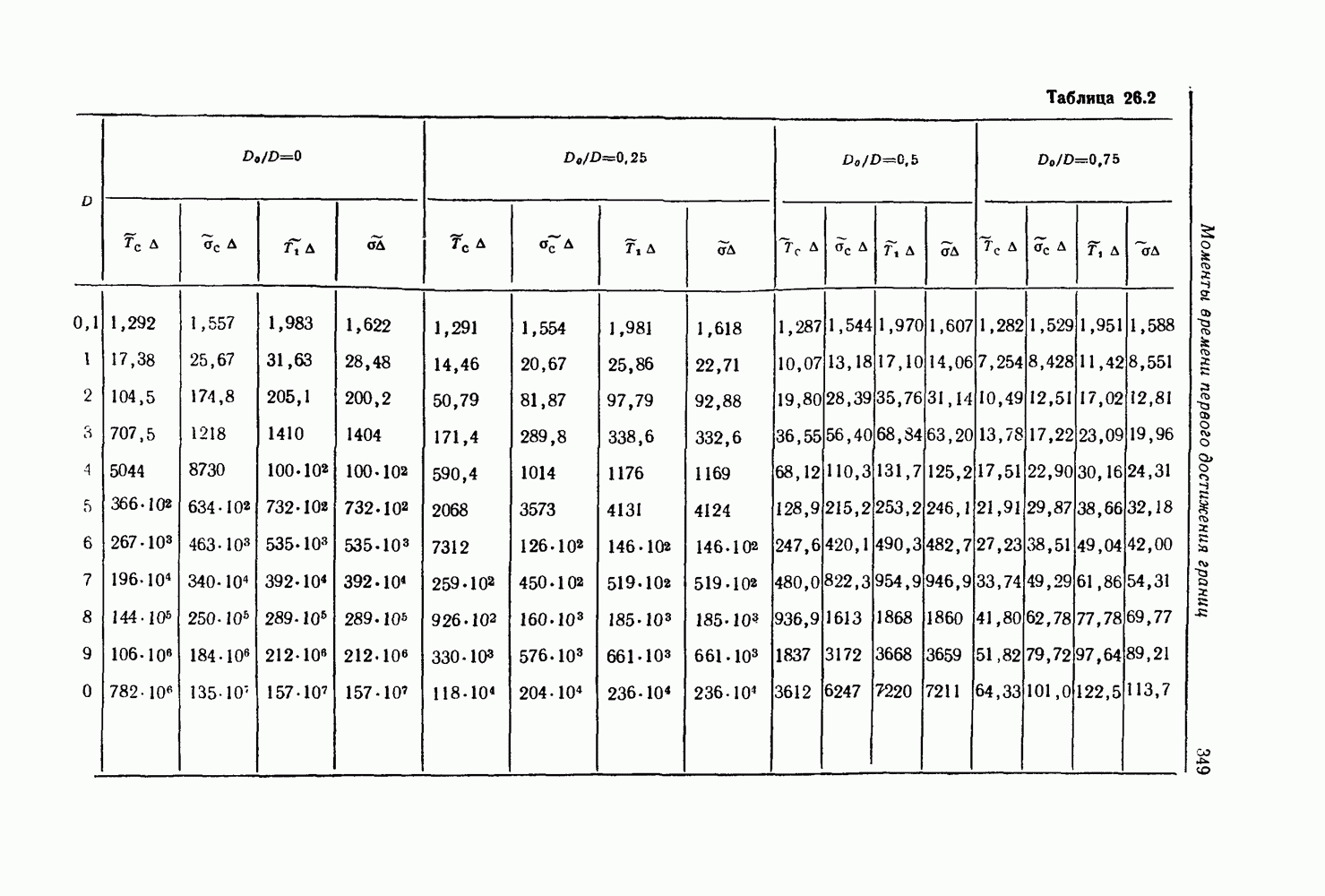
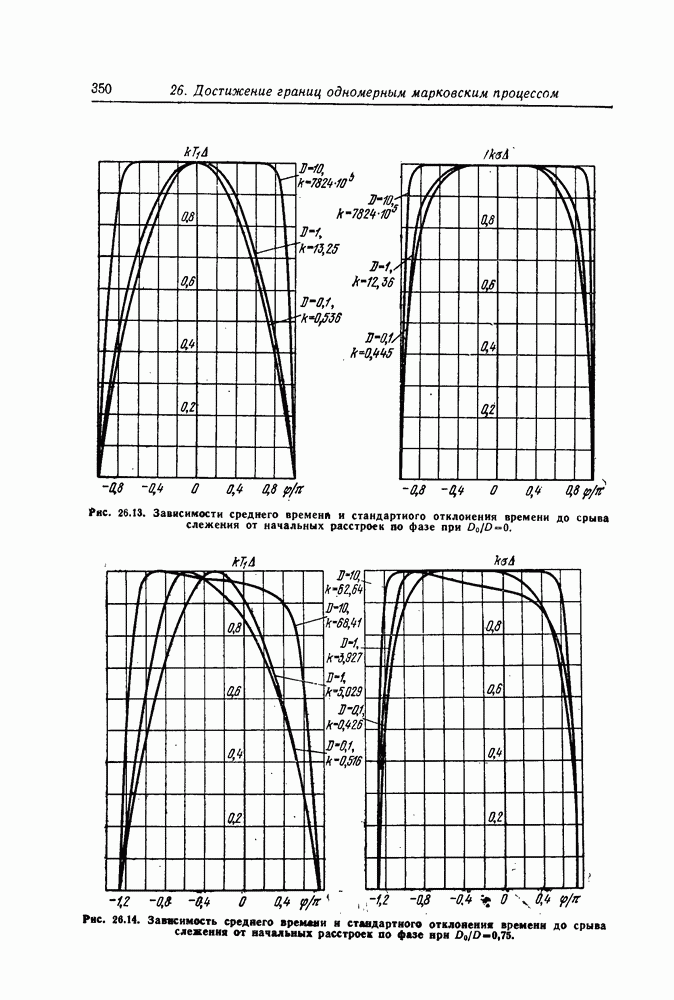
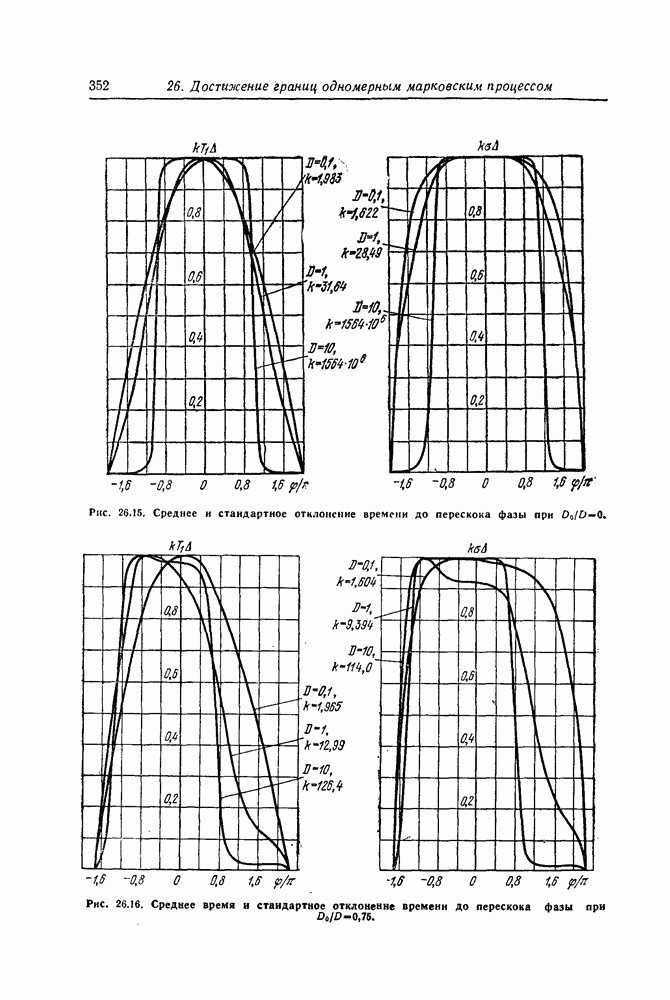
- Моменты времени первого достижения границ
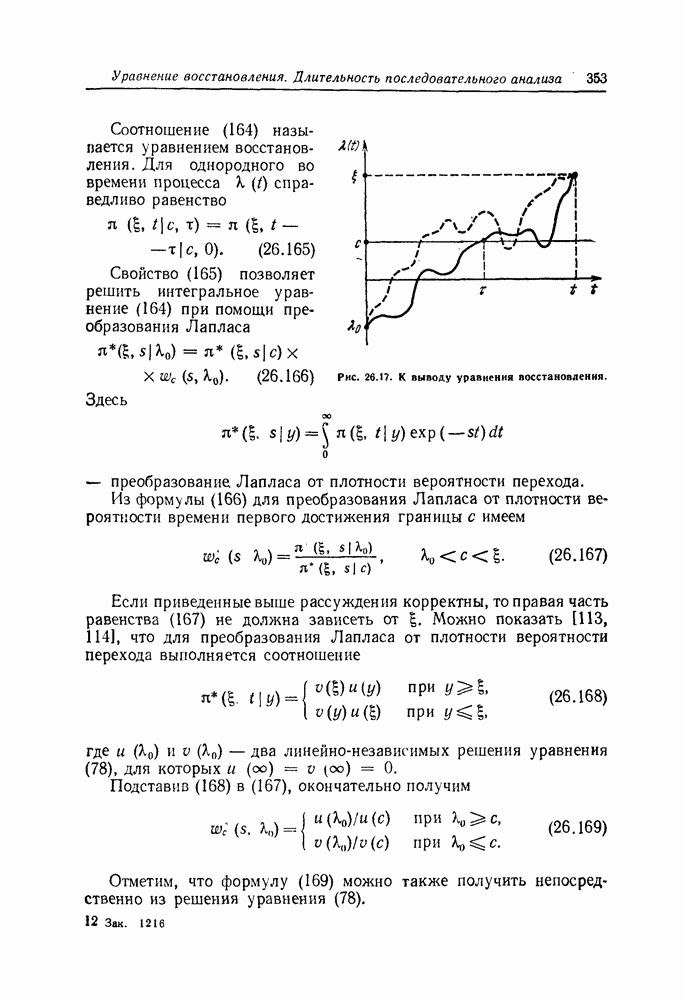
- Уравнение восстановления. Определение длительности процедуры последовательного анализа
- Некоторые смежные вопросы
- 27. Достижение границ многомерным марковским процессом
- Уравнения Понтрягина
- Связь с уравнением Фоккера — Планка — Колмогорова
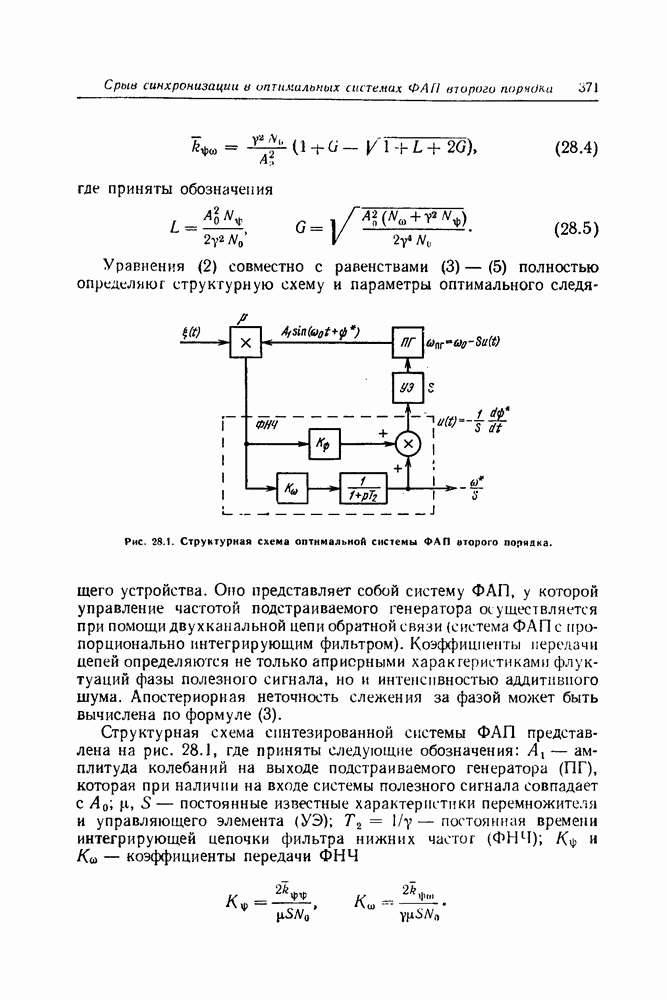
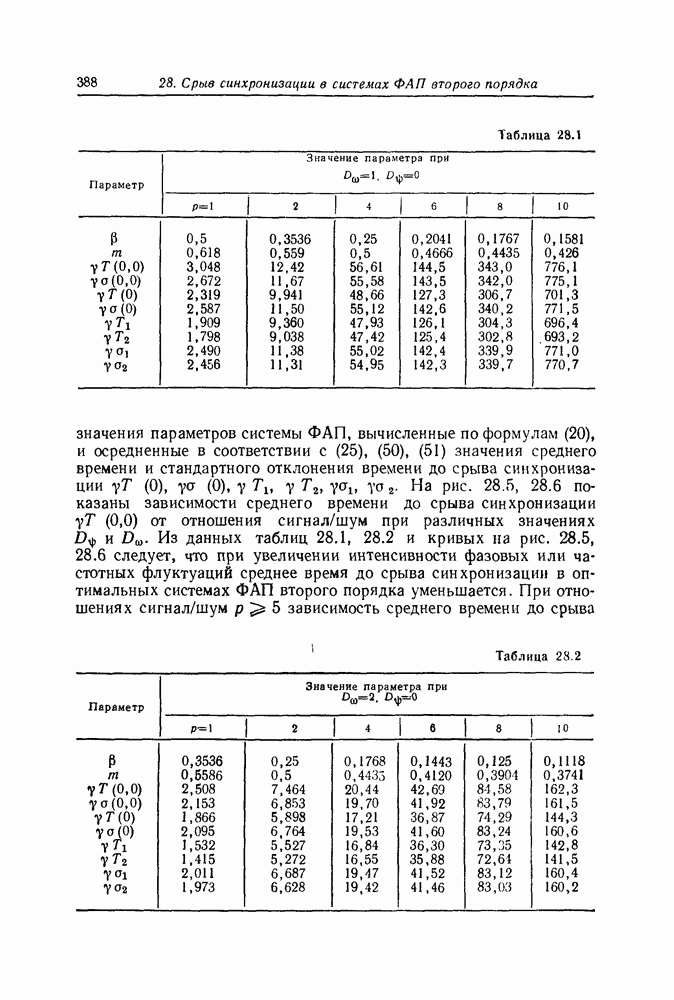
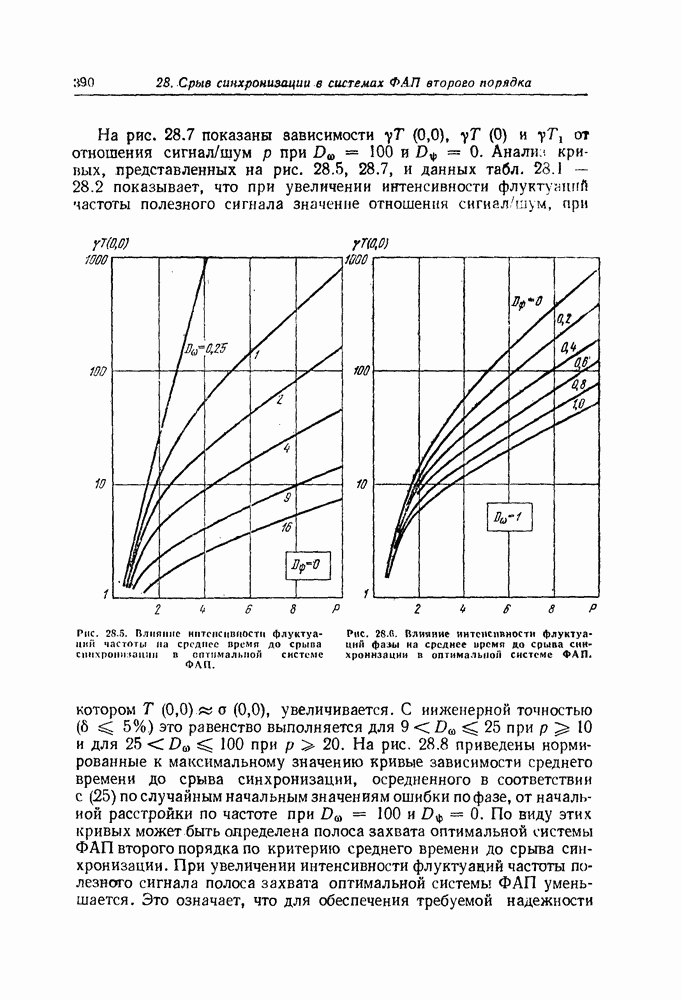
- 28. Срыв синхронизации в системах ФАП второго порядка
- Уравнение для моментов распределения времени до срыва синхронизации в оптимальных системах ФАП второго порядка
- Уравнение для моментов распределения времени до срыва синхронизации в обычных системах ФАП второго порядка
- Численный метод решения дифференциального уравнения в частных производных эллиптического типа
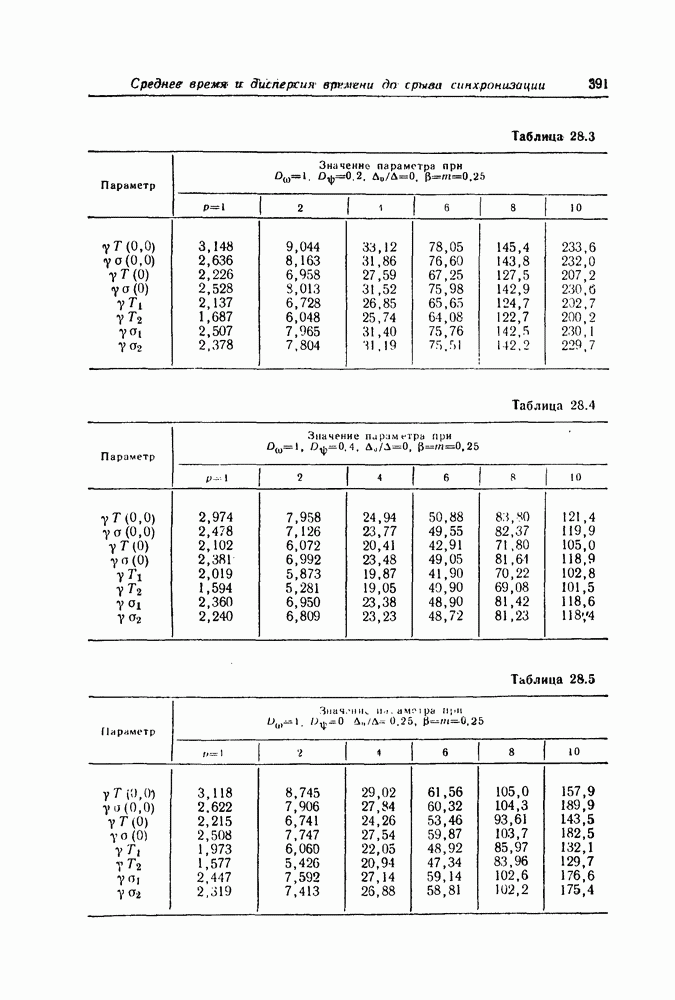
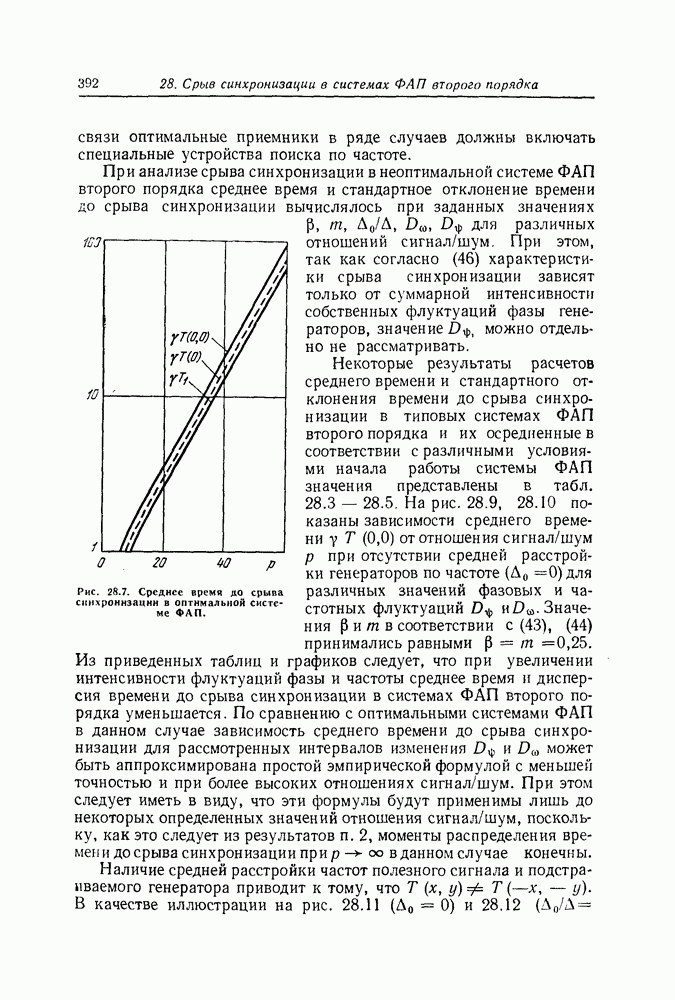
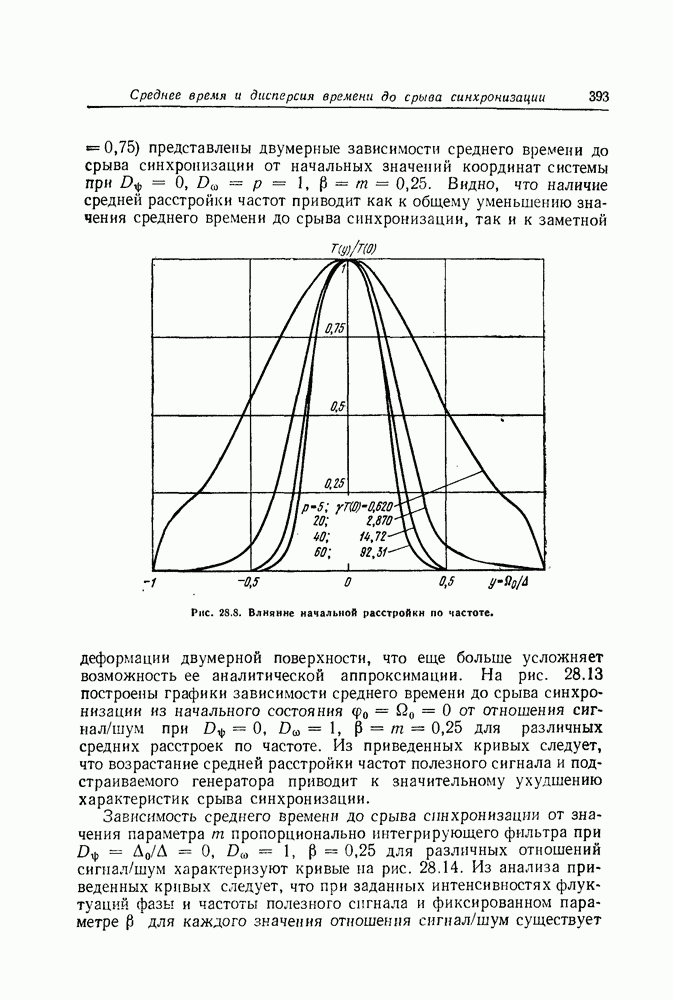
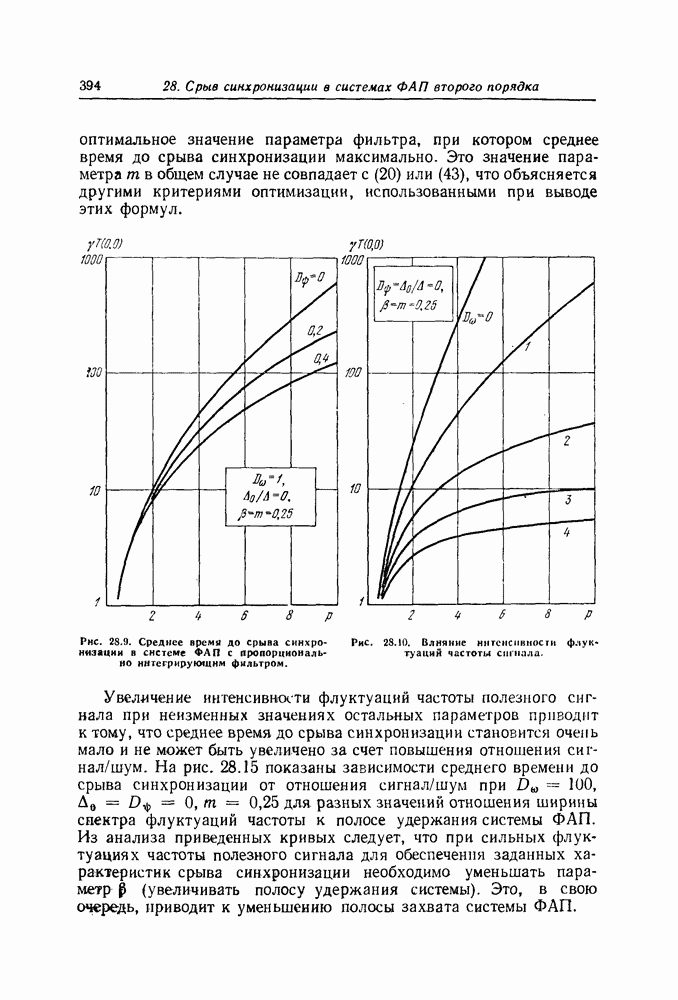
- Среднее время и дисперсия времени до срыва синхронизации в системах ФАП второго порядка
- 29. Общие сведения о случайных точечных процессах
- 30. Пуассоновские процессы
- Обобщения процесса Пуассона
- Простейшие операции над пуассоновским процессом
- 31. Процессы восстановления
- Определение и классификация процессов восстановления
- Основные соотношения
- Функция восстановления
- Плотность восстановления
- Времена возвращения
- Наложение процессов восстановления
- 32. Профильтрованный пуассоповский процесс
- Приложение I. Сведения из теории матриц
- Приложение II. Основные теоремы о производящей функции
- Приложение III. Дельта-функция
- Список литературы