| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
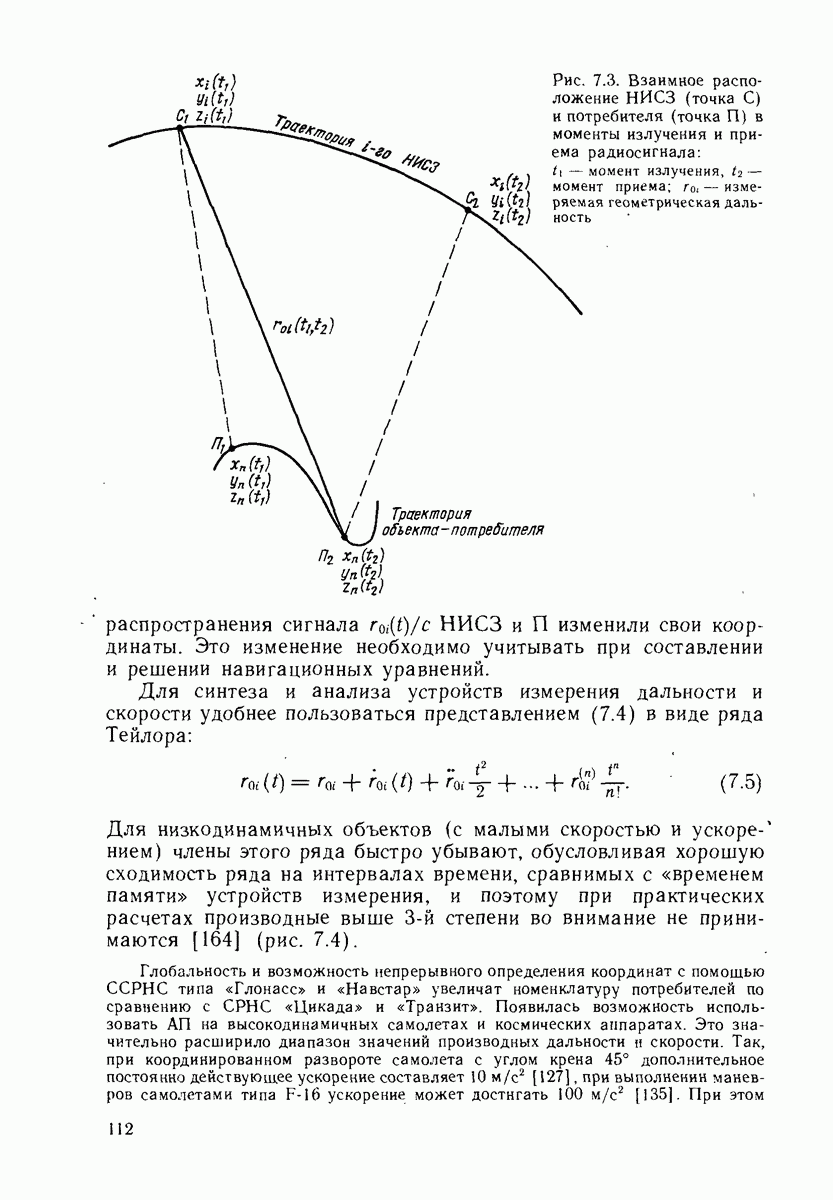
Рассмотрим наложение полос покрытий от двух одинаковых ортогональных цепочек. О качестве такой композиции будем судить по наложению соответствующих дефектов полос. Так, движение двух  -полос будет сопровождаться равномерным перемещением дефектов или, что эквивалентно, осей дефектов (см. § 24.2). Пересечение осей дефектов образует центр композиции дефектов
-полос будет сопровождаться равномерным перемещением дефектов или, что эквивалентно, осей дефектов (см. § 24.2). Пересечение осей дефектов образует центр композиции дефектов  -полос. Для наглядности допустим возможным плоскостное изображение сферических полос цепочек НИСЗ в некоторой окрестности узла сети. Погрешность подобной аппроксимации тем меньше, чем меньшим будет радиус сферического сегмента рассматриваемой окрестности. Различное взаимное фазирование цепочек отразится на траектории центра композиции дефектов.
-полос. Для наглядности допустим возможным плоскостное изображение сферических полос цепочек НИСЗ в некоторой окрестности узла сети. Погрешность подобной аппроксимации тем меньше, чем меньшим будет радиус сферического сегмента рассматриваемой окрестности. Различное взаимное фазирование цепочек отразится на траектории центра композиции дефектов.
При движении полос (рис. 24.2) дефекты  -полос заметают полосы шириной
-полос заметают полосы шириной  Если траектория центра композиции дефектов пересечет общую часть их полос, то это явится реализацией случая наложения дефектов. Поэтому для того, чтобы в сегменте как можно большего радиуса в окрестности узла сети НИСЗ исключить усиление дефектов, необходимо так сфазировать цепочки, чтобы траектория центра композиции дефектов была максимально удалена от начала координат — узла сети. Тогда максимальный радиус упомянутого сегмента будет равен расстоянию этой прямой до начала координат. Действительно, если, например, выбрать такое фазирование, при котором прямая проходит через начало координат, то при вырождении полос, например из-за увеличения
Если траектория центра композиции дефектов пересечет общую часть их полос, то это явится реализацией случая наложения дефектов. Поэтому для того, чтобы в сегменте как можно большего радиуса в окрестности узла сети НИСЗ исключить усиление дефектов, необходимо так сфазировать цепочки, чтобы траектория центра композиции дефектов была максимально удалена от начала координат — узла сети. Тогда максимальный радиус упомянутого сегмента будет равен расстоянию этой прямой до начала координат. Действительно, если, например, выбрать такое фазирование, при котором прямая проходит через начало координат, то при вырождении полос, например из-за увеличения  время прохождения «дырки» будет расти и при максимальном вырождении станет максимальным.
время прохождения «дырки» будет расти и при максимальном вырождении станет максимальным.

Рис. 24.2. Диаграмма, иллюстрирующая композиции дефектов: а — область наложения дефектов;  траектория движения центра композиции дефектов; в — сегмент наблюдаемости
траектория движения центра композиции дефектов; в — сегмент наблюдаемости
Итак, смысл оптимального фазирования состоит в достижении наибольшего значения минимальной кратности покрытия в некоторой, определенным образом заданной области. Как было показано, условие оптимального фазирования двух ортогональных одинаковых цепочек НИСЗ эквивалентно требованию максимально возможного расстояния траектории центра композиции дефектов от узла сети.
Рассмотрим задачу оптимального фазирования всей сети в целом. При этом для окрестности каждого из шести узлов сети нужно построить траекторию центра композиции дефектов (см. рис. 24.2). Однако только три из них, например отвечающие верхним узлам сети, будут различны. В нижних узлах, очевидно, через половину периода обращения будут повторены те же самые изображения.
Пусть фаза первого  цепочки в начальный момент времени
цепочки в начальный момент времени  Тогда через время} требуемое для прохождения от восходящего до первого по ходу движения узла сети, фазы первых НИСЗ относительно первых узлов сети будут такими же, как в начальный момент относительно восходящих узлов. При этом фазы НИСЗ из других цепочек в этих же узлах будут отличаться от фаз в начальный момент относительно восходящих узлов на одно и то же значение
Тогда через время} требуемое для прохождения от восходящего до первого по ходу движения узла сети, фазы первых НИСЗ относительно первых узлов сети будут такими же, как в начальный момент относительно восходящих узлов. При этом фазы НИСЗ из других цепочек в этих же узлах будут отличаться от фаз в начальный момент относительно восходящих узлов на одно и то же значение  равное дробной части числа
равное дробной части числа 
Общий случай фазирования представлен на рис. 24.3. В силу сказанного траектории центров композиции дефектов должны быть максимально удалены от узлов сети. При этом они должны, очевидно, совпадать. Отрезки, отсекаемые от горизонтальных осей этими прямыми, соответственно равны  Приравнивание их приводит к несовместной системе, поскольку в окрестности узла проходит не одна прямая, а две. Вторая, изображенная сплошной линией на третьей картинке, получается, когда для одного и того же НИСЗ из третьей орбиты берется предыдущий, в данном случае НИСЗ из второй цепочки. Поэтому отсекаемый этой прямой отрезок будет равен
Приравнивание их приводит к несовместной системе, поскольку в окрестности узла проходит не одна прямая, а две. Вторая, изображенная сплошной линией на третьей картинке, получается, когда для одного и того же НИСЗ из третьей орбиты берется предыдущий, в данном случае НИСЗ из второй цепочки. Поэтому отсекаемый этой прямой отрезок будет равен 

Рис. 24.3. Диаграммы, поясняющие выбор оптимального фазирования трех цепочек 

Рис. 24.4. Диаграмма, поясняющая условия определения максимального сегмента минимальной кратности покрытия  а — максимальный сегмент; б - плоскость 1-й цепочки; в — плоскость 2-й цепочки; г - предельная граница области видимости 3-й цепочки
а — максимальный сегмент; б - плоскость 1-й цепочки; в — плоскость 2-й цепочки; г - предельная граница области видимости 3-й цепочки
 Приравнивая отрезки, отсекаемые этими прямыми, получаем совместную систему
Приравнивая отрезки, отсекаемые этими прямыми, получаем совместную систему  решением которой будут соотношения
решением которой будут соотношения  определяющие оптимальное фазирование НИСЗ.
определяющие оптимальное фазирование НИСЗ.
Исследуем условие, обеспечивающее заданную минимальную кратность покрытия  Начнем с
Начнем с  Примем за максимальный сферический сегмент узла, обладающий минимальной кратностью покрытия
Примем за максимальный сферический сегмент узла, обладающий минимальной кратностью покрытия  сегмент, вписанный в сферический
сегмент, вписанный в сферический  -угольник, который образуется пересечением двух
-угольник, который образуется пересечением двух  -полос таким образом, что он одновременно касается
-полос таким образом, что он одновременно касается  -полосы 3-й цепочки. Конечно, такое перекрытие может быть обеспечено только при определенных соотношениях параметров сети.
-полосы 3-й цепочки. Конечно, такое перекрытие может быть обеспечено только при определенных соотношениях параметров сети.
Обобщенная картина характера перекрытия некоторой окрестности из узлов сети на рис. 24.4 иллюстрирует условия существования максимально возможного сферического сегмента, в котором минимальная кратность перекрытия  Полоса 3-й цепочки имеет, по определению, очевидно, на границе сегмента
Полоса 3-й цепочки имеет, по определению, очевидно, на границе сегмента  точек нулевой кратности покрытия — узлы 1-го порядка. Полосы
точек нулевой кратности покрытия — узлы 1-го порядка. Полосы  -кратного покрытия не могут быть сделаны уже, в противном случае в упомянутый максимальный сегмент
-кратного покрытия не могут быть сделаны уже, в противном случае в упомянутый максимальный сегмент  -кратного перекрытия попадет узел
-кратного перекрытия попадет узел  -полосы 3-го порядка (см. рис. 24.4). Это понизит минимальную кратность до 3. Вне сегмента кратность перекрытия полос будет увеличиваться за счет перекрытий полосой 3-й цепочки и не может стать меньше 4. С другой стороны, при суждении 3-й полосы и неоптимальном фазировании минимальная кратность может понизиться до 3.
-полосы 3-го порядка (см. рис. 24.4). Это понизит минимальную кратность до 3. Вне сегмента кратность перекрытия полос будет увеличиваться за счет перекрытий полосой 3-й цепочки и не может стать меньше 4. С другой стороны, при суждении 3-й полосы и неоптимальном фазировании минимальная кратность может понизиться до 3.
Принятый способ сопряжения всех трех полос следует признать критическим. Полосы не могут быть сделаны уже без уменьшения заданной минимальной кратности покрытия, а неоптимальное фазирование для определенных таким образом значений критической ширины полос также приводит к уменьшению значения  Последний случай произойдет, очевидно, при совпадении какого-либо узла 3-го порядка первых двух полос с узлом 2-го порядка 3-й полосы.
Последний случай произойдет, очевидно, при совпадении какого-либо узла 3-го порядка первых двух полос с узлом 2-го порядка 3-й полосы.
Сделаем важное для дальнейшего замечание. При оптимальном фазировании вне сегмента наименьшей кратности кратность
покрытия будет практически больше минимальной. Поэтому минимальная кратность в основном будет иметь место только в этом сегменте. Следовательно, оптимальное сопряжение полос требует выполнения равенства  Отсюда определяем наименьшее возможное значение угла 9, выбирая
Отсюда определяем наименьшее возможное значение угла 9, выбирая  согласно (24.2):
согласно (24.2):

Фиксируя определенное значение  находим наименьшее значение радиуса зоны радиовидимости.
находим наименьшее значение радиуса зоны радиовидимости.
Назовем синтезированную таким образом сеть, использующую полосы минимально возможной ширины, экстремальной. Итак, условие экстремальной сети сформулировано в виде выражения (24.6). При этом имеется в виду, что 
Рассмотрим некоторые частные случаи. Пусть  Тогда получим
Тогда получим  Заметим, что в этом же случае для сети, определяемой из достаточных условий, ранее было получено значение
Заметим, что в этом же случае для сети, определяемой из достаточных условий, ранее было получено значение  Видна степень ослабления необходимых условий по сравнению с достаточными. Положим далее
Видна степень ослабления необходимых условий по сравнению с достаточными. Положим далее  Тогда из (24.6) получим
Тогда из (24.6) получим  Примем, наконец,
Примем, наконец,  Тогда
Тогда  В обоих случаях также подтверждается уже отмеченное свойство: уменьшение минимально возможного сферического радиуса зоны радиовидимости НИСЗ при увеличении их числа в цепочке.
В обоих случаях также подтверждается уже отмеченное свойство: уменьшение минимально возможного сферического радиуса зоны радиовидимости НИСЗ при увеличении их числа в цепочке.
Обратимся теперь к случаю обеспечения минимальной кратности, равной нечетному числу. Рассмотрение проведем для  Фазовая картина перекрытия двух полос в окрестности узла сети будет уже иной (рис. 24.5). Траектория центра композиции дефектов определяется однозначно. Модуль отрезка, отсекаемого этой прямой на координатных осях,
Фазовая картина перекрытия двух полос в окрестности узла сети будет уже иной (рис. 24.5). Траектория центра композиции дефектов определяется однозначно. Модуль отрезка, отсекаемого этой прямой на координатных осях,  где
где  дробная часть числа.
дробная часть числа.
При оптимальном фазировании цепочек вырождение полос  -кратного перекрытия приводит к появлению области
-кратного перекрытия приводит к появлению области  -кратного перекрытия. Впервые при монотонном уменьшении ширины полосы эта область появится на траектории центра композиции дефектов в точке пересечения ее с биссектрисой второго координатного октанта. Отсюда выводим условие
-кратного перекрытия. Впервые при монотонном уменьшении ширины полосы эта область появится на траектории центра композиции дефектов в точке пересечения ее с биссектрисой второго координатного октанта. Отсюда выводим условие  которое связывает параметры минимальной сети, обеспечивающей по меньшей мере
которое связывает параметры минимальной сети, обеспечивающей по меньшей мере

Рис. 24.5. Диаграмма, поясняющая определение максимального сегмента минимальной кратности покрытия  : а - траектория центра композиции дефектов; б - максимальный сегмеит
: а - траектория центра композиции дефектов; б - максимальный сегмеит  в — плоскость 1-й цепочки; г - плоскость 2-й цепочки
в — плоскость 1-й цепочки; г - плоскость 2-й цепочки
 Подставляя сюда выражения этих параметров, получаем
Подставляя сюда выражения этих параметров, получаем

Таким образом, экстремальная сеть, обладающая перекрытием кратности  определяется условием, запись которого эквивалентна (24.7):
определяется условием, запись которого эквивалентна (24.7):

Выполним расчеты по приведенной формуле для  Пусть
Пусть  , тогда
, тогда  Приняв
Приняв  получим
получим  Задавшись
Задавшись  будем иметь
будем иметь 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
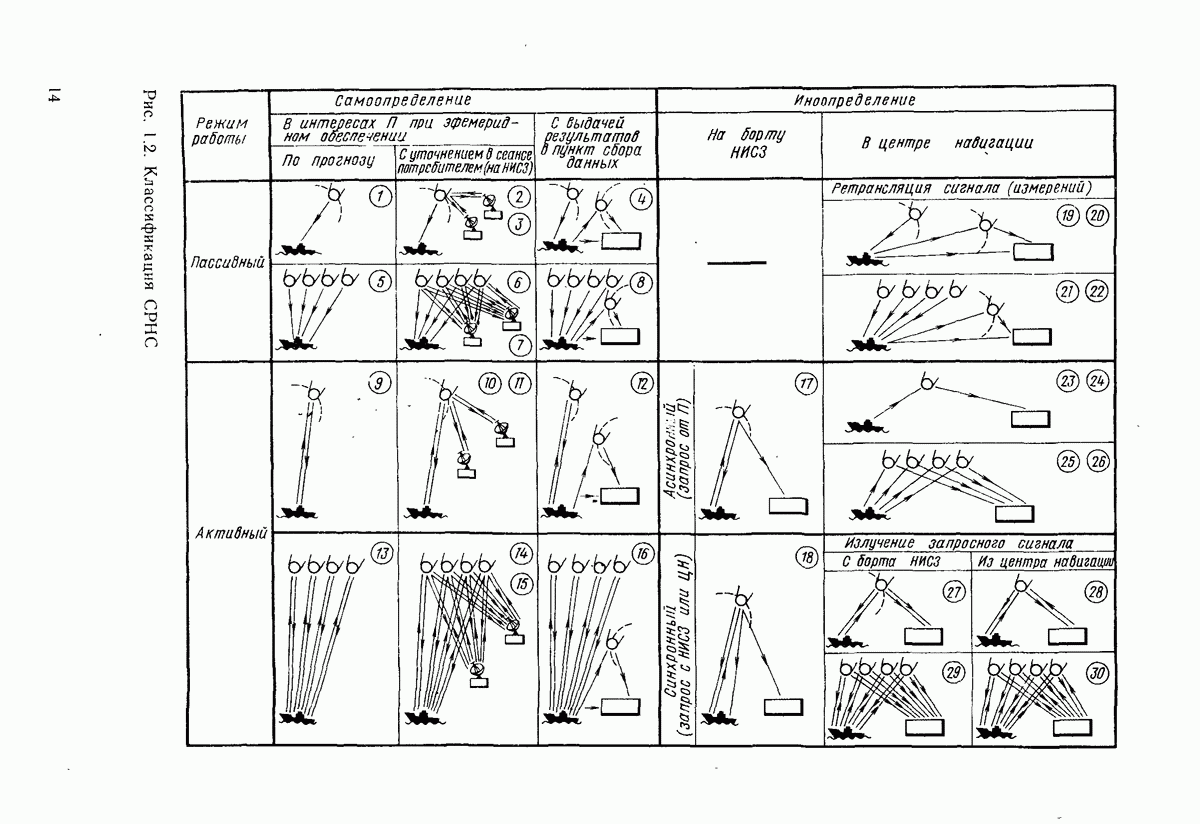
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
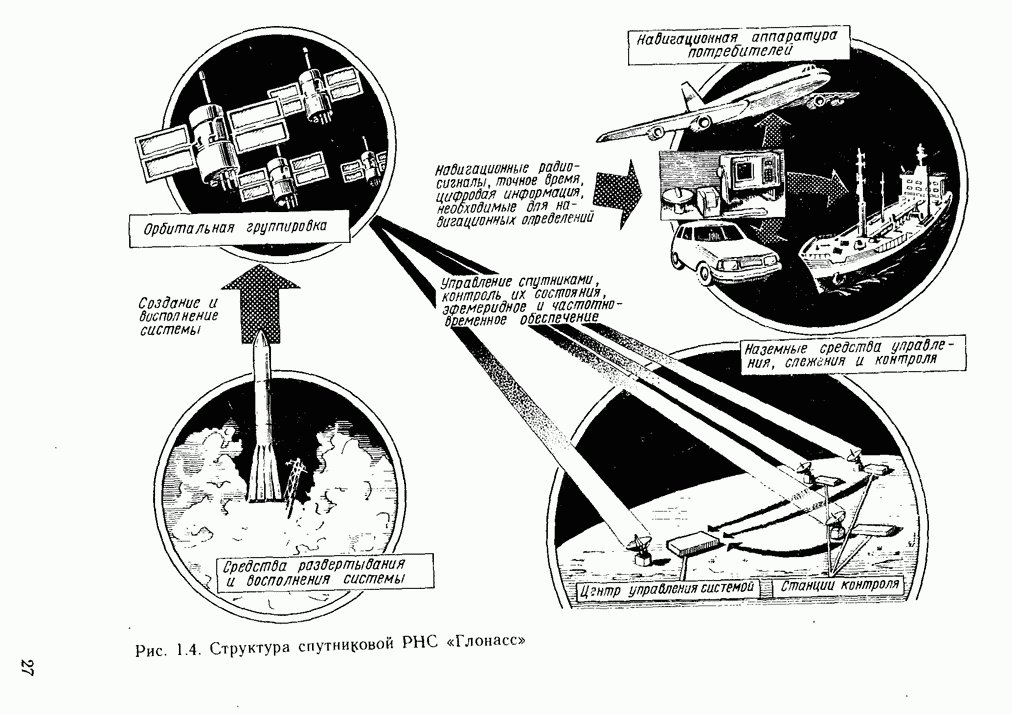
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
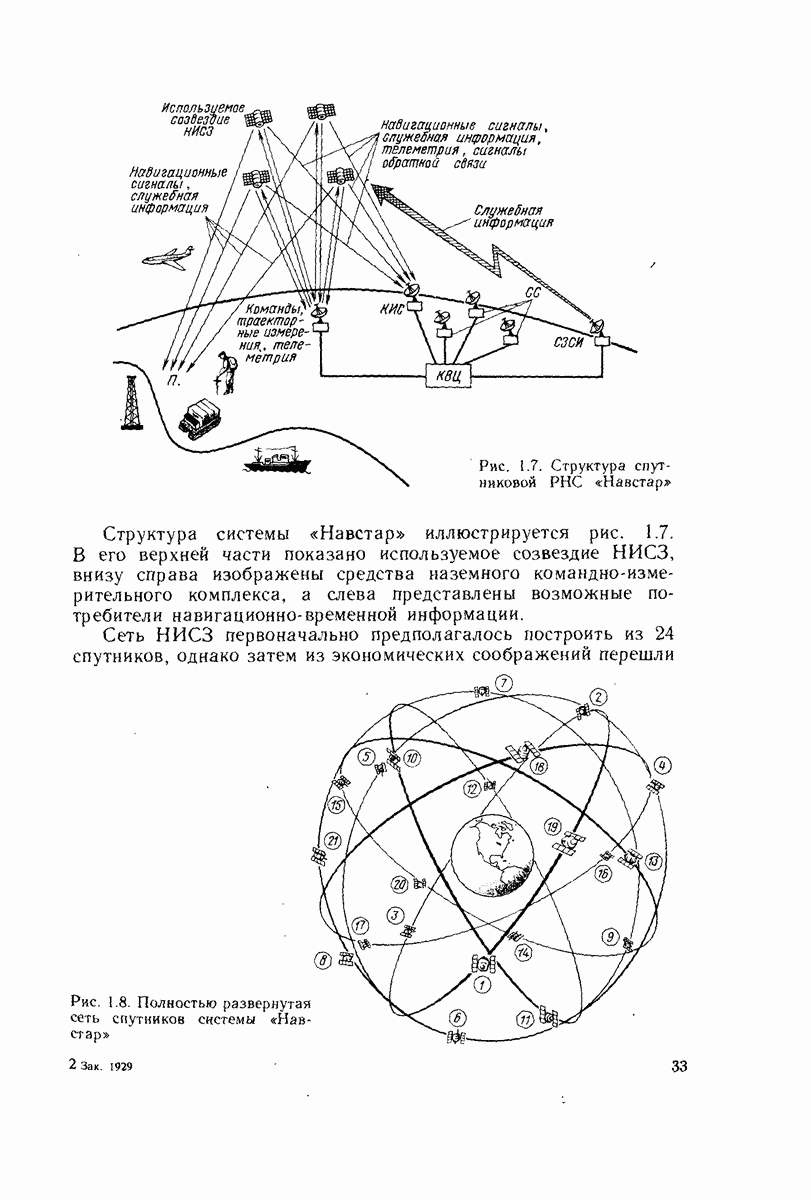
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
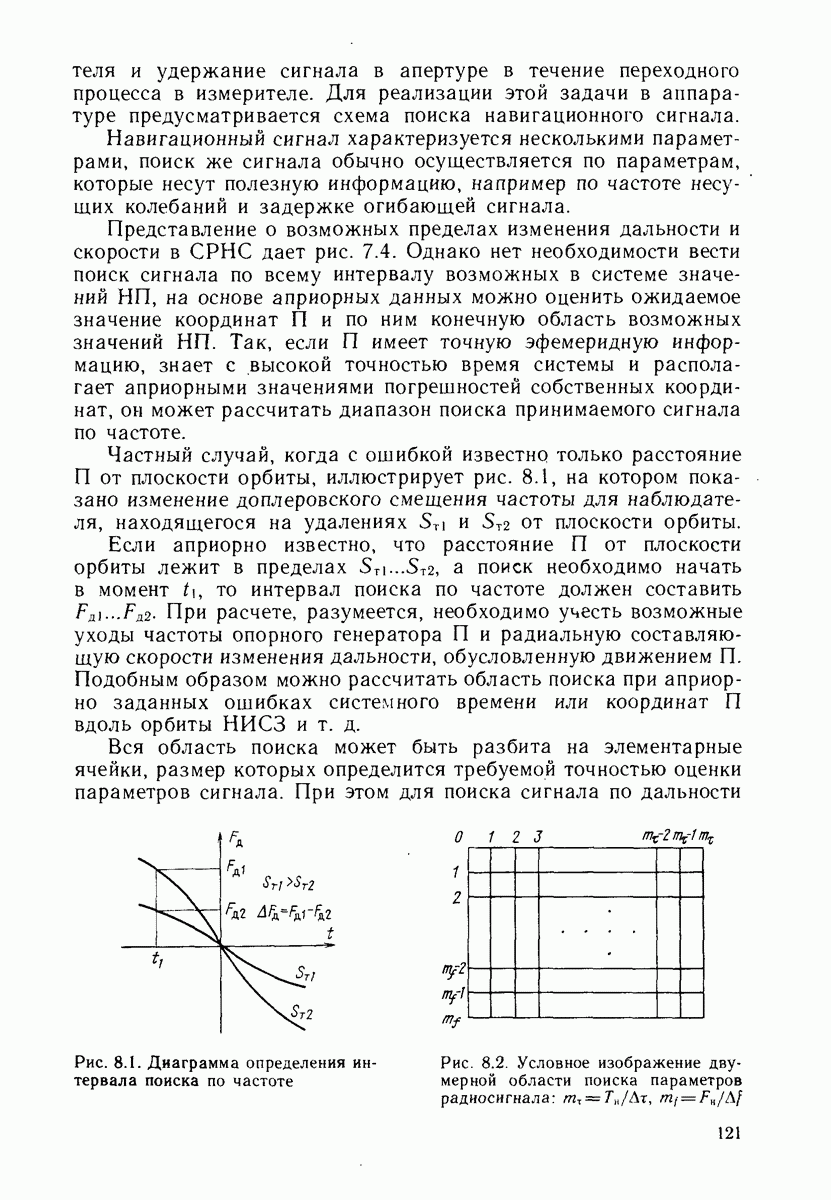
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
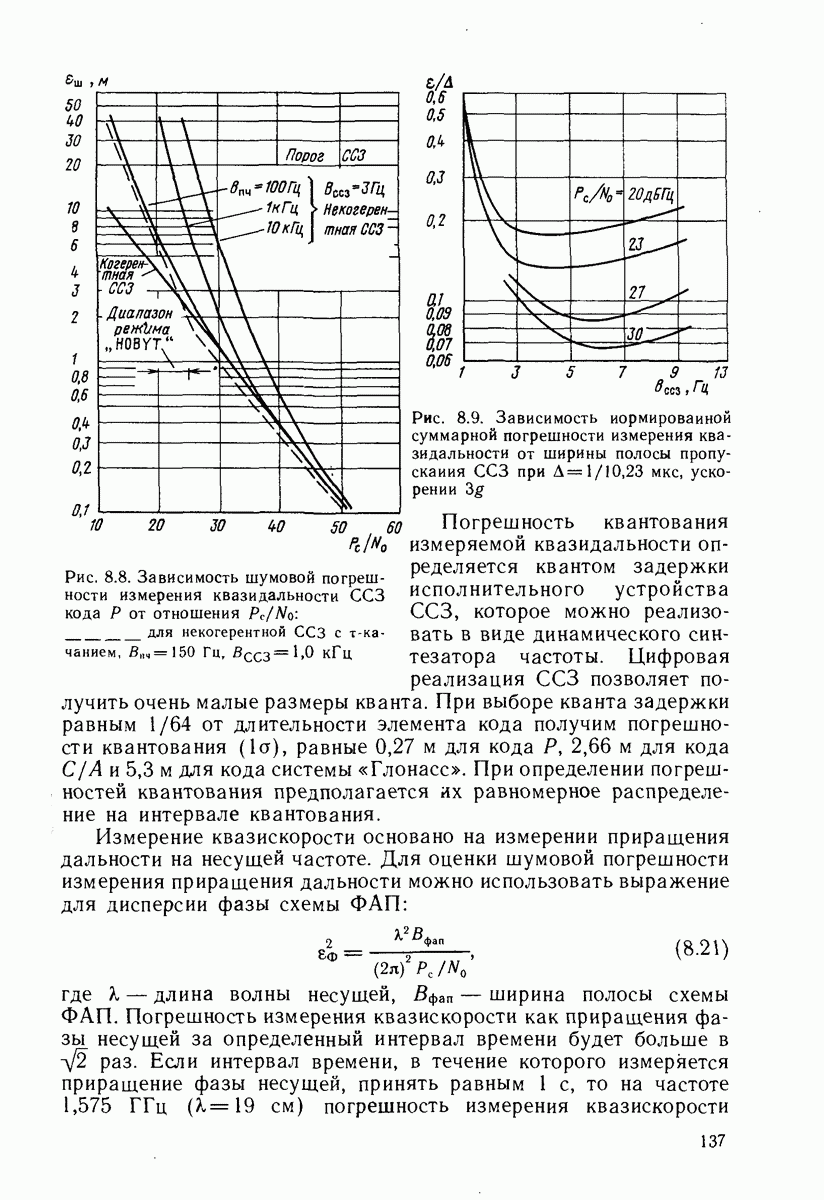
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
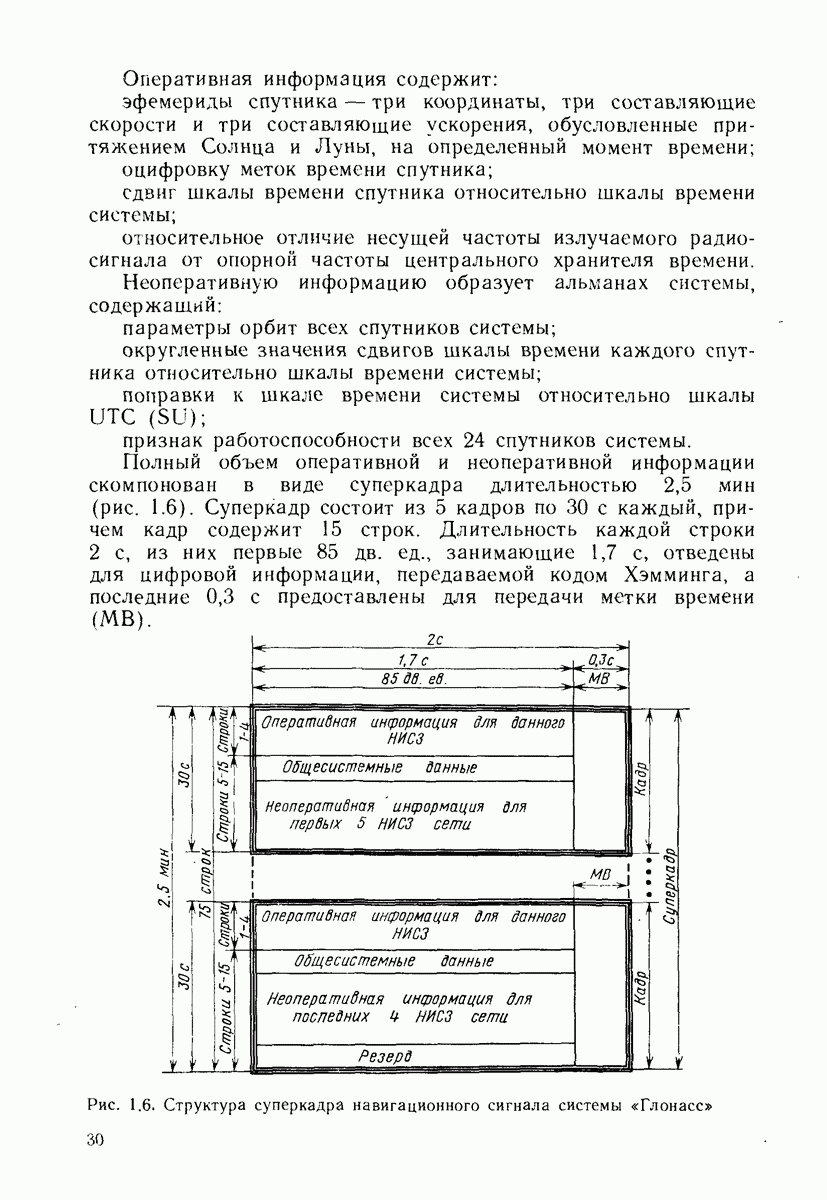
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
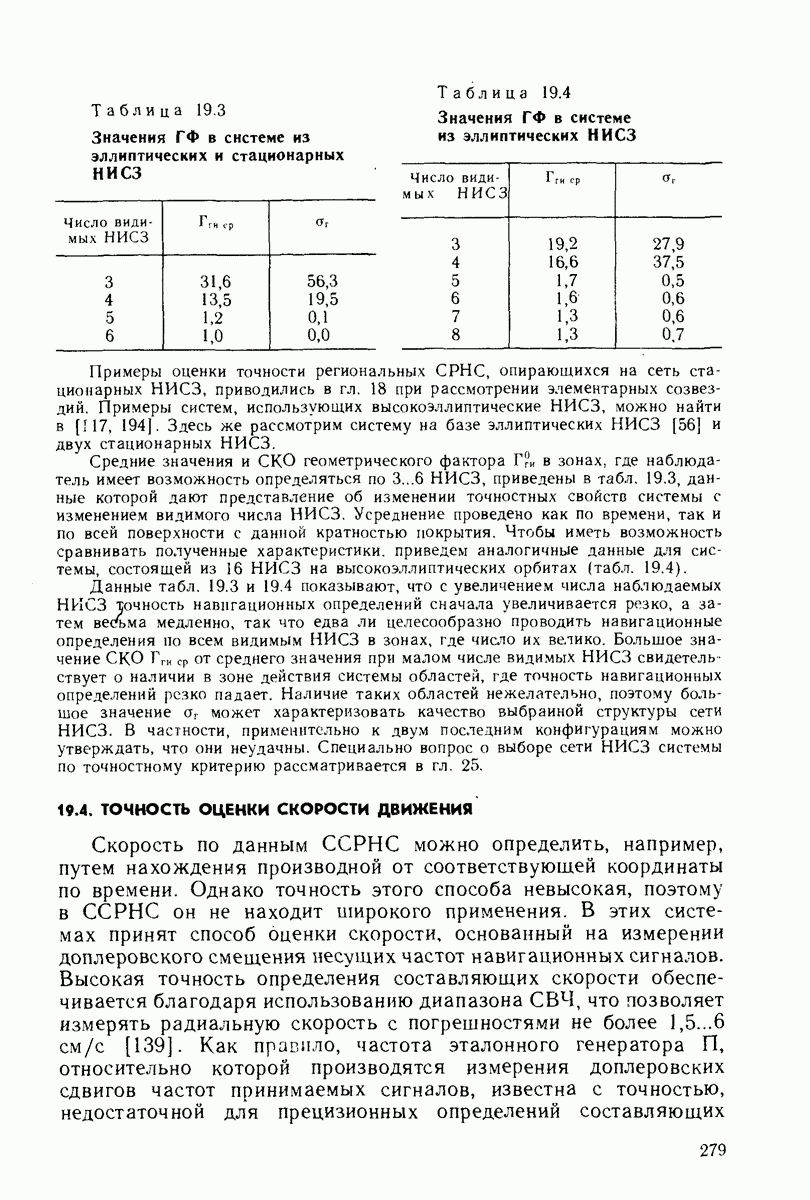
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
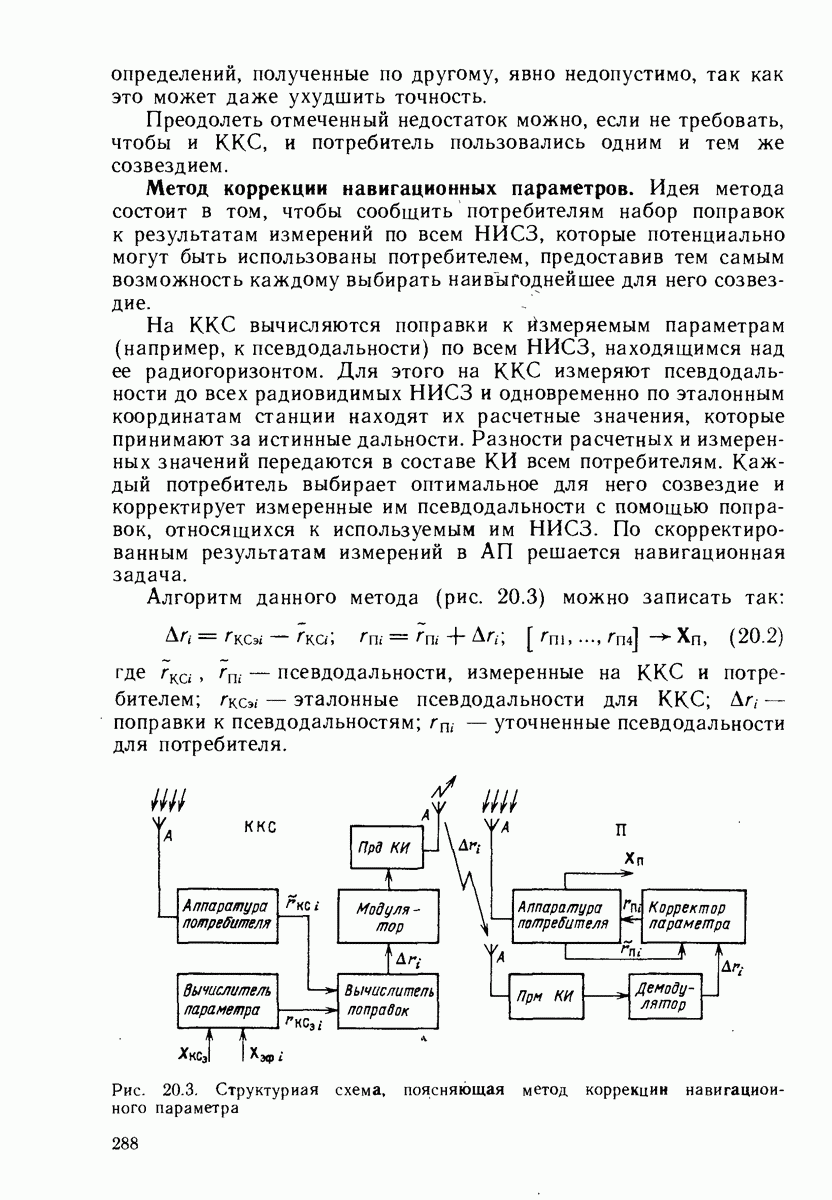
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
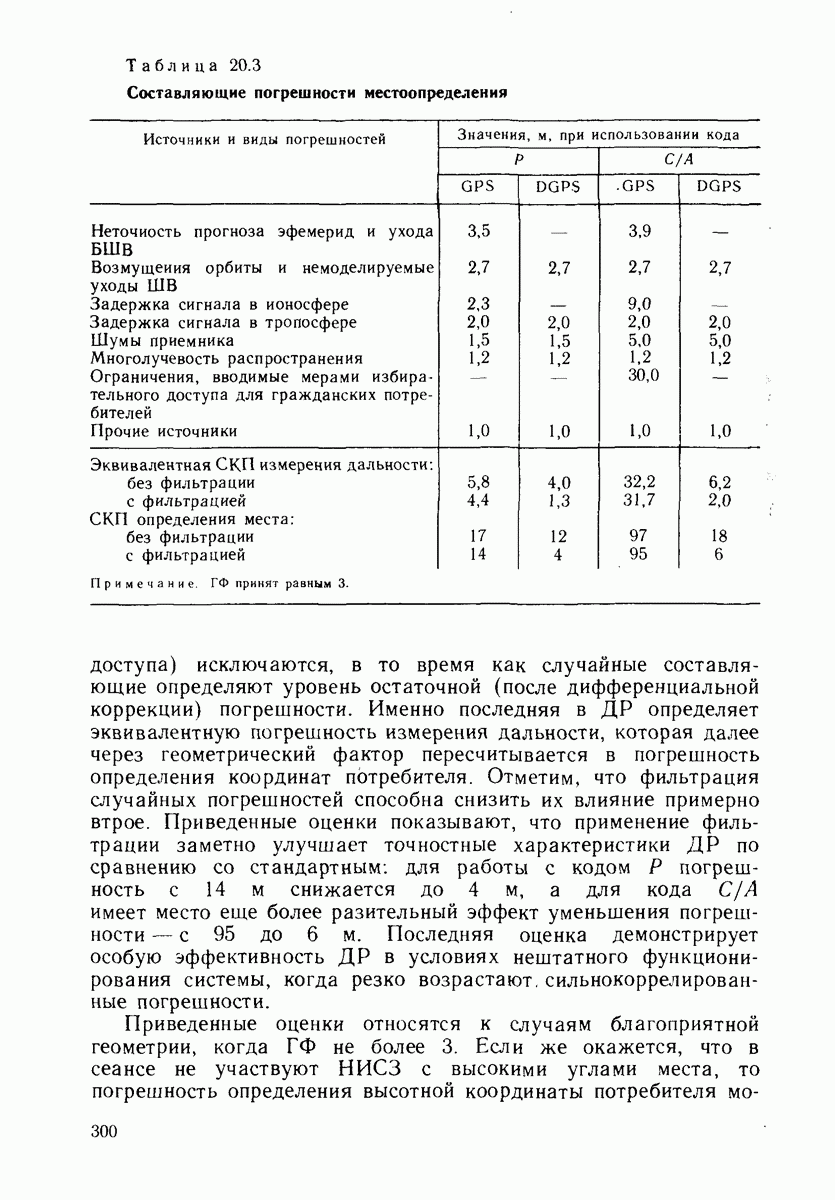
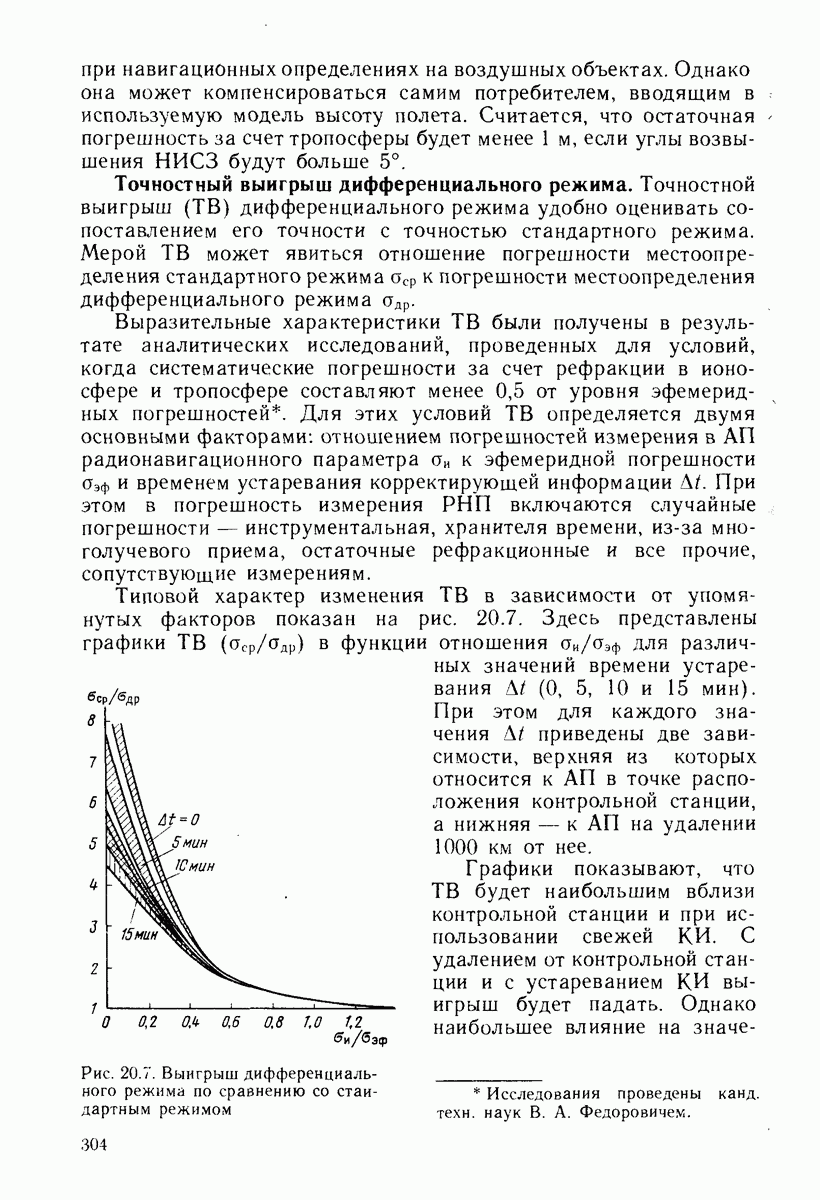
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
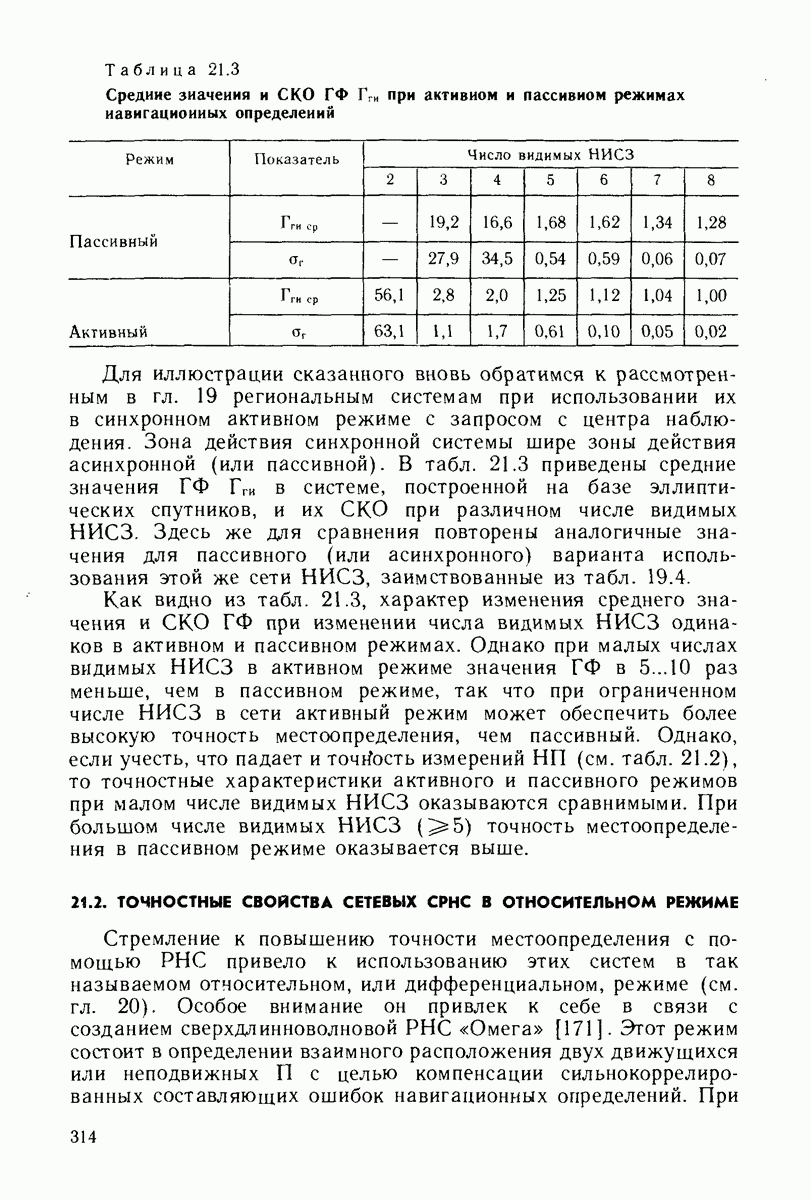
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
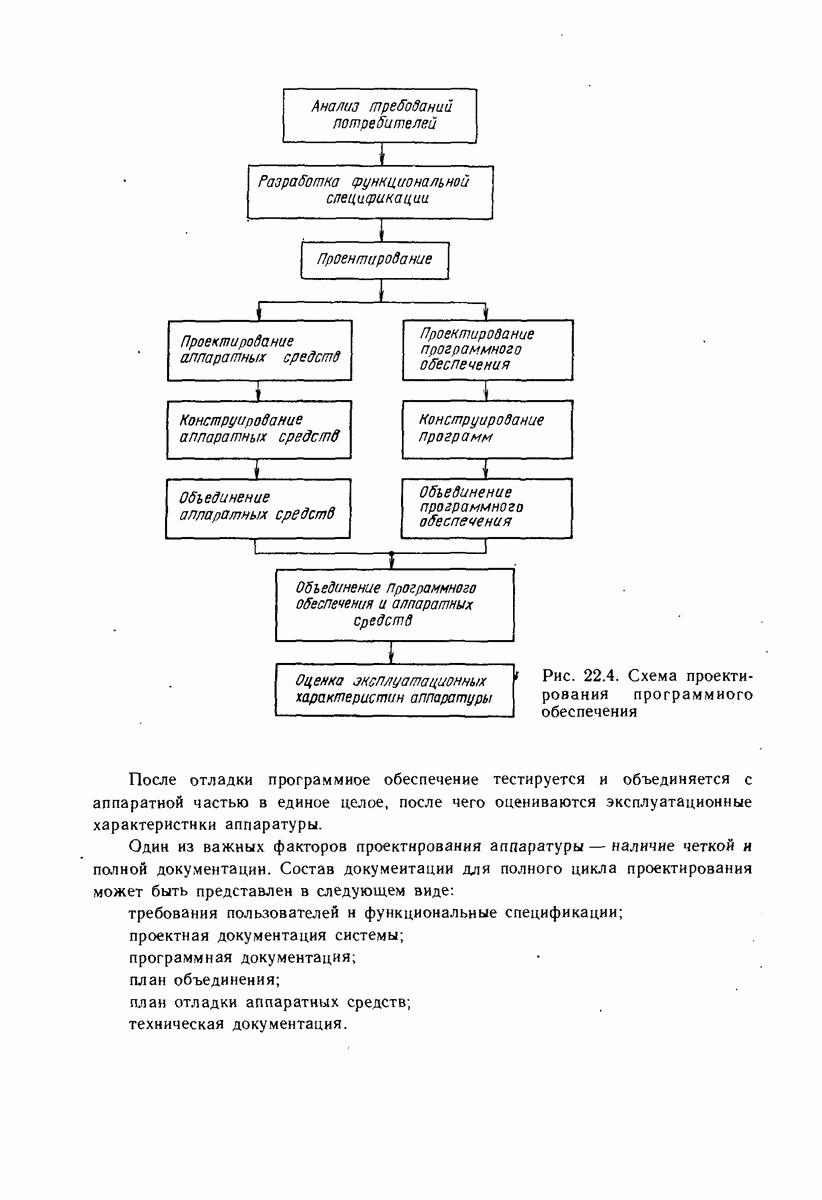
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
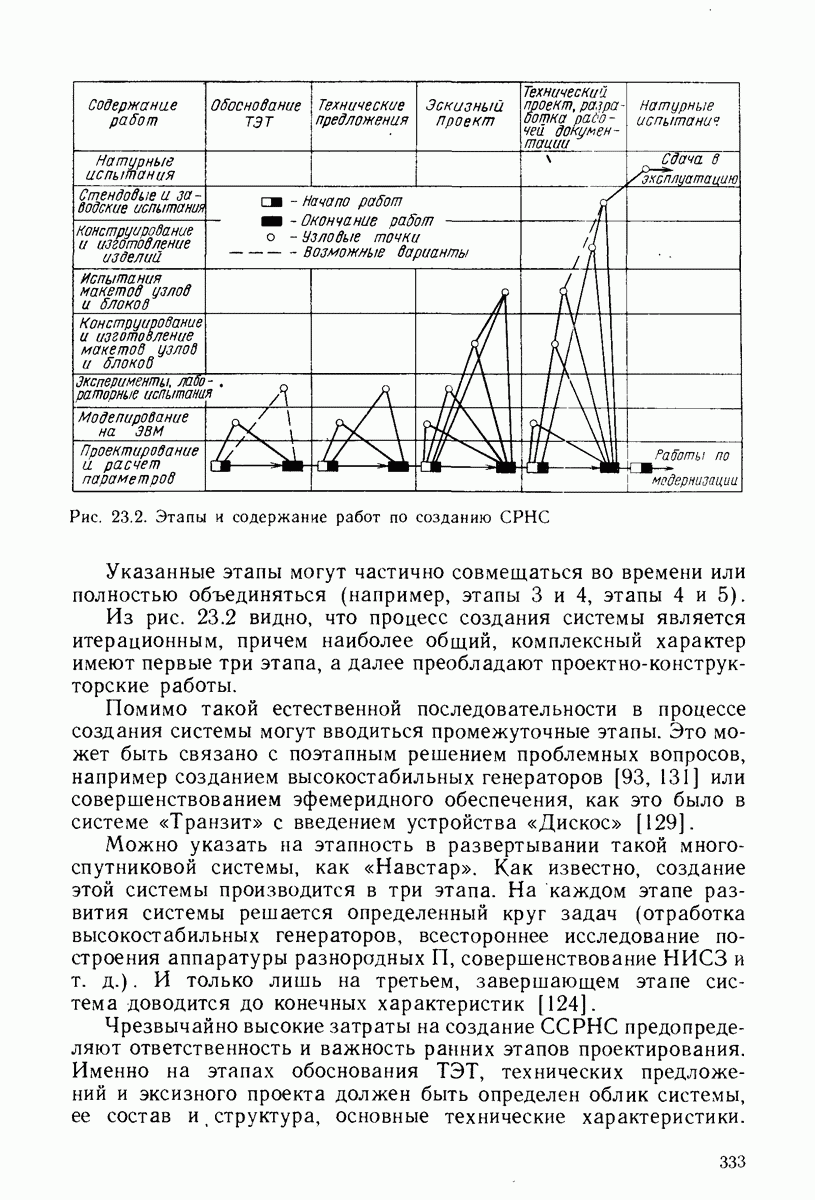
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
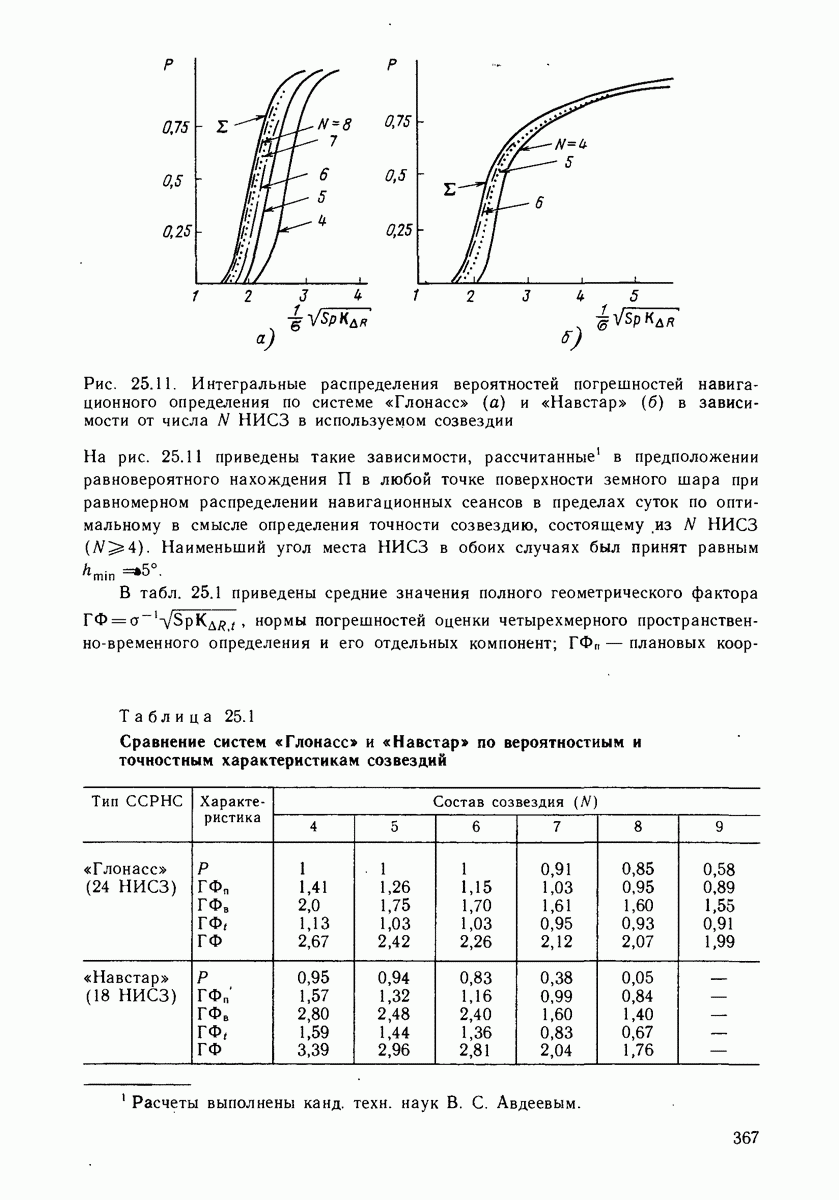
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС