| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
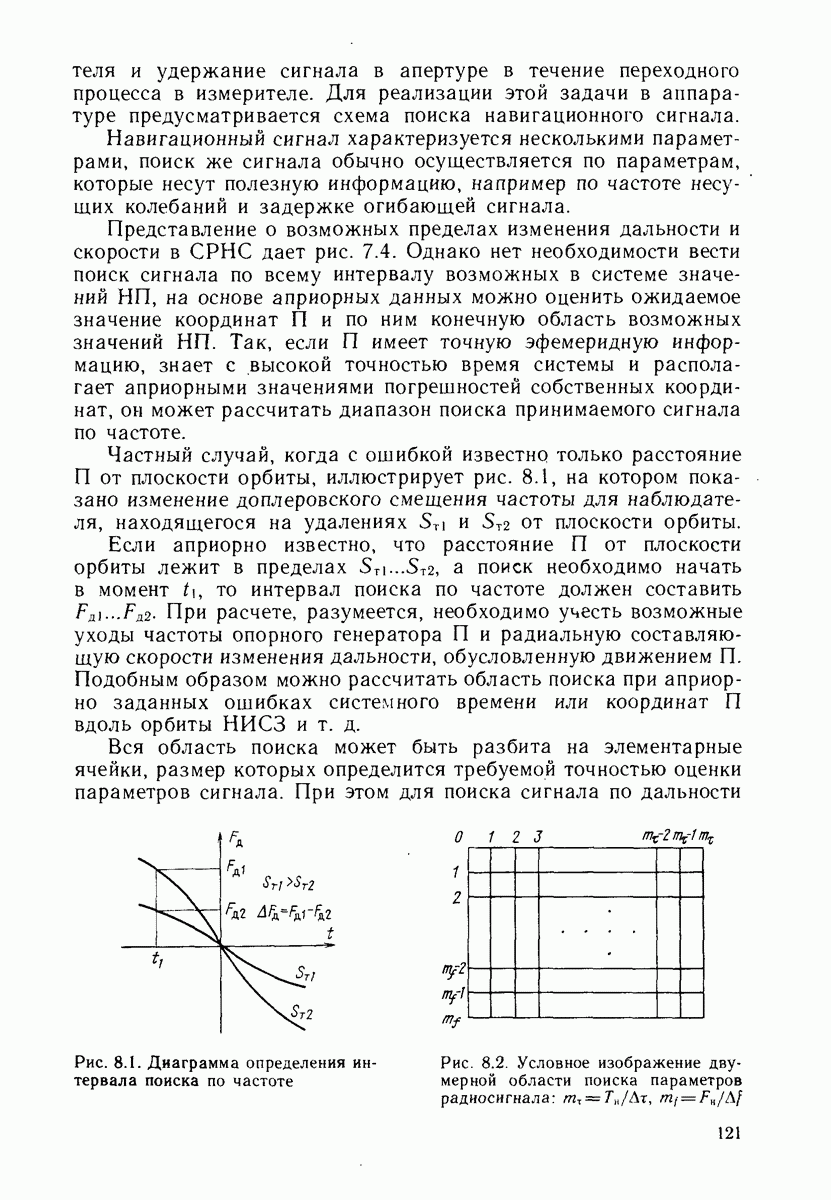
24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
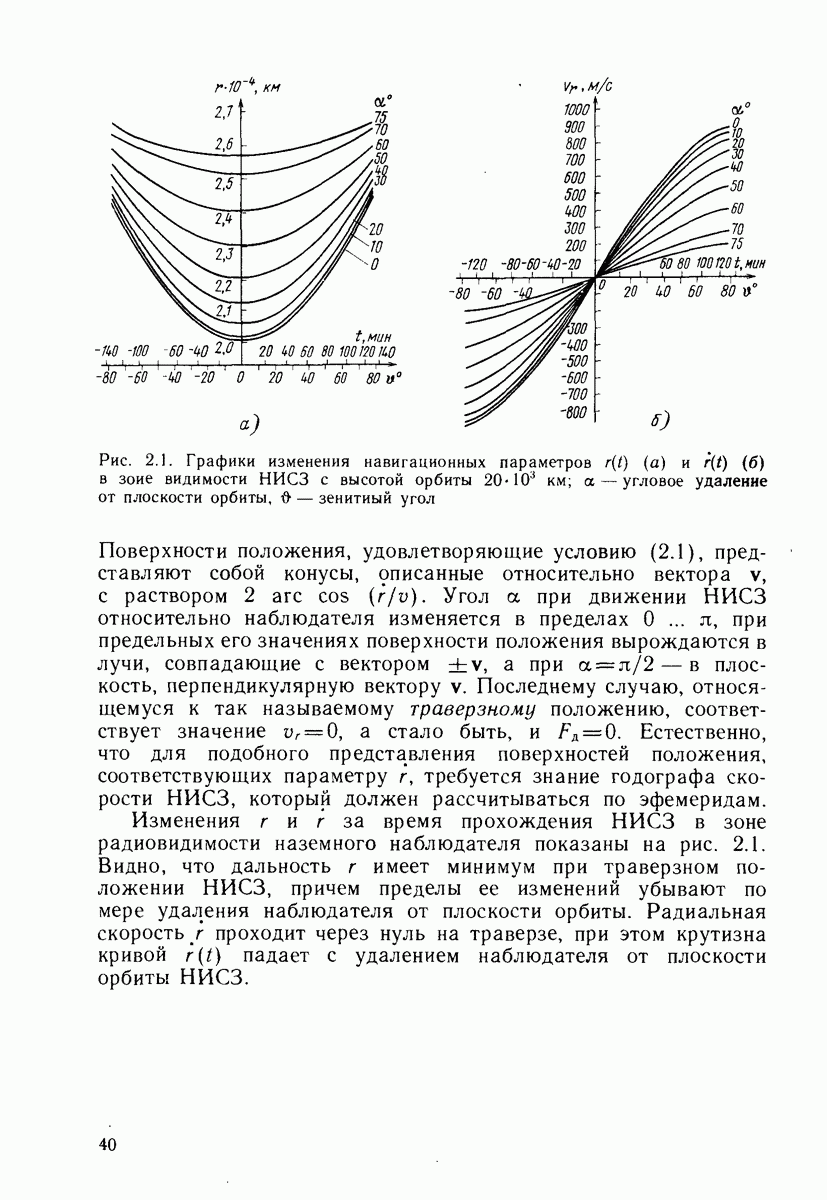
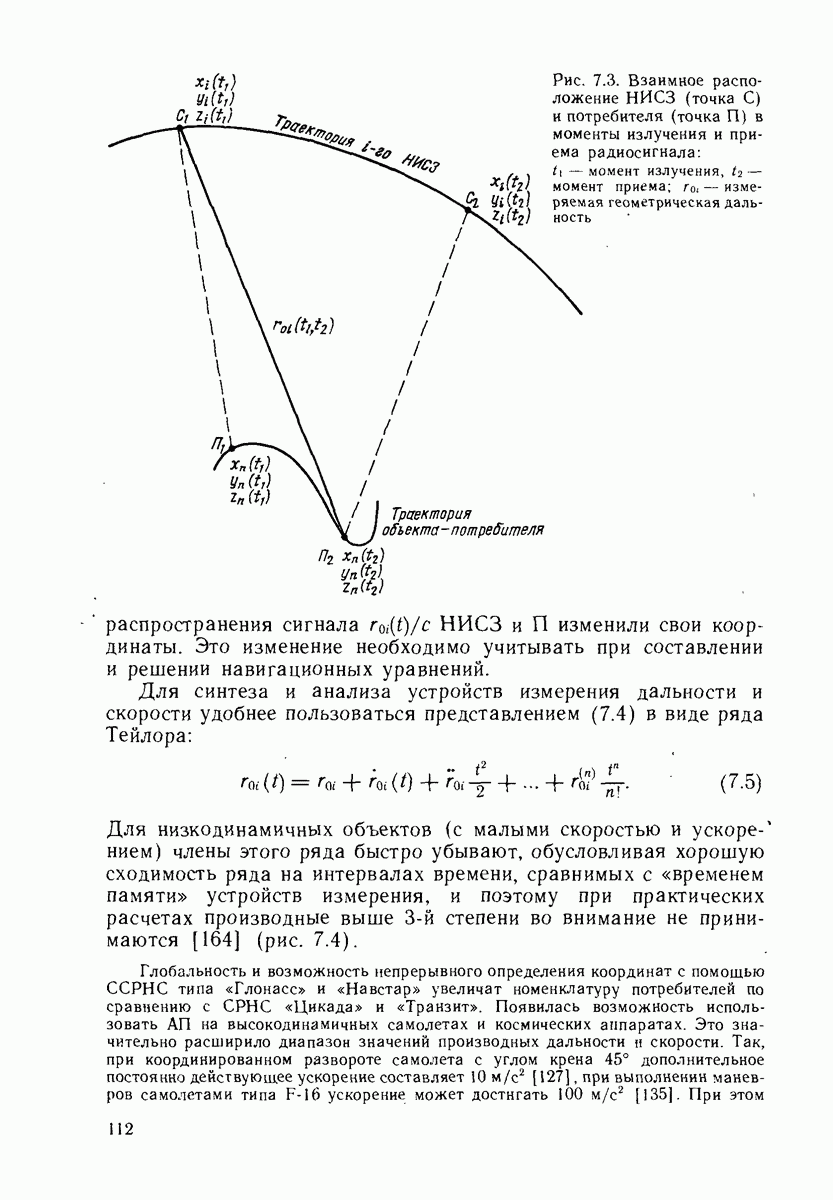
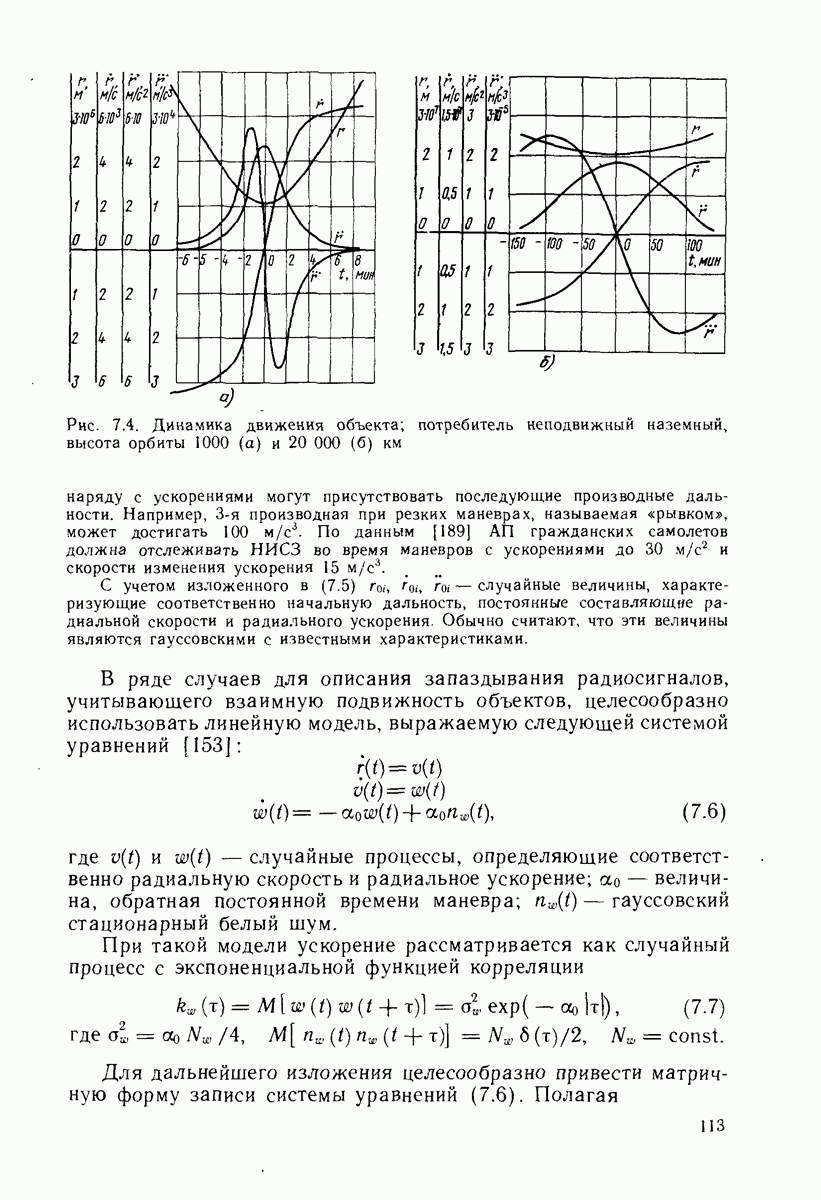
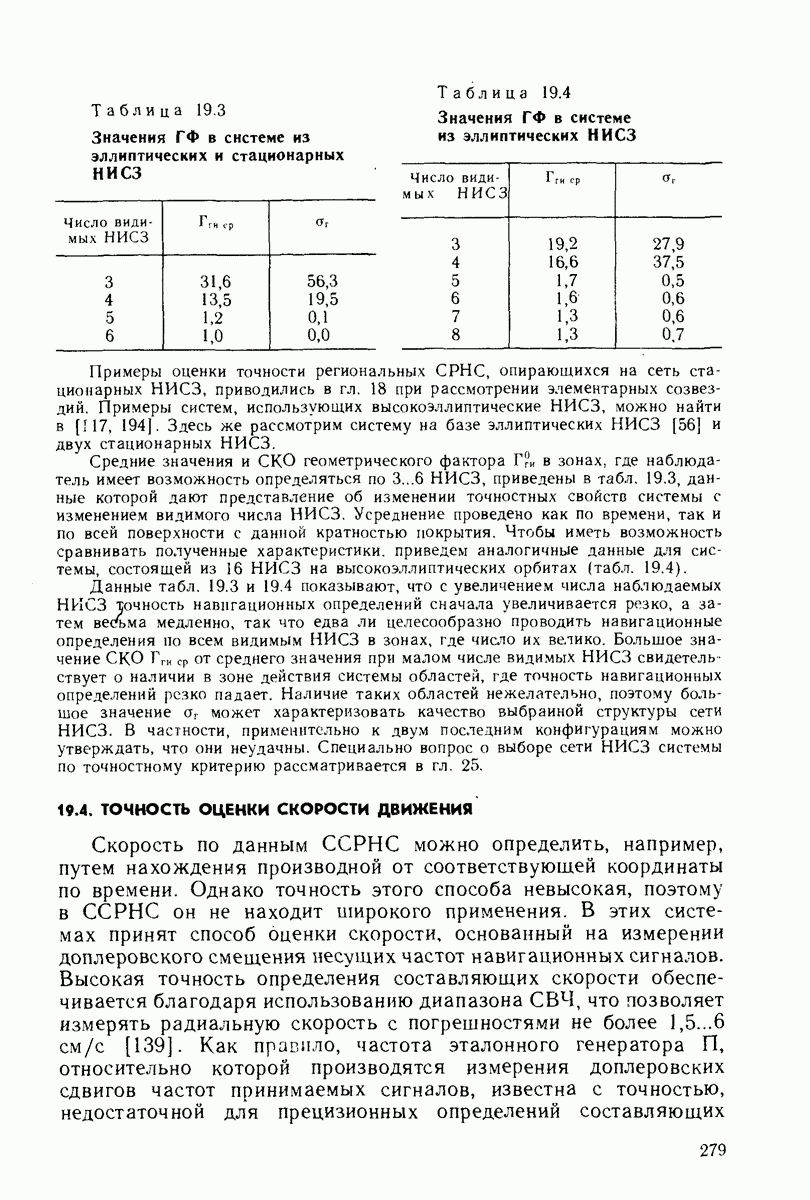
Эволюция движения спутников в процессе эксплуатации системы сопровождается возмущениями номинальной структуры сети НИСЗ. Возникает вопрос о критерии оценки допустимых возмущений в положении НИСЗ относительно его номинального значения. Один из простейших следует из требования обеспечения высокой точности обсерваций всюду в сфере обслуживания системы в течение всего времени ее эксплуатации, что связано с заданием границы максимальной погрешности обсервации. В гл. 25 будет приведена оценка точной верхней границы этой погрешности во всей рабочей зоне, будут выявлены случаи нарушения ограничений этой величины и показано, что критические случаи связаны с появлением областей  -кратного покрытия.
-кратного покрытия.
Используем условие появления областей минимального  -кратного перекрытия в качестве простейшего критерия для оценки допустимой расстройки структуры сети НИСЗ. Введенное ранее понятие полосы цепочки НИСЗ позволяет сформулировать простые геометрические условия для этого критерия.
-кратного перекрытия в качестве простейшего критерия для оценки допустимой расстройки структуры сети НИСЗ. Введенное ранее понятие полосы цепочки НИСЗ позволяет сформулировать простые геометрические условия для этого критерия.
Важной характеристикой полосы является сферический  -угольник, образуемый пересечением границ областей радиовидимости пары НИСЗ, смежной о двумя соседними спутниками. Половина его высоты, обозначенная
-угольник, образуемый пересечением границ областей радиовидимости пары НИСЗ, смежной о двумя соседними спутниками. Половина его высоты, обозначенная  в соотношении (24.2), связана с половиной его ширины у и геоцентрическим радиусом области радиовидимости 9. Этот
в соотношении (24.2), связана с половиной его ширины у и геоцентрическим радиусом области радиовидимости 9. Этот  -угольник представляет собой область
-угольник представляет собой область  -кратного перекрытия полосы, а его вершины определяют одновременно границы области
-кратного перекрытия полосы, а его вершины определяют одновременно границы области  -кратного перекрытия.
-кратного перекрытия.
Можно считать, что на длительных интервалах времени превалирующими возмущениями будут смещения НИСЗ от его

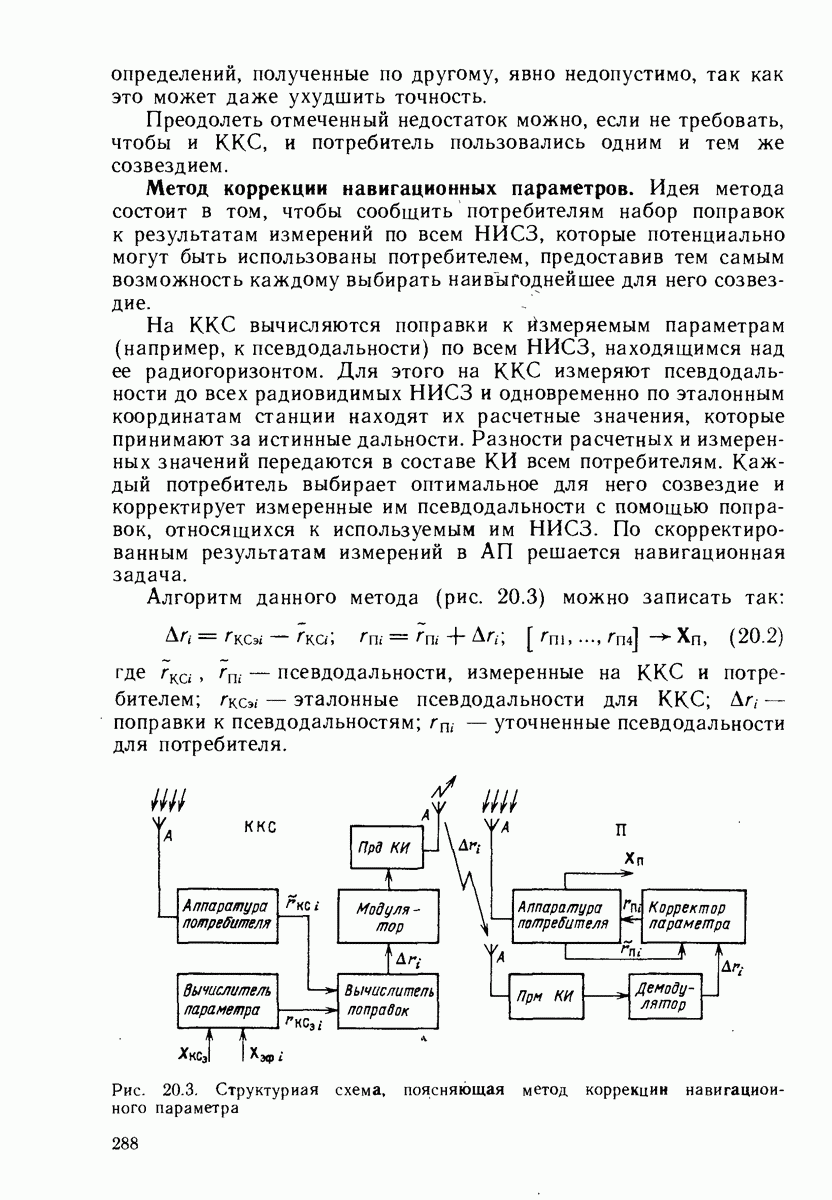
Рис. 24.6. Диаграмма, поясняющая условие вырождения номинальной сети минимальной кратности покрытия  приводящее к появлению области покрытия кратности
приводящее к появлению области покрытия кратности  а — траектория центра композиции дефектов; б - плоскость 1-й цепочки; в — плоскость 2-й цепочки; г - сегмеит
а — траектория центра композиции дефектов; б - плоскость 1-й цепочки; в — плоскость 2-й цепочки; г - сегмеит  в 3-й цепочке
в 3-й цепочке
номинального положения вдоль орбиты. В процессе эволюции НИСЗ полосы цепочек будут подвергаться локальным возмущениям двух типов: трансляциям и деформации. Первые будут приводить к нарушению оптимального фазирования НИСЗ из разных цепочек, а вторые — к изменению кратности покрытия. Локальная деформация полосы, приводящая к вырождению  -угольника, эквивалентна появлению разделяющей полосу области
-угольника, эквивалентна появлению разделяющей полосу области  -кратного покрытия.
-кратного покрытия.
Одновременное пересечение подобных областей из двух полос в одном из сферических сегментов радиуса со, вписанных в 3-ю полосу, означает реализацию области  -кратного покрытия. Ясно, что
-кратного покрытия. Ясно, что 
На рис. 24.6 показана траектория центра композиции дефектов двух полос в сферическом сегменте со 3-й для номинальной системы (в изображении на плоскости). Из приведенного изображения следует, что значение  приводящее к появлению точки
приводящее к появлению точки  -кратного покрытия, будет наибольшим из возможных, когда одновременно для обеих полос
-кратного покрытия, будет наибольшим из возможных, когда одновременно для обеих полос  При этом критическое значение
При этом критическое значение  Для номинальной системы
Для номинальной системы 
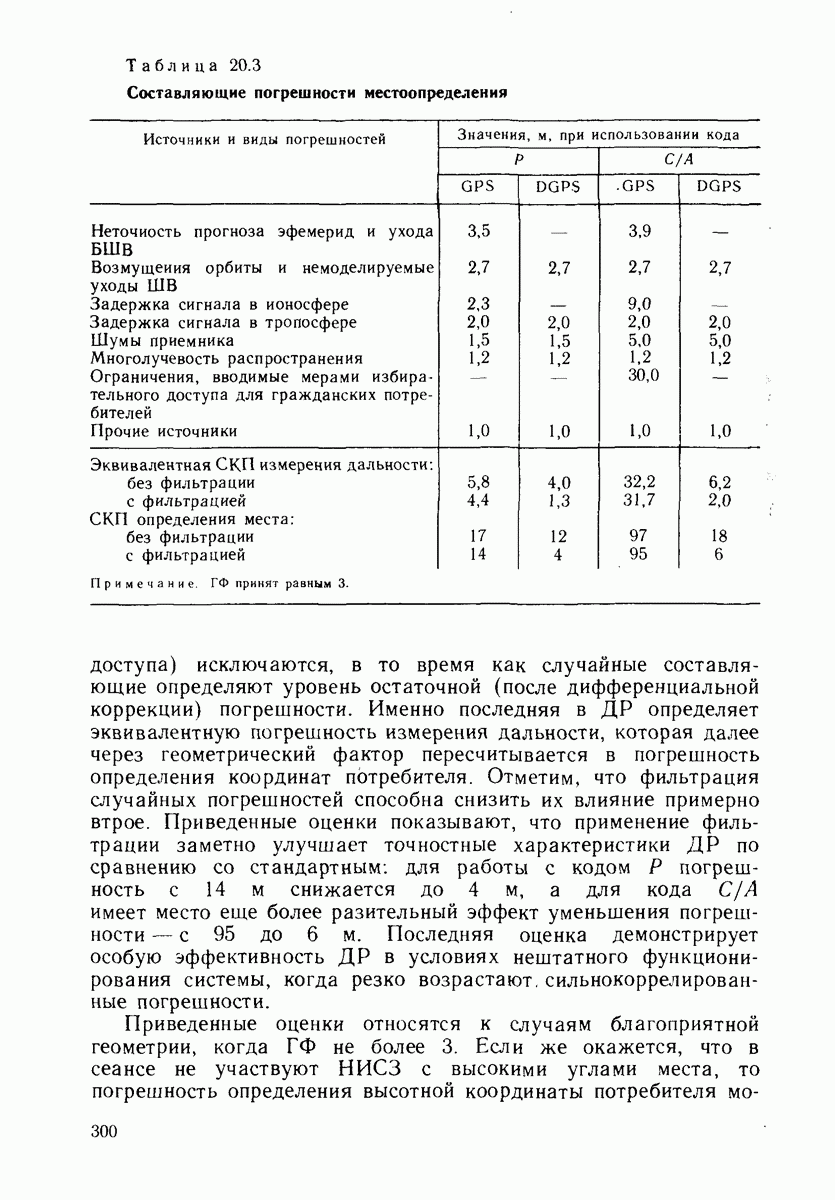
В табл. 24.1 показаны зависимости от  параметров
параметров 
 -угольника полосы, рассчитанные по формулам (24.2) и (24.3), а также сферического радиуса видимости 9 для НИСЗ с периодом
-угольника полосы, рассчитанные по формулам (24.2) и (24.3), а также сферического радиуса видимости 9 для НИСЗ с периодом 
Из таблицы следует, что в номинальной системе при имеет место критический по критерию  -кратного покрытия случай
-кратного покрытия случай  Необходимо также отметить и геометрически очевидное свойство почти скачкообразно изменять
Необходимо также отметить и геометрически очевидное свойство почти скачкообразно изменять  при малых значениях у. Это говорит о сильной зависимости
при малых значениях у. Это говорит о сильной зависимости
Таблица 24.1 (см. скан) Параметры двуугольника  в функции угла
в функции угла 
точностных характеристик (оцениваемых критерием минимума максимальной ошибки обсервации) от небольших возмущений в структуре сети НИСЗ, откуда следует необходимость создавать определенный запас перекрытий.
Получение явных выражений для указанного условия вырождения (в виде появления области  -кратного покрытия) в категориях дрейфа каждого НИСЗ цепочки относительно его номинального положения требует специального исследования.
-кратного покрытия) в категориях дрейфа каждого НИСЗ цепочки относительно его номинального положения требует специального исследования.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
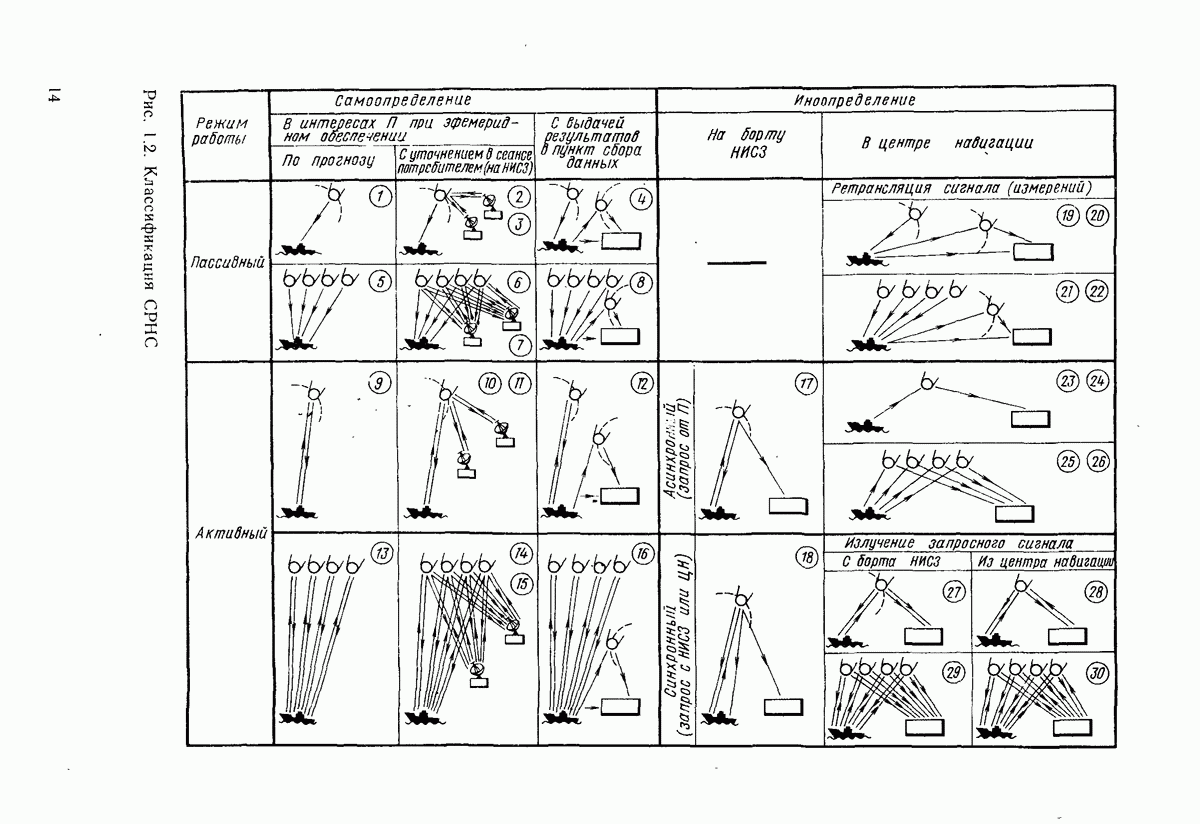
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
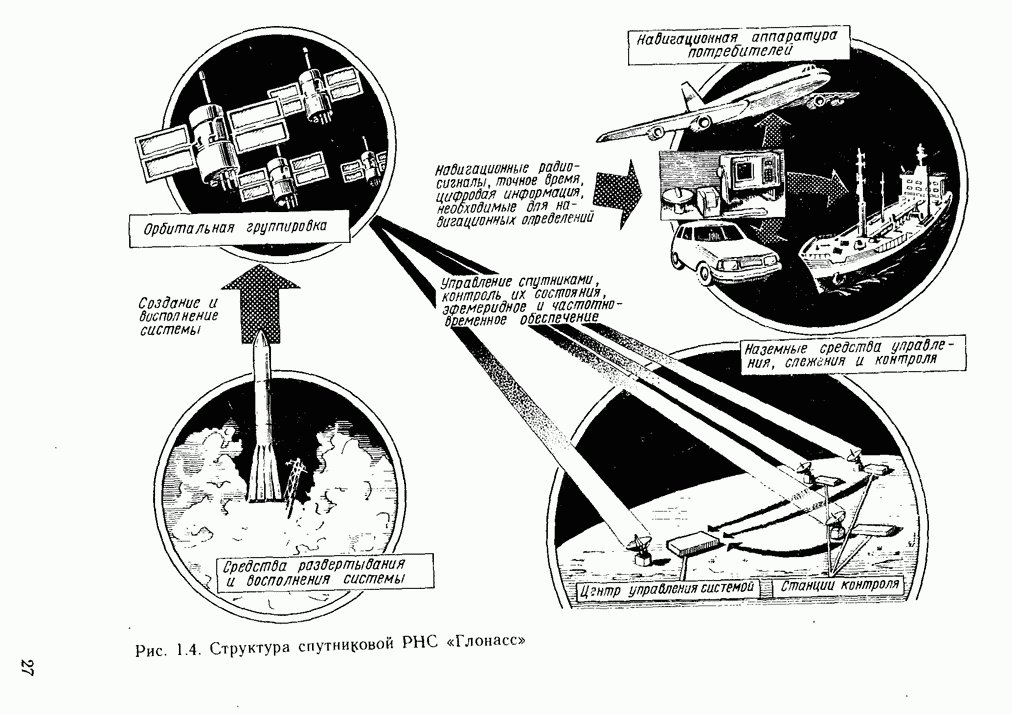
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
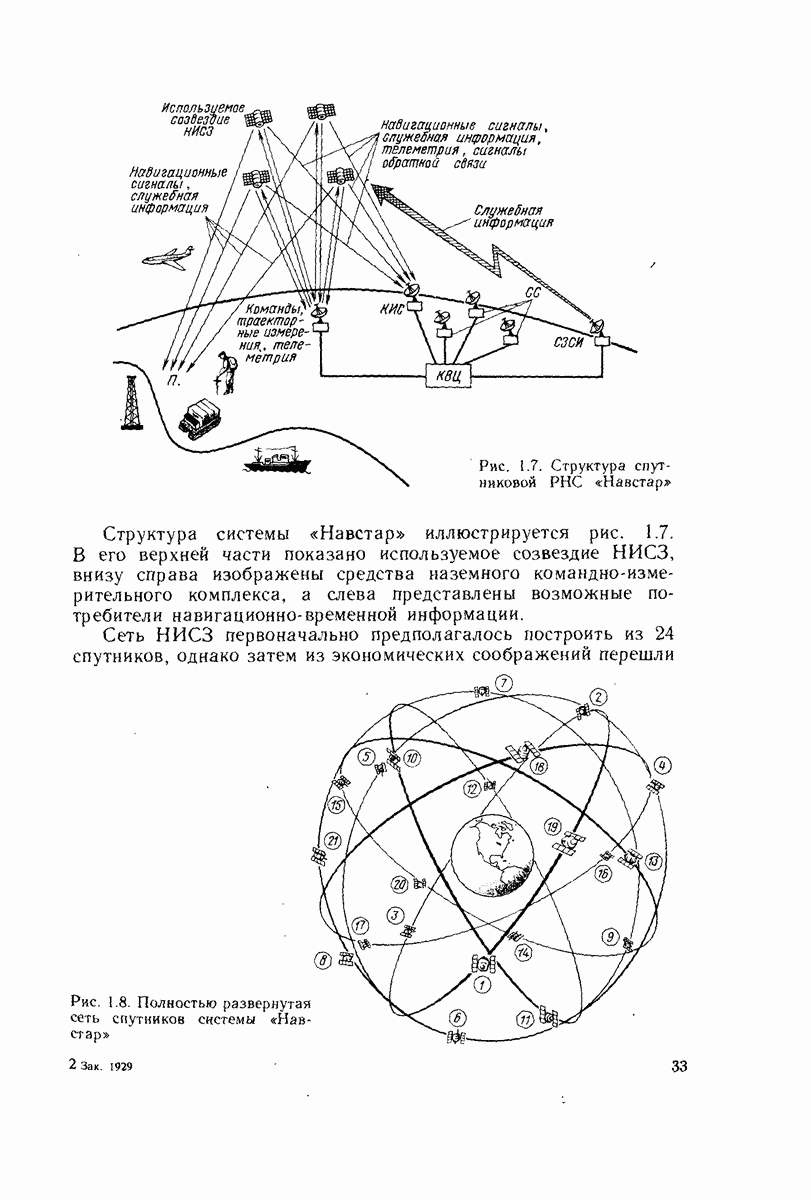
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
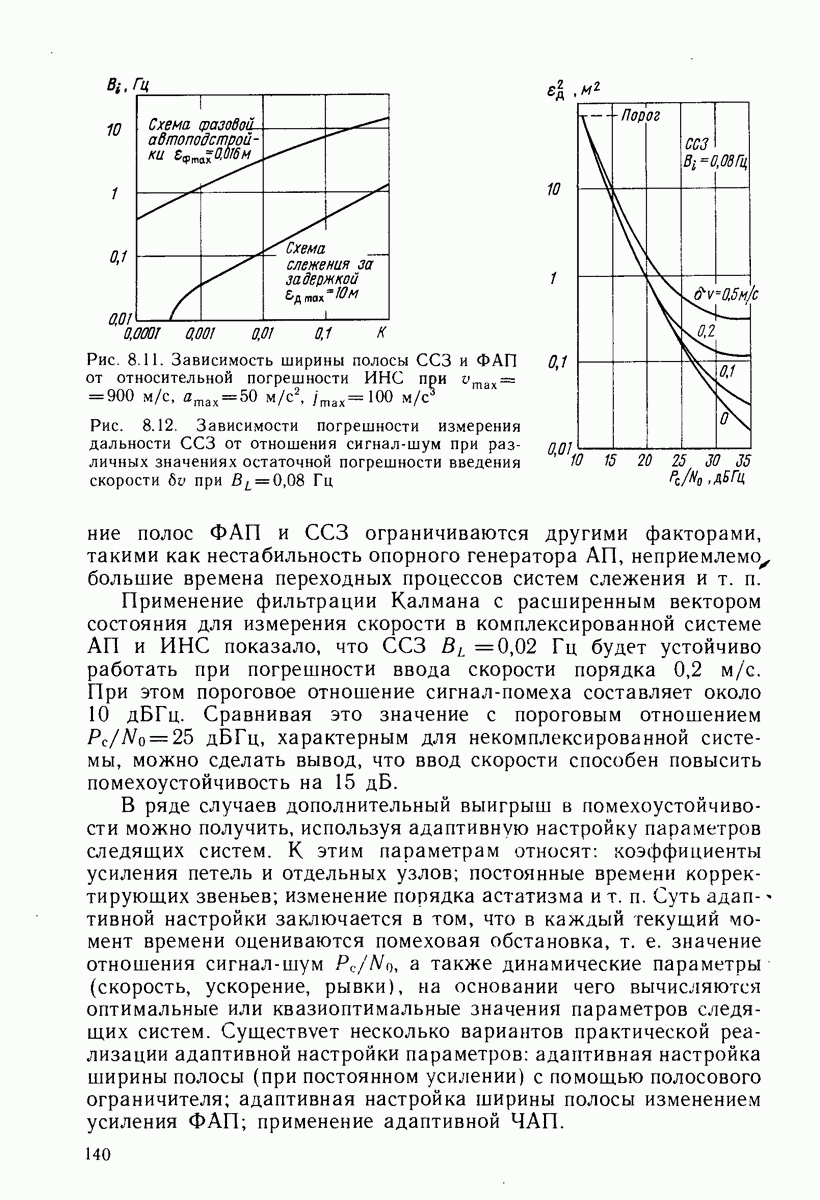
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
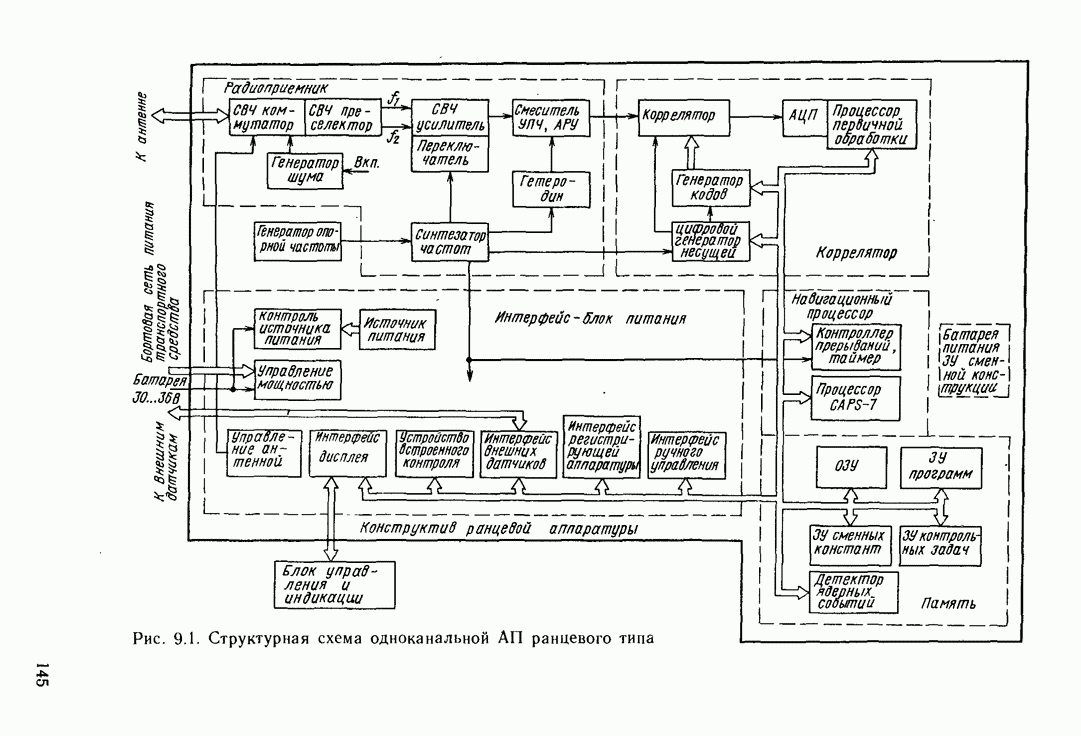
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
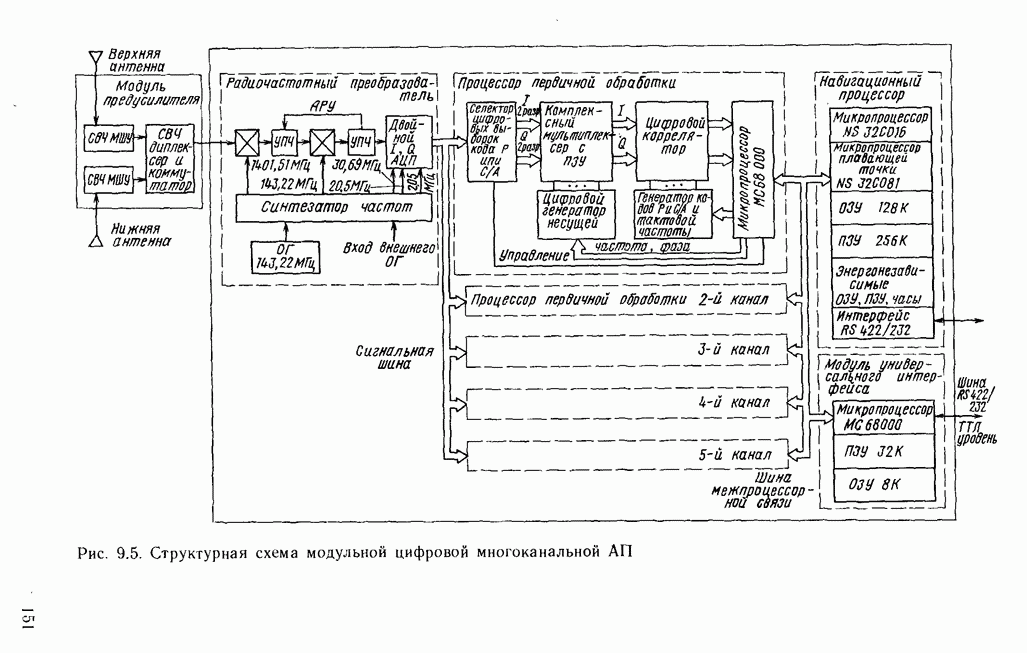
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
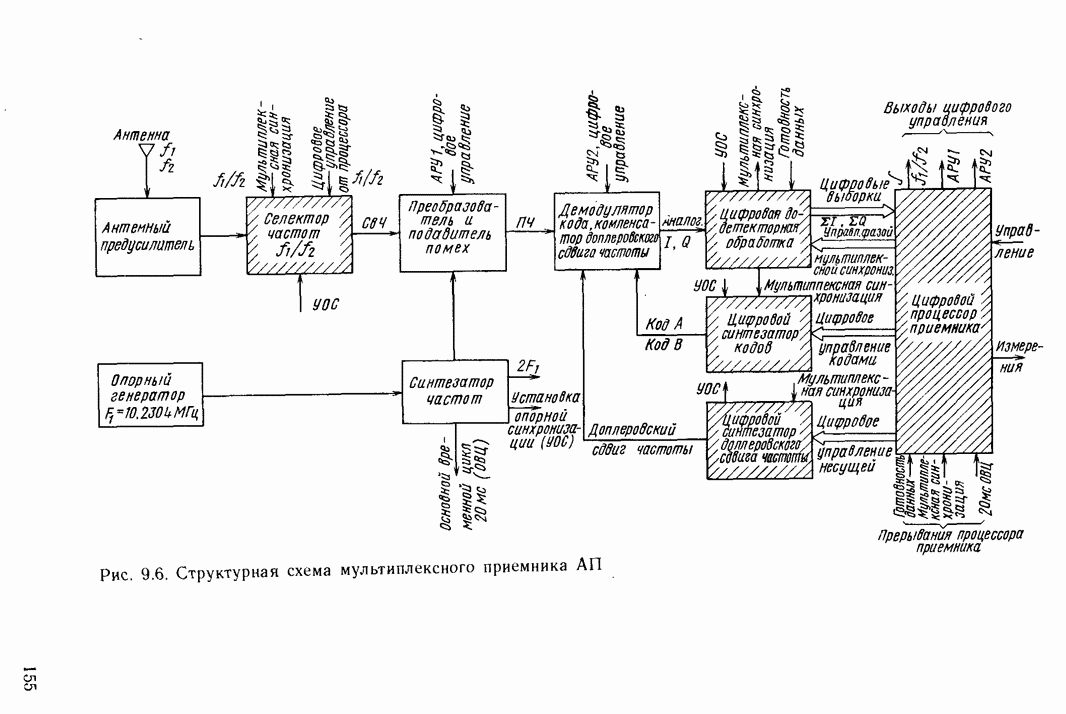
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
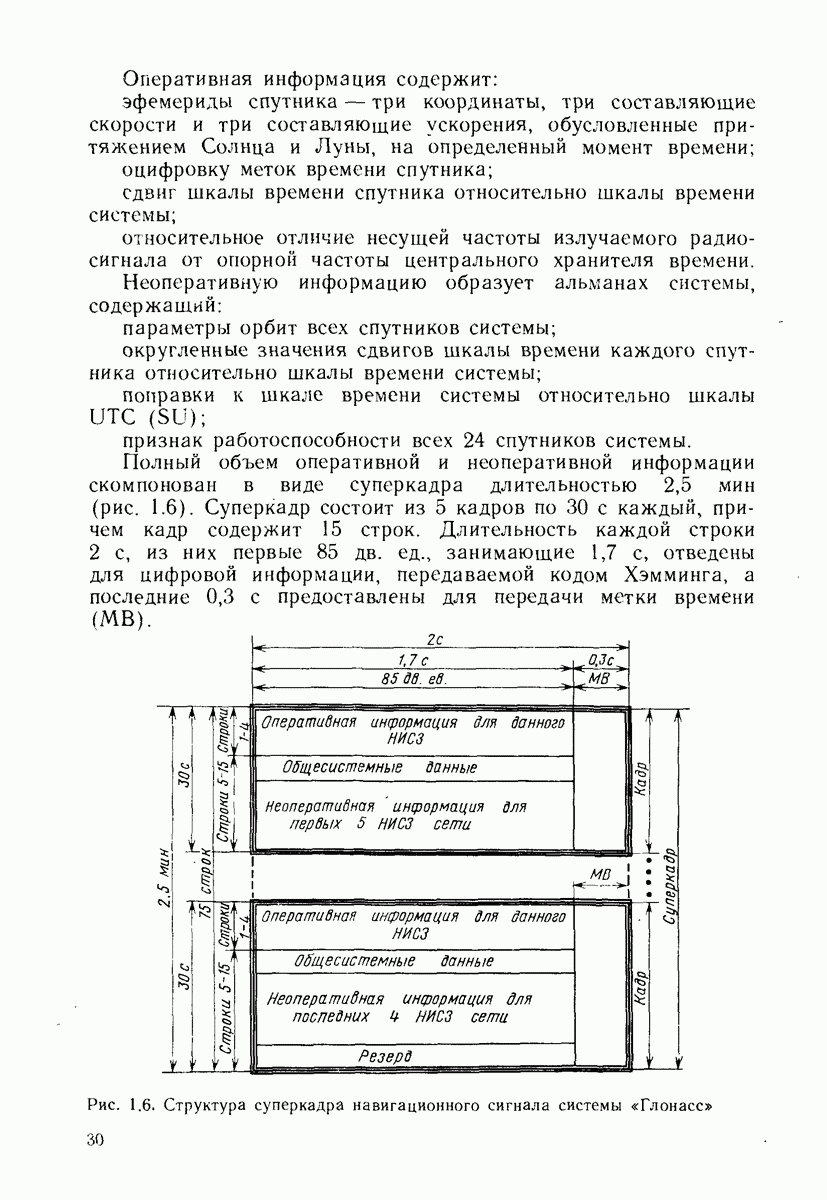
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
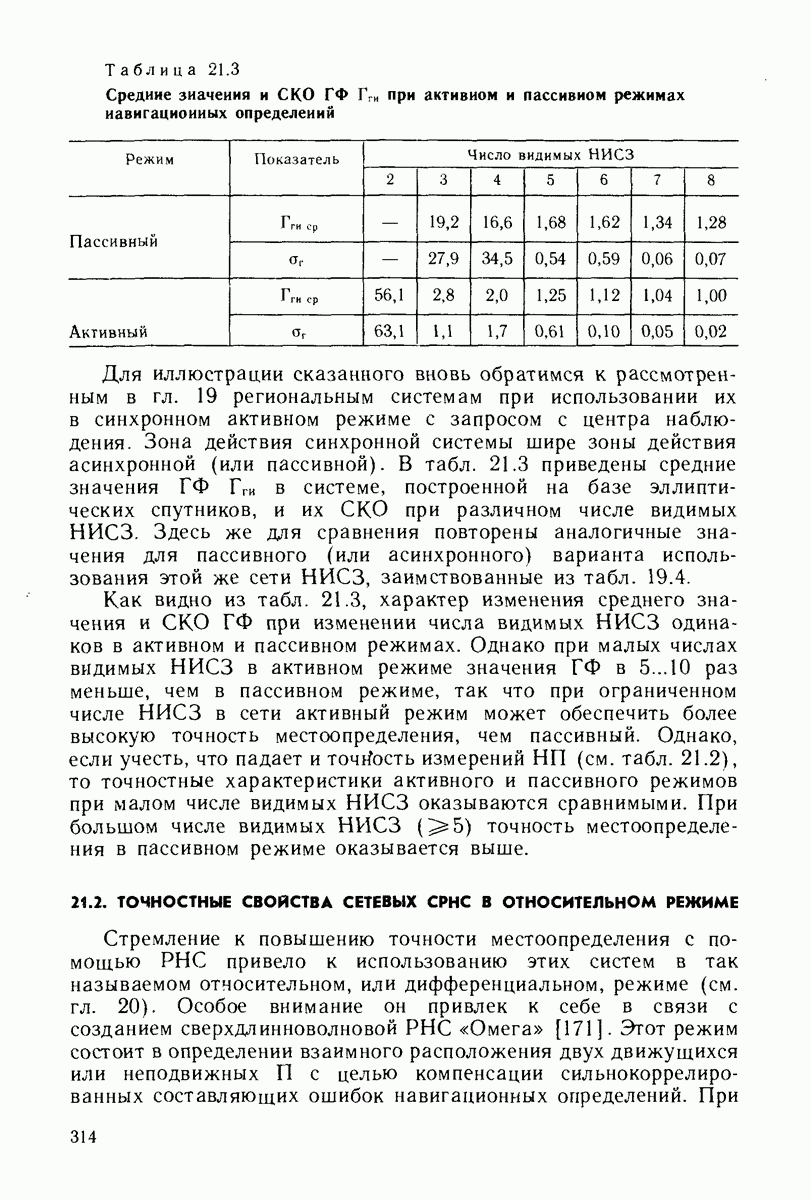
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
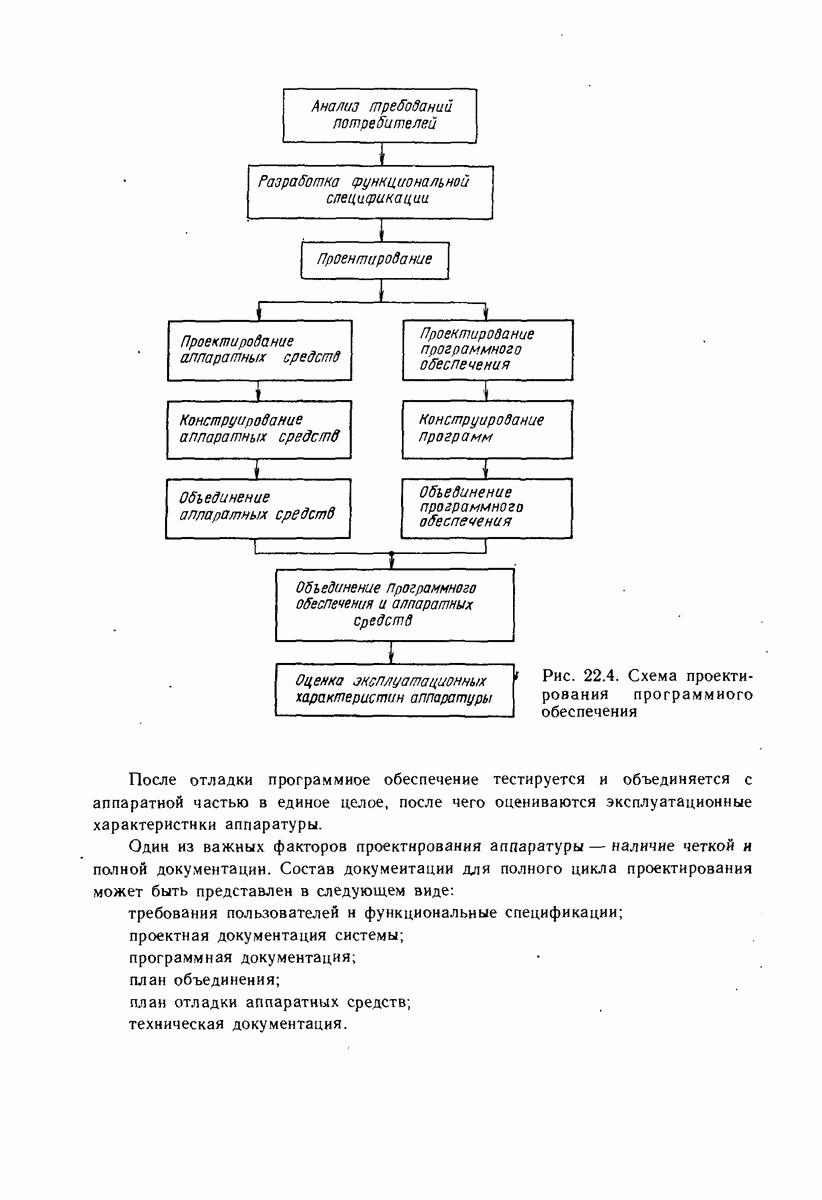
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
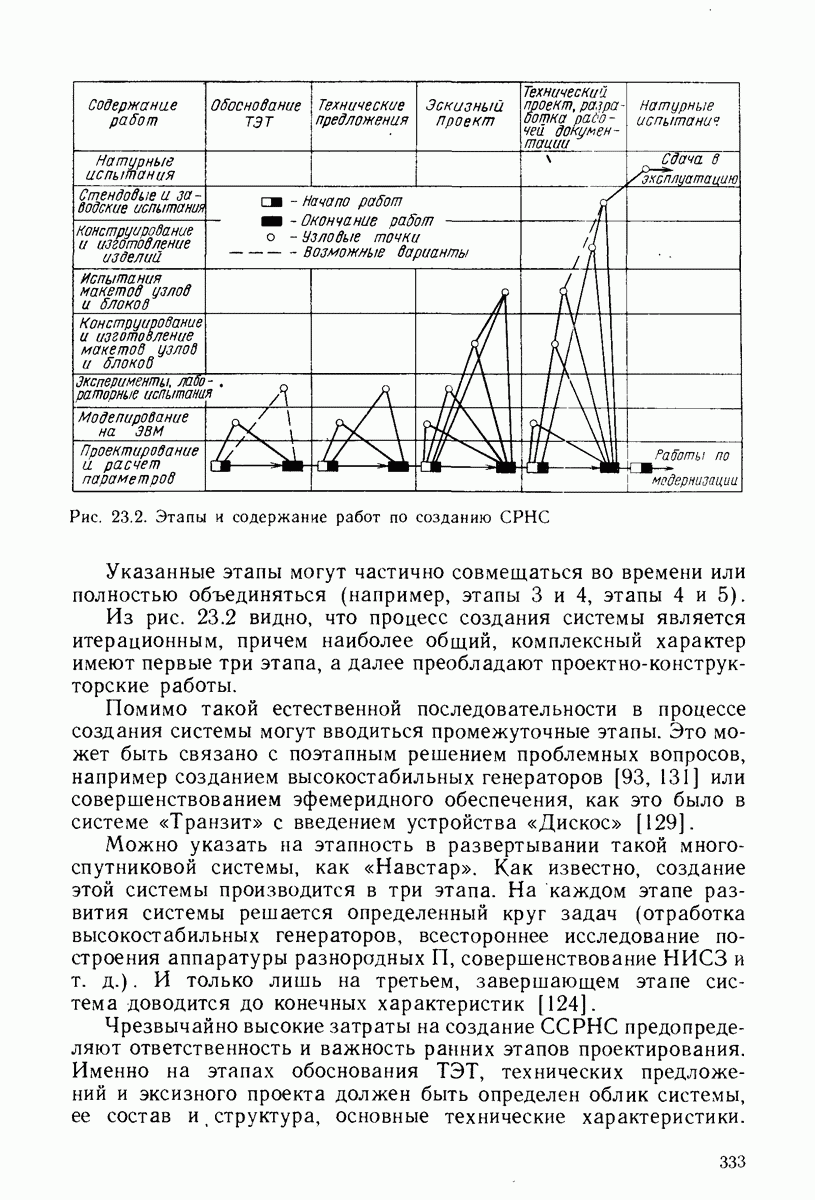
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
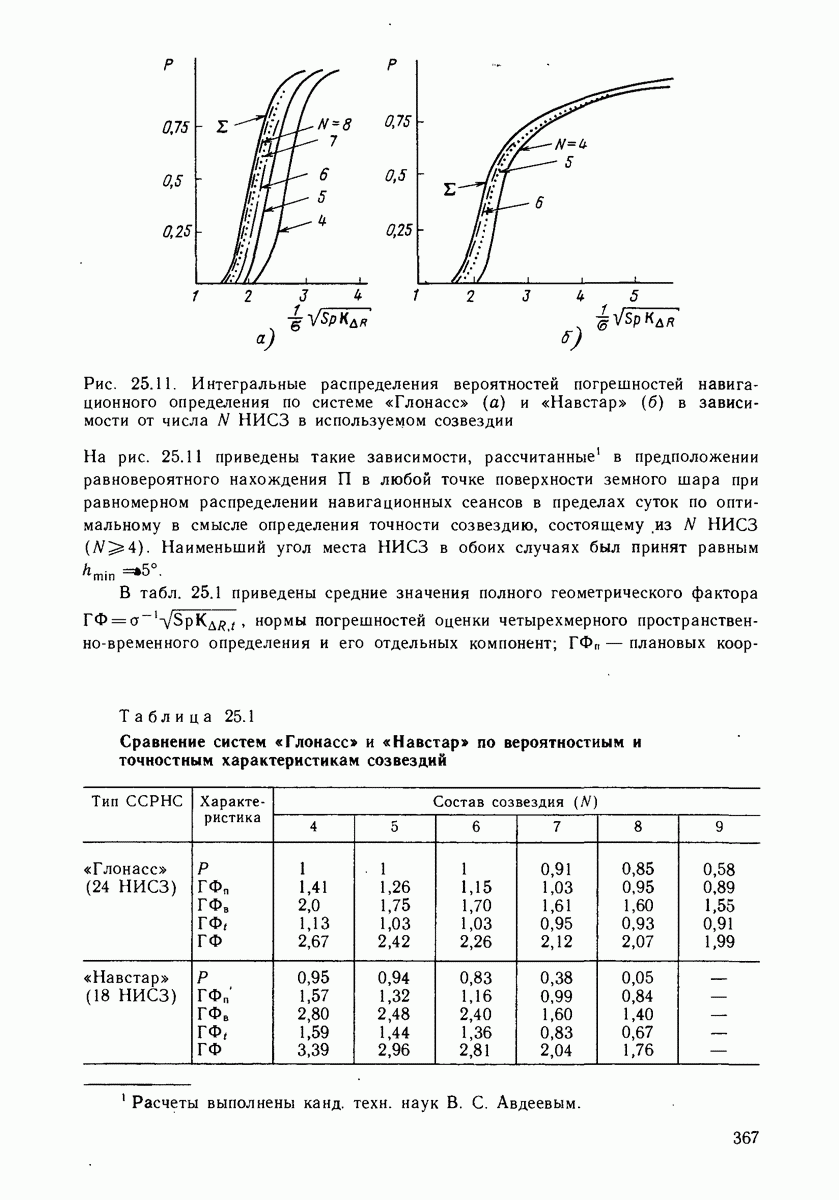
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС