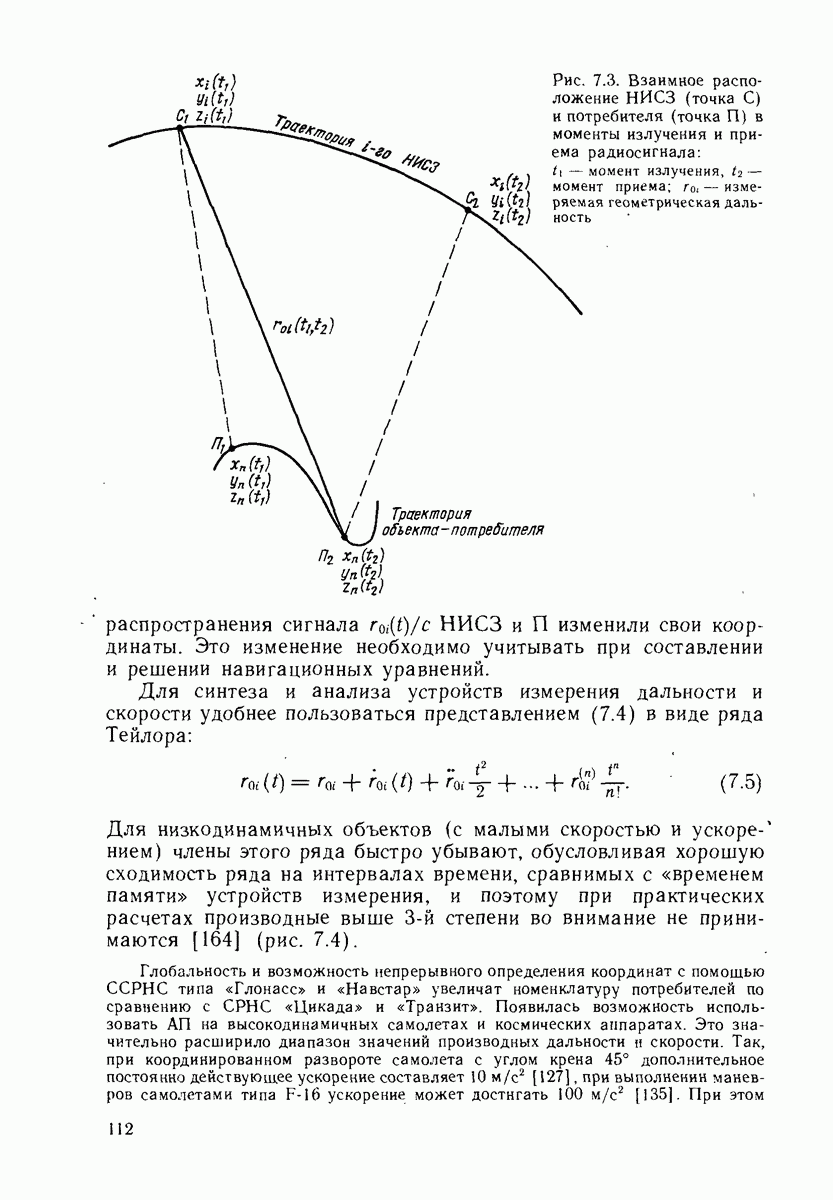
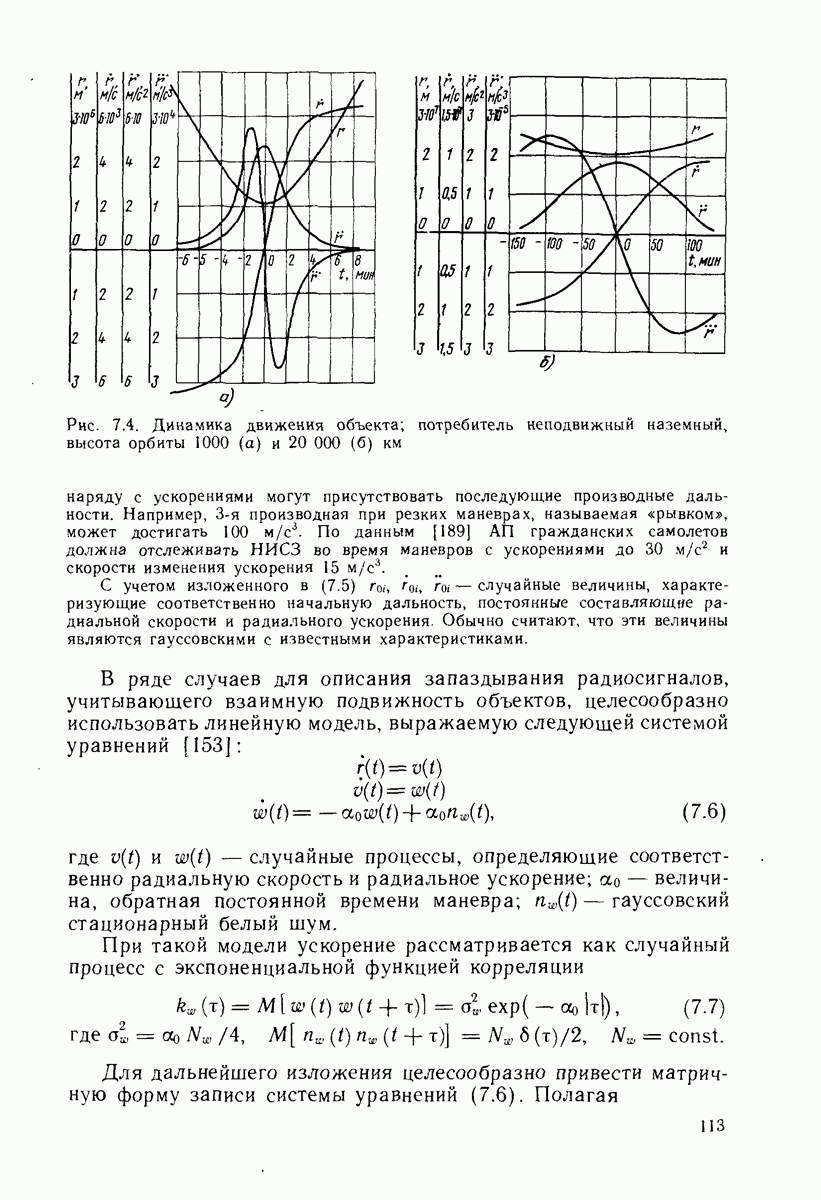
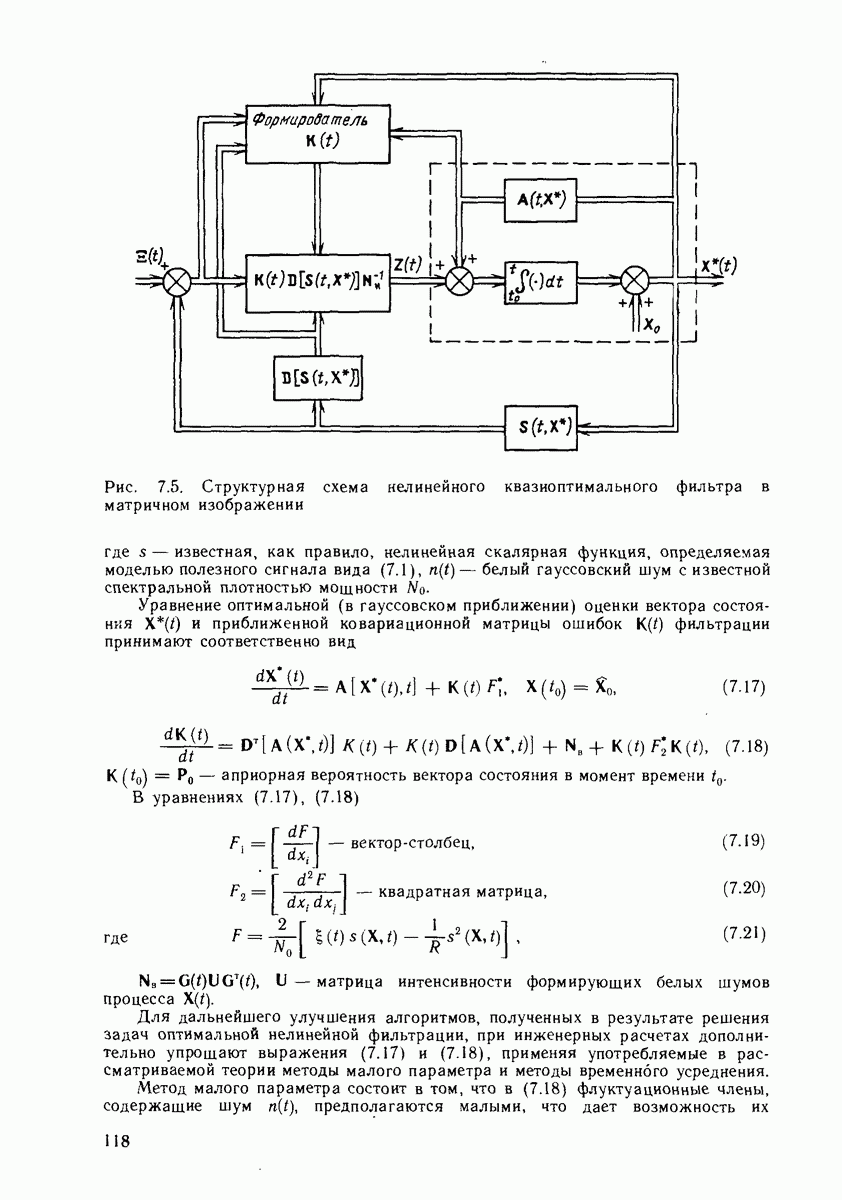
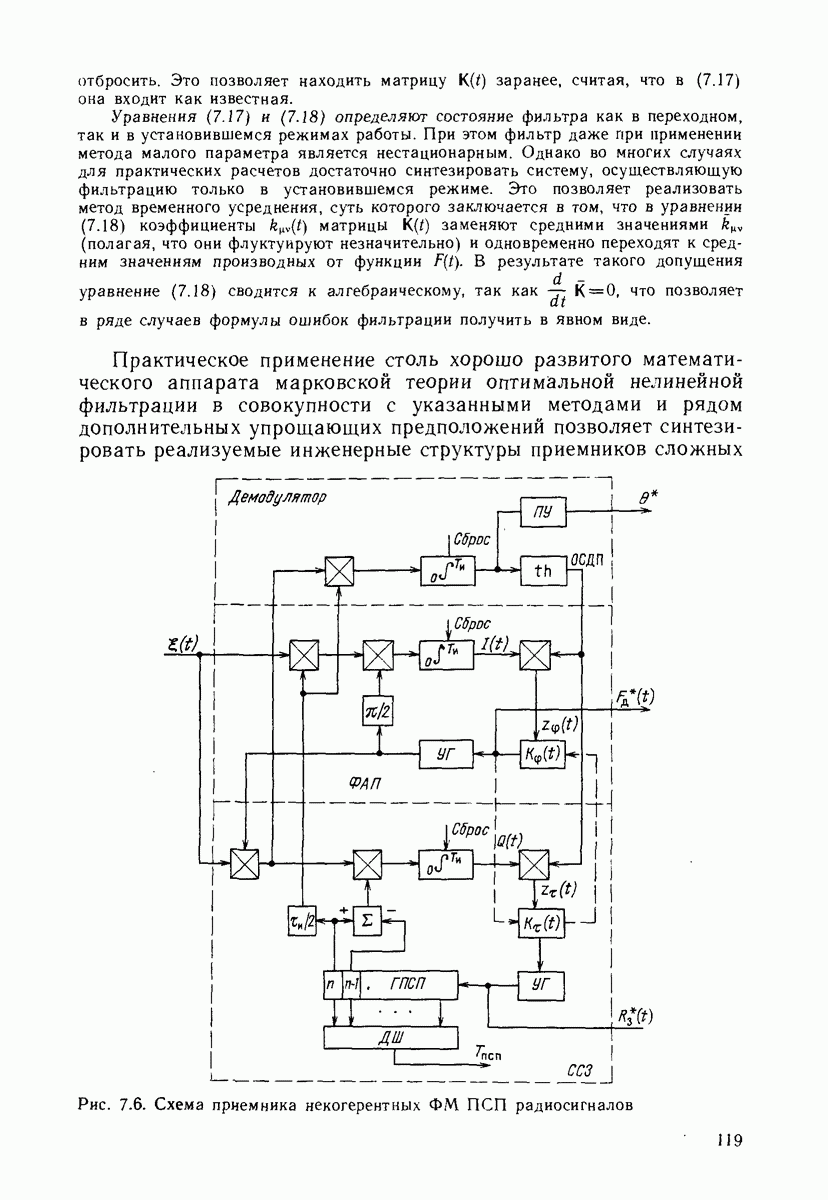
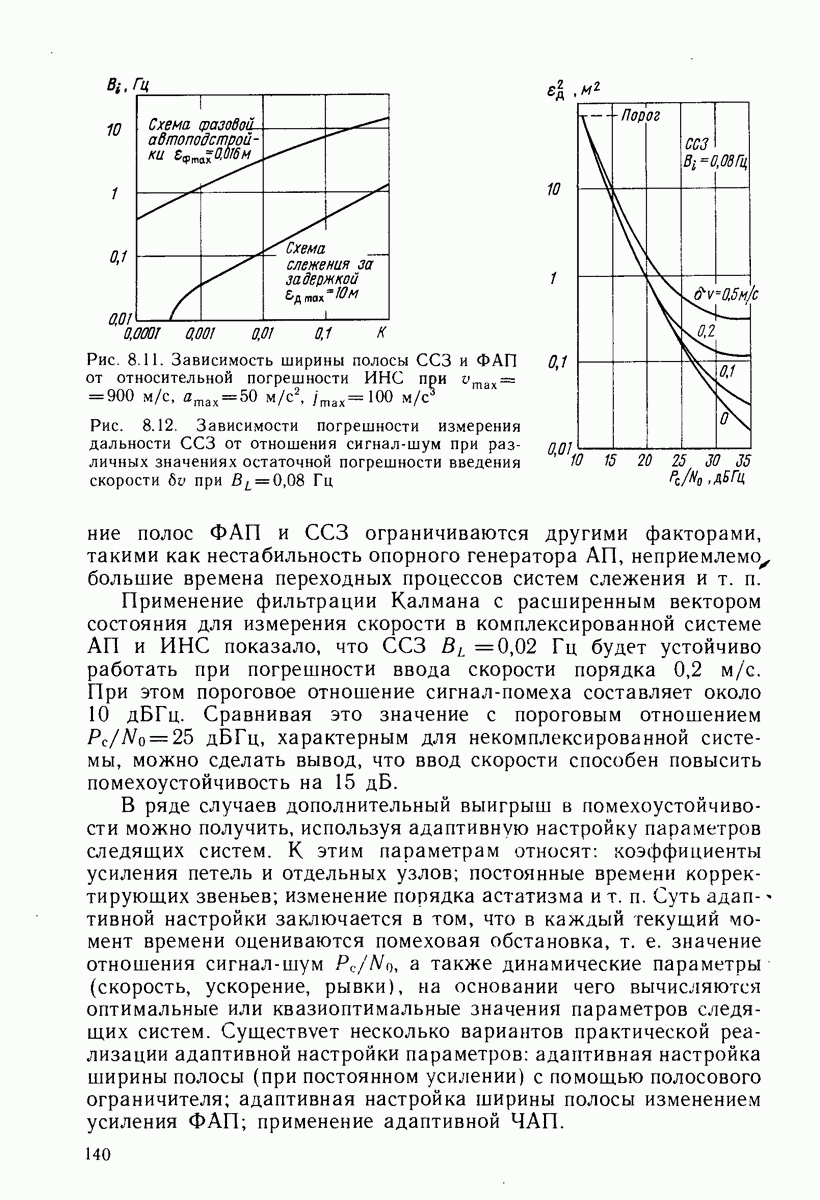
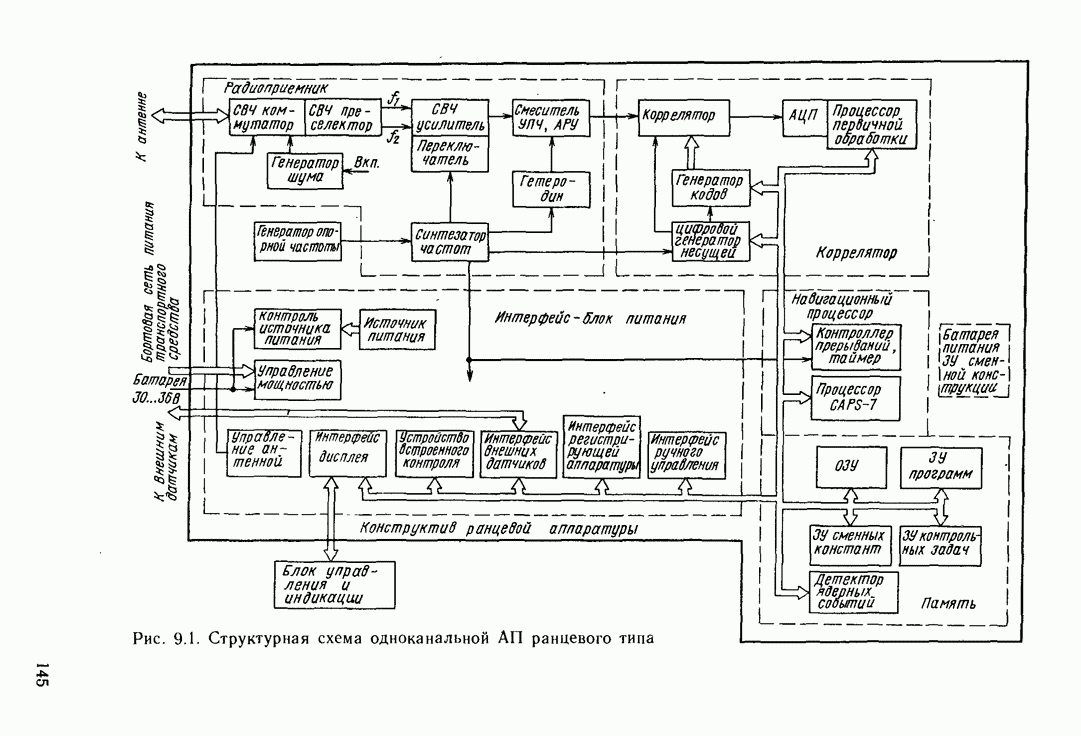
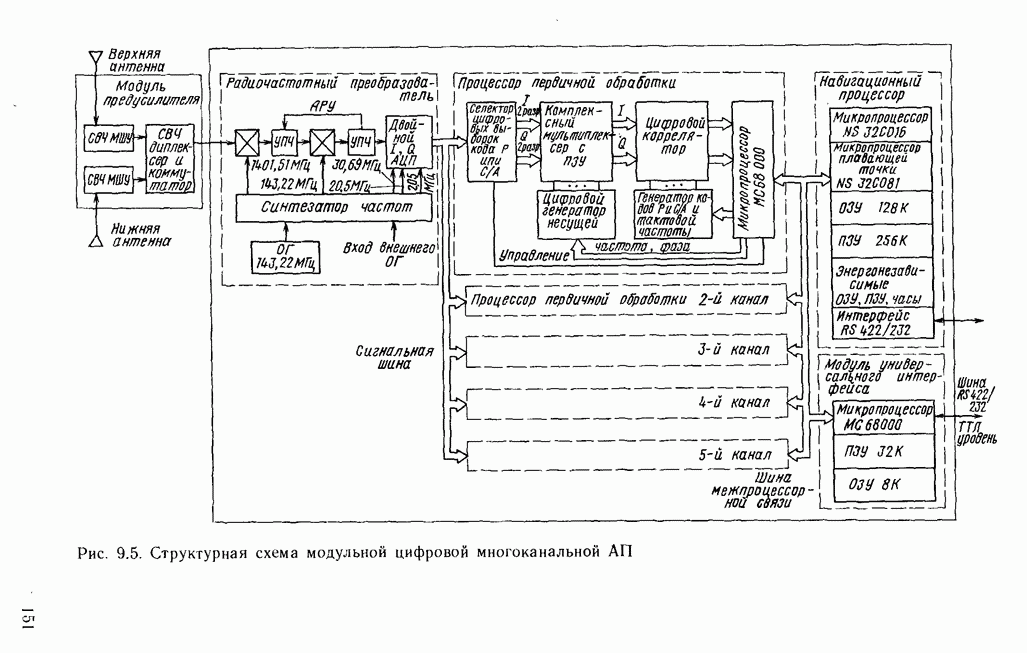
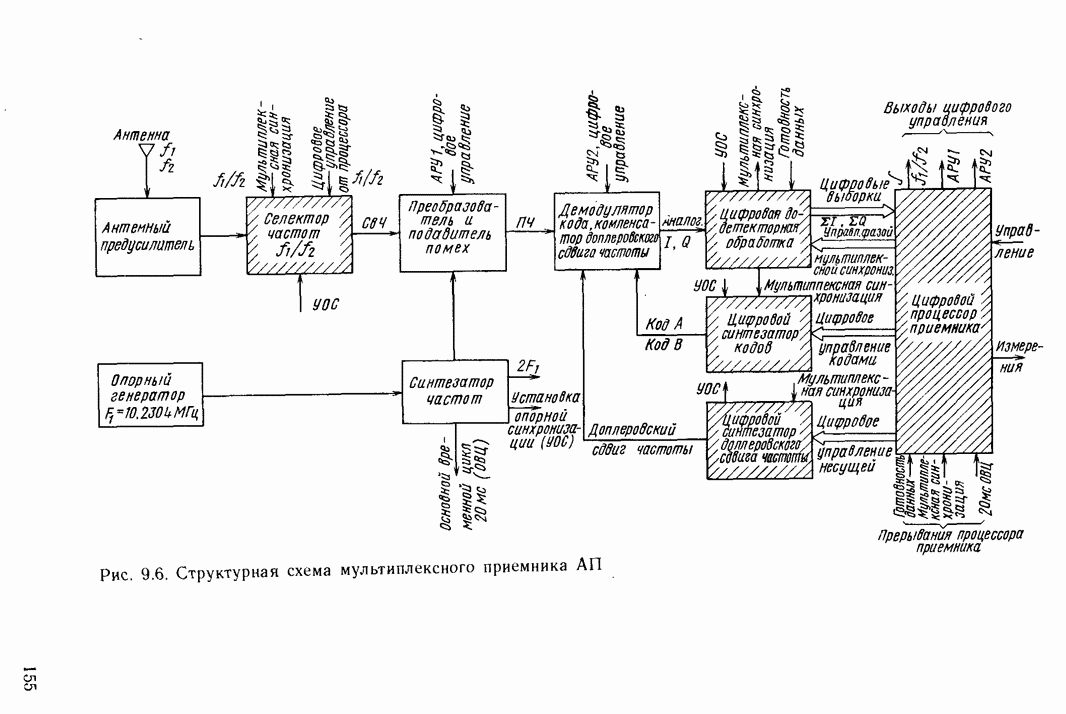
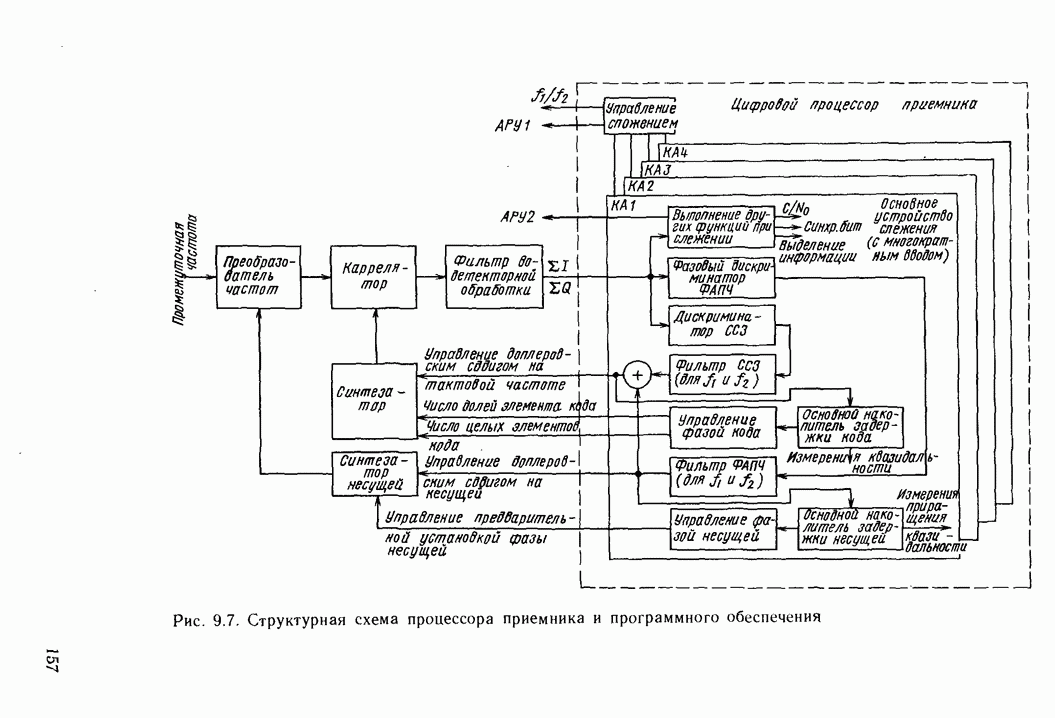
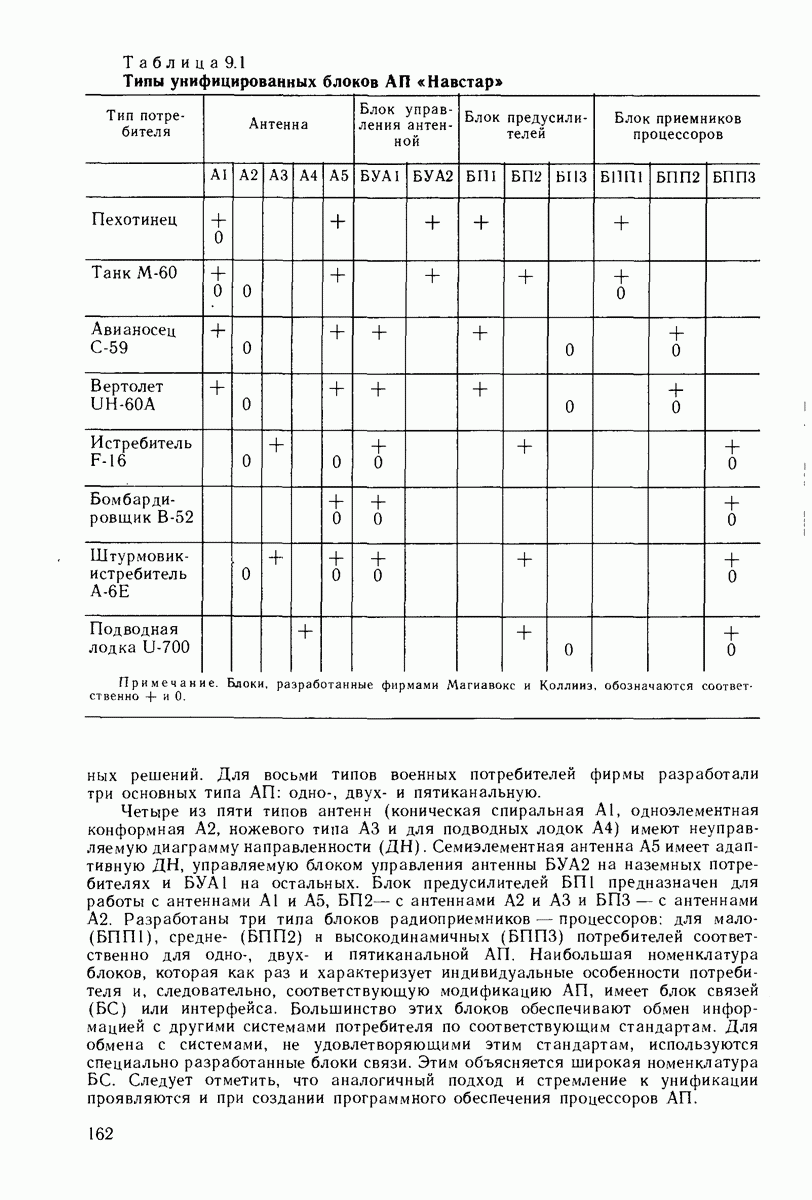
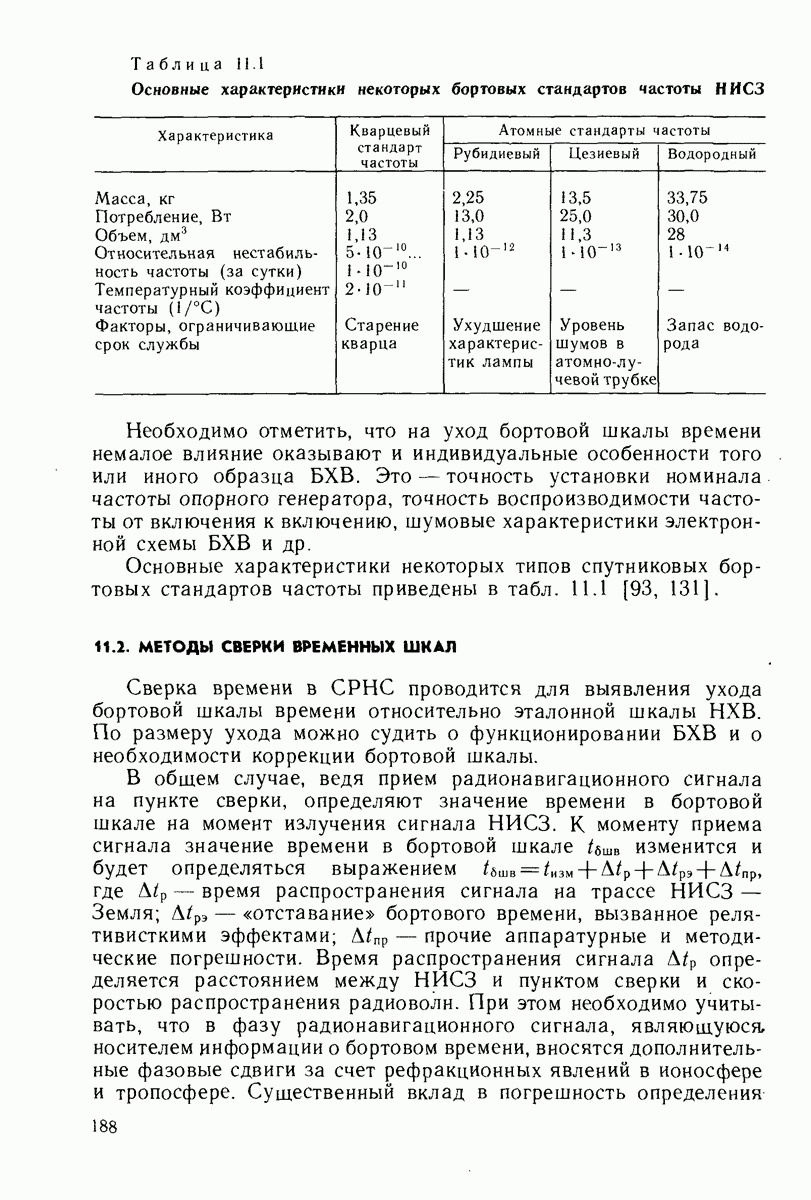
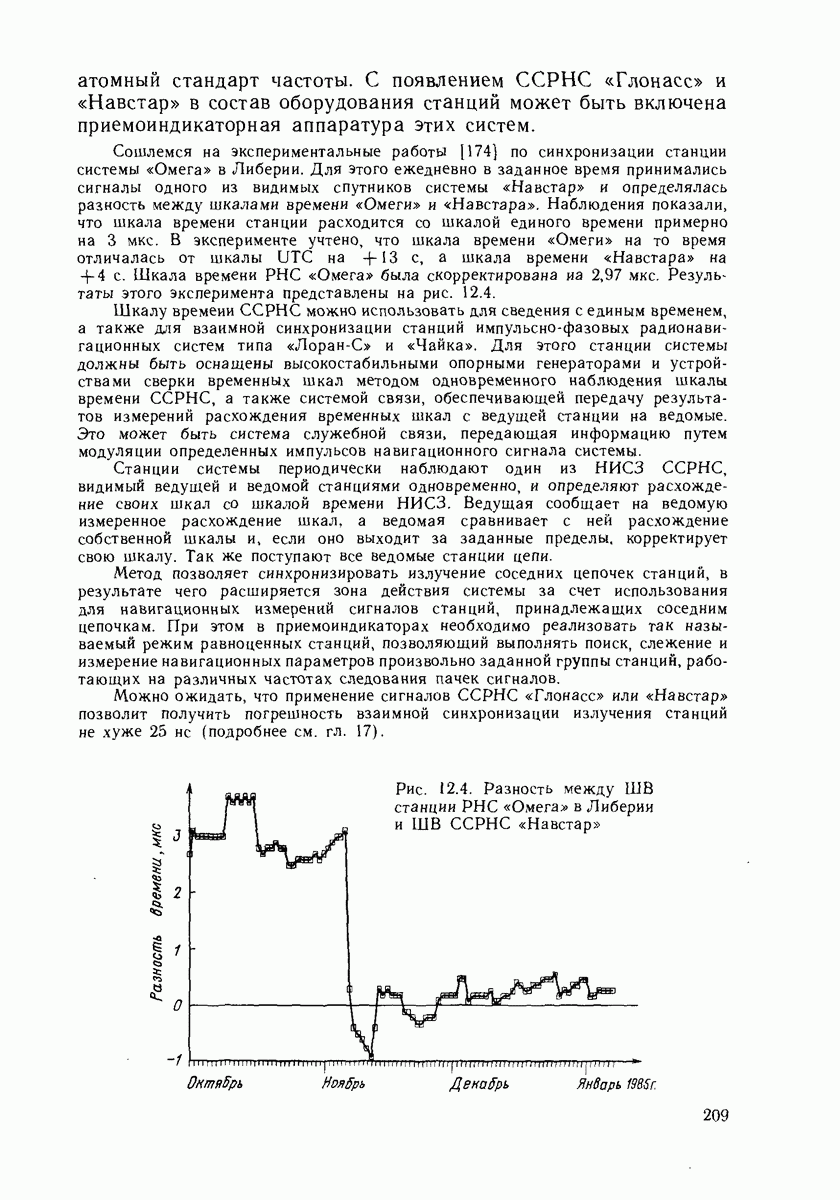
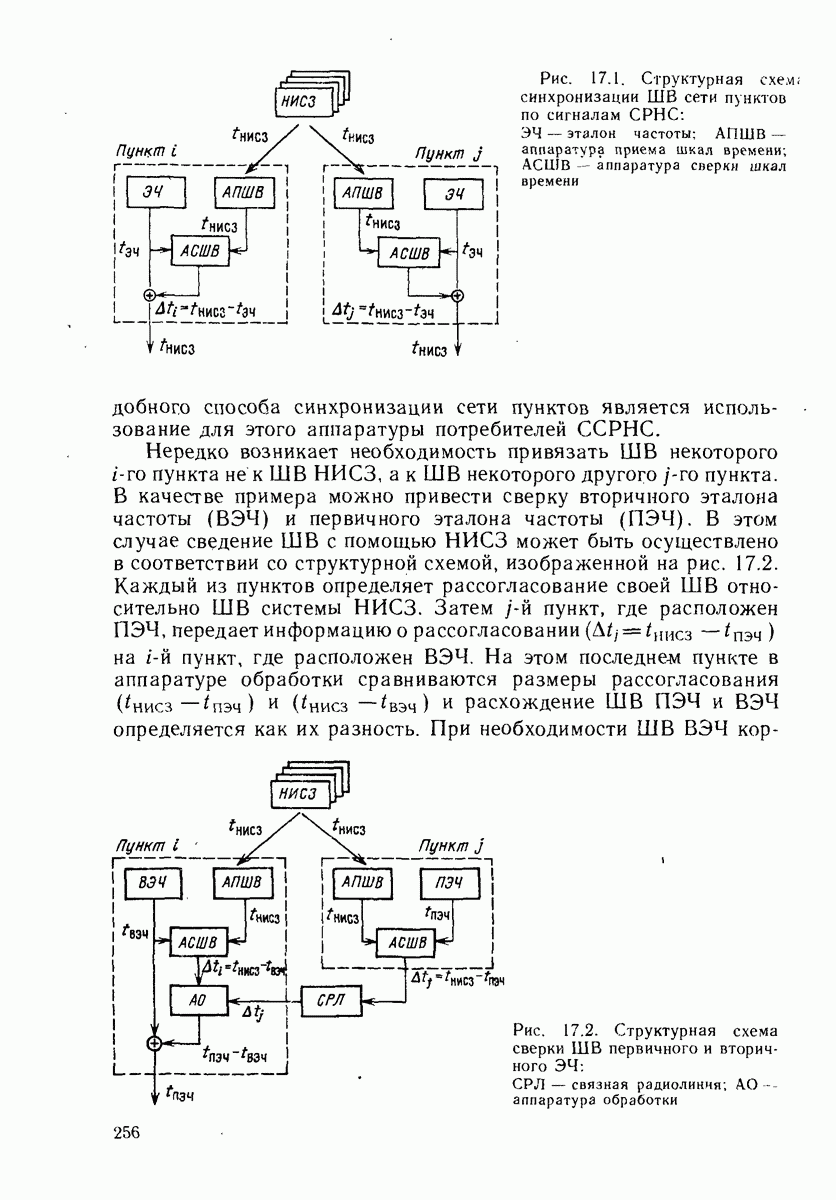
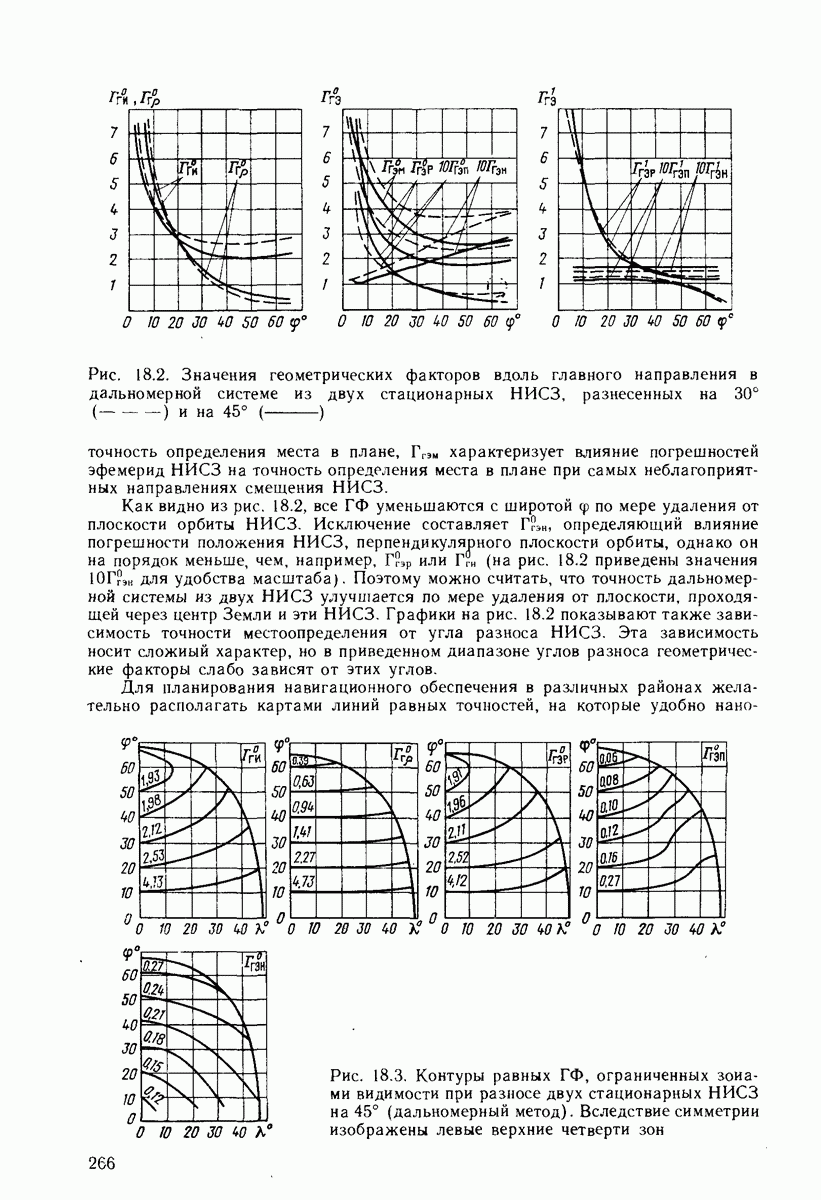
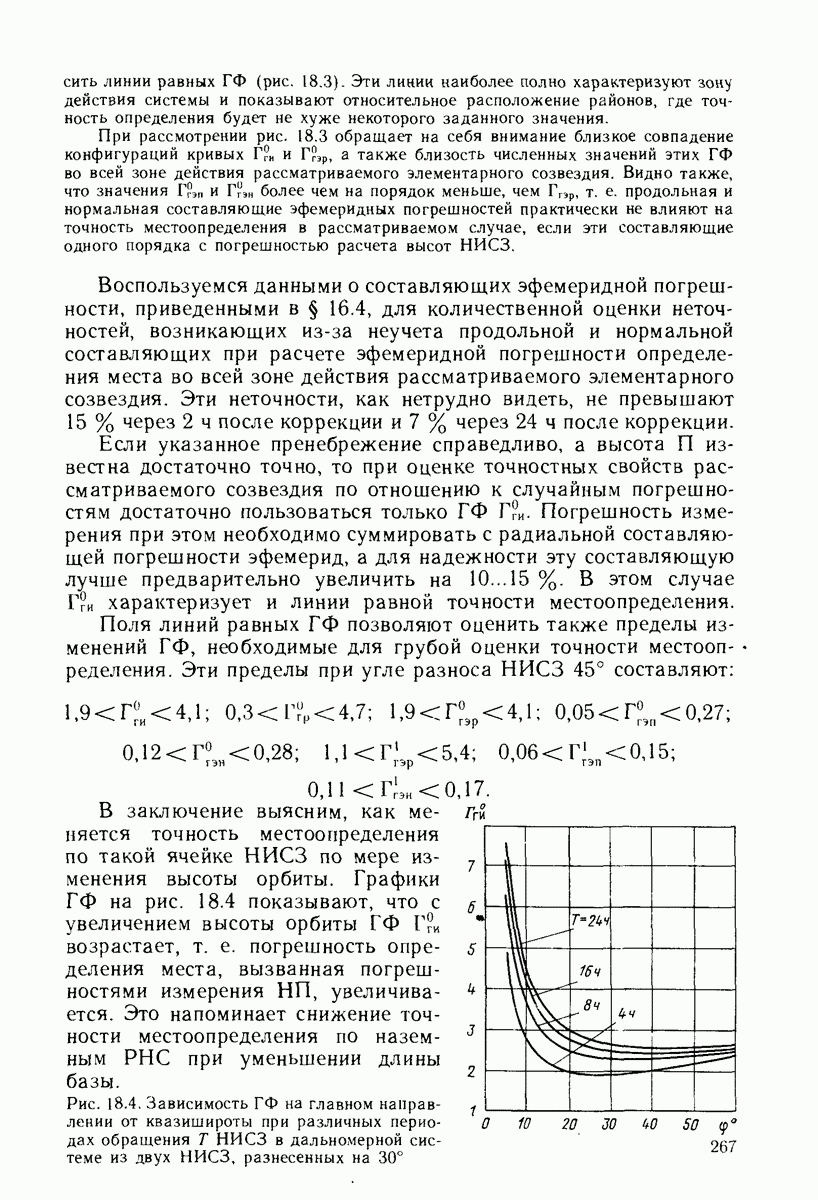
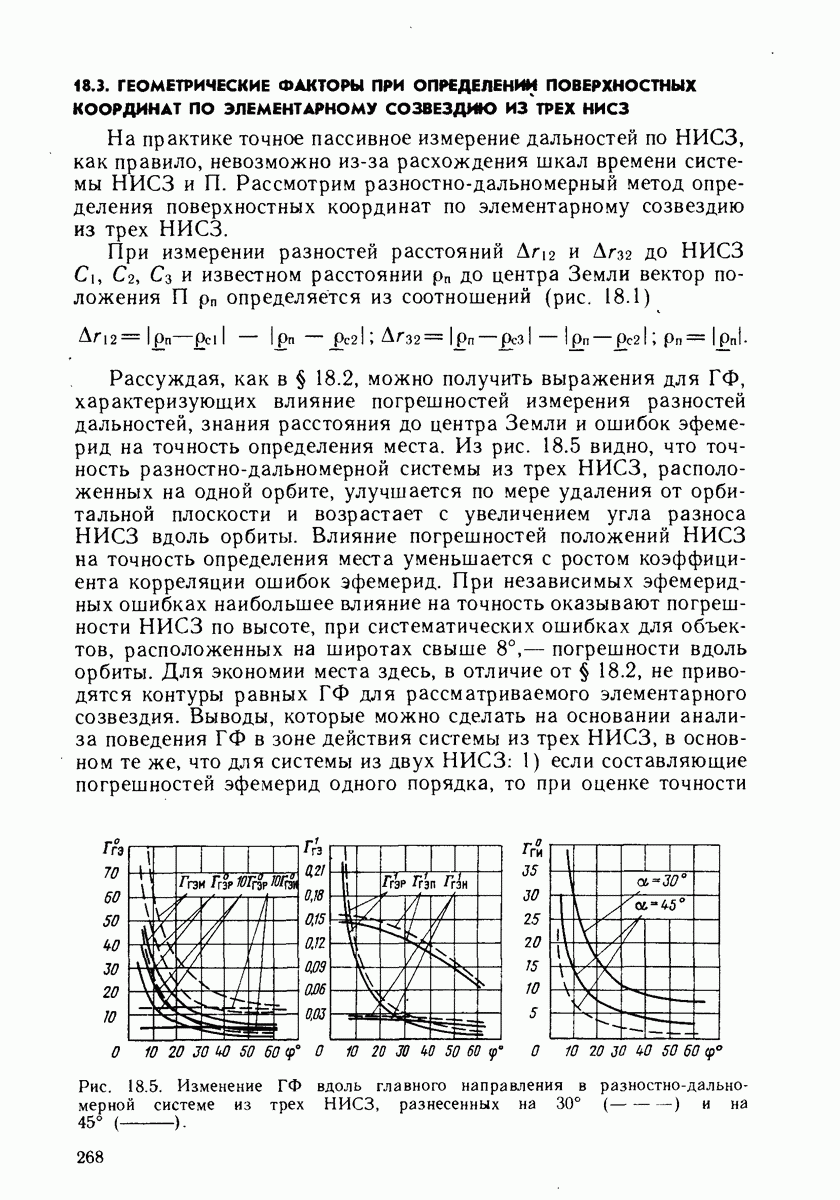
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
Тропосферная коррекция. Основана на предварительной оценке рефракционной погрешности и введении соответствующей поправки в результаты измерений.
Для расчета тропосферной поправки по формулам (5.10), (5.12) необходимо предварительно оценить приземное значение индекса рефракции  При наличии метеоданных для места расположения П значение
При наличии метеоданных для места расположения П значение  можно рассчитать по формуле ! [118]
можно рассчитать по формуле ! [118]

где Т - температура,  полное атмосферное давление, мбар;
полное атмосферное давление, мбар;  парциальное давление водяного пара, мбар;
парциальное давление водяного пара, мбар;  и — коэффициенты, полученные в результате обработки экспериментальных данных:
и — коэффициенты, полученные в результате обработки экспериментальных данных:

Указанные значения  обеспечивают среднеквадратическую погрешность расчета индекса рефракции не более
обеспечивают среднеквадратическую погрешность расчета индекса рефракции не более  на частотах до
на частотах до  при обычно встречающихся вариациях давления, температуры и влажности [118].
при обычно встречающихся вариациях давления, температуры и влажности [118].
Из (5.20) можно получить зависимость погрешности определения значения индекса рефракции от погрешностей измерения метеопараметров. При независимых измерениях параметров  и
и  имеем
имеем

В [118] приводятся значения коэффициентов  с для стандартной атмосферы, рекомендованной ICAO, при относительной влажности воздуха
с для стандартной атмосферы, рекомендованной ICAO, при относительной влажности воздуха  Величины
Величины  с зависят не только от параметров стандартной атмосферы
с зависят не только от параметров стандартной атмосферы  , но и от высоты расположения приемного пункта над уровнем моря
, но и от высоты расположения приемного пункта над уровнем моря  При
При  формула (5.22) согласно данным [118] принимает следующий вид:
формула (5.22) согласно данным [118] принимает следующий вид:

Погрешность расчета индекса рефракции по метеоданным наиболее чувствительна к вариациям относительной влажности и наименее — к изменению давления.
Ионосферная коррекция измерений РНП в системах типа «Навстар» может быть проведена по крайней мере тремя различными способами; алгоритмическим, основанным на использовании дополнительной информации, передаваемой в кадре навигационного сообщения; «полусуммы», использующим квазидальномерные и фазовые измерения; двухчастотным, использующим измерения на двух несущих частотах.
Каждый из указанных способов требует аппаратурных затрат или соответствующего математического обеспечения П. Рассмотрим более подробно каждый из них.
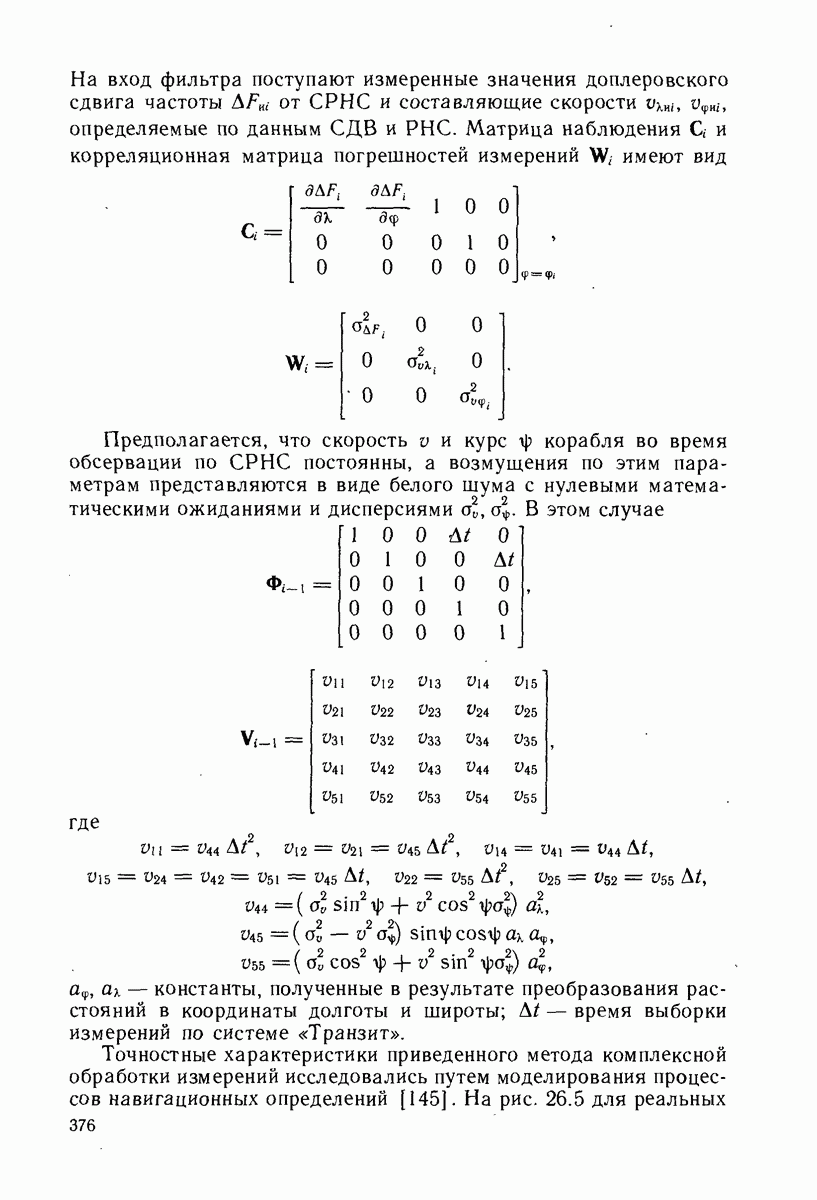
Алгоритмическая ионосферная коррекция. Основывается на упрощенной модели интегральной электронной концентрации, описанной в [160, 178]. В алгоритме используется аппроксимация вариации  положительной полуволной косинуса в дневные часы и постоянной величиной — в ночные. Ионосферная задержка с точностью до постоянного множителя повторяет аппроксимацию интегральной концентрации. На рис. 5.2 приведен пример [160, 178] суточного хода измеренной ионосферной вертикальной задержки и его косинусная аппроксимация. Косинусная функция представляется в виде
положительной полуволной косинуса в дневные часы и постоянной величиной — в ночные. Ионосферная задержка с точностью до постоянного множителя повторяет аппроксимацию интегральной концентрации. На рис. 5.2 приведен пример [160, 178] суточного хода измеренной ионосферной вертикальной задержки и его косинусная аппроксимация. Косинусная функция представляется в виде

где  и
и  (постоянное смещение, амплитуда, фаза и период) — параметры, с помощью которых рассчитывается вертикальная ионосферная задержка
(постоянное смещение, амплитуда, фаза и период) — параметры, с помощью которых рассчитывается вертикальная ионосферная задержка  измеряется в секундах.
измеряется в секундах.
В алгоритме используется разложение косинуса в степенной ряд

где  местное время в подионосферной точке — точке пересечения линией визирования фазового экрана. В алгоритме принята высота фазового экрана
местное время в подионосферной точке — точке пересечения линией визирования фазового экрана. В алгоритме принята высота фазового экрана 

Рис. 5.2. Суточный ход ионосферной задержки и его косинусная аппроксимация
Величины  взяты постоянными:
взяты постоянными:  не,
не,  местного времени. Амплитуда А и период
местного времени. Амплитуда А и период  косинусной аппроксимации представляются полиномами третьей степени от геомагнитной широты подионосферной точки
косинусной аппроксимации представляются полиномами третьей степени от геомагнитной широты подионосферной точки 

Коэффициенты полиномов  и
и  , передаются через спутники в кадре навигационного сообщения; эта информация обновляется каждые 10 дней. Коэффициенты рассчитываются по прогнозу гелиогеофизических условий.
, передаются через спутники в кадре навигационного сообщения; эта информация обновляется каждые 10 дней. Коэффициенты рассчитываются по прогнозу гелиогеофизических условий.
Для расчета геомагнитной широты подионосферной точки необходимы следующие данные: приближенные значения географических координат потребителя  угол места у и азимут из П на
угол места у и азимут из П на 

где  географические координаты подионосферной точки,
географические координаты подионосферной точки,

 центральный угол между П и НИСЗ, аппроксимируемый функцией
центральный угол между П и НИСЗ, аппроксимируемый функцией 
Окончательно ионосферная поправка к квазидальности рассчитывается по формуле

Коэффициент  называемый фактором наклона, учитывает отличие от вертикального распространение радиосигналов от НИСЗ к П и аппроксимируется формулой
называемый фактором наклона, учитывает отличие от вертикального распространение радиосигналов от НИСЗ к П и аппроксимируется формулой

Исходными данными для расчета ионосферных поправок на П по приведенному алгоритму являются приближенные значения координат  время и коэффициенты
время и коэффициенты 
По оценкам, приведенным в [160, 178, 182, 184], алгоритм обеспечивает остаточную среднеквадратическую ионосферную погрешность квазидальности не более  от некомпенсированной погрешности. Это объясняется тем, что алгоритм не воспроизводит вариации
от некомпенсированной погрешности. Это объясняется тем, что алгоритм не воспроизводит вариации  день ото дня, дает усредненные за 10 дней значения. Кроме того, алгоритм плохо воспроизводит поведение ионосферы на экваториальных широтах ввиду ограниченности возможностей кубической аппроксимации. Использовать алгоритм на высоких широтах, по мнению автора [160, 178], нецелесообразно, так как при
день ото дня, дает усредненные за 10 дней значения. Кроме того, алгоритм плохо воспроизводит поведение ионосферы на экваториальных широтах ввиду ограниченности возможностей кубической аппроксимации. Использовать алгоритм на высоких широтах, по мнению автора [160, 178], нецелесообразно, так как при  интегральная электронная концентрация меньше, чем на средних и низких широтах, а ее вариации во времени значительны.
интегральная электронная концентрация меньше, чем на средних и низких широтах, а ее вариации во времени значительны.
Можно построить более точные алгоритмы ионосферной коррекции, однако при этом необходимо сообщать потребителю больший объем ионосферных данных и усложненное математическое обеспечение на потребителе. Алгоритм, разработанный в [160, 178], является в известной степени компромиссным решением между сложностью организации прогноза гелиогеофизических условий и точностью введения коррекции.
Метод полусуммы. Основан на том известном факте, что ионосферные поправки на фазовый и групповой пути одинаковы, но противоположны по знаку:

Действительно, измерив квазидальность по дальномерному коду  по фазе несущей частоты
по фазе несущей частоты  и взяв их полусумму, можно убедиться, что результат не содержит ионосферной составляющей:
и взяв их полусумму, можно убедиться, что результат не содержит ионосферной составляющей:

Шумовая составляющая погрешностей измерений квазидальности  в этом случае определяется в основном шумами измерений по дальномерному коду, так как точность фазовых измерений значительно выше. Однако фазовым измерениям присуща неоднозначность и для практической реализации алгоритма (5.34) на потребителе следует устранить многозначность фазовых измерений, что для подвижных потребителей представляет непростую задачу. С другой стороны, для геодезической аппаратуры, где не требуется быстрого решения навигационной задачи, неоднозначности фазовых отсчетов можно избежать, но получаемая при этом результирующая точность измерения квазидальности определяется точностью не фазовых, а групповых измерений, что неприемлемо для геодезической АП. Метод полусуммы можно использовать для сужения начальной области неопределенности отсчетов при фазовом способе измерения разностей квазидальностей [184].
в этом случае определяется в основном шумами измерений по дальномерному коду, так как точность фазовых измерений значительно выше. Однако фазовым измерениям присуща неоднозначность и для практической реализации алгоритма (5.34) на потребителе следует устранить многозначность фазовых измерений, что для подвижных потребителей представляет непростую задачу. С другой стороны, для геодезической аппаратуры, где не требуется быстрого решения навигационной задачи, неоднозначности фазовых отсчетов можно избежать, но получаемая при этом результирующая точность измерения квазидальности определяется точностью не фазовых, а групповых измерений, что неприемлемо для геодезической АП. Метод полусуммы можно использовать для сужения начальной области неопределенности отсчетов при фазовом способе измерения разностей квазидальностей [184].
Для уменьшения рефракционных погрешностей по результатам дополнительных текущих измерений используется многочастотный способ исключения ионосферной ошибки [25], а также способ, основанный на разностных измерениях по нескольким НИСЗ. Остановимся более подробно на первом способе. В диапазоне длин волн, отведенном для СРНС, обычно излучаются только две частоты. Оценим допустимые аппаратурные погрешности измерений дальности  и скорости
и скорости  при
при  -частотном способе измерения и установим оптимальное распределение мощностей между частотами, обеспечивающее минимум суммарной мощности передающего устройства НИСЗ.
-частотном способе измерения и установим оптимальное распределение мощностей между частотами, обеспечивающее минимум суммарной мощности передающего устройства НИСЗ.
Способ исключения ионосферной ошибки при измерении параметра  причем
причем  соответствует измерению дальности
соответствует измерению дальности  скорости
скорости  по сигналам, излучаемым на двух когерентных частотах, заключается в следующем. В первом приближении измеренное значение параметра
по сигналам, излучаемым на двух когерентных частотах, заключается в следующем. В первом приближении измеренное значение параметра  можно представить в виде
можно представить в виде

где  истинное значение параметра;
истинное значение параметра;  коэффициент, характеризующий состояние ионосферы;
коэффициент, характеризующий состояние ионосферы;  остаточная погрешность измерения параметра, обусловленная рефракцией в тропосфере и неточностью знания скорости света;
остаточная погрешность измерения параметра, обусловленная рефракцией в тропосфере и неточностью знания скорости света;  аппаратурная погрешность.
аппаратурная погрешность.
Второе слагаемое в правой части уравнения представляет собой погрешность измерения параметра обусловленную рефракцией радиоволн в ионосфере [см. (5.10), (5.14)].
Если для измерения используются две когерентные частоты  связанные соотношением
связанные соотношением

то истинное значение параметра № можно получить, совместно решив два уравнения вида (5.35) для каждой из частот с учетом соотношения (5.36):

Ошибки  зависят от частоты и одинаковы в обоих измерительных каналах (индексы «1» и «2» здесь и далее соответствуют первому и второму частотным каналам);
зависят от частоты и одинаковы в обоих измерительных каналах (индексы «1» и «2» здесь и далее соответствуют первому и второму частотным каналам);  аппаратурные погрешности
аппаратурные погрешности  в двух каналах будем считать некоррелированными случайными величинами, отношение дисперсий которых зависит от отношения частот:
в двух каналах будем считать некоррелированными случайными величинами, отношение дисперсий которых зависит от отношения частот:

Параметр  определяется условиями приема в каждом частотном канале
определяется условиями приема в каждом частотном канале  при идентичности сигналов на обеих частотах по всем неэнергетическим параметрам.
при идентичности сигналов на обеих частотах по всем неэнергетическим параметрам.
С учетом изложенного дисперсия оценки параметра  представляется в виде
представляется в виде

и не содержит ионосферной составляющей.
Задаваясь допустимой суммарной погрешностью измерения параметра  с помощью формул (5.37) и (5.38) можно найти допустимые аппаратурные погрешности в каждом частотном канале. Эти погрешности возрастают с увеличением разноса частот и с уменьшением параметра
с помощью формул (5.37) и (5.38) можно найти допустимые аппаратурные погрешности в каждом частотном канале. Эти погрешности возрастают с увеличением разноса частот и с уменьшением параметра  Однако за счет увеличения разноса частот увеличить допустимые аппаратурные погрешности не всегда возможно из-за трудностей использования одной антенны на две частоты. Поэтому дальше рассмотрим вариант увеличения допустимых аппаратурных погрешностей путем выбора оптимального значения параметра
Однако за счет увеличения разноса частот увеличить допустимые аппаратурные погрешности не всегда возможно из-за трудностей использования одной антенны на две частоты. Поэтому дальше рассмотрим вариант увеличения допустимых аппаратурных погрешностей путем выбора оптимального значения параметра  при фиксированном разносе частот между каналами.
при фиксированном разносе частот между каналами.
Оптимальное значение параметра  минимизирующее суммарную мощность передатчика НИСЗ на двух когерентных частотах,
минимизирующее суммарную мощность передатчика НИСЗ на двух когерентных частотах,

различно для режимов измерения  Следовательно, и оптимальное значение суммарной мощности передатчика НИСЗ будет также различным при измерении только дальности
Следовательно, и оптимальное значение суммарной мощности передатчика НИСЗ будет также различным при измерении только дальности  или только скорости
или только скорости  Если же в системе предусмотрено одновременное измерение
Если же в системе предусмотрено одновременное измерение  то значения
то значения  должны быть выбраны такими, при которых мощность передатчика НИСЗ удовлетворяет условию
должны быть выбраны такими, при которых мощность передатчика НИСЗ удовлетворяет условию  Очевидно, при
Очевидно, при  Ргопт значение
Ргопт значение  будет минимальным
будет минимальным  Уравнения (5.38) и (5.39) позволяют сформулировать требования, предъявляемые к допустимым суммарным погрешностям измерения
Уравнения (5.38) и (5.39) позволяют сформулировать требования, предъявляемые к допустимым суммарным погрешностям измерения  при которых
при которых 
Двухчастотный алгоритм ионосферной коррекции обеспечивает наибольшую точность. Однако для его реализации требуется удвоенное число каналов обработки радионавигационных сигналов. Компромиссным решением между аппаратурной сложностью и точностью коррекции является дискретное введение коррекции, поочередно по каждому спутнику, а также дискретная двухчастотная коррекция в сочетании с использованием ионосферных прогнозов.
Можно также уменьшить рефракционные погрешности путем перехода к разностным измерениям, к работе АП в дифференциальном режиме. При этом ошибки, имеющие квазисистематический характер, частично или полностью компенсируются, но подчеркиваются погрешности случайного характера.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
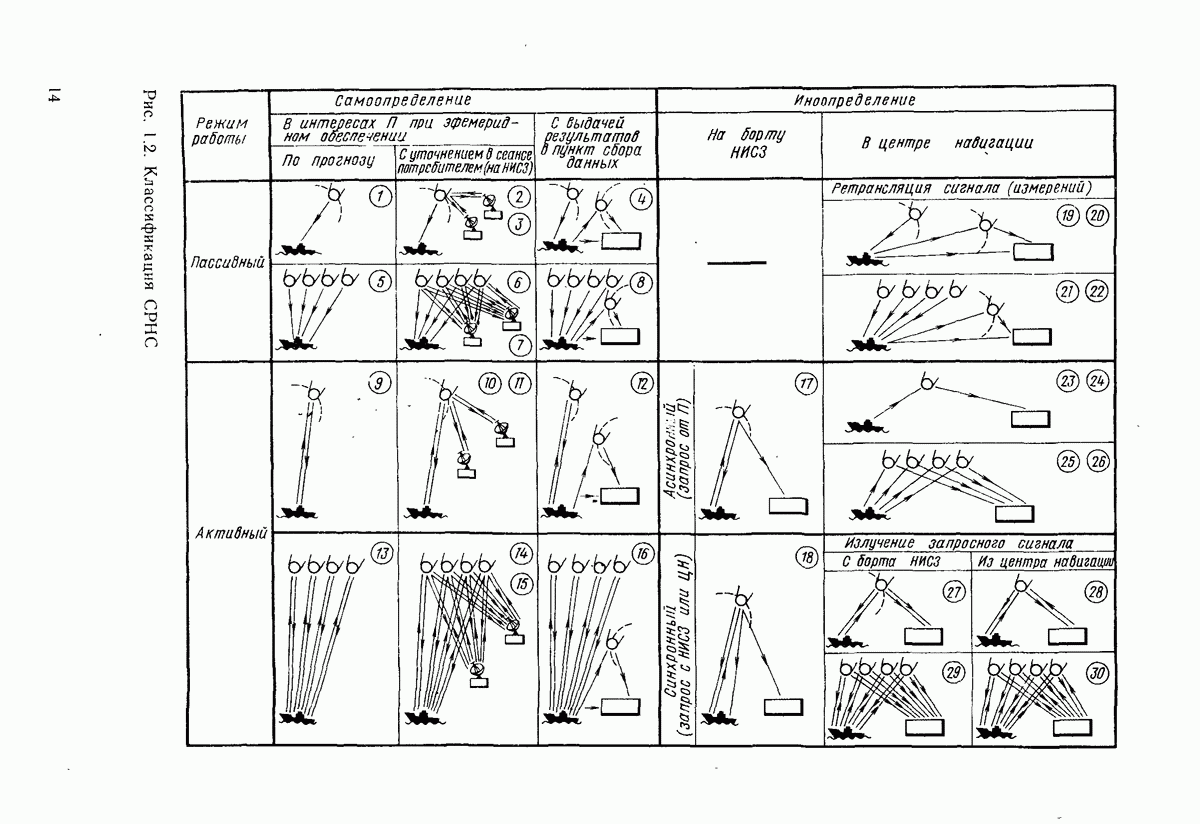
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
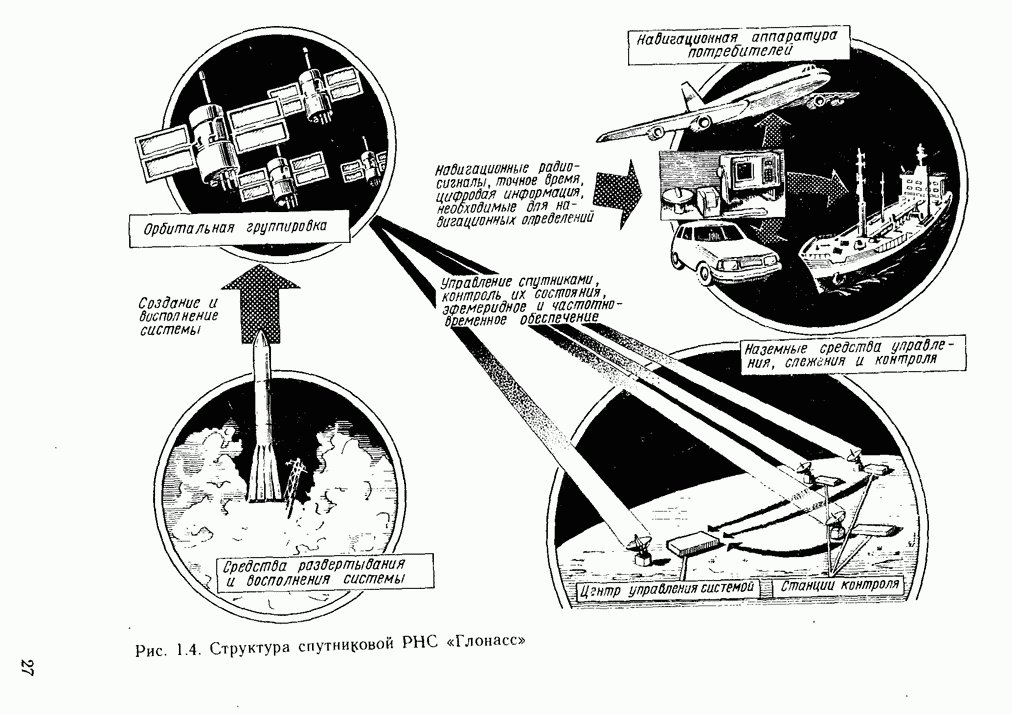
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
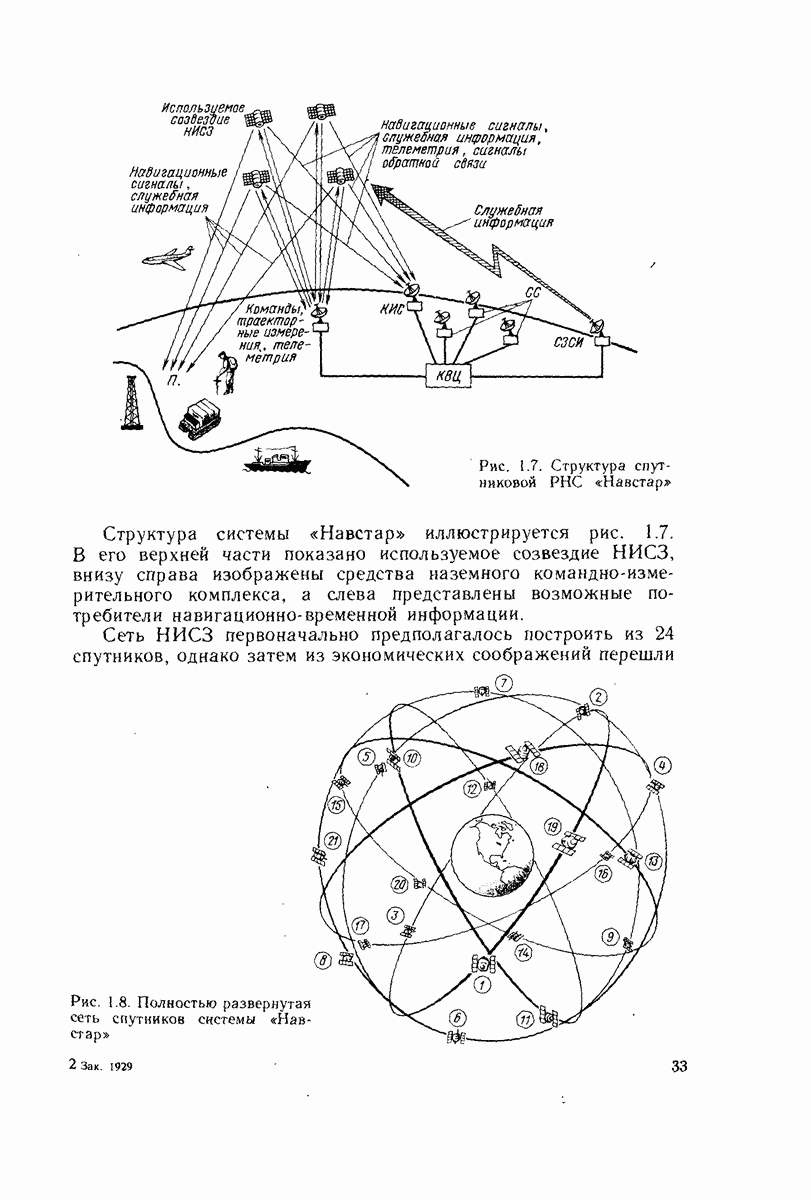
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
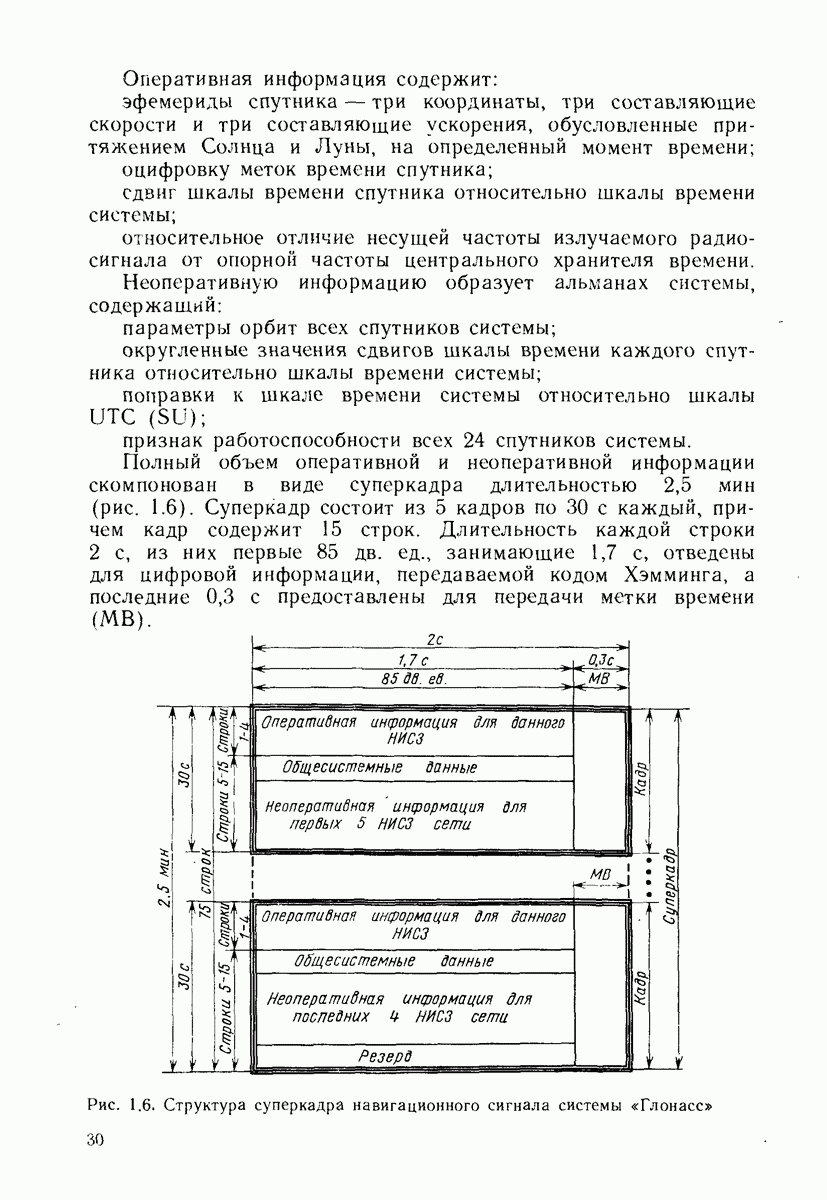
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
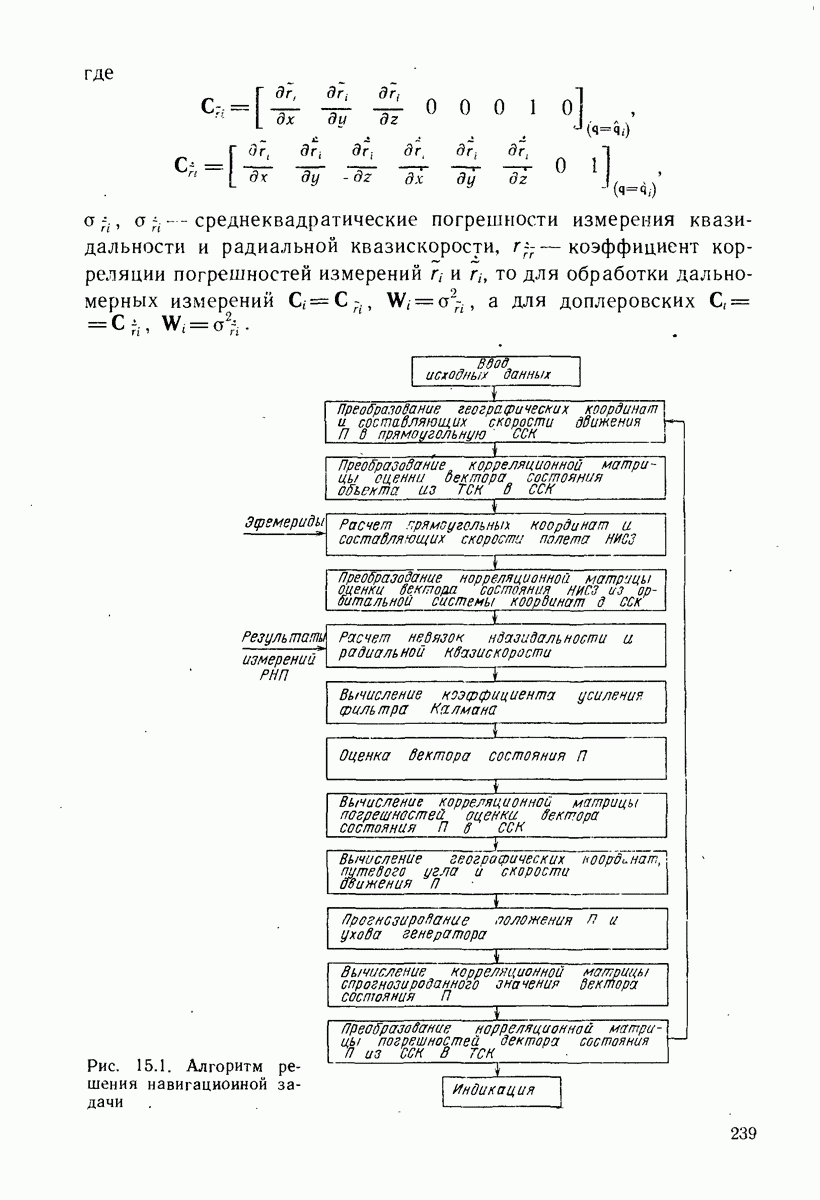
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
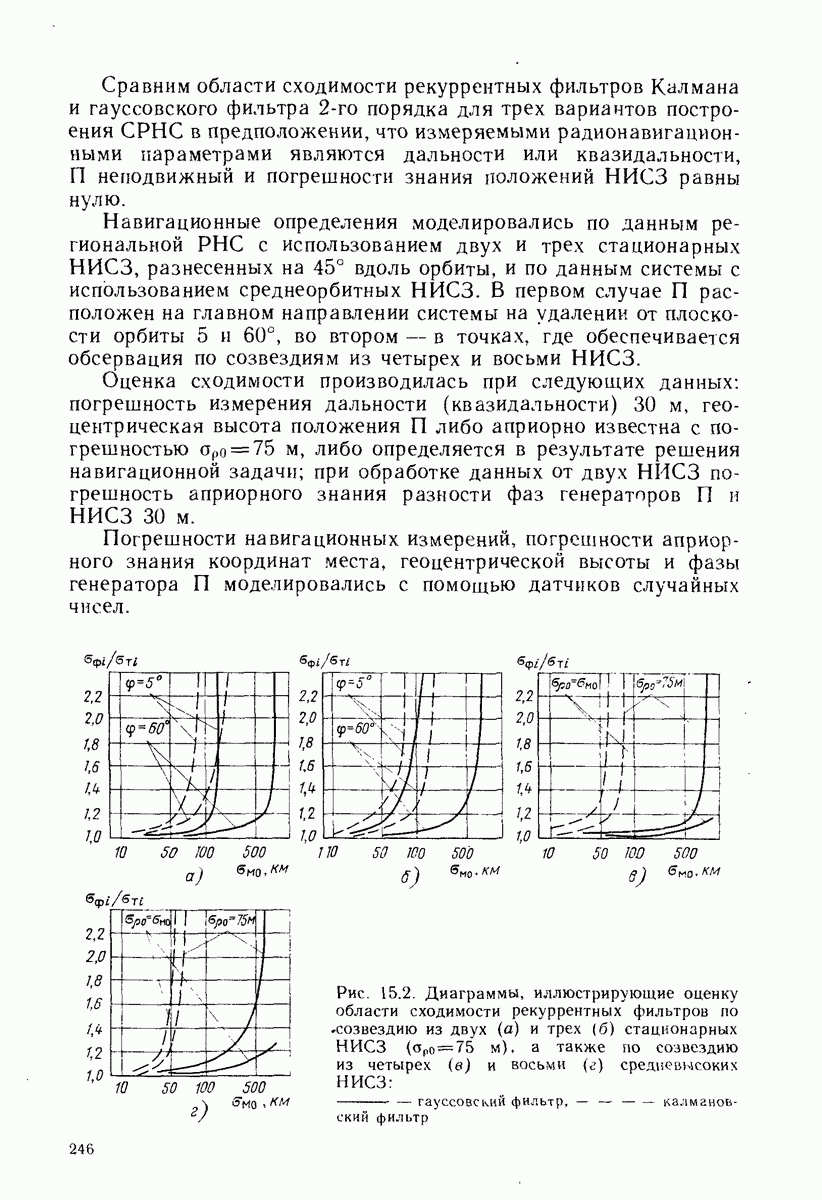
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
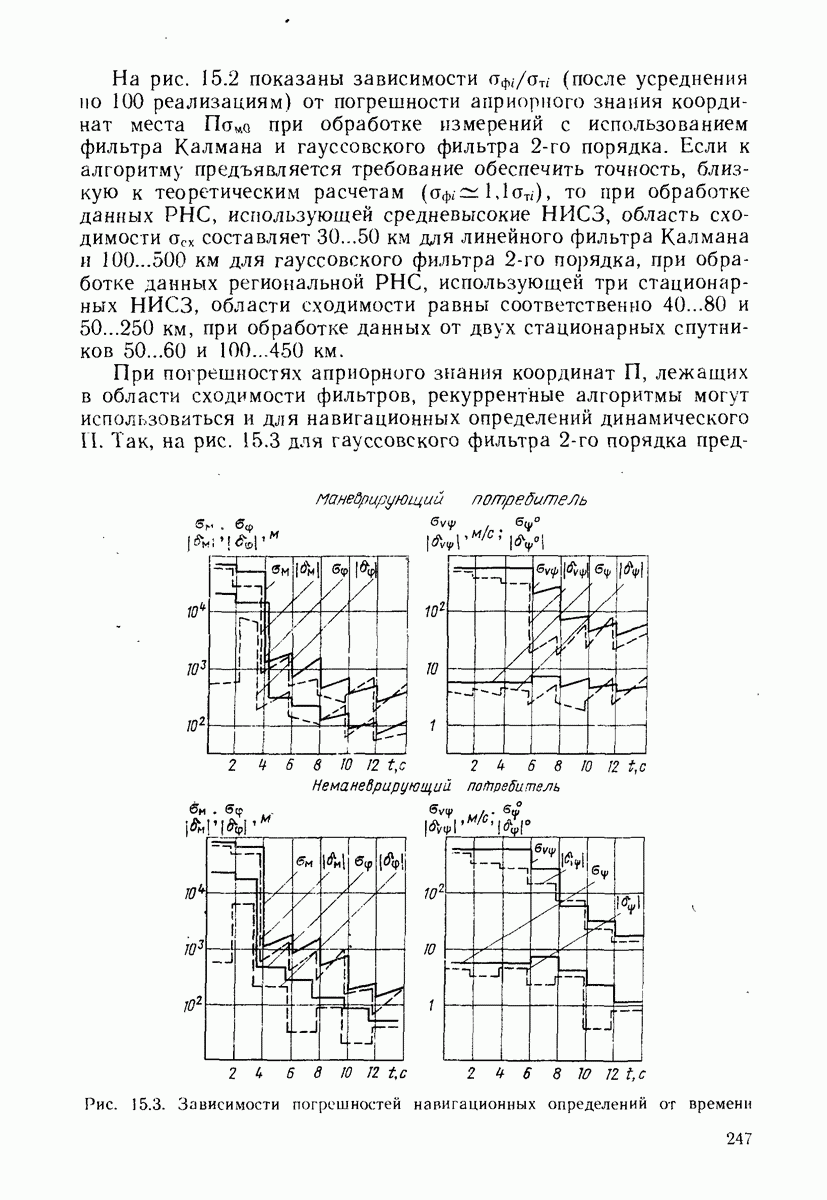
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
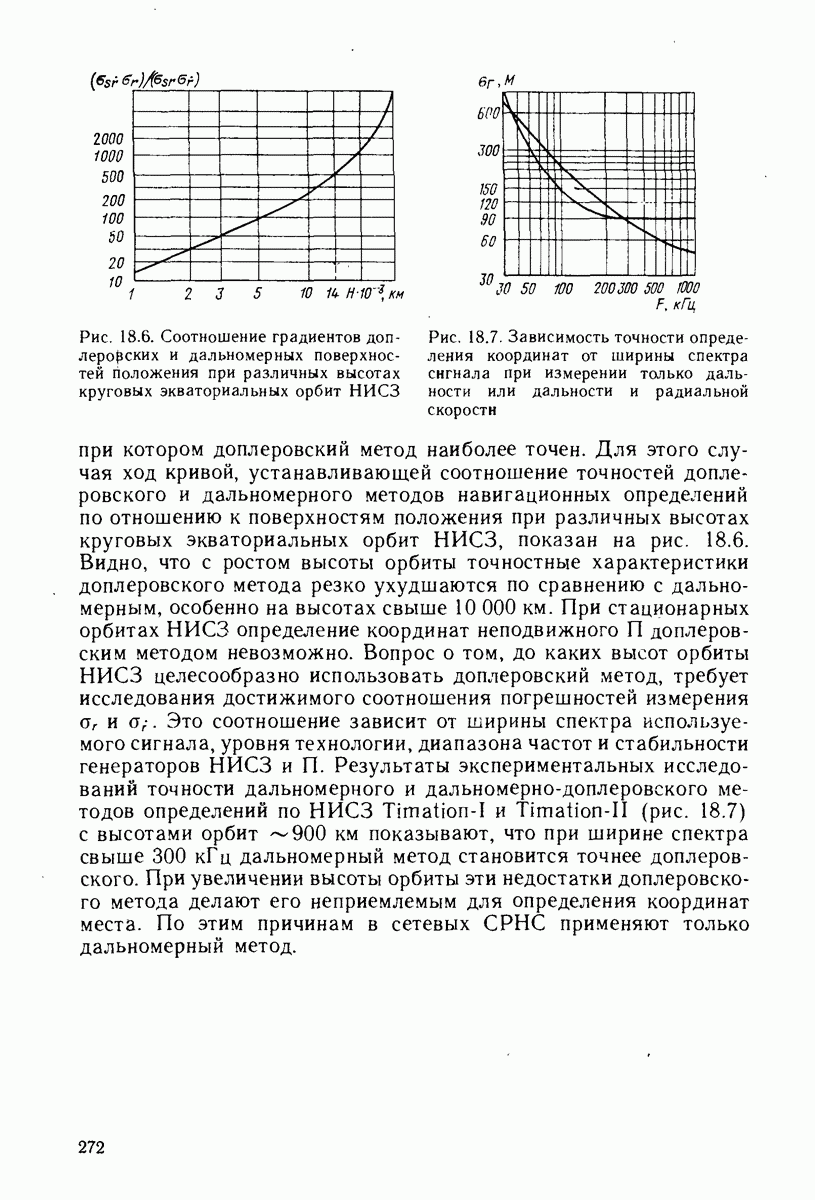
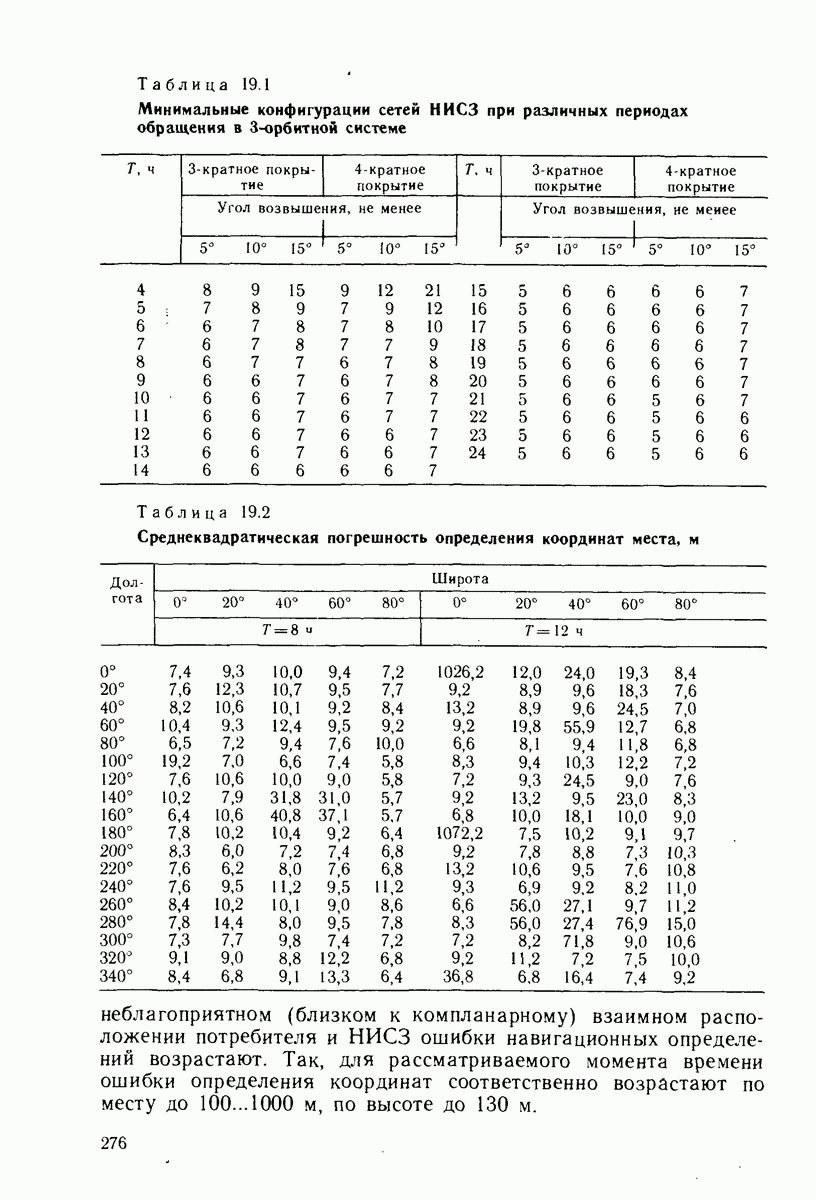
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
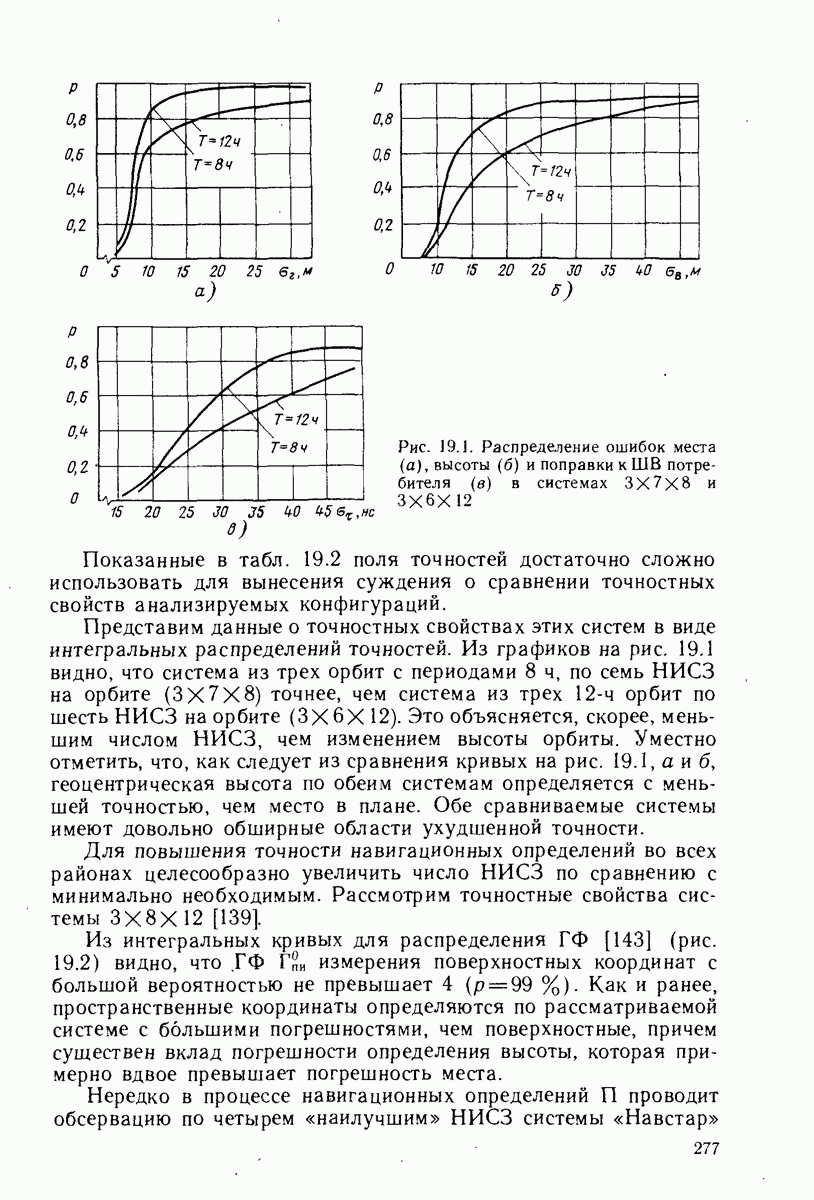
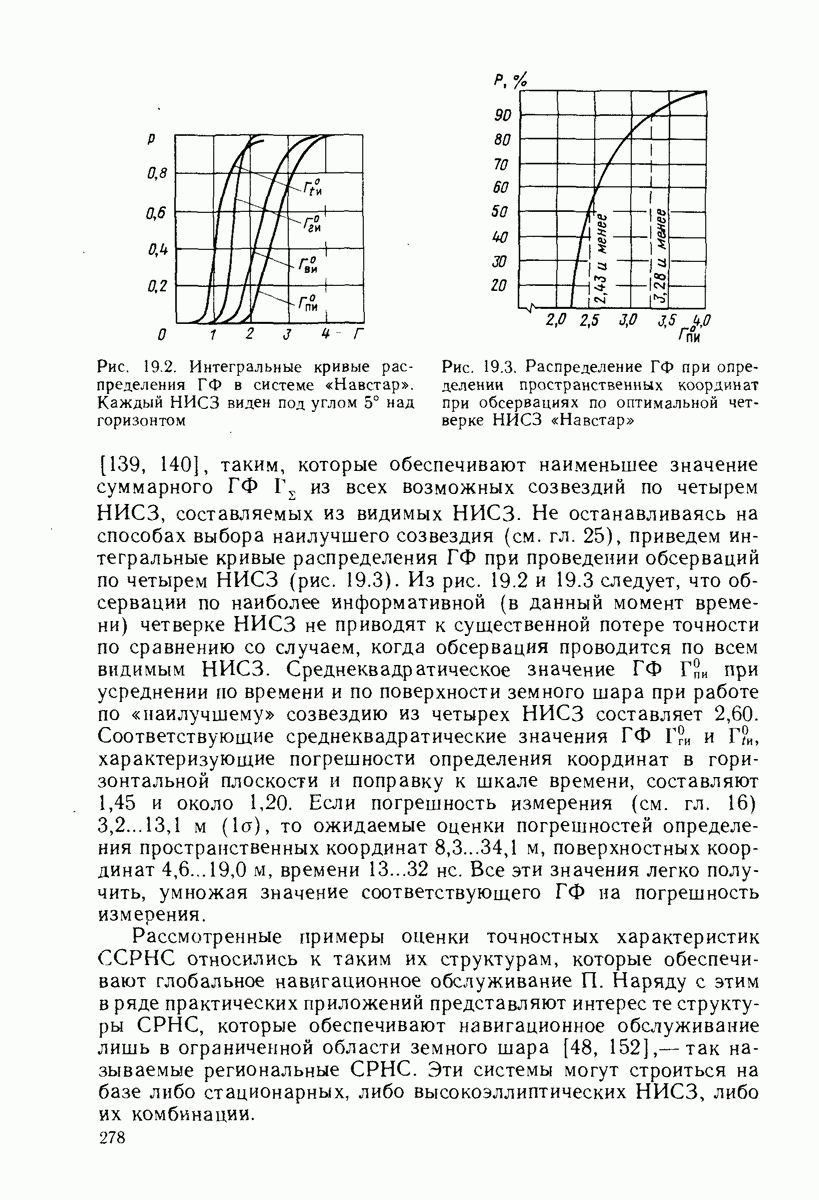
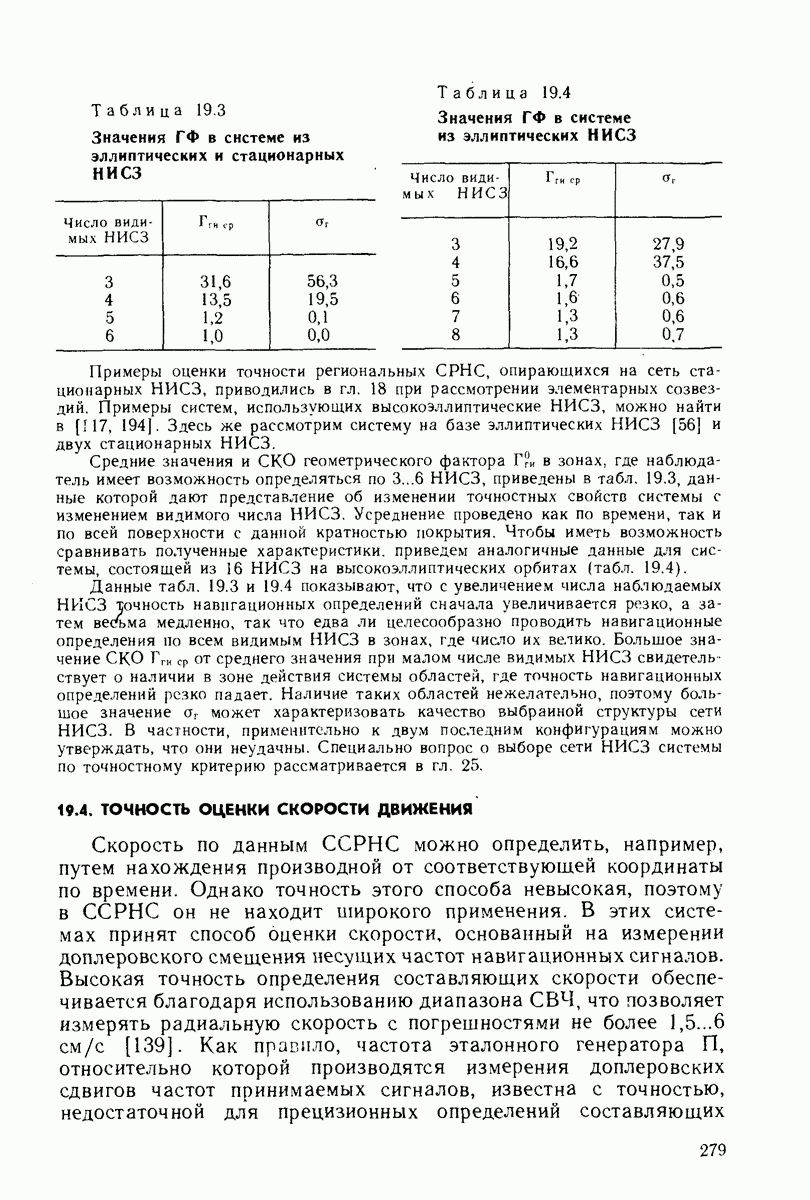
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
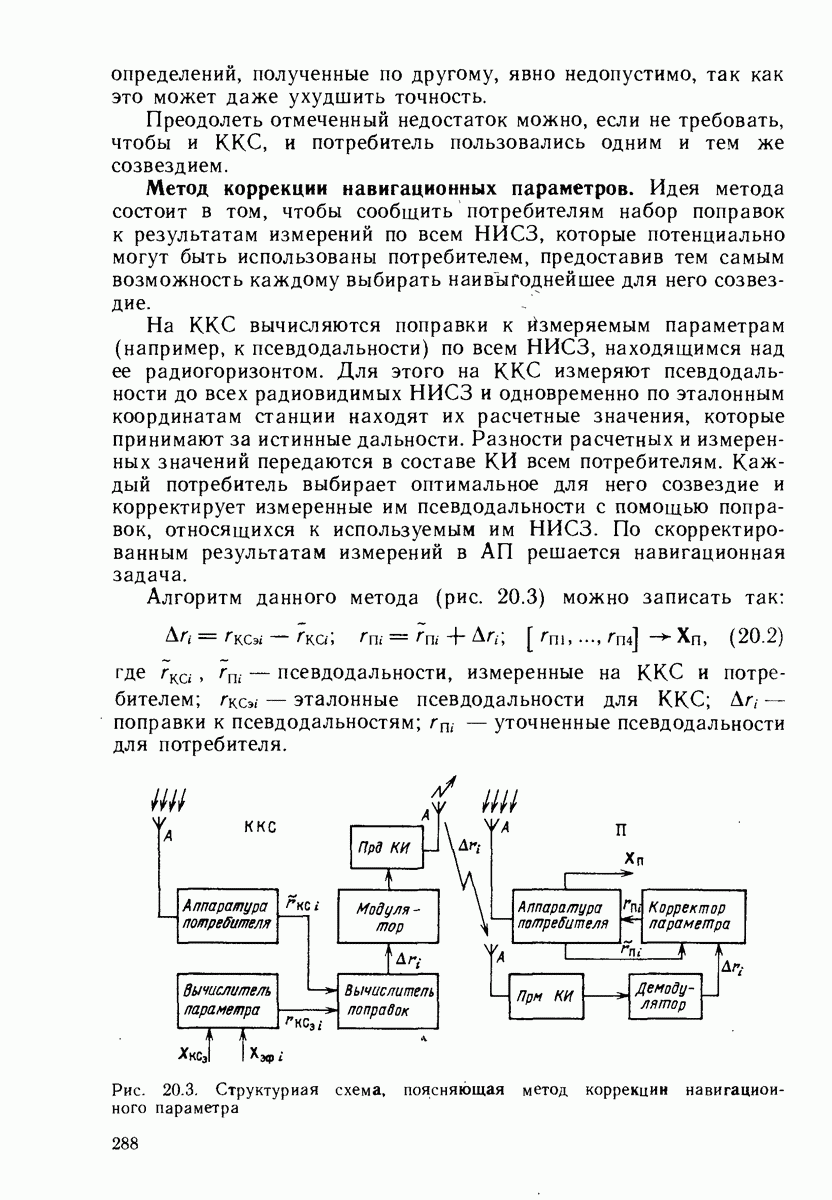
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
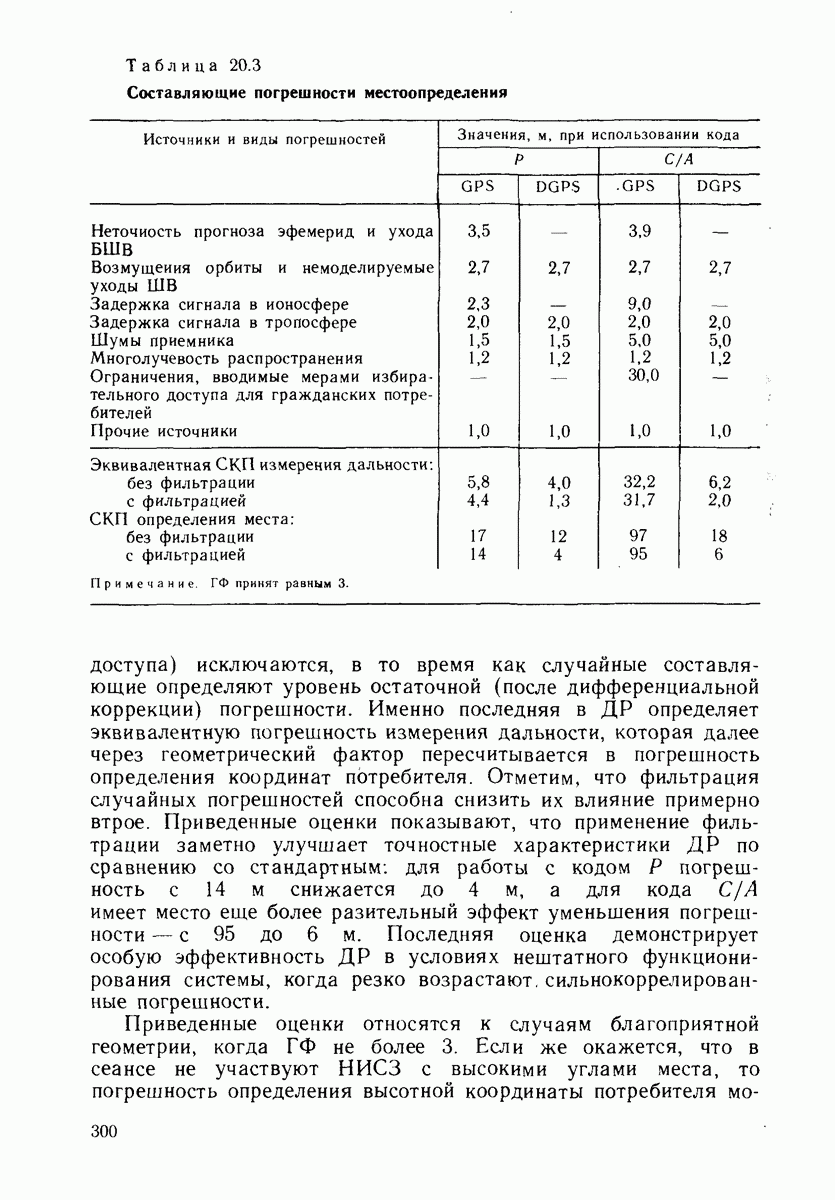
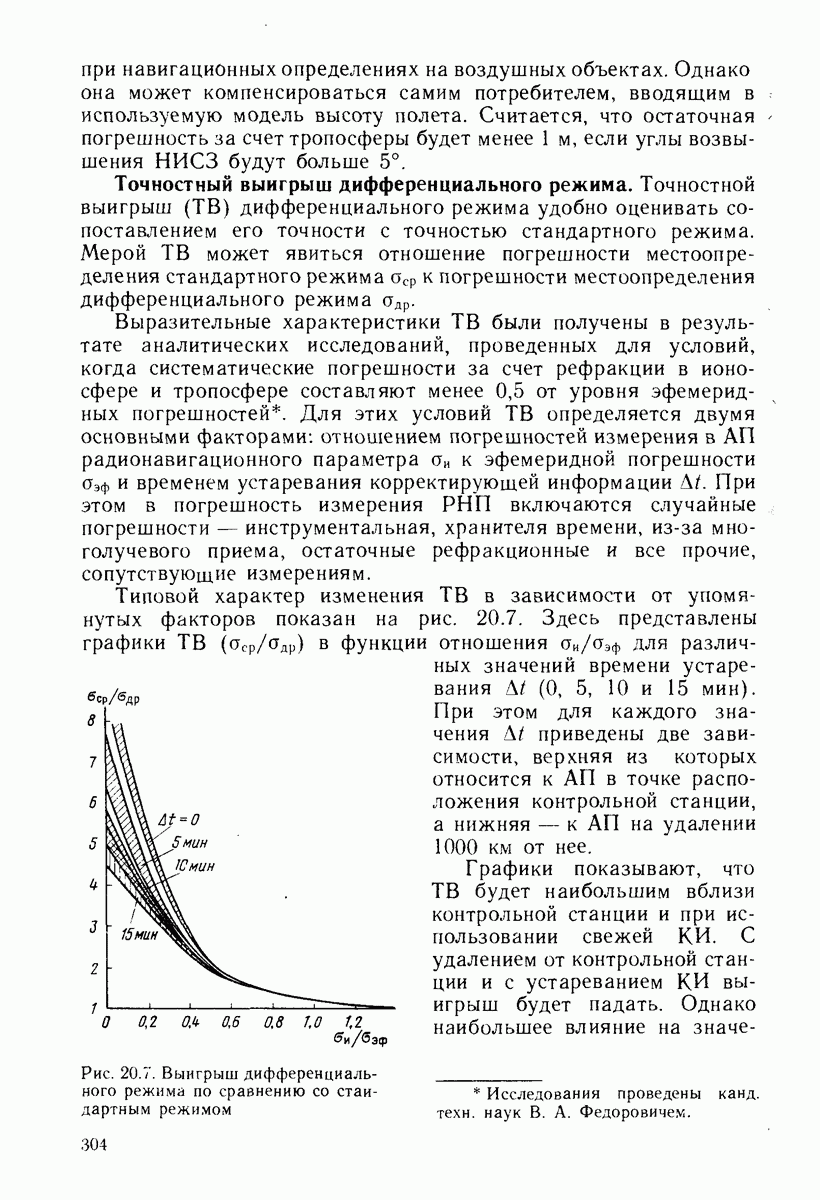
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС